OSNOVE TEHNIČNEGA RISANJA
|
|
|
- Ναβαδίας Δουμπιώτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 OSNOVE TEHNIČNEGA RISANJA POMEN IN NAMEN TEHNIČNEGA RISANJA Izgovorjena ali zapisana beseda ne zadostuje na tehničnem področju pove premalo. Zato se sporazumevamo z risbo, ki ni izdelana poljubno, ampak po zakonitostih in pravilih (standard).s pomočjo risbe izdelamo dolo čen predmet, izvršimo montažo naprave, izdelamo elektroinstalacijo, izvedemo servisni poseg Seveda pa moramo risbo prebrati. STANDARDIZACIJA Standard je dogovor o obliki, velikosti, kakovosti, metodi preizkušanja, poimenovanju in podobnih dogovorjenih znakih terveličinah za najrazličnejše izdelke. Slovenski standardi: Slovenski standardi so praviloma prevzeti mednarodni ali evropski standardi. Označujejo se s kratico SIST in dodatno oznako, ki je enaka oznaki prevzetega standarda. Primer: SIST ISO VRSTE RISB SIST ISO Delitev po načinu prikazovanja predmetov: Ortogonalna risba (osnovni način tehničnega risanja; predmet je v vsaki ravnini prikazan v dveh dimenzijah); Aksonometrična risba (predmet je prikazan v treh dimenzijah). GRAFIČNE ENOTE (cm, palci, pike...) V elektroniki se uporablja palec (palec= 2,54 cm) V strojništvu se uporablja mm V gradbeništvu cm FORMATI RISB (SIST ISO 5457) Format risbe določa ustrezno obliko in velikost papirja. Zaradi praktičnih razlogov pri hranjenju in prenašanju risb, so formati standardizirani. V tehniškem risanju uporabljamo v glavnem skupine A. skupin je večin jih označujemo z velikimi tiskanimi črkami A, B, C Formati skupine A so pravokotne oblike z razmerjem stranic a:b = 1: 2.
2 Oznaka Mere [mm] Površina [m2] A0 841 X A1 594 X 841 ½ A2 420 X 594 ¼ A3 297 X 420 1/8 A4 210 X 297 1/16 Drugi formati: Anglosaški format Zlati rez (zlato razmerje 1 : 1,618) MERILA Risbe rišemo v merilu. Vse mere premeta so v enakem razmerju z dolžinami na risbi. Merila so standardizirana. Merilo (M)=narisana mera:dejanska mera V ACADU rišemo v naravni velikosti oz. v merilu 1:1 Pomanjšano merilo: 1:2, 1:5, 1:10, 1:20, 1:50, 1:100 Povečano merilo: 2:1, 5:1, 10:1, 20:1, 50:1, 100:1 Merilo mora biti zapisano v glavi risbe, glavno merilo zapišemo z večjo pisavo, stranska merila pa z manjšo pisavo (v oklepaju), pri tem moramo stransko merilo navesti tudi ob pogledu oz. podrobnosti, kjer je to uporabljeno. Uporaba drugih meril ni dovoljena. VRSTE ČRT V TEHNIŠKEM RISANJU Oznaka: Oblika: Opis: Uporaba: A debela, polna za vidne robove in obrise predmetov, za podčrtavanje pozicijskih številk, za označevanje konca navoja, za puščice ki kažejo smer prereza ali pogleda; B tanka, polna za šrafure, za označevanje globinenavoja, za kotirne in pomožne kotirne črte, za diagonale, ki označujejo ravne ploskve,
3 za zvrnjene prereze; C tanka, prodtoročna za označevanje prekinitev in prelomov, D cik cak črta šrafura za les; E črtkana, debela za prikaz nevidnih robov na risbah večjega formata; F črtkana, tanka za prikaz nevidnih robov G tanka črta pika - črta za središčnice in simetrale tanka črta pika H črta, odebeljena na koncih in na mestih za označevanje prerezov; spremembe smeri J debela črta pika - za označevanje posebnoobdelanih črta površin predmeta K tanka črta pika - pika črta za označevanje alternativne lege premikajočih delov, za ponazoritev oblike predmeta pred preoblikovanjem za težiščnice
4 KOTIRANJE Kotiranje je predpisano s standardom. Kotiranje je vpisovanje kotov in mer predmeta v risbo. Mero ali kot vpišemo na risbi enkrat in sicer tako, da ni potrebno računanje. Kotiranje nevidnih robov ni dovoljeno. ali Manj, ko premikamo glavo, bolje je. Osnovna pravila kotiranja Kotirna črta leži vzporedno z robom vrazdaljiminimalno 10mm, naslednje pa vrazdalji 7mm. Kotirne in pomožne kotirne črte rišemo s tanko polno črto B. Puščice rišemo praviloma polne, z dolžino, ki je enaka višini kotirnih številk (večja od 3,5 mm). Čez puščico ne smepotekatinobenačrta. Kotirne številke pišemo nad kotirno črto, po možnosti v sredino. Številke morajo biti obrnjene tako, da jih beremo od spodnje ali z desne strani risbe. Vse mere v strojništvu so podane v mm. Pri ravnih delih, ki so izdelani iz pločevine, lepenke itd., zadošča, če narišemo pogled, debelino pa označimo z napisom npr. t = 2.
5 UPORABA ZNAKOV Φ IN S pisanjem znaka Φpred kotirno številko pojasnjujemo, da je kotirni rob projekcija kroga, z znakom pa, da je kotirni rob projekcija kvadrata. Dve diagonali, narisani s črto B, pojasnjujeta, da je ploskev ravna in pravokotne ali trapezaste oblike. Če med pomožnima kotirnima črtama ni prostora za kotimo številko in puščico, rišemo puščici in številko na podaljšku kotirne črte; če tudi to ni mogoče, napišemo številko v bližini, namesto puščic pa pike.. Čez kotirne številke ali med njimi ne sme potekati nobena črta, zato srednjico na takih mestih prekinjamo. Srednjico rišemo pri vseh simetričnih telesih in ponazarja simetralo oziroma težiščnico telesa ali lika (zrcalna slika). Srednjice rišemo s črto G in segajo čez rob telesa le 2 do 4 mm. KOTIRANJE POLMEROV Polmere označujemo s črko R, ki jo postavljamo pred koto polmera.
6 KOTIRANJE KROGLE Kroglo kotiramo tako, da napišemo pred koto z znakom Φbesedo krogla. ZAPOREDNO KOTIRANJE Mere nanizane druga za drugo. Uporabljamo pri jeklenih konstrukcijah in raznih strojnih delih, kjer odstopanja pri posameznih merah nimajo posebnega vpliva. Dolge predmete s konstantnim prerezom rišemo skrajšane; prekinitve omejimo s črto C. VZPOREDNO KOTIRANJE Kote izhajajo iz ene ali večnepremičnih ravnin. Predmete, ki jih stružimo, kotiramo od desnega roba, zaradi poteka obdelava v tej smeri.
7 KOORDINATNO KOTIRANJE (usmerjanje CNC strojev) Koordinatno kotiranje je poenostavljen način vzporednega kotiranja z enim ali večničlišči, le da mere zberemo v tabeli x y Φ Branje mer pri kotiranju v koordinatah: Kot primer obravnavajmo izvrtino 3: izvrtina 3 je oddaljena od levega roba plošče (v smeri x) 175mm, od zgornjega roba plošče (v smeri y) 120mm, njen premer pa znaša 45 mm. KOMBINIRANO KOTIRANJE Pri kombiniranem kotiranju uporabljamo zaporedni in vzporedni način kotiranja. KOTIRANJE KOTOV
8 PROJEKCIJE Risba prikazuje telo v prostoru tridimenzionalno (dolžina, širina in višina). Risalna ravnina je dvodimenzionalna (dolžina in višina). Z načini risanja nadomestimo izpad tretje prostorske dimenzije.poznamo: perspektivno prikazovanje teles (aksonometrična projekcija) prikazovanje teles v večpogledih (ortogonalna projekcija). Aksonometrična projekcija Prikazuje narisani predmet na eni sliki v treh dimenzijah in jo uporabljamo za lažje prikazovanje oblik telesa. Slabost: s kotiranjem postane risba nepregledna. Centralna projekcija Projekcijski žarki izhajajo iz enega, dveh ali treh projekcijskih središč(bežišč). Tako dobimo eno- dvo- ali trosmerno perspektivno projekcijo. Oblika in način prikaza predmete sta odvisna od števila in lege središč. Centralna projekcija je zelo primerna za prikazovanje različnih objektov.
9 Izometrična projekcija Dimetrična projekcija To projekcijo uporabljamo takrat, ko želimo bistvene dele predmeta prikazati v glavnem pogledu. Razmerje stranic a:b:c = 1:1:0,5. Rob a je nagnjen glede na vodoravnico za 7º, rob c za 42º, rob b pa je navpičen. Aksonometrično narisan predmet je za laika nazornejšiod risbe, ki prikazuje predmet v več pogledih. Tak način risanja uporabljamo priizdelavi reklamnih prospektov, prirazlagi navodil za montažo, obratovanje ali servisiranje naprave Pri izdelavi podrobne tehnične dokumentacije tega ne uporabljamo, saj postane risba po kotiranju nepregledna, risanje okroglin (elipse) pa je zamudno. Podrobno tehnično dokumentacijo rišemo v ortogonalni (pravokotni) projekciji.
10 Uporabljena literatura: J. Hrženjak: TEHNIČNO RISANJE, TZS, Ljubljana 1998
Tehniška pisava.. 2 Oznake svinčnikov. 2 Standardi. 4 Vrste tehniških rib. 4 Formati risb.. 6 Glava risbe in kosovnica 6
 Srednja šola tehniških strok Šiška KAZALO Tehnična komunikacija Uvod 2 Tehniška pisava.. 2 Oznake svinčnikov. 2 Standardi. 4 Vrste tehniških rib. 4 Formati risb.. 6 Glava risbe in kosovnica 6 Merila 7
Srednja šola tehniških strok Šiška KAZALO Tehnična komunikacija Uvod 2 Tehniška pisava.. 2 Oznake svinčnikov. 2 Standardi. 4 Vrste tehniških rib. 4 Formati risb.. 6 Glava risbe in kosovnica 6 Merila 7
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
l 5 Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija profila
 referenčna linija profila l=l=l=l=l 1 2 3 4 5... referenčna dolžina l 1 l 2 l 3 l 4 l 5 l n dolžina vrednotenja Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija
referenčna linija profila l=l=l=l=l 1 2 3 4 5... referenčna dolžina l 1 l 2 l 3 l 4 l 5 l n dolžina vrednotenja Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
OPISNA GEOMETRIJA NAVODILA ZA IZDELAVO VAJ V 1. SEMESTRU
 OPISNA GEOMETRIJA NAVODILA ZA IZDELAVO VAJ V 1. SEMESTRU Pravilno rešene in ustrezno narisane vaje so pogoj, da kandidat lahko pristopi k opravljanju kolokvija. Pozitivno opravljen kolokvij je nujen pogoj
OPISNA GEOMETRIJA NAVODILA ZA IZDELAVO VAJ V 1. SEMESTRU Pravilno rešene in ustrezno narisane vaje so pogoj, da kandidat lahko pristopi k opravljanju kolokvija. Pozitivno opravljen kolokvij je nujen pogoj
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
3.letnik - geometrijska telesa
 .letnik - geometrijska telesa Prizme, Valj P = S 0 + S pl S 0 Piramide, Stožec P = S 0 + S pl S0 Pravilna -strana prizma P = a a + av 1 Pravilna -strana prizma P = a + a a Pravilna 6-strana prizma P =
.letnik - geometrijska telesa Prizme, Valj P = S 0 + S pl S 0 Piramide, Stožec P = S 0 + S pl S0 Pravilna -strana prizma P = a a + av 1 Pravilna -strana prizma P = a + a a Pravilna 6-strana prizma P =
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
VARJENJE. 1.1 Definicija varjenja
 VARJENJE 1. SPLOŠNO O VARJENJU 1.1 Definicija varjenja Varjenje je spajanje kovinskih (včasih tudi nekovinskih) strojnih ali konstrukcijskih delov v nerazdružljivo celo to. Nastali spoj naj obdrži čim
VARJENJE 1. SPLOŠNO O VARJENJU 1.1 Definicija varjenja Varjenje je spajanje kovinskih (včasih tudi nekovinskih) strojnih ali konstrukcijskih delov v nerazdružljivo celo to. Nastali spoj naj obdrži čim
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Vaje iz MATEMATIKE 2. Vektorji
 Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
Študij AHITEKTURE IN URBANIZMA, šol. l. 06/7 Vaje iz MATEMATIKE. Vektorji Vektorji: Definicija: Vektor je usmerjena daljica. Oznake: AB, a,... Enakost vektorjev: AB = CD: če lahko vektor AB vzporedno premaknemo
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni izrek.
 DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Koordinatni sistemi v geodeziji
 Koordinatni sistemi v geodeziji 14-1 Koordinatni sistemi v geodeziji Koordinatni sistemi v geodeziji 2 Vrste koordinatnih sistemov Vzpostavitev koordinatnega sistema je potrebna zaradi pridobitve primernega
Koordinatni sistemi v geodeziji 14-1 Koordinatni sistemi v geodeziji Koordinatni sistemi v geodeziji 2 Vrste koordinatnih sistemov Vzpostavitev koordinatnega sistema je potrebna zaradi pridobitve primernega
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Pravokotni koordinatni sistem; ravnina in premica
 Pravokotni koordinatni sistem; ravnina in premica 1. Razmisli, v kakšnih legah so lahko v prostoru: (a) premica in ravnina (b) dve ravnini (c) dve premici.ugotovitve zapiši.. 2. Ali sta premici v prostoru,
Pravokotni koordinatni sistem; ravnina in premica 1. Razmisli, v kakšnih legah so lahko v prostoru: (a) premica in ravnina (b) dve ravnini (c) dve premici.ugotovitve zapiši.. 2. Ali sta premici v prostoru,
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
3. VAJA IZ TRDNOSTI. Rešitev: Pomik v referenčnem opisu: u = e y 2 e Pomik v prostorskem opisu: u = ey e. e y,e z = e z.
 3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
1 3D-prostor; ravnina in premica
 1 3D-prostor; ravnina in premica 1. Razmisli, v kakšnih legah so lahko v prostoru: (a) premica in ravnina (b) dve ravnini (c) dve premici.ugotovitve zapiši.. 2. Ali sta premici v prostoru, ki nimata skupne
1 3D-prostor; ravnina in premica 1. Razmisli, v kakšnih legah so lahko v prostoru: (a) premica in ravnina (b) dve ravnini (c) dve premici.ugotovitve zapiši.. 2. Ali sta premici v prostoru, ki nimata skupne
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
- Geodetske točke in geodetske mreže
 - Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
- Geodetske točke in geodetske mreže 15 Geodetske točke in geodetske mreže Materializacija koordinatnih sistemov 2 Geodetske točke Geodetska točka je točka, označena na fizični površini Zemlje z izbrano
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
GEOMETRIJA V RAVNINI DRUGI LETNIK
 GEOMETRIJA V RAVNINI DRUGI LETNIK 2 1 Geometrija v ravnini 1.1 Osnove geometrije Točka je tisto, kar nima delov. Črta je dolžina brez širine. Ploskev je tisto, kar ima samo dolžino in širino. Osnovni zakoni,
GEOMETRIJA V RAVNINI DRUGI LETNIK 2 1 Geometrija v ravnini 1.1 Osnove geometrije Točka je tisto, kar nima delov. Črta je dolžina brez širine. Ploskev je tisto, kar ima samo dolžino in širino. Osnovni zakoni,
Opisna geometrija II. DVO^RTNI POSTOPEK
 Opisna geometrija II. DVO^RTNI POSTOPEK 1 Dvo~rtni postopek Pridru`ni ortogonalni projekciji na: - tlorisno ravnino π 1, - narisno ravnino π 2, - prese~na os x 12. Imena: - Monge-ov postopek (Gaspard Monge,
Opisna geometrija II. DVO^RTNI POSTOPEK 1 Dvo~rtni postopek Pridru`ni ortogonalni projekciji na: - tlorisno ravnino π 1, - narisno ravnino π 2, - prese~na os x 12. Imena: - Monge-ov postopek (Gaspard Monge,
POROČILO. št.: P 1100/ Preskus jeklenih profilov za spuščen strop po točki 5.2 standarda SIST EN 13964:2004
 Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Osnovna elementa po tolerančnem sistemu ISO a) premer luknje D (notranja mera), b) premer čepa d (zunanja mera)
 TOLERANCE IN UJEMI tolerance dolžin in kotov, geometrične tolerance. Osnovna elementa po tolerančnem sistemu ISO a) premer luknje D (notranja mera), b) premer čepa d (zunanja mera) Veličine za opis toleranc
TOLERANCE IN UJEMI tolerance dolžin in kotov, geometrične tolerance. Osnovna elementa po tolerančnem sistemu ISO a) premer luknje D (notranja mera), b) premer čepa d (zunanja mera) Veličine za opis toleranc
Toke. Sence. Konstrukcija in enote. Posebnosti. Pri drugem programu je rist orientiran horizontalno!
 asist. dr. Domen Kušar OPISNA GEOMETRIJA - NAVODILA ZA IZDELAVO PROGRAMOV 2007/2008 Splošno 12 programov, ki se jih izdeluje v drugem semestru prvega letnika, predstavlja pogoj za pristop k pisnemu delu
asist. dr. Domen Kušar OPISNA GEOMETRIJA - NAVODILA ZA IZDELAVO PROGRAMOV 2007/2008 Splošno 12 programov, ki se jih izdeluje v drugem semestru prvega letnika, predstavlja pogoj za pristop k pisnemu delu
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
1. Splošno o koordinatnih sistemih
 PROJEKTNA NALOGA Avtor: XXX,XXX Šolsko leto: 2009/2010 Kazalo 1. Splošno o koordinatnih sistemih...2 2. Koordinatni sistemi...3 2.1 Kartezični koordinatni sistem ali koordinatni sistem v ravnini...3 2.2.
PROJEKTNA NALOGA Avtor: XXX,XXX Šolsko leto: 2009/2010 Kazalo 1. Splošno o koordinatnih sistemih...2 2. Koordinatni sistemi...3 2.1 Kartezični koordinatni sistem ali koordinatni sistem v ravnini...3 2.2.
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Naloge iz vaj: Sistem togih teles C 2 C 1 F A 1 B 1. Slika 1: Sile na levi in desni lok.
 1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
1 Rešene naloge Naloge iz vaj: Sistem togih teles 1. Tročleni lok s polmerom R sestavljen iz lokov in je obremenjen tako kot kaže skica. Določi sile podpor. Rešitev: Lok razdelimo na dva loka, glej skico.
1 Seštevanje vektorjev in množenje s skalarjem
 Poglavje I Vektorji Seštevanje vektorjev in množenje s skalarjem Za lažjo geometrično predstavo si najprej oglejmo, kaj so vektorji v ravnini. Vektor je usmerjena daljica, ki je natanko določena s svojo
Poglavje I Vektorji Seštevanje vektorjev in množenje s skalarjem Za lažjo geometrično predstavo si najprej oglejmo, kaj so vektorji v ravnini. Vektor je usmerjena daljica, ki je natanko določena s svojo
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune
![11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune 11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune](/thumbs/79/79968210.jpg) 11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
*P172C10113* MATEMATIKA NAVODILA ZA OCENJEVANJE JESENSKI IZPITNI ROK. Petek, 25. avgust Državni izpitni center POKLICNA MATURA
 Državni izpitni center *P7C0* JESENSKI IZPITNI ROK MATEMATIKA NAVODILA ZA OCENJEVANJE Petek, 5. avgust 07 POKLICNA MATURA Državni izpitni center Vse pravice pridržane. P7-C0-- NAVODILA ZA OCENJEVANJE nalog
Državni izpitni center *P7C0* JESENSKI IZPITNI ROK MATEMATIKA NAVODILA ZA OCENJEVANJE Petek, 5. avgust 07 POKLICNA MATURA Državni izpitni center Vse pravice pridržane. P7-C0-- NAVODILA ZA OCENJEVANJE nalog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
L-400 TEHNIČNI KATALOG. Talni konvektorji
 30 50 30-00 TEHIČI KATAOG 300 Talni konvektorji TAI KOVEKTORJI Talni konvektorji z naravno konvekcijo TK Talni konvektorji s prisilno konvekcijo TKV, H=105 mm, 10 mm Talni konvektorji s prisilno konvekcijo
30 50 30-00 TEHIČI KATAOG 300 Talni konvektorji TAI KOVEKTORJI Talni konvektorji z naravno konvekcijo TK Talni konvektorji s prisilno konvekcijo TKV, H=105 mm, 10 mm Talni konvektorji s prisilno konvekcijo
Deljivost naravnih števil
 Deljivost naravnih števil. D = {,,, 4, 6, }, V = {, 4, 6, 48, 60 }. (A) in (E). a) S številom so deljiva števila:, 0, 0 in 060. S številom so deljiva števila: 0, 460, 000 in 46. c) S številom 4 so deljiva
Deljivost naravnih števil. D = {,,, 4, 6, }, V = {, 4, 6, 48, 60 }. (A) in (E). a) S številom so deljiva števila:, 0, 0 in 060. S številom so deljiva števila: 0, 460, 000 in 46. c) S številom 4 so deljiva
Matrike. Poglavje II. Matrika je pravokotna tabela realnih števil. Na primer: , , , 0 1
 Poglavje II Matrike Matrika je pravokotna tabela realnih števil Na primer: [ ] 1 1 1, 2 3 1 1 0 1 3 2 1, 0 1 4 [ ] 2 7, Matrika je sestavljena iz vrstic in stolpcev Vrstici matrike [ ] 1 1 1 2 3 1 [ ]
Poglavje II Matrike Matrika je pravokotna tabela realnih števil Na primer: [ ] 1 1 1, 2 3 1 1 0 1 3 2 1, 0 1 4 [ ] 2 7, Matrika je sestavljena iz vrstic in stolpcev Vrstici matrike [ ] 1 1 1 2 3 1 [ ]
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Univerza v Ljubljani FS & FKKT. Varnost v strojništvu
 Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: srede med 9:00 in 11:30 pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si,
Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: srede med 9:00 in 11:30 pisarna: FS - 414 telefon: 01/4771-414 boris.jerman@fs.uni-lj.si,
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Univerza v Ljubljani FS & FKKT. Varnost v strojništvu
 Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: objavljeno na vratih in na internetu pisarna: FS - 414 telefon: 01/4771-414
Univerza v Ljubljani FS & FKKT Varnost v strojništvu doc.dr. Boris Jerman, univ.dipl.inž.str. Govorilne ure: med šolskim letom: objavljeno na vratih in na internetu pisarna: FS - 414 telefon: 01/4771-414
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Primeri: naftalen kinolin spojeni kinolin
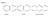 Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
