RJEŠAVANJE PROBLEMA s podzemnom vodom
|
|
|
- Τιτάνια Αξιώτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Inženjersko značenje hidrogeoloških uvjeta: POVRŠINSKA VODA PODZEMNA VODA zagađenje poplava usijedanje zemljišta zbog trajnog sniženja podzemne vode erozija 1 III. HIDROGEOLOŠKI UVJETI RJEŠAVANJE PROBLEMA s podzemnom vodom KONTROLA NEPOVODLJNOG UTJECAJA značajke geološke građe i PODZEMNE VODE 2
2 3 POROZITET = volumen pora / ukupni volumen (kapacitet materijala da primi vodu kad je saturiran) npr. posuda 5 l; 4 l čvrstih čestica + 1 l vode porozitet = 1/5 * 100 = 20% koef. pora = ¼ = 0,25 KOEFICIJENT PORA = volumen pora / volumen čvrstih čestica (inženjerski opis značajki poroziteta tla) 4
3 Gornja zona (u porama zrak i vlaga u sljedećim oblicima): 1. gravitacijska/vadozna voda kreće se pod utjecajem gravitacije; 2. higroskopna vlaga (film vode oko zrna, ne kreće se uslijed gravitacije) 3. lebdeća voda 4. kapilarni pojas (inženjerski problemi!!) 5 OPĆENITO O PODZEMNOJ VODI razina podzemne vode pijezometarska razina/površina hidraulički gradijent 6
4 III. HIDROGEOLOŠKI UVJETI OPĆENITO O PODZEMNOJ VODI hidrostatski tlak propusnost tečenje podzemne vode: HIDRAULIČKI GRADIJENT 7 HIDROSTATIČKI UVJETI HIDROSTATSKI TLAK porni tlak u tlu kada voda miruje Porni tlak P na dubini h u vodi jednak je jediničnoj težini vode (γ w ) * dubina + atmosferski pritisak slide JEDINIČNE TEŽINE RPV horizontalna; ista u tlu i jezeru skica 1: naprezanja u elementu tla od vlastite težine kada je tlo potopljeno 8
5 JEDINIČNA TEŽINA ili gustoća tla γ = težina materijala / volumen materijala γ m = vlažna jedinična težina tla γ d = suha jedinična težina (težina potpuno osušenog tla, u pećnici) γ sat = saturirana jedinična težina (težina potpuno saturiranog tla) γ w = jedinična težina vode = 62.4 lb/ft3 (1 ft3 vode teži 62.4 lb; 9.8 kn/m 3 ) 9 Načelo efektivnih naprezanja SUHO TLO naprezanja se prenose preko čvrstih čestica TLO ISPOD RPV-A naprezanja se prenose preko čvrstih čestica i vode za mehaničko ponašanje tla bitna su EFEKTIVNA NAPREZANJA (σ ), naprezanja koja se prenose preko čvrstih čestica (skeleta tla) efektivno naprezanje je onaj dio totalnog naprezanja koji se prenosi preko skeleta tla 10
6 Načelo efektivnih naprezanja izmjeriti se mogu ukupna (totalna naprezanja) izmjeriti se mogu porni tlakovi (tlakovi u pornoj vodi) EFEKTIVNA NAPREZANJA (σ ) je izvedena veličina σ = σ-u 11 PODZEMNA VODA PORNI TLAK računanje pornog tlaka h = h p + z µ = h p γ w ukupni potencijal (visina potencijalne energije) = piezometarski potencijal + geodetski potencijal PORNI TLAK je umnožak piezometarskog potencijala i jedinične težine vode 12
7 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PARAMETRI PODZEMNA VODA PORNI TLAK h = h p + z µ = h p γ w tlačna visina 13 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PARAMETRI PODZEMNA VODA PORNI TLAK h = h p + z µ = h p γ w 14
8 Načelo efektivnih naprezanja EFEKTIVNA NAPREZANJA (σ ) je σ = σ-u budući da voda ne može prenositi posmična naprezanja vrijedi: τ = τ efektivna naprezanja su važna jer deformacije (slijeganja) tla i čvrstoća ovise upravo o tim naprezanjima 15 PODZEMNA VODA I OTPORNOST TLA nesaturirano tlo kompresija zrak krute čestice međuzrnski pritisak kompresija 16
9 PODZEMNA VODA I OTPORNOST TLA saturirano tlo kompresija voda otpor vode zrak kompresija krute čestice međuzrnski pritisak 17 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PARAMETRI PODZEMNA VODA I OTPORNOST TLA nesaturirano tlo saturirano tlo voda zrak zrak krute čestice međuzrnski pritisak krute čestice međuzrnski pritisak zbog vode - razlika između efektivnih i ukupnih naprezanja 18
10 19 PODZEMNA VODA I OTPORNOST TLA nesaturirano tlo zrak EFEKTIVNA NAPREZANJA krute čestice međuzrnski pritisak saturirano tlo voda PORNI ILI HIDRO- STATIČKI PRITISAK zrak EFEKTIVNA NAPR. krute čestice međuzrnski pritisak UKUPNO = EFEKTIVNO UKUPNO = EFEKTIVNO + PORNI 20 TLAK
11 smicanje PODZEMNA VODA I OTPORNOST TLA saturirano tlo voda nema posmičnu čvrstoću EFEKTIVNA zrak NAPR. krute čestice međuzrnski pritisak smicanje 21 PODZEMNA VODA I OTPORNOST TLA σ = σ u promjene u podzemnoj vodi utječu na efektivna naprezanja σ umanjuju se efektivna naprezanja sposobnost tla da se odupre sili smicanja je manja povećanje razine podzemne vode povećanje pornog tlaka saturirano tlo 22
12 HIDROSTATSKI TLAK I PROCJEĐIVANJE porni tlak u tlu kada je voda nepokretna RPV horizontalna; ista u tlu i jezeru hidraulički gradijent nagib linije 23 porni tlak = tlak vode u porama saturiranog elementa tla uvjeti: nema tečenja, nema naprezanja porni tlak = jedinična težina vode pomnožena s visinom stupca vode (µ = γ w * h p ) µ = 0 kpa µ = 1 kpa µ = 3 kpa 24
13 porni tlak = tlak vode u porama saturiranog elementa tla uvjeti: tečenje prema gore; procjeđivanje uzrokuje povećanje pornog tlaka: na element uronjen u vodu djeluje uzgon koji je jednak razlici tlakova s donje i gornje strane: -za jedinični volumen uzgon je jednak jediničnoj težini vode u = u d u g = γ w µ = 0 kpa µ = 1 kpa µ = 5 kpa vrh uzorka SAMO PORNI TLAK 25 Određivanje potencijala i pornog tlaka je neophodno da bi se predvidjele promjene pornog tlaka i njihovi mogući učinci na inženjerske radove. Kvantifikacija tečenja vode kroz tlo pomoću Darcyjevog zakona: Q=kAh/L. Strujna mreža je grafička metoda za izračun procjeđivanja. 26
14 PODZEMNA VODA: kretanje podzemne vode Brzina TEČENJA podzemne vode KROZ TLO: v = k * i -nagib vodne plohe -propusnost stijene. Darcyjev zakon: 27 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PARAMETRI PODZEMNA VODA PROTOK važno zbog računanja procjeđivanja kroz ili ispod nasipa ANALITIČKA METODA h Q = ka L GRAFIČKA METODA STRUJNA MREŽA 28
15 tečenje vode u tlu modelira se strujnom mrežom; STRUJNICE linije koje pokazuju smjer tečenja EKVIPOTENCIJALA linija jednakih potencijala STRUJNA CIJEV područje između dvije strujnice PODZEMNA VODA PROTOK strujna mreža 29 Upotreba strujne mreže određivanje tlaka vode (pornog tlaka) u bilo kojoj točki mreže: množenje piezometarske visine sa specifičnom težinom vode µ =h p *γ w određivanje protoka (za jednu strujnu cijev : q i =k*( H/ l)* b za kvadratičnu mrežu je l/ b=1 30
16 PODZEMNA VODA PROTOK strujna mreža qi = k* ( H/ l)* b Q = k n n f d H 31 PROPUSNOST TLO zrak zrak voda voda krute čestice krute čestice krute čestice drenirani uvjeti parcijalno drenirani uvjeti nedrenirani uvjeti ili 32 potpuno saturirani
17 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PARAMETRI pore ili šupljine u tlu PROPUSNOST TLO zrak voda krute čestice KOLIČINA VELIČINA POVEZANOST pora uvjetuje propusnost tla 33 PROPUSNOST TLA mjerne jedinice i red veličine 34
18 PODZEMNA VODA SILA STRUJNOG TLAKA...naprezanje u tlu prouzročeno tečenjem vode (= hidraulički gradijent * jedinična težina vode) P s = može prouzročiti istiskivanje individualnih čestica (djeluje u podnožju brana, na padinama ili na dnu iskopa; narušava integritet strukture tla, stvaranje kanala i razvoj još većih pritisaka) pojava ključanja tla kod kritičnog hidrauličkog gradijenta SILA STRUJNOG TLAKA premašuju težinu tla; gubi se međuzrnsko trenje γ T γ w γ b i c = = i γ γ c = γ / γ w w u krupnozrnatim pijescima i c je 0.9-1; FS (likvefakcija)=i c /i i γ w w 35 Hidraulički slom tla u građevinskoj jami može nastupiti slom tla uslijed strujanja vode prema gore tzv. kritični hidraulički gradijent ispiranje čestica iz tla u dnu građevne jame samoubrzavajući proces, jer se ispiranjem čestica smanjuje debljina tla, a time povećava gradijent (proces u građevnoj jami može biti tako brz da mješavina vode i čestica u nekoliko sati ispuni čitav volumen građevne jame) 36
19 povećanje RPV-a; opasnost od hidrauličkog sloma tla 37 slika Daso 38
20 U inženjerskoj geologiji važni: 1. (hidrogeološki) uvjeti koji imaju inženjersko značenje, a odnose se na površinsku i podzemnu vodu; 2. analitički postupci; 3. metode kontrole negativnog utjecaja podzemne vode i procjeđivanja; - (prostorno planiranje) 39 III. HIDROGEOLOŠKI UVJETI Proučavanje podzemne vode u inženjerskoj geologiji VODA KAO INŽENJERSKI PROBLEM (1) problema koje može prouzročiti u građenju; (2) njezinog djelovanja kao agensa erozije; (3) njezinog utjecaja na funkcioniranje građevina; (4) njezinog djelovanja kao medija za prenošenje zagađenja 40
21 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PROBLEMI slom brane Teton (USA) voda kao agens erozije hidraulički slom tla 41 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PROBLEMI slom brane Teton (USA) 42
22 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI PROBLEMI slom brane Teton (USA) Otvorene frakture i pukotine u stijeni desnog potpornjaka bile su inicijalni diskontinuiteti na kojima je započeo proces ispiranja materijala vodom. 43 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI ZAHVATI BARIJERE (različite vrste nasipa) BRTVENI SLOJEVI DRENOVI BUŠOTINE I BUNARI 44
23 sl
24 III. HIDROGEOLOŠKI UVJETI INŽENJERSKI ZAHVATI izbor metode kontrole podzemne vode ovisi o geološkoj građi podzemlja neophodni podaci o značajkama stijena/tala i podzemnoj vodi 47 H y =34y H / h = γ slatke / γ slane h γ = specifična težina 48
Procesi tečenja u tlu i stijeni VODA U TLU
 str. 1 VODA U TLU I. Uvod Kada ne bi bilo vode u tlu, geotehničko bi inženjerstvo bila puno jednostavnija grana građevinarstva. Koliko opterećenje na tlo, tolika promjena ukupnih naprezanja i, kao rezultat,
str. 1 VODA U TLU I. Uvod Kada ne bi bilo vode u tlu, geotehničko bi inženjerstvo bila puno jednostavnija grana građevinarstva. Koliko opterećenje na tlo, tolika promjena ukupnih naprezanja i, kao rezultat,
4 Voda u tlu. 4.1 Pojavnost vode u tlu.
 4 Voda u tlu. 4.1 Pojavnost vode u tlu. Zbog velike važnosti koju prisutnost vode ima na ponašanje tla, ovdje se studenta najprije podsjeća na neka poglavlja hidromehanike, koja se zatim primjenjuju na
4 Voda u tlu. 4.1 Pojavnost vode u tlu. Zbog velike važnosti koju prisutnost vode ima na ponašanje tla, ovdje se studenta najprije podsjeća na neka poglavlja hidromehanike, koja se zatim primjenjuju na
Troosni posmik. Troosni posmik. Troosni posmik. Priprema neporemećenog uzorka. Troosnaćelija. Uzorak je u gumenoj membrani Ćelija se ipuni sa vodom
 Troosnaćelija Ploha loma Priprema neporemećenog uzorka Uzorak je u gumenoj membrani Ćelija se ipuni sa vodom 1 Oprema za troosna ispitivanja (Institut IGH Zagreb) Test Animation σ1= = σdev = σ1= = σdev
Troosnaćelija Ploha loma Priprema neporemećenog uzorka Uzorak je u gumenoj membrani Ćelija se ipuni sa vodom 1 Oprema za troosna ispitivanja (Institut IGH Zagreb) Test Animation σ1= = σdev = σ1= = σdev
Samo se ukupna naprezanja i porni tlak mogu mjeriti, a efektivna naprezanja su izvedena veličina, izravno nemjerljiva, ali
 5 Naprezanja u tlu. 5.1 Načelo efektivnih naprezanja. Ilustracija: položite spužvu u posudu s nešto vode tako da spužva bude potopljena kao na slici i da sve pore budu ispunjene vodom. Dolijevajte vodu
5 Naprezanja u tlu. 5.1 Načelo efektivnih naprezanja. Ilustracija: položite spužvu u posudu s nešto vode tako da spužva bude potopljena kao na slici i da sve pore budu ispunjene vodom. Dolijevajte vodu
Osnovni elementi klizišta
 STABILNOST KOSINA Klizište 1/ Klizanje kao geološki fenomen: - tektonski procesi - gravitacijske i hidrodinamičke sile 2/ Klizanja nastala djelovanjem ljudi: - iskopi, nasipi, dodatno opterećenje kosina
STABILNOST KOSINA Klizište 1/ Klizanje kao geološki fenomen: - tektonski procesi - gravitacijske i hidrodinamičke sile 2/ Klizanja nastala djelovanjem ljudi: - iskopi, nasipi, dodatno opterećenje kosina
P E D O L O G I J A. Tema: Voda u tlu
 MEĐUSVEUČILIŠNI STUDIJ MEDITERANSKA POLJOPRIVREDA P E D O L O G I J A Tema: Voda u tlu Doc.dr.sc. Aleksandra BENSA i Dr.sc. Boško MILOŠ Autorizirana prezentacija Split, 2011/12. Cilj Objasniti odnose između
MEĐUSVEUČILIŠNI STUDIJ MEDITERANSKA POLJOPRIVREDA P E D O L O G I J A Tema: Voda u tlu Doc.dr.sc. Aleksandra BENSA i Dr.sc. Boško MILOŠ Autorizirana prezentacija Split, 2011/12. Cilj Objasniti odnose između
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
Kolegij: Konstrukcije Rješenje zadatka 2. Okno Građevinski fakultet u Zagrebu. Efektivna. Jedinična težina. 1. Glina 18,5 21,
 Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Kolegij: Konstrukcije 017. Rješenje zadatka. Okno Građevinski fakultet u Zagrebu 1. ULAZNI PARAETRI. RAČUNSKE VRIJEDNOSTI PARAETARA ATERIJALA.1. Karakteristične vrijednosti parametara tla Efektivna Sloj
Izravni posmik. Posmična čvrstoća tla. Laboratorijske metode određivanja kriterija čvratoće ( c i φ )
 Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
5. NAPONI I DEFORMACIJE
 MEHANIKA TLA: Naponi i deformacije 59 5. NAPONI I DEFORMACIJE Klasifikacija tla i poznavanje osnovnih pokazatelja fizičkih osobina tla je potrebno ali ne i dovoljno da bi se rešio najveći broj zadataka
MEHANIKA TLA: Naponi i deformacije 59 5. NAPONI I DEFORMACIJE Klasifikacija tla i poznavanje osnovnih pokazatelja fizičkih osobina tla je potrebno ali ne i dovoljno da bi se rešio najveći broj zadataka
HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA JEDNADŽBA KONTINUITETA. s1 =
 HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA Hidrodinamika proučava fluide (tekućine i plinove) u gibanju. Gibanje fluida naziva se strujanjem. Ovdje ćemo razmatrati strujanje tekućina.
HIDRODINAMIKA JEDNADŽBA KONTINUITETA I BERNOULLIJEVA JEDNADŽBA Hidrodinamika proučava fluide (tekućine i plinove) u gibanju. Gibanje fluida naziva se strujanjem. Ovdje ćemo razmatrati strujanje tekućina.
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Q (promjenjivo) P (stalno) c uk=50 (kn/m ) =17 (kn/m ) =20 (kn/m ) 2k=0 (kn/m ) N 60=21 d=0.9 (m)
 L = L 14.1. ZADATAK Zadan je pilot kružnog poprečnog presjeka, postavljen kroz dva sloja tla. Svojstva tla i dimenzije pilota su zadane na skici. a) Odrediti graničnu nosivost pilota u vertikalnom smjeru.
L = L 14.1. ZADATAK Zadan je pilot kružnog poprečnog presjeka, postavljen kroz dva sloja tla. Svojstva tla i dimenzije pilota su zadane na skici. a) Odrediti graničnu nosivost pilota u vertikalnom smjeru.
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
PRILOG. Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C)
 PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
PRILOG Tab. 1.a. Dozvoljena trajna opterećenja bakarnih pravougaonih profila u(a) za θ at =35 C i θ=30 C, (θ tdt =65 C) Tab 3. Vrednosti sačinilaca α i β za tipične konstrukcije SN-sabirnica Tab 4. Minimalni
Slika 5.1 Oblici ponašanja tla pri smicanju
 MEHANIKA TLA: Čvrstoća tla 66 6. ČVRSTOĆA TLA Jedna od najvažnijih inženjerskih osobina tla je svakako smičuća čvrstoća tla. Ona predstavlja najveći smičući napon koji se može naneti strukturi tla u određenom
MEHANIKA TLA: Čvrstoća tla 66 6. ČVRSTOĆA TLA Jedna od najvažnijih inženjerskih osobina tla je svakako smičuća čvrstoća tla. Ona predstavlja najveći smičući napon koji se može naneti strukturi tla u određenom
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
RAD, SNAGA I ENERGIJA
 RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Opšte KROVNI POKRIVAČI I
 1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
1 KROVNI POKRIVAČI I FASADNE OBLOGE 2 Opšte Podela prema zaštitnim svojstvima: Hladne obloge - zaštita hale od atmosferskih padavina, Tople obloge - zaštita hale od atmosferskih padavina i prodora hladnoće
Osnovni elementi mehanike tla
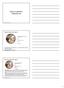 Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami
 BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
GEOTEHNIČKE KONSTRUKCIJE POTPORNE KONSTRUKCIJE. Predavanje: POTPORNE KONSTRUKCIJE Prof.dr.sc. Leo MATEŠIĆ 2012/13
 GEOTEHNIČKE KONSTRUKCIJE POTPORNE KONSTRUKCIJE Predavanje: POTPORNE KONSTRUKCIJE Prof.dr.sc. Leo MATEŠIĆ 2012/13 Sadržaj predavanja 1 TLAK I OTPOR TLA (ponavljanje) 1.1 Općenito - Horizontalni (bočni)
GEOTEHNIČKE KONSTRUKCIJE POTPORNE KONSTRUKCIJE Predavanje: POTPORNE KONSTRUKCIJE Prof.dr.sc. Leo MATEŠIĆ 2012/13 Sadržaj predavanja 1 TLAK I OTPOR TLA (ponavljanje) 1.1 Općenito - Horizontalni (bočni)
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
VOLUMEN ILI OBUJAM TIJELA
 VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
Sistem sučeljnih sila
 Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Gauss, Stokes, Maxwell. Vektorski identiteti ( ),
 Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
BUŠENJE I Fo F r o m r ul u e l
 BUŠENJE I Formule Površina prstenastog presjeka NIZ BUŠAĆIH ALATKI A = π (D 2 4 d 2 ) A površina prstenastog presjeka (m 2 ) D vanjski promjer prstenastog presjeka (m) d unutarnji promjer prstenastog presjeka
BUŠENJE I Formule Površina prstenastog presjeka NIZ BUŠAĆIH ALATKI A = π (D 2 4 d 2 ) A površina prstenastog presjeka (m 2 ) D vanjski promjer prstenastog presjeka (m) d unutarnji promjer prstenastog presjeka
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
GEOTEHNIČKO INŽENJERSTVO
 GEOTEHNIČKO INŽENJERSTVO POMOĆNI DIJAGRAMI, TABLICE I FORMULE ZA ISPIT dopunjeno za ak.god. 016/017 Slika 1. Parcijalni koeficijenti za GEO/STR za djelovanja, parametre materijala i otpore prema EC-7 Slika.
GEOTEHNIČKO INŽENJERSTVO POMOĆNI DIJAGRAMI, TABLICE I FORMULE ZA ISPIT dopunjeno za ak.god. 016/017 Slika 1. Parcijalni koeficijenti za GEO/STR za djelovanja, parametre materijala i otpore prema EC-7 Slika.
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
MJERENJE MALIH DEFORMACIJA U LABORATORIJU
 MJERENJE MALIH DEFORMACIJA U LABORATORIJU RAZLOZI MJERENJA DEFORMACIJA U TLU Pri projektiranju dinamički opterećenih temelja treba odrediti sljedeće: kriterije ponašanja (dozvoljene amplitude, brzine,
MJERENJE MALIH DEFORMACIJA U LABORATORIJU RAZLOZI MJERENJA DEFORMACIJA U TLU Pri projektiranju dinamički opterećenih temelja treba odrediti sljedeće: kriterije ponašanja (dozvoljene amplitude, brzine,
Opća bilanca tvari - = akumulacija u dif. vremenu u dif. volumenu promatranog sustava. masa unijeta u dif. vremenu u dif. volumen promatranog sustava
 Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
MEHANIKA FLUIDA dio 5
 MEHANIKA FLUIDA dio 5 prof. Željko Andreić Rudarsko-geološko-naftni fakultet Sveučilište u Zagrebu zandreic@rgn.hr http://rgn.hr/~zandreic/ Željko Andreić Mehanika fluida P5 1 sadržaj 1-2-3! Tečenje kroz
MEHANIKA FLUIDA dio 5 prof. Željko Andreić Rudarsko-geološko-naftni fakultet Sveučilište u Zagrebu zandreic@rgn.hr http://rgn.hr/~zandreic/ Željko Andreić Mehanika fluida P5 1 sadržaj 1-2-3! Tečenje kroz
Tip ureappleaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 656
 TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
A 2 A 1 Q=? p a. Rješenje:
 8. VJEŽBA - RIJEŠENI ZADACI IZ MEANIKE FLUIDA. Oreite minimalni protok Q u nestlačiom strujanju fluia ko koje će ejektor početi usisaati flui kroz ertikalnu cječicu. Zaano je A = cm, A =,5 cm, h=,9 m.
8. VJEŽBA - RIJEŠENI ZADACI IZ MEANIKE FLUIDA. Oreite minimalni protok Q u nestlačiom strujanju fluia ko koje će ejektor početi usisaati flui kroz ertikalnu cječicu. Zaano je A = cm, A =,5 cm, h=,9 m.
Izbor statističkih testova Ana-Maria Šimundić
 Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
IZVORI DEPRESIJE U VJETRENOJ MREŽI
 IZVORI DEPRESIJE U VJETRENOJ MREŽI Svladavanjeotporatrenja strujanja zraka jamskih provodnika dovodi dogubitkatlaka (tlačne visine, depresije). Gubitke tlaka treba nadoknaditi izvorima depresija. Izvoridepresije
IZVORI DEPRESIJE U VJETRENOJ MREŽI Svladavanjeotporatrenja strujanja zraka jamskih provodnika dovodi dogubitkatlaka (tlačne visine, depresije). Gubitke tlaka treba nadoknaditi izvorima depresija. Izvoridepresije
INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave
 ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave 1.MEHANIKA FLUIDA 1.1 Uvod Fluidima nazivamo tečnosti i gasove (plinove): to su supstance koje lako mijenaju oblik,
ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA II Predavanja za 1. sedmicu nastave 1.MEHANIKA FLUIDA 1.1 Uvod Fluidima nazivamo tečnosti i gasove (plinove): to su supstance koje lako mijenaju oblik,
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
( ) ρ = ρ. Zadatak 141 (Ron, gimnazija) Gustoća leda je 900 kg/m 3, a gustoća morske vode 1000 kg/m 3. Koliki dio ledene sante
 Zadatak 4 (Ron, ginazija) Gustoća leda je 900 /, a gustoća orske vode 00 /. Koliki dio ledene sante voluena viri iznad orske površine? (g = 9.8 /s ) Rješenje 4 ρ l = 900 /, ρ v = 000 /,, =? Akceleracija
Zadatak 4 (Ron, ginazija) Gustoća leda je 900 /, a gustoća orske vode 00 /. Koliki dio ledene sante voluena viri iznad orske površine? (g = 9.8 /s ) Rješenje 4 ρ l = 900 /, ρ v = 000 /,, =? Akceleracija
KONVEKSNI SKUPOVI. Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5. Back FullScr
 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
Metode i instrumenti za određivanje visinskih razlika. Zdravka Šimić
 Metode i instrumenti za određivanje visinskih razlika Zdravka Šimić Visinski prikaz terena - konfiguracija dio plana dio karte 2 Visinski prikaz terena Izohipse ili slojnice povezuju točke iste visine.
Metode i instrumenti za određivanje visinskih razlika Zdravka Šimić Visinski prikaz terena - konfiguracija dio plana dio karte 2 Visinski prikaz terena Izohipse ili slojnice povezuju točke iste visine.
VISKOZNOST TEČNOSTI Viskoznost
 VISKOZNOST VISKOZNOST TEČNOSTI Viskoznost predstavlja otpor kojim se pojedini slojevi tečnosti suprostavljaju kretanju jednog u odnosu na drugi, odnosno to je vrsta unutrašnjeg trenja koja dovodi do protoka
VISKOZNOST VISKOZNOST TEČNOSTI Viskoznost predstavlja otpor kojim se pojedini slojevi tečnosti suprostavljaju kretanju jednog u odnosu na drugi, odnosno to je vrsta unutrašnjeg trenja koja dovodi do protoka
OSNOVE INŽENJERSKE GEOLOGIJA. Snježana Mihalić
 OSNOVE INŽENJERSKE GEOLOGIJA Snježana Mihalić Osnove inženjerske geologije Doc. dr. sc. SNJEŽANA MIHALIĆ http://www.rgn.hr/~smihalic/ Sveučilište u Zagrebu Rudarsko-geološko-naftni fakultet smihalic@rgn.hr
OSNOVE INŽENJERSKE GEOLOGIJA Snježana Mihalić Osnove inženjerske geologije Doc. dr. sc. SNJEŽANA MIHALIĆ http://www.rgn.hr/~smihalic/ Sveučilište u Zagrebu Rudarsko-geološko-naftni fakultet smihalic@rgn.hr
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU
 SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZORAN BAJSIĆ ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU ZAVRŠNI RAD VARAŽDIN, 2012. SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZAVRŠNI RAD ODREĐIVANJE MODULA
SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZORAN BAJSIĆ ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU ZAVRŠNI RAD VARAŽDIN, 2012. SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZAVRŠNI RAD ODREĐIVANJE MODULA
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Fluidi. fluid je bilo koja tvar koja može teći. plinovi i tekućine razlika: plinovi su stlačivi, tekućine nisu (u većini slučajeva)
 MEHANIKA FLUIDA Fluidi fluidi igraju vitalnu ulogu u raznim aspektima naših života pijemo ih, dišemo, plivamo u njima oni cirkuliraju našim tijelima i kontroliraju meteorološke uvjete zrakoplovi lete kroz
MEHANIKA FLUIDA Fluidi fluidi igraju vitalnu ulogu u raznim aspektima naših života pijemo ih, dišemo, plivamo u njima oni cirkuliraju našim tijelima i kontroliraju meteorološke uvjete zrakoplovi lete kroz
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
10. STATIKA FLUIDA Uvod. -ionizirani plin (visoka temperatura) kvantnomehanički. -odreñen oblik i volumen. -poprimaju oblik posude
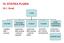 10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
10. STATIKA FLUIDA 10.1. Uvod TVARI KRUTINE TEKUĆINE (KAPLJEVINE) PLINOVI PLAZMA BOSE- EINSTEINOV KONDENZAT -odreñen oblik i volumen -orimaju oblik osude volumennestlačiv -ionizirani lin (visoka temeratura)
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom
 Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
PRETHODNI PRORACUN VRATILA (dimenzionisanje vratila)
 Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
STABILNOST KOSINA. (ponavljanje)
 KLIZIŠTA STABILNOST KOSINA (ponavljanje) Definicija faktora sigurnosti F S τ τ f = τ d ϕ ' ϕ d ' < ϕ ' c ' c d ' < c ' σ Prikaz efektivnih graničnih i mobiliziranih parametara čvrstoće Vrijedi, dakle,
KLIZIŠTA STABILNOST KOSINA (ponavljanje) Definicija faktora sigurnosti F S τ τ f = τ d ϕ ' ϕ d ' < ϕ ' c ' c d ' < c ' σ Prikaz efektivnih graničnih i mobiliziranih parametara čvrstoće Vrijedi, dakle,
TROŠENJE STIJENA REZIDUALNA TLA
 inženjersko tlo TROŠENJE STIJENA REZIDUALNA TLA nastaju trošenjem osnovne stijene profil tla predstavlja povijesni zapis trošenja stijene izdvajanje zona s obzirom na stupanj trošnosti klasifikacije trošnosti
inženjersko tlo TROŠENJE STIJENA REZIDUALNA TLA nastaju trošenjem osnovne stijene profil tla predstavlja povijesni zapis trošenja stijene izdvajanje zona s obzirom na stupanj trošnosti klasifikacije trošnosti
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
7 Deformabilnost i čvrstoća tla.
 7 Deformabilnost i čvrstoća tla. 7.1 Naprezanja i deformacije. Modeli ponašanja elementa tla. Da bismo predvidjeli ponašanje građevine i temeljnog tla, odnosno oblikovali/projektirali građevinu tako da
7 Deformabilnost i čvrstoća tla. 7.1 Naprezanja i deformacije. Modeli ponašanja elementa tla. Da bismo predvidjeli ponašanje građevine i temeljnog tla, odnosno oblikovali/projektirali građevinu tako da
ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD
 GRAĐEVINSKO - ARHITEKTONSKI FAKULTET Katedra za metalne i drvene konstrukcije Kolegij: METALNE KONSTRUKCIJE ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD TLOCRTNI PRIKAZ NOSIVOG SUSTAVA OBJEKTA 2 PRORAČUN
GRAĐEVINSKO - ARHITEKTONSKI FAKULTET Katedra za metalne i drvene konstrukcije Kolegij: METALNE KONSTRUKCIJE ANALIZA DJELOVANJA (OPTEREĆENJA) - EUROKOD TLOCRTNI PRIKAZ NOSIVOG SUSTAVA OBJEKTA 2 PRORAČUN
