ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ

Transcript

1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ολοκληρωµένα Κυκλώµατα µ Έµφαση στη Μικροταινία ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του ΗΜΗΤΡΙΟΥ Ν. ΛΟΪΖΟΥ Επιβλέπων : Ιωάννης Παπανάνος Αναπληρωτής Καθηγητής Ε.Μ.Π. Αθήνα, Ιούλιος 3

2

3 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΕΠΙΚΟΙΝΩΝΙΩΝ, ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ολοκληρωµένα Κυκλώµατα µ Έµφαση στη Μικροταινία ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ του ΗΜΗΤΡΙΟΥ Ν. ΛΟΪΖΟΥ Επιβλέπων : Ιωάννης Παπανάνος Αναπληρωτής Καθηγητής Ε.Μ.Π. Εγκρίθηκ από την τριµλή ξταστική πιτροπή την 6 η Ιουλίου 3. (Υπογραφή) (Υπογραφή) (Υπογραφή) Ιωάννης Παπανάνος Ιωάννης Αβαριτσιώτης Ελυθέριος Καγιάφας Αναπληρωτής Καθηγητής Ε.Μ.Π. Καθηγητής Ε.Μ.Π. Καθηγητής Ε.Μ.Π. Αθήνα, Ιούλιος 3

4 (Υπογραφή)... ΗΜΗΤΡΙΟΣ Ν. ΛΟΪΖΟΣ ιπλωµατούχος Ηλκτρολόγος Μηχανικός και Μηχανικός Υπολογιστών Ε.Μ.Π. 3 All ight eeved

5 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Πρίληψη Πρίληψη Η διπλωµατική αυτή ργασία αποτλί µία µλέτη των, έως σήµρα, γνωστών και πρισσότρο διαδδοµένων τρόπων µοντλοποίησης των γραµµών µταφοράς σ ολοκληρωµένα κυκλώµατα. Η δοµή στην οποία στιάζται το νδιαφέρον ίναι η δοµή της µικροταινίας, της γραµµής µταφοράς, δηλαδή, που αποτλίται από αγωγό σήµατος πάνω από ηµιαγώγιµο υπόστρωµα, το οποίο, µ τη σιρά του, βρίσκται πάνω από αγώγιµη πιφάνια γίωσης. Αρχικά, γίνται µία παρουσίαση των πιο διαδδοµένων µθόδων µοντλοποίησης της µικροταινίας και, ν συνχία, µία θωρητική ανάλυση πλήρους κύµατος της µικροταινίας, χρησιµοποιώντας βασικές ξισώσις της ηλκτροµαγνητικής θωρίας. Παράλληλα, διυκρινίζται ότι η ργασία αυτή θα πικντρωθί στις φυσικές µθόδους µοντλοποίησης. Το κύριο µέρος της ργασίας πραγµατύται την πξήγηση πέντ µθόδων φυσικής µοντλοποίησης, καθώς και των ισοδύναµων κυκλωµατικών µοντέλων και των ξισώσων απλής και κλιστής µορφής που προτίνονται από αυτές. Τα µοντέλα αυτά συγκρίνονται καταρχήν µταξύ τους ώστ να διαπιστωθί κατά πόσο συµφωνούν, νώ στη συνέχια γίνται µία σύγκριση µ ργαστηριακές µτρήσις για συγκκριµένη δοµή µικροταινίας. Η ασυµφωνία µταξύ θωρητικών αποτλσµάτων και πιραµατικών µτρήσων οδηγί στην πρόταση νός καινούριου µοντέλου. Το µοντέλο αυτό βασίζται σ ξισώσις που έχουν ήδη προταθί και λαµβάνι υπόψη τη γωµτρία και τα η- λκτρικά χαρακτηριστικά της µικροταινίας. Το καινούριο µοντέλο συγκρίνται µ τις πιραµατικές µτρήσις και παρατηρίται αρκτά καλή συµφωνία. Λόγω, µάλιστα, του τρόπου ξαγωγής του, το καινούριο µοντέλο µπορί να χρησιµοποιηθί για οποιαδήποτ γωµτρία µικροταινίας. Τέλος, γίνται µία αναφορά στο αν και πότ πρέπι µία γραµµής µταφοράς να θωρίται σαν απλό ή σαν κατανµηµένο κύκλωµα για τον υπολογισµό µγθών διάδοσης νός σήµατος σ αυτήν και παρουσιάζται ο κώδικας τόσο σ HSpice όσο και σ Matlab όλων των µοντέλων που χρησιµοποιήθηκαν.. Ν. Λοΐζος 5

6 Abtact Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Abtact Thi thei contitute a tud of the, up to date, known and mot ued method of tanmiion line modeling in integated cicuit. Inteet i focued on the micotip tuctue: a tanmiion line of a ignal conducto on a emiconducting ubtate, which, in tun, i upon a conducting uface connected to gound. The mot widepead micotip modeling method ae being peented, followed b a theoetical full wave anali of the micotip, uing baic equation fom electomagnetic theo. It i, howeve, claified that thi thei will focu on the phical modeling method. The main pat of thi wok deal with the explanation of five phical modeling method, a well a, the equivalent cicuit model and the imple and cloed-fom equation that ae popoed b thee method. A compaion i fitl made among thee model, in ode to invetigate thei degee of ageement, and then between thee model and laboatoial meauement fo a pecific micotip tuctue. The nonageement between theoetical eult and expeimental data lead to the popoal of a new model. Thi model i baed on alead popoed equation and take into account the geometical and electical chaacteitic of the micotip. Thi new model i compaed with expeimental meauement and a elativel good ageement i obeved. In addition, due to it wa of extaction, thi new model can be ued fo micotip of an geometical chaacteitic. Finall, efeence i made a to if and when a tanmiion line hould be conideed a lumped o ditibuted element fo the calculation of popagation chaacteitic, and the code fo implementing the model ued fo HSpice and Matlab i being peented. 6. Ν. Λοΐζος

7 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Πριχόµνα Πριχόµνα Κφάλαιο : Εισαγωγή 9.. Η σηµασία της σωστής µοντλοποίησης των γραµµών µταφοράς 9.. Γνικές µέθοδοι ανάλυσης και µοντλοποίησης γραµµών µταφοράς... Φυσική µοντλοποίηση 3... Αριθµητικές µέθοδοι ανάλυσης και µοντλοποίησης 3... Ανάλυση Quai-TEM 3... Αναλύσις πλήρους κύµατος (full-wave) 4... Μέθοδος FDTD 4... Μέθοδος SDA (Spectal Domain Appoach - Προσέγγιση Φασµατικού Πδίου) Μέθοδος FEM (Finite-Element Method Μέθοδος ιακριτών Στοιχίων) Μέθοδος Mode-Matching (Ταύτισης Ρυθµών) 9 Κφάλαιο : Θωρητικά Στοιχία.. Θωρητική ανάλυση της δοµής της µικροταινίας.. Φυσικές ιδιότητς διάδοσης στη µικροταινία 3 Κφάλαιο 3: Μοντλοποίηση µικροταινίας Το µοντέλο του Jin και των συνργατών του Το µοντέλο των Eo και Eientadt Το µοντέλο του Weihaa και των συνργατών του Μία τροποποίηση του µοντέλου των Schniede και Heinich Το µοντέλο του Wee και των συνργατών του 5 Κφάλαιο 4: Σύγκριση των µοντέλων Σύγκριση των αποτλσµάτων των µοντέλων µ βάση τα δδοµένα στη δηµοσίυση του Jin και των συνργατών του Σύγκριση των αποτλσµάτων των µοντέλων µ βάση τα δδοµένα στη δηµοσίυση των Eo και Eientadt 6 Κφάλαιο 5: Σύγκριση των µοντέλων µ πραγµατικές µτρήσις και παρουσίαση νός καινούριου µοντέλου Σύγκριση των µοντέλων µ ργαστηριακές µτρήσις Παρουσίαση νός καινούριου µοντέλου Έλγχος της ορθότητας του καινούριου µοντέλου 7 Κφάλαιο 6: Τµαχισµός των γραµµών µταφοράς και χρήση ν σιρά δικτυωµάτων 75 Κφάλαιο 7: Επίλογος Ανακφαλαίωση Συµπράσµατα 77 Βιβλιογραφία 8 Παράρτηµα 83 Π. Κώδικας υλοποιηµένων µοντέλων για Matlab 83 Π.. Το µοντέλο του Jin και των συνργατών του 83 Π.. Το µοντέλο των Eo και Eientadt 84 Π.3. Το µοντέλο του Weihaa και των συνργατών του 85 Π.4. Το µοντέλο των Schniede και Heinich 87 Π.5. Το µοντέλο του Wee και των συνργατών του για µικροταινία µ συνπίπδους αγωγούς γίωσης 89 Π.6. Μία τροποποίηση του µοντέλου του Wee και των συνργατών του για απλή δοµή µικροταινίας 9 Π.7. Το καινούριο µοντέλο που προτίνται στην παράγραφο Π. Κώδικας υλοποιηµένων µοντέλων για HSpice 95 Π.. Το µοντέλο του Jin και των συνργατών του 95 Π.. Το µοντέλο των Eo και Eientadt 97 Π.3. Το µοντέλο του Weihaa και των συνργατών του 99. Ν. Λοΐζος 7

8 Πριχόµνα Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Π.4. Το µοντέλο των Schniede και Heinich µ υπόστρωµα νός στρώµατος Π.5. Το τροποποιηµένο µοντέλο των Schniede και Heinich για υπόστρωµα δύο στρωµάτων 5 Π.6. Το µοντέλο του Wee και των συνργατών του για µικροταινία µ συνπίπδους αγωγούς γίωσης 9 Π.7. Μία τροποποίηση του µοντέλου του Wee και των συνργατών του για απλή δοµή µικροταινίας Π.8. Το καινούριο µοντέλο που προτίνται στην παράγραφο Π3. Βοηθητικά προγράµµατα σ Matlab 6 Π3.. Βοηθητικό πρόγραµµα για τη σύγριση των κυκλωµατικών µγθών που προκύπτουν από το κάθ µοντέλο 6 8. Ν. Λοΐζος

9 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο Κφάλαιο Εισαγωγή Προτού πράσουµ στο κυρίως τµήµα της διπλωµατικής ργασίας, κρίνται αναγκαίο να αναφρθούν, έστω συνοπτικά, κάποια βασικά στοιχία αναφορικά µ τη γραµµή µταφοράς. Για το λόγο αυτό, αρχικά, παρουσιάζται η σηµασία της σωστής µοντλοποίησης των γραµµών µταφοράς και οι λόγοι που έχουν οδηγήσι µγάλο τµήµα της πιστηµονικής κοινότητας που ασχολίται µ τη µοντλοποίηση κυκλωµατικών στοιχίων να στρέψι την προσοχή του στο αντικίµνο αυτό. Εν συνχία, απαριθµούνται γνικά οι µέθοδοι που µπορούν να χρησιµοποιηθούν για ανάλυση και µοντλοποίηση της γραµµής µταφοράς, νώ παράλληλα, σηµιώνονται τα πλονκτήµατα και µιονκτήµατα που έχι η χρήση κάθ µίας από τις διαφορτικές αυτές µθόδους. Στο πόµνο κφάλαιο παρουσιάζονται θωρητικά στοιχία που ισχύουν για την πρίπτωση της γραµµής µταφοράς πάνω από ηµιαγώγιµο υπόστρωµα καθώς και τα φυσικά φαινόµνα που λαµβάνουν χώρα κατά τη διάδοση νός σήµατος σ γραµµή µταφοράς... Η σηµασία της σωστής µοντλοποίησης των γραµµών µταφοράς Η µοντλοποίηση και η προσοµοίωση αποτλούν βασικά στοιχία στοιχία του σύγχρονου τρόπου σχδίασης κυκλωµάτων. Η υρία χρήση των µθόδων αυτών στη σχδίαση οφίλται σ δύο λόγους: Καταρχήν, η µαζική παραγωγή ολοκληρωµένων κυκλωµάτων και το γγονός ότι από τη στιγµή που αυτά κατασκυαστούν δν υπάρχουν πριθώρια διορθώσων, αλλαγών ή τροποποιήσων απαιτί µγάλη προσοχή κατά τη σχδίαση, νώ πριν την παραγωγή, τα οποιαδήποτ κυκλώµατα θα πρέπι να ίναι πλήρως λγµένα ως προς σωστή λιτουργία τους υπό διάφορς συνθήκς. ύτρον, το γγονός ότι κάθ κύκλωµα που πιτλί µία λιτουργία δν κατασκυάζται ξχωριστά αλλά αποτλί τµήµα νός µγαλύτρου ολοκληρωµένου κυκλώµατος, στρί από το σχδιαστη τη δυνατότητα µµονωµένων µτρήσων κάθ τµήµατος και κατ πέκταση τη δυνατότητα αλλαγής νός µόνο τµήµατος από το όλο κύκλωµα διατηρώντας τα υπόλοιπα τµήµατα []. Η αναγκαιότητα τα µοντέλα που πριγράφουν τα διάφορα στοιχία νός κυκλώµατος να ίναι κατά το δυνατό ακριβή στον υπολογισµό των τάσων, ρυµάτων και στην αναπαράσταση των κυ- µατοµορφών, µέσα στα αποδκτά, βέβαια, πίπδα σφάλµατος, ίναι µφανής. Τα πρισσότρα προγράµµατα προσοµοίωσης αδυνατούν να προσγγίσουν την πιθυµητή αυτή ακρίβια χωρίς τη χρήση µοντέλων για γραµµές µταφοράς, για τις γραµµές, δηλαδή, που νώνουν µταξύ τους δύο κυκλωµατικά στοιχία. Η µοντλοποίηση γραµµών µταφοράς, στη γνικότρή της έννοια, αναφέρται στη µοντλοποίηση των αγωγών µτάλλου που βρίσκονται µέσα στην ψηφίδα (chip), των µταλλικών παφών της ψηφίδας, των καλωδίων σύνδσης των παφών της ψηφίδας µ τα pin του πριβλήµατός της, καθώς και των ίδιων των pin. Μία πλήρης πριγραφή της συµπριφοράς των γραµµών µταφοράς µπορί να δοθί µόνο πιλύοντας τις ξισώσις του Maxwell, αναλύοντας, δηλαδή, το ηλκτροµαγνητικό πδίο. Σύµφωνα µ τις ξισώσις του Maxwell, η κατανοµή ρύµατος και φορτίου σ µία δοµή πηράζι και πηράζται από τη ροή ρύµατος και την ύπαρξη φορτίου στις γιτονικές µ αυτή δοµές. ν ίναι δυνατό, ποµένως, να υπάρξι πλήρης αποµόνωση νός στοιχίου σ ένα κύκλωµα, νώ οι αλληλπιδράσις του στοιχίου αυτού µ τις γιτονικές του δοµές έχι σαν αποτέλσµα χωρητικά και παγωγικά φαινόµνα καθώς και φαινόµνα αγωγιµότητας, τα οποία χαρακτηρίζονται γνικά ως παρασιτικά φαινόµνα. Τα φαινόµνα αυτά µταβάλλουν τη συµπριφορά του στοιχίου µ αποτέλσµα αυτή να ίναι διαφορτική από την αναµνόµνη και για το λόγο αυτό αρκτή έρυνα γίνται όσον αφορά την πιρροή των φαινοµένων αυτών στη συµπριφορά νός στοιχίου. Είναι προφανές ότι καθώς η πολυπλοκότητα νός κυκλώµατος αυξάνται τόσο πιο πολύπλοκη θα ίναι και η πίδραση των γιτονικών δοµών σ ένα στοιχίο. Αν πιλγόταν η κατυθίαν πιλυση των ξισώσων του Maxwell, ο υπολογιστικός χρόνος που θα έπρπ να διατθί για τη διργα-. Ν. Λοΐζος 9

10 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία σία αυτή θα ήταν υπρβολικός και αυτό γιατί το κύκλωµα θα έπρπ να διαιρθί σ πολύ µγάλο αριθµό µικρότρων δοµών, οι οποίς µ τη σιρά τους, και χρησιµοποιώντας αριθµητική ανάλυση, θα συνέθταν πολύ µγάλους πίνακς. Για το λόγο αυτό προτιµήθηκ, γνικότρα στη µοντλοποίηση, η πριγραφή νός στοιχίου λαµβάνοντας υπόψη µόνο τις πιδράσις των πολύ κοντινών σ αυτό στοιχίων και µόνο στην πρίπτωση που αυτές ίναι σηµαντικές και µη αγνοήσιµς. Επιδή οι διάφορς πιδράσις που µπορί να έχι ένα στοιχίο από το γιτονικό του πριβάλλον ξαρτώνται από διάφορς παραµέτρους, όπως η συχνότητα ή η γωµτρία του στοιχίου, ίναι σύνηθς για ορισµένα στοιχία να υπάρχουν παραπάνω από ένα µοντέλα, τα οποία βρίσκουν φαρµογή ανάλογα µ τις πικρατούσς συνθήκς. Τα µοντέλα αυτά ίναι απλά αλλά ισχύουν µόνο σ ορισµένς πριπτώσις. Πολλές φορές πιχιρίται και σύνθση των απλών µοντέλων ώστ να προκύψι ένα - νιαίο πολυπλοκότρο µοντέλο το οποίο, όµως, θα ισχύι για πολύ µγαλύτρο ύρος τιµών παραµέτρων του στοιχίου []. Το νδιαφέρον για σωστή και ακριβή µοντλοποίηση των γραµµών µταφοράς έχι µφανιστί έντονα τα τλυταία χρόνια. Η ανάγκη για πιο γρήγορα, πιο αξιόπιστα και πιο µικρά κυκλώµατα έχι οδηγήσι στην όλο και µγαλύτρη ολοκλήρωση των κυκλωµάτων, την προσπάθια δηλαδή, όλο και πρισσότρα κυκλωµατικά στοιχία που βρίσκονται κτός ψηφίδων (off-chip component), να τοποθτηθούν ντός αυτών (on-chip), ούτως ώστ οι γραµµές µταφοράς να µικρύνουν και να µπορέσουν να προσδώσουν στο κύκλωµα τα παραπάνω χαρακτηριστικά. Καθώς, όµως, οι συχνότητς των σηµάτων που διαδίδονται στα κυκλώµατα αυξάνται (οι συχνότητς που χρησιµοποιούνται πλέον φθάνουν τα αρκτά GHz) νώ, παράλληλα, η πυκνότητα των στοιχίων του ολοκληρωµένου κυκλώµατος γίνται όλο και µγαλύτρη, οι καθυστρήσις στην διάδοση των σηµάτων λόγω της ύπαρξης των γραµµών µταφοράς γίνονται όλο και πιο σηµαντικές. Στα ψηφιακά κυκλώµατα η αύξηση των παρουσιαζόµνων καθυστρήσων ίχ αρχικά αποδοθί στην πύλη των τρανζίστορ που οδηγούσ τη συνολική χωρητικότητα του φορτίου και της γραµ- µής µταφοράς. Σταδιακά, όµως, άρχισ να γίνται αντιληπτό ότι το µγαλύτρο τµήµα της καθυστέρησης οφίλονταν στα δίαφορα χωρητικά, παγωγικά και φαινόµνα αγωγιµότητας που παρουσίαζ η γραµµή µταφοράς. Μάλιστα, αποδίχθηκ ότι ακόµα και µέχρι 7% της παρουσιαζόµνης καθυστέρησης οφιλόταν στη γραµµή µταφοράς [3]. Κύρια αιτία στην αύξηση των καθυστρήσων, αρχικά, θωρήθηκ η αντίσταση του αγωγού καθώς και η χωρητικότητα του υποστρώµατος πάνω στο οποίο βρισκόταν η γραµµή µταφοράς. Για το λόγο αυτό, έγιναν έρυνς για την αντικατάσταση των µέχρι τότ χρησιµοποιούµνων υλικών (αλουµίνιο πάνω από οξίδιο του πυριτίου) µ άλλα, όπου ο µν αγωγός να έχι µικρότρη α- ντίσταση, το δ υπόστρωµα µικρότρη διηλκτρική σταθρά. Η ύρση του χαλκού που παρουσιάζι πολύ µικρότρη αντίσταση από το αλουµίνιο και η αντικατάσταση του αλουµινίου από αυτόν δν ίχ σ αρκτές πριπτώσις τα αναµνόµνα αποτλέσµατα στη µίωση των καθυστρήσων. Η αιτία που παρουσιάστηκ η αναντιστοιχία αυτή µταξύ των προσδοκούµνων αποτλσµάτων και των αποτλσµάτων των µτρήσων ίναι ότι µέχρι τότ, το καθολικά αποδκτό µοντέλο για την πριγραφή των καθυστρήσων που οφίλονται σ µία γραµµή µταφοράς ήταν το καταν- µηµένο δικτύωµα RC, που λαµβάνι υπόψη του µόνο την αντίσταση και χωρητικότητα της γραµ- µής. Σ πολλές πριπτώσις, όµως, η καθυστέρηση διάδοσης καθορίζται από τον παγωγικό χαρακτήρα της γραµµής, κάτι που έως τότ δν ίχ ληφθί υπόψη. Παράλληλα, οι απώλις λόγω της µη µηδνικής αγωγιµότητας του υποστρώµατος καθώς και η µφάνιση ορισµένων φυσικών φαινο- µένων που παρουσιάζονται κατά τη διάδοση νός σήµατος και τα οποία θα µλτηθούν στη συνέχια, θα πρέπι πίσης να ληφθούν υπόψη [4]. Τα πρισσότρα απλά προγράµµατα προσοµοίωσης ηλκτρονικών κυκλωµάτων (CAD tool) καθώς και οι πρισσότροι σχδιαστές ηλκτρονικών κυκλωµάτων χρησιµοποιούν ακόµα το κατανµηµένο δικτύωµα RC ως ισοδύναµο της γραµµής µταφοράς, µ αποτέλσµα σοβαρά λάθη στην πρόβλψη του χρόνου καθυστέρησης, του χρόνου ανόδου του διαδιδόµνου σήµατος, τη διαφωνία (cotalk) µταξύ γραµµών µταφοράς καθώς και το θόρυβο κοινού σήµατος (common mode noie). Αυτό συµβαίνι διότι, σ υψηλές συχνότητς (της τάξης των GHz) το µοντέλο RC κάνι µία υπρκτίµηση του χρόνου καθυστέρησης, µ αποτέλσµα να χρησιµοποιηθούν µγαλύτρα στοιχία από αυτά που πραγµατικά χριάζονται. Η χρήση µγαλύτρων στοιχίων έχι µ τη σιρά της. Ν. Λοΐζος

11 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο ως αποτέλσµα µγαλύτρη διαφωνία και υψηλότρα πίπδα απαιτούµνης ισχύος. Παρόλη την ανάπτυξη κάποιων απλών πρακτικών κανόνων για την καλύτρη πρόβλψη των χαρακτηριστικών των γραµµών µταφοράς σ ολοκληρωµένα κυκλώµατα, η πληθώρα των σχδιαστικών παραµέτρων που πηράζουν τη διάδοση νός σήµατος, όπως, τα γωµτρικά χαρακτηριστικά της γραµ- µής, το µήκος της, οι διαφορές των φυσικών χαρακτηριστικών των διαφόρων στρωµάτων που χρησιµοποιούνται, οι χρησιµοποιούµνς τοπολογίς, κ.ά., καθιστά αδύνατη τη χρήση των κανόνων αυτών σ γνικότρη βάση [5]. Τα πρισσότρα προγράµµατα προσοµοίωσης ηλκτρονικών κυκλωµάτων, αγνοούν, συνήθως και την ύπαρξη απωλιών στο υπόστρωµα. Μία τέτοια παράλιψη δν έχι τόση σηµασία όταν το χρησιµοποιούµνο υπόστρωµα έχι χαµηλές απώλις (όπως τα υποστρώµατα από GaA), κάτι που συνήθως συµβαίνι στην πρίπτωση των µικροκυµατικών ολοκληρωµένων κυκλωµάτων. Στην πρίπτωση, όµως, υποστρωµάτων µ αξιοσηµίωτς απώλις (όπως αρκτά νοθυµένο υπόστρωµα πυριτίου), µία τέτοια παράλιψη θα οδηγούσ σ τλίως λανθασµένα αποτλέσµατα. Τα αποτλέσµατα αυτά αρχίζουν να γίνονται αντιληπτά σ υψηλές συχνότητς (τάξης GHz), όπου το απλό µοντέλο του κατανµηµένου RC δικτυώµατος παύι, πλέον, να προσγγίζι σωστά τη λιτουργία της γραµµής µταφοράς. Η ύπαρξη απωλιών στο υπόστρωµα συµβάλλι και στη διασπορά του διαδιδόµνου σήµατος, άλλο ένα σηµίο που θα πρέπι να ληφθί υπόψη κατά τη σχδίαση νός κυκλώ- µατος [6]. Ο τρόπος µ τον οποίο το υπόστρωµα πηράζι τη λιτουργία νός ολοκληρωµένου κυκλώµατος ίναι αρκτά πρίπλοκη. Καταρχήν, ανάλογα µ το πίπδο νόθυσης του υποστρώµατος, η α- γωγιµότητά του µπορί να µταβληθί από ως και 5 S/m. Επίσης, η συχνότητα του µταδιδόµνου σήµατος συνδέται άµσα µ τις ηλκτρικές ιδιότητς που παρουσιάζι το υπόστρωµα. Ακόµα, η ίδια η γωµτρία του αγωγού σήµατος πηράζι τη συµπριφορά του υποστρώµατος: το πλάτος, το πάχος του αγωγού σήµατος, η απόσταση από άλλους αγωγούς ίναι όλοι παράγοντς που θα πρέπι να ληφθούν υπόψη. Τέλος, το υλικό από το οποίο αποτλίται ο αγωγός σήµατος παίζι και αυτό το δικό του ρόλο στη συµπριφορά που θα παρουσιάσι το υπόστρωµα [7]. Μρικά σύγχρονα βοηθητικά ργαλία σχδίασης χρησιµοποιούν για µοντλοποίηση την έννοια του µρικού στοιχίου ισοδύναµου κυκλώµατος (Patial Element Equivalent Cicuit PEEC). Ειδικότρα, προγράµµατα που µοντλοποιούν την παγωγή αποτλσµατικής κατανοµής ισχύος χρησιµοποιούν µοντέλα PEEC για τον υπολογισµό της τιµής της παγωγής στις χαµηλές συχνότητς για µία ολόκληρη δοµή. Τα µοντέλα PEEC, πάντως, µπορούν να προσγγίσουν τη λύση που προκύπτι µ πίλυση των ξισώσων του Maxwell µόνο µ κατάλληλη διαίρση της γραµµής µταφοράς και σ µγάλο αριθµό µικρότρων τµηµάτων, µ αποτέλσµα να µη µπορούν ύκολα και γρήγορα να φαρµοστούν. Όσο, µάλιστα, η πολυπλοκότητα του κυκλώµατος αυξάνται, γίνται φανρό ότι η χρήση τους γίνται όλο και πιο δύσκολη. Θα πρέπι, όµως, να αναφρθί ότι γίνται έρυνα πάνω σ τρόπους µίωσης της πολυπλοκότητας των ξισώσων που προκύπτουν από τη χρήση µοντέλων PEEC στιάζοντας κυρίως σ µίωση της τάξης των ξισώσων. Όσον αφορά τις µθόδους υπολογισµού της χωρητικότητας µίας γραµµής µταφοράς τα πράγ- µατα ίναι κάπως πιο ύκολα. Η θώρηση ότι τα χωρητικά φαινόµνα που µφανίζονται κατά τη διάδοση νός σήµατος σ µία γραµµή µταφοράς οφίλονται κυρίως στη χωρητικότητα των υλικών γύρω από τη γραµµή µταφοράς και ότι ως κατανοµή φορτίου θα πρέπι να θωρηθί η πιφανιακή κατανοµή φορτίου ίναι αποδκτή. Μ τη βάση αυτή και τη χρήση κάποιων πρωτότυπων µθόδων, ο υπολογισµός της χωρητικότητας µπορί να γίνι σχτικά ύκολα και σωστά για όλα τα στοιχία της ψηφίδας. Αντίθτα, για τον υπολογισµό της παγωγής τα πράγµατα γίνονται πιο δύσκολα. Η παγωγική ξάρτηση µταξύ του αγωγού σήµατος και του µονοπατιού πιστροφής του σήµατος, όπου ως µονοπάτι πιστροφής νοίται ο αγωγός µέσω του οποίου κλίνι το κύκλωµα, ίναι πολύπλοκη και ξαρτάται τόσο από τη σχδίαση όσο και από τη χρησιµοποιούµνη τχνολογία. Ε- πιπλέον, δ θα πρέπι να αγνοηθί η ξάρτηση της παγωγής µ τη συχνότητα λόγω της διαφορτικής συµπριφοράς που παρουσιάζι το µονοπάτι πιστροφής ανάλογα µ τη συχνότητα. Από την παραπάνω πριγραφή γίνται φανρή η ανάγκη της σωστής µοντλοποίησης των γραµµών µταφοράς. Αν ληφθί υπόψη και το γγονός της πολλαπλής χρήσης µίας γραµµής µταφοράς σ ένα ολοκληρωµένο κύκλωµα, µπορούµ να διαπιστώσουµ την ακόµα µγαλύτρη σηµα-. Ν. Λοΐζος

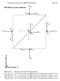
12 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία σία της σωστής µοντλοποίησης. Γνικά, οι γραµµές µταφοράς σ ολοκληρωµένα κυκλώµατα µπορούν να χρησιµοποιηθούν ως βασικά στοιχία για την κατασκυή πηνίων, πυκνωτών ή ως δίκτυα προσαρµογής της χαρακτηριστικής αντίστασης. Το ηλκτρικό µήκος µίας γραµµής µταφοράς, βέβαια, µπορί να ληφθί υπόψη µόνο σ συχνότητς µγαλύτρς των µικροκυµατικών (αφού σ µικρότρς συχνότητς, προκιµένου να λάβουµ ένα αξιοποιήσιµο ηλκτρικό µήκος θα πρέπι να χρησιµοποιηθούν πολύ µακρές γραµµές µταφοράς) µ αποτέλσµα η χρήση των γραµµών µταφοράς ως δίκτυα προσαρµογής να πριορίζται στις υψηλές συχνότητς. Το αντικίµνο της σωστής µοντλοποίησης των γραµµών µταφοράς σ ολοκληρωµένα κυκλώµατα απασχόλησ και απασχολί πολλούς ρυνητές που ίτ υιοθτώντας υρέως χρησιµοποιούµνς µθόδους ίτ προτίνοντας νές, προσπαθούν να δώσουν µία κατά το δυνατό πλήρη (που να ισχύι σ όλς τις συχνότητς ή σ πολύ µγάλο ύρος συχνοτήτων) και όσο το δυνατό πιο σωστή (µικρές αποκλίσις από πραγµατικά δδοµένα) προσέγγιση για τη µοντλοποίηση της γραµ- µής µταφοράς. Μρικές από τις πιο γνωστές µθόδους που χρησιµοποιούνται για την ανάλυση των γραµµών µταφοράς θα αναφρθούν στην πόµνη παράγραφο. Σκοπός - Στόχος Σκοπός της παρούσας διπλωµατικής ργασίας ήταν κατ αρχήν, η βιβλιογραφική µλέτη του τρόπου µοντλοποίησης µίας γραµµής µταφοράς πάνω από υπόστρωµα πυριτίου και κατ πέκταση η θωρητική µλέτη των φυσικών ιδιοτήτων της. Επόµνο στάδιο ήταν η ύρση από τη βιβλιογραφία προτινόµνων µοντέλων ικανών να χρησιµοποιηθούν για νσωµάτωση σ πριβάλλον προσοµοίωσης ηλκτρονικών κυκλωµάτων (προγράµµατα CAD) και ο έλγχος της ακρίβιας και της πιστότητάς τους. Μοντέλα ικανά για νσωµάτωση σ πριβάλλον προσοµοίωσης ηλκτρονικών κυκλωµάτων θωρήθηκαν όσα παρίχαν ξισώσις για τον υπολογισµό των τιµών των διαφόρων στοιχίων του µοντέλου σ κλιστή µορφή, σ µορφή, δηλαδή, που ο υπολογιστής να µπορί να υπολογίσι την τιµή τους σ πολύ µικρό χρονικό διάστηµα και πραγµατοποιώντας απλές πράξις. Ο έλγχος της ακρίβιας και της πιστότητάς των παραπάνω µοντέλων έγιν συγκρίνοντας µ µτρήσις που ίχαν ήδη πραγµατοποιηθί για συγκκριµένη δοµή γραµµής µταφοράς. Τέλος, µ βάση ήδη υπάρχοντα µοντέλα της βιβλιογραφίας, προτάθηκ ένα καινούριο µοντέλο το οποίο υλοποιήθηκ και λέγχθηκ χρησιµοποιώντας τις ίδις µ παραπάνω µτρήσις... Γνικές µέθοδοι ανάλυσης και µοντλοποίησης γραµµών µταφοράς Η παρούσα διπλωµατική ργασία πικντρώνται σ µία ιδική δοµή γραµµή µταφοράς, τη µικροταινία (micotip) και για το λόγο αυτό, φξής και µέχρι το τέλος της ργασίας, αντί του όρου γραµµή µταφοράς, θα χρησιµοποιίται ο όρος µικροταινία. Παρόλο που, σύµφωνα µ το Wheele [8], ο όρος αυτός, που αποτλί συντόµυση της έκφρασης µικροκυµατική γραµµή µταφοράς ( micowave tip line ), δν αποδίδι σωστά το αντικίµνο το οποίο πριγράφι νώ παράλληλα µπορί να προκαλέσι σύγχυση µταξύ δύο διαφορτικών τοπολογιών (αγωγός πάνω από ηµιαγωγό πάνω από πιφάνια γίωσης αγωγός µέσα σ ηµιαγωγό ανάµσα σ πιφάνις γίωσης), έχι πικρατήσι να χρησιµοποιίται για την πριγραφή των τοπολογιών του σχήµατος.. Η διαφορά µταξύ των τοπολογιών αυτών, όπως µπορί να φανί, ίναι η ύπαρξη ή όχι του στρώµατος οξιδίου µταξύ του αγωγού και του υποστρώµατος. Η τοπολογία του σχήµατος.α ίναι γνωστή και ως δοµή MIS (Metal Inulato Semiconducto Μέταλλο Μονωτής Ηµιαγωγός) παρόλο που αντί του µτάλλου µπορί να χρησιµοποιηθί γνικά οποιοδήποτ αγώγιµο υλικό, π.χ. πολυπυρίτιο. Παρακάτω, θα αναφρθούν ν συντοµία ορισµένς από τις βασικότρς µθόδους που χρησιµοποιούνται για την ανάλυση των χαρακτηριστικών διάδοσης της µικροταινίας. Μέσα από τις µθόδους αυτές ίναι δυνατό να προκύψουν ξισώσις για διάφορα χαρακτηριστικά διάδοσης της µικροταινίας. Οι ξισώσις αυτές ίναι κατά κανόνα συναρτήσις των γωµτρικών χαρακτηριστικών της µικροταινίας, καθώς και της συχνότητας, νώ συνήθως τα αποτλέσµατα που προκύπτουν από αυτές δίνονται ανά µονάδα µήκους. Μ τον τρόπο αυτό µπορί να µλτηθί στη συνέχια ο βέλτιστος αριθµός των τµηµάτων στα οποία θα πρέπι να χωριστί µία µικροταινία ανάλογα µ το µήκος της. Ν. Λοΐζος

13 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο ώστ να έχουµ αποτλέσµατα όσο το δυνατό πιο κοντά στην πραγµατικότητα. Το θέµα αυτό θα µας απασχολήσι και παρακάτω. α. β. αγωγός αγωγός οξίδιο/µονωτής ηµιαγωγός ηµιαγωγός Σχήµα. οµές µικροταινίας... Φυσική µοντλοποίηση Στην πρίπτωση της φυσικής µοντλοποίησης, λαµβάνονται υπόψη οι φυσικές ιδιότητς της µικροταινίας και µ τρόπο ίτ αναλυτικό ίτ µπιρικό προτίνονται µοντέλα διακριτών στοιχίων µ αντίστοιχς ξισώσις για την ύρση των τιµών των στοιχίων αυτών. Μ τον τρόπο αυτό µοντλοποίησης µπορούν να προκύψουν απλά και ύκολα στη χρήση µοντέλα τα οποία µπορούν σ πολύ µικρό χρόνο να υπολογίσουν διάφορα µγέθη. Η χρήση τους, κατά κανόνα, πριορίζται σ απλές διατάξις. Πολλές φορές, όµως, χρησιµοποιούνται ως στάδιο αρχικοποίησης άλλων µοντέλων, συνήθως πλήρους κύµατος, που χρησιµοποιούν ισχυρούς αριθµητικούς αλγόριθµους. Πδίο προς µλέτη αποτλί η ύρση τέτοιων µοντέλων τα οποία να µπορούν να χρησιµοποιηθούν για µικροταινίς διαφόρων γωµτρικών µγθών, σ µγάλο ύρος συχνοτήτων και για διάφορς τιµές ηλκτρικών χαρακτηριστικών των υλικών (συντλστής αγωγιµότητας, διηλκτρική σταθρά, κ.ά.). Αυτός ίναι και ο τρόπος µοντλοποίησης που θα µας απασχολήσι στην παρούσα διπλωµατική ργασία. Παρακάτω, αναφέρονται άλλς µέθοδοι µοντλοποίησης και κυρίως ανάλυσης της διάδοσης σηµάτων στη δοµή της µικροταινίας. Οι µέθοδοι αυτές ίναι αριθµητικές και προσβλέπουν στην ύρση του ηλκτροµαγνητικού πδίου που διαδίδται στη µικροταινία, όµως, µρικές από αυτές έχουν χρησιµοποιηθί από ρυνητές και ως βάση για την ύρση φυσικών µοντέλων. Οι παρακάτω µέθοδοι µπορί ναι µν να δίνουν καλύτρα αποτλέσµατα κατά την προσοµοίωση σ σχέση µ τα φυσικά µοντέλα, απαιτούν, όµως, πολύ µγαλύτρο υπολογιστικό χρόνο, ο οποίος, για πολύπλοκς διατάξις, µπορί να µην ίναι καν αποδκτός.... Αριθµητικές µέθοδοι ανάλυσης και µοντλοποίησης Παρακάτω γίνται µία σύντοµη πριγραφή των πιο διαδδοµένων µθόδων ανάλυσης της δοµής της γραµµής µταφοράς. Αρχικά αναφέρται η µέθοδος quai-tem και στη συνέχια διάφορς µέθοδοι πλήρους κύµατος, τόσο στο πδίο του χρόνου όσο και στο πδίο της συχνότητας. Εκτός των παρακάτω µθόδων ανάλυσης, υπάρχουν και άλλς µέθοδοι, άλλς πρισσότρο και άλλς λιγότρο διαδδοµένς. Ενδικτικά, αναφέρουµ κάποις από αυτές: method of line (µέθοδος γραµµών), FDM (Finite Diffeence Method Μέθοδος ιακριτής ιαφοράς), µέθοδος TLM (Tanmiion Line Matix Πίνακα Γραµµής Μταφοράς). Για µία σύντοµη πριγραφή αυτών και άλλων µθόδων, ο αναγνώστης παραπέµπται στην αναφορά [9].... Ανάλυση Quai-TEM Η quai-tem ανάλυση ίναι η πιο διαδδοµένη ανάλυση για το χαρακτηρισµό της µικροταινίας. Βασίζται στις ξισώσις του Maxwell και θωρί ότι το κύµα που διαδίδται στη γραµµή µταφοράς ίναι τύπου TEM (Tanvee Electic and Magnetic ηλκτρικό και µαγνητικό πδίο κάθτα στη διύθυνση διάδοσης). Προφανώς, κάτι τέτοιο, όπως θα φανί και στη συνέχια από τη θ-. Ν. Λοΐζος 3

14 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία ωρητική ανάλυση της µικροταινίας δν ισχύι γνικά. Πολύ σύντοµα, αυτό µπορί να δικαιολογηθί από το γγονός ότι υπάρχουν απώλις νέργιας και ανοµοιογένια στο υλικό διάδοσης. Αξίζι, λοιπόν, να ξταστί σ ποις πριπτώσις ίναι δυνατή η χρήση της προσέγγισης πως το διαδιδό- µνο κύµα στη γραµµή µταφοράς µοιάζι µ TEM. Μ το θέµα αυτό ασχολήθηκαν ο Hono και οι συνργάτς του [], µ αποτέλσµα να καταλήξουν στην παρακάτω συνθήκη όσον αφορά την ισχύ της προσέγγισης αυτής: d << (.) ω µˆ () ˆ () όπου δηλώνι τη µέση τιµή, δηλώνι την απόλυτη τιµή, d ίναι η διάσταση κάθτα στη διύθυνση διάδοσης του κύµατος, ω ίναι η κυκλική συχνότητα, µ και ίναι η µαγνητική διαπρατότητα και διηλκτρική σταθρά αντίστοιχα νώ το σύµβολο ^ δηλώνι τη µιγαδική φύση νός µγέθους. Η συνθήκη αυτή προέκυψ από την απαίτηση η συνιστώσα του ηλκτρικού πδίου κατά µήκος της διύθυνσης διάδοσης να ίναι πολύ µικρότρη από την γκάρσια συνιστώσα του ηλκτρικού πδίου. Στην πρίπτωση που θωρήσουµ ότι το µέσο διάδοσης έχι απώλις (πρίπτωση υποστρώµατος µ απώλις), η παραπάνω συνθήκη παίρνι τη µορφή: d << (.) σ() ω µ () () ω Η ίδια συνθήκη αναφέρται πιο απλά από τον Haegawa και τους συνργάτς του [], σύµφωνα µ τους οποίους, προκιµένου να ισχύσι η quai-tem ανάλυση, το µήκος κύµατος θα πρέπι να ίναι πολύ µγαλύτρο από το πάχος του διπλού στρώµατος που αποτλίται από το οξίδιο και το υπόστρωµα πυριτίου στην πρίπτωση της µικροταινίας του σχήµατος.α, ή απλά του υποστρώµατος πυριτίου στην πρίπτωση της µικροταινίας του σχήµατος.β. Η quai-tem ανάλυση µπορί να ισχύσι για συχνότητς της τάξης µέχρι GHz ή ακόµα και GHz ([], [3]) και για το λόγο αυτό και λόγω της απλότητάς της ίναι αρκτά διαδδοµένη. Συνήθως, στην quai-tem ανάλυση γίνται χρήση του βαθµωτού ηλκτρικού δυναµικού (Φ) και όχι διανυσµατικών µγθών µ αποτέλσµα απλούστρς ξισώσις και γρηγορότρη απόκριση.... Αναλύσις πλήρους κύµατος (full-wave) Προκιµένου να υπάρξι µία λπτοµριακή και πλήρης ανάλυση του τρόπου διάδοσης νός σήµατος κατά µήκος µίας µικροταινίας ίναι αναγκαία η ανάλυση πλήρους κύµατος. Στην ανάλυση αυτή, ξκινώντας από τις ξισώσις του Maxwell για ηλκτροµαγνητικά πδία και χωρίς να γίνται κάποια προσέγγιση για τη µορφή του κύµατος που διαδίδται στη µικροταινία, προκύπτουν ξισώσις που πριγράφουν τα χαρακτηριστικά µγέθη διάδοσης κατά µήκος της µικροταινίας. ιάφοροι ρυνητές έχουν κατά καιρούς χρησιµοποιήσι ορισµένς προσγγίσις της ανάλυσης πλήρους κύ- µατος. Ορισµένς από τις µθόδους αυτές ίναι αρκτά διαδδοµένς και πριγράφονται σύντοµα στη συνέχια.... Μέθοδος FDTD Η µέθοδος FDTD (Finite-Diffeence Time Domain Μέθοδος ιακριτής- ιαφοράς στο Πδίο του Χρόνου) αποτλί στην ουσία µία αριθµητική µέθοδο για την πίλυση των ολοκληρωµατικών ξισώσων του Maxwell. Η µέθοδος ίναι αρκτά διαδδοµένη αφού οι ξισώσις του Maxwell µπορούν να διακριτοποιηθούν µ σαφή τρόπο. Μ την έννοια διακριτοποίηση ννοίται η µτατροπή ολοκληρωµατικών ξισώσων σ ξισώσις αθροίσµατος ( Σ) µ κατάλληλο τρόπο. Χρησιµοποιίται στην πρίπτωση που νδιαφέρι η ξάρτηση των αποτλσµάτων από το χρόνο και όχι από τη συχνότητα και παρουσιάστηκ για πρώτη φορά από τον K.S. Yee. Παρακάτω πα- () 4. Ν. Λοΐζος

15 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο ρουσιάζονται κάποια βασικά σηµία της µθόδου αυτής. Σ πρίπτωση που θωρήσουµ χώρο χωρίς πηγές, οι ξισώσις του Maxwell µπορούν να γραφούν µ τη µορφή υπρβολικών συναρτήσων πρώτης τάξης [4]: de dh dh dh = A x A A z (.3α) dt dx d dz dh de de de = Bx B Bz (.3β) dt dx d dz όπου E = ( E ) T x,e, E z το διάνυσµα της έντασης του ηλκτρικού πδίου και H = ( H ) T x,h, H z το διάνυσµα της έντασης του µαγνητικού πδίου. Επίσης: xx xx = A x, A = και A z = (.4) zz zz όπου xx, και zz ίναι τα διαγώνια στοιχία του τανυστή της ηλκτρικής πιτρπτότητας. Αντίστοιχα, τα Β x, B και B z προκύπτουν και αυτά από την (.4) µ αντικατάσταση των xx, και zz µ τα µ xx, µ και µ zz αντίστοιχα, που αποτλούν τα διαγώνια στοιχία του τανυστή µαγνητικής διαπρατότητας. Σύµφωνα µ τον Yee, κάθ συνάρτηση του χρόνου και του χώρου µπορί να διακριτοποιηθί ως ξής: F n ( i, j,k ) = F( i x, j,k z,n t) (.5) όπου x = = z = l ίναι το διάστηµα αύξησης του µήκους και t ίναι το διάστηµα αύξησης του χρόνου. Οι συνιστώσς της έντασης του ηλκτρικού και µαγνητικού πδίου µπορούν να τοποθτηθούν σ πλέγµα (που ονοµάζται πλέγµα του Yee) µ τον τρόπο που φαίνται στο σχήµα.. z E E x H z (i,j,k) E E x E z E z H H x H E z H x (i,j,k) E z E E x H z (i,j,k) E E x (i,j,k) x Σχήµα. Τοποθέτηση των πδιακών συνιστωσών στο πλέγµα του Yee Υπολογίζοντας µ κατάλληλο τρόπο, βασιζόµνοι στις θέσις τους στο πλέγµα και τις σχέσις (.3), τις συνιστώσς αυτές, χρησιµοποιώντας χρονικά βήµατα ίσα µ το µισό του t, προκύπτουν οι παρακάτω ξισώσις: n n n H ( ) ( ) ( )[ ( x i, j, k = H x i, j, k i, j, k E i, j, k ) µ xx (.6α) n n n E i, j, k E i, j, k E i, j, k H n ( ) ( ) ( )] ( i, j, k n n ) = H ( i, j, k ) ( i, j, k ) E ( i, j, k ) E n z. Ν. Λοΐζος 5 z µ n n ( i, j, k ) E ( i, j, k) E ( i, j, k )] x z x [ z (.6β)

16 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία 6. Ν. Λοΐζος ( ) ( ) ( ) ( ) [ ( ) ( ) ( )] k, j, i E k, j i, E k j,, i E k, j, i E k, j, i µ k, j, i H k, j, i H n n n x n x zz n z n z = (.6γ) ( ) ( ) ( ) ( ) [ ( ) ( ) ( )] n n n z n z xx n x n x k j,, i H k j,, i H k, j, i H k, j, i H k j,, i k j,, i E k j,, i E = (.7α) ( ) ( ) ( ) ( ) [ ( ) ( ) ( )] k, j, i H k, j, i H k, j i, H k, j i, H k, j i, k, j i, E k, j i, E n z n z n x n x n n = (.7β) ( ) ( ) ( ) ( ) [ ( ) ( ) ( )] n x n x n n zz n z n z k, j i, H k, j i, H k j,, i H k j,, i H k j, i, k j, i, E k j, i, E = (.7γ) όπου, ο παράγοντας ισούται µ: l c t = (.8) και c ίναι η ταχύτητα του φωτός. Στις παραπάνω ξισώσις, τα Ε και Η έχουν κανονικοποιηθί µ τέτοιο τρόπο ώστ η χαρακτηριστική αντίσταση να ίναι ίση µ τη µονάδα. Έχοντας βρι τη διακριτή µορφή που θα πρέπι να έχι το ηλκτροµαγνητικό πδίο, παραµένουν δύο σηµία τα οποία θα πρέπι να µλτηθούν προκιµένου να βρθούν οι ξισώσις από τις οποίς θα υπολογιστί το ηλκτροµαγνητικό πδίο. Καταρχήν, θα πρέπι να θωρηθούν κάποις συνοριακές συνθήκς δύτρο, θα πρέπι να δοθούν κάποις αρχικές συνθήκς. Η ύρση των κατάλληλων συνοριακών συνθηκών αποτλί τη µγάλη δυσκολία στη µέθοδο αυτή. Ο µτασχηµατισµός Fouie, που χρησιµοποιίται για τη µτατροπή στο πδίο της συχνότητας των αποτλσµάτων που δίνι η µέθοδος FDTD στο πδίο του χρόνου ίναι ξαιρτικά υαίσθητος στη µορφή των συνοριακών συνθηκών που χρησιµοποιούνται. Έτσι, η όχι και τόσο σωστή πιλογή συνοριακών συνθηκών για την ύρση του ηλκτροµαγνητικού πδίου µ τη µέθοδο FDTD, µπορί να οδηγήσι σ τλίως λανθασµένα αποτλέσµατα στο πδίο της συχνότητας. Το πρόβληµα της ύρσης σωστών συνοριακών συνθηκών για την ύρση του ηλκτροµαγνητικού πδίου στη δοµή της µικροταινίας απασχόλησ πολλούς ρυνητές, νώ πολλές ήταν και οι λύσις που δόθηκαν [5]. Μία από τις πιο διαδδοµένς λύσις ίναι αυτή των συνοριακών συνθηκών α- νοιχτοκυκλώµατος και βραχυκυκλώµατος (open- and hot-cicuit bounda condition). Σύµφωνα µ τη λύση αυτή [6], το ηλκτροµαγνητικό πδίο υπολογίζται δύο φορές: την πρώτη φορά τα ό- ρια θωρούνται ηλκτρικά αγώγιµα (µηδνικές φαπτοµνικές συνιστώσς ηλκτρικού πδίου) τη δύτρη φορά τα όρια θωρούνται µαγνητικά αγώγιµα (µηδνικές φαπτοµνικές συνιστώσς µαγνητικού πδίου). Ο µέσος όρος των δύο αποτλσµάτων δίνι το ζητούµνο ηλκτροµαγνητικό κύµα. Θωρητικά, η µέθοδος αυτή δικαιολογίται ως ξής: ο συντλστής ανάκλασης στην πρίπτωση του βραχυκυκλώµατος ίναι - νώ στην πρίπτωση του ανοιχτοκυκλώµατος ίναι. Αν αθροιστούν, ποµένως, οι λύσις που προκύπτουν σ κάθ µία από τις δύο πριπτώσις, τα ανακλώµνα κύµατα θα πρέπι να απαλιφθούν. Όσον αφορά τις αρχικές συνθήκς που πρέπι να δοθούν, αυτό ξαρτάται από τη µορφή του - κάστοτ προβλήµατος που πρέπι να λυθί. Είναι αρκτά σύνηθς, όµως, να χρησιµοποιίται ίτ ηµιτονική ίτ παλµική διέγρση. Γνικά, η µέθοδος FDTD ίναι αρκτά χρονοβόρα νώ παρουσιάζι δυσκολίς στην πρίπτωση που χριάζται να χρησιµοποιηθούν µγέθη ξαρτώµνα από τη συχνότητα.... Μέθοδος SDA (Spectal Domain Appoach Προσέγγιση Φασµατικού Πδίου) Η µέθοδος SDA αναφέρται γνικά στην φαρµογή ολοκληρωµατικών µτασχηµατισµών, όπως

17 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο ο µτασχηµατισµός Fouie ή ο µτασχηµατισµός Hankel, για την πίλυση προβληµάτων συνοριακών ή αρχικών τιµών. Αποτλί, στην ουσία, ένα ργαλίο µ το οποίο µπορί να µιωθί η πολυπλοκότητα ορισµένων ξισώσων και ιδικότρα των µρικών διαφορικών ξισώσων σ απλές διαφορικές ξισώσις, που µ τη σιρά τους µπορούν να πιδχθούν πιπλέον απλοποιήσις. Μ τη µέθοδο SDA το ηλκτροµαγνητικό πδίο σ µία µικροταινία µπορί να δοθί σαν µία απλή ολοκληρωτική ξίσωση κλιστού τύπου (ξίσωση από την οποία µπορί να προκύψι κατυθίαν λύση χωρίς τη χρήση άλλων ξισώσων). Μ κατάλληλη πιλογή των συντταγµένων, η ξίσωση αυτή µπορί να έχι µία διάσταση λιγότρη από την αρχική µρική διαφορική ξίσωση που προκύπτι µ κατυθίαν χρήση των ξισώσων Maxwell. Η απλή ολοκληρωτική ξίσωση που προκύπτι συνήθως πιλύται µ τη µέθοδο του Galekin, αν και κατά καιρούς έχουν προταθί και άλλς προσγγίσις. Η µέθοδος SDA αποτλί στην ουσία µία υβριδική µέθοδο, µ την έννοια ότι απαιτίται ένα σηµαντικός αριθµός υπολογισµών πριν φαρµοστί, προκιµένου να πιτυχθί υψηλή υπολογιστική απόδοση για ένα συγκκριµένο πρόβληµα ή µία συγκκριµένη οικογένια προβληµάτων. Επίσης, για την ύπαρξη µικρής πολυπλοκότητας στην τλική ξίσωση, απαραίτητη ίναι η κατάλληλη πιλογή συναρτήσων βάσης που θα χρησιµοποιηθούν κατά την φαρµογή της µθόδου Galekin, οι οποίς, µ τη σιρά τους, θα πρέπι να ικανοποιούν τις οριακές συνθήκς της διάταξης που έχι θωρηθί. Για µία πριληπτική αλλά πολύ πρικτική ξήγηση της µθόδου SDA ο αναγνώστης παραπέµπται στην αναφορά [7], νώ για µία σύντοµη πριγραφή στην αναφορά [8] Μέθοδος FEM (Finite-Element Method Μέθοδος ιακριτών Στοιχίων) Η µέθοδος αυτή αποτλί, στην ουσία, την φαρµογή της γνωστής µαθηµατικής µθόδου για την ύρση του ηλκτροµαγνητικού πδίου στη δοµή της µικροταινίας. Σ γνικές γραµµές, η µέθοδος πριλαµβάνι τη διακριτοποίηση της γραµµής µ βάση κάποιο γωµτρικό σχήµα (π.χ. ττράγωνο ή τρίγωνο) και ν συνχία µ χρήση πινάκων και ύρση χαρακτηριστικών ποσών τους (ιδιοτιµές και ιδιοδιανύσµατα), τον υπολογισµό των συνιστωσών του ηλκτροµαγνητικού πδίου. Παρακάτω, παρουσιάζται σ γνικές γραµµές ο τρόπος µ τον οποίο η µέθοδος FEM προσγγίζι την ανάλυση πλήρους κύµατος για τη δοµή της µικροταινίας [9]. Κάποις από τις χρησιµοποιού- µνς σχέσις παρουσιάζονται ή/και αποδικνύονται και στην παράγραφο. όπου γίνται θωρητική ανάλυση της µικροταινίας. Για λόγους, όµως, υκολότρης ανάγνωσης του κιµένου, παρουσιάζονται και στο σηµίο αυτό. Έστω ότι πιθυµούµ να υπολογίσουµ δύο βαθµωτά µγέθη του ηλκτροµαγνητικού πδίου, το βαθµωτό δυναµικό Φ και τη µαγνητική ροή ψ. Σ πρίπτωση που το ηλκτροµαγνητικό πδίο πριγραφί µ τη χρήση του βαθµωτού (Φ) και διανυσµατικού (A ) δυναµικού, η ένταση του ηλκτρικού πδίου και η µαγνητική παγωγή θα δίνονται, αντίστοιχα, από τις σχέσις: B = A (.9α) Ε = Φ jωa (.9β) Από την η ξίσωση του Maxwell (νόµος του Gau για το ηλκτρικό πδίο), θωρώντας ότι δν υπάρχουν φορτία στο χώρο, θα έχουµ, λόγω της (.9β): D = ( Φ) jω A = Φ ( Φ) jω A = (.) Από τη συνθήκη Loentz: A = jωµ Φ (.) όπου η διηλκτρική σταθρά, µπορί να φανί ότι: Φ = j( ωµ ) ( Α) = (.) οπότ η (.) αντικαθιστώντας σ αυτή τις (.), (.) θα πάρι τη µορφή: Φ ω µ Φ = Φ k Φ = (.3) όπου η σχτική διηλκτρική σταθρά και k = ω µ. Επίσης, από την 4 η ξίσωση του Maxwell (νόµος του Ampèe), θα έχουµ ότι:. Ν. Λοΐζος 7

18 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία H = jωd B = jωµ D B = jωµ E (.4) Εφαρµόζοντας τον τλστή στροβιλισµού ( ) στην παραπάνω σχέση και µ βάση την 3 η ξίσωση του Maxwell (νόµος του Faada), η ξίσωση (.4) θα πάρι τη µορφή: ( B) = jωµ E ( B) B = jωµ ( jωb) (.5) Λόγω, όµως, της ης ξίσωσης του Maxwell (νόµος του Gau για το ηλκτρικό πδίο), ισχύι ότι B =, οπότ η (.5) θα γραφτί: B ω µ B = (.6) Όπως γνωρίζουµ, η µαγνητική ροή δίνται από τη σχέση: ψ = B ds (.7) S οπότ, ολοκληρώνοντας τη σχέση (.6) σ µία πιφάνια S θα προκύψι: B ds ω µ B ds = (.8) S S Αλλάζοντας τη σιρά φαρµογής του τλστή της λαπλασιανής και του ολοκληρώµατος, η παραπάνω σχέση θα γραφτί: B ds ω µ B ds = ψ k ψ = (.9) S S Από τις σχέσις (.3) και (.9) µπορί να προκύψι η παρακάτω ξίσωση: Lθ k Mθ = (.) όπου: Φ L =, M = και θ = (.) ψ Πολλαπλασιάζοντας από αριστρά τη σχέση (.) µ τον ανάστροφο του θ και ολοκληρώνοντας σ µία πριοχή S (κάτι που ίναι δυνατό αφού τα θ Τ Lθ και θ Τ Μθ θα ίναι πίνακς-στοιχία, δηλαδή πραγµατικοί αριθµοί) θα έχουµ: Τ Τ k θ LθdS θ MθdS (.) = S Η παραπάνω ξίσωση παρουσιάζι µταβλητότητα και από αυτή µπορί να οριστί το ακόλουθο συναρτησιακό (για την έννοια του συναρτησιακού βλ. [, σλ. -4]): ( ) = ( ) J Φ,ψ Φ ds ψ ds iz Φ ψ ds k Φ ds ψ ds (.3) S S S S Η παραπάνω ανάλυση έγιν έχοντας κάνι την υπόθση ότι δν υπάρχουν φορτία. Όπως θα φανί από την ανάλυση της παραγράφου., οι παραπάνω σχέσις ισχύουν και στην πρίπτωση που υ- πάρχουν φορτία µ αντικατάσταση της διηλκτρικής σταθράς από µία ισοδύναµη διηλκτρική σταθρά. Σύµφωνα µ τη µέθοδο FEM, ντός µίας τυχαίας πριοχής, που δώ θα θωρήσουµ ότι έχι το σχήµα τριγώνου (σχήµα.3), το βαθµωτό δυναµικό Φ και η µαγνητική ροή ψ µπορούν να γραφούν σαν n-τάξης πολυώνυµα ως ξής: Φ ( x, ) = u jσ ijφi και ψ ( x, ) = u jσijψi (.4) όπου u j ίναι ένας πίνακας-γραµµή του οποίου τα στοιχία ίναι οι όροι του πολυωνύµου (π.χ. για τριγωνική πριοχή που αντιπροσωπύι πολυώνυµο ης τάξης και τα σηµία χαρακτηρίζονται από τις συντταγµένς (x, ), θα έχι τη µορφή u j = [ x ]) και σ ij ίναι ένας ττραγωνικός πίνακας τάξης m, όπου m = ( n )( n ) (n η τάξη του πολυωνύµου). Οι όροι Φ i και ψ i ίναι πίνακς-στήλη που πριέχουν τις τιµές των Φ και ψ αντίστοιχα, σ σηµία ντός ή στα όρια της πριοχής που έχι θωρηθί (τριγώνου). Αν ονοµάσουµ v ij τον πίνακα του οποίου οι γραµµές ίναι τα u j στα σηµία αυτά, ο πίνακας σ ij προκύπτι µ αναστροφή του v ij. Αντικαθιστώντας τις σχέσις (.4) στην (.3) και παραγωγίζοντας ως προς τον πίνακα-στήλη Φ k, θα έχουµ: S 8. Ν. Λοΐζος

19 Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία Κφάλαιο J = SikΦi U ikψi k ATikΦ i Φ k = (.5) όπου Α = η πριοχή στην οποία γίνται η ολοκλήρωση T T u j u u l j u l Sik σ jipjlσ kl σ = = ji ds σ kl x x A (.6α) T T u j u u l j u l U ik = σ jir jlσ kl = σ ji ds σ kl x x A (.6β) T Tik = σ jiq jlσ kl = σ ji u ju l ds σ kl A (.6γ) Αν, αντίστοιχα, παραγωγίσουµ την (.3) ως προς ψ k θα προκύψι: Sik ψi UikΦi k ATikψi = (.7) Κάθ στοιχίο των πινάκων S, U και Τ αντιστοιχί στην πριοχή που ορίζται από ένα τριγωνικό στοιχίο. Θωρώντας ότι η προς µλέτη πριοχή έχι διαιρθί σ πολλά τριγωνικά στοιχία και βρίσκοντας τις τιµές S ik, U ik και T ik για κάθ µία από τις πριοχές αυτές, θα προκύψουν οι πίνακς S, U και Τ. Θα πρέπι να σηµιωθί, πίσης, ότι µία πριοχή που αντιστοιχί σ πολυώνυµο n-τάξης µπορί να διαιρθί πραιτέρω σ ακόµα µικρότρς πριοχές ιδίου σχήµατος µέχρις ότου οι µικρότρς αυτές πριοχές αντιπροσωπύσουν πολυώνυµα ης τάξης Σχήµα.3 Τριγωνική πριοχή που αντιστοιχί σ πολυώνυµο 4 ης τάξης Για την πρίπτωση της µικροταινίας µπορούν να γίνουν αρκτές απλοποιήσις λόγω της συµµτρίας που παρουσιάζι η δοµή της. Επίσης, η πιλογή ορθογωνίου τριγώνου ως πριοχής που αντιστοιχί σ πολυώνυµο ης τάξης και κατ πέκταση σ πολυώνυµα µγαλύτρης τάξης, µπορί να µιώσι πολύ την πολυπλοκότητα του προβλήµατος. Αντικαθιστώντας τις τιµές που αντιστοιχούν σ σηµία του τριγωνικού στοιχίου στους πίνακς σ ij και u j για κάθ τριγωνικό στοιχίο που έχι θωρηθί, λαµβάνοντας υπόψη τις αλλαγές της διηλκτρικής (ή ισοδύναµης διηλκτρικής) σταθράς, και βρίσκοντας τους πίνακς S, U και Τ, η τλική ξίσωση που θα προκύψι για το πρόβληµα θα ίναι της µορφής: Ax = λbx (.8) όπου x ίναι ένας πίνακας-στήλη που αντιστοιχί στο Φ ή το ψ. Η παραπάνω διαδικασία πρέπι να πραγµατοποιηθί δύο φορές, µία για το βαθµωτό δυναµικό Φ και µία για τη µαγνητική ροή ψ. Από την (.8) µπορούµ να βρούµ τις ιδιοτιµές της ξίσωσης και τα αντίστοιχα ιδιοδιανύσµατα που θα αποτλούν και λύσις για το x. Πλονκτήµατα της µθόδου αυτής ίναι ότι µπορί να χρησιµοποιηθί για την ανάλυση της µικροταινίας ακόµα και αν θωρηθούν κκλιµένα τα όρια της δοµής. Επίσης, δν παρουσιάζι προβλήµατα σ πρίπτωση που χρησιµοποιηθούν ανοµοιογνή υλικά. Όπως, όµως, και η µέθοδος FDTD απαιτί προσοχή στην πιλογή των συνοριακών συνθηκών.. Ν. Λοΐζος 9

20 Κφάλαιο Μλέτη της Μοντλοποίησης Γραµµών Μταφοράς σ Ο.Κ. µ Έµφαση στη Μικροταινία...4. Μέθοδος Mode-Matching (Ταύτισης Ρυθµών) Η µέθοδος mode-matching ίναι µία αρκτά διαδδοµένη µέθοδος η οποία χρησιµοποιί την ανάπτυξη των ηλκτροµαγνητικών µγθών του πδίου σ ιδιοσυναρτήσις. Ο τρόπος µ τον οποία γίνται η ανάλυση της δοµής της µικροταινίας µ τη µέθοδο αυτή θα φανί καλύτρα µ το παράδιγµα της φαρµογής της στη δοµή του σχήµατος.4 [8]. Πριοχή Πριοχή a t ή x d Πριοχή 3 3 d Πριοχή 4, ρ 4 4 d 3 Πριοχή 5, ρ 5 Πριοχή 6 ή 6 Σχήµα.4 Εγκάρσια τοµή µίας δοµής µικροταινίας Για την ανάλυση της δοµής αυτής, θα θωρήσουµ µόνο τον πικρατούντα ρυθµό ΤΜ = ΤΕΜ [] (παρακάτω θα αναφρθί πότ ο ρυθµός αυτός µπορί να θωρηθί πικρατών) που ίναι άρτιος, οπότ µπορί να τοποθτηθί ένας µαγνητικός τοίχος (µαγνητικά αγώγιµη πιφάνια) στη θέση x= και άρα να αναλυθί µόνο η πριοχή δξιά από το x=. Επιπλέον, προκιµένου το ηλκτροµαγνητικό πδίο να αναπτυχθί σ σιρά Fouie, θωρούµ έναν ηλκτρικό τοίχο (ηλκτρικά αγώγιµη πιφάνια) σ µία θέση x=w, όπου w>>a. Η θώρηση αυτή δν πηράζι το αποτέλσµα, αφού το πδίο πριορίζται κυρίως στην πριοχή κάτω από τον αγωγό πλάτους a. Αν ως χαρακτηριστικά µγέθη του ηλκτροµαγνητικού πδίου χρησιµοποιηθούν το βαθµωτό ηλκτρικό (Φ) και µαγνητικό (Ψ) δυναµικό και αναπτυχθούν σ σιρές Fouie, θα πάρουµ τις παρακάτω σχέσις για κάθ πριοχή της προς µλέτη δοµής (όπως µπορί να φανί και από το σχήµα 5 έχουµ 6 πριοχές ξκινώντας από πάνω προς τα κάτω: αέρας, αγωγός σήµατος, οξίδιο/µονωτής, ηµιαγωγός, αγωγός γίωσης, αέρας): Ψ Φ Ψ Φ M ( x, ) A co( β x) exp[ α ( t) ] = n= Μ n n n ( x, ) Β in( β x) exp[ α ( t) ] N = n= n ( x, ) in( β x) C in( α ) C co( α ) = n= N pn n n ( ) n ( x, ) co( β x) D in( α ) D co( α ) = n= pn n n n ( ) M 6 Ψ = n n 6n n= M 6 Φ x, = L n in β nx exp α 6n d d n= n M ( x, ) K co( β x) exp[ α ( d d d )] ( ) ( ) [ ( d )] n n n 3 3 (.9) Τα A n, B n,, L n ίναι συντλστές προς προσδιορισµό, Ν ίναι ο αριθµός των συναρτήσων βά-. Ν. Λοΐζος