PDH (Plesiochronous Digital Hierarchy) систем
|
|
|
- Εἰλείθυια Λειβαδάς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 PDH (Plesiochronous Digital Hierarchy) систем Импулсно кодно мултиплексирање (РСМ) и хијерархијски комуникациони систем који је објашњен често се назива и PDH систем ( plesiоchronous digital hierarchy). Дигитална мрежа приближне синхронизације (PDH), како би се у слободном преводу могло превести, је технологија која се користи у телекомуникационим мрежама за пренос велике количине података преко дигиталних телекомуникационих медија, као што су оптички и микроталасни радио-системи. Термин потиче од грчке речи плесио, што значи близу, и Хроносвреме, и односи се на чињеницу да PDH мреже раде у различитим деловима мреже готово, али не баш савршено, синхронизовано. PDH обично замењују синхронизоване дигиталне хијерархијске мреже (Synchronous Digital Hierarchy-SDH) или синхроно оптичко умрежавање ( SONET) у већини телекомуникационих мрежа. PDH омогућава пренос података каналима који номинално раде на истој брзини, али омогућава и неке варијације брзине око номиналне вредности. По аналогији, било која два сата номинално раде са истом брзином такта до 60 секунди по минути. Међутим, што је врло вероватно, један ипак ради мало брже од другог, што кориснику није много битно. Основна брзина преноса података је 2048 kbit/s. За пренос говора, користи се тридесет канала са брзином 64 kbit/s по каналу плус два канала за сигнализацију и синхронизацију са брзином 64 kbit/s. Алтернативно, цео пропусни опсег може да се користи за неговорне сврхе, на пример за пренос података. Брзина преноса података је под контролом сата у опреми која генерише податке. Дозвољено је да брзина варира ± 50 ppm на Mbit/s. То значи да пренос различитих података може да се одвија са незнатним међусобним разликама у брзинама. Да би се пренео већи број података са једног места на друго, они су мултиплексирају у групама од по четири. То се чини тако што се користи 1 bit за стримовање податка број 1, затим 1 bit податак број 2, онда број 3, а затим број 4. За предају из мултиплексера додају се додатни битови како би се омогућио пријем демултиплексера за декодирање који бит припада којем податку, и тако правилно реконструише оригиналне податке у каналу. Ови додатни битови се зову "justification" или "stuffing" битови. Због тога што се сваки од четири податка по каналу не преноси обавезно са истом брзином, морале су се увести одређене компензације. При емитовању мултиплексер комбинује четири податка по каналу под претпоставком да се сваки преноси максимално дозвољеном брзином. То значи да повремено (осим ако није стварна тренутна брзина 2 Mbit/s) мултиплексер може пратити и наредни податак. Ово омогућава да сва четири примљена податка мултиплексер може правилно реконструисати у оригиналне податке са брзином од 2 Mbit/s. Укупна брзина преноса података из горе наведеног процеса износи kbit/s (око 8 Mbit/s). Слична техника се користи и за даље комбиновање: четири 8 Mbit/s, заједно, плус за "stuffing", даје 34 Mbit/s, четири 34 Mbit/s даје 140, а четири 140 даје брзину од 565 Mbit/s. 565 Mbit/s је брзина која се обично користи за пренос података преко оптичког система за међуградску комуникацију и комуникацију на већа растојања. Недавно, телекомуни-
2 кационе компаније су замениле своју PDH опрему SDH опремом добијајући много већа брзине преноса од 2048 Mbit/s, 8448 Mbit/s, Mbit/s и Mbit/s Синхронизована дигитална хијерархија (SDH) SDH хијерархија представља једну од три хијерархије са синхронизованим дигиталним мултиплексирањем. Осим ње, у ту категорију спадају још и Т1 и ISDN (о којем ће бити речи у Приступним мрежама). Хијерархија приближне дигиталне синхронизације (PDH) је развијенa као стандард за мултиплексирање рамова (фремова) вишег реда. PDH је омогућио већи број канала при мултиплексирању по европским стандардима од 30 канала по TDM фрему. Ово решење је примењивано неко време, али како PDH има неколико пратећих недостатака то је резултирало развојем синхроне дигиталне хијерархије (SDH). Разлози који су омогућили развој SDH су следећи: - синхронизована-сви сатови у систему морају да се ускладе са референтним тактом; - сервисно-оријентисана - SDH мора усмерити саобраћај од једног до другог краја преносног система између две централе без обзира на пренос између њих, где ће проток бити одржан на истом нивоу током одређеног временског периода; - да дозволи фремове било које величине да буду отклоњени или уметнути у SDH фрем било које величине; - једноставно руковање са могућношћу управљања преносом података преко везе (линка); - обезбеђивање високог нивоа опоравка од грешака; - обезбеђивање високог протока мултиплексираних података било које величине рама, ког ограничава сама технологија; - смањење грешака битова. SDH је тако постао главни протокол за пренос у већини PSTN мрежа, јер омогућава проток од Мbit/s, а у циљу стварања већег SDH преко тога се врши мултиплексирање фремова познатих као Синхрони Транспортни модули (STM). SТМ-1 рам се састоји од мањих протока који су мултиплексирани да остварују рамове брзине 155,52 Мbit/s. Тако SDH могу мултиплексирати пакете фремова за Етернет, PPP и ATM. И док је SDH предвиђен за пренос протокола (Слој 1 у ОSI референтном моделу), он такође обавља и неке функције свича, као што је наведено у једном од разлога његове примене. Најчешће додатне функције SDH хијерархије су: - SDH проспајање(crossconnect) - је SDH верзија време-простор-време пролазног прекидања. Он повезује било који канал са било којег од његових улаза на било који канал од било којег од својих излаза. SDH проспајање се користи у пролазним централама, у којој су сви улази и излази повезани са другим централама; - SDH Add-Drop мултиплексер (АDМ) може да дода или уклони сваки мултиплексирани рам мањи од 1.544Мit. Испод овог нивоа, стандардни ТDМ може се извршити. SDH АDМ-
3 ови могу да изврше задатак SDH проспајања и користе се на крају централе где се канали од претплатника повезују на језгро PSTN мреже. SDH мреже су повезане помоћу оптичких влакана високе брзине, јер оптичка влакна користе светлосне импулсе за пренос података. Модерна оптичка влакна за пренос користе таласно мултиплексирање (WDМ), где се сигнали преносе преко оптичког влакна различитим таласним дужинама, стварајући додатне канале за пренос. То повећава брзину и капацитет линка, што заузврат истовремено смањује и величине и укупне трошкове. Структура SONET/SDH сигнала Синхроне дигиталне мреже SONET (Synchronous Optical Networking-по америчком ANSI стандарду) или SDH (Synchronous Digital Hierarchy по европском ETSI стандарду) често користе различите термине за описивање исте функције или функција. Ово може да доведе до конфузије и претераних разлика. Уз неколико изузетака, SDH се може посматрати као надскуп за SONET. Протокол је изузетно тешка мултиплексирана структура са заглављем уметнутим и преплетеним (интерливираним) између података на сложенији начин, што има за циљ омогућавање заокруженим подацима да имају свој ниво фрема и да буду у стању да круже у односу на структуру фрема и нивоа SDH/SONET. Ово преплитање омогућава веома ниску латентност заокруженим подацима. Подаци који пролазе кроз опрему могу каснити највише 32 микросекунде у односу на фрем од 125 микросекунди и многи протоколи пре слања приближавају податке на најмање један оквир или пакет. Екстра повећање дозвољава мултиплексираним подацима кретање у оквиру целокупног фрема, јер започиње у другом тренутку од основног фрема. Одлука да се ово дозволи на већини нивоа мултиплексираних структура чини протокол сложеним, али даје високе свеукупне перформансе. Основна јединица фремирања у SDH је STM-1 (Дигитални канал ниво а 1), која ради брзином од 155,52 Мbit/s. SONET користи ознаку основне јединице STS-3c (synchronous transport signal 3 concatenated, тј синхрони пренос сигнала 3 уланчан), али висина нивоа функционалности, величина фрема и ниво бит-а су исти као и SТМ-1. SONET нуди и додатну основну јединицу преноса, STS-1 ( synchronous transport signal 1, тј синхрони пренос сигнала - 1), која ради на 51,84 Мbit/s - тачно трећина од STM-1/STS-3c. То је у SONET вези OC-3 сигнал састављен од три STS-1s (или, више коришћен пакет преноса, OC-3 сигнал носи један уланчани STS-3c). Неки произвођачи такође подржавају еквивалент SDH јединици SТМ-0. Фремирање - У пакет оријентисаном преносу података као што су Етернет пакети, фрем се састоји од заглавља и "корисног терета" (садржаја). Заглавље се прво преноси, а затим и садржај (и евентуално претраживач, као што је то CRC). У синхроним оптичким мрежама то је незнатно измењено. Заглавље се назива overhead и уместо да се преноси пре садржаја, он је интерливиран са њим током преноса. Прво се преноси део заглавља, па део садржаја, а онда следећи део заглавља, па онда следећи део садржаја док се цео фрем не пренесе. У случају STS-1 фрем је величине 810 октета, док је STM-1/STS-3c фрем величине 2430 октета. За STS-1, фрем се преноси као 3 октета за заглавље и 87 октета садржаја, што се понавља девет пута док се не пренесе 810 октета за 125 микросекунди. У случају STM- 1/STS-3c, који ради три пута брже од STS-1, прво се преноси 9 октета заглавља, а прати га
4 261 октет садржаја. Ово се такође понавља девет пута, што даје 2,430 послатих октета за 125 микросекунди. И за SONET и за SDH то је нормалан начин фремирања, који би се графички могао приказати као блок од 90 колона и 9 редова за STS-1 и 270 колона и 9 редова за STM-1/STS-3c. Овај пример поравнат је колоном заглавља, тако да заглавље изгледа као гранични блок и за садржај. Унутрашња структура заглавља и садржаја у раму незнатно се разликује код SONET и SDH, а различити термини се користе у стандардима да се опишу ове структуре. Међутим, њихови стандарди су веома слични у примени, што олакшава заједнички рад SDH и SONET у посебним пропусним опсезима. У пракси, термини STS-1 и ОC-1 се понекад користе наизменично, иако се ОC-N формат односи на сигнал у оптичком облику. Због тога је погрешно рећи да ОC-3 садржи 3 ОC-1s, али се може рећи да ОC- 3 садржи 3 STS-1s. SDH фрем SТМ-1 фрем (слике 14. и 15.) је основни преносни формат код SDH или основни рам или први ниво Синхроне Дигиталне Хијерархије (SDH). SТМ-1 фрем се преноси за тачно 125 микросекунди, због тога што постоји 8000 фремова у секунди на фибер-оптичком колу означеним са ОC-3 (Optical Carrier -3). SТМ-1 фрем се састоји од заглавља и поинтера (показивача) плус информација садржаја. Првих 9 колона сваког фрема чине структура заглавља секције (Section Overhead SOH) и поинтери административних јединица (Administrative Unit Pointers-АU поинтери), а 261 наредна колона чине информације садржаја фрема. Поинтери (H1, H2, H3 бајтова) идентификују административне јединице (А U) у оквиру информација садржаја. Слика 14.-Делови SDH фрема
5 Слика 15.-Структура SТМ-1 фрема У оквиру информационог садржаја, који има сопствени фрем структуре од 9 редова и 261 колону, налазе се административне јединице означене као информација садржаја од стране показивача. У саставу административних јединица је један или више виртуелних контејнера ( VC), који садрже секције заглавља пута ( Рath overhead-рон) и VC садржај. Прва колона је за пут, њу прати садржај контејнера, који може да носи и друге контејнере. Административне јединице могу да имају било које фазно поравнање у STM фрему, и то поравнање је означено поинтером у четвртом реду. Заглавље секције SТМ-1 сигнала (SОH) је подељено на два дела: заглавље регенератора секције (RSОH) и заглавља мултиплексa секције (М SOH). Заглавља садрже информације о самом систему, које се користе за широк спектар функција управљања, као што је праћење квалитета преноса, откривање кварова, управљање алармима, подацима комуникационог канала, сервиса канала итд. STM фрем је континуиран и преноси се у серијском моду бајт по бајт, ред по ред. STM 1 фрем садржи: 1 октет = 8 bit укупно : 9 x 270 октета = 2430 октета заглавље : 8 редова x 9 октета поинтери : 1 ред x 9 октета садржај : 9 редова x 261 октета Период трајања : 125 μsec Брзина преноса : Mbps (2430 октета x 8 bitа x 8000 фремова/s ) или 270*9*64Kbps = Mbps Стварни капацитет преноса података: Mbps (2349 x 8 bitа x 8000 фремова/s) Пренос фремова врши се ред по ред, са лева на десно и одозго на доле.
6 Заглавље преноса се користи за сигнализацију и мерење грешака при преносу и састоји се од: - заглавља секције - назване RSOH (регенератор секције) у SDH терминологији: 27 октета који садрже информације о структури фрема потребне терминалне опреме; - заглавља линије - назване МSOH (заглавље мултиплекса секције) у SDH: 45 октета који садрже информације о аларму, одржавање и исправљање грешака које се могу наћи у оквиру мреже и - поинтера - који показују положај Ј1 бајта у садржају фрема. Подаци се преносе са једног краја на други, a пут којим се преносе назива се пут података, који се састоји од две компоненте: - заглавља пута (POH): користи се 9 октета за сигнализацију и грешке мерења од једног до другог краја и - садржаја, тј. корисничких података (774 бајта за STM-0/STS-1, или 2340 октета за STM- 1/STS-3c) За STS-1, садржај се назива енвелопа синхроног садржаја (synchronous payload envelope- SPE), који има 18 додатних бајтова, што доводи до тога да STS-1 има капацитет од 756 бајтова. STS-1 садржај је дизајниран тако да носи пуни PDH DS3 фрем. Када DS3 приступа у SONET мрежу, заглавље пута се додаје, а SONET мрежни елемент (NE-network element) одређује и прекида пут. SONET NE укида линију ако је процесуирано заглавље линије. Треба имати на уму да где год се линија или путања прекида, секција се такође прекида. SONET регенератори прекидају секцију, али не и путање или линије. STS-1 садржај може бити подељен у 7 виртуелних притока групе VTG (virtual tributary group). Такође, сваки VTG може да се подели на 4 VТ1.5 сигнала, од којих сваки може да носи PDH DS1 сигнал. VTG може бити подељен на 3 VТ2 сигнала, од којих сваки може да носи PDH Е1 сигнал. SDH еквивалент VTG је ТUG2, VТ1.5 је еквивалент за VC11, а VТ2 је еквивалент VC12. Три STS-1 сигнала могу бити мултиплексирана временским мултиплексирањем тако да формирају следећи ниво SONЕТ хијерархије, OC-3 (STS-3), тако да ради на 155,52 Мbit/s. Мултиплексирање се изводи преплитањем бајтова (интерливингом) три STS-1 фрема тако да формира један STS-3 фрем, који садржи 2430 бајтова и пренос у 125 микросекунди. Веће брзине се добијају сукцесивном агрегацијом више споријих протока, а њихова брзина се може одмах очитати са самих ознака. На пример, четири STS-3 или АU4 сигнала могу се сакупити тако да формирају 622,08 Мbit/S сигнал, означен као ОC-12 и SТМ-4. Највећа брзина која се обично користи је са ознаком ОC-192 и SТМ-64, која износи нешто мање од 10 Gbps. Брзине преко 10 Gbps су технички могуће и пред усвајањем. (Неколико произвођача већ нуде SТМ-256, са брзинама скоро 40Gbps). На местима где је оптичко влакно преоптерећено, више SONЕТ сигнала може се преносити преко више таласних дужина за шта је неопходно вршити мултиплексирање по таласној дужини, укључујући мул-
7 типлексирање снопа таласне дужине (DVDМ- dense wavelength division multiplexing) и грубо мултиплексирање таласне дужине ( CVDМ- coarse wavelength-division multiplexing). DVDM кола су основа за све савремене трансатлантске кабловске системе и остале протоке на велику удаљеност. SONET/SDH и веза са 10 Gbit Ethernet-ом Још један тип преноса података је 10 Гигабитни Етернет (10GbЕ). Гигабитна Етернет Алијанса креирана је са две 10 Гигабитне Етернет варијанте: локалне варијанте (LAN PHY) са брзином линије од 10,3125 Gbit/S, и широкопојасне варијанте (WAN PHY) са истом брзином као и брзином ОC-192/SТМ-64 од 9,953,280 kbps. VAN PHY варијанта обједињује етернет податке користећи "лагани" SDH/SONЕТ фрем како би били компатибилни на ниском нивоу са опремом дизајнираном за ношење SDH/SONЕТ сигнала, док LAN PHY варијанта обједињује етернет податке користећи 64B/66B кодирање линије. Међутим, 10 Гигабитни Етернет не пружа експлицитно никакву подршку на нивоу битстримовања других SDH/SONЕТ система. Ово се разликује од WDМ система транспондера, укључујући и друге облике WDМ система (CWDМ, DWDМ), који подржавају проток ОC-192 SONЕТ сигнала, a који подржавају танки SONЕТ урамљени 10 Gb Етернет. SONET/SDH нивои брзина У следећој табели приказани су упоредни нивои брзина и ознаке за SONET и SDH: Брзина од 160 Gbit/s ОC-3072/SТМ-1024 још није стандардизована, због високе цене примопредајника и могућности јефтинијег мултиплекса таласне дужине од 10 и 40 Gbit/s. Физички слој Физички слој се састоји од великог броја слојева, од којих је само један оптички/преносни слој (који укључује протоке, jitter спецификације, спецификације оптичких сигнала
8 итд.) SONET и SDH стандарди подразумевају и могућности изоловања и идентификације и порекла недостатака сигнала. SONET/SDH протоколи мрежног управљања SONET опрема се често управља са ТL1 протоколом. ТL1 је традиционални телеком језик управљања и реконфигурације SONЕТ елемената мреже. ТL1 (или било који други језик управљања SONЕТ мрежним елементима) мора се извршити од стране других протокола управљања, укључујући и SNMP, CORBA и ХМL. SDH углавном користи Q3 интерфејс. Најновије имплементације такође користе ТL1 са конвергенцијом SONЕТ и SDH елемената мрежне архитектуре. Постоје неке особине које су прилично универзалнe код управљања SONЕТ мрежом. Пре свега, већина SONЕТ NЕ имају дефинисан ограничен број интерфејса за управљање. То су: Електрични интерфејс. Електрични интерфејс (најчешће 50 Ω) шаље SONЕТ ТL1 команде за локално управљање мрежом, а SONЕТ NЕ мрежни елементи физички се налазе у централи. Ово је за "локално управљање" мрежним елементима ( NЕ) а, евентуално, и за даљинско управљање других SONЕТ NЕ; Craft интерфејс. Локалним "craftspersons" може се приступити SONET мрежним елементима на "craft port" и издати команде преко "немих" терминала или терминала са емулацијом програма који ради на лаптопу. Овај интерфејс може бити прикључен на конзолу сервера и омогућава даљинско управљање и пријављивање. SONET и SDH имају изведене канале за комуникацију података (DCC-data communication channels) унутар заглавља секције и линије за управљање у саобраћају. Генерално, заглавље секције (регенератор секције у SDH) је од велике користи. Према IТU-Т G.7712, постоје три начина за управљање: - IP-only stack, преко PPP као data-link; - OSI-only stack, преко LAP-D као data-link и - Dual (IP+OSI) stack преко PPP или LAP-D са функцијама тунеловања за комуникацију између стекова. Интересантна чињеница о савременим мрежним елементима је та да за обраду и управљање свих канала и сигнала већина NE садржи рутер за рутирање мрежних команди и основних података протокола. Основне функције управљања мрежом укључују: - Мрежну и НЕ резервацију. Да би се извео проток кроз мрежу, сваки NE мора бити конфигурисан. Иако се ово може извршити на локалном нивоу, помоћу craft интерфејса, обично се врши путем система за управљање мрежом (постављањем на виши слој) па се управљање мрежом ипак изводи преко SONЕТ/SDH мреже; - Надоградњу софтвера. NE надоградња софтвера се у модерном NE врши углавном преко SONЕТ/SDH управљања мрежом;
9 - Управљање перформансама. NЕ имају веома велики скуп стандарда за управљање перформансама. PМ критеријуми за праћење омогућавају не само исправност појединих NЕ, него и изолацију и идентификацију већине недостатака или прекида мреже. Софтвер за управљање и мониторинг вишеслојне мреже омогућава правилно филтрирање и решавање проблема у целој мрежи, тако да недостаци и прекиди целе мреже PМ могу бити брзо идентификовани и решени. ОПРЕМА Са скорашњим напретком SONET и SDH чипова, традиционалне категорије мрежне опреме се руше. И поред тога, као и мрежне архитектуре, остале су релативно константне, а чак и новија опрема (Укључујући и "Мултисервисне Резервационе Платформе") може се испитати у светлу подршке архитектури. Дакле, у том погледу и даље се упоређује нова (као и традиционална) опрема према старијим категоријама. Регенератори Традиционални регенератори окончали су заглавље секције, али не и линију или путању. Регенератори су продужили преносне путеве на начин сличан већини регенератора, претварањем у оптички сигнал који се до тада преносио на даљину у електричном формату, а затим се ретрансмитовао регенерисани сигнал велике снаге. Од касних 1990-их, регенератори су у великој мери замењени оптичким појачавачима. Такође, и неке од функција регенератора су пренесене на транспондер за мултиплексирање таласне дужине система. Add-drop multiplexer Add-drop мултиплексери (ADM) су најчешћи тип NЕ. Традиционална АDМ били су дизајнирани за подршку једне од мрежних архитектура, мада системи нове генерације често могу да подржавају више архитектура, понекад и истовремено. АDМ традиционално имају "странице велике брзине" (где је подржана пуна брзина сигнала линије) и "странице мале брзине", који могу да се састоје од електричног и оптичког интерфејса. Страница мале брзине узима малом брзином сигнале које су мрежни елементи мултиплексирали и шаље их на страницу велике брзине и обрнуто. Дигитални проспојни (crossconnect) систем Садашњи Дигитални систем за проспајање (DCS или DXC) подржавају бројчано велике брзине сигнала и омогућавају проспајање DS1, DS3 па чак и STS-3s/12c и тако даље, из било ког улаза на било који излаз. Напредни DCS може истовремено да подржава и наспрамне прстенове. МРЕЖНЕ АРХИТЕКТУРЕ Тренутно, SONET и SDH имају ограничен број дефинисаних архитектура. Ове архитектуре омогућавају ефикасно коришћење пропусне моћи, као и заштиту (тј. могућност пре-
10 носа чак и када је део мреже неисправан), као и могућност разумевања и употребе SONET и SDH широм света. Три основне архитектуре су: - Линеарни АPS (automatic protection switching-аутоматска заштита комутације), такође познат као 1+1: Ово укључује 4 влакна: 2 радна (по 1 у сваком смеру), и два за заштиту влакана. Комутација је базирана на линији стања и може бити једносмерна, у сваком смеру комутација је неовисна о другом смеру, или двосмерна, где су NЕ на сваком крају преклопљени, тако да се саобраћај у оба смера углавном обавља по истом пару влакана. - UPSR (unidirectional path-switched ring-једносмерни пут-комутиран прстен): У UPSR две редудантне копије (на нивоу пута) заштићеног саобраћаја се шаљу у оба смера око прстена. Бирач на изласку чвора одређује квалитетније копирање и бира за коришћење најбоље копије, тако да ако у једном примерку настане слабљење због пуцања или грешке у влакну превазилази проблем. UPSR има тенденцију да стоји близу краја мреже и као такав се понекад назива "колектор прстенова". Зато што се исти подаци шаљу око прстена у оба смера, укупан капацитета UPSR једнак је брзини линије N ОC-N прстена. На пример, ако имамо ОC-3 прстен са 3 STS-1s који се користи за пренос 3 DS-3s од улаза чвора А на излаз чвора D, онда 100% пропусног опсега прстена (N = 3) се користи за проток од чвора А до D. Било који други чворови прстена, рецимо B и C могу само да делују као пролазни чворови. SDH аналогија UPSR -у је унутар заштите подмреже (SNCP-subnetwork connection protection), али SNCP не намеће топологију прстена, иако се може користити у мрежној топологији. - BLSR (bidirectional line-switched ring-двосмерна линија-комутиран прстен): BLSR се јавља у две варијанте, BLSR са 2-влакна и BLSR са 4-влакна. BLSR прекидач је на слоју линије. За разлику од UPSR, BLSR не шаље сувишне копије из улаза на излаз. Уместо тога, чворови прстена при грешкама преусмеравају саобраћај на "дужи пут" око прстена. BLSR је скупљи и сложенији по ефикасности широкопропусног опсега, као и способности за подршку "екстра саобраћаја", која може бити непотребна када се изврши заштита комутације. BLSR могу да раде у оквиру градског региона или, чешће, за комутацију у саобраћају између градова. Због тога што BLSR не шаље сувишне копије од улаза на излаз укупни пропусни опсег који може подржати BLSR није ограничен на брзину линије N ОC-N прстена, а чак може бити и већи од N у зависности од тренутног протока у прстену. У најбољем случају то је кад се одвија сав саобраћај између суседних чворова, а у најгорем када је сав саобраћај на прстену потекао из једног чвора, односно када BLSR служи као колектор прстена. У овом случају подржани проток у прстену једнак је брзини линије N ОC- N прстена. То је ретко и само онда када је постављен као колектор прстена, али се често примењује у прстену између централа. SDH еквивалент BLSR-у се назива Мултиплекс Секције-дељење заштите прстена (МS-SPRING, тј. Multiplex Section- Shared Protection Ring).
11 СИНХРОНИЗАЦИЈА За синхронизацију у телекомуникационим мрежама користи се сат на изворишту, који се оцењују по квалитету, обично под називом "stratum" ниво. Типично, мрежни елемент (NE) користи најквалитетније stratum-е на располагању да би се могло утврдити праћење синхронизације статуса поруке (SSМ) одабраним сатом. Што се тиче синхронизације изворишта на располагању мрежним елементима су: - Локални екстерни тајмер. Ово је атомски сат направљен од Цезијума или сателитски сатни уређај у истој централи као и NЕ. Интерфејс је често DS1, са статусом SSМ која се добија од сата и ставља у заглавље DS1. - Линијски одвојени тајмери. NЕ може да се изабере (или да буде конфигурисан) да одвоји своје време са линијског нивоа, праћењем стања S1 синхронизације бајтова како би се обезбедио квалитет. - Holdover. Као последње средство, у недостатку квалитетнијег тајмера, NЕ могу да иду у "holdover" док квалитетнији екстерни тајмер не буде поново доступан. У овом режиму, NЕ користи сопствени тајмер као референтни. Временска петља Временска петља се ствара када сваки NE у мрежи преузима своје време од других NE, без тога да је било који од њих "главни" извор временског одређивања. Ова мрежна петља види своје текуће време одвојено од било које спољне мреже, због чега настају непознате грешке и на крају, у најгорим случајевима, масивни губитак саобраћаја. Извор ове врсте грешака може бити тешко дијагностикован. У принципу, мрежа које је исправно конфигурисана никада не би требала да се нађе у временској петљи, али неке класе тихих грешака могу ипак проузроковати овај проблем. СЛЕДЕЋА ГЕНЕРАЦИЈА SONET/SDH SONET/SDH развој је првобитно био одређен потребом за пренос више PDH сигнала према DS1, Е1, Е3 DS3 мултиплексираних заједно са другим групама брзином 64 kbps импулсно-кодне модулације говорног саобраћаја. Могућност асиметричног АТМ преноса била је једна од најранијих апликација. У циљу подршке великих пропусних опсега АТМа, развијена је техника уланчавања, при чему су мањи мултиплексирани контејнери (нпр., STS-1) обрнуто мултиплексирани како би се добили већи контејнери (нпр., STS-3c) који су оријентисани ка подршци великих протока података. Међутим, један од проблема са традиционалним уланчавањем је нефлексибилност. Зависно од саобраћаја мешаних података и говора који се морају извршити, не преостаје много неискоришћеног опсега, због фиксне величине уланчаног контејнера. На пример, уградња контејнера од 100 Мbit/s Етернет везе унутар 155 Мbit/s STS-3c доводи до значајног смањења опсега. Још важнија је потреба да сваки средњи NЕ даје подршку новоуведеним величинама ланаца. Овај проблем је касније превазиђен увођењем виртуелног уланчавања. Виртуелно уланчавање (VCAT-Virtual concatenation) омогућава више произвољних склопова за мултиплексирање контејнера нижег реда, уградњу већих контејнера прилично про-
12 извољне величине (на пример 100 Мbit/s), без потребе да средњи NЕ даје подршку овом облику уланчавања. Виртуелно уланчавање повећава моћ Х.86 или протокола Процедуре стварања фремова (GFP-Generic Framing Procedure) како би се садржаји било којег протока могли мапирати у практично уланчани контејнер. Линк Капацитетног подешавања шеме (LCAS-Link Capacity Adjustment Scheme) омогућава динамичку промену протока преко динамичког виртуелног уланчавања, мултиплексирање контејнера на основу краткорочних потреба пропусног опсега у мрежи. Скуп следеће генерације SONЕТ/SDH протокола омогућава етернет пренос који се назива Етернет преко SONET/SDH (ЕoS-Ethernet over SONET/SDH). ЛИНКОВИ ЗА ЛИТЕРАТУРУ: The Queen's University of Belfast SDH/SONET Primer ( /network/sdh-sonet/sdh-sonet.html) SDH Pocket Handbook from Acterna/JDSU ( /technical_resources/pocket_guides/sdh_guide1.html) SONET Pocket Handbook from Acterna/JDSU ( /technical_resources/pocket_guides/sonet_guide.html) The Sonet Homepage ( SONET Interoperability Form (SIF) ( Network Connection Speeds Reference ( Next-generation SDH and MSPP ( The Future of SONET/SDH ( (pdf) Стандарди: Telcordia GR-253-CORE, SONET Transport Systems: Common Generic Criteria ( Telcordia GR-499-CORE, Transport Systems Generic Requirements (TSGR): Common Requirements ( DOCUMENT=GR-499&) ANSI T1.105: SONET - Basic Description including Multiplex Structure, Rates and Formats ( ANSI T1.119/ATIS PP : SONET - Operations, Administration, Maintenance, and Provisioning (OAM&P) - Communications ( ITU-T recommendation G.707: Network Node Interface for the Synchronous Digital Hierarchy (SDH) ( ITU-T recommendation G.783: Characteristics of synchronous digital hierarchy (SDH) equipment functional blocks ( ITU-T recommendation G.803: Architecture of Transport Networks Based on the Synchronous Digital Hierarchy (SDH) (
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
4. АСИНХРОНИ РЕЖИМ ПРЕНОСА (АТМ)
 4. АСИНХРОНИ РЕЖИМ ПРЕНОСА (АТМ) Асинхрони режим преноса (Asynchronous Transfer Mode-АТМ) је ћелијски-базирана техника комутације која користи асинхроно временско мултиплексирање. Код њега се врши кодирање
4. АСИНХРОНИ РЕЖИМ ПРЕНОСА (АТМ) Асинхрони режим преноса (Asynchronous Transfer Mode-АТМ) је ћелијски-базирана техника комутације која користи асинхроно временско мултиплексирање. Код њега се врши кодирање
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
4. ISDN 4.1. УВОД. ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ Page 36
 4. ISDN 4.1. УВОД ISDN (Integrated Services Digital Network) je је скуп комуникационих стандарда за симултани дигитални пренос гласа, видеа, података, као и за друге мрежне услуге преко традиционалних
4. ISDN 4.1. УВОД ISDN (Integrated Services Digital Network) je је скуп комуникационих стандарда за симултани дигитални пренос гласа, видеа, података, као и за друге мрежне услуге преко традиционалних
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
ВИСОКА ШКОЛА ЕЛЕКТРОТЕХНИКЕ И РАЧУНАРСТВА СТРУКОВНИХ СТУДИЈА ДИГИТАЛНИ АУДИО ЗА ДИГИТАЛНУ ВИДЕО РАДИОДИФУЗИЈУ
 ВИСОКА ШКОЛА ЕЛЕКТРОТЕХНИКЕ И РАЧУНАРСТВА СТРУКОВНИХ СТУДИЈА ДИГИТАЛНИ АУДИО ЗА ДИГИТАЛНУ ВИДЕО РАДИОДИФУЗИЈУ Припремила: мр Милица Мишић, дипл. инж. електр. 1 Аудио и видео сигнали су једнако важни елементи
ВИСОКА ШКОЛА ЕЛЕКТРОТЕХНИКЕ И РАЧУНАРСТВА СТРУКОВНИХ СТУДИЈА ДИГИТАЛНИ АУДИО ЗА ДИГИТАЛНУ ВИДЕО РАДИОДИФУЗИЈУ Припремила: мр Милица Мишић, дипл. инж. електр. 1 Аудио и видео сигнали су једнако важни елементи
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
b) Израз за угиб дате плоче, ако се користи само први члан реда усвојеног решења, је:
 Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
SONET/SDH. SDH Synchronous Digital Hierarchy. Εισαγωγή οµή ικτύου SONET/SDH Πλαισίωση Πλαισίωση SONET Πλαισίωση SDH Τοπολογίες SONET/SDH
 ίκτυα Πρόσβασης Ευρείας Ζώνης SDH Synchronous Digital Hierarchy, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών SONET/SDH Εισαγωγή οµή ικτύου SONET/SDH Πλαισίωση Πλαισίωση SONET Πλαισίωση SDH Τοπολογίες SONET/SDH
ίκτυα Πρόσβασης Ευρείας Ζώνης SDH Synchronous Digital Hierarchy, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών SONET/SDH Εισαγωγή οµή ικτύου SONET/SDH Πλαισίωση Πλαισίωση SONET Πλαισίωση SDH Τοπολογίες SONET/SDH
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање. 1. вежба
 Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
Αστικά δίκτυα και δίκτυα κορμού. Αλέξανδρος Σταυδάς Δεύτερος Κύκλος
 Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Δεύτερος Κύκλος Εισαγωγή στα SDH/SONET Εισαγωγή-PDH Δημιουργήθηκε το 1960 για να αντικαταστήσει την αναλογική τηλεφωνική υποδομή. Βασίζεται στο TDM. Χρησιμοποιείται
Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Δεύτερος Κύκλος Εισαγωγή στα SDH/SONET Εισαγωγή-PDH Δημιουργήθηκε το 1960 για να αντικαταστήσει την αναλογική τηλεφωνική υποδομή. Βασίζεται στο TDM. Χρησιμοποιείται
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
КРУГ. У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице.
 КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ
 ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
8.2 ЛАБОРАТОРИЈСКА ВЕЖБА 2 Задатак вежбе: Израчунавање фактора појачања мотора напонским управљањем у отвореној повратној спрези
 Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
5.2. Имплицитни облик линеарне функције
 математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
8. ПИТАГОРИНА ЈЕДНАЧИНА х 2 + у 2 = z 2
 8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
Упутство за избор домаћих задатака
 Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ
 2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
5.ОПТИЧКИ СИСТЕМИ ПРЕНОСА
 5.ОПТИЧКИ СИСТЕМИ ПРЕНОСА 5.1. ПРОБЛЕМ ПОВЕЋАЊА ПРОПУСНОГ ОПСЕГА ОПТИЧКОГ ЛИНКА Све већа потреба корисника за повећањем дотока информација, диктира обавезу проширења пропусног опсега, што је главни проблем
5.ОПТИЧКИ СИСТЕМИ ПРЕНОСА 5.1. ПРОБЛЕМ ПОВЕЋАЊА ПРОПУСНОГ ОПСЕГА ОПТИЧКОГ ЛИНКА Све већа потреба корисника за повећањем дотока информација, диктира обавезу проширења пропусног опсега, што је главни проблем
Вектори vs. скалари. Векторске величине се описују интензитетом и правцем. Примери: Померај, брзина, убрзање, сила.
 Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
Πεδία Πλαισίου SONET (I)
 ίκτυα Πρόσβασης Ευρείας Ζώνης Τεχνολογίες Φυσικού Στρώµατος: SONET/SDH, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών Πεδία Πλαισίου SONET (I) 1 Πεδία Πλαισίου SONET (II) Framing: A1, A = 11110110 00101000 Σηµατοδοτεί
ίκτυα Πρόσβασης Ευρείας Ζώνης Τεχνολογίες Φυσικού Στρώµατος: SONET/SDH, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών Πεδία Πλαισίου SONET (I) 1 Πεδία Πλαισίου SONET (II) Framing: A1, A = 11110110 00101000 Σηµατοδοτεί
Аксиоме припадања. Никола Томовић 152/2011
 Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Αστικά δίκτυα και δίκτυα κορμού. Αλέξανδρος Σταυδάς Πέμπτος Κύκλος
 Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Πέμπτος Κύκλος NG- SDH/SONET Τα προβλήματα του SONET/SDH Τα είδη του φορτίου (traffic) αλλάζουν Κυριαρχία μη-φωνητικών υπηρεσιών Το ζητούμενο είναι η
Αστικά δίκτυα και δίκτυα κορμού Αλέξανδρος Σταυδάς Πέμπτος Κύκλος NG- SDH/SONET Τα προβλήματα του SONET/SDH Τα είδη του φορτίου (traffic) αλλάζουν Κυριαρχία μη-φωνητικών υπηρεσιών Το ζητούμενο είναι η
8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: PI регулација брзине напонски управљаним микромотором једносмерне струје
 Регулација електромоторних погона 8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: регулација брзине напонски управљаним микромотором једносмерне струје Увод Simulik модел На основу упрошћеног блок дијаграма
Регулација електромоторних погона 8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: регулација брзине напонски управљаним микромотором једносмерне струје Увод Simulik модел На основу упрошћеног блок дијаграма
Могућности и планови ЕПС на пољу напонско реактивне подршке. Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије
 Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
ΕΞΕΛΙΞΗ ΔΙΚΤΥΩΝ ΜΕΤΑΔΟΣΗΣ ΣΕ ΔΙΚΤΥΑ ΚΙΝΗΤΗΣ ΤΗΛΕΦΩΝΙΑΣ. Δημουλάς Βασίλειος Δ/νση Δικτύου Πρόσβασης και Μετάδοσης Υποδ/νση Ανάπτυξης Δικτύου Μετάδοσης
 ΕΞΕΛΙΞΗ ΔΙΚΤΥΩΝ ΜΕΤΑΔΟΣΗΣ ΣΕ ΔΙΚΤΥΑ ΚΙΝΗΤΗΣ ΤΗΛΕΦΩΝΙΑΣ Δημουλάς Βασίλειος Εξέλιξη Δικτύων Μετάδοσης σε Δίκτυα Κινητής Τηλεφωνίας Λογική Αρχιτεκτονική Δικτύου GSM/GPRS Βασικές Υφιστάμενες Υπηρεσίες Νέες
ΕΞΕΛΙΞΗ ΔΙΚΤΥΩΝ ΜΕΤΑΔΟΣΗΣ ΣΕ ΔΙΚΤΥΑ ΚΙΝΗΤΗΣ ΤΗΛΕΦΩΝΙΑΣ Δημουλάς Βασίλειος Εξέλιξη Δικτύων Μετάδοσης σε Δίκτυα Κινητής Τηλεφωνίας Λογική Αρχιτεκτονική Δικτύου GSM/GPRS Βασικές Υφιστάμενες Υπηρεσίες Νέες
ЗАШТИТА ПОДАТАКА. Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2 Diffie-Hellman размена кључева први алгоритам са јавним кључем
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2 Diffie-Hellman размена кључева први алгоритам са јавним кључем
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Нивелмански инструмент (нивелир) - конструкција и саставни делови, испитивање и ректификација нивелира, мерење висинских разлика техничким нивелманом
 висинских техничким нивелманом Страна 1 Радна секција: 1.. 3. 4. 5. 6. Задатак 1. За нивелмански инструмент нивелир са компензатором серијски број испитати услове за мерење висинских : 1) Проверити правилност
висинских техничким нивелманом Страна 1 Радна секција: 1.. 3. 4. 5. 6. Задатак 1. За нивелмански инструмент нивелир са компензатором серијски број испитати услове за мерење висинских : 1) Проверити правилност
7.3. Површина правилне пирамиде. Површина правилне четворостране пирамиде
 математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
TAЧКАСТА НАЕЛЕКТРИСАЊА
 TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
Слика 1. Слика 1.2 Слика 1.1
 За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1
 1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
4.4. Паралелне праве, сечица. Углови које оне одређују. Углови са паралелним крацима
 50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ
 ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 2004
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
Хомогена диференцијална једначина је она која може да се напише у облику: = t( x)
 ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ТРЕЋЕ ОТВОРЕНО ПРВЕНСТВО СРБИЈЕ У РЕШАВАЊУ ОПТИМИЗАТОРА 29. НОВЕМБАР ДЕЦЕМБАР ГОДИНЕ
 ТРЕЋЕ ОТВОРЕНО ПРВЕНСТВО СРБИЈЕ У РЕШАВАЊУ ОПТИМИЗАТОРА 29. НОВЕМБАР - 12. ДЕЦЕМБАР 2010. ГОДИНЕ http://puzzleserbia.com/ ДРУГА НЕДЕЉА (6.12. - 12.12.) 7. СУДОКУ АЈНЦ 8. ПЕНТОМИНО УКРШТЕНИЦА 9. ШАХОВСКЕ
ТРЕЋЕ ОТВОРЕНО ПРВЕНСТВО СРБИЈЕ У РЕШАВАЊУ ОПТИМИЗАТОРА 29. НОВЕМБАР - 12. ДЕЦЕМБАР 2010. ГОДИНЕ http://puzzleserbia.com/ ДРУГА НЕДЕЉА (6.12. - 12.12.) 7. СУДОКУ АЈНЦ 8. ПЕНТОМИНО УКРШТЕНИЦА 9. ШАХОВСКЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Први корак у дефинисању случајне променљиве је. дефинисање и исписивање свих могућих eлементарних догађаја.
 СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
Закони термодинамике
 Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Једна од централних идеја рачунарства Метода која решавање проблема своди на решавање проблема мање димензије
 Рекурзија Једна од централних идеја рачунарства Метода која решавање проблема своди на решавање проблема мање димензије Рекурзивна функција (неформално) је функција која у својој дефиницији има позив те
Рекурзија Једна од централних идеја рачунарства Метода која решавање проблема своди на решавање проблема мање димензије Рекурзивна функција (неформално) је функција која у својој дефиницији има позив те
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Писмени испит из Теорије површинских носача. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Погодност за одржавање, Расположивост, Марковљеви ланци
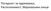 Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни
 ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА
 ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ
 Драган Товаришић, дипл.инж.ел. Скрипта за предавања из предмета ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ за IV разред смера Електротехничар телекомуникација Суботица, 2010.год. ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ Page 1 1. ПОЈАМ
Драган Товаришић, дипл.инж.ел. Скрипта за предавања из предмета ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ за IV разред смера Електротехничар телекомуникација Суботица, 2010.год. ПРИСТУПНЕ МРЕЖЕ И УРЕЂАЈИ Page 1 1. ПОЈАМ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ -
 ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
6.1. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре
 0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
Факултет организационих наука Центар за пословно одлучивање. PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation)
 Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Wide Area Networks - WAN μέρος Α
 24/5/2001 Δίκτυα Ευρείας Περιοχής, xdsl & Συσκευές - Κ. Σ. Χειλάς 1 Wide Area Networks - WAN μέρος Α Κωνσταντίνος Σ. Χειλάς Φυσικός - Ραδιοηλεκτρολόγος - MIS 24/5/2001 Δίκτυα Ευρείας Περιοχής, xdsl & Συσκευές
24/5/2001 Δίκτυα Ευρείας Περιοχής, xdsl & Συσκευές - Κ. Σ. Χειλάς 1 Wide Area Networks - WAN μέρος Α Κωνσταντίνος Σ. Χειλάς Φυσικός - Ραδιοηλεκτρολόγος - MIS 24/5/2001 Δίκτυα Ευρείας Περιοχής, xdsl & Συσκευές
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
У н и в е р з и т е т у Б е о г р а д у Математички факултет. Семинарски рад. Методологија стручног и научног рада. Тема: НП-тешки проблеми паковања
 У н и в е р з и т е т у Б е о г р а д у Математички факултет Семинарски рад из предмета Методологија стручног и научног рада Тема: НП-тешки проблеми паковања Професор: др Владимир Филиповић Студент: Владимир
У н и в е р з и т е т у Б е о г р а д у Математички факултет Семинарски рад из предмета Методологија стручног и научног рада Тема: НП-тешки проблеми паковања Професор: др Владимир Филиповић Студент: Владимир
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
I Наставни план - ЗЛАТАР
 I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
Писмени испит из Метода коначних елемената
 Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c
 6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
Тестирање комуникационих каблова
 Тестирање комуникационих каблова Арсеније Иванишевић Факултет техничких наука, Чачак, Електротехничко и рачунарско инжењерство, даљинско управљање, 2011/2012. arsenije.ivanisevic@gmail.com Ментор рада
Тестирање комуникационих каблова Арсеније Иванишевић Факултет техничких наука, Чачак, Електротехничко и рачунарско инжењерство, даљинско управљање, 2011/2012. arsenije.ivanisevic@gmail.com Ментор рада
Семинарски рад из линеарне алгебре
 Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
Анализа и мерење преносних карактеристика оптичких каблова
 Анализа и мерење преносних карактеристика оптичких каблова Никола Ђорић Факултет техничких наука, Чачак Информационе технологије, 2014/2015 dzonee362@gmail.com Проф.др Ристо Бојовић Апстракт - У раду су
Анализа и мерење преносних карактеристика оптичких каблова Никола Ђорић Факултет техничких наука, Чачак Информационе технологије, 2014/2015 dzonee362@gmail.com Проф.др Ристо Бојовић Апстракт - У раду су
2.1. Права, дуж, полуправа, раван, полураван
 2.1. Права, дуж, полуправа, раван, полураван Човек је за своје потребе градио куће, школе, путеве и др. Слика 1. Слика 2. Основа тих зграда је често правоугаоник или сложенија фигура (слика 3). Слика 3.
2.1. Права, дуж, полуправа, раван, полураван Човек је за своје потребе градио куће, школе, путеве и др. Слика 1. Слика 2. Основа тих зграда је често правоугаоник или сложенија фигура (слика 3). Слика 3.
Штампарске грешке у петом издању уџбеника Основи електротехнике, 1. део, Електростатика
 Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
Слика бр.1 Површина лежишта
 . Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
. Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
ЗАВРШНИ РАД Краљево,фебруар године
 УНИВЕРЗИТЕТ У КРАГУЈЕВЦУ ФАКУЛТЕТ ЗА МАШИНСТВО И ГРАЂЕВИНАРСТВО КРАЉЕВО ЗАВРШНИ РАД Студент: Јелена Живковић, рег. бр. 23/07 Краљево,фебруар 2013. године Живковић Јелена 23/07 1 УНИВЕРЗИТЕТ У КРАГУЈЕВЦУ
УНИВЕРЗИТЕТ У КРАГУЈЕВЦУ ФАКУЛТЕТ ЗА МАШИНСТВО И ГРАЂЕВИНАРСТВО КРАЉЕВО ЗАВРШНИ РАД Студент: Јелена Живковић, рег. бр. 23/07 Краљево,фебруар 2013. године Живковић Јелена 23/07 1 УНИВЕРЗИТЕТ У КРАГУЈЕВЦУ
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1
 КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
PDH ΠΛΗΣΙΟΧΡΟΝΗ ΨΗΦΙΑΚΗ ΙΕΡΑΡΧΙΑ (PLESIOCHRONOUS DIGITAL HIERARCHY)
 1 PDH ΠΛΗΣΙΟΧΡΟΝΗ ΨΗΦΙΑΚΗ ΙΕΡΑΡΧΙΑ (PLESIOCHRONOUS DIGITAL HIERARCHY) ΙΑΠΩΝΙΑ Β.ΑΜΕΡΙΚΗ ΕΥΡΩΠΗ 5η τάξη 397200 Kbit/s 274176 Kbit/s 564992 Kbit/s Χ 4 Χ 6 Χ 4 4η τάξη 97728 Kbit/s Χ 3 Χ 3 139264 Kbit/s Χ
1 PDH ΠΛΗΣΙΟΧΡΟΝΗ ΨΗΦΙΑΚΗ ΙΕΡΑΡΧΙΑ (PLESIOCHRONOUS DIGITAL HIERARCHY) ΙΑΠΩΝΙΑ Β.ΑΜΕΡΙΚΗ ΕΥΡΩΠΗ 5η τάξη 397200 Kbit/s 274176 Kbit/s 564992 Kbit/s Χ 4 Χ 6 Χ 4 4η τάξη 97728 Kbit/s Χ 3 Χ 3 139264 Kbit/s Χ
Динамика. Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе:
 Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Εισαγωγή ΙΙ: Βασικοί τύποι δικτύων
 Εισαγωγή ΙΙ: Βασικοί τύποι δικτύων Tηλεφωνικό δίκτυο Ethernet LAN Internet ATM Τηλεφωνικό ίκτυο (Τ ) Χρονολόγιο σηµαντικών σταθµών: 1839 Τηλέγραφος (Cooke, Wheatstone) 1844 Κώδικας Morse ( --) 1850-1860
Εισαγωγή ΙΙ: Βασικοί τύποι δικτύων Tηλεφωνικό δίκτυο Ethernet LAN Internet ATM Τηλεφωνικό ίκτυο (Τ ) Χρονολόγιο σηµαντικών σταθµών: 1839 Τηλέγραφος (Cooke, Wheatstone) 1844 Κώδικας Morse ( --) 1850-1860
Разлика потенцијала није исто што и потенцијална енергија. V = V B V A = PE / q
 Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
Αρχιτεκτονική Τηλεφωνικού ικτύου
 ίκτυα Πρόσβασης Ευρείας Ζώνης Το ο ίκτυο Πρόσβασης: Το τηλεφωνικό δίκτυο, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών Αρχιτεκτονική Τηλεφωνικού ικτύου Analog / Digital PABX PABX Αναλογικές Συσκευές σε Αναλογικά
ίκτυα Πρόσβασης Ευρείας Ζώνης Το ο ίκτυο Πρόσβασης: Το τηλεφωνικό δίκτυο, Τµήµα Επιστήµης & Τεχνολογίας Τηλ/νιών Αρχιτεκτονική Τηλεφωνικού ικτύου Analog / Digital PABX PABX Αναλογικές Συσκευές σε Αναλογικά
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 2 (13Е013ЕП2) октобар 2016.
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Рачунарске мреже. Александар Картељ
 Рачунарске мреже Александар Картељ kartelj@matf.bg.ac.rs Наставни материјали су преузети од: TANENBAUM, ANDREW S.; WETHERALL, DAVID J., COMPUTER NETWORKS, 5th Edition, 2011 и прилагођени настави на Математичком
Рачунарске мреже Александар Картељ kartelj@matf.bg.ac.rs Наставни материјали су преузети од: TANENBAUM, ANDREW S.; WETHERALL, DAVID J., COMPUTER NETWORKS, 5th Edition, 2011 и прилагођени настави на Математичком
