Opti na koheren na tomografija
|
|
|
- Λαφιδὼθ Παπαϊωάννου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Opti na koheren na tomografija Matevº Caserman Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko Jadranska 19, 1000 Ljubljana Mentor: Primoº Ziherl Povzetek Opti na tomograja je neinvazivna interferometri na zikalna metoda, pri kateri z analizo interference odbitega in referen nega ºarka pridobivamo informacijo o povr²ini, ki jo preiskujemo. S sodobnimi metodami in izbolj²avami lahko preiskujemo tkiva in snovi z mikrometrsko lo ljivostjo 2-3 mm v globino.
2 Uvod v opti no tomograjo Tomograja je vsaka metoda ali postopek, pri katerem opravljamo globinsko slikanje ali slikanje v plasteh. Naprava za slikanje se imenuje tomograf, slika se imenuje tomogram. Uporablja se na razli nih znanstvenih podro jih, predvsem v medicini. Zelo uporabna je tudi v umetni²ko-analitskih sferah, v biologiji, arheologiji, geologiji ipd. Osnova za delovanje metode je postopek, ki se imenuje tomografska rekonstrukcija. Sodobna medicina in tudi ostale naravoslovne vede si od nekdaj ºelijo oblikovati enostavne in u inkovite metode za analizo organov, snovi in povr²in, ki jih no emo po²kodovati, od katerih ne moremo vzeti vzorcev ali moramo rezultate o njihovi strukturi, deformacijah in napakah odkriti hitro in u inkovito. Ob ²tevilnih medicinskih raziskavah, ki jih je medicinska znanost do danes ºe izoblikovala, le malokatera zadovoljuje tudi kriterij cenenosti, dobrega kontrasta, penetracijske globine preiskave in predvsem hitrosti opravljene preiskave. še dolgo vpogled v ºiva tkiva omogo ajo: ra unalni²ka rentgenska tomograja (CT), slikanje z magnetno jedrsko resonanco (MRI), tomograja s pozitronsko emisijo (PET), medicinska ultrasonograja, konfokalna mikroskopija in rentgenska tomograja, vendar imajo tudi te metode svoje slabosti in omejitve. Tako se opti na tomograja (OT) po asi, a vztrajno pribliºuje kvaliteti in uporabnosti bolj znanih medicinskih analitskih metod. Trenutno se metodo najbolj pogosto uporablja pri preiskavah povr²inskih struktur notranjih organov (ºelodec, jetra, srce), struktur in deformacij koºe (do globine nekaj mm) in stanja in deformacij o esne roºenice (predvsem pri bolezenskih po²kodbah), preiskuje se vsebnost kisika v krvi, funkcionalnost nekaterih organov, prekrvavljenost ipd. [1] ƒe se nam je ideja o analizi pacienta z ºarkom iz serije Zveznih stez ²e pred nekaj leti zdela utopija, danes vemo, da je do neke mere uresni ljiva. Prvi poskusi slikanja so posku²ali love²ko telo ali organ v polni meri presvetliti z navadno, belo svetlobo. Kmalu pa se je izkazalo, da bi zaradi previsoke intenzivnosti potrebne svetlobe lahko love²ka tkiva termi no po²kodovali [2], saj so bile za presevanje navadne roke potrebne zelo visoke intenzivnosti svetlobe. Tako se je predlagana metoda za odkrivanje po²kodb prsi, ki jo je leta 1929 predlagal Cutler, ovrgla zaradi prevelike nevarnosti za opekline. Danes OT uporablja zelo speci no svetlobo, s katero laºje in z mnogo manj posledicami za pacienta pridobi informacije [2]. Svetloba iz bliºnjega infrarde ega spektra (Near InfraRed NIR) se namre slabo absorbira v love²kih tkivih, zelo dobro pa ga absorbira naravno barvilo hemoglobin, ki se nahaja v rde ih krvnih 1
3 telescih (eritrocitih), kar omogo a zelo dober kontrast krvi pri slikanju brez dodanih kontrastnih sredstev. Tako lahko nasi enost krvi s kisikom, ki je direktno povezan s koli ino eritrocitov v krvi, direktno spremljamo, ne da bi nam bi bilo vsaki potrebno vzemati vzorce krvi. S preprosto napravo, ki jo namestimo na prst, lahko v realnem asu vsebnost kisika spremljamo tudi pri novorojen kih in po²kodovanih osebah [1]. Seveda OT tudi omogo a slikanje vsebnosti ostalih sestavin love²kih tkiv, npr. vode, nekaterih proteinov in ma² ob. Pri tem sledi strogim varnostnim merilom, ki prepre ujejo moºnost po²kodbe tkiv, dednega zapisa, karcenogenih po²kodb ali termi nih po²kodb [2]. še na za etku moramo upo²tevati tudi slabosti opti ne tomograje in to je penetracijska globina, saj opti ni signal (svetloba) z globino penetracije eksponentno pada, zato so globine meritev omejene. Tako lahko pri slikanju prsi doseºemo maksimalno globino slikanja 12 cm, pri slikanju udov le 8 cm, pri slikanju moºganov komaj 3 cm [3]. Seveda lahko s to metodo preiskujemo le vsaj deloma prosojna tkiva, ki omogo ajo prehod sipane svetlobe. 2
4 Uvod v opti no koherentno tomograjo Predhodna enodimenzionalna metoda, ki je napovedala nadaljna odkritja, je bila OCDR (Optical Coherence-Domain Reectometry), ki je s pomo jo interference bele svetlobe ºe lahko pridobivala informacije o defektih v opti nih vlaknih in mreºnih strukturah, vendar so njeno uporabo kmalu raz²irili na podro je medicine. še pri tej metodi se je s pomo jo interference svetlobe s kratko koheren no dolºino in z natan nim sistemom za zaznavanje interference lahko doseglo visoke lo ljivosti metode [1]. Opti na koherentna tomograja (OCT) je bila sprva odkrita leta 1990, leto kasneje jo je njen izumitelj Naohiro Tanno ºe uspe²no predstavil svetu, vzporedno so jo predstavile tudi druge skupine. Od izuma dalje se je zelo hitro razvijala in se je predvsem uveljavila pri preiskavah o i, saj je ravno pri teh preiskavah potrebna penetracijska globina nekaj centimetrov (kar je pri o eh mogo e) in zelo dobra lo ljivost, ki je pri modernih OCT napravah zlahka dosegljiva. še enostavnej²e OCT naprave namre doseºejo lo ljivost 10 µm in tako zadovoljijo potrebe oftamologov [4]. OCT se je uveljavila tudi kot metoda za preiskovanje umetni²kih del, saj se z njo zlahka identicira ve slojev barve na umetni²kih delih, ne da bi pri tem po²kodovali umetni²ko delo. Uporabna je tudi pri identikaciji razli nih pigmentov v uporabljenih barvah, veliko pa nam metoda pove tudi o tehnikah, ki so jih uporabljali umetniki pri nastajanju umetni²kega dela [5]. Osnovni princip delovanja OCT je interferometrija svetlobe s kratko koherentno dolºino. Ta ra unalni²ka tomograja tako izkori² a koheren ne in interferen ne lastnosti svetlobe. V nasprotju z zelo koherentno svetlobo, s katero delamo pri laserski interferometriji (LI), pri OCT delamo s svetlobo, ki ima zelo ²irok frekven ni spekter (tako kot bela svetloba) v obmo ju NIR. ƒe lahko pri LI opazujemo interferenco svetlobe na razdalji nekaj metrov, so tu interferen ne razdalje kraj²e, lahko so dolge le nekaj µm. Da lahko doseºemo take svetlobne izvore, uporabljamo femtosekundne laserje ali supersvetle diode (superbright LEDs) [2]. OCT deluje na podoben na in kot LI. Osnovni ºarek iz svetlobnega izvora razcepimo na testni in referen ni ºarek in ju vodimo po dveh razli nih opti nih poteh enake dolºine. Ko ºarka ponovno zdruºimo, se pojavi interferenca, e sta bili opti ni poti enako dolgi oz. najve za koheren no razdaljo razli ni. Ker se je manj²i del testnega ºarka odbil od preiskovane povr²ine, referen ni ºarek pa od ogledala, se v interferen nih vzorcih shrani informacija o preiskovani povr²ini. Seveda se svetloba razli no odbija od ma² obnih celic, artefaktov znotraj tkiv, mrtvih celic, ipd., tako da ima vsaka vrsta tkiva svoj zna ilen vzorec odbite svetlobe. S premikanjem ogledala v referen ni veji ºarka lahko doseºemo, da spreminjamo globino preiskovanja v testni veji ºarka. Svetloba bo namre interferirala le, e bo pot, ki jo bo prepotovala po obeh vejah, enaka (znotraj koheren ne dolºine) in bo hkrati imela dovolj visoko intenziteto. Torej bomo lahko s to tehniko, ki se imenuje asovno odvisna OCT (Time Domain OCT TD OCT), posneli informacijo o prostorski postavitvi struktur znotraj vrhnjega 3
5 sloja npr. koºe (slika 1). Slika 1: Iz posameznih odzivov interferen nih funkcij sestavimo posamezen A-scan, ki nam poda informacijo o odbojnosti posamezne podplasti v vzorcu [6]. Prol odbojnosti vzdolº globine, ki mu pravimo tudi A-scan (slika 2), nam tako poda osnovno informacijo o strukturi tkiva vzdolº globine. ƒe take posami ne prole sestavimo skupaj, lahko sestavimo dvodimenzionalne prereze ali celo tridimenzionalne prereze skozi tkivo, ki nam podajo zelo dobro sliko o strukturi preiskovanega tkiva. Tako imenovan prerez imenujemo B-scan (slika 3). ƒe nas zanima stanje tkiva na dolo eni globini, lahko opravimo tudi globinski prerez ali C-scan (slika 4), ki nam poda prerez skozi tkivo na stalni globini. Tudi ta je sestavljen iz informacij iz posami nih A-scanov [1]. Slika 2: A-scan je presek odbojnosti po globini v to ki, v kateri opazujemo vzorec. Poda nam informacijo o globinski strukturi vzorca [6]. 4
6 Slika 3: B-scan je sestavljen iz vzporedno zloºenih informacij o globinski odbojnosti vzorca, ki jih pridobimo iz A-scanov. Tako sestavimo dvodimenzionalno sliko vzorca na podlagi odbojnosti posameznih podplasti. Na sliki je B-scan blazinice na konici prsta [6]. Slika 4: Iz posameznih informacij o strukturah plasti (B-scan) sestavimo tridimenzionalno sliko vzorca ali C-scan, ki je v na²em primeru blazinica na konici prsta [6]. Delovanje OCT Delovanje OCT je zelo podobno delovanju navadnega Michelsonovega interferometra, pri katerem izvajamo klasi no LI. Pri tem svetlobe ne vodimo prosto, ampak jo zapremo v sistem opti nih vlaken, kot je vidno na sliki 5. šarek tako 5
7 Slika 5: Osnovna postavitev OCT je sestavljena iz izvora, ki je v tem primeru supersvetla dioda, iz 50:50 delilnika, ki svetlobo razdeli na dva ºarka, iz referen ne veje, kjer se svetloba odbije od pomi nega zrcala, in vzor ne veje, kjer se svetloba odbije od preiskovanega vzorca. Svetloba iz obeh vej ºarkov se nato zdruºi in zbere na detektorju, ki elektri ni signal posreduje oja evalcu. Oja eni elektri ni signal nato ltriramo in pretvorimo v digitalni signal, ki ga obdelamo z ra unalnikom [1]. potuje od izvora do opti nega delilnika 50:50, ki ºarek razdeli na dva identi na ºarka. Nato enega od teh ºarkov vodimo do vzorca (vzor ni ali testni ºarek), drugega, referen nega, pa vodimo do ogledala, kjer se odbije nazaj. Oba ºarka nato po enaki poti potujeta skozi sistem le nazaj do polprepustnega zrcala in naprej do opti nega vlakna, kjer se zdruºita in interferirata. Interferenca nastane, kadar sta poti obeh ºarkov enaki znotraj koheren ne razdalje. Njuno interferenco zazna detektor, ki vzporedno beleºi tudi poloºaj ogledala pri referen nem ºarku in ta podatek pretvori v podatek o globini slikanja testnega ºarka. Konstruktivna interferenca obeh ºarkov se namre pojavi le takrat, ko sta referen ni in testni ºarek v fazi hrbti obeh valovanj se popolnoma prekrivajo. Tako lahko izmed vseh odbojev iz povr²ine vzorca pridobimo interferenco samo z ºarkom, ki se je odbil na to no dolo eni globini vzorca, kot lahko vidimo na sliki 6. Prvi OCT sistemi so imeli slab²o, a ºe takrat zelo zavidljivo globinsko in pre no lo ljivost, saj so lahko posneli slike z globinsko lo ljivostjo 30 µm s svetlobo, ki je imela valovno dolºino 830 nm in koheren no dolºino 17 µm. Danes so sistemi tehnolo²ko bolj dovr²eni in lahko posnamejo slike z mnogo bolj²o lo ljivostjo, tudi do m. To lo ljivost lahko doseºemo s ²irokopasovnimi viri svetlobe, ki imajo kraj²o koheren no dolºino in tako omogo ajo bolj natan no od itavanje globine slikanja [1]. 6
8 Koheren na dolºina je direktno povezana z lo ljivostjo slikanja in nam poda klju no informacijo o zmogljivosti OCT sistema. Interferenca med referen nim in testnim ºarkom namre nastane le, e se poti obeh ºarkov skoraj popolnoma ujemata najve ja razlika obeh poti je lahko enaka koheren ni dolºini, ki pa je mikrometrska. Zato lahko doseºemo zelo dobro globinsko lo ljivost, saj nam interferenca pove do koheren ne dolºine natan no, katero podplast vzorca opazujemo. Zato pri izbiri svetlobe teºimo k pridobivanju im kraj²e koheren ne dolºine, saj s tem izbolj²amo lo ljivost naprave [2]. Slika 6: Svetloba se od razli nih globinskih nivojev v vzorcu odbija z razli nimi asovnimi zakasnitvami, kar nam omogo a globinsko zaznavanje odbojnosti posamezne plasti v vzorcu. Ker se od vzorca odbije le manj²i del svetlobe, je globina slikanja omejena [7]. ƒasovno odvisna OCT Interakcija med dvema ºarkoma, ki sta iz²la iz istega svetlobnega izvora in sta prepotovala enako pot, imenujemo interferenca (pri Michelsonovem interferometru, kjer imata oba ºarka enako intenziteto, saj se oba odbijeta od enakih ogledal). Razlika pri OCT je, da je testni (vzor ni) ºarek oslabljen, saj vsebuje le od vzorca odbito svetlobo. Ovojnica te interference se spreminja, ko spreminjamo pot enega od ºarkov in doseºe svoj maksimum v to ki, ko oba ºarka prepotujeta natanko enako pot. Intenziteta interference dveh slabo koherentnih ºarkov se lahko izrazi [1]: I = k 1 I S + k 2 I S + 2 (k 1 I S ) (k 2 I S ) Re[γ(τ)], (1) kjer k 1 in k 2 predstavljata koecient delitve ºarka v polprepustnem delilniku interferometra (velja k 1 + k 2 < 1), I S predstavlja intenziteto izvora svetlobe, 7
9 Slika 7: ƒasovno odvisno OCT slikanje, ki analizira strukturo povr²ine koºe v realnem asu. Zaradi razli nih odbojnosti posameznih plasti in mej med plastmi (posledica razli nih lomnih koli nikov plasti) ter zaradi razli nih asovnih zakasnitev od posameznih globin odbitih ºarkov, lahko sestavimo dvodimenzionalno sliko. Ta nam poda informacijo o strukturi tkiv, saj imajo enaka tkiva enako odbojnost [1]. γ(τ) pa predstavlja kompleksno stopnjo koherence, ki jo zasledujemo s tehniko OCT in je direktno odvisna od asovne zakasnitve testnega ºarka τ. Kompleksno stopnjo koherence izra unamo s pomo jo Wiener Kirchine teorema, ki povezuje spekter svetila in avtokorelacijsko funkcijo: S (ω) = 1 Γ (τ) e iωτ dτ (2) 2π kjer S(ω) predstavlja frekven ni spekter svetila, Γ(τ) predstavlja avtokorelacijsko funkcijo v odvisnosti od asovnega zamika τ. Teorem torej poenostavlja zapleteno korelacijsko funkcijo in denira Fourierovo transformacijo kot povezavo med frekven nim spektrom svetila in avtokorelacijsko funkcijo. Lahko razmi²ljamo tudi v obratni smeri. ƒe poznamo spekter svetila in bi iz njega radi izra unali avtokorelacijsko funkcijo, je dovolj opraviti zgolj inverzno Fourierovo transformacijo. ƒe vzamemo raz²irjen spekter svetila okoli centralne frekvence ω 0, ki je Gaussove oblike in ima ²irino δω, lahko spekter svetila zapi²emo kot: 1 S (ω) = (ω ω 2πδω 2 e 0 ) 2 2δω 2 (3) in e na tej funkciji opravimo inverzno Fourierovo transformacijo, dobimo avtokorelacijsko funkcijo, ki je sestavljena iz valujo ega in pojenjajo ega dela: 8
10 γ (τ) = exp ( δω2 τ 2 ) exp ( iω 0 τ) (4) 2 kjer ν predstavlja frekven no spektralno ²irino svetlobnega izvora, ν 0 je centralna opti na frekvenca svetlobnega izvora. Vrh ovojnice se pojavi, ko je τ = 0, velikost intenzitete ovojnice na tem mestu predstavlja odbojnost dela preu evanega vzorca na to no dolo eni globini. Amplituda je odvisna od odbojnih lastnosti plasti in mej med plastmi na tisti globini vzorca. ƒe opazujemo A-scan v frekven nem prostoru (ali v prostoru valovnega vektorja), opazimo nosilno funkcijo, ki je Gaussove oblike (slika 8), na katero se naloºi informacija o tkivu. Razpotegnjenost Gaussove nosilne funkcije je posledica Dopplerjevega efekta in je odvisna od hitrosti premikanja referen nega zrcala [1][6]. Slika 8: Iz reprezentacije v prostoru valovnega vektorja (na sliki zgoraj) naredimo reprezentacijo v x prostoru (na sliki spodaj) s Fourierovo transformacijo. Pri tem upo²tevamo, da dobimo dodatne vrhove zaradi Dopplerjevega efekta, ki nam v frekven ni predstavitvi doda nosilno Gaussovo funkcijo. [6]. Tako ima spreminjanje poti enega ºarka interferometra dve funkciji, ki ju doseºemo z spreminjanjem opti nih poti ºarkov: globinsko slikanje vzorca in ustvarjanje Dopplerjevega efekta in posledi no Gaussove nosilne funkcije v frekven nem prikazu. Frekvenco nosilne funkcije, ki je posledica Dopplerjevega efekta, izrazimo kot [1]: c 1 ( f = f 0 = f 0 c + v s 1 + v s /c f 0 1 v ) s c in lahko izpostavimo samo frekvenco f DN nosilne funkcije, ki je zaradi razloga, da je referen no ogledalce hkrati Dopplerjevo zamaknjen sprejemnik in Dopplerjevo zamaknjen oddajnik, podvojena: (5) 9
11 f DN = 2f 0 v s (6) c kjer v s predstavlja hitrost slikanja, t.j. premikanja na²ega ogledala v referen nem delu interferometra, ν 0 predstavlja centralno opti no frekvenco svetlobnega izvora in c predstavlja hitrost svetlobe. Primer izra una frekvence nosilne funkcije prikazuje slika 10. Slika 9: Na levi sliki je prikazan pojav interference pri asovno odvisnem OCT slikanju, ki se pojavi ob premikanju ogledala v referen nem delu ºarka ob konstantni hitrosti. Na desni sliki je prikazana frekven na slika pri frekven no odvisnem OCT slikanju [1]. Globinska in pre na lo ljivost OCT slikanja sta odvisni od popolnoma lo enih parametrov in sta tako nepovezani. Medtem ko je aksialna ali globinska lo ljvost OCT slikanja v polni meri odvisna od koheren ne dolºine svetlobe, ki jo uporabljamo, je pre na lo ljivost odvisna predvsem od uporabljene optike in mehani nih delov interferometra. Predvsem sta tu pomembna dinami no fokusiranje glede na stati no fokusiranje in globina slikanja, od esar je odvisna tudi koli ina razpr²ene svetlobe, ki moti meritve [1]. Koheren no dolºino svetlobe lahko ocenimo tako, da izra unamo, kdaj se razliki faz dveh ravnih valov tako razlikujeta, da valova nista ve koherentna. ƒe torej zapi²emo ravni val: e φ = e kx ωt (7) in izrazimo razliko med dvema fazama na razdalji x od to ke, kjer sta bila med seboj ²e koherentna (v to ki x 0 ), dobimo: φ = φ 1 φ 2 = (k 1 k 2 )x. (8) ƒe nato vstavimo namesto x kar koherentno dolºino l c in predpostavimo, da je v trenutku, ko dva valova izgubita medsebojno koherentnost, φ = 1, potem dobimo: 10
12 Slika 10: Frekvenca nosilne funkcije zaradi Dopplerjevega pojava v odvisnosti od hitrosti skeniranja, pri valovni dolºini λ = 1300 nm oziroma pri srednji opti ni frekvenci izvora ν 0 = s 1 kar lahko dalje razvijemo v: (k 1 k 2 )l c = 1, (9) 2π λ 0 + λ )l c = 2π nato pa lahko dokon no deniramo koherentno dolºino: 1 = ( 2π λ 0 ( ) λ0 + λ λ 0 λ λ l c, (10) 0 λ l c = 1 2π λ2 0 + λ 0 λ (11) λ kjer λ 0 predstavlja centralno frekvenco in λ frekven no ²irino uporabljene svetlobe. Opazimo, da s svetlobo kratkih valovnih dolºin in z zelo veliko frekven no ²irino doseºemo zelo kratke koheren ne dolºine, ki nam pomagajo pri izbolj²avi globinske lo ljivosti OCT slikanja. Frekven no odvisna OCT Frekven no odvisna OCT (spektralno odvisna ali Fourierovo odvisna koheren na opti na tomograja ali kar FD-OCT) kodira informacijo o odbojnosti tkiva v op- 11
13 ti no frekvenco (valovno dolºino ali valovni vektor razlika je le v reprezentaciji). To omogo a hitrej²e zajemanje podatkov in omogo a primerljivo resolucijo in ob utljivost s asovno odvisnimi OCT sistemi. Merjenje v frekven ni odvisnosti omogo a bolj²i izkoristek informacij zaradi manj²ega ²uma, do katerega pride zaradi ve je ob utljivosti FD-OCT. FD-OCT lahko hkrati posname celotno globino preiskovanega vzorca (A-scan), saj se mu informacija o odbojnosti posamezne podplasti vzorca kodira v posami no frekvenco. Signal interference mora nato le ²e dekodirati, tako da ga lo i na posami ne frekvence in vsako posami no frekvenco analizira. To lahko doseºe z lo itvijo posami nih frekvenc z uklonsko mreºico, frekvence nato posami no zaznamo z linearnim detektorjem z vzdolºno razporejenimi senzorji (slika 11). Isti u inek lahko doseºemo tudi s posami nim detektorjem in brez uklonske mreºice, vendar moramo spreminjati frekvenco svetlobe izvira, s tem pa slikamo posami ne globine preiskovanega tkiva [1]. Slika 11: Shematski prikaz postavitve FD-OCT. Referen no zrcalo je v tej postavitvi ksirano, vzor ni ºarek je krmiljen z posebno optiko za skeniranje vzorca, ki dolo a pre ni premik vzor nega ºarka. Uklonska mreºica ºarka, ki interferirata, razdruºi na posami ne frekvence svetlobe, ki jih nato z linearnim CCD detektorjem posami no analiziramo. Sistem za obdelavo podatkov opravi Fourierovo transformacijo [8]. V FD-OCT je potreben laser s ²irokim frekven nim spektrom. Vpadni laserski ºarek E i delilnik ºarkov razdeli na referen ni E r in na testni ºarek E s. Lega referen nega ogledala dolo a asovno zakasnitev referen nega ºarka τ. Referen ni ºarek in vzor ni ºarek se v delilniku ºarkov zdruºita, rezultat je interferenca. Spektralno vsebino kon nega ºarka analiziramo s spektrometrom in CCD detektorjem, ki sprejema prostorsko kodiran interferen ni spekter. ƒasovno odvisen prol reektivnosti rekonstruiramo preko Fourierove transformacije. Z ve imi zaporednimi posnetki sestavimo tridimenzionalno sliko tkiva. Zaradi Fourierove relacije (Wiener-Khintchinov teorem, ki povezuje avtoko- 12
14 relacijsko funkcijo in spektralno gostoto mo i) lahko globino slikanja v realnem asu izra unamo s Fourierovo transformacijo pridobljenega spektra, ne da bi premikali referen no ogledalce kot pri TD-OCT [1]. ƒeprav se globinska lo ljivost pri tej metodi zmanj²a odvisni smo namre od frekven ne ²irine svetlobnega izvora, celoten postopek postane hitrej²i, hkrati pa zmanj²amo relativni ²um glede na ²tevilo meritev. Prostorsko kodirana frekven no odvisna OCT SEFD-OCT (Spatially Encoded Frequency Domain OCT) izlu² i spektralne informacije tako, da na detektorski sistem linearno zloºenih CCD (Line-Array CCD - LACCD) distribuira razli ne opti ne frekvence preko disperznega elementa uklonske mreºice (slika 12). Tako lahko podatke o globini slike pridobimo ºe samo z enkratnim izpostavljanju OCT. Vendar se v tem primeru razmerje signal/²um (Signal to Noise Ratio - SNR), ki je sicer veliko pri FD- OCT, zmanj²a. Obmo je zaznavanja LACCD je manj²e v primerjavi s fotoob utljivo diodo, s katero doseºemo bistveno ve je razmerje signal/²um (SNR) in sicer ve kot 1000-kratno pri bistveno ve jih hitrostih. Slaba stran te tehnologije je torej v bistveno niºjem SNR, ki je sorazmeren z oddaljenostjo od izhodi² a merjenja (povr²ine vzorca) ter zmanj²anju globinske ob utljivosti. Vzrok je v omejeni detekciji linijske ²irine LADDC. En piksel na LACCD zazna kvazipravokoten del frekven nega opti nega obmo ja in ne to no dolo ene frekvence - Fourierova transformacija nam tako vrne sin(x)/x obna²anje. Poleg tega uklonska mreºica pred spektroskopskem detektorjem navadno ne distribuira svetlobe frekven no prostorsko enakomerno na LACCD, ampak ima inverzno odvisnost. Zato moramo signal ponovno preoblikovati pred procesno obdelavo, vendar se pri tem ne moremo izogniti zmanj²anju kvalitete signala zaradi omejene linijske detekcije LACCD [8]. ƒasovno kodirana frekven no odvisna OCT TEFD OCT (Time Encoded Frequency Domain OCT) posku²a kombinirati prednosti TD OCT in SEFD OCT. V tem primeru spektralne komponente niso kodirane glede na prostorsko razdelitev, ampak glede na as. Spekter svetlobe izvora ltriramo ali generiramo v posami nih diskretnih frekven nih korakih in tako vzorec obsvetimo z razli nimi frekvencami svetlobe (slika 13). Nato spekter interference rekonstruiramo pred Fourierovo transformacijo. Tako pridobimo na SNR, saj lahko uporabljamo fotoob utljive diode (in ne LACCD). Z uporabo frekven no nastavljivega svetlobnega izvora (npr. frekven no nastavljivega laserja) postane opti na postavitev enostavnej²a kot pri SEFD OCT. ƒe je pri TD OCT globinsko slikanje kodirano z zakasnitvijo vzor nega ºarka, je pri TEFD globinsko slikanje kodirano v spreminjajo i frekvenci svetlobnega 13
15 Slika 12: Postavitev za spektralno prostorsko kodirano slikanje. Postavitev vklju uje izvor svetlobe s kratko koheren no dolºino (Low Coherence Source - LCS) in poleg ostalih obi ajnih komponent tudi uklonsko mreºico (Diraction Grating - DG) in kamero, ki deluje kot spektrometer (CAM) [1]. izvora [1]. Prednosti se kaºejo predvsem v dokazano ve jem SNR, saj frekven no nastavljivi laserji ustvarjajo zelo kratke laserske sunke s kratko valovno dolºino pri zelo visokih frekvencah ( Hz) in tako doseºejo manj²o koheren no dolºino. Slabosti so nenatan nost valovne dolºine laserske svetlobe, ²e posebej pri visokih frekvencah in visoka ob utljivost na premike ogrodja naprave in opazovanega vzorca, saj se vzorec med dolgotrajnej²im slikanjem preko ve valovnih dolºin ne sme premikati, da ne pride do zamikov [1]. Polarizacijsko ob utljiva OCT Polarizacijsko ob utljiva OCT (PS-OCT) temelji na metodah klasi ne OCT, le da uporablja polarizirano svetlobo [9]. PS-OCT omogo a meritve dvojnega loma in opti nih osi biolo²kega tkiva. Dvojni lom predstavlja opti no lastnost, ki opisujeje razliko v lomnem koli niku med svetlobo, polarizirano v smeri opti ne osi, in svetlobo, polarizirano pravokotno na opti no os tkiva. Jakost dvojnega loma v snovi lahko izrazimo kot: n = n e n 0, (12) kjer n predstavlja jakost dvojnega loma, n e lomni koli nik izrednega ºarka, t.j. ºarka, ki je polariziran v smeri opti ne osi tkiva, n o lomni koli nik rednega ºarka, t.j. ºarka, ki je polariziran pravokotno na opti no os tkiva [9]. 14
16 Slika 13: Postavitev OCT za slikanje s spremenljivim virom svetlobe npr. nastavljivim laserjem (Swept Source - SS ali Tunable Laser - TL), ki mu lahko nastavljamo valovno dolºino laserske svetlobe. Poleg ostalih komponent imamo prisoten tudi fotodetektor (Photodetector - PD) in digitalno analitsko komponento, ki ra unalni²ko analizira interferiran signal (Digital Signal Processing - DSP) [1]. Do dvojnega loma pride v urejenih vlaknih biolo²kega tkiva, kot npr. v kolagenu ali ºiv nih vlaknih. Za svetlobo valovne dolºine λ = 840 nm je jakost dvojnega loma n na kolagenskih vlaknih od do , kar povzro i fazni zamik δϕ vzor nega ºarka od 0.18 / µm do 0.4 / µm. šarek svetlobe s kratko koheren no dolºino linearno polariziramo in na polprepustnem zrcalu razdelimo na referen ni in vzor ni ºarek interferometra (slika 14). Lambda etrtinska plo² ica na poti referen nega in vzor nega ºarka spremeni polarizacijo ºarka iz linearno polarizirane v kroºno polarizirano in obratno [10]. S spreminjanjem lege referen nega zrcala se spreminja opti na pot referen nega ºarka in s tem opti na pot vzor nega ºarka, ki mora biti pri konstruktivni interferenci enaka poti referen nega ºarka. Kon no sliko sestavimo s primerjavo polarizacij vzor nega in referen nega ºarka, ki pa nista nujno ve enaki. Vzor nemu ºarku se lahko zaradi opti nih lastnosti tkiva, kot npr. razmerja med lomnima koli nikoma dvojnega loma, spremeni polarizacija. Za konstruktivno interferenco morata biti poleg opti nih poti enaki tudi polarizaciji referen nega in vzor nega ºarka [10]. 15
17 Slika 14: Shematski prikaz postavitve PS-OCT[1]. Enoto kovna in paralelna OCT Enoto kovna OCT slikanje temelji na hkratnem slikanju samo ene to ke s tehniko TD OCT. Celotno obmo je vzorca mora naprava preslikati s slikanji globinske odbojnosti posami nih to k, iz katerih nato sestavi dvodimenzionalno sliko (presek) in nato tridimenzionalno sliko, sestavljeno iz posami nih presekov. Medtem mora premikati vzorec s pomo jo elektromehansko vodenih pomi nih mizic, ki premikajo vzorec, ali sistem zrcal, ki preusmerjajo pot vzor nega ºarka (slika 15)[1]. Slika 15: Tipi na postavitev enoto kovnega OCT, s katerim lahko prou ujemo z mikrometrsko lo ljivostjo do 3 mm v globino na²ega vzorca [1]. Paralelni OCT uporablja slikovni senzor CCD oz. posebno kamero (Full- 16
18 Field CCD), s katero popolnoma osvetljen objekt slikajo s sprednje strani in tako hkrati posnamejo interferenco celotne povr²ine, kot je prikazano na sliki 16. Vzorca tako ni ve potrebno premikati v pre nih smereh. S postopnim spreminjanjem lege referen nega ogledala in beleºenju uspe²nih "en face" posnetkov lahko uspe²no konstruiramo tridimenzionalno predstavitev. Vendar je tehnika omejena s hitrostjo CCD naprav, saj morajo biti sposobne slediti frekven ni modulaciji signala pri OCT [1]. Slika 16: Osnovna postavitev OCT vklju uje supersvetlo LED diodo (SLD), konveksne le e, ki ºarek iz opti nega vlakna kolimirajo (L1), delilec ºarka 50:50 (BS), objektiv kamere (CO), CMOS kamera (CAM), ogledalo in referen na pot ºarka (REF) in vzorec z vzor nim ali testnim ºarkom (SMP). S tehnologijo premikanja senzorjev v dveh dimenzijah in z doseganjem globinskega merjenja s pomo jo OCT tehnike lahko doseºemo tridimenzionalno slikanje preiskovanega vzorca [1]. 17
19 Postavitve OCT V osnovi je postavitev OCT vedno enaka, saj za svoje delovanje potrebuje opti ni interferometer, s katerim ºarek razdeli, ga vodi lo eno po referen ni in testni poti, ga nato zdruºi in opazuje njegovo interferenco, kar je predstavljeno na sliki 5. Glede na funkcionalnost in na metodo slikanja poznamo nekaj postavitev, ki se med seboj razlikujejo glede na opti ne in ra unalni²ke komponente sistema. Tako med seboj razlikujemo osnovne postavitve za paralelno slikanje (slika 16), enoto kovno slikanje (slika 15), slikanje s frekven no spremenljivim virom svetlobe (slika 13) in frekven no odvisno slikanje s spektrometrom (slika 12). Obmo je dosega OCT Opti na koheren na tomograja ima doseg 2-3 mm pri globinski lo ljivosti 1-15 µm. Prav zaradi dosega je njena uporaba omejena na dokaj povr²inske preiskave, zato je najbolj uporaben v dermatologiji (slika 17). Velik potencial uporabe se kaºe tudi na drugih medicinskih podro jih, kot na primer raziskave bolezni in po²kodb o i, ipd. [11] Slika 17: Doseg slikanja OCT v primerjavi z ostalimi tomograjami [11]. 18
20 Primeri uporabe in kon en izgled tomograma Tomogram lahko prikaºemo v rno-beli (v sivinah) ali barvni sliki. Pri prikazu s sivimi odtenki je intenzivnost odbojnega signala prikazana v logaritmi ni skali z razli nimi stopnjami osvetlitve. Bela barva ustreza najvi²ji odbojnosti, medtem ko temno siva in rna ustrezata najniºji. Spodnja slika je prikazana v logaritemski skali z razponom od 50 db oz odstotka prvotnega signala pri maksimalni intenzivnosti do 95 db oz. pribliºno odstotka prvotnega signala. Dinami no obmo je razpona slike je tako 45 db in je prilagojeno vzorcu, ki ga slikamo (slika 18). ƒe ºelimo ²e poudariti razlo evanje med razli nimi strukturami na sliki, jo prikaºemo z barvami. V tem primeru je logaritem opti ne reeksije oz. odboja prikazan z razli nimi barvami. Navadno se za prikaz uporablja standardne barve barvne lestvice in sicer tako, da je maksimalna odbojnost prikazan z belo in rde o barvo ( 50 db glede na prvotni signal), minimalna odbojnost pa z modro ali rno barvo (tudi do 100 db glede na prvotni signal). Strukture, ki imajo razli ne odbojnost, bodo obarvane z razli nimi barvami, seveda v skladu z logaritemsko barvno skalo (slika 19) [12]. Slika 18: Slikanje gornjega dela o esa v rno-beli lestvici. Na sliki lahko vidimo o esno le o in ²arenico ter ostale o esne strukture [12]. Slika 19: Slikanje o esa v barvni logaritemski lestvici [12]. OCT je uporabna tehnika pri preiskavah toplotnih po²kodb koºnega tkiva, preko meritve zmanj²anja dvojnega loma, t.j. zmanj²anja razlike med rednim in izrednim ºarkom. Tehnika je ²e posebej uporabna pri ugotavljanju stopnje opeklin, 19
21 kjer je zelo pomembno hitro in pravilno zdravljenje (slika 20). PS-OCT predstavlja nekontaktno tehniko, ki omogo a globinsko slikanje toplotnih posledic na koºi, na podlagi spremembe polarizacije po²kodovane koºe. Slika 20: Slike zdrave in zaradi toplote po²kodovane koºe, narejene z OCT in PS-OCT. a) Zdrava koºa OCT, b) zdrava koºa PS-OCT, c) po²kodovana koºa OCT, d) po²kodovana koºa PS-OCT. Opekline prve stopnje, ki so omejene na po²kodbo epitela koºe ( µm), ne potrebujejo posebnega zdravljenja, saj je koºa sposobna samoregeneracije, pri opeklinah tretje stopnje, kjer je po²kodovana tudi zarodna plast koºe (> 2 mm) pa je potrebna im hitrej²a presaditev koºe. Pri opeklinah druge stopnje pa je zarodna plast koºe le delno po²kodovana ( mm) [13]. Pri PS-OCT sliki normalne koºe so vidna temna polja, ki nakazujejo spremembo polarizacije od tkiva odbite svetlobe. Do spremembe polarizacije pride zaradi dvojnega loma na kolagenskih vlaknih koºe. Ker so kolagenska vlakna v koºi orientirana naklju no, so pri slikanju s PS-OCT temnej²i deli slike porazdeljeni naklju no. Pri toplotno po²kodovani koºi pa pride do po²kodb kolagenskih vlaken. Po²kodovana kolagenska vlakna imajo manj²o razliko med rednim in izrednim ºarkom dvojnega loma, zato je tudi sprememba polarizacije manj²a. Zaradi manj²e spremembe polarizacije je pri PS-OCT sliki manj temnej²ih delov slike ali pa popolnoma izginejo [13]. Razprava in zaklju ek OCT danes omogo a povr²insko slikanje raznovrstnih biolo²kih in medicinskih vzorcev. Stalne izbolj²ave s pridobivanjem novih, bolj²ih in mo nej²ih izvorov svetlobe ter z bolj²imi popravki pri obdelavi podatkov dosegajo strokovnjaki v medicini vedno bolj²e rezultate pri slikanju zunanjih in notranjih love²kih organov [14]. Napredek lahko pri akujemo predvsem na podro ju izdelave novih katetrov iz 20
22 opti nih vlaken. Ti bodo lahko v realnem asu preiskovali ºile in nam posredovali informacijo o po²kodovanih ali poapnelih ºilah. Testira se tudi laserje z druga nimi valovnimi dolºinami, za katere so love²ka tkiva bolj prosojna. Tako bomo lahko s to tehnologijo pogledali ²e globje v povr²ino love²kega telesa z lo ljivostjo nekaj µm. Izbolj²uje se tudi hitrost slikanja, predvsem na ra un izbolj²av elektronike in obdelave podatkov. V bliºnji prihodnosti lahko pri akujemo bistveno zmanj²anje asa obdelave podatkov, ki je trenutno potreben [14]. OCT naprava naj bi v prihodnosti bila del vsake bolni²nice kot odli en pripomo ek zdravnikom, ki bodo ºeleli dobiti vpogled v stanje koºe, ºil ali notranjih organov pacienta. 21
23 Literatura [1] Optical coherence tomography ( Optical_ coherence_ tomography, 2008) [2] M.V.Güngör, Optical Tomography ( BYM504E-2006-optical_tomography.pdf, 2008). [3] NIRx Medical Technologies ( 2008). [4] S. A. Boppart, B. E. Bouma, C. Pitris, J. F. Southern, M. E. Brezinski in J. G. Fujimoto, Natur. m. 4, 861 (1998). [5] M. M. Boyd, T. Zelevinsky, A. D. Ludlow, S. M. Foreman, S. Batt, T. Ido in J. Ye, Sci. 314, 1430 (2006). [6] Biopten imaging systems ( [7] Optical Coherence Tomography ( April 2008). [8] B. Hofer, B. Povaºay, B. Hermann, A. Unterhuber, G. Matz, F. Hlawatsch in W. Drexler, L. of Vienna Uni. of Technology, Austria. ( April 2008). [9] B. Cense, M. Mujat, T. C. Chen, B. H. Park in J. F. de Boer, Opt. Expr. 15, 2421 (2007). [10] D. Stifter, A. D. Sanchis Dufau, E. Breuer, K. Wiesauer, P. Burgholzer, O. Höglinger, E. Götzinger, M. Pircher in C.K.Hitzenberger, Polarizationsensitive optical coherence tomography for material characterisation and testing, ( opticaltechniques/280wiesauer.pdf, April 2008). [11] Introduction to Optical Coherence Tomography, OBEL research ( [12] M. R. Hee, J. A. Izatt, E. A. Swanson, D. Huang, J. S. Schuman, C. P. Lin, C. A. Puliato in J. G. Fujimoto, Arch. Ophthalm. 113 (1995). [13] C. E. Saxer, J. F. de Boer, B. H. Park, Y. Zhao, Z. Chen in J. S. Nelson, Opt. L. 25, 1355 (2000). [14] M. E. Brezinski, G. J. Tearney, B. E. Bouma, J. A. Izatt, M. R. Hee, E. A. Swanson, J. F. Southern in J. G. Fujimoto, Circ. 93, 1206 (1996). 22
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Fotolitograja. Oddelek za ziko. Avtor: Jan Kozjek. Mentor: izred. prof. dr. Igor Poberaj. April Povzetek
 Oddelek za ziko Fotolitograja Avtor: Jan Kozjek Mentor: izred. prof. dr. Igor Poberaj April 2014 Povzetek Fotolitograja je predvsem v industriji polprevodnikov pomemben postopek povr²inskega mikrostrukturiranja.
Oddelek za ziko Fotolitograja Avtor: Jan Kozjek Mentor: izred. prof. dr. Igor Poberaj April 2014 Povzetek Fotolitograja je predvsem v industriji polprevodnikov pomemben postopek povr²inskega mikrostrukturiranja.
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
VALOVANJE UVOD POLARIZACIJA STOJEČE VALOVANJE ODBOJ, LOM IN UKLON INTERFERENCA
 VALOVANJE 10.1. UVOD 10.2. POLARIZACIJA 10.3. STOJEČE VALOVANJE 10.4. ODBOJ, LOM IN UKLON 10.5. INTERFERENCA 10.6. MATEMATIČNA OBDELAVA INTERFERENCE IN STOJEČEGA VALOVANJA 10.1. UVOD Valovanje je širjenje
VALOVANJE 10.1. UVOD 10.2. POLARIZACIJA 10.3. STOJEČE VALOVANJE 10.4. ODBOJ, LOM IN UKLON 10.5. INTERFERENCA 10.6. MATEMATIČNA OBDELAVA INTERFERENCE IN STOJEČEGA VALOVANJA 10.1. UVOD Valovanje je širjenje
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Postavitev hipotez NUJNO! Milena Kova. 10. januar 2013
 Postavitev hipotez NUJNO! Milena Kova 10. januar 2013 Osnove biometrije 2012/13 1 Postavitev in preizku²anje hipotez Hipoteze zastavimo najprej ob na rtovanju preizkusa Ob obdelavi jih morda malo popravimo
Postavitev hipotez NUJNO! Milena Kova 10. januar 2013 Osnove biometrije 2012/13 1 Postavitev in preizku²anje hipotez Hipoteze zastavimo najprej ob na rtovanju preizkusa Ob obdelavi jih morda malo popravimo
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
6 NIHANJE 105. (c) graf pospe²ka v odvisnosti od asa. Slika 32: Graf hitrosti, odmika in pospe²ka v odvisnosti od asa.
 6 NIHANJE 105 6 nihanje 6.1 mehanska 1. Hitrost nekega nihala se spreminja po ena bi: v(t) = 5 cm/s cos(1, 5s 1 t). Nari²i in ozna i kako se spreminjajo odmik hitrost in pospe²ek v odvisnosti od asa! Rp:
6 NIHANJE 105 6 nihanje 6.1 mehanska 1. Hitrost nekega nihala se spreminja po ena bi: v(t) = 5 cm/s cos(1, 5s 1 t). Nari²i in ozna i kako se spreminjajo odmik hitrost in pospe²ek v odvisnosti od asa! Rp:
11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune
![11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune 11. Valovanje Valovanje. = λν λ [m] - Valovna dolžina. hitrost valovanja na napeti vrvi. frekvence lastnega nihanja strune](/thumbs/79/79968210.jpg) 11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
11. Valovanje Frekvenca ν = 1 t 0 hitrost valovanja c = λ t 0 = λν λ [m] - Valovna dolžina hitrost valovanja na napeti vrvi frekvence lastnega nihanja strune interferenca valovanj iz dveh enako oddaljenih
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Hidravli ni oven. Univerza v Ljubljani Fakulteta za matematiko in ziko. Oddelek za ziko
 Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko Hidravli ni oven Seminar Avtor: Marko Kozin Mentor: do. dr. Daniel Sven²ek Ljubljana, mare 2014 Povzetek V seminarju sta predstavljena
Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko Hidravli ni oven Seminar Avtor: Marko Kozin Mentor: do. dr. Daniel Sven²ek Ljubljana, mare 2014 Povzetek V seminarju sta predstavljena
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Svetlobni merilniki odbojnosti
 13. Seminar Optične Komunikacije Laboratorij za Sevanje in Optiko Fakulteta za Elektrotehniko Ljubljana, 1. - 3. februar 2006 Svetlobni merilniki odbojnosti Matjaž Vidmar Seznam prosojnic: Slika 1 Meritev
13. Seminar Optične Komunikacije Laboratorij za Sevanje in Optiko Fakulteta za Elektrotehniko Ljubljana, 1. - 3. februar 2006 Svetlobni merilniki odbojnosti Matjaž Vidmar Seznam prosojnic: Slika 1 Meritev
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA FIZIKO SAGNACOV POJAV. Alenka Bajec
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA FIZIKO SAGNACOV POJAV Alenka Bajec Mentor: prof. dr. Andrej Čadež 29. november 2007 1 NALOGA 1 1 Naloga Opiši Sagnacov pojav. 2 Uvod Sagnacov
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA FIZIKO SAGNACOV POJAV Alenka Bajec Mentor: prof. dr. Andrej Čadež 29. november 2007 1 NALOGA 1 1 Naloga Opiši Sagnacov pojav. 2 Uvod Sagnacov
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Mehurčki v zvočnem polju: Bjerknesove interakcije
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Mehurčki v zvočnem polju: Bjerknesove interakcije Seminar Avtor: Nika Oman Mentor: prof. dr. Rudolf Podgornik Ljubljana, september
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Mehurčki v zvočnem polju: Bjerknesove interakcije Seminar Avtor: Nika Oman Mentor: prof. dr. Rudolf Podgornik Ljubljana, september
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Michelsonov interferometer
 Michelsonov interferometer Namen vaje: Spoznavanje valovnih značilnosti laserske svetlobe Spoznavanje načela delovanja interferometra Brezdotično merjenje kratkih pomikov Eksperimentalne naloge 1. Sestaviti
Michelsonov interferometer Namen vaje: Spoznavanje valovnih značilnosti laserske svetlobe Spoznavanje načela delovanja interferometra Brezdotično merjenje kratkih pomikov Eksperimentalne naloge 1. Sestaviti
S53WW. Meritve anten. RIS 2005 Novo Mesto
 S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Polarizacija laserske svetlobe
 Polarizacija laserske svetlobe Optični izolator izvedba z uporabo λ/4 retardacijske ploščice Odboj polarizirane svetlobe na meji zrak-steklo; Brewster-ov kot Definicija naloge predstavitev teoretičnega
Polarizacija laserske svetlobe Optični izolator izvedba z uporabo λ/4 retardacijske ploščice Odboj polarizirane svetlobe na meji zrak-steklo; Brewster-ov kot Definicija naloge predstavitev teoretičnega
Aerodinamika ºuºelk. Jaka Bobnar. Prof. Dr. Rudi Podgornik. Povzetek. Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko
 Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko Aerodinamika ºuºelk Jaka Bobnar Mentor: Prof. Dr. Rudi Podgornik Povzetek V seminarju bom obravnaval osnove aerodinamike ºuºelk. Predstavil
Univerza v Ljubljani Fakulteta za matematiko in ziko Oddelek za ziko Aerodinamika ºuºelk Jaka Bobnar Mentor: Prof. Dr. Rudi Podgornik Povzetek V seminarju bom obravnaval osnove aerodinamike ºuºelk. Predstavil
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
TRANZITIVNI GRAFI. Katarina Jan ar. oktober 2008
 TRANZITIVNI GRAFI Katarina Jan ar oktober 2008 Kazalo 1 Uvodne denicije........................ 3 2 Vozli² na tranzitivnost.................... 8 3 Povezavna tranzitivnost.................... 10 4 Lo na
TRANZITIVNI GRAFI Katarina Jan ar oktober 2008 Kazalo 1 Uvodne denicije........................ 3 2 Vozli² na tranzitivnost.................... 8 3 Povezavna tranzitivnost.................... 10 4 Lo na
5.2. Orientacija. Aleš Glavnik in Bojan Rotovnik
 Orietacija Aleš Glavik i Boja Rotovik 52 Izvleček: Pred stav lje e so iz bra e te me iz orie ti ra ja v a ra vi, ki jih mo ra poz a ti vsak vod ik PZS, da lah ko var o vo di ude le `e ce a tu ri Pred stav
Orietacija Aleš Glavik i Boja Rotovik 52 Izvleček: Pred stav lje e so iz bra e te me iz orie ti ra ja v a ra vi, ki jih mo ra poz a ti vsak vod ik PZS, da lah ko var o vo di ude le `e ce a tu ri Pred stav
Michelsonov interferometer
 Michelsonov interferometer Uvod Michelsonov interferometer [1] je sestavljen iz treh osnovnih elementov: dveh ravnih zrcal ter polprepustnega zrcala. Shema interferometra je prikazana na sliki 1. Interferenčno
Michelsonov interferometer Uvod Michelsonov interferometer [1] je sestavljen iz treh osnovnih elementov: dveh ravnih zrcal ter polprepustnega zrcala. Shema interferometra je prikazana na sliki 1. Interferenčno
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
predavatelj: doc. Andreja Drobni Vidic
 1 RE ITVE 5. DOMAƒE NALOGE - TOTP - modul MATEMATIKA predavaelj: doc. Andreja Drobni Vidic UPORABA ODVODOV IN INTEGRALI Diferencialni ra un je omogo il re²evanje nalog, za kaere je pred em kazalo, da presegajo
1 RE ITVE 5. DOMAƒE NALOGE - TOTP - modul MATEMATIKA predavaelj: doc. Andreja Drobni Vidic UPORABA ODVODOV IN INTEGRALI Diferencialni ra un je omogo il re²evanje nalog, za kaere je pred em kazalo, da presegajo
Realne funkcije. Elementarne funkcije. Polinomi in racionalne funkcije. Eksponentna funkcija a x : R R + FKKT Matematika 1
 Realne funkcije Funkcija f denirana simetri nem intervalu D = ( a, a) ali D = [ a, a] (i) je soda, e velja f(x) = f( x), x D; (ii) je liha, e velja f(x) = f( x), x D. Naj bo f denirana D f in x 1, x 2
Realne funkcije Funkcija f denirana simetri nem intervalu D = ( a, a) ali D = [ a, a] (i) je soda, e velja f(x) = f( x), x D; (ii) je liha, e velja f(x) = f( x), x D. Naj bo f denirana D f in x 1, x 2
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Nedestruktivne preiskave materialov in konstrukcij
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Seminar Nedestruktivne preiskave materialov in konstrukcij Vid Agrež Mentor: dr. Primož Ziherl 15. 5. 2008 Povzetek Z razvojem industrije in tehnike
Univerza v Ljubljani Fakulteta za matematiko in fiziko Seminar Nedestruktivne preiskave materialov in konstrukcij Vid Agrež Mentor: dr. Primož Ziherl 15. 5. 2008 Povzetek Z razvojem industrije in tehnike
SLIKA 1: KRIVULJA BARVNE OBČUTLJIVOSTI OČESA (Rudolf Kladnik: Osnove fizike-2.del,..stran 126, slika 18.4)
 Naše oko zaznava svetlobo na intervalu valovnih dolžin približno od 400 do 800 nm. Odvisnost očesne občutljivosti od valovne dolžine je različna od človeka do človeka ter se spreminja s starostjo. Največja
Naše oko zaznava svetlobo na intervalu valovnih dolžin približno od 400 do 800 nm. Odvisnost očesne občutljivosti od valovne dolžine je različna od človeka do človeka ter se spreminja s starostjo. Največja
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Ne vron ske mre že vs. re gre sij ski mo de li na po ve do va nje pov pra še va nja na treh vr stah do brin
 Ne vron ske mre že vs. re gre sij mo de li na po ve do va nje pov pra še va nja na treh vr stah do brin An ton Zi dar 1, Ro ber to Bi lo sla vo 2 1 Bo bo vo 3.a, 3240 Šmar je pri Jel šah, Slo ve ni ja,
Ne vron ske mre že vs. re gre sij mo de li na po ve do va nje pov pra še va nja na treh vr stah do brin An ton Zi dar 1, Ro ber to Bi lo sla vo 2 1 Bo bo vo 3.a, 3240 Šmar je pri Jel šah, Slo ve ni ja,
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Effect of Fibre Fineness on Colour and Reflectance Value of Dyed Filament Polyester Fabrics after Abrasion Process Izvirni znanstveni članek
 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
7 Lastnosti in merjenje svetlobe
 7 Lastnosti in merjenje svetlobe Pri tej vaji se bomo seznanili z valovno in delčno naravo svetlobe ter s pojmi spekter, uklon in interferenca. Spoznali bomo, kako se določi valovne dolžine in izmeri gostoto
7 Lastnosti in merjenje svetlobe Pri tej vaji se bomo seznanili z valovno in delčno naravo svetlobe ter s pojmi spekter, uklon in interferenca. Spoznali bomo, kako se določi valovne dolžine in izmeri gostoto
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
2. Širši konceptualni in metodološki okviri
 2. Širši konceptualni in metodološki okviri 11 12 2. Širši konceptualni in metodološki okviri 2.1 Uvod Uspešno reševanje problemov vodenja zahteva po eni strani poglobljeno razumevanje samih sistemov in
2. Širši konceptualni in metodološki okviri 11 12 2. Širši konceptualni in metodološki okviri 2.1 Uvod Uspešno reševanje problemov vodenja zahteva po eni strani poglobljeno razumevanje samih sistemov in
Pulzni sijski sistemi
 Seminar I b - 1. letnik, 2. semester Pulzni sijski sistemi Avtorica: Tanja Kaiba Mentorja: doc. dr. Luka Snoj, dr. Ga²per šerovnik Ljubljana, 21.3.2015 Povzetek V seminarju bom predstavila veriºno reakcijo
Seminar I b - 1. letnik, 2. semester Pulzni sijski sistemi Avtorica: Tanja Kaiba Mentorja: doc. dr. Luka Snoj, dr. Ga²per šerovnik Ljubljana, 21.3.2015 Povzetek V seminarju bom predstavila veriºno reakcijo
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA. ANTENE za začetnike. (kako se odločiti za anteno)
 ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA ANTENE za začetnike (kako se odločiti za anteno) Mentor: univ. dipl. Inž. el. Stanko PERPAR Avtor: Peter
ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA ANTENE za začetnike (kako se odločiti za anteno) Mentor: univ. dipl. Inž. el. Stanko PERPAR Avtor: Peter
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Varjenje polimerov s polprevodniškim laserjem
 Laboratorijska vaja št. 5: Varjenje polimerov s polprevodniškim laserjem Laserski sistemi - Laboratorijske vaje 1 Namen vaje Spoznati polprevodniške laserje visokih moči Osvojiti osnove laserskega varjenja
Laboratorijska vaja št. 5: Varjenje polimerov s polprevodniškim laserjem Laserski sistemi - Laboratorijske vaje 1 Namen vaje Spoznati polprevodniške laserje visokih moči Osvojiti osnove laserskega varjenja
TEORIJA LINIJSKIH KOD
 Fakulteta za elektrotehniko Tržaška 25 1000 Ljubljana Teoretični del iz seminaske naloge ANALIZATOR LASTNOSTI LINIJSKIH KOD TEORIJA LINIJSKIH KOD (2. poglavje seminarja) Asistent: Mag. Matevž Pustišek
Fakulteta za elektrotehniko Tržaška 25 1000 Ljubljana Teoretični del iz seminaske naloge ANALIZATOR LASTNOSTI LINIJSKIH KOD TEORIJA LINIJSKIH KOD (2. poglavje seminarja) Asistent: Mag. Matevž Pustišek
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
7 Lastnosti in merjenje svetlobe
 7 Lastnosti in merjenje svetlobe Pri tej vaji se bomo seznanili z valovno in delčno naravo svetlobe ter s pojmi spekter, uklon in interferenca. Spoznali bomo, kako se določi valovne dolžine, katere valovne
7 Lastnosti in merjenje svetlobe Pri tej vaji se bomo seznanili z valovno in delčno naravo svetlobe ter s pojmi spekter, uklon in interferenca. Spoznali bomo, kako se določi valovne dolžine, katere valovne
DARJA POTOƒAR, FMF
 7. ²olska ura Tema: Ponovitev Oblika: vaje B 1 Kotne funkcije v pravokotnem trikotniku: A V α A 1 B 1 sin α = AA 1 V A = BB 1 V B cos α = V B 1 V B = V A 1 V A tan α = sin α cos α cos α cot α = sin α =
7. ²olska ura Tema: Ponovitev Oblika: vaje B 1 Kotne funkcije v pravokotnem trikotniku: A V α A 1 B 1 sin α = AA 1 V A = BB 1 V B cos α = V B 1 V B = V A 1 V A tan α = sin α cos α cos α cot α = sin α =
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA
 UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA DIPLOMSKO DELO ANITA MANDELJ UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: Matematika in ra unalni²tvo Ravninske mreºe in posplo²itve Pickovega izreka
UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA DIPLOMSKO DELO ANITA MANDELJ UNIVERZA V LJUBLJANI PEDAGO KA FAKULTETA tudijski program: Matematika in ra unalni²tvo Ravninske mreºe in posplo²itve Pickovega izreka
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Gradniki TK sistemov
 Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
2.1. MOLEKULARNA ABSORPCIJSKA SPEKTROMETRIJA
 2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Interakcija DNA, histonskih proteinov in nukleosomov v kromatinu
 UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA FIZIKO Interakcija DNA, histonskih proteinov in nukleosomov v kromatinu Blaº Kav i Mentor: prof. dr. Rudolf Podgornik December 2009 Povzetek
UNIVERZA V LJUBLJANI FAKULTETA ZA MATEMATIKO IN FIZIKO ODDELEK ZA FIZIKO Interakcija DNA, histonskih proteinov in nukleosomov v kromatinu Blaº Kav i Mentor: prof. dr. Rudolf Podgornik December 2009 Povzetek
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
50 odtenkov svetlobe
 50 odtenkov svetlobe Evgenija Burger, Katharina Pavlin, Tamara Pogačar, Mentor: Žiga Krajnik Povzetek Za vsakim dežjem posije sonce. Je pojav mavrice res tako preprost kot ta rek? Kakšna fizikalno-matematična
50 odtenkov svetlobe Evgenija Burger, Katharina Pavlin, Tamara Pogačar, Mentor: Žiga Krajnik Povzetek Za vsakim dežjem posije sonce. Je pojav mavrice res tako preprost kot ta rek? Kakšna fizikalno-matematična
Diagonalni gra. 1 Predstavitev diagonalnih grafov. Zvone Klun. Maj 2007
 Diagonalni gra Zvone Klun Maj 2007 1 Predstavitev diagonalnih grafov Graf je diagonalen (ang. chordal), e ima vsak cikel dolºine 4 ali ve diagonalo. Kjer je diagonala (ang. chord) povezava med dvema vozli²
Diagonalni gra Zvone Klun Maj 2007 1 Predstavitev diagonalnih grafov Graf je diagonalen (ang. chordal), e ima vsak cikel dolºine 4 ali ve diagonalo. Kjer je diagonala (ang. chord) povezava med dvema vozli²
Poliedri Ines Pogačar 27. oktober 2009
 Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
11. Vaja: BODEJEV DIAGRAM
 . Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
. Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
12 Slikanje z jedrsko magnetno resonanco
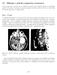 12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
