n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 )
|
|
|
- Δαμιανός Δημητρακόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2 l + 1 m l definiše izgled orbitale u podnivou n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 ) l (angularni) 0, 1, 2,.. n-1 oblik orbitale u podnivou m l (magnetni) -l..0..+l orijentacija orbitale u prostoru
2 Paulijev princip isključenja Zbog posedovanja spinskog kvantnog broja jedna orbitala ne može imati više od dva elektrona Orbitala predstavlja raspodelu verovatnoće nalaženja elektrona u odgovarajućem kvantiranom energetskom stanju, koje definišu kvantni brojevi.
3 Primeri:, Z = 1 n = 1, l = 0, m l = 0, m s = + ½ 1s 1 e, Z = 2 n = 1, l = 0, m l = 0, m s = - ½ 1s 2 Li, Z = 3 n = 2, l = 0, m l = 0, m s = + ½ 1s 2 2s 1 Be, Z = 4 n = 2, l = 0, m l = 0, m s = - ½ 1s 2 2s 2 B, Z = 5 n = 2, l = 1, m l = -1, m s = + ½ 1s 2 2s 2 2p 1
4 Podnivoi su sastavljeni od grupe orbitala u elektronskom nivou Broj orbitala n = 1 1 podnivo (s) 1 n = 2 2 podnivoa (s,p) = 4 n = 3 3 podnivoa (s,p,d) = 9 n = 4 4 podnivoa (s,p,d,f) = 16 n = 5 5 podnivoa (s,p,d,f,g)
5 n = 1, n = 2 i n = 3 nivo n= 3d 3 2 n 2 orbitala u n-tom nivou 1
6 Izgradnja periodnog sistema Svaki naredni element u periodnom sistemu ima po jedan proton u jezgru odnosno po jedan elektron u omotaču više od prethodnog elementa. Taj dodatni elektron se rasporedjuje u raspoloživu orbitalu koja ima najnižu energiju, poštujući pri tome kvantne brojeve i Paulijev princip isključenja. Sve ovo zajedno naziva se pravilom izgradnje (aufbau princip).
7 Valentni elektroni: Elektroni u spoljašnjem nivou ili u orbitali sa najvišim n Mg: 1s 2 2s 2 2p 6 3s 2 As: 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 10 4p 3 Co: 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 7
8 1 valentni elektron 2+5=7 valentnih elektrona 8 elektrona
9 Lewis-ovi simboli elemenata Lewis je predstavio valentne elektrone tačkama. Broj valentnih elektrona se poklapa sa grupom u periodnom sistemu i isti je za elemente u istoj grupi PERIODNOG SISTEMA. e Li Be B C N O F Ne Groups 1A 2A 3A 4A 5A 6A 7A 8A
10
11 Elementi teže da dostignu stabilnu elektronsku konfiguraciju najbližeg plemenitog gasa Ne Atomi teže da izgube, da dobiju ili da podele elektrone dok ne dostignu 8 elektrona u ljusci sa najvišim n Pravilo okteta Vodonik je izuzetak jer ima samo jedan elektron. On gradi vezu samo sa jednim elektronskim parom.
12
13 Elektronegativnost Elektronegativnost je sposobnost atoma u molekulu da privlači elektron.
14 Robert S. Mulliken elektronegativnost je definisana usrednjavanjem vrednosti jonizacionog potencijala i elektron afiniteta. Zato, Mulliken-ove elektronegativnostu izražene su direktno u jedinicama energije, najčešće, elektronvoltima, 1 ev = (14) J Jonizacioni potencijal, ili energija jonizacije je energija potrebna da se atomu ili molekulu oduzme 1 elektron. U hemiji, elektron afinitet je količina energije apsorbovana kada je 1 elektron dodat neutralnom izolovanom atomu gasa da bi se dobio jon gasa sa naelektrisanjem -1. On ima negativnu vrednost ako se energija oslobadja jonizacijom. Većina elemenata ima negativni elektron-afinitet. To znači da većini elemenata nije potrebno dovesti energiju da bi dobili elektron, zapravo, oni jonizacijom oslobadjaju energiju. lor najjače privlače ekstra elektrone, dok ih radon najslabije privlači.
15 Elektronegativnost Paulingova skala elektronegativnosti
16 PRIRODA EMIJSKE VEZE Atomi se medjusobno vezuju u jedinjenja, i na taj način nastaje bogata raznolikost sveta oko nas od samo stotinak elemenata iz periodnog sistema nastalo je do sada oko 12 miliona jedinjenja! Molekuli su odredjeni, definisani razmeštaji atoma u prostoru ovo je stav iz XIX veka, koji je medjutim razvojem modernih eksperimentalnih tehnika dobio svoje dokaze. Pojam molekula uveo je Avogadro od latinske reči moles, što znači teret. Pojam molekula je prvobitno bio predložen da bi se objasnila opažanja o masama elemenata koji se medjusobno povezuju. Pojmove hemijske veze i molekulske strukture prvi je uveo ruski hemičar Butlerov (1861). Cl. Odlučujući doprinosi razumevanju strukture molekula došli su od: G. N. Lewis-a (važnost elektronskog para u formiranju molekula) i Linus-a Paulinga, koji je dao kvantno mehanički doprinos.
17 Danas se molekuli «mogu videti». Eksperimentalno, odredjivanje strukture vrši se upotrebom najmodernijih spektroskopskih metoda ili difrakcijom rendgenskih zraka, kao i detaljnim teorijskim tretmanom. Najmanji molekul je homonuklearni dvoatomski molekul vodonika, a najveći poznati molekul je molekul DNK.
18 Glavna pitanja u razumevanju strukture molekula su: - Zašto se jedinjenja stvaraju? - Zašto molekuli imaju svoje karakteristične oblike? - Zašto se neki atomi retko nalaze u jedinjenjima a neki rado prave čitave atomske mreže i lance? Atomi se vezuju u jedinjenja ako se pri tome oslobadja energija. Energije atoma i njihovih jedinjenja odredjene su načinom na koji su rasporedjeni njihovi elektroni. Dakle, stvaranje jedjinjenja je moguće ukoliko pregrupisavanje elektrona dovodi do postizanja niže energije. Postoje dva načina na koji se mogu menjati medjusobni položaji elektrona: Atom može potpuno predati 1 ili više elektrona drugom atomu. Na taj nači nastaju joni koji se drže zajedno zbog elektrostatičkog privlačenja razlnoimenih naboja. Na ovaj način nastaje JONSKA VEZA. Dva atoma mogu deliti (to jest, zajednički posedovati) elektrone. Na ovaj način nastaje KOVALENTNA VEZA. Jonska i kovalentna veza spadaju u kategoriju EMIJSKI VEZA.
19 Priroda jonske veze Postoje tri stupnja u stvaranju jonske veze, svaki od njih dogadja se uz odredjenju promenu energije sistema. Samo ako je promena energije povoljna, doći će do stvaranje veze. I. Odvajanje elektrona od atoma A: A A + + e - Za ovaj stupanj potrebna je energija jonizacije. II. Dodavanje oslobodjenog elektrona atomu B. U ovom stupnju, odlučujući uticaj ima afinitet prema elektronima. Poseduju ga elementi VII grupe. Ukoliko je afinitet prema elektronima izražen, ovaj stupanj pomaže snižavanju ukupne energije. III. Elektrostatičko privlačenje nastalih jona.
20 Vezuvanje jonskom vezom je zapravo transfer elektrona. Prelaz elektrona se odvija sve dotle dok uključeni atomi ne izgube ili ne prime dovoljno elektrona da postignu popunjene valentne elektronske slojeve. Važi pravilo okteta: atomi teže da postignu elektronske konfiguracije plemenitih gasova. Do stvaranja jonske veze doći će kada A ima malu energiju jonizacije, kada B ima veliki elektron afinitet, i kada su joni na maloj udaljenosti jer se izmedju njih ostvaruje interakcija Coulomb-ovog tipa. Jonska veza nastaje izmedju atoma na levoj i atoma na desnoj strani periodnog sistema elemenata (izmedju metala i nemetala). Na ovaj način nastaju jonski kristali.
21 Na ovaj način nastaju jonski kristali. Nema pojedinačnih molekula nastalih jonskom vezom, već postoje skupine katjona i anjona povezane u kristalne rešetke!
22
23 NaCl jonska jedinjenja se sastoje od rešetke pozitivnih i negativnih jona. CsCl
24 REZIME: Jonska veza -prenos elektrona Ispunjeno oktetno pravilo Privlačna sila izmedju anjona i katjona. Atomi nemetala privlače elektrone mnogo jače od atoma metala tako da jedan ili više elektrona prelazi sa atoma metala na atom nemetala. Atom metala koji da jedan ili više elektrona postaje pozitivno naelektrisana vrsta, katjon. Atom nemetala koji primi jedan ili više elektrona postaje negativno naelektrisana vrsta, anjon.
25 katjoni
26 Anjoni
27 Lewis-ove strukture za jonska jedinjenja Jačine veza u jonskim jedinjenjima su zbog jakih elektrostatičkih sila vrlo visoke i uvek su veće od 1000kJ/mol BaO O Ba Ba O Tačka ključanja MgCl o C MgCl 2 Mg Cl Cl Mg Cl U jonskim jedinjenjima, elektrostatičke sile izmedju naelektrisanih vrsta (anjona i katjona) su vrlo jake što je razlog da ova jedinjenja imaju veoma visoke tačke topljenja, i tačke ključanja.
28 Priroda kovalentne veze Kod kovalentne veze, dva atoma dele elektronski par (ili više elektronskih parova) i na taj način postižu stabilnu elektronsku konfiguraciju inertnih gasova. Kovalentna veza ostvaruje se bez utroška energije za potpuni prelaz elektrona sa jednog na drugi atom.
29 Kovalentna veza - atomi u jedinjenju dele elektronske parove Ispunjeno pravilo okteta ugljenik 1s 2s 2p C u C 4 1s 2s 2p
30 CO 2 O + C + O O C O = O C O Višestruka veza O C O O C O O C O O C O PCl 3 Cl P Cl Cl Cl P Cl Cl Cl P Cl Cl
31 Lewis-ova struktura prikazuje molekul sa simbolima elementa, vezu kao liniju i tačke kao slobodni elektronski par. + Cl + Cl Cl Cl N + N N N number of electrons around each atom = e number of electrons around each atom = Ar Trostruka veza number of electrons around each atom = Ne Pravilo okteta
32 Rezonantne strukture NO NO 2 N O N O Resonace Arrows Rezonantna struktura nastaje kada je moguće napisati više od jedne Lewis-ove strukture za dati molekul (preraspodeliti elektrone) O N O O N O O N O
33 Eksperimentalni dokazi o tome da su elektronski parovi podeljeni dobijeni su primenom raznih metoda. Postavlja se pitanje: zašto dva ista atoma formiraju molekul? I faza: Atomi su daleko i medjusobno se ne privlače II faza: Kako se atomi privlače, jezgro jednog počinje da privlači elektrone drugog ta privlačna interakcija dovodi do pada potencijalne energije. U isto vreme, dešava se i medjusobno odbijanje jezgara, kao i odbijanje elektronskih oblaka. Na nekom internuklearnom rastojanju, postignuto je maksimalno privlačenje, nasuprot rastućem odbijanju sistem je na minimumu energije. Ovo uzajamno privlačenje izmedju jezgara i elektronskih oblaka dovelo je do stvaranja kovalentne veze.
34 MODEL VALENTNE VEZE ibridizacija atomskih orbitala
35 MODEL VALENTNE VEZE + Dva elektrona u s 1s su na nižim energetskim stanjima nego u pojedinačnim atomima što vodi stvaranju kovalentne veze.
36 MODEL VALENTNE VEZE ibridizacija atomskih orbitala 1. sp 3 hibridizacija Detaljnije u organskoj hemiji C 4 facts: C tetrahedral, 4 equivalent bonds C 2s 2p sp 3 hybrid a.o.s: promote electron 2s 4 2p C C(sp 3 ) tetrahedral (sp 3 C + 1s ) hybridize sp 3 hybrid a.o.s
37 MODEL VALENTNE VEZE ibridizacija atomskih orbitala 1. sp 3 hibridizacija Detaljnije u organskoj hemiji C N O lone pairs in sp 3 a.o.s C C N C C O (sp 3 C + sp 3 C) (sp 3 C + sp 3 N) (sp 3 C + sp 3 O)
38 MODEL VALENTNE VEZE ibridizacija atomskih orbitala 2. sp 2 hibridizacija C 2 4 facts: trigonal planar = sp 2 C Detaljnije u organskoj hemiji C Svih šest atoma su u istoj ravni 1s 1s 1s 1s C sp 2 2p C sp 2 2p 2p C C (sp 2 C + 1s ) (sp 2 C + sp 2 C) overlap p orbitals C C bond all atoms coplanar for p orbital overlap = C C double bond = 1 bond + 1 bond
39 MODEL VALENTNE VEZE ibridizacija atomskih orbitala 2. sp 2 hbridizacija C C Detaljnije u organskoj hemiji C O C C C C O O lone pairs in sp 2 a.o.s (sp 2 C + sp 2 C) + (sp 2 C + sp 2 O) +
40 MODEL VALENTNE VEZE ibridizacija atomskih orbitala 3. sp hibridizacija Detaljnije u organskoj hemiji C 2 2 facts: C C linearna = sp 1s 1s C 2p C 2p sp sp 2p 2 bonds C C C C = C C (sp C + 1s ) (sp C + sp C ) triple bond = 2 bonds + 1 bond
41 MODEL VALENTNE VEZE ibridizacija atomskih orbitala sp hibridizacija Detaljnije u organskoj hemiji C N C N N lone pair in sp a.o. (sp C + sp N ) + 2
42 OSOBINE KOVALENTNE VEZE su: Jačina veze; Dužina veze; Red veze (broj zajedničkih elektronskih parova izmedju atoma); Polarnost veze; Prostorni raspored (veza, medjusobno).
43 Jačina veze (bond energy - BE) je energija potrebna da se savlada privlačenje izmedju atoma. Po definiciji, to je standardna molarna entalpija 0 potrebna za raskidanje hemijske veze u 1 molu gasa. Dužina veze predstavlja rastojanje izmedju atomskih jezgara na minimumu potencijalne energije. Ono zavisi od veličine atoma (njihovog radijusa). Postoji veza izmedju reda kovalentne veze, dužine veze i energije veze: Za dati par atoma, viši red veze ima za posledicu kraću dužinu veze i veću energiju veze. Duže veze su često slabije. Takodje, višestruke veze su kraće. Kako svi molekuli neprekidno ispoljavaju vibraciono i rotaciono kretanje, i kako svaka veza vibrira, dužina veze je srednja vrednost izmedju mogućih rastojanja atoma u molekulu.
44 Nepolarna kovalentna veza Izmedju atoma čije se elektronegativnost razlikuju za manje od 0.4). Polarna kovalentna veza Izmedju atoma čije se elektronegativnost razlikuju za izmedju 0.4 i 1.7). Jonska veza Izmedju atoma čije se elektronegativnost razlikuju za više od 1.7, zbog čega dolazi do prenosa elektrona.
45 Elektronegativnost elemenata i polarnost veze = = 0 podjednako privlače par elektrona Cl Cl = nepolarna kovalentna veza Cl = 0.9 nejednako privlače par elektrona = polarna kovalentna veza Na + Cl = 2.1 Prenos elektrona = jonska veza generalno: X< 1.9 kovalentna veza > 1.9 jonska veza nemetal + nemetal metal + nemetal
46 F-F ( = 0) -F ( = 1.9) LiF ( = 3.0) F + - U svim slučajevima se postiže stabilna konfiguracija neona nepolarna kovalentna polarna kovalentna jonska Ne 1s 2, 2s 2, 2p 6 Na + F Na + + [ F ] _ Primer jonske veze
47
48 REZIME: Kovalentna veza - podela elektrona Medjutim, u mnogim jedinjenjima postoje slobodni elektronski parovi. Nevezivni (slobodni) elektronski par Vezivni elektronski par Element Broj veza Broj slobodnih elektronskih parova 1 0 C 4 0 N, P 3 1 O, S, Se 2 2 F, Cl, Br, I 1 3
49 U kovalentnoj vezi, svaki atom poseduje elektronski par (parove) kao da su njegovi. Oblici molekula rezultat su elektrostatičkih odbijanja medju elektronskim parovima. Primer molekul C 4 4 elektronska para se medjusobno odbijaju i zauzimaju energetski najpovoljniji raspored, odnosno, medjusobno najudaljenije položaje, što dovodi do stvaranja tetraedarske konfiguracije.
50 Teorija odbijanja valentnih orbitala (Valence shell electron pair repulsion (VSEPR) theory) objašnjenje oblika kovalentnih molekula. Elektronski parovi se medjusobno odbijaju tako da molekul ima oblik koji odgovara minimumu odbojnih sila izmedju njih.
51 Medjusobni odnos (broj) vezivnih i nevezivnih elektrona oredjuje oblik i polarnost molekula. N: 1s 2 2s 2 2p 3
52
53 Jonska veza i kovalentna veza -poredjenje Molekule nastale kovalentnom vezom karakteriše usmerenost veza. Postoje tačno odredjena mesta u atomima gde oni najuspešnije dele elektronske parove. Kako molekul nastao kovalentnom vezom ima minimalnu potencijalnu energiju kada su atomi u tačno odredjenim položajima, ovi molekuli imaju odredjeni oblik sa odredjenom dužinom veza i uglom izmedju njih. Kada se svi elektroni medjusobno podele izmedju atoma, nema mogućnosti da 1 molekul reaguje sa drugim istovrsnim molekulom kovalentni molekuli su definisani i diskretni.
54 Suprotno tome, jonske veze nemaju svojstvo usmerenosti jer je elektrostatička kulonovska sila usmerena u svim pravcima sferno i podjednako. Jedan jon može privlačiti više od jednog jona i tako nastaju veliki agregati, velike kristalne supstance.
55 Za razliku od prethodnih, metalna veza je uredjena struktura pozitivnih jona u moru elektrona. Pokretljivost elektrona u metalu dovodi do pojave njihovih osobina: provodljivosti, refleksivnosti, kovnosti. Neusmerenost veze dovodi do mogućnostui savijanja, a slobodni elektroni daju električnu i termičku provodljivost. Energija veze, kj/mol: Jonska veza: Kovalentna: Metalna:
56 Unutarmolekulske sile nastao hemijskom vezom jačina veze molekul Jonska veza : J/mol Kovalentna veza: kj/mol
57 Jonska jedinjenja imaju znatno više tačke topljenja i tačke ključanja od kovalentnih MgCl 2(l) Jonska veza 1412 o C PCl 3(l) Polarna kovalentna veza 76 o C
58 Većina materijala poznatih u prirodi postoje u obliku kondenzovanih faza tečnih i čvrstih supstanci. Postavlja se pitanje: Ako je većina supstanci nastala kovalentnom vezom, a kovalentni molekuli postoje kao pojedinačni i zasićni, kako od njih nastaju kondenzovane faze? Zašto sva materija nije u gasovitoj fazi? Kako se drže na okupu čestice čije su valence potpuno zasićene (slučaj kovalentnih molekula)?
59 Medjumolekulske interakcije
60 KOVALENTNA VEZA nepolarna polarna
61 Dipolni moment dipolni moment ( ) se definiše kao: = QR Količina naelektrisanja rastojanje R + centar
62 jedinjenje Polarne kovalentne veze: Dužina veze (Å) Razlika u elektronegativnosti -F Cl Br I Dipolni momenat(d) Polarni molekuli imaju dipolni momenat
63 U molekulima koji imaju dve ili više polarnih veza svaka veza diprinosi ukupnom dipolnom momentu molekula. Ukupni dipolni momenat = vektorskom zbiru pojedinačnih veza. Nepolarni molekuli O C O Linerni molekul CO 2 : dipoli su suprotno orijentisani pa je ukupni dipolni moment jednak nuli molekul nije polaran Polarani molekuli Polarni C 3 Cl CCl 3 Nepolaran CCl 4
64 U električnom polju dipoli se usmeravaju bez polja električno polje Električno polje može da potiče od molekula u okruženju!
65 MEDJUMOLEKULSKE SILE - sile koje deluju izmedju molekula jon - jon kj/mol jon dipol kj/mol dipol dipol 5-25 kj/mol jon - indukovani dipol 3-15 kj/mol dipol - indukovani dipol 2-10 kj/mol Disperzione 0,05-40 kj/mol Sila uzajamnog dejstva van der Waals-ove sile Vodonična veza je posebna klasa dipol-dipol interakcija, i posebno je važna klasa medjumolekulskih interakcija.
66 Jon - dipol interakcija Ostvaruje se kod rastvaranja jonskih kristala u vodi i odgovorna je za pojavu disocijacije. Energija ove interakcije je kj/mol Na + (aq) Na + koordinaciona sfera
67 dipol - dipol interakcija Ostvaruje se kod molekula sličnih veličina. Što je veći dipolni momenat ovim molekula, jače su dipol dipol veze. Očigledan je uticaj medjumolekulskih interakcija na fizičke osobine susptanci. Što su ove veze jače, viša je temperatura ključanja. Energija ove interakcije je 5 25 kj/mol
68 Jon Indukovani dipol Dipol - Indukovani Dipol jon Polarizovana vrsta dipol Polarizovana vrsta jon Indukovani dipol Dipol - Indukovani Dipol kj/mol Fe +2 O 2 - Cl 2-10 kj/mol Cl - Cl
69 Londonove disperzione sile Trenutno indukovana dipoldipol interakcija, vrlo slabe sile uvek prisutne u tečnom i čvrstom stanju.
70 6. Disperzione (London) Disperzione (London) - A + - B + U dužem vremenskom periodu (nepolarno) - + trenutno (polarno) Trenutni dipol Indukovani dipol kj/mol Bilo koja vrsta bilo koja vrsta
71 Jedan trenutno stvoreni dipol indukuje trenutno dipol u najbližem molekulu ili atomu. Sile izmedju trenutno stvorenih dipola zovu se Londonove sile Veći molekuli koji imaju više elektrona se lakše polarišu Londonove disperzione sile: - rastu sa porastom molekulske težine. - postoje izmedju svih molekula. - zavise od oblika molekula. - disperzione sile sfernih molekula su manje od sila izmedju izduženih molekula.
72 Poseban tip dipol-dipol interakcije. Ostvaruje se izmedju atoma u jednom molekulu i atoma (O,F,N) na kojima su slobodni elektronski parovi u drugom molekulu. Atom je mali, izrazito elektronegativan. Energija ove veze je oko 5% od prosečne kovalentne veze (3 5 kj/mol). Vodonična veza
73 VODONIČNA VEZA - posebni slučaj dipol-dipol interakcije Nastaje kada se vodonik vezuje za elektronegativni atom drugog molekula. N- N- O- N- F- N- N- O- O- O- F- O- N- F- O- F- F- F veza Zahteva nespareni elektronski par visoko elektronegativnog elementa
74 Vodonična veza je izuzetno jaka dipol-dipol interakcija koja se javlja kod molekula sa -O, -N, ili F grupama. atom je vrlo mali (r= 37 pm, manji je od bilo kog drugog atoma). U molekulu koji je sastavljen od vodonika i nekog jako elektronegativnog elementa (O, N ili F) elektron biva privučen od strane elektronegativnijeg atoma, i na vodoniku ostaje skoncentrisano jako pozitivno naelektrisanje. Vodonik na kome je skoncentrisano jako pozitivno naelektrisanje sada intenzivno privlači male elektronima bogate atome O, N, F koji se nalaze u drugim molekulima. Jačina vodonične veze u vodi je =19 kj/mol.
75
76 Posledice postojanja vodonične veze A, B su N, O ili F - A - + :B kj/mol Eksperimentalno pokazano da su tačke ključanja supstanci sa vezama -F, -O, i -N veoma visoke. -zahteva da bude vezan za neki elektronegativniji element molekulu F, O, ili N). Elektroni u -X (X = elektronegativni element) se nalaze mnogo bliže X nego. ima samo jedan elektron, tako da je -X veza, uvek polarna + je prisutno na a - na X. -veze su veoma jake.
77 -veza postoji izmedju molekula metanola ali i izmedju metanola i vode C O.....Ọ.. C Zato su ove dve supstance mešljive!
78 zatim... Koji od ova dva alkohola ima višu temperaturu ključanja? C 3 O ili C 3 C 2 O Oba molekula su polarna, oba grade vodonične veze. Veći molekul etanola se više polariše, molekuli medjusobno jače interaguju i zato je 66 o C 78 o C
79 zatim... Koje od ova dva jedinjenja ima višu tačku ključanja? Polarna kovalentna veza C 3 N 2 ili C 3 F Gradi -vezu! Ne gradi -vezu! -6 o C -78 o C
80 STRUKTURA PROTEINA
81 Medjumolekulske sile u proteinima
82 Poseban slučaj - voda
83 Struktura leda odredjena je uredjenom vodoničnom vezom
84 Postojanje vodonične veze objašnjava zašto led pliva po vodi
85
86 Poseban slucaj - alkoholi
87 Molekulski spektri Mnoga jedinjenja (njihovi molekuli) adsorbuju ultravioletno (UV) ili zračenje iz vidljivog dela spektra (Vis). Sledeća slika prikazuje prolazak zraka monohromatske svetlosti (zraka jedne talasne dužine) kroz uzorak. Prolaskom svetlosti, dešava se apsorpcija i intenzitet svetlosti se smanjuje sa upadne vrednosti (I 0 ) na manju vrednost (I).
88 Kada zrak svetlosti odredjene talasne dužine (λ) i upadnog intenziteta I 0 prolazi kroz uzorak koji apsorbuje zračenje, intenzitet svetlosti koja je propuštena zavisiće od tri faktora: -Od toga da li uzorak apsorbuje zračenje na toj talasnoj dužini; -Od dužine puta koji svetlost prolazi (širine kivete l ); -Od koncentracije supstance koja vrši apsorpciju svetlosti u tom rastvoru (c). Frakcija (udeo) zračenja koja je propuštena kroz rastvor, ili transparencija (T) definisana je sa: It gde je I t intenzitet propuštene svetlosti; a I 0 intenzitet upadne svetlosti. Vrednost transparencije kreće se od 1 100%. T I 0
89 Transparencija nekog uzorka menja se logaritamski zavisno od širine kivete i koncentracije uzorka, na sledeći način: log (1/T) = -log T = (konstanta proporcionalnosti) l C Konstanta proporcionalnosti zavisi od hemijske prirode supstance koja apsorbuje, talasne dužine svetlosti i jedinica za l i c. Uobičajeno se l izražava u cm, a c u mol/l; tada je ova konstanta proporcionalnosti nazvana molarna apsorptivnost (izražena u L cm-1 mol-1 i obeležena se ε ili a). Uobičajeno se do vrednosti za ε (a) dolazi merenjem transparencije za rastvor poznate koncentracije. Prethodna relacija odnosi se na količinu svetlosti koja je prošla kroz rastvor. Medjutim, često se izražava i količina svetlosti koja je zadržana (apsorbovana) od strane rastvora, pa definišemo novu veličinu, apsorbanciju (A), kao: A = log (1/T) = -log T
90 Kada izršimo potrebne zamene: A = ε b c (gde je c u mol/l or M) A = a b c (gde je c = g/l) ili: Ova jednačina poznata je kao Berov zakon, i daje linearnu vezu izmedju apsorbancije i koncentracije uzorka. Treba obratiti pažnju na to da postoji opseg važenja ovog zakona!
91 Odredjuje se apsorbancije za tri do pet standarnih rastvora (poznatih koncentracija) i unosi u grafik A = f(c). Tada se meri apsorbancija nepoznatog rastvora I njegova konventracija očitava direktno sa grafika.
92 Kako se odredjuje talasna dužina na kojoj se meri apsorbancija? Ako odredjujemo količinu apsorbovane svetlosti na različitim talasnim dužinama, dobićemo grafik koji nazivamo apsorpcionim spektrom. Ovaj grafik pokazuje specifičnu talasnu dužinu na kojoj kriva dostiže svoj maksimum, odnosno, na kojoj je apsorpcija svetlosti maksimalna. Energija koja odgovara ovoj talasnoj dužini odgovara razlici energija koju elektron ili u molekulu koji apsorbuje svetlost (u uzorku) u normlanom i u pobudjenom stanju.
93 Apsorpcioni spektar supstance može prvenstveno biti upotrebljen da bi bilo odredjenjo prisustvo supstance za kvalitativnu analizu; jer svaka hemijska vrsta imaspecifične energetske nivoe koji mogu da apsorbuju enerigju, zavisno od njene jedinstvene elektronske konfiguracije. Ipak, naješća primena je za kvantitativnu analizu, primenom napred prikazanog Berovog (Lamber-Berovog) zakona.
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Kovalentna veza , CO 2. U molekulima H 2
 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
JONSKA VEZA (metal-nemetal) KOVALENTNA VEZA (nemetal-nemetal) METALNA VEZA (metal-metal) jake H N. prelazne VODONIČNA VEZA H F
 HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
1s 2 2s 2 2p 2. C-atom. Hibridne atomske orbitale. sp 3 hibridizacija. sp 3. Elektronska konfiguracija ugljenika: aktivacija. ekscitovano stanje
 PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
PREAVAJE 2. Ugljenik je u organskim jedinjenjima četvorovalentan. Elektronska konfiguracija ugljenika: 1s 2 2 2p 2 dva nesparena elektrona -atom oc.dr Mirjana Abramović 2p osnovno stanje aktivacija 2p
 Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Ispitna pitanja iz Osnova hemije
 I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance.
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA!
 DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).
![PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ). PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).](/thumbs/74/70316766.jpg) 0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao)
 Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
Teorija molekulskoi orbitala linearna kombinacija atomskih orbitala(lcao) Kada je elektron u blizini jezgre jednog atoma onda njegova valna funkcija sliči atomskoj orbitali tog atoma. Zbrajanjem atomskih
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Spektroskopija u UV-Vis oblasti
 Spektroskopija u UV-Vis oblasti APSORPCIONE METODE EMISIONE METODE Apsorpcija u vidljivom delu spektra zasniva se na stabilnim promenama u elektronskim energetskim nivoima. Apsorpcioni spektar nastaje
Spektroskopija u UV-Vis oblasti APSORPCIONE METODE EMISIONE METODE Apsorpcija u vidljivom delu spektra zasniva se na stabilnim promenama u elektronskim energetskim nivoima. Apsorpcioni spektar nastaje
TALASNO-MEHANI MEHANIČKI MODEL ATOMA
 TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA
 SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA. ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA
 TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA Alfred Verner otac modere neorganske hemije Prusko plavo - Fe 4 [Fe(CN) 6 ] 3, je prvo poznati sintetisani
TEORIJA KRISTALNOG POLJA TEORIJA LIGANDNOG POLJA ili ELETRONSKA STRUKTURA KOORDINACIONIH JEDINJENJA Alfred Verner otac modere neorganske hemije Prusko plavo - Fe 4 [Fe(CN) 6 ] 3, je prvo poznati sintetisani
PERIODNI SISTEM ELEMENATA
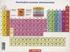 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
mali atomski i kovalentni radijus, velika energija jonizacije, mala stabilnost H - -jona SLIČNOST i sa alkalnim metalima (1 valentni e -,
 VODONIK najrasprostranjeniji element u Vasioni (88,6 at.%) 3. po rasprostranjenosti na Zemlji (iza O i Si), 15 at.% prvi, najlakši i najjednostavniji element (1 p + i 1 e - ) 1s 1 : mali atomski i kovalentni
VODONIK najrasprostranjeniji element u Vasioni (88,6 at.%) 3. po rasprostranjenosti na Zemlji (iza O i Si), 15 at.% prvi, najlakši i najjednostavniji element (1 p + i 1 e - ) 1s 1 : mali atomski i kovalentni
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Kiselo-bazne ravnoteže
 Uvod u biohemiju (školska 2016/17.) Kiselo-bazne ravnoteže NB: Prerađena/adaptirana prezentacija američkih profesora! Primeri kiselina i baza iz svakodnevnog života Arrhenius-ova definicija kiselina i
Uvod u biohemiju (školska 2016/17.) Kiselo-bazne ravnoteže NB: Prerađena/adaptirana prezentacija američkih profesora! Primeri kiselina i baza iz svakodnevnog života Arrhenius-ova definicija kiselina i
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
SPEKTROSKOPIJA SPEKTROSKOPIJA
 Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
U unutrašnja energija H entalpija S entropija G 298. G Gibsova energija TERMOHEMIJA I TERMODINAMIKA HEMIJSKA TERMODINAMIKA
 HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Svojstva veze. Duljina Energija disocijacije Konstanta sile Dipolni moment
 CAPVT II VEZA Svojstva veze Duljina Energija disocijacije Konstanta sile Dipolni moment Duljina veze 1. Udaljenost između jezgara 2. Udaljenost između maksimumâ elektronske gustoće 3. Ravnotežna duljina
CAPVT II VEZA Svojstva veze Duljina Energija disocijacije Konstanta sile Dipolni moment Duljina veze 1. Udaljenost između jezgara 2. Udaljenost između maksimumâ elektronske gustoće 3. Ravnotežna duljina
HEMIJA ELEMENATA VODONIK
 HEMIJA ELEMENATA Najrasprostranjeniji element u Vasioni (88,6 at.%). Na trećem mestu po rasprostranjenosti na Zemlji (15 at.%, iza O i Si). Prvi, najlakši i najjednostavniji element (1 p + i 1 e ). SVOJSTVA
HEMIJA ELEMENATA Najrasprostranjeniji element u Vasioni (88,6 at.%). Na trećem mestu po rasprostranjenosti na Zemlji (15 at.%, iza O i Si). Prvi, najlakši i najjednostavniji element (1 p + i 1 e ). SVOJSTVA
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
