(product-operator) I I cos ω ( t sin ω ( t x x ) + Iy )
|
|
|
- Μέλισσα Παπανδρέου
- 6 χρόνια πριν
- Προβολές:
Transcript
1
2 (product-operator) I I cos( t) + I sin( t) x x y
3 z 2π (rad) y 1 y t x = 2πν x t (rad)
4 sin t Iy# cos t t Ix# Ix# (t ) z Ix# Iy# Ix# (t ) z Ix cos (t ) + Iy sin (t )
5 -x -y t y I-y# I-y# (t ) z (t ) z x I-y# Ix# I-y cos (t ) + Ix sin (t )
6 J- I I cos( πjt) + 2I S sin( πjt) x x y z
7 ± J 2 (Hz) = ± πj ( rad s ) z Ix Sβ Ix Sα z Ix Sβ# y y πjt# x J Hz = 2πJ rad/s x πjt# Ix Sα# IxSβ# IxSβ cos (πjt) IySβ sin (πjt)# IxSα# IxSα cos (πjt) + IySα sin (πjt)#
8 J - + Ix Sα# Ix Sβ# Ix (Sα + Sβ) Ix Sα cos (πjt) + Iy Sα sin (πjt)# Ix Sβ cos (πjt) Iy Sβ sin (πjt)# Ix (Sα + Sβ) cos (πjt) + Iy (Sα Sβ) sin (πjt)# Sα + Sβ = 1 Sα - Sβ = 2 Sz Ix# Ix cos (πjt) + 2 Iy Sz sin (πjt)# Ix Sα S Sβ# Sα# = 1 = 2 Sz S z Ix Sβ
9 -2IxSz -Ix -Iy Iy# -2IySz 2IySz πjt πjt 2IxSz# 2IxSz# 2IxSz# (πjt) 2IzSz (πjt) 2IzSz Ix 2IxSz# Iy# 2IxSz cos (πjt) + Iy sin (πjt)
10 = z + [ I cos( t + φ) + I sin( t φ) ] = I z rf 1 x y
11 z 0 : Larmor z γb 0 = 0 γb = # y γ(b 0 -B) = 0 -# y y x γb = # γβ1 t = 1 t : x γβ1 = 1# 1 :
12 0 -# : # γ(b 0 -B) = 0 -# z θ 2 2 ( ) : cosθ = sinθ = y 2 2 ( ) ( ) γβ1 = 1# x 1 :
13 z ( ) γ(b 0 -B) = 0 -# θ γβ1 = 1# y x
14 z ( ) γ(b 0 -B) = 0 -# x θ γβ1 = 1# y
15 x z y θ θ γ(b 0 -B) = 0 -# γβ1 = 1# ( ) cos θ + = ( ) ( ) ( ) sin θ + = ( ) sin θ + = ( ) ( ) ( ) cos θ + = ( )
16 α α 800 MHz NMR Co (176 ppm) Cα (56 ppm) 800 * * (176-56) = Hz = Hz = 35.9 µs 2
17 z ppm = Hz 2 3 y = Hz x 180
18 I 0 exp( i I t ) 2 exp( i S t ) 1 =I 0 cos I t 2 { ( ) + isin( I t )}{ 2 cos( S t ) 1 + isin( S t )} 1 =I 0 cos I t 2 { ( ) + isin( I t )} 2 cos( S t ) 1 +ii 0 cos I t HSQC --- { ( ) + isin( I t )} 2 sin( S t ) 1
19 ( πj ) δ = δ π/4 ( + πj ) δ = δ + π/4 I S J δ 1 4J δ y π/4 π/4 π/4 π/4 y I x I Sα# Sβ# Sα# Sβ# x S Sα# Sβ# y S -2IxSz sin (πj2δ)
20 x I J 4J y 6 S x 7 6 z I y I z S y S x I x S 2IzSz 7 z I Iα# y I y S 5 x I Iβ# -2IzSy x S
21 8 z I Iα# S t 1 2 x I Iβ# y I y S 9 z I Iα# x S x I Iβ# y I y S I S 7 8 t1 9 x S
22 α β β α S t 1 10 z I Iα# y S y I x I Iβ# x S sin I S t 1 10 cos cos sin
23 10 2IzSy cos ( S t 1 ) 11 2IzSz cos ( S t 1 ) -2IzSx sin ( S t 1 ) -2IzSx sin ( S t 1 ) z S sin cos S t 1 cos sin S t 1 y S cos ( S t 1 ) sin ( S t 1 ) cos ( S t 1 ) sin ( S t 1 ) y S x S x S I S t
24 12-2IySz cos ( S t 1 ) +2IySx sin ( S t 1 ) MQ S 90y z S y I Sα cos ( S t 1 ) x I x S Sβ cos ( S t 1 ) y S I x/y 12 S t 1
25 reverse INEPT I S J δ J δ π/4 π/4 π/4 π/4 y I x I Sα cos ( S t 1 ) Sα cos ( S t 1 ) Sβ cos ( S t 1 ) Sβ cos ( S t 1 ) Ix cos ( S t 1 )
26 --- pulsed field gradient --- ( ) = γb 0 t + γ G( τ) φ t t 0 z( τ)dτ
27 Z - gradient - +3 ΔG +2 ΔG +1 ΔG 0-1 ΔG -2 ΔG -3 ΔG 0 3 ΔG -2 ΔG
28 gradient 30 G/cm for 1 ms ( ) 30 G = T T * (100 MHz / T) = MHz ( 1 H) MHz * 1 ms = 128 (/cm) 1 1cm 128 Gr 30 G/cm 1 cm 1 ms
29 Gradientecho (1) I Gr δ δ 2 3
30 Gradientecho (2) I Gr δ 6 δ 4 5
31 Gradientecho (3) I Gr δ δ 6 7
32 Gradientecho (4) I Gr δ δ 8 y δ Gr x +y
33 ( ) = S t S ( )exp( it)dt
34 FID NMR
35 7 7 x t# Sin 1 t# FID y 1 Cos 8 7 t# 6 5
36
37
38 ( ) = S t S ( )exp( it)dt = S(t) exp(it) dt
39 ( ) = S t S ( )exp( it)dt = S(t) exp(it) dt
40 ( ) = S t S ( )exp( it)dt = S(t) exp(it) dt
41 ( ) = S t S ( )exp( it)dt = S(t)exp(i( )t)dt
42 ( ) = S t S ( )exp( it)dt = S(t)exp(i( )t)dt
43 d = γ Iγ S! 2 r 3 A = I Z S Z 1 3cos 2 θ ( A + B + C + D + E + F) ( ) B = 1 ( 4 I + S + I S + )( 1 3cos 2 θ) C = 3 ( 2 I + S Z + I Z S + )sinθ cosθ exp( iϕ) D = 3 ( 2 I S Z + I Z S )sinθ cosθ exp ( +iϕ) E = 3 4 I + S + sin 2 θ exp( 2iϕ) F = 3 4 I S sin 2 θ exp ( +2iϕ)
44 % d = µ I r 3 ( µ r ( I ' )r * ' 3 r & 5 * µ S ) µ I = γ I!I = γ I! I X, I Y, I Z,. - ( ) = γ I! I + + I r = ( r sinθ cosϕ, r sinθ sinϕ, r cosθ) 2, I + I 2i /, I Z 1 0 B 0 I + = I X + ii Y S d = γ Iγ S! 2 r 3 I = I X ii Y ( A + B + C + D + E + F) I φ# θ# r r sinθ r cosθ
45 z = B0 µ S µ % d = µ I r + 3 ( µ r ( I ' )r * ' 3 r & 5 * µ S ) B 0 I r S $ D I = µ I r + 3 ( µ r ' I & )r ) & 3 r % 5 ) ( µ
46 $ D I = µ I r + 3 ( µ r ' I & )r ) & 3 r % 5 ) ( µ I ( ) r re = µ I r + 3 µ I r cosα 3 r 5 = µ I + 3µ I cosα re r 3 µ I I α µ I cosα re µ I µ I + 3µ I cosα re r S r 3 µ I + 3µ I cosα re
47 S µ I r r µ I + 3µ I cosα re = 2µ I µ I µ I I α = 0 µ I r µ I µ I I r S α = 90! µ I + 3µ I cosα re = µ I
48 µ I r magic- r S µ I µ I 54.7 I
49 B 0 dipole-dipole interaction Sx Iα Iβ Iα Ωs B 0 Iβ Iα Iα Sx Ωs
50 B 0 magic angle Sx Iβ Iα Iα Ωs B 0 B o Iβ Iα Iα Sx Ωs
51 B 0 Iz Sz Iz 2IzSz J(0) S Sz I S I S T 2 I S
52 Ι Σ 0 I x S y x S I y x y x 0 y y y x x y 2I + S + J (2 0 ) x x y
53 % d = µ I r 3 ( µ I r ( ' )r * ' 3 r & 5 * µ S ) µ I = γ I!I = γ I!( I X, I Y, I Z ) r = ( rcosθ X, rcosθ Y, rcosθ Z ) d = γ Iγ S! 2 ( ) r I X S X + I Y S Y + I Z S Z 3I X S X cosθ X cosθ X 3I X S Y cosθ X cosθ Y 3I X S Z cosθ X cosθ Z θ x # B 0 θ z # r θ y # I S 3I Y S X cosθ Y cosθ X 3I Y S Y cosθ Y cosθ Y 3I Y S Z cosθ Y cosθ Z 3I Z S X cosθ Z cosθ X 3I Z S Y cosθ Z cosθ Y 3I Z S Z cosθ Z cosθ Z θ θ θ
54 d = γ Iγ S! 2 ( ) r I X S X + I Y S Y + I Z S Z... 3I Z S Y cosθ Z cosθ Y µ I z I Z 2. cos(θz) 3. µ S y S Y 4. y cos(θy) 3 { µ } I cosθ Z re Z S 3 { µ I } cosθ Z cosθ Y Z { µ } I Z θz I θy θz { µ } I Z I Z S Y ( 3cosθ Z cosθ Y ) { µ I } + 3 µ I Z { } cosθ Z cosθ Z Z I Z S Z ( +1 3cosθ Z cosθ Z )
55 ?? 94 35
56 R 360 R 360 φ R 360 sin φ ( ) φ φ
Basic Theory of Solid-State NMR
 Basic Theory of Solid-State NMR Mei Hong, Department of Chemistry, MIT ˆρ ( t) = ˆρ cosωt ω i Ĥ, ˆρ sinωt 5 th Winter School on Biomolecular Solid-State NMR, Stowe, VT, Jan. 7-12, 218 Magnetic Dipole Moment
Basic Theory of Solid-State NMR Mei Hong, Department of Chemistry, MIT ˆρ ( t) = ˆρ cosωt ω i Ĥ, ˆρ sinωt 5 th Winter School on Biomolecular Solid-State NMR, Stowe, VT, Jan. 7-12, 218 Magnetic Dipole Moment
Τριγωνοµετρική (ή πολική) µορφή µιγαδικού αριθµού. Έστω z = x+ yi ένας µη µηδενικός µιγαδικός αριθµός και OM
 1 Τριγωνοµετρική (ή πολική µορφή µιγαδικού αριθµού Έστω z = x+ yi ένας µη µηδενικός µιγαδικός αριθµός και OM η αντίστοιχη διανυσµατική ακτίνα του Ονοµάζοµε όρισµα του µιγαδικού αριθµού z κάθε µια από τις
1 Τριγωνοµετρική (ή πολική µορφή µιγαδικού αριθµού Έστω z = x+ yi ένας µη µηδενικός µιγαδικός αριθµός και OM η αντίστοιχη διανυσµατική ακτίνα του Ονοµάζοµε όρισµα του µιγαδικού αριθµού z κάθε µια από τις
Αιολική Ενέργεια & Ενέργεια του Νερού
 Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 6: Σχεδίαση Πτερυγίων Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Ιδανικό ρευστό - εξίσωση Laplace Στοιχειώδεις
Αιολική Ενέργεια & Ενέργεια του Νερού Ενότητα 6: Σχεδίαση Πτερυγίων Γεώργιος Λευθεριώτης, Επίκουρος Καθηγητής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Ιδανικό ρευστό - εξίσωση Laplace Στοιχειώδεις
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ. Ενότητα 5 η : Παραδείγµατα 3 µηχανισµών. χώρο (3 )
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Ενότητα 5 η Παραδείγµατα µηχανισµών στο χώρο (3 ) Παράδειγµα 1 ο : Ροµποτικός βραχίονας RPPRR R: revolute pair P: prismatic pair Βραχίονας Τηλεσκοπικός βραχίονας
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Ενότητα 5 η Παραδείγµατα µηχανισµών στο χώρο (3 ) Παράδειγµα 1 ο : Ροµποτικός βραχίονας RPPRR R: revolute pair P: prismatic pair Βραχίονας Τηλεσκοπικός βραχίονας
Solutions - Chapter 4
 Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο ολοκλήρωμα α είδους
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο
ΘΕΜΑ 1. Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες)
 ΘΕΜΑ ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες) ΕΠΙΛΥΣΗ: Ο φορέας χωρίζεται στα τμήματα Α και Β. Το τμήμα Α είναι τριαρθρωτό τόξο. Απομονώνοντας το Α και
ΘΕΜΑ ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες) ΕΠΙΛΥΣΗ: Ο φορέας χωρίζεται στα τμήματα Α και Β. Το τμήμα Α είναι τριαρθρωτό τόξο. Απομονώνοντας το Α και
( ) ) V(x, y, z) Παραδείγματα. dt + "z ˆk + z d ˆk. v 2 =!x 2 +!y 2 +!z 2. F =! "p. T = 1 2 m (!x2 +!y 2 +!z 2
 ΦΥΣ 211 - Διαλ.04 1 Παραδείγματα Κίνηση ενός και μόνο σωματιδίου, χρησιμοποιώντας Καρτεσιανές συντεταγμένες και συντηρητικές δυνάμεις. Οι εξισώσεις Lagrange θα πρέπει να επιστρέφουν τα ίδια αποτελέσματα
ΦΥΣ 211 - Διαλ.04 1 Παραδείγματα Κίνηση ενός και μόνο σωματιδίου, χρησιμοποιώντας Καρτεσιανές συντεταγμένες και συντηρητικές δυνάμεις. Οι εξισώσεις Lagrange θα πρέπει να επιστρέφουν τα ίδια αποτελέσματα
Εισαγωγή στην Τεχνολογία Αυτοματισμού
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ Εισαγωγή στην Τεχνολογία Αυτοματισμού Ενότητα # 3: Μετασχηματισμός Laplace: Συνάρτηση μεταφοράς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑIΟΥ & ΑΕΙ ΠΕΙΡΑΙΑ Τ.Τ. Τμήματα Ναυτιλίας και Επιχειρηματικών Υπηρεσιών & Μηχ. Αυτοματισμού ΤΕ Εισαγωγή στην Τεχνολογία Αυτοματισμού Ενότητα # 3: Μετασχηματισμός Laplace: Συνάρτηση μεταφοράς
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε.
 ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ι 5 Ο ΕΞΑΜΗΝΟ ΔΙΔΑΣΚΩΝ: Δρ ΒΑΣΙΛΕΙΟΣ ΜΠΟΖΑΝΤΖΗΣ Διαμόρφωση Γωνίας Τα είδη διαμόρφωσης γωνίας τα
ΤΕΙ ΠΕΛΟΠΟΝΝΗΣΟΥ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ι 5 Ο ΕΞΑΜΗΝΟ ΔΙΔΑΣΚΩΝ: Δρ ΒΑΣΙΛΕΙΟΣ ΜΠΟΖΑΝΤΖΗΣ Διαμόρφωση Γωνίας Τα είδη διαμόρφωσης γωνίας τα
Μετασχηματισμός Jοukowski κυκλικού κυλίνδρου σε ομοιόμορφη ροή
 Μετασχηματισμός Jοukowski κυκλικού κυλίνδρου σε ομοιόμορφη ροή Κυκλικός κύλινδρος (ακτίνας r ) βρίσκεται εντός επίπεδης, άτριβης, δυναμικής ροής. Η γωνία πρόσπτωσης της αδιατάρακτης (επ άπειρον) ροής είναι
Μετασχηματισμός Jοukowski κυκλικού κυλίνδρου σε ομοιόμορφη ροή Κυκλικός κύλινδρος (ακτίνας r ) βρίσκεται εντός επίπεδης, άτριβης, δυναμικής ροής. Η γωνία πρόσπτωσης της αδιατάρακτης (επ άπειρον) ροής είναι
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
 ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
Homework#13 Trigonometry Honors Study Guide for Final Test#3
 Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 9.1 - Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 01. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 9.1 - Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 01. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός Ax μπορεί να ειδωθεί σαν μετασχηματισ
 Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός
Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Μετασχηματισμοί στον R 2 Μπορούν να παρασταθούν (και να υλοποιηθούν) με πολλαπλασιασμό πινάκων Ο πολλαπλασιασμός
= R{(a + jb)e j2π 3 4 t } (6) a + jb = j2.707 = e j π (7) A = (9) f 0 = 3 4
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
Ολοκληρώματα. ΗΥ111 Απειροστικός Λογισμός ΙΙ
 ΗΥ- Απειροστικός Λογισμός ΙΙ Ολοκληρώματα Εφαρμογές Ολοκληρωμάτων Υπολογισμός μήκους Υπολογισμός εμβαδού Υπολογισμός όγκου Χρήση σε Τύπους/Μετρικές Φυσική Πιθανότητες Γραφική Θέματα Αναγνώρισης προτύπων
ΗΥ- Απειροστικός Λογισμός ΙΙ Ολοκληρώματα Εφαρμογές Ολοκληρωμάτων Υπολογισμός μήκους Υπολογισμός εμβαδού Υπολογισμός όγκου Χρήση σε Τύπους/Μετρικές Φυσική Πιθανότητες Γραφική Θέματα Αναγνώρισης προτύπων
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

Αρµονικοί ταλαντωτές
 Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
Αρµονικοί ταλαντωτές ΦΥΣ 111 - Διαλ. 38 Εκκρεµή - Απλό εκκρεµές θ T mg r F τ = r F = mgsinθ τ = I M d θ α, Ι = M dt = Mgsinθ d θ dt = g sinθ θ = g sinθ Διαφορική εξίσωση Αυτή η εξίσωση είναι δύσκολο να
Ορμή - Κρούσεις. ΦΥΣ Διαλ.23 1
 Ορμή - Κρούσεις ΦΥΣ 111 - Διαλ.3 1 Χτύπημα καράτε ΦΥΣ 111 - Διαλ.3 q Σπάσιμο μιας σανίδας ξύλου με την ώθηση I = FΔt = Δp = mδυ Δt πολύ μικρό και Δp = σταθ. è F μεγάλη Ø Σώματα: ü Χέρι: M xεριού =3Kg,
Ορμή - Κρούσεις ΦΥΣ 111 - Διαλ.3 1 Χτύπημα καράτε ΦΥΣ 111 - Διαλ.3 q Σπάσιμο μιας σανίδας ξύλου με την ώθηση I = FΔt = Δp = mδυ Δt πολύ μικρό και Δp = σταθ. è F μεγάλη Ø Σώματα: ü Χέρι: M xεριού =3Kg,
ITU-R M MHz ITU-R M ( ) (epfd) (ARNS) (RNSS) ( /(DME) MHz (ARNS) MHz ITU-R M.
 ITU-R M.64- (007-005-003) ITU-R M.64- MHz 5-64 (epfd) (RNSS) ().MHz 5-64 MHz 5-960 (RR) ( () (RNSS) ( /(DME) MHz 5-64 (RNSS) (TACAN) ( ITU-R M.639 MHz 5-64 WRC-000 ( (RNSS) (RNSS) () RNSS WRC-03 ( MHz
ITU-R M.64- (007-005-003) ITU-R M.64- MHz 5-64 (epfd) (RNSS) ().MHz 5-64 MHz 5-960 (RR) ( () (RNSS) ( /(DME) MHz 5-64 (RNSS) (TACAN) ( ITU-R M.639 MHz 5-64 WRC-000 ( (RNSS) (RNSS) () RNSS WRC-03 ( MHz
= 0.927rad, t = 1.16ms
 P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
Δρ. Μηχ. Μηχ. Α. Τσουκνίδας. Σχήμα 1
 Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Σχήμα 1 Σχήμα 2 Παραγόμενη Μονάδες S.I. όνομα σύμβολο Εμβαδό Τετραγωνικό μέτρο m 2 Όγκος Κυβικό μέτρο m 3 Ταχύτητα Μέτρο ανά δευτερόλεπτο m/s Επιτάχυνση Μέτρο ανά δευτ/το στο τετράγωνο m/s 2 Γωνία Ακτίνιο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Κλασσική Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Αντίστροφος μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Αντίστροφος μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
NMR for Analytical Chemists. NMR Ch Announcement. Midterm Oct 18 I will give you unknown samples for presentation next Monday
 Chem 56 NMR for Analytial Chemts Leture 1 NMR Ch.1-.3 Announement Midterm Ot 18 I will give you unknown samples for presentation next Monday 1 Quiz Q1 What the expeted motion of M(t) in the rotation frame
Chem 56 NMR for Analytial Chemts Leture 1 NMR Ch.1-.3 Announement Midterm Ot 18 I will give you unknown samples for presentation next Monday 1 Quiz Q1 What the expeted motion of M(t) in the rotation frame
Γραφικά Υπολογιστών: Θέαση στις 3D
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Θέαση στις 3D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Σήμερα θα δούμε τα παρακάτω θέματα: Μετασχηματισμοί
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Θέαση στις 3D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Σήμερα θα δούμε τα παρακάτω θέματα: Μετασχηματισμοί
Ανασκόπηση-Μάθημα 28 Τριπλό ολοκλήρωμα-κυλινδρικές-σφαιρικές συντεταγμένες
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 28 Τριπλό ολοκλήρωμα-κυλινδρικές-σφαιρικές συντεταγμένες Στο μαθήμα 28 (3 /2/28), συνεχίσαμε
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 28 Τριπλό ολοκλήρωμα-κυλινδρικές-σφαιρικές συντεταγμένες Στο μαθήμα 28 (3 /2/28), συνεχίσαμε
Problem 3.16 Given B = ˆx(z 3y) +ŷ(2x 3z) ẑ(x+y), find a unit vector parallel. Solution: At P = (1,0, 1), ˆb = B
 Problem 3.6 Given B = ˆxz 3y) +ŷx 3z) ẑx+y), find a unit vector parallel to B at point P =,0, ). Solution: At P =,0, ), B = ˆx )+ŷ+3) ẑ) = ˆx+ŷ5 ẑ, ˆb = B B = ˆx+ŷ5 ẑ = ˆx+ŷ5 ẑ. +5+ 7 Problem 3.4 Convert
Problem 3.6 Given B = ˆxz 3y) +ŷx 3z) ẑx+y), find a unit vector parallel to B at point P =,0, ). Solution: At P =,0, ), B = ˆx )+ŷ+3) ẑ) = ˆx+ŷ5 ẑ, ˆb = B B = ˆx+ŷ5 ẑ = ˆx+ŷ5 ẑ. +5+ 7 Problem 3.4 Convert
Το ελαστικο κωνικο εκκρεμε ς
 Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
Το ελαστικο κωνικο εκκρεμε ς 1. Εξισώσεις Euler -Lagrange x 0 φ θ z F l 0 y r m B Το ελαστικό κωνικό εκκρεμές αποτελείται από ένα ελατήριο με σταθερά επαναφοράς k, το οποίο αναρτάται από ένα σταθερό σημείο,
u = 0 u = ϕ t + Π) = 0 t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt 2 ϕ = 0
 u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
u = (u, v, w) ω ω = u = 0 ϕ u u = ϕ u = 0 ϕ 2 ϕ = 0 u t = u ω 1 ρ Π + ν 2 u Π = p + (1/2)ρ u 2 + ρgz ω = 0 ( ϕ t + Π) = 0 ϕ t + Π = C(t) C(t) C(t) = K K C(t) ϕ = ϕ 1 + C(t) dt Kt C(t) ϕ ϕ 1 ϕ = ϕ 1 p ρ
( )U 1 ( θ )U 3 ( ) = U 3. ( ) όπου U j περιγράφει περιστροφή ως προς! e j. Γωνίες Euler. ω i. ω = ϕ ( ) = ei = U ij ej j
 Γωνίες Euler ΦΥΣ 11 - Διαλ.3 1 q Όλοι σχεδόν οι υπολογισµοί που έχουµε κάνει για την κίνηση ενός στερεού στο σύστηµα συντεταγµένων του στερεού σώµατος Ø Για παράδειγµα η γωνιακή ταχύτητα είναι: ω = i ω
Γωνίες Euler ΦΥΣ 11 - Διαλ.3 1 q Όλοι σχεδόν οι υπολογισµοί που έχουµε κάνει για την κίνηση ενός στερεού στο σύστηµα συντεταγµένων του στερεού σώµατος Ø Για παράδειγµα η γωνιακή ταχύτητα είναι: ω = i ω
"BHFC8I7H=CB HC &CH=CB 5B8 &CA9BHIA
 ω θ ω = Δθ Δt, θ ω v v = rω ω = v r, r ω α α = Δω Δt, Δω Δt (rad/s)/s rad/s 2 ω α ω α rad/s 2 87.3 rad/s 2 α = Δω Δt Δω Δt α = Δω Δt = 250 rpm 5.00 s. Δω rad/s 2 Δω α Δω = 250 min rev 2π rad rev 60 1 min
ω θ ω = Δθ Δt, θ ω v v = rω ω = v r, r ω α α = Δω Δt, Δω Δt (rad/s)/s rad/s 2 ω α ω α rad/s 2 87.3 rad/s 2 α = Δω Δt Δω Δt α = Δω Δt = 250 rpm 5.00 s. Δω rad/s 2 Δω α Δω = 250 min rev 2π rad rev 60 1 min
COMPLEX NUMBERS. 1. A number of the form.
 COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
Λύσεις στο επαναληπτικό διαγώνισμα 3
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) ιάρκεια 1,38 1,11 0,28 5,55. (h) πειράµατος.
 Γιατί NMR µε παλµούς; Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) Πυρήνας Φυσική αφθονία (%) ν (Hz) Ταχύτητα σάρωσης (Hz/s) Αριθµός σαρώσεων 1 Η 99,985 1000
Γιατί NMR µε παλµούς; Ευαισθησία πειράµατος (Signal to noise ratio = S/N) ιάρκεια πειράµατος (signal averaging)) Πυρήνας Φυσική αφθονία (%) ν (Hz) Ταχύτητα σάρωσης (Hz/s) Αριθµός σαρώσεων 1 Η 99,985 1000
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines
![Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines](/thumbs/51/28406191.jpg) Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
 γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
Section 8.2 Graphs of Polar Equations
 Section 8. Graphs of Polar Equations Graphing Polar Equations The graph of a polar equation r = f(θ), or more generally F(r,θ) = 0, consists of all points P that have at least one polar representation
Section 8. Graphs of Polar Equations Graphing Polar Equations The graph of a polar equation r = f(θ), or more generally F(r,θ) = 0, consists of all points P that have at least one polar representation
= + =. cos ( ) sin ( ) ˆ ˆ ˆ. Άσκηση 4.
 Άσκηση 4 Θεωρείστε και πάλι το σύστημα της άσκησης Τη χρονική στιγμή το σύστημα βρίσκεται στην κατάσταση a (η οποία δεν είναι ιδιοκατάσταση της amilonian) Ποιά είναι η πιθανότητα, μετά από χρόνο, να βρεθεί
Άσκηση 4 Θεωρείστε και πάλι το σύστημα της άσκησης Τη χρονική στιγμή το σύστημα βρίσκεται στην κατάσταση a (η οποία δεν είναι ιδιοκατάσταση της amilonian) Ποιά είναι η πιθανότητα, μετά από χρόνο, να βρεθεί
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 7.1 - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 Copyright ΕΜΠ
Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - 7.1 - Μηχανισμοί & Εισαγωγή στο Σχεδιασμό Μηχανών Ακαδημαϊκό έτος: 214-215 Copyright ΕΜΠ
E = P t = IAt = Iπr 2 t = J (1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Η ενέργεια που παραδίδεται στο αυτί µας σε χρόνο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Η ενέργεια που παραδίδεται στο αυτί µας σε χρόνο
1. Χρονικά Εξαρτημένες Πηγές 2. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση Δικτύων AC
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρθρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΚΥΚΛΩΜΑΤΩΝ Πανεπιστήμιο Ιωαννίνων ΑΝΑΛΥΣΗ ΔΙΚΤΥΟΥ 3 ο Κεφάλαιο Γ. Τσιατούχας Τμήμα Μηχανικών Η/Υ και Πληροφορικής ιάρθρωση. Χρονικά Εξαρτημένες Πηγές. Φάσορες 3. Σύνθετη Αντίσταση 4. Ανάλυση
x 3 D 1 (x 1)dxdy = dydx = (x 1)[y] x x 3 dx + x)dx = 3 x5
![x 3 D 1 (x 1)dxdy = dydx = (x 1)[y] x x 3 dx + x)dx = 3 x5 x 3 D 1 (x 1)dxdy = dydx = (x 1)[y] x x 3 dx + x)dx = 3 x5](/thumbs/100/147787649.jpg) 1 Επαναληπτικές Ασκήσεις 19-1-18 Διπλά Ολοκληρώματα 1. Να υπολογισθεί το ολοκλήρωμα (x 1)dxdy όπου το χωρίο περιέχεται από τις καμπύλες y x και y x. Λύση Οι δύο καμπύλες τέμνονται στα σημεία όπου x x.
1 Επαναληπτικές Ασκήσεις 19-1-18 Διπλά Ολοκληρώματα 1. Να υπολογισθεί το ολοκλήρωμα (x 1)dxdy όπου το χωρίο περιέχεται από τις καμπύλες y x και y x. Λύση Οι δύο καμπύλες τέμνονται στα σημεία όπου x x.
ΜΗΧΑΝΙΣΜΟΙ ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - Β. - Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 06. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΜΗΧΑΝΩΝ - Β. - Copyright ΕΜΠ - Σχολή Μηχανολόγων Μηχανικών - Εργαστήριο Δυναμικής και Κατασκευών - 06. Με επιφύλαξη παντός δικαιώµατος. All rights reserved. Απαγορεύεται
Trigonometry (4A) Trigonometric Identities. Young Won Lim 1/2/15
 Trigonometry (4 Trigonometric Identities 1//15 Copyright (c 011-014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Trigonometry (4 Trigonometric Identities 1//15 Copyright (c 011-014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
xsin ydxdy (α) Εάν το χωρίο R είναι φραγμένο αριστερά και δεξιά από τις ευθείες x=α και x=β και από πάνω και κάτω από τις καμπύλες dr = dxdy
 ΔΙΠΛΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Εφαρμογή Να υολογιστεί το ολοκλήρωμα : cos sin dd Ολοκληρώνουμε ρώτα ως ρος θεωρώντας το σαν σταθερά (αρατηρούμε ότι το «εσωτερικό» ολοκλήρωμα είναι ως ρος, δηλαδή ρώτα εμφανίζεται το
ΔΙΠΛΑ ΟΛΟΚΛΗΡΩΜΑΤΑ Εφαρμογή Να υολογιστεί το ολοκλήρωμα : cos sin dd Ολοκληρώνουμε ρώτα ως ρος θεωρώντας το σαν σταθερά (αρατηρούμε ότι το «εσωτερικό» ολοκλήρωμα είναι ως ρος, δηλαδή ρώτα εμφανίζεται το
11.4 Graphing in Polar Coordinates Polar Symmetries
 .4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry y axis symmetry origin symmetry r, θ = r, θ r, θ = r, θ r, θ = r, + θ .4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry
.4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry y axis symmetry origin symmetry r, θ = r, θ r, θ = r, θ r, θ = r, + θ .4 Graphing in Polar Coordinates Polar Symmetries x axis symmetry
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη users.auth.gr/~katsiki
 ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
ΚΕΦΑΛΑΙΟ 9 «Κυμάνσεις» Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Σχέση δύναμης - κίνησης Δύναμη σταθερή εφαρμόζεται σε σώμα Δύναμη ανάλογη της απομάκρυνσης (F-kx) εφαρμόζεται σε σώμα Το σώμα
e jθ = cos θ j sin θ(1.2)
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκων : Α. Μουχτάρης Εφαρµοσµένα Μαθηµατικά για Μηχανικούς - Λύσεις ης Σειράς Ασκήσεων Ασκηση. Σχέσεις του Euler
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκων : Α. Μουχτάρης Εφαρµοσµένα Μαθηµατικά για Μηχανικούς - Λύσεις ης Σειράς Ασκήσεων Ασκηση. Σχέσεις του Euler
3001 Υδροβορίωση/οξείδωση του 1-οκτενίου σε 1-οκτανόλη
 3001 Υδροβορίωση/οξείδωση του 1-οκτενίου σε 1-οκτανόλη 1. NaBH, I CH H 3 C C. H O /NaOH H 3 OH C 8 H 16 NaBH H O I NaOH C 8 H 18 O (11.) (37.8) (3.0) (53.8) (0.0) (130.) Βιβλιογραφία A.S. Bhanu Prasad,
3001 Υδροβορίωση/οξείδωση του 1-οκτενίου σε 1-οκτανόλη 1. NaBH, I CH H 3 C C. H O /NaOH H 3 OH C 8 H 16 NaBH H O I NaOH C 8 H 18 O (11.) (37.8) (3.0) (53.8) (0.0) (130.) Βιβλιογραφία A.S. Bhanu Prasad,
Answers to practice exercises
 Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
(i) f(x, y) = xy + iy (iii) f(x, y) = e y e ix. f(z) = U(r, θ) + iv (r, θ) ; z = re iθ
 ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
 Ασκήσεις Κεφ. 1, Κινηματική υλικού σημείου Κλασική Μηχανική, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 10 Απριλίου 2012 1. Αν το διάνυσμα θέσης υλικού σημείου είναι: r(t) = [ln(t
Ασκήσεις Κεφ. 1, Κινηματική υλικού σημείου Κλασική Μηχανική, Τμήμα Μαθηματικών Διδάσκων: Μιχάλης Ξένος, email : mxenos@cc.uoi.gr 10 Απριλίου 2012 1. Αν το διάνυσμα θέσης υλικού σημείου είναι: r(t) = [ln(t
Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής. Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Μωσαϊκά-Συρραφή Εικόνων Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή
Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Μωσαϊκά-Συρραφή Εικόνων Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή
Topic 4. Linear Wire and Small Circular Loop Antennas. Tamer Abuelfadl
 Topic 4 Linear Wire and Small Circular Loop Antennas Tamer Abuelfadl Electronics and Electrical Communications Department Faculty of Engineering Cairo University Tamer Abuelfadl (EEC, Cairo University)
Topic 4 Linear Wire and Small Circular Loop Antennas Tamer Abuelfadl Electronics and Electrical Communications Department Faculty of Engineering Cairo University Tamer Abuelfadl (EEC, Cairo University)
I = 1. cos z. dz = = 1 z 2 cos z + 2z sin z + 2 cos z 2. z(z π) 3 dz. f(re iθ. f(z)
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Χρησιμοποιώντας τους ολοκληρωτικούς τύπους Cauchy υπολογίστε το ολοκλήρωμα I = πi z(z π) 3 dz,
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Χρησιμοποιώντας τους ολοκληρωτικούς τύπους Cauchy υπολογίστε το ολοκλήρωμα I = πi z(z π) 3 dz,
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 7: Διαμόρφωση Γωνίας (1/2) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διαμόρφωση γωνίας Ορισμοί Η έννοια της Στιγμιαίας Συχνότητας Διαμόρφωση Φάσης (Phase
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 7: Διαμόρφωση Γωνίας (1/2) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διαμόρφωση γωνίας Ορισμοί Η έννοια της Στιγμιαίας Συχνότητας Διαμόρφωση Φάσης (Phase
Σχεδίαση με Ηλεκτρονικούς Υπολογιστές
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Μετασχηματισμοί συντεταγμένων στις 2 διαστάσεις Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Σχεδίαση με Ηλεκτρονικούς Υπολογιστές Ενότητα # 2: Μετασχηματισμοί συντεταγμένων στις 2 διαστάσεις Καθηγητής Ιωάννης Γ. Παρασχάκης Τμήμα
Αλλαγή µεταβλητής στο τριπλό ολοκλήρωµα ( ) Β R Jordan µετρήσιµα υποσύνολα του U. R, ανοικτό µε. y y y συµβολίζει την ορίζουσα του πίνακα Jacobi
 18 Αλλαγή µεταβλητής στο τριλό ολοκλήρωµα Υενθυµίζουµε ( Θεωρηµα ) το γενικό τύο αλλαγής µεταβλητής στο ολλαλό ολοκλήρωµα: f ( y) dy= f ( g( x) ) det J g( x) dx (1), Β= g Α Α n όου Α, Β R Jodan µετρήσιµα
18 Αλλαγή µεταβλητής στο τριλό ολοκλήρωµα Υενθυµίζουµε ( Θεωρηµα ) το γενικό τύο αλλαγής µεταβλητής στο ολλαλό ολοκλήρωµα: f ( y) dy= f ( g( x) ) det J g( x) dx (1), Β= g Α Α n όου Α, Β R Jodan µετρήσιµα
 1 2 3 4 C n a k max 1 = 92% max 1 = 70% max 1 = 60% max 1 = 50% min(p) = 180 max(p) = 180 min(p) = 90 max(p) = 145 min(p) = 0 max(p) = 90 min(w) = w q min(w) = 2 w q min(w) = 3 w q 1 2 3 X L R Z δ
1 2 3 4 C n a k max 1 = 92% max 1 = 70% max 1 = 60% max 1 = 50% min(p) = 180 max(p) = 180 min(p) = 90 max(p) = 145 min(p) = 0 max(p) = 90 min(w) = w q min(w) = 2 w q min(w) = 3 w q 1 2 3 X L R Z δ
ΜΑΣ002: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση)
 ΜΑΣ: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση) ΟΛΟΚΛΗΡΩΜΑΤΑ:. Να υπολογιστούν τα ολοκληρώματα: 5 d d csc cot d (β) Απάντησεις: C (β) ln C C. Να υπολογιστούν τα ορισμένα ολοκληρώματα: d csc( ) C C d d (β) /5
ΜΑΣ: Μαθηματικά ΙΙ ΑΣΚΗΣΕΙΣ (για εξάσκηση) ΟΛΟΚΛΗΡΩΜΑΤΑ:. Να υπολογιστούν τα ολοκληρώματα: 5 d d csc cot d (β) Απάντησεις: C (β) ln C C. Να υπολογιστούν τα ορισμένα ολοκληρώματα: d csc( ) C C d d (β) /5
ΦΥΣΙΚΗ (ΜΗΧΑΝΙΚΗ-ΚΥΜΑΤΙΚΗ)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ- ΗΛΕΚΤΡΟΝΙΚΩΝ ΦΥΣΙΚΗ (ΜΗΧΑΝΙΚΗ-ΚΥΜΑΤΙΚΗ) ΤΜΗΜΑ Α. ΚΑΘΗΓ. ΖΑΧΑΡΙΑΔΟΥ ΚΑΤΕΡΙΝΑ ΓΡΑΦΕΙΟ ΖΒ4 (ΡΑΓΚΟΥΣΗ-ΖΑΧΑΡΙΑΔΟΥ) E-mail: zacaria@niwa.gr Βιβλιογραφία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΑΤΤΙΚΗΣ ΣΧΟΛΗ ΜΗΧΑΝΙΚΩΝ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ- ΗΛΕΚΤΡΟΝΙΚΩΝ ΦΥΣΙΚΗ (ΜΗΧΑΝΙΚΗ-ΚΥΜΑΤΙΚΗ) ΤΜΗΜΑ Α. ΚΑΘΗΓ. ΖΑΧΑΡΙΑΔΟΥ ΚΑΤΕΡΙΝΑ ΓΡΑΦΕΙΟ ΖΒ4 (ΡΑΓΚΟΥΣΗ-ΖΑΧΑΡΙΑΔΟΥ) E-mail: zacaria@niwa.gr Βιβλιογραφία
fysikoblog.blogspot.com
 fysikobog.bogspot.co Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις ΙΙΙ: Σφαιρικές Αρμονικές Στις σημειώσεις αυτές δίνομε την αναπαράσταση των ιδιοανυσμάτων της
fysikobog.bogspot.co Πανεπιστήμιο Αθηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις ΙΙΙ: Σφαιρικές Αρμονικές Στις σημειώσεις αυτές δίνομε την αναπαράσταση των ιδιοανυσμάτων της
Chapter 1 Complex numbers
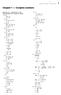 Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
ΣΥΝΤΟΝΙΣΜΟΥ Resonance
 ΤΟΜΟΓΡΑΦΙΑ ΠΥΡΗΝΙΚΟΥ ΜΑΓΝΗΤΙΚΟΥ ΣΥΝΤΟΝΙΣΜΟΥ (MRI-Magnetic Resonance Imaging) Κωνσταντίνα Νικήτα, Ph.D., M.D. Aναπλ.. Καθηγήτρια Περιεχόµενα Εισαγωγή Σύγκριση µε CT Βασικές αρχές NMR Eξίσωση Bloch Χρόνοι
ΤΟΜΟΓΡΑΦΙΑ ΠΥΡΗΝΙΚΟΥ ΜΑΓΝΗΤΙΚΟΥ ΣΥΝΤΟΝΙΣΜΟΥ (MRI-Magnetic Resonance Imaging) Κωνσταντίνα Νικήτα, Ph.D., M.D. Aναπλ.. Καθηγήτρια Περιεχόµενα Εισαγωγή Σύγκριση µε CT Βασικές αρχές NMR Eξίσωση Bloch Χρόνοι
Fourier Analysis of Waves
 Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
( () () ()) () () ()
 ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /011 1 Έστω r = r( t = ( x( t ( t z( t t I = [ a b] συνάρτηση C τάξης και r = r( t = r ( t = x ( t + ( t z ( t είναι μία διανυσματική + Nα αποδείξετε ότι: d 1 1
ΑΝΑΛΥΣΗ ΙΙ- ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ ΦΥΛΛΑΔΙΟ /011 1 Έστω r = r( t = ( x( t ( t z( t t I = [ a b] συνάρτηση C τάξης και r = r( t = r ( t = x ( t + ( t z ( t είναι μία διανυσματική + Nα αποδείξετε ότι: d 1 1
α + ω 0 2 = 0, Lösung: α 1,2
 SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + 2ζω x + ω 2 x = f () m, ω = k m, ζ = c 2 mk... Lehr'sches Dämpfungsmaß AB
SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + 2ζω x + ω 2 x = f () m, ω = k m, ζ = c 2 mk... Lehr'sches Dämpfungsmaß AB
Η απόσταση του σημείου Ρ από τη δεύτερη πηγή είναι: β) Από την εξίσωση απομάκρυνσης των πηγών y = 0,2.ημ10πt (S.I.) έχουμε:
 Γενική άσκηση στη συμβολή κυμάτων (Λύση) α) Η χρονική στιγμή t 1 που το κύμα από την πρώτη πηγή φτάνει στο σημείο Ρ είναι: r1 r1 6 u = => t1 = => t1 = s => t1 = 0, 6s t u 10 1 Τα κύματα φτάνουν στο σημείο
Γενική άσκηση στη συμβολή κυμάτων (Λύση) α) Η χρονική στιγμή t 1 που το κύμα από την πρώτη πηγή φτάνει στο σημείο Ρ είναι: r1 r1 6 u = => t1 = => t1 = s => t1 = 0, 6s t u 10 1 Τα κύματα φτάνουν στο σημείο
Integrals in cylindrical, spherical coordinates (Sect. 15.7)
 Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΝΟΜΟΥ ΤΟΥ ΝΕΥΤΩΝΑ
 ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΝΟΜΟΥ ΤΟΥ ΝΕΥΤΩΝΑ ΑΣΚΗΣΗ 1 Στο πάτωμα ενός ανελκυστήρα βρίσκεται ένας ζυγός. Αν πάνω στο ζυγό τοποθετηθεί ένα αντικείμενο το οποίο έχει μάζα m=85, kg και ο ανελκυστήρας κινείται με σταθερή
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΝΟΜΟΥ ΤΟΥ ΝΕΥΤΩΝΑ ΑΣΚΗΣΗ 1 Στο πάτωμα ενός ανελκυστήρα βρίσκεται ένας ζυγός. Αν πάνω στο ζυγό τοποθετηθεί ένα αντικείμενο το οποίο έχει μάζα m=85, kg και ο ανελκυστήρας κινείται με σταθερή
y = u i t 1 2 gt2 y = m y = 0.2 m
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ) Το χαρτονόµισµα ξεκινά από ηρεµία, u i = 0, και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ) Το χαρτονόµισµα ξεκινά από ηρεµία, u i = 0, και
2 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ ΓΙΑ ΕΞΑΣΚΗΣΗ
 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ ΓΙΑ ΕΞΑΣΚΗΣΗ ΑΠΡΙΛΙΟΣ 00 1. Σφαίρα µάζας m=k προσκρούει µε κατακόρυφη ταχύτητα u 1 =10m/s σε οριζόντιο δάπεδο και αναπηδά µε ταχύτητα u =6m/s. Η διάρκεια επαφής της σφαίρας µε το δάπεδο
η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ ΓΙΑ ΕΞΑΣΚΗΣΗ ΑΠΡΙΛΙΟΣ 00 1. Σφαίρα µάζας m=k προσκρούει µε κατακόρυφη ταχύτητα u 1 =10m/s σε οριζόντιο δάπεδο και αναπηδά µε ταχύτητα u =6m/s. Η διάρκεια επαφής της σφαίρας µε το δάπεδο
Physics 401 Final Exam Cheat Sheet, 17 April t = 0 = 1 c 2 ε 0. = 4π 10 7 c = SI (mks) units. = SI (mks) units H + M
 Maxwell' s Equations in vauum E ρ ε Physis 4 Final Exam Cheat Sheet, 7 Apil E B t B Loent Foe Law: F q E + v B B µ J + µ ε E t Consevation of hage: J + ρ t µ ε ε 8.85 µ 4π 7 3. 8 SI ms) units q eleton.6
Maxwell' s Equations in vauum E ρ ε Physis 4 Final Exam Cheat Sheet, 7 Apil E B t B Loent Foe Law: F q E + v B B µ J + µ ε E t Consevation of hage: J + ρ t µ ε ε 8.85 µ 4π 7 3. 8 SI ms) units q eleton.6
CHAPTER (2) Electric Charges, Electric Charge Densities and Electric Field Intensity
 CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
CHAPTE () Electric Chrges, Electric Chrge Densities nd Electric Field Intensity Chrge Configurtion ) Point Chrge: The concept of the point chrge is used when the dimensions of n electric chrge distriution
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1 3.2: Διαμόρφωση Πλάτους (Amplitude Modulation, AM) 3.3: Διαμόρφωση Πλευρικής Ζώνης με Καταπιεσμένο
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1 3.2: Διαμόρφωση Πλάτους (Amplitude Modulation, AM) 3.3: Διαμόρφωση Πλευρικής Ζώνης με Καταπιεσμένο
ΦΥΣ Διαλ Σήμερα...? q Λογισμό μεταβολών (calculus of variations)
 ΦΥΣ 11 - Διαλ.09 1 Σήμερα...? q Λογισμό μεταβολών (calculus of variations) Λογισμός μεταβολών - εισαγωγικά ΦΥΣ 11 - Διαλ.09 q Εύρεση του ελάχιστου ή μέγιστου μιας ποσότητας που εκφράζεται με τη μορφή ενός
ΦΥΣ 11 - Διαλ.09 1 Σήμερα...? q Λογισμό μεταβολών (calculus of variations) Λογισμός μεταβολών - εισαγωγικά ΦΥΣ 11 - Διαλ.09 q Εύρεση του ελάχιστου ή μέγιστου μιας ποσότητας που εκφράζεται με τη μορφή ενός
Εργαστήριο ΑΠΕ I. Ενότητα 2: Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Β. Πολυζάκης Απόστολος / Καλογήρου Ιωάννης / Σουλιώτης Εμμανουήλ
 Εργαστήριο ΑΠΕ I Ενότητα 2: Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Β Πολυζάκης Απόστολος / Καλογήρου Ιωάννης / Σουλιώτης Εμμανουήλ Με δεδομένο ότι η Ένταση της Ηλιακής ακτινοβολίας εκτός της ατμόσφαιρας
Εργαστήριο ΑΠΕ I Ενότητα 2: Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Β Πολυζάκης Απόστολος / Καλογήρου Ιωάννης / Σουλιώτης Εμμανουήλ Με δεδομένο ότι η Ένταση της Ηλιακής ακτινοβολίας εκτός της ατμόσφαιρας
ΕΝΑΛΛΑΣΣΟΜΕΝΑ ΡΕΥΜΑΤΑ
 ΕΝΑΛΛΑΣΣΟΜΕΝΑ ΡΕΥΜΑΤΑ Ένα ρεύµα ονοµάζεται εναλλασσόµενο όταν το πλάτος του χαρακτηρίζεται από µια συνάρτηση του χρόνου, η οποία εµφανίζει κάποια περιοδικότητα. Το συνολικό ρεύµα που διέρχεται από µια
ΕΝΑΛΛΑΣΣΟΜΕΝΑ ΡΕΥΜΑΤΑ Ένα ρεύµα ονοµάζεται εναλλασσόµενο όταν το πλάτος του χαρακτηρίζεται από µια συνάρτηση του χρόνου, η οποία εµφανίζει κάποια περιοδικότητα. Το συνολικό ρεύµα που διέρχεται από µια
ƒ Œ ˆ Šˆ Œ ˆ Œ ˆŸ ˆ Š Š ˆˆ Œ ˆ Š ˆˆ Š œ Š ˆ Ÿ
 Ó³ Ÿ. 21.. 7, º 7(163).. 748Ä754 ˆ ˆŠ ˆ ˆŠ Š ˆ ƒ Œ ˆ Šˆ Œ ˆ Œ ˆŸ ˆ Š Š ˆˆ Œ ˆ Š ˆˆ Š œ Š ˆ Ÿ.. ± Î,.. ÌÊ Ö ƒ ƒ ˆ, Œμ ± μ μ Ò ±μ² Ö Î É Í Ëμ±Ê ÊÕÐ É ³ ±μ²óí ³ Ò³ Éμ³ μ - Ò ÕÉ Ö ³ ² ÉÊ μ ËÊ ±Í ( É -ËÊ ±Í
Ó³ Ÿ. 21.. 7, º 7(163).. 748Ä754 ˆ ˆŠ ˆ ˆŠ Š ˆ ƒ Œ ˆ Šˆ Œ ˆ Œ ˆŸ ˆ Š Š ˆˆ Œ ˆ Š ˆˆ Š œ Š ˆ Ÿ.. ± Î,.. ÌÊ Ö ƒ ƒ ˆ, Œμ ± μ μ Ò ±μ² Ö Î É Í Ëμ±Ê ÊÕÐ É ³ ±μ²óí ³ Ò³ Éμ³ μ - Ò ÕÉ Ö ³ ² ÉÊ μ ËÊ ±Í ( É -ËÊ ±Í
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΩΤΟΜΕΤΡΙΑΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΩΤΟΜΕΤΡΙΑΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΦΩΤΟΜΕΤΡΙΑΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων
 2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
Review of Single-Phase AC Circuits
 Single-Phase AC Circuits in a DC Circuit In a DC circuit, we deal with one type of power. P = I I W = t2 t 1 Pdt = P(t 2 t 1 ) = P t (J) DC CIRCUIT in an AC Circuit Instantaneous : p(t) v(t)i(t) i(t)=i
Single-Phase AC Circuits in a DC Circuit In a DC circuit, we deal with one type of power. P = I I W = t2 t 1 Pdt = P(t 2 t 1 ) = P t (J) DC CIRCUIT in an AC Circuit Instantaneous : p(t) v(t)i(t) i(t)=i
Εργαστήριο ΑΠΕ I. Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Α
 Εργαστήριο ΑΠΕ I Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Α Ηλεκτρομαγνητική Ακτινοβολία Φάσμα Ηλεκτρομαγνητικής Ακτινοβολίας Γενικά για την Ηλιακή Ακτινοβολία Ο Ήλιος είναι ένα τυπικό αστέρι, αποτελούμενο
Εργαστήριο ΑΠΕ I Ηλιακή Γεωμετρία και Ηλιακό Δυναμικό: Μέρος Α Ηλεκτρομαγνητική Ακτινοβολία Φάσμα Ηλεκτρομαγνητικής Ακτινοβολίας Γενικά για την Ηλιακή Ακτινοβολία Ο Ήλιος είναι ένα τυπικό αστέρι, αποτελούμενο
Σπιν 1/2. Γενικά. 2 Υπενθυμίζουμε ότι τα έξι κουάρκ και τα έξι λεπτόνια του Καθιερωμένου Προτύπου,
 Σπιν / Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική r στροφορμή Jˆ με συνιστώσες Jˆ x, Jˆ
Σπιν / Γενικά Θα χρησιμοποιήσουμε τις γενικές σχέσεις που αποδείξαμε στην ανάρτηση «Εύρεση των ιδιοτιμών της στροφορμής», που, όπως είδαμε, ισχύουν για κάθε γενική r στροφορμή Jˆ με συνιστώσες Jˆ x, Jˆ
Τηλεπικοινωνιακά Συστήματα Ι
 Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 8: Διαμόρφωση Γωνίας (2/2) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εύρος Ζώνης Συχνοτήτων Σημάτων με Διαμόρφωση Γωνίας Δημιουργία Σημάτων Διαμορφωμένων
Τηλεπικοινωνιακά Συστήματα Ι Διάλεξη 8: Διαμόρφωση Γωνίας (2/2) Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Εύρος Ζώνης Συχνοτήτων Σημάτων με Διαμόρφωση Γωνίας Δημιουργία Σημάτων Διαμορφωμένων
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1
 ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1 3.2: Διαμόρφωση Πλάτους (Amplitude Modulation, AM) 3.3: Διαμόρφωση Πλευρικής Ζώνης με Καταπιεσμένο
ΣΤΟΧΑΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ & ΕΠΙΚΟΙΝΩΝΙΕΣ 1o Τμήμα (Α - Κ): Αμφιθέατρο 4, Νέα Κτίρια ΣΗΜΜΥ Διαμόρφωση Πλάτους - 1 3.2: Διαμόρφωση Πλάτους (Amplitude Modulation, AM) 3.3: Διαμόρφωση Πλευρικής Ζώνης με Καταπιεσμένο
και A = 1 Το πρόβλημα των μη ομογενών συνοριακών συνθηκών.
 Στις δύο διαστάσεις αφετηρία είναι η σχέση r + r r r A r + q r q Grr (, = ln ln L L (6 από την οποία μπορούμε να προσδιορίσουμε ότι και επομένως R R q = r, L r = L και A = r (7 r + r r r Grr (, = ln rr
Στις δύο διαστάσεις αφετηρία είναι η σχέση r + r r r A r + q r q Grr (, = ln ln L L (6 από την οποία μπορούμε να προσδιορίσουμε ότι και επομένως R R q = r, L r = L και A = r (7 r + r r r Grr (, = ln rr
Αρχές λειτουργίας απεικονιστικών μηχανημάτων Παραγωγή Ιατρικής Εικόνας
 Αρχές λειτουργίας απεικονιστικών μηχανημάτων Παραγωγή Ιατρικής Εικόνας 2. Μαγνητική Τομογραφία, Υπέρηχοι Παναγιώτης Τσίγκανος ΕΔΙΠ Κλινικό Εργαστήριο Ακτινολογίας Μαγνητική Τομογραφία MRI Magnetic Resonance
Αρχές λειτουργίας απεικονιστικών μηχανημάτων Παραγωγή Ιατρικής Εικόνας 2. Μαγνητική Τομογραφία, Υπέρηχοι Παναγιώτης Τσίγκανος ΕΔΙΠ Κλινικό Εργαστήριο Ακτινολογίας Μαγνητική Τομογραφία MRI Magnetic Resonance
Κεφάλαιο 3 ο : Αναπαράσταση θέσης
 ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Μάθηµα 3 ο Αναπαράσταση θέσης στο επίπεδο (2 ) και στο χώρο (3 ) Οµογενής Μετασχηµατισµός Κεφάλαιο 3 ο : Αναπαράσταση θέσης Μεταφορά αξόνων σε 2 X Ι Ο Ι Y Ι
ΜΗΧΑΝΙΣΜΟΙ & ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕ ΙΑΣΜΟ ΜΗΧΑΝΩΝ Μάθηµα 3 ο Αναπαράσταση θέσης στο επίπεδο (2 ) και στο χώρο (3 ) Οµογενής Μετασχηµατισµός Κεφάλαιο 3 ο : Αναπαράσταση θέσης Μεταφορά αξόνων σε 2 X Ι Ο Ι Y Ι
Ανεξαρτησία κάθετων μεταξύ των κινήσεων
 Ανεξαρτησία κάθετων μεταξύ των κινήσεων ΦΥΣ 111 - Διαλ.08 1 Εξαρτώνται οι τιμές των α x, v x και x από τις τιμές των α y, v y και y την ίδια ή κάποια άλλη χρονική στιγμή? Το ερώτημα που τίθεται είναι κατά
Ανεξαρτησία κάθετων μεταξύ των κινήσεων ΦΥΣ 111 - Διαλ.08 1 Εξαρτώνται οι τιμές των α x, v x και x από τις τιμές των α y, v y και y την ίδια ή κάποια άλλη χρονική στιγμή? Το ερώτημα που τίθεται είναι κατά
α + ω 0 2 = 0, Lösung: α 1,2
 SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + ζω x + ω x = f () m, ω = k m, ζ = c mk... Lehr'sches Dämpfungsmaß AB : x(
SDOFs Der lineare Einmassenschwinger Bewegungsgleichung m x + c x + k x = f () = p()...krafanregung m x g ()...Weganregung x + ζω x + ω x = f () m, ω = k m, ζ = c mk... Lehr'sches Dämpfungsmaß AB : x(
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ 1 ης ΕΡΓΑΣΙΑΣ. Προθεσµία παράδοσης 10/11/09. ασκούνται οι δυνάµεις των ελατηρίων k
 //9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 9- ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ης ΕΡΓΑΣΙΑΣ Προθεσµία παράδοσης //9 Άσκηση Α) Θεωρούµε µετατόπιση της µάζας m, από το σηµείο ισορροπίας του ελατηρίου k, κατά και αντίστοιχα
//9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 9- ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ης ΕΡΓΑΣΙΑΣ Προθεσµία παράδοσης //9 Άσκηση Α) Θεωρούµε µετατόπιση της µάζας m, από το σηµείο ισορροπίας του ελατηρίου k, κατά και αντίστοιχα
Γεωμετρικοί μετασχηματιμοί εικόνας
 Γεωμετρικοί μετασχηματιμοί εικόνας Μάθημα: Υπολογιστική Οραση 1 Γεωμετρικοί Μετασχηματισμοί Ορισμός σημείου στονευκλείδιοχώρο: p=[x p,y p,z p ] T, όπου x p, y p, z p πραγματικοί αριθμοί. ΕστωΕ 3 τοσύνολοτωνp.
Γεωμετρικοί μετασχηματιμοί εικόνας Μάθημα: Υπολογιστική Οραση 1 Γεωμετρικοί Μετασχηματισμοί Ορισμός σημείου στονευκλείδιοχώρο: p=[x p,y p,z p ] T, όπου x p, y p, z p πραγματικοί αριθμοί. ΕστωΕ 3 τοσύνολοτωνp.
Supporting Information for. Update of spectroscopic data for 4-hydroxyldictyolactone and dictyol E isolated from a Halimeda stuposa - Dictyota
 1 Supporting Information for Update of spectroscopic data for 4-hydroxyldictyolactone and dictyol E isolated from a Halimeda stuposa - Dictyota sp. Assemblage Simon P. B. Ovenden, Jonathan L. Nielson,
1 Supporting Information for Update of spectroscopic data for 4-hydroxyldictyolactone and dictyol E isolated from a Halimeda stuposa - Dictyota sp. Assemblage Simon P. B. Ovenden, Jonathan L. Nielson,
1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων
 3 1.1 Διανύσματα 1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων ΑΣΚΗΣΗ 1.1 Να βρεθεί η γωνία που σχηματίζουν τα διανύσματα î + ĵ + ˆk και î + ĵ ˆk. z k i j y x Τα δύο διανύσματα που προκύπτουν από
3 1.1 Διανύσματα 1.1.1 Εσωτερικό και Εξωτερικό Γινόμενο Διανυσμάτων ΑΣΚΗΣΗ 1.1 Να βρεθεί η γωνία που σχηματίζουν τα διανύσματα î + ĵ + ˆk και î + ĵ ˆk. z k i j y x Τα δύο διανύσματα που προκύπτουν από
