1 Ο ΚΕΦΑΛΑΙΟ Ενότητα 1.
|
|
|
- Ασπασία Μιαούλης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 1 Ο ΚΕΦΑΛΑΙΟ Ενότητα 1. Διανύσματα Ισότητα διανυσμάτων Πρόσθεση διανυσμάτων Ερωτήσεις 1. Τ ι ονομάζουμε διάνυσμα;. Τι λέμε μέτρο ενός διανύσματος ;. Τι λέμε μηδενικό διάνυσμα; 4. Τι λέμε φορέα διανύσματος; 5. Τι λέμε συγγραμμικά διανύσματα; 6. Πότε δύο διανύσματα λέγονται ομόρροπα; 7. Πότε δύο διανύσματα λέγονται αντίρροπα; 8. Πότε δύο διανύσματα λέγονται ίσα; 9. Πότε δύο διανύσματα λέγονται αντίθετα; 10. Τι ονομάζουμε γωνία δύο διανυσμάτων και τι τιμές παίρνει; 11. Τι συμπεραίνουμε για τα διανύσματα a, όταν: a, 0 ; a, ; a, ; 1. Πως ορίζουμε το άθροισμα a των διανυσμάτων a και ; 1. Πως προσθέτουμε δύο διανύσματα με τη μέθοδο του παραλληλογράμμου; 14. Ποιες ιδιότητες ισχύουν για το άθροισμα διανυσμάτων; 15. Πως ορίζουμε τη διαφορά a δύο διανυσμάτων a και ; 16.Να λυθεί η εξίσωση a. Σχόλιο Με διανυσματικές ακτίνες λύνονται σύντομα πολλά θέματα του κεφαλαίου αυτού. Ως σημείο αναφοράς επιλέγουμε κατάλληλο σημείο του σχήματος ή του χώρου. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 1
2 Μαθηματικά Κατεύθυνσης Β Λυκείου 1.1 Δίνεται κυρτό τετράπλευρο ΑΒΓΔ. Να αποδειχθεί ότι A B A B. Μέθοδος Για τη λύση των ασκήσεων είναι χρήσιμες και οι επόμενες παρατηρήσεις : Για να αποδείξουμε ότι δύο σημεία Μ και Ν ταυτίζονται, αρκεί να αποδείξουμε ότι MN 0, δηλαδή ότι το διάνυσμα MN είναι μηδενικό. Για να αποδείξουμε ότι δύο ευθύγραμμα τμήματα ΑΒ και ΓΔ είναι ίσα και παράλληλα, αρκεί ν.α.ο. AB ή AB. 1. Δίνονται τα σημεία Α,Β,Γ,Δ ΚΑΙ Ε του χώρου, για τα οποία ισχύει A BE. Ν.α.ο. τα σημεία Α και Β συμπίπτουν. Μέθοδος Σε ορισμένα θέματα ζητείται ο προσδιορισμός ενός σημείου Μ, ώστε να ισχύει κάποια διανυσματική σχέση. Στις περιπτώσεις αυτές προσπαθούμε να εντοπίσουμε ένα σταθερό σημείο Ο τέτοιο, ώστε το διάνυσμα OM να εκφράζεται με τη βοήθεια κάποιων διανυσμάτων, τα οποία όμως δεν έχουν ως άκρο το ζητούμενο σημείο. Η χρήση διανυσματικών ακτίνων οδηγεί συχνά σε σύντομες λύσεις. Ας επισημάνουμε ακόμη ότι: Αν βρούμε AM 0, τότε το Μ ταυτίζεται με το Α. Αν βρούμε MA MB 0, τότε το Μ είναι το μέσο του ευθυγράμμου τμήματος ΑΒ. 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ και τυχαίο σημείο Ρ του χώρου. i) Ν.a.o. PA P PB P. ii) Να προσδιοριστεί η θέση του σημείου Ρ, ώστε να ισχύει PA P P P Δίνεται τρίγωνο ΑΒΓ και τυχαίο σημείο Ρ της πλευράς ΒΓ. Ορίζουμε το σημείο Μ από τη σχέση PM AP PB P. Ν.α.ο. το τετράπλευρο ΑΒΜΓ είναι παραλληλόγραμμο. 1.5 Δίνεται τετράπλευρο ΑΒΓΔ. Ν.α.ο. AB A B Έστω τρίγωνο ΑΒΓ και Ρ τυχαίο σημείο του επιπέδου. Ν.α.ο. το Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
3 διάνυσμα f ( ) A 5B είναι ανεξάρτητο από τη θέση του σημείου Ρ, δηλαδή σταθερό. Ασκήσεις πολλαπλής επιλογής 1.7 Στο παραλληλόγραμμο ΑΒΓΔ είναι: ΑΒ = α, = β. α) Το διάνυσμα ΑΓ ισούται με: Α. α - β Β. β - α Γ. Δ. α + β α - β Ε. β) Το διάνυσμα ΒΔ ισούται με: Α. α + β α + β Β. β - α Δ. Ε. β - α Γ. α + β α - β 1.8 Στο διπλανό σχήμα το διάνυσμα x ισούται με: Α. α - β - γ - δ Β. α + β + γ - δ Γ. α - β + γ - δ Δ. α + β - γ - δ Ε. α - β - γ + δ 1.9 Για κάθε τετράδα σημείων Α, Β, Γ, Δ ισχύει: Α. ΑΔ + ΑΓ = ΒΓ + ΒΔ Β. ΑΔ + ΒΓ = ΑΓ + ΒΔ Γ. ΑΔ + ΒΔ = ΑΓ + ΒΓ Δ. ΑΔ + ΒΓ = ΑΓ + ΒΔ Ε. ΑΔ - ΑΓ = ΒΓ + ΒΔ 1.10 Στο κανονικό εξάγωνο ΑΒΓΔΕΖ είναι: Α. ΑΓ = ΑΕ Β. ΑΓ = - ΕΑ Γ. ΑΓ = - α Δ. ΑΓ = - 4 α Ε. ΑΓ = ΖΔ Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
4 Μαθηματικά Κατεύθυνσης Β Λυκείου 1.11 Στο διπλανό σχήμα το ΑΒΓΔ είναι κυρτό τετράπλευρο και τα Ε, Ζ, Η, Θ μέσα αντιστοίχως των πλευρών ΑΒ, ΓΔ, ΑΓ και ΒΔ. Λανθασμένη είναι η σχέση: Α. ΗΘ = ΑΔ + ΔΘ + ΗΑ Β. ΗΘ = ΒΘ + ΓΒ + ΗΓ Γ. ΗΘ = ΗΑ + ΑΒ + ΒΘ Δ. ΗΘ = ΓΔ + ΔΘ + ΓΗ Ε. ΗΘ = ΑΒ + ΓΔ 4 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
5 Ενότητα. Γινόμενο αριθμού με διάνυσμα Διανυσματική ακτίνα του μέσου ευθύγραμμου τμήματος Ερωτήσεις 1. Πως ορίζεται το γινόμενο του αριθμού λ με το διάνυσμα ;. Τι ιδιότητες έχει ο πολλαπλασιασμός αριθμού με διάνυσμα;. Τι ονομάζεται γραμμικός συνδυασμός διανυσμάτων; 4. Πως αποδεικνύουμε με τη βοήθεια διανυσμάτων ότι δύο ευθείες (ε) και (η) είναι παράλληλες; 5. Πως αποδεικνύουμε ότι τρία σημεία Α,Β,Γ (ή περισσότερα) είναι συνευθειακά; 6. Ποια είναι η διανυσματική ακτίνα του μέσου Μ ενός ευθύγραμμου τμήματος ΑΒ;.1 Δίνεται τρίγωνο ΑΒΓ και οι πραγματικοί αριθμοί α,β,γ με α+β+γ=0. Ν.α.ο. για τυχαίο σημείο Μ του χώρου το διάνυσμα ama MB M είναι σταθερό, δηλαδή ανεξάρτητο από τη θέση του σημείου Μ... Δίνονται τα σημεία Α,Β,Γ,Ρ,Σ για τα οποία ισχύει ότι PA A P B. Ν.α.ο. τα σημεία Α,Β,Γ είναι συνευθειακά με AB B. 4. Δίνονται τα διανύσματα a, με a // και τα σημεία Α,Β,Γ,Ο. Αν OA a, OB 5 a και O 11a ν.α.ο. τα σημεία Α,Β,Γ είναι συνευθειακά και ΒΓ=ΑΒ..4 Δίνονται οι αριθμοί κ,λ,μ με 0 και κ+λ+μ=0.αν OA OB O 0, ν.α.ο. τα σημεία Α,Β,Γ είναι συνευθειακά..5 Αν για τα σημεία Α,Β,Γ,Δ,Ε ισχύει η σχέση 5AB 7EA 10 0 ν.α.ο. τα σημεία Β,Γ,Δ είναι συνευθειακά. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 5
6 Μαθηματικά Κατεύθυνσης Β Λυκείου Σχόλιο Α. Έστω Α,Β,Γ τυχαία σταθερά σημεία και Μ ένα μεταβλητό σημείο. Αν ένας γραμμικός συνδυασμός διανυσμάτων με άκρα τα Α,Β,Γ,Μ ισούται με ένα διάνυσμα στο οποίο δεν εμφανίζεται ως άκρο το μεταβλητό σημείο Μ, τότε το διάνυσμα είναι ένα σταθερό διάνυσμα, ανεξάρτητο δηλαδή από τη θέση του σημείου Μ. Β. Για την απόδειξη τέτοιων θεμάτων επιλέγουμε κάποιο από τα σταθερά σημεία ως αρχή και εκφράζουμε όλα τα διανύσματα με τη βοήθεια των διανυσματικών ακτίνων των άκρων τους. Επιδίωξή μας είναι να μην εμφανιστεί στον τελικό γραμμικό συνδυασμό διανυσμάτων ως άκρο το μεταβλητό σημείο..6 Δίνεται τετράπλευρο ΑΒΓΔ και ένα μεταβλητό σημείο Μ. Ν.α.ο. το διάνυσμα a MA 4 MB M M είναι σταθερό..7 Θεωρούμε τα μη μηδενικά και μη παράλληλα ανά δύο διανύσματα a,,. Αν ισχύουν οι σχέσεις a //( ) και //( a), ν.α.ο. //( a ). Σχόλιο Για την εύρεση του γεωμετρικού τόπου ενός μεταβλητού σημείου Μ τέτοιου, ώστε να ικανοποιείται μια σχέση με διανύσματα, αξίζει να έχουμε κατά νου τις εξής πολύ βασικές πληροφορίες: Αν προκύψει ότι AM a, όπου Α είναι σταθερό σημείο, και το διάνυσμα a είναι σταθερό (έχει σταθερό μέτρο), τότε γράφουμε AM a R και έτσι ο ζητούμενος γεωμετρικός τόπος είναι κύκλος με κέντρο Α και ακτίνα R, Αν προκύψει ότι MA MB, όπου Α,Β είναι σταθερά σημεία, τότε ο ζητούμενος γεωμετρικός τόπος είναι η μεσοκάθετος του ευθύγραμμου τμήματος ΑΒ..8 Δίνεται τρίγωνο ΑΒΓ. Να βρεθεί ο γεωμετρικός τόπος των σημείων Μ για τα οποία ισχύει MA MB MA M. 6 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
7 .9 Δίνεται κυρτό τετράπλευρο ΑΒΓΔ. Να βρείτε τον γεωμετρικό τοπό των σημείων Μ του επιπέδου του ΑΒΓΔ για τα οποία ισχύει MA MB M M..10 Δίνεται τρίγωνο ΑΒΓ. Ν.α.ο. για οποιοδήποτε σημείο Μ το διάνυσμα u MA MB M είναι σταθερό..11 Ν.α.ο. το ευθύγραμμο τμήμα που ενώνει τα μέσα των μη παράλληλων πλευρών ενός τραπεζίου είναι παράλληλο προς τις βάσεις του..1 Στην πλευρά ΒΓ ενός τριγώνου ΑΒΓ θεωρούμε σημείο Ρ τέτοιο, ώστε BP P. Ν.α.ο. AB A 5AP..1 Δίνονται τα σημεία Α, Β και Γ. Ν.α.ο. για οποιοδήποτε σημείο Μ το διάνυσμα MA 5MB M.14 Αν για τα σημεία Α, Β, Γ, Δ, Ε ισχύει η σχέση A BE B A AE B ν.α.ο. τα σημεία Γ, Δ, Ε είναι συνευθειακά..15 Δίνεται τρίγωνο ΑΒΓ με ΒΓ=5 και τυχαίο σημείο Δ του χώρου. Να βρεθεί ο γεωμετρικός τόπος του σημείου Μ του επιπέδου του ΑΒΓ, ώστε να ισχύει MB M M M. Ασκήσεις πολλαπλής επιλογής.16 Στο παραλληλόγραμμο ΑΒΓΔ το Μ είναι μέσο της ΑΒ. Αν = α και ΔΓ = β, τότε: α) Το διάνυσμα ΔΜ ισούται με: α + β β - α Α. Β. Δ. α + 1 β Ε. 1 α + β Γ. - α + 1 β β) Το διάνυσμα ΜΓ ισούται με: Α. α - 1 β Β. 1 Δ. α + 1 β Ε. α + β Γ. 1 α + β α - β Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 7
8 Μαθηματικά Κατεύθυνσης Β Λυκείου γ) Με α + β ισούται το διάνυσμα: Α. ΑΒ Β. ΒΔ Γ. ΔΒ Δ. ΓΑ Ε. ΑΓ δ) Με α - β ισούται το διάνυσμα: Α. ΑΓ Β. ΓΑ Γ. ΒΑ Δ. ΔΒ Ε. ΒΔ.17 Αν α, β ομόρροπα διανύσματα, κ, λ R* διάφοροι του 1 και κ α + λβ = 0, τότε: Α. κ, λ θετικοί Β. κ, λ αρνητικοί Γ. κ, λ αντίστροφοι Δ. κ, λ ετερόσημοι Ε. κανένα από τα προηγούμενα.18 Αν ισχύει: κ α + λβ = 0, κ, λ πραγματικοί αριθμοί διάφοροι του μηδενός, τότε ποια από τις παρακάτω προτάσεις είναι σε κάθε περίπτωση σωστή; Α. Τα α, β έχουν την ίδια φορά Β. Τα α, β είναι κάθετα Γ. Τα α, β είναι αντίρροπα Δ. Τα α, β έχουν το ίδιο μέτρο Ε. Τα α, β έχουν την ίδια διεύθυνση.19 Στο τρίγωνο ΑΒΓ η ΒΕ είναι διάμεσος. Το άθροισμα ΒΑ + ΒΓ ισούται με: Α. ΒΕ Β. ΓΑ Γ. ΕΒ Δ. ΒΕ Ε. ΑΓ 8 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
9 Ενότητα. Ο άξονας Το καρτεσιανό επίπεδο Συνθήκη παραλληλίας διανυσμάτων Συντελεστής διεύθυνσης διανύσματος Ερωτήσεις 1. Τι μορφή έχουν τα σημεία του άξονα x x και τι μορφή τα σημεία του άξονα yý;. Τι ονομάζουμε συντεταγμένες διανύσματος;. Αν Α(x 1,y 1 ) και B(x,y ), ποιες είναι οι συντεταγμένες του διανύσματος AB ; 4. Με τι ισούται το μέτρο του διανύσματος a ( x, y) ; 5. Αν Α(x 1,y 1 ) και B(x,y ), πως υπολογίζεται το (ΑΒ); 6. Με τη βοήθεια της ορίζουσας να γράψετε μια αναγκαία και ικανή συνθήκη, ώστε δύο διανύσματα να είναι συγγραμμικά (παράλληλα). 7. Τι ονομάζουμε γωνία που σχηματίζει ένα μη μηδενικό διάνυσμα a με τον άξονα x x και τι τιμές παίρνει; 8. Τι ονομάζουμε συντελεστή διεύθυνσης ενός διανύσματος a ( x, y) και πότε ορίζεται; 9. Ποια σχέση συνδέει τους συντελεστές διεύθυνσης δύο παράλληλων διανυσμάτων; Ορισμός της ορίζουσας δύο διανυσμάτων: Ονομάζουμε ορίζουσα δύο διανυσμάτων α = (x 1, y 1 ) και β = (x, y ) και τη συμβολίζουμε με x 1 y 1 x y τον πραγματικό αριθμό x 1 y 1 x y = x 1 y - x y 1, όπου η 1 η γραμμή είναι οι συντεταγμένες του διανύσματος α = (x 1, y 1 ) και η η γραμμή είναι οι συντεταγμένες του διανύσματος β = (x, y ). Την ορίζουσα των διανυσμάτων α = (x 1, y 1 ) και β = (x, y ) με την σειρά που δίνονται, τη συμβολίζουμε και με det(α,β ). Δηλαδή det(α,β ) = x 1 y 1 x y = x 1 y - x y 1. Γενικότερα, η παράσταση D = x 1 y 1 x y = x 1 y - x y 1 ονομάζεται ορίζουσα και είναι ένας πραγματικός αριθμός..1 Να βρεθούν οι τιμές του λ R ώστε τα διανύσματα a =(λ -λ+,λ -1) και =(λ +λ+1,λ+1) να είναι ίσα. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 9
10 Μαθηματικά Κατεύθυνσης Β Λυκείου. Να βρεθούν οι τιμές των x, y ώστε τα διανύσματα a =(x +y,x+y) και =(-7,-1) να είναι αντίθετα.. Να γραφεί το διάνυσμα v (4,1) ως γραμμικός συνδυασμός των διανυσμάτων a (,) και (1,)..4 Δίνονται τα σημεία Α(1,), Β(6,8) και Δ(-,). Να βρεθούν οι συντεταγμένες του σημείου Γ, έτσι ώστε το τετράπλευρο ΑΒΓΔ να είναι παραλληλόγραμμο..5 Δίνεται το ευθύγραμμο τμήμα ΑΒ με Α(,-1) και Β(9,5). Να βρεθούν τα σημεία Μ, Ν του ΑΒ ώστε ΑΜ=ΜΝ=ΝΒ..6 Δίνεται το διάνυσμα a =(-6,8). Να βρεθεί: i) το μέτρο του a, ii) ένα διάνυσμα αντίρροπο του a με μέτρο πλάσιο απ το a..7 Να βρεθεί ένα σημείο Μ του άξονα x x το οποίο ισαπέχει από τα σημεία Α(1,) και Β(,-4)..8 Να βρεθούν οι τιμές του x R ώστε τα διανύσματα a =(x,1) και =(9,x) να είναι αντίρροπα..9 Σε ένα τετράπλευρο ΑΒΓΔ είναι Α(-,-1), Β(-5,-), Γ (-4,7) και Δ(-,). i) Ν.α.ο. οι ευθείες ΑΒ και ΓΔ τέμνονται. ii)να βρεθούν οι συντεταγμένες του σημείου τομής Ρ των ΑΒ, ΓΔ..10 Να βρεθούν η γωνία φ την οποία σχηματίζει το διάνυσμα AB, όπου Α(,4) και Β(4,) με τον άξονα x x. Ποιος είναι ο συντελεστής διεύθυνσης του AB ;.11 Αν φ, ω είναι οι γωνίες που σχηματίζουν τα διανύσματα a =(,1) και =(,1) με τον άξονα x x, ν.α.ο. φ+ω=π/4. Σχόλιο Πολλές φορές για την απόδειξη μιας πρότασης ιδιαίτερα αν πρόκειται για γεωμετρικό πρόβλημα τοποθετούμε το σχήμα και 10 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
11 όλα τα δεδομένα της άσκησης σε ένα ορθοκανονικό σύστημα αξόνων. Η τοποθέτηση του σχήματος γίνεται με τέτοιο τρόπο, ώστε να έχουμε όσο το δυνατόν λιγότερους αγνώστους. Αυτό επιτυγχάνεται αν : εκμεταλλευτούμε τις συμμετρίες του σχήματος εκμεταλλευτούμε τις ορθές γωνίες του σχήματος τοποθετήσουμε το μέγιστο δυνατό αριθμό σημείων του σχήματος στους άξονες.1 Να βρεθούν οι x, y R ώστε τα διανύσματα a =(x -xy+y,x+y) και =(-7,-5) να είναι αντίθετα..1 *Να βρεθούν οι x, y R ώστε τα διανύσματα a =(xy+x+y,x y+xy ) και =(11,0) να είναι ίσα.(εργασία).14 Έστω τα διανύσματα a =(1,4), =(,) και =(-,). Να αναλύσετε το διάνυσμα a σε δύο συνιστώσες από τις η μία να είναι παράλληλη στο και η άλλη στο Συμπληρωματική ομάδα..15 Δίνονται τα διανύσματα a =(,) και =(-,-). Na βρεθεί ο συντελεστής διεύθυνσης του διανύσματος γωνία που σχηματίζει το v με τον άξονα x x. v a καθώς και η.16 Δίνεται παραλληλόγραμμο ΑΒΓΔ με Α(4,-1), Β(6,7), Δ(-,-4). Να προσδιορίσετε τις συντεταγμένες της κορυφής Γ..17 Δίνονται τα σημεία Β(1,) και Γ(-1,6). Να βρείτε σημείο Α του άξονα x x ώστε το τρίγωνο ΑΒΓ να είναι ισοσκελές με (ΑΒ)=(ΑΓ)..18 Δίνεται τετράπλευρο ΑΒΓΔ με Α(,), Β(0,-1), Γ(-5,-), Δ(1,7). Ν.α.ο. το ΑΒΓΔ είναι ισοσκελές τραπέζιο..19 Αν Κ, Λ, Μ είναι τα μέσα των πλευρών ΑΒ, ΒΓ, ΓΑ αντίστοιχα του τριγώνου ΑΒΓ και είναι Κ(1,), Λ(,-), Μ(4,0), να προσδιορίσετε τις συντεταγμένες των κορυφών του..0 Δίνονται τα σημεία Α(-,5) και Β(-10,-).Να βρείτε σημείο της ευθείας (ε) : y=-1 που να ισαπέχει από τα Α, Β. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 11
12 Μαθηματικά Κατεύθυνσης Β Λυκείου Ασκήσεις πολλαπλής επιλογής.1 Τα διανύσματα a =(1,λ) και =(4,-λ) είναι παράλληλα όταν: Α. λ=-1 Β. λ=1 Γ. λ=0 Δ. λ=4 Ε. λ=-4. Με a =(1,-), =(-1,), =(,-6) ισχύει: Α. a + = Β. a - = Γ. a - = Δ. - = a Ε. a + =-. Δίνεται το διάνυσμα a =(,- ). Παράλληλο προς το διάνυσμα a είναι το διάνυσμα: 1 Α. (, ) Β. (, ) Γ. (,) Δ. ( 1, ) Ε. (,).4 Το διάνυσμα α (λ - λ - 4, λ - ) είναι μηδενικό με: Α. λ = Β. λ = 1 Γ. λ = - 4 Δ. λ = 0 Ε. για κανένα πραγματικό αριθμό λ.5 Το διάνυσμα α (ημθ, συνθ) είναι το μηδενικό με: Α. θ = κπ Β. θ = κπ + π 4 Γ. θ = κπ + π Δ. θ = κπ + π Ε. καμία τιμή του θ.6 Είναι α (ημθ, συνθ), θ R και κ Ζ. Το α είναι παράλληλο στον άξονα x x με: Α. θ = κπ Β. θ = κπ + π 4 Γ. θ = κπ + π Δ. θ = κπ + π Ε. θ = κπ π.7 Το διάνυσμα α = (ημθ, συνθ), είναι παράλληλο στο β = (συνθ, ημθ) με: Α. θ = 0 Β. θ = π 4 Γ. θ = π Δ. θ = π Ε. θ = π 1 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
13 .8 α διανύσματα α = (λ, λ) και β = (1, - ) είναι παράλληλα. Ο λ ισούται με: Α. - Β. - 1 Γ. Δ. 1 Ε..9 Δίνονται τα διανύσματα α = (-, 4) και β = (, - ). Η σχέση α + κ β = 0 ισχύει με: Α. κ = Β. κ = - Γ. κ = - Δ. κ = Ε. κανένα κ R Ενότητα 4. Εσωτερικό γινόμενο Ερωτήσεις 1. Τι ονομάζεται εσωτερικό γινόμενο a των διανυσμάτων a, ;. Να γράψετε τις ιδιότητες του εσωτερικού γινομένου.. Πως υπολογίζεται η γωνία θ που σχηματίζουν τα διανύσματα a x 1, y ) και x, y ); ( 1 ( 4.1 Έστω ΑΔ το ύψος ενός ισόπλευρου τριγώνου ΑΒΓ με πλευρά α=4. Να υπολογιστούν οι αριθμοί: i) AB ii) A 4. Δίνονται τα μη μηδενικά διανύσματα a και. Αν ν.α.ο. a // και αντιστρόφως. a, 4. Έστω a, δύο διανύσματα με a και 1. Αν τα a, σχηματίζουν γωνία θ=π/4, να βρεθεί το μέτρο του διανύσματος x a. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 1
14 Μαθηματικά Κατεύθυνσης Β Λυκείου 4.4 Δίνονται τα διανύσματα a, με a, Να βρεθεί το μέτρο του διανύσματος a. a. και, 4.5 Δίνονται τα μη μηδενικά διανύσματα a, με a. Αν a ( a ), ν.α.ο. η γωνία των διανυσμάτων a, είναι ίση με π/. 4.6 Δίνεται τετράπλευρο ΑΒΓΔ με Α(0,0), Β(α,β), Γ (α+,β) και Δ(,0).Ν.α.ο.: i) το ΑΒΓΔ είναι παραλληλόγραμμο, ii) αν ΒΓ=ΑΒ και Μ είναι το μέσο της ΑΔ, τότε ΜΒ ΜΓ. 4.7 Να βρεθεί ο γεωμετρικός τόπος των σημείων Μ του επιπέδου ενός τριγώνου ΑΒΓ για τα οποία ισχύει AB AM MA A 4.8 Σε ένα τρίγωνο ΑΒΓ είναι Α(1,),Β(-,1) και Γ (,6).Να υπολογιστεί η γωνία Α του τριγώνου. 4.9 Έστω ΑΔ το ύψος ενός τριγώνου ΑΒΓ. Αν AB B B, ν.α.ο. το τρίγωνο είναι ορθογώνιο Δίνεται παραλληλόγραμμο ΑΒΓΔ και οι προβολές Ε, Ζ του Δ πάνω στις πλευρές ΑΒ, ΑΓ αντίστοιχα. Ν.α.ο. ισχύει η σχέση A AZ AB AE A Να αναλυθεί το διάνυσμα u (9,19) σε δύο κάθετες μεταξύ τους συνιστώσες, από τις οποίες η μία να έχει τη διεύθυνση του διανύσματος a ( 5, ). 4.1 Έστω τρία διανύσματα a,, με 1,, 4, a,, a και, a. Να υπολογίσετε τις παρακάτω παραστάσεις: i) a, ii) a iii) a iv) a a v) a a 4.1 Να βρεθούν τα διανύσματα τα οποία είναι κάθετα στο διάνυσμα a,4 και έχουν μέτρο ίσο με Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
15 4.14 Θεωρούμε τα διανύσματα a, με a, 6. Να βρείτε τις τιμές του λ R, ώστε τα διανύσματα κάθετα. u a και v a να είναι 4.15 Σε ένα τρίγωνο ΑΒΓ είναι Α(4,), Β(1,), Γ(6,7).Να υπολογιστεί η γωνία Α του τριγώνου Έστω τα διανύσματα a και με,,να υπολογιστεί η γωνία,.. a,.αν a και 4.17 Δίνεται τρίγωνο ΑΒΓ. Να προσδιορίσετε το γεωμετρικό τόπο των σημείων Μ για τα οποία ισχύει AB M A Συμπληρωματική ομάδα Έστω τα διανύσματα a και με 1,, a και a,,να υπολογίσετε τη γωνία.αν 4.19 Δίνεται τρίγωνο ΑΒΓ και το τυχαίο σημείο Μ του επιπέδου του. Να αποδείξετε ότι η παράσταση f M MA B είναι ανεξάρτητη από τη θέση του. 4.0 Οι μαθητές σε ένα διαγώνισμα έδωσαν δύο διαφορετικές λύσεις στην παρακάτω άσκηση: Δίνεται το ισοσκελές τρίγωνο ΑΒΓ με ΑΒ=ΑΓ=1 και AB ˆ 10.Να υπολογιστεί το εσωτερικό γινόμενο. 1 η λύση: ΒΓ = ΑΒ + ΑΓ ΑΒΑΓσυν10 Ο = συν10 Ο = +συν60 Ο =+½=, ΒΓ =, 0 Άρα η λύση: Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 15
16 Μαθηματικά Κατεύθυνσης Β Λυκείου 1 10 ( ) , Ποια από τις δύο λύσεις είναι η σωστή; Ασκήσεις πολλαπλής επιλογής 4.1 Δίνονται τα διανύσματα a (, ), (1, 1) και 1 1 (, ). Σωστή είναι η σχέση: Α. a // //, Β., Γ. Δ. Ε. a. 4. Αν,, a και 0,, τότε η γωνία, ισούται με : Α. 0 ο, Β. 0 ο, Γ. 10 ο, Δ.60 ο, Ε. 150 ο 4. Τα διανύσματα α = (λ, 1 λ ) και β = (- 1, 8 λ ) είναι κάθετα με: Α. λ = - 1 Β. λ = 0 Γ. λ = 1 Δ. λ = Ε. λ = Δίνονται τα διανύσματα α = (, - ), β = (1, - 1) και γ = ( 1, - 1 ). Σωστή είναι η σχέση: Α. α = β Β. α. γ = β Γ. α // β // γ Δ. α γ Ε. α = β - γ 4.5 Τα διανύσματα α = (λ, 4) και β = (λ - 4, 1) είναι κάθετα. Ο πραγματικός αριθμός λ ισούται με: Α. 0 Β. - Γ. Δ. 4 Ε Αν κ =, ν =, κ. ν = - και 0 θ = ( κ, ν ) < π, τότε η γωνία θ ισούται με: Α. 0 Β. 0 Γ. 60 Δ. 10 Ε Είναι α. β = 0. Από τις παρακάτω σχέσεις δεν μπορεί να 16 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
17 ισχύει: Α. α = 0 Β. β α Γ. α = β και ( α, β ) = π Δ. ( α, β ) = π 4 Ε. α = β = 1 και ( α, β ) = π Σύμφωνα με το σχήμα, το α. β ισούται με: Α. α. β Β. - α. β Γ. 0 Δ. 1 α. β Ε. - 1 α. β 4.9 Σύμφωνα με το σχήμα, το α. β ισούται με: Α. 0 Β. α. β Γ. - α. β Δ. α. β Ε. - α. β 4.0 Σύμφωνα με το σχήμα, το α. β ισούται με: Α. α. β Β. 1 α. β Γ. Ε. - α. β Δ. - 1 α. β α. β 4.1 Στο σχήμα το ΑΒΓΔ είναι τετράγωνο με πλευρά 4 cm. Ποια από τις παρακάτω ισότητες είναι λανθασμένη; Α. ΑΒ. ΓΒ = 0 Β. ΑΟ. ΑΒ = 8 Γ. ΑΒ. ΑΓ = 16 Δ. ΑΒ. ΓΔ = - 16 Ε. ΟΒ. ΒΑ = 8 4. Αν α είναι μη μηδενικό διάνυσμα και β ένα οποιοδήποτε άλλο διάνυσμα, τότε το γινόμενο α. β ισούται με: Α. α. προβ β α Β. α. προβ α Γ. β. προβ α β Δ. α. προβ α β β Ε. β. προβ β α 4. Τα διανύσματα α και β είναι μη μηδενικά. Το συν ( α, β ) Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 17
18 Μαθηματικά Κατεύθυνσης Β Λυκείου ισούται με: α β Α. α.β Β. α β α.β Γ. α.β α β Δ. α.β α + β Ε. α.β α + β Γενικές ασκήσεις στα διανύσματα. 1. Δίνεται τετράπλευρο ΑΒΓΔ. Να προσδιοριστεί σημείο Ρ για το οποίο είναι 0.. Αν Κ,Λ,Μ είναι τα μέσα των πλευρών ΒΓ, ΓΑ, ΑΒ αντίστοιχα τριγώνου ΑΒΓ, ν.α.ο. για οποιοδήποτε σημείο Ο ισχύει OA OB O. Δίνονται τα διανύσματα a και.ν.α.ο.: i) a, ii). Να ερμηνευτούν γεωμετρικά οι παραπάνω προτάσεις: 4. Δίνονται τα διανύσματα (, ) υπολογιστεί η γωνία θ των a και. a και, με κλ. Να 5. Να αναλυθεί το διάνυσμα u σε δύο κάθετες συνιστώσες, από τις οποίες η μία να έχει τη διεύθυνση γνωστού διανύσματος a. 6. Έστω ΑΔ το ύψος ενός τριγώνου ΑΒΓ. Αν A, Ν.α.ο. O Aˆ Δίνονται τα διανύσματα a, με 1 και,. Να υπολογιστεί η γωνία των διανυσμάτων u 4a και v. 18 Επιμέλεια Σημειώσεων Μανάρας Νικόλαος
19 8. Δίνονται τα διανύσματα,, για τα οποία ισχύουν 1,, και 0. Να υπολογισθεί η τιμή της παράστασης. 9. Ένας κύκλος (Ο,ρ) διέρχεται από την κορυφή Α ενός παραλληλογράμμου και τέμνει τις ΑΒ, ΑΓ και ΑΔ στα σημεία Β,Γ και Δ αντίστοιχα. Ν.α.ο. AB AB 10. Δίνονται τρία διαδοχικά τετράγωνα ΑΒΓΔ, ΒΓΕΖ και ΖΕΘΗ. Ν.α.ο. ˆ ˆ. Επιμέλεια Σημειώσεων Μανάρας Νικόλαος 19
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
AB. Αν το διάνυσμα AB έχει μέτρο 1, τότε λέγεται
 ΔΙΑΝΥΣΜΑΤΑ Στη Γεωμετρία το διάνυσμα ορίζεται ως ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ως ένα ευθύγραμμο τμήμα του οποίου τα άκρα θεωρούνται διατεταγμένα Αν η αρχή και το πέρας ενός διανύσματος
ΔΙΑΝΥΣΜΑΤΑ Στη Γεωμετρία το διάνυσμα ορίζεται ως ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ως ένα ευθύγραμμο τμήμα του οποίου τα άκρα θεωρούνται διατεταγμένα Αν η αρχή και το πέρας ενός διανύσματος
ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ
 ΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ. Να σηµειώσετε το σωστό (Σ) ή το λάθος (Λ) στους παρακάτω ισχυρισµούς:. Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σηµεία Α, Β, Γ είναι συνευθειακά.. Αν α = β, τότε
ΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ. Να σηµειώσετε το σωστό (Σ) ή το λάθος (Λ) στους παρακάτω ισχυρισµούς:. Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σηµεία Α, Β, Γ είναι συνευθειακά.. Αν α = β, τότε
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
 2 ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2015-2016 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΠΙΜΕΛΕΙΑ ΠΑΥΛΟΣ ΧΑΛΑΤΖΙΑΝ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΟ ΔΙΑΝΥΣΜΑΤΙΚΟ ΛΟΓΙΣΜΟ Διάνυσμα λέγεται ένα προσανατολισμένο ευθύγραμμο
2 ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2015-2016 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΠΙΜΕΛΕΙΑ ΠΑΥΛΟΣ ΧΑΛΑΤΖΙΑΝ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΟ ΔΙΑΝΥΣΜΑΤΙΚΟ ΛΟΓΙΣΜΟ Διάνυσμα λέγεται ένα προσανατολισμένο ευθύγραμμο
Αγαπητοί μαθητές, Κάθε κεφάλαιο περιέχει :
 Αγαπητοί μαθητές, αυτό το βιβλίο αποτελεί ένα σημαντικό βοήθημα για τα Μαθηματικά Θετικού Προσανατολισμού της Β Λυκείου, που είναι ένα από τα σημαντικότερα μαθήματα, καθώς περιέχει χρήσιμες γνώσεις για
Αγαπητοί μαθητές, αυτό το βιβλίο αποτελεί ένα σημαντικό βοήθημα για τα Μαθηματικά Θετικού Προσανατολισμού της Β Λυκείου, που είναι ένα από τα σημαντικότερα μαθήματα, καθώς περιέχει χρήσιμες γνώσεις για
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
Μαθηματικά προσανατολισμού Β Λυκείου
 Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
ΔΙΑΝΥΣΜΑΤΑ Ερωτήσεις πολλαπλής επιλογής - Σ Λ - αντιστοίχησης
 Ερωτήσεις πολλαπλής επιλογής 1. * Στο παραλληλόγραµµο ΑΒΓ είναι: ΑΒ = α, Α = β. α) Το διάνυσµα ΑΓ ισούται µε Α. α - β Β. β - α Γ.. α + β Ε. α - β α + β β) Το διάνυσµα Β ισούται µε α + β Α. α + β Β. β -
Ερωτήσεις πολλαπλής επιλογής 1. * Στο παραλληλόγραµµο ΑΒΓ είναι: ΑΒ = α, Α = β. α) Το διάνυσµα ΑΓ ισούται µε Α. α - β Β. β - α Γ.. α + β Ε. α - β α + β β) Το διάνυσµα Β ισούται µε α + β Α. α + β Β. β -
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H
 Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων
 Αρσάκεια Τοσίτσεια Σχολεία Μαθηματικά Κατεύθυνσης Β Λυκείου Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων ) α β α β α//β ) α β α β α β ) α β α β α β 4)
Αρσάκεια Τοσίτσεια Σχολεία Μαθηματικά Κατεύθυνσης Β Λυκείου Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων ) α β α β α//β ) α β α β α β ) α β α β α β 4)
ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ 1 Θέµα: Τα διανύσµατα ❶ ❷ ❸ ❹ ❺ Η έννοια του διανύσµατος Πρόσθεση και αφαίρεση διανυσµάτων Πολλαπλασιασµός αριθµού µε διάνυσµα Συντεταγµένες
ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ 1 Θέµα: Τα διανύσµατα ❶ ❷ ❸ ❹ ❺ Η έννοια του διανύσµατος Πρόσθεση και αφαίρεση διανυσµάτων Πολλαπλασιασµός αριθµού µε διάνυσµα Συντεταγµένες
1.3 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
Μονάδες 5,5 γ) Αν τα διανύσματα a, είναι μη μηδενικά και θ είναι η γωνία των a. λ 0. Για ποια από τις παρακάτω τιμές του λ τα διανύσματα a.
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΘΕΜΑ 1 ο (Πανελλήνιες θετικής κατεύθυνσης Β Λυκείου 1999) Α. Έστω a ( x1,) y1 και ( x,) y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. α) Να εκφράσετε (χωρίς απόδειξη) το
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΘΕΜΑ 1 ο (Πανελλήνιες θετικής κατεύθυνσης Β Λυκείου 1999) Α. Έστω a ( x1,) y1 και ( x,) y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. α) Να εκφράσετε (χωρίς απόδειξη) το
2 Ο ΚΕΦΑΛΑΙΟ Ενότητα 5.
 Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
Ευθεία Ο ΚΕΦΑΛΑΙΟ Ενότητα 5. Εξίσωση γραμμής Συντελεστής διεύθυνσης ευθείας Συνθήκες καθετότητας και παραλληλίας ευθειών Εξίσωση ευθείας ειδικές περιπτώσεις Σχόλιο Το σημείο είναι ο θεμελιώδης λίθος της
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης
 Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. 1. Να αποδείξετε ότι για οποιαδήποτε σημεία Α,Β,Γ,Δ ισχύει ότι : 4 3 4 3 7
 ΒΑΣΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. Να αποδείξετε ότι για οποιαδήποτε σημεία Α,Β,Γ,Δ ισχύει ότι : 4 4 7. Αν ισχύουν να αποδείξετε ότι. Αν ισχύει ότι 5 5 να αποδείξετε
ΒΑΣΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. Να αποδείξετε ότι για οποιαδήποτε σημεία Α,Β,Γ,Δ ισχύει ότι : 4 4 7. Αν ισχύουν να αποδείξετε ότι. Αν ισχύει ότι 5 5 να αποδείξετε
1.3 Εσωτερικό Γινόμενο
 1 Εσωτερικό Γινόμενο 1 Αν α = ( 1, ) i α β iii και β = ( 1, ), να υπολογίσετε τα εσωτερικά γινόμενα: ii ( α )( β ) α β α + β α iv Αν α =, β = 1 και ( αβ, ) = 15 ο, να υπολογίσετε το α β Με βάση το διπλανό
1 Εσωτερικό Γινόμενο 1 Αν α = ( 1, ) i α β iii και β = ( 1, ), να υπολογίσετε τα εσωτερικά γινόμενα: ii ( α )( β ) α β α + β α iv Αν α =, β = 1 και ( αβ, ) = 15 ο, να υπολογίσετε το α β Με βάση το διπλανό
ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ
 Μαθηματικά Κατεύθυνσης Β Λυκείου-Απ Παπανικολάου ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων και και το συμβολίζουμε με α β τον πραγματικό αριθμό αβ
Μαθηματικά Κατεύθυνσης Β Λυκείου-Απ Παπανικολάου ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων και και το συμβολίζουμε με α β τον πραγματικό αριθμό αβ
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΟΡΙΣΜΟΣ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ 1. Να υπολογιστεί το εσωτερικό γινόμενο a δύο διανυσμάτων a και αν: ι) a a 5, 7,(, ) 5, ιι) a 5,,( a, ). 6 6. Το διάνυσμα
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΟΡΙΣΜΟΣ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ 1. Να υπολογιστεί το εσωτερικό γινόμενο a δύο διανυσμάτων a και αν: ι) a a 5, 7,(, ) 5, ιι) a 5,,( a, ). 6 6. Το διάνυσμα
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ. Επιμέλεια Αυγερινός Βασίλης
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Επιμέλεια Αυγερινός Βασίλης ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ο ΔΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΕ ΑΠΑΝΤΗΣΕΙΣ, ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ ΣΕΛΙΔΕΣ 3-36 ΜΕΡΟΣ ο ΕΥΘΕΙΕΣ ΕΡΩΤΗΣΕΙΣ
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Επιμέλεια Αυγερινός Βασίλης ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ο ΔΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΕ ΑΠΑΝΤΗΣΕΙΣ, ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ ΣΕΛΙΔΕΣ 3-36 ΜΕΡΟΣ ο ΕΥΘΕΙΕΣ ΕΡΩΤΗΣΕΙΣ
Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση: Να δίνει τον ορισμό του διανύσματος και των εννοιών που είναι κλειδιά όπως: κατεύθυνση φορά ή διεύθυνση, μηδενικό διάνυσμα,
Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση: Να δίνει τον ορισμό του διανύσματος και των εννοιών που είναι κλειδιά όπως: κατεύθυνση φορά ή διεύθυνση, μηδενικό διάνυσμα,
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
Β Λυκείου- Μαθηματικά Κατεύθυνσης. Μέρος Α Θεωρία. (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις)
 1 Μέρος Α Θεωρία (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις) Η έννοια του διανύσματος Ορισμός του Διανύσματος Διάνυσμα ονομάζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα του
1 Μέρος Α Θεωρία (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις) Η έννοια του διανύσματος Ορισμός του Διανύσματος Διάνυσμα ονομάζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα του
Φυλλάδιο Ασκήσεων 1 Διανύσματα
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΑΝΑΤΟΙΜΟΥ Β ΥΚΕΙΟΥ 07-8 Φυλλάδιο Διανύσματα ο ΓΕ Αγίων Αναργύρων Μαθηματικά Προσανατολισμού Φυλλάδιο Ασκήσεων Διανύσματα Β υκείου ύνθεση Άσκηση Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σημεία Α, Β, Γ είναι
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΑΝΑΤΟΙΜΟΥ Β ΥΚΕΙΟΥ 07-8 Φυλλάδιο Διανύσματα ο ΓΕ Αγίων Αναργύρων Μαθηματικά Προσανατολισμού Φυλλάδιο Ασκήσεων Διανύσματα Β υκείου ύνθεση Άσκηση Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σημεία Α, Β, Γ είναι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου. 2 ο ΘΕΜΑ. Εκφωνήσεις Λύσεις των θεμάτων. Έκδοση 1 η (18/11/2014)
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (8//04) Θέματα ης Ομάδας ο ΘΕΜΑ Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP 8556
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (8//04) Θέματα ης Ομάδας ο ΘΕΜΑ Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP 8556
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ. Επανάληψη Επιμέλεια Αυγερινός Βασίλης. Επιμέλεια : Αυγερινός Βασίλης
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Επανάληψη Επιμέλεια Αυγερινός Βασίλης ΚΕΦΑΛΑΙΟ ο ΔΙΑΝΥΣΜΑΤΑ SOS ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ Θέμα ο Να γράψετε και να αποδείξετε την σχέση της διανυσματικής ακτίνας του μέσου ενός τμήματος
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Επανάληψη Επιμέλεια Αυγερινός Βασίλης ΚΕΦΑΛΑΙΟ ο ΔΙΑΝΥΣΜΑΤΑ SOS ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ Θέμα ο Να γράψετε και να αποδείξετε την σχέση της διανυσματικής ακτίνας του μέσου ενός τμήματος
ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. 1 ο ΚΕΦΑΛΑΙΟ
 Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
Τάξη B. Μάθημα: Η Θεωρία σε Ερωτήσεις. Επαναληπτικά Θέματα. Επαναληπτικά Διαγωνίσματα. Επιμέλεια: Κώστας Κουτσοβασίλης. α Ε
 Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
Ν β K C Ε -α Ο α Ε Τάξη B Μ -β Λ Μάθημα: Η Θεωρία σε Ερωτήσεις Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Επιμέλεια: Διανύσματα Ερωτήσεις θεωρίας 1. Πως ορίζεται το διάνυσμα;. Τι λέγεται μηδενικό διάνυσμα;
) = Απόσταση σημείου από ευθεία. Υπολογισμός Εμβαδού Τριγώνου. και A
 [Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
[Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά. Μαθηματικού
 117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
Επαναληπτικές Ασκήσεις
 Επαναληπτικές Ασκήσεις 1 Έστω Α, Β, Κ, Λ και Μ τυχαία σημεία του χώρου Α ισχύει η σχέση ΑΚ + ΜΑ = ΚΒ 2ΑΒ + ΒΛ, να αποδείξετε ότι: α) τα σημεία Κ, Λ και Μ είναι συνευθειακά, β) ΚΛ ΚΜ, γ) ΚΛ = ΚΜ 2 Έστω
Επαναληπτικές Ασκήσεις 1 Έστω Α, Β, Κ, Λ και Μ τυχαία σημεία του χώρου Α ισχύει η σχέση ΑΚ + ΜΑ = ΚΒ 2ΑΒ + ΒΛ, να αποδείξετε ότι: α) τα σημεία Κ, Λ και Μ είναι συνευθειακά, β) ΚΛ ΚΜ, γ) ΚΛ = ΚΜ 2 Έστω
1.2 Συντεταγμένες στο Επίπεδο
 1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
= π 3 και a = 2, β =2 2. a, β
 1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ. α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β
 O A M B ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ Ο ΘΕΜΑ ον : α α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β. Μονάδες 5 β. Αν α, ν
O A M B ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ Ο ΘΕΜΑ ον : α α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β. Μονάδες 5 β. Αν α, ν
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. ΘΕΜΑ 2ο
 Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Τράπεζα Θεμάτων Διαβαθμισμένης Δυσκολίας-Μαθηματικά Ομάδας Προσανατολισμού Θετικών Σπουδών ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Ι Κ Α ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Σχολικό έτος : 04-05 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων
Μ Α Θ Η Μ Α Τ Ι Κ Α ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Σχολικό έτος : 04-05 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων
Διανύσματα ΚΑΤΗΓΟΡΙΑ 6. Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης. Ασκήσεις προς λύση Παράλληλα διανύσµατα. Οµόρροπα διανύσµατα.
 Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα ΚΑΤΗΓΟΡΙΑ 6 Παράλληλα διανύσµατα. Οµόρροπα διανύσµατα. Αντίρροπα διανύσµατα. Συνθήκη παραλληλίας διανυσµάτων (όλες της οι µορφές). Συνευθειακά
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα ΚΑΤΗΓΟΡΙΑ 6 Παράλληλα διανύσµατα. Οµόρροπα διανύσµατα. Αντίρροπα διανύσµατα. Συνθήκη παραλληλίας διανυσµάτων (όλες της οι µορφές). Συνευθειακά
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε = 5 + 2 α) Να γράψετε το διάνυσμα β) Να δείξετε
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε = 5 + 2 α) Να γράψετε το διάνυσμα β) Να δείξετε
1 x και y = - λx είναι κάθετες
 Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
Κεφάλαιο ο: ΕΥΘΕΙΑ Ερωτήσεις του τύπου «Σωστό-Λάθος» 1. * Συντελεστής διεύθυνσης μιας ευθείας (ε) είναι η εφαπτομένη της γωνίας που σχηματίζει η ευθεία (ε) με τον άξονα. Σ Λ. * Ο συντελεστής διεύθυνσης
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης. Διανύσματα ΚΑΤΗΓΟΡΙΑ 8. Εσωτερικό γινόµενο διανυσµάτων. Ασκήσεις προς λύση 1-50
 Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
Μαθηµατικά Β Λυκείου Θετικής - τεχνολογικής κατεύθυνσης Διανύσματα Εσωτερικό γινόµενο διανυσµάτων. ΚΑΤΗΓΟΡΙΑ 8 Ασκήσεις προς λύση 1-50 1. Θεωρούμε τα σημεία Α(1,2), Β(4,1). Να βρείτε σημείο Μ του άξονα
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Πέμπτη 12 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 0/04/018 ΕΩΣ 14/04/018 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη 1 Απριλίου 018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να αποδείξετε ότι η εφαπτομένη ε του κύκλου
ΑΠΟ 0/04/018 ΕΩΣ 14/04/018 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη 1 Απριλίου 018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Να αποδείξετε ότι η εφαπτομένη ε του κύκλου
1,y 1) είναι η C : xx yy 0.
 ΘΕΜΑ Α ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ο δείγμα Α. Αν α, β δύο διανύσματα του επιπέδου με συντελεστές διεύθυνσης λ και λ αντίστοιχα, να αποδείξετε ότι α β λ λ.
ΘΕΜΑ Α ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΙΟΥ-ΙΟΥΝΙΟΥ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ο δείγμα Α. Αν α, β δύο διανύσματα του επιπέδου με συντελεστές διεύθυνσης λ και λ αντίστοιχα, να αποδείξετε ότι α β λ λ.
Τάξη A Μάθημα: Γεωμετρία
 Τάξη A Μάθημα: Γεωμετρία Η Θεωρία σε Ερωτήσεις Ερωτήσεις Κατανόησης Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Περιεχόμενα Τρίγωνα Α. Θεωρία-Αποδείξεις Σελ.2 Β. Θεωρία-Ορισμοί..Σελ.9 Γ. Ερωτήσεις Σωστού
Τάξη A Μάθημα: Γεωμετρία Η Θεωρία σε Ερωτήσεις Ερωτήσεις Κατανόησης Επαναληπτικά Θέματα Επαναληπτικά Διαγωνίσματα Περιεχόμενα Τρίγωνα Α. Θεωρία-Αποδείξεις Σελ.2 Β. Θεωρία-Ορισμοί..Σελ.9 Γ. Ερωτήσεις Σωστού
Φυλλάδιο 1 - Σημεία Προσοχής στις Παραγράφους 1.1, 1.2 και 1.3
 Φυλλάδιο 1 - Σημεία Προσοχής στις Παραγράφους 1.1, 1.2 και 1.3 1. Σπάμε ένα Διάνυσμα Έστω ότι έχουμε ένα διάνυσμα. Τότε αυτό μπορούμε να το σπάσουμε σε δύο (ή περισσότερα), παρεμβάλλοντας ανάμεσα στα γράμματα
Φυλλάδιο 1 - Σημεία Προσοχής στις Παραγράφους 1.1, 1.2 και 1.3 1. Σπάμε ένα Διάνυσμα Έστω ότι έχουμε ένα διάνυσμα. Τότε αυτό μπορούμε να το σπάσουμε σε δύο (ή περισσότερα), παρεμβάλλοντας ανάμεσα στα γράμματα
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου. 4 ο ΘΕΜΑ. Εκφωνήσεις Λύσεις των θεμάτων. Έκδοση 1 η (19/11/2014)
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου 4 ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (9//4) Θέματα 4 ης Ομάδας Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP_4_866 [παράγραφος
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου 4 ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (9//4) Θέματα 4 ης Ομάδας Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP_4_866 [παράγραφος
ΚΕΦΑΛΑΙΟ 8 ο ΟΜΟΙΟΤΗΤΑ
 ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
ΟΜΟΙΟΤΗΤΑ Ορισμός: Δύο ευθύγραμμα σχήματα ονομάζονται όμοια, αν έχουν τις πλευρές τους ανάλογες και τις γωνίες που σχηματίζονται από ομόλογες πλευρές τους ίσες μία προς μία. ΚΡΙΤΗΡΙΑ ΟΜΟΙΟΤΗΤΑΣ ΤΡΙΓΩΝΩΝ
Γιώργος Νάνος Φυσικός MSc ΕΡΩΤΗΣΕΙΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΘΕΩΡΙΑΣ ΑΣΚΗΣΕΙΣ & ΠΡΟΒΛΗΜΑΤΑ. Μαθηματικά. Θετικής & Τεχνολογικής Κατεύθυνσης.
 Φυσικός MSc ΕΡΩΤΗΣΕΙΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΘΕΩΡΙΑΣ ΑΣΚΗΣΕΙΣ & ΠΡΟΒΛΗΜΑΤΑ Μαθηματικά Θετικής & Τεχνολογικής Κατεύθυνσης Β Ενιαίου Λυκείου Μαθηματικά Κατεύθυνσης B Λυκείου Περιεχόμενα ΚΕΦΑΛΑΙΟ : Διανύσματα Η θεωρία
Φυσικός MSc ΕΡΩΤΗΣΕΙΣ ΠΑΡΑΤΗΡΗΣΕΙΣ ΘΕΩΡΙΑΣ ΑΣΚΗΣΕΙΣ & ΠΡΟΒΛΗΜΑΤΑ Μαθηματικά Θετικής & Τεχνολογικής Κατεύθυνσης Β Ενιαίου Λυκείου Μαθηματικά Κατεύθυνσης B Λυκείου Περιεχόμενα ΚΕΦΑΛΑΙΟ : Διανύσματα Η θεωρία
Ασκήσεις Πράξεις ιανυσµάτων
 Ασκήσεις Πράξεις ιανυσµάτων 1 ίνονται τα διανύσµατα α,, x, y για τα οποία ισχύουν: x+ y= α+ 4 και 4x y= α+ Nδο τα διανύσµατα x, y είναι οµόρροπα Αν ισχύει η ισότητα MA+ 5ΡΑ = 3ΡΜ+ ΡΒ 4ΓΜ νδο τα σηµεία
Ασκήσεις Πράξεις ιανυσµάτων 1 ίνονται τα διανύσµατα α,, x, y για τα οποία ισχύουν: x+ y= α+ 4 και 4x y= α+ Nδο τα διανύσµατα x, y είναι οµόρροπα Αν ισχύει η ισότητα MA+ 5ΡΑ = 3ΡΜ+ ΡΒ 4ΓΜ νδο τα σηµεία
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Θέμα 2 ο (39) -2- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β Λυκείου -3- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤA ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Θέμα 2 ο (39) -2- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β Λυκείου -3- Τράπεζα θεμάτων Μαθηματικών προσανατολισμού Β
και 2, 2 2 είναι κάθετα να βρείτε την τιμή του κ. γ) Αν στο τρίγωνο ΑΒΓ επιπλέον ισχύει Α(3,1), να βρείτε τις συντεταγμένες των κορυφών του Β και Γ.
 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ) 8556 ΘΕΜΑ Δίνονται τα διανύσματα και με, και, 3 α) Να βρείτε το εσωτερικό γινόμενο β) Αν τα διανύσματα γ) Να βρείτε το μέτρο του διανύσματος 8558 ΘΕΜΑ
Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ) 8556 ΘΕΜΑ Δίνονται τα διανύσματα και με, και, 3 α) Να βρείτε το εσωτερικό γινόμενο β) Αν τα διανύσματα γ) Να βρείτε το μέτρο του διανύσματος 8558 ΘΕΜΑ
Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Τρίτη 27 Δεκεμβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ 18/1/016 ΕΩΣ 05/01/017 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη 7 Δεκεμβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Αν ( xy, )
ΑΠΟ 18/1/016 ΕΩΣ 05/01/017 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Τρίτη 7 Δεκεμβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α1. Αν ( xy, )
Λέγεται κάθε προσανατολισμένη ευθεία x x στην οποία ορίζουμε ως αρχή ένα σημείο. Ο και το μοναδιαίο διάνυσμα i ( i = 1)
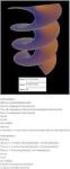 α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
Τράπεζα συναρτήσει των διανυσμάτων α,β,γ. Μονάδες 13 β) να αποδείξετε ότι τα σημεία Α, Β, Γ είναι συνευθειακά. Μονάδες 12
 Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
Τράπεζα 0- Πολλαπλασιασμός αριθμού με διάνυσμα.58 Θεωρούμε τα διανύσματα α,β,γ και τυχαίο σημείο Ο. Αν α β 5γ, α 3β 4γ και 3α β 6γ, τότε: α) να εκφράσετε τα διανύσματα, συναρτήσει των διανυσμάτων α,β,γ.
Σημειώσεις Μαθηματικών 1
 Σημειώσεις Μαθηματικών 1 Διανύσματα Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Διανύσματα 3.1 Έννοια διανύσματος Ορισμός 1 Ονομάζουμε Διάνυσμα ΑΒ ένα προσανατολισμένο ευθύγραμμο τμήμα ΑΒ με αρχή το Α και πέρας
Σημειώσεις Μαθηματικών 1 Διανύσματα Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Διανύσματα 3.1 Έννοια διανύσματος Ορισμός 1 Ονομάζουμε Διάνυσμα ΑΒ ένα προσανατολισμένο ευθύγραμμο τμήμα ΑΒ με αρχή το Α και πέρας
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ. 1. Δίνεται τετράγωνο ΑΒΓΔ.Σε καθεμία από τις παρακάτω περιπτώσεις να βρείτε το άθροισμα
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ 1. Δίνεται τετράγωνο ΑΒΓΔ.Σε καθεμία από τις παρακάτω περιπτώσεις να βρείτε το άθροισμα 2. Να γράψετε ως ένα διάνυσμα τα παρακάτω αθροίσματα :
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ 1. Δίνεται τετράγωνο ΑΒΓΔ.Σε καθεμία από τις παρακάτω περιπτώσεις να βρείτε το άθροισμα 2. Να γράψετε ως ένα διάνυσμα τα παρακάτω αθροίσματα :
Συνοπτική θεωρία. Οι σημαντικότερες αποδείξεις. Ερωτήσεις αντικειμενικού τύπου. Ασκήσεις. Διαγωνίσματα
 Γ Ε Ω Μ Ε Τ Ρ Ι Α Β Λ Υ Κ Ε Ι Ο Υ Συνοπτική θεωρία Οι σημαντικότερες αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα Μαθηματικός Περιηγητής 1 ΚΕΦΑΙΑΟ 9 ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
Γ Ε Ω Μ Ε Τ Ρ Ι Α Β Λ Υ Κ Ε Ι Ο Υ Συνοπτική θεωρία Οι σημαντικότερες αποδείξεις Ερωτήσεις αντικειμενικού τύπου Ασκήσεις Διαγωνίσματα Μαθηματικός Περιηγητής 1 ΚΕΦΑΙΑΟ 9 ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ. 3 2 x. β)
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
Γεωμετρία Βˊ Λυκείου. Κεφάλαιο 9 ο. Μετρικές Σχέσεις
 Γεωμετρία Β Λυκείου Κεφάλαιο 9 Γεωμετρία Βˊ Λυκείου Κεφάλαιο 9 ο Μετρικές Σχέσεις ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Μετρικές σχέσεις ονομάζουμε τις σχέσεις μεταξύ των μέτρων των στοιχείων
Γεωμετρία Β Λυκείου Κεφάλαιο 9 Γεωμετρία Βˊ Λυκείου Κεφάλαιο 9 ο Μετρικές Σχέσεις ΚΕΦΑΛΑΙΟ 9 ο ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΣΕ ΟΡΘΟΓΩΝΙΑ ΤΡΙΓΩΝΑ Μετρικές σχέσεις ονομάζουμε τις σχέσεις μεταξύ των μέτρων των στοιχείων
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του
 ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 4ο Το Θεώρημα του Θαλή και οι Συνέπειές του 198 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α. Αν ΑΔ ΒΓ, ΕΔ ΑΒ τότε το τρίγωνο
Θέματα ενδοσχολικών εξετάσεων Γεωμετρίας Β Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΓΕΩΜΕΤΡΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός Σύμβουλος Μαθηματικών Μαθηματικός Περιηγητής 1 ΠΡΟΛΟΓΟΣ Η συλλογή των θεμάτων
Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση ) ένα σημείο εκτός αυτής. Θέλουμε y (1)
 7 ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ Απόσταση Σημείου από Ευθεία Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση M ( x, y ) ένα σημείο εκτός αυτής Θέλουμε y να υπολογίσουμε την απόσταση d( M, ε) του ε σημείου M από
7 ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ Απόσταση Σημείου από Ευθεία Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση M ( x, y ) ένα σημείο εκτός αυτής Θέλουμε y να υπολογίσουμε την απόσταση d( M, ε) του ε σημείου M από
1.5 ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ.. ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Αν είναι δυο μη μηδενικά διανύσματα τότε ονομάζουμε εσωτερικό γινόμενο των και τον αριθμό : όπου φ είναι η γωνία των
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ.. ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Αν είναι δυο μη μηδενικά διανύσματα τότε ονομάζουμε εσωτερικό γινόμενο των και τον αριθμό : όπου φ είναι η γωνία των
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
 ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
ΙΑΝΥΣΜΑΤΑ. Σ Λ + α = α
 Κεφάλαιο 3ο: ΙΑΝΥΜΑΤΑ Ερωτήσεις του τύπου «ωστό-άθος» 1. * Αν α =, τότε α =. 2. * Αν α, µη µηδενικά διανύσµατα και θ η γωνία τους, τότε 0 θ π 3. * Ισχύει α + 0 = 0 + α = α 4. * Κάθε διάνυσµα µπορεί να
Κεφάλαιο 3ο: ΙΑΝΥΜΑΤΑ Ερωτήσεις του τύπου «ωστό-άθος» 1. * Αν α =, τότε α =. 2. * Αν α, µη µηδενικά διανύσµατα και θ η γωνία τους, τότε 0 θ π 3. * Ισχύει α + 0 = 0 + α = α 4. * Κάθε διάνυσµα µπορεί να
Πολλαπλασιασμός αριθμού με διάνυσμα
 Μαθηματικά Προσανατολισμού Β Λυκείου Επανάληψη Χριστουγέννων Αφού κάνετε μια επανάληψη στο πρώτο κεφάλαιο και θυμηθείτε όλους τους τύπους και τις μεθοδολογίες, να λύσετε τις παρακάτω ασκήσεις από την τράπεζα
Μαθηματικά Προσανατολισμού Β Λυκείου Επανάληψη Χριστουγέννων Αφού κάνετε μια επανάληψη στο πρώτο κεφάλαιο και θυμηθείτε όλους τους τύπους και τις μεθοδολογίες, να λύσετε τις παρακάτω ασκήσεις από την τράπεζα
Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος
 Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ 1. Δίνεται τετράγωνο ΑΒΓΔ.Σε καθεμία από τις παρακάτω περιπτώσεις να βρείτε το άθροισμα.
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ 1. Δίνεται τετράγωνο ΑΒΓΔ.Σε καθεμία από τις παρακάτω περιπτώσεις να βρείτε το άθροισμα.
β = (9, x) να είναι ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια ( ) ΤΑΞΗ...Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΣΗΣ...
 Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ
 Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
Ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 015-016 ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΕΠΙΜΕΛΕΙΑ ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ ΚΕΦΑΛΑΙΟ 9 Ο : ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ ΟΡΘΕΣ ΠΡΟΒΟΛΕΣ Το τμήμα ΒΔ λέγεται προβολή του.. πάνω στην Το τμήμα
ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ
 ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ 1. Α. Έστω x, y και x, y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. i. Να εκφράσετε (χωρίς απόδειξη) το εσωτερικό γινόμενο των διανυσμάτων και συναρτήσει των συντεταγμένων τους.
ΠΡΩΤΟ ΘΕΜΑ ΕΞΕΤΑΣΕΩΝ 1. Α. Έστω x, y και x, y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. i. Να εκφράσετε (χωρίς απόδειξη) το εσωτερικό γινόμενο των διανυσμάτων και συναρτήσει των συντεταγμένων τους.
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2018 A ΦΑΣΗ ΜΑΘΗΜΑΤΙΚΑ
 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν α= ( x,y ), β= ( x,y) γ= x,y α β+ γ =
ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ημερομηνία: Παρασκευή 5 Ιανουαρίου 08 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν α= ( x,y ), β= ( x,y) γ= x,y α β+ γ =
ΦΑΣΜΑ GROUP προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 Σύγχρονο www.fasma.fro.gr ΦΑΣΜΑ GROUP προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. Μαθητικό Φροντιστήριο Κατά το πέρας της εξέτασης οι λύσεις θα αναρτηθούν στο και στο site του φροντιστηρίου. 5ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ
Σύγχρονο www.fasma.fro.gr ΦΑΣΜΑ GROUP προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. Μαθητικό Φροντιστήριο Κατά το πέρας της εξέτασης οι λύσεις θα αναρτηθούν στο και στο site του φροντιστηρίου. 5ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ
Επαναληπτικά συνδυαστικα θέµατα
 Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
Οι γωνίες και που ονομάζονται «εντός εναλλάξ γωνίες» και είναι ίσες. «εντός-εκτός και επί τα αυτά μέρη γωνίες» και είναι ίσες.
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΙΑΝΥΣΜΑΤΑ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. Τι ονοµάζουµε διάνυσµα; αλφάβητου επιγραµµισµένα µε βέλος. για παράδειγµα, Τι ονοµάζουµε µέτρο διανύσµατος;
 ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ 4 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Κάθε διάνυσμα του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή : i j όπου i, j μοναδιαία διανύσματα με κοινή αρχή το
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ 4 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Κάθε διάνυσμα του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή : i j όπου i, j μοναδιαία διανύσματα με κοινή αρχή το
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Φ1 : ΔΙΑΝΥΣΜΑΤΑ ΕΠΙΜΕΛΕΙΑ: ΓΙΑΝΝΗΣ ΧΡΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 Φ1 : ΔΙΑΝΥΣΜΑΤΑ ΕΠΙΜΕΛΕΙΑ: ΓΙΑΝΝΗΣ ΧΡΑΣ 01-01 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΘΕΜΑ Α -ΘΕΩΡΙΑ -ΣΩΣΤΟ-ΛΑΘΟΣ -ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΘΕΜΑ Β - ΑΣΚΗΣΕΙΣ ΘΕΜΑ Γ - ΑΣΚΗΣΕΙΣ ΘΕΜΑ Δ - ΑΣΚΗΣΕΙΣ
Φ1 : ΔΙΑΝΥΣΜΑΤΑ ΕΠΙΜΕΛΕΙΑ: ΓΙΑΝΝΗΣ ΧΡΑΣ 01-01 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΘΕΜΑ Α -ΘΕΩΡΙΑ -ΣΩΣΤΟ-ΛΑΘΟΣ -ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΘΕΜΑ Β - ΑΣΚΗΣΕΙΣ ΘΕΜΑ Γ - ΑΣΚΗΣΕΙΣ ΘΕΜΑ Δ - ΑΣΚΗΣΕΙΣ
Επιμέλεια: Σακαρίκος Ευάγγελος 108 Θέματα - 24/1/2015
 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Επιμέλεια: Σακαρίκος Ευάγγελος 08 Θέματα - 4//05 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσαν. Κεφάλαιο
Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Επιμέλεια: Σακαρίκος Ευάγγελος 08 Θέματα - 4//05 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσαν. Κεφάλαιο
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Β.1.8. Παραπληρωματικές και Συμπληρωματικές γωνίες Κατά κορυφήν γωνίες
 Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
α και γ και να 3. Δίνεται τραπέζιο ΟΑΒΓ με ΟΑ = α, ΟΓ =γ και ΓΒ= 2ΟΑ αποδείξετε ότι ΓΑ = 2ΕΔ ΛΥΣΗ Έχουμε: ΓΑ = ΓΟ + ΟΑ = γ + α
 3 Δίνεται τραπέζιο ΟΑΒΓ με ΟΑ = α, ΟΓ =γ και ΓΒ= ΟΑ Αν Δ και Ε είναι τα μέσα των ΑΒ και ΒΓ αντίστοιχα, να βρείτε τα διανύσματα ΓΑ, ΑΒ και ΕΔ συναρτήσει των α και γ και να αποδείξετε ότι ΓΑ = ΕΔ ΛΥΣΗ Έχουμε:
3 Δίνεται τραπέζιο ΟΑΒΓ με ΟΑ = α, ΟΓ =γ και ΓΒ= ΟΑ Αν Δ και Ε είναι τα μέσα των ΑΒ και ΒΓ αντίστοιχα, να βρείτε τα διανύσματα ΓΑ, ΑΒ και ΕΔ συναρτήσει των α και γ και να αποδείξετε ότι ΓΑ = ΕΔ ΛΥΣΗ Έχουμε:
δίου ορισμού, μέσου του τύπου εξαρτημένης μεταβλητής του πεδίου τιμών που λέγεται εικόνα της f για x α f α.
 3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
3.1 Η έννοια της συνάρτησης Ορισμοί Συνάρτηση f από ένα συνόλου Α σε ένα σύνολο Β είναι μια αντιστοιχία των στοιχείων του Α στα στοιχεία του Β, κατά την οποία κάθε στοιχείο του Α αντιστοιχεί σε ένα μόνο
1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: ii. Το ύψος ΒΚ
 Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
π (α,β). Έστω τα διανύσματα π (α,β) να βρεθούν:
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΚΑΤΕΥΘΥΝΣΗΣ 1. Για τα διανύσματα α, β δίνεται ότι α =1, β = και u α β, v α - β.να υπολογίσετε: π (α,β). Έστω τα διανύσματα α. το εσωτερικό γινόμενο α β β. τα μέτρα u, v των διανυσμάτων
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΚΑΤΕΥΘΥΝΣΗΣ 1. Για τα διανύσματα α, β δίνεται ότι α =1, β = και u α β, v α - β.να υπολογίσετε: π (α,β). Έστω τα διανύσματα α. το εσωτερικό γινόμενο α β β. τα μέτρα u, v των διανυσμάτων
24 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ
 4 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=ΒΓ. Φέρνουμε το ΑΕ ΒΓ και έστω Ζ,Η τα μέσα των ΔΓ και ΑΒ αντίστοιχα. Ν.δ.ο. α) το ΖΓΒΗ είναι ρόμβος ( 9 μον.) β) ΗΖ=ΗΕ ( 8 μον.) γ)
4 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ Δίνεται παραλληλόγραμμο ΑΒΓΔ με ΑΒ=ΒΓ. Φέρνουμε το ΑΕ ΒΓ και έστω Ζ,Η τα μέσα των ΔΓ και ΑΒ αντίστοιχα. Ν.δ.ο. α) το ΖΓΒΗ είναι ρόμβος ( 9 μον.) β) ΗΖ=ΗΕ ( 8 μον.) γ)
Μαθηματικά προσανατολισμού Β Λυκείου. ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ α φάση. Διανύσματα
 Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
Διαίρεση ευθυγράμμου τμήματος σε ν ίσα τμήματα
 ΜΕΡΟΣ Β. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ 7. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ Ίσα τμήματα μεταξύ παραλλήλων ευθειών Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε
ΜΕΡΟΣ Β. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ 7. ΛΟΓΟΣ ΕΥΘΥΓΡΑΜΜΩΝ ΤΜΗΜΑΤΩΝ Ίσα τμήματα μεταξύ παραλλήλων ευθειών Αν παράλληλες ευθείες ορίζουν ίσα τμήματα σε μια ευθεία, τότε θα ορίζουν ίσα τμήματα και σε οποιαδήποτε
Μαθηµατικά Κατεύθυνσης Β Λυκείου Ευθεία. Ασκήσεις Ευθεία
 Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
