|
|
|
- Λυσάνδρα Δασκαλοπούλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Μαρινα Μπομπολακη Κανονικη Μορϕη Jordan Πτυχιακη Εργασια Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Μαρτίου 27
2
3 Εισηγητης: Ευστράτιος Πρασίδης Επιτροπη Βασίλειος Μεταϕτσής Νικόλαος Παπαλεξίου
4
5 Θα ήθελα να ευχαριστήσω θερμά τον επιβλέποντα καθηγητή μου κύριο Ευστράτιο Πρασίδη, για την πολύτιμη βοήθεια και καθοδήγηση στην εκπόνηση της παρούσας πτυχιακής. Με τις υποδείξεις και την προσεκτική θεώρηση της εργασίας και τον πολύτιμο χρόνο που μου διέθεσε, κατάϕερα να προχωρήσω στην περάτωση αυτής της πτυχιακής.
6
7 Περιεχόμενα Εισαγωγή ix Βασικές Εννοιες Διανυσματικοί Χώροι 2 Ιδιοτιμές και Ιδιοδιανύσματα 6 2 Κανονική Μορϕή Jordan 5 Εισαγωγή στην Κανονική Μορϕή 5 2 Παραδείγματα 6 3 Αλγόριθμος Εύρεσης Κανονικής Μορϕής Jordan 27 4 Εϕαρμογές Δυνάμεις Πινάκων Παράδειγματα Το εκθετικό ενός πίνακα 32 Βιβλιογραϕία 33
8
9 Εισαγωγή Οι πίνακες χρησιμοποιούνται στην μοντελοποίηση πολλών ϕαινομένων. Ειδικότερα ϕαίνεται ότι είναι τα καταλληλότερα εργαλεία για την μελέτη μη-αντιμεταθετικών ϕαινομένων. Σ αυτήν την περίπτωση, πολλές ϕορές, είναι απαραίτητο να προβλέψουμε την πορεία του ϕαινομένου στο άπειρο (χρόνο ή χώρο). Σ αυτές τις περιπτώσεις θα θέλαμε να ξέρουμε τις ιδιότητες μεγάλων δυνάμεων του πίνακα. Ενας εύκολος τρόπος είναι να διαγωνοποιήσουμε τον πίνακα και να υπολογίσουμε τις δυνάμεις του. Δυστυχώς δεν είναι όλοι οι πίνακες διαγωνίσιμοι. Ενα άλλος τρόπος είναι να διαγωνοποιήσουμε τον πίνακα έτσι ώστε στην διαγώνιο να μην έχουμε απαραίτητα στοιχεία του σώματος αλλά block πίνακες. Αυτό μπορεί να γίνει για όλους του πίνακες κι αυτή είναι η κανονική μορϕή Jordan. Ο σκοπός αυτής της εργασίας είναι η κατασκευή και η μελέτη των ιδιοτήτων της κανονικής μορϕής Jordan ενός πίνακα. Η έμϕαση είναι στην θεωρητική θεμελίωση της κατασκευής καθώς και ο αλγόριθμος με τον οποίο μπορούμε να καταλήξουμε στην κανονική μορϕή. Στο τέλος δίνουμε κάποιες βασικές εϕαρμογές για τον υπολογισμό δυνάμεων πινάκων χρησιμοποιώντας την κατασκευή μας. Μ. Μπομπολάκη, Σάμος 27.
10
11 Κεϕάλαιο Βασικές Εννοιες Διανυσματικοί Χώροι Εστω K = R, C. Θα μελετήσουμε διανυσματικούς χώρους πάνω από το K και γραμμικές συναρτήσεις μεταξύ τους. Παραδείγματα διανυσματικών χώρων είναι ο K n, ο χώρος των K-διανυσμάτων με n-συντεταγμένες, ο P n (K), ο χώρος των πολυωνύμων με συντελεστές στο K, βαθμού n (n =,,... ), ο M m,n (K), ο χώρος των m n-πινάκων με όρους στο K, ο χώρος C (K) των συνεχών συναρτήσεων από το K στον εαυτό του, ανάμεσα στους άλλους. Εστω V ένας K-διανυσματικός χώρος. Ενα υποσύνολο U του V λέγεται υπόχωρος του V, αν είναι K-διανυσματικός χώρος ως προς τις πράξεις του V. Ο υπόχωρος U συμβολίζεται U V. Μερικά παραδείγματα υπόχωρων είναι τα παρακάτω: (i) Ο K-διανυσματικός χώρος V είναι υπόχωρος του εαυτού του. (ii) Αν V είναι ένας K-διανυσματικός χώρος, το σύνολο {}, όπου = V, είναι υπόχωρος του V και λέγεται μηδενικός ή τετριμμένος υπόχωρος του V. (iii) Κάθε υπόχωρος του K-διανυσματικού χώρου V είναι μη κενό σύνολο. Από αυτά που αναϕέραμε παραπάνω συμπεραίνουμε ότι ένα υποσύνολο του V για να είναι υπόχωρος πρέπει να περιέχει το μηδενικό στοιχείο του V. Αυτό συμβαίνει γιατί, αϕού + u = u για όλα τα στοιχεία του V, θα ισχύει και για τα στοιχεία του υποχώρου. (iv) το σύνολο A = {(a, )/a R} αποτελεί υπόχωρο του R-διανυσματικού χώρου R 2. (v) Το επόμενο κριτήριο προσδιορίζει τους υπόχωρους ενός διανυσματικού χώρου. Το Κριτήριο Υπόχωρου Ι μας λέει ότι αν V ένας K-διανυσματικός χώρος. Ενα υποσύνολο U του V είναι υπόχωρος του V αν και μόνο αν, για κάθε κ K και για όλα τα στοιχεία u, w του U, ισχύει ότι κu U, u + w U
12 2 Βασικες Εννοιες Εστω U και W δύο υπόχωροι του K-διανυσματικού χώρου V. Το άθροισμα U + W των U και W ορίζεται να είναι το εξής: U + W = {u + w/u U, w W } Το άθροισμα U +W είναι υπόχωρος του V. Αν U, U 2,..., U n είναι υπόχωροι του V, τότε το άθροισμα U U n = {u u n /u i U, i n} είναι υπόχωρος του V. Γενικότερα, αν {U i } i I είναι μία οικογένεια υπόχωρων K-διανυσματικού χώρου V, τότε U i = {u i +u i u is /u ij U ij, πεπερασμένο άθροισμα με j s, s N} i I αποτελεί υπόχωρο του V. Το άθροισμα U + W είναι ευθύ αν U W = {} και συμβολίζεται U W. Επίσης, γενικεύουμε τον ορισμό σε ευθύ άθροισμα περισσότερων χώρων. Εστω U, U 2,..., U s πεπερασμένου πλήθους υπόχωροι του V, για s N. Το άθροισμα των U + U U s, λέγεται ευθύ και συμβολίζεται U U 2... U s, αν U i (U U i + U i U s ) = {}, για i s. Παρατήρηση.. Εστω U, U 2,..., U s υπόχωροι του V. Τότε το άθροισμα των υποχώρων είναι ευθύ αν και μόνο αν κάθε στοιχείο u του αθροίσματος έχει μοναδική ανάλυση σε άθροισμα u = u + u u s, όπου u i U i, i s. Να θυμηθούμε ότι αν f : V W είναι μια γραμμική συνάρτηση τότε ο πυρήνας της f ορίζεται ως Ker(f) = {v V : f(v) = W } = f ( W ) και είναι υποχώρος του V. Επίσης η εικόνα Im(f) = f(v ) είναι υποχώρος του W. (i) Ο f ονομάζεται μονομορϕισμός αν είναι -. Εχουμε ότι ο f είναι μονομορ- ϕισμός αν και μόνο αν Ker(f) = { V }. (ii) Ο f ονομάζεται επιμορϕισμός αν είναι επί. Εχουμε ότι ο f είναι επιμορϕισμός αν και μόνο αν Im(f) = W. (iii) Ο f ονομάζεται ισομορϕισμός αν είναι μονομορϕισμός και επιμορϕισμός, δηλαδή αν είναι αντιστρέψιμη γραμμική συνάρτηση. Αν υπάρχει ισομορϕισμός μεταξύ των V και W τότε οι χώροι ονομάζονται ισόμορϕοι και συμβολίζονται με V = W. Επίσης, σε αυτήν την περίπτωση ο f είναι γραμμικός ισομορϕισμός. (iv) Αν ο W είναι υπόχωρος του V τότε η εμϕύτευση i : W V είναι ένας μονομορϕισμός διανυσματικών χώρων. Ορισμός.2. Εστω u, u 2,..., u n στοιχεία του K-διανυσματικού χώρου V.
13 Διανυσματικοι Χωροι 3 (i) Ενας γραμμικός συνδυασμός των u, u 2,..., u n είναι μια παράσταση της μορϕής k u + k 2 u k n u n όπου k, k 2,..., k n K. (ii) Τα u, u 2,..., u n λέγονται γραμμικά ανεξάρτητα αν k u + k 2 u k n u n = = k = k 2 = =. (iii) Τα u, u 2,..., u n λέγονται γραμμικά εξαρτημένα αν δεν είναι γραμμικά ανεξάρτητα, δηλαδή αν υπάρχουν u,..., u n όπου κάποιο k i έτσι ώστε k u + k 2 u k n u n =. (iv) Ενα πεπερασμένο υποσύνολο X του V αποτελούμενο από γραμμικά ανεξάρτητα στοιχεία λέγεται γραμμικά ανεξάρτητο υποσύνολο. Αν το X είναι άπειρο, τότε ονομάζεται γραμμικά ανεξάρτητο αν κάθε πεπερασμένο υποσύνολο του είναι γραμμικά ανεξάρτητο. Ενα υποσύνολο X του V που δεν είναι γραμμικά ανεξάρτητο ονομάζεται γραμμικά εξαρτημένο. (v) Η γραμμική θήκη ενός υποσυνόλου X V είναι το σύνολο των γραμμικών συνδυασμών των στοιχείων του X και συμβολίζεται με X. Επίσης ο X ονομάζεται ο χώρος που παράγεται από το X και είναι ο μικρότερος υπόχωρος του V που περιέχει το X. (vi) Ενας K-διανυσματικός χώρος V λέγεται πεπερασμένης διάστασης, αν υ- πάρχει ένα πεπερασμένο σύνολο που τον παράγει. Διαϕορετικά ο V λέγεται άπειρης διάστασης. Παρατήρηση.3. Για παράδειγμα οι χώροι K n, P n (K) (με n < ), M m,n (K) είναι πεπερασμένης διάστασης ενώ οι P (K) = {p(x)/p(x) K[x]} και C (K) είναι άπειρης διάστασης. Ορισμός.4. Μια βάση B ενός K-διανυσματικού χώρου V είναι ένα γραμμικά ανεξάρτητο υποσύνολο του V που παράγει τον V. Δηλαδή B είναι βάση του V αν είναι γραμμικά ανεξάρτητο και V = B. Παρατήρηση.5. Κάθε διανυσματικός χώρος (πεπερασμένα ή άπειρα παραγόμενος) περιέχει μια βάση. Παρατήρηση.6. Μερικές ιδιότητες των βάσεων είναι οι εξής: Αν ο V είναι ένας πεπερασμένης διάστασης K-διανυσματικός χώρος τότε θα έχουμε ότι: (i) Κάθε πεπερασμένο σύνολο του V που παράγει τον V περιέχει μία βάση του. Επίσης, η βάση είναι το μεγαλύτερο γραμμικά ανεξάρτητο υποσύνολο του V που παράγει τον V. (ii) Κάθε γραμμικά ανεξάρτητο πεπερασμένο υποσύνολο του V επεκτείνεται σε μία βάση του V. Επίσης, η βάση είναι το μικρότερο υποσύνολο του V που παράγει τον V και είναι υποχρεωτικά γραμμικά ανεξάρτητο. Ορισμός.7. Το πλήθος των στοιχείων μιας βάσης του K-διανυσματικού χώρου V πεπερασμένης διάστασης λέγεται διάσταση (dimension) του V ή K- διάσταση του V και συμβολίζεται dim K (V ) ή πιο απλά dim(v ), αν εννοείται το σώμα K. Αν ο χώρος V δεν έχει πεπερασμένη διάσταση τότε λέμε ότι η διάσταση του V είναι άπειρη και γράϕουμε dim K (V ) =.
14 4 Βασικες Εννοιες Παρατήρηση.8. Εστω ότι ο K-διανυσματικός χώρος V είναι πεπερασμένης διάστασης. Τότε: (i) Το μέγιστο πλήθος γραμμικά ανεξάρτητων στοιχείων του V ισούται με dim K (V ). (ii) Το ελάχιστο πλήθος στοιχείων που παράγει τον V είναι dim K (V ). (iii) Οποιοδήποτε γραμμικά ανεξάρτητο υποσύνολο του V με πλήθος στοιχείων ίσο με dim K (V ) αποτελεί μία βάση του V. (iv) Ενα υπόσυνολο του V που τον παράγει με πλήθος στοιχείων ίσο με dim K (V ) αποτελεί μία βάση του V. (v) Εστω W είναι υποχώρος του V, τότε dim(w ) dim(v ). Επίσης dim(w ) = dim(v ) αν και μόνο αν W = V. (vi) (Θεώρημα Διάστασης) Εστω V είναι ένας χώρος πεπερασμένης διάστασης και f : V W μια γραμμική συνάρτηση. Τότε: dim(im(f)) + dim(ker(f)) = dim(v ). (vii) Εστω U και W είναι υποχώροι του V, τότε dim(u + W ) = dim(u) + dim(w ) dim(u W ). (viii) Το άθροισμα U + U U s υποχώρων του V είναι ευθύ αν και μόνο αν dim(u + U U s ) = dim(u ) + dim(u 2 ) + + dim(u s ). (ix) (Ταξινόμηση Διανυσματικών Χώρων Πεπερασμένης Διάστασης) Εστω V και U δυο K-διανυσματικοί χώροι που είναι πεπερασμένα παραγόμενοι. Τότε: V = U dim(v ) = dim(u). Πιο συγκεκριμένα, αν dim(v ) = n τότε η επιλογή μιας διατεταγμένης βάσης ˆα καθορίζει έναν ισομορϕισμό cˆα : V K n που απεικονίζει ένα στοιχείο του V στις συντεταγμένες του ως προς την ˆα. Δηλαδή, V [V ] α ως προ τις συντεταγμένες του. Πόρισμα.9. Σύμϕωνα με το Θεώρημα Διάστασης που αναϕέραμε παραπάνω τα ακόλουθα είναι ισοδύναμα. Εστω f : V V μια γραμμική συνάρτηση. Τότε: (i) Η f είναι -. (ii) Η f είναι επί. (iii) Η f είναι ισομορϕισμός. Εστω A M m n (K). Η διάσταση του υπόχωρου του K m που παράγεται από τις γραμμές του A λέγεται βαθμίδα γραμμών (row rank) του A και η διάσταση του υπόχωρου του K n που παράγεται από τις στήλες του A λέγεται βαθμίδα στηλών (column rank) του A. Ισχύει ότι η βαθμίδα γραμμών ενός πίνακα A M m n (K)
15 Διανυσματικοι Χωροι 5 ισούται με τη βαθμίδα στηλών του. Η κοινή αυτή τιμή ισούται με τη βαθμίδα rank(a) του A. Εστω A M m,n (K). Τότε ο A ορίζει μια γραμμική συνάρτηση r A : K n K m, r A (v) = Av. Ισχύει και το αντίστροϕο. Εστω f : V U είναι μια γραμμική συνάρτηση και ˆα ( ˆβ) είναι μια διατεταγμένη βάση του V (U). Τότε υπάρχει ένας m n πίνακας A = (f : ˆα, ˆβ) έτσι ώστε το παρακάτω διάγραμμα μετατίθεται: V c ˆα f U c ˆβ K m r A K n όπου οι κάθετες συναρτήσεις είναι οι κανονικοί ισομορϕισμοί που ορίζονται από τις βάσεις. Παρατήρηση.. (i) Αν V f U f W είναι δυο γραμμικές συναρτήσεις τότε (gf : ˆα, ˆγ) = (g : ˆα, ˆβ)(gf : ˆβ, ˆγ) ως προς τις αντίστοιχες διατεταγμένες βάσεις. (ii) Η f είναι αντιστρέψιμη αν και μόνο αν ο αντίστοιχος πίνακας είναι αντιστρέψιμος για κάθε επιλογή διατεταγμένων βάσεων. (iii) rank(a) = dim(im(r A )). Δύο πίνακες A, A M m,n (K) για τους οποίους υπάρχουν αντιστρέψιμοι πίνακες S M m (K), T M n (K) έτσι ώστε: A = T AS, ονομάζονται ισοδύναμοι (equivalent). Δύο πίνακες A, A M n (K) για τους οποίους υπάρχει αντιστρέψιμος πίνακας S M n (K) έτσι ώστε: A = S AS λέγονται όμοιοι (similar). Είναι προϕανές ότι όμοιοι πίνακες είναι ισοδύναμοι. Επίσης, ισοδύναμοι πίνακες έχουν την ίδια βαθμίδα. Παρατήρηση.. (i) Δυο πίνακες είναι ισοδύναμοι αν και μόνο αν είναι πίνακες της ίδιας γραμμικής συνάρτησης ως προς διαϕορετικές διατεταγμένες βάσεις. (ii) Δυο πίνακες A, B είναι όμοιοι αν υπάρχει γραμμική συνάρτηση f : K n K n έτσι ώστε A = (f : ˆα, ˆα) και B = (f : ˆβ, ˆβ) για δυο διατεταγμένες βάσεις.
16 6 Βασικες Εννοιες 2 Ιδιοτιμές και Ιδιοδιανύσματα Στην υποενότητα αυτή θα εισάγουμε ορισμένες θεμελιώδεις έννοιες που θα μας χρειαστούν ώστε να κατανοήσουμε καλύτερα το επόμενο κεϕάλαιο. Θα ξεκινήσουμε δίνοντας τον ορισμό της ιδιοτιμής και του ιδιοδιανύσματος μιας γραμμικής απεικόνισης και στην συνέχεια θα δούμε ορισμένες ιδιότητες τους. Ορισμός.2. Εστω V ένας διανυσματικός χώρος και f : V V μια γραμμική απεικόνιση. Ενα στοιχείο λ K ονομάζεται ιδιοτιμή της f αν υπάρχει μη-μηδενικό u V τέτοιο ώστε: f(u) = λu. Το u λέμε ότι είναι ένα ιδιοδιάνυσμα της f που αντιστοιχεί στην ιδιοτιμή λ. Παρατήρηση.3. Εστω V ένας διανυσματικός χώρος επί του K και f : V V μια γραμμική απεικόνιση. Εστω λ K, τότε οι ακόλουθες ιδιότητες είναι ισοδύναμες: (i) Το λ είναι μια ιδιοτιμή της f. (ii) ker(f λ V ). (iii) Η f λ V δεν είναι αντιστρέψιμη. Με βάση τον ορισμό που δώσαμε παραπάνω, μπορούμε εύκολα να ορίσουμε την έννοια της ιδιοτιμής και του ιδιοδιανύσματος ενός πίνακα A. Ορίζουμε το λ να είναι ιδιοτιμή του A αν και μόνο αν το λ είναι ιδιοτιμή της γραμμικής συνάρτησης r A. Ετσι αν υποθέσουμε ότι A M n (K). Αν υπάρχει μη μηδενικό διάνυσμα x τέτοιο ώστε: Ax = λx, για κάποιο λ K. Θα λέμε ότι το λ είναι μια ιδιοτιμή του πίνακα A και το x ένα ιδιοδιάνυσμα του A που αντιστοιχεί στην λ. Παρατήρηση.4. Αν λ K και A M n (K) τότε προκύπτουν οι ακόλουθες ιδιότητες, οι οποίες είναι ισοδύναμες: (i) Το λ είναι μια ιδιοτιμή του A. (ii) Υπάρχει x K n, x, τέτοιο ώστε (A λi)x =. (iii) det(a λi) =. (iv) Ο A λi δεν είναι αντιστρέψιμος. Παρατήρηση.5. Από την τελευταία συνθήκη έχουμε ότι ο A δεν είναι α- ντιστρέψιμος αν και μόνο αν το είναι ιδιοτιμή του A. Ορισμός.6. Εστω f : V V μια γραμμική συνάρτηση του K-διανυσματικού χώρου V. Εστω V λ (f) = {u V : f(u) = λu} = ker(f λ V ) Αν V λ (f) δηλαδή το λ είναι ιδιοτιμή του f τότε ο V λ (f) λέγεται ιδιόχωρος του f για την ιδιοτιμή λ. Παρατήρηση.7. Αν λ λ 2, τότε V λ V λ2 = {}.
17 2 Ιδιοτιμες και Ιδιοδιανυσματα 7 Απόδειξη. Εστω f : V V και έστω u V λ V λ 2 ένα διάνυσμα. Αϕού το u V λ και u V λ2 θα έχω: f(u) = λ u () και f(u) = λ 2 u (2) Άρα από (), (2) αϕού τα πρώτα μέλη είναι ίσα θα είναι και τα δεύτερα, θα έχουμε: λ u = λ 2 u u(λ λ 2 ) = όμως γνωρίζουμε από την αρχική συνθήκη πως λ λ 2 άρα καταλήγουμε ότι u =. Αν A M n (K) ένας πίνακας, είδαμε πριν ότι οι ιδιοτιμές λ του A καθορίζονται από τη σχέση det(a λi) =. Αν A = (a ij ) και x είναι μια μεταβλητή, τότε a x a 2 a n a 2 a 22 x a 2n A xi =.... a n a n2 a nn x Η ορίζουσα det(a xi) είναι ένα πολυώνυμο στη μεταβλητή x με συντελεστές απο το K. Παρατηρούμε ότι το λ K είναι μια ιδιοτιμή του Α αν και μόνο αν είναι ρίζα του det(a xi). Το πολυώνυμο αυτό ονομάζεται χαρακτηριστικό και συμβολίζεται με χ A (x) = det(a xi). Παρατήρηση.8. Εστω A M n (K). Τότε: (i) χ A (x) = χ A t(x) όπου A t είναι ο ανάστροϕος του A. Συνεπώς, οι πίνακες A και A t έχουν τις ίδιες ιδιοτιμές. (ii) Το είναι ρίζα του χ A (x) αν και μόνο αν ο A δεν είναι αντιστρέψιμος. Πρόταση.9. Εστω A M n (K) και χ A (x) = ( ) n x n +a n x n +...+a. Τότε a = deta, a n = ( ) n T ra Απόδειξη. Για την πρώτη ισότητα έχουμε ότι a = χ A () = det(a I) = deta. Εστω A = (a ij ). Εχουμε ότι χ A (x) = (a x)(a 22 x) (a nn x) + β(x) όπου β(x) είναι ένα πολυώνυμο βαθμού το πολύ n 2. Στην παραπάνω ισότητα πολυωνύμων θεωρούμε τους συντελεστές του x n. Στο αριστερό μέλος είναι a n και στο δεξιό είναι ( ) n (a + a a nn ). Άρα a n = ( ) n (a + a a nn ) = ( ) n T ra Πρόταση.2. Αν οι A, B M n (K) είναι όμοιοι, τότε χ A (x) = χ B (x). Απόδειξη. Εστω ότι υπάρχει αντριστρέψιμος P M n (K) με B = P AP. Τότε θα έχουμε: χ B (x) = det(b xi) = det(p AP xi) = det(p (A xi)p ) = detp det(a xi)detp = det(a xi) = χ A (x).
18 8 Βασικες Εννοιες Η χρησιμότητα του θεωρήματος Caley-Hamilton για τις γραμμικές απεικονίσεις αλλά και για τους πίνακες είναι πολύ σημαντική. Για τις γραμμικές απεικονίσεις θα ισχύει το παρακάτω θεώρημα: Θεώρημα.2. (Caley-Hamilton) Εστω f : V V μια γραμμική απεικόνιση. Αν χ f (x) είναι το χαρακτηριστικό πολυώνυμο της f, τότε χ f (f) =. Απόδειξη. Αρκεί να δείξουμε ότι χ f (f)(u) = για κάθε u V. Εστω ένα u V με u (αν u = είναι προϕανές). Αϕού τα n + στοιχεία του V : u = u, u 2 = f(u),..., u n+ = f n (u) είναι γραμμικώς εξαρτημένα, έπεται ότι υπάρχει ένα ελάχιστο k > τέτοιο ώστε το u k+ να είναι γραμμικός συνδυασμός των u,..., u k. Καθώς το k είναι το ελάχιστο με αυτήν την ιδιότητα κανένα από τα u,..., u k δεν είναι γραμμικός συνδυασμός των προηγουμένων του, άρα αυτά είναι γραμμικώς ανεξάρτητα. Επίσης, για κάποια u k+ = a k u k a u, a,..., a k K. Επεκτείνουμε τα γραμμικώς ανεξάρτητα u,..., u k σε βάση â = (u,..., u k, v k+,..., v n ) του V. Παρατηρούμε ότι: ενώ: f(u ) = f(u) = u 2, f(u 2 ) = f 2 (u) = u 3,..., f(u k ) = f(f k 2 (u)) = u k f(u k ) = u k+ = a u + + a k u k έπεται ότι ο πίνακας (f : â) είναι της μορϕής ( A Γ B ), όπου A = και οι Β,Γ είναι κατάλληλοι πίνακες. Εχουμε ότι Αλλά a a 2 a a k M n (K). χ A (x) = ( ) k (x k a k x k a 2 x a ), χ f (x) = χ A (x)χ B (x) ( ) k χ A (f)(u) = f k (u) a k f k (u) a 2 f(u) a u = u k+ a k u k a 2 u 2 a u = Άρα χ f (f)(u) =. Από τα παραπάνω έπεται ότι χ f (f) =. Αντίστοιχα ισχύει το θεώρημα Caley-Hamilton για τους πίνακες. Φυσικά ο βασικός λόγος είναι ότι, για A M n (K), χ ra (x) = χ A (x). Θα δώσουμε μια ακόμη απόδειξη. Υπενθυμίζουμε ότι αν B = (b ij ) ένας n n πίνακας, τότε ο προσαρτημένος πίνακας adjb είναι ένας n n πίνακας του οποίου το στοιχείο στη θέση (i, j) είναι το ( ) i+j d ji όπου d ji είναι η ορίζουσα του (n ) (n ) πίνακα που προκύπτει απο τον Β αν διαγράψουμε την j γραμμή και την i στήλη. Η βασική ιδιότητα είναι ότι B(adjB) = (adjb)b = (detb)i.
19 2 Ιδιοτιμες και Ιδιοδιανυσματα 9 Θεώρημα.22. Εστω A M n, αν χ A (x) είναι το χαρακτηριστικό πολυώνυμο του Α τότε χ A (A) =. Απόδειξη. η Απόδειξη: Θεωρούμε μια γραμμική απεικόνιση f : V V, όπου V ένας διανυσματικός χώρος διάστασης n, και μια διατεταγμένη βάση â του V τέτοια ώστε A = (f : â). Τότε χ A (A) = (χ A (f) : â) και επειδή χ A (x) = χ f (x), από το θεώρημα του Caley-Hamilton για τις γραμμικές απεικονίσεις έχουμε ότι χ A (A) = (χ f (f) : â) =. 2η Απόδειξη: Θα δούμε και μια δεύτερη απόδειξη του θεωρήματος αυτού η οποία χρησιμοποιεί μόνο πίνακες. Εστω A M n (K). Απο τον ορισμό προκύπτει ότι τα στοιχεία του adj(a xi) είναι πολυώνυμα της μεταβλητής x βαθμού το πολύ n. Συνεπώς υπάρχουν πίνακες B i M n (K) τέτοιοι ώστε adj(a xi) = B n x n + B n 2 x n B x + B. Εστω ότι Εχουμε χ A (x) = ( ) n x n + a n x n + + a. (A xi)adj(a xi) = (det(a xi))i = (A xi)(b n x n + B n 2 x n Bo) = (( ) n x n + a n x n + + a )I. Εκτελώντας τις πράξεις και συγκρίνοντας συντελεστές των δυνάμεων του x στα δύο μέλη βλέπουμε ότι B n AB n B n 2 AB n 2 B n 3 AB B AB = ( ) n I = a n I = a n 2 I = a I = a I Πολλαπλασιάζουμε τα δύο μέλη της πρώτης ισότητας απο τις σχέσεις με A n, της δέυτερης με A n,, της προτελευταίας με A και της τελευταίας με I, και στην συνέχεια προσθέτουμε κατά μέλη. Τότε παίρνουμε δηλαδή χ A (A) =. = ( ) n A n + a n A n + + a A + a I, Εισάγουμε την σημασία του ελάχιστου πολυωνύμου ενός τετραγωνικού πίνακα Α (αντίστοιχα μιας γραμμικής απεικόνισης f), το οποίο όπως και το χαρακτηριστικό πολυώνυμο του Α, περιέχει πολλές πληροϕορίες για τον πίνακα Α (αντ. της f). Για κάθε τετραγωνικό πίνακα A M n (K) υπάρχει μοναδικό πολυώνυμο Q A (x) K[x] τέτοιο ώστε (i) Q A (x), Q A (A) = και ο πρώτος συντελεστής του Q A (x) είναι. (ii) Αν ϕ(x) K[x] και ϕ(a) =, τότε Q A (x) ϕ(x).
20 Βασικες Εννοιες Το πολυώνυμο αυτό λέγεται το Ελάχιστο Πολυώνυμο του Α. Παρατήρηση.23. Από αυτά που αναϕέραμε παραπάνω έπεται ότι το ελάχιστο πολυώνυμο μιας γραμμικής απεικόνισης f : V V, Q f (x), είναι το πολυώνυμο με το μικρότερο βαθμό και πρώτο συντελεστή που έχει την ιδιότητα Q f (f) =. Ανάλογα έχουμε ότι αν Α ένας τετραγωνικός πίνακας, A M n (K) τότε υπάρχει ένας ακέραιος ν τέτοιος ώστε οι πίνακες I ν, A, A 2,..., A ν είναι γραμμικά ανεξάρτητα στοιχεία του M n (K) ενώ οι I ν, A, A 2,..., A ν, A ν είναι γραμμικά εξαρτημένα. Άρα ο A ν γράϕεται με μοναδικό τρόπο ως γραμμικός συνδυασμός των I ν,..., A ν, έστω Το πολυώνυμο και έχει τις ιδιότητες A ν = α I ν + α A α ν A ν. Q(x) = α α x... α ν x ν + x ν M n [x] (i) Q(x), Q(A) = και ο πρώτος συντελεστής του Q(x) είναι. (ii) αν ϕ(x) K [x] και ϕ(a) =,τότε Q(x) ϕ(x). Άρα το Q(x) είναι το ελάχιστο πολυώνυμο του A. Οι παρακάτω προτάσεις θα μας βοηθήσουν να καταλάβουμε μερικές ιδιότητες του ελάχιστου πολυωνύμου. Πρόταση.24. Το ελάχιστο πολυώνυμο ενός τετραγωνικού πίνακα A M n (K) διαιρεί το χαρακτηριστικό πολυώνυμο του A, δηλαδή Q A (x) χ A (x). Απόδειξη. Εστω f(x) K[x] ένα πολυώνυμο που ικανοποιεί την σχέση f(a) =. Από την Ευκλείδεια διαίρεση θα έχουμε ότι f(x) = Q A (x)h(x) + u(x), deg u(x) < deg Q A (x). Θέλουμε να δείξουμε ότι u(x) =, οπότε θα ισχύει Q A (x) f(x). Εστω ότι ισχύει u(x), οπότε το u(x) είναι ένα θετικού βαθμού πολυώνυμο, που ικανοποιεί τη σχέση u(a) = f(a) Q A (A)h(A) = που έρχεται σε αντίθεση με τον ορισμό του ελάχιστου πολυωνύμου, αϕού deg u(x) < deg Q A (x) Επομένως θα έχουμε u(x) =. Θεώρημα.25. Τα πολυώνυμα Q f (x) και χ f (x) (αντίστοιχα Q A (x)και χ A (x)) έχουν τις ίδιες ρίζες. Απόδειξη. Αρκεί να δείξουμε ότι κάθε ρίζα του χ f (x) είναι και ρίζα του Q f (x). Εστω λ μια ρίζα του χ f (x). Δηλαδή το λ είναι μια ιδιοτιμή της f άρα υπάρχει u V με u και f(u ) = λu. Ξέρουμε ότι αν ψ(x) K[x] τότε (ψ(f))(u ) = ψ(λ)u. Άρα για ψ(x) = Q f (x) έχουμε (Q f (f))(u ) = Q f (λ)u. Αλλά Q f (f) =, άρα (Q f (f))(u ) = συνεπώς Q f (λ)u =. Ομως u, άρα Q f (λ) =, δηλαδή το λ είναι μια ρίζα του Q f (x). Οπότε δείξαμε ότι οι ιδιοτιμές της f είναι ακριβώς οι ρίζες του Q f (x).
21 2 Ιδιοτιμες και Ιδιοδιανυσματα Πρόταση.26. Ομοιοι πίνακες έχουν το ίδιο ελάχιστο πολυώνυμο. Απόδειξη. Εστω A, B M n (K) είναι όμοιοι πίνακες. Άρα υπάρχει αντιστρέψιμος πίνακας S M n (K) με S AS = B. Αν y(x) = a + a x + + a k x k K[x] τότε, επειδή B n = S A n S, για κάθε ϕυσικό αριθμό n, έχουμε ότι y(b) = a I n + a S AS + a 2 S A 2 S + + a k S A k S = a S I m S + a S AS + + a k S A k S = S (a I m + a A + + a k A k )S = S y(a)s. Άρα y(b) = αν και μόνο αν y(a) =. Συνεπώς Q A (x) = Q B (x). Παρατήρηση.27. Εστω f : V V μια γραμμική απεικόνιση και λ,..., λ k οι διακεκριμένες ιδιοτιμές της, τότε τα παρακάτω θα είναι ισοδύναμα: (i) Η f είναι διαγωνίσιμη (ii) V = V f (λ ) + + V f (λ k ) (iii) V = V f (λ ) V f (λ k ). Το παρακάτω θεώρημα θα μας δώσει ένα κριτήριο διαγωνισιμότητας μέσω του ελαχίστου πολυωνύμου. Θεώρημα.28. Εστω V ένας διανυσματικός χώρος πεπερασμένης διάστασης επί του M n (K) και f : V V μια γραμμική απεικόνιση. Τότε η f είναι διαγωνίσιμη αν και μόνο αν το ελάχιστο πολυώνυμο της f, Q f (x), είναι γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων, δηλαδή είναι της μορϕής Q f (x) = (x λ ) (x λ k ) όπου λ,..., λ k είναι οι διακεκριμένες ιδιοτιμές της f. Απόδειξη. Εστω ότι η f είναι διαγωνίσιμη και ότι λ,..., λ k είναι οι διακεκριμένες ιδιοτιμές της f. Τότε ξέρουμε ότι V = V (λ ) V (λ k ). Άρα αν u V τότε u = u +...+u k όπου u i V (λ i ), i k. Εστω ϕ(x) = (x λ ) (x λ k ) K[x]. Επειδή (f λ i V )(u i ) =, για κάθε i k, έπεται ότι ϕ(f)(u i ) = (f λ V ) (f λ i V ) (f λ k V )(u i ) = για κάθε i k. Άρα ϕ(f)(u) = ϕ(f)(u u k ) = ϕ(f)(u ) ϕ(f)(u k ) =, για κάθε u V. Συνεπώς Q f (x) ϕ(x). Αλλά ξέρουμε ότι οι ιδιοτιμές της f είναι ρίζες του Q f (x), άρα ϕ(x) Q f (x). Επειδή λοιπόν Q f (x) ϕ(x), ϕ(x) Q f (x) και τα πολυώνυμα ϕ(x), Q f (x) έχουν πρώτο συντελεστή, έπεται ότι ϕ(x) = Q f (x). Άρα δείξαμε ότι αν η f είναι διαγωνίσιμη, τότε το ελάχιστο πολυώνυμο της f είναι γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων. Εστω τώρα ότι Q f (x) = (x λ ) (x λ k ) όπου λ,..., λ k οι διακεκριμένες ιδιοτιμές της f. Θα δείξουμε ότι η f είναι διαγωνίσιμη, δηλαδή θα δείξουμε ότι υπάρχει μια βάση του V από ιδιοδιανύσματα της f. Η απόδειξη θα γίνει με επαγωγή ως προς µ = dim F V. Αν dim F V = τότε κάθε γραμμική απεικόνιση f : V V είναι διαγωνίσιμη. Εστω τώρα ότι µ > και ότι κάθε γραμμική απεικόνιση ρ : V V, της οποίας το ελάχιστο πολυώνυμο, Q ρ (x) είναι γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων και dim F V < µ, είναι διαγωνίσιμη. Θεωρούμε μια γραμμική απεικόνιση f : V V με dim F V = µ
22 2 Βασικες Εννοιες και Q f (x) = (x λ ) (x λ k ) όπου λ,..., λ k οι διακεκριμένες ιδιοτιμές της f. Εστω η γραμμική απεικόνιση f λ k V : V V και W = Im(f λ k V ). Ξέρουμε ότι µ = dim F ker(f λ k V ) + dim F Im(f λ k V ) = dim F V (λ k ) + dim F W. Επειδή η λ k είναι μια ιδιοτιμή της f, V (λ k ) = ker(f λ k V ) { V }, άρα dim F V (λ k ) >, συνεπώς dim F W < µ. Αν W = { V }, τότε f = λ k V, άρα η f είναι διαγωνίσιμη. Εστω ότι W { V }, τότε < dim F W < µ. Ο υπόχωρος W = Im(f λ k V ) του V είναι f- αναλλοίωτος, άρα Q fw (x) Q f (x). Συνεπώς το Q fw (x) είναι γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων και επειδή dim F W < µ, από την υπόθεση της επαγωγής έπεται ότι η f W : W W είναι διαγωνίσιμη. Άρα υπάρχει μια βάση B του W που αποτελείται από ιδιοδιανύσματα της f W, συνεπώς και της f. Θα δείξουμε ότι V = W V (λ k ). Επειδή dim F V = µ = dim F W +dim F V (λ k ) αρκεί να δείξουμε ότι W V (λ k ) = { V }. Πράγματι, έστω w W τότε w = (f λ k V )(u ), για κάποιο u V, αϕού W = Im(f λ k V ). Άρα (f λ V ) (f λ k V )(w ) = (f λ V ) (f λ k V )(f λ k V )(u ) = Q f (f)(u ) =. Συνεπώς Q fw (x) (x λ ) (x λ k ), που σημαίνει ότι η λ k δεν είναι ιδιοτιμή της f W, συνεπώς W V (λ k ) = { V }. Ετσι δείξαμε ότι V = W V (λ k ). Αν τώρα B 2 είναι μια βάση του V (λ k ), τότε ξέρουμε ότι B = B B 2 είναι μια βάση του V. Αλλά τα στοιχεία της B είναι ιδιοδιανύσματα της f. Άρα η f είναι διαγωνίσιμη. Πόρισμα.29. Ενας πίνακας A M n (K), είναι όμοιος προς ένα διαγώνιο πίνακα αν και μόνο αν το Q A (x) είναι της μορϕής Q A (x) = (x λ ) (x λ k ), όπου λ,..., λ k είναι οι διακεκριμένες ιδιοτιμές του Α. Απόδειξη. Ο Α είναι όμοιος προς ένα διαγώνιο πίνακα αν και μόνο αν υπάρχει μια βάση του K n από ιδιοδιανύσματα του Α, δηλαδή αν και μόνο αν η γ A είναι διαγωνίσιμη. Επιπλέον επειδή (γ A : Ê) = A ξέρουμε ότι Q A (x) = Q γa (x). Άρα από το Θεώρημα που αναϕέραμε προηγουμένως έπεται ότι ο Α είναι όμοιος ως προς ένα διαγώνιο πίνακα. Παρατήρηση.3. Εστω A M n (K). (i) Αν ο A έχει n διακριτές ιδιοτιμές, τότε ο A είναι διαγωνίσιμος. (ii) Ο K n έχει μια βάση από ιδιοδιανύσματα του A αν και μόνο αν ο A είναι διαγωνίσμος. (iii) Ο A είναι διαγωνίσιμος αν και μόνο αν K n = V λ... V λk, όπου λ i, i =,..., k είναι όλες οι διακριτές ιδιοτιμές του A. Τώρα, αν υποθέσουμε ότι έχουμε δύο τετραγωνικούς πίνακες A και B, τέτοιοι ώστε ο A B να είναι ένας τετραγωνικός πίνακας της μορϕής: [ ] A A B = B
23 2 Ιδιοτιμες και Ιδιοδιανυσματα 3 ο οποίος ονομάζεται το ευθύ άθροισμα των πινάκων Α και Β. Θεώρημα.3. Αν C = A B, όπου Α και Β είναι δυο τετραγωνικοί πίνακες τότε: (i) Τα χαρακτηριστικά πολυώνυμα των δύο αυτών πινάκων ικανοποιούν την παρακάτω σχέση: χ C (λ) = χ A (λ)χ B (λ) (ii) Το ελάχιστο πολυώνυμο Q C (λ) είναι το ελάχιστο κοινό πολλαπλάσιο των ελάχιστων πολυωνύμων Q A (λ) και Q B (λ), το οποίο είναι το μονικό πολυώνυμο Q C (λ) με τον μικρότερο βαθμό τέτοιο ώστε Q A (λ) Q C (λ) και Q B (λ) Q C (λ) Απόδειξη. Το πρώτο αποτέλεσμα προκύπτει από την εξής σχέση: det((λi A) (λi B)) = det(λi A)det(λI B). Για την δεύτερη σχέση, αν C = A B και f(λ) είναι κάποιο πολυώνυμο τότε: f(c) = f(a) = και f(b) = Q A (λ) f(λ) και Q B (λ) f(λ). Άρα Q A (λ) Q C (λ), Q B (λ) Q C (λ) θα είναι το ελάχιστο πολυώνυμο με αυτές τις ιδιότητες. Γενικότερα, έστω ένας τετραγωνικός πίνακας A, θα είναι σε διαγώνια block μορϕή αν ο Α έχει την μορϕή A A 2 A = A k όπου κάθε A i είναι τετραγωνικός πίνακας και οι διαγώνιοι των A i είναι πάνω στην διαγώνιο του πίνακα Α. Κάθε είναι ένας μηδενικός πίνακας κατάλληλου μεγέθους και κάθε A i ονομάζεται block του Α. Παρατήρηση.32. Σύμϕωνα με ότι είπαμε προηγουμένως μπορούμε να πούμε ότι το χαρακτηριστικό πολυώνυμο ενός πίνακα Α με A k στοιχεία στην κύρια διαγώνιο θα είναι: χ A (x) = χ A (x) χ Ak (x) και αντίστοιχα το ελάχιστο πολυώνυμο του θα είναι το ελάχιστο κοινό πολλαπλάσιο των ελάχιστων πολυωνύμων Q A (x),..., Q Ak (x). Στην ουσία κάθε τετραγωνικός πίνακας είναι block διαγώνιου πίνακα. Ομως θα χρησιμοποιούμε αυτήν την έκϕραση όταν υπάρχουν τουλάχιστον δύο blocks σε έναν πίνακα. Ενα παράδειγμα ενός απλού block διαγώνιου πίνακα είναι ο παρακάτω: A =
24 4 Βασικες Εννοιες Οπου αυτός ο πίνακας έχει blocks μεγέθους 3, και 2 καθώς κινούμαστε στην διαγώνιο. Τα τρία blocks στον πίνακα αυτόν είναι: 3 2 A = 7 2, A 2 = [ 6 ] [ ] 2, A 3 =
25 Κεϕάλαιο 2 Κανονική Μορϕή Jordan Στην προηγούμενη ενότητα είδαμε έννοιες οι οποίες θα μας βοηθήσουν να κατανοήσουμε την Κανονική Μορϕή Jordan. Η ενότητα αυτή αποτελεί το κύριο θέμα αυτής της πτυχιακής. Εισαγωγή στην Κανονική Μορϕή Σκοπός είναι να βρούμε έναν τρόπο να μελετήσουμε τους πίνακες που δεν είναι διαγωνίσιμοι. Θα προσπαθήσουμε να κατασκευάσουμε μορϕές που είναι «σχεδόν» διαγώνιοι. Πιο συγκεκριμένα, οι πίνακες θα είναι διαγώνιοι αλλά τα στοιχεία της διαγωνίου δεν θα είναι στοιχεία του σώματος αλλά θα είναι πίνακες, με συγκεκριμένες ιδιότητες. Εστω f : V V γραμμική και λ K n. Ενα διάνυσμα u V θα λέγεται γενικευμένο ιδιοδιάνυσμα της f ως προς το λ αν υπάρχει k ϕυσικός τέτοιος ώστε (f λ V ) k (u) = Το σύνολο V f (λ) = {u V : για κάποιο ϕυσικό k, (f λ V ) k (u) = } ονομάζεται γενικευμένος ιδιόχωρος της f που αντιστοιχεί στο λ. Ως συνήθως, μπορούμε να ορίσουμε τις αντίστοιχες έννοιες για πίνακες. Δίνουμε τις βασικές ιδιότητες των γενικευμένων ιδιοδιανυσμάτων. Λήμμα 2.. Αν V f (λ) {}, τότε το λ είναι ιδιοτιμή της f. Απόδειξη. Πράγματι, αν σ είναι ο ελάχιστος ϕυσικός ώστε (f λ V ) σ (u) = τότε το v = (f λ V ) σ (u) είναι ένα ιδιοδιάνυσμα της f στη λ αϕού: (f λ V )(v) = (f λ V ) σ (u) = Παρατήρηση 2.2. Εστω λ είναι μια γενικευμένη ιδιοτιμή της f. Για κάθε k, ορίζουμε V k f (λ) = {u V : (f λ V ) k (u) = } = ker((f λ V ) k ). Παρατηρούμε ότι έχουμε μια αλυσίδα υποχώρων: V f (λ) V 2 f (λ) V k f (λ),
26 6 Κανονικη Μορϕη Jordan για κάποιο k τέτοιο ώστε V k f 2 Παραδείγματα m (λ) = V (λ), για κάθε m k. Επίσης f V f (λ) = k i= V k f (λ). Το παρακάτω παράδειγμα θα μας βοηθήσει να κατανοήσουμε τον τρόπο εύρεσης των γενικευμένων ιδιοδιανυσμάτων και ιδιόχωρων. Εστω ο πίνακας A = Το χαρακτηριστικό πολυώνυμο θα είναι χ A (x) = (x 2) 3,δηλαδή το 2 θα είναι η μοναδική ιδιοτιμή. Θα υπολογίσουμε τους γενικευμένους ιδιόχωρους V A t (2). Παρατηρούμε ότι 2 2 A 2I = 2. Ομοια, Οπότε: V 3 A(2) = null V A(2) = null V 2 A(2) = null = span. = span, = span,,. = R3. Για την καλύτερη μελέτη των γραμμικών απεικονίσεων είναι πολύ σημαντική η έννοια του αναλλοίωτου υπόχωρου. Δηλαδή, έστω V ένας K n -διανυσματικός χώρος πεπερασμένης διάστασης και f : V V μια γραμμική απεικόνιση. Ενας υπόχωρος W του V λέγεται f-αναλλοίωτος υπόχωρος του V αν f(w ) W. Για να κατανοήσουμε καλύτερα τους f-αναλλοίωτους υπόχωρους του V θα δούμε μερικά παραδείγματα. Παραδείγματα: (i) Αν f : V V μια γραμμική απεικόνιση τότε οι υπόχωροι { V }, V είναι f-αναλλοίωτοι υπόχωροι του V. (ii) Εστω f : V V μια γραμμική απεικόνιση και u V με u. Τότε είναι ϕανερό ότι το u είναι ένα ιδιοδιάνυσμα της f αν και μόνο αν ο υπόχωρος u του V είναι f-αναλλοίωτος. Συνεπώς κάθε υπόχωρος ενός ιδιοχώρου της f είναι f-αναλλοίωτος.
27 2 Παραδειγματα 7 (iii) Εστω f : V V μια γραμμική απεικόνιση. Αν φ(x) K[x], τότε οι υπόχωροι του V, ker(φ(f)) και Im(φ(f)) είναι f-αναλλοίωτοι. Παρατήρηση 2.3. Τώρα, έστω f : V V γραμμική. Αν το λ είναι ρίζα του χ f (x) με πολλαπλότητα m τότε V f (λ) = ker(f λ V ) m και άρα είναι f-αναλλοίωτος υπόχωρος του V. Απόδειξη. Εστω χ f (x) = (x λ) m ψ(x) όπου ψ(λ). Προϕανώς ker(f λ V ) m V f (λ). Εστω u V f (λ) και k ο ελάχιστος ϕυσικός με (f λ V ) k (u) =. Θα δείξουμε ότι k m. Εστω ότι είχαμε k > m. Τότε διαιρώντας το ψ(x) με x λ παίρνουμε ψ(x) = (x λ)π(x) + c όπου c = ψ(λ). Αλλά αϕού k m, από το θεώρημα Caley-Hamilton, έχουμε ότι: άρα (f λ V ) k ψ(λ)(u) = (f λ V ) k m χ f (f)(u) = = (f λ V ) k ((f λ V )π(f)+c)(u) = π(f)(f λ V ) k (u)+c(f λ V ) k (u) = c(f λ V ) k (u) και αϕού c έχουμε (f λ V ) k (u) = που είναι άτοπο από την επιλογή του k. Άρα k m και u ker(f λ V ) m. Επίσης, αν f : V V γραμμική και λ,..., λ k οι διακεκριμένες ιδιοτιμές της f, τότε το άθροισμα W = V f (λ )+...+ V f (λ k ) είναι ευθύ. Αυτό μπορεί να διατυπωθεί και ως εξής: Γενικευμένα ιδιοδιανύσματα που αντιστοιχούν σε διαϕορετικές ιδιοτιμές της f είναι γραμμικώς ανεξάρτητα. Σε αντίθεση όμως με τα ιδιοδιανύσματα, τα γενικευμένα ιδιοδιανύσματα, παράγουν πάντα όλο το χώρο του V. Για να διατυπώσουμε καλύτερα αυτό το αποτέλεσμα, χρειαζόμαστε το επόμενο Λήμμα. Να σημειώσουμε ότι αν E γραμμική και E 2 = E τότε το E ονομάζεται προβολή. Λήμμα 2.4. Αν υπάρχουν E,..., E k ώστε: γραμμικές απεικονίσεις του V τέτοιες (i) E E k = V (ii) E i E j = για i j, τότε E 2 i = E i για κάθε i και V = E V... E k V. Απόδειξη. Αϕού E E k = V και E i E j = αν το i j, τότε έχουμε ότι E i = E i V = E i (E E i E k ) = Ei 2. Αν το v V τότε v = V (v) = [E E k ](v) = E (v) E k (v) το οποίο μας δείχνει ότι το V = E V E k V. Για να δείξουμε την μοναδικότητα, υποθέτουμε ότι = E v E k v k. Πολλαπλασιάζοντας με E i έχουμε ότι = Ei 2v i = E i v i, αϕού E i E j = για i j και Ei 2 = E i. Ετσι, κάθε όρος στην σχέση E v E k v k είναι μηδέν, οπότε V = E V... E k V.
28 8 Κανονικη Μορϕη Jordan Θεώρημα 2.5. Εστω ότι η f : V V είναι γραμμική, πεπερασμένης διάστασης τέτοια ώστε Q f (x) = p (x) ν p 2 (x) ν2 p k (x) ν k όπου τα p (x), p 2 (x),..., p k (x) είναι διακεκριμένα ανάγωγα πολυώνυμα στο K[x] με πρώτο συντελεστή το. Τότε κάθε V i = kerp i (f) ν i είναι ένας f- αναλλοίωτος υπόχωρος του V και V = V V 2 V k. Επιπλέον, Q fvi (x) = p i (x) νi, i k. Απόδειξη. Εστω q i (x) = Q(x)/p i (x) ν i τέτοιο ώστε το q i (x) να περιέχει όλα τα ανάγωγα στοιχεία του Q(x) εκτός από ένα. Να σημειώσουμε ότι αν i j τότε τα q i (x)q j (x) έχουν ως παράγοντα το Q(x). Τα πολυώνυμα q i (x) για i k δεν έχουν κανένα κοινό ανάγωγο στοιχείο και αϕού είναι σχετικά πρώτοι θα πρέπει να k υπάρχουν πολυώνυμα a i (x) με a i (x)q i (x) =. Εστω E i = a i (f)q i (f) τότε i= k E i = V και E i E j = αν i j αϕού E i E j = Q(f)q(f) για κάποιο πολυώνυμο i= q(x). Επιπλέον, V = E i V E k V σύμϕωνα με όσα είπαμε στο προηγούμενο λήμμα. Άρα μας μένει να αποδείξουμε ότι E i V = V i, i. Πρώτα, α δείξουμε ότι E i V V i. Εστω v E i V. Τότε το v = [q i (f)](w) για κάποιο w V και έτσι [p i (f) ν i ](v) = [p i (f) ν i ](q i (f)w) = [p i (f) ν i q i (f)](w) = Q(f)w =. Για να αποδείξουμε ότι V i E i V έστω v V i. Εχουμε ότι [q j (f)](v) = αϕού το q j (f) έχει ως παράγοντα το p i (f) ν i. Επομένως E j (v) =, j i. Ομως V = k E j v = j= k E j (v) = E i (v) E i V. j= Παρατήρηση 2.6. Αν υποθέσουμε ότι έχουμε έναν πίνακα Α ο οποίος είναι 4 4 και έχει μια μόνο επαναλαμβανόμενη ιδιοτιμή λ 2 με ένα ιδιοδιάνυσμα x 2 και ένα γενικευμένο ιδιοδιάνυσμα x (2) 2. Οι άλλες δύο ιδιοτιμές λ και λ 3 να είναι διακεκριμένες με ανεξάρτητα ιδιοδιανύσματα x και x 3. Κατασκευάζουμε έναν πίνακα P = (x, x 2, x (2) 2, x 3) σύμϕωνα με την βάση των τεσσάρων διανυσμάτων που έχουμε (3 ιδιοδιανύσματα και γενικευμένο ιδιοδιάνυσμα). Τώρα, αν πολλαπλασιάσουμε τον πίνακα A με τον πίνακα P θα έχουμε: AP = (λ x, λ 2 x 2, λ 2 x (2) 2, λ 3x 3 ) λ = P λ 2 λ 2 = P J λ 3 Δηλαδή, A = P JP όπου το J είναι σχεδόν διαγώνιος αϕού έχει λ στην κύρια διαγώνιο και μονάδα πάνω από αυτήν, η οποία μονάδα αντιστοιχεί στις στήλες που έχουν γενικευμένα ιδιοδιανύσματα. Αυτή είναι η μορϕή Jordan του πίνακα Α όπως θα εξηγήσουμε αναλυτικά παρακάτω. Να σημειώσουμε ότι ο πίνακας J έχει προϕανώς τις ίδιες ιδιοτιμές με τον πίνακα Α, αϕού ο A και ο J είναι όμοιοι με την ιδιαιτερότητα ότι ο J είναι σε πιο απλή μορϕή απο τον Α. Βέβαια, όταν έχουμε πάνω από μία επαναλαμβανόμενη ιδιοτιμή και η πολλαπλότητα της να είναι μεγαλύτερη του 2, εργαζόμαστε αναλόγως.
29 2 Παραδειγματα 9 Ορισμός 2.7. Ονομάζουμε Jordan Block έναν πίνακα μεγέθους n n της μορϕής: λ. λ.. J n,λ = λ λ λ Μερικά μεγέθη blocks μπορούν να είναι τα εξής: J,λ = (λ), J 2,λ = ( λ λ ), J 3,λ = λ λ λ, J 4,λ = λ λ λ λ Τα Jordan Blocks διάστασης 2 2 ή και μεγαλύτερης είναι τα πιο απλά παραδείγματα τετραγωνικών πινάκων οι οποίοι δεν είναι διαγωνίσιμοι. Μια γραμμική απεικόνιση f : V V λέγεται μηδενοδύναμη αν f k = για κάποιο ϕυσικό αριθμό k. Ο ελάχιστος ϕυσικός αριθμός σ τέτοιος ώστε f σ = λέγεται δείκτης της f. Ενας A M n (K) λέγεται μηδενοδύναμος δείκτου σ αν η r A είναι μηδενοδύναμη δείκτου σ. Προϕανώς η f είναι μηδενοδύναμη δείκτου σ αν και μόνο αν Q f (x) = x σ. Το χαρακτηριστικό πολυώνυμο μιας γραμμικής απεικόνισης f, σε ένα διανυσματικό χώρο διάστασης n θα είναι χ f (x) = ( ) n x n. Σύμϕωνα με τα παραπάνω μπορούμε να πούμε ότι η μοναδική ιδιοτιμή μιας μηδενοδύναμης γραμμικής απεικόνισης είναι το. Παραδείγματα ) B = είναι μηδενοδύναμος δείκτου 3, ενώ ο είναι μηδενοδύναμος δείκτου 2. B 2 = 2 2 2) Εστω A ένας n n πίνακας ο οποίος είναι μηδενοδύναμος δείκτου σ, τότε σ n. Ο πίνακας Α ως μηδενοδύναμος έχει μοναδική ιδιοτιμή λ =, γιατί από την χαρακτηριστική εξίσωση, Ax = λx A σ x = λ σ x λ σ x = λ =, αϕού x. Άρα, χ A (λ) = λ n και Q A (λ) = λ σ, όπου σ n.
30 2 Κανονικη Μορϕη Jordan Πρόταση 2.8. Εστω V ένας διανυσματικός χώρος επί του K πεπερασμένης διάστασης και f : V V μια γραμμική απεικόνιση τέτοια ώστε kerf i kerf i+ kerf i+2 για κάποιο ϕυσικό αριθμό i. Εστω a,..., a σ μια βάση του kerf i+ και a,..., a σ, w,..., w ρ μια βάση του kerf i+2. Αν a,..., a l είναι μια βάση του kerf i τότε τα στοιχεία a,..., a l, f(w ),..., f(w ρ ) είναι γραμμικά ανεξάρτητα στοιχεία του kerf i+. Απόδειξη. Τα στοιχεία f(w ),..., f(w ρ ) ανήκουν στον kerf i+. Εστω γ a + + γ l a l + µ f(w ) + + µ ρ f(w ρ ) =. () Τότε f i (γ a + + γ l a l + µ f(w ) + + µ ρ f(w ρ )) =. Αλλά f i (a j ) = για κάθε j l και άρα f i+ (µ w + + µ ρ w ρ ) =. Συνεπώς µ w + + µ ρ w ρ kerf i+ =< a,..., a σ >. Αν µ w + + µ ρ w ρ, τότε υπάρχουν u,..., u σ K με (u,..., u σ ) (,..., ) έτσι ώστε µ w + + µ ρ w ρ = u a + + u σ a σ, το οποίο είναι άτοπο αϕού a,... a σ, w,..., w ρ είναι γραμμικά ανεξάρτητα. Άρα µ w + +µ ρ w ρ = και καθώς τα w,..., w ρ είναι γραμμικά ανεξάρτητα, πρέπει µ = µ 2 = = µ ρ =. Τώρα από την () έπεται ότι γ a + +γ l a l =, αλλά a,..., a l είναι γραμμικά ανεξάρτητα, άρα γ =... = γ l =, αποδεικνύοντας το ζητούμενο. Θεώρημα 2.9. Εστω dim V = ν και f : V V μηδενοδύναμη γραμμική απεικόνιση δείκτου σ. Τότε υπάρχουν μονοσήμαντα ορισμένοι ϕυσικοί αριθμοί i και σ σ i και μια βάση â του V (όχι μονοσήμαντα ορισμένη) τέτοια ώστε: (f : â) = J σ... J σi Η παραπάνω ονομάζεται κανονική μορϕή Jordan της μηδενοδύναμης απεικόνισης f. Απόδειξη. Εστω W i = kerf i. Τότε επειδή η f είναι μηδενοδύναμη δείκτου σ παίρνουμε την ακολουθία διακεκριμένων υποχώρων του V { V } = W W W 2... W σ W σ = V. Εστω B μια βάση του W. Αυτήν την επεκτείνουμε σε μια βάση του W 2. Εστω λοιπόν Γ 2 W 2 με B Γ 2 μια βάση του W 2. Τώρα επεκτείνουμε αυτή τη βάση του W 2 σε μια βάση του W 3. Εστω Γ 3 W 3 με B Γ 2 Γ 3 μια βάση του W 3. Συνεχίζοντας μάυτό τον τρόπο βρίσκουμε μια βάση B σ = B Γ 2 Γ 3... Γ σ του W σ = V, τέτοια ώστε B i = B Γ 2... Γ i είναι μια βάση του W i για κάθε 2 i σ. Εστω ότι Γ σ = {a σ,..., a σ l σ } W σ. Εχουμε ότι η B σ είναι μια βάση του W σ = kerf σ, η B σ = B σ Γ σ είναι μια βάση του W σ = kerf σ και η B σ 2 είναι μια βάση του W σ 2 = kerf σ 2. Άρα σύμϕωνα και με την προηγούμενη πρόταση έχουμε ότι το σύνολο B σ 2 {f(a σ ),..., f(a σ l σ )}
31 2 Παραδειγματα 2 είναι γραμμικά ανεξάρτητο υποσύνολο του W σ. Αυτό το επεκτείνουμε σε μια βάση B σ του W σ, B σ = B σ 2 {f(a σ ),..., f(a σ l σ )} {a σ,..., a σ l σ }. Αν Γ σ = {f(a σ ),..., f(a σ l σ ), a σ,..., a σ l σ } τότε το B σ 2 είναι μια βάση του W σ 2 = kerf σ 2 και το B σ = B σ 2 Γ σ είναι μια βάση του W σ = kerf σ 3. Άρα από την προηγούμενη πρόταση παίρνουμε ότι: B σ 3 f(γ σ ) = B σ 3 {f 2 (a σ ),..., f 2 (a σ l σ ),..., f(a σ l σ )} είναι ένα γραμμικά ανεξάρτητο υποσύνολο του W σ 2. Αυτό το επεκτείνουμε σε μια βάση B σ 2 του W σ 2, B σ 2 = B σ 3 {f 2 (a σ ),..., f 2 (a σ l σ ), f(a σ ),..., f(a σ l σ )} {a σ 2,..., a σ 2 l σ 2 }. Αν Γ σ 2 = {f 2 (a σ ),..., f 2 (a σ l σ ), f(a σ ),..., f(a σ l σ ), a σ 2,..., a σ 2 l σ 2 } τότε B σ 2 = B σ 3 Γ σ 2 είναι μια βάση του W σ 2. Συνεχίζοντας με τον ίδιο τρόπο, βρίσκουμε μια βάση B i του W i τέτοια ώστε B i = B i Γ i και f(γ i ) Γ i, για κάθε i σ. Ξέρουμε ότι το f(γ 2) είναι ένα γραμμικά ανεξάρτητο υποσύνολο του W το οποίο επεκτείνουμε σε μια βάση Γ του W, Γ = f(γ 2) {a,..., a l() }. Δηλαδή έχουμε V = W σ = W σ < Γ σ >= W σ < a σ,..., a σ l σ > W σ = W σ 2 < Γ σ >, Γ σ = {f(a σ ),..., f(a σ l σ ), a σ,..., a σ l σ } W σ 2 = W σ 3 < Γ σ 2 >, Γ σ 2 = {f 2 (a σ ),..., f 2 (a σ l σ ), f(a σ ),..., f(a σ l σ ), a σ 2,..., a σ 2 l σ 2 }. W 2 = W < Γ 2 >, Γ 2 = {f σ 2 (a σ ),..., f σ 2 (a σ l σ ), f σ 3 (a σ ),..., f σ 3 (a σ l σ ),..., a 2,..., a 2 l 2 } W =< Γ >, Γ = {f σ (a σ ),..., f σ (a σ l σ ), f σ 2 (a σ ),..., f σ 2 (a σ l σ ),..., f(a 2 ),..., f(a 2 l 2 ), a,..., a l } Το σύνολο Γ είναι μια βάση του W = kerf και συνεπώς το σύνολο Γ Γ 2 είναι μια βάση του W 2 και το σ Γ i είναι μια βάση του W σ. Άρα το σύνολο σ i= i= Γ i {aσ,..., a σ l σ } είναι μια βάση του V. Θεωρούμε την ακόλουθη διάταξη αυτής της βάσης â = (f σ (a σ ), f σ 2 (a σ ),..., f(a σ ), f σ (a σ 2 ),..., f(a σ 2 ), a σ 2,..., f σ (a σ l σ ),..., f(a σ l σ ), a σ l σ, f σ 2 (a σ ),..., a σ,..., f(a 2 ), a 2,..., f(a 2 l 2 ), a 2 l 2, a,..., a l ) Εύκολα διαπιστώνουμε ότι ο πίνακας της f ως προς την διατεταγμένη βάση â του V είναι της ζητούμενης μορϕής. Για να διευκρινίσουμε το δείκτη σ, θεωρούμε την κανονική μορϕή Jordan του A και έστω J = diag(j,..., J κ )
32 22 Κανονικη Μορϕη Jordan όπου Ο J i =... Ο n i n i και n n κ = n. Ο πίνακας J i είναι μηδενοδύναμος δείκτου n i και αν σ = max{n,..., n κ } n, τότε έχουμε: διότι J σ =. A σ = P J σ P = Θεώρημα 2.. (Κανονική Μορϕή Jordan) Αν το χαρακτηριστικό πολυώνυμο της f είναι ένα γινόμενο γραμμικών παραγόντων, τότε είναι δυνατόν να βρούμε έναν πίνακα που να είναι όμοιος, ο οποίος είναι της μορϕής Jordan. Πιο συγκεκριμένα, υποθέτουμε ότι χ(x) = (x α ) m (x α s ) m s είναι το χαρακτηριστικό πολυώνυμο της f και ότι το Q(x) = (x α ) e (x α s ) e s είναι το ελάχιστο πολυώνυμο της f. Τότε ο πίνακας για την f έχει κύρια blocks μεγέθους m i m i που αντιστοιχούν σε κάθε ιδιοτιμή α i και σε κάθε κύριο block το μεγαλύτερο δευτερεύον block έχει μέγεθος e i e i. Απόδειξη. Υποθέτουμε ότι το χαρακτηριστικό πολυώνυμο της f θα είναι (x a) m και το ελάχιστο ελάχιστο πολυώνυμο της θα είναι (x a) ν. Εστω g : V V η γραμμική απεικόνιση g = f λ V. Επειδή Q f (x) = (x a) ν έχουμε ότι η g είναι μηδενοδύναμη δείκτου ν. Από το προηγούμενο Θεώρημα έπεται ότι υπάρχει μια διατεταγμένη βάση â του V με (g : â, â) = J,σ... J,σj Αλλά (g : â, â) = (f λ V : â, â) = (f : â, â) (λ V : â, â), άρα (f : â, â) = (g : â, â) + (λ V : â, â) = J,σ λ J λ,σ = =.... Τώρα, απο το Θεώρημα.4 έχουμε ότι V = V V 2... V k όπου V i = ker(f λ i ) ν i J,σj λ J λ,σj και Q fvi = (x λ i ) ν i. Άρα θα υπάρχει μια διατεταγμένη βάση B i = (a i,..., a i ρ i ) του V i με (f Vi : B i, B i ) = J λi,σ (,λi ) J λi,σ (2,λi ) Αν τώρα θεωρήσουμε την διατεταγμένη βάση B του V με... Jλi,σ(jλi,λ i ) B = (a,..., a ρ,..., a 2,..., a 2 ρ 2,..., a k,..., a k ρ k ).
33 2 Παραδειγματα 23 τότε ο πίνακας (f : B, B) = J λ,σ (,λ )... Jλ2,σ(jλ,λ )... Jλk,σ(,λk)... Jλk,σ(jλk,λ k ) είναι μια διατεταγμένη βάση B του V. Ισχύει επιπλέον ότι αν B είναι μια διατεταγμένη βάση του V με J (f : B, B ) =... ( ) και J i στοιχειώδεις πίνακες Jordan τότε οι J,..., J l είναι μια μετάθεση των J λ,σ,..., J (,λ ) λ,σ,..., J (jλ,λ ) λ k,σ,..., J (,λ ) λ k,σ. (jλk,λ k ) Συνεπώς δείξαμε ότι για κάθε γραμμική απεικόνιση f : V V της οποίας το ελάχιστο πολυώνυμο είναι γινόμενο πρωτοβάθμιων παραγόντων, υπάρχει μια διατεταγμένη βάση B του V έτσι ώστε ο πίνακας της f ως προς B, (f : B, B) = J... όπου J l είναι στοιχειώδεις πίνακες Jordan. Επίσης, οι J,..., J l είναι μονοσήμαντα ορισμένοι από την f. Ο πίνακας (*), που όπως είδαμε είναι μονοσήμαντα ορισμένος από την f εκτός από μετάθεση των J,..., J l είναι η κανονική μορϕή Jordan της f. J l J l Παραδείγματα : ) Εστω ο πίνακας A = Ο οποίος έχει ιδιοτιμές το και το 2, αλγεβρικής πολλαπλότητας 2 και 3 αντίστοιχα και γεωμετρικής πολλαπλότητας και. Υπολογίζουμε τους γενικευμένους ιδιοχώρους του πίνακα Α. Πρώτα υπολογίζουμε το ιδιοδιάνυσμα v του A με τους γνωστούς τρόπους: (A I) 3 3 = =
34 24 Κανονικη Μορϕη Jordan Για το ιδιοδιάνυσμα στο V 2 A (), λύνουμε το σύστημα Ax = v. Απλά δίνουμε το αποτέλεσμα, και για να αποϕύγουμε κλάσματα, αντικαθιστούμε το v με το 3v. (A I) = Επαναλαμβάνουμε την διαδικασία για λ = 2: (A 2I) (A 2I) = = = 3 = = Αναλυτικά, θα βρούμε το τελευταίο ιδιοδιάνυσμα που θα ανήκει στο V 3 A (2): (A 2I) x x 2 x 3 x 4 x 5 = x x 2 x 3 x 4 x 5 = Το σύστημα είναι: x = 3x x 2 = 6x + 3x 2 = x + 6x 2 + 3x 3 = 5x + x 2 + 6x 3 + 3x 4 = Άρα έχουμε: Δηλαδή: (A 2I) x = x 2 = x 5 =, x 3 = 3, x 4 = = = 3 Ετσι, βρήκαμε μια βάση για κάθε γενικευμένο ιδιοδιάνυσμα του πίνακα Α. Ολα
35 2 Παραδειγματα 25 μαζί παράγουν τον χώρο και των 5 διαστάσεων των διανυσμάτων των στηλών , Οπότε μπορούμε να βρούμε την κανονική μορϕή Jordan 3 5 P = , J = Οπου AP = P J. 2) Εστω A ο παρακάτω πίνακας Αϕού ο πίνακας A έχει πραγματικές ιδιοτιμές, θα εργαστούμε στον R 5. Αρχικά θα βρούμε το χαρακτηριστικό πολυώνυμο του A. Ο πίνακας A xi μπορεί να χωριστεί σε δυο 2 2 και blocks, για τα οποία μπορούμε εύκολα να βρούμε την ορίζουσα. Το μόνο που χρειάζεται να κάνουμε για να βρούμε το χαρακτηριστικό πολυώνυμο χ(x) είναι να υπολογίσουμε την εξής ορίζουσα: 3 x x = (3 x)( x) + = x2 4x + 4 = (x 2) 2. Λειτουργώντας ανάλογα και για τα υπολόιπα blocks, καταλήγουμε στο ότι το χαρακτηριστικό πολυώνυμο θα ισούται με χ(x) = (x 2) 5. Για να βρόυμε τώρα το ελάχιστο πολυώνυμο του A, εϕόσον γνωρίζουμε ότι θα είναι ίσο με μια δύναμη του (x 2), πρέπει να βρούμε ποιά δύναμη του A 2I μας δίνει τον μηδενικό πίνακα. Ετσι, (A 2I) 2 = =
36 26 Κανονικη Μορϕη Jordan Δηλαδή, το ελάχιστο πολυώνυμο είναι (x 2) 2. Το επόμενο βήμα είναι να βρούμε τον γενικευμένο ιδιόχωρο null(a 2I), δηλαδή τον ιδιόχωρο του 2. Ο γενικευμένος ιδιόχωρος null(a 2I) είναι όλο το R 5. Πρώτα θα βρούμε το block σε άνω τριγωνική μορϕή του πίνακα το οποίο γίνεται αν επιλέξουμε μια βάση για τον αναλλοίωτο υπόχωρο που περιέχει όλα τα ιδιοδιανύσματα. Λύνοντας το σύστημα (A 2I)x = βρίσκουμε ότι x 2 = x, x 4 = x 3. Μπορούμε να διαλέξουμε μια βάση για τον ιδιόχωρο με τον συνηθισμένο τρόπο, δηλαδή αν υποθέσουμε ότι τα x, x 3, x 5 είναι ανεξάρτητες μεταβλητές. Επειτα θα τα επεκτείνουμε για ο- λόκληρο το διάστημα που έχουμε, διαλέγοντας δύο ακόμη γραμμικώς ανεξάρτητα διανύσματα. Αυτό θα μας δώσει την ακόλουθη βάση: u = (,,,, ), u 2 = (,,,, ), u 3 = (,,,, ), u 4 = (,,,, ), u 5 = (,,,, ). Αν κάνουμε τους υπολογισμούς και σύμϕωνα με την βάση που έχουμε, καταλήγουμε στον εξής πίνακα όμοιο του A: Ομως για να υπολογίσουμε την μορϕή Jordan του πίνακα πρέπει να επιλέξουμε τις βάσεις μας πιο προσεκτικά. Θα ξεκινήσουμε με τα u 4, και u 5 εϕόσον είναι στον γενικευμένο ιδιόχωρο και είναι γραμμικώς ανεξάρτητα διανύσματα της βάσης για τον ιδιόχωρο. Τα διανύσματα (A 2I)u 4 και (A 2I)u 5 ανήκουν στον ιδιόχωρο V A (2) και είναι γραμμικώς ανεξάρτητα. Πρέπει να βρούμε μια βάση του ιδιοχώρου και γι αυτό χρειαζόμαστε ακόμα ένα διάνυσμα που είναι γραμμικά ανεξάρτητο με τα άλλα δυο. Μπορούμε να ελέγξουμε ότι το u 3 παραπάνω, ικανοποιεί αυτές τις συνθήκες. Για να βρόυμε την επιθυμητή μορϕή διαλέγουμε w = (A 2I)(u 4 ), w 2 = u 4, w 3 = (A 2I)(u 5 ), w 4 = u 5, w 5 = u 3. Ετσι, κατασκευάζουμε τον πίνακα Α σύμϕωνα με την βάση που έχουμε επιλέξει και γνωρίζοντας ότι A = 2I + (A 2I). Τότε, A(w ) = (2I + (A 2I))(A 2I)(u 4 ) = 2(A 2I)(u 4 ) + (A 2I) 2 (u 4 ) = 2w A(w 2 ) = (2I + (A 2I))(u 4 ) = 2u 4 + (A 2I)(u 4 ) = 2w 2 + w αϕού ξέρουμε ότι (A 2I) 2 =. Ομοια βρίσκουμε ότι A(w 3 ) = 2w 3 και A(w 4 ) = 2w 4 + w 3. Τέλος A(w 5 ) = 2w 5 αϕού το w 5 είναι ένα ιδιοδιάνυσμα και έτσι έχουμε τον ακόλουθο πίνακα σε μορϕή Jordan Πρέπει να έχουμε τουλάχιστον ένα 2 2 block διάστασης 2 (όχι μεγαλύτερο) αϕού το ελάχιστο πολυώνυμο είναι βαθμού 2. Το δεύτερο 2 2 block εμϕανίζεται γιατί η διάσταση του γενικευμένου ιδιόχωρου είναι 2, μεγαλύτερη απο την διάσταση του ιδιόχωρου. Χρειάστηκε να συγκρίνουμε μόνο τους δύο υπόχωρους επειδή ο A 2I είναι μηδενοδύναμος δείκτου 2. Γενικά, συγκρίνοντας τις διαστάσεις όλων των γενικευμένων ιδιόχωρων μπορούμε να βρούμε την κανονική μορϕή Jordan χωρίς να χρειάζεται να βρούμε την βάση.
37 3 Αλγοριθμος Ευρεσης Κανονικης Μορϕης Jordan 27 3 Αλγόριθμος Εύρεσης Κανονικής Μορϕής Jordan Εστω A M n (K) ένας n n πίνακας με στοιχεία από το σώμα K. Υποθέτουμε ότι όλες οι ιδιοτιμές του Α ανήκουν στο σώμα K. Θα περιγράψουμε έναν αλγόριθμο εύρεσης τη κανονικής μορϕής Jordan, J, του πίνακα Α. Βήμα : Υπολογίζουμε το χαρακτηριστικό πολυώνυμο χ A (x) και βρίσκουμε το σύνολο Spec(A) := {λ, λ 2,..., λ κ } των διακεκριμένων ιδιοτιμών του Α. Βήμα 2: Για κάθε ιδιοτιμή λ Spec(A) υπολογίζουμε τις βαθμίδες των πινάκων. (A λi n ), (A λi n ) 2,..., (A λi n ) n Βήμα 3: Για κάθε διοτιμή λ Spec(A) υπολογίζουμε τον ελάχιστο ϕυσικό s := s(λ) για τον οποίο ισχύει: και θέτουμε: rank(a λi n ) s = rank(a λi n ) s+ q m := rank(a λi n ) m rank(a λi n ) m, m =, 2,..., s + Σημειώνουμε ότι: = q s+ < q s q s... q = n rank(a λi n ) Βήμα 4: Για κάθε ιδιοτιμή λ Spec(A) και m =, 2,..., s(λ) θεωρούμε q m q m+ στοιχειώδεις πίνακες Jordan οι οποίοι είναι m m και έχουν διαγώνιο στοιχείο τον αριθμό λ. Βήμα 5: Για κάθε ιδιοτιμή λ Spec(A) θεωρούμε το ευθύ άθροισμα των στοιχειωδών πινάκων Jordan του Βήματος 4. Ο πίνακας που προκύπτει είναι η κανονική μορϕή Jordan του Α. Παράδειγμα Θεωρούμε τον 3 3 πίνακα πραγματικών αριθμών A = Βήμα : Υπολογίζουμε το χαρακτηριστικό πολυώνυμο του Α λ 4 2 χ A (λ) = det 3 8 λ 3 = (λ 2) λ και άρα η μόνη ιδιοτιμή του Α είναι η λ = 2 πολλαπλότητας 3. Spec(A) = 2. θα έχουμε: (A 2I) = Επομένως Άρα μπορούμε να υπολογίσουμε εύκολα τις βαθμίδες που μας χρειάζονται
38 28 Κανονικη Μορϕη Jordan Βημα 2: rank(a 2I) = 3 rank(a 2I) = rank(a 2I) 2 = rank(a 2I) 3 = Βήμα 3: Παρατηρούμε ότι το s = 2 επομένως, q = rank(a 2I) rank(a 2I) = 3 = 2 q 2 = rank(a 2I) rank(a 2I) 2 = = q 3 = rank(a 2I) 2 rank(a 2) 3 = q 4 = Βήμα 4: Οπότε για τον πίνακα Α θα έχουμε ότι: q q 2 = 2 = στοιχειώδη πίνακα Jordan ο οποίος θα είναι μεγέθους και θα έχει το λ = 2 στην διαγώνιο. q 2 q 3 = = στοιχειώδη πίνακα Jordan ο οποίος θα είναι μεγέθους 2 2 και θα έχει το λ = 2 στην διαγώνιο. q 3 q 4 = στοιχειώδη πίνακα Jordan ο οποίος θα είναι μεγέθους 3 3 και θα έχει το λ = 2 στην κύρια διαγώνιο. Βήμα 5: Άρα, η κανονική μορϕή Jordan του πίνακα Α θα είναι ο πίνακας: J = ο οποίος είναι το ευθύ άθροισμα των στοιχειωδών πινάκων Jordan: ( ) 2 (2) 2 Πρόταση 2.. Εστω Α και Β δύο n n πίνακες στο σώμα C των μιγαδικών αριθμών. Τότε ο Α και ο Β είναι όμοιοι αν και μόνο αν έχουν την ίδια κανονική μορϕή Jordan, μέχρι την τάξη των ιδιοτιμών τους. Απόδειξη. Η υπόθεση ότι οι πίνακες πέρνουν και μιγαδικές τιμές μας δείχνει ότι το χαρακτηριστικό πολυώνυμο και στους δύο πίνακες μπορεί να παραγοντοποιηθεί χωρίς κάποιο περιορισμό και έτσι μπορούμε να το χρησιμοποιήσουμε στην κανονική μορϕή Jordan. Αν ο Α και ο Β είναι όμοιοι, τότε έχουν τον ίδιο γραμμικό μετασχηματισμό T. Η κανονική μορϕή Jordan εξαρτάται μόνο από αυτόν τον
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
8.1 Διαγωνοποίηση πίνακα
 Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
βαθμού 1 με A 2. Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
A, και εξετάστε αν είναι διαγωνίσιμη.
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
ΚΕΦΑΛΑΙΟ 5: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
= 7. Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις
 1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
Η ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN
 Η ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Εάν ένας πίνακας δεν διαγωνοποιείται, τότε ο στόχος μας είναι υπολογίσουμε μέσω ενός μετασχηματισμού ομοιότητας, έναν απλούστερο πίνακα, «σχεδόν διαγώνιο» όπως ο παρακάτω πίνακας
Η ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Εάν ένας πίνακας δεν διαγωνοποιείται, τότε ο στόχος μας είναι υπολογίσουμε μέσω ενός μετασχηματισμού ομοιότητας, έναν απλούστερο πίνακα, «σχεδόν διαγώνιο» όπως ο παρακάτω πίνακας
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Ασκήσεις4 48. P AP τριγωνικό. Αφού δείξτε ότι ο A δεν είναι διαγωνίσιμος, βρείτε αντιστρέψιμο A 1 3 1
 Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Μία απεικόνιση από ένα διανυσματικό χώρο V στον εαυτό του, L : V V την ονομάζουμε γραμμικό τελεστή στο V (ή ενδομορφισμό του V ). Ορισμός. L : V V γρα
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
= k. n! k! (n k)!, k=0
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη
 Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ).
 1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
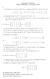 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Κανονική Μορφή Jordan - I Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 35 7 Η Κανονική Μορφή Jordan - I Στην
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Κανονική Μορφή Jordan - I Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 35 7 Η Κανονική Μορφή Jordan - I Στην
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Διαγωνοποίηση μητρών. Στοιχεία Γραμμικής Άλγεβρας
 Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Γραμμική Άλγεβρα II. Ασκήσεις με Υποδείξεις - Απαντήσεις. Περιεχόμενα
 Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Κεφάλαιο 9 1 Ιδιοτιμές και Ιδιοδιανύσματα
 Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
n! k! (n k)!, = k k 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
1 ιαδικασία διαγωνιοποίησης
 ιαδικασία διαγωνιοποίησης Εστω V ένας R-διανυσματικός χώρος (ή έναςc-διανυσματικός χώρος) διάστασης n. Είναι γνωστό ότι κάθε διάνυσμα (,,..., n ) του χώρου V μπορεί να παρασταθεί και σαν πίνακας στήλη
ιαδικασία διαγωνιοποίησης Εστω V ένας R-διανυσματικός χώρος (ή έναςc-διανυσματικός χώρος) διάστασης n. Είναι γνωστό ότι κάθε διάνυσμα (,,..., n ) του χώρου V μπορεί να παρασταθεί και σαν πίνακας στήλη
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Κανονική Μορφή Jordan - II Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 52 9 Η Κανονική Μορφή Jordan - II
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Κανονική Μορφή Jordan - II Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 52 9 Η Κανονική Μορφή Jordan - II
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
Gauss. x + y + z = 2 3x + 3y z = 6 x y + z = 1. x + y + z = r x y = 0 3x + y + sz = s 0
 Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ. (ii) Αν ο Β m+1, με m N, αντιστρέφεται, τότε και ο Β αντιστρέφεται
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
Δακτύλιοι και Πρότυπα Ασκήσεις 6. Η ύλη των ασκήσεων αυτών είναι η Ενότητα6, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα.
 Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-9) ΜΕΡΟΣ 7: ΙΔΙΟΤΙΜΕΣ & ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ ΔΙΑΓΩΝΙΟΠΟΙΗΣΗ ΠΙΝΑΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-9) ΜΕΡΟΣ 7: ΙΔΙΟΤΙΜΕΣ & ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ ΔΙΑΓΩΝΙΟΠΟΙΗΣΗ ΠΙΝΑΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ. ρ Χρήστου Νικολαϊδη
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδηµαϊκό έτος 5-6 ΜΑΘΗΜΑ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Καθηγητής: Σ Πνευµατικός ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ ΟΙ ΚΑΝΟΝΙΚΕΣ ΜΟΡΦΕΣ JORDAN Θεωρούµε ένα n-διάστατο διανυσµατικό χώρο E στο σώµα Κ = ή και
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδηµαϊκό έτος 5-6 ΜΑΘΗΜΑ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Καθηγητής: Σ Πνευµατικός ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ ΟΙ ΚΑΝΟΝΙΚΕΣ ΜΟΡΦΕΣ JORDAN Θεωρούµε ένα n-διάστατο διανυσµατικό χώρο E στο σώµα Κ = ή και
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό
 1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό 1.1 Όρια ακολουθιών Λέμε ότι η ακολουθία { n } συγκλίνει με όριο R αν για κάθε ϵ > 0 υπάρχει ακέραιος N = N(ϵ) τέτοιος ώστε (1.1) n < ϵ για κάθε n > N, και
1 Επανάληψη εννοιών από τον Απειροστικό Λογισμό 1.1 Όρια ακολουθιών Λέμε ότι η ακολουθία { n } συγκλίνει με όριο R αν για κάθε ϵ > 0 υπάρχει ακέραιος N = N(ϵ) τέτοιος ώστε (1.1) n < ϵ για κάθε n > N, και
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ
 Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ 2: ΟΡΙΖΟΥΣΕΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
4 k 2 = 2 ( 1+ 2 k 2. k 2 2 k= k 2. 1.ii) Αν σχηµατίσουµε τον πίνακα µε γραµµές τα δύο διανύσµατα έχουµε: Γ1 Γ1 ---> { }
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
n = dim N (A) + dim R(A). dim V = dim ker L + dim im L.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
Παραδείγματα (2 ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 10
 Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
a b b < a > < b > < a >.
 Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
Βάση και Διάσταση Διανυσματικού Χώρου
 Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii18/laii18html Παρασκευή 9 Μαρτίου 18 Ασκηση 1 Θεωρούµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii18/laii18html Παρασκευή 9 Μαρτίου 18 Ασκηση 1 Θεωρούµε
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 1. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
2 3x 5x x
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
A B. (f; B) = f(x 1 ) = a 11 x 1 + a k1 x k + 0.x k x n f(x 2 ) = a 12 x 1 + a k2 x k + 0.x k x n
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΑΣΚΗΣΕΙΣ III ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN 1 Εστω f : V V γραμμική απεικόνιση Εστω A = ker(f i ) και B = ker(f i+1 ) Δείξτε ότι (i) A B και (ii) f(b) A Αποδ: (i) Εστω x ker(f i ) Τότε f i (x)
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΑΣΚΗΣΕΙΣ III ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN 1 Εστω f : V V γραμμική απεικόνιση Εστω A = ker(f i ) και B = ker(f i+1 ) Δείξτε ότι (i) A B και (ii) f(b) A Αποδ: (i) Εστω x ker(f i ) Τότε f i (x)
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
Ιδιάζουσες τιμές πίνακα. y έχουμε αντίστοιχα τις σχέσεις : Αυτές οι παρατηρήσεις συμβάλλουν στην παραγοντοποίηση ενός πίνακα
 Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου Όνομα συνοπτικές ενδεικτικές λύσεις
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Παναγιώτης Ψαρράκος Αν. Καθηγητής
 Ανάλυση Πινάκων Κεφάλαιο 1: Νόρμες Διανυσμάτων και Πινάκων Παναγιώτης Ψαρράκος Αν. Καθηγητής Δ.Π.Μ.Σ. Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών
Ανάλυση Πινάκων Κεφάλαιο 1: Νόρμες Διανυσμάτων και Πινάκων Παναγιώτης Ψαρράκος Αν. Καθηγητής Δ.Π.Μ.Σ. Εφαρμοσμένες Μαθηματικές Επιστήμες Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Τομέας Μαθηματικών
============================================================== Σχηµατίζουµε τον πίνακα µε στήλες τα διανύσµατα v1,v2,v3,u1,u2:
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
