Производи на бази малине Малиновача Др Бранко Поповић Институт за воћарство, Чачак
|
|
|
- Ῥαάβ Βασιλόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Funded by the European Union s Seventh Framework Programme Производи на бази малине Малиновача Др Бранко Поповић Институт за воћарство, Чачак
2 УНЕСКО Конвенција о заштити нематеријалног културног наслеђа Национални регистар и национална листа нематеријалног културног наслеђа Нематеријално културно наслеђе: Усмена традиција и изрази... Извођачке уметности коло... Друштвени обичаји, ритуали и свечани догађаји слава... Знања и обичаји који се тичу природе и свемира Вештине везане за традиционалне занате Листа знања у коју се уписују традиционална знања, вештине и умећа, технике и праксе, као и њима припадајући предмети, инструменти, артефакти и културни простори који се тичу специфичне производње својствене заједници која то знање носи и/или знања, вештине, веровања и њима одговарајући обичаји и праксе који су настали и развијали се кроз сталну узајамну везу дате заједнице са природом која је окужује.
3 Центар за нематеријално културно наслеђе при Етнографском музеју у Београду Регионални координатори : Народни музеј Чачак за централну Србију Музеј «Старо село» Сирогојно за западну Србију Производња ракије традиционални занат нематеријална културна баштина??????????????????????????
4 Порези на алкохол У производњи и промету алкохолних пића плаћа се: - порез (ПДВ) код нас 20% - акциза (специфичан порез на промет одређених производа) Учешће акцизе у пореским приходима појединих земаља: - Француска 7% - Немачка 9% - Италија 7% - Данска 11% - Финска 17% - Србија 17,4% (2008. година учешће у структури буџета) уз 47,8% од ПДВ чини стуб пореског система
5 Земља ЕУР/100 л а.а. Бугарска 562 Румунија 579 Кипар 598 Словенија 695 Италија 800 Шпанија 830 Словачка 834 Летонија 895 Мађарска 939 Чешка 962 Португал 978 Аустрија 1000 ПДВ 15% Кипар - 21% Португал Земља Луксембург 1041 Естонија 1074 Литванија 1112 Грчка 1135 Пољска 1207 Немачка 1303 Француска 1450 Холандија 1504 Швајцарска 1747 Белгија 1752 Данска 2012 Малта 2329 ЕУР/100 л а.а. ПДВ 7,65% Швајцарска - 25% Данска Земља В. Британија 3061 Финска 3250 Ирска 3925 Шведска 5454 ЕУР/100 л а.а. ПДВ 17,5% В. Британија - 25% Шведска
6 Европа акцизе: Бугарска порез на алкохол 562 Еу/100 л а.а. тј. 2,81 Еу/л ракије 50 вол% Немачка порез на алкохол 1303 Еу/100 л а.а. тј. 6,51 Еу/л ракије 50 вол% Шведска порез на алкохол 5454 Еу/100 л а.а. тј. 27,27 Еу/л ракије 50 вол% Србија акцизе: на ракије од воћа и грожђа 121,89 дин/л тј. 1,00 Еу/л ракије (50 вол%) на ракије од житарица и др. пољ. сировина 309,23 дин/л тј. 2,56 Еу/л ракије (50 %) на жестока алкохолна пића и ликера 198,19 дин/л тј. 1,64 Еу/л ракије (50 %)
7 ПРЕРАДА ВОЋА У ЈАКА АЛКОХОЛНА ПИЋА Квалитет јаких алкохолних пића од воћа (хемијски састав и сензорне карактеристике Сировина - воће Технолошки поступак производње Аутохтоне и одомаћене сорте Класичан (укључује алкохолно врење) Новостворене сорте Класичан (мацерација плодова без алкохолног врења) Интродуковане сорте
8 ПРЕРАДА МАЛИНА У ЈАКА АЛКОХОЛНА ПИЋА РАНИЈЕ НЕУОБИЧАЈЕНО: - ретко доступна сировина до интензивног развоја малинарства, и високе цене малина; ДАНАС: - малина доступна целе године као свежа и смрзнута (око 90% укупног рода малине се смрзава); Спроведена истраживања имају за циљ: развијање новог технолошког поступка за добијање јаког алкохолног пића од малине врхунског квалитета коришћењем сировине која је произвођачима на располагању целе године, чиме се: превазилази сезонски карактер производње, постиже очување и стандардизација примарне ароме ракије пореклом из воћа, повећање обима коришћења малине као сировине за прераду.
9 МАЛИНА КАО СИРОВИНА ЗА ПРОИЗВОДЊУ ЈАКИХ АЛКОХОЛНИХ ПИЋА СОРТЕ: 1 АУТОХТОНЕ И ОДОМАЋЕНЕ ПРВА ПОЛОВИНА XX ВЕКА: ЧАЧАНСКА (ЈЕЛИЧКА), ВАЉЕВСКА (МАРЛБОРО)... 2 НОВОСТВОРЕНЕ СОРТЕ УВЕДЕНЕ У ПРОИЗВОДЊУ 70-ТИХ ГОДИНА XX ВЕКА: ГРАДИНА (Институт за воћарство), ПОДГОРИНА (Институт за воћарство)... 3 ИНТРОДУКОВАНЕ: ВИЛАМЕТ (САД) КРАЈЕМ 70-ТИХ ГОДИНА XX ВЕКА, МИКЕР (САД) ПОЧЕТАК 90-ТИХ ГОДИНА XX ВЕКА, ТЈУЛАМИН (Канада) ПОЧЕТАК XXI ВЕКА - Одгајивачке карактеристике - Квалитет плода - Традиција????? (Ињи блан = Требјано)
10 ВИЛАМЕТ МИКЕР ТЈУЛАМИН
11 Технолошке карактеристике плода малине као сировине за ЈАП: - Низак садржај ферментабилних шећера (5,2-6,7%); - Вредност рн < 3,0 (али и 3,2-3,5); - Специфична и фина, али врло нежна арома; - Свежа малина осетљива на транспорт, кратко се чува; - Смрзнута малина дуго се чува, очуване хемијске карактеристике плода, нема губитка ароме;
12 Арома плода малине: једињење (разне класе: алкохоли, алдехиди, кетони,естри, терпенска једињења...); - Најзаступљенији су: С13 норизопреноиди: β-јонон (око 25%), α-јонон (око 17%) мирис љубичице, малине.. нонанал (око 3-10%) кремасти, воћни мирис; линалол (2-5%) воћно/цветни мирис; кариофилен (3-5%); деканал, α-терпинеол, хексадеканска кис., бензалдехид...
13 Сортна специфичност ароме плода малине: O (3E)-4-(2,6,6-Trimethyl-1-cyclohexen-1-yl)-3-buten-2-on β - јонон Виламет Микер Тјуламин O α - јонон 10 Виламет 4-(2,6,6-Trimethyl-cyclohex-2-enyl)-but-3-en-2-one 5 Микер Тјуламин 0 2,5 O nonanal нонанал 2 1,5 1 0,5 Виламет Микер Тјуламин 0 8 a l p h a - p i n e n e α - пинен 6 4 Виламет Микер 2 Тјуламин 0
14 ПОСТУПЦИ ЗА ПРОИЗВОДЊУ ЈАКИХ АЛКОХОЛНИХ ПИЋА ОД МАЛИНЕ 1 Ферментација кљука Дестилација кљука 2 Ферментација кљука Мацерација кљука Дестилација кљука 3 Мацерација кљука Дестилација кљука Свежа малина ОДГОВАРА!!!!! Смрзнута малина ПРОБЛЕМ??? Смрзнута малина Свежа малина ОДГОВАРА!!!!! Дефростација Активирање ензима LOX пута - повећано стварање С6 алдехида и алкохола мирис на зелено ИНОВАЦИЈА!!!!!!!!! Директна мацерација смрзнуте малине Тачно одређени температура (Т) и време (τ) мацерације, и количина етанола ПРОБЛЕМ??? Дефростација Активирање ензима LOX пута - повећано стварање С6 алдехида и алкохола мирис на зелено
15 Липооксигеназни пут деградације линолне и линолеинске кис.
16 Алкохолна ферментација: - Само свежа малина; - Кратко траје на собној Т (20 ⁰С) 7 дана; - Настанак бројних једињења (тзв. секундарна арома) у зависности од дужине ферментације (само ферментација или ферментација + мацерација); - Лако се квари дестилација одмах по завршеном алкохолном врењу; Алкохолно врење као хемијски процес Моносахариди (глукоза и фруктоза) C 6 H 12 O 6 2C 2 H 5 OH + 2CO 2 + топлота 100 кг 64,6 л а.а. 0,65 Теоријски коефицијент искоришћења шећера Дисахариди (сахароза) C 12 H 22 O 11 + H 2 O 4C 2 H 5 OH + 4CO 2 + топлота 100 кг 68,0 л а.а. 0,68 Теоријски коефицијент искоришћења шећера
17 Алкохолно врење као микробиолошки процес (изазивачи ферментативни квасци) Шећер Главни продукти АФ (етанол, CO 2, топлота) Испарљиви нузпродукти (виши алкохоли, више масне киселине, сирћетна киселина, естри, ацеталдехид, итд.) Неиспарљиви нузпродукти (глицерол, ћилибарна киселина, итд.) Ферментабилни шећери (глукоза, фруктоза и сахароза) Синтеза биомасе квасца Шећер C 2 H 5 OH + CO 2 + топлота + нузпродукти + прекурсори биомасе 100 кг 59,0 л а.а. (58,0 л а.а.) 0,59 (0,58) Стварни теоријски коефицијент искоришћења шећера
18 Алкохолно врење Нестерилни кљук Спонтана Аф Квасци (шећер C 2 H 5 OH + 2CO 2 + топлота + нузпродукти + прекурсори биомасе ) Додатак чистих култура квасца Saccharomyces spp. Kloeckera spp. Metschnikowia spp. Бактерије (шећер киселине + нузпродукти + прекурсори биомасе ) Бактерије млечне Бактерије сирћетне киселине киселине (Lactobacillus, Pediococcus, (Gluconobacter, Oenococcus spp.) Acetobacter spp.) Ферментабилни шећери (глукоза, фруктоза и сахароза) Шећер C 2 H 5 OH + CO 2 + топлота + нузпродукти + прекурсори биомасе 100 кг?????? л а.а. 0,56 Стварни коефицијент искоришћења шећера
19 Мацерација - Користе се и свеже и смрзнуте малине (роленд, гриз...); - Важан квалитет рафинисаног етанола (стандарди и сензорне карактеристике); - Различити односи малине/етанол - Режим мацерације (Т етанола и плодова, дужина мацерације, присуство ваздуха); - Брзо долази до деградације ароме дестилација одмах по завршеној мацерацији;
20 1 Ферментација кљука Дестилација кљука Дестилација 1 Ферментација кљука Дестилација кљука 3 Мацерација кљука Дестилација кљука Уређаји за двократну дестилацију ЦЕНА 3 Мацерација кљука Дестилација кљука Уређаји за једнократну дестилацију ЕВРА РАД ЕВРА АРОМА (ТРОЈНИ ТЕСТ МЕТОД ТРОУГЛА) ДОСТА РАДА ЈЕДНОСТАВАН ЗА РАД 9 ОЦЕЊИВАЧА БОЉА КАЈСИЈЕВАЧА 9 ОЦЕЊИВАЧА БОЉА КАЈСИЈЕВАЧА
21 Сазревање и финализација јаких алкохолних пића од малине БЕЗБОЈНА СТАКЛО INOX ОБОЈЕНА ХРАСТОВА БУРАД СЕДМИЦЕ / МЕСЕЦИ МЕСЕЦИ / ГОДИНЕ СМАЊИВАЊЕ ЈАЧИНЕ ДЕСТИЛАТА: ОМЕКШАНОМ ВОДОМ ДЕСТИЛОВАНОМ ВОДОМ САДРЖАЈ ЕТАНОЛА У ЈАКИМ АЛКОХОЛНИМ ПИЋИМА ОД МАЛИНЕ: 40-43%
22 КАРАКТЕРИСТИКЕ ЈАКИХ АЛКОХОЛНИХ ПИЋА ОД МАЛИНЕ 1 Ферментација кљука Дестилација кљука 2 Ферментација кљука Мацерација кљука Дестилација кљука 3 Мацерација кљука Дестилација кљука Велика варирања у хемијском саставу и сензорним карактеристикама; Често непрепознатљива и покривена примарна арома; Доминирају масне киселине и етил естри масних киселина; Потребно кг/л 40 вол% ракије скупа производња; 228 идентификованих једињења Веома уједначен састав и сензорне карактеристике; Препознатљива и изражена примарна арома малине; Доминирају састојци примарне ароме малине: С13 норизопреноиди (јонони, јонени...), алдехиди (октанал, нонанал, деканал, тридеканал, тетрадеканал...) и др.; Потребно 1,2 кг/л 40 вол% ракије јефтина производња;
23
24 Виламет Микер РОЛЕНД Тјуламин Фине разлике између сортних дестилата: 2-хексенал, бензалдехид, α-јонон, 7,8-дихидро-β-јонон, β-дамасценон, метастигма-4,6,8-триен, едулан, 1,1-диетокси нонан, етилолеат... ГРИЗ Цене: Роленд 3,2 Евра/л, Гриз 2,3 Евра/л,
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
6.1. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре
 0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
I Наставни план - ЗЛАТАР
 I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
Извештај Комисије за оцену урађене докторске дисертације МилетаВељовића, дипл.инж.
 НАСТАВНО-НАУЧНОМ ВЕЋУ ПОЉОПРИВРЕДНОГ ФАКУЛТЕТА УНИВЕРЗИТЕТА У БЕОГРАДУ Датум: 06.05.2016. године Предмет: Извештај Комисије за оцену урађене докторске дисертације МилетаВељовића, дипл.инж. Одлуком Наставно-научног
НАСТАВНО-НАУЧНОМ ВЕЋУ ПОЉОПРИВРЕДНОГ ФАКУЛТЕТА УНИВЕРЗИТЕТА У БЕОГРАДУ Датум: 06.05.2016. године Предмет: Извештај Комисије за оцену урађене докторске дисертације МилетаВељовића, дипл.инж. Одлуком Наставно-научног
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА
 ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
Хемијска, функционална и сензорна својства пива обогаћеног биолошки активним састојцима грожђа
 УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Миле С. Вељовић Хемијска, функционална и сензорна својства пива обогаћеног биолошки активним састојцима грожђа Докторска дисертација Београд, 2016. UNIVERSITY
УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Миле С. Вељовић Хемијска, функционална и сензорна својства пива обогаћеног биолошки активним састојцима грожђа Докторска дисертација Београд, 2016. UNIVERSITY
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Тест за 8. разред. Шифра ученика
 Министарство просвете Републике Србије Српско хемијско друштво Републичко такмичење из хемије 16. мај 2009. године Тест за 8. разред Шифра ученика Пажљиво прочитај текстове задатака. Празне странице теста
Министарство просвете Републике Србије Српско хемијско друштво Републичко такмичење из хемије 16. мај 2009. године Тест за 8. разред Шифра ученика Пажљиво прочитај текстове задатака. Празне странице теста
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Вектори vs. скалари. Векторске величине се описују интензитетом и правцем. Примери: Померај, брзина, убрзање, сила.
 Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Хуманитарна организација Срби за Србе - финансијскo пословање за 2010.год. Стање Стање Стање Датум (+) (-) (+) (-) (+) (-) (Еur.) (Дин.
 Хуманитарна организација Срби за Србе - финансијскo пословање за 2010.год. Стање Стање Стање Датум (+) (-) (+) (-) (+) (-) (Еur.) (Дин.) (КМ) Детаљи 31.12.10 5.615 133.889 Пренесено стање из 2009. 1.1.10
Хуманитарна организација Срби за Србе - финансијскo пословање за 2010.год. Стање Стање Стање Датум (+) (-) (+) (-) (+) (-) (Еur.) (Дин.) (КМ) Детаљи 31.12.10 5.615 133.889 Пренесено стање из 2009. 1.1.10
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
У к у п н о :
 ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
З А Х Т Е В за давање сагласности на реферат о урађеној докторској дисертацији за кандидата на докторским студијама
 УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Број захтева: 33/10-6.9. Датум: 29.06.2016. ВЕЋЕ НАУЧНИХ ОБЛАСТИ БИОТЕХНИЧКИХ НАУКА З А Х Т Е В за давање сагласности на реферат о урађеној докторској дисертацији
УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Број захтева: 33/10-6.9. Датум: 29.06.2016. ВЕЋЕ НАУЧНИХ ОБЛАСТИ БИОТЕХНИЧКИХ НАУКА З А Х Т Е В за давање сагласности на реферат о урађеној докторској дисертацији
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Часопис / Journal ЕКОНОМИКА ПОЉОПРИВРЕДЕ Economics of Agriculture. Основан године / Established 1954
 Часопис / Journal ЕКОНОМИКА ПОЉОПРИВРЕДЕ Economics of Agriculture Основан 1954. године / Established 1954 Издавачи / Publishers Друштво аграрних економиста СЦГ, Београд The Society of Agricultural Economists
Часопис / Journal ЕКОНОМИКА ПОЉОПРИВРЕДЕ Economics of Agriculture Основан 1954. године / Established 1954 Издавачи / Publishers Друштво аграрних економиста СЦГ, Београд The Society of Agricultural Economists
Aнализа производње енергије из отпадне биомасе на фармама у околини града Бора
 Aнализа производње енергије из отпадне биомасе на фармама у околини града Бора Аутор: Јелена Петковић 936/2013 Факултет техничких наука, Чачак Техника и информатика, 2013/14 е-mail: jelenapetkovic.petkovic@gmail.com
Aнализа производње енергије из отпадне биомасе на фармама у околини града Бора Аутор: Јелена Петковић 936/2013 Факултет техничких наука, Чачак Техника и информатика, 2013/14 е-mail: jelenapetkovic.petkovic@gmail.com
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
5.2. Имплицитни облик линеарне функције
 математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
Тест за 7. разред. Шифра ученика
 Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 017/018. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 017/018. година ТЕСТ МАТЕМАТИКА
Предмет: Извештај Комисије за оцену урађене докторске дисертације Саше Деспотовић, дипл. инж. И З В Е Ш Т А Ј 1. ОПШТИ ПОДАЦИ О ДОКТОРСКОЈ ДИСЕРТАЦИЈИ
 НАСТАВНO-НАУЧНОM ВЕЋУ ПОЉОПРИВРЕДНОГ ФАКУЛТЕТА УНИВЕРЗИТЕТА У БЕОГРАДУ Датум: 31.03.2017. године Предмет: Извештај Комисије за оцену урађене докторске дисертације Саше Деспотовић, дипл. инж. Одлуком Наставно-научног
НАСТАВНO-НАУЧНОM ВЕЋУ ПОЉОПРИВРЕДНОГ ФАКУЛТЕТА УНИВЕРЗИТЕТА У БЕОГРАДУ Датум: 31.03.2017. године Предмет: Извештај Комисије за оцену урађене докторске дисертације Саше Деспотовић, дипл. инж. Одлуком Наставно-научног
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
На основу члана 30. став 3. Закона о безбедности хране ( Службени гласник РС, број 41/09),
 На основу члана 30. став 3. Закона о безбедности хране ( Службени гласник РС, број 41/09), Министар пољопривреде, шумарства и водопривреде, доноси П Р А В И Л Н И К О ДЕКЛАРИСАЊУ, ОЗНАЧАВАЊУ И РЕКЛАМИРАЊУ
На основу члана 30. став 3. Закона о безбедности хране ( Службени гласник РС, број 41/09), Министар пољопривреде, шумарства и водопривреде, доноси П Р А В И Л Н И К О ДЕКЛАРИСАЊУ, ОЗНАЧАВАЊУ И РЕКЛАМИРАЊУ
ИЗВЕШТАЈ О AНКЕТИ (одржаној на крају зимског семестра 2008_09 године)
 РЕПУБЛИКА СРБИЈА Висока пословна школа струковних студија Бр. 31.03.2009. год. Лесковац, Дурмиторска 19 Тел. 016/254 961, факс: 016/242 536 e mail: mail@vpsle.edu.rs website: www.vpsle.edu.rs Настaвном
РЕПУБЛИКА СРБИЈА Висока пословна школа струковних студија Бр. 31.03.2009. год. Лесковац, Дурмиторска 19 Тел. 016/254 961, факс: 016/242 536 e mail: mail@vpsle.edu.rs website: www.vpsle.edu.rs Настaвном
ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ
 План наставе и учења: ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ I РАЗРЕД I УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т В Т В Б Т В Т В Б Т В Т В Б Т В Т
План наставе и учења: ТЕХНИЧАР ЗА ДИГИТАЛНУ ГРАФИКУ И ИНТЕРЕНЕТ ОБЛИКОВАЊЕ I РАЗРЕД I УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т В Т В Б Т В Т В Б Т В Т В Б Т В Т
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
10.3. Запремина праве купе
 0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
Питања и задаци за пријемни испит из хемије
 Питања и задаци за пријемни испит из хемије 1. Атоми неког хемијског елемента имају следећу електронску конфигурацију: 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 5. У којој групи и којој периоди ПСЕ се наведени
Питања и задаци за пријемни испит из хемије 1. Атоми неког хемијског елемента имају следећу електронску конфигурацију: 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 5. У којој групи и којој периоди ПСЕ се наведени
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
оп љ ње I полу од т 11. у т полуп е к оп е к у е око т оу л т е a = у л =. 12. т оу лу ABC д то је = =, полуп е к оп о к у R=. у т т е то т оу л.
 оп љ ње I полу од т оу о 1. у т е по у јед кок ко т оу л ко је п о од к к о о е, о. 2. у т по у јед кок ко т оу л о о е cm, ко је кој од о о о јед к од е ку кој п ј ед е о о е к к. 3. Д е т е т оу л у
оп љ ње I полу од т оу о 1. у т е по у јед кок ко т оу л ко је п о од к к о о е, о. 2. у т по у јед кок ко т оу л о о е cm, ко је кој од о о о јед к од е ку кој п ј ед е о о е к к. 3. Д е т е т оу л у
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ -
 ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
Смер: Друмски саобраћај. Висока техничка школа струковних студија у Нишу ЕЛЕКТРОТЕХНИКА СА ЕЛЕКТРОНИКОМ
 Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
Примена првог извода функције
 Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
4.4. Паралелне праве, сечица. Углови које оне одређују. Углови са паралелним крацима
 50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
Закони термодинамике
 Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
НАСТАВНИ ПЛАН И ПРОГРАМ
 НАСТАВНИ ПЛАН И ПРОГРАМ I НАСТАВНИ ПЛАН за образовни профил Техничар мехатронике I РАЗРЕД II РАЗРЕД III РАЗРЕД IV РАЗРЕД УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т
НАСТАВНИ ПЛАН И ПРОГРАМ I НАСТАВНИ ПЛАН за образовни профил Техничар мехатронике I РАЗРЕД II РАЗРЕД III РАЗРЕД IV РАЗРЕД УКУПНО недељно годишње недељно годишње недељно годишње недељно годишње годишње Т
Теорија одлучивања. Анализа ризика
 Теорија одлучивања Анализа ризика Циљеви предавања Упознавање са процесом анализе ризика Моделовање ризика Монте-Карло Симулација Предности и недостаци анализе ризика 2 Дефиниција ризика (квалитативни
Теорија одлучивања Анализа ризика Циљеви предавања Упознавање са процесом анализе ризика Моделовање ризика Монте-Карло Симулација Предности и недостаци анализе ризика 2 Дефиниција ризика (квалитативни
Погодности сорти кајсије за сушење
 УНИВЕРЗИТЕТ У НОВОМ САДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Департман за воћарство, виноградарство, хортикултуру и пејзажну архитектуру Васо Љешковић Погодности сорти кајсије за сушење Мастер рад Нови Сад, 2015. УНИВЕРЗИТЕТ
УНИВЕРЗИТЕТ У НОВОМ САДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Департман за воћарство, виноградарство, хортикултуру и пејзажну архитектуру Васо Љешковић Погодности сорти кајсије за сушење Мастер рад Нови Сад, 2015. УНИВЕРЗИТЕТ
TAЧКАСТА НАЕЛЕКТРИСАЊА
 TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
Могућности и планови ЕПС на пољу напонско реактивне подршке. Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије
 Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
др Милена Марјановић, професор
 РЕПУБЛИКА СРБИЈА Висока пословна школа струковних студија 03.03.2008.год. Лесковац, Дурмиторска 19 Тел. 016/254 961, факс: 016/242 536 e mail: mail@vspm.edu.yu website: www.vspm.edu.yu Настaвном већу Високе
РЕПУБЛИКА СРБИЈА Висока пословна школа струковних студија 03.03.2008.год. Лесковац, Дурмиторска 19 Тел. 016/254 961, факс: 016/242 536 e mail: mail@vspm.edu.yu website: www.vspm.edu.yu Настaвном већу Високе
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
4. Троугао. (II део) 4.1. Појам подударности. Основна правила подударности троуглова
 4 Троугао (II део) Хилберт Давид, немачки математичар и логичар Велики углед у свету Хилберту је донело дело Основи геометрије (1899), у коме излаже еуклидску геометрију на аксиоматски начин Хилберт Давид
4 Троугао (II део) Хилберт Давид, немачки математичар и логичар Велики углед у свету Хилберту је донело дело Основи геометрије (1899), у коме излаже еуклидску геометрију на аксиоматски начин Хилберт Давид
7.3. Површина правилне пирамиде. Површина правилне четворостране пирамиде
 математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
ИЗВЕШТАЈ КОМИСИЈЕ ЗА ИЗБОР У ЗВАЊЕ НАУЧНОГ САРАДНИКА
 УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ ИЗВЕШТАЈ КОМИСИЈЕ ЗА ИЗБОР У ЗВАЊЕ НАУЧНОГ САРАДНИКА ОБЛАСТ: БИОТЕХНИЧКЕ НАУКЕ ГРАНА: ПРЕХРАМБЕНО ИНЖЕЊЕРСТВО НАУЧНА ДИСЦИПЛИНА: ТЕХНОЛОГИЈА АНИМАЛНИХ ПРОИЗВОДА
УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ ИЗВЕШТАЈ КОМИСИЈЕ ЗА ИЗБОР У ЗВАЊЕ НАУЧНОГ САРАДНИКА ОБЛАСТ: БИОТЕХНИЧКЕ НАУКЕ ГРАНА: ПРЕХРАМБЕНО ИНЖЕЊЕРСТВО НАУЧНА ДИСЦИПЛИНА: ТЕХНОЛОГИЈА АНИМАЛНИХ ПРОИЗВОДА
Мониторинг квалитета ваздуха Града Новог Сада у години
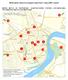 Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
Мониторинг квалитета ваздуха Града Новог Сада у години
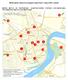 Мониторинг квалитета ваздуха Града Новог Сада у 2010. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад NO
Мониторинг квалитета ваздуха Града Новог Сада у 2010. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад NO
Слика бр.1 Површина лежишта
 . Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
. Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
I Тачка 1. Растојање две тачке: 2. Средина дужи y ( ) ( ) 2. II Права 1. Једначина прамена правих 2. Једначина праве кроз две тачке ( )
 Шт треба знати пре почетка решавања задатака? АНАЛИТИЧКА ГЕОМЕТРИЈА У РАВНИ I Тачка. Растојање две тачке:. Средина дужи + ( ) ( ) + S + S и. Деоба дужи у односу λ: 4. Површина троугла + λ + λ C + λ и P
Шт треба знати пре почетка решавања задатака? АНАЛИТИЧКА ГЕОМЕТРИЈА У РАВНИ I Тачка. Растојање две тачке:. Средина дужи + ( ) ( ) + S + S и. Деоба дужи у односу λ: 4. Површина троугла + λ + λ C + λ и P
ПРОИЗВОДНА, НУТРИТИВНА И АНТИОКСИДАТИВНА СВОЈСТВА СОРТИ РИБИЗЛЕ (Ribes cv.)
 УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Бoбан С. Ђорђевић ПРОИЗВОДНА, НУТРИТИВНА И АНТИОКСИДАТИВНА СВОЈСТВА СОРТИ РИБИЗЛЕ (Ribes cv.) докторска дисертација Београд, 2012. УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ
УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Бoбан С. Ђорђевић ПРОИЗВОДНА, НУТРИТИВНА И АНТИОКСИДАТИВНА СВОЈСТВА СОРТИ РИБИЗЛЕ (Ribes cv.) докторска дисертација Београд, 2012. УНИВЕРЗИТЕТ У БЕОГРАДУ ПОЉОПРИВРЕДНИ
ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ)
 ПРИЛОГ 2. ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ) ДИО А Листа забрањених РОРѕ супстанци из Стокхолмске конвенције о дуготраjним органским загађивачима Назив супстанце CAS
ПРИЛОГ 2. ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ) ДИО А Листа забрањених РОРѕ супстанци из Стокхолмске конвенције о дуготраjним органским загађивачима Назив супстанце CAS
8.2 ЛАБОРАТОРИЈСКА ВЕЖБА 2 Задатак вежбе: Израчунавање фактора појачања мотора напонским управљањем у отвореној повратној спрези
 Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
Семинарски рад из линеарне алгебре
 Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Хуманитарна организација Срби за Србе - финансијскo пословање за 2009.
 Хуманитарна организација Срби за Србе - финансијскo пословање за 2009. Датум Стање Стање (+) (-) (+) (-) (Еur.) (Дин.) Детаљи Напомена 31.12.2008 1.956 20.928 Пренесено стање из 2008. 01.01.2009 31 1 1.986
Хуманитарна организација Срби за Србе - финансијскo пословање за 2009. Датум Стање Стање (+) (-) (+) (-) (Еur.) (Дин.) Детаљи Напомена 31.12.2008 1.956 20.928 Пренесено стање из 2008. 01.01.2009 31 1 1.986
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 016/017. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 016/017. година ТЕСТ МАТЕМАТИКА
ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ
 Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
TРЕНД УКУПНОГ ОБИМА ОТКУПА НЕДРВНИХ ШУМСКИХ ПРОИЗВОДА НА ПОДРУЧЈУ ОПШТИНЕ ИВАЊИЦА
 UDK 630*71:630*89(497.11 Ivanjica) Оригинални научни рад TРЕНД УКУПНОГ ОБИМА ОТКУПА НЕДРВНИХ ШУМСКИХ ПРОИЗВОДА НА ПОДРУЧЈУ ОПШТИНЕ ИВАЊИЦА ЉИЉАНА КЕЧА 1 МИЛИВОЈ БОГОЈЕВИЋ 1 МИЛИЦА МАРЧЕТА 1 Извод: У свету
UDK 630*71:630*89(497.11 Ivanjica) Оригинални научни рад TРЕНД УКУПНОГ ОБИМА ОТКУПА НЕДРВНИХ ШУМСКИХ ПРОИЗВОДА НА ПОДРУЧЈУ ОПШТИНЕ ИВАЊИЦА ЉИЉАНА КЕЧА 1 МИЛИВОЈ БОГОЈЕВИЋ 1 МИЛИЦА МАРЧЕТА 1 Извод: У свету
МЕНАЏМЕНТ ПРОИЗВОДЊЕ ПРЕДУЗЕЋА ЗА ОТКУП И ДОРАДУ ШУМСКИХ ПЛОДОВА
 Стручни рад Економика пољопривреде Број 1/2010. УДК: 331.103:630*28+635.8+582 МЕНАЏМЕНТ ПРОИЗВОДЊЕ ПРЕДУЗЕЋА ЗА ОТКУП И ДОРАДУ ШУМСКИХ ПЛОДОВА Д. Живковић 1, З. Рајић, И. Милијић Сажетак. У раду су разматране
Стручни рад Економика пољопривреде Број 1/2010. УДК: 331.103:630*28+635.8+582 МЕНАЏМЕНТ ПРОИЗВОДЊЕ ПРЕДУЗЕЋА ЗА ОТКУП И ДОРАДУ ШУМСКИХ ПЛОДОВА Д. Живковић 1, З. Рајић, И. Милијић Сажетак. У раду су разматране
УНИВЕРЗИТЕТ У НОВОМ САДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ
 УНИВЕРЗИТЕТ У НОВОМ САДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Департман за пољопривредну технику Крстан Кешељ дипл. инж. пољопривреде КОНВЕКТИВНО СУШЕЊЕ МАЛИНЕ ПРИМЕНОМ РАЗЛИЧИТИХ ПРЕДТРЕТМАНА МАСТЕР РАД Нови Сад, 2017.
УНИВЕРЗИТЕТ У НОВОМ САДУ ПОЉОПРИВРЕДНИ ФАКУЛТЕТ Департман за пољопривредну технику Крстан Кешељ дипл. инж. пољопривреде КОНВЕКТИВНО СУШЕЊЕ МАЛИНЕ ПРИМЕНОМ РАЗЛИЧИТИХ ПРЕДТРЕТМАНА МАСТЕР РАД Нови Сад, 2017.
Факултет организационих наука Центар за пословно одлучивање. PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation)
 Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
61. У правоуглом троуглу АВС на слици, унутрашњи угао код темена А је Угао
 ЗАДАЦИ ЗА САМОСТАЛНИ РАД Задаци за самостлни рад намењени су првенствено ученицима који се припремају за полагање завршног испита из математике на крају обавезног основног образовања. Задаци су одабрани
ЗАДАЦИ ЗА САМОСТАЛНИ РАД Задаци за самостлни рад намењени су првенствено ученицима који се припремају за полагање завршног испита из математике на крају обавезног основног образовања. Задаци су одабрани
ХЕТЕРОЦИКЛИЧНА ЈЕДИЊЕЊА, АЛКАЛОИДИ И АНТИБИОТИЦИ
 ХЕТЕРОЦИКЛИЧНА ЈЕДИЊЕЊА, АЛКАЛОИДИ И АНТИБИОТИЦИ Биохемија је истовремено грана биологије и органске хемије која проучава биологију на молекулском нивоу. Највећи број молекула који учествује у животним
ХЕТЕРОЦИКЛИЧНА ЈЕДИЊЕЊА, АЛКАЛОИДИ И АНТИБИОТИЦИ Биохемија је истовремено грана биологије и органске хемије која проучава биологију на молекулском нивоу. Највећи број молекула који учествује у животним
ДИЈАГРАМИ И ТАБЛИЦЕ ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ОДСЕК ЗА ПРОИЗВОДНО МАШИНСТВО ПРОЈЕКТОВАЊЕ ТЕХНОЛОГИЈЕ ТЕРМИЧКЕ ОБРАДЕ. Приредио: Александар Милетић
 - ПТО ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ОДСЕК ЗА ПРОИЗВОДНО МАШИНСТВО ПРОЈЕКТОВАЊЕ ТЕХНОЛОГИЈЕ ТЕРМИЧКЕ ОБРАДЕ ДИЈАГРАМИ И ТАБЛИЦЕ Приредио: Александар Милетић 1 С т р а н а - ПТО Садржај Пренос топлоте... 3 Цементација...15
- ПТО ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ОДСЕК ЗА ПРОИЗВОДНО МАШИНСТВО ПРОЈЕКТОВАЊЕ ТЕХНОЛОГИЈЕ ТЕРМИЧКЕ ОБРАДЕ ДИЈАГРАМИ И ТАБЛИЦЕ Приредио: Александар Милетић 1 С т р а н а - ПТО Садржај Пренос топлоте... 3 Цементација...15
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА школска 2013/2014. година УПУТСТВО ЗА РАД Тест који треба да решиш
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА школска 2013/2014. година УПУТСТВО ЗА РАД Тест који треба да решиш
МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА
 Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
ПРОРАЧУН СОНИХ КУПАТИЛА
 ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ОДСЕК ЗА ПРОИЗВОДНО МАШИНСТВО ПРОЈЕКТОВАЊЕ ТЕХНОЛОГИЈЕ ТЕРМИЧКЕ ОБРАДЕ ПРОРАЧУН СОНИХ КУПАТИЛА ПРИРЕДИО: АЛЕКСАНДАР МИЛЕТИЋ НОВИ САД, 2011 САДРЖАЈ 1 УВОД... 2 2 КОНСТРУКЦИЈА СОНОГ
ФАКУЛТЕТ ТЕХНИЧКИХ НАУКА ОДСЕК ЗА ПРОИЗВОДНО МАШИНСТВО ПРОЈЕКТОВАЊЕ ТЕХНОЛОГИЈЕ ТЕРМИЧКЕ ОБРАДЕ ПРОРАЧУН СОНИХ КУПАТИЛА ПРИРЕДИО: АЛЕКСАНДАР МИЛЕТИЋ НОВИ САД, 2011 САДРЖАЈ 1 УВОД... 2 2 КОНСТРУКЦИЈА СОНОГ
УТИЦАЈ КОЕФИЦИЈЕНАТА ЕЛАСТИЧНОСТ ТРАЖЊЕ НА ЦЕНЕ ПОЉОПРИВРЕДНО-ПРЕХРАМБЕНИХ ПРОИЗВОДА
 Прегледни рад ЕКОНОМИКА ПОЉОПРИВРЕДЕ Број 4/2007. УДК: 631.153 УТИЦАЈ КОЕФИЦИЈЕНАТА ЕЛАСТИЧНОСТ ТРАЖЊЕ НА ЦЕНЕ ПОЉОПРИВРЕДНО-ПРЕХРАМБЕНИХ ПРОИЗВОДА Д. Момировић 1 Резиме. Како у нашој земљи није рађена
Прегледни рад ЕКОНОМИКА ПОЉОПРИВРЕДЕ Број 4/2007. УДК: 631.153 УТИЦАЈ КОЕФИЦИЈЕНАТА ЕЛАСТИЧНОСТ ТРАЖЊЕ НА ЦЕНЕ ПОЉОПРИВРЕДНО-ПРЕХРАМБЕНИХ ПРОИЗВОДА Д. Момировић 1 Резиме. Како у нашој земљи није рађена
Математика Тест 3 Кључ за оцењивање
 Математика Тест 3 Кључ за оцењивање ОПШТЕ УПУТСТВО ЗА ОЦЕЊИВАЊЕ Кључ за оцењивање дефинише начин на који се оцењује сваки поједини задатак. У општим упутствима за оцењивање дефинисане су оне ситуације
Математика Тест 3 Кључ за оцењивање ОПШТЕ УПУТСТВО ЗА ОЦЕЊИВАЊЕ Кључ за оцењивање дефинише начин на који се оцењује сваки поједини задатак. У општим упутствима за оцењивање дефинисане су оне ситуације
МОГУЋНОСТИ КОРИШЋЕЊЕ ОТПАДА ОД МАЛИНЕ КАО ЕНЕРГЕНАТА У ДОМАЋИНСТВИМА И ИНДУСТРИЈИ Проф. Др Срећко Ћурчић Факултет техничких наука у Чачку
 МОГУЋНОСТИ КОРИШЋЕЊЕ ОТПАДА ОД МАЛИНЕ КАО ЕНЕРГЕНАТА У ДОМАЋИНСТВИМА И ИНДУСТРИЈИ Проф. Др Срећко Ћурчић Факултет техничких наука у Чачку Отпад из пољопривреде као енргент Неки новоформирани засади малине
МОГУЋНОСТИ КОРИШЋЕЊЕ ОТПАДА ОД МАЛИНЕ КАО ЕНЕРГЕНАТА У ДОМАЋИНСТВИМА И ИНДУСТРИЈИ Проф. Др Срећко Ћурчић Факултет техничких наука у Чачку Отпад из пољопривреде као енргент Неки новоформирани засади малине
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1
 1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
1. 2. МЕТОД РАЗЛИКОВАЊА СЛУЧАЈЕВА 1 Метод разликовања случајева је један од најексплоатисанијих метода за решавање математичких проблема. У теорији Диофантових једначина он није свемогућ, али је сигурно
