Lekcija 4 Istosmjerni motori s permanentnim magnetima
|
|
|
- Περσεφόνη Ελευθερόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Lekcij 4 Iomjerni moori permnennim mgneim Prof.dr.c. Jmin Velgić Elekroehnički fkule Srjevo olegij: Akuori
2 4.1. Svojv permnennih mgne Prednoi permnennih mgne imju u zdnjih nekoliko godin znčjn ujecj n rzvoj elekričkih rojev. Ove prednoi u: eliminirnje gubik u bkru, viok guoć energije i efikno, mlen momen inercije roor, mogući veći zrčni rpor zbog veće koerciivne ile. Nedoci permnennih mgne: gubik flekibilnoi uprvljnj mgnekim okom, roškovi vioke guoće ok permnennih mgne u vioki, mgneke krkeriike e mijenjju vremenom, gubik mgnekih vojv mgneizirnj iznd Curiejeve emperure. 2/48
3 Svojv permnennih mgne Permnenni mgneki merijli imju pecijlne krkeriike koje e morju uzei u obzir pri dizjnu roj. Nprimjer, njbolje performne e poižu lomljivom kermikom, neki merijli u hemijki ojeljivi, i vi u emperurno ojeljivi i i većin im ojeljivo n rzmgneizirjuć polj. Odgovrjući dizjn zhijev dobro rzumijevnje merijl. 3/48
4 B-H pelj Tipičn B-H pelj z permnenni mgne je prikzn n ljedećoj lici. 4/48 Dio krivulje zbog koje e permnenni mgnei korie u dizjnirnju moor je gornji lijevi kvdrn. Ovj egmen e nziv krivulj rzmgneizirnj i prikzn je n ljedećem ljdu.
5 rivulj rzmgneizirnj 5/48 Puno operećenje Bez operećenj Recoil line Njlošiji lučj rzmgneizirnj D' C' C B' A' B r - Remnenn indukcij A Linij ere B Gu H c oerciivn il H Oered 0
6 rivulj rzmgneizirnj 6/48 Guoć remnennog zolog ok B r bi će rpoloživ ko je mgne krko pojen. Međuim, zrčnim rporom rzmgneizirnje će rezuliri rdnom čkom bez operećenj ere, B. Ngib linije bez operećenj je mnji većim zrčnim rporom. S prookom ruje kroz or, nje ljedeće rzmgneizirnje permnennog mgne koje uzrokuje pomicnje rdne čke prem C, koj predvlj puno operećenje. Trnzijeni ili kvrovi roj mogu dovei do njlošijeg lučj rzmgneizirnj koji vodi k ukupnom rzmgneizirnju permnennog mgne. Recoil line lijedi rnzijen koji pokzuje mnjenje guoće mgnekog ok u uporedbi originlnom linijom. Popuno je jn vžno uprvljnj rdom mgne kko bi e zdržl rdn čk vn uvje njlošijeg lučj rzmgneizirnj.
7 Rzmgneizirnje mgne moor 7/48 Permnenni mgne e može djelimično ili popuno rzmgneiziri djelovnjem j upronog mgnekog g polj. U lučju moor permnennim mgneim uprono mgneko polje predvlj rekciju rmure, koju proizvode rujom projecni rmurni nmoi. Zbog og dolzi do mnjenj pobudnog polj, koje je, međuim, do izvjene mjere reverzibilno, j. nenkom ruje rmure permnenni mgnei e vrćju u voje prvobino nje. Ako jko ruje oliko pore d komponen jkoi mgnekog g polj rmurne rekcije, koj djeluje n mgne, pone već od vlie koerciivne ile mgne, opdnje pobudnog polj poje ireverzibilno. Proce rzmgneizirnj funkcij je rmurne ruje. Sruj rzmgneizirnj predvlj ruju koj rzmgneizirnjem permnennih mgne mnjuje mgneku konnu moor z 5 %.
8 Rzmgneizirnje mgne moor 8/48 D bi e mnjil opno rzmgneizirnj, konvencionlno je uvojeno d e u moore ugrđuju kvi mgnei koji će bez eškoće izdrži ruju brem edm pu jču od nzivne. Jedn od nčin d e moor zšii od rzmgneizirnj je d e predvidi npjnje rujnim grničnikom. Drugi nčin je d e n čelo kućiš monir polni nvk od mekog željez kroz koji će, zbog mnjenj relukncije, zvorii ilnice i rekcije rmure, p će permnenni mgne oi pošeđen od njihov djelovnj.
9 Permnennomgneki merijli 9/48 Prem ome, permnenni mgnei koji e ugrđuju u iomjerne moore morju imi: šo veći remnenni mgneizm rdi vrnj jkog mgnekog polj, šo veću koerciivnu ilu rdi uprovljnj j ujecjim rzmgneizirnj, šo veći elekrički opor rdi prječvnj vrložnih ruj, šo mnji oplinki koeficijen kko bi mgneki ok bio šo mnje ovin o emperurnim promjenm.
10 Permnennomgneki merijli 10/48 Alnico dobr vojv li premlen koerciivn il i prevelik površin B-H pelje => lhko dolzi do permnennog rzmgneizirnj. Ferii Brij & Sroncij nik cijen, umjereno viok rdn emperur 400 C i prvolinijk ij krivulj rzmgneizirnj. i Međuim, B r je mli => volumen i veličin roj rebju bii veće. Smrijum-obl Sm-Co veom dobr vojv li jko kup budući d je Smrijum rijedk. Neodymium-Željezo-Bor Nd-Fe-B veom dobr vojv oim šo je Curie-jev emperur mo 150 C.
11 Permnennomgneki merijli 11/48 Dijgrm rzmgneizirnj
12 12/ Iomjerni moori permnennim mgneim Cilj: proizvei moore šo većim zkrenim momenom i šo mnjim momenom inercije. Iomjerni moori omogućuju kvlienu regulciju brzine i momen promjenom npon, odnono ruje moor. Od moor e rži d roši šo je moguće mnje energije, d zuzim šo mnji proor i im šo mnju ežinu. Pronlzk nžnih permnennih mgne omogućio je ojeno poboljšnje nvedenih vojv. To e u prvom redu odnoi n veću linerno brzinkomomenne krkeriike koj predvlj ovino brzine moor o operenom momenu. od izvedbi elekromoorom pri većim vrijednoim operenog momen pojvljuje e njezino znno zkrivljenje. od izvedbi permnennim mgneim linerno krkeriike oje u cijelom području.
13 13/48 Momenno-brzinke krkeriike DC moor uzbudnim nmoom elekromoor DC moor permnennim mgneom S uzbudom 100 Permnenni mgne Brzin n 60 n Brzi Momen Momen
14 Iomjerni moori permnennim mgneim Uzrok očuvnj linernoi krkeriike je međudjelovnje orkog i rmurnog roorkog mgnekog polj. od moor permnennim mgneim mgneki polovi or u relizirni kermičkim nvcim. Njihov permebilno goovo je jednk permebilnoi zrk. Tko e mgneke ilnice roor nemju rzlog kroz njih zvri, i p nem deformirnj mgnekih okov ni pojve nelinernoi n brzinko-mgnekoj krkeriici, p ni komucijkih poeškoć u vezi im šo je lučj elekromgneim. Oim og poboljšnj, izvedbe moor kermičkim permnennim mgneim ne rebju energijko npjnje j elekromgnekog vik, ko ni m vik. Poljedic og je mnji obujm i ežin z jednku izlznu ngu u uporedbi moorim elekromgneim. 14/48
15 Iomjerni moori permnennim mgneim 15/48 od moor elekromgnekim polovim n oru ilnice rmurnog mgnekog polj, idući linijom mnjeg mgnekog opor, vijju e prem polnim nvcim or. Zbog og n jednoj rni polnog nvk nje zbrjnje, n drugoj odbijnje mgnekih ilnic orkog i roorkog polj, ime i pojčvnje mgnekog ok or n jednoj rni polnog nvk, i lbljenje n drugoj rni. Poljedic og je ugoni pomk vekor orkog mgnekog ok z određeni ugo α u mjeru upronome okrenju roor, u odnou prem njegovom onovnom položju u nju mirovnj. Poljedic ovog je jednk ugoni pomk zv. neurlne oi roor, koj je po definiciji uvijek okomi n o rocije i n vekor orkog polj.
16 Iomjerni moori permnennim mgneim Umjeo uzbudnih nmo n oru korie e permnenni mgnei. Problemi permnennim mgneim: 16/48 Rzličioi u moorim dolze iz vrijcij j mgnekih merijl koji mogu bii rzmgneizirni prekomjernim emperurm, nponim i mgnekim poljim. Brzin vrnje iomjernog moor ovii o kombinciji npon i ruje koji eku kroz rmuru, e o operećenju. Brzin moor proporcionln je nponu, dok je momen proporcionln ruji. Uprvo zbog ovih vojv e iomjerni i moor vrlo čeo korii u elekromoornim pogonim koji zhijevju uprvljnje brzinom zhvljujući rzvoju energeke elekronike pojednovilo e uprvljnje brzinom i olih vr elekromoor. Brzin moor e može mijenji promjenom opor rmure, koje e izvodi dodvnjem vnjkog promjenjivog opor pojenog u eriju izvorom, ili korišenjem promjenjivog nponkog izvor.
17 Primjer 1 Z moor nzivnim podcim: 17/48 opor rmure: R =0.6 Ω, nzivn ruj rmure: I n =6.5 5A, nzivn nponk konn: v =0.4 V/rd. Porebno je: Nći mkimlni npon z pokrenje moor iz nj mirovnj; b Izrčuni mkimlni npon zuvljnj brzine od 50 rd/, d e moor ne izloži opnoim rzmgneizirnj.
18 Primjer 1 Rješenje: Dopušen ruj iznoi edmorukoj nzivnoj ruji: 18/48 I d 7 I = = = n 45.5 A. U nju mirovnj ruj je ogrničen jedino oporom rmure, p bi mkimlni npon mogo bii: U mx = R I d = = 27.3 V. Rdi igurnoi rzumno je uporijebii dee poo mnji npon, koji izlzi: U = 0.9U mx = = V. Pri zuvljnju vlj uzei u obzir d e priključeni npon j j j p j p zuvljnj u djelovnju zbrj prouelekromoornom ilom, kko je prikzno n ljedećoj lici.
19 Primjer 1 19/48 R R I > 0 I < 0 U p E= e Ω U z E= e Ω Moor u nju pokrenj Moor u nju zuvljnj Njveć prouelekromoorn il pojvljuje j j e pri njvećoj j brzini, j. u renuku poček zuvljnj, vrijedno joj je: E = Ω = = v 20 V. Budući d je vrijedno dopušene ruje, mnjen 10 % rdi igurnoi, iznoi =41 A, npon zuvljnj će bii: U z = R I E = = 4.6 V.
20 Primjeri DC moor čekicm 20/48
21 4.3. Memički model moor 21/48 Ndomjen hem moor z porebe izvođenj memičkog model z DC moor permnennim mgneom prikzn je n ljedećoj lici. i R ω, τ m u L e _
22 Memički model moor 22/48 rug rmure može e opii ljedećom nponkom jedndžbom: u di = R i L e. d gdje je: R - ukupni opor rmurnog krug, [Ω], L - ukupni indukivie rmurnog krug, [H], i - vrijedno ruje rmure, [A], u - vrijedno npon rmure, [V], e -prouelekromoorn il, [V]. Prem ome, npon u pokriv pdove npon n indukivieu i oporu rmure ko i prouelekromoorne ile e.
23 Memički model moor 23/48 Prouelekromoorn il, koj e inducir u nmou rmure zbog vrnje oovine moor proporcionln je nponkoj konni i brzini vrnje oovine moor: e = vωω. gdje je: v nponk konn, [V], v ω ugon brzin vrnje, odnono mehničk brzin vrnje, [1/]. Nponk konn v ovii o konrukcijkim deljim moor i mgnekom oku nmo. Izrz z v je = v gdje je Φ n nzivn vrijedno glvnog mgnekog ok po polu, [V]. e Φ n
24 Memički model moor 24/48 Mehničk ω i elekričk brzin vrnje ω e međuobno u povezne relcijom: ω = p ω e gdje je: p m broj pri polov Primjenom Lplceove rnformcije n izrze dobivju e nponke jedndžbe elekričnog krug rmure u domeni komplekne vrijble prepovlj e kod primjene Lplceove rnformcije d u počeni uvjei jednki nuli. : m U = R L I E E = Ω v
25 Memički model moor 25/48 Mgneki ok Φ i ruj rmure prouzrokuju zkreni momen n rmuri moor momen moor τ m, koji je dn ljedećim izrzom: gdje je: momenn konn moor. τ m = Z opi mehničkog model polzi e od D Aleberov princip d je um vih il koje djeluju n ijel jednk ili inercije dinmičk rvnoež momen: i dω τ m = J m Bω τ d gdje je: τ m momen moor, [kg m -2 ], τ momen ere, [kg m -2 ], J m momen inercije moor, [kg m 2 ], Bω momen vikoznog renj, [kg m -2 ].
26 Memički model moor 26/48 Prelzom u frekvencijko područje dobivju e momenne jedndžbe: Memički model moor j ] [ M B J M m m Ω = Dobivene jedndžbe moor mogu e npii n ljedeći nčin: I M m = j g p j ] [ ] [ 1 ] [ 1 E U E U R E U I ], [ 1 ] [ 1 ] [ E U T E U R L E U L R I = = = ], [ 1, M M B J Ω Ω E m v = =. I M B J m m =
27 Memički model moor U gornjim jedndžbm u: =1/R T = L /R - koeficijen pojčnj rmurnog krug, [A/V], - vremenk konn rmurnog krug, []. N emelju jedndžbi džbi moor dobiv e hem ko n lici. i 27/48 M _ U _ 1 T I M m 1 B J m Ω E v
28 Memički model moor 28/48 Ovinoi promjene brzine brzine vrnje o promjeni npon rmure i momen ere mogu eizrziiljedećim prijenonim Memički model moor g j p j funkcijm: 1 Ω B J T B BT J B U Ω m m v = B B v v J T BT J T B M Ω m m v = Elekromehničk vremenk konn T J / B ovii 1 B B v v Elekromehničk vremenk konn T m =J m / v B ovii o momenu inercije.
29 Memički model moor 29/48 Budući d kod iomjernih moor permnennim mgneim vrijedi d je rmurn vremenk konn Memički model moor mgneim vrijedi d je rmurn vremenk konn znno mnj od elekromehničke vremenke konne moor T << T m, d je oprvdno znemrii djelovnje rmurne vremenke konne p prijenone funkcije poprimju ljedeće oblike: T J B U Ω m m v = = B m v m v 1 T J B M Ω = = T B J B M m v m v 1 1
30 Memički model moor 30/48 Tkođer, budući d je koeficijen vikoznog mehničkog renj B redovno mnogo mnji od koeficijen vikoznog elekričkog renj v /R B << v /R d vrijedi: v v = >> B Tm = R J m v j. B e može znemrii u gornjim izrzim, p e dobiv: Ω 1 = U 1 T m Ω = M 1 T 2 m 1 m 2 T = = 1 v = 1/ J m,, v v.
31 Memički model moor Uzimjući u obzir nveden znemrenj, dobiv e pojednovljen rukurn hem iomjernog moor prikzn n ljedećoj lici. 31/48 M _ U = R _ M m J m 1 Ω E v
32 DC moor bez čekic Ogrničenj moor čekicm: 32/48 Elekričn vez između roor i izvor iomjerne ruje e ovruje ko d e izvor iomjerne ruje poji n grfine čekice koje kližu po komuoru. Prilikom prelk čekice jedne n drugu lmelu komuor pooji renuk kd e izvor nlzi u krkom poju uljed čeg dolzi do ikrenj čekic. Ikrenje čekic dovodi do polgnog unišvnj grfinih čekic, li idookidcije okidcije i rošenj komuor, p je o glvni nedok ove vre moor. Ikrenje e pojčv ukoliko e povećv: brzin vrnje moor pri velikim brzinm eško održvi konk čekic komuorom, npon, operećenje, odnono ruj ko poljedic povećnj npon ili operećenj. Ikrenje oim mog unišvnj komuor i čekic z poljedicu im i vrnje čujnog i elekričkog šum. od velikih rojev komuor je kup i zhijev preciznu ugrdnju mnogih dijelov.
33 DC moor bez čekic N rooru u mješeni permnenni mgnei, or e oji od nmo. predvlj oblik AC moor elekričkom komucijom. Moori ne drže čekice ili komuor mnogo efikniji, mnje renje. 33/48 mogu e pogonii većim brzinm bez rizik ošećenj čekic, šo nije lučj DC moorom čekicm. roz orke nmoe e propuš ruj koj dovodi do zkrenj roor. Srujom koj prolzi kroz orke nmoe e uprvlj izvn elekroničkom klopom, zv. elekroničkim komuorom, koji zmjenjuje klični komuor.
34 DC moor bez čekic Ulog komuor: promjen polrie u vodičim ovino o njihovom položju u odnou n uzbudno polje. Prejek DC moor bez čekic: 34/48
35 35/48 DC moor bez čekic Mehnički rpored dijelov moor Prekpčjući orki polovi Roor od permnennog mgne Svjeloni ši Ugrđene volfrmke lmpe Ugrđene foo diode
36 DC moor bez čekic 36/48 D bi e moglo iprvno odredii kroz koji nmo će elekronički komuor poli ruju, i ruju kojeg mjer, kv moor mor imi enzor položj roor n onovu čeg e uprvlj rdom mog komuor zhijev e dodn elekronik i enzori položj. Ovj enzor korii Hll-ov efek. Brz odziv brzine vrnje. Efikno iomjernog moor bez čekic je 85-90%, dok je iomjernog moor čekicm 75-80%. Dodni energeki prekidči u pojčlu zhijevju znne dodne roškove. orie e u plikcijm gdje e zhijevju velik područj brzin.
37 DC moor bez čekic DC moor permnennim mgneom i čekicm 37/48 DC moor permnennim mgneom bez čekic: Permnenni rjni mgnei n rooru, koji predvljju uzbudu. Sorki npon polifzn nmoi n oru. Već efikno, mnje renje, mnji elekrički šum, zhijev elekronički pogon. Permnenni mgnei n oru, nmoi u uorim rmure n rooru. Umjeo uzbudnih nmo n oru, uzbudu predvljju permnenni mgnei n oru. elekrički šum, zhijev elekronički
38 38/48 Primjer DC moor bez čekic Proizvođč Micromo: DC moor bez čekic: dimenzije 16mm x 28mm Brzin 65,000 rpm obrj u minui Momen: 50 mnm Sng: 11 W Npon: 12 V
39 Specifikcije DC moor bez čekic 39/48
40 Primjene DC moor bez čekic 40/48 Medicin: cenrifuge, orokopki hirurški li, repirori, omološki hirurški li, rnporni pumpni iemi npr. ubrizgvnje inzulin. Modeli vion, uomobil, brodov, helikoper. Mikrokopi. k i CD, DVD i keni pogoni. Umjeno rce.
41 Primjene DC moor bez čekic 41/48 12 upnjev lobode 28 kg62 lb 0.97 m38 in duljin noge
42 Primjene DC moor bez čekic 42/48
43 Primjene DC moor bez čekic 43/48
44 Primjene DC moor bez čekic 44/48
45 4.5. Uprvljnje DC moorom bez čekic Npjnje DC moor bez čekic. 45/48 i 2 B A S N i 3 Ukupn ulzn ruj je iomjern. i 1 C I
46 Uprvljčk rukur Blok hem uprvljčkog krug DC moor bez čekic. 46/48 I G 1 G 2 G 3 i1 I i 2 E i f i 3 E G 4 G 5 G 6 Uprvljčk logik Pozicij roor
47 Prevrčki klop Prevrčki klop je prikzn n ljedećoj lici. 47/48 V Q1 Q3 Q5 D1 D3 D5 0 Q4 i A i B i C Q6 Q2 D4 D6 D2 A B C i 1 i 2 i 3
48 Oblici fznih ruj Oblici fznih ruj u ovinoi od položj roor uzbudnog ok i A i SP elekº 48/48 i B i C Q5 Q1 Q3 Q5 Q6 Q2 Q4 ABC ABC ABC ABC ABC ABC
a) Kosi hitac Krivolinijsko gibanje materijalne toke Sastavljeno gibanje Specijalni sluajevi kosog hica: b) Horizontalni hitac c) Vertikalni hitac
 ) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
Lekcija 3 Istosmjerni motor s nezavisnom uzbudom
 Lekcij 3 tomjerni motor nezvinom uzbudom Prof.dr.c. Jmin Velgić Elektrotehnički fkultet Srjevo olegij: Aktutori 3 1 tomjerni motor nezvinom uzbudom 2/72 Mtemtički opi itomjernog motor nezvinom uzbudom
Lekcij 3 tomjerni motor nezvinom uzbudom Prof.dr.c. Jmin Velgić Elektrotehnički fkultet Srjevo olegij: Aktutori 3 1 tomjerni motor nezvinom uzbudom 2/72 Mtemtički opi itomjernog motor nezvinom uzbudom
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
KUPA I ZARUBLJENA KUPA
 KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
GIBANJE (m h) giba miruje giba giba miruje miruje h 1000 :1000 h 1 h h :1000 1
 GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Osnove elektrotehnike I parcijalni ispit VARIJANTA A. Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti.
 Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]
![c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata] c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]](/thumbs/92/108578155.jpg) Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA
 OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.
 šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi
 Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
A MATEMATIKA Zadana je z = x 3 y + 1
 A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor
 I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su
 ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ČETVOROUGAO. β 1. β B. Četvorougao je konveksan ako duž koja spaja bilo koje dve tačke unutrašnje oblasti ostaje unutar četvorougla.
 Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
m m s s m m Vježba 121 S ruba mosta bacimo vertikalno u vodu kamen brzinom 1 m/s. Nañi visinu mosta i brzinu s s
 dk (Kriijn, ginzij) S rub o bcio eriklno u odu ken brzino.8 /. Nñi iinu o i brzinu kojo ken pdne u odu ko pd 3 ekunde. (g = 9.8 / ) Rješenje =.8 /, = 3, g = 9.8 /, =? Gibnje je jednoliko ubrzno (lobodni
dk (Kriijn, ginzij) S rub o bcio eriklno u odu ken brzino.8 /. Nñi iinu o i brzinu kojo ken pdne u odu ko pd 3 ekunde. (g = 9.8 / ) Rješenje =.8 /, = 3, g = 9.8 /, =? Gibnje je jednoliko ubrzno (lobodni
Elektrostatika. 1. zadatak. Uvodni pojmovi. Rješenje zadatka. Za pločasti kondenzator vrijedi:
 tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
PIRAMIDA I ZARUBLJENA PIRAMIDA. - omotač se sastoji od bočnih strana(najčešće jednakokraki trouglovi), naravno trostrana piramida u omotaču
 PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
 IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Kinematika materijalne toke. 3. dio a) Zadavanje krivocrtnog gibanja b) Brzina v i ubrzanje a
 Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
R: a) x(t)..nejednoliko gibanje duž pravca; y(t)..jednoliko ubrzano gibanje duž pravca s akceleracijom 10 m/s 2. r r r r b) t=0,5 s, ( ) ( ) s
 PRIPREA ZA ZADACU_3 I SEINAR_3 I Gibnje mterijlne točke Riješeni zdtk: I.. Vektor položj mterijlne točke zdn je relcijom: r(t) = ( 6t 3 4t + 3t) i + (5t 3t + ) j Odredite: ) vrtu gibnj u x i y mjeru i
PRIPREA ZA ZADACU_3 I SEINAR_3 I Gibnje mterijlne točke Riješeni zdtk: I.. Vektor položj mterijlne točke zdn je relcijom: r(t) = ( 6t 3 4t + 3t) i + (5t 3t + ) j Odredite: ) vrtu gibnj u x i y mjeru i
1 Ekstremi funkcija više varijabli
 1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA. Prof. dr. sc. Ivica Kladarić
 STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA Prof. dr. sc. Ivic Kldrić Identifikcij i procjen mikrostrukture METALOGRAFIJA je istrživčk metod koj ouhvć optičko istrživnje mikrostrukture
STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA Prof. dr. sc. Ivic Kldrić Identifikcij i procjen mikrostrukture METALOGRAFIJA je istrživčk metod koj ouhvć optičko istrživnje mikrostrukture
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
ŽUPANIJSKO NATJECANJE IZ FIZIKE 2012/2013 Srednje škole 1. skupina. Zadatak 1 (10bodova)
 ŽUPANIJSKO NATJECANJE IZ FIZIKE / Srednje škole. skupin Zdk (bodo) Iic i ric urkuju se n szi duljine s ko d isoremeno kreu s sr. Iic jednoliko ubrz pru peinu ukupnog remen rnj od sr do cilj, posiže brzinu
ŽUPANIJSKO NATJECANJE IZ FIZIKE / Srednje škole. skupin Zdk (bodo) Iic i ric urkuju se n szi duljine s ko d isoremeno kreu s sr. Iic jednoliko ubrz pru peinu ukupnog remen rnj od sr do cilj, posiže brzinu
GEOMETRIJSKA VEROVATNOĆA. U slučaju kada se ishod nekog opita definiše slučajnim položajem tačke u nekoj oblasti, pri čemu je proizvoljni položaj
 GEMETRIJK VERVTNĆ U slučju kd se ishod nekog oi definiše slučjnim oložjem čke u nekoj oblsi, ri čemu je roizvoljni oložj čke u oj oblsi jednko moguć, korisimo geomerijsku verovnoću. ko, recimo, obeležimo
GEMETRIJK VERVTNĆ U slučju kd se ishod nekog oi definiše slučjnim oložjem čke u nekoj oblsi, ri čemu je roizvoljni oložj čke u oj oblsi jednko moguć, korisimo geomerijsku verovnoću. ko, recimo, obeležimo
Kinetička energija: E
 Pime 54 Za iem pikazan na lici odedii ubzanje eea mae m koji e keće naniže kao i ilu u užeu? Na homogeni doboš a dva nivoa koji e obće oko zgloba O dejvuje, zbog neidealnoi ležaja konanni momen opoa M
Pime 54 Za iem pikazan na lici odedii ubzanje eea mae m koji e keće naniže kao i ilu u užeu? Na homogeni doboš a dva nivoa koji e obće oko zgloba O dejvuje, zbog neidealnoi ležaja konanni momen opoa M
Veliine u mehanici. Rad, snaga i energija. Dinamika. Meunarodni sustav mjere (SI) 1. Skalari. 2. Vektori - poetak. 12. dio. 1. Skalari. 2.
 Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
Vele u ehc Rd, g eegj D. do. Sl. Veo 3. Tezo II. ed 4. Tezo IV. ed. Sl: 3 0 pod je jedc (ezo ulog ed). Veo: 3 3 pod je jedc (ezo pog ed) 3. Tezo dugog ed 3 9 pod je jedc 4. Tezoeog ed 3 4 8 pod je jedc
IUPAC nomenklatura cikloalkana Imenuju se tako što se na ime alkana doda prefiks ciklo. Cikloalkil-grupe:
 IKLOALKANI n n iklični ugljovodonici gd su tomi mñusobno povzni vzm. Prstnovi (broj tom u prstnu): mli (-4), obični (5-7), srdnji (8-1), vliki (1...). IUPA nomnkltur ciklolkn Imnuju s tko što s n im lkn
IKLOALKANI n n iklični ugljovodonici gd su tomi mñusobno povzni vzm. Prstnovi (broj tom u prstnu): mli (-4), obični (5-7), srdnji (8-1), vliki (1...). IUPA nomnkltur ciklolkn Imnuju s tko što s n im lkn
MEHANIKA MATERIJALNE ČESTICE
 ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA I -- pednj -- MEHANIKA MATERIJALNE ČESTICE.1 Kinemik meijlne čeice Mehnik je dio fizike koj pouč zkone kenj/gibnj ijel, j. emenku pomjenu položj ijel
ELEKTROTEHNIČKI FAKULTET SARAJEVO INŽENJERSKA FIZIKA I -- pednj -- MEHANIKA MATERIJALNE ČESTICE.1 Kinemik meijlne čeice Mehnik je dio fizike koj pouč zkone kenj/gibnj ijel, j. emenku pomjenu položj ijel
UNIVERZITET U KRAGUJEVCU TEHNIČKI FAKULTET U ČAČKU
 UNVERZTET U KRAGUJEVU TEHNČK FAKULTET U ČAČKU Dr Predrg Perović UPRAVLJANJE ENERGETKM PRETVARAČMA, JEDNOMERNM KORAČNM MOTORMA -skrip- ČAČAK, 26 god. 1 PREDGOVOR krip je zmišljen ko merijl koji pri predme
UNVERZTET U KRAGUJEVU TEHNČK FAKULTET U ČAČKU Dr Predrg Perović UPRAVLJANJE ENERGETKM PRETVARAČMA, JEDNOMERNM KORAČNM MOTORMA -skrip- ČAČAK, 26 god. 1 PREDGOVOR krip je zmišljen ko merijl koji pri predme
Kinematika materijalne toke. 2. Prirodni koordinatni sustav. 1. Vektorski nain definiranja gibanja. Krivocrtno gibanje materijalne toke
 Kioco gibje meijle oke Kiemik meijle oke. dio ) Zje kiocog gibj b) Bi i ubje Položj meijle oke u skom euku eme možemo defiii slijedee ie:. Vekoski i defiij gibj (). Piodi i defiij gibj s s (). Vekoski
Kioco gibje meijle oke Kiemik meijle oke. dio ) Zje kiocog gibj b) Bi i ubje Položj meijle oke u skom euku eme možemo defiii slijedee ie:. Vekoski i defiij gibj (). Piodi i defiij gibj s s (). Vekoski
povratnog napona 6 prekidača na slici 1.
 Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
FURIJEOVI REDOVI ZADACI ( II
 FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
DINAMIKA. u f. Dinamički sistem - pogon sa motorom jednosmerne struje: N: NELINEARAN. m m
 DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, [ i ],, U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA SA
DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, [ i ],, U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA SA
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA
 FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
MEHANIKA FLUIDA I Što valja zapamtiti 9 3. STATIKA FLUIDA. p (izražava ravnotežu masenih sila i sila tlaka).
 MENIK FLUID I Što vlj zpmtiti 9. STTIK FLUID snovn jedndžb sttike (slučj i ) p fi ili f rdp (izržv rvnotežu mseni sil i sil tlk). i Iz osnovne jedndžbe sttike imjući n umu svojstv rdijent zključuje se:
MENIK FLUID I Što vlj zpmtiti 9. STTIK FLUID snovn jedndžb sttike (slučj i ) p fi ili f rdp (izržv rvnotežu mseni sil i sil tlk). i Iz osnovne jedndžbe sttike imjući n umu svojstv rdijent zključuje se:
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Istosmjerni krugovi. 1. zadatak. Na trošilu će se trošiti maksimalna snaga u slučaju kada je otpor čitavog trošila jednak unutrašnjem otporu izvora.
 Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
Regulisani elektromotorni pogoni sa mašinama jednosmerne struje
 Regulisni elektromotorni pogoni s mšinm jednosmerne struje Osnovne krkteristike Regulcij moment - struje indukt Regulcij brzine Nčini relizcije (ktutor) z rd u 2 ili 4 kvdrnt Elektromotorni pogon promenljive
Regulisni elektromotorni pogoni s mšinm jednosmerne struje Osnovne krkteristike Regulcij moment - struje indukt Regulcij brzine Nčini relizcije (ktutor) z rd u 2 ili 4 kvdrnt Elektromotorni pogon promenljive
Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.
 Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
VAŽNO. Posmino naprezanje τ
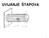 UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Metode rješavanja izmjeničnih krugova
 Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
SIMULIRANJE REGULIRANOG ELEKTROMOTORNOG POGONA PRIMJENOM M FUNKCIJA. Vježba broj 6
 1. VOD 1.1. Cilj vježbe SIMLIANJE EGLIANOG ELEKTOMOTONOG POGONA PIMJENOM M FNKCIJA Vježb broj 6 Prikzti sustv regulirnog istosmjernog elektromotornog pogon u Simulinku. Primjenom mfunkcij zdti prmetre
1. VOD 1.1. Cilj vježbe SIMLIANJE EGLIANOG ELEKTOMOTONOG POGONA PIMJENOM M FNKCIJA Vježb broj 6 Prikzti sustv regulirnog istosmjernog elektromotornog pogon u Simulinku. Primjenom mfunkcij zdti prmetre
Rješenje: F u =221,9 N; A x = F u =221,9 N; A y =226,2 N.
 Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
TROUGAO. - Stranice a,b,c ( po dogovoru stranice se obeležavaju nasuprot temenu, npr naspram temena A je stranica a, itd) 1, β
 TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
Priveznice W re r R e o R p o e p S e l S ing n s
 Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Priveznice Wire Rope Slings PRIVEZNICE OD ČEIČNO UŽEA (RAE) jenosruke SINE WIRE ROPE SINS Sanar EN P P P P P P P P P P P P ozvoljeno operećenje kg elemeni priveznice prekina jenokrako vešanje ) ouvaanje
Slika 4. Zvuni val a) zvuni val se giba kroz mirujui zrak; b) mirujui zvuni val u struji zraka
 . BRZINA ZVUKA. DEFINICIJA BRZINE ZVUKA Iktvo okzje d zvk tje kroz zrk odreenom konnom brzinom. N rimjer, zvk grmljvine dolzi do romtr nekoliko trentk nkon bljek mnje dljini. Brzin zvk je vrlo znjn veliin
. BRZINA ZVUKA. DEFINICIJA BRZINE ZVUKA Iktvo okzje d zvk tje kroz zrk odreenom konnom brzinom. N rimjer, zvk grmljvine dolzi do romtr nekoliko trentk nkon bljek mnje dljini. Brzin zvk je vrlo znjn veliin
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,
 Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
γ = 120 a 2, a, a + 2. a + 2
 Zdtk (Slvi, gimnzij) Duljine strni trokut čine ritmetički niz (slijed) s rzlikom Jedn kut iznosi Koliki je opseg trokut? Rješenje inči udući d duljine strni trokut čine ritmetički niz (slijed) s rzlikom,
Zdtk (Slvi, gimnzij) Duljine strni trokut čine ritmetički niz (slijed) s rzlikom Jedn kut iznosi Koliki je opseg trokut? Rješenje inči udući d duljine strni trokut čine ritmetički niz (slijed) s rzlikom,
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA. školska 2013./2014. godina TEST MATEMATIKA UPUTE ZA RAD
 ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
MEHANIKA FLUIDA. Pritisak tečnosti na ravne površi
 MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
DINAMIKA. Dinamički sistem - pogon sa motorom jednosmerne struje: N: Dinamički sistem Ulazi Izlazi (?)
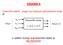 DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
TEHNIČKA MEHANIKA II
 Seučilište u Splitu Seučilišni odjel z stručne studije Bože Plzibt Ado Mtokoić Vldimir Vetm TEHNIČKA MEHANIKA II Split, 06. Predgoor O su skript nmijenjen u prom redu studentim stručnog studij Konstrukcijsko
Seučilište u Splitu Seučilišni odjel z stručne studije Bože Plzibt Ado Mtokoić Vldimir Vetm TEHNIČKA MEHANIKA II Split, 06. Predgoor O su skript nmijenjen u prom redu studentim stručnog studij Konstrukcijsko
DINAMIKA. u f. Dinamički sistem - pogon sa motorom jednosmerne struje: N: NELINEARAN. m m
 DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, ϕ [ i ], ω, θ U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA
DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, ϕ [ i ], ω, θ U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA
Poučak o kosinusu (kosinusov poučak) U trokutu ABC vrijede ove jednakosti b + c a a + c b a + b c.
 Zdtk 4 (4, TUŠ) Kolik je mjer njmnjeg kut u trokutu kojemu su strnie duljin 7 m, 8 m i 9 m? Rješenje 4 Trokut je dio rvnine omeñen s tri dužine Te dužine zovemo strnie trokut Nsuprot većoj strnii u trokutu
Zdtk 4 (4, TUŠ) Kolik je mjer njmnjeg kut u trokutu kojemu su strnie duljin 7 m, 8 m i 9 m? Rješenje 4 Trokut je dio rvnine omeñen s tri dužine Te dužine zovemo strnie trokut Nsuprot većoj strnii u trokutu
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
AKTUATORI U JEDNOSMERNOM POGONU Pojačivači snage
 AKTUATORI U JEDNOSMERNOM POGONU Pojčivči snge Uređji z npjnje električnom energijom jednosmernih motor u pogonim, pre sveg regulisnim. ENERGETSKI ULAZ P eu L d P uu UPRAVLJAČKI ULAZ AKTUATOR + u + e M
AKTUATORI U JEDNOSMERNOM POGONU Pojčivči snge Uređji z npjnje električnom energijom jednosmernih motor u pogonim, pre sveg regulisnim. ENERGETSKI ULAZ P eu L d P uu UPRAVLJAČKI ULAZ AKTUATOR + u + e M
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
OSCILATORNO KRETANJE
 5 OSCILAORNO KREANJE Oscilorno krenje je krenje koje se krkeriše izvesni sepeno ponovljivosi. Nie određeni fizički proces ponvlj se n isi nčin česic (elo) više pu prolzi kroz iso rvnoežno snje. Pre prirodi
5 OSCILAORNO KREANJE Oscilorno krenje je krenje koje se krkeriše izvesni sepeno ponovljivosi. Nie određeni fizički proces ponvlj se n isi nčin česic (elo) više pu prolzi kroz iso rvnoežno snje. Pre prirodi
Strukture GMDH u modeliranju i predikciji vremenskih serija. Ivan Ivek
 Srukure GMDH u modelrnju predkcj vremenskh serj Ivn Ivek Group Mehod of D Hndlng Ivkhnenko, 966. regresj, esmcj, predkcj, konrol... Dobr svojsv: nskoprmersk lgorm smopodešvnje srukure selekcj ulnh vrjbl
Srukure GMDH u modelrnju predkcj vremenskh serj Ivn Ivek Group Mehod of D Hndlng Ivkhnenko, 966. regresj, esmcj, predkcj, konrol... Dobr svojsv: nskoprmersk lgorm smopodešvnje srukure selekcj ulnh vrjbl
4. Relacije. Teorijski uvod
 VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA
 SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
Primjene odreženog integrala
 VJEŽBE IZ MATEMATIKE Ivn Brnović Miroslv Jerković Lekcij 5 Primjen određenog integrl Poglvlje Primjene odreženog integrl. Povr²in rvninskog lik Z dni rvninski lik omežen krivuljm y = f(x) i y = g(x) te
VJEŽBE IZ MATEMATIKE Ivn Brnović Miroslv Jerković Lekcij 5 Primjen određenog integrl Poglvlje Primjene odreženog integrl. Povr²in rvninskog lik Z dni rvninski lik omežen krivuljm y = f(x) i y = g(x) te
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
ELEKTROMOTORNI POGONI - AUDITORNE VJEŽBE
 veučilište u ijeci TEHNIČKI FAKULTET veučilišni preddiplomki tudij elektrotehnike ELEKTOOTONI OGONI - AUDITONE VJEŽBE Ainkroni motor Ainkroni motor inkrona obodna brzina inkrona brzina okretanja Odno n
veučilište u ijeci TEHNIČKI FAKULTET veučilišni preddiplomki tudij elektrotehnike ELEKTOOTONI OGONI - AUDITONE VJEŽBE Ainkroni motor Ainkroni motor inkrona obodna brzina inkrona brzina okretanja Odno n
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Odredjeni integral je granicna vrijednost sume beskonacnog broja clanova a svaki clan tezi k nuli i oznacava se sa : f x dx f x f x f x f x b a f
 Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
O k o OPTIČKI INSTRUMENTI. Oko Tamna komora (camera obscura, pinhole camera) Povećalo (magnifier) Fotoaparat Mikroskop
 OPTIČKI INSTRUMENTI Oko Tmn komor (cmer obscur, pinhole cmer) Povećlo (mgniier) Fotoprt Mikroskop O k o Ljudsko oko je vjerojtno njkompleksniji optički instrument. Ono što g čini još scinntnijim je činjenic
OPTIČKI INSTRUMENTI Oko Tmn komor (cmer obscur, pinhole cmer) Povećlo (mgniier) Fotoprt Mikroskop O k o Ljudsko oko je vjerojtno njkompleksniji optički instrument. Ono što g čini još scinntnijim je činjenic
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA
 TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F
 SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
Difrakcija svetlosti. θ 1. Slika 2. a/2. a/2. (a/2)sinθ 1
 Difrkcij svetlosti Difrkcij je pojv skretnj svetlosnih zrk s prvolinijske putnje pri nilsku n prepreke mlih dimenzij red tlsne dužine svetlosti. Postojnje difrkcije je i dokz o tlsnoj prirodi svetlosti.
Difrkcij svetlosti Difrkcij je pojv skretnj svetlosnih zrk s prvolinijske putnje pri nilsku n prepreke mlih dimenzij red tlsne dužine svetlosti. Postojnje difrkcije je i dokz o tlsnoj prirodi svetlosti.
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. ANALITIČA GEOMETRIJA PROSTORA II. DIO (Pv).. Min Roić Linović 9./. Pv u otou Jenž v Nek je: T (,, ) n točk oto {,, } ni vekto mje Znom točkom oto oli mo v leln nim vektoom. T (,,) - oivoljn točk v
II. ANALITIČA GEOMETRIJA PROSTORA II. DIO (Pv).. Min Roić Linović 9./. Pv u otou Jenž v Nek je: T (,, ) n točk oto {,, } ni vekto mje Znom točkom oto oli mo v leln nim vektoom. T (,,) - oivoljn točk v
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
Osnovna škola. b) Koliko prstenova treba objesiti na kukicu s lijeve strane na slici 2 da bi poluga bila u ravnoteži? 1 3 F/N
 ŠKOLSKO/OPĆINSKO NTJENJE IZ FIZIKE 2.2.2009. Osnovn škol Uut: U svim zdcim gdje je to otrebno koristiti g = 10 N/kg. 1. zdtk (7 bodov) ) Slik 1 rikzuje olugu u rvnoteži n kojoj se nlze dv rsten i neoznti
ŠKOLSKO/OPĆINSKO NTJENJE IZ FIZIKE 2.2.2009. Osnovn škol Uut: U svim zdcim gdje je to otrebno koristiti g = 10 N/kg. 1. zdtk (7 bodov) ) Slik 1 rikzuje olugu u rvnoteži n kojoj se nlze dv rsten i neoznti
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
