10 Determinarea coeficientului de convecție termică la un fascicul de țevi
|
|
|
- Άκανθα Ζαΐμης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 rmothnică Sintză lucrări d laborator 10 Dtrara coficintului d convcți trmică la un d țvi Lucrara d laborator rzintă modul în car s dtră coficintul d convcți trmică la un d țvi. Scoul lucrării st însuşira noţiunilor fundamntal cu rivir la transfrul d căldură rin convcți și a algoritmului d calcul Noțiuni tortic Convcţia trmică st rocsul d transmitr a căldurii rin intrmdiul unui fluid în mişcar car vhiculază nrgia trmică din zonl cu tmratură mai ridicată în altl d tmratură mai scăzută [6]. Proagara căldurii rin convcți rrzintă un rocs comlx d transmitr a căldurii, rocs car ar loc într un fluid aflat în mișcar și un cor solid []. Convcţia rsuun acţiuna combinată a conducţii trmic în stratul limită d fluid d lângă rt, a acumulării d nrgi intrnă şi a mişcării d amstc a articullor d fluid [63]. ransfrul d căldură convctiv (convcția) s ralizază concomitnt cu mișcara uni mas d fluid. Căldura s transmit ca fct al dlasării macroscoic a fluidlor cald în intriorul acliași faz, sau într faz difrit aflat în contact. În majoritata cazurilor ractic, mișcara fluidului ar loc într-un aarat sau într-o conductă. S oat dci afirma că transfrul d căldură convctiv ar loc la dlasara fluidului d-a lungul unui contur solid mai cald sau mai rc [64]. Intnsitata rocsului d convcţi dind în mar măsură d mişcara d amstc a fluidului. Duă natura mişcării s disting două tiuri d mişcar cărora l corsund două tiuri d convcţi: convcți libră (naturală) mișcara fluidului st dtrată numai d difrnțl d dnsitat din masa fluidului, aărut ca urmar a difrnțlor d tmratură xistnt într difrit unct al fluidului [64]. La încălzira fluidului dnsitata lui scad şi l s ridică; la răcir, dnsitata crşt şi fluidul coboară lângă surafaţa d schimb d căldură. Intnsitata mişcării libr st dtrată d natura fluidului, difrnţa d tmratură într fluid şi rt, volumul ocuat d fluid şi câmul gravitaţional [63]. convcți forțată fluidul st us în mișcar rin mijloac xtrn [65]. Mișcara fluidului aar sub acțiuna unor gradinți d rsiun roduși d acțiuna mcanică a unui disozitiv d transort (omă, vntilator, comrsor tc.) sau a unui disozitiv d amstcar (agitator, injctor tc.) [64]. Pntru xrimara fluxului d căldură convctiv s utilizază rlația lui Nwton : Q t t W (10.1) f und: Q [W] st fluxul d căldură transmis rin convcți, α [W/(m K)] coficint d convcți trmică c caractrizază intnsitata transfrului d căldură convctiv, [m ] aria surafți d contact dintr fluid și corul solid, t [ C] tmratura mdi a surafți corului solid, tf [ C] tmratura mdi a fluidului car scaldă surafața corului solid. Dintr mărimil car intră în alcătuira rlații lui Nwton, dtrara coficintului d convcți trmică α rzintă dificultățil cl mai mari, întrucât acsta dind d o sri d factori rintr car: vitza d mișcar a fluidului; tmratura fluidului și a rtlui corului solid; conductivitata trmică a stratului limită d fluid; căldura scifică a fluidului; dnsitata fluidului; viscozitata fluidului; forma și dimnsiunil surafți d contact tc. Pntru dtrara coficintului d convcți trmică α nu s ot folosi rlații analitic ci numai rlații ddus cu ajutorul torii similitudinii. 57
2 Lavinia SOCCIU, Oana GIURGIU Princiiul similitudinii arată că două sistm au o comortar similară dacă raortul dimnsiunilor lor liniar, a fortlor, a vitzlor, st aclași. Similitudina în studiul rocslor d transfr d căldură rsuun asmănar: gomtrică; mcanică și trmică. În cazul convcții forțat în sistm gomtric similar, câmuril vitzlor vor fi similar dacă raortul dintr forțl d inrți și forțl d frcar vâscoas st aclași în ambl fluid [66]. stfl, ntru anumit cazuri ractic, articular, s-au dtrat rlațiil critrial car guvrnază fnomnl rsctiv []. castă tori rmit utilizara rlațiilor obținut modl la fnomnul ral, car st similar cu modlul, rlații în car intrvin ca variabil mărimi indndnt d unitățil d măsură, numit invarianți, numr sau critrii d similitudin. Cl mai utilizat critrii d similitudin sunt: critriul Nusslt (Nu) - rrzintă raortul dintr gradintul tmraturii fluidului la surafata rtlui și un gradint d rfrință al tmraturii. csta st cl mai imortant invariant doarc includ coficintul d convcţi α car trbui dtrat: d (10.) Nu und: λ [W/mK] st coficintul d conducţi trmică a fluidului în stratul limită; iar d [m ] - diamtrul xtrior al conducti [66]. critriul Rynolds (R) caractrizază rgimul d curgr al fluidului și rrzintă raortul dintr forțl d inrți și forțl d viscozitat: w l (10.3) c R und: w [m/s] st vitza d curgr a fluidului; υ [m /s] viscozitata cinmatică a fluidului; lc [m] - lungima caractristică (în cazul rților lani) sau diamtrul xtrior al conducti [66]. critriul Prandtl (Pr) - caractrizază roritățil fizic al fluidului și rrzintă raortul dintr distribuția vitzi și ca a tmraturii: Pr λ υ ρ c 58 (10.4) und: λ [W/mK] st coficintul d conducţi trmică a fluidului în stratul limită; ρ [kg/m 3 ] - dnsitata fluidului; c [J/kgK] - căldura scifică la rsiun constantă a fluidului [66]. Schimbul d căldură într un agnt trmic rimar și un altul scundar rin intrmdiul unui d țvi st un caz d transmitr a căldurii ds utilizat în ractica industrială. În roictara și vrificara schimbătoarlor d căldură car folossc astfl d d țvi, una dintr mărimil rincial car trbui dtrat st coficintul d convcți trmică α d la țvil ului la agntul scundar, coficint c intră în alcătuira rlații coficintului global d schimb d căldură k []. 10. Dscrira instalații și dsfășurara lucrării Instalația xrimntală ntru dtrara coficintului mdiu d transmitr a căldurii rin convcți trmică d la țvil unui la agntul trmic scundar, arul, st rzntată în figura Instalația s comun dintr-un vntilator cntrifugal antrnat d un motor lctric, car asiră arul din mdiul înconjurător și îl rfulază în rzrvorul tamon. P rzrvorul tamon st montată o riză d rsiun statică. Din rzrvorul tamon arul trc mai dart într-un canal aralliidic, car în tronsonul din mijloc ar montat un d țvi. csta st comus din țvi cu diamtrul xtrior d = mm și d lungim 1 = 50 mm. Disoziția țvilor în st în șichir, valoril asurilor transvrsal și longitudinal, rcum și dimnsiunil canalului, fiind dat in figura 10.. gntul trmic rimar, cu circulați intratubulară st înlocuit în instalați cu rzistnț lctric, introdus în intriorul țvilor și lgat la rțaua d nrgi lctrică rin intrmdiul unor born []. Vitza arului înaint și duă ul d țvi st acași. Ea s modifică numai în scțiuna imă d trcr. Pntru dtrara vitzi d circulați a arului duă ul d țvi, s utilizază
3 rmothnică Sintză lucrări d laborator un anmomtru cu cu. Instalația mai st rvazută cu două trmomtr cu lichid ntru măsurara tmraturii arului înaint d ul d țvi, rsctiv tmratura mdi din fascul. Duă vrificara instalații s un sub tnsiun motorul car antrnază vntilatorul și asigură circulația unui dbit d ar rin instalați. Fig Instalația xrimntală ntru dtrara coficintului d convcți trmică la un d țvi Cu ajutorul clati s stabilșt un anumit rgim d curgr al arului. În continuar, s un sub tnsiun rzistnțl lctric din țvil ului. Pntru rvnira accidntlor st obligatoriu ca manvrl să s fctuz în ordina atită mai sus. Duă stabilira unui rgim staționar d transfr d căldură s notază rsiuna statică a arului inaint d ul d țvi st, tmratura ta a arului înaint d și tmratura arului în tf []. Prsiuna baromtrică b s citșt d baromtrul aflat în dotara laboratorului. Mărimil citit s notază în tablul 10., fiind aoi transformat în SI. 59 Fig. 10. Paramtrii gomtrici ai ui d țvi Dnsitata arului înaint d s dtră cu rlația: N st b kg (10.5) N 3 a N m und: ρn st dnsitata arului în condiții normal, ρn=1,98 [kg/m 3 N]; N - tmratura la stara normală, N=73,15K; a [K] - tmratura arului înaint d ul d țvi; st [N/m ] - rsiuna statică a arului înaint d ul d țvi; b [N/m ] - rsiuna baromtrică; N - rsiuna arului în condiții normal, N=10135 N/m. Prsiuna dinamică a arului înaint d ul d țvi: w N (10.6) din m und: w [m/s] st vitza d dlasar a arului înaint / duă ul d țvi, ρ [kg/m 3 ] - dnsitata arului înaint d. Dnsitata arului din s dtră cu rlația: N st b kg (10.7) f N 3 f N m und: f [K] st tmratura mdi a arului din. ria scțiunii transvrsal a canalului: und: L=50 mm și l=30 mm. Ll m (10.8)
4 Lavinia SOCCIU, Oana GIURGIU ria scțiunii im d trcr a arului rin rzultă din figura 10.: Ll n d l m (10.9) und: n [-] st numărul d țvi din scțiuna transvrsală rin, n=3; d [m] - diamtrul xtrior al țvilor, d=mm. Vitza arului în scțiuna imă d trcr rin s dtră cu rlația: w w a f m / s (10.10) Dbitul masic d ar, car st vhiculat rin instalați și car st aclași atât înaint d ul d țvi cât și în scțiuna imă d trcr a arului rin, st dat d rlatia: m w w kg s (10.11) mratura dtrantă, utilizată în stabilira mărimilor car intră în comonnța critriilor d similitudin Nusslt (Nu), Rynolds (R) și Prandtl (Pr), st tmratura mdi din (tf). Proritățil arului uscat la rsiuna stării normal în funcți d tmratura mdi din s obțin din tablul abl 10.1 Proritățil arului uscat la rsiuna stării normal tf [ºC] λ [W/mK] υ [m /s] Pr [-] 5 0, , , ,041 15, , , , , , , , , , , , , , , , , , , , , , , , , , , ,7000 Critriul Rynolds (R) s dtră cu ajutorul rlații: w d R (10.1) und: w [m/s] st vitza d curgr a arului în scțiuna imă d trcr rin ; υ [m /s] viscozitata cinmatică a fluidului; d [m] - diamtrul xtrior al conducti. Figura 10.3 rzintă dndnța coficintului C d rgimul d curgr. Dtrara critriul Nusslt ntru acst caz articular s fctuază utilizând rlația critrială: 0,61 0,31 Nu 0,3 C R Pr (10.13) und: C st un coficint a cărui valoar s obțin din figura Coficintul d convcți s dtră din rlația: W Nu d m K (10.14) Fig Dndnța coficintului C d rgimul d curgr 60
5 rmothnică Sintză lucrări d laborator 10.3 Prlucrara datlor şi rzultatl măsurătorilor Valoril măsurat s cntralizază în tablul 10. ntru ficar măsurătoar în art. csta vor fi aoi transformat în SI. Valoril calculat s vor cntraliza în tablul Nr. crt. abl 10. Valori măsurat ntru dtrara coficintului d convcți Mărima Simbol U.M. 1. Prsiuna baromtrică b Prsiuna statică a arului înaint d mratura arului înaint d mratura mdi a arului în Vitza arului înaint/ duă st ta a tf f w [mbar] [N/m ] [mmho] [N/m ] [ C] [K] [ C] [K] [m/s] Dtrara 1 3 abl 10.3 Mărimi calculat Nr. crt. Mărima Simbol U.M. Dtrara Dnsitata arului înaint d Prsiuna dinamică a arului înaint d ρ [kg/m 3 ] din [N/m ] 3. Dnsitata arului din ρf [kg/m 3 ] ria scțiunii transvrsal a canalului ria scțiunii im d trcr a arului rin Vitza arului în scțiuna imă d trcr rin [m ] [m ] w [m/s] 7. Dbitul masic d ar m [kg/s] 8. Coficintul d conductivitat trmică a arului λ [W/mK] 9. Viscozitata cinmatică a arului υ [m /s] 10. Critriul Prandtl Pr [-] 11. Critriul Rynolds R [-] 1. Coficintul C C [-] 13. Critriul Nusslt Nu [-] 14. Coficintul d convcți trmică α [W/m K] 61
Eşantionarea semnalelor
 Eşantionara smnallor Eşantionara = prlvara d prob dintr-un smnal la momnt d timp dcalat intr l cu cu frcvnta d şantionar, f =/. xˆ t x k t k k = ( = δ ( Smnalul şantionat idal:. Spctrul Xˆ = X ( k k =
Eşantionara smnallor Eşantionara = prlvara d prob dintr-un smnal la momnt d timp dcalat intr l cu cu frcvnta d şantionar, f =/. xˆ t x k t k k = ( = δ ( Smnalul şantionat idal:. Spctrul Xˆ = X ( k k =
Teorema Rezidurilor şi Bucuria Integralelor Reale
 Torma Ridurilor şi Bucuria Intgrallor Ral Prntar d Alandru Ngrscu Intgral cu funcţii raţional c dpind d sin t şi cos t u notaţia it, avm: cos t ( + sin t ( i dt d i, iar intgrara s va fac d-a lungul crcului
Torma Ridurilor şi Bucuria Intgrallor Ral Prntar d Alandru Ngrscu Intgral cu funcţii raţional c dpind d sin t şi cos t u notaţia it, avm: cos t ( + sin t ( i dt d i, iar intgrara s va fac d-a lungul crcului
6.4.Convecţia. unde T s -temperatura termodinamică a suprafeţei corpului solid, -temperatura termodinamică medie a fluidului, 6.
 Trmothnică 77 6..Convcţia Convcţia căldurii st fnomnul lmntar d transfr trmic car s manifstă în mdii fluid şi la supafaţa d sparaţi a fazlor. Est caractristică mdiilor în mişcar, căldura fiind transportată
Trmothnică 77 6..Convcţia Convcţia căldurii st fnomnul lmntar d transfr trmic car s manifstă în mdii fluid şi la supafaţa d sparaţi a fazlor. Est caractristică mdiilor în mişcar, căldura fiind transportată
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
METODE DE DIAGNOSTICARE A PLASMEI
 S.D.Anghl Fizica lasmi şi alicaţii Caitolul VIII METODE DE DIAGNOSTICARE A PLASMEI Duă cum ris chiar din dfiniţia stării d lasmă, a st un mdiu foart comlx, cu mult grad d librtat ntru comonntl i şi cu
S.D.Anghl Fizica lasmi şi alicaţii Caitolul VIII METODE DE DIAGNOSTICARE A PLASMEI Duă cum ris chiar din dfiniţia stării d lasmă, a st un mdiu foart comlx, cu mult grad d librtat ntru comonntl i şi cu
2.CARACTERIZAREA GENERALĂ A RADIOACTIVITǍŢII
 2.CARACTERIZAREA GEERALĂ A RADIOACTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două
2.CARACTERIZAREA GEERALĂ A RADIOACTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
2.CARACTERIZAREA GENERALĂ A RADIOACTIVITǍŢII
 2.CRCTERIZRE GEERLĂ RDIOCTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două fiind
2.CRCTERIZRE GEERLĂ RDIOCTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două fiind
FIZICĂ. Oscilatorul amortizat si oscilatorul fortat. ş.l. dr. Marius COSTACHE
 FIZICĂ Oscilarul amriza si scilarul fra ş.l. dr. Marius COSACHE 3.4 Mişcara scilari amrizaă Oscilarii rali frţ d frcar > amliudina scilaţiilr scad în im Oscilar rsr k, PM d masă m şi frţă d frcar F f rrţinală
FIZICĂ Oscilarul amriza si scilarul fra ş.l. dr. Marius COSACHE 3.4 Mişcara scilari amrizaă Oscilarii rali frţ d frcar > amliudina scilaţiilr scad în im Oscilar rsr k, PM d masă m şi frţă d frcar F f rrţinală
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Senzorul Hall (1) m e (2) Astfel viteza de mişcare a unui electron este datorat forţei
 Snorul all Snorul all Constructi, snorul all st o lăcuţă aralliiică foart subţir in matrial smiconuctor, urtător sarcini oiti şi ngati (lctroni şi goluri). Efctul all în lăcuţă in nu numai concntraţia
Snorul all Snorul all Constructi, snorul all st o lăcuţă aralliiică foart subţir in matrial smiconuctor, urtător sarcini oiti şi ngati (lctroni şi goluri). Efctul all în lăcuţă in nu numai concntraţia
În spectrul de rotaţie al moleculei HCl s-au identificat linii spectrale consecutive cu următoarele lungimi de undă: λ
 PROBLMA 5 În spctrul d rotaţi al molculi HCl s-au idntificat linii spctral conscutiv cu următoarl lungimi d undă: λ 6.4 m; λ 69. m ; λ 8. 4 m ; λ 96. 4 ; λ. 6 m ; 4 5 a Prsupunând molcula un rotator rigid
PROBLMA 5 În spctrul d rotaţi al molculi HCl s-au idntificat linii spctral conscutiv cu următoarl lungimi d undă: λ 6.4 m; λ 69. m ; λ 8. 4 m ; λ 96. 4 ; λ. 6 m ; 4 5 a Prsupunând molcula un rotator rigid
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Fizica Plasmei şi Aplicaţii Probleme
 Fizica Plasmi şi Aplicaţii Problm. Exprimaţi valoara prsiunii atmosfric în difrit unităţi d măsură (N/m, Torr, mm Hg, atm) şi stabiliţi rlaţiil dintr l?. Calculaţi dnsitata unui gaz idal (în m - ) în următoarl
Fizica Plasmi şi Aplicaţii Problm. Exprimaţi valoara prsiunii atmosfric în difrit unităţi d măsură (N/m, Torr, mm Hg, atm) şi stabiliţi rlaţiil dintr l?. Calculaţi dnsitata unui gaz idal (în m - ) în următoarl
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
I 1 I 2 V I [Z] V 1 V 2. Z11 impedanta de intrare cu iesirea in gol 2 I 1 I 21 I
![I 1 I 2 V I [Z] V 1 V 2. Z11 impedanta de intrare cu iesirea in gol 2 I 1 I 21 I I 1 I 2 V I [Z] V 1 V 2. Z11 impedanta de intrare cu iesirea in gol 2 I 1 I 21 I](/thumbs/80/82406840.jpg) urs 5 4/5 ar ca scop sparara unui circuit complx in blocuri individual acsta s analiaa sparat (dcuplat d rstul circuitului) si s caractriaa doar prin intrmdiul porturilor (cuti nagra) analia la nivl
urs 5 4/5 ar ca scop sparara unui circuit complx in blocuri individual acsta s analiaa sparat (dcuplat d rstul circuitului) si s caractriaa doar prin intrmdiul porturilor (cuti nagra) analia la nivl
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
Sistem analogic. Sisteme
 Sistm Smnall pot fi supus prlucrarii in scopul obtinrii unor alt smnal, sau al obtinrii unor paramtri ai acstora. Prlucraril s aplica unui smnal intrar x(t) si s obtin un alt smnal, isir, y(t). Moulara/moulara,
Sistm Smnall pot fi supus prlucrarii in scopul obtinrii unor alt smnal, sau al obtinrii unor paramtri ai acstora. Prlucraril s aplica unui smnal intrar x(t) si s obtin un alt smnal, isir, y(t). Moulara/moulara,
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Mircea Radeş. Vibraţii mecanice. Editura Printech
 Mirca Radş Vibraţii mcanic Editura Printch Prfaţă Lucrara s bazază p cursuril d Vibraţii mcanic prdat la Univrsitata Polithnica Bucurşti, la facultata I.M.S.T. (97-6), la cursul postunivrsitar d Vibraţii
Mirca Radş Vibraţii mcanic Editura Printch Prfaţă Lucrara s bazază p cursuril d Vibraţii mcanic prdat la Univrsitata Polithnica Bucurşti, la facultata I.M.S.T. (97-6), la cursul postunivrsitar d Vibraţii
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
L4. Măsurarea rezistenţelor prin metoda de punte
 L4. Măsurara rzistnţlor prin mtoda d punt. Obictul lucrării În prima part a lucrării s utilizază punta simplă (Whatston) ca mtodă d prcizi ridicată, pntru măsurara rzistnţlor cuprins într 0-0 0 Ω, ralizându-s
L4. Măsurara rzistnţlor prin mtoda d punt. Obictul lucrării În prima part a lucrării s utilizază punta simplă (Whatston) ca mtodă d prcizi ridicată, pntru măsurara rzistnţlor cuprins într 0-0 0 Ω, ralizându-s
VIII Subiectul 1:Fascinația apei
 Olimpiada Națională d Fizică Timișoara 6 Proba tortică Pagina din V Subictul :Fascinația api A. La o fabrică d îmbutlir a api minral plat, apa cu dnsitata dpozitată în rzroar mtalic cu diamtru mar, prăzut
Olimpiada Națională d Fizică Timișoara 6 Proba tortică Pagina din V Subictul :Fascinația api A. La o fabrică d îmbutlir a api minral plat, apa cu dnsitata dpozitată în rzroar mtalic cu diamtru mar, prăzut
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Modele matematice pentru îmbunătăţirea calităţii sistemelor electrice
 Modl matmatic pntru îmbunătăţira calităţii sistmlor lctric Lct.univ.dr.ing. Ghorgh RAŢIU. Introducr Ţinând sama d tndinţl modrn al proictării sistmlor lctric (chipamntlor lctric) d înlocuir a uni proictări
Modl matmatic pntru îmbunătăţira calităţii sistmlor lctric Lct.univ.dr.ing. Ghorgh RAŢIU. Introducr Ţinând sama d tndinţl modrn al proictării sistmlor lctric (chipamntlor lctric) d înlocuir a uni proictări
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Lucrarea de laborator nr. 2 VERIFICARILE METROLOGICE ALE MIJLOACELOR DE MASURARE
 Lucrara d laborator nr. 2 VERIFICARILE METROLOGICE ALE MIJLOACELOR DE MASRARE 1. SCOPL LCRARII Scopul lucrarii îl rprzinta: cunoastra principallor mtod d vrificar mtrologica a unor mijloac d masurar, analogic
Lucrara d laborator nr. 2 VERIFICARILE METROLOGICE ALE MIJLOACELOR DE MASRARE 1. SCOPL LCRARII Scopul lucrarii îl rprzinta: cunoastra principallor mtod d vrificar mtrologica a unor mijloac d masurar, analogic
3. ERORI DE MÃSURARE
 6 Mtrologi, Stadardizar si Masurari 3.. Dfiira rorii d masurar 3. ERORI DE MÃSURARE Î practica, s obsrva ca îtotdaua valoara umrica rala a ui mari fizic masurat st difrita d valoara m idicata d aparatul
6 Mtrologi, Stadardizar si Masurari 3.. Dfiira rorii d masurar 3. ERORI DE MÃSURARE Î practica, s obsrva ca îtotdaua valoara umrica rala a ui mari fizic masurat st difrita d valoara m idicata d aparatul
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
5.7 Modulaţia cu diviziune în frecvenţă ortogonală
 5.7 Modulaţia cu diviziun în frcvnţă ortogonală Transmisiuna datlor cu dbit mar prin modulaţia multinivl a unui purtător, p un canal cu distorsiuni d amplitudin şi d fază, st afctată d intrfrnţa simbolurilor.
5.7 Modulaţia cu diviziun în frcvnţă ortogonală Transmisiuna datlor cu dbit mar prin modulaţia multinivl a unui purtător, p un canal cu distorsiuni d amplitudin şi d fază, st afctată d intrfrnţa simbolurilor.
Lucian Maticiuc. Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 9.
 Capitolul V: Şiruri şi srii d fucţii. Lct. dr. Lucia Maticiuc Facultata d Hidrothică, Godzi şi Igiria Mdiului Matmatici Suprioar, Smstrul I, Lctor dr. Lucia MATICIUC SEMINAR 9. Cap. V Şiruri şi srii d
Capitolul V: Şiruri şi srii d fucţii. Lct. dr. Lucia Maticiuc Facultata d Hidrothică, Godzi şi Igiria Mdiului Matmatici Suprioar, Smstrul I, Lctor dr. Lucia MATICIUC SEMINAR 9. Cap. V Şiruri şi srii d
Transformata Radon. Reconstructia unei imagini bidimensionale cu ajutorul proiectiilor rezultate de-a lungul unor drepte.
 Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
lim lim lim lim (criteriul cu şiruri); lim lim = lim ; Limite de funcńii NotaŃii: f :D R, D R, α - punct de acumulare a lui D;
 Limit d fucńii Aliz mtmtică, cls XI- Limit d fucńii NotŃii: f :D R, D R, α - puct d cumulr lui D DfiiŃii l iti DfiiŃi f ( = l, l R, dcă ptru oric vciătt V lui l istă o vciătt α U lui α stfl îcât D U, α,
Limit d fucńii Aliz mtmtică, cls XI- Limit d fucńii NotŃii: f :D R, D R, α - puct d cumulr lui D DfiiŃii l iti DfiiŃi f ( = l, l R, dcă ptru oric vciătt V lui l istă o vciătt α U lui α stfl îcât D U, α,
4.6. Caracteristicile motoarelor de curent continuu
 Maşia lctrică d curt cotiuu 8D 017 4.6. Caractristicil motoarlor d curt cotiuu Pricipall caractristici al motoarlor d curt cotiuu sut: caractristica mcaică = ( M ) caractristica curtului = ( I i ) caractristica
Maşia lctrică d curt cotiuu 8D 017 4.6. Caractristicil motoarlor d curt cotiuu Pricipall caractristici al motoarlor d curt cotiuu sut: caractristica mcaică = ( M ) caractristica curtului = ( I i ) caractristica
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE
 Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
Capitolul 2 - HIDROCARBURI 2.4.ALCADIENE TEST 2.4.1 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. Rezolvare: 1. Alcadienele sunt hidrocarburi
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE
 Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Capitolul 2 - HIDROCARBURI 2.3.ALCHINE TEST 2.3.3 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Acetilena poate participa la reacţii de
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Capitolul I ECUAŢII DIFERENŢIALE. 1 Matematici speciale. Probleme. 1. Să de integreze ecuaţia diferenţială de ordinul întâi liniară
 Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
Transformata Laplace
 Tranformata Laplace Tranformata Laplace generalizează ideea tranformatei Fourier in tot planul complex Pt un emnal x(t) pectrul au tranformata Fourier ete t ( ω) X = xte dt Pt acelaşi emnal x(t) e poate
Tranformata Laplace Tranformata Laplace generalizează ideea tranformatei Fourier in tot planul complex Pt un emnal x(t) pectrul au tranformata Fourier ete t ( ω) X = xte dt Pt acelaşi emnal x(t) e poate
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
9. Statica solidului rigid...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
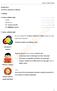 SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
- Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I
 tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
Capitolul 2 - HIDROCARBURI 2.5.ARENE
 Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
Capitolul 2 - HIDROCARBURI 2.5.ARENE TEST 2.5.2 I. Scrie cuvântul / cuvintele dintre paranteze care completează corect fiecare dintre afirmaţiile următoare. 1. Radicalul C 6 H 5 - se numeşte fenil. ( fenil/
LEGI CLASICE DE PROBABILITATE
 7. LEGI CLASICE DE PROBABILITATE Fi (Ω, K, P u câmp d probabilitat şi f : Ω R, o variabilă alatoar. Am văzut că varibili f i s poat asocia o fucţi d rpartiţi F, cotiuă la stâga şi o fucţi caractristică
7. LEGI CLASICE DE PROBABILITATE Fi (Ω, K, P u câmp d probabilitat şi f : Ω R, o variabilă alatoar. Am văzut că varibili f i s poat asocia o fucţi d rpartiţi F, cotiuă la stâga şi o fucţi caractristică
1. ESTIMAREA UNUI SCHIMBĂTOR DE CĂLDURĂ CU PLĂCI
 1. ESTIMAREA UNUI SCHIMBĂTOR DE CĂLDURĂ CU PLĂCI a. Fluidul cald b. Fluidul rece c. Debitul masic total de fluid cald m 1 kg/s d. Temperatura de intrare a fluidului cald t 1i C e. Temperatura de ieşire
1. ESTIMAREA UNUI SCHIMBĂTOR DE CĂLDURĂ CU PLĂCI a. Fluidul cald b. Fluidul rece c. Debitul masic total de fluid cald m 1 kg/s d. Temperatura de intrare a fluidului cald t 1i C e. Temperatura de ieşire
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
METODE DE ANALIZĂ ELASTO-PLASTICĂ DE ORDINUL AL II-LEA A STRUCTURILOR ÎN CADRE 2.1. INTRODUCERE
 MEODE DE AAIZĂ EASO-PASICĂ DE ORDIU A II-EA A SRUCURIOR Î CADRE.. IRODUCERE Prin acctara mtoi stărilor limită ca mtoă roictar în majoritata courilor roictar a structurilor în car, şi ca urmar a zoltărilor
MEODE DE AAIZĂ EASO-PASICĂ DE ORDIU A II-EA A SRUCURIOR Î CADRE.. IRODUCERE Prin acctara mtoi stărilor limită ca mtoă roictar în majoritata courilor roictar a structurilor în car, şi ca urmar a zoltărilor
FIZICA CAPITOLUL: ELECTRICITATE CURENT CONTINUU. Soluţii, indicaţii, schiţe de rezolvare
 FZCA CAPTOLL: LCTCTAT CNT CONTN Souţii, indicţii, schiţ d rzovr. răspuns corct c;. răspuns corct d; 3. răspuns corct b; 4. răspuns corct ; 5. răspuns corct c ( t nrgi ctrică) ; 6. răspuns corct ( putr
FZCA CAPTOLL: LCTCTAT CNT CONTN Souţii, indicţii, schiţ d rzovr. răspuns corct c;. răspuns corct d; 3. răspuns corct b; 4. răspuns corct ; 5. răspuns corct c ( t nrgi ctrică) ; 6. răspuns corct ( putr
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
REZISTENŢE PNEUMATICE NELINIARE. UTILIZAREA DIAFRAGMEI CA ELEMENT DE MĂSURĂ A DEBITULUI DE FLUID
 REZISTENŢE PNEUMATICE NELINIARE. UTILIZAREA DIAFRAGMEI CA ELEMENT DE MĂSURĂ A DEBITULUI DE FLUID - - . OBIECTUL LUCRĂRII Relaţiile de calcul ale rezistenţelor neumatice neliniare. Cunoaşterea diafragmelor,
REZISTENŢE PNEUMATICE NELINIARE. UTILIZAREA DIAFRAGMEI CA ELEMENT DE MĂSURĂ A DEBITULUI DE FLUID - - . OBIECTUL LUCRĂRII Relaţiile de calcul ale rezistenţelor neumatice neliniare. Cunoaşterea diafragmelor,
TERMOSTAT ELECTRONIC DIODA SENZOR
 EPSCOM Rady Prototyping Colccţ ţia Hom Automation EP 0261... Cuprin Przntar Proict Fişa d Aamblar 1. Funcţionar 2 2. Schma 2 3. PCB 3 4. Lita d componnt 3 5. Tutorial dioda miconductoar 4 5 Rgimul trmic
EPSCOM Rady Prototyping Colccţ ţia Hom Automation EP 0261... Cuprin Przntar Proict Fişa d Aamblar 1. Funcţionar 2 2. Schma 2 3. PCB 3 4. Lita d componnt 3 5. Tutorial dioda miconductoar 4 5 Rgimul trmic
2. STATICA FLUIDELOR. 2.A. Presa hidraulică. Legea lui Arhimede
 2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
ENUNŢURI ŞI REZOLVĂRI 2013
 ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
REACŢII DE ADIŢIE NUCLEOFILĂ (AN-REACŢII) (ALDEHIDE ŞI CETONE)
 EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
Complemente teoretice. Limite de funcńii NotaŃii: f :D R, D R, α - punct de acumulare a lui D; DefiniŃii ale limitei DefiniŃia 1.1.
 Analiza matmatică clasa axi-a, problm rzolvat Complmnt tortic Limit d funcńii NotaŃii: f :D R, D R, α - punct d acumular a lui D; DfiniŃii al limiti DfiniŃia lim f = l, l R, dacă pntru oric vcinătat V
Analiza matmatică clasa axi-a, problm rzolvat Complmnt tortic Limit d funcńii NotaŃii: f :D R, D R, α - punct d acumular a lui D; DfiniŃii al limiti DfiniŃia lim f = l, l R, dacă pntru oric vcinătat V
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
TRANSFER DE CĂLDURĂ ŞI MASĂ SEMINAR - probleme propuse şi consideraţii teoretice - 1. CONDUCŢIA TERMICĂ ÎN REGIM STAŢIONAR
 TRANSFER DE CĂLDURĂ ŞI MASĂ SEMINAR - probleme propuse şi consideraţii teoretice -. CONDUCŢIA TERMICĂ ÎN REGIM STAŢIONAR Teoria propagării sau transmiterii căldurii se ocupă cu cercetarea fenomenelor şi
TRANSFER DE CĂLDURĂ ŞI MASĂ SEMINAR - probleme propuse şi consideraţii teoretice -. CONDUCŢIA TERMICĂ ÎN REGIM STAŢIONAR Teoria propagării sau transmiterii căldurii se ocupă cu cercetarea fenomenelor şi
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
CURS 10 ANALIZA PERFORMANŢELOR PE BAZA CONTULUI DE PROFIT ŞI PIERDERE
 CURS ANALIZA PERFORMANŢELOR PE BAZA CONTULUI DE PROFIT ŞI PIERDERE Obictiv: însuşira concptului d cont d profit şi pirdr; însuşira concptului d rntabilitat; dtrminara soldurilor intrmdiar d gstiun; stabilira
CURS ANALIZA PERFORMANŢELOR PE BAZA CONTULUI DE PROFIT ŞI PIERDERE Obictiv: însuşira concptului d cont d profit şi pirdr; însuşira concptului d rntabilitat; dtrminara soldurilor intrmdiar d gstiun; stabilira
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Studiu privind soluţii de climatizare eficiente energetic
 Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
 11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
11.2 CIRCUITE PENTRU FORMAREA IMPULSURILOR Metoda formării impulsurilor se bazează pe obţinerea unei succesiuni periodice de impulsuri, plecând de la semnale periodice de altă formă, de obicei sinusoidale.
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Probleme. c) valoarea curentului de sarcină prin R L şi a celui de la ieşirea AO dacă U I. Rezolvare:
 Pobleme P Pentu cicuitul din fig P, ealizat cu amplificatoae opeaţionale ideale, alimentate cu ±5V, să se detemine: a) elaţia analitică a tensiunii de ieşie valoile tensiunii de ieşie dacă -V 0V +,8V -V
Pobleme P Pentu cicuitul din fig P, ealizat cu amplificatoae opeaţionale ideale, alimentate cu ±5V, să se detemine: a) elaţia analitică a tensiunii de ieşie valoile tensiunii de ieşie dacă -V 0V +,8V -V
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
MOTOARE DE CURENT CONTINUU
 MOTOARE DE CURENT CONTINUU În ultimul timp motoarele de curent continuu au revenit în actualitate, deşi motorul asincron este folosit în circa 95% din sistemele de acţionare electromecanică. Această revenire
MOTOARE DE CURENT CONTINUU În ultimul timp motoarele de curent continuu au revenit în actualitate, deşi motorul asincron este folosit în circa 95% din sistemele de acţionare electromecanică. Această revenire
