10. Lenkimas Bendrosios žinios
|
|
|
- Άγνη Παπαφιλίππου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 10. Lenkimas Bendrosios žinios Lenkimu vadinamas deformavimo tipas, apibūdinamas strpo ašies išsikreivinimu nuo lenkimo momento. Skersinio lenkimo atveu sios ašies išsikreivinimo priežastis ra ir lenkimo momentas, ir skersinė ėga (10.1 pav tekstas, 10. pav. Pagal įrąžas, veikiančias skerspūve, lenkimas skirstomas į grnąį ir skersinį. Lenkimas vadinamas grnuou, kai sios skerspūve veikia tik lenkimo momentas (10.3 pav.. Lenkimas vadinamas skersiniu, kai sios skerspūve veikia ir lenkimo momentas, ir skersinė ėga (10.4 pav.. Pagal sios ašies išsikreivinimo pobūdį lenkimas skirstomas į plokščiąį ir įstrižą. Plokščiuou arba paprastuou vadinamas lenkimas, kai sios ašis išlinksta plokštumoe, sutampančioe su viena iš svarbiausiųų plokštumų, t.. su plokštuma, einančia per sios ašį ir vieną iš centrinių svarbiausiųų skerspūvio ašių (10.5 pav.. Tokią sios deformacią dažniausiai sukelia statmena sios ašiai apkrova, veikianti vienoe iš svarbiausiųų sios plokštumų. Įstrižu vadinamas lenkimas, kai sios ašis išlinksta plokštumoe, nesutampančioe nė su viena iš svarbiausiųų plokštumų (10.6 pav.. Tokią sios deformacią sukelia statmena sios ašiai apkrova, veikianti plokštumoe, kertančioe sios ašį, bet nesutampančioe nė su viena iš svarbiausiųų plokštumų. 10. tekstas 10.1 pav pav pav pav pav. Lenkimas ra sudėtingas deformavimo tipas. Lenkiamo elemento įtemptąą-deformuotąą būseną apibūdinančių ddžių (įrąžų, įtempimų, deformacių ir poslinkių nustatmo metodai ra daug sudėtingesni negu tempiamuose-gniuždomuose, kerpamuose ar sukamuose elementuose. Todėl lenkimo skrius tradiciškai daliamas į dvi dalis: pirmoe dale aptariami bendriei dalkai ir nagrinėamas sios stiprumas, antroe dale nagrinėami sios standumo klausimai. Panašiai padalintas lenkimo skrius ir šiame konspekte: toliau pateikiami įrąžų ir įtempimų nustatmo metodai, o deformacios ir poslinkiai nagrinėami 11 skriue. 77
2 10.. Plokščioo lenkimo įrąžos Plokščioo lenkimo atveu sios skerspūviuose veikia tiek skersinės ėgos, tiek lenkimo momentai. Siekiant geriau suvokti sios deformavimąsi, rasti pavoingus skerspūvius, numatti optimiavimo būdus, sudaromos šių įrąžų diagramos, t.. funkcių f( g, ir f ( g,, f grafikai, vaiduoants atitinkamai skersinės ėgos ir lenkimo momento kitimą išilgai sios ašies. Prieš aptardami įrąžų diagramų sudarmo etapus, nustatsime sios įrąžų ir apkrovos ršį, išsiaiškinsime, kaip randami ekstreminiai lenkimo momentai, kaip brėžiamos parabolės. Bendruou atveu tiek sią (os ruožą veikianti išskirsttoi apkrova, tiek atsiradusios sioe įrąžos ra aplikatės funkcios (10.7 pav.. Ršį tarp šių toldinių funkcių nustatsime nagrinėdami sios elementarioo elemento pusiausvrą. Laiksime, kad nkstamai trumpame ruože d išskirsttoi apkrova ra pastovi (10.8 pav.: 0; + g d + + d 0, d d g. (10.1 0; fb 1 d + g d d + + d 0, d, (10. d nes nars gd 1 d ra antros eilės mažbė. Taigi skersinės ėgos išvestinė skerspūvio aplikatės atžvilgiu lgi sią veikiančiai išskirsttai apkrovai, o lenkimo momento išvestinė skerspūvio aplikatės atžvilgiu lgi skersinei ėgai. Iš šių diferencialinių lgčių gauname, kad lenkimo momento antroi išvestinė skerspūvio aplikatės atžvilgiu lgi sią veikiančiai išskirsttai apkrovai: gf( d ( ( 10.7 pav. d d g. (10.3 Lgts (10.1, (10. ir (10.3 gali būti naudoamos sios įrąžoms skaičiuoti. Tarkime, kad skersinė ėga ( 0 ir lenkimo momentas ( 0 sios pradiniame skerspūve ra žinomi (šios įrąžos nustatomos iš kraštinių sąlgų. Tada d gconst B +d +d g d + 0, (10.4 d+ 0 ( pav. arba g d d (10.6 Integralų išraiška, o kartu skersinės ėgos ir lenkimo momento kitimo dėsniai priklauso nuo išskirsttos apkrovos kitimo dėsnio. ptarkime du dažniausiai pasitaikančius išskirsttosios apkrovos atveus: 78
3 1. Ruožas neapkrautas išskirsttąa apkrova (g0, 10.9 pav.; tada 0 const (ruože skersinė ėga ra pastovi, + 0 (ruože lenkimo momentas kinta tiesiškai. Pasitaiko, kad neapkrautame ruože ir skersinė ėga lgi nuliui (10.10 pav., tada 0 const (ruože lenkimo momentas ra pastovus.. Ruože veikia vienodai išskirstta apkrova ( g const, pav.; tada g + 0 (ruože skersinė ėga kinta tiesiškai, g (ruože lenkimo momentas kinta kvadratiniu dėsniu. Lgts (10.4, (10.5 ir (10.6 galioa tik ruožams, kuriuose išskirsttoi apkrova (kartu ir sios įrąžos kinta toldiškai. Tokius ruožus vieną nuo kito skiria skerspūviai, kuriuose keičiasi išskirsttos apkrovos kitimo dėsnis, taip pat magai, kuriuose pridėta ėga arba momentas pv pav pav. Siekdami išsiaiškinti, kaip kinta įrąžos maguose, panagrinėkime magų pusiausvrą: 1 magas, kuriame veikia ėga (10.1 pav.: 0 ; i + + 0,. i fb 0 ; ( + ( + 0, kai i i i, tai. i i Išvada: pereinant per magą, kuriame veikia ėga, skersinė ėga pasikeičia didumu, lgiu mage veikiančios ėgos didumui, o lenkimo momentas lieka toks pats; magas, kuriame veikia momentas (10.13 pav.: 0 ; i + 0,. i fb 0 ; i i( i + f + 0, kai i, tai i f. Išvada: pereinant per magą, kuriame veikia momentas, skersinė ėga lieka tokia pati, o lenkimo momentas pasikeičia didumu, lgiu mage veikiančio momento didumui. i i i B 10.1 pav. f i i i pav. B pav
4 Proektuotous dažniausiai domina ne bet kokios, bet ekstreminės įrąžos. Tuo atveu, kai ruožas ra apkrautas išskirsttąa apkrova, ekstreminis lenkimo momentas gali veikti ne ruožo galiniuose skerspūviuose, bet kuriame nors kitame o skerspūve. Tokio skerspūvio vieta nustatoma, remiantis matematiniu metodu funkcios ekstremumui skaičiuoti: eigu diferenciuoamos funkcios išvestinė kuriame nors taške lgi nuliui, tai šiame taške duotoi funkcia turi ekstremumą. Prisiminkime, kad d, d taigi ekstreminis lenkimo momentas veiks tame ruožo skerspūve, kuriame skersinė ėga lgi nuliui. Kai ruožas ra apkrautas vienodai išskirstta apkrova, lenkimo momentų diagrama ra kvadratinė parabolė. Parabolei išbrėžti reikia mažiausiai trių taškų. Du taškai gaunami atidėus ruožo galinių skerspūvių lenkimo momentų reikšmes. Trečiasis taškas, t.. taškas, kuriame susikerta lenkimo momentų diagramos galiniuose taškuose nubrėžtos liestinės, nustatomos dveopai. Pirmuou atveu naudoama formulė: i i i 1 l / l/ 3 i/ 1 gconst pav. l/ l/ 3 gconst i gl 4 i/ i / i + g l + 4, (10.7 gl čia indeksas i/ žmi i- ruožo vidurinįį skerspūvį (10.14 pav.. ntruou atveu vienodai išskirstta apkrova pakeičiama atstoamąa, veikiančia viduriniaame ruožo skerspūve, ir skaičiuoamas šiame skerspūve veikiantis lenkimo momentas (10.15 pav.: l i/ i+ i. (10.8 Parabolės liestinių susikirtimo tašką atitinkantis lenkimo momentas i/ vadinamas ruožo tariamuou pav. lenkimo momentu (tai lenkimo momentas, kuris veiktų viduriniaame ruožo skerspūve, ei vienodai išskirstta apkrova būtų pakeista atstoamąa. Sudarant lenkimo momentų diagramas ir siekiant išvengti klaidų (pač maguose, pereinant iš vienos parabolės į kitą arba iš tiesės į parabolę, ir atvirkščiai, pirmiausia reikia sudarti lenkimo momentų diagramą tariamam sios apkrovimo atveui, t.. kai sios ruožuose veikiančios vienodai išskirsttos apkrovos ra pakeistos atstoamosiomis. Po to kiekvieno tokio ruožo liestines (gautas suungus galinius lenkimo momentus su tariamuou lenkimo momentu sudalti į lgų skaičių lgių dalių ir daliimo taškus nuosekliai suungti tiesėmis. Pagaliau per gautų atkarpų vidurius įbrėžti parabolę (10.14, pav.. kivaidu, kad kuo daugiau ra daliimo taškų, tuo parabolė tikslesnė. Dabar ra pakankamai teorinių žinių, kad būtų galima sudarti bet kaip apkrautos sios įrąžų diagramas. Dažniausiai naudoamas toks sios įrąžų diagramos sudarmo algoritmas: 1 skaičiuoami (eigu reikia atraminių reakcių komponentai, skaičiavimo reultatai patikrinami; i i 1 3 i/ 1 3 i l i i/ 80
5 sužmimi skaičiuoamiei skerspūviai, t.. skerspūviai, kuriuose keičiasi įrąžos didumas arba os kitimo dėsnis; tai skerspūviai ties atramomis ir laisvaisiais sios galais, skerspūviai iš abieų ėgos arba momento pridėties taško pusių ir skerspūviai ties išskirsttos apkrovos pradžios ir pabaigos taškais; 3 pūvio metodu (žr. 3.3 poskrį skaičiuoamuosiuose skerspūviuose apskaičiuoamos skersinės ėgos ir lenkimo momentai; 4 apskaičiuotos skersinių ėgų ir lenkimo momentų reikšmės pasirinktu masteliu atidedamos atitinkamose sios ašse; 5 gauti atkarpų galai suungiami, remiantis integraliniu įrąžų ir išskirsttosios apkrovos ršiu; 6 diagramos užbrūkšniuoamos ir užrašomi masteliai (skaičiai, rodants kiek skersinės ėgos ar lenkimo momentų vienetų atidėta brėžinio ilgio vienete, pv., 10 kn/cm, 50 knm/cm; 7 sudartos diagramos patikrinamos. 10. pv. Kartais tenka spręsti atvirkštinį uždavinį, t.. žinant lenkimo momentų diagramą, sudarti skersinių ėgų diagramą ir sios apkrovimo scemą. Toks uždavins, remiantis anksčiau išdėstta medžiaga, sprendžiamas trimis etapais: 1 lenkimo momentų diagramai ties skaičiuoamaisiais skerspūviais nubraižomos liestinės ir apskaičiuoami ų krpties koeficientai ( tg i β ; taip gaunama skersinių ėgų diagrama; i skersinių ėgų diagramai ties skaičiuoamaisiais skerspūviais nubraižomos liestinės ir i apskaičiuoami ų krpties koeficientai ( tgβ g ; taip gaunamos sios ruožuose veikiančios i vienodai išskirsttos apkrovos; 3 iš magų pusiausvros sąlgų nustatomi maguose pridėti momentai ir ėgos ( f i,. i 10.3 pv Grnoo lenkimo normaliniai įtempimai Siekdami gauti normalinių įtempimų pasiskirstmo sios skerspūve formulę, naudosime 3.8 poskre apraštą metodiką. Statikos integralinė s lgts. Grnoo lenkimo atveu skerspūve veikia tik normaliniai įtempimai, lgiagretūs ašiai (10.16 pav.. Todėl iš šešių statikos integralinių lgčių (3.4 lieka tik trs: f f f N σ d, σ d, d σ. (10.9 Užrašę atpautai sios daliai (žr pav. tris pusiausvros lgtis ( 0, f 0, f 0, pav. 81
6 susiesime sios skerspūve veikiančias įrąžas su apkrova: N σ d 0, σ d 0, d σ f. (10.10 Geo metrinė d e f o r m a v i m o l g t i s. Grnoo lenkimo atveu sia išlinksta apskritimo lanku. Viename os krašte sluoksniai pailgėa, kitame sutrumpėa, o vertikalios linios išlieka tiesios. Sluoksnis, kurio ilgis nepasikeičia, vadinamas neutraliuou. Plokštumai, kurioe guli neutralusis sluoksnis, susikirtus su skerspūvio plokštuma, gaunama neutralioi linia (10.17 pav.. Nustatsime ršį tarp sios ašies kreivio κ (κ 1, ρ neutralioo ρ sluoksnio kreivio spinduls ir bet kurio sios sluoksnio liniinės deformacios ε. Tam tikslui išskirkime elementarųį sios elementą ir panagrinėkime o sluoksnio CD, nutolusio atstumu nuo neutralioo sluoksnio B, liniines deformacias (10.18 pav.. kivaidu, kad sluoksnio CD deformacia Cf Df CD Cf Df d ε. Panaudous CD d poslinkių mažumo principą, galima d užrašti, kad tg( dϕ dϕ arba ρ d ρ dϕ. nalogiškai gauname, kad Cf Df ( ρ + dϕ. Dabar galima išreikšti deformacią per sios ašies kreivio spindulį ( ρ + dϕ ρdϕ ( ρ + ρ dϕ 1 ε ρ dϕ ρ dϕ ρ arba per sios ašies kreivį: ε κ. (10.11 NL. Neutralusis sluoksnis pav. f C D C f d Neutralioi linia d d B f D f i i n ė lgtis: σ E ε. ( pav. Dabar belieka išspręsti gautų lgčių sistemą. Į (10.1 lgtį įraškime liniinės deformacios išraišką (10.11: σ E ε Eκ. (10.13 Spręskime pirmąą sistemos (10.10 lgtį: N E κ d 0. Bet skerspūve E κ const, taigi E κ d E κ 0. Kadangi E κ 0, tai S nl 0. Gavome, kad neutraliosios linios S nl 8
7 atžvilgiu skerspūvio statinis momentas lgus nuliui. Taigi neutralioi linia kartu ra ir centrinė skerspūvio ašis. Spręskime antrąą sistemos (10.10 lgtį: E κ d E κ d E κ I 0. Kadangi E κ 0, tai I 0. Gavome, kad skerspūvio išcentrinis inercios momentas lgus nuliui. Taigi ašs ir ra ne tik centrinės, bet ir svarbiausiosios skerspūvio ašs. Spręskime trečiąą sistemos (10.10 lgtį: E κ d E κ d E κ I, κ EI, (10.14 Į (10.13 lgtį įstatę sios ašies kreivio išraišką (10.14, gausime normalinių įtempimų pasiskirstmo sios skerspūve formulę: σ I. (10.15 Čia: nagrinėamo skerspūvio lenkimo momentas, I skerspūvio ašinis inercios momentas neutraliosios linios atžvilgiu, taško, kuriame skaičiuoamas įtempimas, atstumas nuo neutraliosios linios. Iš (10.15 formulės matti, kad normaliniai įtempimai sios skerspūve pasiskirsto tiesės dėsniu: ie lgūs nuliui ties neutraliąa linia, didžiausi kraštiniuose sluoksniuose (10.19 pav.. Dažniausiai proektuotous domina didžiausių normalinių įtempimų absoliutinis didumas. Todėl sios stiprumo sąlga 0 normalinių įtempimų atžvilgiu turi tokį pavidalą: σ ma W R, (10.16 I čia W. ma ormulė (10.15 išvesta grnoo lenkimo atveui. Pasirodo, kad, esant skersiniam lenkimui, skaičiavimo paklaida, naudoant šią formulę, ra nedidelė. Todėl i praktiškai naudoama visiems lenkimo uždaviniams spręsti pav , 10.5 pv Sios tangentiniai įtempimai Tangentinių įtempimų pasiskirstmo sios aukšte dėsnis nustatomas remiantis Žuravskio prielaida, pagal kurią tangentiniai įtempimai sios skerspūvio plote pasiskirsto vienodai, o ų veikimo krptis sutampa su skersinės ėgos veikimo krptimi (iš tikrųų tangentinių įtempimų pasiskirstmas sios plote ir ų veikimo krptis priklauso nuo skerspūvio formos. Žuravskio prielaida geriausiai tinka siauriems ir aukštiems skerspūviams. Esant sudėtingai skerspūvio formai (pv., dvitėui, tangentiniams įtempimams nustatti taikoma speciali metodika. Iš sios (10.0 pav. išskirkime elementarųį elementą. Pūviu, nutolusiu atstumu nuo neutralios linios (ašies, atpaukime apatinę elemento dalį, kurios skerspūvio plotas ω (10.1 pav.. 83
8 +d d d b d 1 d 1+d 10.0 pav pav. Kairiame pūve veiks tangentiniai įtempimai τ ir normaliniai įtempimai σ, dešiniame pūve atitinkamai τ ir (σ + d σ. Horiontaliame pūve dėl tangentinių įtempimų dualumo veiks tangentiniai įtempimai τ τ, o normaliniai įtempimai bus lgūs nuliui, nes vertikalia krptimi sluoksniai vienas kito nespaudžia (galioa poslinkių mažumo principas. tpautam elementui (11. pav. užraškime pusiausvros lgtį 0 : ( σ + dσ τ d b σd + d 0 ω ω d d d τ d b dσd d d S, ω, ω ω I I ω I d S, ω τ τ. d I b, Bet S d, taigi, ω τ d I b Turėdami galvoe, kad tangentinių įtempimų ženklas priklauso tik nuo skersinės ėgos ženklo, gauname tokią galutinę formulę: S τ, (10.17 I b. d b + d čia: τ tangentinis įtempimas, veikiantis plokštumoe ašies krptimi, skersinė ėga, veikianti ašies krptimi, S X skerspūvio dalies, esančios į vieną pusę nuo tiesės, nubrėžtos per nagrinėamąį tašką lgiagrečiai neutraliaai liniai, statinis momentas neutraliosios ašies ( atžvilgiu, b materialusis skerspūvio ties nagrinėamuou tašku plotis, matuoamas krptimi, lgiagrečia neutraliaai liniai. 10. pav pv. 84
9 Iš formulės (10.17 matti, kad tangentinių įtempimų pasiskirstmo sios aukšte dėsnis priklauso nuo santkio S b. ptarsime, kaip pasiskirsto tangentiniai įtempimai įvairių formų skerspūviuose. Stačiakampis (10.3 pav.. Stačiakampiame skerspūve tangentiniai įtempimai kinta kvadratiniu dėsniu, didžiausią reikšmę įgdami ties neutraliąa linia. Skrituls (10.4 pav.. Šiuo atveu tangentinių įtempimų krptis nesutampa su skersinės ėgos veikimo krptimi. Daroma papildoma prielaida, kurioe sakoma, kad tangentinių įtempimų vertikalios proekcios skritulio plote pasiskirsto vienodai. Priėmus tokią prielaidą, vertikalios tangentinių įtempimų proekcios apskaičiuoamos taikant Žuravskio formulę pav pav. Dvitėis (10.5 pav.. Dvitėui tangentiniai įtempimai skaičiuoami atskirai sienutei ir lentnoms. Sienutėe veikiants tangentiniai įtempimai apskaičiuoami pagal Žuravskio formulę, ir ie ra lgiagretūs skersinės ėgos veikimo krpčiai. Lentnose atsiranda dvieų krpčių tangentiniai įtempimai: τ ir τ. Pirmiei ra nedideli, be to, ų nustatmas ra sudėtingas, nes negalioa Žuravskio formulė, todėl ie neskaičiuoami. Tangentiniai įtempimai τ apskaičiuoami pagal Žuravskio formulę darant prielaidą, kad ie lentnos aukšte pasiskirsto vienodai: 10.5 pav. S, w τ, (10.18 I t t čia Sw, t atpautos lentnėlės α α skerspūvio statinis momentas neutralios ašies atžvilgiu (10.6 pav.. Taigi tangentiniai įtempimai lentnose kinta tiesės dėsniu; nuo nulio lentnėlės krašte (0 iki ekstreminės reikšmės ties susikirtimu su sienute. t t d 10.6 pav. d 85
10 Srities, kurioe susikerta lentna su sienute, įtemptoi būsena ra sudėtinga. Joe veikiantiems įtempimams apskaičiuoti nepakanka elementarių medžiagų mecanikos mokslo žinių Sios skaičiavimas Sia gali suirti dėl didžiausių normalinių, dėl didžiausių tangentinių įtempimų arba dėl kompleksinio normalinių ir tangentinių įtempimų poveikio. Normalinių įtempimų atžvilgiu pavoingas tas sios skerspūvis, kuriame veikia didžiausias lenkimo momentas. Šiame skerspūve pavoingiausi ra taškai, labiausiai nutolę nuo neutraliosios linios. Normaliniai įtempimai pavoinguose taškuose turi tenkinti tokią stiprumo sąlgą: ma σ R. (10.19 ma W Tangentinių įtempimų atžvilgiu pavoingas tas skerspūvis, kuriame veikia didžiausia skersinė ėga. Šiame pūve pavoingiausi dažniausiai ra taškai ties neutraliąa linia. Tangentiniai įtempimai pavoinguose taškuose turi tenkinti tokią stiprumo sąlgą: S ma ma τ < Rs. (10.0 ma I b Kompleksinio normalinių ir tangentinių įtempimų poveikio atžvilgiu pavoingas tas skerspūvis, kuriame abieų įrąžų ( ir reikšmės ra pakankamai didelės, pv., skerspūviai ir 5, žr pav. Jeigu tokių įtartinų skerspūvių ra keletas, reikia tikrinti kiekvieną iš ų. Šiuose skerspūviuose pavoingiausi ra taškai, kuriuose įtempimų reikšmė, apskaičiuota priklausomai nuo pasirinktos stiprumo ipoteės, ra didžiausia, pv., taškai ir B, žr pav. Toks kompleksinis normalinių ir tangentinių įtempimų poveikis dažnai pavoingas plonasienio profilio siose. Čia pavoinga šių įtempimų kombinacia veikia sienutėe ties os sandūra su lentna (žr pav.. Ji turi tenkinti stiprumo sąlgą: σ det R, (11.1 čia σ det skaičiuoamiei įtempimai. Stiprumo sąlga, naudoant trečiąą stiprumo teorią, turi tokį pavidalą: σdet σ + 4τ R. ( l l l pav pav. 86
11 Praktiniai skaičiavimai rodo, kad dažniausiai naudoamose gana ilgose siose lemiamą reikšmę turi normaliniai įtempimai, todėl labai dažnai sios skaičiuoamos naudoant tik (10.19 stiprumo sąlgą pv Racionali sios skerspūvio forma. Kintamo skerspūvio sios Sia laikoma racionali, kai i tenkina stiprumo sąlgą, esant minimaliam os svoriui. ažinti sios svorį galima dviem būdais: pirma, keičiant skerspūvio formą, antra, keičiant skerspūvio matmenis. Iš formulės σ R matti, kad esant pastoviam plotui skerspūvio forma ra tuo ma W I geresnė, kuo didesnis skerspūvio atsparumo momentas. Prisiminkime, kad W, I d. Taigi, esant pastoviam aukščiui, atsparumo momentas ra didesnis to skerspūvio, kurio plotas sutelktas kraštiniuose skerspūvio sluoksniuose. Idealiuotas tokio skerspūvio variantas vadinamas idealiuou skerspūviu (10.9a pav.. Iš realių skerspūvių racionaliausias ra dvitėinis skerspūvis (10.9b pav., eigu medžiaga nevienodai stipri tempimui ir gniuždmui (pv., gelžbetonis tėinis skerspūvis (10.9c pav., medinės sios dažniausiai daromos stačiakampio skerspūvio (10.9d pav.. Kitų skerspūvių (skrituls, kržius forma neracionali, ir todėl ie sioms gaminti paprastai nenaudoami (10.9e,f pav.. ptarsime sios optimiavimą, keičiant os skerspūvio matmenis. Pastovaus skerspūvio siose medžiaga visiškai išnaudoama tik tame skerspūve, kuriame veikia maksimalus lenkimo momentas. Visuose kituose skerspūviuose normaliniai įtempimai ra mažesni už proektinį stiprį. Keičiant sios skerspūvio matmenis galima pasiekti, kad bet kuriame os skerspūve didžiausi absoliutiniu didumu normaliniai įtempimai būtų lgūs proektiniam stipriui. Tokios sios vadinamos vienodo stiprumo siomis. Išnagrinėsime, kaip keičiasi skerspūvis gembinės vienodo stiprumo sios, laisvaame gale apkrautos ėga. Sios skerspūvio kitimo lgtį gausime prilginę absoliutiniu didumu didžiausius normalinius įtempimus, veikiančius bet kuriame sios skerspūve, proektiniam stipriui: ( σ ( R. Gavome, kad vienodo stiprumo sios skerspūvio atsparumo momentas turi kisti ma w( tokiu pačiu dėsniu, kaip ir lenkimo momentas: ( w (. (10.3 R ma a b c d e f Nagrinėkime stačiakampio skerspūvio sios du variantus. Tarkime, kad sios skerspūvio aukštis ra pastovus; nustatkime, kaip turi kisti skerspūvio plotis, kad bet kuriame sios skerspūve normaliniai įtempimai absoliutiniu didumu būtų lgūs proektiniam stipriui, t.. kad būtų tenkinama (10.3 lgtis (10.30 pav pav. 87
12 88 Tam tikslui išreikškime atsparumo momentą per skerspūvio matmenis b ir, o užrašę pusiausvros lgtį, lenkimo momentą per ėgą. Įraškime gautas išraiškas į (10.3 lgtį, išspręskime ą kraštinės b atžvilgiu:, ( ( ( R R b w σ. ( R b σ (10.4 Gavome, kad sios skerspūvio plotis kinta tiesiškai (10.31 pav.. Dabar išspręskime kitą variantą: sios skerspūvio plotis pastovus, kinta o aukštis (10.3 pav.:, ( ( ( R R b w σ. ( b R σ (10.5 Gavome antros eilės kreivės lgtį (10.33 pav tekstas l b const pav pav. const b l 10.3 pav pav.
13 10.7. Lenkimo centras Lenkiant sią, kai ėgų veikimo plokštuma sutampa su sios svarbiausiąa plokštuma ( arba, kuri nėra os simetrios plokštuma, sia ne tik išlinksta bet ir susisuka, (pv., lovinio profilio sia, pav.. Jėgą pamažu perkeliant į lovio sienelės pusę galima rasti tokią ėgos padėtį (tašką C e, kuriame pridėus ėgą sia tik išlinks, bet nesusisuks. Šis taškas vadinamas lenkimo centru. Jo padėtis nustatoma nagrinėant tangentinius įtempimus sios skerspūve (10.35 pav.. Sienelėe veikiančių įtempimų atstoamoi aptiksliai (neįvertinus τ veikiančių lentnose lgi skersinei ėgai arba tiesiog ėgai. O tangentinių įtempimų, veikiančių lentnose, atstoamosios sudaro ėgų porą, kuri ir susuka lenkiamą lovinę sią (10.36 pav.. Taigi ėga turi būti pridėta taip, kad i ne tik lenktų sią, bet ir suktų ą ašies atžvilgiu kompensuodama šitaip e dėl tangentinių įtempimų, veikiančių lentnose, susidariusį sukimo momentą. tstumą, kuriuo reikia perstumti ėgą, galima gauti iš K pusiausvros lgties (10.36, pav.: fk 0; 0 e ( 0 + e + ( t 0, e ( t 0. ( pav. 0 e t t c t t c S 0 e c K pav pav pav. Kontroliniai klausimai Kas ra lenkimas? Brėžins Kaip skirstomas lenkimas pagal įrąžas, veikiančias sios skerspūve? Koks lenkimas vadinamas grnuou? Brėžins Koks lenkimas vadinamas skersiniu? Brėžins Kaip skirstomas lenkimas pagal sios išsikreivinimo pobūdį? 89
14 10.6. Koks lenkimas vadinamas plokščiuou? Brėžins Koks lenkimas vadinamas įstrižuou? Brėžins Kas ra skersinių ėgų diagrama? Kas ra lenkimo momentų diagrama? Kas ra skaičiuoamiei skerspūviai? Kur ie žmimi? Kam lgi skersinės ėgos skaitinė reikšmė, kai i skaičiuoama pūvio metodu? Pavds Kam lgi lenkimo momento skaitinė reikšmė, kai i skaičiuoama pūvio metodu? Pavds Užraškite apkrovos ir sios įrąžų diferencialinius ršius Kaip iš skersinių ėgų diagramos galima gauti išskirsttosios apkrovos intensvumą? Pavds Kaip iš lenkimo momentų diagramos galima gauti skersinę ėgą? Pavds Užraškite apkrovos ir sios įrąžų integralinius ršius Parodtai siai aptiksliai nubraižkite skersinių ėgų ir lenkimo momentų diagramas. Naudokite integralinius ršius, susieančius apkrovą su sios įrąžomis Kaip kinta skersinė ėga ir lenkimo momentas sios ruože, kuriame nėra išskirsttosios apkrovos? Brėžins, formulės Kaip kinta skersinė ėga ir lenkimo momentas sios ruože, kuriame veikia vienodai išskirstta apkrova? Brėžins, formulės Kaip kinta lenkimo momentas sios ruože, kuriame skersinės ėgos lgios nuliui? Brėžins, formulė Kokia toldinės funkcios savbė naudoama skaičiuoant ekstreminius lenkimo momentus? 10.. Kokiomis sąlgomis (prielaidomis remiantis gaunama sios normalinių įtempimų formulė? Užraškite lenkimo momento ir normalinio įtempimo integralinį ršį Kas ra neutralusis sluoksnis? Kas ra neutralioi linia? Brėžins Užraškite liniinės deformacios ir sios ašies kreivio spindulio ršį. Brėžins Užraškite lgčių sistemą, iš kurios gaunama normalinių įtempimų pasiskirstmo sios skerspūve formulė Užraškite sios ašies kreivio spindulio ir lenkimo momento ršį Kaip pasiskirsto ir kam lgūs normaliniai įtempimai sios skerspūve? Brėžins Kokių ašių atžvilgiu galima taikti sios normalinių įtempimų formulę? Ką teigia Žuravskio prielaida Užraškite Žuravskio formulę Parodkite, kaip pasiskirsto tangentiniai įtempimai sios stačiakampiame skerspūve. Brėžins Parodkite, kaip pasiskirsto tangentiniai įtempimai dvitėiniame skerspūve. Brėžins Užraškite bendriausias sios stiprumo sąlgų išraiškas Užraškite sios stiprumo sąlgą normalinių įtempimų atžvilgiu Užraškite sios stiprumo sąlgą tangentinių įtempimų atžvilgiu Koks plonasienės sios skerspūvis ir kokie o taškai ra pavoingi sudėtiniam normalinių ir tangentinių įtempimų poveikiui? Brėžins Kokie sios skerspūviai ra racionalūs? Brėžins Kokia sia vadinama vienodo stiprumo sia? Prie gembinės stačiakampio skerspūvio sios laisvoo galo pridėta ėga. Nubraižkite vienodo stiprumo sią, kai const. Paaiškinkite, kodėl gaunate tokios formos gembinę sią Prie gembinės stačiakampio skerspūvio sios laisvoo galo pridėta ėga. Nubraižkite vienodo stiprumo sią, kai bconst. Paaiškinkite, kodėl gaunate tokios formos gembinę sią Ką vadiname sios skerspūvio šlties (lenkimo centru? Brėžins. 90
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
9. Sukimas Bendrosios žinios
 9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
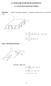 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
Teorinė mechanika I. Uždavinių sprendimo vadovas
 VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
6. Konstrukcijų patikimumo įvertinimo metodai
 6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
DEFORMUOJAMO KŪNO MECHANIKA 1 dalis
 DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
9. KEVALŲ ELEMENTAI. Pavyzdžiai:
 9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
PNEUMATIKA - vožtuvai
 Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
5. Medžiagų mechaninės savybės
 5. Medžiagų mechaninės savybės 5.1. Bendrosios žinios r konstrukcija (jos eementas) yra pakankamai stipri, standi, stabii, gaima spręsti tik tuo atveju, kai šaia įtemptąją ir deformuotąją jos būseną apibūdinančių
5. Medžiagų mechaninės savybės 5.1. Bendrosios žinios r konstrukcija (jos eementas) yra pakankamai stipri, standi, stabii, gaima spręsti tik tuo atveju, kai šaia įtemptąją ir deformuotąją jos būseną apibūdinančių
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra. Gintaras Skersys. Mokymo priemonė
 Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Επώνυμο Όνομα Όνομα Πατρός
 Κωδ. ποψηφ. Επώνυμο Όνομα Όνομα Πατρός χολή Επιτυχίας Ίδρυμ α 15053584 ΑΓΓΕΛΙΔΟ ΤΑΡΟΛΑ ΚΩΤΑΤΙ Ο 15053555 ΑΜΑΑΤΙΔΟ ΗΛΕΚΤΡΑ ΚΩΤΑΤΙ Ο ΤΕΧΟΛΟΓΩ ΓΕΩΠΟΩ (ΦΛΩΡΙΑ) ΠΟΙΜΑΤΙΚΗ ΚΟΙΚ ΘΕΟΛΟΓΙΑ 15053603 ΑΛΑΙΔΟ ΕΘΜΙΑ
Κωδ. ποψηφ. Επώνυμο Όνομα Όνομα Πατρός χολή Επιτυχίας Ίδρυμ α 15053584 ΑΓΓΕΛΙΔΟ ΤΑΡΟΛΑ ΚΩΤΑΤΙ Ο 15053555 ΑΜΑΑΤΙΔΟ ΗΛΕΚΤΡΑ ΚΩΤΑΤΙ Ο ΤΕΧΟΛΟΓΩ ΓΕΩΠΟΩ (ΦΛΩΡΙΑ) ΠΟΙΜΑΤΙΚΗ ΚΟΙΚ ΘΕΟΛΟΓΙΑ 15053603 ΑΛΑΙΔΟ ΕΘΜΙΑ
1 Įvadas Neišspręstos problemos Dalumas Dalyba su liekana Dalumo požymiai... 3
 Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
Skaičių teorija paskaitų konspektas Paulius Šarka, Jonas Šiurys 1 Įvadas 1 1.1 Neišspręstos problemos.............................. 1 2 Dalumas 2 2.1 Dalyba su liekana.................................
ΥΠOΥΡΓΕΙO ΠΑΙΔΕΙΑΣ KAI ΘΡΗΣΚΕΥΜΑΤΩΝ
 ΥΠOΥΡΓΕΙO ΠΑΙΔΕΙΑΣ KAI ΘΡΗΣΚΕΥΜΑΤΩΝ Ε Λ Λ Η Ν Ι Κ Η Δ Η Μ Ο Κ Ρ Α Τ Ι Α Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Π Α Τ Ρ Ω Ν Π Ο Λ Υ Τ Ε Χ Ν Ι Κ Η Σ Χ Ο Λ Η ΤΜΗΜΑ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Πληρ.:Αικατερίνη Λιάπη,Αναπλ.Καθηγήτρια
ΥΠOΥΡΓΕΙO ΠΑΙΔΕΙΑΣ KAI ΘΡΗΣΚΕΥΜΑΤΩΝ Ε Λ Λ Η Ν Ι Κ Η Δ Η Μ Ο Κ Ρ Α Τ Ι Α Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Π Α Τ Ρ Ω Ν Π Ο Λ Υ Τ Ε Χ Ν Ι Κ Η Σ Χ Ο Λ Η ΤΜΗΜΑ ΑΡΧΙΤΕΚΤΟΝΩΝ ΜΗΧΑΝΙΚΩΝ Πληρ.:Αικατερίνη Λιάπη,Αναπλ.Καθηγήτρια
EUROPOS CENTRINIS BANKAS
 2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
ΥΧΡΩΜΑ ΜΟΛΥΒΙΑ. «Γ λ υ κ ό κ α λ ο κ α ι ρ ά κ ι» της Γ ω γ ώ ς Α γ γ ε λ ο π ο ύ λ ο υ
 ΤΑ Π ΥΧΡΩΜΑ ΜΟΛΥΒΙΑ Εφη μ ε ρ ί δ α τ ο υ τ μ ή μ α τ ο ς Β τ ο υ 1 9 ου Δ η μ ο τ ι κ ο ύ σ χ ο λ ε ί ο υ Η ρ α κ λ ε ί ο υ Α ρ ι θ μ ό ς φ ύ λ λ ο υ 1 Ι ο ύ ν ι ο ς 2 0 1 5 «Γ λ υ κ ό κ α λ ο κ α ι ρ
ΤΑ Π ΥΧΡΩΜΑ ΜΟΛΥΒΙΑ Εφη μ ε ρ ί δ α τ ο υ τ μ ή μ α τ ο ς Β τ ο υ 1 9 ου Δ η μ ο τ ι κ ο ύ σ χ ο λ ε ί ο υ Η ρ α κ λ ε ί ο υ Α ρ ι θ μ ό ς φ ύ λ λ ο υ 1 Ι ο ύ ν ι ο ς 2 0 1 5 «Γ λ υ κ ό κ α λ ο κ α ι ρ
r F F r F = STATIKA 1 Q = qmax 2
 STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
Integriniai diodai. Tokio integrinio diodo tiesiogin įtampa mažai priklauso nuo per jį tekančios srov s. ELEKTRONIKOS ĮTAISAI 2009
 1 Integriniai diodai Integrinių diodų pn sandūros sudaromos formuojant dvipolių integrinių grandynų tranzistorius. Dažniausiai integriniuose grandynuose kaip diodai naudojami tranzistoriniai dariniai.
1 Integriniai diodai Integrinių diodų pn sandūros sudaromos formuojant dvipolių integrinių grandynų tranzistorius. Dažniausiai integriniuose grandynuose kaip diodai naudojami tranzistoriniai dariniai.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΧΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Διακριτά Μαθηματικά και Μαθηματική Λογική ΠΛΗ20 Ε ρ γ α σ ί α 1η Συνδυαστική-Σχέσεις-Συναρτήσεις Σκοπός της παρούσας εργασίας είναι η περαιτέρω εξοικείωση με τις σημαντικότερες μεθόδους και ιδέες της Συνδυαστικής
Διακριτά Μαθηματικά και Μαθηματική Λογική ΠΛΗ20 Ε ρ γ α σ ί α 1η Συνδυαστική-Σχέσεις-Συναρτήσεις Σκοπός της παρούσας εργασίας είναι η περαιτέρω εξοικείωση με τις σημαντικότερες μεθόδους και ιδέες της Συνδυαστικής
ΥΠΟΨΗΦΙΟΙ ΓΙΑ ΤΗΝ ΑΝΑΔΕΙΞΗ ΤΩΝ ΜΕΛΩΝ ΤΩΝ ΤΟΠΙΚΩΝ ΔΙΟΙΚΗΣΕΩΝ ΤΩΝ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΤΜΗΜΑΤΩΝ ΤΟΥ ΟΙΚΟΝΟΜΙΚΟΥ ΕΠΙΜΕΛΗΤΗΡΙΟΥ ΤΗΣ ΕΛΛΑΔΑΣ
 Ε Κ Λ Ο Γ Ε Σ 2 0 1 3 Δ Ε Κ Ε Μ Β Ρ Ι Ο Σ 2 0 1 3 55 ΥΠΟΨΗΦΙΟΙ ΓΙΑ ΤΗΝ ΑΝΑΔΕΙΞΗ ΤΩΝ ΜΕΛΩΝ ΤΩΝ ΤΟΠΙΚΩΝ ΔΙΟΙΚΗΣΕΩΝ ΤΩΝ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΤΜΗΜΑΤΩΝ ΤΟΥ ΟΙΚΟΝΟΜΙΚΟΥ ΕΠΙΜΕΛΗΤΗΡΙΟΥ ΤΗΣ ΕΛΛΑΔΑΣ 1ο ΠΕΡΙΦΕΡΕΙΑΚΟ ΤΜΗΜΑ
Ε Κ Λ Ο Γ Ε Σ 2 0 1 3 Δ Ε Κ Ε Μ Β Ρ Ι Ο Σ 2 0 1 3 55 ΥΠΟΨΗΦΙΟΙ ΓΙΑ ΤΗΝ ΑΝΑΔΕΙΞΗ ΤΩΝ ΜΕΛΩΝ ΤΩΝ ΤΟΠΙΚΩΝ ΔΙΟΙΚΗΣΕΩΝ ΤΩΝ ΠΕΡΙΦΕΡΕΙΑΚΩΝ ΤΜΗΜΑΤΩΝ ΤΟΥ ΟΙΚΟΝΟΜΙΚΟΥ ΕΠΙΜΕΛΗΤΗΡΙΟΥ ΤΗΣ ΕΛΛΑΔΑΣ 1ο ΠΕΡΙΦΕΡΕΙΑΚΟ ΤΜΗΜΑ
Rinktiniai informacijos saugos skyriai. 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija
 Rinktiniai informacijos saugos skyriai 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija Paskaitos tikslai Šioje temoje nagrinėjami klausimai: Perstatų šifrai Keitinių šifrai Vienos
Rinktiniai informacijos saugos skyriai 3. Kriptografija ir kriptografijos protokolai: Klasikinė kriptografija Paskaitos tikslai Šioje temoje nagrinėjami klausimai: Perstatų šifrai Keitinių šifrai Vienos
KENGŪRA SENJORAS
 KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS VU MATEMATIKOS IR INFORMATIKOS FAKULTETAS VU MATEMATIKOS IR INFORMATIKOS INSTITUTAS LIETUVOS MATEMATIKŲ DRAUGIJA KENGŪRA 2016. SENJORAS TARPTAUTINIO MATEMATIKOS
Γ49/59 ΕΞ. ΕΠΕΙΓΟΝ Π Ρ Ο Σ :
 Αθήνα, 30-5-2012 Δ Ι Ο Ι Κ Η Σ Η ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΙΟΙΚ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ Δ/ΝΣΗ ΔΙΟΙΚΗΤΙΚΟΥ ΠΡΟΣΩΠΙΚΟΥ ΤΜΗΜΑ : ΕΡΓΑΣΙΑΚΩΝ ΣΧΕΣΕΩΝ Ταχ. Δ/νση : Αγ. Κωνσταντίνου 8 Ταχ. Κώδικας: 102 41 ΑΘΗΝΑ Τηλέφωνο : 210-215289,290,291,292
Αθήνα, 30-5-2012 Δ Ι Ο Ι Κ Η Σ Η ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΙΟΙΚ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ Δ/ΝΣΗ ΔΙΟΙΚΗΤΙΚΟΥ ΠΡΟΣΩΠΙΚΟΥ ΤΜΗΜΑ : ΕΡΓΑΣΙΑΚΩΝ ΣΧΕΣΕΩΝ Ταχ. Δ/νση : Αγ. Κωνσταντίνου 8 Ταχ. Κώδικας: 102 41 ΑΘΗΝΑ Τηλέφωνο : 210-215289,290,291,292
Ι Ο Λ Ο Γ Ι Μ Ο - Α Π Ο Λ Ο Γ Ι Μ Ο Μ Η Ν Ο Γ Δ Κ Δ Μ Β Ρ Ι Ο Υ 2 0 1 5
 Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
Μ Ρ : 0 9 / 0 1 / 2 0 1 6 Ρ. Ρ Ω. : 7 Λ Γ Μ - Λ Γ Μ Μ Η Γ Δ Κ Δ Μ Β Ρ Υ 2 0 1 5 Δ Γ Ρ Ϋ Λ Γ Θ Δ ΚΔ Μ Β Δ Β Ω Θ Δ Δ Ρ Υ Θ Δ 0111 Χ / Γ Δ Θ Μ Θ Δ Ρ Ω Κ - - - 0112 Χ / Γ Λ Ρ Γ Κ Δ 2 3. 2 1 3. 0 0 0, 0 0-2
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Μ Ε Λ Ε Τ Η. Προμήθεια υλικών και φυτοφαρμάκων για τη συντήρηση υφιστάμενων και δημιουργία νέων χώρων πρασίνου Δ.Ε. Χερσονήσου
 Δ/ΝΣΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ & ΑΓΡΟΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΤΙΤΛΟΣ: Προμήθεια υλικών και φυτοφαρμάκων για τη συντήρηση υφιστάμενων και δημιουργία νέων ΑΡ.ΜΕΛΕΤΗΣ: ΔΠΕ9/2015 Μ Ε Λ Ε Τ Η Προμήθεια υλικών και φυτοφαρμάκων
Δ/ΝΣΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ & ΑΓΡΟΤΙΚΗΣ ΠΑΡΑΓΩΓΗΣ ΤΙΤΛΟΣ: Προμήθεια υλικών και φυτοφαρμάκων για τη συντήρηση υφιστάμενων και δημιουργία νέων ΑΡ.ΜΕΛΕΤΗΣ: ΔΠΕ9/2015 Μ Ε Λ Ε Τ Η Προμήθεια υλικών και φυτοφαρμάκων
Α Π Ο Σ Π Α Σ Μ Α από το πρακτικό της υπ' αριθµ. 53 ης /2015 Συνεδρίασης της Οικονοµικής Επιτροπής
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΑΤΤΙΚΗΣ ΗΜΟΣ ΧΑΛΑΝ ΡΙΟΥ /ΝΣΗ ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΑΝΘΡΩΠΙΝΟΥ ΥΝΑΜΙΚΟΥ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΗΜΟΤΙΚΩΝ ΟΡΓΑΝΩΝ ΑΡΜΟ ΙΑ: Κα ΣΟΦΙΑ ΗΛΙΑΚΟΠΟΥΛΟΥ ΤΗΛ.: 2132023905-908 Α Π Ο Σ Π Α Σ Μ
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΑΤΤΙΚΗΣ ΗΜΟΣ ΧΑΛΑΝ ΡΙΟΥ /ΝΣΗ ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΑΝΘΡΩΠΙΝΟΥ ΥΝΑΜΙΚΟΥ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΗΜΟΤΙΚΩΝ ΟΡΓΑΝΩΝ ΑΡΜΟ ΙΑ: Κα ΣΟΦΙΑ ΗΛΙΑΚΟΠΟΥΛΟΥ ΤΗΛ.: 2132023905-908 Α Π Ο Σ Π Α Σ Μ
Μ Ε Λ Ε Τ Η ΠΡΟΜΗΘΕΙΩΝ (σύμφωνα με τις διατάξεις του ΕΚΠΟΤΑ)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΗΡΑΚΛΕΙΟΥ ΔΗΜΟΣ ΜΙΝΩΑ ΠΕΔΙΑΔΑΣ Δ/ΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ Μ Ε Λ Ε Τ Η ΠΡΟΜΗΘΕΙΩΝ (σύμφωνα με τις διατάξεις του ΕΚΠΟΤΑ) αρ. 12/2015 ΥΛΙΚΑ ΑΡΔΕΥΤΙΚΩΝ ΔΙΚΤΥΩΝ προϋπολογισμού:
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΗΡΑΚΛΕΙΟΥ ΔΗΜΟΣ ΜΙΝΩΑ ΠΕΔΙΑΔΑΣ Δ/ΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ Μ Ε Λ Ε Τ Η ΠΡΟΜΗΘΕΙΩΝ (σύμφωνα με τις διατάξεις του ΕΚΠΟΤΑ) αρ. 12/2015 ΥΛΙΚΑ ΑΡΔΕΥΤΙΚΩΝ ΔΙΚΤΥΩΝ προϋπολογισμού:
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
θ) Ο αριθμός των εγκύρων ψηφοδελτίων που έλαβε κάθε ένας συνδυασμός ή μεμονωμένος υποψήφιος ανέρχεται:
 θ) Ο αριθμός των εγκύρων ψηφοδελτίων που έλαβε κάθε ένας συνδυασμός ή μεμονωμένος υποψήφιος ανέρχεται: 6 7 8 9 0 ΝΕΑ ΔΗΜΟΚΡΑΤΙΑ ΣΥΝΑΣΠΙΣΜΟΣ ΡΙΖΟΣΠΑΣΤΙΚΗΣ ΑΡΙΣΤΕΡΑΣ ΠΑΝΕΛΛΗΝΙΟ ΣΟΣΙΑΛΙΣΤΙΚΟ ΚΙΝΗΜΑ (ΠΑ.ΣΟ.Κ)
θ) Ο αριθμός των εγκύρων ψηφοδελτίων που έλαβε κάθε ένας συνδυασμός ή μεμονωμένος υποψήφιος ανέρχεται: 6 7 8 9 0 ΝΕΑ ΔΗΜΟΚΡΑΤΙΑ ΣΥΝΑΣΠΙΣΜΟΣ ΡΙΖΟΣΠΑΣΤΙΚΗΣ ΑΡΙΣΤΕΡΑΣ ΠΑΝΕΛΛΗΝΙΟ ΣΟΣΙΑΛΙΣΤΙΚΟ ΚΙΝΗΜΑ (ΠΑ.ΣΟ.Κ)
2 η δεκάδα θεµάτων επανάληψης
 η δεκάδα θεµάτων επανάληψης 11. Έστω η εξίσωση x + ( λ + )x + 8λ = 0 Να αποδείξετε ότι η εξίσωση έχει πραγµατικές ρίζες για κάθε τιµή του λ R. Πότε οι ρίζες είναι ίσες και πότε άνισες; Αν x 1, x είναι
η δεκάδα θεµάτων επανάληψης 11. Έστω η εξίσωση x + ( λ + )x + 8λ = 0 Να αποδείξετε ότι η εξίσωση έχει πραγµατικές ρίζες για κάθε τιµή του λ R. Πότε οι ρίζες είναι ίσες και πότε άνισες; Αν x 1, x είναι
Γ49/ 35 ΕΞ. ΕΠΕΙΓΟΝ Π Ρ Ο Σ :
 Αθήνα, 19 / 5 / 2010 Δ Ι Ο Ι Κ Η Σ Η ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΙΟΙΚ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ Δ/ΝΣΗ ΔΙΟΙΚΗΤΙΚΟΥ ΠΡΟΣΩΠΙΚΟΥ ΤΜΗΜΑ : ΕΡΓΑΣΙΑΚΩΝ ΣΧΕΣΕΩΝ Ταχ. Δ/νση : Αγ. Κωνσταντίνου 8 Ταχ. Κώδικας: 102 41 ΑΘΗΝΑ Τηλέφωνο : 210-215292,289,290,294
Αθήνα, 19 / 5 / 2010 Δ Ι Ο Ι Κ Η Σ Η ΓΕΝΙΚΗ Δ/ΝΣΗ ΔΙΟΙΚ/ΚΩΝ ΥΠΗΡΕΣΙΩΝ Δ/ΝΣΗ ΔΙΟΙΚΗΤΙΚΟΥ ΠΡΟΣΩΠΙΚΟΥ ΤΜΗΜΑ : ΕΡΓΑΣΙΑΚΩΝ ΣΧΕΣΕΩΝ Ταχ. Δ/νση : Αγ. Κωνσταντίνου 8 Ταχ. Κώδικας: 102 41 ΑΘΗΝΑ Τηλέφωνο : 210-215292,289,290,294
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΥΒΟΙΑΣ ΣΧΟΛΙΚΗ ΕΠΙΤΡΟΠΗ ΜΟΝΑΔΩΝ Α ΒΑΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΕΡΓΑΣΙΑ:
 ΕΡΓΑΣΙΑ: Αναγόμωση συντήρηση Αναγόμωση συντήρηση Μονάδες Α Βάθμιας εκπ/σης ΠΕΡΙΕΧΟΜΕΝΑ 1. Τεχνική περιγραφή 2. Ενδεικτικός Προϋπολογισμός 3. Συγγραφή υποχρεώσεων 1 ΕΡΓΑΣΙΑ: Αναγόμωση συντήρηση Τεχνική
ΕΡΓΑΣΙΑ: Αναγόμωση συντήρηση Αναγόμωση συντήρηση Μονάδες Α Βάθμιας εκπ/σης ΠΕΡΙΕΧΟΜΕΝΑ 1. Τεχνική περιγραφή 2. Ενδεικτικός Προϋπολογισμός 3. Συγγραφή υποχρεώσεων 1 ΕΡΓΑΣΙΑ: Αναγόμωση συντήρηση Τεχνική
Ε Π Ι Τ Ρ Ο Π Η Α Ν Α Π Τ Υ Ξ Η Σ Π Ο Ο Σ Φ Α Ι Ρ Ο Υ ΑΓΩΝΙΣΤΙΚΗ ΠΕΡΙΟ ΟΣ 2014-2015 ΒΑΘΜΟΛΟΓΙΕΣ ΠΡΩΤΑΘΛΗΜΑΤΩΝ ΥΠΟΔΟΜΩΝ
 Ε Π Ι Τ Ρ Ο Π Η Α Ν Α Π Τ Υ Ξ Η Σ Π Ο Ο Σ Φ Α Ι Ρ Ο Υ Κ Α Ι Π Ρ Ω Τ Α Θ Λ Η Μ Α Τ Ω Ν Υ Π Ο Ο Μ Ω Ν ΑΓΩΝΙΣΤΙΚΗ ΠΕΡΙΟ ΟΣ 2014-2015 ΒΑΘΜΟΛΟΓΙΕΣ ΠΡΩΤΑΘΛΗΜΑΤΩΝ ΥΠΟΔΟΜΩΝ Κ Α Τ ΗΚΑΤΗΓΟΡΙΑ Γ Ο Ρ Ι Α ΝΕΩΝ Ν Ε
Ε Π Ι Τ Ρ Ο Π Η Α Ν Α Π Τ Υ Ξ Η Σ Π Ο Ο Σ Φ Α Ι Ρ Ο Υ Κ Α Ι Π Ρ Ω Τ Α Θ Λ Η Μ Α Τ Ω Ν Υ Π Ο Ο Μ Ω Ν ΑΓΩΝΙΣΤΙΚΗ ΠΕΡΙΟ ΟΣ 2014-2015 ΒΑΘΜΟΛΟΓΙΕΣ ΠΡΩΤΑΘΛΗΜΑΤΩΝ ΥΠΟΔΟΜΩΝ Κ Α Τ ΗΚΑΤΗΓΟΡΙΑ Γ Ο Ρ Ι Α ΝΕΩΝ Ν Ε
AIBĖS, FUNKCIJOS, LYGTYS
 AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
AIBĖS, FUNKCIJOS, LYGTYS Aibės sąvoka ir pavyzdžiai Atskirų objektų rinkiniai, grupės, sistemos, kompleksai matematikoje vadinami aibėmis. Šie atskiri objektai vadinami aibės elementais. Kai elementas
ΠΡΩΤΟΔΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ Εκλογικών
 ΠΡΩΤΟΔΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ Εκλογικών Χρήσιμο Β Ο Η Θ Η Μ Α Ο Δ Η Γ Ο Σ του Αντιπροσώπου της Δικαστικής Αρχής (Περιέχονται σχέδια και έντυπα για διευκόλυνση του έργου των Αντιπροσώπων της Δικαστικής Αρχής
ΠΡΩΤΟΔΙΚΕΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ Εκλογικών Χρήσιμο Β Ο Η Θ Η Μ Α Ο Δ Η Γ Ο Σ του Αντιπροσώπου της Δικαστικής Αρχής (Περιέχονται σχέδια και έντυπα για διευκόλυνση του έργου των Αντιπροσώπων της Δικαστικής Αρχής
ΝΕΟ ΛΥΚΕΙΟ 2014 ΕΦΑΡΜΟΓΗ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ ΤΗΣ Α ΤΑΞΗΣ ΛΥΚΕΙΟΥ (ΣΧΟΛΙΚΟ ΈΤΟΣ: 2013-2014)
 ΝΕΟ ΛΥΚΕΙΟ 2014 ΕΦΑΡΜΟΓΗ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ ΤΗΣ Α ΤΑΞΗΣ ΛΥΚΕΙΟΥ (ΣΧΟΛΙΚΟ ΈΤΟΣ: 2013-2014) Α Λ Υ Κ Ε Ι Ο Υ Η Α' τάξη Ημερησίου Γενικού Λυκείου αποτελεί τάξη γενικής παιδείας 35 συνολικά ωρών εβδομαδιαίως
ΝΕΟ ΛΥΚΕΙΟ 2014 ΕΦΑΡΜΟΓΗ ΓΙΑ ΤΟΥΣ ΜΑΘΗΤΕΣ ΤΗΣ Α ΤΑΞΗΣ ΛΥΚΕΙΟΥ (ΣΧΟΛΙΚΟ ΈΤΟΣ: 2013-2014) Α Λ Υ Κ Ε Ι Ο Υ Η Α' τάξη Ημερησίου Γενικού Λυκείου αποτελεί τάξη γενικής παιδείας 35 συνολικά ωρών εβδομαδιαίως
3 modulis. Funkcijos sąvoka. Laipsninė, rodiklinė ir logaritminė funkcija
 P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
Π Ι Ν Α Κ Α Σ Α Μ Ο Ι Β Ω Ν Ε Π Ι Δ Ο Σ Ε Ω Ν
 Π Ι Ν Α Κ Α Σ Α Μ Ο Ι Β Ω Ν Ε Π Ι Δ Ο Σ Ε Ω Ν ΔΙΚΑΣΤΙΚΩΝ ΕΠΙΜΕΛΗΤΩΝ ΕΦΕΤΕΙΩΝ ΑΘΗΝΩΝ & ΠΕΙΡΑΙΩΣ ΔΙΟΡΙΣΜΕΝΩΝ ΣΤΑ ΠΡΩΤΟΔΙΚΕΙΑ ΑΘΗΝΩΝ & ΠΕΙΡΑΙΩΣ ΜΕ ΕΔΡΑ ΤΗΝ ΑΘΗΝΑ Η χιλιομετρική απόσταση υπολογίσθηκε με σημείο
Π Ι Ν Α Κ Α Σ Α Μ Ο Ι Β Ω Ν Ε Π Ι Δ Ο Σ Ε Ω Ν ΔΙΚΑΣΤΙΚΩΝ ΕΠΙΜΕΛΗΤΩΝ ΕΦΕΤΕΙΩΝ ΑΘΗΝΩΝ & ΠΕΙΡΑΙΩΣ ΔΙΟΡΙΣΜΕΝΩΝ ΣΤΑ ΠΡΩΤΟΔΙΚΕΙΑ ΑΘΗΝΩΝ & ΠΕΙΡΑΙΩΣ ΜΕ ΕΔΡΑ ΤΗΝ ΑΘΗΝΑ Η χιλιομετρική απόσταση υπολογίσθηκε με σημείο
ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΝΑΠΤΥΞΗΣ, ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑΣ ΚΑΙ ΝΑΥΤΙΛΙΑΣ ΠΛΑΤΕΙΑ ΣΥΝΤΑΓΜΑΤΟΣ, ΑΘΗΝΑ Α Π Ο Φ Α Σ Η
 ΤΜΗΜΑΤΑΡΧΗΣ : Δ. ΓΡΟΥΖΗΣ ΤΗΛ. 210-3332990 ΠΛΗΡΟΦΟΡΙΕΣ : Ν. ΚΟΡΔΑΛΗ ΤΗΛ.210-3332973 (kordali@mnec.gr) ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΝΑΠΤΥΞΗΣ, ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑΣ ΚΑΙ ΝΑΥΤΙΛΙΑΣ ΠΛΑΤΕΙΑ
ΤΜΗΜΑΤΑΡΧΗΣ : Δ. ΓΡΟΥΖΗΣ ΤΗΛ. 210-3332990 ΠΛΗΡΟΦΟΡΙΕΣ : Ν. ΚΟΡΔΑΛΗ ΤΗΛ.210-3332973 (kordali@mnec.gr) ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΑΝΑΠΤΥΞΗΣ, ΑΝΤΑΓΩΝΙΣΤΙΚΟΤΗΤΑΣ ΚΑΙ ΝΑΥΤΙΛΙΑΣ ΠΛΑΤΕΙΑ
Τ Μ Η Μ Α Φ Ω Τ Ο Γ ΡΑ Φ Ι Α Σ & Ο Π Τ Ι ΚΟ Α ΚΟ Υ Σ Τ Ι Κ Ω Ν Τ Ε Χ Ν Ω Ν / Τ Ε Ι Α Θ Η Ν Α Σ
 IRIS Τ Μ Η Μ Α Φ Ω Τ Ο Γ ΡΑ Φ Ι Α Σ & Ο Π Τ Ι ΚΟ Α ΚΟ Υ Σ Τ Ι Κ Ω Ν Τ Ε Χ Ν Ω Ν / Τ Ε Ι Α Θ Η Ν Α Σ Ο Κ Τ Ω Β Ρ Ι Ο Σ 2011 CULNA ΙΩΑΝΝΗΣ ΤΣΙΑΔΗΣ Η εργασία αυτή αφορά στα ταξίδια των αντικειμένων μέσα σε
IRIS Τ Μ Η Μ Α Φ Ω Τ Ο Γ ΡΑ Φ Ι Α Σ & Ο Π Τ Ι ΚΟ Α ΚΟ Υ Σ Τ Ι Κ Ω Ν Τ Ε Χ Ν Ω Ν / Τ Ε Ι Α Θ Η Ν Α Σ Ο Κ Τ Ω Β Ρ Ι Ο Σ 2011 CULNA ΙΩΑΝΝΗΣ ΤΣΙΑΔΗΣ Η εργασία αυτή αφορά στα ταξίδια των αντικειμένων μέσα σε
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
Π Ι Ν Α Κ Α Σ Κ Α Τ Α Τ Α Ξ Η Σ Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Μ Ε Ρ Ι Κ Η Σ Α Π Α Σ Χ Ο Λ Η Σ Η Σ (Α.Π. ΑΝΑΚΟΙΝΩΣΗΣ 21809/20-11-2009)
 Π Ι Ν Α Κ Α Σ Κ Α Τ Α Τ Α Ξ Η Σ Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Μ Ε Ρ Ι Κ Η Σ Α Π Α Σ Χ Ο Λ Η Σ Η Σ (Α.Π. ΑΝΑΚΟΙΝΩΣΗΣ 21809/20-11-2009) Α/Α ΕΙ ΙΚΟΤΗΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΚΩ. ΚΟΙΝΩΝΙΚΗ ΟΜΑ Α ΕΜΠΕΙΡΙΑ 1 ΠΕ
Π Ι Ν Α Κ Α Σ Κ Α Τ Α Τ Α Ξ Η Σ Ε Π Ι Λ Ο Γ Η Σ Π Ρ Ο Σ Ω Π Ι Κ Ο Υ Μ Ε Ρ Ι Κ Η Σ Α Π Α Σ Χ Ο Λ Η Σ Η Σ (Α.Π. ΑΝΑΚΟΙΝΩΣΗΣ 21809/20-11-2009) Α/Α ΕΙ ΙΚΟΤΗΤΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΚΩ. ΚΟΙΝΩΝΙΚΗ ΟΜΑ Α ΕΜΠΕΙΡΙΑ 1 ΠΕ
Κατά την έναρξη της συνεδρίασης ο Πρόεδρος διαπίστωσε ότι σε σύνολο 27 δημοτικών συμβούλων ήταν:
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΔΙΕΥΘΥΝΣΗ ΔΙΟΙΚΗΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 10/2012 Συνεδρίασης ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ Σήμερα την
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΠΡΕΒΕΖΑΣ ΔΗΜΟΣ ΠΡΕΒΕΖΑΣ ΔΙΕΥΘΥΝΣΗ ΔΙΟΙΚΗΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΥΠΟΣΤΗΡΙΞΗΣ ΑΙΡΕΤΩΝ ΟΡΓΑΝΩΝ Α Π Ο Σ Π Α Σ Μ Α Από το πρακτικό 10/2012 Συνεδρίασης ΔΗΜΟΤΙΚΟΥ ΣΥΜΒΟΥΛΙΟΥ Σήμερα την
ΑΘΡΟΙΣΜΑ ΑΠΕΙΡΩΝ ΟΡΩΝ ΓΕΩΜΕΤΡΙΚΗΣ ΠΡΟΟ ΟΥ. Πρόταση: Το άθροισµα των απείρων όρων µιας γεωµετρικής προόδου που έχει πρώτο όρο α
 ΑΘΡΟΙΣΜΑ ΑΠΕΙΡΩΝ ΟΡΩΝ ΓΕΩΜΕΤΡΙΚΗΣ ΠΡΟΟ ΟΥ Πρότση: Το άθροισµ τω πείρω όρω µις γεωµετρικής προόδου που έχει πρώτο όρο κι λόγο λ, λ < είι Το άθροισµ S = + +... S = λ Εφρµογή : Ν υπολογίσετε το άθροισµ :
ΑΘΡΟΙΣΜΑ ΑΠΕΙΡΩΝ ΟΡΩΝ ΓΕΩΜΕΤΡΙΚΗΣ ΠΡΟΟ ΟΥ Πρότση: Το άθροισµ τω πείρω όρω µις γεωµετρικής προόδου που έχει πρώτο όρο κι λόγο λ, λ < είι Το άθροισµ S = + +... S = λ Εφρµογή : Ν υπολογίσετε το άθροισµ :
ΑΔΑ: ΒΙΕ9ΩΗΑ-5ΒΚ ΑΝΑΡΤΗΤΕΑ ΣΤΟ ΔΙΑΔΙΚΤΥΟ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Χαλκίδα Αριθμ.Πρωτ. : 12577 ΔΗΜΟΣ ΧΑΛΚΙΔΕΩΝ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ ΑΠΟΣΠΑΣΜΑ Αριθ. Αποφ. 91/2014 Από το Πρακτικό της 6ης/2014 Συνεδρίασης της Οικονομικής Επιτροπής του Δήμου Χαλκιδέων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Χαλκίδα Αριθμ.Πρωτ. : 12577 ΔΗΜΟΣ ΧΑΛΚΙΔΕΩΝ ΟΙΚΟΝΟΜΙΚΗ ΕΠΙΤΡΟΠΗ ΑΠΟΣΠΑΣΜΑ Αριθ. Αποφ. 91/2014 Από το Πρακτικό της 6ης/2014 Συνεδρίασης της Οικονομικής Επιτροπής του Δήμου Χαλκιδέων
Ε Ρ Γ Α Σ Ι Α Σ Υ Ν Τ Η Ρ Η Σ Η Α Ν Ε Λ Κ Υ Σ Τ Η Ρ Ω Ν
 Οδός 25 η & Πλ. Αγ. Τριάδας, 16777, Ελληνικό Ε Ρ Γ Α Σ Ι Α Σ Υ Ν Τ Η Ρ Η Σ Η Α Ν Ε Λ Κ Υ Σ Τ Η Ρ Ω Ν ΠΡΟΥΠΟΛΟΓΙΣΜΟΣ : 4.320,00 Φ.Π.Α. 23% : 993,60 ΣΥΝΟΛΙΚΗ ΔΑΠΑΝΗ: 5.313,60 ΕΥΡΩ 1 ΤΕΧΝΙΚΗ ΕΚΘΕΣΗ Η παρούσα
Οδός 25 η & Πλ. Αγ. Τριάδας, 16777, Ελληνικό Ε Ρ Γ Α Σ Ι Α Σ Υ Ν Τ Η Ρ Η Σ Η Α Ν Ε Λ Κ Υ Σ Τ Η Ρ Ω Ν ΠΡΟΥΠΟΛΟΓΙΣΜΟΣ : 4.320,00 Φ.Π.Α. 23% : 993,60 ΣΥΝΟΛΙΚΗ ΔΑΠΑΝΗ: 5.313,60 ΕΥΡΩ 1 ΤΕΧΝΙΚΗ ΕΚΘΕΣΗ Η παρούσα
Ε Υ Α Ρ ΤΕΥΧΟΣ 4 ΗΜΟΤΙΚΗ ΕΠΙΧΕΙΡΗΣΗ Υ ΡΕΥΣΗΣ ΑΠΟΧΕΤΕΥΣΗΣ ΗΜΟΥ ΡΟ ΟΥ. 198.396,00 (χωρίς το Φ.Π.Α.) ΚΑΤΑΣΚΕΥΗ ΣΥΝ ΕΣΕΩΝ ΙΚΤΥΟΥ ΑΠΟΧΕΤΕΥΣΗΣ ΜΕΛΕΤΗ ΕΡΓΟΥ:
 Ε Υ Α Ρ ΗΜΟΤΙΚΗ ΕΠΙΧΕΙΡΗΣΗ Υ ΡΕΥΣΗΣ ΑΠΟΧΕΤΕΥΣΗΣ ΗΜΟΥ ΡΟ ΟΥ Ι Ε Υ Θ Υ Ν Σ Η Ι Κ Τ Υ Ω Ν ΥΠΗΡΕΣΙΑ ΑΠΟΧΕΤΕΥΣΗΣ ΜΕΛΕΤΗ ΕΡΓΟΥ: ΠΡΟΥΠ/ΣΜΟΣ: ΧΡΗΜΑΤΟ ΟΤΗΣΗ: ΚΑΤΑΣΚΕΥΗ ΣΥΝ ΕΣΕΩΝ ΙΚΤΥΟΥ ΑΠΟΧΕΤΕΥΣΗΣ 198.396,00 (χωρίς
Ε Υ Α Ρ ΗΜΟΤΙΚΗ ΕΠΙΧΕΙΡΗΣΗ Υ ΡΕΥΣΗΣ ΑΠΟΧΕΤΕΥΣΗΣ ΗΜΟΥ ΡΟ ΟΥ Ι Ε Υ Θ Υ Ν Σ Η Ι Κ Τ Υ Ω Ν ΥΠΗΡΕΣΙΑ ΑΠΟΧΕΤΕΥΣΗΣ ΜΕΛΕΤΗ ΕΡΓΟΥ: ΠΡΟΥΠ/ΣΜΟΣ: ΧΡΗΜΑΤΟ ΟΤΗΣΗ: ΚΑΤΑΣΚΕΥΗ ΣΥΝ ΕΣΕΩΝ ΙΚΤΥΟΥ ΑΠΟΧΕΤΕΥΣΗΣ 198.396,00 (χωρίς
ΓΙΑ ΕΦΗΒΟΥΣ ΚΑΙ ΕΝΗΛΙΚΟΥΣ Π Ι Σ Τ Ο Π Ο Ι Η Σ Η Ε Π Α Ρ Κ Ε Ι Α Σ Τ Η Σ ΕΛΛΗΝΟΜΑΘΕΙΑΣ Κ Α Τ Α Ν Ο Η Σ Η Γ Ρ Α Π Τ Ο Υ Λ Ο Γ Ο Υ ΔΕΥΤΕΡΗ ΣΕΙΡΑ
 ΓΙΑ ΕΦΗΒΟΥΣ ΚΑΙ ΕΝΗΛΙΚΟΥΣ Ε Π Α Ρ Κ Ε Ι Α Σ Τ Η Σ ΕΛΛΗΝΟΜΑΘΕΙΑΣ Κ Α Τ Α Ν Ο Η Σ Η Γ Ρ Α Π Τ Ο Υ Λ Ο Γ Ο Υ ΔΕΥΤΕΡΗ ΣΕΙΡΑ Δ Ε Ι Γ Μ Α Τ Ω Ν Μ Ν Α Δ Ε Σ Y Π Ο Υ Ρ Γ Ε Ι Ο Π Α Ι Δ Ε Ι Α Σ Κ Α Ι Θ Ρ Η Σ Κ Ε
ΓΙΑ ΕΦΗΒΟΥΣ ΚΑΙ ΕΝΗΛΙΚΟΥΣ Ε Π Α Ρ Κ Ε Ι Α Σ Τ Η Σ ΕΛΛΗΝΟΜΑΘΕΙΑΣ Κ Α Τ Α Ν Ο Η Σ Η Γ Ρ Α Π Τ Ο Υ Λ Ο Γ Ο Υ ΔΕΥΤΕΡΗ ΣΕΙΡΑ Δ Ε Ι Γ Μ Α Τ Ω Ν Μ Ν Α Δ Ε Σ Y Π Ο Υ Ρ Γ Ε Ι Ο Π Α Ι Δ Ε Ι Α Σ Κ Α Ι Θ Ρ Η Σ Κ Ε
Nauji dviejų vamzdžių sistemos balansavimo būdai
 Techninis straipsnis. Hidraulinis sistemų balansavimas Nauji dviejų vamzdžių sistemos balansavimo būdai Kaip pasiekti puikų hidraulinį sistemų balansavimą šildymo sistemose naudojant Danfoss Dynamic Valve
Techninis straipsnis. Hidraulinis sistemų balansavimas Nauji dviejų vamzdžių sistemos balansavimo būdai Kaip pasiekti puikų hidraulinį sistemų balansavimą šildymo sistemose naudojant Danfoss Dynamic Valve
ΑΠΟΦΑΣΗ Ο ΥΠΟΥΡΓΟΣ ΕΣΩΤΕΡΙΚΩΝ KAI ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ KAI ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ ΓΕΝΙΚΗ Δ/ΝΣΗ ΟΙΚΟΝ. ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΥΠΟΣΤΗΡΙΞΗΣ ΔΙΕΥΘΥΝΣΗ ΟΙΚΟΝΟΜΙΚΗΣ & ΑΝΑΠΤΥΞΙΑΚΗΣ ΠΟΛΙΤΙΚΗΣ Τ.Α ΤΜΗΜΑ ΕΠΙΧΟΡΗΓΗΣΕΩΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ KAI ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ ΓΕΝΙΚΗ Δ/ΝΣΗ ΟΙΚΟΝ. ΥΠΗΡΕΣΙΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΥΠΟΣΤΗΡΙΞΗΣ ΔΙΕΥΘΥΝΣΗ ΟΙΚΟΝΟΜΙΚΗΣ & ΑΝΑΠΤΥΞΙΑΚΗΣ ΠΟΛΙΤΙΚΗΣ Τ.Α ΤΜΗΜΑ ΕΠΙΧΟΡΗΓΗΣΕΩΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΥΒΟΙΑΣ ΔΗΜΟΣ ΔΙΡΦΥΩΝ ΜΕΣΣΑΠΙΩΝ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΥΒΟΙΑΣ ΔΗΜΟΣ ΔΙΡΦΥΩΝ ΜΕΣΣΑΠΙΩΝ ΑΠΟΣΠΑΣΜΑ Πρακτικού από τη Δημόσια Τακτική Συνεδρίαση του Δημοτικού Συμβουλίου του Δήμου Διρφύων - Μεσσαπίων, με αριθμό 18/2012 από 17/10/2012.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΕΥΒΟΙΑΣ ΔΗΜΟΣ ΔΙΡΦΥΩΝ ΜΕΣΣΑΠΙΩΝ ΑΠΟΣΠΑΣΜΑ Πρακτικού από τη Δημόσια Τακτική Συνεδρίαση του Δημοτικού Συμβουλίου του Δήμου Διρφύων - Μεσσαπίων, με αριθμό 18/2012 από 17/10/2012.
 ΗΜΕΡΙ Α Περιφερειακή Ανάπτυξη-Αποκέντρωση-Αυτοδιοίκηση και η Αριστερά Λαµία Φθιώτιδας, Ξενοδοχείο Σαµαράς, Κυριακή ώρα 9. 30 π.µ. 2-11-2008 Νοµαρχιακές Επιτροπές ΣΥΝΑΣΠΙΣΜΟΥ Περιφέρειας Στ. Ελλάδας Τµήµατα
ΗΜΕΡΙ Α Περιφερειακή Ανάπτυξη-Αποκέντρωση-Αυτοδιοίκηση και η Αριστερά Λαµία Φθιώτιδας, Ξενοδοχείο Σαµαράς, Κυριακή ώρα 9. 30 π.µ. 2-11-2008 Νοµαρχιακές Επιτροπές ΣΥΝΑΣΠΙΣΜΟΥ Περιφέρειας Στ. Ελλάδας Τµήµατα
Χαρτογράφηση κινδύνου εκδήλωσης κατολίσθησης με τη χρήση GIS Ε Φ Α Ρ Μ Ο Γ Ε Σ Γ Π Σ Σ Τ Η Δ Ι Α Χ Ε Ι Ρ Ι Σ Η Κ Α Τ Α Σ Τ Ρ Ο Φ Ω Ν
 Χαρτογράφηση κινδύνου εκδήλωσης κατολίσθησης με τη χρήση GIS Ε Φ Α Ρ Μ Ο Γ Ε Σ Γ Π Σ Σ Τ Η Δ Ι Α Χ Ε Ι Ρ Ι Σ Η Κ Α Τ Α Σ Τ Ρ Ο Φ Ω Ν Χ. Χ Α Λ Κ Ι Α Σ X Α Ρ Ο Κ Ο Π Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο - Τ Μ.
Χαρτογράφηση κινδύνου εκδήλωσης κατολίσθησης με τη χρήση GIS Ε Φ Α Ρ Μ Ο Γ Ε Σ Γ Π Σ Σ Τ Η Δ Ι Α Χ Ε Ι Ρ Ι Σ Η Κ Α Τ Α Σ Τ Ρ Ο Φ Ω Ν Χ. Χ Α Λ Κ Ι Α Σ X Α Ρ Ο Κ Ο Π Ε Ι Ο Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο - Τ Μ.
ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2015
 ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2015 ΗΜΕΡΟΜΗΝΙΑ ΗΜΕΡΑ ΩΡΑ ΜΑΘΗΜΑ ΚΑΘΗΓΗΤΗΣ ΑΙΘΟΥΣΑ ΕΞΑΜΗΝΟ 03/09/15 ΠΕΜΠΤΗ 12:00-14:00 04/09/15 ΠΑΡΑΣΚΕΥΗ 10:00-12:00 ΕΚΚΛ/ΚΗ ΑΡΧ/ΝΙΚΗ ΒΥΖ/ΝΗΣ Κ' ΜΕΤΑΒΥΖ/ΝΗΣ ΠΕΡΙΟΔΟΥ ΕΙΣΑΓΩΓΗ
ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΣΕΠΤΕΜΒΡΙΟΥ 2015 ΗΜΕΡΟΜΗΝΙΑ ΗΜΕΡΑ ΩΡΑ ΜΑΘΗΜΑ ΚΑΘΗΓΗΤΗΣ ΑΙΘΟΥΣΑ ΕΞΑΜΗΝΟ 03/09/15 ΠΕΜΠΤΗ 12:00-14:00 04/09/15 ΠΑΡΑΣΚΕΥΗ 10:00-12:00 ΕΚΚΛ/ΚΗ ΑΡΧ/ΝΙΚΗ ΒΥΖ/ΝΗΣ Κ' ΜΕΤΑΒΥΖ/ΝΗΣ ΠΕΡΙΟΔΟΥ ΕΙΣΑΓΩΓΗ
 9α ΤΣΙΤΕΙΑ 2010 ΑΓΩΝΙΣΤΙΚΗ ΙΛΙΣΙΑ 25-27 Ιουν 2010 ΑΠΟΤΕΛΕΣΜΑΤΑ 200m ΕΛΕΥΘΕΡΟ - ΝΕΑΝΙ ΩΝ (50) 1 ΜΗΤΡΟΥ ΕΛΕΝΗ 1993 Α.Ο. Ω. ΝΕΑΝ 02:10.79 2 ΖΟΥΜΗ ΣΟΦΙΑ 1993 ΚΟΠΙ ΝΕΑΝ 02:15.82 3 ΕΛΑΣΟΥ Α ΑΝΑΗ 1993 ΓΣΑΙΓΑΛ
9α ΤΣΙΤΕΙΑ 2010 ΑΓΩΝΙΣΤΙΚΗ ΙΛΙΣΙΑ 25-27 Ιουν 2010 ΑΠΟΤΕΛΕΣΜΑΤΑ 200m ΕΛΕΥΘΕΡΟ - ΝΕΑΝΙ ΩΝ (50) 1 ΜΗΤΡΟΥ ΕΛΕΝΗ 1993 Α.Ο. Ω. ΝΕΑΝ 02:10.79 2 ΖΟΥΜΗ ΣΟΦΙΑ 1993 ΚΟΠΙ ΝΕΑΝ 02:15.82 3 ΕΛΑΣΟΥ Α ΑΝΑΗ 1993 ΓΣΑΙΓΑΛ
ΙΚΑΙΟΛΟΓΗΤΙΚΑ ΓΙΑ ΤΗΝ ΜΕΤΕΓΓΡΑΦΗ ΕΛΛΗΝΑ ΠΟ ΟΣΦΑΙΡΙΣΤΗ
 ΙΚΑΙΟΛΟΓΗΤΙΚΑ ΓΙΑ ΤΗΝ ΜΕΤΕΓΓΡΑΦΗ ΕΛΛΗΝΑ ΠΟ ΟΣΦΑΙΡΙΣΤΗ Π Ε Ρ Ι Ο Ο Ι Κ Α Τ Α Θ Ε Σ Η Σ : 1/7/2015 31/10/2015 & 1/01/2016-28/02/2016 1. ΕΛΤΙΟ ΑΘΛΗΤΙΚΗΣ Ι ΙΟΤΗΤΑΣ ΠΟ /ΣΤΗ - Αν δεν το έχει στην κατοχή του,
ΙΚΑΙΟΛΟΓΗΤΙΚΑ ΓΙΑ ΤΗΝ ΜΕΤΕΓΓΡΑΦΗ ΕΛΛΗΝΑ ΠΟ ΟΣΦΑΙΡΙΣΤΗ Π Ε Ρ Ι Ο Ο Ι Κ Α Τ Α Θ Ε Σ Η Σ : 1/7/2015 31/10/2015 & 1/01/2016-28/02/2016 1. ΕΛΤΙΟ ΑΘΛΗΤΙΚΗΣ Ι ΙΟΤΗΤΑΣ ΠΟ /ΣΤΗ - Αν δεν το έχει στην κατοχή του,
Σ Υ Λ Λ Ο Γ Ο Σ Ι Ε Ρ Ο Ѱ Α Λ Τ Ω Ν Α Ι Γ Ι Α Λ Ε Ι Α Σ «Ι Ω Α Ν Ν Η Σ Ο Κ Ο Υ Κ Ο Υ Ζ Ε Λ Η Σ»
 Σ Υ Λ Λ Ο Γ Ο Σ Ι Ε Ρ Ο Ѱ Α Λ Τ Ω Ν Α Ι Γ Ι Α Λ Ε Ι Α Σ «Ι Ω Α Ν Ν Η Σ Ο Κ Ο Υ Κ Ο Υ Ζ Ε Λ Η Σ» Λ Ε Υ Κ Ω Μ Α Σ Υ Λ Λ Ο Γ Ο Υ Π Ε Ρ Ι Ο Ο Υ 1918 2003 Αφιερώνεται σε όλους εκείνους τους αφανείς και φανερούς
Σ Υ Λ Λ Ο Γ Ο Σ Ι Ε Ρ Ο Ѱ Α Λ Τ Ω Ν Α Ι Γ Ι Α Λ Ε Ι Α Σ «Ι Ω Α Ν Ν Η Σ Ο Κ Ο Υ Κ Ο Υ Ζ Ε Λ Η Σ» Λ Ε Υ Κ Ω Μ Α Σ Υ Λ Λ Ο Γ Ο Υ Π Ε Ρ Ι Ο Ο Υ 1918 2003 Αφιερώνεται σε όλους εκείνους τους αφανείς και φανερούς
ΕΚΛΟΓΙΚΑ ΤΜΗΜΑΤΑ ΚΑΙ ΚΑΤΑΣΤΗΜΑΤΑ ΨΗΦΟΦΟΡΙΑΣ ΒΟΥΛΕΥΤΙΚΩΝ ΕΚΛΟΓΩΝ ΤΗΣ 6 ης ΜΑΪΟΥ 2012
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΔΗΜΟΣ ΕΚΛΟΓΙΚΑ ΤΑ ΚΑΙ ΤΑ ΒΟΥΛΕΥΤΙΚΩΝ ΕΚΛΟΓΩΝ ΤΗΣ 6 ης ΜΑΪΟΥ 2012 ΔΗΜΟΥ ΠΕΡΙΦΕΡΕΙΑ ΚΡΗΤΗΣ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΔΗΜΟΣ ΔΗΜΟΤΙΚΗ ΕΝΟΤΗΤΑ ΑΚΡΩΤΗΡΙΟΥ 178ο Αρωνίου 1 ο
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΔΗΜΟΣ ΕΚΛΟΓΙΚΑ ΤΑ ΚΑΙ ΤΑ ΒΟΥΛΕΥΤΙΚΩΝ ΕΚΛΟΓΩΝ ΤΗΣ 6 ης ΜΑΪΟΥ 2012 ΔΗΜΟΥ ΠΕΡΙΦΕΡΕΙΑ ΚΡΗΤΗΣ ΠΕΡΙΦΕΡΕΙΑΚΗ ΕΝΟΤΗΤΑ ΔΗΜΟΣ ΔΗΜΟΤΙΚΗ ΕΝΟΤΗΤΑ ΑΚΡΩΤΗΡΙΟΥ 178ο Αρωνίου 1 ο
Έτος 23ο Αριθ.φύλλου 5944 Τιμή Φυλλου 0.15 Τηλ.24620/28924 e-mail:tsaknaki@otenet.gr Πέμπτη 24 Οκτωβρίου 2013 Δυτική Μακεδονία
 ΚΩΔΙΚΟΣ 1906 Έτος 23ο Αριθ.φύλλου 5944 Τιμή Φυλλου 0.15 Τηλ.24620/28924 e-mail:tsaknaki@otenet.gr Πέμπτη 24 Οκτωβρίου 2013 Δυτική Μακεδονία Με το δάχτυλο Δυτική Μακεδονία Σημαντική ενίσχυση του στόλου
ΚΩΔΙΚΟΣ 1906 Έτος 23ο Αριθ.φύλλου 5944 Τιμή Φυλλου 0.15 Τηλ.24620/28924 e-mail:tsaknaki@otenet.gr Πέμπτη 24 Οκτωβρίου 2013 Δυτική Μακεδονία Με το δάχτυλο Δυτική Μακεδονία Σημαντική ενίσχυση του στόλου
Vilius Stakėnas. Kodavimo teorija. Paskaitu. kursas
 Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
Vilius Stakėnas Kodavimo teorija Paskaitu kursas 2002 2 I vadas Informacija perduodama kanalais, kurie kartais iškraipo informacija Tarsime, kad tie iškraipymai yra atsitiktiniai, t y nėra nei sistemingi,
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos
 Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
Μ Ε Λ Ε Τ Η ΠΡΟΜΗΘΕΙΑ ΠΕΤΡΕΛΑΙΟΥ ΘΕΡΜΑΝΣΗΣ ΓΙΑ ΤΙΣ ΣΧΟΛΙΚΕΣ ΜΟΝΑ ΕΣ ΠΡΩΤΟΒΑΘΜΙΑΣ ΕΚΠΑΙ ΕΥΣΗΣ. Προϋπολογισµού: 43.998,82 σε ΕΥΡΩ
 ΕΛΛΗΝΙΙΚΗ ΗΜΟΚΡΑΤΙΙΑ ΝΟΜΟΣ ΗΡΑΚΛΕΙΙΟΥ ΗΜΟΣ ΑΡΧΑΝΩΝ -- ΑΣΤΕΡΟΥΣΙΙΩΝ /ΝΣΗ ΗΜΟΤΙΙΚΩΝ ΥΠΗΡΕΣΙΙΩΝ ΤΜΗΜΑ ΕΡΓΩΝ ΗΜΟΣ: Αρχανών - Αστερουσίων ΤΙΤΛΟΣ: ΠΡΟΜΗΘΕΙΑ ΠΕΤΡΕΛΑΙΟΥ ΘΕΡΜΑΝΣΗΣ ΓΙΑ ΤΙΣ ΣΧΟΛΙΚΕΣ ΜΟΝΑ ΕΣ ΠΡΩΤΟΒΑΘΜΙΑΣ
ΕΛΛΗΝΙΙΚΗ ΗΜΟΚΡΑΤΙΙΑ ΝΟΜΟΣ ΗΡΑΚΛΕΙΙΟΥ ΗΜΟΣ ΑΡΧΑΝΩΝ -- ΑΣΤΕΡΟΥΣΙΙΩΝ /ΝΣΗ ΗΜΟΤΙΙΚΩΝ ΥΠΗΡΕΣΙΙΩΝ ΤΜΗΜΑ ΕΡΓΩΝ ΗΜΟΣ: Αρχανών - Αστερουσίων ΤΙΤΛΟΣ: ΠΡΟΜΗΘΕΙΑ ΠΕΤΡΕΛΑΙΟΥ ΘΕΡΜΑΝΣΗΣ ΓΙΑ ΤΙΣ ΣΧΟΛΙΚΕΣ ΜΟΝΑ ΕΣ ΠΡΩΤΟΒΑΘΜΙΑΣ
ΧΗΜΕΙΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 4
 ΚΕΦΑΛΑΙΟ 4 ΣΤΟΙΧΕΙΟΜΕΤΡΙΑ ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΠΑΝΤΗΣΕΙΣ: 1. Τι είναι ατομικό και τί μοριακό βάρος; Ατομικό βάρος είναι ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη η μάζα του ατόμου από το 1/12 της
ΚΕΦΑΛΑΙΟ 4 ΣΤΟΙΧΕΙΟΜΕΤΡΙΑ ΕΡΩΤΗΣΕΙΣ ΜΕ ΤΙΣ ΑΠΑΝΤΗΣΕΙΣ: 1. Τι είναι ατομικό και τί μοριακό βάρος; Ατομικό βάρος είναι ο αριθμός που δείχνει πόσες φορές είναι μεγαλύτερη η μάζα του ατόμου από το 1/12 της
Προκαταβλητέα: καταβολές στην αρχή
 Χρηµατοοικονοµική ιοίκηση I ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΡΑΝΤΕΣ 1 ΡΑΝΤΕΣ 2 ΡΑΝΤΕΣ Είναι σειρά (ακολουθία) χρηµατικών καταβολών σε ίσα χρονικά διαστήµατα. Σταθερή και µεταβλητή ράντα Σταθερή: ίσες χρηµατικές
Χρηµατοοικονοµική ιοίκηση I ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΡΑΝΤΕΣ 1 ΡΑΝΤΕΣ 2 ΡΑΝΤΕΣ Είναι σειρά (ακολουθία) χρηµατικών καταβολών σε ίσα χρονικά διαστήµατα. Σταθερή και µεταβλητή ράντα Σταθερή: ίσες χρηµατικές
ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ ΤΟΥ ΙΑΤΡΙΚΟΥ ΣΥΛΛΟΓΟΥ ΑΘΗΝΩΝ
 ΕΝΗΜΕΡΩΣΗ τ ω ν γ ι α τ ρ ω ν ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ ΤΟΥ ΙΑΤΡΙΚΟΥ ΣΥΛΛΟΓΟΥ ΑΘΗΝΩΝ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Δ ι μ η ν ι α ί α Έ κ δ ο σ η Τ Ε Υ Χ Ο Σ 2 1 8 (Τυπώνεται σε 25.500 αντίτυπα) ianoyaριοσ-φεβρουαριοσ
ΕΝΗΜΕΡΩΣΗ τ ω ν γ ι α τ ρ ω ν ΕΝΗΜΕΡΩΤΙΚΟ ΔΕΛΤΙΟ ΤΟΥ ΙΑΤΡΙΚΟΥ ΣΥΛΛΟΓΟΥ ΑΘΗΝΩΝ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Δ ι μ η ν ι α ί α Έ κ δ ο σ η Τ Ε Υ Χ Ο Σ 2 1 8 (Τυπώνεται σε 25.500 αντίτυπα) ianoyaριοσ-φεβρουαριοσ
Χαλκίδα, 6 Ιουνίου 2012 Αρ. Πρωτ.: 57829/2608. Προς. - Περιφερειάρχη Στερεάς Ελλάδας - κ.κ. ηµάρχους Π.Ε Εύβοιας - Πρωτοδικείο Χαλκίδας
 ΚΑΤΕΠΕΙΓΟΝ - ΕΚΛΟΓΙΚΟ ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΣΤΕΡΕΑΣ ΕΛΛΑ ΑΣ ΓΕΝΙΚΗ ΙΕΥΘΥΝΣΗ ΕΣΩΤΕΡΙΚΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΙΕΥΘΥΝΣΗ ΙΟΙΚΗΤΙΚΟΥ-ΟΙΚΟΝΟΜΙΚΟΥ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΕΝΟΤΗΤΑΣ ΕΥΒΟΙΑΣ ΓΡΑΦΕΙΟ ΕΚΛΟΓΩΝ Ταχ. ιεύθυνση:
ΚΑΤΕΠΕΙΓΟΝ - ΕΚΛΟΓΙΚΟ ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΠΕΡΙΦΕΡΕΙΑ ΣΤΕΡΕΑΣ ΕΛΛΑ ΑΣ ΓΕΝΙΚΗ ΙΕΥΘΥΝΣΗ ΕΣΩΤΕΡΙΚΗΣ ΛΕΙΤΟΥΡΓΙΑΣ ΙΕΥΘΥΝΣΗ ΙΟΙΚΗΤΙΚΟΥ-ΟΙΚΟΝΟΜΙΚΟΥ ΠΕΡΙΦΕΡΕΙΑΚΗΣ ΕΝΟΤΗΤΑΣ ΕΥΒΟΙΑΣ ΓΡΑΦΕΙΟ ΕΚΛΟΓΩΝ Ταχ. ιεύθυνση:
MONOLITINIO GELŽBETONIO BALKONO PLOKŠČIŲ ARMAVIMAS ELEMENTAIS SU IZOLIUOJANČIU INTARPU
 VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS HALFEN-DEHA Bronius Jonaitis, Arnoldas Šneideris MONOLITINIO GELŽBETONIO BALKONO PLOKŠČIŲ ARMAVIMAS ELEMENTAIS SU IZOLIUOJANČIU INTARPU Mokomoji knyga Vilnius
VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS HALFEN-DEHA Bronius Jonaitis, Arnoldas Šneideris MONOLITINIO GELŽBETONIO BALKONO PLOKŠČIŲ ARMAVIMAS ELEMENTAIS SU IZOLIUOJANČIU INTARPU Mokomoji knyga Vilnius
Η ΩΡΑΙΑ ΗΜΕΡΑΣ ΤΗΣ ΖΟΖΕΦ ΚΕΣΕΛ. ... γ ι α τ ί ο έ ρ ω τ α ς κ ρ ύ β ε τ α ι σ τ ι ς λ έ ξ ε ι ς Λ Ο Γ Ο Τ Ε Χ Ν Ι Α
 Κ... γ ι α τ ί ο έ ρ ω τ α ς κ ρ ύ β ε τ α ι σ τ ι ς λ έ ξ ε ι ς ΖΟΖΕΦ ΚΕΣΕΛ Η ΩΡΑΙΑ ΤΗΣ ΗΜΕΡΑΣ Ε Ρ Ω Τ Ι Η Λ Ο Γ Ο Τ Ε Χ Ν Ι Α Μ ε τ ά φ ρ α σ η : Ρ ί τ α Κ ο λ α ΐ τ η ΓΙΑ ΤΟ ΒΙΒΛΙΟ Η Ω Ρ Α Ι Α Τ Η Σ
Κ... γ ι α τ ί ο έ ρ ω τ α ς κ ρ ύ β ε τ α ι σ τ ι ς λ έ ξ ε ι ς ΖΟΖΕΦ ΚΕΣΕΛ Η ΩΡΑΙΑ ΤΗΣ ΗΜΕΡΑΣ Ε Ρ Ω Τ Ι Η Λ Ο Γ Ο Τ Ε Χ Ν Ι Α Μ ε τ ά φ ρ α σ η : Ρ ί τ α Κ ο λ α ΐ τ η ΓΙΑ ΤΟ ΒΙΒΛΙΟ Η Ω Ρ Α Ι Α Τ Η Σ
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
Μ Ε Λ Ε Τ Η ΕΚΠΟΤΑ - ΠΡΟΧΕΙΡΟΣ ΔΙΑΓΩΝΙΣΜΟΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΗΡΑΚΛΕΙΟΥ ΔΗΜΟΣ ΑΡΧΑΝΩΝ - ΑΣΤΕΡΟΥΣΙΩΝ Δ/ΝΣΗ ΔΗΜΟΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΔΗΜΟΣ: Αρχανών - Αστερουσίων ΤΙΤΛΟΣ: ΠΡΟΜΗΘΕΙΑ ΥΔΡΑΥΛΙΚΩΝ ΥΛΙΚΩΝ ΑΡ.ΜΕΛΕΤΗΣ: / Μ Ε Λ Ε Τ Η
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΗΡΑΚΛΕΙΟΥ ΔΗΜΟΣ ΑΡΧΑΝΩΝ - ΑΣΤΕΡΟΥΣΙΩΝ Δ/ΝΣΗ ΔΗΜΟΤΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΤΜΗΜΑ ΕΡΓΩΝ ΥΠΟΔΟΜΗΣ ΔΗΜΟΣ: Αρχανών - Αστερουσίων ΤΙΤΛΟΣ: ΠΡΟΜΗΘΕΙΑ ΥΔΡΑΥΛΙΚΩΝ ΥΛΙΚΩΝ ΑΡ.ΜΕΛΕΤΗΣ: / Μ Ε Λ Ε Τ Η
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ 1 η Υ.ΠΕ ΑΤΤΙΚΗΣ Γ.Ν.Α. «Ο ΕΥΑΓΓΕΛΙΣΜΟΣ- ΟΦΘΑΛΜΙΑΤΡΕΙΟ ΑΘΗΝΩΝ- ΠΟΛΥΚΛΙΝΙΚΗ»-Ν.Π.Δ.Δ. ΑΘΗΝΑ 17-07-2015 ΕΤΟΣ ΙΔΡΥΣΗΣ 1884
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ 1 η Υ.ΠΕ ΑΤΤΙΚΗΣ Γ.Ν.Α. «Ο ΕΥΑΓΓΕΛΙΣΜΟΣ- ΟΦΘΑΛΜΙΑΤΡΕΙΟ ΑΘΗΝΩΝ- ΠΟΛΥΚΛΙΝΙΚΗ»-Ν.Π.Δ.Δ. ΑΘΗΝΑ 17-07-2015 ΕΤΟΣ ΙΔΡΥΣΗΣ 1884 ΤΜΗΜΑ ΓΡΑΜΜΑΤΕΙΑΣ ΙΑΤΡΟΙ 08:00 20.00 20.00 08.00 ΓΕΝΙΚΗ ΕΦΗΜΕΡΙΑ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ 1 η Υ.ΠΕ ΑΤΤΙΚΗΣ Γ.Ν.Α. «Ο ΕΥΑΓΓΕΛΙΣΜΟΣ- ΟΦΘΑΛΜΙΑΤΡΕΙΟ ΑΘΗΝΩΝ- ΠΟΛΥΚΛΙΝΙΚΗ»-Ν.Π.Δ.Δ. ΑΘΗΝΑ 17-07-2015 ΕΤΟΣ ΙΔΡΥΣΗΣ 1884 ΤΜΗΜΑ ΓΡΑΜΜΑΤΕΙΑΣ ΙΑΤΡΟΙ 08:00 20.00 20.00 08.00 ΓΕΝΙΚΗ ΕΦΗΜΕΡΙΑ
FRANKO IR HERCO BANDYMAS
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
