DEFORMUOJAMO KŪNO MECHANIKA 1 dalis
|
|
|
- Ἡλί Αλαβάνος
- 5 χρόνια πριν
- Προβολές:
Transcript
1 DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali s lgts 5. Deformuoto būvio teorija 6. Geometri s lgts 7. Tampraus kūo fii s priklausomb s 8. Tamprumo teorijos lgčių sistema
2 . Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais Kotiuumo mechaika viea iš fiikos sudedamųjų dalių ( pav.). Klasiki je fiikoje mechaika arba kotiuumo mechaika agri jama epriklausomai uo kitų jos skrių kaip šilumos fiika, elektra, optika, fii medžiagotra ir t. t. Kotiuumu plačiąja prasme ra vadiama materiali sistema, epertraukiamai pasiskirsčiusi erdv je. Kotiuumas apima e tik materialius kūus, bet ir fiiius laukus. D l šios priežasties kotiuumo mechaika apima e tik medžiagiių terpių mechaiką, bet ir įvairias tarp dalkies disciplias termomechaiką, elektromechaiką ir pa. Prie grai mechaiių disciplių priskiriamos aeromechaika (dujų mechaika), hidromechaika (sksčių mechaika) ir deformuojamojo kūo mechaika (DKM). Taigi deformuojamas kūas ra viea iš pagridiių kotiuumo formų, o deformuojamojo kūo mechaika ra mokslas apie kūų ir jų materialiųjų dalelių pusiausvrą, jud jimą ir deformavimąsi. Kūui deformuojatis keičiasi atstumai tarp jo taškų, kampai tarp liijų, paviršių plotai ir kūų tūriai, materialias dalis siejačios j gos. Deformavimosi d l išoriių poveikių metu atsiradats efektai, vadiami mechaiiais efektais. Deformuojamas kūas ra priešigb teori je mechaikoje agri jamam absoliučiai kietam kūui, kuriam judat atstumai tarp jo taškų esikeičia. Kalbat apie mechaikos disciplias ar jų skrius, sutikami du pavadiimai matemati s ir taikomosios teorijos ar disciplios. Matemati s teorijos skirtos bedriesiems d sigumams aprašti. Taikomosios teorijos įvertia papildomas prielaidas, supaprastia matematies teorijas ir ra skirtos kokrečių ižieriių problemų spredimui. Priklausomai uo agri jamų reiškiių pobūdžio ra skiriamos determiuotos ir statisti s teorijos. Tradiciškai domiavo determiuotos teorijos, kurias mes ir agri sime. Jos audoja matemati s aali s metodus. Vis tik pastaraisiais metais vis didesį vaidmeį vaidia statisti s teorijos, kurios paremtos tikimbiiais metodais. Kotiualiųjų sistemų mechaika agri ja vietisą kūą, audojat matemati s aali s metodus. Nagri jat be galo mažų matmeų diferecialiį elemetą kotiualiųjų sistemų matematiiai modeliai aprašomi difereciali mis lgtimis. Priklausomai uo kūo savbių išskiriamos
3 tamprumo teorija, plastiškumo teorija, valkšumo teorija, klampumo teorija ir kitos disciplios. Pastaruoju metu vis svarbesę vietą užima kūų ir medžiagų irimą agri jati irimo mechaika. Aprašat baigtiių matmeų kūus, audojami diskretiių sistemų mechaikos arba klasiki s statbi s mechaikos metodai, kurie aprašomi kompiuteriiams skaičiavimams labiau pritaiktais algebriiais modeliais. Šiuolaikiiai kompiuteriiai mechaikos ir matemati s fiikos modeliai daugiausia skirti kotiualiųjų sistemų diskretiacijai. Būtet fukciių modelių išreiškimas algebrie forma ir algebriių modelių spredimas ra šio kurso objektas. Savitą DKM modelių ir metodų grupę sudaro ižieri s disciplios, skirtos mechaikos taikmams ižierijoje. Kotiualiųjų sistemų mechaikos pagridas diferecialiio elemeto samprata, kurios pagalba aprašomi makrokūai. Šiuolaiki ms techologijoms pasiekus eįtik tią pažagą, reikia operuoti e tik mikrometrų, bet ir aometrų ddžio medžiagos dalel mis ar et pavieiais atomais, o į diskretiių sistemų modeliavimą įvesti atomies sąvokas. Būtet tomis sąvokomis operuoja moderi mechaikos sritis medžiagų mechaika plačiąja prasme.
4 Fiika Šilumos techika Kotiuumo mechaika Elektra Elektromechaika Fii medžiagotra Termomechaika Aeromechaika Deformuojamojo kūo mechaika Hidromechaika Diskretiių sistemų mechaika (statbi mechaika) Tamprumo teorija Kotiualių sistemų mechaika Plastiškumo teorija Valkšumo teorija Irimo mechaika Ižieri s disciplios (medžiagų atsparumas) pav. Medžiagų mechaika
5 . Tamprumo teorijos sąvokos ir prielaidos Kieto deformuojamo kūo mechaikos dalis agri jati kūų tampriąsias savbes vadiama tamprumo teorija (TT). TT objektas tamprus kūas, kurio taškuose ustatomi įtempimai, deformacijos ir poslikiai, sąlgojami žiomo poveikio. Kūas laikomas tamprus, jeigu pašalius išoriį poveikį jis sugrįžta į pirmkštį būvį. Matemati s TT gimtadieiu priimta laikti 864 m., kai Navje paskelb darbą, kuriame suformulavo TT lgčių sistemą. Pradžioje domiavo pracūų moksliikai. Be Navje, galima pami ti Klaiperoą, Puasoą, Se-Veaą, Košį (Navier, Clapero, Cauch, Poisso, Sait-Veat). Kai kurie iš jų d st Rusijoje, kur v liau irgi susiformavo garsi mechaikos mokkla. TT agri ja tik statikos apkrovas, t.. eįvertiamos j gos atsiradačios judat kūui ir priklausačios uo greičio ar pagreičio. Nagri sime klasikię TT. Tamprus kūas ( pav.) bus laikomas apibūditu, jei žiome jo išoriio paviršiaus S lgtį, tūrį V, tvirtiimo sąlgas bei tamprumo savbes usakačius ddžius (tamprumo modulis E, šlties modulis G ir skersi s deformacijos (Puasoo) koeficietas ν, E G ) ν Kūą veikiats poveikiai gali būti išoriiai, pridedami paviršiuje S arba vidiiai, atsiradats tūrje V. Paviršius S dalijamas į dalis. Dalje S f ( ) {P} S f S pav S u V pridedami j gos poveikiai, o dalje S u judesio poveikiai. Nuliiai poveikiai gali būti agri jami kaip atskiri atvejai: eapkrautas paviršius arba įtvirtitas paviršius.
6 Išori s j gos aprašomos: pavirši mis j gomis { p } { p, p, p } T ir tūri mis j gomis { g } { g, g, g } T, jų dimesija N - 3 m N. m (tai svorio arba iercijos j gos). Nagri sime ekitačias laike apkrovas. Pagridiis TT uždavis ustatti įtempimus, deformacijas, poslikius (apie juos kalb sime v liau) kūo tūrje V, kai kūo paviršius S, jo medžiagos fii s savb s, išoriis statiis poveikis (tūri s bei pavirši s j gos), tvirtiimo sąlgos ra žiomi. Pradiiai duomes gali būti duoti ir kitokia forma, t.. at dalies kūo paviršiaus S vietoje išoriių paviršiių j gų žiomi poslikiai arba priklausomb tarp poslikių ir paviršiių j gų ir paašiai. Kūams agri ti taiksime pjūvio metodą. Juo galima ustatti pjūvje veikiačias vidies j gas. Be to, šis metodas leidžia vidies j gas agri ti kaip išories j gas. Trumpai apie vidies j gas, įtempimą, poslikius ir deformacijas. Vidi s j gos tai papildoma kūo dalelių sąveika, atsiradati uo išoriių j gų. Įtempimas vidiių j gų itesvumo matas. Tai ra vektorius, kurio krptis tokia pati, kaip ties tuo tašku veikiačių vidiių j gų, o didumas prilgsta vidutiei j gai, tekačiai ploto vieetui. A F t A F F w 3 pav. F F lim p pilutiis įtempimas, F lim ormaliis įtempimas, lim t tagetiis įtempimas, A A A A A A p.
7 Poslikiai ir deformacijos (4 pav.) Taško liijiis poslikis - vektorius, kurio pradžia ra edeformuoto kūo taške, o galas deformuoto (vektorius aa ). a s b a π/ s α α ab b c a s s α bc c Atkarpos kampiis poslikis - kampas tarp atkarpos krpties edeformuotame kūe ir tos pačios atkarpos krpties jau deformuotame kūe (kampas α). Liiji deformacija ties kūo tašku kuria ors krptimi tos krpties atkarpos pokčio satkis su pradiiu atkarpos ilgiu, kai tas ilgis kstamai mažas. s lim liiji deformacija s s 4 pav. Kampi deformacija kampo tarp dviejų statmeų kstamai trumpų atkarpų poktis. ( abc a b c ) abc lim - kampi deformacija. ab bc Norit ustatti įtempimų, deformacijų ir poslikių ežiomas fukcijas, reikia dispouoti tam tikrų lgčių sistema. Tos lgts turi susieti ieškomas fukcijas su pradiiais duomeimis, aprašačiais kūą ir jį veikiačias j gas. Tai: - pusiausvros lgts (algebri s ir difereciali s), - geometri s lgts (diferecialiis ršs tarp deformacijų ir poslikių), - fiikos (algebri s) priklausomb s.
8 Prielaidos (pricipai). Medžiagos vietisumo prielaida (hipote ). Teigia, kad medžiaga užpildo kūą tolgiai be tuštumų. Ši prielaida leidžia aprašti kūą toldi mis fukcijomis.. Medžiagos viealtiškumo prielaida. Teigia, kad medžiagos savb s visuose kūo taškuose vieodos. 3. Medžiagos iotropiškumo prielaida. Teigia, kad medžiagos savb s visomis krptimis ra vieodos. 4. Medžiagos idealaus tamprumo prielaida. Teigia, kad ršs tarp apkrovų ir deformacijų ra grįžtamojo pobūdžio. 5. Fiiio tiesiškumo prielaida (Huko d sis). Teigia, kad ršs tarp įtempimų ir deformacijų ra proporcigas. 6. Geometriio tiesiškumo prielaida. Teigia, kad kūo satkiiai pailg jimai maži, palgiti su vieetu, o liijiiai kūo taškų poslikiai maži, palgiti su paties kūo matmeimis. 7. Neįtempto pradiio būvio pricipas. Teigia, kad prieš pridedat išoriius poveikius kūe ra jokių vidiių j gų. 8. Nepriklausomo j gų veikimo (superpoicijos) pricipas. Teigia, kad j gų sistemos poveikio reultatas lgus reultatų uo atskirų j gų sumai. 9. Pusiausvrų išoriių j gų lokaliio efekto (Se Veao) pricipas. Yra dvi šio pricipo formuluot s: a) išoriių j gų sąlgoti įtempimai ir deformacijos kūo taške, pakakamai utolusiame uo j gų prid jimo vietos, epriklauso uo j gų sistemos pobūdžio, o priklauso tik uo j gų sistemos svarbiausiojo vektoriaus ir svarbiausiojo mometo.
9 b) išori s j gos, veikiačios edidel je kūo paviršiaus ar kūo tūrio sritje ir būdamos statiškai ekvivaletiškos, sąlgoja įtempimus ir deformacijas, kurie tolstat uo aptartos srities (uo taško A, žr. 5 pav.) greitai maž ja ir atstumu didesiu už R lgus O. 5 pav. Se-Veao pricipas ra griežtai matematiškai, kiekbiškai pagrįstas, tačiau turimi sprediiai ir eksperimetai visiškai pateisia jo teisigumą. Jis labai svarbus TT, pač agri jat spredimo metodus.
10 3. Įtempimų būvio teorija Įtempimų didumas bet kuriame apkrauto elemeto taške priklauso uo to, kaip orietuotas pjūvis, kuriame tie įtempimai agri jami. Kaitaliodami pjūvio krptį sud tigai apkrautame elemete, ties vieu tuo pačiu tašku gautume įvairių įvairiausias įtempimų reikšmių kombiacijas. Bet kuriai šių kombiacijų usakti pakaka žioti įtempimus kuriose ors trijose statmeose plokštumose ir agri jamo pjūvio orietaciją tų plokštumų atžvilgiu (kampus tarp pjūvio ir tų plokštumų). Įtempimų, veikiačių įvairiose visaip eiačiose per apkrauto kūo tašką plokštumose, visuma ra vadiama įtempimų būviu ties tašku. Ties agri jamuoju apkrauto kūo tašku k statmeais ašims pjūviais, išpjauame be galo mažą stačiakampį gretasieį, kurio briauų ilgis d, d, d (6 pav.). 6 pav. Bedru atveju visuose šešiuose šio gretasieio šouose veikia po tris įtempimų kompoetus (,, ir t.t.).
11 Kadagi atstumai tarp išpjauto gretasieio šoų ra kstamai maži, priešiguose šouose (ematomuose) veikia tokio pat didumo, tik priešigos krpties įtempimai (įtempimai pažm ti štrichu ra lgūs įtempimams be štricho). Taigi įtempimų būviui ties bet kuriuo tašku usakti reikia žioti iš viso devias įtempimų reikšmes. Įtempimų būvis gali būti apraštas vektoriumi {} { } {,,,,,,,, } T () arba įtempimų matrica ~, vadiama teoriumi (stulpeliuose vieodas ra pirmasis ideksas, kuris rodo ormal s krptį) ~ () Nesuku įrodti, kad trs poros tagetiių įtempimų reikšmių ra tarpusavje lgios: Pv: ( M ),, (Tagetiių įtempimų dualumo d sis) (3). Įtempimai ra pasiskirstę visame gretasieio šoo plote. Kadagi tas plotas ra kstamai mažas, galima teigti, kad visuose kiekvieo šoo taškuose įtempimai vieodi ir prilgsta taško k įtempimams. Tod l atstojamąsias gauame daugiat įtempimo kompoetus iš to šoo ploto dd, dd, dd ir t.t. Visos atstojamosios j gos prid tos prie gretasieio šoų cetrų, tod l j gos, kurios susidaro iš ormaliių įtempimų, veikia poromis viea prieš kitą ir visiškai kompesuoja viea kitos poveikį. Tuo tarpu j gos, kurios susideda iš tagetiių įtempimų, sukuria j gų poras. ( ) M, ddd ddd arba
12 Tagetiių įtempimų dualumo d sis,, Dviejuose statmeose plokštumose tagetiių įtempimų kompoetai, statmei tų plokštumų susikirtimo briauai ties tašku ra vieodo didumo ir ukreipti arba abu į briauą arba uo jos Įvertiat tagetiių įtempimų dualumo d sį (3) galime teigti, kad įtempimų būviui ties bet kuriuo tašku usakti reikia žioti e 9, bet 6 įtempimų reikšmes ir kad įtempimų teorius ra simetriškas pagridi s diagoal s atžvilgiu. Tada įtempimų būvis gali būti apraštas vektoriumi { } { } T,,,,, (4) arba teoriumi ~. (5) sim atžvilgiu. Be įtempimų statmeuose (ormali se) ašims,, aikštel se, dažai reikia žioti įtempimus aikštel se bet kaip orietuotose ašių,,
13 Tam ties agri jamuoju apkrauto kūo tašku k išpjauame be galo mažą tetraedrą (7 pav.). 3 tetraedro plokštumos sutampa su koordiati mis plokštumomis, o ketvirtoji ra pasvirusi. Jos pad tis usakoma ormal s {} {,, } T, (6) kur cos(, ), cos(, ), cos (, ). 7 pav. Įtempimas bet kaip orietuotoje plokštumoje (8 pav.) { p } { p, p, p } T (7) 8 pav. Pusiausvros lgtis: ( ) F, (eįvertiat tūriių j gų) p da da da da, kur da da, da da, da da, da bet kaip orietuotos plokštumos plotas.
14 Sutvarkę gauame p. Aalogiškai parašę kitas pusiausvros lgtis gauame p p p (8) Matrici je formoje { } { } ~ p arba { } [ ] { } N p (9) kur N Lgts (9) tai tetraedro pusiausvros algebri s lgts. Kair je pus je vietoje pilojo įtempimo kompoetų gali būti įrašomos pavirši s apkrovos. Aikštel s, kuriose ra tagetiių įtempimų, vadiamos svarbiausiomis. Normaliiai įtempimai, veikiatieji svarbiausioje aikštel je vadiami svarbiausiaisiais. Pasvirusioji aikštel sutaps su svarbiausiąja, kai jos ormal sutaps su p t.. p (žr. 8 pav.), tada p p p p p p () įrašę () į (8) ir pertvarkę gauame: ( ) ( ) ( ) ()
15 Šioje sistemoje ežiomieji,,,. Vieu metu,, egali būti lgūs uliui es. Lgts () sudaro homogeiių lgčių sistemą, kuri turi euliį sprediį, kai jos determiatas lgus uliui det t.. ( )( )( ) ( ) ( ) ( ) () Lgtis () kubi lgtis atžvilgiu, kurią galima užrašti kur I, I 3, det det det det I 3 I I I (3) Kubi s lgties (3) sprediiai ra svarbiausieji įtempimai, kurie žmimi > > 3. Jie apskaičiuojami pagal tikslias Kardao formules, arba skaitiiu Niutoo metodu.
16 4. Pusiausvros difereciali s lgts Rašat algebries pusiausvros lgtis (8) laik me, kad įtempimai priešigose gretasieio plokštumose ra vieodi. Algebri s lgts leidžia įvertiti išories apkrovas ir eįvertia tūriių apkrovų. Dabar agri jimą patiksliame, t.. įvertiame įtempimų teoriaus elemetų pokčius kitat plokštumų koordiat ms (8 pav.). Pokčiams ustatti audojamasi Teiloro eilut s ariais, atmetus aukštesių eilių savbes (9 pav.): d d, d d tikrasis poktis 8 pav. d 9 pav. Užrašomos elemeto, parodto 8 pav., j gų projekcijų sumų į ašis pusiausvros lgts: F, Pavdžiui ( ) dd d dd dd d dd - dd dd g dv pertvarkę ir suprastię iš dv ddd gauame g.
17 Aalogiškai parašę ( ) F gauame g, o parašę ( ) F g. Tokiu būdu gauame diferecialies pusiausvros lgtis g, g, (5) g. arba operatorie-matricie forma { } { } g, (6) kur diferecialiis operatorius. Pusiausvros lgts (5) dar vadiamos Navj (pracūų matematikas, ižiierius Louis Navier, ) vardu. Šios difereciali s pusiausvros lgts ir algebri s pusiausvros lgts (9) leidžia paprastomis operacijomis (diferecijavimo arba algebri mis) tiksliai ustatti, kokios išori s pavirši s j gos {p} ir išori s tūri s j gos {g} sąlgoja įtempimų būvį, apibūdiamą įtempimais {}. Tačiau šių diferecialiių lgčių eužteka pagridiiam TT uždaviiui išspręsti: esat duotoms išori ms j goms, ustatti įtempimų būvį, t.. įtempimų teorių ~, es ra 3 lgts, o ežiomųjų 6. Algebri s lgts tik krašti s sąlgos. Uždavis statiškais eišspredžiamas. Įtempimų vektorius {} {,,,,,,} T vadiamas statiškai galimu, jeigu tekia šias priklausombes.
18 5. Deformuoto būvio teorija Be įtempimų TT agri ja kūo deformacijas ir kūo taškų poslikius. Poslikio kompoetai žmimi u, v, w ( pav.). a v a w u pav. a(,, ), a'( u, v, w) u u(,, ) v v(,, ) w w(,, ) taško poslikiai ra taško koordiačių fukcijos. Remiatis medžiagos vietisumo prielaida teigiame, kad u, v ir w fukcijos gali būti apskaičiuotos visuose taškuose. Laikdami, kad deformacijos mažos, be galo mažojo gretasieio deformaciją galima išreikšti šešiomis deformacijomis (3 liiji s ir 3 kampi s),,,,, ( pav.). d d d d d d d d d tg d tg d tg d pav.
19 Gretasieio deformaciją galima vaiduoti įvairiai, bet kampi deformacija bus ta pati ( pav.). a) b) c) pav. Šiuos deformacijų būvius ( a, b, c pav.) atitika tas pats įtempimų būvis. Aalogiškai įtempimų būviui, deformacijų būvis aprašomas deformacijų vektoriumi ir teoriumi:,,,, deformacijų vektorius { } { } T deformacijų teorius ~,, Deformacijų būvis deformacijų visuma 3 krptimis ir 3-ose plokštumose.
20 Liiji s deformacijos trimis tarpusavje statmeų ašių, status kampas tarp kurių esikeičia, krptimis ra svarbiausiosios deformacijos,, 3, kurios skaičiuojamos iš lgties Kubi s lgties (7) koeficietai apskaičiuojami 3 I I I3. (7) I I I, det. det det det. 3 Aalogija Matome, kad geometriškai deformacija gali būti aprašoma taškų poslikiais arba gretasieių, į kuriuos gali būti sudalitas kūas, deformacijų vektoriumi ir teoriumi.
21 6. Geometri s lgts Lgts siejačios poslikius su deformacijomis vadiamos geometri mis lgtimis. Poslikius laiksime žiomais. Toliau agri jame mažas atkarpas, pv. ilgio d (3 pav.). Teigiame, kad atkarpos ilgio pokčiui įtakos turi tik poslikis u, o poslikiai v ir w ekeičia ilgio, d l jų atkarpa tik pasisuka. Atstumą tarp taškų a ir b galima išreikšti dvejopai ab' u d d (3 pav. viršuti matmeų liija) arba u ab' d u d (3 pav. apati matmeų liija) a u d a 3 pav. d d b u u d u du b u du u d d d u d, arba d d d d d du d u (žr. pav.), tada d d d d u v u, aalogiškai ; Tai pirmosios trs geometri s lgts: u, v u ;
22 a u d Toliau agri jame gretasieio (4 pav.) projekciją į plokštumą -. a d b d u c b α ab v α bc c v d Neįvertiame poslikio w ir matmeų pokčio, įvertiame tik taškų a ir c poslikius ir pradiio stataus kampo poktį. Kampi deformacija α α, kampai ab bc u u α ab tgα ab d / d,. 4 pav v v α bc tgα bc d / d, tada u v. Kitas lgtis gauame aalogiškai agri dami poslikius ir stataus kampo pokčius plokštumose ir. Jas galima užrašti keičiat ašių ir poslikių žm jimus ; u v w u. v w, u w
23 Tokiu būdu gauamos šešios geometri s deformacijų ir poslikių daros lgts : w u w v v u w v u,, ; ; (8) Kūo geometri s lgts (8) dar vadiamos Koši (pracūų matematikas Augusti Cauch, ) vardu. Operatorie-matricie forma Koši lgts užrašomos { } { } u T, (9) kur { } { } T,,,,,, deformacijų vektorius, { } { } T w v u u,, poslikių vektorius, T diferecialiis operatorius. Jeigu žiomi 3 poslikiai tai pagal Koši formules legvai ustatomi 6 deformacijų kompoetai.
24 7. Tampraus kūo fii s priklausomb s Pusiausvros (NAVJE) ir geometri s (KOŠI) lgts galioja ir tampriam ir plastiškam bei valkšiam kūui, jei tik galioja mažų deformacijų prielaida. Kūų skirstmas į tamprius ir etamprius prasideda tik tada, kai usakome ršį tarp deformacijų ir įtempimų. Tai fiiis d sis, arba apibedritas Huko (aglų fiikas Robert Hooke, 63 73) d sis: E E E, G [ ν( )] [ ν( )] [ ν( )] G Operatorie-matricie forma Huko d sis užrašomos { } [ ]{ },, () G D, () arba [ D], kur D E -ν -ν -ν -ν -ν -ν (ν) (ν) (ν) D pasiduodamumo matrica.
25 Kai kada Huko d sis užrašomas { } [ ]{ } [ K]{ } D, () K ( -ν) λ λ λ ν λ ( -ν) λ λ ν λ λ λ ( -ν) ν G G G kur [K] stadumo matrica, λ Lame (matematikas, ižiierius Gabriel Lame, ) koeficietas λ E tamprumo modulis, G šlties modulis, E ν ( ν)( ν) ν Puasoo (pracūų mechaikas, fiikas ir matematikas Simeo Deis Poisso, 78-84) koeficietas,
26 8. Tamprumo teorijos lgčių sistema Duotas kūas. Žiome įtvirtiimo sąlgas ir apkrovas. Reikia rasti 5 ežiomųjų fukcijų. { } {,,,,, } T, { } {,,,,, } T, { u } { u, v, w} T. Šiems ežiomiesiems rasti turime 5 lgčių. Nežiomųjų skaičius Lgts {} {} {u} Lgčių skaičius Statikos ( Navje) { } { } { } g 6 3 Geometri s (Koši) { u} { } T Fii s (Huko) { } [ D ] { } arba { } [ K ] { } Nežiomųjų Lgčių 3665 TT uždavis ra išspredžiamas iš pricipo. Prie šių lgčių būtia prijugti krašties sąlgas: staties ir [ N ]{ } { p} [ N ]{ } { R} at Af, ; at A kiematies {u} {} at A u. u
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
6. Konstrukcijų patikimumo įvertinimo metodai
 6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
6. Kostrukcijų patikimumo įvertiimo metodai 6.1. Bedrieji kostrukcijų patikimumo įvertiimo pricipai 6.1 tekstas Eksploatuojamoje kostrukcijoje, kaip ir visur gamtoje, vyksta priešybių kova: iš vieos pusės,
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
2.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS
 .5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
.5. KLASIKINĖS TOLYDŽIŲ FUNKCIJŲ TEOREMOS 5.. Pirmoji Bolcao Koši teorema. Jei fucija f tolydi itervale [a;b], itervalo galuose įgyja priešigų želų reišmes, tai egzistuoja tos tašas cc, ( ab ; ), uriame
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
Praeita paskaita. Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje. Praeita paskaita. 2D Transformacijos. Grafika ir vizualizavimas, VDU, 2010
 Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Praeita paskaita Grafika ir vizualizavimas Atkirtimai dvimatėje erdvėje Atkarpos Tiesės lgtis = mx+ b kur m krpties koeficientas, o b aukštis, kuriame tiesė kerta ašį Susikirtimo taško apskaičiavimui sulginamos
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
Statistinis ir termodinaminis tyrimo metodai
 MOLEKULINĖS FIZIKOS IR TERMODINAMIKOS PAGRINDAI Statistiis i temodiamiis tyimo metodai Statistiis tyimo metodas Kaip buvo aiškiama medžiagos sadaa Mitį, kad kiekviea medžiaga sudayta iš smulkiausių edalomų
MOLEKULINĖS FIZIKOS IR TERMODINAMIKOS PAGRINDAI Statistiis i temodiamiis tyimo metodai Statistiis tyimo metodas Kaip buvo aiškiama medžiagos sadaa Mitį, kad kiekviea medžiaga sudayta iš smulkiausių edalomų
9. Sukimas Bendrosios žinios
 9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
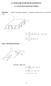 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
7. Geometriniai plokščiųjų figūrų rodikliai
 7. Geometra plokščųjų fgūrų rodkla 7.. Bedrosos žos 7. tekstas 7.. Pagrdės sąvokos Geometras vadam pjūvo (plokščosos fgūros) rodkla, kure prklauso uo pjūvo matmeų, formos e oretacjos r kekška įverta jo
7. Geometra plokščųjų fgūrų rodkla 7.. Bedrosos žos 7. tekstas 7.. Pagrdės sąvokos Geometras vadam pjūvo (plokščosos fgūros) rodkla, kure prklauso uo pjūvo matmeų, formos e oretacjos r kekška įverta jo
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
4 laboratorinis darbas. PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS
 PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS DARBO TIKSLAS - išstudijuoti parametrų taškiių ir itervaliių įverčių radimo, parametriių ir eparametriių hipotezių tikriimo uždaviius ir jų taikymą Teorijos
PARAMETRŲ ĮVERČIAI IR STATISTINĖS HIPOTEZĖS DARBO TIKSLAS - išstudijuoti parametrų taškiių ir itervaliių įverčių radimo, parametriių ir eparametriių hipotezių tikriimo uždaviius ir jų taikymą Teorijos
Skysčiai ir kietos medžiagos
 Skysčiai ir kietos medžiagos Dujos Dujos, skysčiai ir kietos medžiagos Užima visą indo tūrį Yra lengvai suspaudžiamos Lengvai teka iš vieno indo į kitą Greitai difunduoja Kondensuotos fazės (būsenos):
Skysčiai ir kietos medžiagos Dujos Dujos, skysčiai ir kietos medžiagos Užima visą indo tūrį Yra lengvai suspaudžiamos Lengvai teka iš vieno indo į kitą Greitai difunduoja Kondensuotos fazės (būsenos):
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
9. KEVALŲ ELEMENTAI. Pavyzdžiai:
 9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
9. KEVALŲ ELEMENTAI Kealai Tai ploni storio krptii kūnai, sudarti iš kreių plokštuų. Geoetrija nusakoa iduriniu pairšiui ir storiu t. Kiekiena pairšiaus taške galia rasti di kreies, atitinkančias inialius
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
PNEUMATIKA - vožtuvai
 Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
r F F r F = STATIKA 1 Q = qmax 2
 STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
STTIK Mechanika fizinių moksų šaka, naginėjanti mateiaiuosius objektus: kūnus, kūnų sistemas, tų sistemų pusiausvyą, judėjimo dėsnius i mechaninę tapusavio sąveiką. Statika moksas apie pavienius mateiaiuosius
Papildomo ugdymo mokykla Fizikos olimpas. Mechanika Dinamika 1. (Paskaitų konspektas) 2009 m. sausio d. Prof.
 Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
GEOMETRINĖS OPTIKOS PAGRINDAI
 OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
3 modulis. Funkcijos sąvoka. Laipsninė, rodiklinė ir logaritminė funkcija
 P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
P R O J E K T A S VP--ŠMM-0-V-0-00 MOKYMOSI KRYPTIES PASIRINKIMO GALIMYBIŲ DIDINIMAS -9 METŲ MOKINIAMS, II ETAPAS: GILESNIS MOKYMOSI DIFERENCIJAVIMAS IR INDIVIDUALIZAVIMAS, SIEKIANT UGDYMO KOKYBĖS, REIKALINGOS
Integriniai diodai. Tokio integrinio diodo tiesiogin įtampa mažai priklauso nuo per jį tekančios srov s. ELEKTRONIKOS ĮTAISAI 2009
 1 Integriniai diodai Integrinių diodų pn sandūros sudaromos formuojant dvipolių integrinių grandynų tranzistorius. Dažniausiai integriniuose grandynuose kaip diodai naudojami tranzistoriniai dariniai.
1 Integriniai diodai Integrinių diodų pn sandūros sudaromos formuojant dvipolių integrinių grandynų tranzistorius. Dažniausiai integriniuose grandynuose kaip diodai naudojami tranzistoriniai dariniai.
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
PRAKTINIO TAIKYMO VADOVAS ĮVADAS
 STR.05.05:005 prieas PRAKTINIO TAIKYMO VADOVAS ĮVADAS Šiame praktinio nauojimo vaove yra pateikti reikalavimai pastatų ir statinių betonin ms ir gelžbetonin ms konstrukcijoms projektuoti iš sunkaus ir
STR.05.05:005 prieas PRAKTINIO TAIKYMO VADOVAS ĮVADAS Šiame praktinio nauojimo vaove yra pateikti reikalavimai pastatų ir statinių betonin ms ir gelžbetonin ms konstrukcijoms projektuoti iš sunkaus ir
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos
 Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
EKONOMETRIJA 1 (Regresinė analizė)
 EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
EKONOMETRIJA 1 Regresinė analizė Kontrolinis Sudarė M.Radavičius 004 05 15 Kai kurių užduočių sprendimai KOMENTARAS. Kai kuriems uždaviniams tik nusakytos sprendimų gairės, kai kurie iš jų suskaidyti į
SIGNALŲ IR GRANDINIŲ ANALIZĖ
 Dariu MINIOT IGNLŲ IR GRNDINIŲ NLIĖ Projekto koda VP--ŠMM-7-K--47 VGTU Elektroiko fakulteto I pakopo tudijų programų emii ataujiima Viliu Techika VILNIU GEDIMINO TECHNIKO UNIVERITET Dariu MINIOT IGNLŲ
Dariu MINIOT IGNLŲ IR GRNDINIŲ NLIĖ Projekto koda VP--ŠMM-7-K--47 VGTU Elektroiko fakulteto I pakopo tudijų programų emii ataujiima Viliu Techika VILNIU GEDIMINO TECHNIKO UNIVERITET Dariu MINIOT IGNLŲ
KOMPIUTERINIS PROJEKTAVIMAS
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Statybinių konstrukcijų katedra Tatjana Sankauskienė KOMPIUTERINIS PROJEKTAVIMAS AutoCAD sistemoje Mokomoji knyga inžinerinių specialybių
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Statybinių konstrukcijų katedra Tatjana Sankauskienė KOMPIUTERINIS PROJEKTAVIMAS AutoCAD sistemoje Mokomoji knyga inžinerinių specialybių
IV. FUNKCIJOS RIBA. atvira. intervala. Apibrėžimas Sakysime, kad skaičius b yra funkcijos y = f(x) riba taške x 0, jei bet kokiam,
 41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
41 Funkcijos riba IV FUNKCIJOS RIBA Taško x X aplinka vadiname bet koki atvira intervala, kuriam priklauso taškas x Taško x 0, 2t ilgio aplinka žymėsime tokiu būdu: V t (x 0 ) = ([x 0 t, x 0 + t) Sakykime,
Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes.
 Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes. Ji susideda iš vienodų arba skirtingų atomų. Molekulėje
Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes. Ji susideda iš vienodų arba skirtingų atomų. Molekulėje
Taikomieji optimizavimo metodai
 Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Taikomieji optimizavimo metodai 1 LITERATŪRA A. Apynis. Optimizavimo metodai. V., 2005 G. Dzemyda, V. Šaltenis, V. Tiešis. Optimizavimo metodai, V., 2007 V. Būda, M. Sapagovas. Skaitiniai metodai : algoritmai,
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
APKROVŲ IR POVEIKIŲ SKAIČIAVIMO PAGAL DARNIUOSIUS EUROPOS STANDARTUS, PERIMTUS LIETUVOS STANDARTAIS, PRAKTINIO NAUDOJIMO VADOVAS
 LR APLINKOS MINISTERIJA VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS APKROVŲ IR POVEIKIŲ SKAIČIAVIMO PAGAL DARNIUOSIUS EUROPOS STANDARTUS, PERIMTUS LIETUVOS STANDARTAIS, PRAKTINIO NAUDOJIMO VADOVAS II dalis.
LR APLINKOS MINISTERIJA VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS APKROVŲ IR POVEIKIŲ SKAIČIAVIMO PAGAL DARNIUOSIUS EUROPOS STANDARTUS, PERIMTUS LIETUVOS STANDARTAIS, PRAKTINIO NAUDOJIMO VADOVAS II dalis.
III.Termodinamikos pagrindai
 III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
LIETUVOS RESPUBLIKOS APLINKOS MINISTRO Į S A K Y M A S
 LIETUVOS RESPUBLIKOS APLINKOS MINISTRO Į S A K Y M A S DöL LIETUVOS RESPUBLIKOS APLINKOS MINISTRO 003 M. GEGUŽöS 15 D. ĮSAKYMO NR. 33 DöL STATYBOS TECHNINIO REGLAMENTO STR.05.04:003 POVEIKIAI IR APKROVOS
LIETUVOS RESPUBLIKOS APLINKOS MINISTRO Į S A K Y M A S DöL LIETUVOS RESPUBLIKOS APLINKOS MINISTRO 003 M. GEGUŽöS 15 D. ĮSAKYMO NR. 33 DöL STATYBOS TECHNINIO REGLAMENTO STR.05.04:003 POVEIKIAI IR APKROVOS
Ketvirtos eilės Rungės ir Kutos metodo būsenos parametro vektoriaus {X} reikšmės užrašomos taip:
 PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
PRIEDAI 113 A priedas. Rungės ir Kuto metodas Rungės-Kutos metodu sprendiamos diferencialinės lygtys. Norint skaitiniu būdu išspręsti diferencialinę lygtį, reikia žinoti ieškomos funkcijos ir jos išvestinės
Teorinė mechanika I. Uždavinių sprendimo vadovas
 VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
VILNIUS GEDIINO TEHNIKOS UNIVERSITETS R. UŠYS, J. KSNUSKS Teorinė mechania I. Uždavinių sprendimo vadovas OKOOJI KNYG Vilnius Technia 00 R. aušs, J. Kasnausas. TEORINĖ EHNIK I. UŽDVINIŲ SPRENDIO VDOVS
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra. Juozas Navickas FIZIKA. I dalis MOKOMOJI KNYGA
 LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
LIETUVOS ŽEMĖS ŪKIO UNIVERSITETAS Vandens ūkio ir žemėtvarkos fakultetas Fizikos katedra Juozas Navickas FIZIKA I dalis MOKOMOJI KNYGA KAUNAS, ARDIVA 8 UDK 53(75.8) Na95 Juozas Navickas FIZIKA, I dalis
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas. Algirdas Antanavičius. Mokomoji knyga
 Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
Lietuvos žemės ūkio universitetas Vandens ūkio ir žemėtvarkos fakultetas Algirdas Antanavičius GEODEZIJOS PAGRINDAI Mokomoji knyga Akademija, 2007 Redaktorė: M. Židonienė turinys ĮVADAS... 1. Geodezijos
DISKREČIOJI MATEMATIKA
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Valdas Diči ūnas Gintaras Skersys DISKREČIOJI MATEMATIKA Mokymo priemonė Vilnius 2003 Įvadas Išvertus iš lotynu kalbos
ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )
![ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] ) ATSITIKTINIAI PROCESAI. Alfredas Račkauskas. (paskaitų konspektas 2014[1] )](/thumbs/72/67447727.jpg) ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
ATSITIKTINIAI PROCESAI (paskaitų konspektas 2014[1] ) Alfredas Račkauskas Vilniaus universitetas Matematikos ir Informatikos fakultetas Ekonometrinės analizės katedra Vilnius, 2014 Iš dalies rėmė Projektas
ELEMENTARIOJI TEORIJA
 ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
ELEMENTARIOJI TEORIJA Pirmosios kombinatorikos þinios siekia senàsias Rytø ðalis, kuriose mokëta suskaièiuoti këlinius bei derinius ir sudarinëti magiðkuosius kvadratus, ypaè populiarius viduramþiais.
5 klasė. - užduotys apie varniuką.
 5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató Automatická pračka Používateľská príručka
 WMB 71032 PTM Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató utomatická pračka Používateľská príručka Dokumentu Nr 2820522945_LT / 06-07-12.(16:34) 1 Svarbūs
WMB 71032 PTM Skalbimo mašina Vartotojo vadovas Πλυντήριο Ρούχων Εγχειρίδιο Χρήστη Mosógép Használati útmutató utomatická pračka Používateľská príručka Dokumentu Nr 2820522945_LT / 06-07-12.(16:34) 1 Svarbūs
5. Medžiagų mechaninės savybės
 5. Medžiagų mechaninės savybės 5.1. Bendrosios žinios r konstrukcija (jos eementas) yra pakankamai stipri, standi, stabii, gaima spręsti tik tuo atveju, kai šaia įtemptąją ir deformuotąją jos būseną apibūdinančių
5. Medžiagų mechaninės savybės 5.1. Bendrosios žinios r konstrukcija (jos eementas) yra pakankamai stipri, standi, stabii, gaima spręsti tik tuo atveju, kai šaia įtemptąją ir deformuotąją jos būseną apibūdinančių
STOGO ŠILUMINIŲ VARŽŲ IR ŠILUMOS PERDAVIMO KOEFICIENTO SKAIČIAVIMAS
 STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
FRANKO IR HERCO BANDYMAS
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VI SKYRIUS VI SKYRIUS OPTINĖ HOLOGRAFIJA
 180 OPTINĖ HOLOGRAFIJA Holografija vadinamas šviesos bangų struktūros užrašymo ir atgaminimo metodas, grindžiamas koherentinių šviesos pluoštelių difrakcija ir interferencija. Kaip ir fotografijoje, ji
180 OPTINĖ HOLOGRAFIJA Holografija vadinamas šviesos bangų struktūros užrašymo ir atgaminimo metodas, grindžiamas koherentinių šviesos pluoštelių difrakcija ir interferencija. Kaip ir fotografijoje, ji
0.1. Bendrosios sąvokos
 0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
0.1. BENDROSIOS SĄVOKOS 1 0.1. Bendrosios sąvokos 0.1.1. Diferencialinės lygtys su mažuoju parametru F ) x n),x n 1),...,x,x,t;ε = 0, xt;ε) C n T), T [0,+ ), 0 < ε ε 0 ) F x n) t;ε),x n 1) t;ε),...,x t;ε),xt;ε),t;ε
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
15 darbas ŠVIESOS DIFRAKCIJOS TYRIMAS
 15 daras ŠVIESOS DIFRKCIJOS TYRIMS Užduotys 1. Išmatuoti plyšio plotį.. Išmatuoti atstumą tarp dviejų plyšių. 3. Nustatyti šviesos angos ilgį iš difrakcinio vaizdo pro apskritą angą. 4. Nustatyti kompaktinio
15 daras ŠVIESOS DIFRKCIJOS TYRIMS Užduotys 1. Išmatuoti plyšio plotį.. Išmatuoti atstumą tarp dviejų plyšių. 3. Nustatyti šviesos angos ilgį iš difrakcinio vaizdo pro apskritą angą. 4. Nustatyti kompaktinio
Fizika. doc. dr. Vytautas Stankus. Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas
 Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
Modalumo logikos S4 kai kurios išsprendžiamos klasės
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS INFORMATIKOS KATEDRA Magistro baigiamasis darbas Modalumo logikos S4 kai kurios išsprendžiamos klasės Some Decidable Classes of Modal Logic
Elektrotechnikos pagrindai
 Valentinas Zaveckas Elektrotechnikos pagrindai Projekto kodas VP1-2.2-ŠMM 07-K-01-023 Vilnius Technika 2012 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius
Valentinas Zaveckas Elektrotechnikos pagrindai Projekto kodas VP1-2.2-ŠMM 07-K-01-023 Vilnius Technika 2012 Studijų programų atnaujinimas pagal ES reikalavimus, gerinant studijų kokybę ir taikant inovatyvius
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lygčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
KADETAS (VII ir VIII klasės)
 ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
ADETAS (VII ir VIII klasės) 1. E 10 000 Galima tikrinti atsakymus. adangi vidutinė kainasumažėjo, tai brangiausia papūga kainavo daugiau kaip 6000 litų. Vadinasi, parduotoji papūga kainavo daugiau kaip
2008 m. matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija
 008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
008 M MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA 008 m matematikos valstybinio brandos egzamino VERTINIMO INSTRUKCIJA Pagrindinė sesija 7 uždavinių atsakymai I variantas Užd
MECHANINIS DARBAS, GALIA, ENERGIJA. TVERMĖS DĖSNIAI MECHANIKOJE. HIDRODINAMIKA
 LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS MECHANINIS DARBAS, GALIA, ENERGIJA TVERMĖS DĖSNIAI MECHANIKOJE HIDRODINAMIKA III KURSO III TURO METODINIAI NURODYMAI IR UŢDUOTYS
LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS MECHANINIS DARBAS, GALIA, ENERGIJA TVERMĖS DĖSNIAI MECHANIKOJE HIDRODINAMIKA III KURSO III TURO METODINIAI NURODYMAI IR UŢDUOTYS
KURKIME ATEITĮ DRAUGE! FIZ 414 APLINKOS FIZIKA. Laboratorinis darbas SAULĖS ELEMENTO TYRIMAS
 EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Diskrečioji matematika
 VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
VILNIAUS UNIVERSITETAS Gintaras Skersys Julius Andrikonis Diskrečioji matematika Pratybų medžiaga Versija: 28 m. sausio 22 d. Vilnius, 27 Turinys Turinys 2 Teiginiai. Loginės operacijos. Loginės formulės
Laboratorinis darbas Nr. 2
 M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
M A T E M A T I N Ė S T A T I S T I K A Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2005 m. spalio 23 d. Reziumė Antras laboratorinis darbas skirtas išmokti generuoti tikimybinių skirstinių
MONTE KARLO METODAS. Gediminas Stepanauskas IVADAS Sistemos Modeliai Modeliavimas ir Monte-Karlo metodas...
 MONTE KARLO METODAS Gediminas Stepanauskas 2008 Turinys 1 IVADAS 4 1.1 Sistemos.............................. 4 1.2 Modeliai.............................. 5 1.3 Modeliavimas ir Monte-Karlo metodas.............
MONTE KARLO METODAS Gediminas Stepanauskas 2008 Turinys 1 IVADAS 4 1.1 Sistemos.............................. 4 1.2 Modeliai.............................. 5 1.3 Modeliavimas ir Monte-Karlo metodas.............
EUROPOS CENTRINIS BANKAS
 2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2
 DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
DISPERSINĖ, FAKTORINĖ IR REGRESINĖ ANALIZĖ Laboratorinis darbas Nr. 2 Marijus Radavičius, Tomas Rekašius 2010 m. vasario 23 d. Santrauka Antras laboratorinis darbas skirtas išmokti sudarinėti daugialypės
1 iš 8 RIBOTO NAUDOJIMO M. CHEMIJOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 iš 8 RIBT NAUDJIM PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 00 m. birželio 0 d. įsakymu 6.-S- 00 M. EMIJS VALSTYBINI BRANDS EGZAMIN UŽDUTIES VERTINIM INSTRUKIJA Pagrindinė sesija I dalis Kiekvienas
iš 8 RIBT NAUDJIM PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 00 m. birželio 0 d. įsakymu 6.-S- 00 M. EMIJS VALSTYBINI BRANDS EGZAMIN UŽDUTIES VERTINIM INSTRUKIJA Pagrindinė sesija I dalis Kiekvienas
Vandentiekio ir nuotekų tinklų medžiagos Tinklų klojimas Tinklų renovacija. VGTU Vandentvarkos katedra Paruošė doc. dr.
 Vandentiekio ir nuotekų tinklų medžiagos Tinklų klojimas Tinklų renovacija VGTU Vandentvarkos katedra Paruošė doc. dr. Mindaugas Rimeika 1 Pagrindinis reikalavimas vandentiekio vamzdžiams, fasoninėms detalėms,
Vandentiekio ir nuotekų tinklų medžiagos Tinklų klojimas Tinklų renovacija VGTU Vandentvarkos katedra Paruošė doc. dr. Mindaugas Rimeika 1 Pagrindinis reikalavimas vandentiekio vamzdžiams, fasoninėms detalėms,
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
VERTINIMO INSTRUKCIJA 2008 m. valstybinis brandos egzaminas Pakartotinë sesija
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 008 m. birželio 7 d. įsakymu (.3.)-V-37 VERTINIM INSTRUKIJA 008 m. valstybinis brandos egzaminas I dalis Kiekvienas I dalies klausimas vertinamas tašku.
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 008 m. birželio 7 d. įsakymu (.3.)-V-37 VERTINIM INSTRUKIJA 008 m. valstybinis brandos egzaminas I dalis Kiekvienas I dalies klausimas vertinamas tašku.
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra. Gintaras Skersys. Mokymo priemonė
 Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
Vilniaus universitetas Matematikos ir informatikos fakultetas Informatikos katedra Gintaras Skersys Klaidas taisančių kodų teorija Mokymo priemonė Vilnius 2005 I dalis Pagrindinės savokos 1 Įvadas Panagrinėkime
2 laboratorinis darbas. TIKIMYBINIAI MODELIAI
 laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
laboratorns darbas laboratorns darbas. TIKIMYBINIAI MODELIAI DARBO TIKSLAS - šstudjuot atstktnų dydžų r vektorų skrstnus, skrstno (passkrstymo) funkcją, tanko funkcją, skatnes charakterstkas r jų savybes.
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai
 1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė
 Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Ekonometrija. Trendas ir sezoninė laiko eilutės komponentė dėst. T. Rekašius, 2012 m. lapkričio 19 d. 1 Duomenys Visi trečiam laboratoriniam darbui reikalingi duomenys yra tekstinio formato failuose http://fmf.vgtu.lt/~trekasius/destymas/2012/ekomet_lab3_xx.dat,
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
JONAS DUMČIUS TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA
 JONAS DUMČIUS (1905 1986) TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA 1975 metais rotaprintu spausdintą vadovėlį surinko klasikinės filologijos III kurso studentai Lina Girdvainytė Aistė Šuliokaitė Kristina
JONAS DUMČIUS (1905 1986) TRUMPA ISTORINĖ GRAIKŲ KALBOS GRAMATIKA 1975 metais rotaprintu spausdintą vadovėlį surinko klasikinės filologijos III kurso studentai Lina Girdvainytė Aistė Šuliokaitė Kristina
11 klasei Pirmas skyrius MATEMATIKA. tempus. Bendrasis ir išplėstinis kursas
 11 klasei Pirmas skyrius MATEMATIKA tempus Bendrasis ir išplėstinis kursas MATEMATIKA tempus Bendrasis ir išplėstinis kursas 11 klasei Pirmas skyrius UDK 51(075.3) Ma615 Autoriai: VILIJA DABRIŠIENĖ, MILDA
11 klasei Pirmas skyrius MATEMATIKA tempus Bendrasis ir išplėstinis kursas MATEMATIKA tempus Bendrasis ir išplėstinis kursas 11 klasei Pirmas skyrius UDK 51(075.3) Ma615 Autoriai: VILIJA DABRIŠIENĖ, MILDA
