Παίγνια. Κώστας Ρουµανιάς. Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών Οικονοµικό Πανεπιστήµιο Αθηνών. 14 Μαΐου 2015
|
|
|
- Λυσιστράτη Γιάγκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κώστας Ρουµανιάς Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών Οικονοµικό ανεπιστήµιο Αθηνών 14 Μαΐου 21 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 1 / 6
2 Ορισµός Τί είναι παίγνιο; αίγνιο: Μαθηµατική (αυστηρή) αναπαράσταση/ανάλυση συµπεριφοράς δρώντων όταν υπάρχουν ΣΤΡΑΤΗΓΙΚΕΣ ΑΛΛΗΛΕΙ ΡΑΣΕΙΣ. αραπάνω ορισµός: Γενικός. Χρειαζόµαστε κάποια συστατικά για να περιγράψουµε ένα παίγνιο. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 2 / 6
3 Ορισµός Από τί αποτελείται ένα παίγνιο; Για να περιγράψουµε ένα παίγνιο χρειαζόµαστε να ξέρουµε: 1 Τους παίκτες: οιοι συµµετέχουν..χ. λευρά Α και πλευρά Β σε ένα παίγνιο εξοπλισµών. Η δύο ή περισσότερα µέρη σε µία διµερή ή πολυµερή διαπραγµάτευση. Ασπρος-µαύρος στο σκάκι. 2 Τους κανόνες: οιος κινείται και πότε; Τί γνώση έχει ο κάθε παίκτης τη στιγµή που κινείται. οιες κινήσεις επιτρέπονται κλπ..χ. κινείται πρώτα ο µαύρος και πρέπει να κινήσει πιόνια ή ίππους... 3 Τις πιθανές εκβάσεις του παιγνίου: Μπορεί να νικήσει ο Α, ο Μ ή να έρθουν ισοπαλία. 4 Τις αποδόσεις: όσο αποτιµά ο κάθε παίκτης την κάθε πιθανή έκβαση..χ. στοίχηµα 1 για κορώνα γράµµατα: U(Κορώνα) = 1, U(Γράµµατα) = 1. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 3 / 6
4 Είδη παιγνίων Είδη παιγνίων: Συνεργατικά και µή συνεργατικά παίγνια. Με κριτήριο το αν οι παίκτες µπορούν να συνάψουν δεσµευτικά συµβόλαια τα παίγνια διακρίνονται σε: 1 Συνεργατικά (δυνατή η σύναψη δεσµευτικών συµφωνιών) 2 Μή συνεργατικά (δε γίνεται να συναφθούν δεσµευτικές συµφωνίες). Εµείς ϑα ασχοληθούµε µόνο µε µη συνεργατικά παίγνια. Γιατί; Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 4 / 6
5 Είδη παιγνίων Είδη παιγνίων: Στατικά και δυναµικά παίνγια. Με κριτήριο το αν τα παίνγια παίζονται ταυτόχρονα ή δοµούνται στο χρόνο, διακρίνονται σε: 1 Ταυτόχρονα ή στατικά παίγνια (έτρα ψαλίδι χαρτί) 2 υναµικά παίγνια: (π.χ. παίγνια απειλής και αντίδρασης). Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 / 6
6 Είδη παιγνίων Είδη παιγνίων: αίγνια τέλειας και ατελούς πληροφόρησης. Με κριτήριο το αν οι παίκτες έχουν τέλεια ή ατελή πληροφόρηση, τα παίγνια διακρίνονται σε: 1 αίγνια τέλειας πληροφόρησης. 2 αίγνια ατελούς πληροφόρησης. Εµείς ϑα ασχοληθούµε µόνο µε παίγνια τέλειας πληροφόρησης. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 6 / 6
7 Είδη παιγνίων αίγνια Συνεργατικά Μη συνεργατικά Τέλειας πληροφόρησης Ατελούς πληροφόρησης Στατικά Δυναμικά Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 7 / 6
8 Είδη παιγνίων Μορφές αναπαράστασης παιγνίων: αίγνια στρατηγικής ή κανονικής µορφής. Για τα στατικά παίγνια 2 παικτών χρησιµοποιούµε µια απλή µορφή απεικόνισής τους: πίνακας αποδόσεων. χ. αίκτης1 (γραµµή) έχει τρεις κινήσεις:, Μ ή Κ. αίκτης 2 (στήλη) έχει τρεις κινήσεις: Α ή : Κάθε κελί του πίνακα αντιστοιχεί σε µία έκβαση. Μέσα σε κάθε κελί γράφουµε τις αποδόσεις των δύο παικτών (πρώτα του γραµµή). Στα στατικά παίγνια κάθε κίνηση αποτελεί και τη στρατηγική του παίκτη. Α 1,1,3 Μ 3, 2,2 Κ 21, 22,2 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 8 / 6
9 Κυριαρχία Λύσεις παιγνίων: Κυριαρχία. Μερικές ϕορές κάποια παίγνια έχουν προφανή τρόπο να παιχθούν: Μία στρατηγική µου είναι πάντοτε καλύτερη από τις υπόλοιπες: Θα παίξω αυτήν. Μια τέτοια στρατηγική ονοµάζεται κυρίαρχη. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 9 / 6
10 Κυριαρχία Κυριαρχούµενες/Κυρίαρχες στρατηγικές Το δίληµµα του κρατουµένου. «ύο κρατούµενοι ανακρίνονται χωριστά. Αν και οι δύο δε µιλήσουν (αν συνεργαστούν µεταξύ τους), ϕυλακίζονται για ένα χρόνο. Αν ο ένας δώσει στις αρχές ενοχοποιητικά στοιχεία (προδώσει), τότε αυτός που πρόδωσε ελευθερώνεται ενώ ο άλλος ϕυλακίζεται για 9 χρόνια. Αν και οι δύο προδώσουν, τότε ϕυλακίζονται για έξι χρόνια. Οι προτιµήσεις τους εξαρτώνται µόνο από το χρόνο ϕυλάκισης που εκτίουν». αίκτες: Οι δύο κρατούµενοι N = {1, 2}. Στρατηγικές: Τα σύνολα στρατηγικών είναι S i = {Σ,} για κάθε παίκτη i {1, 2}. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 1 / 6
11 Κυριαρχία Κυριαρχούµενες/Κυρίαρχες στρατηγικές Ας δούµε τις αποδόσεις τους σε πίνακα στρατηγικής µορφής: Σ Σ 1, 1 9,, 9 6, 6 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
12 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
13 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
14 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
15 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 1 / 6
16 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
17 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
18 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
19 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
20 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 2 / 6
21 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Σ Σ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
22 Κυριαρχία Κυρίαρχες στρατηγικές στο δίληµµα του κρατουµένου Το είναι αυστηρώς κυρίαρχη στρατηγική για κάθε παίκτη. Το Σ είναι αυστηρώς κυριαρχούµενη στρατηγική. ηλαδή το είναι προτιµότερο του Σ ανεξαρτήτως του τί κάνει ο αντίπαλος. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
23 Το δίληµµα του κρατουµένου Συνεργασία σε περιβάλλον που υποθάλπει την αθέτηση. Γιατί το δίληµµα του κρατουµένου έχει χαίρει τόσης αναγνωρισιµότητας; Αποτυπώνει ευκρινώς καταστάσεις στις οποίες και τα δύο µέρη µπορεί να ωφεληθούν από συνεργασία, αλλά και οι δύο έχουν κίνητρο να «κλέψουν». Κούρσα εξοπλισµών. Σκεφτείτε µια παραλλαγή του διλήµµατος. ύο γείτονες χώρες µε τεταµένες σχέσεις αποφασίζουν αν ϑα επενδύσουν περαιτέρω σε εξοπλισµούς. Αν κανείς από τους δύο δεν επενδύσει και οι δύο µπορούν να κατευθύνουν πόρους σε άλλες δραστηριότητες που προτιµούν. Ωστόσο ό,τι κι αν κάνει ο αντίπαλος ατοµικά προτιµούν να επενδύσουν: αν επενδύσω µόνος µου χαίρω ηγεµονίας. Αν επενδύσεις εσύ ϑέλω να επενδύσω κι εγώ για να αποφύγω την κηδεµονία σου. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
24 Το δίληµµα του κρατουµένου Εξοπλιστικός ανταγωνισµός ως δίληµµα του κρατουµένου Ηνωµένες ολιτείες Αφοπλισµός Εξοπλισµός Σοβιετική Ενωση Αφοπλισµός 3, 3 1, 4 Εξοπλισµός 4, 1 2, 2 Γιατί µας ενδιαφέρει στρατηγική σε πιθανή διαπραγµάτευση; Βλέπουµε ότι ενώ µια συµφωνία σε [Αφοπλισµός, Αφοπλισµός] ϐελτιώνει τη ϑέση και των δύο, έχουµε και οι δύο κίνητρο να ϕύγουµε για να αυξήσουµε τις αποδόσεις µας ΑΝΕΞΑΡΤΗΤΩΣ ΤΟΥ ΤΙ ΚΑΝΕΙ Ο ΑΛΛΟΣ. ώς µπορούµε να κινηθούµε προς συµφωνία; Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
25 Το δίληµµα του κρατουµένου ιδάγµατα από το. του Κ. Το. του Κ. µας δίνει µια καλή αποτύπωση των αντίρροπων δυνάµεων ανάµεσα σε συνεργασία και παρέκκλιση. αρά τα προφανή ωφέλη της συνεργασίας σε ΣΤΑΤΙΚΟ περιβάλλον, όταν το παίγνιο παίζεται µόνο µια ϕορά, υπάρχει ισχυρή ϱοπή προς την παρέκκλιση και τον ανταγωνισµό. Θα πρέπει να ξαναδούµε το Ϲήτηµα υπό το πρίσµα µιας σταθερής διαχρονικής συνεργασίας. Η προοπτική του µέλλοντος (χρόνος) αλλάζει πολλά. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 2 / 6
26 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Οταν µια στρατηγική είναι κυριαρχούµενη σηµαίνει ότι ανεξαρτήτως του τί παίζουν οι άλλοι παίκτες, η στρατηγική αυτή είναι χειρότερη από τουλάχιστον µία άλλη. αρένθεση. Οταν είναι κυρίαρχη, είναι καλύτερη από ΟΛΕΣ ΤΙΣ ΑΛΛΕΣ, ανεξαρτήτως του τι παίζουν οι άλλοι παίκτες. Αυτό σηµαίνει ότι µια κυριαρχούµενη (αυστηρώς) στρατηγική δε ϑα την επιλέγει ποτέ ένας ορθολογικός παίκτης. Ας πούµε ότι ο παίκτης 1 είναι ορθολογικός. Αυτό σηµαίνει ότι αν έχει κυριαρχούµενη στρατηγική, µπορούµε να τη διαγράψουµε. Αρα και ο παίκτης 2 ϑα ξέρει ότι η κυριαρχούµενη στρατηγική του παίκτη 1 δε ϑα παικτεί ποτέ και άρα είναι σα να διαγράφεται από το παιχνίδι. Στο νέο παιχνίδι που µένει µπορούµε να διαγράψουµε τις στρατηγικές που είναι κυριαρχούµενες κ.ο.κ. έως ότου να µην υπάρχουν πια κυριαρχούµενες στρατηγικές. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
27 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
28 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
29 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
30 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 3 / 6
31 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
32 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
33 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
34 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
35 Το δίληµµα του κρατουµένου Επαναλαµβανόµενη διαγραφή κυριαρχούµενων στρατηγικών Α Κ Δ M 3 6 Κ 2 8 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 3 / 6
36 Ισορροπία Nash Η µάχη των ϕύλων ολλές ϕορές δεν είναι προφανές ότι πρέπει να παίξουµε πάντοτε (ό,τι κι αν κάνει ο αντίπαλος) µε ένα συγκεκριµένο τρόπο. Ο Γιάγκος και η Βαλεντίνη είναι ένα νέο Ϲευγάρη που ϑέλει να ϐγει το ϐράδυ. Βασικό τους µέληµα να ϐρεθούν. Εχουν δύο επιλογές: Box ή Opera. Ο Γιάγκος (γραµµή) και η Βαλεντίνη (στήλη) έχουν τις εξής αποδόσεις: Βαλεντίνη Box Opera Γιάγκος Box 2, 1, Opera, 1, 2 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
37 Ισορροπία Nash Η µάχη των ϕύλων Βαλεντίνη Box Opera Γιάγκος Box 2, 1, Opera, 1, 2 Τώρα δεν είναι ξεκάθαρο ότι ο Γιάγκος ή η Βαλεντίνη προτιµάει πάντοτε τη µία στρατηγική. Το τί ϑέλει να παίξει εξαρτάται και από το τί ϑα παίξει ο άλλος παίκτης (στρατηγική αλληλεξάρτηση). Αν είµαστε σίγουροι ότι η Βαλεντίνη ϑα παίξει Opera ( εξιά), προτιµάµε να παίξουµε κι εµείς Opera, γιατί ενδιαφερόµαστε πιο πολύ να ϐρεθούµε. Βασικός στόχος να «ϐρεθούµε» και δευτερευόντως στο χώρο που προτιµάµε. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
38 αραδείγµατα παιγνίων Ισορροπία Nash Βαλεντίνη Box Opera Γιάγκος Box 2, 1, Opera, 1, 2 εν υπάρχει καταφανώς κυρίαρχη στρατηγική. ώς λύνεται το παίγνιο; ΙΣΟΡΡΟΙΑ NASH. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
39 αραδείγµατα παιγνίων Ισορροπία Nash Βαλεντίνη Box Opera Γιάγκος Box 2, 1, Opera, 1, 2 Το {Box, Box} είναι ισορροπία Nash. Το ίδιο και το {Opera, Opera } (δύο ισορροπίες στο παίγνιο). Ισορροπία Nash: Κανένας δε ϑέλει να ϕύγει ΜΟΝΟΜΕΡΩΣ. Το {Box} είναι άριστο για το Γιάγκο δεδοµένου του {Box} της Ιταλίας και αντιστρόφως. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
40 αραδείγµατα παιγνίων αίγνιο σύγκρουσης: Chicken ή το γεράκι και το περιστέρι ύο µέλη µιας συµµορίας διεκδικούν την αρχηγία. Κινούνται ο ένας προς τον άλλον µε ταχύτητα µέσα σε αυτοκίνητα. Κάθε µαχητής µπορεί είτε να συνεχίσει επιθετικά ως το τέλος (να παίξει το «γεράκι»), είτε να υποταχθεί (να παίξει «περιστέρι»). Αν και οι δύο παίξουν περιστέρι µοιράζονται την αρχηγία. Αν ο ένας παίξει γεράκι και ό άλλος περιστέρι, το γεράκι νικάει το περιστέρι. Αν και οι δύο παίξουν Γεράκι, διαλύουν τα αυτοκίνητά τους, καταλήγουν στο νοσοκοµείο και χάνουν την αρχηγία. αίκτες: Οι δύο µαχητές. N = {1, 2}. Στρατηγικές: κάθε παίκτης επιλέγει Γεράκι ή εριστέρι: S i = {Γεράκι, εριστέρι} για i = 1, 2. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 4 / 6
41 αραδείγµατα παιγνίων αραδείγµατα Ισορροπιών Nash. Chicken ή «το γεράκι και το περιστέρι» Αποδόσεις: δίνονται από τον παρακάτω πίνακα µαζί µε τις ισορροπίες Nash. Γεράκι εριστέρι Γεράκι 1, 1 1, εριστέρι, 1, Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
42 αραδείγµατα παιγνίων Οταν η δύναµη είναι αδυναµία αράδειγµα από ψυχολογία Ϲώων. Τα γουρούνια εδραιώνουν σχέσεις κυριαρχίας. Μεταξύ δύο γουρουνιών το ένα είναι κυρίαρχο και το άλλο υποτελές Βιολόγοι έβαλαν 2 γουρούνια σε µακρόστενο κλουβί. Στη µία άκρη µοχλός που ελευθέρωνε ϕαΐ στην άλλη άκρη. οιο γουρούνι ϑα έσπρωχνε το µοχλό και ποιο ϑα έτρωγε το ϕαΐ; Με έκπληξη διαπιστώθηκε ότι το κυρίαρχο γουρούνι τραβούσε το µοχλό και το υποτελές έτρωγε τη µερίδα του «λέοντος». Γιατί; Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
43 αραδείγµατα παιγνίων Οταν η δύναµη είναι αδυναµία και το αντίστροφο Κυρίαρχο Γουρούνι εν πιέζει ιέζει Υποτελές γουρούνι εν πιέζει, 4, 1 ιέζει 1, 2, 3 Το υποτελές γουρούνι (γραµµή) συγκρίνει τις στρατηγικές του και ϐλέπει ότι το συµφέρει να µην πιέσει. Αν πιέσει το κυρίαρχο ϑα προλάβει να πάει στο ϕαΐ και το υποτελές ϑα υποστεί το κόστος του να πιέσει χωρίς να ϕάει. Συγκρίνει (,4) µε ( 1, 2) και ϐλέπει ότι το συµφέρει να µην πιέσει. Αν το κυρίαρχο γουρούνι µπορούσε να κρατηθεί και να αφήσει το υποτελές να ϕάει, το υποτελές ϑα ήθελε να πιέσει. Αλλά δε µπορούν να υπογράψουν συµβόλαιο και δε µπορούν να πάψουν να είναι γουρούνια! Μοναδική ισορροπία Nash το [ εν πιέζει, πιέζει]. Το υποτελές τρώει το περισσότερο ϕαΐ. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
44 αραδείγµατα παιγνίων Κυνήγι ελαφιού/λαγού Κυνήγι ελαφιού: υο κυνηγοί ταυτόχρονα αποφασίζουν αν ϑα κυνηγήσουν ελάφι ή λαγό. Για να πιάσουν ελάφι χρειάζεται συντονισµός: πρέπει και οι δύο να κυνηγήσουν µαζί στην ίδια περιοχή. Το ελάφι δίνει πολύ κρέας. Λαγό µπορεί να κυνηγήσει ο καθένας µόνος αλλά ϑα έχει λιγότερο κρέας, ιδιαίτερα αν κυνηγήσουν και οι δύο λαγό. αίκτες: Οι δύο κυνηγοί N = {1, 2}. Στρατηγικές: Τα σύνολα στρατηγικών είναι S i = {Ε, Λ} για κάθε παίκτη i {1, 2}. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
45 αραδείγµατα παιγνίων Το κυνήγι του ελαφιού και του λαγού ληρωµές. Ας δούµε τις πληρωµές τους σε πίνακα στρατηγικής µορφής: Ε Λ Ε 1,1,3 Λ 3, 2,2 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 4 / 6
46 αραδείγµατα παιγνίων ροφίλ στρατηγικών Ορισµός (ροφίλ στρατηγικών) Για ένα παίγνιο n παικτών, προφίλ στρατηγικών είναι ένα διάνυσµα n στρατηγικών, µίας για κάθε παίκτη. αραδείγµατος χάριν, ένα προφίλ ϑα µπορούσε να είναι για το παίγνιο του ελαφιού το διάνυσµα {Ε,Λ}. Ενα άλλο προφίλ το διάνυσµα {Λ,Λ} κ.ο.κ. Αν ο π.αίκτης 1 έχει 3 στρατηγικές και ο παίκτης 2 στρατηγικές, ϑα έχουµε συνολικά 2 3 = 6 προφίλ στρατηγικών στο παίγνιο. Ενα προφίλ (αµιγών) στρατηγικών συµβολίζεται [s 1, s 2..., s i..., s n ] Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
47 αραδείγµατα παιγνίων Αριστες αποκρίσεις Ορισµός ( Αριστη απόκριση) Αριστη απόκριση για τον παίκτη i είναι ένας κανόνας που µας δίνει ποια είναι η πιο συµφέρουσα στρατηγική για τον i ως απάντηση σε ένα προφίλ στρατηγικών όλων των άλλων παικτών ( i). Με άλλα λόγια: Η άριστη συνάρτηση δίνει τη άριστη στρατηγική s i του παίκτη i όταν οι άλλοι παίκτες παίζουν s i. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
48 αραδείγµατα παιγνίων Αριστες αποκρίσεις-best responses: το κυνήγι του ελαφιού Ας δούµε όµως τις άριστες αποκρίσεις των παικτών. ληρωµές: Οι πληρωµές (κάτω αριστερά για τον γραµµή και πάνω δεξιά για τον στήλη) είναι η συνάρτηση χρησιµότητας του καθενός: u : S R. Ε Λ Ε Λ Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
49 αραδείγµατα παιγνίων Αριστες αποκρίσεις Ας συµβολίσουµε τις άριστες αποκρίσεις του γραµµή µε πράσινο. Ε Λ Ε 1,1,3 Λ 3, 2,2 και τις άριστες αποκρίσεις του στήλη µε κόκκινο. Ε Λ Ε 1,1,3 Λ 3, 2,2 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου / 6
50 αραδείγµατα παιγνίων Αριστες αποκρίσεις Ας δούµε άριστες αποκρίσεις για το παιχνίδι έτρα, Ψαλίδι, Χαρτί. Ψ Χ, 1,,1 Ψ,1, 1, Χ 1,,1, ίνακας : Το παιχνίδι πέτρα, ψαλίδι, χαρτί σε κανονική µορφή. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 / 6
51 αραδείγµατα παιγνίων Αριστες αποκρίσεις Ορισµός (Ισορροπία Nash-σε αµιγείς στρατηγικές) Μια ισορροπία Nash ενός παιγνίου είναι ένα προφίλ στρατηγικών s S τέτοιο ώστε για κάθε παίκτη i N: u i (s i, s i ) u i(s i, s i ) 3 ερµηνείες της ισορροπίας Nash: Η ισορροπία Nash είναι ένα προφίλ στρατηγικών (µια για κάθε παίκτη), τέτοιο ώστε η στρατηγική του κάθε παίκτη είναι άριστη απόκριση στις υπόλοιπες στρατηγικές του προφίλ. Αν δηλαδή οι υπόλοιποι παίκτες παίζουν το προφίλ ισορροπίας, τότε και ο παίκτης i ϑέλει να παίξει τη στρατηγική του προφίλ. Αλλιώς: αν όλοι παίζουν το προφίλ, κανένας δεν ϑέλει να ϕύγει από το προφίλ ΜΟΝΟΜΕΡΩΣ. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 1 / 6
52 Τί προσφέρει η ισορροπία Nash; Ισορροπία Nash όσο καλή λύση είναι; Μπορούµε να δούµε την ισορροπία Nash ως πρόβλεψη του πώς ϑα παιχτεί ένα παίγνιο; ολλές ϕορές σε παίγνια υπάρχουν δύο ισορροπίες Nash. Αυτό σηµαίνει ότι το παίγνιο παίζεται µε δύο τρόπους; Εν µέρει ναι. Σκεφτείτε το πώς οδηγούµε. Ας πούµε ότι δεν υπήρχε νόµος να οδηγούµε δεξιά και αύριο το πρωί ϑα έπρεπε δύο από εµάς να επιλέξουν σε ποια πλευρά του δρόµου ϑα οδηγούσαν. Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 2 / 6
53 Τί προσφέρει η ισορροπία Nash; Απόφαση πλευράς οδήγησης Α Α 1, 2 1, 1 1, 1 1, 2 Αν οι δύο παίκτες συντονιστούν (παίξουν (Α,Α) ή (, ) ) ϑα ϕτάσουν στη δουλειά τους. Ο γραµµή ϑα κερδίσει µισθό 1 και ο στήλη µισθό 2. Αν δε συντονιστούν ϑα συγκρουστούν και ϑα πληρώσουν από 1 για επισκευές των αυτοκινήτων τους. Ισορροπίες Nash: (Α,Α) και (, ). Η ισορροπία ash προβλέπει ότι κάποιοι ϑα συντονιστούν αριστερά (Ελλάδα) και κάποιοι δεξιά (Αγγλία). ροβλέπει ότι ως κοινωνική σύµβαση ϑα υιοθετήσουµε ή τη µία ή την άλλη ισορροπία. ε µπορεί να προβλέψει µε ποιον από τους δύο τρόπους ϑα παιχτεί αλλά λέει ότι ϑα παιχτεί µε έναν από τους δύο. Οπως και παίζεται σε όλες τις χώρες του κόσµου! Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 3 / 6
54 Τί προσφέρει η ισορροπία Nash; Ισορροπία Nash όσο καλή λύση είναι; Οταν δεν υπάρχει ισορροπία σε ένα παίγνιο; Σκεφτείτε το παίγνιο ενός τερµατοφύλακα µε έναν επιθετικό που χτυπάει πέναλτυ. Ας απλουστεύσουµε υποθέτοντας ότι αν ο τερµατοφύλακας πέσει στη σωστή µεριά πιάνει τη µπάλα, ενώ αν όχι µπαίνει γκολ. Το στοίχηµα είναι 1 Τερµατοφύλακας Α Επιθετικός Α 1, 1 1, 1 1, 1 1, 1 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 4 / 6
55 Τί προσφέρει η ισορροπία Nash; Οταν δεν υπάρχει ισορροπία Αποκλείεται και οι δύο να ϑέλουν να µείνουν στο ίδιο κελί. εν υπάρχει ισορροπία σε αµιγείς στρατηγικές. άντοτε κάποιος ϑέλει να ϕύγει ΜΟΝΟΜΕΡΩΣ. Α Τερματοφύλακας Δ Α 1 1 Επιθετικός Δ 1 1 Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 / 6
56 Τί προσφέρει η ισορροπία Nash; Οταν δεν υπάρχει ισορροπία Τερµατοφύλακας Α Επιθετικός Α 1, 1 1, 1 1, 1 1, 1 Αυτό σηµαίνει ότι η ϑεωρία παιγνίων δεν προβλέπει πώς ϑα παιχτεί το παίγνιο; Οχι, προβλέπεται ότι ϑα παιχτεί στην τύχη. Ορίζονται ισορροπίες Nash σε µεικτές (τυχαίες) στρατηγικές. Οπως αποδεικνύεται κάνουν προβλέψεις πολύ κοντά στην αλήθεια. Αλλά αυτό είναι έξω από το αντικείµενό µας... Κώστας Ρουµανιάς (Ο..Α.) αίγνια 14 Μαΐου 21 6 / 6
Notes. Notes. Notes. Notes Ε 10,10 0,3 Λ 3,0 2,2
 Θεωρία παιγνίων: Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία παιγνίων: 3 Δεκεμβρίου 2012 1 / 21 -best responses Κυνήγι ελαφιού: Δυο κυνηγοί ταυτόχρονα
Θεωρία παιγνίων: Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία παιγνίων: 3 Δεκεμβρίου 2012 1 / 21 -best responses Κυνήγι ελαφιού: Δυο κυνηγοί ταυτόχρονα
Notes. Notes. Notes Σ -1,-1-9,0 Π 0,-9-6,-6. Notes Σ Π
 Θεωρία αιγνίων-υριαρχία ώστας Ρουμανιάς Ο..Α. Τμήμα Δ. Ε. Ο.. Δεκεμβρίου 1 ώστας Ρουμανιάς (Δ.Ε.Ο..) Θεωρία αιγνίων-υριαρχία Δεκεμβρίου 1 1 / Λύσεις αιγνίων. υριαρχούμενες/υρίαρχες στρατηγικές Το δίλημμα
Θεωρία αιγνίων-υριαρχία ώστας Ρουμανιάς Ο..Α. Τμήμα Δ. Ε. Ο.. Δεκεμβρίου 1 ώστας Ρουμανιάς (Δ.Ε.Ο..) Θεωρία αιγνίων-υριαρχία Δεκεμβρίου 1 1 / Λύσεις αιγνίων. υριαρχούμενες/υρίαρχες στρατηγικές Το δίλημμα
Κυριαρχία και μεικτές στρατηγικές Μεικτές στρατηγικές και κυριαρχία Είδαμε ότι μια στρατηγική του παίκτη i είναι κυριαρχούμενη, αν υπάρχει κάποια άλλη
 Θεωρία παιγνίων: Μεικτές στρατηγικές και Ισορροπία Nash Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 18 Μαρτίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Μεικτές στρατηγικές 18 Μαρτίου 2012 1 / 9 Κυριαρχία και μεικτές
Θεωρία παιγνίων: Μεικτές στρατηγικές και Ισορροπία Nash Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 18 Μαρτίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Μεικτές στρατηγικές 18 Μαρτίου 2012 1 / 9 Κυριαρχία και μεικτές
Κεφάλαιο 29 Θεωρία παιγνίων
 HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 29 Θεωρία παιγνίων Ύλη για τη Μίκρο ΙΙ: κεφάλαιο 29.1, 29.2, 29.4, 29.7, 29.8 Κεφάλαιο 29 Θεωρία παιγνίων Ταυτόχρονα
HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 29 Θεωρία παιγνίων Ύλη για τη Μίκρο ΙΙ: κεφάλαιο 29.1, 29.2, 29.4, 29.7, 29.8 Κεφάλαιο 29 Θεωρία παιγνίων Ταυτόχρονα
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 2: Έννοιες λύσεων σε παίγνια κανονικής μορφής. Ε. Μαρκάκης. Επικ. Καθηγητής
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 2: Έννοιες λύσεων σε παίγνια κανονικής μορφής Ε. Μαρκάκης Επικ. Καθηγητής Λύσεις παιγνίων 2 Επιλέγοντας στρατηγική... Δεδομένου ενός παιγνίου, τι στρατηγική πρέπει
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 2: Έννοιες λύσεων σε παίγνια κανονικής μορφής Ε. Μαρκάκης Επικ. Καθηγητής Λύσεις παιγνίων 2 Επιλέγοντας στρατηγική... Δεδομένου ενός παιγνίου, τι στρατηγική πρέπει
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 3: Παίγνια με περισσότερους παίκτες και μέθοδοι απλοποίησης παιγνίων. Ε. Μαρκάκης. Επικ.
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 3: Παίγνια με περισσότερους παίκτες και μέθοδοι απλοποίησης παιγνίων Ε. Μαρκάκης Επικ. Καθηγητής Παίγνια πολλών παικτών 2 Παίγνια με > 2 παίκτες Όλοι οι ορισμοί που
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 3: Παίγνια με περισσότερους παίκτες και μέθοδοι απλοποίησης παιγνίων Ε. Μαρκάκης Επικ. Καθηγητής Παίγνια πολλών παικτών 2 Παίγνια με > 2 παίκτες Όλοι οι ορισμοί που
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 ΚΟΙΝΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ Players-Παίκτες Rules- Κανόνες. Τιµωρείσαι εάν τους παραβιάσεις.
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΕΥΤΕΡΟ- ΚΥΡΙΑΡΧΟΥΜΕΝΗ ΣΤΡΑΤΗΓΙΚΗ- PRISONER S DILLEMA ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 ΚΟΙΝΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ Players-Παίκτες Rules- Κανόνες. Τιµωρείσαι εάν τους παραβιάσεις.
Μικτές Στρατηγικές σε Παίγνια και σημεία Ισορροπίας Nash. Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1
 Μικτές Στρατηγικές σε Παίγνια και σημεία Ισορροπίας Nash Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1 Σημεία ισορροπίας Nash: Yπάρχουν πάντα; Έχουν όλα τα παίγνια σημείο ισορροπίας; - Ναι, στην εξιδανικευμένη
Μικτές Στρατηγικές σε Παίγνια και σημεία Ισορροπίας Nash Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1 Σημεία ισορροπίας Nash: Yπάρχουν πάντα; Έχουν όλα τα παίγνια σημείο ισορροπίας; - Ναι, στην εξιδανικευμένη
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 4: Μεικτές Στρατηγικές. Ε. Μαρκάκης. Επικ. Καθηγητής
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 4: Μεικτές Στρατηγικές Ε. Μαρκάκης Επικ. Καθηγητής Μεικτές στρατηγικές σε παίγνια 2 Σημεία ισορροπίας: Ύπαρξη Δεν έχουν όλα τα παίγνια σημείο ισορροπίας Π.χ. Το Matching
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 4: Μεικτές Στρατηγικές Ε. Μαρκάκης Επικ. Καθηγητής Μεικτές στρατηγικές σε παίγνια 2 Σημεία ισορροπίας: Ύπαρξη Δεν έχουν όλα τα παίγνια σημείο ισορροπίας Π.χ. Το Matching
Κεφάλαιο 5 R (2, 3) R (3, 0)
 Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
10/3/17. Μικροοικονομική. Κεφάλαιο 29 Θεωρία παιγνίων. Μια σύγχρονη προσέγγιση. Εφαρµογές της θεωρίας παιγνίων. Τι είναι τα παίγνια;
 HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 29 Θεωρία παιγνίων Θεωρία παιγνίων Η θεωρία παιγνίων βοηθά στην ανάλυση της στρατηγικής συμπεριφοράς από φορείς που κατανοούν ότι οι
HA. VAIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 29 Θεωρία παιγνίων Θεωρία παιγνίων Η θεωρία παιγνίων βοηθά στην ανάλυση της στρατηγικής συμπεριφοράς από φορείς που κατανοούν ότι οι
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 2 η Διάλεξη Παίγνια ελλιπούς πληροφόρησης Πληροφοριακά σύνολα Κανονική μορφή παιγνίου Ισοδύναμες στρατηγικές Παίγνια συνεργασίας και μη συνεργασίας Πεπερασμένα και
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 2 η Διάλεξη Παίγνια ελλιπούς πληροφόρησης Πληροφοριακά σύνολα Κανονική μορφή παιγνίου Ισοδύναμες στρατηγικές Παίγνια συνεργασίας και μη συνεργασίας Πεπερασμένα και
Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες
 Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Μαρτίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες 4 Μαρτίου 214 1 / 14 Ενα απλούστατο παίγνιο
Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Μαρτίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες 4 Μαρτίου 214 1 / 14 Ενα απλούστατο παίγνιο
Κεφάλαιο 4. Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία
 Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Κεφάλαιο 4 Στο προηγούµενο κεφάλαιο ορίσαµε την ισορροπία κατά Nash και είδαµε ότι µια ισορροπία κατά Nash είναι: (α) ένα διάνυσµα από στρατηγικές, έτσι ώστε δεδοµένων των υπολοίπων στρατηγικών, ο παίκτης
Βασικές Αρχές της Θεωρίας Παιγνίων
 Βασικές Αρχές της Θεωρίας Παιγνίων - Ορισμός. Αν οι επιλογές μιας επιχείρησης εξαρτώνται από την αναμενόμενη αντίδραση των υπόλοιπων επιχειρήσεων που συμμετέχουν στην αγορά, τότε υπάρχει στρατηγική αλληλεπίδραση
Βασικές Αρχές της Θεωρίας Παιγνίων - Ορισμός. Αν οι επιλογές μιας επιχείρησης εξαρτώνται από την αναμενόμενη αντίδραση των υπόλοιπων επιχειρήσεων που συμμετέχουν στην αγορά, τότε υπάρχει στρατηγική αλληλεπίδραση
Κεφάλαιο 9 ο Κ 5, 4 4, 5 0, 0 0,0 5, 4 4, 5. Όπως βλέπουµε το παίγνιο δεν έχει καµιά ισορροπία κατά Nash σε αµιγείς στρατηγικές διότι: (ΙΙ) Α Κ
 Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
Κεφάλαιο ο Μεικτές Στρατηγικές Τώρα θα δούµε ένα παράδειγµα στο οποίο κάθε παίχτης έχει τρεις στρατηγικές. Αυτό θα µπορούσε να είναι η µορφή που παίρνει κάποιος µετά που έχει απαλείψει όλες τις αυστηρά
HAL R. VARIAN. Μικροοικονομική. Μια σύγχρονη προσέγγιση. 3 η έκδοση
 HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 29 Θεωρία παιγνίων Θεωρία παιγνίων Η θεωρία παιγνίων βοηθά στην ανάλυση της στρατηγικής συμπεριφοράς από φορείς που κατανοούν ότι
HAL R. VARIAN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 29 Θεωρία παιγνίων Θεωρία παιγνίων Η θεωρία παιγνίων βοηθά στην ανάλυση της στρατηγικής συμπεριφοράς από φορείς που κατανοούν ότι
Κοινωνικά Δίκτυα Θεωρία Παιγνίων
 Κοινωνικά Δίκτυα Θεωρία Παιγνίων Ν. Μ. Σγούρος Τμήμα Ψηφιακών Συστημάτων, Παν. Πειραιώς sgouros@unipi.gr Ορισμοί Ένα Παίγνιο (game) ορίζεται ως μια δραστηριότητα με τα ακόλουθα τρία χαρακτηριστικά: Υπάρχει
Κοινωνικά Δίκτυα Θεωρία Παιγνίων Ν. Μ. Σγούρος Τμήμα Ψηφιακών Συστημάτων, Παν. Πειραιώς sgouros@unipi.gr Ορισμοί Ένα Παίγνιο (game) ορίζεται ως μια δραστηριότητα με τα ακόλουθα τρία χαρακτηριστικά: Υπάρχει
Κεφάλαιο 2ο (α) Αµιγείς Στρατηγικές (β) Μεικτές Στρατηγικές (α) Αµιγείς Στρατηγικές. Επαναλαµβάνουµε:
 Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
Κεφάλαιο 2 ο Μέχρι τώρα δώσαµε τα στοιχεία ενός παιγνίου σε µορφή δέντρου και σε µορφή µήτρας. Τώρα θα ορίσουµε τη στρατηγική στην αναλυτική µορφή του παιγνίου (η στρατηγική ορίζεται από κάθε στήλη ή γραµµή
Διάλεξη 7. Θεωρία παιγνίων VA 28, 29
 Διάλεξη 7 Θεωρία παιγνίων VA 28, 29 Θεωρία παιγνίων Στη θεωρία παιγνίων χρησιμοποιούμε υποδείγματα για τη στρατηγική συμπεριφορά των οικονομικών μονάδων που καταλαβαίνουν ότι οι ενέργειές τους επηρεάζουν
Διάλεξη 7 Θεωρία παιγνίων VA 28, 29 Θεωρία παιγνίων Στη θεωρία παιγνίων χρησιμοποιούμε υποδείγματα για τη στρατηγική συμπεριφορά των οικονομικών μονάδων που καταλαβαίνουν ότι οι ενέργειές τους επηρεάζουν
Kεφάλαιο 10. Πόσα υποπαίγνια υπάρχουν εδώ πέρα; 2 υποπαίγνια.
 Kεφάλαιο 10 Θα δούµε ένα δύο παραδείγµατα να ορίσουµε/ µετρήσουµε τα υποπαίγνια και µετά θα λύσουµε και να βρούµε αυτό που λέγεται τέλεια κατά Nash ισορροπία. Εδώ θα δούµε ένα παίγνιο όπου έχουµε µια επιχείρηση
Kεφάλαιο 10 Θα δούµε ένα δύο παραδείγµατα να ορίσουµε/ µετρήσουµε τα υποπαίγνια και µετά θα λύσουµε και να βρούµε αυτό που λέγεται τέλεια κατά Nash ισορροπία. Εδώ θα δούµε ένα παίγνιο όπου έχουµε µια επιχείρηση
δημιουργία: http://macedonia.uom.gr/~acg επεξεργασία: Ν.Τσάντας
 Θεωρία Παιγνίων Μελέτη στοιχείων που χαρακτηρίζουν καταστάσεις ανταγωνιστικής άλληλεξάρτησης με έμφαση στη διαδικασία λήψης αποφάσεων περισσοτέρων από ένα ληπτών απόφασης (αντιπάλων). Παίγνια δύο παικτών
Θεωρία Παιγνίων Μελέτη στοιχείων που χαρακτηρίζουν καταστάσεις ανταγωνιστικής άλληλεξάρτησης με έμφαση στη διαδικασία λήψης αποφάσεων περισσοτέρων από ένα ληπτών απόφασης (αντιπάλων). Παίγνια δύο παικτών
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 3 η Διάλεξη-Περιεχόμενα (1/2) Σημείο ή ζεύγος ισορροπίας κατά Nash Λύση ακολουθιακής κυριαρχίας και σημεία ισορροπίας Nash Αλγοριθμική εύρεση σημείων ισορροπίας
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 3 η Διάλεξη-Περιεχόμενα (1/2) Σημείο ή ζεύγος ισορροπίας κατά Nash Λύση ακολουθιακής κυριαρχίας και σημεία ισορροπίας Nash Αλγοριθμική εύρεση σημείων ισορροπίας
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Λύσεις 2η σειράς ασκήσεων Προθεσμία παράδοσης: 18 Μαίου 2015 Πρόβλημα 1. (14
Παιγνιακά Μοντέλα Σύγκρουσης και Συνεργασίας
 Επίκουρος Καθηγητής Ιωάννης Παραβάντης Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ Μάρτιος 2010 Παιγνιακά Μοντέλα Σύγκρουσης και Συνεργασίας 1. Εισαγωγή Στο παρόν φυλλάδιο παριστάνουµε περιπτώσεις
Επίκουρος Καθηγητής Ιωάννης Παραβάντης Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ Μάρτιος 2010 Παιγνιακά Μοντέλα Σύγκρουσης και Συνεργασίας 1. Εισαγωγή Στο παρόν φυλλάδιο παριστάνουµε περιπτώσεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Παρασκευή 16 Οκτωβρίου 2007 ιάρκεια εξέτασης: 3 ώρες (15:00-18:00) ΘΕΜΑ 1
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Παρασκευή 16 Οκτωβρίου 2007 ιάρκεια εξέτασης: 3 ώρες (15:00-18:00) ΘΕΜΑ 1
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενα Μαθήµατα: Παίχτες: είναι αυτοί που λαµβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΠΕΜΠΤΟ ΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενα Μαθήµατα: Παίχτες: είναι αυτοί που λαµβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
Κεφάλαιο 7ο. max(p 1 c)(α bp 1 +dp 2 )
 Κεφάλαιο 7ο Μιλήσαµε στο προηγούµενο κεφάλαιο για το τι θα συµβεί αν οι επιχειρήσεις ανταγωνίζονται σε τιµές. Επιπλέον µιλήσαµε για το πως αποδεικνύεται το παράδοξο του Bertrand και καθώς επίσης και για
Κεφάλαιο 7ο Μιλήσαµε στο προηγούµενο κεφάλαιο για το τι θα συµβεί αν οι επιχειρήσεις ανταγωνίζονται σε τιµές. Επιπλέον µιλήσαµε για το πως αποδεικνύεται το παράδοξο του Bertrand και καθώς επίσης και για
3 ΙΣΟΡΡΟΠΙΕΣ 3 ΙΣΟΡΡΟΠΙΕΣ
 Kεφάλαιο 11 Θα επαναλάβουµε αυτά που είχαµε πει την προηγούµενη φορά. Παραστατικά αν έχουµε το εξής παίγνιο όπου οι δύο παίχτες παίρνουν ταυτόχρονα τις αποφάσεις τους αφού αποφασίσει ο Ι, θα δούµε πόσα
Kεφάλαιο 11 Θα επαναλάβουµε αυτά που είχαµε πει την προηγούµενη φορά. Παραστατικά αν έχουµε το εξής παίγνιο όπου οι δύο παίχτες παίρνουν ταυτόχρονα τις αποφάσεις τους αφού αποφασίσει ο Ι, θα δούµε πόσα
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ EKΤΟ ΔΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ II ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ EKΤΟ ΔΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ II ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούμενα Μαθήματα: Παίχτες: είναι αυτοί που λαμβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ EKΤΟ ΔΥΝΑΜΙΚΑ ΠΑΙΓΝΙΑ ΠΛΗΡΟΥΣ ΠΛΗΡΟΦΟΡΗΣΗΣ II ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούμενα Μαθήματα: Παίχτες: είναι αυτοί που λαμβάνουν τις αποφάσεις. Ένα παίγνιο πρέπει
Λήψη απόφασης σε πολυπρακτορικό περιβάλλον. Θεωρία Παιγνίων
 Λήψη απόφασης σε πολυπρακτορικό περιβάλλον Θεωρία Παιγνίων Αβεβαιότητα παρουσία άλλου πράκτορα Μια άλλη πηγή αβεβαιότητας είναι η παρουσία άλλου πράκτορα στο περιβάλλον, ακόμα κι όταν ένας πράκτορας είναι
Λήψη απόφασης σε πολυπρακτορικό περιβάλλον Θεωρία Παιγνίων Αβεβαιότητα παρουσία άλλου πράκτορα Μια άλλη πηγή αβεβαιότητας είναι η παρουσία άλλου πράκτορα στο περιβάλλον, ακόμα κι όταν ένας πράκτορας είναι
Δεύτερο πακέτο ασκήσεων
 ΕΚΠΑ Τμήμα Οικονομικών Επιστημών Μικροοικονομική Θεωρία ΙΙ Εαρινό εξάμηνο Ακαδ. έτους 08-09 Αν. Παπανδρέου, Φ. Κουραντή, Ηρ. Κόλλιας Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 0 Μαϊου. Θα υπάρξει
ΕΚΠΑ Τμήμα Οικονομικών Επιστημών Μικροοικονομική Θεωρία ΙΙ Εαρινό εξάμηνο Ακαδ. έτους 08-09 Αν. Παπανδρέου, Φ. Κουραντή, Ηρ. Κόλλιας Δεύτερο πακέτο ασκήσεων Προθεσμία παράδοσης Παρασκευή 0 Μαϊου. Θα υπάρξει
* τη µήτρα. Κεφάλαιο 1o
 Κεφάλαιο 1o Θεωρία Παιγνίων Η θεωρία παιγνίων εξετάζει καταστάσεις στις οποίες υπάρχει αλληλεπίδραση µεταξύ ενός µικρού αριθµού ατόµων. Άρα σε οποιαδήποτε περίπτωση, αν ο αριθµός των ατόµων που συµµετέχουν
Κεφάλαιο 1o Θεωρία Παιγνίων Η θεωρία παιγνίων εξετάζει καταστάσεις στις οποίες υπάρχει αλληλεπίδραση µεταξύ ενός µικρού αριθµού ατόµων. Άρα σε οποιαδήποτε περίπτωση, αν ο αριθµός των ατόµων που συµµετέχουν
Κεφάλαιο 8 ο Τ 3, 1-1, -1 Χ -1, -1 1, 3
 Κεφάλαιο 8 ο Συνεχίζουµε µε τις µεικτές στρατηγικές. Θα δούµε τώρα ένα παράδειγµα στο οποίο υπάρχουνε ισορροπίες κατά Nash σε αµιγείς στρατηγικές αλλά πέρα από αυτό υπάρχει και µια ισορροπία κατά Nash
Κεφάλαιο 8 ο Συνεχίζουµε µε τις µεικτές στρατηγικές. Θα δούµε τώρα ένα παράδειγµα στο οποίο υπάρχουνε ισορροπίες κατά Nash σε αµιγείς στρατηγικές αλλά πέρα από αυτό υπάρχει και µια ισορροπία κατά Nash
- Παράδειγμα 2. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να
 - Παράδειγμα. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να αποκρούσει ένας τερματοφύλακας. - Αν οι δύο παίκτες επιλέξουν
- Παράδειγμα. Εκτέλεση Πέναλτι ή Κορώνα-Γράμματα (Heads or Tails) - Ένας ποδοσφαιριστής ετοιμάζεται να εκτελέσει ένα πέναλτι, το οποίο προσπαθεί να αποκρούσει ένας τερματοφύλακας. - Αν οι δύο παίκτες επιλέξουν
Συνδυαστικά Παίγνια. ιαµόρφωση Παιγνίων. Θέµατα σε Πάιγνια Μηδενικού Αθροίσµατος
 Συνδυαστικά Παίγνια 1. Σε ένα παιγνίδι 2 παικτών µηδενικού αθροίσµατος οι παίκτες αναγγέλουν εναλλάξ ένα αριθµό µεταξύ {2,3,4}. Ο παίκτης που κάνει το άθροισµα των αριθµών που έχουν αναγγελθεί να φθάσει
Συνδυαστικά Παίγνια 1. Σε ένα παιγνίδι 2 παικτών µηδενικού αθροίσµατος οι παίκτες αναγγέλουν εναλλάξ ένα αριθµό µεταξύ {2,3,4}. Ο παίκτης που κάνει το άθροισµα των αριθµών που έχουν αναγγελθεί να φθάσει
Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Games)
 Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Gaes) Το δίληµµα των φυλακισµένων, όπως ξέρουµε έχει µια και µοναδική ισορροπία η οποία είναι σε αυστηρά κυρίαρχες στρατηγικές. C N C -8, -8 0, -10 N -10,
Κεφάλαιο 13ο Eπαναλαµβανόµενα παίγνια (Repeated Gaes) Το δίληµµα των φυλακισµένων, όπως ξέρουµε έχει µια και µοναδική ισορροπία η οποία είναι σε αυστηρά κυρίαρχες στρατηγικές. C N C -8, -8 0, -10 N -10,
 Θεωρία παιγνίων Δημήτρης Χριστοφίδης Εκδοση 1η: Παρασκευή 3 Απριλίου 2015. Παραδείγματα Παράδειγμα 1. Δυο άτομα παίζουν μια παραλλαγή του σκακιού όπου σε κάθε βήμα ο κάθε παίκτης κάνει δύο κανονικές κινήσεις.
Θεωρία παιγνίων Δημήτρης Χριστοφίδης Εκδοση 1η: Παρασκευή 3 Απριλίου 2015. Παραδείγματα Παράδειγμα 1. Δυο άτομα παίζουν μια παραλλαγή του σκακιού όπου σε κάθε βήμα ο κάθε παίκτης κάνει δύο κανονικές κινήσεις.
Γενική Ισορροπία-Ευηµερία. 2ο Θεµελιώδες Θεώρηµα των Οικονοµικών της ευηµερίας. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
 Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Ασκήσεις. Ιωάννα Καντζάβελου. Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1
 Ασκήσεις Ιωάννα Καντζάβελου Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1 1. Επιλογή Διαδρομής 2. Παραλλαγή του Matching Pennies 3. Επίλυση Matching Pennies με Βέλτιστες Αποκρίσεις 4. Επίλυση BoS με Βέλτιστες
Ασκήσεις Ιωάννα Καντζάβελου Τµήµα Μηχανικών Πληροφορικής και Υπολογιστών 1 1. Επιλογή Διαδρομής 2. Παραλλαγή του Matching Pennies 3. Επίλυση Matching Pennies με Βέλτιστες Αποκρίσεις 4. Επίλυση BoS με Βέλτιστες
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΡΙΤΟ-ΙΣΟΡΡΟΠΙΑ ΚΑΤΑ NASH ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΡΙΤΟ-ΙΣΟΡΡΟΠΙΑ ΚΑΤΑ NASH ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Συνέχεια από πριν.. Στο προηγούμενο μάθημα είδαμε ότι μπορούμε να επιλύσουμε παίγνια με την μέθοδο της απαλοιφής
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΡΙΤΟ-ΙΣΟΡΡΟΠΙΑ ΚΑΤΑ NASH ΑΚΑΔΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Συνέχεια από πριν.. Στο προηγούμενο μάθημα είδαμε ότι μπορούμε να επιλύσουμε παίγνια με την μέθοδο της απαλοιφής
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ. Ενότητα 2: Ισορροπία Nash. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 2: Ισορροπία Nash Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Ενότητα 2: Ισορροπία Nash Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 3 η Διάλεξη-Περιεχόμενα (1/2) Σημείο ή ζεύγος ισορροπίας κατά Nash Λύση ακολουθιακής κυριαρχίας και σημεία ισορροπίας Nash Αλγοριθμική εύρεση σημείων ισορροπίας
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 3 η Διάλεξη-Περιεχόμενα (1/2) Σημείο ή ζεύγος ισορροπίας κατά Nash Λύση ακολουθιακής κυριαρχίας και σημεία ισορροπίας Nash Αλγοριθμική εύρεση σημείων ισορροπίας
3. Παίγνια Αλληλουχίας
 3. Παίγνια Αλληλουχίας Τα παίγνια αλληλουχίας πραγµατεύονται περιπτώσεις όπου οι κινήσεις των παικτών διαδέχονται η µια την άλλη, σε αντίθεση µε τα παίγνια όπου οι αποφάσεις των παικτών γίνονται ταυτόχρονα
3. Παίγνια Αλληλουχίας Τα παίγνια αλληλουχίας πραγµατεύονται περιπτώσεις όπου οι κινήσεις των παικτών διαδέχονται η µια την άλλη, σε αντίθεση µε τα παίγνια όπου οι αποφάσεις των παικτών γίνονται ταυτόχρονα
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ. Βfi 1 2 Αfl 1 1, 2 0, 1 2 2, 1 1, 0
 ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Παίγνιο: Συμμετέχουν τουλάχιστον δύο παίκτες με τουλάχιστον δύο στρατηγικές ο καθένας και αντίθετα συμφέροντα. Το αποτέλεσμα για κάθε παίκτη καθορίζεται από τις συνδυασμένες επιλογές όλων
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Παίγνιο: Συμμετέχουν τουλάχιστον δύο παίκτες με τουλάχιστον δύο στρατηγικές ο καθένας και αντίθετα συμφέροντα. Το αποτέλεσμα για κάθε παίκτη καθορίζεται από τις συνδυασμένες επιλογές όλων
A 2 B 2 Γ 2. u 1 (A 1, A 2 ) = 3 > 1 = u 1 (B 1, A 2 ) u 1 (A 1, Γ 2 ) = 1 > 0 = u 1 (B 1, Γ 2 ) A 2 B 2
 Κεφάλαιο 2 Στατικά παίγνια με πλήρη πληροφόρηση 2.1 Εισαγωγή Η πιο απλή, αλλά και θεμελιώδης, κατηγορία παιγνίων είναι αυτή των στατικών παιγνίων με πλήρη πληροφόρηση. Στα παίγνια αυτά οι συμμετέχοντες
Κεφάλαιο 2 Στατικά παίγνια με πλήρη πληροφόρηση 2.1 Εισαγωγή Η πιο απλή, αλλά και θεμελιώδης, κατηγορία παιγνίων είναι αυτή των στατικών παιγνίων με πλήρη πληροφόρηση. Στα παίγνια αυτά οι συμμετέχοντες
Βασικές Έννοιες Θεωρίας Παιγνίων
 Παύλος Σ. Εφραιμίδης Έκδοση 05/11/2013 Περιεχόμενα Τι είναι η θεωρία παιγνίων Ο ρόλος ενός μαθηματικού μοντέλου Το δίλημμα του φυλακισμένου Σημείο ισορροπίας Nash Θεωρία Παιγνίων Η θεωρία παιγνίων (game
Παύλος Σ. Εφραιμίδης Έκδοση 05/11/2013 Περιεχόμενα Τι είναι η θεωρία παιγνίων Ο ρόλος ενός μαθηματικού μοντέλου Το δίλημμα του φυλακισμένου Σημείο ισορροπίας Nash Θεωρία Παιγνίων Η θεωρία παιγνίων (game
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ ΠΑΙΓΝΙΑ ΜΗ ΕΝΙΚΟΥ ΑΘΡΟΙΣΜΑΤΟΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012
 ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ ΠΑΙΓΝΙΑ ΜΗ ΕΝΙΚΟΥ ΑΘΡΟΙΣΜΑΤΟΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενο Μάθηµα: Κυρίαρχη Στρατηγική- Κυριαρχούµενη στρατηγική-nash equilibrium Μια στρατηγική
ΕΠΙΧΕΙΡΗΣΙΑΚΑ ΠΑΙΓΝΙΑ ΕΡΓΑΣΤΗΡΙΟ ΜΑΘΗΜΑ ΤΕΤΑΡΤΟ ΠΑΙΓΝΙΑ ΜΗ ΕΝΙΚΟΥ ΑΘΡΟΙΣΜΑΤΟΣ ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2011-2012 Προηγούµενο Μάθηµα: Κυρίαρχη Στρατηγική- Κυριαρχούµενη στρατηγική-nash equilibrium Μια στρατηγική
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Εξεταστική περίοδος Ιουνίου 2015 16 Ιουνίου 2015 Διάρκεια εξέτασης: 2,5 ώρες
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ - ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ Θεωρία Παιγνίων και Αποφάσεων Διδάσκων: Ε. Μαρκάκης, Εαρινό εξάμηνο 2015 Εξεταστική περίοδος Ιουνίου 2015 16 Ιουνίου 2015 Διάρκεια εξέτασης: 2,5 ώρες
Μεταξύ του µονοπωλίου και του τέλειου ανταγωνισµού
 Ολιγοπώλιο Μεταξύ του µονοπωλίου και του τέλειου ανταγωνισµού Ο ατελής ανταγωνισµός αναφέρεται σε εκείνες τις δοµές µ της αγοράς που κυµαίνονται µεταξύ του τέλειου ανταγωνισµού και του µονοπωλίου. Μεταξύ
Ολιγοπώλιο Μεταξύ του µονοπωλίου και του τέλειου ανταγωνισµού Ο ατελής ανταγωνισµός αναφέρεται σε εκείνες τις δοµές µ της αγοράς που κυµαίνονται µεταξύ του τέλειου ανταγωνισµού και του µονοπωλίου. Μεταξύ
Α2 Β2 Γ2 2 Α1 1,0 5,-1-1,-2 9,-2 Β1 2,1-2,0 0,2 0,-1 Γ1 0,3 14,2 2,1 8,1 1 1,2 0,1 3,0-1,0
 ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ ιδάσκων: Ε. Πετράκης. Επαναληπτική Εξέταση: 15/09/99 Απαντήστε στα τρία από τα τέσσερα θέµατα. Όλα τα υποερωτήµατα βαθµολογούνται το ίδιο. 1. Θεωρήσατε ένα ολιγοπωλιακό κλάδο όπου τρεις
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ ιδάσκων: Ε. Πετράκης. Επαναληπτική Εξέταση: 15/09/99 Απαντήστε στα τρία από τα τέσσερα θέµατα. Όλα τα υποερωτήµατα βαθµολογούνται το ίδιο. 1. Θεωρήσατε ένα ολιγοπωλιακό κλάδο όπου τρεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜ ΕΦΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙ ΠΙΓΝΙΩΝ Εξετάσεις 13 Φεβρουαρίου 2004 ιάρκεια εξέτασης: 2 ώρες (13:00-15:00) ΘΕΜ 1 ο (2.5) α) Για δύο στρατηγικές
ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜ ΕΦΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙ ΠΙΓΝΙΩΝ Εξετάσεις 13 Φεβρουαρίου 2004 ιάρκεια εξέτασης: 2 ώρες (13:00-15:00) ΘΕΜ 1 ο (2.5) α) Για δύο στρατηγικές
Θεωρία Παιγνίων και Αποφάσεων
 Θεωρία Παιγνίων και Αποφάσεων Ε. Μαρκάκης Επικ. Καθηγητής Τι είναι η Θεωρία Παιγνίων? Quote από το βιβλίο του Osborne: Game Theory aims to help us understand situawons in which decision makers interact
Θεωρία Παιγνίων και Αποφάσεων Ε. Μαρκάκης Επικ. Καθηγητής Τι είναι η Θεωρία Παιγνίων? Quote από το βιβλίο του Osborne: Game Theory aims to help us understand situawons in which decision makers interact
Οµάδες ψηφοφόρων Αρ. Μελών Οµάδων Προτιµήσεις Α 1 x > y > z Β 1 y > z >x Γ 1 z > x > y
 0. Mη Μεταβατικές Συλλογικές Προτιµήσεις Το αξίωµα της µεταβατικότητας στην περίπτωση των προτιµήσεων ενός µεµονωµένου φορέα αποφάσεων, επιτρέπει την επέκταση της ικανότητας σύγκρισης ζευγών επιλογών στο
0. Mη Μεταβατικές Συλλογικές Προτιµήσεις Το αξίωµα της µεταβατικότητας στην περίπτωση των προτιµήσεων ενός µεµονωµένου φορέα αποφάσεων, επιτρέπει την επέκταση της ικανότητας σύγκρισης ζευγών επιλογών στο
ΜΟΝΟΠΩΛΙΑΚΟΣ ΑΝΤΑΓΩΝΙΣΜΟΣ, ΟΛΙΓΟΠΩΛΙΑ, ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΜΟΝΟΠΩΛΙΑΚΟΣ ΑΝΤΑΓΩΝΙΣΜΟΣ, ΟΛΙΓΟΠΩΛΙΑ, ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Κεφάλαιο 7 Ε. Σαρτζετάκης Μονοπωλιακός ανταγωνισμός Η μορφή αγοράς του μονοπωλιακού ανταγωνισμού περιέχει στοιχεία πλήρους ανταγωνισμού (ελεύθερη
ΜΟΝΟΠΩΛΙΑΚΟΣ ΑΝΤΑΓΩΝΙΣΜΟΣ, ΟΛΙΓΟΠΩΛΙΑ, ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Κεφάλαιο 7 Ε. Σαρτζετάκης Μονοπωλιακός ανταγωνισμός Η μορφή αγοράς του μονοπωλιακού ανταγωνισμού περιέχει στοιχεία πλήρους ανταγωνισμού (ελεύθερη
Ασκήσεις μελέτης της 6 ης διάλεξης
 Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
Οικονομικό Πανεπιστήμιο Αθηνών, Τμήμα Πληροφορικής Μάθημα: Τεχνητή Νοημοσύνη, 2016 17 Διδάσκων: Ι. Ανδρουτσόπουλος Ασκήσεις μελέτης της 6 ης διάλεξης 6.1. (α) Το mini-score-3 παίζεται όπως το score-4,
ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Τρίτη 15 Ιανουαρίου 2008 ιάρκεια εξέτασης: 3 ώρες (13:00-16:00) ΘΕΜΑ 1 ο (2,5
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Τρίτη 15 Ιανουαρίου 2008 ιάρκεια εξέτασης: 3 ώρες (13:00-16:00) ΘΕΜΑ 1 ο (2,5
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις 8 Σεπτεµβρίου 005 ιάρκεια εξέτασης: 3 ώρες (:00-4:00 ΘΕΜΑ ο (.5 Το παράδοξο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις 8 Σεπτεµβρίου 005 ιάρκεια εξέτασης: 3 ώρες (:00-4:00 ΘΕΜΑ ο (.5 Το παράδοξο
ΑΣΚΗΣΗ 1 Βρείτε την ισορροπία των ακόλουθων παιγνίων απαλείφοντας διαδοχικά τις κυριαρχούµενες στρατηγικές.
 ΑΣΚΗΣΗ 1 Βρείτε την ισορροπία των ακόλουθων παιγνίων απαλείφοντας διαδοχικά τις κυριαρχούµενες στρατηγικές. Α 1 Α 2 Α 3 Β 1 Β 2 Β 3 1, -1 0, 0-1, 0 0, 0 0, 6 10, -1 2, 0 10, -1-1, -1 Α 1 Α 2 Α 3 Β 1 Β
ΑΣΚΗΣΗ 1 Βρείτε την ισορροπία των ακόλουθων παιγνίων απαλείφοντας διαδοχικά τις κυριαρχούµενες στρατηγικές. Α 1 Α 2 Α 3 Β 1 Β 2 Β 3 1, -1 0, 0-1, 0 0, 0 0, 6 10, -1 2, 0 10, -1-1, -1 Α 1 Α 2 Α 3 Β 1 Β
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 8: Παίγνια πλήρους και ελλιπούς πληροφόρησης Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Notes. Notes. Notes. Notes
 Θεωρία Καταναλωτή: Αβεβαιότητα Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 0 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή: Αβεβαιότητα 9 Οκτωβρίου 0 / 5 Ανάγκη θεωρίας επιλογής υπό αβεβαιότητα
Θεωρία Καταναλωτή: Αβεβαιότητα Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 0 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή: Αβεβαιότητα 9 Οκτωβρίου 0 / 5 Ανάγκη θεωρίας επιλογής υπό αβεβαιότητα
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
 ΑΣΚΗΣΗ 3 (θεωρία παιγνίων) Οι δύο μεγαλύτερες τράπεζες μιας χώρας, Α και Β, εκτιμούν ότι μια άλλη τράπεζα, η Γ, θα κλείσει στο προσεχές διάστημα και πρόκειται να προχωρήσουν σε διαφημιστικές εκστρατείες
ΑΣΚΗΣΗ 3 (θεωρία παιγνίων) Οι δύο μεγαλύτερες τράπεζες μιας χώρας, Α και Β, εκτιμούν ότι μια άλλη τράπεζα, η Γ, θα κλείσει στο προσεχές διάστημα και πρόκειται να προχωρήσουν σε διαφημιστικές εκστρατείες
Chess Academy Free Lessons Ακαδημία Σκάκι Δωρεάν Μαθήματα. Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης
 Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης Παρατήρηση: Μόνο σε αυτό το μάθημα όταν λέμε κομμάτι εννοούμε κομμάτι ή πιόνι και όταν λέμε κομμάτια εννοούμε κομμάτια
Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης Παρατήρηση: Μόνο σε αυτό το μάθημα όταν λέμε κομμάτι εννοούμε κομμάτι ή πιόνι και όταν λέμε κομμάτια εννοούμε κομμάτια
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ. Ενότητα 8: Πεπερασμένα επαναλαμβανόμενα παίγνια. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 8: Πεπερασμένα επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα 8: Πεπερασμένα επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Έστω ότι έχουµε 2 µάρκες υπολογιστών: A (Apricot), B (Banana) [ ιαρκή Αγαθά].
![Έστω ότι έχουµε 2 µάρκες υπολογιστών: A (Apricot), B (Banana) [ ιαρκή Αγαθά]. Έστω ότι έχουµε 2 µάρκες υπολογιστών: A (Apricot), B (Banana) [ ιαρκή Αγαθά].](/thumbs/59/42714237.jpg) 2.2. ΥΟΠΩΛΙΟ ΙΑΦΟΡΕΤΙΚΩΝ ΠΡΟΪΟΝΤΩΝ ΜΕ ΕΤΕΡΟΓΕΝΕΙΣ ΚΑΤΑΝΑΛΩΤΕΣ Έστω ότι έχουµε 2 µάρκες υπολογιστών: (pricot), (anana) [ ιαρκή Αγαθά]. Υποθέτουµε µηδενικό κόστος παραγωγής και P, P, οι τιµές για το Α, αντίστοιχα.
2.2. ΥΟΠΩΛΙΟ ΙΑΦΟΡΕΤΙΚΩΝ ΠΡΟΪΟΝΤΩΝ ΜΕ ΕΤΕΡΟΓΕΝΕΙΣ ΚΑΤΑΝΑΛΩΤΕΣ Έστω ότι έχουµε 2 µάρκες υπολογιστών: (pricot), (anana) [ ιαρκή Αγαθά]. Υποθέτουµε µηδενικό κόστος παραγωγής και P, P, οι τιµές για το Α, αντίστοιχα.
ΑΛΓΟΡΙΘΜΙΚΗ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Πανεπιστήµιο Αθηνών Εαρινό Εξάµηνο 2007 ιδάσκων : Ηλίας Κουτσουπιάς
 ΑΛΓΟΡΙΘΜΙΚΗ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Πανεπιστήµιο Αθηνών Εαρινό Εξάµηνο 007 ιδάσκων : Ηλίας Κουτσουπιάς Μάθηµα : Overview Of The Algorithmic Game Theory Ηµεροµηνία : 007/04/19 Σηµειώσεις : Ελενα Χατζηγιωργάκη,
ΑΛΓΟΡΙΘΜΙΚΗ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Πανεπιστήµιο Αθηνών Εαρινό Εξάµηνο 007 ιδάσκων : Ηλίας Κουτσουπιάς Μάθηµα : Overview Of The Algorithmic Game Theory Ηµεροµηνία : 007/04/19 Σηµειώσεις : Ελενα Χατζηγιωργάκη,
Πλειστηριασμός Για να πλειοδοτήσει κάποιος άξονας θα πρέπει να αναλάβει την υποχρέωση
 Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
Πλειστηριασμός Προκειμένου να περιγράψουμε το χέρι μας στο συμπαίκτη, χρησιμοποιούμε μια ειδική διεθνή γλώσσα τα Μπριτζικά ή Μπριτζιακά. Τα καλά νέα είναι ότι αυτή η γλώσσα έχει μόνο λίγες λεξούλες. Πλειστηριασμός
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ
 ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
ΗΜΙΟΥΡΓΙΑ ΠΑΙΧΝΙ ΙΟΥ ΣΤΟ SCRATCH ΒΗΜΑ ΠΡΟΣ ΒΗΜΑ ΣΕΝΑΡΙΟ ΠΑΙΧΝΙ ΙΟΥ Το παιχνίδι θα αποτελείται από δυο παίκτες, οι οποίοι θα βρίσκονται αντικριστά στις άκρες ενός γηπέδου δεξιά και αριστερά, και µια µπάλα.
Οικονομία των ΜΜΕ. Ενότητα 8: Παίγνια και ολιγοπωλιακές επιχειρήσεις
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Παίγνια και ολιγοπωλιακές επιχειρήσεις Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή Οικονομικών
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Παίγνια και ολιγοπωλιακές επιχειρήσεις Γιώργος Τσουρβάκας, Αναπληρωτής Καθηγητής Τμήμα Δημοσιογραφίας και ΜΜΕ Σχολή Οικονομικών
ΑΝΑΛΥΣΗ ΓΚΟΛ Πρόκληση ανισορροπίας στην αμυντική γραμμή του αντιπάλου: Αξιοποιώντας τις αδυναμίες της αντίπαλης άμυνας
 ΑΝΑΛΥΣΗ ΓΚΟΛ Πρόκληση ανισορροπίας στην αμυντική γραμμή του αντιπάλου: Αξιοποιώντας τις αδυναμίες της αντίπαλης άμυνας 03-Σεπ-10: Ευρωπαϊκό πρωτάθλημα 2012, προκριματικά Λιχτενστάιν 0-4 Ισπανία (1ο γκολ):
ΑΝΑΛΥΣΗ ΓΚΟΛ Πρόκληση ανισορροπίας στην αμυντική γραμμή του αντιπάλου: Αξιοποιώντας τις αδυναμίες της αντίπαλης άμυνας 03-Σεπ-10: Ευρωπαϊκό πρωτάθλημα 2012, προκριματικά Λιχτενστάιν 0-4 Ισπανία (1ο γκολ):
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ 1. Κοινά χαρακτηριστικά
 ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ 1 Εφαρµόζονται σε αγορές που δεν είναι Walrasian. ηλαδή σε αγορές που οι πρωταγωνιστές δεν είναι λήπτες τιµών π.χ. ολιγοπώλιο. Τέτοιες αγορές τις µελετούµε µε παίγνια. Κοινά χαρακτηριστικά
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ 1 Εφαρµόζονται σε αγορές που δεν είναι Walrasian. ηλαδή σε αγορές που οι πρωταγωνιστές δεν είναι λήπτες τιµών π.χ. ολιγοπώλιο. Τέτοιες αγορές τις µελετούµε µε παίγνια. Κοινά χαρακτηριστικά
 Πάνω στον πίνακα έχουµε γραµµένο το γινόµενο 1 2 3 4 595. ύο παίκτες Α και Β παίζουν το εξής παιχνίδι. Ο ένας µετά τον άλλο, διαγράφουν από έναν παράγοντα του γινοµένου αρχίζοντας από τον παίκτη Α. Νικητής
Πάνω στον πίνακα έχουµε γραµµένο το γινόµενο 1 2 3 4 595. ύο παίκτες Α και Β παίζουν το εξής παιχνίδι. Ο ένας µετά τον άλλο, διαγράφουν από έναν παράγοντα του γινοµένου αρχίζοντας από τον παίκτη Α. Νικητής
Mικροοικονοµικές Πολιτικές της ΕΕ. Χρυσοβαλάντου Μήλλιου Οικονοµικό Πανεπιστήµιο Αθηνών
 Mικροοικονοµικές Πολιτικές της ΕΕ Χρυσοβαλάντου Μήλλιου Οικονοµικό Πανεπιστήµιο Αθηνών 2. Οικονοµική Θεµελίωση: Δοµές Αγοράς Χ. Μήλλιου - ΟΠΑ 2 Αγορά Τι είναι η αγορά; Στην αγορά κάθε προϊόντος υπάρχουν
Mικροοικονοµικές Πολιτικές της ΕΕ Χρυσοβαλάντου Μήλλιου Οικονοµικό Πανεπιστήµιο Αθηνών 2. Οικονοµική Θεµελίωση: Δοµές Αγοράς Χ. Μήλλιου - ΟΠΑ 2 Αγορά Τι είναι η αγορά; Στην αγορά κάθε προϊόντος υπάρχουν
Θέματα Τ.Θ.Δ.Δ. ΘΕΜΑ Β
 Θέματα Τ.Θ.Δ.Δ. ΘΕΜΑ Β 1. Δίνονται δύο ενδεχόμενα A, B ενός δειγματικού χώρου και οι πιθανότητες: 3 5 1 P( A), P( A B) και P( B) 4 8 4 α) Να υπολογίσετε την P( A B) β) i) Να παραστήσετε με διάγραμμα Venn
Θέματα Τ.Θ.Δ.Δ. ΘΕΜΑ Β 1. Δίνονται δύο ενδεχόμενα A, B ενός δειγματικού χώρου και οι πιθανότητες: 3 5 1 P( A), P( A B) και P( B) 4 8 4 α) Να υπολογίσετε την P( A B) β) i) Να παραστήσετε με διάγραμμα Venn
ΑΣΚΗΣΗ 1 ΑΣΚΗΣΗ 2 ΑΣΚΗΣΗ 3
 ΑΣΚΗΣΗ 1 Δύο επιχειρήσεις Α και Β, μοιράζονται το μεγαλύτερο μερίδιο της αγοράς για ένα συγκεκριμένο προϊόν. Καθεμία σχεδιάζει τη νέα της στρατηγική για τον επόμενο χρόνο, προκειμένου να αποσπάσει πωλήσεις
ΑΣΚΗΣΗ 1 Δύο επιχειρήσεις Α και Β, μοιράζονται το μεγαλύτερο μερίδιο της αγοράς για ένα συγκεκριμένο προϊόν. Καθεμία σχεδιάζει τη νέα της στρατηγική για τον επόμενο χρόνο, προκειμένου να αποσπάσει πωλήσεις
Μικροοικονοµική Θεωρία. Τιµές και εισόδηµα. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 22 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Γενική Ισορροπία. Γενική ισορροπία και παραγωγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013
 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 013 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη αντιστοιχία
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 013 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη αντιστοιχία
Μικροοικονοµική Θεωρία. Γενική ισορροπία και παραγωγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 24 Σεπτεµβρίου 2014
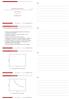 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Ένα Παίγνιο (game) ορίζεται ως μια δραστηριότητα με τα ακόλουθα τρία χαρακτηριστικά:
 Γενικοί Ορισμοί Η Θεωρία Παιγνίων (game theory) εξετάζει δραστηριότητες στις οποίες το αποτέλεσμα της απόφασης ενός ατόμου εξαρτάται όχι μόνο από τον τρόπο με τον οποίο επιλέγει ανάμεσα από διάφορες εναλλακτικές
Γενικοί Ορισμοί Η Θεωρία Παιγνίων (game theory) εξετάζει δραστηριότητες στις οποίες το αποτέλεσμα της απόφασης ενός ατόμου εξαρτάται όχι μόνο από τον τρόπο με τον οποίο επιλέγει ανάμεσα από διάφορες εναλλακτικές
Μελέτη πάνω στην εφαρμογή της θεωρίας παιγνίων σε θέματα πολεμικών τακτικών και στρατηγικής.
 Μελέτη πάνω στην εφαρμογή της θεωρίας παιγνίων σε θέματα πολεμικών τακτικών και στρατηγικής. Ιστορική αναδρομή 1713 Ο Francis Waldegrave, σε ένα γράμμα του, παρουσίασε την πρώτη μικτή στρατηγική μεγίστου
Μελέτη πάνω στην εφαρμογή της θεωρίας παιγνίων σε θέματα πολεμικών τακτικών και στρατηγικής. Ιστορική αναδρομή 1713 Ο Francis Waldegrave, σε ένα γράμμα του, παρουσίασε την πρώτη μικτή στρατηγική μεγίστου
6. Παίγνια αλληλοδιαδοχικών κινήσεων και η αξία του περιορισμού των επιλογών κάποιου ατόμου
 Θεωρία παιγνίων 1 1. Παρακίνηση: Honda και Toyota 2. Ισορροπία κατά Nash 3. Το δίλημμα του φυλακισμένου 4. Ισορροπία με κυρίαρχη στρατηγική 5. Μειονεκτήματα της ισορροπίας κατά Nash 6. Παίγνια αλληλοδιαδοχικών
Θεωρία παιγνίων 1 1. Παρακίνηση: Honda και Toyota 2. Ισορροπία κατά Nash 3. Το δίλημμα του φυλακισμένου 4. Ισορροπία με κυρίαρχη στρατηγική 5. Μειονεκτήματα της ισορροπίας κατά Nash 6. Παίγνια αλληλοδιαδοχικών
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών
 Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Πληροφοριακά Συστήματα Διοίκησης (ΜΒΑ) Ενότητα 9: Λύσεις παιγνίων δύο παικτών Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΘΕΜΑ 1 ο (2.5) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Δευτέρα 3 Σεπτεμβρίου 2012 Διάρκεια εξέτασης: 3 ώρες (16:30-19:30)
ΘΕΜΑ 1 ο (2.5) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις Δευτέρα 3 Σεπτεμβρίου 2012 Διάρκεια εξέτασης: 3 ώρες (16:30-19:30)
EMOJITO! 7 Δίσκοι Ψηφοφορίας. 100 Κάρτες Συναισθημάτων. 1 Ταμπλό. 7 Πιόνια παικτών. 2-7 Παίκτες
 o Emojito! είναι ένα παιχνίδι παρέας, για 2 έως 14 άτομα, όπου οι παίκτες προσπαθούν να εκφράσουν συναισθήματα που απεικονίζονται σε κάρτες, είτε χρησιμοποιώντας το πρόσωπό τους, είτε ήχους ή και τα 2.
o Emojito! είναι ένα παιχνίδι παρέας, για 2 έως 14 άτομα, όπου οι παίκτες προσπαθούν να εκφράσουν συναισθήματα που απεικονίζονται σε κάρτες, είτε χρησιμοποιώντας το πρόσωπό τους, είτε ήχους ή και τα 2.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις 1 Φεβρουαρίου 26 ιάρκεια εξέτασης: 3 ώρες (15:-18:) ΘΕΜΑ 1 ο (2.5) Κάθε ένας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ Τελικές Εξετάσεις 1 Φεβρουαρίου 26 ιάρκεια εξέτασης: 3 ώρες (15:-18:) ΘΕΜΑ 1 ο (2.5) Κάθε ένας
Ολιγοπώλιο. Εισαγωγή στην Οικονομική Επιστήμη Ι. Αρ. Διάλεξης: 11
 Ολιγοπώλιο Εισαγωγή στην Οικονομική Επιστήμη Ι Αρ. Διάλεξης: 11 Μορφές Αγορών μεταξύ Μονοπωλίου και Τέλειου Ανταγωνισμού Ο Ατελής Ανταγωνισμός αναφέρεται στην διάρθρωση της αγοράς εκείνης η οποία βρίσκεται
Ολιγοπώλιο Εισαγωγή στην Οικονομική Επιστήμη Ι Αρ. Διάλεξης: 11 Μορφές Αγορών μεταξύ Μονοπωλίου και Τέλειου Ανταγωνισμού Ο Ατελής Ανταγωνισμός αναφέρεται στην διάρθρωση της αγοράς εκείνης η οποία βρίσκεται
δ 2 s Το είναι η προσφορά από τον παίχτη ΙΙ στον παίχτη Ι. Παίρνει ο Ι y
 Κεφάλαιο 1 Το τελευταίο που κάναµε ήταν µια ιαπραγµάτευση στην οποία υπάρχουν ύο παίκτες, κάνει ο ένας µια προσφορά, ο άλλος τη έχεται ή όχι. Αν εν την εχτεί κάνει αντιπροσφορά την οποία ο πρώτο παίχτης
Κεφάλαιο 1 Το τελευταίο που κάναµε ήταν µια ιαπραγµάτευση στην οποία υπάρχουν ύο παίκτες, κάνει ο ένας µια προσφορά, ο άλλος τη έχεται ή όχι. Αν εν την εχτεί κάνει αντιπροσφορά την οποία ο πρώτο παίχτης
Αλγοριθμική Θεωρία Παιγνίων: Εισαγωγή και Βασικές Έννοιες
 Αλγοριθμική Θεωρία Παιγνίων: Εισαγωγή και Βασικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πολύπλοκα Συστήματα αποτελούνται από πολλές
Αλγοριθμική Θεωρία Παιγνίων: Εισαγωγή και Βασικές Έννοιες ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πολύπλοκα Συστήματα αποτελούνται από πολλές
Τεχνητή Νοημοσύνη. 6η διάλεξη ( ) Ίων Ανδρουτσόπουλος.
 Τεχνητή Νοημοσύνη 6η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Τεχνητή Νοημοσύνη 6η διάλεξη (2016-17) Ίων Ανδρουτσόπουλος http://www.aueb.gr/users/ion/ 1 Οι διαφάνειες αυτής της διάλεξης βασίζονται στα βιβλία Τεχνητή Νοημοσύνη των Βλαχάβα κ.ά., 3η έκδοση, Β. Γκιούρδας
Chess Academy Free Lessons Ακαδημία Σκάκι Δωρεάν Μαθήματα. Ματ με δύο βαριά κομμάτια Ματ με Βασίλισσα Επιμέλεια: Γιάννης Κατσίρης
 Ματ με δύο βαριά κομμάτια Ματ με Βασίλισσα Επιμέλεια: Γιάννης Κατσίρης Σημείωση: Βαριά κομμάτια = Πύργοι και Βασίλισσα Ελαφρά κομμάτια = Ίπποι και Αξιωματικοί Κομμάτια = Βασιλιάς, Βασίλισσα, Πύργοι, Ίπποι
Ματ με δύο βαριά κομμάτια Ματ με Βασίλισσα Επιμέλεια: Γιάννης Κατσίρης Σημείωση: Βαριά κομμάτια = Πύργοι και Βασίλισσα Ελαφρά κομμάτια = Ίπποι και Αξιωματικοί Κομμάτια = Βασιλιάς, Βασίλισσα, Πύργοι, Ίπποι
B 1 A 1 B 2 A 2. t 1. t 3 w. t 2 A 3 B 3. t 4. t 5
 Κεφάλαιο 3 Δυναμικά παίγνια 3.1 Εισαγωγή Μέχρι στιγμής έχουμε αναλύσει παίγνια στα οποία όλοι οι παίκτες επιλέγουν τις στρατηγικές τους ταυτόχρονα. Αυτή η υπόθεση όμως δεν είναι πάντα κατάλληλη. Σε πολλές
Κεφάλαιο 3 Δυναμικά παίγνια 3.1 Εισαγωγή Μέχρι στιγμής έχουμε αναλύσει παίγνια στα οποία όλοι οι παίκτες επιλέγουν τις στρατηγικές τους ταυτόχρονα. Αυτή η υπόθεση όμως δεν είναι πάντα κατάλληλη. Σε πολλές
Παραδείγματα Παιγνίων
 Παραδείγματα Παιγνίων Παύλος Σ. Εφραιμίδης v1.3, 01/06/2014 Τι περιλαμβάνει ένα παίγνιο: Παίγνιο Παίκτες Πιθανές κινήσεις για κάθε παίκτη Απόδοση ή όφελος για κάθε παίκτη σε κάθε πιθανή έκβαση του παιγνίου
Παραδείγματα Παιγνίων Παύλος Σ. Εφραιμίδης v1.3, 01/06/2014 Τι περιλαμβάνει ένα παίγνιο: Παίγνιο Παίκτες Πιθανές κινήσεις για κάθε παίκτη Απόδοση ή όφελος για κάθε παίκτη σε κάθε πιθανή έκβαση του παιγνίου
Condorcet winner. (1) Αν U j (x) > U j (y) τότε U i (x) > U i (y) και (2) Αν U i (y) > U i (x) τότε U j (y) > U j (x).
 Οικονοµικό Πανεπιστήµιο Αθηνών Άνοιξη 2012 Τµήµα Οικονοµικής Επιστήµης ηµόσια Οικονοµική ΙI Η διαδικασία της ψηφοφορίας Ως µεθόδου παροχής των δηµοσίων αγαθών (για τα ιδιωτικά αγαθά, ο µηχανισµός των τιµών).
Οικονοµικό Πανεπιστήµιο Αθηνών Άνοιξη 2012 Τµήµα Οικονοµικής Επιστήµης ηµόσια Οικονοµική ΙI Η διαδικασία της ψηφοφορίας Ως µεθόδου παροχής των δηµοσίων αγαθών (για τα ιδιωτικά αγαθά, ο µηχανισµός των τιµών).
Κεφ. 9 Ανάλυση αποφάσεων
 Κεφ. 9 Ανάλυση αποφάσεων Η θεωρία αποφάσεων έχει ως αντικείμενο την επιλογή της καλύτερης στρατηγικής. Τα αποτελέσματα κάθε στρατηγικής εξαρτώνται από παράγοντες, οι οποίοι μπορεί να είναι καταστάσεις
Κεφ. 9 Ανάλυση αποφάσεων Η θεωρία αποφάσεων έχει ως αντικείμενο την επιλογή της καλύτερης στρατηγικής. Τα αποτελέσματα κάθε στρατηγικής εξαρτώνται από παράγοντες, οι οποίοι μπορεί να είναι καταστάσεις
Θεωρία Παιγνίων και Αποφάσεων. Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος. Ε. Μαρκάκης. Επικ. Καθηγητής
 Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
Θεωρία Παιγνίων και Αποφάσεων Ενότητα 5: Εύρεση σημείων ισορροπίας σε παίγνια μηδενικού αθροίσματος Ε. Μαρκάκης Επικ. Καθηγητής Περίληψη Παίγνια μηδενικού αθροίσματος PessimisIc play Αμιγείς max-min και
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή
 Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Παίγνια Δύο Αντιπάλων Τα προβλήματα όπου η εξέλιξη των καταστάσεων εξαρτάται
Τεχνητή Νοημοσύνη (ΥΠ23) 6 ο εξάμηνο Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Ουρανία Χατζή raniah@hua.gr 1 Παίγνια Δύο Αντιπάλων Τα προβλήματα όπου η εξέλιξη των καταστάσεων εξαρτάται
ΘΕΩΡΙΑ ΠΑΙΓΝΙΩΝ. Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια. Ρεφανίδης Ιωάννης Τμήμα Εφαρμοσμένης Πληροφορικής
 Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα 9: Απείρως επαναλαμβανόμενα παίγνια Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Επίλυση Προβλημάτων 1
 Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Επίλυση Προβλημάτων 1 Επίλυση Προβλημάτων Περιγραφή Προβλημάτων Αλγόριθμοι αναζήτησης Αλγόριθμοι τυφλής αναζήτησης Αναζήτηση πρώτα σε βάθος Αναζήτηση πρώτα σε πλάτος (ΒFS) Αλγόριθμοι ευρετικής αναζήτησης
Ενημερωτική Διαφοροποίηση Προϊόντος: Ο Ρόλος της Διαφήμισης
 Ενημερωτική Διαφοροποίηση Προϊόντος: Ο Ρόλος της Διαφήμισης - Οι επιχειρήσεις δεν ανταγωνίζονται μόνο ως προς τις τιμές στις οποίες επιλέγουν να πουλήσουν τα προϊόντα τους. - Ο μη-τιμολογιακός ανταγωνισμός
Ενημερωτική Διαφοροποίηση Προϊόντος: Ο Ρόλος της Διαφήμισης - Οι επιχειρήσεις δεν ανταγωνίζονται μόνο ως προς τις τιμές στις οποίες επιλέγουν να πουλήσουν τα προϊόντα τους. - Ο μη-τιμολογιακός ανταγωνισμός
