|
|
|
- Δημήτηρ Αγγελίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Διπλωματική Εργασία Παναγιώτης Σπανός Εξωτερικοί Αυτομορφισμοί Ομάδων Επιφανειών Τριμελής Επιτροπή: Ευάγγελος Ράπτης Δημήτριος Βάρσος Μιχαήλ Συκιώτης (Επιβλέπων) Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Μαθηματικών Αθήνα 2017
2
3 Περίληψη Εστω S g η επιφάνεια γένους g 1. Η επεκτεταμένη ομάδα κλάσεων απεικονίσεων Mod ± (S g ) ορίζεται να είναι η ομάδα πηλίκο των ομοιομορφισμών της S g προς τους ομοιομορφισμούς που είναι ομοτοπικοί με την ταυτοτική απεικόνιση. Στην παρούσα εργασία θα παρουσιάσουμε μία απόδειξη του θεωρήματος Dehn, Nielsen, Baer. Το θεώρημα αυτό ισχυρίζεται πως η Mod ± (S g ) είναι ισόμορφη με την ομάδα Out(π 1 (S g )) των εξωτερικών αυτομορφισμών της π 1 (S g ) θεμελιώδους ομάδας της επιφάνειας S g. Τα βασικά εργαλεία της απόδειξης πηγάζουν από την υπερβολική δομή της επιφάνειας όταν g 2. iii
4 Summary Let S g be a surface of genus g 1. The extended mapping class group Mod ± (S g ) is dened as the quotient group of homeomorphisms from S g to itself modulo homeomorphisms homotopic to the identity. In this master's thesis we present a proof of the Dehn, Nielsen, Baer theorem, which states that Mod ± (S g ) is isomorphic to the group Out(π 1 (S g )) of outer automorphisms of π 1 (S g ), where π 1 (S g ) denotes the fundamental group of the surface S g. The basic tools used in the proof come from the hyperbolic structure of the surface, when g 2. iv
5
6
7 Εισαγωγή Κύριο εργαλείο για τη μελέτη των επιφανειών είναι η ομάδα κλάσεων απεικονίσεων (mapping class group). Η ομάδα αυτή ορίζεται ως η ομάδα πηλίκο των ομοιομορφισμών από την επιφάνεια στον εαυτό της, που διατηρούν τον προσανατολισμό, ως προς τους ομοιομορφισμούς που είναι ομοτοπικοί με την ταυτοτική απεικόνιση. Αν θεωρήσουμε και ομοιομορφισμούς που δε διατηρούν τον προσανατολισμό τότε έχουμε την επεκτεταμένη ομάδα κλάσεων απεικονίσεων. Για κάθε ομάδα G, εσωτερικός αυτομορφισμός της G, λέγεται ένας φ αυτομορφισμός της μορφής φ(g) = hgh 1. Οι εσωτερικοί αυτομορφισμοί αποτελούν κανονική υποομάδα της ομάδας αυτομορφισμών και επομένως ορίζεται η ομάδα πηλίκο. Η ομάδα πηλίκο των εσωτερικών αυτομορφισμών στην ομάδα αυτομορφισμών καλείται ομάδα εξωτερικών αυτομορφισμών. Στην παρούσα εργασία θα παρουσιάσουμε μία απόδειξη του θεωρήματος Dehn, Nielsen, Baer. Το θεώρημα αυτό ισχυρίζεται πως για επιφάνεια γένους μεγαλύτερου ή ίσου με 1, η επεκτεταμένη ομάδα κλάσεων απεικονίσεων είναι ισόμορφη με την ομάδα των εξωτερικών αυτομορφισμών της θεμελιώδους ομάδας της επιφάνειας. Το θεώρημα αυτό αποτελεί μία όμορφη ανάμιξη διαφορετικών κλάδων των μαθηματικών και είναι σημαντικό γιατί μέσω αυτού η μελέτη ενός τοπολογικού αντικειμένου, της ομάδας κλάσεων απεικονίσεων, ανάγεται στη μελέτη ενός πλήρως αλγεβρικού αντικειμένου, της ομάδας εξωτερικών αυτομορφισμών. Μάλιστα αυτή η ανάμειξη γίνεται μέσω της υπερβολικής γεωμετρίας. Η αρχική μορφή του θεωρήματος ήταν η ύπαρξη ενός επιμορφισμού από την ομάδα κλάσεων απεικονίσεων στη θεμελιώδη ομάδα της επιφάνειας. Πρώτη φορά αποδείχθηκε η ύπαρξη του επιμορφισμού από τον Max Dehn το 1922, παρ όλα αυτά η απόδειξη αυτή δε δημοσιεύτηκε. Ο Jakob Nielsen ήταν ο πρώτος που δημοσίευσε μία απόδειξη του αρχικού θεωρήματος το Η απόδειξη του Nielsen αποτελείται από δύο μέρη, το πρώτο μέρος αποδίδεται στον Dehn. Το 1928 το θεώρημα αποδείχθηκε σε όλη του τη γενικότητα από τον Reinhold Baer, ο οποίος έδειξε την ύπαρξη ισομορφισμού. Το 1931 ο Nielsen αποδεικνύει ξανά το θεώρημα, συντομότερα και πιο κομψά, η απόδειξη αυτή όμως δε δημοσιεύεται. Οvii
8 viii λες οι προαναφερθήσες αποδείξεις βασίζονται στην υπερβολική δομή της επιφάνειας γένους μεγαλύτερου ή ίσου με 2. Το 1937 ο Herbert Seifert αποδεικνύει το θεώρημα χρησιμοποιώντας αποκλειστικά τοπολογία και όχι υπερβολική γεωμετρία, με αποτέλεσμα να ξεχαστεί η ιδέα από την οποία προήλθε το θεώρημα. Ενα εξ ίσου σημαντικό εργαλείο για τη μελέτη των υπερβολικών επιφανειών είναι ο χώρος Teichmüller. Ο χώρος Teichmüller ορίζεται ως ο χώρος πηλίκο του χώρου των υπερβολικών μετρικών της επιφάνειας ως προς ισοδυναμία, όπου δύο μετρικές d 1, d 2 είναι ισοδύναμες όταν υπάρχει ισομετρία της επιφάνειας, ισοτοπική με την ταυτοτική απεικόνιση που απεικονίζει την d 1 στην d 2. Είναι σημαντικό να αναφερθεί ότι υπάρχει το Θεώρημα ταξινόμησης των Jakob Nielsen και William Thurston, το οποίο δίνει έναν αντιπρόσωπο με συγκεκριμμένες ιδιότητες για κάθε στοιχείο της ομάδας κλάσεων απεικονίσεων. Στην α- πόδειξη της ταξινόμησης από τον Lipman Bers χρησιμοποιείται η δράση της ομάδας κλάσεων απεικονίσεων στον χώρο Teichmüller. Ακολουθεί μία σύντομη περιγραφή της απόδειξης του Θεωρήματος Dehn, Nielsen, Baer. Πρώτα δείχνουμε το θεώρημα για επιφάνεια γένους 1, και έπειτα για επιφάνεια γένους g, όπου g 2. Η απόδειξη της πρώτης περίπτωσης μοιάζει με αυτήν της δεύτερης. Επομένως θα περιγράψουμε την απόδειξη για S g επιφάνεια γένους g, με g 2. Σταθεροποιούμε ένα σημείο βάσης και κατασκευάζουμε έναν ομομορφισμό σ : Mod ± Out(π 1 (S g, x 0 ). Επιλέγουμε μία συλλογή καμπυλών γ 1, γ 2,..., γ 2g, των οποίων οι κλάσεις ομοτοπίας παράγουν την π 1 (S g, x 0 ), ως εξής: γ 1 γ 2 γ 3 Δείχνουμε ότι η σ είναι μονομορφισμός παίρνοντας τυχαίο [φ] ker σ και κατασκευάζοντας ομοτοπία από αντιπρόσωπο φ [φ] στην ταυτοτική απεικόνιση id Sg. Τέλος για να δείξουμε ότι είναι επιμορφισμός παίρνουμε τυχαίο [Φ] Out Out(π 1 (S g )), έστω Φ [Φ] Out. Το [Φ] Out δρα στις κλάσεις συζυγίας, [Φ] Out Cl([γ i ]) = Cl(Φ([γ i ])). Δείχνουμε ότι οι {Φ([γ i ])} είναι αλυσίδα κλάσεων ελεύθερης ομοτοπίας απλών κλειστών καμπυλών με σταθερό αλγεβρικό αριθμό τομής ±1. Από αυτή την ιδιότητα προκύπτει ότι υπάρχει ομοιομορφισμός φ που απεικονίζει τις γ i σε αντιπροσώπους του Φ([γ i ]). Τέλος δείχνουμε για αντιπρόσωπο φ σ([φ] f ), ότι η σύνθεση φ 1 Φ είναι εσωτερικός αυτομορφισμός, το οποίο ολοκληρώνει την απόδειξη. Εν κατακλέιδι θα κάνουμε μία σύνοψη των κεφαλαίων. Στο Κεφάλαιο 1 παρουσιάζουμε
9 ix βασικές έννοιες της θεωρίας ομάδων, δράσεις ομάδων, αυτομορφισμοί και το γράφημα του Cayley. Στο Κεφάλαιο 2 μελετούμε τον δισδιάστατο υπερβολικό χώρο και δείχνουμε ότι κάθε επιφάνεια γένους g 2 επιδέχεται υπερβολική δομή. Αυτό σημαίνει ότι ο καθολικός χώρος επικάλυψής κάθε τέτοιας επιφάνειας είναι το υπερβολικό επίπεδο. Στο Κεφάλαιο 3 ασχολούμαστε με καμπύλες και τόξα στις επιφάνειες και δίνουμε μία ταξινόμησή τους, εισάγεται επίσης η έννοια της ισοτοπίας. Στο Κεφάλαιο 4 δίνεται ο ορισμός της ομάδας κλάσεων απεικονίσεων, πραγματοποιούμε τους υπολογισμούς μερικών απλών περιπτώσεων. Στο ίδιο κεφάλαιο παρουσιάζουμε το Θεώρημα του Nielsen και τη μέθοδο του Alexander, τα οποία χρησιμεύουν για τον υπολογισμό ομάδων κλάσεων απεικονίσεων. Στο Κεφάλαιο 5 δίνονται τα βασικά εργαλεία για την απόδειξη του Θεωρήματος Dehn, Nielsen, Baer, δηλαδή οι έννοιες της σχεδόν ισομετρίας και της σύνδεσης στο άπειρο. Τέλος παρουσιάζεται η απόδειξη του Θεωρήματος όπως περιγράφθηκε προηγουμένως.
10
11 Περιεχόμενα 1 Στοιχεία θεωρίας ομάδων και αλγεβρικής τοπολογίας Δράσεις Ομάδων Αυτομορφισμοί Γράφημα Cayley Υπερβολική γεωμετρία Το Επίπεδο του Lobachevski Ο Δίσκος του Poincaré Το σύνορο του H 2 και του D Ταξινόμηση ισομετριών Η υπερβολική γεωμετρία των επιφανειών S g Καμπύλες και τόξα Απλές κλειστές καμπύλες Αριθμοί τομής Τόξα Ισοτοπία Ταξινόμηση απλών κλειστών καμπυλών Ομάδα κλάσεων απεικονίσεων Mod(S) Επεκτεταμένη ομάδα κλάσεων απεικονίσεων Υπολογισμοί ομάδων κλάσεων απεικονίσεων Μέθοδος Alexander Εξωτερικοί αυτομορφισμοί ομάδων επιφανειών Σχεδόν ισομετρίες Σύνδεση στο άπειρο xi
12 xii ΠΕΡΙΕΧΟΜΕΝΑ 5.3 Θεώρημα Dehn, Nielsen, Baer
13
14
15 Κεφάλαιο 1 Στοιχεία θεωρίας ομάδων και αλγεβρικής τοπολογίας 1.1 Δράσεις Ομάδων Ορισμός Μία ομάδα G λέμε ότι δρα σε ένα σύνολο S, αν υπάρχει ομομορφισμός ρ : G Sym(S), όπου Sym(S) = {f : S S όπου f 1-1 και επί} (η ομάδα μεταθέσεων επί του S). 2. Μία ομάδα G λέμε ότι δρα σε έναν τοπολογικό χώρο X, αν υπάρχει ομομορφισμός ρ : G Homeo(X), όπου Homeo(X) = {f : X X όπου f ομοιομορφισμός} (Homeo(X) Sym(X)). 3. Μία ομάδα G λέμε ότι δρα σε έναν μετρικό χώρο (X, d) με ισομετρίες, αν υπάρχει ισομετρία ρ : G Isom(X), όπου Isom(X) = {f : X X όπου f ισομετρία} (Isom(X) Homeo(X) Sym(X)). Σημείωση. Οπως παρατηρούμε από το Isom(X) Homeo(X) Sym(X), σε κάθε μία από τις περιπτώσεις ικανοποιείται η 1. Συμβολισμός. Οταν μια ομάδα G δρα στο X (είτε είναι σύνολο, τοπολογικός χώρος ή μετρικός χώρος) τότε αντί να γράφουμε ρ(g)(x) θα γράφουμε απλούστερα g x ή gx, αντίστοιχα ga = ρ(g)(a) και GA = ρ(g)(a). g G 1
16 ΑΥΤΟΜΟΡΦΙΣΜΟΙ Ορισμός Εστω G μία ομάδα που δρα σε ένα σύνολο X 1. Λέμε ότι μία δράση ρ είναι πιστή (ή αποτελεσματική) αν kerρ = {1 G }. 2. Λέμε ότι η δράση είναι ελεύθερη αν για κάθε x X και κάθε g G \ {1} ισχύει gx x. 3. Λέμε ότι η δράση είναι μεταβατική αν για κάθε x, y X υπάρχει g G τέτοιο ώστε y = gx. 4. Για κάθε x X ορίζεται η σταθεροποιούσα του x, Stab G (x) = {g G gx = x}. 5. Αν ο X είναι τοπολογικός χώρος (ή επιπλέον μετρικός χώρος) η ομάδα Stab G (x) καλείται ομάδα ισοτροπιών του x X και συμβολίζεται με G x (isotropy group). 1.2 Αυτομορφισμοί Ορισμός Εστω G μία ομάδα. Το σύνολο των αυτομορφισμών της G (ισομορφισμών από την G στον εαυτό της), με πράξη τη σύνθεση συναρτήσεων, είναι ομάδα και καλείται ομάδα αυτομορφισμών της G. Συμβολίζεται Aut(G) = {φ : G G φ ομομορφισμός, 1-1 και επί}. Παρατήρηση Για κάθε g G η συνάρτηση T g : G G με x gxg 1 είναι ομομορφισμός, 1-1 και επί, δηλαδή αυτομορφισμός, άρα T g Aut(G). Επίσης ισχύει (T g ) 1 = T g 1 και T g1 T g2 = T g1 g 2, επομένως το σύνολο {T g : G G : g G} είναι υποομάδα της Aut(G). Ορισμός Η ομάδα Inn(G) = {T g : G G : g G} καλείται ομάδα εσωτερικών αυτομορφισμών και τα στοιχεία της, εσωτερικοί αυτομορφισμοί. Παρατήρηση Εστω φ Aut(G) και T g Inn(G) τότε για κάθε x G ισχύει: φ T g φ 1 (x) = φ(gφ 1 (x)g 1 ) = φ(g)xφ(g 1 ) = T φ(g) (x) για κάθε x G Επομένως Inn(G) Aut(G).
17 ΚΕΦΑΛΑΙΟ 1. Στοιχεία θεωρίας ομάδων και αλγεβρικής τοπολογίας 3 Ορισμός Η ομάδα πηλίκο Aut(G)/Inn(G) καλείται ομάδα εξωτερικών αυτομορφισμών της ομάδας G και συμβολίζεται με Out(G). Παρατήρηση Με άλλα λόγια η Out(G) είναι η ομάδα αυτομορφισμών της G modulo συζυγία. Επίσης, σε αντίθεση με το όνομά της, τα στοιχεία της δεν είναι αυτομορφισμοί της G. Αν σκεφτούμε ότι η ομάδα Aut(G) δρα στην G με τον προφανή τρόπο, τότε αντίστοιχα η Out(G) δρα στις κλάσεις συζυγίας της G, Cl G (x) = {h G h = gxg 1 }. Εστω T Out(G) τότε T = φinn(g) για κάποιον αντιπρόσωπο φ Aut(G) της T. Η φυσιολογική δράση που ορίζεται είναι η T Cl G (x) = Cl G (φ(x)). 1.3 Γράφημα Cayley Ορισμός (Γράφημα). Ενα γράφημα X αποτελείται από ένα μη-κενό σύνολο V (X) (σύνολο κορυφών), ένα σύνολο E(X) (σύνολο ακμών) (V (X), E(X) ξένα) και τρεις απεικονίσεις: (i) αντιστροφή: : E(X) E(X) (ii) αρχή: ι : E(X) V (X) (iii) τέλος: τ : E(X) V (X) Ετσι ώστε ē = e για κάθε e E(X), ē e για κάθε e E(X) και τέλος ι(ē) = τ(e) για κάθε e E(X). Ορισμός Ενας προσανατολισμός ενός γραφήματος X είναι ένα υποσύνολο O του E(X) τέτοιο ώστε η τομή O {e, ē} να είναι μονοσύνολο για κάθε e E(X). Ενα γράφημα λέγεται προσανατολισμένο αν έχει επιλεγεί ένας προσανατολισμός. Ορισμός (Δράση ομάδας σε γράφημα). Λέμε ότι μία ομάδα G δρα σ ένα γράφημα X αν η G δρα στα σύνολα κορυφών V (X) και ακμών E(X) έτσι ώστε για κάθε g G και e E(X) να ισχύει:
18 ΓΡΑΦΗΜΑ CAYLEY (i) ge = gē (ii) ι(ge) = gι(e) (iii) τ(ge) = gτ(e) Λέμε ότι η δράση είναι χωρίς αντιστροφές αν ge ē, για κάθε g G, e E(X). Σημείωση. Το (iii) μπορεί να προκύψει από τα (i) και (ii). Παρατήρηση Στην περίπτωση που η G δρα στο γράφημα X χωρίς αντιστροφές ορίζεται το γράφημα πηλίκο X G ως εξής: (i) Κορυφές του X G είναι οι τροχιές κορυφών. (ii) Ακμές του X G είναι οι τροχιές ακμών. και ορίζουμε ι([e]) = [ι(e)], τ([e]) = [τ(e)] και [e] = [ē]. Θέλουμε η δράση να είναι χωρίς αντιστροφές προκειμένου να έχουμε [e] [ē] για κάθε ακμή του γραφήματος πηλίκο. Ορισμός Ενα γράφημα X λέγεται συνεκτικό αν για κάθε δύο κορυφές v και u του X υπάρχει μονοπάτι που τις συνδέει. Δηλαδή υπάρχει μονοπάτι με άκρα το v και u. Δηλαδή μία ακολουθία p = e 1,..., e n με e 1,..., e n E(X) και τ(e i ) = ι(e i+1 ) για i = 1,..., n 1, ι(e 1 ) = v και τ(e n ) = u. Παρατήρηση Αν μία ομάδα G δρα χωρίς αντιστροφές σε ένα συνεκτικό γράφημα X τότε και το γράφημα πηλίκο είναι συνεκτικό. Ορισμός (Γεωμετρική αναπαράσταση). Εστω X ένα γράφημα, θεωρούμε την ξένη ένωση T = V (X) (E(X) [0, 1]) = {v} ({e} [0, 1]) v V (X) e E(X) με τη διακριτή τοπολογία. Στον χώρο T ορίζουμε τη σχέση ισοδυναμίας που περιγράφεται ως εξής : ι(e) (e, 0), τ(e) (e, 1), (e, t) (ē, 1 t) για κάθε e E(X). Ο αντίστοιχος χώρος πηλίκο T λέγεται γεωμετρική αναπαράσταση του γραφήματος X.
19 ΚΕΦΑΛΑΙΟ 1. Στοιχεία θεωρίας ομάδων και αλγεβρικής τοπολογίας 5 Ορισμός Εστω X ένα συνεκτικό γράφημα. Ορίζουμε μετρική d : V (X) V (X) [0, ) ως εξής d(u, v) = το ελάχιστο μήκος μονοπατιού που συνδέει τις κορυφές u και v = min{μήκος(p) : ι(p) = v, τ(p) = u} Την παραπάνω μετρική την επεκτείνουμε σε όλο το γράφημα (στη γεωμετρική του αναπαράσταση) γραμμικά στις ακμές, με τέτοιο τρόπο ώστε κάθε ακμή να ειναι ισομετρική με το [0, 1] με τη συνήθη μετρική. Παρατήρηση Ενα γράφημα X είναι συνεκτικό αν και μόνο αν η γεωμετρική του αναπαράσταση με τη μετρική του Ορισμού είναι συνεκτικός χώρος. Παρατήρηση Η τοπολογία που προκύπτει από τη μετρική δεν είναι η διακριτή τοπολογία. Παρατήρηση Αν X είναι ένα συνεκτικό γράφημα στο οποίο δρα μία ομάδα G χωρίς αντιστροφές τότε η απεικόνιση X X G είναι απεικόνιση πηλίκο τοπολογικών χώρων (αν τα θεωρήσουμε μετρικούς χώρους με τη γεωμετρική αναπαράσταση των γραφημάτων και μετρική τη μετρική του Ορισμού 1.3.8). Σημείωση. Από εδώ και πέρα όταν μιλάμε για γράφημα X θα εννοούμε τη γεωμετρική του αναπαράσταση και αν είναι συνεκτικό θα το θεωρούμε αντίστοιχα μετρικό χώρο. Παρατήρηση Αν μία ομάδα G δρα σε ενα συνεκτικό γράφημα X, τότε η G δρα με ισομετρίες στον μετρικό χώρο X. Ορισμός Εστω G πεπερασμένα παραγόμενη ομάδα και S = {s 1, s 2... s n } πεπερασμένο σύνολο γεννητόρων της G. Το γράφημα Cayley της G ως προς S, συμβολίζεται Γ(G, S), είναι το γράφημα με: (i) κορυφές: τα στοιχεία της G (ii) ακμές: για κάθε κορυφή (στοιχείο) g G και κάθε s S υπάρχει μια γεωμετρική ακμή με αρχή το g και τέλος το gs.
20 ΓΡΑΦΗΜΑ CAYLEY Παρατήρηση Δύο κορυφές g και h του Γ(G, S) συνδέονται με μία ακμή αν και μόνο αν g 1 h S ±1. Για κάθε ακμή υπάρχει και η αντίστροφή της. 2. Το γράφημα Γ(G, S) είναι συνεκτικό. (Αφού το S παράγει την G.) Ορισμός Εστω G πεπερασμένα παραγόμενη ομάδα, S = {s 1, s 2,..., s n } πεπερασμένο σύνολο γεννητόρων της G. Ορίζουμε την μετρική της λέξης d S (1, g) = g S = min{k g = s 1 s 2... s k με s i S ±1 } και d S (g, h) = g 1 h S = min{k g 1 h = s 1 s 2... s k με s i S ±1 }. Παρατήρηση Αν Γ(G, S) είνα το γράφημα Cayley μίας πεπερασμένα παραγόμενης ομάδας G. Η ομάδα G με τη μετρική της λέξης εμφυτεύεται ισομετρικά στο Γ(G, S). (δηλαδή η μετρική της λέξης μπορεί να οριστεί και ως η απόσταση των αντίστοιχων κορυφών στο γράφημα Caley) 2. Προφανώς η μετρική της λέξης, όπως και το γράφημα Cayley, εξαρτώνται από το σύνολο γεννητόρων S. 3. Η G δρα με ισομετρίες φυσικά στο Γ(G, S) δηλαδή στις κορυφές με πολλαπλασιασμό g x = gx και στις ακμές ως εξής: αν e = (x, xs) τότε ge = g(x, xs) = (gx, gxs). 4. Η παραπάνω δράση είναι ελεύθερη και μεταβατική στις κορυφές. 5. Το γράφημα πηλίκο Γ(G, S) G αποτελείται λοιπόν από μία κορυφή και S το πλήθος γεωμετρικές ακμές (βρόγχους). (Είναι συμπαγής μετρικός χώρος)
21 Κεφάλαιο 2 Υπερβολική γεωμετρία 2.1 Το Επίπεδο του Lobachevski Το άνω ημιεπίπεδο H 2 := {z C : Im(z) > 0} εφοδιασμένο με τη μετρική Riemann dx ds = 2 + dy 2 = 4dzd z είναι το επίπεδο του Lobachevski που αποτελεί ένα μοντέλο y (z z) 2 του υπερβολικού επιπέδου. Ορισμός (Υπερβολικό μήκος). Εστω α : [0, 1] H 2 ένα κατά τμήματα διαφορίσιμο τόξο α(t) = x(t) + iy(t) H 2 για κάθε t [0, 1]}. Ορίζουμε το υπερβολικό μήκος l H 2 l H 2(α) = 1 0 ( dx dt Ορισμός (Υπερβολική μετρική). ) 2 ( + dy ) 2 1 dt dt = y(t) 0 Η υπερβολική απόσταση δύο σημείων z, w H 2 ορίζεται ως Παρατήρηση Εύκολα βλέπουμε ότι η d H 2 του τόξου α ως εξής: α (t) dt y(t) d H 2(z, w) = inf{l H 2(α) : α κατά τμήματα διαφορίσιμο τόξο}. είναι μετρική. Πράγματι είναι τετριμμένο ότι είναι μη αρνητική και συμμετρική, επίσης αν είναι μηδέν τότε το τόξο είναι η σταθερή απεικόνιση, δηλαδή z = w. Τέλος ικανοποιεί την τριγωνική ανισότητα αφού αν α 1, α 2 τόξα από το z 1 στο z { 2 α1 (2t), αν t [0, 1/2] και z 2 στο z 3 αντίστοιχα, το α(t) = είναι τόξο από το z 1 α 2 (2t 1), αν t [1/2, 1] στο z 3. 7
22 ΤΟ ΕΠΙΠΕΔΟ ΤΟΥ LOBACHEVSKI Ορισμός Μία απεικόνιση της μορφής T (z) = az+b cz+d μετασχηματισμός Möbius. όπου a, b, c, d C με ad bc 0 λέγεται Σημείωση. Ενας μετασχηματισμός Möbius T (z) = az+b cz+d επεκτείνεται σε μία 1-1 και επί, σύμμορφη απεικόνιση της σφαίρας του Riemann. Οπου αν c 0 τότε T ( d/c) = και T ( ) = a/c, και αν c = 0 τότε T ( ) =. (Περισσότερες πληροφορίες ο αναγνώστης μπορεί να αναζητήσει στο [24] ή σε κάποιο άλλο βιβλίο μιγαδικής ανάλυσης.) Παρατήρηση Θέλουμε να περιορίσουμε τις απεικονίσεις στο άνω ημιεπίπεδο, επομένως αναζητάμε εκείνες που το διατηρούν. Θεωρούμε το υποσύνολο των μετασχηματισμών Möbius, PSL 2 (R) := {T : C C : T (z) = az+b cz+d, με a, b, c, d R και ad bc = 1}, το σύνολο αυτό είναι ομάδα με πράξη τη σύνθεση. Υπάρχει ένας καλώς ορισμένος ομομορφισμός από την ομάδα των πραγματικών πινάκων με ορίζουσα 1, SL(2, R) στην ομάδα PSL 2 (R). Αν A = ( ) a b SL(2, R), τότε ο φυσικός ομομορφισμός είναι A T A με T A (z) = az+b cz+d c d. Παρατηρούμε ότι ο ομομορφισμός είναι επί και ότι ο πυρήνας του είναι η υποομάδα I = {I 2, I 2 }, όπου I 2 είναι ο ταυτοτικός πίνακας. Άρα PSL 2 (R) = SL(2, R) I. Επομένως κάθε στοιχείο της PSL 2 (R) αντιστοιχεί σε δύο πίνακες A και A, άρα μπορούμε να ορίσουμε το ίχνος των στοιχείων της PSL 2 (R), T r(t A ) = tr(a) έτσι ώστε να είναι καλά ορισμένη συνάρτηση στην ομάδα πηλίκο. Παρατηρούμε επίσης ότι στην PSL 2 (R) περιέχονται όλοι οι μετασχηματισμοί Möbius της μορφής z az+b cz+d με a, b, c, d R και ad bc > 0, αφού διαιρώντας αριθμητή και παρονομαστή με ad bc έχουμε τον ίδιο μετασχηματισμό, με a d b c = 1. Θεώρημα Η PSL 2 (R) δρα στον H 2 με ομοιομορφισμούς. Απόδειξη. Θα δείξουμε αρχικά ότι ένας μετασχηματισμός Möbius T PSL 2 (R) απεικονίζει τον H 2 στον εαυτό του. Εστω λοιπόν T με T (z) = az+b cz+d. Τότε έχουμε (2.1.1) (2.1.2) T (z) = az + b (az + b)(c z + d) = cz + d cz + d 2 Im(T (z)) = (T (z) T (z)) 2i = = ac z 2 + adz + bc z + bd cz + d 2, επομένως (z z)(ad bc) 2i cz + d 2 = z z 2i cz + d 2 = Im(z) i cz + d 2 Δηλαδή Im(z) > 0 αν και μόνο αν Im(T (z)) > 0. Η απόδειξη του θεωρήματος ολοκληρώνεται από τη συνέχεια της T και της T 1 = dz b cz+a.
23 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 9 Θεώρημα Η PSL 2 (R) δρα στον H 2 με ισομετρίες. Απόδειξη. Δείξαμε ήδη ότι κάθε στοιχείο της PSL 2 (R) απεικονίζει τον H 2 στον εαυτό του. Θα δείξουμε ότι αν το α : [0, 1] H 2 είναι κατά τόξα διαφορίσιμο, τότε για κάθε T PSL 2 (R) έχουμε ότι l H 2(T (α)) = l H 2(α). Εστω α τόξο με α(t) = z(t) = x(t)+iy(t) και T (α(t)) = w(t) = az(t)+b cz(t)+d = u(t)+iv(t). Εχουμε ότι (2.1.3) dw dz = d dz ( ) az + b a(cz + d) c(az + b) = cz + d (cz + d) 2 = 1 (cz + d) 2 Οπως στο Θεώρημα στις σχέσεις 2.1.1, έτσι και εδώ έχουμε (2.1.4) v = Im(T (z)) = (T (z) T (z)) 2i = (z z)(ad bc) 2i cz + d 2 = Im(z) i cz + d 2 = y cz + d 2 Άρα από και έχουμε dw dz = v y, επομένως l H 2(T (α)) = 1 0 dw dt 1 v(t) dt = dw dz dz 0 v(t) dt dt = 1 0 v(t) y(t) dz dt v(t) dt = 1 0 dz dt y(t) dt = l H 2(α) Άρα η απεικόνιση T διατηρεί το υπερβολικό μήκος, επομένως και την υπερβολική μετρική, άρα είναι ισομετρία. Για X τυχαίο μετρικό χώρο, I R και α : I X καμπύλη, η α καλείται γεωδαισιακή καμπύλη ή απλώς γεωδαισιακή, αν για κάθε x, y I ισχύει d(α(x), α(y)) = x y. Για μία Riemann πολλαπλότητα, επειδή η απόσταση μεταξύ δύο σημείων ορίζεται ως το inmum των μηκών όλων των καμπυλών που διέρχονται από τα σημεία, γεωδαισιακή καμπύλη λέμε την καμπύλη που είναι τοπικά ελαχίστου μήκους. Εν γένει δεν είναι ισοδύναμοι ορισμοί. Δηλαδή γεωδαισιακή καμπύλη μεταξύ δύο σημείων είναι η καμπύλη που το μήκος της επιτυγχάνει την απόσταση των σημείων. Αν το I = [a, b], τότε η α καλείται γεωδαισιακό τόξο. Αν I = [0, ), τότε η α καλείται γεωδαισιακή ακτίνα και τέλος αν I = R, τότε καλείται γεωδαισιακή γραμμή. Θα δείξουμε ότι οι γεωδαισιακές σ αυτόν τον χώρο είναι οι ευθείες γραμμές οι οποίες είναι κάθετες στον άξονα των πραγματικών αριθμών και αντίστοιχα τα ημικύκλια που είναι κάθετα στον άξονα των πραγματικών αριθμών, R = {z C : Im(z) = 0}.
24 ΤΟ ΕΠΙΠΕΔΟ ΤΟΥ LOBACHEVSKI Κάθε δύο σημεία επομένως μπορούν να ενωθούν με γεωδαισιακή, και η απόστασή τους δίνεται από την αντίστοιχη γεωδαισιακή. Αν επιλέξουμε ένα τρίτο σημείο εκτός αυτής της γεωδαισιακής, τότε υπάρχουν περισσότερες από μία γεωδαισιακές που δεν την τέμνουν και διέρχονται από το σημείο. Αυτό σημαίνει ότι η υπερβολική γεωμετρία δεν είναι ευκλείδεια, δηλαδή το πέμπτο αξίωμα των στοιχείων του Ευκλείδη, το αξίωμα της παραλληλίας δεν ικανοποιείται. Θεώρημα Οι γεωδαισιακές καμπύλες στον H 2 είναι τα ημικύκλια που είναι κάθετα στον άξονα R και οι ευθείες που είναι κάθετες στον άξονα R. Απόδειξη. Εστω z 1, z 2 H 2. Υποθέτουμε αρχικά ότι z 1 = ia και z 2 = ib (b > a). Αν γ(t) = x(t) + iy(t) είναι ένα κατά τμήματα διαφορίσιμο τόξο που ενώνει το z με το w τότε: ( 1 dx dt l H 2(γ) = 0 ) 2 ( + dy ) 2 1 dt dy dt dt 1 y(t) 0 y(t) dt 0 dy b dt y(t) dt = 1 a y dy = ln b a Ομως ln b είναι το υπερβολικό μήκος του ευθύγραμμου τμήματος που ενώνει τα σημεία ia a και ib. Άρα η γεωδαισιακή που ενώνει τα σημεία z 1, z 2 {z C : Re(z) = 0} είναι ευθεία κάθετη στον άξονα των πραγματικών R. Εστω τώρα δύο τυχαία σημεία z 1, z 2 H 2 διακρίνουμε περιπτώσεις. Αν τα z 1, z 2 ανήκουν στην ίδια, κάθετη στον άξονα R, ευθεία τότε Re(z 1 ) = Re(z 2 ) = b, ο μετασχηματισμός Möbius T (z) = z b μετακινεί τα z 1, z 2 στον άξονα {z C : Re(z) = 0} και T PSL 2 (R). Άρα η γεωδαισιακή που ενώνει τα T (z 1 ), T (z 2 ) είναι ευθεία ε, κάθετη στον άξονα των πραγματικών R. Επομένως επειδή ο μετασχηματισμός T 1 (z) = z + b πάει την ευθεία ε σε μία παράλληλη ευθεία T 1 (ε) και διατηρεί τις γεωδαισιακές, έπεται ότι η γεωδαισιακή που ενώνει τα z 1, z 2 είναι ευθεία κάθετη στον άξονα των πραγματικών R.
25 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 11 Αν τα z 1, z 2 δεν ανήκουν στην ίδια, κάθετη στον άξονα R, ευθεία τότε υπάρχει μοναδικός κύκλος C κάθετος στον άξονα R που διέρχεται από τα z 1, z 2. Εστω c 1, c 2 R (c 2 > c 1 ) τα σημεία τομής του κύκλου με τον R. Τότε θεωρούμε τους εξής μετασχηματισμούς Möbius: T 1 (z) = z c 1, επομένως ( c 1 ) = 1, άρα T 1 PSL 2 (R) 1 T 2 (z) = z (c 2 c 1 ), επομένως 0 ( (c 2 c 1 )) ( 1) 1 = 1, άρα T 2 PSL 2 (R) 1 T 3 (z) = z, επομένως ( 1 ) = 1 άρα T3 PSL 2 (R) c 2 c 1 c 2 c 1 Η σύνθεση T = T 3 T 2 T 1 είναι στοιχείο του PSL 2 (R) και άρα διατηρεί το άνω ημιεπίπεδο. Παρατηρούμε ότι ο T απεικονίζει τον κύκλο C στον άξονα I := {z C : Re(z) = 0, Im(z) > 0}: πράγματι αν z C και αν w := z c 1 και c := c 2 c 1 2, τότε έχουμε z c 2 +c 1 2 = c 2 c 1 2 w + c1 c 2+c 1 2 = c w c 2 c 1 2 = c και T (z) = 1 z c 2 1 c 2 c 1 = (Re(w) c) 2 + (Im(w)) 2 = c 2 (Re(w)) 2 2cRe(w) + (Im(w)) 2 = 0 1 w 2c 1 2c = 1 2c w 1 2c = w w(2c w) 2cw w 2 = = = 2c(2c w) 2c 2c w 2c 2c w = = 2cRe(w) + 2iIm(w) (Re(w))2 + (Im(w)) 2 = 2c 2c w = 2iIm(w) 2c 2c w 2c (2c w) 2c(2c w) 2c(2c w) = Άρα T (z) I. Αφού ο T είναι μετασχηματισμός Möbius διατηρεί τα μήκη, και αφού η ε είναι γεωδασιακή, έπεται ότι και ο C είναι γεωδαισιακή καμπύλη. Συμβολισμός. I := {z C : Re(z) = 0, Im(z) > 0} Πόρισμα Κάθε δύο σημεία z, w H 2 μπορούν να ενωθούν με μοναδική γεωδαισιακή και η υπερβολική απόσταση μεταξύ των z και w είναι ίση με το υπερβολικό μήκος της μοναδικής γεωδαισιακής που τα ενώνει. Συμβολισμός. Συμβολίζουμε με [z, w] τη μοναδική γεωδαισιακή που ενώνει το z με το w.
26 ΤΟ ΕΠΙΠΕΔΟ ΤΟΥ LOBACHEVSKI Πόρισμα Αν z και w είναι δύο διαφορετικά σημεία του H 2 τότε d H 2(z, w) = d H 2(z, ξ) + d H 2(ξ, w) αν και μόνο αν ξ [z, w]. Πόρισμα Κάθε μετασχηματισμός στην PSL 2 (R) απεικονίζει γεωδαισιακές σε γεωδαισιακές στον H 2. Απόδειξη. Υπάρχουν δύο εύκολοι τρόποι να το δούμε. Εστω z, w H 2 και T PSL 2 (R). Αν ξ [z, w] τότε d H 2(z, w) = d H 2(z, ξ)+d H 2(ξ, w) άρα d H 2(T (z), T (w)) = d H 2(T (z), T (ξ))+ d H 2(T (ξ), T (w)), άρα T (ξ) [T (z), T (w)]. Άρα ο T απεικονίζει τη γεωδαισιακή [z, w] σε γεωδαισιακή. Ενας δεύτερος τρόπος είναι γεωμετρικής φύσης. Ξέρουμε από τη μιγαδική ότι οι μετασχηματισμοί Möbius απεικονίζουν κύκλους και ευθείες σε κύκλους και ευθείες, επίσης διατηρούν γωνίες. Το υποσύνολό τους, PSL 2 (R) διατηρεί τον άξονα των πραγματικών R, επομένως οι PSL 2 (R) απεικονίζουν ευθείες κάθετες στο R και κύκλους κάθετους στο R πάλι σε ευθείες και κύκλους κάθετους στο R, άρα γεωδαισιακές σε γεωδαισιακές. Λήμμα Εστω z, w H 2. Τότε sinh ( ) 1 2 d H2(z, w) = z w 2 Im(z)Im(w). Απόδειξη. Παρατηρούμε ότι το αριστερό μέλος της προς απόδειξη ισότητας είναι αναλλοίωτο από τον ισομορφισμό T PSL 2 (R). Θα δείξουμε στη συνέχεια ότι και το δεξιό μέλος της ισότητας είναι επίσης αναλλοίωτο από τον ισομορφισμό T. Εστω T (z) = az+b cz+d τότε: az+b T (z) T (w) 2 Im(T (z))im(t (w)) = 2 = = 2 cz+d aw+b cw+d Im( az+b cz+d = aw+b )Im( cw+d ) adz+bcw bcz adw (cz+d)(cw+d) 2 Im( adz+bc z adw+bc w )Im( ) cz+d 2 cw+d 2 adz+bcw bcz adw cz+d cw+d adim(z) bcim(z) cz+d 2 = = adim(w) bcim(w) cw+d 2 (ad bc)(z w) = 2 (ad bc)(im(z)im(w)) = z w = 2 Im(z)Im(w)
27 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 13 Άρα η σχέση είναι αναλλοίωτη ως προς τη δράση της T στα z, w. Υπάρχει μετασχηματισμός T PSL 2 (R) όπως στην απόδειξη του Θεωρήματος ο οποίος μεταφέρει τα z, w στον άξονα των φανταστικών I. Επομένως αρκεί να δείξουμε τη σχέση για z = ia και w = ib. ) Εστω a, b R με b > a > 0, τότε sinh( 1 2 d H 2(ia, ib)) = sinh( 1 2 ln b a (ln ) = sinh όμως a = z και b = w. Να θυμήσουμε ότι ισχύει η ταυτότητα sinh 1 (x) = ( ln x + ) x άρα x = sinh(ln(x + x 2 z w + 1)), άρα για x = 2 Im(z)Im(w) έχουμε ( ) z w 2 Im(z)Im(w) = sinh ln z w z w Im(z)Im(w) + 4Im(z)Im(w) = ( ) = sinh ln a b a b ab = 4ab ( ( )) ( ( )) a b = sinh ln 2 a + b 2b + ab 2 = sinh ln ab 2 = ab ( ( )) ( ) b 1 = sinh ln = sinh a 2 d H2(z, w) b a Θεώρημα Η ομάδα PSL 2 (R) είναι ισόμορφη με την ομάδα ισομετριών του υπερβολικού επιπέδου H 2, που διατηρούν τον προσανατολισμό και η οποία συμβολίζεται με Isom + (H 2 ) Απόδειξη. Εστω φ Isom + (H 2 ) μία ισομετρία του H 2. Οπως το Πόρισμα , η φ απεικονίζει γεωδαισιακές σε γεωδαισιακές. Επομένως η εικόνα φ(i) είναι μία γεωδαισιακή. Εχουμε όμως ότι υπάρχει μία ισομετρία T 1 PSL 2 (R) που απεικονίζει την φ(i) στην I (αυτό το δείχνουμε όπως στην απόδειξη του Θεωρήματος 2.1.8). Εχουμε ότι T 1 φ(i) = λi, για λ > 0, και συνθέτουμε με T 2 (z) = λ 1 z, όπου T 2 PSL 2 (R). Εχουμε επομένως ότι T 2 T 1 φ(i) = i. Αν T 2 T 1 φ((0, i)) = (i, ) τότε συνθέτουμε με T 3 (z) = 1 z, όπου T 3 PSL 2 (R), αλλιώς αν T 2 T 1 φ((0, i)) = (0, i) την αφήνουμε έτσι. Θέτουμε T = T 3 T 2 T 1 φ (αντίστοιχα αν αφήνει αναλλοίωτο το (0, i) θέτουμε T = T 2 T 1 φ). Παρατηρούμε ότι T (i) = i, T ((0, i)) = (0, i) και T ((i, )) = (i, ). Επίσης d H 2(ia, ib) = ln b a για b > a > 0, άρα d H 2(T (ia), i) = d H 2(T (ia), T (i)) = d H2(ia, i), επομένως για a > 1 Im(T (ia)) έχουμε ln = ln a T (ia) = ia, όμοια για a < i. Δηλαδή η ισομετρία T αφήνει 1 1 κατά σημείο σταθερό τον άξονα I.
28 Ο ΔΙΣΚΟΣ ΤΟΥ POINCARÉ Εστω τώρα z = x + iy τυχαίο σημείο z H 2 και T (z) = u + iv. Για κάθε t > 0 έχουμε d H 2(z, it)) = d H 2(T (z), T (it))) = d H 2(T (z), it)) από το Λήμμα έχουμε x 2 + (y t) 2 y = u2 + (v t) 2 v x2 + (y t) 2 t 2 v = u2 + (v t) 2 t 2 y όμως η σχέση ισχύει για κάθε t > 0, παίρνοντας όρια lim t x 2 + (y t) 2 u 2 + (v t) 2 v = lim y v = y t t 2 Επομένως δείξαμε ότι v = y και αντικαθιστώντας παίρνουμε x 2 = u 2. Ομως η συνάρτηση είναι συνεχής επομένως x = u ή x = u. Δηλαδή T (z) = z ή T (z) = z. Ομως η T είναι σύνθεση ισομετριών που διατηρούν τον προσανατολισμό, επομένως διατηρεί τον προσανατολισμό, ενώ T (z) = z τον αντιστρέφει, άρα T (z) = z. Δηλαδή φ PSL 2 (R). Παρατήρηση Αν θεωρήσουμε PSL ± 2 t 2 (R) = {T (z) = a z+b c z+d : με ad bc = 1} PSL 2(R), τότε: PSL ± 2 (R) = {A R2 2 : det(a) = ±1} I = GL(2, R) {λi2 : λ R} έχουμε PSL 2 (R) PSL ± 2 (R) και μάλιστα [PSL± 2 (R) : PSL 2(R)] = 2. Γιατί αν θεωρήσουμε ψ : H 2 H 2 με ψ(z) = z, τότε ψ ψ = id H 2 Μπορούμε επίσης να δείξουμε ότι PSL ± 2 (R) = Isom(H2 ). και PSL ± 2 (R) = PSL 2(R) ψpsl 2 (R). Ακολουθώντας την ίδια διαδικασία του Θεωρήματος καταλήγουμε σε T (z) = z ή T (z) = z. Αν ισχύει η πρώτη περίπτωση όπως πριν τελειώσαμε. Αν ισχύει η δεύτερη περίπτωση τότε T 3 T 2 T 1 φ(z) = z άρα φ(z) = a( 1) z + b c( 1) z + d και a( 1)d c( 1)b = ( 1)(ad cb) = 1 άρα φ PSL± 2 (R). 2.2 Ο Δίσκος του Poincaré Τώρα θα περιγράψουμε το μοντέλο του δίσκου του Poincaré για το υπερβολικό επίπεδο, το οποίο καλείται υπερβολικός δίσκος. Εστω D 2 = {z C : z < 1}. Η απεικόνιση f(z) = zi + 1 είναι ολόμορφη, 1-1 και επί απεικόνιση από τον H 2 στον D 2. Εχουμε z + i επίσης f (z) 0 για κάθε z H 2 και f 1 (z) = iz 1 i z. Επειδή η f είναι σύμμορφη απεικόνιση, διατηρεί και τις γωνίες. Ορίζουμε για z, w D 2 μετρική στην D 2 ως d D 2(z, w) = d H 2(f 1 (z), f 1 (w)). Με αυτή τη μετρική ο δίσκος ονομάζεται υπερβολικός δίσκος.
29 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 15 Σημείωση. Ο φυσιολογικός τρόπος να οριστεί μετρική στον δίσκο D 2 είναι ορίζοντας τη μετρική Riemann ds = 2 dx 2 + dy 2 1 x 2 + y 2 = 2 dz 1 z 2. Προκύπτει τότε για δύο σημεία z, w D2 η μετρική d D 2(z, w) = cosh (1 1 2 z w 2 ) + (1 z 2 )(1 w 2. Η f(z) = zi + 1 τότε είναι ) z + i ισομετρία από τον H 2 στον D 2. Πόρισμα Η ομάδα ισομετριών του υπερβολικού δίσκου D 2 είναι { ( ) } z a Isom(D 2 ) = φ : D 2 D 2 : φ(z) = e iθ, a C, a < 1, θ [0, 2π). āz 1 Απόδειξη. Αρκεί να δείξουμε ότι η f T f 1 η οποία είναι ισομετρία του υπερβολικού δίσκου είναι της παραπάνω μορφής. Πράγματι, έστω T PSL(2, R) με T (z) = az+b cz+d όπου ad bc = 1 τότε T (f 1 zi(a + ib) (a ib) (z)) = zi(c + id) (c id) Θέτουμε x := a + ib και y := c + id. Τότε: f(t (f 1 (z))) = w 1 z w 2 w 2 z 1 όπου w 1 = x iy x + iȳ = x iy (x iy) και w 2 = ȳ + i x x + iy. Επομένως w 1 = 1 και άρα το w 1 γράφεται ως w 1 = e iθ. Εφ όσον ȳ + i x = a 2 + b 2 + c 2 + d 2 2 και x + iy = a 2 + b 2 + c 2 + d 2 + 2, έχουμε ότι w 2 < 1. Πόρισμα Κάθε ισομετρία φ Isom + (D 2 ) είναι σύμμορφη συνάρτηση. Λήμμα Εστω φ Isom + (D 2 ) μία ισομετρία. Αν η φ σταθεροποιεί ένα διάνυσμα και ένα σημείο, τότε η φ είναι η ταυτοτική απεικόνιση id D 2. Απόδειξη. Εστω φ = e iθ z a μία ισομετρία, η οποία σταθεροποιεί ένα σημείο και ένα āz 1 διάνυσμα. Χωρίς βλάβη της γενικότητας, μπορούμε να υποθέσουμε ότι σταθεροποιεί το 0 iθ a και ένα διάνυσμα. Αν σταθεροποιεί το 0, τότε φ(0) = 0, δηλαδή e = 0, άρα a = 0. 1 Επομένως φ = e iθ z, επειδή η φ σταθεροποιεί ενα διάνυσμα δεν γίνεται να το περιστρέφει. Επομένως φ = id D 2.
30 ΤΟ ΣΥΝΟΡΟ ΤΟΥ H 2 ΚΑΙ ΤΟΥ D 2 Πόρισμα Οι γεωδαισιακές στον D 2 είναι τμήματα κύκλων που τέμνουν κάθετα τον κύκλο S 1 = { z D 2 : z = 1 } και οι διάμετροι. Απόδειξη. Για κάθε κύκλο που τέμνει τον άξονα των πραγματικών R αντιστοιχεί μία καμπύλη της μορφής που ειπώθηκε. Αν έχουμε μία ευθεία που τέμνει τον άξονα R κάθετα στο σημείο x, τότε αντιστοιχεί σε καμπύλη που ένα της άκρο είναι το i και το άλλο xi + 1 x + i. Επομένως μπορούμε να κάνουμε μία περιστροφή κατά γωνία θ, με θ 0 και θ π xi+1 2 Arg( x+i ), που είναι ισομετρία και διατηρεί τις γωνίες, άρα προκύπτει καμπύλη που τέμνει σε δύο σημεία τον κύκλο, έστω z 1, z 2 διάφορα του i. Η αντίστροφη της f απεικονίζει τα z 1, z 2 σε σημεία του R και την καμπύλη σε γεωδαισιακή άρα σε ημικύκλιο, άρα τέμνει το R κάθετα. Επομένως η αρχική καμπύλη έτεμνε τον S 1 κάθετα. 2.3 Το σύνορο του H 2 και του D 2 Θα παρουσιάσουμε δύο διαφορετικούς τρόπους για να πάρει κάποιος το σύνορο του H 2 και του D 2. Ο πρώτος είναι χρησιμοποιώντας το γεγονός ότι και οι δύο αυτοί χώροι είναι τοπολογικοί υπόχωροι του C με την ιδιότητα η τοπολογία που προκύπτει απο τη μετρική τους συμπίπτει με την τοπολογία που προκύπτει από το C. Ο δεύτερος τρόπος είναι κοιτώντας τους χώρους ως ανεξάρτητους μετρικούς χώρους. Παρατηρούμε ότι η υπερβολική απόσταση στον υπερβολικό δίσκο D 2 από την αρχή του 0 εξαρτάται μόνο από το μέτρο του z, z. Επομένως η ανοικτή μπάλα B D 2(0, R) είναι η ευκλείδεια μπάλα B D 2(0, R) = B C (0, R ). Επίσης έχουμε ότι οι ισομετρίες του δίσκου Isom(D 2 ) διατηρούν του κύκλους, άρα και τις μπάλες, επομένως οι ανοικτές μπάλες με την υπερβολική μετρική είναι ευκλείδειες. Επομένως η τοπολογία του D 2 που προκύπτει από τη μετρική συμπίπτει με την τοπολογία του σαν υποσύνολο του C. Λόγω της ισομετρίας f
31 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 17 έπεται ότι και η τοπολογία του H 2 που προκύπτει από τη μετρική συμπίπτει με την τοπολογία που προκύπτει ως υποσύνολο του C. Σαν τοπολογικοί χώροι, το επίπεδο H 2 C C είναι ανοικτός υπόχωρος τους μιγαδικού επιπέδου και κατ επέκταση της σφαίρας του Riemann C = C { }. Ο δίσκος D 2 C είναι ανοικτός υπόχωρος του μιγαδικού επιπέδου. Παρατηρούμε επίσης ότι το H 2 σαν υποσύνολο της σφαίρας του Riemann είναι ένας ανοικτός δίσκος που το σύνορό του διέρχεται από το επ άπειρον σημείο { }. Επομένως H 2 = H 2 \ H 2 = R { }. Τοπολογικά είναι κύκλος, δηλαδή R { } = S 1 και καλείται κύκλος του απείρου. Αυτό προκύπτει αμέσως από την παρατήρηση ότι το R { } είναι συνεκτικό σύνολο. Αν δεν ήταν θα υπήρχε ένα ανοικτό σύνολο U που θα περιείχε το { } και R U c, αφού τα B c (0, R) είναι σύστημα περιοχών του { }, B c (0, R) U όμως B c (0, R) R για κάθε R > 0, άρα είναι συνεκτκό σύνολο. Για τον δίσκο άμεσα βλέπουμε ότι D 2 = D 2 \ D 2 = {z C : z = 1} = S 1. Σημείωση. Σημειώνουμε ότι και στις δύο περιπτώσεις τα σύνορα είναι συνεκτικοί χώροι ομοιομορφικοί με το S 1 = {z C : z = 1. Πόρισμα Μία γεωδαισιακή γραμμή γ : (, + ) H 2 καθορίζεται πλήρως από τα σημεία της στο σύνορο H 2 (όμοια για D 2 ). Τώρα θα κοιτάξουμε τοπολογικά το σύνορο των δύο αυτών χώρων. Ορισμός (Απόσταση Hausdor). Η απόσταση Hausdor δύο υποσυνόλων A, B X ορίζεται ως d H (A, B) = inf{ε : A N ε (B) και B N ε (A)}, όπου N ε (C) = {x X : dist(x, C) < ε}, για C x. Ορισμός Εστω X = H 2 ή D 2. Δύο γεωδαισιακές ακτίνες γ 1, γ 2 : [0, ) X λέγονται ασυμπτωτικές και συμβολίζουμε γ 1 H γ 2 αν d H (γ 1, γ 2 ) <. Παρατήρηση Η σχέση H είναι σχέση ισοδυναμίας στο σύνολο των γεωδαισιακών ακτίνων. Ορισμός (Σύνορο Gromov). Το σύνορο του Gromov X είναι το σύνολο των κλάσεων ισοδυναμίας X = {γ : γ γεωδαισιακή ακτίνα } H
32 ΤΟ ΣΥΝΟΡΟ ΤΟΥ H 2 ΚΑΙ ΤΟΥ D 2 Τώρα θα περιγράψουμε την δ-περιοχή μιας γεωδαισιακής γραμμής γ στον H 2, δηλαδή το σύνολο N δ (γ). Εστω, όπως πριν, I = {z C : Re(z) = 0, Im(z) > 0}, τότε το σύνολο N δ (I) φράσσεται από δύο ευθείες γραμμές από το 0 στο συμμετρικές ως προς τον άξονα των y που σχηματίζουν στο 0 γωνία θ από το I. Πρόταση Η δ-περιοχή της I είναι N δ (I) = {x + iy : y > x cot(θ)} όπου η θ προκύπτει από τη σχέση tanh( δ 2 ) = tan( θ 2 ). Απόδειξη. Αν z N δ (I), τότε d H 2(z, I) < δ. Αφού για κάθε λ R >0 η υπερβολική ισομετρία T λ = λz αφήνει τον I αναλλοίωτο, έχουμε d H 2(λz, I) = d H 2(λz, T λ (I)) = d H 2(z, I) < δ. Επομένως αν z N δ (I), τότε ολόκληρη η ευθεία {λz : λ R >0 } περιέχεται στην περιοχή N δ (I). Για να δείξουμε ότι η δ-περιοχή N δ (I) είναι συμμετρικό σύνολο ως προς τον I, αρκεί να παρατηρήσουμε ότι d H 2(x + iy, I) = d H 2( x + iy, I), x R, y > 0. Για να βρούμε τον τύπο του θ, έστω w = e i( π 2 θ) ένα σημείο του συνόρου του N δ (I). (i 1)(w + 1) Από τον τύπο της υπερβολικής απόστασης έχουμε δ = d H 2(i, w) = ln (i + 1)(w 1) = 1 + ieiθ ln i e iθ. Δηλαδή e δ 1 + ieiθ = i e iθ. Επομένως tanh( δ 2 ) = tan( θ 2 ). Χρησιμοποιώντας τις T PSL 2 (R) μπορούμε να κατασκευάσουμε όλες τις δ-περιοχές γεωδαισιακών γραμμών. Παρατηρούμε λοιπόν ότι για να ανήκει στην δ-περιοχή της γεωδαισιακής ακτίνας γ 1 = {z C : Re(z) = 0 Im(z) (0, 1]} μία άλλη γεωδαισιακή ακτίνα γ 2 πρέπει lim γ 2 (t) = 0. Από αυτό προκύπτει ότι το R { } είναι σε 1-1 και επί αντιστοιχία t με το σύνολο H 2 = {γ : γ γεωδαισιακή ακτίνα } H.
33 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία Ταξινόμηση ισομετριών Θα γίνει μία ταξινόμηση των ισομετριών που διατηρούν τον προσανατολισμό του H 2, κοιτώντας τον αριθμό των σταθερών σημείων της ισομετρίας στο H 2. Πρόταση (Επέκταση μετασχηματισμών Möbius). Κάθε μετασχηματισμός Möbius T PSL 2 (R) επεκτείνεται σε ομοιομορφισμό της σφαίρας του Riemann. Απόδειξη. Ενας μετασχηματισμός T (z) = az + b όπου a, b, c, d R και ad bc = 1 είναι { } cz + d d { a } σύμμορφη απεικόνιση T : C \ C \, αν c 0, και T : C C, αν c = 0. c c ( ) d Επεκτείνεται επομένως σε σύμμορφη T : C C θέτοντας T = και T ( ) = a c c, αν c 0, και T ( ) =, αν c = 0. Αν c 0 βλέπουμε ότι σε οποιοδήποτε σημείο διάφορο του d έχουμε T (z) = c ad bc (cz + d) 2 = 1 d (cz + d) 2 0, ενώ στο σημείο κοιτάμε την f(z) = 1 c T (z) = cz + d az + b, ( ) f da cb (z) = (az + b) 2 = 1 d d όπου στο σημείο z = είναι f c = (az + b) 2 c c ad + cb 0. ( ) 1 Και τέλος για το σημείο z = κοιτάμε την g(z) = T = bz + a z dz + c όπου g (z) = bc ad (dz + c) 2 στο σημείο z = 0 γίνεται g (0) = 1 c 2 0. Ομοια και για την περίπτωση c = 0. Επομένως ο μετασχηματισμός T PSL 2 (R) επεκτείνεται σε σύμμορφη απεικόνιση T : C C. Πόρισμα Κάθε T PSL 2 (R) επεκτείνεται σε σύμμορφη απεικόνιση T : H 2 H 2. Πρόταση Κάθε ισομετρία T PSL 2 (R) έχει σταθερό σημείο στον H 2. Πιο συγκεκριμένα για T id H 2 ισχύει μία από τις παρακάτω τρεις περιπτώσεις: Η T έχει ακριβώς ένα σταθερό σημείο στον H 2. Η T δεν έχει σταθερό σημείο στον H 2 και έχει ακριβώς ένα σταθερό σημείο στον H 2. Η T δεν έχει σταθερό σημείο στον H 2 και έχει ακριβώς δύο σταθερά σημεία στον H 2.
34 ΤΑΞΙΝΟΜΗΣΗ ΙΣΟΜΕΤΡΙΩΝ Απόδειξη. Εστω T PSL 2 (R) με T (z) = az+b cz+d id H 2. Αν η T έχει σταθερό σημείο στον H 2, τότε είναι λύση της εξίσωσης (2.4.1) az + b cz + d = z και αντίστροφα αν z λύση της εξίσωσης, τότε είναι σταθερό σημείο. Διακρίνουμε περιπτώσεις. Αν c 0, τότε το δεν είναι λύση της Επομένως η γράφεται ως cz 2 + (d a)z b = 0. Αν η διακρίνουσα = (d a) 2 4c( b) < 0, τότε η έχει δύο μιγαδικές συζυγείς λύσεις, η μία θα έχει θετικό φανταστικό μέρος, άρα θα ανήκει στον H 2 και η άλλη αρνητικό. Επομένως σε αυτή την περίπτωση θα έχει ακριβώς ένα σταθερό σημείο που ανήκει στον H 2. Αν η διακρίνουσα = (d a) 2 4c( b) = 0, τότε η εξίσωση έχει μόνο μία πραγματική λύση την a d 2c, η οποία επειδή είναι πραγματική ανήκει στο R H2. Άρα σε αυτή την περίπτωση θα έχει ακριβώς ένα σταθερό σημείο που ανήκει στο H 2. Τέλος αν η διακρίνουσα = (d a) 2 4c( b) > 0, τότε η εξίσωση έχει δύο πραγματικές λύσεις οι οποίες ανήκουν επίσης στο R H 2. Δηλαδή σε αυτή την περίπτωση θα έχει ακριβώς δύο σταθερά σημεία που ανήκουν στο H 2. Αν c = 0, τότε η έχει πάντα μία λύση το και γράφεται (2.4.2) az + b = dz Αν (d a) 0, τότε η έχει λύση και το b d a, άρα δύο λύσεις μία το H2 και την b πραγματική d a R H2, δηλαδή δύο σταθερά σημεία στο H 2. Αν (d a) = 0, τότε η έχει μοναδική λύση το το οποίο είναι στο H 2, δηλαδή ένα σταθερό σημείο στο H 2. Ορισμός Εστω T PSL 2 (R), με T id H 2. Αν η T έχει ένα ακριβώς σταθερό σημείο στον H 2, τότε καλείται ελλειπτική ισομετρία. Αν η T δεν έχει σταθερά σημεία στον H 2 και έχει ένα ακριβώς σταθερό σημείο στο H 2, τότε καλείται παραβολική ισομετρία. Αν η T δεν έχει σταθερά σημεία στον H 2 και έχει ακριβώς δύο σταθερά σημεία στο H 2, τότε καλείται υπερβολική ισομετρία.
35 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 21 Σημείωση. Στην επόμενη πρόταση χρησιμοποιούμε της συνάρτηση T r( ) που έχει ορισθεί στην Παρατήρηση Πρόταση Εστω T PSL 2 (R), με T id H 2 τότε: T ελλειπτική ισομετρία αν και μόνο αν T r(t ) < 2. T παραβολική ισομετρία αν και μόνο αν T r(t ) = 2. T υπερβολική ισομετρία αν και μόνο αν T r(t ) > 2. Απόδειξη. Εστω T (z) = az+b cz+d, με ad bc = 1 και a, b, c, d R. Αν c 0, τότε έχουμε: (T r(t )) 2 = ( tr ( )) 2 a b = a 2 + d 2 + 2ad = (a d) 2 + 4ad = c d = (d a) 2 4(bc bc ad) = = (d a) 2 4(c( b) 1) = = (d a) 2 4(c( b)) + 4 = = + 4 Τα σημεία που μένουν σταθερά δίνονται από την εξίσωση cz 2 + (d a)z b = 0. Διακρίνουμε περιπτώσεις, αν > 0 ισοδύναμα T r(t ) > 2, τότε η εξίσωση έχει δύο διακεκριμένες πραγματικές ρίζες, επομένως η ισομετρία T έχει δύο σταθερά σημεία στο σύνορο, άρα είναι υπερβολική. Αν = 0 ισοδύναμα T r(t ) = 2, τότε η εξίσωση έχει ακριβώς μία πραγματική ρίζα και άρα η ισομετρία T έχει ένα ακριβώς σταθερό σημείο στο σύνορο, δηλαδή είναι παραβολική. Αν < 0 ισοδύναμα T r(t ) < 2, τότε η εξίσωση έχει μόνο δύο συζυγείς μιγαδικές ρίζες, εκ των οποίων μόνο η μία είναι στοιχείο της H 2, άρα η ισομετρία είναι ελλειπτική. Αν c = 0, τότε έχουμε ότι ad = ad bc = 1 άρα (d a) 2 = d 2 + a 2 2ad = d 2 + a 2 2 και επομένως (T r(t )) 2 = a 2 + d = (d a) Αν λοιπόν a = d, τότε όπως δείξαμε πριν έχει μόνο ένα σταθερό σημείο η ισομετρία T, το, που είναι στοιχείο του συνόρου, επομένως είναι παραβολική ισομετρία. Οταν όμως a = d παίρνουμε T r(t ) = 2. Τέλος αν a d, τότε πάλι όπως δείξαμε και πριν έχει δύο σταθερά σημεία στο σύνορα το b a και το, τότε όμως T r(t ) > 2. Επομένως σε κάθε περίπτωση το αποτέλεσμα συμβαδίζει με την εκφώνηση της πρότασης.
36 Η ΥΠΕΡΒΟΛΙΚΗ ΓΕΩΜΕΤΡΙΑ ΤΩΝ ΕΠΙΦΑΝΕΙΩΝ S g Ορισμός (Άξονας υπερβολικής ισομετρίας). Εστω T PSL 2 (R) μία υπερβολική ισομετρία. Άξονας της ισομετρίας T, συμβολίζεται με Axis(T ), είναι η γεωδαισιακή γραμμή με πέρατα τα σταθερά σημεία της T. Παρατήρηση Εξ ορισμού έχουμε ότι Axis(gT g 1 ) = g (Axis(T )) για κάθε g PSL 2 (R). (Η PSL 2 (R) είναι ομάδα και τα στοιχεία της δρουν στα στοιχεία του H 2, επομένως ο συμβολισμός g βοηθάει να δούμε τους μετασχηματισμούς ως δράσεις). Αφού ο T στέλνει τη γεωδαισιακή Axis(T ) σε γεωδαισιακή γραμμή με τα ίδια πέρατα, έπεται T (Axis(T )) = Axis(T ). 2.5 Η υπερβολική γεωμετρία των επιφανειών S g Ορισμός Εστω S μία επιφάνεια. Αν ο καθολικός χώρος επικάλυψης της S είναι ο H 2, τότε η επιφάνεια καλείται υπερβολική. Παρατήρηση Μία υπερβολική επιφάνεια S μπορεί να οριστεί ως μία λεία επιφάνεια εφοδιασμένη με μία μετρική Riemann σταθερής καμπυλότητας -1. Αν η επιφάνεια είναι επιπλέον κλειστή, τότε καλούμε υπερβολική δομή της επιφάνειας, {(U i, φ i ) : φ i (U i ) H 2 } μία συλλογή λείων χαρτών έτσι ώστε τα U i να καλύπτουν την επιφάνεια S και κάθε απεικόνιση αλλαγής χαρτών φ i φ 1 j στο φ j (U i U j ) να είναι ο περιορισμός μιας ισομετρίας του H 2, που διατηρεί τον προσανατολισμό. Μπορεί να δειχθεί ότι μία τέτοια επιφάνεια έχει καθολικό χώρο επικάλυψης το H 2. Α- ντίστροφα αν μία επιφάνεια έχει καθολικό χώρο επικάλυψης το H 2, τότε μπορεί να εφοδιαστεί με μία μετρική Riemann σταθερής καμπυλότητας -1. Επειδή είναι πιο βολικός λόγο συμμετρίας, θα δείξουμε ότι ο καθολικός χώρος επικάλυψης της κλειστής προσανατολίσιμης επιφάνειας γένους g 2 είναι ο υπερβολικός δίσκος D 2, το οποίο είναι ισοδύναμο με το να δείχναμε ότι είναι το υπερβολικό επίπεδο H 2. Επομένως για κάθε g 2 η επιφάνεια S g είναι υπερβολική.
37 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 23 Θεώρημα (Η υπερβολική δομή των επιφανειών S g ). Για κάθε g 2 η επιφάνεια γένους g, S g, επιδέχεται υπερβολική δομή. Απόδειξη. Η επιφάνεια S g είναι το πηλίκο ενός κανονικού ευκλειδείου 4g-γώνου, ταυτίζοντας τα ζεύγη των απέναντι πλευρών. Αν συμβολίσουμε με a 1, b 1, a 2, b 2,..., b g a g, τότε η αλγεβρική σχέση στο σύνορο δίνεται από την a 1 b 1... a g b g a 1 1 b 1 1 a 1 g b 1 g. a 1 b 1 2 b 1 a 1 2 a 1 1 b 2 b 1 1 a 2 Θα ταυτίσουμε την επιφάνεια S g με το πηλίκο μίας συμπαγούς περιοχής του D 2, φραγμένης από ένα γεωδαισιακό πολύγωνο (πολύγωνο με πλευρές γεωδαισιακές στον υπερβολικό δίσκο D 2 ) του οποίου οι πλευρές θα έχουν ίσα μήκη και οι γωνίες που σχηματίζουν στα σημεία τομής θα είναι όλες ίσες (ένα κανονικό γεωδαισιακό πολύγωνο). Ξεκινάμε με 4g σημεία (z 0, z 1,..., z 4g 1, z 4g = z 0 ) ισομοιρασμένα σε ένα τυχαίο ευκλείδειο κύκλο με κέντρο το 0, z i = r, με r < 1. Τα ενώνουμε με γεωδαισιακά τμήματα [z i, z i+1 ]. Επειδή η d D 2 είναι αναλλοίωτη από τις ισομετρίες της μορφής e iθ, δηλαδή από τις περιστροφές, τα γεωδαισιακά αυτά τμήματα έχουν όλα ίσο μήκος και σχηματίζουν ίσες γωνίες στα σημεία τομής τους (αφού οι ισομετρίες αυτές, διατηρούν τις γωνίες). Άρα η ένωση αυτών των γεωδαισιακών τμημάτων είναι ένα κανονικό γεωδαισιακό πολύγωνο. έχουμε Θεωρούμε θ(r) την εσωτερική γωνία δύο διαδοχικών πλευρών του πολυγώνου. Τότε lim θ(r) = 0 και lim θ(r) = π π r 1 r 0 2g Η πρώτη ισότητα προκύπτει επειδή καθώς η ακτίνα του κύκλου τείνει στο 1 τα γεωδαισιακά τμήματα τείνουν να γίνουν τμήματα κύκλου που τέμνουν κάθετα την S 1, άρα γεωδαισιακές που εφάπτονται, δηλαδή η γωνία μεταξύ τους τείνει στο 0. Η δεύτερη ισότητα προκύπτει επειδή καθώς η ακτίνα του κύκλου τείνει στο 0 τα γεωδαισιακά τμήματα τείνουν να γίνουν
38 Η ΥΠΕΡΒΟΛΙΚΗ ΓΕΩΜΕΤΡΙΑ ΤΩΝ ΕΠΙΦΑΝΕΙΩΝ S g τμήματα διαμέτρων, δηλαδή ευθυγράμμων τμημάτων, επομένως το πολύγωνο τείνει να γίνει ευκλείδειο, επομένως η γωνία τείνει να γίνει η γωνία του κανονικού ευκλείδειου 4g-γωνου, η οποία είναι π π 2g. θ 0 θ = π/4 θ 3π/4 Η θ(r) είναι συνεχής απεικόνιση, (μπορεί να εκφραστεί ως συνεχή συνάρτηση του r και του g, μέσω του νόμου των συνημιτόνων) επομένως λόγω συνέχειας από το θεώρημα ενδιάμεσης τιμής υπάρχει r 0 τέτοιο ώστε θ(r 0 ) = π. Αυτό δε μπορεί να ισχύσει για g = 1 2g καθώς η θ δε μπορεί να πάρει την τιμή π 2. Εστω P το συμπαγές υποσύνολο του D 2 που αποτελείται από το κανονικό γεωδαισιακό πολύγωνο γωνίας π 2g και τη φραγμένη συνιστώσα. Επιλέγουμε μία ακμή v 0 και ταυτίζουμε διαδοχικά τις ακμές με a 1, b 1, a1 1, b , a g, b g, a 1 g, b 1 g με αντίστροφη φορά από τους δείκτες του ρολογιού, ξεκινώντας από το v 0. Για κάθε a i, i = 2, 3,..., g ορίζουμε ως αρχή του γεωδαισιακού τμήματος την κορυφή ανάμεσα στην a i και b 1 i 1 και για a 1 ορίζουμε ως αρχή την κορυφή ανάμεσα στην a 1 και b 1 g, δηλαδή την v 0. Για κάθε b i, i = 1, 2,..., g ορίζουμε ως αρχή του γεωδαισιακού τμήματος την κορυφή ανάμεσα στην b i και την a i. Παρόμοια για αρχή των γεωδαισιακών τμημάτων a 1 i, i = 1, 2,..., g, την κορυφή που βρίσκεται ανάμεσα στην a 1 i και την b 1 i i = 1, 2,..., g 1 την κορυφή που βρίσκεται ανάμεσα στην b 1 i b 1 g την v 0.. Τέλος για αρχή των γεωδαισιακών τμημάτων b 1 i, και στην a i+1, και αρχή της Για κάθε ζεύγος a j, a 1 j υπάρχει μοναδική ισομετρία έστω α j που πάει την ακμή με ετικέτα a 1 j στην ακμή με ετικέτα a j καλώς ορισμένη ως προς την αρχή του γεωδαισιακού τμήματος (δηλαδή απεικονίζει την αρχή σε αρχή). Ομοια για κάθε b j υπάρχει η ισομετρία β j που πάει την b j στην b 1 j καλώς ορισμένη ως προς την αρχή του γεωδαισιακού τμήματος. Εστω Γ < Isom + (D 2 ) η υποομάδα που παράγεται από {α i, β i : i = 1, 2,..., g}. Καλούμε τους γεννήτορες α i, β i και τους αντίστροφούς τους, μετασχηματισμούς ταύτισης ακμών
39 ΚΕΦΑΛΑΙΟ 2. Υπερβολική γεωμετρία 25 (edge pairing tranformation). Ισχυρισμός Για κάθε μετασχηματισμό ταύτισης ακμών φ Γ έχουμε ότι η τομή P φ(p ) αποτελείται ακριβώς από μία ακμή του P. Πράγματι, έστω e η ακμή που μετακινεί η φ και την πηγαίνει στην ακμή e (εξ ορισμού υπάρχει μία τέτοια ακμή). Κάθε γεωδαισιακή γραμμή γ στον D 2 χωρίζει τον δίσκο σε δύο συνεκτικές συνιστώσες D 2 \ γ, οι οποίες καλούνται πλευρές της γεωδαισιακής. Κάθε γεωδαισιακή ακμή του P ανήκει σε μία γεωδαισιακή γραμμή γ και το P, επειδή είναι συνεκτικό σύνολο, ανήκει σε μία από τις δύο πλευρές D 2 \ γ. Επομένως το ίδιο ισχύει για το φ(p ). Για κάθε γεωδαισιακή ακμή του, το φ(p ) ανήκει σε μία από τις δύο πλευρές της γεωδαισιακής γραμμής στην οποία ανήκει η ακμή. Η γεωδαισιακή ακμή e του P ανήκει σε μία γεωδαισιακή γραμμή, έστω ε. Η ε έχει δύο πλευρές. Η ε είναι γεωδαισιακή γραμμή στην οποία ανήκει ακμή του P άρα το P ανήκει σε μία πλευρά της ε. Ομως το ε είναι γεωδαισιακή γραμμή στην οποία ανήκει και ακμή του φ(p ) άρα και το φ(p ) ανήκει σε μια από τις δύο πλευρές της ε. Επειδή η φ διατηρεί τον προσανατολισμό και τις γωνίες επομένως έχουμε ότι τα φ(p ) και P ανήκουν σε διαφορετικές πλευρές. Άρα P φ(p ) = (P ε) (φ(p ) ε) = e. Επειδή το P είναι ομοιομορφικό με ευκλείδειο κανονικό πολύγωνο, το πηλίκο του P υπό τις ταυτοποιήσεις από τους μετασχηματισμούς ταύτισης ακμών είναι ομοιομορφικό με την επιφάνεια S g. Ισχυρισμός Οι μετασχηματισμοί ταύτισης ακμών ικανοποιούν τις ίδιες σχέσεις με τους γεννήτορες της θεμελιώδους ομάδας της επιφάνειας, π 1 (S g ). Πράγματι, αρκεί να δείξουμε ότι α 1 β 1 α 1 1 β α g β g αg 1 β 1 g = id D 2. Είναι πιο βολικό να δείξουμε την ισοδύναμη σχέση β g α g βg 1 αg 1... β 1 α 1 β1 1 α 1 1 = id D 2, που προκύπτει από την αντιστροφή. Ονομάζουμε για ευκολία τους μετασχηματισμούς ως φ 4g := β g, φ 4g 1 := α g, φ 4g 2 := βg 1, φ 4g 3 := αg 1,..., φ 2 := β1 1, φ 1 := α1 1. Εξ ορισμού η α1 1 = φ 1 παίρνει την v 0 (αρχή της a 1 και την πηγαίνει στην αρχή της a 1 1. Αν ονομάσουμε τις κορυφές, ξεκινώντας από την v 0 και πηγαίνοντας αντίστροφα στους δείκτες του ρολογιού, ως v 0, v 3, v 2, v 1, v 4. Βλέπουμε ότι η φ i πάει την v i 1 στην v i για i = 1, 2, 3, 4. Αφού η v 4 είναι η αρχή του γεωδαισιακού τμήματος a 2, μπορούμε να συνεχίσουμε με επαγωγή να ονομάζουμε τις υπόλοιπες κορυφές, ως v 5,..., v 4g 1 καταλήγοντας v 4g = v 0, έτσι ώστε φ i (v i 1 ) = v i, για κάθε i = 1,..., 4g 1 και φ 4g (v 4g 1 ) = v 0. Ειδικότερα βλέπουμε ότι φ 4g... φ 1 (v 0 ) = v 0. Για κάθε κορυφή v i βρίσκεται ανάμεσα σε δύο ακμές, θα μετράμε τις
t : (x, y) x 2 +y 2 y x
 Σύνοψη Κεφαλαίου 5: Αντιστροφική Γεωμετρία Αντιστροφή 1. Η ανάκλαση σε μία ευθεία l στο επίπεδο απεικονίζει ένα σημείο A σε ένα σημείο A που απέχει ίση απόσταση από την l αλλά βρίσκεται στην άλλη πλευρά
Σύνοψη Κεφαλαίου 5: Αντιστροφική Γεωμετρία Αντιστροφή 1. Η ανάκλαση σε μία ευθεία l στο επίπεδο απεικονίζει ένα σημείο A σε ένα σημείο A που απέχει ίση απόσταση από την l αλλά βρίσκεται στην άλλη πλευρά
1 m z. 1 mz. 1 mz M 1, 2 M 1
 Σύνοψη Κεφαλαίου 6: Υπερβολική Γεωμετρία Υπερβολική γεωμετρία: το μοντέλο του δίσκου 1. Στο μοντέλο του Poincaré της υπερβολικής γεωμετρίας, υπερβολικά σημεία είναι τα σημεία του μοναδιαίου δίσκου, D =
Σύνοψη Κεφαλαίου 6: Υπερβολική Γεωμετρία Υπερβολική γεωμετρία: το μοντέλο του δίσκου 1. Στο μοντέλο του Poincaré της υπερβολικής γεωμετρίας, υπερβολικά σημεία είναι τα σημεία του μοναδιαίου δίσκου, D =
Modular καµπύλες. Αριστείδης Κοντογεώργης. 1 εκεµβρίου Τµήµα Μαθηµατικών Πανεπιστηµίου Αθηνών. , 1/26
 Modular καµπύλες Αριστείδης Κοντογεώργης Τµήµα Μαθηµατικών Πανεπιστηµίου Αθηνών. 1 εκεµβρίου 2014, 1/26 Το υπερβολικό επίπεδο H = {z : I(z) > 0} Το Θεώρηµα σύµµορφης απεικόνισης του Riemann (Riemann mapping
Modular καµπύλες Αριστείδης Κοντογεώργης Τµήµα Μαθηµατικών Πανεπιστηµίου Αθηνών. 1 εκεµβρίου 2014, 1/26 Το υπερβολικό επίπεδο H = {z : I(z) > 0} Το Θεώρηµα σύµµορφης απεικόνισης του Riemann (Riemann mapping
Δώδεκα Αποδείξεις του. Θεμελιώδους Θεωρήματος της Άλγεβρας
 Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
6 Συνεκτικοί τοπολογικοί χώροι
 36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
f(f 1 (B)) f(f 1 (B)) B. X \ (f 1 (C)) = X \ f 1 (C) = f 1 (Y \ C) X \ (f 1 (C)) f 1 (Y \ C). f 1 (Y \ C) = f 1 (Y \ C ) = X \ f 1 (C ).
 Κεφάλαιο 4 Συναρτήσεις μεταξύ μετρικών χώρων 4.1 Συνεχείς συναρτήσεις Εστω (X, ρ) και (Y, σ) δύο μετρικοί χώροι. Στην 2.2 δώσαμε τον ορισμό της συνέχειας μιας συνάρτησης f : X Y σε κάποιο σημείο x 0 X:
Κεφάλαιο 4 Συναρτήσεις μεταξύ μετρικών χώρων 4.1 Συνεχείς συναρτήσεις Εστω (X, ρ) και (Y, σ) δύο μετρικοί χώροι. Στην 2.2 δώσαμε τον ορισμό της συνέχειας μιας συνάρτησης f : X Y σε κάποιο σημείο x 0 X:
ή κανονικός ( regular ), αν για κάθε x και κάθε κλειστό αντιπαραδείγματα με τα οποία αποδεικνύεται ότι οι αντίστροφες συνεπαγωγές δεν ισχύουν.
 93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
93 4 Διαχωριστικά αξιώματα Στο κεφάλαιο αυτό εισάγουμε τα λεγόμενα διαχωριστικά αξιώματα και εξετάζουμε τις βασικές ιδιότητές τους. Ένα από αυτά το έχουμε ήδη εισαγάγει δηλαδή το αξίωμα Husdorff ( ορισμός
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
i=1 i=1 i=1 (x i 1, x i +1) (x 1 1, x k +1),
 Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
x 2 + y 2 + z 2 = R 2.
 Σημειώσεις μαθήματος Μ2324 Γεωμετρική Τοπολογία Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2011 Εισαγωγή Η Γεωμετρική Τοπολογία είναι ο κλάδος των μαθηματικών που μελετάει τα ολικά χαρακτηριστικά
Σημειώσεις μαθήματος Μ2324 Γεωμετρική Τοπολογία Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2011 Εισαγωγή Η Γεωμετρική Τοπολογία είναι ο κλάδος των μαθηματικών που μελετάει τα ολικά χαρακτηριστικά
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ας ξεκινήσουμε υπενθυμίζοντας τον ορισμό της συνέχειας σε μετρικούς χώρους. διατυπώνεται και με τον ακόλουθο τρόπο: για κάθε σφαίρα
 33.4.Συνεχείς συναρτήσεις Η έννοια της συνεχούς συνάρτησης είναι θεμελιώδης και μελετάται κατ αρχήν για συναρτήσεις μιας και κατόπιν δύο ή περισσότερων μεταβλητών στα μαθήματα του Απειροστικού Λογισμού.
33.4.Συνεχείς συναρτήσεις Η έννοια της συνεχούς συνάρτησης είναι θεμελιώδης και μελετάται κατ αρχήν για συναρτήσεις μιας και κατόπιν δύο ή περισσότερων μεταβλητών στα μαθήματα του Απειροστικού Λογισμού.
R ισούται με το μήκος του. ( πρβλ. την ιστορική σημείωση 3.27 στο τέλος
 73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
4 Ασθενείς τοπολογίες σε χώρους με νόρμα. 4.1 θεωρήματα Mazur, Alaoglou, Goldstine.
 8 Έστω (, ) 4 Ασθενείς τοπολογίες σε χώρους με νόρμα 4. θεωρήματα Mazur, Alaoglou, Goldste. χώρος με νόρμα. Υπενθυμίζουμε ότι η ασθενής τοπολογία T του έχει ως βάση ( ανοικτών ) περιοχών του όλα τα σύνολα
8 Έστω (, ) 4 Ασθενείς τοπολογίες σε χώρους με νόρμα 4. θεωρήματα Mazur, Alaoglou, Goldste. χώρος με νόρμα. Υπενθυμίζουμε ότι η ασθενής τοπολογία T του έχει ως βάση ( ανοικτών ) περιοχών του όλα τα σύνολα
από t 1 (x) = A 1 x A 1 b.
 Σύνοψη Κεφαλαίου 2: Ομοπαραλληλική Γεωμετρία Γεωμετρία και μετασχηματισμοί 1. Μία ισομετρία του R 2 είναι μία απεικόνιση από το R 2 στο R 2 που διατηρεί αποστάσεις. Κάθε ισομετρία του R 2 έχει μία από
Σύνοψη Κεφαλαίου 2: Ομοπαραλληλική Γεωμετρία Γεωμετρία και μετασχηματισμοί 1. Μία ισομετρία του R 2 είναι μία απεικόνιση από το R 2 στο R 2 που διατηρεί αποστάσεις. Κάθε ισομετρία του R 2 έχει μία από
ι3.4 Παραδείγματα T ) έχει την ιδιότητα Heine-Borel, αν κάθε κλειστό και φραγμένο υποσύνολό του είναι συμπαγές.
 6 ι3.4 Παραδείγματα Στην παράγραφο αυτή θα μελετήσουμε κάποια σημαντικά παραδείγματα, για τις εφαρμογές, χώρων συναρτήσεων οι οποίοι είναι τοπικά κυρτοί και μετρικοποιήσιμοι αλλά η τοπολογία τους δεν επάγεται
6 ι3.4 Παραδείγματα Στην παράγραφο αυτή θα μελετήσουμε κάποια σημαντικά παραδείγματα, για τις εφαρμογές, χώρων συναρτήσεων οι οποίοι είναι τοπικά κυρτοί και μετρικοποιήσιμοι αλλά η τοπολογία τους δεν επάγεται
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ
 Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
Μιχάλης Παπαδημητράκης. Αναλυτική χωρητικότητα Συνεχής αναλυτική χωρητικότητα
 Μιχάλης Παπαδημητράκης Αναλυτική χωρητικότητα Συνεχής αναλυτική χωρητικότητα 1 Παράγωγος στο. Ας θυμηθούμε ότι μια μιγαδική συνάρτηση f ορισμένη σε ένα υποσύνολο του μιγαδικού επιπέδου λέμε ότι είναι
Μιχάλης Παπαδημητράκης Αναλυτική χωρητικότητα Συνεχής αναλυτική χωρητικότητα 1 Παράγωγος στο. Ας θυμηθούμε ότι μια μιγαδική συνάρτηση f ορισμένη σε ένα υποσύνολο του μιγαδικού επιπέδου λέμε ότι είναι
Η Γεωμετρία της Αντιστροφής Η βασική θεωρία. Αντιστροφή
 Αντιστροφή Υποθέτουμε ότι υπάρχει ένας κανόνας ο οποίος επιτρέπει την μετάβαση από ένα σχήμα σε ένα άλλο, με τέτοιο τρόπο ώστε το δεύτερο σχήμα να είναι τελείως ορισμένο όταν το πρώτο είναι δοσμένο και
Αντιστροφή Υποθέτουμε ότι υπάρχει ένας κανόνας ο οποίος επιτρέπει την μετάβαση από ένα σχήμα σε ένα άλλο, με τέτοιο τρόπο ώστε το δεύτερο σχήμα να είναι τελείως ορισμένο όταν το πρώτο είναι δοσμένο και
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Εισαγωγή στην Τοπολογία
 Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT
 ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΜΕΣΩ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ CLAIRAUT Αρβανιτογεώργος Ανδρέας Πατέρας Ιωάννης ΓΕΩΔΑΙΣΙΑΚΕΣ ΚΑΜΠΥΛΕΣ Στόχος Εργασίας Η εύρεση των γεωδαισιακών καμπυλών πάνω σε μια επιφάνεια.
3.5 Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους.
 7 3.5 Το θεώρημα Hah-Baach σε τοπολογικούς διανυσματικούς χώρους. Εξετάζουμε καταρχήν τη σχέση μεταξύ ενός μιγαδικού διανυσματικού χώρου E και του υποκείμενου πραγματικού χώρου E R. Έστω E μιγαδικός διανυσματικός
7 3.5 Το θεώρημα Hah-Baach σε τοπολογικούς διανυσματικούς χώρους. Εξετάζουμε καταρχήν τη σχέση μεταξύ ενός μιγαδικού διανυσματικού χώρου E και του υποκείμενου πραγματικού χώρου E R. Έστω E μιγαδικός διανυσματικός
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΠΕΙΚΟΝΙΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΑΠΕΙΚΟΝΙΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
αβ (, ) τέτοιος ώστε f(x
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΘΕΜΑ Α Άσκηση α) Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ αβ., ] Αν η f είναι συνεχής στο [ αβ, ]
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
Έχοντας υπόψιν το Λήμμα του Urysohn, είναι φυσικό να θέσουμε το ακόλουθο ερώτημα: Αν
 3 4.3 Τελείως κανονικοί χώροι ( ). 3 2 Έχοντας υπόψιν το Λήμμα του Urysoh, είναι φυσικό να θέσουμε το ακόλουθο ερώτημα: Αν κανονικός χώρος, x και κλειστό ώστε x. Υπάρχει τότε συνεχής συνάρτηση f :, ώστε
3 4.3 Τελείως κανονικοί χώροι ( ). 3 2 Έχοντας υπόψιν το Λήμμα του Urysoh, είναι φυσικό να θέσουμε το ακόλουθο ερώτημα: Αν κανονικός χώρος, x και κλειστό ώστε x. Υπάρχει τότε συνεχής συνάρτηση f :, ώστε
f 1 (A) = {f 1 (A i ), A i A}
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΕΜ Χειμερινό εξάμηνο 2017-18 ΜΕΜ231-ΤΟΠΟΛΟΓΙΑ, 11Η ΔΙΑΛΕΞΗ ΣΥΜΠΑΓΕΙΑ ΔΙΔΑΣΚΩΝ: Ι.Δ. ΠΛΑΤΗΣ Μετά τη συνεκτικότητα, όπου είδαμε κάπως αναλυτικά την ιδιότητα εκείνη που επιτρέπει σύνολα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΕΜ Χειμερινό εξάμηνο 2017-18 ΜΕΜ231-ΤΟΠΟΛΟΓΙΑ, 11Η ΔΙΑΛΕΞΗ ΣΥΜΠΑΓΕΙΑ ΔΙΔΑΣΚΩΝ: Ι.Δ. ΠΛΑΤΗΣ Μετά τη συνεκτικότητα, όπου είδαμε κάπως αναλυτικά την ιδιότητα εκείνη που επιτρέπει σύνολα
Κ X κυρτό σύνολο. Ένα σημείο x Κ
 8 5 Το θεώρημα Kre-Mlm Βασικές ιδιότητες συμπαγών και κυρτών συνόλων. Ορισμός 5. Έστω X διανυσματικός χώρος και Κ X κυρτό σύνολο. Ένα σημείο x Κ λέγεται ακραίο ( extreme ) σημείο του Κ, αν δεν είναι γνήσιος
8 5 Το θεώρημα Kre-Mlm Βασικές ιδιότητες συμπαγών και κυρτών συνόλων. Ορισμός 5. Έστω X διανυσματικός χώρος και Κ X κυρτό σύνολο. Ένα σημείο x Κ λέγεται ακραίο ( extreme ) σημείο του Κ, αν δεν είναι γνήσιος
Όταν δεν υπάρχει κίνδυνος σύγχυσης γράφουμε συνήθως ο τοπολογικός χώρος X και χρησιμοποιούμε την σύντμηση τ.χ. (= τοπολογικός χώρος).
 4 Τοπολογικοί χώροι. Στοιχειώδεις έννοιες της τοπολογίας Στην παράγραφο αυτή εισάγουμε τις βασικές έννοιες της τοπολογίας, δηλαδή αυτές του ανοικτού και κλειστού συνόλου, της κλειστότητας και του εσωτερικού
4 Τοπολογικοί χώροι. Στοιχειώδεις έννοιες της τοπολογίας Στην παράγραφο αυτή εισάγουμε τις βασικές έννοιες της τοπολογίας, δηλαδή αυτές του ανοικτού και κλειστού συνόλου, της κλειστότητας και του εσωτερικού
1 Η εναλλάσσουσα ομάδα
 Η εναλλάσσουσα ομάδα Η εναλλάσσουσα ομάδα Όπως είδαμε η συνάρτηση g : S { } είναι ένας επιμορφισμός ομάδων. Ο πυρήνας Ke g {σ S / g σ } του επιμορφισμού συμβολίζεται με A περιέχει όλες τις άρτιες μεταθέσεις
Η εναλλάσσουσα ομάδα Η εναλλάσσουσα ομάδα Όπως είδαμε η συνάρτηση g : S { } είναι ένας επιμορφισμός ομάδων. Ο πυρήνας Ke g {σ S / g σ } του επιμορφισμού συμβολίζεται με A περιέχει όλες τις άρτιες μεταθέσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
f x 0 για κάθε x και f 1
 06 4.2 Το Λήμμα του Uysoh το Λήμμα της εμφύτευσης και το θεώρημα μετρικοποίησης του Uysoh. Ο κύριος στόχος αυτής της παραγράφου είναι η απόδειξη ενός θεμελιώδους αποτελέσματος γνωστού ως το Λήμμα του Uysoh.
06 4.2 Το Λήμμα του Uysoh το Λήμμα της εμφύτευσης και το θεώρημα μετρικοποίησης του Uysoh. Ο κύριος στόχος αυτής της παραγράφου είναι η απόδειξη ενός θεμελιώδους αποτελέσματος γνωστού ως το Λήμμα του Uysoh.
Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ. Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις
 Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις ẋ 1 f 1 (x 1 x 2 ) ẋ 2 f 2 (x 1 x 2 ) (501) Το σύστημα αυτό γράφεται σε διανυσματική
Κεφάλαιο 5 ΔΙΔΙΑΣΤΑΤΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ενα αυτόνομο δυναμικό σύστημα δύο διαστάσεων περιγράφεται από τις εξισώσεις ẋ 1 f 1 (x 1 x 2 ) ẋ 2 f 2 (x 1 x 2 ) (501) Το σύστημα αυτό γράφεται σε διανυσματική
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Ε Μέχρι 18 Μαΐου 2015.
 Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
 Κεφάλαιο 7 Ισομετρίες, Συμμετρίες και Πλακοστρώσεις Οπως είδαμε στην απόδειξη του πρώτου κριτηρίου ισότητας τριγώνων, ο Ευκλείδης χρησιμοποιεί την έννοια της εφαρμογής ενός τριγώνου σε ένα άλλο, χωρίς
Κεφάλαιο 7 Ισομετρίες, Συμμετρίες και Πλακοστρώσεις Οπως είδαμε στην απόδειξη του πρώτου κριτηρίου ισότητας τριγώνων, ο Ευκλείδης χρησιμοποιεί την έννοια της εφαρμογής ενός τριγώνου σε ένα άλλο, χωρίς
B = F i. (X \ F i ) = i I
 Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Συνεκτικά σύνολα. R είναι συνεκτικά σύνολα.
 4 Συνεκτικά σύνολα Έστω, Ι διάστηµα και f : Ι συνεχής, τότε η f έχει την ιδιότητα της ενδιαµέσου τιµής, δηλαδή, η f παίρνει κάθε τιµή µεταξύ δύο οποιονδήποτε διαφορετικών τιµών της, συνεπώς το f ( Ι )
4 Συνεκτικά σύνολα Έστω, Ι διάστηµα και f : Ι συνεχής, τότε η f έχει την ιδιότητα της ενδιαµέσου τιµής, δηλαδή, η f παίρνει κάθε τιµή µεταξύ δύο οποιονδήποτε διαφορετικών τιµών της, συνεπώς το f ( Ι )
ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
v y = 12x 2 y + 4y v(x, y) = 6x 2 y 2 + y 4 + y + c(x). f(z) = u(z, 0) + iv(z, 0) = z + i(z 4 + c), f(z) = iz 4 + z i.
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Α 0 Ιουλίου, 0 Θέμα. (αʹ) Να βρεθεί η τιμή του a R για την οποία η συνάρτηση u(x, y) ax 3 y +4xy
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Εξετάσεις στη Μιγαδική Ανάλυση ΟΜΑΔΑ: Α 0 Ιουλίου, 0 Θέμα. (αʹ) Να βρεθεί η τιμή του a R για την οποία η συνάρτηση u(x, y) ax 3 y +4xy
f I X i I f i X, για κάθεi I.
 47 2 Πράξεις σε τοπολογικούς χώρους 2. Η τοπολογία γινόμενο Σε προηγούμενη παράγραφο ορίσαμε την τοπολογία γινόμενο στο καρτεσιανό γινόμενο Y δύο τοπολογικών χώρων Y, ( παράδειγμα.33 () ). Στην παρούσα
47 2 Πράξεις σε τοπολογικούς χώρους 2. Η τοπολογία γινόμενο Σε προηγούμενη παράγραφο ορίσαμε την τοπολογία γινόμενο στο καρτεσιανό γινόμενο Y δύο τοπολογικών χώρων Y, ( παράδειγμα.33 () ). Στην παρούσα
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
Το Θεώρημα Stone - Weierstrass
 Το Θεώρημα Stone - Weierstrass Θεώρημα 1 Έστω ¹ X συμπαγής χώρος Hausdorff και έστω C R (X η πραγματική άλγεβρα όλων των συνεχών συναρτήσεων f : X R. Έστω ότι ένα υποσύνολο A C R (X (1 το A είναι υπάλγεβρα
Το Θεώρημα Stone - Weierstrass Θεώρημα 1 Έστω ¹ X συμπαγής χώρος Hausdorff και έστω C R (X η πραγματική άλγεβρα όλων των συνεχών συναρτήσεων f : X R. Έστω ότι ένα υποσύνολο A C R (X (1 το A είναι υπάλγεβρα
f(x) = lim f n (t) = d(t, x n ) d(t, x) = f(t)
 Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
1 + t + s t. 1 + t + s
 Κεφάλαιο 1 Μετρικοί χώροι Ομάδα Α 1.1. Εστω (X, ) χώρος με νόρμα. Δείξτε ότι η νόρμα είναι άρτια συνάρτηση και ικανοποιεί την ανισότητα x y x y για κάθε x, y X. Υπόδειξη. Για κάθε x X έχουμε x = ( 1)x
Κεφάλαιο 1 Μετρικοί χώροι Ομάδα Α 1.1. Εστω (X, ) χώρος με νόρμα. Δείξτε ότι η νόρμα είναι άρτια συνάρτηση και ικανοποιεί την ανισότητα x y x y για κάθε x, y X. Υπόδειξη. Για κάθε x X έχουμε x = ( 1)x
V x, y W x, y, y συνιστούν προφανώς ένα ανοικτό
 81 3.2 Το θεώρημα Tychooff. Στην παράγραφο αυτή θα ασχοληθούμε με το θεώρημα Tychooff, δηλαδή ότι ένα αυθαίρετο καρτεσιανό γινόμενο συμπαγών χώρων είναι, με την τοπολογία γινόμενο, συμπαγής χώρος. Το θεώρημα
81 3.2 Το θεώρημα Tychooff. Στην παράγραφο αυτή θα ασχοληθούμε με το θεώρημα Tychooff, δηλαδή ότι ένα αυθαίρετο καρτεσιανό γινόμενο συμπαγών χώρων είναι, με την τοπολογία γινόμενο, συμπαγής χώρος. Το θεώρημα
Θεωρία Galois. Πρόχειρες σημειώσεις (εκδοχή )
 Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
Μαθηματική Ανάλυση ΙI
 Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Μαθηματική Ανάλυση ΙI Δρ. Θεόδωρος Ζυγκιρίδης 25 Μαΐου 211 2 Περιεχόμενα 1 Ο χώρος R n 1 1.1 Ο Ευκλείδιος n-χώρος..................................
Π Δ Μ Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Μαθηματική Ανάλυση ΙI Δρ. Θεόδωρος Ζυγκιρίδης 25 Μαΐου 211 2 Περιεχόμενα 1 Ο χώρος R n 1 1.1 Ο Ευκλείδιος n-χώρος..................................
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων.
 πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων. Αριστείδης Κοντογεώργης -Τμήμα Μαθηματικών ΕΚΠΑ Πρότυπο Λύκειο Ευαγγελικής Σχολής Σμύρνης 21 Οκτωβρίου 2015 1 το τελευταίο θεώρημα του
πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων. Αριστείδης Κοντογεώργης -Τμήμα Μαθηματικών ΕΚΠΑ Πρότυπο Λύκειο Ευαγγελικής Σχολής Σμύρνης 21 Οκτωβρίου 2015 1 το τελευταίο θεώρημα του
Θεωρία Τελεστών. Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert. Αριστείδης Κατάβολος. Τµήµα Μαθηµατικών
 Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert Αριστείδης Κατάβολος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ενότητα: Χώροι µε νόρµα - Χώροι Hilbert Αριστείδης Κατάβολος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
j=1 x n (i) x s (i) < ε.
 Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Κεφάλαιο 0. Μεταθετικοί ακτύλιοι, Ιδεώδη
 Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
h(x, y) = card ({ 1 i n : x i y i
 Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
H Θεωρία των Dessins d'enfants του Grothendieck
 H Θεωρία των Dessins d'enfants του Grothendieck Μανώλης Τζωρτζάκης Εθνικό Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Μαθηματικών March 8, 2014 Ιστορία/ Motivation Αλγεβρικές Καμπύλες και το Θεώρημα Belyi
H Θεωρία των Dessins d'enfants του Grothendieck Μανώλης Τζωρτζάκης Εθνικό Καποδιστριακό Πανεπιστήμιο Αθηνών Τμήμα Μαθηματικών March 8, 2014 Ιστορία/ Motivation Αλγεβρικές Καμπύλες και το Θεώρημα Belyi
ΑΣΚΗΣΕΙΣ. 1. Στο ομοπαραλληλικό επίπεδο δίνεται το σύστημα συντεταγμένων S { A, A, A }.
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΠΘ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ Ι ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0-3 ΑΣΚΗΣΕΙΣ. Στο ομοπαραλληλικό επίπεδο δίνεται το σύστημα συντεταγμένων S { A, A, A }. 0 ' Θεωρούμε τα σημεία A, A, A που ορίζονται
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΑΠΘ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ Ι ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 0-3 ΑΣΚΗΣΕΙΣ. Στο ομοπαραλληλικό επίπεδο δίνεται το σύστημα συντεταγμένων S { A, A, A }. 0 ' Θεωρούμε τα σημεία A, A, A που ορίζονται
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ. Πολλαπλότητες. & Γεωμετρία των τριών διαστάσεων
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Πολλαπλότητες & Γεωμετρία των τριών διαστάσεων Οι οκτώ γεωμετρίες του 3-διάστατου χώρου ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Φωτεινός Μεργούπης-Ανάγνου
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ Πολλαπλότητες & Γεωμετρία των τριών διαστάσεων Οι οκτώ γεωμετρίες του 3-διάστατου χώρου ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ Φωτεινός Μεργούπης-Ανάγνου
Μιχάλης Παπαδημητράκης. Μιγαδική Ανάλυση. Τμήμα Μαθηματικών. Πανεπιστήμιο Κρήτης
 Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και
Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Τμήμα Μαθηματικών Πανεπιστήμιο Κρήτης Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. με νόρμα, με τις ακόλουθες νόρμες οι οποίες ορίζονται μέσω των νορμών των X και Y.
 2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω ( X, ) και (, ) X Y {( x, ) : x X και Y} Y χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω ( X, ) και (, ) X Y {( x, ) : x X και Y} Y χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται
Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1. Μιγαδικοί αριθμοί. ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά Μιγαδική Ανάλυση Α 1 Μιγαδική ανάλυση Μέρος Α Πρόχειρες σημειώσεις 1 Μιγαδικοί αριθμοί Τι είναι και πώς τους αναπαριστούμε Οι μιγαδικοί αριθμοί είναι μια επέκταση του συνόλου
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ Γ. Π. Β. ΦΡΟΝΤΙΣΤΗΡΙΑΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΛΥΜΕΝΕΣ & ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ Επιμέλεια: Γ. Π. Βαξεβάνης (Γ. Π. Β.) (Μαθηματικός) ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ
f x x, ν Ν-{0,1} είναι παραγωγίσιμη στο R
 ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
834. Θεωρία Ομάδων Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα, 2013
 834. Θεωρία Ομάδων Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα, 2013 Περιεχόμενα 1 Βασικές Έννοιες 1 1.1 Ορισμοί - παραδείγματα.............................. 1 1.2 Υποομάδες και Σύμπλοκα..............................
834. Θεωρία Ομάδων Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Αθήνα, 2013 Περιεχόμενα 1 Βασικές Έννοιες 1 1.1 Ορισμοί - παραδείγματα.............................. 1 1.2 Υποομάδες και Σύμπλοκα..............................
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
ΣΥΜΜΟΡΦΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ MÖBIUS ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΥΝΟΡΙΑΚΩΝ ΤΙΜΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΥΜΜΟΡΦΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ MÖBIUS ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΥΝΟΡΙΑΚΩΝ ΤΙΜΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΚΑΤΣΑΝΕΒΑΚΗ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΣΥΜΜΟΡΦΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ MÖBIUS ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΥΝΟΡΙΑΚΩΝ ΤΙΜΩΝ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΚΑΤΣΑΝΕΒΑΚΗ
Α Δ Ι. Παρασκευή 20 Δεκεμβρίου GL n (R) / SL n (R)
 Α Δ Ι Α - Φ 8 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 20 Δεκεμβρίου
Α Δ Ι Α - Φ 8 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 20 Δεκεμβρίου
EukleÐdeiec emfuteôseic: ˆnw frˆgmata
 EukleÐdeiec emfuteôseic: ˆnw frˆgmata Εστω f : X Y μια εμφύτευση του μετρικού χώρου (X, ρ) στο χώρο με νόρμα (Y, ). Η παραμόρφωση της f ορίζεται ως εξής: f(x) f(y) ρ(x, y) dist(f) = sup sup x y ρ(x, y)
EukleÐdeiec emfuteôseic: ˆnw frˆgmata Εστω f : X Y μια εμφύτευση του μετρικού χώρου (X, ρ) στο χώρο με νόρμα (Y, ). Η παραμόρφωση της f ορίζεται ως εξής: f(x) f(y) ρ(x, y) dist(f) = sup sup x y ρ(x, y)
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΤΟΙΧΕΙΩΔΕΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΤΟΙΧΕΙΩΔΕΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Διδάσκων : Επίκ. Καθ. Κολάσης Χαράλαμπος Άδειες Χρήσης Το παρόν εκπαιδευτικό
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 24-25, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: ΜΔΕ ο φύλλο προβλημάτων Α. Τόγκας
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
π B = B και άρα η π είναι ανοικτή απεικόνιση.
 3 Παράρτημα 2 Παρατηρήσεις, ασκήσεις και Διορθώσεις Παράγραφος ) Σελίδα, : Παρατηρούμε τα ακόλουθα για το χώρο πηλίκο / Y : Y = / Y και (α) { } (β) = Y / Y { } Επίσης από τον τύπο () έπεται ιδιαίτερα ότι
3 Παράρτημα 2 Παρατηρήσεις, ασκήσεις και Διορθώσεις Παράγραφος ) Σελίδα, : Παρατηρούμε τα ακόλουθα για το χώρο πηλίκο / Y : Y = / Y και (α) { } (β) = Y / Y { } Επίσης από τον τύπο () έπεται ιδιαίτερα ότι
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Αντίστροφος Μετασχηματισμός Laplace Στην
Α Δ Ι Θ Θ Α Ε Ι Μ : https://sites.google.com/site/maths4edu/home/algdom114
 Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
(i) f(x, y) = xy + iy (iii) f(x, y) = e y e ix. f(z) = U(r, θ) + iv (r, θ) ; z = re iθ
 ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΜΑΘΗΜΑΤΙΚΗ ΦΥΣΙΚΗ (ΜΕΤΑΠΤΥΧΙΑΚΟ) 6 Νοεμβρίου 07 Αναλυτικές συναρτήσεις Άσκηση (i) Δείξτε ότι η συνάρτηση f(z) είναι αναλυτική σε χωρίο D του μιγαδικού επιπέδου εάν και μόνο εάν η if(z) είναι αναλυτική
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
1 Χώροι πηλίκα { } x = y x y Y. Με τις πράξεις της πρόσθεσης και του βαθμωτού πολλαπλασιασμού που ορίζονται με τον
 Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
irr Q,b (x) = x 3 2, irr Q,ω (x) = x 2 + x + 1 irr (Q(ω),b) (x) = irr (Q,b) (x) = x 3 2,
 Θεωρία Galois Θεοδώρα Θεοχαρη-Αποστολιδη Χαρά Χαραλαμπους Οι σημειωσεις αυτες θα συμπληρωνονται κατα τη διαρκεια των μαθηματων. 13 Δεκεμβρίου 2014 Περιεχόμενα 3 Μεταθέσεις και ομάδες Galois 41 3.1 Οι ρίζες
Θεωρία Galois Θεοδώρα Θεοχαρη-Αποστολιδη Χαρά Χαραλαμπους Οι σημειωσεις αυτες θα συμπληρωνονται κατα τη διαρκεια των μαθηματων. 13 Δεκεμβρίου 2014 Περιεχόμενα 3 Μεταθέσεις και ομάδες Galois 41 3.1 Οι ρίζες
4.2 Αυτοπάθεια και ασθενής συμπάγεια * * X, x X, είναι επί του. X. Σημειώνουμε ότι υπάρχουν παραδείγματα μη
 94 Ένας χώρος με νόρμα (, ( ( ( ϕ : : ϕ =, ( 4. Αυτοπάθεια και ασθενής συμπάγεια λέγεται αυτοπαθής ( refleive, αν η κανονική εμφύτευση,, είναι επί του, δηλαδή ϕ =. Παρατηρούμε ότι ένας αυτοπαθής χώρος
94 Ένας χώρος με νόρμα (, ( ( ( ϕ : : ϕ =, ( 4. Αυτοπάθεια και ασθενής συμπάγεια λέγεται αυτοπαθής ( refleive, αν η κανονική εμφύτευση,, είναι επί του, δηλαδή ϕ =. Παρατηρούμε ότι ένας αυτοπαθής χώρος
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. με νόρμα, με τις ακόλουθες νόρμες οι οποίες ορίζονται μέσω των νορμών των X και Y.
 2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω (, ) και (, ) {( x, ) : x και } χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται χώρος με
2 Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα. Έστω (, ) και (, ) {( x, ) : x και } χώροι με νόρμα. Τότε ο διανυσματικός χώρος = ( με τις συνήθεις κατά σημείο πράξεις ) γίνεται χώρος με
Θεωρία Γραφημάτων 7η Διάλεξη
 Θεωρία Γραφημάτων 7η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 7η Διάλεξη
Θεωρία Γραφημάτων 7η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 7η Διάλεξη
Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ
 Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Το Σύνολο C των Μιγαδικών Αριθμών Είναι γνωστό ότι η εξίσωση x δεν έχει λύση στο σύνολο IR των πραγματικών αριθμών, αφού το τετράγωνο κάθε πραγματικού αριθμού είναι μη αρνητικός
Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Το Σύνολο C των Μιγαδικών Αριθμών Είναι γνωστό ότι η εξίσωση x δεν έχει λύση στο σύνολο IR των πραγματικών αριθμών, αφού το τετράγωνο κάθε πραγματικού αριθμού είναι μη αρνητικός
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Θεωρία Sylow. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Παράρτηµα Β. Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης [ ) ( )
 Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1
 Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1 Ιάκωβος Ανδρουλιδάκης users.uoa.gr/ iandroul iandroul@math.uoa.gr Πανεπιστήμιο Αθηνών, Τμήμα Μαθηματικών, Τομέας Άλγεβρας-Γεωμετρίας Περίληψη Στη διάλεξη
Ο αναλυτικός δείκτης και η χαρακτηριστική του Euler 1 Ιάκωβος Ανδρουλιδάκης users.uoa.gr/ iandroul iandroul@math.uoa.gr Πανεπιστήμιο Αθηνών, Τμήμα Μαθηματικών, Τομέας Άλγεβρας-Γεωμετρίας Περίληψη Στη διάλεξη
Μιχάλης Παπαδημητράκης. Μιγαδική Ανάλυση
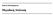 Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και η σφαίρα του Riemann............ 0
Μιχάλης Παπαδημητράκης Μιγαδική Ανάλυση Περιεχόμενα Οι μιγαδικοί αριθμοί.. Οι μιγαδικοί αριθμοί..................................2 Το Ĉ, η στερεογραφική προβολή και η σφαίρα του Riemann............ 0
