%H I J ª J z{w ~ 7 ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/
|
|
|
- Τισιφόνη Γιαννακόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 "!# %$&')(*+ %$& #')((*+ %$& #,)(*- /.10-*2, FHGJILKNMPOQKSRTG/UWVXMYOQK Z\[^]_a`cbedfbgàh ifhjfkh^z\_l]m[ n/ op2$q srn(t.1 u vlw>xqy?z{wb }y?~z 9 89< wb } 7 ƒ w }~ ˆ 9 Š9 % Œ E ~ ˆ 9JŽ 7 y>z{~ ˆ 9 5 % 6 > =?? š 4 ~ œ 9 z ~ 7Jž z}w 48Ÿ y?~ wbx 9 w>~ 2w>z 89< z}w 46 6ƒ y 4 E?;>=?= Ž % 5 ~ 469 t 6 E :ª ˆ 4 ~ œ A }y?ˆ8z :ª «z
2 %H I J ª J z{w ~ 7 ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª D J ª ; x {9 z œbwb 9 ˆ6z ªJªJªJªJª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ª KŒ ew> 9 A 9:ƒ ML w ~7:9:4 ª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J vy?~ 489-N }y 4 ~ : 69 w 4 w ƒ ~ oˆ 9 ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª O J ª D KŒ ew> 9 A 9:ƒ Nƒ ~ 4QP y NN 3P ~ 9:4 ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J = J ª vy?~ z 9: wb }~ œ ~ 9: Š 69 w 4 w ƒ ~ ˆ 9 ª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J R SUT'V:WX<;Y?'AZ7[#$:WE?'Y8;!]\W!7'<^#$!"# <;:WE &_ ; ª J vy?~ ` wb { {z}w> }~y 4aL z}wœo~ }wb }~y z ~ 4 ~ 9 ` 7 ˆ6~ œ>w 9:4 9u«w>~ x 9 ªJªJª/ªJª ª J O ; ª ; b7 z{~dc6 wb {~ y 46 T92e 7 z{~ ƒ 9 4 }w 9 N ˆQ 6z{~ 4 :~ 9u ` 7 ˆ6~ œbw 9 4 9u«w>~x 9 ªJª/ªJªJª/ªJª ª ; J ; ª K oˆ6wb }~y 4Q 69 6zgf ~ 4QL?9 z 9 6z{~ 4 :~ 9u ` 7 ˆ6~ œbw 9 4 9u«w>~x 9 ªJª/ªJª/ªJªJª/ªJª ª ;> ; K oˆ6wb }~y 46 Š4692N }y 4 ~ 9:46489: ˆ ƒ y?ˆ8œ 9:ƒ9:4 ` ˆ 4ih ˆ6~ 69 ªJªJªJªJª/ªJª/ªJªJª/ªJª ª ;?D ; ª D j57 :w w L?9u 69: N«z 7 ˆ 9:4 9: w 46 ˆ 4 ew ƒ 69kL z}wœo~ }wb }~y 4 ªJªJª/ªJª/ªJªJª/ªJª ª ; l Rs_ 8ª J 35dL0x x6z y?z ~ 9 95 ` ˆ 4 9 ew> 9 œ 9 }y?z ~ 9:ª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª ;yo 8ª ; Œz{y ˆ6~ w w>~z 9u w 48 ˆ 4 9 ew> 9 œ 9 }y?z ~ 9 jªjªjª/ªjª/ªjªjªjªjªjª/ªjª/ªjªjª/ªjª ª E; 8ª KŒ ew> 9 wxz 489J9 9: ew> 9 w(z 469 ƒ7 }z ~ ˆ 9 ª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª? x:ƒ9: 69 :yoy?z y 46467:9 :ˆ6z œ ~ ~ L?469: ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª { tv& &E=# <;&8p8;i?q}~%HEHQ!QX<;V#rV J b w>z{~ 7 7 ~d 7 z 9:4 }~ w>x9hª/ªjª/ªjªjª/ªjª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ; ew ƒ 69 œ 9 9 ˆ6z % {9 ˆ6z jª 7 {z{~ oˆ 9J9 7: 7 ƒ œ?y ˆ ƒ 9 ~ 46 ˆ6~ @ j57 z ~œ 7:9 69 v~ 9u9 Nœ 9 9 ˆ6z 69 ~ ~ 4"L D y e ~ y 4" ~ 467 w>~z 9Bš {y?z ~ y 4Q9 Š 9:46 9 ˆ6z 69 :y>ˆ6z{x6ˆ8z 9sªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª y e ~ y 4 z{~ 9:ƒ w 464 ~ 9: N 9 46 {9 ˆ6z 89 ~ 9 ƒ w 464Hª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª D?; I SUT'V:WX<;&64oV#r(<>G %'&@?HA8;!]\sX!7'<^#$!"#$<>:WE IsI D ª J z{~ L ~ 469 YªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª D?D D ª ; KŒ ew> 9 A 9:ƒ N9 ~ 46 9 ~ 4 ~ 9 4"9 6z{~ 4 :~ 9 89 yœ>wbz{~ w 4 9WªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª D? D ª x {9 z œbwb 9 ˆ6z 9:4 ˆ8 9J ~x6z 99 6z{~ 4 :~ 9u ` 7 ˆ6~ œbw `ƒk ~ 46 9 ~ 4 ª/ªJªJª/ªJª ª DyO ;
3 D y ƒ ew>z}wb~ y 419:4 }z 9J9: 9 ƒ Š 69: y?x 9 z œbwb 9 ˆ6z fªjª/ªjªjªjªjªjª/ªjª/ªjªjª/ªjª ª ; D ª D y?ˆ6 w L?9u 69p` 7 9 }z y ƒ w L?467 {~ ƒ 9 # w L z}wœo~ }wb }~y 4Qª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª D D ª y?ˆ6 w L?9u ` ˆ 4"ƒ ~ ~ 9 ˆ ƒ wb 7 z{~ 9: w L z}wœo~ }wb }~y 4fªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª? D ª ž y?z ƒ w ~ {ƒ9% w L z{w 4QL ~ 9:4W w 46 N 9 w ` ˆ 4 ew ƒ " w { ~ ˆ 9/ªJªJª/ªJª/ªJªJª/ªJª ª SUT'V:WX<;Y?t} mn<peh-#$&<>e?'a8;!b\s!7'<^#$!"# <;:WE :W% &8>!"#$<;'<^#$V \sv&ehv!/8; ª J K oˆ6wb }~y 46 Š `ƒk ~ 46 9 ~ 4 89J w L z}wœo~ }wb }~y 4WªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ª ; ž y?z ƒ w ~ {ƒ9% w L z{w 4QL ~ 9:4W ˆ" ew ƒ L z}wœo~ }wb }~y ª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª > ª w>z}wb x z 9 E o 9 z{xqy ~ oˆ 9u 69: 7 êwb {~ y 48 ` K ~ 48 9 ~ 4 ª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª?D 3 6 8z{y e ~ ƒ wb }~y 4W4692N }y 4 ~ 9:46489/ 69 w< } 7 y?z{~ 9u ` K ~ 46 9 ~ 4 ªJªJªJªJª/ªJª/ªJªJª/ªJª ª ª D 7 {z{~ oˆ 9J9 e 7 z ~ 9 ˆ6z 9 qy A 4692N }y 4 ~ 9:46489J ` ˆ 4 :y>z{ ƒ w { ~ «TªJªJª/ªJª/ªJªJª/ªJª ª? ª 3 œbw 4 9 ˆ" 7 z{~ 7: ~ 9 69/ 9 z{ :ˆ8z 9 ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª > ª j57 œo~ wb }~y w ˆ ƒ ~ x z 9%9 ƒ ~ z}w L?9 L z{wœo~ wb {~ y 46489: ª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª?= :W,94o!/rr< M##$ :W%?'uW -#$!+# <pg %H&@7# ö-c'4ov#r(<;i,thvx<pg %H sl ª J 7 {z{~ oˆ 9J wb {~ ˆ 9u9 # ƒ7 {z{~ 9u 6 7 z{~ ˆ 9uªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª? ª ; y?z{ ƒ w ~ «# ƒ7 }z ~ 9u 6 7 z ~ ˆ 9 ª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª >@ ª 7 {z{~ oˆ 9J wb {~ ˆ 9u 69 N w>z 6~ ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª Ẽ Ž z y?ˆ 69 œ 9 z wb {~ ˆ 9 9 # ƒ7 }z ~ 9u 6 7 z ~ ˆ 9 ª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª 0O m t:we?' &45&E=#6\W!7'<^#$!"# <;:WEE'&8q7#6#$ :W%EH:W<; ö-c'4ov#r(<;, T'VX<pG %' _D 8ª J x {9 z œbwb 9 ˆ6z 9:4 ˆ8 9J ~x6z 9 w 46 N w ƒ7 }z ~ ˆ 9u 69 N w>z 6~ ªJª/ªJªJª/ªJª ª O J 8ª ; K y 48 z 9 ƒ 9 4 L z{wœ ~ wb {~ y 48469: ` ˆ 469 xy?ˆ 9u 69nh ˆ6~ 69 6z 9 { ~y 4"4 ˆ 9lªJª/ªJª ª O? 8ª Ž z y?ˆ 4 y?~z 69 N w>z 6~ jªjªjª/ªjª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª O K e 9:46 ~ y 4"ƒ w e ~ ƒ w 9 69 z ˆ gp w ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª OE _ av&e'v&!/8><^#$v&6%h 8>& #$ :W%E':=<;X ' O8ª J j ~ w L z}w ƒƒ95 69 w>z 9 z A 9:4 z y {9^ª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J = J O8ª ; Œz{y? 6z ~ 7 7: L>7:467 z}w9: N 69: }z y?ˆ Š4 y>~ z ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J =B@ O8ª Ž z y?ˆ 4 y?~z w }~ y 464 w>~z 9 69 u9 z z ª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J =? Œz{yo 9: ˆ ` 92e }z{w> {~ y 4" ` 7:469 z L ~ 9sªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J0J = ASUT'V:WX<;Y8><pE'V!QX<p-V&?'A8>!A &8;!"# <^'<;#rvi\sv&e'v&!/8; W&l J =8ª J ew ƒ L z}wœo~ }wb }~y ` w> 6 6z y e ~ ƒ w }~ y 4W ~ 467 w>~z 9jª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J0J J =8ª ;K oˆ6wb }~y 46 Š `ƒk ~ 46 9 ~ 4 ~ 467 w>z{~ {7 9: ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J =8ª y ˆ8 }~y 4 z 9 w>z 67:9J 69 7 êwb }~y 46 N `ƒk ~ 46 9 ~ 4Q ~ 487 w>z ~ {7 9: ªJªJªJª/ªJª/ªJªJª/ªJª ª J0J J w 469nL z}wœo~ }wb }~y % w 46 N 9 œo~ 69 ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J0J O s!7cw:=ehe'+4o+ew#9\s!7'<^#$!"# <;:WEE'&8 7#6:W$Q!"#$<>:WEH +RD J0J ª J {9 ˆ y A 9:46 9 ˆ6z 7:489 z L ~ 9 A ~ ƒ 6ˆ ~ y 4 L z}wœo~ }wb }~y ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ; J J0J ª ;KŒ469 z L ~ 9nL z{wœ ~ wb {~ y 48469: 9 z{w?y 46487:9 ª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ;>D J0J ª K e89 ƒ 9u ` ˆ 4 :y?z z ~ L ~ z y> w }~ y 4ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ;> J0J ž y?z{ 9u 69 z 7 wb }~y 4Q 69 z}w?y 46469:ƒ9:4 L z}wœo~ }wb }~y ª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ;B J0J ª D Œˆ w>zšx6~ 4 w>~ z 9 8 J O J J ªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J >=
4 J0J ª Œz{~ 4 :~ 9: Š 89J 87 9 {~ y 4Q ` ˆ 469 y w 469nL z{wœ ~ wb {~ y 48469: 9 ªJª/ªJª/ªJªJª/ªJª ª J?; &Rumn,H!/.0&213#$&45, 6?'A8>!B.0:Wr45:W8;:s\=<; +l J ; ª J v 9 6z{y?x x:ƒ9 :y {ƒ y y L ~ ˆ 9fªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J J ; ª ; x {9 z œbwb 9 ˆ6z N«y 46 w ƒ 9 4 w>ˆ ew9 ƒ7 }z ~ ˆ 9 y {ƒ y y L ~ ˆ 9 /ªJªJª/ªJª/ªJªJª/ªJª ª J > J ; ª K 9 ˆ6x6x9u ˆ 67 :w w L>9 œ 9 z %9 z{y?ˆ L?9 ª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J J ; 9 wb {~ y 4 9:4 }z 9/ ˆ ƒ ~ 4 y ~ 7 w> 6 6w>z 9 4 9/9 ˆ ƒ ~ 4 y ~ 7 w>x y ˆ 9WªJª/ªJª/ªJªJª/ªJª ª J ; ª D y Qx:9: :y {ƒ y y L ~ ˆ 9: Š9 7 œ>y ˆ8 {~ y 4Q 69p` 4 ~œ 9 z ^ª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ; ª %y?z ~ y 41 69: ew>z }~ :ˆ9: Š9 89:46 ~ 7 z{~ {~ ˆ 9 ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J ; ª 4"h wb {~ y 419 9: 6w> 9tA 9 ƒ % ~ { 9 z ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J D J :=4o, #9?'Y &8>!"#$<;'<^#$V \sv&ehv!/8; +I 3<ª J 35dL0x x6z 9u92e 7 z{~ 9 ˆ6z 9J9 ~d 7 z 9:4 }~ wb }~y 4192e 7 z{~ 9 ˆ6z 9YªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J D> 3<ª ; J A «y>z ƒ95 69 :y e ~ y 4 ª/ªJª/ªJªJª/ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J D(O 3<ª K oˆ6wb }~y 4Q 69 j ~ z{w> 9:4"9: ew> 9tA 9:ƒ y?ˆ6z x 9 ªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J = y?ˆ6z x6ˆ6z 9 9 e {z{~ 46 gx oˆ 9/ ` ˆ 469 E o 9 z ˆ8z «w> 9cªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J 3<ª D y 46 ~ }~y z{w> : y?z 69 ƒ 9 4 œo~ 69 A ƒ wb {~ x z 9 ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J D 3<ª ž y?z ƒ w ~ {ƒ9 6w ƒ ~ {y 4 ~ 9 4 ˆQœo~ 69 ªJª ª/ªJª/ªJªJª/ªJª/ªJªJªJªJªJª/ªJª/ªJªJª/ªJª ª J
5 1 Wii i w i D D i V"!$#&% I'NM y?ˆ +4 ` w y 48 ew 9:4 9 z-ˆ 469Š«y?z ƒ ˆ wb {~ y 4 w e ~ y ƒ wb {~ ˆ 9T 89Š w 4 y> {~ y :ƒ Œ9 ` 9 ewb 9 ƒ w>~ ~ ƒ 9:ƒ9:4 X~ 4 {z{y ˆ6~z 9 ˆ œ>y :w>x6ˆ w>~ z 9>ª y?ˆ wœ?y 46 ˆ 469 ~ 4 {ˆ6~ {~ y 4 6z 9 ƒ ~ x z 9T 69N w 4 yb }~ y 4 ` ~ 46 w Š ~ 9 ˆ ª 2w>z ˆ6~ 9>š>4 y?ˆ qy?ˆ8œ>y 46 :y 46 ~ 67 z 9 z 9Tƒ y> 7 œ 7 469:ƒ9:4 )(? ` 9-9 ˆ6~e 9 ˆ ˆ8z œ 9 4 ~ z 9:4 ˆ 4 ~ 9 ˆ 9 ˆ 4 ~ 46 }w 4 ª v 9#ƒ 9 ~ 9 ˆ8z 92e 9 ƒ 9#9: / 9 ˆ6~ 89 w1 :y ~ ~ y ˆ e ew>z }~ :ˆ9: :šoƒ w>~ x6~ 9 4W +* z ~q ` w L ~ ` ˆ 4 y w>x }z{w>~ ˆ6~ { ~ 9 6w ˆ 4 8 7:4 y ƒ9x E ~ oˆ 9 z 7:9: ª v ` 9 ew> 9 A 9:ƒ "9: w z 7 ˆ 4 ~y 4 69 }y?ˆ 19: 17 œ 7:489:ƒ9:4 y { ~x 9 :ª u -` w L ~ y 4 ` ˆ 4 9:48 {9:ƒ x 9N 69 qy?~ 4 ª?Ž y?ˆ8 9 {z}wœbw>~6 ˆ 6 E ~ :~ 9:4 :y 46 ~ 9uƒ 9 { }z 9N ˆ6z- 9 ˆ6~ A ~8ˆ 469 {z{ˆ6 }ˆ6z 9 ƒ wb } 7 ƒ w }~ ˆ 9Bª -ˆ8~ ˆ 9 4 y?ˆ w y? 8 {y 46 ˆ 489W 69: :z ~ 8 {~ y 4 y 4 }~ 4 ˆ 9W 69Wp` 9 ew> 9 A 9:ƒ š 4 y>ˆ 69 œ?y 46 / 9 ƒ ˆ 4 ~ z ` ˆ 469 }y> y y L ~ 9>ª y?ˆ z 9 }z 9 ~ L?4 y 46 w1 {y? qy y L ~ 9 69#p` 9 ew> 9 A 9:ƒ, }z 9 yo w 9:ƒ9:4 6y ƒ7 y ƒ y?z 6 9 IR 4š 67 c 4 ~ { w 4 ˆ 469 œbw>z ~ 7 7 {y? qy y L ~ ˆ 9>ª vlw ~ ƒ9:46 ~ y 4 êwb }z 9 9: ˆ 469 E o yb } x {9 6 E ~ ˆ 9 {z x: «y>z 9Bª y?ˆ8z{z}wb~ 9 e ~ 9 z 69 u ~ ƒ9:48 ~ y 46 5 ˆ6 6 7:ƒ9:4 w>~z 9 ˆ6~ 469 {9 z}w>~ 9:4 ew ~ ƒƒ7: ~ wb 9 ƒ 9 4 T 9 z{ 9 8 {~ x9: 4 y> }z 9u7 9 9 wb }ˆ 9: 9u ` y?x {9 z œbwb {~ y 4.-tª y?ˆ qy?ˆ6z z{~ y 46 N ~ z 9 9:ƒ9:4 % y }ˆ9 z w }z{ˆ8 }ˆ8z 9UL>7 y ƒ7 {z{~ ˆ 9 69J ` 9: ew> 9 A 9:ƒ N9 9 y>~ 6 E ~ oˆ 9: ˆ6~Lz 7-L ~ {9:4 9: y ƒ6x:469 5 w ewb 9 A 9 ƒ ª 9/ {9 z}w>~ w y? 7 z 9: : :y 48 {7 ˆ e 7 z ~ ƒ9:4 w9:ƒ9:4 uœ 7 z{~c 7:9 ˆ6~ 9:4 w ˆ6z 9 z}wb~ 9:4 w0/ ˆ }~ce wb {~ y 4ª y>ˆ 6z 7 «7 z y 46 N 67-L w L?9 z 69: :y š y ƒƒ 9 9: ˆ6~ ` y?x 9 z œbwb 9 ˆ6z ª y?ˆ 9:48 y 46 ˆ ` ~g9 ~ ƒ y>z A w 4 69 y ƒ 8z 9:48 z 9 :y ƒ ƒ9:4-9 ˆ6~ A ~ 9: + y 4"L?7Š w 46 -p` 9 ew> 9 A 9:ƒ ª y?ˆ z 9 }z y?ˆ8œ 9 z{y 46 9 :y w 48 X 9 2 ~ œ 9 z {9 :y {~ y 48 X ` 9: 6w> 9 A 9:ƒ ˆ6~8y 4 7 7T ˆ6 9: ~ œ 9:ƒ9:4 + 6z y? y {7:9 w>ˆq :y>ˆ6z 69 ` 6~ }y?~z 9% 69 w 6 E ~ ˆ 9 qy?ˆ6z 67 :z{~z 9 w z 7 w ~ 7 6 E ~ ˆ 9Bª 10 [ FIBC="\6M>=A7]9CR6QXJABIMV=PR6BC="QXK&R6B;_^MV7FC=PBI5L?`FIMVKL7GaLBI5ZYbMVFI5cFIMVKL7676=P;V;>='de5&REFC=f3g^=UhEQXJABIMV=P7:?U=+958REij3E=+9C9CK&R:93E= :9<;>=@?A5&36BC=D3E=D;>5GFIH6JAKLBCM>=N9OFI5&7:365&BI303E=P9"Q:5&BOFIM>?AR6;>=P9<JA;>JA2D=A7FS58M>BC=+9T2@5&M>9"?U=AFOFI=@JP?SH6=P;V;>=WQXK&R:YZ5&7F 4 2lk D
6 MK V l! ILKNUWV2M v ` 9 ew> 9 A 9:ƒ Š 9 z ` w>z x 469 w>ˆ e ƒ y?ˆ8œ 9 ƒ :y>z{ ƒ wb 7 z{~ 9: :ª y 4 Šx8~ 9:4 y?ˆ8œ 9:4 ~ 87 w ~ {7 ewbz w 4 y> }~y 4W 69 6w>z {~ :ˆ 9: y 4 {ˆ 9: 9: ª v 9ƒ y?ˆ8œ 9:ƒ9:4 ` ˆ 469 ewbz }~ :ˆ9 qy 4 }ˆ 9 9 9: 67 :z ~ y ƒƒ 9 ˆ 469 ˆ6 9: ~y 4 :y 4 {~ 4 ˆ 9 ` 7 œ 7:489:ƒ9:4 ewbz<ˆ 469 :y?ˆ8z{x 9>š ` 9: A A ~ z 9 ˆ 469 w> 6 ~ :wb }~y 4 y 4 }~ 4 ˆ 9u 69 œ 9 z ª IR w 48 Š w<œbw>z{~ 7 7 }y? qy y L ~ ˆ 9Bš ˆ 9 4 y>ˆ w> 6 9: y 46 ˆ 489J ~ L?4895 ` ˆ 4 ~ A y?ˆ w { ~ ƒ ~ y <ƒ y?ˆ œ 9:ƒ9:4 ` ˆ 4 y?x {9 z œbwb 9 ˆ6z 9 ˆ6~ ` ˆ 489 6w>z {~ :ˆ 9 qy 4 }ˆ 9 9 ~ 9: 67 z{~ u ew>zˆ 469 ~ L?469< ` ˆ 4 ~œ 9 z O w 46 up` 9 ew> 9 A 9:ƒ ª w>~ ˆ 4 y?x 9 z œ>w 9 ˆ8z w ` wbˆ8 }z 9: wb }z{~x6ˆ8 :š }~z 7 69 ` 92e 7 z ~ 9:4 9 ˆ ˆ 9 9 ` y?x {9 z œbwb }~y 4gš w>z-~ w/ :y 46Ÿ ˆ 69: w> 6 ew>z 9 ~ Œ 69 ƒ 9 ˆ6z 9 qy?ˆ6z 9 e y?z 9 z y 49:4 œo~ z y ƒ 9 4 ª y?ˆ6z wb }~ «w>~z 9J4 y> }z 9 9 z{ 9 8 {~ y 4 ~ 4 }ˆ6~ }~ œ 9<9 p` w>~ 69J 69 :y ˆ ` ~g«w>ˆ8 N y 46 ~ 67 z 9 zn :y ƒ ƒ9 6z y œo~ y?~z 9: še4 y?ˆ N ~ y 48 :ª J ª y { gx 69 ˆ 489 6y?z y L>9>ª ` 9 uˆ 4) x:ƒ9 6 E ~ oˆ 9 :y 48 ˆ6~ w 4 ˆ y ƒ6x:469 6z 7tA 9:46 ˆ o ~ ˆ 9>ª vlw ~d 7 z ƒ 59:4 }z 9 69 ˆ e)7 œ 7:469 ƒ w ~ L?489< ` ˆ 4 ~ œ 9 z 9 ˆ 4Qƒ ˆ }~ 95 89u w 7 z{~y 89>š 6y>~ ~ 9 :y ƒƒ9 ˆ 4 ~ 7>š8 ` ˆ 4 8 7:4 y ƒ9x 469 o ~ ˆ 9>ªe3 6z x 69 p` y>x {9 z œbwb 9 ˆ6z ª ` 9 N/ ˆ CA ˆ 4 8y?~ e w>z{x6~ }z{w>~ z 9/ ` y?z ~ L ~ 469>š& ` 6y?z y L>9< y :ƒ t ˆ ` 6z 7 {9 4 ˆ 4 «w>~ ` 92e 7 z{~ 9:4 9 ˆ 9 }y>ˆ <9: 6 7:4 y ƒ6x:489: ~ oˆ 9: :š w { ~ ˆ 9: y?ˆ êw 4 {~ ˆ 9: š& y uƒ, ƒ 9 9:ƒ t ª ; ª X ~ qy 9 ` ˆ 469 z x-l? 9 L z}w ˆ 7:9 w 48 u y 4 œ?y>~ ~ 4 w L?9 ~ ƒƒ 7 ~ wb ª y?ˆ w 6ƒ 9 { {y 46 ˆ ` w>ˆ y?ˆ6z " ĵ 9:ƒ ~ 9 ˆ8 w 67 w> 9 z w 46 :y 4 {z}w>~ 4 9>ª ~ 69 ˆ ej7 œ 7:469 ƒ ˆ8œ 9:4, }z 9 z 9: ~ 7: ew>z ` ~ 4 9 z ƒ7: ~ w>~z { 9 z xl?9 w y>z ~ < y 4 ~ ~ ƒ ˆ }w 467 y>ˆ6z 9 y?x {9 z œbwb 9 ˆ6z ª v ` 9 46 {9 ƒ x 9 69 {y?ˆ <9: J7 œ 7:469 ƒ 9 4 ~ ƒ ˆ }w 467 wœ 9 Wˆ 4 qy?~ 4 69 w ~ L>469# ` ˆ 4 ~œ 9 z w>ˆ 9 ƒ t 9: #w> 6 9:7p` 9 ewb 9 w>ˆ 9 ƒ 69Wp` y?x {9 z œbwb 9 ˆ6z ª y?ˆ qy {ˆ y 48 <9:4 :y 46 7 ˆ t ˆ 9 ew> ˆ 9"9: ew> 9 w>ˆ 9:ƒ 89"p` y>x {9 z œbwb 9 ˆ6z š2 67 c 4 ~ w 46 # y 4 œ>y?~ ~ 4 w L?9 ~ ƒƒ7: ~ wb šl9: 4 t y> {z 9%9: 6w> 9 ˆ ˆ 9 š ` 9 A A ~ z 9%9 Šˆ 4 9 }~ y?ˆ8œ 9 z 695p` 9 ewb 959 ˆ6 ~ ~ 9:4 }z y?~ + ~ ƒ9:48 ~ y 46 :ª K œo~ 69 ƒ ƒ9:4 šœ wz xl> 9 L z}w ˆ 7:9iL w>z 69 w>ˆ y?ˆ6z ˆ 9 ƒ w ƒ,:ƒ9q y 4"L ˆ 9 ˆ8z qy?ˆ6z w ƒ7 A }z ~ ˆ 9#9 ˆ8 ~ ~ # 69 ew> ˆ 9 9: ew> 9Bª v ` 9: ew> 9 9: w>~ 46 ~2ˆ 469 :y 46 }z ˆ6 {~ y 4 69: }~ 487:9 ` y?x 9 z œ>w 9 ˆ8z w 46 N w z 9 6z 7 {9 4 }wb }~y 4 ewb {~ y A 9:ƒ qy?z y œo~z{y 46489:ƒ9:4 ~ ƒƒ 7 ~ wb ª y?ˆ8zz 9 7 z 9 z%ˆ 47 œ 7:469 ƒ 9 4 w 46 % ` 9: 6w> 9tA 9 ƒ :šq4 y?ˆ ~ 46 ~ {y 46 ˆ6z9J«wB~ % oˆ 9 ` y?x 9 z A œbwb 9 ˆ6z y?~ 9J y zšˆ 4 z 9 x z 9u w 46 6w> ˆ 9 9: 6w> 9 9 ˆ8 ~ ~ 9 4gªQKŒ4 ew> ˆ 9 qy?~ 4 89u w ~ L?469 ` ˆ 4 ~ œ 9 z O še4 y>ˆ 6y?~ ~ y 46 ˆ 4 }z ~ x z 9 69 œ 9 9 ˆ6z y?z { 6y 4 y>z ƒ7: :ª y?~ c 9 e i (i = 1, 2, 3) qy?~ w ~ L?469N ` ˆ 4 ~ œ 9 z 9:4 t 9 Š ˆ 4 y?~ 4 69% ` 9: ew> 9 w>ˆ 9:ƒ 69% ` y?x 9 z œbwb 9 ˆ6z ª q9: t z 9 7 z 7 ewbz 9 }z y?~ :yoy?z y : wbz 7 ~ 9:46469 y i (i = 1, 2, 3) 67 c 4 ~ 9: ew>z 9 z 9 x z 9 š 69 e ` 9: ew> 9J9 ˆ6 ~ ~ 9:4 i OP = v 9: :yoy?z y 46467:9 L?9 4 y 9 ew> ˆ 9 œ 9 9 ˆ6z 69" w xew 9 3 y i e i soit OP = y i e i. i=1 w>~ 69 z i y 4 / ˆ 9:ƒ9:4 ƒ 9 ˆ6z 7:9: ew>z w#z xl> 9 L z}w ˆ 7:9/ 9J y 4QL 69< w z{y?~ 9 w 4 A e i 69p` 9 ewb 9"9 ˆ6 ~ ~ 9:4ª y ƒ ˆ 69: 6z{y? 8z{~ 7 7 KLR:9REFIMV;>M>9CK&7 9;>5D?UKL7bY&=A7FIMVKL7G3g^ M>7:9 FI=AM>7]Q KLR6B; 5N9CK&2D2@5cFIMVKL7 36=P9M>7:3EM?U=P9'BCJPQ JAFCJP9Pk
7 O O C O t O e 2 P origine du temps espace au temps e 1 t y i (t) ˆ8 6 y {7:9 < 69#p` y?x {9 z œbwb 9 ˆ6z šg9: y y?z y 46487:9: 9 z }w>~ 469u y 4QL ˆ 9 ˆ6z l i y?~œ 9:4, {z 9 x 9 w>ˆ6 y?ˆ6 ˆ 9 {~ 9: ˆ ` ˆ 469 y y i l y 4 w<œbw9 ˆ6z 4 ˆ ƒ7 z ~ ˆ z}w 69 w ~ }ˆ6wB }~y 4 6 E ~ ˆ 9 :y 46 ~ 67 z 7:9>ª KŒ4W«w>~ š ew>zt 9 9 E o yb } x {9>š84 y?ˆ wœ>y 46 ` 9 ƒ x 7 9 w 8ƒ ~ ˆ z{~ }~ y 4 Ŵ y 4 A L?9 ƒ ` y?x 9 z œ>w 9 ˆ8z w 48 Œ ` 9: 6w> 9tA 9 ƒ X4 ` 9: X ew z ~ L y?ˆ8z 9 ˆ {9:ƒ9:4 9 e w> 9>ª7KŒ 9 9 ` w>ˆ A w 4 ƒ9 ~ 9 ˆ6z 9 ˆ 9# 9 œ>y?~ ~ 4 w L>9 9: / 9 {~ š 1 w ~ ƒ ~ 9 ~ 4 c 4 ~ 7: ~ ƒ w ª v ` 9 e 9:46 ~ y 4 6wB }~ w 9/ 69 ` 6y?z y L> wz xl> 9uL z}w ˆ 7:9 y?~, }z 9 x 9 w>ˆ6 :y>ˆ6 ˆ 9 }~ 9 ˆ 9 w y 4"L ˆ 9 ˆ8z l w }~ «w>~ z 9 9 6z y? 6z ~ 7 7: z 9 oˆ8~ {9 < 69 9 { 9 69 :z ~ 8 {~ y 4ª +9 4m 9 z}w 69ƒ, ƒ 9 qy?ˆ6z 9: w>ˆ }z y?ˆ8z 9 w> 6 6w>z 9 ~ # 69"ƒ9: ˆ8z 9>š ew>z 92e 9 ƒ 9 ˆ 4 } 7 y y ~ 9 qy?ˆ6z ƒ 9 ˆ6z 9 zˆ 4 w 4QL> 9 ew>zz}w> 8 y?z w>ˆ }z ~ x z 9 ª e v ` y?x {9 i z œbwb 9 ˆ6z š&ƒ ˆ 4 ~ ˆQ 9:ƒ t 9 ` ˆ 4 {z{~ x: z 9 š z 9 x z 9 w>~ 48 ~w>ˆ }y?ˆ6z 89J ˆ6~gˆ 4"7 œ 7:469tA ƒ9:4 e 89< ` 9: ew> 9 A 9:ƒ 6w>z i 69 ` t 9 y iª y?ˆ 5 y ƒƒ 9 % y 4 < ew { {7 ˆ8x6z 9 8 }~ 9:ƒ9:4 ˆ 9 ƒ t 6y?z y L?9 ˆ 469 :yoy?z y :ƒ y?z 9: 9 t ª v 9: :yoy?z y 46467:9 yišƒ9: ˆ6z 7 9: wœ 9 wjz xl?9ml z}w A ˆ 7 9>š y 4 ewb {~ w9: :ª 9 w y?z{z 9: qy 46 4 y> {z 9/«w Ÿ y 4 ˆ ˆ 9 9J {9 zˆ 4 z 7 «7 z 9:4 }~ 9: ªWj w 46 9 y y?z y 46487:9: šbp` (t, y i ) y?x {9 z œbwb 9 ˆ6z O 67 z{~ w ~ L?469- ` ˆ 4 ~œ 9 z ` ˆ 469 ewbz }~ :ˆ9 qy 4 }ˆ 9 9 C ew>zp` 7 êwb }~y 4 ª y>ˆ y?ˆ œ?y 46 N 67 c 4 ~z ˆ 469 œ ~ 9 { {9 z 9 wb {~œ 99 ˆ 469 w> 7 7 z{wb }~y 4 z 9 wb {~œ 9 y i (t) v i = dyi dt et a i = d2 y i dt 2. z 9: 9 ˆ 4 y?~ 4 9 { 9:4 }~ 9: ª êw ˆ e y?x 9 z œ>w 9 ˆ8z 9 ˆ œ 9:4 5z 9 7 z 9 z ˆ 4"7 œ 7 469:ƒ9:4 69 ` 9: ew> 9 A 9:ƒ z 9: 9 {~œ 9 ƒ 9 4 Š ew>z (t, y i ) 9 J ` w>~ 69Š ` 6y>z y L?9: z xl?9: ql z}w ˆ 7:9 (t, y i ) ~ 89:4 }~ oˆ 9: :š ˆ 9 9 9: w z 9 wb {~ y 4 9:4 }z 9 9: ~ 7 z 9:4 9: :yoy?z y : y?ˆ6z z 7 y 46 z 9 ~ «w>ˆ :y 464 w }z 9Š w {z{ˆ6 }ˆ6z 9 L>7 y ƒ7 {z{~ ˆ 9T 69N ` 9: 6w> 9tA 9 ƒ Œ9 wœ?y>~ zœ :y ƒ ƒ9:4 p` y?x {9 z œbwb 9 ˆ6z š wœ 9 {9 wb 6 ew>z 9 ~ 69 ƒ9: ˆ8z 9>š 9: % y 4QL?7Bª
8 ª [jm!/rtk ILK "M!$#L%&#&ŠK vlw L?7 y ƒ 7 }z ~ 9Š 69 ` 9: ew> 9tA 9:ƒ L w ~7:9 4 9: 9 9 ` ˆ 4 9: 6w> 9 w(z 469 êwb }z 9% ~ ƒ9:46 ~ y 46 ƒ ˆ 4 ~ ` ˆ 469J«w ƒ ~ 9 69J y?ˆ A 9 ewb 9: w(z 469: }z{y>~ Š ~ ƒ 9 46 ~y 46 ew>z{w dx:9: 9 4 {z 9J9 ˆ e"9 %w?w 4 9:4 y?ˆ8 }z 9 ˆ 489 L?7 y ƒ 7 }z{~ 9N ` 9 ewb 9u9 ˆ8 ~ ~ 9 4gª y?ˆ wœ?y 48 y 4 %ˆ 469 wb 6 ~ wb {~ y 4 9 ƒ L w ~ 7:9 4W w 48 oˆ8~ ew>z}w ƒ 7 }z{~ {9 9 { 9u«w ƒ ~ 9% 69 y?ˆ A 9: ew> 9 :ª IR b y?y 46 :y ƒ ƒ9:4 ` y?x 9 z œ>w 9 ˆ8z 9 y 4QL?7u w 46 N ` 9: 6w> 9tA 9 ƒ L w ~ 7:9 4gª J ª v 9 9:ƒ T t T 69% ` 9: 6w> 9tA 695p` 8y?z y L?9N 69 ` y?x {9 z œbwb 9 ˆ6z :y 4 :~ 69>š ˆ 469 y 46 }w 4 9 w 6 ~ {~œ 9 8z x: š wœ 9 ƒ y ˆ yjˆ 4 6y>~ e ` ˆ 4 ~ ƒ ª vlw ~ z 9 {~ y 4 ˆ «ˆ8 {ˆ6z 9 w 46 T95 9:46 z{y?~ { w 4 69 T ; ª v ` 9: 6w> 9 w>ŵ 9:ƒ 69p` y?x {9 z œbwb 9 ˆ6z :y 4 ~ 69 wœ 9 ` 9: ew> 9u9 ˆ6 ~ ~ 9:4 69 w «w ƒ ~ 9Š 69 t y?ˆ A 9: ew> 9 qy?ˆ6z T = t ª y?ˆ y 46 }wb }y 46 oˆ 9/9 9:ƒ N9: wbx y ˆ ª vlw ~ ƒ ˆ }w 467 ~ 7% 69: 7 œ 7:469 ƒ 9 4 9: w ƒ, ƒ 9 qy?ˆ6zn }y?ˆ 9 y>x {9 z œbwb 9 ˆ6z (q ˆ ` ˆ 4)7 œ 7 469:ƒ9:4 y?~ %wœbw 4 y?ˆ w> 6z x ˆ 4 w>ˆ8 {z 9J469/ 87 9:46 ew 69 ` y?x 9 z œbwb 9 ˆ6z ª ~ 69 ˆ e y?x {9 z œbwb 9 ˆ6z 69% ~ L?489Š ` ˆ 4 ~œ 9 z O 9 6z 9: w ƒ,:ƒ9 y>z{~ L ~ 469 O ˆ1 9 ƒ Š9:4 w y?z 9 ˆ6z 6y?z y L>9 ~ 48 ~ ˆ 9 z}w 95ƒ, ƒ 9 9:ƒ êw 48 "9 ˆ6z Š ~ L?469: ` ˆ 4 ~œ 9 z 9 z 9 :y?ˆ8 9 z{y 4 ª O O t t = 0 O KŒ4 {y?ˆ8 1 9 ƒ š ˆ 4 z 9 x z 9 69 ` 9: ew> 9 9 ˆ6 ~ ~ 9:4 9: «y?z ƒ7 ˆ qy?~ 4 k 69 w ~ L?469 t ` ˆ 4 ~ œ 9 z O w>ĵ 9 ƒ t 9 ĵ }z ~ x: z 9 y?z { 6y 4 y?z ƒ 7 ª KŒ4 y 46 7 ˆ 9:4 9>š ˆ 4 y?x {9 z œbwb 9 ˆ6z e 9 ˆ8 Šz 9 7 z 9 zt {y?ˆ 9: T7 œ 7 469:ƒ9:4 N 695 ` 9: 6w> 9tA 9 ƒ L w i ~ 7 9:4 ( ˆ 417 œ 7 469:ƒ9:4 {9 {z{y?ˆ œ 9 w 46 ˆ 4 9: ew> 9 ˆ «9 ˆ6~ 9 w L?9 :y?z z 9 qy 46 w 4 w>ˆ 9:ƒ 9 w ˆ 9 ~59 Qz 9 7 z 7 6w>z 9 t :yoy?z y : wbz 7 ~ 9:46469 (y i ) z 9 wb {~œ 9: w>ˆ {z{~ x z 9 ª u4 ` w ew Q ~ 9 ˆ ` ~ 4 }z{y ˆ6~z 9 ˆ 469 e y 4QL ˆ 9 ˆ6z i l ª y?ˆ y>ˆ8œ?y 48 ƒ wb~ w 4 wœ?y?~z w 48 ` 9: ew> 9tA 9:ƒ L w ~7:9:4 y ƒ ƒ9:4 69 ˆ e y?x 9 z œ>w A 9 ˆ6z z 9 9 }~œ 9:ƒ9:4 69/ ~ L?489: Š ` ˆ 4 ~ œ 9 z O }z ~ x: z 9: 9 z 9 x z 9 4 5ˆ 4 ƒ, ƒ 9 O e i e i 7 œ 7:469 ƒ 9 4 ew>z9: y y?z y 46487:9: (t, y i ) 9 ªsjU` w> 6z x: N4 y E o y> { x: 9: š4 y>ˆ wœ>y 46 (t, y i ) t = t + d 0 KLR:9QXK&R6YLK&7:9?SH6KLM>9CMVBR67:=f58REFIBC="Q:5&BI5&2NJAFCBIM>9I5cFIMVKL7 T = at + b 5ZYL=P? a > 0k
9 y d 9 uˆ 469 :y 46 }w 4 9 ˆ 9 4 y?ˆ 8z 9:4 y 46 4 ˆ 9<9 9: {z{~ x: z 9: 9 0 e z{yb wb {~ y 41 69p` 9 ew> 9 œ 9 }y?z ~ 9 9 ˆ6 ~ ~ 9: w 4 ˆ" 9:ƒ i (t) e i = 3 j =1 R j i R j i (t)e j soit e i = R j i (t)e j. KŒ4) 67 ~ L>4 w 4 ewbz 9 :yoy?z y : :w>z 7: ~ 9:48469: ˆ) y>~ 4 d i (t) :y>ˆ6z N ˆQ 9 ƒ še4 y?ˆ y?x 9:4 y 46 qy?ˆ6z e i y 4 uz 9 ~ 7: ew>z5ˆ 469 ` y?x 9 z œbwb 9 ˆ6z O w>ˆ y i = R i j (t)yj + d i (t). 9 9:46 w 4 š 89: 8 7:4 y ƒ9x 469: 6 E ~ ˆ 9 7 ~dce ˆ 9 w> 6 6w>z}w>~ { 9:4 qy?ˆ6zn 9 z }w>~ 46 y?x 9 z œ>w A 9 ˆ6z oˆ 9W4 y?ˆ w> 6 9: 9 z y 46 w> : 7:7 z 7 :š ƒ w>~ wb : 7 7 z 7: ew>z<z{w> 6 qy?z ˆ6y?~ vlw"z 7 qy 46 9W9: «y?ˆ6z 4 ~ 9 ew>z ` 92e ~ 9 4 9N ` ˆ 469 w {9 6z{~ œo~ 7-L ~ 7 9T ` y?x 9 z œ>w 9 ˆ8z :š ~ ~ 469 z }~ 9: 2 w 46 - ` 7 {ˆ 69Š 69 y>~ 69 w 4 w ƒ ~ ˆ 9>ª y?ˆ N 9 w>z{w> 7 z ~ y 46 N 69 w «w Ÿ y 4" ˆ6~œBw 4 9>ª J ª v 9 ˆ8z ~ L?469u ` ˆ 4 ~ œ 9 z 9 ˆ 469< z y?~ 9/ 89/p` 9 ew> 9 A 9:ƒ L w ~ 7 9:4gš64 y 4 ~ 4 ˆ {9J w 46 ` 9: CA ewb 9>ªe3 ˆ6 :ˆ 469/4 ` 9 6z{~ œo~ 7-L ~ 7 9 ew>zšz{w> 6 qy?z w «w ƒ ~ 9N 69: N y>ˆ A 9: 6w> 9 59 ˆ8 ~ ~ 9 46 :ª ; ª ewb oˆ 9 œ 9 9 ˆ8z û }z ~ x z 9Œ 9 {z}w 48 qy?z 9 ew>z ew>z{w 7: ~ {ƒ9l 9Œ y 4QLŠ 69Œ w ~ L>469X ` ˆ 4 ~ œ 9 z e w 46 5p` 9 ew> 9 A 9:ƒ i L w ~ 7 9:4gª v 9 y 4 5y?z { 6y 4 y?z ƒ 7 N w 46 ew> ˆ 9 9 ew> 9<9 ˆ6 ~ ~ 9:4gª e i y?ˆ y>ˆ8œ?y 48 ~ z 9 ˆ ` ~ :y 48 {9 z œ 9 4 5ˆ 469J ~ z 9 }~ y 41 ` 9 ewb 9 c e 9 w>ˆq y?ˆ6z N ˆQ 9 ƒ :ª v 9: :yoy?z y : (y i ) w yo :~ 7:9: W ` y?x {9 z œbwb 9 ˆ6z%~ 469 z }~ 9: y 4 w> 6 9:7:9 L w ~ 7 9:46489: :ª vlw O ~ L?469 ` ˆ 4 ~œ 9 z ` ˆ 4 wbˆ8 }z 9 y>x {9 z œbwb 9 ˆ6zN~ 469 z {~ 9: w# y>ˆ6z 7 êwb {~ y 4Q9 4"«y 4 }~y 4Q ˆQ 9:ƒ O y 9 x i (t) = v i t + x i 0 4 ` x wœ?y i 046 ew x 9 y?~ 4 ` ˆ 4 y?x 9 z œbwb 9 ˆ6zu~ 469 z }~ 9: 6z{~ œ ~ 7-L ~ 7Bš 8z 7: 9:4 467 w 46ƒ y>~ 46 % w 46 u w 9:46 7:9 v i y 4 69: y 46 w 4 9 :ª vlw œo~ 9: { 9 z 9: wb }~ œ 9 69 O 6w>z z}wb 6 y>z O 9: viª y>ˆ 69 9-N {y 4gš 6w>z z}wb 6 y>z Tw>ˆ6 ˆ 9:4 y?ˆ w>ˆ6z ~ y 46 ~ 4 y?ˆ y ƒƒ 9 w 4 ~ ƒ 7 ` ˆ 469 œo~ 9: {9BªQKŒ4 z 9tA œbw 4 9Bš>4 y>ˆ qy?ˆ8œ?y 46 Xƒ w>~ w 4 67 c 4 ~ z2ˆ 4 y?x 9 z œbwb 9 ˆ6zXw> : 7: 7 z z{y> }wb }~y 4 ew>z2z{w> 6 qy?z w>ˆ e y?x {9 z œbwb 9 ˆ6z ~ 469 z }~ 9 ª vlwz 9: w }~ y 4"9 4 }z 9J 9 y y>z y 48467:9 (t, y i ) 9 (t, y i ) ˆ e 9 y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9: O 9: Nˆ 4 w 6w>z {~ :ˆ ~ 9 z 89u w «y?z ƒ ˆ 9 L?7:487 z}w 9 6z 7 7: 69 ƒ ƒ9:4 7 }w>x ~ 9 ˆ6~g 8z 9:48 94 y ƒ 69 O }z{w 46 «y?z ƒ wb }~y 4W 69/ w ~ 7 9 y R j i t = t et y i = R i j ( y j v j t y j 0) 9: ˆ 489 z y> w }~ y 4 :y 46 w 4 9/ 69p` 9 ew> 9 œ 9 }y?z ~ 9 9 ˆ6 ~ ~ 9:4 9: 9 ˆ 9 ] G0% M 1K ILG % K 1KNM O1K #! O! % U1K e i = R j i e j ª ` 9 1 6w>z z{w> 6 qy?z w w {9 6z ~œo~7l ~ 7:91 69 y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9: 69 ` 9: 6w> 9tA 9 ƒ L w ~7:9:4 oˆ 9/9: Š y>~ 4692N }y 4 ~ 9:48469: 69 w 4 w ƒ ~ oˆ 9J y 4 «y?z ƒ ˆ 7:9 :ª O
10 ª J ª vlw 6z 9 ƒ ~ x z 9Q y?~ {~ 6ˆ9 oˆ ` ˆ 489 ew>z }~ :ˆ9 qy 4 }ˆ 9 9" y?ˆ ƒ ~ 9 w>ˆ6 ˆ 469"«y?z{ 9 9 9:4 ƒ y?ˆ8œ 9:ƒ9:4 69 }z}w 46 { wb }~y 4 ˆ 4 ~ «y?z ƒ 9 qy?ˆ6z<ˆ 4 y?x {9 z œbwb 9 ˆ6z ~ 469 z }~ 9: ª ` 9: 9 6z{~ 4 :~ 9 ` ~ 489 z {~ 9 ˆ6~T :w>z}w> 7 z{~ 9 / ˆ 9 ƒ 9 4 9: y?x 9 z œbwb 9 ˆ6z ~ 489 z {~ 9 :ª 469 w>ˆ8 {z 9«w Ÿ y 4m 69W 9 ~z 9u9 ˆ 9/ w ~ L>469 ` ˆ 4 ~ œ 9 z %9 ˆ 469J z y?~ 9 w 46 Np` 9 ew> 9 A 9:ƒ ML w ~7:9:4ª ; ª vlw 69 ˆ e ~ x:ƒ9 y?~ 9: w y?~ «y 48 w ƒ9:4 w9œ 69+ w 4 w ƒ ~ ˆ 9 qy?ˆ6zˆ 469 ew>z {~ ˆ 9 qy 4 }ˆ ƒ w { 9 ~ 469 z 9 m y?ˆ ƒ ~ {9 ˆ 4 ew ƒ 69u«y?z 9 9 e 7 z ~ 9 ˆ6z 9 f i (x j ) m d2 x i dt = f i (x j (t)). 2 y?ˆ Š92e ~ L?9 y 48 ˆ ` ~4 ` 1w>~ Š 6w Š ` y?x {9 z œbwb 9 ˆ6z 6z ~œo~7l ~ 7: ª w>zš :y 48 {7 ˆ 9 4 šq w y>~ «y 4 A w ƒ 9 4 }w 9u 89/ w 4 w ƒ ~ oˆ 9J y?~, {z 9 ~ 4 œbw>z ~ w «y?z ƒ 9 qy?ˆ6zn }y?ˆ 9: y?x 9 z œbwb 9 ˆ6z ~ 469 z }~ 9 ª83 ~ 46 ~ w «y?z{ 9u {9 }z{w 46 «y>z ƒ9u ˆ6~ œ>w 4 w y?~ f i (x k ) = Rj i f j (x l (x k, t)) y L x l (x k, t) w ~7: >ª"KŒ4"«w>~ š 9: ˆ6~ A :~ y?~, }z 9 œoz{w>~ y>ˆ6z }y?ˆ 9: N9: N y?~ T 69 w# 8 ~ ˆ 9>ª 9 p` ~ 4 œ 9 z {9 69 wš }z{w 46 «y?z ƒ wb }~y 4J 69Š w ~ 7 9>ª ` 9: 9 6z{~ 4 :~ z 9: wb }~ œo~ 7 8ª vlw {z{y?~ ~ x:ƒ9/ y?~ 9: u 9 9J 69 p` wb }~y 4"9 89< wz 7 w> {~ y 4 w 46 ˆ 4) x:ƒ9 69 6w>z {~ :ˆ 9: qy 4 }ˆ 9 9 T9 4 ~ 4 9 z}w> }~ y 4gª ~ˆ 4 y?z{ a 92e 9 z 9 ˆ 469«y>z{ 9 ˆ6z ˆ 4 :y?z f(ab) i b w y?z w «y?z 9 92e 9 z 7:9 ew>z9 :y?z f(ba) i b ˆ6z9 :y?z a 9: N 9: 9 ˆ 9 f(ba) i = f (ab) i 9 e ~ 9u 694 y ƒ x6z 9 ˆ {9 9 e 7 z{~ ˆ6~ ƒ y 4 }z 9 4 Š ˆ 9u 9 :y 48 {7 ˆ % 89 9 Š y?~ T4692N A }y 4 ~ : % y 4 ƒ ~ 9: %9:4) 67 «w>ˆ8 ª 9 w {y?ˆ6 9 w L?7 y ƒ7 }z ~ 9 69 p` 9 ewb 9 A 9 ƒ L w ~ 7 9:4 w>z%~ 4 ` w 9:4 z 7 w ~ 7 6w ƒ w>x y ˆ y?ˆ8z9: y>x {9 z œbwb 9 ˆ6z ª 469<7 œ ~ 69:4 9 ~z 9 9 6z{yœo~ e 7 z{~ 9:4 9: Š ˆ6z 9 9 ƒ T 69 œo~ ƒ ˆ6y 48 T9 9 }ˆ 7 9: Š w 46 9 w 48467:9 êw>z}w 4 9 w 48 9 z}w >y 46 :y ƒ ~ oˆ 9: N9 N ˆ z 7 9:ƒƒ9:4 w 46 N 9 w> : 7:7 z}w 9 ˆ8z N 69 ew>z }~ ˆ 9 :ª [jm!/rtk ILK "M % <G M % K v ` 9 ew> 9 A 9:ƒ 1ƒ ~ 4QP y NN gp ~ 9 4 9: Wˆ 4 9: ew> 9 wxz 489 êwb {z 9) ~ ƒ 9 46 ~y 46 y 4 p` 9 ew> 9 η 9 w ~ L?4 ~c 9 ˆ ` ~ 92e ~ 9 œ 9 {y?z{~ 9: z 7:9: w { yo :~ 7 9: ƒ ˆ 4 ~ ` ˆ 4 8z{y ˆ6~ w w>~z 9< y?z 9 4 :~ 9:4 ˆ 469 xew {9 69p` 9 ew> 9 œ 9 }y?z ~ 9 9: 9 ˆ 9 e a (a = 0, 1, 2, 3) η(e a, e b ) = η ab avec η ab = diag( 1, 1, 1, 1). 9 9 xew 9 y 46 }~ {ˆ 9u w 7 }z{w 69 y>z 9:4 :~ Bª y?~ y X = X 3 X a e a soit X = X a e a. a=0 ˆ 4 œ 9 9 ˆ6z š&4 y?ˆ 7 z{~œ>y 46 X a y 4 9: y ƒ y w 4 9 T 69 X w 46 9 { 9 xew 9>ª vlw 4 y?z ƒ95 89 X η(x, X) = 3 a=0 3 η ab X a X b soit η(x, X) = η ab X a X b. b=0 J = wbŵ w>z z 7%9: y 46487:9 ewbz
11 y>ˆ6znˆ 4 œ 9 9 ˆ8z še4 y?ˆ wœ?y 46 N9: N 67 c 4 ~ {~ y 46 Š ˆ6~œBw 4 9: X y?z{~ 9:4 7 w 46 N 9 9 ƒ η(x, X) < 0 X η(x, X) = 0 X ~ y?z{~ y> }z y? 9:4 7 9 w 46 N ` 9: 6w> 9Bª η(x, X) > 0 X 469 :y>ˆ6z{x 9 ˆ 9 y 4 ˆ 9 89p` 9 ew> 9 A 9:ƒ ƒ ~ 4QP y NN 3P ~ 9:4 9: 67 :z ~ 9 ew>z#ˆ oˆ6wb }~y 4 x µ (τ) y τ 9 #ˆ 4 ewbz}w ƒ6x {z 9>ª v 9 œ 9 9 ˆ6z A 67 z ~œ 7:9 ) w" :y?ˆ6z x 919 dx µ /dτ ª v 9 ~ L>469W 69W w 4 y?z ƒ 9u ˆ"œ 9 9 ˆ6z A 67 z{~ œ 7:9/9: %~ w 4 ˆ" 6y?~ e1 ˆQ ew>z}w ƒ 7 }z}w L?9>ª y?ˆ N4 y> {y 46 dx µ /dτ {y?ˆ:/ y?ˆ6z y?z{~ 9:4 7u w 46 N 9 9 ƒ :y?ˆ8z{x 9 ˆ L>9:4 z 9 9:ƒ x µ (τ) dx µ /dτ {y?ˆ:/ y?ˆ6z ~ yb }z{y> 9 :y?ˆ8z{x 9 ˆ L>9:4 z 9J ˆ ƒ ~ x z 9 x µ (τ) dx µ dτ }y>ˆ:/ y?ˆ6z y>z{~ 9 4 7u w 48 p` 9 ewb 9 :y?ˆ8z{x 9 ˆ L>9:4 z 9J9 ewb 9>ª x µ (τ) 4 z 9 x z 9Š 69Šp` 9 ewb 9 A 9 ƒ Œƒ ~ 4"P y NN gp ~ 9 4#9: - y 46 }~ {ˆ 7 ` ˆ 469 y?z ~ L ~ 469T j9 ` ˆ {z}w 89 y>z 9:4 :~ L z > 9 w z 9: w }~ y 419:4"9: 6w> 9 w(z 469 e a ª 4 7 œ 7:469 ƒ 9 4 S9: z 9 7 z 7 ew>z 9: êwb {z 9 y y>z y 48467:9 x µ (µ = 0, 1, 2, 3) OM = x 0 e 0 + x i e i. v 9: :yoy?z y : y 4 %w> 6 9:7:9 ƒ ~ 4"P y NN gp ~ :ª (x µ ) y?ˆ wœ?y 46 w 4 y> }~y ~ w 4 9 ƒ ~ 4"P y NN gp ~ :4 }z 9 89 ˆ e qy?~ 4 9 ƒ ƒ ~ 4"P y NN gp ~ 9 4gše 67 c 4 ~ 9 wbˆ :w>z{z 7 6w>z M 1 9 M ` 9: 6w> 9tA s 2 (M 1, M 2 ) = η(m 1 M 2, M 1 M 2 ). j w 48 ˆ 4 z 9 x z 9>š9: y y?z y 46487:9: ƒ ~ 4QP y NN gp ~ : u 89 9 M 9 4 y?ˆ wœ?y 46 ` 92e 6z 9: ~ y y y?z y 46487:9: 69 w ~ }w 1 4 9Jƒ ~ 4"P y NN gp ~ x µ 2 M 2 y 4 z 9: 9 }~ œ 9:ƒ9:4 x µ 1 9 s 2 (M 1, M 2 ) = η µν (x µ 1 x µ 2)(x ν 1 x ν 2). y>ˆ w> 6 9: y 46 w ƒ7 }z ~ ˆ 91ƒ ~ 4QP y NN gp ~ >ª y?ˆ #4 y> {y 46 ƒ η µν ds ~ 4QP y NN 3P ~ 9: :4 }z 9/ 69 ˆ e qy?~ 4 ~ 4 c 4 ~ ƒ 9 4 œ?y?~ ~ 46 Š 69 :yoy?z y : -«w>ˆ8 «w>~ z 9 w { 9 4 }~ y 4 ˆ 9 ds 2 = η µν dx µ dx ν. 29 w>z z 7Q 69Q w ~ }w 4 9 x µ 9 x µ + dx µ 9 ˆ8, }z 9 4 ˆ š487l wb {~ «y?ˆm qy ~ }~ «Cª y?~ Jˆ 4 y?~ 4 š ` 9:48 {9:ƒ s 2 (M 1, M 2 ) x 9-69 qy?~ 4 ˆ 469+ ~ w 4 9+ƒ ~ 4QP y NN 3P ~ 9: ˆ 9Œ 69T 9 2w> 6 9: 7Œ ˆ ƒ ~ x z 9 ª C M ~ ˆ 69/ še4 y> 7 y?ˆ w y c 4 ~z)ˆ 469 y>z{~ 9 4 wb {~ y 4 9:ƒ qy?z 9 9Bª y?ˆ 67 :~ y 46 ˆ 9 qy?ˆ6z)ˆ 4 z 9 x z 9 (O, e a ) š 9) 89:ƒ ~ A 469 oˆ8~ :y 4 {~ 9:4 9: 9) 89:ƒ ~ A 469"«ˆ8 }ˆ6z ª v ` w>ˆ8 }z 9 69:ƒ ~ A e 0 C : 9 89:ƒ ~ A 469 ew {7 ªŽ y?ˆ8 Jœ 9 9 ˆ6z y?z ~ 9 4 7# w 46 J 9 9:ƒ / 9 Mz{w ~ y?~ ~ z ~ L?7 œ 9 z < 9 «C M X ˆ8 {ˆ6z ~ X 0 > 0 š ` 9: A A ~z 9 š6 y?~ ~z{~ L?7 œ 9 z 9 ew { {7J w 48 9 w y 4 }z}wb~ z 9Bª η(x, e 0 ) < 0 y?ˆ qy {ˆ y 48 ˆ 9 w ~ L>469- ` ˆ 4 ~œ 9 z ` ˆ 469 6w>z {~ :ˆ 9 y 4 {ˆ 9: 9+9: ˆ 469 :y?ˆ8z{x 9T ˆ L?9:4 z 9 9 ƒ :ª y?ˆ z 9 ƒ wbz{ ˆ6y 46 ˆ 9<4 y?ˆ y?ˆ œ?y 46 ew>z{w ƒ 7 }z 9 z w# :y?ˆ8z{x 9 ` w>~ 69u ` ˆ 4 ew>z}w ƒ9x }z 9 s 9: ˆ 9J 9 œ 9 9 ˆ6z A 67 z{~ œ 7:9 dx µ /ds y>~ 69 4 y?z ƒ 9 9 ~z{~ L?7 œ 9 z 9«ˆ8 {ˆ6z 1 η µν dx µ ds dx ν ds = 1 et dx 0 J0J ds > 0,
12 7 w 4 67 c 4 ~ ˆ 469 :y 48 w 4 9 w 8 ~ {~œ 9 6z x: ª y?ˆ w> 6 9: y 46 9 œ 9 9 ˆ6z A 67 z{~œ 7:9 # w ~ L?469 s ` ˆ 4 ~ œ 9 z % w êw z ~ A œo~ 9: {9 69 w 6w>z {~ :ˆ 9 qy 4 {ˆ 9: 9Bš8 y>ˆ8œ :4 y> 7 9 u y?ˆ w y 46 }y?ˆ8 69u ˆ8~ 9 ~ 4 }z y ˆ8~ z 9 ˆ 469 w {9 8z{~œo~ 7L ~ 7:9N ` y?x 9 z œ>w 9 µª ˆ8z :še ~ ~ 469 z {~ 9: :š 69 ` 9: ew> 9 A 9:ƒ Nƒ ~ 4QP y NN 3P ~ 9:4gª y 46 ~ 67 z y 46 ˆ 4 z 9 x z 9 (O, e a ) wœ 9 ~z{~ L?7 œ 9 z 9«ˆ8 {ˆ6z ª e y>ˆ T 67 c 4 ~ { y 46 9 y 4QL?9 ƒ % ` y?x 9 z œbwb 9 ˆ6z w { y ~ 7 9 z 9 x z w «w Ÿ y 4W ˆ8~œBw 4 9Bª O J ª w ~ L>469 ` ˆ 4 ~œ 9 z 9 w z y?~ 9 ˆ L?9:4 z 9 9 ƒ < ` 7 êwb {~ y 4 x i = 0 (i = 1, 2, 3) êw z{~ A œo~ 9 { 9 ª vlw y 4 :~ 89 wœ w>z}w ƒ6x {z 9 e 0 s y?z{z 9: qy 46 x0ª y?ˆ w 6ƒ9 }y 48 ˆ 9 9 9:ƒ 69p` 6y>z y L? y?x 9 z œbwb 9 ˆ6z 9: t t = 1 y?~ w>ˆ { ~ c x0 t = s c y 9 Œˆ 489 :y 48 w 4 9 ˆ 4 ~ œ 9 z {9 9 ˆ6~ -` ~ 4 9 z 6z 7 9 z}wˆ 7 z ~ 9 ˆ6z 9 ƒ :y ƒƒ9 w œo~ 9: { 9 c 69 w ˆ ƒ ~ x z 9>ª ; ª v ` 9: 6w> 9 w>ˆ) 9:ƒ 69 p` t y?x {9 z œbwb 9 ˆ6z 9: ` 9: ew> 9 9 ˆ6 ~ ~ 9:4) 87 c 4 ~2 ew>z x 0 = ct y?z } 6y L y 4 w " w ~ L?469 ` ˆ 4 ~œ 9 z ª v 9 }z ~ x: z 9 89p` y?x {9 z œbwb 9 ˆ6z ~ 469 z }~ 9: ª 29 y 4 :~ 89 wœ 9 e 9: ˆ8~ 87 c 4 ~& ewbz9: 69 wu 7 }z{w 69 y?z 9:4 ~ 9:48469%9N i y 4QLJ 69 w z{y>~ 9N ` 7 êw }~ y 4 e ewb oˆ 9 œ 9 9 ˆ6z {9 i }z{w 46 y?z 9 y 4 J 6w>zŠ ew>z{w 7: ~ {ƒ9%9u y 4"L 89J w ~ L?469 ` ˆ 4 ~ œ 9 z :ª e i e 0 O x i = 0 ª e 2 x 0 = 0 e 1 x i = 0 espace au temps t = x 0 / c v ` y?x {9 z œbwb 9 ˆ6zN~ 469 z }~ 9: 9 ˆ8 Nz 9 7 z 9 z }y?ˆ T 9: T7 œ 7 469:ƒ9:4 % 69up` 9 ewb 9 A 9 ƒ Šƒ ~ 4"P y NN gp ~ 9 4 L z > 9 w>ˆ e :yoy?z y : Wƒ ~ 4QP y NN gp ~ : (x µ ) w 46 W 9 ˆ 9 9 x 9 0 c «y?~ 9 9:ƒ t ` y?x 9 z œ>w 9 ˆ8z x i y 4 ~ wœ 9 9: y y>z y 48467:9 L w ~ 7: /p` i y?x {9 z œbwb 9 ˆ6z ª y 4 w>ˆ8 }z 9 y?x {9 z œbwb 9 ˆ6z+~ 469 z {~ 9: O š ~ ƒ ~ :~ 9:ƒ9:4 2wœ 9 69: 6y?z y L?9 Œ9 69 z xl?9: tl z}w ˆ 7:9 ~ 89:4 }~ oˆ 9: :š9: u w>z{w> 7 z ~ {7 ew>zˆ 4 z 9 x z š wœ 9 w y 46 ~ }~y 4 ~ z ~ L?7 œ 9 z u9/«ˆ8 {ˆ6z ª e a e 0 v 9: :yoy?z y : ƒ ~ 4QP y NN gp ~ 9:46469 w yo :~ 7:9: y 4 ª vlw z 9: w }~ y 4 9:4 }z 9 9 :yoy?z y 46467:9 (x µ ) (x µ ) 9 ` ˆ 4 ƒ,:ƒ9u7 œ 7:469 ƒ 9 4 9: y w>z w< }z{w 46 «y?z ƒ wb }~y 4W 69 y?~ 4 :w>z 7 (x µ ) x µ = L µ ν x ν + D µ avec L 0 0 > 0 y D y 4 9: :yoy?z y 46467:9 5 ˆ y?~ 4 qy?ˆ6z ` y?x {9 z œbwb 9 ˆ6z 6z{~ ƒ 7J9 µ 5y y 4 9: }z{w 46 CA L «y?z ƒ wb {~ y 48 T 69 vy?z 9 4 b še ~ 9 y?z { 6y 8z{y 469 :š& w }~ «w>~ w 4 a e a = L b a e b KLR:95cFCFCM>BCKL7:9D;_^ 58FOFC=P7FCM>K&7 9OR:B@;V=lFIJA;>=P9I?UK&Q 58a&=l3E=$9CMVaL76=]5ZY&=+?); 53EM 9 FS587:?A= 2DM>7 &K '9 bmv=p7676=lm>7:76mvfcj+9om>2@58;>= ds 2 = η µν dx µ dx νk c = 2, ;_^ R67:M FIJf3E="FC=P2NQ 9'3E=AQ:R6M>96k 8 2 kc9 1kj; 9A^ 58aLM F 3g^R676=NYZ5&;V=PR6B"=Uh65&?UFC= R6M 9O=PBOF J ; 3EJABIMVYL=AB";_^R67:M FIJD36=N;>K&7:a&R6=PR6B<36=
13 wœ 9 η ρσ = L µ ρ L ν σ η µ ν η ρ σ = η ª=KŒ4 w6/ y?ˆ8 }w 4 ρσ ˆ 9N 9 }z{w 46 «y>z ƒ wb }~y 46 y 46 9 z œ 9:4 ` y?z{~ 9:4 wb {~ y 4/ 69: 7 {z}w 69 9 š ` 9: A A ~z 9 e a e a š4 det L y?ˆ y?x8 9 4 y 46 J 9 }z}w 46 «y?z ƒ w }~ y 46 6z y? 6z 9 y>z } 8y 6z y 469 / ˆ L z y?ˆ vy?z 9:4 µ š4 y> 7 9: ˆ6~ :y 46 9 z œ 9:4 w ƒ7 {z{~ oˆ 9Jƒ ~ 4"P y NN gp ~ ª ` w L ~ ˆ y?ˆ CA L z y?ˆ6 9 :y e 9 ` ~ 69 4 {~ 7 ˆ L z{y?ˆ vy?z 9 4 L 0 (4) y?ˆmx6~ 9 4 L :y ƒ 9 +(4) L(4) vlw «y?z ƒ9il?7:467 ª z}w9 69 }z{w 46 «y?z ƒ wb }~y 46 9 ˆ8, }z 9 y?x8 9:4 ˆ 9>ª y?ˆ W4 y?ˆ :y }y y z w< {z}w 48 «y?z ƒ wb {~ y 41 7 :~ w 9u 69 vy?z 9:4 x 0 = x0 wx 1 1 w 2 x 1 = x1 wx 0 1 w 2 x 2 = x 2 x 3 = x 3 y 9 Xˆ 469 y 46 w 4 9 ˆ 9 }~ 9 ˆ 9 ˆ 4/9:4 œbw9 ˆ6zw>x y ˆ 9>ª v ` 7 oˆ6wb }~y 4/ 89T w ~ L?469- ` ˆ 4 ~ œ 9 z w 69Šp` y?x {9 z œbwb 9 ˆ6z O 9: x 1 = 0 y?~ x 1 (x 0 ) = wx0ª 9 :~ y 46469N w%œo~ 9: {9 z 9 wb {~œ 9 ew>zœz{w> 6 qy?z mp` y?x {9 z œbwb 9 ˆ6z O ˆ6~uwm qy?ˆ6z 92e 6z 9 { ~ y 4 ª+3 ~ 48 ~ š+ w œo~ 9 { 9 z 9: wb }~ œ 9"9:4 }z 9 69 ˆ e v 1 = cw y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9 O 9 9: }y>ˆ:/ y?ˆ6z ˆ 9 {~ 9 ˆ 9 O c ª ~ v 1 /c 1 9 v 1 x 1 /c x w y?z Š4 y>ˆ z 9 {z{y?ˆ œ?y 46 N w {z}w 48 «y?z ƒ wb {~ y 4 7 :~ w 9u 89< w ~ 7 9>ª 0 y?ˆ wœ?y < ~ w L w ƒ ƒ9 69 ~ 4QP y NN 3P ~ 69 ` 9: ew> 9 A 9:ƒ 5ƒ ~ 4"P y NN gp ~ 9 4gš z 7: ˆ8~ 69 ˆ e ~ ƒ 9 46 ~y 46 2 ˆ6z9T 7:ƒ w :~ A 69: y?ˆ :š qy?ˆ6z 9: 69 ˆ e y?x 9 z œ>w 9 ˆ8z ~ 489 z {~ 9 69 ~ L?469 2 ` ˆ 4 ~ œ 9 z x 1 = 0 9 x 1 = 0 ª ν = x 0 x 0 cone de lumière x 1 e 0 e 0 e 1 O e 1 y?ˆ :y 48 w }y 46 oˆ 9 9 «9 ˆ6~ 9 w L>9 ` 9 ew> 9: Š9 ˆ6 ~ ~ 9:46 š ewbz}w x:9: -9:4 {z 99 ˆ eš Q ˆ 6y?~ e 69%p` y>x {9 z œbwb 9 ˆ6zT~ 469 z }~ 9: ª>3 ~ 48 ~q oˆ ` ˆ 4 7 œ 7 469:ƒ9:4 y?~ wœbw 4 y?ˆ w> 6z x ˆ 4 w>ˆ8 }z p` y?x {9 z œbwb 9 ˆ6z ªDKŒ4 z 9 œbw 4 9Bš ~Xˆ 4 7 œ 7:469 ƒ w 46 u9 69 ƒ ~ A 469<«ˆ8 {ˆ6z~ ˆ ` ˆ 4 7 œ 7:469 ƒ 9 4 w y?z }y>ˆ 9: y?x {9 z œbwb 9 ˆ6z z 9 x z œbw wbx 9 qy?ˆ6z {y?ˆ8 Ny?x {9 z œbwb 9 ˆ6z ª 1 1 w> 6z x: X x 1 2 ª ` 9 w 4 yb }~ y 4/ 69 w>ˆ w ~ 7 4 y?x {9 z œbwb 9 ˆ6zL ˆ 9: :y 4 oˆ 9>š ~ w> 7 7 z 7>š 9: 67 z{~ w 46 p` 9 ewb 9 A 9 ƒ Lƒ ~ 4QP y NN gp ~ 9 4 ewbz ˆ 469u ~ L?489% ` ˆ 4 ~ œ 9 z Š ˆ L?9 4 z 9 9:ƒ :ª"KŒ4 ew> ˆ 9 y>~ w ~ L?469 ` ˆ 4 ~ œ 9 z N 69 ` y?x 9 z œ>w 9 ˆ8z ˆ 9: :y 4 oˆ 9>š 4 y?ˆ qy?ˆ8œ?y 46 {z{y?ˆ œ 9 z"ˆ 4 9 z wb~ 4 y?x {9 z œbwb 9 ˆ6z"~ 469 z {~ 9: w 4QL>9:4 " oˆ8~j y 4 :~ 89 ~ 48 w 4 }w 467 ƒ 9 4 š ` 9: A A ~ z 9 9: ˆ 9 e µ 0 = u y 9: µ µ w" êw z{~ A œo~ 9 { 9 69 ` y?x 9 z œ>w 9 ˆ8z u w> 7:7 z 7 wœ 9 ª 9 w ˆ L0Lyx z 9 ˆ 9<4 y>ˆ «w { ~y 46 9 E o yb } x {9: 5 ˆ6~ œ>w 4 9: y?ˆ8z 87 c 4 ~z u 0 > 0 9 9:ƒ N9 p` 9 ew> 9/ 89 9 y?x 9 z œ>w 9 ˆ8z ª J
14 w x 0 O O cone de lumière e 0 e 1 e 0 O e 1 x 1 Ž y>ˆ8 ` w>xy>z gš?9 9 ƒ t ˆ" ew>z{w ƒ9x }z 9 69 w ~ L?4695 ` ˆ 4 ~œ 9 z ewbz t s y ew>zp` 8y?z y L?9T 89Š ` y?x {9 z œbwb 9 ˆ6z-w> 7 7 z 7Š ` 92e 6z ~ ƒ9 ` w>~ 69 = s c. 3 ~ 46 ~ ` 6y?z y L?9 469N 69 œoz}wb~ - ew, }z 9 wx ew>z y 4 wb : 7 7 z}wb {~ y 4 {y?ˆ8 +w>ˆ ƒ y?~ 46 w 6z 7 :~ ~ y 4 w> }ˆ 9 9u 89: 6y?z y L?9 :ª v 9 ew>z{w ƒ6x }z 9 s 9 %w> 6 9:7J9 9 ƒ 8z{y? 6z 9 ª ~ 69 ˆ e y?x {9 z œbwb 9 ˆ6z šœ y 4 ˆ 4 9: # 6w>z 92e 9:ƒ 9 ~ 469 z }~ 9: š 8z 9:48469:4 w ƒ,:ƒ9 y?z ~ L ~ 4691 ˆm 9:ƒ qy?ˆ6z 9 ˆ6z< 6y>z y L?9 w y?z :š êw 46 ~ {9 z 9 y?ˆ6 9:4 š ` 6y?z y L?9# 69Wp` y>x {9 z œbwb 9 ˆ6z 4 y 4 ~ 489 z {~ 9 ~ 46 ~ ˆ 9 z}w5ˆ 469 ˆ6z 7:9 ˆ 9 {~ 9 ˆ p` y?x {9 z œbwb 9 ˆ6zX~ 489 z {~ 9 ª ˆ6z 9 ~ w L z{w ƒ ƒ9 ` 9: ew> 9tA 9:ƒ 69 ~ 4QP y NN 3P ~ š84 y?ˆ wœ?y 46 :y 4 {z}w>~z 9 ƒ 9 4 w>ˆ e w> 6 6w>z ª ` 9: s < x 9 6w>z}w y e 9# 69 / ˆ ƒ 9 w>ˆ e y>ˆ9 œ?y Ew L?9 ˆ6z 69 vlw 4QL>9 œo~ 4gª 4 / ˆ ƒ 9 w>ˆ ew>z }~ 9 4 œ>y Ew L?99: /w>ˆ z 9 }y?ˆ8zt ˆ / 9 ˆ 469 oˆ 9 9 ˆ6~&z 9 7 ~ 469 z {~ 9: ª y?ˆ8z 9 6z y?ˆ8œ 9 z 4 y>ˆ w y 48 +ƒ y 4 }z 9 z+ ˆ ƒ x 0 x 0 O s 6z y? 6z 9 vlw ~d 7 z 9: ƒ 6z{y> 6z 9 qy?ˆ6z 92e 6z 9: ~ y 4 x 1 s 9: 92e }z 9:ƒ ˆ ƒ qy?ˆ6z w z{y?~ 9Bª y?ˆ :y 46 ~ 67 z{y 48 ˆ 469 :y?ˆ6z x 9% ˆ L?9 4 z 9 9:ƒ x µ (τ) ª s 9 4 }z 9Q9: 69 ˆ e 7 œ 7 469:ƒ9:4 wbz}w> 7 z ~ 7: ew>z τ i 9 s = ~ :46 w 4 95 ˆ 6y?~ e ˆ 6w>z}w ƒ6x {z 9 τf τ i η µν dx µ dτ j; G5NR67]5&\6R:93E="Y&KE?P58\6R6; 58M>BI=<?P58BM>; de58ref 3EM>YbM>9C=ABQ 58B ck dx ν dτ dτ, τ ª&KŒ4 6z 9:4 w 4 :y ƒƒ9 6w>z}w ƒ6x {z 9 wu :yoy?z y x 0 69 τ f
15 ` y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9: šo4 y?ˆ y>x8 9 4 y 46 s = x 0 f x 0 i 1 v2 c 2 dx0 car dx i dx = vi 0 c et donc s < x 0. 9 œ 9 4 y 46 p` 9 ewb 9 69< ` y?x {9 z œbwb 9 ˆ6z5w> : 7: 7 z 7Bª 2wBzuw 4 w y L ~ 9 wœ 9 ` y?x 9 z œ>w 9 ˆ8z5~ 489 z {~ 9 š 4 y?ˆ Š y?ˆ6 6w>~ 9 z{~y 46 ˆ 9up` 9 ewb Ny?x 9 z œbwb 9 ˆ6z š ˆ6~ 9: Nˆ 4Q9: ew> 9 9 ˆ6 ~ ~ 9:4gšo y?~ Šy?z } 6y A L y 4 w w êw z{~ A œo~ 9: { 9Š9:4 }y?ˆ - y?~ 4 69Š w ~ L?489 ` ˆ 4 ~œ 9 z :ª 9 9:48 w 4 š 9-9: 6w> 9 469Š y 4 ew 6w>z}w x 9: 9:4 {z 9 9 ˆ e 9 u~ œ?y 4 {9 y?ˆ6 9 z ª y?ˆ wbˆ6z{y : w>~z 9:ƒ9:4 Jˆ 469 ~ ƒ ~ }wb }~y 4 69Q ` 9: ew> 9>ª 9 z 9 :š-4 y?ˆ y?ˆ œ?y 46 ~ 4 {z{y ˆ6~z 9 ˆ 4 {z{~ x z 9 y>z } 8y 4 y?z ƒ 7 ˆ6~ y?~ w : e ew> 9: 9 67 c 4 ~ z9: y y>z y 48467:9 w { yo :~ 7:9 ƒ wb~ w ˆ 9 }~y 49: 69 i wœ?y?~z ~ 9: 9: y 4 (y i ) ˆ 469 ~ 4 9 z{ 6z 7 }wb }~y 4 8 ~ ˆ 9>ª vlw ~z :ˆ 7 œ ~ 9:4 ˆ «w>~ N oˆ 9<4 y?ˆ 5469 y>ˆ8œ?y 48 ˆ %ƒ9: ˆ6z 9 z wœ 9 %ˆ 489 z xl?9 L z}w ˆ 7:9 :w>z-~64 ` 92e ~ 9 ew + 89 ƒ y?ˆ8œ 9:ƒ9:4 +z{~ L ~ 69 oˆ 9: y 4 ˆ 9 9:49: ew> 9tA 9:ƒ ƒ ~ 4QP y NN 3P ~ 9:4 :y ƒƒ9jp` w ƒ y 4 }z 7 y>z 4"9:4 J O>=0O8š6ƒ y ˆ y#ˆ 469J 67 c 4 ~ {~ y 4" ` ˆ 4 ƒ y?ˆ8œ 9:ƒ9:4 %z{~ A L ~ 69>ª y?ˆ N4 ` w y 46 ew N y z w 67 ƒ y 46 {z}wb {~ y 4Q 69 9 w ª g«wbˆ8 y?ˆ ~ L?489 zš ˆ 9J w ~ }êwb {~ y 4 9: +z}w ~ w9:ƒ9:4 ~ 7 z 9 4 9Š oˆ8~e 6z 7 œ>wbˆ8 w 46 -p` 9 ew> 9 A 9:ƒ tl w ~7:9:4 y ` y 4 67 w> 9 ~x6z 9 ƒ 9 4 ˆ 4 y?z{ / y ~ 69 9 z œ>w 4 69 z 7 «7 z 9 4 {~ 9 ª 7 w 46ƒ y?~ 48 :š4 y?ˆ qy?ˆ8œ>y 46 w 6ƒ 9 { {z 9 ˆ 9 9 :yoy?z y : 6z 9:46 z y 4 9 ˆ8z {9:48 ˆ ˆ 9: qy?ˆ6zšˆ 4 z 7 «7 z 9:4 }~ 9: w 48 w ~ ƒ ~ 9 y (y i ) y i l avec l = c2 a i l 9 w {9 ˆ 9u y 4QL ˆ 9 ˆ6z ~ qy 4 ~x 9 qy?ˆ6zšˆ 4 y?x {9 z œbwb 9 ˆ6z ` w> 7 7 z{wb }~y 4 z 9 wb {~œ 9 a i ª y?ˆ w y 46 6z 9 46 z 9 ` 92e 9:ƒ 9 69 ` y?x 9 z œ>w 9 ˆ8z ˆ 4 ~ «y?z ƒ7:ƒ9:4 Ww> : 7: 7 z 7) w 46 z y> wb {~ y 4 ` w> : 7:7 z}w }~ y 4 z 9 wb {~œ 9 9 w oˆ6w z{~ A œo~ 9: {9 y>ˆ 6y?~ ~ y 46 y ƒ ƒ9 œ 9 9 ˆ6z u vlw5 êw z ~ A w> : 7: 7 z}wb {~ y 4 9 }z{~ x: z 9 6ˆ8~ ˆ 9 e i (a, 0, 0) ªXj w 46 X9 w 4 x 2 = x 3 = 0 x 0 (s) = c2 as sinh, x 1 (s) = c2 a c 2 a µ w y?ˆ8zš :y ƒ y w 4 9 u 0 = cosh as, u 1 = sinh as c 2 c. 2 šb w ~ L?469+ ` ˆ 4 ~œ 9 z w5 qy?ˆ6z 7 êwb }~y 4 cosh as c 2 e 1 ˆ" {z{~ x z 9u9 œ 9 9 ˆ6z 89 y ƒ y w 4 9 e 0 1 = sinh as c 2, e 1 1 = cosh as c 2. a µ = du µ /dsªdj š y?z } 6y L y 4 w9 u µš w5 y>ˆ6z2 y ƒ qy w 4 9: (a/c 2, 0, 0) w 46 u 9 w 4 š ` 9: ew> ˆ 4 y>~ 4 69 w 46 w a µ = (a/c 2 )e µ 1 x 2 = x 3 = 0 ~ L?469 ` ˆ 4 ~œ 9 z 9: w 69:ƒ ~ A z{y>~ 9 ew w 4 % ew>zš 9 qy?~ 4 9 5w?w 4 % qy?ˆ6zny?z ~ L ~ 469u ª 9 w>~ z ˆ8z9+ ~ w L z{w ƒƒ 9Œ 69T ~ 4QP y NN gp ~o ˆ 9 9 y?x {9 z œbwb 9 ˆ6z ˆ 2 ew z 9 7 z 9 z {y?ˆ 9: 7 œ 7:469 ƒ / ` 9: 6w> 9tA 9 ƒ %ƒ ~ 4QP y NN gp ~ 9 4gª y?ˆ y ƒƒ9: 9 9:48 w 4 u~ ~ w 46 ˆ 4 :w ewbz }~ :ˆ ~ 9 zš w>z ~ ` w L ~ ` ˆ 4 ƒ y?ˆ8œ 9:ƒ9:4 z{~ L ~ 69 ˆ 4 ~ «y>z ƒ7:ƒ9:4 Nw> 7:7 z 7>ª KLR:9'5ZY&KL7:9 3E= ;>5N2@58BIa&="Q6R:M>9 R6= l QXK&R6BR:76=f5&?P?UJA;>JABS5cFIMVKL7G3E= 10 2 kc9 2k J D
16 x 0 cone de lumière observateur u e 1 espace orthogonal O x 1 ] G0% MYV K@#!uI'% % MgILKNMlO1K #! O! % U1K vlwj 6z 9:ƒ ~ x z 9Š y>~ 69 w 4 w ƒ ~ ˆ 9N ~ - ˆ ` ˆ 469 ewbz }~ :ˆ9 y 4 {ˆ 9: 9Š y>ˆ ƒ ~ {9 w>ˆ6 ˆ 469N«y?z{ 9 9: 9 4 ƒ y?ˆ8œ 9:ƒ9:4 89 {z}w 46 wb {~ y 4 ˆ 4 ~ «y?z ƒ 9 qy?ˆ6zš {y?ˆ 9: y?x {9 z œbwb 9 ˆ6z ~ 469 z }~ 9: :š w>ˆ }z 9 ƒ 9 4 ~ w ~ L?469 ` ˆ 4 ~ œ 9 z 9: ˆ 489/ z y?~ 9 ˆ L?9:4 z 9 9 ƒ N w 46 N ` 9: 6w> 9tA 9 ƒ ƒ ~ 4"P y NN gp ~ 9 4gª KŒ4 L>7:467 z}w š w 69: :z ~ 8 {~ y 4 69 ` ~ 4 9 z}w> }~ y 4 qy?ˆ6z ˆ 4 x ƒ 9Q 69 ew>z {~ ˆ 9 qy 4 {ˆ 9: «w>~ 9 z w> 9:ƒ9:4 J ˆ 9# w 46 u9 w z 9 ` ˆ 469 { 7 y?z ~ 9 w ~ oˆ 9 69: ew ƒ ªDj w 48 J9 :w 6z 7: {9 4 š?4 y>ˆ w y 46 L ~ ƒ 9 ƒ 9 4 :y 46 ~ 67 z 9 zxˆ 489 ew>z }~ ˆ 9 qy 4 {ˆ 9: ƒ w { 9 ~ 489 z 9 m ˆ 4 6w ƒ 69 «y>z{ 9 <9 e 7 z ~ 9 ˆ8z 9: ª vlw y?~-z 9 wb {~œo~ 9 69 w 4 w ƒ ~ ˆ 9 9 «y?z ƒ ˆ 7:9 qy?ˆ6z/ˆ w 46 4 y?x 9 z œ>w 9 ˆ8z2~ 489 z {~ 9 š ` 9 A A ~ z 9 w 46 ˆ 4< x:ƒ9t 89 y y?z y 46487:9: ƒ ~ 4QP y NN 3P ~ 9:46489: (x µ ) ˆ 4 ew ƒ 69 êw z{~ A «y?z 9: 92e 7 z{~ 9 ˆ6z 9: š>4 y?ˆ wœ?y 48 Œ w y?~ z 9: wb }~ œ ~ 9 69T w 4 w ƒ ª ~ oˆ y?~ 9 F µ (x λ ) m duµ ds = F µ (x λ (s)) avec η µν u µ F ν = 0 y x µ (s) 9: w ~ L?469 ` ˆ 4 ~ œ 9 z + 69N wu ew>z }~ ˆ 9 wœ 9 s 9 9:ƒ 6z y? 6z 9N9 µ wu oˆ6w z{~ A œo~ 9: {9>ª u vlw :y 46 ~ }~y 4 wdl?7 x6z ~ ˆ 9u : w>~z 9 y?ˆ8znw { ˆ6z 9 z w :y ƒ ewb {~ x6~ ~ 7 :w>z v 9 œ 9 9 ˆ6z z L ~ 9tA ~ ƒ 6ˆ ~y 4 d ds (η µνu µ u ν ) = 0 soit mη µν u µ duν ds = 0. p µ 69 w ew>z }~ :ˆ9>š y>ˆ êw z{~ A ~ ƒ 6ˆ ~ y 4gš9: 67 c 4 ~ 9 6w>z p µ = mcu µ. J
17 ª vlw y?~z 9: wb }~ œo~ 95 69u w 4 w ƒ ~ ˆ 9 w>ˆ6z}w w ƒ, ƒ 9 «y?z ƒ9 qy?ˆ6zt {y?ˆ Š9: y?x {9 z œbwb 9 ˆ6z ~ 489 z A }~ 9: J ~9 ew ƒ 69 êw z{~ A «y?z{ 9: /9: <x6~ 9 4 ˆ 4 ew ƒ 69 œ 9 9 ˆ8z 69 ` 9: 6w> 9tA 9 ƒ <ƒ ~ 4 A P y NN 3P ~ 9:4gš ` 9 A A ~ z 9u ~ ew>zn ew 4"L?9:ƒ9:4 69 :yoy?z y : ƒ ~ 4QP y NN gp ~ 9:46469 y 4 w F µ (x ρ ) = L µ ν F ν (x σ (x ρ )). w }ˆ6z 9: 9:ƒ9:4 w y 46 ~ }~ y 4 w L?7 x6z{~ oˆ 99: 9:4 :y?z 9 œ 7 z{~c 7:9 ª 4 ` jw 6w η µ ν ` uµ F ν = 0 y?x 9 z œbwb 9 ˆ6z ~ 469 z }~ 9: 6z{~ œ ~ 7-L ~ 7 :ª ` 9 9 6z ~ 4 ~ 9Š 69 z 9 wb {~œo~ 7>ª(K-4#«w>~ š 9 ~ 9 -œoz}w>~8 y?ˆ8z }y>ˆ8 9 Œ 9: 2 y?~ 2 69Š w 6 E ~ ˆ 9BšE7 œ 9 4 }ˆ 9 9 ƒ 9 4 9:4# {9N ~ ƒ ~ w 4 w>ˆ e }z{w 46 «y>z ƒ wb }~y vy?z 9 4 6z y? 6z 9 L 0 (4) ª vlw ˆ ƒ ~ x z 9 w ˆ 4Q }wb }ˆ N ew>z {~ ˆ ~ 9 z w 46 N ` 9: ew> 9tA 9:ƒ Šƒ ~ 4QP y NN 3P ~ 9:4gª v ` ~ 4 œbw>z ~ w 4 9 z 9 w A }~ œo~ 9< 69 7 êwb {~ y w e&n 9: ~ ƒ ~ oˆ 9 ˆ 9# w :y 46 }w wœ ~ 9 { {9 89 w ˆ ƒ ~ x z 9>ª c y ƒƒ 9 ˆ 469 :y 48 {7 ˆ êw }~ y 46 :š& 9 œ 9 9 ˆ6z 89 6z y? ew L w }~ y 4 69/ µ w ˆ ƒ ~ x z 9u9: k ~ y> }z y? 9>ª 9: :y ƒ qy w 4 9: Š y 4 N y 46 w 4 9 y?ˆ8zšˆ 4 y?x {9 z œbwb 9 ˆ6zŠ~ 469 z }~ 9 ª vlw ~ L?4895 ` ˆ 4 ~ œ 9 z ` ˆ 4 6 6y> {y 4gš y 46 ~ 67 z 7 :y ƒƒ9 ˆ 469 ewbz }~ :ˆ9 qy 4 }ˆ ƒ w {94 ˆ 9>š 9: Qˆ 469 z{y>~ 9 ˆ L>9:4 z 9 ˆ ƒ ~ x z 9>ª N9:4 z 7: ˆ 9 ˆ 9) w œo~ 9: {9 z 9: wb }~ œ 9Q 69 w ˆ ƒ ~ x z 9Q9: y>ˆ6z {y?ˆ 9 c y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9: :ªQKŒ4"9 9 še9:4 6z 9 4 w 4 w ~ z 9 }~ y 4 :z{y>~ { w 4 9 1še4 y?ˆ wœ>y 46 x 0 (λ) = k 0 λ (k 0 > 0) x 1 (λ) = k 1 λ mais k 0 = k 1 donc x 1 (x 0 ) = x 0. KŒ4 :yoy?z y 46467:9 ƒ ~ 4QP y NN 3P ~ 9:48469: }~ ˆ 9 ew>z w «y 4 {~ y 4 :y ƒ 92e 9 (x µ ) š 4 y>ˆ z 9 6z 7 {9 4 {y 46 ˆ 469 y w 4895ƒ y 4 yo 6z{y ƒ w A A(x ν ) = a 0 exp( iη µν k µ x ν ) y k 9: 9 œ 9 9 ˆ8z 89 6z{y> ew L wb {~ y 4 oˆ8~ 9: Š~ y> }z y? 9 µ η µν k µ k ν = 0 ª y>ˆ 6z 9 4 y 46 k 0 > 0 ª v 9 y>ˆ qy?ˆ8œ>y c 4 ~ z w «z 7 oˆ 9:4 9 ƒ9: ˆ6z 7 9 6w>z ˆ 4 y?x 9 z œ>w 9 ˆ8z2~ 489 z {~ 9? 69 êw z{~ A œo~ 9: { 9 qy?~ 4 Œ~ ƒ qy?z }w ˆ 9N w% 6 ew 9Š 69Š ` y 46 69T9: -ˆ 469 «y 4 }~ y 4 69Š ` 9: ew> 9tA 9:ƒ Œƒ ~ 4QP y NN 3P ~ 9:4gª ν[u] u µ ew>zp` 9 e 6z 9 { ~y 4 ν[u] = c 9:4«w>~ w 4 wb 9 4 {~ y 4 ˆ 9 η µν u µ k ν < 0 2π η µνu µ k ν, š ˆ6~ 9 /œ>w w>x9# w 46 }y?ˆ8 x:ƒ9w 69 :yoy?z y : ƒ ~ 4QP y NN 3P ~ 9:48469: ª y?ˆ qy?ˆ8œ>y 46 %7L w9:ƒ9:4 ~ 4 }z y ˆ6~ z 9u w ~ z 9 {~ y 4" 69 6z{y> ew L wb {~ y 4 ` y w 489 z 9: wb }~ œ 9 ` y?x 9 z œ>w 9 ˆ8z ~ 469 z }~ 9: µ 6w>z ` 92e 6z 9: { ~ y 4 u n µ 1 [u] = ( η ρσ k ρ u σ ) (kµ + η ρσ k ρ u σ u µ ) x n µ [u] 69 ª ` 9 ˆ 4 œ 9 9 ˆ6z y?z ~ w 48 ` 9: ew> 9Bš ˆ6~ wb }~ «w>~ η αβ n α [u]n β [u] = 1 9 η αβ n α [u]u β = 0 qy?ˆ8œbw 4 y 4 ` 92e 6z ~ ƒ9 z w 46 N 9 }z ~ x z 9 e4 y>ˆ wœ>y 46 e i n µ = n i e v ` ~ 4 9 z 6z 7 wb {~ y 4 L?7 y ƒ7 {z{~ oˆ 9m 69 9: êw 4 {~ 7: ) w 46 p` 9 ew> 9 µ ia 9:ƒ )ƒ ~ 4"P y NN gp ~ 9 4 9: w>~ z 9>ªDKŒ 9 :y>z{z 9 qy 46 " w 87 :y ƒ qy ~ }~y 4 ˆ œ 9 9 ˆ6z k ˆ6z 9 µ µ ˆ6z 9# y?ˆ A 9: ew> 9 y?z A u } 8y L y 4 w oˆ8~ 9 p` 9 ewb 9< 89/p` y?x {9 z œbwb 9 ˆ6z ª vlw «w Ÿ y 4 y 4 % 9 êw 4 }~ 7 % ` u y?x 9 z œ>w }~ y µ 4 9 p` 7 ƒ ~ { ~y 4 :y 46 ˆ6~ w>ˆ e"«y?z ƒ ˆ 9 % 69/ ` 9 9 j y? 6 9 z%z 9 wb {~œo~ u ` µ w>x 9 z z}wb {~ y 4gª+KŒ4 6w>z {~ :ˆ ~ 9 z š 4 y?ˆ wœ?y 48 % w «y?z ƒ ˆ 9 ˆ 67 w w L?9u 69 «z 7 ˆ 9:4 9: ν e = η µνk µ u ν e. ν o η µν k µ u ν o J
18 u µ observateur k µ n µ [u] espace orthogonal v ` 9 e 6z 9 { ~y 4 w y? 8 7:9-69 c A e 9 k µª 9 9:46 w 4 w 46 L wš 6z}w }~ ˆ 9Bš 9 œ 9 9 ˆ6z 69 6z y? ew L w }~ y 4u 69 w ˆ ƒ ~ x z 954 ` 9: y ˆ ` ˆ 469 :y 46 }w 4 9 ƒ ˆ }~ ~ :wb }~ œ 9 6z x: :ª ~ 9: :48 ˆ š 9 w 4 ` w( 9 9 ew Np` 9 9 j y? 6 9 znz 9 wb {~œo~ 9 ν e /ν o ª y?ˆ8z5ˆ 4 y?x {9 z œbwb 9 ˆ6zw> 7 7 z 7< 69 êw z ~ A œo~ 9: {9 u µšq4 y?ˆ w>ˆ6z y 46 59: %ƒ, ƒ 9 %9 e 8z 9: ~y 46 69u w «z 7 ˆ ν[u] 9 89u w ~z 9 }~y z y? ew L w }~ y 4 w 46 Š ` 9: ew> 9u 89Jp` y>x {9 z œbwb 9 ˆ6z š n µ [u] wœ 9 }y?ˆ 69 ƒ, ƒ 9 w"z 9 }z ~ }~ y 4 {y?ˆ8 9 } 7 y?z{~ ˆ 9 6ˆ6~ ˆ 9 qy?ˆ6z «w>~ z 9 ˆ 469 ν[u] a i /c ƒ9: ˆ8z 9 69+«z 7 oˆ 9:4 9 ~E«w>ˆ8 2ˆ z w>~ 469T9 e 9:46 ~ y 4 9:ƒ y>z 9: 9Bª 469 wbˆ8 }z 9 «w Ÿ y T ~ z 9+9: ˆ 9 ` y 4W469 9 ˆ N ˆ y 46 ~ 67 z 9 zšˆ 4 y>x {9 z œbwb 9 ˆ6zŠ~ 489 z {~ 9 :y 4 ~ w 4 Š~ 46 }w 4 w 487:ƒ9:4 ˆ6z{w 4 9 9:ƒ N 69 w ƒ9: ˆ6z 9 69 w «z 7 ˆ wœ 9 ` y?x 9 z œbwb 9 ˆ6z w> 7 7 z 7>ª 9 9ML?7 y ƒ 7 }z{~ 9T 69T ` 9: 6w> 9tA 9 ƒ Œƒ ~ 4QP y NN gp ~ 9:4 9: Œ }y?ˆ 5«w>~ wb {~ «w>~ w 4 9 qy?ˆ6z 87 :z ~ z 9 w 8 ~ ˆ 9 }w 4 N ˆ 9/9: Š9 9 L z}wœo~ }wb }~y T489J y 4 ew 6z{~ Š9:4" ~ L? y ƒ 9>ª J
19 š Wii u D W i ] G0% Ö `! IIV<!/R+I'% G0 JV<! % I!uI'% G 1K@#L# K K I QVT%L"RW% K Ö ` U % l!# KQRTK!$% # K j w 46 5 ` 9: 6w> 9tA 9 ƒ L w ~7:9:4še4 y?ˆ wœ>y 46 5«y>z ƒ ˆ7/p` 7 êwb }~y 4Q«y 46 w ƒ9:4 }w 9J 69< w 4 w A ƒ ~ ˆ 9 qy?ˆ6z 69: y?x 9 z œ>w 9 ˆ8z ~ 489 z {~ 9 :ª y>ˆ6z ˆ 469 6w>z {~ :ˆ 9 qy 4 }ˆ 9 9 y 4 w ~ L?489 ` ˆ 4 ~œ 9 z %9 67 c 4 ~ 9 ew>z še4 y?ˆ wœ>y 46 qy?ˆ6z ˆ 4 ew ƒ 69 «y?z 9 W92e 7 z{~ 9 ˆ6z 9: }z{w 46 «y?z ƒ wb }~y 4W 69/ w ~ 7 9>ª x i a(t) d 2 x i a m a = f i (x k dt 2 a (t)) a 69uƒ w { {9 ~ 469 z 9 m a f i oˆ8~ {9 {z}w 48 «y?z ƒ 9 :y ƒƒ 9 ˆ 4 œ 9 9 ˆ6z y?ˆ ˆ 469 vlw y>~ ` w { }z{w> {~ y 4 L z{wœ ~ wb {~ y 48469: 9>š 6ˆ6x ~ 7 9 6w>z 9-N {y 4 9:4 J Ẽ w 48 9: >š {~ 6ˆ 9 ˆ 9 w «y?z{ 9 y 48467:9 ew>z f i 92e 9 z{ 7 9 ˆ6z1 9 { 9 ew>z {~ ˆ 9 f i = m (p) ga g i a ew>z ˆ 4 9:46 9:ƒ x9 69 ew>z }~ :ˆ9: W9 y 9 w ƒ w { 96L z}wœ 9 ew ~œ 9 89 wq 6w>z {~ :ˆ 9 m (p) ga a 9 Jy 9: i 9 ew ƒ L z{wœ ~ wb {~ y 48469: g 69 w>ˆ8 {z 9: ew>z }~ ˆ 9 :ªWj w 48 9 w % ` ˆ ˆ9 w>ˆ8 {z 9 ew>z {~ ˆ 9 y 4 {ˆ 9: 9 89<ƒ w { 9UL z{wœ 9 b w> }~œ 9 m (a) gb g i w# qy?ˆ6z 9 e 8z 9: ~y 4 g i (x k ) = Gm (a) gb (x k x k b ) x i x i b 3 y 9: Tˆ 469 :y 46 w 4 9% 69 :y>ˆ6 w L?9 L z}wœo~ }wb }~y ª y?ˆ -4 yb }y 46 ˆ 9 9 9N y>~ 9: T~ 4 œbw>z ~ w 4 9 G 69u«y?z ƒ 9u y?ˆ ˆ 469 }z}w 46 «y?z ƒ w }~ y 4W 69< w ~7:9>ª y>ˆ ~ 4 }z y ˆ8~ y 46 Š 9 qy> 9 4 }~ N {y 4 ~ 9:4" 69 L z{wœo~ wb {~ y 4W ˆ y?z{ b U(x k ) = Gm (a) gb v ` z L ~ 9 qy> 9 4 }~ 9 95 ` ~ 4 9 z}w> }~y 4 y?ˆ8z w ew>z }~ ˆ 9 J O 1 x i x i b. a 9: V a = m (p) ga U ª
20 1 9 9:46 w 4 9:4 œ 9 z {ˆ 69- ` 7L w ~ 7X 69-p` w> }~y 4u9 69+ w z 7 w> }~ y 4gš4 y?ˆ œ>y >y 46 ~ ƒƒ 7 ~ wb 9:ƒ9:4 ˆ 9 m (p) ga m (a) gb = ª y?ˆ y y 46 9 z}w> 8 y?z 89: 2ƒ w {9: L z}wœ 9: w> }~ œ 9: 9 2 ew { ~œ 9: X7-L w 9 ˆ 419 Š~q92e ~ 95 {9 m(p) gb ˆ 9:ƒ9:4 m(a) ga 9: ƒ w {9 L z}wœ 9 9 ª 9 6y>~ e c e 9 w/œbw9 ˆ6z 4 ˆ ƒ 7 z{~ oˆ 9 69% m ga m w :y 46 w N {y 4gª 9: 9 A :~ z ƒ ~ w>z gb 89: T9 e 7 z{~ :4 w>xqy?z}w }y?~z 9 w 46 9 ˆ w «y?z{ 9 L z}wœo~ w }~ y 46469: }z 9 69 ˆ e xy?ˆ 9: -9 ƒ9: ˆ6z 7 9>ª 9N«ˆ8 Tz 7 w ~ 7Š w 6z 9 ƒ ~ x z 9 «y?~ ew>z wœ 9 46 ~ 9 4 J (O? 8ªQKŒ 99 N }z y?ˆ8œ 7 9 wœ 9 Jˆ 469u«w>~ x 9 8z 7 ~ ~ y 4Q4 ˆ ƒ7 z{~ ˆ 9-9 N y?ˆ8z ˆ 469 w L>9% 69% ~ w {z 99: 69 ˆ e ƒ w { 9: 9 ˆ ˆ 9BªQj w 48 9% x:ƒ9 y w>~ z 9>š {9 ˆ 9 6z y ˆ8~ Gm y 9: w ƒ w {9 ˆ# y?z{ 7:9: 9Š y 4 - y 464 ˆ wœ 9 Šˆ 469 }z x: *L z{w z 7 ~ ~ y 4gª m 9 œ 9 4 y 46 #p` 7 êwb }~y w 4 w ƒ ~ oˆ 9u ` ˆ 469 6w>z {~ :ˆ 9 qy 4 }ˆ 9 9u7 :z ~ 9u y?ˆ w «y?z ƒ 9 m d2 x i dt 2 = m gg i. KŒ 9 9 ˆ8 ` w> 6 ~ ˆ 9 z w 46 T9 :w y 69N w Ž9 z z 9>ª z-~ wjˆ 4#«w>~ 92e 7 z{~ ƒ 9 4 }w z 9 :y 464 Ŵ ew>z w ~ 7 9>š qy? 6ˆ w>z ~ {7 wœ 9 ` 92e 7 z{~ 9:4 9 9: i Š 6z{wB }~ oˆ 9:ƒ9:4 T y 46 w 4 š ew>z 92e 9:ƒ 9 < w ˆ6z «w> 9 g ƒ } 8~ ˆ 9N 69 w5 }y>ˆ6z 69 Œ~ {9>š ˆ 9 }y>ˆ - 9: y?z{ ˆ8 9:4 69 w ƒ,:ƒ9 «w Ÿ y 4 ~ :48 w ƒƒ ˆ6z ƒ w { 9J ˆ8zŠ :y ƒ y ~ {~ y 4 ~ 4 9 z 469Bª 9: w 6z y?ˆ8œ 9 ˆ 9 9 ~ 9: {y?ˆ8 W«w>~ z 9:ƒ w>z oˆ6w>x 9 6ˆ6~ ˆ 9 m = m g. m 9 y 4 69: y :y ƒ dx 9:ƒ9:4 ~d 7 A m z 9 4 :ª ` 9: 5 9 ˆ ` y 4 w> 6 9: 9u9 8z{~ 4 :~ 9 ` ˆ 4 ~œ 9 z w g ~ 7 69J w ˆ8 9< ~x6z 9Bª 9 z ƒ9 ` 7 :z ~ z 9 ` 7 êw }~ y 41 ˆ ƒ y?ˆ8œ 9:ƒ9:4 ` ˆ 469 ew>z {~ ˆ 9 w 46 ˆ 4 ew ƒ 69kL z{wœ ~ wb {~ y 4 g i y?ˆ N w «y?z ƒ 9 d 2 x i dt 2 = gi. ` 9: ˆ 4 7 }wb 69"«wB~ 9 4 { 7 y?z ~ 9Q 69 92N }y 4 69Q w L z{wœo~ wb {~ y 4 ƒ w>~ ~ 9 z}w>~ y 464 w>x :46 9 z oˆ 9 9 ~ 9 ˆ 4Q«w>~ :z{ˆ8 :~ w ª y 46 ~ 67 z{y 46 1ƒ w>~ 4 9:4 w 4 ˆ 4 y?x {9 z œbwb 9 ˆ6z w 48 z{y> }wb }~y 4 9 ` w> : 7:7 z}w }~ y 4 :y 48 w 4 9 ˆ6~ w y?ˆ8z 7 oˆ6wb }~y 4 y?ˆ8z 69 œbw 9 ˆ6z ~ 4 ~ }~ w 9: w 67 êwb 9: ª 4 ` 9 ew < ~ «A x i (t) = a i t 2 /2 ce ~ 9< 69 œ?y?~zu ˆ ` ˆ 47 œ 7:489:ƒ9:4 <z 9 7 z 7 ew>z (t, y i ) 9: /z 9 7 z 7 ew>z 9 :yoy?z y : (t, y i ) ` y?x 9 z œ>w 9 ˆ8z%wB : 7 7 z 7 ˆ6~ œbw 4 w «y?z ƒ ˆ 9 69 a i 489 6w>z {~ :ˆ 9u ~x6z 95 ` 7 êwb }~y 4 :y>ˆ6z{x 9 ˆ6~œ 7 z ~dc 9p` 7 oˆ6wb }~y 41 ˆ6~ œbw 4 9 y i (t) t = t et y i = y i 1 2 ai t 2. y i (t) = v i t + y i z{~ 9 ew>z ` y?x 9 z œ>w 9 ˆ8zNw> : 7: 7 z 7 ew>z w d 2 y i = a i. dt oˆ6wb }~y 4 ˆ ƒ y?ˆ8œ 9:ƒ9:4 9: z{w> 6 6z y 9 z 69 9: 9 ` ˆ 489 ew>z {~ ˆ 9 w 46 ˆ 4 ew ƒ 69BL z}wœo~ }wb }~y 4 6z}w }~ ˆ 9 ƒ 9 4 y 46 w 4 ª KŒ4 y 46 7 ˆ 9:4 9>š%4 y?ˆ "469 qy?ˆ8œ?y 46 6w wœ?y?~z g i G 6, k ba 1 kc9 2k ;>=
21 yo w 9:ƒ9:4 ~ 4 y?ˆ y ƒƒ 9 ˆ 4 y?x {9 z œbwb 9 ˆ6zL~ 489 z {~ 9 y?x 9 z œ>w 4 ˆ 469 6w>z {~ :ˆ 9Œ ˆ8x6~ w 4 ` w> {~ y 4 ` ˆ 4 ew ƒ L z}wœo~ }wb }~y ˆ 4 ~ «y>z ƒ9 i y?ˆ<x8~ 9:4/ ~ 4 y?ˆ y ƒƒ9: ˆ 4 y?x {9 z œbwb 9 ˆ6z w 46 z y> wb {~ y 4 g ƒ w>~ wb : 7 7 z 7>šŒ ` w> 7 7 z{wb }~y 4 a i = giš y?x {9 z œbw 4 ˆ 469 ew>z }~ ˆ 9 ~ x8z 9>ª 9 9Q«y?z ƒ ˆ wb {~ y 4 ` w> 6 9: 9 w y?z T 9 6z ~ 4 ~ 9u ` 7 ˆ6~œBw9:4 9 «wb~ x9>ª j59t«w Ÿ y 4 7 oˆ8~œbw 9 4 9>š ` 9: wn 7 x x6z 9 8~ {y?~ z 9 89T ` w 9:48 {9 ˆ8z 9:4 ˆ8 9Š ~x6z 9- w 48 X 9 ew ƒ L z{wœo~ wb {~ y 46489:L 69 w Ž 9 z{z 9>š z 7:9: 9 ƒ 9 4 %œ 7 :ˆ 9 p` ~ 4 7 z ~ 9 ˆ8z ` ˆ 4 wœo~ y 4)ƒ ~ %9:4 ˆ8 9 ~ x8z 9J9:4 :y>ˆ6 ew 4 {9 Nƒ y> 9 ˆ6z ˆ 9: oˆ 9: N ~ :w>~ 489: 69u 9 y :ªWKŒ4"9 9 š qy?ˆ6ztˆ 4 y?x {9 z œbwb 9 ˆ6zNw> 7 7 z 7 ` 7 êw }~ y 41 ˆ ƒ y?ˆ8œ 9:ƒ9:4 ` ˆ 469 ew>z {~ ˆ 9 ~ x6z 99: qy?ˆ6zuˆ 469 9: w 4 9 ˆ8z/ y 46 }w 4 9 d 2 y i dt 2 = a i + g i g iª z a i + g i = 0 w 46 9 z 7 «7 z 9 4 {~ 9 Œ9:4 oˆ 9 ~ x8z 9 ` 9 qy?ˆ6z{ ˆ6y>~ 9/ƒ y>ˆ8œ 9 ƒ 9 4 ` ˆ 469 ew>z }~ :ˆ9<9: uz 9 {~ ~ L?469J9 5ˆ 4 ~ «y>z ƒ9< w 48 9 z 7 «7 z 9:4 {~ 9: x6~ 9 4 ˆ ` ~ + y?~ w> 7 7 z 7W ˆ qy?~ 4 69 œoˆ 91 ` ˆ 4 y?x {9 z œbwb 9 ˆ6z ~ 469 z }~ 9: ª 4 ~ < ˆ ` ~ +9: yo w 9:ƒ9:4 ~ 489 z {~ 9 ªQKŒ4 z 7 w ~ 7 69 ˆ e ew>z }~ :ˆ9: Š9:4 ˆ8 9J ~x6z 9u 9 z}w> 6 8z{yo 9:4 % w>zn 9 :~ 4 ` 9: %œbw w>x9 ˆ 9 ~p` y 4"487L? ~ L?9 š ` 9: A A ~z 9u 9 N9 9 N 69 ƒ w>z 7 9>ª ij U d VT% RD!uI'% G0QM K V<% K I!# KNM OQU 1VT%QRN% K Ö S U % ]! # KQRTK X!$% # K vlw) 6z 9 ƒ ~ x z 9 œ 7 z ~dce :wb }~y 4 9 e 7 z ~ ƒ9:4 w 9W 691p` 7-L w ~ 7# 691 w ƒ w { 9 ~ 469 z 9W9 691 w ƒ w { 9 L z{wœ 9 w 7 7J«w>~ 9 6w>z w ~ 7 9 œ 9 z J J = wœ 9 69 w 46 ~ 4 ~ 467 6ˆ6~ p` w>~ 69 ˆ) 9:46 ˆ 9Bª ~ L 67 ~ L?469 w y 4QL ˆ 9 ˆ6z ˆ" 9 46 ˆ9>še w 7 z{~ y 69 T y g ( m T = 2π m g 69: 9 }~ 9: y :~ wb }~y 4 9 y 46487:9 ew>z ) 1/2 ( ) 1/2 L g 9: ` w> : 7: 7 z}wb {~ y 4/ 69Š w 9: w 4 9 ˆ6z ª v ` y?x {9 z œbwb {~ y 4 ƒ y 4 }z 9 ˆ 9 9 9tA ~ 9: -~ :46 w 4 9 ˆ z}w> 6 qy?z m/m g ª 9-N {y 4 z 9 6z 9:46 z{w< 9 { 9%9 e 7 z ~ 9 4 9Bª vlw 6z 7 :~ ~ y 49: }~ ƒ z{w>~ ª 9 9:46 w 4 69: z 7: ˆ w ˆ 8z 7 ~ 9 ˆ œ 9:4, }z 9 y?x8 9 4 ˆ ` w>~ 89 ` ˆ 469 xew w }y>z ~y 4 ˆ8~œBw 4 #ˆ 469 ~ 67:91 ˆ 9AK f> œ0f wuc 4 ˆ J O J ~ x 9>ª v 9 92e 7 z{~ 9:4 9: z 7 9:4 9: xew 7:9 ˆ6z# 9 6z{~ 4 :~ 9 y z 7 ~ ~ y 46 w w 4 )/ ˆ ˆ ` 10 12ª b ˆp` ~ ƒ qy?z w { 9 92e 7 z ~ 9:4 9>š&4 y>ˆ w y w>~ 9 zt ˆ 9 ˆ 9 9 ˆ9 6z{~ 4 :~ ` 92e 7 z{~ 9:4 9>ª ~ {ˆ 7:9 wbˆ e 92e {z 7:ƒ ~ 7: #3l9 ˆ he7 w>ˆ ` ˆ 489 xew w y?~ 9:4 69 ˆ e ƒ w {9: a 9 b }y>z ~y 4 ˆ6~ 9: Šz 9 ~ 7 9 4" w>ˆ cq 69 }y?z ~ y 4gš ˆ6~ A ƒ,:ƒ9 c e 7 w>ŵx }~ ª v 9 ƒ w { {9 69 :y>z{ a y 4 ˆ6 6 qy {7 9: }z x: œ>y?~ ~ 469 :ª v 9 xb }~ 69 w xew w }y?z ~ y 4)9: c e 7 w z 7 «7 z 9 4 {~ 9 9 b ~ 7 w ˆ6z «wb 9J 69< w Ž9 z z 9Bª 9 y 4 9:4 z y> w }~ y 4 6w>z%z{w> 6 qy?z %w>ˆ"z 7 «7 z 9:4 }~ 9: 'L?7 yo 9 4 }z{~ ˆ 9 ˆ8 6 y {7 ~ 469 z }~ 9: ª w y 4 ˆ 469 w> : 7: 7 z}wb {~ y 4 9:4 }z ~ «ˆ L?9 ` c 894 y?z ƒ9 i c i = Rω 2 cos φ w> 7:7 z{wb }~y 4 9 g g 9, 8 2 ki9 2k i * w>ˆ 6w ƒ L z{wœ ~ wb {~ y 48469:g 89J w Ž 9 z{z 9>ª ; J
tel , version 1-21 Mar 2013
 ! "#! $"%" &'()* +*,-./-01/ 2 3 45 467 68 9:; 6?87 @ 6 =
! "#! $"%" &'()* +*,-./-01/ 2 3 45 467 68 9:; 6?87 @ 6 =
 ! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
2?nom. Bacc. 2 nom. acc. S <u. >nom. 7acc. acc >nom < <
 K+P K+P PK+ K+P - _+ l Š N K - - a\ Q4 Q + hz - I 4 - _+.P k - G H... /.4 h i j j - 4 _Q &\\ \\ ` J K aa\ `- c -+ _Q K J K -. P.. F H H - H - _+ 4 K4 \\ F &&. P H.4 Q+ 4 G H J + I K/4 &&& && F : ( -+..
K+P K+P PK+ K+P - _+ l Š N K - - a\ Q4 Q + hz - I 4 - _+.P k - G H... /.4 h i j j - 4 _Q &\\ \\ ` J K aa\ `- c -+ _Q K J K -. P.. F H H - H - _+ 4 K4 \\ F &&. P H.4 Q+ 4 G H J + I K/4 &&& && F : ( -+..
REGION 4 (Fault) REGION 5 REGION 1 REGION 2. (Aquifer) REGION 3
 È r!"!# $%&' (&)*+,&.-#/!. 021435176%8:9 ;6=A@ B:CD>FEHGI
È r!"!# $%&' (&)*+,&.-#/!. 021435176%8:9 ;6=A@ B:CD>FEHGI
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #
 Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
a,b a f a = , , r = = r = T
 !" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
!" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
 ) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Ó³ Ÿ , º 7(156).. 62Ä69. Š Œ œ ƒˆˆ ˆ ˆŠ. .. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ 2. μ ± Ê É É Ê Ò μ μ, Œμ ±
 Ó³ Ÿ. 009.. 6, º 7(156.. 6Ä69 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŒ ˆ - ˆ ƒ ˆ ˆ ˆŸ Š -Œ ˆ Šˆ ˆ.. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ μ ± Ê É É Ê Ò μ μ, Œμ ± É ÉÓ μ Ò ÕÉ Ö ²μ Í Ò - μ Ò ² É Ö ³ ÖÉÓ Ì ÒÎ ² ÖÌ, μ²ó ÊÕÐ Ì ±μ ± 4- μ Ò. This paper
Ó³ Ÿ. 009.. 6, º 7(156.. 6Ä69 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŒ ˆ - ˆ ƒ ˆ ˆ ˆŸ Š -Œ ˆ Šˆ ˆ.. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ μ ± Ê É É Ê Ò μ μ, Œμ ± É ÉÓ μ Ò ÕÉ Ö ²μ Í Ò - μ Ò ² É Ö ³ ÖÉÓ Ì ÒÎ ² ÖÌ, μ²ó ÊÕÐ Ì ±μ ± 4- μ Ò. This paper
Les gouttes enrobées
 Les gouttes enrobées Pascale Aussillous To cite this version: Pascale Aussillous. Les gouttes enrobées. Fluid Dynamics. Université Pierre et Marie Curie - Paris VI,. French. HAL Id: tel-363 https://tel.archives-ouvertes.fr/tel-363
Les gouttes enrobées Pascale Aussillous To cite this version: Pascale Aussillous. Les gouttes enrobées. Fluid Dynamics. Université Pierre et Marie Curie - Paris VI,. French. HAL Id: tel-363 https://tel.archives-ouvertes.fr/tel-363
"!$#&%('*),+.- /,0 +/.1),032 #4)5/ /.0 )80/ 9,: A B C <ED<8;=F >.<,G H I JD<8KA C B <=L&F8>.< >.: M <8G H I
 "!$#&%('*),+.- /,0 +/.1),032 #4)5/.-076 4/.0 )80/ 9,: ;=@?4: A B C
"!$#&%('*),+.- /,0 +/.1),032 #4)5/.-076 4/.0 )80/ 9,: ;=@?4: A B C
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2004.. 35.. 5 Š 539.12.01 ˆ ˆ Š œ Ÿ Š Ÿ ˆŸ Ÿ ƒ.. Ë ³µ Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 1116 Š ˆ ˆ ŒŸ Œ ˆŠ 1119 Š Ÿ ˆŸ Ÿ ˆ Œ Š œ ˆ 1121 Š Ÿ ˆŸ Ÿ Š œ Œ ˆŒ ˆ Œ 1130 Š ˆ Œ ˆ Š Ÿ Š Ÿ ˆŸ Ÿ 1134 ˆ ˆ œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2004.. 35.. 5 Š 539.12.01 ˆ ˆ Š œ Ÿ Š Ÿ ˆŸ Ÿ ƒ.. Ë ³µ Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 1116 Š ˆ ˆ ŒŸ Œ ˆŠ 1119 Š Ÿ ˆŸ Ÿ ˆ Œ Š œ ˆ 1121 Š Ÿ ˆŸ Ÿ Š œ Œ ˆŒ ˆ Œ 1130 Š ˆ Œ ˆ Š Ÿ Š Ÿ ˆŸ Ÿ 1134 ˆ ˆ œ
!! "#$%& '( )(*%+%#,+ -. / / 0 1/ /2/ " / : /2 4 ;<("= **( /> / ?1 /?1 3/ / / : 4 / 4 5 2// -
 ! "! # $%% &'' ('#)* + &'', -./012 34567489:; 945 >4? >@A B %C #''%CD! B C %) &'' ('#)* + &'', -./012 3E @FGAGF:; 945 >4? >@A M#* N, OPPQ +!H! II J $*) ) &'' ('#)* + &'', -./012 K484E:G8L >945
! "! # $%% &'' ('#)* + &'', -./012 34567489:; 945 >4? >@A B %C #''%CD! B C %) &'' ('#)* + &'', -./012 3E @FGAGF:; 945 >4? >@A M#* N, OPPQ +!H! II J $*) ) &'' ('#)* + &'', -./012 K484E:G8L >945
Ó³ Ÿ , º 3(180).. 313Ä320
 Ó³ Ÿ. 213.. 1, º 3(18).. 313Ä32 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ˆŸ ƒ ƒ Ÿ ˆ Š ˆ Šˆ Š ŒŒ ˆ ˆ ˆ ˆ ˆ Œ ˆŠ.. μ a, Œ.. Œ Í ± μ,. ƒ. ²Ò ± a ˆ É ÉÊÉ Ö ÒÌ ² μ μ ±μ ± ³ ʱ, Œμ ± ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ
Ó³ Ÿ. 213.. 1, º 3(18).. 313Ä32 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ˆŸ ƒ ƒ Ÿ ˆ Š ˆ Šˆ Š ŒŒ ˆ ˆ ˆ ˆ ˆ Œ ˆŠ.. μ a, Œ.. Œ Í ± μ,. ƒ. ²Ò ± a ˆ É ÉÊÉ Ö ÒÌ ² μ μ ±μ ± ³ ʱ, Œμ ± ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ
Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 636 ˆ ˆ Šˆ Œ ˆŸ ˆŒˆ - Šˆ Œ Š ˆ ˆ 638 Š ˆ ˆ ˆ : ˆ ˆŸ 643 ˆ ˆ Šˆ Š 646 Œ ˆ Šˆ 652 Œ ˆ Šˆ Š ˆ -2 ˆ ˆ -2Œ 656 ˆ ˆ Šˆ Š œ Š ˆ Œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Š ˆ ˆ ˆ Š ˆ ˆ Œ.. μ É Ó Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 636 ˆ ˆ Šˆ Œ ˆŸ ˆŒˆ - Šˆ Œ Š ˆ ˆ 638 Š ˆ ˆ ˆ : ˆ ˆŸ 643 ˆ ˆ Šˆ Š 646 Œ ˆ Šˆ 652 Œ ˆ Šˆ Š ˆ -2 ˆ ˆ -2Œ 656 ˆ ˆ Šˆ Š œ Š ˆ Œ
 !"# $%! & ')( +*!-,% &.!"/& 0132/1547698:2/; D0E2/8FG>@?/IHJH>IJH % +K " "/L% MN( & O') +MP& Q.R SUT9V W X:YOZ [\W ]^ W+_ `Babc5dfegb@h)ikjmlnoCc5o p#qlr-s icc5outoecavecwccfgb@h)icxzy{awc
!"# $%! & ')( +*!-,% &.!"/& 0132/1547698:2/; D0E2/8FG>@?/IHJH>IJH % +K " "/L% MN( & O') +MP& Q.R SUT9V W X:YOZ [\W ]^ W+_ `Babc5dfegb@h)ikjmlnoCc5o p#qlr-s icc5outoecavecwccfgb@h)icxzy{awc
d 2 y dt 2 xdy dt + d2 x
 y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
www.absolualarme.com met la disposition du public, via www.docalarme.com, de la documentation technique dont les rιfιrences, marques et logos, sont
 w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
w. ww lua so ab me lar m.co t me la sit po dis ion du c, bli pu via lar ca do w. ww me.co m, de la ion nta t do cu me on t ed hn iqu tec les en ce s, rι fιr ma rq ue se t lo go s, so nt la pr op riι tι
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2013.. 44.. 5 ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ É μë Î ± É ÉÊÉ ³.. ƒ. ±μ, ˆ É ÉÊÉ Ö μ Ë ± Š, ²³ - É, Š Ì É ˆ 1535 Œ 1537 μ² Ò Î Ö Ì É 1537 μé Í ²Ò μ² μ Ò ËÊ ±Í 1539 ² Ò ³ Éμ Ò Î É 1541
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2013.. 44.. 5 ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ É μë Î ± É ÉÊÉ ³.. ƒ. ±μ, ˆ É ÉÊÉ Ö μ Ë ± Š, ²³ - É, Š Ì É ˆ 1535 Œ 1537 μ² Ò Î Ö Ì É 1537 μé Í ²Ò μ² μ Ò ËÊ ±Í 1539 ² Ò ³ Éμ Ò Î É 1541
Š Š Œ Š Œ ƒˆ. Œ. ϵ,.. ÊÏ,.. µ ±Ê
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2003.. 34.. 7 Š 524.8+[530.12:531.51] Š Š Œ Š Œ ƒˆ. Œ. ϵ,.. ÊÏ,.. µ ±Ê Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 138 Š Šˆ Š Š ˆ ˆ Š Œ ƒˆˆ 140 Š Œ ƒˆÿ œ 141 Š Ÿ Š Œ ƒˆÿ 143 ˆ Ÿ Š Œ ƒˆÿ ˆ Œ 144 ˆŸ Ä ˆ Œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2003.. 34.. 7 Š 524.8+[530.12:531.51] Š Š Œ Š Œ ƒˆ. Œ. ϵ,.. ÊÏ,.. µ ±Ê Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 138 Š Šˆ Š Š ˆ ˆ Š Œ ƒˆˆ 140 Š Œ ƒˆÿ œ 141 Š Ÿ Š Œ ƒˆÿ 143 ˆ Ÿ Š Œ ƒˆÿ ˆ Œ 144 ˆŸ Ä ˆ Œ
Œ ˆ Œ Ÿ Œˆ Ÿ ˆŸŒˆ Œˆ Ÿ ˆ œ, Ä ÞŒ Å Š ˆ ˆ Œ Œ ˆˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 018.. 49.. 4.. 907Ä917 Œ ˆ Œ Ÿ Œˆ Ÿ ˆŸŒˆ Œˆ Ÿ ˆ œ, Ä ÞŒ Å Š ˆ ˆ Œ Œ ˆˆ.. ³μ, ˆ. ˆ. Ë μ μ,.. ³ ʲ μ ± Ë ²Ó Ò Ö Ò Í É Å μ ± ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö μ ² Ìμ μé Ê Ö ±
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 018.. 49.. 4.. 907Ä917 Œ ˆ Œ Ÿ Œˆ Ÿ ˆŸŒˆ Œˆ Ÿ ˆ œ, Ä ÞŒ Å Š ˆ ˆ Œ Œ ˆˆ.. ³μ, ˆ. ˆ. Ë μ μ,.. ³ ʲ μ ± Ë ²Ó Ò Ö Ò Í É Å μ ± ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö μ ² Ìμ μé Ê Ö ±
Ax = b. 7x = 21. x = 21 7 = 3.
 3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
March 14, ( ) March 14, / 52
 March 14, 2008 ( ) March 14, 2008 1 / 52 ( ) March 14, 2008 2 / 52 1 2 3 4 5 ( ) March 14, 2008 3 / 52 I 1 m, n, F m n a ij, i = 1,, m; j = 1,, n m n F m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a
March 14, 2008 ( ) March 14, 2008 1 / 52 ( ) March 14, 2008 2 / 52 1 2 3 4 5 ( ) March 14, 2008 3 / 52 I 1 m, n, F m n a ij, i = 1,, m; j = 1,, n m n F m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a
Œ ˆ ˆŸ Šˆ œ ˆŒŒ ˆˆ ˆ..
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 ˆ ˆ Šˆ ˆ ˆ ˆ Šˆ Š Œ ˆ ˆŸ Šˆ œ ˆŒŒ ˆˆ ˆ.. Î ± É ÉÊÉ ³..., Œμ ± ˆ 103 Šˆ œ Œ Š ˆ ˆ 106 ˆˆ ˆ ˆŸ Šˆ œ ˆ 114 Š Š ˆˆ ˆˆ Ÿ ˆ œ ƒ Œ Šˆ- œ œ? 116 ˆ ƒ Œ Šˆ œ œ œ Œ Ÿ ˆ ˆ ˆŸ ˆ ˆ Š ƒ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 ˆ ˆ Šˆ ˆ ˆ ˆ Šˆ Š Œ ˆ ˆŸ Šˆ œ ˆŒŒ ˆˆ ˆ.. Î ± É ÉÊÉ ³..., Œμ ± ˆ 103 Šˆ œ Œ Š ˆ ˆ 106 ˆˆ ˆ ˆŸ Šˆ œ ˆ 114 Š Š ˆˆ ˆˆ Ÿ ˆ œ ƒ Œ Šˆ- œ œ? 116 ˆ ƒ Œ Šˆ œ œ œ Œ Ÿ ˆ ˆ ˆŸ ˆ ˆ Š ƒ
x3 + 1 (sin x)/x d dx (f(g(x))) = f ( g(x)) g (x). d dx (sin(x3 )) = cos(x 3 ) (3x 2 ). 3x 2 cos(x 3 )dx = sin(x 3 ) + C. d e (t2 +1) = e (t2 +1)
 x sin x cosx e x lnx x3 + (sin x)/x e x {}}{ (f(g(x))) = f ( g(x)) g (x). }{{}}{{} f(g(x)) 3x cos(x 3 ). 3x cos(x 3 ) x 3 3x sin(x 3 ) (sin(x3 )) = cos(x 3 ) (3x ). 3x cos(x 3 ) = sin(x 3 ) + C. e ( +).
x sin x cosx e x lnx x3 + (sin x)/x e x {}}{ (f(g(x))) = f ( g(x)) g (x). }{{}}{{} f(g(x)) 3x cos(x 3 ). 3x cos(x 3 ) x 3 3x sin(x 3 ) (sin(x3 )) = cos(x 3 ) (3x ). 3x cos(x 3 ) = sin(x 3 ) + C. e ( +).
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ä ƒ ² ± Ñ Ò É ÉÊÉ Ô É Î ± Ì Ö ÒÌ ² μ Å μ Ò Í μ ²Ó μ ± ³ ʱ ²μ Ê, Œ ±
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 017.. 48.. 6.. 934Ä940 ˆ Š Ÿ Š ˆ ˆ ˆ ˆ ƒ Ÿ.. ƒ ² ± Ñ Ò É ÉÊÉ Ô É Î ± Ì Ö ÒÌ ² μ Å μ Ò Í μ ²Ó μ ± ³ ʱ ²μ Ê, Œ ± μ μ Ò ÕÉ Ö μ ³μ μ ÉÓ ±ÉÊ ²Ó μ ÉÓ É μ É ²Ó É É μ μ É ±- Éμ Ö μ³ ²μ Ê ±μ.
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 017.. 48.. 6.. 934Ä940 ˆ Š Ÿ Š ˆ ˆ ˆ ˆ ƒ Ÿ.. ƒ ² ± Ñ Ò É ÉÊÉ Ô É Î ± Ì Ö ÒÌ ² μ Å μ Ò Í μ ²Ó μ ± ³ ʱ ²μ Ê, Œ ± μ μ Ò ÕÉ Ö μ ³μ μ ÉÓ ±ÉÊ ²Ó μ ÉÓ É μ É ²Ó É É μ μ É ±- Éμ Ö μ³ ²μ Ê ±μ.
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ²
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 2 ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ² ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ, Œƒ, Œμ ± μ ³Ê² Ê É Ö μ É Ö μ²ê³ ± μ ±μ Î ± Ö ³μ ²Ó, μ μ²öõð Ö ÊÎ ÉÓ ² Ö Ëμ - ³ Í μ ÒÌ,
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 2 ŒˆŠ Š ˆ Š ˆ ˆ ˆ œ ƒ ƒˆƒ Š ƒ.. ˆÏÌ μ,.. ² ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²ÓÍÒ, Œƒ, Œμ ± μ ³Ê² Ê É Ö μ É Ö μ²ê³ ± μ ±μ Î ± Ö ³μ ²Ó, μ μ²öõð Ö ÊÎ ÉÓ ² Ö Ëμ - ³ Í μ ÒÌ,
Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2010.. 41.. 1 Š ƒ ˆ ˆŸ Å Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê. ÉÉÊ,. Ê μ μ ± Ö μ Í Ö Ö ÒÌ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2010.. 41.. 1 Š ƒ ˆ ˆŸ Å Š Šˆ ATLAS: ˆ ˆŸ ˆ Šˆ, Œ ˆ Œ ˆ.. ƒê ±μ,. ƒ ² Ï ², ƒ.. Š ± ²,. Œ. Ò,.. ŒÖ²±μ ±,.. Ï Ìμ μ,.. Ê ±μ Î,.. ±μ,. Œ. μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê. ÉÉÊ,. Ê μ μ ± Ö μ Í Ö Ö ÒÌ
T T T T %'&)(H*., -0/ 1 ˆ Q Žy yÿtš ž u _Ž ˆ6Š [ Q h 6 _ 6 P h Ž J )Ž Ñ J Š ] 6Š HŽ ˆ6Š J ]Ž Ž QŠ ÉH užyšž {ššq
![T T T T %'&)(H*., -0/ 1 ˆ Q Žy yÿtš ž u _Ž ˆ6Š [ Q h 6 _ 6 P h Ž J )Ž Ñ J Š ] 6Š HŽ ˆ6Š J ]Ž Ž QŠ ÉH užyšž {ššq T T T T %'&)(H*., -0/ 1 ˆ Q Žy yÿtš ž u _Ž ˆ6Š [ Q h 6 _ 6 P h Ž J )Ž Ñ J Š ] 6Š HŽ ˆ6Š J ]Ž Ž QŠ ÉH užyšž {ššq](/thumbs/67/56491238.jpg) ! " $ $ %'&)(+*,.-0/ 1 2436587:9:7:;67=< >@?AD?FH;67=OWV
! " $ $ %'&)(+*,.-0/ 1 2436587:9:7:;67=< >@?AD?FH;67=OWV
 !"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ ƒ. ˆ. μ μ. Í μ ²Ó Ò ² μ É ²Ó ± Í É ŠÊ Î Éμ ± É ÉÊÉ, Œμ ± Ÿ ˆ ˆ Š Ÿ ˆ ˆ Š Ÿ ˆ Œ ˆ ˆ Š Ÿ ˆŸ - ˆˆ 1375
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 5 ˆ Šˆ ˆ Š ˆŒ œ ˆ ˆ Šˆ Œ - ˆˆ ƒ. ˆ. μ μ Í μ ²Ó Ò ² μ É ²Ó ± Í É ŠÊ Î Éμ ± É ÉÊÉ, Œμ ± ˆ 1372 Ÿ ˆ ˆ Š Ÿ ˆ ˆ Š Ÿ ˆ Œ ˆ ˆ Š Ÿ ˆŸ - ˆˆ 1375 Š ˆŒ œ ˆ ˆ Šˆ Œ - - ˆˆ 1409 Œˆ ˆ ˆ Šˆ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 5 ˆ Šˆ ˆ Š ˆŒ œ ˆ ˆ Šˆ Œ - ˆˆ ƒ. ˆ. μ μ Í μ ²Ó Ò ² μ É ²Ó ± Í É ŠÊ Î Éμ ± É ÉÊÉ, Œμ ± ˆ 1372 Ÿ ˆ ˆ Š Ÿ ˆ ˆ Š Ÿ ˆ Œ ˆ ˆ Š Ÿ ˆŸ - ˆˆ 1375 Š ˆŒ œ ˆ ˆ Šˆ Œ - - ˆˆ 1409 Œˆ ˆ ˆ Šˆ
 J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ
Multi-GPU numerical simulation of electromagnetic waves
 Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
œ T 1? Š6? Š ZŠ 1ŠŒ T ŠŒ 1ŽZ Š= Œ < T rž =ŽZ Ž j Z G 1Ž 2 Š6 Z \ ŽZ Œ?Š : T 1 ŽZ œ T Œ 6Ž Z Œ < T 1 2 Š=ªŽZŽ? Œ Ž ; 3 ' - X 3 3 "! $#&% 2 4 Ž =Ž <
 ! " #%$&!'() * ) +,%-/.102-134-65087:9A@B> CEDGFIH J8K?LNMODQP R:DTSVUXW YAJZH[FIHAP\K?L?H] ^N_ `a bcc!d cfehgji c kl bm n bo k_jiprq n dts c uhipjvh_ n ds l wrc!bxy `c uhipjvh_ n ds gjic!kl a x
! " #%$&!'() * ) +,%-/.102-134-65087:9A@B> CEDGFIH J8K?LNMODQP R:DTSVUXW YAJZH[FIHAP\K?L?H] ^N_ `a bcc!d cfehgji c kl bm n bo k_jiprq n dts c uhipjvh_ n ds l wrc!bxy `c uhipjvh_ n ds gjic!kl a x
Mixed Distributions = + k k. = n. k k k. ρ k Χ Χ ] e [ ] Χ i
![Mixed Distributions = + k k. = n. k k k. ρ k Χ Χ ] e [ ] Χ i Mixed Distributions = + k k. = n. k k k. ρ k Χ Χ ] e [ ] Χ i](/thumbs/53/31856315.jpg) p d d Mxd Dstrbutos ρν ( ( ρ Ν( ρ ( ρ ρ ρ ( L ( ρ [ ρ ( ( ρ ( ]! " # $&% ' * - 3 4&5 6 7 8 9: ;A@CB < DFE G IKJLNM OFP QRS TU V S WTNX ρ Y[Z!\LZ!]^]`_ ab!c L! d!! ρ ( ρ Ρ( ρ ρ gh Cḧ l l ρ log L ρ log!
p d d Mxd Dstrbutos ρν ( ( ρ Ν( ρ ( ρ ρ ρ ( L ( ρ [ ρ ( ( ρ ( ]! " # $&% ' * - 3 4&5 6 7 8 9: ;A@CB < DFE G IKJLNM OFP QRS TU V S WTNX ρ Y[Z!\LZ!]^]`_ ab!c L! d!! ρ ( ρ Ρ( ρ ρ gh Cḧ l l ρ log L ρ log!
 B G [0; 1) S S # S y 1 ; y 3 0 t 20 y 2 ; y 4 0 t 20 y 1 y 2 h n t: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 1; 3: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 2; 4: r = 10 5 ; a = 10 6 t = 20
B G [0; 1) S S # S y 1 ; y 3 0 t 20 y 2 ; y 4 0 t 20 y 1 y 2 h n t: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 1; 3: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 2; 4: r = 10 5 ; a = 10 6 t = 20
m i N 1 F i = j i F ij + F x
 N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
Ó³ Ÿ , º 7(170) Ä1091 ˆŒ ˆ. Œ. ˆ. Ò μí± 1. ˆ É ÉÊÉ É μ É Î ±μ Ô± ³ É ²Ó μ Ë ±, Œμ ±
 Ó³ Ÿ. 011.. 8, º 7(170.. 1038Ä1091 Š ˆˆ ˆˆ Š ˆŒ ˆ Œ. ˆ. Ò μí± 1 ˆ É ÉÊÉ É μ É Î ±μ Ô± ³ É ²Ó μ Ë ±, Œμ ± Î ÉÒ Ì ² ±Í ÖÌ ² É Ö É μ Ö Ô² ±É μ ² ÒÌ ³μ É. Theory of electroweak interactions is given in 4 lectures.
Ó³ Ÿ. 011.. 8, º 7(170.. 1038Ä1091 Š ˆˆ ˆˆ Š ˆŒ ˆ Œ. ˆ. Ò μí± 1 ˆ É ÉÊÉ É μ É Î ±μ Ô± ³ É ²Ó μ Ë ±, Œμ ± Î ÉÒ Ì ² ±Í ÖÌ ² É Ö É μ Ö Ô² ±É μ ² ÒÌ ³μ É. Theory of electroweak interactions is given in 4 lectures.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
 3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
A.x = b. x X. x p X P. C.x p A.x p c p a p. p X,
 j! #" $%&'()* +, -. /0 $ 2,+ 3,$.45 26798:-; 26? 7,-@, +AB +C, +7,$+ DB 6+ 2E-F5+?0-G+ 7,-G HEIJLKNMMOQP:RTSUWVXM&Y[ZF\JLU]I_^`RaS\JLb ced UWVXfMKhgaiXiXi kxl m;noeprq`stm;uo l v;wexzy{ ~}a & ƒ
j! #" $%&'()* +, -. /0 $ 2,+ 3,$.45 26798:-; 26? 7,-@, +AB +C, +7,$+ DB 6+ 2E-F5+?0-G+ 7,-G HEIJLKNMMOQP:RTSUWVXM&Y[ZF\JLU]I_^`RaS\JLb ced UWVXfMKhgaiXiXi kxl m;noeprq`stm;uo l v;wexzy{ ~}a & ƒ
]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1
![]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1 ]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1](/thumbs/84/90712514.jpg) ! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /
! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /
Š Œ Š, ƒˆ ƒ ˆ ˆ Œ.. Œμ μ μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 016.. 47.. 5 Š Œ Š, ƒˆ ƒ ˆ ˆ Œ.. Œμ μ μ ˆ É ÉÊÉ μ ² ³ Î Ëμ ³ Í, Œμ ± Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± ˆ 149 Š Œ Ÿ ˆŸ Ÿ 1440 ƒ - ˆ 1484 ˆŸ ˆ ˆ ƒ œ ƒ 1505 ˆŸ Ä Œ 1518 Š ˆ 1538 ˆ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 016.. 47.. 5 Š Œ Š, ƒˆ ƒ ˆ ˆ Œ.. Œμ μ μ ˆ É ÉÊÉ μ ² ³ Î Ëμ ³ Í, Œμ ± Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± ˆ 149 Š Œ Ÿ ˆŸ Ÿ 1440 ƒ - ˆ 1484 ˆŸ ˆ ˆ ƒ œ ƒ 1505 ˆŸ Ä Œ 1518 Š ˆ 1538 ˆ
MAS310. MAS310 1 Question 1 continued on next page SCHOOL OF MATHEMATICS AND STATISTICS Continuum Mechanics. e 1, e 2, e 3 e i = a ij e.
 MAS10 SCHOOL OF MATHEMATICS AND STATISTICS Autumn Semeter 011 1 Continuum Mechanic hour!#"$ % &"('$)*+*,'.-/01"$ 4 % 576 "$ 98:; & ';*?@ BAC>>; 9D E8:; F G7A7AHD.I; B,'( J KL7M N1OPRQBS$TUP@VWPYXYZ%[$\,T][$^Z%OP1_
MAS10 SCHOOL OF MATHEMATICS AND STATISTICS Autumn Semeter 011 1 Continuum Mechanic hour!#"$ % &"('$)*+*,'.-/01"$ 4 % 576 "$ 98:; & ';*?@ BAC>>; 9D E8:; F G7A7AHD.I; B,'( J KL7M N1OPRQBS$TUP@VWPYXYZ%[$\,T][$^Z%OP1_
ΜΕΤΑΠΤΥΧΙΑΚΗ ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ. Ελευθερίου Β. Χρυσούλα. Επιβλέπων: Νικόλαος Καραμπετάκης Καθηγητής Α.Π.Θ.
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΕΛΕΓΧΟΥ Αναγνώριση συστημάτων με δεδομένη συνεχή και κρουστική συμπεριφορά
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ ΚΑΙ ΕΛΕΓΧΟΥ Αναγνώριση συστημάτων με δεδομένη συνεχή και κρουστική συμπεριφορά
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
(x y) = (X = x Y = y) = (Y = y) (x y) = f X,Y (x, y) x f X
 X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
X, Y f X,Y x, y X x, Y y f X Y x y X x Y y X x, Y y Y y f X,Y x, y f Y y f X Y x y x y X Y f X,Y x, y f X Y x y f X,Y x, y f Y y x y X : Ω R Y : Ω E X < y Y Y y 0 X Y y x R x f X Y x y gy X Y gy gy : Ω
( ) ( ) ( ) ( ) ( ) β ( ) ... Χ 2 Υ 11 Χ 12. Χ... p Χ 22 Υ 21 Υ 1. Χ... np ... ,..., ˆ. i,
 "! #%$ &(' )*- /" 3 45687495:;< >?@AB DE"F G HIJ KL"MNONP QRTVUW"XZYZ[U\8Q ] ^`_ a_bcdfe _ cghjk_ e e l ezmh o`qqr stujvwxzryz"o{"q }~ u Vƒ Š ~Œ Ž w %š wœ" "žÿš Vœ` % % Z ž œ% œ Ÿ ž 8 œ9 w " 9 œ Vª«w f
"! #%$ &(' )*- /" 3 45687495:;< >?@AB DE"F G HIJ KL"MNONP QRTVUW"XZYZ[U\8Q ] ^`_ a_bcdfe _ cghjk_ e e l ezmh o`qqr stujvwxzryz"o{"q }~ u Vƒ Š ~Œ Ž w %š wœ" "žÿš Vœ` % % Z ž œ% œ Ÿ ž 8 œ9 w " 9 œ Vª«w f
Ó³ Ÿ , º 4(181).. 501Ä510
 Ó³ Ÿ. 213.. 1, º 4(181.. 51Ä51 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ Š ˆ ƒ ˆ ˆŸ Ÿ ƒ Ÿ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ Š.. Œμ Éμ 1,.. Ê 2 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± ƒ ÒÎ ² É μ Ô - ³ Ê²Ó ²Ö ³ É ± Š. Ò Ï É Í μ Ò Ô Ö ³μ³
Ó³ Ÿ. 213.. 1, º 4(181.. 51Ä51 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ Š ˆ ƒ ˆ ˆŸ Ÿ ƒ Ÿ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ Š.. Œμ Éμ 1,.. Ê 2 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± ƒ ÒÎ ² É μ Ô - ³ Ê²Ó ²Ö ³ É ± Š. Ò Ï É Í μ Ò Ô Ö ³μ³
ˆˆ ƒ ˆ ˆˆ.. ƒ ÏÉ,.. μ Ê μ, Œ.. Œ É Ï ²,.. ± Î ±μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2005.. 36.. 5 Š 539.12.01 ˆŸ ˆˆ ƒ ˆ ˆˆ.. ƒ ÏÉ,.. μ Ê μ, Œ.. Œ É Ï ²,.. ± Î ±μ ˆ É ÉÊÉ Ë ± Ò μ± Ì Ô, μé μ, μ Ö ˆ 1004 ˆ ˆŠ ƒ ˆ ˆ ƒ Ÿ ˆ ƒ Œ ˆ - ˆŸ 1006 œ ƒ ˆ ƒ ˆ ˆ- ƒ Ÿ 1013 ˆŸ ƒ ˆ ˆ ƒ Ÿ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2005.. 36.. 5 Š 539.12.01 ˆŸ ˆˆ ƒ ˆ ˆˆ.. ƒ ÏÉ,.. μ Ê μ, Œ.. Œ É Ï ²,.. ± Î ±μ ˆ É ÉÊÉ Ë ± Ò μ± Ì Ô, μé μ, μ Ö ˆ 1004 ˆ ˆŠ ƒ ˆ ˆ ƒ Ÿ ˆ ƒ Œ ˆ - ˆŸ 1006 œ ƒ ˆ ƒ ˆ ˆ- ƒ Ÿ 1013 ˆŸ ƒ ˆ ˆ ƒ Ÿ
ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ
 Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
Š ˆ ˆ Š ˆ ˆˆ. ˆŸ Š ˆ Œ Š ˆ. ƒ. Š ³ ±
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2003.. 34.. 4 Š 539.12.04 ƒ Ÿ ˆ ˆ Š ˆ ˆ Š ˆ ˆ Š ˆ ˆˆ. ˆŸ Š ˆ Œ Š ˆ. ƒ. Š ³ ± ƒ ˆˆŒ, Šµ µ², Œµ ±µ ± Ö µ ²., µ Ö.. ³ Ê Ï ± µ Ê É Ò Ê É É, µ± Ò, µ Ö.. ʲ µ ÊÎ µ- ² µ É ²Ó ± É ÉÊÉ Ö µ Ë ±
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2003.. 34.. 4 Š 539.12.04 ƒ Ÿ ˆ ˆ Š ˆ ˆ Š ˆ ˆ Š ˆ ˆˆ. ˆŸ Š ˆ Œ Š ˆ. ƒ. Š ³ ± ƒ ˆˆŒ, Šµ µ², Œµ ±µ ± Ö µ ²., µ Ö.. ³ Ê Ï ± µ Ê É Ò Ê É É, µ± Ò, µ Ö.. ʲ µ ÊÎ µ- ² µ É ²Ó ± É ÉÊÉ Ö µ Ë ±
P Ò±,. Ï ± ˆ ˆŒˆ Š ƒ ˆŸ. Œ ƒ Œ ˆˆ γ-š Œˆ ƒ ƒˆ 23 ŒÔ. ² μ Ê ². Í μ ²Ó Ò Í É Ö ÒÌ ² μ, É μí±, μ²óï
 P15-2012-75.. Ò±,. Ï ± ˆ Œ ˆŸ ˆ, š Œ ˆ ˆŒˆ Š ƒ ˆŸ ˆ ˆ, Œ ƒ Œ ˆˆ γ-š Œˆ ƒ ƒˆ 23 ŒÔ ² μ Ê ² Í μ ²Ó Ò Í É Ö ÒÌ ² μ, É μí±, μ²óï Ò±.., Ï ±. P15-2012-75 ˆ ³ Ö μ Ì μ É, μ Ñ ³ ÒÌ μ É Ì ³ Î ±μ μ μ É μ Íμ Ö ÕÐ
P15-2012-75.. Ò±,. Ï ± ˆ Œ ˆŸ ˆ, š Œ ˆ ˆŒˆ Š ƒ ˆŸ ˆ ˆ, Œ ƒ Œ ˆˆ γ-š Œˆ ƒ ƒˆ 23 ŒÔ ² μ Ê ² Í μ ²Ó Ò Í É Ö ÒÌ ² μ, É μí±, μ²óï Ò±.., Ï ±. P15-2012-75 ˆ ³ Ö μ Ì μ É, μ Ñ ³ ÒÌ μ É Ì ³ Î ±μ μ μ É μ Íμ Ö ÕÐ
L A TEX 2ε. mathematica 5.2
 Διδασκων: Τσαπογας Γεωργιος Διαφορικη Γεωμετρια Προχειρες Σημειωσεις Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Εαρινό Εξάμηνο 2005 στοιχεοθεσια : Ξενιτιδης Κλεανθης L A TEX 2ε σχεδια : Dia mathematica
Διδασκων: Τσαπογας Γεωργιος Διαφορικη Γεωμετρια Προχειρες Σημειωσεις Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Εαρινό Εξάμηνο 2005 στοιχεοθεσια : Ξενιτιδης Κλεανθης L A TEX 2ε σχεδια : Dia mathematica
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
(... )..!, ".. (! ) # - $ % % $ & % 2007
 (! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
MÉTHODES ET EXERCICES
 J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
!"#!$% &' ( )*+*,% $ &$ -.&01#(2$#3 4-$ #35667
 !"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
!"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
P ƒ. ÉÕÌ 1,,.. ± 1,.Œ. 1,2, ƒ. Š ³ ± 1,3, ƒ.. Šμ μ ±μ 1,..Š²Ò 1,.. μ μ Íμ 1,2,. ³Î ³ 1,4,. ƒ. É 1,.. Î ± 1.
 P7-2007-8. ƒ. ÉÕÌ 1,,.. ± 1,.Œ. 1,2, ƒ. Š ³ ± 1,3, ƒ.. Šμ μ ±μ 1,..Š²Ò 1,.. μ μ Íμ 1,2,. ³Î ³ 1,4,. ƒ. É 1,.. Î ± 1 Š Š ˆŸ Œ Š ƒ Ÿ ƒšˆ Œ ² μ Ê ² μ Ò É Ì ± Ô± ³ É 1 2ˆ É ÉÊÉ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 3ˆ É ÉÊÉ
P7-2007-8. ƒ. ÉÕÌ 1,,.. ± 1,.Œ. 1,2, ƒ. Š ³ ± 1,3, ƒ.. Šμ μ ±μ 1,..Š²Ò 1,.. μ μ Íμ 1,2,. ³Î ³ 1,4,. ƒ. É 1,.. Î ± 1 Š Š ˆŸ Œ Š ƒ Ÿ ƒšˆ Œ ² μ Ê ² μ Ò É Ì ± Ô± ³ É 1 2ˆ É ÉÊÉ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 3ˆ É ÉÊÉ
ˆ ˆ Œ Ÿ Š Œ ƒˆ Šˆ ˆ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ
 Ó³ Ÿ. 2015.. 12, º 2(193).. 281Ä298 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ˆ ˆ Œ Ÿ Š Œ ƒˆ Šˆ ˆ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± Í Œ Ì ²ÖÉ É ±μ É μ É Í ( ƒ) μ μ²ö É μ μ ÉÓ É ²Ó- ÊÕ ² ±Í
Ó³ Ÿ. 2015.. 12, º 2(193).. 281Ä298 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ˆ ˆ Œ Ÿ Š Œ ƒˆ Šˆ ˆ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± Í Œ Ì ²ÖÉ É ±μ É μ É Í ( ƒ) μ μ²ö É μ μ ÉÓ É ²Ó- ÊÕ ² ±Í
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure
 Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure Hervé Rivano To cite this version: Hervé Rivano. Algorithmique et télécommunications
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure Hervé Rivano To cite this version: Hervé Rivano. Algorithmique et télécommunications
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. )!#)! ##%' " (&! #!$"/001
 !"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. ') '#*#(& )!#)! ##%' " (&! #!$"/001 ')!' &'# 2' '#)!( 3(&/004&' 5#(& /006 # '#)! 7!+8 8 8 #'%# ( #'## +,-'!$%(' & ('##$%('9&#' & ('##$%('9')
!"#! $%&'$% %(' ') '#*#(& ( #'##+,-'!$%(' & ('##$%(' &#' & ('##$%('. ') '#*#(& )!#)! ##%' " (&! #!$"/001 ')!' &'# 2' '#)!( 3(&/004&' 5#(& /006 # '#)! 7!+8 8 8 #'%# ( #'## +,-'!$%(' & ('##$%('9&#' & ('##$%('9')
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Ó³ Ÿ , º 1(199).. 66Ä79 .. Ê 1. Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ±
 Ó³ Ÿ. 216.. 13, º 1(199).. 66Ä79 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ Œ Ÿ ƒˆÿ ˆ Œ ƒ ˆ ˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μé ³± Ì ²ÖÉ É ±μ É μ É Í ³μÉ Î μ ²μ± ²Ó μ³ μ- Éμ± Ö ² ±É ± ³ ÏÉ Ì ±μ²ó± Ì ³ ±, Ò
Ó³ Ÿ. 216.. 13, º 1(199).. 66Ä79 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ Œ Ÿ ƒˆÿ ˆ Œ ƒ ˆ ˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μé ³± Ì ²ÖÉ É ±μ É μ É Í ³μÉ Î μ ²μ± ²Ó μ³ μ- Éμ± Ö ² ±É ± ³ ÏÉ Ì ±μ²ó± Ì ³ ±, Ò
Artificial Intelligence. 8. Inductive Logic Programming
 Artificial Intelligence Artificial Intelligence 8. Inductive Logic Programming Lars Schmidt-Thieme Information Systems and Machine Learning Lab (ISMLL) Institute of Economics and Information Systems &
Artificial Intelligence Artificial Intelligence 8. Inductive Logic Programming Lars Schmidt-Thieme Information Systems and Machine Learning Lab (ISMLL) Institute of Economics and Information Systems &
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
ƒ Š ˆ Šˆ Š Œˆ Šˆ Š ˆŒ PAMELA ˆ AMS-02
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2017.. 48.. 5.. 582Ä588 œ ˆ Œ ˆ Š Ÿ Š Œ ƒ Š ˆ Šˆ Š Œˆ Šˆ Š ˆŒ PAMELA ˆ AMS-02.. ² ± 1, Š. Œ. ²μͱ 2,.. μ μ³μ²μ 1,. ˆ. Ê 2,.Œ.ƒ ²Ó 2,.. Ê 1,.. Š ²²μ 1, 2,.. ŠÊ Íμ 1,,.. ʱÓÖ μ 1,. ƒ. Œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2017.. 48.. 5.. 582Ä588 œ ˆ Œ ˆ Š Ÿ Š Œ ƒ Š ˆ Šˆ Š Œˆ Šˆ Š ˆŒ PAMELA ˆ AMS-02.. ² ± 1, Š. Œ. ²μͱ 2,.. μ μ³μ²μ 1,. ˆ. Ê 2,.Œ.ƒ ²Ó 2,.. Ê 1,.. Š ²²μ 1, 2,.. ŠÊ Íμ 1,,.. ʱÓÖ μ 1,. ƒ. Œ
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Im{z} 3π 4 π 4. Re{z}
 ! #"!$%& '(!*),+- /. '( 0 213. $ 1546!.17! & 8 + 8 9:17!; < = >+ 8?A@CBEDF HG
! #"!$%& '(!*),+- /. '( 0 213. $ 1546!.17! & 8 + 8 9:17!; < = >+ 8?A@CBEDF HG
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Accept. Feed. Reject. axis of rotation
 p ï Ã! #"$% '& &(%&)&* +, "-./ 0/1325476!8:9#;/@A13@CBAD1FEHG=2JI,47KC251FL MNC3Y[ZR47\]K 13@CGP\^13FY[fUS?GPLXG=6XKATU>3
p ï Ã! #"$% '& &(%&)&* +, "-./ 0/1325476!8:9#;/@A13@CBAD1FEHG=2JI,47KC251FL MNC3Y[ZR47\]K 13@CGP\^13FY[fUS?GPLXG=6XKATU>3
P μ,. Œμ α 1,. ²μ ± 1,.. ϱ Î, Ÿ. Ê Í± 2 Œˆ ˆ Œ Š Ÿ Š Ÿ ˆ ˆŒ ˆˆ. ² μ Ê ² μ Ò É Ì ± Ô± ³ É
 P13-2009-117.. μ,. Œμ α 1,. ²μ ± 1,.. ϱ Î, Ÿ. Ê Í± 2 Œˆ ˆ Œ Š Ÿ Š Ÿ ˆ ˆŒ ˆˆ ² μ Ê ² μ Ò É Ì ± Ô± ³ É 1ˆ É ÉÊÉ Éμ³ μ Ô, ±Ä Ï, μ²óï 2 Ì μ²μ Î ± Ê É É, Õ ², μ²óï μ... P13-2009-117 μ ³ μ ³μ² ±Ê²Ö ÒÌ Êαμ
P13-2009-117.. μ,. Œμ α 1,. ²μ ± 1,.. ϱ Î, Ÿ. Ê Í± 2 Œˆ ˆ Œ Š Ÿ Š Ÿ ˆ ˆŒ ˆˆ ² μ Ê ² μ Ò É Ì ± Ô± ³ É 1ˆ É ÉÊÉ Éμ³ μ Ô, ±Ä Ï, μ²óï 2 Ì μ²μ Î ± Ê É É, Õ ², μ²óï μ... P13-2009-117 μ ³ μ ³μ² ±Ê²Ö ÒÌ Êαμ
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
 F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
())*+,-./0-1+*)*2, *67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3*
 ! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
! " # $ $ %&&' % $ $! " # ())*+,-./0-1+*)*2,-3-4050+*67()(,01-+4(-8 9 0:,*2./0 30 ;+-7 3* *),+*< 7+)0 3* *),+-30 *5 35(2(),+-./0 30 *,0+ 3* (=24(-) 04(-() 18(4-3-) 3-2(>*+)(3-3* *3*+-830-+-2?< +(*2,-30+
Š Š ˆˆ Š ˆ ˆ Š Ÿ ˆ ˆ œ ƒ ˆŒ ˆŸ. ƒ. Š μì,.. ŠμÉ ±μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 Š Š ˆˆ Š ˆ ˆ Š Ÿ ˆ ˆ œ ƒ ˆŒ ˆŸ. ƒ. Š μì,.. ŠμÉ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 226 ƒ Š ƒ Ÿ ˆ Ÿ - 228 KX ˆ ˆˆ Š ƒ 240 Š ˆ œ ƒ ˆŒ ˆŸ 260 ˆ Š ˆ œ ƒ ˆŒ - ˆŸ ˆ ƒ Š ƒ Œ Ÿ ˆ Ÿ 267 Š
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 Š Š ˆˆ Š ˆ ˆ Š Ÿ ˆ ˆ œ ƒ ˆŒ ˆŸ. ƒ. Š μì,.. ŠμÉ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 226 ƒ Š ƒ Ÿ ˆ Ÿ - 228 KX ˆ ˆˆ Š ƒ 240 Š ˆ œ ƒ ˆŒ ˆŸ 260 ˆ Š ˆ œ ƒ ˆŒ - ˆŸ ˆ ƒ Š ƒ Œ Ÿ ˆ Ÿ 267 Š
m r = F m r = F ( r) m r = F ( v) F = F (x) m dv dt = F (x) vdv = F (x)dx d dt = dx dv dt dx = v dv dx
 m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
m r = F m r = F ( r) m r = F ( v) x F = F (x) m dv dt = F (x) d dt = dx dv dt dx = v dv dx vdv = F (x)dx 2 mv2 x 2 mv2 0 = F (x )dx x 0 K = 2 mv2 W x0 x = x x 0 F (x)dx K K 0 = W x0 x x, x 2 x K 2 K =
TALAR ROSA -. / ',)45$%"67789
 TALAR ROSA!"#"$"%$&'$%(" )*"+%(""%$," *$ -. / 0"$%%"$&'1)2$3!"$ ',)45$%"67789 ," %"(%:,;,"%,$"$)$*2
TALAR ROSA!"#"$"%$&'$%(" )*"+%(""%$," *$ -. / 0"$%%"$&'1)2$3!"$ ',)45$%"67789 ," %"(%:,;,"%,$"$)$*2
ˆ ˆ Š Ÿ Œ ˆŠ ˆ ˆ ˆŠ Œ ƒ ˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 ˆ ˆ Š Ÿ Œ ˆŠ ˆ ˆ ˆŠ Œ ƒ ˆ Œ œ ˆ Œ.. ŠÊ ³ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 6 Š Ÿ ˆ ˆ Š Ÿ Œ ˆŠ ˆ ˆ ˆŠ ƒ 7 Œ ƒ ˆ Œ ˆ Œ ˆ Œ ƒ ˆ Œ 9 Š Ÿ ˆŸ Œ ƒ ˆ Œ 14 Œ Œ œ ƒ Œˆ œ ˆ 16 ˆŸ ˆ Œ Œ ƒˆ ˆŒ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 7 ˆ ˆ Š Ÿ Œ ˆŠ ˆ ˆ ˆŠ Œ ƒ ˆ Œ œ ˆ Œ.. ŠÊ ³ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 6 Š Ÿ ˆ ˆ Š Ÿ Œ ˆŠ ˆ ˆ ˆŠ ƒ 7 Œ ƒ ˆ Œ ˆ Œ ˆ Œ ƒ ˆ Œ 9 Š Ÿ ˆŸ Œ ƒ ˆ Œ 14 Œ Œ œ ƒ Œˆ œ ˆ 16 ˆŸ ˆ Œ Œ ƒˆ ˆŒ
ˆˆ ŸŒ ƒ ˆŸ CP- ˆŒŒ ˆˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 5 ˆˆ ŸŒ ƒ ˆŸ CP- ˆŒŒ ˆˆ œ Š.. Š ± ²,.. Œ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1163 ˆ ˆ ˆ Œ œ Š 1166 Š ˆŒ œ Re (ɛ /ɛ) Š Š - ˆŒ NA48 ˆ KTeV 1172 Š ˆŒ NA48 1178 ˆ Œ ˆ Re(ɛ /ɛ) Š ˆŒ KTeV
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2007.. 38.. 5 ˆˆ ŸŒ ƒ ˆŸ CP- ˆŒŒ ˆˆ œ Š.. Š ± ²,.. Œ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1163 ˆ ˆ ˆ Œ œ Š 1166 Š ˆŒ œ Re (ɛ /ɛ) Š Š - ˆŒ NA48 ˆ KTeV 1172 Š ˆŒ NA48 1178 ˆ Œ ˆ Re(ɛ /ɛ) Š ˆŒ KTeV
An approach is given in relativistic nuclear physics which is based on the application of the similarity laws, symmetry of solutions and other
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 1998, Œ 29,.3 Š 539.171.1 Ÿ ˆ ˆ Š Ÿ Ÿ Ÿ ˆ ˆŠ : ˆ œ 4- Š, ˆŒŒ ˆˆ ˆ, ˆ ˆ ˆŸ Š Ÿ ˆ, ˆ, Œ ˆŒ ˆŠˆ.Œ. ²,.. ² Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 578 ˆ Œ Œ ˆ Šˆ Œ. ˆŒŒ ˆŸ Œ ˆ ˆŠ 581 ˆ ˆ ˆŸ Š Ÿ ˆ. ˆ œ Š 593
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 1998, Œ 29,.3 Š 539.171.1 Ÿ ˆ ˆ Š Ÿ Ÿ Ÿ ˆ ˆŠ : ˆ œ 4- Š, ˆŒŒ ˆˆ ˆ, ˆ ˆ ˆŸ Š Ÿ ˆ, ˆ, Œ ˆŒ ˆŠˆ.Œ. ²,.. ² Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 578 ˆ Œ Œ ˆ Šˆ Œ. ˆŒŒ ˆŸ Œ ˆ ˆŠ 581 ˆ ˆ ˆŸ Š Ÿ ˆ. ˆ œ Š 593
Jeux d inondation dans les graphes
 Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Ó³ Ÿ , º 3(194).. 673Ä677. Š Œ œ ƒˆˆ ˆ ˆŠ. ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ±
 Ó³ Ÿ. 2015.. 12, º 3(194.. 673Ä677 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŸ ˆ Šˆ ˆ ˆ Œ ˆŠ ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ É ÉÊÉ Ö μ Ë ± μ²ó ±μ ± ³ ʱ, Š ±μ, μ²óï μé É ² Ò Ê Ö Ö Î ² Ò Ê²ÓÉ ÉÒ,
Ó³ Ÿ. 2015.. 12, º 3(194.. 673Ä677 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŸ ˆ Šˆ ˆ ˆ Œ ˆŠ ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ É ÉÊÉ Ö μ Ë ± μ²ó ±μ ± ³ ʱ, Š ±μ, μ²óï μé É ² Ò Ê Ö Ö Î ² Ò Ê²ÓÉ ÉÒ,
ZZ (*) 4l. H γ γ. Covered by LEP GeV
 : 33 9! " 5< 687 235 # #) " " &( $ # $!" K I K T S R N \ N \ ] N ^ K V 63 7 "" ` 2 9 a C C E D # C B A @ " "? > H N OQP N M Y WX U V H O ( N O_P b i h i h h 63 7 "" ` C C E D # C B A @ " "? > b d e f f
: 33 9! " 5< 687 235 # #) " " &( $ # $!" K I K T S R N \ N \ ] N ^ K V 63 7 "" ` 2 9 a C C E D # C B A @ " "? > H N OQP N M Y WX U V H O ( N O_P b i h i h h 63 7 "" ` C C E D # C B A @ " "? > b d e f f
P Œ ²μ, Œ.. ƒê Éμ,. ƒ. ²μ,.. μ. ˆ ˆŸ Œˆ ˆŸ ˆ Š Œ ˆŸ Ÿ - ˆ ˆ ŠˆŒˆ Œ Œˆ ˆ œ ˆ Œ ˆ ŒˆŠ Œ -25
 P6-2011-64.. Œ ²μ, Œ.. ƒê Éμ,. ƒ. ²μ,.. μ ˆ ˆŸ Œˆ ˆŸ ˆ Š Œ ˆŸ Ÿ - ˆ ˆ ŠˆŒˆ Œ Œˆ ˆ œ ˆ Œ ˆ ŒˆŠ Œ -25 Œ ²μ... P6-2011-64 ² μ Ö ²Õ³ Ö ± ³ Ö μ Í Ì μ Ò Ö μ-ë Î ± ³ ³ Éμ ³ μ²ó μ ³ ³ ± μé μ Œ -25 μ³μðóõ Ö μ-ë
P6-2011-64.. Œ ²μ, Œ.. ƒê Éμ,. ƒ. ²μ,.. μ ˆ ˆŸ Œˆ ˆŸ ˆ Š Œ ˆŸ Ÿ - ˆ ˆ ŠˆŒˆ Œ Œˆ ˆ œ ˆ Œ ˆ ŒˆŠ Œ -25 Œ ²μ... P6-2011-64 ² μ Ö ²Õ³ Ö ± ³ Ö μ Í Ì μ Ò Ö μ-ë Î ± ³ ³ Éμ ³ μ²ó μ ³ ³ ± μé μ Œ -25 μ³μðóõ Ö μ-ë
ˆ œ ˆ ˆ ˆ Šˆ Œ ˆ ˆ Š ˆ Ÿ Œˆ ˆ Œˆ ŒŠ Œ ˆ Ÿ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 6 ˆ œ ˆ ˆ ˆ Šˆ Œ ˆ ˆ Š ˆ Ÿ Œˆ ˆ Œˆ ŒŠ Œ ˆ Ÿ ˆ Œ.. Ê μ, ƒ. ƒ. ³Ö,.. Éμ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1603 ˆ ˆ ˆŸ ˆ ˆ œ Š Œ ˆ Ÿ 1614 Î μ μ Ö É ²Ó μ μ μ É É±. 1614 μöé μ ÉÓ μ μ Ö
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 6 ˆ œ ˆ ˆ ˆ Šˆ Œ ˆ ˆ Š ˆ Ÿ Œˆ ˆ Œˆ ŒŠ Œ ˆ Ÿ ˆ Œ.. Ê μ, ƒ. ƒ. ³Ö,.. Éμ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1603 ˆ ˆ ˆŸ ˆ ˆ œ Š Œ ˆ Ÿ 1614 Î μ μ Ö É ²Ó μ μ μ É É±. 1614 μöé μ ÉÓ μ μ Ö
Œ ˆ ˆ Š ƒ ƒˆˆ: Š ˆŸ ˆŸ Š
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2015.. 46.. 3 Ÿ - ˆ ˆ Šˆ Œ ˆ Œ ˆ ˆ Š ƒ ƒˆˆ: Š ˆŸ ˆŸ Š œ Š.. ƒμ Ê μ 1,. Œ. Ö Ê μ 1,. ˆ. ± 1, Œ.. μ É Ó 2,,.. ²μ 2, ˆ.. ˆ²ÓÎ ±μ 3 1 ƒ μ²μ Î ± É ÉÊÉ, Œμ ± 2 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 3 ÊÎ μ-
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2015.. 46.. 3 Ÿ - ˆ ˆ Šˆ Œ ˆ Œ ˆ ˆ Š ƒ ƒˆˆ: Š ˆŸ ˆŸ Š œ Š.. ƒμ Ê μ 1,. Œ. Ö Ê μ 1,. ˆ. ± 1, Œ.. μ É Ó 2,,.. ²μ 2, ˆ.. ˆ²ÓÎ ±μ 3 1 ƒ μ²μ Î ± É ÉÊÉ, Œμ ± 2 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 3 ÊÎ μ-
Déformation et quantification par groupoïde des variétés toriques
 Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
#%" )*& ##+," $ -,!./" %#/%0! %,!
 -!"#$% -&!'"$ & #("$$, #%" )*& ##+," $ -,!./" %#/%0! %,! %!$"#" %!#0&!/" /+#0& 0.00.04. - 3 3,43 5 -, 4 $ $.. 04 ... 3. 6... 6.. #3 7 8... 6.. %9: 3 3 7....3. % 44 8... 6.4. 37; 3,, 443 8... 8.5. $; 3
-!"#$% -&!'"$ & #("$$, #%" )*& ##+," $ -,!./" %#/%0! %,! %!$"#" %!#0&!/" /+#0& 0.00.04. - 3 3,43 5 -, 4 $ $.. 04 ... 3. 6... 6.. #3 7 8... 6.. %9: 3 3 7....3. % 44 8... 6.4. 37; 3,, 443 8... 8.5. $; 3
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ ˆ ² μ É ²Ó ± Í É μ²õé É, μ É μ ±, ± ˆŸ Œ 246 Š 248. Œ Œ ˆŒ œ ˆ ˆ 258 ˆŸ ˆ 260 Š ˆ Ÿ Œ ˆ Š 262 ˆ ˆ Œˆ Šˆ ˆŸ 263
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2012.. 43.. 1 ˆŸ Œ Ÿ ˆ ˆ Ÿ.. É μ ˆ ² μ É ²Ó ± Í É μ²õé É, μ É μ ±, ± ˆŸ Œ 246 Œ ˆ Œ ˆ Ÿ Š 248 ˆ Ÿ Ÿ 252 ˆ ˆ œ ˆ Œ 256 Œ Œ ˆŒ œ ˆ ˆ 258 ˆŸ ˆ 260 Š ˆ Ÿ Œ ˆ Š 262 ˆ ˆ Œˆ Šˆ ˆŸ 263 ˆ ˆ ˆ Œ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2012.. 43.. 1 ˆŸ Œ Ÿ ˆ ˆ Ÿ.. É μ ˆ ² μ É ²Ó ± Í É μ²õé É, μ É μ ±, ± ˆŸ Œ 246 Œ ˆ Œ ˆ Ÿ Š 248 ˆ Ÿ Ÿ 252 ˆ ˆ œ ˆ Œ 256 Œ Œ ˆŒ œ ˆ ˆ 258 ˆŸ ˆ 260 Š ˆ Ÿ Œ ˆ Š 262 ˆ ˆ Œˆ Šˆ ˆŸ 263 ˆ ˆ ˆ Œ
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
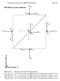 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
3 + tanx 100 Differentiate G(t) = Answer: G (t) = Differentiate f (x) = lnx + ex 2. Differentiate F(s) = ln ( cos(2s) + 2 ) Answer: F (s) =
 Differentiate y xcos(2x 2 ( x 1 2 3 Differentiate f (x sinx f (x cos(1 + x - 2*xˆ2 + x*(-1 + 4*x*sin(1 + x - 2*xˆ2 Differentiate y -24*cot(x*csc(xˆ3 3 + tanx 100 Differentiate G(t (cost 4 1 (sec(xˆ2/(2*sqrt(3
Differentiate y xcos(2x 2 ( x 1 2 3 Differentiate f (x sinx f (x cos(1 + x - 2*xˆ2 + x*(-1 + 4*x*sin(1 + x - 2*xˆ2 Differentiate y -24*cot(x*csc(xˆ3 3 + tanx 100 Differentiate G(t (cost 4 1 (sec(xˆ2/(2*sqrt(3
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ ˆ ˆ ˆ ˆŠ Œ.. Š ². Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Œ ˆ ˆŸ ˆ ˆ Š ˆ ˆ ˆ ˆŠ Œ.. Š ² Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ ˆ Œ Œ 579 μ²μ Î ± Ö μ²ó ² μ. 579 ³ ² μ Ë ³ Í É ±. Œ Éμ Ò ² μ Ö É Ê±ÉÊ Ò μ É ² ÒÌ 581 ³ ³ ² ÒÌ μî É Í. 584 Œ ˆŒ ˆŸ ƒ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2011.. 42.. 2 Œ ˆ ˆŸ ˆ ˆ Š ˆ ˆ ˆ ˆŠ Œ.. Š ² Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ ˆ Œ Œ 579 μ²μ Î ± Ö μ²ó ² μ. 579 ³ ² μ Ë ³ Í É ±. Œ Éμ Ò ² μ Ö É Ê±ÉÊ Ò μ É ² ÒÌ 581 ³ ³ ² ÒÌ μî É Í. 584 Œ ˆŒ ˆŸ ƒ
 k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)

 " #%$& ' ( *%- T U
" #%$& ' ( *%- T U  8 7!"$#!%') ""! -/.$ -324654 )! 98/:/; < E <
8 7!"$#!%') ""! -/.$ -324654 )! 98/:/; < E <