PRAVILA ZA PRIPREMU I POLAGANJE USMENOG ISPITA IZ BIOHEMIJE
|
|
|
- Μαργαρίτες Βικελίδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Fakultet veterinarske medicine, Univerzitet u Beogradu Katedra za fiziologiju i biohemiju Predmet: Biohemija PRAVILA ZA PRIPREMU I POLAGANJE USMENOG ISPITA IZ BIOHEMIJE Nakon analize ispitnih rezultata u protekle dve školske godine, procene kretanja realnog znanja i razumevanja studenata i ostvarenosti ciljeva predmeta, Kolegijum nastavnika na predmetu Biohemija doneo je odluku da, počev od decembarskog ispitnog roka god. uvede usmeno ispitivanje kandidata. 1. U periodu od decembra do juna godine za usmeni ispit dolazi u obzir 20 "velikih" pitanja koja su se od ranije koristila za Test, sa pridodatih 4 pitanja koja su se u frakcionisanoj formi ranije pojavljivala kao "mala" ili "test" pitanja. Počev od juna godine biće aktiviran pun spisak pitanja usklađen sa materijom sa predavanja. Spisak pitanja se nalazi na kraju ovog dokumenta. 2. Usmeni ispit je javan i mogu mu prisustvovati studenti koji planiraju polaganje u nekom kasnijem roku. 3. Studenti treba da obrate pažnju na to da ubuduće prosto nabrajanje golih činjenica ne garantuje pozitivnu ocenu. Od velike važnosti je poznavanje biološkog i metaboličkog konteksta zadate teme. 4. Studentima se sugeriše da za pripremanje ispita koriste neki od brojnih zvaničnih kvalitetnih udžbenika biohemije. Princip kojeg se držimo je da ne ocenjujemo iz kojeg udžbenika su kandidati učili, već koliko znaju i razumeju programom predviđeno gradivo. 5. Struktura ispitnog procesa: a) Prvo se polaže praktični ispit (datum i grupe se zakazuju unapred). Forma i rok važenja praktičnog ispita se ne menjaju u odnosu na prethodni period. Praktični ispit položen u bilo kom ispitnom roku jedne šk. godine važi zaključno sa oktobarskim II ispitnim rokom naredne školske godine. b) U svakom ispitnom roku, svi kandidati koji imaju važeći praktični ispit polažu mali test čija je svrha da eliminiše studente koji nisu ovladali osnovnim činjenicama. Pitanja na eliminacionom testu će biti ista kao dosadašnja testpitanja. Test se radi dan/dva nakon praktičnog ispita (datum i grupe se zakazuju unapred); sadrži 10 pitanja koja se boduju sa po 1 poenom; trajanje 20 minuta; minimum za prolaz je 6 ostvarenih poena. 1
2 c) Potvrda izlaska na ispit i izvlačenje ispitivača: u zakazanom terminu studenti koji su stekli pravo izlaska na usmeni ispit okupljaju se radi potvrde izlaska i javnog izvlačenja ispitivača. Student izvlači ceduljicu sa imenom i upisuje se na spisak datog ispitivača u nekom od termina predviđenih za usmeni ispit. Broj kandidata u jednom terminu je ograničen na 5. Promena termina je moguća samo u dogovoru sa ispitivačem. d) Usmeni ispit: kandidat izvlači karticu koja sadrži ispitnu kombinaciju od 4 pitanja i dobija min. da se pripremi za izlaganje, koje treba da traje dodatnih min. Ispitne kombinacije su napravljene u više varijanti i redovno će se menjati. Zamena pitanja nije dozvoljena. Svaki odgovor se posebno ocenjuje ocenom od Na sva ispitna pitanja potrebno je odgovoriti za pozitivnu ocenu. Ispitivač zadržava pravo da kandidatu postavi dopunska pitanja ukoliko ocena balansira. 6. Odnos broja osvojenih bodova i konačne ocene: - Prisustvovanje nastavi 2x2 max. 4 poena - Provera rada na vežbama 3x2 max. 6 poena - Kolokvijumi u semestru 2x10 max. 20 poena Ukupno iz nastave max. 30 poena min. 15 poena - Praktični ispit 2x6 max. 12 poena min. 2 poena - Mali test 10x1 max. 10 poena min. 6 poena - Usmeni ispit 4x12 max. 48 poena min. 28 poena UKUPNO ZA OCENU max. 100 poena min. 51 poen Beograd, god. Glavni predmetni nastavnik Prof. dr Ivan B. Jovanović 2
3 SPISAK PITANJA ZA PERIOD OD DECEMBRA VAŽENJE: ZAKLJUČNO SA APRILOM god PITANJA ZA OVAJ PERIOD SU ODŠTAMPANA CRNOM BOJOM I - BIOLOŠKI MOLEKULI (5) 1. - Aminokiseline Opšta struktura, glavne fizikohemijske osobine i klasifikacija aminokiselina; priroda peptidne veze; biološki značajni peptidi Građa proteina Nivoi građe proteina uz odgovarajući primer: primarna, sekundarna, suprasekundarna, tercijarna i kvaternarna struktura Struktura i funkcija proteina: mioglobin (Mb) i hemoglobin (Hb) Trodimenzionalna građa apoproteinskog dela Mb i Hb i funkcionalna struktura hema; mehanizam vezivanja i otpuštanja O2 sa kinetičkim svojstvima; alosterni efekat kod Hb Struktura i funkcija proteina: kolegen i imunoglobulin G (IgG) Opisati trodimenzionalnu građu i biološku funkciju kolagena i IgG Mehanizam i optimalni uslovi za delovanje enzima Modeli funkcionisanja katalitičkog centra (Fišer, Košland); mehanizam uticaja temperature, ph, aktivatora i inhibitora na enzimsku aktivnost sa kinetičkim posledicama Izoenzimi i multienzimski kompleksi Pojam i biološki smisao izoenzima, građa i funkcija LDH; pojam i biološki smisao multienzimskih kompleksa, navesti primer Energetika i kinetika enzim-katalizovane reakcije Osnovni termodinamički pojmovi: ukupna energija ( H), slobodna energija ( G) i entropija ( S); endergone i egzergone reakcije, kuplovane reakcije, značaj energije aktivacije ( G*) pri enzimskoj katalizi; Mihaelis-Menten kinetika enzimske reakcije (kinetika zasićenja) Modulacija enzimske aktivnosti Alosterna i kovalentna modulacija enzimske reakcije sa odgovarajućim primerima; kovalentna aktivacija zimogena Struktura bioloških membrana Opšta struktura i fizikohemijske osobine glicerofosfatida; fosfolipidni dvosloj; proteini membrane; glikokaliks Transport kroz membranu Pore, kanali, pasivni i aktivni transport, endo i egzocitoza. 11. Prenos (transdukcija) hormonskih signala na ćelijskoj membrani Receptori, mehanizmi transdukcije, sekundarni glasnici, biološki efekti. II - METABOLIZAM (15) A. Konvergencija kataboličkih puteva Transportni (respiracioni) lanac elektrona i sinteza ATP Metabolički smisao i povezanost sa drugim metaboličkim procesima; sakupljane, pretvaranje i konzervacija metaboličke energije; ključne komponente RL i njihova organizacija; proton-motorna sila i sinteza ATP. 3
4 13. - Ciklus limunske kiseline komponente CLK i njihova organizacija; energetski bilans (ATP); katabolički aspekti CLK i anaplerotske reakcije; osnove regulacije i suština "respiracione kontrole CLK". B. Metabolizam ugljenih hidrata Varenje ugljenih hidrata Enzimska razgradnja u digestivnom traktu, resorpcija i transport; unos glukoze u ćelije, međusobno pretvaranje (interkonverzija) heksoza Pentozofosfatni put komponente PFP i njihova organizacija (oksidativna i neoksidativna grana i metabolički scenariji za njihovu aktivaciju). 16. Glikoliza komponente glukolize i njihova organizacija (pripremna i oksidativna faza); aerobna i anaerobna glukoliza; energetski bilans (ATP); osnove regulacije Glukoneogeneza i resinteza glukoze Pojam i metabolički smisao glukoneogeneze i resinteze glukoze, povezanost sa drugim metaboličkim procesima; glukoplastični molekuli; ključne komponente procesa i njihova organizacija Glikogenoliza (razlaganje glikogena) i regulacija Metabolički smisao glikogenolize i povezanost sa drugim metaboličkim procesima; ključne komponente procesa i njihova organizacija; regulacija glikogenolize (detaljno) Glikogeneza (sinteza glikogena) i regulacija Metabolički smisao glikogeneze i povezanost sa drugim metaboličkim procesima; ključne komponente procesa i njihova organizacija; regulacija glikogeneze (detaljno). C. Metabolizam lipida Varenje lipida Emulgovanje i enzimska razgradnja u digestivnom traktu; resorpcija i reesterifikacija; transport u krvi: lipoproteini krvne plazme klasifikacija građa i uloge Metabolizam triglicerida i glicerofosfatida Mobilizacija triglicerida u adipocitima (sa osnovama regulacije) i transport do tkiva; sinteza triglicerida i glicerofisfatida β-oksidacija masnih kiselina komponente β-omk i njihova organizacija; oksidacija polinezasićenih MK i MK sa neparnim brojem C-atoma; energetski bilans (ATP) Sinteza acetonskih tela Metabolički smisao i povezanost sa drugim metaboličkim procesima; poremećaji matabolizma koji uslovljavaju nastanak ketoze; ključne komponente sinteze AcT i njihova organizacija Sinteza masnih kiselina komponente multienzimskog kompleksa sintaze masnih kiselina i organizacija 4
5 procesa sinteze Sinteza holesterola komponente i organizacija procesa (nastanak HMG-KoA, polimerizacija i ciklizacija); alosterna regulacija HMK-KoA reduktaze. D. Metabolizam azotnih jedinjenja Varenje proteina Enzimska razgradnja u digestivnom traktu, resorpcija i transport Metabolizam proteina i aminokiselina Pul (rezervoar) AK u organizmu; metaboličko poreklo i sudbina slobodnih aminokiselina; strategija razgradnje aminokiselina u jetri: transaminacija, oksidativna dezaminacija, dekarboksilacija; sudbina aminoazota i C-skeleta AK Sinteza uree Metabolički smisao uree i povezanost sa drugim metaboličkim procesima; ključne komponente procesa i njihova organizacija; energetski bilans (ATP) Katabolozam aminokiselina koje daju piruvat Katabolizam aromatičnih aminokislina, fenilketonurija i alkaptonurija Katabolizam hemoglobina Razlaganje u RES, žučne boje (pojam i značaj direktnog i indirektnog bilirubina) transport bilirubina u krvnom serumu; konjugacija i lučenje; transformacije u crevima i entero-hepatorenalno kruženje Katabolizam purinskih nukleotida komponente procesa i njihova organizacija; mokraćna kiselina (urat) i njen klinički značaj. E. Integracija metabolizma Insulin i glukagon u regulaciji metabolizma Metabolička sudbina piruvata i acetil-koa Međusobno pretvaranja ugljenih hidrata i masti (tov životinja) Specifičnosti metabolizma preživara Biološki značaj preživanja, mikroflora buraga, metabolizam ugljenih hidrata, lipida i proteina u buragu, metaboličke adaptacije preživara. III - OSNOVI MOLEKULSKE GENETIKE (4) Struktura RNK i DNK a) Biohemijski sastav i morfologija polinukleotidnih lanaca; Votson-Krikovi principi građe DNK. b) Građa i uloga histona; pakovanje DNK u jedru eukariota Replikacija (udvajanje) udvajanje i reparacija (popravka) DNK a) Biološki smisao replikacije; osnovni principi replikacije; ključne komponente procesa i njihova organizacija; tok replikacije: inicijacija, elongacija i terminacija. b) Tačkasta oštećenja i reparacija DNK Transkripcija (sinteza RNK) i posttranskripciona obrada a) Biološki smisao transkripcije; osnovni principi transkripcije; ključne komponente procesa i njihova organizacija; tok transkripcije: inicijacija, elongacija i terminacija. 5
6 b) Posttranskripciona obrada primarnog transkripta irnk (5'-cap, splajsing, 3'- poliadenilacija), trnk i rrnk u eukariotskim ćelijama Translacija (sinteza proteina) a) Biološki smisao tranlacije; osnovni principi translacije; ključne komponente procesa i njihova organizacija; tok tranlacije: inicijacija, elongacija i terminacija. b) Mehanizam delovanja antibiotika na nivou translacije. 6
ISPITNA PITANJA ZA USMENI DIO ISPITA
 UNIVERZITET CRNE GORE MEDICINSKI FAKULTET MEDICINSKA BIOHEMIJA ISPITNA PITANJA ZA USMENI DIO ISPITA STUDIJSKI PROGRAM MEDICINA I ENZIMOLOGIJA 1. Opšte osobine enzima i struktura molekula enzima 2. Izoenzimi.
UNIVERZITET CRNE GORE MEDICINSKI FAKULTET MEDICINSKA BIOHEMIJA ISPITNA PITANJA ZA USMENI DIO ISPITA STUDIJSKI PROGRAM MEDICINA I ENZIMOLOGIJA 1. Opšte osobine enzima i struktura molekula enzima 2. Izoenzimi.
PITANJA ZA USMENI ISPIT IZ BIOHEMIJE
 PITANJA ZA USMENI ISPIT IZ BIOHEMIJE PROTEINI STRUKTURA I FUNKCIJE 1. Struktura proteina nivoi organizacije molekula 2. Proteini koji transportuju kiseonik hemoglobin i mioglobin ENZIMI 1. Opšte osobine
PITANJA ZA USMENI ISPIT IZ BIOHEMIJE PROTEINI STRUKTURA I FUNKCIJE 1. Struktura proteina nivoi organizacije molekula 2. Proteini koji transportuju kiseonik hemoglobin i mioglobin ENZIMI 1. Opšte osobine
VODA ELEKTROLITI I ACIDO-BAZNA RAVNOTEŽA...
 SADRŽAJ UVOD 1 1. BIOHEMIJA ĆELIJE... 1-1 1.1 UVOD... 1-2 1.2 ĆELIJA KAO OSNOVNA ŽIVA JEDINICA TELA... 1-2 1.3 VANĆELIJSKA TEČNOST UNUTRAŠNJA OKOLINA... 1-2 1.4 BIOELEMENTI I BIOMOLEKULI... 1-3 1.5 ĆELIJA
SADRŽAJ UVOD 1 1. BIOHEMIJA ĆELIJE... 1-1 1.1 UVOD... 1-2 1.2 ĆELIJA KAO OSNOVNA ŽIVA JEDINICA TELA... 1-2 1.3 VANĆELIJSKA TEČNOST UNUTRAŠNJA OKOLINA... 1-2 1.4 BIOELEMENTI I BIOMOLEKULI... 1-3 1.5 ĆELIJA
Aminokiseline. Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina 22.12.2014
 Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
ISPITNA PITANJA OSNOVI BIOHEMIJE
 UNIVERZITET PRIVREDNA AKADEMIJA, NOVI SAD STOMATOLOŠKI FAKULTET PANČEVO ISPITNA PITANJA OSNOVI BIOHEMIJE Prof. dr Esma R. Isenović 1. Biohemija kao nauka, zadaci izučavanja i discipline 1. Koja je definicija
UNIVERZITET PRIVREDNA AKADEMIJA, NOVI SAD STOMATOLOŠKI FAKULTET PANČEVO ISPITNA PITANJA OSNOVI BIOHEMIJE Prof. dr Esma R. Isenović 1. Biohemija kao nauka, zadaci izučavanja i discipline 1. Koja je definicija
FARMACEUTSKO-BIOKEMIJSKI FAKULTET SVEUČILIŠTA U ZAGREBU. IZVEDBENI PLAN akademska godina 2012./2013. ljetni semestar
 FARMACEUTSKO-BIOKEMIJSKI FAKULTET SVEUČILIŠTA U ZAGREBU IZVEDBENI LAN akademska godina 2012./2013. ljetni semestar Naziv kolegija: Biokemija Naziv studija: Medicinska biokemija Godina i semestar studija:
FARMACEUTSKO-BIOKEMIJSKI FAKULTET SVEUČILIŠTA U ZAGREBU IZVEDBENI LAN akademska godina 2012./2013. ljetni semestar Naziv kolegija: Biokemija Naziv studija: Medicinska biokemija Godina i semestar studija:
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
IZVEDBENI NASTAVNI PLAN
 Medicinski fakultet Sveučilišta u Rijeci Kolegij: BIOKEMIJA Voditelj: prof. dr.sc. Robert Domitrović Suradnici: prof.dr.sc Jadranka Varljen, doc.dr.sc. Dijana Detel, doc.dr.sc. Jelena Marinić, dr.sc. Sunčica
Medicinski fakultet Sveučilišta u Rijeci Kolegij: BIOKEMIJA Voditelj: prof. dr.sc. Robert Domitrović Suradnici: prof.dr.sc Jadranka Varljen, doc.dr.sc. Dijana Detel, doc.dr.sc. Jelena Marinić, dr.sc. Sunčica
IZVEDBENI NASTAVNI PLAN
 Medicinski fakultet Sveučilišta u Rijeci Kolegij: Biokemija Voditelj: Doc. dr.sc. Dijana Detel Suradnici: Prof.dr.sc. Robert Domitrović, doc.dr.sc. Jelena Marinić, dr.sc. Sunčica Buljević Katedra: Zavod
Medicinski fakultet Sveučilišta u Rijeci Kolegij: Biokemija Voditelj: Doc. dr.sc. Dijana Detel Suradnici: Prof.dr.sc. Robert Domitrović, doc.dr.sc. Jelena Marinić, dr.sc. Sunčica Buljević Katedra: Zavod
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Biohemija proteina i nukleinskih kiselina
 Biohemija proteina i nukleinskih kiselina Biohemija proteina i nukleinskih kiselina Predavanja: Profesor Vesna Niketić vniketic@chem.bg.ac.rs Docent Natalija Polović polovicn@chem.bg.ac.rs Vežbe: Dr Natalija
Biohemija proteina i nukleinskih kiselina Biohemija proteina i nukleinskih kiselina Predavanja: Profesor Vesna Niketić vniketic@chem.bg.ac.rs Docent Natalija Polović polovicn@chem.bg.ac.rs Vežbe: Dr Natalija
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
IZVEDBENI NASTAVNI PLAN
 Medicinski fakultet Sveučilišta u Rijeci Kolegij: Biokemija II Voditelj: red. prof. dr. sc. Robert Domitrović Suradnici: doc. dr. sc. Dijana Detel, doc. dr. sc. Jelena Marinić, dr. sc. Sunčica Buljević,
Medicinski fakultet Sveučilišta u Rijeci Kolegij: Biokemija II Voditelj: red. prof. dr. sc. Robert Domitrović Suradnici: doc. dr. sc. Dijana Detel, doc. dr. sc. Jelena Marinić, dr. sc. Sunčica Buljević,
CIKLUS LIMUNSKE KISELINE (CLK)
 SVEUČILIŠTE U ZAGREBU FAKULTET KEMIJSKOG INŽENJERSTVA I TEHNOLOGIJE CIKLUS LIMUNSKE KISELINE (CLK) Doc. dr. sc. Dragana Vuk Metabolička sudbina piruvata 1. Oksidacijska dekarboksilacija piruvata 2. Ciklus
SVEUČILIŠTE U ZAGREBU FAKULTET KEMIJSKOG INŽENJERSTVA I TEHNOLOGIJE CIKLUS LIMUNSKE KISELINE (CLK) Doc. dr. sc. Dragana Vuk Metabolička sudbina piruvata 1. Oksidacijska dekarboksilacija piruvata 2. Ciklus
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Lobulus: Funkcionalna jedinica jetre
 Fiziologija jetre ANATOMIJA JETRE PORTNI HILUS Lobulus: Funkcionalna jedinica jetre Nepravilna poliedarna prizma ( 0.7x2.0 mm) v.portae a.hepatica laminae hepatis,lamina terminalis Portna trijada Žučni
Fiziologija jetre ANATOMIJA JETRE PORTNI HILUS Lobulus: Funkcionalna jedinica jetre Nepravilna poliedarna prizma ( 0.7x2.0 mm) v.portae a.hepatica laminae hepatis,lamina terminalis Portna trijada Žučni
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
NIVOI ORGANIZACIJE I EKSPRESIJE GENOMA
 NIVOI ORGANIZACIJE I EKSPRESIJE GENOMA ANIMACIJE!!! REPLIKACIJA https://www.youtube.com/watch?v=tnkwgcfphqw TRANSKRIPCIJA https://www.youtube.com/watch?v=jqiwwjqf5d0 TRANSKRIPCIJA I TRANSLACIJA https://www.youtube.com/watch?v=-k8y0atkkai
NIVOI ORGANIZACIJE I EKSPRESIJE GENOMA ANIMACIJE!!! REPLIKACIJA https://www.youtube.com/watch?v=tnkwgcfphqw TRANSKRIPCIJA https://www.youtube.com/watch?v=jqiwwjqf5d0 TRANSKRIPCIJA I TRANSLACIJA https://www.youtube.com/watch?v=-k8y0atkkai
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
HORMONSKA REGULACIJA METABOLIZMA
 HORMONSKA REGULACIJA METABOLIZMA HORMONSKA REGULACIJA METABOLIZMA - Definicija - Bazalni metabolizam - Faktori od uticaja: METABOLIZAM - Zastupljenost skeletnih mišića u ukupnoj telesnoj masi - Uzrast
HORMONSKA REGULACIJA METABOLIZMA HORMONSKA REGULACIJA METABOLIZMA - Definicija - Bazalni metabolizam - Faktori od uticaja: METABOLIZAM - Zastupljenost skeletnih mišića u ukupnoj telesnoj masi - Uzrast
Organele života i smrti
 MITOHONDRIJE Organele života i smrti OTKRIĆE MITOHONDRIJA 1857. Albert Kolliker uređeni nizovi granula u mišićnim ćelijama 1893. Richard Altman bioblasti vrsta bakterija? 1. menjaju oblik 2. umnožavaju
MITOHONDRIJE Organele života i smrti OTKRIĆE MITOHONDRIJA 1857. Albert Kolliker uređeni nizovi granula u mišićnim ćelijama 1893. Richard Altman bioblasti vrsta bakterija? 1. menjaju oblik 2. umnožavaju
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
 100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
IZVEDBENI NASTAVNI PLAN
 Sveučilište u Rijeci Medicinski fakultet University of Rijeka Faculty of Medicine Braće Branchetta 20 51000 Rijeka CROATIA Phone: +385 (0)51 651 111 www.medri.uniri.hr Kolegij: Biokemija Voditelj: doc.dr.sc.
Sveučilište u Rijeci Medicinski fakultet University of Rijeka Faculty of Medicine Braće Branchetta 20 51000 Rijeka CROATIA Phone: +385 (0)51 651 111 www.medri.uniri.hr Kolegij: Biokemija Voditelj: doc.dr.sc.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
CILJNA MESTA DEJSTVA LEKOVA
 FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
FARMACEUTSKA HEMIJA 1 CILJNA MESTA DEJSTVA LEKVA Predavač: Prof. dr Slavica Erić Ciljna mesta dejstva leka CILJNA MESTA NA MLEKULARNM NIVU: lipidi (lipidi ćelijske membrane) ugljeni hidrati (obeleživači
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
3/25/2016. Hemijske komponente ćelije
 Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA
 Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
TRANSLACIJA. Doc. dr Snežana Marković
 TRANSLACIJA Doc. dr Snežana Marković Institut za biologiju i ekologiju Prirodno-matematički fakultet Univerzitet u Kragujevcu BIOSINTEZA PROTEINA - TRANSLACIJA U toku translacije dolazi do specifičnog
TRANSLACIJA Doc. dr Snežana Marković Institut za biologiju i ekologiju Prirodno-matematički fakultet Univerzitet u Kragujevcu BIOSINTEZA PROTEINA - TRANSLACIJA U toku translacije dolazi do specifičnog
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
METABOLIZAM PROTEINA
 METABOLIZAM PROTEINA PREGLED METABOLIZMA AMINO KISELINA Hranom unijeti proteini se razgrađuju do amino kiselina, koje se apsorbuju, prenose cirkulacijom i preuzimaju u ćelije različitih tkiva. Amino kiseline
METABOLIZAM PROTEINA PREGLED METABOLIZMA AMINO KISELINA Hranom unijeti proteini se razgrađuju do amino kiselina, koje se apsorbuju, prenose cirkulacijom i preuzimaju u ćelije različitih tkiva. Amino kiseline
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore
 Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore OLIMPIJADA ZNANJA 2018. Rješenja zadataka iz HEMIJE za IX razred osnovne škole 1. Koju zapreminu, pri standardnim uslovima, zauzimaju
Prirodno-matematički fakultet Društvo matematičara I fizičara Crne Gore OLIMPIJADA ZNANJA 2018. Rješenja zadataka iz HEMIJE za IX razred osnovne škole 1. Koju zapreminu, pri standardnim uslovima, zauzimaju
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama. Hloroplast
 Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama Hloroplast Procesom ćelijskog disanja deponovana energija u šećerima erima prevodi se u ATP i druge energetske metabolite. Istovremeno se
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama Hloroplast Procesom ćelijskog disanja deponovana energija u šećerima erima prevodi se u ATP i druge energetske metabolite. Istovremeno se
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
METABOLIZAM PROTEINA
 METABOLIZAM PROTEINA PREGLED METABOLIZMA AMINO KISELINA Hranom unijeti proteini se razgrađuju do amino kiselina, koje se apsorbuju, prenose cirkulacijom i preuzimaju u ćelije različitih tkiva. Amino kiseline
METABOLIZAM PROTEINA PREGLED METABOLIZMA AMINO KISELINA Hranom unijeti proteini se razgrađuju do amino kiselina, koje se apsorbuju, prenose cirkulacijom i preuzimaju u ćelije različitih tkiva. Amino kiseline
OSNOVI ELEKTRONIKE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA
 ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
ELEKTROTEHNIČKI FAKULTET U BEOGRADU KATEDRA ZA ELEKTRONIKU OSNOVI ELEKTRONIKE SVI ODSECI OSIM ODSEKA ZA ELEKTRONIKU LABORATORIJSKE VEŽBE VEŽBA BROJ 1 OSNOVNA KOLA SA DIODAMA Autori: Goran Savić i Milan
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
METABOLIZEM OGLJIKOVIH HIDRATOV
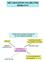 METABOLIZEM OGLJIKOVIH HIDRATOV KAKO CELICA DOBI GLUKOZO IN OSTALE MONOSAHARIDE? HRANA ZNOTRAJCELIČNI GLIKOGEN ali ŠKROB razgradnja s prebavnimi encimi GLUKOZA in ostali monosaharidi fosforilitična cepitev
METABOLIZEM OGLJIKOVIH HIDRATOV KAKO CELICA DOBI GLUKOZO IN OSTALE MONOSAHARIDE? HRANA ZNOTRAJCELIČNI GLIKOGEN ali ŠKROB razgradnja s prebavnimi encimi GLUKOZA in ostali monosaharidi fosforilitična cepitev
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Biohemija nukleinskih kiselina. Genetska informacija
 Biohemija nukleinskih kiselina Genetska informacija deoksiribonukleinske kiseline (DNK) ribonukleinske kiseline (RNK) DNK je nosilac naslednih informacija u ćeliji, dok RNK učestvuju u prenošenju tih informacija
Biohemija nukleinskih kiselina Genetska informacija deoksiribonukleinske kiseline (DNK) ribonukleinske kiseline (RNK) DNK je nosilac naslednih informacija u ćeliji, dok RNK učestvuju u prenošenju tih informacija
Regulacija ekspresije gena kod prokariota
 Regulacija ekspresije gena kod prokariota Bakterije Jednoćelijski organizmi koji nemaju jedro i druge organele. Geni u najvećem broju slučajeva ne poseduju introne i većina gena organizovana je u operone.
Regulacija ekspresije gena kod prokariota Bakterije Jednoćelijski organizmi koji nemaju jedro i druge organele. Geni u najvećem broju slučajeva ne poseduju introne i većina gena organizovana je u operone.
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
METABOLIZAM UGLJENIH HIDRATA
 METABOLIZAM UGLJENIH HIDRATA 14.02.2018. Zbirni pregled glikolize i ciklusa trikarboksilnih kiselina Glikoliza omogućava oksidaciju glukoze u uslovima sa ili bez O 2. U uslovima prisustva O 2,
METABOLIZAM UGLJENIH HIDRATA 14.02.2018. Zbirni pregled glikolize i ciklusa trikarboksilnih kiselina Glikoliza omogućava oksidaciju glukoze u uslovima sa ili bez O 2. U uslovima prisustva O 2,
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
uniformno konvergira na [ 2, 2]?
![uniformno konvergira na [ 2, 2]? uniformno konvergira na [ 2, 2]?](/thumbs/69/60733220.jpg) Građevinski fakultet Univerziteta u Beogradu 27.6.2015. ZAVRXNI ISPIT IZ MATEMATIKE 3 Prezime i ime: Broj indeksa: 1. Definisati diferencijabilnost funkcije u = u(x, y, z) u taqki (0, 1, 2). 2. Definisati
Građevinski fakultet Univerziteta u Beogradu 27.6.2015. ZAVRXNI ISPIT IZ MATEMATIKE 3 Prezime i ime: Broj indeksa: 1. Definisati diferencijabilnost funkcije u = u(x, y, z) u taqki (0, 1, 2). 2. Definisati
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
KATABOLIZAM UGLJENIH HIDRATA
 KATABOLIZAM UGLJENIH HIDRATA 20.02.2018. SINTEZA I RAZGRADNJA GLIKOGENA Glikogen je homopolimer glukoze, oblik u kojem se ugljeni hidrati čuvaju u životinja. Čuvanjem glukoze u obliku glikogena
KATABOLIZAM UGLJENIH HIDRATA 20.02.2018. SINTEZA I RAZGRADNJA GLIKOGENA Glikogen je homopolimer glukoze, oblik u kojem se ugljeni hidrati čuvaju u životinja. Čuvanjem glukoze u obliku glikogena
STVARANJE VEZE C-C POMO]U ORGANOBORANA
![STVARANJE VEZE C-C POMO]U ORGANOBORANA STVARANJE VEZE C-C POMO]U ORGANOBORANA](/thumbs/55/37829094.jpg) STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Inzulin, glukagon i. Prof. dr. Zoran Valić Katedra za fiziologiju Medicinski fakultet u Splitu
 Inzulin, glukagon i šećerna erna bolest Prof. dr. Zoran Valić Katedra za fiziologiju Medicinski fakultet u Splitu sudjelovanje u probavi dva važna hormona: inzulin i glukagon (važni za regulaciju metabolizma
Inzulin, glukagon i šećerna erna bolest Prof. dr. Zoran Valić Katedra za fiziologiju Medicinski fakultet u Splitu sudjelovanje u probavi dva važna hormona: inzulin i glukagon (važni za regulaciju metabolizma
UZDUŽNA DINAMIKA VOZILA
 UZDUŽNA DINAMIKA VOZILA MODEL VOZILA U UZDUŽNOJ DINAMICI Zanemaruju se sva pomeranja u pravcima normalnim na pravac kretanja (ΣZ i = 0, ΣY i = 0) Zanemaruju se svi vidovi pobuda na oscilovanje i vibracije,
UZDUŽNA DINAMIKA VOZILA MODEL VOZILA U UZDUŽNOJ DINAMICI Zanemaruju se sva pomeranja u pravcima normalnim na pravac kretanja (ΣZ i = 0, ΣY i = 0) Zanemaruju se svi vidovi pobuda na oscilovanje i vibracije,
ENZIMI KAO CILJNA MESTA DEJSTVA LEKOVA. Enzimi kao ciljna mesta dejstva lekova
 FARMACEUTSKA HEMIJA 1 ENZIMI KAO CILJNA MESTA DEJSTVA LEKOVA Predavač: Prof. dr Slavica Erić Enzimi kao ciljna mesta dejstva lekova -enzimi učestvuju u hemijskoj reakciji ali pri tome ostaju nepromenjeni
FARMACEUTSKA HEMIJA 1 ENZIMI KAO CILJNA MESTA DEJSTVA LEKOVA Predavač: Prof. dr Slavica Erić Enzimi kao ciljna mesta dejstva lekova -enzimi učestvuju u hemijskoj reakciji ali pri tome ostaju nepromenjeni
Osnovne karakteristike 3-D strukture molekula DNK i RNK
 Osnovne karakteristike 3-D strukture molekula DNK i RNK Rendgenska strukturna analiza (vlakana) DNK Watson-Crickov model (B) DNK Zašto dvostruki heliks? Polimorfizam DNK: kanonske (standardne/prosečne)
Osnovne karakteristike 3-D strukture molekula DNK i RNK Rendgenska strukturna analiza (vlakana) DNK Watson-Crickov model (B) DNK Zašto dvostruki heliks? Polimorfizam DNK: kanonske (standardne/prosečne)
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
