NANOTEHNOLOGIJA. Dr. Maja Remškar; Nanodelci in nanovarnost, 2009 NANODELCI
|
|
|
- Σαλώμη Δαγκλής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 NANOTEHNOLOGIJA Dr. Maja Remškar; Nanodelci in nanovarnost, 2009 NANODELCI
2 Kaj so nanodelci?* Nanodelci so drobni skupki materiala,ki so (v vsaj eni dimenziji) manjši od 100 nanometrov = 0.1mikrometra. V obliki tanke plasti, ali pa tanki igličasti kristali ali nitke. Nanodelci so premajhni, da bi jih videli s prostim očesom!
3 Da delec dobi predpono nano- mora biti vsaj v eni dimenziji manjši od 100nm. Nanodelci so lahko zelo tanka vlakna, ki so dolga tudi več metrov, lahko so to igličasti kristali ali nitke, pa tudi majhne kroglice in zrnca. Pri samih nanodelcih in v materialih, ki le-te vsebujejo, so opazili lastnosti, ki se močno razlikujejo od lastnosti, ki jih imajo večji delci enake kemijske sestave. Fizikalno-kemijske lastnosti, ki so v nanodelcih drugačne, so spremenjena kemična reaktivnost, električna prevodnost, termična razteznost, optična prevodnost, trdnost... Posamezni nanodelci nimajo vseh teh lastnosti, je pa pogosto, da ima delec na nanoskali zgoraj navedene značilnosti drugačne kot delec, ki je za velikostni red ali dva večji. Razmerje med površino in prostornino delca je zelo pomemben podatek, saj kaže kako (kemično) reaktiven je delec. Večje kot je razmerje, bolj je delec reaktiven. Kemijske sile med delci so posledica reaktivnosti površinskih atomov. Če je atomov na površini več oz. imajo atomi več prostih vezi, se delci lahko hitreje in močneje vežejo.
4 Dejstvo je, da varnih nanodelcev ni. Je pa zelo težko reči, kakšen vpliv imajo na okolje. Njihova glavna lastnost je, da so majhni in lahki, da lahko dolgo časa lebdijo v zraku. Zaradi velikega števila atomov na površini, ki nimajo vseh sosednjih atomov in zato tudi ne zapolnjenih kemijskih vezi, imajo nanodelci povečano kemijsko aktivnost. Pomembna je seveda tudi kemijska sestava. Poleg namensko narejenih nanodelcev moramo biti pozorni tudi na nenamensko proizvedene nanodelce, še posebej v gradbeništvu, ki nastajajo kot stranski produkt proizvodnje oz. rušenja objektov, betoniranja, brušenja, rezanja, mletja, lomljenja, menjave kritin (posebno azbestnih) in tudi brušenja sten za končno obdelavo. Pri vseh teh postopkih nastajajo nanodelci, ki gredo v prostor. V človeško telo pridejo nanodelci skozi kožo, prebavila in predvsem dihala. V notranjih prostorih je precej velika koncentracija nanodelcev že zaradi t.i. ozadja. Ti delci, ki so vedno prisotni v zraku, so predvsem posledica gorenja in izpuhov avtomobilskih motorjev, predvsem dizelskih. Naravno proizvedeni nanodelci nastanejo kot posledica vulkanskih izbruhov, erozij ali puščavskega prahu. Tudi virusi so naravno proizvedeni nanodelci, vendar je njihov delež v prostoru precej manjši od delcev zaradi gorenja. V nekem stanovanju v mestu je od 10 tisoč do 40 tisoč nanodelcev v cm3 zraka. Na podeželju je to število nekoliko manjše. Nanodelci pridejo v prostor tudi iz odprtih kaminov, zelo priljubljene so tudi sveče (v lokalih in doma), ki sproščajo zelo velike količine nanodelcev, premera nm. Dokazano je, da nanodelci ogljika skrajšujejo življenjsko dobo in povzročajo bolezni srca in ožilja. Kajenje je, kot vemo, toksično, kancerogeno, v cm3 izdihanega zraka kadilcev je 100 milijonov nanodelcev. V vdihanem zraku kadilcev so nanodelci mešani z večjimi delci, ki se tudi nalagajo v pljučih in so kemijsko manj aktivni, vendar so veliko bolj obremenilni zaradi nalaganja v pljučih. Toksično je tudi pasivno kajenje, kjer je delež nanodelcev v vdihanem zraku povečan. Še posebej so občutljivi otroci. V prostoru, kjer je nekdo kadil, ostajajo nanodelci v ozračju tudi po več tednov. Največji onesnaževalci, predvsem v prometu so dizelski avtomobili, poleg avtomobilov za zasebno rabo tudi vsa tovorna vozila na dizelski pogon. Potrebno pa je poudariti to, da se nanodelcev ne smemo bati in se»skrivati«pred njimi. Potrebno je, da z njimi živimo v sožitju, saj se jim popolnoma izogniti ne moremo. Nimajo pa samo negativnih učinkov, obstajajo tudi raziskave o učinku nanodelcev na npr. kožnega raka. Žal pa to področje ni dobro raziskano zato ne vemo, kaj je pravzaprav res
5 Vsi zelo majhni delci niso nevarni človeku, razen če pridejo v organizem v prevelikem številu. Človeško telo je razvilo obrambne mehanizme pred raznimi boleznimi, virusi in majhnimi delci. Toksični so tisti delci, ki ob prihodu v telo kemijsko reagirajo s posameznimi celicami, jih spremenijo ali uničijo, ali pa spremenijo ali ovirajo njihovo delovanje. Majhni delci lahko poškodujejo epitelijsko tkivo, povzročijo vnetja, alergije in odziv celic na oksidativni stres. V človeško telo lahko delci pridejo skozi kožo, prebavila in predvsem dihala. Delci lahko tudi preidejo skozi celične membrane. Pri težje topnih delcih, kot so recimo kovinski oksidi, je odstranjevanje delcev iz organizma precej zapleteno, saj se začnejo zbirati v ledvicah. Delci lahko tudi pridejo v krvni obtok ter možgane. Kot eden izmed najbolj prepoznavnih primerov ogrožanja zdravja se pogosto omenja azbest. Njegova toksičnost poleg reaktivnosti je v tem, da se material pogosto pojavlja v obliki vlaken, ki so lahko široka zgolj 10 nm, ob tem pa dolga tudi po več μm. Taka vlakna lahko kljub svoji velikosti pridejo globoko v pljuča.
6 Nanohrana je beseda, s katero označujemo hrano, ki je bila pridelana, predelana ali pakirana s pomočjo nanotehnologije ali v katero so primešani nanomateriali.to ni več stvar znanstvene fantastike, ampak je že na prodajnih policah, ne da bi bilo na izdelkih sploh označeno, da vsebujejo nanomateriale. Nekaj primerov uporabe nanotehnologije v prehrani: nanosrebro uporabljajo zaradi njegove antibakterijske aktivnosti, na primer v embalaži za hrano, v hladilnikih, lončkih za otroško hrano in čaj, kuhinjski posodi,.. ; nanodelci silicijevega oksida so dodani polimernim kompozitom, da povečajo njihovo gostoto in preprečijo prepustnost plastike za kisik ter tako podaljšajo obstojnost hrane; nanokroglice škroba z velikostjo od 50 do 150 nanomestrov so dodelane lepilu za embalažo, saj s svojo kar 400-krat večjo površino od običajnega škroba za pripravo zahtevajo manj vode in ustrezno krajši čas za sušenje; nanodelci železa so zaradi povečane reaktivnosti in biološke koristnosti dodelani visokoenergijskim pijačam; Aluminijevi silikati se uporabljajo za preprečitev zlepljanja v procesu pridelave hrane v prašni obliki. Nanotehnologi so razvili užitne nanoprevleke z debelino 5nm, ki so povsem prosojne za človeško oko. Te prevleke se lahko nanašajo na meso, sire, sadje in zelenjavo, da se prepreči izguba vlage in zmanjša vpliv ozračja. So tudi nosilke barv, okusa, vsebujejo antioksidante, encime in podaljšajo življenjsko dobo izdelka, tudi po tem, ko je bila vidna embalaža odprta. V prehrani se znajde veliko delcev tudi kot posledica obrabe orodij pri pridelavi hrane in zaradi onesnaženega okolja med pridelavo. Povsem vsakdanje brušenje noža, proizvede veliko količino nanodelcev v ozračju. Nekatere nanodelce lahko tudi jemo, a ti dokaj hitro pridejo v stik s slino in želodčno sluznico ter jih telo praviloma lažje izloči kot tiste, ki se z vdihavanjem nabirajo v pljučih in niso biološko razgradljivi
7 debelina človeškega lasu potem, ko bi ga podolgem razcepili na nitk.
8 Glavna orodja nanotehnologije in nekatere možnosti njihove uporabe* nanopore (nosilci zdravil oziroma aktivnih snovi v reverzibilnih baterijah), nanocevke (nova generacija maziv, ojačitvena vlakna), nanodelci (samočistilni premazi,zaščitni premazi, barve), nanokristali (keramika, prikazalniki na poljsko emisijo), nanovlakna (tekstil, neprebojne tkanine), Ogljikove nanocevke so bile odkrite leta 1991 in so takoj vzbudile široko paleto napovedi možne uporabe. nanovrste (senzorika, sončne celice), nanoelektronika (tranzistor na tunelski efekt), nanotipala (mikroskopija, biosenzorika), nanoročice (detekcija razstreliv), nanolupine (prenos zdravilnih učinkovin), nanotrakovi (električni prevodniki), nanokompoziti (samomazalne prevleke, sončne celice, umetne mišice) itd. Razvoj novih orodij in njihove uporabe je silovit. Vedno več je tudi predvidevanj, da se bodo v prihodnosti pojavile povsem drugačne rešitve v nanoelektroniki, shranjevanju informacij, pridobivanju energije na osnovi bioloških procesov itd.
9 Za zgodnje odkrivanje raka so v razvoju senzorji, ki delujejo na osnovi nanomaterialov. Gre za drobne nitke ali cevke, ki se zaradi vezave na določene molekule upognejo. Z merjenjem tega upogiba bi bilo mogoče odkriti rakave spremembe že na celični ravni. Nanomedicina Nanorobotki, ki bi jih preprosto vbrizgali v kri in bi sami našli obolela mesta, postavili diagnozo, pozdravili okvaro in potem še nadzorovali, da se bolezen ne bi ponovila, so sanje nanomedicine. Razvoj nanodelcev kot nosilcev zdravilnih učinkovin ali kot senzorjev sprememb v organizmu spada v uresničljivi del teh sanj. Nanodelci so zaradi izjemne majhnosti zelo uporabni v onkologiji, za zdaj zlasti pri slikanju in diagnostiki, saj povečajo kontrast na slikah tumorjev, posnetih z jedrsko magnetno resonanco ali z rentgenskim slikanjem.
10 Izvor nanodelcev in kje jih* najdemo: naravni: erozija, puščavski prah, vulkanski izbruhi, virusi; proizvedeni: namensko proizvedeni: kozmetika, hrana, detergenti, tekstil, zaščitne vodoodbojne prevleke; nenamensko proizvedeni: stranski produkt pri industrijski proizvodnji (mletje, varjenje, brušenje, gradbeništvo, tehnologije razpršil; izgorevanje biomase in fosilnih goriv; izpuh motorjev z notranjim izgorevanjem, še zlasti dizelskih motorjev.
11
12 Posebne lastnosti nanodelcev: povečana kemična aktivnost, spremenjene fizikalne lastnosti, velika površina glede na maso, lebdenje v zraku; zaradi termične energije dosegajo hitrosti do več metrov na sekundo in trkajo z molekulami zraka, številčnost nanodelcev v cm3: pisarna: (deset do štirideset tisoč), varjenje: (4 milijoni), brušenje: (dvesto tisoč), izdih kadilca: > (sto milijonov).
13 Zakaj je velikost tako pomembna?* 70 nm delci prodrejo v pljučne mešičke. 50 nm delci prodrejo v celice. 30 nm delci prodrejo v celično jedro. ni podatkov o potovanju delcev, ki so manjši od 20 nm.
14 Kaj se zgodi, če nanodelci pridejo v živ organizem?* V človeško telo lahko delci pridejo skozi kožo, prebavila in predvsem dihala. Na vse tri načine lahko pridejo v krvni obtok, ki jih raznese po vsem telesu. Vse več je izsledkov, da lahko nanodelci iz krvnega obtoka ali prek živčnih poti zaidejo tudi v možgane. Povečane koncentracije nevrodegenerativnih bolezni v okoljih, obremenjenih z visokimi koncentracijami ultrafinih prašnih delcev, kažejo na možnost vpliva teh delcev v ozračju na razvoj nekaterih obolenj, kot sta npr. Parkinsonova in Alzheimerjeva bolezen.
15 Ali veste pri zgorevanju navadne sveče pride do sproščanja nanodelcev z velikostjo do 30 nanometrov.
16 Vsakih dodatnih 10 μg ogljika v m3 zraka za en odstotek poveča smrtnost zaradi bolezni srca. Skupki nanodelcev ogljika, ki nastajajo pri zgorevanju. Ali veste da naj bi pri gorenju vseh goriv, ki vsebujejo ogljik (npr. biomase, fosilna goriva), prihajalo do popolne oksidacije ogljika v ogljikov dioksid. Vendar popolne oksidacije v praksi ni, del ogljika ostane neoksidiran in se združuje v zelo majhne skupke z velikostjo okrog 10 nanometrov. Ti skupki se nato združujejo v nekoliko večje, do 100 nanometrov, in se izločajo v okolje okrog kurišča.
17 Ali veste da pri uporabi pirotehnike in razstreliv, uporabljenih v rudarstvu, gradbeništvu, pri vojaških vajah in vojaških operacijah nanodelci dobijo veliko hitrost vstran od središča eksplozije, kar jih med seboj oddalji in prepreči združevanje in s tem ohranja njihovo povečano kemično aktivnost.
18 Ali veste da je poleg gorenja največji onesnaževalec ozračja z nanodelci promet. Večina delcev v izpuhu avtomobilov ima velikost pod 100 nm, velik del celo pod 10 nm. Živeti v bližini prometnic ni zdravo ravno zaradi ogljika. Dizelski motorji so veliki onesnaževalci ozračja z nanodelci. Pri bencinskih motorjih je manj nanodelcev in manj nenasičenih strupenih dušikovih oksidov, medtem ko je prednost dizelskih motorjev ta, da proizvajajo manj ogljikovega dioksida.
19
20 Računalniška simulacija lotusovega površja in kapljica vode na katero se je nalepila umazanija. Lotusov list Najlepši primer hidrofobne površine v naravi je lotosov list, ki je izredno hidrofoben oz. skoraj že superhidrofoben. Čeprav raste v blatnem ribniškem okolju je vedno čist, saj se umazanija ponavadi v obliki vodnih raztopin sploh ne prime na površino. Kontaktna površina z listom je samo od 2 do 3% površine dežne kaplje. Zato da se list čisti sam je kriv hidrofoben zgornji sloj na listu in sama sestava lotusovega lista. Ta ima obliko igličastega sloja-površino pokrivajo strukture, ki imajo obliko hribčka in so visoke in široke okoli 10μm. Na teh igličastih strukturah pa se nahajajo še od nekaj nanometrov do enega mikrometra velike cevaste tvorbe iz hidrofobnega materiala. Taka površina kapljici ne ponuja nobenega dobrega oprijemališča zato se kapljica odkotali z nje in pri tem nase prilepi umazanijo z lista. Čeprav je fenomen lotosovega list znan in čaščen v Aziji že preko let sta botanika C. Neinhuis in W. Barthlott šele v 70-desetih ugotovila posebno sestavo lotosove površine. V zadnjih desetletjih se ta koncept uporablja tudi pri razvijanju materialov s hidrofobni mi lastnostmi.
21 FOTOSINTEZA!
22 Nanotehnologija proizvodna tehnologija, s katero dosežemo izredno natančnost in ultramajhne dimenzije. Nanotehnologija nam omogoča izdelavo materialov ali naprav, ki so lažje, hitrejše, močnejše, ki imajo popolnoma nove ali pa dodatne, specifične lastnosti.
23 Nanomateriali v površinski obdelavi lesa nanoaditivi boljša odpornost na abrazijo, odpornost na zlepljanje, odpornost na kemikalije, hitrejše sušenje in hitrejše utrjevanje. nanooksidi za zaščito lesa pred UV žarki; nano TiO2, nano ZnO, izboljšanje transparentnosti, stabilnosti, učinkovitosti in zniževanja stroškov proizvodnje. Z uporabo različnih nanodelcev bi tako dosegali različne efekte in izboljšave lastnosti ob znatno zmanjšani količini delcev in večji stabilnosti sistema. Kemično vezani nanodelci tudi ne morejo predstavljati nikakršne nevarnosti za ljudi.
24 NEVARNOSTI NANOTEHNOLOGIJ Nevarnost nano delcev narašča s padanjem njihove velikosti. Najnevarnejši so prosti nanodelci velikosti pod 50 nm, ker zlahka prodrejo skozi celično steno. uporaba je do neke mere lahko problematična za same proizvajalce, ki take materiale vgrajujejo v premaz, zaradi varovanja zaposlenih v delovnem okolju. Ko pa so nanodelci vgrajeni v premaz v večini primerov ne bi smelo biti kakih nepredvidljivih posledic za uporabnike premazov, saj so nanodelci v premazu vezani na polimerne matrice in ni verjetno, da bi se v dobi uporabe lahko sproščali v okolje v neaglomerirani obliki.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
The Thermal Comfort Properties of Reusable and Disposable Surgical Gown Fabrics Original Scientific Paper
 24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Effect of Fibre Fineness on Colour and Reflectance Value of Dyed Filament Polyester Fabrics after Abrasion Process Izvirni znanstveni članek
 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe 8 Učinek finosti filamentov na barvne vrednosti in odbojnost svetlobe barvanih poliestrskih filamentnih tkanin po drgnjenju July November
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
LIPIDI IN PREHRANA ŠPORTNIKA. Žiga Drobnič, Filip Zupančič, 1.b
 LIPIDI IN PREHRANA ŠPORTNIKA Žiga Drobnič, Filip Zupančič, 1.b Lipide delimo na: maščobe (masti,olja) - kombinacija molekule glicerola s tremi dolgoverižnimi organskimi kislinami - maščobnimi kislinami
LIPIDI IN PREHRANA ŠPORTNIKA Žiga Drobnič, Filip Zupančič, 1.b Lipide delimo na: maščobe (masti,olja) - kombinacija molekule glicerola s tremi dolgoverižnimi organskimi kislinami - maščobnimi kislinami
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Zemlja in njeno ozračje
 Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
2.1.2 Sestava mleka in primerjava z ovčjim in kravjim mlekom
 8 2.1.2 Sestava mleka in primerjava z ovčjim in kravjim mlekom Sestava mleka različnih sesalcev se močno razlikuje po količini posameznih sestavin, po njihovih lastnostih in porazdelitvi ter je povezana
8 2.1.2 Sestava mleka in primerjava z ovčjim in kravjim mlekom Sestava mleka različnih sesalcev se močno razlikuje po količini posameznih sestavin, po njihovih lastnostih in porazdelitvi ter je povezana
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
vaja Izolacija kromosomske DNA iz vranice in hiperkromni efekt. DNA RNA Protein. ime deoksirbonukleinska kislina ribonukleinska kislina
 transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
FLEKSIBILNA ZVOČNA IZOLACIJA ZA AKUSTIČNO UDOBNOST
 Powered by TCPDF (www.tcpdf.org) FLEKSIBILNA ZVOČNA IZOLACIJA ZA AKUSTIČNO UDOBNOST Specialno namenjena za zmanjšanje hrupa cevi odpadnih vod in deževnice Tanka in učinkovita zvočna izolacija z odličnimi
Powered by TCPDF (www.tcpdf.org) FLEKSIBILNA ZVOČNA IZOLACIJA ZA AKUSTIČNO UDOBNOST Specialno namenjena za zmanjšanje hrupa cevi odpadnih vod in deževnice Tanka in učinkovita zvočna izolacija z odličnimi
MIKROSKOP IN MIKROSKOPIRANJE
 Gimnazija Murska Sobota POROČILO K LABORATORIJSKI VAJI MIKROSKOP IN MIKROSKOPIRANJE Sandra Gorčan, 4.c prof. Edita Vučak Murska Sobota,8.10.2003 UVOD: Mikroskop je naprava, ki služi za gledanje mikroskopsko
Gimnazija Murska Sobota POROČILO K LABORATORIJSKI VAJI MIKROSKOP IN MIKROSKOPIRANJE Sandra Gorčan, 4.c prof. Edita Vučak Murska Sobota,8.10.2003 UVOD: Mikroskop je naprava, ki služi za gledanje mikroskopsko
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Polimerni nanokompoziti z glinenimi delci
 Polimerni nanokompoziti z glinenimi delci M. Huskić Kemijski inštitut Laboratorij za polimerno kemijo in tehnologijo Glineni materiali Gline: Alumosilikati, ki vsebujejo še Na, Ca, Mg, Fe, Zn Naravni glineni
Polimerni nanokompoziti z glinenimi delci M. Huskić Kemijski inštitut Laboratorij za polimerno kemijo in tehnologijo Glineni materiali Gline: Alumosilikati, ki vsebujejo še Na, Ca, Mg, Fe, Zn Naravni glineni
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
NALOGE K PREDMETU DELOVNO OKOLJE -PRAH
 NALOGE K PREDMETU DELOVNO OKOLJE -PRAH 1. Kakšna je povprečna hitrost molekul CO 2 pri 25 C? 2. Kakšna je povprečna hitrost molekul v zraku pri 25 C, kakšna pri 100 C? M=29 g/mol 3. Pri kateri temperaturi
NALOGE K PREDMETU DELOVNO OKOLJE -PRAH 1. Kakšna je povprečna hitrost molekul CO 2 pri 25 C? 2. Kakšna je povprečna hitrost molekul v zraku pri 25 C, kakšna pri 100 C? M=29 g/mol 3. Pri kateri temperaturi
Zemlja in njeno ozračje
 Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
Zemlja in njeno ozračje Pojavi v ozračju se dogajajo na zelo različnih časovnih in prostorskih skalah Prostorska skala Pojav 1 cm Turbulenca, sunki vetra 1 m 1 km 10 km 100 km 1000 in več km Tornadi Poplave,
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
za delo z nevarnimi kemičnimi snovmi I. SPLOŠNI UKREPI ZA VARNO DELO S KEMIČNIMI SNOVMI
 Na podlagi 14. člena pravilnika o varovanju delavcev pred tveganji zaradi izpostavljenosti kemičnim snovem pri delu (Uradni list RS, št. 100/01) izdaja minister za delo, družino in socialne zadeve P R
Na podlagi 14. člena pravilnika o varovanju delavcev pred tveganji zaradi izpostavljenosti kemičnim snovem pri delu (Uradni list RS, št. 100/01) izdaja minister za delo, družino in socialne zadeve P R
Katedra za farmacevtsko kemijo. Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks. 25/11/2010 Vaje iz Farmacevtske kemije 3 1
 Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
MERJENJE Z MIKROSKOPOM
 1. laboratorijska vaja MERJENJE Z MIKROSKOPOM Uvod Mikroskop Mikroskop (iz grških besed mikrós majhno in skopeîn gledati, videti) je posebna optična naprava, ki je sestavljena iz sistema leč, za opazovanje
1. laboratorijska vaja MERJENJE Z MIKROSKOPOM Uvod Mikroskop Mikroskop (iz grških besed mikrós majhno in skopeîn gledati, videti) je posebna optična naprava, ki je sestavljena iz sistema leč, za opazovanje
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
ENERGETSKI STROJI. Energetski stroji. UNIVERZA V LJUBLJANI, FAKULTETA ZA STROJNIŠTVO Katedra za energetsko strojništvo
 ENERGETSKI STROJI Uvod Pregled teoretičnih osnov Hidrostatika Dinamika tekočin Termodinamika Podobnostni zakoni Volumetrični stroji Turbinski stroji Energetske naprave Podobnostni zakoni Kriteriji podobnosti
ENERGETSKI STROJI Uvod Pregled teoretičnih osnov Hidrostatika Dinamika tekočin Termodinamika Podobnostni zakoni Volumetrični stroji Turbinski stroji Energetske naprave Podobnostni zakoni Kriteriji podobnosti
ZGRADBA ATOMA IN PERIODNI SISTEM
 ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
Aleš Mrhar. kinetični ni vidiki. Izraženo s hitrostjo in maso, dx/dt očistkom
 Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
Izločanje zdravilnih učinkovin u iz telesa: kinetični ni vidiki Biofarmacija s farmakokinetiko Univerzitetni program Farmacija Aleš Mrhar Izločanje učinkovinu Izraženo s hitrostjo in maso, dx/ k e U očistkom
S programom SPSS se, glede na število ur, ne bomo ukvarjali. Na izpitu so zastavljena neka vprašanja, zraven pa dobimo računalniški izpis izračunov. T
 2. predavanje RVM Kvantitativne metode Borut Kodrič, Koper 21.5.2010 Ključ za dostop do e-učilnice: RMD2009 Tekom srečanj bodo zadeve osvežene v smislu, da bodo okleščene. Morda bo dodan še kak rešen primer.
2. predavanje RVM Kvantitativne metode Borut Kodrič, Koper 21.5.2010 Ključ za dostop do e-učilnice: RMD2009 Tekom srečanj bodo zadeve osvežene v smislu, da bodo okleščene. Morda bo dodan še kak rešen primer.
FOTOSINTEZA Wan Hill primerjal rastlinsko fotosintezo s fotosintezo BAKTERIJ
 FOTOSINTEZA FOTOSINTEZA je proces, pri katerem s pomočjo svetlobne energijje nastajajo v živih celicah organske spojine. 1772 Priestley RASTLINA slab zrak dober zrak Rastlina s pomočjo svetlobe spreminja
FOTOSINTEZA FOTOSINTEZA je proces, pri katerem s pomočjo svetlobne energijje nastajajo v živih celicah organske spojine. 1772 Priestley RASTLINA slab zrak dober zrak Rastlina s pomočjo svetlobe spreminja
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Delavno okolje-aerosoli PRAH
 Delavno okolje-aerosoli PRAH P R A V I L N I K o varovanju delavcev pred tveganji zaradi izpostavljenosti kemičnim snovem pri delu 4. člen (mejne vrednosti za poklicno izpostavljenost in biološke mejne
Delavno okolje-aerosoli PRAH P R A V I L N I K o varovanju delavcev pred tveganji zaradi izpostavljenosti kemičnim snovem pri delu 4. člen (mejne vrednosti za poklicno izpostavljenost in biološke mejne
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
CAPD IN KOSTI. Miha Benedik UKC KON, Center za dializo
 CAPD IN KOSTI Miha Benedik UKC KON, Center za dializo Fosfat Izločanje fosfata pri PD Fosfat je intracelularni anion M.t.: 96 daltonov Molekula obdana z vodnim obročem Obnaša se kot srednja molekula D/P
CAPD IN KOSTI Miha Benedik UKC KON, Center za dializo Fosfat Izločanje fosfata pri PD Fosfat je intracelularni anion M.t.: 96 daltonov Molekula obdana z vodnim obročem Obnaša se kot srednja molekula D/P
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Nanosenzorji iz nanožic in nanocevk (Nanotube and nanowire nanosensors)
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Nanosenzorji iz nanožic in nanocevk (Nanotube and nanowire nanosensors) Miha Devetak Mentor: prof. dr. Dragan Mihailović Ljubljana, marec 2006 1 1
Univerza v Ljubljani Fakulteta za matematiko in fiziko Nanosenzorji iz nanožic in nanocevk (Nanotube and nanowire nanosensors) Miha Devetak Mentor: prof. dr. Dragan Mihailović Ljubljana, marec 2006 1 1
Zgodba vaše hiše
 1022 1040 Zgodba vaše hiše B-panel strani 8-11 Osnovni enobarvni 3020 3021 3023 paneli 3040 3041 Zasteklitve C-panel strani 12-22 S-panel strani 28-35 1012 1010 1013 2090 2091 1022 1023 1021 1020 1040
1022 1040 Zgodba vaše hiše B-panel strani 8-11 Osnovni enobarvni 3020 3021 3023 paneli 3040 3041 Zasteklitve C-panel strani 12-22 S-panel strani 28-35 1012 1010 1013 2090 2091 1022 1023 1021 1020 1040
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
KOENCIM Q 10 Kaj je koencim Q 10? Kje najdemo Q 10? Ali pridobimo dovolj Q10 po naravni poti? Kako deluje? 1. Koencim Q10 velja za enega najmo
 KOENCIM Q 10 Kaj je koencim Q 10? Koencim je naravna substanca in pomembna komponenta vsake žive celice. Najdemo ga tako v človeškem organizmu kakor tudi v živalskih in rastlinskih celicah. Vse naše celice
KOENCIM Q 10 Kaj je koencim Q 10? Koencim je naravna substanca in pomembna komponenta vsake žive celice. Najdemo ga tako v človeškem organizmu kakor tudi v živalskih in rastlinskih celicah. Vse naše celice
Simbolni zapis in množina snovi
 Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Simbolni zapis in množina snovi RELATIVNA MOLEKULSKA MASA ON MOLSKA MASA Relativna molekulska masa Ker so atomi premajhni, da bi jih merili z običajnimi tehtnicami, so ugotovili, kako jih izračunati. Izražamo
Autor: Rama Kanduri Traduzione in Italiano a cura di:
 Autor: Rama Kanduri Traduzione in Italiano a cura di: www.prendersicura.it info@prendersicura.it " Ponovno smo odkrili da srebro uničuje bakterije, kar je znano dejstvo že stoletja... vendar so z odkritjem
Autor: Rama Kanduri Traduzione in Italiano a cura di: www.prendersicura.it info@prendersicura.it " Ponovno smo odkrili da srebro uničuje bakterije, kar je znano dejstvo že stoletja... vendar so z odkritjem
Izločanje zdravilnih učinkovin iz telesa:
 Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
Izločanje zdravilnih učinkovin iz telesa: kinetični vidiki Biofarmacija s farmakokinetiko Aleš Mrhar Izločanje učinkovin Izraženo s hitrostjo in maso, dx/dt = k e U očistkom in volumnom, Cl = k e V Hitrost
UNIVERZA V LJUBLJANI FAKULTETA ZA ELEKTROTEHNIKO. Ana Urh in Andrej Kocjan. Lambda sonda
 UNIVERZA V LJUBLJANI FAKULTETA ZA ELEKTROTEHNIKO Ana Urh in Andrej Kocjan Lambda sonda Seminarska naloga pri predmetu Merilni pretvorniki Laboratorij za regulacijsko tehniko in močnostno elektroniko (LRTME)
UNIVERZA V LJUBLJANI FAKULTETA ZA ELEKTROTEHNIKO Ana Urh in Andrej Kocjan Lambda sonda Seminarska naloga pri predmetu Merilni pretvorniki Laboratorij za regulacijsko tehniko in močnostno elektroniko (LRTME)
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
AZBEST. NIKOLI dokončana ZGODBA
 AZBEST NIKOLI dokončana ZGODBA 2015 Urednica: Maja Južnič Sotlar Besedila: Erika Koncut, Maja Južnič Sotlar, Marko Vudrag Recenzentka: Metoda Dodič Fikfak Oblikovanje: Nina Dekleva Grafična zasnova naslovnice:
AZBEST NIKOLI dokončana ZGODBA 2015 Urednica: Maja Južnič Sotlar Besedila: Erika Koncut, Maja Južnič Sotlar, Marko Vudrag Recenzentka: Metoda Dodič Fikfak Oblikovanje: Nina Dekleva Grafična zasnova naslovnice:
AZBEST. NIKOLI dokončana ZGODBA
 AZBEST NIKOLI dokončana ZGODBA 2015 Urednica: Maja Južnič Sotlar Besedila: Erika Koncut, Maja Južnič Sotlar, Marko Vudrag Recenzentka: Metoda Dodič Fikfak Oblikovanje: Nina Dekleva Grafična zasnova naslovnice:
AZBEST NIKOLI dokončana ZGODBA 2015 Urednica: Maja Južnič Sotlar Besedila: Erika Koncut, Maja Južnič Sotlar, Marko Vudrag Recenzentka: Metoda Dodič Fikfak Oblikovanje: Nina Dekleva Grafična zasnova naslovnice:
podlago, bo najprej potrebna celotna odstranitev starega fasadnega sloja in zatem izvedba novega toplotnoizolativnega sistema. Pred namestitvijo noveg
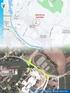 Nova fasada na hiši Poleg ogrevalnega sistema je najbolj pomemben dejavnik prihranka stroškov ogrevanja dovolj debel fasadni sloj. Znano je, da 5 in nekaj več centimetrov debela fasada že dolgo več ne
Nova fasada na hiši Poleg ogrevalnega sistema je najbolj pomemben dejavnik prihranka stroškov ogrevanja dovolj debel fasadni sloj. Znano je, da 5 in nekaj več centimetrov debela fasada že dolgo več ne
Varjenje polimerov s polprevodniškim laserjem
 Laboratorijska vaja št. 5: Varjenje polimerov s polprevodniškim laserjem Laserski sistemi - Laboratorijske vaje 1 Namen vaje Spoznati polprevodniške laserje visokih moči Osvojiti osnove laserskega varjenja
Laboratorijska vaja št. 5: Varjenje polimerov s polprevodniškim laserjem Laserski sistemi - Laboratorijske vaje 1 Namen vaje Spoznati polprevodniške laserje visokih moči Osvojiti osnove laserskega varjenja
SONČNE CELICE. Primož Hudi. Mentor: doc. dr. Zlatko Bradač. V seminarju sem predstavil sestavo ter delovanje sončnih celic.
 SONČNE CELICE Primož Hudi V seminarju sem predstavil sestavo ter delovanje sončnih celic. Mentor: doc. dr. Zlatko Bradač Maribor, 2009 Kazalo 1 UVOD...3 2 SONČNE CELICE...4 2.1 SESTAVA SONČNE CELICE...4
SONČNE CELICE Primož Hudi V seminarju sem predstavil sestavo ter delovanje sončnih celic. Mentor: doc. dr. Zlatko Bradač Maribor, 2009 Kazalo 1 UVOD...3 2 SONČNE CELICE...4 2.1 SESTAVA SONČNE CELICE...4
STANDARD1 EN EN EN
 PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA. ANTENE za začetnike. (kako se odločiti za anteno)
 ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA ANTENE za začetnike (kako se odločiti za anteno) Mentor: univ. dipl. Inž. el. Stanko PERPAR Avtor: Peter
ŠOLSKI CENTER ZA POŠTO, EKONOMIJO IN TELEKOMUNIKACIJE Celjska 16, 1000 Ljubljana SEMINARSKA NALOGA ANTENE za začetnike (kako se odločiti za anteno) Mentor: univ. dipl. Inž. el. Stanko PERPAR Avtor: Peter
Energije in okolje 1. vaja. Entalpija pri kemijskih reakcijah
 Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
KOLI»INSKI ODNOSI. Kemik mora vedeti, koliko snovi pri kemijski reakciji zreagira in koliko snovi nastane.
 KOLI»INSKI ODNOSI Kemik mora vedeti koliko snovi pri kemijski reakciji zreagira in koliko snovi nastane 4 Mase atomov in molekul 42 tevilo delcev masa in mnoæina snovi 43 RaËunajmo maso mnoæino in πtevilo
KOLI»INSKI ODNOSI Kemik mora vedeti koliko snovi pri kemijski reakciji zreagira in koliko snovi nastane 4 Mase atomov in molekul 42 tevilo delcev masa in mnoæina snovi 43 RaËunajmo maso mnoæino in πtevilo
PROTITELESA IN IMUNSKI ODGOVOR BIOKEMIJA ČUTIL
 PROTITELESA IN IMUNSKI ODGOVOR BIOKEMIJA ČUTIL Povzetek dveh predavanj pri predmetu Biokemija študijski program Kemija 2008/2009 doc. dr. Marko Dolinar Pred vami je del gradiva, ki ga pripravljam za naslednje
PROTITELESA IN IMUNSKI ODGOVOR BIOKEMIJA ČUTIL Povzetek dveh predavanj pri predmetu Biokemija študijski program Kemija 2008/2009 doc. dr. Marko Dolinar Pred vami je del gradiva, ki ga pripravljam za naslednje
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
17. Električni dipol
 17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
MOTORJI Z NOTRANJIM ZGOREVANJEM
 MOTORJI Z NOTRANJIM ZGOREVANJEM Dvotaktni Štititaktni Motorji z notranjim zgorevanjem Motorji z zunanjim zgorevanjem izohora: Otto motor izohora in izoterma: Stirling motor izobara: Diesel motor izohora
MOTORJI Z NOTRANJIM ZGOREVANJEM Dvotaktni Štititaktni Motorji z notranjim zgorevanjem Motorji z zunanjim zgorevanjem izohora: Otto motor izohora in izoterma: Stirling motor izobara: Diesel motor izohora
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
