Elektronska paramagnetna resonanca (EPR)
|
|
|
- Τισιφόνη Αλαβάνος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Elektronska paramagnetna resonanca (EPR) Pregled predavanja o EPR snovni princip delovanja EPR v primerjavi z NMR Instrumentacija Analiza EPR signala Primeri praktične uporabe EPR Posebne metode, ki temeljijo na EPR Instrumentalna farmacevtska analiza 1
2 Kaj je EPR? Elektronska paramagnetna resonanca (EPR) Elektronska spinska resonanca (ESR) { Elektronska magnetna resonanca (EMR) } Spektroskopija: ne-destruktivna analizna tehnika dkritje EPR Yevgeny Zavoisky, Kazan 1944 CuCl 2, CuS 4, MnS 4 Instrumentalna farmacevtska analiza 2
3 Kakšne spojine lahko analiziramo? Zvrsti z enim ali več nesparjenimi elektroni Radikali (stabilnost!) Spojine z elementi prehodnih kovin Defekti v kristalnih rešetkah H H H H EPR Princip delovanja B 0 E h Instrumentalna farmacevtska analiza 3
4 Zeemanov efekt Degenerirano stanje Magnetno polje Magnetni momenti elektronov se v zunanjem magnetnem polju skoraj naključno porazdelijo na dva energijska nivoja. Ko je sistem v termičnem ravnovesju jih je nekoliko več na energijskem nivoju z nižjo energijo, saj sledijo Boltzmannovi porazdelitvi. Kaj povzroči razliko med energijskimi nivoji? B 0 Razcep energijskih nivojev elektronov v zunanjem magnetnem polju (B 0 ). Nižji energijski nivo: magnetni moment elektrona je poravnan z zunanjim magnetnim poljem B 0 (oz. precesira okoli smeri zunanjega mag. polja) Instrumentalna farmacevtska analiza 4
5 Kako opišemo energijska nivoja? S pomočjo elektronskega spina in z njim povezanega magnetnega momenta Za molekulo z enim nesparjenim elektronom: V zunanjem magnetnem polju je razlika med elektronskima energijskima nivojema enaka: E = g B B 0 M S g = sorazmernostni faktor M S = elektronsko spinsko kvantno število (+½ ali -½) B = Bohrov magneton B 0 = Magnetno polje Prehodi med energijskima nivojema B 0 E h Absorpcija mikrovalov Med spreminjanjem magnetnega polja (an. sweep) postanejo elektronski spini resonantni s frekvenco mikrovalov s katerimi obsevamo paramagnetni vzorec. Vzorec zato absorbira moč (energijo) mikrovalov, kar vodi v EPR prehod. Ta se slednjič po spin-lattice relaksaciji pretvori v toploto. Instrumentalna farmacevtska analiza 5
6 EPR meritev Energija M s ±½ M s = +½ E=h =g B B pp B = 0 B > 0 M s = -½ Magnetno polje (B) h Planckova konstanta x erg.s frekvenca (GHz ali MHz) g g-faktor (približno 2.0) Bohrov magneton ( x erg.g -1 ) B magnetno polje (G ali mt) Pri EPR meritvi paramagnetni vzorec v zunanjem magnetnem polju absorbira elektromagnetno valovanje (mikrovalove), ko je izpolnjen resonančni pogoj: pri izbrani frekvenci mora biti ustrezna jakost magnetnega polja. Frekvenca in polje EPR meri prehode elektronskih spinov med energijskimi nivoji Prehod inducira elektromagnetno valovanje z ustrezno frekvenco (mikrovalovi), s katerim vzorec obsevamo Frekvenca elektromagnetnega valovanja, ki je potrebna za prehod je odvisna od jakosti magnetnega polja Pas mikrovalov L S X K Q W Frekvenca [GHz] B res (za g=2) [G] bmočje mikrovalov GHz G = 1 T (gauss) (tesla) Instrumentalna farmacevtska analiza 6
7 Časovno okno EPR nsčasovna skala Za EPR so vse spremembe vezi prehitre, zato jih vidi povprečene. Spremembe konformacij kratkih verig (lipidi!) pa so ravno v časovnem oknu EPR, zato je EPR tako občutljiv na anizotropijo njihovega opletanja. Spremembe konformacij daljših polimerov (proteini) so za EPR prepočasne, zato jih zazna kot superpozicijo konformacij. EPR spekter Absorpcija, A Prvi odvod absorpcije, da/db Polje, B Polje, B EPR spekter je prvi odvod absorpcijskega spektra Instrumentalna farmacevtska analiza 7
8 g faktor Izmerjen iz sredine signala Za prost elektron Za organske radikale Pogosto blizu vrednosti za prosti elektron g = h / B Za spojine z elementi prehodnih kovin Večja odstopanja zaradi sklopitev s spinskimi orbitalami in zero-field splitting g faktor Mo(SCN) 5 2- V(acetilacetonat) e CH C 14 H 10 + (antracen) kation C 14 H 10 - (antracen) anion Cu(acetilacetonat) Instrumentalna farmacevtska analiza 8
9 g faktor g -factor 2 Manganese Plastocyanin Ferredoxin Metmyoglobin Magnetic field, mt Identifikacija kovinskih ionov preko njihovih g faktorjev EPR Instrumentacija Izvor Vzorec Detektor Instrumentalna farmacevtska analiza 9
10 Kako deluje EPR spektrometer? Mikrovalovni most dprtina za vzorec Resonator Elektromagnet Konzola Mikrovalovni most - diagram Magnet Instrumentalna farmacevtska analiza 10
11 Mikrovalovno polje v resonatorju Modulacija Če bi vzorec v resonatorju obsevali z enako močjo mikrovalov in spreminjali magnetno polje (an. sweep), bi bil izstopni tok na diodi sorazmeren absorpcijskemu spektru in ne prvemu odvodu. Prvi odvod dobimo z modulacijo zunanjega magnetnega polja (B 0 ), ki vodi do oscilacije absorpcijskega signala. Amplitudo oscilacije absorpcijskega signala detektiramo s fazno odvisnim detektorjem. Prednost tega dodatnega koraka je filtracija šuma, ki ne niha z modulacijsko frekvenco in neresonančne absorpcije mikrovalov, ki ni odvisna od magnetnega polja. Nadalje s prvim odvodom dosežemo boljšo resolucijo v primerjavi s samim absorpcijskim spektrom. Instrumentalna farmacevtska analiza 11
12 Potek EPR meritve EPR Multipliciteta EPR signala - hiperfina interakcija Instrumentalna farmacevtska analiza 12
13 Hiperfina interakcija Hiperfina interakcija Elektron S (½) Jedro I (½) M s +½ M I +½ a M S =±½ -½ E 1 E 2 B -½ E = g BS z + (ha 0 )S z I z E = g BS z + (a)s z I z (ha 0 (Hz) a (G) preko g-faktorja) -½ +½ Selekcijsko pravilo M S = ±1 (elektron) M I = 0 (jedro) dublet E 1 = g B + a/2 E 2 = g B -a/2 E 1 E 2 = a Instrumentalna farmacevtska analiza 13
14 Elektron S (½) Jedro I (1) M s M I M S =±½ +½ a E 1 E 2 E 3 -½ triplet B E = g BS z + (ha 0 )S z I z E = g BS z + (a)s z I z (ha 0 (Hz) a (G) preko g-faktorja) Selekcijsko pravilo M S = ±1 (elektron) M I = 0 (jedro) E 1 = g B + a E 2 = g B E 3 = g B -a Hiperfina interakcija EPR signal se razcepi zaradi sosednjih jedrer To imenujemo hiperfine interakcije Nam da informacije o: Številu in identiteti jeder Razdalji od nesparjenega elektrona Interakcije s sosednjimi jedri E = g B B 0 M S + am s m I a = hiperfina konstanta sklopitve m I = jedrsko spinsko kvantno število a - izmerjena kot razdalja med centroma dveh signalov Instrumentalna farmacevtska analiza 14
15 Katera jedra vstopajo v interakcijo? Enaka selekcijska pravila kot pri NMR Vsak izotop vsakega elementa ima jedersko spinsko kvantno število osnovnega stanja, I ki ima vrednost n/2, n je celo število Izotopi s sodim atomskim številom in sodim masnim številom imajo I = 0, in nimajo EPR spektra 12 C, 28 Si, 56 Fe, Izotopi z lihim atomskim številom in sodim masnim številom imajo sod n 2 H, 10 B, 14 N, Izotopi z lihim masnim številom imajo lih n 1 H, 13 C, 19 F, 55 Mn, Katera jedra vstopajo v interakcijo? 1 H I =1/2 13 C I =1/2 14 N I =1 15 N I =1/2 High spin Fe(III) I = 5/2 Low spin Fe(III) I =1/2 63 Cu(II) I =3/2 55 Mn(II) I =5/2 95 Mo(V) I =5/2 97 Mo(V) I =5/2 61 Ni(III) I =3/2 51 V I =7/2 Instrumentalna farmacevtska analiza 15
16 Hiperfina interakcija primer H H mt Atomarni vodik: interakcija e - z jedrom (protonom) s spinom ½ Hiperfina interakcija Sklopitveni vzorci enaki kot pri NMR Pogosteje vidimo sklopitve z jedri s spinom večjim od ½ Število črt: 2NI + 1 N = število ekvivalentnih jeder I = jedersko spinsko kvantno število Določa samo število črt ne pa intenzitet Instrumentalna farmacevtska analiza 16
17 Hiperfina interakcija Relativne intenzitete so določene s številom jeder, ki vstopajo v interakcijo Če vstopa v interakcijo samo eno jedro Imajo vse črte enako intenziteto Če vstopa v interakcijo več jeder Distribucije izpeljane na podlagi spina Za spin ½ (najpogosteje), sledijo interakcije binominalni porazdelitvi Relativne intenzitete I = ½ N Relativne intenzitete 1 1 : 1 1 : 2 : 1 1 : 3 : 3 : 1 1 : 4 : 6 : 4 : 1 1 : 5 : 10 : 10 : 5 : 1 1 : 6 : 15 : 20 : 15 : 6 : 1 Instrumentalna farmacevtska analiza 17
18 Relativne intenzitete I = ½ Relativne intenzitete I = 1 N Relativne intenzitete 1 1 : 1 : 1 1 : 2 : 3 : 2 : 1 1 : 3 : 6 : 7 : 6 : 3 : 1 1 : 4 : 10 : 16 : 19 : 16 : 10 : 4 : 1 1 : 5 : 15 : 20 : 45 : 51 : 45 : 20 : 15 : 5 : 1 1 : 6 : 21 : 40 : 80 : 116 : 141 : 116 : 80 : 40 : 21 : 6 : 1 Instrumentalna farmacevtska analiza 18
19 Relativne intenzitete I = 1 Hiperfine interakcije primer 1 Primer: V(acetilacetonat) 2 Interakcija e - z vanadijevim jedrom Za vanadij, I = 7/2 Zato, 2NI + 1 = 2(1)(7/2) + 1 = 8 Pričakujemo, da bomo videli 8 črt enake intenzitete Instrumentalna farmacevtska analiza 19
20 Hiperfine interakcije primer 1 EPR spekter vanadil acetilacetonata Hiperfine interakcije primer 2 Primer: Benzen radikal anion [C 6 H 6 ] - Elektron je delokaliziran čez vseh šest ogljikovih atomov Sklaplja se s šestimi ekvivalentnimi vodikovimi atomi Zato, 2NI + 1 = 2(6)(1/2) + 1 = 7 Zato ima spekter sedem črt z relativnimi intenzitetami 1:6:15:20:15:6:1 Instrumentalna farmacevtska analiza 20
21 Hiperfine interakcije primer 2 EPR spekter benzen radikal aniona Hiperfine interakcije Sklopitve z več seti jeder: Prva sklopitev z najbližjim setom jeder Največja vrednost a Razcep vsake od teh črt zaradi sklopitve z naslednjim najbližjim jedrom Naslednja največja vrednost a Nadaljuj 2-3 vezi vstran od lokacije nesparjenega elektrona Instrumentalna farmacevtska analiza 21
22 Hiperfine interakcije primer 3 Primer: Pirazin anion radikal Elektron je delokaliziran čez obroč Sklaplja se z dvema ekvivalentnima jedroma N (I = 1) 2NI + 1 = 2(2)(1) + 1 = 5 Nato se sklaplja s štirimi ekvivalentnimi H (I = ½) 2NI + 1 = 2(4)(1/2) + 1 = 5 Zato mora biti spekter kvintet z intenzitetami 1:2:3:2:1 in vsaka od teh črt se mora razcepiti v kvintet z intenzitetami 1:4:6:4:1 Hiperfine interakcije primer 3 EPR spekter pirazin radikal aniona Instrumentalna farmacevtska analiza 22
23 EPR Primeri praktične uporabe EPR 5P 7P 10P 12P 12C 14P 1 mt Kvantitativna & kvalitativna analiza Kvantitativna analiza signala: intenziteta (h), površina pod krivuljo Kinetika redukcije nitroksidov Kvantifikacija paramagnetnih centrov d 1 d 0 d -1 h 1 h 0 h -1 Kvalitativna analiza signala: oblika signala, širina črt (d), a N Nitroksidni radikali poročajo o svoji okolici: kisik, polarnost, ph, viskoznost, urejenost (ureditveni parameter) a N g 0 Instrumentalna farmacevtska analiza 23
24 Nitroksidi kot merilci reduktivnega statusa tkiva EPR Intenziteta t ½ ~ min EPR aktiven EPR neaktiven Čas (min) Kinetika redukcije nitroksidnega radikala ksimetrija brez 2 prisoten zračni 2 5P 1 mt Instrumentalna farmacevtska analiza 24
25 ksimetrija + Na - C S R R R R S S S C - Na + S R R R S S S S S R R R R S S R C - Na + LiPc (Lithium Phthalocyanine) Spojina občutljiva na kisik preko (T 2 ) Vpliv kisika na širino črte EPR širina črte v (G) naklon = 8.9 mg / mmhg Kisik (p 2 ) Ilangovan, G., Li, H., Zweier, J.L., Kuppusamy, P. J. Phys. Chem. B 104, 4047 (2000); 104, 9404 (2000); 105, 5323 (2001) 21% Kisik 0 % dziv na kisik Zrak zrak zrak N 2 N čas (sec) Instrumentalna farmacevtska analiza 25
26 GSH vsebnost glutationa ph H N R N R 15 N 15 N Instrumentalna farmacevtska analiza 26
27 ph-občutljivi nitroksidi ph Instrumentalna farmacevtska analiza 27
28 ph Polarnost okolice Instrumentalna farmacevtska analiza 28
29 Viskoznost Anizotropija Kristal Viskozna raztopina Neviskozna raztopina Kristalinična trdna snov je rigiden material s translacijsko simetrijo na dolge razdalje (ponavljanje osnovnih celic) Paramagnetni center v trdnem materialu nima rotacijskih ali translacijskih prostostnih stopenj zato se izrazi anizotropija magnetnih interakcij Instrumentalna farmacevtska analiza 29
30 Dinamika v bioloških membranah rotacija vezi s rotacijska difuzija»wobbling«10-8 s protruzija 10-9 s flip-flop s oscilacija vezi s lateralna difuzija 10-7 s undulacija 10-7 s 1 s Anizotropija spinskih označevalcev v bioloških membranah Gibanje amfifilne spinske probe je v lipidnem dvosloju omejeno. π orbitala nitroksida z nesparjenim e - je usmerjena v prostoru. Instrumentalna farmacevtska analiza 30
31 Anizotropno vs. izotropno gibanje S je ureditveni parameter c = korelacijsko rotacijski čas Izotropno gibanje c = 4 r³ / 3kT [Debye] Ureditveni parameter (S) Instrumentalna farmacevtska analiza 31
32 Primer spinske sonde v celični membrani N P PP 5P 7P 10P N P N 5P 12P 12C 14P N N N P P P N 7P N 10P N 12P rder parameter S 0,75 0,70 0,65 0,60 0,55 0,50 0,45 1 mt liposomes erytocyte MCF-7 cells N 0,40 P 14P N 0, Position of doxyl group Simulacija molekulske dinamike Instrumentalna farmacevtska analiza 32
33 EPR dozimetrija Hidroksiapatit sestavlja: ~95% mase zobnega emajla 70-75% dentina 60-70% kasti Klinični EPR spektrometri MAGNETIC FLUX LINES PATIENT SPHERE F HMGENEITY MAGNET CILS Instrumentalna farmacevtska analiza 33
34 EPR Posebne metode, ki temeljijo na EPR Spinske pasti (an. spin traps) DMP, 5,5-dimetilpirolin-N-oksid H 3 C H 3 C N H R. H 3 C H 3 C N. H R nitron nitroksid (ni radikal) (radikal) Instrumentalna farmacevtska analiza 34
35 Spinske pasti (an. spin traps) Site directed spin labeling (SDSL) Metantiosulfonatni spinski označevalec (SL) specifično reagira z SH skupino AK metionin v proteinu. SL poroča o dinamiki in svoji okolici. Instrumentalna farmacevtska analiza 35
36 Site directed spin labeling (SDSL) SDSL metoda je uporabna zlasti za študij (trans)membranskih proteinov, ki jih ne moremo kristalizirati ali pa so preveliki za študij z NMR. Site directed spin labeling (SDSL) Vpliv gibljivosti (zgoraj) in magnetne dipolarne interakcije na EPR spekter nitroksida (spodaj). Magnetna dipolarna interakcija med dvema radikaloma (nitroksidnima spinskima označevalcema) prispeva k širitvi črt. Tako lahko izmerimo razdaljo (r) med dvema nitroksidoma. Instrumentalna farmacevtska analiza 36
37 Primer: Rodopsin Aktivacija rodopsina s svetlobo: model razporeditve vijačnic rodopsina v mirujočem (modra vijačnica zgoraj) in aktiviranem stanju (rdeča vijačnica spodaj). Vsak mutant vsebuje samo en (levo) ali dva (desno) SL, zaradi preglednosti pa so prikazani vsi. ΔM s je sprememba v mobilnosti SL po aktivaciji s svetlobo. EPR Imaging Histološka slika organa in in vivo EPR slika. Presek debla Instrumentalna farmacevtska analiza 37
38 EPR Imaging Magnetic Resonance Insights 2008: Instrumentalna farmacevtska analiza 38
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Spektroskopija elektronska paramagnetna resonanca (EPR) - spinsko označevanje in spinsko lovljenje pri študiju supramolekularnih sistemov
 Spektroskopija elektronska paramagnetna resonanca (EPR) - spinsko označevanje in spinsko lovljenje pri študiju supramolekularnih sistemov Janez Štrancar Laboratory of Biophysics, IJS / C AMASTE Zakaj EPR?
Spektroskopija elektronska paramagnetna resonanca (EPR) - spinsko označevanje in spinsko lovljenje pri študiju supramolekularnih sistemov Janez Štrancar Laboratory of Biophysics, IJS / C AMASTE Zakaj EPR?
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Spektroskopija. S spektroskopijo preučujemo lastnosti snovi preko njihove interakcije z različnimi področji elektromagnetnega valovanja.
 Spektroskopija S spektroskopijo preučujemo lastnosti snovi preko njihove interakcije z različnimi področji elektromagnetnega valovanja. Posamezna tehnika ima ime po območju uporabljenega elektromagnetnega
Spektroskopija S spektroskopijo preučujemo lastnosti snovi preko njihove interakcije z različnimi področji elektromagnetnega valovanja. Posamezna tehnika ima ime po območju uporabljenega elektromagnetnega
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Elektron u magnetskom polju
 Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
INSTRUMENTALNA FARMACEVTSKA ANALIZA
 INSTRUMENTALNA FARMACEVTSKA ANALIZA Vaje in seminarji Nace Zidar, Rok Frlan, Janez Mravljak, Simon Žakelj, Jurij Trontelj, Zoran Lavrič ENOVITI MAGISTRSKI ŠTUDIJSKI PROGRAM FARMACIJA KAZALO 1. NMR-SPEKTROSKOPIJA...
INSTRUMENTALNA FARMACEVTSKA ANALIZA Vaje in seminarji Nace Zidar, Rok Frlan, Janez Mravljak, Simon Žakelj, Jurij Trontelj, Zoran Lavrič ENOVITI MAGISTRSKI ŠTUDIJSKI PROGRAM FARMACIJA KAZALO 1. NMR-SPEKTROSKOPIJA...
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/
 ZGRADBA ATOMA 1.1 - DALTON atom (atomos nedeljiv) antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/ dokaz izpred ~ 200 let Temelj so 3 zakoni: ZAKON O OHRANITVI MASE /Lavoisier, 1774/ ZAKON
ZGRADBA ATOMA 1.1 - DALTON atom (atomos nedeljiv) antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/ dokaz izpred ~ 200 let Temelj so 3 zakoni: ZAKON O OHRANITVI MASE /Lavoisier, 1774/ ZAKON
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Naloge iz Atomov, molekul, jeder 15 februar 2017, 1. rešitev Schrödingerjeve enačbe za radialni del valovne funkcije. Kolikšna je normalizacijska
 Naloge iz Atomov, molekul, jeder 15 februar 2017, 1 1 Vodikov atom 1.1 Kvantna števila 1. Pokaži, da je Y 20 (ϑ) = A(3 cos 2 ϑ 1) rešitev Schrödingerjeve enačbe za kotni del valovne funkcije. Kolikšna
Naloge iz Atomov, molekul, jeder 15 februar 2017, 1 1 Vodikov atom 1.1 Kvantna števila 1. Pokaži, da je Y 20 (ϑ) = A(3 cos 2 ϑ 1) rešitev Schrödingerjeve enačbe za kotni del valovne funkcije. Kolikšna
MAGNETNI MATERIALI. 1. Mehkomagnetni materiali 2. Trdomagnetni materiali
 MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
ZGRADBA ATOMA IN PERIODNI SISTEM
 ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE
 OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE Elektronska paramagnetna rezonancija (EPR), takođe poznata kao elektronska spinska rezonancija (ESR) ili elektronska magnetna rezonancija (EMR), je rezonantna
OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE Elektronska paramagnetna rezonancija (EPR), takođe poznata kao elektronska spinska rezonancija (ESR) ili elektronska magnetna rezonancija (EMR), je rezonantna
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Slika 5.1 Magnetenje različnih vrst snovi
 5. Magnetni materiali in njihove lastnosti Če opazujemo različne snovi v magnetnem polju, lahko pri vsaki ugotovimo magnetne lastnosti. Glede na izraženost magnetnih lastnosti oz. glede na obnašanje snovi
5. Magnetni materiali in njihove lastnosti Če opazujemo različne snovi v magnetnem polju, lahko pri vsaki ugotovimo magnetne lastnosti. Glede na izraženost magnetnih lastnosti oz. glede na obnašanje snovi
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Poglavje 10. Molekule Kovalentna vez
 Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Gradniki TK sistemov
 Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana,
 logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana, 1 Kazalo 1 UVOD 3 2 OSNOVE JEDRSKE MAGNETNE RESONANCE 3 2.1 Magnetne lastnosti jeder in resonanca............... 3 2.2 Radiofrekvenčni pulz.........................
logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana, 1 Kazalo 1 UVOD 3 2 OSNOVE JEDRSKE MAGNETNE RESONANCE 3 2.1 Magnetne lastnosti jeder in resonanca............... 3 2.2 Radiofrekvenčni pulz.........................
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU
 NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
2.1. MOLEKULARNA ABSORPCIJSKA SPEKTROMETRIJA
 2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
2.1. MOLEKULARNA ABSORPCJSKA SPEKTROMETRJA Molekularna absorpcijska spektrometrija (kolorimetrija, fotometrija, spektrofotometrija) temelji na merjenju absorpcije svetlobe, ki prehaja skozi preiskovano
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
4. Z električnim poljem ne moremo vplivati na: a) α-delce b) β-delce c) γ-žarke d) protone e) elektrone
 1. Katera od naslednjih trditev velja za katodne žarke? a) Katodni žarki so odbijajo od katode. b) Katodni žarki izvirajo iz katode c) Katodni žarki so elektromagnetno valovanje z kratko valovno dolžino.
1. Katera od naslednjih trditev velja za katodne žarke? a) Katodni žarki so odbijajo od katode. b) Katodni žarki izvirajo iz katode c) Katodni žarki so elektromagnetno valovanje z kratko valovno dolžino.
ANALITIČKA KEMIJA II BOLTZMANNOVA RASPODJELA. nositelj: prof.dr.sc. P. Novak održao: doc.dr.sc.t. Jednačak; ak.god. 2017/18.
 ANALITIČKA KEMIJA II BOLTZMANNOVA RASPODJELA nositelj: prof.dr.sc. P. Novak održao: doc.dr.sc.t. Jednačak; ak.god. 2017/18. Ludwig Boltzmann rođen umro boravio nacionalnost struka 20. veljače 1844. Beč
ANALITIČKA KEMIJA II BOLTZMANNOVA RASPODJELA nositelj: prof.dr.sc. P. Novak održao: doc.dr.sc.t. Jednačak; ak.god. 2017/18. Ludwig Boltzmann rođen umro boravio nacionalnost struka 20. veljače 1844. Beč
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
S53WW. Meritve anten. RIS 2005 Novo Mesto
 S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Mehanizem feromagnetnih domen in magnetne aplikacije
 Seminar- 4. letnik Mehanizem feromagnetnih domen in magnetne aplikacije Avtor: Jože BUH Mentor: Dr. Denis ARČON 7. januar 2011 Povzetek Za permanentne (trde) magnete je značilno, da ostanejo namagneteni,
Seminar- 4. letnik Mehanizem feromagnetnih domen in magnetne aplikacije Avtor: Jože BUH Mentor: Dr. Denis ARČON 7. januar 2011 Povzetek Za permanentne (trde) magnete je značilno, da ostanejo namagneteni,
12 Slikanje z jedrsko magnetno resonanco
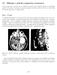 12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
11 Slikanje z jedrsko magnetno resonanco
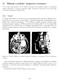 11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Specifičnost spektrov. Princip emisijske spektrometrije. Atomizacija in vzbujanje
 Princip emisijske spektrometrije Emisijska spektrometrija temelji na nastanku in detekciji spektrov, ki so posledica radiacijske deekscitacije vzbujenih elektronov. Pri teh procesih sodelujejo zunanji
Princip emisijske spektrometrije Emisijska spektrometrija temelji na nastanku in detekciji spektrov, ki so posledica radiacijske deekscitacije vzbujenih elektronov. Pri teh procesih sodelujejo zunanji
e 2 4πε 0 r i r j Ze 2 4πε 0 r i j<i
 Poglavje 9 Atomi z več elektroni Za atom z enim elektronom smo lahko dobili analitične rešitve za lastne vrednosti in lastne funkcije energije. Pri atomih z več elektroni to ni mogoče in se moramo zadovoljiti
Poglavje 9 Atomi z več elektroni Za atom z enim elektronom smo lahko dobili analitične rešitve za lastne vrednosti in lastne funkcije energije. Pri atomih z več elektroni to ni mogoče in se moramo zadovoljiti
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA
 Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Katedra za elektroniku Elementi elektronike Laboratorijske vežbe Vežba br. 2 STATIČKE KARAKTERISTIKE DIODA I TRANZISTORA Datum: Vreme: Studenti: 1. grupa 2. grupa Dežurni: Ocena: Elementi elektronike -
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
UNIVERZA V LJUBLJANI, FAKULTETA ZA STROJNIŠTVO Katedra za energetsko strojništvo VETRNICA. v 2. v 1 A 2 A 1. Energetski stroji
 Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
Katedra za energetsko strojništo VETRNICA A A A Katedra za energetsko strojništo Katedra za energetsko strojništo VETRNICA A A A Δ Δp p p Δ Katedra za energetsko strojništo Teoretična moč etrnice Določite
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Molekularna spektrometrija
 Molekularna spektrometrija Absorpcija Fluorescenca Pojavi v snovi (posledica interakcije EM valovanje- snov): Elektronski prehodi Vibracije Rotacije Spekter Izvor svetlobe prizma Spekter Material, ki deloma
Molekularna spektrometrija Absorpcija Fluorescenca Pojavi v snovi (posledica interakcije EM valovanje- snov): Elektronski prehodi Vibracije Rotacije Spekter Izvor svetlobe prizma Spekter Material, ki deloma
PRENOS SIGNALOV
 PRENOS SIGNALOV 14. 6. 1999 1. Televizijski signal s pasovno širino 6 MHz prenašamo s koaksialnim kablom na razdalji 4 km. Dušenje kabla pri f = 1 MHz je,425 db/1 m. Koliko ojačevalnikov z ojačenjem 24
PRENOS SIGNALOV 14. 6. 1999 1. Televizijski signal s pasovno širino 6 MHz prenašamo s koaksialnim kablom na razdalji 4 km. Dušenje kabla pri f = 1 MHz je,425 db/1 m. Koliko ojačevalnikov z ojačenjem 24
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
 28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
dt 2 I tretiramo kvantno-mehani ki, pokazati da vaºi
 Kvantna mehanika zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 31. avgust 015. 1. Kruti rotator u ravni momenta inercije I i elektri nog dipolnog momenta d se nalazi u elektri nom polju
Kvantna mehanika zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 31. avgust 015. 1. Kruti rotator u ravni momenta inercije I i elektri nog dipolnog momenta d se nalazi u elektri nom polju
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Katedra za farmacevtsko kemijo. Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks. 25/11/2010 Vaje iz Farmacevtske kemije 3 1
 Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone
 UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone Bojan Žunkovič mentor: doc. dr. Matjaž Žitnik 7. maj 2007 Povzetek V preteklosti je bilo sinhrotronsko sevanje pri pospeševanju
UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone Bojan Žunkovič mentor: doc. dr. Matjaž Žitnik 7. maj 2007 Povzetek V preteklosti je bilo sinhrotronsko sevanje pri pospeševanju
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Nuklearna Magnetna Rezonancija NMR
 ANALITIČKA KEMIJA II uvodno predavanje općenito uzorkovanje; norme i standardi; intelektualno vlasništvo STATISTIKA osnove EKSTRAKCIJA, KROMATOGRAFIJA - osnove ELEKTROANALITIČKE METODE BOLTZMANNOVA RAZDIOBA
ANALITIČKA KEMIJA II uvodno predavanje općenito uzorkovanje; norme i standardi; intelektualno vlasništvo STATISTIKA osnove EKSTRAKCIJA, KROMATOGRAFIJA - osnove ELEKTROANALITIČKE METODE BOLTZMANNOVA RAZDIOBA
ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΗΛΕΚΤΡΟΝΙΑΚΟΥ ΠΑΡΑΜΑΓΝΗΤΙΚΟΥ ΣΥΝΤΟΝΙΣΜΟΥ (EPR)
 ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΗΛΕΚΤΡΟΝΙΑΚΟΥ ΠΑΡΑΜΑΓΝΗΤΙΚΟΥ ΣΥΝΤΟΝΙΣΜΟΥ (EPR) Τι μελετάμε; Ελεύθερες ρίζες σε στερεά, υγρά ή αέρια Άτομα με μη συμπληρωμένη εξωτερική στοιβάδα (Η, Ν) ή μόρια με ασύζευκτα e Ιόντατωνμετάλλωνμετάπτωσηςπου
ΦΑΣΜΑΤΟΣΚΟΠΙΑ ΗΛΕΚΤΡΟΝΙΑΚΟΥ ΠΑΡΑΜΑΓΝΗΤΙΚΟΥ ΣΥΝΤΟΝΙΣΜΟΥ (EPR) Τι μελετάμε; Ελεύθερες ρίζες σε στερεά, υγρά ή αέρια Άτομα με μη συμπληρωμένη εξωτερική στοιβάδα (Η, Ν) ή μόρια με ασύζευκτα e Ιόντατωνμετάλλωνμετάπτωσηςπου
Atomi, molekule, jedra
 Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma........................... 5 1.2 Schrödingerjeva enačba za vodikov atom.................. 5 Nastavek
Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma........................... 5 1.2 Schrödingerjeva enačba za vodikov atom.................. 5 Nastavek
Mehurčki v zvočnem polju: Bjerknesove interakcije
 Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Mehurčki v zvočnem polju: Bjerknesove interakcije Seminar Avtor: Nika Oman Mentor: prof. dr. Rudolf Podgornik Ljubljana, september
Univerza v Ljubljani Fakulteta za matematiko in fiziko Oddelek za fiziko Mehurčki v zvočnem polju: Bjerknesove interakcije Seminar Avtor: Nika Oman Mentor: prof. dr. Rudolf Podgornik Ljubljana, september
1 Lastna nihanja molekul CO in CO 2 : model na zračni
 1 Lastna nihanja molekul CO in CO 2 : model na zračni drči Pri vaji opazujemo lastna nihanja molekul CO in CO 2 na preprostem modelu na zračni drči. Pri molekuli CO 2 se omejimo na lastna nihanja, pri
1 Lastna nihanja molekul CO in CO 2 : model na zračni drči Pri vaji opazujemo lastna nihanja molekul CO in CO 2 na preprostem modelu na zračni drči. Pri molekuli CO 2 se omejimo na lastna nihanja, pri
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
KEMIJA PRVEGA LETNIKA
 KEMIJA naravoslovna znanost oz. veda, ki proučuje zakonitosti v naravi družboslovje proučuje zakonitosti v medčloveških odnosih matematika je veda, ki služi kot pripomoček k drugim naravoslovnim in družboslovnim
KEMIJA naravoslovna znanost oz. veda, ki proučuje zakonitosti v naravi družboslovje proučuje zakonitosti v medčloveških odnosih matematika je veda, ki služi kot pripomoček k drugim naravoslovnim in družboslovnim
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Eksperimenti iz Atomov, molekul in jeder
 Eksperimenti iz Atomov, molekul in jeder Gregor Bavdek, Bojan Golli, Matjaž Koželj Pedagoška fakulteta UL Ljubljana 2017 Kazalo 1 Franck-Hertzov poskus 2 2 Lastna nihanja molekul CO in CO 2 : model na
Eksperimenti iz Atomov, molekul in jeder Gregor Bavdek, Bojan Golli, Matjaž Koželj Pedagoška fakulteta UL Ljubljana 2017 Kazalo 1 Franck-Hertzov poskus 2 2 Lastna nihanja molekul CO in CO 2 : model na
Atomi, molekule, jedra
 Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma............................. 5 1.2 Schrödingerjeva enačba za vodikov atom.................... 5 Nastavek
Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma............................. 5 1.2 Schrödingerjeva enačba za vodikov atom.................... 5 Nastavek
