Glava 4 ANALIZA I OBRADA SIGNALA U VREMENSKOM DOMENU
|
|
|
- Κλωπᾶς Φαίδρος Αλεξιάδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Glava 4 ANALIZA I OBRADA SIGNALA U VREMENSKOM DOMENU Obrada sgala u vremeskom domeu podrazumjeva određvaje odzva a pobudu prozvoljog oblka. Damčk lear sstem opsa su dferecjalm jedačama određvaje odzva jhovm drektm rješavajem u opštem slučaju je jedostava problem. M ćemo se zadržat a aalz obrad sgala learm, vremesk varjatm (Lear Tme Ivarat - LTI) sstemma. Vdjećemo da se LTI sstem u potpuost može opsat preko jegovog odzva a jedču mpulsu fukcju, odoso mpulsog odzva. Ukolko zamo mpuls odzv, operacja kovolucje, do koje se dolaz predstavljajem sgala prozvoljog oblka jedčm mpulsm fukcjama, omogućava am da proađemo odzv a prozvolju pobudu. Aalzrajuć osobe LTI sstema vdjećemo da se, osm mpulsm odzvom, LTI sstem može okaraktersat drugm fukcjama sstema, od kojh je pr obrad sgala u vremeskom domeu ajzačajj jedč odskoč odzv, defsa kao odzv a jedču odskoču fukcju.
2 GLAVA 4 4. Impuls odzv LTI sstema Impuls odzv h() t learog, vremesk varjatog sstema se defše kao odzv a pobudu u vdu jedče mpulse (Drakove) fukcje δ () t : () LTI { δ () t} ht = T, (4.) gdje je sa T LTI ozače operator kojm LTI sstem trasformše pobud sgal u sgal odzva. 4.2 Kovolucja Matematčka operacja ozačea kao kovolucja omogućava proalažeje odzva LTI sstema a pobud sgal prozvoljog oblka, ako je pozat mpuls odzv sstema. Kako bsmo to pokazal, prvo ćemo predstavt pobud sgal kao tegral mpulsh fukcja, a zatm odredt odzv a tako zapsa sgal, korsteć osobu superpozcje LTI sstema Predstavljaje sgala mpulsm fukcjama Posmatrajmo stepeastu aproksmacju ˆx() t sgala xt, () kao a Slc 4.. Ova aproksmacja se može zrazt kao leara kombacja pomjereh pravougaoh mpulsa: a sljedeć ač: δ Δ t () t Δt, t < Δt 2 = Δt 0, t > 2 (4.2) xt ˆ () = xk ( Δt) δδ t ( t kδt) Δt. (4.3) k = 56
3 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) (d) (e) Slka 4. (a) Stepeasta aproksmacja kotualog sgala. (b-e)) Elemet sume (4.): prmjer pomjereh pravougaoh mpulsa. 57
4 GLAVA 4 Kada Δ t 0, jedč pravougao mpuls δ Δ t () t postaje jedak Drakovoj fukcj δ () t. Razmac tačaka kδ t a vremeskoj os postaju beskoačo mal, te kδ t postaje kotuala varjabla τ, a suma (4.3) prelaz u tegral. Aproksmacja sgala ˆx() t u tom gračom slučaju postaje: lm xt ˆ lm xk tδ t t k t t xτ δ t τ dτ () = ( Δ ) Δ ( Δ ) Δ = ( ) ( ). (4.4) Δ t 0 Δ t 0 k = Posmatrajuć Slku 4. možemo prmjett da smajejem Δ t aproksmacja ˆx() t tež sgalu xt. () Pokazaćemo da se pr tome zapravo smajuje razlka površa koje sa vremeskom osom zaklapaju sgal xt () jegova aproksmacja ˆx() t. Δt Δt U tervalu vremea mδt < t < mδ t+ samo čla sume (4.3) za 2 2 k = m je razlčt od ule. To je grafčk lustrovao a Slc 4.2. Prmjetmo da pravougao mpuls δ Δ t ( t kδt) Δ t u (4.3) maju jedču ampltudu. Aproksmacja sgala ˆx() t u posmatraom tervalu je kostata jedaka = mδ t: vrjedost sgala xt () u tačk t Δt Δt xt ˆ () = xk ( Δt) δ Δ t ( t kδt) Δ t = xm ( Δt), mδt < t< mδ t+. (4.5) k= m 2 2 Posmatrajuć Slku 4.2(c) možemo zaključt da je vrjedost sgala u tačk mδ t jedaka površ posmatraog pravougaoog mpulsa šre Δ t x( mδt) ampltude. Ako su vrjedost sgala u posmatraom tervalu Δt koače, u gračom slučaju, kada Δ t 0, površa posmatraog pravougaoog mpulsa tež površ koju sa vremeskom osom a xt () posmatraom tervalu zatvara fukcja, odoso jeom tegralu: Δ t Δt mδ+ t 2 x( mδ t) = x( mδt) δδ t ( t mδt) Δ t = x( τ) dτ, Δt 0 Δt. (4.6) Δt mδ t 2 58
5 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) Slka 4. 2 Grafčkaa terpretacja jedačee (4.3): (a) sgal x( t ) prozvoljog oblka; (b) jed č pravougao mpuls pomjere u tačkuu t = mδt Δt Δ t (c) aproksmacja sgala u tervalu mδ t < t < mδt Izraz (4. 5) se eće promjet ako prošrmo grace tegralaa pr tome pomožmo podtegralu fukcju sa pravougaom mpulsom jedče ampltude m Δ t Δ t : ( δ Δt τ ) (mδt) = Δt x( x( ( τ ) δ Δt (τ mδt) Δtdτ, Δt 0. (4.7) 59
6 GLAVA 4 Kada Δ t 0, mδ t postaje kotuala varjabla t. U svakom treutku vremea vrjed da je: () = ( τ) δ( τ ) xt x tdτ, (4.8) što je zbog parost Drakove fukcje koačo jedako: () = ( ) ( ) xt xτ δ t τ dτ. (4.9) Izraz (4.9) je jedak aproksmacj sgala datoj sa (4.4). Na ovaj ač smo pokazal da je x() t = lm xˆ t () t, ako sgal xt () ma koače vrjedost, kao da Δ 0 se smajvajem Δ t smajuje razlka površa koje sa vremeskom osom zaklapaju sgal jegova aproksmacja. Razmatrajuć aproksmacju sgala proašl smo ač predstavljaja sgala mpulsm fukcjama dat sa (4.9). Jedakost (4.9) am govor da je sgal prozvoljog oblka moguće zrazt preko tegrala jedčh mpulsh fukcja koje su pomjeree u vremeu čje su teže (jače udara) jedake vrjedostma sgala u treucma u koje su pomjeree. Ilustracja ove jedakost je data a Slc 4.3, gdje je prkaza prozvolj sgal x( τ ), jedča δ t τ kao fukcja od τ sa fksm t jhov prozvod. mpulsa fukcja ( ) Jedakost (4.9) smo mogl jedostavje dokazat pozavajuć osobe Drakove fukcje: τ δ τ τ δ τ τ δ τ τ x( ) ( t ) d = x( t) ( t ) d = x( t) ( t ) d = x( t). (4.0) Prethodo provedeo šre razmatraje ma za clj da aglas terpretacju sgala xt () preko jedčh mpulsh fukcja. Iako sama po seb ovakva terpretacja sgala prozvoljog oblka ema svrhu, oa je veoma korsa prlkom zvođeja zraza za kovolucju kao metoda za određvaje odzva a prozvolju pobudu. 60
7 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) Slka 4. 3 Grafčkaa terpretacja jedačee (4.9): (a) sgal x( τ ) prop zvoljog oblka; (b) pom mjerea jedča mpulsa fukcja δ (t τ ) kao fukcja od τ sa fksm t (c) prozvod ova dva sgala Kovoluco tegral Kao što smo već raje stakl,, clj am je da proađemo odzv LTIL sstema a pobuduu prozvoljm sgalom. Vdje el smo da sgal prozvoljog oblka mož žemo aproksmrat pomoću jedčh mpulsh fukcja: ( ) ˆx t = x( k = ) kδt δ δ Δt ( ) t kδ t Δ t, (4.) 6
8 GLAVA 4 te da ova aproksmacja u gračom slučaju, kada Δ t 0, postaje jedaka sgalu xt: () xt xk tδ t k t t xτ δ t τ dτ () = lm ( Δ ) Δt ( Δ ) Δ = ( ) ( ). (4.2) Δ t 0 k = Proađmo prvo odzv a aproksmacju sgala ˆx() t. Ozačmo sa hδ t () t odzv a jedč pravougao mpuls δ Δ () t : Δt () { δ Δt() } Za vremesk varjate ssteme vrjed da je: gdje je sa sstem. t h t = T t. (4.3) ( Δ ) = { δ Δ ( Δ )} h t k t T t k t, (4.4) Δt TI t T TI ozačea trasformacja koju uos vremesk varjata Osoba superpozcje LTI sstema dopušta am da odzv a aproksmacju sgala ˆx() t apšemo u oblku: yˆ() t = T { ˆ LTI x() t } = T LTI x( kδt) δ Δt ( t kδt) Δ t= k = { Δ } ( ) Δ ( ) ( ) T δ ( ) = x kδt t kδt Δ t = x kδt h t kδt Δt. k= LTI t t k= (4.5) U gračom slučaju, kada Δ t 0, jedč pravougao mpuls δ Δ t () t postaje jedak Drakovoj fukcj δ () t, pa stoga odzv a jedč pravougao mpuls hδ t () t postaje jedak mpulsom odzvu ht. () Uz to, kδt postaje kotuala varjabla τ suma prelaz u tegral. Buduć da u ovom gračom slučaju ˆx() t xt (), odzv a ˆx() t postaje odzv a xt: () 62
9 Aalza obradaa kotualh sgalaa u vremeskom domeu y( ( t) = T = lm Δ t 0 k = = lm Δ t 0 k = = x τ h t τ dτ. LTI { x ( ) ()} t x ( ( ( } = T ) x kδ t T ) kδ t h ) LTI t Δ 0 k = LTII Δt lmm ( { δ Δt ( t k Δt Post tupak određvajaa odzva a sgal prozvoljog oblka putem odzva a jegovu stepeastu aproksmacju lustrova je a Slc Posebo su prkaza odzv a pojedače pravougaoe mpulse kojma se s aproksmra pobud sgal. Aproksmacjaa odzva jedaka je zbru th pojedačh odzva. ) ( x k Δt t kδ t Δ t = )} ) ) δ Δ t Δ t = (t kδt) Δt = (4.6) (a) (b)) Slka 4. 4 Grafčkaa terpretacja određvajaa odzva: (a) pobuda x t prozvoljog oblka (b) mpuls odzv sljedećoj strac) ); h( t ) ( ) (astavakk a 63
10 GLAVAA 4 (c) (d) (e) (f) Slka 4.4 (astavak): (c-e) ek od pojedačh pravougaoh mpulsa kojmaa se apr roksmra pobuda (f) aproksmacjaa pobude ˆx ( t) (astavakk a sljedećoj strac); 64
11 Aalza obradaa kotualh sgalaa u vremeskom domeu (g) (h) () (j) Slka 4.4 (astavak): (g-) odzv a pojdače pravougaoe mpulse (j) aproksmatv odzvv ŷ ( t ) (astavak a sljedećoj strac); 65
12 GLAVAA 4 (k) Slka 4.4 (astavak): (k)) odzv y ( t ). Dakle, odzv y ( t ) learog, vremesk varjatog sstema a pobudu x( ( t ) prozvoljog oblka može se dobt a osovu jedačee (4.6). U svom koačom oblku: ( y t = ova jedača je ozačeaa kao kovoluco tegral. Matematčka operacjaa kovolucje dva sgala x( t) smbolčk ozačavaa sa: ) x( τ )h(t τ ) )dτ h( ( t ) (4.7) data sa (4.7) se ( ) y t = x( ( t) h( ( ) Kovolucja je komutatva, asocjatvaa dstrbutva operacja. Ove osobe koje sljedee drekto z defcje kovolucje preko tegrala olakšavaju aalzu složeh sstema. Osoba komk mutatvost am govor da ulaz sgal mpuls odzv mogu zamjet uloge, a da se zlaz sgal e promje: t. (4.8) y( t) = x( t ) h( ) = h( ( t) x( ( t) t =. (4.9) 666
13 Aalza obrada kotualh sgala u vremeskom domeu () T { } { } xt T LTI y() t LTI 2 Slka 4.5 Blok šema kaskade veze dva LTI sstema. Osobu asocjatvost možemo korstt za proalažeje mpulsog odzva kaskade veze LTI sstema. Posmatrajmo kaskadu vezu dva LTI sstema sa mpulsm odzvma h () t h2 () t, prkazau a Slc 4.5. Za pojedače ssteme vrjed da je y() t = x() t h() t y2() t = x2() t h2() t. Kako je ulaz u prv sstem jedak ulazu u cjel sstem x () t = x() t, ulaz u drug sstem jedak zlazu z prvog sstema x2() t = y() t, a zlaz z cjelog sstema jedak zlazu z y t = y t, sljed: drugog sstema () () 2 () = () = () () = () () = () () () y t y2 t x2 t h2 t y t h2 t x t h t h2 t. (4.20) Osoba asocjatvost kovolucje am omogućava promjeu redosljeda operacja, tako da je: () () () () () () () y t = x t h t h t = x t h t h t 2 2. (4.2) Iz (4.2) zaključujemo da je mpuls odzv kaskade veze dva LTI sstema jedak kovolucj jhovh mpulsh odzva: () () () ht = h t h t. (4.22) 2 Posmatrajmo sada paralelu vezu dva LTI sstema sa mpulsm odzvma h2 t, prkazau a Slc 4.6. Kod paralele veze se st pobud sgal x t = x t = x t, dok je zlaz h () t () stovremeo dovod a ulaz oba sstema () 2() () cjelog sstema jedak zbru zlaza pojedačh sstema y() t y () t y () t Sljed da je odzv paralele veze jedak: () () () () () () () = +. 2 y t = y t + y t = x t h t + x t h t. (4.23) 67
14 GLAVA 4 T LTI { } xt () y() t T LTI { } 2 Slka 4.6 Blok šema paralele veze dva LTI sstema. Na osovu osobe dstrbutvost kovolucje, z (4.23) sljed da je: () () () () () () () () y t = x t h t + x t h2 t = x t h t + h2 t, (4.24) te je mpuls odzv paralele veze dva LTI sstema jedak zbru mpulsh odzva pojedačh sstema koj če paralelu kofguracju: () () () ht = h t + h t. (4.25) Grafčko rješavaje kovolucje Posmatrajuć kovoluco tegral: () = ( ) ( ) y t x τ h t τ dτ, (4.26) zaključujemo da je u svakom treutku t sgal y() t jedak težskom tegralu sgala x( τ ), pr čemu su teže jedake h( t τ ). Kako bsmo došl do grafčkog metoda za određvaje kovolucje za specfču vrjedost h t τ h τ, koj je fukcja varjable t, prvo geeršmo sgal ( ) z sgala ( ) 68
15 Aalza obrada kotualh sgala u vremeskom domeu ezavse varjable τ, tako što ćemo uradt refleksju sgala h( τ ) oko shodšta pomjert ga udeso za t ako je t > 0, l uljevo za t ako je t < 0. Podtegral sgal dobjemo možejem x( τ ) sa h( t τ ) za razlčte vrjedost t. Za jedu specfču vrjedost ezavse varjable t, kovolucja y() t se dobje tegrrajuć prozvod x( τ) h( t τ) u gracama od do, što u geometrjskom smslu zač račuajuć površu spod prozvoda x( τ) h( t τ). Možemo zamslt kao da sgal h( t τ ) "klz" po τ os pr tome gledamo kolko je jegovo preklapaje sa x( τ ). Kovolucja je mjera tog preklapaja zražea površom koju sa τ osom zaklapa prozvod x( τ) h( t τ). U slučajevma kada se rad sa jedostavm sgalma, površa se lako odred geometrjskm metodma. Postupak je potrebo poovt za svaku vrjedost ezavse varjable t, odoso za svak vremesk treutak u kom želmo da odredmo sgal odzva. Pr zboru tačaka u kojma će se račuat kovolucja potrebo je prekrt čtav opseg u kome je prozvod x( τ) h( t τ) razlčt od ule, što za sgale koačog trajaja zač u početom koraku pomjert reflektova sgal dovoljo uljevo da se zbjege preklapaje sa sgalom x( τ ), a sa račuajem prestat kada prlkom pomjeraja reflektovaog sgala udeso prestae preklapaje th sgala. Ukolko trajaje bar jedog od sgala koj učestvuju u kovolucj je koačo, kovolucja se račua za sve vrjedost ezavse varjable t od do. Postupak grafčkog rješavaja kovolucje lustrova je a Slc 4.7 a prmjeru kovolucje sgala xt () mpulsog odzva h() t. Oba sgala su u oblku pravougaoog mpulsa, al razlčth ampltuda. Rezultat kovolucje u tačkama u kojma se vrš račuaje su a rezultujućoj Slc 4.7(z) aglaše samo rad boljeg razumjevaja. 69
16 GLAVAA 4 (a) (b) (c) (d) (e) (f) Slka 4.7 Ilustracjaa grafčkog rješavajaa kovolucje: (a) sgal t ; (b) st sgal prkaza a τ os (c-f) strac); pomjere reflektova mpuls odzv (astavak a sljedećoj x( ) 70
17 Aalza obradaa kotualh sgalaa u vremeskom domeu (g) (h) () (j) (k) (l) Slka 4.7 (astavak): (g) mpuls odzv h ; (h) reflektova mpuls odzv prkaza a τ os (-l)) prozvod sgalaa x( τ ) pomjereh reflektovah mpulsh odz va (astavak a sljedećoj stras ac); () t 7
18 GLAVAA 4 (m) () (o) (p) (q) Slka 4.7 (astavak): (m-qstrac); pomjere reflektova mpuls odzv (astavak a sljedećoj 72
19 Aalza obradaa kotualh sgalaa u vremeskom domeu (r) (s) (t) (u) (v) Slka 4.7 (astavak): (r-v) prozvod sgala x τ pomjerehh reflektovah mpulsh odz zva (astavak a sljedećoj strac); ( ) 73
20 GLAVAA 4 (z) Slka 4.7 (astavak): (z) rezultat kovolucje. Prmjer 4.: Grafčkm putem odredt odzv LTI sstema sa mpulsm odzvom datm a Slc 4.8(a) a pobudu prkazau a Slc 4. 8(b). (a) (b) Slka 4. 8 (a) Impuls odzv LTII sstema (b) pobuda. 74
21 Aalza obradaa kotualh sgalaa u vremeskom domeu Rješe eje: Odz zv LTI sstema je dat kovolucjom mpulsog odzva pobudog sgala. Ako se grafčkom rješavaju kovolucje u ovom zadatku prstup tako da se reflektuje pobud sgal, taj sgal se ako reflektovaja pomjera uljevo dok e prestae preklapaje sa mpulsm odzvom. Preklapaje sa mpulsm odzvom počje kadaa se predjaa vca reflektovaog pobudog sgala ađe u tačk T, što odgovara sgalu x ( T τ ). Za svako t < TT ema preklapaja mpulsog odz va sa pomjerem reflektovam pobudm sgalom, pa je rezultatt kovolucje jedak ul. U tervalu TT < t < 0 površa spod prozvoda h( τ ) x( t τ ) raste jerr se sa porastom vremea t povećava šra tervala a kom je taj prozvod razlr lčt od ule. Međutm, u tervalu 0 < t < T površa ostaje kostata jerr see za svako t z tog trevala sgal x(t τ ) u potpuost preklapa sa h( τ ). Tek za t > T preklapaje se postepeo smajuje potpuo prestaje za t = 2TT. Rezultatt kovolucje je prkaza a Slc 4.9. Prm mjetmo da se odzv LTI sstema sa mpulsm odzvom koj je jedak ul za t < 0 pojavo prje pobude. Slka 4.9 Kovolucja sgalaa sa Slke
22 GLAVAA 4 Prmjer 4.2: Impuls odz v LTI sstema dat je a Slc 4.0(a). Grafčkmm putem odredt odzv a pobud sgal prk kaza a Slc 4.0(b) ). Rješeje: Istm postupkom kao u Prmjeru 4. dobjamo sgal odzva dat a Slc 4.. Buduć da je mpuls odzv LTI sstema jedak ul za t < 0, odzv počje od treutka pobuđvaja sstema. (a) (b) Slk ka 4.0 (a) Impuls odzv kauzalog LTI sste ema (b) kauzalaa pobuda. 76
23 Aalza obradaa kotualh sgalaa u vremeskom domeu Slka 4. Kovolucja sgalaa sa Slke 4.0. Prm mjer 4.3: Za kauzal LTI sstem datt a Slc 4. 2( (a) a pobu ud sg al prkaza a Slc 4.2(b) ). grafčkm putem odredt odzv (a) (b) Slka 4. 2 (a) Impuls odzv kauzalog LTI sstema (b) pobud sgal. 77
24 GLAVAA 4 Rješeje: Prmjetmo da se pobud sgal može razložt a elemetare sgale x( ( t) = x ( t ) + x 2 ( t ) kao a Slc Potražćemo odzv sstema korsteć prcp superpozcje. Graf fčkm putem odredmo pojedače kovolucje mpulsog odzva sa pravougaom mpulsma sa Slke 4.3. Rezultat ovh kovolucja su dat a Slc 4..4(a,b). Prmjetmo da je pravougao mpuls x2 ( t ) pomjerea verzja pravougaoog mpulsa x ( t ) pomožea sa -, tj. x 2 ( t ) = x (t T ). Pozavajuć ko volucju y () t = h( t ) x ( t), kovolucju mpulsog odzva pravougaoog mpulsa x2 ( t ) smo mogl dobt korsteć prcp learost vremeske varjatost kao y 2 () t = h ( t ) x 2 ( t ) = y ( t T ). Na Slc 4. 4( (c) dat je rezultat kovolucje kao y t = + y t. ( ) y () t 2 ( ) Slka 4.3 Razlagaje sgala x( t ) a pravougaoe mpulse x ( t ) x 2 ( ) t. 78
25 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) Slka 4.4 (a) Kovolucja y t = t x ; (b) kovolucja y 2 ( t ) = h() t x 2 ( ) (c) kovolucja y () t = h ( t ) x ( t ). 2 t ( ) = h( ) () t 79
26 GLAVA 4 U aalz obrad sgala posebo mjesto zauzma kovolucja prozvoljog sgala sa Drakovm mpulsma. Posmatrajmo kovolucju sgala xt () prozvoljog oblka sa pomjerem Drakovm mpulsom δ ( t t 0 ). Na osovu defcoog zraza za kovolucju: dobjamo da je: () = () () = ( ) ( ) y t x t h t x τ h t τ dτ, (4.27) y() t = x() t δ ( t t ) = x( τ) δ ( t t τ) dτ. (4.28) 0 0 Po svojstvu odabraja Drakove fukcje zamo da je: te je kovolucja (4.28) jedaka: ( τ) δ( τ) ( ) δ( τ) x t t = x t t t t, (4.29) () = ( ) ( ) y t x t t δ t t τ dτ. (4.30) 0 0 Itegral Drakovog mpulsa od do jedak je jedc, eovso od toga u koju tačku vremea je Drakov mpuls pomjere. Dakle, kovolucja sgala xt () prozvoljog oblka sa Drakovm mpulsom pomjerem u tačku t 0 jedaka je sgalu xt, () pomjereom u tačku t 0 : ( ) ( ) δ ( ) ( ) yt = xt t t = xt t. (4.3) 0 0 Na Slc 4.5 lustrovao je grafčko rješavaje kovolucje prozvoljog sgala xt () sa pomjerem Drakovm mpulsom ht () = δ ( t t 0 ). Prlkom formraja prozvoda x( τ) h( t τ) za svaku vrjedost ezavse varjable t dobjamo prozvod x( τ) δ( t t 0 τ), koj je po svojstvu odabraja Drakove xt t δ t t τ. Kovolucja u tačk t je jedaka površ fukcje jedak ( ) ( )
27 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) (d) (e) (f) Slka 4.5 Kovolucja sgala prozvoljog oblka pomjereog Drakovog mpulsa: (a) sgal prozvoljog oblka (b) mpuls odzv prkaza a τ os; (c)( reflektova mpuls odzv; ( d,e) pomjere reflektova mpuls odzv (f) rezultat kovolucje. 8
28 GLAVA 4 koju prozvod xt ( t0) δ( t t0 τ) udara Drakove fukcje zos xt ( t 0 ), te je y() t x( t t 0 ) zatvara sa τ osom. Ta površa je jača =. Posmatrajmo sada kovolucju prozvoljog sgala xt () poovljem Drakovm mpulsma δ() t = δ( t kt) k = smo ozačl sa T. Zajuć da je xt ( ) δ ( t kt) xt ( kt) lear operator, dobjamo da je: sa perodčo. Perod sgala δ () t = da je kovolucja () = () δ () = () δ( ) = () δ( ) = ( ) xt xt t xt t kt xt t kt xt kt k= k= k=.(4.32) Dakle, kovolucjom prozvoljog sgala xt () sa perodčo poovljem Drakovm mpulsma dobjamo jegovo perodčo prošreje: () = ( ) xt xt kt. (4.33) k = Za lustracju je a Slc 4.6 prkazaa kovolucja trougaoog mpulsa sa perodčo poovljem Drakovm mpulsma. Rezultat te kovolucje su perodčo poovlje trougao mpuls sa stm perodom. 4.3 Jedč odskoč odzv LTI sstema Osm mpulsm odzvom, sstem je potpuo određe ako pozajemo jedč odskoč odzv, tj. odzv a jedču odskoču fukcju u() t. Korsteć kovoluco tegral, jedč odskoč odzv a() t dobjamo kao: () = () () = ( ) ( ) = ( ) at ut ht uτ ht τ dτ ht τ dτ. (4.34) 0 82
29 Aalza obradaa kotualh sgalaa u vremeskom domeu (a) (b) (c) Slka 4. 6 Ko volucja sgalaa saa perodčoo poovljem Drakovm mpulsma: (a) sgal x ( t); (b) povorka Drakovh mpulsa (c) rezultatt kovolucje. Za kauzale ssteme je h( t τ ) = 0 umjesto, pos staje t : za τ > t, pa gorja graca tegrala, a( ( ) t t = h( ( τ )dτ. (4.35) Dakle, jedč odskoč odzv je jedak tegralu mpulsog odzva, dok see mpuls odz v može proać kao k zvod jedčog odskočog odzva: da ( t ) h( t ) =. (4.36) dt 83
30 GLAVA Osobe LTI sstema Vdjel smo da se odzv kotualog LTI sstema a prozvolju pobudu može dobt kovolucjom ulazog sgala mpulsog odzva. Stoga možemo reć da je kotual LTI sstem u potpuost okaraktersa svojm mpulsm odzvom h() t. Osove osobe sstema, koje smo aalzral u Glav 3, sada ćemo posmatrat pod uslovom da je sstem leara vremesk varjata LTI sstem bez memorje Podsjetmo se da je sstem bez memorje oaj sstem kod koga zlaz u ekom treutku zavs od vrjedost ulaza samo u tom treutku. Jed ač da ovo bude tačo za LTI ssteme je da sstem bude opsa sa: () Kx() t y t =. (4.37) Impuls odzv se defše kao odzv sstema a pobud sgal u vdu Drakovog mpulsa x() t = δ () t, te je za LTI ssteme bez memorje mpuls odzv oblka: () δ () ht = K t. (4.38) Na zlazu sstema bez memorje sgal može bt samo pojača l oslablje u odosu a ulaz sgal. Za K = rad se o sstemu kod koga je mpuls odzv ht () = δ () t, te je sgal a zlazu ovog LTI sstema jedak sgalu a jegovom ulazu. Blo koj LTI sstem sa drugačjm mpulsm odzvom je LTI sstem sa memorjom Ivertblost LTI sstema Posmatrajmo LTI sstem sa mpulsm odzvom () h t. Napomemo da je sstem po defcj vertbla ako je moguće proać verz sstem koj, kad 84
31 Aalza obrada kotualh sgala u vremeskom domeu se veže kaskado sa orgalm sstemom, formra takav slože sstem a čjem je zlazu odzv jedak ulazom sgalu. Ako sa hi () t ozačmo mpuls odzv verzog sstema, da b LTI sstem bo vertbla mora da vrjed: () () δ () ht h t = t. (4.39) I Buduć da je pod ovm uslovom mpuls odzv kaskade veze Drakov mpuls: K () () () δ () h t = h t h t = t, (4.40) I a zamo da je kovolucja prozvoljog sgala sa Drakovm mpulsom jedaka tom sgalu, zaključujemo da je odzv kaskade veze jedak sgalu a ulazu u kaskadu vezu sstema, koj je stovremeo ulaz sgal u orgal sstem sa mpulsm odzvom h() t Kauzalost LTI sstema Kada smo uvodl kocept kauzalost rekl smo da je sstem kauzala ako odzv zavs samo od treute prošlh vrjedost sgala a ulazu u sstem. Zbog toga kod kauzalh LTI sstema gorja graca kovolucoog tegrala: () = ( ) ( ) y t x τ h t τ dτ, (4.4) e smje da bude veća od vrjedost ezavse varjable t za koju se račua vrjedost odzva, jer b u suprotom u račuaju odzva učestvovale x τ za τ > t, te je: vrjedost pobudog sgala ( ) t () = ( ) ( ) Smjeom t τ τ tegral (4.42) se svod a: y t x τ h t τ dτ. (4.42) 85
32 GLAVA 4 () = ( ) ( ) Zaključujemo da će opšt zraz za kovolucju: y t h τ x t τ dτ. (4.43) 0 () = ( ) ( ) y t h τ x t τ dτ, (4.44) koj je ekvvaleta sa (4.4), postat jedak (4.43) samo ako je ht () = 0 za t < 0, te je uslov kauzalost kotualh LTI sstema da jhov mpuls odzv bude jedak ul za t < Stablost LTI sstema Sstem je stabla ako ograče pobud sgal prozvod ograče sgal odzva. Da bsmo odredl uslove pod kojma je LTI sstem stabla, posmatraćemo LTI sstem sa mpulsm odzvom h() t a koj djeluje ograče pobud sgal. Kad kažemo da je sgal ograče oda postoj eka poztva kostata B < za koju je xt () < B, t. Tada je: yt hτ xt τ dτ hτ xt τ dτ B hτ dτ () = ( ) ( ) ( ) ( ) ( ). (4.45) Prema tome, sgal odzva će bt ograče kotual LTI sstem će bt stabla ako je jegov mpuls odzv apsoluto tegrabla: ( τ) h dτ <. (4.46) Kao prmjer stablog LTI sstema možemo avest sstem čja je uloga samo da zakas ulaz sgal, pa je jegov mpuls odzv ht () = δ ( t t 0 ). Određujuć da l je sstem stabla sptujemo apsolutu tegrablost mpulsog odzva: h( τ) dτ = δ ( τ t0 ) dτ =. (4.47) 86
33 Aalza obrada kotualh sgala u vremeskom domeu Vdmo da je mpuls odzv ovog LTI sstema apsoluto tegrabla pa je sstem stabla, što je blo za očekvat jer je odzv ovog sstema a blo koju ogračeu pobudu jedak pomjereoj verzj pobude, dakle ograče. Posmatrajmo sada sstem opsa sa: t () ( τ) y t = x dτ, (4.48) koj azvamo tegrator. Da bsmo proašl mpuls odzv sstema pretpostavmo da je x() t = δ () t. Tada je odzv jedak mpulsom odzvu, što je u ovom kokretom slučaju jedča odskoča fukcja: t () = () = δ ( τ) τ = () y t h t d u t. (4.49) Isptujuć apsolutu tegrablost mpulsog odzva dobjamo beskoaču vrjedost, jer je tegral jedče odskoče fukcje sgal agba r() t koj beskoačo raste sa porastom vremea: ( ) ( ) h τ dτ = u τ dτ = dτ =, (4.50) te zaključujemo da se rad o establom LTI sstemu Ops LTI sstema dferecjalm jedačama U clju opsa sstema potrebo je fzčkm sstemma prdružt parametre varjable relevate za jegovo poašaje, te uspostavt relacje zmeđu jh. Veze zmeđu parametara varjabl sstema, kao relacje koje povezuju ulaze zlaze sgale, određuju se a osovu prrodh zakoa l ekspermetalo. U realm fzčkm sstemma za varjable bramo mjerljve velče. Vdjel smo da je kod LTI sstema odzv dat kovolucom tegralom. Dakle, relacje zmeđu ulazh zlazh sgala u sstemu se mogu opsat tegralo-dferecjalm jedačama. U slučaju da sgal u sstemu zavse 87
34 GLAVA 4 samo od jede ezavse varjable (vremea) to su obče dferecjale jedače. Sstem čje varjable zavse od vše ezavsh varjabl (pr. mjejaju se u vremeu u prostoru), opsuju se parcjalm dferecjalm jedačama. Kod LTI sstema bez memorje dferecjale jedače se svode y t = Kx t. a algebarske, jer je kod ovh sstema () () 4.5. Jedače staja Pretpostavmo da je za ops poašaja ekog sstema dovoljo pozavaje fzčkh velča koje ćemo ozačt kao varjable staja. U tom slučaju su sve ostale velče u sstemu, zuzev ulazh sgala, zavse varjable. Pretpostavmo da sstem može da bude pobuđe sa m ulazh sgala (ulazh varjabl) da ma l zlazh sgala, odoso zlazh varjabl. Vektor varjabl staja T x () t, x2() t,, x () t ćemo ozačt kao vektor staja x () t, dok ćemo T vektore ulazh e() t, e2() t,, em () t zlazh sgala T y() t, y2() t,, yl () t ozačt sa e () t y () t, respektvo. Svak od elemeata ovh vekora je fukcja vremea kao ezavse varjable. Sa T su ozače traspoova vektor. Relacje koje povezuju varjable staja ulaze varjable opsuju se skupom smultah dferecjalh jedača prvog reda, koje se ozačavaju kao sstem jedača staja. U matrčoj form sstem jedača staja u vremeskom domeu ma oblk: () = () + () Dx t Ax t Be t, (4.5) pr čemu operator D ozačava prvu dervacju, pa je Dx () t vektor prvh zvoda varjabl staja, A kvadrata matrca staja B pravougaoa matrca koefcjeata uz ulaze sgale. Izlaze varjable sstema su određee matrčom jedačom: () t = () t + () t y Cx De, (4.52) gdje su C D matrce koje povezuju zlaze varjable sa varjablama staja ulazm varjablama. Elemet matrca A, B, C D zavse od parametara 88
35 Aalza obrada kotualh sgala u vremeskom domeu strukture šeme sstema. Ukolko se rad o vremesk varjatm sstemma, elemet matrca A, B, C D se e mjejaju u toku vremea. Ako je ek od elemeata ovh matrca fukcja ulazog l zlazog sgala, oda se rad o elearm sstemma Ops LTI sstema dferecjalm jedačama všeg reda Za obradu sgala LTI sstemma posebo su važ sstem sa jedm ulazom jedm zlazom, jer prlkom rada sa složejm sstemma korstmo prcp superpozcje. Stoga se ećemo zadržavat a aalz sstema metodama varjabl staja, već ćemo z jedača staja odredt relacju koja povezuje jeda zlaz sgal yj () t sa jedm ulazm sgalom ek () t. Gledao matematčk, sstem od smultah dferecjalh jedača (4.5) prvog reda svodmo a jedu dferecjalu jedaču -tog reda sa kostatm koefcjetma: () () () () m d yj t dyj t d ek t dek t a + + a + a0yj() t = bm + + b m + b0ek () t. (4.53) dt dt dt dt Pr tome korstmo jedače (4.52) koje povezuju zlaze varjable sa varjablama staja pobudama. Uobčajea otacja pr radu sa varjablama staja je da se sa x () t ozačavaju varjable staja, tj. elemet vektora staja x () t, a sa e () t pobud sgal (ekstacje), dok se pr aalz sstema sa jedm ulazom jedm zlazom sa xt () občo ozačava ulaz, a sa y() t zlaz sgal sgal. Zbog toga ćemo u daljjem zlagaju, kada budemo korstl ops sstema dferecjalm jedačama všeg reda, korstt sljedeć oblk: () () () () m d y t dy t d x t dx t () = m + + m + 0 a a a y t b b b x t. (4.54) dt dt dt dt Sažet oblk dferecjale jedače (4.54) se može zapsat sa: k k d y m () t d x() t ak = b k k. (4.55) k dt k= 0 k= 0 dt () 89
36 GLAVA 4 U lteratur se korst zaps dferecjale jedače (4.54) sa operatorma k D kojma se ozačava k -ta dervacja, pa se dferecjala jedača (4.54) može zapsat u oblku: () () m m ad + a D + + ad + a 0 y t = bmd + am D + + bd + b 0 x t. (4.56) Koefcjet a k b k su poveza sa vrjedostma elemeata matrca A, B, C D jer se dferecjala jedača (4.54) može zvest z sstema jedača (4.5) (4.52). Ako su koefcjet a k b k kostate, rad se o learm vremesk varjatm sstemma. Ako ek od ovh koefcjeata zavs od vremea, oda se poašaje sstema u toku vremea mjeja, te oblk zlazog sgala e zavs samo od oblka ulazog sgala, već od treutka pobuđvaja sstema, te kažemo da je sstem vremesk zavsa. Ako postoj ek koefcjet u jedač (4.54) koj je fukcja ulazog l zlazog sgala, oda je ta dferecjala jedača eleara, te se rad o elearm sstemma. Dferecjala jedača (4.54) je ehomogea jer je jea desa straa razlčta od ule. Desa straa (4.54) je fukcja pobude, koja u opštem slučaju sadrž ulaz sgal xt () jegove dervacje do m -tog reda. Uslov fzčke ostvarljvost sstema je da je m. Kod LTI sstema bez memorje sv koefcjet osm a 0 b 0 su jedak ul, te se leara dferecjala jedača (4.54) svod a algebarsku jedaču: b0 y() t = x() t = Kx() t, (4.57) a0 tako da je određvaje odzva u ovakvm sstemma jedostavo. Reale kauzale LTI ssteme sa memorjom aalzramo u koačom vremeskom tervalu, koj je ograče početm treutkom t 0 kada počje pobuda krajjm treutkom t, koj može bt promjeljv ako želmo da odredmo poašaje sstema u blo kom treutku vremea ako početog treutka posmatraja t 0. Postupak tražeja odzva LTI sstema sa memorjom svod se a tražeje rješeja ehomogee leare dferecjale jedače -tog reda sa kostatm koefcjetma, čj je opšt oblk dat u form ( ). Odzv se sastoj od rješeja odgovarajuće homogee dferecjale jedače 90
37 Aalza obrada kotualh sgala u vremeskom domeu partkularog djela, a za kompleto rješavaje eophodo je specfcrat počete uslove u ekom treutku vremea. Rješeje homogee dferecjale jedače: d y t () dy() t a + + a + a0y t = 0, (4.58) dt dt koje se azva sopstve odzv sstema, je leara kombacja svh jeh partkularh rješeja. Svaku homogeu learu dferecjalu jedaču sa st kostatm koefcjetma će zadovoljt fukcja oblka e, s. Uvrštavajem ovog pretpostavljeog rješeja u (4.58) dobjamo: ( ) () as a s as a e. (4.59) st = 0 Vrjedost s za koje je jedača (4.59) zadovoljea dobjaju z: as + a s + + as + a0 = 0. (4.60) Jedača (4.60) se zove karakterstča jedača sstema, a komplekse učestaost s koje je zadovoljavaju zovu se sopstvee učestaost sstema. Buduć da je karakterstča jedača tog reda, postoj ukupo korjea karakterstče jedače s = p, =,2,,, odoso sopstveh učestaost. Kada su sve sopstvee učestaost razlčte, pojedača rješeja homogee dferecjale jedače (4.58) su: pt p2t () () () pt y t = K e, y t = K e,, y t = K e. (4.6) 2 2 Opšte rješeje homogee dferecjale jedače je: gdje su s () = pt, (4.62) = y t K e K kostate koje zavse od početh uslova. U slučaju všestrukh korjea zraz postaju složej. Pretpostavmo da je korje karakterstče jedače p reda r, tj. p = p2 = = pr. Tada se može pokazat da su pojedača rješeja homogee dferecjale jedače vezaa za ovu sopstveu učestaost oblka: r r 2 (), (),, (), () y t = K t e y t = K t e y t = K te y t = K e. (4.63) p t p 2 2 t p t p t r r r r 9
38 GLAVA 4 Opšt oblk sopstveog odzva je u ovom slučaju: r s = = r+ r pt pt () = +. (4.64) y t Kt e K e Ukolko postoj vše všestrukh sopstveh učestaost, za svaku od jh se formra po jeda suma a ač kao što je rađeo za všestruk korje p u (4.64). Sopstve odzv može da bude potakut pobudom, al o postoj kada je pobuda fukcja jedaka ul, jer predstavlja rješeje homogee dferecjale jedače. Sopstveo rješeje opsuje razmjeu eergje u sstemu koja se odvja bez utcaja vajske pobude u smslu da vajska pobuda e utče a oblk sopstveog odzva. Pojam "sopstveo" potče od čjece da jegove kompoete Ke p t oscluju sključvo sopstvem učestaostma p, koje zavse samo od strukture šeme parametara sstema a e od vajske pobude. Vdjećemo kasje da jedo kostate K sopstveog rješeja zavse od pobudog sgala zatečeog staja, odoso akumulsae eergje u treutku pobuđvaja sstema. Prud odzv sstema je partkular do rješeja ehomogee dferecjale jedače koj zavs od pobude. Taj partkular do odzva se proalaz tako da se pretpostav rješeje u vdu leare kombacje člaova koj se pojavljuju s dese strae dferecjale jedače. Pr tome su koefcjet leare kombacje epozat određuju se uvrštavajem pretpostavljeog rješeja u ehomogeu dferecjalu jedaču. Kada se rad sa složem oblcma ekstacje, kod LTI sstema ema potrebe da se određuje partkularo rješeje a ovaj ač. Dovoljo je proać mpuls odzv sstema, pa odzv a prozvolju pobudu odredt kao kovolucju pobudog sgala mpulsog odzva. Kompleta odzv jedak je zbru sopstveog prudog odzva. U slučaju razlčth sopstveh učestaost kompleta odzv je jedak: p. (4.65) = pt () = + () yt Ke y t Kod stablh sstema prv čla ščezava tokom vremea u sstemu se uspostavlja ustaljeo staje kada je odzv jedak prudom odzvu. Zbog toga kažemo da prv čla opsuje prelaz proces. Ako je pobuda kostata l 92
39 Aalza obrada kotualh sgala u vremeskom domeu prostoperodča (traja) fukcja, ustaljeo staje se često azva stacoaro staje. Kako b odzv bo jedozačo određe, eophodo je odredt kostate K. Oe se mogu odredt z sstema od jedača koje se dobju dervrajem rješeja (4.65) puta uvrštavajem pozath vrjedost kompletog partkularog odzva, kao jhovh zvoda u treutku pobuđvaja sstema t 0. Rad jedostavost, gdje god to prroda problema dopušta, uzma se da je t 0 = 0. Buduć da rješeje (4.65) vrjed za t 0+, jegovm dervrajem puta uvrštavajem t = 0+, formramo sstem od algebarskh jedača: ( 0 ) ( 0 ) y y = K dy dt + p + p ( 0 ) ( 0 ) = = y p ( 0 ) ( 0 ), + p K + = dt p = d dt dy = dt + + dy pk (4.66) z kojh je moguće odredt kostat K. Vdmo da je za proalažeje odzva eophodo pozavaje vrjedost odzva eposredo ako dy dovođeja ekstacje, tj. vrjedost ( 0 ), 0,,, + =. Dakle, potrebo dt je proać ač kako z pozath vrjedost odzva u treutku t = 0 eposredo prje pobuđvaja sstema odredt počete vrjedost odzva u treutku t = 0+. U slučaju kada su odzv sve jhove dervacje kotuale dy dy dy fukcje, rješeje je jedostavo jer je ( 0 ) ( 0 ) ( 0 = + = ), za dt dt dt = 0,,,. Kod eregularh komutacja, kod kojh ovo je uvjek zadovoljeo, problem se usložjava ećemo ga razmatrat u vremeskom domeu, jer se lakše rješava u domeu Laplasove trasformacje, što ćemo vdjet u Poglavlju 7. Iz ovako postavljeog sstema (4.66) se jaso vd da kostate K zavse od razlke početh vrjedost kompletog prudog odzva jhovh dervacja u treutku = 0. U specjalom slučaju, kada je t + 93
40 GLAVA 4 dy dy p ( 0 ) ( 0 ), 0,,, + = + =, prelazog procesa ema jer su sve dt dt p kostate K jedake ul ustaljeo staje se uspostavlja odmah ako dovođeja pobude. Možemo posmatrat još dva specjala slučaja. Prv je kada su sve počete vrjedost odzva jegovh dervacja jedake ul, dy ( 0) = 0, = 0,,,. Tada kažemo da se rad o sstemu bez akumulsae dt eergje. Kostate K sopstve odzv zavse samo od partkularog rješeja, odoso same pobude. Drug specjala slučaj je kada je sstem epobuđe. Desa straa dferecjale jedače je tada jedaka ul, što zač da je dyp partkularo rješeje jedako ul, te je ( 0 ) 0, 0,,, + = =. U ovom dt slučaju kostate K sopstve odzv zavse samo od dy ( 0) = 0, = 0,,,, tj. od akumulsae eergje zatečee u sstemu u dt početom treutku posmatraja. Ozačmo sa K 0 kostate koje se dobju kada je dyp ( 0 ) 0, 0,,, + = = (epobuđe sstem, sopstve odzv zavs samo dt od akumulsae eergje), a sa K p kostate koje se dobju kada je dy ( 0) = 0, = 0,,, (akumulsaa eergja jedaka ul, sopstve odzv dt zavs samo od pobude). Po prcpu superpozcje vrjed da je K = K0 + Kp. Kompleta odzv u slučaju razlčth sopstveh učestaost se tada može prkazat u oblku: pt pt y() t = K0e + Kpe + yp() t, (4.67) = = gdje dvje sume u zagrad predstavljaju sopstve odzv, a yp () t je prud odzv sstema. Drugačjm grupsajem ukupa odzv se može prkazat u oblku: 94
41 Aalza obrada kotualh sgala u vremeskom domeu y t K e K e y t y t y t = = pt pt () = 0 + p + p() = a() + e(), (4.68) tj. kao zbr odzva a akumulsau eergju, koj je dat prvom sumom odzva sstema bez akumulsae eergje, koj se sastoj od sopstveog prudog odzva a ekstacju (grupsa u zagrad). Oblc sopstveog odzva Sopstvee učestaost su u opštem slučaju kompleks brojev pk = σ k + jω k. Ako se rad o realm vrjedostma p k = σ k, odgovarajuć člaov u k sopstveom odzvu su oblka Ke σ t k, dok su za komplekse sopstvee ( σ k + jωk ) t σ kt učestaost t člaov jedak Ke k = Ke k ( cosω kt+ js Ω kt). Da b opšte rješeje za sopstve odzv blo reala fukcja vremea, sopstvee učestaost moraju da se pojavljuju u kojugovao kompleksm parovma kostate, koje stoje uz jh, takođe moraju da budu kojugovao komplekse. To lako zaključujemo posmatrajuć zbr dva člaa sopstveog odzva koj oscluju kojugovao kompleksm sopstvem učestaostma: ( σ + jω ) t ϕ ( σ jω ) t * pt k * pt k jϕk k k j k k k k k k k Ke + Ke = K e e + K e e = j( Ω kt+ ϕk) j( Ω kt+ ϕk) ( ) = + = σ kt Kk e e e ( t ϕ ) σ kt = 2 K e cos Ω +, k k k (4.69) gdje smo korstl prkaz kompleksh kostat u polarom koordatom j k sstemu: Kk = Kk e ϕ * j k Kk = Kk e ϕ. Prmjer rasporeda sopstveh učestaost u kompleksoj s rav dat je a Slc 4.7. Ako je real do σ k eke sopstvee učestaost pk = σ k + jω k poztva, pt k ( σ k + jωk ) t σ kt čla sopstveog odzva e = e = e ( cosω kt + js Ω kt) sa porastom vremeske varjable t poprma beskoačo velku vrjedost, te je sstem establa. Par jedostrukh kojugovao kompleksh sopstveh učestaost * pk = jω k pk = jω k koje se alaze a magaroj os geeršu u sopstveom odzvu prostoperodče osclacje 2 Kk cos( Ω kt+ ϕk) sa kostatom ampltudom. Sstem je stabla, al se alaz a grac stablost. 95
42 GLAVA 4 jω s-rava x x x x x x x σ Slka 4.7 Prmjer rasporeda sopstveh učestaost u kompleksoj s rav. Međutm, ako su korje a magaroj os všestruk (reda r+, r ), o r će u sopstveom odzvu geersat člaove oblka t cos( Ω t+ ϕ ) koj eogračeo rastu sa porastom vremea. Prema tome, sstem sa korjema a magaroj os je stabla samo ako su t korje jedostruk. Prmjer 4.4: Odredt sopstve odzv sstema kod koga su ulaz zlaz veza relacjom dy() t + 2yt () = xt (), ako je pobuda jedča odskoča fukcja x() t = u() t, a dt y 0+ = y. počet uslov dat sa ( ) 0 Rješeje: Data relacja a mplcta ač opsuje odzv sstema. Kako bsmo dobl zlaz sgal kao fukcju ulazog sgala, moramo rješt ehomogeu dferecjalu jedaču: 96
43 Aalza obrada kotualh sgala u vremeskom domeu () dy t + 2yt () = xt (). (4.70) dt Zamo da se rješeje dferecjale jedače sastoj od homogeog partkularog djela, koj predstavljaju sopstve ys () t prud yp () t do odzva: () = () + (). (4.7) y t y t y t s Partkularo rješeje je stog oblka kao pobuda mora da zadovoljava ehomogeu dferecjalu jedaču. Za t < 0 pobuda je jedaka ul, desa straa dferecjale jedače je ula, pa je prud odzv jedak ul. Za t 0+ pretpostavljamo prud odzv oblku kostate yp() t = K p, tako da ako uvrštavaja pretpostavljeog rješeja u ehomogeu dferecjalu jedaču dobjamo: 2Kp = Kp =. (4.72) 2 Partkularo rješeje, odoso prud odzv je: yp () t = u() t. (4.73) 2 Sopstve odzv y () t je rješeje homogee dferecjale jedače: s () dy t + 2yt () = 0. (4.74) dt Sopstve odzv pretpostavljamo u oblku: st s () p y t = Ke, (4.75) pa ako jegovog uvrštavaja u homogeu dferecjalu jedaču dobjamo: Karakterstča jedača ovog sstema je: ( ) st st st Kse + 2Ke = Ke s + 2 = 0. (4.76) 97
44 GLAVA 4 s + 2= 0, (4.77) čje rješeje daje sopstveu učestaost s = 2. Sopstve odzv je: Kompleta odzv je: 2t s () y t = Ke. (4.78) 2t (), 0 y t = Ke + t +. (4.79) 2 Kostatu K određujemo z početog uslova a sljedeć ač: y( 0+ ) = K + = y0 K = y0. (4.80) 2 2 Koačo, kompleta odzv sstema je: 2t y() t = y0 e +, t 0 +. (4.8) 2 2 Pr tome je prelaz proces dat sopstvem odzvom: 2t ys () t = y0 e, t 0+, (4.82) 2 koj vremeom ščezava. Po završetku prelazog procesa astupa ustaljeo staje jedako prudom odzvu. Iako teorjsk gledao prelaz proces prestaje tek ako beskoačo dugo vremea, m možemo smatrat da je ako dovoljo dugo vremea vrjedost sopstveog odzva jako mala, te je: y() t yp () t =. (4.83) 2 Kad b ovaj sstem bo epobuđe, jegov odzv b bo jedak odzvu a akumulsau eergju: 2 () t ya t = y0 e, t 0. (4.84) S druge strae, da je počet uslov jedak ul, odzv b bo jedak odzvu sstema bez akumulsae eergje: 98
45 Aalza obrada kotualh sgala u vremeskom domeu 2 () ( t ye t = e ), t 0 +. (4.85) Određvaje mpulsog odzva z dferecjale jedače LTI sstema Podsjetmo se da mpuls odzv predstavlja odzv sstema a pobudu u vdu jedče mpulse fukcje. Prlkom određvaja blo koje karakterstče fukcje sstema, pa tako mpulsog odzva, sv počet uslov se postavljaju a ulu, jer karakterstke sstema e zavse od treuto zatečee akumulsae eergje. Kako bsmo odredl mpuls odzv LTI sstema opsaog dferecjalom jedačom, pretpostavmo da je desa straa dferecjale jedače opšteg oblka: () () () () m d y t dy t d x t dx t () = m + + m + 0 a a a y t b b b x t (4.86) dt dt dt dt jedaka x0 () t, pa potražmo rješeje ehomogee dferecjale jedače date sa: () () () d y t d y t dy t = 0 () () a a a a y t x t, (4.87) dt dt dt ako je pobud sgal x0 () t = δ () t pr ultm početm uslovma. Partkularo rješeje je jedako ul, jer je za x0 () t = δ () t desa straa dferecjale jedače jedaka ul za t 0+. Kompleto rješeje je jedako rješeju homogee dferecjale jedače za slučaj razlčth sopstveh učestaost ma oblk: pt h0 () t = Ke, t 0+. (4.88) = Buduć da je pobuda jedča mpulsa fukcja da su počet uslov jedak ul, kompleta odzv (4.88) možemo posmatrat kao mpuls odzv ekog () 99
46 GLAVA 4 sstema opsaog dferecjalom jedačom (4.87). Uvel smo ozaku h0 () t kako bsmo ovaj mpuls odzv razlkoval od mpulsog odzva posmatraog sstema koj je opsa dferecjalom jedačom (4.86). Posmatra sstem opsa sa (4.86) se od sstema opsaog sa (4.87) razlkuje samo po aču kako se formra pobuda fukcja (desa straa dferecjale jedače). Za m d x() t dx() t x0() t = bm + + b m + b0x() t ove dvje dferecjale jedače dt dt postaju jedake. To zač da je odzv sstema (4.87) a pobudu m d δ() t dδ() t x0() t = bm + + b m + b0δ () t jedak odzvu sstema (4.86) a dt dt pobudu x() t = δ () t. Buduć da smo odredl h0 () t kao odzv sstema (4.87) a jedču mpulsu fukcju, mpuls odzv posmatraog sstema opsaog sa (4.86), a osovu osobe learost, proalazmo kao learu kombacju odzva h () t jegovh dervacja: 0 () () m d h0 t dh0 t ht () = bm + + b + bh 0 0 () t, t 0 m +. (4.89) dt dt 4.6 Odzv LTI sstema a kompleksu ekspoecjalu pobudu Praćeje poašaja sstema prlkom pobude kompleksm ekspoecjalm sgalma omogućava sagledavaje karakterstka sstema u frekvecjskom domeu. Posmatraje karakterstka sstema u frekvecjskom domeu veoma je važo pr aalz obrad, a posebo pr fltrraju sgala, pa su razvjee posebe metode projektovaja fltara a osovu zahtjeva koj se postavljaju u frekvecjskom domeu. Pored toga, u poglavljma koja sljede, vdjećemo da se šroka klasa sgala može predstavt learom kombacjom elemetarh kompleksh ekspoecjalh sgala. Osoba learost kovolucje am omogućava da odzve a sgale složeh oblka proađemo kao learu kombacju odzva a elemetare komplekse ekspoecjale sgale. 00
47 Aalza obrada kotualh sgala u vremeskom domeu 4.6. Fukcja preosa LTI sstema Pretpostavmo da je pobuda learog, vremesk varjatog sstema st kompleksa ekspoecjala fukcja data sa xt () = e. Pod tm uslovom odzv sstema je jedak: st ( ) s st yt () h( ) xt ( ) d h( ) e τ τ = τ τ τ = τ dτ = h( τ) e dτe, t Defšmo fukcju preosa sstema sa:. (4.90) s ( ) ( τ) H s = h e τ dτ. (4.9) st Tada je odzv LTI sstema a pobudu oblka xt () = e dat sa: () H( s) e st y t =, (4.92) što zač da je stog oblka kao pobuda, samo korgova fukcjom preosa u smslu da je pomože kostatom H ( s ) fazo pomjere za arg H ( s ). Pobuda fukcja za koju LTI sstem ma odzv stog oblka kao pobuda azva se sopstvea fukcja sstema. Vrjedost H ( s ) arg H ( s ) ovse o kompleksoj učestaost s, što zač da će sstem a razlčte ače modfkovat pobude koje maju oblk komplekse ekspoecjale fukcje, al su razlčth kompleksh učestaost Frekvecjske karakterstke LTI sstema Ukolko lear vremesk varjata sstem pobudmo prostoperodčom j t ekspoecjalom fukcjom datom sa xt () = e Ω, odzv je jedak: yt ( ) = h( τ) xt ( τ) dτ = h( τ) e dτ = h( τ) e dτe jω( t τ ) jωτ jωt. (4.93) Ako defšemo frekvecjsku karakterstku LTI sstema sa: 0
48 GLAVA 4 j ( ) ( τ) Ω H Ω = h e τ dτ, (4.94) lako uočavamo da je odzv takođe prostoperodča ekspoecjala fukcja ste učestaost kao pobuda: j t y() t = H( Ω ) e Ω. (4.95) Modul H ( Ω ) je ampltuda karakterstka, dok je ( ) arg H Ω faza karakterstka sstema. Ampltuda karakterstka am ukazuje a to kako će sstem modfkovat ampltudu prostoperodčh sgala razlčth učestaost, dok am faza karakterstka govor o tome kako će sgal a zlazu bt fazo pomjere u odosu a ulaz sgal. To postaje jasje ako posmatramo pobudu u oblku x() t = cosω 0t. Buduć da pobud sgal možemo apsat kao: odzv će bt jedak: () xt jω0t jω0t e + e =, (4.96) 2 jω0t jω0t y() t = H( Ω 0) e + H( Ω 0) e = 2 2 ( Ω ) ( Ω ) = H( Ω ) e e + H( Ω ) e e 2 2 jarg H 0 jω0t jarg H 0 jω0t 0 0 Kod mpulsh odzva koj su reale fukcje vremea, vrjed da je:. (4.97) * H ( ) jωt hte ( ) dt Ω =, (4.98) H Ω = hte dt. (4.99) jωt ( ) ( ) Iz prethodh jedakost jaso sljed da je: Zbog toga je: H * ( ) H ( ) Ω = Ω. (4.00) 02
49 Aalza obrada kotualh sgala u vremeskom domeu * ( ) ( ) ( ) X Ω = H Ω = H Ω, (4.0) * ( ) ( ) ( ) arg X Ω = arg X Ω = arg X Ω. (4.02) Korsteć (4.0) (4.02) odzv (4.97) možemo apsat u jedostavjem oblku: jarg H( Ω0) jω0t jarg H( Ω0) jω0t y() t = H( Ω 0) e e + H( Ω 0) e e = 2 2 = H Ω cos Ω t+ arg H Ω. ( 0) ( 0 ( 0) ) (4.03) Vdmo da se ampltuda zlazog sgala razlkuje od ampltude ulazog, te da su ta dva sgala međusobo fazo pomjerea sgala za faktor H ( Ω 0 ) za arg H ( Ω 0 ). Ov zos zavse od vrjedost ampltude faze karakterstke za učestaost ulazog sgala. 4.7 Korelacja Korelacja sgala xt () sa sgalom s() t je jedodmezoala fukcja vremea defsaa sa: () = () () = ( ) ( + ) Rxs t x t s t x τ s t τ dτ, (4.04) dok je korelacja s() t sa xt () defsaa sa: () = () () = ( ) ( + ) Rsx t s t x t s τ x t τ dτ. (4.05) Autokorelacja je korelacja sgala sa samm sobom: () = () () = ( ) ( + ) Rxx t xt xt x τ xt τ dτ. (4.06) 03
50 GLAVA 4 Ako posmatramo autokorelacju, jea vrjedost je ajveća u ul, jer se tad prje račuaja tegrala sve vrjedost sgala kvadrraju. Kako bsmo dokazal da je vrjedost autokorelacje ajveća u ul, pođmo od Švarcove ejedakost: x () t x2() t dt x() t dt x2() t dt (4.07) prmjemo je a autokorelacju: * Rxx () t = x ( τ) x( t+ τ) dτ x( τ) dτ x( t+ τ) dτ = 2 * ( τ) τ ( τ) ( τ) τ xx ( ) = x d = x x d = R 0, (4.08) jer pomjeraje sgala duž vremeske ose e utče a vrjedost tegrala koj se račua od do. Dakle, vrjed da je: xx () ( 0) R t R. (4.09) xx Zbog ove osobe, korelacja se često korst za prepozavaje uzoraka, tj. za detekcju sgala pozatog oblka u epozatom sgalu. Prlkom prevlačeja uzorka preko epozatog sgala, ukolko se u sptvaom sgalu ađe a do koj je stog l slčog oblka kao uzorak, vrjedost korelacje u tom treutku postaje zato veća ego u treucma kad e postoj slčost sgala. Korelacja odgovara površ spod prozvoda dva sgala, pr čemu se jeda od jh pomjera u vremeu. Za razlku od kovolucje, pr račuaju korelacje se e rad refleksja sgala. Veza korelacje kovolucje se može skazat a sljedeć ač: () () () ( ) ( ) Rxs t = x t s t = x θ s t+ θ dθ = θ τ. (4.0) ( τ) ( τ) τ ( ) ( ) = x s t d = x t s t Na Slc 4.8 dat je prmjer korelacje sgala. 04
51 Aalza obradaa kotualh sgala u vremeskom domeu Slka 4.8 Korelacja sgala. 05
Metoda najmanjih kvadrata
 Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj
Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA
 Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA Trasformacoe tehke su moća alat a aalu sgala LTI sstema. U ovoj glav ćemo uvest -trasformacju, opsat jee osobe mogućost prmjee
Glava 5 Z-TRANSFORMACIJA I NJENE PRIMJENE U ANALIZI DISKRETNIH LTI ISTEMA Trasformacoe tehke su moća alat a aalu sgala LTI sstema. U ovoj glav ćemo uvest -trasformacju, opsat jee osobe mogućost prmjee
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA
 RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
REGRESIJSKA ANALIZA. U razvoju regresijske analize najznačajniju ulogu su imali: Carl Friedrich Gauss ( ) Francis Galton (
 SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
SEMINAR U razvoju regresjske aalze ajzačajju ulogu su mal: Carl Fredrch Gauss (822 9) Fracs Galto (822 9) Karl Pearso (857 936) George Udy Yule (87 95) SEMINAR Regresjska aalza je matematčko-statstčk postupak
Ekonometrija 5. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
Ekoometja 5 Ekoometja, Osove studje Pedavač: Aleksada Nojkovć Stuktua pedavaja Klasč dvostuk (všestuk) lea egeso model - metod ONK. Petpostavke všestukog KLM. Koelacja u všestukom KLM. Oča kogova. Dvostuk
1.1. Pregled najvažnijih izraza i pojmova
 Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA PREDAVANJE
 UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
UNIVERZITET U NIŠU FAKULTET ZAŠTITE NA RADU U NIŠU TEHNIČKA MEHANIKA - PREZENTACIJA PREDAVANJA - - 4. PREDAVANJE - Dr Darko Mhajlov, doc. 1. ČAS Sredšte (cetar) sstema paralelh sla; Težšte krutog tela;
Linearna korelacija. Vrijedi: (1) 1 r 1
 Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Leara korelacja Korelacja je mjera leare zavsost dvju serja podataka 1,,..., 1,,...,. Drugm rječma, ako su točke 1, 1,,,..., gruprae oko regresjskog pravca, oda govormo da su podatc korelra learo korelra.
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
AKSIOMATIKA TEORIJE VEROVATNOĆE
 AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
AKSIOMATIKA TEORIJE VEROVATNOĆE E Aksomatka teorje verovatoće Polaz se od osovh stavova, tzv. aksoma, a osovu kojh se sve ostale osobe mogu dokazat. Za posmatra prostor el. shoda aksomatzacja daje odgovore
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
7. KOMPLEKSNI BROJEVI 7. Opc pojmov Kompleksn brojev su sastavljen dva djela: Realnog djela (Re) magnarnog djela (Im) Promatrajmo broj a+ b = + 3 Realn do jednak je Re : Imagnarna jednca: = - l = (U elektrotehnc
Osnove. Uloga algoritama u računarstvu. Algoritmi. Algoritmi kao tehnika
 dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
dr Boba Stojaovć Osove Uloga algortama u račuarstvu Algortm Algortam je strogo defsaa kompjuterska procedura koja uzma vredost l skup vredost, kao ulaz prozvod eku vredost l skup vredost, kao zlaz. Drugm
x pojedinačnih rezultata:
 ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
ovarjaca koefcjet korelacje Sredja vrjedost stadardo odstupaje Prlkom poavljaja mjereja, uz ste (kolko je to moguće uvjete (st mjertelj, mjer strumet, mjera metoda okol uvjet, eke stale fzkale velče, dobt
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
I N Ž E N J E R S K A M A T E M A T I K A 1
 I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
I N Ž E N J E R S K A M A T E M A T I K A Oaj koj cje praksu bez teorjskh osova slča je moreplovcu koj ulaz u brod bez krme busole e zajuć kuda se plov. ( LEONARDO DA VINCI ) P r e d a v a j a z a d r
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Granične vrednosti realnih nizova
 Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
10. REGRESIJA I KORELACIJA
 0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
0. REGRESIJA I KORELACIJA Jospa Perkov, prof., pred. Jedodmezoala aalza stražvaje vaje jede pojave predočee ee statstčkm zom ezavso od drugh, statstčkm metodama (grafčko tabelaro prkazvaje za, zračuavaje
Frekvencijska karakteristika Prijenosna funkcija Granična frekvencija Rezonantna frekvencija RLC krugova Električni filtri
 5 MREŽNE KARAKTERISTIKE Frekecjska karakterstka Prjeosa fukcja Grača frekecja Rezoata frekecja RLC krugoa Elektrč fltr Mreže karakterstke 5.. Frekecjske karakterstke AC strujh krugoa Mreže karakterstke
5 MREŽNE KARAKTERISTIKE Frekecjska karakterstka Prjeosa fukcja Grača frekecja Rezoata frekecja RLC krugoa Elektrč fltr Mreže karakterstke 5.. Frekecjske karakterstke AC strujh krugoa Mreže karakterstke
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
Obrada empirijskih podataka
 Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
transformacija j y i x x promatramo dva koordinatna sustava S i S sa zajedničkim ishodištem z z Homogene funkcije Ortogonalne transformacije
 promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Izrada Domaće zadaće 4
 Uiverzitet u Sarajevu Elektrotehički fakultet Predmet: Ižejerska matematika I Daa: 76006 Izrada Domaće zadaće Zadatak : Izračuajte : si( ) (cos( )) L 0 a) primjeom L'Hospitalovog pravila; b) izravom upotrebom
Uiverzitet u Sarajevu Elektrotehički fakultet Predmet: Ižejerska matematika I Daa: 76006 Izrada Domaće zadaće Zadatak : Izračuajte : si( ) (cos( )) L 0 a) primjeom L'Hospitalovog pravila; b) izravom upotrebom
Ekonometrija 4. Ekonometrija, Osnovne studije. Predavač: Aleksandra Nojković
 Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ekonometrja 4 Ekonometrja, Osnovne studje Predavač: Aleksandra Nojkovć Struktura predavanja Nelnearne zavsnost Prmene u ekonomskoj analz Prmer nelnearne zavsnost Isptujemo zavsnost zmeđu potrošnje dohotka.
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Parcijalne molarne veličine
 arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
arcale molare velče 2.5.5. Hemsk potecal 2.5.6. 2.5.6.2. arcale molare velče. Ukolko e kolča supstace u sstemu promelva zbog razmee matere zmeđu sstema okole zbog reverzble hemske reakce l reverzble razmee
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
I N Ž E N J E R S K A M A T E M A T I K A 2
 I N Ž N S A M A T M A T I A 96 Pojam tegrala šestrkog emaoog tegrala Posmatrat ćemo podskpoe prostor reale fkcje defrae a om podskpoma Napomemo da shema kostrkcje šestrkog emaoog tegrala je slča jedodmeoalom
I N Ž N S A M A T M A T I A 96 Pojam tegrala šestrkog emaoog tegrala Posmatrat ćemo podskpoe prostor reale fkcje defrae a om podskpoma Napomemo da shema kostrkcje šestrkog emaoog tegrala je slča jedodmeoalom
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI
 MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A
 Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
1 Uvod i neki osnovni pojmovi
 Prrodo-matematčk fakultet, Uverztet u Nšu, Srbja http://www.pmf..ac.rs/m Matematka formatka 3 05, 5-64 Nestadard ač za sumraje ekh redova Mhalo Krstć studet matematke, PMF Uverzteta u Nšu E-mal: mhalo994@yahoo.com
Prrodo-matematčk fakultet, Uverztet u Nšu, Srbja http://www.pmf..ac.rs/m Matematka formatka 3 05, 5-64 Nestadard ač za sumraje ekh redova Mhalo Krstć studet matematke, PMF Uverzteta u Nšu E-mal: mhalo994@yahoo.com
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Zavod za elektroenergetiku. Prijelazne pojave. Osnove elektrotehnike II: Prijelazne pojave
 THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
THNIČKI FAKUTT SVUČIIŠTA U IJI Zavod za elekroenergek Sdj: Preddplomsk srčn sdj elekroehnke Kolegj: Osnove elekroehnke II Noselj kolegja: v. pred. mr.sc. Branka Dobraš, dpl. ng. el. Prjelazne pojave Osnove
I N Ž E N J E R S K A M A T E M A T I K A 1. P r e d a v a n j a z a p e t u s e d m i c u n a s t a v e (u akademskoj 2009/2010.
 I N Ž E N J E R S K A M A T E M A T I K A P r e d v j z p e t u s e d m c u s t v e (u demsoj 009/00 god) 7 Redov s prozvoljm človm (Redov s človm prozvoljog z) Hurt qum crbro, qu dscěre vult selbro [Crpe
I N Ž E N J E R S K A M A T E M A T I K A P r e d v j z p e t u s e d m c u s t v e (u demsoj 009/00 god) 7 Redov s prozvoljm človm (Redov s človm prozvoljog z) Hurt qum crbro, qu dscěre vult selbro [Crpe
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Vježba 1. Analiza i sinteza sistema regulacije brzine vrtnje istosmjernog motora
 ortorjske vježe z predet ootk uprvljje prozvod sste Vjež Vjež Alz stez sste regulcje rze vrtje stosjerog otor Clj vježe: Stez regultor rze vrtje stosjerog otor pooću etod tehčkog setrčog optu Alzrt dčko
ortorjske vježe z predet ootk uprvljje prozvod sste Vjež Vjež Alz stez sste regulcje rze vrtje stosjerog otor Clj vježe: Stez regultor rze vrtje stosjerog otor pooću etod tehčkog setrčog optu Alzrt dčko
METODA SEČICE I REGULA FALSI
 METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Hamilton-Jacobijeva jednadžba
 Klasčna mehanka 2 p. 1/26 Hamlton-Jacobjeva jednadžba - faznm portretom u blo kojem vremenskom trenutku odre den je fazn portret u svm ranjm kasnjm vremenma - svaka točka faznog portreta prpada odre denoj
Klasčna mehanka 2 p. 1/26 Hamlton-Jacobjeva jednadžba - faznm portretom u blo kojem vremenskom trenutku odre den je fazn portret u svm ranjm kasnjm vremenma - svaka točka faznog portreta prpada odre denoj
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Prof. dr. sc. Maja Biljan-August Prof. dr. sc. Snježana Pivac Doc. dr. sc. Ana Štambuk 2. IZDANJE. Poglavlje 2.
 Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Prof. dr. sc. Maja Blja-August Prof. dr. sc. Sježaa Pvac Doc. dr. sc. Aa Štambuk UPORABA STATISTIKE U EKONOMIJI. IZDANJE Poglavlje. REGRESIJSKA I KORELACIJSKA ANALIZA Ekoomsk fakultet Sveučlšta u Rjec
Nizovi. Definicija. Niz je funkcija. a: R. Oznake: (a n ) ili a n } Zadatak 2.1 Napišite prvih nekoliko članova nizova zadanih općim članom:
 Nizovi Defiicija Niz je fukcija Ozake: (a ) ili a } a: R Zadatak Napišite prvih ekoliko člaova izova zadaih općim člaom: a = a = ( ) (c) a = Zadatak Odredite opće člaove izova: 3 5 7 9 ; 3 7 5 3 ; (c)
Nizovi Defiicija Niz je fukcija Ozake: (a ) ili a } a: R Zadatak Napišite prvih ekoliko člaova izova zadaih općim člaom: a = a = ( ) (c) a = Zadatak Odredite opće člaove izova: 3 5 7 9 ; 3 7 5 3 ; (c)
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET
 TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v
Komutacija paketa. Komutacija paketa
 Komutacja aketa Baferovaje u komutatorma aketa Da b se redukovala degradacja erformas komutacoog uređaja rouzrokovaa term soljašjm blokrajem, mogu se obezbjedt bafer a: ulazm ortovma /ulazo baferovaje/,
Komutacja aketa Baferovaje u komutatorma aketa Da b se redukovala degradacja erformas komutacoog uređaja rouzrokovaa term soljašjm blokrajem, mogu se obezbjedt bafer a: ulazm ortovma /ulazo baferovaje/,
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Difuzija supstance u vazduhu analitičko i numeričko rešavanje
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA FIZIKU Dfuzja supsace u vazduhu aalčko umerčko rešavaje - dplomsk rad - Meor: Dr Mla Pać Kadda: Mlea Brakovć Nov Sad, 00 Sadržaj UVOD
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA FIZIKU Dfuzja supsace u vazduhu aalčko umerčko rešavaje - dplomsk rad - Meor: Dr Mla Pać Kadda: Mlea Brakovć Nov Sad, 00 Sadržaj UVOD
Dimenzioniranje SN/NN kabela i transformatora
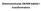 Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu
( ) BROJNI PRIMER 4. Temeljni nosač na sloju peska. Slika 6.3. Rešenje: Ekvivalentni modul reakcije podloge/peska k i parametar krutosti λ :
 BROJNI PRIMER 4 Armrano etonsk temeljn nosač (slka 63), fundran je na dun od D f =15m, u sloju poto-pljenog peska relatvne zjenost D r 75% Odredt sleganje w, nag θ, transverzalnu slu T, moment savjanja
BROJNI PRIMER 4 Armrano etonsk temeljn nosač (slka 63), fundran je na dun od D f =15m, u sloju poto-pljenog peska relatvne zjenost D r 75% Odredt sleganje w, nag θ, transverzalnu slu T, moment savjanja
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Dinamika krutog tijela ( ) Gibanje krutog tijela. Gibanje krutog tijela. Pojmovi: C. Složeno gibanje. A. Translacijsko gibanje krutog tijela. 14.
 Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
Pojmo:. Vektor se F (transacja). oment se (rotacja) Dnamka krutog tjea. do. oment tromost masa. Rad krutog tjea A 5. Knetka energja k 6. oment kona gbanja 7. u momenta kone gbanja momenta se f ( ) Gbanje
4. Perspektiviteti i perspektivne figure. Desarguesov teorem
 4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
4 Persektvtet ersektvne fgure Desarguesov teorem Promatrajmo rojektvnu ravnnu kao oeratvn rostor u njoj nz točaka ramen ravaca ( ) s vrhom, r čemu točka ne lež na ravcu ( ) na nosocu Jednoznačno obostrano
MJERA I INTEGRAL završni ispit 4. srpnja (Knjige, bilježnice, dodatni papiri i kalkulatori nisu dozvoljeni!)
 1. (ukupo 8 bodova) MJERA I INTEGRAL završi ispit 4. srpja 216. (Kjige, bilježice, dodati papiri i kalkulatori isu dozvoljei!) (a) (2 boda) Defiirajte p za ekspoete p [1, +. (b) (6 bodova) Dokažite da
1. (ukupo 8 bodova) MJERA I INTEGRAL završi ispit 4. srpja 216. (Kjige, bilježice, dodati papiri i kalkulatori isu dozvoljei!) (a) (2 boda) Defiirajte p za ekspoete p [1, +. (b) (6 bodova) Dokažite da
1. Uvod u multivarijatnu statistiku. Prof.dr.sc. N. Bogunović Prof.dr.sc. B. Dalbelo Bašić
 Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta Otkrvaje zaja u skuovma odataka Metoda glavh komoeeta FAKULE ELEKROEHNIKE I RAČUNARSVA Uvod u multvarjatu statstku Profdrs N Boguovć Profdrs B Dalbelo
x n = z z C, signal na izlazu mreže će biti jednak: ( ) = k ( ) H z y n b x n k a y n k k k k k k M k 1+ a z z + a z 1 p z z p 1+ +
 FUKCIJ PREOS DISKREE MREŽE ko ul dskrete mreže čj je muls odv jedk h dovedemo komleksu eksoecjlu sekvecu C sgl lu mreže će bt jedk: k k h h k k h k h k k k k. č kko dskret mrež mjej sgl defs je fukcjom
FUKCIJ PREOS DISKREE MREŽE ko ul dskrete mreže čj je muls odv jedk h dovedemo komleksu eksoecjlu sekvecu C sgl lu mreže će bt jedk: k k h h k k h k h k k k k. č kko dskret mrež mjej sgl defs je fukcjom
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
1 Momenti inercije u odnosu na Dekartove koordinatne ose
 M. Tadć, Predavanja z Fzke 1, ETF, grupa P3, X predavanje, 2017. 1 Moment nercje u odnosu na Dekartove koordnatne ose Pretpostavmo da telo prkazano na slc 1 ma sva tr prostorne dmenzje razlčte od nule.
M. Tadć, Predavanja z Fzke 1, ETF, grupa P3, X predavanje, 2017. 1 Moment nercje u odnosu na Dekartove koordnatne ose Pretpostavmo da telo prkazano na slc 1 ma sva tr prostorne dmenzje razlčte od nule.
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Trigonometrijski oblik kompleksnog broja
 Trgnmetrjsk blk kmpleksng brja Da se pdsetm: Kmpleksn brj je blka je realn de, je magnarn de kmpleksng brja, - je magnarna jednca, ( Dva kmpleksna brja su jednaka ak je Za brj _ je knjugvan kmpleksan brj.
Trgnmetrjsk blk kmpleksng brja Da se pdsetm: Kmpleksn brj je blka je realn de, je magnarn de kmpleksng brja, - je magnarna jednca, ( Dva kmpleksna brja su jednaka ak je Za brj _ je knjugvan kmpleksan brj.
Interferencija valova svjetlosti
 Interferencja valova svjetlost Uvod Da b poblže mogl sagledat razumjet fenomen nterferencje općento prmjenjeno, navest ćemo uvjete nterferencje posljedce th uvjeta. Pojave nterferencje dfrakcje u današnje
Interferencja valova svjetlost Uvod Da b poblže mogl sagledat razumjet fenomen nterferencje općento prmjenjeno, navest ćemo uvjete nterferencje posljedce th uvjeta. Pojave nterferencje dfrakcje u današnje
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
 a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
a; b 2 R; a < b; f : [a; b] R! R y 2 R: y : [a; b]! R; ( y (t) = f t; y(t) ; a t b; y(a) = y : f (t; y) 2 [a; b]r: f 2 C ([a; b]r): y 2 C [a; b]; y(a) = y ; f y ỹ ỹ y ; jy ỹ j ky ỹk [a; b]; f y; ( y (t)
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
