ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΤΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΤΩΝ q-κατανομων
|
|
|
- Αοιδή Λειβαδάς
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ & ΣΥΓΧΡΟΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΤΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΤΩΝ q-κατανομων ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΙΑ ΤΗΝ ΑΠΟΚΤΗΣΗ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΔΙΠΛΩΜΑΤΟΣ ΕΙΔΙΚΕΥΣΗΣ ΣΤΑ ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ Μεταπτυχιακή Φοιτήτρια: Δήμητρα Καρατζιά Επιβέπων: Καθηγητής Αναστάσιος Μπούντης ΠΑΤΡΑ 06
2
3 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΤΩΝ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΙ ΕΦΑΡΜΟΓΕΣ ΤΩΝ q-κατανομων ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΓΙΑ ΤΗΝ ΑΠΟΚΤΗΣΗ ΜΕΤΑΠΤΥΧΙΑΚΟΥ ΔΙΠΛΩΜΑΤΟΣ ΕΙΔΙΚΕΥΣΗΣ ΣΤΑ ΕΦΑΡΜΟΣΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ ΤΡΙΜΕΛΗΣ ΕΞΕΤΑΣΤΙΚΗ ΕΠΙΤΡΟΠΗ Α. Μπούντης Ιάκωβος Βαν Ντερ Βέιε Χ. Κοκοογιαννάκη Καθηγητής Τμήματος Καθηγητής Τμήματος Αναπηρώτρια Καθηγήτρια Μαθηματικών Μαθηματικών Τμήματος Μαθηματικών Μεταπτυχιακή Φοιτήτρια: Δήμητρα Καρατζιά Επιβέπων: Καθηγητής Αναστάσιος Μπούντης ΠΑΤΡΑ 06
4
5 Δήμητρα Καρατζιά Πτυχιούχος Τμήματος Μαθηματικών Πανεπιστημίου Πατρών Copyright Δήμητρα Καρατζιά, 06 Με επιφύαξη παντός δικαιώματος. All rights reserved. Απαγορεύεται η αντιγραφή, αποθήκευση και διανομή της παρούσας εργασίας, εξ οοκήρου ή τμήματος αυτής, για εμπορικό σκοπό. Επιτρέπεται η ανατύπωση, αποθήκευση και διανομή για σκοπό μη κερδοσκοπικό, εκπαιδευτικής ή ερευνητικής φύσης, υπό την προϋπόθεση να αναφέρεται η πηγή προέευσης και να διατηρείται το παρόν μήνυμα. Ερωτήματα που αφορούν τη χρήση της εργασίας για κερδοσκοπικό σκοπό πρέπει να απευθύνονται προς την συγγραφέα. Οι απόψεις και τα συμπεράσματα που περιέχονται σε αυτό το έγγραφο εκφράζουν την συγγραφέα και δεν πρέπει να ερμηνευτεί ότι εκφράζουν τις επίσημες θέσεις του Πανεπιστημίου Πατρών.
6
7 Αφιερωμένο στη μνήμη του πατέρα μου
8
9 ΕΥΧΑΡΙΣΤΙΕΣ Η παρούσα μεταπτυχιακή διατριβή εκπονήθηκε στα παίσια του Μεταπτυχιακού Προγράμματος «Μαθηματικά και Σύγχρονες Εφαρμογές» του Τμήματος Μαθηματικών του Πανεπιστημίου Πατρών υπό την επίβεψη του Καθηγητή Αναστασίου Μπούντη, στον οποίο θα ήθεα να εκφράσω ένα θερμό ευχαριστώ για την πούτιμη βοήθεια, την άψογη συνεργασία και την υποδειγματική καθοδήγηση καθ όη τη διάρκεια εκπόνησης της παρούσας εργασίας. Επίσης, θα ήθεα να ευχαριστήσω τα υπόοιπα μέη της τριμεούς εξεταστικής επιτροπής την Αναπηρώτρια Καθηγήτρια κα. Κοκοογιαννάκη και τον Καθηγητή κ. Βαν Ντερ Βέιε για την προσεκτική ανάγνωση της διατριβής και τις εύστοχες παρατηρήσεις τους. Ιδιαίτερες ευχαριστίες θέω να εκφράσω προς την οικογένειά μου για την απέραντη αγάπη τους και για τη συνεχή ενθάρρυνση και υποστήριξη σε κάθε στάδιο των σπουδών μου.
10
11 Περιεχόμενα Περίηψη. 5 Abstract... 7 Κεφάαιο : Εισαγωγή.. 9 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και οι q-συναρτήσεις.... Η υπεργεωμετρική εξίσωση.. 3. Λύσεις της υπεργεωμετρικής εξίσωσης και σχέσεις με τις εξισώσεις Fokker- Planck, Schrödingerκαι Klein-Gordon Η Εξίσωση Fokker-Planck. 4.. Οι Εξισώσεις Schrödinger και Klein-Gordon Οι μη γραμμικές εξισώσεις Fokker-Planck, Schrödinger και Klein-Gordon που περιέχουν q-παράμετρο Συμπεράσματα Κεφάαιο 3: Γενικότερες Εφαρμογές των q- Συναρτήσεων Το πρόβημα του τυχαίου περιπατητή μέσω του μοντέου RRW Η συνεχής μορφή της Masterεξίσωσης για την κατανομή Η αναυτική ύση της κατανομής του χρόνου επιστροφής P R (0,t) Αριθμητική επίυση του διακριτού περιπατητή χρησιμοποιώντας τις q- εκθετικές Συμπεράσματα Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε προβήματα σεισμοογίας Ανάυση της Εηνικής σεισμικής δραστηριότητας Ανάυση της κατανομής συχνότητας-μεγέθους της σεισμικότητας Ανάυση της κατανομής του χρόνου μεταξύ των σεισμικών γεγονότων Συνάρτηση επικινδυνότητας και δυνατότητες πρόβεψης Συμπεράσματα
12 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε προβήματα οικονομικών επιστημών Οικονομικά δεδομένα αποδόσεων και q-συναρτήσεις Συνάρτηση επικινδυνότητας και δυνατότητες πρόβεψης Συμπεράσματα... 8 Κεφάαιο 6: Συμπεράσματα και Ανοικτά Ερωτήματα.. 8 Βιβιογραφία
13 Περίηψη Θέμα της παρούσας μεταπτυχιακής διατριβής είναι οι Συνήθεις Διαφορικές Εξισώσεις (Σ.Δ.Ε.) της Μαθηματικής Φυσικής και οι q-συναρτήσεις. Όπως είναι γνωστό, οι Σ.Δ.Ε. εμφανίζονται σε μαθηματικά μοντέα που περιγράφουν προβήματα φυσικών, βιοογικών, τεχνοογικών και οικονομικών προβημάτων. Στη διατριβή αυτή επιχειρούμε μια εισαγωγή στις γραμμικές και μηγραμμικές εξισώσεις Fokker-Planck, Schrödinger και Klein-Gordon, οι οποίες σχετίζονται με την εκθετική ύση e z της εγόμενης «συρρέουσας» υπεργεωμετρικής εξίσωσης με κατάηη επιογή της μεταβητής z. Η δεύτερη γραμμικώς ανεξάρτητη ύση της «συρρέουσας» δεν ικανοποιεί καμία από τις παραπάνω εξισώσεις. Παρόα αυτά, χρησιμοποιώντας τη δεύτερη αυτή ύση και θέτοντας το z ίδιο με αυτό της εξίσωσης Fokker-Planck οδηγούμαστε σε μια νέα Μ.Δ.Ε την οποία ονομάσαμε Fokker-Planck κυματική εξίσωση. Στη συνέχεια δίνουμε έμφαση στις μη γραμμικές εξισώσεις που περιέχουν την εγόμενη q-παράμετρο και αναφερόμαστε στις εφαρμογές τους. Εξηγούμε ότι οι q- εκθετικές και q-gaussians συναρτήσεις σχετίζονται με ημι-σταθερές καταστάσεις ισορροπίας συστημάτων και μεγιστοποιούν την εντροπία του Tsallis. Η εφαρμογή των q-εκθετικών καταδεικνύεται μέσα από την περιγραφή τριών προβημάτων: α) το μοντέο του περιπατητή, β) τη πρόγνωση σεισμικών συμβάντων και γ) τη πρόβεψη οικονομικών αποδόσεων. Πιο συγκεκριμένα, το μοντέο του περιπατητή ή RRW (Restricted Random Walker) αναφέρεται στην κατανομή του χρόνου επιστροφής ενός τυχαίου περιπατητή στο σημείο μηδέν. Αποδεικνύεται ότι η πιθανότητα μετατόπισης από το σημείο αυτό μπορεί να προσεγγιστεί, για δεδομένες συνθήκες, από την q-εκθετική συνάρτηση. Η επόμενη εφαρμογή των q-εκθετικών αφορά ένα πρόβημα σεισμοογίας. Εξετάζοντας ένα μεγάο δείγμα σεισμικών καταγραφών από τον εηνικό χώρο, διερευνάται η κατανομή της συχνότητας ως προς το μέγεθος του σεισμού, η κατανομή των χρόνων μεταξύ των σεισμικών γεγονότων, η συνάρτηση επικινδυνότητας και η δυνατότητα πρόβεψης. Η τεευταία εφαρμογή αναφέρεται στον τομέα της οικονομίας, όπου μεετώνται οικονομικά δεδομένα αποδόσεων. Η 5
14 χρήση των q-εκθετικών συναρτήσεων επιτρέπει την εκτίμηση της συνάρτησης επικινδυνότητας και παρέχει δυνατότητες πρόβεψης. 6
15 Abstract The objective of this master thesis is the Ordinary Differential Equations (O.D.E) of Mathematical Physics and q-equations. Commonly, (O.D.Es) are an integral part of mathematical models describing many science problems in physics, biology, engineering and economics. In the present work, we make an attempt to present linear and non-linear Fokker-Planck, Schrödinger, and Klein-Gordonequations associated with the exponential solution e z of the confluent hypergeometric equation, depending on the choice of the variable z. The second solution of the confluent hypergeometric equation does not satisfy any of the above equations. Nevertheless, using the second solution and setting z equal to that employed in the Fokker-Planck equation yields a novel Partial Differential Equation which we call Fokker-Planck wave equation. Emphasis is given to non-linear equations involving a so-called q-parameter and their applications. It is worth mentioning that q-exponential and q-gaussians functions are related to semi-stable equilibrium systems and maximize the entropy of Tsallis. Three application examples are discussed here: a) the problem of Restricted Random Walker (RRW), b) prediction of seismic events, and c) prediction of financial returns, all of which highlight the importance of the q-exponential function. Specifically, the distribution of first return times of the RRW is investigated. It is proved that by employing the numerical solution of the problem and assuming certain additional conditions, the return distribution is given by a q-exponential. The next example refers to a problem of seismology. By analyzing a number of seismic events within Greece the frequency us magnitude and the inter-event times distribution is studied. It is also discovered that this data is approximated by a statistical distribution of q-exponential type which leads to the computation of a risk function for earthquake prediction. The last application refers to a financial problem concerning the distribution of the interoccurence times between daily losses below a negative threshold value. This distribution is also associated with a q-exponential which facilitates the estimation of a risk function and provides the possibility of improving the prediction of certain economic events. 7
16 8
17 ΚΕΦΑΛΑΙΟ Εισαγωγή Οι διαφορικές εξισώσεις είναι ένας κάδος των Μαθηματικών που αποτεεί το σημαντικότερο ίσως εργαείο στη μαθηματική περιγραφή προβημάτων που προέρχονται από τα πεδία της φυσικής, της τεχνοογίας, της βιοογίας, των οικονομικών και άων επιστημών. Για το όγο αυτό, τα τεευταία 40 χρόνια έχουν δημοσιευτεί ποές επιστημονικές μεέτες που σχετίζονται με νέες έννοιες και εφαρμογές καθώς και μεθόδους επίυσης των εξισώσεων αυτών. Αρχικά, στην παρούσα διατριβή αναφέρουμε κάποιες βασικές Συνήθεις Διαφορικές Εξισώσεις (Σ.Δ.Ε.) τις οποίες χρειαζόμαστε στην παρούσα εργασία, τις εγόμενες υπεργεωμετρικές. Έτσι, στη αρχή θα ορίσουμε τις εξισώσεις αυτές και θα χρησιμοποιήσουμε τις ύσεις τους για να τις συνδέσουμε με ορισμένες γνωστές γραμμικές και μη γραμμικές Σ.Δ.Ε. Πιο συγκεκριμένα, θα ασχοηθούμε με τη εγόμενη «συρρέουσα» υπεργεωμετρική εξίσωση (confluent hypergeometric equation). Ξεκινώντας με τις ύσεις της εξίσωσης αυτής και κάνοντας τις κατάηες επιογές για την μεταβητή της ως συνάρτηση των x, t θα συνδέσουμε τις ύσεις αυτές με τις εξισώσεις Fokker-Planck, Schrödinger, Klein-Gordon και επεκτάσεις αυτών. Έπειτα, θα εισαγάγουμε τον ορισμό των q-εκθετικών συναρτήσεων και θα δειχθεί η συσχέτισή τους με την υπεργεωμετρική συνάρτηση και τις αντίστοιχες μη γραμμικές εξισώσεις των Fokker-Planck, Schrödinger και Klein-Gordon. Περιηπτικά, αναφέρουμε ότι οι q-εκθετικές και q-gaussians κατανομές είναι συναρτήσεις σχετικές με ημι-σταθερές καταστάσεις συστημάτων και το 9
18 Κεφάαιο : Εισαγωγή χαρακτηριστικό τους είναι ότι μεγιστοποιούν την εντροπία του Tsallis. Όπως γνωρίζουμε παρακάτω η φυσική σημασία της εντροπίας μπορεί να θεωρηθεί ότι είναι η έκφραση του μέτρου της αταξίας ενός συστήματος σύμφωνα με τη στατιστική μηχανική ή αιώς στατιστική θερμοδυναμική. Η στατιστική μηχανική είναι ο κάδος της Μαθηματικής Φυσικής που βασίζεται στη θεωρία πιθανοτήτων και περιαμβάνει ισχυρά μαθηματικά εργαεία για την αντιμετώπιση μεγάων συστημάτων του πεδίου της μηχανικής, η οποία ασχοείται με την ομαδική κίνηση αντικειμένων ή σωματιδίων που υπόκεινται σε εσωτερικές δυνάμεις. Με άα όγια συνδέει τις μικροσκοπικές ιδιότητες των μορίων ή ατόμων με τις μακροσκοπικές ιδιότητες των υικών που παρατηρούνται στην καθημερινή ζωή. Στα επόμενα κεφάαια, δίνονται τρία παραδείγματα εφαρμογής των q-εκθετικών συναρτήσεων. Πιο συγκεκριμένα, στο πρώτο παράδειγμα μεετάται το μοντέο RRW (Restricted Random Walker), όπου σκοπός είναι να βρεθεί η κατανομή του χρόνου επιστροφής ενός τυχαίου περιπατητή στο σημείο μηδέν, P R (0,t) (β. Tinarkli et. al.). Η πιθανότητα ααγής από το σημείο αυτό δίνεται από τον τύπο n/l α, όπου α είναι μια ανεξάρτητη μεταβητή. Όταν το αє[0,] η πιθανότητα P R (0,t) μπορεί να προσεγγιστεί ικανοποιητικά από την q-εκθετική συνάρτηση για την τιμή δε α= παίρνουμε ακριβώς την q-εκθετική καθώς το L. Το μοντέο RRW έχει μια αναυτική ύση και μια αριθμητική. Η ακριβής αναυτική ύση, που αντιστοιχεί στο συνεχές μοντέο, P R (0,t) δίνεται με τη βοήθεια των σειρών Bessel και είναι εξαρτώμενη από την τιμή του α. Η διακριτή αριθμητική ύση προέρχεται από τις συνεχείς επαναήψεις της αντίστοιχης (διακριτής) Master εξίσωσης, όπου επιβεβαιώνουμε ότι μόνο για α= η κατανομή είναι ακριβώς η q-εκθετική και μια πού μικρή ααγή της παραμέτρου α κάνει την κατανομή να αποκίνει. Η επόμενη εφαρμογή αφορά σε ένα πρόβημα σεισμοογίας (β. Antonopoulos et al., 04), όπου και εδώ χρησιμοποιούνται οι q-κατανομές. Μεετάται η σεισμική δραστηριότητα από το 976 μέχρι το 009 στην Εάδα με βάση το σύνοο των δεδομένων που κατέγραψαν οι Μακρόπουος και άοι (0), για την ανάυση των οποίων χρησιμοποιούνται έννοιες της μη-εκτατικής στατιστικής φυσικής. Εξετάζοντας το σύνοο όων των δεδομένων,αά και εκείνο από το οποίο έχουν εξαιρεθεί οι μετασεισμοί αναφερόμαστε στην κατανομή συχνότητας και μεγέθους σεισμών και δείχνουμε ότι και τα δύο σύνοα μπορούν να προσεγγιστούν από ένα φυσικό μοντέο προερχόμενο από το παίσιο των μεθόδων της μη-εκτατικής 0
19 Κεφάαιο : Εισαγωγή στατιστικής φυσικής. Στη συνέχεια, μεετάμε την κατανομή των χρόνων μεταξύ σεισμικών γεγονότων για διαφορετικά μεγέθη σεισμού και δείχνουμε ότι τα δεδομένα προσεγγίζονται από μια στατιστική κατανομή της q-εκθετικής μορφής η οποία επιτρέπει τον αναυτικό υποογισμόμιας συνάρτησης επικινδυνότητας. Μέσω αυτής της ανάυσης παίρνουμε στοιχεία για τη δυναμική ενός σεισμού που σχετίζεται με ένα είδος μη γραμμικής μνήμης. Η τεευταία εφαρμογή των q-εκθετικών συναρτήσεων αναφέρεται στον τομέα της οικονομίας και βασίζεται στην εργασία των Ludesceret. al, 0. Θεωρώντας 6 αντιπροσωπευτικά οικονομικά στοιχεία (μετοχές, δείκτες, εμπορεύματα και συνααγματικές ισοτιμίες), υποογίζουμε στην κατανομή P Q (r) των χρόνων μεταξύ των ημερήσιων απωειών, με κατώτερο όριο το Q και σταθερή μέση τιμή R Q. Δείχνουμε ότι για όες τις περιπτώσεις η κατανομή P Q (r) ακοουθεί τη μορφή P Q (r) /[+(q-)βr] /(q-), όπου β και q είναι «δομικές» σταθερές που εξαρτώνται μόνο από τη μέση τιμή R Q και όχι από κάποιο συγκεκριμένο κεφάαιο (οικονομικό στοιχείο). Παρατηρείται ότι η μεταβητή q όχι απά εξαρτάται από τη μέση τιμή R Q όπως το β, αά αυξάνεται ογαριθμικά ως προς αυτήν μέσω της σχέσης q=+q 0 ln(r Q /), έτσι ώστε όταν το R Q η κατανομή P Q (r) προσεγγίζει μια απή εκθετική συνάρτηση. Η αναυτική μορφή της κατανομής P Q επιτρέπει την εκτίμηση μιας συνάρτησης επικινδυνότητας έτσι ώστε να βετιωθεί η εκτίμηση του χρηματοοικονομικού κινδύνου.
20 ΚΕΦΑΛΑΙΟ Συνήθεις Διαφορικές Εξισώσειςτης Μαθηματικής Φυσικής και οι q-συναρτήσεις Στο κεφάαιο αυτό, αρχικά θα δοθεί ο ορισμός της υπεργεωμετρικής εξίσωσης και η ύση της, και θα αναφερθεί η εγόμενη «συρρέουσα» υπεργεωμετρική εξίσωση (confluent hypergeometric equation) ως ειδική περίπτωση η οποία θα μας απασχοήσει στα επόμενα εδάφια. Στη συνέχεια, θα μεετήσουμε τις σχέσεις μεταξύ των ύσεων της προαναφερθείσας εξίσωσης με τις γνωστές γραμμικές και αντίστοιχα μη γραμμικές εξισώσεις Fokker- Planck, Schrödinger και Klein- Gordon. Για τις μη γραμμικές εξισώσεις απαραίτητη προϋπόθεση είναι η εισαγωγή της q-εκθετικής συνάρτησης. Σε επόμενο κεφάαιο θα μιήσουμε εκτενέστερα για τη συνάρτηση αυτή ενώ εδώ θα περιοριστούμε να αναφέρουμε ότι: (α) εκφράζει σύγκιση στο μηδέν που ακοουθεί νόμο αγεβρικής (και όχι εκθετικής) μείωσης και (β) συνδέεται άμεσα με τη μη γραμμικότητα των παραπάνω εξισώσεων, μέσω της q- παραμέτρου που περιέχει.
21 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις. Η υπεργεωμετρική εξίσωση Ορισμός: Η υπεργεωμετρική συνήθης διαφορική εξίσωση (Σ.Δ.Ε.) του Gauss [37] είναι η ακόουθη: z( z) y '' + { c ( a + b + ) z} y ' aby = 0 (.) όπου z είναι γενικά μια μιγαδική μεταβητή, y(z) είναι οι ύσεις που ικανοποιούν την (.) και οι τόνοι δηώνουν παραγώγιση ως προς z. Αν οι c, a b και c a b δεν είναι ακέραιοι, η γενική ύση της (.) για z < είναι η ακόουθη: y= cfabcz + cz Fa c+ b c+ cz (.) c (, ; ; ) (, ; ; ) όπου F(a,b;c;z) είναι η υπεργεωμετρική συνάρτηση της μορφής, a b z F abcz z (.3α) n n n (, ; ; ) =, <, α,b C, c C\Z0 n= 0 cn n! και τα a n,b n,c n είναι τα σύμβοα του Pochhammer, η (.3α) ορίζεται και ως ακοούθως: ab aa ( + ) bb ( + ) aa ( + )( a+ ) bb ( + )( b+ ) Fabcz z z z c cc ( + ) 3 cc ( + )( c+ ) 3 (, ; ; ) = (.3β) με a,b,c πραγματικές σταθερές και c, c αυθαίρετους συντεεστές που προσδιορίζονται από τις συνθήκες y(0)= y 0 και y (0)= y. Όπως είναι γνωστό [37] αν η σειρά έχει άπειρους όρους, συγκίνει (ομοιόμορφα και απόυτα) στο διάστημα <z<. Γενικότερα, στο μιγαδικό επίπεδο συγκίνει για z <, ενώ για z > αποκίνει. Για z = η σύγκιση εξαρτάται από την ποσότητα s = c (a + b): αν s -, η σειρά αποκίνει, αν - <s 0, η σειρά συγκίνει υπό συνθήκες, εκτός από z= αν s > 0, η σειρά συγκίνει απόυτα. 3
22 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Η υπεργεωμετρική συνάρτηση F(a,b;c;z) ως ύση της Σ.Δ.Ε. δευτέρου βαθμού (.), ανήκει στις εγόμενες ειδικές συναρτήσεις της Μαθηματικής Ανάυσης. Η επόμενη ενότητα, βασίζεται στις ύσεις της αποκαούμενης «συρρέουσας» υπεργεωμετρικής εξίσωσης (confluent hypergeometric equation). Θα διερευνήσουμε τις ύσεις αυτές κάνοντας κατάηες επιογές για τη μεταβητή μας και θα μεετήσουμε πώς μέσω αυτών των ύσεων οδηγούμαστε στις γραμμικές εξισώσεις Fokker- Planck, Schrödinger και Klein- Gordon.. Λύσεις της υπεργεωμετρικής εξίσωσης και σχέσεις με τις εξισώσεις Fokker-Planck, Schrödinger και Klein-Gordon.. Η εξίσωση Fokker-Planck Στη στατιστική μηχανική, η εξίσωση Fokker-Planck είναι μια μερική διαφορική εξίσωση (Μ.Δ.Ε), η οποία περιγράφει την χρονική εξέιξη της συνάρτησης πυκνότητας πιθανότητας της ταχύτητας ενός σωματιδίου υπό την επίδραση τυχαίων δυνάμεων όπως στην περίπτωση της κίνησης Brown. Ένα παράδειγμα της κίνησης Brown είναι όταν ένα σωματίδιο σκόνης συγκρούεται με ένα μεγάο σύνοο σωματιδίων έστω μόρια του αέρα, τα οποία κινούνται με διαφορετικές ταχύτητες σε διαφορετικές τυχαίες κατευθύνσεις. Η εξίσωση Fokker- Planck πήρε το όνομα της από τους Adriaan Fokker και Max Planck, ωστόσο είναι και γνωστή ως η «προς τα εμπρός» εξίσωση Kolmogorov εν ονόματι του Andrey Kolmogorov [38]. Στην παρούσα παράγραφο θα δείξουμε ότι η εξίσωση Fokker-Planck = [ KxF ( ) ] + t x x F Q F (.4) συνδέεται με μια υπεργεωμετρική διαφορική εξίσωση «συρρέουσας» μορφής. Στην εξίσωση αυτή, F είναι η συνάρτηση κατανομής, K(x) είναι ο συντεεστής μετατόπισης και Q μια θετική ποσότητα, που αποτεεί τον συντεεστή διάχυσης. Ο δεύτερος όρος στο δεξί μέρος της εξίσωσης περιγράφει τα αποτεέσματα των 4
23 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις διακυμάνσεων των δυνάμεων, είναι δηαδή ο εγόμενος διαχυτικός όρος. Εδώ θα περιοριστούμε κυρίως στην περίπτωση όπου το K(x) είναι σταθερό. Όπως προαναφέρθηκε η συνήθης υπεργεωμετρική συνάρτηση (.3α-.3β) είναι μια ιδιαίτερη συνάρτηση, που δίνεται με τη βοήθεια υπεργεωμετρικών σειρών. Η παραπάνω συνάρτηση περιαμβάνει πήθος ειδικών περιπτώσεων. Μία από αυτές είναι η «συρρέουσα»μορφή την οποία θα χρησιμοποιήσουμε στο συγκεκριμένο εδάφιο. Ειδικότερα, ο τύπος της «συρρέουσας» μορφής δίνεται ως: n an z φ( abz ; ; ) =, ab, R (.5) b n! n= 0 n με a n, b n τα σύμβοα Pochhammer και n μη αρνητικό ακέραιο. Το a n δίνεται ως εξής: a0 =, an = aa ( + )( a+ )...( a+ n ) αντίστοιχα και το b n. Η «συρρέουσα» υπεργεωμετρική συνάρτηση επομένως, ικανοποιεί τη διαφορική εξίσωση: zφ''( abz ; ; ) + ( b z) φ'( abz ; ; ) aφ( abz ; ; ) = 0, (.6) η οποία για a = b παίρνει τη μορφή: zφ''( aaz ; ; ) + ( a z) φ'( aaz ; ; ) aφ( aaz ; ; ) = 0, (.7) οπότε a n =b n και η (.5) γίνεται: n z z φ( aaz ; ; ) = = e. (.8) n! n= 0 Η εξίσωση (.7) είναι δεύτερης τάξης, γραμμική, με μη σταθερούς συντεεστές. Με άα όγια η διαφορική εξίσωση έχει δύο γραμμικώς ανεξάρτητες ύσεις. Η πρώτη είναι η εκθετική και δίνεται από την (.8). Εμείς θα αναφερθούμε εδώ στην πήρη ύση της εξίσωσης, αναυτικά, βρίσκοντας και τη δεύτερη ύση. Η βασική μας αναφορά στο παρόν κεφάαιο είναι τα άρθρα των Plastino και Rocca [-3]. 5
24 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Θα χρησιμοποιήσουμε τη μέθοδο των δυναμοσειρών, δηαδή θα προσπαθήσουμε να εκφράσουμε τη ύση της δεδομένης εξίσωσης υπό μορφήν δυναμοσειράς και όχι μέσω γνωστών συναρτήσεων. Η μέθοδος αυτή είναι μια βετιωμένη και πιο γενική μορφή της μεθόδου Taylor. Έτσι, γράφοντας τη σειρά μας στη μορφή: k φ( z) = az (.9) k = 0 k προσδιορίζουμε τους συντεεστές a k υποογίζοντας τις παραγώγους όων των τάξεων στο z = 0, εισάγοντας την (.9) στην διαφορική μας εξίσωση. Θέοντας να μεετήσει ιδιαίτερες περιπτώσεις παρόμοιων εξισώσεων ο Frobenius έδωσε την επέκταση της μεθόδου των σειρών γράφοντας τη ύση υπό τη μορφή μιας πιο γενικής δυναμοσειράς του τύπου: s k φ( z) = z az (.0) k = 0 k όπου ο εκθέτης s μπορεί να πάρει μια οποιαδήποτε πραγματική τιμή καθοριζόμενη από την ίδια την εξίσωση. Η ιδέα του Frobenius ήταν ότι η τυχόν ανωμαία που θα προκαέσει στη ύση ο απειρισμός των συντεεστών της εξίσωσης δεν θα είναι εντονότερη από μία δύναμη του z. Έτσι, αν η ανωμαία αυτή «απορροφηθεί» ως εναρκτήρια δύναμη το υπόοιπο κομμάτι της ύσης θα είναι ομαό ώστε να αναπτυχθεί σε συγκίνουσα δυναμοσειρά τύπου Taylor. Επομένως, για μικρά z η ύση θα είναι της μορφής φ~ z s αφού οι ανώτερες δυνάμεις της σειράς μπορούν να αγνοηθούν. Αντικαθιστώντας τη ύση αυτή στην εξίσωση και κρατώντας τη χαμηότερη από τις δυνάμεις που θα εμφανιστούν βρίσκουμε: s s s s( s ) z z + ( z) sz z = 0 s s s s s( s ) z + sz sz z = 0. (.) Η χαμηότερη δύναμη θα είναι αυτή της δευτέρας παραγώγου, τάξεως s, οπότε η εναρκτήρια δύναμη θα πρέπει να ικανοποιεί τη συνθήκη, [s(s-)+s]z s- =0. Για να ισχύει η προηγούμενη ισότητα ο συντεεστής της δύναμης πρέπει να είναι 6
25 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις ίσος με το μηδέν, δηαδή s -s+s = 0 s = 0 s = s =0. Παρατηρούμε ότι, όγω της διπής ρίζας, μία μόνο ύση μπορεί να κατασκευαστεί με τη μέθοδο δυναμοσειρών η οποία είναι η ακόουθη: z z φ ( z) = z φ ( z) = e. (.) k 0 k k! Έχοντας τώρα τη μία ύση μπορούμε να κατασκευάσουμε και τη δεύτερη με τη μέθοδο της βρονσκιανής, a z a P( z) dz dz ( ) dz z z z aln z a z W( z) = e = e = e = ee = z e. (.3) Ο τύπος για την δεύτερη ύση συνεπώς είναι: z ζ W z e = dz = e d a φ (.4) ζ φ φ ζ ή αιώς υπό τη μορφή σειρών έχουμε, φ ( z) = e z n ( n+ ) a ( ) z (.5) [( n+ ) an ]! n= 0 αφού το αόριστο οοκήρωμα της (.4) δεν είναι στοιχειώδης συνάρτηση και πρέπει να υποογιστεί με ανάπτυξη του e ζ σε δυναμοσειρά και οοκήρωση όρο προς όρο. Έχοντας βρει τις δύο ύσεις της συρρέουσας υπεργεωμετρικής εξίσωσης, θα εξετάσουμε αν έχουν κάποια σχέση με την εξίσωση Fokker-Planck για κατάηο z. Ξεκινάμε με την πρώτη ύση ϕ=ϕ (z) της (.8), στην οποία θέτουμε []: x z = t (.6) οπότε προκύπτει, x x ( t ) ( aa,, ( t )) e + φ + = (.7) όπου το, όπως θα δείξουμε, σχετίζεται με τις σταθερές K και Q της εξίσωσης Fokker-Planck. 7
26 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Αντικαθιστώντας την (.7) στην εξίσωση Fokker-Planck (.4), ως F = ϕ και βρίσκοντας τις μερικές παραγώγους ως προς t, ως προς x και τη δεύτερη μερική παράγωγο ως προς x, έχουμε: F t = x ( t ) + e. (.8α) Η μερική παράγωγος ως προς x είναι: F x = e x ( t+ ) (.8β) και η δεύτερη μερική παράγωγος ως προς x είναι: F x = e x ( t+ ). (.8γ) Επομένως, με αντικατάσταση των παραπάνω στην εξίσωση (.4) προκύπτει: F Q F = [ KF] + t x x (όπου K= σταθερό) x x x ( t+ ) ( t+ ) Q ( t+ ) e + K( ) e e = 0 Q K 0 = Q 3 + K + = 0. (.9) Έτσι, καταήξαμε, σε μια σχέση μεταξύ των παραμέτρων, Κ και Q η οποία αν ισχύει υποδηώνει ότι η πρώτη ύση της υπεργεωμετρικής συνάρτησης όντως ικανοποιεί την εξίσωση Fokker-Planck. Ένας άος τρόπος να καταήξουμε στο αποτέεσμα αυτό είναι να βρούμε τις σχέσεις μεταξύ της πρώτης και της δεύτερης παραγώγου της «συρρέουσας» υπεργεωμετρικής συνάρτησης ως προς z, με τις μερικές παραγώγους της ϕ ως προς x και t. Έπειτα, αντικαθιστώντας στην διαφορική εξίσωση (.7) και μετά από υποογισμούς να οδηγηθούμε στην εξίσωση Fokker-Planck. 8
27 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Η μερική παράγωγος της ϕ ως προς t συνδέεται με τις ϕ, ϕ μέσω της σχέσης: dφ φ t φ φ φ' = = = φ' = φ dz t z t t (.0α) Αντιστοίχως, η μερική παράγωγος της ϕ ως προς x οδηγεί στην dφ φ x dφ φ = = dz x z dz x. (.0β) Η δεύτερη παράγωγος της ϕ ως προς z δίνει: d φ dφ dφ x φ x φ φ φ'' = = ( ) = ( ) = ( ) = ( )( ) = dz z dz x dz z x x z x x x φ'' = φ. (.0γ) x Αντικαθιστώντας τα παραπάνω αποτεέσματα στη διαφορική εξίσωση (.7) οδηγούμαστε στη σχέση: zφ''( aaz,, ) + ( a z) φ'( aaz,, ) aφ( aaz,, ) = 0 φ z + ( a z) φ' aφ = 0 x φ z + aφ' zφ' aφ = 0 x (όμως φ =φ) φ φ φ φ' = 0 + = 0 x x t 3 φ φ 0 + = x t (.) Στο σημείο αυτό, χρησιμοποιούμε τη σχέση μεταξύ των σταθερών (.9). Λύνουμε ως προς 3 και κάνοντας ίγες πράξεις έχουμε: όµως ισχύει ότι φ = φ δηαδ ή x t x x Q ( K + ) φ + φ = 0 (, φ = φ ) 9
28 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Q φ φ ( K + )( ) = 0 x t K φ Q φ φ = 0 x x t K φ Q φ φ + + = 0 x x t φ ( Kφ) Q φ + = 0. (.) t x x Παρατηρούμε ότι, η (.) δεν είναι άη από την εξίσωση Fokker-Planck, όταν ο συντεεστής μετατόπισης Κ είναι σταθερός. Στις περιπτώσεις όπου το K εξαρτάται από το x αναφερόμαστε στη εγόμενη διαδικασία Ornstein-Uhlenbeck. Η διαδικασία αυτή είναι μια στοχαστική διαδικασία η οποία περιγράφει την ταχύτητα ενός Brownian σωματιδίου υπό την επίδραση «τριβής» που είναι είτε σταθερή, είτε γκαουσιανή (κανονική κατανομή) είτε μαρκοβιανή, επιτρέποντας γραμμικούς μετασχηματισμούς των χωροχρονικών μεταβητών. Ξεκινάμε από τη εξίσωση Fokker-Planck, F [ KxF ( ) ] Q F + = 0, t x x και αναζητούμε ύσεις μέσω χωριζομένων μεταβητών: F( xt,) = GtH () ( x) (.3) όπου για την διαδικασία Ornstein- Uhlenbeck επιέγεται K( x) = x. (.4) Αντικαθιστώντας την F στην προαναφερθείσα εξίσωση οδηγούμαστε στα ακόουθα κάνοντας τις απαραίτητες πράξεις: ( ) H G + G KH QG H = 0 t x x G G ( KH ) QG H + = 0 t H x H x G Q H ( KH ) G t H x H x = G Q H ( KH ) G t H x x = ( ) = (.5) όπου >0, αυθαίρετη σταθερά. 0
29 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Προφανώς, από την παραπάνω εξίσωση προκύπτει: G + G = 0 t (.6) της οποίας η ύση είναι, Gt () = e t. (.7) Η δεύτερη διαφορική εξίσωση (.5) γίνεται υπό αυτές τις συνθήκες: Q H KH x ( ) + H = 0. (.8) x Για τη γραμμική περίπτωση K(x)= x, εφαρμόζοντας τον μετασχηματισμό Fourier η (.8) παίρνει τη μορφή: Q ˆ ˆ H + ˆ = 0 a ah a H (.9) όπου Ĥ είναι ο μετασχηματισμός Fourier της συνάρτησης Η ως προς τη μεταβητή α. Λύνοντας τώρα την παραπάνω διαφορική εξίσωση βρίσκουμε την Ĥ ως ακοούθως: Q ˆ ˆ ˆ H ˆ 0 Q ˆ H a H + a H = ah + Hˆ = 0 a a a Hˆ Q + ( a ) H ˆ = 0 a a Q Qa ( a ) da ( ln a) a 4 Hˆ = e = e Qa 4 Ha ˆ ( ) = a e. (.30) Εφόσον υποογίσαμε την Ĥ, μπορούμε τώρα με τον αντίστροφο μετασχηματισμό Fourier να βρούμε την H και κατ επέκταση τη συνάρτηση F(x,t), + ˆ iax + Qa 4 iax H ( x) = H ( a) e da H ( x) = a e e da π π, (.3) αντικαθιστώντας την H(x) στη συνάρτηση F(x,t) και οοκηρώνοντας για όα τα >0:
30 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις + Qa t 4 0 iax F(,) x t = a( ) e a e e dad π (.3) όπου το α() πρέπει να ικανοποιεί την ακόουθη συνθήκη κανονικοποίησης: a( ) d =. (.33) 0 Συμπεραίνουμε, οιπόν, εκ των ανωτέρω ότι η πρώτη ύση της «συρρέουσας» υπεργεωμετρικής εξίσωσης είναι και ύση της εξίσωσης Fokker-Planck εφόσον ικανοποιείται όπως είδαμε μια σχέση μεταξύ των παραμέτρων και K, Q. Επομένως, έχοντας βρει και τη δεύτερη ύση της (.7) υπό τη μορφή της (.4), μπορούμε να θέσουμε το εξής ερώτημα: τι είδους Μ.Δ.Ε. θα μπορούσε να έχει αυτή την ύση με την προϋπόθεση ότι επιβάουμε και πάι τη συνθήκη: x z = t. Με την συνθήκη αυτή, η ύση μας παίρνει τη μορφή: x ( t+ ) x ( t+ ) ζ x e φ( aa,, ( t+ )) = e dζ α (.34) ζ όπου σκοπός μας και πάι είναι να καταήξουμε σε μια σχέση μεταξύ του και των παραμέτρων Κ, Q, αν βέβαια υπάρχει τέτοια ύση της εξίσωσης Fokker-Planck. Αντικαθιστώντας οιπόν τη (.34) στην εξίσωση Fokker-Planck (.4) με F=ϕ, βρίσκουμε τις μερικές παραγώγους ως προς t, ως προς x και τη δεύτερη μερική παράγωγο ως προς x. Η μερική παράγωγος ως προς t, είναι: x ( t+ ) x t+ x ζ x ( t ) ( t ) F + e + e = e dζ + e ( ) α t ζ x α ( t ) x ( t+ ) x ( t ) e ζ + F = e dζ α t ζ x. (.35α) α ( t )
31 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Η μερική παράγωγος ως προς x, είναι: x ( t+ ) x ( t+ ) x ζ x ( t ) ( t ) F + e + e = e dζ + e ( ) α x ζ x α ( t ) x ( t+ ) x ζ ( t+ ) F e = e dζ α x ζ x, (.35β) α ( t ) και η δεύτερη μερική παράγωγος ως προς x, είναι: x ( t+ ) x ( t+ ) x ζ x ( t ) ( t ) F + e + e α x α = e dζ + e ( t ) α x ζ x a ( t ) x ( t+ ) x ζ F ( t+ ) e x e α α dζ ( t ) α x. (.35γ) a = + x ζ ( t ) Επομένως, με αντικατάσταση των παραπάνω στην εξίσωση (.4) προκύπτει: F = [ KF] + Q F t x x (όπου K = σταθερό) x x ( t+ ) ( t+ ) x x ζ ( t+ ) ( t+ ) ζ e e e dζ + K[ e dζ ] α α ζ x α x α ( t ) ζ ( t ) x ( t+ ) x ζ ( t+ ) α α [ e dζ ( t ) ] 0. α x a Q e x + = ζ ( t ) (.36) Ποαπασιάζουμε την παραπάνω με και παίρνουμε: x x ( t+ ) ( t+ ) x 3 x ζ ( t+ ) ( t ) 3 + α x α ζ e e K e dζ + + Ke dζ + + α ζ x α ( t ) ζ ( t ) 3
32 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις x ( t+ ) x ζ ( t+ ) Q e Q Q a + e 0 dζ + = α ζ x α x α+ ( t ) ( t ) x ( t+ ) x ( t ) 3 Q e ζ + ( + K+ ) e dζ + α ζ 3 K Q Q a = 0. (.37) x a x a x a x a+ ( t ) ( t ) ( t ) ( t ) Όμως, από τη (.9) γνωρίζουμε ότι, 3 Q + K+ = 0. Άρα, πρέπει να μηδενιστεί και ο όρος, Q a = 0. (.38) x ( ) a+ t Η παραπάνω ισότητα ισχύει για την περίπτωση όπου ο διαχυτικός όρος Q=0 ή το α=0. Όμως, και οι δύο αυτές ύσεις απορρίπτονται διότι αν το Q=0 θα παίρναμε την εξίσωση της διάχυσης ενώ αν το α=0 θα καταήγαμε η ύση να είναι μία σταθερά. Άρα, η δεύτερη ύση της συρρέουσας δεν ικανοποιεί την εξίσωση Fokker-Planck για το z που θέσαμε. Στη συνέχεια, θα δείξουμε ότι, η δεύτερη ύση της συρρέουσας θα ικανοποιούσε την εξίσωση Fokker-Planck εάν ο τύπος της ήταν ο ακόουθος: [ ] + = + ν t x x t F KF Q F F (.39) Η εξίσωση (.39) είναι μια Μ.Δ.Ε. την οποία ονομάσαμε Fokker-Planck κυματική εξίσωση για όγους που θα εξηγήσουμε πιο κάτω. Αντικαθιστώντας τις μερικές παραγώγους επιχειρούμε να προσδιορίσουμε τα K, Q και ν. Υποθέτουμε ότι το K είναι μια σταθερά ενώ το ν μπορεί να είναι είτε σταθερά είτε συνάρτηση του x ή του t. 4
33 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Πιο αναυτικά, θέτοντας z=μx+t με μ, σταθερές, στη δεύτερη ύση της «συρρέουσας» μορφής η (.39) μετατρέπεται στην ακόουθη εξίσωση: Q ( φ + ) + Kµ ( φ + ) + K'( x) φ = µ ( φ + ) + ν ( φ + ) α α α α+ α α+ z z z z z z Q Q Q ( + Kµ + K'( x) µ ν ) φ + ( + Kµ µ ν ) ( µ + ν ) = 0 α α+ z z (.40) Για να ικανοποιείται η εξίσωση αυτή συμπεραίνουμε ότι, Q + Kµ + K' µ ν = 0 Q ν K' + K = µ + (.4α) µ µ Q + Kµ µ ν Q ν K = µ + (.4β) µ µ και Q ν µ + ν = 0 Q =. µ (.4γ) Από τις (.4α), (.4β) φαίνεται ότι το K =0 δηαδή το K σταθερά. Παρατηρούμε, ωστόσο ότι αν το ν είναι σταθερά θα είναι αντιστοίχως και το Q ενώ αν είναι συνάρτηση του x ή t προφανώς θα είναι και το Q. Άρα, σύμφωνα με τα παραπάνω έχουμε K ν = και Q =. (.4) µ µ Το ότι, για Q>0, το ν είναι αρνητικό, δικαιοογεί την ονομασία της (.39) ως κυματική εξίσωση. 5
34 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Πριν συνεχίσουμε και έχοντας αναφέρει την περίπτωση όπου το K δεν είναι σταθερά, μπορούμε να επανέθουμε στην (.39) και να αναζητήσουμε ύσεις χωριζομένων μεταβητών θεωρώντας F( xt,) = H( xgt ) () (.43) και K( x) = x. Τότε συνεπάγεται ότι: F [ KF ] Q F F + = + ν t x x t () ( ) ( ) () ( ) Gt '( ) ( ) ( ) H x ( ) Q H x H x + K xh xgt + K Gt = Gt ( ) + ν Gt H( x) t x x t Διαιρώντας με HG την εξίσωση αυτή παίρνουμε: G' G'' QH'' H' K K' k G G H H ν = = (.44) όπου ν, k σταθερές. Προφανώς, για να ισχύει η εξίσωση αυτή πρέπει: G G k 0 G = t ν t ν (.45) η οποία είναι μια Σ.Δ.Ε. δεύτερης τάξης με σταθερούς συντεεστές, της οποίας το χαρακτηριστικό πουώνυμο είναι: r k r 0 ν ν = και οι ύσεις που προκύπτουν είναι οι ακόουθες,. (.46) ν ν ν ν ν 4k r = ± + r = ± + 4 k ν Για να έχουμε πραγματικές ύσεις αυτής της μορφής πρέπει το υπόρριζο να είναι μεγαύτερο ή ίσο του μηδενός, δηαδή ν -(/4k ). Αν συμβαίνει αυτό τότε 6
35 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις προκύπτει μια θετική και μια αρνητική ρίζα r. Η ύση της διαφορικής εξίσωσης (.45) δίνεται επομένως ως εξής: + + 4k ν t + 4k ν t ν ν ν ν Gt () Gtk (, ) ce ce = = + (.47) όπου c και c σταθερές που υποογίζονται από τις αρχικές συνθήκες. Παρατηρούμε ότι, αφού ν<0, οι ως άνω ύσεις οδηγούν σε G(t) 0, καθώς t. Η Μ.Δ.Ε (.44) μας οδηγεί σε μία ακόμα εξίσωση της μορφής, Q H [ KH ] kh x + = 0 x η οποία είναι η ίδια με αυτή που ύσαμε παραπάνω με τη βοήθεια μετασχηματισμών Fourier. Άρα, απευθείας παίρνουμε Q ˆ H + ˆ ˆ = 0. a ah a kh Η ύση της οποίας είναι η ακόουθη: Qa k ˆ 4 H a e =. Στη συνέχεια, υποογίζουμε την H με τον αντίστροφο μετασχηματισμό Fourier και προκύπτει: + ˆ iax + k Qa 4 iax H ( x) = H ( a) e da H ( x) = a e e da π π. Έχοντας υποογίσει και τις δύο συναρτήσεις H(x) και G(t) μπορούμε εύκοα να βρούμε την F(x,t) με μια αντικατάσταση των παραπάνω στη (.43): + Qa k 4 iax 0 F( x,) t = G(, t k ) k a( k ) a e e dadk π (.48) όπου οοκηρώνουμε ως προς k για να συμπεριάβουμε όες τις δυνατές περιπτώσεις, επιβάοντας και τη συνθήκη κανονικοποίησης 7
36 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις a( k ) dk =. 0.. Οι Εξισώσεις Schrödinger και Klein-Gordon Μια άη εξίσου σημαντική εξίσωση η οποία συνδέεται με υπεργεωμετρική συνάρτηση είναι η εξίσωση του Schrödinger. Η εξίσωση αυτή προτάθηκε από τον Αυστριακό φυσικό Erwin Schrödinger το 95 για να περιγράψει τη χρονική και χωρική εξάρτηση κβαντομηχανικών συστημάτων. Παίζει σημαντικό ρόο στη κβαντομηχανική θεωρία με σημασία ανάογη του δεύτερου νόμου του Νεύτωνα στην κασική μηχανική. Στην κασική φυσική για να προσδιορίσουμε την κατάσταση ενός σώματος χρησιμοποιούμε τις συντεταγμένες της θέσης του καθώς και την ταχύτητα του. Στον μικρόκοσμο, όπου κυριαρχεί η κβαντική φυσική, η κατάσταση ενός σωματιδίου προσδιορίζεται μέσω μιας μιγαδικής κυματοσυνάρτησης Ψ, της οποίας το μέτρο στο τετράγωνο Ψ(x,t) αποτεεί την πιθανότητα το σωμάτιο να βρίσκεται στη θέση x για χρόνο t. Με άα όγια χρειάζεται να ύσουμε μια κυματοσυνάρτηση σε αναογία με την εξίσωση ενός μηχανικού ή ηεκτρομαγνητικού κύματος. Η κυματοσυνάρτηση Ψ την οποία αναζητούμε στην κβαντική φυσική προσδιορίζεται από την εξίσωση του Schrödinger: Ψ Ψ i = + V( x) Ψ (.49) t m x όπου ħ η σταθερά του Planck, m η μάζα του σωματιδίου και V(x) το δυναμικό στο οποίο κινείται. Χρησιμοποιώντας και σε αυτή την περίπτωση τη «συρρέουσα» υπεργεωμετρική συνάρτηση, ακοουθούμε την ίδια διαδικασία όπως παραπάνω, θέτοντας όμως στην εξίσωση (.8): i p z = ( px Et) με E= m (.50) όπου Ε είναι η ενέργεια και p η ορμή του εεύθερου σωματιδίου με V(x)=0. Η υπεργεωμετρική συνάρτηση που προκύπτει είναι της μορφής, 8
37 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις i i ( px Et) φ( a, a, ( px Et)) = e φ (.5) με φ E = φ t i. (.5) Υποογίζουμε τώρα τις παραγώγους της συρρέουσας υπεργεωμετρικής συνάρτησης ως προς z, βρίσκοντας τις σχέσεις τους με τις μερικές παραγώγους της ϕ ως προς t και x, ώστε να αντικαταστήσουμε στην διαφορική εξίσωση (.7) και μετά από υποογισμούς να οδηγηθούμε στην εξίσωση Schrödinger. Για τη ϕ/ t παρατηρούμε ότι: dφ φ t φ i φ φ' = = = φ' = φ dz t z ie t E t (.53α) ενώ η μερική παράγωγος της ϕ ως προς x ικανοποιεί: d x d φ φ φ = = φ dz x z dz ip x (.53β) Παραγωγίζοντας την ϕ δεύτερη φορά ως προς z βρίσκουμε: d φ dφ dφ x φ x φ φ φ '' = = ( ) = ( ) = ( ) = ( )( ) = dz z dz x dz z x ip x z x ip x ip p x φ '' = p φ. (.53γ) x Σύμφωνα με τα παραπάνω αποτεέσματα συνεπάγεται ότι, zφ''( aaz,, ) + ( a z) φ'( aaz,, ) aφ( aaz,, ) = 0 φ z + ( a z) φ' aφ = 0 p x φ z + aφ' zφ' aφ = 0 p x (όμως ϕ =ϕ) φ ' 0 φ = p x 9
38 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις φ i φ = p x E t 0. (.54) Ισοδύναμα μπορούμε να γράψουμε την (.54) στη μορφή: φ φ i = (.55) t m x Ωστόσο, αν θέσουμε, H = m x 0 (.56) οδηγούμαστε στην τεική μορφή της εξίσωσης, η οποία είναι η μερική εξίσωση Schrödinger για V(x)=0 και ϕ(x,t)=ψ(x,t), που δίνεται από τον τύπο: φ i = H 0 φ. (.57) t Είναι φανερό οιπόν από τα παραπάνω ότι ξεκινώντας από μια ειδική ύση της υπεργεωμετρικής εξίσωσης οδηγούμαστε σε ύσεις άων εξισώσεων της Μαθηματικής Φυσικής. Θα κείσουμε το παρόν εδάφιο με μία ακόμη εφαρμογή που μας οδηγεί στην εξίσωση Klein-Gordon. Η εξίσωση Klein-Gordon ονομάστηκε έτσι προς τιμήν των θεωρητικών φυσικών Oskar Klein και Walter Gordon αποτεεί μια σχετικιστική γενίκευση της εξίσωσης Schrödinger της κβαντικής μηχανικής. Η βασική ιδέα για τη δημιουργία της εξίσωσης αυτής είναι να αξιοποιηθούν οι ίδιοι τεεστές που χρησιμοποιούνται για την θέση, την ορμή και την ενέργεια στην εξίσωση Schrödinger αά επιπέον αντί της κασικής σχέσης ενέργειας E=p /m να χρησιμοποιηθεί η σχετικιστική E =(pc) +(mc ). Θέτουμε, οιπόν, z = i( kx ωt) με mc h 4 ω = kc + (.58) και αναζητούμε ύσεις επίπεδων κυμάτων i( kx ωt ) e a a i kx t = φ[, ; ( ω )] = φ (.59) 30
39 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις για την «συρρέουσα» υπεργεωμετρική διαφορική εξίσωση η οποία παίρνει τη μορφή: i( kx ωt) φ'' + [ a i( kx ωt)] φ' aφ = 0. (.60) Στη συνέχεια, ακοουθώντας την ίδια διαδικασία όπως προηγουμένως υποογίζουμε τις παραγώγους ως προς z και τις συνδέουμε με τις μερικές παραγώγους ως προς x και t, καθώς και τη δεύτερη μερική παράγωγο ως προς x ώστε να τις αντικαταστήσουμε στην διαφορική μας εξίσωση. Για την μερική παράγωγο της ϕ ως προς t έχουμε: dφ φ t φ i φ φ' = = = φ' = φ dz t z iω t ω t (.6α) ενώ η μερική παράγωγος της ϕ ως προς x ικανοποιεί: d x d d i φ φ φ φ φ = = = φ dz x z dz ik x dz k x (.6β) Η δεύτερη μερική παράγωγος της ϕ ως προς x συνδέεται με την ϕ ως εξής: d φ dφ dφ x i φ x i φ i φ φ '' = = ( ) = ( ) = ( ) = ( )( ) = dz z dz x dz z x k x z x k x k k x φ '' = k φ. (.6γ) x Ως αποτέεσμα των ανωτέρω η διαφορική εξίσωση (.60) οδηγεί στις σχέσεις: i( kx ωt) φ'' + [ a i( kx iωt)] φ aφ = 0 (αφού ϕ =ϕ) i( kx ωt) φ'' + aφ i( kx ωt) φ aφ = 0 φ i φ φ'' φ' = 0 = 0 k x ω t (.6) όμως φ φ = t ω t (.63) οπότε, φ φ = 0. (.64) k x ω t 3
40 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Χρησιμοποιώντας τις ισότητες: φ x = k φ (.65) και mc h 4 ω = kc +. η διαφορική εξίσωση (.64) παίρνει την τεική της μορφή: φ φ ω φ φ = 0 = 0 k x ω t k x t 4 kc mc φ φ ( + ) = 0 c k kh x t 4 φ mc φ φ + = 0 x kh x t 4 φ mc φ c + ( k ) φ = 0 c x kh t 4 φ mc φ φ = 0 x h t φ φ mc + φ = 0. (.66) c t x h Έτσι, φτάνουμε στην επιθυμητή εξίσωση Klein-Gordon η οποία όπως είδαμε συνδέεται και αυτή με μια υπεργεωμετρική εξίσωση. Θα ήταν ενδιαφέρον να μεετήσουμε σε μια μεοντική εργασία σε ποιες Μ.Δ.Ε. παρόμοιες με τις Schrödinger και Klein-Gordon οδηγεί η δεύτερη (γραμμική ανεξάρτητη) ύση της «συρρέουσας» υπεργεωμετρικής εξίσωσης..3 Οι μη γραμμικές εξισώσεις Fokker-Planck, Schrödinger και Klein- Gordon που περιέχουν q-παράμετρο. Σε μια ποικιία φυσικών συστημάτων παρατηρείται συχνά το φαινόμενο της εγόμενης ανώμαης διάχυσης [36]. Το κύριο χαρακτηριστικό της διάχυσης αυτής είναι ότι η μέση τετραγωνική μετατόπιση εξαρτάται μη γραμμικά από τον χρόνο. Με 3
41 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις τον όρο μέση τετραγωνική μετατόπιση εννοούμε το μέσο όρο του τετραγώνου της απόστασης που διανύει ένα σωματίδιο από την αρχική θέση όπου είχε τοποθετηθεί, π.χ. x(0)=0. Δηαδή, αν <x (t)>=dt, αυτή είναι ανάογη του χρόνου, οπότε η διάχυση ονομάζεται ομαή, με συντεεστή διάχυσης D. Μια νέα μη γραμμική Fokker-Planck εξίσωση [36] προτάθηκε για να περιγράψει αυτού του είδους τα φυσικά συστήματα στα οποία παρατηρείται ανώμαη διάχυση. Στη συνέχεια, θα αναφερθούμε σε μια τέτοια μη γραμμική εξίσωση διάχυσης και θα δείξουμε τη σχέση της με την γενική υπεργεωμετρική συνάρτηση. Αρχικά, πρέπει να τονίσουμε ότι η διαδικασία που ακοουθούμε για την εξαγωγή της μη γραμμικής Fokker- Planck εξίσωσης, μέσω της ύσης της γενικής υπεργεωμετρικής συνάρτησης, σχετίζεται με μια βασική συνάρτηση, την γνωστή ως q-εκθετική, ο τύπος της οποίας είναι: + q q z + q z > e ( ) [ ( ) ], αν ( ) 0 q z = 0, αιώς (.67) Η συνήθης υπεργεωμετρική συνάρτηση F(α,β;γ;z) περιέχει τρία σύμβοα Pochhammer και δίνεται από: n αβ n n z F( αβγ, ; ; z) = για z < (.68) γ n! n= 0 n όπου α n =α(α+)(α+) (α+n-) και αντίστοιχους ορισμούς των β n, γ n μέσω των παραμέτρων β, γ αντιστοίχως. Η σειρά συγκίνει εάν τα α και b είναι μη αρνητικοί ακέραιοι. Έστω ότι μεετάμε την υπεργεωμετρική συνάρτηση F(α,β;γ;z) η οποία ικανοποιεί την διαφορική εξίσωση: z( zf ) ''( αβγ, ; ; z) + [ γ ( α+ β+ ) zf ] '( αβγ, ; ; z) αβf( αβγ, ; ; z) = 0. (.69) Αν θεωρήσουμε ότι β=γ τότε για α -α, z -z, η F παίρνει τη μορφή, [,40]: F( αγγ, ; ; z) = ( + z) α. (.70) Εστιάζοντας την προσοχή μας στη συνάρτηση, 33
42 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις x f( xt, ) = [ + ( q )( t+ )] q, (.7) θεωρούμε ότι το είναι το ίδιο με την προηγούμενη ενότητα, δηαδή υπακούει στη σχέση: 3 Q + K+ = 0 (.7) όπου K και Q οι σταθερές της εξίσωσης Fokker-Planck. Επιστρέφοντας στην (.69) για α=/(q-) και z= (q-)(t+x/) η ύση F μετατρέπεται στην: x x F[, γγ ; ;( q)( t+ )] = [ + ( q )( t+ )] q q. (.73) Για β=γ όμως, δεν αάζει μόνο η μορφή της ύσης F αά και η διαφορική υπεργεωμετρική συνάρτηση η οποία γίνεται ως εξής: z( zf ) ''( αγγ, ; ; z) + [ γ ( α+ γ+ ) zf ] '( αγγ, ; ; z) αγf( αγγ, ; ; z) = 0. (.74) Ακοούθως, υποογίζουμε τις μερικές παραγώγους της F ως προς x και t συναρτήσει της F και των οικών παραγώγων της F, F. Η οική παράγωγος της F ως προς z δίνει: ' df F t F F = = = F' = F F. (.75α) dz t z ( q) t ( q) t Η μερική παράγωγος της F ως προς x συνδέεται με την F μέσω της: df F x df F = = dz x z dz ( q) x (.75β) και αντιστοίχως η δεύτερη μερική παράγωγος της F ως προς x ικανοποιεί: F '' = = ( ) ( ) = ( ) d F d df df x F x dz z dz x dz z x ( q) x z F F ( )( ) = x ( q) x ( q) ( q) x 34
43 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις F '' = ( q) F x. (.75γ) Στη συνέχεια, αντικαθιστούμε τα παραπάνω στην (.74) και οδηγούμαστε στην παρακάτω εξίσωση: F z( z) + ( γ α z γ z zf ) ' αγ F= 0 ( q) x F z( z) + γ ( zf ) ' z( α + ) F' αγ F= 0 ( q) x z( + ) F q F γ z( z) + γ ( zf ) ' + F= 0 q x q t q ( ) ( ) F qz F γ z( z) + + γ ( zf ) ' F= 0. (.76) q x q t q ( ) ( ) Ποαπασιάζοντας με ( q) η ως άνω παράσταση αποποιείται στην 3 F F γ ( z) + q + ( q) [( zf ) ' F] = 0. (.77) x t z q Παρατηρούμε ότι η εξίσωση αυτή ικανοποιείται αν θεωρήσουμε ότι η F ικανοποιεί όγω της (.73) την ακόουθη σχέση ( zf ) ' F= 0 q (.78) οπότε έχουμε, F x F t 3 ( z) + q = 0. Ισοδύναμα, η τεευταία γράφεται: 3 ( ) F F q + q F = 0 x t (.79) αφού ισχύει F (-q) (z)=-z και πιο συγκεκριμένα, 35
44 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις q 3 F F + = 0 x t. (.80) Τώρα είμαστε σε θέση να αντικαταστήσουμε το από τη σχέση (.7) με αποτέεσμα: q Q F F ( K + ) + = 0 x t q q F ( KF ) Q F + = 0 t x x (.8) επισημαίνοντας ότι η συνάρτηση F υπακούει στις σχέσεις: q F F F K = K = x x x. (.8) Καταήξαμε έτσι σε μία μη γραμμική εξίσωση Fokker-Planck η οποία συμπίπτει με αυτή του Plastino [] σε σχέση με το νόμο δύναμης των q εντροπιών εάν θέσουμε, g = F q q* = / q με αποτέεσμα η εξίσωση να έχει τη μορφή: q* g ( Kg) Q g + = 0. t x x Επίσης, στην περίπτωση όπου η F είναι ανεξάρτητη του t η (.8) μετατρέπεται, προφανώς, στην ακόουθη: q ( KxF ( ) ) Q F = 0 x x (.83) της οποίας η ακριβής ύση δίνεται ως εξής: ( q ) F( x) = [ + V( x)] q (.84) Q όπου dv ( x) = K( x). (.85) dx 36
45 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Συμπεραίνουμε ότι, η μη γραμμική γενίκευση της εξίσωσης Fokker-Planck περιέχεται στη δομή των υπεργεωμετρικών διαφορικών εξισώσεων. Σε περίπτωση που ο συντεεστής μετατόπισης, K, δεν είναι σταθερά αά εξαρτάται από το x τότε ακοουθούμε την ίδια σειρά βημάτων. Μια νέα μη γραμμική εξίσωση Schrödinger έχει πρόσφατα μεετηθεί από τους Nobre, Rego Monteiro και Tsallis (NRT). Η εν όγω NRT εξίσωση συμβάει σημαντικά στη συνεχιζόμενη έρευνα μη γραμμικών εξισώσεων της φυσικής. Συγκεκριμένα, οι μη γραμμικές εξισώσεις Schrödinger έχουν βρει σημαντικές εφαρμογές σε διάφορους τομείς. Η πιο μεετημένη μη γραμμική Schrödinger εξίσωση περιέχει μια κυβική μη γραμμικότητα στην κυματική συνάρτηση. Γενικά, έχει εφαρμοστεί σε οπτικές ίνες και στη μεέτη των κυμάτων του νερού. Στην κβαντική μηχανική εξισώσεις αυτού του είδους ίσως να μπορούν να περιγράψουν τη συμπεριφορά μιας κυματικής συνάρτησης η οποία θα αναπαριστά την κατάσταση ενός κβαντικού συστήματος ποών σωμάτων. Για να δούμε όμως πώς καταήγουμε σε μια μη γραμμική εξίσωση Schrödinger, χρησιμοποιούμε από τις υπεργεωμετρικές συναρτήσεις τη σχέση, F( αγγ, ; ; z) = ( + z) α Πιο συγκεκριμένα, q i i [ + ( q)( px Et)] = F[, γγ ; ; ( q )( px Et)] q (.86) όπου, p E = και z = i ( q )( px Et). (.87) m Η υπεργεωμετρική συνάρτηση υπακούει τότε στη διαφορική εξίσωση: z( zf ) ''( αβγ, ; ; z) + [ γ ( α+ β+ ) zf ] '( αβγ, ; ; z) αβf( αβγ, ; ; z) = 0. Όταν β=γ η παραπάνω εξίσωση παίρνει τη μορφή, z( zf ) ''( αγγ, ; ; z) + [ γ ( α+ γ+ ) zf ] '( αγγ, ; ; z) αγf( αγγ, ; ; z) = 0. 37
46 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Αντικαθιστούμε το z και τα α,γ της συνάρτησης F, και προκύπτει: i i ( q )( px Et)[ ( q )( px Et)] F '' + i γ + [ γ ( + γ + ) ( q )( px Et)] F ' 0 q q F =. (.88) Στη συνέχεια, θα υποογίσουμε τις παραγώγους της F σε σχέση με τις μερικές παραγώγους ως προς t και x. Αρχικά, παραγωγίζουμε την F ως προς t, ie( q ) F = F' t i F' = F ( q ) E t. (.89α) Έπειτα, βρίσκουμε τη μερική παράγωγο ως προς x, ip( q ) F = F' x i F' = F. (.89β) ( q) p x Υποογίζουμε εύκοα και τη δεύτερη παράγωγο ως προς x, x p ( q ) F = F'' F'' = ( q ) p x F. (.89γ) Σύμφωνα με τα παραπάνω η διαφορική υπεργεωμετρική εξίσωση γίνεται: i i ( q )( px Et)[ ( q )( px Et)] F + ( ) q p x i i + [ γ ( + γ + ) ( q )( px Et)] F q ( q ) E t γ 0 q F =. (.90) Ποαπασιάζοντας τους όρους της εξίσωσης με E(q-) αποποιείται στην ακόουθη έκφραση: i i ( q )( px Et)[ ( q )( px Et)] F + ( ) q m x i + [ γ ( + γ + ) ( q )( px Et)] i F γ EF = 0. (.9) q t 38
47 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Παραγωγίζοντας τη σχέση (.86) ως προς t, παίρνουμε: i t q E = F F (.9) οπότε ο τεευταίος όρος της (.9) ισούται με: ( ) ( γef = i γ F q) F. (.93) t Τότε η (.9) παίρνει τη μορφή: ( q) ( q) ( q) ( q) [ F ] F F + i γ ( γ )[ F ] F i γf F = mq ( ) x q t t Αποποιώντας την τεευταία εξίσωση φτάνουμε στην ακόουθη: ( q) ( q) ( q) ( q) [ F ] F F i γ ( γ )[ F ] γf = mq ( ) x t q ( q) ( q) ( q) ( q) ( q) [ F ] F F i γ F γf F ) + mq ( ) x t q ( q) + + γ + + γf } = 0 q ( q) ( q) ( q) ( q) q [ F ] F F i F F 0 + =. (.94) mq ( ) x t q q Ποαπασιάζουμε με(q-)και διαιρούμε με [-F (-q) ] οπότε: ( q) F F i q F = 0 (.95) m x t ή ισοδύναμα, = (.96) t ( q) iq F F HF 0 όπου H 0 είναι H = m x 0. (.97) 39
48 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Ακοούθως, θα δούμε τι προκύπτει εάν θεωρήσουμε μια χρονικά ανεξάρτητη συνάρτηση H και μια F(x,t)=f(t)g(x). Έστω, F( xt,) = f() tg( x). (.98) Επομένως, χωρίζοντας τις χωρικές από τις χρονικές μεταβητές προκύπτουν οι ακόουθες δύο εξισώσεις. Θέτουμε επιπέον ψ(0,0)=και μετατρέπονται στις : q i [ f()] t = f() t (.99) t και d q ( ) [ ( )] gx = gx. (.00) m dx Είναι εύκοο να διαπιστωθεί ότι μια πιθανή ύση είναι: i ( q) f ( t) = [ + Et] q q (.0α) i ( q) g( x) = [ + px] ( q + ) q (.0β) για p E = m =. (.0γ) Όταν το q=οι ως άνω συναρτήσεις οδηγούν στη ύση για τη συνήθη Schrödinger εξίσωση. Από τα παραπάνω προκύπτει ότι, ο τύπος της NRT εξίσωσης είναι: i q xt H xt t ψ ψ ( ) (,) = [ (,)] q (.0) οπότε μπορούμε, παίρνοντας μια χρονικά ανεξάρτητη χαμιτόνια συνάρτηση H, να ακοουθήσουμε την παραπάνω διαδικασία, να χωρίσουμε δηαδή τις χωρικές από τις χρονικές μεταβητές με αποτέεσμα να καταήξουμε στις ακόουθες συναρτήσεις: i ( q) f ( t) = [ + Et] q q (.03α) 40
49 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις i ( q) g( x) = [ + px] ( q)(3 q) q (.03β) για p E = m =. (.03γ) Κείνουμε το κεφάαιο αυτό με τη μη γραμμική εξίσωση Klein-Gordon, χρησιμοποιώντας την q-εκθετική όπως και στην εξίσωση Schrödinger. Πιο συγκεκριμένα, q [ + i( q)( kx ωt)] = F[, γγ ; ; i( q )( kx ωt)] q (.04) όπου, z = i( q )( kx ωt) και mc h 4 ω = kc + (.05) Η υπεργεωμετρική συνάρτηση υπακούει στη διαφορική εξίσωση: z( zf ) ''( αβγ, ; ; z) + [ γ ( α+ β+ ) zf ] '( αβγ, ; ; z) αβf( αβγ, ; ; z) = 0. Όταν β=γ η παραπάνω εξίσωση παίρνει τη μορφή, z( zf ) ''( αγγ, ; ; z) + [ γ ( α+ γ+ ) zf ] '( αγγ, ; ; z) αγf( αγγ, ; ; z) = 0. Αντικαθιστούμε το z και τα α,γ της συνάρτησης F, και προκύπτει: i( q )( kx ωt)[ i( q )( kx ωt)] F '' + + [ γ ( + γ + ) i( q )( kx ωt)] F ' q γ 0 q F =. (.06) Στη συνέχεια, θα υποογίσουμε τις παραγώγους της F σε σχέση με τις μερικές παραγώγους ως προς t και x. Αρχικά, παραγωγίζουμε την F ως προς t, F = iω( q ) F' t i F' = F. (.07α) ω( q ) t 4
50 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις Ισχύει βεβαίως ότι, ( q) F F F ' = ω qq ( ) t και i F = F ω ( q) F t. Έπειτα, βρίσκουμε υποογίζοντας τη μερική παράγωγο ως προς x F = ik( q ) F ' F' = F x ik( q ) x (.07β) ενώ εύκοα παίρνουμε και τη δεύτερη παράγωγο ως προς x, F = k ( q ) F'' F'' = x k ( q ) x F. (.07γ) Σύμφωνα με τα παραπάνω η διαφορική υπεργεωμετρική εξίσωση γίνεται: ( ) i( q )( kx ωt)[ i( q )( kx ωt)] F + k ( q ) x i + [ γ ( + γ + ) i( q )( kx ωt)] F q ( q ) ω t γ 0 q F =. (.08) ή ισοδύναμα, z( z) F qz F iγ ( q) F γ z F + [ ( ) ( )] + = 0. (.09) k ( q ) x q iω( q ) t ω( q ) t Από την σχέση (.04) παρατηρούμε ότι -z=f (-q) επομένως, ( q) zf F ( q) qz F iγ ( q) F γ F F + [ ( )] + = 0, (.0) k ( q ) x q iω t ω t και κάνοντας πράξεις η εξίσωση αποποιείται στην ακόουθη, ( q) zf F iqz F 0 + = k ( q ) x ω( q ) t 4
51 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις + = k x ω t ( q) F F iq F 0. (.) Χρησιμοποιώντας τη σχέση της δεύτερης παραγώγου προκύπτει: ( q) ( q) F F F F = 0 k x ω t F F = 0. (.) k x ω t Η δεύτερη μερική παράγωγος ως προς x ισούται με: F x = k qf (q ). (.3) Έτσι κάνοντας τις πράξεις καταήγουμε στην μη γραμμική εξίσωση Klein-Gordon: F F qm c F c t x h (q ) + = 0. (.4) Αν τώρα αντί για την (.04) έχουμε τη συνάρτηση: ϕ( x, t) = A[ + i( q)( kx ωt] q (.5) προφανέστατα φ(0,0)=a. Η εξίσωση παίρνει τη μορφή: ϕ(,) xt ϕ(,) xt qmc ϕ(,) xt (q ) [ ] [ ] + [ ] = 0 c t ϕ(0,0) x ϕ(0,0) h ϕ(0,0) (.6) ή ισοδύναμα, qm c c t x h (q ) [ ϕ( xt, )] [ ϕ( xt, )] + [ ϕ( xt, )] = 0. (.7) 43
52 Κεφάαιο : Συνήθεις Διαφορικές Εξισώσεις της Μαθηματικής Φυσικής και q-συναρτήσεις. Συμπεράσματα Μεετήσαμε τις γραμμικές και μη γραμμικές ειδικές περιπτώσεις διαφορικών εξισώσεων Fokker-Planck, Schrödinger και Klein-Gordon, οι οποίες σχετίζονται με τη ύση της «συρρέουσας» υπεργεωμετρικής εξίσωσης. Παρατηρήσαμε ότι, στις γραμμικές η ύση της συρρέουσας που χρησιμοποιήσαμε περιέχει δύο σύμβοα του Pochhammer ενώ στις q-μη γραμμικές τρία, χρησιμοποιώντας βέβαια τη γενική υπεργεωμετρική εξίσωση. Από τις τρεις αυτές παραμέτρους η πρώτη ονομάζεται μη εκτατική παράμετρος q του Tsallis. Η q-εκθετική μέσω της ιδιότητας, F( αγγ, ; ; z) = ( + z) α είδαμε ότι σχετίζεται με μια υπεργεωμετρική συνάρτηση. Οι q-εκθετικές συναρτήσεις παίζουν πρωταγωνιστικό ρόο στα επόμενα κεφάαια αφού θα αναύσουμε φυσικά προβήματα στα οποία εφαρμόζεται. Η q-εκθετική συνάρτηση είναι μια κατανομή πιθανοτήτων που προκύπτει από τη μεγιστοποίηση της εντροπίας του Tsallis υπό κατάηους περιορισμούς. Όπως θα αναφερθεί παρακάτω είναι μια γενίκευση των εκθετικών συναρτήσεων με τρόπο ανάογο με αυτόν όπου η εντροπία του Tsallis είναι μια γενίκευση του προτύπου εντροπίας των Boltzmann-Gibbs. 44
53 ΚΕΦΑΛΑΙΟ 3 Γενικότερες Εφαρμογές των q- Συναρτήσεων Ένα σύστημα μετά από μια μεταβοή (π.χ. στην ενέργεια ή/και στον όγκο ή/και στον αριθμό των μορίων ή/και στη χημική σύσταση), υποθέτουμε ότι έχει έρθει σε ισορροπία εάν κάνοντας διαφορετικές μετρήσεις των φυσικών ποσοτήτων, χωρίς να μεταβηθεί κάποια από τις παραμέτρους του, βρίσκουμε ότι παραμένει στην ίδια κατάσταση. Με άα όγια, οι αποκίσεις είναι τόσο μικρές που στην πράξη δεν μπορούν να μετρηθούν. Οι θερμοδυναμικές καταστάσεις είναι καταστάσεις ισορροπίας και οι φυσικές ποσότητες που τις περιγράφουν ονομάζονται καταστατικές συναρτήσεις. Ένας άος τρόπος να περιγράψουμε τις καταστάσεις ισορροπίας είναι να θεωρήσουμε ότι μέσα σε μεγάο χρονικό διάστημα κάθε μόριο του συστήματος θα περάσει από όες τις δυνατές μικροκαταστάσεις συμβατές με την οική ενέργεια, δηαδή όες αυτές οι καταστάσεις έχουν ίση πιθανότητα να εμφανισθούν. Στην περίπτωση αυτή, έμε ότι το σύστημα πηροί την εργοδική υπόθεση της θερμοδυναμικής (ή εργοδικότητα). Οι Boltzmann-Gibbs στατιστικές προσεγγίζουν θερμοστατιστικά τα εργοδικά συστήματα. Όταν διαταραχθεί όμως η εργοδικότητα και το σύστημα μετατοπιστεί σε καταστάσεις μη-ισορροπίας, τότε οι στατιστικές Boltzmann-Gibbs αποτυγχάνουν. Όπως έχει αποκαύψει η έρευνα των τεευταίων 30 ετών, οι κατανομές που περιγράφουν τις στατιστικές αυτές σχετίζονται με q-εκθετικές συναρτήσεις και q-συναρτήσεις του Gauss, που μεγιστοποιούν την εντροπία του Tsallis. 45
54 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Στη Στατιστική Φυσική, εντροπία είναι η έννοια μέσω της οποίας μετράται η αταξία, όπου η μέγιστη τιμή της αντικατοπτρίζει την πήρη αποδιοργάνωση και ισοδυναμεί τεικά με την παύση της ζωής ή αιώς της εξέιξης. Τις τεευταίες 3 δεκαετίες η κασική θεωρία των Boltzmann-Gibbs και των Gaussian κατανομών έχει γενικευθεί σε καταστάσεις μακράν ισορροπίας μέσω ενός νέου παισίου γνωστού ως θερμοστατιστική Tsallis. Πράγματι, υπάρχει μια μεγάη κατηγορία συστημάτων με ημι-σταθερές καταστάσεις ισορροπίας ώστε να είναι απαραίτητη για την αντιμετώπιση τους η γενίκευση της στατιστικής Boltzmann-Gibbs, (B-G). Οι συνήθεις εκθετικές συναρτήσεις και οι συναρτήσεις του Gauss αντικαθίστανται τώρα από τις q-εκθετικές και q- Gaussians, οι οποίες ορίζονται αντίστοιχα ως: exp q + qu u = 0, αιώς /( q) [ ( ) ], +(-q)u 0 (3.) και Pu = A u = A + q u (3.) /( q) ( ) exp q ( β ) [ ( ) β ], <q<3 όπου β>0 μια θετική παράμετρος και A σταθερά κανονικοποίησης ώστε + P( u) du =. Συγκεκριμένα η q-gaussian (3.) μεγιστοποιεί την εντροπία του Tsallis η οποία δίνεται από τον τύπο: q Sq k( pi ) / ( q ) (3.3) i υπό κατάηες συνθήκες. Αξίζει να σημειωθεί ότι για q οι q-εκθετικές συναρτήσεις και οι q- Gaussians γίνονται οι γνωστές εκθετικές συναρτήσεις και συναρτήσεις του Gauss αντίστοιχα. Έτσι, οι q συναρτήσεις περιγράφουν το σύστημα κάθε φορά που η επιογή των παραμέτρων ή αρχικών συνθηκών οδηγεί σε μη B-G συμπεριφορά. Επομένως, η q στατιστική είναι η γενίκευση της B-G στατιστικής και η οικογένεια των αντίστοιχων κατανομών επεκτείνεται από απές συναρτήσεις του Gauss σε q- Gaussians. Σε ποιά προβήματα όμως γίνονται όα αυτά πραγματικότητα; 46
55 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Στο Κεφάαιο αναφερθήκαμε στο φαινόμενο της ανώμαης διάχυσης. Η διάχυση μπορεί να μεετηθεί είτε μακροσκοπικά με την εφαρμογή των νόμων του Fick (ή κάποιων πιο πρόσφατων γενικεύσεων τους στα παίσια της θερμοδυναμικής), είτε σωματιδιακά, μέσω των τυχαίων βηματισμών που εκτεούν τα διαχεόμενα σωματίδια. Οι νόμοι του Fick εκφράζουν το γεγονός ότι η ροή ύης οφείεται σε διαφορά συγκέντρωσης των σωματιδίων και κατευθύνεται από περιοχές μεγαύτερης συγκέντρωσης προς περιοχές μικρότερης συγκέντρωσης. Από την ατομιστική σκοπιά η διάχυση θεωρείται ότι οφείεται στους τυχαίους βηματισμούς των σωματιδίων. Γενικά, ο όρος διάχυση χρησιμοποιείται σε κάθε περίπτωση όπου αμβάνει χώρα τυχαίος βηματισμός ενός συνόου ατόμων. Το φαινόμενο της διάχυσης συχνά μεετάται με την βοήθεια του μοντέου των τυχαίων βηματισμών. Ο όρος τυχαίος βηματισμός (ή τυχαίος περίπατος) εισήχθη για πρώτη φορά από τον Karl Pearson το 905. Ο τυχαίος βηματισμός μικρών σωματιδίων αιωρούμενων σε αέριο ή υγρό ανακαύφθηκε από τον Robert Brown το 87. Η θεωρία της κίνησης Brown και της ατομιστικής διάχυσης αναπτύχθηκε αργότερα από τον Albert Einstein. Ένας τυχαίος περίπατος μπορεί να περιγραφεί ως η μαθηματική μοντεοποίηση μιας αηουχίας τυχαίων βημάτων. Για παράδειγμα, η διαδρομή ενός μορίου σε ένα υγρό ή ένα αέριο (κίνηση Brown), αποτεεί τυπικά συστήματα της φυσικής που μπορούν να μοντεοποιηθούν από έναν τυχαίο περίπατο. Έτσι οι τυχαίοι περίπατοι έχουν χρησιμοποιηθεί σε ποούς διαφορετικούς τομείς όπως η οικονομία, η χημεία, η βιοογία, η οικοογία, η ψυχοογία, και η επιστήμη των υποογιστών. Για να κατανοήσουμε καύτερα τα παραπάνω οι J. Tinarkli και H. Jensen μαζί με τον C. Tsallis μεέτησαν το μονοδιάστατο μοντέο RRW (Restricted Random Walker) [33]. Το μοντέο αυτό αποτεείται από έναν τυχαίο περιπατητή με μια απορροφητική συνοριακή συνθήκη στο σύνοο των ακεραίων {0,,, L}, όπου η πιθανότητα ο περιπατητής να κάνει ένα βήμα δίνεται από τον τύπο g(n)=(n/l) α. Η Master εξίσωση ύνει απευθείας το μοντέο αυτό αριθμητικά, με οποιαδήποτε ακρίβεια θέουμε. Μεετάμε το άθροισμα των θέσεων ενός περιπατητή μετά από Τ βήματα. Κάνοντας με μεγάη ακρίβεια τις αριθμητικές πράξεις καταήγουμε στο συμπέρασμα ότι το όριο της κατανομής αυτού του αθροίσματος για L και για συγκεκριμένα Τ και L, δεν συγκίνει στη συνήθη εκθετική συνάρτηση αά σε μια q- εκθετική. Η ακριβής μορφή της q-gaussian αμβάνεται για α=. Για α το όριο της 47
56 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων κατανομής του αθροίσματος των θέσεων δεν περιγράφεται ούτε από την εκθετική ούτε από την q-εκθετική συνάρτηση. Το α= είναι μια ειδική περίπτωση και σκοπός μας είναι να δείξουμε γιατί είναι τόσο σημαντική. Για την επίτευξη αυτού του στόχου μεετάμε την κατανομή της πρώτης φοράς που επιστρέφει στο ίδιο σημείο ο περιπατητής (το μοντέο RRW). Οι συγγραφείς του άρθρου [33] αρχικά ύνουν αναυτικά τη συνεχή Master εξίσωση για να βρουν αναυτικά την πιθανότητα ο περιπατητής να είναι στη θέση n μετά από χρόνο t. Κατόπιν χρησιμοποιώντας τη διακριτή μορφή της Master εξίσωσης προσδιορίζουν αντιστοίχως την αριθμητική ύση του προβήματος. Από την αναυτική ύση η οποία δίνεται σε όρους σειρών Bessel μπορούμε να αναγνωρίσουμε γιατί η τιμή α= είναι μοναδική. Επίσης, η αριθμητική ύση υποδηώνει ότι για α= η κατανομή επιστροφής δίνεται από μια q-εκθετική καθώς L, ενώ για α η κατανομή προσεγγίζει τις q-εκθετικές αά δεν είναι ακριβώς μια από αυτές. Αρχικά, θα παρουσιάσουμε την αναυτική ύση της συνεχούς Master εξίσωσης για το μοντέο RRW και έπειτα θα τη χρησιμοποιήσουμε για να δείξουμε την εξάρτηση των κατανομών από τη μεταβητή α. Επόμενο βήμα είναι να συγκρίνουμε την αναυτική ύση με την αριθμητική και τέος να δούμε πως οι q- συναρτήσεις σχετίζονται με τις μη B-G στατιστικές. 3. Το πρόβημα του τυχαίου περιπατητή μέσω του μοντέου RRW Θεωρούμε ένα μονοδιάστατο μοντέο στο οποίο ένας περιπατητής μετακινείται από τη θέση n s στην n s+, όπου οι θέσεις αυτές ανήκουν στο σύνοο των ακεραίων {0,,.L} και s είναι η διακριτή μεταβητή του χρόνου. Η κίνηση των βημάτων του περιπατητή δίνεται από τον ακόουθο τύπο: n s+ ns + με πιθανότητα g(n)/ = ns με πιθανότητα g(n)/ ns με πιθανότητα -g(n) (3.4) 48
57 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων όπου, α n gn ( ) =, α (0,) (3.5) L Σημειώνουμε ότι για τον κανονικό τυχαίο περιπατητή απαιτούμε g(n)= ώστε η πιθανότητα να μετακινηθεί δεξιά ή αριστερά είναι ίση με ½. Η Master εξίσωση για την κατανομή δίνεται από τον τύπο: Pn( n, s+ ) = Pn( n, s) + g( n ) Pn( n, s) + g( n+ ) Pn( n+, s) g( n) Pn( n, s). (3.6) Στο n=l υποθέτουμε ότι έχουμε μια «αντανακαστική» συνοριακή συνθήκη ενώ στο n=0 επιβάουμε μια «απορροφητική» συνοριακή συνθήκη. Η πιθανότητα επιστροφής επομένως του RRW στη θέση n=0 δίνεται από τον τύπο: P (0, s+ ) = P (0, s+ ) P (0, s). (3.7) RD n n 3. Η συνεχής μορφή της Master εξίσωσης για την κατανομή Στη παράγραφο αυτή, θα δείξουμε πώς φτάνουμε στη συνεχή μορφή της κατανομής της Master εξίσωσης. Για την επίτευξη του σκοπού αυτού, θέτουμε, x = L οπότε { 0,/, /,...} x= n x L L. Ομοίως, κιμακώνουμε τον χρόνο, t = / L ή t=s/l. Αυτό επιβεβαιώνει ότι η συνεχής προσέγγιση προέρχεται ακριβώς καθώς το L. Τέος, αντικαθιστούμε το g(n) με g(x) όπου g(x)= x α. 49
58 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων διάχυσης: Καθώς το L η Master εξίσωση παίρνει τη μορφή της Μ.Δ.Ε. της Pxt (,) α = [ x Pxt (, )] t L x (3.8) Η ύση για τη πιθανότητα P(x,t) δίνεται από τον τύπο για θετικά: Pxt (, ) = ΑP( x)exp( t) (3.9) 8L Υποθέτοντας ότι: α Q ( x) = x P ( x) (3.0) αντικαθιστούμε την (3.9) στην (3.8) και χρησιμοποιώντας τη σχέση (3.0) παίρνουμε: [ Α P ( x)exp( t)] = [ x Α P ( x)exp( t)] t L L x L α 8 8 AP( x) [exp( ) t] = A exp( ) t [ Q( x)] t 8L L 8L x AP( x)exp( ) t= A exp( ) t [ Q( x)] 8L 8L L 8L x P( x) = [ Q ( x)] 8L L x α x Q() x Pxt (,) 0 + =, α x 4x δηαδή, d ( ) ( ) 0 Q x + Q x =. (3.) α dx 4x Η γενική ύση της προκύπτουσας εξίσωσης δίνεται με τη βοήθεια των σειρών Bessel αφού είναι της μορφής: ''( ) + ( ) '( ) + { βγ + ( α νγ )} ( ) = 0 (3.) γ x y x a xy x x y x 50
59 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων όπως διαπιστώνουμε αν ποαπασιάσουμε τη διαφορική μας εξίσωση με το x : α x Q ( x) x Q ( x) 0 + = x 4 (3.3) Συγκρίνοντας τους συντεεστές της (3.) με της (3.3) προκύπτει ότι τα α=/, β=/(-α), γ=(-α)/ και ν=/(-α), με αποτέεσμα η ύση της (3.3) να γράφεται ως εξής: α/ α/ x x Q( x) =Α xj/( α) ( ) +Β xυ/( α) ( ). (3.4) α α όπου J /(-α) και Y /(-α) είναι συναρτήσεις Bessel πρώτου και δευτέρου είδους αντίστοιχα. Από τις συνοριακές συνθήκες έχουμε ότι για x=0 το P (x) είναι πεπερασμένο, Q (x=0)=0 και για x= έχουμε μια αντανακαστική συνοριακή συνθήκη, όπου το J για x= είναι μηδέν, J(x) x= =0. Προφανώς, όταν η / x[q (x)] x= =0 η συνθήκη ικανοποιείται. Η συνοριακή συνθήκη για x=0 συνεπάγεται ότι Β=0 ενώ για x= συνεπάγεται ότι το /(-α) είναι η μηδενική ρίζα της συνάρτησης Bessel τάξης {/(-α) -}. Έτσι, τα στην (3.9) παίρνουν διακριτές τιμές n = α j/( α ), n, n=,,3... (3.5) όπου j /(-α)-,n είναι η n-στη μηδενική ρίζα της συνάρτησης Bessel τάξης {/(-α)-}. Εφόσον βρήκαμε την Q (x) είμαστε σε θέση να υποογίσουμε την κατανομή P(x,t). Αντικαθιστώντας την Q (x) στην P(x,t), η κατανομή παίρνει τη μορφή: Q ( x) Pxt (, ) = A exp( t) = α x 8L α / A x x = A[ J/( α( )]exp( t) α = x α 8L α / J/( α) ( j/( α), nx ) ( α) j/( α), n = An exp( t). α / x 8L n= 5
60 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Άρα, α / J/( α) ( j/( α), nx ) ( α) j/( α), n Pxt (, ) = An exp( t). (3.6) α / x 8L n= Ωστόσο για την ειδική περίπτωση α= προκύπτει η πού απή μορφή: J( j0, n x) j0, n Pxt (, ) = An exp( t). (3.7) x 8L n= Η αρχική μας συνθήκη για το πρόβημα είναι ότι τη χρονική στιγμή t=0 όοι οι περιπατητές βρίσκονται στη θέση n=. Θα προσπαθήσουμε να βρούμε το συντεεστή A n για αυτή την αρχική συνθήκη που έχουμε υποθέσει. Για t=0 η κατανομή P(x,t) είναι: α / J/( α) ( j/( α), nx ) Px (,0) = An (3.8) α / x n= Εδώ παρουσιάζεται μια τροποποιημένη έκδοση των σειρών Bessel. Η (3.) είναι η εξίσωση Sturn-Liouville και έχει ως αποτέεσμα οι ιδιοσυναρτήσεις να είναι ορθογώνιες. Επομένως, αν τα a και b είναι διάφορα του μηδενός στη συνάρτηση Bessel βαθμού ν- τότε Jν( α x) Jν( bx) xdx = 0 (3.9) Αν α b τότε η ύση αυτού του οοκηρώματος είναι J ν (α)/. Έτσι, δ mn, J( 0 ν jν, mxj ) ν( jν, nxxdx ) = [ Jν ( jν, m)] (3.0) όπου δm,n=0 για m n και δn,n=. Χρησιμοποιώντας το αποτέεσμα αυτό καταήγουμε, αντιστρέφοντας τη σχέση (3.0), στο ακόουθο αποτέεσμα: A n j = ( ). (3.) J j L ( α / ) /( α ), n J /( α ) α / /( )( /( ), n) L α α 5
61 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Για την ειδική περίπτωση α= έχουμε: A n j0, n = J( ). (3.) J ( j ) L L 0, n Το μόνο που απομένει είναι να μεετήσουμε την ασυμπτωτική συμπεριφορά για μεγάα t. Χρησιμοποιώντας την ασυμπτωτική έκφραση για το J ν (z) καθώς το n, το A n ασυμπτωτικά είναι ίσο με j α /4 /( α ), n π π An π j/( α ), n( α / ) L cos( ). (3.3) α / L ( α) 4 Από τα παραπάνω συνεπάγεται ότι όσο το πηίκο t/l δεν είναι μικρό, οι όροι υψηότερης τάξης στην (3.8) μπορούν να αγνοηθούν και η κατανομή P(x,t) μπορεί να μειώνεται εκθετικά για t>l ή σε όρους του διακριτού μεταβητού χρόνου βήματος s>l. 3.3 Η αναυτική ύση για την πιθανότητα επιστροφής P R (0,t) Αφού η συνοριακή συνθήκη για x=0 είναι απορροφητική, η πιθανότητα ο περιπατητής να επιστρέψει πρώτη φορά στο σημείο x=/l δίνεται από τη σχέση: α J(,) xt = [ x Pxt (,)] L x και η τεική κατανομή γράφεται: j ( α) j PR(0, t) = AJ ( )exp( t) (3.4) L /( α), n /( α), n /( ) / n n α = L α 8L 53
62 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Σχήμα : Σύγκριση της διακριτής ύσης της Master εξίσωσης (3.6) με την συνεχή ύση, (3.4), για την κατανομή του χρόνου της πρώτης επιστροφής όπου (a) α=0.75; (b) α= και; (c) α=.5. 54
63 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Στο παραπάνω γράφημα σύμφωνα με το άρθρο [33] παρατηρούμε τη σύγκριση της ακριβούς αναυτικής ύσης της Master εξίσωσης της (3.6) με την αναυτική ύση της (3.4). Ο αριθμός N=000 (των όρων) είναι ικανοποιητικός ώστε η γραφική παράσταση της αναυτικής ύσης να είναι αποδεκτή, έχοντας ακρίβεια μικρότερη από το πάτος της απεικόνισης του γραφήματος. Δυστυχώς δεν είναι δυνατόν να συμπτύξουμε τους όρους της (3.4) σε μια πιο απή έκφραση. Συγκεκριμένα, είναι αδύνατον να συσχετίσουμε αναυτικά την κατανομή P R (0,t) με τις q-εκθετικές μορφές της (3.). Εφόσον, οι συναρτήσεις Bessel στις σειρές για την κατανομή P R (0,t) είναι ομαές συναρτήσεις τάξεως /(-α) και /[(-α)-], δεν θα περίμενε κανείς ότι θα μπορούσαν να περιγραφούν με όρους q- εκθετικών συναρτήσεων για τις διάφορες τιμές του εκθέτη α στην (3.3). 3.4 Αριθμητική επίυση του διακριτού περιπατητή χρησιμοποιώντας τις q-εκθετικές Στον ακόουθο πίνακα παρατηρούμε τα αριθμητικά αποτεέσματα για την κατανομή του χρόνου επιστροφής στο σημείο μηδέν του περιπατητή της εξίσωσης (3.6), τα οποία προκύπτουν με αριθμητική επίυση της διακριτής Master εξίσωσης, (3.7). Τα αποτεέσματα αυτά φαίνονται παρακάτω με ακρίβεια: Πίνακας : Οι κατανομές P RD (0,s) κανονικοποιημένες για διάφορες τιμές του βήματος L με α=. 55
64 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Στον παραπάνω πίνακα [33] θυμίζουμε ότι το L=ts και η κανονικοποιήση αναφέρεται στην κατανομή P RD (0,s). Χρησιμοποιώντας τον ορισμό των q-εκθετικών στην (3.) μπορεί κάποιος να εκφράσει την κανονικοποιημένη κατανομή της πρώτης επιστροφής ως: P (0, s) = P (0,0) exp ( β s) = P (0,0)[ + ( q ) β s] (3.5) RD RD q q + RD q q όπου β q είναι η μόνη εεύθερη παράμετρος αφού η τιμή της q μπορεί να ηφθεί από την ασυμπτωτική συμπεριφορά της κίσης, η οποία είναι ίση με /(-q). Η σύγκριση μεταξύ των διακριτών και αναυτικών αποτεεσμάτων της (3.6) και των q-εκθετικών της (3.5) δίνεται στο επόμενο Σχήμα. 56
65 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Σχήμα : Σύγκριση της διακριτής ύσης Master εξίσωσης και των q-εκθετικών συναρτήσεων για κανονικοποιημένες κατανομές του χρόνου της πρώτης επιστροφής για (a) α=0.75; (b) α=; και (c) α=.5. Επειδή στην αριθμητική μεέτη ο χρόνος είναι πεπερασμένος, η κανονικοποίηση της κατανομής μπορεί να μην είναι ακριβής, δεδομένου ότι για μεγάους χρόνους χάνονται κάποιες κατανομές επιστροφής. Έτσι εέγχουμε το βαθμό στον οποίο ικανοποιείται η κανονικοποίηση για τους χρόνους επιστροφής που είμαστε ικανοί να χειριστούμε. Μπορούμε να τα αντιηφθούμε καύτερα τα παραπάνω κάνοντας ένα επιπέον βήμα. Ορίζουμε μια ποσότητα Δ, η οποία δηώνει την απόυτη διαφορά μεταξύ του ακριβούς διακριτού αποτεέσματος και μιας q-εκθετικής συνάρτησης. Γνωρίζουμε ότι για πεπερασμένο L η κατανομή του χρόνου επιστροφής τέμνει την εκθετική για χρόνο μεγαύτερο από L. Αυτό σημαίνει ότι η μορφή μιας q-εκθετικής θα ισχύει για όους τους χρόνους καθώς το L. Αν η κατανομή είναι ακριβώς η q- εκθετική τότε το Δ πησιάζει το μηδέν καθώς το σύστημα τείνει στο άπειρο. 57
66 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων Σχήμα 3: Η ποσότητα Δ ως συνάρτηση αποκίσεων του συστήματος. Σχεδιάζουμε στο Σχήμα 3 την παραπάνω ποσότητα ως συνάρτηση ενός συστήματος για α= και για δύο πού μικρές απομακρύνσεις από αυτή την περίπτωση. Σημειώνουμε ότι για α= το όριο L είναι ίδια με την q-εκθετική. Για α παίρνουμε μια μικρή ποσότητα lim L Δ>0 με αποτέεσμα η κατανομή του χρόνου επιστροφής να μην είναι ίση με την q-εκθετική. 3.5 Συμπεράσματα Μεετήθηκε αναυτικά και αριθμητικά ένας απός τυχαίος περίπατος με θέση που εξαρτάται από το ρυθμό μετάβασης, με στόχο την κατανόηση των ερωτημάτων, πότε και γιατί οι μορφές των q-συναρτησιακών κατανομών περιγράφουν στατιστικές ιδιότητες μη συμβατών συστημάτων, εστιάζοντας στην πρώτη κατανομή του χρόνου επιστροφής του περιπατητή. Από την αναυτική ύση απεδείχθη ότι οι κατανομές επιστροφής είναι ομαά εξαρτώμενες από την παράμετρο α η οποία καθορίζει τις πιθανότητες επιστροφής του RRW μοντέου. Επειδή ήταν αδύνατο να βρεθεί αναυτικά η σχέση μεταξύ της 58
67 Κεφάαιο 3: Γενικότερες Εφαρμογές των q-συναρτήσεων κατανομής του χρόνου επιστροφής με την q-εκθετική, βρέθηκε αριθμητικά ότι η q- εκθετική ταιριάζει ακριβώς με την αριθμητική ύση. Για την ειδική περίπτωση όπου α= η αριθμητική ανάυση δείχνει ότι η κατανομή επιστροφής είναι ίση με την q- εκθετική με q=3/, όταν ο βαθμός του συστήματος αμβάνεται από το άπειρο. Μπορεί κάποιος να εντοπίσει αρκετούς όγους που κάνουν το α= ειδικό. Ο μέσος όρος επιστροφής μπορεί να υποογιστεί άμεσα χωρίς να είναι γνωστή η κατανομή οόκηρου του χρόνου επιστροφής. Ο μέσος όρος του αριθμού βημάτων του διακριτού χρόνου για την πρώτη επιστροφή από τη θέση n= στη n=0 εκφράζεται από τον τύπο, L/ ( a) για 0<α< sr = Lln L για α= a L / ( a ) για <α< Από το μέσο όρο συμπεραίνουμε ότι για α=έχουμε μια οριακή τιμή. Οι q-εκθετικές συναρτήσεις που αμβάνονται για την τιμή α= με q=3/ αντιστοιχούν σε μια πού απή συναρτησιακή μορφή f(x)=α/(+x). Με βάση αυτές τις παρατηρήσεις είναι δύσκοο να αποφασίσει κανείς κατά πόσον η επιτυχία της προσέγγισης από q-εκθετικές συναρτήσεις προκαείται από κάποια θεμειώδη βασική αρχή ή είναι τυχαίας προέευσης. 59
68 ΚΕΦΑΛΑΙΟ 4 Εφαρμογές q-συναρτήσεων σε προβήματα σεισμοογίας Ο φοιός της γης μπορεί να θεωρηθεί ως ένα πούποκο δυναμικό σύστημα οι αηεπιδράσεις του οποίου εκτείνονται σ ένα ευρύ φάσμα του χώρου και παράγουν σεισμούς, όγω της σχετικής κίνησης των τεκτονικών πακών. Ο χρόνος, η τοποθεσία, η επικεντρική απόσταση (απόσταση από το ρήγμα) και το μέγεθος των σεισμικών γεγονότων καταγράφονται σε βάσεις δεδομένων. Τα δεδομένα αυτά είναι εύκοα προσβάσιμα για να μπορεί κάποιος να τα επεξεργαστεί και να εξαγάγει χρήσιμα συμπεράσματα για τη σεισμικότητα μιας περιοχής. Η κατανόηση του μηχανισμού δημιουργίας ενός σεισμού εξακοουθεί να παραμένει ένας από τους κύριους στόχους των γεωφυσικών επιστημών. Παρά την πουποκότητα που προκύπτει μέσα από την ανάυση των σεισμικών δεδομένων, παρατηρείται συσχέτιση μεταξύ κάποιων χαρακτηριστικών του σεισμού (π.χ. συχνότητα μέγεθος) που υποδεικνύει κάποιου είδους αυτό-ομοιότητας στα δεδομένα των παρατηρήσεων. Για το όγο αυτό, κάποια χαρακτηριστικά των σεισμών μπορούν να περιγραφούν από απές εμπειρικές σχέσεις όπως των Guterberg-Richter [4], που περιγράφει τη σχέση μεταξύ της συχνότητας εμφάνισης του σεισμού και του μεγέθους αυτού, καθώς και του Omori [0], που σχετίζεται με τη χρονική κατανομή των σεισμών. Στο παρόν κεφάαιο αναπτύσσουμε το περιεχόμενο μιας εργασίας [3] στην οποία διερευνάται η σεισμική δραστηριότητα από το 976 έως το 009 στην περιοχή της Εάδος, αμβάνοντας υπόψη τα μεγαύτερα μεγέθη σεισμών που συνέβησαν κατά τη διάρκεια αυτής της περιόδου. Η Εάδα βρίσκεται στο σύνορο δύο 60
69 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας τεκτονικών πακών, της Ευρασιατικής και της Αφρικανικής με αποτέεσμα η περιοχή να είναι εντόνως σεισμογενής. Το 75% των εηνικών σεισμών αμβάνουν χώρα είτε κάτω από τη θάασσα μακριά από κατοικημένες περιοχές είτε σε βάθος ποών χιιομέτρων με μειωμένη επικινδυνότητα. Έτσι, οι σεισμικοί κατάογοι ή οι βάσεις δεδομένων που είναι σχετικά ακριβείς και πήρεις είναι χρήσιμοι για μια εμπεριστατωμένη αξιοόγηση του σεισμικού κινδύνου μια περιοχής. Στους σεισμούς αυτούς έχει δειχθεί σε μια σειρά πρόσφατων δημοσιεύσεων ότι αξίζει να χρησιμοποιήσουμε μη-εκτατικές φυσικές στατιστικές (NESP) για την κατανόηση τους. Οι NESP περιγράφουν μεγάα συστήματα και δεν εξαρτώνται από τον αριθμό των μορίων (ενέργεια και όγκος). Τις χρησιμοποιούμε για να μεετήσουμε την κατανομή συχνότητας πιθανότητας του μεγέθους και την κατανομή του χρόνου μεταξύ των σεισμικών γεγονότων. Οι NESP προτάθηκαν από τον Tsallis [9], σκοπός του οποίου ήταν να προτείνει μια μη-προσθετική γενίκευση της κασικής εντροπίας S BG της Boltzmann Gibbs θερμοδυναμικής. Με τον όρο μη προσθετική εννοούμε ότι το σύστημα δεν μπορεί να θεωρηθεί ως άθροισμα ανεξάρτητων υποσυστημάτων, για παράδειγμα η συνοική ενέργεια (του όγκου ή του αριθμού των μορίων) δεν είναι άθροισμα των ενεργειών των επιμέρους συστημάτων. Οι NESP έχουν εφαρμοστεί με επιτυχία σε ένα ευρύ φάσμα μη γραμμικών φυσικών, κοινωνικών και τεχνητών συστημάτων όπου η μεγάης εμβέειας σχέσεις οδηγούν σε ένα νόμο δύναμης ασυμπτωτικής συμπεριφοράς των στατιστικών κατανομών της. Έτσι, στη ενότητα αυτή, αρχικά μεετάται η κατανομή της συχνότητας μεγέθους της σεισμικότητας στην Εάδα. Για τη μεέτη αυτή, όμως χρησιμοποιείται ένα μοντέο σύμφωνα με το οποίο η ενέργεια που απεευθερώνεται από το ρήγμα είναι ανάογη του όγκου των θραυσμάτων τα οποία γεμίζουν το χώρο ανάμεσα στα επίπεδα του ρήγματος. Το μοντέο αυτό εφαρμόστηκε πρόσφατα σε διάφορα τοπικά και περιφερειακά σεισμικά δεδομένα άων χωρών και με βάση τα αποτεέσματα προέκυψε ότι μπορεί να εφαρμοστεί και στην περιοχή της Εάδας. Στη συνέχεια, μεετάται η κατανομή των χρόνων P Μ (T) μεταξύ των σεισμικών γεγονότων για διάφορα μεγέθη M και προκύπτει ότι σε όες τις περιπτώσεις μπορεί να προσεγγιστεί από μια q-εκθετική συνάρτηση γνωστή από τις NESP. Το αποτέεσμα αυτό δίνει τη δυνατότητα να εκτιμηθεί αναυτικά η συνάρτηση επικινδυνότητας W M (T,ΔΤ), η οποία ορίζεται ως η πιθανότητα 6
70 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας τουάχιστον ένας σεισμός με μέγεθος μεγαύτερο του Μ να συμβεί στο επόμενο χρονικό διάστημα Δt εάν ο τεευταίος σεισμός συνέβη t ημέρες πριν. 4. Ανάυση της Εηνικής σεισμικής δραστηριότητας Στην εργασία [3] χρησιμοποιείται μια πρόσφατη βάση σεισμικών δεδομένων σύμφωνα με το άρθρο [6] και περιαμβάνει σεισμικά γεγονότα που έαβαν χώρα σε όη την Εάδα από το 90 μέχρι το 009. Πιο συγκεκριμένα, οι σεισμικές καταγραφές αφορούν επιφανειακούς σεισμούς δηαδή εστιακού βάθους μικρότερου των 40km και περιοχές με γεωγραφικά πάτη από 34 ο N έως4 ο N και γεωγραφικά μήκη από 9 ο E έως 9 ο E. Προκύπτουν 353 δεδομένα έχοντας θεωρήσει ως κατώτατο όριο μεγέθους του σεισμού το M c =4.. Έπειτα, χρησιμοποιώντας τη εγόμενη window method [], δημιουργήθηκε ένα σύνοο δεδομένων μόνο με τους κύριους σεισμούς, δηαδή εξαιρέθηκαν οι μετασεισμοί. Το σύνοο αυτό περιαμβάνει 53 σεισμικά γεγονότα, μεγέθους Μ Μ c και ανώτατο όριο μεγέθους το 6.9. Επίσης, αφού δεν περιέχονται οι μετασεισμοί, προκύπτει η δυνατότητα να μεετηθεί πιο εύκοα η συνάρτηση πιθανότητας του χρόνου μεταξύ των σεισμικών γεγονότων καθώς και η συνάρτηση επικινδυνότητας. Τα αποτεέσματα από την ανάυση του παραπάνω συνόου (χωρίς τους μετασεισμούς), μπορούν να συγκριθούν με την αντίστοιχη ανάυση του συνόου που περιαμβάνει τους μετασεισμούς, για να δούμε πώς δημιουργούνται οι μετασεισμοί και πώς μπορούν να επηρεάσουν την κατανομή του χρόνου μεταξύ των σεισμικών γεγονότων, την εκτιμώμενη συνάρτηση επικινδυνότητας και τη σχέση μεταξύ του δείκτη q [β. (4.5)], του μεγέθους Μ και της μέσης τιμής R M των κατανομών του χρόνου μεταξύ των σεισμικών γεγονότων. 4.. Ανάυση της κατανομής συχνότητας-μεγέθους της σεισμικότητας Το 004 οι Sotolongo Costa και Posadas ανέπτυξαν ένα φυσικό μοντέο για το μηχανισμό δημιουργίας ενός σεισμού. Σε αυτό το μοντέο, η τοπική σύγκρουση 6
71 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας και η μετατόπιση των θραυσμάτων ανάμεσα στα επίπεδα ρήγματος είναι βασικές αιτίες απεευθέρωσης ενέργειας του σεισμού. Επομένως, η ενέργεια που απεευθερώνεται μπορεί να θεωρηθεί ανάογη του όγκου των θραυσμάτων και η συνάρτηση κατανομής ενέργειας αντιστοιχεί σε όρους της κατανομής μεγέθους των θραυσμάτων. Οι συγγραφείς έαβαν υπόψη την αηεπίδραση των θραυσμάτων και θεώρησαν ότι είναι συμβατή με το μοντέο που ανέπτυξαν στα παίσια των NESP [3]. Αν θεωρηθεί ότι το μέγεθος της επιφάνειας ενός θραύσματος είναι σ και η αντίστοιχη πιθανότητα p(σ), τότε η εντροπία S q του Tsallis εκφράζεται ως : S q q p ( σ) dσ = k, (4.) q όπου k είναι η σταθερά του Boltzmann και το q είναι ο δείκτης εντροπίας. Θέτοντας k=και εφαρμόζοντας κατάηους περιορισμούς προκύπτει η πιθανότητα p(σ). Σχήμα : Κανονικοποιημένη αθροιστική κατανομή μεγέθους: (a) για το σύνοο σεισμών που περιέχει και τους μετασεισμούς (κουκκίδες) και πρόβεψη από το μοντέο της εξίσωσης (4.4) (q M =.443±0.08, a = ± ); (b) για το σύνοο σεισμών χωρίς τους μετασεισμούς (κουκκίδες) και πρόβεψη από το μοντέο της (4.4) (q M =.46±0.08, a = ± ). [3] Η συνάρτηση κατανομής μεγέθους του θραύσματος δίνεται ως: q P( σ) = [ ( )( σ σq )] q q. (4.) Υποθέτοντας τώρα, ότι η απεευθέρωση της ενέργειας Ε είναι ανάογη των θραυσμάτων Ε~r 3 [9] και η σχέση της ενέργειας Ε με το μέγεθος Μ είναι 63
72 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας Μ=/3[log(E)], οοκηρώνοντας την (4.) προκύπτει η αθροιστική κατανομή, με τύπο: M N( > M) q 0 = [ ( )( )] /3 N q a q q. (4.3) Η παραπάνω εξίσωση περιγράφει την αθροιστική κατανομή Ν σεισμών με μέγεθος Μ Μ c μεγαύτερο δηαδή από το κατώτατο όριο που έχει τεθεί για τη σεισμική περιοχή της Εάδας, συμβοικά Ν(>Μ). Λαμβάνοντας υπόψη το εάχιστο μέγεθος Μ 0 του σεισμικού καταόγου, όπου στη συγκεκριμένη περίπτωση ισχύει Μ 0 =Μ c, η (4.3) μετατρέπεται στην ακόουθη: N M q q a { } M /3 ( > ) [( ) / ( )](0 / ) = M0 /3 N [( q) / ( q)](0 / a ) q q. (4.4) Το παραπάνω μοντέο εφαρμόζεται σε μεγέθη σεισμών που καταγράφηκαν στον εαδικό χώρο. Αρχικά, έγινε ανάυση στο σύνοο των δεδομένων που περιείχε όους τους σεισμούς και έπειτα στο σύνοο χωρίς τους μετασεισμούς. Για οόκηρο το σύνοο δεδομένων, το μοντέο περιγράφει αρκετά καά την κατανομή μεγέθους ενός σεισμού που απεικονίζεται στο Σχ.(a) για τις τιμές q M =.443±0.08 και a = ± και αντιστοίχως για το σύνοο χωρίς τους μετασεισμούς στο Σχ.(b) για τις τιμές q M =.46±0.08 και a = ± Και στις δύο περιπτώσεις οι τιμές του q και α παρατηρείται ότι είναι αρκετά κοντά. Το συμπέρασμα οιπόν, που προκύπτει είναι ότι οι μετασεισμοί δεν μεταβάουν σημαντικά την αθροιστική κατανομή συχνότητας του μεγέθους στην περιοχή της Εάδας για την περίοδο μεταξύ του Ανάυση της κατανομής του χρόνου μεταξύ των σεισμικών γεγονότων Η χρονική εξέιξη των σεισμικών γεγονότων σε μια γεωγραφική περιοχή χαρακτηρίζεται από ένα σύνοο διακριτών χρόνων Τ i μεταξύ των σεισμικών γεγονότων για i=,,n. Για κάθε μέγεθος Μ Μ c μεετάται η συνάρτηση κατανομής 64
73 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας μεγέθους P M (T) του αντίστοιχου χρόνου T μεταξύ των σεισμικών γεγονότων. Δεδομένου ότι έχουμε ένα πεπερασμένο και διακριτό αριθμό καταγεγραμμένων σεισμικών γεγονότων και μεγεθών, υποογίζεται αριθμητικά η μέση τιμή R M των αντίστοιχων χρόνων T μεταξύ των σεισμικών γεγονότων, δηαδή βρίσκουμε την πιθανότητα κατανομής P M (T) για κάθε χρόνο ξεχωριστά και έπειτα παίρνουμε το μέσο όρο αυτών. Θεωρούμε ότι τα μεγέθη των σεισμικών γεγονότων κυμαίνονται μεταξύ του Μ και του 6.9, το οποίο είναι το ανώτατο όριο μεγέθους και για τα δύο σύνοα που αναύονται. Ο αριθμός των δεδομένων είναι αρκετά ικανοποιητικός ώστε να εξαχθούν αξιόπιστα στατιστικά στοιχεία για τον υποογισμό της κατανομής μεγέθους P M (T). Σχήμα :(a) Η κατανομή μεγέθους P M (T) με το χρόνο T (σε ημέρες) των συμβάντων, για σεισμούς μεγέθους Μ Μ c για το σύνοο σεισμών που περιέχει τους μετασεισμούς, και η πρόβεψη της (4.5) για q r =.4±0.054 (διακεκομμένη καμπύη); (b) Αντίστοιχη κατανομή P M (T) για το σύνοο των κύριων σεισμών και πρόβεψη της (4.5) για q r =.4± [3] της μορφής: Η συνάρτηση κατανομής μεγέθους P M (T) προσεγγίζεται από μια συνάρτηση P ( T) = M A [ + ( q ) βt] q (4.5) όπου Α είναι μια σταθερά και παράμετροι β, q εξαρτώνται από την σταθερή μέση τιμή R M των χρόνων μεταξύ των σεισμικών γεγονότων. Η μορφή αυτή της κατανομής μεγέθους P M (T) για q> δείχνει ότι η κατανομή του χρόνου μεταξύ των σεισμικών γεγονότων μειώνεται με πιο αργό ρυθμό από την εκθετική απομείωση (long-range 65
74 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας dependence). Ο παραπάνω τύπος της εξίσωσης (4.5) έχει τη μορφή μιας γενικευμένης κατανομής Pareto (κατανομή νόμου δύναμης), η οποία συχνά ονομάζεται q-εκθετική κατανομή. Η q-εκθετική κατανομή προέρχεται από μεγιστοποίηση της εντροπίας S q του Tsallis και περιγράφει επιτυχώς την κατανομή του χρόνου μεταξύ των σεισμικών γεγονότων. Σε περίπτωση που αντικαταστήσουμε το Τ με Τ στον παρονομαστή της (4.5), η εξίσωση η οποία προκύπτει είναι μια q-gaussian συνάρτηση πιθανότητας κατανομής, γνωστή από τη μη-εκτατική στατιστική μηχανική. Στο Σχ. (a) απεικονίζεται η γραφική παράσταση της συνάρτησης κατανομής μεγέθους P M (T), των χρόνων μεταξύ των σεισμικών γεγονότων με το χρόνο Τ (εκφρασμένο σε ημέρες). Το γράφημα αυτό προκύπτει για το σύνοο δεδομένων που περιέχει και τους μετασεισμούς για μεγέθη Μ Μ c. Η διακεκομμένη καμπύη είναι η αριθμητική προσέγγιση για τα σεισμικά δεδομένα από την q-εκθετική συνάρτηση της (4.5) χρησιμοποιώντας την τιμή q r =.4± Στο Σχ. (b) βέπουμε το αντίστοιχο γράφημα της κατανομής P M (T) με το χρόνο T για ίδιες τιμές μεγέθους με το Σχ. (a) αά για το σύνοο δεδομένων χωρίς τους μετασεισμούς. Η q-εκθετική της (4.5) προσεγγίζει τα δεδομένα για q r =.4±0.057, (όπου q r< q r ). Από τη σύγκριση των δύο γραφημάτων προκύπτει ότι στην περίπτωση όπου συμπεριαμβάνονται οι μετασεισμοί, αυξάνεται η τιμή της μεταβητής q στην κατανομή του χρόνου των σεισμικών γεγονότων. Πιθανότατα αυτό συμβαίνει εξαιτίας των επιδράσεων ομαδοποίησης που παρατηρήθηκαν στις ακοουθίες των μετασεισμών που οδηγούν σε μεγαύτερες αποκίσεις από τα αντίστοιχα αποτεέσματα της απής εκθετικής συνάρτησης (4.5) στην οριακή περίπτωση q. Από τα παραπάνω προκύπτει ότι ο δείκτης q στην (4.5) αμβάνει τιμές μεγαύτερες από q= της απής εκθετικής κατανομής e -βt στην περίπτωση που το σύνοο δεδομένων αποτεείται από τους κύριους σεισμούς και μετασεισμούς. Με βάση αυτό, το συμπέρασμα που προκύπτει είναι ότι οι κύριοι σεισμοί μαζί με τις μετασεισμικές δονήσεις είναι μεταξύ τους αρκετά χρονικά εξαρτώμενοι και επομένως, δεν είναι δυνατό να προσεγγιστούν από τις απές εκθετικές στατιστικές, που οδηγούν σε χαοτική συμπεριφορά καθώς το q. 66
75 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας 4. Συνάρτηση επικινδυνότητας και δυνατότητες πρόβεψης Έχοντας μια αναυτική έκφραση για την κατανομή μεγέθους P M (T) του χρόνου T μπορεί να μεετηθεί η συνάρτηση επικινδυνότητας W M (T,ΔΤ). Η συνάρτηση αυτή ορίζεται ως η πιθανότητα τουάχιστον ένας σεισμός με μέγεθος μεγαύτερο από Μ c να συμβεί στο επόμενο χρονικό διάστημα ΔT εάν ο τεευταίος σεισμός συνέβη T ημέρες πριν. Πιο συγκεκριμένα, τα W M και P M συνδέονται με την ακόουθη έκφραση: W ( T, T) M T+ T T = T PM () t dt. (4.6) P () t dt M Αντικαθιστώντας την κατανομή P M (Τ) της (4.5) στην (4.6) και οοκηρώνοντας οδηγούμαστε στην ακόουθη εξίσωση: q q β ( q ) T WM ( T, T) = [ + ]. (4.7) + β ( q ) T Για εκθετικά φθίνουσες κατανομές P M (Τ), η συνάρτηση επικινδυνότητας είναι W M (T,ΔT)=-e -βδt και είναι ανεξάρτητη του χρόνου T ενώ για τις συναρτήσεις κατανομής πιθανότητας που φθίνουν με νόμο δύναμης ισχύει W M (T,ΔT) ΔT/T όπου ΔΤ<<Τ. Σχήμα 3: Συνάρτηση επικινδυνότητας W M (T,ΔT) με το χρόνο T (σε ημέρες) για Μ Μ c, για τέσσερις διαφορετικές τιμές του ΔΤ: a) για το σύνοο με τους μετασεισμούς και παραμέτρους β, q ίδιες με αυτές του Σχ.(a); (b) για το σύνοο χωρίς τους μετασεισμούς και παραμέτρους β, q ίδιες με αυτές του Σχ.(b). [3] 67
76 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας Στο Σχ.3 απεικονίζεται η συνάρτηση επικινδυνότητας W M (T,ΔT) της (4.7) για τέσσερα διαφορετικά χρονικά διαστήματα ΔΤ για τα δύο σύνοα δεδομένων που αναύονται. Σε κάθε σύνοο δεδομένων χρησιμοποιούνται οι αντίστοιχες τιμές β,q, Μ που θεωρούνται και στο Σχ.. Είναι προφανές, ότι και για τα δύο σύνοα δεδομένων και για ένα σταθερό διάστημα ΔΤ η πιθανότητα τουάχιστον ένας σεισμός με μέγεθος Μ Μ c να συμβεί στο επόμενο χρονικό διάστημα ΔΤ (εάν ο τεευταίος σεισμός συνέβη Τ ημέρες πριν) μειώνεται καθώς το Τ αυξάνεται. Εάν αυξηθεί το ΔΤ, η πιθανότητα της συνάρτησης επικινδυνότητας W M (T,ΔT) αυξάνεται. Η καμπύη της συνάρτησης επικινδυνότητας αποτεείται από δύο τμήματα, το αριστερό τμήμα το οποίο αντιστοιχεί σε εκθετική μείωση της πιθανότητας W M (T,ΔT) και το δεξί τμήμα που φθίνει με νόμο δύναμης. Βάσει των παραπάνω, προκύπτει μια συναρτησιακή σχέση μεταξύ των R M και M, ξεχωριστά για τα δύο σύνοα. Το ενδιαφέρον των ερευνητών επικεντρώνεται στη σχέση αυτή διότι οποιαδήποτε συσχέτιση του q με το Μ ή/και του q με το R M δίνει μεγάη απόκιση από τα δεδομένα και επομένως, δεν θα παρείχε ασφαείς προβέψεις. Έτσι, η σχέση μεταξύ των R M και M και για τα δύο σύνοα δεδομένων είναι ιδιαίτερα χρήσιμη καθώς μπορεί να ειτουργήσει ως προγνωστικός παράγοντας μιας μέσης τιμής του χρόνου εμφάνισης ενός σεισμικού γεγονότος με μέγεθος Μ Μ c στην Εάδα. Στο Σχ. 4 απεικονίζονται οι γραφικές παραστάσεις μεταξύ των q και Μ, των qκαι R M και των R M και Μ, για το σύνοο που περιαμβάνει τους κύριους σεισμούς και τους μετασεισμούς καθώς και οι αντίστοιχες γραφικές παραστάσεις για το σύνοο χωρίς τους μετασεισμούς. Από τα γραφήματα (d) και (e), δηαδή για το σύνοο χωρίς τους μετασεισμούς, προκύπτει ότι το q παραμένει σχεδόν σταθερό με τη μεταβοή των R M και Μ, ενώ στην περίπτωση του συνόου με τους μετασεισμούς (a) και (b), το q μειώνεται, τείνοντας στη μονάδα, καθώς αυξάνεται το Μ και το R M. Από τα δεδομένα του Σχ. 4(c)-(f) και τη χρήση ογαριθμικού κατακόρυφου άξονα και για τα δύο σύνοα που μεετώνται προκύπτει η ακόουθη πιθανή σχέση μεταξύ R M και Μ: log( R ) = log( a) + bm (4.8) M Για το σύνοο χωρίς τους μετασεισμούς στο Σχ. 4(c) οι τιμές των α και b είναι α= ±. 0-4 και b=.38±0. ενώ οι αντίστοιχες τιμές για το σύνοο με 68
77 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας τους μετασεισμούς είναι α= ± και b=.5±0.4. Παρατηρούμε ότι οι τιμές για το b και των δύο συνόων είναι περίπου ίδιες, γεγονός που σημαίνει ότι το R M αυξάνεται μονότονα καθώς αυξάνεται τοm. Εξισώσεις όπως η (4.8) μπορούν να αποτεέσουν προγνωστικό παράγοντα μιας μέσης τιμής του χρόνου εμφάνισης ενός σεισμικού συμβάντος μεγέθους Μ 4.στην Εάδα. Σχήμα 4:(a) Γραφική απεικόνιση του q με το M για μεγέθη σεισμών Μ Μ c για το σύνοο με τους μετασεισμούς; (b) Απεικόνιση του q με το R M ; (c) Απεικόνιση του R M με το M; (d),(e) και (f) Αντίστοιχα των (a),(b) και (c) για το σύνοο σεισμών χωρίς τους μετασεισμούς. Για τα (a),(b),(d) και (e) με διακεκομμένες γραμμές απεικονίζονται οι γραμμικές προσεγγίσεις των δεδομένων ενώ στα σχήματα (c) και (f) τα δεδομένα προσεγγίζονται από την (4.8) (ο κατακόρυφος άξονας είναι ογαριθμικός). [3] Επομένως, για το σύνοο με τους μετασεισμούς, προκύπτει ότι καθώς αυξάνεται το μέγεθος Μ του σεισμού αά και η μέση τιμή R M του χρόνου του σεισμού, το q μεταβάεται από τιμές μεγαύτερες του και σταδιακά πησιάζει το της απής κατανομής. Αυτό σημαίνει ότι η δημιουργία ενός σεισμικού συμβάντος παρουσιάζει έντονη χαοτική συμπεριφορά. Αντιθέτως, για το σύνοο σεισμών που έχουν εξαιρεθεί οι μετασεισμοί, το q αμβάνει τιμές πού κοντά στο. Τα παραπάνω υποδεικνύουν ότι οι μετασεισμικές δονήσεις προσθέτουν ντετερμινισμό στην χαοτική συμπεριφορά του φαινομένου, ενώ αν αφαιρεθούν η κατανομή των κυρίως σεισμών φαίνεται ότι είναι «τυχαία». 69
78 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας 4.3 Συμπεράσματα Σε αυτό το κεφάαιο, μεετήθηκε η σεισμικότητα της Εάδας χρησιμοποιώντας έννοιες από τις μη-εκτατικές φυσικές στατιστικές και εφαρμόζοντάς τις στο σύνοο δεδομένων που αναφέρεται στο άρθρο [6]. Χρησιμοποιήθηκαν δύο σύνοα σεισμών, το πρώτο περιείχε κύριους σεισμούς και μετασεισμούς και το δεύτερο περιείχε μόνο τους κύριους σεισμούς. Η χρονική περίοδος μεέτης των δεδομένων ήταν από το 976 έως το 009 και ήφθηκαν υπόψη μόνο σεισμοί με μέγεθος Μ 4.. Αρχικά, έγινε διερεύνηση της κατανομής συχνότητας του μεγέθους του σεισμού και για τα δύο σύνοα και μετά από σύγκριση προέκυψε ότι μπορούν να προσεγγιστούν αρκετά καά από ένα φυσικό μοντέο το οποίο προέρχεται από τις NESP στατιστικές για παρόμοιες τιμές των παραμέτρων προσαρμογής. Οι τιμές των q και a εκτιμάται ότι είναι κατάηες για να δώσουν την κατανομή μεγέθους των σεισμών στην Εάδα για την εξεταζόμενη περίοδο. Στη συνέχεια, είδαμε την πιθανότητα κατανομής του χρόνου εμφάνισης Τ ενός σεισμού με μέγεθος μεγαύτερο του Μ c και παρατηρήθηκε ότι και για τα δύο σύνοα τα δεδομένα προσεγγίζονται από μια στατιστική κατανομή της μορφής q- εκθετικής (4.5). Αυτή η μορφή κατανομής επιτρέπει να υποογιστεί αναυτικά η συνάρτηση επικινδυνότητας, που είναι η πιθανότητα να συμβεί τουάχιστον ένας σεισμός με μέγεθος μεγαύτερο του Μ στο επόμενο χρονικό διάστημα ΔΤ, εάν ο τεευταίος σεισμός συνέβη Τ ημέρες πριν. Έγινε μεέτη της συνάρτησης επικινδυνότητας και για τα δύο σύνοα δεδομένων και προέκυψε ότι για ένα σταθερό χρονικό διάστημα ΔΤ η πιθανότητα να συμβεί τουάχιστον ένας σεισμός με μέγεθος Μ 4. στο επόμενο χρονικό διάστημα ΔΤ (εάν ο τεευταίος σεισμός συνέβη Τ ημέρες πριν), μειώνεται καθώς το Τ αυξάνεται ενώ με την αύξηση του χρονικού διαστήματος ΔΤ η συνάρτηση W M (T,ΔT) αυξάνεται. Τέος, βρέθηκε μια κατά προσέγγιση συναρτησιακή σχέση (ογαριθμικής μορφής) ανάμεσα στο R M και M η οποία είναι σημαντική διότι μπορεί να χρησιμοποιηθεί ως παράγοντας εκτίμησης μιας μέσης τιμής R M του χρόνου εμφάνισης ενός σεισμού μεγέθους Μ 4.στον εαδικό χώρο. Ένα άο κύριο 70
79 Κεφάαιο 4: Εφαρμογές q-συναρτήσεων σε Προβήματα Σεισμοογίας συμπέρασμα, είναι ότι οι μετασεισμοί των κύριων σεισμικών γεγονότων είναι υπεύθυνοι για την αύξηση του δείκτη q, που υποδηώνει την ύπαρξη χαοτικής συμπεριφοράς στο φαινόμενο δημιουργίας σεισμών. Ο χρόνος δημιουργίας ενός σεισμού είναι ένα μη-γραμμικό φαινόμενο και παρουσιάζει φθίνουσα κατανομή που περιγράφεται από νόμο δύναμης. 7
80 ΚΕΦΑΛΑΙΟ 5 Εφαρμογές των q-συναρτήσεων σε προβήματα οικονομικών επιστημών Ένα από τα σημαντικότερα ζητήματα των οικονομοόγων είναι ο προσδιορισμός των νόμων που διέπουν την δυναμική εξέιξη των χρηματοοικονομικών αγορών, διότι η κατανόηση των νόμων αυτών επιτρέπει μια καύτερη εκτίμηση του οικονομικού κινδύνου. Με βάση την πρωτοποριακή εργασία των Granger [3] και Mandelbrot [7] έγινε αποδεκτό ότι οι χρηματοοικονομικές αγορές είναι πούποκα συστήματα που εμφανίζουν δομή αυτοομοιότητας υπό ααγή κίμακας. Παρά την πουποκότητα, κάποια χαρακτηριστικά της δυναμικής συμπεριφοράς των αγορών είναι δυνατόν να περιγραφούν από απούς εμπειρικούς νόμους. Βασιζόμενοι στους νόμους αυτούς μπορούμε να προσδιορίσουμε μια συνάρτηση επικινδυνότητας που επιτρέπει τη βετίωση των προβέψεων. Στην παρούσα ενότητα, οι ερευνητές της εργασίας [5] με X i θεωρούν τις αποδόσεις ενός κεφααίου που κυμαίνονται μεταξύ δευτεροέπτων και χρόνων. Η σχέση μεταξύ των αποδόσεων των οικονομικών αγορών και της τιμής P i ενός κεφααίου δίνεται ως εξής: X = ( P P )/ P. (5.) i i i i Εξ ορισμού οι θετικές αποδόσεις είναι τα κέρδη και οι αρνητικές είναι οι απώειες. Η εργασία εστιάζει στις καθημερινές τιμές κεισίματος των P i όπου i-και i δηώνουν διαδοχικές μέρες που πραγματοποιείται η συνααγή. Είναι γνωστό ότι οι 7
81 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών αποδόσεις X i δε συσχετίζονται γραμμικά και έτσι η συνάρτηση αυτοσυσχέτισης μηδενίζεται για χρόνους καθυστέρησης s, της τάξης των επτών. Η μεταβητότητα η οποία ορίζεται ως η απόυτη τιμή των αποδόσεων παρουσιάζει σταθερότητα μακράς εμβέειας (long-term persistency), πράγμα που αντανακά την ύπαρξη μη γραμμικότητας και πουποκότητας, στις οικονομικές αγορές. Η χρονική εξέιξη των αγορών μπορεί να χαρακτηριστεί από το σύνοο των χρόνων r i μεταξύ των απωειών κάτω από ένα εάχιστο αρνητικό όριο -Q συγκεκριμένα από τη μέση τιμή R Q των χρόνων και τη συνάρτηση κατανομής τους P Q (r). Για κάθε καταγραφή υπάρχει μία προς μία αντιστοιχία ανάμεσα στο Q και το R Q της μορφής R Q = D() r dr (5.) Q όπου D(r) είναι η κατανομή των αποδόσεων. Έχει δειχθεί πρόσφατα από τους Bogachev και Bunde [8], ότι κατά την ανάυση 6 κεφααίων, που χωρίζονται σε 4 κατηγορίες (μετοχές, δείκτες μετοχών, εμπορεύματα, νομίσματα), οι χρόνοι μεταξύ των απωειών r i σχετίζονται με μια συνάρτηση αυτοσυσχέτισης η οποία μειώνεται με νόμο δύναμης και αντανακά μια μη γραμμική μνήμη των αγορών. Αποδεικνύεται ότι για σταθερούς χρόνους απωειών R Q 0 (σε ημέρες συνααγών), η συνάρτηση κατανομής P Q (r) εξαρτάται μόνο από το R Q αά όχι από το εξεταζόμενο οικονομικό στοιχείο (κεφάαιο) και μειώνεται ασυμπτωτικά με νόμο δύναμης ο εκθέτης του οποίου εξαρτάται από το R Q. Παρατηρείται ότι σε όες τις περιπτώσεις η συναρτησιακή μορφή της κατανομής P Q (r) σε όο το εύρος των τιμών r και R Q μπορεί να προσεγγιστεί αρκετά καά από q-εκθετικές συναρτήσεις γνωστές από την μη εκτατική στατιστική μηχανική. Η τιμή της μεταβητής q αυξάνεται ογαριθμικά με το R Q έτσι ώστε για μεγάα R Q η P Q (r) ακοουθεί ένα νόμο δύναμης ενώ για R Q = προκύπτει μια απή εκθετική. Χρησιμοποιώντας την q-εκθετική μορφή της P Q (r) εξάγεται μια αναυτική μορφή για τη συνάρτηση επικινδυνότητας W Q (t;δt), η οποία ορίζεται ως η πιθανότητα τουάχιστον ένα γεγονός μικρότερο του Q να συμβεί στο επόμενο διάστημα Δt εάν το τεευταίο γεγονός συνέβη t ημέρες πριν. Η συνάρτηση επικινδυνότητας παίζει σημαντικό ρόο στην εκτίμηση της τιμής του κινδύνου η οποία είναι ίσως το πιο συνηθισμένο εργαείο για την αξιοόγηση οικονομικών συνααγών. 73
82 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών Σχ. : Γραφική απεικόνιση των καθημερινών τιμών αποδόσεων X i για μετοχές της IBM για (a) Ιανουάριο 000 και Ιούνιο 00 για Q και R Q =70 (κόκκινη γραμμή); (b) 7 Αυγούστου και 3 Οκτώβρη 00 (τα βέη αντιστοιχούν στα χρονικά διαστήματα). 5. Οικονομικά δεδομένα αποδόσεων και q- συναρτήσεις Το Σχ. (a) δείχνει τις αποδόσεις της IBM καταγραφής ανάμεσα στον Ιανουάριο του 000 και τον Ιούνιο του 00. Η κόκκινη οριζόντια γραμμή απεικονίζει τις καθημερινές απώειες κάτω από το -Q , όπου η μέση τιμή των χρόνων R Q είναι 70 ημέρες συνααγών. Το Σχ. (b) δείχνει, για το χρονικό παράθυρο μεταξύ 7 Αυγούστου και 3 Οκτωβρίου του 00, τους χρόνους μεταξύ 74
83 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών των απωειών. Οι χρόνοι αυτοί, αντικατοπτρίζουν τη δυναμική του κεφααίου. Στην περίοδο μεταξύ του Απριίου 005 και του Σεπτέμβρη 008 δεν συνέβησαν καθημερινές απώειες μικρότερες από , δηαδή το μεσοδιάστημα αυτό είναι,5 χρόνια ενώ στην επόμενη μεταβητή περίοδο συνέβησαν απώειες με υψηή συχνότητα με χρόνους απωειών της τάξης ημερών και εβδομάδων. Σχ. : Γραφική απεικόνιση της μέσης τιμής R Q με την απόυτη τιμή απωειών Q για διαφορετικά οικονομικά στοιχεία. Το Σχ. απεικονίζει την εξάρτηση του R Q από το Q για ένα παράδειγμα από καθεμία από τις κάσεις των κεφααίων που θεωρήθηκαν. Δεδομένου ότι για μεγάες απώειες το D(r) μειώνεται με νόμο δύναμης [39], η μέση τιμή R Q των χρόνων των απωειών αυξάνεται με ίδιο νόμο για μεγάα Q. Όταν συγκρίνουμε διαφορετικές καταγραφές είναι βασικό να κρατάμε σταθερό το R Q. 75
84 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών Σχ. 3: (a) Η συνάρτηση κατανομής των χρόνων μεταξύ των απωειών για τις καθημερινές τιμές αποδόσεων X i από τις καταγραφές της IBM για το 96-00, για μέση τιμή R Q =, 5, 0, 30 και 70, και οι προσεγγίσεις από τις q-εκθετικές (συνεχείς γραμμές); (b) Η εξάρτηση της παραμέτρου β και της τιμής q από το R Q στις q-εκθετικές;(c) Η κατανομή για R Q = (απή εκθετική). Το Σχ.3(a) δείχνει, αναφορικά με την IBM καταγραφή, τη συνάρτηση κατανομής P Q (r) των χρόνων μεταξύ των απωειών για πέντε τιμές της μέσης τιμής R Q =, 5, 0, 30 και 70. Τα αριθμητικά αποτεέσματα απεικονίζονται με κύκους. Οι συμπαγείς καμπύες είναι η προσέγγιση μέσω της q-εκθετικής. P () r = Q A ( + ( q ) βr) q (5.3) όπου Α είναι μια σταθερά κανονικοποίησης. Στη μαθηματική βιβιογραφία αυτή η κατανομή συνήθως αναφέρεται ως «generalized Pareto» [39] κατανομή. Περιστασιακά αναφέρεται και ως «Zipf Mandelbrot» κατανομή. Παρατηρούμε ότι η προσέγγιση είναι εξαιρετική. Το Σχ. 3(b) δείχνει την εξάρτηση του β (τετράγωνα) και 76
85 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών του q (κύκοι) από το R Q. Η ημι-ογαριθμική παράσταση του β αρχικά μειώνεται εαφρώς με την αύξηση του R Q και στη συνέχεια για R Q =6 φτάνει σε ένα πατό με β 0.3. Επίσης, το σχήμα δείχνει ότι η τιμή της παραμέτρου q αυξάνεται ογαριθμικά με R Q μέσω της σχέσης: q= + q ln( R Q / ) (5.4) 0 με q Συνεπώς, για R Q (όπου το Q 0) το q και η q-εκθετική τείνει σε μια απή εκθετική P(r)= -r δηαδή P Q (r) exp(-βr) όπου β ln. Στο Σχ.3(c) όταν το R Q = η κατανομή του χρόνου απωειών έχει τη μορφή της απής εκθετικής, δηαδή όα τα σημεία είναι κοντά σε μια ευθεία γραμμή επιβεβαιώνοντας τη μορφή αυτή. Σχ. 4: Η συνάρτηση κατανομής των χρόνων μεταξύ των απωειών για τις καθημερινές τιμές αποδόσεων από 6 δεδομένα (μετοχές, δείκτες, νομίσματα) διαφορετικών κάσεων οικονομικών στοιχείων (με χρώματα) και οι προσεγγίσεις από τις q-εκθετικές (μαύρες γραμμές). Το Σχ. 4 απεικονίζει για όες τις 6 καταγραφές που θεωρήθηκαν τη συνάρτηση κατανομής των χρόνων μεταξύ των απωειών για τις ίδιες τιμές του R Q όπως και στο Σχ. 3. Το σχήμα αυτό, επιβεβαιώνει ότι για μεγάες τιμές του R Q η συνάρτηση κατανομής συμπεριφέρεται με τον ίδιο τρόπο για όα τα χαρακτηριστικά μεγέθη που μεετώνται. Το σχήμα δείχνει ότι ισχύει το ίδιο και για μικρές τιμές του R Q. Τα δεδομένα προσεγγίζονται από την q-εκθετική του Σχ.3. Για την ίδια τιμή R Q 77
86 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών όγω του πεπερασμένου μεγέθους των αποτεεσμάτων τα δεδομένα αποκίνουν περισσότερο για μεγάες τιμές του r αά περιγράφονται εξαιρετικά καά από την q- εκθετική. 5. Συνάρτηση επικινδυνότητας και δυνατότητες πρόβεψης Η συνάρτηση κατανομής των χρόνων μεταξύ των απωειών είναι ένα σημαντικό εργαείο για την εκτίμηση του κινδύνου από τη στιγμή που συνδέεται με τη συνάρτηση επικινδυνότητας W Q (t,δt). Η συνάρτηση επικινδυνότητας ορίζεται ως η πιθανότητα ένα τουάχιστον γεγονός μικρότερο του Q να συμβεί στο επόμενο χρονικό διάστημα Δt εάν το τεευταίο συμβάν συνέβη t ημέρες πριν. Επομένως, το W Q σχετίζεται με το P Q μέσω του τύπου, W (; t t) Q t+ t t = + t P () r dr Q P () r dr Q (5.5) Με απή οοκήρωση της παραπάνω σχέσης προκύπτει: q q β ( q ) t WQ ( t; t) = ( + ) (5.6α) + β ( q ) t Στο Σχ. 5 απεικονίζεται η γραφική παράσταση της συνάρτησης επικινδυνότητας για R Q = 00 και Δt=, 5, 0 και 00. Η συνάρτηση επικινδυνότητας W Q μπορεί να εκφραστεί σε όρους q-εκθετικών ως εξής: e W (; t t) = Q ( β / q)( t+ t) q ( β / q) t eq (5.6β) με q =/(-q). Είναι εύκοο να δει κανείς ότι για εκθετικά μειούμενες συναρτήσεις κατανομών το W Q είναι σταθερό και ίσο W Q (t,δt)=-exp(-βδt) ενώ για κατανομές που μειώνονται με νόμο δύναμης ισχύει W Q (t,δt) Δt/t για Δt<<t. 78
87 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών Σχ. 5: Η καθοική συνάρτηση επικινδυνότητας W Q (t,δt) της (5.6α) για τη μέση τιμή R Q =00 και Δt=, 5, 0 και 00 (ημέρες). Επισημαίνεται ότι W Q (t,δt) μπορεί να χρησιμοποιηθεί για ποά οικονομικά στοιχεία - κεφάαια στην εκτίμηση του κινδύνου. Ένα γνωστό παράδειγμα είναι το Value-at-Risk (Var). Το Var ορίζεται ως η σχετική απώεια η οποία στη δεδομένη μονάδα χρόνου μπορεί να επιτευχθεί με συγκεκριμένη μικρή πιθανότητα p. Αυτό σημαίνει ότι οι αναμενόμενες αποδόσεις με πιθανότητα -p είναι μεγαύτερες από Q. Χαρακτηριστικές τιμές της πιθανότητας -p είναι 0.95 και 0.99 και χαρακτηριστικές μονάδες χρόνου και 0 ημέρες. Ακοούθως, θεωρούμε ως μονάδα χρόνου τη ημέρα. Σε μια μηδενικής τάξης προσέγγιση που τα φαινόμενα μνήμης παραείπονται η τιμή του Var μπορεί να καθοριστεί από την κατανομή D(r) των ημερήσιων αποδόσεων, D () r dr = p (5.7) Q Για να άβουμε την τιμή του Var από τις (5.6) και (5.7) ακοουθούμε τον αγόριθμο που πρότειναν οι Bogachev και Bunde και τον εφαρμόζουμε επαναηπτικά. ) Στο πρώτο βήμα επιέγουμε το p και καθορίζουμε από την (5.7) την αντίστοιχη απώεια Q. Έπειτα, προσδιορίζουμε το χρόνο t που παρήθε από την τεευταία απόδοση η οποία ήταν μικρότερη από το Q και χρησιμοποιούμε την (5.6) για να 79
88 Κεφάαιο 5: Εφαρμογές q-συναρτήσεων σε Προβήματα Οικονομικών Επιστημών προσδιορίζουμε μια νέα πιθανότητα W -Q. Εάν W -Q είναι μέσα σε ένα καθορισμένο διάστημα σφάματος p±δp, τότε ο αγόριθμος σταματά. ) ΕάνW -Q είναι μεγαύτερο του p+δp τότε ποαπασιάζουμε το Q με (+ΔQ) και προσδιορίζουμε το νέο χρόνο t που παρήθε από την τεευταία απόδοση η οποία ήταν μικρότερη του -Q(+ΔQ). Εάν το W -Q είναι ακόμη μεγαύτερο του p+δp επανααμβάνουμε το ίδιο βήμα μέχρι στο νιοστό βήμα όπου η W n -Q(+ΔQ) είναι μικρότερη του p+δp. Ο αγόριθμος σταματά και επιέγουμε σαν εκτίμηση της Var το Q=-Q(+ΔQ) n. 3) Εάν το W -Q είναι μικρότερο του p-δp ακοουθούμε τη διαδικασία του βήματος n αά με αρνητική αύξηση ΔQ<0 μέχρις ότου η τιμή του W -Q(+ΔQ) να είναι μεγαύτερη από το p-δp. Σχ. 6: Υποογισμός της Value-at-Risk από τις IBM καταγραφές από το για πιθανότητες (a) -p=0.99 (πράσινες καμπύες); (b) -p=0.95 (κόκκινες καμπύες); (μαύρες) καμπύες η απόυτη τιμή των ημερήσιων απωειών για τιμές που υπερβαίνουν το Το Σχ. 6 απεικονίζει τη τιμή της Var της ΙΒΜ μετοχής για δύο πιθανότητες p=0.05 και p=0.0. Για να εκτιμηθεί η Var έχει επιεγεί Δp=0.000και ΔQ =0.0. Το σχήμα δείχνει ότι η εκτίμηση της Var έχει βετιωθεί αμβάνοντας υπόψη τα φαινόμενα μη γραμμικής μνήμης. Η Var ενισχύεται μετά τις μεγάες απώειες και μειώνεται με την αύξηση του χρόνου μετά από την τεευταία μεγάη απώεια. 80
Το πρόβλημα των μηδενικών ιδιοτιμών.
 Το πρόβημα των μηδενικών ιδιοτιμών. Από την προηγούμενη συζήτηση έχει γίνει φανερό ότι αν η ομογενής διαφορική εξίσωση L ϕ ( = 0έχει μη μηδενική ύση (ή ύσεις που να ικανοποιεί τις (ομογενείς συνοριακές
Το πρόβημα των μηδενικών ιδιοτιμών. Από την προηγούμενη συζήτηση έχει γίνει φανερό ότι αν η ομογενής διαφορική εξίσωση L ϕ ( = 0έχει μη μηδενική ύση (ή ύσεις που να ικανοποιεί τις (ομογενείς συνοριακές
TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ
 TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ. ΕΙΣΑΓΩΓΗ Ας θεωρήσουμε το σύστημα ανοικτού βρόχου που περιγράφεται από τις εξισώσεις κατάστασης (.) και (.2): x Ax+ Bu (.)
TO ΠΡΟΒΛΗΜΑ ΤΗΣ ΤΟΠΟΘΕΤΗΣΗΣ ΠΟΛΩΝ ΜE ΑΝΑΤΡΟΦΟΔΟΤΗΣΗ ΤΩΝ ΜΕΤΑΒΛΗΤΩΝ ΚΑΤΑΣΤΑΣΗΣ. ΕΙΣΑΓΩΓΗ Ας θεωρήσουμε το σύστημα ανοικτού βρόχου που περιγράφεται από τις εξισώσεις κατάστασης (.) και (.2): x Ax+ Bu (.)
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα Επιμέεια: Ι. Λυχναρόπουος. Έστω ο πίνακας 3. Δείξτε ότι το διάνυσμα v (,3) είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Ιδιοτιμές - Ιδιοδιανύσματα Επιμέεια: Ι. Λυχναρόπουος. Έστω ο πίνακας 3. Δείξτε ότι το διάνυσμα v (,3) είναι ένα ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή
Έστω η πραγµατική συνάρτηση f(t) της πραγµατικής µεταβλητής t (π.χ χρόνος). Ο µετασχηµατισµός Laplace της συνάρτησης f(t) δίνεται από τη σχέση:
 ΜΑΘΗΜΑ : Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE. Εισαγωγή Ο µετασχηµατισµός pl και ο µετασχηµατισµός Z είναι δύο πού χρήσιµα µαθηµατικά εργαεία για την ανάυση και σχεδίαση συστηµάτων αυτοµάτου και ιδιαίτερα ΓΧΑ Γραµµικών
ΜΑΘΗΜΑ : Ο ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ APACE. Εισαγωγή Ο µετασχηµατισµός pl και ο µετασχηµατισµός Z είναι δύο πού χρήσιµα µαθηµατικά εργαεία για την ανάυση και σχεδίαση συστηµάτων αυτοµάτου και ιδιαίτερα ΓΧΑ Γραµµικών
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουλος
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουος Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα 3. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές ποαπότητες
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Ι. Λυχναρόπουος Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα 3. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές ποαπότητες
2.3 Στάσιμο κύμα. ημ 2π. συν = 2A. + τα οποία T. t x. T λ T λ ολ
 .3 Στάσιμο Κύμα.3 Στάσιμο κύμα.3.1 Μαθηματική Επεξεργασία Ας υποθέσουμε ότι έχουμε μία χορδή και σε αυτήν την χορδή διαδίδονται δύο πανομοιότυπα κύματα σε αντίθετες κατευθύνσεις. Δηαδή αν το δούμε από
.3 Στάσιμο Κύμα.3 Στάσιμο κύμα.3.1 Μαθηματική Επεξεργασία Ας υποθέσουμε ότι έχουμε μία χορδή και σε αυτήν την χορδή διαδίδονται δύο πανομοιότυπα κύματα σε αντίθετες κατευθύνσεις. Δηαδή αν το δούμε από
Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα.
 ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
ΕΙΣΑΓΩΓΗ ΕΝΝΟΙΑ ΤΟΥ ΚΥΜΑΤΟΣ Τι ονομάζουμε κύμα; Κύμα ονομάζουμε τη διάδοση μιας διαταραχής από σημείο σε σημείο του χώρου με ορισμένη ταχύτητα. Η διαταραχή μπορεί να είναι α. Η ταάντωση των μορίων του
Τεχνικές Εκτίμησης Υπολογιστικών Συστημάτων Ακαδημαϊκό έτος Λύσεις για την Προαιρετική Εργασία
 Τεχνικές Εκτίμησης Υποογιστικών Συστημάτων Ακαδημαϊκό έτος 2016-17 Λύσεις για την Προαιρετική Εργασία Φεβρουάριος 2017 Πρόβημα 1 Δίνεται το παρακάτω μητρώο με τις πιθανότητες μετάβασης μιας Μαρκοβιανής
Τεχνικές Εκτίμησης Υποογιστικών Συστημάτων Ακαδημαϊκό έτος 2016-17 Λύσεις για την Προαιρετική Εργασία Φεβρουάριος 2017 Πρόβημα 1 Δίνεται το παρακάτω μητρώο με τις πιθανότητες μετάβασης μιας Μαρκοβιανής
, όπου x = 0,1,...,300000. Έτσι, για την πιθανότητα σε ένα έτος να μην υπάρξουν θάνατοι ζώων από τον εμβολιασμό έχουμε, 2! 299998!
 Η Κατανομή Poisso Ας δούμε ένα πρόβημα: Σε μια κτηνοτροφική περιοχή υπάρχουν 3 αιγοπρόβατα. Κάθε χρόνο όα τα αιγοπρόβατα εμβοιάζονται για προστασία από κάποια ασθένεια. Σύμφωνα με την άδεια χρήσης του
Η Κατανομή Poisso Ας δούμε ένα πρόβημα: Σε μια κτηνοτροφική περιοχή υπάρχουν 3 αιγοπρόβατα. Κάθε χρόνο όα τα αιγοπρόβατα εμβοιάζονται για προστασία από κάποια ασθένεια. Σύμφωνα με την άδεια χρήσης του
ΚΕΦΑΛΑΙΟ 4: ΙΔΙΟΤΙΜΕΣ ΚΑΙ ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΟΡΙΣΜΟΙ Δίνεται ο πίνακας Παρατηρήστε τι γίνεται όταν ποαπασιάζουμε τον Α με το διάνυσμα u u u παίρνουμε δηαδή ένα διάνυσμα ποαπάσιο του u. Η αναζήτηση διανυσμάτων που έχουν παρόμοια
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΟΡΙΣΜΟΙ Δίνεται ο πίνακας Παρατηρήστε τι γίνεται όταν ποαπασιάζουμε τον Α με το διάνυσμα u u u παίρνουμε δηαδή ένα διάνυσμα ποαπάσιο του u. Η αναζήτηση διανυσμάτων που έχουν παρόμοια
Αριθµητικά χαρακτηριστικά µιάς τυχαίας µεταβλητής
 Αριθµητικά χαρακτηριστικά µιάς τυχαίας µεταβητής (Α) Mέση τιµή Ορισµός Η µέση τιµή ή µαθηµατική επίδα µιας τ.µ. Χ µε πυκνότητα πιθανότητας f (x) είναι ο αριθµός: µ E() + xf (x) xf (x)dx διακριτή συνεχής
Αριθµητικά χαρακτηριστικά µιάς τυχαίας µεταβητής (Α) Mέση τιµή Ορισµός Η µέση τιµή ή µαθηµατική επίδα µιας τ.µ. Χ µε πυκνότητα πιθανότητας f (x) είναι ο αριθµός: µ E() + xf (x) xf (x)dx διακριτή συνεχής
( ) ( ) ( ) ( ) ( ) ( )
 ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο Αρχιμήδης" ΣΑΒΒΑΤΟ, ΦΕΒΡΟΥΑΡΙΟΥ 009 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜΑ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n Α n 7 είναι
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο Αρχιμήδης" ΣΑΒΒΑΤΟ, ΦΕΒΡΟΥΑΡΙΟΥ 009 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜΑ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n Α n 7 είναι
3. Χαρακτηριστικές Παράμετροι Κατανομών
 . Χαρακτηριστικές Παράμετροι Κατανομών - Αναμενόμενη ή μέση τιμή μιας διακριτής τυχαίας μεταβητής. Θα ήταν αρκετά χρήσιμο να γνωρίζουμε γύρω από ποια τιμή «κυμαίνεται» η τ.μ. Χ. γύρω από την οποία «απώνεται»
. Χαρακτηριστικές Παράμετροι Κατανομών - Αναμενόμενη ή μέση τιμή μιας διακριτής τυχαίας μεταβητής. Θα ήταν αρκετά χρήσιμο να γνωρίζουμε γύρω από ποια τιμή «κυμαίνεται» η τ.μ. Χ. γύρω από την οποία «απώνεται»
14. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ
 4. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ 4. Η µέθοδος Newn-Raphsn για µη γραµµική ανάυση Η γενική εξίσωση ισορροπίας ενός µη γραµµικού συστήµατος γράφεται: F ( ) = F q () όπου είναι οι εσωτερικές
4. ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΜΗ-ΓΡΑΜΜΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ 4. Η µέθοδος Newn-Raphsn για µη γραµµική ανάυση Η γενική εξίσωση ισορροπίας ενός µη γραµµικού συστήµατος γράφεται: F ( ) = F q () όπου είναι οι εσωτερικές
ΕΑΠ ΦΥΕ 34. ( γ ) Βρείτε την ενέργεια σε ev του φωτονίου της σειράς Balmer, που έχει το
 ΕΑΠ ΦΥΕ 4 Σύντοµες Απαντήσεις στην Εξέταση Ιουνίου 4 στο µάθηµα «Από την Κασική στην Σύγχρονη Φυσική» ) Η σειρά Balmer του γραµµικού φάσµατος του ατόµου του υδρογόνου αντιστοιχεί σε µεταβάσεις ηεκτρονίων
ΕΑΠ ΦΥΕ 4 Σύντοµες Απαντήσεις στην Εξέταση Ιουνίου 4 στο µάθηµα «Από την Κασική στην Σύγχρονη Φυσική» ) Η σειρά Balmer του γραµµικού φάσµατος του ατόµου του υδρογόνου αντιστοιχεί σε µεταβάσεις ηεκτρονίων
Εξαιτίας της συμβολής δύο κυμάτων του ίδιου πλάτους και της ίδιας συχνότητας. που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό ελαστικό μέσο
 ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
ΣΤΑΣΙΜΑ ΚΥΜΑΤΑ Τι ονομάζουμε στάσιμο κύμα f()=0.5sin() Εξαιτίας της συμβοής δύο κυμάτων του ίδιου πάτους και της ίδιας συχνότητας που διαδίδονται ταυτόχρονα στο ίδιο γραμμικό εαστικό μέσο με αντίθετη φορά,
2( ) ( ) ψ είναι οι ιδιοκαταστάσεις του τελεστή. ψ x, θα πάρουµε
 ΟΙ Ι ΙΟΚΑΤΑΣΤΑΣΕΙΣ ΤΟΥ ΤΕΛΕΣΤΗ ΚΑΤΑΣΤΡΟΦΗΣ ΩΣ ΚΑΤΑΣΤΑΣΕΙΣ ΕΛΑΧΙΣΤΗΣ ΑΒΕΒΑΙΟΤΗΤΑΣ ΣΥΝΟΧΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ (COHERENT STATES) ΤΟΥ ΑΡΜΟΝΙΚΟΥ ΤΑΛΑΝΤΩΤΗ Στην προηγούµενη ανάρτηση, δείξαµε ότι στην αναπαράσταση
ΟΙ Ι ΙΟΚΑΤΑΣΤΑΣΕΙΣ ΤΟΥ ΤΕΛΕΣΤΗ ΚΑΤΑΣΤΡΟΦΗΣ ΩΣ ΚΑΤΑΣΤΑΣΕΙΣ ΕΛΑΧΙΣΤΗΣ ΑΒΕΒΑΙΟΤΗΤΑΣ ΣΥΝΟΧΙΚΕΣ ΚΑΤΑΣΤΑΣΕΙΣ (COHERENT STATES) ΤΟΥ ΑΡΜΟΝΙΚΟΥ ΤΑΛΑΝΤΩΤΗ Στην προηγούµενη ανάρτηση, δείξαµε ότι στην αναπαράσταση
3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]
![3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1] 3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]](/thumbs/79/79263211.jpg) 20 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει ότι
20 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει ότι
R 1. e 2r V = Gauss E + 1 R 2
 : Γραμμική πυκνότητα φορτίου βρίσκεται στον άξονα αγώγιμου κυινδρικού φοιού εσωτερικής ακτίνας και εξωτερικής α) Να υποογιστεί η επαγόμενη πυκνότητα φορτίου στις δύο όψεις του φοιού, αν το συνοικό του
: Γραμμική πυκνότητα φορτίου βρίσκεται στον άξονα αγώγιμου κυινδρικού φοιού εσωτερικής ακτίνας και εξωτερικής α) Να υποογιστεί η επαγόμενη πυκνότητα φορτίου στις δύο όψεις του φοιού, αν το συνοικό του
ΙΔΙΟΤΗΤΕΣ ΜΟΝΟΤΟΝΙΑΣ ΣΕ ΑΝΑΝΕΩΤΙΚΕΣ ΑΝΕΛΙΞΕΙΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ ΙΔΙΟΤΗΤΕΣ ΜΟΝΟΤΟΝΙΑΣ ΣΕ ΑΝΑΝΕΩΤΙΚΕΣ ΑΝΕΛΙΞΕΙΣ Κωνσταντίνος Ν. Μακρής Διπωματική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΕΦΑΡΜΟΣΜΕΝΗ ΣΤΑΤΙΣΤΙΚΗ ΙΔΙΟΤΗΤΕΣ ΜΟΝΟΤΟΝΙΑΣ ΣΕ ΑΝΑΝΕΩΤΙΚΕΣ ΑΝΕΛΙΞΕΙΣ Κωνσταντίνος Ν. Μακρής Διπωματική
Κβαντική Φυσική Ι. Ενότητα 4: Εξίσωση Schro dinger. Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 4: Εξίσωση Schro dinger Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η εξαγωγή της εξίσωσης Schro dinger καθώς και μια πρώτη
Κβαντική Φυσική Ι Ενότητα 4: Εξίσωση Schro dinger Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η εξαγωγή της εξίσωσης Schro dinger καθώς και μια πρώτη
6. ΑΡΙΘΜΗΤΙΚΗ ΟΛΟΚΛΗΡΩΣΗ
 6. ΑΡΘΜΗΤΚΗ ΟΛΟΚΛΗΡΩΣΗ. Αριθµητική Οοκήρωση Οπως αναφέραµε στην εισαγωγή, είναι συχνά δύσκοο να υποογιστεί ο αναυτικός τύπος, ή δεν υπάρχει αναυτικός τύπος, που δίνει το ορισµένο οοκήρωµα µιας συνεχούς
6. ΑΡΘΜΗΤΚΗ ΟΛΟΚΛΗΡΩΣΗ. Αριθµητική Οοκήρωση Οπως αναφέραµε στην εισαγωγή, είναι συχνά δύσκοο να υποογιστεί ο αναυτικός τύπος, ή δεν υπάρχει αναυτικός τύπος, που δίνει το ορισµένο οοκήρωµα µιας συνεχούς
ΣΤΟΙΧΕΙΑ ΑΡΙΘΜΗΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΝΙΚΟΛΑΟΥ ΙΩ ΔΑΡΑ ΕΠΙΚΟΥΡΟΥ ΚΑΘΗΓΗΤΗ ΣΤΡΑΤΙΩΤΙΚΗΣ ΣΧΟΛΗΣ ΕΥΕΛΠΙΔΩΝ ΣΤΟΙΧΕΙΑ ΑΡΙΘΜΗΤΙΚΗΣ ΑΝΑΛΥΣΗΣ ΤΟΜΟΣ ος ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ ΑΡΙΘΜΗΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ ΙΔΙΟΤΙΜΩΝ ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΑΛΓΕΒΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
ΝΙΚΟΛΑΟΥ ΙΩ ΔΑΡΑ ΕΠΙΚΟΥΡΟΥ ΚΑΘΗΓΗΤΗ ΣΤΡΑΤΙΩΤΙΚΗΣ ΣΧΟΛΗΣ ΕΥΕΛΠΙΔΩΝ ΣΤΟΙΧΕΙΑ ΑΡΙΘΜΗΤΙΚΗΣ ΑΝΑΛΥΣΗΣ ΤΟΜΟΣ ος ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ ΑΡΙΘΜΗΤΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ ΙΔΙΟΤΙΜΩΝ ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΑΛΓΕΒΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ
3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]
![3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1] 3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]](/thumbs/92/110100632.jpg) 0 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω E διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A E. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει
0 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω E διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A E. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει
1. Υποθέτοντας ότι η τριβή είναι αρκετά μεγάλη, το σημείο επαφής θα έχει συνεχώς
 Διονύσης Μητρόπουος Άνοδος κάθοδος κυιόμενου αρχικά σώματος σε κεκιμένο επίπεδο, με ή χωρίς οίσθηση ΕΚΦΩΝΗΣΗ Ένα «στρογγυό» σώμα έχει μάζα m, ακτίνα R και ροπή αδράνειας Ι cm m R². Οι τιμές του είναι ⅖
Διονύσης Μητρόπουος Άνοδος κάθοδος κυιόμενου αρχικά σώματος σε κεκιμένο επίπεδο, με ή χωρίς οίσθηση ΕΚΦΩΝΗΣΗ Ένα «στρογγυό» σώμα έχει μάζα m, ακτίνα R και ροπή αδράνειας Ι cm m R². Οι τιμές του είναι ⅖
ΝΙΚΟΛΑΟΥ ΙΩ. ΔΑΡΑ ΕΠΙΚΟΥΡΟΥ ΚΑΘΗΓΗΤΟΥ ΣΤΡΑΤΙΩΤΙΚΗΣ ΣΧΟΛΗΣ ΕΥΕΛΠΙΔΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΚΑΙ ΣΤΡΑΤΙΩΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΥΤΗΣ. ΤΟΜΟΣ 2 ΟΣ ΒΙΒΛΙΟ 1 ο
 ΝΙΚΟΛΑΟΥ ΙΩ. ΔΑΡΑ ΕΠΙΚΟΥΡΟΥ ΚΑΘΗΓΗΤΟΥ ΣΤΡΑΤΙΩΤΙΚΗΣ ΣΧΟΛΗΣ ΕΥΕΛΠΙΔΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΚΑΙ ΣΤΡΑΤΙΩΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΥΤΗΣ ΤΟΜΟΣ ΟΣ ΒΙΒΛΙΟ ο ΣΤΡΑΤΗΓΙΚΗ ΑΜΥΝΑ ΕΛΛΗΝΙΚΟ ΚΕΝΤΡΟ ΕΛΕΓΧΟΥ ΟΠΛΩΝ www.rmscotrol.fo
ΝΙΚΟΛΑΟΥ ΙΩ. ΔΑΡΑ ΕΠΙΚΟΥΡΟΥ ΚΑΘΗΓΗΤΟΥ ΣΤΡΑΤΙΩΤΙΚΗΣ ΣΧΟΛΗΣ ΕΥΕΛΠΙΔΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΚΑΙ ΣΤΡΑΤΙΩΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ ΑΥΤΗΣ ΤΟΜΟΣ ΟΣ ΒΙΒΛΙΟ ο ΣΤΡΑΤΗΓΙΚΗ ΑΜΥΝΑ ΕΛΛΗΝΙΚΟ ΚΕΝΤΡΟ ΕΛΕΓΧΟΥ ΟΠΛΩΝ www.rmscotrol.fo
Σεµινάριο Αυτοµάτου Ελέγχου
 Σεµινάριο Αυτοµάτου Εέγχου Μάθηµα 9 Ευστάθεια κατά Lyaunv Η έννοια της ευστάθειας κατά Lyaunv Γενικό κριτήριο ευστάθειας Παραδείγµατα Καιγερόπουος 9 Ευστάθεια κατά Lyaunv Εισαγωγή Η έννοια της ευστάθειας
Σεµινάριο Αυτοµάτου Εέγχου Μάθηµα 9 Ευστάθεια κατά Lyaunv Η έννοια της ευστάθειας κατά Lyaunv Γενικό κριτήριο ευστάθειας Παραδείγµατα Καιγερόπουος 9 Ευστάθεια κατά Lyaunv Εισαγωγή Η έννοια της ευστάθειας
ΚΕΦΑΛΑΙΟ 4. Προσομοίωση Βασικών Στοχαστικών Ανελίξεων : Ανέλιξη Poisson και Κίνηση Brown
 ΚΕΦΑΛΑΙΟ 4 Προσομοίωση Βασικών Στοχαστικών Ανείξεων : Ανέιξη Pi και Κίνηση Bw Είναι γνωστό ότι, αν το αποτέεσμα ενός τυχαίου πειράματος είναι ένας αριθμός στο R, τότε αυτό να μπορεί να εκφραστεί χρησιμοποιώντας
ΚΕΦΑΛΑΙΟ 4 Προσομοίωση Βασικών Στοχαστικών Ανείξεων : Ανέιξη Pi και Κίνηση Bw Είναι γνωστό ότι, αν το αποτέεσμα ενός τυχαίου πειράματος είναι ένας αριθμός στο R, τότε αυτό να μπορεί να εκφραστεί χρησιμοποιώντας
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ
 ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑΙΟΥ ΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ Σηµειώσεις Μη Γραµµικού Προγραµµατισµού Β Κούτρας ΧΙΟΣ Β Κούτρας ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΙΣΜΟΣ ΕΙΣΑΓΩΓΗ Στο κοµµάτι αυτό
ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑΙΟΥ ΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΙΙ Σηµειώσεις Μη Γραµµικού Προγραµµατισµού Β Κούτρας ΧΙΟΣ Β Κούτρας ΜΗ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΙΣΜΟΣ ΕΙΣΑΓΩΓΗ Στο κοµµάτι αυτό
όπου α (β) = η αναλογία των μη εμπορεύσιμων αγαθών στο συνολικό εγχώριο (ξένο) δείκτη τιμών.
 Κεφάαιο 6 ο : Προσδιορισμός πραγματικής ισοτιμίας Εισαγωγή Η ανάυση στα προηγούμενα κεφάαια αναφερόταν στους προσδιοριστικούς παράγοντες της ονομαστικής συνααγματικής ισοτιμίας. Στο παρόν κεφάαιο θα ασχοηθούμε
Κεφάαιο 6 ο : Προσδιορισμός πραγματικής ισοτιμίας Εισαγωγή Η ανάυση στα προηγούμενα κεφάαια αναφερόταν στους προσδιοριστικούς παράγοντες της ονομαστικής συνααγματικής ισοτιμίας. Στο παρόν κεφάαιο θα ασχοηθούμε
Διπλωματική Εργασία. Εφαρμοσμένη Θεωρία Πινάκων
 Πανεπιστήμιο Μακεδονίας Τ.Ε.Ι. Δυτικής Μακεδονίας Π.Μ.Σ Εφαρμοσμένης Πηροφορικής Διπωματική Εργασία Θέμα Εφαρμοσμένη Θεωρία Πινάκων Επιβέπον Καθηγητής Πετράκης Ανδρέας Μεταπτυχιακός Φοιτητής Τσαγκαρή Αθηνά
Πανεπιστήμιο Μακεδονίας Τ.Ε.Ι. Δυτικής Μακεδονίας Π.Μ.Σ Εφαρμοσμένης Πηροφορικής Διπωματική Εργασία Θέμα Εφαρμοσμένη Θεωρία Πινάκων Επιβέπον Καθηγητής Πετράκης Ανδρέας Μεταπτυχιακός Φοιτητής Τσαγκαρή Αθηνά
ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΕΝΔΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ
 Επώνυμο: Όνομα: ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ ΤΗΛ : 777 94 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ ΤΗΛ : 99 9494 www.syghrono.gr Τμήμα: Ημερομηνία: Α Βαθ. Β Βαθ. Μ.Ο. ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ --7 ΕΝΔΕΙΚΤΙΚΕΣ
Επώνυμο: Όνομα: ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ ΤΗΛ : 777 94 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ ΤΗΛ : 99 9494 www.syghrono.gr Τμήμα: Ημερομηνία: Α Βαθ. Β Βαθ. Μ.Ο. ΔΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ --7 ΕΝΔΕΙΚΤΙΚΕΣ
( ) ( ) ( ) ( ) ( ) ( )
 ΕΠΙΤΡΟΠΗ ΔΙΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο ρχιμήδης" ΣΒΒΤΟ, ΦΕΒΡΟΥΡΙΟΥ 9 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n n 7 είναι ρητός n
ΕΠΙΤΡΟΠΗ ΔΙΓΩΝΙΣΜΩΝ η Εηνική Μαθηματική Ουμπιάδα "Ο ρχιμήδης" ΣΒΒΤΟ, ΦΕΒΡΟΥΡΙΟΥ 9 ΟΙ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΤΩΝ Θέματα μεγάων τάξεων ΠΡΟΒΛΗΜ Να προσδιορίσετε τις τιμές του θετικού ακέραιου 9n n 7 είναι ρητός n
γ. είναι η απόσταση που διανύει το κύμα σε χρόνο T, όπου Τ η περίοδος του κύματος.
 ΕΥΤΕΡΟ ΚΕΦΑΛΑΙΟ ΚΥΜΑΤΑ Ερωτήσεις ποαπής επιογής Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις ποαπής επιογής αρκεί να γράψετε στο φύο απαντήσεων τον αριθμό της ερώτησης και δεξιά από αυτόν το γράμμα
ΕΥΤΕΡΟ ΚΕΦΑΛΑΙΟ ΚΥΜΑΤΑ Ερωτήσεις ποαπής επιογής Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις ποαπής επιογής αρκεί να γράψετε στο φύο απαντήσεων τον αριθμό της ερώτησης και δεξιά από αυτόν το γράμμα
0. Σύντοµη επισκόπηση θεωρίας πιθανοτήτων
 . Σύντοµη επισκόπηση θεωρίας πιθανοτήτων Α. Τυχαίες µεταβητές Τυχαία µεταβητή καείται µια µεταβητή η τιµή της οποίας καθορίζεται από το αποτέεσµα κάποιου στοχαστικού πειράµατος. Αν Ω ο δειγµατικός χώρος
. Σύντοµη επισκόπηση θεωρίας πιθανοτήτων Α. Τυχαίες µεταβητές Τυχαία µεταβητή καείται µια µεταβητή η τιµή της οποίας καθορίζεται από το αποτέεσµα κάποιου στοχαστικού πειράµατος. Αν Ω ο δειγµατικός χώρος
Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης
 Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης 2010-2011 kolako@ced.upatras.gr 10 Μαρτίου 2011 Πρόβημα 1 Ερώτημα ) Έστω W S και W B ο μέσος χρόνος αναμονής στην ουρά του σταθμού S και B αντίστοιχα. Λαμβάνοντας
Λύσεις Προαιρετικής Eργασίας Τεχνικές Εκτίμησης 2010-2011 kolako@ced.upatras.gr 10 Μαρτίου 2011 Πρόβημα 1 Ερώτημα ) Έστω W S και W B ο μέσος χρόνος αναμονής στην ουρά του σταθμού S και B αντίστοιχα. Λαμβάνοντας
ΕΦΑΡΜΟΓΕΣ ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ (ΜΜ618)
 ΕΦΑΡΜΟΓΕΣ ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ (ΜΜ6) Διδάσκων: Δρ. Χρήστος Τάντος, Εαρινό εξάμηνο 7- ΕΡΓΑΣΙΑ #: Θερμική ακτινοβοία Ημερομηνία ανάρτησης εργασίας στην ιστοσείδα του μαθήματος: -- Ημερομηνία παράδοσης εργασίας:
ΕΦΑΡΜΟΓΕΣ ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ (ΜΜ6) Διδάσκων: Δρ. Χρήστος Τάντος, Εαρινό εξάμηνο 7- ΕΡΓΑΣΙΑ #: Θερμική ακτινοβοία Ημερομηνία ανάρτησης εργασίας στην ιστοσείδα του μαθήματος: -- Ημερομηνία παράδοσης εργασίας:
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ» ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 o ΔΙΑΓΩΝΙΣΜΑ ΦΕΒΡΟΥΑΡΙΟΣ 0: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτεείς προτάσεις - να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπα το γράμμα
o ΔΙΑΓΩΝΙΣΜΑ ΦΕΒΡΟΥΑΡΙΟΣ 0: ΘΕΜΑΤΑ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις ημιτεείς προτάσεις - να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπα το γράμμα
Κβαντική Φυσική Ι. Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική. Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την εφαρμογή της
Κβαντική Φυσική Ι Ενότητα 15: Η έννοια του κυματοπακέτου στην Kβαντομηχανική Τερζής Ανδρέας Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει την εφαρμογή της
Στάσιμα Κύματα. Εξίσωση κύματος που διαδίδεται προς τη θετική φορά του άξονα xox :
 Στάσιμα Κύματα Εξίσωση κύματος που διαδίδεται προς τη θετική φορά του άξονα xox : y 1 = Aημ2π( t x ) Εξίσωση κύματος που διαδίδεται προς την αρνητική φορά του άξονα xox : y 2 = Aημ2π( t + x ) Η συμβοή
Στάσιμα Κύματα Εξίσωση κύματος που διαδίδεται προς τη θετική φορά του άξονα xox : y 1 = Aημ2π( t x ) Εξίσωση κύματος που διαδίδεται προς την αρνητική φορά του άξονα xox : y 2 = Aημ2π( t + x ) Η συμβοή
ΠΕΠΕΡΑΣΜΕΝΕΣ ΙΑΦΟΡΕΣ ΚΑΙ ΕΞΙΣΩΣΕΙΣ ΙΑΦΟΡΩΝ
 ΠΕΠΕΡΑΣΜΕΝΕΣ ΙΑΦΟΡΕΣ ΚΑΙ ΕΞΙΣΩΣΕΙΣ ΙΑΦΟΡΩΝ Α. Πεπερασµένες διαφορές Εστω δεδοµένος πραγµατικός αριθµός. Για τυχούσα συνάρτηση f = f() ορίζουµε ως διαφορά (πρώτης τάξης) της f() την συνάρτηση f µε f() =
ΠΕΠΕΡΑΣΜΕΝΕΣ ΙΑΦΟΡΕΣ ΚΑΙ ΕΞΙΣΩΣΕΙΣ ΙΑΦΟΡΩΝ Α. Πεπερασµένες διαφορές Εστω δεδοµένος πραγµατικός αριθµός. Για τυχούσα συνάρτηση f = f() ορίζουµε ως διαφορά (πρώτης τάξης) της f() την συνάρτηση f µε f() =
website:
 Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
Αλεξάνδρειο Τεχνολογικό Εκπαιδευτικό Ιδρυμα Θεσσαλονίκης Τμήμα Μηχανικών Αυτοματισμού Μαθηματική Μοντελοποίηση Αναγνώριση Συστημάτων Μαάιτα Τζαμάλ-Οδυσσέας 6 Μαρτίου 2017 1 Εισαγωγή Κάθε φυσικό σύστημα
ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός
 ηµήτρης Τσίνογου ρ. Μηχανοόγος Μηχανικός ΤΕΙ Σερρών Τµήµα Μηχανοογίας Αγωγή Μόνιµη κατάσταση Κεφάαιο 3 ΤΕΙ Σερρών Τµήµα Μηχανοογίας Το επίπεδο τοίχωµα Τοιχοποιία σπιτιών (τοίχοι, παράθυρα, στέγες) Τοιχώµατα
ηµήτρης Τσίνογου ρ. Μηχανοόγος Μηχανικός ΤΕΙ Σερρών Τµήµα Μηχανοογίας Αγωγή Μόνιµη κατάσταση Κεφάαιο 3 ΤΕΙ Σερρών Τµήµα Μηχανοογίας Το επίπεδο τοίχωµα Τοιχοποιία σπιτιών (τοίχοι, παράθυρα, στέγες) Τοιχώµατα
ˆ Αποτελείται από σωµατίδια, τα οποία πληρούν το µέσο χωρίς διάκενα. ˆ Τα σωµατίδια αυτά συνδέονται µεταξύ τους µε ελαστικές δυνάµεις.
 6 Κύµατα 6.1 Ορισµός του κύµατος Κύµα ονοµάζεται η διάδοση µιας διαταραχής που µεταφέρει ενέργεια και ορµή µε στα- ϑερή ταχύτητα. Εαστικό µέσο ονοµάζεται κάθε υικό µέσο που, για όγους απότητας, δεχόµαστε
6 Κύµατα 6.1 Ορισµός του κύµατος Κύµα ονοµάζεται η διάδοση µιας διαταραχής που µεταφέρει ενέργεια και ορµή µε στα- ϑερή ταχύτητα. Εαστικό µέσο ονοµάζεται κάθε υικό µέσο που, για όγους απότητας, δεχόµαστε
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κυματική εξίσωση Schrödiger Η δυνατότητα ενός σωματιδίου να συμπεριφέρεται ταυτόχρονα και ως κύμα, δηλαδή να είναι εντοπισμένο
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KΒΑΝΤΟΜΗΧΑΝΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ Κυματική εξίσωση Schrödiger Η δυνατότητα ενός σωματιδίου να συμπεριφέρεται ταυτόχρονα και ως κύμα, δηλαδή να είναι εντοπισμένο
Κύματα (Βασική θεωρία)
 Κύματα (Βασική θεωρία) Λεεδάκης Κωστής ( koleygr@gmailcom ) 10 Δεκεμβρίου 015 1 1 Βασικά στοιχεία Κύμα ονομάζεται οποιαδήποτε διαταραχή διαδίδεται μέσα στο χώρο Τα ηεκτρομαγνητικά κύματα είναι τα μόνα
Κύματα (Βασική θεωρία) Λεεδάκης Κωστής ( koleygr@gmailcom ) 10 Δεκεμβρίου 015 1 1 Βασικά στοιχεία Κύμα ονομάζεται οποιαδήποτε διαταραχή διαδίδεται μέσα στο χώρο Τα ηεκτρομαγνητικά κύματα είναι τα μόνα
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ. Ασκήσεις Κεφαλαίου Ι
 ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου Ι Άσκηση 1: Θεωρήστε δύο ορθοκανονικά διανύσματα ψ 1 και ψ και υποθέστε ότι αποτελούν βάση σε ένα χώρο δύο διαστάσεων. Θεωρήστε επίσης ένα τελαστή T που ορίζεται στο χώρο
ΚΒΑΝΤΟΜΗΧΑΝΙΚΗ Ασκήσεις Κεφαλαίου Ι Άσκηση 1: Θεωρήστε δύο ορθοκανονικά διανύσματα ψ 1 και ψ και υποθέστε ότι αποτελούν βάση σε ένα χώρο δύο διαστάσεων. Θεωρήστε επίσης ένα τελαστή T που ορίζεται στο χώρο
Μηχανικά Κύματα. ελαστικού μέσου διάδοσης στο οποίο διαδίδεται το κύμα.
 Μηχανικά Κύματα Τρέχον αρμονικό κύμα Ταχύτητα διάδοσης: υ δ = Δx Δt απόσταση που διένυσε το κύμα χρονικό διάστημα για την απόσταση αυτή ΣΗΜΑΝΤΙΚΟ: η ταχύτητα διάδοσης εξαρτάται ΜΟΝΟ από τις ιδιότητες του
Μηχανικά Κύματα Τρέχον αρμονικό κύμα Ταχύτητα διάδοσης: υ δ = Δx Δt απόσταση που διένυσε το κύμα χρονικό διάστημα για την απόσταση αυτή ΣΗΜΑΝΤΙΚΟ: η ταχύτητα διάδοσης εξαρτάται ΜΟΝΟ από τις ιδιότητες του
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ. Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής
 ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
ΜΙΓΑΔΙΚΟ ΔΥΝΑΜΙΚΟ ΓΕΝΙΚΑ Έστω σωμάτιο, στις τρεις διαστάσεις, που βρίσκεται υπό την επίδραση μιγαδικού δυναμικού της μορφής Re Im V r V r i V r, όπου οι συναρτήσεις Re,Im V r V r είναι πραγματικές συναρτήσεις
Έστω μια συνεχής (και σχετικά ομαλή) συνάρτηση f( x ), x [0, L]
![Έστω μια συνεχής (και σχετικά ομαλή) συνάρτηση f( x ), x [0, L] Έστω μια συνεχής (και σχετικά ομαλή) συνάρτηση f( x ), x [0, L]](/thumbs/53/31520444.jpg) c Σειρές Fourier-Μετασχηματισμός Fourier Έστω μια συνεχής (και σχετικά ομαλή) συνάρτηση f( ) [ ] για την οποία ξέρουμε ότι f() = f( ) =. Μια τέτοια συνάρτηση μπορούμε πάντα να τη γράψουμε : π f( ) = A
c Σειρές Fourier-Μετασχηματισμός Fourier Έστω μια συνεχής (και σχετικά ομαλή) συνάρτηση f( ) [ ] για την οποία ξέρουμε ότι f() = f( ) =. Μια τέτοια συνάρτηση μπορούμε πάντα να τη γράψουμε : π f( ) = A
Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1
 Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1 Μη- Σχετικιστική Κβαντομηχανική Η μη- σχετικιστική έκφραση για την ενέργεια: Στην QM αντιστοιχούμε την ενέργεια και την ορμή με Τελεστές:
Η εξίσωση Dirac (Ι) Σπύρος Ευστ. Τζαμαρίας Στοιχειώδη Σωμάτια 1 Μη- Σχετικιστική Κβαντομηχανική Η μη- σχετικιστική έκφραση για την ενέργεια: Στην QM αντιστοιχούμε την ενέργεια και την ορμή με Τελεστές:
ΚΕΦΑΛΑΙΟ 5 ΡΟΠΟΓΕΝΝΗΤΡΙΕΣ
 ΚΕΦΑΛΑΙΟ 5 ΡΟΠΟΓΕΝΝΗΤΡΙΕΣ 5 Εισαγωγή Σ αυτό το κεφάαιο θα δούµε ότι οι ροπές µιας τυχαίας µεταβητής µπορούν να υποογιστούν µε τη βοήθεια κατάηων συναρτήσεων Αυτές οι συναρτήσεις καούνται ροπογεννήτριες
ΚΕΦΑΛΑΙΟ 5 ΡΟΠΟΓΕΝΝΗΤΡΙΕΣ 5 Εισαγωγή Σ αυτό το κεφάαιο θα δούµε ότι οι ροπές µιας τυχαίας µεταβητής µπορούν να υποογιστούν µε τη βοήθεια κατάηων συναρτήσεων Αυτές οι συναρτήσεις καούνται ροπογεννήτριες
ETY-202 ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ ETY-202 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ. Στέλιος Τζωρτζάκης 1/11/2013
 stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ Στέλιος Τζωρτζάκης 1 3 4 Ο διανυσματικός χώρος των φυσικών καταστάσεων Η έννοια
stzortz@iesl.forth.gr 1396; office Δ013 ΙΤΕ 2 ΎΛΗ & ΦΩΣ 02. ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΕΡΓΑΛΕΙΑ ΤΗΣ ΚΒΑΝΤΟΜΗΧΑΝΙΚΗΣ Στέλιος Τζωρτζάκης 1 3 4 Ο διανυσματικός χώρος των φυσικών καταστάσεων Η έννοια
Παράρτημα Αʹ. Ασκησεις. Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός.
 Παράρτημα Αʹ Ασκησεις Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός. Άσκηση 1. Συμβατικά στην περιοχή του ηλεκτρομαγνητικού ϕάσματος μακρινό υπέρυθρο (far infrared, FIR) έχουμε μήκος
Παράρτημα Αʹ Ασκησεις Αʹ.1 Ασκήσεις Κεϕαλαίου 1: Εισαγωγή στη κβαντική ϕύση του ϕωτός. Άσκηση 1. Συμβατικά στην περιοχή του ηλεκτρομαγνητικού ϕάσματος μακρινό υπέρυθρο (far infrared, FIR) έχουμε μήκος
[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)
![[1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x) [1] είναι ταυτοτικά ίση με το μηδέν. Στην περίπτωση που το στήριγμα μιας συνάρτησης ελέγχου φ ( x)](/thumbs/52/30132893.jpg) [] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
[] 9 ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Η «συνάρτηση» δέλτα του irac Η «συνάρτηση» δέλτα ορίζεται μέσω της σχέσης φ (0) αν 0 δ[ φ ] = φ δ dx = (9) 0 αν 0 όπου η φ είναι μια συνάρτηση που ανήκει
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Συνήθεις Διαφορικές Εξισώσεις Ι ΣΔΕ Bernoulli, Riccati, Ομογενείς Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων
Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών
 ΤΕΙ ΛΑΡΙΣΑΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών Χρήστου Νικοαΐδη Φεβρουάριος 5 Χρήστος Νικοαΐδης Διδάκτωρ του Πανεπιστημίου της Οξφόρδης Στοιχεία Πιθανοτήτων
ΤΕΙ ΛΑΡΙΣΑΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών Χρήστου Νικοαΐδη Φεβρουάριος 5 Χρήστος Νικοαΐδης Διδάκτωρ του Πανεπιστημίου της Οξφόρδης Στοιχεία Πιθανοτήτων
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ 1. Μέσο μήκος ροής στα διαγράμματα ελέγχου τύπου Shewhart
 ΚΕΦΑΛΑΙΟ Μέσο μήκος ροής στα διαγράμματα εέγχου τύπου Shwhar. Διάγραμμα εέγχου τύπου Shwhar Στις παραγωγικές διεργασίες μας ενδιαφέρει η παρακοούθηση της συμπεριφορά μιας κρίσιμης ποσότητας ενός μετρήσιμου
ΚΕΦΑΛΑΙΟ Μέσο μήκος ροής στα διαγράμματα εέγχου τύπου Shwhar. Διάγραμμα εέγχου τύπου Shwhar Στις παραγωγικές διεργασίες μας ενδιαφέρει η παρακοούθηση της συμπεριφορά μιας κρίσιμης ποσότητας ενός μετρήσιμου
Τίτλος Μαθήματος: Μοριακή Κβαντική Χημεία. Ενότητα 10: Ερμηνεία Κυματοσυναρτήσεως Αριστείδης Μαυρίδης Τμήμα Χημείας
 Τίτλος Μαθήματος: Ενότητα 10: Ερμηνεία Κυματοσυναρτήσεως Αριστείδης Μαυρίδης Τμήμα Χημείας 1. Ερμηνεία Κυματοσυναρτήσεως.... Το κλασσικό όριο... 6 Σελίδα 1. Ερμηνεία Κυματοσυναρτήσεως Σε προηγούμενο μάθημα
Τίτλος Μαθήματος: Ενότητα 10: Ερμηνεία Κυματοσυναρτήσεως Αριστείδης Μαυρίδης Τμήμα Χημείας 1. Ερμηνεία Κυματοσυναρτήσεως.... Το κλασσικό όριο... 6 Σελίδα 1. Ερμηνεία Κυματοσυναρτήσεως Σε προηγούμενο μάθημα
Κβαντική Φυσική Ι. Ενότητα 5: Κυματομηχανική. Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 5: Κυματομηχανική Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η ερμηνεία της κυματοσυνάρτησης, δηλαδή της λύσης της εξίσωσης
Κβαντική Φυσική Ι Ενότητα 5: Κυματομηχανική Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοπός ενότητας Σκοπός της ενότητας είναι η ερμηνεία της κυματοσυνάρτησης, δηλαδή της λύσης της εξίσωσης
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ ΙΙ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΝΟΜΙΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΣΠΟΥΔ ΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΤΙΚΗΣ ΔΥΝΑΜΙΚΗΣ Μεθοδολογία Κλεομένης Γ. Τσιγάνης Λέκτορας ΑΠΘ Πρόχειρες
6.8 Συµβολή Κυµάτων. y = y 1 + y 2 +... http : //perif ysikhs.wordpress.com 55 Μιχάλης Ε. Καραδηµητριου
 6.8 Συµβοή Κυµάτων Οταν δύο ή περισσότερα κύµατα διαδίδονται ταυτόχρονα στο ίδιο εαστικό µέσο έµε ότι συµβάουν. Εχει διαπιστωθεί ότι για την κίνηση των σωµατιδίων του µέσου τα κύµατα ακοουθούν την αρχή
6.8 Συµβοή Κυµάτων Οταν δύο ή περισσότερα κύµατα διαδίδονται ταυτόχρονα στο ίδιο εαστικό µέσο έµε ότι συµβάουν. Εχει διαπιστωθεί ότι για την κίνηση των σωµατιδίων του µέσου τα κύµατα ακοουθούν την αρχή
Κβαντική Φυσική Ι. Ενότητα 25: Μαθηματική μελέτη του κβαντικού αρμονικού ταλαντωτή. Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 25: Μαθηματική μελέτη του κβαντικού αρμονικού ταλαντωτή Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την μελέτη
Κβαντική Φυσική Ι Ενότητα 25: Μαθηματική μελέτη του κβαντικού αρμονικού ταλαντωτή Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσιάσει την μελέτη
x y x z για κάθε x, y, . Ένας δακτύλιος R καλείται μεταθετικός αν
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο Θα περιοριστούμε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο Θα περιοριστούμε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
4. Όρια ανάλυσης οπτικών οργάνων
 4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
Αρµονική Ανάλυση. Ενότητα: Ο µετασχηµατισµός Hilbert στον L p (T) Απόστολος Γιαννόπουλος. Τµήµα Μαθηµατικών
 Ενότητα: Ο µετασχηµατισµός Hilbert στον L () Απόστοος Γιαννόπουος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υικό, όπως εικόνες,
Ενότητα: Ο µετασχηµατισµός Hilbert στον L () Απόστοος Γιαννόπουος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υικό, όπως εικόνες,
=, όπου Τ είναι η περίοδος του 12
 Ερωτήσεις στα κύματα 1. Εγκάρσιο αρμονικό κύμα, διαδίδεται πάνω σε εαστική χορδή μεγάου μήκους. Μετά την διάδοση του κύματος οι τααντώσεις που έχουν πραγματοποιηθεί κάποια χρονική στιγμή t 1 σε δυο σημεία
Ερωτήσεις στα κύματα 1. Εγκάρσιο αρμονικό κύμα, διαδίδεται πάνω σε εαστική χορδή μεγάου μήκους. Μετά την διάδοση του κύματος οι τααντώσεις που έχουν πραγματοποιηθεί κάποια χρονική στιγμή t 1 σε δυο σημεία
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ., 1 i n, με σταθερό όρο b F και συντελεστές a i
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Γραμμικά συστήματα Μία εξίσωση της μορφής K () καείται γραμμική εξίσωση μεταητών i i με σταθερό όρο F και συντεεστές i F όπου το F θα είναι το σώμα των πραγματικών ή μιγαδικών αριθμών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Γραμμικά συστήματα Μία εξίσωση της μορφής K () καείται γραμμική εξίσωση μεταητών i i με σταθερό όρο F και συντεεστές i F όπου το F θα είναι το σώμα των πραγματικών ή μιγαδικών αριθμών
+ παριστάνει : α. διάσπαση β β. διάσπαση γ γ. σύντηξη δ. σχάση. Μονάδες 5
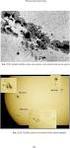 ΘΜ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Η πυρηνική αντίδραση 35 4 9 + 9 U 56 Ba 36 Kr + 3 + ενέργεια α. διάσπαση
ΘΜ ο Στις ερωτήσεις -4 να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Η πυρηνική αντίδραση 35 4 9 + 9 U 56 Ba 36 Kr + 3 + ενέργεια α. διάσπαση
Μερικές Διαφορικές Εξισώσεις
 Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
Πανεπιστήμιο Πατρών, Τμήμα Μαθηματικών Μερικές Διαφορικές Εξισώσεις Χειμερινό εξάμηνο ακαδημαϊκού έτους 14-15, Διδάσκων: Α.Τόγκας ο φύλλο προβλημάτων Ονοματεπώνυμο - ΑΜ: Πρόβλημα 1. Για κάθε μια από τις
E = 1 2 k. V (x) = Kx e αx, dv dx = K (1 αx) e αx, dv dx = 0 (1 αx) = 0 x = 1 α,
 Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μαθηματική Μοντελοποίηση Ι 1. Φυλλάδιο ασκήσεων Ι - Λύσεις ορισμένων ασκήσεων 1.1. Άσκηση. Ενα σωμάτιο μάζας m βρίσκεται σε παραβολικό δυναμικό V (x) = 1/2x 2. Γράψτε την θέση του σαν συνάρτηση του χρόνου,
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών (ΜΕΜ 274) Λύσεις Θεμάτων Εξέτασης Ιούνη 2019
 Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
Μέϑοδοι Εφαρμοσμένων Μαϑηματιϰών ΜΕΜ 74 Λύσεις Θεμάτων Εξέτασης Ιούνη 9 Ζήτημα Α Α. Δείξτε ότι αν p, q πραγματιϰά πολυώνυμα ίδιου βαϑμού, τότε p q ϰαϑώς ±. Λύση. Αρϰεί να δείξουμε ότι για με αρϰετά μεγάλο
ΦΥΕ34 Λύσεις 6 ης Εργασίας Ασκήσεις
 ΦΥΕ4 Λύσεις 6 ης Εργασίας Ασκήσεις ) α)η διακριτική ικανότητα του φράγµατος ορίζεται ως ο όγος, όπου, +δ, δ δύο µήκη κύµατος που µόις διακρίνονται µε γυµνό οφθαµό και δ πού µικρό Αυτό συµβαίνει σύµφωνα
ΦΥΕ4 Λύσεις 6 ης Εργασίας Ασκήσεις ) α)η διακριτική ικανότητα του φράγµατος ορίζεται ως ο όγος, όπου, +δ, δ δύο µήκη κύµατος που µόις διακρίνονται µε γυµνό οφθαµό και δ πού µικρό Αυτό συµβαίνει σύµφωνα
Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μιγαδικός λογισμός και ολοκληρωτικοί Μετασχηματισμοί ΣΥΝΑΡΤΗΣΙΑΚΟΙ ΧΩΡΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER Διδάσκων : Επίκ Καθ Κολάσης Χαράλαμπος Άδειες Χρήσης
Με αφορμή την άσκηση 2.47
 Με αφορμή την άσκηση 2.47 Σε κάποιο σημείο ενός ομογενούς εαστικού μέσου βρίσκεται μία πηγή Π παραγωγής εγκαρσίων κυμάτων d με εξίσωση y=a ημ(ωt). Στο σημείο Σ βρίσκεται δέκτης κυμάτων που απέχει απόσταση
Με αφορμή την άσκηση 2.47 Σε κάποιο σημείο ενός ομογενούς εαστικού μέσου βρίσκεται μία πηγή Π παραγωγής εγκαρσίων κυμάτων d με εξίσωση y=a ημ(ωt). Στο σημείο Σ βρίσκεται δέκτης κυμάτων που απέχει απόσταση
) = 2lnx lnx 2
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Σεπτέµβριος 8 Τµήµα Οικονοµικών Επιστηµών Μάθηµα: Μικροοικονοµική Ι ιδάσκοντες: Β. Ράπανος-Ι Χειάς Εξέταση στη Μικροοικονοµική Ι Στην εξέταση αυτή δίνονται δύο σύνοα το Α και το Β.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Σεπτέµβριος 8 Τµήµα Οικονοµικών Επιστηµών Μάθηµα: Μικροοικονοµική Ι ιδάσκοντες: Β. Ράπανος-Ι Χειάς Εξέταση στη Μικροοικονοµική Ι Στην εξέταση αυτή δίνονται δύο σύνοα το Α και το Β.
Το Ελεύθερο Σωμάτιο Ρεύμα Πιθανότητας
 Το Ελεύθερο Σωμάτιο Ρεύμα Πιθανότητας Δομή Διάλεξης Χρονική εξέλιξη Gaussian κυματοσυνάρτησης σε μηδενικό δυναμικό (ελέυθερο σωμάτιο): Μετατόπιση και Διασπορά Πείραμα διπλής οπής: Κροσσοί συμβολής για
Το Ελεύθερο Σωμάτιο Ρεύμα Πιθανότητας Δομή Διάλεξης Χρονική εξέλιξη Gaussian κυματοσυνάρτησης σε μηδενικό δυναμικό (ελέυθερο σωμάτιο): Μετατόπιση και Διασπορά Πείραμα διπλής οπής: Κροσσοί συμβολής για
ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 o ΔΙΑΓΩΝΙΣΜΑ ΦΕΒΡΟΥΑΡΙOΣ 0: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. γ.. α. 3. γ.. β. 5. α-λ, β-σ, γ-σ, δ-σ, ε-λ. ΘΕΜΑ Β. Σωστή είναι
o ΔΙΑΓΩΝΙΣΜΑ ΦΕΒΡΟΥΑΡΙOΣ 0: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α. γ.. α. 3. γ.. β. 5. α-λ, β-σ, γ-σ, δ-σ, ε-λ. ΘΕΜΑ Β. Σωστή είναι
e είναι ακέραια ρίζα του Ρ(χ), να βρεθούν
 Σύογος Θετικών Επιστηµόνων ράµας ιαγωνισµός στη µνήµη του καθηγητή: Βασίη Ξανθόπουου Μαθηµατικά : Τάξη: Β ράµα 30 Μαρτίου 01 Θέµα Α ίνεται το πουώνυµο P ( x) = x κ x+ κ κ: θετικός ακέραιος. Α 1. Να βρεθούν
Σύογος Θετικών Επιστηµόνων ράµας ιαγωνισµός στη µνήµη του καθηγητή: Βασίη Ξανθόπουου Μαθηµατικά : Τάξη: Β ράµα 30 Μαρτίου 01 Θέµα Α ίνεται το πουώνυµο P ( x) = x κ x+ κ κ: θετικός ακέραιος. Α 1. Να βρεθούν
Κεφάλαιο 6 Τυπικές συναρτήσεις κατανομής στην τεχνική υδρολογία
 Κεφάαιο 6 Τυπικές συναρτήσεις κατανομής στην τεχνική υδροογία Στο κεφάαιο αυτό περιγράφουμε τις τρεις βασικές οικογένειες συναρτήσεων κατανομής που χρησιμοποιούνται στην τεχνική υδροογία. Η πρώτη περιαμβάνει
Κεφάαιο 6 Τυπικές συναρτήσεις κατανομής στην τεχνική υδροογία Στο κεφάαιο αυτό περιγράφουμε τις τρεις βασικές οικογένειες συναρτήσεων κατανομής που χρησιμοποιούνται στην τεχνική υδροογία. Η πρώτη περιαμβάνει
Φυσική Γενικής Παιδείας Γ Λυκείου 2001
 Φυσική Γενικής Παιδείας Γ Λυκείου 00 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα ο Στις ερωτήσεις - να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Η πυρηνική αντίδραση:
Φυσική Γενικής Παιδείας Γ Λυκείου 00 ΕΚΦΩΝΗΣΕΙΣ Ζήτηµα ο Στις ερωτήσεις - να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Η πυρηνική αντίδραση:
Ασκηση 1: Να διατυπώσετε το πρόβλημα οριακών τιμών το οποίο απαιτείται για τη μαθηματική επίλυση του φυσικού μοντέλου που φαίνεται στο σχήμα: y Λ 2
 Ασκήσεις Κεφααίου 5 Ασκηση : Να διατυπώσετε το πρόβημα οριακών τιμών το οποίο απαιτείται για τη μαθηματική επίυση του φυσικού μοντέου που φαίνεται στο σχήμα: y K κυματιστήρας b b 4 M M 4 b 3 3 K κάτοψη
Ασκήσεις Κεφααίου 5 Ασκηση : Να διατυπώσετε το πρόβημα οριακών τιμών το οποίο απαιτείται για τη μαθηματική επίυση του φυσικού μοντέου που φαίνεται στο σχήμα: y K κυματιστήρας b b 4 M M 4 b 3 3 K κάτοψη
ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΜΕΛΕΤΗ ΣΤΑΣΙΜΟΥ ΚΥΜΑΤΟΣ ΣΕ ΧΟΡΔΗ ΣΤΕΡΕΩΜΕΝΗ ΣΤΑ ΑΚΡΑ ΤΗΣ
 ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ &ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΜΕΛΕΤΗ ΣΤΑΣΙΜΟΥ ΚΥΜΑΤΟΣ ΣΕ ΧΟΡΔΗ ΣΤΕΡΕΩΜΕΝΗ ΣΤΑ ΑΚΡΑ ΤΗΣ ΒΑΡΗ 2010 Κωνσταντίνος Μπίιας
ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ &ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΜΕΛΕΤΗ ΣΤΑΣΙΜΟΥ ΚΥΜΑΤΟΣ ΣΕ ΧΟΡΔΗ ΣΤΕΡΕΩΜΕΝΗ ΣΤΑ ΑΚΡΑ ΤΗΣ ΒΑΡΗ 2010 Κωνσταντίνος Μπίιας
Μηχανική ΙI. Μετασχηματισμοί Legendre. διπλανό σχήμα ότι η αντίστροφη συνάρτηση dg. λέγεται μετασχηματισμός Legendre της f (x)
 Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
Τμήμα Π Ιωάννου & Θ Αποστολάτου 7/5/000 Μηχανική ΙI Μετασχηματισμοί Legendre Έστω μια πραγματική συνάρτηση f (x) Ορίζουμε την παράγωγο συνάρτηση df (x) της f (x) : ( x) (η γραφική της παράσταση δίνεται
KATANOMEΣ- ΚΑΤΑΝΟΜΗ MAXWELL ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KATANOMEΣ- ΚΑΤΑΝΟΜΗ MAXWELL ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα 1. Στατιστικές Συλλογές. Κατανομή Gibbs 3. Από την Κατανομή Gibbs στις Κατανομές Maxwell
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 KATANOMEΣ- ΚΑΤΑΝΟΜΗ MAXWELL ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα 1. Στατιστικές Συλλογές. Κατανομή Gibbs 3. Από την Κατανομή Gibbs στις Κατανομές Maxwell
L2 {mk. K Z 1Z 2 e 2. v 8 ě 4 ˆ 10 7 m/s. Z 2 79, e 1.6ˆ10 19 C, 9ˆ10 9 Nm 2 /C 2
 Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βαχάκη, Ιανουαρίου Διάρκεια εξέτασης 3 ώρες, Καή επιτυχία ( = bonus ερωτήματα),
Ονοματεπώνυμο: Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βαχάκη, Ιανουαρίου Διάρκεια εξέτασης 3 ώρες, Καή επιτυχία ( = bonus ερωτήματα),
Κεφάλαιο 3. Γραµµικές ιαφορικές Εξισώσεις 2 ης (και ανώτερης) τάξης. Στο Κεφάλαιο αυτό θα ασχοληθούµε κυρίως µε γραµµικές δ.ε. 2 ης τάξης, διότι:
 Κεφάαιο 3 Γραµµικές ιαφορικές Εξισώσεις ης (και ανώτερης) τάξης Στο Κεφάαιο αυτό θα ασχοηθούµε κυρίως µε γραµµικές δε ης τάξης, διότι: οι γραµµικές δε ης τάξης έχουν ποές φυσικές εφαρµογές, η θεωρία των
Κεφάαιο 3 Γραµµικές ιαφορικές Εξισώσεις ης (και ανώτερης) τάξης Στο Κεφάαιο αυτό θα ασχοηθούµε κυρίως µε γραµµικές δε ης τάξης, διότι: οι γραµµικές δε ης τάξης έχουν ποές φυσικές εφαρµογές, η θεωρία των
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Φυσική Σημασία του Μετασχηματισμού Fourier Ο μετασχηματισμός Fourier
Κινητικότητα στα στάσιμα ή μαντεύω και επαληθεύω
 Κινητικότητα στα στάσιμα ή μαντεύω και επαηθεύω Αντί να προσθέσω κάποιες ασκήσεις μαζί με τις εκατοντάδες των ασκήσεων που μέχρι τώρα έχετε δει, προτιμώ να δούμε μαζί μια μικρή μεέτη στις διάφορες μορφές
Κινητικότητα στα στάσιμα ή μαντεύω και επαηθεύω Αντί να προσθέσω κάποιες ασκήσεις μαζί με τις εκατοντάδες των ασκήσεων που μέχρι τώρα έχετε δει, προτιμώ να δούμε μαζί μια μικρή μεέτη στις διάφορες μορφές
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
Κβαντική Φυσική Ι. Ενότητα 23: Σκέδαση σε τετραγωνικά δυναμικά. Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής
 Κβαντική Φυσική Ι Ενότητα 23: Σκέδαση σε τετραγωνικά δυναμικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να μελετήσει την περίπτωση σκέδασης σε σκαλοπάτι
Κβαντική Φυσική Ι Ενότητα 23: Σκέδαση σε τετραγωνικά δυναμικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να μελετήσει την περίπτωση σκέδασης σε σκαλοπάτι
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 26/10/2017. Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς
 Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
Συνθεις Διαφορικές Εξισώσεις Ι Ασκσεις - 26/0/207 Διαφορικές Εξισώσεις Bernoulli, Riccati και Ομογενείς Οι εξισώσεις Bernoulli αποτελούν την κλάση των μη γραμμικών διαφορικών εξισώσεων πρώτης τάξης της
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
5 Σχετικιστική μάζα. Στο Σ Πριν Μετά. Στο Σ
 Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
Α Τόγκας - ΑΜ333: Ειδική Θεωρία Σχετικότητας Σχετικιστική μάζα 5 Σχετικιστική μάζα Όπως έχουμε διαπιστώσει στην ειδική θεωρία της Σχετικότητας οι μετρήσεις των χωρικών και χρονικών αποστάσεων εξαρτώνται
S T (x) = exp. (α) m n q x = m+n q x m q x. (β) m n q x = m p x m+n p x. (γ) m n q x = m p x n q x+m. tp x = S Tx (t) = S T (x + t) { x+t
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΣΗΣ ΘΝΗΣΙΜΟΤΗΤΑΣ ΙΩΑΝΝΗΣ Σ. ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ, ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2013-2014
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΑΝΑΛΥΣΗΣ ΘΝΗΣΙΜΟΤΗΤΑΣ ΙΩΑΝΝΗΣ Σ. ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ, ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 2013-2014
