Telesá v pohybe. Kapitola 7
|
|
|
- Φωσφόρος Καψής
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Kapitola 7 Telesá v pohybe Aby sme mohli študovať správanie sa pohybujúcich sa telies, musíme preskúmať základný význam pojmu pohyb. Ktoré vlastnosti, charakteristiky pohybu vieme merať prípadne spočítať, aby nám pomohli v popise pohybujúcich sa telies? Dvojica takých činiteľov je zrejme dráha a čas potrebný na prejdenie dráhy, kým tretím je pojem priemernej rýchlosti. Zvykli sme si na to už všetci: ak do mesta, ktoré sa nachádza vo vzdialenosti 200 kilometrov dorazíme za 5 hodín, priemerná rýchlosť je 200 km/5 h = 40 km/h. Aj keď na to nemyslíme, tak používame nasledujúci vzťah, vzorec v priem = s t, kde v označuje rýchlosť, s prejdenú dráhu a t čas potrebný na prejdenie dráhy s. Vynásobme obidve strany tejto rovnosti t a dostaneme s = v priem t. Ak je napríklad priemerná rýchlosť 30 km/h, potom za 4 hodiny sa dostaneme do vzdialenosti 30 km/h 4 h = 120 km. Je úplne zrejmé, že v priem nám nehovorí nič o skutočnej rýchlosti v jednotlivých okamihoch. Auto spomalí, zastaví, zrýchli počas štvorhodinovej cesty mnohokrát, potrebujeme preto nájsť nejaký iný spôsob pre popis pohybujúceho sa telesa popis, ktorý zohľadní meniacu sa rýchlosť telesa. Za týmto účelom zavádzame pojem zrýchlenia, ktoré definujeme ako mieru zmeny rýchlosti. Poznamenávame, že kedykoľvek povieme rýchlosť, neznamená to len veľkosť rýchlosti, ale tiež jej smer: rýchlosť je vektorová veličina. Neskôr uvidíme, že v prípade telies pohybujúcich sa po kružnici existuje zrýchlenie aj vtedy, ak veľkosť rýchlosti je stále rovnaká, mení sa ale jej smer Veličiny popisujúce pohyb
2 Kapitola Nechajme však bez povšimnutia zmenu smeru a zaoberajme sa len s takými zmenami rýchlosti, pri ktorých sa mení veľkosť rýchlosti. Ak stlačíme plynový pedál auta, rýchlosť začne rásť, napríklad z 5 km/h na 40 km/h za 10 sekúnd. Vzorec zodpovedajúci definícii zrýchlenia je a = v t (, veľké grécke písmeno delta jedna z matematických skratiek znamená skoro vždy zmenu. Táto zmena je pozitívna, ak príslušná veličina rastie, je negatívna, ak klesá.) Dosaďme do nášho vzorca naše údaje a = 40 km/h 5 km/h 10 sec =. 35 km/h 10 sec = 3,5 km/h/sec, čo znamená, že rýchlosť vzrastie každú sekundu o 3,5 km/h. Toto je dosť nešikovná (aj keď naprosto správna) veličina; zrýchlenie udávame skôr v jednotkách m/sec/sec, teda m/sec 2 (prípadne v cm/sec 2 ). Ak sa teleso dostáva do pohybu z pokoja a pohybuje sa so stálym zrýchlením a m/sec 2, potom na konci druhej sekundy sa bude pohybovať rýchlosťou 2a m/sec 2 a tak ďalej. Úplne všeobecne môžeme písať, že na konci t tej sekundy sa bude pohybovať rýchlosťou v t = at. Tento vzťah sa dá úspešne použiť v mnohých prípadoch, ale často potrebujeme taký vzorec, v ktorom vystupuje aj vzdialenosť telesa od východiskového bodu. Aby sme sa k tomuto vzorcu dostali, pozrime si obrázok 7.1a, na ktorom sme graficky znázornili priebeh rýchlosti v závislosti od času v prípade rovnomerného zrýchlenia tj. v prípade, keď zrýchlenie a sa nemení, je konštantné. Keďže prírastok rýchlosti za každú sekundu je rovnaký, graf je priamka a priemerná rýchlosť (v priem ) v nejakom časovom intervale sa rovná rýchlosti uprostred tohoto časového intervalu. Napríklad v časovom intervale, ktorý trvá od t = 2 do t = 4 je priemerná rýchlosť 3a, je rovná rýchlosti, ktorá patrí k časovému okamihu t = 3. Ak pohyb začína z pokoja v okamihu t = 0, potom priemerná rýchlosť pohybujúceho sa telesa za prvých t sekúnd sa rovná 1 2 at. Na obrázku 7.1b môžeme vidieť aj číselný príklad. Dráhu, ktorú teleso prejde dostaneme tak, že priemernú rýchlosť vynásobíme dobou pohybu. (Auto s priemernou rýchlosťou 40 km/h prejde za 5 hodín 200 kilometrov.) Môžeme teda písať, že s = v priem čas = 1 2 at t = 1 2 at2.
3 Biofyzika a radiológia 117 Obr. 7.1: Rýchlosť pohybu pri rovnomernom zrýchlení v závislosti od času. Z rovníc, ktoré sme dostali doteraz, sa dostaneme k tretej vylúčením času. Je známe, že v t = at, odtiaľ t = v t /a a takto t 2 = v 2 t /a2. Dosaďme tento výsledok do vzťahu s = 1 2 at2 s = 1 2 a v2 t a 2 = v2 t 2a a v 2 t = 2as. Pohybové rovnice, ktoré sme obdržali môžeme používať len vtedy, ak zrýchľujúce sa teleso vyrážalo z pokoja. Vzťahy však chceme zapísať aj pre také telesá, ktoré sa pred zrýchlením už pohybovali určitou rýchlosťou v 0. Vzťah v t = at hovorí, že ako sa zväčšuje rýchlosť v dôsledku zrýchlenia. K tejto veličine musíme jednoducho pridať rýchlosť v 0, ktorú teleso malo na začiatku a okamžite dostávame obecnejší výraz: v t = v 0 + at. Nasledujúci vzťah s = 1 2 at2 udáva do akej vzdialenosti sa dostalo zrýchľujúce sa teleso. Keby sa pohybovalo bez zrýchlenia s počiatočnou rýchlosťou v 0, za t sekúnd by prešlo dráhu v 0 t. Sčítajme tieto dva údaje: s = v 0 t+ 1 2 at2. Podobne sa dostaneme aj k našej tretej rovnici: v 2 t = v as. Napíšme si tieto tri rovnice s krátkymi poznámkami 1. v t = v 0 + at (nevystupuje prejdená dráha); 2. s = v 0 t at2 (nevystupuje konečná rýchlosť); 3. vt 2 = v as (nevystupuje konečný čas).
4 Kapitola To, že ktorý (ktoré) zo vzťahov použijeme závisí len od toho, že čo je v danej úlohe dané a čo hľadáme. Hľadajme napríklad zrýchlenie auta, ktoré zrýchli za 15 sekúnd z rýchlosti 20 m/s na rýchlosť 80 m/s. Poznáme teda v 0, v t a t; nepoznáme a. V našej prvej rovnici máme všetky tieto veličiny, preto píšeme, že 7-2 Príčina pohybu 80 = a 15a = = 60 a = = 4 m/sec2. Ďalej by sme chceli vedieť, že koľko metrov auto prešlo počas zrýchľovania. Nakoľko zrýchlenie už poznáme, môžeme použiť tretiu rovnicu 80 2 = s 8s = = 6000 s = 6000 = 750 m. 8 (Mohli by sme sa k tomuto výsledku dopracovať aj inou cestou?) V tomto príklade má zrýchlenie, rýchlosť a posunutie (dráha) všade súhlasný smer. Často je však situácia odlišná a v takých prípadoch sa musíme poriadne pozrieť kam napísať znamienko + a kam. Nech sa pohybuje auto v severnom smere rýchlosťou 30 m/sec. Šofér brzdí a znižuje rýchlosť v každú sekundu o 5 m/sec. Toto zníženie rýchlosti je spomalenie, čo zo stávajúcej rýchlosti musíme odčítať, ale môžeme na neho hľadieť aj ako na zrýchlenie v južnom smere. Ak znamienko + priradíme vektoru ukazujúcemu v severnom smere, potom zrýchlenie bude: a = 5 m/s 2. Za aký čas sa autu podarí zastaviť zistíme z rovnice v t = v 0 + at. Nakoľko konečná rýchlosť je v t = 0, 0 = +30 5t a t = 6 sec. Už aj malé deti vedia, že medzi silou a pohybom je nejaká súvislosť tlak, alebo ťah často hýbe s vecami. Avšak to, že aký je vzťah medzi silou a pohybom, zďaleka nie je samozrejmé. V skutočnosti základné princípy vzťahujúce sa na pohyb do 17-ho storočia neskúmali. Súvislosť medzi posunutím, rýchlosťou a časom skúmal prvý krát taliansky prírodovedec Galilei, asi tak, ako sme to urobili mi v predchádzajúcom odseku; pravdepodobne bol to on, kto prvý krát povedal, že čo je zrýchlenie a rozpoznal jeho dôležitosť pri skúmaní pohybu. Galilei zomrel v roku 1642 v Taliansku a v tom istom roku sa narodil veľký fyzik a matematik, Isaac Newton. Jeho práca stavala na základy položené Galileim a dopracoval sa k trom základným zákonom pohybu.
5 Biofyzika a radiológia 119 Newtonov prvý pohybový zákon: Každé teleso zostane v pokoji, alebo bude vykonávať priamočiary a rovnomerný pohyb, kým nejaká vonkajšia sila ho neprinúti zmeniť svoj pohybový stav. Tento zákon vyjadruje tzv. zotrvačnosť hmoty, ktorá vyjadruje odpor telies voči akejkoľvek zmene rýchlosti. Zákon vyslovuje aj to, že rýchlosť telesa sa môže zmeniť len vtedy, ak na neho pôsobí nejaká sila. Vráťme sa ku knihe, ktorá leží na stole a potlačme ho z boku. Ak je táto sila tlačenia malá, kniha sa nepohne vieme, že prečo: sile tlačenia odoláva, vyrovnáva ju rovnako veľká, ale opačne orientovaná trecia sila. Kniha sa začne pohybovať až vtedy, ak sila tlaku prevýši treciu silu. Situácia je menej zrejmá, ak knihu tlačíme po doske stola nemennou rýchlosťou po priamočiarej dráhe jej rýchlosť sa teda nemení. V tomto prípade sme dokonale vyvážili treciu silu, výslednica sily tlačenia a trecej sily je nulová. Ak knihu tlačíme väčšou silou, väčšou než je trecia sila, potom sa pohyb knihy zrýchľuje; ak prestaneme tlačiť, brzdiaca trecia sila knihu rýchlo zastaví. Toto je všetko správne a dobré ale nedostal nás bližšie k vyriešeniu problému, k vyjasneniu toho, že čo sa presne deje vtedy, ak vektorová výslednica síl pôsobiaca na teleso nie je nulová. Vedci a filozofovia nepochopili podstatu tejto otázky dlhé storočia, nakoľko vo svojej neistote hľadali súvislosť medzi silou a rýchlosťou, predpokladajúc, že príčinou rýchlosti je sila. Galileimu sa takmer podarilo problém uchopiť, a Newton ho jasne rozpoznal: bezprostredná súvislosť nie je medzi rýchlosťou a silou, ale medzi zrýchlením a silou. Newtonov druhý pohybový zákon: Zrýchlenie telesa, ktoré vyvoláva sila na neho pôsobiaca, je priamo úmerné sile a jeho smer je súhlasný so smerom sily. Ak tá istá sila pôsobí na telesá rôznej hmotnosti, ňou vyvolané zrýchlenie je nepriamo úmerné hmotnosti telesa. Než by sme napísali Newtonov druhý zákon aj pomocou vzťahu, zastavme sa na minútku a povedzme si pár slov o pojme hmotnosť, o hmotnosti, ktorá má v tomto zákone tak dôležitú rolu. Akákoľvek hmota, hmotné teleso má dve všeobecné charakteristiky: pôsobí na neho gravitačná sila má teda nejakú tiaž, a kladie odpor zrýchleniu teda má zotrvačnosť. Obidve vlastnosti sa dajú využiť k určeniu hmotnosti telesa. Tiaž telesa je niečo, čo môžeme merať bezprostredne pomocou pružinových váh. Zoberme napríklad vzorový kilogram (veľkou obozretnosťou vyrobenú kópiu prakilogramu stráženého v pivnici v Sèvres) a zavesme ho na pružinové váhy bez stupnice. Uvedomme si, než by sme zaznamenali polohu ručičky, že merania budeme robiť na rôznych miestach najprv v meste 3-3 Hmotnosť a tiaž Obr. 7.2: Tiaž kilogramového závažia závisí od zemepisnej polohy.
6 Kapitola Boulder, vo výške 1500 metrov nad morom (štát Colorado), potom na hladine mora v meste San Francisco. Druhé z uvedených miest je máličko bližšie k stredu Zeme gravitačná príťažlivosť je väčšia, vzorový kilogram je ťažší, ručička pružinových váh sa zastaví máličko nižšie, než v prvom prípade. Ak s našimi váhami vyjdeme na vrchol Mount Everestu, do výšky 4346 metrov, tiaž vzorového kilogramu bude menšia, na váhach musíme nakresliť k tiaži toho istého vzorového kilogramu tretiu rysku (obrázok 7.2). Ktorú z trojice rysiek budeme považovať za definitívnu? Akou stupnicou vybavia váhy výrobcovia? Nakoľko väčšina ľudskej populácie žije vo výškach blízkych morskej výške, rysku označujúcu 1 kilogram vyryjú mierne nad znak, ktorý sme namerali v San Franciscu, zdá sa, že takto to musí byť správne. V každodennom živote používané váhy nie sú precízne prístroje a ani väčšiu presnosť nevyžadujú. Ak v rôznych výškach ukazujú váhy o chlp iné hodnoty, to nie je nebezpečné, lebo tí, ktorí používajú pružinové váhy, sú spokojní ich presnosťou. Podstatou nášho bádania je, že tiaž gramu alebo kilogramu je závislá od miesta, kde ho meriame. Existujú samozrejme aj váhy iného druhu napríklad jednoduché rovnoramenné váhy, alebo precízne analytické váhy (pozri obrázok 7.3) používaním takýchto váh sa zbavíme spomínaných rušivých vplyvov okamžite. Zoberme napríklad kameň, ktorý je v meste Boulder vyvážený na rovnoramenných váhach presne našim vzorovým kilogramom. Tento kameň bude na rovnoramenných váhach v presnej rovnováhe aj v San Franciscu, aj na Mount Evereste. Pôsobenie gravitácie na kameň sa síce mení z miesta na miesto, ale vždy bude rovnaké, ako pôsobenie gravitácie na vzorový kilogram. Na základe takýchto úvah môžeme prijať za fakt, že hmotnosť kameňa je rovnaká, ako hmotnosť vzorového kilogramu. Ešte kratšie: hmotnosť kameňa je 1 kilogram. Aká je skutočná tiaž kameňa? To nie sme schopní povedať ani vypočítať dovtedy, pokiaľ nejakou inou cestou nie sme schopný zmerať, alebo vypočítať silu gravitačnej príťažlivosti na tom mieste, kde sme na túto tiaž zvedaví. Tiaž je teda sila a to je niečo iné, než hmotnosť napriek tomu, že v bežnom živote a v obchode veľmi často hovoríme o váhe (tiaži) niečoho a pritom máme na mysli hmotnosť. Gram a kilogram sú hmotnostné jednotky, ale ich tiaž meraná na 45 zemepisnej šírky na úrovni hladiny mora je jednotkou sily. Vyjadrujeme to aj v ich názvoch: tiaž 1 gramu je 1 pond a tiaž 1 kilogramu je 1 kilopond. (V predchádzajúcej kapitole sme tieto jednotky už používali.) Predstavme si, že v neznámej nadmorskej výške zoberieme kameň a položíme ho na jeden z misiek rovnoramenných váh, a prikladaním závaží (aj toto je nesprávne pomenovanie, ale nič proti nemu nedokážeme urobiť) na druhú misku kameň vyvážime. Týmto spôsobom presne určíme hmotnosť
7 Biofyzika a radiológia 121 kameňa v kilogramoch, alebo v gramoch, ale jeho tiaž nie. Ak použijeme presne ociachované pružinové váhy, sme schopní povedať aká je tiaž kameňa v kilopondoch, alebo v pondoch, ale nevieme aká je jeho hmotnosť. Aby sme dokázali ozrejmiť súvislosť medzi hmotnosťou a tiažou telies, musíme skúmať podrobnejšie zotrvačnosť (inerciu) telies. Obr. 7.3: Kilogramové závažie pri porovnaní s etalónom je na každom zemepisnom mieste rovnaké Newtonov druhý pohybový zákon hovorí, že (v prípade rovnakých hmotností) zrýchlenie je priamo úmerné sile a (v prípade rovnakých síl) zrýchlenie je nepriamo úmerné hmotnosti. Pomocou vzorca to môžeme zapísať nasledovne a = k F m. Jednotku vzdialenosti a času sme už definovali, tie sú potrebné k meraniu zrýchlenia a, definovali sme aj jednotku hmotnosti (v sústave CGS a tiež MKS, gram a kilogram). Ak chceme určiť jednotku sily, je účelné koeficient k vystupujúci v rovnici považovať za 1 (aj vedci 19-ho storočia to tak robili). V tomto prípade a = F/m, čo máme vo zvyku zapisovať vo forme F = ma.
8 Kapitola Táto jednotka sily v sústave CGS sa nazýva dyn, v sústave MKS newton. Jednotka sily kilopond, ktorú sme použili už v predchádzajúcej kapitole je jednotkou sily v tzv. technickej sústave. V tejto sústave je jednotka sily základná veličina, inými slovami: neodvádza sa od jednotiek hmotnosti a zrýchlenia. V technickej sústave je to naopak: z jednotiek sily a zrýchlenia dostávame jednotku hmotnosti, ktorého názov je technická jednotka hmotnosti (Tjh). Neskôr sa tejto otázke budeme venovať podrobnejšie, teraz len poznamenáme, že 1 Tjh = 9, 81 kg. Zhrňme doteraz známe jednotky do tabuľky teda Sústava Hmotnosť Zrýchlenie Sila CGS gram cm/sec 2 dyn MKS kilogram m/sec 2 newton Technická techn. jedn. hmotnosti m/sec 2 kilopond 1 dyn = 1 g cm/sec 2 1 newton = 1 kg m/sec 2 = 10 5 dyn 1 kilopond = 9,81 kg m/sec 2 = 9,81 newton = 9, dyn. Vypočítajme v rámci cvičenia, že akou veľkou silou musíme brzdiť vlakovú súpravu s hmotnosťou 200 ton a pohybujúcu sa rýchlosťou 24 m/sec, aby sa zastavila za 2 minúty. Ak smer pohybu považujeme za kladný smer, potom potrebná zmena rýchlosti je zrýchlenie je teda Hmotnosť sústavy v sústave MKS je a hľadaná sila je v = 0 24 = 24 m/sec, v/t = 24/120 = 0,20 m/sec 2. m = = kg, F = ma = ( 0,20) = newton. Záporné znamienko výsledku ukazuje, že smer sily je opačný, ako smer pohybu. K zastaveniu vlakovej súpravy je potrebná brzdiaca sila.
9 Biofyzika a radiológia 123 V druhom príklade uvažujme vozidlo, ktorého hmotnosť je 1500 kg a rýchlosť 20 m/sec. Koľko metrov prejde vozidlo, než sa zastaví ak brzdiaca sila bude newtonov? Túto vzdialenosť vieme ľahko vypočítať, ak poznáme zrýchlenie; na základe Newtonovho druhého pohybového zákona ho vieme vypočítať z hmotnosti vozidla a z brzdiacej sily F = ma; a = F m = = 8 m/sec 2. Ďalej v 2 t = v as 0 = s, s = = 25 m. (V tomto príklade sme mlčky uvažovali o zrýchlení ako o kladnej veličine, nakoľko za kladný smer sme zobrali smer brzdiacej sily. Tento smer je opačný, ako smer pohybu vozidla. Znamienko vo výsledku 25 m ukazuje, že vozidlo postupovalo pri brzdení v opačnom smere, než pôsobila brzdiaca sila a než sa zastavilo, postúpilo dopredu 25 metrov.) Pozrime sa v rámci tretieho príkladu na to, že aké bude zrýchlenie elektrónu, ak elektrické pole pôsobí na elektrón s hmotnosťou gram silou 1, dyn. F = ma; a = F m = 1, = cm/sec 2. Šikmá veža v Pise, jedna z architektonických divov, je nerozlučne spätá s dejinami fyziky, nakoľko hrala úlohu v jednom experimente, ktorý údajne vykonal práve tu pred viac než 300 rokmi slávny taliansky prírodovedec Galilei. Podľa vyprávania nechal padnúť z najvyššieho balkónu veže súčasne dve gule: jednu ťažkú železnú a jednu ľahkú drevenú (obrázok 7.4). Napriek veľkému váhovému rozdielu medzi telesami zaryli sa do zeme skoro súčasne. Očakávali by sme aj mi rovnaký výsledok aký dosiahol Galilei? Predpokladajme, že hmotnosti gúľ sú 10 kg a 1 kg, železná guľa je teda 10 krát ťažšia, ako drevená. Tiaž gúľ je tá sila, ktorá spôsobuje ich zrýchlenie smerom dole a dostávame sa k záveru, že železná guľa síce má desaťkrát väčšiu hmotnosť, ale aj sila spôsobujúca zrýchlenie je desaťnásobná: zrýchlenie oboch gúľ je potom rovnaké, musia padať jedna vedľa druhej a musia dopadnúť naraz. Skúmajme však voľný pád telies ďalej a zmerajme zrýchlenie 1 kilogramového telesa v Eagle City na Aljaške. Metóda, pomocou ktorej sa zrýchlenie dá zmerať veľkou presnosťou je síce iná, ale zrýchlenie určíme v podstate 7-4 Tiaž a voľný pád
10 Kapitola tak, že starostlivo zmeriame dobu, za ktorú voľne padajúce teleso dopadne na zem z presne určenej výšky. Zrýchlenie sa potom dá vypočítať na základe vzťahu s = 1 2 at2.
11 Biofyzika a radiológia 125 Obr. 7.4: Galileiho experiment s voľne padajúcimi telesami. Zrýchlenie voľne padajúceho telesa smerujúce smerom dole (ktoré je zvykom na celom svete značiť g) má na Aljaške hodnotu 982,18 cm/sec 2, teda 9,8218 m/sec 2. Z toho, čo sme povedali o definícii jednotky sily vieme, že sila veľkosti 1 newton udelí telesu s hmotnosťou 1 kilogram zrýchlenie 1 m/sec 2 ; k tomu, aby zrýchlenie bolo 9,8218 m/sec 2 potrebujeme silu
12 Kapitola 9, 8218 newtonov. Môžeme teda povedať, že v Eagle City je tiaž kilogramového závažia presne 9, 8218 newtonov. Zopakujme náš experiment v Panama City, v oblasti kanálov; tu zistíme, že g = 9,7824 m/sec 2, z čoho môžeme usúdiť, že kilogramové závažie má na tomto mieste tiaž 9, 7824 newtona. Vo všeobecnosti môžeme povedať, že pre každé teleso platí tiaž = hmotnosť násobená gravitačným zrýchlením = m g. (7.1) Obr. 7.5: Atwoodov pádostroj na zmiernenie gravitácie, na spomalenie voľného pádu. (Nezabudnime, že výpočty musíme robiť vždy v tej istej sústave jednotiek, teda buď dyn, gram a cm/sec 2, alebo newton, kilogram a m/sec 2 ; alebo kilopond, Thj. a m/sec 2.) Skúmanie voľne padajúcich telies je výbornou metódou k spoznaniu základných pohybových zákonov. Nakoľko voľný pád je dosť rýchly, aby sme ho mohli pozorovať pohodlne, vymyslelo sa k jeho spomaleniu mnoho dôvtipných zariadení: takým zariadením je napríklad Atwoodov pádostroj (obrázok 7.5). Jedná sa v podstate o dlhú zvislú tyč s ľahkou kladkou na vrchu točiacou sa bez trenia doplnený súborom kovových závaží overenej hmotnosti; tieto môžeme zavesiť v ľubovoľnom množstve na konce šnúry vedenej cez kladku. S týmto zariadením v závislosti od toho, že aké je jeho prevedenie (väčšinou sa jedná o 2 metre vysokú tyč vybavenú s presnými stopkami) môžeme približne, alebo presnejšie merať dĺžku dráhy s a čas t, čím môžeme študovať vzťah medzi silou, hmotnosťou a zrýchlením. Predpokladajme, že na jednom konci vlákna Atwoodovho pádostroja vytvoríme zo závaží záťaž s hmotnosťou 900 gramov a na druhom konci záťaž s celkovou hmotnosťou 800 gramov. Je zrejmé, že ak pustíme šnúru, ťažšia strana (záťaž s hmotnosťou 900 gramov) začne klesať. Aké veľké bude zrýchlenie smerujúce smerom dole? Keby bola na oboch stranách záťaž 800 gramov, záťaže by boli vyvážené a nebolo by zrýchlenie; ak však rovnováha nie je, potom zrýchľujúcou silou bude tiaž prebytku 100 gramov na jednej strane. Problém je v tom, že nepoznáme presne tiaž závažia s hmotnosťou 100 gramov. Keby túto knihu čítali výhradne len v Eagle City na Aljaške, mohli by sme s najväčším kľudom prehlásiť, že každé závažie s hmotnosťou 100 gramov má tiaž m g dyn, teda , 18 = dyn. V blízkosti Panamského prieplavu však bude mať hmotnosť 100 gramov tiaž dyn. Pokiaľ si však môžeme dovoliť chybu niekoľko desatín percenta, môžeme počítať tak, akoby g = 980 cm/sec 2, alebo 9,8 m/sec 2 všade na zemskom povrchu. V Atwoodovom pádostroji bude urýchľujúca sila = dyn, tj. 0, 98 newtona.
13 Biofyzika a radiológia 127 Obr. 7.6: Záťaže zavesené na konce vlákna Atwoodovho zariadenia. Táto sila urýchľuje obidve hmotnosti, teda celkom = 1700 gramov, čo je 1,7 kilogramu. Zrýchlenie je potom alebo a = F m = = 57,6 cm/sec 2 0,980 1,700 = 0,576 m/sec2. Ak poznáme zrýchlenie, vieme určiť prejdenú dráhu, čas, rýchlosť atď. v každom prípade. V súvislosti s Atwoodovým pádostrojom, s ktorým sme sa zoznámili, sa môžeme pýtať aj na iné veci. Aké napätie vzniká vo vlákne? Ak chytíme 900 gramové závažie a zabránime mu v pohybe, vlákno drží len tiaž 800 gramového závažia a tá budí vo vlákne napätie = dyn. Ak chytíme 800 gramové závažie, napätie vo vlákne sa rovná tiaži 900 gramového závažia, čo je dyn. Je správny náš predpoklad, že keď závažia sa budú môcť pohybovať na pádostroji, tak napätie vlákna bude niekde medzi týmito dvomi hodnotami? Úloha sa dá vyriešiť, pokiaľ hľadíme len na jednu zo závaží napríklad na 800 gramové, a ostatné časti zariadenia necháme úplne bez povšimnutia (to je metóda, keď zložitý problém skúmame oddelením, izolovaním jednej je časti; pozri obrázok 7.6).
14 Kapitola Pozrime sa teda na 800 gramové závažie, ktoré sa pohybuje smerom hore so zrýchlením 57,6 cm/sec 2. Toto zrýchlenie spôsobuje sila F = ma = ,6 = dyn smerujúca hore. Táto sila je výslednicou dvoch síl pôsobiacich na závažie: (1) napätia T vo vlákne ukazujúceho smerom hore a (2) tiaže dyn závažia smerujúcej dole. Nakoľko napätie T je väčšie ako tiaž závažia, môžeme písať nasledujúce 1 T mg = T = mg = = dyn. Rovnakým spôsobom môžeme skontrolovať výsledok s izolovaným 900 gramovým závažím. Nakoľko toto závažie zrýchľuje smerom dole, jeho tiaž je väčšia ako napätie vo vlákne a preto mg T = ma T = ,6 = ,6 T = = dyn. 7-5 Naklonené roviny Na obrázku 7.7 chlapec sa šmýka na sánkach po svahu so sklonom 20. Ak sneh je znečistený blatom, koeficient trenia môžeme považovať za 0,25. V tomto príklade sa deje pohyb pozdĺž svahu, naklonenej roviny. Zrýchlenie chlapca a aj sila vyvolávajúce zrýchlenie pôsobí v tomto smere, je rovnobežné s dĺžkou naklonenej roviny. Gravitačná príťažlivosť G je však aj v tomto prípade zvislá. Toto G môžeme ľahko rozdeliť na dve zložky: jedna je rovnobežná s dĺžkou naklonenej roviny (F l ), druhá je na ňu kolmá (F n ). Zložka F l zrýchľuje sánky; F n je kolmá na smer pohybu, preto sama priamo pohyb ani neovplyvňuje. Táto zložka kolmá k rovine nazývaná tiež: normálová zložka, zložka ukazujúca v smere normály roviny však pritláča sánky k snehu; je to presne tá zložka sily, ktorú potrebujeme k výpočtu trecej sily brzdiacej sánky. Môžeme vypočítať silu, ktorá urýchľuje sánky smerom dole F = F l F t = = F l µf n = Gsin 20 0,25 Gcos 20 = = G 0,342 0,25 G 0,940 = 0,107G. 1 Nakoľko hodnota g (980 cm/sec 2 ) je v našich výpočtoch už zaťažená chybou, nie je presná, nebolo by opodstatnené uvádzať ani výsledok presnosťou na viac ako tri platné cifry; výsledok sme preto zaokrúhlili na
15 Biofyzika a radiológia 129 Obr. 7.7: Rozloženie gravitačnej príťažlivosti na dve zložky: jedna je rovnobežná so smerom pohybu druhá je na neho kolmá. Hmotnosť saní sme neudali; predpokladajme, že v nejakej sústave jednotiek je táto hmotnosť m. V tej istej sústave je tiaž saní rovná G = mg. Potom F = ma 0, 107mg = ma. Hmotnosť sa nám vykráti, napovedajúc, že výsledok bude rovnaký pre sane s ľubovoľnou hmotnosťou a = 0,107g. Presne k tomu istému výsledku sa môžeme dopracovať aj úvahou, že ak sila rovnajúca sa tiaži telesa spôsobuje zrýchlenie g, potom sila rovnajúca sa 0, 107 násobku tiaže telesa meranej v ľubovoľnej sústave jednotiek spôsobí zrýchlenie 0, 107g. Nakoľko každé nepodopreté teleso má v dôsledku gravitačnej príťažlivosti rovnaké zrýchlenie smerujúce dole, rovnice rovnomerného zrýchlenia (voľného pádu) možno použiť pre všetky voľne padajúce telesá, či sa už jedná o raketu, golfovú loptičku, alebo strelu vystrelenej z pušky. Pozrime si napríklad jednoduchý príklad, keď chlapec stojací na moste 10 metrov nad vod- 7-6 Vrh
16 Kapitola nou hladinou vyhodí do vzduchu smerom zvislo hore kameň s počiatočnou rýchlosťou 20 m/sec. Do akej výšky sa dostane kameň? Tu sa na chvíľku musíme zastaviť, aby sme zvážili tú časť problému, ktorú sme v úlohe vyslovene nepovedali menovite to, že kameň v bode, v ktorom dosiahne svoju najväčšiu výšku, sa na okamih zastaví. Otázku môžeme teraz vysloviť v inej podobe: Ak poznáme počiatočnú rýchlosť v 0 (+20 m/sec, nakoľko v 0 ukazuje smerom hore) a zrýchlenie a ( 9,8 m/sec 2, nakoľko smer gravitačného zrýchlenia ukazuje smerom dole), aká dlhá je tá dráha s, na konci ktorej bude rýchlosť kameňa rovná nule? Veľmi jednoducho odkiaľ 0 2 = ,8s, s = ,6 = +20,4 metra. Kladné znamienko ukazuje, že najvyšší bod sa nachádza nad bodom hodu, nakoľko za kladný smer sme zvolili smer hore. Môžeme si tiež položiť otázku, že za akú dobu kameň dopadne do vody (berme to tak, že most neprekáža v páde kameňa). Ak kameň dopadne do vody, bude 10 metrov pod mostom, teda s = 10 m. (Táto dráha s teraz neznačí celkovú dráhu, ktorú kameň preletí, len vzdialenosť kameňa od miesta hodu teraz v okamihu dopadu; napr. v okamihu, keď kameň pri páde zhora dosiahne úroveň mosta, je s = 0.) K tomuto výpočtu použijeme našu druhú rovnicu odkiaľ 4,9t 2 20t 10 = 0, t 1 = 0,45 sec, 10 = 20t 1 2 9,8t2, t 2 = +4,53 sec. Je evidentné, že hľadaným riešením je druhý výsledok, nakoľko dopad do vody musí nastať po vyhodení kameňa do vzduchu. Vo väčšine prípadov nestačí zvážiť pohyby vo zvislom smere (hore a dole). Čo sa stane napríklad vtedy, ak chlapec kameň nezahodí zvislo smerom hore, ale zahodí ho s počiatočnou rýchlosťou 20 m/sec presne vo vodorovnom smere?
17 Biofyzika a radiológia 131 Obr. 7.8: Dráha vodorovne zahodenej lopty. Ak zanedbáme trenie pochádzajúce z odporu vzduchu, jedinou silou ktorou pôsobí na kameň je gravitačná príťažlivosť a preto kameň má zrýchlenie výhradne smerujúce dole, a veľkosť zrýchlenia je 9,8 m/sec 2. Nakoľko zrýchlenie nemá vodorovnú zložku, nijakým spôsobom neovplyvňuje vodorovný pohyb kameňa a ten sa vo vodorovnom smere pohybuje so stálou rýchlosťou 20 m/s až dovtedy, než dopadne na hladinu rieky. Obdobným spôsobom ani vodorovná zložka rýchlosti nijakým spôsobom nevplýva na pohyb v smere hore-dole, na gravitačné zrýchlenie. Na obrázku 7.8 vidíme dve lopty: prvú z nich zahodíme vo vodorovnom smere práve v tom okamihu, keď druhú pustíme a necháme voľne padať. Nakoľko vodorovne odhodená lopta v okamihu hodu nemá zvislú zložku rých-
18 Kapitola Obr. 7.9: Rýchlosť šikmo vrhnutej lopty má vodorovnú aj zvislú zložku.
19 Biofyzika a radiológia 133 losti, jej pohyb smerom dole je presne rovnaký, ako voľne padajúcej lopty. Pohyb vo vodorovnom smere prebieha nezávisle od pohybu vo zvislom smere tak, že výsledná dráha vznikne zložením rovnomerného pohybu vo vodorovnom smere a rovnomerne zrýchleného pohybu vo zvislom smere. V úlohách riešiacich vrhy môžeme o vodorovnej a zvislej zložke pohybu uvažovať oddelene od seba. Ako príklad si pozrieme golfového hráča na obrázku 7.9. Svojim úderom udeľuje golfovej loptičke rýchlosť 36 m/s v smere uzatvárajúcom 30 s vodorovným smerom a miesto jeho úderu sa nachádza o 15 metrov nižšie, než cieľová rovinka s jamkou. Ako ďaleko doletí táto loptička v dôsledku popísaného úderu? (Hľadáme vzdialenosť x vyznačenú na obrázku.) Rozdeľme rýchlosť v na vodorovnú zložku v v a zvislú zložku v z. a v v = 36cos 30 = 31,2 m/s v z = 36cos 30 = 18 m/s. Skutočná dráha lopty je oblúk OBAC. Priemet tohoto oblúku na zvislý smer je OB A C, ktorú by popísala fiktívna lopta vyhodená zvislo hore s počiatočnou rýchlosťou 18 m/sec. Koľko času uplynie, než sa dostane z bodu O do bodu C táto fiktívna lopta? Za tú istú dobu dorazí skutočná lopta do C a zaryje sa do pôdy. Ak sledujeme len zvislú zložku pohybu lopty, tak môžeme písať odkiaľ 4,9t 2 18t + 15 = 0 s = v 0 t at2 15 = 18t 4,9t 2 t = 18 ± , ,9 t 1 = 1,28 sec, t 2 = 2,40 sec. Prvá hodnota, 1,28 sec je doba, za ktorú lopta dosiahne výšku 15 metrov nad miestom úderu, ale to je zatiaľ len výstupná fáza, bod B; Podľa riešenia je potrebných 2,40 sec k tomu, aby lopta doletela do bodu C. Po túto dobu je hodnota v v konštantná a rovná 31,2 m/sec, preto lopta vo vodorovnom smere preletí vzdialenosť x = 2,40 31,2 = 74,9 metra.
20 Kapitola (7-1) (7-3) Úlohy 7.1. Stojacie auto zrýchli za 10 sekúnd na rýchlosť 60 km/h. (a) Aké je jeho priemerné zrýchlenie počas 10-ich sekúnd? (b) Akú dlhú dráhu prejde za tento čas? 7.2. Cyklista zrýchli za 40 sekúnd z rýchlosti 5 km/h na 30 km/h. (a) Aké je jeho priemerné zrýchlenie? (b) Akú vzdialenosť prejde počas 40 sekúnd zrýchlenia? 7.3. Stojacie auto zrýchli na vzdialenosti 120 m na rýchlosť 30 m/sec. Aké je jeho zrýchlenie? 7.4. Elektrón s rýchlosťou m/sec vletí do elektrického poľa, ktoré ho zastaví na vzdialenosti 4 cm. Aké je jeho zrýchlenie? 7.5. Elektrón s rýchlosťou cm/sec vstúpi do elektrického poľa, ktoré ho ďalej urýchľuje so zrýchlením cm/sec 2. (a) Za akú dobu zrýchli elektrón na dvojnásobok svojej pôvodnej rýchlosti? (b) Akú dlhú dráhu preletí za túto dobu? 7.6. V úlohe 7.5 má zrýchlenie evidentne súhlasný smer s pôvodnou rýchlosťou elektrónu. Vykonajme výpočty za predpokladu, že zrýchlenie je orientované opačne, než smer pôvodnej rýchlosti elektrónu Vlaková súprava pohybujúca sa rýchlosťou 20 m/s aby dodržala cestovný poriadok musí doraziť ku kontrolnému stanovisku vo vzdialenosti 10 km za 6 minút. (a) Aké rovnomerné zrýchlenie musí mať vlaková súprava, aby ku kontrolnému stanovisku dorazila včas? (b) Akou rýchlosťou presviští okolo kontrolného stanoviska? 7.8. Zväzok iónov vstupuje do urýchľujúceho elektrického poľa rýchlosťou 2, cm/sec. Na katódu vo vzdialenosti 30 cm musí dopadnúť presne za 8 µsec (a) Akým stálym zrýchlením sa musia ióny urýchľovať, aby sa to stalo? (b) Akou rýchlosťou dopadnú ióny na katódu? 7.9. Lopta sa skotúľa po svahu dlhom 2,0 metra za 4 sec. (a) Aké je jej zrýchlenie? (b) Aká je jej rýchlosť na dolnom konci svahu? Elektrón v pokoji, pod vplyvom rovnomerne zrýchľujúceho elektrického poľa preletí vzdialenosť 2 cm za 2, sec než dopadne na anódu. (a) Aké je jeho zrýchlenie? (b) Akou rýchlosťou doletí k anóde? Ak niekto chce zarobiť na tom, že nakúpi fazule v určitej nadmorskej výške a predá ho v tej istej cene na inej nadmorskej výške, nakupuje alebo predáva vo väčšej nadmorskej výške? (Váženie sa deje pružinovými váhami.)
21 Biofyzika a radiológia Predpokladajme, že 500 gramov zlata stojí 600 dolárov. Predávajúci aj kupujúci používajú pružinové váhy. Ten, ktorý na obchode chce zarobiť bude kupovať v Eagle City na Aljaške a predávať v Panamskom prielive, alebo naopak? Koľko zlata musí kúpiť, aby zarobil 100 dolárov? Akou silou musíme pôsobiť na teleso s hmotnosťou 450 gramov, aby sme ho urýchlili so zrýchlením 12 cm/sec 2? Aká veľká sila je potrebná k zrýchleniu 12 m/sec 2? Aká veľká sila udelí hmotnosti 250 kg zrýchlenie 30 cm/sec 2? Aká veľká sila je potrebná k zrýchleniu 30 m/sec 2? Na vodorovnej klzkej podložke (tj. podložke bez trenia) urýchľuje sila 0,25 newtonov teleso so zrýchlením 4 m/sec 2. Aká je hmotnosť telesa? Na vodorovnej klzkej podložke (tj. podložke bez trenia) urýchľuje sila 3,0 kilopond teleso so zrýchlením 15 m/sec 2. Aká je hmotnosť telesa? Na teleso s hmotnosťou 300 gram, ktoré je na začiatku v pokoji, pôsobí sila F, pod vplyvom ktorej sa teleso, na stole bez trenia, presunie za 3 sekundy o 2 metre. (a) Aké je zrýchlenie telesa? (b) Aká veľká je sila F? Na teleso s hmotnosťou 12 kilogramov, ktoré je na začiatku v pokoji, pôsobí sila F, pod vplyvom ktorej sa teleso, na stole bez trenia, presunie za 4 sekundy o 6 metrov. (a) Aké je zrýchlenie telesa? (b) Aká veľká je sila F? Ako sa zmení úloha 7.17, ak koeficient trenia medzi predmetom a stolom je 0,20? Vyriešme úlohu 7.18 s koeficientom trenia 0, Rušeň s hmotnosťou 25 ton ťahá rýchlosťou 72 km/h súpravu s hmotnosťou 300 ton.(a) Aké môže byť maximálne spomalenie súpravy, ak koeficient trenia medzi kolesami a koľajnicami je 0,20? (b) Aká vzdialenosť je potrebná k zastaveniu vlaku, pokiaľ predpokladáme, že na jednotlivých vozňoch sú zrovna také brzdy, ako na rušni? Rušeň s hmotnosťou 30 ton ťahá rýchlosťou 60 km/h súpravu s hmotnosťou 500 ton.(a) Aké môže byť maximálne spomalenie súpravy, ak koeficient trenia medzi kolesami a koľajnicami je 0,15? (b) Aká vzdialenosť je potrebná k zastaveniu vlaku, pokiaľ predpokladáme, že na jednotlivých vozňoch sú zrovna také brzdy, ako na rušni? Za akú dobu dopadne na dno 40 metrov hlbokej šachty kameň, ktorý do nej upustíme? Šálka na kávu nám vypadne z ruky vo výške 1,5 metra nad zemou. Za akú dobu dopadne na zem? (7-4)
22 Kapitola Kameň upustený z vrcholu skaly dopadne k jeho úpätiu za 4 sekundy. Ako vysoko vyčnieva vrch skaly nad úpätie? Kvetináč zo strechy budovy dopadne na zem za 3 sekundy. Aká vysoká je budova? Kameň upustený na planéte X padne z výšky 24 metrov za 2 sekundy. (a) Aká je hodnota g na tejto planéte? (b) Aká je tiaž 5 kilogramového telesa na planéte X? Na planéte U padne kameň z výšky 20 metrov za 3 sekundy. (a) Aká je hodnota g na tejto planéte? (b) Aká je hmotnosť telesa s tiažou 100 kilopond na planéte U? Na konce vlákna Atwoodovho pádostroja (vedeného kladkou bez trenia) zavesíme záťaže s hmotnosťou 1000 gramov a 1020 gramov. (a) Aké veľké je zrýchlenie väčšej záťaže smerujúceho dole? (b) Za akú dobu poklesne väčšia záťaž o 200 centimetrov, ak záťaže pustíme z pokoja? Na konce vlákna Atwoodovho pádostroja (vedeného kladkou bez trenia) zavesíme záťaže s hmotnosťou 20 gramov a 18 gramov. (a) Aké veľké je zrýchlenie väčšej záťaže smerujúceho dole? (b) Za akú dobu poklesne väčšia záťaž o 1 meter, ak záťaže pustíme z pokoja? Aké veľké je napätie vo vlákne úlohy 7.29? Aké veľké je napätie vo vlákne úlohy 7.30? Predpokladajme, že na okraj stola bez trenia umiestnime kladku ktorá sa pretáča bez trenia. Od 2000 gramového závažia na stole vedieme vlákno vodorovným smerom cez kladku a na jeho druhý visiaci koniec zavesíme závažie s hmotnosťou 250 gramov. Akým zrýchlením bude klesať 250 gramové závažie? Predpokladajme, že na okraj stola bez trenia umiestnime kladku ktorá sa pretáča bez trenia. Od 2,5 kilogramového telesa na stole vedieme vlákno vodorovným smerom cez kladku a na jeho druhý visiaci koniec zavesíme závažie s hmotnosťou 0,6 kilogramov. Akým zrýchlením sa bude pohybovať teleso na stole? V úlohe 7.33 je koeficient trenia medzi závažím a stolom 0,10. Aká bude rýchlosť 2000 gramového závažia na stole na konci prvej sekundy, ak svoj pohyb začne z pokoja? V úlohe 7.33 je koeficient trenia medzi predmetom a stolom 0,15. O koľko poklesne závažie na konci visiaceho vlákna za dve sekundy? Aké veľké je napätie vlákna v úlohe 7.35?
23 Biofyzika a radiológia Aké veľké je napätie vlákna v úlohe 7.36? Muž s tiažou 80 kilopond stojí vo výťahu na pružinových váhach. Výťah sa pohybuje smerom dole. Koľko ukážu pružinové váhy pred zastavením výťahu, ak ten spomaľuje 1 m/sec 2? Žena s tiažou 50 kilopond stojí vo výťahu na pružinových váhach. Výťah sa pohybuje smerom hore. Výťah pred zastavením spomaľuje 2 m/sec 2. Čo ukazujú pružinové váhy? (Stupnica pružinových váh je robená v newtonoch; túto jednotku používame len v laboratóriach a v učebniciach.) Žena v Paríži stojí na pružinových váhach v pohybujúcom sa výťahu. Pred zastavením váhy namiesto 60 kilopondov ukazujú 45 kilopondov a po zastavení znova 60 kilopondov. (a) V ktorom smere sa pohyboval výťah: smerom hore, alebo smerom dole? (b) Vypočítajme spomalenie Muž stojí na pružinových váhach v pohybujúcom sa výťahu. Keď výťah začne spomaľovať, tak namiesto 80 kilopondov ukáže 95 kilopondov a po zastavení znova 80 kilopondov. (a) Pohyboval sa výťah smerom hore, alebo smerom dole? (b) Aké bolo zrýchlenie pred zastavením? Teleso kĺže bez trenia po naklonenej rovine so sklonom 20. Aké je jeho zrýchlenie pozdĺž naklonenej roviny? Naklonená rovina bez trenia uzatvára s vodorovným smerom uhol 25. Akým zrýchlením skĺzne teleso po tejto naklonenej rovine? Zopakujme úlohu 7.43, ak koeficient trenia je 0, Ako sa zmenia výsledky úlohy 7.44, ak koeficient trenia bude 0,15? Na rampe naklonenej o 15 je čln s tiažou 500 kilopond, koeficient trenia je 0,30. Skĺzne čln do vody sám od seba? Akou silou (rovnobežne s dĺžkou naklonenej rampy) musíme čln potlačiť, ak nie? Na naklonenej rovine so sklonom 20 je debna s nadpisom Pozor krehké!. Koeficient trenia je 0,20. Akou veľkou silou (rovnobežnou s dĺžkou naklonenej roviny) musíme debnu zadržiavať, aby skĺzla dole konštantnou rýchlosťou? Kniha kĺže dole s konštantnou rýchlosťou po naklonenej rovine, ktorá zviera s vodorovným smerom uhol α. Ukážme, že koeficient trenia medzi knihou a naklonenou rovinou musí byť rovný tg α Koeficient trenia medzi predmetom a povrchom naklonenej roviny je µ. Aký bude vzťah medzi koeficientom trenia a tangensom uhla sklonu naklonenej roviny ak predmet kĺže dole po naklonenej rovine s konštantnou rýchlosťou? (7-5)
24 Kapitola (7-6) Naklonená rovina s dĺžkou 130 cm má horný koniec o 50 centimetrov vyššie, ako dolný. Muž cvrnkol do krabičky cigariet tak, že tá sa začala pohybovať smerom hore po naklonenej rovine a na jej hornom konci sa práve zastavila. Aká bola počiatočná rýchlosť krabičky cigariet, ak koeficient trenia medzi naklonenou rovinou a krabičkou cigariet je µ = 0,15? Žoch surovej gumy neskĺzne po naklonenej rovine s uhlom sklonu 15, lebo koeficient trenia je 0,40. Akú rýchlosť musíme dať žochu na vrchu naklonenej roviny, aby skĺzol až dole a na dolnom konci naklonenej roviny sa zastavil? Muž stojí na okraji 120 metrov hlbokej šachty a vyhodí zvislo hore do vzduchu kameň s počiatočnou rýchlosťou 20 m/s. Kameň vyletí do vzduchu a potom spadne na dno šachty. Koľko času uplynie od okamihu hodu do okamihu dopadu kameňa na dno šachty? Na streche 50 metrov vysokej budovy stojí človek, ktorý vystrelí z praku smerom hore kameň, ktorého počiatočná rýchlosť je 30 m/s. Za akú dobu dopadne kameň na pôdu pri základoch budovy? Na planéte X vyhodí kozmonaut zvislo hore kameň s počiatočnou rýchlosťou 20 m/sec a ten mu dopadne naspäť do dlane o 20 sekúnd. Aká je tiaž kameňa na tejto planéte, ak jeho hmotnosť je 500 gramov? Predmet s hmotnosťou 2 kilogramy vyhodené zvislo hore s počiatočnou rýchlosťou 10 m/s sa na planéte Y vráti za 8 sekúnd. Aká je tiaž 2 kilogramového závažia na tejto planéte? Loptu zahodíme s počiatočnou rýchlosťou 40 m/s pod uhlom 37. (a) Do akej výšky vyletí lopta? (b) Ako ďaleko lopta doletí vo vodorovnom smere? Golfovú loptičku odpália s počiatočnou rýchlosťou 40 m/s pod uhlom 30. (a) Do akej výšky vyletí lopta? (b) Ako ďaleko lopta doletí vo vodorovnom smere? Hráč odkopne loptu pod uhlom 60 (počítajúc od vodorovného smeru). (a) Akú počiatočnú rýchlosť získala lopta pri kope, ak odletela do vzdialenosti 45 metrov vo vodorovnom smere? (b) Do akej výšky lopta vyletela? Brankár vykopol loptu pod uhlom 45 a tá doletela do vzdialenosti 30 metrov vo vodorovnom smere. (a) Do akej výšky lopta vystúpila? (b) S akou veľkou počiatočnou rýchlosťou opustila nohu brankára? Bombardér klesá pod uhlom 30 (počítajúc od vodorovného smeru) rýchlosťou 150 m/sec, keď vo výške 1000 metrov nad zemou vypustí bombu. (a) Za akú dobu bomba dopadne na zem? (b) Ako ďaleko (vo vodorovnom smere) od miesta jej vypustenia dopadne bomba na zem?
25 Biofyzika a radiológia Bombardér stúpa pod uhlom 30 (počítajúc od vodorovného smeru) rýchlosťou 300 m/sec. Vo výške 1200 metrov nad zemou vypustí bombu. (a) Za akú dobu bomba dopadne na zem? (b) Ako ďaleko (vo vodorovnom smere) od miesta jej vypustenia dopadne bomba na zem?
26 Kapitola
2. Dva hmotné body sa navzájom priťahujú zo vzdialenosti r silou 12 N. Akou silou sa budú priťahovať zo vzdialenosti r/2? [48 N]
![2. Dva hmotné body sa navzájom priťahujú zo vzdialenosti r silou 12 N. Akou silou sa budú priťahovať zo vzdialenosti r/2? [48 N] 2. Dva hmotné body sa navzájom priťahujú zo vzdialenosti r silou 12 N. Akou silou sa budú priťahovať zo vzdialenosti r/2? [48 N]](/thumbs/55/37806266.jpg) Gravitačné pole 1. Akou veľkou silou sa navzájom priťahujú dve homogénne olovené gule s priemerom 1 m, ktoré sa navzájom dotýkajú? Hustota olova je 11,3 g cm 3. [2,33 mn] 2. Dva hmotné body sa navzájom
Gravitačné pole 1. Akou veľkou silou sa navzájom priťahujú dve homogénne olovené gule s priemerom 1 m, ktoré sa navzájom dotýkajú? Hustota olova je 11,3 g cm 3. [2,33 mn] 2. Dva hmotné body sa navzájom
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
GYMNÁZIUM V ŽILINE, HLINSKÁ 29 ALTERNATÍVNA ZBIERKA ÚLOH Z FYZIKY PRE 1. ROČNÍK. Spracovali: Mgr. Andrea Bednárová, PhD., Mgr.
 GYMNÁZIUM V ŽILINE, HLINSKÁ 29 ALTERNATÍVNA ZBIERKA ÚLOH Z FYZIKY PRE 1. ROČNÍK Spracovali: Mgr. Andrea Bednárová, PhD., Mgr. Zuzana Durná 27 Milá študentka, milý študent. Dostáva sa Vám do rúk Alternatívna
GYMNÁZIUM V ŽILINE, HLINSKÁ 29 ALTERNATÍVNA ZBIERKA ÚLOH Z FYZIKY PRE 1. ROČNÍK Spracovali: Mgr. Andrea Bednárová, PhD., Mgr. Zuzana Durná 27 Milá študentka, milý študent. Dostáva sa Vám do rúk Alternatívna
Motivácia pojmu derivácia
 Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Úloha 3.7 Teleso hmotnosti 2 kg sa pohybuje pozdĺž osi x tak, že jeho dráha je vyjadrená rovnicou
 3 Dynamika Newtonove pohybové zákony Úloha 3.1 Teleso tvaru kvádra leží na horizontálnej doske stola. Na jeho prednej stene sú pripevnené dve lanká v strede steny. Lanká napneme tak, že prvé zviera s čelnou
3 Dynamika Newtonove pohybové zákony Úloha 3.1 Teleso tvaru kvádra leží na horizontálnej doske stola. Na jeho prednej stene sú pripevnené dve lanká v strede steny. Lanká napneme tak, že prvé zviera s čelnou
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín. Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť.
 Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
,Zohrievanie vody indukčným varičom bez pokrievky,
 Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
ELEKTRICKÉ POLE. Elektrický náboj je základná vlastnosť častíc, je viazaný na častice látky a vyjadruje stav elektricky nabitých telies.
 ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
ZADANIE 1_ ÚLOHA 3_Všeobecná rovinná silová sústava ZADANIE 1 _ ÚLOHA 3
 ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
RIEŠENIA 3 ČASŤ
 RIEŠENIA 3 ČASŤ - 2009-10 1. PRÁCA RAKETY Raketa s hmotnosťou 1000 kg vystúpila do výšky 2000 m nad povrch Zeme. Vypočítajte prácu, ktorú vykonali raketové motory, keď predpokladáme pohyb rakety v homogénnom
RIEŠENIA 3 ČASŤ - 2009-10 1. PRÁCA RAKETY Raketa s hmotnosťou 1000 kg vystúpila do výšky 2000 m nad povrch Zeme. Vypočítajte prácu, ktorú vykonali raketové motory, keď predpokladáme pohyb rakety v homogénnom
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
6 Gravitačné pole. 6.1 Keplerove zákony
 89 6 Gravitačné pole Pojem pole patrí k najzákladnejším pojmom fyziky. Predstavuje formu interakcie (tzv. silového pôsobenia) v prostredí medzi materiálnymi objektmi ako sú častice, atómy, molekuly a zložitejšie
89 6 Gravitačné pole Pojem pole patrí k najzákladnejším pojmom fyziky. Predstavuje formu interakcie (tzv. silového pôsobenia) v prostredí medzi materiálnymi objektmi ako sú častice, atómy, molekuly a zložitejšie
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE. Chemickotechnologická fakulta. Doc. RNDr. Viliam Laurinc, CSc. a kolektív FYZIKA I
 SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE Chemickotechnologická fakulta Doc. RNDr. Viliam Laurinc, CSc. a kolektív FYZIKA I Zbierka príkladov a problémov Predslov Cieľom výpočtových cvičení z fyziky
SLOVENSKÁ TECHNICKÁ UNIVERZITA V BRATISLAVE Chemickotechnologická fakulta Doc. RNDr. Viliam Laurinc, CSc. a kolektív FYZIKA I Zbierka príkladov a problémov Predslov Cieľom výpočtových cvičení z fyziky
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
4 Dynamika hmotného bodu
 61 4 Dynamika hmotného bodu V predchádzajúcej kapitole - kinematike hmotného bodu sme sa zaoberali pohybom a pokojom telies, čiže formou pohybu. Neriešili sme príčiny vzniku pohybu hmotného bodu. A práve
61 4 Dynamika hmotného bodu V predchádzajúcej kapitole - kinematike hmotného bodu sme sa zaoberali pohybom a pokojom telies, čiže formou pohybu. Neriešili sme príčiny vzniku pohybu hmotného bodu. A práve
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
ZBIERKA ÚLOH Z FYZIKY PRE 3. ROČNÍK
 Kód ITMS projektu: 26110130519 Gymnázium Pavla Jozefa Šafárika moderná škola tretieho tisícročia ZBIERKA ÚLOH Z FYZIKY PRE 3. ROČNÍK (zbierka úloh) Vzdelávacia oblasť: Predmet: Ročník: Vypracoval: Človek
Kód ITMS projektu: 26110130519 Gymnázium Pavla Jozefa Šafárika moderná škola tretieho tisícročia ZBIERKA ÚLOH Z FYZIKY PRE 3. ROČNÍK (zbierka úloh) Vzdelávacia oblasť: Predmet: Ročník: Vypracoval: Človek
7 Derivácia funkcie. 7.1 Motivácia k derivácii
 Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
Kontrolné otázky z jednotiek fyzikálnych veličín
 Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
[ v 0 = at r + (at r ) 2 + 2as = 16,76 m/s ]
![[ v 0 = at r + (at r ) 2 + 2as = 16,76 m/s ] [ v 0 = at r + (at r ) 2 + 2as = 16,76 m/s ]](/thumbs/91/106924523.jpg) Posledná aktualizácia: 22. mája 202. Čo bolo aktualizované (oproti predošlej verzii zo 6. marca 2009): Rozsiahle zmeny, napr.: Dodané postupy riešení ku niektorým príkladom. Dodané niektoré nové príklady.
Posledná aktualizácia: 22. mája 202. Čo bolo aktualizované (oproti predošlej verzii zo 6. marca 2009): Rozsiahle zmeny, napr.: Dodané postupy riešení ku niektorým príkladom. Dodané niektoré nové príklady.
23. Zhodné zobrazenia
 23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
A) práca, mechanická energia
 A) práca, mechanická energia (MMF, s. 95) 1. Vypočítajte prácu, ktorú vykoná sila pri urýchlení telesa z 0 na rýchlosť v. Uvažujte nasledovné sily: 1 a) F konšt. mv 1 b) F k.t mv 1 c) F F 0 + k.x mv (MMF,
A) práca, mechanická energia (MMF, s. 95) 1. Vypočítajte prácu, ktorú vykoná sila pri urýchlení telesa z 0 na rýchlosť v. Uvažujte nasledovné sily: 1 a) F konšt. mv 1 b) F k.t mv 1 c) F F 0 + k.x mv (MMF,
Kinematika hmotného bodu
 Kinematika hmotného bodu 1. Automobil potrebuje na vykonanie cesty dlhej 120 km spolu s 15-minútovou prestávkou celkove 2h 40 min. Časť cesty išiel rýchlosťou v 1 = 40 km/h a časť rýchlosťou v 2 = 60 km/h.
Kinematika hmotného bodu 1. Automobil potrebuje na vykonanie cesty dlhej 120 km spolu s 15-minútovou prestávkou celkove 2h 40 min. Časť cesty išiel rýchlosťou v 1 = 40 km/h a časť rýchlosťou v 2 = 60 km/h.
DOMÁCE ZADANIE 1 - PRÍKLAD č. 2
 Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
3 Kinematika hmotného bodu
 29 3 Kinematika hmotného bodu Pohyb vo všeobecnosti zahŕňa všetky zmeny a procesy, ktoré prebiehajú vo vesmíre. Je neoddeliteľnou vlastnosťou hmoty. Časť fyziky, ktorá sa zaoberá popisom pohybu telies,
29 3 Kinematika hmotného bodu Pohyb vo všeobecnosti zahŕňa všetky zmeny a procesy, ktoré prebiehajú vo vesmíre. Je neoddeliteľnou vlastnosťou hmoty. Časť fyziky, ktorá sa zaoberá popisom pohybu telies,
5 Trecie sily. 5.1 Šmykové trenie
 79 5 Trecie sily S trením sa stretávame doslova na každom kroku. Bez trenia by nebola možná naša chôdza, pohyb auta či bicykla, nemohli by sme písať perom, prípadne ho držať v ruke. Skrutky by nespĺňali
79 5 Trecie sily S trením sa stretávame doslova na každom kroku. Bez trenia by nebola možná naša chôdza, pohyb auta či bicykla, nemohli by sme písať perom, prípadne ho držať v ruke. Skrutky by nespĺňali
Úvod. Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...
 Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Základné poznatky molekulovej fyziky a termodynamiky
 Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
FYZIKA DUSˇAN OLCˇA K - ZUZANA GIBOVA - OL GA FRICˇOVA Aprı l 2006
 FYZIKA DUŠAN OLČÁK - ZUZANA GIBOVÁ - OL GA FRIČOVÁ Apríl 2006 2 Obsah 1 o-g-f:mechanický pohyb tuhého telesa 5 1.1 Kinematika hmotného bodu......................... 6 1.1.1 Rýchlost a zrýchlenie pohybu....................
FYZIKA DUŠAN OLČÁK - ZUZANA GIBOVÁ - OL GA FRIČOVÁ Apríl 2006 2 Obsah 1 o-g-f:mechanický pohyb tuhého telesa 5 1.1 Kinematika hmotného bodu......................... 6 1.1.1 Rýchlost a zrýchlenie pohybu....................
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
KATEDRA DOPRAVNEJ A MANIPULAČNEJ TECHNIKY Strojnícka fakulta, Žilinská Univerzita
 132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
132 1 Absolútna chyba: ) = - skut absolútna ochýlka: ) ' = - spr. relatívna chyba: alebo Chyby (ochýlky): M systematické, M náhoné, M hrubé. Korekcia: k = spr - = - Î' pomerná korekcia: Správna honota:
STRIEDAVÝ PRÚD - PRÍKLADY
 STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
A) kladky. Zbierka príkladov k predmetu Mechanika
 A) kladky (N 1999/000, ) 1. Určite veľkosť zrýchlenia telesa m1 na obrázku. Trenie ani hmotnosť kladky neuvažujte. m g a1 = 4m1 + m (N 009/010, 0). Jedna z techník vyťahovania bezvládneho človeka z ľadovcovej
A) kladky (N 1999/000, ) 1. Určite veľkosť zrýchlenia telesa m1 na obrázku. Trenie ani hmotnosť kladky neuvažujte. m g a1 = 4m1 + m (N 009/010, 0). Jedna z techník vyťahovania bezvládneho človeka z ľadovcovej
URČENIE MOMENTU ZOTRVAČNOSTI FYZIKÁLNEHO KYVADLA
 54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
Mocniny : 1. časť. A forma. B forma. 1. Kontrolná práca z matematiky 8. ročník
 1. Kontrolná práca z matematiky 8. ročník Mocniny : 1. časť 1. Vypočítajte pomocou tabuliek : a) 100 ; 876 ; 15,89 ; 1, ; 0,065 ; b) 5600 ; 16 ; 0,9 ;,64 ; 1,4 ; c) 1,5 ; 170 ; 0,01 ; 148 0, 56 ; 64, 5
1. Kontrolná práca z matematiky 8. ročník Mocniny : 1. časť 1. Vypočítajte pomocou tabuliek : a) 100 ; 876 ; 15,89 ; 1, ; 0,065 ; b) 5600 ; 16 ; 0,9 ;,64 ; 1,4 ; c) 1,5 ; 170 ; 0,01 ; 148 0, 56 ; 64, 5
Chí kvadrát test dobrej zhody. Metódy riešenia úloh z pravdepodobnosti a štatistiky
 Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Priamkové plochy. Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava
 Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
Priamkové plochy Priamkové plochy Ak každým bodom plochy Φ prechádza aspoň jedna priamka, ktorá (celá) na nej leží potom plocha Φ je priamková. Santiago Calatrava Priamkové plochy rozdeľujeme na: Rozvinuteľné
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Einsteinove rovnice. obrázkový úvod do Všeobecnej teórie relativity. Pavol Ševera. Katedra teoretickej fyziky a didaktiky fyziky
 Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
y K K = (x K ) K= ( cos α, sin α) x = cos α y = sin α ,y K x K Klasická dynamika
 Študijná poôcka: Zostroje jednotkovú kružnicu, t.j. kružnicu s poloero R = y K K x α x K K = (x K,y K ) K= ( cos α, sin α) x = cos α y = sin α y Poocou jednotkovej kružnice je veľi jednoduché odhadnúť
Študijná poôcka: Zostroje jednotkovú kružnicu, t.j. kružnicu s poloero R = y K K x α x K K = (x K,y K ) K= ( cos α, sin α) x = cos α y = sin α y Poocou jednotkovej kružnice je veľi jednoduché odhadnúť
Priezvisko: Ročník: Katedra chemickej fyziky. Krúžok: Meno: Dátum cvičenia: Dvojica:
 Katedra chemickej fyziky Dátum cvičenia: Ročník: Krúžok: Dvojica: Priezvisko: Meno: Úloha č. 7 URČENIE HUSTOTY KVPLÍN Známka: Teória Tabuľka Výpočet Zaokrúhľovanie Záver Meranie 1. Úlohy: a) Určte hustotu
Katedra chemickej fyziky Dátum cvičenia: Ročník: Krúžok: Dvojica: Priezvisko: Meno: Úloha č. 7 URČENIE HUSTOTY KVPLÍN Známka: Teória Tabuľka Výpočet Zaokrúhľovanie Záver Meranie 1. Úlohy: a) Určte hustotu
Pracovný zošit z fyziky
 Gymnázium Antona Bernoláka Námestovo Pracovný zošit z fyziky Mgr. Stanislav Kozák Mgr. Stanislav Kozák, 2011 Mgr. Stanislav Kozák Pracovný zošit z fyziky pre 1. ročník gymnázia Vydavateľ: Tlačiareň Kubík
Gymnázium Antona Bernoláka Námestovo Pracovný zošit z fyziky Mgr. Stanislav Kozák Mgr. Stanislav Kozák, 2011 Mgr. Stanislav Kozák Pracovný zošit z fyziky pre 1. ročník gymnázia Vydavateľ: Tlačiareň Kubík
Matematický model robota s diferenciálnym kolesovým podvozkom
 Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
Termodynamika. Doplnkové materiály k prednáškam z Fyziky I pre SjF Dušan PUDIŠ (2008)
 ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
CHÉMIA Ing. Iveta Bruončová
 Výpočet hmotnostného zlomku, látkovej koncentrácie, výpočty zamerané na zloženie roztokov CHÉMIA Ing. Iveta Bruončová Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov
Výpočet hmotnostného zlomku, látkovej koncentrácie, výpočty zamerané na zloženie roztokov CHÉMIA Ing. Iveta Bruončová Moderné vzdelávanie pre vedomostnú spoločnosť/projekt je spolufinancovaný zo zdrojov
Zrýchľovanie vesmíru. Zrýchľovanie vesmíru. o výprave na kraj vesmíru a čo tam astronómovia objavili
 Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
18. kapitola. Ako navariť z vody
 18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
Zložené funkcie a substitúcia
 3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
A) výpočet momentu zotrvačnosti
 A) výpočet momentu zotrvačnosti (N /, 8). Vypočítajte moment zotrvačnosti symetricky splackateného kotúčika toaletného papiera s hmotnosťou m, výškou h, s vonkajšou stranou dĺžky a a vnútornou stranou
A) výpočet momentu zotrvačnosti (N /, 8). Vypočítajte moment zotrvačnosti symetricky splackateného kotúčika toaletného papiera s hmotnosťou m, výškou h, s vonkajšou stranou dĺžky a a vnútornou stranou
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Príklady z Fyziky týždeň
 Príklady z Fyziky 1 1. týždeň 1. Uvažujme vektory A = 3i + 3j, B = i j, C = 2i + 5j umiestnené v jednej rovine. Prepíšte vektory do súradnicového tvaru a graficky ich znázornite a graficky ich spočítajte.
Príklady z Fyziky 1 1. týždeň 1. Uvažujme vektory A = 3i + 3j, B = i j, C = 2i + 5j umiestnené v jednej rovine. Prepíšte vektory do súradnicového tvaru a graficky ich znázornite a graficky ich spočítajte.
1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2
 1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2 Rozdiel LMT medzi dvoma miestami sa rovná rozdielu ich zemepisných dĺžok. Pre prevod miestnych časov platí, že
1 Prevod miestneho stredného slnečného času LMT 1 na iný miestny stredný slnečný čas LMT 2 Rozdiel LMT medzi dvoma miestami sa rovná rozdielu ich zemepisných dĺžok. Pre prevod miestnych časov platí, že
Fyzikálna olympiáda. 52. ročník. školský rok 2010/2011. Kategória D. Úlohy školského kola
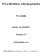 Fyzikálna olympiáda 52. ročník školský rok 2010/2011 Kategória D Úlohy školského kola (ďalšie informácie na http://fpv.utc.sk/fo a www.olympiady.sk) Odporúčané študijné témy pre kategóriu D 52. ročníka
Fyzikálna olympiáda 52. ročník školský rok 2010/2011 Kategória D Úlohy školského kola (ďalšie informácie na http://fpv.utc.sk/fo a www.olympiady.sk) Odporúčané študijné témy pre kategóriu D 52. ročníka
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Úloha č.:...viii... Název: Meranie momentu zotrvačnosti kolesa Vypracoval:... Viktor Babjak... stud. sk... F 11.. dne...
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I Úloha č.:...viii... Název: Meranie momentu zotrvačnosti kolesa Vypracoval:... Viktor Babjak... stud. sk... F 11.. dne...
Margita Vajsáblová. ρ priemetňa, s smer premietania. Súradnicová sústava (O, x, y, z ) (O a, x a, y a, z a )
 Mrgit Váblová Váblová, M: Dekriptívn geometri pre GK 101 Zákldné pom v onometrii Váblová, M: Dekriptívn geometri pre GK 102 Definíci 1: onometri e rovnobežné premietnie bodov Ε 3 polu prvouhlým úrdnicovým
Mrgit Váblová Váblová, M: Dekriptívn geometri pre GK 101 Zákldné pom v onometrii Váblová, M: Dekriptívn geometri pre GK 102 Definíci 1: onometri e rovnobežné premietnie bodov Ε 3 polu prvouhlým úrdnicovým
Odporníky. 1. Príklad1. TESLA TR
 Odporníky Úloha cvičenia: 1.Zistite technické údaje odporníkov pomocou katalógov 2.Zistite menovitú hodnotu odporníkov označených farebným kódom Schématická značka: 1. Príklad1. TESLA TR 163 200 ±1% L
Odporníky Úloha cvičenia: 1.Zistite technické údaje odporníkov pomocou katalógov 2.Zistite menovitú hodnotu odporníkov označených farebným kódom Schématická značka: 1. Príklad1. TESLA TR 163 200 ±1% L
Ján Buša Štefan Schrötter
 Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Analýza údajov. W bozóny.
 Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH
 6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH 6. Otázky Definujte pojem produkčná funkcia. Definujte pojem marginálny produkt. 6. Produkčná funkcia a marginálny produkt Definícia 6. Ak v ekonomickom procese počet
6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH 6. Otázky Definujte pojem produkčná funkcia. Definujte pojem marginálny produkt. 6. Produkčná funkcia a marginálny produkt Definícia 6. Ak v ekonomickom procese počet
16. Základne rovinné útvary kružnica a kruh
 16. Základne rovinné útvary kružnica a kruh Kružnica k so stredom S a polomerom r nazývame množinou všetkých bodov X v rovine, ktoré majú od pevného bodu S konštantnú vzdialenosť /SX/ = r, kde r (patri)
16. Základne rovinné útvary kružnica a kruh Kružnica k so stredom S a polomerom r nazývame množinou všetkých bodov X v rovine, ktoré majú od pevného bodu S konštantnú vzdialenosť /SX/ = r, kde r (patri)
Numerické metódy Učebný text pre bakalárske štúdium
 Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
M O N I T O R 2004 pilotné testovanie maturantov MONITOR Fyzika I. oddiel
 M O N I T O 2004 pilotné testovanie maturantov MONITO 2004 Fyzika I. oddiel Test je určený maturantom na všetkých typoch stredných škôl, ktorí sa pripravujú na maturitnú skúšku z fyziky. EXAM, Bratislava
M O N I T O 2004 pilotné testovanie maturantov MONITO 2004 Fyzika I. oddiel Test je určený maturantom na všetkých typoch stredných škôl, ktorí sa pripravujú na maturitnú skúšku z fyziky. EXAM, Bratislava
MECHANIKA TEKUTÍN. Ideálna kvapalina je dokonale tekutá a celkom nestlačiteľná, pričom zanedbávame jej vnútornú štruktúru.
 MECHANIKA TEKUTÍN TEKUTINY (KVAPALINY A PLYNY) ich spoločnou vlastnosťou je tekutosť, ktorá sa prejavuje tým, že kvapaliny a plynné telesá ľahko menia svoj tvar a prispôsobujú sa tvaru nádoby, v ktorej
MECHANIKA TEKUTÍN TEKUTINY (KVAPALINY A PLYNY) ich spoločnou vlastnosťou je tekutosť, ktorá sa prejavuje tým, že kvapaliny a plynné telesá ľahko menia svoj tvar a prispôsobujú sa tvaru nádoby, v ktorej
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Analytická geometria pre tých, ktorí jej potrebujú rozumieť
 Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 831 02 Bratislava Anino BELAN Analytická geometria pre tých, ktorí jej potrebujú rozumieť učebný text pre septimu osemročného gymnázia BRATISLAVA
Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 831 02 Bratislava Anino BELAN Analytická geometria pre tých, ktorí jej potrebujú rozumieť učebný text pre septimu osemročného gymnázia BRATISLAVA
Súčtové vzorce. cos (α + β) = cos α.cos β sin α.sin β cos (α β) = cos α.cos β + sin α.sin β. tg (α β) = cotg (α β) =.
 Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Test. Matematika. Forma A. Štátny pedagogický ústav, Bratislava NUPSESO. a.s.
 Test Matematika Forma A Štátny pedagogický ústav, Bratislava Ò NUPSESO a.s. 1. Koľkokrát je väčší najmenší spoločný násobok čísel 84 a 16 ako ich najväčší spoločný deliteľ. A. B. 3 C. 6 D.1. Koľko záporných
Test Matematika Forma A Štátny pedagogický ústav, Bratislava Ò NUPSESO a.s. 1. Koľkokrát je väčší najmenší spoločný násobok čísel 84 a 16 ako ich najväčší spoločný deliteľ. A. B. 3 C. 6 D.1. Koľko záporných
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
RIEŠENIE WHEATSONOVHO MOSTÍKA
 SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
Kvalitatívne úlohy vo vyučovaní fyziky na ZŠ
 METODICKO-PEDAGOGICKÉ CENTRUM V PREŠOVE Mária Krajčová Kvalitatívne úlohy vo vyučovaní fyziky na ZŠ - 2006 - OBSAH Úvod... 3 1 Pohyb telesa... 5 2 Sila a jej meranie... 9 3 Skladanie síl... 12 4 Posuvné
METODICKO-PEDAGOGICKÉ CENTRUM V PREŠOVE Mária Krajčová Kvalitatívne úlohy vo vyučovaní fyziky na ZŠ - 2006 - OBSAH Úvod... 3 1 Pohyb telesa... 5 2 Sila a jej meranie... 9 3 Skladanie síl... 12 4 Posuvné
4 DYNAMIKA SÚSTAVY HMOTNÝCH BODOV 1
 Posledná aktualizácia: 14. apríla 2012. Čo bolo aktualizované (oproti predošlej verzii z 11. februára 2011): Preusporiadané poradie úvodných 9 príkladov. Kompaktnejšia prezentácia príkladu 4.7, najmä bez
Posledná aktualizácia: 14. apríla 2012. Čo bolo aktualizované (oproti predošlej verzii z 11. februára 2011): Preusporiadané poradie úvodných 9 príkladov. Kompaktnejšia prezentácia príkladu 4.7, najmä bez
u R Pasívne prvky R, L, C v obvode striedavého prúdu Činný odpor R Napätie zdroja sa rovná úbytku napätia na činnom odpore.
 Pasívne prvky, L, C v obvode stredavého prúdu Čnný odpor u u prebeh prúdu a napäta fázorový dagram prúdu a napäta u u /2 /2 t Napäte zdroja sa rovná úbytku napäta na čnnom odpore. Prúd je vo fáze s napätím.
Pasívne prvky, L, C v obvode stredavého prúdu Čnný odpor u u prebeh prúdu a napäta fázorový dagram prúdu a napäta u u /2 /2 t Napäte zdroja sa rovná úbytku napäta na čnnom odpore. Prúd je vo fáze s napätím.
6. V stene suda naplneného vodou je v hĺbke 1 m pod hladinou otvor veľkosti 5 cm 2. Aká veľká tlaková sila pôsobí na zátku v otvore?
 Mechanika tekutín 1. Aká je veľkosť tlakovej sily na kruhový poklop ponorky s priemerom 1 m v hĺbke 50 m? Hustota morskej vody je 1,025 g cm 3. [402 kn] 2. Obsah malého piesta hydraulického zariadenia
Mechanika tekutín 1. Aká je veľkosť tlakovej sily na kruhový poklop ponorky s priemerom 1 m v hĺbke 50 m? Hustota morskej vody je 1,025 g cm 3. [402 kn] 2. Obsah malého piesta hydraulického zariadenia
STATIKA STAVEBNÝCH KONŠTRUKCIÍ I Doc. Ing. Daniela Kuchárová, PhD. Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov
 Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov zaťaženia Prostý nosník Konzola 31 Príklad č.14.1 Vypočítajte a vykreslite priebehy vnútorných síl na nosníku s previslými koncami,
Priebeh vnútorných síl na prostom nosníku a na konzole od jednotlivých typov zaťaženia Prostý nosník Konzola 31 Príklad č.14.1 Vypočítajte a vykreslite priebehy vnútorných síl na nosníku s previslými koncami,
REZISTORY. Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických
 REZISTORY Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických obvodoch. Základnou vlastnosťou rezistora je jeho odpor. Odpor je fyzikálna vlastnosť, ktorá je daná štruktúrou materiálu
REZISTORY Rezistory (súčiastky) sú pasívne prvky. Používajú sa vo všetkých elektrických obvodoch. Základnou vlastnosťou rezistora je jeho odpor. Odpor je fyzikálna vlastnosť, ktorá je daná štruktúrou materiálu
Špeciálna teória relativity v Loedelových diagramoch. Boris Lacsný, Aba Teleki
 Špeciálna teória relativity v Loedelových diagramoch Boris Lacsný, Aba Teleki Nitra, august 2007 Kapitola 1 Špeciálna teória relativity Teória relativity je cesta poznania nášho sveta. Hovorí nie len o
Špeciálna teória relativity v Loedelových diagramoch Boris Lacsný, Aba Teleki Nitra, august 2007 Kapitola 1 Špeciálna teória relativity Teória relativity je cesta poznania nášho sveta. Hovorí nie len o
Škola pre mimoriadne nadané deti a Gymnázium. Teória 2 Mechanika hmotného bodu 2.1 Kinematika
 Meno a priezvisko: Škola: Školský rok/blok: Predmet: Skupina: Trieda: Dátum: Škola pre mimoriadne nadané deti a Gymnázium Teória 2 Mechanika hmotného bodu 2.1 Kinematika 2.1.0 Úvod do kinematiky Najstarším
Meno a priezvisko: Škola: Školský rok/blok: Predmet: Skupina: Trieda: Dátum: Škola pre mimoriadne nadané deti a Gymnázium Teória 2 Mechanika hmotného bodu 2.1 Kinematika 2.1.0 Úvod do kinematiky Najstarším
Goniometrické substitúcie
 Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Mechanika hmotného bodu
 Meno a priezvisko: Škola: Školský rok/blok: Skupina: Trieda: Dátum: Bilingválne gymnázium C. S. Lewisa, Beňadická 38, Bratislava 2008-2009 / B Teória Mechanika hmotného bodu Kinematika Dynamika II. Mechanika
Meno a priezvisko: Škola: Školský rok/blok: Skupina: Trieda: Dátum: Bilingválne gymnázium C. S. Lewisa, Beňadická 38, Bratislava 2008-2009 / B Teória Mechanika hmotného bodu Kinematika Dynamika II. Mechanika
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
II. SILA A POHYB. PRÁCA. ENERGIA. Skúmanie pôsobenia sily. 2.1 Telesá pôsobia na seba silou. Účinky sily
 II. SILA A POHYB. PRÁCA. ENERGIA Skúmanie pôsobenia sily Stáva sa, že víchor poláme stromy či zničí strechy domov. Prúd vody pri povodni odplaví autá, zeminu, mosty. Zvykneme hovoriť, že silný vietor či
II. SILA A POHYB. PRÁCA. ENERGIA Skúmanie pôsobenia sily Stáva sa, že víchor poláme stromy či zničí strechy domov. Prúd vody pri povodni odplaví autá, zeminu, mosty. Zvykneme hovoriť, že silný vietor či
