PRIJENOS i DISTRIBUCIJA ELEKTRIČNE ENERGIJE
|
|
|
- Κρειος Δοξαράς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 TEHNIČKI FAKULTET SVEUČILIŠTA U RIJECI Sveučilišni diploki tudij elektrotehnike PRIJENOS i DISTRIBUCIJA ELEKTRIČNE ENERGIJE. KONSTRUKCIJSKI RAD ODREĐIVANJE KONSTANTI NADEMNOG VODA Odredite jedinične uzdužne ipedncije te poprečne ditncije u utvu ietričnih koponent z kv dlekovod, čij je geoetrij glve tup zdn liko , dni u još i ljedeći podci: Frekvencij reže: 5 Hz Mterijl vodič: Alučel Prejek vodič: 4/4 Broj vodič u nopu: Rzk vodič u nopu: Provje vodič: Broj trojki n ito tupu: Izoltorki lnc: xk7/8 Mterijl zštitnog užet: Alučel Prejek zštitnog užet: 7/ Broj zštitnih užet: Provje zštitnog užet:,5 Specifični otpor tl: Ω - -
2 .. Općenito o kontnt vod Kontnte vod u onovn električn vojtv ndzenog vod, iz njih lijede v otl njegov vojtv i krkteritike, o koji će oviiti električne prilike n vodu. Kontnte vod ovie o vojtvi terijl od kojih je vod izveden (npr. pecifični otpor terijl z vodiče), o geoetrijki vojtvi vod (npr. dienzije vodič, udljenot i rpored eđu vodiči), i o okolni prilik (npr. tepertur, kiš). Vodovi koji u inče izvedeni n iti nčin, općenito e rzlikuju po duljini, p zbog tog kontnte vod definiro po jedinici duljine, obično po kiloetru. Kontnte vod u otpor (Ω/k), induktivitet (H/k), kpcitet (F/k) i odvod (S/k). Kod trofznih vodov kontnte e zdju po fzi, dkle z jedn fzni vodič, tie d e ko povrtni dio trujnog krug uze zišljeni neutrlni vodič. N lici. u z odječk vod duljine dx kontnte vod prikzne pooću grfičkih ibol, i to otpor i induktivitet u fzno vodiču (uzdužne kontnte), kpcitet i odvod izeđu fznog i neutrlnog vodič (poprečne kontnte). U zdtku trebo odrediti ietrične koponente ipedncije i ditncije ndzenih vodov, odnono direktne, inverzne i nulte koponente tih veličin. Kod ndzenih vodov u, budući d ne rotcionih dijelov, direktn i inverzn ipedncij eđuobno jednke (ito vrijedi i z ditncije). npone i truje nultog utv je krkteritično d u ite u vi vodiči po iznou i kutu. Slik. Kontnte vodov Budući d njihov u nije jednk nuli, one i orju nći povrtni put. Tj povrtni put je zelj i dozen užd. Pri prorčunu nultog utv tog e orju uzeti u obzir i utjecj zelje i vi eđuobni utjecji eđu vodiči dlekovod. - -
3 .. Tok prorčun N teelju podtk o vodiči izrčunt ćeo njprije tricu uzdužnih ipedncij i tricu potencijlnih koeficijent. ti vršio redukciju zštitnih užet i nopov vodič. N krju rčuno ietrične koponente utv koji izrvno dju jedinične uzdužne ipedncije ko i poprečne ditncije vodov. Izvršeni prorčuni u provedeni n teelju jednopolne hee vod, koji je pretpotvljen jednki po izvedbi od početk do krj.. Podci vodič Frekvencij 5 Hz Mterijl vodič lučel Prejek vodič 4/4 Broj vodič u nopu Rzk vodič u nopu. Njveći provje vodič. Broj trojki Izoltorki lnc *K7/8 Mterijl zštitnih užet lučel Prejek zštitnih užet 7/ Broj zštitnih užet Njveći provje zštitnih užet.5 Otpor tl. Ω 4 4 8, Slik. Geoetrij glve tup - -
4 N onovi broj trojki određujeo broj vodič (ne rčunjući vodiče u nopu) n. Iz tblice podci o izvedbi fznih vodič (prilog I) izvdio ljedeće podtke z jedn vodič (z nehoogene vodiče): vnjki rdiju vodič r.9 tvrni prejek vodič (bez čelične jezgre) A Al 4.5 Rdiju čelične jezgre rčuno iz broj čeličnih žic i njihovog projer, poznvjući prvilo d e u vko lijedeće loju hoogenog užet broj žic poveć z šet. rdiju čelične jezgre r 4. Iz zdnih podtk z zštitno uže i iz tblice. (prilog I) određujeo ljedeće vrijednoti: vnjki rdiju vodič r g 5.86 tvrni prejek vodič A AlČe Otpor vod Otpor vod rčuno z proječnu pogonku teperturu od o C. Iz tblic (prilog I) izvdio otpor kod itojerne truje: R o.87 Ω/k Otpor zštitnog užet je: R g.4 Ω/k Povećnje otpor ulijed kin-efekt kod izjenične truje e rčun pre foruli: R nrjo ( nr) r r Re + R o J ( nr) gdje u: J o (nr), J (nr) Beelove funkcije nultog i prvog red μ μ r o ρ R ωμ ρ ω πf o 4π / r ωπr ρ π 4 H / k pec. otpor trujnice r μ πf ρ fμ R o - 4 -
5 Končno e dobije z djeltni otpor kod izjenične truje: R R o π + f R.459 R.87 + R.99 Ω / k 8 o 4 4π f R 4 o [ Ω / k] To je djeltni otpor z jedn vodič. Ako e fz jedne trojke toji od više vodič koji u vezni u nop, ond treb izrčunti djeltni otpor po fzi z čitv vod dijeljenje otpor broje vodič u nopu. Končno, djeltni otpor po fzi ( vodič u nopu) iznoi: R f.99/.597 Ω/k.5. Rpored vodič N teelju zdne geoetrije glve tup, odnono ovjeišt izoltorkih lnc i pričvršćenj zštitnih užet odredit ćeo ve potrebne eđuobne udljenoti z ntvk prorčun. Pošto u nši dljnji prorčuni uzio u obzir i utjecj zelje, vžn je i viin vodič iznd tl. Pri toe obično rčuno neko proječno viino, pre izrzu koji približno vrijedi z lnčnicu, koju dobijeo ko od viine ovjeišt n tupu odbijeo 7/ njvećeg provje vodič: h H.7f x Ne ijeo zneriti ni duljinu izoltor i noč vodov. U zdtku je zdn broj člnk i tip izoltor: K 7/8 U nše lučju e korite ovjeni kpti izoltori. Duljinu izoltor određujeo znjući dienzije jednog člnk. kpti izoltor tip K 7/8 viin jednog člnk iznoi.7. N tj nčin izrčunvo proječne viine vodič jedne trojke iznd tl: h y (.7 f x ).56 h y (.7 f x ) 5.56 h y (.7 f x ) 6.56 Noč vod, odnono zštitnog užet je duljine
6 Proječne viine zštitnih užet e rčunju n identičn nčin, o izotvljo duljinu izoltor: h 4 y 4 (.7 f gx +.) 4.9 N onovu podtk rpored i proječnih viin vodič odredit ćeo koordinte zrclnih lik vodič i zštitnih užet u zelji: z vodič ' : x -8.5 z vodič ' : x 4. z vodič ' : x 6. zštitno uže 4' : x -. y -.56 y y y -4.9 Međuobne udljenoti vodič i zštitnih užet koje u potrebne z prorčun induktivitet odnono ipedncije i kpcitet odnono uceptncije rčuno pre Pitgorino teoreu: D 4 D 4 D ij ( x x ) + ( y y ) ( ) i j i j D H ij i, j,,,4. ( x x ) + ( y y ) ( ) i j i j Međuobne udljenoti oznčene D odnoe e n eđuobne udljenoti vodič i zštitnih užet u prorčunu induktivitet, eđuobne udljenoti oznčene H odnoe e n ve eđuobne udljenoti vodič i zštitnih užet pre njihovi zrclni lik. H ' H ' 4. H ' H ' 4.78 H 4' 65. H ' 5. H ' 4.7 H 4' H '. H 4' H 44' 85.8 D. D 5.4 D 4.97 D 9. D D 4 7. ' H 4' H ' H ' ' ' 4' - 6 -
7 .6. Induktivitet.6.. Mtric uzdužnih ipedncij Kd trofzni vodovi teku truje nultog redolijed, tj. truje jednke u vkoj fzi, one e orju ztvoriti kroz zelju i kroz dozenu užd. Pod pretpotvko d ne dozenih užet povrtni vodič je o zelj. Cron je 96.g. izrdio etodu koj počiv n pretpotvci d povrtn nult truj kroz zelju protječe zišljeni vodiče, koji je prleln vodiče vod, prolzi ipod površine zelje udljen od njih z D i i reducirni geoetrijki rdiju. Tko e ogu korititi izvodi z prorčun induktivitet. N teelju velikog broj ekperientlnih jerenj Cron je došo do ljedećih izrz z ipednciju petlje što je čine jedn vodič i povrtni put kroz zelju. ii-z R I + R z + jx ii-z R ii-z + jx ii-z πfμ Otpor R ii-z predtvlj otpor vodič uvećn z otpor zlje R z. 4 Rektncij X ii-z predtvlj unutršnju rektnciju vodič uvećnu z vnjku rektnciju petlje vodič zelj X i z.78 μf ln. r kμf.78 X ii z μf ln + X r kμf.78 D kμf X i z X μf ln i D μf ln r r D D r D X ii z μf ln + μf ln μf ln r D D i D r v ' k r v je vltit SGU vodič; k je kontnt ovin o broju žic vodič..78 D - kvdrt ekvivlentne viine po Cronu μ kf R [Ω/k] - djeltni otpor vodič kod o C - 7 -
8 iiz πfμ D R + + μf ln i,,,4. 4 D negnetke terijle iz kojih e izvode fzni vodiči i zštitn užd, ukoliko zštitn užd nije izveden iz čelik, μ μ o 4π -4 H/k gnetk perebilnot vkuu. Uzevši to u obzir, ko i vrijednot z frekvenciju f 5 Hz, z D e dobiv:.78 D 9.6 ρ 7 4π 5k k /ρ; ρ je pecifični otpor vodič Tie i izrz z vltitu ipednciju vodič utjecje zelje prelzi u oblik: 9. R j.68ln ii z, D ρ izrz z vltitu ipednciju jednog zštitnog užet utjecje zelje: 9. R j.68ln ii z g. Dg ρ D g [] vltit SGU zštitnog užet R g [Ω/k] djeltni otpor zštitnog užet kod o C Međuobn ipedncij dviju petlji vodič zelj πμf 4 ij z + ijz.78 jμf ln D kμf πμf D + jμf ln 4 D ij ij i, j,,,4. Uvrtivši μ μ o 4π -4 H/k i f 5 Hz u gornju forulu dobivo: j.68ln ij z. Dij ρ D ij [] udljenot izeđu vodič odnono zštitnog užet i i vodič odnono zštitnog užet j (vodič i zštitno uže u rvnoprvno tretirni) - 8 -
9 Vez izeđu npon i truj u trofzni utvi je definirn Ohovi zkono u trično obliku: vodic vodic vodic [ V ] [ ] [ I ] vodic gdje u: [ V ] - vektor pdov npon vodič vodic [ ] vodic [ I ] - vektor truje vodič - tric uzdužnih ipedncij vodič U rzvijeno obliku tričn jedndžb gli: d dx V V M V M Vn n L n L ( n+ ) I L n L ( n+ ) I M M M n n L nn L n ( n+ ) In M M M ( ) ( ) ( ) ( )( ) n+ n+ L n+ n L n+ n+ In+ + Mtric ipedncij je red n+, gdje je n broj vodič, broj zštitnih užet. Dijgonlni člnovi trice ipedncij ii R ii + jωlii predtvljju vltite ipedncije petlji koje tvore vodič, odnono zštitno uže i povrtn tz kroz zelju, vndijgonlni člnovi ij R ij + jωlij predtvljju uzdužne eđuipedncije izeđu petlji i -ti vodič zelj i j -ti vodič zelj. Eleenti trice ipedncije e jednotvno određuju iz geoetrij tup i podtk o vodiči i zštitni užeti. Mtric uzdužnih ipedncij vodič ovko određen je jediničn, tj. i dienziju Ω/k. Pojedini člnovi trice uzdužnih ipedncij e određuju iz već nvedenih forul: 9. ρ ii z R j.68ln z vodiče D + 9. ii z R g +.5 j.68ln z zštitn užet Dg ρ 9. ρ ij z.5 + j.68ln z vodiče i zštitn užet D ij - 9 -
10 Tvorb trice ipedncije odvij e u kldu ljedeći prvili:. Mtric uzdužnih ipedncij je red n+, gdje u n broj vodič (ne rčunjući poebno vodiče u nopovi) ukupni broj zštitnih užet. Vodiči iju nji redni broj od zštitnih užet, tj. vodiči e nvode od do n, zštitn užd od n+ do n+.6.. Metod SGU U gornji e izrzi koriti poj SGU vodič (rednj geoetrijk udljenot) i u dljnje tektu će tj poj biti pobliže objšnjen. U prorčunu induktivivitet okruglog hoogenog vodič vltit SGU vodič je funkcij rdiju vodič i perebilitet vodič. reltivni perebilitet vodič μ r izlzi d je vltit SGU vodič: r 4 ' re μ r.7788r Veličinu r' nzivo reducirni rdiju. Uz itu truju I forirt će e u lučju punog hoogenog vodič rdiju r iti obuhvtni tok, ko u lučju šupljeg vodič bekončno tnke tijenke, li rdiju r' < r. Izrčuno vltitu SGU o jednog vodič pre izrzu: d k r gdje je r vnjki rdiju vodič, fktor k ćeo izvditi iz tblice (prilog II). hoogene vodiče dn je tj fktor u ovinoti o broju žic u vodiču. vodiče od lučel (ldreyčel) e rčun dovoljno točno ko e koritio grfo z određivnje vltite SGU z šuplje vodiče u obliku cijevi, prikzn je u obliku tblice (prilog II). Grf predtvlj funkciju d /r f (r /r ), dkle vrijedi pove općenito (r i r u vnjki i unutrnji rdiju šuplje cijevi). Alučel e ože prikzti ko šuplj cijev uz pretpotvku d v truj teče luinijki plšto. Unutrnji rdiju cijevi odgovr rdijuu čelične jezgre. Vnjki rdiju r.9 Unutrnji rdiju r 4. r /r.68 iz tblice izvdio k d /r.8 d k r Veličinu r 4. dobijeo ko zbrojio polujer centrlne čelične žice i projer jedne od šet preotlih čeličnih žic, koje e nlze u drugo loju. Dkle: r / d č /
11 D e rdilo o prejeku 5/8, kod kojeg je čeličn jezgr izveden 9 žic, rpoređenih koncentrično u loj oko centrlne žice, rčunli bi r ko 5/ d č. zštitno uže: Vnjki rdiju r 5.86 Unutrnji rdiju r.6 r /r.686 iz tblice izvdio k d /r.87 d k r Redukcij vodič u nopu Određivnje trice ipedncije kod vodov vodiči u nopu je dug rčun, p ćeo e polužiti etodo SGU. Kko e rdi o vodiči n loj eđuobnoj udljenoti, obično e nop zijeni jedni vodiče odgovrjućeg rednjeg geoetrijkog rdiju. Pogrešk je zneriv. nči potrebno je izrčunti vltitu SGU vodič. Vodiče nop rzještene n eđuobnoj udljenoti D nop ožeo zijeniti jedni vodiče. Reducirn vltit SGU z tipične nopove dn je u prilogu III. U nše lučju io dv vodič u nopu p e vltiti SGU vodič (reducirni rdiju nop vodič) rčun po izrzu: D d Dnop Sd io ve potrebne pretre z izrčunvnje trice uzdužnih ipedncij : i i i i i i.5+.58i.5+.78i i.5+.58i i i i.5+.78i i i.6.4. Redukcij zštitnih užet Io vod n vodič i zštitnih užet. Mtric ipedncije vodič it će n+ redk i n+ tupc, p je rčunnje ovkvi tric neoguće. to je potrebno d iz trice fznih vodič eliiniro zštitnu užd, i dobijeo tricu ekvivlentnih fznih vodič. štitn užd u uzeljen, p je npon n nji jednk nuli. To n oogućuje d e riješio redk i tupc zštitnih užet blok trnforcijo. - -
12 V V b d V c dx b c d q b bb cb db qb c bc cc dc qc p bp cp dp qp q bq cq dq qq I I I I I b c p q ili krćeno d dx V bc I III II bc I IV pq I d dx d dx d dx bc I bc II pq [ V ] [ ][ I ] + [ ][ I ] III bc IV pq IV [] [ ][ I ] + [ ][ I ][ ] pq IV III bc [ I ] [ ] [ ][ I ] bc I bc II IV III bc [ V ] [ ][ I ] [ ][ ] [ ][ I ] bc I II IV III bc [ V ] ([ ] [ ][ ] [ ])[ I ] Končno e tric, koj uzi u obzir oi zelje još i dozenu užd, dobiv pooću ljedećeg izrz i i onoliko redk i tupc, koliko je fznih vodič: Mtric I (obuhvć o fzne vodiče): I II IV III [ ] [ ] [ ][ ] [ ] i i i i i.5+.58i i.5+.58i i Mtric II : (obuhvć utjecj zštitnog užet n fzne vodiče): i.5+.78i i - -
13 bog činjenice d je vod izveden o jedni zštitni užeto, tric II nije prv tric, već je vektor-tupc eleentin 4, 4, 4. Mtric III : (obuhvć utjecj zštitnog užet n fzne vodiče): i.5+.78i i Ponovno zbog činjenice d je vod izveden o jedni zštitni užeto, tric III nije prv tric, već je vektor-redk eleentin 4, 4, 4. Mtric IV : (obuhvć o zštitno uže): i Obziro d potoji o jedno zštitno uže tric koj bi opiivl eđuobni utjecj zštitne uždi vodi e n jedn eleent iz trice odnono n 44. D je vod bio izveden dv zštitn užet, tric IV il bi dienzije x. Inverzij trice IV zbog tog je neuporedivo jednotvnij budući e ( IV ) - rčun ko / 44. Budući d redukcij zštitnih užet predtvlj pecijlni lučj redukcije, z koju je npon zštitnih uždi jednk nuli, nije potrebno vršiti nikkve trnforcije n vektoru npon. Pre toe z provedbu redukcije zštitnih užet dovoljn je forul redukcije z ipedncije. Ipiivnje Cronovih forul z vki vodič, vezivnje vodič u nop, te izdvjnje dozene uždi dolzio do utv ekvivlentnih fznih vodič. jednotruki vod to je tric x, z dvotruki vod 6 x 6. d dx V Vb V c b c b bb cb c bc cc I I I b c bc [ ] I I I b c Dijgonlni eleenti ove trice u uzdužne vltite ipedncije petlje ekvivlentnih fznih vodič i i zelje ko povrtnog vodič n jedinicu duljine petlje. Vndijgonlni eleenti predtvljju uzdužne eđuobne ipedncije izeđu ekvivlentnih fznih vodič i i j. - -
14 Nš tric ekvivlentnih fznih vodič izgled ovko: i i i i i i i i i.6.5. Preplet vod Ako u oi triju vodič trofznog vod ještene u vrhovi itotrničnog trokut, kžeo d je vod ietričn i v tri vodič, ko i je prejek iti, iti će iti induktivitet. Međuti, kontrukcijo vodov e t ietrij rijetko potiže. Pojedini vodiči itog vod td iju nejednke induktivitete, p zbog tog i nejednke rektncije. Rzličiti pdovi npon u pojedini fz dovode u pogonu do izobličenj zvijezde npon i do pogonkih poteškoć. bog tog e kontruktivno oigurv električn ietrij vodov, koji u geoetrijki neietrični, cikličko zjeno položj vodič n tupu odnono tkozvni preplitnje. Vod e po dužini podijeli n tri dijel. Potrebn u dv preplitnj d bi vki vodič zuzeo ve oguće položje. Kod nšeg vod pretpotvljo potpuni preplet. Slik 4. Potpuni preplet jednotrukog vod Slik 5. Potpuni preplet dvotrukog vod - 4 -
15 Neietrične vodove ietriro preplitnje. Td je uzdužn tric ipedncij projek tric ipedncij vih triju ekcij preplitnj kod jednotrukog ili vih devet ekcij preplitnj kod potpunog preplet dvotrukog vod Prijen ietričnih koponent Mtric ietričnih koponent izlzi iz trice ekvivlentnih fznih vodič prijeno linernih trnforcij. Mtric ekvivlentnih fznih vodič je ietričn. prepleteni vod treb tricu ekvivlentnih fznih vodič ietrirti. Mtric e ietrir n tj nčin d e uze rednj vrijednot vndijgonlnih eleent, ujeto d e rčun poebn tric z vku dionicu preplitnj, ito tko e rčun rednj vrijednot dijgonlnih eleent. Ako e uze u obzir d je tric ipedncij ekvivlentnih fznih vodič ietričn tric, tj. d je b b c c bc cb dobiju e rednje vrijednoti z vltite i eđuobne ipedncije ( + + ) ( + + ) b Mtric ekvivlentnih fznih vodič z prepleteni vod gli: bb bc cc c bc [ ] prep Mtric trnforcije z jednotruke vodove gle: [] S [] S - 5 -
16 - 6 - Mtrice trnforcije z dvotruk vodove gle: [ ] [] [] S S SS [ ] [] [] S S SS U gornji izrzi u opertori i : Mtricu [ ] bc trnforiro u ietrične koponente: [ ] [] [ ] [ ] S S prep bc Sitei koponent prepletenog vod u nezvini. Sietrične koponente ipedncije vod jeu: i d o + + j.5 j.5 +
17 Trnforciju u ietrične koponente lko proširio n dvotruke vodove. Tko npr. z dvotruki vod ožeo npiti trične jedndžbe: d d dx VI V bc bc II [ S] [ VI ] [] S [ V ] bc I,I bc II,I bc I,II bc II,II I I bc bc [ I,I ] [ I,II ] bc bc [ ] [ ] bc I bc II [ S] [ I ] [] [ ] I S I II dx II II,I II,II [ S] d dx [ VI ] [ V ] bc bc [ I,I ] [ I,II ] bc bc [ ] [ ] [ S] [ I ] [ ] I III [] S II,I II,II [] S II Kko je: [] S [] S [ S] dobijeo: [] S, [ ] [ S] [] S [ ] [ ] bc,bc S [] S Nkon trnforcije trice ekvivlentnih fznih vodič dobivo u nše zdtku uzdužnu tricu z ietrične koponente: i i i Ko što o prije poenuli, dijgonlni eleenti trice u redo nult, direktn i inverzn ipedncij. nultu ipednciju jedne fze dobivo: R + jω L j.6594 Ω / k. o o o Nult ipedncij jednog vodič je dv put već (zbog dv vodič u nopu) i iznoi: o j.88 Ω / k - 7 -
18 Djeltni otpor nultog utv (po vodiču) iznoi: R o Ω/k Induktivitet nultog utv (po vodiču) iznoi: L o H/k Direktn i inverzn ipedncij jedne fze vod iznoi: R + jω L j.4 / k Ω Djeltni otpor direktnog utv (po fzi) iznoi: R.5977 Ω/k Induktivitet direktnog i inverznog utv (po fzi) iznoi: L.98 - H/k.7. Kpcitet.7.. Utjecj zelje Površinu zelje ožeo trti površino vodljivog tijel, n kojoj e pod utjecje nboj vodič tkođer kupi električni nboj. Vžn je viin vodič iznd tl. Metod zrcljenj n pože d u rčun uključio zelju bez potrebe z određivnje nboj n površini zelje. Slik polj izeđu vodič i zelje it je ko i dio like polj izeđu dv vodič n dvotrukoj udljenoti..7.. Odvod vod i koron bog teškog tetičkog definirnj, ko i zbog znerivog utjecj n rezultte prorčun, odvod vod i koron niu uzeti u obzir. Pre toe pretpotvljo toko prorčun d je odvod G. Krkteritične veličine odvod po fzi jedne trojke iznoe.. μs/k..7.. Mtric potencijlnih koeficijent Vez npon i nboj vodič ože e izrziti jedndžbo koj definir tricu potencijlnih koeficijent: [ V] [ P] [ Q] gdje u: [ V ] - vektor npon n vodiči - 8 -
19 [ P ] - tric potencijlnih koeficijent [ Q ] - vektor nboj n vodiči Potencijli vodič pre zelji u funkcij nboj n vodiči. U tcionrno tnju vrijedi izrz: d dx V V M V M Vn n P P L Pn L P ( n+ ) Q P P L Pn L P ( n+ ) Q M M M Pn Pn L Pnn L Pn ( n+ ) Qn M M M ( ) ( ) ( ) ( )( ) P n+ P n+ L P n+ n L P n+ n+ Qn+ + Vrijedi ponovno d je tric potencijlnih koeficijent red n+, gdje n i iju već rnije opino znčenje. Mtric [P] je reln kvdrtn ietričn tric, čiji e člnovi jednotvno određuju iz geoetrije tup i podtk o vodiči i zštitni užeti. Dijgonlni člnovi trice potencijlnih koeficijent z vodiče određuju e iz izrz: 6 Hii Pii 8 ln [ k / F] Dc odnono, z zštitn užet: 6 Hii Pii 8 ln [ k / F] Dgc Vndijgonlni člnovi trice potencijlnih koeficijent određuju e iz izrz: P ij H 6 8 ln D ij ij [ k / F] U gornji izrzi pojedine oznke predtvljju ljedeće (oi već nvedenih oznk): H ii [] udljenot vodič, odnono zštitnog užet, od voje zrclne like, H ij [] udljenot vodič, odnono zštitnog užet, i od zrclne like vodič, odnono zštitnog užet j (vodiči i zštitno uže u rvnoprvno tretirni). Tvorb trice potencijlnih koeficijent podliježe vi prvili ko i tric ipedncij. Kod određivnj vltite SGU vodič z prorčun kpcitet (reducirni rdiju nop) rčuno n iti nčin ko kod induktivitet, o što ujeto vltite SGU vodič d uzeo u prorčun vnjki rdiju vodič r. N tj nčin izrčuno vltitu SGU vodič: D r D c nop 4-9 -
20 U prorčunu z zštitno uže tkođer rčuno vnjki rdijuo vodič ujeto reducirni rdijuo: D gc r g 5.86 Mtric potencijlnih koeficijent z nš prijer gli:.94e e+7.794e+7.997e e+7.4e+8.766e+7.47e+7.794e+7.766e+7.449e+8.494e+7.997e+7.47e+7.494e e+8 Ako jedndžbu [ V] [ P][ Q] [ Q] [ P] [ V] [ [ K][ V] ponožio [ P] [ K] [ P] dobijeo: Mtric [ K ] je tric kpcitivnih koeficijent. On dje vezu izeđu nboj n vodiči i npon vodič pre zelji. Ponožio gornju jedndžbu jω: jω[ Q] jω[ K][ V] [] I jω[ K][ V] [] I j[ B][ V] Množenje trice [ K ] ω dobijeo tricu kpcitivnih uceptncij [ B ]: odnono: [ B ] ω[ K] ω [ B] [ P] Dkle, budući d želio odrediti tricu ditncij, odnono uceptncij, već u prvo korku e člnovi trice potencijlnih koeficijent dijele kružno frekvencijo ω π f, odnono: - -
21 [ B ] Dobiven je inverzn tric kpcitivnih uceptncij. Potupko blok trnforcije eliiniro zštitnu užd, te n krju rpolžeo inverzno trico ekvivlentnih fznih uceptncij. Potupk blok trnforcije itovjetn je ono pokzno z redukciju zštitnog užet iz trice ipedncije vodič. Dkle: ekv I II IV III [ B ] [ B ] [ B ][ B ] [ B ] Mtric B I (obuhvć o fzne vodiče): Mtric B II : (obuhvć utjecj zštitnog užet n fzne vodiče): bog činjenice d je vod izveden o jedni zštitni užeto, tric B II nije prv tric, već je vektor-tupc eleentin B - 4, B - 4, B - 4. Mtric B III : (obuhvć utjecj zštitnog užet n fzne vodiče): Ponovno zbog činjenice d je vod izveden o jedni zštitni užeto, tric B III nije prv tric, već je vektor-redk eleentin B - 4, B - 4, B - 4. Mtric B IV : (obuhvć o zštitno uže):
22 Obziro d potoji o jedno zštitno uže tric koj bi opiivl eđuobni utjecj zštitne uždi vodi e n jedn eleent iz trice B - odnono n B D je vod bio izveden dv zštitn užet, tric B IV il bi dienzije x. Inverzij trice B IV zbog tog je neuporedivo jednotvnij budući e (B IV ) - rčun ko /B Inverzn tric ekvivlentnih fznih uceptncij iznoi: Inverzn tric ekvivlentnih fznih uceptncij e poto invertir i rezultt je tric vltitih i eđuobnih uceptncij ekvivlentnih fznih vodič..7948e E-7 -.4E E-7.8E E-7 -.4E E-7.954E-6 Mtricu ietričnih koponent z utv ekvivlentnih fznih uceptncij vodič dobivo n iti nčin ko i tricu ietričnih koponent z utv ekvivlentnih fznih ipedncij. gdje je: [ B ] [] S [ B ] [] S [ B ] prep prep B B B B B B B o B d B B B B i tric ekvivlentnih fznih uceptncij prepletenog vod. Srednje vrijednoti z vltite i eđuobne uceptncije prepletenog vod u: B B ( B + B + B ) ( B + B + B ) 4.7 b bb bc cc c - -
23 ietrične ditncije jeu: B o B + B B d B i B B U gornje izrzu dijgonlni čln B o predtvlj jediničnu nultu, B d i B i direktnu i inverznu poprečnu uceptnciju, izrženu u S/k. B d i B i u jednki, jer ne rotcionih dijelov. U nše prorčunu dobivo tricu ietričnih koponenti kpcitivnih uceptncij ekvivlentnih fznih vodič:.6e-6.57e-6.57e-6 Ko što o prije poenuli, dijgonlni eleenti trice u redo nult, direktn i inverzn uceptncij. nulti kpcitet (po vodiču) dobivo: C o B o /( ω ).4-9 F/k Direktni i inverzni kpcitet po fzi gli: C B /ω.7-8 F/k.8. Nzivni npon vod Nzivni npon vod e očit iz broj člnk izoltorkog lnc: U nz kv..9. Jkot električnog polj n površini vodič Koron ntje kd jkot električnog polj n površini vodič prekorči električnu čvrtoću uzduh. Jkot električnog polj kontroliro n površini vodič jer je to jkot polj njveć. trofzni vod više vodič, izrz z kilnu vrijednot polj je: E U x ( + ( ) r / r ) nop kv c x D r ln D gdje je: U x njviš vrijednot npon koj e u norlni pogonki uvjeti ože pojviti u bilo koje trenutku i u bilo kojoj točki reže: U x. U n. 4 kv broj vodič u nopu - -
24 r.9 c vnjki rdiju vodič r nop - rdiju kružnice nop (vodiči u redovito prvilno rpoređeni po kružnici). U nše lučju e vodiči nlze n projeru kružnice opine oko vodič, p je: Dnop rnop 5 D eđuobn SGU fznih vodič D D D D D 5.9 vltit SGU vodič Uvrtivši dobivene podtke izrčunvo kilnu jkot polj: ( + ( ).9 /5) 4 Ex ln 5.9 kv c.. Kritični npon Kritični npon je onj pogonki npon kod kojeg jkot električnog polj n površini vodič tn doegne vrijednot električne čvrtoće uzduh. Ako je, dkle, pogonki npon nji od kritičnog nećeo iti pojvu korone. Ako je pogonki npon veći od kritičnog iti ćeo pojvu korone, i to utoliko jču što je rzlik izeđu pogonkog i kritičnog npon već. Izrz z kritični npon je izveden uz pretpotvku d je jkot električnog polj n površini vodič jednk električnoj čvrtoći uzduh, koj u norlni prilik iznoi kv/c. Dobivo linijki kritični npon U kr iz jedndžbe: U kr. + r ln ( D / D ) ( ) ( r / r ) nop [ kv ].9 ln ( 9 / 5.9) ( ) (.9 /5). U kr kv - 4 -
25 PRILOG I Tblic. Alučeličn i ldreyčeličn užet Nzivni prejek Ukupni projer Broj i projer žic plšt Al ili E-AlMg čeličn jezgr Rčunki prejek užet plšt jezgr ukupno Al/Fe Srednji oki otpor (Ω/k kod o C) E-AlMg Fe 6/ x.8 x / x.5 x / x.7 x / x. x /.65 x. 7 x /.7 6 x.85 7 x / x. 9 x /5.6 6 x.5 7 x /55 6. x. 7 x / x.44 7 x /7 8. x.6 7 x / x.7 7 x /4 8.9 x.7 7 x / x. 7 x /5.7 6 x. 7 x / x.8 9 x /54.5 x.5 7 x / x.45 7 x /55.4 x. 7 x / x.6 9 x /8 6.9 x.85 9 x / x 4. 9 x / x.8 7 x /9 9. x 4. 9 x / x.7 9 x / x.4 7 x /.85 x x / x.5 7 x / x 4. 9 x / x x
26 Tblic. Vodiči od čelik. luinij i E-AlMgSi (ldrej) Nzivni Rčunki Kontrukcij Vnjki Srednji oki otpor (Ω/k kod o C) prejek prejek broj projer projer žic žic [] čelik E-Al E-AlMgSi
27 PRILOG II Vltiti SGU vodič (d ) ) Hoogen užet ( r - vnjki rdiju) Broj žic d žic.779 r 7 žic.77 r 9 žic.758 r 7 žic.768 r 6 žic.77 r ) Cijevi (r - vnjki. r - unutrnji rdiju) Vrijedi probližno i z užet - 7 -
28 r/r d/r r/r d/r r/r d/r r/r d/r r/r d/r
29 PRILOG III Vltit SGU vodič u nopu Proječni pecifični otpor tl: ork vod očvr zelj vlžn krupn pijek itni uhi pijek uhi krupni šljunk kenito tlo Ω Ω Ω Ω 5 Ω Ω Ω - 9 -
30 PRILOG IV Glve tupov - -
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
PIRAMIDA I ZARUBLJENA PIRAMIDA. - omotač se sastoji od bočnih strana(najčešće jednakokraki trouglovi), naravno trostrana piramida u omotaču
 PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA
 OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]
![c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata] c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]](/thumbs/92/108578155.jpg) Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
A MATEMATIKA Zadana je z = x 3 y + 1
 A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
KUPA I ZARUBLJENA KUPA
 KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
Rješenje: F u =221,9 N; A x = F u =221,9 N; A y =226,2 N.
 Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi
 Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.
 šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su
 ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
GIBANJE (m h) giba miruje giba giba miruje miruje h 1000 :1000 h 1 h h :1000 1
 GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
Osnove elektrotehnike I parcijalni ispit VARIJANTA A. Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti.
 Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F
 SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
Istosmjerni krugovi. 1. zadatak. Na trošilu će se trošiti maksimalna snaga u slučaju kada je otpor čitavog trošila jednak unutrašnjem otporu izvora.
 Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,
 Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
povratnog napona 6 prekidača na slici 1.
 Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ELEKTROMOTORNI POGONI - AUDITORNE VJEŽBE
 veučilište u ijeci TEHNIČKI FAKULTET veučilišni preddiplomki tudij elektrotehnike ELEKTOOTONI OGONI - AUDITONE VJEŽBE Ainkroni motor Ainkroni motor inkrona obodna brzina inkrona brzina okretanja Odno n
veučilište u ijeci TEHNIČKI FAKULTET veučilišni preddiplomki tudij elektrotehnike ELEKTOOTONI OGONI - AUDITONE VJEŽBE Ainkroni motor Ainkroni motor inkrona obodna brzina inkrona brzina okretanja Odno n
γ = 120 a 2, a, a + 2. a + 2
 Zdtk (Slvi, gimnzij) Duljine strni trokut čine ritmetički niz (slijed) s rzlikom Jedn kut iznosi Koliki je opseg trokut? Rješenje inči udući d duljine strni trokut čine ritmetički niz (slijed) s rzlikom,
Zdtk (Slvi, gimnzij) Duljine strni trokut čine ritmetički niz (slijed) s rzlikom Jedn kut iznosi Koliki je opseg trokut? Rješenje inči udući d duljine strni trokut čine ritmetički niz (slijed) s rzlikom,
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor
 I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
Elektrostatika. 1. zadatak. Uvodni pojmovi. Rješenje zadatka. Za pločasti kondenzator vrijedi:
 tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
MEHANIKA FLUIDA. Isticanje kroz velike otvore
 MEANIKA FLUIDA Isticnje krz velike tvre 1.zdtk. Krz veliki ptvr u bčn zidu rezervr blik rvnkrkg trugl snve i keficijent prtk µ, ističe vd. Odrediti prtk krz tvr k su pznte veličine 1 i (v.sl.). Eleentrni
MEANIKA FLUIDA Isticnje krz velike tvre 1.zdtk. Krz veliki ptvr u bčn zidu rezervr blik rvnkrkg trugl snve i keficijent prtk µ, ističe vd. Odrediti prtk krz tvr k su pznte veličine 1 i (v.sl.). Eleentrni
Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.
 Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Lekcija 3 Istosmjerni motor s nezavisnom uzbudom
 Lekcij 3 tomjerni motor nezvinom uzbudom Prof.dr.c. Jmin Velgić Elektrotehnički fkultet Srjevo olegij: Aktutori 3 1 tomjerni motor nezvinom uzbudom 2/72 Mtemtički opi itomjernog motor nezvinom uzbudom
Lekcij 3 tomjerni motor nezvinom uzbudom Prof.dr.c. Jmin Velgić Elektrotehnički fkultet Srjevo olegij: Aktutori 3 1 tomjerni motor nezvinom uzbudom 2/72 Mtemtički opi itomjernog motor nezvinom uzbudom
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA
 SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. ANALITIČA GEOMETRIJA PROSTORA II. DIO (Pv).. Min Roić Linović 9./. Pv u otou Jenž v Nek je: T (,, ) n točk oto {,, } ni vekto mje Znom točkom oto oli mo v leln nim vektoom. T (,,) - oivoljn točk v
II. ANALITIČA GEOMETRIJA PROSTORA II. DIO (Pv).. Min Roić Linović 9./. Pv u otou Jenž v Nek je: T (,, ) n točk oto {,, } ni vekto mje Znom točkom oto oli mo v leln nim vektoom. T (,,) - oivoljn točk v
a) Kosi hitac Krivolinijsko gibanje materijalne toke Sastavljeno gibanje Specijalni sluajevi kosog hica: b) Horizontalni hitac c) Vertikalni hitac
 ) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA. Prof. dr. sc. Ivica Kladarić
 STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA Prof. dr. sc. Ivic Kldrić Identifikcij i procjen mikrostrukture METALOGRAFIJA je istrživčk metod koj ouhvć optičko istrživnje mikrostrukture
STRUKTURA I SVOJSTVA MATERIJALA METALOGRAFIJA ŽELJEZNIH LEGURA Prof. dr. sc. Ivic Kldrić Identifikcij i procjen mikrostrukture METALOGRAFIJA je istrživčk metod koj ouhvć optičko istrživnje mikrostrukture
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
1 Ekstremi funkcija više varijabli
 1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
Priprema za ispit - RJEŠENJA
 Priprem z ispit - RJEŠENJA 1. Odredi duljinu strnie i kutove trokut ABC ko je = 16 m, = 11.2 m te + = 93⁰. = 16 m = 11.2 m + = 93⁰,,, =? Njprije ćemo izrčunti kut jer je = 180⁰ - ( + ) = 87⁰ No, sd znmo
Priprem z ispit - RJEŠENJA 1. Odredi duljinu strnie i kutove trokut ABC ko je = 16 m, = 11.2 m te + = 93⁰. = 16 m = 11.2 m + = 93⁰,,, =? Njprije ćemo izrčunti kut jer je = 180⁰ - ( + ) = 87⁰ No, sd znmo
Metode rješavanja izmjeničnih krugova
 Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 17. VEKORI I KVADRANE MARICE 17.1 Opcenito o vektorim Vektor je usmjeren duzin i zto im: pocetk (hvtiste), krj i smjer. Vektor se ozncv s oznkom n pr.: rpq,, Duzin PQ ili r nziv se duzin vektor, intenzitet
17. VEKORI I KVADRANE MARICE 17.1 Opcenito o vektorim Vektor je usmjeren duzin i zto im: pocetk (hvtiste), krj i smjer. Vektor se ozncv s oznkom n pr.: rpq,, Duzin PQ ili r nziv se duzin vektor, intenzitet
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
Odredjeni integral je granicna vrijednost sume beskonacnog broja clanova a svaki clan tezi k nuli i oznacava se sa : f x dx f x f x f x f x b a f
 Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
R: a) x(t)..nejednoliko gibanje duž pravca; y(t)..jednoliko ubrzano gibanje duž pravca s akceleracijom 10 m/s 2. r r r r b) t=0,5 s, ( ) ( ) s
 PRIPREA ZA ZADACU_3 I SEINAR_3 I Gibnje mterijlne točke Riješeni zdtk: I.. Vektor položj mterijlne točke zdn je relcijom: r(t) = ( 6t 3 4t + 3t) i + (5t 3t + ) j Odredite: ) vrtu gibnj u x i y mjeru i
PRIPREA ZA ZADACU_3 I SEINAR_3 I Gibnje mterijlne točke Riješeni zdtk: I.. Vektor položj mterijlne točke zdn je relcijom: r(t) = ( 6t 3 4t + 3t) i + (5t 3t + ) j Odredite: ) vrtu gibnj u x i y mjeru i
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Osnovna škola. b) Koliko prstenova treba objesiti na kukicu s lijeve strane na slici 2 da bi poluga bila u ravnoteži? 1 3 F/N
 ŠKOLSKO/OPĆINSKO NTJENJE IZ FIZIKE 2.2.2009. Osnovn škol Uut: U svim zdcim gdje je to otrebno koristiti g = 10 N/kg. 1. zdtk (7 bodov) ) Slik 1 rikzuje olugu u rvnoteži n kojoj se nlze dv rsten i neoznti
ŠKOLSKO/OPĆINSKO NTJENJE IZ FIZIKE 2.2.2009. Osnovn škol Uut: U svim zdcim gdje je to otrebno koristiti g = 10 N/kg. 1. zdtk (7 bodov) ) Slik 1 rikzuje olugu u rvnoteži n kojoj se nlze dv rsten i neoznti
OBRASCI ELEMENTARNE MATEMATIKE SY jun 2008.
 OBRASCI ELEMENTARNE MATEMATIKE SY347 9. ju 008. Priroi rojevi u kup vih pozitivih elih rojev, N {,, 3,...}. Celi rojevi u kup vih pozitivih i etivih elih rojev i ule, Z {...,, 3, 0,,, 3,...}. Rioli rojevi
OBRASCI ELEMENTARNE MATEMATIKE SY347 9. ju 008. Priroi rojevi u kup vih pozitivih elih rojev, N {,, 3,...}. Celi rojevi u kup vih pozitivih i etivih elih rojev i ule, Z {...,, 3, 0,,, 3,...}. Rioli rojevi
Primer 3.1 Ugaona brzina i ugaono ubrzanje prenosnog elementa:
 Pie 3.1 Mehnički ite, ikzn n lici, keće e u vni ctež. Ketnje enonog eleent definiše njegov ugo otcije ϕ ( t) eltivno ketnje definiše koodint ( ) t. Podci u: ϕ( t ) t, ( t) 3t t, b 1, ( t[ ], [ ], ϕ[ d
Pie 3.1 Mehnički ite, ikzn n lici, keće e u vni ctež. Ketnje enonog eleent definiše njegov ugo otcije ϕ ( t) eltivno ketnje definiše koodint ( ) t. Podci u: ϕ( t ) t, ( t) 3t t, b 1, ( t[ ], [ ], ϕ[ d
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
x y 2 9. Udaljenost točke na osi y od pravca 4x+3y=12 jednaka je 4. Koja je to točka?
 MATEMATIKA Zdci s držvne mture viš rzin Brojevi i lgebr Funkcije Jedndžbe i nejedndžbe Geometrij Trigonometrij LINEARNA FUNKCIJA 1. Uz koji uvjet jedndžb A+By+C=0 predstvlj prvc?. Koje je znčenje broj
MATEMATIKA Zdci s držvne mture viš rzin Brojevi i lgebr Funkcije Jedndžbe i nejedndžbe Geometrij Trigonometrij LINEARNA FUNKCIJA 1. Uz koji uvjet jedndžb A+By+C=0 predstvlj prvc?. Koje je znčenje broj
Gravitacija ZADACI ZA SAMOSTALNI RAD STUDENATA OSNOVE FIZIKE 1
 Oje z fiziku eučiište Joi Juj toye itcij ADACI A AOALNI AD UDENAA ONOVE IIKE. Oeite eio obik jeec oko eje ko zno je enji ouje eje 670 k, je enj ujenot izeñu eje i jeec,8 0 8 i oć (uniezn) gitcijk kontnt
Oje z fiziku eučiište Joi Juj toye itcij ADACI A AOALNI AD UDENAA ONOVE IIKE. Oeite eio obik jeec oko eje ko zno je enji ouje eje 670 k, je enj ujenot izeñu eje i jeec,8 0 8 i oć (uniezn) gitcijk kontnt
 IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
38. Savezno takmiqenje iz fizike za uqenike srednjih xkola xkolske 2002/2003. god. II razred
 Zdtke pripreil: Zoric Pjovi Recenzent: dr Gorn Popri Predednik koiije: dr Mi o Mitrovi JUGOLOVENKO DRUXVO FZQR MNRVO PROVJEE NUKE REPULKE CRNE GORE MNRVO PROVEE POR REPULKE RJE MNRVO Z PROVJEU NUKU KULURU
Zdtke pripreil: Zoric Pjovi Recenzent: dr Gorn Popri Predednik koiije: dr Mi o Mitrovi JUGOLOVENKO DRUXVO FZQR MNRVO PROVJEE NUKE REPULKE CRNE GORE MNRVO PROVEE POR REPULKE RJE MNRVO Z PROVJEU NUKU KULURU
DINAMIKA. Dinamički sistem - pogon sa motorom jednosmerne struje: N: Dinamički sistem Ulazi Izlazi (?)
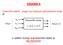 DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
Kinematika materijalne toke. 3. dio a) Zadavanje krivocrtnog gibanja b) Brzina v i ubrzanje a
 Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
α =. n n n Vježba 001 Koliko stranica ima pravilni mnogokut ako jedan njegov unutarnji kut iznosi 144? Rezultat: n = 10.
 Zdtk (Mrij, gimzij) Koliko stric im prvili mogokut ko jed jegov uutrji kut izosi 8? Rješeje Formul z veličiu jedog uutrjeg kut prvilog mogokut je: ( ) 8 α = ( ) 8 8 = / 8 = ( ) 8 8 = 8 6 8 8 = 6 7 = 6
Zdtk (Mrij, gimzij) Koliko stric im prvili mogokut ko jed jegov uutrji kut izosi 8? Rješeje Formul z veličiu jedog uutrjeg kut prvilog mogokut je: ( ) 8 α = ( ) 8 8 = / 8 = ( ) 8 8 = 8 6 8 8 = 6 7 = 6
STATISTIKA S M E I M N I AR R 7 : METODE UZORKA
 Fakultet za menadžment u turizmu i ugotiteljtvu, Opatija Sveučilišni preddiplomki tudij Polovna ekonomija u turizmu i ugotiteljtvu Noitelj kolegija: Prof. dr. c. Suzana Marković Aitentica: Jelena Komšić
Fakultet za menadžment u turizmu i ugotiteljtvu, Opatija Sveučilišni preddiplomki tudij Polovna ekonomija u turizmu i ugotiteljtvu Noitelj kolegija: Prof. dr. c. Suzana Marković Aitentica: Jelena Komšić
MEHANIKA FLUIDA. Pritisak tečnosti na ravne površi
 MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA
 FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Formule iz Matematike II. Mandi Orlić Tin Perkov
 Formule iz Mtemtike II Mndi Orlić Tin Perkov INTEGRALI NEODREDENI INTEGRALI Svojstv 1. (f(x) ± g(x)) = ± g(x) 2. = Tblic integrl f(x) F(x) + C x + C x x +1 +1 + C 1 x ln x + C 1 x+b ln x + b + C e x e
Formule iz Mtemtike II Mndi Orlić Tin Perkov INTEGRALI NEODREDENI INTEGRALI Svojstv 1. (f(x) ± g(x)) = ± g(x) 2. = Tblic integrl f(x) F(x) + C x + C x x +1 +1 + C 1 x ln x + C 1 x+b ln x + b + C e x e
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Zadatak 1
 PISMENI ISPIT IZ KLASIČNE MEHANIKE I 3.. 9. Zdtk Čestic mse m izbčen je s površine Zemlje pod kutem α brzinom v. Ako je otpor zrk proporcionln trenutnoj brzini konstnt proporcionlnosti je ), izrčunjte
PISMENI ISPIT IZ KLASIČNE MEHANIKE I 3.. 9. Zdtk Čestic mse m izbčen je s površine Zemlje pod kutem α brzinom v. Ako je otpor zrk proporcionln trenutnoj brzini konstnt proporcionlnosti je ), izrčunjte
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA
 TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA. školska 2013./2014. godina TEST MATEMATIKA UPUTE ZA RAD
 ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
Poučak o kosinusu (kosinusov poučak) U trokutu ABC vrijede ove jednakosti b + c a a + c b a + b c.
 Zdtk 4 (4, TUŠ) Kolik je mjer njmnjeg kut u trokutu kojemu su strnie duljin 7 m, 8 m i 9 m? Rješenje 4 Trokut je dio rvnine omeñen s tri dužine Te dužine zovemo strnie trokut Nsuprot većoj strnii u trokutu
Zdtk 4 (4, TUŠ) Kolik je mjer njmnjeg kut u trokutu kojemu su strnie duljin 7 m, 8 m i 9 m? Rješenje 4 Trokut je dio rvnine omeñen s tri dužine Te dužine zovemo strnie trokut Nsuprot većoj strnii u trokutu
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Seminar 13 i 14: Laplaceove tranformacije
 Seinar i : Laplaceove tranforacije Koritio izvadak iz dva tudentka rada koje donoio na ljede ih pet tranica ovih aterijala. Sljede u tablicu oºete korititi na ipitia. Takožer oºete korititi tablicu koju
Seinar i : Laplaceove tranforacije Koritio izvadak iz dva tudentka rada koje donoio na ljede ih pet tranica ovih aterijala. Sljede u tablicu oºete korititi na ipitia. Takožer oºete korititi tablicu koju
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami
 BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
 27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
Specijalna vrsta nepravih integrala jesu oni koji sadrze potencije ili geometrijski red u podintegralnoj funkciji.
 Mt Vijug: Rijsni zdci iz vis mtmti 9. NEPRAVI INTEGRALI 9. Opcnito o nprvim intgrlim Intgrl oli f d s nziv nprviln o: ) jdn ili oj grnic intgrcij nisu oncn vc soncn:, ) pod intgrln funcij f j prinut u
Mt Vijug: Rijsni zdci iz vis mtmti 9. NEPRAVI INTEGRALI 9. Opcnito o nprvim intgrlim Intgrl oli f d s nziv nprviln o: ) jdn ili oj grnic intgrcij nisu oncn vc soncn:, ) pod intgrln funcij f j prinut u
 Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
 ! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
Zdaci iz trigonometrije trokuta Izračunaj ostale elemente trokuta pomoću zadanih:
 Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
TROUGAO. - Stranice a,b,c ( po dogovoru stranice se obeležavaju nasuprot temenu, npr naspram temena A je stranica a, itd) 1, β
 TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
