Mehanika fluida... Osnovna jednačina hidrostatike... Vežba br. 1
|
|
|
- Ἀριστόβουλος Ζάχος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Mehnik fluid Osnovn jednčin hidrosttike Vežb br ZDTK ) Z svki od fluid u prikznim sudovim usvojiti i ncrtti n slici referentni sistem z=0, ztim odrediti pijezometrsku kotu b) Izrčunti hidrosttički (p) i psolutni (p ps ) pritisk u oznčenim tčkm (-E) c) Izrčunti čitnj n mnometrim p M i p M u drugom sudu d) Ncrtti slobodn nivo fluid u pijezometrim drugog sud i npisti vrednost C p M p M NFT VOD D = α+ β 50 m / VOD E ρ 3 VODE =0 kg/dm α+ β ρ NFTE = ( 0 - ) kg/dm 00 3 ZDTK N slici su prikzn dv spojen sud u kojim se nlze fluidi gustin ρ =083 kg/dm 3, ρ =0 kg/dm 3 i ρ 3 =097 kg/dm 3 Iznd fluid gustine ρ 3 nlzi se vzduh, čij se gustin znemruje Z dtu instlciju izrčunti: ) Pijezometrske kote svih fluid N skici ncrtti položj kot i upisti vrednosti b) Pritisk u vzduhu ) Čitnje n otvorenom (p M ) i diferencijlnom (p M ) mnometru VZDUH p M p M ρ 3 ρ 05 ρ ρ = αβ - 0 m
2 Mehnik fluid Hidrosttičk sil horizontln komponent Vežb br ZDTK Odrediti intenzitet, prvc i smer horizontlne komponente hidrosttičke sile koj deluje n - zid rezervor z tri rzličit slučj Ukupnu silu odrediti ko zbir pojedinčnih komponenti (vektorski sbrti) i odrediti mesto delovnj rezultnte Npomen: Silu rčunti po nčelim z rvnski zdtk tmo gde to nčelo vži ) presek - = α+ β 50 m ρ v ρ v ρ 3 v =0 kg/dm b) presek - ρ ρ = α 0 m ρ 3 =085 kg/dm ρ =0 kg/dm 3 ρ ρ 0 c) presek - vzduh vzduh = β 5 m 4 ρvz 0 ρ 3 v =0 kg/dm h=/4 ` ρ` ρ v ρ v 3 ρ` =36 kg/dm 3
3 Mehnik fluid Hidrosttičk sil vertikln komponent i ukupn sil Vežb br 3 ZDTK 3 Odrediti vertiklnu komponentu hidrosttičke sile (intenzitet, smer i npdnu tčku) koj deluje n zid širine L Ukupnu ve rtiklnu silu rčunti ko zbir pojedinčnih komponenti 5 ρ = = α+ β 50 m α+ β ( +07) kg/dm ρ = ( α+ β 00 +0) kg/dm3 ρ ρ 4 3 L=5 00 ZDTK 3 N slici je prikzn rezervor u kojem se nlzi vod gustine ρ=0 kg/dm 3 i vzduh znemrljive gustine ) N osnovu čitnj n mnometru odrediti pijezometrsku kotu vode b) Z svki od tri oznčen del površine (-3) izrčunti vertiklnu komponentu hidrosttičke sile p M= ( α+ β)/4 kp () 07 () VZDUH (3) 07 presek VOD = α+ β 30 m 4 ZDTK 33 N osnovu slike iz zdtk 3 izrčunti ukupnu hidrosttičku silu n polusferno ispupčenje (3) u slučju d je čitnje n mnometru p M = -06(α+β) kp
4 Mehnik fluid Tečenje u cevim pod pritiskom Vežb br 4 ZDTK 4 Iz rezervor vod dotiče u rezervor kroz horizontlnu cev prečnik 50 mm i koso crevo prečnik 00 mm ) ko je protok kroz horizontlnu cev Q =5+(α+β)/5 L/s izrčunti pijezometrsku kotu Π u rezervoru b) Izrčunti protok kroz crevo Q ko se mlznic n krju crev nlzi n koti Z ml =(α+β)/0+03 m c) U odgovrjućoj rzmeri ncrtti energetsku i pijezometrsku liniju Π =? Z ul=( α+ β)/0 m ξ ul =05 ξ ul =05 λ =0030 D =00 mm Q=? λ =000 D=50 mm L=0 ( α+ β) m ξ ml =005 Z ml = ( α+ β)/0+03 m Π=( α+ β)/0 m ZDTK 4 Iz rezervor vod se isporučuje nselju s potrošnjom Q 3 =(α+β)+5 L/s, deo se koristi z punjenje rezervor ) ko je ukupn protok vode iz rezervor Q =5(α+β) L/s, odrediti koeficijent loklnog gubitk energije n ztvrču n cevi ξ zt tko d nselje dobije odgovrjuću količinu vode b) Odrediti protok Q i pijezometrsku kotu u rezervoru c) U odgovrjućoj rzmeri ncrtti energetsku i pijezometrsku liniju d) ko bi se nselje snbdevlo vodom smo iz rezervor (ztvrč n cevi se potpuno ztvori), koliki bi bio protok kroz cevovod? 5m 5m 5m D=300 mm ξ zt =? ξ kol =03 D=00 mm 3 D=5 0 mm ξ ul =05 Q=5( α+ β) L/s ξ rc =0 m ξ zt =5 8m m Q 3=( α+ β)+5 L/s
5 Mehnik fluid Tečenje u cevi - Dinmičk jednčin Vežb br 5 ZDTK 5 ) Odrediti protok kroz cev ko očitn rzlik pijezometrskih kot u presecim i (pre i n suženju) iznosi Π=(α+β)/0 m b) Odrediti silu kojom vod deluje n mlznik oblik konus od presek 3 do presek 4, ko je ukupn gubitk energije duž konus 5% brzinske visine u preseku 4 Znemriti linijski gubitk energije duž konus Π=( α+ β)/0m 3 4 D=5( α+ β)mm D=3( α+)mm β D=5( α+ β)mm z=0 d ml=( α+ β)mm ξ - =0 3 5D 4 ZDTK 5 ) N osnovu očitnog pritisk n mnometru izrčunti protok u cevim b) Odrediti presečne sile (M, N i T) u preseku - Pri prorčunu uzeti u obzir i sopstvenu težinu cevi p M=5( α+ β) kp Koeficijent trenj z obe cevi λ=00 Sopstven te`in cevi G 4 C=300 N/m 5 ξ kol =04 ξ ml =0 D=50mm 00 d ml=00mm D=50mm 80 ξ ul =05 Q
6 Mehnik fluid Tečenje u cevi Hidruličke mšine Vežb br 6 ZDTK 6 Iz rezervor vod se pomoću pumpe prebcuje u rezervor (gornji cevovod) Iz rezervor vod se grvitciono vrć u rezervor (donji cevovod) ) ko je protok kroz donji cevovod Q =3(α+β) L/s izrčunti pijezometrsku kotu u rezervoru Pretpostviti d su rezervori dovoljno veliki tko d je nivo u njim konstntn b) ko je protok kroz gornji cevovod jednk protoku kroz donji Q =Q izrčunti visinu diznj i sngu pumpe c) U odgovrjućoj rzmeri ncrtti energetsku i pijezometrsku liniju z gornji cevovod 00 m 500 m Π =? Π= α/0 m m ξ ul =05 λ =005 η=07 D=500 mm ξzt= αβ λ =005 D =300 mm Q=3( α+ β) L/s λ 3 =005 D 3=300 mm ξ ul =05 m ξ kol =0 00 m Q=3( α+) β L/s 600 m ξ kol =0 ZDTK 6 ) Izrčunti potrebnu energiju vode n potisu pumpe (presek -), tko d se n poslednjem (četvrtom) prskču održi pritisk od p 4 =50 kp Protok i pritisk kroz prskče su vezni jednčinom Q i = C p, gde je protok u m3 /s, pritisk (p) u brim C=β/(α) Referentn rvn, z=0 m, je n osi cevovod Nizvodno od presek 4 potrebno je obezbediti protok od 0 L/s b) Izrčunti minimln nivo u rezervoru d se n usisu pumpe (presek -), ne pojvi negtivn pritisk c) Izrčunti visinu diznj pumpe d) Ncrtti energetsku i pijezometrsku liniju z grnični slučj (minimlni nivo vode u rezervoru) (br=0 5 P) Π R =? ξ ul =05 Koeficijent trenj z obe cevi λ=00 D=350 mm D =300 mm p =50 kp 4 Q Q Q 3 Q 4 z=0 0 m 30 m α+ β α+ β α+ β 0 L/s
7 Mehnik fluid Tečenje u cevi Kombinovni zdci Vežb br 7 ZDTK 7 Iz ztvorenog rezervor, u kome se nlzi vzduh pod pritiskom p vz = [(α+β)/5]-8 kp, vod teče u rezervor Gustin vode je ρ=000 kg/m 3 d) Iz uslov d ukupni dotok u rezervor iznosi Q =00+α/ L/s odrediti proticje u svim cevim i kotu nivo u rezervoru e) Odrediti rezultujuću silu n koleno n cevi 3 (između presek - i -) U prorčunu znemriti sopstvenu težinu vode i cevi f) U odgovrjućoj rzmeri ncrtti energetsku i pijezometrsku liniju z donju cev Vzduh D=035 m λ =00 ξ rc - =05 ξ rc -3 =03 D=00 m λ = ξ ul =05 00 ξ zt =50 D =05 m 3-0 ξ kol =0 λ 3 =005 ξ kol = ZDTK 7 Iz rezervor vod se pomoću pumpe prebcuje u rezervor Potrebno je d u rezervor konstntno dotiče Q =00 L/s U tčki K n cevovodu postoji konstntn potrošnj vode od Q cvor = α L/s Nivo vode u rezervoru je konstntn, dok nivo vode u rezervoru može d vrir između kot Π min i Π mx ) Ncrtti dijgrm zvisnosti snge pumpe od kote u rezervoru Dijgrm ncrtti n osnovu 4 pr tčk (Π, Np), z Π = Π min ; Π min +5m; Π min +30m; Π mx ( m) 0m D=030 m 0m 00m D D K ξ ul =05 ξ kol =05 Q cvor= α L/s D=05 m
8 Mehnik fluid Tečenje u cevi Hidrodinmički otpori Vežb br 8 ZDTK 8 Iz rezervor u rezervor teče vod kroz cev prem slici ) Ispitivnjim n prikznoj lbortorijskoj instlciji utvrđeno je d se lminrno tečenje u cevi može ostvriti i z Reynolds-ove brojeve do 5000 (obično se smtr s pri Re= nstje turbulentno tečenje) Iz uslov d se u cevi pri Re=5000 ostvruje lminrni režim tečenje, izrčunti mksimlnu rzliku nivo u rezervorim b) Z tko dobijenu rzliku nivo, izrčunti protok kroz cev z slučj d je zbog nestbilnosti lminrno tečenje prešlo u turbulentno tečenje u hidrulički gltkoj cevi Koliki je sd Re broj? Npomen: Sve loklne gubitke znemriti u odnosu n linijske Π=? ρ=000 kg/m 3 ν=0-6 m /s D=30 mm L=( α+ β)/0 m ZDTK 8 U horizontlnoj položenoj kružnoj cevi rspored brzin je dt izrzom: u r =u mx (-4r /D ) gde je u mx brzin u osovini cevi izmeren pomoću Pitot-ove cevi Tečenje je ustljeno i lminrno ) Izrčunti protok kroz cev i srednju brzinu u cevi Odrediti Re broj i proveriti pretpostvku o lminrnom tečenju b) Nći izrz z npon σ r =σ r, srčunti σ r =σ r n rstojnju r=0 i r=d/, (npon n zidu τ= σ r =σ r je z r=d/) c) Izrčunti koeficijent tngencijlnog npon C τ i koeficijent trenj λ d) Izrčunti čitnje n mnometru (M) u=u (-4r r mx /D ) D 7D h 7D+h h= α/5 mm D=( α+ β)/5 mm µ =0 - gr/cm s ρ=000 kg/m3 presek - u mx 5D D/ r D p M 00 0D 05D
9 Mehnik fluid Hidrodinmički otpori trenj i oblik Vežb br 9 ZDTK 9 Proučv se otpor trenj uz rvnu ploču dužine L=α/4 m velike širine (problem je rvnski), koj je postvljen prlelno s fluidnom strujom ) Oko ploče, brzinom U = (α+β)/ m/s, struji vzduh gustine ρ = kg/m 3 i dinmičke viskoznosti µ = x0-4 gr/cms - Pokzti d je grnični sloj celom dužinom lminrn - Odrediti silu trenj F n m širine ploče - Odrediti tngencijlni npon τ i debljinu grničnog sloj δ u tčkm i b) Oko ploče, brzinom U = (α+β)/3 m/s, struji vod gustine ρ = 0 kg/dm 3 i dinmičke viskoznosti µ = x0 - gr/cms - Pokzti d je grnični sloj turbulentn n više od 90% dužine ploče - Odrediti silu trenj F n m širine ploče - Ncrtti dijgrme promene debljine grničnog sloj δ(x) i tngecijlnog npon τ(x) koristeći podtke dobijene u sledećim tčkm: x =05 L, x =05 L, x 3 =075 L i x 4 =L U y k=0 mm L/ L/3 L/6 L x ZDTK 9 N modelu se ispituje uticj vetr n stub trougonog poprečnog presek čije su dimenzije dte n skici rzin rvnomerne vzdušne struje je U m = (α+β)/ m/s (gustin vzduh je ρ = kg/m 3 ) U oznčenim tčkm su mereni pritisci, dobijeni koeficijenti pritisk Cp su dti u tbeli ) Srčunti pritiske u oznčenim tčkm b) Srčunti silu otpor oblik u prvcim X i Y, ko i odgovrjuće koeficijente sile otpor (ko merodvn površin poprečnog presek se uzim mksimln površin poprečnog presek stub, normlnog n prvc strujnj) c) Koristeći rezultt pod b), srčunti ukupnu silu otpor koj će delovti n stub u prirodi koji je 5 put veći od model, koji se nlzi u vodi brzine U o = (α/) m/s (gustin vode je ρ = 0 kg/dm 3 ) U Y 6 X 3 / 5 4 / t~k Cp =( α+ β)/ cm
10 Mehnik fluid Otvoreni tokovi Jednoliko tečenje i hidrulički skok Vežb br 0 ZDTK 0 Z prizmtični knl poprečnog presek prikznog n slici izrčunti: ) Protok u knlu Q ko kritičn dubin iznosi h K =α/0 m b) Normlnu dubinu h N ko podužni ngib dn knl iznosi I D =05 o / oo, z vrednost protok se usvoji podtk dobijen pod ) c) Režim tečenj u knlu pri normlnoj dubini 45 o n=004 m -/3 s 04 h ZDTK 0 Z knl trougonog poprečnog presek ngib strnic : izrčunti: ) Kritičnu dubinu u knlu h K pri protoku od Q=(α-β) m 3 /s b) Dubinu iz hidruličkog skok h ko je protok u knlu Q, ispred skok je izmeren dubin h =h K /3 m c) Gubitk energije n skoku E d) Froude-ov broj Fr z dubine h, h i h K : h Q h h K : h
MEHANIKA FLUIDA. Pritisak tečnosti na ravne površi
 MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
Osnove elektrotehnike I parcijalni ispit VARIJANTA A. Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti.
 Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Relativno mirovanje tečnosti. Translatorno kretanje suda sa tečnošću
 Reltivno irovnje tečnosti Trnsltorno kretnje sud s tečnošću Zdtk Cistern čiji je orečni resek elis oluos i b nunjen je tečnošću ustine i kreće se rvolinijski jednklo ubrzno ubrznje w o orizontlnoj rvni
Reltivno irovnje tečnosti Trnsltorno kretnje sud s tečnošću Zdtk Cistern čiji je orečni resek elis oluos i b nunjen je tečnošću ustine i kreće se rvolinijski jednklo ubrzno ubrznje w o orizontlnoj rvni
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
MEHANIKA FLUIDA. Isticanje kroz velike otvore
 MEANIKA FLUIDA Isticnje krz velike tvre 1.zdtk. Krz veliki ptvr u bčn zidu rezervr blik rvnkrkg trugl snve i keficijent prtk µ, ističe vd. Odrediti prtk krz tvr k su pznte veličine 1 i (v.sl.). Eleentrni
MEANIKA FLUIDA Isticnje krz velike tvre 1.zdtk. Krz veliki ptvr u bčn zidu rezervr blik rvnkrkg trugl snve i keficijent prtk µ, ističe vd. Odrediti prtk krz tvr k su pznte veličine 1 i (v.sl.). Eleentrni
Rješenje: F u =221,9 N; A x = F u =221,9 N; A y =226,2 N.
 Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu
Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.
 Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
a) Kosi hitac Krivolinijsko gibanje materijalne toke Sastavljeno gibanje Specijalni sluajevi kosog hica: b) Horizontalni hitac c) Vertikalni hitac
 ) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
) Kosi hic Kriolinijsko ibnje merijlne oke Ssljeno ibnje 5. dio 3 4 Specijlni slujei koso hic: b) orizonlni hic c) Veriklni hic b) orizonlni hic c) Veriklni hic 5 6 7 ) Kosi hic 8 Kosi hic (bez opor zrk)
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
Elektrostatika. 1. zadatak. Uvodni pojmovi. Rješenje zadatka. Za pločasti kondenzator vrijedi:
 tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Metode rješavanja izmjeničnih krugova
 Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
Strnic: V - u,i u(t) i(t) etode rešvn izmeničnih kruov uf(t) konst if(t)konst etod konturnih stru etod npon čvorov hevenin-ov teorem Norton-ov teorem illmn-ov teorem etod superpozicie t Strnic: V - zdtk
Otpori trenja i otpori oblika
 4 Otpori trenja i otpori oblika Zadatak 4.. Na osnovu pritisaka izmerenih duž konture prikazanog stuba, izloženog homogenoj vazdušnoj struji, odre deni su koeficijenti pritisaka C p (dati u tabeli). Izračunati
4 Otpori trenja i otpori oblika Zadatak 4.. Na osnovu pritisaka izmerenih duž konture prikazanog stuba, izloženog homogenoj vazdušnoj struji, odre deni su koeficijenti pritisaka C p (dati u tabeli). Izračunati
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
 IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA
 SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
Savijanje elastične linije
 //00 Svijnje estične inije Anitičk metod odreďivnj estične inije Irčunvnje ugi i ngi u pomoć tic Prv jednčin svijnj Normni npon u nekoj tčki poprečnog presek s M moment spreg s M I x I x ksijni moment
//00 Svijnje estične inije Anitičk metod odreďivnj estične inije Irčunvnje ugi i ngi u pomoć tic Prv jednčin svijnj Normni npon u nekoj tčki poprečnog presek s M moment spreg s M I x I x ksijni moment
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F
 SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
MEHANIKA FLUIDA. Zakon o količini kretanja
 MEHANIKA FLUIDA Zakon o količini kretanja zadatak Odrediti intenzitet sile kojom mlaz vode deluje na razdelnu račvu cevovoda hidroelektrane koja je učvršćena betonskim blokom (vsl) Prečnik dovodnog cevovoda
MEHANIKA FLUIDA Zakon o količini kretanja zadatak Odrediti intenzitet sile kojom mlaz vode deluje na razdelnu račvu cevovoda hidroelektrane koja je učvršćena betonskim blokom (vsl) Prečnik dovodnog cevovoda
Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.
 šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
Podužno ukrućenje na rebru nosača (na h/4 od vrha rebra) vruće valjani L profil: L100x100x MPa 1 E 210GPa ν 0.3 G 81GPa f y.
 5. zdtk Izvrši sve potrebne kontrole nosivos i stbilnos z srednje polje krnskog nosč rspon L=6 m po kome se kreće točk dizlice s prorčunskom vrednošću mksimlne sile Q Ed =600 kn. Poprečni presek nosč čine
5. zdtk Izvrši sve potrebne kontrole nosivos i stbilnos z srednje polje krnskog nosč rspon L=6 m po kome se kreće točk dizlice s prorčunskom vrednošću mksimlne sile Q Ed =600 kn. Poprečni presek nosč čine
A MATEMATIKA Zadana je z = x 3 y + 1
 A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]
![c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata] c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]](/thumbs/92/108578155.jpg) Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Istosmjerni krugovi. 1. zadatak. Na trošilu će se trošiti maksimalna snaga u slučaju kada je otpor čitavog trošila jednak unutrašnjem otporu izvora.
 Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
NEKE POVRŠI U. Površi koje se najčešće sreću u zadacima su: 1. Elipsoidi. 2. Hiperboloidi. 3. Paraboloidi. 4. Konusne površi. 5. Cilindrične površi
 NEKE POVŠI U Pvrši kje se njčešće sreću u dcim su:. Elipsidi. Hiperlidi. Prlidi 4. Knusne pvrši 5. Cilindrične pvrši. Elipsidi Osnvn jednčin elipsid ( knnsk) je : + + = c, i c su dsečci n, i si. Presek
NEKE POVŠI U Pvrši kje se njčešće sreću u dcim su:. Elipsidi. Hiperlidi. Prlidi 4. Knusne pvrši 5. Cilindrične pvrši. Elipsidi Osnvn jednčin elipsid ( knnsk) je : + + = c, i c su dsečci n, i si. Presek
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
PIRAMIDA I ZARUBLJENA PIRAMIDA. - omotač se sastoji od bočnih strana(najčešće jednakokraki trouglovi), naravno trostrana piramida u omotaču
 PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
ČETVOROUGAO. β 1. β B. Četvorougao je konveksan ako duž koja spaja bilo koje dve tačke unutrašnje oblasti ostaje unutar četvorougla.
 Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
Mnogougo oji im četii stnice nziv se četvoougo. ČETVOROUGAO D δ δ γ C A α β B β Z svi četvoougo vži im je zi unutšnji i spoljšnji uglov isti i iznosi 0 0 α β γ δ 0 0 α β γ δ 0 0 Njpe žemo četvoouglovi
FURIJEOVI REDOVI ZADACI ( II
 FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
MEHANIKA FLUIDA. Složeni cevovodi
 MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE)
 Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Zada~i za program 2 po predmetot МЕХАНИКА НА ФЛУИДИ (AFI, TI, EE) Предметен наставник: Проф. д-р Методија Мирчевски Асистент: Виктор Илиев (rok za predavawe na programot - 07. i 08. maj 2010) (во термини
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
KUPA I ZARUBLJENA KUPA
 KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su
 ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
4. Relacije. Teorijski uvod
 VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
Zadatak 1
 PISMENI ISPIT IZ KLASIČNE MEHANIKE I 3.. 9. Zdtk Čestic mse m izbčen je s površine Zemlje pod kutem α brzinom v. Ako je otpor zrk proporcionln trenutnoj brzini konstnt proporcionlnosti je ), izrčunjte
PISMENI ISPIT IZ KLASIČNE MEHANIKE I 3.. 9. Zdtk Čestic mse m izbčen je s površine Zemlje pod kutem α brzinom v. Ako je otpor zrk proporcionln trenutnoj brzini konstnt proporcionlnosti je ), izrčunjte
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor
 I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
DINAMIKA. u f. Dinamički sistem - pogon sa motorom jednosmerne struje: N: NELINEARAN. m m
 DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, [ i ],, U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA SA
DINAMIKA Dinmički sistem - pogon s motorom jednosmerne struje: N: u u m m i, [ i ],, U opštem slučju ovj dinmički sistem je U opštem slučju ovj dinmički sistem je NELINEARAN MATEMATIČKI MODEL POGONA SA
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
TEKSTOVI ZADATAKA (2. kolokvijum) iz Elektromagnetike (studijski program EEN, 2012/1)
 TEKSTOV ZADATAKA (2. kolokvijum) iz Elektomgnetike (stuijski pogm EEN, 22/). Oeiti silu koj eluje n tčksto opteećenje Q smešteno izn polusfeične povone izočine nultog potencijl. 2. Oeiti elimične kpcitivnosti
TEKSTOV ZADATAKA (2. kolokvijum) iz Elektomgnetike (stuijski pogm EEN, 22/). Oeiti silu koj eluje n tčksto opteećenje Q smešteno izn polusfeične povone izočine nultog potencijl. 2. Oeiti elimične kpcitivnosti
OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA
 OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Многоугао, странице и дијагонале. Број дијагонала многоугла. Obele`i svaki mnogougao, a zatim napi{i kojoj vrsti po broju stranica pripada.
 Многоугао Многоугао, странице и дијагонале. Број дијагонала многоугла 1 Obele`i svki mnogougo, ztim npi{i kojoj vrsti po broju strnic pripd. Petougo Ncrtj osmougo FGH. Obele`i wegov temen. ) Npi{i temen
Многоугао Многоугао, странице и дијагонале. Број дијагонала многоугла 1 Obele`i svki mnogougo, ztim npi{i kojoj vrsti po broju strnic pripd. Petougo Ncrtj osmougo FGH. Obele`i wegov temen. ) Npi{i temen
Definicije i osobine statičkog momenta površine poprečnog preseka za proizvoljnu osu. Definicija. - statički moment površine A za osu y.
 Definicije i osobine sttičkog moment površine poprečnog presek z proizvoljn os Definicij - sttički moment površine z os Zbog ( ) ( ) immo je - sttički moment površine z os ( ) i i ( ) Ovo tkođe znči je
Definicije i osobine sttičkog moment površine poprečnog presek z proizvoljn os Definicij - sttički moment površine z os Zbog ( ) ( ) immo je - sttički moment površine z os ( ) i i ( ) Ovo tkođe znči je
Tečenje sa slobodnom
 3 Tečenje sa slobodnom površinom Zadatak 3.1. Pri ustaljenom jednolikom tečenju u kanalu trapeznog poprečnog preseka, izmerena je dubina vode H = 1.0 m. Nagib dna kanala je I D =0.5% a Manning-ov koeficijent
3 Tečenje sa slobodnom površinom Zadatak 3.1. Pri ustaljenom jednolikom tečenju u kanalu trapeznog poprečnog preseka, izmerena je dubina vode H = 1.0 m. Nagib dna kanala je I D =0.5% a Manning-ov koeficijent
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
povratnog napona 6 prekidača na slici 1.
 Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
Prktikum iz elektroenergetike Lortorij Elektro Mgneti Trnzient Progrm (EMTP) Zdtk Primjer prorčun prelznog povrtnog npon (prekidnje liskog krtkog spoj) Potreno je prorčunti prijelzni povrtni npon n kontktim
TEORIJA BETONSKIH KONSTRUKCIJA 79
 TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Odredjeni integral je granicna vrijednost sume beskonacnog broja clanova a svaki clan tezi k nuli i oznacava se sa : f x dx f x f x f x f x b a f
 Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
MEHANIKA FLUIDA I Što valja zapamtiti 9 3. STATIKA FLUIDA. p (izražava ravnotežu masenih sila i sila tlaka).
 MENIK FLUID I Što vlj zpmtiti 9. STTIK FLUID snovn jedndžb sttike (slučj i ) p fi ili f rdp (izržv rvnotežu mseni sil i sil tlk). i Iz osnovne jedndžbe sttike imjući n umu svojstv rdijent zključuje se:
MENIK FLUID I Što vlj zpmtiti 9. STTIK FLUID snovn jedndžb sttike (slučj i ) p fi ili f rdp (izržv rvnotežu mseni sil i sil tlk). i Iz osnovne jedndžbe sttike imjući n umu svojstv rdijent zključuje se:
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA
 TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Mašinsko učenje. Regresija.
 Mašinsko učenje. Regresija. Danijela Petrović May 17, 2016 Uvod Problem predviđanja vrednosti neprekidnog atributa neke instance na osnovu vrednosti njenih drugih atributa. Uvod Problem predviđanja vrednosti
Mašinsko učenje. Regresija. Danijela Petrović May 17, 2016 Uvod Problem predviđanja vrednosti neprekidnog atributa neke instance na osnovu vrednosti njenih drugih atributa. Uvod Problem predviđanja vrednosti
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
TROUGAO. - Stranice a,b,c ( po dogovoru stranice se obeležavaju nasuprot temenu, npr naspram temena A je stranica a, itd) 1, β
 TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA. školska 2013./2014. godina TEST MATEMATIKA UPUTE ZA RAD
 ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu
= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi
 Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Sistem sučeljnih sila
 Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
Tip ureappleaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 656
 TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
TehniËki podaci Tip ureappeaja: ecovit Jedinice VKK 226 VKK 286 VKK 366 VKK 476 VKK 66 Nazivna topotna snaga (na /),122,,28, 7,436,,47,6 1,16,7 Nazivna topotna snaga (na 60/) 4,21,,621, 7,23,,246,4 14,663,2
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
VISKOZNOST TEČNOSTI Viskoznost
 VISKOZNOST VISKOZNOST TEČNOSTI Viskoznost predstavlja otpor kojim se pojedini slojevi tečnosti suprostavljaju kretanju jednog u odnosu na drugi, odnosno to je vrsta unutrašnjeg trenja koja dovodi do protoka
VISKOZNOST VISKOZNOST TEČNOSTI Viskoznost predstavlja otpor kojim se pojedini slojevi tečnosti suprostavljaju kretanju jednog u odnosu na drugi, odnosno to je vrsta unutrašnjeg trenja koja dovodi do protoka
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE
 SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE Do sd smo već definisli skup Ω elementrnih dogđj Ako se elementrni dogđji ω mogu predstviti ko relni brojevi, ond se eksperiment može zmisliti ko izbor jedne promenljive
SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE Do sd smo već definisli skup Ω elementrnih dogđj Ako se elementrni dogđji ω mogu predstviti ko relni brojevi, ond se eksperiment može zmisliti ko izbor jedne promenljive
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
DINAMIKA. Dinamički sistem - pogon sa motorom jednosmerne struje: N: Dinamički sistem Ulazi Izlazi (?)
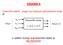 DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
DINAMIKA Dinički siste - pogon s otoro jednoserne struje: N: u u f Dinički siste Ulzi Izlzi (?) i, [ i ],, f f U opšte slučju ovj dinički siste je NELINEARAN MATEMATIČKI MODEL POGONA SA NEZAVISNO POBUĐENOM
PRETHODNI PRORACUN VRATILA (dimenzionisanje vratila)
 Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Predet: Mašinski eleenti Proračun vratila strana Dienzionisati vratilo elektrootora sledecih karakteristika: oinalna snaga P = 3kW roj obrtaja n = 400 in Shea opterecenja: Faktor neravnoernosti K =. F
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
38. Savezno takmiqenje iz fizike za uqenike srednjih xkola xkolske 2002/2003. god. II razred
 Zdtke pripreil: Zoric Pjovi Recenzent: dr Gorn Popri Predednik koiije: dr Mi o Mitrovi JUGOLOVENKO DRUXVO FZQR MNRVO PROVJEE NUKE REPULKE CRNE GORE MNRVO PROVEE POR REPULKE RJE MNRVO Z PROVJEU NUKU KULURU
Zdtke pripreil: Zoric Pjovi Recenzent: dr Gorn Popri Predednik koiije: dr Mi o Mitrovi JUGOLOVENKO DRUXVO FZQR MNRVO PROVJEE NUKE REPULKE CRNE GORE MNRVO PROVEE POR REPULKE RJE MNRVO Z PROVJEU NUKU KULURU
Kinematika materijalne toke. 3. dio a) Zadavanje krivocrtnog gibanja b) Brzina v i ubrzanje a
 Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
Kinemik meijlne oke 3. dio ) Zdnje kiocnog gibnj b) Bzin i ubznje 1 Kiocno gibnje meijlne oke Položj meijlne oke u skom enuku emen možemo definii n slijedee nine: 1. Vekoski nin defininj gibnj (). Piodni
GIBANJE (m h) giba miruje giba giba miruje miruje h 1000 :1000 h 1 h h :1000 1
 GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
GIBANJE ( h) gibnje gibnje ijel je projen položj ijel ili dijelo ijel u odnou pre neko drugo ijelu z koje o ujeno (dogoorno) uzeli d iruje U odnou n liječnik: gib iruje gib iruje gib gib iruje iruje gib
Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu.
 VISKOZNOST VISKOZNOST Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu. VISKOZNOST Da li očekujete da će glicerol imati veću ili manju
VISKOZNOST VISKOZNOST Viskoznost predstavlja otpor tečnosti pri proticanju. Viskoznost predstavlja unutrašnje trenje između molekula u fluidu. VISKOZNOST Da li očekujete da će glicerol imati veću ili manju
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
 27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Proračunski model - pravougaoni presek
 Proračunski model - pravougaoni presek 1 ε b 3.5 σ b f B "" ηx M u y b x D bu G b h N u z d y b1 a1 "1" b ε a1 10 Z au a 1 Složeno savijanje - VEZNO dimenzionisanje Poznato: statički uticaji za (M i, N
Proračunski model - pravougaoni presek 1 ε b 3.5 σ b f B "" ηx M u y b x D bu G b h N u z d y b1 a1 "1" b ε a1 10 Z au a 1 Složeno savijanje - VEZNO dimenzionisanje Poznato: statički uticaji za (M i, N
Matematika za ekonomiste Časlav Pejdić, (064)
 Mtemtik z ekonomiste Čslv Pejdić, (06) 09 0 SADRŽAJ SADRŽAJ UVOD DEO RELACIJE I FUNKCIJE DEO ALGEBRA 6 DEO NIZOVI I REDOVI DEO NEPREKIDNOST I DIFERENCIJABILNOST FUNKCIJE 7 5 DEO LIMESI I IZVODI 9 6 DEO
Mtemtik z ekonomiste Čslv Pejdić, (06) 09 0 SADRŽAJ SADRŽAJ UVOD DEO RELACIJE I FUNKCIJE DEO ALGEBRA 6 DEO NIZOVI I REDOVI DEO NEPREKIDNOST I DIFERENCIJABILNOST FUNKCIJE 7 5 DEO LIMESI I IZVODI 9 6 DEO
