ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
|
|
|
- Ἀδράστεια Φραγκούδης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου εγκλισµού θεωρούµε τη κλάση E { F: Ω σ( C)} Για τη κλάση υποσυόλω E παρατηρούµε ότι C E διότι για τυχό C ισχύει Ω C σ( C ) Επίσης η κλάση E είαι σ-άλγεβρα υποσυόλω του Ω διότι :. ) Ω σ(c σ ( C) είαι σ-άλγεβρα υποσυόλω του Ω. \ Ω σ( C). Οµως ( Ω\ ) Ω Ω \ Ω και άρα Ω Ω σ C ) Ω Ω αφού η ) Α E τότε κατά το ορισµό της E είαι Ω σ( C ) και συεπώς Ω ( \ ) ( ) ) Α {, } E τότε Ω σ ( C ) και άρα ( Ω) σ( C) Συεπώς ( ) Ω σ( C ), δηλαδή, E. Ωστε η Ε είαι σ-άλγεβρα και περιέχει τη C και συεπώς περιέχει και σ ( C) F. Α τώρα Ω, F είαι τυχό στοιχείο της F τότε Eδηλαδή Ω σ( C ), δηλαδή F σ( C) γ) εύκολο Άσκηση 3. σελ. 3 Έστω D έα σύστηµα Dy. Θα δείξουµε ότι ικαοποιούται οι ()-(v) της άσκησης. Οι () και () από το ορισµό. Για τη () αρκεί α παρατηρήσουµε ότι... και αφού δύο οποιαδήποτε σύολα της έωσης... έχου τοµή το κεό συµπεραίουµε ότι D. Αποµέει η (v). Πράγµατι θέτουµε..., \,3 3 \, Από τη () συµπεραίουµε ότι D. Επίσης τα σύολα είαι ξέα αά δύο και ισχύει άρα κατά το ορισµό D. Ατίστροφα έστω ότι η κλάση D ικαοποιεί τις ()-(v) της άσκησης. Θα δείξουµε ότι ικαοποιούται οι (),(),() του ορισµού του συστήµατος Dy. Αρκεί α γίει για τη (). Έστω { : } D µε. Θέτουµε, και γεικά έχουµε(εύκολα µε επαγωγή) ότι τη (v) ότι D. Όµως.. Από τη () της άσκησης D και αφού + θα έχουµε από
2 Άσκηση 3.4 σελ. 3 α) Α το µέτρο P έχει τη ιδιότητα (3.3) συµπεραίουµε ότι Ρ (Ε)Ρ(Ε) για κάθε Ε P. Όµως η κλάση P είαι ηµιδακτύλιος και σ ( P ). Αρκεί α επικαλεστούµε τη πρόταση 3.3 σελ.. β) Για τυχό Ι(α,β] P ' θεωρούµε τη κλάση φ { Α : P( I) P () P ()} Θα δείξουµε ότι η κλάση φ είαι έα σύστηµα Dy υποσυόλω του. Πράγµατι (, + ] κα άρα P( I) P(( (, + ] ) I) P( (, + ] I) P( (, + ]) I) P ((, + ]) P (I) P (I) P ((, + ]) P (I) P ( ) άρα φ. Α τώρα Α, Β φ µε τότε βέβαια P( I) P ()P (I) άρα P( I) P ()P (I) P( I) P( I) P()P(I) P()P(I) και συεπώς P( I \ I) P ( \ ) P (I). Όµως I\ I (\) I (εύκολο) Τελικά \ φ. Έστω τώρα {, } φ µε Από τη P( I) P ()P (I) συµπεραίουµε ότι και αφού τα I είαι ξέα αά δύο P( ( I)) P (I) P ( ). Όµως Τελικά ( I) ( ) I (επαληθεύστε) P(( ) I) P ( )P (I) άρα (3.3) P( I) P ( )P (I) φ. Ώστε φ είαι σύστηµα Dy και προφαώς λόγω της (3.3) περιέχει τα σύολα της P άρα φ d( P ) σ ( P ). Αφού η κλάση φ περιέχει τη έχουµε αποδείξει ότι P( I) P ()P (I). () Για τυχό Α θεωρούµε τη κλάση ε { Β : P( ) P( )P() } Όπως προηγουµέως αποδεικύεται ότι η ε είαι σύστηµα Dy υποσυόλω του που λόγω της () περιέχει P και άρα ε d( P ) δηλαδή ε (µάλιστα ) Και άρα έχουµε αποδείξει ότι: P( ) P()P() Β. Άσκηση 4. σελ. 4 Επαγωγικά στο κ Για κ είαι προφαές από το ορισµό του ηµιδακτυλίου. Έστω τώρα ότι ισχύει για κ λδηλ. \ λ Α Β (*)
3 Τότε λ+ λ+ λ λ λ λ+ λ+ (*) ( ) λ+ ( λ+ ) ( \ λ+). \ Α ( Α ) Α ( Α ) (\ ) κάθε έα από τα \λ + υποσυόλω από το ηµιδακτύλιο και άρα ( \ ) ξέα µεταξύ τους αφού Άσκηση 4.3 σελ. 5 Θέτουµε \ λ+ Από το ορισµό του ηµιδακτυλίου (,,..,) γράφεται ως έωση ξέω µεταξύ τους λ + \ λ +,,, είαι ξέα.. Από υπόθεση Α F. Σύµφωα µε τη άσκηση 4. (*) όπου,,..., ξέα µεταξύ τους και συεπώς Γ όπου Γ,,, Α ( ). Από υπόθεση επίσης τα σύολα,,..., είαι ξέα µεταξύ τους και από τη (*) προκύπτει ότι (,..., αφού η ) ( ) και συεπώς τα σύολα,,..., είαι ξέα µεταξύ τους άρα P( ) P( ) + P() είαι απλώς προσθετική από υπόθεση. Από τη τελευταία συµπεραίουµε ότι P( ) P( ) για κάθε και άρα P( ) P(). P Από τη εκφώηση έχουµε ήδη τη ατίθετη αισότητα και τελικά τη ζητούµεη ισότητα. Άσκηση 4.5 σελ. 6 Θέτουµε Α Τότε Α ( \ ) ( ) και συεπώς Όµως ( \ ) (επαληθεύστε) και η ακολουθία \ είαι P() P( \ ) + P( ) (*) φθίουσα και συεπώς κατά τη εκφώηση l P( \ ) Επίσης l P( ) P( ) και συεπώς από τη (*) παίρουµε ότι
4 P() P( ) Άσκηση 4.8 σελ. 9 Θέτουµε φ σ ( F N ). Θα δείξουµε ότι F φ. Έστω τυχό Ε F µε το ορισµό της F το E Nµε Α F και Ν N και άρα Α, Ν F N. Συεπώς Α Ν σ (F N) φ. είξαµε λ οιπό ότι F σ ( F N) F. Άσκηση 5. σελ. 9. Τότε σύµφωα φ. Επε ιδή από το ορισµό της F βλέπουµε άµ εσα ότι F, N F συµπεραίουµ ε ότι F N F και άρα Εύκολα διαπιστώεται ότι { } (,) και επειδή η ακολουθία (, ] είαι φθίουσα έχουµε P({}) l P(, ] l P(F() F( )) F() l F( ) F() F( ) Άσκηση 6. σελ. 6 Εύκολα διαπιστώουµε ότι οι κλάσεις C { Ω},..., C { Ω} Θεωρούµε τις παρακάτω κλάσεις υποσυόλω ε { : C { Ω} για,,,} είαι αεξάρτητες. ε { : C { Ω} + για +,,,} Τότε οι κλάσεις ε, ε είαι κλειστές ως προς τη πεπερασµέη τοµή δηλ. α Α,Β ε τότε Α Β ε (ι,). Επίσης είαι αεξάρτητες όπως διαπιστώεται αµέσως και άρα σ ( ε), σ( ε) είαι αεξάρτητες κατά τη πρόταση 6.. Όµως ε C... C, ε C+... C και ε F και ε F. Άρα σ ( ε ) F, σ( ε ) F. Γείκευση Έστω C, Ι αεξάρτητες κλάσεις κλειστές για πεπερασµέες τοµές και Ι σύολο δεικτώ για το οποίο γωρίζουµε ότι Ι J λ όπου J λ, λ Λ είαι ξέα µεταξύ τους (Λ άλλο σύολο δεικτώ). Θέτουµε F σ ( C ), λ Λ. Τότε οι σ-άλγεβρες F λ, λ Λ είαι αεξάρτητες. (Υπόδειξη : Θέτουµε ε { Λ : Λ λ K λ λ Λ Jλ C { Ω}, Κ πεπερασµέο υποσύολο του } Τότε οι ε λ, λ Λ είαι αεξάρτητες και κλειστές για πεπερασµέες τοµές. Άσκηση 6.4 σελ.3 J λ
5 Έχουµε P( ) και P ( ) < άρα P( ) και P ( ) > Από τη τελευταία έχουµ ε ότι l l P ( ) και άρα P Συεπώς l P( ) και λόγω αεξαρτησίας l ( ) l l P( ) () Εξ άλλου µε l sup P ( ) P ( ) P( ) lp( ) ll P( ) ll P ( ) l le Οπότε λαµβάοτας υπόψι τη σχέση () έχουµε P ( ) l P( ) l P( ) ll e Άσκηση 6.5 σελ.3 Έχουµε l P ( ) και P ( \ + ) < τώρα διαδοχικά l P(lsup ) P( ) l P( ) ll P( ) l όµως ( \ ) ( \ )... ( \ ) και συεπώς l l χρησιµοποιώτας τη αισότητα oole και τη ιδιότητα P ( \ ) P ( ) P ( ) P(lsup ) ll[ P ( ) + P ( ) P ( ) + P ( ) P ( ) l... +P( l) P ( l l )] επαληθεύστε ότι το ετός τω αγκυλώ άθροισµα γράφεται P ( \ ) + P ( \ ) P ( \ ) + P ( ) και συεπώς l l l l P(lsup ) ll( P ( \ ) + P ( )) l( P ( \ ) + l P ( )) + l + l l l( P ( \ )) αφού + P ( \ ) < + Άσκηση.4 σελ.34 l l Θέτουµε {( x,..., x ) : x a} τότε και συεπώς η συάρτηση
6 ( x,..., x ) I ( x,..., x ) είαι συάρτηση orel. ( x,..., x ) Με τη σειρά της η συάρτηση I ( ) είαι τυχαία µεταβλητή ως σύθεση της τ.µ. ( x,..., x ) και της συάρτησης orel I (βλέπε πρόταση.4 ) Επειδή Y * I ( ) (επαληθεύστε το) συµπεραίουµε ότι η Y είαι τ.µ. Άσκηση.5 σελ.34 Θέτουµε C { :, Τ ο τυχό στοιχείο E P + είαι της µορφής E ( a, b]... ( a, b] ( a+, b+ ]... ( a+, b+ ] όπου ( a, b]... ( a, b ] και ( a+, b+ ]... ( a+, b+ ] άρα E C δηλαδή P + C σ( P + ) σ( C) + } εξ άλλου το τυχό στοιχείο C γράφεται ( ) ( ) θεωρούµ g : + ε τώρα τη µ ε τύπο gx (,..., x, x,..., x ) ( x,..., x ) και + τη h : µε τύπο hx (,...,,,..., + + x x+ x+ ) ( x+,..., x+ ) δηλαδή τις + προβολές του στο και ατίστοιχα. Τότε εύκολα διαπιστώεται ότι g ( ) και h ( ) και επειδή οι συαρτήσεις g,h είαι συεχείς θα + είαι και orel δηλαδή g ( ), h ( ) και συεπώς + g ( ) h ( ) C + και άρα σ ( C) Άσκηση.5 σελ.39 κ Y P-σ.β. σηµαίει ότι υπάρχει N αι ( ω) Υ( ω), ω Ω \ N α τώρα τεθεί N N τότε N F και F µε PN ( ) + PN ( ) PN ( ) δηλαδή PN ( ) και βέβαια ισχύ ει ( ω ) Y( ω ), ω Ω \ N άρα sup ( ω) Y( ω), ω Ω \ N Άσκηση : Έστω { : } ακολουθία εδεχοµέω µε l P ( ). Α Χ τυχαία µεταβλ ητή µε E[ ]< δείξτε ότι l dp. Απόδειξη : (εις άτοπο απαγωγή) Αρκεί α δείξουµε ότι ( ε > )( δε ( ) > ): < ε, ότα P( ) < δε ( ) Έστω ότι δε ισχύει τότε ( ε > )( δ > ): µε P ( ) < και < ε, ( ) θέτουµε και άρα P
7 Τώρα θέτουµε τότε I I και άρα I I στο Ω και µε βάση το παρακάτω θε ώρηµα έπεται ότι I I Ω Ω Συεπώς I dp l I dp l dp l( dp+ dp) Ω Ω l f Από τη µία dp I dp dp. Ω + I dp > ε και από τη άλλη επειδή P() > Ω - άτοπο. Θεώρηµα : Έστω, ακολουθία τ.µ. τέτοια ώστε ) l P-σχεδό πατού ) Υπάρχει τ.µ. Υολοκληρώσιµη ως προς P τέτοια ώστε για κάθε α ισχύει Y P-σχεδό πατού. Τότε η τ.µ. Χ είαι ολοκληρώσιµη ως προς P και µάλιστα l dp dp. Άσκηση : Έστω {, } ακολουθία τ.µ. είξτε ότι σβ.. P(lsu p{ > ε}), ε > (). Απόδειξη : Από Αρχιµήδειο ιδιότητα ε >, : < ε τότε { > ε} { > } l sup{ > ε} lsup{ > } Και άρα α η () ισχύει για κάθε ε της µορφής θα ισχύει και για κάθε ε γεικά. Το ατίστροφο είαι προφαές ώστε P(lsup{ > ε}), ε > P(lsup{ > }), P(lsup{ > }), P( { > }), P( { }), () επειδή η ακολουθία { } είαι φθίουσα συµπεραίουµε ότι P( ) l P( ) αλλά και ατίστροφα α
8 P( ) τότε P) (, αφού.ώστε τελικά η () ισοδυαµεί µε P( { } ) P(l ). Άσκηση : Έστω { : } ακολουθία αεξάρτητω τ.µ. µε P ( ) και P ( ). είξτε ότι P αλλά δε ισχύει σβ... Απόδειξη : P( > ε) P( > ε) P( ) l P( > ε ) ότι / θα δειχθεί µε εις άτοπο απαγωγή. Έστω ότι ισχύει τότε σύµφωα µε προηγούµ εη άσκηση θα πρέπει P(lsup{ > ε }). Από τη άλλη επειδή τα εδεχόµεα { > ε}, σβ..,,... είαι αεξάρτητα έπεται ότι P( > ε ) P( ) orel-catell θα έχ ω P(lsup{ > ε}) -άτοπο P οπότε από το δεύτερο λήµµα Άσκηση : Α οι τ.µ. { E [ ] µ, Var[ ] σ τότε µ. Απόδειξη : : } είαι ισόοµες και αεξάρτητες µ ε S L S S µ Ε[ µ ] Ε[ ] Ε [ S µ ] { Var[ S µ ] + ( E[ S µ ]) } Όµως ES [ µ ] E [ ] µ µ µ και Var[ S µ ] Var[ µ µ ] Var[ µ ] Var[ µ ] σ λόγω αεξαρτησίας S σ S [ µ ] σ [ S L Τελικά Ε lε µ ] Άσκηση : Έστω ακολουθία τ.µ. { : } και S δείξτε ότι L S L α τότε Λύση :
9 L E[ ] έχουµε διαδοχ ικά S E[( ) ] E E( ) E ( + ) ( E( ) E( +,,, + ( ( ) ( )) ( ) E E E )) S Συεπώς E( ) E( ) Όµως l E ( ) και από γωστό λήµµα της αάλυσης l E ( ) Άσκηση : Έστω { : } αεξάρτητες, ισόοµες µε καταοµή οµοιόµ ορφη στο (,). Θέτουµε Y {,..., }, Z ( ax{,..., }). είξτε ότι D D Y Y, Z Z όπου Υ,Ζ τ.µ. µε εκθετική καταοµή. Λύση : Z ( ax{,..., }),,, Οι τ.µ.,..., έχου τη ίδια καταοµή, οµοιόµορφη στο (,), και συεπώς έχου α.σ.κ., x < F( x) x, x<, x Η καταοµή της τ.µ. T ax{,..., } είαι Όσο αφορά τη καταοµή της τ.µ. PT ( x) P(ax{,..., } x) P( x,,..., ) P( { x}) και λόγω αεξαρτησίας έπεται ότι P( T x) P({ x}) F( x) [ F( x)] x F( x) P( Z x) P( ( T) x) P( T ) x x PT ( ) PT ( < ) Z έχουµε
10 x και συεπώς F ( ) [ ( )] x F, x x ή ισοδύαµα F ( x) ( ), < x, x Για τυχό x > υπάρχει τέτοιο ώστε < x, οπότε F ( x ) ( x ) x, και βέβαια l F ( x) e. x Για τυχό x l F ( x ). Ώστε l F ( x) e, x ηλα δή Z Z ε () Άσκηση : Έστω ακολουθία τ.µ. { : } µε τιµές στο. είξτε ότι υπάρχει ακολουθία > : Λύση : ( ε > )( M( ε) > ): P( > M) < ε άρα για ε υπάρχει M : P( > ) <, άρα P( > ) <, P ( > ) < < εφαρµόζω το λήµµα orel-caell για τα σύολα { > } κι έχω P up{ (ls > }) P( { > }) Θέτω Ω { }. Τότε P ( Ω ) και για τυχό ω Ω ( ω) τέτοιο ώστε υπάρχει ω { }, δηλαδή ω { },. Ώστε για τυχό ( ω) ω Ω α θέτω αφού P ( Ω ) Άσκηση Έστω πείραµα τύχης µε δύο ισοπίθαα δυατά αποτελέσµατα επιτυχία αποτυχία. Το πείραµα επααλαµβάεται επ άπειρο. Ποια η πιθαότητα α συατώται επ άπειρο διαδοχές επιτυχιώ τουλάχιστο διπλάσιες σε πλήθος από το πλήθος τω δοκιµώ που προηγούται;
11 Λύση Θεωρείστε το δ.χ. Ω {,} όπως στο παράδειγµα 6.3 σελ. 8 εφοδιασµέο µε το µέτρο πιθαότητας P για το οποίο ισχύει P( x... x {,}) Q( )...Q( ), {,} + όπου Q το µέτρο πιθαότητας στο {,} το οριζόµεο από τις σχέσεις Q({})Q({}). To εδεχόµεο της εκφώησης είαι Αlsup Τότε Ρ( ) ( ) + 3(-) όπου {ω(ω,ω,...): ω, ω,...,ω }, - {,}x{}x...x{}x {,} και συεπώς κ 3- - ( ) Από τ η τελευταία συάγουµε ότι Άσκηση P( ) < και άρα P() Έστω p η πιθαότητα επιτυχούς έκβ ασης της προσπάθειας α τεθεί σε λειτουργία έα σύστηµα κατά τη -οστή απόπειρα και Χ ο αριθµός αποπειρώ µέχρι τη πρώτη επιτυχή απόπειρα. Υποθέτοτας ότι p < α) Να δοθεί ο κατάλληλος δ.χ. και α ορισθεί η τ.µ. Χ β) Υπολογίστε τη P(< ) και τη καταοµή της τ.µ. Χ γ) ώστε µια απλή ικαή συθήκη ώστε P( < ) δ) Υπολογίστε επακριβώς τη P( < ) ότα : ) p p,< p< ) p, και p ) p, και p Λύση α) Ω {,} και P οριζόµεο από τη P( P( x x...x x {,}) P ( )...P ( ) + στο {,} από τη P ({}) P,P ({}) P για {,} και P οριζόµεο Για τυχό ω( ω, ω,...) ορίζουµε:
12 f{ : ω } α { : ω } Χω ( ) α ω(,,...) β) P( < ) P( ) P(,,...). Οµως {(,...)} µε { ω ( ω, ω,...) : ω,..., ω } {}x {}x...x{}x Συεπώς Η καταοµή της τ.µ. Χ είαι : P( ) ( P ) γ) P( <) ότα και µόο ότα + {,} P( < ) P( ) lp( ) l ( P ) ( P ) P( ) P({}x...x{}x{}x {,}) + ) P( < ) αφού P ( P )P ( P ) επειδή P e P συµπεραίουµε ότι η συθήκη P συεπάγεται ότι δ) ( P ) ) P( < ) αφού P ( )( + ) P( < ) ( ) l l ) ( ) ( + ) l
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
{[ 140,150 ),[ 160,170 ),...,[ 200, 210]
![{[ 140,150 ),[ 160,170 ),...,[ 200, 210] {[ 140,150 ),[ 160,170 ),...,[ 200, 210]](/thumbs/91/106977432.jpg) Σημειώσεις στις Πιθαότητες Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
Σημειώσεις στις Πιθαότητες Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
ΜΑΘΗΜΑ 9 Γενικές ασκήσεις µιγαδικών
 ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
Παρατηρήσεις 1 Για α ααζητήσουµε το όριο της f στο, πρέπει η f α ορίζεται όσο θέλουµε κοτά στο, δηλαδή η f α είαι ορισµέη σ έα σύολο της µορφής ( α, )
 Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
ΛΥΚΕΙΟ ΜΕΤΑΜΟΡΦΩΣΗΣ 2014 ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΟΡΙΑ. 0 : Παραγοντοποιώ αριθµητή και παρονοµαστή και διώχνω τους παράγοντες x, x 0 που προκύπτουν.
 ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
5 η ΕΚΑ Α ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 41.
 ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ AA A A
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Ε 1. Διαφορικός λογισμός (Κανόνες παραγώγισης)
 Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει α είαι σε θέση: 1 Να μπορεί α βρίσκει απο τη γραφική παράσταση μιας συάρτησης το πεδίο ορισμού της το σύολο τιμώ της τη τιμή της σε έα σημείο x 2
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει α είαι σε θέση: 1 Να μπορεί α βρίσκει απο τη γραφική παράσταση μιας συάρτησης το πεδίο ορισμού της το σύολο τιμώ της τη τιμή της σε έα σημείο x 2
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΚΕΦΑΛΑΙΟ ο. Τι οοµάζεται συάρτηση ; Είαι µια διαδικασία µε τη οποία κάθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα ακριβώς στοιχείο κάποιου άλλου συόλου Β.. Ποιες είαι οι κυριότερες γραφικές παραστάσεις
ΚΕΦΑΛΑΙΟ ο. Τι οοµάζεται συάρτηση ; Είαι µια διαδικασία µε τη οποία κάθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα ακριβώς στοιχείο κάποιου άλλου συόλου Β.. Ποιες είαι οι κυριότερες γραφικές παραστάσεις
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ. ΘΕΜΑ Ι ίνεται η συνεχής συνάρτηση f : R
 ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
xf(y) + yf(x) = (x + y)f(x)f(y)
 ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι 1,,, k είαι οι τιµές µιας µεταβλητής Χ, που αφορά Β.1. τα άτοµα εός δείγµατος µεγέθους,
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι 1,,, k είαι οι τιµές µιας µεταβλητής Χ, που αφορά Β.1. τα άτοµα εός δείγµατος µεγέθους,
Επαναληπτικό Διαγώνισμα Μαθηματικών Γενικής Παιδείας Γ Λυκείου
 Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
{[ 140,150 ),[ 160,170 ),...,[ 200, 210]
![{[ 140,150 ),[ 160,170 ),...,[ 200, 210] {[ 140,150 ),[ 160,170 ),...,[ 200, 210]](/thumbs/92/110200214.jpg) Σημειώσεις στη Πληροφορική ΙΙΙ 1. Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο. Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
Σημειώσεις στη Πληροφορική ΙΙΙ 1. Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο. Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
ΑΠΑΝΤΗΣΕΙΣ. Επιµέλεια: Οµάδα Μαθηµατικών της Ώθησης
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
4. Δεσμευμένη Πιθανότητα - Ανεξαρτησία Ενδεχομένων
 Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
(c f (x)) = c f (x), για κάθε x R
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ Ασκήσεις : 1, 2, 3, σελ. 107.
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]
![ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β] ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]](/thumbs/20/426829.jpg) ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
Πανελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γενικης Παιδειας
 ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΚΕΦΑΛΑΙΟ ΙΙ. αντιστοιχίζεται ο αριθµός Χω= ω+ ω δηλαδή ορίζεται η συνάρτηση Χ : Ω µε Χω,ω ω ω Α 3, 2, 2,3, 4,1, 1, 4
 ΚΕΦΑΛΑΙΟ ΙΙ. Η έννοια της τυχαίας µεταβλητής Συχνά αυτό το οποίο παρατηρούµε σε ένα πείραµα τύχης δεν είναι το όποιο αποτέλεσµα ω Ω αλλά µια µαθηµατική ποσότητα Χ εξαρτώµενη από το αποτέλεσµα ω Ω. Ας εξετάσουµε
ΚΕΦΑΛΑΙΟ ΙΙ. Η έννοια της τυχαίας µεταβλητής Συχνά αυτό το οποίο παρατηρούµε σε ένα πείραµα τύχης δεν είναι το όποιο αποτέλεσµα ω Ω αλλά µια µαθηµατική ποσότητα Χ εξαρτώµενη από το αποτέλεσµα ω Ω. Ας εξετάσουµε
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
β± β 4αγ 2 x1,2 x 0.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Λυµένες Ασκήσεις * * *
 Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
Κι όµως, τα Ρολόγια «κτυπούν» και Εξισώσεις: Η Άλγεβρα των εικτών του Ρολογιού
 Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
Μαθηµατική Επαγωγή 175.
 Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικών αριθµών. Μιγαδικό επίπεδο. Γεωµετρική παράσταση του αθροίσµατος µιγαδικών αριθµών.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
78 Ερωτήσεις Θεωρίας Στα Μαθηματικά Γενικής Παιδείας
 Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ
 ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
Α2. Πότε μια συνάρτηση f λέγεται γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της; Μονάδες 4
 (http://edu.klmaka.gr) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
(http://edu.klmaka.gr) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
Δ/νση Β /θµιας Εκπ/σης Φλώρινας Κέντρο ΠΛΗ.ΝΕ.Τ. (Πρόοδοι) ΠΡΟΟΔΟΙ
 ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ A =. Σύµφωνα µε την Πρόταση 5.7 (σελ. 119), η συµπληρωµατική (δυϊκή)
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
ονοµάζεται γεωµετρική πολλαπλότητα αυτής. Τα ιδιοδιανύσµατα αυτά είναι βάση του διανυσµατικού υποχώρου E ( λ 0 ), που ονοµάζεται ιδιόχωρος
 Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΙΟΥΝΙΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΙΟΥΝΙΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
Λύση. Λύση Άσκηση 3. Λύση. ( Α Α Α Ι ) Α. Α Α=Ιν. Άσκηση 4. επαληθεύει τη σχέση Χ. Λύση.
 Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
ν ν Άσκηση 1. Α =Α, Β =Β. Λύση Άσκηση Α Β =Β Α, Α Β=ΒΑ. Β Α= ( Β Β)( ΑΒ ) Β Α=Ι( ΑΒ ) Β Α=ΑΒ. Άσκηση = Α Α Α Α=.
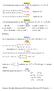 Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Όταν πραγματοποιείται το Α πραγματοποιείται και το Β.
 Βασικές έοιες και τύποι πιθαοτήτω Πείραμα τύχης - Η έοια του τυχαίου Δειγματικός χώρος Ω εός πειράματος τύχης (πεπερασμέος, απείρως αριθμήσιμος, συεχής) Εδεχόμεα Α, Β, (απλά, σύθετα) Βέβαιο εδεχόμεο Αδύατο
Βασικές έοιες και τύποι πιθαοτήτω Πείραμα τύχης - Η έοια του τυχαίου Δειγματικός χώρος Ω εός πειράματος τύχης (πεπερασμέος, απείρως αριθμήσιμος, συεχής) Εδεχόμεα Α, Β, (απλά, σύθετα) Βέβαιο εδεχόμεο Αδύατο
i) Αν ο φυσικός αριθμός n δεν είναι τετράγωνο ακεραίου, τότε ο n είναι άρρητος.
 Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
ΕΡΩΤΗΣΕΙΣ ΜΕ ΥΠΑΡΧΕΙ ( ) τέµνει σε άπειρα σηµεία την πλάγια ασύµπτωτή της; 9. Υπάρχει συνάρτηση που να µην είναι η σταθερή η οποία έχει άπειρες
 ΕΡΩΤΗΣΕΙΣ ΜΕ ΥΠΑΡΧΕΙ. Υάρχει συάρτηση f : R R : f ( ) + f( ) =, για άθε. Υάρχει συάρτηση f ορισµέη αι συεχής [,+ ), η οοία δε αρουσιάζει αρότατο στο 3. ίεται συάρτηση f τέτοια ώστε f f = +, R. Υάρχει συάρτηση
ΕΡΩΤΗΣΕΙΣ ΜΕ ΥΠΑΡΧΕΙ. Υάρχει συάρτηση f : R R : f ( ) + f( ) =, για άθε. Υάρχει συάρτηση f ορισµέη αι συεχής [,+ ), η οοία δε αρουσιάζει αρότατο στο 3. ίεται συάρτηση f τέτοια ώστε f f = +, R. Υάρχει συάρτηση
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Μαθηματικά κατεύθυνσης Γ Λυκείου. Όλη η θεωρία και οι ασκήσεις των πανελλαδικών εξετάσεων. Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς
 Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
Τι είναι εκτός ύλης. Σχολικό έτος
 Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Στατιστική. μονάδα και ισχύει: i. ν ν. = ή ως ποσοστό % οπότε % = i fi
 Στατιστική "Υπάρχου τα μικρά ψέματα, τα μεγάλα ψέματα και οι στατιστικές" Μαρκ Τουαί Σε κάθε πρόβλημα της Στατιστικής υπάρχει έας «πληθυσμός» Ω τα στοιχεία του οποίου (άτομα) εξετάζοται ως προς έα χαρακτηριστικό
Στατιστική "Υπάρχου τα μικρά ψέματα, τα μεγάλα ψέματα και οι στατιστικές" Μαρκ Τουαί Σε κάθε πρόβλημα της Στατιστικής υπάρχει έας «πληθυσμός» Ω τα στοιχεία του οποίου (άτομα) εξετάζοται ως προς έα χαρακτηριστικό
ΑΠΑΝΤΗΣΕΙΣ. ευτέρα, 17 Μα ου 2010 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ. Οµάδα Μαθηµατικών της Ώθησης. Επιµέλεια:
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014 ÊÏÑÕÖÁÉÏ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 04 Ε_.ΜλΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Ηµεροµηία: Κυριακή 7 Απριλίου 04 ιάρκεια Εξέτασης: ώρες ΑΠΑΝΤΗΣΕΙΣ Α. α) Λάθος (βλέπε σελίδα 4 του σχολικού βιβλίου, Το σωστό
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 04 Ε_.ΜλΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Ηµεροµηία: Κυριακή 7 Απριλίου 04 ιάρκεια Εξέτασης: ώρες ΑΠΑΝΤΗΣΕΙΣ Α. α) Λάθος (βλέπε σελίδα 4 του σχολικού βιβλίου, Το σωστό
Μάθημα: Γεωργικός Πειραματισμός-Βιομετρία (Κωδ. 2860) 2. Τυχαίες μεταβλητές-βασικές κατανομές
 Μάθημα: Γεωργικός Πειραματισμός-Βιομετρία (Κωδ 860) Τυχαίες μεταβλητές-βασικές καταομές Σύτομη αασκόπηση βασικώ εοιώ, προτάσεω και τύπω Ο κλασικός ορισμός της πιθαότητας (Laplace, 181) Ο στατιστικός ορισμός
Μάθημα: Γεωργικός Πειραματισμός-Βιομετρία (Κωδ 860) Τυχαίες μεταβλητές-βασικές καταομές Σύτομη αασκόπηση βασικώ εοιώ, προτάσεω και τύπω Ο κλασικός ορισμός της πιθαότητας (Laplace, 181) Ο στατιστικός ορισμός
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 7-05-00 ΘΕΜΑ Α Α. ος τρόπος Οι παρατηρήσεις t, t,..., t έχου μέση τιμή. Οι έες παρατηρήσεις είαι της μορφής: yi = ti, όπου i =,,...,
ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 7-05-00 ΘΕΜΑ Α Α. ος τρόπος Οι παρατηρήσεις t, t,..., t έχου μέση τιμή. Οι έες παρατηρήσεις είαι της μορφής: yi = ti, όπου i =,,...,
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
1. Το σύνολο των μιγαδικών αριθμών
 Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
lim lim Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Ορισµός Μία συνάρτηση f είναι παραγωγίσιµη σε ένα σηµείο x του πεδίου ορισµού της, όταν υπάρχει στο R, το
 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΠΑΡΑΓΡΑΦΟΣ Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Ορισµός Μία συάρτηση είαι παραγωγίσιµη σε έα σηµείο του πεδίου ορισµού της, ότα υπάρχει στο R, το lim ( ( Το όριο αυτό οοµάζεται παράγωγος της στο και
ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΠΑΡΑΓΡΑΦΟΣ Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ Ορισµός Μία συάρτηση είαι παραγωγίσιµη σε έα σηµείο του πεδίου ορισµού της, ότα υπάρχει στο R, το lim ( ( Το όριο αυτό οοµάζεται παράγωγος της στο και
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2003 ΕΚΦΩΝΗΣΕΙΣ
 ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
2.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
www.fr-anodos.gr (, )
 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές»
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Το σύνολο των πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας) α)
4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ
 1.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ ΘΕΩΡΙΑ 1. Αρχή της Μαθηµατιής Επαγωγής Έστω ισχυρισµός Ρ(), όπου θετιός αέραιος. Α (i) Ρ αληθής αι (ii) Ρ() Ρ( + 1) για άθε, τότε Ρ() αληθής για άθε.. Αισότητα Bernoulli (1 +α
1.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ ΘΕΩΡΙΑ 1. Αρχή της Μαθηµατιής Επαγωγής Έστω ισχυρισµός Ρ(), όπου θετιός αέραιος. Α (i) Ρ αληθής αι (ii) Ρ() Ρ( + 1) για άθε, τότε Ρ() αληθής για άθε.. Αισότητα Bernoulli (1 +α
ΘΕΜΑ Α Α1. Έστω t 1,t 2,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν, που έχουν
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
Ι δ ι ο τ η τ ε ς Π ρ ο σ θ ε σ η ς - Π ο λ λ α π λ α σ ι α σ μ ο υ ΙΔΙΟΤΗΤΑ ΠΡΟΣΘΕΣΗ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ. Λυµένες Ασκήσεις
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5 σελ 9 Ασκήσεις : 3 4 8 9 σελ 98 Λυµέες Ασκήσεις Άσκηση 8 Να βρείτε τη ιδιάζουσα παραγοτοποίηση
Αάλυση Πιάκω και Εφαρµογές Σελίδα από Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5 σελ 9 Ασκήσεις : 3 4 8 9 σελ 98 Λυµέες Ασκήσεις Άσκηση 8 Να βρείτε τη ιδιάζουσα παραγοτοποίηση
2.3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ. 1. Μέση τιµή x = Σταθµικός Μέσος x = 3. ιάµεσος (δ) ενός δείγµατος ν παρατηρήσεων, οι οποίες έχουν διαταχθεί σε
 .3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ ΘΕΩΡΙΑ. Μέση τιµή x = x = x = + + + t t... t = x + x +... + x + +... + x κ κ = f x κ t κ κ = κ κ x = κ x. Σταθµικός Μέσος x = xw + x w +... + x w w + w +... + w = x w w όπου
.3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ ΘΕΩΡΙΑ. Μέση τιµή x = x = x = + + + t t... t = x + x +... + x + +... + x κ κ = f x κ t κ κ = κ κ x = κ x. Σταθµικός Μέσος x = xw + x w +... + x w w + w +... + w = x w w όπου
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 8 Νοεμβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση 3 η (//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 8 Νοεμβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση 3 η (//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ. ορισµοί. Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 )
 ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ. Εισαγωγή
 4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εισαγωγή Η Θεωρία Αριθμώ, δηλαδή η μελέτη τω ιδιοτήτω τω θετικώ ακεραίω, έθεσε από πολύ ωρίς τους μαθηματικούς μπροστά στο εξής πρόβλημα: Κάποια πρόταση αληθεύει
4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εισαγωγή Η Θεωρία Αριθμώ, δηλαδή η μελέτη τω ιδιοτήτω τω θετικώ ακεραίω, έθεσε από πολύ ωρίς τους μαθηματικούς μπροστά στο εξής πρόβλημα: Κάποια πρόταση αληθεύει
φ = 2ω = = 2 2(ν 2) + 4 = 2 + 4
 Γιατί οι μέλισσες κάου εξαγωικές τις κηρήθρες τους ; Χριστία Δασκαλάκη Α.Μ. 99 Ημερομηία παράδοσης 9-10-014 Θεωρούμε έα καοικό -γωο και σημειώουμε μια γωία του καθώς και τις γωίες του ισοσκελούς τριγώου
Γιατί οι μέλισσες κάου εξαγωικές τις κηρήθρες τους ; Χριστία Δασκαλάκη Α.Μ. 99 Ημερομηία παράδοσης 9-10-014 Θεωρούμε έα καοικό -γωο και σημειώουμε μια γωία του καθώς και τις γωίες του ισοσκελούς τριγώου
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ
 ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Ρωτήσαμε 50 μαθητές μιας τάξης για το αριθμό τω αδελφώ τους Οι απατήσεις που πήραμε είαι: 0,,,,4,5 Α v, v, v, v4, v5, v 6 είαι οι ατίστοιχες συχότητες τους
ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Ρωτήσαμε 50 μαθητές μιας τάξης για το αριθμό τω αδελφώ τους Οι απατήσεις που πήραμε είαι: 0,,,,4,5 Α v, v, v, v4, v5, v 6 είαι οι ατίστοιχες συχότητες τους
ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
 015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
c f(x) = c f (x), για κάθε x R
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
Δεσμευμένη πιθανότητα και Ανεξαρτησία ενδεχομένων
 Δεσμευμέη πιθαότητα και Αεξαρτησία εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας 4 Ο πολλαπλασιαστικός τύπος 4 Το θεώρημα ολικής πιθαότητας 44 Το θεώρημα Bayes 45 Αεξαρτησία εδεχομέω
Δεσμευμέη πιθαότητα και Αεξαρτησία εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας 4 Ο πολλαπλασιαστικός τύπος 4 Το θεώρημα ολικής πιθαότητας 44 Το θεώρημα Bayes 45 Αεξαρτησία εδεχομέω
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος
 Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ασκήσεις7 80. AU διαγώνιο. αποτελούμενη από ιδιοδιανύσματα του A. Πρόσθετες ιδιότητες κανονικών πινάκων: Έστω A o
 Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ. 1. Τι ονομάζουμε σύνολο Μιγαδικών Αριθμών; Τι ονομάζουμε πραγματικό μέρος - φανταστικό μέρος ενός μιγαδικού αριθμού z = α + βi.
 ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΜΑΘΗΜΑ Η έννοια του µιγαδικού αριθµού Πράξεις
 ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2015 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συνδυασμός ν στοιχείων ανά κ είναι μια μη διατεταγμένη συλλογή κ στοιχείων από τα ν.
 13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
Αρµονική Ανάλυση. Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις. Απόστολος Γιαννόπουλος. Τµήµα Μαθηµατικών
 Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό υλικό, όπως εικόνες,
εδάφιο 3, σελ. 181 υπερβολή ή παραβολή. Η ταξινόµηση αυτή παρουσιάζεται στον 1 ο πίνακα, T
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεων
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
lim f (x) = +. ΣΗΜΕΙΩΣΕΙΣ Μη πεπερασμένο όριο στο x 0 R
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
