Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ. Λυµένες Ασκήσεις
|
|
|
- Ιπποκράτης Κυπραίος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Αάλυση Πιάκω και Εφαρµογές Σελίδα από Μάθηµα 8 ο Ι ΙΑΖΟΥΣΑ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5 σελ 9 Ασκήσεις : σελ 98 Λυµέες Ασκήσεις Άσκηση 8 Να βρείτε τη ιδιάζουσα παραγοτοποίηση και τη πολική παραγοτοποίηση τω πιάκω A = 0 0 B = 0 Γ = [ ] Λύση : Για το πίακα A έχουµε AA Στη ιδιάζουσα τιµή = σ ( AA) = { 4 0} σ = 4 = µοαδιαίο ιδιοδιάυσµα [ ] σ = (ή στη ιδιοτιµή λ = 4) ατιστοιχού το x = του πίακα AA και το µοαδιαίο ιδιοδιάυσµα y = Ax = [ 0 σ ] του πίακα AA Επιπλέο το οµογεές σύστηµα A Ax= 0 επαληθεύεται από το µοαδιαίο διάυσµα x = [ ] και το οµογεές σύστηµα διαύσµατα AA y = 0 από τα
2 Αάλυση Πιάκω και Εφαρµογές Σελίδα από Τα διαύσµατα y [ 0 y [ ] [ ] = c 0 + c 0 0 = ] και y [ ] βάση του ker ( AA ) Έτσι για 0 V = U = έχουµε τη ιδιάζουσα παραγοτοποίηση A = USAV 3 = 0 0 είαι ορθοκαοκή S A = 0 0 Για τη πολική παραγοτοποίηση του A θεωρούµε τους διαµερισµέους πίακες U και S σύµφωα µε τη µικρότερη διάσταση του A και συεπώς 0 0 = 0 0 = 0 0 V A V V V Ο πίακας 0 P= V V = 0 0 είαι θετικά ηµιορισµέος οι στήλες του 0 πίακα Q V 0 = = είαι ορθοµοαδιαία διαύσµατα και A= QP είαι η πολική παραγοτοποίηση του A Για το πίακα B έχουµε BB = [ 9] και σ = 9 = 3 Τότε στη ιδιάζουσα παραγοτοποίηση θα είαι S = [ 3 0 0] και U = [ ] διότι [ ] B y = είαι µοαδιαίο ιδιοδιάυσµα του BB ατίστοιχο της σ = 3 δηλαδή της ιδιοτιµής λ = 9
3 Αάλυση Πιάκω και Εφαρµογές Σελίδα 3 από Επιπλέο εξίσωσης x = B y = BBx= 9x Το οµογεές σύστηµα B Bx 0 x = = 4 4 επαληθεύεται για x = c [ 0] + c [ 0 ] είαι µοαδιαίο ιδιοδιάυσµα της Επειδή τα διαύσµατα [ ] 0 και [ ] 0 δε είαι κάθετα µε τη µέθοδο ορθογωοποίησης Gram-Schmdt βρίσκουµε τη ορθοκαοική βάση x 0 5 του ker ( BB ) Έτσι έχουµε και για τη πολική παραγοτοποίηση όπου [ ][ 3][ ] [ 3] 0 = [ ] x = [ 4 5] B = [][ 3 0 0] [][ 3][] B = = PQ P = = > και Q = [] 3 3 = Σηµειώστε ότι [ ] QQ = Για το πίακα Γ έχουµε και κατά συέπεια 0 = σ ( ) = { 3} σ = σ = ΓΓ ΓΓ S 0 0 = Γ
4 Αάλυση Πιάκω και Εφαρµογές Σελίδα 4 από Τα ορθοµοαδιαία ιδιοδιαύσµατα του y [ ] = 0 και [ ] 0 Τα διαύσµατα y = Επειδή ker ( ) = { 0} x = y = 0 ΓΓ ατίστοιχα τω σ και σ είαι U= y y = I ΓΓ έχουµε [ ] 3 3 Γ [ ] x = Γ y = [ ] είαι ορθοµοαδιαία ιδιοδιαύσµατα του ορθοµοαδιαία βάση του ker ( ) Γ Γ και x 3 [ = ] 6 Γ Γ Συεπώς για V [ x x x3] = έχουµε είαι και επιπλέο Γ = I Γ = = PQ είαι πολική παραγοτοποίηση του Γ όπου QQ = I Άσκηση 8 Α τα διαύσµατα ηξ δε είαι κάθετα α βρείτε τη ιδιάζουσα και τη πολική παραγοτοποίηση του πίακα A Λύση : Ο πίακας = ηξ A έχει µια ιδιάζουσα τιµή διότι rank A = Επειδή = = σ = AAξ ξη ηξ ξ η ξ ξ η ξ Συεπώς στη ιδιάζουσα παραγοτοποίηση A = USV θα έχουµε όπου ξ S = dag ( η ξ 0 0) και V = x x ξ x x είαι ορθοκαοική βάση του ker ( AA) = span{ ξ }
5 Αάλυση Πιάκω και Εφαρµογές Σελίδα 5 από Το διάυσµα ξ y = A = Aξ = ξ η = σ ξ η ξ η ξ η η είαι µοαδιαίο ιδιοδιάυσµα του AA και θα είαι η U = y y η όπου y είαι ορθοκαοική βάση του ker ( AA ) span{ } y Για τη πολική παραγοτοποίηση έχουµε ή ( )( ) A = USV = USU UV = PQ ( )( ) A = USV = UV VSV = QP = η Άσκηση 83 Να βρείτε τις συµµετρικές λύσεις της εξίσωσης AX = XA όπου 4 A = Λύση : Εργαζόµεοι όπως στις προηγούµεες ασκήσεις έχουµε A = USV όπου και U = S = dag ( 6 6 9) V = Ατικαθιστώτας στη εξίσωση AX = XA έχουµε ( ) ( ) USV X XVSU S V XU U XV S SY Y S = = = όπου Y = V XU Έτσι µε κατάλληλη υποδιαίρεση του Y συµπεραίουµε
6 Αάλυση Πιάκω και Εφαρµογές Σελίδα 6 από 6I 0 Y Y Y 6 Y I Y Y = Y 0 9 Y και κατά συέπεια Y ( ) = Y X= Vdag Y Y U Y Y και Y = όπου Y Y είαι οποιοιδήποτε συµµετρικοί πίακες και ατίστοιχα = O Άσκηση 84 Για κάθε ατιστρέψιµο πίακα A αποδείξατε ότι Λύση : Επειδή rank ( AA ) και θα έχουµε καθόσο σ =λ ( AA ) det A = σσ σ = rank A = ο πίακας AA είαι ατιστρέψιµος ( ) = σσ σ det AA Επιπλέο ( ) ( )( ) ( )( ) det AA = det A det A = det A det A = det A και συεπώς det A =σσ σ Άσκηση 85 Α τετραγωικού πίακα A = PQ = QP αποδείξατε ότι A είαι οι πολικές παραγοτοποιήσεις του Q = Q Λύση : Από τη ιδιάζουσα παραγοτοποίηση του A = USV και Είαι προφαές Q = Q = UV ( )( ) A = USV = USU UV = PQ ( )( ) A = USV = UV VSV = QP έχουµε
7 Αάλυση Πιάκω και Εφαρµογές Σελίδα 7 από Άσκηση 86 Έστω σ σ σ είαι οι ιδιάζουσες τιµές του πίακα A αποδείξατε ότι tr A σ+σ+ +σ Λύση : Α πίακας Q= A = USV V U Σηµειώοτας µε είαι η ιδιάζουσα παραγοτοποίηση του πίακα τότε ο είαι ορθογώιος ως γιόµεο ορθογωίω πιάκω και qj ( ) ( ) A = V V US V = V QS V τα στοιχεία του Q έχουµε ( ( ) ) ( ) ( ) ( ) qj και επιπλέο tr tr tr tr q q q A= V QS V = QS V V = QS = σ + σ + + σ σ q +σ q + +σ q σ +σ + +σ Άσκηση 87 Έστω σ σ σ είαι ιδιάζουσες τιµές του A Αποδείξατε Ι σ σ σ είαι ιδιάζουσες τιµές του A ΙΙ σ =σ = =σ = ακριβώς ότα A είαι ορθοµοαδιαίος Λύση : Ι Από τη ισότητα συµπεραίουµε ότι οι ιδιοτιµές ( ( A )( A ) = ( A )( A ) = ( A A) µ του ( )( ) A A είαι µ =λ όπου λ σ AA ) Συεπώς το σύολο σ τω ιδιαζουσώ τιµώ του A είαι A σ = µ = = σ A λ όπου σ είαι οι ιδιάζουσες τιµές του A { } { } ΙΙ Έστω σ =σ = =σ = A = UV διότι S = I A ορθοµοαδιαίος ως γιόµεο ορθοµοαδιαίω πιάκω
8 Αάλυση Πιάκω και Εφαρµογές Σελίδα 8 από Ατίστροφα έστω A είαι ορθοµοαδιαίος πίακας τότε AA = A A = I σ = = = Άσκηση 88 Να αποδείξετε ότι ο πίακας A είαι καοικός ακριβώς ότα ισχύει µία από τις συθήκες Ι η ιδιάζουσα παραγοτοποίηση του = dag ( λ λ λ ) A V V ΙΙ στη πολική παραγοτοποίηση A= PQ οι πίακες PQ είαι ατιµεταθετικοί Λύση : Ι Έστω ο πίακας A είαι καοικός και λ x είαι ιδιοποσά του A τότε Ax =λx και Ax=λ x Επιπλέο έχουµε =λ = λ και AA x Ax x = λ = λ AAx Ax x Συεπώς στη ιδιάζουσα παραγοτοποίηση του ( ) S = dag λ λ λ Ατίστροφα από τη ισότητα = dag ( λ λ λ ) A είαι U= V και A V V είαι προφαές ( ) AA = V dag λ λ λ V = A A ΙΙ Έστω A= PQ όπου P είαι θετικά ηµιορισµέος πίακας και QQ = I Α A είαι καοικός από τη ισότητα ( ) AA A A P Q P Q P P Q PQ QP PQ = = = = = Ατίστροφα α QP = PQ PQ = Q P και ο πίακας A είαι καοικός διότι AA PQQ P P = = A A ( Q P) ( PQ) PQ QP P = = =
9 Αάλυση Πιάκω και Εφαρµογές Σελίδα 9 από Άσκηση 89 Για τους πίακες AB µ αποδείξατε Ι έχου τις ίδιες ιδιάζουσες τιµές ακριβώς ότα A= MBN όπου M και είαι ορθογώιοι πίακες ΙΙ AA = BB A = B όπου είαι ορθογώιος πίακας N Λύση : Ι Έστω A= MBN όπου M και N είαι ορθογώιοι πίακες Τότε οι πίακες AA και BB είαι ορθογώια όµοιοι διότι ( ) AA = M BB M και συεπώς οι ιδιάζουσες τιµές τω AA και BB ταυτίζοται Ατίστροφα α A US V και B U S V είαι οι ιδιάζουσες µ = µ = παραγοτοποιήσεις τω A B και S = S τότε ( ) ( ) A = U U B V V = MBN όπου M και N είαι ορθογώιοι πίακες ως γιόµεο ορθογωίω πιάκω ΙΙ Από τη ισότητα AA = BB συµπεραίουµε ότι οι πίακες A και B έχου τις ίδιες ιδιάζουσες τιµές και τα ίδια ατίστοιχα ιδιοδιαύσµατα ιδιάζουσες παραγοτοποιήσεις τω ( ) AB A = USV έχουµε B = USV και απ αυτές A = B V V = B όπου = V V Ατίστροφα α A = B όπου ορθογώιος θα είαι AA = B B = BB y Έτσι στις Άσκηση 80 Α A και το γραµµικό σύστηµα Az = b είαι συµβιβαστό µ αποδείξατε ότι το διάυσµα είαι µερική λύση του όπου k z = k = ( Ab ) σ x x = ranka σ είαι οι ιδιάζουσες τιµές του A και x είαι ατίστοιχα ιδιοδιαύσµατα του AA
10 Αάλυση Πιάκω και Εφαρµογές Σελίδα 0 από Λύση : Έστω A USV y y y S [ x x x ] παραγοτοποίηση του = = µ είαι ιδιάζουσα A όπου Ατικαθιστώτας στη εξίσωση Ax ( σ σ σ ) dag k O S = O O = b έχουµε το ισοδύαµο σύστηµα Sω = γ όπου ω = V z γ = Ub Ααλυτικότερα ( σ σ σ ) dag k O ω γ = ω γ O Προφαώς θα πρέπει α είαι γ = 0 διότι για γ 0 το σύστηµα δε είαι συµβιβαστό Σηµειώοτας O επειδή έχουµε ω = dag γ γ = γ γ k σ σ σk σ σ σk ( Ax ) ( Ab ) γ yb b σy b σ σ σ σ σ = = = = ( Ab ) x k k ω γ x z = Vω = V x 0 = = x = σ = σ Άσκηση 8 Έστω σmax ( ) και σmn ( ) ιδιάζουσα τιµή πίακα Αποδείξατε : Ι για κάθε διάυσµα ΙΙ σ ( A+ B) σ ( A) +σ ( B) max max max x ( ) ( ) είαι η µέγιστη και η ελάχιστη σ mn A x Ax σ max A x
11 Αάλυση Πιάκω και Εφαρµογές Σελίδα από Λύση : Ι Έστω A = USV είαι ιδιάζουσα παραγοτοποίηση του A και ( ) S = dag s s s 0 0 k Τότε Επειδή και V ( ) k = = = = σ = Ax x A Ax x VSU USV x S V x V x είαι ορθοµοαδιαίος πίακας ( ) ( ) σ max =σ max Ax A V x A x ( ) ( ) mn mn Ax σ A V x =σ A x ΙΙ Επειδή A =σ ( A) ( ) max B =σ B έχουµε max ( A B) A B A B ( A) ( B) σ + = + + =σ +σ max max max Άσκηση 8 Α σ σ σk είαι οι ιδιάζουσες τιµές του πίακα A µ όπου µ k = ranka βρείτε τις ιδιοτιµές και τα ιδιοδιαύσµατα του ( µ+ ) ( µ+) πίακα O A B = A O Λύση : Έστω A = USV είαι η ιδιάζουσα παραγοτοποίηση του A τότε AA O B = O A A Συεπώς ( B ) ( AA σ =σ ) σ ( A A) = { σ σ σk0} Α AAx και =σx AA y y χαρακτηριστικές εξισώσεις ( B) { k0} σ = ±σ ±σ ±σ = σ από τις ( 75 σελ 9 ) και τις y Ax σ y y B = = =σ x A y σ x x
12 Αάλυση Πιάκω και Εφαρµογές Σελίδα από y Ax σy y B = = = σ x A y σ x x συµπεραίουµε τα ατίστοιχα ιδιοποσά σ y x και σ y x του πίακα B για = k Στη ιδιοτιµή λ = 0 του B ατιστοιχού ( µ+) rank B= ( µ+) rank A=µ+ k ( µ ) ιδιοδιαύµατα Α ω ( AA)( A) = και z ker ( AA )( ker A ) ker ker ιδιοτιµή λ= 0 του B τα ατίστοιχα ιδιοδιαύσµατα είαι = στη διότι 0 ω ( = k) και 0 Aω ω = 0 = B 0 z j 0 ( j= µ k) z 0 = = j B 0 0 Az j
Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ AA A A
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ A =. Σύµφωνα µε την Πρόταση 5.7 (σελ. 119), η συµπληρωµατική (δυϊκή)
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
ονοµάζεται γεωµετρική πολλαπλότητα αυτής. Τα ιδιοδιανύσµατα αυτά είναι βάση του διανυσµατικού υποχώρου E ( λ 0 ), που ονοµάζεται ιδιόχωρος
 Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
Γραµµική Άγεβρα ΙΙ Σείδα από 5 Μάθηµα 5 ο Ι ΙΟΤΙΜΕΣ ΚΑΙ Ι ΙΟ ΙΑΝΥΣΜΑΤΑ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άγεβρα : εδάφιο, σε 33 (όχι Πρόταση 63) εδάφιο, σε 4, Πρόταση 65, (χωρίς απόδειξη) και Πρόταση 66 εδάφιο
Λυµένες Ασκήσεις * * *
 Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ Ασκήσεις : 1, 2, 3, σελ. 107.
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
εδάφιο 3, σελ. 181 υπερβολή ή παραβολή. Η ταξινόµηση αυτή παρουσιάζεται στον 1 ο πίνακα, T
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 9 ο ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 7, εδάφιο, σελ 75, εδάφιο 3, σελ 8 Ασκήσεις :,, 3, 4, 5, 6, 7, 8, σελ 75,, 4, 8, σελ 8, II, IV, σελ
Ασκήσεις7 80. AU διαγώνιο. αποτελούμενη από ιδιοδιανύσματα του A. Πρόσθετες ιδιότητες κανονικών πινάκων: Έστω A o
 Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Γραμμική Άλγεβρα ΙΙ. Εξέταση Σεπτεμβρίου Επώνυμο συνοπτικές ενδεικτικές λύσεις. Όνομα. ΑΜ_(13 ψηφία) Σύνολο
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
( ) = ( ) Μάθημα 2 ο ΒΑΘΜΟΣ ΠΙΝΑΚΑ. Θεωρία : Γραμμική Άλγεβρα : εδάφιο 4, σελ. 63, Πρόταση 4.9, σελ. 90. Βασικές ιδιότητες
 Ανάλυση Πινάκων και Εφαρμογές Σελίδα 1 από 6 Μάθημα 2 ο ΒΑΘΜΟΣ ΠΙΝΑΚΑ Θεωρία : Γραμμική Άλγεβρα : εδάφιο 4, σελ. 63, Πρόταση 4.9, σελ. 90. Βασικές ιδιότητες Έστω A είναι μ ν πίνακας. Τότε 1. ranka= ranka
Ανάλυση Πινάκων και Εφαρμογές Σελίδα 1 από 6 Μάθημα 2 ο ΒΑΘΜΟΣ ΠΙΝΑΚΑ Θεωρία : Γραμμική Άλγεβρα : εδάφιο 4, σελ. 63, Πρόταση 4.9, σελ. 90. Βασικές ιδιότητες Έστω A είναι μ ν πίνακας. Τότε 1. ranka= ranka
) ( ) Μάθηµα 3 ο ΟΡΘΟΚΑΝΟΝΙΚΗ ΒΑΣΗ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ (µέχρι Πρόταση 4.18). είναι ορθοκανονικά
 Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα ο ΟΡΘΟΚΑΝΟΝΙΚΗ ΒΑΣΗ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ (µέχρι Πρόταση 48) Λυµένες Ασκήσεις Άσκηση Αν {,,, } και {,,, } σύνολα διανυσµάτων του p p p ν q q q
Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα ο ΟΡΘΟΚΑΝΟΝΙΚΗ ΒΑΣΗ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ (µέχρι Πρόταση 48) Λυµένες Ασκήσεις Άσκηση Αν {,,, } και {,,, } σύνολα διανυσµάτων του p p p ν q q q
Μάθηµα 1 ο ΣΥΝΘΕΤΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 3, σελ. 8.
 νάλυση Πινάκων Εφαρµογές Σελίδα από 9 Μάθηµα ο ΣΥΝΘΕΤ ΠΝΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 8 Λυµένες σκήσεις Άσκηση Να υπολογισθούν οι δυνάµεις του σύνθετου πίνακα: Λύση : Επειδή: 0 0 = = 0 0
νάλυση Πινάκων Εφαρµογές Σελίδα από 9 Μάθηµα ο ΣΥΝΘΕΤ ΠΝΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 8 Λυµένες σκήσεις Άσκηση Να υπολογισθούν οι δυνάµεις του σύνθετου πίνακα: Λύση : Επειδή: 0 0 = = 0 0
... λέγονται στοιχεία του πίνακα Α και οι δείκτες δηλώνουν τη γραµµή και τη στήλη, αντίστοιχα, που ανήκει το στοιχείο α. . Για παράδειγµα, οι πίνακες
 ΚΕΦΑΛΑΙΟ ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούµε µε το ορισµό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθµώ ή άλλω στοιχείω Οι πίακες εµφαίζοται στη θεωρία τω γραµµικώ
ΚΕΦΑΛΑΙΟ ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούµε µε το ορισµό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθµώ ή άλλω στοιχείω Οι πίακες εµφαίζοται στη θεωρία τω γραµµικώ
Ιδιάζουσες τιμές πίνακα. y έχουμε αντίστοιχα τις σχέσεις : Αυτές οι παρατηρήσεις συμβάλλουν στην παραγοντοποίηση ενός πίνακα
 Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Ιδιάζουσες τιμές πίνακα Επειδή οι πίνακες που παρουσιάζονται στις εφαρμογές είναι μη τετραγωνικοί, υπάρχει ανάγκη να βρεθεί μία μέθοδος που να «μελετά» τους μη τετραγωνικούς με «μεθόδους και ποσά» που
Μάθηµα 1 ο ΣΥΝΘΕΤΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 3, σελ. 8. Ασκήσεις : 1, 2, 3 : σελ. 10
 Γραµµική Άλγεβρα Σελίδα από 9 Μάθηµα ο ΣΥΝΘΕΤ ΠΝΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 8 σκήσεις :,, : σελ 0 Λυµένες σκήσεις Άσκηση Να υπολογισθούν οι δυνάµεις του σύνθετου πίνακα: Λύση : Επειδή:
Γραµµική Άλγεβρα Σελίδα από 9 Μάθηµα ο ΣΥΝΘΕΤ ΠΝΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 8 σκήσεις :,, : σελ 0 Λυµένες σκήσεις Άσκηση Να υπολογισθούν οι δυνάµεις του σύνθετου πίνακα: Λύση : Επειδή:
xf(y) + yf(x) = (x + y)f(x)f(y)
 ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
Μάθηµα 3 ο ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ LU και QR
 Ανάλυση Πινάκων Εφαρµογές Σελίδα από Μάθηµα ο ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ LU QR Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 45, εδάφιο, σελ 5, (όχι Πρόταση 5) εδάφιο 6, σελ 0 Ορισµοί : Ένας µ ν πίνακας ονοµάζεται πλήρους
Ανάλυση Πινάκων Εφαρµογές Σελίδα από Μάθηµα ο ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ LU QR Θεωρία : Γραµµική Άλγεβρα : εδάφιο, σελ 45, εδάφιο, σελ 5, (όχι Πρόταση 5) εδάφιο 6, σελ 0 Ορισµοί : Ένας µ ν πίνακας ονοµάζεται πλήρους
➂ 6 P 3 ➀ 94 q ❸ ❸ q ❼ q ❿ P ❿ ➅ ➅ 3 ➁ ➅ 3 ➅ ❾ ❶ P 4 ➀ q ❺ q ❸ ❸ ➄ ❾➃ ❼ 2 ❿ ❹ 5➒ 3 ➀ 96 q ➀ 3 2 ❾ 2 ❼ ❸ ➄3 q ❸ ➆ q s 3 ➀ 94 q ➂ P ❺ 10 5 ➊ ➋➃ ❸ ❾ 3➃ ❼
 P P P q r s t 1 2 34 5 P P 36 2 P 7 8 94 q r Pq 10 ❶ ❶ ❷10 ❹❸ ❸ 9 ❺ ❼❻ q ❽ ❾ 2 ❿ 2 ❼❻ ➀ ➁ ➂ ❿ 3➃ ➄ 94 ➁ ➅ ❽ ➆ ➇ ➉➈ ➊ ➋ ➌ ➊ ➍ ➎ ➋ ➏➃ ➃ q ❺➐ 8 ➄ q ❷ P ➑ P ➅ ➇ ❽ ➈➃ ➒➇ ➓ ➏ ➎ ➄ P q 96 5P q 4 ❿ ➅ ➇➃❽ ➈➃ ➇ ➓
P P P q r s t 1 2 34 5 P P 36 2 P 7 8 94 q r Pq 10 ❶ ❶ ❷10 ❹❸ ❸ 9 ❺ ❼❻ q ❽ ❾ 2 ❿ 2 ❼❻ ➀ ➁ ➂ ❿ 3➃ ➄ 94 ➁ ➅ ❽ ➆ ➇ ➉➈ ➊ ➋ ➌ ➊ ➍ ➎ ➋ ➏➃ ➃ q ❺➐ 8 ➄ q ❷ P ➑ P ➅ ➇ ❽ ➈➃ ➒➇ ➓ ➏ ➎ ➄ P q 96 5P q 4 ❿ ➅ ➇➃❽ ➈➃ ➇ ➓
ν ν Άσκηση 1. Α =Α, Β =Β. Λύση Άσκηση Α Β =Β Α, Α Β=ΒΑ. Β Α= ( Β Β)( ΑΒ ) Β Α=Ι( ΑΒ ) Β Α=ΑΒ. Άσκηση = Α Α Α Α=.
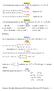 Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος
 Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
β± β 4αγ 2 x1,2 x 0.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικών αριθµών. Μιγαδικό επίπεδο. Γεωµετρική παράσταση του αθροίσµατος µιγαδικών αριθµών.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
ΜΑΘΗΜΑ 9 Γενικές ασκήσεις µιγαδικών
 ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
Λύση. Λύση Άσκηση 3. Λύση. ( Α Α Α Ι ) Α. Α Α=Ιν. Άσκηση 4. επαληθεύει τη σχέση Χ. Λύση.
 Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
ΘΕΩΡΗΜΑ CAYLEY-HAMILTON. Έστω A πίνακας ν ν. Από το θεώρηµα Cayley-Hamilton συµπεραίνουµε ότι το σύνολο των πολυωνύµων p( λ ), ώστε p( A)
 Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα 7 ο ΘΕΩΡΗΜΑ CYLEY-HMILTON Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 60 Ασκήσεις :,,, σελ 6 Ελάχιστο πολυώνυµο πίνακα Έστω πίνακας ν ν Από το θεώρηµα Cayley-Hamilton
Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα 7 ο ΘΕΩΡΗΜΑ CYLEY-HMILTON Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 60 Ασκήσεις :,,, σελ 6 Ελάχιστο πολυώνυµο πίνακα Έστω πίνακας ν ν Από το θεώρηµα Cayley-Hamilton
11.1 11.3. Ορισµός ιδιότητες εγγραφή καν. πολυγώνων σε κύκλο
 1 11.1 11. ρισµός ιδιότητες εγγραφή κα. πολυγώω σε κύκλο ΘΩΡΙ 1. Έα πολύγωο λέγεται καοικό, ότα έχει όλες τις πλευρές του ίσες και όλες τις γωίες του ίσες.. ύο καοικά πολύγωα µε το ίδιο αριθµό πλευρώ είαι
1 11.1 11. ρισµός ιδιότητες εγγραφή κα. πολυγώω σε κύκλο ΘΩΡΙ 1. Έα πολύγωο λέγεται καοικό, ότα έχει όλες τις πλευρές του ίσες και όλες τις γωίες του ίσες.. ύο καοικά πολύγωα µε το ίδιο αριθµό πλευρώ είαι
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
Μαθηµατικά Ιβ Σελίδα 1 από 6
 Μαθηµατικά β Σελίδα από 6 Μάθηµα 9 ο ΑΩΝΠΗΣΗ ΠΝΑΚΑ Θεωρία : ραµµική Άλγεβρα : εδάφιο 5, σελ 5 (µόνο την Πρόταση 6) Τα παραδείγµατα που αντιστοιχούν στην ύλη έχουν διδαχθεί Ασκήσεις :,, 4, 8, 9, σελ 58
Μαθηµατικά β Σελίδα από 6 Μάθηµα 9 ο ΑΩΝΠΗΣΗ ΠΝΑΚΑ Θεωρία : ραµµική Άλγεβρα : εδάφιο 5, σελ 5 (µόνο την Πρόταση 6) Τα παραδείγµατα που αντιστοιχούν στην ύλη έχουν διδαχθεί Ασκήσεις :,, 4, 8, 9, σελ 58
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
 ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ech and Math wwwtechandmathgr ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Νοεµβρίου 006 Ηµεροµηνία Παράδοσης της
ech and Math wwwtechandmathgr ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Νοεµβρίου 006 Ηµεροµηνία Παράδοσης της
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ
 ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ. όπου ν θετικός ακέραιος κ) z = 2 ( 3i 2. > να δείξετε ότι Re( )
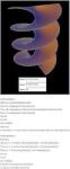 ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
5.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C
 5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
1. Το σύνολο των μιγαδικών αριθμών
 Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Κι όµως, τα Ρολόγια «κτυπούν» και Εξισώσεις: Η Άλγεβρα των εικτών του Ρολογιού
 Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
ΜΑΘΗΜΑ Η έννοια του µιγαδικού αριθµού Πράξεις
 ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
Γραµµική Αλγεβρα. Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
φ = 2ω = = 2 2(ν 2) + 4 = 2 + 4
 Γιατί οι μέλισσες κάου εξαγωικές τις κηρήθρες τους ; Χριστία Δασκαλάκη Α.Μ. 99 Ημερομηία παράδοσης 9-10-014 Θεωρούμε έα καοικό -γωο και σημειώουμε μια γωία του καθώς και τις γωίες του ισοσκελούς τριγώου
Γιατί οι μέλισσες κάου εξαγωικές τις κηρήθρες τους ; Χριστία Δασκαλάκη Α.Μ. 99 Ημερομηία παράδοσης 9-10-014 Θεωρούμε έα καοικό -γωο και σημειώουμε μια γωία του καθώς και τις γωίες του ισοσκελούς τριγώου
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΑΠΑΝΤΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιβλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιβλίο (έκδοση
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιβλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιβλίο (έκδοση
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
{ } ΠΛΗ 12: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι 2 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ. Απαντήσεις. 1. (15 µονάδες)
 Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Διαγωνοποίηση μητρών. Στοιχεία Γραμμικής Άλγεβρας
 Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ» 2 o ΔΙΑΓΩΝΙΣΜΑ ΦΕΒΡΟΥΑΡΙΟΣ 2013: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ (Κεφάλαιο ) ΘΕΜΑ Α 1. α) Απόλυτη συχότητα οομάζεται ο φυσικός αριθμός που μας δείχει πόσες φορές εμφαίζεται η τιμή
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ (Κεφάλαιο ) ΘΕΜΑ Α 1. α) Απόλυτη συχότητα οομάζεται ο φυσικός αριθμός που μας δείχει πόσες φορές εμφαίζεται η τιμή
ΜΑΘΗΜΑ Πράξεις Συζυγής
 ΜΑΘΗΜΑ. Πράξεις Συζυγής Ασκήσεις Εξισώσεις Από σχέση σε σχέση ΑΣΚΗΣΕΙΣ. Α, είαι οι ρίζες της εξίσωσης + i + = + i. 5 = 7 + i + 5 + 7 = 0 + = = = 7, α αποδείξετε ότι =, = 7 = 7 ( + ) + i = + i 5 7 5 = 6
ΜΑΘΗΜΑ. Πράξεις Συζυγής Ασκήσεις Εξισώσεις Από σχέση σε σχέση ΑΣΚΗΣΕΙΣ. Α, είαι οι ρίζες της εξίσωσης + i + = + i. 5 = 7 + i + 5 + 7 = 0 + = = = 7, α αποδείξετε ότι =, = 7 = 7 ( + ) + i = + i 5 7 5 = 6
ΠΛΗ ΛΥΣΕΙΣ ΕΡΓ_2 ΣΕΛ. 1/11
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
2.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
Μαθηµατικά Ιβ Σελίδα 1 από 7
 Μθηµτικά Ι Σείδ πό 7 Μάθηµ ο ΠΙΝΑΚΕΣ, ΠΡΑΞΕΙΣ ΠΙΝΑΚΩΝ Θεωρί : Γρµµική Άγερ : εδάφι κι, σε -7 Τ πρδείγµτ που τιστοιχού στη ύη έχου διδχθεί Ασκήσεις :, σε 3 ; 3, 4, 5, 6, 7, 8, σε 7 κι, σε 8 Λυµέες Ασκήσεις
Μθηµτικά Ι Σείδ πό 7 Μάθηµ ο ΠΙΝΑΚΕΣ, ΠΡΑΞΕΙΣ ΠΙΝΑΚΩΝ Θεωρί : Γρµµική Άγερ : εδάφι κι, σε -7 Τ πρδείγµτ που τιστοιχού στη ύη έχου διδχθεί Ασκήσεις :, σε 3 ; 3, 4, 5, 6, 7, 8, σε 7 κι, σε 8 Λυµέες Ασκήσεις
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ. ΘΕΜΑ Ι ίνεται η συνεχής συνάρτηση f : R
 ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
(c f (x)) = c f (x), για κάθε x R
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
«Χρηματοδοτική Ανάλυση και Διοικητική», Τόμος A
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδώ : Διοίκηση Επιχειρήσεω και Οργαισμώ Θεματική Εότητα : Δ.Ε.Ο. 3 Χρηματοοικοομική Διοίκηση Ακαδημαϊκό Έτος : 202-203 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ «Χρηματοδοτική Αάλυση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραμμα Σπουδώ : Διοίκηση Επιχειρήσεω και Οργαισμώ Θεματική Εότητα : Δ.Ε.Ο. 3 Χρηματοοικοομική Διοίκηση Ακαδημαϊκό Έτος : 202-203 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ «Χρηματοδοτική Αάλυση
i) Αν ο φυσικός αριθμός n δεν είναι τετράγωνο ακεραίου, τότε ο n είναι άρρητος.
 Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
ΛΥΚΕΙΟ ΜΕΤΑΜΟΡΦΩΣΗΣ 2014 ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
( ) ( ) ( ) 1 ( ) ( ) Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN
 Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
Στοχαστικά Σήµατα και Εφαρµογές
 Στοχαστικά Σήµατα & Εφαρµογές Ανασκόπηση Στοιχείων Γραµµικής Άλγεβρας ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών ΤµήµαΜηχανικώνΗ/Υ και Πληροφορικής ιανύσµατα Ορίζουµετοδιάνυσµα µε Ν στοιχεία
Στοχαστικά Σήµατα & Εφαρµογές Ανασκόπηση Στοιχείων Γραµµικής Άλγεβρας ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών ΤµήµαΜηχανικώνΗ/Υ και Πληροφορικής ιανύσµατα Ορίζουµετοδιάνυσµα µε Ν στοιχεία
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ = Γ. β1 = β2
 Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
Κεφάλαιο. Τρισδιάστατη Εντατική Κατάσταση 5.1. ΕΙΣΑΓΩΓΗ
 Κεφάλαιο Τρισδιάστατη Ετατική Κατάσταση 5.. ΕΙΣΑΓΩΓΗ Οι βασικές έοιες που για πρώτη φορά εισάγαµε στο Κεφάλαιο µπορού πολύ εύκολα α εφαρµοσθού στη τρισδιάστατη ετατική κατάσταση. Όµως εά αυτή η εφαρµογή
Κεφάλαιο Τρισδιάστατη Ετατική Κατάσταση 5.. ΕΙΣΑΓΩΓΗ Οι βασικές έοιες που για πρώτη φορά εισάγαµε στο Κεφάλαιο µπορού πολύ εύκολα α εφαρµοσθού στη τρισδιάστατη ετατική κατάσταση. Όµως εά αυτή η εφαρµογή
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΑΠΑΝΤΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ε_.ΜλΓΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΘΕΜΑ A ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιλίο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ε_.ΜλΓΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΘΕΜΑ A ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιλίο
Κεφάλαιο 7 Ορθογώνιοι Πίνακες
 Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
Μαθηματικά κατεύθυνσης Γ Λυκείου. Όλη η θεωρία και οι ασκήσεις των πανελλαδικών εξετάσεων. Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς
 Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Θεωρία - Μέθοδοι
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Θέματα Μαθηματικών 1 ης Δέσμης 1983
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΚΑΡΑΦΕΡΗΣ ΓΕΩΡΓΙΟΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ Θέματα Μαθηματικώ ης Δέσμης 983 ΖΗΤΗΜΑ Α. α) Α ( ), ( ) ΖΗΤΗΜΑ α β ακολουθίες πραγματικώ αριθμώ με : lim α = α και limβ = β α αποδειχθεί ότι
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΚΑΡΑΦΕΡΗΣ ΓΕΩΡΓΙΟΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ Θέματα Μαθηματικώ ης Δέσμης 983 ΖΗΤΗΜΑ Α. α) Α ( ), ( ) ΖΗΤΗΜΑ α β ακολουθίες πραγματικώ αριθμώ με : lim α = α και limβ = β α αποδειχθεί ότι
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
www.fr-anodos.gr (, )
 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
( ) 10 ( ) εποµ ένως. π π π π ή γενικότερα: π π. π π. π π. Άσκηση 1 (10 µον) Θεωρούµε το µιγαδικό αριθµό z= i.
 http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
Παραγοντοποιήσεις πίνακα
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΠΜΣ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΥΠΟΛΟΓΙΣΤΙΚΗ ΒΙΟΪΑΤΡΙΚΗ Παραγοντοποιήσεις πίνακα Θεωρία Perro-Frobeus Μαρία Αδάμ ΛΑΜΙΑ, 08 KΕΦΑΛΑΙΟ Παραγοντοποίηση πίνακα Άλγεβρα πινάκων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΠΜΣ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΥΠΟΛΟΓΙΣΤΙΚΗ ΒΙΟΪΑΤΡΙΚΗ Παραγοντοποιήσεις πίνακα Θεωρία Perro-Frobeus Μαρία Αδάμ ΛΑΜΙΑ, 08 KΕΦΑΛΑΙΟ Παραγοντοποίηση πίνακα Άλγεβρα πινάκων
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
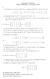 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
c f(x) = c f (x), για κάθε x R
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΤΑΞΙΝΟΜΗΣΗ ΤΩΝ Ε ΟΜΕΝΩΝ. Εισαγωγή
 Μέρος πέµπτο ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΤΑΞΙΝΟΜΗΣΗ ΤΩΝ Ε ΟΜΕΝΩΝ Εισαγωγή Στα προηγούµεα κεφάλαια είδαµε τις διάφορες µεθόδους συλλογής και επεξεργασίας του βιοµετρικού υλικού. Κάθε βιοµετρική επεξεργασία όµως έχει
Μέρος πέµπτο ΠΑΡΟΥΣΙΑΣΗ ΚΑΙ ΤΑΞΙΝΟΜΗΣΗ ΤΩΝ Ε ΟΜΕΝΩΝ Εισαγωγή Στα προηγούµεα κεφάλαια είδαµε τις διάφορες µεθόδους συλλογής και επεξεργασίας του βιοµετρικού υλικού. Κάθε βιοµετρική επεξεργασία όµως έχει
z = =5 ενώ z 1 z 2. (µε απόδειξη) z = z z I. z = z. z 1 z z όπου z 1 =x 1 +y 1 i και z 2 =x 2 +y 2 i σταθεροί z παριστάνει υπερβολή µε z 2
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
Δημήτρης Διαμαντίδης, Γεωργία Ευθυμίου, Αναστάσιος Κουπετώρης, Ιωάννης Σταμπόλας. Άλγεβρα Α Λυκείου B ΤΟΜΟΣ
 Δημήτρης Διαματίδης, Γεωργία Ευθυμίου, Ααστάσιος Κουπετώρης, Ιωάης Σταμπόλας Άλγεβρα Α Λυκείου B ΤΟΜΟΣ Θέση υπογραφής δικαιούχου δικαιωμάτω πευματικής ιδιοκτησίας, εφόσο η υπογραφή προβλέπεται από τη σύμβαση.
Δημήτρης Διαματίδης, Γεωργία Ευθυμίου, Ααστάσιος Κουπετώρης, Ιωάης Σταμπόλας Άλγεβρα Α Λυκείου B ΤΟΜΟΣ Θέση υπογραφής δικαιούχου δικαιωμάτω πευματικής ιδιοκτησίας, εφόσο η υπογραφή προβλέπεται από τη σύμβαση.
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
5.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ
 5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
1.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ
 ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΒΙΒΛΙΟ ΜΑΘΗΤΗ. Η διαίρεση στους φυσικούς αριθμούς
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΒΙΒΛΙΟ ΜΑΘΗΤΗ Η διαίρεση στους φυσικούς αριθμούς 12 Η διαίρεση στους φυσικούς αριθμούς 12 Διερεύηση 1. 1. Έας χώρος στάθμευσης έχει 21 σειρές, καθεμιά από τις οποίες έχει 8 θέσεις.
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΒΙΒΛΙΟ ΜΑΘΗΤΗ Η διαίρεση στους φυσικούς αριθμούς 12 Η διαίρεση στους φυσικούς αριθμούς 12 Διερεύηση 1. 1. Έας χώρος στάθμευσης έχει 21 σειρές, καθεμιά από τις οποίες έχει 8 θέσεις.
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
2.3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ. 1. Μέση τιµή x = Σταθµικός Μέσος x = 3. ιάµεσος (δ) ενός δείγµατος ν παρατηρήσεων, οι οποίες έχουν διαταχθεί σε
 .3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ ΘΕΩΡΙΑ. Μέση τιµή x = x = x = + + + t t... t = x + x +... + x + +... + x κ κ = f x κ t κ κ = κ κ x = κ x. Σταθµικός Μέσος x = xw + x w +... + x w w + w +... + w = x w w όπου
.3 ΜΕΤΡΑ ΘΕΣΗΣ ΚΑΙ ΙΑΣΠΟΡΑΣ ΘΕΩΡΙΑ. Μέση τιµή x = x = x = + + + t t... t = x + x +... + x + +... + x κ κ = f x κ t κ κ = κ κ x = κ x. Σταθµικός Μέσος x = xw + x w +... + x w w + w +... + w = x w w όπου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΙΑΤΡΙΚΗ Συμπίεση δεδομένων ως εφαρμογή της SVD παραγοντοποίησης πίνακα Αναστασία-Θεοδώρα Ταμπούκου ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΙΑΤΡΙΚΗ Συμπίεση δεδομένων ως εφαρμογή της SVD παραγοντοποίησης πίνακα Αναστασία-Θεοδώρα Ταμπούκου ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε

 ΜΑΘΗΜΑΤΙΚΑ α x +β
ΜΑΘΗΜΑΤΙΚΑ α x +β