OPĆA FIZIKA 1. I. DIO (pitanja 1 56) odgovori na ispitna pitanja prema predavanjima. prof. Emila Babića
|
|
|
- Άιμον Αλεξάνδρου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 OPĆA FIZIKA odgovori na ispitna pitanja prema predavanjima prof. Emila Babića I. DIO (pitanja 56)
2
3 OPĆA FIZIKA odgovori na ispitna pitanja (I. dio) Sažetak Ovo je prvi dio odgovora na pitanja iz kolegija Opća fizika, na prvoj godini istraživačkog smjera studija fizike. Odgovorena su pitanja od do 56 koja se mogu pronaći na Osnovna literatura su predavanja profesora Emila Babića iz Opće fizike, uz koja ide udžbenik Mehanika (Berkeley) []. Korištene su još zbirka zadataka Numeričko modeliranje složenih gibanja [] i Riješeni zadaci iz opće fizike [3]. Namjena ove skripte jest lakše praćenje predavanja te lakše pripremanje usmenog djela ispita. Ne može zamijeniti profesorova predavanja i propisanu literaturu za kolegij. Skriptu je recenzirao i grafički uredio Krešimir Cindrić, a Bruno Klajn ju je pažljivo pročitao i uočio mnogo grešaka. Od srca im zahvaljujem na trudu, a za greške koje su eventualno ostale preuzimam odgovornost. U Zagrebu, 007. Dijana Tolić Literatura [] C. Kittel, W. D. Knight, M. A. Ruderman, Mehanika, Tehnička knjiga, 003. [] E. Babić, Numeričko modeliranje složenih gibanja, Školska knjiga, 988. [3] E. Babić, R. Krsnik, M. Očko, Riješeni zadaci iz opće fizike, Školska knjiga,
4 4
5 Sadržaj Sažetak 3 Uvod i osnovni pojmovi. Predmet proučavanja fizike i veza s ostalim znanostima. 7. Fizikalne veličine dimenzije i jedinice SI sustav Relativnost gibanja, sustav i objekt opažanja (dimenzije). Referentni i koordinatni sustav Dimenzija i jedinica brzine, ubrzanja, količine gibanja, sile i energije u SI sustavu Dugodosežne interakcije, ovisnost sila o dimenzionalnosti prostora. 0 Vektori 6. Skalarni produkt dvaju vektora. Kosinusni poučak. 7. Vektorski produkt dvaju vektora. Sinusni poučak. 8. Operacije s vektorima. Derivacija vektora Četiri osnovna meñudjelovanja. 5 Newtonovi zakoni 0. I Newtonov zakon. Pokus. 6. Drugi Newtonov zakon. Pokus. Značenje i ograničenja. Relacije neodreñenosti. 6. Treći Newtonov zakon. Pokusi. Problem istovremenog odreñivanja sile. Problem elektromagnetnih sila. 8 Referentni sustavi i Galilejeva invarijantnost 3. Apsolutna i relativna brzina Apsolutna i relativna akceleracija. Machov princip Galilejeve tranformacije. Hipoteza Galilejeve invarijantnosti Ubrzani sustav. Fiktivne (inercijalne) sile. Mjerač ubrzanja Sustav koji rotira. Brzina i ubrzanje čestice koja se vrti. 8. Centrifugalna i Coriolisova sila Centrifugalna sila na površini Zemlje. Ovisnost o geografskoj širini. 4 Trenje 0. Zakoni trenja izmeñu suhih površina. Trenje na kosini. Proklizavanje i porijeklo trenja kotrljanja. 5 Jednadžbe gibanja. Jednadžba gibanja. Rješavanje u slučaju stalne sile. Numeričko rješavanje. 7. Slobodni pad. Atwoodov ureñaj. Pokusi Neovisnost gibanja. Vodoravni hitac. Pokusi i film Kosi hitac. Pokusi. Lovac i majmun Utjecaj otpora zraka na padanje tijela. Pokusi. Granična brzina Put i brzina pri slobodnom padu s trenjem razmjernim brzini. 33 5
6 Zakoni očuvanja energije 7. Zakoni očuvanja. Porijeklo, svojstva, primjene Izvod kinetičke energije preko impulsa i rada sile. Film Pretvorba potencijalne energije u kinetičku pri slobodnom padu Pretvorbe energije pri slobodnom padu Sačuvanje mehaničke energije. Pokusi Rad i snaga. Rad kao linijski integral sile Konzervativne sile i rad izvršen konzervativnom silom Potencijalna energija. Veza izmeñu sile i potencijalne energije Skok s motkom. Film. Pretvorbe energije Istraživanje sile i potencijalne energije iz ovisnosti o položaju. Granice gibanja Unutarnja energija sustava čestica Brzina potrebna da tijelo zauvijek napusti Zemlju. 47 Zakoni očuvanja količine gibanja 39. Očuvanje količine gibanja. Izvod i pokusi Sudari i raspršenja čestica. Vrste i značajke Savršeno elastični centralni sudar dviju čestica iste mase i jedna miruje. Pokusi Očuvanje količine gibanja i homogenost prostora Savršeno neelastični sudar dviju čestica iste mase: jedna miruje. Pokusi Sustav centra mase (SCM). Brzina i ubrzanje centra mase Karakteristike sudara u SCM i LS Veza izmeñu kuta sudara u LS i SCM Veza izmeñu količina gibanja i kinetičkih energija dviju čestica u SCM i LS Endo i egzotermne reakcije. Neelastični sudar dva tijela: promjena unutrašnje energije Potisak i konačna brzina rakete. Potisak mlaznog motora Očuvanje kutne količine gibanja. Veza sa momentom sile. Pokusi Moment centralne sile. Primjer Momenti unutrašnjih sila u sustavu N čestica Drugi Keplerov zakon. Geometrijsko značenje sačuvanja kutne količine gibanja Kutna količina gibanja i kinetička energija tijela koje kruži Oblik galaksije. Efektivna potencijalna energija tijela koje kruži Očuvanje kutne količine gibanja i izotropnost prostora. 66 6
7 Uvod i osnovni pojmovi. Predmet proučavanja fizike i veza s ostalim znanostima Fizika je znanost koja proučava strukturu svemira i prirodne mehanizme. Ona predstavlja veliko poopćenje prirode i prirodnih zakona. Priroda, kao golem i složen aparat znatno se pojednostavljuje u svojim dijelovima koje smo uspjeli teorijski objasniti. Tako na primjer dio fizike koji proučava gibanje dijelova Sunčevog sustava, mehanizme nastanka zvijezda i galaksija te ostala gibanja u svakodnevnom životu, svrstavamo u zakone klasične mehanike (tri Newtonova zakona, sila gravitacije, zakon očuvanja energije, količine gibanja i kutne količine gibanja) i ti zakoni vrijede za sva makroskopska tijela. Klasična mehanika se proširuje na specijalnu i opću teoriju relativnosti. Imamo dio fizike koji proučava atomske pojave, sastav tvari, zračenje svjetlosti odnosno zakone kvantne mehanike (Schrödingerova jednadžba i temeljna načela koja su relativno neodreñena). Zakoni klasične elektrodinamike (četiri Maxwellove jednadžbe, Lorentzova sila u vakuumu u tvari je potreban Ohmov zakon za vodiče te polarizacija tvari za izolatore) izvrsno objašnjavaju razne električke i magnetske pojave te meñudjelovanje svjetlosti i tvari. Četiri zakona termodinamike fenomenološki opisuju makroskopske sustave, toplinske strojeve i procese u živim bićima. Svi zakoni fizike koje smo uspjeli shvatiti odlikuju se jednostavnošću i ljepotom. Fizika je temelj svim prirodnim znanostima. U kemiji, koja se dijeli na anorgansku (fizikalnu i teorijsku) te organsku (biokemiju i molekularnu) kemiju, koristimo kvantnu mehaniku i termodinamiku. Zatim u biologiji, takoñer kvantnu mehaniku i termodinamiku, a u astronomiji koja je zapravo i starija od fizike, kvantnu i klasičnu mehaniku. Matematika je pak jezik fizike, ona nije njezin dio. Ona omogućuje da fizikalni zakoni budu jasno zapisani. Smisao teorijske fizike jest da nañe pravu formulu kojom će opisati prirodnu pojavu i to pomoću matematike (matematičkog formalizma). 7
8 . Fizikalne veličine, dimenzije i jedinice. SI sustav. Da bismo razmjenjivali informacije o gibanjima potrebni su nam etaloni ili standardi za duljinu, vrijeme i masu. Silu, rad i bilo koju fizikalnu veličinu uopće (dakle sve karakteristike sustava/tijela) moramo moći izraziti pomoću tri temeljne jedinice za vrijeme, duljinu i masu. Meñutim, često se zbog praktičnih razloga uvode i dodatne mjerne jedinice, kao npr. za električnu struju ili za temperaturu. U SI sustavu jedinica meñunarodno su dogovorene i priznate sljedeće osnovne mjerne jedinice, koje se danas definiraju ovako : 8 sekunda (s) vrijeme potrebno da se u atomu cezija izvrši oscilacija. metar (m) duljina koju svjetlost prevali u vakuumu za vrijeme od sekundi. amper (A) električna struja koja, ako konstantno teče kroz dva paralelna, metar udaljena, beskonačno duga vodiča zanemarivog presjeka, proizvodi meñu njima silu koja po metru 7 duljine iznosi 0 N. kelvin (K) jedinica za temperaturu. Skala se definira preko dvije točke apsolutne nule (0 K) i trojne točke specijalno pripremljene vode (73.6 K). mol jedinica za količinu tvari (množinu): mol sadrži 3 Avogadrov broj (približno ) čestica. kandela (Cd) je intenzitet svjetlosti u odreñenom smjeru izvora monokromatskog zračenja frekvencije Hz, ener- getske jakost 683 W sr u tom smjeru. kilogram (kg) masa valjka od platine i olova koji se čuva u Sevresu u Francuskoj. Osim ovih sedam službenih jedinica imamo brojne izvedene kao što su primjerice: tona, minuta, sat i litra. One su izvan SI ali dozvoljene. Prefiksi odreñuju red veličine. Najćešće korišteni prefiksi su: tera (T) giga (G) mega (M) = 0 kilo (k) 9 3 = 0 deci (d) = 0 mikro (µ) = = 0 hekto (h) = 0 centi (c) = 0 nano (n) = 6 = 0 deka (da) = 0 mili (m) = 0 3 piko (p) = U toku provoñenja složenih proračuna vrlo je važno biti siguran da se jedinice na jednoj strani dobivene jednadžbe podudaraju sa jedinicama druge strane. Analiza ove vrste naziva se dimenzijska analiza: nije uopće potrebno kazati kojim se mjernim jedinicama služimo već samo voditi računa da se radi o dimenziji mase [M], duljine [L] ili vremena [T]. Ovdje su, zbog kompletnosti, navedeni etaloni SI sustava. Naravno, te podatke nije potrebno pamtiti.
9 3. Relativnost gibanja, sustav i objekt opažanja (dimenzije). Referentni i koordinatni sustav. Budući da gibanje definiramo kao premještanje nekog tijela u odnosu na ostala tijela koja miruju, kažemo da samo relativna gibanja imaju smisla. Slično, samo relativni prostor ima smisla, odnosno o prostoru možemo govoriti samo kao o prostoru koji je ispunjen nekim objektima. Stanje sustava u mehanici potpuno je opisano s položajem i brzinom { r, v} te uobičajeno još i sa masom m, { r, p}. Referentni sustav je dogovorno odreñen sustav kojega izabiremo proizvoljno u smislu pogodnosti. Objekt se u svom vlastitom referentnom sustavu ne giba. Opis gibanja ovisi o izboru referentnog sustava (dok samo gibanje naravno ostaje isto). Primjerice, za opis gibanja Zemlje oko Sunca ishodište našeg referentnog sustava postavit ćemo u Sunce, dok ćemo za promatranje kosog hica na površini Zemlje naravno uzeti neki pogodniji sustav. Osnovne pretpostavke su da postoji jedinstveno, homogeno vrijeme te da je prostor ravni euklidski, homogeni. Imamo dvije klase referentnih sustava: inercijalni i neinercijalni sustavi. ) inercijalni: u njemu vrijede Newtonovi zakoni. Ne možemo nikakvim pokusom utvrditi mirujemo li ili se gibamo. Primjeri dovoljno dobrih inercijalnih sustava su zrakoplov koji leti konstantnom brzinom i soba u kući. ) neinercijalni: sustav koji naspram nekog inercijalnog sustava ubrzava. Postoje vanjske sile te ne vrijedi drugi Newtonov zakon u standardnom obliku, već ga treba prilagoditi i uključiti postojanje inercijskih pseudo-sila (primjer: npr. zrakoplov koji ubrzava). Referentni i koordinatni sustav su različiti pojmovi, premda se referentni sustavi mogu koordinatizirati. Koordinatni sustav naprosto se odnosi na potrebu popisivanja svih točaka prostora u kojima je boravila materijalna točka tijekom gibanja. Kartezijev koordinatni sustav opisuje položaj pomoću koordinata { x, y, z }, cilindrični sustav pomoću koordinata { ρφz,, }, a sferni sustav pomoću koordinata { rθφ,, }. I na kraju, za vektorski prikaz ne treba nam koordinatni sustav nego naprosto ishodište 0 i radijus vektor r. Vrijedi r ( t) = x( t) xˆ + y( t) yˆ + z( t) zˆ, gdje vrh vektora r ( t) opisuje putanju objekta kojeg promatramo. Ako ga deriviramo po vremenu t dobit ćemo brzinu objekta v( t), a brzinu dalje deriviramo po t za akceleraciju a( t). Da bi se razlikovale od skalarnih, vektorske veličine se označuju sa strelicom: a. Modul vektora (tj. njegova duljina ili norma) označuje se ovako: a, ili budući da je to skalar, jednostavno bez strelice: a. Jedinični vektori označuju se s kapicom: a ˆ. Vrijedi: a = aaˆ. 9
10 4. Dimenzija i jedinica brzine, ubrzanja, količine gibanja, sile i energije u SI sustavu. Brzina: v [L][T] m s (vektor) Ubrzanje: a [L][T] m s (vektor) Količina gibanja: p [M][L][T] kg m s = N s (vektor) Sila: F [M][L][T] kg m s N (njutn 3 ) (vektor) Energija: E [M][L] [T] kg m s = N m J (džul) (skalar) [F][L] 5. Dugodosežne interakcije, ovisnost sila o dimenzionalnosti prostora. Četiri su temeljne interakcije: gravitacijska, elektromagnetska, slaba i jaka sila 4. Doseg ovih sila uvjetovan je masom prijenosnika, što je masa prijenosnika veća doseg sile je manji i obrnuto, što je masa manja sila ima veći doseg. Fotoni i gravitoni su prijenosnici bez mase, tako su elektromagnetska i gravitacijska sila beskonačnog dosega nazivamo ih dugodosežnim interakcijama 5. Dugodosežne sile obje opadaju sa kvadratom udaljenosti. Gravitacijska sila je vrlo slaba, za oko 40 redova veličine je slabija od elektromagnetske (efekt gravitacije osjećamo samo zahvaljujući činjenici da je gravitacijska sila uvijek privlačna tj. nema negativne mase, a budući da je naš okoliš više ili manje električki neutralan, elektromagnetsku silu ne osjećamo tako jako). Elektromagnetska sila ima relativnu jakost 0 (ako uzmemo da je jakost jake (nuklearne) 39 sile jednaka ), a gravitacijska 0. Elektromagnetska sila je jako važna u atomima, a gravitacijska odreñuje gibanja na Zemlji, gibanja zvijezda i galaksija (tzv. gibanja na velikoj skali). Ovisnost sila o dimenziji prostora može se opisati kao F r D, gdje je D dimenzionalnost prostora,, ili 3. U jednoj dimenziji sila je tako proporcionalna D 0 sa r = r =, tj. konstantna je. U dvodimenzionalnom svijetu imamo F r, a u 3D sila opada sa kvadratom udaljenosti: F r (Coulombova, gravitacijska). 3 Relaciju N kg m s čitamo: jedan njutn definiramo kao silu potrebnu da tijelu od kilograma da ubrzanje od m s 4 Stariji naziv za jaku i slabu silu je nuklearne sile. 5 vidi pitanje 9. 0
11 Vektori 6. Skalarni produkt dvaju vektora. Kosinusni poučak. Skalarni produkt dvaju vektora definiramo kao broj koji dobijemo množeći iznos prvog vektora sa iznosom drugog vektora te kosinusom kuta meñu njima: a b a b cos ( a, b) (6.) Iz (6.) vidimo da, ako je skalarni produkt nula, onda su vektori okomiti. Ovakav skalarni umnožak ne oslanja se ni na kakav koordinatni sustav. Budući da je kosinus kuta izmeñu prvog i drugog vektora isti kao kosinus kuta izmeñu drugog i prvog (tj. cosφ = cos( φ), odnosno, kosinus je parna funkcija), skalarni produkt je komutativan (vrijedi a b = b a). Skalarni produkt dvaju jediničnih vektora upravo je kosinus kuta meñu njima. Skalarni produkt u Kartezijevim komponentama: xˆ xˆ = yˆ yˆ = zˆ zˆ = xˆ yˆ = yˆ zˆ = zˆ xˆ = 0 a b = ( a xˆ + a yˆ + a zˆ )( b xˆ + b yˆ + b zˆ ) = a b + a b + a b x y z x y z x x y y z z (6.) Primjer: primjena skalarnog produkta za izvod kosinusnog poučka Neka je razlika dvaju vektora a i b neki treći vektor c : a b = c. b Uzimajući skalarni produkt svake strane tog izraza sa samim sobom, dobivamo: ( a b) ( a b) = c c a + b a b = c γ = ( a, b) a Slika 6. : Kosinusni poučak c = a b što daje poznatu relaciju za trokut, zvanu kosinusni poučak: a + b ab cosγ = c (6.3) Ostale primjene: jednadžba ravnine, rad sile na nekom putu, električni i magnetski vektori u elektromagnetskom valu, brzina vršenja rada, brzina promjene volumena koji nastaje gibanjem dijela ravne plohe itd.
12 7. Vektorski produkt dvaju vektora. Sinusni poučak. Vektorski produkt definira se na sljedeći način: a b a b sin ( a, b) cˆ (7.) Iznos mu je a b sin ( a, b), što je jednako površini paralelograma sa stranicama duljina a i b, a smjer ĉ je vektor koji je okomit na ravninu u kojoj leže a i b. Hoće li ĉ gledati prema gore ili dolje iz te ravine, odreñujemo pravilom desne ruke (dogovor, tzv. pravilo desne ruke). c = a b a a b b c = b a Slika 7. : Vektorski produkt Budući da je sinus kuta izmeñu prvog i drugog vektora suprotnog predznaka od sinus kuta izmeñu drugog i prvog (tj. sinφ = sin( φ), sinus je neparna funkcija) vektorski produkt je antikomutativan (vrijedi a b = b a). Vektorski produkt vektora sa samim sobom jednak je nuli, jer je sin ( a, a ) = sin 0 = 0. Vektorski produkt u Kartezijevim komponentama: xˆ yˆ zˆ ay az ax az ax ay a b = a ˆ ˆ x ay az = x y + zˆ = by bz bx bz bx bz b b b x y z = xˆ ( a b a b ) + yˆ ( a b a b ) + zˆ ( a b a b ) y z z y z x x z x y y x (7.) Primjer: primjena vektorskog produkta za izvod sinusnog poučka Promotrimo trokut definiran sa c = a + b. Množimo vektorski s lijeva obje strane jednakosti s a : a c a = a + a b uzevši u obzir da je a a = 0 i da obje strane moraju imati iznos, slijedi a c sin ( a, c) = a b sin ( a, b) što je poznati sinusni poučak za trokut: sin ( a, c) sin ( a, b) = (7.3) b c
13 8. Operacije s vektorima. Derivacija vektora. Raspis u Kartezijevim koordinatama Zbrajanje vektora a a + b b ax a = a ˆ ˆ y = axx + ay y + azzˆ a z Zbroj dvaju vektora a + b definira se geometrijskom konstrukcijom koja se često naziva pravilom paralelograma. Zbrajanje vektora je komutativno i asocijativno. a + b = b + a (komutativnost) a + ( b + c) = ( a + b) + c (asocijativnost) U Kartezijevim koordinatama: a + b = ( a + b ) xˆ + ( a + b ) yˆ + ( a + b ) zˆ Množenje sa skalarom Slika 8.: Raspis u Kartezijevim koordinatama x x y y z z λa = aλ ( λ + µ ) a = λa + µa λ( a + b) = λa + λb Skalarno i vektorsko množenje a b a b cos ( a, b) a b a b sin ( a, b) cˆ (komutativnost) (distributivnost) (distributivnost) Deriviranje vektora A( s) - vektorska funkcija skalarne varijable s da d A( s + s) A( s) = A( s) = lim = ds ds s 0 s d A ( ) d Ay ( s) x s d Az ( s) = xˆ + yˆ + zˆ ds ds ds Vrijedi: d da db ( A + B) = + (derivacija zbroja) ds ds ds d d d ( ) λ A λa = A + λ (d. produkta sa skalarom) ds ds ds x z ẑ ˆx a y ŷ a a x a z y 3
14 d d d ( ) A B A B = B + A ds ds ds d d d ( ) A B A B = B + A ds ds ds Parcijalno deriviranje A = A( λ, η, µ ): A Aλ ˆ Aη A λ η µ = + ˆ + µ ˆ λ λ λ λ A Aλ ˆ Aη A λ η µ = + ˆ + µ ˆ η η η η A Aλ ˆ Aη A λ η µ = + ˆ + µ ˆ µ µ µ µ (d. skalarnog produkta) (d. vektorskog produkta) (po λ) (po η) (po µ) Totalni diferencijal d A : A( λη,, µ ) Aλη (,, µ ) A( λη,, µ ) da = dλ + dη + d µ. λ η µ 4
15 9. Četiri osnovna meñudjelovanja/interakcije. Sve što postoji u svemiru meñudjeluje, a sve što znamo o prirodi i svijetu znamo iz posljedica tih meñudjelovanja. Kvantitativna mjera jakosti interakcije jest sila. U prirodi postoji obilje zakona naspram kojeg je ovaj broj temeljnih interakcija doista malen. Te četiri temeljne interakcije su gravitacijska sila, elektromagnetska, slaba nuklearna i jaka nuklearna. 39 Gravitacijska sila. Što se tiče relativne jakosti ovo je vrlo slaba sila (0 ), no doseg joj je velik te je uvijek privlačna pa je odgovorna za gibanja u svemiru (zvijezde, planeti, galaksije). Ova sila poput elektromagnetske opada sa kvadratom udaljenosti, no za oko 40 redova je slabija od nje. Pretpostavlja se (postoje vrlo dobri teorijski razlozi) da su čestice prijenosnici gravitoni, no tek ih je potrebno eksperimentalno potvrditi. Elektromagnetska sila je važna u atomima. Njena relativna jakost je 0 (vrlo jaka sila). Takoñer je dugodosežna poput gravitacijske. Prijenosnik: foton (γ). Slaba sila javlja se kod raspada atomske jezgre. Ovo je kratkodosežna sila koja 5 ima isto porijeklo kao i elektromagnetska. Relativna jakost joj je 0, a djeluje na 5 ± 0 0 m. Prijenosnici: W, Z bozoni. Jaka sila drži na okupu protone i neutrone te cijelu atomsku jezgru. Na fundamentalnoj skali ima beskonačan doseg, no ostatak te sile koji drži atomsku jezgru zajedno ima vrlo mali doseg (postoji eksponencijalni član u jednadžbi) 5 0. Relativne je jakosti. Prijenosnici: meñu nukleonima djeluju mezoni ±,0 ±,0 (π, K,...), a fundamentalni prijenosnici (meñu kvarkovima) su gluoni (g). Nebeska gravitacija Zemaljska gravitacija Opća gravitacija Newton (686. g.) Električna sila Magnetska sila Elektromagnetska sila Maxwell (864. g.) Salam, Glashow, Weinberg (979. g.) Elektroslaba sila? Slaba sila Jaka sila Slika 9.: Četiri fundamentalne sile 5
16 Newtonovi zakoni 0. Prvi Newtonov zakon. Pokus. Kad je ukupna sila na neko tijelo nula, onda je i akceleracija kojom se to tijelo giba nula. Brzina je u tom slučaju konstantna, a vektor akceleracije ima sve komponente jednake nuli, i tangecijalnu i radijalnu. Prvi Newtonov zakon glasi: F uk = 0 a = 0 v = const. (I. N.z.) ''Tijelo ostaje u stanju mirovanja ili jednolikog gibanja po pravcu kad na njega ne djeluju vanjske sile.'' Prvi Newtonov zakon je nužna pretpostavka drugom i trećem. On definira inercijalni referentni sustav (sustav na koji ne djeluju vanjske sile). Samo u inercijalnom referentnom sustavu Newtonovi zakoni vrijede u obliku u kojem ćemo ih napisati. Pokusi: zračna klupa, kotrljanje kuglice po uglančanoj i hrapavoj podlozi, Galilejev pokus.. Drugi Newtonov zakon. Pokus. Značenje i ograničenja. Relacije neodreñenosti. F = ( mv) = m = m = ma dt dt dt. d m= const dv d v (II. N.z.) ''Promjena količine gibanja tijela proporcionalna je sili koja djeluje na to tijelo.'' Količina gibanja je definirana kao umnožak mase i brzine. Kada govorimo o sili F mislimo na ukupnu silu koja djeluje na tijelo i to na silu koja djeluje izvana (sila teža, reakcija podloge, sila trenja, ), a ne primjerice na pogonsku silu motora, koja djeluje iznutra. Drugi Newtonov zakon kaže da je ta ukupna sila koja djeluje na tijelo jednaka umnošku njegove mase i akceleracije. Ovaj zakon nije definicija operativne sile, on samo govori što će se dogoditi ako sila djeluje na tijelo. Kada su brzine bliske brzinama svjetlosti, Newtonov zakon u gornjem obliku još uvijek je prikladan jer F = dp dt uvijek vrijedi pa i za v c uz uvjet 6 p = γ( mv) gdje je γ. (.) v c 6 Besmisleno je tu relaciju promatrati kao p = ( γm) v i umnožak ( γm ) smatrati relativističkom masom koncept relativističke mase je besmislen. 6
17 Ograničenja: ne vrijedi za kvantne čestice. Primjerice u atomu nam koncept putanje potpuno beskoristan. Zatim, u slučaju v c uvodimo specijalnu teoriju relativnosti i Lorentzov faktor γ. Pokus: pokazali smo na malim kolicima i utezima, da ubrzanje uz konstantnu silu ovisi o masi kolica odnosno masi utega - što smo više utega upotrijebili, kolica su imala manje ubrzanje a (odnosno ubrzanje je obrnuto proporcionalno masi m): F F = ma a = (.) m Relacije neodreñenosti 7 odnose se na nemogućnost točnog poznavanja (neodreñenost) brzine i položaja čestice, odnosno količine gibanja i položaja čestice. Iste relacije postoje u kombinaciji vrijeme i energija, a u pitanju su uvijek parovi veličina. Javljaju se kod kvantnih (vrlo sitnih 8 ) čestica i tamo nam jednadžba gibnja tj. koncept putanje, nije korisna. Neodreñenost u količini gibanja i položaju prikazujemo relacijom: px x ħ (.3) Uzmimo da istovremeno trebamo izmjeriti položaj i količinu gibanja neke čestice (kvantnog objekta). Javit će se neodreñenost položaja x koja je razmjerna valnoj duljini λ svjetlosti kojom obasjavamo tu česticu. Samim obasjavanjem čestice mi smo joj promijenili brzinu (količinu gibanja). Obasjavanjem sa svjetlošću neke valne duljine česticu udaramo sa fotonima svjetlosti te ju time skrećemo sa njene prvotne putanje, odnosno utvrñivanjem položaja čestice mi smo istovremeno promijenili njezinu količinu gibanja. Dakle istovremeno nije moguće poznavati položaj i količinu gibanja, jer se samim odreñivanjem položaja mijenja količina gibanja. U kvantnoj mehanici sam čin mjerenja drastično utječe na sustav. Ovo ne znači da čestica doista ima točno odreñenu količinu gibanja i točno odreñen položaj istovremeno, a da ga mi naprosto ne možemo odrediti zbog nedovoljno preciznog mjerenja. Konceptualno ne postoji mjerenje koje ne bi poremetilo sustav te zato nije fizikalno pitati se o njihovim istovremenim vrijednostima sustav po svojoj prirodi doista niti nema istovremeni položaj i količinu gibanja. Heisenbergova relacija neodreñenosti javlja se kada istovremeno pokušamo odrediti položaj i količinu gibanja objekta. 9 7 odnosno Heisenbergove relacije neodreñenosti. 8 Javljaju se i kod makroskopskih čestica, samo što u makrosvijetu nisu tako zamjetne. 9 Policajac zaustavlja automobil na cesti zbog prekoračenja dozvoljene brzine. Automobilom upravlja Heisenberg. Policajac ga upita: Gospodine, znate li vi koliko ste brzo vozili? na što mu Heisenberg odgovara: Ne znam. Ali znam gdje sam. 7
18 . Treći Newtonov zakon. Pokusi. Problem istovremenog odreñivanja sile. Problem elektromagnetnih sila. F = F ''Kad dva tijela djeluju jedno na drugo, sila F kojom prvo tijelo djeluje na drugo, jednaka je po iznosu ali suprotnog smjera od sile F kojom drugo tijelo djeluje na prvo.'' Ako primjerice ispustimo kredu na pod, tijela će meñusobno djelovati jedno na drugo, ona će se ubrzavati. No, budući da je Zemlja puno tromija od krede njena će akceleracija biti puno manja od akceleracije krede. Sve sile su meñudjelovanja, sve što je u svemiru meñudjeluje. Najbolji primjer trećeg Newtonovog zakona je pritisak prsta o podlogu, ne bismo se doista uvjerili da postoji sila protureakcije. Ovaj zakon nam govori kada više ne vrijede zakoni klasične mehanike, tj. odstupanja od trećeg Newtonovog zakona su najbolji pokazatelji neadekvatnosti klasične mehanike. On nikada ne vrijedi za elektromagnetska djelovanja. Relacija zakona očuvanja količine gibanja proizlazi upravo iz ovog zakona. Problem istovremenog odreñivanja sila sastoji se u tome što se meñudjelovanja svemirom zapravo beskonačno šire pa nismo nikada sigurni da li na tijelo djeluju neke sile ili ne. Teško je uzeti u obzir sve utjecaje na neki objekt, tj. odrediti postoje li učinci udaljenih dijelova svemira. Problem elektromagnetnih sila se odnosi na to da treći Newtonov zakon naprosto ne vrijedi za magnetske sile. Ako se dva naboja gibaju, osim Coulombove sile meñu njima se javlja i magnetska sila koja ovisi o brzini kojom se naboji gibaju, pa ukupne sile koje djeluju izmeñu dva naboja nisu nužno jednake i suprotne. 8
19 Referentni sustavi i Galilejeva invarijantnost 3. Apsolutna i relativna brzina. Relativnost brzina je potvrñena nizom pokusa. Apsolutna brzina nema nikakvog smisla. Dolazimo do temeljne hipoteze o Galilejevoj invarijantnosti: zakoni fizike u svim inercijalnim sustavima su jednaki. Prema ovoj hipotezi nikakvim pokusom ne možemo utvrditi da li se motritelj jednoliko giba s obzirom na zvijezde stajačice ili miruje. Brzina je relativna i zbog toga nije moguće razlikovati inercijalne sustave. Ovo načelo bilo je u temeljima Newtonove slike svemira i jedno je od glavnih oslonaca specijalne teorije relativnosti. 4. Apsolutna i relativna akceleracija. Machov princip. Newtonov zamišljeni pokus sa kantom vode: kantu s vodom objesimo na nit i zavrtimo. Promatramo iz sustava kante i sustava promatrača (mi). Voda se u početku vrti u odnosu na kantu, a u odnosu na nas miruje i ima ravan oblik. Voda se ubrzava i počinje se gibati u odnosu na nas, a mirovati u odnosu na kantu vidimo kako poprima paraboličan oblik. Naš sustav je inercijalan, a sustav kante nije jer kanta akcelerira u odnosu na naš sustav. Isto tako možemo reći da i naš sustav akcelerira u odnosu na sustav kante, pa bi onda voda trebala biti ravna i parabolična u obrnutim slučajevima no nije tako. Ovo je Newtona navelo da zaključi da je prostor apsolutan, tj. da je sustav kante nije onaj pravi sustav, nego je naš. Newton je zastupao apsolutno ubrzanje. Suprotni nazor, da samo ubrzanje s obzirom na zvijezde stajačice ima smisla naziva se Machov princip. Zasad nije naišao ni na potvrdu ni na prigovor sa eksperimentalne strane, no neki fizičari poput Macha i Einsteina su relativnom ubrzanju ipak davali prednost pred apsolutnim. Ekvivalentna formulacija Machovog principa: uvijek se kao protudjelovanje bilo kojoj gravitacijskoj sili može naći odgovarajuća inercijska pseudosila (npr. ubrzava li dizalo prema gore sa a = g poništit će g ). Uvijek postoji sustav u kojem su tijela u bestežinskom stanju. Posljedica toga je da je masa, tj. inercija svojstvo prostora. 0 To je temelj opće teorije relativnosti. 0 Još jedna ekvivalentna formulacija: ako maknemo svu masu, nema više prostora. 9
20 5. Galilejeve tranformacije. Hipoteza Galilejeve invarijantnosti. Promatramo dva sustava, S i S i pitamo se čime je dan položaj čestice P gledano iz oba sustava. Vrijeme t = t = 0 u oba sustava počnemo mjeriti od nule. Galilei je zaključio da je vrijeme invarijanta fizikalna veličina koja se ne mijenja pri prelasku iz jednog sustava u drugi: uvijek je t = t. Pretpostavimo da se ishodišta 0 i 0 oba sustava poklapaju. Sustav S se sada započinje gibati stalnom brzinom V u x smjeru. U tom slučaju imamo sljedeće transformacije koordinata: t = t x = x + Vt y = y z = z (5.) Ovo su tzv. Galilejeve transformacije koordinata i za njih vrijedi hipoteza Galilejeve invarijantnosti: Osnovni zakoni fizike imaju oblik u svim sustavima povezanim Galilejevim transformacijama (sustavima koji se stalnom brzinom V gibaju jedni prema drugima). Takoñer, pokusi pokazuju da je ubrzanje nekog objekta jednako u S i S tj. a = a (pokažite), a duljina objekta se ne mijenja nego je L jednak L. Neposredna posljedica ovih jednadžbi je pravilo zbrajanja brzina: dx dx dx vx = = = + V = v x + V vi = v i + V dt dt dt (5.) Provjera Galilejevih transformacija se svodi na provjeru slaganja brzina (da je čovjek u vlaku doista brži za brzinu vlaka). Galilejeve transformacije su dobre za brzine mnogo manje od c, tj. u nerelativističkoj granici. Za brzine bliske c, morat ćemo koristiti Lorentzove transformacije specijalna teorija relativnosti. 6. Ubrzani sustav. Fiktivne (inercijalne) sile. Mjerač ubrzanja. Ubrzani ili neinercijalni sustav klasa je referentnog sustava. U takvom sustavu postoje vanjske sile koje djeluju na sustav, u njemu vrijeme nije jedinstveno, a prostor nije više euklidski homogeni. Što se tiče Newtonovih zakona, bitno je reći da se akceleracija a iz F = ma odnosi na ubrzanje mjereno u odnosu na neubrzani sustav. Smatramo li Zemlju neubrzanim odnosno inercijalnim sustavom dok pratimo neki pokus na njenoj površini, ubrzanje a objekta koji promatramo doista jest a inercijalno i vrijedi Newtonov zakon u obliku F = ma. Zemlja doista i jest približno dobar inercijalni sustav, jer je njezina centrifugalna akceleracija vrlo mala. Ali, ako bismo htjeli biti jako precizni, F = ma na površini Zemlje (gdje je a primjerice akceleracija nekog kamena čije gibanje promatramo) Newtonov zakon moramo pisati kao F = m( a + a ) gdje je a centrifugalna Zemljina akceleracija. 0
21 Dakle, ako smo u ubrzanom sustavu moramo uzeti u obzir i ubrzanje tog sustava. Odavde odmah vidimo da ako je a = 0 sustav je inercijalan i Newtonov zakon se svodi na F = ma: F = m( a + a ) = ma + ma = ma F0 (6.) Korisno je označiti F0 = ma0 što je upravo i definicija fiktivne (inercijalne) sile. Ova sila se dakle uvijek javlja u neinercijalnim sustavima zbog njihovog ubrzanja. Svakom tijelu u neinercijalnom sustavu daje ubrzanje jednakog iznosa kao ubrzanje sustava i suprotnog smjera. Dakle u svakom neinercijalnom sustavu se osjeća fiktivna sila koja se treba dodati pravoj sili F da bi dobili ma koja se doista opaža: ma = F + F 0 Opća svojstva inercijalnih sila: ne postoje u inercijalnom sustavu, nisu posljedica meñudjelovanja (primjerice centrifugalna sila nije nekakva reakcija na centripetalnu silu!) i a je neovisno o masi. Mjerač ubrzanja (akcelerometar, slika 6.) je ureñaj koji se sastoji od opruge neke konstante elastičnosti i mase pričvršćene na tu oprugu ograničene na gibanje u samo jednom smjeru. Tako se pomakom mase može mjeriti ubrzanje neinercijalnog sustava. Opruga u a inercijalnom sustavu (lijevo na slici) miruje pa a = 0. Akceleracije sustava a takoñer nema. Sila na masu m je F = kx = 0, jer je x = 0. U neinercijalnom sustavu (desno) imamo F = m( a + a ) = ma. Slijedi da je: m kx = ma, odnosno akceleracija neinercijalnog sustava jednaka je a = kx m. Primjerice, čovjek unutar rakete mjereći x x m može saznati točnu vrijednost ubrzanja rakete. Slika 6.: Akcelerometar bez obzira radilo se o ping-pong loptici ili primjerice o sumo hrvaču, jer ubrzanje a naravno ne ovisi o masi.
22 7. Sustav koji rotira. Brzina i ubrzanje čestice koja se vrti. Sustav se vrti oko svoje osi kutnom brzinom ω. svake čestice u takvom sustavu će biti: v = ω r Linearna ili obodna brzina (7.) gdje je r udaljenost čestice od središta vrtnje. Zamislimo kuglicu koja se vrti na niti duljine r. Znamo da na česticu djeluje napetost niti T koja vuče česticu prema središtu vrtnje. Dakle sila T preuzima ulogu centripetalne sile (ulogu centripetalne sile uvijek igra neka druga sila, recimo u slučaju vrtnje planeta oko Sunca to je gravitacijska sila izmeñu Sunca i planeta): T = F = ma (7.) cp v Fcp = m, (7.3) r tj. centripetalna akceleracija je po iznosu v acp = = ω r, (7.4) r a usmjerena je prema središtu vrtnje (zato minus): a = ω r (7.5) cp cp. Ako bismo istu ovu vrtnju promatrali iz samog sustava vrtnje, tj. neinercijalnog sustava (zamislit ćemo si da smo muha mase m i da sjedimo na loptici koja se na niti vrti ukrug) imamo sljedeću situaciju: budući da smo u ubrzanom sustavu, nužno se javlja nekakva fiktivna sila koja je posljedica ubrzanja sustava. Znamo već (iz svakodnevnog iskustva na vrtuljcima) da nas ta sila gura prema van i da se moramo napregnuti točno odreñenom silom ako želimo mirovati i ako ne želimo izletjeti van s vrtuljka. Rekli smo već da je sila u neinercijalnom sustavu zapravo uvećana za neku fiktivnu silu koja ovisi o ubrzanju sustava, iznosi F0 = ma : ma = F + F 0 (7.6) s tim da se muha sama od sebe ne ubrzava pa je sila F = 0 (odnosno rekli smo da želimo mirovati na vrtuljku pa stavimo da je naša akceleracija a = 0). Ostaje ma = F 0 (7.7) gdje je F 0 odreñena ubrzanjem vrtuljka a cp i masom muhe: a = acp F0 = ma = m( ω r) ma = mω r cp (7.8) Dobili smo fiktivnu silu koja nas doista gura prema van (predznak je sada pozitivan). Ova sila naziva se centrifugalna sila i zamjećuje se isključivo iz samog ubrzanog sustava tj. zamjećuje ju samo muha na loptici ili mi na vrtuljku.
23 8. Centrifugalna i Coriolisova sila. Recimo da naša muha (vidi 7.) pokuša hodati po loptici u isto vrijeme dok se loptica vrti na niti. Ako se tijelo giba u neinercijalnom sustavu koji rotira, na njega osim centrifugalne sile djeluje i tzv. Coriolisova sila. Ova sila ovisi o brzini kojom se tijelo (muha) giba. Njeni učinci se opažaju katkad u letovima aviona, jer je i Zemlja takoñer slabo neinercijalan sustav zbog dnevne vrtnje oko svoje osi. I centrifugalna i Coriolisova sila su dakle fiktivne sile. Muha se počinje gibati brzinom v, uz brzinu v = ω r, koju već ima zbog vrtnje (na nekoj udaljenosti r od središta, što je u ovom slučaju duljina niti). Ukupna brzina muhe je sada: u = v + v. Sila koju muha osjeća u neinercijalnom sustavu: što nakon kvadriranja postaje: F0 = ma u ( v + v) = macp = m = m r r ( v ' + ω r ) = m, r v ma m mωv r mω r r (8.) =. (8.) Prvi član predstavlja realnu interakciju centripetalnu silu kao što je primjerice sila trenja. Druge dvije sile su fiktivne, Coriolisova i centrifugalna (zadnji član). Zemljina centrifugalna akceleracija na ekvatoru dana je sa v acp = = R Z ω RZ. 3
24 9. Centrifugalna sila na površini Zemlje. Ovisnost o geografskoj širini. ω Kutna brzina Zemlje je vrlo mala pa je r = R cosθ Z centrifugalna akceleracija još manja: a = ω r g a cf θ udaljenost do osi vrtnje Zemlje r možemo napisati kao R Z r = RZ cos θ. Kut θ mjerimo iz središta Zemlje tako da je na ekvatoru 0 a na polu 90 stupnjeva. Vidimo da centrifugalna akceleracija ovisi o mjestu na površini Zemlje (jer ovisi o njenom radijusu): Slika 9.: Centrifugalna sila a = ω na površini Zemlje R cos θ. (9.) cf Z Pa i ukupno akceleracija slobodnog pada g uk = g + a cf ovisi o mjestu na površini Zemlje, jer centrifugalna akceleracija ovisi. Akceleracija slobodnog pada je uvijek umanjena za akceleraciju centrifugalne sile (jedna nas privlači ka središtu, druga nas gura od središta). Centrifugalna akcele-racija je prema gornjoj relaciji najveća za θ = 0, što je na ekvatoru. Prema tome, na ekvatoru je g umanjen za najveći iznos i tamo je najmanji ( g E = 9.78 m s ), a na polovima je g najveći ( g E = 9.83 m s ). Da zaključimo, što je geografska širina veća, centrifugalna sila je manja. Na polovima je nema, a na ekvatoru je najveća. No, čak i na ekvatoru radi se o zanemarivo malenom ubrzanju ( a cf = m s ). Meñu druge, još manje doprinose akceleraciji slobodnog pada možemo navesti i činjenicu da Zemlja nije savršena kugla, već spljošteni elipsoid te da raspored kopnenih masa nije homogen na Zemlji. Meñutim, ti doprinosi su jedva mjerljivi. cf 4
25 Trenje 0. Zakoni trenja izmeñu suhih površina. Trenje na kosini. Proklizavanje i porijeklo trenja kotrljanja. F tr = µn. (0.) Kad god površina jednog tijela klizi preko površine drugoga, svako od ta dva tijela djeluje na drugo silom trenja. Sila trenja djeluje u smjeru paralelnom sa dodirnim površinama. Općenito je trenje posljedica djelovanja molekularnih sila na površini tijela, i detaljni mehanizam trenja bio bi vrlo složen. Suho trenje je sila koja se javlja pri kontaktu krutih i približno glatkih površina. Razlika izmeñu suhog trenja i trenja s fluidom jest da suho trenje ne raste sa brzinom: F tr F tr v v Slika 0.. Lijevo: suho klizanje: stick slip: malo se zalijepi pa malo krene. Desno: trenje s fluidom. Neke pojave vezane uz suho trenje su stagnacija, odnosno tijela miruju i u neravnotežnim položajima, te proklizavanje. Sila trenja za dano tijelo ne ovisi o površini u kontaktu. Može djelovati i kada nema relativnog gibanja. Zamislimo teški drveni sanduk na podu. Postoji cijeli spektar sila za koji sanduk uopće ne možemo pomaknuti (možemo napraviti i pokus sa dinamometrom ne bi li se uvjerili.) Silu koja ovo uzrokuje nazivamo silom statičkog trenja. Ona može poprimiti sve vrijednosti od nula do µ stn. Dok god je primijenjena sila jednaka statičkoj sili trenja nema gibanja. Dakle statičko trenje može doseći samo neku konačnu vrijednost nakon koje više ne može rasti, tako da djelovanje primijenjene sile može pretegnuti (s vremenom ipak uspijemo pomaknuti sanduk). No, u principu se sila trenja uvijek malo smanjuje kada se tijelo počne jednoliko gibati po podlozi zbog deformacije. Statička deformacija uvijek je veća od dinamičke (kada tijela miruju propadanje u podlogu je najveće). 5
26 Trenje na kosini. Ako želimo da tijelo miruje na kosini, moramo vidjeti kada će sile koje djeluju na njega biti u ravnoteži. 3 Niz kosinu imamo sinusnu komponentu sile teže, a uz kosinu imamo kosinusnu komponentu sile trenja. Lako se uvjerimo da u ravnoteži vrijedi: µ = tgα Ako tijelo miruje na kosini u ravnotežnom položaju, i ako ga pokušamo pomaknuti u bilo kojem smjeru, ono će proklizati jer će se poremetiti ravnoteža sila. Porijeklo trenja kotrljanja je deformacija podloge. Zbog te deformacije javljaju se lijeve i desne sile koje djeluju prema centru kotrljajućeg tijela. Kad ne bi bilo deformacije, tijelo bi se stalno gibalo (jer ne bi bilo trenja kotrljanja). 3 Sile u x smjeru: mg sinα Nµ = 0, sile u y smjeru: N mg cosα = 0 N = mg cosα (uvrstimo u prvu jednadžbu) 6
27 Jednadžbe gibanje. Jednadžba gibanja. Rješavanje u slučaju stalne sile. Numeričko rješavanje. Jednadžba gibanja sastoji se od drugog Newtonovog zakona i izraza za silu F. Pod utjecajem ukupne sile F čestica stalne mase podliježe ubrzanju u skladu sa drugim Newtonovim zakonom. Jednadžba gibanja: F ma m d r = = d t (II. N.z.) Integracijom ove diferencijalne jednadžbe dobivamo izraze za vektor brzine i položaja čestice kao funkcije vremena. Da bismo uopće riješili jednadžbu, moramo poznavati silu, tj. izraz za silu: ( ) F v t = d t r ( t) = v( t)dt (.,.) m Rješavanjem ovih izraza dobit ćemo samo opća rješenja sve moguće krivulje r ( t) i v( t). Na nama je onda da izborom početnih uvjeta odaberemo i naše rješenje. Vidimo da lakoća rješavanja problema zapravo ovisi o samom izrazu za silu F. Primjer stalne sile. Ako je sila stalna i ubrzanje je stalno. Pogledajmo primjer gravitacijske sile (slobodan pad, vertikalni ili kosi hitac, sve ovisno o početnim uvjetima). F = mg uvrstimo u prvi integral (.): F v( t) = dt = g dt m (.3) v( t) = gt + C r ( t) = ( gt + C)dt = + + r ( t) gt Ct C Uzmimo početne uvjete za vertikalni hitac prema dolje (dolje je minus, gore plus smjer): v( t = 0) = v, r( t = 0) = h. 0 (.4) 7
28 i uvrstimo ih u (.3) i (.4): v(0) g 0 C C v v( t) = ( gt + v ) = + = 0 0 = + + = = = 0 r(0) g 0 C 0 C h C h r( t) h gt v t (.5) Numeričko rješavanje uvijek je primjenjivo i danas su ga jako olakšala računala. Ako je sila F poznata, numeričko rješenje je moguće. Svodi se na odreñivanje položaja čestice u trenutku t + t, ako ga poznajemo u trenutku t. r( t + t) = r( t) + v( t) t (.6) Da bismo odredili brzinu u svakom trenutku moramo znati akceleraciju: dakle položaj u t + tće biti: v( t + t) = v( t) + a( t) t (.7) r( t + t) = r( t + t) + v( t + t) t = r( t + t) + v( t) + a( t) t itd. Uzastopnom primjenom prvog izraza se može odrediti numerički položaj čestice u bilo kojem trenutku, što je zapravo njezina putanja. Problem se svodi na poznavanje akceleracije, a najveća pogreška dolazi otud što koristimo brzinu iz prethodnog trenutka. (Grešku možemo smanjiti ako umjesto s t računamo s manjim vremenskim intervalom, npr. t.). Slobodni pad. Atwoodov ureñaj. Pokusi. Slobodni pad je vrsta gibanja blizu površine Zemlje tijelo postavimo na neku visinu i bez početne brzine pustimo da vertikalno padne na Zemlju. Samo tijela velike gustoće padaju slobodnim padom, jer se jedino onda trenje sa zrakom može u potpunosti zanemariti. Rješavamo jednadžbu gibanja: F v( t) = dt = g dt m v( t) = gt + C y( t) = ( gt + C)dt = + + y( t) gt Ct C 8
29 Početni uvjeti za slobodni pad: v( t = 0) = 0, y( t = 0) = h, daju jednadžbu gibanja za slobodni pad: v(0) g 0 C C 0 v( t) = gt = + = = + + = = = (.) y(0) g 0 C 0 C h C h y( t) h gt Pokusi. Sva tijela padaju jednakim ubrzanjem jer ono ne ovisi o masi. Napravili smo pokuse sa Newtonovom cijevi, sa Galilejevom kosinom i dvije kuglice različite mase smo puštali da padaju na stol. Sa Atwoodovim strojem smo pokazali da brzina ovisi linearno sa vremenom, a put ne. s v t Graf 0.: Ovisnost prijeñenog puta o vremenu pri jednolikom ubrzanom gibanju. t Graf 0.: Ovisnost brzine o vremenu pri jednolikom ubrzanom gibanju. Atwoodov ureñaj. Problem rada ovog stroja temelji se na I. i II. Newtonovom zakonu. Dvije nejednake mase, m > m, obješene su pomoću konopca preko koloture. Za koloturu i konopac pretpostavljamo da su bez trenja i da im je masa zanemarivo mala. Zbog nerastezljivosti konopca i zanemarive mase koloture, napetosti su nužno jednake s obje strane koloture. Iznos ubrzanja će biti jednak za obje mase. Popišimo sve sile koje djeluju na prvu i drugu masu: m a = T m g =. m a m g T Zbrojimo li gornje jednadžbe dobit ćemo ( m + m ) a = ( m m ) g, tj. ubrzanje bilo koje od masa je: m m a = g. m + m T + m m m g T mg Slika 0.: Atwoodov ureñaj. 9
30 3. Neovisnost gibanja. Vodoravni hitac. Pokusi i film. Gibanja u x i y smjeru bit će neovisna onda kada na tijelo djeluje jedna ili više sila s komponentama u oba smjera koje nisu meñusobno povezane. Dakle neovisnost gibanja odnosi se na činjenicu da konkretno vodoravni hitac možemo rastaviti na slobodni pad i jednoliko gibanje u vodoravnom smjeru. Ta dva gibanja možemo potpuno zasebno promatrati i računati. Ako sila nema komponenata u nekom smjeru onda ona u tom smjeru ne može ni djelovati. Neovisnost gibanja posljedica je toga što sila teža djeluje samo u y smjeru, pa će padanje biti jednako i za slobodni pad i za vodoravni hitac. Zanimljiva posljedica neovisnosti gibanja: ispustimo li istovremeno neki predmet sa visine y, a istovremeno bacimo drugi predmet prema prvom s neke udaljenosti x i s iste visine y, oni će se uvijek susresti (uz pretpostavku da prije toga ne udare u tlo). Jednadžba gibanja za vodoravni hitac dobije se integrirajući odvojeno silu u x smjeru (nula) i silu u y smjeru (silu težu). Dobit ćemo izraze za x( t ) i y( t ): d d d d ˆ ma = m x + yˆ mgy x 0 i g = = = dt dt dt dt g y( t) = h t (3.) x( t) = v0xt (3.) To je parametarski oblik jednadžbe gibanja. Ako izrazimo vrijeme iz (3.) i uvrstimo u (3.) dobit ćemo jednadžbu putanje 4 tijela: g y( x) = h x v Pokusi. Istovremeno bacamo jednu kuglicu vodoravno, a drugu puštamo padati sa iste visine obje kuglice zajedno udaraju u pod. Domet bačene kuglice proporcionalan je brzini v 0 i korijenu visine h. 0 4 Jednadžba putanje je samo drugačiji zapis jednadžbi gibanja u kojem ne postoji eksplicitna ovisnost o t. Parametarski oblik jednadžbi gibanja koristan je kad želimo znati položaj tijela u nekom trenutku t, a jednadžba putanje je korisna kad želimo nacrtati putanju kojom se tijelo giba. 30
31 4. Kosi hitac. Pokusi. Lovac i majmun. Tijelo izbacimo sa ili bez početne visine pod nekim kutom u odnosu na horizontalu. Ono se giba pod utjecajem jednolikog gravitacijskog polja. Zanemarujemo druge sile (kao što je trenje sa zrakom) i iz drugog Newtonovog zakona dobijemo jednadžbu gibanja: d x d y ma = m xˆ + yˆ mg 0 a g = + = dt dt (4.) Vidimo da opet treba posebno integrirati x i y smjer sile (nezavisnost gibanja). Smjerovi komponenata su okomiti pa jednadžbu razdvajamo na dvije jednadžbe za komponente. Integriramo izraze: uz početne uvjete za kosi hitac: d x d y = 0 i = g (4., 4.3) dt dt v = v cos α, v = v sin α gt, x = 0, y = 0, x jednadžbe gibanja za x i y smjer su: 0 y x( t) = v t cosα (4.4) 0 g y( t) = v0t sin α t. (4.5) Iz jednadžbi gibanja (4.4) i (4.5) možemo dobiti i jednadžbu putanje kojom se tijelo giba, eliminirajući vrijeme: Uočimo da je (3.6) jednadžba parabole. g y( x) tgα x x v cosα = (4.6) 0 3
32 Lovac i majmun. Skica problema: h α Lovac nišani majmuna na visini h. Postavlja se pitanje hoće li tane pogoditi majmuna ako u trenutku kada lovac opali, majmun ispusti granu (tane se giba kao kosi hitac). Hoće, jer kada tane nakon nekog vremena t stigne na udaljenost d (vodoravna udaljenost izmeñu lovca i majmuna), majmun i tane će zbog sile teže pasti za jednak iznos ( gt ). Tane ima sljedeće jednadžbe gibanja: a majmun sljedeće: d g yt ( t) = v0t sin α t, xt ( t) = v0t cos α, g, ( ). ym = h t xm t = d Tane i majmun će se susresti u trenutku τ, kad je yt ( τ) = ym ( τ) i xt ( τ) = xm ( τ): x T ( τ ) = vτ 0 cos α d = vτ 0 cosα τ = d xm ( τ) = d v0 cosα Uvrštavajući τ u yt ( t) ili ym ( t ) dobit ćemo visinu na kojoj će tane pogoditi majmuna: g d d g d ym ( τ) = h T ( ) 0 sin. y τ v α v0 cosα = = v0 cosα v0 cosα Uočimo da će lovac pogoditi majmuna samo ako je gañao pod kutom α takvim da vrijedi h = d tan α, gdje je h visina s koje je majmun počeo padati, a d vodoravna udaljenost izmeñu majmuna i lovca. 3
33 5. Utjecaj otpora zraka na padanje tijela. Pokusi. Granična brzina. i 6. Put i brzina pri slobodnom padu s trenjem razmjernim brzini. Ako se tijelo giba kroz fluid na njega djeluje sila trenja koja ovisi o njegovoj veličini, obliku, brzini, itd. te naravno o karakteristikama samog fluida (gustoća, viskoznost, itd.). Općenito izrazi za silu trenja imaju dva člana, linearnog i kvadratičnog u v. Pri malim brzinama prevladava prvi član, a pri velikim drugi. F cv kv tr (5.) F tr kv cv Graf 5.. Dva doprinosa iznosu sile trenja u fluidu o brzini. Prvi član (linearni) povezan je sa viskoznošću fluida, dok je drugi posljedica stvaranja vrtloga. Ako promatramo vrlo sitna tijela vidimo da se u slučaju vrlo malog polumjera doprinos kvadratičnog člana sili trenja može zanemariti. Zato čestice prašine i magla padaju s trenjem Ftr cv, a krupna tijela poput kamena, kapi kiše i padobranca s trenjem Ftr kv. Promotrimo utjecaj otpora zraka ako je trenje linearno proporcionalno brzini. dv c ma = mg cv a = g v dt = m (5.) cv mg S vremenom će, zbog djelovanja sile trenja prema gore, doći do jednolikog gibanja i čestica više neće ubrzavati dok pada. Drugi izraz dakle moramo izjednačiti sa nulom. Čestica ostatak puta pada jednolikom brzinom koju nazivamo v g (graničnom brzinom): dv c = 0 g = vg (5.3) dt m Uvrstimo g nazad u jednadžbu gibanja: dv c c c c = g v = vg v = ( vg v). (5.4) dt m m m m v 33
34 Ovu diferencijalnu jednadžbu rješavamo integrirajući lijevu stranu po dv, a desnu po dt. dv c = dt (5.5) ( v v) m Uzimajući supstituciju g y = vg v dobije se sljedeće rješenje gornjeg integrala: c ln( vg v) = t + K. (5.6) m Početni uvjet je v( t = 0) = 0 pa je ln vg = K. Lako dobijemo da je konačni izraz za brzinu čestice: v = v g e = v e c g t t m vg g. (5.7) v za F tr = 0 v g za Ftr v Graf 5.. Brzina slobodnog pada u slučaju kada nema trenja te kada je trenje proporcionalno s brzinom Ako pogledamo graf 5. vidjet ćemo da u slučaju kada zanemarimo trenje, brzina čestice jednoliko raste s vremenom. To je jednoliko ubrzano gibanje odnosno slobodni pad u ovom slučaju. U slučaju trenja proporcionalnog sa brzinom, brzina čestice ne može rasti više od granične brzine v g. Pogledajmo sada kako bi izgledao s-t graf: s za F tr = 0 za Ftr v t t Graf 5.3. Funkcija s( t ) u slučaju bez trenja (parabola) i slučaju s trenjem gdje prvo ide približno kao parabola, a zatim postaje linearna. 34
35 Izraz za put dobijemo integriranjem izraza za brzinu: / s( t) v ( t t ( e t t )) k = (5.8) g a akceleraciju lako dobijemo deriviranjem istog izraza. Ubrzanje slobodnog pada u slučaju trenja nije konstantno: k gdje je t k vg m =. v c a t tk. a = ge (5.9) za F tr = 0 g za Ftr v t Graf 5.4. Funkcija ubrzanja a( t ) u usporedbi sa konstantnom akceleracijom g kada nema trenja Izrazi za brzinu, akceleraciju i put u slučaju trenja proporcionalnog sa kvadratom brzine dobiju se iz izraza: ma = mg kv (5.0) jednakim postupkom, odnosno integracijom jednadžbe gibanja. Dobit ćemo nešto kompliciranije izraze (integrale rješavamo pomoću Bronštejna): v t s = g k gt vg ( ) e + ln, gt vg e gt vg e v = vg gt vg, e + k a = g v m. s za F tr = 0 za Ftr v v za F tr = 0 v g a za F tr = 0 za Ftr v za Ftr v t t t 35
36 Zakon očuvanja energije 7. Zakoni očuvanja. Porijeklo, svojstva, primjene. Stanje sustava zadano je njegovim položajem i brzinom. Zakoni očuvanja pomažu nam naći to stanje kada je zakon sile nepoznat. Postoji mnogo zakona očuvanja i svi su posljedica neke odreñene simetrije sustava u kojem vrijede 5. Oni su nam posebno korisni za kvantne čestice (u atomu nam je putanja potpuno beskoristan pojam). Pomažu nam donijeti zaključke o stanju sustava bez da moramo rješavati jednadžbu gibanja. Dakle svi zakoni očuvanja imaju neka dobra svojstva: ne ovise o pojedinostima putanje, njima lako prikazujemo posve općenite (i vrlo značajne) posljedice jednadžbi gibanja, mogu nam unaprijed reći je li nešto moguće ili nemoguće, upotrebljavamo ih kada su sile potpuno nepoznate (npr. u fizici elementarnih čestica), u bliskoj su vezi s transformacijama, odnosno mogu nas uputiti na ideje o invarijantnosti. 6 Neki važniji zakoni očuvanja: ) Zakon očuvanja energije ukupna energija izoliranog sustava je konstantna. Ovo je posljedica homogenosti vremena (sekunda danas traje jednako dugo kao i sekunda prije sto godina). ) Zakon očuvanja količine gibanja (impulsa) ukupna količina gibanja izoliranog sustava takoñer je konstantna. Slijedi iz homogenosti prostora (svojstva objekta se ne smiju mijenjati translacijom tog objekta u prostoru). 3) Zakon očuvanja kutne količine gibanja ukupna kutna količina gibanja izoliranog sustava je očuvana. Ovo je posljedica izotropnosti prostora (svojstva objekta se ne mijenjaju rotacijom u prostoru). Postoje još i zakoni očuvanja ukupne količine naboja, mase, broja bariona, leptona, stranosti, itd. Neki vrijede egzaktno, a neki su aproksimativni 7. 5 Matematički iskaz te tvrdnje zove se Noetherin teorem. 6 Primjer: očuvanje impulsa se može tumačiti i kao neposredna posljedica invarijantnosti s obzirom na Galilejeve transformacije. Takoñer primjer za Noetherin teorem. 7 To ovisi o tome je li simetrija sustava savršena ili samo približna. 36
Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika
 1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
Gravitacija. Gravitacija. Newtonov zakon gravitacije. Odredivanje gravitacijske konstante. Keplerovi zakoni. Gravitacijsko polje. Troma i teška masa
 Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
šupanijsko natjecanje iz zike 2017/2018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova)
 šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
šupanijsko natjecanje iz zike 017/018 Srednje ²kole 1. grupa Rje²enja i smjernice za bodovanje 1. zadatak (11 bodova) U prvom vremenskom intervalu t 1 = 7 s automobil se giba jednoliko ubrzano ubrzanjem
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Algebra Vektora. pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske
 Algebra Vektora 1 Algebra vektora 1.1 Definicija vektora pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske veličine za opis skalarne veličine trebamo zadati samo njezin iznos (npr.
Algebra Vektora 1 Algebra vektora 1.1 Definicija vektora pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske veličine za opis skalarne veličine trebamo zadati samo njezin iznos (npr.
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Dinamika tijela. a g A mg 1 3cos L 1 3cos 1
 Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Repetitorij-Dinamika. F i Zakon očuvanja impulsa (ZOI): i p i = j p j. Zakon očuvanja energije (ZOE):
 Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Gauss, Stokes, Maxwell. Vektorski identiteti ( ),
 Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Fizika 1. Auditorne vježbe 5. Dunja Polić. Dinamika: Newtonovi zakoni. Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva
 Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Školska godina 2006/2007 Fizika 1 Auditorne vježbe 5 Dinamika: Newtonovi zakoni 12. prosinca 2008. Dunja Polić (dunja.polic@fesb.hr)
Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstva Školska godina 2006/2007 Fizika 1 Auditorne vježbe 5 Dinamika: Newtonovi zakoni 12. prosinca 2008. Dunja Polić (dunja.polic@fesb.hr)
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Neka je a 3 x 3 + a 2 x 2 + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka.
 Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Rad, energija i snaga
 Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Rotacija krutog tijela
 Rotacija krutog tijela 6. Rotacija krutog tijela Djelovanje sile na tijelo promjena oblika tijela (deformacija) promjena stanja gibanja tijela Kruto tijelo pod djelovanjem vanjskih sila ne mijenja svoj
Rotacija krutog tijela 6. Rotacija krutog tijela Djelovanje sile na tijelo promjena oblika tijela (deformacija) promjena stanja gibanja tijela Kruto tijelo pod djelovanjem vanjskih sila ne mijenja svoj
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
2. Ako je funkcija f(x) parna onda se Fourierov red funkcije f(x) reducira na Fourierov kosinusni red. f(x) cos
 . KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
. KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Kružno gibanje. Pojmovi. Radijus vektor (r), duljina luka (s) Kut (φ), kutna brzina (ω), obodna brzina (v)
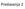 Predavanja 2 Kružno gibanje Pojmovi Kod kružnog gibanja položaj čestice jednoznačno je određen kutom kojeg radijus vektor zatvara s referentnim pravcem Radijus vektor (r), duljina luka (s) Kut (φ), kutna
Predavanja 2 Kružno gibanje Pojmovi Kod kružnog gibanja položaj čestice jednoznačno je određen kutom kojeg radijus vektor zatvara s referentnim pravcem Radijus vektor (r), duljina luka (s) Kut (φ), kutna
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Nastavna jedinica. Gibanje tijela je... tijela u... Položaj točke u prostoru opisujemo pomoću... prostor, brzina, koordinatni sustav,
 1. UVOD 1. * Odgovorite na sljedeća pitanja tako da dopunite tvrdnje. 1.1 Što je gibanje tijela? Gibanje tijela je... tijela u... 1.2 Osnovni parametri u kinematici su... i... 1.3 Na koji način opisujemo
1. UVOD 1. * Odgovorite na sljedeća pitanja tako da dopunite tvrdnje. 1.1 Što je gibanje tijela? Gibanje tijela je... tijela u... 1.2 Osnovni parametri u kinematici su... i... 1.3 Na koji način opisujemo
Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika
 3. Dinamika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji opisuje
3. Dinamika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji opisuje
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
( ) ( ) Zadatak 001 (Ines, hotelijerska škola) Ako je tg x = 4, izračunaj
 Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Izradio: Željan Kutleša, mag.educ.phys. Srednja tehnička prometna škola Split
 DINAMIKA Izradio: Željan Kutleša, mag.educ.phys. Srednja tehnička prometna škola Split Ova knjižica prvenstveno je namijenjena učenicima Srednje tehničke prometne škole Split. U knjižici su korišteni zadaci
DINAMIKA Izradio: Željan Kutleša, mag.educ.phys. Srednja tehnička prometna škola Split Ova knjižica prvenstveno je namijenjena učenicima Srednje tehničke prometne škole Split. U knjižici su korišteni zadaci
Sume kvadrata. mn = (ax + by) 2 + (ay bx) 2.
 Sume kvadrata Koji se prirodni brojevi mogu prikazati kao zbroj kvadrata dva cijela broja? Propozicija 1. Ako su brojevi m i n sume dva kvadrata, onda je i njihov produkt m n takoder suma dva kvadrata.
Sume kvadrata Koji se prirodni brojevi mogu prikazati kao zbroj kvadrata dva cijela broja? Propozicija 1. Ako su brojevi m i n sume dva kvadrata, onda je i njihov produkt m n takoder suma dva kvadrata.
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
( x) ( ) ( ) ( x) ( ) ( x) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
 Zadatak 08 (Vedrana, maturantica) Je li unkcija () = cos (sin ) sin (cos ) parna ili neparna? Rješenje 08 Funkciju = () deiniranu u simetričnom području a a nazivamo: parnom, ako je ( ) = () neparnom,
Zadatak 08 (Vedrana, maturantica) Je li unkcija () = cos (sin ) sin (cos ) parna ili neparna? Rješenje 08 Funkciju = () deiniranu u simetričnom području a a nazivamo: parnom, ako je ( ) = () neparnom,
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Determinante. a11 a. a 21 a 22. Definicija 1. (Determinanta prvog reda) Determinanta matrice A = [a] je broj a.
![Determinante. a11 a. a 21 a 22. Definicija 1. (Determinanta prvog reda) Determinanta matrice A = [a] je broj a. Determinante. a11 a. a 21 a 22. Definicija 1. (Determinanta prvog reda) Determinanta matrice A = [a] je broj a.](/thumbs/72/66829778.jpg) Determinante Determinanta A deta je funkcija definirana na skupu svih kvadratnih matrica, a poprima vrijednosti iz skupa skalara Osim oznake deta za determinantu kvadratne matrice a 11 a 12 a 1n a 21 a
Determinante Determinanta A deta je funkcija definirana na skupu svih kvadratnih matrica, a poprima vrijednosti iz skupa skalara Osim oznake deta za determinantu kvadratne matrice a 11 a 12 a 1n a 21 a
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Newtonov opdi zakon gravitacije
 Predavanje 3 Newtonov opdi zakon gravitacije F=Gm 1 m 2 /R 2 r Jedinični vektor G=6.67 10-11 Nm 2 kg -2 gravitacijska konstanta (Sir Henry Cavendish 1798) G nije isto što i g Gravitacijska sila djeluje
Predavanje 3 Newtonov opdi zakon gravitacije F=Gm 1 m 2 /R 2 r Jedinični vektor G=6.67 10-11 Nm 2 kg -2 gravitacijska konstanta (Sir Henry Cavendish 1798) G nije isto što i g Gravitacijska sila djeluje
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
Silu trenja osećaju sva tela koja se nalaze u blizini Zemlje i zbog nje tela koja se puste padaju nadole. Ako pustimo telo da slobodno pada, ono će
 Silu trenja osećaju sva tela koja se nalaze u blizini Zemlje i zbog nje tela koja se puste padaju nadole. Ako pustimo telo da slobodno pada, ono će se bez obzira na masu kretati istim ubrzanjem Zanimljivo
Silu trenja osećaju sva tela koja se nalaze u blizini Zemlje i zbog nje tela koja se puste padaju nadole. Ako pustimo telo da slobodno pada, ono će se bez obzira na masu kretati istim ubrzanjem Zanimljivo
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton,
 Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu
 Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Impuls i količina gibanja
 FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba 4 Impuls i količina gibanja Ime i prezime prosinac 2008. MEHANIKA
FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba 4 Impuls i količina gibanja Ime i prezime prosinac 2008. MEHANIKA
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
MATEMATIKA Pokažite da za konjugiranje (a + bi = a bi) vrijedi. a) z=z b) z 1 z 2 = z 1 z 2 c) z 1 ± z 2 = z 1 ± z 2 d) z z= z 2
 (kompleksna analiza, vježbe ). Izračunajte a) (+i) ( i)= b) (i+) = c) i + i 4 = d) i+i + i 3 + i 4 = e) (a+bi)(a bi)= f) (+i)(i )= Skicirajte rješenja u kompleksnoj ravnini.. Pokažite da za konjugiranje
(kompleksna analiza, vježbe ). Izračunajte a) (+i) ( i)= b) (i+) = c) i + i 4 = d) i+i + i 3 + i 4 = e) (a+bi)(a bi)= f) (+i)(i )= Skicirajte rješenja u kompleksnoj ravnini.. Pokažite da za konjugiranje
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
- osnovni zakoni gibanja (Newtonovi aksiomi) - gibanja duž ravne podloge i kosine - sila trenja - vrste sila
 Dinamika - osnovni zakoni gibanja (Newtonovi aksiomi) - gibanja duž ravne podloge i kosine - sila trenja - vrste sila Osnovni zakoni gibanja: Newtonovi aksiomi Sir Isaac Newton (1642. 1727.) by Sir Godfrey
Dinamika - osnovni zakoni gibanja (Newtonovi aksiomi) - gibanja duž ravne podloge i kosine - sila trenja - vrste sila Osnovni zakoni gibanja: Newtonovi aksiomi Sir Isaac Newton (1642. 1727.) by Sir Godfrey
M086 LA 1 M106 GRP Tema: Uvod. Operacije s vektorima.
 M086 LA 1 M106 GRP Tema:.. 5. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 2 M086 LA 1, M106 GRP.. 2/17 P 1 www.fizika.unios.hr/grpua/
M086 LA 1 M106 GRP Tema:.. 5. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 2 M086 LA 1, M106 GRP.. 2/17 P 1 www.fizika.unios.hr/grpua/
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Prikaz sustava u prostoru stanja
 Prikaz sustava u prostoru stanja Prikaz sustava u prostoru stanja je jedan od načina prikaza matematičkog modela sustava (uz diferencijalnu jednadžbu, prijenosnu funkciju itd). Promatramo linearne sustave
Prikaz sustava u prostoru stanja Prikaz sustava u prostoru stanja je jedan od načina prikaza matematičkog modela sustava (uz diferencijalnu jednadžbu, prijenosnu funkciju itd). Promatramo linearne sustave
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Vektorska analiza doc. dr. Edin Berberović.
 Vektorska analiza doc. dr. Edin Berberović eberberovic@mf.unze.ba Vektorska analiza Vektorska algebra (ponavljanje) Vektorske funkcije (funkcije sa vektorima) Jednostavna analiza (diferenciranje) Učenje
Vektorska analiza doc. dr. Edin Berberović eberberovic@mf.unze.ba Vektorska analiza Vektorska algebra (ponavljanje) Vektorske funkcije (funkcije sa vektorima) Jednostavna analiza (diferenciranje) Učenje
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
Primjeri zadataka iz Osnova fizike
 Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
Mjerne jedinice 1. Koja je od navedenih jedinica osnovna u SI-sustavu? a) džul b) om c) vat d) amper 2. Koja je od navedenih jedinica osnovna u SI-sustavu? a) kut b) brzina c) koncentracija d) količina
Linearna algebra I, zimski semestar 2007/2008
 Linearna algebra I, zimski semestar 2007/2008 Predavanja: Nenad Bakić, Vježbe: Luka Grubišić i Maja Starčević 22. listopada 2007. 1 Prostor radijvektora i sustavi linearni jednadžbi Neka je E 3 trodimenzionalni
Linearna algebra I, zimski semestar 2007/2008 Predavanja: Nenad Bakić, Vježbe: Luka Grubišić i Maja Starčević 22. listopada 2007. 1 Prostor radijvektora i sustavi linearni jednadžbi Neka je E 3 trodimenzionalni
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
ASIMPTOTE FUNKCIJA. Dakle: Asimptota je prava kojoj se funkcija približava u beskonačno dalekoj tački. Postoje tri vrste asimptota:
 ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
9. GRANIČNA VRIJEDNOST I NEPREKIDNOST FUNKCIJE GRANIČNA VRIJEDNOST ILI LIMES FUNKCIJE
 Geodetski akultet, dr sc J Beban-Brkić Predavanja iz Matematike 9 GRANIČNA VRIJEDNOST I NEPREKIDNOST FUNKCIJE GRANIČNA VRIJEDNOST ILI LIMES FUNKCIJE Granična vrijednost unkcije kad + = = Primjer:, D( )
Geodetski akultet, dr sc J Beban-Brkić Predavanja iz Matematike 9 GRANIČNA VRIJEDNOST I NEPREKIDNOST FUNKCIJE GRANIČNA VRIJEDNOST ILI LIMES FUNKCIJE Granična vrijednost unkcije kad + = = Primjer:, D( )
Analitička geometrija i linearna algebra
 1. VEKTORI POJAM VEKTORA Svakodnevno se susrećemo s veličinama za čije je određivanje potrean samo jedan roj. Na primjer udaljenost, površina, volumen,. Njih zovemo skalarnim veličinama. Međutim, postoje
1. VEKTORI POJAM VEKTORA Svakodnevno se susrećemo s veličinama za čije je određivanje potrean samo jedan roj. Na primjer udaljenost, površina, volumen,. Njih zovemo skalarnim veličinama. Međutim, postoje
