Osnovni fiziološki procesi u biljkama
|
|
|
- Ἁλκυόνη Ράγκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Modul: Osnove agroekologije Tematska cjelina: Ekofiziologija bilja prof. dr. sc. Irena Jug Osnovni fiziološki procesi u biljkama FOTOSINTEZA Fotosinteza je u živom svijetu jedinstveni fizikalno kemijski mehanizam energetskog inputa kojim biljke, alge i fotosintetske bakterije koriste svjetlosnu energiju za sintezu organske tvari. To je temeljni fiziološki proces koji omogućuje cjelokupan život na Zemlji. S kemijskog aspekta fotosinteza predstavlja niz reakcija oksidacije i redukcije u kojima se pomoću svjetlosne energije iz niskomolekularnih organskih spojeva, vode i ugljik(iv) oksida, u zelenim biljkama sintetizira složena organska tvar, najprije ugljikohidrati iz kojih transformacijama i resintezama nastaju svi ostali organski spojevi. Samo neznatan dio fotosintetske produkcije na Zemlji koristi se kao hrana, dio se koristi kao gorivo ili sirovina za industriju i dr. Velik je značaj ovog procesa za kruženje ugljika i drugih elemenata u prirodi. Kako je koncentracija CO 2 u atmosferi vrlo mala (0,03 % volumno ili 0,04 % težinski) svake godine 10 % cjelokupnog CO 2 atmosfere reducira se do ugljikohidrata fotosintetskim organizmima. Fotosinteza je vrlo kompleksan set fizikalno kemijskih reakcija podržan vrlo složenom organskom strukturom unutar kloroplasta i zbog toga je energetski relativno nisko efikasan proces. Npr., za sintezu molekule šećera potrebno je 30 ak različitih proteina i vrlo kompliciran sustav biomembrana. 6 CO + 12 H O CH O+ 6 O + 6 H O hν kj mol Teorijski koeficijent iskorištenja usvojene svjetlosne energije iznosi oko 22,4 %, a u praksi prosječno iskorištenje iznosi tek 0,5 2,0 % (za cijelu godinu) pa tu leže velike mogućnosti poboljšanja primarne produkcije što je temeljni zadatak ratarstva. Kloroplasti su stanične organele, ovalnog ili elipsoidnog oblika, dužine 4 6 μm, širine 1 2 μm. Broj kloroplasta u stanici lisnog parenhima je različit, ovisno o vrstibiljkeitkiva,starostiitd., a kreće se od nekoliko (spužvasti parenhim, mezofil) do 200 (palisadni parenhim)
2 Za fotosintezu viših biljaka značajni su klorofili i karotenoidi, pigmenti smješteni u kloroplaste. Klorofila ima pet: a, b, c, d i e, ali kod viših biljaka u fotosintezi sudjeluju samo klorofili a i klorofili b koji su kemijski esteri dikarbonske kiseline klorofilina gdje je vodik u jednoj karboksilnoj grupi esterificiran metanolom, a u drugoj fitolom Apsorpcija energije odvija se porfirinskom jezgrom koja je građena iz četiri pirolova prstena, povezana metinskim mostovima i s atomom Mg u središtu, vezanim s dvije kovalentne i dvije koordinatne veze na N atome pirolovih prstena. Učinkovit dio spektra za fotosintezu je u području plave i crvene svjetlosti koju apsorbiraju klorofili. Spektar apsorpcije klorofila ima dva maksimuma i to jedan u plavom, a drugi u crvenom dijelu. Valne duljine zelene i žute svjetlosti uglavnom se reflektiraju što rezultira bojom klorofila koja je plavo zelena (klorofil a) ili žutozelena (klorofil b). Klorofil a maksimalno apsorbira svjetlost valnih duljina 430 i 662 nm, a klorofil b, čija koncentracija može iznositi do 1/3 koncentracije klorofila a, maksimalno apsorbira svjetlost valnih duljina 453 i 642 nm U sastav fotosustava ulaze i karotenoidi koji se dijele na karotene i ksantofile. Po kemijskoj strukturi to su ugljikovodici, sastavljeni od 8 molekula izoprena, kondenziranih u dugački niz s više dvostrukih veza (alkeni) i s jononskim prstenovima na oba kraja. Poznato je više od 80 karotenoida, a zajednička im je osnovna građafitoen(40catoma). Boja im je narančasta do žuta, a najpoznatiji od karotena su, ß karoten i γ karoten, likopen itd. ß karoten je provitamin vitamina A. Ksantofili su oksidirani oblici karotena i sadrže kisik u okviru hidroksilne, keto, epoksi, metoksi i karboksi grupe. Poznati su lutein, violaksantin, neoksantin, zeaksantin. Karotenoidi mogu vezati višak kisika (kod intenzivne osvjetljenosti) pa tako štitite klorofile od fotooksidacije ULOGA KLOROPLASTNIH PIGMENATA apsorpcija svjetlosne energije i njeno usmjeravanje na akceptor elektrona čime započinje fotokemijska faza fotosinteze. klorofili karotenoidi Fotosustav ksantofili
3 klorofili se nalaze u tilakoidnim membranama u nakupinama od nekoliko stotina molekula od 200 molekula samo jedna molekula može predati ekscitirani elektron primarnom akceptoru e mjesto gdje se ta molekula nalazi naziva se reakcijsko središte ostale molekule klorofila antene za hvatanje svjetlosti MEHANIZAM I KEMIZAM FOTOSINTEZE Proces fotosinteze dijeli se na: 1. svijetlu fazu u tilakoidnom sustavu uz učešće pigmenata i sastoji se od fotofizičkih i fotokemijskih reakcija 2. tamnu fazu Fotofizičke reakcije: apsorpcija svjetlosne energije ekscitacija i deekscitacija klorofila prijenos energije do reakcijskog centra fotosustava Fotokemijske reakcije: transport elektrona fotoliza vode sinteza ATP i NADPH Oba fotosustava (FS I i FS II) funkcioniraju zajednički kako bi podigli elektrone s razine molekula donora elektrona niskog potencijala (voda), do razine akceptora visokog potencijala (NADP+). Razlika u potencijalu kreće se od do 0.4 ev. Niz komponenti koje sudjeluju u transportu elektrona uklopili su Hill i Bendall u tzv. "Z" shemu Tamna faza fotosinteze (Calvin Bensonov ciklus) Energija akumulirana u svjetloj fazi u spojevima ATP i NADPH nije stabilna i transformira se u energiju ugljikohidrata u tamnom dijelu fotosinteze. Tamna faza fotosinteze obuhvaća redukciju CO 2 do ugljikohidrata uz pomoć ATP i NADPH Calvin Bensonov ciklus odvija se u stromi kloroplasta. Najvažniji enzim Calvin Bensonovog ciklusa je ribulozadifosfat karboksilaza/ oksigenaza (RUBISCO) Calvin Bensonov ciklus se sastoji iz tri faze : karboksilacija redukcija regeneracija prvi produkt šećer s 3 C atoma (3 PGA = fosfoglicerin aldehid), pa otuda naziv C 3 tip fotosinteze 6 CO + 12 NADPH + 12 HO + 18 ATP CH O + 18 ADP + 18 P i
4 FOTORESPIRACIJA kod C 3 tipa biljaka, paralelno s fotosintezom odvija se i proces fotorespiracije (primanje i trošenje kisika i oslobađanje CO 2 na svjetlosti u fotosintetski aktivnim stanicama) koja je često intenzivnija u odnosu na disanje u mraku za razliku od pravog disanja koje se odvija u mitohondrijima, fotorespiracija se odvija u peroksizomima (mikrotjela), a prema nekim mišljenjima i u kloroplastima. Fotorespiracija je usko povezana s fotosintezom jer se odvija u uvjetima intenzivne osvjetljenosti i visoke koncentracije kisika u odnosu na CO 2 Kod C 3 biljaka temperatura značajno utječe na fotorespiraciju jer pri visokim temperaturama dolazi do smanjenja relativne vlažnostizrakaipovećanja gradijenta vlažnosti između biljkei zraka, što rezultira povećanim gubitkom vode. Činitelji koji podstiču fotorespiraciju su: visoka konc. O 2 niska konc. CO 2 visoka temperatura. Enzim RUBISCO koji katalizira vezanje CO 2 na ribulozu 1,5 bifosfat (RBP) u tamnoj fazi fotosinteze, u procesu fotorespiracije djeluje kao oksigenaza, pa uz prisustvo kisika razlaže RBP na 3 PGK i fosfoglikolnu kiselinu iz koje djelovanjem fosfataze nastaje glikolna kiselina Glikolna kiselina je supstrat fotorespiracije. Ona difundira iz kloroplasta u peroksizome koji su u kontaktu s kloroplastima. Oksidaza glikolne kiseline transformira je u glioksalnu kiselinu uz izdvajanje H 2 O 2 koji neutralizira katalaza razlažući navodui kisik. Glioksalna kiselina se manjim djelom oksidira do CO 2 i mravlje kiseline,avećim djelom se prevodi u glicin transaminacijom. Glicin se prenosi u mitohondrije, gdje se dvije molekule kondenziraju u serin, uz izdvajanje molekule CO 2 inh 4+. OvareakcijakojaseodvijaumitohondrijimaglavnijeizvorCO 2 u fotorespiraciji. Serin se nizom reakcija prevodi u 3 PGK, uz učešće ATP i dezaminaciju. Nastala 3 PGK u kloroplastima se uključuje u sintezu saharoze i škroba
5 Kod nekih biljnih vrsta primarni produkt fotosinteze nije fosfoglicerat (3C atoma), već malat i aspartat (4C atoma). Specifično zaovebiljkejetakođer da imaju tzv. kranz anatomiju (njem. kranz vijenac), tj. dvije vrste fotosintetskih stanica Stanice mezofila ne razlikuju se od stanica kod C 3 tipa biljaka, dok stanice parenhimske sare (omotača provodnih snopova), osim uobičajenih granularnih kloroplasta, imaju i agranularne. U mezofilnim stanicama CO 2 se veže na fosfo enolpirogrožđanu kiselinu (PEP), odnosno na fosfoenolpiruvat, pri čemu nastaje oksaloctena kiselina od koje hidrogenacijom nastaje malat ili vezivanjem amonijaka malatom aspartat, dakle C4 spoj. Pokazatelji fotosinteze prosječna godišnja efikasnost fotosinteze je 0,5 % za kukuruz, pšenicu i dr. usjeve, jer na intenzitet fotosinteze utječe vrlo velik broj biotskih i abiotskih čimbenika kao što su koncentracija klorofila, veličina, trajnost i zdravstveno stanje asmilacijske površine, prostorna orjentacija lišća, aktivnost enzima fotosinteze i disanja, svojstva provodnog tkiva, intenzitet osvjetljenosti, temperatura, raspoloživost vode i biogenih elemenata i dr. Pokazatelji fotosinteze su : 1) Intenzitet (brzina) fotosinteze je količina usvojenog CO 2 po jedinici površine lista u jedinici vremena, 2) Fotosintetska efikasnost je odnos između akumulirane i apsorbirane energije, 3) Produktivnost fotosinteze je količinastvoreneorgansketvaripo jedinici lisne površine u određenom vremenu, 4) Biološki prinos je ukupna masa organske tvari po jedinici površine tla dok je poljoprivredni prinos masa organske tvari određenih biljnih organa zbog koje se biljka uzgaja. Produktivnost fotosinteze ovisi o djelotvornosti sustava "source" "sink", odnosno uzajamnih odnosa između fotosintetskih tkiva i organa te mjesta potrošnje, odnosno pohranjivanja asimilata, 5) Koeficijent efikasnosti fotosinteze je odnos čiste produktivnosti fotosinteze i usvojenog CO 2, 6) Koeficijent poljoprivredne efikasnosti fotosinteze je odnos mase suhe organske tvari u poljoprivrednom dijelu prinosa i ukupne organske tvari (biološki prinos) (PP/BP), 7) Koeficijent energetske efikasnosti je odnos količine usvojenog CO 2 po jedinici površine usjeva i količine primljene svjetlosne energije, 8) Kompenzacijska točka je kad je intenzitet fotosinteze jednak intenzitetu disanja, tj. količina usvojenog CO 2 jednaka je količini izdvojenog O 2 9) Neto fotosinteza je intenzitet fotosinteze umanjen za intenzitet disanja. DISANJE Disanje je suprotan proces fotosintezi koji predstavlja energetski output, također kontroliran enzimatskim sustavima. Tijekom disanja elektroni se premještaju niz energetski gradijent, od organskih komponenti prema H +,kojiskisikomtvoristabilnu anorgansku molekulu vode. C 6 H 12 O 6 + 6O 2 6CO 2 +6H 2 O kj mol 1 U disanju se cjepaju lanci ugljikohidrata, masti, organskih kiseline, rezervnih proteina, ili čak i konstitucijskih proteina, kad nedostaje visokoenergetskih molekula.
6 1. Stanično disanje Stanično disanje je niz oksidoredukcijskih reakcija koje prati oslobađanje energije. Pored aerobnog disanja i sve vrste fermentacija (alkoholno, mlječno, maslačno vrenje itd.) kao i oksidacije neorganskih tvari, smatraju se disanjem. Žive stanice neprestano imaju potrebu za energijom, te je temeljni biološki smisao disanja održavanje života Stadiji staničnogdisanjasu: Glikoliza (cjepanje glukoze u dvije 3C molekule) Krebsov ciklus (3C molekule razlažu se do CO 2 ) ili ciklus limunske kiseline Elektron transportni sustav i sinteza ATP Formiranje vode Prenositelji vodika: NADH, NADPH i FADH 2 1. Glikoliza anaerobna razgradnja glukoze do pirogrožđne kiseline uz oslobađanje energije. Za glikolizu nije potreban kisik, što je pogodno za biljna tkiva izložena deficitu kisika, a prethodi potpunoj oksidaciji u Krebsovom ciklusu Glikoliza (glyco = sladak, lysis = podjela) je anaerobni dio staničnog disanja koji se odvija u citosolu (tekući dio protoplazme) svih živih stanica, a njeni enzimi su uglavnom vodotopljivi i ne vežu se na biološke membrane. 2. Krebsov ciklus Pirogrožđana kiselina, kao krajni produkt glikolize u aerobnim uvjetima, difundira u mitohondrije i oksidira se potpuno do CO 2 ivodeukrebsovom ciklusu ili ciklusu trikarbonskih kiselina (TCA) ili ciklusu limunske kiselne. Pri tome se oslobođena energija organske tvari akumulira u ATP. 1) Acetil CoA kondenzira s oksalacetatom pri čemu nastaje citrat (limunska kiselina) (2C atoma acetilne grupe s 4C oksaloctene kiseline grade 6C limunsku kiselinu), 2) Limunska kiselina se izomerizira do izolimunske kiseline, 3) Izolimunska kiselina gubi CO 2 te se 5C ketoglutarne kiseline oksidira uz NAD + koji se reducira do NADH, 4) Multienzimski kompleks (α ketoglutarat dehidrogenaza) katalizira odvajanje CO 2 uz oksidaciju preostale C 4 sukcinilne (jantarne) kiseline (uz sukcinil CoA) i redukciju NAD + do NADH,
7 5) Supstrat fosforilacija (u nizu reakcija) prvo dovodi do odvajanja sukcinil CoA od sukcinilne kiseline, fosfatna grupa veže se na GDP (gvanozin difosfat) i nastaje GTP (gvanozin trifosfat) koji prenosi fosfatnu grupu na ADP gradećiatp, 6) Sukcinilna kiselina se oksidira do fumarne kiseline uz redukciju FAD 7) Fumarna kiselina veže vodu uz rearanžiranje kemijskih veza, tako da nastaje maleinska (jabučna) kiselina, Sumarno, Krebsov ciklus je niz reakcija koje dovode do potpune oksidacije supstrata, od acetil CoA (piruvat se transformira u acetat, acetat u acetil CoA, a acetil CoA ulazi u Krebsov ciklus) koji ulazi u ciklus i veže se s 4C oksalacetatom gradeći 6C citrat, zatim se postupno obavlja dekarboksilacija i unizureakcijaizdvajaseco 2 uz sintezu 1 ATP, 3 NADH i 1 FADH 2 te preostaje oksalacetat koji reagira s novim acetil CoA. 8) Jabučna kiselina se oksidira uz redukciju NAD do NADH i konačno nastaje, zapravo se regenerira oksaloctena kiselina. 3. Elektron transportni sustav, transport protona, sinteza ATP i formiranje vode Citokromi u kristama mitohondrija cijepaju vodikov atom: te elektroni otpuštaju višak slobodne energije u više koraka uz pomoć četiri kompleksna proteina integrirana u membrane mitohondrija Istovremeno se prenose elektroni i protoni koji grade vodu u posljednjoj (terminalnoj) fazi prijenosa, pri čemu se koristi njihov protok iz matriksa u unutarnji membranski prostor uz sintezu ATP. Cijanid otporno disanje Aerobno disanje može biti inhibirano prisustvom aniona koji reagiraju s heminskim željezom citokromoksidaze itakoblokiraju transport do kisika kao terminalnog (krajnjeg) akceptora elektrona. Naročito su efikasni CN (cijanid) i N 3 (azid) neke biljne vrste i tkiva nastavljaju disanje unatoč blokadi citokromoksidaze, jer posjeduju alternativni transport elektrona, koji počinje s ubikinonom (poznati kaokoenzim Q10 ufarmaciji). Takvo disanje se naziva cijanid otporno ili cijanid rezistentno i čini prosječno % kod biljaka od ukupnog disanja. CN otporno disanje pokazuju pšenica, kukuruz, krumpir, grašak i druge biljke, mlado korijenje, plod rajčice, a primjećuje se često u oplodnji kad oslobođena toplina pospješuje izlučivanje aromatskih tvari (amina) u cvatnji privlačećiinsekte. Prisutnost cijanidnih glikozida u sjemenkama ima korektivnu ulogu pri klijanju, kao i obrambenu ulogu od strane predatora. Značaj kisika za disanje i fotosintezu samo potpunom oksidacijom glukoze stanica oslobađa dovoljno energije, ali se (uglavnom kod biljaka) održavanje minimalnih životnih funkcija može postići i anaerobnom oksidacijom Metabolizam masti usko je povezan s prisustvom kisika jer se nakon hidrolize razgrađuju do acetil CoA ( oksidacija masti) za što je potreban kisik. Metabolizam proteina zahtjeva kisik jer nakon hidrolize do aminokiselina one moraju biti oksidativno dezaminirane (uklonjen N).
8 Disanjem se proizvodi CO 2 i H 2 O, tvari neophodne za fotosintezu u kojoj se sintetizira glukoza i izdvaja O 2 potreban za disanje. Intenzitet disanja predstavlja količinu vezanog kisika i oslobođenog CO 2 u jedinici vremena po jedinici mase biljnog tkiva. Ovisno o supstratu za disanje (ugljikohidrati, proteini, masti, organske kiseline) biljne tvari će u procesima oksidativne razgradnje trebatiirazličite količinekisika
CIKLUS LIMUNSKE KISELINE (CLK)
 SVEUČILIŠTE U ZAGREBU FAKULTET KEMIJSKOG INŽENJERSTVA I TEHNOLOGIJE CIKLUS LIMUNSKE KISELINE (CLK) Doc. dr. sc. Dragana Vuk Metabolička sudbina piruvata 1. Oksidacijska dekarboksilacija piruvata 2. Ciklus
SVEUČILIŠTE U ZAGREBU FAKULTET KEMIJSKOG INŽENJERSTVA I TEHNOLOGIJE CIKLUS LIMUNSKE KISELINE (CLK) Doc. dr. sc. Dragana Vuk Metabolička sudbina piruvata 1. Oksidacijska dekarboksilacija piruvata 2. Ciklus
Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija
 Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija MITOHONDRIJI -u svim eukariotskim stanicama -njihov broj ovisi o metaboličkoj aktivnosti stanice (nekoliko stotina
Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija MITOHONDRIJI -u svim eukariotskim stanicama -njihov broj ovisi o metaboličkoj aktivnosti stanice (nekoliko stotina
Kloroplasti. Fotosinteza Mitohondriji Stanično disanje
 Kloroplasti Fotosinteza Mitohondriji Stanično disanje http://en.wikipedia.org/wiki/plas tid PLASTIDI Organeli biljnih stanica i stanica algi Proizvodnja i pohranjivanje šećera i drugih molekula Pigmenti
Kloroplasti Fotosinteza Mitohondriji Stanično disanje http://en.wikipedia.org/wiki/plas tid PLASTIDI Organeli biljnih stanica i stanica algi Proizvodnja i pohranjivanje šećera i drugih molekula Pigmenti
VISOKO GOSPODARSKO UČILIŠTE U KRIŽEVCIMA
 VISOKO GOSPODARSKO UČILIŠTE U KRIŽEVCIMA Dr.sc. Marija Vukobratović Križevci, 2009. 1 UVOD U METABOLIZAM Svi živi organizmi za svoje aktivnosti (održavanje života, rast i razvoj) zahtijevaju energiju,
VISOKO GOSPODARSKO UČILIŠTE U KRIŽEVCIMA Dr.sc. Marija Vukobratović Križevci, 2009. 1 UVOD U METABOLIZAM Svi živi organizmi za svoje aktivnosti (održavanje života, rast i razvoj) zahtijevaju energiju,
Fotosinteza. Fotosinteza. Biljke. Autotrofi. Izv. prof. dr. sc. Lidija Šver. fotoautotrofi
 Fotosinteza Izv. prof. dr. sc. Lidija Šver Fotosinteza Pretvara sunčevu energiju u kemijsku Autotrofi koriste anorganske tvari i energiju da bi proizveli organske molekule; proizvođači kemoautotrofi (neke
Fotosinteza Izv. prof. dr. sc. Lidija Šver Fotosinteza Pretvara sunčevu energiju u kemijsku Autotrofi koriste anorganske tvari i energiju da bi proizveli organske molekule; proizvođači kemoautotrofi (neke
Fotosinteza. Fotosinteza. Biljke. Autotrofi. Izv. prof. dr. sc. Lidija Šver. fotoautotrofi
 Fotosinteza Izv. prof. dr. sc. Lidija Šver Fotosinteza Pretvara sunčevu energiju u kemijsku Autotrofi koriste anorganske tvari i energiju da bi proizveli organske molekule; proizvođači kemoautotrofi (neke
Fotosinteza Izv. prof. dr. sc. Lidija Šver Fotosinteza Pretvara sunčevu energiju u kemijsku Autotrofi koriste anorganske tvari i energiju da bi proizveli organske molekule; proizvođači kemoautotrofi (neke
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Put pentoza fosfata. B. Mildner. Put pentoza fosfata
 Put pentoza fosfata B. Mildner Put pentoza fosfata Svrha ovog puta je: A) da se stanici omogući dovoljno NADPH, koji služi kao reducens u biosintetskim reakcijama kao i u zaštiti stanica od kisikovih radikala.
Put pentoza fosfata B. Mildner Put pentoza fosfata Svrha ovog puta je: A) da se stanici omogući dovoljno NADPH, koji služi kao reducens u biosintetskim reakcijama kao i u zaštiti stanica od kisikovih radikala.
Ciklus limunske kiseline-2
 Ciklus limunske kiseline-2 Boris Mildner Katabolizam proteina, masti i ugljikohidrata u tri faze staničnog disanja. Faza 1.: oksidacija masnih kiselina, masti i ugljikohidrata kako bi nastao acetil-coa.
Ciklus limunske kiseline-2 Boris Mildner Katabolizam proteina, masti i ugljikohidrata u tri faze staničnog disanja. Faza 1.: oksidacija masnih kiselina, masti i ugljikohidrata kako bi nastao acetil-coa.
Uvod u metabolizam - procesi izgradnje i razgradnje u živoj stanici
 Metabolizam Uvod u metabolizam - procesi izgradnje i razgradnje u živoj stanici Izv. prof. dr. sc. Lidija Šver jelokupnost svih kemijskih pretvorbi u stanici ili organizmu Pretvorba (transformacija) tvari
Metabolizam Uvod u metabolizam - procesi izgradnje i razgradnje u živoj stanici Izv. prof. dr. sc. Lidija Šver jelokupnost svih kemijskih pretvorbi u stanici ili organizmu Pretvorba (transformacija) tvari
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Ciklus limunske kiseline-1 KOMPLEKS PIRUVAT DEHIDROGENAZE
 Ciklus limunske kiseline-1 KOMPLEKS PIRUVAT DEHIDROGENAZE Boris Mildner Citratni ciklus /Krebsov ciklus Piruvat koji nastaje glikolizom, umjesto da se reducira u laktat, odnosno u etanol, dalje se oksidira
Ciklus limunske kiseline-1 KOMPLEKS PIRUVAT DEHIDROGENAZE Boris Mildner Citratni ciklus /Krebsov ciklus Piruvat koji nastaje glikolizom, umjesto da se reducira u laktat, odnosno u etanol, dalje se oksidira
Fotosinteza. 1. Sinteza NADPH+H + in ATP 2. Fiksacija CO 2
 Fotosinteza 1. Sinteza NADPH+H + in ATP 2. Fiksacija CO 2 Oris 1 Fotoreaktivnost klorofila 2 Z-shema fotosinteze 3 Svetlobno-gnana ATP-sinteza - Fotofosforilacija 4 Fiksacija ogljikovega dioksida 5 Calvin-Bensonov
Fotosinteza 1. Sinteza NADPH+H + in ATP 2. Fiksacija CO 2 Oris 1 Fotoreaktivnost klorofila 2 Z-shema fotosinteze 3 Svetlobno-gnana ATP-sinteza - Fotofosforilacija 4 Fiksacija ogljikovega dioksida 5 Calvin-Bensonov
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama. Hloroplast
 Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama Hloroplast Procesom ćelijskog disanja deponovana energija u šećerima erima prevodi se u ATP i druge energetske metabolite. Istovremeno se
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama Hloroplast Procesom ćelijskog disanja deponovana energija u šećerima erima prevodi se u ATP i druge energetske metabolite. Istovremeno se
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
Glukoneogeneza i regulacija glukoneogeneze
 Glukoneogeneza i regulacija glukoneogeneze Boris Mildner Glukoneogeneza Sinteza ugljikohidrata iz jednostavnih preteča Put od fosfoenolpiruvata do glukoza 6-fosfata zajednički je za mnoge preteče ugljikohidrata.
Glukoneogeneza i regulacija glukoneogeneze Boris Mildner Glukoneogeneza Sinteza ugljikohidrata iz jednostavnih preteča Put od fosfoenolpiruvata do glukoza 6-fosfata zajednički je za mnoge preteče ugljikohidrata.
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Aminokiseline. Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina 22.12.2014
 Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
DIHANJE. Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo. Agronomija - VSŠ 2005/06
 DIHANJE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Fotosinteza + Dihanje + Svetlobno dihanje Dihanje Substrat: škrob saharoza fruktani drugi sladkorji lipidi organske kisline proteini
DIHANJE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Fotosinteza + Dihanje + Svetlobno dihanje Dihanje Substrat: škrob saharoza fruktani drugi sladkorji lipidi organske kisline proteini
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Vodik. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZVOR EMISIJE
 Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Disanje (Respiracija)
 Disanje (Respiracija) Osim fotosinteze, deo primarnog metabolizma biljaka je i proces ćelijskog disanja (respiracija). Dok se u fotosintezi procesima redukcije iz CO2 i vode sintetišu organska jedinjenja,
Disanje (Respiracija) Osim fotosinteze, deo primarnog metabolizma biljaka je i proces ćelijskog disanja (respiracija). Dok se u fotosintezi procesima redukcije iz CO2 i vode sintetišu organska jedinjenja,
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Svi živi organizmi imaju potrebu za konstantnim prilivom energije kako bi održali ćelijsku strukturu i rast. 4/17/2013
 Metabolizam Svi živi organizmi imaju potrebu za konstantnim prilivom energije kako bi održali ćelijsku strukturu i rast. Kemotrofni organizmi; dobivaju slobodnu energiju gj oksidacijom hranjivih tvari
Metabolizam Svi živi organizmi imaju potrebu za konstantnim prilivom energije kako bi održali ćelijsku strukturu i rast. Kemotrofni organizmi; dobivaju slobodnu energiju gj oksidacijom hranjivih tvari
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
METABOLIZEM OGLJIKOVIH HIDRATOV
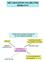 METABOLIZEM OGLJIKOVIH HIDRATOV KAKO CELICA DOBI GLUKOZO IN OSTALE MONOSAHARIDE? HRANA ZNOTRAJCELIČNI GLIKOGEN ali ŠKROB razgradnja s prebavnimi encimi GLUKOZA in ostali monosaharidi fosforilitična cepitev
METABOLIZEM OGLJIKOVIH HIDRATOV KAKO CELICA DOBI GLUKOZO IN OSTALE MONOSAHARIDE? HRANA ZNOTRAJCELIČNI GLIKOGEN ali ŠKROB razgradnja s prebavnimi encimi GLUKOZA in ostali monosaharidi fosforilitična cepitev
lat: nucleus = jezgra
 JEZGRA lat: nucleus = jezgra glavna karakteristika koja označava razliku između eukariotskih i prokariotskih stanica je prisutnost jezgre kod eukariota. U njemu se nalazi DNK, u kojoj su uskladištene informacije
JEZGRA lat: nucleus = jezgra glavna karakteristika koja označava razliku između eukariotskih i prokariotskih stanica je prisutnost jezgre kod eukariota. U njemu se nalazi DNK, u kojoj su uskladištene informacije
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
DIHANJE. Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo. Agronomija - UNI
 DIHANJE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - UNI Fotosinteza + Dihanje + Svetlobno dihanje Dihanje Fotosinteza 6CO 2 + 6H 2 O C 6 H 12 O 6 + 6O 2 Fotosintetski
DIHANJE Univerza v Ljubljani Biotehniška fakulteta Oddelek za agronomijo Agronomija - UNI Fotosinteza + Dihanje + Svetlobno dihanje Dihanje Fotosinteza 6CO 2 + 6H 2 O C 6 H 12 O 6 + 6O 2 Fotosintetski
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Glukoneogeneza. Glukoneogeneza. Glukoneogeneza. poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih.
 poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih. Izhodne spojine:, laktat, in drugi intermediati cikla TKK glukogene aminokisline, glicerol Kaj pa maščobne kisline? Ireverzibilne
poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih. Izhodne spojine:, laktat, in drugi intermediati cikla TKK glukogene aminokisline, glicerol Kaj pa maščobne kisline? Ireverzibilne
STVARANJE VEZE C-C POMO]U ORGANOBORANA
![STVARANJE VEZE C-C POMO]U ORGANOBORANA STVARANJE VEZE C-C POMO]U ORGANOBORANA](/thumbs/55/37829094.jpg) STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
CIKLUS AZOTA I SUMPORA U PRIRODI
 CIKLUS AZOTA I SUMPORA U PRIRODI Asimilacija azota i sumpora zahtevaju niz biohemijskih reakcija koje spadaju u reakcije sa velikim energetskim zahtevima. Za asimilaciju azota iz nitrata (NO 3- ) potrebna
CIKLUS AZOTA I SUMPORA U PRIRODI Asimilacija azota i sumpora zahtevaju niz biohemijskih reakcija koje spadaju u reakcije sa velikim energetskim zahtevima. Za asimilaciju azota iz nitrata (NO 3- ) potrebna
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Opća bilanca tvari - = akumulacija u dif. vremenu u dif. volumenu promatranog sustava. masa unijeta u dif. vremenu u dif. volumen promatranog sustava
 Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
UVOD CIKLUS CITRONSKE KISLINE (CCK) = KREBSOV CIKLUS = CIKLUS TRIKARBOKSILNIH KISLIN
 CIKLUS CITRONSKE KISLINE (CCK) = KREBSOV CIKLUS = CIKLUS TRIKARBOKSILNIH KISLIN Glavne metabolične poti oglj. hidratov pri rastlinah in živalih GLIKOGEN, ŠKROB Riboza 5-fosfat + NADPH+H + katabolizem fosfoglukonatna
CIKLUS CITRONSKE KISLINE (CCK) = KREBSOV CIKLUS = CIKLUS TRIKARBOKSILNIH KISLIN Glavne metabolične poti oglj. hidratov pri rastlinah in živalih GLIKOGEN, ŠKROB Riboza 5-fosfat + NADPH+H + katabolizem fosfoglukonatna
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
IMOBILIZACIJA AKTIVNIH TVARI ZA BIOLOŠKO PREPOZNAVANJE
 IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
Supstituisane k.k. Sinteza Aminokiseline Biodegradabilni polimeri Peptidi. Industrijska primena Aminokiseline Stočarstvo Hiralni katalizatori
 Supstituisane k.k. Značaj Sinteza Aminokiseline Biodegradabilni polimeri Peptidi Industrijska primena Aminokiseline Stočarstvo Hiralni katalizatori Hidroksikiseline Kozmetička industrija kreme Biološki
Supstituisane k.k. Značaj Sinteza Aminokiseline Biodegradabilni polimeri Peptidi Industrijska primena Aminokiseline Stočarstvo Hiralni katalizatori Hidroksikiseline Kozmetička industrija kreme Biološki
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
 100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Nastanek NADH in NADPH Prenos elektronov in nastanek ATP
 Nastanek NADH in NADPH Prenos elektronov in nastanek ATP Glavne metabolične poti glukoze Glikoliza (Embden Meyerhofova metabolna pot) Fosfoglukonatna (pentozafosfatna) pot: nekatere živali Katabolizem
Nastanek NADH in NADPH Prenos elektronov in nastanek ATP Glavne metabolične poti glukoze Glikoliza (Embden Meyerhofova metabolna pot) Fosfoglukonatna (pentozafosfatna) pot: nekatere živali Katabolizem
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
PRERADA GROŽðA. Sveučilište u Splitu Kemijsko-tehnološki fakultet. Zavod za prehrambenu tehnologiju i biotehnologiju. Referati za vježbe iz kolegija
 Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
METABOLIZAM UGLJENIH HIDRATA
 METABOLIZAM UGLJENIH HIDRATA 14.02.2018. Zbirni pregled glikolize i ciklusa trikarboksilnih kiselina Glikoliza omogućava oksidaciju glukoze u uslovima sa ili bez O 2. U uslovima prisustva O 2,
METABOLIZAM UGLJENIH HIDRATA 14.02.2018. Zbirni pregled glikolize i ciklusa trikarboksilnih kiselina Glikoliza omogućava oksidaciju glukoze u uslovima sa ili bez O 2. U uslovima prisustva O 2,
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
OKSIDACIJSKA FOSFORILACIJA
 OKSIDACIJSKA FOSFORILACIJA Sinteza ATP B. Mildner & M. Kekez 2012. 1. Što od navedenog nije dio Mittchelove kemiosmotske hipoteze? a) Dio energije koji se dobiva transportom elektrona koristi se za dobivanje
OKSIDACIJSKA FOSFORILACIJA Sinteza ATP B. Mildner & M. Kekez 2012. 1. Što od navedenog nije dio Mittchelove kemiosmotske hipoteze? a) Dio energije koji se dobiva transportom elektrona koristi se za dobivanje
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
