Tablica za odreappleivanje postotaka trajnog invaliditeta kao posljedice nesretnog sluëaja (nezgode)
|
|
|
- Κύρα Κυπραίος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Tablica za odreappleivanje postotaka trajnog invaliditeta kao OP E ODREDBE 1. Ova Tablica za odreappleivanje postotka trajnog invaliditeta kao posljedice nesretnog sluëaja (nezgode) (u nastavku teksta: Tablica invaliditeta) sastavni je dio OpÊih i Posebnih uvjeta i svakoga pojedinog ugovora o osiguranju osoba od posljedica nesretnog sluëaja koji ugovaratelj osiguranja sklopi s Generali osiguranjem d.d. za trajni invaliditet kao posljedicu nesretnog sluëaja. 2. KonaËni postotak trajnog invaliditeta odreappleuje se nakon zavrπenog lijeëenja i rehabilitacije na temelju cjelokupne medicinske dokumentacije, ukljuëujuêi i sve rendgenske snimke koje je osiguranik duæan podnijeti osiguratelju na uvid uz prijavu nesretnog sluëaja. KonaËni postotak invaliditeta na udovima, kraljeπnici ili organima odreappleuje se najranije 3 mjeseca nakon zavrπenog cjelokupnog lijeëenja i rehabilitacije, osim kod amputacija i toëaka Tablice invaliditeta gdje je u posebnim odredbama drukëije odreappleeno. Ako osiguranik ne provodi ili zanemaruje lijeëniëke upute o lijeëenju, terapiji i uzimanju lijekova, osiguratelj Êe konaëni postotak invaliditet iz Tablice invaliditeta umanjiti za 1/3. Kod pseudoartroza, natuëenja koπtano-miπiênih struktura i sindroma prenaprezanja ne odreappleuje se invaliditet. Kod degenerativnih promjena, natuëenja miπiënih i zglobnih struktura, istegnuêa koπtano-zglobno-miπiënih struktura ne odreappleuje se invaliditet. 3. Kod viπestrukih ozljeda pojedinog uda, kraljeπnice ili organa uslijed jednog nesretnog sluëaja, ukupan invaliditet na odreappleenom udu, kraljeπnici ili organu, ocjenjuje se tako da se za najveêu posljedicu oπteêenja uzima postotak predviappleen u ovoj Tablici invaliditeta, od sljedeêe najveêe posljedice uzima se 1/2 postotka odreappleenog u ovoj Tablici invaliditeta te redom 1/4, 1/8 itd. Ukupan postotak invaliditeta ne moæe biti veêi od postotka koji je odreappleen ovom Tablicom invaliditeta za potpuni gubitak tog uda ili organa. 4. U osiguranju osoba od posljedica nesretnog sluëaja kod ocjene invaliditeta primjenjuje se iskljuëivo postotak odreappleen ovom Tablicom invaliditeta. Osigurateljna obveza ne postoji za posljedice nesretnog sluëaja koje nisu odreappleene ovom Tablicom invaliditeta ili su njenim odredbama iskljuëene iz osiguranja. 5. Posljedice povreda jednog organa ne zbrajaju se i ne mogu biti ocijenjene po viπe toëaka Tablice invaliditeta, invaliditet se ocjenjuje po onoj toëki koja odreappleuje najveêi postotak za tu posljedicu. 6. U sluëaju gubitka ili oπteêenja viπe udova ili viπe organa zbog jednog nesretnog sluëaja, postoci invaliditeta za svaki pojedini ud ili organ se zbrajaju, ali ne mogu iznositi viπe od 100%. 7. Ako je kod osiguranika postojao trajni invaliditet prije nastanka nesretnog sluëaja, obveza osiguratelja odreappleuje se prema novom invaliditetu, neovisno o ranijem, osim u sljedeêim sluëajevima: a) ako je prijavljeni nesretni sluëaj prouzroëio poveêanje dotadaπnjeg invaliditeta, obveza osiguratelja utvrappleuje se prema razlici izmeappleu ukupnog postotka invaliditeta i ranijeg postotka; b) ako osiguranik prilikom nesretnog sluëaja izgubi ili ozljedi jedan od ranije ozlijeappleenih organa ili udova, obveza osiguratelja utvrappleuje se samo prema poveêanom invaliditetu; c) ako su radioloπkim pretragama dokazane degenerativne bolesti koπtanozglobnog sustava postojale i prije nastanka nesretnog sluëaja, osiguratelj Êe konaëni invaliditet iz Tablice invaliditeta umanjiti za 1/3 procijenjenog invaliditeta; d) ako se dokaæe da osiguranik boluje od πeêerne bolesti, bolesti srediπnjeg ili perifernog æivëanog sustava, gluhoêe, slabovidnosti, bolesti krvoæilja ili kroniëne pluêne bolesti te ako navedene bolesti utjeëu na poveêanje invaliditeta nakon nesretnog sluëaja, osiguratelj Êe konaëni invaliditet iz Tablice invaliditeta umanjiti za 1/2 procijenjenog invaliditeta; e) ako je ranija kroniëna bolest uzrok nastanka nesretnog sluëaja, osiguratelj Êe konaëni invaliditet iz Tablice invaliditeta umanjiti za 1/2 procijenjenog invaliditeta; 8. Osiguranikove subjektivne tegobe u smislu bolova, miπiêne slabosti, otoka na mjestu ozljede, trnaca, straha, koænih oæiljaka koji ne uzrokuju funkcijska oπteêenja te svih drugih smetnji psihiëke naravi koje su nastale nakon neke nezgode (posttraumatski stresni poremeêaj, strah, nesanice, promjene raspoloæenja itd.) ne uzimaju se u obzir pri odreappleivanju postotka trajnog invaliditeta. Individualne sposobnosti, socijalni poloæaj ili zanimanje (profesionalna sposobnost) ne uzimaju se u obzir pri odreappleivanju postotka invaliditeta. I. GLAVA 1. Æariπna ili difuzna oπteêenja mozga s posljediënom dekortikacijom, odnosno decerebracijom dokazana tijekom bolniëkog lijeëenja u odgovarajuêoj kirurπkoj, neuroloπkoj ili neuropsihijatrijskoj ustanovi: - trajno vegetativno stanje; - hemiplegija s afazijom i agnozijom; - obostrani Parkinsonov sindrom; - triplegija, tetraplegija; - teπka posttraumatska demencija s psihoorganskim sindromom; - psihoza nakon ozljede mozga...do 100 % 2. Æariπna ili difuzna oπteêenja mozga s trajnim neuroloπkim ispadima dokazanim tijekom bolniëkog lijeëenja u odgovarajuêoj neurokirurπkoj ili neuroloπkoj ustanovi: - hemiplegija; - hemipareza s izraæenim spasticitetom; - ekstrapiramidalna simptomatologija (nemoguênost koordinacije pokreta ili postojanje grubih nehotiënih pokreta); - pseudobulbarna paraliza s prisilnim plaëem ili smijehom; - oπteêenje malog mozga s izraæenim poremeêajem hoda ili koordinacije...do 90 % 3. Pseudobulbarni sindrom...do 80 % 4. Posttraumatska epilepsija dokazana objektivnim dijagnostiëkim metodama i. bolniëki lijeëena u neuroloπkoj ili psihijatrijskoj ustanovi: a) s uëestalim napadima usprkos urednoj medikaciji, uz promjene liënosti dokazane tijekom lijeëenja...do 60 % b) s povremenim napadima usprkos medikaciji...do 20 % 5. Æariπna ili difuzna oπteêenja mozga s posljediënim psihoorganskim sindromom dokazanim tijekom bolniëkog lijeëenja objektivnim dijagnostiëkim postupcima s nalazima psihijatra i psihologa: a) blaæi stupanj...do 30 % b) srednji stupanj...do 40 % c) izraæeni stupanj...do 60 % 6. Stanje nakon nagnjeëenja mozga dokazanog tijekom bolniëkog lijeëenja objektivnim dijagnostiëkim postupcima dijagnostiëke obrade (CT, EEG): a) bez neuroloπkih ispada...do 5 % b) s blaæim neuroloπkim ispadima...do 20 % c) s neuroloπkim ispadima u srednjem stupnju...do 35 % d) s neuroloπkim ispadima u jakom stupnju...do 50 % 7. OπteÊenje malog mozga s adiadohokinezom i asinergijom...40 % 8. Stanje poslije trepanacije svoda lubanje i/ili prijeloma baze lubanje radioloπki dokazano bez neuroloπkih ispada...do 5 % 9. Operirani intracerebralni hematom bez neuroloπkih ispada...do 5 % 1. Za karniocerebralne ozljede koje nisu bolniëki utvrappleene u prva 24 sata nakon ozljeappleivanja ne priznaje se invaliditet po toëkama Sve posljedice kraniocerebralnih ozljeda moraju biti potvrappleene odgovarajuêom dijagnostiëkom obradom tijekom bolniëkog lijeëenja. 3. Za posljedice potresa mozga ne odreappleuje se invaliditet. 4. Kod razliëitih posljedica kraniocerebralnih ozljeda zbog jednog nesretnog sluëaja postoci invaliditeta se ne zbrajaju, veê se postotak invaliditeta odreappleuje samo po toëki koja je najpovoljnija za osiguranika. 5. Trajni invaliditet po toëkama odreappleuje se najranije nakon isteka godine dana od ozljeappleivanja, a za posttraumatske epilepsije najranije nakon dvije godine od ozljeappleivanja uz promjene u EEG-u. 10. Gubitak vlasiπta: a) treêina povrπine vlasiπta...do 5 % b) polovina povrπine vlasiπta...do 15 % c) Ëitavo vlasiπte...do 30 % II. O»I 11. Potpuni gubitak vida na oba oka % 12. Potpuni gubitak vida na jedno oko...30 % 13. Oslabljenje vida jednog oka zbog ozljede: za svaku desetinu smanjenja vidne oπtrine...3 % 14. U sluëaju da je na drugom oku vidna oπtrina oslabljena za viπe od tri desetine, za svaku desetinu umanjenja vida ozlijeappleenog oka...6 % 15. Trajna dvoslika nastala zbog ozljede oka: a) vanjska oftalmoplegija...10 % b) potpuna oftalmoplegija...20 %
2 16. Gubitak oëne leêe: a) afakija jednostrana...20 % b) afakija obostrana...30 % 17. DjelomiËno oπteêenje mreænice i staklastog tijela: a) djelomiëni ispad vidnog polja zbog posttraumatskog odljuπtenja mreænice...3 % b) zamuêenje staklastog tijela zbog traumatskog krvarenja...3 % 18. Pseudofakija: a) jednostrana...5 % b) obostrana...10 % 19. Trajno proπirenje zjenice nakon direktnog udara u oko...3 % 20. Nepotpuna unutarnja oftalmoplegija...do 10 % 21. Ozljeda suznog aparata i oënih vjeapplea: a) epifora...3 % b) entropium, ektropium...3 % c) ptoza vjeapplee...3 % 22. KoncentriËno suæenje vidnog polja na preostalom oku: a) od 80 do 60 stupnjeva...do 10 % b) do 40 stupnjeva...do 30 % c) do 20 stupnjeva...do 50 % d) do 5 stupnjeva...do 60 % 23. Jednostrano koncentriëno suæenje vidnog polja: a) do 40 stupnjeva...do 5 % b) do 30 stupnjeva...do 15 % c) do 5 stupnjeva...do 30 % 24. Homonimna hemianopsija...do 30 % 1. Invaliditet se nakon traumatskog odljuπtenja mreænice odreappleuje po toëkama 12., 13., 14. ili 17. najranije mjesec dana od zavrπenog lijeëenja. 2. Ozljeda oëne jabuëice koja je uzrokovala odljuπtenje mreænice mora biti bolniëki utvrappleena. 3. Trajna oπteêenja oka ocjenjuju se nakon zavrπenog lijeëenja osim za ozljede iz toëaka 15. i 20. koje se mogu procjenjivati tek nakon isteka godine dana od ozljeappleivanja. 4. Invaliditet iz toëke 19. ocjenjuje se po Maπkeovim tablicama, a primjenom toëke 13. Tablice invaliditeta. 5. Invaliditet po toëkama ne odreappleuje se ako se radi o posljedici potresa mozga ili posljedici ozljede mekih struktura vrata (tzv. trzajna ozljeda vratne kraljeπnice). 6. Invaliditet po toëkama 22. i 23. odreappleuje se nakon roka iz toëke 3. ovih Posebnih odredbi, uz nove nalaze vidnog polja uëinjene metodom kompjuterizirane perimetrije. III. U I 25. Potpuna gluhoêa na oba uha s urednom kaloriëkom reakcijom vestibularnog organa...40 % 26. Potpuna gluhoêa na oba uha s ugaslom kaloriëkom reakcijom vestibularnog organa...60 % 27. Potpuna gluhoêa na jednom uhu s urednom kaloriëkom reakcijom vestibularnog organa...15 % 28. Potpuna gluhoêa na jednom uhu s ugaslom kaloriëkom reakcijom vestibularnog organa...20 % 29. Obostrana nagluhost s urednom kaloriëkom reakcijom vestibularnog organa obostrano; ukupni gubitak sluha (Fowler-Sabine): a) %...do 5 % b) %...do 10 % c) %...do 20 % 30. Obostrana nagluhost s ugaslom kaloriëkom reakcijom vestibularnog organa, ukupni gubitak sluha ( Fowler-Sabine): a) %...do 10 % b) %...do 20 % c) %...do 30 % 31. Jednostrana jaka nagluhost s urednom kaloriëkom reakcijom vestibularnog organa; gubitak sluha na razini od decibela...10 % 32. Jednostrana jaka nagluhost s ugaslom kaloriëkom reakcijom vestibularnog organa; gubitak sluha na razini decibela...do 12 % 33. Ozljeda uπne πkoljke: a) djelomiëan gubitak...do 5 % b) potpuni gubitak...10 % 1. Za sve posljedice ozljeda iz glave III. invaliditet se odreappleuje nakon zavrπenog lijeëenja, ali ne ranije od 6 mjeseci nakon ozljede, osim toëke 33. koja se odreappleuje odmah po zavrπenom lijeëenju. 2. Ako je u osiguranika postojalo prije ozljede oπteêenje sluha tipa akustiëke traume, invaliditet zbog gubitak sluha po Fowler-Sabine nastao nesretnim sluëajem umanjuje se za 1/2. 3. Invaliditet po toëkama ne odreappleuje se ako se radi o posljedici potresa mozga ili posljedici ozljede mekih struktura vrata (tzv. trzajna ozljeda vratne kraljeπnice). IV. LICE 34. Oæiljno-deformirajuÊa oπteêenja koæe lica s funkcijskim smetnjama i/ili postraumatski deformiteti kostiju lica: a) u lakom stupnju...do 2 % b) u srednjem slupnju...do 5 % c) u teπkom stupnju...do 15 % 35. OgraniËeno otvaranje usta (razmak gornjih i donjih zuba): a) od 5 cm do 3 cm...do 10 % b) do 1,5 cm...do 25 % 36. Traumatska oπteêenja Ëeljusnih kostiju, jezika ili nepca s funkcijskim smetnjama: a) u srednjem stupnju...do 10 % b) u teπkom stupnju...do 20% 37. Odstranjenje donje Ëeljusti...30% 38. Pareza liënog æivca uzrokovana prijelomom sljepooëne kosti ili ozljedom parotidne regije: a) u srednjem stupnju...do 5 b) u jakom stupnju s kontrakturom i tikom mimiëke muskulature...do 20 % c) paraliza liënog æivca...30 % 39. Gubitak stalnog zuba: a) svaki zub...1 % b) prijelom zuba, za svaki zub...0,5 % 1. Za kozmetiëke i estetske oæiljke na licu bez funkcijskih smetnji ne odreappleuje se invaliditet. 2. Invaliditet iz toëke 38. procjenjuje se nakon zavrπenog lijeëenja, ali najranije 24 mjeseca po ozljedi i uz obvezno EMNG praêenje. V. NOS 40. Ozljede nosa: a) djelomiëan gubitak nosa...do 10 % b) gubitak Ëitavog nosa...30 % 41. Anosmija uzrokovana dokazanim prijelomom gornjeg unutarnjeg dijela nosnih kostiju...do 5 % 42. Oteæano disanje nakon prijeloma nosnog septuma koji je utvrappleen kliniëki i radioloπki neposredno nakon ozljede...do 3 % 1. Kod razliëitih posljedica ozljede nosa zbog jednog nesretnog sluëaja, postoci invaliditeta se ne zbrajaju, veê se invaliditet odreappleuje po toëki najpovoljnijoj za osiguranika. 2. Invaliditet iz toëke 41. utvrappleuje se nakon zavrπenog lijeëenja, ali ne prije isteka jedne godine od ozljeappleivanja ili operacije. 3. Za toëke 40., 41., 42. osiguranik je obvezan osiguratelju na uvid dostaviti RTG snimku. VI. DU NIK I JEDNJAK 43. Ozljeda duπnika: a) stanje nakon traheotomije poslije ozljede...do 5 % b) stenoza duπnika poslije ozljede grkljana i poëetnog dijela duπnika...do 10 % 44. Stenoza duπnika zbog koje se mora trajno nositi kanila...60 %
3 45. Suæenje jednjaka radioloπki dokazano: a) u srednjem stupnju...do 5 % b) u teπkom stupnju...do 30 % 46. Potpuno suæenje jednjaka s trajnim gastrostomom...85 % VII. PRSNI KO 47. Ozljede rebara: a) radioloπki dokazan prijelom dva rebra ili prijelom prsne kosti zarastao s pomakom bez smanjenja pluêne ventilacije restritktivnog tipa...2 % b) prijelom tri ili viπe rebra zarastao s pomakom bez smanjenja pluêne ventilacije restritktivnog tipa...5 % 48. Stanje nakon torakotomije...5 % 49. OπteÊenje pluêne funkcije restriktivnog tipa zbog prijeloma rebara, otvorenih ozljeda prsnog koπa, posttraumatskih priraslica, hematotoraksa i pneumotoraksa : a) vitalni kapacitet umanjen za 20% -30%...do 10 % b) vitalni kapacitet umanjen za 31%- 50%...do 30 % c) vitalni kapacitet umanjen za 51% i viπe...do 50 % 50. Fistula nakon empijema...10 % 1. Kapacitet pluêa odreappleuje se ponovljenom spirometrijom, po potrebi i detaljnom pulmoloπkom obradom i ergometrijom. 2. Ako uz invaliditet iz toëaka 47., 48. i 50. postoji poremeêaj pluêne funkcije restriktivnog tipa, invaliditet se ne ocjenjuje navedenim toëkama, veê toëkom Invaliditet iz toëaka 49. i 50. ocjenjuje se nakon zavrπenog lijeëenja, ali ne ranije od jedne godine nakon ozljeappleivanja. 4. Invaliditet se ne odreappleuje za prijelom jednog rebra. 5. Ako je spirometrijom dokazan mijeπani poremeêaj pluêne funkcije (opstruktivni i restriktivni), invaliditet se umanjuje razmjerno ispadu funkcije zbog bolesti. 51. Gubitak jedne dojke: a) u æivotnoj dobi do 50 godina...10 % b) u æivotnoj dobi iznad 50 godina...5 % c) teπko oπteêenje dojke u æivotnoj dobi do 50 godina...5 % 52. Gubitak obje dojke: a) u æivotnoj dobi do 50 godina...30 % b) u æivotnoj dobi iznad 50 godina...15 % c) teπko oπteêenje obje dojke u æivotnoj dobi do 50 godina...10 % 53. Posljedice penetrantnih ozljeda srca i velikih krvnih æila prsnog koπa: a) srce s normalnim EKG-om i ultrazvukom...20 % b) srce s promijenjenim EKG-om i ultrazvukom, ovisno o teæini promjene...do 50 % c) aneurizma aorte s implantatom...40 % VIII. KOÆA 54. Dublji oæiljci na tijelu nakon opeklina ili ozljeda bez funkcijskih smetnji koji zahvaêaju: a) od 10 do 20 % povrπine tijela...do 5 % b) viπe od 20 % povrπine tijela...15 % 55. Duboki oæiljci na tijelu nakon opeklina ili ozljeda, a zahvaêaju: a) od 5% do 10 % povrπine tijela...do 5 % b) do 20 % povrπine tijela...do 15 % c) viπe od 20 % povrπine tijela...25 % 1. Za estetske oæiljke i naruæenje ne odreappleuje se invaliditet. 2. Za dublje oæiljke koji zahvaêaju do 10% povrπine tijela, a ne uzrokuju funkcijske smetnje, ne odreappleuje se invaliditet. 3. SluËajevi iz toëaka 54. i 55. izraëunavaju se primjenom pravila devetke. 4. Dublji oæiljak nastaje nakon intermedijalne opekline (II. b stupanj) i/ili ozljede s veêim defektom koæe. 5. Duboki oæiljak nastaje nakon duboke opekline (III. stupanj) ili potkoæne subdermalne opekline (IV. stupanj) i/ili velike ozljede koænog pokrivaëa. 6. Za posljedice epidermalne opekline (I. stupanj) i povrπne ozljede koæe (II.a stupanj) ne odreappleuje se invaliditet. 7. Funkcijske smetnje izazvane opeklinama ili ozljedama iz toëke 55. ocjenjuju se prema odgovarajuêim toëkama Tablice invaliditeta. IX. TRBU NI ORGANI 56. Traumatska hernija i kile prednje trbuπne stjenke nakon laparotomijskih rana nastalih uslijed ozljede...5 % 57. Ozljeda oπita: a) stanje nakon prsnuêa oπita bolniëki dokazanog neposredno nakon ozljede i kirurπki zbrinutog...20 % b) dijafragmalna hernija- recidiv nakon kirurπki zbrinute dijafragmalne traumatske hernije...25 % 58. Ozljede crijeva ili æeluca s resekcijom...10 % 59. Ozljeda jetre s resekcijom...do 15 % 60. Gubitak slezene (splenektomija): a) u æivotnoj dobi do 20 godina...20 % b) u æivotnoj dobi iznad 20 godina...10 % 61. Ozljeda guπteraëe s funkcijskim oπteêenjem...do 10 % 62. Anus praeternaturalis (trajni)...50 % 63. Incontinentio alvi (trajna): a) djelomiëna...do 20 % b) potpuna...60 % X. MOKRA NI ORGANI 64. Gubitak jednog bubrega uz normalnu funkciju drugog...30 % 65. Gubitak jednog bubrega uz oπteêenje funkcije drugog: a) u lakom stupnju do 30 % oπteêenja funkcije...do 40 % b) u srednjem stupnju do 50 % oπteêenja funkcije...do 55 % c) u jakom stupnju preko 50 % oπteêenja funkcije...do 80 % 66. Funkcijska oπteêenja jednog bubrega: a) u lakom stupnju do 30 % oπteêenja funkcije...do 10 % b) u srednjem stupnju do 50 % oπteêenja funkcije...do 15 % c) u jakom stupnju preko 50 % oπteêenja funkcije...do 20 % 67. Funkcijska oπteêenja oba bubrega: a) u lakom stupnju do 30 % oπteêenja funkcije...do 20 % b) u srednjem stupnju do 50 % oπteêenja funkcije...do 30 % c) u jakom stupnju preko 50 % oπteêenja funkcije...do 60 % 68. PoremeÊaj ispuπtanja mokraêe zbog ozljede uretre klasificirane prema Charriereu: a) ispod 18 CH...do 10 % b) ispod 14 CH...do 20 % c) ispod 6 CH...do 35 % 69. Ozljeda mokraênog mjehura sa smanjenim kapacitetom: - za svaku 1/3 smanjenog kapaciteta...10 % 70. Potpuna inkontinencija urina - trajno...40 % 71. Urinarna fistula: a) uretralna...20 % b) perinealna i vaginalna...30 % XI. GENITALNI ORGANI 72. Gubitak jednog testisa: a) u æivotnoj dobi do 60 godina...15 % b) u æivotnoj dobi iznad 60 godina...5 % 73. Gubitak oba testisa: b) u æivotnoj dobi iznad 60 godina...25 % 74. Gubitak penisa: b) u æivotnoj dobi iznad 60 godina...30 % 75. Deformacija penisa s onemoguêenom kohabitacijom: b) u æivotnoj dobi iznad 60 godina...25 % 76. Gubitak maternice i jajnika u æivotnoj dobi do 55 godina: a) gubitak maternice...30 % b) gubitak jednog jajnika...10 % c) gubitak oba jajnika...30 % 77. Gubitak maternice i jajnika u æivotnoj dobi iznad 55 godina: a) gubitak maternice...10 % b) gubitak svakog jajnika...5 % 78. OπteÊenja vulve i vagine koja onemoguêavaju kohabitaciju: b) u æivotnoj dobi iznad 60 godina...15 % c) potpuna oftalmoplegija...20 %
4 XII. KRALJE NICA 79. Ozljeda kraljeπnice s trajnim potpunim oπteêenjem kraljeπniëne moædine ili perifernih æivaca (paraplegija, triplegija, tetraplegija) s gubitkom kontrole defekacije i uriniranja % 80. Ozljeda kraljeπnice s potpunom paralizom donjih ekstremiteta bez smetnje defekacije i uriniranja...80 % 81. Ozljeda kraljeπnice s trajnim djelomiënim oπteêenjem kraljeπniëne moædine ili perifernih æivaca (tetrapareza, tripareza) bez gubitka kontrole defekacije i uriniranja, dokazana EMG-om...do 50 % 82. Ozljeda kraljeπnice s parezom donjih ekstremiteta, dokazana EMG-om...do 40 % OπteÊenja koja spadaju pod toëke 79. i 80. ocjenjuju se nakon utvrappleivanja trajnih neuroloπkih oπteêenja, a iz toëaka 81. i 82. ocjenjuju se po zavrπenom lijeëenju, ali ne ranije od 2 godine od dana ozljede. 83. Posljedice prijeloma najmanje dva kraljeπka uz promjenu fizioloπke zakrivljenost kraljeπnice (kifoza,skolioza): a) u srednjem stupnju...do 15 % b) u jakom stupnju...do 30 % 84. Umanjena pokretljivost kraljeπnice nakon prijeloma korpusa (trupa) vratnog kraljeπka...do 3 % 85. Umanjena pokretljivost kraljeπnice nakon prijeloma korpusa (trupa) slabinskog segmenta - u jakom stupnju...do 10 % 86. Serijski prijelom popreënih nastavaka tri ili viπe kraljeπka...do 3 % 1. Za ocjenu po toëkama 83., 84., 85. i 86. obvezno je osiguratelju dostaviti rendgenske snimke na uvid. 2. Invaliditet poslije ozljede kraljeπnice iz toëaka 84., 85. i 86. ocjenjuje se uz obvezno mjerenje pokretljivosti 6 mjeseci nakon zavrπenog lijeëenja i rehabilitacije. 3. Za retrofleksiju vratne kraljeπnice koja je iznad 6 cm ne odreappleuje se invaliditet. 4. Nisu obuhvaêene osiguranjem, te se ne ocjenjuje invaliditet, zbog degenerativnih promjena kraljeπnice koje ukljuëuju: herniju disci intervertebralis, sve vrste lumbalgija, diskopatija, spondiloza, spondiolisteza, spondioliza, sakralgija, miofascitisa, kokcigodinija, ishialgija, fibrozitisa i sve patoanatomske promjene slabinsko-kriæne regije oznaëene analognim terminima, kao i bolni sindromi vratne kraljeænice. 5. Ne ocjenjuje se invaliditet nakon istegnuêa zglobno-ligamentarnih struktura vratne kraljeπnice, odnosno nakon trzajnih ozljeda vratne kraljeπnice. XIII. ZDJELICA 87. Viπestruki prijelom zdjelice s teæom deformacijom ili denivelacijom sakroilijakalnih zglobova ili simfize...30 % 88. Simfizeoliza s horizontalnim i/ili vertikalnim pomakom: a) veliëine 1 cm...do 10 % b) veliëine 2 cm...do 15 % c) veliëine preko 2 cm...do 25 % 89. Prijelom jedne crijevne kosti zarastao s pomakom...do 5 % 90. Prijelom obje crijevne kosti zarastao s pomakom...do 10 % 91. Prijelom stidne ili sjedne kosti zarastao s pomakom...do 5 % 92. Prijelom dvije kosti: stidne, sjedne ili stidne i sjedne, zarastao s pomakom...do 10 % 93. Prijelom kriæne kosti zarastao s pomakom...do 5 % 1. Za prijelome kostiju zdjelice koji su zarasli bez pomaka i bez objektivnih funkcijskih smetnji ne odreappleuje se invaliditet. 2. Za prijelom trtiëne kosti ne odreappleuje se invaliditet. XIV. RUKE 94. Gubitak obje ruke ili obje πake % 95. Gubitak ruke u ramenu (eksartikulacija)...70 % 96. Gubitak ruke u podruëju nadlaktice...65 % 97. Gubitak ruke ispod lakta s oëuvanom funkcijom lakta...60 % 98. Gubitak jedne πake...55 % 99. Gubitak svih prstiju: a) na obje πake...90 % b) na jednoj πaci...45 % 100. Gubitak palca...20 % 101. Gubitak kaæiprsta...10 % 102. Gubitak: a) srednjeg prsta...5 % b) domalog ili malog prsta, za svaki prst...3 % 103. Gubitak metakarpalne kosti palca...4 % 104. Gubitak metakarpalne kosti kaæiprsta...3 % 105. Gubitak metakarpalne kosti srednjeg, domalog i malog prsta, za svaku kost...2 % 1. Za gubitak jednog Ëlanka palca odreappleuje se 1/2, a za gubitak jednog Ëlanka ostalih prstiju odreappleuje se 1/3 postotka odreappleenog za gubitak tog prsta. 2. DjelomiËan gubitak koπtanog dijela Ëlanka odreappleuje se kao potpuni gubitak Ëlanka tog prsta. 3. Za gubitak jagodice prsta odreappleuje se 1/2 postotka odreappleenog za gubitak Ëlanka tog prsta Potpuna ukoëenost ramenog zgloba: a) u funkcijski nepovoljnom poloæaju (abdukcija od stupnjeva)...35 % b) u funkcijski povoljnom poloæaju (abdukcija do 20 stupnjeva)...do 25 % 107. Radioloπki dokazani prijelomi u podruëju ramena zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju ramenog zgloba...do 3 % 1. Invaliditet iz toëaka 106. i 107. ocjenjuje se 6 mjeseci nakon zavrπenog 108. Labavost ramenog zgloba s koπtanim defektom zglobnih tijela...do 10 % 109. Endoproteza ramenog zgloba...30 % 110. KroniËni osteomijelitis kostiju ruke s fistulom...do 10 % 111. Paraliza akcesornog æivca...15 % 112. Paraliza brahijalnog pleksusa...60 % 113. DjelomiËna paraliza brahijalnog pleksusa (ERB - gornji dio ili KLUMPKE - donji dio)...35 % 114. Paraliza perifernih æivaca ruke: a) aksilarnog æivca...15 % b) radijalnog æivca...30 % c) medijalnog æivca % d) ulnarnog æivca...30 % 115. Paraliza dva æivca jedne ruke...50 % 116. Paraliza tri æivca jedne ruke...60 % 1. Za uganuêe akromioklavikularnog ili sternoklavikularnog zgloba te za pseudoartrozu (nadlaktiëne kosti) ne odreappleuje se invaliditet. 2. Za posljedice prijeloma kljuëne kosti ne odreappleuje se invaliditet. 3. Za parezu æivca odreappleuje se najviπe do 2/3 invaliditeta odreappleenog za paralizu toga æivca. 4. Invaliditet iz toëaka odreappleuje se nakon zavrπenog lijeëenja i rehabilitacije, ali ne prije isteka dvije godine od ozljeappleivanja, s obveznim nalazom EMG-om dokazanog oπteêenja, ne starijim od 3 mjeseca. 5. Za oπteêenje korjenova spinalnih æivaca vratne kraljeænice (tzv. radikularna oπteêenja) ne odreappleuje se invaliditet Potpuna ukoëenost lakatnog zgloba: a) u funkcijski nepovoljnom poloæaju...do 25 % b) u funkcijski povoljnom poloæaju od stupnjeva...do 15 % 118. Radioloπki dokazani prijelomi u podruëju lakta zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju lakatnog zgloba...do 3 % 119. Nestabilni lakatni zglob- sloboda pokreta u popreënom pravcu viπe od 20 stupnjeva...do 5 %
5 1. Invaliditet iz toëaka ocjenjuje se 6 mjeseci nakon zavrπenog 120. Endoproteza lakta...25 % 121. Potpuna ukoëenost podlaktice: a) u supinaciji...do 25 % b) u srednjem poloæaju...do 15 % c) u pronaciji...do 20 % 122. Potpuna ukoëenost ruënog zgloba: a) u poloæaju ekstenzije...do 15 % b) u osovini podlaktice...do 20 % c) u poloæaju fleksije...do 30 % 123. Radioloπki dokazani prijelomi u podruëju ruënog zgloba zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju ruënog zgloba...do 3 % 124. Endoproteza Ëunjaste kosti i/ili mjeseëaste kosti % 1. Za pseudoartrozu podlaktice, palëane ili lakatne kosti, te Ëunjaste ili mjeseëaste kosti, ne odreappleuje se invaliditet. 2. Invaliditet iz toëaka ocjenjuje se 6 mjeseci nakon zavrπenog 3. Za posljedice prijeloma metakarpalnih kostiju ne odreappleuje se invaliditet Potpuna ukoëenost svih prstiju jedne ruke...40 % 126. Potpuna ukoëenost pojedinih prstiju: a) Ëitavog palca...12 % b) Ëitavog kaæiprsta...8 % c) Ëitavog srednjeg prsta...4 % d) domalog ili malog prsta, za svaki prst...2 % 1. Za potpunu ukoëenost jednog zgloba palca odreappleuje se 1/2, a za potpunu ukoëenost jednog zgloba ostalih prstiju 1/3 postotka odreappleenog za potpunu ukoëenost tog prsta. 2. Zbroj postotaka za ukoëenost pojedinih zglobova jednog prsta ne moæe biti veêi od postotka odreappleenog za potpunu ukoëenost tog prsta. 3. Ukupan invaliditet za ozljede prstiju ne moæe iznositi viπe od invaliditeta za gubitak πake. 4. Za posljedice ozljede prstiju invaliditet se odreappleuje bez primjene naëela iz toëke 3. OpÊih odredbi Tablice invaliditeta. XV. NOGE 127. Gubitak obje natkoljenice % 128. Eksartikulacija noge u kuku % 129. Gubitak natkoljenice u gornjoj treêini, bataljak nepodesan za protezu...60 % 130. Gubitak natkoljenice ispod gornje treêine...50 % 131. Gubitak obje potkoljenice, bataljak podesan za protezu...80 % 132. Gubitak potkoljenice, bataljak manji od 6 cm...45 % 133. Gubitak potkoljenice, bataljak veêi od 6 cm...40 % 134. Gubitak oba stopala...80 % 135. Gubitak jednog stopala...35 % 136. Gubitak stopala u Chopartovoj liniji...35 % 137. Gubitak stopala u Lisfrancovoj liniji...30 % 138. Transmetatarzalna amputacija...25 % 139. Gubitak prve ili pete metatarzalne kosti...5 % 140. Gubitak druge, treêe ili Ëetvrte metatarzalne kosti, za svaku kost...3 % 141. Gubitak svih prstiju stopala na jednoj nozi...20 % 142. Gubitak palca stopala: a) distalnog Ëlanka palca...2,5 % b) Ëitavog palca...5 % 143. Gubitak Ëitavog II.-V. prsta na nozi, za svaki prst...2 % 144. DjelomiËni gubitak II.-V. prsta na nozi, za svaki prst...1 % UkoËenost interfalangealnih zglobova II.-V. prsta u ispruæenom poloæaju ili umanjena pokretljivost ovih zglobova ne predstavlja invaliditet Potpuna ukoëenost kuka: a) u funkcijski nepovoljnom poloæaju...40 % b) u funkcijski povoljnom poloæaju...30 % 146. Radioloπki dokazani prijelomi u podruëju kuka zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju kuka...do 5 % 147. Potpuna ukoëenost oba kuka...70 % 148. Nereponirano zastarjelo traumatsko uganuêe kuka...do 35 % 149. Umanjena pokretljivost kuka nakon radioloπki dokazanog prijeloma, i/ili posttraumatske artroze nakon prijeloma usporeappleeno sa zdravim, umanjenje viπe od 2/3 opsega pokreta...do 20 % 150. Nepravilno zarastao prijelom bedrene kosti uz angulaciju za: a) od stupnjeva...do 10 % b) viπe od 20 stupnjeva...do 15 % 151. KroniËni osteomijelitis kostiju nogu s fistulom...do 10 % 1. Za pseudoartrozu bedrene kosti i vrata bedrene kosti ne odreappleuje se invaliditet. 2. Invaliditet iz toëaka ocjenjuje se 6 mjeseci nakon zavrπenog 152. Endoproteza kuka: a) parcijalna...do 15 % b) totalna...do 30 % 153. SkraÊenje noge nakon prijeloma: a) 2-4 cm...do 10 % b) 4,1-6 cm...do 15 % c) viπe od 6 cm...do 20 % 154. Potpuna ukoëenost koljena: a) u funkcijski nepovoljnom poloæaju...do 30 % b) u funkcijski povoljnom poloæaju (do 10 stupnjeva fleksije)...do 25 % 155. Umanjena pokretljivost zgloba koljena nakon radioloπki dokazanog prijeloma, i/ili posttraumatske artroze nakon prijeloma usporeappleeno sa zdravim, umanjenje viπe od 2/3 opsega pokreta...do 20 % 156. Radioloπki dokazani prijelomi u podruëju koljena zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju koljena...do 3 % 157. Nestabilnost koljena nakon ozljede ligamentarnih struktura, usporeappleeno sa zdravim, potrebno stalno noπenje ortopedskog aparata...do 10 % 1. Invaliditet iz toëaka ocjenjuje se 6 mjeseci nakon zavrπenog 2. Invaliditet se ne odreappleuje za oπteêenje i/ili operativno odstranjenje meniska. 3. Invaliditet se ne odreappleuje za nestabilnost koljena koja je posljedica operativnog odstranjenja meniska Endoproteza koljena: a) parcijalna...do 15 % b) totalna...do 30 % 159. Slobodno zglobno tijelo nastalo nakon ozljede koljena, radioloπki dokazano...do 3 % 160. Funkcijske smetnje poslije odstranjenja ivera: a) djelomiëno odstranjen iver...do 5 % b) potpuno odstranjen iver...do 15 % 161. Nepravilno zarastao prijelom potkoljenice, radioloπki dokazan s valgus, varus ili recurvatum deformacijom - usporeappleeno sa zdravom viπe od 15 stupnjeva...do 15 % 162. Potpuna ukoëenost skoënog zgloba: a) u funkcijski nepovoljnom poloæaju...do 25 % b) u funkcijski povoljnom poloæaju (5-10 stupnjeva plantarne fleksije)...do 20 % 163. Radioloπki dokazani prijelomi u podruëju skoënog zgloba zarasli s pomakom ili intraartikularni prijelomi uz urednu funkciju zgloba...do 3 % 1. Za pseudoartrozu patele ili tibije ne odreappleuje se invaliditet. 2. Invaliditet iz toëaka odreappleuje se 6 mjeseci nakon zavrπenog 3. Kod ozljeda ligamentarnih struktura zgloba (distorzije) invaliditet se ne odreappleuje
6 164. Endoproteza skoënog zgloba...25 % 165. Traumatsko proπirenje maleolarne vilice stopala - usporeappleeno sa zdravim...do 5 % 166. Deformiteti stopala: pes excavatus, pes planovalgus, pes varus, pes equinus u teπkom stupnju:...do 5 % 167. Deformacija petne kosti poslije kompresivnog prijeloma...do 5 % 168. Deformacija talusa poslije prijeloma, uz deformirajuêu artrozu, radioloπki dokazano...do 5 % 169. Deformacija metatarzusa nakon prijeloma metatarzalnih kostiju (za svaku metatarzalnu kost 1%)...do 5 % 1. Za ocjenu invaliditeta po toëkama osiguranik je obvezan dostaviti na uvid RTG snimke. 2. Invaliditet iz toëaka odreappleuje se 6 mjeseci nakon zavrπenog 170. Potpuna ukoëenost distalnog zgloba palca na nozi...2 % 171. Potpuna ukoëenost proksimalnog zgloba palca na nozi ili oba zgloba...4 % 172. Velik oæiljci na peti ili tabanu poslije ozljede mekih dijelova - viπe od 1/2 povrπine tabana...do 10 % 173. Paraliza æivaca noge: a) ishijadiënog æivca...do 40 % b) femoralnog æivca...do 30 % c) tibijalnog æivca...do 25 % d) peronealnog æivca...do 25 % e) glutealnog æivca...do 10 % 174. Potpuni prekid Ahilove tetive...5 % 1. Invaliditet iz toëke 173. odreappleuje se nakon zavrπenog lijeëenja i rehabilitacije, ali ne prije isteka dvije godine od ozljeappleivanja, s nalazom EMG-om dokazanog oπteêenja, ne starijim od 3 mjeseca. 2. Za pareze æivaca na nozi odreappleuje se najviπe do 2/3 postotka odreappleenog za paralizu toga æivca. 3. Za oπteêenje korijenova spinalnih æivaca slabinske regije (tzv. radikularna oπteêenja) ne odreappleuje se invaliditet. 4. Nepotpuni prekid Ahilove tetive ocjenjuje se prema toëki 163. uz predoëenje UZV i pregleda lijeënika sa utvrappleenim funkcijskim oπteêenjem. PROCJENA OPE»ENE POVR INE PO WALLACE-ovom PRAVILU PRAVILO DEVETKE -Vrat i glava...9 % -Jedna ruka...9 % -Prednja strana trupa...2 x 9 % -Zadnja strana trupa...2 x 9 % -Jedna noga...2 x 9 % -Perineum i genitalije...1 % U primjeni od
UVJETI ZA OSIGURANJE OSOBA OD POSLJEDICA NEZGODE [01.01-EH-1]
![UVJETI ZA OSIGURANJE OSOBA OD POSLJEDICA NEZGODE [01.01-EH-1] UVJETI ZA OSIGURANJE OSOBA OD POSLJEDICA NEZGODE [01.01-EH-1]](/thumbs/66/56148995.jpg) UVJETI ZA OSIGURANJE OSOBA OD POSLJEDICA NEZGODE [01.01-EH-1] TABLICA ZA ODRE IVANJE POSTOTKA TRAJNOG INVALIDITETA KAO POSLJEDICE NESRETNOG SLU»AJA [NEZGODE] [01.T-2-1.1] EUROHERC EUROHERC TABLICA
UVJETI ZA OSIGURANJE OSOBA OD POSLJEDICA NEZGODE [01.01-EH-1] TABLICA ZA ODRE IVANJE POSTOTKA TRAJNOG INVALIDITETA KAO POSLJEDICE NESRETNOG SLU»AJA [NEZGODE] [01.T-2-1.1] EUROHERC EUROHERC TABLICA
TABLICA ZA ODRE IVANJE POSTOTKA TRAJNOG INVALIDITETA KAO POSLJEDICE NESRETNOG SLU»AJA (NEZGODE)
 Osiguranje na Vaπoj strani TABLICA ZA ODRE IVANJE POSTOTKA TRAJNOG INVALIDITETA KAO POSLJEDICE NESRETNOG SLU»AJA (NEZGODE) OP E ODREDBE 1. Ova Tablica invaliditeta za odreappleivanje postotka trajnog invaliditeta
Osiguranje na Vaπoj strani TABLICA ZA ODRE IVANJE POSTOTKA TRAJNOG INVALIDITETA KAO POSLJEDICE NESRETNOG SLU»AJA (NEZGODE) OP E ODREDBE 1. Ova Tablica invaliditeta za odreappleivanje postotka trajnog invaliditeta
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
ΚΑΝΟΝΙΣΜΟΣ (EE) 2019/1238 ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΚΟΙΝΟΒΟΥΛΙΟΥ ΚΑΙ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ
 198/1 L I ( (EE) 2019/1238 20 2019 (PEPP) ( ), 114,,, ( 1 ), ( 2 ), : (1),.. (2),., 25, :. (3),,.,,,. ( 1 ) C 81 2.3.2018,. 139. ( 2 ) 4 2019 ( ) 14 2019. EL L 198/2 25.7.2019 (4).,,. H,, ( ). (5) 2015,
198/1 L I ( (EE) 2019/1238 20 2019 (PEPP) ( ), 114,,, ( 1 ), ( 2 ), : (1),.. (2),., 25, :. (3),,.,,,. ( 1 ) C 81 2.3.2018,. 139. ( 2 ) 4 2019 ( ) 14 2019. EL L 198/2 25.7.2019 (4).,,. H,, ( ). (5) 2015,
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
C M Y CM MY CY CMY K. Ortoze i ortopedske potpore. Composite
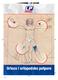 Ortoze i ortopedske potpore Odlika urbanog Ëovjeka je da se tjelesnim aktivnostima bavi povremeno i neredovito. Vrlo Ëesto se tjelesnim naporima pristupa nepripremljeno i nakon duæe stanke. Tjelesna nepripremljenost,
Ortoze i ortopedske potpore Odlika urbanog Ëovjeka je da se tjelesnim aktivnostima bavi povremeno i neredovito. Vrlo Ëesto se tjelesnim naporima pristupa nepripremljeno i nakon duæe stanke. Tjelesna nepripremljenost,
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
TABLICE AKTUARSKE MATEMATIKE
 Na temelju članka 160. stavka 4. Zakona o mirovinskom osiguranju («Narodne novine», br. 102/98., 127/00., 59/01., 109/01., 147/02., 117/03., 30/04., 177/04., 92/05., 43/07., 79/07., 35/08., 40/10., 121/10.,
Na temelju članka 160. stavka 4. Zakona o mirovinskom osiguranju («Narodne novine», br. 102/98., 127/00., 59/01., 109/01., 147/02., 117/03., 30/04., 177/04., 92/05., 43/07., 79/07., 35/08., 40/10., 121/10.,
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Program za tablično računanje Microsoft Excel
 Program za tablično računanje Microsoft Excel Teme Formule i funkcije Zbrajanje Oduzimanje Množenje Dijeljenje Izračun najveće vrijednosti Izračun najmanje vrijednosti 2 Formule i funkcije Naravno da je
Program za tablično računanje Microsoft Excel Teme Formule i funkcije Zbrajanje Oduzimanje Množenje Dijeljenje Izračun najveće vrijednosti Izračun najmanje vrijednosti 2 Formule i funkcije Naravno da je
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo
 Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Pismeni dio ispita iz Matematike Riješiti sistem jednačina i diskutovati rješenja u zavisnosti od parametra a:
 Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
DUALNOST. Primjer. 4x 1 + x 2 + 3x 3. max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 (P ) 1/9. Back FullScr
 DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 (D)
DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 DUALNOST Primjer. (P ) 4x 1 + x 2 + 3x 3 max x 1 + 4x 2 1 3x 1 x 2 + x 3 3 x 1 0, x 2 0, x 3 0 1/9 (D)
1. Duljinska (normalna) deformacija ε. 2. Kutna (posmina) deformacija γ. 3. Obujamska deformacija Θ
 Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
Deformaije . Duljinska (normalna) deformaija. Kutna (posmina) deformaija γ 3. Obujamska deformaija Θ 3 Tenor deformaija tenor drugog reda ij γ γ γ γ γ γ 3 9 podataka+mjerna jedinia 4 Simetrinost tenora
KONVEKSNI SKUPOVI. Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5. Back FullScr
 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK
 OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
EKSPONENCIJALNE i LOGARITAMSKE FUNKCIJE
 **** MLADEN SRAGA **** 0. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE EKSPONENCIJALNE i LOGARITAMSKE FUNKCIJE α LOGARITMI Autor: MLADEN SRAGA Grafički urednik: Mladen Sraga
**** MLADEN SRAGA **** 0. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE EKSPONENCIJALNE i LOGARITAMSKE FUNKCIJE α LOGARITMI Autor: MLADEN SRAGA Grafički urednik: Mladen Sraga
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Στοιχεία και έγγραφα που απαιτούνται για την εγγραφή στο ΓΕΜΗ
 Στοιχεία και έγγραφα που απαιτούνται για την εγγραφή στο ΓΕΜΗ Σύμφωνα με την αριθμ. Κ1-941 οικ./27.4.12 και την Κ1-1484/12.6.2012 του Υπουργείου Ανάπτυξης & Ανταγωνιστικότητας πρέπει να γίνει εγγραφή των
Στοιχεία και έγγραφα που απαιτούνται για την εγγραφή στο ΓΕΜΗ Σύμφωνα με την αριθμ. Κ1-941 οικ./27.4.12 και την Κ1-1484/12.6.2012 του Υπουργείου Ανάπτυξης & Ανταγωνιστικότητας πρέπει να γίνει εγγραφή των
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
