PRIJENOS i DISTRIBUCIJA ELEKTRIČNE ENERGIJE

Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:

Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b

Vježba 1. Analiza i sinteza sistema regulacije brzine vrtnje istosmjernog motora

ortorjske vježe z predet ootk uprvljje prozvod sste Vjež Vjež Alz stez sste regulcje rze vrtje stosjerog otor Clj vježe: Stez regultor rze vrtje stosjerog otor pooću etod tehčkog setrčog optu Alzrt dčko

Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza

Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog

ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА

ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote

Metoda najmanjih kvadrata

Metoda ajmajh kvadrata Moday, May 30, 011 Metoda ajmajh kvadrata (MNK) MNK smo već uvel u proučavaju leare korelacje; gdje smo tražl da suma kvadrata odstupaja ekspermetalh točaka od pravca koj h a ajbolj

Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam

Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema

Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,

Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište

Moguća i virtuelna pomjeranja

Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +

Dimenzioniranje SN/NN kabela i transformatora

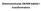Dmezoraje SN/NN kabela trasformatora Za NN mrežu prkazau slkom potrebo je odredt presjek glavh adzemh trofazh zvoda te moofazh podzvoda obzrom a dozvolje pad apoa kod krajjeg potrošača od 6% dozvoljeu

METODE OPTIMIZACIJE NELINEARNO PROGRAMIRANJE

MEODE OPIMIZACIJE NELINEARNO PROGRAMIRANJE Dr Dšć Dr Mloš Stć Grđevsk kultet Uverztet u Beogrdu 4. UVOD FORMULACIJA PROBLEMA Zdtk optmzcje je prolžeje promeljvh pr kojm clj krterjumsk ukcj uzm ekstremu

FURIJEOVI REDOVI ZADACI ( II

FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos

4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i

Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine

odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa

.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi

n n su realni brojevi, a n, koji mora biti cjelobrojna

Aproksmrnje podtk Aproksmrnje podtk krvuljom Aproksmrnje podtk krvuljom (engl. curve ttng), nzv se još regresjsk nlz (engl. regresson nlss), je postupk uklpnj unkcje u skup točk koje predstvljju određene

1.4 Tangenta i normala

28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x

4. Trigonometrija pravokutnog trokuta

4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz

2.6 Nepravi integrali

66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,

Rijeseni neki zadaci iz poglavlja 4.5

Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz

Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,

PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,

α =. n n n Vježba 001 Koliko stranica ima pravilni mnogokut ako jedan njegov unutarnji kut iznosi 144? Rezultat: n = 10.

Zdtk (Mrij, gimzij) Koliko stric im prvili mogokut ko jed jegov uutrji kut izosi 8? Rješeje Formul z veličiu jedog uutrjeg kut prvilog mogokut je: ( ) 8 α = ( ) 8 8 = / 8 = ( ) 8 8 = 8 6 8 8 = 6 7 = 6

F (t) F (t) F (t) OGLEDNI PRIMJER SVEUČILIŠTE J.J.STROSSMAYERA U OSIJEKU ZADATAK

OGLEDNI PRIMJER ZADAAK Odredte dnamčke karakterstke odzv armranobetonskog okvra C-C prkazanog na slc s prpadajućom tlorsnom površnom, na zadanu uzbudu tjekom prve tr sekunde, ako je konstrukcja prje djelovanja

IZVODI ZADACI (I deo)

IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a

GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo

GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;

Riješeni zadaci: Nizovi realnih brojeva

Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički

VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su

ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk

- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)

MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile

7 neg. ( - ) neg. ( - ) poz. (+ ) poz. (+ )

X. gimzij Iv Supek Zgre, Klićev 7. lipj 000. godie Mturl zdć iz mtemtike Rješej zdtk. ) Riješi jeddžu 7 Rješeje: Njprije se tre riješiti psolutih vrijedosti tko d z svki izrz uutr psolute vrijedosti odredimo

II. ANALITIČKA GEOMETRIJA PROSTORA

II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim

I N Ž E N J E R S K A M A T E M A T I K A 2

I N Ž E N J E R S K A M A E M A I K A P r e d v j G L A V A 8 OURIEROVI REDOVI, OURIEROVI INEGRALI I OURIEROVA RANSORMACIJA 8.. U v o d m cresc eudo. [Gs rse šrejem.] Lsk posovc ourerov red je jed od jvžjh

Elektrostatika. 1. zadatak. Uvodni pojmovi. Rješenje zadatka. Za pločasti kondenzator vrijedi:

tnic:iii- lektosttik lektično polje n gnici v ielektik. Pločsti konenzto. Cilinični konenzto. Kuglsti konenzto. tnic:iii-. ztk vije mete ploče s zkom ko izoltoom ile su spojene n izvo npon, ztim ospojene

MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI

MODELI TEMELJENI NA DIFERENCIJALNIM JEDNADŽBAMA VIŠEG REDA I NA SUSTAVIMA DIFERENCIJALNIH JEDNADŽBI MATEMATIČKO NJIHALO Jedadžba koja osuje gbaje matematčkog jala rozlaz z drugog Newtoovog zakoa r ma F

Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.

Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),

Elektrotehnički fakultet univerziteta u Beogradu 16.maj Odsek za Softversko inžinjerstvo

Elektrotehnčk fakultet unverzteta u Beogradu 6.maj 8. Odsek za Softversko nžnjerstvo Performanse računarskh sstema Drug kolokvjum Predmetn nastavnk: dr Jelca Protć (35) a) () Posmatra se segment od N uzastonh

Numerička integracija

umerčk tegrcj Zdtk umerčke tegrcje umerčk tegrcj je postupk zrčuvj prlže vredost određeog tegrl: < d. z vredost podtegrle ukcje dt uređeom telom čemu pretpostvljmo d je: pr... Bzr se ko umerčko derecrje

Aritmetički i geometrijski niz

Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.

M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost

M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.

Dvanaesti praktikum iz Analize 1

Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.

KUPA I ZARUBLJENA KUPA

KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p

= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi

Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim

c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]

Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom

Rješenje: F u =221,9 N; A x = F u =221,9 N; A y =226,2 N.

Osnove strojrstv Prvilo izolcije i uvjeti rvnoteže Prijeri z sostlno rješvnje 1. Gred se, duljine uležišten je u točki i obješen je n svoje krju o horizontlno uže. Izrčunjte horizontlnu i vertiklnu koponentu

3.1 Granična vrednost funkcije u tački

3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili

( ) p a. poklopac. Rješenje:

5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p

Eliminacijski zadatak iz Matematike 1 za kemičare

Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska

Pismeni ispit održan

Pisei ispit održ 69 4 Kostrkcij prikz skici je, pored sopstvee težie, optereće i jedko rspodeljei povreei opterećeje p /, koje ože delovti proizvoljo položj ploči Dejstvo vetr je predstvljeo kpi horizotli

Kinematika materijalne toke. 2. Prirodni koordinatni sustav. 1. Vektorski nain definiranja gibanja. Krivocrtno gibanje materijalne toke

Kioco gibje meijle oke Kiemik meijle oke. dio ) Zje kiocog gibj b) Bi i ubje Položj meijle oke u skom euku eme možemo defiii slijedee ie:. Vekoski i defiij gibj (). Piodi i defiij gibj s s (). Vekoski

2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x

Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:

pismeni br : Odrediti interval konvergencije reda = 11.2: Metodom varijacije konstante odrediti opće rješenje jednadžbe ( x

Piedio D.Joičić pismei b..: Odediti itel koegecije ed..: Metodom ijcije kostte odediti opće ješeje jeddžbe e.: Ičuti d, gdje je K goj poloic elipse peđe od K b točke A, do B,..: Ičuti pom okttu. I d, gdje

7 Algebarske jednadžbe

7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.

METODA SEČICE I REGULA FALSI

METODA SEČICE I REGULA FALSI Zadatak: Naći ulu fukcije f a itervalu (a,b), odoso aći za koje je f()=0. Rešeje: Prvo, tražimo iterval (a,b) a kome je fukcija eprekida, mootoa i važi: f(a)f(b)

PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,

PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati

Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.

šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td

1.1. Pregled najvažnijih izraza i pojmova

Teorja formacje, kapactet dskretog komukacjskog kaala, Markovljev lac Pregled ajvažjh zraza pojmova Dskreto bezmemorjsko zvoršte Izvoršte X X = {x,,x,,x } [p(x ) = [p(x) = [p(x ) p(x ) p(x ) X dskreta

Obrada empirijskih podataka

Obrada emprjskh podataka deskrptva statstka opsvaje podataka z uzorka l populacje u form osovh parametara osove vrste podataka po astaku varjable (upotreba razlčth mjerh ljestvca) se mogu klasfcrat a:.

21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI

21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka

PIRAMIDA I ZARUBLJENA PIRAMIDA. - omotač se sastoji od bočnih strana(najčešće jednakokraki trouglovi), naravno trostrana piramida u omotaču

PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu

IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)

IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO

IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo

IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai

ZBIRKA POTPUNO RIJEŠENIH ZADATAKA

**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.

SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F

SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost

RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA

RAČUNANJE SA PRIBLIŽNIM VREDNOSTIMA BROJEVA PRIBLIŽNI BROJ I GREŠKA tača vredost ekog broja X prblža vredost ekog broja X apsoluta greška Δ = X X graca apsolute greške (gorja graca) relatva greška X X

I N Ž E N J E R S K A M A T E M A T I K A 1. P r e d a v a n j a z a p e t u s e d m i c u n a s t a v e (u akademskoj 2009/2010.

I N Ž E N J E R S K A M A T E M A T I K A P r e d v j z p e t u s e d m c u s t v e (u demsoj 009/00 god) 7 Redov s prozvoljm človm (Redov s človm prozvoljog z) Hurt qum crbro, qu dscěre vult selbro [Crpe

Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A

Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.

Istosmjerni krugovi. 1. zadatak. Na trošilu će se trošiti maksimalna snaga u slučaju kada je otpor čitavog trošila jednak unutrašnjem otporu izvora.

Strnic: X stosmjerni krugovi Prilgođenje n mksimlnu sngu. Rješvnje linernih mrež: Strnic: X. zdtk Otpor u kominciji prem slici nlzi se u posudi u kojoj vld promjenjiv tempertur. Pri temperturi ϑ = 0 C,

( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )

Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija

( ) Φ = Hɺ Hɺ. 1. zadatak

7.vježba iz ermodiamike rješeja zadataka. zadatak Komresor usisava 30 m 3 /mi zraka staja 35 o C i 4 bar te ga o ravotežoj romjei staja v kost. komrimira a tlak 8 bar. Komresor se hladi vodom koja tijekom

UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka

UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju

ELEKTROTEHNIČKI ODJEL

MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,

Reverzibilni procesi

Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože

INTELIGENTNO UPRAVLJANJE

INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila

Računanje sa približnim brojevima

čuje s prblžm brojevm. IZVOI GEŠK Hemjsko-žejersk prorču u opštem slučju obuhvt dve e: Formulsje eophodh jedč mtemtčkog model ešvje mtemtčkog model Nek je lj prorču određvje eke velče, koj je ukj prmetr

PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).

PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo

1 Ekstremi funkcija više varijabli

1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,

A MATEMATIKA Zadana je z = x 3 y + 1

A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte

POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE

**** MLADEN SRAGA **** 00. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTENCIJE α M-- uiverzl zbirk potpuo riješeih zdtk Rješej svih zdtk s kopleti postupko i uput. Koristio

Dinamika krutog tijela. 14. dio

Dnaka kutog tjela 14. do 1 Pojov: 1. Vekto sle F (tanslacja). Moent sle (otacja) 3. Moent toost asa 4. Rad kutog tjela A 5. Knetka enegja E k 6. Moent kolna gbanja 7. u oenta kolne gbanja oenta sle M (

dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor

I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto

Matematika 1 - vježbe. 11. prosinca 2015.

Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.

1 PRORAČUN PLOČE POS 1

KRSTST PLOČ JEDNO POLJE P9/ PRORČUN PLOČE POS Ploča dimezija 6.0 7.m u osovi oslojea je a dva para paralelih greda POS,, koje su oslojee a stubove POS S u uglovima ploče. Pored sopstvee težie, ploča je

Interferencija valova svjetlosti

Interferencja valova svjetlost Uvod Da b poblže mogl sagledat razumjet fenomen nterferencje općento prmjenjeno, navest ćemo uvjete nterferencje posljedce th uvjeta. Pojave nterferencje dfrakcje u današnje

II. ANALITIČKA GEOMETRIJA PROSTORA

II. ANALITIČA GEOMETRIJA PROSTORA II. DIO (Pv).. Min Roić Linović 9./. Pv u otou Jenž v Nek je: T (,, ) n točk oto {,, } ni vekto mje Znom točkom oto oli mo v leln nim vektoom. T (,,) - oivoljn točk v

(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.

1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,

IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv

Linearna algebra 2 prvi kolokvij,

1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika

DINAMIKA. Dinamički sistem - pogon sa motorom jednosmerne struje: N: u f Ulazi Izlazi (?) U opštem slučaju ovaj DS je NELINEARAN!!!!

DINAMIKA Dnčk sste - ogon s otoro jednoserne struje: N: { DS } u u Ulz Izlz (?),,, [ ] θ U ošte slučju ovj DS je NELINEAAN!!!! BLOK DIJAGAM MAEMAIČKOG MODELA POGONA Iz jednčne ndukt u e e Iz Njutnove jednčne

18. listopada listopada / 13

18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu

KONSTRUKTIVNI ZADACI (TROUGAO) Rešavanje konstruktivnih zadataka je jedna od najtežih oblasti koja vas čeka ove godine.

KONSRUKIVNI ZI (ROUGO) Rešvje kotruktivih zdtk je jed od jtežih olti koj v ček ove godie. Zhtev doro predzje, pozvje odgovrjuće teorije. Zto vm mi preporučujemo d e jpre podetite teorije veze z trougo

Numerička matematika 2. kolokvij (1. srpnja 2009.)

Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni

Παρασκευή 1 Νοεμβρίου 2013 Ασκηση 1. Λύση. Παρατήρηση. Ασκηση 2. Λύση.

(, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R

Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.

Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34

Vektori u ravnini. - Nije bitan redoslijed AB ili BA

Vektor u rnn. Osnon pomo o ektorm Skup sh tok prc p zmeu ukluuu nh sme ne dužnu Ne tn redosled l e poetn tok e zršn tok odsek n prcu p Defnc: Usmeren odsek od toke ko poetne toke do toke ko zršne toke

Iterativne metode - vježbe

Iterativne metode - vježbe 5. Numeričke metode za ODJ Zvonimir Bujanović Prirodoslovno-matematički fakultet - Matematički odjel 21. studenog 2010. Sadržaj 1 Eulerove metode (forward i backward). Trapezna

radni nerecenzirani materijal za predavanja

Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je

ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA. školska 2013./2014. godina TEST MATEMATIKA UPUTE ZA RAD

ZAVRŠNI ISPIT NA KRAJU OSNOVNOG OBRAZOVANJA I ODGOJA školsk 0./04. godin TEST MATEMATIKA UPUTE ZA RAD Test koji trebš riješiti im 0 zdtk. Z rd je predviđeno 0 minut. Zdtke ne morš rditi prem redoslijedu

1.PRIZMA ( P=2B+M V=BH )

.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti

TRIGONOMETRIJA TROKUTA

TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane

Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju

RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)

Operacije s matricama

Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M

PRESECI SA PRSLINOM - VELIKI EKSCENTRICITET

TEORJA ETONSKH KONSTRUKCJA 1 PRESEC SA PRSLNO - VELK EKSCENTRCTET ČSTO SAVJANJE - SLOODNO DENZONSANJE Poznato: Nepoznato: - statčk tcaj za pojedna opterećenja ( ) - sračnato - kvaltet materjala (, σ v

2.7 Primjene odredenih integrala

. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu