ПЛАНИНЕ РЕПУБЛИКЕ СРБИЈЕ И ИЗАБРАНА РАСТОЈАЊА У ОДНОСУ НА ЊИХОВЕ ВРХОВЕ
|
|
|
- Κηφάς Ζέρβας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Јован Илић 1 Сава Станковић 2 ПЛАНИНЕ РЕПУБЛИКЕ СРБИЈЕ И ИЗАБРАНА РАСТОЈАЊА У ОДНОСУ НА ЊИХОВЕ ВРХОВЕ Географски положај, граница, географски центар и број становника Републике Србије Републикa Србијa се налази већим делом на Балканском полуострву (део државе јужно од река Саве и Дунава - површина km 2 или 74,8 % укупне површине) и мањим делом у Средњој Европи (дао државе северно од поменутих река - површина km 2 или 25,2 %). Површина Републике Србије је km 2 [1]. Србија се граничи са Црном Гором (дужина границе 236,0 km), Босном и Херцеговином (382,8 km), Хрватском (259,3 km), Мађарском (174,4 km), Румунијом (546,5 km), Бугарском (367,1 km) Македонијом (273,0 km) и Албанијом (111,1 km). Укупна дужина границе Србије је 2.350,2 km [2]. Географски центар [3] Србије, израчунат методом мреже тачака, налази се у насељу Гривац, општина Кнић, у делу сеоског атара Бакчине, на њиви Раденка Петровића. Географске координате центра су: северна географска ширина (СГШ) f = 43 31' 15" и источна географска дужина (ИГД) λ = 20 43' 36". Према попису становништва из године, Република Србија је имала становника (просечна густина 111 становника/km 2 ), а године Централна Србија и Војводина становника [4]. Основне висинске и просторне карактеристике рељефа Србије Рељеф Србије ја разнолик. Подаци у табели 1 показују да ја најзаступљенији планински рељеф. Површина те категорије рељефа је km 2 или 38,5 % укупне површина Србије. У склопу планинског рељефа највеће пространство има нископланински рељеф (27,3 %). На брдовито земљиште долази скоро једна четвртина (24,7 %), а на низијско земљиште више од једне трећине (36,8 %) површине Србије. Низијско земљиште налази се у Војводини, те у Посавини и Поморављу Централне Србије. 1 Др Јован Илић, редовни професор Географског факултета у пензији, Београд. 2 Сава Станковић, Служба за границе Министарства спољних послова СЦГ. 147
2 Табела 1. Висинска категоризација рељефа (земљишта) у Србији и површина појединих висинских зона (појасева) Висинска Категорија рељефа Површина зона (m) (земљишта) km 2 % Низијско , Брдско , Нископланинско , ,59 Средњепланинско ,37 Преко 2000 Високопланинско 206 0,23 У К У П Н О Извор: др Томислав Младеновић: Висинска структура земљишта у СФР Југославији, Зборник радова, Војногеографски институт, Београд, 1984, стр. 71. По географском положају, правцу пружања, старости, геолошкој грађи, начину постанка и облицима рељефа, планине Србије лоциране су у више планинских система и група. На истоку Србије су Карпатско-балканске планине, које се протежу од Дунава на северу до Заплањско-лужничке котлине и Руј-планине на југу. Према истоку сежу до бугарске границе, а на западу до Велике и Јужне Мораве. Мироч (768 m) је најсевернији, а Стара планина је највиша (Миџор m). Ртањ (1.560 m) има средишњи положај у овом планинском систему. На југоистоку Србије су Родопске планине (Дукат, Бесна кобила, Чемерник и др.), а северозападно од њих је Копаоничка група планина (Копаоник, Жељин, Гоч и Столови). На југу Србије, на граници према Македонији је Шар планина (Љуботен m), а на тромеђи Србије, Црне Горе и Албаније су Проклетије са врхом Ђеравица (2.656 m). То је највиши планински врх у Србији. На југозападу Србије је Старовалшко-рашка планинска област, омеђена Дрином на западу, Ђетињом и Западном Моравом на северу, Ибром на истоку и југоистоку и Лимом на југозападу. Најзначајније планине овог простора су Златибор, Тара, Златар, Јадовник, Голија и Јавор. У овом простом су и Пештерска висораван и Новопазарски басен. Шумадијске планине налазе се у средишњем делу Србије, између Дунава и Саве на северу, Западне Мораве и Ђетиње на југу, Велике Мораве на истоку и Колубаре, Љига и Дичине на западу. Чине их Авала, Космај, Букуља, Венчац, Рудник и Гледићке планине. Рудне и флишне планине протежу се од Саве на северу до Ђетиње на југу и од Дрине на западу до Колубаре, Љига и Дичине на истоку. У групу рудних планина спадају Гучево, Борања, Соколске планине, Повлен, Маљен и Сувобор, а у групу флишних планина Цер и Влашић [5]. 148
3 Основне географске особености важних планина Србије Ми смо у овом раду укратко географски обрадили 11 планина Србије које су, по нашем мишљењу, врло интересантне за велики број љубитеља планина и других посетилаца, па и ђачких екскурзија. То су: Фрушка гора, Цер, Златибор, Авала, Рудник, Ртањ, Стара планина, Копаоник, Голија, Проклетије и Шар-пианина. За највише врхове тих планина дали смо више статистичких података. Основне оријентирне податке дајемо у табели 2. Следи приказ основних географских карактеристика наведених планина. Фрушка гора је ниска планина, јер њен највиши врх, Црвени чот, има надморску висину 539 m (Таб. 2). Налази се у северном Срему, јужно од Дунава и Новог Сада. Пружа се у смеру запад-исток у дужини од око 80 km. На линији Ириг - Сремска Каменица широка је 15 km. Виши делови планине су под дивном листопадном шумом, а нижи делови под њивама, воћњацима и ливадама. Фрушка гора је посебно позната по томе што се на њој и у њеном подножју налази 17 српско-православних манастира, и то: Крушедол, Велика Ремета, Гргетег, Ново Хопово, Старо Хопово, Раваница, Фенек, Јазак, Мала Ремета, Бешеново, Шишатовац, Петковица, Кувеждин, Ђипса, Привина Глава, Беочин и Раковац [6]. Зато ову планину, због великог броја манастира, многи називају Српска Света Гора. На Фрушкој гори постоји више излетничких центара, односно излетишта (Иришки Венац, Чортановци, Стражилово и др.). Посебан значај и атрактивност има средишњи део Фрушке горе, на површини од хектара, који је год. проглашен за национални парк. Због свега наведеног Фрушку гору радо посећује велики број туриста и других заинтерсованих лица. Цер је такође ниска планина, пошто његов највиши врх, Тодоров рт, има надморску висину 687 m. На истом врху су остаци старе тврђаве - Косанин град, па се и тај назив користи као ознака највишег врха ове планине. Цер се налази на северозападу Централне Србије, јужно од Мачве и северно од реке Лешнице. У историји је познат по чувеној Церској бици из августа године. Том битком почео је рат између Аустро-угарске Монархије и Краљевине Србије, односно почео је Први светски рат. Срби су били победници. То је била прва српска и прва савезничка победа у I светском рату. Златибор је средњевисока планина, односно благо заталасана висораван у југозападној Србији. Налази се југозападно и јужно од Ужица, између река Ђетиње на северу, Увца на југу и Великог Рзава на истоку. Торник је највише узвишење са надморском висином од m. Више је под ливадама и пашњацима него под шумама. Има благу субпланинску 149
4 климу, са доста сунчаних дана. Златибор je због повољне климе, питомих и живописних пејзажа, дивних терена за шетњу, излете и спортске активности (посебно зимске), повољних саобраћајних веза, изграђене и разноврсне туристичко-угоститељске инфраструктуре, постао врло важно туристичко подручје у Србији. На Златибору се често одржавају разни научни и стручни скупови. Врло је важно одредиште ђачких екскурзија. Авала је ниска планина (надморска висина 506 m). Налази се јужно од Београда, поред пута за Крагујевац. Удаљена је од главног града Србије 15 km. Обрасла је добро очуваном листопадном шумом, a има и четинара, који су засађени у новије време. Помиње се у више докумената из римског периода. У средњем веку и у време турских освајања спомиње се као утврђење Жрнов. Године на врху Авале подигнут је и свечано је откривен Споменик незнаном јунаку, односно ту погинулом српском војнику године. Године довршен је садашњи, грандиозни Споменик незнаном јунаку, аутора вајара Ивана Мештровића. На Авали је године, после двогодишње градње, пуштен у рад један од најлепших телевизијских репетитора у Европи и свету - Авалски торањ, висок 202,87 m, (са антенама). На висини од 101 m налазио се ексклузивни ресторан из кога се пружао видик на панораму Београда и Шумадије. Ремек дело архитектуре осмисли су архитекти Угљеша Богдановић и Слободан Јањић, и конструктор академик Милан Крстић. У торањ је уграђено око 4000 t армираног бетона. Ово дело, чија је изградња коштала око 20 милиона долара, најпре је 25. априла године оштећено, а четири дана касније и срушено у НАТО бомбардовању. На пету годишњицу рушења Авалског торња, Удружење љубитеља Авалског торња и Удружење новинара Србије започела су прикупљање средстава за обнову торња, симбола Београда, у његовом изворном облику. Авала је омиљено излетиште Београђана и других бројних посетилаца. Врло је често посећују и ђачке екскурзије. Рудник се налази у средишњем делу Шумадије, северно од Горњег Милановца, поред друма Београд - Чачак. Спада у групу средњевисоких планина, пошто је надморска висина највишег врха m. Посебно треба нагласити да је највиши врх ове планине добио назив по најзначајнијем српском географу, академику Јовану Цвијићу ( ), дакле Цвијићев врх. Рудник је највиша планина у Шумадији. Виши делови планине су под густом шумом, а нижи под ливадама, пашњацима, воћњацима, виноградима и њивама. У његовом подножју извиру реке Јасеница, Лепеница, Гружа и Љиг. У новије време, добија све већи значај у туризму. Ртањ се налази у источној Србији, између Црног Тимока на северу и Моравице на југу. Пружа се у смеру југозапад-североисток у дужини од око 30 km. Купасти врх Шиљак има надморску висину m, што значи да Ртањ спада у средњепланинску висинску категорију. Припада Карпат- 150
5 ско-балканском планинском систему. Близу њега је познато здравственотуристичко насеље Соко Бања, што значи да посетиоци Бање и друга лица, када се попну на врх ове планине имају врло велики видик. Он обухвата знатан део Тимочке крајине и Поморавља и суседне планине (Кучај, Озрен, Тупижница и др.). Стара планина се налази на српско-бугарској граници. Пружа се у смеру северозапад-југоисток, на дужини око око 90 km. Њен највиши врх Миџор има надморску висину m, што значи да планина спада у високопланинску рељефну категорију. Са Миџора се види већи део Тимочке крајине и Понишавља и знатан део бугарског Подунавља. Преко те високе и дугачке планине прелази су увелико отежани. Ипак, олакшање за прелаз преко те планине омогућава постојање више планинских превоја, међу којима је најважнији Кадибогаз. На странама планине има доста шуме и пространих ливада и пашњака. Отуда је овај предео одавно познат као значајно сточарско подручје. Копаоник је једна од најдужих, највиших и за посетиоце најинтересантнијих планина Србије. Пружа се углавном правцем север-југ, на дужини од око 90 km. Развође је између Лаба, Топлице и Расине на истоку и Ибра на западу. Највећа му је надморска висина m. То је Панчићев врх, назван по Јосипу Панчићу ( ), нашем истакнутом научнику (ботаничару) и првом председнику Српске академије наука. Он је био неуморни истраживач наших планина, па и Копаоника. Ова планина, са својим плећатим странама, листопадним и четинарским шумама, цветним ливадама, многобројним изворима, потоцима и речицама, представља једну од најлепших планина Србије. Постоје и пространи пашњаци. У његовој грађи учествују разноврсне стене, од којих посебан значај имају вулканске стене. За њих је везана појава разних руда, посебно оловно-цинканих. На Копаонику постоје бројне жичаре, скијашке стазе, већи број хотела и других туристичких објеката, због чега га током целе године радо посећује велики број домаћих и страних туриста. Омиљено је одредиште и бројних ђачких екскурзија. Голија се налази на југозападу Србије, између градова Рашке и Сјенице. Пружа се у правцу запад-исток. Има, заправо, полукружни облик. Важан је хидрографски чвор, јер у њеном подножју извиру реке Студеница и Моравица и неке притоке Рашке и Увца. Највиши врх је Јанков камен, чија је надморска висина m. То је највиша планина у југозападној Србији, са које се виде пространи и географски разнолики предели (Пештер, Стари Влах и др.). Планина је већим делом под листопадном и четинарском шумом. Има и пашњака и ливада, па је Голија са суседним пределима, познато сточарско подручје. Радо је посећују планинари. Проклетије се налазе у граничном подручју Србије, Црне Горе и 151
6 Албаније, на крајњем југоистоку Динарског планинског система. Већим делом се налазе у Албанији. У Србији (Метохија) налази се њен најисточнији део, са планинским врхом Ђеравицом. Надморска висина Ђеравице је m, па је то, како смо већ истакли, највиши планински врх Србије. Проклетије су и највиша планина у читавом Динарском планинском систему. Највиши планински врхови су назубљени, кршевити и голи. Нижи делови планине су под листопадном, а виши под четинарском шумом. Изнад појаса шума налазе се травни предели. Има доста трагова плеистоцене глацијације. У њеном метохијском подножју извире више притока Белог Дрима. Ту се налази и манастир Високи Дечани. Између Проклетија и Мокре планине налази се Чакор, највиши друмски превој у Србији и Црној Гори. Висина му је m. Ту се налази важан друм Колашин-Пећ, односно Подгорица-Приштина. Шар-планина (Шара) налази се у западном граничном подручју између Републике Србије и Републике Македоније. Лоцирана је између Метохијске, Косовске и Полошке котлине. На југозападу се граничи са планином Кораб, а на североистоку је омеђена Качаничком клисуром, којом протиче река Лепенац, лева притока Вардара. Северне падине планине припадају Србији, а јужне Македонији. Највиши врх Шар-планине је Титов врх (2.748 m). Налази се у Македонији. Шар-планина има више врхова изнад m, који се налазе на граничној линији Србија-Македонија. Најисточнији високи врх је Љуботен (2.496 m), који се налази изнад Качаничке клисуре. Дужина планине је око 85, а ширина km. Заступљен је и глацијални рељеф вирмске старости. Неки циркови испуњени су водом, односно постали су планинска језера (Ливадичко, Јажиначко и др. језера). Шуме су увелико искрчене ради добијања ливада и пашњака. Зато је Шара одавно позната као сточарски предео. У новије време развија се туризам (Брезовица, Попова Шапка и др.). Математичко-географски положај и најкраћа растојања између највиших врхова и између тих врхова и важнијих градова Србије и света и битних математичко-оријентирних тачака на Земљи У табелама 2, 3, 4 и 5 дали смо за највише врхове датих планина (11 планина) Србије податке о надморској висини, математичко-географском положају, најкраћим међусобним растојањима, најкраћим растојањима између њих и важних градова Србије и света и битним математичкооријентирних одредишта на Земљи. Подаци у табелама су довољно прегледни и јасни, па није потребна њихова обимнија анализа. Почећемо са табелом 2. Подаци у њој показују да врх Авале (
7 m) има најмању, а врх Проклетија Ђеравица (2656 m) највећу надморску висину. Фрушка гора (Црвени чот, f = 45 09' 06") има најсевернији, Шарпланина (Љуботен, f = 42 12' 22") најјужнији, Цер (Тодоров рт, λ = 19 29' 59") најзападнији и Стара планина (Миџор, λ = 22 40' 58") најисточнији географски положај међу посматраним планинама Србије. Врх Рудника (Цвијићев врх) је најближи географском центру Србије (село Гривац, општина Кнић). Табела 2. Основни географски подаци за обрађене планине Планина Назив врха Надморска висина врха (m) Географске координате врха Северна Источна географска географска ширина - СГШ дужина - ИГД ϕ ( ' ") λ ( ' ") Фрушка гора Црвени чот Цер Тодоров рт Златибор Торник Авала Врх Авале Рудник Цвијићев врх Ртањ Шиљак Стара планина Миџор Копаоник Панчићев врх Голија Јанков камен Проклетије Ђеравица Шар-планина Љуботен Напомена: Износи надморских висина наведених планина узети су из Географског атласа за V, VI, VII и VIII разред основне школе. Издавачи: Завод за издавање уџбенике и наставна средства и Завод за картографију Геокарта, Београд, 2000, стр. 89. Износе за географске координате одредили су аутори овога рада. Подаци у табели 3 су посебно интересантни. Ти подаци су, заправо, најважнији, јер показују међусобно најкраће растојање између највиших врхова 11 посматраних планина. Највеће растојање у смеру север-југ је између Црвеног чота (Фрушка гора) и Љуботена (Шар-планина). Износи 346,3 km. То је истовремено и највеће праволинијско растојање у склопу свих растојања датих у табели 3. Најкраће растојање је између Панчићевог врха (Копаоник) и Јанковог камена (Голија) 41,3 km. За карактеристично најкраће растојање смера запад-исток узели смо размак између Торника (Златибор) и Миџора (Стара планина). Износ је 247,1 km. За пет врхова: Црвени чот, Торник, Цвијићев врх, Миџор и Љуботен израчунали смо и њихове просечне удаљености у односу на све врхове дате у табели 3. Износи су: Црвени чот 205,2 km, Торник 142,1 km, Цвијићев врх 127,5 km, 153
8 Миџор 218,2 km и Љуботен 206,5 km. Најмањи износ је за Цвијићев врх, пошто се планина Рудник налази у средишњем делу Србије. Највећи износи су за гранично-периферне планине - Стару планину и Шар-планину. Табела 3. Најкраћа (праволинијска) растојања између највиших планинских врхова датих планина Напомена: Растојања између планинских врхова срачуната су из правоуглих координата (Гаус-Кригерова пројекција, елипсоид Бесел 1841). Одређена су алатом ArcView GIS 3.3 на дигиталној Прегледно-топографској карти 1: ВГИ у Београду (GIS_PTK 300). Из табеле 4 сазнајемо колико износе најкраћа растојања између највиших врхова датих планина и важних одредишта (локација) у 10 најзначајнијих градова Србије. У обзир су узете важне и разноврсне локације, 154
9 у Београду Споменик кнезу Михаилу Обреновићу, у Новом Саду Споменик Светозару Милетићу, Нишу Споменик Стевану Синћелићу, Шапцу Црква Светог Ђорђа, Ужицу Град-тврђава, Приштини хотел Гранд итд. Табела 4. Најкраћа (праволинијска) растојања између највиших планинских врхова и одабраних оријентирних локација у наведеним градовима Србије Оријентационе локације у градовима: Београд - Споменик кнезу Михаилу Обреновићу (44 49' 07" СГШ, 20 28' 00", ИГД), Ниш - Споменик Стевану Синђелићу (43 19' 19" СГШ, 21 54' 29" ИГД), Крагујевац - Народни музеј, Ул.Вука Караџића 1 (44 00' 54", СГШ 20 55' 26" ИГД), Смедерево - Јужни улаз у тврђаву (44 40' 04" СГШ, 20 56' 03" ИГД), Шабац - Црква Светог Ђорђа (44 52' 42" СГШ, 18 48' 15" ИГД), Ужице - Град - тврђава (43 51' 29" СГШ, 19 50' 18" ИГД), Нови Сад - Споменик Светозару Милетићу (45 15' 25" СГШ, 19 50' 36" ИГД), Суботица - Градска кућа (46 06' 02" СГШ, 19 40' 11" ИГД), Приштина - Хотел Гранд (42 39' 27" СГШ, 21 09' 54" ИГД), Призрен - Српска богословија (42 12' 34" СГШ, 20 44' 15" ИГД). Напомена. Растојања између пл. врхова и оријентационих локација у градовима Србије мерена су алатом ArcView GIS 3.3 на дигиталној Прегледно-топографској карти 1: ВГИ у Београду. 155
10 Табела 5. Најкраћа растојања између највиших врхова датих планина и основних оријентирних одредишта на Земљи и важних локација у највећим градовима света Напомена. Најкраћа растојања дата у овој табели мерена су по локсодроми великом кругу са центром у центру Земље, на Microsoft Encarta Interactive World Atlas Подаци у табели 5 функционално су слични подацима у табели 4. У њој су садржане најкраће удаљености између највиших врхова датих 156
11 планина у Србији и основних оријентирних одредишта на Земљи и интересантних одредишта (локација) у највећим градовима света. Сматрамо да ће за читаоца Глобуса, када се попне на врх Копаоника или неке друге наведене планине, бити интересантно да сазна, колико је удаљен (најкраће) од екватора, Ајфелове Куле у Паризу, Палате Уједињених нација у Њујорку, Царске палате у Токију итд. Дакле, читалац овога рада, ако се, на пример, налази на Торнику (Златибор), брзо и лако може да добије информацију о томе колико је његово стојиште најкраће удаљено од 10 важних планинских врхова у Србији, од 10 најважнијих градова Србије, од 4 најважније оријентирне тачке на Земљи и од 8 највећих градова у свету. То значи, да укупно добија 32 даљинске информације. Закључак Ми смо у овом раду укратко обрадили: 1) Географски положај, дужину границе, географски центар и број становника Србије, 2) Основне висинске и просторне карактеристике рељефа Србије, 3) Основне географске особености важних планина Србије (11 планина) и 4) Математичко-географски положај и најкраћа растојања (у km) између највиших врхова важних планина Србије и између тих врхова и важних градова Србије и света и битних математичко-оријентирних тачака на Земљи. Зато сматрамо да ће овај рад, а посебно бројчани износи у табелама 3, 4 и 5, бити интересантни и корисни за читаоце Глобуса. Литература и напомене [1] Статистички годишњак Србије и Црне Горе Завод за статистику Србије и Црне Горе. Београд, 2003, стр. 16. [2] Јован Илић - Сава Станковић, Политичко-географске карактеристике и значај државне границе Србије. Зборник Србија и савремени процеси у Европи и свету. Издавачи: Географски факултет Универзитета у Београду, Департман за географију, туризам и хотелијерство ПМФ Универзитета у Новом Саду, Одсек за географију ПМФ Универзитета у Приштини (са привременим седиштем у Косовској Митровици) и Одсек за географију Универзитета у Нишу, Београд, 2005, стр [3] Географски центар дате територије дефинисали смо као одредиште (тачку) које је, у просеку, најближе свим одредиштима посматране територије. [4] Статистички годишњак Србије и Црне Горе 2003, стр. 63. Године 157
12 2002. на Косову и Метохији није обављен попис становништва због неповољних безбедоносно-политичких прилика. [5] Драган Родић, Географија за III разред средње школе. Завод за уџбенике и наставна средства. Београд, 2003, стр ; Географски атлас за V, VI, VII и VIII разред основне школе. Издавачи: Завод за уџбенике и наставна средства и Завод за картографију Геокарта, Београд, 2000, стр. 89. [6] Монографија Кроз Србију и Гору Гору. Прво издање. Приредио др Слободан Ристановић, Београд, 1995, стр Као извор података за поједине планине коришчена су и ова дела: 1. Др Јован Ђ. Марковић, Географске области Социјалистичке Федеративне Републике Југославије. Београд, 1970; 2. Мала енциклопедија Просвета. Књига 1, 2. и 3. Београд, 1978; 3. Благо на путевима Југославије. Енциклопедијско-туристички водич. Београд, 1983; 4. Споменичко наслеђе Србије, Београд, 1998; 5. Монографија Културна ризница Србије. Београд, 2001; 6. Наведени уџбеник Драгана Родића Географија за III разред средње школе и 7. Разноврсни туристичко-информативни материјали добијени у Планинарском савезу Србије. Београд. 158
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
(од 4. до 155. стране) (од 4. до 73. стране) ДРУГИ, ТРЕЋИ И ЧЕТВРТИ РАЗРЕД - Европа и свет у другој половини 19. и почетком 20.
 Драгољуб М. Кочић, Историја за први разред средњих стручних школа, Завод за уџбенике Београд, 2007. година * Напомена: Ученици треба да се припремају за из уџбеника обајвљених од 2007 (треће, прерађено
Драгољуб М. Кочић, Историја за први разред средњих стручних школа, Завод за уџбенике Београд, 2007. година * Напомена: Ученици треба да се припремају за из уџбеника обајвљених од 2007 (треће, прерађено
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
7.3. Површина правилне пирамиде. Површина правилне четворостране пирамиде
 математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
математик за VIII разред основне школе 4. Прво наћи дужину апотеме. Како је = 17 cm то је тражена површина P = 18+ 4^cm = ^4+ cm. 14. Основа четворостране пирамиде је ромб чије су дијагонале d 1 = 16 cm,
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
КРУГ. У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице.
 КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА
 ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
10.3. Запремина праве купе
 0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
5.2. Имплицитни облик линеарне функције
 математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни
 ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
I Наставни план - ЗЛАТАР
 I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
Примена првог извода функције
 Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Аксиоме припадања. Никола Томовић 152/2011
 Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
8. ПИТАГОРИНА ЈЕДНАЧИНА х 2 + у 2 = z 2
 8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ -
 ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Оријентација старих православних цркава у Републици Србији северно од Саве и Дунава Милутин Тадић, Ивана Нешић
 ЗБОРНИК РАДОВА Географски факултет Универзитета у Београду: Свеска LXI COLLECTION OF PAPERS Faculty of Geography at the University of Belgrade: Vol. LXI Оријентација старих православних цркава у Републици
ЗБОРНИК РАДОВА Географски факултет Универзитета у Београду: Свеска LXI COLLECTION OF PAPERS Faculty of Geography at the University of Belgrade: Vol. LXI Оријентација старих православних цркава у Републици
Нивелмански инструмент (нивелир) - конструкција и саставни делови, испитивање и ректификација нивелира, мерење висинских разлика техничким нивелманом
 висинских техничким нивелманом Страна 1 Радна секција: 1.. 3. 4. 5. 6. Задатак 1. За нивелмански инструмент нивелир са компензатором серијски број испитати услове за мерење висинских : 1) Проверити правилност
висинских техничким нивелманом Страна 1 Радна секција: 1.. 3. 4. 5. 6. Задатак 1. За нивелмански инструмент нивелир са компензатором серијски број испитати услове за мерење висинских : 1) Проверити правилност
Слика 1. Слика 1.2 Слика 1.1
 За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Први корак у дефинисању случајне променљиве је. дефинисање и исписивање свих могућих eлементарних догађаја.
 СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ
 2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
Вектори vs. скалари. Векторске величине се описују интензитетом и правцем. Примери: Померај, брзина, убрзање, сила.
 Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
6.3. Паралелограми. Упознајмо још нека својства паралелограма: ABD BCD (УСУ), одакле је: а = c и b = d. Сл. 23
 6.3. Паралелограми 27. 1) Нацртај паралелограм чији је један угао 120. 2) Израчунај остале углове тог четвороугла. 28. Дат је паралелограм (сл. 23), при чему је 0 < < 90 ; c и. c 4 2 β Сл. 23 1 3 Упознајмо
6.3. Паралелограми 27. 1) Нацртај паралелограм чији је један угао 120. 2) Израчунај остале углове тог четвороугла. 28. Дат је паралелограм (сл. 23), при чему је 0 < < 90 ; c и. c 4 2 β Сл. 23 1 3 Упознајмо
МАТЕМАТИЧКИ ЛИСТ 2017/18. бр. LII-3
 МАТЕМАТИЧКИ ЛИСТ 07/8. бр. LII- РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ . III разред. Обим правоугаоника је 6cm + 4cm = cm + 8cm = 0cm. Обим троугла је 7cm + 5cm + cm =
МАТЕМАТИЧКИ ЛИСТ 07/8. бр. LII- РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ . III разред. Обим правоугаоника је 6cm + 4cm = cm + 8cm = 0cm. Обим троугла је 7cm + 5cm + cm =
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
I Тачка 1. Растојање две тачке: 2. Средина дужи y ( ) ( ) 2. II Права 1. Једначина прамена правих 2. Једначина праве кроз две тачке ( )
 Шт треба знати пре почетка решавања задатака? АНАЛИТИЧКА ГЕОМЕТРИЈА У РАВНИ I Тачка. Растојање две тачке:. Средина дужи + ( ) ( ) + S + S и. Деоба дужи у односу λ: 4. Површина троугла + λ + λ C + λ и P
Шт треба знати пре почетка решавања задатака? АНАЛИТИЧКА ГЕОМЕТРИЈА У РАВНИ I Тачка. Растојање две тачке:. Средина дужи + ( ) ( ) + S + S и. Деоба дужи у односу λ: 4. Површина троугла + λ + λ C + λ и P
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 1 МАТЕМАТИКА УПУТСТВО
6.1. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре
 0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
ТАНГЕНТА. *Кружница дели раван на две области, једну, спољашњу која је неограничена и унутрашњу која је ограничена(кружницом).
 СЕЧИЦА(СЕКАНТА) ЦЕНТАР ПОЛУПРЕЧНИК ТАНГЕНТА *КРУЖНИЦА ЈЕ затворена крива линија која има особину да су све њене тачке једнако удаљене од једне сталне тачке која се зове ЦЕНТАР КРУЖНИЦЕ. *Дуж(OA=r) која
СЕЧИЦА(СЕКАНТА) ЦЕНТАР ПОЛУПРЕЧНИК ТАНГЕНТА *КРУЖНИЦА ЈЕ затворена крива линија која има особину да су све њене тачке једнако удаљене од једне сталне тачке која се зове ЦЕНТАР КРУЖНИЦЕ. *Дуж(OA=r) која
НАЦРТ ГЕНЕРАЛНОГ УРБАНИСТИЧКОГ ПЛАНА КРАЉЕВО 2020.
 НАЦРТ ГЕНЕРАЛНОГ УРБАНИСТИЧКОГ ПЛАНА КРАЉЕВО 2020. Одељење за урбанизам, грађевинарство и стамбено-комуналне делатности градске управе Краљево Број: Дана: Н А Ч Е Л Н И К Звонко Ковачевић, дипл.инж.грађ.
НАЦРТ ГЕНЕРАЛНОГ УРБАНИСТИЧКОГ ПЛАНА КРАЉЕВО 2020. Одељење за урбанизам, грађевинарство и стамбено-комуналне делатности градске управе Краљево Број: Дана: Н А Ч Е Л Н И К Звонко Ковачевић, дипл.инж.грађ.
АНАЛИТИЧКА ГЕОМЕТРИЈА. - удаљеност између двије тачке. 1 x2
 АНАЛИТИЧКА ГЕОМЕТРИЈА d AB x x y - удаљеност између двије тачке y x x x y s, y y s - координате средишта дужи x x y x, y y - подјела дужи у заданом односу x x x y y y xt, yt - координате тежишта троугла
АНАЛИТИЧКА ГЕОМЕТРИЈА d AB x x y - удаљеност између двије тачке y x x x y s, y y s - координате средишта дужи x x y x, y y - подјела дужи у заданом односу x x x y y y xt, yt - координате тежишта троугла
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
САВРЕМЕНИ АТЛАСИ СРБИЈЕ
 Доступно онлајн на www.gi.sanu.ac.rs Зборник радова Географског института Јован Цвијић САНУ 61(1) (105-114) Оригинални научни рад УДК: 912(497.11) САВРЕМЕНИ АТЛАСИ СРБИЈЕ Мирчета Вемић 1 *, Сузана Ловић*
Доступно онлајн на www.gi.sanu.ac.rs Зборник радова Географског института Јован Цвијић САНУ 61(1) (105-114) Оригинални научни рад УДК: 912(497.11) САВРЕМЕНИ АТЛАСИ СРБИЈЕ Мирчета Вемић 1 *, Сузана Ловић*
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање. 1. вежба
 Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
Универзитет у Београду, Саобраћајни факултет Предмет: Паркирање ОРГАНИЗАЦИЈА ПАРКИРАЛИШТА 1. вежба Место за паркирање (паркинг место) Део простора намењен, технички опремљен и уређен за паркирање једног
ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ
 Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
2.1. Права, дуж, полуправа, раван, полураван
 2.1. Права, дуж, полуправа, раван, полураван Човек је за своје потребе градио куће, школе, путеве и др. Слика 1. Слика 2. Основа тих зграда је често правоугаоник или сложенија фигура (слика 3). Слика 3.
2.1. Права, дуж, полуправа, раван, полураван Човек је за своје потребе градио куће, школе, путеве и др. Слика 1. Слика 2. Основа тих зграда је често правоугаоник или сложенија фигура (слика 3). Слика 3.
b) Израз за угиб дате плоче, ако се користи само први члан реда усвојеног решења, је:
 Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА СВЕСКА LXXXVII - Бр. 1 YEAR 2007 TOME LXXXVII - N о 1
 ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА 2007. СВЕСКА LXXXVII - Бр. 1 YEAR 2007 TOME LXXXVII - N о 1 Оригиналан научни рад UDC 911.3:314 (497.11) БРАНИСЛАВ
ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА 2007. СВЕСКА LXXXVII - Бр. 1 YEAR 2007 TOME LXXXVII - N о 1 Оригиналан научни рад UDC 911.3:314 (497.11) БРАНИСЛАВ
Упутство за избор домаћих задатака
 Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Од површине троугла до одређеног интеграла
 Природно-математички факултет, Универзитет у Нишу, Србија http://www.pmf.i.ac.rs/mii Математика и информатика (4) (5), 49-7 Од површине троугла до одређеног интеграла Жарко Ђурић Париске комуне 4-/8, Врање
Природно-математички факултет, Универзитет у Нишу, Србија http://www.pmf.i.ac.rs/mii Математика и информатика (4) (5), 49-7 Од површине троугла до одређеног интеграла Жарко Ђурић Париске комуне 4-/8, Врање
4. Троугао. (II део) 4.1. Појам подударности. Основна правила подударности троуглова
 4 Троугао (II део) Хилберт Давид, немачки математичар и логичар Велики углед у свету Хилберту је донело дело Основи геометрије (1899), у коме излаже еуклидску геометрију на аксиоматски начин Хилберт Давид
4 Троугао (II део) Хилберт Давид, немачки математичар и логичар Велики углед у свету Хилберту је донело дело Основи геометрије (1899), у коме излаже еуклидску геометрију на аксиоматски начин Хилберт Давид
МАТЕМАТИЧКИ ЛИСТ 2016/17. бр. LI-4
 МАТЕМАТИЧКИ ЛИСТ 06/7. бр. LI-4 РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ III разред. а) 50 4 = 00; б) 0 5 = 650; в) 0 6 = 6; г) 4 = 94; д) 60 : = 0; ђ) 0 : = 40; е) 648 :
МАТЕМАТИЧКИ ЛИСТ 06/7. бр. LI-4 РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ III разред. а) 50 4 = 00; б) 0 5 = 650; в) 0 6 = 6; г) 4 = 94; д) 60 : = 0; ђ) 0 : = 40; е) 648 :
Скрипта ријешених задатака са квалификационих испита 2010/11 г.
 Скрипта ријешених задатака са квалификационих испита 00/ г Универзитет у Бањој Луци Електротехнички факултет Др Момир Ћелић Др Зоран Митровић Иван-Вања Бороја Садржај Квалификациони испит одржан 9 јуна
Скрипта ријешених задатака са квалификационих испита 00/ г Универзитет у Бањој Луци Електротехнички факултет Др Момир Ћелић Др Зоран Митровић Иван-Вања Бороја Садржај Квалификациони испит одржан 9 јуна
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 016/017. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 016/017. година ТЕСТ МАТЕМАТИКА
ПЛАН ДЕТАЉНЕ РЕГУЛАЦИЈЕ
 ПЛАН ДЕТАЉНЕ РЕГУЛАЦИЈЕ В Е Т Р О П А Р К И Н Ђ И Ј А НА ЛОКАЦИЈИ БЕШКА КРЧЕДИН У ОПШТИНИ ИНЂИЈА Носилац израде Плана детаљне регулације: Д и р е к т о р : ЗЛАТКО ГРКОВИЋ дипл.инж.арх. 1 Носилац израде
ПЛАН ДЕТАЉНЕ РЕГУЛАЦИЈЕ В Е Т Р О П А Р К И Н Ђ И Ј А НА ЛОКАЦИЈИ БЕШКА КРЧЕДИН У ОПШТИНИ ИНЂИЈА Носилац израде Плана детаљне регулације: Д и р е к т о р : ЗЛАТКО ГРКОВИЋ дипл.инж.арх. 1 Носилац израде
КЛИМАТСКЕ КАРАКТЕРИСТИКЕ ФРУШКЕ ГОРЕ
 UDK 630*111.82(497.113 Fruška gora) Оригинални научни рад КЛИМАТСКЕ КАРАКТЕРИСТИКЕ ФРУШКЕ ГОРЕ ВИОЛЕТА БАБИЋ 1 Извод: У раду су приказане климатске карактеристике Фрушкe горе, на основу података са климатолошких
UDK 630*111.82(497.113 Fruška gora) Оригинални научни рад КЛИМАТСКЕ КАРАКТЕРИСТИКЕ ФРУШКЕ ГОРЕ ВИОЛЕТА БАБИЋ 1 Извод: У раду су приказане климатске карактеристике Фрушкe горе, на основу података са климатолошких
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c
 6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
6. ЛИНЕАРНА ДИОФАНТОВА ЈЕДНАЧИНА ах + by = c Ако су а, b и с цели бројеви и аb 0, онда се линеарна једначина ах + bу = с, при чему су х и у цели бројеви, назива линеарна Диофантова једначина. Очигледно
TAЧКАСТА НАЕЛЕКТРИСАЊА
 TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
Динамика. Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе:
 Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Математика Тест 3 Кључ за оцењивање
 Математика Тест 3 Кључ за оцењивање ОПШТЕ УПУТСТВО ЗА ОЦЕЊИВАЊЕ Кључ за оцењивање дефинише начин на који се оцењује сваки поједини задатак. У општим упутствима за оцењивање дефинисане су оне ситуације
Математика Тест 3 Кључ за оцењивање ОПШТЕ УПУТСТВО ЗА ОЦЕЊИВАЊЕ Кључ за оцењивање дефинише начин на који се оцењује сваки поједини задатак. У општим упутствима за оцењивање дефинисане су оне ситуације
ЗАВРШНИ РАД КЛИНИЧКА МЕДИЦИНА 5. школска 2016/2017. ШЕСТА ГОДИНА СТУДИЈА
 ЗАВРШНИ РАД КЛИНИЧКА МЕДИЦИНА 5 ШЕСТА ГОДИНА СТУДИЈА школска 2016/2017. Предмет: ЗАВРШНИ РАД Предмет се вреднује са 6 ЕСПБ. НАСТАВНИЦИ И САРАДНИЦИ: РБ Име и презиме Email адреса звање 1. Јасмина Кнежевић
ЗАВРШНИ РАД КЛИНИЧКА МЕДИЦИНА 5 ШЕСТА ГОДИНА СТУДИЈА школска 2016/2017. Предмет: ЗАВРШНИ РАД Предмет се вреднује са 6 ЕСПБ. НАСТАВНИЦИ И САРАДНИЦИ: РБ Име и презиме Email адреса звање 1. Јасмина Кнежевић
КОМБИНОВАНИ ТЕСТ из природних и друштвених наука
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2016/2017. година
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2016/2017. година
Слика бр.1 Површина лежишта
 . Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
. Конвенционалне методе процене.. Параметри за процену рудних резерви... Површина лежишта Површине лежишта ограничавају се спајањем тачака у којима је истражним радом утврђен контакт руде са јаловином.
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ
 ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
Слика 1 Ако се са RFe отпорника, онда су ова два температурно зависна отпорника везана на ред, па је укупна отпорност,
 Температурно стабилан отпорник састоји се од два једнака цилиндрична дела начињена од различитих материјала (гвожђе и графит) У ком односу стоје отпорности ова два дела отпорника ако се претпостави да
Температурно стабилан отпорник састоји се од два једнака цилиндрична дела начињена од различитих материјала (гвожђе и графит) У ком односу стоје отпорности ова два дела отпорника ако се претпостави да
РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА
 РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА 006. Задатак. Одредити вредност израза: а) : за, и 69 0, ; б) 9 а) Како је за 0 и 0 дати израз идентички једнак изразу,, : : то је за дате вредности,
РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА 006. Задатак. Одредити вредност израза: а) : за, и 69 0, ; б) 9 а) Како је за 0 и 0 дати израз идентички једнак изразу,, : : то је за дате вредности,
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Факултет организационих наука Центар за пословно одлучивање. PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation)
 Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Факултет организационих наука Центар за пословно одлучивање PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) Студија случаја D-Sight Консултантске услуге за Изградња брзе пруге
Решења задатака са првог колоквиjума из Математике 1Б II група задатака
 Решења задатака са првог колоквиjума из Математике Б II група задатака Пре самих решења, само да напоменем да су решења детаљно исписана у нади да ће помоћи студентима у даљоj припреми испита, као и да
Решења задатака са првог колоквиjума из Математике Б II група задатака Пре самих решења, само да напоменем да су решења детаљно исписана у нади да ће помоћи студентима у даљоj припреми испита, као и да
Испитвање тока функције
 Милош Станић Техничка школа Ужицe 7/8 Испитвање тока функције Испитивање тока функције y f подразумева да се аналитичким путем дође до сазнања о понашању функције, као и њеним значајним тачкама у координантном
Милош Станић Техничка школа Ужицe 7/8 Испитвање тока функције Испитивање тока функције y f подразумева да се аналитичким путем дође до сазнања о понашању функције, као и њеним значајним тачкама у координантном
МАСТЕР РАД УНИВЕРЗИТЕТ У БЕОГРАДУ МАТЕМАТИЧКИ ФАКУЛТЕТ. Тема: ГОРЊА И ДОЊА ГРАНИЧНА ВРЕДНОСТ НИЗА И НИЗА СКУПОВА И ЊИХОВЕ ПРИМЕНЕ У РЕЛНОЈ АНАЛИЗИ
 УНИВЕРЗИТЕТ У БЕОГРАДУ МАТЕМАТИЧКИ ФАКУЛТЕТ МАСТЕР РАД Тема: ГОРЊА И ДОЊА ГРАНИЧНА ВРЕДНОСТ НИЗА И НИЗА СКУПОВА И ЊИХОВЕ ПРИМЕНЕ У РЕЛНОЈ АНАЛИЗИ МЕНТОР: КАНДИДАТ: Проф. др Драгољуб Кечкић Милинко Миловић
УНИВЕРЗИТЕТ У БЕОГРАДУ МАТЕМАТИЧКИ ФАКУЛТЕТ МАСТЕР РАД Тема: ГОРЊА И ДОЊА ГРАНИЧНА ВРЕДНОСТ НИЗА И НИЗА СКУПОВА И ЊИХОВЕ ПРИМЕНЕ У РЕЛНОЈ АНАЛИЗИ МЕНТОР: КАНДИДАТ: Проф. др Драгољуб Кечкић Милинко Миловић
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
УПУТСТВО ЗА ОДРЕЂИВАЊЕ ВРСТЕ ДОКУМЕНАТА КОЈЕ ИЗРАЂУЈЕ ОПЕРАТЕР СЕВЕСО ПОСТРОЈЕЊА. август 2010.
 УПУТСТВО ЗА ОДРЕЂИВАЊЕ ВРСТЕ ДОКУМЕНАТА КОЈЕ ИЗРАЂУЈЕ ОПЕРАТЕР СЕВЕСО ПОСТРОЈЕЊА август 2010. I. УВОД Сврха овог Упутства је да помогне оператерима који управљају опасним материјама, како да одреде да
УПУТСТВО ЗА ОДРЕЂИВАЊЕ ВРСТЕ ДОКУМЕНАТА КОЈЕ ИЗРАЂУЈЕ ОПЕРАТЕР СЕВЕСО ПОСТРОЈЕЊА август 2010. I. УВОД Сврха овог Упутства је да помогне оператерима који управљају опасним материјама, како да одреде да
МАТЕМАТИЧКИ ЛИСТ 2014/15. бр. XLIX-4
 МАТЕМАТИЧКИ ЛИСТ 0/5. бр. XLIX- РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ III разред. а) 70 5 = 50; б) 0 = 80; в) 0 = 9; г) 5 = 850; д) 60 : = 0; ђ) 0 : 8 = 0; е) 86 : = ;
МАТЕМАТИЧКИ ЛИСТ 0/5. бр. XLIX- РЕЗУЛТАТИ, УПУТСТВА ИЛИ РЕШЕЊА ЗАДАТАКА ИЗ РУБРИКЕ ЗАДАЦИ ИЗ МАТЕМАТИКЕ III разред. а) 70 5 = 50; б) 0 = 80; в) 0 = 9; г) 5 = 850; д) 60 : = 0; ђ) 0 : 8 = 0; е) 86 : = ;
4.4. Паралелне праве, сечица. Углови које оне одређују. Углови са паралелним крацима
 50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
50. Нацртај било које унакрсне углове. Преношењем утврди однос унакрсних углова. Какво тврђење из тога следи? 51. Нацртај угао чија је мера 60, а затим нацртај њему унакрсни угао. Колика је мера тог угла?
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 2004
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
Могућности и планови ЕПС на пољу напонско реактивне подршке. Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије
 Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
6.7. Делтоид. Делтоид је четвороугао који има два пара једнаких суседних страница.
 91.*Конструиши трапез у размери 1:200, ако је дато: = 14 m, = 6 m, = 8 m и β = 60. 92.*Ливада има облик трапеза. Нацртај је у размери 1:2000, ако су јој основице 140 m и 95 m, један крак 80 m, и висина
91.*Конструиши трапез у размери 1:200, ако је дато: = 14 m, = 6 m, = 8 m и β = 60. 92.*Ливада има облик трапеза. Нацртај је у размери 1:2000, ако су јој основице 140 m и 95 m, један крак 80 m, и висина
РЕЉЕФНЕ КАРАКТЕРИСТИКЕ ГОЧА И ПОДГОРИНЕ
 Зборник радова Департмана за географију, туризам и хотелијерство 36/2007. Оригинални научни рад UDK 551.4.03 (497.11) РЕЉЕФНЕ КАРАКТЕРИСТИКЕ ГОЧА И ПОДГОРИНЕ CHARACTERISTICS OF RELIEF OF GOC MOUNTAIN AND
Зборник радова Департмана за географију, туризам и хотелијерство 36/2007. Оригинални научни рад UDK 551.4.03 (497.11) РЕЉЕФНЕ КАРАКТЕРИСТИКЕ ГОЧА И ПОДГОРИНЕ CHARACTERISTICS OF RELIEF OF GOC MOUNTAIN AND
Мониторинг квалитета ваздуха Града Новог Сада у години
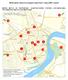 Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
Хомогена диференцијална једначина је она која може да се напише у облику: = t( x)
 ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ОЦЕНА КОНКУРЕНТНОСТИ ТУРИСТИЧКИХ ДЕСТИНАЦИЈА НА ПРИМЕРУ КЉУЧНИХ РЕСУРСА ГРАДОВА У СРБИЈИ
 Зборник радова Географски факултет Универзитета у Београду 62 (145-174) Оригинални научни рад УДК 338.487(497.11) ОЦЕНА КОНКУРЕНТНОСТИ ТУРИСТИЧКИХ ДЕСТИНАЦИЈА НА ПРИМЕРУ КЉУЧНИХ РЕСУРСА ГРАДОВА У СРБИЈИ
Зборник радова Географски факултет Универзитета у Београду 62 (145-174) Оригинални научни рад УДК 338.487(497.11) ОЦЕНА КОНКУРЕНТНОСТИ ТУРИСТИЧКИХ ДЕСТИНАЦИЈА НА ПРИМЕРУ КЉУЧНИХ РЕСУРСА ГРАДОВА У СРБИЈИ
Разлика потенцијала није исто што и потенцијална енергија. V = V B V A = PE / q
 Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
Key words: river basin, characteristics, terminology, meaning, use.
 Мирослав Оцокољић Драгана Милијашевић 1 ЕЛЕМЕНТИ РЕЧНОГ СЛИВА ТЕРМИНОЛОГИЈА ИЗРАЗА, ЗНАЧЕЊЕ И УПОТРЕБА Извод: У раду су обрађене и коментарисане бројне физичко географске и друге карактеристике речне мреже
Мирослав Оцокољић Драгана Милијашевић 1 ЕЛЕМЕНТИ РЕЧНОГ СЛИВА ТЕРМИНОЛОГИЈА ИЗРАЗА, ЗНАЧЕЊЕ И УПОТРЕБА Извод: У раду су обрађене и коментарисане бројне физичко географске и друге карактеристике речне мреже
