Radni materijal 17 PRIZME
|
|
|
- Κλείτος Γαλάνη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Radni materijal 17 PRIZME Odreži i zalijepi slike u bilježnicu, izvedi formule za oplošje i obujam, označi i izvedi formule za plošne i prostorne dijagonale. Oplošje OBP = + Volumen ili obujam V = Bv slika 1 KOCKA slika KVADAR slika PRAVILNA ŠESTEROSTRANA PRIZMA slika 4 TROSTRANA PRIZMA
2 Radni materijal 15 PRIZME zadaci za vježbu 1. Oplošje kocke iznosi 18 cm. Izračunaj njen brid, obujam, duljinu dijagonale baze, prostornu dijagonalu i površinu dijagonalnog presjeka.. Kocki s dijagonalom baze d = cm uveća se brid za cm. Za koliko će se povećati oplošje, a za koliko obujam?. Kocka brida 8.5 cm je od bakra gustoće ρ = 8.8 g/ cm, a kocka brida 9 cm je od čelika gustoće ρ = 7.8 g/ cm. Koja ima veću masu i za koliko? 4. Izračunaj prostornu dijagonalu, oplošje i obujam kvadra kojem je brid c = 4cm, dijagonala osnovice 10 cm, a bridovi osnovice se odnose kao :4. 5. Izračunaj oplošje i obujam kvadra kojem je prostorna dijagonala 7 cm, a bridovi se odnose kao 4:8:1. 6. Dijagonala osnovke kvadra jednaka je visini i ima duljinu 5 cm. Osnovni bridovi se odnose kao :4. Izračunaj površine sva dijagonalna presjeka. 7. Dijagonalni presjek kvadra bridom b je kvadrat površine 6 cm, a duljina brida a je 4 cm. Izračunaj oplošje i obujam. 8. Izračunaj obujam trostrane prizme kojoj su bridovi osnovice 15 cm, 8 cm i 41 cm i oplošje 445 cm. 9. Izračunaj oplošje trostrane prizme kojoj su bridovi osnovice 5 cm, 7 cm i 8 cm i obujam 100 cm. 10. Izračunaj obujam pravilne trostrane prizme kojoj se osnovni brid i visina odnose kao 1:, a pobočje ima površinu P= 7cm Izračunaj osnovni brid pravilne trostrane prizme ako je O= cm i v= 5cm. 1. Izračunaj nepoznate elemente pravilne trostrane prizme kojoj je oplošje O= 6 cm i pobočje P= 18 cm. 1. Osnovni brid pravilne trostrane prizme odnosi se prema visini kao :, a obujam je 4 cm. Izračunaj oplošje. 14. Oplošje pravilne trostrane prizme iznosi + 18, a osnovni brid se prema visini odnosi kao :. Izračunaj obujam. 15. Izračunaj visinu i obujam pravilne četverostrane prizme osnovnog brida 18 cm i oplošja 160 cm. 16. Dijagonala baze pravilne četverostrane prizme ima duljinu 0 cm, a prostorna dijagonala 5 cm. Izračunaj obujam i oplošje. 17. Površina dijagonalnog presjeka pravilne četverostrane prizme dijagonalom baze je 7 cm. Izračunaj oplošje i obujam ako je dijagonala baze jednaka visini prizme. 18. Izračunaj oplošje i obujam pravilne šesterostrane prizme kojoj je visina 10 5 cm, a veća prostorna dijagonala je 0 cm. 19. Volumen pravilne šesterostrane prizme je 75 cm, a pobočni brid je dva puta veći od osnovnog. Izračunaj oplošje, dijagonale baze i prostorne dijagonale. 0. Površina dijagonalnog presjeka većom dijagonalom baze je 160 cm, a osnovni brid je duljine 8 cm. Izračunaj oplošje i obujam.
3 Radni materijal 18 PIRAMIDE Odreži i zalijepi slike u bilježnicu, izvedi formule za oplošje i obujam. Označi i izvedi formule za visinu piramide i visinu pobočke te kutove α i β. Oplošje OBP = + Volumen ili obujam V = Bv slika 1 PRAVILNA ČETVEROSTRANA PIRAMIDA slika PRAVILNA TROSTRANA PIRAMIDA slika PRAVILNA ŠESTEROSTRANA PIRAMIDA
4 Radni materijal 19 KRNJE PIRAMIDE Odreži i zalijepi slike u bilježnicu, izvedi formule za oplošje i obujam. Označi i izvedi formule za visinu piramide i visinu pobočke. Oplošje OBbP Volumen ili obujam = + + V = ( B+ Bb + b) v slika 1 PRAVILNA ČETVEROSTRANA KRNJA PIRAMIDA slika PRAVILNA TROSTRANA KRNJA PIRAMIDA
5 Radni materijal 16 PIRAMIDE zadaci za vježbu 1. Izračunaj oplošje i obujam pravilne trostrane piramide kojoj je visina pobočke u = pobočni brid b = 9.. Izračunaj oplošje i obujam pravilne trostrane piramide kojoj je kut pobočke i baze α = 45, a visina duljine v =.. Odredi oplošje i obujam pravilne trostrane piramide kojoj je visina 1 cm, a visina pobočke 15 cm. 4. Ako je oplošje pravilne trostrane piramide 4 i visina pobočke u =, koliki je obujam? 5. Odredi oplošje i obujam pravilne četverostrane piramide kojoj je osnovni brid 48 cm i visina pobočke 5 cm. 6. Ako je obujam pravilne četverostrane piramide , a osnovni brid 0, oplošje je? 7. Ako je obujam pravilne četverostrane piramide 6, a visina pobočke je jednaka osnovnom bridu, kolika je duljina pobočnog brida? 8. Površina pobočja pravilne četverostrane piramide je 60 cm, a osnovni brid se prema visini pobočke odnosi kao 4 : 5. Izračunaj obujam. 9. Izračunaj obujam i oplošje pravilne četverostrane piramide ako je osnovni brid 1 cm, a kut pobočke i baze Pobočni brid pravilne šesterostrane piramide tri puta je veći od osnovnog brida, a visina ima duljinu 4. Izračunaj oplošje i obujam. 11. Odredi oplošje i obujam pravilne šesterostrane piramide kojoj je osnovni brid cm, a visina pobočke 19 cm. 1. Površina pobočja pravilne šesterostrane piramide iznosi 16 cm, a osnovni se brid prema visini pobočke odnosi kao :. Odredi oplošje i obujam, 1. Visina pravilne šesterostrane piramide iznosi 1.5 cm, a visina pobočke je jednaka osnovnom bridu. Odredi duljinu pobočnog brida, oplošje i obujam. 14. Visina pravilne šesterostrane piramide se prema bočnom bridu odnosi kao 1: 5, a osnovni brid je za 1.5 cm veći od visine. Izračunaj osnovni i bočni brid te obje visine. 15. Odredi oplošje pravilne šesterostrane piramide kojoj je bočni brid dva puta dulji od osnovnog brida. 16. Odredi volumen pravile četverostrane krnje piramide ako se osnovni bridovi i visina pobočke odnose kao 4 : 1 :, a oplošje je 148 cm. 17. Odredi oplošje i volumen pravile četverostrane krnje piramide ako su: a. Duljine osnovnih bridova 9 cm i cm, a visina pobočke 5 cm b. Duljine osnovnog brida 1 cm i pobočnog brida 10 cm, a visina pobočke 8 cm 18. Odredi oplošje i volumen pravile trostrane krnje piramide ako su: a. Duljine osnovnih bridova 5 cm i cm, a duljina visine 4 cm b. Duljine osnovnog brida 15 cm i pobočnog brida 0 cm, a visina 16 cm 19. Zbroj osnovnih bridova pravilne trostrane krnje piramide iznosi 10 cm. Ako je bočni brid 58 cm, a visina pobočke 4 cm, koliko je oplošje? 0. Zbroj površina baza pravilne trostrane krnje piramide iznosi 9, a razlika polumjera njima upisanih kružnica je. Izračunaj osnovne bridove. 7, a
6 Radni materijal 0 VALJAK I STOŽAC Odreži i zalijepi slike u bilježnicu, izvedi formule za oplošje i obujam. slika 1 VALJAK slika KOSI VALJAK slika STOŽAC slika 4 KOSI STOŽAC slika 5 KRNJI STOŽAC slika 6 KOSI KRNJI STOŽAC
7 Radni materijal 1 Valjak, stožac i kugla zadaci za vježbu 1. Izračunaj promjer baze i obujam valjka visine 1 cm i oplošja 16π cm.. Promjer baze valjka jednak je visini (jednakostranični valjak), a površina plašta je 64π. Izračunaj oplošje i volumen.. U valjak oplošja 8π cm upisana je kvadratska prizma. Odredi volumen prizme ako je visina valjka za 1 veća od promjera baze. 4. U kocku osnovnog brida a upisan je i opisan valjak. Kolika je razlika volumena opisanog i upisanog valjka? 5. Odredi oplošje i obujam uspravnog stošca kojem je osni presjek jednakokračan trokut površine 6 cm i jednim kutom Izračunaj volumen stošca kojemu je polumjer jednak visini, a oplošje je 5π ( 1+ ) cm. 7. Volumen stošca je 9π cm. Ako je polumjer baze stošca jednak visini, koliko je oplošje? 8. Odredi oplošje uspravnog stošca visine 1 cm i obujma 4π cm. Koliki je središnji kut u plaštu stošca? 9. Polumjer baze stošca jednak je visini, a oplošje iznosi O= 16π ( 1+ ) cm. Izračunaj obujam 10. Površina plašta stošca iznosi 60π cm. Polumjer baze stošca se prema izvodnici odnosi :5. Izračunaj oplošje i volumen. 11. U valjkastoj posudi polumjera 1 cm i visine 40 cm nalazi se kugla polumjera 1 cm potpuno pokrivena vodom. Za koliko se smanji razina vode kada se izvadi kugla? 1. U jednakostraničan valjak upisana je kugla. Kako se odnose oplošja valjka i kugle? 1. Kolika je visina jednakostraničnog valjka koji je dobiven od željezne kugle volumena 100π cm?
8 VALJAK, STOŽAC I KUGLA zadaci za vježbu RM 1. Izračunaj promjer baze i obujam valjka visine 1 cm i oplošja 16π cm.. Promjer baze valjka jednak je visini (jednakostranični valjak), a površina plašta je 64π. Izračunaj oplošje i volumen.. U valjak oplošja 8π cm upisana je kvadratska prizma. Odredi volumen prizme ako je visina valjka za 1 veća od promjera baze. 4. Odredi oplošje i obujam uspravnog stošca kojem je osni presjek jednakokračan trokut površine 6 cm i jednim kutom Izračunaj volumen stošca kojemu je polumjer jednak visini, a oplošje je 5π ( 1+ ) cm. 6. Volumen stošca je 9π cm. Ako je polumjer baze stošca jednak visini, koliko je oplošje? 7. Odredi oplošje uspravnog stošca visine 1 cm i obujma 4π cm. Koliki je središnji kut u plaštu stošca? 8. Površina plašta stošca iznosi 60π cm. Polumjer baze stošca se prema izvodnici odnosi :5. Izračunaj oplošje i volumen. 9. U valjkastoj posudi polumjera 1 cm i visine 40 cm nalazi se kugla polumjera 1 cm potpuno pokrivena vodom. Za koliko se smanji razina vode kada se izvadi kugla? 10. U jednakostraničan valjak upisana je kugla. Kako se odnose oplošja valjka i kugle? 11. Kolika je visina jednakostraničnog valjka koji je dobiven od željezne kugle volumena 100π cm? 1. Kolika je masa zraka u plasteniku u obliku šatora ako je gustoća zraka 1.9 kg/ m? 1. Izračunaj obujam i oplošje tijela na slikama. 14. Ako je duljina brida kocke jednak a, odredi oplošje i obujam poliedara na slici.
9 RM priprema za ispit znanja Poliedri i rotacijska tijela 1. Duljina prostorne dijagonale kocke je 5cm. Odredi oplošje te kocke. (Rj: 50cm ). Duljine bridova kvadra su u omjeru 1::. Ako je obujam kvadra 16cm koliko je oplošje kvadra? (Rj: O= 198cm). Površina baze uspravne šesterostrane prizme je 8cm. Ako je visina prizme cm, izračunaj oplošje prizme. (Rj: O= cm ) 4. Najveći dijagonalni presjek pravilne šesterostrane prizme je kvadrat površine 6cm. Izračunaj obujam te prizme. 5. Odredi obujam trostrane piramide duljina osnovnih bridova 5cm, cm i 5cm, te duljine bočnog brida 5cm. 6. Uspravna pravilna četverostrana piramida ima obujamcm. Duljina visine jednaka log x 1 + log x = 1. Izračunaj oplošje je pozitivnom rješenju jednadžbe ( ) ( ) piramide. (Rj: 6 6 vcma O cm =, = 4, = (84) + ) 7. Krnja piramida obujma 74dm ima površine osnovki B1 = 16dm i B = 9dm. Izračunaj duljinu visine piramide. (Rj: 6dm) 8. Oplošje uspravnog valjka je 84π cm, a visina mu je za 5 cm veća od promjera osnovice. Odredi plašt i obujam valjka. (Rj: P = 66 πcm, V = 99πcm) 9. Pravokutnik stranica 10 i 15 rotira oko kraće i duže stranice. Odredi oplošje i obujam tih rotacijskih tijela. ( V1 =50π cm, O1 =750π cm, V =1500π cm, O =500π cm ) 10. Trokut stranica 1,14 i 15 rotira oko srednje stranice. Odredi obujam tako dobivenog rotacijskog tijela. ( V =19π cm ) RM priprema za ispit znanja Poliedri i rotacijska tijela 1. Duljina prostorne dijagonale kocke je 5cm. Odredi oplošje te kocke. (Rj: 50cm ). Duljine bridova kvadra su u omjeru 1::. Ako je obujam kvadra 16cm koliko je oplošje kvadra? (Rj: O= 198cm). Površina baze uspravne šesterostrane prizme je 8cm. Ako je visina prizme cm, izračunaj oplošje prizme. (Rj: O= cm) 4. Najveći dijagonalni presjek pravilne šesterostrane prizme je kvadrat površine 6cm. Izračunaj obujam te prizme. 5. Odredi obujam trostrane piramide duljina osnovnih bridova 5cm, cm i 5cm, te duljine bočnog brida 5cm. 6. Uspravna pravilna četverostrana piramida ima obujamcm. Duljina visine jednaka log x 1 + log x = 1. Izračunaj oplošje je pozitivnom rješenju jednadžbe ( ) ( ) piramide. (Rj: 6 6 vcma O cm =, = 4, = (84) + ) 7. Krnja piramida obujma 74dm ima površine osnovki B1 = 16dm i B = 9dm. Izračunaj duljinu visine piramide. (Rj: 6dm) 8. Oplošje uspravnog valjka je 84π cm, a visina mu je za 5 cm veća od promjera osnovice. Odredi plašt i obujam valjka. (Rj: P= 66 πcm, V = 99πcm) 9. Pravokutnik stranica 10 i 15 rotira oko kraće i duže stranice. Odredi oplošje i obujam tih rotacijskih tijela. ( V1 =50π cm, O1 =750π cm, V =1500π cm, O =500π cm ) 10. Trokut stranica 1,14 i 15 rotira oko srednje stranice. Odredi obujam tako dobivenog rotacijskog tijela. ( V =19π cm )
10 Stereometrija Priprema za ispit znanja RM Osnovni bridovi trostrane prizme imaju duljine 6cm, 8cm i 0cm. Ako je oplošje prizme 151 cm, koliki je obujam?. Bridovi četverostrane prizme odnose se kao : 4 : 1, a prostorna dijagonala iznosi 6 cm. Izračunaj oplošje i obujam kvadra.. Odredi obujam pravilne četverostrane piramide osnovnog brida 10 cm i kuta pobočke i baze Odredi oplošje pravilne trostrane piramide pobočnog brida 9cm i visine 6 cm. 5. Odredi oplošje i obujam valjka ako je opseg osnog presjeka 0 cm, a površina 16 cm 6. U jednakostraničan valjak upisana je kugla. Kako se odnose oplošja valjka i kugle? 7. Odredi oplošje uspravnog stošca visine 1 cm i obujma 4π cm. koliki je središnji kut u plaštu stošca? 8. U valjkastoj posudi polumjera 1 cm i visine 40 cm nalazi se kugla polumjera 1 cm potpuno pokrivena vodom. Za koliko se smanji razina vode kada se izvadi kugla? 9. Željeznu kuglu obujma1000 π cm pretopimo u jednakostraničan valjak. U kojem su omjeru oplošja kugle i valjka? 10. U kocku osnovnog brida a upisan je i opisan valjak. Kolika je razlika volumena opisanog i upisanog valjka? 11. Izračunaj promjer baze i obujam valjka visine 1 cm i oplošja 16π cm. 1. Odredi oplošje i obujam uspravnog stošca kojem je osni presjek jednakokračan trokut površine 6 cm i jednim kutem Površina pobočaka uspravne trostrane prizme jednake su 9, 10 i 17 cm, a površina osnovke iznosi 4 cm. Koliki je obujam ove prizme? 14. Površina dijagonalnog presjeka većom dijagonalom baze pravilne šesterostrane prizme iznosi 160 cm, a osnovni je brid duljine 8 cm. Izračunaj oplošje.
11 STEREOMETRIJA ZADACI SA PRIJEMNIH ISPITA 1.Kocka ABCDA 1 B 1 C 1 D 1 je stranice a. Zapremina piramide čija su temena DCA 1 D 1 isnosi:.dužina ivice kocke je 1, a rastojanje temena B od dijagonale AC 1 jednako je:.zapremina paralelopipeda čije su sve strane rombovi stranice a i <60 jednaka je: 4.Osnova piramide je jednakostranični trougao stranice a, a projekcija vrha je težište.ako bočne strane grade ugao od 60, površina piramide je: 5.U piramidi ABCD međusobno normalne strane ABC i ABD su jednakostranični trouglovi. Ako je AB=, tada je površina te piramide jednaka: 6.Ako zapremina pravilnog tetraedra iznosi 7, onda je njegova visina: 7.Jednakokraki trapez čija je visina 1, krak 1 a srednja linija 15, obrće se oko svoje manje osnovice. Zapremina dobijenog obrtnog tele je: 8.Ugao između izvodnice i visine prave kupe je 60, a razlika njihovih dužina je m. Zapremina kupe je: 9.Poluprečnik osnove prave kupe je r, a dve uzajamno normalne izvodnice dele omotač re kupe u odnosu 1:. Zapremina te kupe je: 10.Omotač prave kupe je kružni isečak površine M=10π i centralnim uglom α=6.zapremina te kupe je: 11.U pravu kupu poluprečnika osnove r i visine H=r upisana je kocka. Odnos zapremina kupe i kocke je: 1.U pravu kupu poluprečnika osnove r=5cm i visine H=1cm upisana je lopta. Zapremina lopte je: 1.Izvodnica prave zarubljene kupe je s=5cm, a poluprečnici osnova r=5cm i r1=cm.u kupu je upisana pravilna četvorostrana zarubljena piramida.zapremina piramide je: 14.Dužina dijagonale kvadrata je cm. Zapremina tog kvadra ( u cm )je: cm, a dužine dijagonala njegovih bočmih strana su 5cm i A) 4 B)0 C)8 D)0 E)0 15.Dužina dijagonale kvadra je 6cm, a njegova površina je 7cm. Zbir dužina svih ivica u kvadru (u cm) je: A)16 B)18 C)0 D)1 E)4 16.Četvorostrana piramida čija je osnova kvadrat stranice 8cm ima međusobno jednake bočne ivice. Ako je visina piramide 7cm, onda je dužina bočne ivice (u cm) jednaka: A)5 B)9 C)6 D)8 E)10 17.Zapremina pravilne četvorostrane piramide je 4 cm. Ako bočna ivica piramide gradi ugao od 45 sa osnovom piramide, onda je dužina bočne ivice (u cm) jednaka: A) B) C) D) E) 18.Osnova prave piramide je kvadrat čija je stranica dužine 4 dm, a bočne strane su joj jednakostranični trouglovi. Zapremina te piramide (u dm ) je: A)9 B)8 C) D) E)
12 19.Zapremina pravilne četvorostrane jednakoivične piramide, čije su sve ivice dužine dm, jednaka je (u dm ): A) B)4 C) D) E) 0.Zapremina pravilne trostrane piramide osnovne ivice cm i visine 4cm je (u cm ): A)1 B)6 C) D) E)7 1.Osnova prave piramide je jednakostranični trougao(visina piramide prolazi kroz ortocentar trougla).ako je dužina bočne ivice piramide 5cm, a dužina visine 4cm, zapremina piramide je (u cm ): A)9 B)18 C)6 D)16 E)8.Ako je dužina ivice jednakoivičnog tetraedra jednaka naspramnih ivica tog tetraedra (u cm) jednako: A) B) C) D)1 E) cm, onda je rastojanje između središta.dužina ivice pravilnog tetraedra je 4cm. Površina preseka tetraedra sa ravni koja sadrži jednu njegovu ivicu i sredinu naspramne ivice je: A)4 B) C) D)9 4.Ako je φ ugao diedra pravilnog tetraedra, onda je: A)sinφ= B)cosφ= C)cosφ= D) sinφ= E) cosφ= 5.Osnova prave četvorostrane prizme je romb površine 1m, a površine njenih dijagonalnih preseka su m i 6m. Površina prizme je (u m ): A) B) C) D) E) 6.Bočne ivice pravilne zarubljene trostrane piramide nagnute su prema osnovi pod uglom od 60, a ivice osnove su 6 i. Zapremina zarubljene piramide je: A) B) C) D) E) 7Dijagonala kvadra je 44cm, a njegove ivice odnose se kao :6:9.Zapremina kvadra je (u cm ): A)108 B)4 C)864 D)888 E)691 8.Osnova piramide je trougao sa stranicama 1cm, 14cm i 15cm, a svaka bočna strana piramide nagnuta je pod ulom od 60 prema ravni osnove. Površina piramide je (u cm ): A)504 B)40 C)10 D)5 E)5 9.Osni presek pravog valjka je pravougaonik čija je dijagonala 5m.Ako je poluprečnik osnove valjka za 1m manji od njegove visine, onda je zapremina tog valjka (u m ): A)16π B)1π C)14π D)0π E)18π 0.Omotač pravog valjka rasečen duš jedne izvodnice i razvijen u ravni daje kvadrat stranice dužine 10cm. Zapremina tog valjka (u cm ) je: A) B)50π C)00π D) E)15π 1.U prav valjak poluprečnika osnove m i visine 4m upisana je pravilna četvorostrana prizma, tako da osnove prizme pripadaju osnovama valjka. Površina te prizme je (u m ): A)0 B)16+ C)16 D)16+ E)16.Ugao između izvodnice i visine prave kupe je 60.Ako je izvodnica za 1m duža od visine zapremina date kupe iznosi (u cm ): A)π B) C) D) π E)π.Površina prave kupe je četiri puta veća od površine njene osnove.odnos visine i poluprečnika osnove date kupe jednak je: A):1 B)4:1 C)4: D)4: E) :1
13 4.Površina prave kružne kupe je 16πcm, a izvodnica je za 6cm duža od poluprečnika osnove. Zapremina kupe je (u cm ): A)40π B)76π C)4π D)60π E)64π 5.U datu pravu kupu upisana je lopta, pri čemu je odnos visine kupe i poluprečnika lopte 4:1.Odnos zapremina kupe i lopte je: A):1 B):1 C): D)4: E)8:5 6.Dve paralelne ravni čije je međusobno rastojanje dm, seku sferu poluprečnika Rdm po dvema kružnim linijama, poluprečnika r1=6dm i r=8dm, pri čemu centar sfere nije između tih ravni. Tada je poluprečnik R jednak ( u dm): A)6 B)9 C)10 D)1 E)16 7.Dužine osnovica jednakokrakog trapeza su 16cm i 4cm, a dužina kraka 10cm.Zapremina tela koje nastaje rotacijom tog trapeza oko duže osnovice je (u cm ): A)640π B)84π C)56π D)51π E)104π 8.Jednakokraki trapez sa osnovicama cm i 6cm i površinom 48cm, rotira oko duži koja spaja središta osnovica. Zapremina dobijenog tela iznosi ( u cm ): A)6π B)5π C)104π D)08π E)64π 9Ako je površina lopte 4π, njena zapremina je: A) B)88π C)916π D) E)97π 40.U pravu kupu poluprečnika osnove 5cm i visine 1cm upisana je lopta.površina lopte je (u cm ): A) B) C) D) E) 41.Osnova pravilne šestostrane piramide upisana je u donju osnovu pravog valjka, a njen vrh se poklapa sa centrom gornje osnove.ako je visina piramide 6cm, a njena zapremina 1 cm, površina valjka je (u cm ): A)16π B)0π C)4π D)π E)4π 4.Trapez rotira jednom oko veće, a drugi put ooko svoje manje osnovice.zapremine dobijenih obrtnih tela odnose se kao :4. Razmera osnovica trapeza je: A)7: B)4: C):1 C):1 E)5: 4.Od polukruga poluprečnika r sačinjen je omotač kupe.zapremina te kupe je: A) B) C) D) E) 44.Metalna zarubljena kupa čiji su poluprečnici osnova 1 i 4 pretopi se u valjak iste visine.poluprečnik osnove dobijenog valjka je: A)4 B) C) D) E) 45.U jednakostranični trougao čija je stranica a= cm upisan je krug.ako ova figura rotira oko visine trougla, onda je odnos zapremina rotacionih tele dobijenih rotacijom trougla i kruga: A)4: B)9:4 C)4:π D)16:9 E)π: 46.Visina i izvodnica prave kupe odnose se kao 4:5, a njena zapremina je jednaka 96πcm.Površina te kupe iznosi (u cm ): A)96 B)156 C) D)84π E)96π 47.Romb stranice a i oštrog ugla 60 obrćr se redom, oko kraće i oko duže dijagonale.razlika zapremina tako nastalih dvaju tela je: A) B) C) D)1 E) 48.Zapremina prave kupe je A) B) C) D) E), a nje osni presek je pravougli trougao.dužina izvodnice te kupe je:
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Racionalni algebarski izrazi
 . Skratimo razlomak Racionalni algebarski izrazi [MM.4-()6] 5 + 6 +. Ako je a + b + c = dokazati da je a + b + c = abc [MM.4-()] 5 6 5. Reši jednačinu: y y y + + = 7 4 y = [MM.4-(4)] 4. Reši jednačinu:
. Skratimo razlomak Racionalni algebarski izrazi [MM.4-()6] 5 + 6 +. Ako je a + b + c = dokazati da je a + b + c = abc [MM.4-()] 5 6 5. Reši jednačinu: y y y + + = 7 4 y = [MM.4-(4)] 4. Reši jednačinu:
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Planimetrija. Sličnost trouglova. GF 000 Dužine stranica trougla su 5cm, cm i 8cm. Dužina najduže stranice njemu sličnog
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Planimetrija. Sličnost trouglova. GF 000 Dužine stranica trougla su 5cm, cm i 8cm. Dužina najduže stranice njemu sličnog
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
9 Elementarni zadaci: Prizma i kvadar
 9 Elementarni zadaci: Prizma i kvadar Elementarna pitanja: 1. Kako glasi formula za računanje površine prizme? 2. Kako glasi formula za računanje zapremine prizme? [V = B H] 3. Kako glasi formula za računanje
9 Elementarni zadaci: Prizma i kvadar Elementarna pitanja: 1. Kako glasi formula za računanje površine prizme? 2. Kako glasi formula za računanje zapremine prizme? [V = B H] 3. Kako glasi formula za računanje
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
Zdaci iz trigonometrije trokuta Izračunaj ostale elemente trokuta pomoću zadanih:
 Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
Zdaci iz trigonometrije trokuta... 1. Izračunaj ostale elemente trokuta pomoću zadanih: a) a = 1 cm, α = 66, β = 5 ; b) a = 7.3 cm, β =86, γ = 51 ; c) b = 13. cm, α =1 48`, β =13 4`; d) b = 44.5 cm, α
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika
 Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
Repetitorij matematike zadaci za maturu 2008.
 Repetitorij matematike zadaci za maturu 008 Izračunaj : 7 : 5 + : = 5 5 8 Izračunaj : a ( 05 y ) = y b 8 n 7 9 n+ n n Rastavi na faktore : 5 a + a 8a 6= Skrati razlomke : a ( ) + + a b a b a + a b+ ab
Repetitorij matematike zadaci za maturu 008 Izračunaj : 7 : 5 + : = 5 5 8 Izračunaj : a ( 05 y ) = y b 8 n 7 9 n+ n n Rastavi na faktore : 5 a + a 8a 6= Skrati razlomke : a ( ) + + a b a b a + a b+ ab
POLIEDRI. Ivana Bojović 171/03
 POLIEDRI Ivana Bojović 171/03 Sadržaj Poliedarske površi...2 Prizma...5 Piramida...8 Zarubljena piramida...10 Pravilni poliedri...11 Površina poliedara...12 Površina prizme...12 Površina pravouglog paralelopipeda...13
POLIEDRI Ivana Bojović 171/03 Sadržaj Poliedarske površi...2 Prizma...5 Piramida...8 Zarubljena piramida...10 Pravilni poliedri...11 Površina poliedara...12 Površina prizme...12 Površina pravouglog paralelopipeda...13
2s v A. 0 B. 1 C. 2 D. 4 E. A. 4 B. 3 C. 2 D. 1 E. 0
 17 1989 1 1.1. Ako je v = gt + v 0 i s = g 2 t2 + v 0 t, onda je t jednak A. 2s B. v + v 0 2s C. v v 0 s D. v v 0 2s v E. 2s v 1.2. Broj rješenja jednadžbe x + 1 x = 10 u skupu realnih brojeva x R, iznosi
17 1989 1 1.1. Ako je v = gt + v 0 i s = g 2 t2 + v 0 t, onda je t jednak A. 2s B. v + v 0 2s C. v v 0 s D. v v 0 2s v E. 2s v 1.2. Broj rješenja jednadžbe x + 1 x = 10 u skupu realnih brojeva x R, iznosi
Zadaci iz trigonometrije za seminar
 Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Analitička geometrija 1. Tačka 1. MF000 Neka su A(1, 1) i B(,11) tačke u koordinatnoj ravni Oxy. Ako tačka S deli duž AB
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Analitička geometrija 1. Tačka 1. MF000 Neka su A(1, 1) i B(,11) tačke u koordinatnoj ravni Oxy. Ako tačka S deli duž AB
VOLUMEN ILI OBUJAM TIJELA
 VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
Elementarni zadaci iz Euklidske geometrije II
 Elementarni zadaci iz Euklidske geometrije II Sličnost trouglova 1. Neka su dati krugovi k 1 (O 1, r 1 ), k 2 (O 2, r 2 ) i k 3 (O 3, r 3 ) takvi da k 1 dodiruje krug k 2 u tački P, k 2 dodiruje krug k
Elementarni zadaci iz Euklidske geometrije II Sličnost trouglova 1. Neka su dati krugovi k 1 (O 1, r 1 ), k 2 (O 2, r 2 ) i k 3 (O 3, r 3 ) takvi da k 1 dodiruje krug k 2 u tački P, k 2 dodiruje krug k
Zadaci iz Geometrije 4
 Zadaci iz Geometrije 4 - za rad na vežbama - 3. maj 2017. 1 Stereometrija 1. Data je kocka ABCDA 1 B 1 C 1 D 1 ivice a. Dokazati da je tetraedar ACB 1 D 1 pravilan i odrediti mu dužinu ivice. 2. Dat je
Zadaci iz Geometrije 4 - za rad na vežbama - 3. maj 2017. 1 Stereometrija 1. Data je kocka ABCDA 1 B 1 C 1 D 1 ivice a. Dokazati da je tetraedar ACB 1 D 1 pravilan i odrediti mu dužinu ivice. 2. Dat je
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
7.1 Međusobni položaji točaka, pravaca i ravnina
 Poglavlje 7 Stereometrija Stereometrijom nazovamo geometriju (trodimenzionalnog euklidskog) prostora. Osnovni elementi prostora su točke, pravci i ravnine. Aksiome geometrije prostora nećemo navoditi.
Poglavlje 7 Stereometrija Stereometrijom nazovamo geometriju (trodimenzionalnog euklidskog) prostora. Osnovni elementi prostora su točke, pravci i ravnine. Aksiome geometrije prostora nećemo navoditi.
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
11. GEOMETRIJA. Zadaci:
 11. GEOMETRIJA elementarna geometrija likova u ravnini drediti mjeru kuta razlikovati vrste trokuta rabiti poučke o sukladnosti trokuta rabiti Pitagorin poučak i njegov obrat rabiti osnovna svojstva paralelograma
11. GEOMETRIJA elementarna geometrija likova u ravnini drediti mjeru kuta razlikovati vrste trokuta rabiti poučke o sukladnosti trokuta rabiti Pitagorin poučak i njegov obrat rabiti osnovna svojstva paralelograma
12 Elementarni zadaci: Računanje površine tijela u ravni i trigonometrija
 12 Elementarni zadaci: Računanje površine tijela u ravni i trigonometrija Elementarna pitanja: 1. Nabrojati sve geometriske figure prikazane na slici ispod. [kocka, kvadar, četverostrana piramida, sfera
12 Elementarni zadaci: Računanje površine tijela u ravni i trigonometrija Elementarna pitanja: 1. Nabrojati sve geometriske figure prikazane na slici ispod. [kocka, kvadar, četverostrana piramida, sfera
PRIMJERI ZADATAKA ZA TEST IZ MATEMATIKE
 PRIMJERI ZADATAKA ZA TEST IZ MATEMATIKE . 0.: 0.0 0. 0.0 je: 5000 0.0 5 0.00. Izračunajte 0.% od : 0. 4 0. 0.0 0.00 0.. Skratite razlomak a a a 4a + 4 + a a a a a a 0.77 4. Rješenje jednadžbe =. 5 je -
PRIMJERI ZADATAKA ZA TEST IZ MATEMATIKE . 0.: 0.0 0. 0.0 je: 5000 0.0 5 0.00. Izračunajte 0.% od : 0. 4 0. 0.0 0.00 0.. Skratite razlomak a a a 4a + 4 + a a a a a a 0.77 4. Rješenje jednadžbe =. 5 je -
2n 2, 2n, 2n + 2. a = 2n 2, b = 2n, c = 2n + 2. a b c. a P =
 Zadatak (Tomislav gimnazija) Nađite sve pravokutne trokute čije su stranice tri uzastopna parna roja Rješenje inačica pća formula za parne rojeve je n n N udući da se parni rojevi povećavaju za možemo
Zadatak (Tomislav gimnazija) Nađite sve pravokutne trokute čije su stranice tri uzastopna parna roja Rješenje inačica pća formula za parne rojeve je n n N udući da se parni rojevi povećavaju za možemo
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
1. APSOLUTNA GEOMETRIJA
 1. APSOLUTNA GEOMETRIJA Euklidska geometrija izvedena sintetičkim metodom zasniva se na aksiomama koje su podeljene u pet grupa i to: aksiome rasporeda, aksiome incidencije, aksiome podudarnosti, aksiome
1. APSOLUTNA GEOMETRIJA Euklidska geometrija izvedena sintetičkim metodom zasniva se na aksiomama koje su podeljene u pet grupa i to: aksiome rasporeda, aksiome incidencije, aksiome podudarnosti, aksiome
Elementarni zadaci iz predmeta Euklidska geometrija 1
 Elementarni zadaci iz predmeta Euklidska geometrija 1 Trougao Računanje uglova u trouglu 1. Težišnica i visina iz vrha A u ABC djele ugao α na tri jednaka dijela. Koliki su uglovi trougla ABC. 2. U trouglu
Elementarni zadaci iz predmeta Euklidska geometrija 1 Trougao Računanje uglova u trouglu 1. Težišnica i visina iz vrha A u ABC djele ugao α na tri jednaka dijela. Koliki su uglovi trougla ABC. 2. U trouglu
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Ispit održan dana i tačka A ( 3,3, 4 ) x x + 1
 Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Ministarstvo prosvete i sporta Republike Srbije Druxtvo matematiqara Srbije Prvi razred A kategorija
 18.02006. Prvi razred A kategorija Dokazati da kruжnica koja sadrжi dva temena i ortocentar trougla ima isti polupreqnik kao i kruжnica opisana oko tog trougla. Na i najve i prirodan broj koji je maƭi
18.02006. Prvi razred A kategorija Dokazati da kruжnica koja sadrжi dva temena i ortocentar trougla ima isti polupreqnik kao i kruжnica opisana oko tog trougla. Na i najve i prirodan broj koji je maƭi
RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Ako dva trougla imaju dvije stranice proporcionalne i podudaran ugao izme du njih tada su ta dva trougla slična.
 Sličnost trouglova i Talesova teorema Definicija sličnosti trouglova Dva trougla ABC i A B C su slična ako su im sva tri ugla redom podudarna i ako su im a odgovarajuće stranice proporcionalne tj. = b
Sličnost trouglova i Talesova teorema Definicija sličnosti trouglova Dva trougla ABC i A B C su slična ako su im sva tri ugla redom podudarna i ako su im a odgovarajuće stranice proporcionalne tj. = b
MATEMATIKA EKSTERNA PROVJERA ZNANJA UČENIKA NA KRAJU III CIKLUSA OSNOVNE ŠKOLE
 MATEMATIKA EKSTERNA PROVJERA ZNANJA UČENIKA NA KRAJU III CIKLUSA OSNOVNE ŠKOLE UPUTSTVO VRIJEME RJEŠAVANJA TESTA: 70 MINUTA Pribor: grafitna olovka i gumica, hemijska olovka, geometrijski pribor. Upotreba
MATEMATIKA EKSTERNA PROVJERA ZNANJA UČENIKA NA KRAJU III CIKLUSA OSNOVNE ŠKOLE UPUTSTVO VRIJEME RJEŠAVANJA TESTA: 70 MINUTA Pribor: grafitna olovka i gumica, hemijska olovka, geometrijski pribor. Upotreba
Konstruktivni zadaci. Uvod
 Svaki konstruktivni zadatak ima četri dijela: 1. Analiza 2. Konstrukcija 3. Dokaz 4. Diskusija Konstruktivni zadaci Uvod U analizi pretpostavimo da je zadatak riješen, i na osnovu slike (skice) rješenja,
Svaki konstruktivni zadatak ima četri dijela: 1. Analiza 2. Konstrukcija 3. Dokaz 4. Diskusija Konstruktivni zadaci Uvod U analizi pretpostavimo da je zadatak riješen, i na osnovu slike (skice) rješenja,
GIMNAZIJA LAZAREVAC ZADACI IZ MATEMATIKE ZA MATURSKI ISPIT
 GIMNAZIJA LAZAREVAC ZADACI IZ MATEMATIKE ZA MATURSKI ISPIT I RACIONALNI ALGEBARSKI IZRAZI I POLINOMI Uprostiti izraz ab abab : ab ba ab yy y y y y y y Uprostiti izraz : Uprostiti izraz Uprostiti izraz
GIMNAZIJA LAZAREVAC ZADACI IZ MATEMATIKE ZA MATURSKI ISPIT I RACIONALNI ALGEBARSKI IZRAZI I POLINOMI Uprostiti izraz ab abab : ab ba ab yy y y y y y y Uprostiti izraz : Uprostiti izraz Uprostiti izraz
EUKLIDSKA GEOMETRIJA
 EUKLIDSKA GEOMETRIJA zadaci za vežbe AKSIOMATSKO ZASNIVANJE EUKLIDSKE GEOMETRIJE 1. Ako dve razne ravni imaju zajedničku tačku tada je njihov presek prava. Dokazati. 2. Za svake dve prave koje se seku
EUKLIDSKA GEOMETRIJA zadaci za vežbe AKSIOMATSKO ZASNIVANJE EUKLIDSKE GEOMETRIJE 1. Ako dve razne ravni imaju zajedničku tačku tada je njihov presek prava. Dokazati. 2. Za svake dve prave koje se seku
Pismeni ispit iz predmeta Euklidska geometrija 1
 Univerzitet u Zenici Pedagoški fakultet Odsjek: Matematika i informatika Zenica, 27.01.2010. Pismeni ispit iz predmeta Euklidska geometrija 1 Zadatak br. 1 a) U oštrouglom trouglu ABC (AC < BC) visina
Univerzitet u Zenici Pedagoški fakultet Odsjek: Matematika i informatika Zenica, 27.01.2010. Pismeni ispit iz predmeta Euklidska geometrija 1 Zadatak br. 1 a) U oštrouglom trouglu ABC (AC < BC) visina
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET. Marjan M. Matejiæ Lidija V. Stefanoviæ Branislav M. Ranðeloviæ Igor. Milovanoviæ MATEMATIKA
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Marjan M. Matejiæ Lidija V. Stefanoviæ Branislav M. Ranðeloviæ Igor. Milovanoviæ MATEMATIKA KOMPLETI ZADATAKA ZA PRIJEMNI ISPIT 011. Edicija: Pomoæni ud benici Marjan
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Marjan M. Matejiæ Lidija V. Stefanoviæ Branislav M. Ranðeloviæ Igor. Milovanoviæ MATEMATIKA KOMPLETI ZADATAKA ZA PRIJEMNI ISPIT 011. Edicija: Pomoæni ud benici Marjan
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Aksiome podudarnosti
 Aksiome podudarnosti Postoji pet aksioma podudarnosti (tri aksiome podudarnosti za duži + dvije aksiome podudarnosti za uglove) III 1 Za svaku polupravu a sa početnom tačkom A i za svaku duž AB, postoji
Aksiome podudarnosti Postoji pet aksioma podudarnosti (tri aksiome podudarnosti za duži + dvije aksiome podudarnosti za uglove) III 1 Za svaku polupravu a sa početnom tačkom A i za svaku duž AB, postoji
ALFA List - 1. Festival matematike "Split 2013." Otvoreno ekipno natjecanje učenika osnovnih i srednjih škola Split, 10. svibnja 2013.
 ALFA List - 1 Točan odgovor: 10 bodova Pogrešan odgovor: 5 bodova Bez odgovora: 0 bodova 1. Ako je (x+ 3): 4=( x ):3, onda je x jednako: A) 1 B) 1 C) 17 D) 17 E) 6. Kut od 1º30' gleda se kroz povećalo
ALFA List - 1 Točan odgovor: 10 bodova Pogrešan odgovor: 5 bodova Bez odgovora: 0 bodova 1. Ako je (x+ 3): 4=( x ):3, onda je x jednako: A) 1 B) 1 C) 17 D) 17 E) 6. Kut od 1º30' gleda se kroz povećalo
Euklidska geometrija II (1. dio)
 Univerzitet u Zenici Pedagoški fakultet Odsjek: Matematika i informatika Akademska 2012/2013. (sveska je skinuta sa stranice pf.unze.ba\nabokov U svesci je mogu a pojava grešaka. Za uo ene greške pisati
Univerzitet u Zenici Pedagoški fakultet Odsjek: Matematika i informatika Akademska 2012/2013. (sveska je skinuta sa stranice pf.unze.ba\nabokov U svesci je mogu a pojava grešaka. Za uo ene greške pisati
Ministarstvo prosvete i sporta Republike Srbije Druxtvo matematiqara Srbije OPXTINSKO TAKMIQENjE IZ MATEMATIKE Prvi razred A kategorija
 18.1200 Prvi razred A kategorija Neka je K sredixte teжixne duжi CC 1 trougla ABC ineka je AK BC = {M}. Na i odnos CM : MB. Na i sve proste brojeve p, q i r, kao i sve prirodne brojeve n, takve da vaжi
18.1200 Prvi razred A kategorija Neka je K sredixte teжixne duжi CC 1 trougla ABC ineka je AK BC = {M}. Na i odnos CM : MB. Na i sve proste brojeve p, q i r, kao i sve prirodne brojeve n, takve da vaжi
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Primjer prizme je u π 1. Osnovka uspravne kvadratne piramide EFGHV je u π 2. Tlocrt i nacrt tijela dan je na slici. Odredimo prodor tih tijela.
 S. Varošanec, Nacrtna geometrija, 4. Mongeovo projiciranje 90 Primjer 4.56. Osnovka ABCD uspravne četverostrane prizme je u π 1. Osnovka uspravne kvadratne piramide EFGHV je u π 2. Tlocrt i nacrt tijela
S. Varošanec, Nacrtna geometrija, 4. Mongeovo projiciranje 90 Primjer 4.56. Osnovka ABCD uspravne četverostrane prizme je u π 1. Osnovka uspravne kvadratne piramide EFGHV je u π 2. Tlocrt i nacrt tijela
PROBNI TEST ZA PRIJEMNI ISPIT IZ MATEMATIKE
 Fakultet Tehničkih Nauka, Novi Sad PROBNI TEST ZA PRIJEMNI ISPIT IZ MATEMATIKE 1 Za koje vrednosti parametra p R polinom f x) = x + p + 1)x p ima tačno jedan, i to pozitivan realan koren? U skupu realnih
Fakultet Tehničkih Nauka, Novi Sad PROBNI TEST ZA PRIJEMNI ISPIT IZ MATEMATIKE 1 Za koje vrednosti parametra p R polinom f x) = x + p + 1)x p ima tačno jedan, i to pozitivan realan koren? U skupu realnih
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Sli cnost trouglova i Talesova teorema
 Sli cnost trouglova i Talesova teorema Denicija. Dva trougla ABC i A B C su sli cna ako su im sva tri ugla redom podudarna a i ako su im odgovaraju ce stranice proporcionalne tj. a = b b = c c. Stav 1.
Sli cnost trouglova i Talesova teorema Denicija. Dva trougla ABC i A B C su sli cna ako su im sva tri ugla redom podudarna a i ako su im odgovaraju ce stranice proporcionalne tj. a = b b = c c. Stav 1.
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 5. GEOMETRIJA 5.1 Opcenito o kutevima Poznate su slijedece vrste kuteva: siljasti kut α < 90 pravi kut α = 90 tupi kut 90 < α < 180 ravni kut α = 180 izboceni kut 180 < α < 360 puni kut α = 360 Komplementi
5. GEOMETRIJA 5.1 Opcenito o kutevima Poznate su slijedece vrste kuteva: siljasti kut α < 90 pravi kut α = 90 tupi kut 90 < α < 180 ravni kut α = 180 izboceni kut 180 < α < 360 puni kut α = 360 Komplementi
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Antene. Srednja snaga EM zračenja se dobija na osnovu intenziteta fluksa Pointingovog vektora kroz sferu. Gustina snage EM zračenja:
 Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
Anene Transformacija EM alasa u elekrični signal i obrnuo Osnovne karakerisike anena su: dijagram zračenja, dobiak (Gain), radna učesanos, ulazna impedansa,, polarizacija, efikasnos, masa i veličina, opornos
4 Sukladnost i sličnost trokuta
 4 Sukladnost i sličnost trokuta 4.1 Sukladnost trokuta Neka su ABC i A B C trokuti sa stranicama duljina a b c odnosno a b c. Kažemo da su ti trokuti sukladni ako postoji bijekcija f : {A B C} {A B C }
4 Sukladnost i sličnost trokuta 4.1 Sukladnost trokuta Neka su ABC i A B C trokuti sa stranicama duljina a b c odnosno a b c. Kažemo da su ti trokuti sukladni ako postoji bijekcija f : {A B C} {A B C }
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Pošto se trebaju napisati sve nastavne cjeline i gradivo sva četiri razreda (opće i jezično) potrajati će duži vremenski period.
 Zadaci s rješenjima, a ujedno i s postupkom rada biti će nadopunjavani tokom čitave školske godine. Tako da će u slijedećem vremenskom periodu nastati mala zbirka koja će biti popraćena s teorijom. Pošto
Zadaci s rješenjima, a ujedno i s postupkom rada biti će nadopunjavani tokom čitave školske godine. Tako da će u slijedećem vremenskom periodu nastati mala zbirka koja će biti popraćena s teorijom. Pošto
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Pitanja za usmeni dio ispita iz matematike
 PITANJA ZA MATURALNI ISPIT Pitanja za usmeni dio ispita iz matematike. Dokazati da je zbroj unutarnjih kutova u trokutu 80 0,a spoljnjih 60 0.. Dokazati da je spoljnji kut trokuta jednak zbroju dva nesusjedna
PITANJA ZA MATURALNI ISPIT Pitanja za usmeni dio ispita iz matematike. Dokazati da je zbroj unutarnjih kutova u trokutu 80 0,a spoljnjih 60 0.. Dokazati da je spoljnji kut trokuta jednak zbroju dva nesusjedna
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
TAČKA i PRAVA. , onda rastojanje između njih računamo po formuli C(1,5) d(b,c) d(a,b)
 TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje između dve tačke Ako su nam date tačke Ax (, y) i Bx (, y ), onda rastojanje između njih računamo po formuli
TAČKA i PRAVA Najpre ćemo se upoznati sa osnovnim formulama i njihovom primenom.. Rastojanje između dve tačke Ako su nam date tačke Ax (, y) i Bx (, y ), onda rastojanje između njih računamo po formuli
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Elektronske lekcije o stereometriji u osmom razredu osnovne škole kreirane korišćenjem programskog paketa GeoGebra
 Matematički fakultet Univerzitet u Beogradu Elektronske lekcije o stereometriji u osmom razredu osnovne škole kreirane korišćenjem programskog paketa GeoGebra -master rad- Mentor: prof. dr Miroslav Marić
Matematički fakultet Univerzitet u Beogradu Elektronske lekcije o stereometriji u osmom razredu osnovne škole kreirane korišćenjem programskog paketa GeoGebra -master rad- Mentor: prof. dr Miroslav Marić
Zadaci za pripremu prijemnog ispita
 UNIVERZITET U KRAGUJEVCU PRIRODNOMATEMATI^KI FAKULTET INSTITUT ZA MATEMATIKU I INFORMATIKU Zadaci za pripremu prijemnog ispita KRAGUJEVAC, 2017 GODINE INSTITUT ZA MATEMATIKU I INFORMATIKU Zadaci za pripremu
UNIVERZITET U KRAGUJEVCU PRIRODNOMATEMATI^KI FAKULTET INSTITUT ZA MATEMATIKU I INFORMATIKU Zadaci za pripremu prijemnog ispita KRAGUJEVAC, 2017 GODINE INSTITUT ZA MATEMATIKU I INFORMATIKU Zadaci za pripremu
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Druxtvo matematiqara Srbije OPXTINSKO TAKMIQENjE IZ MATEMATIKE Prvi razred A kategorija. f(x + 1) x f(x) + 1.
 09.0200 Prvi razred A kategorija Ako je n prirodan broj, dokazati da 3n 2 + 3n + 7 nije kub nijednog prirodnog broja. U trouglu ABC je ABC = 60. Neka su D i E redom preseqne taqke simetrala uglova CAB
09.0200 Prvi razred A kategorija Ako je n prirodan broj, dokazati da 3n 2 + 3n + 7 nije kub nijednog prirodnog broja. U trouglu ABC je ABC = 60. Neka su D i E redom preseqne taqke simetrala uglova CAB
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
2. Bez kalkulatora odredi vrijednosti trigonometrijskih funkcija za brojeve (kutove) iz točaka u 1.zadatku.
 . Na brojevnoj kružnici označi točke: A (05π), A 2 ( 007π 2 ), A 3 ( 553π 3 ) i A 4 ( 40 o ). 2. Bez kalkulatora odredi vrijednosti trigonometrijskih funkcija za brojeve (kutove) iz točaka u.zadatku. 3.
. Na brojevnoj kružnici označi točke: A (05π), A 2 ( 007π 2 ), A 3 ( 553π 3 ) i A 4 ( 40 o ). 2. Bez kalkulatora odredi vrijednosti trigonometrijskih funkcija za brojeve (kutove) iz točaka u.zadatku. 3.
Ako prava q prolazi kroz koordinatni početak i gradi ugao φ [0, π) sa x osom tada je refleksija S φ u odnosu na tu pravu:
 Refleksija S φ u odnosu na pravu kroz koordinatni početak Ako prava q prolazi kroz koordinatni početak i gradi ugao φ [0, π) sa x osom tada je refleksija S φ u odnosu na tu pravu: ( ) ( ) ( ) x cos 2φ
Refleksija S φ u odnosu na pravu kroz koordinatni početak Ako prava q prolazi kroz koordinatni početak i gradi ugao φ [0, π) sa x osom tada je refleksija S φ u odnosu na tu pravu: ( ) ( ) ( ) x cos 2φ
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
ODREĐIVANJE TEŽIŠTA KRUTOG TELA Korišćenjem Varinjonove teoreme, dobija se: = Gi. = G z
 TEŽIŠTE Svako kruto telo je sačinjeno od velikog brojačestica (elementarnih delova). Kada se telo nalazi u blizini Zemljine površine na svaku od tihčestica dejstvuje sila njene težine koja je usmerena
TEŽIŠTE Svako kruto telo je sačinjeno od velikog brojačestica (elementarnih delova). Kada se telo nalazi u blizini Zemljine površine na svaku od tihčestica dejstvuje sila njene težine koja je usmerena
Masa i gustina. zadaci
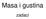 Masa i gustina zadaci 1.)Vaga je u ravnote i dok je na jednom njenom tasu telo, a na drugom su tegovi od: 10 g, 2 g, 500 mg i 200 mg.kolika je masa ovog tela? 2.)Na jednom tasu vage se nal azi telo i teg
Masa i gustina zadaci 1.)Vaga je u ravnote i dok je na jednom njenom tasu telo, a na drugom su tegovi od: 10 g, 2 g, 500 mg i 200 mg.kolika je masa ovog tela? 2.)Na jednom tasu vage se nal azi telo i teg
O trouglu. mr Radmila Krstić, asistent Prirodno-matematički fakultet, Niš
 O trouglu mr Radmila Krstić, asistent Prirodno-matematički fakultet, Niš O trouglu 2 O TROUGLU Trougao je nezaobilazna tema kako osnovne tako i srednje škole. O trouglu se skoro sve zna. Navodimo te činjenice.
O trouglu mr Radmila Krstić, asistent Prirodno-matematički fakultet, Niš O trouglu 2 O TROUGLU Trougao je nezaobilazna tema kako osnovne tako i srednje škole. O trouglu se skoro sve zna. Navodimo te činjenice.
Analitička geometrija
 1 Analitička geometrija Neka su dati vektori a = a 1 i + a j + a 3 k = (a 1, a, a 3 ), b = b 1 i + b j + b 3 k = (b 1, b, b 3 ) i c = c 1 i + c j + c 3 k = (c 1, c, c 3 ). Skalarni proizvod vektora a i
1 Analitička geometrija Neka su dati vektori a = a 1 i + a j + a 3 k = (a 1, a, a 3 ), b = b 1 i + b j + b 3 k = (b 1, b, b 3 ) i c = c 1 i + c j + c 3 k = (c 1, c, c 3 ). Skalarni proizvod vektora a i
Aksiomatsko zasnivanje euklidske geometrije
 Aksiomatsko zasnivanje euklidske geometrije 1. Postoji jedna i samo jedna prava koja sadrži dve razne tačke A i B. 2. Postoji jedna i samo jedna ravan koja sadrži tri nekolinearne tačke A, B, C. 3. Ako
Aksiomatsko zasnivanje euklidske geometrije 1. Postoji jedna i samo jedna prava koja sadrži dve razne tačke A i B. 2. Postoji jedna i samo jedna ravan koja sadrži tri nekolinearne tačke A, B, C. 3. Ako
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
Ljetno kolo 2017./2018.
 Ljetno kolo 217./218. ŠKOLA EKIPA KATEGORIJA POVJERENIK NATJECANJA C3 R. IME I PREZIME UČENIKA RAZRED IME I PREZIME MENTORA 1. 2. 3.. ODGOVORI: 1. 11. 26. 2. 12. 27. 3. 13. 28.. 1. 29. 5. 15. 3. 6. 16.
Ljetno kolo 217./218. ŠKOLA EKIPA KATEGORIJA POVJERENIK NATJECANJA C3 R. IME I PREZIME UČENIKA RAZRED IME I PREZIME MENTORA 1. 2. 3.. ODGOVORI: 1. 11. 26. 2. 12. 27. 3. 13. 28.. 1. 29. 5. 15. 3. 6. 16.
ISPITNI ZADACI FORMULE. A, B i C koeficijenti (barem jedan A ili B različiti od nule)
 FORMULE Implicitni oblik jednadžbe pravca A, B i C koeficijenti (barem jedan A ili B različiti od nule) Eksplicitni oblik jednadžbe pravca ili Pravci paralelni s koordinatnim osima - Kada je u općoj jednadžbi
FORMULE Implicitni oblik jednadžbe pravca A, B i C koeficijenti (barem jedan A ili B različiti od nule) Eksplicitni oblik jednadžbe pravca ili Pravci paralelni s koordinatnim osima - Kada je u općoj jednadžbi
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
10. Koji od brojeva -9,007; -8; 1 ; 0,018 je cijeli broj? 11. Razlomak 1 napiši u decimalnom obliku. 12. Broj 0,5 napiši u obliku razlomka.
 MATEMATIKA Brojevi Osnovni nivo 1. Koji od navedenih brojeva: 8, -2, 0, 3, 2, 61, 5 su prirodni brojevi? 3 2. Koji od brojeva 2, -4, 5, -6, 0, -3 su negativni cijeli brojevi? 3. Koji od brojeva 12, -4,
MATEMATIKA Brojevi Osnovni nivo 1. Koji od navedenih brojeva: 8, -2, 0, 3, 2, 61, 5 su prirodni brojevi? 3 2. Koji od brojeva 2, -4, 5, -6, 0, -3 su negativni cijeli brojevi? 3. Koji od brojeva 12, -4,
Univerzitet u Beogradu, Matematički fakultet. Predmet:Metodika nastave i računarstva Tema:Sličnost
 Univerzitet u Beogradu, Matematički fakultet Predmet:Metodika nastave i računarstva Tema:Sličnost Profesor Student Nebojša Ikodinović Marina Stanković 270/2011 Anđela Milijašević 132/2011 Datum:15.12.2014
Univerzitet u Beogradu, Matematički fakultet Predmet:Metodika nastave i računarstva Tema:Sličnost Profesor Student Nebojša Ikodinović Marina Stanković 270/2011 Anđela Milijašević 132/2011 Datum:15.12.2014
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Prof. Mira Mihajlović Petković 1
 Prof. Mira Mihajlović Petković 1 TRIGONOMETRIJSKE FUNKCIJE ŠILJASTOG KUTA sin nasuprotna kateta a hipotenuza c cos priležeća kateta b hipotenuza c tg nasuprotna kateta a priležeća kateta b ctg Definicijski
Prof. Mira Mihajlović Petković 1 TRIGONOMETRIJSKE FUNKCIJE ŠILJASTOG KUTA sin nasuprotna kateta a hipotenuza c cos priležeća kateta b hipotenuza c tg nasuprotna kateta a priležeća kateta b ctg Definicijski
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Općinsko natjecanje. 4. razred
 9 1. Općinsko natjecanje iklus susreta i natjecanja mladih matematičara, učenika osnovnih i srednjih škola Republike Hrvatske i u 1998. godini sastojao se od školskih natjecanja, gradskih i općinskih natjecanja,
9 1. Općinsko natjecanje iklus susreta i natjecanja mladih matematičara, učenika osnovnih i srednjih škola Republike Hrvatske i u 1998. godini sastojao se od školskih natjecanja, gradskih i općinskih natjecanja,
MOJ QAS. Ljubixa Dini. POVRXINA LOPTE (SFERE) Qas obrade novog gradiva u OX,, ele kula u Nixu
 MOJ QAS Ljubixa Dini POVRXINA LOPTE (SFERE) Qas obrade novog gradiva u OX,, ele kula u Nixu Uvodni deo qasa Podsetimo se da smo u sedmom razredu obrađivali obim i povrxinu kruga, kao i obim i povrxinu pravilnih
MOJ QAS Ljubixa Dini POVRXINA LOPTE (SFERE) Qas obrade novog gradiva u OX,, ele kula u Nixu Uvodni deo qasa Podsetimo se da smo u sedmom razredu obrađivali obim i povrxinu kruga, kao i obim i povrxinu pravilnih
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
DRŽAVNO NATJECANJE IZ MATEMATIKE
 DRŽAVNO NATJECANJE IZ MATEMATIKE. razred srednja škola B kategorija Pula, 30. ožujka 009. Zadatak B-.. (0 bodova) Tomislav i ja, reče Krešimir, možemo završiti posao za 0 dana. No, ako bih radio s Ivanom
DRŽAVNO NATJECANJE IZ MATEMATIKE. razred srednja škola B kategorija Pula, 30. ožujka 009. Zadatak B-.. (0 bodova) Tomislav i ja, reče Krešimir, možemo završiti posao za 0 dana. No, ako bih radio s Ivanom
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Repetitorij-Dinamika. F i Zakon očuvanja impulsa (ZOI): i p i = j p j. Zakon očuvanja energije (ZOE):
 Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Repetitorij-Dinamika Dinamika materijalne točke Sila: F p = m a = lim t 0 t = d p dt m a = i F i Zakon očuvanja impulsa (ZOI): i p i = j p j i p ix = j p jx te i p iy = j p jy u 2D sustavu Zakon očuvanja
Zbirka testova za polaganje maturskog i stručnog ispita iz MATEMATIKE. Zavod za udžbenike i nastavna sredstva PODGORICA
 Zbirka testova za polaganje maturskog i stručnog ispita iz MATEMATIKE Zavod za udžbenike i nastavna sredstva PODGORICA Zbirka testova za polaganje maturskog i stručnog ispita iz MATEMATIKE Zavod za udžbenike
Zbirka testova za polaganje maturskog i stručnog ispita iz MATEMATIKE Zavod za udžbenike i nastavna sredstva PODGORICA Zbirka testova za polaganje maturskog i stručnog ispita iz MATEMATIKE Zavod za udžbenike
OPĆINSKO/ŠKOLSKO NATJECANJE IZ MATEMATIKE
 Ministarstvo znanosti, obrazovanja i športa Republike Hrvatske Agencija za odgoj i obrazovanje Hrvatsko matematičko društvo OPĆINSKO/ŠKOLSKO NATJECANJE IZ MATEMATIKE 1. razred srednja škola A kategorija
Ministarstvo znanosti, obrazovanja i športa Republike Hrvatske Agencija za odgoj i obrazovanje Hrvatsko matematičko društvo OPĆINSKO/ŠKOLSKO NATJECANJE IZ MATEMATIKE 1. razred srednja škola A kategorija
