ISPIT GRUPA A - RJEŠENJA
|
|
|
- Παρθενορή Λύτρας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L, odrediti: a) sile i napone u štapovima A i B, b) deformacije štapova A i B, c) nagib krute poluge. q 0 A B Podaci: q kn/m; poluga AB 1 m; štapovi E 00 GPa, A A A B 100 cm, L 300 mm. ( %). Puno čelično vratilo sastavljeno iz dva dijela 1 i opterećeno je momentima uvijanja kao na slici desno. Odrediti: L 1 L a) ugao uvijanja u presjeku D u odnosu na presjek A, b) maksimalan napon u presjeku C. A 1 B C T B D T D Podaci: E 00 GPa, ν 0.3, D 1 1.5D 15 mm, L 1 L 500 mm, T B T D 0 knm. D 1 D 3. Za gredu s prepustom pravougaonog poprečnog presjeka, b h, opterećenu kao na slici desno provjeri da li su normalni i tangencijalni naponi u dozvoljenim granicama. Dozvoljeni napon na savijanje je σ doz 15 MPa, a dozvoljeni tangencijalni napon je τ doz MPa. Podaci: 0.3 m, L AC 0.6 m, L AD 0.8 m, M 1 knm, q 10 kn/m, dimenzije grede b h 0 80 mm. (15+50%) M A B C D L AC L AD q (5%). Za dio na slici desno u tački A odrediti: a) tangencijalne napone, 300 mm 00 mm b) normalne napone. usljed djelovanja sile F 5 kn. Prečnik dijela je D 50 mm. Napomena: ugao koji sila F zaklapa s horizontalnom osom je tg(ϕ) 3 :. 3 5 A B 5 kn Probs. 8 /3 ( %) Vrijeme izrade minuta MF-UNZE, 013-Jan-8
2 ISPIT GRUPA A - RJEŠENJA 1. ZADATAK : 1m E : 00GPa q max : 100 kn m A A : 100cm A A A B : mm L : 0.3m a) Sile i naponi u štapovima Problem je statički određen pa se sile mogu dobiti iz uslova ravnoteže: q max F i 0 F A + F B L AB 0 ( 1) i M i i 0 A F B q max 1 L AB 0 ( ) 3 F B : F A : q max 6 q max kn F B kn pa su naponi (sile imaju suprotan smjer od onog koji djeluje na polugu): σ A : σ B : F A Pa A A F B Pa A B b) Deformacije u štapovima ε A : σ A E σ B ε B : E
3 c) nagib krute poluge S obzirom da su deformacije štapova jednake, poluga će ostati u horizontalnom položaju.. ZADATAK D 1 π D 1 : 15mm I o1 : mm L 1 : 500mm D 1 D π D : 100 mm I 1.5 o : mm L 1 L : 50 mm : 50mm L BC : L 1 50 mm E : 00GPa ν : 0.3 G : E ( 1 + ν) GPa T B : 0kN m T D : 0kN m Na osnovu slike se može postaviti uslov ravnoteže (T A ima suprotan smjer od smjera T B i T D ): T A T B T D 0 pa je T A : T B + T D 10 N m Također se mogu razlikovati dva područja djelovanja konstantnih momenata uvijanja i to: T AB : T A 10 N m T BD : T A T B 10 N m a) Ugao uvijanja u presjeku D jednak je zbiru uglova uvijanja pojedinih segmenata, i to
4 φ AB : T AB G I o φ BC : T BD L BC G I o T BD L φ CD : G I o φ : φ AB + φ BC + φ CD 0.85 b) Maksimalni napon u presjeku C je za minimalan prečnik u tom presjeku, tj. za D τ max : D T BD I o MPa ************************************************************************************************************** 3. ZADATAK Podaci: : 0.3m L AC : 0.6m L AD : 0.8m L CD : L AD L AC q : 10 kn M m B : 1kN m σ doz : 1MPa b : 0mm h : 80mm τ doz : MPa b h 3 I : mm A : b h mm 1 a)
5 Posmatrajmo raspodjelu transferzalnih sila i momenata savijanja za gredu ACD. Reakcije u osloncima A i C (pretpostavlja se da sile F A i F C djeluju prema gore). F i 0 F A + F C q L CD 0 (1) i L CD M i 0 M B F C L AC + q L CD L AC + 0 () i L CD M B + L CD q L AC + Iz () sijedi: F C : L AC kn Iz (1) slijedi: F A : q L CD F C kn (pogrešno pretpostavljen smjer) Sada se mogu nacrtati dijagrami momenata savijanja i transferzalnih sila 1 F, kn M, knm x, m x, m Maksimalni momenti savijanja je na mjestu djelovanja momenta savijanja u tački B, i to s lijeve strane, pa je M max : F A 0.6 kn m dok je maksimalna transferzalna sila uzduž dijela grede AC i jednaka je reakciji u A F max : F A kn Provjera normalnih napona
6 σ max M max h I M max h b h 3 1 6M max b h σ doz 6M max σ max : b h 1.06 MPa σ max < σ doz Provjera tangencijalnog napona: 3F max τ max : MPa τ A max < τ doz Dakle, greda će izdržati dato opterećenje. **************************************************************************************************************. ZADATAK Podaci: F : 5kN L 1 : 300mm L : 00mm D : 50mm D π I : mm A : 6 tg( φ) 3 φ : atan D π mm U ravni kojoj propadaju tačke A i B vladaju tangencijalni i normalni naponi usljed momenta savijanja i smicanja koje izazivaju komponente sile F u pravcu vertikalne i horizontalne ose, i to: F y : ( F sin( φ) ) 3 kn F x : F cos( φ) kn Sila F y u tački A izaziva pritisne normalne napone usljed savijanja, dok nema djelovanja tangencijalnih napona, pošto se tačka nalazi na donjoj površini.
7 σ : F y L 1 I D MPa Sila F x u tački A izaziva maksimalne tangencijalne napone usljed smicanja pošto se tačka nalazi na neutralnoj osi, dok iz istog razloga nema normalnih napona usljed savijanja τ : F x 3 A.716 MPa **************************************************************************************************************
8 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa B 1. Kruta poluga ABC oslonjena je na dva elastična štapa AD i CE i može da se okreće u osloncu B, kao što je prikazano na slici desno. Ako je poluga opterećena silom F 10 kn koja djeluje na polovini dijela poluge AB, odrediti: a) sile i napone u štapovima AD i CE, b) deformacije štapova AD i CE, c) nagib krute poluge ABC. F A B C D L AC E Podaci: poluga ABC 1 m, L AC 3 m; štap AD E AD 7 GPa, A AD 1 cm, L AD 300 mm; štap CE E CE GPa, A CE 1.5 cm, L CE 00 mm. ( %). Za konzolu kružnog poprečnog presjeka opterećenu kao na slici desno provjeri da li su normalni i tangencijalni naponi u dozvoljenim granicama. Dozvoljeni napon na savijanje je σ doz 150 MPa, a dozvoljeni tangencijalni napon je τ doz 100 MPa. Podaci: 0.6 m, L AC 0.9 m, M 1 knm, F 1 kn, prečnik konzole d 50 mm. A M L AC B F C (5%) 3. Za dio na slici desno u tački B odrediti: a) tangencijalne napone, 300 mm 00 mm b) normalne napone. usljed djelovanja sile F 5 kn. Prečnik dijela je D 5 mm. Napomena: ugao koji sila F zaklapa s horizontalnom osom je tg(ϕ) 3 : 3 5 A B 5 kn Probs. 8 /3 ( %) 50 MPa. Za element napona nekog elementa od duktilnog čelika provjeriti da li će doći do pucanja elementa, ako je R eh 100 MPa. 5 MPa 90 MPa (15%) Vrijeme izrade minuta MF-UNZE, 013-Jan-8
9 ISPIT GRUPA B - RJEŠENJA 1. ZADATAK : 1m L AC : 3m L BC : L AC E AD : 7GPa L AD : 300mm A AD : 1cm E CE : GPa L CE : 00mm A CE : 1.5cm F : 10kN a) Problem je statički neodređen, pa pored uslova ravnoteže moramo postaviti i uslove kompatibilnosti. Pretpostavimo da se štap AD izdužuje, a štap CE skraćuje, tj. da sila F A djeluje prema dole, a sila F C prema gore na krutu polugu. Uslov ravnoteže je: M i i 0 B F A F + F C L BC 0 ( 1) Uslov kompatibilnosti (pomjeranja u tačkama A i C s tačkom B čine slične truglove, ali treba paziti na znak "-" s obzirom da se jedan štap skraćuje a drugi izdužuje) δ A δ C ( ) L BC Takođe vrijedi: F A L AD F C L CE δ A δ E AD A C ( 3) AD E CE A CE Uvrštravajući (3) u () dobija se F A L CE E AD L AD E CE A AD F A CE L C BC 1 9 F C ( )
10 Sada se uvrštavanjem () u (1) dobija 9 F F C : 1.06 kn (djeluje prema gore) L BC F F C L BC F A :.188 kn (djeluje prema dole) pa su naponi u štapovima A i D (sile djeluju suprotno od onih koje djeluju na krutu gredu) σ AD : F A MPa A AD istezanje σ CE : F C MPa A CE pritisak b) Deformacije štapova ε AD : σ AD δ E AD : ε AD L AD m AD izduženje ε CE : σ CE δ E CE : ε CE L CE m CE skraćenje c) Nagib poluge γ : atan δ AD + δ CE L AC 0.05 **************************************************************************************************************. ZADATAK Podaci: : 0.6m L AC : 0.9m L BC : L AC F : 1kN M A : 1kN m
11 σ doz : 150MPa d : 50mm τ doz : 100MPa d π I : mm A : 6 d π mm a) Posmatrajmo raspodjelu transferzalnih sila i momenata savijanja za konzolu ABC. Reakcije u uklještenju C (pretpostavlja se da sila F A djeluju prema gore, a moment u smjeru kazaljke na satu). F i F + F C 0 (1) i M i M + F L BC + M C 0 () i Iz (1) sijedi: F C : F 1 kn (pogrešno pretpostavljen smjer) Iz () slijedi: M C : M A F L BC 1.3 kn m (pogrešno pretpostavljen smjer) Sada se mogu nacrtati dijagrami momenata savijanja i transferzalnih sila F, kn M, knm x, m x, m
12 Maksimalni momenti savijanja je u uklještenju C, i to s lijeve strane, pa je M max : M C 1.3 kn m dok je maksimalna transferzalna sila uzduž dijela grede BC i jednaka je reakciji u uklještenju F max : F C 1 kn Provjera normalnih napona σ max M max h I M max d π 6 d 3M max d 3 π σ doz 3M max σ max : MPa σ max < σ doz d 3 π Provjera tangencijalnog napona: F max τ max : MPa τ 3A max < τ doz Dakle, greda će izdržati dato opterećenje. ************************************************************************************************************** 3. ZADATAK Podaci: F : 5kN L 1 : 300mm L : 00mm D : 5mm D π I : mm A : 6 tg( φ) 3 φ : atan D π mm
13 U ravni kojoj propadaju tačke A i B vladaju tangencijalni i normalni naponi usljed momenta savijanja i smicanja koje izazivaju komponente sile F u pravcu vertikalne i horizontalne ose, i to: F y : ( F sin( φ) ) 3 kn F x : F cos( φ) kn Sila F x u tački B izaziva pritisne normalne napone usljed savijanja, dok nema djelovanja tangencijalnih napona, pošto se tačka nalazi na donjoj površini. F x L 1 D σ : MPa I Sila F y u tački A izaziva maksimalne tangencijalne napone usljed smicanja pošto se tačka nalazi na neutralnoj osi, dok iz istog razloga nema normalnih napona usljed savijanja τ : F y 3 A 8.19 MPa **************************************************************************************************************. ZADATAK Podaci: σ x : 90MPa R eh : 100MPa σ y : 50MPa τ xy : 5MPa Da bismo primijenili zadate teorije neophodno je prvo izračunati glavne normalne napone σ x + σ y σ 1 : σ x σ y + + τ xy MPa σ x + σ y σ : σ x σ y + τ xy MPa
14 a) Teorija najvećeg tangencijalnog napona (glavni naponi su istog znaka) σ ekv : max σ 1, σ ( ) MPa σ ekv > σ doz b) Teorija najvećeg specifičnog deformacionog rada σ ekv : σ 1 σ 1 σ + σ MPa σ ekv < σ doz **************************************************************************************************************
15 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa C 1. Kruta poluga ABC oslonjena je na dva elastična štapa AD i CE i može da se okreće u osloncu B, kao što je prikazano na slici desno. Ako se štap AD zagrije za T 0 C, odrediti sile i napone u štapovima AD i CE. Podaci: poluga ABC 1 m, L AC 3 m; štap AD E AD 7 GPa, A AD 1 cm, L AD 300 mm, α AD / C ; štap CE E CE GPa, A CE 1.5 cm, L CE 00 mm.. Vratilo sastavljeno iz dva dijela od različitih materijala 1 i, opterećeno je momentima uvijanja kao na slici desno. Odrediti: A B C D L AC (5+530%) E a) ugao uvijanja u presjeku D u odnosu na presjek A, b) maksimalan napon u presjeku C. TA A L1 L 1 B C TB LAB D TD Podaci: E 1 00 GPa, ν 1 0.3, E 150 GPa, ν 0.35, D 1 D 15 mm, L 1 L 500 mm, 3T A T B 1.5T D 10 Nm. D1 D (15+50%) 3. Za konzolu kvadratnog poprečnog presjeka opterećenu kao na slici desno provjeri da li su normalni i tangencijalni A B C naponi u dozvoljenim granicama. Dozvoljeni napon na savijanje je σ doz 100 MPa, a dozvoljeni tangencijalni napon je τ doz 50 MPa. L AC F B Podaci: 0.6 m, L AC 0.9 m, F A kn, F B 1 kn, stranica poprečnog presjeka konzole b 60 mm. F A (5%). Za dio na slici desno u tački H odrediti: a) tangencijalne napone, b) normalne napone. usljed djelovanja sile F 150 N. Prečnik dijela je D 15 mm. 150 N 150 mm 50 mm ( %) Vrijeme izrade minuta MF-UNZE, 013-Jan-8
16 ISPIT GRUPA C - RJEŠENJA 1. ZADATAK : 1m L AC : 3m L BC : L AC E AD : 7GPa L AD : 300mm A AD : 1cm E CE : GPa L CE : 00mm A CE : 1.5cm T : 0 C α : C a) Problem je statički neodređen, pa pored uslova ravnoteže moramo postaviti i uslove kompatibilnosti, pri čemu treba paziti na utjecaj temperature. Pretpostavimo da se štap AD izdužuje, a štap CE skraćuje, tj. da sila F A djeluje prema dole, a sila F C prema gore na krutu polugu. Uslov ravnoteže je: M i i 0 B F A + F C L BC 0 ( 1) Uslov kompatibilnosti (pomjeranja u tačkama A i C s tačkom B čine slične truglove, no treba paziti na znak "-" s obzirom da se jedan štap skraćuje a drugi izdužuje). Također, ukupno izduženje štapa AD je jednako izduženju usljed povećanja temperature, δ AT α TL AD, te utjecaja sile F A (δ AF ), dok je izduženje štapa C E uzrokovano samo silom F C (δ CF ), pa imamo odnos δ AT + δ AF δ CF ( ) L BC Takođe vrijedi: F A L AD F C L CE δ AT : α T L AD δ AF δ E AD A CF ( 3) AD E CE A CE Uvrštravajući (3) u () dobija se A AD E AD L CE F A A AD E AD α T + F A CE E CE L BC L C 61.6N + 1 AD 9 F C ( )
17 Sada se uvrštavanjem () u (1) dobija A AD E AD α T F C : kn (djeluje prema gore) A AD E AD L CE L BC + L A CE E CE L BC AD F C L BC F A : 0.35 kn (pogrešno pretpostavljen smjer, djeluje prema gore na krutu polugu) pa su naponi u štapovima A i D (sile djeluju suprotno od onih koje djeluju na krutu gredu) σ AD : F A 3.96 MPa A AD pritisak (jer sila djeluje prema dole na štap) σ CE : F C MPa A CE pritisak b) Deformacije štapova δ AD : α T L AD + F A L AD δ AD mε E AD A AD : AD L AD izduženje F C L CE δ CE δ CE : m ε E CE A CE : skraćenje CE L CE. ZADATAK D 1 π D 1 : 15mm I o1 : mm L 1 : 500mm D π D : D 1 15 mm I o : 3 L : L mm mm W 0 : I o1 D 1 : 50mm L BC : L 1 50 mm
18 E 1 E 1 : 00GPa ν 1 : 0.3 G 1 : 1 + ν 1 E ( ) E : 150GPa ν : 0.35 G : 1 + ν ( ) GPa GPa T B T B T B : 10kN m T D : 80 kn m T 1.5 A : 3 10 J Na osnovu slike se mogu razlikovati dva područja djelovanja konstantnih momenata uvijanja i to: T AB : T A 0 kn m T BD : T A T B 80 kn m a) Ugao uvijanja u presjeku D jednak je zbiru uglova uvijanja pojedinih segmenata, i to T AB φ AB : φ G 1 I AB o1 T BD L BC φ BC : 0.6 φ G 1 I BC o1 T BD L φ CD : 1.71 φ G I CD 0.03 o φ : φ AB + φ BC + φ CD.03 b) Maksimalni napon u presjeku C je jednak za oba dijela pošto su momenti uvijanja i karakteristike presjeka jednake za oba dijela:
19 τ max : D T BD MPa I o ************************************************************************************************************** 3. ZADATAK Podaci: : 0.6m L AC : 0.9m L BC : L AC 0.3m F A : kn F B : 1kN b σ doz : 100MPa b : 60mm I : 1 τ doz : 50MPa mm A : b mm a) Posmatrajmo raspodjelu transferzalnih sila i momenata savijanja za konzolu ABC. Reakcije u oklještenju C (pretpostavlja se da sila F AC djeluje na gore, a moment savijanja M C u pravcu okretanja kazaljke na satu). F i 0 F A i M i 0 F A L AC i + F B + F C 0 (1) F B L BC M C 0 () Iz (1) sijedi: F C : F A F B 3 kn Iz () slijedi: M C : F A L AC F B L BC 3.3 kn m
20 Sada se mogu nacrtati dijagrami momenata savijanja i transferzalnih sila 0 0 F, kn 1 3 M, knm x, m x, m Maksimalni momenti savijanja je u uklještenju M max : M C 3.3 kn m dok je maksimalna transferzalna sila uzduž dijela grede AB i jednaka je F A F max : F A kn Provjera normalnih napona σ max M max h I M max b 1 h 6M max b 3 σ doz 6M max σ max : MPa σ max < σ doz b 3 Provjera tangencijalnog napona: 3F max τ max : MPa τ A max < τ doz Dakle, konzola će izdržati dato opterećenje. **************************************************************************************************************. ZADATAK
21 Podaci: F : 150N L 1 : 50mm L : 150mm D : 15mm D π I : mm A : 6 I 0 : I I mm D π mm U ravni kojoj propada tačka H vladaju tangencijalni naponi usljed uvijanja momentom uvijanja FL 1, tangencijalnih napona usljed smicanja silom F nema, jer je tačka H na gornjoj površini, te normalni naponi usljed savijanja momentom savijanja FL. - tangencijalni napon usljed uvijanja D F L 1 τ : MPa I 0 - normalni napon usljed savijanja (zatezanje) σ : F L I D MPa **************************************************************************************************************
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A
 Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Psmen spt z OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga ABC se oslanja pomoću dvje špke BD CE kao na slc desno. Špka BD, dužne 0.5 m, zrađena je od čelka (E AB 10 GPa) ma poprečn presjek od 500 mm.
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona.
 Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Aksijalno napregnuti elementi su elementi izloženi samo na zatezanje ili pritisak.
 * Aksijalno napregnuti elementi su elementi izloženi samo na zatezanje ili pritisak. JM Gere, BJ Goodno, Mechanics of Materials,, Cengage g Learning, Seventh Edition, 2009. *RC Hibbeler, Mechanics of Materials,
* Aksijalno napregnuti elementi su elementi izloženi samo na zatezanje ili pritisak. JM Gere, BJ Goodno, Mechanics of Materials,, Cengage g Learning, Seventh Edition, 2009. *RC Hibbeler, Mechanics of Materials,
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
20 mm. 70 mm i 1 C=C 1. i mm
 MMENT NERJE ZDTK. Za površinu prema datoj slici odrediti: a centralne težišne momente inercije, b položaj glavnih, centralnih osa inercije, c glavne, centralne momente inercije, d glavne, centralne poluprečnike
MMENT NERJE ZDTK. Za površinu prema datoj slici odrediti: a centralne težišne momente inercije, b položaj glavnih, centralnih osa inercije, c glavne, centralne momente inercije, d glavne, centralne poluprečnike
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
 Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
PROSTA GREDA (PROSTO OSLONJENA GREDA)
 ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
PRIMJERI TEST PITANJA iz OTPORNOSTI MATERIJALA I 1
 PRIMJERI TEST PITANJA iz OTPORNOSTI MATERIJALA I 1 Napomene: Pitanja služe kao priprema za izradu testova iz Otpornosti Materijala I, koji se polažu parcijalno i integralno. Testovi su koncipirani kao
PRIMJERI TEST PITANJA iz OTPORNOSTI MATERIJALA I 1 Napomene: Pitanja služe kao priprema za izradu testova iz Otpornosti Materijala I, koji se polažu parcijalno i integralno. Testovi su koncipirani kao
GRAĐEVINSKI FAKULTET U BEOGRADU Modul za konstrukcije PROJEKTOVANJE I GRAĐENJE BETONSKIH KONSTRUKCIJA 1 NOVI NASTAVNI PLAN
 GRAĐEVINSKI FAKULTET U BEOGRADU pismeni ispit Modul za konstrukcije 16.06.009. NOVI NASTAVNI PLAN p 1 8 /m p 1 8 /m 1-1 POS 3 POS S1 40/d? POS 1 d p 16 cm 0/60 d? p 8 /m POS 5 POS d p 16 cm 0/60 3.0 m
GRAĐEVINSKI FAKULTET U BEOGRADU pismeni ispit Modul za konstrukcije 16.06.009. NOVI NASTAVNI PLAN p 1 8 /m p 1 8 /m 1-1 POS 3 POS S1 40/d? POS 1 d p 16 cm 0/60 d? p 8 /m POS 5 POS d p 16 cm 0/60 3.0 m
4. PREDAVANJE ČISTO PRAVO SAVIJANJE OTPORNOST MATERIJALA I
 4. PREDAVANJE ČISTO PRAVO SAVIJANJE OTPORNOST MATERIJALA I Čisto pravo savijanje Pod čistim savijanjem grede podrazumeva se naprezanje pri kome su sve komponente unutrašnjih sila jednake nuli, osim momenta
4. PREDAVANJE ČISTO PRAVO SAVIJANJE OTPORNOST MATERIJALA I Čisto pravo savijanje Pod čistim savijanjem grede podrazumeva se naprezanje pri kome su sve komponente unutrašnjih sila jednake nuli, osim momenta
Zadatak 4b- Dimenzionisanje rožnjače
 Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadatak 4b- Dimenzionisanje rožnjače Rožnjača je statičkog sistema kontinualnog nosača raspona L= 5x6,0m. Usvaja se hladnooblikovani šuplji profil pravougaonog poprečnog preseka. Raster rožnjača: λ r 2.5m
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
3525$&8158&1(',=$/,&(6$1$92-1,095(7(120
 Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
Srednja masinska skola OSOVE KOSTRUISAJA List1/8 355$&8158&1(',=$/,&(6$1$9-1,095(7(10 3ROD]QLSRGDFL maksimalno opterecenje Fa := 36000 visina dizanja h := 440 mm Rucna sila Fr := 350 1DYRMQRYUHWHQR optereceno
, 81, 5?J,. 1o~",mlt. [ BO'?o~ ~Iel7L1 povr.sil?lj pt"en:nt7 cf~ ~ <;). So. r~ ~ I~ + 2 JA = (;82,67'11:/'+2-[ 4'33.10'+ 7M.
 J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
OTPORNOST MATERIJALA
 3/8/03 OTPORNOST ATERIJALA Naponi ANALIZA NAPONA Jedinica u Si-sistemu je Paskal (Pa) Pa=N/m Pa=0 6 Pa GPa=0 9 Pa F (N) kn/cm =0 Pa N/mm =Pa Jedinična površina (m ) U tečnostima pritisak jedinica bar=0
3/8/03 OTPORNOST ATERIJALA Naponi ANALIZA NAPONA Jedinica u Si-sistemu je Paskal (Pa) Pa=N/m Pa=0 6 Pa GPa=0 9 Pa F (N) kn/cm =0 Pa N/mm =Pa Jedinična površina (m ) U tečnostima pritisak jedinica bar=0
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
5. PREDAVANJE ČISTO KOSO SAVIJANJE EKCENTRIČNO NAPREZANJE OTPORNOST MATERIJALA I
 5. PREDAVANJE ČISTO KOSO SAVIJANJE EKCENTRIČNO NAPREZANJE OTPORNOST MATERIJALA I ČISTO KOSO SAVIJANJE Pod pravim savijanjem podrazumeva se slučaj kada se ravan savijanja poklapa sa jednom od glavnih ravni
5. PREDAVANJE ČISTO KOSO SAVIJANJE EKCENTRIČNO NAPREZANJE OTPORNOST MATERIJALA I ČISTO KOSO SAVIJANJE Pod pravim savijanjem podrazumeva se slučaj kada se ravan savijanja poklapa sa jednom od glavnih ravni
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
TEORIJA BETONSKIH KONSTRUKCIJA 79
 TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
30 kn/m. - zamenimo oslonce sa reakcijama oslonaca. - postavimo uslove ravnoteže. - iz uslova ravnoteže odredimo nepoznate reakcije oslonaca
 . Za zadati nosač odrediti: a) Statičke uticaje (, i T) a=.50 m b) Dimenzionisati nosač u kritičnom preseku i proveriti normalne, smičuće i uporedne napone F=00 k F=50 k q=30 k/m a a a a Kvalitet čelika:
. Za zadati nosač odrediti: a) Statičke uticaje (, i T) a=.50 m b) Dimenzionisati nosač u kritičnom preseku i proveriti normalne, smičuće i uporedne napone F=00 k F=50 k q=30 k/m a a a a Kvalitet čelika:
Vrijedi relacija: Suma kvadrata cosinusa priklonih kutova sile prema koordinatnim osima jednaka je jedinici.
 Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
Za adani sustav prostornih sila i j k () oktant i j k () oktant koje djeluju na materijalnu toku odredite: a) reultantu silu? b) ravnotežnu silu? a) eultanta sila? i j k 8 Vektor reultante: () i 8 j k
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Geometrijske karakteristike poprenih presjeka nosaa. 9. dio
 Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
l r redukovana dužina (zavisno od dužine i načina vezivanja)
 Vežbe 6 IZVIJANJE 1 IZVIJANJE Izvijanje se javlja kod aksijalno napregnutih štapova na pritisak, kada imaju relativno veliku dužinu u odnosu na površinu poprečnog preseka. Zbog postojanja geometrijskih
Vežbe 6 IZVIJANJE 1 IZVIJANJE Izvijanje se javlja kod aksijalno napregnutih štapova na pritisak, kada imaju relativno veliku dužinu u odnosu na površinu poprečnog preseka. Zbog postojanja geometrijskih
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
Osnovne vrste naprezanja: Aksijalno naprezanje Smicanje Uvijanje. Savijanje. Izvijanje
 Osnovne vrste napreanja: ksijalno napreanje Smicanje Uvijanje Savijanje Ivijanje 1 SVIJNJE GREDE SI Greda je opterećena na desnom kraju silom paralelno jednoj od glavnih centralnih osa inercije (y osi).
Osnovne vrste napreanja: ksijalno napreanje Smicanje Uvijanje Savijanje Ivijanje 1 SVIJNJE GREDE SI Greda je opterećena na desnom kraju silom paralelno jednoj od glavnih centralnih osa inercije (y osi).
Totalni napon u tački preseka. Normalni i tangencijalni napon.
 Totalni napon u tački preseka. Normalni i tangencijalni napon. Zamislimo da je opterećeno elastično telo nekom proizvoljnom ravni presečeno na dva dela. Odbačeni desni deo tela, na posmatrani levi, na
Totalni napon u tački preseka. Normalni i tangencijalni napon. Zamislimo da je opterećeno elastično telo nekom proizvoljnom ravni presečeno na dva dela. Odbačeni desni deo tela, na posmatrani levi, na
Izvođenje diferencijalne jednačine elastične linije elastična linija kod proste grede elastična linija kod konzole
 Izvođenje diferencijalne jednačine elastične linije Elastična linija, čija je jednačina y(z), je krivolinijski oblik ose nosača izazvan opterećenjem. Koordinatni sistem ćemo uvek uzimati tako da je koordinatni
Izvođenje diferencijalne jednačine elastične linije Elastična linija, čija je jednačina y(z), je krivolinijski oblik ose nosača izazvan opterećenjem. Koordinatni sistem ćemo uvek uzimati tako da je koordinatni
Teorija betonskih konstrukcija 1. Vežbe br. 4. GF Beograd
 Teorija betonskih konstrukcija 1 Vežbe br. 4 GF Beograd Teorija betonskih konstrukcija 1 1 "T" preseci - VEZANO dimenzionisanje Poznato: statički uticaji (M G,Q ) sračunato kvalitet materijala (f cd, f
Teorija betonskih konstrukcija 1 Vežbe br. 4 GF Beograd Teorija betonskih konstrukcija 1 1 "T" preseci - VEZANO dimenzionisanje Poznato: statički uticaji (M G,Q ) sračunato kvalitet materijala (f cd, f
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD Osijek, 15. rujan 2017. Ivan Kovačević SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD Osijek, 15. rujan 2017. Ivan Kovačević SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Savijanje statički neodređeni nosači
 Savijanje statički neodređeni nosači Statička neodređenost nosača Uslovi neprekidnosti elastične linije Prva jednačina savijanja Normalni napon u nekoj tački poprečnog preseka s M moment sprega s z M I
Savijanje statički neodređeni nosači Statička neodređenost nosača Uslovi neprekidnosti elastične linije Prva jednačina savijanja Normalni napon u nekoj tački poprečnog preseka s M moment sprega s z M I
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Savijanje nosaa. Savijanje ravnog štapa prizmatinog poprenog presjeka. a)isto savijanje. b) Savijanje silama. b) Savijanje silama.
 Štap optereen na savijanje naivamo nosa ili grea. Savijanje nosaa a) Napreanja ( i τ) b) Deformacije progib (w) Os štapa se ko savijanja akrivljuje to je elastina ili progibna linija nosaa. Savijanje ravnog
Štap optereen na savijanje naivamo nosa ili grea. Savijanje nosaa a) Napreanja ( i τ) b) Deformacije progib (w) Os štapa se ko savijanja akrivljuje to je elastina ili progibna linija nosaa. Savijanje ravnog
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Konvencija o znacima za opterećenja grede
 Konvencija o znacima za opterećenja grede Levo od preseka Desno od preseka Savijanje Čisto savijanje (spregovima) Osnovne jednačine savijanja Savijanje silama Dimenzionisanje nosača izloženih savijanju
Konvencija o znacima za opterećenja grede Levo od preseka Desno od preseka Savijanje Čisto savijanje (spregovima) Osnovne jednačine savijanja Savijanje silama Dimenzionisanje nosača izloženih savijanju
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Proračun štapova na zatezanje i pritisak. Osnova za proračun je zadovoljenje nejednačine σ σ, σ d
 Proračun štapova na zatezanje i pritisak Osnova za proračun je zadovojenje nejednačine, max d gde je max maksimum apsoutne vrednosti normanog napona štapa a d je dozvojeni normani napon Ovakva nejednakost
Proračun štapova na zatezanje i pritisak Osnova za proračun je zadovojenje nejednačine, max d gde je max maksimum apsoutne vrednosti normanog napona štapa a d je dozvojeni normani napon Ovakva nejednakost
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA
 ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
GRAĐEVINSKI FAKULTET U BEOGRADU pismeni ispit ODSEK ZA KONSTRUKCIJE TEORIJA BETONSKIH KONSTRUKCIJA. grupa A. p=60 kn/m. 7.
 ODSEK ZA KONSTRUKCIJE 28.01.2015. grupa A g=50 kn/m p=60 kn/m 60 45 15 75 MB 35, RA 400/500 7.5 m 5 m 25 1.1 Odrediti potrebnu površinu armature u karakterističnim presecima (preseci na mestima maksimalnih
ODSEK ZA KONSTRUKCIJE 28.01.2015. grupa A g=50 kn/m p=60 kn/m 60 45 15 75 MB 35, RA 400/500 7.5 m 5 m 25 1.1 Odrediti potrebnu površinu armature u karakterističnim presecima (preseci na mestima maksimalnih
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
TEHNIČKA MEHANIKA I 9. PREDAVANJE SILE U PRESEKU GREDNOG NOSAČA. Str knjiga Poglavlje 12 Unutrašnje sile
 5.5.2016 1 TEHNIČKA MEHANIKA I 9. PREDAVANJE SILE U PRESEKU GREDNOG NOSAČA Str 267-290 knjiga Poglavlje 12 Unutrašnje sile 5.5.2016 2 ŠTA ĆEMO NAUČITI U OVOM POGLAVLJU? Određivanje unutrašnjih sila u presecima
5.5.2016 1 TEHNIČKA MEHANIKA I 9. PREDAVANJE SILE U PRESEKU GREDNOG NOSAČA Str 267-290 knjiga Poglavlje 12 Unutrašnje sile 5.5.2016 2 ŠTA ĆEMO NAUČITI U OVOM POGLAVLJU? Određivanje unutrašnjih sila u presecima
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD
![35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD 35(7+2'1,3525$&8195$7,/$GLPHQ]LRQLVDQMHYUDWLOD](/thumbs/60/45174330.jpg) Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
Predmet: Mašinski elementi Proraþun vratila strana 1 Dimenzionisati vratilo elektromotora sledecih karakteristika: ominalna snaga P 3kW Broj obrtaja n 14 min 1 Shema opterecenja: Faktor neravnomernosti
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
Ispit održan dana i tačka A ( 3,3, 4 ) x x + 1
 Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
STATIČKI ODREĐENI SUSTAVI
 STTIČKI ODREĐENI SUSTVI STTIČKI ODREĐENI SUSTVI SVOJSTV SUSTV Kod statički određenih nosača rješenja za reakcije i unutrašnje sile su jednoznačna. F C 1. F x =0 C 2. M =0 3. F y =0 Jednoznačno rješenje
STTIČKI ODREĐENI SUSTVI STTIČKI ODREĐENI SUSTVI SVOJSTV SUSTV Kod statički određenih nosača rješenja za reakcije i unutrašnje sile su jednoznačna. F C 1. F x =0 C 2. M =0 3. F y =0 Jednoznačno rješenje
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
BETONSKE KONSTRUKCIJE 2
 BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
LOGO ISPITIVANJE MATERIJALA ZATEZANJEM
 LOGO ISPITIVANJE MATERIJALA ZATEZANJEM Vrste opterećenja Ispitivanje zatezanjem Svojstva otpornosti materijala Zatezna čvrstoća Granica tečenja Granica proporcionalnosti Granica elastičnosti Modul
LOGO ISPITIVANJE MATERIJALA ZATEZANJEM Vrste opterećenja Ispitivanje zatezanjem Svojstva otpornosti materijala Zatezna čvrstoća Granica tečenja Granica proporcionalnosti Granica elastičnosti Modul
SILE U PRESEKU GREDNOG NOSAČA
 SIE U PRESEKU GREDNOG NOSAČA DEFINICIJE SIA U PRESECIMA Projektovanje bilo kog konstruktivnog elemenata podrazumeva određivanje unutrašnjih sila u tom elementu da bi se obezbedilo da materijal od koga
SIE U PRESEKU GREDNOG NOSAČA DEFINICIJE SIA U PRESECIMA Projektovanje bilo kog konstruktivnog elemenata podrazumeva određivanje unutrašnjih sila u tom elementu da bi se obezbedilo da materijal od koga
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
SVEUČILIŠTE U MOSTARU GRAĐEVINSKI FAKULTET
 SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
SVEUČILIŠTE U MOSTRU GRĐEVINSKI FKULTET Kolegij: Osnove betonskih konstrukcija k. 013/014 god. 8. pismeni (dodatni) ispit - 10.10.014. god. Zadatak 1 Dimenzionirati i prikazati raspored usvojene armature
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
Osnovni pojmovi, spoljašnje i unutrašnje sile, definicije napona i deformacije, vrste naprezanja. Osnovni pojmovi
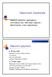 Osnovni pojmovi, spoljašnje i unutrašnje sile, definicije napona i deformacije, vrste naprezanja Osnovni pojmovi Kruto telo Rastojanje ma koje tačke je stalno, ne menja se, telo se ne deformiše predmet
Osnovni pojmovi, spoljašnje i unutrašnje sile, definicije napona i deformacije, vrste naprezanja Osnovni pojmovi Kruto telo Rastojanje ma koje tačke je stalno, ne menja se, telo se ne deformiše predmet
Proračunski model - pravougaoni presek
 Proračunski model - pravougaoni presek 1 ε b 3.5 σ b f B "" ηx M u y b x D bu G b h N u z d y b1 a1 "1" b ε a1 10 Z au a 1 Složeno savijanje - VEZNO dimenzionisanje Poznato: statički uticaji za (M i, N
Proračunski model - pravougaoni presek 1 ε b 3.5 σ b f B "" ηx M u y b x D bu G b h N u z d y b1 a1 "1" b ε a1 10 Z au a 1 Složeno savijanje - VEZNO dimenzionisanje Poznato: statički uticaji za (M i, N
Univerzitet u Beogradu 20. januar Elektrotehnički fakultet
 Univerzitet u eograu. januar 1. Elektrotehnički fakultet EHNIK 1. Telekomunikacioni kabl je potrebno zategnuti između ve vertikalne konzole (stuba) koje su ubetonirane u sreišta krovova ve susene zgrae,
Univerzitet u eograu. januar 1. Elektrotehnički fakultet EHNIK 1. Telekomunikacioni kabl je potrebno zategnuti između ve vertikalne konzole (stuba) koje su ubetonirane u sreišta krovova ve susene zgrae,
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
