viacrozmerných a nekonečnorozmerných priestoroch. A ako nasvedčuje jej názov, pôjde o rovnice nelineárne.
|
|
|
- Νικολίτα Κεδίκογλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Nelineárna analýza 1. Úvod Na začiatok by bolo načim ako-tak vymedzit, čím sa nelineárna analýza zaoberá. Čitatel by už mal však mat dostatok skúseností, aby vedel, že je to dost t ažké u l ubovol nej matematickej disciplíny. U nelineárnej analýzy je to o to t ažšie, že na rozdiel povedzme od geometrie či integrálneho počtu ide o disciplínu, ktorá sa ako-tak sformovala v svojej súčasnej polohe až v druhej polovici tohoto storočia. Predsa však sa dá povedat, že nelineárna analýza sa točí okolo riešenia rovníc vo viacrozmerných a nekonečnorozmerných priestoroch. A ako nasvedčuje jej názov, pôjde o rovnice nelineárne. Presnejšie povedané, základnú otázku nelineárnej analýzy možno postavit takto: Nech X, Z sú konečno- alebo nekonečnorozmerné priestory, U X, F : U Z a z Z. Ako vyzerá F 1 (z)? Ako príklad si vezmime najjednoduchšiu verziu vety o implicitnej funkcii. Nech X = R 2, Z = R, (x, y ) R 2, U je okolie bodu (x, y ) a F : U Z je C r -diferencovatel ná. F (x, y ) = z, F/ y(x, y ). Potom, (vol ne povedané), lokálne v okolí bodu (x, y ) možno z implicitnej rovnice F (x, y) = z premennú y vyjadrit ako jednoznačnú C r funkciu y = ϕ(x), t.j. lokálne F (x, y) = z platí práve vtedy, ak y = ϕ(x). Vel mi často má otázka štruktúry množiny riešení rovnice F (x) = z podobu otázky závislosti riešení rovnice na parametroch. V takomto prípade je X = Y P, kde P chápeme ako priestor parametrov úlohy. Pýtame sa na závislost riešenia od parametrov: ak poznáme riešenie pre istú hodnotu p = p, čo sa s ním stane, ak zmeníme p? V aplikáciách rovnice spravidla predstavujú ustálené stavy nejakej dynamiky. Napríklad môže íst o tyč, na ktorej os pôsobíme tlakom. Za priestor riešení môžeme považovat funkciu, ktorá dl žkovej súradnici tyče prirad uje jej priečnu výchylku, za parameter môžeme vziat silu, ktorou tyč stláčame. Pre malé hodnoty parametra - sily, bude jediným riešením funkcia identicky rovná nule (a teda malá zmena parametra neovplyvní riešenie). Pri istej medznej hodnote parametra však tyč z priamej polohy vybočí a nie je zrejmé, na ktorú stranu. Hovoríme, že príde k vetveniu, bifurkácii riešení. 2. Diferenciálny počet v Banachových priestoroch Príklad vety o implicitnej funkcii napovedá, že sotva bude možné niečo o množine riešení rovnice F (x) = z povedat, ak sa nebude od nej žiadat nejaký stupeň regularity. Všeobecne povedané, čím regulárnejšia (hladšia) je funkcia F, tým jemnejšie môžu byt naše výpovede o štruktúre množiny riešení. Pretože vo všeobecnosti nám pôjde o rovnice v Banachových priestoroch, potrebujeme v nich najprv zaviest derivácie a naučit sa s nimi pracovat. 2.1 Derivácia v smere Kým v prípade funkcie jednej premennej je definícia derivácie bez nejasností a stotožňuje sa s diferenciálom, už v prípade z R 2 do R (teda reálnej funkcie dvoch Typeset by AMS-TEX 1
2 2 reálnych premenných) sa definujú prinajmenej dva pojmy, ktoré s diferencovaním súvisia - parciálne derivácie, (úplný) diferenciál. Tieto pojmy sa zväzujú tajomnou formulou df = ( f/ x 1 )dx 1 + ( f/ x 2 )dx 2. Túto tajomnú formulu samozrejme možno rozšírit na funkcie z R m do R n (teda n reálnych funkcií s m premennými). Čo však s funkciami na nekonečnorozmerných priestoroch? Pripomeňme si však, že parciálne derivácie na f/ x i (x) je vlastne derivácia funkcie jednej premennej, ktorá vznikne zúžením funkcie f na rovnobežku s osou x i cez bod x, teda funkcie ϕ(t) = f(x + te i ), kde e i je i-tý jednotkový súradnicový vektor. Z geometrického hl adiska však niet nijakého dôvodu privilegovat súradnicové osi - analogicky môžeme derivovat funkciu, ktorá vznikne zúžením funkcie na l ubovol nú priamku cez bod x. Vyjadrením toho je pojem derivácie v smere: Definícia. Nech X, Y sú Banachove priestory, U X je otvorená a F : U Y. Nech x U a h X. Ak existuje limita 1 lim [F (x + ϑh) F (x)], ϑ ϑ nazývame ju deriváciou funkcie F v bode x v smere h a označujeme ju h F (x) Poznámka. Ak X = R m, potom zrejme ei F (x) = F/ x i (x) Aplikácia. Derivácie v smere hrajú významnú úlohu pri odvodzovaní nutných podmienok pre lokálne extrémy reálnych funkcií na konečnorozmerných a Banachových priestoroch v prítomnosti ohraničení. Nech F : X R, kde X je Hilbertov priestor a nech K = {x X :< a i, x > b i, i = 1,..., n}, kde <.,. > je skalárny súčin, a i X a b i R sú dané. Nech ˆx K je taký bod, že F (ˆx) = min x K F (x). Potom hodnota F zrejme nemôže klesat pozdl ž nijakej polpriamky cez bod ˆx, ktorá v blízkosti bodu ˆx leží v množine K. To vedie k podmienke h F (ˆx) pre každé h také, že h F (ˆx) existuje a < a i, h > pre všetky i I(ˆx) = {i :< a i, ˆx >= b i }. Ak sa starostlivo do dôsledkov využijú tieto podmienky minima, dostane sa spravidla formálne dostatok podmienok na jeho určenie (kol ko neznámych, tol ko rovníc) Cvičenia. 1. Dokážte, že h h F (x) je homogénna v h. 2. Dokážte tvrdenie Nech F : R m R a nech ˆx je lokálne minimum funkcie F. Odvod te z známe nutné podmienky minima F/ x i (ˆx) =, i = 1,..., m.
3 3 4. Nech F : R m R a nech F je diferencovatel ná v bode x R m. Dokážte, že platí h F (x) = F/ x 1 (x)h F/ xm (x)h m. 5. Nech f : R 2 R, (x, y) f(x, y) je diferencovatel ná. Definujme F : C[, 1] C[, 1] predpisom F (ϕ)(x) = f(x, ϕ(x)) (2.1) Zobrazenie F nazývame Nemyckého operátorom generovaným funkciou f. Dokážte, že h F (ϕ)(x) = f (x, ϕ(x))h(x). y 6. Dokážte, že rovnaká formula ako v cvičení 5. platí aj vtedy, ak F chápeme ako zobrazenie L p [, 1] L p [, 1], p Gâteauxov diferenciál Nech F : U Y, kde U X a X, Y sú Banachove priestory. Predpokladajme, že pre x U existuje h F (x) pre každé h. Podl a cvičenia je h F (x) homogénnou funkciou h. Ak je navyše aditívnou funkciou h, potom je lineárna v h Definícia. Ak je zobrazenie h h F (x) lineárne a ohraničené, potom ho nazývame Gâteauxovým diferenciálom funkcie F v bode x a označujeme ho df (x). Gâteauxov (G-) diferenciál je teda definovaný predpisom df (x)h = h F (x) pre h X (2.2) Poznámky. 1. Gâteauxov diferenciál je prvkom priestoru L(X, Y ) ohraničených lineárnych operátorov z X do Y. 2. Ak je dim X <, netreba ohraničenost operátora h h F (ˆx) osobitne predpokladat, vyplýva totiž z linearity. 3. G-diferenciál budeme nazývat tiež G-deriváciou a nebudeme medzi týmito pojmami robit rozdiel. 4. Mystickej formule df (x) = F/ x 1 (x)dx F/ x n (x)dx n možno teraz dat zmysel rovnosti diferenciálov, pričom dx i chápeme ako diferenciál zobrazenia, ktoré bodu x = (x 1,..., x n ) R n prirad uje jeho i-tú zložku x i. 5. Nech F : U R n, U R m a nech F je diferencovatel ná v bode x U. Potom matica G-diferenciálu F v bode x je df (x) = F 1/ x 1 (x)... F 1 / x m (x).... F n / x 1 (x)... F n / x m (x) Takto možno l avú stranu (2.2) chápat ako násobenie vektora h maticou df (ˆx).
4 Cvičenia. 1. Nájdite príklad spojitej funkcie R 2 R 1, ktorá má v nejakom bode derivácie vo všetkých smeroch, nie je však v ňom G-diferencovatel ná. 2. Dokážte tvrdenia poznámok a Za predpokladov cvičení a dokážte, že F je G-diferencovatel ná (či už ako zobrazenie C[, 1] C[, 1], alebo L p (, 1) L p (, 1), p 1) a že platí [df (ϕ)h](x) = f/ y(x, ϕ(x))h(x). 4. Ak je funkcia v nejakom bode G-diferencovatel ná, je v ňom aj spojitá? 2.3. Fréchetov diferenciál Definičnú rovnicu (2.2) pre Gâteauxov diferenciál môžeme prepísat aj v tvare F (x + ϑh) = F (x) + ϑ[df (x)h + ω(h, ϑ)] (2.3) kde lim ω(h, ϑ) = (2.4) ϑ pre každé pevné h. Vzt ahy (2.3), (2.4) môžeme interpretovat tak, že G-diferenciál je najlepšou lineárnou aproximáciou ( lokálnou linearizáciou ) funkcie F v bode x. To umožňuje všeličo usúdit o správaní sa funkcie F v okolí bodu x zo správania jej G-diferenciálu. Je to dôležité preto, že lineárne zobrazenia sa vyšetrujú ovel a pohodlnejšie. Skúsenost však ukazuje, že tesnost priblíženia F jej linearizáciou v zmysle (2.2) - (232) nie je pre takéto účely dostatočná. Preto sa zavádza pojem Fréchetovho diferenciálu Definícia. Nech X, Y sú Banachove priestory, U X je otvorená, F : U Y a x U. Hovoríme, že zobrazenie F je Fréchetovsky diferencovatel náv bode x, ak existuje lineárny ohraničený operátor DF (x) (nazývaný Fréchetovým (F-) diferenciálom) taký, že lim h 1 [F (x + h) F (x) DF (x)h] = h Poznámky. 1. Aj v prípade Fréchetovho diferenciálu budeme alternatívne používat termín Fréchetova (F-) derivácia. Pokial vynecháme prívlastok, budeme vždy mat na mysli F-diferenciál. 2. Diferenciál, ako sa definuje v diferenciálnom počte je Fréchetov diferenciál. 3. Ak existuje Fréchetov diferenciál, potom je rovný Gâteauxovmu (a preto je jediný). Gâteauxov diferenciál je Fréchetovým vtedy, ak je konvergencia v (8.2) rovnomerná vzhl adom na h, spl ňajúce h G-diferenciál budeme dôsledne značit písmenom d, F-diferenciál zasa písmenom D; upozorňujeme však, že táto konvencia nie je všeobecne prijatá a značenia sú všakovaké. V teórii a aplikáciách sa pracuje takmer výlučne s F-diferenciálom. Zmysel G-diferenciálu je v tom, že jeho definícia je na rozdiel od F-diferenciálu konštruktívna a je ho možné počítat aj pri zobrazení z nekonečnorozmerných priestorov, ako napr. v cvičení Kedy je G-diferenciál aj F-diferenciálom, o tom hovorí nasledujúca veta:
5 Veta. Nech X, Y sú Banachove priestory, U X otvorená F : U Y a x U. Ak F je G-diferencovatel ná a df je spojitý v okolí V bodu x (ako zobrazenie V L(X, Y )), potom F je v bode x F -diferencovatel ná. K dôkazu tejto vety nám poslúži nasledujúca lema, ktorú budeme aj v d alšom často používat Lema (Hadamardova). Nech F spl ňa predpoklady vety. Ak x + ϑh U pre ϑ 1, potom platí F (x + h) F (x) = kde integrál chápeme ako Riemannov. Dôkaz. Označíme 1 1 ( = df (x + ϑh)hdϑ ϕ(ϑ) = F (x + ϑh). df (x + ϑh)dϑ h) (2.5) Potom ϕ : [, 1] Y je diferencovatel ná. Podl a Newtonovej-Leibnizovej formuly platí F (x + h) F (x) = ϕ(1) ϕ() = Priamo z definícií a však dostávame z čoho vyplýva (2.5). 1 ϕ (ϑ) = h F (x + ϑh) = df (x + ϑh)h, ϕ (ϑ)dϑ Poznámka. Ak dim Y > 1, neplatí vo všeobecnosti veta o strednej hodnote diferenciálneho počtu - F (x + h) F (x) = df (x + ˆϑh)h nemusí platit pre nijaké ˆϑ 1. Nahradzuje ju Hadamardova lema. Dôkaz vety Predpoklad spojitosti df značí, že k zvolenému ε > existuje δ > také, že ak k X, k δ, potom F (x + k) U a platí df (x + k) df (x) ε alebo, v zmysle definície normy lineárneho operátora, (df (x + k) df (x))h ε h (2.6) pre každé h X. Nech teraz h δ. Podl a Lemy a (2.6) platí F (x + h) F (x) df (x)h = = 1 To dokazuje vetu. 1 [ 1 [df (x + ϑh) df (x)]hdϑ df (x + ϑh)dϑh df (x)h = ] (df (x + ϑh) df (x)) dϑ h ε h
6 Príklad. Veta nám umožňuje počítat F-diferenciál zobrazenia F na nekonečnorozmernom priestore v danom bode takto: 1. Vypočítame derivácie v smeroch v bodoch nejakého okolia U bodu x. 2. Overíme, že h h F (x) je prvkom priestoru L(X, Y ) pre všetky x U (a teda funkcia je G-diferencovatel ná v U). 3. Overíme, že G-diferenciál df je spojitý na U. Postup si ukážeme na prípade derivácie Nemyckého operátora z Cvičení , Dokážeme, že ak je funkcia f spojito diferencovatel ná, potom je G-diferenciál jej Nemyckého operátora z C[, 1] do C[, 1] z Cvičenia jeho F-diferenciálom. Kroky 1, 2 sú predmetom spomínaných cvičení. Vykonáme teda krok 3. Označme normu v C[, 1]. Treba dokázat, že pre l ubovol nú funkciu u C[, 1] a l ubovol né ε > existuje δ > také, že ak v C[, 1], u v < δ, potom pre každé h C[, 1] platí [ ] f f (, u( )) (, v( )) h( ) ε h, y y t.j. [ ] f f sup (x, u(x)) (x, v(x)) h(x) ε sup h(x). (2.7) x [,1] y y x [,1] Nerovnost u v < δ značí u(x) v(x) < δ pre každé x [, 1]. Podl a predpokladu je f/ y spojitá, a teda je aj rovnomerne spojitá na každej kompaktnej množine. Preto existuje také δ >, že f f (x, u(x)) (x, v(x)) < ε y y pre každé x [, 1]. Pre toto δ zrejme platí aj (2.7) Varovanie. Tvrdenie z Príkladu vo všeobecnosti neplatí, ak F chápeme ako zobrazenie z L 2 [, 1] do L 2 [, 1]. Dá sa dokázat, že F : L 2 [, 1] L 2 [, 1] daná predpisom (2.1) je diferencovatel ná práve vtedy, ak f je afinná v y, t.j. f(x, y) = a(x) + b(x)y. Pri výpočte derivácie možno často využit nasledovnú vetu o derivácii kompozície zobrazení Veta. Nech X, Y, Z sú B-priestory a nech U X, V Y sú otvorené, F : U Y, G : V Z. Nech F (x) V a nech F, G sú (F-)diferencovatel né v bode x resp. F (x). Potom funkcia G F je (F-)diferencovatel ná v bode x a platí D(G F )(x) = DG(F (x))df (x). (2.8) Dôkaz tejto vety je takmer doslovným prepisom zodpovedajúcej vety z elementárneho diferenciálneho počtu a preto ho prenechávame na čitatel a.
7 Cvičenia. 1. Zostrojte reálnu funkciu dvoch premenných, ktorá je v nejakom bode spojitá a G-, ale nie F-diferencovatel ná. 2. Dokážte tvrdenie z Dokážte detailne Vetu Dokážte, že ak F je v bode x F-diferencovatel ná, potom je v ňom aj spojitá. 4. Platí Veta aj pre G-diferenciály? 5. Dokážte, že ak existuje F-diferenciál, potom je jediný Multilineárne zobrazenia Ako definovat vyššie derivácie funkcií na Banachových priestoroch? V prípade funkcie jednej reálnej premennej niet problémov: ak F : X Y je diferencovatel ná a X = R, potom x DF (x) je opät funkcia jednej reálnej premennej a má zmysel hovorit o jej derivácii. To je preto, že priestor lineárnych operátorov L(X, Y ) je izomorfný priestoru X, ak X = R. Akonáhle však dim X > 1, potom to nie je pravda. Ak F : U Y je diferencovatel ná a U X, potom DF : U L(X, Y ). Ak chceme hovorit o druhej derivácii funkcie F, teda o derivácii jej derivácie, ide o deriváciu funkcie s hodnotami v priestore L(X, Y ), teda v úplne inom priestore, než je Y. To je samozrejme možné, ukazuje sa však užitočným chápat aj vyššie derivácie funkcií z X do Y ako funkcie s hodnotami v tom istom priestore Y. To je možné takto: Ak DF : X L(X, Y ), potom D 2 F (x) = D(DF )(x) L(X, L(X, Y )). Ak P L(X, L(X, Y )) potom pre zvolené h X je Q = P h L(X, Y ). Pre zvolené k X je Qk = (P h)k Y. (2.9) Každé zobrazenie P L(X, (X.Y )) teda predpisom (2.9) môžeme stotožnit s istým zobrazením z X X do Y. Toto zobrazenie je zrejme bilineárne, t.j. pri pevnej hodnote jednej z premenných je lineárne v druhej z nich. Nie je už t ažko si predstavit, že takto možno pokračovat k vyšším deriváciám. Vedie k zobrazeniam viacerých premenných, ktoré sú lineárne v každej z nich - k multilineárnym zobrazeniam. Aby sme mohli pracovat s deriváciami vyšších rádov, potrebujeme si teda čo-to povedat o multilineárnych zobrazeniach. Ich teória je v mnohom analogická teórii lineárnych operátorov Definícia. Nech X 1,..., X n, Y sú B-priestory. Hovoríme, že zobrazenie A : X 1 X n Y je multilineárne (presnejšie n-lineárne), ak A(x 1,..., x i 1,, x i+1,..., x n ) : X i Y je lineárne pre každé i a pre každé pevné x 1,..., x i 1, x i+1,..., x n. Podobne, ako u lineárnych zobrazení, budeme často zátvorku za symbolom multilineárneho zobrazenia vynechávat. Platí
8 Veta. Nech X 1,..., X n, Y sú B-priestory a nech A : X 1 X n Y je multilineárne zobrazenie. Potom nasledujúce tvrdenia sú ekvivalentné. (i) A je spojitá v každom bode x X = X 1 X n (ii) A je spojitá v bode. (iii) existuje K > také, že Ax 1... x n K x 1... x n (2.1) pre každé (x 1,..., x n ) X (iv) A je diferencovatel ná v každom bode X a jej derivácia je spojitou funkciou x. Dôkaz povedieme po trase (iv) (i) (ii) (iii) (i), (i) (iii) (iv). Zrejme (iv) (i) (ii). Dôkazy ostatných implikácií: (ii) (iii) Pretože A = a A je spojitá v, existuje δ > také, že platí Ay 1... y n 1 ak y i δ pri i = 1,..., n. Z toho pre l ubovol né x i X i, i = 1,..., n dostávame A δx 1 x 1,..., δx n x n 1 (pretože δx i / x i δ). Z multilinearity vyplýva teda (2.11) platí s K = δ n. (iii) (i) Tvrdenie (i) vyplýva z nerovnosti Ax 1... x n δ n x 1... x n, A(x x ) K x 1 x 1... x n x n, ktorá je bezprostredným dôsledkom (iii). (i) (iii) (iv) Dôkaz vykonáme pre n = 2, jeho rozšírenie pre n > 2 je zrejmé. Nech x, h X. h A(x) = lim ϑ ϑ 1 [A(x 1 + ϑh 1, x 2 + ϑh 2 ) Ax 1 x 2 ] = = lim ϑ ϑ 1 [Ax 1 x 2 + ϑ(ah 1 x 2 + Ah 2 x 1 ) + ϑ 2 Ah 1 h 2 Ax 1 x 2 ] = = Ah 1 x 2 + Ah 2 x 1. Zobrazenie h Ah 1 x 2 + Ah 2 x 1 je zrejme lineárne a podl a (iii) aj ohraničené a teda podl a definície G-diferenciálu je A G-diferencovatel né v bode x a platí da(x)h = Ah 1 x 2 + Ah 2 x 1 (2.11)
9 9 F-diferencovatel nost A vyplynie z Vety ak ukážeme, že zobrazenie A(, x 2 ) + A(x 1, ) : X 1 X 2 Y, (h 1, h 2 ) Ah 1 x 2 + Ax 1 h 2 ) je spojité ako zobrazenie z X 1 X 2 do L(X, Y ). Toto zobrazenie je zrejme lineárne a teda stačí dokázat, že je ohraničené. Podl a (i) však platí Ah 1 x 2 + Ax 1 h 2 K( h 1 x 2 + x 1 h 2 ) 2K( x 1 + x 2 )( h 1 + ( h 2 ), čím je dôkaz ukončený Definícia. Multilineárne zobrazenie, spl ňajúce podmienku (2.12) (alebo l ubovol nú z jej ekvivalentných podmienok) nazývame ohraničeným. Najmenšiu z konštánt K, pre ktorú platí (2.13) nazývame normou zobrazenia A a označujeme A (resp. rovnakým symbolom, akým označujeme normu v priestore Y ) Poznámky. 1. Všimnime si analógie medzi ohraničenými multilineárnymi formami a ohraničenými lineárnymi operátormi (napr. ekvivalencia ohraničenosti (2.13) a spojitosti, definíciu normy). 2. Ak X 1,..., X n sú konečnorozmerné priestory, potom každé multilineárne zobrazenie z X 1 X n je ohraničené. Pre dané B-priestory X 1,..., X n, Y je množina multilineárnych foriem z X 1 X n do Y s normou zavedenou v Definícii opät B-priestorom; označujeme ho L(X 1, X 2,..., X n ; Y ). Dôkaz je rovnaký ako pre priestor ohraničených lineárnych operátorov, preto ho ponechávame čitatel ovi ako cvičenie. Rovnako ponechávame na čitatel a dôkaz nasledovnej vety: Veta. Priestor L(X 1,..., X n ; Y ) je izometricky izomorfný priestoru L(X 1, L(X 2,... (L(X n, Y )... )). Ak X 1 = X 2 = = X n = X, označujeme L n (X, Y ) = L(X 1,..., X n ; Y ) Definícia. Multilineárne zobrazenie A L n (X, Y ) nazývame symetrickou, ak pre l ubovol nú permutáciu σ : {1,..., n} {1,..., n} a l ubovol né x 1,..., x n X platí Ax σ(1)... x σ(n) = Ax 1... x n. Ak A L n (X, Y ) a x 1 = x 2 = = x n X, píšeme Ax 1... x n = Ax n Veta. K l ubovol nej multilineárnemu zobrazeniu A L n (X, Y ) existuje symetrické SymA L n (X, Y ) také, že (i) (SymA)x n = Ax n pre každé x X (ii) SymA = A ak A je ohraničené. Definujeme ju vzt ahom (SymA)x 1... x n = 1 n! Ax σ(1)... x σ(n) (2.12) σ permutácie Dôkaz prenechávame čitatel ovi ako cvičenie.
10 Cvičenia. 1. Nájdite trilineárnu funkciu z R 1 R 2 R 3 do R 2, ktorá nie je konštantná v nijakej z premenných. 2. Urobte detailne indukčný krok v závere dôkazu Vety Dokážte tvrdenie Poznámky Dokážte Vetu [ Návod: použite indukciu ] 5. Dokážte, že zobrazenie SymA, definované vzt ahom (2.13) spl ňa (i), (ii) Vety. Je to jediná symetrické zobrazenie, ktoré ich spl ňa? [ Návod: Ukážte, že n n n A t j x j = (SymA)x 1... x n t 1... t n j=1 6. Dokážte, že priestor L(X 1,..., X n ; Y ) so zavedenou normou je Banachov. 7. Dokážte, že pre ohraničené multilineárne zobrazenie A L(X 1,..., X n ; Y ) platí A = sup Ax 1... x n. x i Derivácie vyšších rádov Definícia. Nech X, Y sú B-priestory, U X je otvorená a F : U Y je diferencovatel ná v každom x U. Hovoríme, že F má druhú deriváciu v bode x U, ak funkcia DF : U (X, Y ) má deriváciu v bode x. Vtedy píšeme D 2 F (x) = D(DF )(x). Pripomeňme si, že DF : U L(X, Y ), takže D 2 F (x) L(X, L(X, Y )). Podl a Vety môžeme D 2 F (x) chápat ako prvok L 2 (X, Y ), pričom D 2 F (x )hk = D(DF (x)h) x=x k. Pre porozumenie je užitočné rozmysliet si prípad X = R n, Y = R. V takomto prípade môžme každé zobrazenie A L n (R, R) reprezentovat takto: Označíme a ij = Ae i e j, kde {e i } n i=1 sú bazové vektory Rn. Z multilinearity pre l ubovol né h, k bezprostredne vyplýva Ahk = h T Ak, kde A na pravej strane je matica s prvkami a ij. Ak A = D 2 F (x ), ij-tý prvok
11 11 matice [D 2 F (x )] je D 2 F (x )e i e j = D(DF (x)e i ) x=x e j = 1 [ ] = lim (DF (x)ei ) x=x +εe ε ε j (DF (x)e i ) x=x [ 1 F (x + εe j + ϑe i ) F (x + εe j ) = lim lim ε ε ϑ ϑ ] F (x + ϑe i ) F (x ) lim ϑ ϑ [ 1 F = lim (x + εe j ) F ] (x ) = ε ε x i x i = 2 F x i x j (x ); teda [D 2 F (x )] ij = 2 F x i x j (x ). (2.13) Z elementárneho diferenciálneho počtu vieme, že za istých podmienok regularity si s poradím derivovania v (2.13) nemusíme robit starosti, t.j. matica D 2 F (x) je symetrická. Nasledujúca veta rozširuje tento výsledok na l ubovol né Banachove priestory. Podmienky sú však trochu iné, než sa obvykle udávajú. V prípade X = R n, Y = R, pretože vo všeobecnosti diferenciál nie je určený konečným počtom parciálnych derivácií Veta. Nech F : U Y, U X otvorená, X, Y - B-priestory. Ak D 2 F existuje v okolí bodu x U a v bode x je spojitá, potom je D 2 F (x) symetrická Poznámka. Tvrdenie vety platí aj za predpokladu samotnej existencie D 2 F v bode x. Dôkaz je však zložitejší a pre naše účely bude veta postačovat vo formulácii, v ktorej je uvedená. V prípade X = R n možno zamenitel nost druhých parciálnych derivácií dokázat za predpokladu spojitosti prvých parciálnych derivácií v okolí bodu x, z čoho však nevyplýva existencia 2. diferenciálu. Naopak, z jeho existencie nevyplýva spojitost 1. parciálnych derivácií v okolí bodu x. Dôkaz. Potrebujeme dokázat, že pre l ubovol né h, k X platí kde lim lim Φ(t, s) = lim lim Φ(s, t), t s s t Φ(t, s) = 1 [F (x + sh + tk) F (x + sh) F (x + tk) F (x)]. st Nech h, k X sú také, že D 2 F je spojitá v každom bode x+sh+tk pre s 1
12 12 a t 1. Potom dvojnásobným použitím Lemy dostaneme kde Φ(1, 1) = ω 1 (h, k) = = 1 [DF (x + h + tk) DF (x + tk)]kdt [D 2 F (x + sh + tk)hkdsdt 1 D 2 F (x)hkdsdt + ω 1 (h, k) = D 2 F (x)hk + ω 1 (h, k), 1 1 ak h, k sú zvolené tak malé, že D 2 F (x + sh + tk) D 2 F (x) dsdt h k ε h k, (2.14) D 2 F (x + sh + tk) D 2 F (x) ε pre s 1 a t 1. Zámenou h za k dostaneme rovnakým postupom Φ(1, 1) = D 2 F (x)hk + ω 2 (h, k), (2.15) kde ω(h, k) = ω 2 (h, k) ω 1 (h, k) spl ňa (2.14). Označme A multilineárne zobrazenie, definované predpisom Ahk = D 2 F (x)kh. Z rovnosti (2.15) vyplýva (D 2 F (x) A)hk = ω(h, k). Nech teraz h, k X sú l ubovol né. Ak δ zvolíme dost malé, vzhl adom na (2.14) platí δ 2 (D 2 F (x) A)hk = (D 2 F (x) A)δhδk ω(δh, δk) δ 2 ε a teda Ked že ε bolo l ubovol né, platí čo je tvrdením vety. D 2 F (x) A < ε. D 2 F (x) = A,
13 Veta. Nech X, Y, Z sú B-priestory, U X, V Y sú otvorené a nech F : U V, G : V Z. Ak D r F (x) a D r G(F (x)) existujú, potom existuje aj D r (G F )(x). Ak sú navyše D r F, D r G spojité na U resp. V, potom je aj D r (G F ) spojité na U. K dôkazu budeme potrebovat nasledovnú lemu Lema. Nech X, Y, Z sú B-priestory. Potom zobrazenie Φ : L(X, Y ) L(Y, Z) L(X, Z) dané predpisom Φ(A, B) = B A má derivácie všetkých rádov a tieto derivácie sú spojité. Dôkaz. Zobrazenie Φ je zrejme ohraničené bilineárne zobrazenie a ako také je podl a Vety (iv) aj diferencovatel né a jeho derivácia je spojitá. Z výrazu (2.11) pre deriváciu bilineárnej funkcie vidno, že DΦ : (A, B) DΦ(A, B) je súčtom dvoch funkcií, z ktorých prvá je lineárna v A a nezávisí od B a druhá je lineárna v B a nezávisí od A. Preto je druhý diferenciál D 2 Φ konštantný a d alšie sú nulové. Dôkaz Vety Vetu dokážeme indukciou. Pre r = 1 veta vyplýva z Vety Predpokladajme, že veta platí pre r 1 namiesto r. Ak G má r-tú deriváciu v bode F (x), potom DG má r 1-tú deriváciu v bode F (x). Zobrazenie x DG(F (x)) DF (x) (2.16) je teda kompozíciou r 1 razy diferencovatel ného zobrazenia x (DF (x)), DG(F (x)) z X do L(X, Y ) L(Y, Z) a bilineárneho zobrazenia Φ : L(X, Y ) L(Y, Z) L(X, Z), ktoré je (r 1)-krát diferencovatel né podl a Lemy Z formuly (2.8) teda vyplýva, že D(G F ) má (r 1)-ú deriváciu v bode x, čo značí, že G F má r-tú deriváciu v bode x. Analogicky, použitím indukcie dokážeme aj spojitost r-tej derivácie G F za predpokladu spojitosti r-tých derivácií funkcií F a G. Derivácie vyšších rádov sa definujú indukciou analogicky ako druhá derivácia: D k+1 F (x) = D(D k F )(x). Z definície indukciou vyplýva, že D k F (x) je prvkom priestoru L(X, L(X,..., L(X, Y ))... ), ktorý je podl a Vety izometricky izomorfný kkrát priestoru L k (X, Y ). Indukciou sa z Vety odvodí, že ak D k F existuje v okolí bodu x a v bode x je spojitá, potom je D k F (x) symetrická Cvičenia. 1. Dokážte detailne tvrdenie o symetrii D k F (x). 2. Dokážte detailne spojitost D r (G F ) za predpokladu spojitosti D r G a D r F. 3. Dokážte, že f : R 2 R je C r -diferencovatel ná, potom ňou generovaný Nemyckého operátor (Cvičenie ) je C r ako zobrazenie z C[, 1] do C[, 1] a platí (D r F (ϕ)h r )(s) = D r ϕ(s)(h(s)) r.
14 Taylorova veta Taylorova veta ako ju poznáme z elementárneho diferenciálneho počtu, platí aj v Banachových priestoroch. Formulácia sa takmer zhoduje s formuláciou pre reálne funkcie, koeficienty - derivácie však majú zmysel multilineárnych zobrazení. V d alšom budeme používat obvyklú symboliku. Ak X, Y sú B-priestory U X je otvorená a F : U X, V U, potom pre F C r (V, Y ) bude značit, že F má r-tú deriváciu v bodoch U a táto derivácia je spojitá vo V. C (V, Y ) = r Cr (V, Y ). Pre úplnost uvádzame, že C ω (V, Y ) označujeme množinu analytických funkcií V Y. Hoci vel a z teórie možno rozšírit na analytický prípad, ponecháme ho v tomto texte bokom. Preto ani neuvádzame presnú definíciu analytickej funkcie vo viacrozmernom priestore. Ďalej, ak ρ : U R a x U, píšeme F = O(ρ) v x resp. F = o(ρ) v x, ak platí F (ξ) K ρ(ξ) v okolí x pre nejaké K > resp. F (ξ)/ρ(ξ) pre ξ x Veta (Taylorova). Nech X, Y sú B-priestory U X otvorená, F C n (U, Y ). Potom pre každé x U a h X dostatočne malé platí F (x + h) = F (x) + DF (x)h + + kde Podobne platí R n (x, h) = 1 (n 1)! 1 1 (n 1)! Dn 1 F (x)hn 1 + R n (x, h), (2.17) (1 s) n D n F (x + sh)h n ds = O( h n ). F (x + h) = F (x) + DF (x)h n! Dn F (x)h n + R n+1 (x, h), (2.18) kde R n+1 (x, h) = o( h n ). Dôkaz. Zobrazenie t D n F (x + th)h n je spojité pre t 1 a dost malé h. Z Lemy dostávame < y, F (x + h) > =< y, F (x) + 1 =< y, F (x) > + 1 =< y, F (x) > +D DF (x + ϑh)hdϑ > 1 < y, DF (x + ϑh)h > dϑ < y, F (x + ϑh) > dϑh. Funkcia ϑ < y, F (x + ϑh) > je C n reálna funkcia jednej reálnej premennej, preto ju môžeme rozvinút podl a Taylorovej vety pre takéto funkcie. Takto dostaneme rovnost < y, F (x+h) >=< y 1, F (x)+df (x)h+ + (n 1)! Dn 1 F (x)h n 1 +R n (x, h) >
15 15 a analogickú rovnost zodpovedajúcu rovnosti (2.18). Pretože rovnosti platia pre l ubovol ný lineárny funkcionál, platia aj pre ich argumenty. Tým sú rovnosti (2.17) a (2.18) dokázané. Menej známe je obrátenie Taylorovej vety, ktoré je niekedy užitočné. Uvádzame ho bez dôkazu Veta. Nech X, Y sú B-priestory, U X je otvorená, F : U Y a nech ϕ k : U L k (X, Y ), k =, 1,..., n sú symetrické. Pre x U označme n 1 ρ(x, h) = F (x + h) k! ϕ k(x)h k. k= Predpokladajme, že (1) ϕ k sú spojité na U (2) lim (ξ,h) (x,) ρ(ξ, h)/ h n = pre každé x U. Potom F C n (U, Y ) a platí D k F = ϕ k na U. Nasledujúci príklad, ktorého výsledok použijeme v nasledujúcej kapitole, slúži na ilustráciu možnosti použitia Vety Príklad. Nech X je B-priestor. Potom množina R operátorov L(X, X), ktoré majú ohraničený inverzný je otvorená a zobrazenie A A 1 je na nej C. Dôkaz. Zvol me < r <. Nech A, B L(X, X) a nech A R. Platí A + B = A(I + A 1 B). (2.19) Ak B < 1/ A 1, potom A 1 B < 1 a podl a známej vety z funkcionálnej analýzy má operátor I + A 1 B ohraničený inverzný; podl a (2.19) má ohraničený inverzný operátor aj A + B. Ďalej platí (A + B) 1 = I + A 1 B) 1 A 1 = ( 1) k (A 1 B) k A 1 kde a teda ρ(a, B) = A 1 = k=r+1 r k= ρ(a, B) A 1 r+2 B r+1 k= 1 k! ϕ k(a)b k + ρ(a, B), ϕ k (A) = k!( 1) k A k 1 ( 1) k (A 1 B) k A 1 (A 1 B) r+1 k= k= ( 1) k (A 1 B) k, A 1 B k = (1 A 1 B ) 1 A 1 r+2 B r+1. Sú teda splnené predpoklady Vety 2.6.2, podl a ktorej je zobrazenie A A 1 C r. Pretože r bolo zvolené l ubovol ne, je táto funkcia aj C.
16 16 3. Rovnomerne kontraktívne zobrazenia 3.1. Lokálna verzia Banachovej vety o pevnom bode Banachova veta o pevnom bode kontraktívnych zobrazení sa pre svoje bohaté aplikácie stala všeobecne známym užitočným nástrojom. Pri jej používaní sa spravidla stáva, že zobrazenie, ktorého pevný bod chceme dokázat, nie je kontraktívne na celom priestore. V takom prípade je často možné použit postup, ktorý teraz sformulujeme vo všeobecnosti. Nech X je B-priestor, x X a δ >. Označíme G(x, δ) = {x : x x < δ} Veta. Nech X je B-priestor a nech T : G(x, δ) X je kontraktívne zobrazenie s konštantou α < 1 také, že T x x < δ(1 α). Potom T má jediný pevný bod a tento bod leží v G(x, δ). Dôkaz. Pre x G(x, δ) platí T x x T x T x + T x x < α x x + δ(1 α) δ, teda T : G(x, δ) G(x, δ). Množina G(x, δ) je uzavretou podmnožinou Banachovho priestoru X a preto je úplným metrickým priestorom. Zobrazenie T zobrazuje G(x, δ) kontraktívne do seba a má teda podl a Banachovej vety o pevnom bode jediný pevný bod v G(x, δ). Pretože T (G(x, δ)) G(x, δ), tento pevný bod musí ležat v G(x, δ) Poznámka. Zrejmá analógia Vety (so vzdialenost ou namiesto normy rozdielu) platí aj v úplnom metrickom priestore Princíp rovnomernej kontrakcie V tomto odseku nám pôjde o závislost pevného bodu na parametroch, od ktorých závisí kontraktívne zobrazenie. Výsledok má bohaté aplikácie a dajú sa z neho odvodiť užitočné nástroje lokálnej nelineárnej analýzy Definícia. Nech X je B-priestor, U X a nech P je množina. Hovoríme, že zobrazenie T : U P X je rovnomerne (vzhl adom na y P ) kontraktívne, ak existuje α < 1 také, že pre každé x, x U a každé y P. T (x, y) T (x, y) α x x Označenie. Ak T je funkciou dvoch premenných x, y, potom budeme značit D x T (x, y) = DT (, y), teda D x T (x, y) značí deriváciu funkcie premennej x v bode (x, y) pri pevnom y; podobný význam má D y T (x, y).
17 Veta (princíp rovnomernej kontrakcie). Nech U, V sú otvorené podmnožiny B-priestorov X resp. P, T : Ū V X je rovnomerná kontrakcia a nech T (, y) má jediný pevný bod ϕ(y) U pre každé y V. Potom platí (i) Ak T je lipschitzovská vzhl adom na y s konštantou L a α je konštanta rovnomernej kontrakcie, potom ϕ je lipschitzovská s konštantou L/(1 α). (ii) Ak T C r (U V, X) pre r, potom aj ϕ C r (V, X); ak r 1, platí Dϕ(y) = (I D x T (ϕ(y)y)) 1 D y T (ϕ(y), y). (3.1) Všimnime si, že vo vete nepredpokladáme, že obrazy T sú obsiahnuté v Ū a preto musíme existenciu pevného bodu v Ū predpokladat ; samozrejme, že ak existuje, tak je jediný. Dôkaz vety. (i) Pre y 1, y 2 P platí ϕ(y 1 ) ϕ(y 2 ) = T (ϕ(y 1 ), y 1 ) T (ϕ(y 2 ), y 2 ) z čoho vyplýva T (ϕ(y 1 ), y 1 ) T (ϕ(y 1 ), y 2 ) + T (ϕ(y 1 ), y 2 ) T (ϕ(y 2 ), y 2 ) L y 1 y 2 + α ϕ(y 1 ) ϕ(y 2 ), ϕ(y 1 ) ϕ(y 2 ) L 1 α y 1 y 2 (ii) Pre r = je dôkaz podobný dôkazu (i) a prenechávame ho čitatel ovi ako cvičenie. Najprv si ukážeme, že z kontraktívnosti vyplýva D x T (x, y) α pre x, y U V. Naozaj, podl a Vety platí pre h X D x T (x, y)h = h T (x, y) = lim lim t 1 t 1 α x + th x = α h, t (T (x + th, y)) T (x, y) t čo je podl a definície normy operátora tvrdením. Tvrdenie (ii) dokážeme najprv pre r = 1. Formálnym (zatial neodôvodneným) derivovaním rovnosti T (ϕ(y), y) = ϕ(y) podl a y dostávame z čoho vyplýva D x T (ϕ(y), y)dϕ(y) + D y T (ϕ(y), y) = Dϕ(y); Dϕ(y) = (I D x T (ϕ(y), y)) 1 D y T (ϕ(y), y) (3.2) Pretože D x T (ϕ(y)y) α < 1, je podl a známej vety o existencii inverzného operátora výraz na pravej strane dobre definovaný a predstavuje jediného možného kandidáta na Dϕ(y). Musíme však ešte dokázat, že je naozaj deriváciou. Použijeme
18 18 postup z Príkladu To znamená, že ak označíme pravú stranu (3.2) potrebujeme dokázat, že pre každé h P platí lim t a že je spojitou funkciou y. Použitím Lemy dostávame 1 [ϕ(y + th) ϕ(y)] = h (3.3) t ϕ(y + th) ϕ(y) =T (ϕ(y + th), y + th) T (ϕ(y), y) [ 1 ] = D x T (ϕ(y) + ϑ(ϕ(y + th) ϕ(y), y)dϑ (ϕ(y + th) ϕ(y)) z čoho vyplýva + t 1 [ 1 ϕ(y + th) ϕ(y) =t I Pravá strana má zmysel, pretože D y T (ϕ(y + th), y + ϑth)dϑh, ] 1 D x T (ϕ(y) + ϑ(ϕ(y + th) ϕ(y)), y)dϑ [ 1 ] D y T (ϕ(y + th), y + ϑth)dϑ h. (3.4) 1 D x T (ϕ(y) + ϑ(ϕ(y) + th) ϕ(y), y)dϑ 1 sup D x T (x, y) dϑ α < 1. x Ū y P Pretože podl a Príkladu je funkcia operátora A A 1 spojitou na svojom definičnom obore, dostávame (3.3) z (3.4) limitným prechodom pre t. Spojitost vzhl adom na y vyplýva z toho, že je kompozíciou spojitých funkcií. Nech teraz T C r (U, V ), r > 1. Indukciou dokážeme, že y C r (V ). Predpokladajme, že tvrdenie platí pre r 1 miesto r. Pravá strana (3.1) je kompozíciou lineárnych zobrazení y (I D x T (ϑ(y), y)) 1 a y D y T (ϕ(y), y). Tieto sú C r 1 podl a indukčného predpokladu, Príkladu a Vety Podl a Vety a Lemy je C r 1 aj ich kompozícia a teda aj Dϕ. To ale značí, že ϕ je C r Poznámka. Platí aj analytické rozšírenie princípu rovnomernej kontrakcie: ak T C ω, potom aj ϕ je C ω Príklad. Diferencovatel ná závislost riešenia diferenciálnej rovnice od počiatočných dát. Štandardnou ilustráciou aplikácie Banachovej vety o pevnom bode je existenčná veta pre diferenciálne rovnice. V tomto príklade ukážeme, že z princípu rovnomernej
19 19 kontrakcie možno vyt ažit ovel a viac - diferencovatel nú závislost riešenia od počiatočných podmienok. Táto veta hrá kl účovú úlohu v geometrickej teórii diferenciálnych rovníc a jej elementárny dôkaz je technicky dost komplikovaný. Uvažujme diferenciálnu rovnicu dx/dt = f(t, x) (3.5) v R n, f C r (U, R n ), U R R n otvorená, r > s počiatočnou podmienkou x(τ) = ξ, (3.6) kde (τ, ξ) U. Zvol me (t, x ) U. Budeme sa zaujímat nielen o existenciu a jednoznačnost riešenia rovnice (3.5), prechádzajúceho cez bod (t, x ), ale aj o regularitu jeho závislosti od bodu (τ, ξ) v okolí bodu (t, x ). Zvol me otvorenú množinu B U takú, že (t, x ) B a B U. Označme a zvol me R, T tak malé, že M = sup B f, L = sup D x f B Q = {(t, x) : t t 2T, x x 4R} B, 4LT < 1 a 2MT < R. Spojitá funkcia x : [t T, t + T ] R n je riešením rovnice (3.5), spl ňajúcim (3.6) (pri τ t T, ξ x R) vtedy a len vtedy, ak rieši integrálnu rovnicu x(t) = ξ + t τ f(s, x(s))ds pre t T t t + T, t.j. ak je pevným bodom zobrazenia T : C[t T, t + T ] C[t T, t + T ], daného vzt ahom T (x; ξ, τ)(t) = ξ + t τ f(s, x(s))ds, (3.7) závislého od parametrov ξ a τ. Všimnime si, že podl a Príkladu je T C 1 v x; jej C 1 závislost na parametroch τ a ξ je zrejmá. Označme x (t) x. Pre ξ x R a τ t T a t T t t + T platí T (x, ξ, τ)(t) x ξ x + Ďalej, ak x, x G(x, 4R), potom T (x; ξ, τ) T (x ; ξ, τ) L t τ t τ t x(s) x (s) ds 2LT τ f(s, x ) ds R + 2MT 2R, f(s, x(s)) f(s, x (s)) ds sup x(t) x (t), t T t t +T
20 2 Podl a Vety (s α = 1/2, δ = 4R) je teda T kontrakcia na G(x, 4R) s koeficientom α = 2LT 1/2, rovnomerne vzhl adom na ξ ξ R a τ t < T. Z Cvičenia vyplýva, že T je C r funkciou x, ξ, τ. Podl a Vety existuje pre tieto hodnoty parametrov jediný pevný bod ϕ(τ, ξ) G(x, 4R), ktorý je C r funkciou parametrov ξ a τ. Ekvivalentne, funkcia t ϕ(ξ, τ)(t) je jediným riešením úlohy (3.5), (3.6) na intervale [t T, t + T ] s hodnotami v množine {(x x ) 4R}. Počítajme teraz deriváciu D ξ ϕ podl a Vety Označme ˆx(t) = ϕ(ξ, τ)(t) a Y (t) = D ξ ϕ(ξ, τ)(t). Z formuly (3.2) vyplýva [(I D x T (ˆx; ξ, τ))y ](t) = D ξ T (ˆx, ξ, τ)(t). (3.8) Zrejme platí a podl a Príkladu D ξ T (ˆx, ξ, τ) = Id (3.9) D x T (ˆx; ξ, τ)(t) = t Dosadením (3.9) a (3.1) do (3.8) dostávame Y (t) t τ τ D x f(s, ˆx(s))ds. (3.1) D x f(s, ˆx(s))Y (s)ds = Id. Derivovaním tejto rovnice podl a t dostávame, že Y (t) L(R n, R n ) rieši diferenciálnu rovnicu Ẏ (t) = D x f(s, ˆx(s))Y (3.11) s počiatočnou podmienkou Y (τ) = I. (3.12) Rovnica (3.11) sa nazýva variačnou rovnicou (alebo linearizáciou rovnice (3.5) pozdl ž riešenia ˆx. Je to lineárna neautonómna rovnica. Stl pce matice Y sú jej lineárne nezávislými (vzhl adom na (3.12)) riešeniami, matica Y (t) je teda fundamentálnou maticou riešení rovnice (3.11) Cvičenia. 1. Dokážte tvrdenie Vety pre r =. 2. Vyjadrite D 2 ϕ(y) z Vety pomocou prvých a druhých derivácií T. [Návod: Derivujte formálne vzt ah Dϕ = D x T Dϕ + D y T podl a y a dosad te za Dϕ z (3.1).] 3. Overte detailne diferencovatel nost T z Príkladu vo všetkých premenných. 4. Dokážte, že z(t) = D τ ϕ(t, τ, ξ) je riešením variačnej rovnice (31.1) s počiatočnou podmienkou z(τ) = f(τ, ξ). Aký je vzt ah z a Y? [Návod: z je riešením lineárnej rovnice, pre ktorú je Y fundamentálna matica riešení.]
21 21 5. V Príklade predpokladajme, že U = R n+1 a že Df je globálne ohraničené. Použitím Vety dokážte globálnu existenciu, jednoznačnost a hladkú závislost riešenia na τ, ξ. [Návod: Hl adajte riešenie ako pevný bod v priestore spojitých funkcií R R n s normou x L = sup e L t t x(t), <t< kde Df L] 6. V nadväznosti na Príklad pri jeho označeniach a predpokladoch predpokladajte navyše, že funkcia f je C r závislá od parametra µ R p. Dokážte, že u(t) = D µ φ(ξ, τ, µ)(t) je riešením nehomogénnej lineárnej rovnice u = D x f(s, ˆx(s), µ)u + D µ f(s, ˆx(s), µ) vyhovujúce podmienke u(τ) =. Ako môžeme u vyjadrit pomocou Y (t)? 4. Veta o implicitnej funkcii a jej aplikácie 4.1. Vety o implicitnej a inverznej funkcii Vetu o implicitnej funkcii možno považovat za primárny netriviálny kvalitatívny poznatok diferenciálneho počtu. Predstavuje základný nástroj lokálnej nelineárnej analýzy diferencovatel ných objektov Veta (o implicitnej funkcii). Nech X, Y, Z sú B-priestory, U X, V Y sú otvorené, F : U V Z je C r, < r, (x, y ) U V, F (x, y ) =. Predpokladajme, že D y F (x, y ) má spojitý inverzný operátor. Potom existuje okolie U 1 V 1 U V bodu (x, y ) a funkcia f C r (U 1, V 1 ) taká, že f(x ) = y a že F (x, y) = pre (x, y) U 1 V 1 platí práve vtedy, ak y = f(x). Ďalej platí Df(x ) = [D y F (x, y )] 1 D x F (x, y ). (4.1) Poznámka. Znenie vety presne zodpovedá zneniu elementárnej vety o implicitnej funkcii pre reálnu funkciu dvoch premenných Poznámka. Veta o implicitnej funkcii je prototypom tvrdení, ktorých schému by sme mohli vol ne vyjadrit termínom princíp linearizácie : Ak linearizácia v bode x nejakého hladkého matematického objektu Ω má vlastnost V a táto vlastnost je robustná, potom lokálne vlastnost V má aj samotný objekt. Robustnost ou rozumieme, že vlastnost okrem objektu Ω majú aj objekty jemu blízke vo vhodnej topológii. V konkrétnom prípade Vety objektom je funkcia F, vlastnost ou V je možnost vyjadrit z podmienky F (x, y) = y ako funkciu x. Táto vlastnost je (globálne) splnená pre linearizáciu F v bode (x, y ) (rovnica D x F (x, y )h +
22 22 D y F (x, y )k = má jednoznačné riešenie k = [D y F (x, y )] 1 D x F (x, y )h ), jej lokálne splnenie pre funkciu F je predmetom tvrdenia vety. Robustnost vlastnosti V je predmetom Cvičenia Iným výrazom princípu linearizovanej stability je napr. Veta o asymptotickej stabilite na základe prvého priblíženia (čo je iné pomenovanie linearizácie). Princíp linearizácie má obrovský koncepčný význam pre aplikácie matematiky, pretože podmienečne odobruje používanie zjednodušených linearizovaných modelov nielen po kvantitatívnej, ale aj po kvalitatívnej stránke. Na druhej strane nás varuje, že v nerobustných kritických prípadoch (ako napr. ak D y F (x, y ) nemá spojitý inverzný), lokálna podoba množiny F (x, y) = je podstatne ovplyvnená členmi vyššieho stupňa Taylorovho rozvoja funkcie F (x, y) v bode (x, y ) Poznámka. Ak X, Y, Z sú konečnorozmerné priestory, podmienka invertovatel nosti D y F (x, y ) je splnená práve vtedy, ak hodnost D y F (x, y ) = dim Y = dim Z Poznámka. Metóda dôkazu dáva odhad na vel kost množín U 1, V 1 (Cvičenie ), ktorý je niekedy dôležitý Poznámka. Platí aj analytická verzia Vety o implicitnej funkcii. Dôkaz Vety je motivovaný myšlienkou iteračného riešenia rovnice F (x, y) = pri pevne zvolenom x Newtonovou metódou: Zvolíme (x, y) a pri rovnakom x hl adáme novú iteráciu y tak, aby platilo F (x, y ) =. (4.2) Linearizáciou v bode (x, y) dostávame z (4.2) pre y predpis alebo, ak D y F je invertovatel ný, F (x, y) + D y F (x, y)(y y) =, y = y [D y F (x, y)] 1 F (x, y). (4.3) V (4.3) nahradíme premennú hodnotu D y F (x, y) konštantnou hodnotou D y F (x, y ), čím dostaneme y = y [D y F (x, y )] 1 F (x, y). (4.4) Je zrejmé, že za predpokladov vety je y pevným bodom pravej strany (4.4), t.j. zobrazenia T (y, x) = y [D y F (x, y )] 1 F (x, y) práve vtedy, ak (x, y) je riešením rovnice F (x, y) =. Zrejme T má rovnaký stupeň hladkosti ako F. Aby sme vetu dokázali, stačí teda podl a Vety overit, že pri vhodnej vol be okolí U 1, V 1 je T kontrakcia v y V 1, ktorá je rovnomerná vzhl adom na x U 1 ; formula (4.1) už potom vyjde formálnym derivovaním vzt ahu F (x, f(x)) = vzhl adom na x. Podl a Lemy platí pre x U 1, y 1, y 2 V T (y 1, x) T (y 2, x) M 1 1 I DF (x, y ) 1 DF (x, y 1 + ϑ(y 2 y 1 ) y 1 y 2 dϑ DF (x, y ) DF (x, y 1 + ϑ(y 2 y 1 )) y 1 y 2 dϑ,
23 23 kde M = (DF (x, y ) 1. Ked že DF (x, y) je spojitou funkciou x, y, existuje okolie U 1 bodu x a okolie V 1 bodu y (ktoré môžeme vziat ako gul u G(y, R)) také, že pre zvolené α < 1 platí DF (x, y ) DF (x, y ) αm 1 (DF (x, y )) 1, pre každé x, y U 1 V 1. Ked že V 1 sme zvolili konvexným, patrí spolu s y 1 a y 2 do V 1 aj y 1 + ϑ(y 2 y 1 ) pre l ubovol né ϑ 1. Preto pre x U 1, y 1, y 2 V 1 platí T (y 1, x) T (y 2, x) α y 1 y 2. Ďalej platí T (y, x) y M F (x, y ) r(1 α), ak bolo U 1 zvolené dost malé. Podl a Viet a teda pre x U 1 existuje jediný pevný bod y = f(x) U, ktorý je C r funkciou x. Vel mi závažným dôsledkom vety o implicitnej funkcii je Veta o inverznej funkcii. Takisto ako Veta o implicitnej funkcii je rozšírením lokálnej Vety o inverznej funkcii pre reálne funkcie bez dodatočných podmienok Veta (lokálna o inverznej funkcii). Nech X, Y sú B-priestory, U X je otvorená, f C r (U, Y ), r >, x U. Predpokladajme, že Df(x ) má ohraničený inverzný operátor. Potom f je lokálny difeomorfizmus, t.j. existuje okolie W = V U 1 bodu (f(x ), x ) a g C r (V, U 1 ) také, že g f = id U1 af g = id V. Dôkaz. Použijeme Vetu pre zobrazenie F : Y U Y F (y, x) = y f(x). Platí F (f(x ), x ) = a D x F (f(x ), x ) = Df(x ); podl a Vety existuje okolie V bodu f(x ), okolie Ũ U bodu x a funkcia g : V Ũ taká, že F (y, x) = pre (y, x) V Ũ práve vtedy, ak x = g(y). Položme U 1 = {x Ũ : f(x) V }. L ahko si overíme, že f g a g f sú identické zobrazenia na V resp. U 1.A to je vlastne tvrdením vety Cvičenia. 1. Za predpokladu F C 2 vypočítajte D 2 f(x ). 2. Dokážte robustnost vlastnosti Ohraničený operátor A : X Y má ohraničený inverzný. 3. Urobte odhad vel kosti okolí U 1, V 1 z Vety pomocou M = (DF (x, y )) 1 a modulu spojitosti DF. 4. Ak navyše k predpokladom Vety platí D j yf (x, y ) = pre j =,..., k r, potom D j f(x ) = pre j =,..., k; ak k < r, potom Dokážte. D k+1 f(x ) = [D y F (x, y ] 1 D k+1 x F (x, y ).
24 Príklady použitia vety o implicitnej funkcii Obsahom kapitoly je exkurzia po rozličných aplikáciách vety o implicitnej funkcii - či už v konečnorozmerných, alebo nekonečnorozmerných priestoroch. Na záver si ukážeme úskalie, ktoré číha pri používaní vety vo funkcionálnych priestoroch. Príklady z literatúry ukazujú, že pri nedbalom overovaní predpokladov vety ho l ahko možno prehliadnut Príklad. Spojitá závislost algebraicky jednoduchej vlastnej hodnoty matice a jej vlastného vektora od jej prvkov. Vlastný vektor nie je jednoznačnou funkciou matice (je určený modulo násobenie nenulovou konštantou). Aby úloha dostala zmysel, budeme navyše požadovat, aby mal danú (jednotkovú) normu. Matice A : R n R n sú dané ich n 2 prvkami, ich množinu môžeme stotožnit s R n2. Skutočnost, že λ je vlastnou hodnotou A a v je jej jednotkový vlastný vektor môžeme vyjadrit tak, že dvojica y = (v, λ) R n+1 je nulou funkcie F = (F 1,..., F n+1 ) : R n2 R n+1, danej predpisom { (A λi)v F (A, y) = < v, v > 1 (4.5) kde <, > je skalárny súčin. Funkcia F je zrejme C funkciou svojich premenných. Nech teda A je matica, ktorá má algebraicky jednoduchú vlastnú hodnotu λ s vlastným vektorom v, < v, v >= 1; platí teda F (A, y ) =. Použitím Vety chceme dokázat, že lokálne pre l ubovol né A blízke A existuje jediná dvojica y = (v, λ) blízka y taká, že platí (4.5) a táto y je C funkciou A. K tomu nám stačí overit, že ( ) A λi v D y F (A, y ) = 2v T. je regulárnou maticou, alebo ekvivalentne, že det D y F (A, y ). Ked že λ je jednoduchou vlastnou hodnotou, existuje regulárna matica S = (s 1,..., s n ) taká, že S 1 v = e n = (,,..., 1) T, t. j. s n = v, C = S 1 A S λ I spl ňa c nj = c jn = pre j = 1,..., n a minor prvku c nn je. Platí Označme S = ( S 1 ). det( S 1 ) det D y F (A, y ) det S = det( S 1 D y F (A, y ) S) ( ) C en = det. w
25 25, kde w = (w 1,..., w n ) je riadkový vektor taký, že w n = 2 < v, v > Tým je overené, že sú splnené predpoklady Vety V príkladoch tohoto odseku sa budú vyskytovat aj zobrazenia na nekončnorozmerných priestoroch, ktorých diferencovatel nost treba overovat. Spravidla sa to robí postupom z Príkladu Ten je síce priamočiary, ale často dost zdl havý. Prenechávame ho preto na čitatel a a obmedzíme sa na formálny výpočet diferenciálu a overenie podmienky z Vety 4.1.1, že D y F (x, y ) má ohraničený inverzný. Ked že deriváciu zobrazenia na nekonečnorozmernom priestore nemožno reprezentovat konečnou tabul kou hodnôt, spravidla ho treba zapísat ako zobrazenie, povedzme h DF (x)h. V súlade s premennou zobrazenia F, podl a ktorej sa derivuje, budeme premennú zobrazenia DF (x) spravidla označovat pridaním symbolu δ k premennej. (teda povedzme δx DF (x)δx. Symbol δx, atd. treba teda chápat chápat ako symbol pre jednu premennú Príklad. Funkcia ako parameter. Vetu o implicitnej funkcii môžme interpretovat ako výpoved o tom, ako sa správa riešenie y rovnice F (x, y) = pri zmene jej vonkajšieho parametra x. Skúmajme teraz riešenia x rovnice f(x) =. (4.6) V tejto rovnici zdanlivo nijaké parametre nevystupujú. Môže nás však zaujímat, čo sa s riešeniami rovnice (4.6) stane, ak v nejakom funkcionálnom priestore zmeníme funkciu f. Takto vlastne za funkcionálny parameter v rovnici (4.6) môžeme považovat samotnú funkciu f! Dokážeme nasledovné tvrdenie: Nech X, Y sú B-priestory, U X je otvorená a f C 1 (Ū, Y ). Nech f(x ) = pri x U. Predpokladajme že Df(x ) má ohraničený inverzný. Potom existuje okolie W funkcie f v C 1 (Ū, Y ) a okolie V bodu x také, že pre každé g W existuje jediný bod ϕ(g) V taký, že g(ϕ(g)) = ; funkcia ϕ je C 1 funkciou g. Aby sme tvrdenie dokázali, použijeme Vetu na funkciu F : C 1 (C 1 (Ū, Y ) U, Y ), danú predpisom F (g, x) = g(x). Vypočítame diferenciál funkcie F v smere: (δg,δx) F (g, x) = lim t 1 = lim t 1 t 1 [F (g + tδg, x + tδx) F (g, x)] t [g(x + tδx) + tδg(x + tδx) g(x)] t = lim [g(x) + t(dg(x)δx + δg(x)) + o(t) g(x)] t = Dg(x)δx + δg(x). Zobrazenie (δg, δx) Dg(x)δx + δg(x) je zrejme lineárne ohraničené a preto predstavuje df (g, x). Overenie, že DF (g, x) existuje, ponecháme podl a dohody na čitatel a.
26 26 Podl a predpokladu platí F (f, x ) = f(x ) =, tvrdenie teda vyplynie z Vety 4.1.1, ak overíme, že D x F (f, x ) má inverzný spojitý. Zrejme platí D x F (f, x ) = Df(x ), Df(x ) však má spojitý inverzný operátor podl a predpokladu Príklad. Lokálna existencia, jednoznačnost a spojitá závislost riešení diferenciálnej rovnice na počiatočných dátach. Túto úlohu sme už riešili v Príklade pomocou princípu rovnomernej kontrakcie. Vtipné škálovanie nám umožní riešit ju pomocou vety o implicitnej funkcii. Ako v Príklade hl adajme riešenie diferenciálnej rovnice (závislej od parametra µ), spl ňajúce podmienku ẋ = f(t, x, µ), (4.7) x(τ) = ξ. (4.8) K predpokladom o x, f, τ, ξ z Príkladu pridáme, že f je C 1 funkciou premenných t, x, µ pre (t, x) U a µ W, kde W je otvorenou podmnožinou Banachovho priestoru P. Ciel dôkazu z Príkladu doplníme o ciel Cvičenia dokázat aj C r -závislost riešenia od parametra µ. Ak x je riešením (4.1), (4.2) na intervale [τ α, τ + α] a y(σ) = x(ασ + τ) ξ, potom y(σ) spl ňa rovnicu na intervale [ 1, 1] a počiatočnú podmienku označíme dy/dσ = αf(ασ + τ, ξ + y, µ) (4.9) y() = (4.1) Y ={ϕ C 1 ([ 1, 1], R n ) : y() = } Z =C([ 1, 1], R n ) X =R U W a funkciu F : X Y Z definujeme predpisom F (α, τ, ξ, µ, y)(σ) = y (σ) αf(ασ+ τ, ξ + y(σ), µ) pre 1 σ 1. Zrejme y spl ňa (4.9), (4.1) práve vtedy ak Pre l ubovol né (τ, ξ, µ ) U W zrejme platí F (α, τ, ξ, µ, y) =. (4.11) F (, τ, ξ, µ, ) =.
27 27 Ak overíme splnenie d alších predpokladov Vety C r -diferencovatel nost F a existenciu spojitého inverzného operátora k D y F (, τ, ξ, µ ), z Vety 4.1.1, dostaneme lokálnu (v (τ, ξ, µ) existenciu funkcie y = y(α, τ, ξ, µ), spl ňajúcu rovnicu (4.11) a jej C r -závislost od α, τ, ξ, µ. No a to značí, že funkcia ( ) t τ x(t) = ξ + y α je riešením problému (4.7), (4.8) pre malé α (všimnime si, že dl žka intervalu, na ktorom dostaneme riešenie, je iba 2α!). Obmedzíme sa opät na výpočet smerových derivácií F v bode (, ξ, τ, µ, ). Overenie splnenia podmienky existencie spojitej inverzie D y F z Vety a diferencovatel nosti v zmysle krokov 2 a 3 z Príkladu ponecháme na čitatel a. Platí F (α + ϑδα, τ + ϑδτ, ξ + ϑδξ, µ + ϑδµ, y + ϑδy)(σ) F (α, τ, ξ, µ, y)(σ) =y (σ) + ϑδy (σ) (α + ϑδα)f((α + ϑδα)σ + τ + ϑδτ, ξ + δξ + y(σ) + ϑδy(σ), µ + ϑδµ) y (σ) + αf(ασ + τ, ξ + y(σ), µ) = =ϑ [(δy) (σ) αd t f(ασ + τ, ξ + y(σ), µ)((δα)σ + δτ) αd x f(ασ + τ, ξ + y(σ), µ)(δξ + δy(σ)) αd µ f(ασ + τ, ξ + y(σ), µ)δµ δαf(ασ + τ, ξ + y(σ), µ)] + o(ϑ), z čoho (za predpokladu existencie DF ) vyplýva [D F (α, τ, ξ, µ, y)(δα, δτ, δξ, δµ, δy)](σ) =δy (σ) [αd t f(ασ + τ, ξ + y(σ), µ) + f(ασ + τ, ξ + y(σ), µ)] δα αd t f(ασ + τ, ξ + y(σ), µ)δτ αd x f(ασ + τ, ξ + y(σ), µ)δξ αd µ f(ασ + τ, ξ + y(σ), µ)δµ αd x f(ασ + τ, ξ + y(σ), µ)δy(σ). Pre α =, τ = τ, ξ = ξ, µ = µ dostávame DF (, τ, ξ, µ, )(,,,, δy)(σ) = δy (σ), čo znamená D y F (, τ, ξ, µ, )δy = δy. Tento operátor má zrejme ohraničený inverzný zo Z Y, [D y F (, τ, ξ, µ, )] 1 δz(σ) = σ Tým je overovanie predpokladov Vety ukončené. δz(ϑ)dϑ.
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich
 Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
Tuesday 15 th January, 2013, 19:53 Základy tenzorového počtu M.Gintner Vektorový priestor V : Množina prvkov (vektory), na ktorej je definované ich sčítanie a ich násobenie reálnym číslom tak, že platí:
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
Motivácia pojmu derivácia
 Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
FUNKCIE N REÁLNYCH PREMENNÝCH
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Matematika 2. časť: Funkcia viac premenných Letný semester 2013/2014
 Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR. Michal Zajac. 3 T b 1 = T b 2 = = = 2b
 VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
VLASTNÉ ČÍSLA A JORDANOV KANONICKÝ TVAR Michal Zajac Vlastné čísla a vlastné vektory Pripomeňme najprv, že lineárny operátor T : L L je vzhl adom na bázu B = {b 1, b 2,, b n } lineárneho priestoru L určený
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
7 Derivácia funkcie. 7.1 Motivácia k derivácii
 Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prednáška Fourierove rady. Matematická analýza pre fyzikov IV. Jozef Kise lák
 Prednáška 6 6.1. Fourierove rady Základná myšlienka: Nech x Haφ 1,φ 2,...,φ n,... je ortonormálny systém v H, dá sa tento prvok rozvinút do radu x=c 1 φ 1 + c 2 φ 2 +...,c n φ n +...? Ako nájdeme c i,
Prednáška 6 6.1. Fourierove rady Základná myšlienka: Nech x Haφ 1,φ 2,...,φ n,... je ortonormálny systém v H, dá sa tento prvok rozvinút do radu x=c 1 φ 1 + c 2 φ 2 +...,c n φ n +...? Ako nájdeme c i,
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus
 1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
1. prednáška Lineárna algebra I - pole skalárov, lineárny priestor, lineárna závislosť, dimenzia, podpriestor, suma podpriestorov, izomorfizmus Matematickým základom kvantovej mechaniky je teória Hilbertových
BANACHOVE A HILBERTOVE PRIESTORY
 BANACHOVE A HILBERTOVE PRIESTORY 1. ZÁKLADNÉ POJMY Normovaným lineárnym priestorom (NLP) nazývame lineárny (= vektorový) priestor X nad telesom IK, na ktorom je daná nezáporná reálna funkcia : X IR + (norma)
BANACHOVE A HILBERTOVE PRIESTORY 1. ZÁKLADNÉ POJMY Normovaným lineárnym priestorom (NLP) nazývame lineárny (= vektorový) priestor X nad telesom IK, na ktorom je daná nezáporná reálna funkcia : X IR + (norma)
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Reálna funkcia reálnej premennej
 (ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
(ÚMV/MAN3a/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 18.10.2012 Úvod V každodennom živote, hlavne pri skúmaní prírodných javov, procesov sa stretávame so závislosťou veľkosti niektorých veličín od
Funkcie - základné pojmy
 Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Obsah. 1.1 Reálne čísla a ich základné vlastnosti... 7 1.1.1 Komplexné čísla... 8
 Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Obyčajné diferenciálne rovnice
 (ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
(ÚMV/MAN3b/10) RNDr. Ivan Mojsej, PhD ivan.mojsej@upjs.sk 14.3.2013 Úvod patria k najdôležitejším a najviac prepracovaným matematickým disciplínam. Nielen v minulosti, ale aj v súčastnosti predstavujú
Spojitosť a limity trochu inak
 Spojitosť a limity trochu inak Štefan Tkačik Abstrakt Spojitosť funkcie alebo oblastí je základným stavebným kameňom matematickej analýzy. Pochopenie jej podstaty uľahčí chápanie diferenciálneho a integrálneho
Spojitosť a limity trochu inak Štefan Tkačik Abstrakt Spojitosť funkcie alebo oblastí je základným stavebným kameňom matematickej analýzy. Pochopenie jej podstaty uľahčí chápanie diferenciálneho a integrálneho
Diferenciálny a integrálny počet funkcií viac premenných v príkladoch
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Diferenciálny a integrálny počet funkcií viac premenných v príkladoch Martin Kollár, L ubica Kossaczká a Daniel Ševčovič Vysokoškolský
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Diferenciálny a integrálny počet funkcií viac premenných v príkladoch Martin Kollár, L ubica Kossaczká a Daniel Ševčovič Vysokoškolský
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c)
 Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Mini minimaliz acia an BUˇ Koˇ sice 2011
 Mini minimalizácia Ján BUŠA Košice 2011 RECENZOVALI: Prof. RNDr. Noname, CSc. Doc. RNDr. Emanname, PhD. Prvé vydanie Za odbornú stránku učebného textu zodpovedá autor. Rukopis neprešiel redakčnou ani jazykovou
Mini minimalizácia Ján BUŠA Košice 2011 RECENZOVALI: Prof. RNDr. Noname, CSc. Doc. RNDr. Emanname, PhD. Prvé vydanie Za odbornú stránku učebného textu zodpovedá autor. Rukopis neprešiel redakčnou ani jazykovou
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Podmienenost problému a stabilita algoritmu
 Podmienenost problému a stabilita algoritmu Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Podmienenost a stabilita 1/19 Obsah 1 Vektorové a
Podmienenost problému a stabilita algoritmu Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Podmienenost a stabilita 1/19 Obsah 1 Vektorové a
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
Goniometrické substitúcie
 Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
MATEMATICKÁ ANALÝZA 1
 UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied Božena Mihalíková, Ján Ohriska MATEMATICKÁ ANALÝZA Vysokoškolský učebný text Košice, 202 202 doc. RNDr. Božena
Metódy vol nej optimalizácie
 Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/28 Motivácia k metódam vol nej optimalizácie APLIKÁCIE p. 2/28 II 1. PRÍKLAD: Lineárna regresia - metóda najmenších štvorcov Na základe dostupných
Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/28 Motivácia k metódam vol nej optimalizácie APLIKÁCIE p. 2/28 II 1. PRÍKLAD: Lineárna regresia - metóda najmenších štvorcov Na základe dostupných
Matematická analýza pre fyzikov IV.
 119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
1 Úvod Predhovor Sylaby a literatúra Základné označenia... 3
 Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
Obsah 1 Úvod 3 1.1 Predhovor...................................... 3 1.2 Sylaby a literatúra................................. 3 1.3 Základné označenia................................. 3 2 Množiny a zobrazenia
4 Reálna funkcia reálnej premennej a jej vlastnosti
 Reálna unkcia reálnej premennej a jej vlastnosti Táto kapitola je venovaná štúdiu reálnej unkcie jednej reálnej premennej. Pojem unkcie patrí medzi základné pojmy v matematike. Je to vlastne matematický
Reálna unkcia reálnej premennej a jej vlastnosti Táto kapitola je venovaná štúdiu reálnej unkcie jednej reálnej premennej. Pojem unkcie patrí medzi základné pojmy v matematike. Je to vlastne matematický
Numerické metódy matematiky I
 Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
G. Monoszová, Analytická geometria 2 - Kapitola III
 text obsahuje znenia viet, ktoré budeme dokazovat na prednáškach text je doplnený aj o množstvo poznámok, ich ciel om je dopomôct študentom k lepšiemu pochopeniu pojmov aj súvislostí medzi nimi text je
text obsahuje znenia viet, ktoré budeme dokazovat na prednáškach text je doplnený aj o množstvo poznámok, ich ciel om je dopomôct študentom k lepšiemu pochopeniu pojmov aj súvislostí medzi nimi text je
Integrovanie racionálnych funkcií
 Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Úvod 2 Predhovor... 2 Sylaby a literatúra... 2 Označenia... 2
 Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
Obsah Úvod Predhovor Sylaby a literatúra Označenia Euklidovské vektorové priestory 3 Skalárny súčin 3 Gram-Schmidtov ortogonalizačný proces 8 Kvadratické formy 6 Definícia a základné vlastnosti 6 Kanonický
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II. Zbierka riešených a neriešených úloh
 Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II Zbierka riešených a neriešených úloh Anna Grinčová Jana Petrillová Košice 06 Technická univerzita v Košiciach Fakulta
Technická univerzita v Košiciach Fakulta elektrotechniky a informatiky MATEMATIKA II Zbierka riešených a neriešených úloh Anna Grinčová Jana Petrillová Košice 06 Technická univerzita v Košiciach Fakulta
Príklady na precvičovanie Fourierove rady
 Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
Príklady na precvičovanie Fourierove rady Ďalším významným typom funkcionálnych radov sú trigonometrické rady, pri ktorých sú jednotlivé členy trigonometrickými funkciami. Konkrétne, jedná sa o rady tvaru
NUMERICKÁ MATEMATIKA. Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ. Fakulta elektrotechniky a informatiky
 Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA Fakulta elektrotechniky a informatiky Štefan Berežný Táto publikácia vznikla za finančnej podpory
Moderné vzdelávanie pre vedomostnú spoločnosť/ Projekt je spolufinancovaný zo zdrojov EÚ NUMERICKÁ MATEMATIKA Fakulta elektrotechniky a informatiky Štefan Berežný Táto publikácia vznikla za finančnej podpory
Definícia parciálna derivácia funkcie podľa premennej x. Definícia parciálna derivácia funkcie podľa premennej y. Ak existuje limita.
 Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti
 4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Numerické metódy Učebný text pre bakalárske štúdium
 Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Imrich Pokorný Numerické metódy Učebný text pre bakalárske štúdium Strana 1 z 48 1 Nepresnosť numerického riešenia úloh 4 1.1 Zdroje chýb a ich klasifikácia................... 4 1.2 Základné pojmy odhadu
Úvod. Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...
 Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
(IP3) (f, g) = (g, f) (symetria), (IP4) (f, f) > 0 pre f 0 (kladná definitnosť). Z podmienok (IP1) (IP4) sa ľahko dokážu rovnosti:
 Hilbertove priestory Veľké množstvo aplikácií majú lineárne normované priestory, v ktorých norma je odvodená od skalárneho (vnútorného) súčinu, podobne ako v bežnom trojrozmernom euklidovskom priestore.
Hilbertove priestory Veľké množstvo aplikácií majú lineárne normované priestory, v ktorých norma je odvodená od skalárneho (vnútorného) súčinu, podobne ako v bežnom trojrozmernom euklidovskom priestore.
Metódy vol nej optimalizácie
 Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/52 Metódy minimalizácie funkcie jednej premennej Metódy minimalizácie funkcie jednej premennej p. 2/52 Metódy minimalizácie funkcie jednej
Metódy vol nej optimalizácie Metódy vol nej optimalizácie p. 1/52 Metódy minimalizácie funkcie jednej premennej Metódy minimalizácie funkcie jednej premennej p. 2/52 Metódy minimalizácie funkcie jednej
Numerické metódy, pravdepodobnosť a matematická štatistika
 Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Strana 1 z 262 Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Strana
Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Strana 1 z 262 Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Strana
Planárne a rovinné grafy
 Planárne a rovinné grafy Definícia Graf G sa nazýva planárny, ak existuje jeho nakreslenie D, v ktorom sa žiadne dve hrany nepretínajú. D sa potom nazýva rovinný graf. Planárne a rovinné grafy Definícia
Planárne a rovinné grafy Definícia Graf G sa nazýva planárny, ak existuje jeho nakreslenie D, v ktorom sa žiadne dve hrany nepretínajú. D sa potom nazýva rovinný graf. Planárne a rovinné grafy Definícia
Numerické metódy, pravdepodobnosť a matematická štatistika. Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER
 Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Prvé vydanie Za
Numerické metódy, pravdepodobnosť a matematická štatistika Ján BUŠA Viktor PIRČ Štefan SCHRÖTTER Košice 2006 RECENZOVALI: Prof. RNDr. Jozef Doboš, CSc. Doc. RNDr. Vladimír Penjak, CSc. Prvé vydanie Za
Spojité rozdelenia pravdepodobnosti. Pomôcka k predmetu PaŠ. RNDr. Aleš Kozubík, PhD. 26. marca Domovská stránka. Titulná strana.
 Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Spojité rozdelenia pravdepodobnosti Pomôcka k predmetu PaŠ Strana z 7 RNDr. Aleš Kozubík, PhD. 6. marca 3 Zoznam obrázkov Rovnomerné rozdelenie Ro (a, b). Definícia.........................................
Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej transformácie,
 Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
Kapitola Riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie Cieľom cvičenia je zvládnuť riešenie diferenciálnych rovníc pomocou Laplaceovej tranformácie, keď charakteritická rovnica má rôzne
1-MAT-220 Algebra februára 2012
 1-MAT-220 Algebra 1 12. februára 2012 Obsah 1 Grupy 3 1.1 Binárne operácie.................................. 3 1.2 Cayleyho veta.................................... 3 2 Faktorizácia 5 2.1 Relácie ekvivalencie
1-MAT-220 Algebra 1 12. februára 2012 Obsah 1 Grupy 3 1.1 Binárne operácie.................................. 3 1.2 Cayleyho veta.................................... 3 2 Faktorizácia 5 2.1 Relácie ekvivalencie
Symbolická logika. Stanislav Krajči. Prírodovedecká fakulta
 Symbolická logika Stanislav Krajči Prírodovedecká fakulta UPJŠ Košice 2008 Názov diela: Symbolická logika Autor: Doc. RNDr. Stanislav Krajči, PhD. Vydala: c UPJŠ Košice, 2008 Recenzovali: Doc. RNDr. Miroslav
Symbolická logika Stanislav Krajči Prírodovedecká fakulta UPJŠ Košice 2008 Názov diela: Symbolická logika Autor: Doc. RNDr. Stanislav Krajči, PhD. Vydala: c UPJŠ Košice, 2008 Recenzovali: Doc. RNDr. Miroslav
zlomok poznatel nej časti skutočnosti. Robí tak prostredníctvom svojich pojmov (tento proces môžeme nazvat formalizácia), jej hlavnou úlohou je potom
 0 Úvod 1 0 Úvod 0 Úvod 2 Matematika (a platí to vo všeobecnosti pre každú vedu) sa viac či menej úspešne pokúša zachytit istý zlomok poznatel nej časti skutočnosti. Robí tak prostredníctvom svojich pojmov
0 Úvod 1 0 Úvod 0 Úvod 2 Matematika (a platí to vo všeobecnosti pre každú vedu) sa viac či menej úspešne pokúša zachytit istý zlomok poznatel nej časti skutočnosti. Robí tak prostredníctvom svojich pojmov
2. prednáška. Teória množín I. množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin
 2. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Verzia: 27. 9. 2009 Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi
2. prednáška Teória množín I množina operácie nad množinami množinová algebra mohutnosť a enumerácia karteziánsky súčin Verzia: 27. 9. 2009 Priesvtika: 1 Definícia množiny Koncepcia množiny patrí medzi
Nelineárne optimalizačné modely a metódy
 Nelineárne optimalizačné modely a metódy Téma prednášky č. 8 Metódy transformujúce úlohu naviazaný extrém na úlohu na voľný extrém Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie
Nelineárne optimalizačné modely a metódy Téma prednášky č. 8 Metódy transformujúce úlohu naviazaný extrém na úlohu na voľný extrém Prof. Ing. Michal Fendek, CSc. Katedra operačného výskumu a ekonometrie
II. Diferencovateľné variety
 II. Diferencovateľné variety 1. Potreba diferenciálneho počtu na množinách bez lineárnej štruktúry 1.1. Príklad. Ideálne kyvadlo. Ide o pohyb hmotného bodu na nehmotnej niti v zvislej rovine pod vplyvom
II. Diferencovateľné variety 1. Potreba diferenciálneho počtu na množinách bez lineárnej štruktúry 1.1. Príklad. Ideálne kyvadlo. Ide o pohyb hmotného bodu na nehmotnej niti v zvislej rovine pod vplyvom
primitívnoufunkcioukfukncii f(x)=xnamnožinereálnychčísel.avšakaj 2 +1 = x, tedaajfunkcia x2
 Neurčitý integrál. Primitívna funkcia a neurčitý integrál Funkcia F(x)sanazývaprimitívnoufunkcioukfunkcii f(x)naintervale(a,b),akpre každé x (a,b)platí F (x)=f(x). Z definície vidíme, že pojem primitívnej
Neurčitý integrál. Primitívna funkcia a neurčitý integrál Funkcia F(x)sanazývaprimitívnoufunkcioukfunkcii f(x)naintervale(a,b),akpre každé x (a,b)platí F (x)=f(x). Z definície vidíme, že pojem primitívnej
Numerické metódy Zbierka úloh
 Blanka Baculíková Ivan Daňo Numerické metódy Zbierka úloh Strana 1 z 37 Predhovor 3 1 Nelineárne rovnice 4 2 Sústavy lineárnych rovníc 7 3 Sústavy nelineárnych rovníc 1 4 Interpolačné polynómy 14 5 Aproximácia
Blanka Baculíková Ivan Daňo Numerické metódy Zbierka úloh Strana 1 z 37 Predhovor 3 1 Nelineárne rovnice 4 2 Sústavy lineárnych rovníc 7 3 Sústavy nelineárnych rovníc 1 4 Interpolačné polynómy 14 5 Aproximácia
Riešenie sústavy lineárnych rovníc. Priame metódy.
 Riešenie sústavy lineárnych rovníc. Priame metódy. Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Priame metódy 1/16 Obsah 1 Základy 2 Systémy
Riešenie sústavy lineárnych rovníc. Priame metódy. Ing. Gabriel Okša, CSc. Matematický ústav Slovenská akadémia vied Bratislava Stavebná fakulta STU G. Okša: Priame metódy 1/16 Obsah 1 Základy 2 Systémy
p(α 1 ) = u 1. p(α n ) = u n. Definícia (modulárna reprezentácia polynómu). Zobrazenie
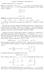 1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
1. Rychlá Fourierová transformácia Budeme značiť teleso T a ω jeho prvok. Veta 1.1 (o interpolácií). Nech α 0, α 1,..., α n sú po dvoch rôzne prvky telesa T[x]. Potom pre každé u 0, u 1,..., u n T existuje
Úvod. Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...
 Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
23. Zhodné zobrazenia
 23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
23. Zhodné zobrazenia Zhodné zobrazenie sa nazýva zhodné ak pre každé dva vzorové body X,Y a ich obrazy X,Y platí: X,Y = X,Y {Vzdialenosť vzorov sa rovná vzdialenosti obrazov} Medzi zhodné zobrazenia patria:
Základy matematickej štatistiky
 1. Náhodný výber, výberové momenty a odhad parametrov Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. mája 2015 1 Náhodný výber 2 Výberové momenty 3 Odhady parametrov
1. Náhodný výber, výberové momenty a odhad parametrov Katedra Matematických metód Fakulta Riadenia a Informatiky Žilinská Univerzita v Žiline 6. mája 2015 1 Náhodný výber 2 Výberové momenty 3 Odhady parametrov
Obsah. 1.1 Základné pojmy a vzťahy Základné neurčité integrály Cvičenia Výsledky... 11
 Obsah Neurčitý integrál 7. Základné pojmy a vzťahy.................................. 7.. Základné neurčité integrály............................. 9.. Cvičenia..........................................3
Obsah Neurčitý integrál 7. Základné pojmy a vzťahy.................................. 7.. Základné neurčité integrály............................. 9.. Cvičenia..........................................3
Derivácia funkcie. Pravidlá derivovania výrazov obsahujúcich operácie. Derivácie elementárnych funkcií
 Derivácia funkcie Derivácia funkcie je jeden z najužitočnejších nástrojov, ktoré používame v matematike a jej aplikáciách v ďalších odboroch. Stručne zhrnieme základné informácie o deriváciách. Podrobnejšie
Derivácia funkcie Derivácia funkcie je jeden z najužitočnejších nástrojov, ktoré používame v matematike a jej aplikáciách v ďalších odboroch. Stručne zhrnieme základné informácie o deriváciách. Podrobnejšie
1. POLIA A VEKTOROVÉ PRIESTORY. V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom
 1. POLIA A VEKTOROVÉ PRIESTORY V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom ďalšom výklade kľúčovú úlohu, a dokážeme o nich niekoľko jednoduchých základných tvrdení.
1. POLIA A VEKTOROVÉ PRIESTORY V tejto kapitole zavedieme dva druhy algebraických štruktúr, ktoré budú hrať v celom ďalšom výklade kľúčovú úlohu, a dokážeme o nich niekoľko jednoduchých základných tvrdení.
Zložené funkcie a substitúcia
 3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
Gramatická indukcia a jej využitie
 a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
Prirodzené čísla. Kardinálne čísla
 Prirodzené čísla Doteraz sme sa vždy uspokojili s tým, že sme pod množinou prirodzených čísel rozumeli množinu N = { 1, 2,3, 4,5, 6, 7,8,9,10,11,12, } Túto množinu sme chápali intuitívne a presne sme ju
Prirodzené čísla Doteraz sme sa vždy uspokojili s tým, že sme pod množinou prirodzených čísel rozumeli množinu N = { 1, 2,3, 4,5, 6, 7,8,9,10,11,12, } Túto množinu sme chápali intuitívne a presne sme ju
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
Teória funkcionálneho a logického programovania
 Prírodovedecká fakulta UPJŠ Košice Teória fucionálneho a logického programovania (poznámky z prednášok z akademického roka 2002/2003) prednáša: Prof. RNDr. Peter Vojtáš, DrSc. 2 TEÓRIA FUNKCIONÁLNEHO A
Prírodovedecká fakulta UPJŠ Košice Teória fucionálneho a logického programovania (poznámky z prednášok z akademického roka 2002/2003) prednáša: Prof. RNDr. Peter Vojtáš, DrSc. 2 TEÓRIA FUNKCIONÁLNEHO A
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Technická univerzita v Košiciach. Zbierka riešených a neriešených úloh. z matematiky. pre uchádzačov o štúdium na TU v Košiciach
 Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
Technická univerzita v Košiciach Zbierka riešených a neriešených úloh z matematiky pre uchádzačov o štúdium na TU v Košiciach Martin Bača Ján Buša Andrea Feňovčíková Zuzana Kimáková Denisa Olekšáková Štefan
1 Polynómy a racionálne funkcie Základy Polynómy Cvičenia Racionálne funkcie... 17
 Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
Obsah 1 Polynómy a racionálne funkcie 3 11 Základy 3 1 Polynómy 7 11 Cvičenia 13 13 Racionálne funkcie 17 131 Cvičenia 19 Lineárna algebra 3 1 Matice 3 11 Matice - základné vlastnosti 3 1 Cvičenia 6 Sústavy
Úvod do lineárnej algebry
 Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
Katedra matematiky Fakulta elektrotechniky a informatiky Technická Univerzita v Košiciach Úvod do lineárnej algebry Monika Molnárová, Helena Myšková 005 RECENZOVALI: RNDr. Štefan Schrötter, CSc. RNDr.
TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA 1. Funkcia jednej premennej a jej diferenciálny počet
 TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA časťa Funkcia jednej premennej a jej diferenciáln počet Dušan Knežo, Miriam Andrejiová, Zuzana Kimáková 200 RECENZOVALI: prof. RNDr. Jozef
TECHNICKÁ UNIVERZITA V KOŠICIACH STROJNÍCKA FAKULTA MATEMATIKA časťa Funkcia jednej premennej a jej diferenciáln počet Dušan Knežo, Miriam Andrejiová, Zuzana Kimáková 200 RECENZOVALI: prof. RNDr. Jozef
MATEMATICKÁ OLYMPIÁDA
 S MATEMATICÁ OLYMPIÁDA skmo.sk 2008/2009 58. ročník Matematickej olympiády Riešenia úloh IMO. Nech n je kladné celé číslo a a,..., a k (k 2) sú navzájom rôzne celé čísla z množiny {,..., n} také, že n
S MATEMATICÁ OLYMPIÁDA skmo.sk 2008/2009 58. ročník Matematickej olympiády Riešenia úloh IMO. Nech n je kladné celé číslo a a,..., a k (k 2) sú navzájom rôzne celé čísla z množiny {,..., n} také, že n
Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Řízení lineárních systémů Katedra matematické analýzy Vedoucí bakalářské práce: Studijní program: Studijní obor: doc. RNDr. Jaroslav
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Řízení lineárních systémů Katedra matematické analýzy Vedoucí bakalářské práce: Studijní program: Studijní obor: doc. RNDr. Jaroslav
Diferenciálne rovnice
 Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Kompilátory. Cvičenie 6: LLVM. Peter Kostolányi. 21. novembra 2017
 Kompilátory Cvičenie 6: LLVM Peter Kostolányi 21. novembra 2017 LLVM V podstate sada nástrojov pre tvorbu kompilátorov LLVM V podstate sada nástrojov pre tvorbu kompilátorov Pôvodne Low Level Virtual Machine
Kompilátory Cvičenie 6: LLVM Peter Kostolányi 21. novembra 2017 LLVM V podstate sada nástrojov pre tvorbu kompilátorov LLVM V podstate sada nástrojov pre tvorbu kompilátorov Pôvodne Low Level Virtual Machine
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
ZÁPISKY Z MATEMATICKEJ ANALÝZY 1
 UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied 4 3 4 n 6 4 3 2 3 2 4 3 6 5 6 7 3 4 2 3 3/5 /2 2/5 /3 /4 /5 /0 d 0/ /0 /5 /4 /3 2/5 6 3 2 3 2 6 5 6 7 3 4 2
UNIVERZITA PAVLA JOZEFA ŠAFÁRIKA V KOŠICIACH Prírodovedecká fakulta Ústav matematických vied 4 3 4 n 6 4 3 2 3 2 4 3 6 5 6 7 3 4 2 3 3/5 /2 2/5 /3 /4 /5 /0 d 0/ /0 /5 /4 /3 2/5 6 3 2 3 2 6 5 6 7 3 4 2
MATEMATIKA I ZBIERKA ÚLOH
 TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA ÚSTAV TECHNOLÓGIÍ, EKONOMIKY A MANAŽMENTU V STAVEBNÍCTVE KATEDRA APLIKOVANEJ MATEMATIKY RNDr. Pavol PURCZ, PhD. Mgr. Adriana ŠUGÁROVÁ MATEMATIKA I ZBIERKA
TECHNICKÁ UNIVERZITA V KOŠICIACH STAVEBNÁ FAKULTA ÚSTAV TECHNOLÓGIÍ, EKONOMIKY A MANAŽMENTU V STAVEBNÍCTVE KATEDRA APLIKOVANEJ MATEMATIKY RNDr. Pavol PURCZ, PhD. Mgr. Adriana ŠUGÁROVÁ MATEMATIKA I ZBIERKA
,Zohrievanie vody indukčným varičom bez pokrievky,
 Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
