ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
|
|
|
- ÉΘεοκλής Κοντόσταυλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ Αθήνα, Ιούνιος 206 Επιβλέπων Καθηγηής : Μιχαήλ Λουλάκης
2
3 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ου ΒΑΣΙΛΕΙΟY ΖΑΧΑΡΙΑΔΗ Επιβλέπων : Μιχαήλ Λουλάκης Επικ. Καθηγηής Ε.Μ.Π. Εγκρίθηκε από ην ριμελή εξεασική επιροπή ην 27 η Ιουνίου 206 (Υπογραφή) (Υπογραφή) (Υπογραφή) Μιχαήλ Λουλάκης Δημήριος Φουσκάκης Βασίλειος Κοκκίνης Επικ. Καθηγηής Ε.Μ.Π. Αναπλ Καθηγηής Ε.Μ.Π. Αναπλ Καθηγηής Ε.Μ.Π. Αθήνα, Ιούνιος 206
4 Περίληψη Οι Σοχασικές Ανελίξεις μελεούν πιθανοθεωρηικά μονέλα και περιγράφουν φαινόμενα που εξαρώναι από ο χρόνο και υπόκειναι σε υχαιόηα. Είναι λογικό επομένως να έχουν εφαρμογή σε διάφορους κλάδους επισημών και να προσελκύουν κάθε μαθημαικό. Οι martigale προσεγγίσεις είναι καηγορία Σοχασικών Ανελίξεων που έχουν ενυπωσιακές εφαρμογές σα Οικονομικά Μαθημαικά. "Martigale" είναι γαλλικό ακρωνύμιο που προέρχεαι από η σραηγική που ακολουθεί ένας παίκης για να κερδίσει ο παιχνίδι. Οι Σοχασικές Ανελίξεις που έχουν ην ιδιόηα να καασκευάζουν ην πιθανοθεωρηική δομή ους για ο μέλλον με βάση μόνο η γνώση μέχρι ο παρόν, ονομάζοναι Markovia προσεγγίσεις. Οι Μαρκοβιανές αλυσίδες είναι ίσως η πιο σημανική καηγορία Σοχασικών Ανελίξεων Σκοπός ης εργασίας αυής είναι να παρουσιάσουμε ην βέλιση σραηγική διακοπής για διακριό χρόνο χρησιμοποιώνας martigale και Markovia προσεγγίσεις. Σην πραγμαικόηα ο χρονικός ορίζονας ενός προβλήμαος μπορεί να είναι πεπερασμένος αλλά και μη πεπερασμένος. Γι'αυό ον λόγο θα παρουσιάσουμε και ις δύο περιπώσεις με δύο εφαρμογές. Πιο αναλυικά σο πρώο κεφάλαιο αναλύεαι η θεωρία ης βέλισης διακοπής. Θα παρουσιάσουμε martigale και Markovia προσεγγίσεις για διακριό χρόνο και α αποελέσμαα ους. Αρχικά θα αναφερθούμε σην martigale προσέγγιση και σην συνέχεια θα ακολουθήσει η Markovia. Σο δευερο κεφάλαιο κάνουμε μία γρήγορη εισαγωγή σα χρημαοοικονομικά μαθημαικά για ην ευκολόερη καανόηση ης εφαρμογής μας για πεπερασμένο χρονικό ορίζονα. Αναφερόμασε σα ευρωπαϊκού και αμερικανικού ύπου δικαιώμαα, όπως επίσης και σον αλγόριθμο ιμολόγησης ους. Αναφέρουμε ο διωνυμικό υπόδειγμα πολλών περιόδων και αναλύουμε ην βέλιση σραηγική άσκησης ενός αμερικανικού δικαιώμαος. Σο έλος υπάρχει και η ανίσοιχη εφαρμογή με ον κώδικα και α αποελέσμαα ου. Σο ρίο κεφάλαιο αναλύεαι μία εφαρμογή για μη πεπερασμένο χρονικό ορίζονα. Το πρόβλημα που παρουσιάζουμε, είναι ένα "παιχνίδι ζαριού". Βρίσκουμε ην βέλιση σραηγική που πρέπει να ακολουθήσουμε, όπως και ις πιθανόηες "νίκης". Το κεφάλαιο κλείνει με ον μέσο χρόνο διάρκειας ης σραηγικής μας. Για όλα αυά υπάρχουν και οι ανίσοιχοι κώδικες με α αποελέσμαα ους. Σο ελευαίο κεφάλαιο έχουμε ις αριθμηικές μεθόδους βελισοποίησης. Γίνεαι αναφορά σην μέθοδο Mote Carlo, με ην οποία προσομοιώνουμε ο "παιχνίδι ζαριού" ου ρίου κεφαλαίου. Σο έλος εφαρμόζουμε ην μέθοδο δειγμαοληψίας με κριήριο σημανικόηας σο πρόβλημά μας. Όλοι οι κώδικες που χρησιμοποιήθηκαν καασκευάσηκαν σην Java. Λέξεις κλειδιά: martigale, Markovia, βέλιση σραηγική διακοπής, βέλισος χρόνος διακοπής, αναμενόμενο κέρδος, υπάρχον κέρδος, Mote Carlo, δειγμαοληψία με κριήριο σημανικόηας, αρχή ης μη επιηδειόηας, αμερικανικό δικαίωμα.
5 Abstract Stochastic Processes study probability models ad describe time-depedet pheomea that are subject to radomess. Therefore, it is reasoable that they have applicatio to may differet disciplies ad attract every mathematicia. Martigale approach are a brach of Stochastic processes that have impressive applicatios to Mathematical Ecoomics. Martigale is a Frech acroym that comes from the strategy that a player follows to wi the game. Stochastic Processes that have the property to costruct their ow probabilistic structure for the future based oly o the kowledge of the preset, are called as Markovia approach. Markovia chais are probably the most importat sectio of Stochastic processes The purpose of this dissertatio is to preset the optimal strategy with stoppig rule for discrete time usig martigale ad Markovia approaches. I reality the time horizo of a problem could either be fiite or ifiite. For that reaso we will preset both cases with two applicatios. Specifically, i the first chapter we aalyze the theory of optimal stoppig. We will preset martigale ad Markovia approximatios for discrete time ad their results. At first we will refer to the martigale approximatio ad the to the Markovia. I the secod chapter, we are makig a itroductio to Mathematical Ecoomics i order to better expad o our applicatio for the fiite time horizo. We refer to the Europea ad America optios, as well as, their pricig algorithms. We will metio the biomial model for may times ad will aalyze the optimal strategy of implemetatio of the America optio. I the ed, there is also the correspodig applicatio with the code ad its outputs. I the third chapter, a implemetatio for the ifiite time horizo is beig aalyzed. The problem that we preset is a dice game. We fid the optimal strategy that eeds to be followed ad the victory probabilities. This chapter is cocluded with mea time of the duratio of our strategy. For all of these there are ad the relevat codes with their outputs. I the last chapter, we have the optimizatio umerical methods. We metio the Mote Carlo method with which we simulate the dice game of the third chapter. I the ed we implemet the importace samplig method i our problem. All the codes used were created with Java. Key words: martigale, Markovia, optimal strategy with stoppig rule, optimal stoppig time, expected profit, existig profit, Mote Carlo, importace samplig, priciple of o arbitrage, America optio.
6 Ευχαρισίες Θα ήθελα να ευχαρισήσω θερμά ον επιβλέπων καθηγηή κ. Μιχαήλ Λουλάκη για ην εμπισοσύνη που μου έδειξε αναθέονας μου ην εργασία αυή. Τον ευχαρισώ για ην υπομονή και ην αμέριση καθοδήγησή ου με καίριες υποδείξεις καθ όλη ην διάρκεια ης εκπόνησης ης διπλωμαικής μου εργασίας. Τέλος, θα ήθελα να ευχαρισήσω ιδιαίερα ην οικογενειά μου για ην υποσήριξη ους και ην πολύιμη βοήθεια ους σε όλη ην διάρκεια ων σπουδών μου.
7 Πίνακας περιεχομένων ΚΕΦΑΛΑΙΟ (Βέλιση Διακοπή: Γενική Θεωρία) Martigale προσέγγιση Μαρκοβιανή προσέγγιση... 5 ΚΕΦΑΛΑΙΟ 2 (Εφαρμογή με πεπερασμένο χρονικό ορίζονα) Εισαγωγή Βασικά χρημαοοικονομικά παράγωγα και η αρχή ης μη επιηδειόηας Γενικά Βασικά χρημαοοικονομικά παράγωγα Αρχή ης μη επιηδειόηας Διωνυμικό υπόδειγμα πολλών περιόδων Αναδρομικός αλγόριθμος ιμολόγησης και ανισάθμισης Δικαιώμαα αμερικανικού ύπου Αλγόριθμος ιμολόγησης αμερικανικών δικαιωμάων Χρόνοι διακοπής Βέλιση σραηγική άσκησης Εφαρμογή ης βέλισης σραηγικής άσκησης... 4 ΚΕΦΑΛΑΙΟ 3 (Εφαρμογή με μη πεπερασμένο χρονικό ορίζονα) Εισαγωγή Παρουσίαση Προβλήμαος (Παιχνίδι ζαριού) Βέλιση σραηγική Μέσος χρόνος αφίξεως ( Ε(Τ) ) Πιθανόηες εμφάνισης και νίκης ΚΕΦΑΛΑΙΟ 4 (Αριθμηικοί Μέθοδοι Βελισοποίησης) Εισαγωγή Σοιχεία Σαισικής Σην Mote Carlo Μείωση ης Διασποράς Εφαρμογή ης Mote Carlo Δειγμαοληψία με κριήριο Σημανικόηας (Importace Samplig)....6 Βιβλιογραφία...65
8 2
9 3 ΚΕΦΑΛΑΙΟ ΒΕΛΤΙΣΤΗ ΔΙΑΚΟΠΗ: Γενική Θεωρία Σo πρώο κεφάλαιο θα αναφερθούμε σην θεωρία ης βέλισης διακοπής. Θα παρουσιάσουμε martigale και Markovia προσεγγίσεις για διακριό χρόνο και α αποελέσμαα ους. Αρχικά θα αναφερθούμε σην martigale προσέγγιση και σην συνέχεια θα ακολουθήσει η Markovia.
10 4. Martigale προσέγγιση Έσω G = ( G) 0 είναι μια ακολουθία υχαίων μεαβληών που ορίζοναι σον φιλραρισμένο χώρο πιθανόηας ( Ω, F,( F) 0, P). G είναι ο κέρδος που λαμβάνουμε αν η παραήρηση μας G σαμαίσει σε χρόνο. Κάθε G είναι μερήσιμη. Τυπικά η ( F) 0 συμπίπει με ην ( F G ) 0, αλλά γενικά είναι μεγαλύερη. F - F είναι οι διαθέσιμες πληροφορίες που έχουμε μέχρι ην χρονική σιγμή. Όλες οι αποφάσεις μας για ην βέλιση διακοπή θα πρέπει να βασίζοναι σε αυές ις πληροφορίες. Ορισμός (Markov time): Μαρκοβιανός χρόνος είναι η υχαία μεαβληή : Ω {0,,..., }, αν { } F, 0. Ο χρόνος ονομάζεαι χρόνος διακοπής αν <, P as... Το σύνολο ων χρόνων διακοπής συμβολίζεαι με M και ο σύνολο όλων ων Μαρκοβιανών χρόνων με M. Τα υποσύνολα ου M είναι: M = { M : }, 0 Η συνάρηση που θα μελεηθεί σα προβλήμαα βέλισης διακοπής είναι : V* = sup EG Όπου V * είναι η συνάρηση αξίας που πρέπει να υπολογίσουμε και * είναι ο βέλισος χρόνος διακοπής σο μέγισο ης συνάρησης. Για να εξασφαλίσουμε ην ύπαρξης ης EG προϋποθέουμε όι E( sup Gk ) <, k οε είναι καλά ορισμένη M (με G 0 αν = ). Ωσόσο σε πολλές περιπώσεις μπορούμε να ανικαασήσουμε ο G k με G + k ή G k.για λόγους απλόηας υποθέουμε όι η παραπάνω προϋπόθεση ισχύει πάνα. Εισάγωνας ο υποσύνολο V M σο πρόβλημα μας, η συνάρηση γίνεαι: = sup EG, 0 (..) M
11 5 Μερικές φορές διαπισώνουμε όι ο χρόνος μας, παίρνει ην ιμή ο οποίο ανήκει σο M. Σε αυή ην περίπωση υπάρχουν ρείς επιλογές, που ωσόσο για καμία δεν μπορούμε να πούμε όι είναι καλύερη από ην άλλη. Αν limsup G όε G είναι η αξία που θα λάβουμε. Ένας άλλος ρόπος είναι να ορίσουμε αυθαίρεα ην G σαν μία σαθερά. Τέλος για περισσόερη ευκολία να ορίσουμε όι G = limsup G. Μέθοδος πίσω επαγωγής (backward iductio) Για να λύσουμε ην (..) με <, θα χρησιμοποιήσουμε ην μέθοδο πίσω επαγωγής για να δημιουργήσουμε μια ακολουθία υχαίων μεαβληών ( S ) 0 που θα λύσει ο πρόβλημα μας σοχασικά. Η συνάρηση (..) γράφεαι : V = sup EG, 0 (..2) με να είναι ο χρόνος διακοπής. Για να λυθεί ο πρόβλημα πρέπει να αφήσουμε ον χρόνο να πάει προς α πίσω και να προχωρήσει αναδρομικά ως εξής: Αν = όε σαμαάμε και ο κέρδος μας είναι S = G. Για = μπορούμε να συνεχίσουμε ή να σαμαήσουμε. Σην περίπωση που σαμαήσουμε ο κέρδος S είναι ίσο με G, αν όμως συνεχίσουμε ο βέλισο κέρδος μας είναι S = ES ( F ). Η απόφαση αυή, αν θα συνεχίσουμε ή θα σαμαήσουμε, πρέπει να βασίζεαι μόνο σην πληροφορία ης F. Πιο συγκεκριμένα, αν G ES ( F ) πρέπει να σαμαήσουμε ην χρονική σιγμή =, ενώ για G < ES ( F ) συνεχίζουμε. Ομοίως εργαζόμασε και για = 2,...,0. Η μέθοδος δημιουργεί μια ακολουθία υχαίων μεαβληών ( S ) 0 που ορίζεαι ως εξής: S = G, = (..3) S = max( G, ES ( F)), =,...,0 + (..4) Επίσης μας δίνει ον χρόνο διακοπής: = if{ k : S = G }, 0 k k
12 6 Θεώρημα (Για Πεπερασμένο χρόνο): Εξεάζονας ο πρόβλημα ης βέλισης διακοπής (..2) και θεωρώνας όι η υπόθεση μας ( E( sup Gk ) < ) ισχύει, έχουμε 0 : k S EG ( F), M S = EG ( F) (..5)-(..6) Επιπλέον αν 0 είναι δεδομένο και σαθερό όε έχουμε: i. Ο χρόνος διακοπής είναι ο βέλισος. ii. Αν * είναι ο βέλισος χρόνος διακοπής, όε *. iii. Η ακολουθία ( Sk ) k είναι η μικρόερη supermartigale ( Sk ) k που κυριαρχεί ης ( Gk) k iv. Η ακολουθία διακοπής ( S ) k είναι martigale. Απόδειξη: k Η απόδειξη θα πραγμαοποιηθεί με επαγωγή για =,,...,0. Σημειώσε όι και οι δύο σχέσεις (..5)-(..6) είναι εριμμένες και ικανοποιούναι όαν για =, λόγω ης (..3). Θα υποθέσουμε όι ισχύουν για =,,..., k, με k, και θα δείξουμε όι ισχύουν και για = k. (..5): Παίρνουμε M k και ορίζουμε = k. Σην συνέχεια με M k και { k} Fk έχουμε: EG ( F ) = EI ( ( kg ) F ) + EI ( ( = k ) G F ) k k k k = I( = k ) G + I( keeg ) ( ( F) F ) k k k.(α) Από ην επαγωγική υπόθεση, η ανισόηα (..5) ισχύει για = k. Όμως M k ο οποίο σημαίνει όι EG ( Fk) S k. Από ην άλλη πλευρά, η (..4) μας δείχνει όι Gk Sk και ES ( k Fk ) Sk. Με ην εφαρμογή ων ριών αυών ανισοήων σην παραπάνω σχέση έχουμε: EG ( F ) I( = k ) S + I( kes ) ( F ) k k k k I( = k ) S + I( ks ) = S k k k.(β)
13 7 Το οποίο μας δείχνει όι η (..5) ισχύει και για = k. (..6): Για να αποδείξουμε όι η (..6) ισχύει για = k είναι αρκεό να ελέγξουμε αν οι ανισόηες (α) και (β) γίνοναι ισόηες για = k. Από = if{ k : Sk = Gk}.(γ) σημειώνουμε όι = k k για { k k}, έσι ώσε από ην (α) με = k και με ην υπόθεση επαγωγής (..6) για = k έχουμε: EG ( F ) = I( = k ) G + I( keeg ) ( ( F) F ) k k k k k k k k = I( = k ) G + I( kes ) ( F ) k k k k k = I( = k ) S + I( ks ) = S k k k k k όπου σην προελευαία ισόηα χρησιμοποιούμε όι Gk = Sk για { = k κ } απο (γ), καθώς επίσης και ES ( k Fk ) = Sk για { k κ} απο ην (γ) και (..4). Αυό δείχνει όι η (..6) ισχύει για = k. (i): Λαμβάνονας Ε σην (..5) βρίσκουμε όι ως εκ ούου με η ES ES λήψη ου supremum για όλα α EG για όλα α M και V. Από ην άλλη πλευρά από ην (..6) έχουμε ES M βλέπουμε όι = EG ο οποίο μας φανερώνει όι ES V και από ην σιγμή που ισχύει. Οι δύο ανισόηες μας δίνουν ην ισόηα ES = EG, θα ισχύε και V EG =. V = ES, (ii): Ισχυριζόμασε όι η βελισοποίηση ου * σημαίνει όι S,.. = G P as * * Πράγμαι, αν αυό δεν συνέβαινε, χρησιμοποιώνας όι Sk Gk, k από (..3)-(..4), βλέπουμε όι S G * * με PS ( > G ) 0 * > *. Έσι προκύπει όι EG < ES ES = V. Η αυσηρή ανισόηα έρχεαι σε ανίθεση με ο γεγονός * * όι ο * είναι βέλισο. Επομένως S,. = G P as * * όπως ισχυρισήκαμε και δεδομένου όι * P as.. προκύπει από ον ορισμό ης (γ). (iii): Από ην (β) έχουμε S ES ( F) k+ k
14 8 για όλα α k δείχνει όι ( S ) k είναι supermartigale. Από ην (..3) και (..4) προκύπει όι Sk Gk P as.. για όλα α k πράγμα που σημαίνει όι ( S ) k επικραεί ης ( Gk) k. Επιπλέον αν ( S k ) k είναι μία άλλη supermartigale που επικραεί ης ( Gk) k, όε ο ισχυρισμός όι Sk S P as.. μπορεί να επαληθευεί με επαγωγη για k =,,..., l. Πράγμαι αν k = όε ο ισχυρισμός είναι ακόλουθως από ην (..3). Υποθέουμε όι Sk S P as.. για k =,,..., l με l + από ην (..4) έχουμε όι : S = max( G, ES ( F )) max( G, ES ( )) l F Sl P as.. l l l l l l xρησιμοποιώνας ην ιδιόηα ης supermartigale και ον ισχυρισμό. ( S k ) k ο ποιο αποδεικνύει (iv): Για να αποδείξουμε ην martigale ιδιόηα ES ( F ) = S ( k+ ) k k με k δοσμένο και σαθερό, σημειώνουμε όι ES ( F ) = EI ( ( ks ) F ) + EI ( ( k + ) S F + ) ( k+ ) k k k k k = I( k) S + I( k+ ) Ε( S + F ) k k k = I ( k ) S + I ( k + ) S = S k k k όπου η προελευαία ισόηα προκύπει από ο γεγονός όι Sk = ES ( k+ Fk) για { k + }, ενώ { k+ } Fk από ην σιγμή που Άρα η απόδειξή μας είναι πλήρης. είναι χρόνος διακοπής. Από ο παραπάνω θεώρημα διακρίνουμε όι η λύση ου προβλήμαος μας V0 (βέλιση διακοπή), μπορεί να πραγμαοποιηθεί λύνονας επαγωγικά α προβλήμαα V για =,,...,0. Μία γενική αρχή που λαμβάνεαι σο πρόβλημα μας είναι: Αν ο κανόνας διακοπής 0 είναι βέλισος για ην V0 και δεν ήαν βέλισος για να σαμαήσει σο χρονικό διάσημα {0,,..., }, όε ξεκινώνας ην παραήρησή μας σο χρόνο και βασιζόμενοι σην πληροφορία ης F, αυός ο κανόνας διακοπής θα είναι βέλισος και για ην V.
15 9 Μέθοδος σημανικού άνω πέραος (essetial supremum) Η μέθοδος πίσω επαγωγής χρειάζεαι να έχει πεπερασμένο. Ώσόσο οι.μ που ορίζοναι από δύο επαναλαμβανόμενες σχέσεις (..3)-(..4), φανερώνουν ένα χαρακηρισικό ο οποίο δύνααι να επεκαθεί και σε μη πεπερασμένο και θα αποελεί ην βάση για αυή ην μέθοδο. Τα παραπάνω μαζί με α (..5)-(..6) δείχνουν όι ισχύει η ακόλουθος ύπος: S S = sup EG ( F) M (..7) Όπως βλέπουμε προκύπει ένα πρόβλημα σην περίπωση που ο εξαιρούμενο σύνολο P-ull εξαράαι από συγκεκριμένο M. Έσι μπορεί να απούχει η παραπάνω αυόηα, αν παίρνει μη μερήσιμα γιαί ο δεξί μέρος δεν χρειάζεαι να ορίζεε από μία μερήσιμη συνάρηση. Για να ξεπεράσουμε αυό ο πρόβλημα χρησιμοποιούμε ην μέθοδο ου σημανικού άνω πέραος (essetial supremum). Λήμμα (essetial supremum): Έσω όι { Za : a I} είναι μια οικογένεια υχαίων μεαβληών που ορίζοναι σο ( Ω, GP, ), όπου I είναι ένα αυθαίρεο σύνολο. Τόε J I μερήσιμο, έοιο ώσε η υχαία μεαβληή Z * : και πληροί ις ακόλουθες ιδιόηες: i. PZ Z = a I ii. Αν Z : * ( a ), Ω R ορίζεαι ως εξής: Z * = sup Z a J a Ω R είναι μια άλλη.μ που ικανοποιεί ην προηγούμενη ιδιόηα σην θέση ης * Z, όε PZ * ( Z) =. Η.μ. εξής: * Z ονομάζεαι σημανικό άνω πέρας ης { Za : a I} και συμβολίζεαι ως * Z = ess sup a I Z a Επιπλέον ο σύνολο { Za : a I} είναι άνω καευθυνόμενο, με ην έννοια όι ab, I, c I έοιο ώσε Z a Z b Z c P-a.s, όε ο σύνολο J = { a : }
16 0 μπορεί να επιλεγεί έσι ώσε (iii). Z * = lim Za P-a.s. όπου Za Z... a 2 P-a.s.. Αυό θα μας φανεί χρήσιμο για ην απόδειξη σε μη-πεπερασμένο. Απόδειξη: Από ην σιγμή που x (2 / π )arcta( x) είναι μια γνησίως αύξουσα συνάρηση από σο [,], δεν μας περιορίζει κανένας να υποθέσουμε όι Za για όλα α a T. Σε ανίθεη περίπωση ανικαθισούμε ην Z a με (2 / π )arcta( Z a ) για a I. Ας θέσουμε ως ην οικογένεια όλων ων μερήσιμων υποσυνόλων C ων I. Επιλέγουμε μια αύξουσα ακολουθία { C : } σο έσι ώσε a = sup E(sup Z ) = sup E(sup Z ) a C a C a C a Τόε ο σύνολο J : C = ισχυριζόμασε όι Z * ορίζεαι από ην = είναι ένα μερήσιμο υποσύνολο ου I και Z * = sup Z a J και ικανοποιεί ις ιδιόηες. Για να επαληθεύσουμε ον ισχυρισμό μας παίρνουμε αυθαίρεα ένα α I. Αν α J όε Za Z * a Από ην άλλη πλευρά, αν a J υποθέουμε όι * ( a ) a< EZ Z a από ην σιγμή που a PZ * ( a Z) 0 * = EZ [,] και J {} a > >, όε ανήκει σο. Επειδή η αυσηρή ανισόηα είναι προφανώς αδύναη, βλέπουμε όι η (i) ισχύειε για όλα α a I όπως ισχυρισήκαμε. Επιπλέον ο (ii) είναι φυσικό ακόλουθο για J μερήσιμο. Τέλος αν η (iii) ικανοποιείε όε ο αρχικό αριθμήσιμο σύνολο J = { a, a,...} μπορεί να ανικαασαθεί με ένα καινούργιο αριθμήσιμο σύνολο J = { a, a2,...} αν ορίσουμε a = a, και σην συνέχεια επιλέξουμε επαγωγικά 0 γ α β ανισοιχούν σε Z, Z, Z α β γ a a a για όπου έσι ώσε Zα Zβ Zγ P as.. Επομένως με ο essetial supremum οι (..5) και (..6) μπορούν να γραφούν και ως εξής:
17 S = ess sup E( G F ), 0 Αυή η αυόηα μας παρέχει ένα επιπλέον χαρακηρισικό για ην ακολουθία ( S ) 0. Το πλεονέκημα ης είναι όι μπορεί να επεκαθεί και σε μηπεπερασμένο. Ας εξεάσουμε ο πρόβλημα (..) για =. Έχουμε : V = sup EG, 0 (..8) Με να είναι ο χρόνος διακοπής. Για να ο λύσουμε θα πρέπει να εξεάσουμε ην ακολουθία ( S) 0 που ορίζεαι ως εξής: S = ess sup E( G F ) (..9) με χρόνο διακοπής = if{ k : Sk = Gk}, 0 (..0) όπου if =. Θεώρημα (Για Μη Πεπερασμένο Χρόνο) Για ο βέλισο πρόβλημα διακοπής (..9), θεωρώνας όι ισχύει E( sup Gk ) <, ισχύουν και οι ακόλουθοι ύποι: S = max( G, ES ( + F)), 0 (..) k Υπέθεσε επίσης όι χρειάζεαι όι P( < ) =, 0 Τόε έχουμε για όλα α 0 : S EG ( F), M (..2) S = EG ( F) (..3) Επιπλέον αν ο 0 είναι δοσμένο και σαθερό,έχουμε:
18 2 i. Ο είναι ο βέλισος χρόνος διακοπής για ην (..9) ii. Αν * είναι ο βέλισος χρόνος διακοπής για ην (..9) όε * P-a.s. iii. Η ( Sk) k είναι η μικρόερη supermartigale ακολουθία που κυριαρχεί ης ( Gk) k. iv. Η σαμαημένη ακολουθία ( Sk ) k είναι martigale. Εν έλει διαπισώνουμε όι δεν υπάρχει βέλισος χρόνος σην (..9), αν η συνθήκη P( < ) = Απόδειξη: απούχει, έσι ώσε P( = ) > 0. Αρχικά θα δείξουμε όι αρισερή πλευρά είναι μικρόερη από ην δεξιά όαν ο 0 είναι δοσμένο και σαθερό. Παίρνουμε M και ο σύνολο = ( + ). Τόε M+ από η σιγμή που { + } F, έχουμε: EG ( F) = EI ( ( = G ) F) + EI ( ( + ) G F) = I( = G ) + I( + ) EG ( F) = I( = G ) + I( + ) EEG ( ( F + ) F) I( = G ) + I( + ) ES ( + F) max( G, ES ( + F)) Από αυή ην ανισόηα προκύπει όι ess sup E( G F ) max( G, E( S F )) + που είναι η επιθυμηή. Για να αποδείξουμε ανίσροφα ην ανισόηα αρχικά σημειώνουμε όι S G, P as.. από ον ορισμό ης S επομένως S ES ( + F), που είναι supermartigale ιδιόηα ης ( S) 0. Για ην επαλήθευση ης ανισόηας ας δείξουμε αρχικά όι η οικογένεια { EG ( F + ): M + } ικανοποιεί ο (iii) ου λήμμαος. Σημειώνουμε όι αν σ και σ 2 είναι από M + και θέσουμε σ3 = σia + σ2i C, όπου A A= { EG ( σ F+ ) EG ( σ F+ )}, όε ο σ 3 ανήκει σο M + και έχουμε 2 EG ( F ) = EG ( I + G I F ) σ σ σ 3 + C A 2 A + = I EG ( F ) + I EG ( F ) A σ + C A σ2 + = EG ( F ) EG ( F ) σ + σ2 +
19 3 που ο ικανοποιεί. Από Z ώσε όπου * = lim Za υπάρχει μία ακολουθία { σ k : k } σο M + έοια + + σ2 + esssup EG ( F ) = lim EG ( F ) + σk + k EG ( F ) EG ( F )..., P as.. Από ην σιγμή που ο αρισερό μέρος ης σ ισόηας, ισούαι με S +, από ην συνθήκη ου θεωρήμαος μονόονης σύγκλισης έχουμε: ES ( F) E(lim EG ( F ) F) = lim ( ( ) ) = lim EG ( F) S + = σ k + EEGσ F k k + F k k σ k Όπου η ελευαία ανισόηα είναι από ον ορισμό ης πλήρης. (..2): Η ανισόηα προκύπει άμεσα από ον ορισμό. S. Η απόδειξη ης (..) είναι (..3): Η απόδειξη για ο (iv) που ακολουθεί δείχνει όι η ακολουθία ( Sk ) k είναι martigale. Επιπλέον θέωνας G = sup G έχουμε * k k Για όλα α k. Επειδή η Sk k ανισόηα όι η ( ) S ess E G F E G F * k sup ( k ) ( k) k * G είναι ολοκληρώσιμη, προκύπει από ην παραπάνω είναι ομοιόμορφα ολοκληρώσιμη. Εφαρμόζονας ην optioal samplig σην ( M ) = ( ) με χρόνο διακοπής έχουμε S k k k k M = EM ( F). M = S και Με M = S βλέπουμε όι ισούαι με ην (..3). (i): Αποδεικνύεαι με ον ίδιο ρόπο όπως σο θεώρημα για πεπερασμένο Ν. (ii): Αποδεικνύεαι με ον ίδιο ρόπο όπως σο θεώρημα για πεπερασμένο Ν. S k (iii): Έχουμε αποδείξει όι η ( ) είναι supermartigale. Επιπλέον από ην (..9) έχουμε όι S G, P as.. για όλα α k που σημαίνει όι η ( ) k k ( G ). Ας υποθέσω σο έλος όι ( ) k ης ( G ), όε έχουμε k S k S k κυριαρχεί επι ης είναι μία άλλη supermartigale που κυριαρχει S = EG ( F) ES ( F) S k k k k k για όλα α k όπου η ελευαία ανισόηα προκύπει από ο θεώρημα optioal samplig. k
20 4 (iv): Αποδεικνύεαι με ον ίδιο ρόπο όπως σο θεώρημα για πεπερασμένο Ν. Ένα ελευαίο θεώρημα που χρειάζεαι να αναφέρουμε είναι ο συνδιασμός ων δύο παραπάνω μεθόδων. Όαν δηλαδή έχουμε πεπερασμένο που είνει σο άπειρο. Σε αυή ην περίπωση από ην (..8) σημειώνουμε όι αυξάνοναι έσι ώσε: S και S = lim S, = lim υπάρχει P-a.s. 0. Όπως επίσης και V με V = lim V, 0 Από S = ess sup E( G F), S = ess sup E( G F) Έχουμε : Ομοίως 0. S V S, V Θεώρημα (Από πεπερασμένο σε μη πεπερασμένο ορίζονα): Εξεάζονας α προβλήμαα βέισης διακοπής (..2), (..9) και ισχύονας E( sup Gk ) < k. Ισχύουν οι ύποι : Απόδειξη: S S,, V V, 0. Αφήνουμε ο και χρησιμοποιώνας ις προϋποθέσεις ου θεωρήμαος μονόονης σύγκλισης, έχουμε ις ακόλουθες επαναλαμβανόμενες σχέσεις:
21 5 S = max( G, ES ( F)) + για όλα α 0. Συγκεκριμένα, έπεαι όι ( ) 0 είναι supermatigale. Από ην σιγμή S που S G, P as.., βλέπουμε όι ( S ) G sup 0 G, P as.. για όλα α 0 ο οποίο σημαίνει από ην E( sup G ) < όι η (( ) ) 0 k ολοκληρώσιμη. Επιπλέον από optioal samplig έχουμε για M. Όμως Sk Gk S G, P as.. για όλα α M και k S ES ( F) S είναι ομοιόμορφα για όλα α k από ο οποίο συνεπάγεαι όι ES ( F) EG ( F) για όλα α M. Συνδυάζονας ις δύο παραπάνω ανισόηες, από ην (..9) έχουμε όι S S.. P as για 0. Δεδομένου όι ισχύει και ο ανίσροφο ης ανισόηας έχουμε S = S.. P as για 0. Από αυό επίσης προκύπει όι =.. P as για 0. Τέλος η ρίη αυόηα, V = V προκύπει από ο θεώρημα μονόονης σύγκλισης. Άρα η απόδειξη είναι πλήρης..2 Μαρκοβιανή προσέγγιση Υποθέουμε όι έχουμε μια χρονικά-ομοιογενή Μαρκοβιανή αλυσίδα Χ= ( Χ ) 0 που ορίζεαι σον φιλραρισμένο χώρο πιθανόηας ( Ω, F,( F) 0, Px) και παίρνει ιμές από ον μερήσιμο χώρο ( E, ) όπου για απλόηα θα υποθέσουμε όι d d E = για κάποια d και = ( ) είναι σ-άλγεβρα Borel σο όι η αλυσίδα ξεκινάει από ο x υπο ην d. Εικάζεαι P x για x E. Θεωρείε επίσης όι η απεικόνιση x Px ( f) είναι μερήσιμη f F και ακολουθεί όι η απεικόνιση x E ( ) x Z είναι μερήσιμη για κάθε.μ. Z. Εν έλει χωρίς βλάβη ης γενικόηας θεωρούμε όι ( Ω, F) ισούαι με ον κανονικό χώρο 0 0 ( E, ) με αποέλεσμα η εκιμήρια μεαόπισης θ : Ω Ω να είναι καλά ορισμένη από θ( ω)( k) = ω( + k) για ω = ( ω( k)) k 0 Ω και k, 0. (Υπενθύμιση 0 = {0} )
22 6 Έσω μια μερήσιμη συνάρηση G: E, που ικανοποιεί ην συνθήκη GX ( ) = 0, αν = ): (με Ex( sup GX ( ) ) <, x E (.2.) 0 Εξεάζουμε ο πρόβλημα βέλισης διακοπής: V ( x) = sup EG x ( X ) (.2.2) 0 Με x E και ο supremum επιλέγεαι από όλους ους χρόνους διακοπής ης X. Να σημειώσουμε όι εδώ μπορεί να είναι ο άπειρο. Σε αυή ην περίπωση ακόμα ισχυριζόμασε όι ο supremum επιλέγεαι από ους χρόνους διακοπής, δηλαδή από ους χρόνους Markov με < P-a.s. Με αυό ον ρόπο οποιαδήποε περιγραφή ης GX ( ) είναι άνευ σημασίας για ο προβλημά μας (.2.2). Για να λύσουμε ο πρόβλημα (.2.2) όαν <, θέουμε : G = GX ( ) Για 0 η (.2.2) απλοποιείαι σο πρόβλημα (..2), όπου σις θέσεις ων P και E έχουμε P x και E x ανίσοιχα με x E. Έχονας απλοποιήσει ο προβλημά μας μπορούμε πλέον να εφαρμοσουμε και ην μέθοδο πίσω επαγωγής που μας οδηγεί σε μία ακολουθία.μ. ( S ) 0 και χρόνο διακοπής. Η S είναι : Και χρόνο διακοπής έχουμε θέσει με 0. S = V ( X), 0 (.2.3) D = if{0 : X D} (.2.4) C = { x EV : ( x) > Gx ( )} (.2.5) D = { x EV : ( x) = Gx ( )} (.2.6) Τέλος ο ελεσής μεάβασης T ης X είναι:
23 7 TF( x) = E F( X ) με x E και F: E να είναι μια μερήσιμη συνάρηση έσι ώσε η F( X) να είναι ολοκληρώσιμη σε σχέση με ην P x, x E. x Θεώρημα (Πεπερασμένο Ν: Ομοιογενής χρόνος): Έχουμε ο πρόβλημα βέλισης διακοπής (.2.2) ισχύονας η συνθήση (.2.), όε η συνάρηση αξίας V ικανοποιεί ις εξισώσεις Wald-Bellma. V ( x) = max( G( x), TV ( x)) (.2.7) με x E και =,.,. ΌπουV 0 = G. Επιπλέον έχουμε: i. Ο χρόνος διακοπής D είναι βέλισος. ii. Αν * είναι βέλισος χρόνος διακοπής, όε D * P-a.s. για κάθε x E. iii. Η ακολουθία ( V ( X )) 0 είναι η μικρόερη supermartigale που κυριαρχεί ης ( GX ( )) 0 υπο ην P x για x E δεδομένο και σαθερό. D iv. Η σαμαημένη ακολουθία ( V ( X )) 0 είναι martigale υπο ην Απόδειξη: P x για κάθε x E. Για να επαληθεύσουμε ην (.2.3) αναρέχουμε σην (..6) και έχουμε S = E( GX ( ) F), 0 x D Από ην σιγμή που S θ = S, παίρνουμε όι ο k + k ικανοποιεί ην σχέση : = if{ k : S = GX ( )} = + θ, 0 k k 0 Από α παραπάνω και χρησιμοποιώνας ην ιδιόηα Markov έχουμε S = E( GX ( ) F) = E( GX ( ) F) x x θ θ = E GX ( ) = V ( X) X 0 με ην ελευαία ισόηα να προκύπει από (..5) και (..6) από ο οποίο συνεπάγεαι ES = E ( GX ( ) = sup EGX ( ) = V ( x ) x 0 x x 0 0 με 0 και x E. Επομένως η (.2.3) ισχύει.
24 8 Για να επαληθεύσουμε ην (.2.7) αναρέχουμε σην (..4) και χρησιμοποιώνας ην (.2.3) όπως επίσης και ην ιδιόηα Markov έχουμε: V X GX E V X F ( ) = max( ( ), x( ( + ) )) = max( GX ( ), Ex( V ( X) θ F)) = max( GX ( ), EX ( V ( X))) = max( G( X ), TV ( X )) για όλα α 0. Για = 0 και χρησιμοποιώνας X0 = x υπο ην P x, η παραπάνω ισόηα μας δίνει ην (.2.3). Επομένως η απόδειξη είναι πλήρης. Θέουμε έναν ελεσή Q : QF( x) = max( G( x), TF( x)) (.2.8) με x E και F: E να είναι μια μερήσιμη συνάρηση για ην οποία ισχύει F( X) L( P x ) για x E. Τόε οι εξισώσεις (.2.7) γράφοναι : V ( x) = QGx ( ), (.2.9) Q είναι η νιοσή δύναμη ου Q. Ο παραπάνω αναδρομικός υπος είναι μια αποελεσμαική μέθοδος για να βρούμε ο V όαν Law( X P x ) με x E. X (Σημείωση: Px = Law( X X 0 = x) ) Ας μελεήσουμε ώρα ην περίπωση που έχουμε μη-ομογενή χρόνο. Θέουμε Z = ( X, ) με 0 γνωρίζουμε όι Z = ( Z) 0 είναι Μαρκοβιανή αλυσίδα ομογενής χρονικά. Δίνεαι μερήσιμη συνάρηση G:{0,,..., } E που ικανοποιεί ην σχέση : και η (.2.2) γίνεαι ( sup ( +, ) ) <, 0, x E (.2. ) Ex, G kx + k 0 k V ( x, ) sup E G (, X ) = x, + + (.2.2 ) 0
25 9 ο supremum επιλέγεαι από όλους ους χρόνους διακοπής ης X και υπο ην P x, με 0, x E δεδομένα και σαθερά. X = x Ένα από α παραπάνω επιβεβαιώνει όι S+ k= V ( + k, X+ k), 0 (.2.0) Αν λάβουμε υπόψιν και ον (..4) όπως επίσης και μία ιδιόηα Markov έχουμε: V ( + kx, + k) = max( GZ ( + k), EZ ( V ( Z))), 0 k (.2.) + k με z= ( x, ),0 και x E. Θέονας k = 0 και χρησιμοποιώνας Z = z= ( x, ) υπο ην P z παίρνουμε ην: V ( x, ) = max( Gx (, ), TV ( x, )), =,...,,0 (.2.2) TV (, x) = E G(, X ) και T είναι ο ελεσής μεάβασης ης Z που με, x δίνεαι από: TFx (, ) = E F ( +, X + ), 0, x E x, Να σημειώσουμε όι οι αναδρομικοί ύποι (.2.) είναι εξισώσεις Wald-Bellma για προβλήμαα με μη ομογενείς χρόνους. Επίσης όαν για ομογενή χρόνους και G= Gx ( ), έχουμε V ( x, ) = V ( x) και η (.2.2) απλοποιείαι σην (.2.7). Σην συνέχεια δίνεαι ένας πολύ σημανικός ορισμός για ην επίλυση ης (.2.2 ). Ορισμός (Υπεραρμονικής) Μια μερήσιμη συνάρηση F:{0,,..., } E ονομάζεαι υπεραρμονική αν TFx (, ) Fx (, ), ( x, ) {0,,..., } E (.2.3) Θεωρούμε όι η TF(, x) είναι καλά ορισμένη, δηλαδή F ( +, X+ ) L( Px, ), ( x, ). Επιπλέον αν F ( + kx, + k) L( Px, ), 0 k και ( x, ) {0,,..., } E, όε επαληθεύεαι άμεσα από ιδιόηα ου Markov ο παρακάω χαρακηρισμός για ην υπεραρμονική συνάρηση: Η F είναι υπεραρμονική αν και μόνο αν η F ( + kx, + ) 0 k k υπο ην P x, ( x, ) {0,,..., } E. (.2.4) είναι υπεραρμονική
26 20 Συνοψίζονας α παραπάνω σε ένα θεώρημα προκύπει ο ακόλουθο. Θεώρημα (Πεπερασμένο Ν: Μη Ομοιογενής Χρόνος): Έσω ένα πρόβλημα βέλισης διακοπής (.2.2 ) και με ην (.2. ) να ισχύει, η συνάρηση αξίας V Ν ικανοποιεί ις εξισώσεις Wald-Bellma με V ( x, ) = max( Gx (, ), TV ( x, )), =,...,,0 (.2.5) όπου TV (, x) = E, xg(, X ) και x E. Περαιέρω βλέπουμε όι : Ο χρόνος διακοπής D είναι βέλισος για ην (.2.2 ) Αν * είναι ένας βέλισος χρόνος διακοπής σην (.2.2 ) όε D * Px, as.. ( x, ) {0,,..., } E. Η συνάρηση αξίας V συνάρησης κέρδους G σο {0,,..., } είναι η μικρόερη υπεραρμονική που κυριαρχεί ης E. Η σαμαημένη ακολουθία ( V (( + k) D, X( + k) )) 0 k είναι μία Απόδειξη: martigale υπο ην P x,, ( x, ) {0,,..., } E. Η απόδειξη είναι ίδια με ου θεωρήμαος για πεπερασμένο και και ομογενή χρόνο. Το κλειδί ης αυόηας ης (.2.2 ) που ην συνδέει με ην (..2) είναι η S + = V ( + k, X + ). k D Σην συνέχεια θα ασχοληθούμε για μη πεπερασμένο. Σε αυή ην περίπωση η (.2.2) γίνεαι : V( x) = sup EG x ( X ) (.2.6) Με να είναι ο χρόνος διακοπής και P ( ), x X0 = x = x E. Επίσης έχουμε α σύνολα C και D, που είναι α σύνολα ων x για α οποία συνεχίζουμε και διακόπουμε ανίσοιχα. C= { x EVx : ( ) > Gx ( )} D= { x EVx : ( ) = Gx ( )}
27 2 Προσθέουμε ους αρχικούς χρόνους εισόδου D σο D θέονας = if{ t 0 : X D} D Ο παρακάω ορισμός είναι πόλυ σημανικός για ην λύση ης (.2.6) Ορισμός: Έσω μία μερήσιμη συνάρηση F: E, ονομάζεαι υπεραρμονική αν TF( x) F( x), x E (.2.7) t η TF( x) είναι καλά ορισμένη, δηλαδή F( X) L( Px), 0, x E, όε ισχύει : F X L P x ( ) ( ), αν επίσης έχουμε Η F είναι υπεραρμονική αν και μόνο αν η ( F( X)) 0 είναι supermartigale υπο ην P x, x E. (.2.8) Σην περίπωση μη πεπερασμένου δεν είναι απαραίηο να ασχοληθούμε ξεχωρισά για ομογενής και μη ομογενής χρόνους, γιαί ο χρόνος διακοπής μας δεν επηρεάζεαι όπως συμβαίνει για πεπερασμένο. Θεώρημα( Για Μη πεπερασμένο ): Έσω ο πρόβλημα βέλισης διακοπής (.2.6), με ην υπόθεση (.2.) να ισχύει, όε η συνάρηση αξίας V ικανοποιεί ις εξισώσεις Wald-Bellma: V( x) = max( G( x), TV( x)), x E (.2.9) Υποθέουμε όι απαιείαι: Px( D < ) =. Έσι έχουμε: Ο χρόνος διακοπής D είναι βέλισος για ην (.2.6) Αν * είναι ένας βέλισος χρόνος διακοπής για ην (.2.6) όε D * Px as., x E. Η συνάρηση αξίας V είναι η μικρόερη υπεραρμονική συνάρηση που επικραεί ης συνάρησης κέρδους G σην E Η σαμαημένη ακολουθία ( V( X )) D 0 είναι μία martiagale υπο ην P x, x E. Σε περίπωση που ισχύει Px( D = ) > 0 για μερικά x E, όε δεν έχουμε σίγουρα βέλισο χρόνο διακοπής για ην (.2.6).
28 22 Απόδειξη: Η αυόηα που είναι ο «κλειδί» για να προσαρμόσουμε ο προβλημά μας (.2.6) σο πρόβλημα (..8) είναι S = V( X ) για 0. Αυό μπορεί να αποδειχθεί με ο πέρασμα σο όριο για ην (.2.3) και χρησιμοποιώνας ο θεώρημα από πεπερασμένο σε μη πεπερασμένο. Με ον ίδιο ακριβώς ρόπο απορρέει η (.2.9) από ην (.2.7). Οι υπόλοιπες καασάσεις προκύπουν από ο θεώρημα για μη πεπερασμένο Ν (martigale-o μέρος). Η (iii) ελειοποιεί ην (iii) ου θεωρήμαος για μη πεπερασμένο Ν (martigale-o μέρος). Η απόδειξη είναι πλήρης. Πόρισμα (Επαναληπική Μέθοδο) Σύμφωνα με ην αρχική υπόθεση ου παραπάνω θεωρήμαος έχουμε: V( x) = lim QGx ( ), x E (.2.20) Για να μην υπάρχει σύγχυση για πεπερασμένο και μη πεπερασμένο, αναφέρουμε ο παρακάω θεώρημα. Θεώρημα (Η Μοναδικόηα Σην Wald-Bellma Εξίσωση): Σύμφωνα με ην υπόθεση ου θεωρήμαος για μη πεπερασμένο, έχουμε F: E είναι μια συνάρηση που λύνει ην εξίσωση Wald-Bellma F( x) = max( G( x), TF( x)), x E (.2.2) Θεωρείαι όι η F είναι μερήσιμη και υποθέουμε όι η F ικανοποιεί ην F( X) L( P x ), x E. Επιπλέον E(sup F( X)) < (.2.22) 0 Η F ισούαι με ην συνάρηση αξίας V αν και μόνο αν ισχύει η παρακάω οριακή συνθήκη σο άπειρο: lim sup FX ( ) = lim sup GX ( ), x E Px as.. (.2.23) Σε αυή ην περίπωση ο αρισερό limsup ισούαι με limif., δηλαδή η ακολουθία ( F( X)) 0 είναι συγκλίνουσα Px as.., x E.
29 23 Απόδειξη: Αν F = V όε η (iii) από ο θεώρημα για μη πεπερασμένο Ν (markοvia) παραπάνω, γνωρίζουμε όι η F είναι η μικρόερη υπεραρμονική συνάρηση που κυριαρχεί ης G σο E. Θα δείξουμε όι μία έοια συνάρηση πρέπει να ικανοποιεί ην (.2.23). Από η σιγμή που F G ισχύει, είναι προφανές όι ο αρισερό μέρος ης (.2.34) είναι μεγαλύερο από ο δεξί. Για να αποδείξουμε ην ανίσροφη φορά ης ανισόηας θα μελεήσουμε ην συνάρηση H : E που ορίζεαι ως Hx ( ) = E(sup GX ( )), x E x 0 Η σημανική ιδιόηα ης H είναι όι είναι υπεραρμονική. Αυό αποδεικνύεαι με ον ακόλουθο ρόπο. Από ην ιδιόηα Markov έχουμε: TH ( x) = E H ( X ) = E ( E (sup G( X ))) z x X 0 = E( E(sup GX ( ) F)) = E(sup GX ( )) H( x) x x θ x για όλα α x E. Επιπλέον, για X0 = x υπο ην P x βλέπουμε όι Hx ( ) Gx ( ) για όλα α x E.Ωσόσο F( x) H( x) για όλα α x E από ην υπόθεση. Ως εκ ούου από ην ιδιόηα Markov προκύπει FX ( ) HX ( ) = E (sup GX ( )) X k k 0 = E(sup GX ( ) θ F) x k k 0 = E(sup GX ( ) F) x k+ k 0 E(sup GX ( ) F).(α) x l l m για κάθε m δοσμένο και σαθερό όπου x E. Η ελική έκφραση ου παραπάνω, ορίζει μία γενικευμένη martigale για υπο ην P, είναι γνωσό όι P as.. συγκλίνει για και κάθε x E με ο όριο που ικανοποιεί ην ανισόηα : lim E(sup GX ( ) F) E(sup GX ( ) F) = sup GX ( ).(β) x l x l l l m l m l m όπου η ελικλη αυόηα προκύπει από ο γεγονός όι sup l mgx ( l) είναι F - μερήσιμη. Για σην (α) και χρησιμοποιώνας ην (β) έχουμε: limsup FX ( ) sup GX ( ) P as.. l m l x x x
30 24 για όλα α m 0 και x E. Τέλος για m σην πάνω ανισόηα, κααλήγουμε να έχουμε ην (.2.23). Αυό είναι ο πρώο κομμάι ης απόδειξης. Ανίσροφα, ας υποθέσουμε όι η F ικανοποιεί ις (.2.2)-(.2.23), θα δείξουμε όι η F θα πρέπει να είναι ίση με ην V. Ας σημειώσουμε όι η F είναι υπεραρμονική από ην (.2.2) και όι F G. Επιπλέον από (iii) ου θεώρημαος για μη πεπερασμένο Ν (markοvia), έχουμε όι F V. Για να δείξουμε όι F V θα εξεάσουμε ον χρόνο διακοπής = if{ 0: FX ( ) GX ( ) + ε} Dε με ε > 0 δοσμένο και σαθερό. Ση συνέχεια από ην (.2.23) βλέπουμε όι D ε < Px ην as.. για x E. Επιπλέον ισχυριζόμασε όι η ( F( X )) 0 είναι μία martigale υπο x D ε P για x E. Από ην ιδιόηα Markov και ην (.2.2) συνεπάγεαι E ( F( X ) F ) = E ( F( X ) I( F ) + E ( F( X ) I( < ) F ) x D x D ε ε x D Dε ε = E ( F( X ) I( F ) + E ( F( X ) I( < ) F ) x Dε x D Dε ε = E ( F ( X ) F ) I ( ) + E ( F ( X ) I ( = k ) F ) x Dε x k = 0 k Dε = E ( F ( X )) I ( ) + F ( X ) I ( = k ) X Dε k = 0 k Dε = TF( X ) I( ) + F( X ) I( < ) = F( X ) I( D ) + F( X ) I( D < ) Dε D D ε ε = F( X ) I( ) + F( X ) I( < ) = F( X ( ) ) D ( ) Dε D ( ) D ε ε ε για όλα α και x E αποδεικνύει ον ισχυρισμό μας. Ως εκ ούου για 0 και x E. Επίσης E ( F( X )) F( x) x D = ε Ex( F( X )) = Ex( F( X ) I( D )) + Ex( F( X) I( D > )) D ε D ε με 0. Για, και χρησιμοποιώνας (.2.22) και (.2.) με F G, έχουμε Ex ( F( X )) = F( x), x E. Τέλος, αφού η V είναι υπεραρμονική, έχουμε όι Dε V( x) EV( X ) E G( X ) E F( X ) ε = F( x) ε x D x D x ε ε Dε ε ε Dε ε Dε ε ε > 0, x E. Για πολύ μικρό ε 0 έχουμε F V. Η απόδειξη είναι πλήρης.
31 25 Έσω όι έχουμε ένα δοσμένο a (0,] και μία φραγμένη μερήσιμη συνάρηση g: E και c: E +, εξεάζουμε ο πρόβλημα βέλισης διακοπής : ( ) sup k x( ( ) ( k )) k = V x = E agx a cx (.2.24) είναι ο χρόνος διακοπής ης X και P ( ) x X0 = x =. Η cx ( ) είναι η συνάρηση που μας δείχνει ο κόσος για να πάμε σην επόμενη παραήρηση ου X όαν X k = x. Το a cx ( k )) εξ ορισμού είναι 0 όαν = 0. Θέουμε X = ( X ) 0, k = που χαρακηρίζει μία Μαρκοβιανή αλυσίδα που διακόπεαι με ρυθμό a. Ο ελεσής μεάβασης ης X είναι : TF ( x) = atf( x), x E (.2.25) Όαν F( X) L( P x ). Έσι ο πρόβλημα μας γίνεαι : = x k = Vx ( ) sup E( gx ( ) ( cx k )) με να είναι ο χρόνος διακοπής για ην X και 0 P ( ) x X = x =. Εισάγουμε ην ακολουθία I με και για 0 και Z = ( X, I ) I 0 I a cx ( k ) = + k = = a σο. Τόε η Z (, = X I) ορίζει μια Μαρκοβιανή αλυσίδα Z 0 = ( X0, I0) = ( xa, ) υπο ην P xa,. Ο ελεσής μεάβασης ης ισούαι με: TF( xa, ) = E F( X, I ) Z xa, για ( xa, ) E και F( X, I ) L( P xa, ). Εν συνεχεία ξαναγράφουμε ην V(x) ως εξής: W xa = Exa, GZ Με Gz ( ) = gx ( ) aγια z= ( xa, ) E. (, ) sup ( ) Αφαιρώνας ο a και από α δύο μέλη ης V(x) έχουμε:
32 26 W( xa, ) = V( x) a, ( xa, ) E Όπως διακρίνουμε η W είναι παρόμοιο πρόβλημα με ην V σην εξίσωση (.2.6). Επομένως ισχύει και ο θεώρημα για μη πεπερασμένο. Σημειώνουμε επίσης όι : TW( xa, ) = E W( X, I ) = E ( V( X ) I ) = EV( X ) a cx ( ) = atv( x) a cx ( ) Z xa, xa, x Έσι χρησιμοποιώνας α παραπάνω η (.2.9) γράφεαι σαφέσερα ως : Και απαλείφονας ο α έχουμε: Επίσης η (.2.7 ) παίρνει ην μορφή : V( x) a = max( g( x) a, atv( x) a c( x)) V( x) = max( g( x), atv( x) c( x)) atf( x) c( x) F( x) για x E. Η F ικανοποιεί ην ανισόηα αν και μόνο αν ( xa, ) F( x) a είναι υπεραρμονική σε σχέση με ην Z = ( X, I ).
33 27 ΚΕΦΑΛΑΙΟ 2 ΕΦΑΡΜΟΓΗ ΜΕ ΠΕΠΕΡΑΣΜΕΝΟ ΧΡΟΝΙΚΟ ΟΡΙΖΟΝΤΑ 2. Εισαγωγή Σο παρόν κεφάλαιο θα κάνουμε μία εισαγωγή σα Χρημαοοικονομικά Μαθημαικά. Αρχικά θα παρουσιάσουμε α βασικόερα χρημαοοικονομικά παράγωγα και ην αρχή ης μη επιηδειόηας. Θα αναφερθούμε σα ευρωπαϊκού και αμερικανικού ύπου δικαιώμαα αγοράς και πώλησης. Εν συνεχεία θα εξηγήσουμε ι είναι ο διωνυμικό υπόδειγμα και πώς εφαρμόζεαι σε πολλές περιόδους. Θα παρουσιάσουμε ον αλγόριθμο ιμολόγησης ων αμερικανικών δικαιωμάων, όπως επίσης και ην βέλιση σραηγική ου δικαιώμαος. Σο έλος ου κεφαλαίου θα παραθέσουμε ένα παράδειγμα που θα εφαρμόζουμε ην βέλιση σραηγική άσκηση ου αμερικανικού δικαιώμαος. 2.2 Βασικά χρημαοοικονομικά παράγωγα και η αρχή ης μη επιηδειόηας.
34 Γενικά Επικαλούμενοι ην εμπειρία μας με ις ράπεζες, είε ως κααθέες είε ως δανειολήπες, γνωρίζουμε ην ύπαρξη ου όκου και ου επιοκίου. Τόκος είναι ο κέρδος που αποφέρει η επένδυση που γίνεαι ( ως κααθέσης από ην πλευρά ου πολίη και ως δανείου από ην πλευρά ων ραπεζών) και επιόκιο είναι ο ρυθμός απόδοσής ης. Ορισμός Ονομάζουμε προϊόν χωρις κίνδυνο με σαθερό επιόκιο r ένα προϊόν που η αξία ου μεαβάλλεαι σον χρόνο με η σχέση At ( ) = A(0) e rt Το βασικό χαρακηρισικό ου προϊόνος χωρίς κίνδυνο είναι όι γνωρίζουμε από σήμερα ην αξία ου σο μέλλον. Ανίσοιχα για ένα ποσό Α που θα πληρωθεί η rt χρονική σιγμή Τ, έχει σημερινή αξία Ae. Ένα απλό ομόλογο, με χρόνο ωρίμανσης Τ και ιμή όψεως Α, δίνει σον κάοχό ου ο δικαίωμα να εισπράξει από ον εκδόη ου ο ποσό Α σην χρονική σιγμή Τ. Ο κάοχος θεωρούμε όι έχει ην θεική θέση και ο εκδόης ην αρνηική σε αυή ην συμφωνία. Επομένως για να γίνει μία έοια συμφωνία θα πρέπει ο εκδόης ου ομολόγου να εισπράξει ένα ποσό για ην παραχώρηση ου Βασικά χρημαοοικονομικά παράγωγα Παράγωγα προϊόνα είναι α συμβόλαια που καθορίζουν μια συμφωνία, η οποία θα πραγμαοποιηθεί σον μέλλον και η αξία ης εξαράαι από άλλο προϊόν που ονομάζεαι πρωογενές. Τα προθεσμιακά συμβόλαια είναι δικαιώμαα προαίρεσης που συνάποναι μεαξύ δύο μερών. Είναι προκαθορισμένη η ποσόηα αγοραπωλησίας ου πρωογενούς προϊόνος ην χρονική σιγμή Τ και με προσυμφωνημένη ιμή παράδοσης Κ. Τα δικαιώμαα προαίρεσης είναι ευρωπαϊκού και αμερικανικού ύπου αγοράς και πώλησης. Το ευρωπαϊκό δικαίωμα αγοράς, με χρόνο ωρίμανσης Τ και ιμή άσκησης Κ, δίνει ην δυναόηα σον κάοχο ου να αγοράσει από ον ανισυμβαλλόμενο ο προκαθορισμένο ποσοσό πρωογενούς προϊόνος ην χρονική σιγμή Τ σην ιμή
35 29 Κ. Το δικαίωμα ασκείαι εφόσον η ιμή ου προϊόνος ην χρονική σιγμή Τ, S T είναι μεγαλύερη από ην Κ. Επομένως η απόδοση ου δικαιώμαος για ον κάοχο + ου είναι ( S K) = max{ S K, 0} και είναι πάνοε μη αρνηική. T T Σο αμερικανικό δικαίωμα αγοράς, μπορούμε να ασκήσουμε ο δικαίωμα μας οποιαδήποε σιγμή μέχρι ο πέρας ου χρόνου Τ. Σο ευρωπαϊκό μπορεί να ασκηθεί μόνο σο πέρας ου, δηλαδή ην χρονική σιγμή Τ. Το ευρωπαϊκό δικαίωμα πώλησης, με χρόνο ωρίμανσης Τ και ιμή άσκησης Κ, δίνει ην δυναόηα σον κάοχο ου να πουλήσει σον ανισυμβαλλόμενο ο προκαθορισμένο ποσοσό πρωογενούς προϊόνος ην χρονική σιγμή Τ σην ιμή Κ. Το δικαίωμα ασκείαι εφόσον η ιμή ου προϊόνος ην χρονική σιγμή Τ, ST είναι μικρόερη από ην Κ. Επομένως η απόδοση ου δικαιώμαος για ον κάοχο ου είναι ( K S ) + και είναι πάνοε μη αρνηική. T Το αμερικανικό δικαίωμα πώλησης, όπως και σην περίπωση ου δικαιώμαος αγοράς, μπορεί να ασκηθεί οποιαδήποε σιγμή μέχρι ο πέρας ου χρόνου. Σο ευρωπαϊκό μπορεί να ασκηθεί μόνο σο πέρας ου, δηλαδή ην χρονική σιγμή Τ. Είναι καανοηό όι ένα δικαίωμα αγοράς ή πώλησης, μόνο θεικό μπορεί να αποβεί για ον κάοχο ου. Αυός ακριβώς είναι και ο λόγος που πρέπει να κααβάλει κάποιο αρχικό ποσό για ην απόκηση ου. Για α αμερικανικά δικαιώμαα είναι εύλογο όι ο ποσό αυό θα είναι μεγαλύερο Αρχή ης μη επιηδειόηας Η αρχή ης μη επιηδειόηας αξιώνει όι δεν μπορεί να υπάρξει δυναόηα κέρδους χωρίς ην ανάληψη ρίσκου. Σα Χρημαοοικονομικά Μαθημαικά δεχόμασε ην αρχή αυή ως αξίωμα. Η ιμολόγηση παραγώγων βασίζεαι σην αρχή ης μη επιηδειόηας. Οι παρακάω προάσεις είναι οι περιορισμοί που εξάγοναι από ην αρχή ης μη επιηδειόηας για ην αρχική αξία ων ευρωπαϊκών δικαιωμάων. Πρόαση ) Αν η σιγμή T 0 ένα χαροφυλάκιο Α έχει σε κάθε πιθανό ενδεχόμενο μη αρνηική αξία, όε η αρχική αξία ου είναι μη αρνηική VT ( A) 0 V0 ( A) 0 2) Αν η σιγμή T 0 η αξία ενός χαροφυλακίου Α είναι σε κάθε πιθανό ενδεχόμενο όση η αξία ενός χαροφυλακίου Β, όε η αρχική αξία ου Α πρέπει να είναι ουλάχισον όση αυή ου Β.
36 30 V ( A) V ( B) V ( A) V ( B) T T 0 0 3) Η παραπάνω ανισοισόηα μπορεί να σαθεί και μόνο με ισόηα Πρόαση 2 V ( A) = V ( B) V ( A) = V ( B). T T 0 0 Η αξία FS ( 0, TK, ) ενός προθεσμιακού συμβολαίου με ωρίμανση Τ και ιμή παράδοσης Κ είναι Πρόαση 3 F( S, T, K) = S Ke rt. 0 0 Η αξία cs ( 0, TK, ) ενός ευρωπαϊκού δικαιώμαος αγοράς με ωρίμανση Τ και ιμή άσκησης Κ ικανοποιεί ις ανισόηες Πρόαση 4 ( S Ke ) c( S, T, K) S. rt Οι αρχικές αξίες cs ( 0, TK, ) και ps ( 0, TK, ) ων ευρωπαϊκών δικαιωμάων αγοράς και πώλησης ανίσοιχα, συνδέοναι με η σχέση F( S, T, K) = c( S, T, K) p( S, T, K) Σην συνέχεια θα αναφερθούμε, με βάση ην αρχή ης μη επιηδειόηας, σην αρχική αξία ενός αμερικανικού δικαιώμαος. Είναι προφανές, όπως αναφέραμε, όι ο αμερικανικό δικαίωμα αγοράς ( CS ( 0, TK, )) πρέπει να αξίζει ουλάχισον όσο ο ευρωπαϊκό, γιαί μπορεί να ασκηθεί οποιαδήποε σιγμή. Θεώρημα : Αν η καοχή ου πρωογενούς προϊόνος δεν έχει κόσος ή αποφέρει έσοδα, οι αξίες ενός ευρωπαϊκού και ενός αμερικανικού δικαιώμαος αγοράς είναι ίσες. C( S, T, K) = c( S, T, K). 0 0 Ένα άμεσο συμπέρασμα για ο παραπάνω θεώρημα είναι όι ο καοχός ενός έοιου δικαιώμαος, η βέλιση σραηγική που μπορεί να ακολουθήσει είναι να μην ο ασκήσει πρώιμα. Σην περίπωση όμως ενός αμερικανικού δικαιώμαος πώλησης, η πρώιμη άσκηση ου είναι η βέλιση σραηγική.
37 3 Θεώρημα 2: Σην περίπωση ων αμερικανικών δικαιωμάων η ισοιμία αγοράς και πώλησης (για προϊόνα που η καοχή ους δεν επιφέρει κόσος ή έσοδα) εκφράζεαι με ην ακόλουθη σχέση S K C( S, T, K) P( S, T, K) S Ke rt Οι αποδείξεις ων παραπάνω θεωρημάων και προάσεων σκοπίμως παραλείποναι. Σόχος μας είναι η γρήγορη εισαγωγή σο κομμάι ων Χρημαοοικονομικών Μαθημαικών που θα ασχοληθούμε (για περαιέρω πληροφορίες αναρέξε σην βιβλιογραφία). Σε όλες ις περιπώσεις ο πρωογενές προϊόν δεν αποδίδει μερίσμαα σε χρονο t < T, σε περίπωση που αποδίδει όε οι σχέσεις αλλάζουν. 2.3 Διωνυμικό υπόδειγμα πολλών περιόδων Κάθε ρεαλισικό υπόδειγμα θα πρέπει να εμπεριέχει ην υχαιόηα ως προς ην χρονική εξέλιξη ης αξίας ου πρωογενούς προϊόνος και να λαμβάνει υπ όψιν ην μεαβολή ης αξίας ου χρήμαος με ην πάροδο ου χρόνου. Με αυό ον ρόπο θέλουμε να κάνουμε ακριβέσερη ιμολόγηση ων παραγώγων με βάση ην αρχη ης μη επιηδειόηας. Σην ενόηα αυή θα παρουσιάσουμε ένα διακριό και ρεαλισικό υπόδειγμα αγοράς. Σο υπόδειγμα αυό θα εξεάσουμε δύο προϊόνα, ένα προϊόν χωρίς κίνδυνο και ένα με κίνδυνο. Το προϊόν με κίνδυνο θα αναφέρουμε ως πρωογενές προϊον και συνήθως αυού ο παράγωγο θέλουμε να ιμολογήσουμε. Έσω όι έχουμε χρόνο ωρίμανσης Τ, μπορούμε να χωρίσουμε ο χρονικό διάσημα [0, T ] σε Ν μικρόερα και ίσα διασήμαα. Κάθε έοιο διάσημα έχει εύρος h= T /. Για ο προϊόν χωρίς κίνδυνο υποθέουμε όι η σημερινή αξία ου είναι B 0 =, και μεαβάλλεαι με σαθερό ρυθμό σο χρόνο, επομένως ισχύει η σχέση rh Λ= B B = e, με r ο σαθερό επιόκιο. Για ο πρωογενές προϊόν, η σημερινή / tk+ tk ου αξία είναι S 0 > 0, ενώ η εξέλιξη ης σο χρόνο είναι σοχασική. Την σιγμή t k η αξία ου πρωογενούς προϊόνος είναι S t k και ισχύει S = S ξ tk+ tk k+
38 32 με { ξ k } μία ακολουθία με ανεξάρηες και ισόνομες υχαίες μεαβληές που έχουν καανομή: με p να είναι η πιθανόηα μεάβασης. u,0< p< ξk = d,0< p< Λαμβάνονας υπ όψιν ην αρχή ης μη επιηδειόηας προκύπει ο ακόλουθος περιορισμός: rh d < e < u. Πρέπει να σημειώσουμε επίσης όι d > 0, ώσε η ιμή ου πρωογενούς προϊόνος να είναι πάνα θεική. Μία γραφική απεικόνιση ου πρωογενούς προϊόνος σο υπόδειγμα μας είναι : Όπως βλέπουμε οι πιθανές ροχιές ης αξίας ου πρωογενούς προϊόνος σο διάσημα [0, T ] είναι 2, όσες και οι συνδυασμοί ιμών που παίρνουν οι υχαίες μεαβληές { ξ k }. Τα χρημαοοικονομικά μαθημαικά θεωρούν ο μονέλο μας σαν ένα χώρο πιθανόηας Ω, α σημεία ου οποίου είναι α πιθανά σενάρια εξέλιξης ης αγοράς. Είναι ξεκάθαρο πλέον και όι η αξία ου πρωογενούς προϊόνος ην χρονική σιγμή t k, S t k είναι υχαία μεαβληή όπως επίσης και μία σοχασική διαδικασία ορισμένη σον Ω εφοδιασμένο με ένα μέρο πιθανόηας P (ο μέρο πιθανόηας μας δείχνει πόσο πιθανή είναι κάθε ιμή ης.μ, δηλαδη ην καανομή ης). Το μονέλο μας ολοκληρώνεαι με ην έννοια ης διήθησης. Θεωρούμε ον Ω ως ένα σύνολο από όλες ις δυναές εκβάσεις ης αγοράς που εξελίσσοναι σον χρόνο. Σην αρχή είναι αδύναο να αναφέρουμε ποιό σενάριο θα πραγμαοποιηθεί, αν όμως περιμένουμε ως ο πέρας ου χρόνου μπορούμε να πούμε ποιό είναι ο σενάριο. Αν πάλι θελήσουμε να ο μελεήσουμε για ους ενδιάμεσους χρόνους π.χ. t, όε μπορούμε να αποφανθούμε σε ποιό ενδεχόμενο ανήκει.
39 33 K = { ω,.., ω } ή σο Kd = { ω( /2) +,.., ω}. u /2 Η εξέλιξη ης αγοράς αναπαρίσααι γραφικά k θα είναι η διαμέριση ου Ω και ισούαι: 0 = { Ω} = { K, K }.. T u d = {{ ω},..{ ω }} 2 Η απόδοση, X ( ω ), ενός παραγώγου με ωρίμανση Τ είναι μία υχαία μεαβληή που εξαράαι μόνο από ο ω, δηλαδή ο πιθανό σενάριο ης αγοράς. Σα ευρωπαϊκού ύπου (π.χ αγοράς) εξαράαι μόνο από ην ιμή ου πρωογενούς + προϊόνος σην ωρίμανση, X( ω) = ( ST ( ω) K). Σε περίπωση όμως ύπαρξης φράγμαος Μ, όε εξαράαι από όλη ην ροχιά ης ιμής, δηλαδή αποδίδει όσο ένα απλό μόνο αν δεν ξεπεράσει η ιμή ου πρωογενούς προϊόνος ο φράγμα μας. Σο συγκεκριμένο σημείο είναι απαραίηο να αναφέρουμε ι είναι χαροφυλάκιο και ι είναι αυοχρημαοδοούμενο χαροφυλάκιο. Χαροφυλάκιο είναι ο σύνολο ων περιουσιακών σοιχείων που έχει ένας πελάης σην καοχή ου πχ. Μεοχές, ομόλογα, δικαιώμαα προαίρεσης κλ. Ένα χαροφυλάκιο που εξελίσσεαι σον χρόνο με μια σειρά από συναλλαγές, οι οποίες εξαρώναι μονο από ην πληροφορία που είναι διαθέσιμη μέχρι η σιγμή εκείνη και δεν μεαβάλουν ην αξία ου χαροφυλακίου η σιγμή που συνελούναι, ονομάζεαι αυοχρημαοδοούμενο. Για ην ιμολόγηση ενός παραγώγου πρέπει να αναπαραγάγουμε ην απόδοση ου με ένα χαροφυλάκιο με δύο προϊόνα. Είναι αδύναο όμως να ανισαθμίσουμε ο χαροφυλάκιο μας ην σιγμή t = 0 με ην απόδοση ου παραγώγου ην σιγμή Τ. Γι αυό ο λόγο χρησιμοποιούμε ένα αυοχρημαοδοούμενο χαροφυλάκιο
40 34 ( α, β ) ο οποίο επιρέπει ις συναλλαγές και κα επέκαση ην θέση μας σε αυό. Σην επόμενη παράγραφο θα δούμε πώς καασκευάζουμε ένα έοιο χαροφυλάκιο που αναπαράγει ην απόδοση και ιμολόγηση ου παραγώγου με ωρίμανση Τ Αναδρομικός αλγόριθμος ιμολόγησης και ανισάθμισης Μια υχαία μεαβληή Χ είναι k -μερήσιμη, όαν η ιμή ης εξαράαι μόνο από ις ιμές ου πρωογενούς προϊόνος μέχρι η σιγμή t k, δηλαδή X( ω) = Φ ( S ( ω),..., S ( ω)) t0 t k Φ είναι συνάρηση. Επίσης 0 -μερήσιμη υχαία μεαβληή είναι σαθερά. Ορισμός Μια αυοχρημαοδοούμενη σραηγική θα είναι μια ακολουθία χαροφυλακίων {( ϕk, ψ k)} k έσι ώσε k = 0,...,, έχουμε. Οι ϕk, ψ k είναι k -μερήσιμες υχαίες μεαβληές 2. ϕ S + ψ B = ϕ S + ψ B k tk+ k tk+ k+ tk+ k+ tk+ Σην πρώη συνθήκη είναι φανερό όι η θέση που έχουμε ην σιγμή t k, εξαράαι από ην εξέλιξη ης αγοράς μέχρι αυή η σιγμή. Η δεύερη συνθήκη μας δείχνει ην αλλαγή θέσης που μπορούμε να κάνουμε ην χρονική σιγμή t k +, ο αρισερό μέρος είναι η αξία ου χαροφυλακίου πριν ην αλλαγή και ο δεξί η αξία ου μεά. Έσω όι θέλουμε να ιμολογήσουμε ένα παράγωγο με δεδομένη απόδοση η σιγμή Τ ίση με V = U ( S,..., S ). Καασκευάζουμε μία αυοχρημαοδοούμενη T t t0 t σραηγική που αναπαράγει ην απόδοση ου σην ωρίμανση. ϕ S + ψ B = V T T T Η σχέση πρέπει να ισχύει και για { ξ = u} όσο και για { ξ = d}. Έσι ορίζουμε V = U ( S,..., S u ) και V = U ( S,..., S d ) T t t0 t T t t0 t έχουμε ϕ VT VT = S ( u d) t VT u VT d και ψ = B ( u d) t Από ις παραπάνω σχέσεις προκύπει αμέσως όι οι ( ϕ, ψ ) είναι - μερήσιμες υχαίες μεαβληές. Μπορούμε λοιπόν να ορίσουμε ην αξία ου
41 35 παραγώγου η σιγμή t ως ην αξία ου χαροφυλακίου μας ην χρονική σιγμή t. V = U ( S,..., S ) : = ϕ S + ψ B. t t t0 t t t Με ανικαάσαση ων ϕ, ψ έχουμε V = e ( qv + ( q) V ) rh t όπου q = d u d rh e. Επαναλαμβάνονας ην διαδικασία οπισθοδρομώνας μέχρι ον χρόνο t, 0 προκύπει ο αλγόριθμος rh V = e ( qv + ( q) V ). tk k k Η αρχή ης μη επιηδειόηας μας επιβάλλει ην αρχική αξία ου παραγώγου προκειμένου να μην υπάρχει σραηγική επιηδειόηας. Η αξία αυή πρέπει να είναι V = ϕ S + ψ. t0 0 t Δικαιώμαα αμερικανικού ύπου Σε αυή ην ενόηα θα δείξουμε πώς γίνεαι η ιμολόγηση ων αμερικανικών δικαιωμάων σο διωνυμικό υπόδειγμα πολλών περιόδων. Όπως επίσης θα μιλήσουμε για ους χρόνους διακοπής και ο θεώρημα επιλεκικής διακοπής Αλγόριθμος ιμολόγησης αμερικανικών δικαιωμάων Θα παρουσιάσουμε έναν αλγόριθμο ιμολόγησης και ανισάθμισης αμερικανικών δικαιωμάων που ξεκινά από ον χρόνο ωρίμανσης ου παραγώγου και καασκευάζει ένα αυοχρημαοδοούμενο χαροφυλάκιο που ανισαθμίζει ις απαιήσεις ου καόχου ου. Για ην γρηγορόερη καανόηση ου, θα δούμε πώς λειουργεί σο διωνυμικό υπόδειγμα μίας περιόδου. Έσω όι έχουμε δύο προϊόνα σην αγορά, ένα χωρίς κίνδυνο με επιόκιο r όπου η rtk αξία ου προϊόνος είναι Bt = e η σιγμή t t k, και ένα προϊόν με κίνδυνο που έχει αρχική αξία s o, ην αμέσως επόμενη χρονική σιγμή h s με πιθανόηα p ή s 2 με
42 36 πιθανόηα -p. Η αρχή ης μη επιηδειόηας μας επιβάλλει ον περιορισμό s < se < s. rh 2 0 Ένα δικαίωμα αμερικανικού ύπου σην ωρίμανση, αποδίδει σον κάοχο ου f αν η ιμή ου πρωογενούς προϊόνος είναι s ή f 2 αν η ιμή είναι s 2. Σε περίπωση όμως που ασκηθεί άμεσα αποδίδει f 0. Αν επιλέξουμε να μην ασκήσουμε άμεσα ο δικαίωμα, όε η παρούσα αξία ου δικαιώμαος είναι : rh rh e s2 u0 = e ( qf+ ( q) f2), με q =. s s 2 Είναι προφανές όι αν f0 u0 μας συμφέρει να ασκήσουμε άμεσα ο δικαίωμα ειδάλλως θα πρέπει να περιμένουμε μέχρι ην ωρίμανση h. Επομένως η αξία ου αμερικανικού παραγώγου σήμερα είναι: V = max{ f, u } = f u = f e ( qf + ( q) f ) = u + ( f u ). rh Είναι η μόνη ιμή ου δικαιώμαος που είναι συμβαή με ην αρχή ης μη επιηδειόηας. Ένα αμερικανικό δικαίωμα μπορεί να ασκηθεί οποιαδήποε σιγμή όαν πρόκειαι για διωνυμικό υπόδειγμα πολλών περιόδων. Το αμερικανικό παράγωγο ην χρονική σιγμή t k αποδίδει σον κάοχο ου Y k. Η { Y k } 0 k ονομάζεαι εγγενής αξία και επιπλέον k [0, ] είναι μία k -μερήσιμη υχαία μεαβληή. Ισχύει δηλαδή με Y = Y ( S,..., S ) k k 0 k S k να είναι η ιμή ου πρωογενούς προϊόνος η σιγμή tk = kh. Αν έχουμε ένα αμερικανικού ύπου δικαίωμα πώλησης, όε η εγγενής αξία ου είναι Yk = K Sk, όπου Κ η ιμή άσκησης. Αν ο αμερικανικό δικαίωμα δεν ασκηθεί μέχρι ην ωρίμανση ου η αξία ου θα είναι V = Y +. Κάι έοιο είναι λογικό γιαί ο κάοχος ου θα ο ασκήσει μόνο αν έχει θεική εσωερική αξία. Έσω t είναι η χρονική σιγμή που μελεάμε. Η ιμή ου πρωογενούς προϊόνος είναι S, η εσωερική αξία ου αμερικανικού δικαιώμαος είναι Y. Αν δεν ασκηθεί σην ωρίμανση θα έχει απόδοση V = Y( S0,..., S u ) αν η αξία ου προϊόνος γίνει S u, ειδάλλως V = Y( S0,..., S d ) για S d. Για να αποφασίσει ο κάοχος ου αν θα ο ασκήσει ή όχι θα πρέπει να συγκρίνει ην εσωερική αξία Y με ην αξία ου παραγώγου αν δεν ασκηθεί. Η αξία ου ην χρονική σιγμή t μπορεί να υπολογισεί δημιουργώνας ένα χαροφυλάκιο
43 37 ( α, β ) ο οποίο θα έχει ίδια απόδοση με ο παράγωγο. Επομένως η αξία ου παραγώγου αν δεν ασκηθεί θα είναι rh rh U = e ( q V + ( q ) V ) = e EV [ ]. Αν Y U όε ο κάοχος ου δικαιώμαος θα ασκήσει ο δικαίωμα ην σιγμή t, σε ανίθεη περίπωση θα περιμένει ως ην ωρίμανση. Μην ξεχνάμε όι Y, U είναι μερήσιμες υχαίες μεαβληές, μπορεί να εξαρώναι από ην ισορία ης αγοράς μέχρι εκείνη ην σιγμή αλλά είναι διαφορεικές σους κόμβους ανάμεσα. Αυό σημαίνει όι είναι πιθανό σε κάποιους κομβους να συμφέρει ον κάοχο ου να ο ασκήσει. Ορίζουμε V = Y U = Y e E [ V ]. rh Q Οπισθοδρομώνας για t 2,..., t0 βρίσκουμε ον αλγόριθμο. Ο αλγόριθμος περιγράφει ην εξής διαδικασία: + Ορίζουμε U = 0, V = Y U = Y( S0,.., S) Για k =,,..,, έχονας ορίσει ην Vk = Vk( S0,.., S) 0. Βρίσκουμε χαροφυλάκιο ( αk, βk ) ώσε αk, β k k - rhk μερήσιμες υχαίες μεαβληές και αk Sk + βk e = Vk 2. Βρίσκουμε ην αξία ου χαροφυλακίου rh rh k k k k k k k U = e ( q V + ( q ) V ) = e EV [ ]. 3. Συγκρίνουμε ην U k με ην Yk και ορίζουμε ην Vk Yk Uk Uk ( Yk U k ) + = = +. Για k = 0,..., ορίζουμε ο χαροφυλάκιο ( ϕk, ψ k), με ϕk = αk και Λήμμα k + rjh ψ = β + ( Y U ) e. k k j j j= 0 Το χαροφυλάκιο {( ϕk, ψk)} 0 k χρονική σιγμή t k είναι : είναι αυοχρημαοδοούμενο και η αξία ου η k ϕ + r( k j) h k = k + ( j j). j= 0 V V Y U e
44 38 Ένα πολύ σημανικό θεώρημα που θα χρησιμοποιήσουμε σην εφαρμογή μας είναι ο ακόλουθο. Θεώρημα 3: I. Η μόνη αρχική αξία σο αμερικανικό δικαίωμα με εσωερική αξία { Y k } 0 k που δεν αφήνει περιθώριο για επιηδειόηα είναι η V 0 από ον παραπάνω αλγόριθμο. rh Q II. Η βέλιση περίοδος άσκησης είναι k* = if{ k: Yk Uk = e E [ Vk+ k]}. III. Η σραηγική ανισάθμισης ου αμερικανικού δικαιώμαος από ον πωληή ου δίνεαι από ο χαροφυλάκιο {( ϕk, ψk)}. 0 k Παραηρούμε δηλαδή όι η βέλιση σραηγική που πρέπει να ακολουθήσει ο κάοχος ενός αμερικανικού δικαιώμαος, είναι να ο ασκήσει όαν η εσωερική αξία ου δικαιώμαος είναι ουλάχισον όση η αναμενόμενη αξία ου δικαιώμαος ην αμέσως επόμενη χρονική σιγμή. Κάι επίσης που πρέπει να αναφέρουμε είναι όι η βέλιση περίοδος διακοπής k * είναι και αυή μια υχαία μεαβληή Χρόνοι διακοπής Ορισμός Θα λέμε όι ένα ενδεχόμενο A ανήκει σην οικογένεια ενδεχομένων δείκρια συνάρηση ου A είναι k -μερήσιμη k, αν η, ω A A( ω) = 0, ω A Ο ορισμός μας λέει όι ο ενδεχόμενο A ανήκει σην κλάση γνωρίζουμε ις ιμές S,..., 0 S. t k k, αν αρκεί να Πρόαση 5 Οι ιδιόηες ων ενδεχομένων { } είναι: 0 έχουμε +. Ω, 0 Αν A, όε c A 0
45 39 Αν AB,, όε A B και A B. Ορισμός Θα ονομάζουμε ην υχαία μεαβληή T : Ω 0 { } ως χρόνος διακοπής ης { St } αν 0, ο ενδεχόμενο { T = } ανήκει σην. 0 Ο χρόνος διακοπής μπορεί να χρησιμοποιηθεί ως μία σραηγική σαμαήμαος που βέβαια δεν ης επιρέπεαι να δει ο μέλλον. Αν και η σραηγική εξαράαι από ην ροχιά ου πρωογενούς προϊόνος, ο ορισμός επιβάλλει όι η απόφαση που θα παρθεί για ην διακοπή, εξαράαι μονο από ις ιμές μέχρι εκείνη ην σιγμή S,..., 0 S και όχι από ις επόμενες ιμές ου πρωογενούς προϊόνος. t k Λήμμα 2 Η υχαία μεαβληή T : Ω 0 { } είναι χρόνος διακοπής, αν και μόνο αν, 0 ο ενδεχόμενο { T } ανήκει σην. Απόδειξη: Έσω Τ ο χρόνος διακοπής. Για 0 έχουμε { T } = { T = k}. Όμως { T = k} k για k = 0,,...,. Επιπλέον η είναι κλεισή ως προς ις ενώσεις άρα έχουμε { T }. Ανισρόφως, Υποθέουμε όι { T }, 0. Έχουμε { T = 0} = { T 0} 0 ενώ για { T = } = { T } { T } c αφού όλες οι είναι κλεισές ως προς συμπληρώμαα και ομές. Επομένως ο Τ είναι χρόνος διακοπής. Πόρισμα Αν οι T, S είναι χρόνοι διακοπής, όε οι T S με ( T S)( ω) = mi{ T( ω), S( ω)} και με ( T S)( ω) = max{ T( ω), S( ω)}, είναι και αυοί χρόνοι διακοπής. k = 0
46 40 Θεώρημα 4 (optioal stoppig): Αν η διαδικασία { V } 0 είναι -martigale και ο υχαίος χρόνος Τ είναι φραγμένος χρόνος διακοπής ης { S }, όε t 0 EV [ ] = EV [ ]. T 0 Παραήρηση: Η προεξοφλημένη αξία οποιουδήποε αυοχρημαοδοούμενου χαροφυλακίου είναι martigale ως προς ο μέρο martigale Q. 2.5 Βέλιση σραηγική άσκησης Σε αυήν ην παράγραφο θα παρουσιάσουμε πώς επιυγχάνουμε ην βέλιση σραηγική άσκησης ου δικαιώμαος μας. Λήμμα 3 Έσω ο χρόνος διακοπής k * που είδαμε σην προηγούμενη ενόηα, η αρχική αξία ου χαροφυλακίου {( ϕk, ψ k)} k από ον αλγόριθμο ιμολόγησης αμερικανικών δικαιωμάων είναι V = V = E e Y, * = k*. ϕ Q r * 0 0 [ + ] * Απόδειξη: Από ο Λήμμα έχουμε όι ο χαροφυλάκιο είναι αυοχρημαοδοούμενο και από ένα θεώρημα που λέει όι, αν ο Q είναι μέρο martigale σον Ω, όε η rtk προεξοφλημένη αξία κάθε αυοχρημαοδοούμενου χαροφυλακίου e V t είναι k ( Q, k )-martigale, η προεξοφλημένη αξία ου είναι martigale rkh Mk = e V ϕ k Ο χρόνος k* = if{ k 0 : Yk Uk} είναι χρόνος διακοπής. Επίσης από ο πόρισμα είδα όι ο * είναι ένας φραγμένος χρόνος διακοπής. Επομένως, από ο Θεώρημα (optioal stoppig) έχουμε V = E M = E e V. ϕ Q Q r * 0 [ ] [ ϕ ] * *
47 4 Από ο λήμμα έχουμε όι V ϕ k = Vk, αν k* k. Συμπεραίνουμε όι παραπάνω σχέση γίνεαι V ϕ = V και η * * V E e V ϕ Q rh * 0 = [ ] * + + Αν * =, έχουμε V = V = Y = Y. Αν * < και Vk = Yk Uk = Yk = Y + k αφού 0 Uk Y * k* * *. Σε κάθε περίπωση έχουμε από ην προηγούμενη εξίσωση. V * * * * * * * + = Y και ο ισχυρισμός μας προκύπει Λήμμα 4 ϕ Έσω ο χρόνος διακοπής ης { S } με. Τόε Q rh + V0 E [ e Y ]. Απόδειξη: t k k Από ο λήμμα έχουμε όι V ϕ k Vk, k. Γνωρίζουμε όι U k 0, άρα έχουμε Vk Yk Uk Y + ϕ = k. Είναι προφανές όι προκύπει V Y α δύο μέλη με e Q έχουμε rh +. Πολλαπλασιάζονας και και σην συνέχεια παίρνονας ην αναμενόμενη ιμή ως προς Q rh ϕ Q rh + E [ e V ] E [ e Y ]. ϕ Q rh ϕ Q rh + Από ο θεώρημα (optioal stoppig) έχουμε όι V0 = E [ e V ] E [ e Y ]. Παραήρηση: Συνδυάζονας α λήμμαα 3 και 4 έχουμε όι ϕ Q rh + V0 = sup E [ e Y ] και ο supremum επιυγχάνεαι για χρόνο διακοπής * = k*. 2.6 Εφαρμογή ης βέλισης σραηγικής άσκησης. Σε αυή ην ενόηα θα εφαρμόσουμε α όσα αναφέραμε μέχρι ώρα. Θα σχοληθούμε με ένα αμερικανικό δικαίωμα πώλησης. Θα δείξουμε πόε και πού πρέπει να ασκήσουμε ο δικαίωμα που θα έχουμε σην καοχή μας, ώσε να έχουμε ακολουθήσει ην βέλιση δυναή σραηγική. Έσω λοιπόν όι καέχουμε ένα αμερικανικό δικαίωμα πώλησης με ιμή άσκησης Κ=90, r=0.0325, σ=0, , Ν=00 για χρόνο. Το πρωογενές μας προϊόν έχει αρχική ιμή 00.
48 42 Καασκευάζουμε έναν κώδικα που ασκεί ην βέλιση σραηγική και να μας υπώνει ους κόμβους άσκησης ου δικαιώμαος. Υποσημείωση: Ο κώδικας, όπως και όλοι οι κώδικες ης υπάρχουσας εργασίας είναι σε γλώσσα προγραμμαισμού JAVA. ΚΩΔΙΚΑΣ public class Fuc { public static void mai(strig[] args) { double S[][]=ew double[0][0]; double Y[][]=ew double[0][0]; double V[][]=ew double[0][0]; double q=(math.exp( )-math.exp( ))/(Math.exp( )-Math.exp( )); it So=00; it a=000; for(it j=0;j<0;j++) { for(it i=0; i<j+; i++) { S[j][i]=So*Math.pow(Math.exp( ),ji)*Math.pow(Math.exp( ),i); System.out.pritl(j+" "+S[j][i]); } }//System.out.prit(S[99][33]);System.out.pritl(); for(it j=0;j<0;j++) { for(it i=0; i<j+; i++) { Y[j][i]=90-S[j][i]; } } //System.out.prit(Y[00][33]);System.out.pritl(); for(it i=0;i<0;i++) {if (90-S[00][i]<=0) {V[00][i]=0; } if (90-S[00][i]>0) {V[00][i]=90-S[00][i]; //System.out.pritl("Kombos askisews eiai:"+"["+00+","+i+"]"+s[00][i]); if (a>i) {a=i; System.out.pritl("Call optio:"+00+" "+(a)); } } //System.out.prit(V[00][i]);System.out.pritl(); } for(it j=99;j>=0;j--) {it b=000; for(it i=0; i<j+; i++) {
49 43 if (Math.exp( )*(q*V[j+][i]+(- q)*v[j+][i+])<=y[j][i]) {V[j][i]=Y[j][i]; //System.out.pritl("Kombos askisews eiai:"+"["+j+","+i+"]"+s[j][i]); if(b>i) {b=i; System.out.pritl("Call optio:"+j+" "+(b)); } } if(math.exp( )*(q*v[j+][i]+(- q)*v[j+][i+])>y[j][i]) {V[j][i]=Math.exp( )*(q*V[j+][i]+(- q)*v[j+][i+]);} }} //System.out.prit(V[2][2]);System.out.pritl(); } } Γράφημα κόμβων και αποελέσμαα: Call optio00 53 Call optio:99 53 Call optio:98 53 Call optio:97 53 Call optio:96 53 Call optio:95 53 Call optio:94 52 Call optio:93 52 Call optio:92 52 Call optio:9 5 Call optio:90 5 Call optio:89 5 Call optio:88 50 Call optio:87 50 Call optio:86 49 Call optio:85 49 Call optio:84 49 Call optio:83 48 Call optio:82 48 Call optio:8 47 Call optio:80 47 Call optio:79 46 Call optio:78 46 Call optio:77 46 Call optio:76 45 Call optio:75 45 Call optio:74 44 Call optio:73 44 Call optio:72 43 Call optio:7 43 Call optio:70 43 Call optio:69 42
50 44 Call optio:68 42 Call optio:67 4 Call optio:66 4 Call optio:65 40 Call optio:64 40 Call optio:63 39 Call optio:62 39 Call optio:6 39 Call optio:60 38 Call optio:59 38 Call optio:58 37 Call optio:57 37 Call optio:56 36 Call optio:55 36 Call optio:54 35 Call optio:53 35 Call optio:52 34 Call optio:5 34 Call optio:50 34 Call optio:49 33 Call optio:48 33 Call optio:47 32 Call optio:46 32 Call optio:45 3 Call optio:44 3 Call optio:43 30 Call optio:42 30 Call optio:4 29 Call optio:40 29 Call optio:39 28 Call optio:38 28 Call optio:37 28 Call optio:36 27 Call optio:35 27 Call optio:34 26 Call optio:33 26 Call optio:32 25 Call optio:3 25 Call optio:30 24 Call optio:29 24 Call optio:28 23 Call optio:27 23 Call optio:26 22 Call optio:25 22 Call optio:24 2 Call optio:23 2 Call optio:22 20 Call optio:2 20 Call optio:20 20 Call optio:9 9
51 45 Συμπεράσμαα: Κοιάζονας ο γράφημα, παραηρούμε καλύερα ους κόμβους άσκησης. Οι κόμβοι άσκησης είναι με κόκκινο χρώμα. Η πρώη χρονική σιγμή που μας συμφέρει να ασκήσουμε ο δικαίωμα είναι για Ν=8 όπου ο πρωογενές προϊόν κοσίζει S = Επίσης διακρίνουμε όι η καμπύλη που t8 δημιουργείαι από ους κόμβους άσκησης, πλησιάζει σιγά σιγά ον κόμβο σον οποίο η ιμή άσκησης ισούαι με ην ιμή ου πρωογενούς προϊόνος, όπου και εν έλει ον φάνει σο πέρας ων περιόδων μας.
52
53 46 ΚΕΦΑΛΑΙΟ 3 ΕΦΑΡΜΟΓΗ ΜΕ ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΧΡΟΝΙΚΟ ΟΡΙΖΟΝΤΑ 3. Εισαγωγή Σο προηγούμενο κεφάλαιο κάναμε μια εισαγωγή σην χρημαοοικονομική θεωρία, για ην καλύερη καανόηση ης εφαρμογής που παρουσιάσαμε με πεπερασμένο χρονικό ορίζονα. Σο παρόν κεφάλαιο θα ασχοληθούμε με πρόβλημα μη πεπερασμένου χρονικού ορίζονα. Θα βρούμε ην βέλιση σραηγική με βάση ην θεωρία ου ου κεφαλαίου. Θα υπολογίσουμε ον μέσο χρόνο άφιξης, όπως επίσης και ις πιθανόηες εμφάνισης ους.
54 Παρουσίαση Προβλήμαος (Παιχνίδι ζαριού) Το πρόβλημα μας είναι ένα «παιχνίδι ζαριού». Έσω ένας παίχης ρίχνει ένα «δίκαιο» εξάεδρο ζάρι, δηλαδή είναι ισοπίθανα όλα α ενδεχόμενα,,6. Αν ο παίχης φέρει αποέλεσμα {2,3,4,5,6}, μπορεί είε να σαμαήσει και να πάρει αυό που έφερε, είε να συνεχίσει να ρίχνει αθροίζονας όλα α επόμενα αποελέσμαα. Όαν ο παίχης φέρει όε είναι αναγκασμένος να σαμαήσει και χάνει όι έχει «κερδίσει» μέχρι εκείνη ην σιγμή, δηλαδή 0 κέρδος. Ο παίχης μπορεί να σαμαήσει οποιαδήποε σιγμή θελήσει έχονας κραήσει ο άθροισμα ων ρίψεων που έφερε. 3.3 Βέλιση σραηγική Όπως διαπισώνουμε ο πρόβλημα μας είναι μη πεπερασμένου χρονικού ορίζονα. Η βέλιση σραηγική λοιπόν που πρέπει να ακολουθήσουμε, είναι να σαμαήσουμε όαν ο αναμενόμενο κέρδος μας ισούαι με ο υπάρχον κέρδος. Δηλαδή θα ψάξουμε να βρούμε ποιο είναι ο άθροισμα που πρέπει να έχουμε συλλέξει ώσε να ισχύει η ισόηα. Ο παρακάω κώδικας μας βοηθάει να βρούμε αυό ο άθροισμα. public class Fuc { public static void mai(strig[] args) { double h[]=ew double[4]; for(it j=8;j<40;j++) { double G[]=ew double[j]; for(it i=j-7; i>0; i--) { G[j-6]=j-6; G[j-]=j-; G[j-2]=j-2; G[j-3]=j-3; G[j-4]=j-4; G[j-5]=j-5; G[i]=(G[i+2]+G[i+3]+G[i+4]+G[i+5]+G[i+6])/ 6; }
55 48 G[0]=(G[2]+G[3]+G[4]+G[5]+G[6])/6; System.out.pritl(G[0]); } } } Αποελέσμαα: Συμπεράσμαα Όπως παραηρούμε σα αποελέσμαα μας, η ισόηα επιυγχάνεαι για κ=20 και κ=2. Δηλαδή η βέλιση σραηγική που πρέπει να ακολουθήσουμε είναι να συνεχίσουμε να ρίχνουμε ο ζάρι έως όου φάσει ο άθροισμα μας να είναι 20 ή 2.
56 Μέσος χρόνος αφίξεως ( E[T] ) Είδαμε ποια είναι η βέλιση σραηγική για ο πρόβλημα μας. Ποιός είναι όμως ο μέσος χρόνος άσκησης αυής ης σραηγικής; Πόσο χρόνο θα χρειασούμε για να φάσουμε άθροισμα 20 ή 2; Ακόμα καλύερα πόσες ρίψεις θα χρειασούμε; Ο ακόλουθος κώδικας μας διευκολύνει να δώσουμε ην απάνηση. public class Mpilos { public static void mai(strig[] args) { float g[]=ew float[22]; g[2]=(float); g[3]=(float); g[4]=(float)7/6; g[5]=(float)8/6; g[6]=(float)55/36; g[7]=(float)7/4; float p; for(it i=8; i<g.legth; i++) { g[i]=((g[i-2]+g[i-3]+g[i-4]+g[i-5]+g[i-6])/6)+; System.out.pritl(g[i]); } System.out.pritl("E(T) for k= 20 or 2 is :g[20]="+g[20]+","+"g[2]="+g[2]); } } Αποελέσμαα:
57 E(T) for k= 20 or 2 is :g[20]= ,g[2]= Συμπεράσμαα Όπως διαπισώνουμε ο μέσος χρόνος ή καλύερα ο μέσος αριθμός ρίψεων είναι έσσερις φορές. 3.5 Πιθανόηες εμφάνισης και νίκης Ένα πολύ ενδιαφέρον σοιχείο για ο πρόβλημα μας, είναι να υπολογίσουμε ην πιθανόηα να «κερδίσουμε». Δηλαδή ποια είναι η πιθανόηα να έχουμε άθροισμα πάνω απο 20. Επίσης θα βρούμε ις πιθανόηες να έχουμε ακριβώς άθροισμα 20 και 2. Υπενθυμίζουμε όι ο ζάρι είναι δίκαιο επομένως κάθε ενδεχόμενο {,2,3,4,5,6} έχει πιθανόηα εμφάνισης /6. Επομένως ο πίνακας μεάβασης πιθανοήων είναι : Πίνακας μεάβασης
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
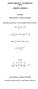 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
n 5 = 7 ε (π.χ. ορίζοντας n0 = 1+ ε συνεπώς (σύμϕωνα με τις παραπάνω ισοδυναμίες) an 5 < ε. Επομένως a n β n 23 + β n+1
 Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
sup(a + B) = sup A + sup B inf(a + B) = inf A + inf B.
 Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
 Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
B = {x A : f(x) = 1}.
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
f(x) = lim f n (t) = d(t, x n ) d(t, x) = f(t)
 Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
Κεφάλαιο 7 Ακολουθίες και σειρές συναρτήσεων 7.1 Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση Ορισμός 7.1.1. Εστω X σύνολο, (Y, ρ) μετρικός χώρος και f n, f : X Y (n = 1, 2,...). Λέμε ότι η ακολουθία συναρτήσεων
Το Θεώρημα Stone - Weierstrass
 Το Θεώρημα Stone - Weierstrass Θεώρημα 1 Έστω ¹ X συμπαγής χώρος Hausdorff και έστω C R (X η πραγματική άλγεβρα όλων των συνεχών συναρτήσεων f : X R. Έστω ότι ένα υποσύνολο A C R (X (1 το A είναι υπάλγεβρα
Το Θεώρημα Stone - Weierstrass Θεώρημα 1 Έστω ¹ X συμπαγής χώρος Hausdorff και έστω C R (X η πραγματική άλγεβρα όλων των συνεχών συναρτήσεων f : X R. Έστω ότι ένα υποσύνολο A C R (X (1 το A είναι υπάλγεβρα
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Μέθοδοι ανάλυσης οικονοµικής σκοπιµότητας έργων. Κοινωνικο- οικονοµικές. Ο ορισµός του έργου. Τεχνική αξιολόγησης έργων
 Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Κεφάλαιο 4. Θεωρήµατα οµής
 Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
1. For each of the following power series, find the interval of convergence and the radius of convergence:
 Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ
 ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Έστω [, b] ένα κλειστό διάστημα με < b. Διαμέριση του [, b] είναι ένα οποιοδήποτε πεπερασμένο υποσύνολο του [, b] το οποίο περιέχει τουλάχιστον
ΑΝΑΛΥΣΗ 2 ΣΕ 37 ΜΑΘΗΜΑΤΑ Μ. Παπαδημητράκης. ΠΡΩΤΟ ΜΑΘΗΜΑ Έστω [, b] ένα κλειστό διάστημα με < b. Διαμέριση του [, b] είναι ένα οποιοδήποτε πεπερασμένο υποσύνολο του [, b] το οποίο περιέχει τουλάχιστον
5 Σύγκλιση σε τοπολογικούς χώρους
 121 5 Σύγκλιση σε τοπολογικούς χώρους Στο κεφάλαιο αυτό πρόκειται να μελετήσουμε την έννοια της σύγκλισης σε γενικούς τοπολογικούς χώρους, πέραν των μετρικών χώρων. Όπως έχουμε ήδη διαπιστώσει ( πρβλ.
121 5 Σύγκλιση σε τοπολογικούς χώρους Στο κεφάλαιο αυτό πρόκειται να μελετήσουμε την έννοια της σύγκλισης σε γενικούς τοπολογικούς χώρους, πέραν των μετρικών χώρων. Όπως έχουμε ήδη διαπιστώσει ( πρβλ.
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
ΑΝΑΛΥΣΗ 1 ΕΙΚΟΣΤΟ ΕΒΔΟΜΟ ΜΑΘΗΜΑ, 6-12-13 Μ. Παπαδημητράκης. 1 Τώρα θα δούμε την απόδειξη του Θεωρήματος που διατυπώσαμε στο τέλος του προηγούμενου μαθήματος. Απόδειξη. [α] Θεωρούμε συνάρτηση f : A R και
i=1 i=1 i=1 (x i 1, x i +1) (x 1 1, x k +1),
 Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
0 1 0 0 0 1 p q 0 P =
 Στοχαστικές Ανελίξεις - Σεπτέμβριος 2015 ΟΔΗΓΙΕΣ (1) Απαντήστε σε όλα τα θέματα. Τα θέματα είναι ισοδύναμα. (2) Οι απαντήσεις να είναι αιτιολογημένες. Απαντήσεις χωρίς να φαίνεται η απαιτούμενη εργασία
Στοχαστικές Ανελίξεις - Σεπτέμβριος 2015 ΟΔΗΓΙΕΣ (1) Απαντήστε σε όλα τα θέματα. Τα θέματα είναι ισοδύναμα. (2) Οι απαντήσεις να είναι αιτιολογημένες. Απαντήσεις χωρίς να φαίνεται η απαιτούμενη εργασία
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Παράρτηµα Α. Στοιχεία θεωρίας µέτρου και ολοκλήρωσης.
 Παράρτηµα Α Στοιχεία θεωρίας µέτρου και ολοκλήρωσης Α Χώροι µέτρου Πέραν της «διαισθητικής» περιγραφής του µέτρου «σχετικά απλών» συνόλων στο από το µήκος τους (όπως πχ είναι τα διαστήµατα, ενώσεις/τοµές
Παράρτηµα Α Στοιχεία θεωρίας µέτρου και ολοκλήρωσης Α Χώροι µέτρου Πέραν της «διαισθητικής» περιγραφής του µέτρου «σχετικά απλών» συνόλων στο από το µήκος τους (όπως πχ είναι τα διαστήµατα, ενώσεις/τοµές
Apì ton diakritì kôbo ston q ro tou Gauss
 Apì ton diaritì Ôbo ston q ro tou Gauss 1 Isoperimetri anisìthta sto diaritì Ôbo Θεωρούμε την οικογένεια J των συναρτήσεων J : [0 1] [0 ) που ικανοποιούν τα εξής: J0) = J1) = 0. Για κάθε a b [0 1] a +
Apì ton diaritì Ôbo ston q ro tou Gauss 1 Isoperimetri anisìthta sto diaritì Ôbo Θεωρούμε την οικογένεια J των συναρτήσεων J : [0 1] [0 ) που ικανοποιούν τα εξής: J0) = J1) = 0. Για κάθε a b [0 1] a +
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Υπόδειξη. (α) Άµεσο αφού κάθε υποσύνολο µηδενικού συνόλου είναι µετρήσιµο.
 Κεφάλαιο 2 Ολοκλήρωµα Lebesgue 2.1 Οµάδα Α 1. Αν η f : (a, b) R είναι παραγωγίσιµη, τότε η f είναι µετρήσιµη. Υπόδειξη. Θεωρούµε την ακολουθία f : (a, b) R µε f (x) = [f(x + 1/) f(x)]. Εφόσον, η f είναι
Κεφάλαιο 2 Ολοκλήρωµα Lebesgue 2.1 Οµάδα Α 1. Αν η f : (a, b) R είναι παραγωγίσιµη, τότε η f είναι µετρήσιµη. Υπόδειξη. Θεωρούµε την ακολουθία f : (a, b) R µε f (x) = [f(x + 1/) f(x)]. Εφόσον, η f είναι
Αρµονική Ανάλυση. Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις. Απόστολος Γιαννόπουλος. Τµήµα Μαθηµατικών
 Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ενότητα: Ολοκλήρωµα Lebesgue - Ασκήσεις Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό υλικό, όπως εικόνες,
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
x < A y f(x) < B f(y).
 Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
j=1 x n (i) x s (i) < ε.
 Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
2πσ 2 e (x µ)2 /2σ 2 dx = 1. (13.1) e x2 dx. e y2 dy, I = 2. e (y2 +z 2) dy dz.
 Κεφάλαιο 3 Κ.Ο.Θ.: Λίγη θεωρία και αποδείξεις Σε αυτό το κεφάλαιο θα δούμε τέσσερις αποδείξεις αποτελεσμάτων που σχετίζονται με την κανονική κατανομή και το Κ.Ο.Θ., οι οποίες είναι αρκετά πιο απαιτητικές,
Κεφάλαιο 3 Κ.Ο.Θ.: Λίγη θεωρία και αποδείξεις Σε αυτό το κεφάλαιο θα δούμε τέσσερις αποδείξεις αποτελεσμάτων που σχετίζονται με την κανονική κατανομή και το Κ.Ο.Θ., οι οποίες είναι αρκετά πιο απαιτητικές,
Το φασματικό Θεώρημα
 Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
Το φασματικό Θεώρημα 1 Το φάσμα ενός τελεστή Λήμμα 1.1 Έστω A B(H) φυσιολογικός τελεστής. Αν x H είναι ιδιοδιάνυσμα του A με ιδιοτιμή λ, τότε A x = λx. Έπεται ότι οι ιδιόχωροι ενός φυσιολογικού τελεστή
1 Χώροι πηλίκα { } x = y x y Y. Με τις πράξεις της πρόσθεσης και του βαθμωτού πολλαπλασιασμού που ορίζονται με τον
 Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
Χώροι πηλίκα Έστω διανυσματικός χώρος και Y διανυσματικός υπόχωρος του. Για κάθε θεωρούμε το σύμπλοκο σχετικά με τον Y, = + y y Y = + Y ορ { : } δηλαδή το είναι η παράλληλη μεταφορά του Y κατά το διάνυσμα.
θ. Bolzano θ. Ενδιάμεσων τιμών θ. Μεγίστου Ελαχίστου και Εφαρμογές
 Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ (Τεύχος 35) θ Bolzano θ Ενδιάμεσων τιμών θ Μεγίστου Ελαχίστου και Εφαρμογές Στο άρθρο αυτό επιχειρείται μια προσέγγιση των βασικών αυτών θεωρημάτων με εφαρμογές έ- τσι ώστε να
Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ (Τεύχος 35) θ Bolzano θ Ενδιάμεσων τιμών θ Μεγίστου Ελαχίστου και Εφαρμογές Στο άρθρο αυτό επιχειρείται μια προσέγγιση των βασικών αυτών θεωρημάτων με εφαρμογές έ- τσι ώστε να
Φ(s(n)) = s (Φ(n)). (i) Φ(1) = a.
 1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
ΘΕΜΑ Α Α1. Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αν F είναι μια παράγουσα της f στο Δ, να αποδείξετε ότι:
 ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΟΝΟΜΑ ΤΜΗΜΑ Διαγώνισμα Προσομοίωσης Μαθηματικών Προσανατολισμού 11/5/19 Γ Λυκείου ΕΚΠΑΙΔΕΥΤΗΡΙΟ ΔΙΑΡΚΕΙΑ ΘΕΜΑ Α Α1. Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αν F είναι
ΜΑΘΗΜΑ - ΕΞΕΤΑΖΟΜΕΝΗ ΥΛΗ ΟΝΟΜΑ ΤΜΗΜΑ Διαγώνισμα Προσομοίωσης Μαθηματικών Προσανατολισμού 11/5/19 Γ Λυκείου ΕΚΠΑΙΔΕΥΤΗΡΙΟ ΔΙΑΡΚΕΙΑ ΘΕΜΑ Α Α1. Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ. Αν F είναι
Dunamoseirèc A. N. Giannakìpouloc, Tm ma Statistik c OPA
 Dunamoseirèc A. N. Giannakìpouloc, Tm ma Statistik c OPA Eisagwg Οι δυναμοσειρές είναι μια πολύ ενδιαφέρουσα κατηγορία σειρών. Βρίσκουν πολύ σημαντικές εφαρμογές στον ορισμό συναρτήσεων καθώς και σε διάφορες
Dunamoseirèc A. N. Giannakìpouloc, Tm ma Statistik c OPA Eisagwg Οι δυναμοσειρές είναι μια πολύ ενδιαφέρουσα κατηγορία σειρών. Βρίσκουν πολύ σημαντικές εφαρμογές στον ορισμό συναρτήσεων καθώς και σε διάφορες
f(x) f(c) x 1 c x 2 c
 Μαθηματικός Λογισμός Ι Φθινόπωρο 2014 Σημειώσεις 1-12-14 Μ. Ζαζάνης 1 Πραγματικές Συναρτήσεις και Ορια Εστω S R ένα υποσύνολο του R και f : S R μια συνάρτηση με πεδίο ορισμού το S και τιμές στους πραγματικούς
Μαθηματικός Λογισμός Ι Φθινόπωρο 2014 Σημειώσεις 1-12-14 Μ. Ζαζάνης 1 Πραγματικές Συναρτήσεις και Ορια Εστω S R ένα υποσύνολο του R και f : S R μια συνάρτηση με πεδίο ορισμού το S και τιμές στους πραγματικούς
4 Ασθενείς τοπολογίες σε χώρους με νόρμα. 4.1 θεωρήματα Mazur, Alaoglou, Goldstine.
 8 Έστω (, ) 4 Ασθενείς τοπολογίες σε χώρους με νόρμα 4. θεωρήματα Mazur, Alaoglou, Goldste. χώρος με νόρμα. Υπενθυμίζουμε ότι η ασθενής τοπολογία T του έχει ως βάση ( ανοικτών ) περιοχών του όλα τα σύνολα
8 Έστω (, ) 4 Ασθενείς τοπολογίες σε χώρους με νόρμα 4. θεωρήματα Mazur, Alaoglou, Goldste. χώρος με νόρμα. Υπενθυμίζουμε ότι η ασθενής τοπολογία T του έχει ως βάση ( ανοικτών ) περιοχών του όλα τα σύνολα
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ. Το 1ο Θέμα στις πανελλαδικές εξετάσεις
 Επιμέλεια Καραγιάννης Β. Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Το ο Θέμα στις πανελλαδικές εξετάσεις Ερωτήσεις+Απαντήσεις
Επιμέλεια Καραγιάννης Β. Ιωάννης Σχολικός Σύμβουλος Μαθηματικών ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Το ο Θέμα στις πανελλαδικές εξετάσεις Ερωτήσεις+Απαντήσεις
Pr(10 X 15) = Pr(15 X 20) = 1/2, (10.2)
 Κεφάλαιο 10 Συνεχείς τυχαίες μεταβλητές Σε αυτό το κεφάλαιο θα εξετάσουμε τις ιδιότητες που έχουν οι συνεχείς τυχαίες μεταβλητές. Εκείνες οι Τ.Μ. X, δηλαδή, των οποίων το σύνολο τιμών δεν είναι διακριτό,
Κεφάλαιο 10 Συνεχείς τυχαίες μεταβλητές Σε αυτό το κεφάλαιο θα εξετάσουμε τις ιδιότητες που έχουν οι συνεχείς τυχαίες μεταβλητές. Εκείνες οι Τ.Μ. X, δηλαδή, των οποίων το σύνολο τιμών δεν είναι διακριτό,
