Κεφάλαιο 4. Θεωρήµατα οµής
|
|
|
- Αδελφά Βασιλόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο σοιχείο περιοδιού σε άθροισα ων p-συνισωσών ου Έσω Μ ένα πεπερασένα παραγόενο R-πρόυπο Να υπενθυίσουε όι ένα m 0 έγεαι περιοδιό αν r R ε r 0 αι rm 0 = 0 αι ένα m έγεαι εεύθερο σρέψης αν m 0 αι η σχέση συνεπάγεαι όι r = 0 Ξέρουε όι αν είναι εεύθερο σρέψης T rm = 0 T = { m m περιοδιό σοιχείο ου Μ} όε T αι Ένα R πρόυπο Ν έγεαι περιοδιό R-πρόυπο αν άθε σοιχείο ου είναι περιοδιό δηαδή N = T N Ένα R-πρόυπο Κ έγεαι εεύθερο σρέψης R-πρόυπο αν άθε η ηδενιό σοιχείο ου Κ είναι εεύθερο σρέψης Πχ είναι εεύθερο σρέψης Ÿ -πρόυπο Ÿ n είναι περιοδιό Ÿ -πρόυπο Ÿ n δεν είναι ούε περιοδιό ούε εεύθερο σρέψης Ÿ -πρόυπο
2 4 Πρόαση Αν Ν είναι ένα πεπερασένο παραγόενο R-πρόυπο ο οποίο είναι εεύθερο σρέψης όε ο Ν είναι ένα εεύθερο R-πρόυπο Απόδειξη Έσω N =< x,, xk > Τόε άθε k -σοιχεία ου Ν είναι γραιά εξαρηένα έσω Πράγαι έσω + F ένας R-επιορφισός ε F εεύθερο διάσασης k αι π y,, yk+ όε a,, ak+ F ε π ( a ) = y Επειδή F εεύθερο διάσασης k έπεαι όι α α,, α k + είναι γραιά εξαρηένα άρα r,, ) (0,,0) ε r a + r k a 0, άρα r y + r k y 0 ( r k + Συνεπώς α y,, y k k+ = είναι γραιά εξαρηένα + + k+ = Έσω οιπόν ρ ο έγισο πήθος γραιά αναξαρήων σοιχείων ου Ν Σύφωνα ε α προηγούενα Ν, έσω z z,, Για άθε x,, z ρ εξαρηένα άρα r R ε r 0 αι r x < z,, z ρ > ρ k Θεωρούε ρ γραιά ανεξάρηα σοιχεία ου k α σοιχεία x, z,, z είναι γραιά Έσω r = r όε r 0 επειδή R είναι αέραια περιοχή αι r ρ rx < z,, z ρ > k αι επειδή N =< x,, xk > έπεαι όι rw < z,, z ρ > w N Θεωρούε ον R-οοορφισό Επειδή ο Ν είναι εεύθερο σρέψης έπεαι όι ο N Imθ r z ρ z,, Imθ r Αά ε βάση α προηγούενα θ r θ ρ r N N w rw είναι R-ονοορφισός άρα Imθ z,, z N αι επειδή είναι εεύθερο R-πρόυπο, ως υποπρόυπο εεύθερου έπεαι όι αι ο είναι εεύθερο R-πρόυπο ως υποπρόυπο εεύθερου Άρα εεύθερο R-πρόυπο r ρ N Imθr είναι 4 Πρόαση Έσω Μ πεπερασένα παραγόενο R-πρόυπο αι ο σύνοο ων περιοδιών σοιχείων ου Μ Τόε T
3 () T αι = T F όπου F εεύθερο R-πρόυπο ε rkf = ο έγισο πήθος γραιά ανεξάρηων σοιχείων ου Μ () Αν = T F, όπου T περιοδιό υποπρόυπο ου Μ αι F εεύθερο υποπρόυπο ου Μ όε T = T αι F F () Αν T F όπου T περιοδιό R-πρόυπο αι F εεύθερο όε T T αι F F Η απόδειξη ης Πρόασης αφήνεαι ως άσηση Το αόουθο Πόρισα είναι άεση συνέπεια ης Πρόασης 4 Πόρισα Έσω Μ, Ν πεπερασένα παραγόενα R-πρόυπα Τόε N αν αι όνο αν T T N αι ο έγισο πήθος γραιά ανεξάρηων σοιχείων ου Μ ισούαι ε ο έγισο πήθος γραιά ανεξάρηων σοιχείων ου Ν αι Αν Μ πεπερασένα παραγόενο R-πρόυπο όε από ην Πρόαση έπεαι όι T είναι πεπερασένα παραγόενο R-πρόυπο Έσω T =< w,, wk > Επειδή w είναι ένα περιοδιό σοιχείο έπεαι όι r R ε r 0 αι rw = 0, k Συνεπώς αν r = r όε r 0 αι rt = 0 r k Η επόενη Πρόαση ας δίνει ια ανάυση ου ως ευθύ άθροισα ων pσυνισωσών ου T 44 Πρόαση Έσω Ν ένα περιοδιό R-πρόυπο αι έσω όι υπάρχει d R ε = k k k d 0 αι dn = 0 Αν d up p, ε u ανισρέψιο, αι p,, p η συνροφιούς πρώους αι Np = { x N p x = 0}, k Τόε + k () Np d N όπου d = up p p p, k = () N = Np Np k + k
4 4 Απόδειξη () Προφανώς p ( d, ) = συνεπώς έχουε όι d N Np Έσω ώρα x Np άρα p x = 0 Επειδή = r d + r p για άποια r r, R Άρα x = r d x + r p x, x = dr x d N, άρα Np = d N () Επειδή ( d,, d k ) = έπεαι όι = d + + k dk για άποια,, k R Άρα αν x N Έσω ώρα όε x = dx + d x + + k d k x άρα N = Np + + Npk w Np σ Np Προφανώς για άθε σ για j, άρα w = 0 αφού σ d σ ( p σ, d ) = άρα w = 0 Συνεπώς σ σ x N j έχουε όι x d = 0 w Np αι pσ σ w = 0 αφού w Npσ Αά N = Np Np k Παράδειγα Έσω ο Ÿ -πρόυπο = Ÿ Τόε = 0 αι όπου = Ÿ = ] {[0],[],[6] [9] } = = 4 = 4 Ÿ [ = = [ 4] = {[0],[4],[8] } = 45 Ορισός Έσω Ν ένα R-πρόυπο αι p ένα πρώο σοιχείο ου R Το υποσύνοο Np = { x N p x = 0 για άποιο 0} ου Ν είναι ένα υποπρόυπο ου Ν αι έγεαι η p-συνισώσα ου Ν 46 Θεώρηα πρωαρχιής ανάυσης Έσω Μ ένα πεπερασένα παραγόενο περιοδιό R-πρόυπο ε 0 Τόε υπάρχει πεπερασένο πήθος η συνροφιών πρώων σοιχείων ου R, p,, ε p αι = p pk p k 0 Επιπέον αν Ν είναι ένα πεπερασένα παραγόενο περιοδιό R-πρόυπο όε N αν αι όνο αν p Np για άθε πρώο σοιχείο p ου R
5 5 Η απόδειξη ου θεωρήαος που αφήνεαι ως άσηση, σηρίζεαι σην προηγούενη πρόαση αι σο όι αν φ : N είναι ένας R-οοορφισός όε φ( p) Np αι αφήνεαι ως άσηση Θα δείξουε όι αν Μ είναι ένα πεπερασένα παραγόενο περιοδιό R-πρόυπο όε άθε p-συνισώσα, p, ου Μ, ε p 0 είναι ευθύ άθροισα υιών υποπρούπων Πριν δείξουε αυό θα εεήσουε ορισένες βασιές ιδιόηες ων υιών R-προύπων 4 Κυιά Πρόυπα αι οναδιόηα ανάυσης p-περιοδιού σε άθροισα υιών Όπως ξέρουε ένα R-πρόυπο Μ έγεαι υιό R-πρόυπο αν παράγεαι από φ : R ένα σοιχείο Έσω = Rm 0 αι όε ο φ είναι ένας R-επιορφισός, r rm άρα R ker φ Επειδή ο R είναι απι, ker φ = Rx0 αι ο σοιχείο x 0 ου R είναι οναδιό ως προς συνροφιόηα Τώρα ο ιδεώδες ker φ = { r R rm0 = 0} = { r R rm = 0 m } έγεαι ο ηδενισής ου Μ ή ο ιδεώδες άξης ου Μ αι συβοίζεαι ε σοιχείο άξη ου 0 o( ) Το δε x ου R, για ην αρίβεια η άση συνροφιόηας ου, έγεαι η 0 σοιχείο ου Προφανώς 0 αν αι όνο αν η άξη ου Μ δεν ένα ανισρέψιο R Αν Μ ένα R-πρόυπο αι m 0 όε ορίζεαι η άξη ου m 0 ως η άξη ου Rm 0 αι συβοίζεαι ε o ( m0 ) Συνεπώς o ( m0 ) = [ d] αν αι όνο αν dm0 = 0 αι αν rm0 = 0 όε d r Για παράδειγα η άξη ου Ÿ -προύπου Ÿm είναι m, για ην αρίβεια είναι η άση συνροφιόηας { m, m} Η άξη ου [x]- x 0
6 6 προύπου [ x] < x + > { q( x + ) q (0)} είναι x +, για ην αρίβεια η άση συνροφιόηας Η επόενη πρόαση ας έει όι η άξη ενός υιού προύπου ο χαραηρίζει ως προς ισοορφισό 4 Πρόαση ύο υιά R-πρόυπα Μ, Ν είναι ισόορφα αν αι όνο αν έχουν ην ίδια άξη Απόδειξη Έσω : N ένας R-ισοορφισός Θα δείξουε όι o ( ) = o( N) Έσω r o( ) αι x N Τόε y ε x = φ(y) αι rx = rφ) y) = φ( ry) = φ ( 0) = 0 άρα r o(n) Παρόοια δείχνουε όι o( N) o( ) άρα o ( ) = o( N) Αν ώρα o ( ) = o( N) όε R R o( ) = o( N) συνεπώς N Σχόιο Εδώ ουσιασιά δείξαε όι αν Ι, J ιδεώδη ου R όε ισόορφα ως R-πρόυπα αν αι όνο αν I = J R, R είναι I J Άσηση Να βρεθεί παράδειγα δαυίου R, ιδεωδών είναι ισοόρφοι δαύιοι αι I J I, J έσι ώσε R, R να I J Εύοα βέπουε όι άθε υποπρόυπο υιού είναι υιό αι άθε πρόυπο πηίο υιού είναι υιό 4 Πρόαση Έσω A = A Ak όπου A η εριένα υιά R-πρόυπα άξης r, k αι ( r, ) = για άθε, j ε j Τόε ο Α είναι ένα υιό r j R-πρόυπο άξης r = r r r k
7 7 Απόδειξη Έσω A = Ra, αι η άξη ου Ra είναι r x αι a = a + + ak Ισχυριζόασε όι A = Ra Πράγαι, sa 0 sa = 0 για άθε k r s k Τώρα = επειδή ( r, ) = για j έπεαι όι r s συνεπώς o ( Ra) = Rr άθε r j Τώρα θα δείξουε όι k Ra = A Προφανώς αρεί να δείξουε όι a Ra για Έσω r = r r r + rk όε ( r, r ) =, άρα υπάρχουν, R ε r r αι συνεπώς a = r a, αά r a = r ( a + + ak ) = r a, άρα + a r a = άξης = r a Ra Σην επόενη πρόαση βρίσουε α υποπρόυπα ενός υιού R-προύπου p, όπου p είναι ένα πρώο σοιχείο ου R 4 Πρόαση Έσω Α ένα υιό R-πρόυπο άξης p, όπου p πρώο σοιχείο ου R Τόε α υποπρόυπα ου Α είναι 0 = p A p A p A pa A φ : R A Απόδειξη Έσω όι A = Ra 0 αι όε ker φ p R Έσω r ra K 0 K A όε K = φ( φ ( )) όπου φ ( K) = { r R φ( r) K} Το φ ( K) είναι ένα υποπρόυπο ου φ K R που περιέχει ον ker K Επειδή ( ) είναι ένα υποπρόυπο ου R έπεαι όι φ ( K) = dr για άποιο K d R αι επειδή ker φ φ ( ) έπεαι όι R dr p Συνεπώς d p, άρα d = p, ν αι εποένως K = φ( φ ( K)) = φ( p R) = p A Μένει να δείξουε όι αν όε p A p A Επειδή p A είναι υιό ( 0 R-πρόυπο ε p A = R p a ), αρεί να δείξουε όι η άξη ου A είναι διαφορειή από ην άξη ου A Αά η άξη ου A είναι p p p p
8 8 Ένα άεσο συπέρασα είναι ο αόουθο 44 Πόρισα Έσω Α υιό R-πρόυπο άξης p, όπου p πρώο σοιχείο ου R Αν A = B Γ όε B = 0 ή Γ = 0 Ασήσεις 4 Έσω Α υιό R-πρόυπο άξης p, p πρώο Τόε άθε υποπρόυπο αι πρόυπο πηίο ου Α είναι άξης p για άποιο Έσω A = A όπου A υιά R-πρόυπα άξης p, σοιχείο ου R αι 0 A k όε να δειχθεί όι k Αν A p πρώο a έοιο ώσε p a = 0, όπου a = p a για άποιο a A 4 Ανάυση p-περιοδιού σε άθροισα υιών αι Θεωρήαος οής 4 Ορισός Ένα R-πρόυπο Μ έγεαι p -περιοδιό, όπου p ένα πρώο σοιχείο ου R, αν για άθε x, x = 0 για άποιο p Θα δείξουε όι αν ένα p -περιοδιό R-πρόυπο αναύεαι ως ευθύ άθροισα πεπερασένου πήθους υιών όε η ανάυση είναι οναδιή ως προς ο πήθος αι ις άξεις ων η ηδενιών υιών Γι αυό θα χρειασούε ο αόουθο Λήα 4 Λήα Έσω Μ ένα p -περιοδιό R-πρόυπο, όπου p πρώο σοιχείο ου R αι ( p) = { x px = 0}
9 9 () Αν = όε ( = αι ( p) k ( p) ( p) k ( p) p) k k ( p) () Αν = όπου η εριένα υιά R-πρόυπα, k, k όε k = dm ( p) R pr Απόδειξη Είναι προφανές από άσηση όι ο ( p) είναι ένα R -πρόυπο αι pr επειδή p είναι ένα πρώο σοιχείο ου R έπεαι όι είναι ένας R -διανυσαιός χώρος pr R είναι ένα σώα άρα pr Η () είναι άεση αι η () έπεαι από ην () αι ο όι αν ( p) είναι υιό, όε είναι υιό άξης p, για άποιο Τώρα ( p) = p, ο οποίο είναι υιό άξης p, άρα ( p) R pr 4 Θεώρηα Έσω A = A A = A A όπου A υιά άξης ε αι = αι = j p A υιά άξης p ε Τόε Απόδειξη Από () ου προηγούενου ήαος έπεαι όι = = dm A( p) Θα δείξουε όι = ε επαγωγή σο Αν = όε pa = 0 άρα = = = = Έσω > Θεωρούε ο R-πρόυπο προηγούενου ήαος έχουε όι A A A p) ( A A ( p) A A ( p) A ( R pr = = A Από () ου A( p) A p) A ( p)
10 0 Εύοα βέπουε όι p ) A A A ( p) ανισ ι είναι υιό άξης p (ανι Aι ( p) Από ο () ου προηγούενου ήαος έπεαι όι ο πήθος ων ηδενιών A ισούαι ε ο πήθος ων ηδενιών A ( p) A A A έσω Τ Άρα = 0 ( p) A ( p) A για αι = 0, Συνεπώς A ( p) = = = = = = αι όπου j p A Συνεπώς A A A + + ( p) A + ( p) A ( p) A + ( p) + A + A A ( p) A j A j A j ( p) ανισ A είναι η εριένα υιά άξης p j (ανισ j ( p) ) + j, άρα από υπόθεση επαγωγής =, = j j + j 44 Θεώρηα Κάθε πεπερασένα παραγόενο p-περιοδιό R-πρόυπο αναύεαι ως ευθύ άθροισα υιών υποπρούπων ου Απόδειξη Έσω Μ ένα πεπερασένα παραγόενο περιοδιό p-πρόυπο αι x,, x ένα σύνοο γεννηόρων ου Μ ε x άξης p, αι m m m Θα m = δείξουε ε επαγωγή σο όι υπάρχουν σοιχεία y,, ου Μ ε άξη ου y n, p όπου n m, αι όι αν m = Ry Ry Ry Να παραηρήσουε n = 0 για άποιο όε Ry = 0 Για = 0 έπεαι όι = 0 Έσω m = > αι m > 0 Έσω m = > 0 Χωρίς βάβη ης γενιόηας πορούε να υποθέσουε όι = Rx + Rx + Από υπόθεση επαγωγής επειδή y
11 m < m, αφού m > 0, υπάρχουν y,, y σοιχεία ου ε άξη ου y, = = n p όπου n m, αι Τώρα α σοιχεία Ry Ry = x, y,, y παράγουν ο Μ αφού = Rx +, αι αν n < m για άποιο {,, } όε m + n < m, άρα από υπόθεση επαγωγής θα είχαε ια ανάυση ου Μ ως ευθύ άθροισα υιών Έσω οιπόν όι m = n, Rx = {0} ή = = =,, Έχουε όι = Rx + Αν Rx όε έχουε εειώσει Έσω όι Rx {0}, άρα r R ε rx αι rx 0, αι έσω όι x Ψάχνουε να βρούε ένα y έοιο ώσε rx + = Ry + αι αν ry όε ry = 0 Επειδή η άξη ου x γ + είναι p ε γ m αι επειδή x, γ > 0 Άρα rx p γ r γ m Έσω m γ = p, όε p m = x = 0 αι επειδή x p m m m = n έχουε όι n γ n p m = 0 Αά m = Ry Ry αι η άξη ου y είναι p, γ αι n n, άρα από Άσηση 4, m = p για άποιο y n y Έσω ώρα Ry = {0} Αν Τόε y = x y Προφανώς Ry + = Rx + = Θα δείξουε όι w Ry όε w = r y για άποιο r R r x = r ( y + y) = r y + r y, άρα p γ γ γ r, αά p y = p ( x y) = γ γ p x p y = m m = 0 Συνεπώς w = r y = 0 αι εποένως Ry = {0} απ αυό έπεαι όι = Ry η Απόδειξη ου Θεωρήαος 44 Για ην απόδειξη αυή θα χρειασούε ο αόουθο Λήα
12 45 Λήα Έσω Α ένα R-πρόυπο ε p A = 0 αι p A 0, όπου p ένα πρώο 0 p a0 0 Ra0 σοιχείο ου R Αν a A ε αι A όε () β A ε β 0 αι Ra Rβ 0 () Γ A ε A Ra Γ = 0 0 = Απόδειξη () Επειδή A Ra 0, υπάρχει c A \ Ra0 Επειδή c = 0 Ra 0 αι p 0 p c = c Ra0 υπάρχει j ιρόερος θειός ε ην ιδιόηα c Ra0 αι p j c Ra 0 (, p) = Έσω p j c = r a 0 αι έσω r = p r όπου j j j = 0 0 p c = p p c = p p ra 0 έπεαι όι j +, άρα j Έσω j p j r αι 0 Τώρα αι επειδή η άξη ου a είναι p αι ( r, p) = β = p c rp a, όε p β = 0 αι αν Ra Rβ 0 αι s R ε 0 0 sβ 0 όε έπεαι όι ( s, p) = άρα = s + p αι = sβ pβ Συνεπώς β = sβ Ra 0 p j 0 Ra0 Rβ = 0 β + Άρα c Ra ο οποίο είναι άοπο από ην επιογή ου j, άρα () Έσω S = { A 0 αι Ra 0 = 0} από () S Φ αι από ο Λήα Zorn έπεαι όι ο S έχει εγισιό σοιχείο, έσω Γ p A αι p ( ) 0 Αν Γ a 0 + Γ A R( a 0 Γ) Γ + όε από () υπάρχει Τώρα ( ) = 0 β0 + Γ 0 ε R ( a0 + Γ) R( β0 + Γ) = 0, άρα Ra 0 Rβ0 + Γ = 0, επειδή Ra0 Γ = 0 Αά Γ Rβ + Γ 0 αι Ra Rβ + Γ 0 άοπο, επειδή Γ εγισιό 0 0 = σοιχείο ου S Άρα όι A Ra Γ = 0 A = R( a + Γ A = Ra Γ Γ 0 ) 0 + αι επειδή Ra0 Γ = 0 έπεαι Απόδειξη Θεωρήαος 44 Έσω Μ x,, x ε x 0 Θα δείξουε ο = Θεώρηα ε επαγωγή σο Για = είναι άεσο
13 Έσω > αι έσω όι η άξη ου x να είναι p ε Τόε p = 0 αι p x ο φυσιός επιορφισός Προφανώς 0, άρα από προηγούενο Λήα π : Μ Rx w w + Rx = π( x ),, π( x ) = π ( x ),, ( ) Rx π x = Rx Έσω άρα από υπόθεση επαγωγής ο είναι ευθύ άθροισα υιών, συνεπώς ο Μ αναύεαι ως ευθύ άθροισα υιών 46 Θεώρηα Κάθε πεπερασένα παραγόενο p-περιοδιό R-πρόυπο αναύεαι ως ευθύ άθροισα πεπερασένου πήθους υιών προύπων αι η ανάυση αυή είναι οναδιή ως προς ο πήθος αι ις άξεις ων (η ηδενιών) υιών προύπων Απόδειξη Το Θεώρηα 44 ας δίνει ην ανάυση αι ο Θεώρηα 4 ην οναδιόηα Συβοισός Αν r R όε ο υιό R-πρόυπο 0 r0 R Έσω Μ, Ν πεπερασένα παραγόενα p-περιοδιά Θεώρηα υπάρχει ια αοουθία δυνάεων ου p, Cp N Cp Cp Cp σ ε ε R ο συβοίζουε ε Cr 0 R-πρόυπα Τόε από ο p,, p έσι ώσε αι ια αοουθία, p,, p έσι ώσε σ Επειδή ένας R-ισοορφισός διαηρεί ην ανάυση σε ευθύ άθροισα, από ο Θεώρηα 4 παίρνουε όι σ 47 Θεώρηα Με ους προηγούενους συβοισούς έχουε όι N αν αι όνο αν = σ αι η αοουθία p,, p ισούαι ε ην αοουθία p,, p
14 4 Έσω ώρα Α, Β πεπερασένα παραγόενα R-πρόυπα Από α Θεωρήαα 4 (), 46 αι 44 έπεαι όι υπάρχει πεπερασένο πήθος πρώων σοιχείων ου R, p,, p αι για άθε πρώο p ια πεπερασένη αοουθία δυνάεων ου, p ρ p έσι ώσε wa φορές ρ A R R Cp Cp Cp Cp όπου w A ο έγισο πήθος γραιών ανεξάρηων σοιχείων ου Α Παρόοια για ο Β υπάρχει ια πεπερασένη αοουθία πρώων σοιχείων ου R q,, q αι για άθε πρώο j σ q,, q σ έσι ώσε wb φορές q ρ για πεπερασένη αοουθία δυνάεων ου σ σ Cq B R R Cq Cq Cq όπου w B ο έγισο πήθος γραιών ανεξάρηων σοιχείων ου Β Από α Θεωρήαα 4 (), 46 αι 47 έπεαι όι σ σ 48 Θεώρηα (Θεώρηα οής Ι) Με ους προηγούενους συβοισούς έχουε όι A B αν αι όνο αν w A = wb, { p,, p} = { q,, q } αι για άθε,, αν p = q z(), όε ρ = z( ) αι η αοουθία p ρ, p,, p ισούαι ε ην αοουθία σz( ) z( ),, σz( ) z ( ) z( ) q q 49 Ορισός Τα σοιχεία ου R: T A έγοναι οι σοιχειώδεις διαιρέες ου ρ ρ p,, p, p,, p,, p,, p Συνεπώς ο Θεώρηα οής Ι έει όι αν Α, Β είναι πεπερασένα παραγόενα R- πρόυπα όε A B αν αι όνο αν w A = wb αι οι σοιχειώδεις διαιρέες ου T B είναι οι ίδιοι ε ους σοιχειώδεις διαιρέες ου ρ T A
15 5 Το αόουθο θεώρηα, εφράζει η οναδιόηα ως προς ο πήθος αι ις άξεις, ης ανάυσης ενός πεπερασένα παραγόενου περιοδιού R-προύπου σε ευθύ άθροισα η ηδενιών υιών, ε διαφορειό ρόπο 40 Θεώρηα (Θεώρηα οής ΙΙ) Έσω Μ ένα πεπερασένα παραγόενο περιοδιό R-πρόυπο Τόε υπάρχουν ανισρέψια,, d d d αι d,, d σοιχεία ου R ε d 0, d η Cd Cd Επιπέον αν Cr Cr αι r 0, r η ανισρέψια, αι r r r όε = αι Cr = Cd, Απόδειξη Επειδή Μ είναι ένα πεπερασένα παραγόενο περιοδιό υπάρχει πεπερασένο πήθος πρώων σοιχείων R-πρόυπο p,, p ου R ε p {0} αι = p p Τώρα από ο Θεώρηα 44 άθε p είναι ευθύ άθροισα υιών Αν είναι ο πήθος ων η ηδενιών υιών όρων που εφανίζεαι σην ανάυση ου p, έσω = max{, } Τόε όπου j j Cp p = p = p = αι, Μεριά από α πορεί να είναι 0 δηαδή = 0, απά α θεωρούε σην j αρχή ώσε να έχουε ο ίδιο πήθος όρων σε άθε ανάυση Προφανώς για άθε j {,, } υπάρχει {,, } ε 0 Έσω ώρα j = j j j j Τόε = p p = Μ
16 6 Από ην Πρόαση 4 j j j Cd όπου d = p p p αι επειδή j j, έχουε όι d d d Επιπέον από ην επιογή ου έπεαι όι d 0 αι d η ανισρέψια, Έσω ώρα όι = N N όπου N Cr, r η ανισρέψιια, r 0, αι r r r Έσω p,, p γινόενο πρώων ων αι r Αν j οι η συνροφιοί πρώοι που εφανίζοναι σις αναύσεις σε d όε επειδή έχουε όι d = p a a p a d = p p αι Cd Cp j= a r = p r = p β β p p β β aj β j j αι Crj Cp = = = N N Cd Cd Cr Cr Cp = j= Από ο Θεώρηα 46 έχουε όι για άθε Cp a Cp a a j j Cp j= = α β Cp Cp β j Cp Επειδή d είναι 0 αι η ανισρέψιο υπάρχει ουάχισον ένα πρώο σοιχείο σην ανάυσή ου, δηαδή άποιο από α a είναι 0 Έσω πχ όι a 0 Επειδή d d d έχουε όι 0 a a a β < άρα από ο Θεώρηα 4 έπεαι όι η δεξιά πευρά ης (*) έχει η ηδενιούς όρους για = άρα (*)
17 7 Παρόοια επειδή αι r είναι 0 αι η ανισρέψιο ααήγουε όι άρα = ν Συνεπώς η (*) γίνεαι αι a Άρα από ο Θεώρηα 4 a β Cp Cp β Cp Cp, j a β a a β β a = β για άθε, j Συνεπώς d ] = [ r ] j [ 4 Ορισός Τα σοιχεία d,,d ου R έγοναι οι αναοίωοι παράγονες ου Μ Συνεπώς ο Θεώρηα οής ΙΙ έει όι αν Α, Β είναι πεπερασένα παραγόενα R- πρόυπα, όε A B αν αι όνο αν w A = wb αι οι αναοίωοι παράγονες ου είναι οι ίδιοι ε ους αναοίωους παράγονες ου T B T A Παραδείγαα Έσω η αβειανή οάδα A = Ÿ5 Ÿ5 Ÿ5 Ÿ6 Ÿ54 Να βρεθούν οι σοιχειώδεις διαιρέες αι οι αναοίωοι παράγονες ης Α Έχουε όι Ÿ 5 Ÿ Ÿ5 Ÿ6 Ÿ4 Ÿ9 Ÿ54 Ÿ Ÿ Άρα A A Α Α5 Ÿ Ÿ4 Ÿ Ÿ Ÿ Ÿ5 Ÿ 5 άρα οι σοιχειώδεις διαιρέες είναι παράγονες 5 5 5,,,, = 5 = = 5 5, 5, Πόσες ανά δύο η ισόορφες αβειανές οάδες υπάρχουν άξης p d d d αι οι αναοίωοι
18 8 Από ο Θεώρηα οής Ι (σοιχειώδεις διαιρέες) έπεαι όι υπάρχουν όσες η ισόορφες αβειανές οάδες άξης p όσες αι αοουθίες p, p,, p ε = Ÿp Ÿp 5, άρα Ÿp, Ÿp, Ÿp Ÿ, Ÿp, p, Ÿp Ÿ, p Ÿp Πόσες ανά δύο η ισόορφες αβειανές οάδες υπάρχουν άξης 5 Υπάρχουν επιογές για ις -συνισώσες, Υπάρχουν επιογές για ις -συνισώσες,,, Υπάρχει επιογή για ις 5 συνισώσες 5 Άρα υπάρχου η ισόορφες αβειανές οάδες άξης 5 Ασήσεις 4 Πόσες ανά δύο η ισόορφες αβειανές οάδες υπάρχουν άξης 6 Ποιοι είναι οι αναοίωοι παράγονες αι οι σοιχειώδεις διαιρέες ης A = Ÿ Ÿ45 Ÿ6 Ÿ9 Έσω Α αβειανή οάδα ε A = αι Να δειχθεί όι υπάρχει K A ε άξη ης K να είναι 4 Να δειχθεί όι ια πεπερασένη αβειανή οάδα Α δεν είναι υιή αν αι όνο αν υπάρχει K A ε K Ÿ Ÿ για άποιο πρώο p 5 Ποιοι είναι οι αναοίωοι παράγονες ης Ÿm Ÿn p p
19 9 6 Έσω Α εεύθερη αβειανή διάσασης αι B A Να δειχθεί όι πεπερασένη αν αι όνο αν η Β είναι εεύθερη διάσασης A είναι B 7 Έσω Α αβειανή ε αναοίωους παράγονες d d Να δειχθεί όι η Α δεν πορεί να παραχθεί από ιγόερα από ρ σοιχεία 8 Έσω Α πεπερασένα παραγόενη αβειανή οάδα αι f : A A ένας επιορφισός Να δειχθεί όι η f ένας ισοορφισός d ρ
Κεφάλαιο 1. Πρότυπα. Στο κεφάλαιο αυτό εισαγάγουµε την έννοια του προτύπου πάνω από δακτύλιο που θα παίξει σηµαντικό ρόλο στα επόµενα κεφάλαια.
 Κεφάαιο Πρότυπα Στο κεφάαιο αυτό εισαγάγουµε την έννοια του προτύπου πάνω από δακτύιο που θα παίξει σηµαντικό ρόο στα επόµενα κεφάαια Στις σηµειώσεις αυτές όοι οι δακτύιοι περιέχουν µοναδιαίο στοιχείο
Κεφάαιο Πρότυπα Στο κεφάαιο αυτό εισαγάγουµε την έννοια του προτύπου πάνω από δακτύιο που θα παίξει σηµαντικό ρόο στα επόµενα κεφάαια Στις σηµειώσεις αυτές όοι οι δακτύιοι περιέχουν µοναδιαίο στοιχείο
Κεφάλαιο 3. Ελεύθερα Πρότυπα. στοιχείων του Μ καλείται βάση του e λ παράγει το Μ, και ii) κάθε m M γράφεται κατά µοναδικό
 Κεφάαιο 3 Εεύθερα Πρότυπα 3.1 Εεύθερα Πρότυπα Έστω Μ ένα R-πρότυπο. Μια οικογένεια Μ αν ) το σύνοο { Λ} τρόπο ως άθροισµα της µορφής πεπερασµένο πήθος από τα ( e ) στοιχείων του Μ καείται βάση του e παράγει
Κεφάαιο 3 Εεύθερα Πρότυπα 3.1 Εεύθερα Πρότυπα Έστω Μ ένα R-πρότυπο. Μια οικογένεια Μ αν ) το σύνοο { Λ} τρόπο ως άθροισµα της µορφής πεπερασµένο πήθος από τα ( e ) στοιχείων του Μ καείται βάση του e παράγει
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ. 1. Εισαγωγικά. Υποθέτουµε ότι ο αναγνώστης γνωρίζει τα περιεχόµενα στην ενότητα Γραµµικές Μορφές.
 ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ Εισαγωγιά Υποθέτουε ότι ο ααγώστης γωρίζει τα περιεχόεα στη εότητα Γραιές Μορφές Γειές υποθέσεις Συβοισοί Ο χώρος, στοιχεία του οποίου χρησιοποιούε, είαι έας γραιός (αυσατιός) χώρος V
ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ Εισαγωγιά Υποθέτουε ότι ο ααγώστης γωρίζει τα περιεχόεα στη εότητα Γραιές Μορφές Γειές υποθέσεις Συβοισοί Ο χώρος, στοιχεία του οποίου χρησιοποιούε, είαι έας γραιός (αυσατιός) χώρος V
x y x z για κάθε x, y, . Ένας δακτύλιος R καλείται μεταθετικός αν
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο Θα περιοριστούμε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο Θα περιοριστούμε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
ικαιώατα αερικανικού τύπου
 Κεφάλαιο 5 ικαιώατα αερικανικού τύπου 5.1 Εισαγωγή Σε αυτό το κεφάλαιο θα δούε πώς πορούε να τιολογήσουε δικαιώατα αερικανικού τύπου ε βάση το διωνυικό υπόδειγα πολλών περιόδων. Θα δούε επίσης την έννοια
Κεφάλαιο 5 ικαιώατα αερικανικού τύπου 5.1 Εισαγωγή Σε αυτό το κεφάλαιο θα δούε πώς πορούε να τιολογήσουε δικαιώατα αερικανικού τύπου ε βάση το διωνυικό υπόδειγα πολλών περιόδων. Θα δούε επίσης την έννοια
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
λ n-1 λ n Σχήµα 1 - Γράφος µεταβάσεων διαδικασίας γεννήσεων- θανάτων
 Κεφάαιο 4. Απά οντέα συστηάτων αναονής Στο κεφάαιο αυτό παρουσιάζουε απά οντέα αναονής (συστήατα ε ένα σταθό εξυπηρέτησης) ενώ τα οντέα δικτύων αναονής θα εξεταστούν σε επόενο κεφάαιο. 4. Μοντέα αναονής
Κεφάαιο 4. Απά οντέα συστηάτων αναονής Στο κεφάαιο αυτό παρουσιάζουε απά οντέα αναονής (συστήατα ε ένα σταθό εξυπηρέτησης) ενώ τα οντέα δικτύων αναονής θα εξεταστούν σε επόενο κεφάαιο. 4. Μοντέα αναονής
ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ
 ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ Α. ΑΣΦΑΛΙΣΕΙΣ ΕΠΙ ΠΟΛΛΩΝ ΚΕΦΑΛΩΝ Ορισένες φορές ένα ασφαλιστήριο καλύπτει περισσότερες από ία ζωές. Ένα προφανές παράδειγα είναι η ασφάλιση θανάτου για δύο συζύγους, καθένας
ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ Α. ΑΣΦΑΛΙΣΕΙΣ ΕΠΙ ΠΟΛΛΩΝ ΚΕΦΑΛΩΝ Ορισένες φορές ένα ασφαλιστήριο καλύπτει περισσότερες από ία ζωές. Ένα προφανές παράδειγα είναι η ασφάλιση θανάτου για δύο συζύγους, καθένας
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
3. Χαρακτηριστικές Παράμετροι Κατανομών
 . αρακτηριστικές Παράετροι Κατανοών - Αναενόενη ή έση τιή ιας διακριτής τυχαίας εταβητής. Στο προηγούενο κεφάαιο είδαε ότι σε κάθε τ.. αντιστοιχεί ία κατανοή. Αν και η συνάρτηση κατανοής F ή ισοδύναα η
. αρακτηριστικές Παράετροι Κατανοών - Αναενόενη ή έση τιή ιας διακριτής τυχαίας εταβητής. Στο προηγούενο κεφάαιο είδαε ότι σε κάθε τ.. αντιστοιχεί ία κατανοή. Αν και η συνάρτηση κατανοής F ή ισοδύναα η
Μέτρα martingale. Κεφάλαιο Εισαγωγή. 4.2 εσευένη έση τιή
 Κεφάλαιο 4 Μέτρα martingale 4.1 Εισαγωγή Είδαε στο Κεφάλαιο 2 ότι σε αγορές ιας περιόδου, αν ένα παράγωγο πορεί να αναπαραχθεί, τότε πορούε να το τιολογήσουε σύφωνα ε την αρχή της η επιτηδειότητας και
Κεφάλαιο 4 Μέτρα martingale 4.1 Εισαγωγή Είδαε στο Κεφάλαιο 2 ότι σε αγορές ιας περιόδου, αν ένα παράγωγο πορεί να αναπαραχθεί, τότε πορούε να το τιολογήσουε σύφωνα ε την αρχή της η επιτηδειότητας και
Υποδείγατα αγορών ιας περιόδου
 Κεφάλαιο 2 Υποδείγατα αγορών ιας περιόδου 2.1 Εισαγωγή Θα αρχίσουε τώρα να κάνουε υποθέσεις για τη δυναική των πρωτογενών προϊόντων και θα ερευνήσουε αν ε αυτές τις επιπλέον υποθέσεις πορούε να εξαγάγουε
Κεφάλαιο 2 Υποδείγατα αγορών ιας περιόδου 2.1 Εισαγωγή Θα αρχίσουε τώρα να κάνουε υποθέσεις για τη δυναική των πρωτογενών προϊόντων και θα ερευνήσουε αν ε αυτές τις επιπλέον υποθέσεις πορούε να εξαγάγουε
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΣΤ. ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΑΣΦΑΛΙΣΤΡΑ ΓΙΑ GOMPERTZ ΚΑΙ MAKEHAM
 ΣΤ ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΑΣΦΑΛΙΣΤΡΑ ΓΙΑ GOMPERTZ ΚΑΙ MAKEHAM Όπως σηειώσαε παραπάνω, οι πιθανότητες που εξαρτώνται από τη σειρά των θανάτων πορούν να εφρασθούν συναρτήσει "πιθανοτήτων πρώτου θανάτου" Κατά συνέπεια,
ΣΤ ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΑΣΦΑΛΙΣΤΡΑ ΓΙΑ GOMPERTZ ΚΑΙ MAKEHAM Όπως σηειώσαε παραπάνω, οι πιθανότητες που εξαρτώνται από τη σειρά των θανάτων πορούν να εφρασθούν συναρτήσει "πιθανοτήτων πρώτου θανάτου" Κατά συνέπεια,
Η. ΑΣΚΗΣΕΙΣ ( T) ( 1) ( 2) 3 x =
 Αν είναι "εκ προοιίου φανερό" ότι η παραπάνω διαδικασία είναι συνεπής προς τον υπολογισό της Παραγράφου ΣΤ το προηγούενο παράδειγα επελέγη ε στόχο την επίδειξη αυτής της συνέπειας Η ΑΣΚΗΣΕΙΣ Σε ένα πίνακα
Αν είναι "εκ προοιίου φανερό" ότι η παραπάνω διαδικασία είναι συνεπής προς τον υπολογισό της Παραγράφου ΣΤ το προηγούενο παράδειγα επελέγη ε στόχο την επίδειξη αυτής της συνέπειας Η ΑΣΚΗΣΕΙΣ Σε ένα πίνακα
1) Μη συνεργατική ισορροπία
 ΠΑΡΑΡΤΗΜΑ: ΔΙΕΘΕΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΕΣ ΣΥΜΩΝΙΕΣ ΩΣ ΕΝΑ ΠΑΙΓΝΙΟ «ΔΙΛΛΗΜΑΟ ΤΟΥ ΦΥΛΑΚΙΣΜΕΝΟΥ» Υποθέτουε ότι υπάρχουν Ν χώρες, όπου N={,, }, η κάθε ία από τις οποίες παράγει αγαθά και εκπέπει e τόνους διοξειδίου
ΠΑΡΑΡΤΗΜΑ: ΔΙΕΘΕΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΕΣ ΣΥΜΩΝΙΕΣ ΩΣ ΕΝΑ ΠΑΙΓΝΙΟ «ΔΙΛΛΗΜΑΟ ΤΟΥ ΦΥΛΑΚΙΣΜΕΝΟΥ» Υποθέτουε ότι υπάρχουν Ν χώρες, όπου N={,, }, η κάθε ία από τις οποίες παράγει αγαθά και εκπέπει e τόνους διοξειδίου
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Ένας δακτύλιος είναι ένα σύνολο R εφοδιασµένο µε δύο πράξεις, + : R R και : R R R, έτσι ώστε i) ( R, + ) είναι αβελιανή οµάδα,
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα ασχοηθούµε µε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο R Θα περιοριστούµε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάαιο αυτό θα ασχοηθούµε µε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύιο R Θα περιοριστούµε στα πέον απαραίτητα για αυτά που ακοουθούν στα άα κεφάαια Η κατευθυντήρια
Ασαφής Λογική και Αναγνώριση Προτύπων
 Ασαφής Λογική και Αναγνώριση Προτύπων Ορισός Έστω Χ ένα τυπικό σύνολο αντικειένων, που το καλούε σύπαν, του οποίου τα στοιχεία τα συβολίζουε ε. Η σχέση του περιέχεσθε για ένα τοπικό υποσύνολο του Α του
Ασαφής Λογική και Αναγνώριση Προτύπων Ορισός Έστω Χ ένα τυπικό σύνολο αντικειένων, που το καλούε σύπαν, του οποίου τα στοιχεία τα συβολίζουε ε. Η σχέση του περιέχεσθε για ένα τοπικό υποσύνολο του Α του
ΕΙ ΙΚΑ ΘΕΜΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΚΕΦ. 2 ΑΛΥΣΙ ΕΣ MARKOV
 ΕΙ ΙΚΑ ΘΕΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΚΕΦ ΑΛΥΣΙ ΕΣ MARKOV Πίνακας Περιεχοένων Γενικά3 Εργοδικότητα 3 Πιθανότητες πρώτης ετάβασης Αναενόενος χρόνος8 4 Κλάσεις Ισοδυναίας Κατάταξη Καταστάσεων6 5 Γενική δοή
ΕΙ ΙΚΑ ΘΕΑΤΑ ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΚΕΦ ΑΛΥΣΙ ΕΣ MARKOV Πίνακας Περιεχοένων Γενικά3 Εργοδικότητα 3 Πιθανότητες πρώτης ετάβασης Αναενόενος χρόνος8 4 Κλάσεις Ισοδυναίας Κατάταξη Καταστάσεων6 5 Γενική δοή
35 = (7+ 109) =
 Άλγεβρα Α Λυείου Στεφανής Παναγιώτης Συνδυαστιές Ασήσεις Ασήσεις δηµοσιευµένες στο περιοδιό τεύχος 8 Άσηση α) Να δείξετε ότι: 7 + + + +... + 9 = β) Να λυθεί η ανίσωση: 7 7x + x + x +... +
Άλγεβρα Α Λυείου Στεφανής Παναγιώτης Συνδυαστιές Ασήσεις Ασήσεις δηµοσιευµένες στο περιοδιό τεύχος 8 Άσηση α) Να δείξετε ότι: 7 + + + +... + 9 = β) Να λυθεί η ανίσωση: 7 7x + x + x +... +
ΕΡΓΑΣΙΑ 2 (Παράδοση:.) Λύση Ι. Το πεδίο ορισµού Α, θα προκύψει από την απαίτηση ο παρονοµαστής να είναι διάφορος του µηδενός.
 ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ C.A.M.
 ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ C.A.M. Aναονητικά Συστήατα, Γραές Παραγωγής, F.M.S. Γιάννης Α. Φίης Ιανουάριος 3 Πουτεχνείο Κρήτης Π Ε Ρ Ι Ε X Ο Μ Ε Ν Α EIΣΑΓΩΓΗ...3 ΟΥΡΕΣ H ΣΥΣΤΗΜΑΤΑ ΑΝΑΜΟΝΗΣ...6. Μοντέα Γέννησης Θανάτου...
ΙΚΤΥΑ ΠΑΡΑΓΩΓΗΣ C.A.M. Aναονητικά Συστήατα, Γραές Παραγωγής, F.M.S. Γιάννης Α. Φίης Ιανουάριος 3 Πουτεχνείο Κρήτης Π Ε Ρ Ι Ε X Ο Μ Ε Ν Α EIΣΑΓΩΓΗ...3 ΟΥΡΕΣ H ΣΥΣΤΗΜΑΤΑ ΑΝΑΜΟΝΗΣ...6. Μοντέα Γέννησης Θανάτου...
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ. Περίληψη της Ύλης της Επιχειρησιακής Έρευνας
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραα Σπουδών: ΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ και ΟΡΓΑΝΙΣΜΩΝ Θεατική Ενότητα: ΕΟ-3 Ποσοτικές Μέθοδοι Περίηψη της Ύης της Επιχειρησιακής Έρευνας Ακαδηαϊκό Έτος 003-004 Πρόογος Το φυάδιο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Πρόγραα Σπουδών: ΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ και ΟΡΓΑΝΙΣΜΩΝ Θεατική Ενότητα: ΕΟ-3 Ποσοτικές Μέθοδοι Περίηψη της Ύης της Επιχειρησιακής Έρευνας Ακαδηαϊκό Έτος 003-004 Πρόογος Το φυάδιο
Εισαγωγή. 1. Παράµετρος, εκτιµητής, εκτίµηση
 Εκτίηση Σηείου Εκτίηση Σηείου Εισαγωγή Σε πολλές περιπτώσεις στη στατιστική έχουε συναντήσει προβλήατα για τα οποία απαιτείται να εκτιηθεί ια παράετρος. Η έθοδος που ακολουθεί στις περιπτώσεις αυτές κανείς
Εκτίηση Σηείου Εκτίηση Σηείου Εισαγωγή Σε πολλές περιπτώσεις στη στατιστική έχουε συναντήσει προβλήατα για τα οποία απαιτείται να εκτιηθεί ια παράετρος. Η έθοδος που ακολουθεί στις περιπτώσεις αυτές κανείς
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
4 η δεκάδα θεµάτων επανάληψης
 1 η δεκάδα θεάτων επανάληψης 1. ίνεται ισόπλευρο τρίγωνο πλευράς α. Στις πλευρές,, παίρνουε σηεία, Ε, Ζ αντίστοιχα τέτοια ώστε Ε Ζ 1 α Να υπολογίσετε συναρτήσει του α το εβαδόν Του τριγώνου Ζ Του τριγώνου
1 η δεκάδα θεάτων επανάληψης 1. ίνεται ισόπλευρο τρίγωνο πλευράς α. Στις πλευρές,, παίρνουε σηεία, Ε, Ζ αντίστοιχα τέτοια ώστε Ε Ζ 1 α Να υπολογίσετε συναρτήσει του α το εβαδόν Του τριγώνου Ζ Του τριγώνου
τις διαφορετικές μεταξύ τους τιμές της Y ( λ ν )
 Διδιάστατες Καταομές Διδιάστατες Καταομές Πίαας συοτήτω διδιάστατης αταομής Θεωρούμε δύο τυαίες μεταβητές X, Y αι ζεύγη παρατηρήσεω,,,,,, από δείγμα μεγέθους Τόσο τα,,, όσο αι τα,,, δε είαι απαραιτήτως
Διδιάστατες Καταομές Διδιάστατες Καταομές Πίαας συοτήτω διδιάστατης αταομής Θεωρούμε δύο τυαίες μεταβητές X, Y αι ζεύγη παρατηρήσεω,,,,,, από δείγμα μεγέθους Τόσο τα,,, όσο αι τα,,, δε είαι απαραιτήτως
Α θ ή ν α, 7 Α π ρ ι λ ί ο υ
 Α θ ή ν α, 7 Α π ρ ι λ ί ο υ 2 0 1 6 Τ ε ύ χ ο ς Δ ι α κ ή ρ υ ξ η ς Α ν ο ι κ τ ο ύ Δ ι ε θ ν ο ύ ς Δ ι α γ ω ν ι σ μ ο ύ 0 1 / 2 0 1 6 μ ε κ ρ ι τ ή ρ ι ο κ α τ α κ ύ ρ ω σ η ς τ η ν π λ έ ο ν σ υ μ
Α θ ή ν α, 7 Α π ρ ι λ ί ο υ 2 0 1 6 Τ ε ύ χ ο ς Δ ι α κ ή ρ υ ξ η ς Α ν ο ι κ τ ο ύ Δ ι ε θ ν ο ύ ς Δ ι α γ ω ν ι σ μ ο ύ 0 1 / 2 0 1 6 μ ε κ ρ ι τ ή ρ ι ο κ α τ α κ ύ ρ ω σ η ς τ η ν π λ έ ο ν σ υ μ
34 34 1.641 357 1.373
 Α -- Ο Η Α Α-Η Η Α -- Α Α 5 Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α Α..... Ο Α 599 Α & Α Α Α Α Α Α Α Α Α 21 21 1.495 343 1.351 601 Α & Α Α / Α Α Α Α 24 24 1.418 313 1.053 661 Α Α Α Α Α Α Α Α Α
Α -- Ο Η Α Α-Η Η Α -- Α Α 5 Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α Α..... Ο Α 599 Α & Α Α Α Α Α Α Α Α Α 21 21 1.495 343 1.351 601 Α & Α Α / Α Α Α Α 24 24 1.418 313 1.053 661 Α Α Α Α Α Α Α Α Α
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
Το οντέλο Black & Scholes ως όριο διωνυικών υποδειγάτων
 Κεφάλαιο 6 Το οντέλο Blac & Scoles ως όριο διωνυικών υποδειγάτων 61 Εισαγωγή Σ αυτό το κεφάλαιο θα θεωρήσουε διωνυικά υποδείγατα για τη δυναική του πρωτογενούς προϊόντος στο διάστηα [0,T], όπου το πλήθος
Κεφάλαιο 6 Το οντέλο Blac & Scoles ως όριο διωνυικών υποδειγάτων 61 Εισαγωγή Σ αυτό το κεφάλαιο θα θεωρήσουε διωνυικά υποδείγατα για τη δυναική του πρωτογενούς προϊόντος στο διάστηα [0,T], όπου το πλήθος
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]
![3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1] 3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]](/thumbs/79/79263211.jpg) 20 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει ότι
20 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει ότι
Μάθημα: Ρομποτικός Έλεγχος
 Διαηαικό Πρόγραα Μεαπυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδηαϊκό Έος - Μάθηα: Ροποικός Έλεγχος Σαική και Δυναική Ανάλυση Ροποικών Χειρισών Κωνσανίνος Τζαφέσας Τοέας Σηάων, Ελέγχου & Ροποικής
Διαηαικό Πρόγραα Μεαπυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδηαϊκό Έος - Μάθηα: Ροποικός Έλεγχος Σαική και Δυναική Ανάλυση Ροποικών Χειρισών Κωνσανίνος Τζαφέσας Τοέας Σηάων, Ελέγχου & Ροποικής
4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ ΘΕΩΡΙΑ ΣΧΟΛΙΑ ΜΕΘΟ ΟΙ
 .1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ ΘΕΩΡΙΑ 1. Αρχή της Μαθηµατιής Επαγωγής Έστω ισχυρισµός Ρ(ν), όπου ν θετιός αέραιος. Αν i) Ρ αληθής αι ii) Ρ(ν) Ρ(ν + 1) για άθε ν, τότε Ρ(ν) αληθής για άθε ν.. Ανισότητα Bernoulli
.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ ΘΕΩΡΙΑ 1. Αρχή της Μαθηµατιής Επαγωγής Έστω ισχυρισµός Ρ(ν), όπου ν θετιός αέραιος. Αν i) Ρ αληθής αι ii) Ρ(ν) Ρ(ν + 1) για άθε ν, τότε Ρ(ν) αληθής για άθε ν.. Ανισότητα Bernoulli
Θεωρητική μηχανική ΙΙ
 ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
ΟΣΑ ΓΡΑΦΟΝΤΑΙ ΕΔΩ ΝΑ ΤΑ ΔΙΑΒΑΖΕΤΕ ΜΕ ΣΚΕΠΤΙΚΟ ΒΛΕΜΜΑ. ΜΠΟΡΕΙ ΝΑ ΠΕΡΙΕΧΟΥΝ ΛΑΘΗ. Θεωρητική μηχανική ΙΙ Να δειχθεί ότι αν L x, L y αποτελούν ολοκληρώματα της κίνησης τότε και η L z αποτελεί ολοκλήρωμα της
Παράδειγμα Το γνωστό παράδειγμα με τα βάρη 30 ατόμων ταξινομημένα σε 5 ομάδες. Η μέση τιμή για το δείγμα έχει βρεθεί x = 77. = =
 Παράδειγα Το γωστό παράδειγα ε τα βάρη 0 ατόω ταξιοηέα σε 5 οάδες. Η έση τιή για το δείγα έχει βρεθεί 77. Τάξη Απόλυτες συχότητες Κετρική τιή τάξης Απόκλιση από το έσο 65-69 67,5 9,5 70-7 6 7,5,5 75-79
Παράδειγα Το γωστό παράδειγα ε τα βάρη 0 ατόω ταξιοηέα σε 5 οάδες. Η έση τιή για το δείγα έχει βρεθεί 77. Τάξη Απόλυτες συχότητες Κετρική τιή τάξης Απόκλιση από το έσο 65-69 67,5 9,5 70-7 6 7,5,5 75-79
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]
![3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1] 3Τοπολογικοί διανυσματικοί χώροι. y A, για κάθε λ [ 0,1]](/thumbs/92/110100632.jpg) 0 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω E διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A E. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει
0 3Τοποογικοί διανυσματικοί χώροι 3. Βασικές έννοιες και ορισμοί. Έστω E διανυσματικός χώρος υπεράνω του σώματος K ( K Rή C) = και A E. (α) Το A έγεται κυρτό αν, για κάθε x, y A, για κάθε [ 0,] ισχύει
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
3. Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών)
 Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών) Μια «πολύπλοη» συνάρτηση f, δυό μεταβλητών, μπορεί να προσεγγιστεί (στην γειτονιά ενός σημείου (,y)) από μια πολυωνιμιή συνάρτηση με την βοήθεια του αναπτύγματος
Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών) Μια «πολύπλοη» συνάρτηση f, δυό μεταβλητών, μπορεί να προσεγγιστεί (στην γειτονιά ενός σημείου (,y)) από μια πολυωνιμιή συνάρτηση με την βοήθεια του αναπτύγματος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Martingales. Κεφάλαιο Εισαγωγή. 4.2 εσευένη έση τιή
 Κεφάλαιο 4 Martingales 4.1 Εισαγωγή Στο κεφάλαιο αυτό θα εισαγάγουε την έννοια της δεσευένης έσης τιής για διακριτές τυχαίες εταβλητές και θα δούε πότε χαρακτηρίζουε ια στοχαστική διαδικασία διακριτού
Κεφάλαιο 4 Martingales 4.1 Εισαγωγή Στο κεφάλαιο αυτό θα εισαγάγουε την έννοια της δεσευένης έσης τιής για διακριτές τυχαίες εταβλητές και θα δούε πότε χαρακτηρίζουε ια στοχαστική διαδικασία διακριτού
2.3 Στάσιμο κύμα. ημ 2π. συν = 2A. + τα οποία T. t x. T λ T λ ολ
 .3 Στάσιμο Κύμα.3 Στάσιμο κύμα.3.1 Μαθηματική Επεξεργασία Ας υποθέσουμε ότι έχουμε μία χορδή και σε αυτήν την χορδή διαδίδονται δύο πανομοιότυπα κύματα σε αντίθετες κατευθύνσεις. Δηαδή αν το δούμε από
.3 Στάσιμο Κύμα.3 Στάσιμο κύμα.3.1 Μαθηματική Επεξεργασία Ας υποθέσουμε ότι έχουμε μία χορδή και σε αυτήν την χορδή διαδίδονται δύο πανομοιότυπα κύματα σε αντίθετες κατευθύνσεις. Δηαδή αν το δούμε από
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
(1A) Ε ΟΜΕΝΑ 2Φ10 Σ. Η. ΔΡΙΤΣΟΣ. Yλικά : Άνοιγµα δοκού: l 0-2 = l 2-3 = 4,40 m ΖΗΤΟΥΜΕΝΑ: Σ..Η ΔΡΙΤΣΟΣ
 (A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
(A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ = Ο. Μαγνητικό πεδίο ευθύγραµµου ρευµατοφόρου αγωγού. Μαγνητικό πεδίο κυκλικού ρευµατοφόρου αγωγού.
 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ Μαγνητικό πεδίο είναι ο χώρος που έχει την ιδιότητα να ασκεί αγνητικές δυνάεις σε κατάλληλο υπόθεα (αγνήτες, ρευατοφόροι αγωγοί ) Το αγνητικό πεδίο το ανιχνεύουε ε την βοήθεια ιας αγνητικής
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ Μαγνητικό πεδίο είναι ο χώρος που έχει την ιδιότητα να ασκεί αγνητικές δυνάεις σε κατάλληλο υπόθεα (αγνήτες, ρευατοφόροι αγωγοί ) Το αγνητικό πεδίο το ανιχνεύουε ε την βοήθεια ιας αγνητικής
Ενδεικτικές Λύσεις Θεµάτων Εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34
 Σύγχρονη ΦΥΕ4 4/7/ Ελληνικό Ανοικτό Πανεπιστήιο Ενδεικτικές Λύσεις Θεάτων Εξετάσεων στη Θεατική Ενότητα ΦΥΕ4 ΣΥΓΧΡΟΝΗ ιάρκεια: 8 λεπτά Ονοατεπώνυο: Τήα: Θέα ο (Μονάδες:.5) Από τη συνέχεια της κυατοσυνάρτησης
Σύγχρονη ΦΥΕ4 4/7/ Ελληνικό Ανοικτό Πανεπιστήιο Ενδεικτικές Λύσεις Θεάτων Εξετάσεων στη Θεατική Ενότητα ΦΥΕ4 ΣΥΓΧΡΟΝΗ ιάρκεια: 8 λεπτά Ονοατεπώνυο: Τήα: Θέα ο (Μονάδες:.5) Από τη συνέχεια της κυατοσυνάρτησης
Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο Λιαροκάπης Ευθύιος Άδεια
Σχολή Εφαροσένων Μαθηατικών και Φυσικών Επιστηών Εθνικό Μετσόβιο Πολυτεχνείο Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών Κεφάλαιο 9: Ελεύθερα Ηλεκτρόνια σε Μαγνητικό Πεδίο Λιαροκάπης Ευθύιος Άδεια
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
/ % / Α. Α 6 6 14.958 14,90 31,40 9.863 10,00 17,70 121 Α Α % / Α. Α 17 17 17.595 17,80 34,90 17.222 17,40 33,20
 Α -- Ο Η %, Α -- Α Α 5 Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α... Α..Α...... Ο Α... Α..Α...... 127 Α Α Α Α Α Α Α % / Α. Α 8 8 19.884 16,72 29,20 19.161 16,53 31,30 129 Α Α Α Α Α Α % / Α. Α 6 6
Α -- Ο Η %, Α -- Α Α 5 Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α... Α..Α...... Ο Α... Α..Α...... 127 Α Α Α Α Α Α Α % / Α. Α 8 8 19.884 16,72 29,20 19.161 16,53 31,30 129 Α Α Α Α Α Α % / Α. Α 6 6
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
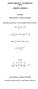 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΕΛΕΓΧΟΙ ΥΠΟΘΕΣΕΩΝ ΓΙΑ ΜΕΣΕΣ ΤΙΜΕΣ ΚΑΙ ΑΝΑΛΟΓΙΕΣ ΚΑΝΟΝΙΚΩΝ ΠΛΗΘΥΣΜΩΝ
 ΚΕΦΑΛΑΙΟ 18 ΕΛΕΓΧΟΙ ΥΠΟΘΕΣΕΩΝ ΓΙΑ ΜΕΣΕΣ ΤΙΜΕΣ ΚΑΙ ΑΝΑΛΟΓΙΕΣ ΚΑΝΟΝΙΚΩΝ ΠΛΗΘΥΣΜΩΝ Στο κεφάλαιο αυτό θα ας απασχολήσουν έλεγχοι στατιστικών υποθέσεων που αναφέρονται στις έσες τιές και αναλογίες πληθυσών
ΚΕΦΑΛΑΙΟ 18 ΕΛΕΓΧΟΙ ΥΠΟΘΕΣΕΩΝ ΓΙΑ ΜΕΣΕΣ ΤΙΜΕΣ ΚΑΙ ΑΝΑΛΟΓΙΕΣ ΚΑΝΟΝΙΚΩΝ ΠΛΗΘΥΣΜΩΝ Στο κεφάλαιο αυτό θα ας απασχολήσουν έλεγχοι στατιστικών υποθέσεων που αναφέρονται στις έσες τιές και αναλογίες πληθυσών
Α 9.543 9.720-177 -1,8% Α Α 3.327 5.644-2.317-41,1% Α 9.448 9.629-181 -1,9% Α Α 3.758 3.174 584 18,4% Page 1 of 8
 Ο Ο Α Α Α Α 817 Α % Α 10.338 10.651-313 -2,9% Α Α Α 817 Α % Α 8.708 8.136 572 7,0% Α Α Α 817 Α % Α. Α. % 8.981 8.651 330 3,8% Α Α Α 817 Α % Α. Α. % 10.078 10.430-352 -3,4% Α Α Α 817 Α % Α. Α.. 9.288 Α
Ο Ο Α Α Α Α 817 Α % Α 10.338 10.651-313 -2,9% Α Α Α 817 Α % Α 8.708 8.136 572 7,0% Α Α Α 817 Α % Α. Α. % 8.981 8.651 330 3,8% Α Α Α 817 Α % Α. Α. % 10.078 10.430-352 -3,4% Α Α Α 817 Α % Α. Α.. 9.288 Α
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
103 Α Α Α % Α 22 22 15,777 15.53 33.5 11,839 11.67 25.9
 %- & Α -Η Η Α- Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α... Α..Α.... Ο Α... Α..Α.. 127 Α Α Α Α Α Α Α % Α 21 21 20,924 18.40 36.8 19,434 17.15 34.2 127 Α Α Α Α Α Α Α %.. α 2 2 18,978 16.57 33.0 17,638
%- & Α -Η Η Α- Ω Ο Α Ο Ω Ο Α Ο Α Ο Ο Ο Α ΧΟ Η Α Ο Η / ΧΟ Η Ο Α... Α..Α.... Ο Α... Α..Α.. 127 Α Α Α Α Α Α Α % Α 21 21 20,924 18.40 36.8 19,434 17.15 34.2 127 Α Α Α Α Α Α Α %.. α 2 2 18,978 16.57 33.0 17,638
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
Κεφάλαιο 3. Ιδιότητες μονάδων - συστήματος που βασίζονται σε διάφορους τύπους γήρανσης
 Κεφάλαιο Ιδιότητες ονάδων - συστήατος που βασίζονται σε διάφορους τύπους γήρανσης Έχουε ήδη αναφερθεί στην έννοια της «γήρανσης» ιας ονάδας ή ενός συστήατος κατά την ελέτη IF / DF χρόνων ζωής Συγκεκριένα
Κεφάλαιο Ιδιότητες ονάδων - συστήατος που βασίζονται σε διάφορους τύπους γήρανσης Έχουε ήδη αναφερθεί στην έννοια της «γήρανσης» ιας ονάδας ή ενός συστήατος κατά την ελέτη IF / DF χρόνων ζωής Συγκεκριένα
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
ΚΕΦΑΛΑΙΟ 6 ΑΣΑΦHΣ ΛΟΓΙΚΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΤΙΚΟΣ ΣΥΛΛΟΓΙΣΜΟΣ
 ΚΕΦΑΛΑΙΟ 6 ΑΣΑΦHΣ ΛΟΓΙΚΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΤΙΚΟΣ ΣΥΛΛΟΓΙΣΜΟΣ 6. ΑΠΟ ΤΗΝ ΚΛΑΣΙΚΗ ΣΤΗΝ ΑΣΑΦΗ ΛΟΓΙΚΗ Η θεωρία της λογικής (Logc theory) ελετά τις εθόδους και τις αρχές του συλλογισού (Reasog), δηλαδή, ε ποιο τρόπο
ΚΕΦΑΛΑΙΟ 6 ΑΣΑΦHΣ ΛΟΓΙΚΗ ΚΑΙ ΠΡΟΣΕΓΓΙΣΤΙΚΟΣ ΣΥΛΛΟΓΙΣΜΟΣ 6. ΑΠΟ ΤΗΝ ΚΛΑΣΙΚΗ ΣΤΗΝ ΑΣΑΦΗ ΛΟΓΙΚΗ Η θεωρία της λογικής (Logc theory) ελετά τις εθόδους και τις αρχές του συλλογισού (Reasog), δηλαδή, ε ποιο τρόπο
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Θ έ λ ω ξ ε κ ι ν ώ ν τ α ς ν α σ α ς μ ε τ α φ έ ρ ω α υ τ ό π ο υ μ ο υ ε ί π ε π ρ ι ν α π ό μ ε ρ ι κ ά χ ρ ό ν ι α ο Μ ι χ ά λ η ς
 9. 3. 2 0 1 6 A t h e n a e u m I n t e r C o Ο μ ι λ ί α κ υ ρ ί ο υ Τ ά σ ο υ Τ ζ ή κ α, Π ρ ο έ δ ρ ο υ Δ Σ Σ Ε Π Ε σ τ ο ε π ί σ η μ η δ ε ί π ν ο τ ο υ d i g i t a l e c o n o m y f o r u m 2 0 1
9. 3. 2 0 1 6 A t h e n a e u m I n t e r C o Ο μ ι λ ί α κ υ ρ ί ο υ Τ ά σ ο υ Τ ζ ή κ α, Π ρ ο έ δ ρ ο υ Δ Σ Σ Ε Π Ε σ τ ο ε π ί σ η μ η δ ε ί π ν ο τ ο υ d i g i t a l e c o n o m y f o r u m 2 0 1
Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηµα ασκήσεων 11/12/2006
 Τήα Επιστήης και Τεχολογίας Υλικώ Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηα ασκήσεω //006 Μελέτη οοδιάστατου στοιχειακού στερεού ε δύο τροχιακά αά άτοο ε χρήση υβριδικώ ατοικώ τροχιακώ Θεωρούε δύο τροχιακά
Τήα Επιστήης και Τεχολογίας Υλικώ Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηα ασκήσεω //006 Μελέτη οοδιάστατου στοιχειακού στερεού ε δύο τροχιακά αά άτοο ε χρήση υβριδικώ ατοικώ τροχιακώ Θεωρούε δύο τροχιακά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ. «Μοντέλα βάσης της Bayesienne Ανάλυσης και Σύµφυτες Απώλειες»
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ιωαική εργασία «Μονέα άσς ς Ανάυσς και Σύφυες Αώειες» ς Θεοώρας Καρααάκ Ειέων καγής : ούκισσα Κρικού Εξεασική ειροή. Κρικού. Κοσιώρς Ε. Τσοάκ Ηράκειο Μάιος 4 ΜΟΝΤΕΛΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ιωαική εργασία «Μονέα άσς ς Ανάυσς και Σύφυες Αώειες» ς Θεοώρας Καρααάκ Ειέων καγής : ούκισσα Κρικού Εξεασική ειροή. Κρικού. Κοσιώρς Ε. Τσοάκ Ηράκειο Μάιος 4 ΜΟΝΤΕΛΑ
14SYMV
 14SYMV002401220 2014-11-13 Α Α: 469 6 - Ω α α ήθ α/α 354 σ ο ιβ ίο ίσ αι ο ώ ής ς σίας ας α α ιά σή α οίο α ύ : Α 1. αθη η ή ι ο άο ι ο αΐ η, Α αή ύ α Οι ο ο ι ού οαα ισ ού αι Α ά ς ο ο ίο ής, ο ο οίος
14SYMV002401220 2014-11-13 Α Α: 469 6 - Ω α α ήθ α/α 354 σ ο ιβ ίο ίσ αι ο ώ ής ς σίας ας α α ιά σή α οίο α ύ : Α 1. αθη η ή ι ο άο ι ο αΐ η, Α αή ύ α Οι ο ο ι ού οαα ισ ού αι Α ά ς ο ο ίο ής, ο ο οίος
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
Το διωνυικό υπόδειγα πολλών περιόδων
 Κεφάλαιο Το διωνυικό υπόδειγα πολλών περιόδων.1 Εισαγωγή Στο κεφάλαιο αυτό θα παρουσιάσουε ένα διακριτό αλλά περισσότερο ρεαλιστικό υπόδειγα αγοράς, το διωνυικό υπόδειγα πολλών περιόδων. Θα διαερίσουε
Κεφάλαιο Το διωνυικό υπόδειγα πολλών περιόδων.1 Εισαγωγή Στο κεφάλαιο αυτό θα παρουσιάσουε ένα διακριτό αλλά περισσότερο ρεαλιστικό υπόδειγα αγοράς, το διωνυικό υπόδειγα πολλών περιόδων. Θα διαερίσουε
22,875 17,944. 25.7 Central line associated bloodstream infection 18,432 1,257
 Α Α Η Α Ο CHECKLIST Α Η Ω Η Ο Α Ω GRAMΩ Α Ο Ο Ω Α Ο Ο Ο Ο Ο * αά ος α ί ος., *, ο ια ί ι ς οι ώ, αά ο Έ α, α ίβ ας α α ιώ ς.. α ιίας, α ιία, ή α οη ε ι ής..ι., Αθή α, ή α Πα ε βάεω ε Χώ ο ς Πα η.π., Πά
Α Α Η Α Ο CHECKLIST Α Η Ω Η Ο Α Ω GRAMΩ Α Ο Ο Ω Α Ο Ο Ο Ο Ο * αά ος α ί ος., *, ο ια ί ι ς οι ώ, αά ο Έ α, α ίβ ας α α ιώ ς.. α ιίας, α ιία, ή α οη ε ι ής..ι., Αθή α, ή α Πα ε βάεω ε Χώ ο ς Πα η.π., Πά
οποίο ανήκει και π ο γνωστός αριθµός.
 1 ΜΗΚΟΣ ΤΟΞΟΥ ΘΕΩΡΙ Μήκος τόξου : Το ήκος ενός τόξου ο δίνεται από τον τύπο = πρ όπου ρ η ακτίνα του κύκλου στον οποίο ανήκει και π ο γνωστός αριθός.. Το ακτίνιο (rad): Ονοάζουε τόξο ενός ακτινίου (rad)
1 ΜΗΚΟΣ ΤΟΞΟΥ ΘΕΩΡΙ Μήκος τόξου : Το ήκος ενός τόξου ο δίνεται από τον τύπο = πρ όπου ρ η ακτίνα του κύκλου στον οποίο ανήκει και π ο γνωστός αριθός.. Το ακτίνιο (rad): Ονοάζουε τόξο ενός ακτινίου (rad)
Η. ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ A ΚΑΙ Α. Στην Άσκηση IV.ΣΤ.14 δείξαµε ότι, κάτω από την υπόθεση οµοιόµορφης κατανοµής των
 Η ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ ΚΑΙ Α Στην Άσηση IVΣΤ4 είξε ότι, άτω πό την πόθεση οοιόορφης τνοής των + θνάτων σε άθε έτος ηλιίς (UDD, + q Η ισότητ τή είχνει ότι, άτω πό την πόθεση UDD, τ ενιί σφάλιστρ ι ινοποιούν τη
Η ΣΧΕΣΕΙΣ ΜΕΤΑΞΥ ΚΑΙ Α Στην Άσηση IVΣΤ4 είξε ότι, άτω πό την πόθεση οοιόορφης τνοής των + θνάτων σε άθε έτος ηλιίς (UDD, + q Η ισότητ τή είχνει ότι, άτω πό την πόθεση UDD, τ ενιί σφάλιστρ ι ινοποιούν τη
Η Μέθοδος Παραγοντοποίησης Ακεραίων Αριθών Number Field Sieve: Θεωρία και Υλοποίηση. Νικόλαος Καραπάνος
 Η Μέθοδος Παραγοντοποίησης Ακεραίων Αριθών Number Field Sieve: Θεωρία και Υλοποίηση Νικόλαος Καραπάνος Master Thesis Επιβλέπων: Παύλος Σπυράκης, Καθηγητής Τήα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήιο Πατρών
Η Μέθοδος Παραγοντοποίησης Ακεραίων Αριθών Number Field Sieve: Θεωρία και Υλοποίηση Νικόλαος Καραπάνος Master Thesis Επιβλέπων: Παύλος Σπυράκης, Καθηγητής Τήα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήιο Πατρών
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
 RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Ενότητα 7: Ανάλυση ιασποράς µε έναν παράγοντα (One way Analysis of Variance)
 Ενότητα 7: Ανάλυση ιασποράς ε έναν παράγοντα Oe wy yss of Vrce Σε αυτή την ενότητα θα εξετάσουε ένα ειδικό πρόβληα γραικής παλινδρόησης το ο- ποίο εφανίζεται αρκετά συχνά στις εφαρογές. Συγκεκριένα θέλουε
Ενότητα 7: Ανάλυση ιασποράς ε έναν παράγοντα Oe wy yss of Vrce Σε αυτή την ενότητα θα εξετάσουε ένα ειδικό πρόβληα γραικής παλινδρόησης το ο- ποίο εφανίζεται αρκετά συχνά στις εφαρογές. Συγκεκριένα θέλουε
όπου α (β) = η αναλογία των μη εμπορεύσιμων αγαθών στο συνολικό εγχώριο (ξένο) δείκτη τιμών.
 Κεφάαιο 6 ο : Προσδιορισμός πραγματικής ισοτιμίας Εισαγωγή Η ανάυση στα προηγούμενα κεφάαια αναφερόταν στους προσδιοριστικούς παράγοντες της ονομαστικής συνααγματικής ισοτιμίας. Στο παρόν κεφάαιο θα ασχοηθούμε
Κεφάαιο 6 ο : Προσδιορισμός πραγματικής ισοτιμίας Εισαγωγή Η ανάυση στα προηγούμενα κεφάαια αναφερόταν στους προσδιοριστικούς παράγοντες της ονομαστικής συνααγματικής ισοτιμίας. Στο παρόν κεφάαιο θα ασχοηθούμε
Πα κ έ τ ο Ε ρ γ α σ ί α ς 4 Α ν ά π τ υ ξ η κ α ι π ρ ο σ α ρ µ ο γ ή έ ν τ υ π ο υ κ α ι η λ ε κ τ ρ ο ν ι κ ο ύ ε κ π α ι δ ε υ τ ι κ ο ύ υ λ ι κ ο
 ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
ΣΥΜΒΑΝΤΑ ΖΩΗΣ ΚΑΙ ΘΑΝΑΤΟΥ Ι & ΙΙ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΝΑΛΟΓΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Κ Ι ΚΟΥΤΣΟΠΟΥΛΟΣ ΣΥΜΒΑΝΤΑ ΖΩΗΣ ΚΑΙ ΘΑΝΑΤΟΥ Ι & ΙΙ (ΠΕΡΙΛΗΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΤΩΝ ΠΑΡΑ ΟΣΕΩΝ ΚΑΙ ΑΣΚΗΣΕΙΣ) ΣΕΠΤΕΜΒΡΙΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΝΑΛΟΓΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Κ Ι ΚΟΥΤΣΟΠΟΥΛΟΣ ΣΥΜΒΑΝΤΑ ΖΩΗΣ ΚΑΙ ΘΑΝΑΤΟΥ Ι & ΙΙ (ΠΕΡΙΛΗΠΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΤΩΝ ΠΑΡΑ ΟΣΕΩΝ ΚΑΙ ΑΣΚΗΣΕΙΣ) ΣΕΠΤΕΜΒΡΙΟΣ
Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών
 ΤΕΙ ΛΑΡΙΣΑΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών Χρήστου Νικοαΐδη Φεβρουάριος 5 Χρήστος Νικοαΐδης Διδάκτωρ του Πανεπιστημίου της Οξφόρδης Στοιχεία Πιθανοτήτων
ΤΕΙ ΛΑΡΙΣΑΣ ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Στοιχεία Πιθανοτήτων και Θεωρίας Ουρών Χρήστου Νικοαΐδη Φεβρουάριος 5 Χρήστος Νικοαΐδης Διδάκτωρ του Πανεπιστημίου της Οξφόρδης Στοιχεία Πιθανοτήτων
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
