Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
|
|
|
- Ἀπολλωνία Νικολάκος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα χρησιμοποιήσουμε για ην ερώηση αυή είναι ο διάγραμμα pareto, λαμβάνονας υπόψη και ις ιμές. Τόμος Δ σελ:31 Είδος Οριζόνια ψυγεία Τιμή Συνολικό κόσος ελαώμαος Βλάβη θερμοσάη Διαρροή συμπυκνωή Θραύση ζαμιού ψυγείου Βλάβη ελαηρίων πόρας Βλάβη λάμπας Για ποιο ευκολία και αφού δεν υπάρχει περιορισμός σο ερώημα αυό βάζουμε α δεδομένα σο minitab και παίρνουμε α παρακάω αποελέσμαα οι ενολές είναι οι παρακάω. Stat>quality tools >Pareto chart defects table Και ση θέση labels βάζουμε α ονόμαα ων προβλημάων που α έχουμε βάλει σε μια σήλη και ση θέση frequencies βάζουμε α συνολικά κόση. και παίρνουμε α παρακάω αποελέσμαα.
2 Pareto Chart of C3 9 1 C4 C Θραύση ζαμιού ψυγείου βλάβη ελαηρίων πόρας βλάβη θερμοσάη βλάβη λάμπας Other Percent C Percent 33,8 3,8 18,5 13,5 3,3 Cum % 33,8 64,7 83, 96,7 1, Σο παραπάνω διάγραμμα παραηρούμε όι η θραύση ζαμιού ψυγείου είναι περισσόερο δαπανηρή και αμέσως μεά η βλάβη ελαηρίων πόρας για α οριζόνια ψυγεία. Το παρακάω διάγραμμα προκύπει με ις ίδιες ενολές όμως ο πίνακας είναι ο επόμενος Είδος Καακόρυφα Τιμή Συνολικό κόσος ελαώμαος ψυγεία Βλάβη 4 48 θερμοσάη Διαρροή συμπυκνωή Θραύση ζαμιού ψυγείου Βλάβη ελαηρίων πόρας Βλάβη λάμπας
3 Pareto Chart of C15 C16 C Θραύση ζαμιού ψυγείου κάθεων βλάβη λάμπας κάθεων βλάβη ελαηρίων πόρας κάθεων βλάβη θερμοσάη κάθεων διαρροή συμπυκνωή κάθεων Percent C Percent 45,1 15, 14,4 13,1 1,3 Cum % 45,1 6, 74,6 87,7 1, Σο παραπάνω διάγραμμα παραηρούμε όι η θραύση ζαμιού ψυγείου είναι περισσόερο δαπανηρή και αμέσως μεά η βλάβη λάμπας για α καακόρυφα ψυγεία Και ώρα θα αναλύσουμε και ους δύο ύπους ψυγείου μαζί σα να υπάρχουν 1 είδη ελαωμάων Είδος Οριζόνια ψυγεία Τιμή Συνολικό κόσος ελαώμαος Βλάβη θερμοσάη Διαρροή συμπυκνωή Θραύση ζαμιού ψυγείου Βλάβη ελαηρίων πόρας Βλάβη λάμπας Βλάβη 4 48 θερμοσάη Διαρροή συμπυκνωή Θραύση ζαμιού ψυγείου Βλάβη ελαηρίων πόρας Βλάβη λάμπας
4 Pareto Chart of C3 C4 C βλάβη θερμοσάη οριζονιων Θραύση ζαμιού ψυγείου οριζονιων βλάβη λάμπας οριζονιων Θραύση ζαμιού ψυγείου κάθεων βλάβη ελαηρίων πόρας οριζονιων βλάβη θερμοσάη κάθεων βλάβη λάμπας κάθεων βλάβη ελαηρίων πόρας κάθεων διαρροή συμπυκνωή κάθεων Ot her Percent C Percent 4,, 13,3 1,9 9,7 4,3 4,1 3,7 3,5,3 Cum % 4, 46, 59,5 7,4 8,86,3 9,4 94, 97,71, παραηρούμε όι η θραύση ζαμιού ψυγείου οριζόνιων είναι περισσόερο δαπανηρή και αμέσως μεά η βλάβη ελαηρίων πόρας οριζόνιων αν πάρουμε και ις δύο περιπώσεις μαζί. Β) Σο ερώημα αυό θα ακολουθήσουμε ις ίδιες ενολές αλλά θα βάλουμε ις παρακάω παραμέρους. Είδος ελαώμαος Βλάβη θερμοσάη Διαρροή συμπυκνωή Θραύση ζαμιού ψυγείου Βλάβη ελαηρίων πόρας Καακόρυφα ψυγεία και οριζόνια Τιμή Συνολικό κόσος
5 Βλάβη λάμπας Θα προσθέσουμε δηλαδή και α οριζόνια με α καακόρυφα ψυγεία. Pareto Chart of C3 C Percent C3 Θραύση ζαμιού ψυγείου βλάβη ελαηρίων πόρας βλάβη θερμοσάη βλάβη λάμπας διαρροή συμπυκνωή C Percent 37,1 6,1 17, 14, 5,8 Cum % 37,1 63, 8, 94, 1, επομένως θεωρούμε όι δεν υπάρχουν διαφορεικού ύπου ψυγεία. Παραηρούμε όι η θραύση ζαμιού ψυγείου είναι περισσόερο δαπανηρή και αμέσως μεά η βλάβη ελαηρίων πόρας ανεξάρηα από ον ύπο ψυγείου. Άσκηση α) ο σωσό είναι ο (iv) αυό υπάρχει σο βιβλίο γ όμος ση σελίδα Σην αρχή έκανε μικρομερική ρύθμιση ης ζυγαριάς δηλαδή σανάρισμα ενός οργάνου δηλαδή ο μηδενισμός ου σελ 66 και μεά έκανε βαθμονόσηση δηλαδή εγγραφή ων ενδείξεων αφού ξεκόλλησε η εικέα β) Το σωσό είναι ο (i) βρίσκεαι ση σελίδα 16 όμος Δ η καανομή μπορεί να είναι εσφαλμένη γιαί δεν έχουμε πάρει ο σωσό αριθμό κλάσεων Το (ii) είναι λάθος γιαί ση σελίδα 18 ου ίδιου όμου λέει για η διαδικασία ων κλάσεων και ις μέγισες ιμές ους. Το (iii) είναι λάθος γιαί από ον κανόνα ου Sturges οι κλάσεις πρέπει να είναι 6 και όχι 7 σελ 17. Προσοχή σον κανόνα αυόν δεν κάνουμε σρογγυλοποίηση αλλά παίρνουμε ο ακέραιο μέρος ου αποελέσμαος αν και ο κανόνας αυός είναι καθαρά εμπειρικός ύπος Και ο (iv) δεν είναι σωσό γιαί η κενρική ιμή ης 3 ης κλάσης είναι 145 και όχι 14. σελ 17.
6 γ) Το σωσό είναι ο (iii) σελ 114 όμος Γ Για να ελαχισοποιήσουμε ο σφάλμα μέρησης πρέπει να ελέγχουμε συχνά ην ακμή σήριξης ου βραχίονα και ων δίσκων, για να διαπισώνουμε αν έχει φθαρεί ή όχι. 7 Το (ii) είναι λάθος γιαί μπορεί να μερήσει μάζα μέχρι 1 και είναι πολύ ακριβής. Το έαρο δεν ισχύει γιαί ο ζυγός είναι ακριβής απλά μπορεί να παρουσιάσει σοβαρά μειονεκήμαα σην αποκαάσαση ης ισορροπίας ων δυνάμεων. Το πρώο δεν είναι σωσό γιαί αν δημιουργηθεί πρόβλημα σην ισορροπία όε και σύνομα αν γίνουν οι μερήσεις δεν θα μερηθούν σωσά. δ) Το σωσό είναι ο (iv) ο (i) απορρίπεαι και αυό βρίσκεαι ση σελ138 γ όμου (ii) απορρίπεαι και βρίσκεαι ση σελίδα 7 καθώς και ο (iii) βρίσκεαι σην ίδια σελίδα και δεκό είναι ο (iv) αυό βρίσκεαι ση σελίδα 136. ε) Το σωσό είναι ο (ii) ο πρώο απορρίπεαι γιαί δεν μπορούμε να βρούμε η μέση ιμή ου εύρους σελ 58 ο ρίο δεν είναι σωσό γιαί ακόμα και αν ήαν μέσα σα όρια υπάρχει επαναληπικόηα και 7 συνεχείς παραηρήσεις θα είναι πάνω από ην κενρική ιμή άρα θα είναι εκός ελέγχου. Και ο έαρο είναι λάθος γιαί σαν κενρική γραμμή δεν βάζουμε ην πραγμαική ιμή (751cm) αλλά αυή που μεράμε από α δεδομένα μας. Άρα καλά κάναμε και βάλαμε σαν ιμή η ιμή 75 cm Το σωσό είναι ο δεύερο και αυό γιαί ση σελίδα 6 λέει πόε μια διαδικασία είναι εκός ελέγχου και ση συγκεκριμένη περίπωση ένα ουλάχισον σημείο βρίσκεαι πάνω από ο όριο ελέγχου, επίσης υπάρχουν επαναλαμβανόμενες μορφές κλ άρα η διαδικασία είναι εκός ελέγχου και σωσό είναι ο δεύερο. Άσκηση 3 α) Για να μελεήσουμε η συμμερικόηα ης καανομής ου μήκους ου προφίλ κάθε πριονιού θα εφαρμόσουμε ένα ισόγραμμα συχνοήων για κάθε ένα πριόνι. Τόμος δ σελ 14. Graph> histogram και σο κενό θα βάλω η μεαβληή με ις δοθείσες ιμές ου μήκους προφίλ για ο πριόνι Α
7 3, Histogram of C,5 Frequency, 1,5 1,,5, 5, 5, 5,4 5,6 5,8 C 51, 51, 51,4 Η μορφή ου παραπάνω ισογράμμαος φανερώνει όι ο προφίλ για ο πριόνι Α επηρεάζεαι σημανικά από κάποιον παράγονα, ο οποίος έχει ην άση να διαφοροποιείαι περνώνας από διαφορεικές καασάσεις Graph> histogram και σο κενό θα βάλω η μεαβληή με ις δοθείσες ιμές ου μήκους προφίλ για ο πριόνι Β 7 Histogram of C1 6 5 Frequency , 49,5 5, C1 5,5 51, 51,5
8 Η καανομή ου παραπάνω ισογράμμαος δεν είναι συμμερική μια και υπάρχουν πολύ λιγόερες ιμές αρισερά ης ψηλόερης σήλης. Τέοιου είδους καανομές λέγοναι λοξή προς α δεξιά (ασύμμερη προς α δεξιά). β) Για να βρούμε ο ποσοσό ων προφίλ αλουμινίου που παράγοναι «ενός προδιαγραφών» δηλαδή μεαξύ ων ιμών [49, 51] μεράμε ις ιμές που βρίσκοναι εκός οι οποίες είναι 5 και όε ο ποσοσό που βρίσκεαι εκός είναι 5/ =,5 δηλαδή ο 5% βρίσκεαι εκός άρα ο 75% θα βρίσκεαι ενός ων προδιαγραφών. γ) οι ενολές είναι graph>scatterplot > simple και βάζουμε ις δυο ιμές σον X και Y άξονα και παάω οκ. 51,5 Scatterplot of C1 vs C 51, 5,5 C1 5, 49,5 49, 5, 5, 5,4 5,6 5,8 C 51, 51, 51,4 51,6 Από ο παραπάνω διάγραμμα διασκόρπισης μπορούμε να δούμε αν υπάρχει σχέση μεαξύ ων δύο μηκών προφίλ πριονιών. Παραηρούμε όι υπάρχει θεική συσχέιση μεαξύ ων δυο μηκών προφίλ ων πριονιών αυό σημαίνει όι όαν μεγαλώνει ο ένα μήκος θα μεγαλώνει και ο άλλο μήκος. Βέβαια δύο ιμές αποκλίνουν από ο επιθυμηό αποέλεσμα αλλά είναι μόνο δύο οπόε ο συμπέρασμα συνεχίζει να ισχύει. δ)
9 Θα εφαρμόσουμε διάγραμμα αιίου αποελέσμαος σο ερώημα αυό. Οι ενολές για να γίνει ο παραπάνω διάγραμμα αιίου αποελέσμαος είναι οι παρακάω. Stat>quality tools> cause-and-effect Σον πίνακα που ανοίγει θα πρέπει να φιάξεε σήλες από πριν ανοίξεε ο causeand-effect Αρχικά θα φιάξεε 4 σήλες με α ονόμαα άνθρωπος υλικά μέθοδος μηχανές μεά θα φιάξεε άλλες 4 που θα έχουν 1 η κόπωση εχνηών έλλειψη εκπαίδευσης εχνηών η υπερβολική αχύηα κοπικού εργαλείου 3 η μη λίπανση ου σημείου κοπής υψηλή παραγωγικόηα ακααλληλόηα βαμμένης επιφάνειας 4 η ακαάλληλων προσμίξεων σο κράμα αλουμινίου έλλειψη λιπανικού υγρού αμφιβόλου ποιόηας βαφής προφίλ και α βάζουμε ο ένα διπλά σο άλλο δηλαδή άνθρωπος με ην πρώη ομάδα υλικά με ην έαρη,μέθοδος με ην ρίη και μηχανές με η δεύερη. Και παάμε οκ.
10 Cause-and-Effect Diagram μέθοδος άνθρωπος μη λιπανση ου σημείου κοπής κόπω ση εχνηών υψηλή παραγωγικόηα ακααλληλόηα βαμέν ης επιφ άν ειας υπερβολική αχύηα κοπικού εργ αλείου έλλειψη εκπαίδευσης εχνηών παραγωγή ελαωμαικ ών προφίλ αλουμινίου αμφ ιβόλου ποιόηας βαφ ής προφ ίλ έλλειψη λιπανικού υγ ρού ακαάλληλων προσμίξεω ν σο κράμμα αλουμιν ίου μηχανές υλικά Άσκηση 4 α) Λάθος γιαί α παρασιικά δεν είναι υχαία αλλά συσημαικά σφάλμαα σελ 45 β) Σωσό σελ58 γ) Λάθος σελ 73 Η επαναδιακρίβωση δεν μπορεί να γίνεαι συνέχεια και αυό γιαί ο κόσος είναι πολύ μεγάλο. Ο καλύερος ρόπος για να γίνεαι η επαναδιακρίβωση είναι να γίνεαι σε μια χρονική σιγμή και αν βρεθεί εκός ορίων να γίνεαι συχνόερα μέχρι να βελιωθεί. Μόλις γίνει αυό ο χρόνος για ην επαναδιακρίβωση γίνεαι μεγάλος. Έσι, ο κόσος μικραίνει όσο ο δυναόν περισσόερο. δ) Λάθος σελ 89 Μπορεί βέβαια να γίνει ο σχημαισμός ου σύνθεου μήκους από άλλους συνδυασμούς έσι ώσε να δημιουργηθεί ο πρόυπο σύνθεο μήκος 6,91mm ε) Σωσό σ) Σωσό σελ 45 ζ) Λάθος σελ και βέβαια υπάρχει συσχέιση μπορεί έσι όπως φαίνοναι να δημιουργούν ένα απλωμένο νέφος αν όμως α πάρουμε ανά ομέα Α και Β θα παραηρήσουμε όι και σις δυο περιπώσεις υπάρχει μια θεική συσχέιση μεαξύ ων δύο μεαβληών βάθους ενανθράκωσης και ανοχής σην ριβή.
11 η) Σωσό σελ 46 Άσκηση 5 α) Σο ερώημα αυό μας ζηείαι να υπολογίσουμε ην ελασικόηα ενός υλικού μέσω ου χρόνου διέλευσης υπερήχων από ένα δοκίμιο με βάρος Β=1, ±, g L=5 ±,1mm t=, ±,1s w=1 ±,1mm h=1 ±,1mm και η ελασικόηα δίνεαι από ον ύπο E = LB thw E = = = g s mm, , 6 15 /( ) θα βρούμε η μέγιση ιμή και ην ελάχιση ιμή ης ελασικόηας. Η μέγιση ιμή που μπορεί να πάρει η ελασικόηα είναι 5,1*1, E = = 15, άρα ( 15+, ),199 *9,99*9,99 Η ελάχιση ιμή που μπορεί να πάρει η ελασικόηα είναι 49,99*1,18 E = = 14, άρα (15-, ),1 *1,1*1,1 άρα η ελασικόηα είναι 15 ±, βάζουμε ο μεγαλύερο διάσημα. β) Για να υπολογίσουμε ο σύνθεο υχαίο σφάλμα θα πρέπει να πάρουμε ον ύπο που δίνει ο σύνθεο υχαίο σφάλμα. Ε Ε Ε Ε Ε Ε= Β δ δ δ L δ t δ h δ w Β L t h w (1) δ Β=, =,4 δ L =,1 =,1 δ t =, 1 =, 1 δ h =,1 =,1 δ w =,1 =,1
12 Ε L 5 = 1,5 = = Β thw, 11 Ε B 1, =,3 = L t hw, 11 Ε LB 5 1, 1 = 15 3 = 3 = = t hw t 1 1,,8 Ε LB 1 5 1, 1 6 = 1, 5 = = = h t w h, Ε LB 1 5 1, 1 = 1, 5 = = w t h w, 1 1 Άρα ο σύνθεο υχαίο σφάλμα θα είναι ο επόμενο,ανικαθισώνας ις ιμές που βρήκαμε παραπάνω και χρησιμοποιώνας ον ύπο (1) δε=,65 +,9 +,5 +,5 +,5 =,85459 =, γ) Το σχεικό σύνθεο υχαίο σφάλμα δίνεαι από ην παρακάω σχέση δ E = E δ Β+ δ + δ + δ + δ Ε Ε Ε Ε Ε L t h w Β L t h w LB, 8549, 93 = = =, , 15, 1 1 thw Άσκηση 6 Η διακριική ικανόηα ου ζυγού ακριβείας που χρησιμοποιείαι για ην εύρεση ου βάρους ου καυσικού ναρίου είναι,1και ακολουθεί ομοιόμορφη καανομή. Συνεπώς η υπική αβεβαιόηα θα είναι u 1 =,5 gr με άπειρους βαθμούς 3 ελευθερίας.
13 Το βάρος ου NaOH έχει υπική αβεβαιόηα u =,5 gr με ν=4-1=3 β.ε. 4 Η ακρίβεια ης ογκομερικής φιάλης έχει υπική αβεβαιόηα u 3 =, ml με 6 άπειρους βαθμούς ελευθερίας. H αβεβαιόηα πλήρωσης ης ογκομερικής φιάλης έχει υπική αβεβαιόηα,3 u 4 = ml με ν=5-1=4 β.ε. 5 δεν υπάρχει αβεβαιόηα ης θερμοκρασίας λόγω ων συσάσεων που έκανε ο καθηγηής. α) Ο θεωρηικός ύπος ης συνδυασμένης υπικής αβεβαιόηας ου ειδικού βάρους είναι ο επόμενος. p p p u ( p) = ( ) * u ( x ) = ( ) u ( B) + ( ) u ( V) = c i i= 1 xi B V 1 B ( ) u ( B) + ( ) u ( V) v v Συνεπώς 1 B uc ( p) = ( ) u ( B) + ( ) u ( V) v v β) Για να βρούμε η συνδυασμένη υπική αβεβαιόηα που ανισοιχεί σον υπολογισμό ου ειδικού βάρους ου διαλύμαος Θα βρούμε ην υπική αβεβαιόηα ου βάρους ην υπική αβεβαιόηα ου όγκου Για ο βάρος η υπική αβεβαιόηα,5,5 UB = u1 + u = + =, 83+, 65 =, 8365gr 3 4 Για ον όγκο η υπική αβεβαιόηα θα είναι,,3 UV = u3 + u4 = + =, 667 +, 18 =, 467ml 6 5
14 επομένως, 1 B uc ( p ) = ( ) u ( B) ( ) u ( V) διαλυμαος v + v = 1 4 uc ( p διαλυμαος ) = ( ), ( ),467 = 1 1 8,365 * ,947* 1-11 =8,365 *1-1 +,3947* 1-1 u c ( p διαλυμαος ) = 8,757 *1-1 u ( p διαλυμαος ) 8,757*1,95 1 c 1 1 = = =,95 gr\ml γ) Η εκεαμένη υπική αβεβαιόηα θα δίνεαι από ον ύπο U=K*U C (P διαλύμαος ) Για να υπολογίσουμε ον ύπο αυό θα πρέπει να υπολογίσουμε ο Κ V eff 4 = Uc u1 u u3 u = επομένως από πίνακα.8 ο Κ=1,96 άρα η εκεαμένη υπική αβεβαιόηα θα δίνεαι από ον ύπο U=K*U C (P διαλύμαος )=1,96*,95 =,578 Έσι η αβεβαιόηα που σχείζεαι με ον υπολογισμό ου ειδικού βάρους ου διαλύμαος σε 95% επίπεδο εμπισοσύνης είναι ±,578 gr\ml
15 Άσκηση 7 α) Σο ερώημα αυό θα πρέπει να βρούμε ην κενρική γραμμή και α όρια ελέγχου καάλληλου διαγράμμαος ελέγχου για ην παρακολούθηση ης διαδικασίας παραγωγής κινηήρων και θα ελέγξουμε αν η διαδικασία παραγωγής είναι υπό έλεγχο. Ημέρα Αριθμός ελεγχόμενων Αριθμός ελαωμάων κινηήρων Σο ερώημα αυό ο σαισικό εργαλείο που θα χρησιμοποιήσουμε είναι διάγραμμα ελέγχου και πιο συγκεκριμένα υ-διάγραμμα γιαί δεν έχουμε σαθερό δείγμα. Αυό συμβαίνει γιαί έχουμε αριθμό ελαωμάων ανά αριθμό ελεγχόμενων κινηήρων. Θα πάρουμε ους λόγους ελαωμάων ανά αριθμό ελεγχόμενων κινηήρων. Ημέρα Αριθμός Ucl Lcl ελαωμάων ανά κινηήρα. 1 3/1=,3 3,15968,569 18/7=, ,4157, /1=, ,468,68186
16 4 34/15=,6667,9198, /8=1,875 3,3157, /1=,3333 3,468, /14=1,5,9591, /9=, ,975, /1=3,4 3,15968, /1=1, ,468, /1=1,75 3,468, /13=1,6931 3,43, /15=1,73333,9198, /15=1,6,9198, /17=1,359,8578, /13=,769 3,43, /17=1,6476,8578, /14=1,9857,9591, /18=1,16667,8983, /15=1,6,9198,867 Επομένως u = ( ) /( ) =481/58=1,86434 Επομένως α πάνω και α κάω όρια δίνοναι από ους ύπους. UCL = u + 3 u και UCL = u 3 u για κάθε ένα δείγμα n n ξεχωρισά ανικαθισώνας σους ύπους ις ιμές που βρήκαμε παραπάνω παίρνουμε α παραπάνω αποελέσμαα. Που φαίνοναι σην 3 η και 4 η σήλη ου πίνακα. Και ο γράφημα μέσω ου excel είναι ο επόμενο
17 4 3,5 3 Σειρά1 Σειρά Σειρά3 Σειρά4,5 1,5 1, ο επόμενο είναι εναλλακικό ου πρώου 4 3,5 3,5 1,5 1 Σειρά1 Σειρά Σειρά3 Σειρά4, παραηρούμε όι πάνω από ο,9 υπάρχει μόνο μια ιμή και κάω από ο,87 καμία η διεργασία παρουσιάζει σαφείς ενδείξεις όι είναι εκός σαισικού ελέγχου. β) θα γίνει ο ίδιο γράφημα αλλά με ο Minitab οι ενολές που πρέπει να γίνουν είναι οι παρακάω. Stat> control chart> attribute chart > u
18 Βάζουμε ις παραηρήσεις σο φύλλο εργασίας και σο label βάζουμε ο πλήθος ων ελαωμάων και ση σήλη size βάζουμε ο πλήθος κάθε υποομάδας. Επίσης πάμε σο options chart >testκαι παάμε όλα α διαθέσιμα κριήρια και παάμε οκ. και οκ. 3,5 U Chart of C18 1 Sample Count Per Unit 3,,5, 1,5 1,,5 UCL=,9 _ U=1,864 LCL=,87, Sample Tests performed with unequal sample sizes α ίδια αποελέσμαα επιβεβαιώνοναι και σο ερώημα αυό. παραηρούμε όι πάνω από ο,9 υπάρχει μόνο μια ιμή και κάω από ο,87 καμία η διεργασία παρουσιάζει σαφείς ενδείξεις όι είναι εκός σαισικού ελέγχου. Συγνώμη σε όλους αλλά κανείς δεν μου είχε δώσει ο υποσηρικικό υλικό και ις διορθώσεις ου καθηγηή. Ευχαρισώ ο φοιηή που μου α έσειλε
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ
 Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Ελληνικό Σαισικό Ινσιούο Πρακικά 8 ου Πανελληνίου Συνεδρίου Σαισικής (5) σελ.35-34 ΑΘΡΟΙΣΤΙΚΗ ΑΜΟΙΒΑΙΑ ΠΛΗΡΟΦΟΡΙΑ ΩΣ ΣΤΑΤΙΣΤΙΚΟ ΕΛΕΓΧΟΥ ΜΗ-ΓΡΑΜΜΙΚΟΤΗΤΑΣ ΧΡΟΝΟΣΕΙΡΩΝ Παπάνα Αγγελική και Κουγιουμζής Δημήρης
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
3 Συσχετίσεις σε χρονοσειρές
 3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
3 Συσχείσεις σε χρονοσειρές Η χρονοσειρά ενός χρημαισηριακού δείκη { y, y,, yn } ως πραγμαοποίηση μιας σοχασικής διαδικασίας { t } t= ης μεαβολής ων ιμών ου δείκη { x, x,, xn} πραγμαοποίηση μιας άλλης
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
d k dt k a ky(t) = dt k b kx(t) (3.1)
 Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Κεφάλαιο 3 Ανάλυση Σημάων και Συσημάων σο Πεδίο ου Χρόνου 3. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Είδαμε σο προηγούμενο κεφάλαιο κάποια εισαγωγικά
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
Ανάπτυξη και Αξιολόγηση Στρατηγικής Κεντρικού Ελέγχου Ροών σε Αποχετευτικά ίκτυα µε Έµφαση στην Εφαρµογή της στον Ελλαδικό Χώρο
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ: Μηχανικών Παραγωγής & ιοίκησης Ανάπυξη και Αξιολόγηση Σραηγικής Κενρικού Ελέγχου Ροών σε Αποχεευικά ίκυα µε Έµφαση σην Εφαρµογή ης σον Ελλαδικό Χώρο ιαριβή που υπεβλήθη για ην
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Α Σ Κ Η Σ Η 1 ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY
 Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
Α Σ Κ Η Σ Η ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΚΑΛΩΔΙΟΥ ΜΕ ΤΗ ΜΕΘΟΔΟ MURRAY Γενικά Με η μέθοδο Murray, όπου χρησιμοποιούναι οι ιδιόηες ης γέφυρας Wheatstone, μπορούν να προσδιορισούν σφάλμαα διαρροής προς η γη και
ΚΕΦΑΛΑΙΟ IΙΙ: TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. 1. Τάσεις σε συνεχή μέσα (ε πανάληψη) 2. Τάσεις σε α-συνεχή. μέσα. 3. Ενεργός και Ολική τάση
 ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΚΕΦΑΛΑΙΟ IΙΙ: 3. Ενεργός και Ολική άη TAΣΕΙΣ ΣΤΟ Ε ΑΦΟΣ. Τάεις ε υνεχή μέα (ε πανάληψη). Τάεις ε α-υνεχή μέα 4. Γεωαικές άεις (λόγω ιδίου βάρους) 5. Τάεις λόγω εξωερικών φορίων Θεωρία Ελαικόηας Καανομή
ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ
 Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
Ελληνικό Σαισικό Ινσιούο Πρακικά ου Πανελληνίου Συνεδρίου Σαισικής (7), σελ 39-336 ΑΞΙΟΛΟΓΗΣΗ ΕΚΤΙΜΗΤΩΝ ΑΜΟΙΒΑΙΑΣ ΠΛΗΡΟΦΟΡΙΑΣ ΑΠΟ ΙΣΤΟΓΡΑΜΜΑ ΣΕ ΧΡΟΝΟΣΕΙΡΕΣ Παπάνα Αγγελική, Κουγιουμζής Δημήρης Γενικό Τμήμα
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
1 Κεφάλαιο 1 ΟΡΘΕΣ ΚΑΙ ΔΙΑΤΜΗΤΙΚΕΣ ΤΑΣΕΙΣ, ΣΧΕΔΙΑΣΜΟΣ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ 1.1 Εισαγωγή Ένα από α βασικόερα ανικείμενα σο επάγγελμα ου μηχανικού είναι η λεγόμενη διασασιολόγηση ή σχεδιασμός δομικών σοιχείων
y(t) = T [x(t)] (7.1)
![y(t) = T [x(t)] (7.1) y(t) = T [x(t)] (7.1)](/thumbs/93/114087149.jpg) Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
Κεφάλαιο 7 Ανάλυση Συσημάων σο Πεδίο ου Χρόνου 7. Εισαγωγή Σε αυό ο κεφάλαιο, θα συζηήσουμε για ο πως μπορούμε να μελεάμε συσήμαα σο πεδίο ου χρόνου. Τι είναι όμως α συσήμαα και γιαί α χρησιμοποιούμε;
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΦΙΛΟΣΟΦΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ ΚΑΙ ΠΑΙΔΑΓΩΓΙΚΗΣ Πανελή Α. Δείρογλου Πυχιούχου Παιδαγωγικού Τήαος Δηοικής Εκπαίδευσης Το Ολοήερο Δηοικό Σχολείο από η σκοπιά ων
ΚΗΠΟΣ & ΒΕΡΑ. τα «πώς ντας σε όλα μας ό πλούσιο φωτογρ. λίδα 3. όλης. Διαβάστε στη σελ. 7 για ένα βιβλίο που θα κάνει τις ιδέες σας...
 μ Κηπο ανία Π ΕΡ Ι Ο Δ Ι ΚΗ ΕΚ Δ ΟΣΗ ΓΙΑ ΤΗ ΦΥΣΗ ΚΑ Ι ΤΟ ΠΕ ΡΙ ΒΑ ΛΛΟ Ν Αγαπηοί φίλοι ου πράσινου, Όλοι μας διαπισώνουμε καθημερινά ο έλλειμμα που υπάρχει σε καθαρό νερό και αέρα, σο πράσινο, ση διαχείριση
μ Κηπο ανία Π ΕΡ Ι Ο Δ Ι ΚΗ ΕΚ Δ ΟΣΗ ΓΙΑ ΤΗ ΦΥΣΗ ΚΑ Ι ΤΟ ΠΕ ΡΙ ΒΑ ΛΛΟ Ν Αγαπηοί φίλοι ου πράσινου, Όλοι μας διαπισώνουμε καθημερινά ο έλλειμμα που υπάρχει σε καθαρό νερό και αέρα, σο πράσινο, ση διαχείριση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ ΝΙΚΟΛΑΟΣ Κ. ΜΠΕΚΙΑΡΗΣ ΛΥΜΠΕΡΗΣ ΤΕΧΝΙΚΕΣ ΓΡΑΜΜΙΚΩΝ ΚΑΙ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΛΕΓΚΤΩΝ ΣΥΣΤΗΜΑΤΩΝ
Κεφάλαιο 4 Ιδανικοί χημικοί αντιδραστήρες
 Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
Κεφάλαιο 4 Ιδανικοί χημικοί ανιδρασήρες Με βάση α σοιχεία για ην κινηική και η σοιχειομερία ων ανιδράσεων, μπορούμε ώρα να προχωρήσουμε σην ανάλυση ορισμένων βασικών ύπων χημικών ανιδρασήρων. Η ανάλυση
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
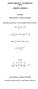 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Πανεπιστήµιο Θεσσαλίας
 Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Πανεπισήιο Θεσσαλίας Τήα Ηλεκρολόγων Μηχανικών & Μηχανικών Υπολογισών Άσκηση : Λυένες Ασκήσεις Έσω ένα σύσηα νήης, σο οποίο έχουε προσθέσει ια κρυφή νήη θυάων 6 θέσεων εαξύ ης κρυφής νήης δεδοένων L και
Σειρά Ασκήσεων στην Αντοχή των Υλικών
 Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
Σιρά Ακήων ην Ανοχή ων Υλικών Άκηη η Σο ημίο Α μιας πίπδης μαλλικής πιφάνιας μ μέρο λαικόηας 00 GP και λόγο Pissn 0.5 μρήθηκαν οι πιμηκύνις ις καυθύνις, και μ η διάαξη ων πιμηκυνιομέρων ου χήμαος, ως 900,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
3. ΦΑΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΤΩΝ (ΑΝΑΛΥΣΗ FOURIER)
 3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
3. ΦΑΣΜΑΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΑΩΝ (ΑΝΑΛΥΣΗ FOURIER) 3.. Γενικά Ένα σήμα μπορεί να αναπαρασαθεί με έναν από ους παρακάω ισοδύναμους ρόπους: Ως χρονικά μεαβαλλόμενη άση (κυμαομορφή) x(t) (αναπαράσαση σο πεδίο ου
Μάθημα 3- Εργαλεία ποιότητας-ασκήσεις-ερωτήσεις
 E D A 5 C 3 4 B 2 Μάθημα 3- Εργαλεία ποιότητας-ασκήσεις-ερωτήσεις Επτά+ βασικά εργαλεία ποιότητας (χρησιμοποιούνται για βελτίωση μιας διεργασίας-διαδικασίας) Εργαλείο Τι κάνει Σχήμα Ανάλυση Παρέτο- Pareto
E D A 5 C 3 4 B 2 Μάθημα 3- Εργαλεία ποιότητας-ασκήσεις-ερωτήσεις Επτά+ βασικά εργαλεία ποιότητας (χρησιμοποιούνται για βελτίωση μιας διεργασίας-διαδικασίας) Εργαλείο Τι κάνει Σχήμα Ανάλυση Παρέτο- Pareto
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ. Μέρος Α (2007-08)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Ολοκλήρωση διεργασίας χρησιμοποιώντας την τεχνολογία σύγκλισης (Pinch Technology)
 Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
Θέμα: Ολοκλήρωση διεργασίας χρησιμοποιώνας ην εχνολογία σύγκλισης (Pinch Technology) Εισηγηές: Εμμανουήλ Κοζαμπασάκης, Πανεπισήμιο ου Maπchester, Ινσιούο Ε πισήμης και Τεχνολογίας, UMST, U.K. καθηγ. Bodo
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ
 1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕΔΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΛΟΓΙΣΤΙΚΗΣ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΗΣ Προσδιορισμός ης αξίας που δημιουργείαι για ους μεόχους με βάση ο οικονομικό και λογισικό κέρδος σα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Βέλισες σραηγικές διακοπής μιας Μαρκοβιανής αλυσίδας ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ ΒΑΣΙΛΕΙΟΣ ΖΑΧΑΡΙΑΔΗΣ
Πανεπιστήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεταπτυχιακών Σπουδών «Πληροφορική»
 Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
Πανεπισήμιο Πειραιώς Τμήμα Πληροφορικής Πρόγραμμα Μεαπυχιακών Σπουδών «Πληροφορική» Μεαπυχιακή Διαριβή Τίλος Διαριβής Αλγόριθμοι Αποικίας Μυρμηγκιών Ονομαεπώνυμο Φοιηή Φρανζέσκος Νομικός Παρώνυμο Γεώργιος
? Συμπεριφορά ψαθυρών υλικών 11/6/2018. Δρ. Σωτήρης Δέμης. Σημειώσεις Εργαστηριακής Άσκησης Κριτήρια Αστοχίας Διάτμηση Τοιχοποιίας
 11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
11/6/018 Σημειώεις Εργαηριακής Άκηης Κριήρια Αοχίας Διάμηη Τοιχοποιίας Δρ. Σωήρης Δέμης Πολιικός Μηχανικός (Πανεπιημιακός Υπόροφος) Έως ώρα Καααικός νόμος όλκιμων υλικών (αξονική κααπόνιη ε μία διεύθυνη)
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής και ση συνέχεια χρησιµοοιείαι ολλαλασιασµός
Παραγωγή Κυµατοµορφών FM:
 Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παραγωγή Κυµαοµορφών ύο βασικές µέθοδοι για ην αραγωγή κυµαοµορφών : - Έµµεση (inir ) - όου ο σήµα διαµόρφωσης χρησιµοοιείαι αρχικά για ην αραγωγή κυµαοµορφής σενής ζώνης και ση συνέχεια χρησιµοοιείαι
Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος
 Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος Χρησιμοποιείται μόνο όταν οι τιμές της μεταβλητής έχουν ένα σταθερό άθροισμα (συνήθως 100%, όταν μιλάμε για σχετικές συχνότητες) Είναι χρήσιμο μόνο
Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος Χρησιμοποιείται μόνο όταν οι τιμές της μεταβλητής έχουν ένα σταθερό άθροισμα (συνήθως 100%, όταν μιλάμε για σχετικές συχνότητες) Είναι χρήσιμο μόνο
Ενότητα Ζ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ
 Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Ενόηα Ζ ΚΑΜΠΤΟΔΙΑΤΜΗΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ Η ΕΝΝΟΙΑ, ΟΙ ΤΥΠΟΙ ΚΑΙ ΤΑ ΚΡΙΤΗΡΙΑ ΑΣΤΟΧΙΑΣ 1. ΚΑΜΠΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΦΟΡΕΩΝ 1.1.1 Παραμορφώσεις Καθύψος ης Διαομής 1.1 MΗΧΑΝΙΣΜΟΣ ΑΝΑΛΗΨΗΣ ΔΡΩΣΑΣ ΡΟΠΗΣ Όπως φαίνεαι
Με αντένσταση απαντά ο Χρ. Βλαχογιάννης
 Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 17 Δεκεμβρίου 2010 Φύλλο 140 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 17 Δεκεμβρίου 2010 Φύλλο 140 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
Κεφάλαιο 8: Μαγνητικά Υλικά και Ιδιότητες ΙΙ. Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Σχολή Εφαρμοσμένν Μαθημαικών και Φυσικών Εισημών Εθνικό Μεσόβιο Πολυεχνείο Διηλεκρικές Οικές Μαγνηικές Ιδιόηες Υλικών Κεφάλαιο 8: Μαγνηικά Υλικά και Ιδιόηες ΙΙ Λιαροκάης Ευθύμιος Άδεια Χρήσης Το αρόν εκαιδευικό
Ανάλυση της µηχανικής συµπεριφοράς της συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα
 Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
Ανάλυση ης µηχανικής συµπεριφοράς ης συνάφειας ράβδων οπλισµού FRP µε σκυρόδεµα Β. Καραζαφέρης MΕ, Υποψήφιος διδάκωρ ΕΜΠ Μ. Καής Επίκουρος Καθηγηής ΕΜΠ Λέξεις κλειδιά: FRP, συνάφεια, πεπερασµένα σοιχεία
ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ
 1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ Α. ΣΤΟΧΟΙ Η συνειδητή χρήση των κανόνων ασφαλείας στο εργαστήριο. Η εξοικείωση στη χρήση του υποδεκάμετρου και του διαστημόμετρου
1 ο ΕΚΦΕ (Ν. ΣΜΥΡΝΗΣ) Δ Δ/ΝΣΗΣ Δ. Ε. ΑΘΗΝΑΣ 1 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΧΡΟΝΟΥ ΜΑΖΑΣ ΔΥΝΑΜΗΣ Α. ΣΤΟΧΟΙ Η συνειδητή χρήση των κανόνων ασφαλείας στο εργαστήριο. Η εξοικείωση στη χρήση του υποδεκάμετρου και του διαστημόμετρου
Περί χασμάτων. Ελένη Μάνου, νεφρολόγος Επιμελήτρια Α' ΓΝ Παπαγεωργίου Θεσσαλονίκη
 Περί χασμάων Ελένη Μάνυ, νεφρλόγς Επιμελήρια Α' ΓΝ Παπαγεωργίυ Θεσσαλνίκη Χάσμα ανιόνων (ΧΑ) ρύ: ένα δύσκλ και παραμελημέν κεφάλαι! "Gamblegram" Η σημασία ης ηλεκρικής υδεερόηας σε σχέση με η σύγχυση πυ
Περί χασμάων Ελένη Μάνυ, νεφρλόγς Επιμελήρια Α' ΓΝ Παπαγεωργίυ Θεσσαλνίκη Χάσμα ανιόνων (ΧΑ) ρύ: ένα δύσκλ και παραμελημέν κεφάλαι! "Gamblegram" Η σημασία ης ηλεκρικής υδεερόηας σε σχέση με η σύγχυση πυ
ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ
 8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
8ο Πανελλήνιο Συμποσιο Ωκεανογαφίας & Αλιείας ΥΠΟΛΟΓΙΣΤΙΚΑ ΜΟΝΤΕΛΑ ΚΥΚΛΟΦΟΡΙΑΣ ΚΑΙ ΔΙΑΔΟΣΗΣ ΠΕΤΡΕΛΑΪΚΗΣ ΡΥΠΑΝΣΗΣ ΣΤΗΝ ΠΕΡΙΟΧΗ ΤΟΥ ΛΙΜΕΝΑ ΘΕΣΣΑΛΟΝΙΚΗΣ Χισόφοος Γ. Κουίας*, Αχιλλέας Γ. Σαμαάς** *Ο.Λ.Θ. Α.Ε.,
Ορισμός: u(t) = 0 (t < 0) και u(t) = 1 (t 0) (4.1) Από τις (4.3) και (4.4), προκύπτει ότι το βηματικό σήμα u(t) είναι σήμα ισχύος.
 4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
4. ΑΝΑΛΥΣΗ ΒΑΣΙΚΩΝ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΗΜΑΤΩΝ 4.. To βημαικό σήμα (step signal) u(t) Ορισμός: u(t) = 0 (t < 0) και u(t) = (t 0) (4.) Μέση ιμή: = (4.) Ενέργεια: Ε = lim [T ] [-, ] u (t).dt (4.3) Μέση
Αρχίζοντας με το ΜΙΝΙΤΑΒ 15
 Αρχίζοντας με το ΜΙΝΙΤΑΒ 15 Βήματα: 1. Ανοίγουμε το φύλλο εργασίας (Worksheet) του Minitab 15. 2. Ανοίγουμε το φύλλο εργασίας του Excel με το όνομα data Ν115.xls. 3. Μαρκάρουμε τα δεδομένα μας από το φύλλο
Αρχίζοντας με το ΜΙΝΙΤΑΒ 15 Βήματα: 1. Ανοίγουμε το φύλλο εργασίας (Worksheet) του Minitab 15. 2. Ανοίγουμε το φύλλο εργασίας του Excel με το όνομα data Ν115.xls. 3. Μαρκάρουμε τα δεδομένα μας από το φύλλο
Μέθοδοι ανάλυσης οικονοµικής σκοπιµότητας έργων. Κοινωνικο- οικονοµικές. Ο ορισµός του έργου. Τεχνική αξιολόγησης έργων
 Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Το ανικείµενο ων µεθόδων αξιολόγησης έργων: 7 Μέθοδοι ανάλυσης κοινωνικο-οικονοµικής οικονοµικής σκοπιµόηας έργων Να αναλύσει και εκιµήσει ποσοικά ις ωφέλειες και ις δαπάνες που δηµιουργούναι από ην υλοποίηση
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
Πυκνότητα στερεών σωμάτων κυλινδρικού σχήματος
 Χρήση διαστημόμετρου για εύρεση πυκνότητας στερεών σωμάτων γεωμετρικού σχήματος Προκειμένου να υπολογιστεί η πυκνότητα σε στερεά σώματα γεωμετρικού σχήματος πραγματοποιούνται μετρήσεις α) της μάζας τους
Χρήση διαστημόμετρου για εύρεση πυκνότητας στερεών σωμάτων γεωμετρικού σχήματος Προκειμένου να υπολογιστεί η πυκνότητα σε στερεά σώματα γεωμετρικού σχήματος πραγματοποιούνται μετρήσεις α) της μάζας τους
Multi Post. Ενδοριζικοί άξονες ανασύστασης
 Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
«Προσβλητική» και «απαξιωτική» ενέργεια
 Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 1 Οκωβρίου 2010 Φύλλο 127 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου 67 ΧΡΟΝΙΑ αφιερωµένα σην ενηµέρωση Παρασκευή 1 Οκωβρίου 2010 Φύλλο 127 www.fonitisparou.gr Έος 65 ο Νέα Περίοδος
Τι είναι η Πυκνότητα;
 ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας Μέτρηση Πυκνότητας Τι είναι η Πυκνότητα; Ένας κόκκος πλαστελίνης έχει την ίδια πυκνότητα με ένα μεγάλο κομμάτι από το ίδιο υλικό. Ένα ρίνισμα σιδήρου έχει την ίδια πυκνότητα
ΦΥΣΙΚΗ Α ΓΥΜΝΑΣΙΟΥ Φύλλο Εργασίας Μέτρηση Πυκνότητας Τι είναι η Πυκνότητα; Ένας κόκκος πλαστελίνης έχει την ίδια πυκνότητα με ένα μεγάλο κομμάτι από το ίδιο υλικό. Ένα ρίνισμα σιδήρου έχει την ίδια πυκνότητα
Μεταλλική συμπεριφορά
 Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Μεαλλική συμπεριφορά Χαρακηρισικά μεαλλικής συμπεριφοράς Μεγάλη θερμική και ηλεκρονιακή αγωγιμόηα Μεγάλο μέρο ελασικόηας όγκου (Β=10 11 Pa) Μεαλλική λάμψη Ι. Μονέλο Drude (Jelliu) Σύμβαση προσήμου: e:
Δύο κύριοι τρόποι παρουσίασης δεδομένων. Παράδειγμα
 Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
25 χρόνια από την πτώση του τείχους του Βερολίνου
 25 χρόνια από ην πώση ου είχους ου Βερολίνου Πόσα γνωρίζουμε για ο είχος που χώριζε ην σημανικόερη πόλη ης Γερμανίας σε Αναολικό και Δυικό μπλοκ; Με αφορμή ην 25η επέειο ης πώσης ου είχους ου Βερολίνου
25 χρόνια από ην πώση ου είχους ου Βερολίνου Πόσα γνωρίζουμε για ο είχος που χώριζε ην σημανικόερη πόλη ης Γερμανίας σε Αναολικό και Δυικό μπλοκ; Με αφορμή ην 25η επέειο ης πώσης ου είχους ου Βερολίνου
(1A) Ε ΟΜΕΝΑ 2Φ10 Σ. Η. ΔΡΙΤΣΟΣ. Yλικά : Άνοιγµα δοκού: l 0-2 = l 2-3 = 4,40 m ΖΗΤΟΥΜΕΝΑ: Σ..Η ΔΡΙΤΣΟΣ
 (A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
(A) κός Οπλισένυ Σκυρδέας Ενισχυένη ε Σρώση Οπλισένυ Σκυρδέας- Έλεγχς άρκειας ιφάνειας Ε ΟΜΕΝΑ Άνιγα δκύ: l 0- l -3 4,40 m Φ0 Η. Πλάς δκύ: b 0 mm Πλάς σήριξης: b. ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ σ 0mm 0
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ - 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Μαΐου 2010 Ώρα : 10:00-12:30 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) θέματα. 2) Να απαντήσετε σε όλα τα θέματα. 3)
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 6 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Μαΐου 2010 Ώρα : 10:00-12:30 Οδηγίες: 1) Το δοκίμιο αποτελείται από επτά (7) θέματα. 2) Να απαντήσετε σε όλα τα θέματα. 3)
Στατιστική για Οικονομολόγους ΙΙ ΛΥΜΕΝΑ ΘΕΜΑΤΑ παλαιοτέρων ετών από «ανώνυμο φοιτητή» (Στις ΛΥΣΕΙΣ ενδεχομένως να υπάρχουν λάθη. )
 Στατιστική για Οικονομολόγους ΙΙ ΛΥΜΕΝΑ ΘΕΜΑΤΑ παλαιοτέρων ετών από «ανώνυμο φοιτητή» (Στις ΛΥΣΕΙΣ ενδεχομένως να υπάρχουν λάθη. ) Πίνακας Περιεχομένων Εργασία η... Θέμα ο :... Θέμα ο :... 4 Θέμα 3 ο :...
Στατιστική για Οικονομολόγους ΙΙ ΛΥΜΕΝΑ ΘΕΜΑΤΑ παλαιοτέρων ετών από «ανώνυμο φοιτητή» (Στις ΛΥΣΕΙΣ ενδεχομένως να υπάρχουν λάθη. ) Πίνακας Περιεχομένων Εργασία η... Θέμα ο :... Θέμα ο :... 4 Θέμα 3 ο :...
ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Βασικά Εργαλεία και Μέθοδοι για τον Έλεγχο της Ποιότητας [ΔΙΠ 50], ΕΡΓΑΣΙΑ 4. Ενδεικτική Λύση
![ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Βασικά Εργαλεία και Μέθοδοι για τον Έλεγχο της Ποιότητας [ΔΙΠ 50], ΕΡΓΑΣΙΑ 4. Ενδεικτική Λύση ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Βασικά Εργαλεία και Μέθοδοι για τον Έλεγχο της Ποιότητας [ΔΙΠ 50], ΕΡΓΑΣΙΑ 4. Ενδεικτική Λύση](/thumbs/71/64440698.jpg) ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Βασικά Εργαλεία και Μέθοδοι για τον Έλεγχο της Ποιότητας [ΔΙΠ 50], 2012-13 Άσκηση 1 ΕΡΓΑΣΙΑ 4 Ενδεικτική Λύση (α-1.5) Σωστό. Το διάγραμμα στελέχους φύλλου, ως ειδική περίπτωση ιστογράμματος,
ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ Βασικά Εργαλεία και Μέθοδοι για τον Έλεγχο της Ποιότητας [ΔΙΠ 50], 2012-13 Άσκηση 1 ΕΡΓΑΣΙΑ 4 Ενδεικτική Λύση (α-1.5) Σωστό. Το διάγραμμα στελέχους φύλλου, ως ειδική περίπτωση ιστογράμματος,
4. Το βάρος ενός αντικειμένου είναι 98Ν. Πόση είναι η μάζα του; a. 9,8kg b. 46kg c. 10kg d. 1kg
 1. Στη θέση Α είναι ένα ελατήριο με κρεμασμένο στην άκρη του ένα σώμα. Στη θέση Β είναι το ίδιο ελατήριο με το ίδιο σώμα στην άκρη. Τι μπορεί να συμβαίνει ώστε η επιμήκυνση στη θέση Α να μην είναι ίδια
1. Στη θέση Α είναι ένα ελατήριο με κρεμασμένο στην άκρη του ένα σώμα. Στη θέση Β είναι το ίδιο ελατήριο με το ίδιο σώμα στην άκρη. Τι μπορεί να συμβαίνει ώστε η επιμήκυνση στη θέση Α να μην είναι ίδια
IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHELL MOMENTUM BALANCES) ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VELOCITY DUSTRIBUTION) ΣΤΡΩΤΗ ΡΟΗ (LAMINAR FLOW)
 IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHE MOMENTUM BAANCES ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VEOCITY DUSTIBUTION ΣΤΡΩΤΗ ΡΟΗ (AMINA FOW Σε αό ο κεφάλαιο θα εξεάσοµε πως µπορούµε να εφαρµόσοµε ο ισοζύγιο ορµής σε ένα διαφορικό όγκο (differential
IΣΟΖΥΓΙΑ ΟΡΜΗΣ (SHE MOMENTUM BAANCES ΚΑΤΑΝΟΜΗ ΤΑΧΥΤΗΤΑΣ (VEOCITY DUSTIBUTION ΣΤΡΩΤΗ ΡΟΗ (AMINA FOW Σε αό ο κεφάλαιο θα εξεάσοµε πως µπορούµε να εφαρµόσοµε ο ισοζύγιο ορµής σε ένα διαφορικό όγκο (differential
Χρειάζεται επείγουσα...νοσηλεία!
 αφιερωµένα σην ενηµέρωση Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Φύλλο 95 Έος 65ο Νέα Περίοδος Έος Ίδρυσης 1945 ΑΝΤΩΝΗΣ ΑΝΤΩΝΙΑΔΗΣ Αποκλεισική συνένευξη
αφιερωµένα σην ενηµέρωση Εβδομαδιαία πολιική εφημερίδα Πάρου - Ανιπάρου Σκέψου ον πλανήη σου... ανακύκλωσε η ΦΩΝΗ σου Φύλλο 95 Έος 65ο Νέα Περίοδος Έος Ίδρυσης 1945 ΑΝΤΩΝΗΣ ΑΝΤΩΝΙΑΔΗΣ Αποκλεισική συνένευξη
ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών
 ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών Βασιλεία Ι. Σινάνογλου Ειρήνη Φ. Στρατή Παναγιώτης Ζουμπουλάκης Σωτήρης Μπρατάκος Εξώφυλλο Εργαστηριακό Τμήμα (ημέρα ώρα)
ΕΡΓΑΣΤΗΡΙΟ ΕΝΟΡΓΑΝΗΣ ΑΝΑΛΥΣΗΣ ΤΡΟΦΙΜΩΝ Οδηγός Συγγραφής Εργαστηριακών Αναφορών Βασιλεία Ι. Σινάνογλου Ειρήνη Φ. Στρατή Παναγιώτης Ζουμπουλάκης Σωτήρης Μπρατάκος Εξώφυλλο Εργαστηριακό Τμήμα (ημέρα ώρα)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΜΒΑ «Νέες Αρχές ιοίκησης Επιχειρήσεων» ΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ υναµικά Μονέλα Χωροθέησης σο Σχειασµό Εφοιασικής Αλυσίας ΕΠΙΜΕΛΕΙΑ: ΛΑΜΠΡΟΠΟΥΛΟΣ
Εισαγωγή στην Στατιστική (ΔΕ200Α-210Α)
 Τμήμα Διοίκησης Επιχειρήσεων (Α. Ν.), Τ.Ε.Ι. Κρήτης Εργαστήριο Στατιστική-Ασκ2, Εαρ. 2018 Σελίδα 1 από 11 2η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση, χρησιμοποιώντας ως δεδομένα, μεγέθη
Τμήμα Διοίκησης Επιχειρήσεων (Α. Ν.), Τ.Ε.Ι. Κρήτης Εργαστήριο Στατιστική-Ασκ2, Εαρ. 2018 Σελίδα 1 από 11 2η Εργαστηριακή Άσκηση Σκοπός: Η παρούσα εργαστηριακή άσκηση, χρησιμοποιώντας ως δεδομένα, μεγέθη
ΜΑΘΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΘΡΑΚΩΣΗ ΚΑΙ ΣΚΥΡΟΔΕΜΑΤΟΣ
 ΜΑΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΡΑΚΩΣΗ ΚΑΙ ΤΗ ΧΛΩΡΙΩΣΗ ΣΚΥΡΟΔΕΜΑΤΟΣ Η Διπλωμαική Εργαία παρουιάηκε ενώπιον ου Διδακικού Προωπικού ου Πανεπιημίου Αιγαίου Για ην Εκπλήρωη ων Απαιήεων για ο Δίπλωμα Ειδίκευης
ΜΑΗΜΑΤΙΚΑ ΜΟΝΤΕΛΑ ΓΙΑ ΤΗΝ ΕΝΑΝΡΑΚΩΣΗ ΚΑΙ ΤΗ ΧΛΩΡΙΩΣΗ ΣΚΥΡΟΔΕΜΑΤΟΣ Η Διπλωμαική Εργαία παρουιάηκε ενώπιον ου Διδακικού Προωπικού ου Πανεπιημίου Αιγαίου Για ην Εκπλήρωη ων Απαιήεων για ο Δίπλωμα Ειδίκευης
