! "#$%&'!()'"" %*+,-.+* "(*/0(/*'1 %+%/&2(#+)" 3#(4 0+)(#)/+/" (*2#("5 3#(4 02"' "(/1#'" +) (4' '6+&/(#+) +. 42%&+71#%&+#1" 2)1 8')'(#0 1#$+*%4#"$"
|
|
|
- Αριάδνη Μιχαηλίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"#$ %& '"$ (& )*+,- (.//& /02/3.! "#$%&'!()'"" %*+,-.+* "(*/0(/*' %+%/&2(#+)" 3#(4 0+)(#)/+/" (*2#("5 3#(4 02"' "(/#'" +) (4' '6+&/(#+) +. 42%&+7#%&+#" 2) 8')'(#0 #$+*%4#"$" 4$5$4$ )678 *,9,, : *;< =$ >6?@*+ <,6 a %02*2#23 "( )*"'"+. &%4 5&263/&2*,&' %02*2#237 83*43% 9%*:3$0*2.7 ;<=< )">?@AB7 BCDDEF 83*43%7 G63 H3263$'&%40I b J:"'#2*"% &%4 J,"'"+. ;$"+$&/7 FKF7 FLBCMA 8&>3%N#$+7 F#02$*&I c -3O&$2/3%2 "( 5&263/&2*,0 &%4 K2&2*02*,07 9%*:3$0*2. "( P3'0*%Q*7 ;<=< )"> MR SLDDDAT7 S*%'&%4I d -3O&$2/3%2 "( U""'"+.7 K2",Q6"'/ 9%*:3$0*2.7 KJLADM?A K2",Q6"'/7 KV343%I e W*003%0,6&(20Q"''3+ X# )3$'*%7 W&''"202$&003 A?7 -LATA?C )3$'*%7 Y3$/&%. AE3,3*:34 CA =,2"N3$ BDD?I!%&' :3$0*"% $3,3*:34 Z!#%3 BDADB C"+ D7+E,7E+6< F"FE#*7?";D?; 6GE?#?9+?E@ H?7-6I6+J9"<J 9"+; 6GE*#& #;AR. B?D * ED6KE#!7;6DD F+"LJ K"+ 6I"#E7?";*+?#J D76*<J D7+*76MJ ANOOB *<*F7?I6 <J;*@?,D,*#,E#*7?";D& H?7- R. 7-6 *I6+*M6 #?K67?@6 ;E@96+ "K "KKDF+?;M?; 7-6,#";*# *;< -*F#"?<,*D6D& *;< -*#K 7-6 *I6+*M6 #?K67?@6 ;E@96+ "K "KKDF+?;M K*7-6+6< K"+ )6;<6#?*; <?F#"?<D$ P-6;?;<?I?<E*#D -*I6 I*+?*9#6 9?+7- D7*76D& *D?D& K"+ 6L*@F#6& 7-6,*D6?; R.?D?7D6#K *; 6?M6;I*#E6& H-?,- EDE*##J,*;;"7 96 6LF+6DD6< 6LF#?,?7#J?; *?7 I6,7"+D E;<6+,";D?<6+*7?";$ Q; 7-*7,*D6& Q(Y X) := <67(Q >(Y X)),*; "K76; 96 ED6< *D!7;6DD F+"LJ& H? K"+ * 9J *?7 I6,7"+ Y?; 7-6 A,";D7*;7B 6;I?+";@6;7 6;M6;<6+6< 9J * +6D?<6;7,-*+*,76+?86< 9J X$ QK *?7 DF*,6?D,";;6,76<& M#"9*# E;?;I*<*9?#?7J,*; 96 <676+@?;6< K+"@?7$ )"+6"I6+&?7,*; 96 ED6<?; *## 7-6 EDE*# #",*#,*#,E#*7?";D #?S6 7-6 <676+@?;*7?"; "K 6I"#E7?";*+?#J D?;ME#*+ 7+*?7 I6,7"+D *;< 7-6?+ #",*#?;I*<*9?#?7J *;< *77+*,7?I?7J$ P6,";,#E<6 H? L76;<6<,*D6 D7E<?6D <6@";D7+*7?;M 7-6 ED6KE#;6DD "K QT 7-6,*#,E#*7?"; "K NOOD E;<6+ -*F#"R<?F#"?< M6;67?,D AQB& "K 6I"#E7?";*+?#J D76*<J M6;67?, <?@"+F-?D@D ANOUDB H?7- & O$*"$* F+"F"+7?";*#?7J "E7FE7D A*; *DDE@F7?"; 7-*7?D 9E7 7-6 KE#!#@6;7 "K H-?,-?D * F+?"+? -?M-#J 6L,6F7?";*#B AQQB& *;< "K NOUD H?7-"E7 DE,- F+"F"+7?";*#?7J AQQQB$ V-6D6,*D6 D7E<?6D D-"E#< *#D" -*I6 D"@6?;76+6D7?; 7-6?+ "H; +?M-7 K"+ 7-6 DF6##6< "E7,*#,E#*7?"; +6,?F6D *;< :'-3+*";!7;6DDW!7;6DD F+"LJW -*F#"R<?F#"?< NOOW 6I"#E7?";*+?#J D76*<J M6;67?, <?@"+F-?D@W 6I"#ER 7?";*+?#J D7*9#6 M6;67?, <?@"+F-?D@W?<6*#RK+66 M6;67?, <?@"+F-?D@W 6I"#E7?";*+?#J D76*<J F"#J@"+F-?D@W 6I"#E7?";*+?#J D7*9#6 F"#J@"+F-?D@W?<6*#RK+66 F"#J@"+F-?D@ <= >'(4++&+8#02& %*'2$?&' V-?D F*F6+?D *9"E7 *; 6K!,?6;7 7""# K"+ *;*#JD?;M +6#*7?I6#J,"@F#?,*76< )"<6#D D7+E,7E+6D F#ED?;76+F+67*7?"; +E#6DW 7-6"+?6D *+6 +E#6D K"+,";D7+E,7?;M *;< V-6"+67?,*# 6I"#E7?";*+J 9?"#"MJ *?@D 7" F+6<?,7 7-6 F+"F6+7?6D "K "+M*;?D@D K+"@ 6I"#E7?";*+J,";D?<6+*7?";D$ V-6+6K"+6& H6 H*;7 "E+ F"FE#*7?"; <J;*@?,*# :X"++6DF";<?;M *E7-"+$ N@*?#T Y$*$Y$@678Z9?"#"MJ$#6?<6;E;?I$;#$ [;"H; *D \*;D )678$ 5E7-"+ N@*?#T "#"K$#6?@*+Z8""#"M?$DE$D6 QOO' /]%/R]%^ F+?;7/QOO' /]%/R]00 ";#?;6 _ (.// V*J#"+ ` C+*;,?D U=QT /.$/.^.//]%/]%^$(./.$%.((%0-77FT//HHH$?;K"+@*H"+#<$,"@
2 !"#!"#"!" $%&' ()* +",%-.(/ $%&'( )%*$+(,-.%/0 -% './-'*2*'-,(',- -3' ('4'( %)./&.4.&+,( $,7'0-3' /,-+*,( )*,$'8%*7 )%* %+* &.09%+*0' -3,- %) -3' -3'%*: %) 0-*+9-+*'& 2%2+(,-.%/0; )+/&,$'/-,((: &.))'*'/- )*%$ -3' 9(,00.9,( &.))'*'/-.,( '<+,-.%/,/& &.09*'-'=-.$' )%*$,(.0$05 63' %/(:./&.4.&+,(=('4'( 2,*,$'-'*0-3,-,*' 8'(( *'2*'0'/-'&./ -3' (,--'* )%*$,(.0$0,*' $.>*,-.%/ *,-'05?/ %-3'*,02' )'8 %*>,/.0$0 0,-.0): -3',00+$2-.%/0.$2(.9.-(: $,&'./ -3' 9%/0-*+9-.%/ %) &.09*'-'=-.$' $%&'( /%/=%4'*(,22./> >'/'*,-.%/0;,/& /% %*>,/.0$ 9%$'0 9(%0' -% -3' (.)' 3.0-%*.'0.$2(.9.-(:,00+$'&./ &.))'*'/-.,( '<+,-.%/ 2%2+(,-.%/ $%&'( (&-4) 5/49&:5 A.-3-3'./&.4.&+,(=%*.'/-'& 9%/9'2- %) '/4.*%/$'/- '02%+0'&./ -3' -3'%*: %) 0-*+9-+*'& 2%2+= (,-.%/0; -3' 9(,00.9,( (%>.0-.9 '<+,-.%/ 8.-3 n B-3' 02,-.,( &'/0.-: %)./&.4.&+,(0C 9,/ ' *'8*.--'/,0 &n/&t = r(e)n; 8.-3 E = n/k,/& r(e) = r D (! E); -% *./> %+- -3,- -3' /%/=9%/0-,/9: %) r 03%+(& ' &+' -%, *',9-.%/ %) -3'./&.4.&+,(0 -% -3'.* 0+**%+/&./> '/4.*%/$'/-5 6% &'(4', (.--(' &''2'*./ -3.0 *',9-.%/; r 03%+(& ' &'9%$2%0'&./-%, 0+$ %) 2'* 9,2.-,.*-3,/& &',-3 *,-'0; r(e) = b(e) d(e);,0-3'0' -8% 9%/-*.+-.%/0 *'2*'0'/- *,&.9,((: &.))'*'/- $%&'0./ /&.4.&+,(=('4'( $'93,/.0$0 9,/,))'9- r5 A' (',4' %2'/ -3' 0%$'83,-,878,*& <+'0-.%/ %) 3%8-3' E=&'2'/&'/9' %) r 03%+(& ' -3%+>3- %),0 './> &'*.4'& )*%$,/ E=&'2'/&'/9' %) b,/& d B-3.0 &'2'/&'/9' ',0.(: '9%$'0 9%$2(.9,-'& 0./9' /'>,-.4'.*-3 *,-'0,*' /%-,((%8'&C5?/0-',&; 8' >% )%* -3' $.9*%09%2.9 2'*02'9-.4'5 6% -3.0 '/& 9%/0.&'*, -3%+>3- 'E2'*.$'/-./ E.0 7'2-,*-.!9.,((: 9%/0-,/-; '5>5 : 3,*4'0-./> %*,&&./>./&.4.&+,(0; &'2'/&./> %/ 83'-3'* n.0 0$,(('* %* (,*>'* -3,/ K5?/ -3,- 9,0'; b,/& d '9%$' 9%/0-,/-05 F%* -3' &', $',/0-3,-./&.4.&+,(0 &.',- *,/&%$G )%* -3'.* $',/0-3,- :%+/>,*' %*/./ 9(+-93'0 %),4'*,>' 0.H' c B8.-3 2%00.(: c =!C -3,-,*' 2*%&+9'&./, I%.00%/ 2*%9' *,-' bjc5 63'*' 'E.0- /% %*>,/.0$ (.)' 3.0-%*:5 < K(,00.9,( &.))'*'/-.,( '<+,-.%/ 2%2+(,-.%/ $%&'(0 9,/ ' 4'*: +0')+( )%* >'/'*,-./>.&',0,%+- 83,- *',( 2%2+(,-.%/ $%&'(0 $.>3- &%5 L%8'4'*; -3'.* 2,*,$'-'*0,*',0.9,((: 23'/%$'/%(%>.9,(,/&,/: *'(,-.%/ /&.4.&+,(=('4'( 2,*,$'-'*0,*',- '0- )+&>'& (,97 %) 0+)!9.'/-(: 9(',*=9+-./-'*2*'-,-.%/ *+('0 -%, $,-93./>.%(%>.9,( *',(.-: $,7'0-3,- -3': 9,//%- ' 9%/0.&'*'& $%&'(0./ -3' 0-*.9-0'/0' %) -3' 8%*&,/& 03%+(& *,-3'* ' 9,(('& $'-,23%*0 %* -%: $%&'(05 M(-3%+>3./ -3'.*.$$'&.,-'./-'*2*'-,-.%/; -3' '2.0-'$%(%>.9,( 0-,-+0 %) 9(,00.9,( &.09*'-'=-.$' 2%2+(,-.%/ $%&'(0 ),*'0 +-, (.--(' '--'* -3,/ -3,- %) -3' &.))'*'/-.,( '<+,-.%/ $%&'(0; -3':,*' )+*-3'* 0,4'& : -3' ),9- -3,-,- '<+.(.*.+$ -3'.*-3 *,-' >'/'*,((: 0,-.0!'0,/ '<+,-.%/ -3,-.0 '<+,( -% -3' '<+.(.*.+$ '<+,-.%/ )%* -3' 2%2+(,-.%/ &'/0.-.'0 %), &.09*'-' >'/'*,-.%/ $%&'( 8.-3 $,-93./> 'E2'9-'& (.)'-.$' %))02*./> /+$'*05 N/&'* -3',00+$2-.%/ %) *,/&%$ $,-./>; ,-'$'/-,(0% 'E-'/&0 -% -3' $%&'(0 %) 9(,00.9,( 2%2+(,-.%/ >'/'-.905 O%- %/(: -3,-;,(0% -3'./4,0.%/ %), /'8 -:2'./-%,/ 'E.0-./> '<+.(.*.+$;.) (%%7'&,- %/, >'/'*,-.%/,0 %22%0'& -%, *',(=-.$',0.0;.0 &'09*.'& : '<+,-.%/0-3,- $,-93-3%0' %) ),$.(.,* &.09*'-'=-.$' $%&'(05 P%,(-3%+>3-3*%+>3%+- 8' +0' -3' (,/>+,>' %) 0-*+9-+*'& 2%2+(,-.%/ $%&'(0; :%+ $,:./ -3' 9%/9*'-' 'E,$2('0!*0- *',& -3'./-'*2*'-,-.%/ %) -3' 4,*.%+0 0:$%(0 %/(: 9+*0%*.(: ')%*' -+*/./> -% -3' '<+,-.%/0 -% *'>,./ :%+* 0'/0' %) ),$.(.,*.-:,/& -3'*',)-'* *'*',& -3' &'!/.-.%/0 -%,9<+,./- :%+*0'() ' 0-*+9-+*'& 2%2+(,-.%/ 2'*02'9-.4'5 Q',(./> ' &:/,$.90 %) 0-*+9-+*'& 2%2+(,-.%/ $%&'(0 %)-'/ (',&0 -% +/9%$)%*-,(: 3',4: $,-3'$,-.9,( )%*$,(.0$5 R+97.(:; -3' 0+S'9- %) ,2'* ('-0 +0 *'0-*.9- %+*0'(4'0 -% 2%2+(,-.%/ &:/,$.9,( '<+.(.*.,,/& >'/'*,-.%/=8.0',*>+$'/-; 83'*' -3' '<+,-.%/0 0.$2(.): -% $%*' ),$.(.,* %/'0; %/(:./-'*2*'-'& 8.-3, $%*' 2*%2'*,--'/-.%/ -%.%(%>.9,( *',(.-: T!UV5!" #$% &'(&%)*+ ', -(./+-'(!*(%++ /(0!*(%++ )'2-%+ W9%(%>.9,((:;!-/'00 9,/ ' &'!/'&,0-3' 3:2%-3'-.9,(,0:$2-%-.9 -.$'=,4'*,>'& *,-' %) 'E2%/'/= -.,( >*%8-3 ρ(y, E) *'0+(-0 )*%$, -3%+>3- 'E2'*.$'/-./ %/' ('-0, 9(%/' %) -:2' Y
3 .!"#$%&' "( )*"'"+*,&' -.%&/*,0!"# mutant population size population sizes of other species mutant population size population sizes of other species resident population size resident population size $%&'()!* +,,'-.(/.%0 02.3) %4)/ 02.(/-5)(-/, )%&)5/,') /4 67/8'05 )980).* +.3) -8):%/, :/-) 02 / -:/,/( 808',/.%0 -./.);.3).(/-5)(-/, 67/8'05 )980). :/ <) :/,:',/.)4 /-.3).%=) /5)(/&) 02.3) ='./. &(0>.3 (/.)- /..3) :0=='%.7 /..(/:.0(* &(0> % / )(&04%: )5%(0=). E?@A;B@C* D)();.3).)(= E)5%(0=).F %-; %.3).(/4%.%0 02.3).3)0( (':.'()4 808',/.%0- G)*&*?!!;!@;BHCI; -'880-)4.0 ()2)(.0 )5)(7.3%&; >3).3)( <%0.%: 0( /<%0.%:; 0'.-%4) / %4%5%4'/,.3/. 3/-.3) 80.).%/,.0 %!'):) %.- 808',/.%0 47/=%:/,,7 (),)5/. <)3/5%0'(* +2; /- 4)8%:.)4 % $%&'()!;.3) )5%(0=). %- 4).)(=%)4 <7.3) /..(/:.0( 02 / ()-%4). 808',/.%0; E = E /..( (X); 0) -8)/J- 02 %5/-%0 ".)-- G0( %5/-%0 )980).?B"CI* K0.3)( /=) %- 40=%/..(/-5)(-/, 67/8'05 )980).; 0( %.3) -8):%/, :/-).3/..3) )5%(0=). %- :0-./.; 40=%/..(/-5)(-/, )%&)5/,')?@@C* +5/-%0 ".)-- %-.3) =/%.00, 20( 4)/,%& >%.3,0&L.)(= M/(>%%/ )50,'.%0; >%.3 ='./.- %.3) (0,) 02 G8(0-8):.%5)I %5/4)(-* N) ()/-0 20( '-%&.3) /4O):.%5) E3780.3).%:/,F%.3) 08)%& -).):) %-.3/. = ',/.%0-02 %.)() ()8(04':) :,0/,,7 <'. 20,,0> -0=) P)4),%/ 8/..)(* Q/(. 02.3) =)./, :0-.(':.% ).%:/, :,0/, %4%5%4'/,- 0'. 02 4%8,0%4 P)4),%/ 0)- %-.0 4%=%%-3.3) /5)(/&) 022-8(%& '=<)( 02 / <%0,0&%:/, %4%5%4'/, <7 / 2/:.0( 0)L3/,2.0 =/J) '8 20(.3) 2/:..3/. %..(/-=%.- 0,7 3/,2 02 %.- /,,),)-.0 )/:3 02 % (%&* D):);.3) ".)-- 02 / 4%8,0%4 83)0.78) %- 4)")4 /-.3) /-7=8.0.%:.%=)L/5)(/&)4 (),/.%5) &(0>.3 (/.) 02.3) -0 4%=%%-3)4 '=<)( 02 4)-:)4/.-; % /.30'&3. )98)(%=). >3)().3)-) 4)-:)4/.- /,, 3/5).3) -/=),%2)L 3%-.0(7 8/(/=).)(- /-.3)%( /:)-.0(* R3)-) 8/(/=).)(- %:,'4) =/.%& 8(08)-%.%)- >3%,) =/.%& 0880(.'%.%)- /() :0-%4)()4 / :0=80). 02.3) )5%(0=).* R3%- :0-.(':.%0 >0(J-; /.,)/-. 20( = ) ):0,0&%:/, -:)/(%0- :0-%4)()4-0 2/(; %.3/. <7 =)/- 02.3%- ".)-- :0:)8.; 0) /((%5)- /..3) -/=) )50,'.%0/(7 8()4%:.%0-20( 83)0.78)- /- <7 >0(J%&.3(0'&3.3) 2',, %.(%:/:%)- 02 P)4),%/ %3)(%./:)?@AC* S) />/().30'&3.3/. >3) %. :0=)-.0 :/,:',/.%& 80,7=0(83%: )50,'.%0/(7 0'.:0=)- %.3) 8()-):) 02 &)).%: :0-.(/%.-; /4 /,-0 20( -0=) :0=8,%:/.)4 -)9'/, %.)(/:.%0-?!#C;.3%- -30(.:'. 0,0&)( >0(J-; /4.3)() %- 0 /,.)(/.%5) <'..0 &0 </:J.0.3) </-%:- /4 :/,:',/.).3) %5/-%0 ".)-- 02 /,,),)- 0,0:% 80.).%/,,7 /22):.%&.3).(/%.- '4)( :0-%4)(/.%0.0 /((%5) /..3) :0(():. 8()4%:.%0* N,7 %.3) -%=8,)-. :/-)-; %. %- 80--%<,).0 "4 )98,%:%. 20(=',/- 20(.3) %5/-%0 ".)--* D0>L )5)(; 20( -0=) 02.3) -%=8,)( ):0,0&%:/, -:)/(%0-;.3)() )9%-. &004 8(09%)- G>3%:3 '20(.'/.),7 02.) /() %:0(():.,7 ()2)(()4.0 /- O'-. ".)--I* T%.3 8(097 >) =)/ 3)() / U'/.%.7.3/. % /,, 0::/-%0- U'/.%./.%5),7 )U'/,.0 ".)--; 7). :/ <) -'<-.%.'.)4 20( %. % -0=) )50,'.%0/(7 :/,:',/.%0-* +.3%- 8/8)(; >) >%,, 4)(%5) 0) 2'(.3)( 8(097; 0( (/.3)( / )5) -%=8,)( 8(097 20( / :0==0,7 '-)4 8(097;.3/. -30',4 )/-) )50,'.%0/(7 :/,:',/.%0-20( /,/(&) :,/-- 02 :0=8,%:/.)4 ):0,0&%:/, /4 808',/.%0 &)).%:/, -:)/(%0-* T3/. U'/.%.%)- :/ <) '-)4 /- ".)-- 8(097 4)8)4-0.3) '-) 0) >/.-.0 =/J) 02 ".)--* R3) =/% '-) 02 %5/-%0 ".)-- %- %.3) )50,'.%0/(%,7 -.)/47 -.(/.)&7 GVWWI.3)0(7 /4 /4/8.%5) 47/=%:-; -':3 /-.3) :/,:',/.%0 02 8/%(>%-) %5/-%<%,%.7 8,0.- GQ+Q-I; / :05)%)..00, 20( //,7-%& VWW- /4.3)%( )50,'.%0/(7 -./<%,%.7 8(08)(.%)- 20( -:/,/(.(/%.- G-)) >) -3/,, %.)(8()..3) /:(07= VWW 3)() /- )50,'.%0/(%,7 -.)/47; %*)*; '%5/4/<,); -.(/.)&7 -%:).3) 4)"%.%0 02.3) VWW :0:)8. 40)- 0. %=8,7.3/. VWW- /() )50,'.%0/(%,7 -./<,)I* $0(.30-)
4 !""!"#"!" $%&' ()* +",%-.(/ evolutionarily stable global ESS evolutionarily unstable global ESS mutant trait value resident trait value local ESS branching point #$%&'( )* +,$'-$.( $/0,.$$2$ $%/8,. $/9$:,3(9 $/ 3;( &55(' 2(<3 5,/(28 6< 3;(!3/(.. 6< 563(/3$,2 =&3,/3.,., <&/:3$6/ 6< 3;( =&3,/3,/9 3;( '(.$9(/3 3',$3.* >;( <6&' 5,/(2..;6-.6=(,23('/,3$0( 56..$2( :6/!%&',3$6/.8 $/9$:,3$0( 6< :6''(.56/9$/%24 9$<<('(/3 (062&3$6/,'4 5;(/6=(/,* >;( &55(' '$%;3 5,/(2 (?52,$/. 6&' &.( 6<.3(,94 $/.3(,9 6< 3;(.3$22 =6'( :6==6/.3,2(,. $/3('5'(3,3$6/ <6' 3;( =$992(.4=62 $/ 5,'3$:&2,' &.(.8 6<3(/,22 6/( /((9. $., D&,/3$34 3;,3 $..$%/ (D&$0,2(/3 36!3/(..7.$%/@5'6?4C =.$%/(ρ)* >;( =,$/ 345( 6< (:626%$:,2.:(/,'$6 -;('(, %669 9(,2 6< $626%$:,2 9(3,$2 :,/ ( $/:6'56',3(9,/9 4(3, %669!3/(.. 5'6?4 $.,0,$2,2( $. -;('( 3;( :6==&/$34.3,3( :6/0('%(. 36,/ (D&$2$'$&= 56$/38 %$0$/% '$.( 36, :6''(.56/9$/%24 /6/E"&:3&,3$/% (/0$'6/=(/3* F/ 3;,3 :,.(8 3;(,55'65'$,3(8 <6' (,.$24 $/3('5'(3,2(,/9 $<,22 $/9$0$9&,2.,'( 6'/ (D&,2 (,.$24 :,2:&2,2(8!3/(.. 5'6?4 $. 2/@R G C8 3;( 26%,'$3;= 6< 3;(,0(',%( 2$<(3$=( 6<<.5'$/% /&=('8 6',.$: '(5'69&:3$6/ ',3$68 R G * 0/23423& &-5 6(6%/7 8% 92)5-*%/ 2):; )2)<!39&3(&-)4 /%5-*%)& %)=-/2).%)&5" # 5%92)* (553.6&-2) -5 &(& &% *%.24/(6-9 6(/(.%&%/57 ()* %)9% R G ()* ρ (/% 5.22& -) &% H!"IC* F/ %(/(',28 $/9$0$9&,2. :,/ ( 6'/ $/ =6'( 3;,/ 6/( 56..$2(.3,3(8,. $.8 <6' (?,=52(8 3;( :,.( $/.5,3$,224 9$.3'$&3(9 565&2,3$6/. -;$:; ;,0( 36 ( 9(,23 -$3; 4 3,J$/%.5,3$,2 26:,3$6/ 6/ 6,'9,., :6=56/(/3 6< 3;( h@%&%/24%)%-&;c<5&(&% 6< $/9$0$9&,2.8 -;$:; 3;(/ :6/.$.3. 6<, 26:,3$6/,/9, 5;4.$626%$:,2.3,3(8 52&. 56..$24, =,'J(' 6<.6:$,2.3,3&.8 (3:* K&( 36 6&',..&=53$6/ 6< (/0$'6/=(/3,2 :6/.3,/:48 3;( 5;4.$626%$:,2.3,3( :,/ ( '(52,:(9 4, 5'6?4.3,3( :6/.$.3$/% 6<,%( 36%(3;(' -$3; 3;(.3,3( 6< $'3;* F/3(%',3$/% 6&3 60(',%( %$0(. 3;( /(?3E%(/(',3$6/ 65(',36'!* R G :6''(.56/ ;( 96=$/,/3 ($%(/0,2&( 6< 3;$. 65(',36'* L..5(22$/% 6&3 3;( %(/(',2,'%&=(/3 $/ =,3;(=,3$:,2, (9 3;( ;(&'$.3$: 3('=. '(D&$'(. 3;( $/3'69&:3$6/ 6< 3(:;/$:,2 =,3;(=,3$:. 3;,3 $. /63 %('=,/( 36 3;( =(..,%( 6< 3;$. 5,5('8 -( 6/24 %$0( 3-6 (?,=52(..;6-$/% 3;( (..(/3$,2. $/ 3;(.$=52( $2( :,.(* >;( =,3;(=,3$:,2 9(3,$2. 6< 3;( 9(!/$3$6/,/9 :,2:&2,3$6/ 6< R G $/ 3;( %(/(',2 :,.( =,4 ( <6&/9 $/ H!G8!)I8 -$3; 3;( 2,3(.3 %(/(',2$M,3$6/ $/ HN"I* >?(.6:% #$/$3( he.3,3(.5,:(.,/9 :26/,2 '(5'69&:3$6/* >;( %'6-3; 6<, 565&2,3$6/ 6<!/$3(.3,3( $/9$0$9&,2. $/ :6/3$/&6&. 3$=( $. %$0(/ 4 9 N = (" + #)N, 9t
5 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"# $%&'& N () *%& +&,*-' -. )/0*(0 2&3)(*(&) -. (32(+(240) (3 2(..&'&3* )*0*&) ' /'&)&3*,-3*&8*9 N '&.&') *- *%& :4*03*)5 ;- <&&/ *%& 3-*0*(-30 =4'2&3 -$9 $& )4//'&)) 2&/&32&3,&) -3 *%& *'0(* +&,*-' -. *%& :4*03*) 032 '&)(2&3* &3+('-3:&3*5> ;%& :0*'(,&)! 032 " 0'& =4(* 4/.'-: /&',0/(*0 '0*&)5 ;%& -..?2(0@-30,-:/-3&3*) -. " &A40 *%& *'03)(*(-3 '0*&) =&*$&&3 *%&,-''&)/-32(3@ %?)*0*&)9 *%& 2(0@-30,-:/-3&3*) &A40 :(34) *%& -+&'0 '0*&) -. )*0*& *'03)(*(-3).'-: *%& %? )*0*&) :(34) *%& %?)*0*&?2&/&32&3* 2&0*% '0*&)5 ;%&,-:/-3&3*) -.! &A40 *%& 0+&'0@& /&',0/(*0 =('*% '0*&) (3 2&/&32&3,& -3 *%& %?)*0*& -. *%& /0'&3* )/(* 0,,-'2(3@ *- *%& %?)*0*& -. *%& -..)/'(3@5 ;%& (3+0)(-3!*3&)) ρ,-''&)/-32) *- *%& '(@%*:-)* &(@&3+04& -.! + "5 B'@4(3@ -3 =0)().'-: =('*%) *- =('*%) () /-))(=& -3C.-',-3)*03* &3+('-3:&3*)5 ;%& '&0)-3.-',%--)(3@ *%& =('*%) 0) '&.&'&3,& /-(3*) () *%0* 4)40C *%& )&* -. =('*% )*0*&) (),-3)(2&'0=C ):0&' *%03 *%&.4,-:/&:&3* -. )*0*&) 3&,&))0'C *- 2&),'(=& %-$ 03 (32(+(240 /0))&) *%'-4@% (*) (.&5 ;%&!')*,-:/-3&3*) -. N $( '&.&' *- *%& =('*% )*0*&)5 ;- )*&/ =0,< 032.-'*% =&*$&&3 0 /-/40*(-3 )*0*& =('*% '0*&?=0)&2.-':0():9 $& 3&&2 0 :0*'(8 # (3D&,*(3@ *%& +&,*-' -. =('*% '0*&) (3*- *%& )/0,& -.,%03@&) (3 2&3)(*(&) -. 0 (32(+(240)9 C-43@ (<&E! F F F F. # ; = F F... F F! F F B),03 =& )&&3.'-: *%().-':409 # ; /'-D&,*) *%& )/0,& -. /-/40*(-3 '0*&) -3*- *%& )/0,& -. =('*% '0*&)5 ;%& G(&<:033HIC&3=&'@HJ&*K =('*%?'0*&?=0)&2 0//'-0,% *- )*'4,*4'&2 /-/40*(-3) () *- /4* (32(+(240),&3*'& )*0@&5 73 *%& /'&)&3*,0)&9 *%& )*0*& (32(+(240 :-+&) 0,,-'2(3@ *- 0 J0'<-+,%0(3 $(*% <((3@9 032 *%& /'-=0=((*C *%0* (32(+(240) =-'3 (3,&'*0(3 =('*% )*0*&) 0* 0@& a 0'& 0(+& 032 '&)(2& (3,&'*0(3 )*0*&) =C *%& :0*'(8 & a" #5 L&3,&9 *%& 0+&'0@& =('*% '0*& 0* 0@& a )/(* -4* 0,,-'2(3@ *- *%& =('*% )*0*& -. *%& /0'&3* 032 *%0* -. *%& <(2) () (a) = # ;!& a" #5 ;%() &8/'&))(-3 )%-$) *%& :&,%03(): 0) &:=-2(&2 (3 *%& :0*'(,&)!9 " 032 #9 (* () /-))(=& *-,0,40*& *%& 0+&'0@& =('*% '0*& (32(+(240.'-: (*) =('*% )*0*&) 032 a5 L&3,&9 0@& 032 =('*% )*0*& *-@&*%&' 0'& 0 /'-8C )*0*&.-' -.,0,40*(3@ *%& 0+&'0@& =('*% '0*&) -. (32(+(240) -+&' *%&(' (.&5 ;%& +&,*-' -. /-/40*(-3 =('*% '0*&) )0*()!&) 0 :0*'(8 +&')(-3 -. M-*<0N) (3*&@'0 &A40*(-3 B(t) = $%(,%.-' τ '&24,&) *- t+τ F B(t a) (a) 2a + # ;!e (t+τ)" N( τ) B(t) = F B(t a) (a) 2a. O4=)*(*4*( &8/-3&3*(0 *'(0 )-4*(-3 & ρa *%0* *%& (3+0)(-3!*3&)) ρ,03 =&,0,40*&2.'-: =C )-+(3@,%0'0,*&'()*(, &A40*(-3E 2-:(303* &(@&3+04& -. (ρ) =!, $(*% (z) := F & za (a) 2a 032 *%0* U &A40) *%& &(@&3+&,*-' $(*% &(@&3+04&! -. (ρ). *%&-'C -. '&3&$0 &A40*(-3) *&) *%0*.-' τ (32&&2 B(t) (<& & ρa U5 P'-: *%&.0,* *%0* 0)- B(t) = # ;!N(t)9 (*.--$) *%0* *%& ρ.-432 (3 *%() :033&' 0)- )0*()!&) 2&*(! + " ρ$) = F5
6 !"#!"#"!" $%&' ()* +",%-.(/ $%& '()* +%,-.! := / (a),a = (/) 0, R / =,%+)0' -) %5!. 6) %+8%-'* %5 (z) 0&- 8%*)')3-0,,-7&-0*- 9)'( z: 0.*% )'*,%+)0' -) ,-7&-0*-* 9)'( z; <-7-: ρ )* 8%*)')3-9(- R / >! 0, )* -20')3-9(- R / <!; $)0..=: '(- 5%..%9)2 0&24+-' *(%9* '(0' '()* R / &)2('54..= 70 >- )'-&8&-'-, 0* 0 03-&02-.)5-')+- %55*8&)2 4+>-&;?(- 03-&02-.)5-')+- 4+>-&* %5 %55*8&)2 >= ),)3),40.* >%& ),)55-&-' *'0'-* -@40. "?!: 9(-&- " )* 0 3-7'%& '(0' (0* 0.. )'* 7%+8%-'* -@40. '%!;?(- 0'4&0. 8&%>0>).)'=,)*'&)>4')% '% 03-&02- '(-*- 4+>-&* %3-& )* '(- *'0')%0&=,)*'&)>4')% 2--&0'-, >= '(- 2--&0')% 8&%7-** )'*-.5: );-;: '(- &)2(' -)2-3-7'%& U %5! 7%&&-*8%,)2 '% R / : %&+0.)A-, *47( '(0' "? U =!; B%)2 *% 2)3-* "?!U = "? R / U = R / "? U = R / ; 0(.23% C-,-.)0,)8.%),* 9)'( -3-&=>%,= >%& -@40.: >4' 8%'-')0..= 5%& 0,)*')7')% >-' * 0, *; D '(- 70*- %5,)8.%), (-&+08(&%,)'-* 9)'( >4' 0 *)2.- >)&'( *'0'-: R / -@40.* (0.5 '(- *4+ %5 '(- 03-&02-4+>-&* %5 %55*8&)2 50'(-&-, %& +%'(-&-,;?(- 507'%& %-E( ) 7%+-* 5&%+ '(- 9)*( '%,-!- R / *47( '(0' '(- %4'7%+- 5&%+ 0)3- -3%.4')%0&= ')%* >0*-, % '()* F%55*8&)2 4+>-&G 5%& ),)3),40.* +0'7(-* '(- %4'7%+- 5&%+ +%&-,-'0).-, 2--')70..= >0*-, ')%*; H(- '(- *-I-* 0&- *-80&0'-: '(- *-I,)55-&-7-7%+-* % '%8 %5 '(- 8(=*)%.%2)70. *'&47'4&-; 6% ) '(- *)+8.-*' 70*-: '(- (E*'0'- -@40.* '(- 80)& J*-I: 8(=*)%.%2)70. *'0'-K; D,)8.%),*: )5-3-&=>%,= )* >%& -@40. >4' 5%& '(-)& *-I: '(- 7%&&-*8%,)2 -I'E2--&0')% %8-&0'%& )*! =! ( ) l55 l 5+, L l +5 l ++ 9)'( l 55 '(-.)5-')+- 4+>-& %5,042('-&* % : l 5+ '(-.)5-')+- 4+>-& %5,042('-&* % : l +5 '(-.)5-')+- 4+>-& %5 *%* % : 0, l ++ '(-.)5-')+- 4+>-& %5 *%* % : 0.. 5%& '(- +4'0': 0* '(-= (088- '% %774& ) '(- -3)&%+-'0. 0, 2--')7 >07M2&%4, 8&%3),-, >= '(- &-*),-' 8%84.0')%;?(- *)+8.-*' 70*- )* 9(- '(- *-I,-'-&+)0')% )* ),-8-,-' %5 '(-.%74* ) 9()7( '(- +4'0',)55-&* 5&%+ '(- &-*),-' 0* '( &)'- l 55 = p 5 f : l +5 = p + f : l 5+ = p 5 m: l ++ = p + m: 9)'( m 0, f '(- 4+>-&* %5 %55*8&)2 50'(-&-, 0, +%'(-&-, %3-& 0.)5-')+-: 0, p + 0, p 5 '(- 8&%>0>).)'= %5 >-)2 >%& %& ; D '(0' 70*-:! (0* &0M %- 0, R / =! L (p 5f + p + m). <?()* &-*4.' 7%4., 0.*% (03- >-- %>'0)-, +%&-,)&-7'.= >= %>*-&3)2 '(0' -3-&=>%,= )* >%& *'%7(0*')70..= -@40.: (03)2 -I07'.= '(- *0+- 8&%>0>).)'= %5 >-)2 >%& +0.- %& ; H- '(- 2-' R / >= N4*' 03-&02)2 %3-& '(- 8%**)>).)')-*; O* 0 74&)%*)'=: 9- +-')% '(0' 9(- '(-.%74* % 9()7( '(- +4'0',)55-&* (0* 0 )"4-7- % '(- *-I,-'-&+)0')%: 9-70 *').. -, 48 9)'( '(- *0+- 5%&+4.0 >=,-!)2 p + 0, p 5 '% >- '(- 0*=+8'%')7 8&%>0>).)')-* %5 >-)2 >%& %& : );-;: >= 7(%%*)2 5%& p + 0, p 5 '(- 7%+8%-'* %5 '(- &)2(' -)2-3-7'%& U %5!: 0,,-!)2 m 0, f 020) 0* '(- 4+>-& %5 %55*8&)2 50'(-&-, %& +%'(-&-, %3-& 0.)5-')+-: );-;: f = l 55 + l +5 : m = l 5+ + l ++ ;?(-: >= 4*)2 R / = "?!U: -I07'.= '(- *0+- 5%&+4.0 5%& R / )* %>'0)-,; P.= '(- *)+).0&)'= %5 '(- -I8&-**)%* )* 8.-0*)2Q '% '- p + 0, p 5 : 9-!&*' (03- '% '- R / ; O%'(-& +0''-& )* '(0' 9(- )' 7%+-* '% 7%*),-&)2 '&0)' -3%.4')%: 9-9).. (03- '% 077%4' 5%& '(- 507' '(0': 7%'&0&= '% '(- *)'40')% ) (-&+08(&%,)'-*: '(-,-3-.%8+-'0. 80''-&* %5 *-80&0'-
7 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"# $%&%$ '(% )%*%$$'(+,-.+//%(%)0 2%)*%3 0('+0 4%*05($ 6+,, 7%)%(',,- *5)$+$0 5/ 065 *5895)%)0$3 0:% 0('+0$ 5/ 0:% 8',%3 Y 8 5( X 8 3 '). 0:5$% 5/ 0:% /%8',%3 Y / 5( X / ;) 7%)%(',3 0:%$% 065 $%&<.%9%).%)0 0('+0 4%*05($.5 )50 %45,4% +).%9%).%)0,- '$ 0:%- '(% *5=9,%. >- 0:%+( 7%)%0+* *54'(+')*%?5( 8=0'0+5)', *54'(+')*%3.%9%).+)7 5) 6:%0:%( 5)% /5*=$%$ 5) +)0%(8%.+'0% 0%(8 %45,=0+5) $0'(0+)7 6+0: %)5=7: '**%$$+>,% 7%)%0+* 4'(+'0+5)3 5( 5) %45,=0+5) $0'(0+)7 /(58 ' 7%)%0+*',, %(+$:%. 959=,'0+5) 5( 75+)7 5) /5( $5,5)7 0:'0 +0 (=)$ 5=0 5/ 0:% +)+0+', 4'(+'0+5)@ A),- +) 0:% %&0(%8% *'$% 0:'0 0:% *54'(+')*%$ >%06%%) 8',% '). /%8',% 0('+0$ '(% ',, B%(53 0:% /%8',% '). 8',% *5<%45,4% '$ +/ 0:%- 6%(% $%9'('0% $9%*+%$ ;) 0:% 50:%( %&0(%8% *'$%3 X 8 = G(X / )3 0:% $0').+)7 '). 8=0'0+5)', 4'(+'0+5) +) 0:% 8',% '). /%8',% 0('+0 4%*05($ +$ /=,,- *5((%,'0%.3 '). 6% *') $9%'C 5/ ' $+)7,% %45,=0+5)'(- 0('+0 4%*05(3 %&9(%$$%..+//%(%)0,- +) 8',%$ '). /%8',%$?%&*%90 6:%) G +$ %D=', 05 0:% +.%) ) 6:+*: *'$% 6% :'4% E=$0 ' $+)7,% 0('+0 4%*05(@ < ;) 7%)%(',3 0:'0 +$3 +/ 0:%-.5 )50 (%.=*% 05 ' 8'0(+& 6+0: $58% $9%*+', *5)4%)+%)0 $0(=*0=(%3 )%&0<7%)%('0+5) 59%('05($.5 )50 ',,56 %&9,+*+0 %&9(%$$+5)$ /5( 0:%+(.58+)')0 %+7%)4',=% 2%)*%3 0:%(% +$ ' )%%. /5( ' )%&0,'-%( 5/ 9(5&+%$3 0:+$ 0+8% /5( R F G:% 8'+) 0:%5(%8 5/ 0:% 9'9%(3 0%,,+)7 :56 0:% *:'('*0%(+$0+* 95,-)58+', 5/ 0:% )%&0<7%)%('0+5) 8'0(+& %4',='0%. '0! *') >% =$%. 05.%*+.% '>5=0 7,5>', =)+)4'.'>+,+0-3 +$ $0'0%. '). 9(54%. +) H%*0+5) I ;) H%*0+5) J3 6% $C%0*: 0:% %$$%)0+', 7%58%0(+*', )'0=(% 5/ 0:% (%$=,0 /5( 0:% $9%*+', *'$% 5/ K K 8'0(+*%$3 '$ 0:+$ +$ 0:% 5),- *'$% ',,56+)7 )%'0 9+*0=(%$ ;) H%*0+5) L3 6% $=88'(+B%,5*', *',*=,'0+5) (%*+9%$ 6:+*: *') '85)7 50:%( 0:+)7$ >% =$%. /5( 0:%.%0%(8+)'0+5) 5/?,5*', 9(59%(0+%$ 5/@ %45,=0+5)'(+,- $+)7=,'( 95+)0$3 0:'0 +$3 95+)0$ X 6:%(% [ ρ/ Y ](X, E '00( (X)) = F?0:%.%(+4'0+4% >%+)7 0'C%) /5( 0:%!($0 '(7=8%)0 5/ ρ3 6(+00%) '$ Y 6:%) ρ 6'$!($0 +)0(5.=*%.3 '/0%( 6:+*: 0:% (%$=,0+)7 /=)*0+5) +$ %4',='0%. '0?X, E '00( (X))@ G:%$% 065,+)%$ 5/ '(7=8%)0 *=,8+)'0% +) H%*0+5) " +) 0:% +)0(5.=*0+5) 5/ 0:% )%6!0)%$$ 9(5&- Q(Y X) ;) H%*0+5)$ MN#3 6% 9(%$%)0 0:(%% *'$% $0=.+%$ 5/ :56 0:% '>$0('*0 (%$=,0$ *') >% 9= =$%!" #$%! & '()*+%)*,-.,) *-/0*,- 0-2 *+ %3+%-*,-.,) -,-'-%40+*/% )*(% G:% (%$=,0 0:'0 6% '(% '/0%( +$ >'$+*',,- 0595,57+*', +) )'0=(% ;) 0:+$ $%*0+5)3 6%,'- >'(% 0:% =).%(,-+)7 $0(=*0=(% /5( 0:% *'$% 5/ K K 8'0(+*%$3 6:%(% %4%(-0:+)7 *') %'$+,- >% 4+$=',+B%. G:+$ ',$5 ',,56$ =$ 05 $:56 :56 0:% 7%)%(',!0)%$$ 9(5&- 05 >%.%$*(+>%. +) 0:% )%&0 $%*0+5) *') >% $%%) '$ ' )'0=(', %&0%)$+5) 5/ 0:% R F <! )5)<+)4'$+5) *(+0%(+5) /5( O%$,+% 8'0(+*%$ G:% 7%)%(', (%$=,0 +$.%$*(+>%. +) H%*0+5) I G:% 9(55/ 0:%(% 8'C%$ )5 =$% 5/ 0:% +.%'$.%4%,59%. +) 0:+$ $%*0+5) ;/ -5= '(% 8'+),- +)0%(%$0%. +) '99,+*'0+5)$ 5( +) 0:% 7%)%(', 9(55/3-5= 8'- E=$0 '$ 6%,,.+(%*0,- 854% 05 0:'0 $%*0+5) G:+$ $%*0+5) +$ 5),- 8%')0 /5( 0:5$% 6:5 7% '0%. >- $%%+)7 :56.+//%(%)0 (%$=,0$ *5))%*0 G5 C%%9 5=( '(7=8%)0$ (%,'0+4%,- =)*,=00%(%.3 6% $:',, *5=*: 0:%8 +) 0:% /5(8 5/ 0:%.%(+4'0+5) 5/ %$0+8'0%$ /5( 0:% $+7) 5/ 0:% +)4'$+5)!0)%$$ /5( $+89,%.+$*(%0%<0+8% 85.%,$ +) 8'0(+& /5(8 G:% +)$+7:0$ 0:=$ 5>0'+)%. '99,- 6+0:5=0 *:')7% 05 %$0+8'0+)7 0:% $+7) 5/,)?R +) 85(% *589,+*'0%. 85.%,$ 0:'0 ',,56 0:% )%&0<7%)%('0+5) 59%('05( 5/ 0:%,+)%'(+B%. 8=0')0.-)'8+*$ 05 >% (%9(%$%)0%. '$ ' 8'0(+& P5)$+.%( 0:%,+/% :+$05(- 7('9:+*',,- (%9(%$%)0%. +) Q+7=(% J3 6+0: 0:% $=(4+4', 9(5>'>+,+0+%$ F s F 3 s!! '). /%(0+,+0+%$ f! 3 f K F3.%0%(8+)%. >- 0:% %)4+(5)8%)0 $%0 >- 0:% *588=)+0- '$ 6%,, '$ >- ' 950%)0+',,- %45,4+)7 0('+0 4%*05(?G5 '45+. *,=00%(3 6% $:',, +) 0:+$ $%*0+5) :+.% 0:% %4%(<9(%$%)0 '(7=8%)0$ (Y X)@ G+8% +$ $=995$%. 05 (=) +) $0%9$ '). 0:% +).+*%$! '). K 5/ 0:% 959=,'0+5) $+B%$ n i (%/%( 05 '7% %&9(%$$%. +) )=8>%( 5/ 0+8% $0%9$ G:% 959=,'0+5) (%*=((%)*% *5((%$95).+)7 05 0:+$,+/% :+$05(- +$ N = 7N 6+0: N = ( n! n K ), 7 = ( sf f! s F f K F s! ).
8 !"#!"#"!" $%&' ()* +",%-.(/ s n n 2 f s 0 f 2 newborns $%&'() *+,%-./) /%0) %234(5 '2)6 34 %//'23(73) 48 R # 97: ;) %:3)(.()3)6 72! P <!=+ >) 97(793)(%23%9 )?'73%4: 04( 7 -'37:3 %: 7 94:237:3 ):@%(4:-):3 2)3 ;5 7 ()2%6):3 94--':%35 %2 P (λ) := λ A f! s # λ f A s! s # = #, 7:6 ρ = /:(λ 6 ), 8)() λ 6 %2 3) 94(()2.4:6%:& 64-%:7:3 )%&):@7/') <%+)+B λ 6 λ i )+ >)() %2 4:/5 7 2%:&/) ;%(3 2373)B 24 C5 ()8(%3%:& 3) 97(793)(%23%9 )?'73%4: 72 %3 %2 ) )) <$%&'() D= 373 E: 3%2 )F7-./) >)()04() R # (=!) = f! s # + f A s! s #.! = f! s # λ! + f A s! s # λ A R #! ρ #. P (!) =! R #. P (!) # ρ #. G48)@)(B ':04(3':73)/5 3) /733)( ()2'/3 64)2 :43 )F3):6 34-4() &):)(7/ -46)/2 /79H%:& 3) 9('9%7/ I)(4 %: 3) -73(%F "+ $%&'() J 6).%932 3) '2'7/ 9(%3)(%7 04( 8): 3) -46'/'2 40 3) 64-%:7:3 )%&):@7/') 40 7 A A -73(%F %2 2-7//)( 37:!+ E0 8) %:6%973) %: 3) 27-).%93'() 3) 40 3) 3(79) 7:6 6)3)(-%:7:3 04( A A K)2/%) -73(%9)2 <$%&'() L=B %3 ;)94-)2 9/)7( 85 04( 2'9-73(%9)2 3%2 94-./%973)6 94-;%:73%4: 40 9(%3)(%7 97: ;) ()./79)6 ;5 3) 2%-./) R # M9(%3)(%4:+ f s 0 λ - + f 2 s s 0 λ -2 R 0 0 λ d λ $%&'() D+ N)/73%4: ;)38)): R # 7:6 λ 6 04( 3) /%0) %234(5 40 $%&'() A+
9 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"! det -2 λ d < trace - #$%&'( )* +,( -./&(0 2 3,( 3'.4(.56 6(3('7$ '$9 2' :,$4, $30 67$5.53 ($%(5-./&( $0 07.//(' 3,.5!* +,( ;.'.</. 0(;.'.3(0 3,( '(%$50 :$3, '(./.56 47;/(9 ($%(5-./&(0* =5 3,( /$5( 6(3 = 3'.4(!>. '(./ ($%(5-./&( 4'00(0!? 5 3,( /$5( 6(3 = 3'.4(!>. '(./ ($%(5-./&( 4'00(0!>.56 2' 47;/(9 ($%(5-./&(0 4'00$5% 3,( /$5( 6(3 =! 4''(0; ,($' 76&/&0 2&'3,(' 6(3.$/0.<&3 3,( /4.3$5 2 3,( '(./ ($%(5-./&(0.'( %$-(5 $5 #$%&'( A* -2 - ( ) A = 0 θ 2 θ 0 det non-feasible region 0 λ d < 0 λ d > P() > 0 P() = 0 P() < 0 R 0 = - 2 A = ( λ θ 0 0) #$%&'( B* +,( -./&(0 2 3,( 3'.4(.56 6(3('7$5.53 3, <( '(./$C(6 <D 8 8 E(0/$( 7.3'$4(0!* +,( 2'7&/.0 4''(0;56 3 3,( %(5('$4 2'7 2! 5 3,( 4&'-( $56$4.3(6 <D 3,(.'':> :$3, λ.56 F3,(G θ( i ) 2'(( ;.'.7(3('0* H3( 3,.3 P (!) =! 3'.4( + 6(3* #' E(0/$( 7.3'$4(0 ( a b c I) > P (!) =! J a J,* trace K2 :( 3,(5./0 /L :,$4, '(%$50 $5 3,( F3'.4(>6(3GM;/.5( 4.5 <( '(./$C(6 <D %(5('./ 55M 5(%.3$-( 7.3'$4(0 F#$%&'( "G> $3 <(47(0 4/(.' :,D 3,( P (!) > I 4'$3('$5 6(0 53 (93(56 3 %(5('./ 55M5(%.3$-( '$4(0* +,( 3'&</( 47(0 2'7 3,( '$%,3 &;;(' '(%$5 <(3:((5 3,( /$5( P (!) = I.56 3,( ;.'.</. 6(3 =! N 3'.4(8 $5 :,$4,./0 3,( 0(456 ($%(5-./&( $0 /.'%(' 3,.5 5(* #$%&'( "./0 0&%%(030,: 5( 7.D 03$// ;&3 3,( P (!) > I 4'$3('$5 3 %6 &0( (-(5 :,(5 3,( &56('/D$5% ;;&/.3$5 6D5.7$40 /( '( %(5('./ '$4(0.0 <.0$0 2' 3,( 4./4&/.3$5 2 3,( 5((6(6 $5-.0$5!35(00(0O.5D '(0$6(53> $54/&6$5%.5D ;'0;(43$-( P@@>,.0 $5-.0$5!35(00 C('* Q(54(>.5D 7&3.53 (R&./ 3 3,( '(0$6(53!560 $30(/2 5 3,( /$5( 0(%7(53 2'7 (3'.4(>6(3) = (I,!) 3 (3'.4(>6(3) = (8,!)* S( 0,.//.00&7(!'03 3,.3.3 3,( '(0$6(53 ;,(53D;( 3'.4( 8 = N 6(3* F+,$0 456$3$5 $0 %&.'.53((6 :,(5 2' 3,( '(0$6(53! $0 $''(6&4$</(*GT00&7( 5: 3,.3 3,( 03'.3(%$(0 &56(' 450$6('.3$5.'( 4,.'.43('$C(6 <D. 3'.$3 -(43' 2'7 07( R n * K2 3,( /$2(M,$03'D ;.'.7(3('0
10 !"#!"#"!" $%&' ()* +",%-.(/ det non-feasible region A = ( λ θ 0 λ ) -2-0 θ 2 A = ( θ 0 ) 0 λ d < 0 - λ d > 2 trace P() > 0 P() = 0 P() < 0 λ d = $%&'() "* +,-.%/%,0 ()&%2 3( - &)2)(-/ 2242)&-,%5) # # 6-,(%7!* 89) 3(6'/-: ;(():<2=,,9) &)2)(%; 3(6 3! 2,9) ;'(5) %2=%;-,)=.0,9) -((>? >%,9 λ θ( i ) 3()) <-(-6),)(:* =)<)2= ;2,%2'':/0 2,9),(-%, 5);,(? -20 ;2,%2'': ;'(5) %2,(-%, :<-;) >%// 6-<, - ;2,%2'': ;'(5) B3 3( 2 -/,)(2-,%5) :,(-,)&0,9) ;(():<2=%2& <%2, )5)( /%): %2,9) ()&%2 P (!) = C?,9)2,9),('./):6) ()&%2 ;-2 2)5)(.) ()-;9)=.0 3//>%2& - ;2,%2'': <-,9 %2,(-%, :<-;) :,-(,%2& 3(6,9) ():%=)2,* D)2;)? 2 :,(-,)&0 ;-2 %25-=),9-, %: ;22);,)=, %,.0 - ;2,%2'': <-,9 %2,(-%, :<-;)* 89) ;2;/':%2 %:,9-, %3 3( -// :,(-,)&%):.', - <(:<);,%5) E++ P (!) > C?,9)2 2 :,(-,)&0,9-, ;-2.) ;22);,)= ;2,%2'':/0,,9%: <(:<);,%5) E++ ;-2 %25-=)* D)2;)? '2=)(,9):) ;2=%,%2:? %3,9),(-%, :<-;) %: ;22);,)=,9) <(:<);,%5) E++ %: %2=))= '2%25-=-./)* F> ;2:%=)(,9) ;-:) >9)() 3(,9) ():%=)2,,(-;) # = G =),* +%2;),9) <<'/-,%2 %: -, )H'%4 /%.(%'6?!,9)2 9-:,9) 3(6 (! C C! ) %2:,)-= 3,9) 6() &)2)(-/ 3(6 %2=%;-,)= %2 $%&'() " 3( det 0 non-feasible region 0 0 λ d < 2 trace P λ d > ( resident) λ $%&'() I* J;-,%2 3,9) ;9-(-;,)(%:,%; </026%-/ %2 =)<)2=)2;) 2,(-;) -2= =),*
11 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"# $%&'()*+,(&- &'%)*. = / 0*& 2+ %3 *4%$56*7 89: $%8 &-(3; 9< % 595:6%&(93 6(=(3> (3 &,9 5%&)-*+,(&- &-* +&'%&*>8 5%'%$*&*'?*(3> &-* $(>'%&(93 '%&*?*&,**3 &-9+* 5%&)-*+ %30 39 $(>'%&(93 <9' &-* B3 &-%& )%+*7 &-* 5'*=(9:+ %'>:$*3& >9*+ &-'9:>- 93 &-* )930(&(93 &-%& )69+* &9 &-* 0*& <!7 9' *C:(=%6*3&68 &'%)* <. B3 &-* <9669,(3> +*)&(937,* +-%66 *4&*30 &-* %?9=* '*+:6& <9'.. $%&'()*+ &9 >*3*'%6 n n $%&'()*+ 2+ % 5'*5%'%&(937 D(>:'* E +-9,+ $9'* 0*&%(6+ 9< -9, (3 &-*.. )%+* &-* 69)%&(93 9< &-* )-%'%)&*'(+&() $(%67 %30 -*3)* 9< (&+ '99&+7 )-%3>*+,(&- &'%)* %30 0*&!" #$% P(&) > ' ()*+%)*,-.,) /%-%)0 n n 20+)*(%3 F*& P (λ; Y X) := 0*&(λ4 5(Y X)) 0*39&* &-* )-%'%)&*'(+&() $(%6 9< &-* 3*4&G>*3*'%&(93 $%&'(4 9< &-* 6(3*%'(H*0 083%$()+ 9< % Y $:&%3& (3 %3 X '*+(0*3& )9$$:3(&8 I*45'*++*0 +9 &-%& &-* 6*%0(3> )9*<!)(*3& (+ 59+(&(=*J Theorem 23 $30*43%5 6 *0 #%*%7&4&8'3 *( (i) /"+$&92*, 9&$&/353$0 4393%4,"%5*%#"#0'. "% 523 5$&*5, (ii) 523 5$&*5 09&,3 *0,"%%3,534, (iii) P (!; Y X) > K f or all Y = X, &%4 I(=J ( P / λ)(!; X X) = K (:2*,2 *0 &':&.0 523,&03 *(!(X X) *0 *$$34#,*8'3) "$ ( P / λ)(!; X X) = K &%4 R K <! ("$ Y,'"03 5" X (523 '&553$,"%4*5*"% *0 +#&$&%5334, ("$ 3;&/9'3, 8. (. P / λ. )(!; X X) = K &%4 ( P / λ)(!; Y X) > K ("$ Y,'"03 5" X). <% 523 "523$ 2&%4 *( 523% 52&5 Y,&% *%7&43 X. P (!; Y X) < K f or some Y, =$""( B3=%+(93!&3*++ %30 R K %'* )93&(3:9:+ (3 &-* 0*$9>'%5-() 5%'%$*&*'+ %30 -*3)* (3 &-* &'%(&+ R K 9< &-* '*+(0*3& *C:%6+! L8 %++:$5&(937 %66 %6&*'3%&(=* +&'%&*>(*+ )%3?* '*%)-*0 <'9$ &-* '*+(0*3&?8 <9669,(3> % )93&(3:9:+ 5%&- &-'9:>- &'%(& +5%)* M-*'*<9'* =%6:*+ 9< R K )%3 9)):' &-%& )%3?* '*%)-*0 &-'9:>-?(<:')%&(93+ )9$5%&(?6*,(&- R K?*(3> &-* 09$(3%3& *(>*3=%6:* 9< % 393G3*>%&(=* $%&'(4 %30 &-* %++:$5&(93 &-%& P (!; Y X) > K M-* *4(+&*3)* 9< +:)- %3 *(>*3=%6:* (+ >:%'%3&**0?8 &-* N*''93OD'9?*3(:+ &-*9'*$ M-* %++:$5&(93+ 9< 393G3*>%&(=(&8 $%;* &-* 09$(3%3& *(>*3=%6:* 393G3*>%&(=* '*%6 %30 -*3)* % )93&(3:9:+ <:3)&(93 9< &-* 0*$9>'%5-() 5%'%$*&*'+ %30 9< &-* &'%(&+ I@(>*3=%6:*+ %'* +$99&- <:3)&(93+ *4)*5& <9' %3 (30*&*'$(3%)8,-*'* &-*8 )'9++P >(=*3 &-%& &-* 09$(3%3& *(>*3=%6:* (+ %6,%8+ '*%67 (& (+ 3*)*++%'(68 )93&(3:9:+7 %6&-9:>- 39& +$99&-7 9=*' +:)- % )'9++(3>J M-* %++:$5&(93 &-%& P (!; Y X) > K $%;*+ &-%& &-* 09$(3%3& *(>*3=%6:* (+ 39& %669,*0 &9 $9=* )93&(3:9:+68 &9 %?9=*! (3 &-* $%33*' (30()%&*0 (3 &-* 69,*' 6*<& 5%3*6 9< D(>:'* Q D9' &-* +*)930 5%'&7 (< P (!; Y X) < K <9' +9$* Y &-*'* $:+&?* +9$* '*%6 λ >! +:)- &-%& P (λ; Y X) = K A(3)* &-(+ λ (+ %3 *(>*3=%6:* %30 +(3)* R K (Y X) (+ 09$(3%3&7 *(&-*' R K (Y X) = λ >! 9' R K (Y X) > λ >! ID9' >*3*'% $(%6+ P,(&- 59+(&(=* 6*%0(3> &*'$7 &-*'* (+ %6+9 %,%8 &9 5'90:)* % 59+(&(=* '*%6 '99& %?9=*! <'9$ % +&%'&(3> +(&:%&(93,-*'* &-*'* %'* 39 +:)- '99&+,-(6* %66 &-* &($* ;**5(3> P (!; Y X) > K7 &9,(& &-'9:>- &-*?(<:')%&(93 0*5()&*0 (3 &-* 69,*' '(>-& 5%3*6 9< D(>:'* Q R9,*=*'7 <9' 393G3*>%&(=* $%&'()*+7 &-(+?(<:')%&(93 (+ ':6*0 9:&?8 9?+*'=(3> &-%& S:+&?*<9'* +:)- %?(<:')%&(93,9:60 9)):' &-*'* -%=* &9 *4(+& )9$56*4 *(>*3=%6:*+,(&- $90:6:+ 6%'>*' &-%3 &-* 393G3*>%&(=* '*%6 09$(3%3& *(>*3=%6:*7,-()-,9:60 )93&'%0()& (&+ 09$(3%3)*J
12 !"#!"#"!" $%&' ()* +",%-.(/ Y = X: other Y: P λ not allowed by assumption: impossible: $%&'() *+,-.(-%/& 0(2. 3%-'.-%/ 45)() -5) 62%/./- )%&)/7.8') )9'.83!: ;)(-.%/ <%0'(;.-%/3 0-5) (- =.--)(/ 0-5) ;5.(.;-)(%3-%; =8>/2%.8 0. =3%-%7) 2.-(%?.() )?;8'6)6 <> -5).33'2=-%/ -5.- Y X) > B+ C/ -5) /)?- 3);-%/: 4) ;/3%6)( %/ 2() 6)-.%8-5) -8<? 0( 5%&5)( 6%2)/3%/.8 -(.%- 3=.;)3: 45%;5 %3 <.3)6 8.(&)8> / 8;.8 ;.8;'8.-%/3+ D)(): 4) /8> 6%3;'33-5) %2=8%;.-%/3 0-5).<7) -5)()2 0( -5) 6(.4%/& 0 ECE3+ $( -5) ;.8;'8.-%/ 0 ECE3 /) ;./ 8.(&)8> ;/;)/-(.-) / 387%/& 0( Y %/ P (!; Y X) = C0 /): %/.66%-%/: G/43 32) =%/- %/ Y FH=8./) 0( 45%;5-5) %/7.3%/!-/)33 %3 /)&.-%7): -5)/ -5) %/7.3%/!-/)33 %3.83 /)&.-%7) %/.88 =%/ ;//);- - -5%3 =%/- <>. ;/-%/''3 = )3 /- ;(33 /) 0-5) 38'-%/ ;'(7)3 0 P (!; Y X) = B+ I3 3/.3 3';5. ;'(7) %3 ;(33)6: -5)!-/)33 ;5./&)3 0(2 /)&.-%7) - =3%-%7)+,%2%8.(8>: %0 /) G/43. =%/- 0( 45%;5 %/7.3%/!-/)33 %3 =3%-%7): -5)/ %/7.3%/!-/)33 %3.83 =3%-%7) %/.88 =%/ ;//);- - -5%3 =%/- <>. ;/-%/''3 = )3 /- ;(33 /) 0-5) 38'-%/ ;'(7)3 0 P (!; Y X) = B+,%/;) %/ -5%3 ;.3).83 32) -5)( )%&)/7.8') 2.> =.33-5('&5! 45)/. 38'-%/ ;'(7) %3 ;(33)6:!-/)33 2.> ( 2.> /- ;5./&) 3%&/ -5)()+ since: Im i Re + +? P(;Y X) = 0 $%&'()!B+ J5) %/0(2.-%/ &%7)/ <> -5) 38'-%/3 0-5) )9'.-%/ P (!; Y X) = B %/ -5) (X, Y )H=8./).<'- -5) 3%&/3 0-5) %/7.3%/!-/)33+
13 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"#!" #$%&' ()*$+, $%& '&(&)*+,%&-). -/ 0&,2-( &6&(5&(, -(+. -(,%& -((&,272,. -/,%&,)*2, 46*&8 9:, 2,4 *66+2*,2-( 24 4:9;&,,- -(4,)*2(,4< =( 6*),2:+*)8 42>6+& ')*6%2*+,--+4 )&A:2)&,%&,)*2,4,- 9& 4*+*)< $%&)&/-)&8 /-) %2'%&) 52>&(42-(48 *(5 /-) >-4, (:>&)2*+ B-)?8 +-*+ *+:+*,2-(4 5->2(*,&,%&,)*5&< C4 /*) *4 B& *)& *B*)&8,%&!)4, *:,%-)4,- 5&)27& +-*+ 2(7*5*92+2,. 6)-6&),2&4 52)&,+. /)->,%& %*)*,&)24,2 6-+.(->2*+ -/,%& +2(&*)2D&5 2(7*42-( 5.(*>24 B&)& $*.+-) *(5 E:+>&) F3#G< $%&2) *+:+*,2-(4 B&)&,*?&( /:),%&) 9. H-:),&*: *(5 I&44*)5 FJG< C4,%&4&,&%(2A:&4 *)& &K,)&>&+. :4&/:+ 2( *66+2*,2-(48 B& 4:>>*)2D& %&)&,%&2) &K,&(42-(,- %2'%&) 52>&(42-(*+,)*2, 46*&4< $-?&&6,%& *+:+*,2-(4 42>6+&8 B& 4%*++,%)-:'%-:,,%24 4&,2-( *44:>&,%*,,%& (&K,L'&(&)*,2-( >*,)2K 24 *+B*.4 2))&5:29+&< I&, s(y X) := ρ(y E *,,) 2(,)*2, 46*& B%&)& [ s/ Y ](Y X) = M *)& *++&5 &7-+:,2-(*)2+. 42(':+*) F!"8NNG< OK*>6+&4 *)& *++,%& 46&2*+ 6-2(,4 2(52*,&5 2( P2':)& Q< $%& '-*+ -/,%24 4&,2-( 24,- *+:+*,& O0@4 *(5,- 5&)27& 2(52*,-)4 /-),%&2) +-*+ 2(7*5*92+2,. *(5 *,,)*,272,. /)->,%& %*)*,&)24,2 6-+.(->2*+< C4 9&/-)&8 B& *44:>&,%*, E *,,) (X) 5-&4 (-, ":,:*,&< 02(& *++ *+:+*,2-(4 9&+-B *)& +-*+8 2, 6*.4!)4,,- B)2,& -:, * (:>9&) -/ )&+*,2-(4,%*, %-+5 '--5 +-*++. /-),%& %*)*,&)24,2 6-+.(->2*+ -/,%& (&K,L'&(&)*,2-( >*,)2K *(5 /-) 2(7*42-(!,(&44 *(5 R M R P (R M (Y X); Y X) = M, B2,% P (λ; Y X) := 5&,(λ- #(Y X))8 *(5 /-) Y 4:/!2&(,+. +-4&,- X8 [ ] P (R M (Y X); Y X) > M, λ s(y X) +((R M(Y X)), T ) (X X) 2( 6*),2:+*) [ ] s s (X X) = Y X (X X) = RM / Y (X X) T ) *(58 B%&( ( s/ Y )(X X) = M, Q s Y Y $ (X X) = [ Q R M /( Y Y $ ) T ) ] Q s (X X), X X (X X) = $ [ Q R M /( X X $ ) T ) ] (X X) [ B2,% T ) (Y X),%& >&*( *'& *, )&6)-5:,2-( -/ Y L2(52725:*+4 2( E *,,) (X)8 T ) (Y X) = M a. $ (a)/ 5a ] (Y X)8 [ (a)](y X),%& >*,)2K -/ *7&)*'& 6&) *62,* 92),% )*,&4 *, *'& a -/ * Y L2(52725:*+ 2( E *,,) (X) 52//&)&(,2*,&5 *-)52(',- 92),% 4,*,&48 *(5 U *(5 V,%& )2'%, *(5 +&/, &2'&(7&,-)4 -/,%& (&K,L'&(&)*,2-( >*,)2K # = M (a) 5a8 -L(-)>*+2D&5 4:%,%*,! $ U =!8 V $ U =! F!NG<
14 !"#!"#"!" $%&' ()* +",%-.(/ $%&'( ')*' +)(, X -. * /&02, 3(/'&45 [./ Y ](Y X) -. * 4&+ 3(/'&4 *,6 [ 7./( Y Y 8 )](Y X) *,6 [ 7.(Y X)/( X X 8 )](Y X) *4(.9*4( 2*'4-/(.:; <&4(&3(45.-,/( s(x X) = = *,6 R = (X X) =!, s s (X X) = X Y (X X) *,6 R = X (X X) = R = Y (X X). >? 6-@@(4(,'-*'-,A ')4&A) ')( (9*0-'? P (R = (Y X); Y X) = =5 &,( A('. P λ (R =(Y X); Y X) R = P (Y X) + Y Y (R =(Y X); Y X) = =. &, +-')&' (CD0-/-' *4A2(,'.5 ( ) R = P! Y = P λ Y. 8)(4(@&4(5 (3&0'-&,*4-0?.-,A0*4 D&-,'.5 D4-2*4-0? /)*4*/'(4-E(6 F? [ s/ Y ](X X) = =5 /*, *0'(4,*'-3(0? F( /)*4*/'(4-E(6,&' &,0? F? [ R = / Y ](X X) = =5 F' *0.& F? P (!; X X) = =. Y 0% 2(&&%/ 3(/(3&%/-'(&-4)5 5462* /5% 8% (99/49/-(&%2:.4*-!%* ;%) &% <=> -5 9(/&-(22: *%&%/.-)%* 8: 34)5&/(-)&5 $/:@: G7HI;: #5 4&%/;-5% ;% ;462* (?% &4 /%9%(& -&.(): &-.%55 92%(5% -)5%/& &% 2(5& 9/(5% ;%/% )%%*%* -) (22 &% 74224;-)@ *%2-8%/(&-4)5" J4')(4 6-@@(4(,'-*'-,A ')4&A) ')( /)*4*/'(4-.'-/ (9*'-&, A-3(. *,6 7 ( ) R = P! [ 7 Y Y = P R = 8 λ λ Y T Y + 7 ( ) R = P! [ 7 X X = P R = 8 λ λ X T X + 7 P Y Y 8 7 P X X 8 +)-/) *'.-,A0*4 D&-,'. X5.-,/( ')(4( [ R = / Y ](X X) = [ R = / X](X X) = =5 4(6/(. '& [ ( P 7 ) ] R! = Y Y (X X) = 7 P (!; X X), 8 λ Y Y 8 ], ], *,6 [ ( P 7 ) ] R! = X X (X X) = 7 P (!; X X). 8 λ X X 8 B(,/(5 *.-,A0*4.'4*'(A? X -.,-,3*6*F0( -@ ')(.?22('4-/.9*4( 2*'4-C 7 P (!; X X) -.,(A*'-3( 6(!,-'(, Y Y 8 *,6 &,0? -@ -' -.,&,KD&.-'-3( 6(!,-'(: D4&D(4'-(. &@ (3&0'-&,*4?.-,A0*4 D&-,'. *4(.'4&,A /&,3(4A(,/(.'*K F-0-'?5 *,6 2'*0 -,3*6*F-0-'? &@ *' 0(*.'.&2(,(-A)F&4-,A.'4*'(A-(. ')( F-06KD &@ * D&0?2&4D)-.2;:
15 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"" #$%&'( )&'*+%(+')+,$-./0/$ -2&3'$, $& -$$%-)$/*/$ &4 $5+,/'(30-% 6&/'$ 75-$+*+% $5+ 23$-8 $/&'-0 )&*-%/-')+ 2-$%/9 4&% $5+ :+$+%2/'/,$/) +*&03$/&'-% :'-2/), $5-$ %+,30$, 75+' $5+ 23$-$/&'-0,$+6, -%+ '&$ &'0 %-%+.3$ -0,& *+%,2-00 -': $/2+ /, %+,)-0+: -))&%:/'(0 A' $5+ )-,+ &4 &'+8:/2+',/&'-0 $%-/$,6-)+,B -$$%-)$/*/$ &4 $5+,/'(30-% 6&/'$ /, /':+6+':+'$ &4 $5+ 23$-$/&'-0 *-%/-')+ -': $5+ )&':/$/&' 4&%,$%&'( )&'*+%(+')+,$-./0/$ %+:3)+, $& $5+ 3,3-0 )&'8 :/$/&' 4&% )&'$/'3&3,,$-./0/$ D+/2-%E, ;<=><"? %+,30$ /, $5-$ /' )0&'-00 %+6%&:3)/'( &%(-'/,2,B 5-60&/:, -': :/60&/:, F.3$ '&$ /' 5-60&8:/60&/:,B,++ #+)$/&' "GB X /,,$%&'(0 )&'*+%8 (+')+,$-.0+ /4 $5+,22+$%/) 2-$%/9 [ < s/( X X H ) < s/( Y Y H )](X X) /, 6&,/$/*+ :+!'/$+ -': &'0 /4 /$ /, '&'8'+(-$/*+ :+!'/$+@ I+')+B 3':+% $5+ (/*+' %+,$%/)$/&', &' $5+ %+6%&:3)$/*+,,$+2B -' +*&03$/&'-%/0,/'(30-%,$%-$+( X /,,$%&'(0 )&'*+%(+')+,$-.0+ /4 $5+,22+$%/) 2-$%/9 [ < P X X H < P Y Y H ] (!; X X) /, 6&,/$/*+ :+!'/$+. -': &'0 /4 /$ /, '&'8'+(-$/*+ :+!'/$+@ H5+ )%/$+%/- 4&% 23$3-0 /'*-:-./0/$ -%+ :/44+%+'$ /'B &' $5+ &'+ 5-':B $5+ )0&'-0 -': &/: J+':+0/-' -':B &' $5+ &$5+% 5-':B $5+ :/60&/: J+':+0/-' )-,+@ A' $5+ )0&'-0 -': 5-60&/: )-,+B $5+%+ +9/,$ 6-/%, &4 23$3-00 /'*-:-.0+,$%-$+(/+, -%&3': -,/'(30-%,$%-$+( X /4 $5+ 2-$%/9 [ < s/( X X H ) + < s/( Y Y H )](X X) /, '+(-$/*+ :+!'/$+ -': &'0 /4 /$ /, '&'86&,/$/*+ :+!'/$+B &% +K3/*-0+'$0 /4 $5+,22+$%/) 2-$%/9 [ < P Y Y + H < P X X H ] (!; X X) /, '+(-$/*+ :+!'/$+, -': &'0 /4 /$ /, '&'86&,/$/*+ :+!'/$+@ A' $5+ :/60&/: )-,+B $5/, /, $5+ )-,+ /4 $5+ 2-$%/9 [ < s/( X X H )](X X) /, 6&,/$/*+ :+!'/$+ -': &'0 /4 /$ /, '&'8'+(-$/*+ :+!'/$+ ;CL?B &% +K3/*-0+'$0 /4 $5+,22+$%/) 2-$%/9 < P -': &'0 /4 /$ /, '&'8'+(-$/*+ :+!'/$+@ (!; X X) /, 6&,/$/*+ :+!'/$+, X XH!" #$%!&'%(( )*+,-. H5+ 6%+)+:/'( &.,+%*-$/&', )-'.+,322-%/M+: /' $5+,$-$+2+'$ $5-$ Q(Y X) := P (!; Y X) )-' -)$ -,!$'+,, 6%&9 /' -00 0&)-0 )-0)30-$/&', %+0-$+: $& +*&03$/&'-%/0,/'(30-% 6&/'$,@ A4 $5+ $%-/$,6-)+ /, )&''+)$+:B Q )-' -0,& -)$ -,!$'+,, 6%&9 4&% $5+ )5+)N/'( &4 (0&.-0 3'/'*-:-./0/$@ A' $5+ '+9$,+)$/&',B 7+ 6%+,+'$ $5%++ )-,+,$3:/+, :+2&',$%-$/'( $5+ 3,+430'+,, &4 Q@ A' -::/$/&'B +-)5 &4 $5+,+,$3:/+, 5-,,&2+ /'$+%+,$ /' /$, &7' %/(5$@ /" 0(% (& ( 8' $)9+:38)9+83( O0$5&3(5 $5+ &66&,/$+ 6&,,/./0/$ /, '&$ +9)03:+:. %30+, &4 0&(/) -0&'+B 7+,5-00 4&% :+!'/$+'+,, $-N+ $5+ 52+'&6$+%-',/$3-$/&' -, %+4+%+')+ -': -,,32+ $5-$ , -%+ :/60&/: -': 2-0+, -%+ 5-60&/:@ A' $5-$ )-,+B &'0 $ %+6%&:3)$/*+ &3$63$ '++:, $&.+ :/,)&3'$+: 7/$5! P+
16 !"#!"#"!" $%&' ()* +",%-.(/ $%%&' $() *+),-&%&.-/$%,02/0234 $(5 &(%) $,,263 0+$0 373)8&5) -, 8&( 392$% 820 :& 0+3,3; 5-::33(/34 $(5 6$0-(. -, $(5&6< =+3,3 $,,26*0-&(, %3$5 0& 0+3 (3;0>.3(3$0-&( 6$0-; (!?! = f ) :(Y X) m(y X)!? f 6(Y '-0+ f : -, 0+3 3;*3/035 %-:30-63 (2683 &: :36$%3 &::,*-(. &: $ :36$%34 f ;*3/035 %-:30-63 (2683 &: 6$%3 &::,*-(. &: $ :36$%34 $(5 m 0+3 3;*3/035 %-:30-63 (2683 &: A:36$%3B &::,*-(. &: $ 6$%3< C: 0+3,3 92$(0-0-3,4 f : $(5 f 6 53*3(5 &(%) &( 0+3 :36$%3 0$-0,4 $(5 m &(%) &( 0+3 6$%3 0$-0,< D, -, 2,2$% -( 6&53%, '-0+ 6&3 0+$( &(3 8-0+,0$034 '-0+,&63,*$0-$% 6&53%, '-0+ $.&&5 $6&2(0 &:,)6630) $, &(%) 3;/3*0-&( ;*3,,-&( :& =! E f :(Y X) +! E f? : (Y X) +!? mf 6(Y X) 5&3, (&0 3;/3% -( 0$(,*$3(/)< F-(/3! +$, 0+3,02/023 &: $ G3,%-3 6$0-;4 Q(Y X) =!? [f : + f 6 m](y X)! -, $ :2%%!0(3,, *&;)4 '-0+&20 $() (335 :& 3,0-/0-&(, &( 0+3 ($023 &: 0+3 0$-0,*$/3< =+3 92$(0-0) T : = Q +! =!? (f : + f 6 m) $%%&', $ (-/3 5-3/0 -(03*30$0-&( $, 0+3 $73$.3 (2683 &: $%%3%3, 0$(, :&6 :36$%3 0& :36$%34 5-3/0 & 0+&2.+ $ 6$%3 73/0&< A=+3 3$,&( :& &2 /+&-/3 &: 0+3 (&0$0-&( T : -, 0+$0,-6-%$%) /&(,02/035 92$(0-0-3, '33 -(0&52/35 ' , (&0$0-&( -( HEIJ $(5 -( H?@J 2( ($63 &: 0)*3 3*&52/0-&( (2683<B K7&%20-&($-%),-(.2%$,0$03.-3, /$( 83 /$%/2%$035 8),300-(. Q Y (X X) =!? [ f: Y + m f 6 Y + f m 6 Y ] (X X) =+-, 392$0-&( /$( 83 '-003( -( $ 6&3 3%3.$(0 $, '3%% $, 63$(-(.:2% :&6 8) &8,37-(. 0+$0,-(/3 $0 *&*2%$0-&( 5)($6-/$% 392-% ,-53(0 :36$%3,,+&2%5 L2,0 3*%$/3 0+36,3%73,4 0+3 *&*2%$0-&(,3; $0-& 392$%, f 6 (X X)/f : (X X)4 $(5 0+3 :36$%3, $3 $%% &::,*-(. &: 6$%3,4 0+$0 -,4 f : (X X) =!, f 6 (X X) = r(x), m(x X) = r! (X), '+33 r(x) -, 0+3 3,-53(0,3; $0-& A-<3<4 53(,-0) &: 6$%3, ) 53(,-0) &: :36$%3,B< K;*3,,35 -( 0+3 /&(0-820-&(, &: 0+3 0'&,3;3,M [ %((f: ) + %((f ] [ ] 6) %((m) (X : X :, X 6 ) (X 6 X :, X 6 ) Y : Y : Y 6 & $%03($0-73%) [ ] f : f 6 p 6 + p : (X : X :, X 6 ) Y : Y : [ m Y 6 ] (X 6 X :, X 6 ) '-0+p 6 (X) $(5 p : (X) 0+3 3,-53(0 :$/0-&(, 6$%3, $(5 :36$%3,4 p 6 = r/(! + r)4 p : =!/(! + r)<
17 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"# $%&'(')*+*,-.+/0,/ ' 0*%23+'4 0,4',2- X.'% ) (,45*%( 64/5 7 Q Y Y (X X) =! [ 7 f Y Y + m 7 f 5 8 Y Y + f 7 ] m 8 5 (X X), Y Y 8 /49 :4*,,% /3, *%,; 5'+ '%( 65'+./5</%%,0 7 f 6 7 Q Y Y (X X) =! Y 6 Y 8 + r! 7 f 5 6 Y 6 Y 8 = m (X X). = r Y 5 Y5 8 ><<'4%,+- *%,;?@@./%(*,*/%09 5'+0 '%( 65'+0 );'& '0 0<'4', 0<.*0 :*,; '0 /%+-./3<+*%2,; 6()'.A +//<,;4/32; E ',,4 (X)B 8; (,45*%',*/% /6./%(*,*/%0 6/4 0,4/%2./%&42%. 6/4 ;'<+/C(*<+/*(0 *0 '% /<% <4/)+5B 8; 4'0/% *0,;',,;.'%/%*.'+ D3',*/% /6 '('<,*& (-%'5*.0 E0 FG9HI9 '%( *% <'4,*.3+'4 F!JIK9 :;*.; :'0 30( )- L*5'4 F7MN7"I,/ (4*& ;*0.4*,4*'9,'A0 '% 3%303'+ 6/45 6/4 ;'<+/C(*<+/*(0 FJ!IB $% (*<+/*(09 *6,;4 '4 %/ <'4%,'+ 66.,09 2% O<400*/% )./50 '((*,*& 6/4 05'++ %/32; 53,',*/%'+ 0,<0B $%&'0*/%!,%00 *0 ' <4/<4,- /6 ;,4/P-2/,0B Q/:&49 '6,4 ' 03)0,*,3,*/%9,; </<3+',*/% '2'*%./%0*0,0 /6 ;/5/P-2/,0B 8; &%,3'+ 03)0,*,3,*/% 0,< *0,;46/4,:*. '0 +'42 '0,; <;%/,-<*. 0,< 30( *%.'+.3+',*%2,; *%&'0*/%!,%00B 8;*0 +'(0,/ '% '((*,*/%'+ 6'.,/4 7 *%,;.'%/%*.'+ D3',*/% 6/4 (*<+/*(0 :;%./5<'4( :*,; ;'<+/*(0 /4.+/%'+ 4<4/(3.40B R,;4:*0,;.'%/%*.'+ D3',*/% 6/4 (*<+/*(0 *0 '% O'.,./<- /6,;.'%/%*.'+ D3',*/% 6/4.+/%'+ 4<4/(3.40B 8;*0 6'.,/4 7 '<<'40 *% 64/%, /6,; 53,',*/%'+./&'4*'%. '++,;', ;'<<%0./5<'4( :*,;,;.+/%'+.'0 *0,;',,; 53,',*/%'+./&'4*'%. 5',4*O *0 66.,*&+- 4<+'.( )- ' 5',4*O,;', *0,:*. '0 +'42B 8;46/49 L*5'4S0 E+B..) 403+,0 '<<+- D3'++-,/,;.+/%'+ '%(,; 0,'%('4( T%(+*'%.'0B $% ;'<+/C(*<+/*(09,; 6'.,/4 7./50 *% 6/4,; (*<+/*( 0O9 )3, %/, 6/4,; ;'<+/*( /%B 8;46/49,;*0 6'.,/4.'%%/, ) ')0/4)( *%,; 53,',*/%'+./&'4*'%. 5',4*OB R%+- :;%,; 53,',*/%'+ 0,<0 /6,;,:/ 0O0 ' %./44+',(9,; *6 <'4,9 )3, %/,,; /%+- *6 <'4,9 /6,; L*5'4,;/45 '<<+*0 :*,;/3, 634,;4 '(/B 8; 0*,3',*/% 6/4 53,3'+ *%&'(')*+*,- *0 0*5*+'4,/,;', 6/4 0,4/%2./%&42%.B $%,;9 ',!40, 0*2;, 5'-) ',,4'.,*& )3, /% 0./%(,;/32;, 4',;4./%,4*&(9.'0,;', X m = G(X 6 )9 Q(Y 6, Y 5 X 6 ) =! 7 [f 6(Y 6 X 6 ) + f 5 (Y 6 X 6 )m(y 5 X 6 )]!, :*,; Y 5 = G(X 6 )9 X 6,;,4'*, &'+3 /6,; '((*,*/%'+ ;/5/P-2/,./440</%(*%2,/,; ;,4/P-C 2/, Y 6 '%( ;/5/P-2/, X 6 B E$% ;'<+/C(*<+/*( 0<.*09,; (&+/<5%,'+ 0-0,50 /6,; 5'+0 '%( 65'+0 '4 )/3%(,/ ) &% 5/4 (*664%,,;'% *% (*<+/*(0 '0,;- 0,'4, 64/5 (*664%,./5<+5%,0 /6 2%0BK $6,;4 '4 %/ <'4%,'+ 66.,0 /% 2% O<400*/%9 6/4 05'++ 53,',*/%'+ 0,<0 X 6 = X 6 + 7(Y 6 X 6 ) + /( Y 6 X 6 ) '%( ;%. Y 5 X 5 = 7 (G (X (X 6)(Y 6 X 6 ) + /( Y 6 X 6 ). 8;46/49,; D3',*/% 6/4,; &/+3,*/%'4*+- 0*%23+'4 0,4',2*0 )./50 f 6 Y 6 (X 6 X 6 ) + r! f 5 Y 6 (X 6 X 6 ) + r m Y 5 (X 5 X 6 )7 (G (X 6 (X 6 ) = =. 8;*4 *%&'(')*+*,-.'% ) (,45*%( 64/5,;.4*,4*' 2*&% M9 30*%2,; 0./%( (4*&'C,*&0 /6 Q(Y 6, Y 5 X 6 ) 6/4 Y 6 '%( X 6.'+.3+',( '0 *6 (Y 5 /(Y 6 = 7[(G/(X](X)B $% &*: /6,;./%,4*&(%00 /6,; '0035<,*/% X m = G(X 6 )9 : 464'*% 64/5 2*&*%2,; +/%2 '%( 32+- O<+*.*, 6/453+'B
18 !"#!"#"!" $%&' ()* +",%-.(/!" #$%& %'()* ++, +-.$%/0-0 $ 2&-&'/3 )/40567/%4 8* &/'7&5 $ )/&5&-' $99&9& 05 $ 40)/!&5 (-)&5 :$5)*;<&/-8&52 30-)/'/0-% $% &'() *%+ &', %,-& ),.&(/%0, )'*22./%)(+,3 &',,4/25&(/% /6 * +(7/38'()7 /% * 2/.5).*22,+ A9 $% *:3,,7,%& (&' &', (782(.(& 83*.&(., /6 8/852*&(/% :,%,&(.*2 7/+,22,3)0, *))57, &', %/%;6/.*2 2/.( &/ <,,(&',3 (&'/5& 8',%/&=8(.,66,.&) /3 7/%/7/38'(.0 *& 2,*)& (% &', 3,)(+,%& 8/852*&(/%9 >', +(7/38'()7 7*=,4/24, <=,(&',3 &', )5<)&(&5&(/% /6 *2&,3%*&(4, *22,2,) /% &', 6/.*2 2/.5) /3 <= )5<)&(&5&(/%) /% /&',3 2/.(0 3,6,33,+ &/ *) 7/+(!,3) *%+ :,%,3(.*22=.*22,+ B9?22 (%+(4(+5*2) *3, *))57,+ &/ <, </3%,@5*2 <5& 6/3 :,%,&(. +(66,3,%.,)0 *%+ &/ <, 6/37,+ <= 3*%+/7 7*&(%:9 A&',3(), &',3, *3, %/ 3,)&3(.&(/%) /% &', 8'=)(/2/:(.*2 )&35.&53,9 $% &'() ),.&(/%0, )'*22 7/3,/4,3 &*B, /% </*3+ /%, 653&',3 )&*%+*3+ *))578&(/% /6 8/852*&(/% :,%,&(.)C &', %57<,3) /6 7*.3/; *%+ 7(.3/;:*7,&,) &'*&,%+ 58 (% D=:/&,) *3, *& *22 &(7,) 83/8/3&(/%*2 E(9,90 6/3 *22 :,%/&=8,) *%+ '; )&*&,)F9 >'() *))578&(/% () 5)5*22=,%./5%&,3,+ (% (&),@5(4*2,%& 6/37 *) &', *))578&(/% &'*& 5%+,3 3*%+/7 5%(/% /6 :*7,&,) %,2= 6/37,+ D=:/&,) /..53 (% G*3+=HI,(%<,3: 83/8/3&(/%)9 E?.&5*22=0 *), )'*22 /%2=./%)(+,3,@5(2(<3(* *%+ &',(3 (%4*+*<(2(&=0 (& )56!.,) &/ *))57, 83/8/3&(/%*2(&= /6 &', 2(6,&(7,,66,.&(4, 7(.3/; *%+ 7*.3/;:*7,&(. /5&85&)9F I',%,./%)(+,3 *22,2(.,4/25&(/%0 &', (%+(4(+5*2) E(9,90 /<J,.&) &/ &', &=8, /6 '(.', *))(:%!&%,)),)F &/./%)(+,3 *3, &', :,%,./8(,)9 >',(3 ';)&*&,./%)()&) /6 &', ';)&*&, /6 &',(3.*33(,3 &/:,&',3 (&' &', &=8, /6 &', /&',3 *22,2, (&' '/7 &',= )'*3, &'().*33(,30 '(.' 7*= <, a /3 A9 $% &',.*), /6 7/+(!,3,4/25&(/%0 &', (%+(4(+5*2)./33,)8/%+ &/ &', 5)5*2 <(/2/:(.*2 /%,)0 <5& %/ (&' *) *++(&(/%*2 <(3&' )&*&,./78/%,%& &', :,%/&=8, /% &', A;2/.5)9 K/&*&(/%C *22,2,) /% &', +(7/38'(. 2/.5)C A, a E3,)(+,%&)F0 α E75&*%&F0 3,)(+,%& *22,2, /% * 7/+(!,3 2/.5)C b E:,%,3*22= )5883,)),+ (% &', %/&*&(/%F0 75&*%& *22,2, /% * 7/+(!,3 2/.5)C BL 3,)(+,%& &3*(& 4,.&/3)C X aa X aabb, X AA X AAbb X aa = X Aa X aabb = X Aabb, 75&*%& ',&,3/D=:/&, &3*(& 4,.&/3)C Y = X aα, X Aα, X aab, X aab, X AAB, (&' X aab := X aabb, X aab := X aabb, X AAB := X AAbB L 3,2*&(4, 63,@5,%.= /6 '*82/&=8,)C p a 0 p A E3,)(+,%&)L +,8,%+ /% X aa, X aa, X AA )0 p α 0 p ab 0 p AB E75&*%&)FL 2(6,&(7, /66)83(%: %57<,3)C Mw(Y X aa, X aa, X AA ) (&' )8,.(!..*),) *<<3,4(*&,+ *) w aα := w(x aα X aa, X aa, X AA )0 w aab := w(x aab X aa, X aa, X AA ),,&.9L 3,./7<(%*&(/% 83/<*<(2(&= /6?NC c0 (&' # c! M 9 $& () 8/))(<2, &/ +,4,2/8 *./%)()&,%& 8/852*&(/% +=%*7(.*2 6/37*2()7 <*),+ /% &', 7,%&*2./%; )&35.&(/% /6 E:,%,3*2(D,+F (%+(4(+5*2) +,).3(<,+ (% &', (%&3/+5.&(/% OMPQ9 G/,4,30 ',% :,%,&(. +(66,3,%&(*&(/% () (%4/24,+0 (& () 5)5*22= 6*3,*)(,3 &/ 5), &', )&*%+*3+ 8/852*&(/% :,%,&(.*2 6/3; 7*2()7 *) &'() 7/3,,66,.&(4,2=,-82/(&) &', )=77,&3= (%',3,%& (% R,%+,2S) 2*)9?6&,3 /3B(%: /5& &', 3,2,4*%& 2(%,*3(D*&(/%) /%,,%+) 58 (&',-*.&2= &', )*7, 6/3752*) *) 6/3 &', 8/852*&(/% +=%*7(.*2 6/37*2()79 >', 2(%,*3(D,+ :,%,3*&(/% +=%*7(.) /6 &', :,%, 63,@5,%.= /6 * 75&*%& (% /%, /6 &', *22,2,)./%)&(&5&(%: &', 8/2=7/38'()7 () p α = = αp α = w α p α (&' w α := p a w aα + p A w Aα. $% 8/852*&(/% :,%,&(.)0 w α () B%/% *) &', 7*3:(%*2!&%,)) /6 &', a;*22,2,9 G,%.,0 (( ) ( ) ( )) Xaα Xaa XAa R #,α, = w X Aα X aa X α, AA
19 !"#$%&' "( )*"'"+*,&' -.%&/*,0!"! #$%&% '$% ()&* )( '$% ()&*+,-.&/02 )+' '$-' '$% 3$%0)'43% %0%05%&% ,,%,% 6)02/2'2 )( '#) 6)*3)0%0'27 %83&%22/0 '$% 5%3%05%06% )0 '$% '#) /0'&-9/05/:/5+-, %0:/&)0*%0'2 '$-' /' *-4 %06)+0'%&; <$%,/0%-&/=%5 %0%&-'/)0 540-*/62 )( '$% %0% (&%>+%064 )( - *+'-0' )0 - *)5/!%&,)6+2 /2 p ab = w aabp a p ab + w aab (! c)p A p ab + w aab cp a p AB, p AB = w AABp A p AB + w aab (! c)p a p AB + w aab cp A p ab. <$/2 6-0.% &%#&/''%0 /0 :%6')&9*-'&/8 ()&* -2 ( ) ( ) pab pab =! p B AB p AB #/'$! B =! B,2%, + c! B,&%6 = ( ) ( ) w ab? waab +c (p? w AB w A p a ) aab -05 w ab = p a w aab + p A w aab, w AB = p a w aab + p A w 0)'% '$-' /0 E%'= FG"H -&% #&)0-05 $-:% ').% &%3,-6%5 #/'$ '$% )0%2 -.):%;C I%06% X aab X aa Q B c, X aab X aa = (w ab!)(w AB!) + cw aab (p a w ab + p A w AB!) X AAB X AA #$%&% '$% ()&* )( '$% ()&*+,-.&/02 )+' '$-' - *+'-0' *)5/!%& -,,%,% /2 6$-&-6'%&/=%5.4-3$%9 0)'43% '$-' 6)02/2'2 )( '$&%% 6)*3)0%0'2 %83&%22/0 '$% 5%3%05%06% )0 '$% '$&%% /0'&-9/05/:/5+-, %0:/&)0*%0'2 '$-' /' *-4 %06)+0'%& -2 #%,, -2 '$% &%6)*./0-'/)0 (&-6'/)0.%'#%%0 /'2-05 '$% ()6-,,)6+2; J 5/*)&3$/2* /2 %:),+'/)0-&/,4 2'%-54 /( /' /2 +0/0:-5-.,%.4.)'$ -,'%&0-'/:% -,,%,%2-05 *)59 /!%&2; <$%!&2' 6-0.% K+5%5 (&)* #$%'$%& w α <! ()& -,, 3)22/.,% :-,+%2 )( X aα -05 X Aα 7 '$% 2%6)05 (&)* Q B ; L/&2' 6)02/5%& '$% 6-2% #$%&% c =?; <$/2 6-2% /2 2/*/,-& ') '$-' )( /0:-2/)0 -''%*3'2.4 -,'%&0-'/:% -,,%,%27.+' 3)22/.,4 ()& - 5/((%&%06% /0 '$% 2%' )( -66%22/.,% 3$%0)'43%2; I%06% /(.)'$ w ab <! -05 w AB <!7 '$% 5/*)&3$/2* /2 +0/0:-5-.,%.4 *)5/!%&2 #/'$ c =?; J 6,)2%&,))M -' '$% ()&*+,- ()& Q B 2$)#2 '$-' /0 '$-' 6-2% Q B /2 -,2) 0%-'/:% #$-'%:%& '$% :-,+% )( c; N) w ab <! -05 w AB <! ()& -,, 3)22/.,% *)5/!%&2 /2-2+(!6/%0' 6)05/'/)0 ()& - 5/*)&3$/2* ').%,).-,,4 +0/0:-5-.,%; O/'$)+' -04 6)02'&-/0' )0 '$% %0%'/6 -&6$/'%6'+&%7 '$/2 6)05/'/)0 #/'$ '$% 2'&/6' /0%>+-,/'4 2/02 &%3,-6%5 #/'$ '$%/& 0)092'&/6' 6)+0'%&3-&'2 /2 -,2) 0%6%29 2-&4; E)&% 3&%6/2%,47 /( '$% %0%'/6-05 5%:%,)3*%0'-, -&6$/'%6'+&% -,,)#2 ()& -,,%,%2 )& *)5/!%&2 ()& #$/6$ w ab >! )& w AB >!7-057 /0 '$% 23%6/-, 6-2% '$-' '$%&% $-33%0 ').% 0) 2+6$ -,,%,%2-05 '$%&% )0,4 %8/2' 2+6$ *)5/!%&2 ()& #$/6$ p a w ab + p A w AB <!7 -',%-2' )0% )( '$%2% /2 2+(!6/%0',4 6,)2%,4,/0M%5 ') '$% ()6-,,)6+27 '$%0 '$% 5/*)&3$/2* /2 /0:-5-.,%; 2/&$3 E)5/!%&2 %0'%&/0 %0%'/6 5/*)&3$/2*2 3&%2%0' -0 /0'%&%2'/0 2+.',%'4 #/'$ &%23%6' ') '$% +2% )( Q '$-' /0 )'$%& 6,-22%2 )( 3&).,%*2 '%052 ').% 0)09%0%&/6; P0 '$% 23%6/-, 6-2% #$%&% c =?7 '$% 0%8'9%0%&-'/)0 *-'&/8 )( '$% &%2/5%0' $-2 *)&% '$-0 )0% %/%0:-,+% %>+-, ')!; P0 L/+&% "7 '$% &%2/5%0'2 -&%,)6-'%5 -' '$% 3)/0' ('&-6%7 5%') = (G,!) 6)00%6'/0 '$% 2'-.,% &%/)0 #/'$ '$% '&)+.,%2)*% &%/)0 #$%&%.)'$ =%&) 6&)22/02 )( '$% 6$-&-6'%&/2'/6 3),40)*/-, -&%,-&%& '$-0!; I%06%7 '$%!&2' -,'%&0-'/:% )( /0 '$% '$%)&%* /0 N%6'/)0 D 5)%2 0)' $),5 '&+%7-05 /' /2 3)22/.,% ()& '$% '&-/' :%6')& Y )( - 3-/& )( 4)C ') *):% -#-4 (&)* '$% &%2/5%0' :-,+% X 5/&%6',4 /0') '$% '&)+.,%2)*% &%/)0; I)#%:%&7 /(.)'$ w ab <! -05 w AB <! ()& -,, 3)22/.,% *)5/!%&27 '$% 2%6)05 -,'%&0-'/:% )( /0 '$% '$%)&%* /0 N%6'/)0 D $),52 '&+%; E)&%):%&7 Q B (c, Y X) <? ()& -,, *)5/!%&2; Q0 '$% )'$%& $-057 /( '$%&% -&%
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Parts Manual. Trio Mobile Surgery Platform. Model 1033
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
! " #! $ % & $ ' ( % & # ) * +, - ) % $!. /. $! $
[ ] # $ %&$'( %&#) *+,-) %$./.$ $ .$0)(0 1 $( $0 $2 3. 45 6# 27 ) $ # * (.8 %$35 %$'( 9)$- %0)-$) %& ( ),)-)) $)# *) ) ) * $ $ $ %$&) 9 ) )-) %&:: *;$ $$)-) $( $ 0,$# #)$.$0#$ $8 $8 $8 $8,:,:,:,: :: ::
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!" #$! '() -*,*( *(*)* *. 1#,2 (($3-*-/*/330%#& !" #$ -4*30*/335*
!" #$ %#&! '( (* + #*,*(**!',(+ *,*( *(** *. * #*,*(**( 0* #*,*(**(***&, 1#,2 (($3**330%#&!" #$ 4*30*335* ( 6777330"$% 8.9% '.* &(",*( *(** *. " ( : %$ *.#*,*(**." %#& 6 &;" * (.#*,*(**( #*,*(**(***&,
!"! # $ %"" & ' ( ! " # '' # $ # # " %( *++*
!"! # $ %"" & ' (! " # $% & %) '' # $ # # '# " %( *++* #'' # $,-"*++* )' )'' # $ (./ 0 ( 1'(+* *++* * ) *+',-.- * / 0 1 - *+- '!*/ 2 0 -+3!'-!*&-'-4' "/ 5 2, %0334)%3/533%43.15.%4 %%3 6!" #" $" % & &'"
! "#! & "0/! ).#! 71 1&$ -+ #" &> " %+# "1 2$
"#$" &""'(() *+ , -------------------------------------------------------------------------------------------------------------------. / 0-1 2 $1 " 1 /& 1------------------------------------------------------------------------------------------------------------------------3
! " #$% & '()()*+.,/0.
! " #$% & '()()*+,),--+.,/0. 1!!" "!! 21 # " $%!%!! &'($ ) "! % " % *! 3 %,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,0 %%4,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,5
J! "#$ %"& ( ) ) ) " *+, -./0-, *- /! /!+12, ,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/<3/ +15;+ 5/<3=9 -!.1!-9 +17/> ) ) &
J! "#$ %"& J ' ( ) ) ) " *+, -./0-, L *- /! /!+12,3-4 % +15,. 6 /72-, 0,,3-8 / ',913-51:-*/;+ 5/01 ',913-51:--
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 31 η Ελληνική Μαθηματική Ολυμπιάδα "Ο Αρχιμήδης" 22 Φεβρουαρίου 2014
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 4 106 79 ΑΘΗΝΑ Τηλ. 6165-617784 - Fax: 64105 e-mail : info@hms.gr www.hms.gr GREEK MATHEMATICAL SOCIETY 4, Panepistimiou (Εleftheriou Venizelou)
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
-! " #!$ %& ' %( #! )! ' 2003
-! "#!$ %&' %(#!)!' ! 7 #!$# 9 " # 6 $!% 6!!! 6! 6! 6 7 7 &! % 7 ' (&$ 8 9! 9!- "!!- ) % -! " 6 %!( 6 6 / 6 6 7 6!! 7 6! # 8 6!! 66! #! $ - (( 6 6 $ % 7 7 $ 9!" $& & " $! / % " 6!$ 6!!$#/ 6 #!!$! 9 /!
9 1. /001/2 27 /8? /89 16 < / B? > DEE F
!" #$ %! &!$ % ' $ ($ $ ) #%*!! +!(, % -. /001/2 03 4 /1. / 5 /6 0/078/2 27 91 1:3 /14 10 72 91.1;11 27 < 2 82 27 = 9 /62025 9> / = 9> 0/80 > /8? /89 16 < 3 9 4 24 4 /11 / 89 ;1 @ = 271002 A1? B 602 C
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
!"#$ "%&$ ##%&%'()) *..$ /. 0-1$ )$.'-
!!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
!!"#$"%&'()%*$& !! )!+($,-./,0. !! )!"% $&)#$+($1$ !!2)%$34#$$)$ !!+(&%#(%$5$( #$%
!!"#$"%&'()%*$&!! )!+($,-./,0.!"#!! )!"% $&)#$+($1$!!2)%$34#$$)$!!+(&%#(%$5$( #$% & !"# $ $ % # &#$ '()*+, -,./ $* 0" 10#')230##445$&% ##* % 0# ' 4#, ) 0# $, 0# 6 7% % # #* # 8#10&29,:# )) )# )#
]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1
![]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1](/thumbs/84/90712514.jpg "]Zp _[ I 8G4G /<4 6EE =A>/8E>4 06? E6/<; 6008:6> /8= 4; /823 ;1A :40 >176/812; 98/< ;76//40823 E182/;G g= = 4/<1")
! " #$ # %$ & ' ( ) *+, ( -+./0123 045067/812 15 96:4; 82 /178/? = 1@4> 82/01@A74; B824= 6/87 60/8567/; C 71 04D47/10; C 82/1 /
! "#" "" $ "%& ' %$(%& % &'(!!")!*!&+ ,! %$( - .$'!"
! "#" "" $ "%& ' %$(%&!"#$ % &'(!!")!*!&+,! %$( -.$'!" /01&$23& &4+ $$ /$ & & / ( #(&4&4!"#$ %40 &'(!"!!&+ 5,! %$( - &$ $$$".$'!" 4(02&$ 4 067 4 $$*&(089 - (0:;
http://www.mathematica.gr/forum/viewtopic.php?f=109&t=15584
Επιμέλεια: xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΕΚΦΩΝΗΣΕΙΣ ΤΕΥΧΟΣ 5ο ΑΣΚΗΣΕΙΣ 401-500 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς
"#$%%!&' ( *+,%%- !%!%!*&."$%%/-0! !%!%4!*&."$((,%/ !%!%(!*&."$,1,$,%/,!%!%"!*&."$"%%%%!!%!%$!*&."$"(,/$!!%!%2!*&."$",%%%/%0 !%!%!*&.
"#$%% &' ( )* *+,%%- %%*&."$%%/-0 %%,*&."$((,%%%/ %%(*&."$,1,$,%/, %%"*&."$"%%%% %%$*&."$"(,/$ %%1*&."$"(%%%/23 %%2*&."$",%%%/%0 %%4*&."$((,%/ %%-*&."$"",%%/4 %%*&."$(%%%/% 56)7)89)7:;8
!! "#$%& ! " # $ &%"+,(-. (# / 0 1%23%(2443
"#$& " # $ & ' &( &)* &"# &"+,(-. (# / 0 123(2443 2443 56 1 7 & '()(()(*+( ),)(-.(/)((,),24420 8.94: -; :53&:54::549 '()((0)(#'(1)(' ( )(-.(/)((,),24460..94: < * 94&5=>6 '()( 2( )(3(1)((0)('.( )4)((,)
!"#$%& '!(#)& a<.21c67.<9 /06 :6>/ 54.6: 1. ]1;A76 _F -. /06 4D26.36 <> A.:4D6:6C C4/4 /06 D:43? C</ O=47?6C b*dp 12 :1?6:E /< D6 3:4221N6C 42 D:A6 O=
![!#$%& '!(#)& a<.21c67.<9 /06 :6>/ 54.6: 1. ]1;A76 _F -. /06 4D26.36 <> A.:4D6:6C C4/4 /06 D:43? C</ O=47?6C b*dp 12 :1?6:E /< D6 3:4221N6C 42 D:A6 O=](/thumbs/72/67457957.jpg "!#$%& '!(#)& a<.21c67.<9 /06 :6>/ 54.6: 1. ]1;A76 _F -. /06 4D26.36 <> A.:4D6:6C C4/4 /06 D:43? C</ O=47?6C b*dp 12 :1?6:E /< D6 3:4221N6C 42 D:A6 O=")
! " #$% & '( )*+, -. /012 3045/67 8 96 57626./ 4. 4:;74= 69676.36 D426C
!"!# ""$ %%"" %$" &" %" "!'! " #$!
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
! " #! $ %! & & $ &%!
!" #! $ %!&&$&%! ! ' ( ')&!&*( & )+,-&.,//0 1 23+ -4&5,//0 )6+ )&!&*( '(7-&8 )&!&9!':(7,&8 )&!&2!'1;
)))*+,-!-)#..!""-#)/..+-$-*..-!--+ -*
ψ!"#$%&'&( )))*+,-!-)#..!""-#)/..+-$-*..-!--+ -* ψ #-).#!./ #0)1 #2#)--#3#-..-4#32+4#.#34.#-)3$$-!-315$-#+-")3"6.+-32-#-#3-#3#0-.3 ")!4 31-))!7.-3"#*).#03+ --38-#)3#.-!9.-#*-.$-3!#-)#)3!""-#)3#!-*)#!4:--.)))#!-##-.6+#!#+*-.*+.--)-!
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
Sheet H d-2 3D Pythagoras - Answers
1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
'!!$%+(!$,-%+./!'#' 0$1! 2$,13
!"#$% & '#$!!(!)* '!!$%+(!$,-%+./!'#' 0$1! 2$,13 % 5*! "#$%&%'(')&%&*++)&,&,&**) $ # 6 7!!"# $%& $ '()$ )$ *+$, -.#/01023101!!3141413.. % 5 6 ## -7 72$ 3!"48-%!8049"0:"3: ;#????????? -. /0-0!
!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%
" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @
a,b a f a = , , r = = r = T
!" #$%" &' &$%( % ) *+, -./01/ 234 5 0462. 4-7 8 74-9:;:; < =>?@ABC>D E E F GF F H I E JKI L H F I F HMN E O HPQH I RE F S TH FH I U Q E VF E WXY=Z M [ PQ \ TE K JMEPQ EEH I VF F E F GF ]EEI FHPQ HI E
March 14, ( ) March 14, / 52
March 14, 2008 ( ) March 14, 2008 1 / 52 ( ) March 14, 2008 2 / 52 1 2 3 4 5 ( ) March 14, 2008 3 / 52 I 1 m, n, F m n a ij, i = 1,, m; j = 1,, n m n F m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a
Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.
Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
!"#!$% &' ( )*+*,% $ &$ -.&01#(2$#3 4-$ #35667
!"#!$% & &' ( )*+*,% $ -*(-$ -.*/% $- &$ -.&01#(2$#3 4-$ #35667 5051 & 00000000000000000000000000000000000000000000000000000000000000000000000000000 9 508&:;&& 0000000000000000000000000000000000000000000000000
SPFC: a tool to improve water management and hay production in the Crau region
SPFC: a tool to improve water management and hay production in the Crau region J.C. Mailhol, A. Merot To cite this version: J.C. Mailhol, A. Merot. SPFC: a tool to improve water management and hay production
,, #,#, %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, )
!! "#$%&'%( (%)###**#+!"#$ ',##-.#,,, #,#, /01('/01/'#!2#! %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, ) 6###+! 4! 4! 4,*!47! 4! (! 8!9%,,#!41! 4! (! 4!5),!(8! 4! (! :!;!(7! (! 4! 4!!8! (! 8! 4!!8(!44!
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
TALAR ROSA -. / ',)45$%"67789
TALAR ROSA!"#"$"%$&'$%(" )*"+%(""%$," *$ -. / 0"$%%"$&'1)2$3!"$ ',)45$%"67789 ," %"(%:,;,"%,$"$)$*2
A A O B C C A A. A0 = A 45 A 1 = B Q Ak 2. Ak 1
! " " #$%&'(&) *+,-. /01 34 564784 37964 :4 ; ?@ 34 E156F57E1 GHE H567JF4 H5F:7H4 K06 LF37:4 M4N45F415 30 6PG34 0F EK0 F17JF4415 R465071 K6ES3P4 :4 E156F57E1 3M07:4 :4 4 4F3 7156F415 4 E15 6H9H3H 7KE7S34
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 31 η Ελληνική Μαθηματική Ολυμπιάδα "Ο Αρχιμήδης" 22 Φεβρουαρίου 2014
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 106 79 ΑΘΗΝΑ Τηλ. 361653-3617784 - Fax: 364105 e-mail : info@hms.gr, GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Εleftheriou Venizelou)
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
... * +, . >1 " W1 X &=:C.1 3.% 2 *! > 8. $( >1 $.: " G YJ ZC1 G! 1.
1... #) %# "#$%& '%(! 3 2 1 ()*+, &! # $% &!" 5 6!7 8 9 4 2 3 /$01 &,. 2 =! > 8 3.%
!! " &' ': " /.., c #$% & - & ' ()",..., * +,.. * ' + * - - * ()",...(.
..,.. 00 !!.6 7 " 57 +: #$% & - & ' ()",..., * +,.. * ' + * - - * ()",.....(. 8.. &' ': " /..,... :, 00. c. " *+ ' * ' * +' * - * «/'» ' - &, $%' * *& 300.65 «, + *'». 3000400- -00 3-00.6, 006 3 4.!"#"$
OILGEAR TAIFENG. (ml/rev) (bar) (bar) (L/min) (rpm) (kw)
PVWW!"#$ PVWW!"#$%&'()*+!"#$% 12!"#$%&'()*!!"#$%&'(!"#$!"#$%&'()*+!"#$%!!"#!$%&'()*+!"#$%!"!"#$%&'!"#$%&'!"#!"#$%!" SE!"!"#$%&'!"#!"#$%&'!"#$%&'!"#$!"#$!"#$%&'!"#$%&'!"#$%&!"#$%&'!"!"#$%&!"#$%&!"!"#$%!"#$%!"#$%&'(!"#$%&'!!"#!"#!"#$%&!"#$%&'(
ΚΥΚΛΟΙ ΚΑΤΕΡΓΑΣΙΑΣ. κατά τον άξονα Ζ.
ΚΥΚΛΟΙ ΚΑΤΕΡΓΑΣΙΑΣ Οι κύκλοι κατεργασίας χρησιµοποιούνται για ξεχόνδρισµα - φινίρισµα ενός προφίλ χωρίς να απαιτείται να προγραµµατίζουµε εµείς τα διαδοχικά πάσα της κατεργασίας. Έτσι, στο πρόγραµµα περικλείουµε
( ) ΘΕ ΑΝ4 / 2 0. α) β) f(x) f ( x) cos x
Η ΑΝΕΠ Η Η Ν Ω Ν Ω ΑΘΗ Α ΑΝIV Ε ε ά ει Ν επ ε β ί 5 (3-9-5) Επώ : Ό α: ΑΝ Ν: ΘΕ ΑΝ Τα π α Chebyshev T ( ) α π ω μ ( ) y y y (,,, ) π [,] Η ω α α α π α μ / d d T ( ) Tm ( ) [ T ( )] Α απ f ( ) 3, [,], α
WXEY Z Z [\ ] ^] Y _A` Z aebec(y ] ] [Ẍ d _A\e] fe[xe[ga\ [[_Ad
![WXEY Z Z [\ ] ^] Y _A` Z aebec(y ] ] [Ẍ d _A\e] fe[xe[ga\ [[_Ad](/thumbs/83/87388510.jpg "WXEY Z Z [\ ] ^] Y _A` Z aebec(y ] ] [Ẍ d _A\e] fe[xe[ga\ [[_Ad")
% &! (')*+,$-!., -$!#$ /1032547686)479;:-
,,-# $% &.(#./ %0 ) &, ((# ).!#3 8( # #2!*
&'(!"# $% ) *+(#$%#,,-# $% &.(#./ %0 ) &, ((#.1 2 3.4235*6#)7 1 #$%1 &#& "#$ ).!#3 8(. 423 6# #2!* % /%% (:% % $%# ;(# ("% (6 )# $%1# #2 @! ) 372
! "# " #!$ &'( )'&* $ ##!$2 $ $$ 829 #-#-$&2 %( $8&2(9 #."/-0"$23#(&&#
! "# " #!$ %""! &'( )'&* $!"#$% &$'#( )*+#'(,#* /$##+(#0 &1$( #& 23 #(&&# +, -. % ($4 ($4 ##!$2 $567 56 $$ 829 #-#-$&2 %( $8&2(9 #."/-0"$23#(&&# 6 < 6 6 6 66 6< <
500 JournalofNingxiaMedicalUniversity : (2014) $ A L 1, MNO 2 (1. c, ; 2., ) : = 2 % (SDF) 2 ) 012I,CDB 23 S
500 JouralofNigxiaMedicalUiversity 36 5 2014 5 :1674-6309(2014)05-0500-05 $ A L 1, MNO 2 (1. c, 750004; 2., 750001) : = 2 (SDF)2 )012I,CDB 23 SD) 70E,60E, STZ"2,10E, 0" 2 ) 53E, 2 I(DMI,25E ) SDF'I(SDLI,14E),SDF'I(SDSI,
!"#$"%$&'(%$ ) * +!,, #'%(((% -.-)+ /,/ # $'( %.$0. % !!1/3$"$&4.$ /,,. % %% 0 !1,,,'($ ) /) +. %, 03 ) /) +. %, %.$0.
! ""#$ %%$&!!' $ $(( )* "')* "%+ ""!%%$, "'%%%$ "!% *-$ % %)*!"#$"%$&'(%$ ) * +!,, #'%(((% -.-)+ /,/ # $'( %.$0. % -.-1 2!!1/3$"$&4.$.+ 2!!1)3$"$&4 " $$#(% $#& 0) 256578 /,,. % %% 0 +49':!1,,,'($ %.$0.0
SWOT 1. Analysis and Planning for Cross-border Co-operation in Central European Countries. ISIGInstitute of. International Sociology Gorizia
SWOT 1 Analysis and Planning for Cross-border Co-operation in Central European Countries ISIGInstitute of International Sociology Gorizia ! " # $ % ' ( )!$*! " "! "+ +, $,,-,,.-./,, -.0",#,, 12$,,- %
MÉTHODES ET EXERCICES
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
Florida State University Libraries
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2005 A New Examination of Service Loyalty: Identification of the Antecedents and Outcomes of an Attitudinal
B G [0; 1) S S # S y 1 ; y 3 0 t 20 y 2 ; y 4 0 t 20 y 1 y 2 h n t: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 1; 3: r = 10 5 ; a = 10 6 ei n = ỹi n y i t n ); i = 2; 4: r = 10 5 ; a = 10 6 t = 20
!"!"!!#" $ "# % #" & #" '##' #!( #")*(+&#!', & - #% '##' #( &2(!%#(345#" 6##7
!"!"!!#" $ "# % #" & #" '##' #!( #")*(+&#!', '##' '# '## & - #% '##'.//0 #( 111111111111111111111111111111111111111111111111111 &2(!%#(345#" 6##7 11111111111111111111111111111111111111111111111111 11111111111111111111111111111111111111111111111111
DC BOOKS. a-pl½-z-v iao-w Da-c-n
a-pl½-z-v iao-w Da-c-n 1945 P-q-s-s-e 24þ\-v I-mkÀ-t-I-m-U-v aq-s-w-_-b-e-nâ P-\-n -p. {-K-Ù-I-À- -mh-v-, h-n-hà- I³-, d-n-«. A-²-y-m-]-I³. C-c-p-]- -n-\-m-e-p hàj-s- A-²-y-m-]-IP-o-h-n-X- -n-\-pt-i-j-w
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
k k ΚΕΦΑΛΑΙΟ 1 G = (V, E) V E V V V G E G e = {v, u} E v u e v u G G V (G) E(G) n(g) = V (G) m(g) = E(G) G S V (G) S G N G (S) = {u V (G)\S v S : {v, u} E(G)} G v S v V (G) N G (v) = N G ({v}) x V (G)
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
ΚΙ Ν Υ Ν Ο Σ ΜΑΘΗΜΑ ΕΠΙ ΗΜΙΟΛΟΓΙΑΣ. Εκτίµηση κινδύνου ανάπτυξης νόσου Παράγοντες κινδύνου Τρόποι σύγκρισης των παραµέτρων κινδύνου
ΜΑΘΗΜΑ ΕΠΙ ΗΜΙΟΛΟΓΙΑΣ Epidemiology and Public Health Dept of Epidemiology and Public Health N. TZANAKIS M.D. Consultant in Respiratory Medicine Assistant Professor in Epidemiology P.O. Box 1352, 71110
m i N 1 F i = j i F ij + F x
N m i i = 1,..., N m i Fi x N 1 F ij, j = 1, 2,... i 1, i + 1,..., N m i F i = j i F ij + F x i mi Fi j Fj i mj O P i = F i = j i F ij + F x i, i = 1,..., N P = i F i = N F ij + i j i N i F x i, i = 1,...,
!"#$%&'()*+%,)-$%.')*+)-+/0&"-%.')+.'"-$%.')+
&7'*IJ?; '67'8'%9-%&7'*/&-%''-%' %&'*%-%'*-/&-%''-%' 3%45 *7-R-%R-&*/%-37'&3%ST R'*9U%*7'MWK-%X'& 7-A*&**-*9 39YY[-W%_D37F&-%'D[Y*7-RD33`%L5?5 '-%4;?>@4;?>37-*'/&-%''-%' B'%46'%>>@4;>>D**-%/-*'3F*%'*%*%'
tel , version 1-7 Feb 2013
!"## $ %&' (") *+ '#),! )%)%' *, -#)&,-'" &. % /%%"&.0. )%# "#",1 2" "'' % /%%"&30 "'' "#", /%%%" 4"," % /%%5" 4"," "#",%" 67 Y% !"!"# $ %& & # &$ ' '#( ''# ))'%&##& *'#$ ##''' "#$ %% +, %'# %+)% $
Διευθύνοντα Μέλη του mathematica.gr
Το «Εικοσιδωδεκάεδρον» παρουσιάζει ϑέματα που έχουν συζητηθεί στον ιστότοπο http://www.mathematica.gr. Η επιλογή και η ϕροντίδα του περιεχομένου γίνεται από τους Επιμελητές του http://www.mathematica.gr.
'( )*(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((( +
! " # $ %&&' '( )*(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((( + %( ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((('& %('(,,
Πίνακας ρυθμίσεων στο χώρο εγκατάστασης
1/8 Κατάλληλες εσωτερικές μονάδες *HVZ4S18CB3V *HVZ8S18CB3V *HVZ16S18CB3V Σημειώσεις (*5) *4/8* 4P41673-1 - 215.4 2/8 Ρυθμίσεις χρήστη Προκαθορισμένες τιμές Θερμοκρασία χώρου 7.4.1.1 Άνεση (θέρμανση) R/W
!"# '1,2-0- +,$%& &-
"#.)/-0- '1,2-0- "# $%& &'()* +,$%& &- 3 4 $%&'()*+$,&%$ -. /..-. " 44 3$*)-),-0-5 4 /&30&2&" 4 4 -&" 4 /-&" 4 6 710& 4 5 *& 4 # 1*&.. #"0 4 80*-9 44 0&-)* %&9 4 %&0-:10* &1 0)%&0-4 4.)-0)%&0-44 )-0)%&0-4#
Space weather influences on atmospheric electricity
Space weather influences on atmospheric electricity Article Accepted Version Nicoll, K. A. (2014) Space weather influences on atmospheric electricity. Weather, 69 (9). pp. 238-241. ISSN 1477-8696 doi:
Φροντιστήριο #4 Λυμένες Ασκήσεις σε Σχέσεις 30/03/2017
Φροντιστήριο #4 Λυμένες Ασκήσεις σε Σχέσεις 30/03/2017 Άσκηση Φ4.1: Θεωρείστε τις ακόλουθες σχέσεις επί του συνόλου Α={1, 2, 3} 1. R={(1, 1), (1, 2), (1, 3), (3, 3)} 2. S={(1, 1), (1, 2), (2, 1), (2, 2),
Στοιχειώδεις τελεστές στην άλγεβρα των adjointable τελεστών σε Hilbert πρότυπα
Στοιχειώδεις τελεστές στην άλγεβρα των adjointable τελεστών σε Hilbert πρότυπα Χαράλαμπος Μαγιάτης Ανάλυση & Κβαντική Θεωρία Πληροφορίας Σεμινάριο Τμήματος Μαθηματικών ΕΚΠΑ 17/05/2019 1 / 56 Hilbert C
Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =
C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
η η η η GAR = 1 F RR η F RR F AR F AR F RR η F RR F AR µ µ µ µ µ µ Γ R N=mxn W T X x mean X W T x g W P x = W T (x g x mean ) X = X x mean P x = W T X d P x P i, i = 1, 2..., G M s t t
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Answers to practice exercises
Answers to practice exercises Chapter Exercise (Page 5). 9 kg 2. 479 mm. 66 4. 565 5. 225 6. 26 7. 07,70 8. 4 9. 487 0. 70872. $5, Exercise 2 (Page 6). (a) 468 (b) 868 2. (a) 827 (b) 458. (a) 86 kg (b)
1 Adda247 No. 1 APP for Banking & SSC Preparation Website:store.adda247.com
Adda47 No. APP for Banking & SSC Preparation Website:store.adda47.com Email:ebooks@adda47.com S. Ans.(d) Given, x + x = 5 3x x + 5x = 3x x [(x + x ) 5] 3 (x + ) 5 = 3 0 5 = 3 5 x S. Ans.(c) (a + a ) =
ALFA ROMEO. Έτος κατασκευής
145 1.4 i.e. AR33501 66 90 10/94-01/01 0802-1626M 237,40 1.4 i.e. 16V AR33503 76 103 12/96-01/01 0802-1627M 237,40 1.6 i.e. AR33201 76 103 10/94-01/01 0802-1628M 237,40 1.6 i.e. 16V AR67601 88 120 12/96-01/01
AC 1 = AB + BC + CC 1, DD 1 = AA 1. D 1 C 1 = 1 D 1 F = 1. AF = 1 a + b + ( ( (((
? / / / o/ / / / o/ / / / 1 1 1., D 1 1 1 D 1, E F 1 D 1. = a, D = b, 1 = c. a, b, c : #$ #$ #$ 1) 1 ; : 1)!" ) D 1 ; ) F ; = D, )!" D 1 = D + DD 1, % ) F = D + DD 1 + D 1 F, % 4) EF. 1 = 1, 1 = a + b
ρ ρ s ::= sd sd ::= K x sk xotse se sk ::= K (sk x) se ::= x K se se se x = se xotse se xotse se x sp se se l lo sp ::= x l K sp x(x ) l ::= char number lo ::= se (+ = = < > ) se se se ot ::= τ ɛ τ
Αυτό το κεφάλαιο εξηγεί τις ΠΑΡΑΜΕΤΡΟΥΣ προς χρήση αυτού του προϊόντος. Πάντα να μελετάτε αυτές τις οδηγίες πριν την χρήση.
Αυτό το κεφάλαιο εξηγεί τις ΠΑΡΑΜΕΤΡΟΥΣ προς χρήση αυτού του προϊόντος. Πάντα να μελετάτε αυτές τις οδηγίες πριν την χρήση. 3. Λίστα Παραμέτρων 3.. Λίστα Παραμέτρων Στην αρχική ρύθμιση, μόνο οι παράμετροι
! " #$ (!$ )* ' & )* # & # & ' +, #
! " #$ %%%$&$' %$($% (!$ )* ' & )* # & # & ' +, # $ $!,$$ ' " (!!-!.$-/001 # #2 )!$!$34!$ )$5%$)3' ) 3/001 6$ 3&$ '(5.07808.98: 23*+$3;'$3;',;.8/ *' * $
( N m 2 /C 2 )( C)( C) J
Electrical Energy and Capacitance Practice 8A, p. 669 Chapter 8. PE electric = 6.3 0 9 J q = q = q p + q n = ().60 0 9 C + ()(0) = 3.0 0 9 C kcqq (8.99 0 9 N /C )(3.0 0 9 C) r = = P Ee lectric 6.3 0 9
C F E E E F FF E F B F F A EA C AEC
Proceedings of the International Multiconference on Computer Science and Information Technology pp. 767 774 ISBN 978-83-60810-27-9 ISSN 1896-7094 CFEEEFFFEFBFFAEAC AEC EEEDB DACDB DEEE EDBCD BACE FE DD
Α Δ Ι. Παρασκευή 20 Δεκεμβρίου GL n (R) / SL n (R)
Α Δ Ι Α - Φ 8 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2013/asi2013.html, https://sites.google.com/site/maths4edu/home/algdom114 Παρασκευή 20 Δεκεμβρίου
Evaluation et application de méthodes de criblage in silico
Evaluation et application de méthodes de criblage in silico Hélène Guillemain To cite this version: Hélène Guillemain. Evaluation et application de méthodes de criblage in silico. Sciences agricoles. Conservatoire
HONDA. Έτος κατασκευής
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
SIEMENS Squirrel Cage Induction Standard Three-phase Motors
- SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
Ammonium, nitrate, and nitrite in the oligotrophic ocean: Detection methods and usefulness as tracers
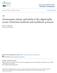University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School 2005 Ammonium, nitrate, and nitrite in the oligotrophic ocean: Detection methods and usefulness as tracers
! "! #" # $ #% !!*$( & +( $#!,-'( . $ ), ( )* / $ 5- (6 7# 8,6 - - /& 4&! '
! "! #" # $ #% & '#()!!*$( & +( $#!,-'(. $ ), ( )* /0 1234 $ 5- (6 7# 8,6 - - /& 4&! ' 6,!(*$(- (,('& 9 !" # $% $% $$!" #$ # % # &'&&&&&'& &() #* $$ & '' $( $) * $ +"&,-&!" +$ )$ " ## +," )- )) ## &. ''
! " #! $ %&! '( #)!' * +#, " -! %&! "!! ! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / # ' -. + &' (, % # , 2**.
! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;
ΚΕΦΑΛΑΙΟ 1 ο ΔΙΑΝΥΣΜΑΤΑ
taexeiolag ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΑΣΚΗΣΗ 1 uuuu uuuu uuuu Αν OA OB 3O 0 και ΚΕΦΑΛΑΙΟ 1 ο ΔΙΑΝΥΣΜΑΤΑ uuuu uuuu uuuu OA OB 1, O α Να δείξετε ότι τα σημεία Α, Β, Γ είναι συνευθειακά
Δημήτριος Σπαθάρας Σχολικός Σύμβουλος Μαθηματικών
. Δημήτριος Σπαθάρας Σχολικός Σύμβουλος Μαθηματικών www.pe03.gr. Δημήτριος Σπαθάρας Σχολικός Σύμβουλος Μαθηματικών, Φθιώτιδας και Ευρυτανίας www.pe03.gr Day: 1 49th INTERNATIONAL MATHEMATICAL OLYMPIAD
M p f(p, q) = (p + q) O(1)
l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
ΓΕΝΙΚΗ ΦΥΣΙΚΗ IV: ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ
Τμήμα Φυσικής Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης ΓΕΝΙΚΗ ΦΥΣΙΚΗ IV: ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ Ι. ΑΡΒΑΝΙΤΙ ΗΣ jarvan@physcs.auth.gr 2310 99 8213 ΘΕΜΑΤΙΚΕΣ ΕΝΟΤΗΤΕΣ ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ ΠΟΛΩΣΗ ΣΥΜΒΟΛΗ ΠΕΡΙΘΛΑΣΗ
#&' ()* #+#, 2 )' #$+34 4 )!' 35+,6 5! *,#+#26 37)*! #2#+#42 %8')* #44+#%$,)88) 9 #,6+-55 $)8) -53+2#5 #6) :&' 2#3+23- ##) :* 232+464 #-) ''7 465+436
! "#$$% #& ()* #+#, -./0*1 2 ) #$+34 4 )! 35+,6 5! *,#+#26 37)*! #2#+#42 %8)* #44+#%$,)88) 9 #,6+-55 $)8) -53+2#5 #6) :& 2#3+23- ##) :* 232+464 #-) 7 465+436 .* &0* 0!*07 ;< =! ))* *0*>!! #6&? @ 8 (? +
1 B0 C00. nly Difo. r II. on III t o. ly II II. Di XR. Di un 5.8. Di Dinly. Di F/ / Dint. mou. on.3 3 D. 3.5 ird Thi. oun F/2. s m F/3 /3.
. F/ /3 3. I F/ 7 7 0 0 Mo ode del 0 00 0 00 A 6 A C00 00 0 S 0 C 0 008 06 007 07 09 A 0 00 0 00 0 009 09 A 7 I 7 7 0 0 F/.. 6 6 8 8 0 00 0 F/3 /3. fo I t o nt un D ou s ds 3. ird F/ /3 Thi ur T ou 0 Fo
Αρχεία και Βάσεις Δεδομένων Φροντιστήριο Κανονικές Μορφές
ΗΥ-360 Αρχεία και Βάσεις Δεδομένων Φροντιστήριο Κανονικές Μορφές 1 Κλειστότητα Συναρτησιακών Eξαρτήσεων: Πώς συμβολίζεται: F + Τι σημαίνει : Το ΣΥΝΟΛΟ των Σ.Ε. που μπορούν να παραχθούν από ένα σύνολο εξαρτήσεων
CONSULTING Engineering Calculation Sheet
E N G I N E E R S Consulting Engineers jxxx 1 Structure Design - EQ Load Definition and EQ Effects v20 EQ Response Spectra in Direction X, Y, Z X-Dir Y-Dir Z-Dir Fundamental period of building, T 1 5.00
ITU-R SF ITU-R SF ( ) GHz 14,5-14,0 1,2.902 (WRC-03) 4.4. MHz GHz 14,5-14 ITU-R SF.1585 ( " " .ITU-R SF.
1 (008-003) * (ITU-R 54/4 ITU-R 6/9 ). 1. 4. 3. GHz 14,5-14,0 1,.90 (WRC-03) ( 4.4 ( - ) MHz 6 45-5 95 GHz 14,5-14 ( 4.4 " " ( ( ( ( ITU-R SF.1585 ( ( (ATPC) ( (.ITU-R SF.1650-1 " " * ITU-R SM.1448 / (
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure
Algorithmique et télécommunications : Coloration et multiflot approchés et applications aux réseaux d infrastructure Hervé Rivano To cite this version: Hervé Rivano. Algorithmique et télécommunications