ΚΕΦΑΛΑΙΟ 4 Ο ΜΕΛΕΤΗ ΕΥΣΤΑΘΕΙΑΣ ΚΑΙ ΣΥΓΚΛΙΣΗΣ ΑΡΙΘΜΗΤΙΚΟΥ ΑΛΓΟΡΙΘΜΟΥ ΤΟΥ ΑΝΤΙΣΤΡΟΦΟΥ ΠΡΟΒΛΗΜΑΤΟΣ
|
|
|
- Ευγένεια Δράκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 9 ΚΕΦΑΛΑΙΟ Ο ΜΕΛΕΤΗ ΕΥΣΤΑΘΕΙΑΣ ΚΑΙ ΣΥΓΚΛΙΣΗΣ ΑΡΙΘΜΗΤΙΚΟΥ ΑΛΓΟΡΙΘΜΟΥ ΤΟΥ ΑΝΤΙΣΤΡΟΦΟΥ ΠΡΟΒΛΗΜΑΤΟΣ. ΕΥΣΤΑΘΕΙΑ ΑΡΙΘΜΗΤΙΚΟΥ ΑΛΓΟΡΙΘΜΟΥ.. Εισαγωγή Έστω ~ (, ~ ~ (, η ακιβής λύση ός ποβλήµατος αχικώ και συοιακώ τιµώ και η λύση τω ξισώσω ππασµέω διαφοώ. Το σφάλµα της ποσέγγισης τότ ίαι: F( (. ~ Το σφάλµα της ποσέγγισης µας διαφέι ως πος δύο σηµία: α Ποια ίαι η συµπιφοά του σφάλµατος καθώς η αιθµητική παάµτος τίι στο άπιο για δδοµέα, ; β Ποια ίαι η συµπιφοά του σφάλµατος καθώς ο αιθµητικός κάαβος γίται λπτότος δηλαδή, τίι στο 0 για δδοµέο ; Η δύτη ώτηση ίαι πιο σηµατική για τη ποσέγγιση αφού σκοπός τέτοιω ποσγγίσω ίαι το σφάλµα στο όιο α πλησιάζι στο 0. Και για τις δύο ωτήσις ο αιθµός τω χοικώ βηµάτω τίι στο άπιο, το οποίο µποί α οδηγήσι σ απιόιστη µγέθυση του σφάλµατος. Εώτηση: Για τη απάτηση στα πααπάω ωτήµατα για απλά ποβλήµατα, όπως η πίλυση της ξίσωσης θµότητας σ οθογωικό χωίο, στη αχή υποθέτουµ τη ύπαξη ακιβούς λύσως αλλά και τη δυατότητα στη ακιβή λύση του διαχωισµού τω µταβλητώ. Υπό κατάλληλς ποϋποθέσις η ακιβής λύση µποί α γαφί ως σιά Forir: ΘΕΩΡΗΜΑ []: Έστω η συάτηση ( και οι παάγωγοι της, οι οποίς ίαι κατά τµήµατα συχίς στο διάστηµα [-π, π] και η ( πιοδική µ πίοδο π. Τότ η ( µποί α γαφί µ µοαδικό τόπο ως σιά Forir. Στη πίπτωση σηµίου ασυέχιας οι σχέσις διαµοφώοται αάλογα. Σηµίωση: Η ποϋπόθση της κατά τµήµατα συέχιας απαιτί ππασµέο πλήθος σηµίω ασυέχιας και για τη ( αλλά και για τις πααγώγους της. Έστω το πόβληµα αχικώ και συοιακώ τιµώ: όπου (,, (.α > 0, 0 π, 0 (.β
2 9 µ κ (,0 φ( κ( π ( 0, 0 και ( π, 0 π 0 π π (.γ όπου κ σταθά. Τότ α θωήσουµ ότι η φ( -φ(- για π<<0 η ακιβής λύση του ποβλήµατος µποί α γαφί: (, ( m A m p(im m (. µ π 0 m λ, λ N m φ( p( im i (. (m π ( m λ, λ N π πm A Η σχέση (. ίαι η γικυµέη λύση του ποβλήµατος αχικώ και συοιακώ τιµώ µόο α η σιά Forir για τη φ( συγκλίι απόλυτα. ηλαδή ποκιµέου α υπάχι η αάλυση της ( σ σιές Forir ίαι απααίτητο οι αχικές συθήκς α ικαοποιού τη ολοκλήωση (.. Στο σηµίο αυτό παουσιάζται το σχήµα ππασµέω διαφοώ που χησιµοποιίται για τη αιθµητική λύση του ποβλήµατος αχικώ και συοιακώ τιµώ:,,...,j 0,... (.5α 0, 0, 0, (.5β 0 0 ϕ(, 0,,...J (.5γ Υποθέτουµ ότι µία µη ππλγµέη λύση τω ξισώσω ππασµέω διαφοώ µποί α γαφί ως σιά Forir. Έστω Α, και m σταθές µ m φυσικό: im A (.6 Α η πααπάω σχέση ατικατασταθί στο σχήµα ππασµέω διαφοώ (.5α τότ ικαοποιί τη διαφοική ξίσωση (.α α:
3 9 ( m (.7 ( ( os( m Α η σταθά Α πάι κατάλληλς τιµές (. τότ το άπιο άθοισµα ή σιά Forir, im (m A m [ (m ] (.8 ίαι η ακιβής λύση του ποβλήµατος µ τη µοφή τω ππασµέω διαφοώ (.5(α-γ, αφού: (α Η σιά συγκλίι οµοιόµοφα γιατί συγκλίι για τη φ( και η (m ίαι φαγµέη (β Κάθ όος της σιάς ικαοποιί τη ξίσωση ππασµέω διαφοώ, άα και το άθοισµα (γ Για 0 αάγται στη φ( άα ικαοποιούται οι αχικές συθήκς του ποβλήµατος (δ Λόγω της ιδιότητας της ( α ίαι πιττή ικαοποιούται και οι συοιακές συθήκς. Συγκίοτας τη ακιβή λύση µ αυτή που ποκύπτι από το σχήµα ππασµέω διαφοώ παατηούµ ότι διαφέου ως πος το όο που αφοά τη χοική µταβολή. Στη ακιβή λύση ο συτλστής αποµίωσης µ το χόο της ( ίαι ίσος µ p(-m. Για τη µη ππλγµέη του σχήµατος ππασµέω διαφοώ, µποούµ α παατηήσουµ ότι το (m αποτλί το συτλστή µγέθυσης ή αποµίωσης της m αµοικής για κάθ βήµα. Α οι πααπάω ααφόµοι συτλστές ααλυθού σ σιές Taylor γύω από το m 0 για τη κθτική σχέση και m0 για τη συάτηση του συηµίτοου, παατηούµ ότι συµφωού στους όους πώτης τάξως: ( ( m m m (.9α m m m (.9β Άα για ακτά µικά και αλλά και m, η λύση του σχήµατος ππασµέω διαφοώ αποτλί καλή ποσέγγιση της λύσης της διαφοικής ξίσωσης. Είαι όµως φαό ότι για συγκκιµές απαιτήσις ακίβιας όλς οι αµοικές πέα από κάποια συγκκιµέη τιµή, δηλαδή για ακτά µγάλς αµοικές δηλαδή για m>m 0 ίαι αποκλίουσς από τη ακιβή λύση αφού από τις σχέσις (.9α, (.9β η διαφοά στους όους δυτέας τάξως γίται σηµατική για οποιαδήποτ και. Μποούµ α τις αποκλίσουµ αυτές τις αµοικές θέτοτας πιοισµό ως πος τη µγέθυση σύµφωα µ βασική ιδιότητα τω κθτικώ συατήσω. Οίζουµ λοιπό ως συθήκη υστάθιας: Ma ( m (m (.0
4 9 Α η συθήκη (.0 ικαοποιίται καµία αµοική του δ µγθύται. Η απάτηση λοιπό στη πώτη ώτηση ίαι ότι το σφάλµα ποσέγγισης πααµέι φαγµέο α ισχύι η συθήκη υστάθιας (.0[]. Απόδιξη []: Ακί α αποδίξουµ ότι τόσο η ακιβής λύση όσο και η λύση που ποκύπτι από το σχήµα ππασµέω διαφοώ ίαι φαγµές. Από τη σχέση (., (. και λόγω της απολύτου σύγκλισης της φ( η ακιβής λύση (, ίαι φαγµέη καθώς τίι στο άπιο. Όσο αφοά τη αιθµητική λύση, ακί η α ίαι φαγµέη καθώς τίι στο άπιο. Είαι: [ (m ] A [ (m ] (. im (m A m (m m Αφού ισχύι η (.0 ίαι: A (. (m m Είαι όµως για τη φ( η σιά Forir απολύτως συγκλίουσα οπότ το άπιο άθοισµα που µφαίζται στη πααπάω σχέση συγκλίι, οπότ ίαι και φαγµέο. Άα και η αιθµητική λύση ίαι φαγµέη. Εφαµόζοτας τη συθήκη υστάθιας στο πόβληµα (.5 παατηούµ ότι ο συτλστής µγέθυσης (.7 ίαι παγµατικός αιθµός µικότος του. Για α ισχύι η συθήκη ακί α µη γίται µικότος του. Για α συµβαίι αυτό ακί α ισχύι: (. Η πααπάω µέθοδος υστάθιας µ τη χήση σιώ Forir ίαι γωστή και ως µέθοδος vo Nma και µποί α πκταθί και σ ποβλήµατα όπου µία συιστώσα της ακιβούς λύσης α αυξάται κθτικά στο χόο, χησιµοποιώτας αάλογη συθήκη που α πιτέπι όµως τη αύξηση στο χόο, όπως θα δούµ παακάτω. Εώτηση : Όπως ποααφέαµ πιο σηµατική από τις ωτήσις ίαι αυτή που αφοά τη συµπιφοά του σφάλµατος όσο ο αιθµητικός κάαβος γίται όλο και πιο λπτός. Έστω το σηµίο (, ίαι έα σηµίο σ έα κάαβο µ βήµατα και για το οποίο έχι υπολογιστί η λύση του ποβλήµατος αχικώ και συοιακώ τιµώ µ το σχήµα τω ππασµέω διαφοώ. Ποκιµέου α βλτιώσουµ τους υπολογισµούς δηµιουγούµ όλο και λπτότους κάαβους και ξαακάουµ τους υπολογισµούς. Η τιµή του για το συγκκιµέο χόο τίι στο άπιο και ίαι ξκάθαο ότι και σ αυτή τη πίπτωση πέπι α αποφυχθού συτλστές µγέθυσης µ απόλυτη τιµή µγαλύτη του, όπως και στη ποηγούµη πίπτωση, αφού από τη σχέση (.8 η ακιβής λύση του σχήµατος ππασµέω διαφοώ αποκλίι για τιµές του µγαλύτς από. Για το λόγο αυτό θωούµ
5 95 κάαβο µ βήµατα /Κ και /Κ όπου Κ φυσικός µ και τέτοια ώστ α ισχύι η συθήκη (. οπότ και η (.0. Έστω (, η λύση του σχήµατος ππασµέω διαφοώ στο σηµίο (, και (, η ακιβής λύση στο σηµίο αυτό, όπου. Τότ α ισχύι η (.0, η λύση (, συγκλίι στη (, για κάθ καθώς το Κ τίι στο άπιο. Απόδιξη []: Έστω m 0 έας θτικός ακέαιος. Για δοσµέο Κ ίαι: / m ( im / (m (m A m m m m m 0 0 (. Για το δύτο άθοισµα λόγω της (.0 και του αητικού κθέτη της κθτικής συάτησης, ισχύι: m > A (.5 m 0 (m m Το πααπάω άθοισµα µποί α γίι οσοδήποτ µικό ακί α πιλέξουµ ακτά µγάλο m 0 αφού η σιά Forir για τη φ( ίαι απολύτως συγκλίουσα. Για α υπολογίσουµ το πώτο άθοισµα παατηούµ ότι έχι τη µοφή αθοισµάτω ( λ όπου, λ οι συτλστές µγέθυσης. Όµως ισχύι: ( λ ( - λ ( - - λ... λ - (.6 Αφού τα και λ ίαι µικότα του, ο δύτος παάγοτας ίαι µικότος του. Για το πώτο παάγοτα χησιµοποιώτας τα ααπτύγµατα σ σιές Taylor (.9α, (.9β έχουµ m P (m m ( ( (.7 όπου Ρ κάποιο πολυώυµο µ µταβλητή τη παάσταση στη παέθση. Η πααπάω παάσταση ίαι φαγµέη καθώς η µταβλητή του πολυωύµου βίσκται στη πιοχή αάπτυξης τω σιώ (.9α, (.9β αφού ο τίτος όος τίι στο 0, ο δύτος και ο πώτος όος ίαι σταθοί σύµφωα µ τη υπόθση που έχι γίι για τη υποδιαίση του καάβου. Έστω το φάγµα α ίαι Β. Τότ: m m 0 m B A m B ( m ( m 0 ( m A m (.8 Επιλέγοτας µγάλο m 0 ποκιµέου α κάουµ ακτά µικό το άθοισµα Σ πιλέγουµ µικό για α κάουµ µικό το άθοισµα Σ. Μ αυτό το τόπο
6 96 µποούµ α έχουµ οσοδήποτ µικό σφάλµα ποσέγγισης θέλουµ πιλέγοτας το Κ α ίαι ικαοποιητικά µγάλο. Συοπτικά, δύο πιπτώσις υστάθιας έχου µλτηθί. Στη µία πίπτωση µ σταθό αφήσαµ το α τίι στο άπιο ή ατίστοφα, στη δύτη πίπτωση κατώτας το σταθό αφήσαµ το α τίι στο άπιο. Και στις δύο πιπτώσις ίαι ααγκαία η συθήκη (. ποκιµέου α αποφύγουµ τα κάθ ίδους λάθη, στο υπολογισµό της λύσης αιθµητικά µ το σχήµα ππασµέω διαφοώ, α γίου τόσο πολύ µγάλα ώστ τα αποτλέσµατα του υπολογισµού α γίου ααξιόπιστα. Στη παγµατικότητα η ααξιοπιστία τω αποτλσµάτω χιάζται µικούς κύκλους υπολογισµού για α µφαιστί α δ ισχύι η πααπάω ααφόµη συθήκη. Οπότ κάθ φοά που χησιµοποιούµ σχήµατα ππασµέω διαφοώ για το υπολογισµό ποσγγιστικώ λύσω σ ποβλήµατα αχικώ και συοιακώ συθηκώ ίαι απααίτητο α γωίζουµ τις συθήκς που πέπι α ισχύου ώστ α ίαι υσταθής... Συτλστής µγέθυσης Στο παάδιγµα πίλυσης ποβλήµατος αχικώ και συοιακώ συθηκώ µ χήση σχήµατος ππασµέω διαφοώ που χησιµοποιήσαµ (.5α ο συτλστής µγέθυσης ποέκυψ α ίαι µοαδικός. ηλαδή, το στο συγκκιµέο πόβληµα ποκύπτι ως η µοαδική λύση από τη ξίσωση που ποκύπτι α ατικαταστήσουµ τη σχέση (.6 στη (.5α. Αυτό οφίλται στο γγοός ότι το πόβληµα ίαι µοοδιάστατο στο χώο αφός και αφτέου ότι το χησιµοποιούµο σχήµα ππασµέω διαφοώ ίαι δύο βηµάτω ως πος το χόο δηλαδή µποί α γαφί ως: B B0 (.9 όπου Β 0 Β 0 (, και Β Β (,, τλστές πάω στη συάτηση. Α γικά υπάχι B τότ υποθέτοτας ότι f( ίαι Β 0 Β 0 (, Β 0 (, Β Β (, Β ( και C B Β 0 η πααπάω σχέση γίται: C( (.0 Η πααπάω σχέση όπως ααφέαµ οοµάζται σχέση δύο βηµάτω γιατί µόο δύο χοικά βήµατα πιλαµβάοται σ αυτή, το ( και το. Στη πίπτωση που το πόβληµα αχικώ και συοιακώ τιµώ αφοά χωικές µταβλητές, (,(,..,( τότ η ακιβής λύση του ποβλήµατος µ χήση τω σιώ Forir παίι τη παακάτω µοφή, όσο αφοά τη λύση ως πος τη χωική παάµτο: ( A p(ik (. ( k k
7 97 Όπου k έα διάυσµα-παάµτος τω σιώ Forir, διάστασης που στη απλή πίπτωση που ίαι φυσικός αιθµός. Στη αιθµητική λύση οι πααπάω σιές παίου τη µοφή: i( k (, A (. (k k όπου A οι συτλστές τω σιώ Forir ατίστοιχοι µ τη (. και ( k p[ i(k ] p{i[k ( k (.. k ( ]} (. Τότ στη σχέση (.0 λόγω χωικής πολυδιάστασης ατιστοιχί και ο όος k: ( C(, k ( (. όπου C πίακας τλστής. O πααπάω πίακας καλίται τλστής µγέθυσης. Στη πίπτωση του ποβλήµατος πααδίγµατος (.5 πιδή αποτλίται από έα στοιχίο κφυλίζται σ συτλστή µγέθυσης. Στη πίπτωση που το πόβληµα αχικώ και συοιακώ τιµώ που µλτάµ στη µοφή ππασµέω διαφοώ που έχουµ πιλέξι πιλαµβάι πλέο τω δύο χοικώ βηµάτω, τότ ίαι της µοφής B B.. B q q q q 0 0 (.5 όπου B q,,b 0 ααφέοται στους τλστές ππασµέω διαφοώ. Μ αάλογς συοιακές συθήκς η πααπάω σχέση µποί α λυθί µοαδικά ως πος τη q. Θωώτας C C ( B q B 0,..., q (.6 και q q v~ (.7 : Τότ ίαι Cq I C ~ 0 : 0 C q 0 I : :... : I C0 0 0 : 0 (.8
8 98 και τλικά v~ C ~ (, k v~ (.9 Σ κάθ πίπτωση λοιπό η σχέση (. µας δίι το πίακα τλστή µγέθυσης. Η καοικότητα ή µη του πίακα αυτού καθοίζι και τη συθήκη υστάθιας η οποία στη γική πίπτωση έχι τη µοφή C (, k για 0 < < τ 0 Τ (.0 όπου τ ίαι η µέγιστη τιµή που µποί α πάι το. Μ τη πααπάω σχέση ααφέται ότι ο τλστής πίακας αυτής της µοφής πέπι α ίαι οµοιόµοφα φαγµέος. Στη Θωία Τλστώ [] α F ίαι έας τλστής στο χώο τλστώ B, ο οποίος έχι τη µοφή πίακα F(k µέσω µιας ξίσωσης της µοφής: w (k F(kv(k (. τότ ο τλστής φάσσται µ το παακάτω τόπο: F Ma F(k (. F (k όπου για δοσµέο k το φάγµα του πίακα F(k δίται από: F(k F(kv Ma F(kv Ma (. v v 0 v Οπότ F (k ίαι το µέτο ή όµα του πίακα F(k που υπολογίζται µέσω µτασχηµατισµού του πίακα. Άα η συθήκη υστάθιας αφοά και τη παάµτο διάυσµα k. Οπότ η συθήκη υστάθιας απαιτί για κάποιο θτικό αιθµό τ οι πίακς : (, k C για 0 < < τ 0 Τ k (. α ίαι οµοιόµοφα φαγµέοι. Όπου N στη πίπτωση που. Α F ίαι έας τταγωικός πίακας διάστασης και λ i, i,.., οι ιδιοτιµές του πίακα, η µέγιστη τω ιδιοτιµώ κατά απόλυτη τιµή οοµάζται φασµατική ακτία. Α R(, k ίαι η φασµατική ακτία του F, τότ ισχύι: Αγγλ. Spral rais
9 99 F R (.5 αφού ο λόγος Fv v δ ίαι µικότος από τη τιµή που ποκύπτι α στη θέση του v ατικαταστήσουµ το ιδιοδιάυσµα που ποκύπτι από τη φασµατική ακτία. Είαι γωστό από τη Γαµµική Άλγβα ότι η φασµατική ακτία του F ίαι R. Επίσης ισχύι: F Ma v 0 F(Fv Fv Fv v Ma v 0 w 0 Fw w Fv v F F F (.6 Οπότ τλικά η συθήκη υστάθιας απαιτί για κάποιο χόο ο συτλστής µγέθυσης: R (, k C(, k C(, k για 0 < < τ 0 < Τ k (.7 α ίαι οµοιόµοφα φαγµέος. Το απλούστο παάδιγµα αιθµητικής πίλυσης ποβλήµατος µ τη µέθοδο ππασµέω διαφοώ, του οποίου η µλέτη του συτλστή µγέθυσης α καταλήγι σ πίακα-τλστή, ίαι η κυµατική ξίσωση:, os.>0 (.8 Χησιµοποιώτας το παακάτω σχήµα ππασµέω διαφοώ ( (.9 παατηούµ ότι δ έχουµ τη πίπτωση ποβλήµατος δύο βηµάτω, δηλαδή δ έχουµ µόο και, αλλά και -. Θέτοτας y (.0 η ξίσωση.9 διαµοφώται σ πόβληµα δύο βηµάτω, αφού διαµοφώται στο παακάτω σύστηµα ξισώσω: y y ( (. Το πααπάω σύστηµα µ τη χήση τω σχέσω
10 00 y A Aξ im im (. καταλήγι στο παακάτω τλστή-πίακα µγέθυσης G a (, m 0 (. όπου a / και -os(m. Το χαακτηιστικό πολυώυµο του πααπάω πίακα ίαι λ λ 0 (. όπου a. Οι ίζς που ποκύπτου ίαι: λ ± (.5, Α τότ ma(λ i ίαι µγαλύτο του οπότ δ ισχύι η συθήκη (.0. Α < οι λύσις ίαι συζυγίς µιγαδικές µ µέτο. Άα η σχέση που ποκύπτι από τη φαµογή της συθήκης (.0 ίαι ( os( m < (.6 Από τη οποία ποκύπτι η τλική συθήκη υστάθιας για τη κυµατική ξίσωση: < (.7 Εαλλακτικά η ατικατάσταση τω σιώ Forir στο σχήµα ππασµέω διαφοώ, στη πίπτωση πολυβηµατικού αλγοίθµου (.5 µας δίι µια πολυωυµική ξίσωση τάξως q ως πος η οποία ατιστοιχί στη χαακτηιστική ξίσωση του τλστή µγέθυσης... Συθήκη Vo Nma Στη ποηγούµη παάγαφο καταλήξαµ στο συµπέασµα ότι η λύση ός ποβλήµατος αχικώ και συοιακώ τιµώ µ τη αιθµητική µέθοδο τω ππασµέω διαφοώ, ποκιµέου α ίαι υσταθής µ τη έοια που δώσαµ στη υστάθια στη ατίστοιχη παάγαφο αυτής της γασίας, απααίτητη συθήκη ίαι η ύπαξη µιας σταθάς C έτσι ώστ
11 0 R 0 < < τ για 0 < Τ k (, k C (.8 Τότ θα ισχύι: R (,k C, Τ 0 (.9 οπότ Τ (, k R (.50 C Γικά µποί α ισχύι C και τλικά λ. Η συθήκη υστάθιας (.0 ποέκυψ από τις ιδιότητς της κθτικής συάτησης (.9 για το συτλστή µγέθυσης της ακιβούς λύσης του ποβλήµατος (.. Αάλογα για κάποιο άλλο πόβληµα µποί ο συτλστής µγέθυσης α έχι κθέτη θτικό αιθµό οπότ η συθήκη (.0 δ θα αταποκίται στις αάγκς του ποβλήµατος. Παακάτω πιγάφται ααλυτικά µία τέτοια φαµογή. Τ Για στο διάστηµα 0 < < τ, η έκφαση C στη πίπτωση αυτή ίαι φαγµέη από τη γαµµική έκφαση της µοφής C, όπου C σταθός αιθµός ξατώµος αποκλιστικά από το τ και το C. Από το οισµό της φασµατικής ακτίας ποκύπτι τότ ( R(, k λ O για 0 < < τ i,..., p (.5 όπου λ,...,λ G, k σ φθίουσα σιά. Η πααπάω σχέση αποτλί τη συθήκη υστάθιας vo Nma. Στη ισαγωγή της υστάθιας χησιµοποιήθηκ ως συθήκη η σχέση (.0 η οποία κατέληξ µ τη θωία που ααπτύξαµ α έχι ατίστοιχα τη παακάτω µοφή: ίαι οι ιδιοτιµές του τλστή µγέθυσης ( λ (.5 Πολλές κατηγοίς ποβληµάτω συοιακώ και αχικώ τιµώ, όπως ήδη ααφέαµ αφοού κθτική αύξηση για κάποια από τις συιστώσς της ακιβούς λύσης ως πος το χόο. Συθήκς υστάθιας όπως η (.0 δ πιτέπου σ αυτού του ίδους τα ποβλήµατα τέτοια αύξηση. Για αυτό το λόγο χησιµοποιίται η γικυµέη συθήκη υστάθιας (.5 η οποία πιτέπι ικαή αύξηση. Εφαµογή: Εφαµογή της πααπάω συθήκης (.5 αποτλί το τοποποιηµέο πόβληµα διάχυσης
12 0, > 0, > 0 (.5 Α γάψουµ τη ξίσωση ππασµέω διαφοώ της πααπάω διαφοικής ξίσωσης, τότ ποκύπτι: ( (.5 Τότ ο συτλστής µγέθυσης ποκύπτι από τη ατικατάσταση της (.6 στη (.5. Η λύση της ξίσωσης που ποκύπτι ως πος ίαι: m G(,m si (.55 ( και ίαι φαό ότι η συθήκη υστάθιας vo Nma ικαοποιίται α ισχύι: ( os. / (.56 όπως ίχ υπολογιστί για τη µη τοποποιηµέη ξίσωση διάχυσης.. ΕΦΑΡΜΟΓΗ ΜΕΘΟΟΥ ΕΥΣΤΑΘΕΙΑΣ ΑΛΓΟΡΙΘΜΟΥ VON NEUMANN ΣΤΗΝ ΕΠΙΛΥΣΗ ΤΟΥ ΑΝΤΙΣΤΡΟΦΟΥ ΠΡΟΒΛΗΜΑΤΟΣ.. Εισαγωγή Η συθήκη υστάθιας vo Nma ααφέται στη αιθµητική υστάθια της µθόδου τω ππασµέω διαφοώ. Αάλογα µ τη µοφή του ποβλήµατος η αιθµητική υστάθια πιτυγχάται υπό ποϋποθέσις. Οι ποϋποθέσις αυτές ποκύπτου από τους πιοισµούς που θέτουµ στη «βοηθητική» ααλυτική λύση που ποκύπτι από σιές Forir και συγκκιµέα στο µέος της λύσης που αφοά τη χοική µταβολή. Αάλογα µ τη µοφή του διαχυτικού χαακτήα του ποβλήµατος ποκύπτου και οι πιοισµοί για το συτλστή µγέθυσης που ποκύπτι από τη ατικατάσταση της σχέσης (.6 στο χησιµοποιούµο σχήµα ππασµέω διαφοώ. Ειδικά όµως η ααφόµη συθήκη µποί α φαµοστί σ πολλά ποβλήµατα χωίς α πηάζται από το διαχυτικό χαακτήα του ποβλήµατος. Θα φαµόσουµ τη συθήκη υστάθιας vo Nma στη αιθµητική λύση µ τη µέθοδο τω ππασµέω διαφοώ του ατιστόφου ποβλήµατος βαθιάς καθίζησης µ τη µέθοδο καοικοποίησης. Το πόβληµα αχικώ και συοιακώ τιµώ ίαι το ακόλουθο
13 0 για ( (.57α 0 ; 0 < (.57β και (,0 (, (α.σ. (.57γ (, 0 (σ.σ. (.57δ ( (0, 0 (σ.σ. (.57 ( (, 0 (σ.σ. (.57στ όπου η λύση στο υθύ πόβληµα βαθιάς καθίζησης και η λύση του ατιστόφου ποβλήµατος. Το πααπάω πόβληµα σύµφωα µ τη διαχυτική µοφή που µφαίστηκ στο υθύ πόβληµα ααµέται α όχι πιβάλλται α µφαίζι αύξηση τω υπολογιστικώ τιµώ ως πος το χόο. Συθήκς υστάθιας όπως η (.0 αποτέπου τη ύπαξη όπως έχουµ δίξι αυτής της διαχυτικής συµπιφοάς του ποβλήµατος. Στο συγκκιµέο πόβληµα οι απαιτήσις για πιοισµέα αυξαόµο καταλήγου στη συθήκη που µαθηµατικά κφάζται από τη σχέση (.5. Σύµφωα µ τη συθήκη vo Nma η υστάθια της αιθµητικής λύσης του ατιστόφου ποβλήµατος διαχύσως ξασφαλίζται α υπό ποϋποθέσις, οι οποίς ξατώται από τις αιθµητικές πααµέτους του ποβλήµατος, ισχύι (,, κ (.58 µ (, M 0 κ (.59 για µικά,. Η πααπάω ααφόµη συθήκη διαµοφώται αάλογα µ τη µοφή κάθ ποβλήµατος και ατίστοιχα κάθ ξίσωσης... Εφαµογή στο ατίστοφο πόβληµα Μέθοδος καοικοποίησης Η διακιτοποιηµέη µοφή της µικής διαφοικής ξίσωσης µτά από ατικατάσταση της (.6 µτατέπται στη ξίσωση της υστάθιας για το συτλστή µγέθυσης. Οπότ από τη σχέση
14 0 ( ( ( 6 ( ( (.60 µ τη ατικατάσταση της (.6 έχι τη µοφή im( im( im im( im( im( im im( im( im( im im (.6 η οποία καταλήγι στη παακάτω ξίσωση: i i i i i i i i (.6 όπου [0.8,.0]- (.6 0. (.6 ], [ (.65 [0,.0] (.66 Στις πααπάω ααφόµς πααµέτους παατηούµ ότι συµπιλαµβάοται οι όοι και οι οποίοι ατιστοιχού στις µταβλητές του ποβλήµατος αχικώ και συοιακώ τιµώ - και. Η υστάθια όµως πιβάλι ως µταβλητές α ίαι τα αιθµητικά στοιχία του ποβλήµατος. Για αυτό το λόγο θωούµ τις πααπάω µταβλητές ως πααµέτους µ τιµές, αυτές που παίου σ όλς τις χοικές και χωικές φάσις του ποβλήµατος. Σύµφωα µ τη υστάθια που µλτήσαµ σ ποηγούµη παάγαφο µας διαφέι η συµπιφοά της/τω ίζας/ιζώ της ξίσωσης καθώς τα, κιούται πος το 0. Είαι
15 05 i si f f si 6 si (.67 Για το οποίο πέπι α ισχύι: 0 (.68 το οποίο ξασφαλίζται α R( f 0. Η πααπάω συθήκη ξασφαλίζται α ισχύι: 0 (.69 όπως ύκολα ποκύπτι από τη (.67 αφού η σχέση (si (λ/ (λ ίαι πολύ κοτά στο για τις χησιµοποιούµς τιµές. Η σχέση (.69 ξασφαλίζι τη ισχύ τόσο της (.57, όσο και τη ισχύ του αιστού µέλους της αισότητας (.59 αφού ίαι ισοδύαµς. Στη πίπτωση όµως που δ ισχύι η πααπάω συθήκη, όπως στη πίπτωση που µλτάµ θα πέπι α διυήσουµ πισσότο και α καταλήξουµ σ πιο πίπλοκη αλλά πίσης µη ππλγµέη σχέση για το. Πέπι α ισχύι: R( f R(f Im(f 0 (.70 Α Im( f τότ η πααπάω σχέση ισχύι πάτα. Εαλλακτικά πέπι α ισχύι: Im (f si ( / < για (.7 Στη πίπτωση τη οποία µλτάµ ισχύι η δύτη πίπτωση της πααπάω σχέσης. Το µέτο της f ίαι φθίουσα συάτηση του στο διάστηµα (0, οπότ το µικότο άω φάγµα του µέτου της f ίαι το (Παάτηµα Η: lim ( f 0 (.7 Στο Παάτηµα Η µφαίζοται πίσης οι πιθαές τιµές που µποί α πάι η πααπάω παάσταση. Η πααπάω ποσότητα αποτλί δικτικό συτλστή µγέθυσης για τη χοική µταβολή της (,. Όσο πιο µγάλος ίαι ο πααπάω συτλστής τόσο πιο πολύ αποκλίι η αιθµητική λύση από τη παγµατική.
16 06.. Μτπξγασία πίλυσης Εισαγωγή στη σύγκλιση Για ικαοποιητική υστάθια στο πόβληµα που ατιµτωπίζουµ δ µας διαφέι µόο η συθήκη (.58 όπως µφαίζται αλλά ακόµη πισσότο θα µλτήσουµ το αποτέλσµα της πίλυσης. Αφού έχουµ ξασφαλίσι τη συθήκη υστάθιας του ποβλήµατος όπως και στη πίπτωση της σύθτης πααγώγου θα µλτήσουµ τη ταχύτητα σύγκλισης του αλγοίθµου. Είαι φαό ότι ο παάγοτας µ το οποίο γίται µτήσιµη η ταχύτητα σύγκλισης ίαι το µέτο της f το οποίο ξατάται από το si(. Στο Παάτηµα Η µφαίζται η µοφή τω συατήσω, si(, si(/. Είαι φαό ότι πολύ κοτά στο 0 και πίπου για τιµές < 0. ίαι: f O( (.7.. Εφαµογή στο ατίστοφο πόβληµα Μέθοδος καοικοποίησης Η φαµογή της συθήκης υστάθιας vo Nma στη αιθµητική λύση µ τη µέθοδο τω ππασµέω διαφοώ του ατιστόφου ποβλήµατος βαθιάς καθίζησης µ τη µέθοδο καοικοποίησης ατιµτωπίζται σ αυτή τη παάγαφο. Το πόβληµα αχικώ και συοιακώ τιµώ ίαι το ακόλουθο για ( (.7α 0 ; 0 < (.7β και (,0 (, (α.σ (.7γ ( (0, 0 (σ.σ. (.7ζ (, 0 (σ.σ. (.7στ ( (,0 (, (α.σ (.7δ Οι απαιτήσις υστάθιας ίαι κοιές µ αυτές της καοικοποιήσως της µθόδου (,, κ (.75 µ
17 07 ( M, 0 κ (.76 για µικά,. Εφαµόζουµ τη µέθοδο υστάθιας στο έο σχήµα ππασµέω διαφοώ: ( ( (.77 δηλαδή ατικαθιστούµ τη (.6 στο σχήµα που ποκύπτι από το οποίο έχι απαλιφθί ο συτλστής Α: m i( im m i( m i( im m i( m i( im m i( ( (.78 καταλήγουµ σ µια δυτοβάθµια ξίσωση (Παάτηµα Θ ως πος το συτλστή µγέθυσης µ τη παακάτω µοφή: ( ( 0 (.79 όπου >0 (.80 >0 (.8 ( ( ( si i (.8
18 08 µ ( os( (.8 [0.8,.0]- (.8 0. (.85 [0,.0] (.86 [ ], (.87 Όµως si( και (.88 για µικές τιµές του. Οπότ >0 (.89 >0 (.90 ( i ( (.9 και µ απαλοιφή του ίαι >0 (.9 >0 (.9 ( i ( (.9 Η λύση της πααπάω ξίσωσης ίαι, ( ± ( ( ( ± ( ( ( (.95 Είαι φαό πως ότα τίι στο 0 τότ οι ίζς τίου στο. Παατηούµ ότι
19 09 >0, >0, R( >0, Im( >0 (.96 Οπότ ( ( ( ( ma ( ( ma ( ( ma ( ( ma (.97 όπου >0 (.98 i µ R( >0, Im( >0 (.99 Η αάπτυξη σ σιές γύω από το τω πααπάω πααστάσω µας δίι (Παάτηµα Θ: ( ( ( O O ( Μτπξγασία πίλυσης Εισαγωγή στη σύγκλιση Για ικαοποιητική υστάθια στο πόβληµα που ατιµτωπίζουµ δ µας διαφέι µόο η συθήκη (.58 όπως µφαίζται αλλά ακόµη πισσότο θα µλτήσουµ το αποτέλσµα της πίλυσης. Αφού έχουµ ξασφαλίσι τη συθήκη υστάθιας του ποβλήµατος όπως και στη πίπτωση της σύθτης πααγώγου θα µλτήσουµ τη ταχύτητα σύγκλισης του αλγοίθµου. Είαι φαό ότι η µταβλητή ως πος τη οποία γίται µτήσιµη η ταχύτητα σύγκλισης ίαι η. Από τη σχέση (.99 ίαι καθώς το τίι στο 0 ( O O( (.0
20 0. ΥΠΟΛΟΓΙΣΜΟΣ ΣΦΑΛΜΑΤΟΣ ΠΡΟΣΕΓΓΙΣΗΣ ΑΝΤΙΣΤΡΟΦΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΜΕ ΧΡΗΣΗ ΣΕΙΡΩΝ TAYOR ΣΥΓΚΛΙΣΗ.. Εισαγωγή Σύµφωα µ τις υποθέσις που έγια για τη υστάθια, η λύση του ός ποβλήµατος µ τη χήση ππασµέω διαφοώ συγκλίι στη ακιβής λύση, ά για, (ατίστοιχα τίου στο 0, ικαοποιίται η συθήκη υστάθιας του αιθµητικού αλγοίθµου. µας διαφέι όµως µόο η σύγκλιση αιθµητικής και ακιβούς λύσης αλλά για πακτικούς λόγους και η ταχύτητα σύγκλισης τω δύο λύσω. Στη παάγαφο αυτή µλτάται το θωητικό υπόβαθο της µλέτης της ταχύτητας σύγκλισης στη βάση του σφάλµατος ποσέγγισης µ χήση σιώ Taylor. Έστω ~, ~ ( (, ~ (.0 η ακιβής λύση του ποβλήµατος µ συχής µικές πααγώγους. Από τη χήση τω σιώ Taylor µ υπόλοιπο έχουµ: ~! ~ ~ ~ θ (.0 ~! ~! ~! ~ ~ ~ θ (.0 ~! ~! ~! 6 ~! ~! ~! ~! ~! ~! ~! ~! ~! ~ ~ ~ ~ θ θ θ θ θ θ θ θ θ θ (.05 και παόµοις κφάσις για τα ~, ~ και τις υπόλοιπς µοφές τω πος τα πίσω ππασµέω διαφοώ και θ κ, κ.. αιθµοί µταξύ 0 και. Θωούµ ως παάδιγµα τη ξίσωση Eisi Kolmogorov: Αγγλ. raio rror
21 , >0 (.06 µ «µπός» σχήµα ππασµέω διαφοώ για µική παάγωγο ως πος το χόο. Αφού η ακιβής λύση ικαοποιί τη διαφοική ξίσωση θωούµ το τλστή: Φ( ~ ~ ~ ~ ~ ~ (.07 Ατικαθιστώτας τις πααπάω σχέσις στο τλστή καταλήγουµ: ( ( ( [ ] O O ~ ~ ~ ( ~ Φ θ θ θ (.08 Το πααπάω αποτέλσµα µποί α µηυθί ως ακολούθως: Υπάχου δύο σταθές Κ και Κ ξατώµς από τη ~, έτσι ώστ η απόλυτη τιµή του τλστή Φ α ίαι µικότη η ίση από Κ ( Κ ( για οσοδήποτ µικά,. Καλούµ το αποτέλσµα του τλστή Φ σφάλµα ποσέγγισης. Το αποτέλσµα του τλστή µας δίι τη πληοφοία της ταχύτητας σύγκλισης της αιθµητικής λύσης στη ακιβή καθώς ο αιθµητικός κάαβος γίται όλο και πιο λπτός []. Οπότ µ τη χήση της υστάθιας και του τλστή Φ αποδικύται η σύγκλιση, ός από τα τία στοιχία που χιάζοται για το ποσδιοισµό ός ποβλήµατος, που από τη αχική του µοφή θωίται µη καλώς οισµέο, ως καλώς οισµέου... Εφαµογή στη µέθοδο καοικοποίησης Ατικαθιστώτας στο παακάτω σχήµα ( ( ( 6 ( ( (.09 το αιθµητικό λάθος ίαι (Παάτηµα Ι: ( O( O( ~ ~ 6 ~ ~ Φ (.0 Άα υπάχου δύο σταθές Κ και Κ ξατώµς από τις πααµέτους του ποβλήµατος, έτσι ώστ η απόλυτη τιµή του τλστή Φ α ίαι µικότη η ίση από Κ ( Κ ( για οσοδήποτ µικά,. Όσο µικότς τιµές του και
22 θωήσουµ για τη λύση του ποβλήµατος µ τη µέθοδο τω ππασµέω διαφοώ τόσο καλύτη σύγκλιση παγµατικής και αιθµητικής λύσης θα έχουµ. Κατά συθήκη η πιλογή αιθµητικώ πααµέτω πιβάλλι <<<. Παατηώτας τη σχέση (.0 µποούµ α συµπάουµ ότι ο κύιος παάγοτας που πηάζι το σφάλµα ποσέγγισης ίαι αυτός που αφοά το. Ο συτλστής Κ ξατάται από τις πααγώγους της ως πος, τη χωική µταβλητή και τη χοική µταβλητή -. Το χωικό σηµίο τω αιθµητικώ υπολογισµώ το οποίο πηάζται σηµατικά από το αιθµητικό λάθος ίαι κοτά στο δξιό σύοο όπου οι παάγωγοι της ως πος ίαι σηµατικές και στη αχή της φαµογής του αλγοίθµου όπου πίσης η χοική µταβλητή παίι σηµατικά χαµηλές τιµές. Αυτό φαίται στα αποτλέσµατα όπου κοτά στο δξιό σύοο υπάχι σηµατική ασυµβατότητα στα αποτλέσµατα από το υθύ µ το ατίστοφο πόβληµα (Εικ.-α -γ. Ως πος τη κτική καθίζηση ίαι φαό ότι δ πηάζται από το σφάλµα ποσέγγισης, όπως και στη ποηγούµη µέθοδο... Εφαµογή στη µέθοδο καοικοποίησης Σύµφωα µ τα πααπάω ατικαθιστώτας στο τλστή Φ, όπου: (. Έχουµ ως αποτέλσµα (Παάτηµα ΙΑ: ( O( O( ~ 6 ~ ~ Φ (. Άα υπάχου δύο σταθές Κ και Κ ξατώµς από τις πααµέτους του ποβλήµατος, έτσι ώστ η απόλυτη τιµή του τλστή Φ α ίαι µικότη η ίση από Κ ( Κ ( για οσοδήποτ µικά,. Όσο µικότς τιµές του και θωήσουµ για τη λύση του ποβλήµατος µ τη µέθοδο τω ππασµέω διαφοώ τόσο καλύτη σύγκλιση παγµατικής και αιθµητικής λύσης θα έχουµ. Κατά συθήκη η πιλογή αιθµητικώ πααµέτω πιβάλλι <<<. Παατηώτας τη σχέση (. µποούµ α συµπάουµ ότι ο κύιος παάγοτας που πηάζι το σφάλµα ποσέγγισης ίαι αυτός που αφοά το. Ο συτλστής Κ ξατάται από τη δύτης τάξης παάγωγο της ως πος, τη
23 χωική µταβλητή και τη χοική µταβλητή -. Το χωικό σηµίο τω αιθµητικώ υπολογισµώ το οποίο πηάζται σηµατικά από το αιθµητικό σφάλµα ίαι και σ αυτή τη πίπτωση κοτά στο δξιό σύοο, λιγότο από τη ποηγούµη µέθοδο αφού η παάµτος, ίαι στη δύαµη. Στο σηµίο αυτό οι παάγωγοι της ως πος ίαι σηµατικές ώ στη αχή της φαµογής του αλγοίθµου η «χοική» µταβλητή παίι σηµατικά χαµηλές τιµές. Αυτό φαίται στα αποτλέσµατα (Εικ. -α -γ, όπου κοτά στο δξιό σύοο υπάχι σηµατική ασυµβατότητα στα αποτλέσµατα από το υθύ µ το ατίστοφο πόβληµα. Ως πος τη κτική καθίζηση ίαι φαό ότι δ πηάζται από το σφάλµα ποσέγγισης, όπως και στη ποηγούµη µέθοδο καοικοποίησης.
24 . ΣΥΜΠΕΡΑΣΜΑΤΑ ΚΕΦΑΛΑΙΟΥ Στο Κφάλαιο µλτάται η υστάθια και η σύγκλιση του αιθµητικού αλγοίθµου για το ατίστοφο πόβληµα βαθιάς καθίζησης το οποίο στο ποηγούµο Κφάλαιο πιλύθηκ αιθµητικά µ χήση καοικοποιήσω. Η υστάθια µλτάται στη βάση τω σιώ Forir µ χήση της γικυµέης συθήκης υστάθιας vo Nmma. Παουσιάζται το θωητικό υπόβαθο για τη µλέτη υστάθιας και φαµόζται για τις δύο καοικοποίησις που φαµόστηκα στο ποηγούµο Κφάλαιο. Η υστάθια, κατά vo Nma, του αιθµητικού αλγοίθµου της καοικοποίησης µ τη µέθοδο πιτυγχάται µ κατάλληλς πιλογές της πααµέτου καοικοποίησης και κατάλληλη πιλογή του βάθους για το οποίο πιλύται αιθµητικά το ατίστοφο πόβληµα, το οποίο πηάζι τη παάµτο. Η ξασφάλιση της αιστής αισότητας της σχέσης (.59 δ αφοά µόο στη υστάθια του αλγοίθµου όσο αφοά στη σύγκλιση αιθµητικής και ακιβούς λύσης αφού η µοφή της χοικής µταβολής του ποβλήµατος ίαι αυξητική. Όσο πιο µικό ίαι το φάγµα του συτλστή f το οποίο πίσης πηάζται από τις πααπάω ααφόµς πααµέτους και, τόσο πισσότο πιτυγχάται η υστάθια αλλά και υθµίζται ο συτλστής µγέθυσης της αιθµητικής ποσέγγισης του ποβλήµατος ώστ α συγκλίι στα αποτλέσµατα της ακιβούς λύσης. Κατά όµοιο τόπο ποκύπτι και η συθήκη υστάθιας για το αιθµητικό αλγόιθµο πίλυσης του ατιστόφου ποβλήµατος µ τη µέθοδο καοικοποίησης. Οι παάµτοι από τις οποίς ξατάται η υστάθια ίαι η παάµτος καοικοποίησης και η χοική µταβλητή. Σύµφωα µ τις υποθέσις που έγια για τη υστάθια, η λύση του ποβλήµατος µ τη χήση τω ππασµέω διαφοώ συγκλίι στη ακιβής λύση ά για, τίου στο 0, η συθήκη υστάθιας ικαοποιίται. Στο Κφάλαιο η ταχύτητα σύγκλισης στη βάση του σφάλµατος ποσέγγισης µ χήση σιώ Taylor, για τις δύο µθόδους καοικοποίησης του ατιστόφου ποβλήµατος βαθιάς καθίζησης. Για τη µέθοδο καοικοποίησης ποκύπτι ότι υπάχου οι παάµτοι Κ και Κ ξατώµς από τις πααµέτους του ποβλήµατος, έτσι ώστ η απόλυτη τιµή του τλστή Φ α ίαι µικότη η ίση από Κ ( Κ ( για οσοδήποτ µικά,. Όσο µικότς τιµές του και θωήσουµ για τη λύση του
25 5 ποβλήµατος µ τη µέθοδο τω ππασµέω διαφοώ τόσο καλύτη σύγκλιση παγµατικής και αιθµητικής λύσης θα έχουµ. Ο συτλστής Κ ξατάται από τις πααγώγους της ως πος, τη χωική µταβλητή και τη χοική µταβλητή -. Το χωικό σηµίο τω αιθµητικώ υπολογισµώ το οποίο πηάζται σηµατικά από το αιθµητικό λάθος ίαι κοτά στο δξιό σύοο όπου οι παάγωγοι της ως πος ίαι σηµατικές και στη αχή της φαµογής του αλγοίθµου όπου πίσης η χοική µταβλητή παίι σηµατικά χαµηλές τιµές. Αυτό φαίται στα αποτλέσµατα όπου κοτά στο δξιό σύοο υπάχι σηµατική ασυµβατότητα στα αποτλέσµατα από το υθύ µ το ατίστοφο πόβληµα (Εικ.-0α -0γ. Ως πος τη κτική καθίζηση ίαι φαό ότι δ πηάζται από το σφάλµα ποσέγγισης. Όσο αφοά τη µέθοδο καοικοποίησης ποκύπτι ότι υπάχου οι παάµτοι Κ και Κ ξατώµς από τις πααµέτους του ποβλήµατος, έτσι ώστ η απόλυτη τιµή του τλστή Φ α ίαι µικότη η ίση από Κ ( Κ ( για οσοδήποτ µικά,. Όσο µικότς τιµές του και θωήσουµ για τη λύση του ποβλήµατος µ τη µέθοδο τω ππασµέω διαφοώ, τόσο καλύτη σύγκλιση παγµατικής και αιθµητικής λύσης θα έχουµ. Κατά συθήκη η πιλογή αιθµητικώ πααµέτω πιβάλλι <<<. Ο συτλστής Κ ξατάται από τη δύτης τάξης παάγωγο της ως πος, τη χωική µταβλητή και τη χοική µταβλητή -. Το χωικό σηµίο τω αιθµητικώ υπολογισµώ το οποίο πηάζται σηµατικά από το αιθµητικό σφάλµα ίαι και σ αυτή τη πίπτωση κοτά στο δξιό σύοο, λιγότο από τη ποηγούµη µέθοδο αφού η παάµτος, ίαι στη δύαµη. Στο σηµίο αυτό οι παάγωγοι της ως πος ίαι σηµατικές ώ στη αχή της φαµογής του αλγοίθµου η «χοική» µταβλητή παίι σηµατικά χαµηλές τιµές. Αυτό φαίται στα αποτλέσµατα (Εικ. -α -γ, όπου κοτά στο δξιό σύοο υπάχι σηµατική ασυµβατότητα στα αποτλέσµατα από το υθύ µ το ατίστοφο πόβληµα. Ως πος τη κτική καθίζηση ίαι φαό ότι δ πηάζται από το σφάλµα ποσέγγισης, όπως και στη ποηγούµη µέθοδο καοικοποίησης.
26 6
27 7 ΒΙΒΛΙΟΓΡΑΦΙΑ ΚΕΦΑΛΑΙΟΥ. Rihmyr, R.D. a Moro, K.W., Diffr mhos for iiial val prolms, Joh Wily & Sos, 967
28 8
ΚΕΦΑΛΑΙΟ 3 Ο ΤΟ ΑΝΤΙΣΤΡΟΦΟ ΠΡΟΒΛΗΜΑ ΒΑΘΙΑΣ ΚΑΘΙΖΗΣΗΣ ΕΥΣΤΑΘΕΙΑ ΙΑΦΟΡΙΚΩΝ
 69 ΚΕΦΑΛΑΙΟ 3 Ο ΤΟ ΑΝΤΙΣΤΡΟΦΟ ΠΡΟΒΛΗΜΑ ΒΑΘΙΑΣ ΚΑΘΙΖΗΣΗΣ ΕΥΣΤΑΘΕΙΑ ΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. ΑΝΤΙΣΤΡΟΦΟ ΠΡΟΒΛΗΜΑ ΙΑΧΥΣΗΣ-ΜΕΤΑ ΟΣΗΣ ΒΑΘΙΑΣ ΚΑΘΙΖΗΣΗΣ.. Εισαγωγή Η διαδικασία της άτλησης πτρλαίου ή ρού σ µγάλης
69 ΚΕΦΑΛΑΙΟ 3 Ο ΤΟ ΑΝΤΙΣΤΡΟΦΟ ΠΡΟΒΛΗΜΑ ΒΑΘΙΑΣ ΚΑΘΙΖΗΣΗΣ ΕΥΣΤΑΘΕΙΑ ΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. ΑΝΤΙΣΤΡΟΦΟ ΠΡΟΒΛΗΜΑ ΙΑΧΥΣΗΣ-ΜΕΤΑ ΟΣΗΣ ΒΑΘΙΑΣ ΚΑΘΙΖΗΣΗΣ.. Εισαγωγή Η διαδικασία της άτλησης πτρλαίου ή ρού σ µγάλης
2. ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ
 . ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. Εισαγωγή Στο παόν κφάλαιο θα παουσιάσουµ αιθµητικές µθόδους για την πίλυση µη γαµµικών αλγβικών ξισώσων, ξισώσων δηλαδή της µοφής 0. όπου η συνάτηση ίναι
. ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. Εισαγωγή Στο παόν κφάλαιο θα παουσιάσουµ αιθµητικές µθόδους για την πίλυση µη γαµµικών αλγβικών ξισώσων, ξισώσων δηλαδή της µοφής 0. όπου η συνάτηση ίναι
αριθμητή και παρονομαστή επί γ + δi. Οι γνωστές αλγεβρικές ταυτότητες ισχύουν όπως και στους πραγματικούς.
 Μθοδολογία ασκήσων ο φάλαιο Άλγβας Μιγαδικοί ιθμοί Μιγαδικοί αιθμοί Τα πόμνα σχόλια αναφέονται στις πααγάφους.1 ως και.3 σλ. 83 ως 100 του σχολικού βιβλίου των μαθηματικών θτικής τχνολογικής κατύθυνσης
Μθοδολογία ασκήσων ο φάλαιο Άλγβας Μιγαδικοί ιθμοί Μιγαδικοί αιθμοί Τα πόμνα σχόλια αναφέονται στις πααγάφους.1 ως και.3 σλ. 83 ως 100 του σχολικού βιβλίου των μαθηματικών θτικής τχνολογικής κατύθυνσης
Οικονοµετρία Ι..Σηµειώσεις ικ. Τσερκέζου.
 Οικονοµτία Ι..Σηµιώσις ικ. Τσκέζου. ΑΥΤΟΣΥΣΧΕΤΙΣΗ ΤΩΝ ΤΙΜΩΝ ΤΟΥ ΙΑΤΑΡΑΚΤΙΚΟΥ ΟΡΟΥ.. Παουσίαση του Πολήµατος.. Που οφίλται.. Ποις ίναι οι Επιπτώσις της Αυτοσυσχέτισης του ιαταακτικού Όου.. Πως λέγχται.
Οικονοµτία Ι..Σηµιώσις ικ. Τσκέζου. ΑΥΤΟΣΥΣΧΕΤΙΣΗ ΤΩΝ ΤΙΜΩΝ ΤΟΥ ΙΑΤΑΡΑΚΤΙΚΟΥ ΟΡΟΥ.. Παουσίαση του Πολήµατος.. Που οφίλται.. Ποις ίναι οι Επιπτώσις της Αυτοσυσχέτισης του ιαταακτικού Όου.. Πως λέγχται.
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
Παρατηρήσεις 1 Για α ααζητήσουµε το όριο της f στο, πρέπει η f α ορίζεται όσο θέλουµε κοτά στο, δηλαδή η f α είαι ορισµέη σ έα σύολο της µορφής ( α, )
 Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Πηγές Κατανομή χωικής d
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Πηγές Κατανομή χωικής d
2.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ
 94 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αιθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβικό λογισμό Για αάδειγμα,
94 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αιθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβικό λογισμό Για αάδειγμα,
ΠΡΟΣΤΑΣΙΑ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 Κεφάλαιο 5 ΠΡΟΣΤΑΣΙΑ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Εισαωή Η αυξημέη αησυχία τω σύχοω κοιωιώ ια τις καταστοφικές επιπτώσεις στη ποιότητα του πειβάλλοτος από τη ααία και άαχη αάπτυξη, που παατηείται τα τελευταία χόια,
Κεφάλαιο 5 ΠΡΟΣΤΑΣΙΑ ΤΟΥ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Εισαωή Η αυξημέη αησυχία τω σύχοω κοιωιώ ια τις καταστοφικές επιπτώσεις στη ποιότητα του πειβάλλοτος από τη ααία και άαχη αάπτυξη, που παατηείται τα τελευταία χόια,
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ
 ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
ΚΑΤΑΣΚΕΥΑΣΙΜΟΤΗΤΑ ΚΑΝΟΝΙΚΩΝ ΠΟΛΥΓΩΝΩΝ ΓΙΑΝΝΗΣ ΞΕΙ ΑΚΗΣ ΘΕΩΡΗΜΑ : Ααγκαία συθήκη για α κατασκευάζεται µε καόα και διαβήτη έα καοικό πολύγωο είαι το πλήθος τω πλευρώ του α είαι της µορφής ( + )...( + ) όπου
ΜΑΘΗΜΑ Η έννοια του µιγαδικού αριθµού Πράξεις
 ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΘΕΜΑ 1ο. Α.1. Δίνονται οι μιγαδικοί αριθμοί z 1, z 2. Να αποδείξετε ότι: Μονάδες 5
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1ο ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 15 ΣΕΠΤΕΜΒΡΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ TEXΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Α.1. Δίοται
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΘΕΜΑ 1ο ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 15 ΣΕΠΤΕΜΒΡΙΟΥ 2000 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ TEXΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) Α.1. Δίοται
Ασκήσεις7 80. AU διαγώνιο. αποτελούμενη από ιδιοδιανύσματα του A. Πρόσθετες ιδιότητες κανονικών πινάκων: Έστω A o
 Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ AA A A
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
x όπου Ε είναι η ολική ενέργεια ανά µονάδα µάζας και Η είναι η ολική ενθαλπία για τις οποίες ισχύει
 ΜΕΘΟ ΟΙ ΑΕΡΟ ΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Κ.Χ. ΓΙΑΝΝΑΚΟΓΛΟΥ, Αν. Καθηγητής, Τοµέας Ρευστών, Σχολή Μηχανολόγων Ε.Μ.Π. ΜΟΝΟ ΙΑΣΤΑΤΕΣ ΕΞΙΣΩΣΕΙΣ EULER ιαφοετικές Γαφές των Εξισώσεων
ΜΕΘΟ ΟΙ ΑΕΡΟ ΥΝΑΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ Κ.Χ. ΓΙΑΝΝΑΚΟΓΛΟΥ, Αν. Καθηγητής, Τοµέας Ρευστών, Σχολή Μηχανολόγων Ε.Μ.Π. ΜΟΝΟ ΙΑΣΤΑΤΕΣ ΕΞΙΣΩΣΕΙΣ EULER ιαφοετικές Γαφές των Εξισώσεων
z = =5 ενώ z 1 z 2. (µε απόδειξη) z = z z I. z = z. z 1 z z όπου z 1 =x 1 +y 1 i και z 2 =x 2 +y 2 i σταθεροί z παριστάνει υπερβολή µε z 2
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ A =. Σύµφωνα µε την Πρόταση 5.7 (σελ. 119), η συµπληρωµατική (δυϊκή)
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 7 Μάθηµα 6 ο ΥΪΚΕΣ ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ Θεωρία : Γραµµική Άλγεβρα : σελ. 8 (από τη 4 η γραµµή) και σελ. 9, εδάφιο 5, σελ. 7, Πρόταση 6.8, σελ. 4 Παράδειγµα : Στη
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηγοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηγοί - Μάθηµα 9o
 Μάθηµα Γαµµές Μταφοάς Κυµατοδηοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 9o ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πξασίας Σήµατος Τµήµα Πληοφοικής & Τηλπικοινωνιών
Μάθηµα Γαµµές Μταφοάς Κυµατοδηοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 9o ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πξασίας Σήµατος Τµήµα Πληοφοικής & Τηλπικοινωνιών
Παράρτηµα Γ Eνότητα Γ.1 Απόδειξη θεωρήµατος 1.5 Kεφαλαίου 1.
 Παράρτηµα Γ νότητα Γ. Απόδιξη θωρήµατος.5 Kφαλαίου. στω f ίναι συνχής και πραγµατική συνάρτηση στο κανονικοποιηµένη (αφαιρώντας µια σταθρά) ώστ f ( x) dx= u = Pr f αρµονική µ (,) v (,) =. Τότ η. στω u
Παράρτηµα Γ νότητα Γ. Απόδιξη θωρήµατος.5 Kφαλαίου. στω f ίναι συνχής και πραγµατική συνάρτηση στο κανονικοποιηµένη (αφαιρώντας µια σταθρά) ώστ f ( x) dx= u = Pr f αρµονική µ (,) v (,) =. Τότ η. στω u
Κι όµως, τα Ρολόγια «κτυπούν» και Εξισώσεις: Η Άλγεβρα των εικτών του Ρολογιού
 Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
Κι όµως, τα Ρολόγια «κτυπού» και Εξισώσεις: Η Άλγεβρα τω εικτώ του Ρολογιού Εισαγωγικά ηµήτρης Ι. Μπουάκης Σχ. Σύµβουλος Μαθηµατικώ Σε ορισµέα βιβλία Αριθµητικής, αλλά κυρίως Άλγεβρας Β Γυµασίου και Α
Συµπάγεια και οµοιόµορφη συνέχεια
 35 Συµπάγια και οµοιόµορφη συνέχια Μια πολύ σηµαντική έννοια στην Ανάλυση ίναι αυτή της συµπάγιας. Όπως θα δούµ τα συµπαγή υποσύνολα του Ευκλίδιου χώρου R συµπριφέρονται λίγο πολύ ως ππρασµένα σύνολα.
35 Συµπάγια και οµοιόµορφη συνέχια Μια πολύ σηµαντική έννοια στην Ανάλυση ίναι αυτή της συµπάγιας. Όπως θα δούµ τα συµπαγή υποσύνολα του Ευκλίδιου χώρου R συµπριφέρονται λίγο πολύ ως ππρασµένα σύνολα.
x D 350 C D Co x Cm m m
 Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 3 Μάθηµα 5 ο NΟΡΜΑ ΠΙΝΑΚΑ Για κάθε αριθµό, η -όρµα του διαύσµατος [ ] = συµβολίζεται και ισούται µε το θετικό αριθµό = = (5) Αποδεικύοται για τη -όρµα οι παρακάτω
Εισαγωγή στην Αστρονομία
 Παπαδόπουλος Μιλτιάδης ΑΕΜ: 4 Εξάμηο: 7 ο Ασκήσεις: -4 Εισαγωγή στη Αστοομία Έα ομογεές μεσοαστικό έφος έχει μάζα Μ ΜΗ (μία μάζα Ηλίου) και πυκότητα ^ mp/m^ Η πείοδος αξοικής πειστοφής του είαι έτη Ποια
Παπαδόπουλος Μιλτιάδης ΑΕΜ: 4 Εξάμηο: 7 ο Ασκήσεις: -4 Εισαγωγή στη Αστοομία Έα ομογεές μεσοαστικό έφος έχει μάζα Μ ΜΗ (μία μάζα Ηλίου) και πυκότητα ^ mp/m^ Η πείοδος αξοικής πειστοφής του είαι έτη Ποια
Συμπλήρωμα 2 εδαφίου 3.3: Το γενικό μεταβολικό πρόβλημα για συναρτησιακό ολοκληρωτικού τύπου με ολοκληρωτέα συνάρτηση F κατά 2
 ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
(4) γενικής λύσης το x με το -x. και θα έχουμε : y ομ (x)=c 1 (-x) -1 +c 2 (-x) 3
 0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ. ΘΕΜΑ Ι ίνεται η συνεχής συνάρτηση f : R
 ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
ΧΡΗΣΗ ΑΚΟΛΟΥΘΙΩΝ ΣΕ ΣΥΝΑΡΤΗΣΕΙΣ ΘΕΜΑ Ι ίεται η συεχής συάρτηση f : R Να δείξετε ότι f = ΛΥΣΗ R µε τη ιδιότητα αf α = f + α α+, α Η αρχική γράφεται: α f α α + = f + Έστω g = f +.Τότε: g g Η () α ( α ) =α
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
Μαθηματι ά ατεύθυνσης
 Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
Β Λυκείου Μαθηματι ά ατεύθυνσης Ο Κύκλος Θεωία Μεθοδολογία -Ασκήσεις Σ υ ν ο π τ ι κ ή Θ ε ω ί α Ονομασία Διατύπωση Σχόλια Σχήμα Α. Κύκλος Οισμός: Ονομάζεται κύκλος με κέντο Ο και ακτίνα το σύνολο των
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΜΕΘΟΔΟΛΟΓΙΑ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΡΕΥΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΘΕΡΜΙΚΩΝ ΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ιπλωµατική Εγασία : ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΚΩ ΙΚΑ ΕΠΙΛΥΣΗΣ ΑΞΟΝΟΣΥΜΜΕΤΡΙΚΩΝ ΠΕ ΙΩΝ ΡΟΗΣ ΓΙΑ ΟΜΗΜΕΝΑ ΚΑΙ
Περιστροφική Φασματοσκοπία
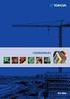 Πριστροική Φασματοσκοία Κλασσική ριγραή της ριστροικής κίησης Κλασσική ριγραή της ριστροικής κίησης T T υ υ γωιακή ορμή ή στροορμή γραμμική ορμή ροή αδραίας ω γωιακή ταχύτητα λ μήκος κύματος T ω ω T λ
Πριστροική Φασματοσκοία Κλασσική ριγραή της ριστροικής κίησης Κλασσική ριγραή της ριστροικής κίησης T T υ υ γωιακή ορμή ή στροορμή γραμμική ορμή ροή αδραίας ω γωιακή ταχύτητα λ μήκος κύματος T ω ω T λ
Ανοικτά και κλειστά σύνολα
 5 Ανοικτά και κλιστά σύνολα Στην παράγραφο αυτή αναπτύσσται ο µηχανισµός που θα µας πιτρέψι να µλτήσουµ τις αναλυτικές ιδιότητς των συναρτήσων πολλών µταβλητών. Θα χριαστούµ τις έννοις της ανοικτής σφαίρας
5 Ανοικτά και κλιστά σύνολα Στην παράγραφο αυτή αναπτύσσται ο µηχανισµός που θα µας πιτρέψι να µλτήσουµ τις αναλυτικές ιδιότητς των συναρτήσων πολλών µταβλητών. Θα χριαστούµ τις έννοις της ανοικτής σφαίρας
στους μιγαδικούς αριθμούς
 Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
1) Ηλεκτρικό πεδίο φορτισμένου φύλλου απείρων διαστάσεων
 1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
www.fr-anodos.gr (, )
 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
Η παραπάνω ιδιότητα γενικεύεται και για περισσότερους από δύο πραγµατικούς αριθµούς. Έτσι έχουµε: αβγ α β γ = β β. d a β = α
 ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΠΟΡΕΙΑ ΤΗΣ ΕΥΡΥΖΩΝΙΚΟΤΗΤΑΣ ΣΤΗΝ ΕΛΛΑ Α Β Εξάµηνο 2016
 ΙΕΥΘΥΝΣΗ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΓΟΡΑΣ ΚΑΙ ΑΝΤΑΓΩΝΙΣΜΟΥ ΠΟΡΕΙΑ ΤΗΣ ΕΥΡΥΖΩΝΙΚΟΤΗΤΑΣ ΣΤΗΝ ΕΛΛΑ Α Β Εξάµηο 26 ΜΑΪΟΣ 27 Συτάκτης: Πρσφόη Αποστολέλλη ΠΕΡΙΕΧΟΜΕΝΑ. Σύοψη... 3 2. Εξέλιξη υρυζωικώ
ΙΕΥΘΥΝΣΗ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΠΑΡΑΚΟΛΟΥΘΗΣΗΣ ΑΓΟΡΑΣ ΚΑΙ ΑΝΤΑΓΩΝΙΣΜΟΥ ΠΟΡΕΙΑ ΤΗΣ ΕΥΡΥΖΩΝΙΚΟΤΗΤΑΣ ΣΤΗΝ ΕΛΛΑ Α Β Εξάµηο 26 ΜΑΪΟΣ 27 Συτάκτης: Πρσφόη Αποστολέλλη ΠΕΡΙΕΧΟΜΕΝΑ. Σύοψη... 3 2. Εξέλιξη υρυζωικώ
1.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ
 ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
( ) ( ) ( ) 1 ( ) ( ) Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN
 Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
Γαµµική Άλγεβα ΙΙ Σελίδα από Μάθηµα 8 ο ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDN Έστω λ είναι ιδιοτιµή του ν ν πίνακα, αλγεβικής πολλαπλότητας ν > Ένα διάνυσµα τάξης x, διάφοο του µηδέν, ονοµάζεται γενικευµένο ιδιοδιάνυσµα,,
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΑΠΑΝΤΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ε_.ΜλΓΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΘΕΜΑ A ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιλίο
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ε_.ΜλΓΑ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΘΕΜΑ A ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιλίο
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ. 1. Τι ονομάζουμε σύνολο Μιγαδικών Αριθμών; Τι ονομάζουμε πραγματικό μέρος - φανταστικό μέρος ενός μιγαδικού αριθμού z = α + βi.
 ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
Γραμμική Άλγεβρα ΙΙ. Εξέταση Σεπτεμβρίου Επώνυμο συνοπτικές ενδεικτικές λύσεις. Όνομα. ΑΜ_(13 ψηφία) Σύνολο
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 00 Επώυμο συοπτικές εδεικτικές λύσεις Όομα ΑΜ_( ψηφία) Ημ/ία Αίθουσα Α 4 Σύολο Η εξέταση αποτελείται από 4 Θέματα Κάθε θέμα αξίζει μοάδες Το άριστα είαι 0 μοάδες
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΑΠΑΝΤΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιβλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιβλίο (έκδοση
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή Απριλίου ΑΠΑΝΤΗΣΕΙΣ Α.. Θεωρία Σχολικό Βιβλίο (έκδοση ) σελίδα 9. Α.. Θεωρία Σχολικό Βιβλίο (έκδοση
β και για τις οποίες το σύστημα (Σ) έχει λύση.
 ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι (Συαρτήσεις μιας μεταβλητής-γραμμική Άλγεβρα) -- Θέμα ο Δίοται οι ευθείες 4 : z +, : 4 y ε = y = ε = = z 4 (α) Να αοδείξετε ότι οι ευθείες ε και ε είαι συείεδες (β)
ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι (Συαρτήσεις μιας μεταβλητής-γραμμική Άλγεβρα) -- Θέμα ο Δίοται οι ευθείες 4 : z +, : 4 y ε = y = ε = = z 4 (α) Να αοδείξετε ότι οι ευθείες ε και ε είαι συείεδες (β)
Λυµένες Ασκήσεις * * *
 Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
ΑΛΓΕΒΡΑ Α' ΛΥΚΕΙΟΥ. Η ΕΞΙΣΩΣΗ αx+β=0
 Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Η επίδραση της κοινωνικής διάστασης των ρομπότ στη σχολική επίδοση
 Η πίδαση της κοινωνικής διάστασης των ομπότ στη σχολική πίδοση Νικόλαος Φαχαντίδης 1, Τιανταφυλλίδου Πολυξένη 2 nfaxanti@uowm.gr, jennypg30@yahoo.gr 1 Τμήμα Μηχανικών Πληοφοικής και Τηλπικοινωνιών, Παν.
Η πίδαση της κοινωνικής διάστασης των ομπότ στη σχολική πίδοση Νικόλαος Φαχαντίδης 1, Τιανταφυλλίδου Πολυξένη 2 nfaxanti@uowm.gr, jennypg30@yahoo.gr 1 Τμήμα Μηχανικών Πληοφοικής και Τηλπικοινωνιών, Παν.
5.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C
 5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ
 ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
ΘΕΩΡΙΑ ΠΙΘΑΝΟΤΗΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ Επιµέλεια: Ι. Σπηλιώτης,. Λεπίπας, Π. Αγγελόπουλος Άσκηση.3 σελ. 4 α) εύκολο β) Αφού C F θα είαι σ( C) σ( F) και λόφω του α) θα είαι σ( C) F. Για τη απόδειξη του ατίθετου
lim f (x) = +. ΣΗΜΕΙΩΣΕΙΣ Μη πεπερασμένο όριο στο x 0 R
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2003 ΕΚΦΩΝΗΣΕΙΣ
 ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Θεωρία - Μέθοδοι
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηγοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηγοί - Μάθηµα 10o-11o
 Μάθηµα Γαµµές Μταφοάς Κυµατοδηγοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουος Κυµατοδηγοί - Μάθηµα o-o ΕΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τοµέας Επικοινωνιών και Επξγασίας Σήµατος Τµήµα Πηοφοικής & Τηπικοινωνιών
Μάθηµα Γαµµές Μταφοάς Κυµατοδηγοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουος Κυµατοδηγοί - Μάθηµα o-o ΕΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τοµέας Επικοινωνιών και Επξγασίας Σήµατος Τµήµα Πηοφοικής & Τηπικοινωνιών
ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ
 ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ υ δ υ α σ τ ι κ ή Πειραιάς 7 Μάθημα 8ο ΣΥΝΔΥΑΣΤΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Μ. Κούτρας Συδυαστική 7-8 8 Το διωυμικό θεώρημα μπορεί α αποτελέσει τη βάση για τη απόδειξη
ΤΜΗΜΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΑΙ ΑΣΦΑΛΙΣΤΙΚΗΣ ΕΠΙΣΤΗΜΗΣ Σ υ δ υ α σ τ ι κ ή Πειραιάς 7 Μάθημα 8ο ΣΥΝΔΥΑΣΤΙΚΕΣ ΤΑΥΤΟΤΗΤΕΣ Μ. Κούτρας Συδυαστική 7-8 8 Το διωυμικό θεώρημα μπορεί α αποτελέσει τη βάση για τη απόδειξη
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ = Γ. β1 = β2
 Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
ΟΡΙΑ. 0 : Παραγοντοποιώ αριθµητή και παρονοµαστή και διώχνω τους παράγοντες x, x 0 που προκύπτουν.
 ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙI ΥΛΗ ΣΤΟ ΠΕ ΙΟ
 III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
Ειδικά Θέµατα Μηχανικής! (Μηχανική Σύνθετων Υλικών) Κεφάλαιο 2 (2.1)
 Ειδικά Θέµατα Μηχαικής Μηχαική Σύτω Υλικώ Κφάλαιο. / Μηχαική υµπριφορά οροτρόπου µέου. onaxis ορότροπο offaxis ορότροπο Στο κύριο ύτηµα onaxis του οροτρόπου µέου οι υιτώς του λατικού µητρώου δόως ίαι 9
Ειδικά Θέµατα Μηχαικής Μηχαική Σύτω Υλικώ Κφάλαιο. / Μηχαική υµπριφορά οροτρόπου µέου. onaxis ορότροπο offaxis ορότροπο Στο κύριο ύτηµα onaxis του οροτρόπου µέου οι υιτώς του λατικού µητρώου δόως ίαι 9
Μάθημα: Ρομποτικός Έλεγχος
 Διατμηματικό Πόγαμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 0 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
Διατμηματικό Πόγαμμα Μεταπτυχιακών Σπουδών «ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΙΣΜΟΥ» Ε.Μ.Π., Ακαδημαϊκό Έτος 0 Μάθημα: Ρομποτικός Έλεγχος Αυτόματος Έλεγχος Ρομπότ Κων/νος Τζαφέστας Τομέας Σημάτων, Ελέγχου & Ρομποτικής
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
Δ/νση Β /θµιας Εκπ/σης Φλώρινας Κέντρο ΠΛΗ.ΝΕ.Τ. (Πρόοδοι) ΠΡΟΟΔΟΙ
 ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
Σειρά Προβλημάτων 2 Λύσεις
 ΕΠΛ2: Θωρία Υπολογισμού και Πολυπλοκότητα Σιρά Προβλημάτων 2 Λύσις Άσκηση Να μτατρέψτ τα πιο κάτω DFA στις κανονικές κφράσις που τα πριγράφουν χρησιμοποιώντας τη διαδικασία που πριγράφται στις διαφάνις
ΕΠΛ2: Θωρία Υπολογισμού και Πολυπλοκότητα Σιρά Προβλημάτων 2 Λύσις Άσκηση Να μτατρέψτ τα πιο κάτω DFA στις κανονικές κφράσις που τα πριγράφουν χρησιμοποιώντας τη διαδικασία που πριγράφται στις διαφάνις
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
2.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
5.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ
 5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
University of Crete. School of Science Department of Mathematics. Master Thesis. Lie Groups, Lie Algebras and the Hydrogen Atom
 Πανεπιστήµιο Κήτης Σχολή Θετικών Επιστηµών Τµήµα Μαθηµατικών Μεταπτυχιακή εγασία Le οµάδες, Le άλγεβες και το Άτοµο του Υδογόνου Νίκος Κωνσταντίνου Ανδιανός Επιβλέπων καθηγητής Μιχάλης Κολουντζάκης Ηάκλειο
Πανεπιστήµιο Κήτης Σχολή Θετικών Επιστηµών Τµήµα Μαθηµατικών Μεταπτυχιακή εγασία Le οµάδες, Le άλγεβες και το Άτοµο του Υδογόνου Νίκος Κωνσταντίνου Ανδιανός Επιβλέπων καθηγητής Μιχάλης Κολουντζάκης Ηάκλειο
Γραπτές ανακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις
 Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Εύρωστοι Γεωμετρικοί Αλγόριθμοι Robust algorithms in Computational Geometry
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ Εύωστοι Γεωμετικοί Αλγόιθμοι Roust lgorithms in Computtionl Geometr Ζαχάου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΤΩΝ ΑΠΟΦΑΣΕΩΝ Εύωστοι Γεωμετικοί Αλγόιθμοι Roust lgorithms in Computtionl Geometr Ζαχάου
Ι δ ι ο τ η τ ε ς Π ρ ο σ θ ε σ η ς - Π ο λ λ α π λ α σ ι α σ μ ο υ ΙΔΙΟΤΗΤΑ ΠΡΟΣΘΕΣΗ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
Α2. Πότε μια συνάρτηση f λέγεται γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της; Μονάδες 4
 (http://edu.klmaka.gr) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
(http://edu.klmaka.gr) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
και ( n) 1 R. Αν ε > 0, επιλέγουµε για κάθε k 1 ένα καλύπτουµε τότε την ευθεία Α µε την ακολουθία των ορθογωνίων .
 80 Σύνολα µέτρου µηδέν στον και ο χαρακτηρισµός του Lebesgue των iema ολοκληρωσίµων συναρτήσων 7. Ορισµός. Έστω για κάθ 0 Α, λέµ ότι το Α έχι διάστατο µέτρο µηδέν αν, > υπάρχι ακολουθία ανοικτών διάστατων
80 Σύνολα µέτρου µηδέν στον και ο χαρακτηρισµός του Lebesgue των iema ολοκληρωσίµων συναρτήσων 7. Ορισµός. Έστω για κάθ 0 Α, λέµ ότι το Α έχι διάστατο µέτρο µηδέν αν, > υπάρχι ακολουθία ανοικτών διάστατων
β± β 4αγ 2 x1,2 x 0.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
Συλλογή Ασκήσεων Υδροστατικής
 Συλλογή Ασκήσεων Υδοστατικής Άσκηση. ℵ Να βεθεί η τιμή της πίεσης που δείχνει το πιεσόμετο, σε mmhg. Δίνονται οι πυκνότητες υδαγύου Hg 600kg/m, νεού Ν 000 kg/m και αέα Α,9 kg/m. 0 cm cm + 0 Επίλυση Αχικά
Συλλογή Ασκήσεων Υδοστατικής Άσκηση. ℵ Να βεθεί η τιμή της πίεσης που δείχνει το πιεσόμετο, σε mmhg. Δίνονται οι πυκνότητες υδαγύου Hg 600kg/m, νεού Ν 000 kg/m και αέα Α,9 kg/m. 0 cm cm + 0 Επίλυση Αχικά
ΥΠΟ ΕΙΓΜΑΤΑ TRANSFER
 ΥΠΟ ΕΙΓΜΑΤΑ TRANSFER Tα υποδίγµατα Transfer αποτλούν µία καλύτρη προσέγγιση στην κτίµηση µονοµταβλητών υποδιγµάτων, στο κφάλαιο αυτό παρουσιάζονται πρισσότρο αναλυτικά. REGRESSION ANALYSIS OF TIME SERIES
ΥΠΟ ΕΙΓΜΑΤΑ TRANSFER Tα υποδίγµατα Transfer αποτλούν µία καλύτρη προσέγγιση στην κτίµηση µονοµταβλητών υποδιγµάτων, στο κφάλαιο αυτό παρουσιάζονται πρισσότρο αναλυτικά. REGRESSION ANALYSIS OF TIME SERIES
6 η ΕΡΓΑΣΙΑ. Ημερομηνία Παράδοσης: 1/7/2007
 6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
Τι είναι εκτός ύλης. Σχολικό έτος
 Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ. Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
B ρ (0, 1) = {(x, y) : x 1, y 1}
 Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
2.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
3.3 Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους. x y E (υποπροσθετικότητα ) ) και p( x) p( x)
 4 3.3 Το συναρτησοιδές του Mikowski και μτρικοποιησιμότητα σ τοπικά κυρτούς χώρους. Υπνθυμίζουμ ότι αν E διανυσματικός χώρος, μια συνάρτηση : E R λέγται υπογραμμικό συναρτησοιδές αν (ι) ( λ) λ ( ) =, λ
4 3.3 Το συναρτησοιδές του Mikowski και μτρικοποιησιμότητα σ τοπικά κυρτούς χώρους. Υπνθυμίζουμ ότι αν E διανυσματικός χώρος, μια συνάρτηση : E R λέγται υπογραμμικό συναρτησοιδές αν (ι) ( λ) λ ( ) =, λ
ΜΙΓΑΔΙΚΟΙ 9o ΓΕΛ ΠΕΡΙΣΤΕΡΙΟΥ είναι τέλεια, να υπολογίσετε την τιμή της παράστασης: Α = (1 + i) v - (1 - i) v. 15. Αν z μιγαδικός και f (ν) = i
 Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]
![ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β] ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]](/thumbs/20/426829.jpg) ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
Άσκηση 1. R y. R x. Επίλυση (2.1) (2.2) Q 1 1 = 1 1
 Ασκήσεις εφαµογής ισοζυγίου οής γαµ. οµής Άσκηση Ακοφύσιο Α εκτοξεύει κυλινδική φλέβα νεού διαµέτου d c µε υθµό l/. H φλέβα του νεού εισέχεται σε ένα διαχύτη και χωίζεται σε κυλινδικές φλέβες µε διατοµές
Ασκήσεις εφαµογής ισοζυγίου οής γαµ. οµής Άσκηση Ακοφύσιο Α εκτοξεύει κυλινδική φλέβα νεού διαµέτου d c µε υθµό l/. H φλέβα του νεού εισέχεται σε ένα διαχύτη και χωίζεται σε κυλινδικές φλέβες µε διατοµές
, όµως z ΚΑ =3.5 cm, αστάθεια
 Άσκηση : Ένας ξύλινος κύος µε πλευά 0cm και ειδικό άος SG0.7 επιπλέει σε νεό. Να υπολογισθούν:. Το ύψος του τµήµατος του κύου που είναι υθισµένο στο νεό. Το µετακεντικό ύψος. Να µελετηθεί η ισοοπία του
Άσκηση : Ένας ξύλινος κύος µε πλευά 0cm και ειδικό άος SG0.7 επιπλέει σε νεό. Να υπολογισθούν:. Το ύψος του τµήµατος του κύου που είναι υθισµένο στο νεό. Το µετακεντικό ύψος. Να µελετηθεί η ισοοπία του
Δυνάμεις πραγματικών αριθμών
 Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
i) Αν ο φυσικός αριθμός n δεν είναι τετράγωνο ακεραίου, τότε ο n είναι άρρητος.
 Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
Πρόλογος 3 Πρόλογος Τ ο βιβλίο αυτό απευθύεται σε κάθε συάδελφο Μαθηματικό, αλλά κυρίως σε κάθε έο συάδελφο που πρόκειται α συμμετάσχει στο διαγωισμό του Α.Σ.Ε.Π. Επίσης, απευθύεται σε μαθητές με υψηλούς
Βασικές γνώσεις Μαθηµατικών Α και Β Λυκείου που πρέπει να ξέρουµε για να ξεκινήσουµε τις σπουδές µας στο TEI
 Βασικές γώσεις Μαθηµατικώ Α και Β Λυκείου που πρέπει α ξέρουµε για α ξεκιήσουµε τις σπουδές µας στο TEI Επιµέλεια Όµηρος Κορακιαίτης Προσθήκες διορθώσεις: Θεολόγος Πααγιωτίδης Άλγεβρα και πράξεις: (ή το
Βασικές γώσεις Μαθηµατικώ Α και Β Λυκείου που πρέπει α ξέρουµε για α ξεκιήσουµε τις σπουδές µας στο TEI Επιµέλεια Όµηρος Κορακιαίτης Προσθήκες διορθώσεις: Θεολόγος Πααγιωτίδης Άλγεβρα και πράξεις: (ή το
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
( ) y ) άγνωστη συνάρτηση, f (, )
 6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ
 ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ 1. Α. Να βρεθού οι κ,λ R για τους οποίους είαι ίσα τα πολυώυµα ( λ + 1) x ( κ ) x λ + 1 (x) = και Q(x) = κx λx + κ Β. Να βρείτε τους πραγµατικούς αριθµούς α, β, γ R για τους
ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ 1. Α. Να βρεθού οι κ,λ R για τους οποίους είαι ίσα τα πολυώυµα ( λ + 1) x ( κ ) x λ + 1 (x) = και Q(x) = κx λx + κ Β. Να βρείτε τους πραγµατικούς αριθµούς α, β, γ R για τους
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
