Primer: gas ili smeša gasova p = 1 tečnost ili smeša mešljivih tečnosti p = 1 dve delimično mešljive ili nemešljive tečnosti p = 2 kristal p = 1
|
|
|
- Ἔραστος Ονησίφορος Βασιλειάδης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 RAVNOTEŽA FAZA 1
2 Faza, p svaki homogeni deo sistema, uniforman po svojim fizičkim osobinama i hemijskom sastavu u celoj zapremini, koji od ostalih homogenih delova razdvajaju granice, tj. površine na kojima dolazi do nagle promene osobina ili sastava. Primer: gas ili smeša gasova p = 1 tečnost ili smeša mešljivih tečnosti p = 1 dve delimično mešljive ili nemešljive tečnosti p = 2 kristal p = 1 Različite čvrste supstance istog ili različitog hemijskog sastava, ako imaju različitu kristalnu strukturu sačinjavaju različite faze. jednofazni (homogeni) sistemi višefazni (heterogeni) sistemi 2
3 Broj nezavisnih komponenti, c najmanji broj nezavisno promenljivih sastojaka neophodnih da se odredi sastav svake pojedine faze. Ako postoji samo fizička ravnoteža (prisutne vrste međusobno hemijski ne reaguju) broj nezavisnih komponenata jednak je ukupnom broju prisutnih hemijskih vrsta. Primer: led, voda i vodena para u ravnoteži c = 1 (H 2 O), p = 3 U sistemima u kojima se dešavaju hemijske promene, broj nezavisnih komponenti je manji od broja hemijskih vrsta za broj uspostavljenih ravnoteža. Primer: CaCO 3 (s) CaO(s) + CO 2 (g) c = 2 (npr. CaO i CO 2 ) p = 3 (dve čvrste i jedna gasovita faza) broj prisutnih hemijskih vrsta = 3 c = 2 (broj prisutnih hemijskih vrsta broj hemijskih ravnoteža = 3-1) 3
4 Stepen slobode, f - broj promenljivih ili parametara (pritisak, temperatura, molski udeo komponenata) koje se mogu nezavisno menjati a da se pri tome ne promeni ukupan broj faza posmatranog sistema. Uslovi koji se mogu menjati su intenzivne veličine (p, T, sastav). Sistemi: jednokomponentni jednofazni dvofazni trofazni dvokomponentni polikomponentni 4
5 USLOV RAVNOTEŽE FAZA Termodinamička ravnoteža u heterogenom sistemu određena je mehaničkom, termičkom i hemijskom ravnotežom. mehanička ravnoteža - ne postoji kretanja unutar sistema P I P II termička ravnoteža ne postoji prenos toplote između faza T I T II hemijska ravnoteža nema promene sastava u bilo kojoj tački sistema i,i i,ii Za sistem van ravnoteže: i,i i,ii 5
6 MEHANIČKA RAVNOTEŽA Ne postoji kretanje unutar sistema, što je ispunjeno kada je pritisak u svim fazama sistema isti. T const. const. Uslov ravnoteže: dadadapdvpdv I I I I 0 dapromena Helmohcove funkcije rada P I P II p-pritisak dv-promena zapremine I-odnosi se nafazu I II-odnosi se nafazu II
7 TERMIČKA RAVNOTEŽA Ne postoji prenošenje toplote između faza, jer je temperatura u svim fazama ista. V n const. i const. Uslov ravnoteže: ds ds IdS I0 dq dq 0 T T I T I II T II ds promena entropije dq - razmenjena toplota T - temperatura
8 HEMIJSKA RAVNOTEŽA Nema promene sastava u bilo kojoj tački, što je ispunjeno kada su hemijski potencijali svake od komponenata isti u svakoj od faza. p const. T const. Uslov ravnoteže: dgdgdg I I0 i,i dn i i,i dn i 0 i,i i,ii dg promena Gibsove slobo ene i -hemijski potencija -ite vrste dn -promena broja molova -ite vrst i
9 USLOVI RAVNOTEŽE FAZA Ravnoteža je termodinamička Ravnotežni uslovi između faza I i II Oblik ravnoteže Ekstenzivni parametar Intenzivni parametar Ravnotežni uslov Mehanička V p p I = p II Termička S T T I = T II Hemijska n i i I = II
10 Fazni prelaz promene faze u jednokomponentim sistemima predstavljaju fizičke transformacije čistih supstanci (ne hemijske). Primer: topljenje/mržnjenje isparavanje/kondenzacija sublimacija/depozicija prelaz između dve čvrste faze iste supstance 10
11 TERMODINAMIČKA RAVNOTEŽA I HEMIJSKI POTENCIJAL Koja je faza prisutna na datom pritisku i temperaturi? Spontani procesi imaju negativnu promenu Gibsove slobodne energije. Faza sa najnižim hemijskim potencijalom je najstabilnija.
12 TERMODINAMIČKA RAVNOTEŽA I HEMIJSKI POTENCIJAL Jednokomponentni sistem Temperaturska zavisnost ( μ/ T)p = -Sm Kako temperatura raste, hemijski potencijal čiste supstancije opada, uvek. Kada done do faznog prelaza, relativne vrednosti hemijskih potencijala različitih faza se modifikuju i postaju jednaki.
13 GIBSOVO PRAVILO FAZA Gibbs (Josiah Willard Gibbs), god Uslov termodinamičke ravnoteže: ( dg) 0 TP, Stanje sistema sa p faza i c komponenata u ravnoteži je određeno ako su određeni temperatura, pritisak i sastav u svakoj fazi. Gibsovo pravilo faza f c p 2 f stepen slobode c- broj komponenti p broj faza u sistemu 13
14 F = Ukupan broj promenjlivih Broj zavisno promenjljivih Sistem sa c komponenti u svakoj od p faza broj parametara koji određuje stanje sistema = cp Broj komponenti c jednak je broju svih koncentracija komponenata, koje se u jednoj fazi mogu izraziti preko molskih udela, čiji je zbir jednak 1 - broj parametara koji određuje stanje sistema = (c - 1)p + 2 Stanje sistema određeno je pritiskom i temperaturom broj parametara koji određuje stanje sistema = cp + 2 Ukupan broj promenljivih = p (c - 1) + 2
15 Iz uslova ravnoteže faze i, I i, II... 1,I 1,II 1, p... 2,I 2,II 2, p c,i c,ii c, p Za svaku komponentu distribuiranu u p faza ima p-1 ovakvih relacija,,,..., i,i i,ii i,ii i,iii i,iii i,iv i, p1 i, p Za c komponenti ovakvih relacija ukupno ima c (p 1) To je broj zavisnih koncentracija komponenata u sistemu jer su ravnotežne koncentracije jedne komponente u dve faze povezane relacijom i, I i, II Broj zavisno promenljivih = c (p - 1) 15
16 Maksimalan broj parametara koji se mogu menjati a da se pri tom ne promeni broj faza u ravnoteži, tj. broj stepeni slobode: F = Ukupan broj promenjlivih Broj zavisno promenjljivih F= p (c 1) + 2 c (p 1) = c p + 2 GIBSOVO PRAVILO FAZA F c p 2 f stepen slobode c- broj komponenti p broj faza u sistemu 16
17 Primer: Koliko stepeni slobode ima jednokomponenti: jednofazni, dvofazni ili trofazni sistem? a) Jednokomponentni jednofazni sistemi c = 1, p = 1 Primer: gas b) Jednokomponentni dvofazni sistemi c = 1, p = 2 Primer: tečno gas čvrsto gas F = c p + 2 F = = 2 F = c p + 2 F = = 1 (dvovarijantni sistem) (monovarijantni sistem) c) Jednokomponentni trofazni sistemi c = 1, p = 3 Primer: čvrsto - tečno - gas (led - voda vodena para) F = c p + 2 F= = 0 (nonvarijantni sistem)
18 FAZNI PRELAZI PO Ehrenfest-u Fazni prelaz je praćen promenom odgovarajućih termodinamičkih parametara i termodinamičkih funkcija. Paul Ehrenfest Erenfest: fazni prelaz je istog reda kao i izvod Gibsove energije po temperaturi i/ili pritisku koji pokazuje diskontinualnu promenu na temperaturi faznog prelaza. Fazni prelaz prvog reda Fazni prelaz drugog reda Fazni prelaz višeg reda 18
19 FAZNI PRELAZI PO Ehrenfest-u Fazni prelaz prvog reda dg SdT VdP G G dg dt dp T P P T G G S ; T P P T V G P G T G T T P P V S S V m, m, S S fp fp fp V S S T fp fp H 2 i G V V P Pn n Tn, j i Tn, i j Tn, j 2 i G S S T T n n Pn, i j Pn, i j Pn, j i i d d V II V I trsv dp dp T, II T, I S II S I trs S T T T P, II P, I 19 trs trs H
20 FAZNI PRELAZ PRVOG REDA H Nagli porast cp T je posledica konačne vrednosti promene H sa beskonačno malom promenom T. p Primeri faznih prelaza prvog reda: topljenje i očvršćavanje isparavanje i kondenzacija sublimacija i resublimacija polimorfni prelazi Ilustracija promena Gibsove slobodne energije, zapremine, entropije, entalpije i toplotnog kapaciteta sa temperaturom za fazne prelaze prvog reda; T t je temperatura prelaza T trs
21 VRSTE FAZNIH PRELAZA SdT Vdp dg Fazni prelaz drugog reda koeficijent termičkog širenja koeficijent kompresibilnosti fp p p p p T T T c T S T G V T V T p G V p V p G
22 FAZNI PRELAZ DRUGOG REDA Primer faznog prelaza drugog reda: provodljivost superprovodljivost Ilustracija promena Gibsove slobodne energije, zapremine, entropije, entalpije i toplotnog kapaciteta sa temperaturom za fazne prelaze drugog reda; T t je temperatura prelaza T trs
23 Ilustracija promene toplotnog kapaciteta za fazne prelaze prvog (levo) i fazne prelaze drugog reda (desno). 23
24 RAVNOTEŽA FAZA JEDNOKOMPONENTNIH SISTEMA Klajperonova i Klauzijus Klajperonova jendačina Klajperonova (Benoît Paul Émile Clapeyron) jednačina služi za analitičko opisivanje stanja jednokomponentnog dvofaznog sistema u ravnoteži: dp trs H dt T V trs trs dp promena pritiska dt promena temperature Δ Δ T trs trs trs H- promena parcija ln e molarne entalpije fazne transformacije V - promena parcija ln e molarne zapre min e fazne transformacije - temperatura fazne transformacije Klauzijus Klajperonova (Rudolph Clausius, Benoît Paul Émile Clapeyron) jednačina važi za jednokomponentne dvofazne sisteme od kojih je jedna gasna faza. dln P dt H vap 2 vap RT p pritisak ln prirodni log aritam dt promena temperature Δ R univerza ln a gasna konstan ta T vap vap H- promena parcija ln e molarne entalpije isparavanja - temperatura isparavanja 24
25 Klajperonova JEDNAČINA - izvođenje Za istovremenu malu promenu pritiska i temperature dve faze u ravnoteži sistema: dg SdT VdP d di S IdT V IdP d S dt V dp II II II U stanju ravnoteže: d I = d II S I dt V I dp S ( S II S I ) dt ( V II V dp dt trs trs II S V dt V I ) dp II dp S V II II S V I I trs trs S V S 2 S 1 S H T trs S T trs trs H Klajperonova jednačina dp trs H dt T V trs trs 25
26 Klajperonova JEDNAČINA 26
27 Klauzijus - Klajperonova JEDNAČINA - izvođenje Pretpostavka: Gasna faza se ponaša kao idealan gas, tj. važi zakon idealnog gasnog stanja: Molarna zapremina kondenzovane faze je zanemarljivo mala u odnosu na molarnu zapreminu gasne faze. Entalpija je nezavisna od temperature pv nrt p - pritisak V - zapremina n broj molova R - univerzalna T - temperatura gasna konstanta Za ravnotežu tečne, l, i gasne, g, faze: (ekvivalentna jednačina važi i za ravnotežu čvrste i gasne faze) V V V V g l g vap trs vap 2 vap g vap RT P trs trs dp H P H vap isparavanje dt T V RT Klauzijus - Klajperonova jednačina dln P dt 27 RT H vap 2 vap
28 Klajperonova jednačina dp trs H dt T V trs trs Nagib promene napona pare sa temperaturom faznog prelaza. opšti slučaj: uzak temp. interval: fp fp H H f f T T,, fp fp V V f f T T 28
29 Entropija isparavanja Trutonov (Trouton) zakon: mnoge tečnosti čije su relativne molekulske mase oko 100, na normalnoj tački ključanja pokazuju približno istu vrednost entropije od oko 88 J/molK. vap H vap S 8JKmol T vap 11 Važi za: većinu nepolarnih tečnosti tečnosti koje imaju molekulske mase manje od 100 tečnosti koje imaju relativno umerene tačke ključanja, između 150 i 1000 K (npr. hloroform i benzen) Odstupanja se javljaju kod: polarnih jedinjenja tečnosti sa izraženim vodoničnim vezama (npr. voda) tečnosti sa niskim tačkama ključanja, ispod 150 K (npr. helijum i vodonik) ili relativno visokih tački ključanja iznad 1000 K. 29
30 Entropija topljenja Kod supstanci koje se sastoje iz atoma kao npr metali, entropija topljenja je obično u opsegu između 8 i 38 J/molK Kod supstancu čiji su molekuli npr. dugi lanci ugljovodonika, entropija topljenja iznosi i do 120 J/molK 30
31 Pregled Definicija faze faznog prelaza nezavisne komponenete stepena slobode Termodinamički uslov ravnoteže faza Gibsovo pravilo faza Ravnoteža faza jednokomponentnih sistema: Klajperonova jednačina Klauzijus - Klajperonova jednačina 31
32 FAZNI DIJAGRAM Fazni dijagram (ravnotežni dijagram ili dijagram stanja) grafički prikaz uslova ravnoteže između raličitih faza sistema. Vrsta koordinatnog sistema koji se koristi za ovakvo prikazivanje zavisi od složenosti posmatranog sistema, odnosno broja stepeni slobode koji se za svaki sistem izračunava prema Gibsovom pravilu faza. Jednokomponentni sistemi c 1, Jednokomponenti jednofazni sistem f = 2 Jednokomponenti dvofazni sistem f = 1 Jednokomponenti trofazni sistem f = F c p 2 3 p p 1, p 2, p 3, F 2 F 1 F 0 dvovarijantni sistem jednovarijantni sistem nonvarijantni sistem Stanje ravnoteže jednokomponentog sistema može se predstaviti tačkom u dvodimenzionalnom prostoru ili ravni. promenljive veličine: p i T Fazni dijagram jednokomponentnog sistema 32
33 FAZNI DIJAGRAM - nastavak Kriva napona pare ili kriva tačke ključanja AC kriva linija koja pokazuje uslove ravnoteže tečnosti i pare. Kriva sublimacije OA - kriva linija koja pokazuje uslove ravnoteže čvrste faze i pare. Kriva topljenja AD - kriva linija koja pokazuje uslove ravnoteže čvrste faze i tečnosti. Za stanje sistema duž kriva sublimacije/isparavnja/topljenja: c = 1, p = 2 i f = 1 Fazni dijagram jednokomponentnog sistema Trojna tačka A tačka u preseku tri krive linije koja definiše temperaturu na kojoj su u ravnoteži sve tri faze: čvrsta, tečnost i gas. Za stanje sistema u trojnoj tački: c = 1, p = 3 i f = 0 33
34 FAZNI DIJAGRAM - nastavak Fazni dijagram jednokomponentnog sistema 34
35 FAZNI DIJAGRAM - nastavak Kriva napona pare ili kriva tačke ključanja AC kriva linija koja pokazuje uslove ravnoteže tečnosti i pare. Kriva sublimacije OA - kriva linija koja pokazuje uslove ravnoteže čvrste faze i pare. Kriva topljenja AD - kriva linija koja pokazuje uslove ravnoteže čvrste faze i tečnosti. Za stanje sistema duž kriva sublimacije/isparavnja/topljenja: c = 1, p = 2 i f = 1 Fazni dijagram jednokomponentnog sistema Trojna tačka A tačka u preseku tri krive linije koja definiše temperaturu na kojoj su u ravnoteži sve tri faze: čvrsta, tečnost i gas. Za stanje sistema u trojnoj tački: c = 1, p = 3 i f = 0 35
36 FAZNI DIJAGRAM - nastavak Tačka ključanja temperatura pri kojoj se napon pare izjednači sa spoljašnjim pritiskom. Normalna tačka ključanja temperatura pri kojoj se napon pare izjednači sa spoljašnjim pritiskom od 1 atm (101,325 kpa). Standardna tačka ključanja temperatura pri kojoj se napon pare izjednači sa spoljašnjim pritiskom od 1 bar (100 kpa). Primer: NTK vode = 100,0ºC, STK vode = 99,6ºC Fazni dijagram jednokomponentnog sistema Kritična temperatura temperatura pri kojoj se izjednačuju gustine tečne i parne faze i iznad koje postoji samo jedna, gasovita faza. Primer: KT vode = 374ºC i p = 22 MPa 36
37 POLIMORFNI SISTEMI Polimorfizam pojava da se jedna supstancija može javiti u različitim kristalnim oblicima, koji su termodinamički stabilni u datom domenu temperature i pritiska. Alotropija polimorfizam elemenata. Dva tipa polimorfizam: enantropija i monotropija Enantioropija pojava polimorfizma gde svaki od kristalnih oblika jedne supstance ima svoju oblast stabilnosti, a promena od jednog do drugog oblika na određenoj temperaturi dešava se u oba smera. Prelazna tačka polimorfne transformacije temperatura na kojoj postoji ravnoteža između dva enantioropna kristalnog oblika sa parom. Monotropija pojava polimorfizma gde je jedan od kristalnih oblika stabilan, a drugi metastabilan. Spontana promena vrši se samo u smeru od metastabilnog do stabilnog oblika. Pojava ne jedne nego više stabilnih trojnih tačaka kod polimorfnih sistema. Pojava metastabilnih trojnih tačaka, u kojima se susreću metastabilne koegzistentne krive, kod polimorfnih sistema. 37
38 MONOTROPIJA Kriva ab uslov ravnoteže stabilnog α-oblika Kriva de uslov ravnoteže β-oblika Fazni dijagram sa pojavom monotropije c Napon pare β-oblika veći od napona pare α-oblika na svim temperaturama njegovog postojanja te je β-oblik metastabilan. Kriva Bc - kriva napona pare tečnosti B trojna tačka α-oblika (odgovara tački topljenja α-oblika) E - tačka topljenja metastabilnog β-oblika F - hipotetička tačka prelaza Primer: crveni (stabilni) i beli (metastabilni) fosfor + dva oblika belog fosfora koja su enantioropna jedan u odnosu na drugi kvarc dva enantioropna oblika, α i β-kvarc + dva metastabilna oblika α i β-kristobalit koji su enantropni jedan u odnosu na drugi 38
39 DIJAGRAM FAZA ZA SUMPOR Dva polimorfna (enantropna) oblika sumpora: rombični i monoklinični sumpor Prelazna tačka polimorfne transformacije B (95.5ºC) Kriva AC - kriva napona pare rombičnog sumpora stabilnog ispod 95.5ºC Kriva BC - kriva napona pare monokliničnog oblika stabilnog iznad 95.5ºC Napon pare rombičnog oblika niži od napona pare monokliničnog oblika na temperaturama nižim od temperature prelaza. Pojava metastabilnih oblika (zadržana transformacija) Metastabilna trojna tačka H (114.5ºC) Tri stabilne trojne tačke: B (95.5ºC), C (119.2ºC) i D (151ºC) Fazni dijagram sumpora Enantropija kod živa(ii)jodida : crveni α-hgi 2 i žuti β- HgI 2 sa T prelaza = 127 ºC 39
40 Prehlađena voda?! FAZNI DIJAGRAM VODE Led (čvrsta faza), voda (tečna faza) i vodena para (gasna faza): trojna tačka A K i 611 Pa Kriva BA - kriva napona pare sublimacije daje uslove pri kojima su dve faze, čvrsta i gas, u ravnoteži Kriva AC - kriva napona pare tečne vode ili kriva isparavanja Kriva AE kriva metastabilnog napona pare prehlađene vode Kriva AD kriva mržnjenja ili topljenja sa negativnim nagibom (porast pritiska vodi opadanju vrednosti tačke topljenja leda) Fazni dijagram vode pri relativno niskim pritiscima (do 1 mpa) Kriva AE je kriva napona pare prehlađene tečnosti. Topljenje lednika! 40
41 DIJAGRAM FAZA ZA VODU Temperatura topljenja opada sa porastom pritiska (vodonične veze). Nastanak mraza: kada temperatura vlažnog vazduha opada, para se kondenzuje i nastaje rosa. Daljim spuštanjem temperature, rosa očvršćava i nastaje mraz. Nastanak inja: kada je vlažnost vazduha vrlo niska (za vreme hladnih zimskih dana) sniženje temperature vodi pravo iz područja pare u područje čvrste faze. Vodena para direktno očvršćava u led, odn. inje.
42 POLIMORFIZAM LEDA Javlja se na pritiscima od oko bar kao posledica modifikacije međumolekulskih sila pod dejstvom pritiska. Obični led (led I) kristališe u heksagonalnom sistemu jedino može kao čvrsta faza postojati pri pritiscima manjim od bar. Promenom pritiska i temperature iz tečne vode se mogu dobiti led I, led III, led V, led VI i led VII. Led IV egzistira u istoj oblasti kao i led V. Led II se ne može dobiti iz tečne vode već iz neke od čvrstih modifikacija (iz leda I, III, V ili VI). Led I Fazni dijagram vode za slučaj šireg domena pritisaka. Četiri trojne tačke u kojima postoji ravnoteža između dve čvrste i jedne tečne faze. Četiri trojne tačke u kojima postoji ravnoteža između tri čvrste faze. 42
43 43
44 DIJAGRAM FAZA ZA UGLJEN DIOKSID A C 0 B Pozitivan nagib krive tačke topljenja od pritiska (OA), tj. porast pritiska povećava tačku topljenja. Trojna tačka se javlja na pritisku od 5,18 bar (tečni ugljen dioksid ne može postojati na atmosferskom pritisku bez obzira na temperaturu) Čvrsta faza sublimuje pri uslovima atmosferskog pritiska i sobne temperature ( suvi led ) Na sobnoj temperaturi, gas i tečnost su u ravnoteži pri pritisku od 68 bar 44
45 DIJAGRAM FAZA ZA UGLJEN DIOKSID Superkritični ugljen dioksid komprimovani ugljen dioksid i zagrejan iznad kritične tačke. Primena u superkritičnoj hromatografiji (koristi se kao mobilna faza) i u ekstrakciji, npr. za dobijanje kafe bez kofeina. Espreso: mg/l Filter kafa: mg/l Kafa bez kofeina: mg/l Molekul kofeina 45
46 DIJAGRAM FAZA ZA UGLJENIK Tri alotropske modifikacije kristalnog ugljenika: grafit dijamant fularen (C 60, Harold W. Kroto, UK, i Richard E. Smalley, USA, Nobelova nagrada za hemiju g) Grafit Dijamant Fularen 46
47 DIJAGRAM FAZA ZA UGLJENIK Za postojanje tečnog ugljenika potrebna npr. na atmosferskom pritisku temperatura iznad 4000 K ili pritisak od 550 kbar i temperatura od 2000 K Za dobijanje dijamanta potrebna je: temperatura od 1000 K i pritisak od 400 kbar Za prevođenje grafita u dijamant potrebna je temperatura oko 4000 K. Razvijanje novih tehnologija proizvodnje dijamanta 47
48 DIJAGRAM FAZA ZA HELIJUM Na niskim T čvrsto i gas nikad nisu u ravnoteži: He atomi su tako laki da vibriraju ogromnim amplitudama. Čvrst He se može dobiti samo na vrlo niskoj T i visokom pritisku hcp i bcc označavaju heksagonalno pakovanje i zapreminski centrirano kubno pakovanje. λ-linija označava specijalni fazni prelaz gde toplotni kapacitet postaje beskonačan označavajući fluid - superfluidni prelaz tečnog He He-II tečna faza je superfluid, teče bez viskoznosti 48
49 RAVNOTEŽA FAZA - pregled Definicija faze, faznog prelaza, nezavisne komponenete, stepena slobode. Termodinamički uslov ravnoteže faza Gibsovo pravilo faza Ravnoteža faza jednokomponentnih sistema: Clapeyron-ova jednačina Clausius - Clapeyron-ova jednačina Fazni dijagram Polimorfizam: enantropija i monotropija Primeri faznih dijagrama: fazni dijagram sumpora fazni dijagram vode fazni dijagram ugljen dioksida fazni dijagram ugljenika 49
RAVNOTEŽA FAZA.
 RAVNOTEŽA FAZA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Definicija faze faznog prelaza nezavisne komponenete stepena slobode Termodinamički uslov ravnoteže faza Gibsovo pravilo faza Ravnoteža
RAVNOTEŽA FAZA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Definicija faze faznog prelaza nezavisne komponenete stepena slobode Termodinamički uslov ravnoteže faza Gibsovo pravilo faza Ravnoteža
BROJ NEZAVISNIH KOMPONENTI
 RAVNOTEŽA FAZA FAZA p-homogeni deo nekog heterogenog sistema, uniforman po svojim fizičkim osobinama i hemijskom sastavu u celoj zapremini a koji je od ostalih delova sistema odvojen granicom faza. Granica
RAVNOTEŽA FAZA FAZA p-homogeni deo nekog heterogenog sistema, uniforman po svojim fizičkim osobinama i hemijskom sastavu u celoj zapremini a koji je od ostalih delova sistema odvojen granicom faza. Granica
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Sumpor (enantiotropija i monotropija) Ugljenik
 Ravnoteža faza: JEDNOKOMPONENTNI SISTEMI-čiste supstancije Poglavlje 7 u knjizi 7.1.Opšti uslovi ravnoteže faza 7.1.1. Faza, komponenta, stepen slobode 7.1.2. Termodinamički uslovi ravnoteže faza 7.1.3.
Ravnoteža faza: JEDNOKOMPONENTNI SISTEMI-čiste supstancije Poglavlje 7 u knjizi 7.1.Opšti uslovi ravnoteže faza 7.1.1. Faza, komponenta, stepen slobode 7.1.2. Termodinamički uslovi ravnoteže faza 7.1.3.
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
U unutrašnja energija H entalpija S entropija G 298. G Gibsova energija TERMOHEMIJA I TERMODINAMIKA HEMIJSKA TERMODINAMIKA
 HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: S čvrsto < S tečno << S gas
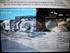 ,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Drugi zakon termodinamike
 Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
TOPLOTA. Primjeri. * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem.
 1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
BIOFIZIKA TERMO-FIZIKA
 BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
RAVNOTEŽA TEČNO-PARA
 RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Termodinamika se bavi materijom u svim agregatnim stanjima.
 Termodinamika - Termo toplota - Dinamika promena, snaga Termodinamika je oblast fizike koja se bavi odnosima između toplote i drugih oblika energije. Konkretno objašnjava kako se toplotna energija pretvara
Termodinamika - Termo toplota - Dinamika promena, snaga Termodinamika je oblast fizike koja se bavi odnosima između toplote i drugih oblika energije. Konkretno objašnjava kako se toplotna energija pretvara
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
TERMODINAMIKA.
 TERMODINAMIKA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Termodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama
TERMODINAMIKA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Termodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Energetska priroda toplote Mejer i Džul (R. Mayer, , i J. Joul, ) W. Thomson S. Carnot J. W. Gibbs
 ERMODINAMIKA ermodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje u njima. ermodinamika je
ERMODINAMIKA ermodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje u njima. ermodinamika je
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
8 Funkcije više promenljivih
 8 Funkcije više promenljivih 78 8 Funkcije više promenljivih Neka je R skup realnih brojeva i X R n. Jednoznačno preslikavanje f : X R naziva se realna funkcija sa n nezavisno promenljivih čiji je domen
8 Funkcije više promenljivih 78 8 Funkcije više promenljivih Neka je R skup realnih brojeva i X R n. Jednoznačno preslikavanje f : X R naziva se realna funkcija sa n nezavisno promenljivih čiji je domen
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
TERMOENERGETIKA. Boričić Aleksandra
 TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Termohemija. C(s) + O 2 (g) CO 2 (g) H= -393,5 kj
 Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
NULTI I PRVI ZAKON TERMODINAMIKE
 NULTI I PRVI ZAKON TERMODINAMIKE NULTI ZAKON (princip)termodinamike ako su dva sistema A i B u međusobnom termičkom kontaktu, i u ravnoteži sa trećim sistemom C onda su u ravnoteži i jedan sa drugim Ako
NULTI I PRVI ZAKON TERMODINAMIKE NULTI ZAKON (princip)termodinamike ako su dva sistema A i B u međusobnom termičkom kontaktu, i u ravnoteži sa trećim sistemom C onda su u ravnoteži i jedan sa drugim Ako
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
 27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
Uvod Nafte su veoma kompleksne heterogene disperzne smeše razli itih ugljovodni
 Uvod Nafte su veoma kompleksne heterogene disperzne smeše različitih ugljovodničnih jedinjenja parafinskog, naftenskog i aromatskog tipa i neorganskih komponenata. Hemijski sastav nafti je relativno ujednačen,
Uvod Nafte su veoma kompleksne heterogene disperzne smeše različitih ugljovodničnih jedinjenja parafinskog, naftenskog i aromatskog tipa i neorganskih komponenata. Hemijski sastav nafti je relativno ujednačen,
Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač:
 RASTVORI 1 Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač: Rastvarač je komponenta koja ima isto agregatno stanje kao i dobijeni rastvor.
RASTVORI 1 Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač: Rastvarač je komponenta koja ima isto agregatno stanje kao i dobijeni rastvor.
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
Matematka 1 Zadaci za drugi kolokvijum
 Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
za reverzibilan kružni proces količina toplote koju je sistem na svojoj nižoj temperaturi T 1 predao okolini i ponovo prešao u početno stanje
 ENROPIJA Spontani procesi u prirodi se uvek odvijaju u određenom smeru (npr. prelazak toplote sa toplijeg na hladnije telo) što nije moguće opisati termodinamičkim funkcijama do sad obrađenim. Nulti zakon
ENROPIJA Spontani procesi u prirodi se uvek odvijaju u određenom smeru (npr. prelazak toplote sa toplijeg na hladnije telo) što nije moguće opisati termodinamičkim funkcijama do sad obrađenim. Nulti zakon
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Gibbs-ova slobodna energija
 ibbs-ova slobodna energija Reakcija će se odvijati spontano ili ne, zavisno od toga de li je praćena porastom entropije univerzuma ili ne: ri = const: S S S univerzuma sistema okruzenja S univerzuma H
ibbs-ova slobodna energija Reakcija će se odvijati spontano ili ne, zavisno od toga de li je praćena porastom entropije univerzuma ili ne: ri = const: S S S univerzuma sistema okruzenja S univerzuma H
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
OSNOVI ELEKTRONIKE. Vežbe (2 časa nedeljno): mr Goran Savić
 OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
TERMODINAMIKA osnovni pojmovi energija, rad, toplota
 TERMODINAMIKA osnovni pojmovi energija, rad, toplota TERMODINAMIKA TERMO TOPLO nauka o kretanju toplote DINAMO SILA Termodinamika-nauka odnosno naučna disciplina koja ispituje odnose između promena u sistemima
TERMODINAMIKA osnovni pojmovi energija, rad, toplota TERMODINAMIKA TERMO TOPLO nauka o kretanju toplote DINAMO SILA Termodinamika-nauka odnosno naučna disciplina koja ispituje odnose između promena u sistemima
1 Afina geometrija. 1.1 Afini prostor. Definicija 1.1. Pod afinim prostorom nad poljem K podrazumevamo. A - skup taqaka
 1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
= T 2. AgBr (s) + ½ Cl 2(g) + ½ Br 2(g) = AgCl (s) O (l) O (g) +1/2O 2(g) H 2(g) =H 2. značaj navođenja agregatnog stanja
 TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
TOPLOTA I RAD, PRVI ZAKON TERMODINAMIKE
 TOPLOTA I RAD, PRI ZAKON TERMODINAMIKE Mehanički rad u termodinamici uvek predstavlja razmenu energije izmedju sistema i okoline. Mehanički rad se javlja kao rezultat delovanja sile duž puta: W Fdl W Fdl
TOPLOTA I RAD, PRI ZAKON TERMODINAMIKE Mehanički rad u termodinamici uvek predstavlja razmenu energije izmedju sistema i okoline. Mehanički rad se javlja kao rezultat delovanja sile duž puta: W Fdl W Fdl
