Ανταγωνιστικές Οικονοµίες Ανταλλαγής

Transcript

1 Κεφάλαιο 1 Ανταγωνιστικές Οικονοµίες Ανταλλαγής 1.1 Οικονοµία Ανταλλαγής Οπως και στο προηγουµενο κεφάλαιο, υποθέτουµε ότι ο χώρος αγα- ϑών είναι διατεταγµένος χώρος µε norm E και το σύνολο κατανάλωσης ο ϑετικός κώνος E + του E. Στο κεφάλαιο αυτό υποθέτουµε ότι στην οικονοµία έχουµε l καταναλωτές και µελετούµε τη συµπεριφορά των καταναλωτών σε σχέση µε τις προτιµήσεις τους, τις τιµές και το συνολικό διαθέσιµο αγαθό. Το µοντέλο είναι δύο περιόδων, 0 και 1. Υποθέτουµε ότι η χρονική στιγµή 0 έ- χει ολοκληρωθεί και ότι ο κάθε καταναλωτής είναι έτοιµος να µπεί στην επόµενη περίοδο (χρονική στιγµή 1) µε κάποιο αρχικό αγαθό (πλούτο) που έχει αποκτηθεί την χρονική στιγµή 0 και µε µια σχέση προτίµησης µε την οποία ϑα κάνει τις επιλογές του την χρονική στιγµή 1. Επίσης υποθέτουµε ότι την χρονική στιγµή 1 οι καταναλωτές ϑα ανταλλάξουν τα προϊόντα τους µε στόχο να ικανοποιήσουν τις ανάγκες τους. Καθοριστικό ϱόλο στην ανταλλαγή ϑα παίξουν οι τιµές των αγαθών κατά την χρονική στιγµή 1. Γενικά είναι άγνωστο τι ϑα συµβεί τη χρονική στιγµή 1 και στόχος µας είναι να µελετήσουµε τα διάφορα δυνατά ενδεχόµενα για τις διάφορες τιµές των αγαθών. Οι τιµές είναι ο µεγάλος άγνωστος και κα- ϑορίζουν τι πρόκειται να συµβεί την επόµενη περίοδο. 1

2 2 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής Στο µοντέλο που µελετούµε υποθέτουµε ότι στο τέλος της χρονικής στιγµής 0 ο i καταναλωτής έχει αρχικό εισόδηµα ω i E +, ω i 0 και σχέση προτίµησης i. Το αρχικό είσόδηµα είναι µια δέσµη (διάνυσµα) αγαθών και το άθροισµά των ω i συµβολίζεται µε ω και ονοµάζεται ολικό αγαθό, δηλαδή ω = ω i. Το ολικό αγαθό των καταναλωτών είναι αυτό που ϑα διατεθεί και ϑα ανταλλαγεί την χρονική στιγµή 1. Η οικονοµία αυτή ονοµάζεται οικονοµία ανταλλαγής και ϑα συµ- ϐολίζεται µε E. Επίσης χρησιµοποιούµε τον συµβολισµό E = ( E, E, {(ω i, i ) i = 1, 2,..., l}), όπου δυϊκό εύγος E, E παριστάνει το χώρο των αγαθών και τιµών και τα εύγη (ω i, i ) παριστάνουν το αρχικό εισόδηµα και την σχέση προτίµησης των καταναλωτών. Επίσης υπενθυµίζουµε ότι σύµφωνα µε την αρχική µας υπόθεση, µε τον όρο σχέση προτίµησης εννοούµε πάντοτε λογική σχέση προτίµησης. Αν υποθέσουµε ότι p είναι το διάνυσµα τιµών τη χρονική στιγµή 1, τότε w i = p(ω i ), είναι η αξία του αρχικού αγαθού του i καταναλωτή µε το οποίο εισέρχεται στην αγορά τη χρονική στιγµή 1. Το σύνολο B ωi (p) = {x E m + p(x) p(ω i )}, είναι το σύνολο προϋπολογισµού του i καταναλωτή υπό την τιµή p. 1.2 Η Εννοια της Κατανοµής Στην οικονοµία ανταλλαγής υποθέτουµε ότι την επόµενη χρονική στιγ- µή, που ονοµάζεται χρινική στιγµή ένα, οι καταναλωτές ανταλλάσουν

3 1.2. Η Εννοια της Κατανοµής 3 τα προϊόντα τους µε σκοπό να ϐελτιώσουν την ϑέση τους. Υποθέτουµε επίσης ότι (ω 1, ω 2,..., ω l ) είναι η κατανοµή του συνολικού αγαθού στο τέλος της χρονικής στιγµής µηδέν. Το συνολικό εισόδηµα ω = l ω i ϑα ανταλλαγεί κατά την χρονική στιγµή 1 και υποθέτουµε ότι x 1 είναι το διάνυσµα αγαθών που ϑα αποκτήσει ο πρώτος καταναλωτής, x 2 το διάνυσµα αγαθών που ϑα αποκτήσει ο δεύτερος καταναλωτής και γενικά υποθέτουµε ότι x i, i = 1, 2,..., l, είναι το διάνυσµα αγαθών που ϑα αποκτήσει ο i καταναλωτής την χρονική στιγµή 1. Τα διανύσµατα x i δεν είναι κατανάγκη εκείνα που µεγιστοποιούν τις προτιµήσεις των καταναλωτών. Τότε τα διανύσµατα x 1, x 2,..., x l µε την σειρά που αναγράφονται δηλώνουν την κατανοµή του συνολικού αγαθού κατά την περίοδο 1. Ετσι δίνουµε τον ορισµό : Αν x 1, x 2,..., x l E + ώστε x 1 + x x l = ω, το στοιχείο (x 1, x 2,..., x l ) του (E + ) l ονοµάζεται κατανοµή και συµβολίζεται µε x = (x 1, x 2,..., x l ). Οι κατανοµές ϑα συµβολίζονται µε καλλιγραφικά έντονα γράµµατα όπως x, y, z,... Το σύνολο των κατανοµών της οικονοµίας ανταλλαγής E συµβολίζεται µε A, δηλαδή A = {x = (x 1, x 2,..., x l ) (E + ) l x i = ω}. Εστω x = (x 1, x 2,..., x l ), y = (y 1, y 2,..., y l ) (E) l. διάταξη του (E) l ορίζεται ως εξής : Η σηµειακή x y αν και µόνο αν x i y i για κάθε i = 1, 2,..., l. Επίσης ορίζουµε : (i) x y αν και µόνο αν x i i y i για κάθε i = 1, 2,..., l, (ii) x y αν και µόνο αν x i i y i για κάθε i = 1, 2,..., l και x i i y i για ένα τουλάχιστον i,

4 4 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής (iii) x y αν και µόνο αν x i i y i για κάθε i = 1, 2,..., l, και (iv) x y αν και µόνο αν x y και y x. Η σχέση του (E + ) l ονοµάζεται ολική προτίµηση, και είναι ανακλστική και µεταβατική αλλά δεν είναι πλήρης. Η κατανοµή x = (x 1, x 2,..., x l ) ονοµάζεται : (i) ατοµικά λογική αν x i i ω i για κάθε i, (ii) άριστη κατά Pareto αν δεν υπαρχει κατανοµή y = (y 1, y 2,..., y l ) τέτοια ώστε y x, δηλαδή y i x i για κάθε i και y i i x i για ένα τουλάχιστον i, και (iii) άσθενώς άριστη κατά Pareto αν δεν υπάρχει κατανοµή y = (y 1, y 2,..., y l ) τέτοια ώστε y i x, δηλαδή y i x i για κάθε i. Αν υποθέσουµε ότι οι σχέσεις προτίµησης i αναπαρίστανται από τις συναρτήσεις χρησιµότητας u i ορίζουµε τη συνάρτηση ώστε u : (E + ) l R l, u(x 1, x 2,..., x l ) = (u 1 (x 1 ), u 2 (x 2 ),..., u l (x l )). Η u ονοµάζεται ολική συνάρτηση χρησιµότητας και ορίζει την συνολική προτίµηση στον (E + ) l. ηλαδή αν x = (x 1, x 2,..., x l ), y = (y 1, y 2,..., y l ) (E + ) l έχουµε : x y αν και µόνο αν u(x) u(y). Επίσης έχουµε x y αν και µόνο αν u(x) > u(y), x y αν και µόνο αν u(x) u(y) x y αν και µόνο αν u(x) = u(y). Θα συµβολίζουµε µε Λ το σύνολο των ατοµικά λογικών κατανοµών, δηλαδή Λ = {x A x i i ω i, για κάθε i}. και

5 1.2. Η Εννοια της Κατανοµής 5 Επίσης ϑα συµβολίζουµε µε K το σύνολο K = {x = (x 1, x 2,..., x l ) (E + ) l x i ω}. Κάθε στοιχείο του K ϑα ονοµάζεται κατορθωτή κατανοµή και το K ϑα αναφέρεται ως το σύνολο των κατορθωτών κατανοµών. Για κάθε (x 1, x 2,..., x l ) (E + ) l ϑέτουµε S(x 1, x 2,..., x l ) = x i. Η απεικόνιση S είναι συνεχής γραµµικός τελεστής του (E + ) l στον E και ϑα αναφέρεται ως ο τελεστής του αθροίσµατος. Εχουµε S(x) = ω, για κάθε x A, και Ακόµη ϑα συµβολίζουµε µε 0 S(x) ω, για κάθε x K. w = (ω 1, ω 2,..., ω l ), την αρχική κατανοµή και µε w δ το στοιχείο w δ = (ω, ω,..., ω), του (E + ) l, όπου οι συντεταγµένες του w δ είναι το συνολικό αγαθό ω. Εδώ ϑα πρέπει να σηµειώσουµε την διαφορά µεταξυ των συµβόλων w και ω. Το πρώτο είναι η αρχική κατανοµή και το δεύτερο το συνολικό εισόδηµα. Προφανώς έχουµε ω = S(w). Με [0, w δ ] ϑα συµβολίζουµε το διατεταγµένο διάστηµα του (E) l µε άκρα τα 0, w δ δηλαδή [0, w δ ] = {x = (x 1, x 2,..., x l ) (E + ) l 0 x i ω για κάθε i}.

6 6 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής Εχουµε όπου [0, w δ ] = [0, ω] [0, ω]..., [0, ω], [0, ω] = {x E 0 x ω}. Στη περίπτωση όπου E = R m, το διάστηµα [0, w δ ] είναι κλειστό και ϕραγµένο, άρα συµπαγές, υποσύνολο του (R m +) l. Πρόταση 1.1. Αν το διατεταγµένο διάστηµα [0, ω] του E είναι συµπαγές, τότε το σύνολο των κατορθωτών κατανοµών K και το σύνολο των κατανοµών A της οικονοµίας ανταλλαγής είναι συµπαγή και κυρτά υποσύνολα του [0, w δ ]. Αν οι σχέσεις προτίµησης i είναι άνω ηµισυνεχείς, το συνόλο των ατοµικά λογικών κατανοµών Λ είναι συµπαγές και αν οι σχέσεις προτίµησης i είναι κυρτές το Λ είναι κυρτό. Απόδειξη. Εστω x = (x 1, x 2,..., x l ) K. Τότε 0 l x i ω, ε- ποµένως 0 x i ω για κάθε i, άρα x [0, w δ ]. Εποµένως K [0, w δ ] και εύκολα διαπιστώνουµε ότι K = [0, w δ ] S 1 ([0, ω]). Επειδή το διάστηµα [0, ω] του E + είναι συµπαγές, το [0, w δ ] είναι συµπαγές. Η απεικόνιση S είναι συνεχής, άρα S 1 ([0, ω]) είναι κλειστό και το σύνολο K ως κλειστό υποσύνολο συµπαγούς είναι είναι συµπαγές. Επίσης έχουµε A = [0, w δ ] S 1 ({ω}), άρα το σύνολο A είναι συµπαγές. Υποθέτουµε ότι x = (x 1, x 2,..., x l ), y = (y 1, y 2,..., y l ) K. Τότε για κάθε λ (0, 1) έχουµε (λx i + (1 λ)y i ) = λ x i + (1 λ) y i λω + (1 λ)ω = ω, εποµένως λx + (1 λ)y K. Ανάλογα αν υποθέσουµε ότι x, y A, έχουµε ότι λx + (1 λ)y A, άρα τα σύνολα A, K είναι κυρτά.

7 1.2. Η Εννοια της Κατανοµής 7 Εστω x = (x 1, x 2,..., x l ) Λ. Τότε x i i ω i για κάθε i, εποµένως έχουµε ότι x i Λ i = {x [0, ω] x i ω i } και είναι εύκολο να δείξουµε ότι : Λ = (Λ 1 Λ 2..., Λ l ) A. Επειδή οι σχέσεις i είναι άνω ηµισυνεχείς έχουµε ότι τα σύνολα Λ i είναι κλειστά άρα το σύνολο Λ είναι συµπαγές σαν κλειστό υποσύνολο του συµπαγούς συνόλου A. Αν υποθέσουµε ότι οι σχέσεις προτίµησης είναι κυρτές, γιά κάθε x, y Λ έχουµε x i, y i i ω i για κάθε i, εποµένως, γιά κάθε λ (0, 1) έχουµε λx i + (1 λ)y i i ω i, για κάθε i. Εποµένως λx + (1 λ)y Λ, άρα το σύνολο Λ είναι κυρτό. Πρόταση 1.2. Αν τουλάχιστο µια από τις σχέσεις προτίµησης i είναι µονότονη, για κάθε κατορθωτή κατανοµή x υπάρχει κατανοµή y A (που εξαρτάται από την x) ώστε y x. Απόδειξη. Εστω x = (x 1, x 2,..., x l ) και έστω z = ω x i. Επειδή x K έχουµε ότι z 0. Αν z = 0, τότε x A και η πρόταση ισχύει για y = x. Αν z > 0 ϑεωρούµε τη κατανοµή y = (y 1, y 2,..., y l ) όπου y j = x j + z για κάποιο j γιά το οποίο έχουµε ότι η σχέση j είναι µονότονη και y i = x i για κάθε i j. Τότε η y είναι κατανοµή µε y x, εποµένως ισχύει η πρόταση. Υποθέτουµε ότι D (E + ) l και x D. Θα λέµε ότι το x είναι µεγιστικό στοιχείο του D ως προς την ολική σχέση προτίµησης αν δεν υπάρχει y D ώστε y x. Πρόταση 1.3. Εστω η κατανοµή x = (x 1, x 2,..., x l ). Τότε

8 8 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής (i) Η κατανοµή x είναι άριστη κατά Pareto αν και µόνο αν το x είναι µεγιστικό στοιχείο του συνόλου των κατανοµών A ως προς την ολική προτίµηση. (ii) Αν τουλάχιστο µιά από τις σχέσεις προτίµησης είναι µονότονη, η κατανοµή x είναι άριστη κατά Pareto αν και µόνο αν το x είναι µεγιστικό στοιχείο του συνόλου των κατορθωτών κατανοµών K ως προς την ολική προτίµηση Απόδειξη. Η (i) είναι άµεση συνέπεια του ορισµού.γιά την απόδειξη της (ii) υποθέτουµε ότι τουλάχιστο µιά από τις σχέσεις προτίµησης είναι µονότονη. Αν η κατανοµή x είναι άριστη κατά Pareto και υποθέσουµε ότι υπάρχει y K, ώστε y x, έχουµε ότι υπάρχει κατανοµή z ώστε z y x, άτοπο γιατί η x είναι άριστη κατά Pareto. Αρα το x είναι µεγιστικό στοιχείο του συνόλου K. Αντίστροφα αν υποθέσουµε ότι η κατανοµή x είναι µεγιστικό στοιχείο του K δεν υπάρχει κατανοµή y ώστε y x, άρα η x ειναι άριστη κατά Pareto. Εστω ότι x είναι µεγιστικό στοιχείο του Λ. Τότε το x είναι και µεγιστικό στοιχείο του A γιατί αν υποθέσουµε ότι υπάρχει y A µε y x, έχουµε ότι y i i x i i ω i για κάθε i, άρα y Λ, άτοπο γιατί υποθέσαµε ότι το x είναι µεγιστικό στοιχείο του Λ. Αρα η κατανοµή x είναι άριστη κατά Pareto. Θεώρηµα 1.4. Αν το διατεταγµένο διάστηµα [0, ω] του E είναι συµπαγές και οι προτιµήσεις i της οικονοµίας ανταλλαγής E είναι άνω ηµισυνεχείς, υπαρχει κατανοµή που είναι ατοµικά λογική και άριστη κατά Pareto. Απόδειξη. Θα δείξουµε ότι το σύνολο των ατοµικά λογικών κατανοµών Λ έχει µεγιστικά στοιχεία ως προς την ολική σχέση προτίµησης. Υποθέτουµε ότι το Λ είναι µερικά διατεταγµένο µε τη σχέση ολικής προτίµησης και υποθέτουµε ότι Γ είναι ένα ολικά διατεταγµένο υποσύνολο του Λ, δηλαδή ότι για κάθε γ 1, γ 2 Γ έχουµε γ 1 γ 2 ή γ 2 γ 1. Για να εφαρµοσουµε το λήµµα του Zorn ϑα δείξουµε ότι υπάρχει κατανοµή x Λ ώστε x γ, για κάθε γ Γ. Επειδή το σύνολο Λ είναι συµπαγές, το σύνολο Γ έχει συγκλίνον υποδίκτυο. Ετσι υποθέτουµε ότι το Γ Γ είναι υποδίκτυο του Γ που συγκλίνει στο x. Το x

9 1.3. Ο Πυρήνας της Οικονοµίας 9 είναι άνω ϕράγµα του Γ, γιατί είναι εύκολο να δείξουµε ότι x γ για κάθε γ Γ. Επίσης για κάθε γ Γ υπάρχει γ Γ ώστε γ γ, άρα x γ, εποµένως το x είναι άνω ϕράγµα του Γ. Άρα από το λήµµα του Zorn το Λ έχει µεγιστικά στοιχεία ως προς την ολική σχέση προτίµησης. Από τη Πρόταση 1.3, έχουµε ότι κάθε µεγιστικό στοιχείο του Λ είναι κατανοµή άριστη κατά Pareto, άρα ισχύει η πρόταση. Θεώρηµα 1.5. Αν οι σχέσεις προτιµήσεις i είναι άνω ηµισυνεχείς, το σύνολο των ασθενώς άριστων κατά Pareto κατανοµών είναι κλειστό. Απόδειξη. Εστω {x n } ακολουθία από ασθενώς άριστες κατά Pareto κατανοµές και έστω ότι x n x. Τότε x A, γιατί το σύνολο των κατανοµών A είναι κλειστό. Αν υποθέσουµε ότι η x δεν είναι ασθενώς άριστη κατά Pareto, υπάρχει κατανοµή y ώστε y x. Επειδή οι i είναι άνω ηµισυνεχείς, τα σύνολα P (y i ) είναι ανοικτά. Επίσης x i P (y i ) για κάθε i. Επειδή η ακολουθία {x n i } συγκλίνει στο x i, υπάρχει n 0 τετοιο ώστε y i x n i για κάθε n n 0 και µπορούµε να υποθέσουµε ότι το n 0 είναι κοινό για όλα τα i, δηλαδή ότι y i x n i για κάθε i = 1, 2,..., l και κάθε n n 0. Τότε ϑα έχουµε ότι y x n, για κάθε n n 0, άτοπο γιατί έχουµε υποθέσει ότι οι κατανοµές x n είναι ασθενώς άριστες κατά Pareto. 1.3 Ο Πυρήνας της Οικονοµίας Υποθετουµε ότι στην οικονοµία ανταλλαγής E είναι δυνατόν ορισµένοι καταναλωτές να µην ενεργούν ατοµικά αλλά να ενώνονται σε οµάδες (συνασπισµούς) µε στόχο να ϐελτιώσουν την ϑέση τους όλοι οι καταναλωτές του συνασπισµού, ανεξάρτητα από τους υπόλοιπους. Ετσι κάθε υποσύνολο S του {1, 2,..., l} είναι και ένας συνασπισ- µός υπό την έννοια ότι για κάθε i S ο i καταναλωτής είναι µέλος του συνασπισµού. Εποµένως το σύνολο των µη κενών υποσυνολων του {1, 2,..., l} είναι το σύνολο όλων των συνασπισµών που εµφανίζονται στην οικονοµία. Με την δηµιουργία συνασπισµών τα µέλη τους επιδιώκουν να

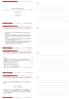
10 10 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής ϐελτιώσουν την ϑέση τους ανακατανέµοντας µεταξύ τους το αρχικό τους εισόδηµα. Θα λέµε ότι ο συνασπισµός S ϐελτιώνει την κατανοµή x = (x 1, x 2,..., x l ) της E, ή ότι η κατανοµή x ϐελτιώνεται από το συνασπισµό S, αν υπάρχει κατανοµή y = (y 1, y 2,..., y l ) της οικονοµίας E ώστε y i i x i για κάθε i S και y i = ω i. i S i S Αν η κατανοµή x = (x 1, x 2,..., x l ) δεν µπορεί να ϐελτιωθεί από κανένα συνασπισµό ονµάζεται κατανοµή πυρήνα. Το σύνολο των κατανοµών πυρήνα της E ονοµάζεται πυρήνας της οικονοµίας E και συµβολίζεται µε core (E). Πρόταση 1.6. Κάθε κατανοµή πυρήνα είναι ατοµικά λογική και ασθενώς άριστη κατά Pareto Απόδειξη. Εστω ότι x = (x 1, x 2,..., x l ) είναι κατανοµή πυρήνα. Αν υποθέσουµε ότι x i i ω i για κάποιο i, τότε ο συνασπισµός {i} ϐελτιώνει την κατανοµή x = (x 1, x 2,..., x l ) γιατί (ω 1, ω 2,..., ω l ) είναι κατανοµή και ισχύει ω i i x i, άτοπο. Εποµένως έχουµε ότι x i i ω i για κάθε i άρα η x = (x 1, x 2,..., x l ) είναι ατοµικά λογική κατανοµή. Αν υποθέσουµε ότι η x = (x 1, x 2,..., x l ) δεν είναι ασθενώς άριστη κατά Pareto, υπαρχει κατανοµή y = (y 1, y 2,..., y l ) ώστε y i i x i για κάθε i, εποµένως ο συνασπισµός S = {1, 2,..., l} όλων των καταναλωτών ϐελτιώνει την κατανοµή, άτοπο. Αρα η x = (x 1, x 2,..., x l ) είναι και ασθενώς άριστη κατά Pareto. 1.4 Το κουτί του Edgeworth Γιά να παραστήσουµε γραφικά τις κατανοµές σε οικονοµία αταλλαγής µε δυό αγαθά και δυο καταναλωτές χρησιµοποιούµε τη παρακάτω µέθοδο που είναι γνωστή ως «κουτί του Edgeworth». Υποθέτουµε ότι έχουµε δυο καταναλωτές µε αρχικό αγαθό α = (α 1, α 2 ) και β = (ϐ 1, ϐ 2 ) αντίστοιχα.

11 1.4. Το κουτί του Edgeworth 11 y 1 Γ x 2 y 1 u 1 (z 1, z 2 ) = u 1 (x 1, x 2 ) A = (x x 1, x 2 ) 2 y 2 E Θ H Z 0 x 1 u 2 (w 1, w 2 ) = u 2 (y 1, y 2 ) y 2 B x 1 Σχήµα 1.1: Το κουτί του Edgeworth Θεωρούµε το σύστηµα αξόνων x 1 0x 2 του R 2 και ένα νεο σύστηµα αξόνων y 1 Ay 2 µε κορυφή το σηµείο A του επιπέδου x 1 0x 2 που ορίζεται από το διάνυσµα ω = α + β του συνολικού αγαθού µε άξονες παράλληλους σε αυτούς του x 1 0x 2 και µε ϕορά αντίθετη µε αυτή των αξόνων του x 1 0x 2. Τότε για το τυχαίο σηµείο του ορθογωνίου 0BAΓ έχουµε : Αν (x 1, x 2 ) είναι οι συντεταγµένες του στο x 1 0x 2 και (y 1, y 2 ) οι συντεταγµένες του στο y 1 Ay 2, έχουµε άρα το ευγάρι των διανυσµάτων x 1 + y 1 = ω 1 και x 2 + y 2 = ω 2, ((x 1, x 2 ), (y 1, y 2 )) είναι κατανοµή. Ετσι το τυχαίο σηµείο του 0BAΓ, αντιστοιχίζεται στή κατανοµή

12 12 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής ((x 1, x 2 ), (y 1, y 2 )), όπου (x 1, x 2 ) είναι οι συντεταγµένες του στο x 1 0x 2 και (y 1, y 2 ) οι συντεταγµένες του στο y 1 Ay 2. Εποµένως σύµφωνα µε αυτή την παραδοχή, τα σηµεία του ορθογωνίου 0BAΓ παριστάνουν τις κατανοµές της οικονοµίας. Εστω ότι u 1 (x 1, x 2 ) και u 2 (y 1, y 2 ) είναι οι συναρτήσεις χρησιµότητας των καταναλωτών. Τότε τα αγαθά τα προτιµότερα του = (x 1, x 2 ) για τον πρώτο καταναλωτή είναι τα σηµεία (z 1, z 2 ) του x 1 0x 2 ώστε u 1 (z 1, z 2 ) u 1 (x 1, x 2 ). Γ y 1 A = (x x 1, x 2 ) 2 y 2 E Θ H Z 0 x 1 Καµπύλη Συµφωνίας B Σχήµα 1.2: Καµπύλη Συµφωνίας στο κουτί του Edgeworth Τα προτιµότερα αγαθά γιά το δεύτερο καταναλωτή είναι τα σηµεία (w 1, w 2 ) του y 1 Ay 2 ώστε u 2 (w 1, w 2 ) u 2 (y 1, y 2 ). Τότε αν το Θ είναι σηµείο του EZH και Θ = (θ 1, θ 2 ) στο x 1 0x 2 και Θ = (θ 1, θ 2) στο y 1 Ay 2, τότε ((θ 1, θ 2 ), (θ 1, θ 2)) είναι κατανοµή µε (θ 1, θ 2 ) 1 (x 1, x 2 ) και (θ 1, θ 2) 2 (y 1, y 2 ). Αν το Θ δεν είναι σηµείο της καµπύλης HZ έ- χουµε ότι (θ 1, θ 2 ) 1 (x 1, x 2 ) και αν το Θ δεν είναι σηµείο της καµπύλης

13 1.4. Το κουτί του Edgeworth 13 EZ έχουµε ότι (θ 1, θ 2) 2 (y 1, y 2 ). Αν το σηµείο Θ του EZH ανήκει ταυτόχρονα και στις δύο καµπύλες αδιαφορίας, (π.χ. αν οι καµπύλες αδιαφορίας εφάπτονται ) τότε η κατανοµή ((θ 1, θ 2 ), (θ 1, θ 2)), δεν ϐελτιώνεται από καµιά άλλη κατανοµή, δηλαδή είναι ϐέλτιστη κατά Pareto. Τα σηµεία του ορθογώνιου OBAΓ που εφάπτονται οι καµπύλες αδιαφορίας είναι το σύνολο των κατανοµών που είναι ϐέλτιστες κατά Pareto. Το σύνολο αυτό ονοµάζεται καµπύλη συµφωνίας. Αν = (α 1, α 2 ), Γ ϐ 1 A = (α α 1, α 2 ) = (ϐ 1, ϐ 2 ) 2 ϐ 2 E Θ H Z 0 α 1 Κατανοµή Πυρήνα B Σχήµα 1.3: Κατανοµή Πυρήνα στο κουτί του Edgeworth δηλαδή αν το ως σηµείο του x 1 0x 2 παριστάνει τα αρχικό αγαθό του πρώτου καταναλωτή, τότε το ως σηµείο του y 1 Ay 2 είναι = (ϐ 1, ϐ 2 ), δηλαδή παριστάνει το αρχικό αγαθό του του δεύτερου καταναλωτή. Ε- ποµένως το είναι η αρχική κατανοµή ((α 1, α 2 ), (ϐ 1, ϐ 2 )) και το EZH παριστάνει το σύνολο των ατοµικά λογικών κατανοµών. Επειδή κάθε κατανοµή πυρήνα είναι και ατοµικά λογική και ασθενώς άριστη κατά

14 14 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής Pareto, εχουµε ότι οι κατανοµές πυρήνα ανήκουν στην τοµή της καµπύλης συµφωνίας µε το EZH. Ειδικά στην περίπτωση µας η τοµή αυτή είναι το σύνολο των κατανοµών πυρήνα. 1.5 Θεωρήµατα Ευηµερίας Ενα από τα σηµαντικότερα προβλήµατα της οικονοµίας είναι ο προσδιορισµός κατανοµών x = (x 1, x 2,..., x l ) και τιµών p ώστε για κάθε i, το x i να είναι το προτιµότερο στοιχείο του καταναλωτή i υπό την τιµή p. ηλαδή ϑέλουµε να προσδιορίσουµε τιµή p και κατανοµή x = (x 1, x 2,..., x l ) τέτοια ώστε για κάθε i = 1, 2,..., m να ισχύει x i B ωi (p) και x B ωi (p) x i i x. Αν ισχύουν τα παραπάνω, το ευγάρι κατανοµή διάνυσµα τιµών επιφέρουν την ευηµερία όλων των καταναλωτών ταυτόχρονα γιατί κάθε ένας από αυτούς κατέχει ένα διάνυσµα αγαθών x i που είναι προτιµότερο ή ίδιο από κάθε άλλο διάνυσµα αγαθών που µπορεί να αποκτήσει υπό τη τιµή p. Ορισµός 1.7. Το διάνυσµα p E στηρίζει την κατανοµή x = (x 1, x 2,..., x l ) αν p 0 και για κάθε x E + και κάθε i ισχύει η συνεπαγωγή x i x i p(x) p(x i ). Μια ισοδύναµη διατύπωση του ορισµού είναι η ακόλουθη : Το διάνυσµα p στηρίζει την κατανοµή x = (x 1, x 2,..., x l ) αν για κάθε i = 1, 2,..., l το διάνυσµα p στηρίζει την σχέση i στο x i. Πρόταση 1.8. Αν το διάνυσµα p στηρίζει την κατανοµή x = (x 1, x 2,..., x l ), έχουµε : (i) Αν τουλάχιστον µια από τις σχέσεις προτίµησης i τότε p E+ είναι µονότονη, (ii) Αν οι σχέσεις προτίµησης i είναι κατω ηµισυνεχείς, p E+ και p(ω) > 0, τότε η κατανοµή x = (x 1, x 2,..., x l ) είναι ασθενώς άριστη κατά Pareto.

15 1.5. Θεωρήµατα Ευηµερίας 15 Απόδειξη. (i.) Εστω ότι η σχέση προτίµησης i είναι µονότονη. Τότε για κάθε x E + έχουµε x + x i x i, εποµένως x + x i x i, άρα p(x + x i ) p(x i ). Εποµένως p(x) 0. Άρα p E +. (ii.) Υποθέτουµε ότι η κατανοµή δεν είναι ασθενώς άριστη κατά Pareto. Τότε υπάρχει κατανοµή (y 1, y 2,..., y l ) ώστε y i i x i για κάθε i. Εποµένως p(y i ) p(x i ) για κάθε i, επειδή το διάνυσµα p στηρίζει τη κατανοµή. Επειδή οι σχέσεις προτίµησης i είναι κάτω ηµισυνεχείς τα σύνολα P (x i ) είναι ανοικτά εποµένως υπάρχει 0 < λ < 1 ώστε λy i i x i για κάθε i. Ετσι έχουµε λp(y i ) p(x i ) για κάθε i, εποµένως λ p(y i ) p(x i ) = p(ω) > 0. Επειδή η y = (y 1, y 2,..., y l ) είναι κατανοµή έχουµε p(y i ) = p(ω) εποµένως λp(ω) p(ω) > 0, άτοπο γιατί 0 < λ < 1. κατανοµή x είναι ασθενώς άριστη κατά Pareto. Ορισµός 1.9. Εστω η κατανοµή x = (x 1, x 2,..., x l ). Εποµένως η (i) Αν υπαρχει p E +, p 0 ώστε για κάθε x E + και για κάθε i = 1, 2,..., l ισχύουν x i B ωi (p) και x i x i p(x) > p(ω i ), η κατανοµή x είναι κατανοµή ισορροπίας (κατά Walras) που στηρίζεται από το διάνυσµα p. (ii) Αν υπάρχει p E+, p 0, ώστε για κάθε i = 1, 2,..., l και για κάθε x E + να ισχύει η συνεπαγωγή x i x i p(x) p(ω i ), η κατανοµή x είναι κατανοµή σχεδόν ισορροπίας που στηρίζεται από το διάνυσµα p.

16 16 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής Πρόταση Εστω η κατανοµή x = (x 1, x 2,..., x l ) και διάνυσµα p E+, p 0. Οι παρακάτω προτάσεις είναι ισοδύναµες : (i) Για κάθε i η σχέση προτίµησης i παίρνει µέγιστη τιµή στο B ωi (p) στο σηµείο x i, (ii) η x είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p. Απόδειξη. Εστω ότι ισχύει η (i). Τότε x i B ωi (p) για κάθε i. Επειδή η i παίρνει µέγιστη τιµή στο B ωi (p) στο x i έχουµε ότι x i x i p(x) > p(ω i ) γιατί αν υποθέσουµε ότι p(x) p(ω i ) έχουµε ότι x B ωi (p), άτοπο. Αρα η x = (x 1, x 2,..., x l ) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p. Γιά το αντίστροφο υποθέτουµε ότι η (ii) είναι αληθής. Επειδή x είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p, έχουµε ότι x i B ωi (p) για κάθε i. Επειδή για κάθε x E +, έχουµε ότι x i x i p(x) > p(ω i ), η σχέση i παίρνει µέγιστη τιµή στο B ωi (p) στο σηµείο x i, γιατί αν υποθέσουµε ότι υπάρχει x B ωi (p) ώστε x i x i, έχουµε ότι p(x) > p(ω i ), άτοπο. Πρόταση Αν x = (x 1, x 2,..., x l ) είναι κατανοµή σχεδον ισορροπίας που στηρίζεται από το διάνυσµα p E +, τότε p(x i) = p(ω i ), για κάθε i = 1, 2,..., l. Απόδειξη. Επειδή x i i x i έχουµε p(x i ) p(ω i ) για κάθε i. Επίσης έχουµε ότι p(x i ), p(ω i ) 0 για κάθε i και x i = ω i, επειδή η x = (x 1, x 2,..., x l ) είναι κατανοµή. Από τα παραπάνω έπεται ότι p(x i ) = p(ω i )

17 1.5. Θεωρήµατα Ευηµερίας 17 και από την παρατήρηση ότι p(x i ) p(ω i ) έχουµε ότι p(x i ) = p(ω i ) για κάθε i γιατί διαφορετικά ϑα είχαµε p(x i ) > p(ω i ), άτοπο. Πρόταση Αν x = (x 1, x 2,..., x l ) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p, τότε (i) η x = (x 1, x 2,..., x l ) είναι ατοµικά λογική, και (ii) αν οι σχέσεις προτίµησης i είναι τοπικά µη κορεσµένες η κατανοµή x είναι σχεδόν ισορροπία που στηρίζεται από την τιµή p. Απόδειξη. (i) Εστω ότι ω i i x i, για κάποιο i. Επειδή x είναι κατανοµή ισορροπίας κατά Walras έχουµε ότι p(ω i ) > p(ω i ), άτοπο. Αρα x i i ω i για κάθε i, εποµένως η κατανοµή x = (x 1, x 2,..., x l ) είναι ατοµικά λογική. (ii) Εστω z E + µε z i x i για κάποιο i. Επειδή οι σχέσεις προτίµησης i είναι τοπικά µη κορεσµένες, υπάρχει ακολουθία {z ν } του E + ώστε z ν i z για κάθε ν και lim ν z ν = z. Επίσης έχουµε z ν i z i x i p(z ν ) > p(ω i ), για κάθε ν N. Από την συνέχεια του p έχουµε ότι p(z) p(ω i ), άρα η κατανοµή x = (x 1, x 2,..., x l ) είναι σχεδόν ισορροπία που στηρίζεται από την τιµή p. Θεώρηµα 1.13 (Ισοδυναµία ισχυρής και ασθενούς ισορροπίας). Εστω η κατανοµή x = (x 1, x 2,..., x l ) και έστω διάνυσµα p E +, p 0. Αν οι σχέσεις προτίµησης i είναι κάτω ηµισυνεχείς και τοπικά µη κορεσ- µένες, οι παρακάτω προτάσεις είναι ισοδύναµες (i) η x είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p,

18 18 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής (ii) η x = (x 1, x 2,..., x l ) είναι κατανοµή σχεδόν ισορροπίας που στηρίζεται από το διάνυσµα p. Απόδειξη. Από τη Πρόταση 1.12 προκύπτει το ευθύ. Γιά το αντίστροφο υποθέτουµε ότι η (ii) είναι αληθής. Επειδή η x είναι σχεδον ισορροπία που στηρίζεται από το διάνυσµα p, από την Πρόταση 1.11 έχουµε ότι p(x i ) = p(ω i ) για κάθε i, άρα x i B ωi (p). Υποθέτουµε ότι x E + και x i x i. Θα δείξουµε ότι p(x) > p(ω i ). Επειδή x i x i έχουµε p(x) p(ω i ). Εστω p(x) = p(ω i ). Επειδή οι σχέσεις προτίµησης i είναι κάτω ηµισυνεχείς το P (x i ) είναι ανοικτό, εποµένως υπάρχει περιοχή V του x που περιέχεται στο P (x i ). Η περιοχή αυτή τέµνει και τους δύο ανοικτούς ηµιχώρους που ορίζει το υπερεπίπεδο L = {z E p(z) = p(ω i }, γιατί αν a E ώστε p(a) = 1, τότε x + λa V και x λa V για κάποιο λ > 0 και x + λa, x λa ανήκουν σε διαφορετικούς ηµιχώρους. Άρα υπαρχει y V µε p(y) < p(ω i ). Αυτό είναι άτοπο γιατί y i x i, εποµένως p(y) p(ω i ). Αρα έχουµε ότι p(x) > p(ω i ). Εποµένως η x = (x 1, x 2,..., x l ), είναι ισορροπία κατά Walras που στηρίζεται από το p. Θεώρηµα 1.14 (Πρώτο Θεώρηµα Ευηµερίας). Αν οι σχέσεις προτίµησης i είναι αυστηρά κυρτές, τότε κάθε κατανοµή ισορροπίας κατα Walras είναι άριστη κατά Pareto Απόδειξη. Υποθέτουµε ότι x = (x 1, x 2,..., x l ) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p. Για να δείξουµε ότι η x είναι άριστη κατά Pareto ϑα δείξουµε ότι δεν υπάρχει κατανοµή y = (y 1, y 2,..., y l ) ώστε y i x i για κάθε i και y j j x j για ένα τουλάχιστον j. Υποθέτουµε ότι υπάρχει τέτοια κατανοµή y. Από την αυστηρή κυρτότητα των σχέσεων προτίµησης έχουµε ότι 1 2 y j x j j x j. Επειδή η x είναι κατανοµή ισορροπίας κατά Walras έχουµε, 1 2 p(y j) p(x j) > p(ω j ).

19 1.5. Θεωρήµατα Ευηµερίας 19 Επειδή το x j ανήκει στο σύνολο προϋπολογισµού του j-καταναλωτή έ- χουµε p(ω j ) p(x j ) και αν αντικαταστήσουµε στη προηγούµενη ανισότητα έχουµε p(y j ) > p(x j ). Από την προηγούµενη σχέση, την ισότητα p(y i ) = p(x i ), και από το γεγονός ότι στα παραπάνω αθροίσµατα οι προσθεταίοι είναι µη αρνητικοί πραγµατικοί αριθµοί, έπεται ότι p(y k ) < p(x k ) γιά ένα τουλάχιστο k. Οµως y k x k και y k x k και από την αυστηρή κυρτότητα, όπως προηγουµένως, έχουµε p(y k ) > p(x k ), άτοπο. Άρα η κατανοµή x είναι άριστη κατά Pareto. Θεώρηµα 1.15 ( εύτερο Θεώρηµα Ευηµερίας). Εστω ότι ο ϑετικός κώνος E + του E έχει εσωτερικά σηµεία. Αν οι σχέσεις προτίµησης i είναι κάτω ηµισυνεχείς, µη κορεσµένες και αυστηρά κυρτές, τότε κάθε ασθενώς άριστη κατανοµή κατά Pareto (άρα κάθε άριστη κατά Pareto κατανοµή) στηρίζεται από µη µηδενικό διάνυσµα p E +. Απόδειξη. Εστω ότι η κατανοµή x = (x 1, x 2,..., x l ) είναι ασθενώς άριστη κατά Pareto. Επειδή οι σχέσεις i είναι µη κορεσµένες τα σύνολα P (x i ) = {x E + x i x i }, είναι µη κενά για κάθε i = 1, 2,..., l. Εστω F = P (x 1 ) + P (x 2 ) + + P (x l ). Τότε το F είναι µη κενό υποσύνολο του E +. Ακόµη το σύνολο F είναι κυρτό και ανοικτό υποσύνολο του E + ως άθροισµα πεπερασµένουπλήθους κυρτών και ανοικτών υποσυνόλων του E +. Επίσης ω F, γιατί αν υποθέσουµε ότι ω F, τότε ω = y 1 + y y l µε y i i x i για κάθε i, άτοπο γιατί η κατανοµή x = (x 1, x 2,..., x l ) είναι ασθενώς άριστη κατά Pareto. Προκειµένου να διαχωρίσουµε τα ω και F µε συνεχές γραµµικό συναρτησιακό του E αρκεί να δείξουµε ότι το F ως υποσύνολο του E έχει εσωτερικά

20 20 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής σηµεία. Αν υποθέσουµε ότι y = y 1 + y y l F µε y i i x i για κάθε i και ότι z είναι εσωτερικό σηµείο του E + και z i = z για κάθε l i = 1, 2,.., l, έχουµε ότι y i + z i i x i, άρα x + z F. Αν B(z, ρ) E +, έχουµε ότι B(y + z, ρ) F. Πραγµατικα B(y + z, ρ) = y + B(z, ρ), ε- ποµένως γιά κάθε u B(y + z, ρ) έχουµε u = y + y, y B(z, ρ) E +. Αν y i = y έχουµε ότι y l i + y i i x i, άρα u F, άρα το y + z είναι εσωτερικό σηµείο του F. Άρα υπάρχει p E, p 0 που διαχωρίζει τα ω και F, δηλαδή έχουµε p(x) p(ω), για κάθε x F. Θα δείξουµε πρώτα ότι p E+. Ανάλογα µε τη παραπάνω απόδειξη, αν υποθέσουµε ότι x F, γιά κάθε y E + και λ R +, έχουµε x + λy F, εποµένως p(x + λy) p(ω). Άρα λp(y) p(ω) p(x), γιά κάθε λ R + από όπου προκύπτει ότι p(y) 0 γιά κάθε y E +, άρα p E +. Θα δείξουµε τώρα ότι το διάνυσµα p στηρίζει την κατανοµή x = (x 1, x 2,..., x l ). Υποθέτουµε ότι x j x j και ϑέλουµε να δείξουµε ότι p(x) p(x j ). Επειδή τα σύνολα P (x i ) είναι µη κενά, για κάθε i υπάρχει y i i x i. Επειδη οι σχέσεις προτίµησης i είναι αυστηρά κυρτές έχουµε ότι ty i + (1 t)x i i x i για κάθε i j και για κάθε t (0, 1) και Εποµένως άρα ty j + (1 t)x + ty j + (1 t)x j x j. (ty i + (1 t)x i ) F, i j tp(y j ) + (1 t)p(x) + t p(y i ) + (1 t) i j p(x i ) p(ω), i j

21 1.6. Ασκήσεις 21 για κάθε t (0, 1). Στην προηγούµενη σχέση παίρνουµε όρια όταν t τείνει στο µηδέν και έχουµε p(x) + p(x i ) p(ω) = i j p(x i ), από όπου προκύπτει ότι p(x) p(x j ). Αρα το διάνυσµα p στηρίζει την κατανοµή x = (x 1, x 2,..., x l ). 1.6 Ασκήσεις Ασκηση Εστω οικονοµία ανταλλαγής µε τρία αγαθά και τρεις καταναλωτές µε αρχικά αγαθά ω 1 = (5, 3, 2), ω 2 = (4, 2, 5), ω 3 = (6, 1, 3) και συναρτήσεις χρησιµότητας u i = (x 1 + x 2 + x 3 )x i για κάθε i = 1, 2, 3 και έστω η κατανοµή x = ((8, 1, 1), (4, 4, 1), (3, 1, 8)). Εξετάστε αν η κατανοµή x ϐελτιώνει την κατανοµή y = ((7, 3, 2), (2, 2, 5), (6, 1, 3)) υπό το συνασπισ- µό {1, 2} και αν είναι άριστη ή ασθενώς άριστη κατά Pareto. Απόδειξη. x 1 + x 2 = (8, 1, 1) + (4, 4, 1) = (12, 5, 2) ω 1 + ω 2 = (9, 5, 7), άρα σύµφωνα µε τον ορισµό, η x δεν ϐελτιώνει την y υπό το συνασπισµό {1, 2}. Εστω η κατανοµή z = (a, b, c) = ((15, 0, 0), (0, 6, 0), (0, 0, 10)). Είναι u 1 (a) = 225 > 80 = u 1 (x 1 ), u 2 (b) = 36 = u 2 (x 2 ), u 3 (c) = 100 > u 3 (x 3 ) = 96. Άρα η κατανοµή x δεν είναι άριστη κατά Pareto. Εστω η κατανοµή k = (a, b, c) = ((14, 0, 0), (1, 6, 0), (0, 0, 10)). Είναι u 1 (a) = 196 > 80 = u 1 (x 1 ), u 2 (b) = 42 > 36 = u 2 (x 2 ), u 3 (c) = 100 > u 3 (x 3 ) = 96. Άρα η κατανοµή x δεν είναι ούτε ασθενώς άριστη κατά Pareto. Ασκηση Σε οικονοµία ανταλλαγής µε δυο αγαθά και δυο καταναλωτές µε συνάρτησης χρησιµότητας u 1 (x, y) = u 2 (x, y) = xy και αρχικά διαθέσι- µα ω 1 = (5, 4), ω 2 = (3, 6). Με χρήση του κουτιού του Edgeworth παραστήστε γραφικά το σύνολο των ατοµικά λογικών κατανοµών και προσδιορίστε

22 22 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής τα σηµεία τοµής των καµπύλων που ορίζουν το σύνολο αυτό. Επίσης προσδιορίστε δυο ατοµικά λογικές κατανοµές. Απόδειξη. Το συνολικό διαθέσιµο στην οικονοµία είναι ω = ω 1 + ω 2 = (5, 4) + (3, 6) = (8, 10). Υποθέτουµε ότι οι δυο καταναλωτές είναι στις κορυφές του κουτιού του Edgeworth. Η συνάρτηση χρησιµότητας του πρώτου καταναλωτή ως προς το σύστηµα αξόνων xy είναι u 1 (x, y) = xy, ενώ η συνάρτηση χρησιµότητας του δεύτερου καταναλωτή ως προς το σύστηµα αξόνων st είναι u 2 (s, t) = st = (8 x)(10 y). Το σηµείο (5, 4) του xy- συστήµατος αξόνων είναι το σηµείο (3, 6) του st- συστήµατος αξόνων και συµβολίζει την αρχική κατανοµή. Ετσι η καµπύλη αδιαφορίας του πρώτου καταναλωτή ως προς το xy- σύστηµα αξόνων δίνεται από τα σηµεία του συνόλου {(x, y) R 2 + xy = 20} ενώ η καµπύλη αδιαφορίας του δεύτερου καταναλωτή ως προς το st- σύστηµα αξόνων είναι τα σηµεία του συνόλου {(s, t) R 2 + st = 18}. Το σύνολο των ατοµικά λογικών κατανοµών ειναι το σύνολο των κατανοµών που ϐελτιώνουν την αρχική κατανοµή, δηλαδή το σύνολο των κατανοµών για τις οποίες η καµπύλη αδιαφορίας του πρώτου καταναλωτή ϐρίσκεται πάνω από την καµπύλη αδιαφορίας που περνά από το αρχικό του διαθέσιµο (4, 5) ως προς το xyσύστηµα αξόνων, ενώ η καµπύλη αδιαφορίας του δεύτερου καταναλωτή ως προς το st- σύστηµα αξόνων είναι πάνω από την καµπύλη αδιαφορίας που διέρχεται από το αρχικό του διαθέσιµο ως προς το ίδιο σύστηµα αξόνων. ηλαδή είναι το σύνολο των ευγών (x, y) ως προς το αντίστοιχο σύστηµα αξόνων που περικλείεται από τις καµπύλες xy = 20, (8 x)(10 y) = 18. Εστω (x, y) σηµείο τοµής. Τότε οι συντεταγµένες του ϑα επαληθεύουν και τις δυο εξισώσεις, οπότε λύνοντας την πρώτη ως προς x και αντικαθιστώντας στη δεύτερη έχουµε y = 20 20, (8 x)(10 ) = 18. Το τριώνυµο που προκύπτει x x είναι το 5x 2 41x + 80 = 0 µε ϱίζες x = 5 και x = 3.2. Οι λύσεις αυτές υποδεικνύουν και δυο αντίστοιχες ατοµικά λογικές κατανοµές ((5, 4), (3, 6)), (( 16 5, ), ( 4 5, 15 4 )). Ασκηση είξτε ότι σε οικονοµία ανταλλαγής µε δυο αγαθά και δυο καταναλωτές µε αρχικά αγαθά ω 1 = ( 3 2, 1 2 ), ω 2 = ( 3 2, 3 ) και συναρτήσεις 2 χρησιµότητας u 1 (x, y) = xy, u 2 (x, y) = x 2 y η κατανοµή x = ((1, 1), (2, 1)) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα

23 1.6. Ασκήσεις 23 p = (1, 1). Απόδειξη. Εύκολα διαπιστώνουµε ότι τα διανύσµατα (1, 1), (2, 1) ανήκουν στα αντίστοιχα σύνολα προϋπολογισµού. Εστω (x, y) 1 (1, 1) ή ισοδύναµα xy > 1. Θα δείξουµε ότι p (x, y) = x + y > p (1, 1) = 2. Εχουµε x + y > x Επίσης εξετάζουµε αν x (x, y) 2 (2, 1) = x + y > p (2, 1) = 3. (x, y) 2 (2, 1) = x + y x + 4. Αρκεί να δείξουµε ότι x Αν f (x) = x 3 3x 2 +4, x > 0 x 2 x 2 έχουµε ότι f (x) = 3x 2 6x = 3x(x 2), άρα f (x) f (2) = 0, για κάθε x 0. Εποµένως η ((1, 1), (2, 1)) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα (1, 1). Ασκηση Εστω οικονοµία ανταλλαγής µε δυο αγαθά και δυο καταναλωτές µε αρχικά αγαθά ω 1 = (5, 3), ω 2 = (4, 2) και συναρτήσεις χρησιµότητας u 1 (x, y) = u 2 (x, y) = x 2 y. Προσδιορίστε (i) τις συναρτήσεις ήτησης των καταναλωτών, (ii) τη συνάρτηση υπερβάλλουσας ήτησης και µία τιµή ισορροπίας, (iii) µιά κατανοµή ισορροπίας. Απόδειξη. (i): Για τον προσδιορισµό της συνάρτησης ήτησης του πρώτου καταναλωτή έχουµε : Μεγιστοποίησε τη συνάρτηση u(x, y) = xy, υπό τους περιορισµούς p 1 x + p 2 y 5p 1 + 3p 2, x 0, y 0. Επειδή η 1 είναι συνεχής, αυστηρά κυρτή και τοπικά µη κορεσµένη το µέγιστο λαµβάνεται στον εισοδηµατικό περιορισµό. ηλαδή έχουµε p 1 x + p 2 y = 5p 1 + 3p 2 y = 5p 1+3p 2 p 1 x p 2. Άρα έχουµε το ισοδύναµο πρόβληµα : Μεγιστοποίησε τη συνάρτηση f (x) = (5p 1 + 3p 2 )x p 1 x 2 p 2, υπό τους περιορισµούς x 0, y = 4p 1+3p 2 p 1 x p 2 0. Μελετώντας το πρόσηµο της f (x) διαπιστώνουµε ότι το x = 5p 1+3p 2 2p 1 είναι ϑέση µεγίστου για την f υπό τους περιορισµούς που ϑέσαµε. Άρα

24 24 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής η συνάρτηση ήτησης του πρώτου καταναλωτή είναι x 1 (p) = ( 5p 1 + 3p 2 2p 1, 5p 1 + 3p 2 2p 2 ), p 1 > 0, p 2 > 0. Για το δεύτερο καταναλωτή έχουµε : Μεγιστοποίησε τη συνάρτηση u(x, y) = x 2 y υπό τους περιορισµούς p 1 x + p 2 y 4p 1 + 2p 2, x 0, y 0. Ανάλογα µε την προηγούµενη περίπτωση έχουµε ότι το µέγιστο λαµβάνεται στον εισοδηµατικό περιορισµό, εποµένως y = 4p 1+2p 2 p 1 x p 2. Εποµένως προκύπτει το ισοδύναµο πρόβληµα : Μεγιστοποίησε τη συνάρτηση f (x) = x 2 ( 4p 1 + 2p 2 p 1 x p 2 ), υπό τους περιορισµούς x 0, y = 4p 1+2p 2 p 1 x p 2 0. Από τον τελευταίο περιορισµό έχουµε x 4p 1+2p 2 p 1. Μελετώντας το πρόση- µο της f (x) διαπιστώνουµε ότι x = 8p 1+4p 2 3p 1 είναι ϑέση µεγίστου για την f υπό τους περιορισµούς που ϑέσαµε. Άρα η συνάρτηση ήτησης του δεύτερου καταναλωτή είναι x 2 (p) = ( 8p 1 + 4p 2 3p 1, 4p 1 + 2p 2 3p 2 ), p 1 > 0, p 2 > 0. (ii) ω = (9, 5) είναι το συνολικό διαθέσιµο αγαθό και ζ (p) = x 1 (p) + x 2 (p) ω = ( 23p p 2 6p 1, 23p 1 17p 2 6p 2 ), είναι η συνάρτηση υπερβάλλουσας ήτησης. Κάθε διάνυσµα τιµών p µε ζ (p) = 0 είναι τιµή ισορροπίας. Αν κάνουµε τις πράξεις έχουµε ότι κάθε p = (t, 23 t), t > 0 είναι τιµή ισορροπίας. Γιά t = 17 έχουµε p = (17, 23) 17 είναι ένα διάνυσµα τιµών ισορροπίας. Τότε είναι κατανοµή ισορροπίας. (x 1 (p), x 2 (p)) = ( ( , 462 ), ( , )),

25 1.6. Ασκήσεις 25 Ασκηση Εστω οικονοµία ανταλλαγής µε δυο αγαθά και δυο καταναλωτές µε αρχικό αγαθό ω 1 = (4, 5), ω 2 = (3, 7) και συναρτήσεις χρησιµότητας u 1 (x, y) = x 2 y, u 2 = xy 2. Εξετάστε αν η κατανοµή x = ((5, 3), (2, 9)) είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το διάνυσµα p = (2, 1). Απόδειξη. Παρατηρούµε ότι (2, 1) (5, 3) = 13 = (2, 1) (4, 5), (2, 1) (2, 9) = 13 = (2, 1) (3, 7) άρα τα διανύσµατα αγαθών (5, 3), (2, 9) ανήκουν στους αντίστοιχους εισοδηµατικούς περιορισµούς. Εξετάζουµε αν ή ισοδύναµα αν u 1 (x, y) > u 1 (5, 3) (2, 1) (x, y) > (2, 1) (5, 3), Εστω y > 75 x 2. Θα εξετάσουµε αν x 2 y > 75 2x + y > 13. 2x + y > 2x + 75 x 2 = 2x x Εξετάζουµε αν f (x) = 2x x 2 0, x 0. Είναι f (x) = 6x 2 26x = 2x(3x 13). Οι λύσεις της f (x) = 0 είναι το 0 και το Αποδεικνύεται ότι η f παίρνει ελάχιστο για x = 3 3. Είναι f ( 13 3 ) = 2(13 3 ) ( 13 3 )2 = (2 3 1) + 75 = 75 (13 3 )3 < 0. Για x = 13 3 u 1 (5, 3) = 75 και και y = 75 ( 13 3 )2 + ɛ όπου ɛ > 0 έχουµε ότι u 1 (x, y) = x 2 y > (2, 1) ( 13 3, 75 ( 13 + ɛ) < 13 )2 3 για ɛ αρκούντως µικρό. Άρα η x δεν είναι κατανοµή ισορροπίας κατά Walras που στηρίζεται από το p. Ασκηση Εστω οικονοµία ανταλλαγής µε δυο αγαθά και τρεις καταναλωτές των οποίων τα αρχικά διαθέσιµα είναι ω 1 = (3, 2), ω 2 = (1, 4), ω 3 = (5, 2) και συναρτήσεις χρησιµότητας u 1 (x, y) = xy, u 2 (x, y) = x 2 y, u 3 (x, y) = xy 2. Προσδιορίστε τη συνάρτηση υπερβάλλουσας ήτησης και µια τιµή ισορ- ϱοπίας. Προσδιορίστε επίσης κατανοµή ισορροπίας κατά Walras.

26 26 Κεφάλαιο1. Ανταγωνιστικές Οικονοµίες Ανταλλαγής Απόδειξη. Οι σχέσεις προτίµησης των καταναλωτών που ορίζονται µέσω των αντίστοιχων συναρτήσεων χρησιµότητας είναι αυστηρά µονότονες και άρα οι συναρτήσεις χρησιµότητας λαµβάνουν τη µέγιστη τιµή τους στον εισοδηµατικό περιορισµό του συνόλου προϋπολογισµού B(p, w), p >> 0. Αν κάνουµε τις πράξεις έχουµε ότι οι συναρτήσεις ήτησης των καταναλωτών είναι x 1 (p) = ( 3p 1 + 2p 2 2p 1, 3p 1 + 2p 2 2p 2 ), x 2 (p) = ( 2p 1 + 8p 2 3p 1, p 1 + 4p 2 3p 2 ), x 3 (p) = ( 5p 1 + 2p 2 3p 1, 10p 1 + 4p 2 3p 2 ), για p >> 0. Η συνάρτηση υπερβάλλουσας ήτησης της οικονοµίας είναι ζ (p) = x 1 (p) + x 2 (p) + x 3 (p) ω 1 ω 2 ω 3 = = ( 26p 2 31p 1 6p 1, 31p 1 26p 2 6p 2 ). Μια τιµή ισορροπίας είναι η p = (26, 31) και για την τιµή αυτή οι δέσµες κατανάλωσης είναι x 1 = ( 70 26, ), x 2 = ( , ), x 3 = ( 64 26, 128) 31 που ορίζουν κατανοµή ισορροπίας. Ασκηση Εστω οικονοµία παραγωγής µε δυο αγαθά. παραγωγής της εταιρίας είναι Το σύνολο Y = {(x, y) R 2 x 100, y 1 e x }. Προσδιορίστε το αποτελεσµατικό σύνορο του Y και τη συνάρτηση εφοδιασ- µού y(p). Επίσης προσδιορίστε ένα άνω ϕράγµα του Y. Απόδειξη. Ενα άνω ϕράγµα του Y είναι το a = (100, 1). Εχουµε ότι το αποτελεσµατικό σύνορο του Y είναι Eff (Y ) = {(x, y) R 2 y = 1 e x, x 100}. Επίσης το Y είναι αυστηρά κυρτό. Άρα O(p) = p 1 x +p 2 y =

27 1.6. Ασκήσεις 27 p 1 x + p 2 (1 e x ) = f (x). Είναι f (x) = p 1 p 2 e x. Μελετώντας το πρόσηµο της f (x) διαπιστώνουµε ότι το x = ln p 1 p 2 είναι ϑέση ολικού µεγίστου. Αν x = ln p 1 p 2 τότε y = 1 p 1 p 2. Εποµένως η συνάρτηση εφοδιασµού είναι y(p) = (ln p 1 p 2, 1 p 1 p 2 ), ln p 1 p 2 100, p 1, p 2 > 0.