Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΕΡΙΕΧΟΜΕΝΑ
|
|
|
- Νατάσα Ζάνος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 :
2 Έκδοση Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΠΕΡΙΕΧΟΜΕΝΑ ΣΕΛΙ Α ΚΕΦΑΛΑΙΟ 1 - ΙΑΝΥΣΜΑΤΑ 1.1 Η ΕΝΝΟΙΑ ΤΟΥ ΙΑΝΥΣΜΑΤΟΣ 1 Μέτρο διανύσµατος 1 ιεύθυνση διανύσµατος Φορά διανύσµατος Ίσα διανύσµατα 3 Αντίθετα διανύσµατα 3 Γωνία δύο διανυσµάτων 3 1. ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΙΑΝΥΣΜΑΤΩΝ 4 ιάνυσµα θέσης 6 Μέτρο αθροίσµατος διανυσµάτων ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΕΠΙ ΙΑΝΥΣΜΑ 7 Γραµµικός συνδυασµός διανυσµάτων 8 1η συνθήκη παραλληλίας διανυσµάτων 8 ιανυσµατική ακτίνα µέσου τµήµατος ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο 9 Υπολογισµός µέτρου διανύσµατος από τις συντεταγµένες του 1 η συνθήκη παραλληλίας διανυσµάτων 1 Γωνία διανύσµατος µε τον άξονα 1 Συντελεστής διεύθυνσης διανύσµατος 13 3η συνθήκη παραλληλίας διανυσµάτων ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΙΑΝΥΣΜΑΤΩΝ 14 Αναλυτική έκφραση εσωτερικού γινοµένου 16 Συνηµίτονο γωνίας δύο διανυσµάτων 17 Προβολή διανύσµατος σε διάνυσµα 17 ΠΙΝΑΚΑΣ ΑΝΑΚΕΦΑΛΑΙΩΣΗΣ 18 ΜΕΘΟ ΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΣΤΑ ΙΑΝΥΣΜΑΤΑ 1 ΛΥΜΕΝΑ ΠΑΡΑ ΕΙΓΜΑΤΑ 8 ΚΕΦΑΛΑΙΟ Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕ Ο.1 Η ΕΞΙΣΩΣΗ ΤΗΣ ΕΥΘΕΙΑΣ 37 Γωνία κλίσης ευθείας 37 Συντελεστής διεύθυνσης ευθείας 38 Συνθήκες παραλληλίας και καθετότητας ευθειών 38 Ειδικές µορφές εξίσωσης ευθείας 39. ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ 40 ιάνυσµα παράλληλο ή κάθετο σε ευθεία 40.3 ΑΠΟΣΤΑΣΗ ΣΗΜΕΙΟΥ ΑΠΟ ΕΥΘΕΙΑ ΕΜΒΑ ΟΝ ΤΡΙΓΩΝΟΥ 4 ΠΙΝΑΚΑΣ ΑΝΑΚΕΦΑΛΑΙΩΣΗΣ 43 ΜΕΘΟ ΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΣΤΗΝ ΕΥΘΕΙΑ 44 ΛΥΜΕΝΑ ΠΑΡΑ ΕΙΓΜΑΤΑ 49
3 ΣΕΛΙ Α ΚΕΦΑΛΑΙΟ 3 ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΣΥΝΟΠΤΙΚΟΣ ΠΙΝΑΚΑΣ ΚΩΝΙΚΩΝ ΤΟΜΩΝ 56 ΜΕΘΟ ΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΣΤΙΣ ΚΩΝΙΚΕΣ ΤΟΜΕΣ 59 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 66 ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 16 ΥΠΟ ΕΙΞΕΙΣ ΑΣΚΗΣΕΩΝ 18
4 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 1 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 1. ΙΑΝΥΣΜΑΤΑ 1.1 Η έννοια του διανύσµατος Τα µεγέθη στις επιστήµες χωρίζονται σε δύο κατηγορίες: Σε µονόµετρα ή βαθµωτά τα οποία είναι πλήρως ορισµένα αν γνωρίζουµε µόνο το µέτρο τους και την αντίστοιχη µονάδα µέτρησης (όπως η µάζα, ο όγκος, ο χρόνος, η θερµοκρασία, η πυκνότητα κ.τ.λ.) και Σε διανυσµατικά ή απλά διανύσµατα για τον προσδιορισµό των οποίων εκτός από το µέτρο τους και τη µονάδα µέτρησης χρειαζόµαστε επιπλέον τη διεύθυνση και τη φορά τους (όπως είναι η µετατόπιση, η δύναµη, η ταχύτητα, η επιτάχυνση, η ένταση του ηλεκτρικού ρεύµατος κ.τ.λ.). Κάθε διανυσµατικό µέγεθος παριστάνεται µε ένα διάνυσµα το οποίο είναι ένα προσανατολισµένο ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται διατεταγµένα. Το πρώτο σηµείο λέγεται αρχή ή σηµείο εφαρµογής και το δεύτερο λέγεται πέρας του διανύσµατος. Στην παράσταση του διανύσµατος χρησιµοποιούµε ένα ευθύγραµµο τµήµα που το πέρας του έχει τη µορφή βέλους. Στο Α (αρχή) διπλανό σχήµα παριστάνεται ένα διάνυσµα µε αρχή το σηµείο Α και πέρας το σηµείο Β, το οποίο συµβολίζεται µε AB. Εναλλακτικά για το συµβολισµό ενός διανύσµατος µπορούµε να χρησιµοποιούµε πεζά γράµµατα του Ελληνικού ή του Λατινικού αλφαβήτου επιγραµµισµένα µε ένα βέλος, όπως α, β, u, v κ.τ.λ. AB Β (πέρας) Μέτρο διανύσµατος Το µήκος του ευθυγράµµου τµήµατος ΑΒ που έχει άκρα την αρχή και το πέρας του διανύσµατος ονοµάζεται µέτρο ή µήκος του διανύσµατος και συµβολίζεται µε AB. Ένα διάνυσµα του οποίου αρχή και πέρας συµπίπτουν, όπως το AA, λέγεται µηδενικό διάνυσµα, έχει µέτρο ίσο µε 0 και µπορεί να συµβολιστεί ως 0. Ένα διάνυσµα που έχει µέτρο ίσο µε τη µονάδα µέτρησης λέγεται µοναδιαίο διάνυσµα.
5 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ιεύθυνση διανύσµατος Φορέας ενός µη µηδενικού διανύσµατος AB ονοµάζεται η ευθεία ε πάνω στην οποία βρίσκεται το διάνυσµα. Β Αν ο φορέας του AB συµπίπτει ή είναι παράλληλος µε µια Α ευθεία ε, λέµε ότι το AB είναι παράλληλο µε την ε και ε γράφουµε AB //ε. ε Ως διεύθυνση ενός διανύσµατος AB ονοµάζουµε τον φορέα του ή οποιαδήποτε άλλη ευθεία παράλληλη σ αυτόν. ύο διανύσµατα που έχουν ίδια διεύθυνση Γ ονοµάζονται παράλληλα ή συγγραµµικά και για να το δηλώσουµε συµβολικά, γράφουµε τα δύο Β διανύσµατα µε το σύµβολο της παραλληλίας (//) Ζ Α ανάµεσά τους. Ε Έτσι στο διπλανό σχήµα έχουµε AB //Γ και AB //ΕΖ. Ως φορέα ενός µηδενικού διανύσµατος AA θεωρούµε οποιαδήποτε ευθεία που διέρχεται από το Α. Φορά διανύσµατος Ως φορά του διανύσµατος AB ονοµάζουµε την πορεία που ακολουθούµε, µετακινούµενοι πάνω στον φορέα του, από την αρχή Α προς το πέρας Β του διανύσµατος. Ως φορά ενός µηδενικού διανύσµατος µπορούµε να θεωρήσουµε οποιαδήποτε. ύο µη µηδενικά συγγραµµικά διανύσµατα AB και Γ µπορεί να είναι: Β α) Οµόρροπα, όταν βρίσκονται προς το ίδιο ηµιεπίπεδο ως προς την ευθεία ΑΓ που διέρχεται Α από τις αρχές τους (δηλαδή όταν έχουν την ίδια Γ Γ φορά) ή όταν έχουν ίδιο φορέα και µία από τις Β ηµιευθείες ΑΒ, Γ περιέχει την άλλη και Α Β β) Αντίρροπα, όταν δεν είναι οµόρροπα (αντίθετη Α φορά). Γ ΠΡΟΣΟΧΗ: Οι έννοιες «οµόρροπα» και «αντίρροπα» αφορούν µόνο σε συγγραµµικά Β Α διανύσµατα (ίδιο φορέα ή παράλληλους φορείς). ύο διανύσµατα ΑΒ και Γ που είναι οµόρροπα (ίδια διεύθυνση και φορά) λέµε ότι έχουν ίδια κατεύθυνση και γράφουµε συµβολικά AB Γ, ενώ αν είναι αντίρροπα Γ ΑΒ Γ ΑΒ Γ
6 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 3 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός (ίδια διεύθυνση αλλά αντίθετες φορές) λέµε ότι έχουν αντίθετη κατεύθυνση και γράφουµε συµβολικά AB Γ. Το µηδενικό διάνυσµα µπορεί να θεωρηθεί ως οµόρροπο ή αντίρροπο µε κάθε άλλο διάνυσµα. Ίσα διανύσµατα ύο µη µηδενικά διανύσµατα ΑΒ και Γ λέγονται ίσα αν έχουν ίσα µέτρα και ίδια κατεύθυνση (δηλαδή ίδια διεύθυνση και φοράοµόρροπα). Συµβολικά τότε γράφουµε ΑΒ=Γ. Α Β Γ ΣΗΜΑΝΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Αν ΑΒ= Γ τότε ισχύουν και οι σχέσεις BA= Γ, ΑΓ= Β και Β= ΓΑ. Γ Α Β Α Μ Β Αν Μ είναι το µέσον του τµήµατος ΑΒ, τότε ΑM= MB και αντίστροφα. Αντίθετα διανύσµατα ύο µη µηδενικά διανύσµατα ΑΒ και Γ λέγονται αντίθετα αν έχουν ίσα µέτρα αλλά αντίθετη κατεύθυνση (ίσα µέτρα αλλά αντίρροπα). Συµβολικά τότε γράφουµε ΑΒ=-Γ. Είναι προφανείς οι ιδιότητες: ΑΒ= ΒΑ και αν AB= Γ τότε AB= Γ Α Β Γ Γωνία δύο διανυσµάτων Θεωρούµε δύο µη µηδενικά διανύσµατα α και β και ένα σηµείο Ο του επιπέδου. Με αρχή το Ο κατασκευάζουµε διανύσµατα ΟΑ= α και ΟΒ= β (δηλαδή µεταφέρουµε τα αρχικά διανύσµατα παράλληλα ώστε να προκύψουν διανύσµατα ίσα µε αυτά µε κοινή αρχή το Ο). Ως γωνία των διανυσµάτων α και β ονοµάζουµε την κυρτή γωνία ΑΟΒ ˆ που σχηµατίζουν οι ηµιευθείες ΟΑ και ΟΒ. Λ Λ Η γωνία των α και β συµβολίζεται ως (α,β) ή (β,α) ή θ σε περίπτωση που δεν προκαλείται σύγχυση. Ισχύουν: 0 θ π θ=0 α θ=π α Ο Α θ β α Β α β θ=0 α β θ=π β β
7 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 4 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ύο διανύσµατα α και β ονοµάζονται ορθογώνια ή κάθετα αν σχηµατίζουν γωνία θ= π. Τότε συµβολικά γράφουµε α β. Αν ένα από τα α, β είναι το µηδενικό διάνυσµα, τότε µπορούµε να θεωρήσουµε ως γωνία των α και β οποιαδήποτε θ [0,π]. Άρα µπορούµε να θεωρήσουµε ότι το µηδενικό διάνυσµα είναι επίσης κάθετο µε κάθε άλλο διάνυσµα. 1. Πρόσθεση Αφαίρεση διανυσµάτων Μπορούµε να προσθέσουµε ή να αφαιρέσουµε διανύσµατα και το «αποτέλεσµα» καθεµιάς από αυτές τις πράξεις είναι ένα διάνυσµα. Α. ΠΡΟΣΘΕΣΗ ΙΑΝΥΣΜΑΤΩΝ Η πρόσθεση δύο διανυσµάτων α και β µπορεί να γίνει µε δύο τρόπους: α) Καθιστώντας τα διαδοχικά: Με αρχή σηµείο Ο του επιπέδου θεωρούµε διάνυσµα OA= α και µε αρχή το πέρας Α αυτού διάνυσµα ΑΒ= β. Τότε το διάνυσµα ΟΒ είναι το άθροισµα ή αλλιώς η συνισταµένη των α και β και συµβολίζεται µε α+β. α Ο β Α α+β Β β) Με τον κανόνα του παραλληλογράµµου: Με κοινή αρχή σηµείο Ο του επιπέδου θεωρούµε δύο διανύσµατα OA= α και ΟΒ= β. Τότε το άθροισµα α+ β ορίζεται από τη διαγώνιο του παραλληλογράµµου που έχει προσκείµενες α Ο Α α+β Β Μ πλευρές τις ΟΑ και ΟΒ, δηλαδή είναι το διάνυσµα ΟΜ. β Και στους δύο παραπάνω τρόπους αποδεικνύεται ότι το άθροισµα των α και β είναι ανεξάρτητο από την επιλογή του σηµείου Ο. Ιδιότητες της πρόσθεσης Αν α, β και γ είναι τρία διανύσµατα, τότε ισχύουν οι ιδιότητες: 1. α+ β= β+ α Αντιµεταθετική
8 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 5 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός. (α+ β) + γ= α + (β+ γ) 3. α+ 0= α 4. α + ( α) = 0 Προσεταιριστική Ιδιότητα Ουδετέρου στοιχείου Ιδιότητα Αντιθέτου διανύσµατος Επειδή κατά την πρόσθεση τριών ή περισσοτέρων διανυσµάτων δεν παίζει ρόλο η σειρά των προσθετέων, µπορούµε αντί της πρόσθεσης (α+ β) + γ ή α + (β+ γ) να γράφουµε απλά α+ β+ γ. Μια απλή µέθοδος πρόσθεσης πολλών διανυσµάτων Αν έχουµε να προσθέσουµε περισσότερα των δύο διανυσµάτων, τότε αντί να βρούµε το άθροισµα των δύο πρώτων και µετά το άθροισµα αυτού µε το τρίτο κ.τ.λ., µπορούµε να βρούµε το άθροισµα όλων απ ευθείας µε δύο βήµατα: Τα καθιστούµε διαδοχικά µε τη σειρά που µας τα δίνουν (ή όποια άλλη σειρά επιθυµούµε) και το άθροισµά τους είναι το διάνυσµα που έχει ως αρχή την αρχή του πρώτου και πέρας το πέρας του τελευταίου (βλέπε σχήµα). α α+β+γ+δ β δ γ Β. ΑΦΑΙΡΕΣΗ ΙΑΝΥΣΜΑΤΩΝ Ως διαφορά α-β δύο διανυσµάτων α και β ορίζουµε το διάνυσµα που προκύπτει από το άθροισµα του α µε το αντίθετο του β. Έτσι: α-β=α+(-β) Αν µας δώσουν δύο διανύσµατα α και β µπορούµε να βρούµε τη διαφορά α-β : α) Προσθέτοντας στο α το β όπως περιγράψαµε κατά την περιγραφή της πρόσθεσης διανυσµάτων (καθιστώντας διαδοχικά τα α και β ) ή α β α-β β α β) Να τα καταστήσουµε µε κοινή αρχή, οπότε το α-β είναι το διάνυσµα της «άλλης» διαγωνίου του παραλληλογράµµου, αυτής που έχει ως αρχή το πέρας του αφαιρετέου (β ) και ως πέρας το πέρας του µειωτέου (α ). α α β β α-β
9 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 6 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ιάνυσµα θέσης Έστω Ο σταθερό σηµείο του χώρου. Τότε για κάθε σηµείο Μ του χώρου ορίζεται ένα µοναδικό διάνυσµα ΟΜ το οποίο ονοµάζεται διάνυσµα θέσης του σηµείου Μ ή διανυσµατική ακτίνα του Μ. Το σταθερό σηµείο Ο ως προς το οποίο ορίζουµε τις διανυσµατικές ακτίνες κάθε σηµείου, ονοµάζεται σηµείο αναφοράς στο χώρο. Επειδή για δύο σηµεία Α και Β του χώρου ισχύει ότι ΟΑ+ ΑΒ= ΟΒ προκύπτει µια σχέση πολύ χρήσιµη σε ασκήσεις, γιατί µας επιτρέπει να αναλύουµε κάθε διάνυσµα µε τη βοήθεια των διανυσµατικών ακτίνων των άκρων του: ΑΒ=ΟΒ-ΟΑ δηλαδή κάθε διάνυσµα µπορεί να γραφεί ως διαφορά της διανυσµατικής ακτίνας του πέρατός του µείον τη διανυσµατική ακτίνα της αρχής του. Ο Ο Α Μ Β ΣΗΜΑΝΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Σε πολλές περιπτώσεις συναντάµε διαφορά διανυσµάτων µε κοινό πέρας π.χ. ΑΟ ΒΟ. Για συντοµία µπορούµε να θυµόµαστε πρακτικά το αποτέλεσµα µιας τέτοιας διαφοράς, το οποίο είναι το διάνυσµα ΑΒ που προκύπτει από τις αρχές των διανυσµάτων µε τη σειρά που δίνονται. Έτσι συµβολικά ΑΟ ΒΟ= ΑΒ. Ισχύει ότι ΑΒ= ΑΧ+ ΧΒ όπου Χ οποιοδήποτε σηµείο του καρτεσιανού επιπέδου. 3. Στο παραλληλόγραµµο ΑΒΓ το άθροισµα ΑΒ+ Α είναι η διαγώνιος Β ΑΓ, ενώ η διαφορά ΑΒ Α είναι η άλλη διαγώνιος Β. 4. Για να δείξουµε ότι ένα τετράπλευρο ΑΒΓ είναι παραλληλόγραµµο, αρκεί να δείξουµε ότι ΑΒ= Γ (σχηµατικά ΑΒΓ ). Α Γ Μέτρο Αθροίσµατος ιανυσµάτων Καθιστώντας διαδοχικά δύο διανύσµατα α και β και σχεδιάζοντας το διάνυσµα α+ β, από την τριγωνική ανισότητα στο τρίγωνο που προκύπτει, θα ισχύει για τα µέτρα τους η σχέση: α-β α+β α+β α β α+ β ΠΑΡΑΤΗΡΗΣΕΙΣ Από την προηγούµενη σχέση θέτοντας όπου β το β και αφού β = β, εύκολα προκύπτει και η α-β α β α+ β. Γενικά για ν διανύσµατα α 1, α,..., αν ισχύει: α1+ α α ν α 1 + α α ν
10 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 7 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Ισχύουν (προσοχή: Αφού τις αποδείξουµε πρώτα, καθόσον δεν αναφέρονται στο σχολικό βιβλίο) οι παρακάτω ισοδυναµίες: α β α+ β = α + β α β α β = α+ β α= 0 ή β= 0 α β = α+ β = α + β Η απόδειξη µπορεί να γίνει µε τη βοήθεια της θεωρίας του εσωτερικού γινοµένου (βλέπε 1.5) 1.3 Πολλαπλασιασµός αριθµού µε διάνυσµα Έστω λ πραγµατικός αριθµός µε λ 0 και α µη µηδενικό διάνυσµα. Ως γινόµενο λ α ορίζουµε ένα διάνυσµα το οποίο: Είναι οµόρροπο του α αν λ>0 και αντίρροπο του α αν λ<0 και Έχει µέτρο λ α α 3 α Στην περίπτωση που λ=0 ή α =0, τότε ως γινόµενο λ α ορίζουµε το µηδενικό διάνυσµα 0. Ένα γινόµενο µορφής 1 α λ (µε λ 0) µπορούµε να το συµβολίζουµε και µε α λ. Ιδιότητες του πολλαπλασιασµού αριθµού µε διάνυσµα Για κάθε λ, µ R ισχύουν: 1. λ (α+ β) = λ α+ λ β. λ (α β) = λ α λ β 3. (λ + µ) α= λ α + µ α 4. (λ µ) α= λ α µ α 5. λ (µ α) = (λ µ) α 6. ( λ α) = (λ α) = λ ( α) Ιδιότητες χρήσιµες σε εξισώσεις µε διανύσµατα 1. λ α= 0 λ= 0 ή α= 0. Αν λ α= λ β και λ 0, τότε α= β 3. Αν λ α = µ α και α 0, τότε λ=µ.
11 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 8 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Γραµµικός συνδυασµός διανυσµάτων Αν δοθούν δύο διανύσµατα α και β κάθε διάνυσµα ν που παράγεται από το άθροισµα των διανυσµάτων κ α και λ β όπου κ, λ R ονοµάζεται γραµµικός συνδυασµός των α και β. Έτσι ν=κ α+λ β. Μπορούµε ανάλογα να έχουµε γραµµικούς συνδυασµούς περισσοτέρων από δύο διανυσµάτων, όπως για παράδειγµα το διάνυσµα u= 3 α β+ γ δ που είναι ένας γραµµικός συνδυασµός των διανυσµάτων α, β, γ και δ. 1η Συνθήκη παραλληλίας διανυσµάτων Η ικανή και αναγκαία συνθήκη ώστε α και β (µε β 0) να είναι παράλληλα (συγγραµµικά, ίδια διεύθυνση) είναι να υπάρχει πραγµατικός αριθµός λ τέτοιος ώστε α= λ β. Άρα αν α και β (µε β 0) δύο διανύσµατα ισχύει η ισοδυναµία: α//β α=λ β, µε λ R ΠΑΡΑΤΗΡΗΣΕΙΣ Στην περίπτωση που τα διανύσµατα είναι συγγραµµικά αποδεικνύεται εύκολα ότι ο αριθµός λ είναι µοναδικός. Ειδικότερα η παραπάνω ισοδυναµία ισχύει ως εξής: α α β α= λ β, µε λ= > 0 β α α β α= λ β, µε λ= < 0 β Αν δοθεί α 0 τότε µπορούµε εύκολα να σχηµατίσουµε δύο µοναδιαία διανύσµατα συγγραµµικά του α, ένα οµόρροπο και ένα αντίρροπο µε το α, 1 1 που είναι αντίστοιχα τα α 1= α και α =- α. α α Στην παραπάνω συνθήκη παραλληλίας υπάρχει η προϋπόθεση β 0, γιατί αν β= 0 και α 0 δεν υπάρχει αριθµός λ τέτοιος ώστε α= λ β, αλλά παρ όλα αυτά τα α και β είναι συγγραµµικά, καθώς το µηδενικό διάνυσµα (β) µπορεί να θεωρηθεί ως συγγραµµικό οποιουδήποτε διανύσµατος. ΣΗΜΑΝΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Μπορούµε να αποδείξουµε (καθώς δεν αναφέρεται στο σχολικό βιβλίο) ότι: Αν α//β, µε β 0, τότε τα διανύσµατα α+ β, α β αλλά και γενικότερα κάθε γραµµικός συνδυασµός µ α+ ν β των α και β είναι διάνυσµα συγγραµµικό µε αυτά. ΑΠΟ ΕΙΞΗ Θα αποδείξουµε τη γενική περίπτωση του γραµµικού συνδυασµού.
12 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 9 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Έστω ότι τα διανύσµατα α και β είναι συγγραµµικά. Τότε θα υπάρχει αριθµός λ R τέτοιος ώστε α= λ β. Έτσι µ α+ ν β = µ (λ β) + ν β = (µλ+ ν) β= κ β, όπου κ=µλ+ν. Η τελευταία αυτή σχέση δηλώνει ότι το διάνυσµα µ α+ ν β β (οπότε και του α ). είναι συγγραµµικό του. Αποδεικνύεται ότι (δεν το χρησιµοποιούµε καθώς δεν υπάρχει στο σχολικό βιβλίο): Αν α και β δύο µη συγγραµµικά διανύσµατα και κ,λ,κ,λ R τότε: α) Αν ισχύει κ α+ λ β= 0 συµπεραίνουµε ότι κ=λ=0 β) Αν ισχύει κ α+ λ β= κ' α+ λ'β συµπεραίνουµε ότι κ=κ και λ=λ. ιανυσµατική ακτίνα µέσου τµήµατος Θεωρώντας ευθύγραµµο τµήµα ΑΒ και το µέσον του Α Μ, ισχύει ότι η διανυσµατική ακτίνα του µέσου Μ του τµήµατος ΑΒ είναι ίση µε το ηµιάθροισµα των διανυσµατικών ακτίνων των άκρων του (Α Ο και Β) ως προς το ίδιο σηµείο αναφοράς, δηλαδή: ΟΑ+ΟΒ ΟΜ= Ισχύει επίσης και η αντίστροφη πρόταση, δηλαδή αν για τρία σηµεία Α, Β και Μ ισχύει η ΟΑ+ ΟΒ σχέση ΟΜ=, τότε το Μ είναι το µέσον του ΑΒ. // Μ // Β 1.4 Συντεταγµένες στο επίπεδο Καρτεσιανό επίπεδο - συντεταγµένες Άξονας ονοµάζεται µια ευθεία πάνω στην οποία έχουµε ορίσει ένα σηµείο Ο και ένα διάνυσµα OI= i που ανήκει στην ηµιευθεία Ο και έχει µέτρο 1. Το σηµείο Ο λέγεται αρχή του άξονα και το διάνυσµα i µοναδιαίο διάνυσµα. Η ηµιευθεία Ο λέγεται θετικός ηµιάξονας και η Ο αρνητικός ηµιάξονας. Για κάθε σηµείο Μ του άξονα, επειδή OM//i, υπάρχει µοναδικός πραγµατικός αριθµός τέτοιος ώστε OM= i. Αντίστροφα για κάθε πραγµατικό αριθµό υπάρχει ένα µοναδικό σηµείο Μ του άξονα, τέτοιο ώστε OM= i. Ο αριθµός ονοµάζεται τετµηµένη του Μ και το σηµείο Μ συµβολίζεται µε Μ(). O I M()
13 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 10 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Καρτεσιανό επίπεδο ονοµάζεται ένα σύστηµα δύο αξόνων και y y κάθετων µεταξύ τους, που έχουν κοινή αρχή Ο και αντίστοιχα µοναδιαία διανύσµατα i και j. Ένα τέτοιο επίπεδο συµβολίζεται µε Οy και λέγεται αλλιώς σύστηµα συντεταγµένων. Συνήθως θεωρούµε ως ισοµήκη τα µοναδιαία διανύσµατα στους δύο άξονες οπότε το y M j M(,y) O i M1 σύστηµα συντεταγµένων λέγεται ορθοκανονικό σύστηµα συντεταγµένων. Επίσης συνηθίζεται να σχεδιάζουµε τον άξονα οριζόντιο και τον άξονα y y κατακόρυφο. Κάθε σηµείο µ στο καρτεσιανό επίπεδο έχει δύο προβολές Μ 1 και Μ πάνω στους άξονες και y y αντίστοιχα. Η τετµηµένη του Μ 1 (ως προς τον άξονα ) λέγεται τετµηµένη του σηµείου Μ και η τετµηµένη y του Μ (ως προς τον άξονα y y) λέγεται τεταγµένη του σηµείου Μ. Η τετµηµένη και η τεταγµένη του Μ λέγονται συντεταγµένες του Μ. Κάθε σηµείο Μ στο καρτεσιανό επίπεδο έχει ένα µοναδικό ζεύγος συντεταγµένων (,y), αλλά και αντίστροφα κάθε ζεύγος συντεταγµένων (,y) ορίζει ένα µοναδικό σηµείο. Στο εξής κάθε σηµείο Μ µε συντεταγµένες (,y) θα συµβολίζεται µε Μ(,y) ή απλούστερα (,y). y Συντεταγµένες διανύσµατος Σε σύστηµα συντεταγµένων Οy θεωρούµε σηµείο y Α(,y) και τις προβολές του Α 1 και Α στους άξονες και y y αντίστοιχα. Αν σχεδιάσουµε το διάνυσµα OA= α ισχύουν οι σχέσεις: ΟΑ = i, ΟΑ = y j και ΟΑ= ΟΑ + ΟΑ. Από 1 1 αυτές συµπεραίνουµε ότι: α= i+y j Έτσι το α γράφεται ως γραµµικός συνδυασµός των i και j µε i=(1,0) και j=(0,1). α Α(,y) Αποδεικνύεται ότι οι παραπάνω αριθµοί και y είναι µοναδικοί. Είναι προφανές ότι και κάθε άλλο διάνυσµα ίσο µε το α γράφεται µε τη µοναδική παραπάνω µορφή. Έτσι τελικά κάθε διάνυσµα του επιπέδου µπορεί να γραφτεί µε µοναδικό τρόπο ως γραµµικός συνδυασµός των µοναδιαίων διανυσµάτων i και j. Α j α O i Α1 y
14 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 11 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Οι αριθµοί και y λέγονται συντεταγµένες του διανύσµατος α (τετµηµένη τεταγµένη), ενώ τα διανύσµατα i και y j λέγονται συνιστώσες του α κατά την διεύθυνση των i και j αντίστοιχα. ΠΡΟΤΑΣΗ ύο διανύσµατα είναι ίσα αν και µόνο αν είναι ίσες οι αντίστοιχες συντεταγµένες τους. Κάθε διάνυσµα µε συντεταγµένες και y µπορούµε να το συµβολίζουµε απλά µε το διατεταγµένο ζεύγος (,y). ΣΗΜΕΙΩΣΗ: Επειδή µε τον παραπάνω τρόπο συµβολίζουµε και ένα σηµείο στο καρτεσιανό επίπεδο, το αν το ζεύγος (,y) σε µια πρόταση παριστάνει σηµείο ή διάνυσµα θα φαίνεται από τα συµφραζόµενα της πρότασης (το νόηµα της πρότασης). Συντεταγµένες γραµµικού συνδυασµού διανυσµάτων Αν δοθούν δύο διανύσµατα α= 1i+ y1j, β= i+ yj και δύο αριθµοί λ, µ R, τότε για τις συντεταγµένες των διανυσµάτων α+ β, λ α αλλά και κάθε γραµµικού συνδυασµού λ α + µ β των α και β ισχύουν οι σχέσεις: α+ β = (1+ )i + (y1+ y )j λ α= λ1i+ λy1j λ α + µ β = (λ + µ )i + (λy + µy )j 1 1 ή απλούστερα ( 1, y 1 )+(, y )=( 1 +, y 1 +y ) λ ( 1, y 1 )=(λ 1, λy 1 ) λ ( 1, y 1 )+µ (, y )=(λ 1 +µ, λy 1 +µy ) Συντεταγµένες µέσου τµήµατος Ας υποθέσουµε ότι δίνονται δύο σηµεία Α( 1,y 1 ) και Β(,y ) του καρτεσιανού επιπέδου και Μ(,y) το µέσον του τµήµατος ΑΒ. Επειδή ισχύει ΟΑ+ ΟΒ ΟΜ=, για τις συντεταγµένες του Μ θα y Ο Α( 1,y 1 ) // Μ(,y) // Β(,y ) έχουµε: 1+ y 1+y = και y=
15 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 1 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Συντεταγµένες διανύσµατος µε γνωστά άκρα Ας υποθέσουµε ότι δίνονται δύο σηµεία Α( 1,y 1 ) και Β(,y ) του καρτεσιανού επιπέδου. Οι συντεταγµένες (,y) του διανύσµατος AB δίνονται από τις σχέσεις: = - 1 και y=y -y 1 δηλαδή τετµηµένη διανύσµατος = τετµηµένη πέρατος τετµηµένη αρχής τεταγµένη διανύσµατος = τεταγµένη πέρατος τεταγµένη αρχής Παρατήρηση Οι συντεταγµένες (, y) διανύσµατος Β µας δείχνουν τον τρόπο µε τον οποίο µπορούµε να µεταβούµε από την αρχή στο πέρας ενός διανύσµατος, κινούµενοι µόνο οριζόντια (παράλληλα Α µε τον ) και κατακόρυφα (παράλληλα µε τον y y). Έτσι αν π.χ. AB =(-3, ), για να µεταβούµε από το Α στο Β θα πρέπει να κινηθούµε 3 µονάδες αριστερά (λόγω του «-») και µονάδες επάνω (ή αντίστροφα επάνω και 3 αριστερά). Υπολογισµός του µέτρου διανύσµατος από τις συντεταγµένες του Αν δοθεί ένα διάνυσµα α = (,y) του καρτεσιανού επιπέδου, τότε το µέτρο του δίνεται µε τη βοήθεια των συντεταγµένων του από τη σχέση: α = +y Αν δοθούν δύο σηµεία Α( 1,y 1 ) και Β(,y ) του καρτεσιανού επιπέδου, τότε η απόστασή τους ΑΒ (δηλαδή το µέτρο του AB ) δίνεται από τη σχέση: (AB)= (- 1) +(y-y 1) η Συνθήκη παραλληλίας διανυσµάτων Έστω δύο διανύσµατα α =( 1,y 1 ) και β =(,y ) του καρτεσιανού επιπέδου. Ονοµάζουµε ορίζουσα των διανυσµάτων α και β και τη συµβολίζουµε µε det(α,β) την ορίζουσα y 1 1 y και ως δεύτερη γραµµή τις συντεταγµένες του β. που έχει ως πρώτη γραµµή τις συντεταγµένες του α
16 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 13 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Ισχύει ότι τα διανύσµατα α και β είναι συγγραµµικά αν και µόνο αν η ορίζουσά τους είναι ίση µε µηδέν, δηλαδή: α//β det(α,β)=0 Γωνία διανύσµατος µε τον άξονα Έστω α = (,y) ένα µη µηδενικό διάνυσµα του καρτεσιανού επιπέδου και Α ένα σηµείο για το οποίο ισχύει OA= α. Ονοµάζουµε γωνία που σχηµατίζει το διάνυσµα α µε τον άξονα τη γωνία φ που πρέπει να διαγράψει ο θετικός ηµιάξονας Ο, αν στραφεί κατά τη θετική φορά για να συµπέσει µε την ηµιευθεία ΟΑ. Προφανώς είναι 0 φ < π. ΠΡΟΣΟΧΗ να µη γίνεται σύγχυση της προηγούµενης έννοιας της γωνίας διανύσµατος µε τον άξονα, µε την έννοια «γωνία δύο διανυσµάτων» που αναφέραµε στην 1.1 και η οποία δεν παίρνει τιµές στο [0, π) αλλά στο [0,π]. Α(,y) y O φ α Συντελεστής διευθύνσεως διανύσµατος Έστω διάνυσµα α = (, y) µε 0. Ονοµάζουµε συντελεστή διεύθυνσης λ του α το πηλίκο y. Αν φ η γωνία που σχηµατίζει το διάνυσµα α µε τον άξονα τότε ισχύει: y λ= =εφφ Είναι προφανές ότι αν α // τότε y=0 οπότε λ=0 και αντίστροφα. Στην περίπτωση που για το διάνυσµα α = (,y) ισχύει =0, δηλαδή α //y y τότε δεν ορίζεται συντελεστής διεύθυνσης. 3η Συνθήκη παραλληλίας διανυσµάτων Αν θεωρήσουµε δύο διανύσµατα α = ( 1,y 1) και β = (,y ) µε αντίστοιχους συντελεστές διεύθυνσης λ 1 και λ, ισχύει ότι τα διανύσµατα είναι συγγραµµικά αν και µόνο αν έχουν ίσους συντελεστές διεύθυνσης, δηλαδή: α//β λ 1 =λ Προφανώς για τα π.χ. α = (0,1) και β = (0,4) ισχύει α//β//y'y (δεν ορίζεται λ).
17 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 14 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 1.5 Εσωτερικό γινόµενο διανυσµάτων Έστω δύο διανύσµατα α και β του καρτεσιανού επιπέδου. Ονοµάζουµε εσωτερικό γινόµενο των α και β και το συµβολίζουµε µε α β τον πραγµατικό αριθµό που ορίζεται ως εξής: α β συνφ, αν α 0 και β 0 α β=, 0, αν α= 0 η β= 0 (1η µορφή εσωτερικού γινοµένου) όπου φ η γωνία των α και β. ΠΡΟΣΟΧΗ: Το εσωτερικό γινόµενο δύο διανυσµάτων, σε αντίθεση µε τις υπόλοιπες πράξεις των διανυσµάτων, δεν δίνει ως αποτέλεσµα ένα διάνυσµα αλλά έναν πραγµατικό αριθµό. Έτσι ενώ µια πράξη µορφής α+ δεν έχει νόηµα, η πράξη α β+ είναι µια πρόσθεση δύο πραγµατικών αριθµών. Προφανώς αν α,β µη µηδενικά, ισχύουν οι ισοδυναµίες α β>0 φ οξεία και α β<0 φαµβλεία, καθώς το πρόσηµο του α β καθορίζεται από το πρόσηµο του συνφ. Ιδιότητες του εσωτερικού γινοµένου 1. α β= β α Αντιµεταθετική ιδιότητα. α β α β = α β 3. α β α β = α β 4. α β α β= 0 5. α β λ1 λ= 1, όπου λ 1, λ οι συντελεστές διεύθυνσης των α και β αντίστοιχα µε την προϋπόθεση ότι αυτοί ορίζονται (δηλαδή ότι α,β // y'y) 6. (λ α) β= α (λ β) = λ (α β) 7. α (β+ γ) = α β+ α γ Επιµεριστική ιδιότητα 8. α α= α = α Τετράγωνο του α 9. i = j = 1 και i j= j i= 0 όπου i και j τα µοναδιαία διανύσµατα των αξόνων και y y αντίστοιχα. ΣΗΜΑΝΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1. Λόγω της ιδιοµορφίας του εσωτερικού γινοµένου, δεν ισχύουν γενικά κάποιες ιδιότητες που χρησιµοποιούµε συχνά σε άλλες πράξεις όπως π.χ. στον πολλαπλασιασµό αριθµών (όλες οι ιδιότητες που θα αναφερθούν εδώ και οι οποίες
18 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 15 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός δεν ισχύουν γενικά, δεν αποκλείεται να ισχύουν για κάποιες ειδικές περιπτώσεις διανυσµάτων, κάτι που συνήθως αναφέρεται ως «ΣΗΜΕΙΩΣΗ»). Έτσι: α) εν ισχύει γενικά η προσεταιριστική ιδιότητα, δηλαδή (α β) γ α (β γ) Μη συγχέουµε την παραπάνω σχέση µε την ιδιότητα 6. του εσωτερικού γινοµένου µια που εκεί το λ ήταν πραγµατικός αριθµός και όχι διάνυσµα. Έτσι ισχύει ότι (β α) β= β (α β) µια που το β είναι πραγµατικός αριθµός. ΣΗΜΕΙΩΣΗ: Η προσεταιριστική ιδιότητα µε την παραπάνω σειρά των διανυσµάτων ισχύει µόνο αν α//γ. Άµεσες συνέπειες της µη ισχύος της προσεταιριστικής ιδιότητας είναι και οι παρακάτω σχέσεις: (α β) β α β, β (α β) β α, (α β) α β ΣΗΜΕΙΩΣΗ: Οι παραπάνω σχέσεις ισχύουν ως ισότητες αν και µόνο αν α//β. Ειδικά για την τελευταία ισχύει πάντα ότι : (α β) α β. β) Γενικά είναι: α β α β ΣΗΜΕΙΩΣΗ: Η προηγούµενη σχέση ισχύει ως ισότητα αν και µόνο αν α//β. Σε κάθε περίπτωση ισχύει η ανισότητα Cauchy-Schwartz δηλαδή ότι α β α β. γ) εν ισχύει ο νόµος της διαγραφής στον πολλαπλασιασµό (καθώς το εσωτερικό γινόµενο δεν είναι η γνωστή µας πράξη του πολλαπλασιασµού). Έτσι: Αν α β=0 α=0 ή β=0 Αν α =β α=β και 0 Αν α β=0 β=0 και α 0 ΣΗΜΕΙΩΣΗ: Ο νόµος της διαγραφής στον πολλαπλασιασµό ισχύει µόνο αν όλα τα διανύσµατα που συµµετέχουν στην ιδιότητα είναι συγγραµµικά.
19 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 16 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός. Οι δυνάµεις ενός διανύσµατος α είναι άλλοτε διανύσµατα και άλλοτε πραγµατικοί αριθµοί και µάλιστα εναλλάξ. Έτσι α διάνυσµα, αριθµός κ.τ.λ. α αριθµός, 3. Στα διανύσµατα ισχύουν οι ταυτότητες µε άρτιους εκθέτες (π.χ. (α + β) = α + β + α β ) 3 α διάνυσµα, αλλά όχι και οι ταυτότητες µε περιττούς εκθέτες (π.χ. (α+ β) α + 3α β+ 3α β + β ) 4. Αν α β = τότε α = β αλλά όχι αντίστροφα. 5. Προσοχή χρειάζεται επίσης στο ότι αν ισχύει α= γ τότε α γ= 0 (διάνυσµα), ενώ αν α β= γ δ τότε α β γ δ= 0 (αριθµός) γιατί οι α β και γ δ είναι αριθµοί. α 4 ΑΠΟ ΕΙΞΗ ΤΩΝ Ι ΙΟΤΗΤΩΝ που αναφέραµε στην α β α+ β = α + β. α β α β = α+ β, 3. α= 0 η β= 0 α β = α+ β = α + β 1. α+ β = α + β α+ β = ( α + β ) (α+ β) = α + β + α β α + β + α β= α + β + α β α β = α β α β από ιδιότητα. του εσωτερικού γινοµένου.. Παρόµοια 3. Παίρνοντας τη σχέση α β = α+ β = α + β µε ισοδυναµίες και υψώνοντας στο τετράγωνο τα τρία µέλη, καταλήγουµε στη σχέση α β = α β = α β η οποία µε βάση τις ιδιότητες. και 3. του εσωτερικού γινοµένου καταλήγει ισοδύναµα στο σύστηµα α β, και ισοδύναµα α= 0 η β= 0, γιατί µόνο το µηδενικό διάνυσµα µπορεί α β να είναι ταυτόχρονα οµόρροπο και αντίρροπο ως προς ένα άλλο διάνυσµα. Αναλυτική έκφραση εσωτερικού γινοµένου Έστω δύο διανύσµατα α = ( 1,y 1) και β = (,y ) στο καρτεσιανό επίπεδο. Μια άλλη έκφραση του εσωτερικού τους γινοµένου µε τη βοήθεια των συντεταγµένων τους είναι η: α β=1 +y1 y (η µορφή εσωτερικού γινοµένου) και ονοµάζεται αναλυτική έκφραση του εσωτερικού γινοµένου των α και β.
20 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 17 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ιανύσµατα κάθετα στο α( 1, y 1) Αν α = ( 1, y 1), µε τη βοήθεια της παραπάνω σχέσης µπορούµε να δείξουµε ότι δύο διανύσµατα κάθετα στο α είναι τα α 1=(-y 1, 1) και α =(y 1,- 1). Συνηµίτονο γωνίας δύο διανυσµάτων Έστω δύο µη µηδενικά διανύσµατα α = ( 1,y 1) και β = (,y ) στο καρτεσιανό επίπεδο τα οποία σχηµατίζουν γωνία θ. Τότε α β = α β συνθ και εποµένως: α β 1 +y1y συνθ= ή µε τη βοήθεια των συντεταγµένων τους συνθ= α β +y +y 1 1 Προβολή διανύσµατος σε διάνυσµα Έστω δύο διανύσµατα α και β του καρτεσιανού επιπέδου µε α 0. Με αρχή ένα σηµείο Ο του επιπέδου θεωρούµε τα διανύσµατα ΟΑ = α και ΟΒ = β. Από το Β β β Β α φέρνουµε κάθετη στη διεύθυνση ΟΑ και έστω Β1 το ίχνος της κάθετης. Το διάνυσµα ΟΒ1 ονοµάζεται προβολή του β στο α Ο α Β 1 Α και συµβολίζεται µε προβ β α. Έτσι ΟΒ1 = προββ. α Αποδεικνύεται ότι η προβολή του β στο α είναι ανεξάρτητη από τη θέση του σηµείου Ο. Τότε µια άλλη έκφραση του εσωτερικού γινοµένου των α και β είναι η παρακάτω: α β=α προβ β α (3η µορφή εσωτερικού γινοµένου) ΠΑΡΑΤΗΡΗΣΕΙΣ Φυσικά ισχύει και η σχέση α β= β α= β προβ α β γ β Σύµφωνα µε τα παραπάνω αν οι προβολές κάποιων διανυσµάτων π.χ. β και γ πάνω σε ένα διάνυσµα α είναι ίσες, τότε θα ισχύει α β = α γ. Ο α
21 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 18 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΠΙΝΑΚΑΣ ΑΝΑΚΕΦΑΛΑΙΩΣΗΣ Στον παρακάτω πίνακα εννοείται ότι τα κεφαλαία γράµµατα παριστάνουν σηµεία του καρτεσιανού επιπέδου και τα διανύσµατα α και β έχουν συντεταγµένες (1, y 1 ) και (, y ) αντίστοιχα και σχηµατίζουν γωνία φ. Όταν σε µια ιδιότητα αναφέρεται µόνο το διάνυσµα α προς χάριν απλούστευσης ως συντεταγµένες του θεωρούνται οι (,y). ΑΘΡΟΙΣΜΑ - ΙΑΦΟΡΑ ΙΑΝΥΣΜΑΤΩΝ ΜΕΤΡΟ ΙΑΝΥΣΜΑΤΟΣ Αν ΑΒ= Γ τότε ΑΓ= Β και ΓΑ= Β ΑΒ= ΟΒ-ΟΑ ΑΟ ΒΟ= ΑΒ α+ β = (1+,y1+ y ) α β = (1,y1 y ) α = + y α-β α+ β α+ β ΑΠΟΣΤΑΣΗ ΣΗΜΕΙΩΝ Α( 1,y 1 ) και Β(,y ) ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΜΕΣΟ Μ ΤΜΗΜΑΤΟΣ ΑΒ ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΙΑΝΥΣΜΑΤΟΣ ΙΣΟΤΗΤΑ ΙΑΝΥΣΜΑΤΩΝ ΣΥΝΤΕΛΕΣΤΗΣ ΙΕΥΘΥΝΣΕΩΣ ΙΑΝΥΣΜΑΤΟΣ α 1 1 (AB) = ( - ) + (y -y ) λ α = (λ, λy) Ι ΙΟΤΗΤΕΣ 1. λ α= 0 λ= 0 ή α= 0. Αν λ α= λ β και λ 0, τότε α= β 3. Αν λ α = µ α και α 0, τότε λ=µ. ΟΑ+ ΟΒ ΟΜ=, όπου Ο σηµείο αναφοράς 1+ y1+ y Αν Α( 1, y 1 ) και Β(, y ) τότε Μ(, ) Αν Α( 1, y 1 ) και B(, y ) δύο σηµεία, τότε ΑΒ = (, y y ) 1 1 τετµηµ. διανύσµατος = τετµηµ. πέρατος τετµηµ. αρχής τεταγµ. διανύσµατος = τεταγµ. πέρατος τεταγµ. αρχής = α= β y = y 1 1 δηλαδή y λ= = εφφ όπου φ η γωνία του διανύσµατος µε τον άξονα (φ [0,π))
22 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 19 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΣΥΝΘΗΚΕΣ ΣΥΓΓΡΑΜΜΙΚΟΤΗΤΑΣ α//β υπάρχει λ R, τέτοιος ώστε α= λ β (β 0) 1 y1 α//β det(α,β) = 0 = 0 y α//β λ1= λ, όπου λ 1, λ οι συντελεστές διεύθυνσης α//β α β =± α β και µάλιστα α β α β = α β και α β α β = α β ΜΕ ΑΠΟ ΕΙΞΗ α β α+ β = α + β και α β α β = α+ β ΜΟΝΑ ΙΑΙΑ ΙΑΝΥΣΜΑΤΑ 1 1,οµόρροπο του α και α,αντίρροπο του α ΣΥΓΓΡΑΜΜΙΚΑ ΤΟΥ α 1 = α α =- α α α ΙΑΝΥΣΜΑΤΑ ΚΑΘΕΤΑ ΣΤΟ α Αν α = ( 1, y 1), δύο διανύσµατα κάθετα στο α είναι τα α 1= ( y 1, 1) και α = (y 1, 1) ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ α β συνφ, αν α 0 και β 0 ΙΑΝΥΣΜΑΤΩΝ α β=, 0, αν α= 0 η β= 0 όπου φ η γωνία των α και β (µε φ [0,π]) α β = 1 + y1 y α β= α προββ α Ι ΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ 1. α β= β α Αντιµεταθετική ιδιότητα ΓΙΝΟΜΕΝΟΥ. α β α β = α β 3. α β α β = α β 4. α β α β= 0 5. α β λ1 λ= 1, όπου λ 1, λ οι συντελεστές διεύθυνσης των α και β αντίστοιχα µε την προϋπόθεση ότι αυτοί ορίζονται (δηλαδή ότι α,β // y'y) 6. (λ α) β= α (λ β) = λ (α β) 7. α (β+ γ) = α β+ α γ Επιµεριστική ιδιότητα 8. α α= α = α Τετράγωνο του α 9. i = j = 1 και i j= j i= 0 όπου i και j τα µοναδιαία διανύσµατα
23 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 0 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΣΥΝΗΜΙΤΟΝΟ ΓΩΝΙΑΣ ΥΟ ΙΑΝΥΣΜΑΤΩΝ ΣΥΝΘΗΚΕΣ ΚΑΘΕΤΟΤΗΤΑΣ ΥΟ ΙΑΝΥΣΜΑΤΩΝ ΠΡΟΣΟΧΗ Γενικά (α β) γ α (β γ) (α β) β α β β (α β) β α (α β) α β αλλά (α β) α β Αν α β=0 α=0 ή β=0 Αν α =β α=β και 0 Αν α β=0 β=0 και α 0 α β α β αλλά α β α β Οι παραπάνω ιδιότητες, εκτός της πρώτης, ισχύουν ως ισότητες ή συνεπαγωγές αντίστοιχα, αν τα διανύσµατα που συµµετέχουν σε αυτές είναι συγγραµµικά. Η πρώτη ισχύει ως ισότητα αν είναι συγγραµµικά τα α και γ. α β 1 + y1y συνφ = συνφ = α β 1 + y1 + y α β α β= 0 α β λ1 λ= 1, µε την προϋπόθεση ότι α,β // y'y α β + y y = 0 1 1
24 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 1 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΜΕΘΟ ΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ ΣΤΑ ΙΑΝΥΣΜΑΤΑ ΖΗΤΟΥΜΕΝΟ 1. Συγγραµµικότητα Έστω ότι ζητάµε να δείξουµε πως α//β (µε α,β 0) Παραδείγµατα 1,,3 ΜΕΘΟ ΟΙ είχνουµε ότι υπάρχει λ R τέτοιος ώστε α= λ β. Ειδικότερα αν λ>0 τότε α β, ενώ αν λ<0 τότε α β. είχνουµε ότι det(α,β) = 0 είχνουµε ότι α β = α β (οπότεα β) ή. Καθετότητα 1 Έστω ότι ζητάµε να δείξουµε πως α β ή ζητάµε να υπολογίσουµε τις τιµές κάποιων παραµέτρων ώστε να συµβαίνει αυτό. Παραδείγµατα 4,5 α β = α β (οπότε α β) είχνουµε ότι το συνηµίτονο της γωνίας τους είναι 1 (οπότεα β ) ή 1 (οπότε α β). είχνουµε ότι λα = λ. β είχνουµε ότι α//γ και β//γ όπου γ κατάλληλο διάνυσµα. Χρησιµοποιούµε κάποια από τις ισοδυναµίες: α β α β= 0 α β λ1 λ= 1, µε την προϋπόθεση ότι α,β // y'y α β + y y = 0 1 1
25 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 3. Καθετότητα Σε γεωµετρικές ασκήσεις που περιέχουν ορθές γωνίες Παράδειγµα 6 4. Ισότητα Έστω ότι ζητάµε να δείξουµε πως ΑΒ=Γ Παράδειγµα 7 5. Απόδειξη σχέσεων µε µέτρα Παράδειγµα 8 Μπορούµε να εκµεταλλευτούµε την ορθή γωνία ενός σχήµατος µε δύο κυρίως τρόπους: Ή για τη γραφή του εσωτερικού γινοµένου µε τη βοήθεια προβολών Ή εκφράζοντας το εσωτερικό γινόµενο των κάθετων διανυσµάτων (που είναι 0) µε τη µορφή (κ λ) (κ + λ) = κ λ χρησιµοποιώντας διανυσµατικές ακτίνες. Έτσι στο παρακάτω σχήµα έχουµε: Α \\ Γ ΒΑ Β = ΒΑ προβ Β = ΒΑ ΒΑ = ΒΑ ΒΑ ΑΒ Α ΑΒ Α = 0 (ΟΒ ΟΑ) (Ο ΟΑ) = 0 (ΟΒ ΟΑ) ( ΟΒ ΟΑ) = 0 (ΟΒ ΟΑ) (ΟΒ+ ΟΑ) = 0 ΟΒ ΟΑ = 0 κ.τ.λ. Αρκεί να δείξουµε ότι έχουν ίδιες συντεταγµένες. Αρκεί να δείξουµε ότι ΑΒ Γ και ΑΒ = Γ Αρκεί να δείξουµε ότι ΑΓ = Β. Αρκεί να δείξουµε ότι Β = ΓΑ. Β Αρκεί να δείξουµε, συνήθως µε υπολογισµούς, ότι τα διανύσµατα αυτά είναι ίσα προς ένα τρίτο διάνυσµα ή ότι είναι ίσα µε την ίδια παράσταση. \\ O Αρκεί να δείξουµε ότι το ΑΒ Γ είναι παραλληλόγραµµο Συνήθως υψώνουµε τα µέλη της σχέσης στο τετράγωνο για να «φύγουν» τα µέτρα και κάνουµε τις πράξεις.
26 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 3 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 6. Απόδειξη γραµµικών σχέσεων 1 Έστω ότι ζητάµε να δείξουµε πως α +α +...+α =ν α, ν Ν*, 1 ν δηλαδή το πλήθος των προσθετέων ίσο µε το συντελεστή του α. Παράδειγµα 9 7. Απόδειξη γραµµικών σχέσεων Έστω ότι ζητάµε να δείξουµε πως α +α +...+α =β +β +...+β 1 κ 1 λ µε κ,λ Ν* Παράδειγµα Συγγραµµικότητα 3 σηµείων Έστω ότι ζητάµε να δείξουµε πως τα σηµεία Α, Β, Γ είναι συνευθειακά. Παραδείγµατα 11,1 Συνήθως εκφράζουµε το α µε ν διαφορετικούς τρόπους, κάθε φορά µε τη βοήθεια ενός εκ των α 1,α,...,αν. Γράφουµε τα α 1,α,...,α κ,β 1,β,...,βλ ως διαφορές των διανυσµατικών ακτίνων των άκρων τους, αναλύοντάς τα µε τη βοήθεια σηµείου αναφοράς(*) π.χ. Ο (ΑΒ = ΟΒ ΟΑ ) και αποδεικνύουµε τη σχέση που προκύπτει. Κάνουµε πράξεις στο ένα µέλος και καταλήγουµε στο άλλο. είχνουµε ότι (α1 + α α κ) (β1 + β β λ) = 0 είχνουµε ότι α1 + α ακ = κ α, β + β β = λ β και κ α= λ β (βλέπε 1 λ µεθοδολογία 6). Αρκεί να αποδείξουµε ότι δύο από τα ΑΒ,ΒΓ ή ΑΓ είναι συγγραµµικά (βλέπε µεθοδολογία 1). ΣΗΜΑΝΤΙΚΗ ΠΑΡΑΤΗΡΗΣΗ Ειδικά στην περίπτωση που δίνεται σχέση µορφής κ ΟΑ+ λ ΟΒ + µ ΟΓ = 0 (1) µε κ+λ+µ=0 χωρίς τα κ, λ, µ να είναι όλα µηδέν, τότε τα Α, Β, Γ είναι πάντα συνευθειακά. Η απόδειξη µπορεί να γίνει εκφράζοντας έναν από τους συντελεστές στην (1) µε τη βοήθεια των άλλων δύο (π.χ. µ=-κ-λ). Για να δείξουµε ότι περισσότερα από τρία σηµεία είναι συνευθειακά, αρκεί να δείξουµε ότι είναι συνευθειακά ανά τρία. (*) Η ανάλυση ενός διανύσµατος σε διαφορά διανυσµάτων µε τη βοήθεια σηµείου αναφοράς, είναι µια πολύ χρήσιµη µέθοδος, η οποία µπορεί να εφαρµοστεί σε πολλές ασκήσεις. Ως σηµείο αναφοράς συνήθως εξυπηρετεί να χρησιµοποιήσουµε ένα από τα σηµεία της άσκησης.
27 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 4 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 9. Ταύτιση δύο σηµείων Έστω ότι ζητάµε να δείξουµε πως τα σηµεία Α και Β ταυτίζονται. Παραδείγµατα 13, Προσδιορισµός σηµείου Ρ το οποίο επαληθεύει δοσµένη γραµµική διανυσµατική σχέση Παράδειγµα Προσδιορισµός των συντεταγµένων σηµείων τα οποία έχουν κάποια ιδιότητα Παράδειγµα Ανάλυση γνωστού διανύσµατος ν=( ν,y ν) σε δύο συνιστώσες α και β µε γνωστές διευθύνσεις. Αρκεί να δείξουµε ότι ΑΒ = 0 Αρκεί να δείξουµε ότι ΟΑ = ΟΒ όπου Ο τυχαίο σηµείο του χώρου. ΠΑΡΑΤΗΡΗΣΗ: Η παραπάνω µεθοδολογία εφαρµόζεται και στην περίπτωση που ζητάµε να δείξουµε πως δύο ή περισσότερα τµήµατα έχουν κοινό µέσο. Έτσι αν Μ 1, Μ,,Μ ν τα µέσα των τµηµάτων, αρκεί αν δείξουµε ότι ΟΜ = ΟΜ =... = ΟΜ 1 ν Υπολογίζουµε µε τη βοήθεια γνωστών (σταθερών) διανυσµάτων τη διανυσµατική ακτίνα ΟΡ του Ρ, όπου Ο κατάλληλο (δοσµένο) σηµείο του σχήµατος. Συµβολίζουµε µε αγνώστους τις συντεταγµένες των σηµείων αυτών, εκφράζουµε µε συντεταγµένες τις ιδιότητες που έχουν τα σηµεία και λύνουµε τις σχέσεις που προκύπτουν Γράφουµε το ν µε τη βοήθεια συντεταγµένων ως γραµµικό συνδυασµό των α και β, δηλαδή ν = κ α+ λ β και προσδιορίζουµε τα κ και λ. ΕΙ ΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ Α. Να αναλυθεί το ν=( ν,y ν) σε δύο συνιστώσες παράλληλες προς δύο γνωστά διανύσµατα α=(,y ) και β=(,y ) α α β β (Ή αλλιώς: Να γραφεί το ν ως γραµµικός συνδυασµός των α και β ). Παράδειγµα 17 ύο διανύσµατα παράλληλα προς τα α και β είναι τα κ α και λ β αντίστοιχα. Έστω ότι υπάρχουν κ, λ R τέτοιοι ώστε ν = κ α+ λ β. Με τη βοήθεια των συντεταγµένων και της προηγούµενης ισότητας, δηµιουργούµε σύστηµα, από όπου υπολογίζουµε τα κ και λ. Τότε οι ζητούµενες συνιστώσες είναι η κ α και η λ β.
28 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 5 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Β. Να αναλυθεί το ν=( ν,y ν) σε δύο συνιστώσες κάθετες προς δύο γνωστά διανύσµατα α=(,y ) και β=(,y ) α α β β Παράδειγµα 18 Γ. Να αναλυθεί το ν=( ν,y ν) σε δύο συνιστώσες, µία παράλληλη και µία κάθετη προς γνωστό διάνυσµα α=(,y ) α α Παράδειγµα Ασκήσεις που αφορούν στη γωνία δύο διανυσµάτων Παραδείγµατα 0,1 14. Ασκήσεις που µας δίνουν τα Λ α, ν και (α,ν) την προβ ν α και µας ζητούν Παράδειγµα ύο διανύσµατα κάθετα προς τα α και β είναι τα α = ( y, ) και β = ( y, ) αντίστοιχα 1 α α 1 β β (γιατί λα λα 1 = 1 και λβ λβ 1 = 1). Γράφουµε το ν ως γραµµικό συνδυασµό των α1 και β1, ν = κ α 1 + λ β1. Μετατρέπουµε τη σχέση αυτή σε σχέση συντεταγµένων. Προσδιορίζουµε µε λύση συστήµατος τα κ και λ, οπότε οι ζητούµενες συνιστώσες είναι η κ α και η λ β. 1 1 Με ανάλογο συλλογισµό, ένα διάνυσµα κάθετο µε το α είναι το α 1 = ( y α, α). Άρα ν = κ α+ λ α1. Μετατρέπουµε τη σχέση αυτή σε σχέση συντεταγµένων. Προσδιορίζουµε µε λύση συστήµατος τα κ και λ, οπότε οι ζητούµενες συνιστώσες είναι η κ α και η λ α1. α β Χρησιµοποιούµε τη σχέση συνθ = ή τη α β 1 + y1y σχέση συνθ= + y + y 1 1 Ειδικά για την πρώτη σχέση, πολλές φορές, δεν µπορούµε να υπολογίσουµε απ ευθείας τα µέτρα των διανυσµάτων. Τότε υπολογίζουµε τα τετράγωνά τους και από εκεί προσδιορίζουµε τα µέτρα. Αν µας ζητούν να αποδείξουµε ότι δύο γωνίες είναι ίσες, υπολογίζουµε µε τις παραπάνω σχέσεις το συνηµίτονο της καθεµιάς. Επειδή προβν//α α θα υπάρχει λ R, ώστε προβν= λ α (1). Άρα θα ισχύει α α ν= α προβν α ν= α λ α α ν= λ α α α ν= λ α. Από τη σχέση αυτή βρίσκουµε το λ και από την (1) την προβ ν α..
29 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 6 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 15. Ασκήσεις γεωµετρικών τόπων Έστω ότι ζητάµε το γεωµετρικό τόπο (γ.τ.) σηµείου Μ το οποίο επαληθεύει κάποια σχέση που περιέχει διανύσµατα ή µέτρα διανυσµάτων. Παραδείγµατα 3,4,5,6 Η αντιµετώπιση τέτοιων ασκήσεων εξαρτάται από τη µορφή της σχέσης: Αν η σχέση εκφράζεται µε µέτρα διανυσµάτων και έχει µορφή: ΜΑ = ΜΒ, όπου Α και Β σταθερά σηµεία, τότε ο γ.τ. του Μ είναι η µεσοκάθετος του ΑΒ. ΜΑ =ρ>0, όπου Α σταθερό σηµείο, τότε ο γ.τ. του Μ είναι ο κύκλος (Α, ρ). Αν η σχέση έχει µορφή ΑΜ=λ α, όπου Α σταθερό σηµείο, α γνωστό διάνυσµα και λ R, τότε ο γ.τ. του Μ είναι η ευθεία ε που διέρχεται από το Α και έχει τη διεύθυνση του α. Αν Α,Β δοσµένα σηµεία και η σχέση εκφράζεται µε εσωτερικό γινόµενο διανυσµάτων της µορφής: MA MB=0 τότε (µε απόδειξη*) ο γ.τ. του Μ είναι κύκλος διαµέτρου ΑΒ AM AB=0 τότε (µε απόδειξη*) ο γ.τ. του Μ είναι η κάθετη ευθεία στην ΑΒ στο Α * ΑΠΟ ΕΙΞΕΙΣ ΤΩΝ ΤΕΛΕΥΤΑΙΩΝ Γ.Τ. Μ Έστω Ο το µέσον του ΑΒ. ΤότεΜΑ ΜΒ = 0 (ΜΟ+ ΟΑ) (ΜΟ+ ΟΒ) = 0,, (ΜΟ+ ΟΑ) (ΜΟ ΟΑ) = 0 ΜΟ ΟΑ = 0 ΜΟ = ΟΑ Α Ο Β ΜΟ = ΟΑ ΜΟ = ΟΑ. Έτσι το Μ απέχει σταθερή απόσταση από το σταθερό Ο και εποµένως ο γ.τ. είναι ο κύκλος µε διάµετρο ΑΒ. ΑΛΛΙΩΣ: Η σχέση ΜΑ ΜΒ = 0 σηµαίνει ότι ΜΑ ΜΒ, οπότε AMB ˆ = 90. Άρα το Μ «βλέπει» µε ορθή γωνία το σταθερό τµήµα ΑΒ και εποµένως ανήκει σε κύκλο µε διάµετρο το ΑΒ. Αφού ΑΜ ΑΒ = 0, τα ΑΜ και ΑΒ είναι κάθετα και επειδή έχουν κοινή αρχή το Α, ο γ.τ. του Μ είναι η σταθερή ευθεία ε που είναι κάθετη στην ΑΒ στο Α. ε Μ Α Β
30 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 7 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΣΗΜΑΝΤΙΚΗ ΠΑΡΑΤΗΡΗΣΗ ΑΝΑΛΥΤΙΚΗ ΜΕΘΟ ΟΣ ΑΠΟ ΕΙΞΗΣ Πολλές φορές η λύση µιας άσκησης επιτυγχάνεται ευκολότερα αν κατασκευάσουµε και εργαστούµε πάνω σε ένα καρτεσιανό σύστηµα συντεταγµένων (ιδιαίτερα αν τα διανύσµατα µας δίνονται µε συντεταγµένες) ή όπως λέµε εφαρµόζοντας την αναλυτική µέθοδο απόδειξης. Έτσι: Κατασκευάζουµε ένα σύστηµα συντεταγµένων Τοποθετούµε πάνω σε αυτό όλα τα σηµεία στα οποία αναφέρεται η άσκηση. Σε σηµεία που δεν είναι δοσµένα θέτουµε παραµετρικές συντεταγµένες. Η τοποθέτηση καλό είναι να γίνεται µε τέτοιο τρόπο ώστε όσο το δυνατόν περισσότερα σηµεία να έχουν τετµηµένες ή τεταγµένες µηδέν. Εκφράζουµε τα δεδοµένα και τα ζητούµενα µε συντεταγµένες και προσπαθούµε να φτάσουµε στο επιθυµητό αποτέλεσµα. Μερικές ιδέες για τη δηµιουργία συστηµάτων συντεταγµένων σε διάφορα βασικά σχήµατα είναι οι παρακάτω: Ορθογ. τρίγωνο Ορθογώνιο Τετράγωνο Ισοσκελές τρίγωνο Α(0,α) Γ(0,γ) (0,δ) Γ(β,δ) (0,β) Γ(β,β) Α(0,0) Β(β,0) Α(0,0) Β(β,0) Α(0,0) Β(β,0) Β(-β,0) Γ(β,0) Τρίγωνο Α(α,β) Παραλληλόγραµµο Ισοσκελές τραπέζιο Τυχαίο τετράπλευρο (-β,γ) Γ(β,γ) (δ,ε) (β,γ) Γ(α+β,γ) Β(0,0) Γ(γ,0) Α(0,0) Β(α,0) Α(-α,0) Β(α,0) Α(0,0) Γ(γ,0) Β(α,β)
31 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 8 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός ΛΥΜΕΝΑ ΠΑΡΑ ΕΙΓΜΑΤΑ 1. ίνονται τα σηµεία Α, Β, Γ και µε διανύσµατα θέσης α, β, 4α β και α+ β ως προς σηµείο αναφοράς Ο αντίστοιχα. Να δείξετε ότι τα διανύσµατα ΑΒ και Γ είναι συγγραµµικά. ΑΒ = ΟΒ ΟΑ = β α Γ = Ο ΟΓ = α+ β (4β β) = 3β 3α= 3 (β α) Άρα Γ = 3 ΑΒ οπότε Γ //ΑΒ.. Να βρείτε τον πραγµατικό αριθµό ώστε τα διανύσµατα α(,) και β(16,) να είναι οµόρροπα. Για να είναι οµόρροπα τα α και β πρέπει και αρκεί det(α,β)=0 και να υπάρχει θετικός αριθµός λ έτσι ώστε α= λ β. det( α,β )= = -3=0 =16 =± 4. Για =4 είναι α = (4,) και β = (16,8) = 4 (4,) = 4 α οπότε α και β οµόρροπα. Για =-4 είναι α = ( 4,) και β = (16, 8) = 4 ( 4,) = 4 α αντίρροπα. οπότε α και β Άρα η ζητούµενη τιµή του είναι το Αν α =, β = 1, γ = 3 και α+ β+ γ = 0 να δείξετε ότι β γ. Είναι α+ β+ γ = 0 (β+ γ) = α οπότε (*) (β+ γ) = ( α) β + β γ+ γ = 4 α β + β γ + γ = 4 α 1+ β γ +9=16 β γ =6 β γ=3. Όµως και β γ = 3 οπότε β γ = β γ εποµένως β γ. (*)ΠΡΟΣΟΧΗ: Οι σχέσεις (β+ γ) = α και (β+ γ) = ( α) συνδέονται µε συνεπαγωγή και όχι ισοδυναµία γιατί γενικά αν α = β τοτε α = β αλλά όχι αντίστροφα. 4. Έστω ΟΑ και ΟΒ δύο κάθετα διανύσµατα µε ΟΑ = α+ β και ΟΒ = α β. Αν α β = 6 και β = 5 να υπολογιστεί το α. ΟΑ ΟΒ ΟΑ ΟΒ = 0 (α+ β) (α β) = 0 α + 3 α β β = 0 α + 3 α β β = 0 α = β 3 α β α = α = 16 α = 4
32 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 9 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 5. Έστω τα διανύσµατα α= i j, β = 6i+ yj και γ = i+ 4j. Αν α β τότε: α) Να προσδιοριστεί το β β) Να δείξετε ότι β γ α) α β α β = ( ) y = 0 6 y = 0 y = 3. Άρα β= 6i+ 3j. β) β γ = 6 ( ) = 0. Άρα β γ. ΣΗΜΕΙΩΣΗ: Το ότι β γ θα µπορούσε να προκύψει και αλλιώς αν παρατηρήσουµε ότι γ = α.έτσι γ//α και αφού α β, τότε προφανώς β γ. 6. ίνεται ορθογώνιο τρίγωνο ΑΒΓ και Α το ύψος του. είξτε ότι ισχύει η ισοδυναµία: ˆΑ = 90 ΑΒ = ΒΓ Β ΕΥΘΥ: Έστω ˆΑ = 90. Θα δείξουµε ότι ΑΒ = ΒΓ Β. Έχουµε κατά σειρά ΑΒ = ΑΒ ΑΒ = ΑΒ (ΑΓ+ ΓΒ) = = ΑΒ ΑΓ+ ΑΒ ΓΒ= 0+ ΑΒ ΓΒ== προβ ΑΒ ΓΒ= ΓΒ = Β ΓΒ = Β ( ΒΓ) = ΒΓ Β. Γ Α Β ΑΝΤΙΣΤΡΟΦΟ: Έστω ότι ισχύει ΑΒ = ΒΓ Β (1). Θα δείξουµε ότι ˆΑ = 90. ΑΒ = ΑΒ ΑΒ = (ΑΓ+ ΓΒ) (Α + Β) = ΑΓ Α + ΑΓ Β+ ΓΒ Α + ΓΒ Β = = ΑΓ Α + ΑΓ Β+ 0+ ΓΒ Β= ΑΓ Α + ΑΓ Β+ ΓΒ Β= ΑΓ (Α + Β) + ΓΒ Β= = ΑΓ ΑΒ+ ΒΓ Β (). Από (1) και () έχουµε: ΒΓ Β = ΑΓ ΑΒ+ ΒΓ Β ΑΓ ΑΒ= 0 ΑΓ ΑΒ Αˆ = Έστω τετράπλευρο ΑΒΓ και Α 1, Α τα συµµετρικά του Α ως προς και Γ αντίστοιχα. Αν Β 1, Β τα συµµετρικά του Β ως προς και Γ αντίστοιχα, να δείξετε Α Β = Α Β και Α Α = Β Β. ότι Τα τετράπλευρα ΑΒΑ 1 Β 1 και ΑΒΑ Β είναι παραλληλόγραµµα για τι οι διαγώνιές τους διχοτοµούνται. Άρα ισχύουν: Α1Β 1 = ΑΒ και Α1Β1 ΑΒ οπότε Α Β = ΑΒ 1 1 και ΑΒ = ΑΒ και ΑΒ ΑΒ οπότε ΑΒ = ΑΒ Εποµένως Α1Β1 = ΑΒ άρα Α1Α = Β1Β. Β 1 / / Β ν Γ ν Β = Α 1 χ χ Α = Α
33 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 30 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 8. Αν α = β = α+ β να δειχθεί ότι α β = α 3. Είναι α = α+ β α = α+ β α = (α+ β) α = α + α β+ β α = β α = α + α β + β α Τότε = α + α β + α α β = α (1) α β = α β = (α β) = α α β+ β = α α β + β = α + α + α = 3 α Άρα α β = α Αν Μ και Ν τα µέσα των πλευρών ΑΒ και Γ τετραπλεύρου ΑΒΓ να δείξετε ότι Α + ΒΓ = ΜΝ. Ισχύουν: ΜΝ= ΜΑ+ Α + Ν ΜΝ= ΜΒ+ ΒΓ+ ΓΝ Με πρόσθεση κατά µέλη έχουµε: ΜΝ= ΜΑ+ Α + Ν+ ΜΒ+ ΒΓ+ ΓΝ= = ΜΑ + Α + Ν ΜΑ Ν Γ + ΒΓ+ Ν = Α + ΒΓ 10. Αν ΑΒΓ ΕΖ κανονικό εξάγωνο δείξτε ότι ΑΓ+ ΑΕ= Α + ΒΓ Με κέντρο αναφοράς το κέντρο Ο του εξαγώνου έχουµε: ΟΕ= ΟΒ ΑΓ+ ΑΕ= ΟΓ ΟΑ+ ΟΕ ΟΑ = ΟΓ ΟΒ ΟΑ = ΑΟ= Α = ΒΓ+ ΑΟ = ΒΓ+ Α. (1) Α Α Μ Β Ζ Ο Γ Β Ε 11. ίνονται τρία σηµεία Α, Β, Γ για τα οποία ισχύει ΟΒ+ 4 ΟΓ = 5 ΟΑ, όπου Ο τυχαίο σηµείο αναφοράς. Να δείξετε ότι τα Α, Β, Γ είναι συνευθειακά. ΟΒ+ 4 ΟΓ = 5 ΟΑ ΟΒ+ 4 ΟΓ 5 ΟΑ = 0 (1) Επειδή οι συντελεστές (1, 4, -5) έχουν άθροισµα 0, σύµφωνα µε τη µεθοδολογί,α διασπάµε το 5 µε τη βοήθεια των 1 και 4. Έτσι: (1) ΟΒ+ 4 ΟΓ ΟΑ 4 ΟΑ = 0 (ΟΒ ΟΑ) + (4 ΟΓ 4 ΟΑ) = 0 ΑΒ+ 4 ΑΓ = 0 ΑΒ = 4 ΑΓ που σηµαίνει ότι ΑΒ, ΑΓ συγγραµµικά, οπότε Α, Β, Γ συνευθειακά.
34 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 31 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 1. Σε τρίγωνο ΑΒΓ προεκτείνουµε τις διαµέσους ΒΚ και ΓΛ κατά τµήµατα Κ =ΒΚ και ΛΕ=ΓΛ αντίστοιχα. Να δείξετε ότι τα σηµεία Ε, Α και είναι συνευθειακά. Θα προσπαθήσουµε να υπολογίσουµε τα ΑΕ και Α µε στόχο να δείξουµε ότι ΑΕ = λ Α Είναι ΑΕ = ΑΓ+ ΓΕ = ΑΓ+ ΓΛ. Ε Α Όµως Λ µέσο ΑΒ οπότε ΓΛ = ΓΑ + ΓΒ. _ // Άρα ΑΕ = ΑΓ+ ΓΑ+ ΓΒ = ΓΒ (1). Επίσης Λ Κ Κ µεσο ΑΓ _ // Α = ΑΒ+ Β = ΑΒ+ ΒΚ = ΑΒ+ ΒΑ+ ΒΓ = = ΒΓ (). Β Γ Από (1) και () προκύπτει ότι ΑΕ = Α οπότε ΑΕ//Α και εποµένως Ε, Α, συνευθειακά. 13. ίνονται τα σηµεία Α, Β, Γ για τα οποία ισχύει η σχέση ΑΒ+ 004 ΑΓ = (λ+ ) ΒΓ (1). Να προσδιοριστεί η τιµή του λ R ώστε τα Α και Γ να συµπίπτουν. Για να συµπίπτουν τα Α και Γ πρέπει και αρκεί προσθετουµε στα δυο µελη (1) το ΒΓ ΑΓ= 0 ΑΒ+ 0 = (λ+ ) ΒΓ ΑΒ+ ΒΓ = (λ+ ) ΒΓ+ ΒΓ ΑΓ = (λ+ 3) ΒΓ λ+ 3= 0, Β Γ 0 = (λ+ 3) ΒΓ η λ+ 3= 0 λ = 3. ΒΓ = Να δείξετε ότι τα ευθύγραµµα τµήµατα που έχουν άκρα τα µέσα των απέναντι πλευρών κυρτού τετραπλεύρου διχοτοµούνται (έχουν κοινό µέσο) Μία µέθοδος επίλυσης της άσκησης αυτής είναι µε συντεταγµένες ορίζοντας ένα κατάλληλο σύστηµα συντεταγµένων όπως αυτό που φαίνεται στο διπλανό σχήµα. Έστω Κ, Λ, Μ και Ν τα µέσα των απέναντι πλευρών του τετραπλεύρου (βλέπε σχήµα), Ο 1 το µέσον της ΚΝ και Ο το µέσον της ΝΛ. Θα δείξουµε ότι Ο 1 Ο. Έχουµε κατά σειρά: Συντεταγµένες Κ: ( α+ γ, β+ δ ) Συντεταγµένες Μ: ( 0+ ε, 0+ 0 ε )=(,0 ) Β(α,β) Ν Κ Γ(γ,δ) Α(0,0) Μ (ε,0) Λ
35 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 3 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Άρα συντεταγµένες του µέσου Ο 1 του ΚΜ: Συντεταγµένες Ν: ( 0+ α, 0+ β α )=(, β ) Συντεταγµένες Λ: ( γ+ ε, δ+ 0 γ + ε )=(, δ ) Άρα συντεταγµένες του µέσου Ο του ΛΝ: Εποµένως Ο 1 Ο αφού έχουν τις ίδιες συντεταγµένες. α+ γ ε β+ δ α+ γ+ ε β+ δ (, ) = (, ). 4 4 α γ+ ε β δ + + α+ γ+ ε β+ δ (, ) = (, ). 4 4 ΣΗΜΕΙΩΣΗ: Φυσικά µπορούµε να λύσουµε την άσκηση χωρίς να χρησιµοποιήσουµε 1 συντεταγµένες, όπως να υπολογίσουµε τα ΚΛ και ΝΜ δείχνοντας ότι ΚΛ = ΝΜ= ΑΓ, οπότε το ΚΛΜΝ είναι παραλληλόγραµµο και εποµένως οι διαγώνιές του ΚΜ και ΝΛ διχοτοµούνται. 15. Αν ΑΒΓ ορθογώνιο να προσδιορίσετε σηµείο Μ τέτοιο ώστε να ισχύει ΜΑ+ ΜΒ+ ΜΓ = Μ Έχουµε κατά σειρά: ΜΑ+ ΜΒ+ ΜΓ= Μ ΜΑ+ ΜΓ= Μ ΜΒ ΜΟ= Β ΜΟ= ΒΟ ΜΟ= ΒΟ. Άρα το Μ ταυτίζεται µε το σηµείο Β. 16. ίνεται τρίγωνο ΑΒΓ µε Α(0,3), Β(-1,3) και Γ(1,1). Να βρεθούν οι συντεταγµένες: α) Σηµείου Κ για το οποίο ισχύει ΓΚ = ΒΓ β) Σηµείου Λ της ευθείας ΑΓ για το οποίο ισχύει ΚΛ//ΑΒ. α) Έστω Κ(,y). Τότε ΓΚ = ( 1,y 1) και ΒΓ = (1+ 1,1 3) = (, ). Έτσι: = = ΓΚ = ΒΓ ( 1,y 1) = (, ). Άρα Κ(,0). y = y = 0 β) Έστω Λ(α,β). Για να ανήκει το Λ στην ευθεία ΑΓ πρέπει και αρκεί ΑΛ//ΑΓ det(αλ, ΑΓ) = 0. Για να ισχύει ΚΛ//ΑΒ πρέπει και αρκεί ΚΛ//ΑΒ det(κλ,αβ) = 0 Όµως ΚΛ = (α,β), ΑΒ = ( 1,0), ΑΛ = (α,β 3) και ΑΓ = (1, ). Α Ο Β Μ Γ Έτσι: α β 3 = 0 det(αλ, ΑΓ) = 0 1. det(κλ, ΑΒ) = 0 α β = Λύνοντας το σύστηµα έχουµε ότι 3 α= και β= 0. Άρα Λ=( 3,0).
36 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 33 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 17. Να αναλυθεί το διάνυσµα γ = (, 3) σε δύο συνιστώσες µε διευθύνσεις τις διευθύνσεις των διανυσµάτων α = (1, ) και β = (, 3). Έστω u και v οι ζητούµενες συνιστώσες του γ µε u//α και v//β. Τότε υπάρχουν πραγµατικοί αριθµοί κ και λ, τέτοιοι ώστε u= κ α, v = λ β και γ = κ α+ λ β κ+ λ = (, 3) = κ (1, ) + λ (,3) (, 3) = (κ+ λ, κ+ 3λ). κ + 3λ = Λύνοντας το σύστηµα έχουµε ότι κ = και λ = Άρα u = (1, ) και v = (, 3) Να αναλυθεί το διάνυσµα γ = (, 3) σε δύο συνιστώσες κάθετες στις διευθύνσεις των διανυσµάτων α = (1, ) και β = (,3). Ένα διάνυσµα κάθετο προς το α = (1, ) είναι το α 1 = (,1) και ένα διάνυσµα κάθετο προς το β = (,3) είναι το β 1 = ( 3,). Έστω ότι υπάρχουν πραγµατικοί αριθµοί κ και λ τέτοιοι ώστε γ = κ α1 + λ β1 κ 3λ = (, 3) = κ (,1) + λ ( 3,). κ + λ = Λύνοντας το σύστηµα έχουµε ότι κ = και λ = Άρα u = (,1) και v = ( 3,) Να αναλυθεί το διάνυσµα γ = (, 3) σε δύο συνιστώσες, µιας παράλληλης προς το διάνυσµα α = (1, ) και µιας κάθετης σ αυτό. Η µέθοδος είναι ανάλογη εκείνης που εφαρµόσαµε στα προηγούµενα παραδείγµατα. Έτσι: Ένα διάνυσµα παράλληλο µε το α = (1, ) είναι το u= κ α, όπου κ πραγµατικός αριθµός. Ένα διάνυσµα κάθετο στο α = (1, ) είναι το α 1 = (,1) και ένα τυχαίο διάνυσµα παράλληλο µε το α 1 (άρα κάθετο στο α ) είναι το v = λ α1, όπου λ πραγµατικός κ+ λ = αριθµός. Άρα γ = κ α+ λ α 1 (, 3) = κ (1, ) + λ (,1). κ + λ = Λύνοντας το σύστηµα βρίσκουµε ότι κ = και λ = Άρα u = (1, ) και v = (,1). 5 5
37 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 34 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός Λ π 0. Έστω α και β δύο διανύσµατα µε α = 3, β = 1 και (α,β) = φ=. Να βρεθεί 6 η γωνία των διανυσµάτων u= α+ β και v = α β. u v Αν είναι θ η γωνία των u και v τότε συνθ = (1). Άρα αρκεί να υπολογίσουµε u v το εσωτερικό γινόµενο u v και τα µέτρα των u και v. Είναι: u v = (α+ β) (α β) = α β = α β = 3 1= (). Για να υπολογίσουµε τα µέτρα των u και v πρέπει πρώτα να βρούµε τα τετράγωνα των µέτρων αυτών. π u = u = (α+ β) = α + α β+ β = α + α β συνφ + β = συν + 1= 6 3 = = 7. Άρα u = 7 (3). Όµοια: v = v = (α β) =... = 1. Άρα v = 1 = 1 (4). (),(3) 7 (1) συνθ= = 0, 756οπότε η γωνία θ είναι περίπου 41. (4) Έστω α,β,w και v διανύσµατα µε α = β = 1, w = 3 α+ β, v = 7 α+ 8 β Λ και w v. Να βρεθεί η γωνία (α,β). Αφού w v είναι w v = 0 (3α+ β) ( 7α+ 8β) = 0 1α + 10α β+ 16β = 0 Λ Λ 1 α + 10 α β συν(α,β) + 16 β = συν(α,β) = 0 Λ Λ 1 Λ συν(α,β) + 16= 0 συν(α,β) = και αφού 0 (α,β) π έχουµε ότι Λ π. (α,β) = 3 Λ π. Αν α =, ν = 1 και (α,ν) = να εκφραστεί µε τη βοήθεια του α η προβολή του 3 ν πάνω στο α. Επειδή προβν//α θα υπάρχει λ R, ώστε προβν= λ α (1). Άρα θα ισχύει α Λ α ν= α προβ ν α ν= α λ α α ν= λ α α ν= λ α α ν συν(α,ν) = λ α α 1 συν π 3 =λ 1 =4λ λ=1 1. Άρα από (1) προβν= α α. 4 4 α
38 Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣ. 35 ΙΑΚΟΥΜΑΚΟΣ ΓΙΩΡΓΟΣ - Μαθηµατικός 3. ίνεται τετράπλευρο ΑΒΓ. Να βρεθεί ο γεωµετρικός τόπος των σηµείων Μ για τα οποία ισχύει MA+ M = ΜΒ+ ΜΓ. Έστω Κ µέσον της Α και Λ µέσον της ΒΓ. Τότε: MA+ M = ΜΚ και MΒ+ MΓ = ΜΛ. Έτσι η δοσµένη σχέση γίνεται: ΜΚ = ΜΛ ΜΚ = ΜΛ ΜΚ = ΜΛ. Άρα το Μ ισαπέχει από τα σταθερά σηµεία Κ και Λ οπότε ο γεωµετρικός του τόπος είναι η µεσοκάθετος ε του ΚΛ. Β Α Λ Κ Μ ε Γ 4. ίνεται τρίγωνο ΑΒΓ. Να βρεθεί ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου για τα οποία ισχύει ΑΜ= 3λ ΓΑ + (1+ 3λ) ΑΒ µε λ>0. Είναι: ΑΜ= 3λ ΓΑ + (1+ 3λ) ΑΒ ΑΜ= 3λ ΓΑ+ ΑΒ+ 3λ ΑΒ ΑΜ ΑΒ = 3λ (ΓΑ + ΑΒ) ΒΜ= 3λ ΓΒ. Άρα ΒΜ//ΓΒ και µάλιστα ΒΜ ΓΒ αφού 3λ>0. Άρα ο γεωµετρικός τόπος του Μ είναι η ηµιευθεία Β. 5. Έστω ορθοκανονικό σύστηµα αναφοράς Οy και σταθερό σηµείο Α του επιπέδου µε OA = 3. Να βρεθεί ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου για τα οποία είναι OM (OM OA) = 7. ΘΕΜΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ Προσπαθούµε να εµφανίσουµε στη δοσµένη σχέση το µέτρο του OA που είναι γνωστό καθώς και κάποιο άλλο διάνυσµα που να περιέχει ως άκρο το µεταβλητό σηµείο Μ. OM (OM OA) = 7 (OA+ AM) (OA+ AM OA) = 7 (OA+ AM) (AM OA) = 7 (AM) (OA) = 7 AM OA = 7 AM 3 = 7 AM = 16 AM = 4. Άρα το Μ απέχει από το σταθερό σηµείο Α σταθερή απόσταση 4, οπότε ανήκει στον κύκλο (Α,4). 6. ίνονται τρία σταθερά σηµεία Α, Β, Γ και δύο µεταβλητά σηµεία Μ και Κ. Αν ισχύει ότι ΜΚ = ΜΑ+ ΜΒ+ ΜΓ, δείξτε ότι η ΜΚ διέρχεται από σταθερό σηµείο. Αν είναι Λ το µέσον του ΑΒ τότε: ΜΑ+ ΜΒ = ΜΛ οπότε η δοσµένη σχέση γίνεται ισοδύναµα: ΜΚ = ΜΛ+ ΜΓ ΜΚ = (ΜΛ+ ΜΓ). Αν είναι Ρ το µέσον της του ΛΓ τότε ΜΛ+ ΜΓ = ΜΡ και η προηγούµενη σχέση γίνεται ισοδύναµα: A M B Γ
ΙΑΝΥΣΜΑΤΑ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. Τι ονοµάζουµε διάνυσµα; αλφάβητου επιγραµµισµένα µε βέλος. για παράδειγµα, Τι ονοµάζουµε µέτρο διανύσµατος;
 ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΙΝΥΣΜΤ ΘΕΩΡΙ ΘΕΜΤ ΘΕΩΡΙΣ Τι ονοµάζουµε διάνυσµα; AB A (αρχή) B (πέρας) Στη Γεωµετρία το διάνυσµα ορίζεται ως ένα προσανατολισµένο ευθύγραµµο τµήµα, δηλαδή ως ένα ευθύγραµµο τµήµα του οποίου τα άκρα θεωρούνται
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
 2 ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2015-2016 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΠΙΜΕΛΕΙΑ ΠΑΥΛΟΣ ΧΑΛΑΤΖΙΑΝ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΟ ΔΙΑΝΥΣΜΑΤΙΚΟ ΛΟΓΙΣΜΟ Διάνυσμα λέγεται ένα προσανατολισμένο ευθύγραμμο
2 ο ΓΕΛ ΣΤΑΥΡΟΥΠΟΛΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2015-2016 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΠΙΜΕΛΕΙΑ ΠΑΥΛΟΣ ΧΑΛΑΤΖΙΑΝ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΟ ΔΙΑΝΥΣΜΑΤΙΚΟ ΛΟΓΙΣΜΟ Διάνυσμα λέγεται ένα προσανατολισμένο ευθύγραμμο
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης
 Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
Μαθηματικά Προσανατολισμού Β Λυκείου Στάμου Γιάννης Αναλυτική θεωρία Λυμένα παραδείγματα Ερωτήσεις κατανόησης Ασκήσεις Επαναληπτικά διαγωνίσματα ΠΕΡΙΕΧΟΜΕΝΑ Κεφάλαιο ο : Διανύσματα Ενότητα I: Η έννοια
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ Διανύσματα-Ευθεία-Κύκλος Αναλυτική Θεωρία 500 Ασκήσεις Επιμέλεια : ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ ΝΙΚΟΣ Κ. ΡΑΠΤΗΣ Σελίδα 2 1. Η Έννοια του Διανύσματος Ορισμός Διανύσματος Το διάνυσμα ορίζεται ως
AB. Αν το διάνυσμα AB έχει μέτρο 1, τότε λέγεται
 ΔΙΑΝΥΣΜΑΤΑ Στη Γεωμετρία το διάνυσμα ορίζεται ως ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ως ένα ευθύγραμμο τμήμα του οποίου τα άκρα θεωρούνται διατεταγμένα Αν η αρχή και το πέρας ενός διανύσματος
ΔΙΑΝΥΣΜΑΤΑ Στη Γεωμετρία το διάνυσμα ορίζεται ως ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ως ένα ευθύγραμμο τμήμα του οποίου τα άκρα θεωρούνται διατεταγμένα Αν η αρχή και το πέρας ενός διανύσματος
Μαθηματικά προσανατολισμού Β Λυκείου
 Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
Μαθηματικά προσανατολισμού Β Λυκείου Συντεταγμένες Διανύσματος wwwaskisopolisgr wwwaskisopolisgr Συντεταγμένες στο επίπεδο Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι το διάνυσμα i OI
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
1.1 Η Έννοια του Διανύσματος
 ΙΝΥΣΜΤΙΚΟΟΙΣΜΟΣ 11 Η Έννοια του ιανύσματος ΜΘΗΣΙΚΟΙ ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να κατανοήσει τις έννοιες : διάνυσµα, µηδενικό διάνυσµα, φορέας-διεύθυνση, κατεύθυνση - φορά, µέτρο διανύσµατος, ϖαραλληλία
ΙΝΥΣΜΤΙΚΟΟΙΣΜΟΣ 11 Η Έννοια του ιανύσματος ΜΘΗΣΙΚΟΙ ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να κατανοήσει τις έννοιες : διάνυσµα, µηδενικό διάνυσµα, φορέας-διεύθυνση, κατεύθυνση - φορά, µέτρο διανύσµατος, ϖαραλληλία
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
34 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Άξονας Πάνω σε μια ευθεία επιλέγουμε δύο σημεία Ο και Ι, έτσι ώστε το διάνυσμα OI να έχει μέτρο και να βρίσκεται στην ημιευθεία O Λέμε τότε ότι έχουμε έναν άξονα με αρχή
ΕΝΝΟΙΑ ΤΟΥ ΙΑΝΥΣΜΑΤΟΣ
 ΕΝΝΟΙ ΤΟΥ ΙΝΥΣΜΤΟΣ Όπως είναι γνωστό από τη φυσική, τα διάφορα µεγέθη διακρίνονται σε βαθµωτά και διανυσµατικά. αθµωτά είναι τα µεγέθη τα οποία χαρακτηρίζονται µόνο από το µέτρο τους. Τέτοια µεγέθη είναι
ΕΝΝΟΙ ΤΟΥ ΙΝΥΣΜΤΟΣ Όπως είναι γνωστό από τη φυσική, τα διάφορα µεγέθη διακρίνονται σε βαθµωτά και διανυσµατικά. αθµωτά είναι τα µεγέθη τα οποία χαρακτηρίζονται µόνο από το µέτρο τους. Τέτοια µεγέθη είναι
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Αγαπητοί μαθητές, Κάθε κεφάλαιο περιέχει :
 Αγαπητοί μαθητές, αυτό το βιβλίο αποτελεί ένα σημαντικό βοήθημα για τα Μαθηματικά Θετικού Προσανατολισμού της Β Λυκείου, που είναι ένα από τα σημαντικότερα μαθήματα, καθώς περιέχει χρήσιμες γνώσεις για
Αγαπητοί μαθητές, αυτό το βιβλίο αποτελεί ένα σημαντικό βοήθημα για τα Μαθηματικά Θετικού Προσανατολισμού της Β Λυκείου, που είναι ένα από τα σημαντικότερα μαθήματα, καθώς περιέχει χρήσιμες γνώσεις για
Παρουσίαση 1 ΙΑΝΥΣΜΑΤΑ
 Παρουσίαση ΙΑΝΥΣΜΑΤΑ Παρουσίαση η Κάθετες συνιστώσες διανύσµατος Παράδειγµα Θα αναλύσουµε το διάνυσµα v (, ) σε δύο κάθετες µεταξύ τους συνιστώσες από τις οποίες η µία να είναι παράλληλη στο α (3,) Πραγµατικά
Παρουσίαση ΙΑΝΥΣΜΑΤΑ Παρουσίαση η Κάθετες συνιστώσες διανύσµατος Παράδειγµα Θα αναλύσουµε το διάνυσµα v (, ) σε δύο κάθετες µεταξύ τους συνιστώσες από τις οποίες η µία να είναι παράλληλη στο α (3,) Πραγµατικά
1 Ο ΚΕΦΑΛΑΙΟ Ενότητα 1.
 1 Ο ΚΕΦΑΛΑΙΟ Ενότητα 1. Διανύσματα Ισότητα διανυσμάτων Πρόσθεση διανυσμάτων Ερωτήσεις 1. Τ ι ονομάζουμε διάνυσμα;. Τι λέμε μέτρο ενός διανύσματος ;. Τι λέμε μηδενικό διάνυσμα; 4. Τι λέμε φορέα διανύσματος;
1 Ο ΚΕΦΑΛΑΙΟ Ενότητα 1. Διανύσματα Ισότητα διανυσμάτων Πρόσθεση διανυσμάτων Ερωτήσεις 1. Τ ι ονομάζουμε διάνυσμα;. Τι λέμε μέτρο ενός διανύσματος ;. Τι λέμε μηδενικό διάνυσμα; 4. Τι λέμε φορέα διανύσματος;
ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. 1 ο ΚΕΦΑΛΑΙΟ
 Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
Ο ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΟΡΕΣΤΙΑΔΑΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ο ΚΕΦΑΛΑΙΟ Διάνυσμα ορίζεται ένα ευθύγραμμο τμήμα στο οποίο έχει ορισθεί ποια είναι η αρχή, ή σημείο εφαρμογής του
ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ 1 Θέµα: Τα διανύσµατα ❶ ❷ ❸ ❹ ❺ Η έννοια του διανύσµατος Πρόσθεση και αφαίρεση διανυσµάτων Πολλαπλασιασµός αριθµού µε διάνυσµα Συντεταγµένες
ΦΥΛΛΑ ΙΑ ΣΗΜΕΙΩΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ 1 Θέµα: Τα διανύσµατα ❶ ❷ ❸ ❹ ❺ Η έννοια του διανύσµατος Πρόσθεση και αφαίρεση διανυσµάτων Πολλαπλασιασµός αριθµού µε διάνυσµα Συντεταγµένες
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ. Επιμέλεια Αυγερινός Βασίλης
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Επιμέλεια Αυγερινός Βασίλης ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ο ΔΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΕ ΑΠΑΝΤΗΣΕΙΣ, ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ ΣΕΛΙΔΕΣ 3-36 ΜΕΡΟΣ ο ΕΥΘΕΙΕΣ ΕΡΩΤΗΣΕΙΣ
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ Επιμέλεια Αυγερινός Βασίλης ΠΕΡΙΕΧΟΜΕΝΑ ΜΕΡΟΣ ο ΔΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΕ ΑΠΑΝΤΗΣΕΙΣ, ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ ΣΕΛΙΔΕΣ 3-36 ΜΕΡΟΣ ο ΕΥΘΕΙΕΣ ΕΡΩΤΗΣΕΙΣ
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
1.2 Συντεταγμένες στο Επίπεδο
 1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
1 Συντεταγμένες στο Επίπεδο Τι εννοούμε με την έννοια άξονας; ΑΠΑΝΤΗΣΗ Πάνω σε μια ευθεία επιλέγουμε δύο σημεία και Ι έτσι ώστε το διάνυσμα OI να έχει μέτρο 1 και να βρίσκεται στην ημιευθεία O Λέμε τότε
5 Γενική µορφή εξίσωσης ευθείας
 5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
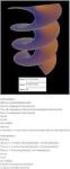
Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση: Να δίνει τον ορισμό του διανύσματος και των εννοιών που είναι κλειδιά όπως: κατεύθυνση φορά ή διεύθυνση, μηδενικό διάνυσμα,
Ο μαθητής που έχει μελετήσει το κεφάλαιο των διανυσμάτων θα πρέπει να είναι σε θέση: Να δίνει τον ορισμό του διανύσματος και των εννοιών που είναι κλειδιά όπως: κατεύθυνση φορά ή διεύθυνση, μηδενικό διάνυσμα,
ΘΕΜΑ ίνονται τα διανύσµαταα, β. α) Να υπολογίσετε τη γωνία. β) Να αποδείξετε ότι 2α+β= β) το συνηµίτονο της γωνίας των διανυσµάτων
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ! ΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣΜΑ ΘΕΜΑ 005 Θεωρούµε τα σηµεία Ρ, Λ, Κ και Μ του επιπέδου για τα οποία ισχύει η σχέση 5ΡΛ
ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ
 ΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ. Να σηµειώσετε το σωστό (Σ) ή το λάθος (Λ) στους παρακάτω ισχυρισµούς:. Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σηµεία Α, Β, Γ είναι συνευθειακά.. Αν α = β, τότε
ΙΑΝΥΣΜΑΤΑ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ ΕΡΩΤΗΣΕΙΣ ΑΞΙΟΛΟΓΗΣΗΣ. Να σηµειώσετε το σωστό (Σ) ή το λάθος (Λ) στους παρακάτω ισχυρισµούς:. Αν ΑΒ + ΒΓ = ΑΓ, τότε τα σηµεία Α, Β, Γ είναι συνευθειακά.. Αν α = β, τότε
Μαθηματικά. Β'Λυκείου. Προσανατολισµού Θετικών Σπουδών. Μαρίνος Παπαδόπουλος
 Μαθηματικά 'Λυκείου Προσανατολισµού Θετικών Σπουδών Μαρίνος Παπαδόπουλος ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΟΣ 5 Σελ. ΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΙΣΜΟΣ Ενότητα 1 Η έννοια του διανύσµατος 7 Πράξεις διανυσµάτων 11 Ενότητα 2 Πολλαπλασιασµός
Μαθηματικά 'Λυκείου Προσανατολισµού Θετικών Σπουδών Μαρίνος Παπαδόπουλος ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΟΣ 5 Σελ. ΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΙΣΜΟΣ Ενότητα 1 Η έννοια του διανύσµατος 7 Πράξεις διανυσµάτων 11 Ενότητα 2 Πολλαπλασιασµός
ΙΑΝΥΣΜΑΤΑ. Σ Λ + α = α
 Κεφάλαιο 3ο: ΙΑΝΥΜΑΤΑ Ερωτήσεις του τύπου «ωστό-άθος» 1. * Αν α =, τότε α =. 2. * Αν α, µη µηδενικά διανύσµατα και θ η γωνία τους, τότε 0 θ π 3. * Ισχύει α + 0 = 0 + α = α 4. * Κάθε διάνυσµα µπορεί να
Κεφάλαιο 3ο: ΙΑΝΥΜΑΤΑ Ερωτήσεις του τύπου «ωστό-άθος» 1. * Αν α =, τότε α =. 2. * Αν α, µη µηδενικά διανύσµατα και θ η γωνία τους, τότε 0 θ π 3. * Ισχύει α + 0 = 0 + α = α 4. * Κάθε διάνυσµα µπορεί να
ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Λέγεται κάθε προσανατολισμένη ευθεία x x στην οποία ορίζουμε ως αρχή ένα σημείο. Ο και το μοναδιαίο διάνυσμα i ( i = 1)
 α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
α.. Άξονας Λέγεται κάθε προσανατολισμένη ευθεία στην οποία ορίζουμε ως αρχή ένα σημείο Ο και το μοναδιαίο διάνυσμα i ( i 1). Ο i I Οι ημιευθείες Ο και O λέγονται αντίστοιχα θετικός ημιάξονας και αρνητικός
ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ
 Μαθηματικά Κατεύθυνσης Β Λυκείου-Απ Παπανικολάου ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων και και το συμβολίζουμε με α β τον πραγματικό αριθμό αβ
Μαθηματικά Κατεύθυνσης Β Λυκείου-Απ Παπανικολάου ÅÓÙÔÅÑÉÊÏ ÃÉÍÏÌÅÍÏ ÄÉÁÍÕÓÌÁÔÙÍ ΟΡΙΣΜΟΣ Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων και και το συμβολίζουμε με α β τον πραγματικό αριθμό αβ
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ - ΤΕΧΝ/ΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ - ΤΕΧΝ/ΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Περιέχει: Όλη την ύλη της Β Λυκείου, σύµφωνα µε το αναλυτικό πρόγραµµα του Υπουργείου Παιδείας σε (3) ΒΙΒΛΙΟµαθήµατα που το καθένα περιέχει: Α. Απαραίτητες
ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ - ΤΕΧΝ/ΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Περιέχει: Όλη την ύλη της Β Λυκείου, σύµφωνα µε το αναλυτικό πρόγραµµα του Υπουργείου Παιδείας σε (3) ΒΙΒΛΙΟµαθήµατα που το καθένα περιέχει: Α. Απαραίτητες
ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΙΑΝΥΣΜΑΤΟΣ
 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΙΑΝΥΣΜΑΤΟΣ Άξονας Έστω η ευθεία x x (σχ. 21) και τα σηµεία Ο, Ι πάνω σ αυτή, ώστε ΟΙ= i όπου i το µοναδιαίο διάνυσµα, δηλαδή ένα διάνυσµα που θεωρούµε ότι η φορά του είναι θετική και το µέτρο
ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΙΑΝΥΣΜΑΤΟΣ Άξονας Έστω η ευθεία x x (σχ. 21) και τα σηµεία Ο, Ι πάνω σ αυτή, ώστε ΟΙ= i όπου i το µοναδιαίο διάνυσµα, δηλαδή ένα διάνυσµα που θεωρούµε ότι η φορά του είναι θετική και το µέτρο
Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 1ο κεφάλαιο: Διανύσματα Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος
1ο κεφάλαιο: Διανύσματα Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος
Επαναληπτικά συνδυαστικα θέµατα
 Επαναληπτικά συνδυαστικα θέµατα Θέµα ο A. Αν α, β µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: i. αβ και ii. Αν α β τότε ισχύει α + β =. 4 4 B. Να βρεθούν οι τιµές του λ ώστε η
Επαναληπτικά συνδυαστικα θέµατα Θέµα ο A. Αν α, β µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: i. αβ και ii. Αν α β τότε ισχύει α + β =. 4 4 B. Να βρεθούν οι τιµές του λ ώστε η
1. ** ίνεται τρίγωνο ΑΒΓ. Αν Μ και Ν είναι τα µέσα των πλευρών ΒΓ και ΓΑ να αποδείξετε ότι:
 Ερωτήσεις ανάπτυξης 1. ** ίνεται τρίγωνο ΑΒΓ. Αν Μ και Ν είναι τα µέσα των πλευρών ΒΓ και ΓΑ να αποδείξετε ότι: α) ΑΜ = 1 2 ( ΑΒ + ΑΓ ) β) ΜΝ = 1 2 ΒΑ 2. ** ίνονται τα διανύσµατα ΑΒ και Α Β. Αν Μ και Μ
Ερωτήσεις ανάπτυξης 1. ** ίνεται τρίγωνο ΑΒΓ. Αν Μ και Ν είναι τα µέσα των πλευρών ΒΓ και ΓΑ να αποδείξετε ότι: α) ΑΜ = 1 2 ( ΑΒ + ΑΓ ) β) ΜΝ = 1 2 ΒΑ 2. ** ίνονται τα διανύσµατα ΑΒ και Α Β. Αν Μ και Μ
Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ)
 3. Η ΠΑΡΑΒΟΛΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ). Εξίσωση παραβολής p, όπου
3. Η ΠΑΡΑΒΟΛΗ ΘΕΩΡΙΑ. Ορισµός Ονοµάζουµε παραβολή µε εστία σηµείο Ε και διευθετούσα ευθεία (δ) το γεωµετρικό τόπο των σηµείων του επιπέδου τα οποία ισαπέχουν από το Ε και τη (δ). Εξίσωση παραβολής p, όπου
= π 3 και a = 2, β =2 2. a, β
 1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1 of 68 Δίνονται τα διανύσματα a και β με a, β = π 3 και a =, β =. α) Να βρείτε το εσωτερικό γινόμενο a β. (Μονάδες 8) β) Αν τα διανύσματα a + β και κ a + β είναι κάθετα να βρείτε την τιμή του κ. γ) Να
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο
 . ΣΥΝΤΕΤΑΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο ΘΕΩΡΙΑ. Άξονας (Ο, i ) λέγεται κάθε ευθεία εφοδιασµένη µε αρχή Ο και µοναδιαίο διάνυσµα i.. Τετµηµένη σηµείου Μ που ανήκει σε άξονα (Ο, i ) λέγεται ο αριθµός, για τον οποίο ισχύει
. ΣΥΝΤΕΤΑΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕ Ο ΘΕΩΡΙΑ. Άξονας (Ο, i ) λέγεται κάθε ευθεία εφοδιασµένη µε αρχή Ο και µοναδιαίο διάνυσµα i.. Τετµηµένη σηµείου Μ που ανήκει σε άξονα (Ο, i ) λέγεται ο αριθµός, για τον οποίο ισχύει
Οµοιότητα Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Β. ΜΕΘΟ ΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ
 Οµοιότητα Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Όµοια λέγονται δύο πολύγωνα που έχουν τις πλευρές τους ανάλογες και τις αντίστοιχες γωνίες τους ίσες. Λόγος οµοιότητας δύο όµοιων πολυγώνων λέγεται ο λόγος δύο
Οµοιότητα Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Όµοια λέγονται δύο πολύγωνα που έχουν τις πλευρές τους ανάλογες και τις αντίστοιχες γωνίες τους ίσες. Λόγος οµοιότητας δύο όµοιων πολυγώνων λέγεται ο λόγος δύο
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά. Μαθηματικού
 117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
117 ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Μανώλη Ψαρρά Μαθηματικού Περιεχόμενα 1. Διανύσματα (47) ελ. - 9. Ευθεία (18) ελ. 10-1 3. Κύκλος (13).ελ. 13-15 4. Παραβολή (14) ελ. 16-18 5. Έλλειψη (18)..
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ. Επανάληψη Επιμέλεια Αυγερινός Βασίλης. Επιμέλεια : Αυγερινός Βασίλης
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Επανάληψη Επιμέλεια Αυγερινός Βασίλης ΚΕΦΑΛΑΙΟ ο ΔΙΑΝΥΣΜΑΤΑ SOS ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ Θέμα ο Να γράψετε και να αποδείξετε την σχέση της διανυσματικής ακτίνας του μέσου ενός τμήματος
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ Επανάληψη Επιμέλεια Αυγερινός Βασίλης ΚΕΦΑΛΑΙΟ ο ΔΙΑΝΥΣΜΑΤΑ SOS ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ Θέμα ο Να γράψετε και να αποδείξετε την σχέση της διανυσματικής ακτίνας του μέσου ενός τμήματος
Σημειώσεις Μαθηματικών 1
 Σημειώσεις Μαθηματικών 1 Διανύσματα Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Διανύσματα 3.1 Έννοια διανύσματος Ορισμός 1 Ονομάζουμε Διάνυσμα ΑΒ ένα προσανατολισμένο ευθύγραμμο τμήμα ΑΒ με αρχή το Α και πέρας
Σημειώσεις Μαθηματικών 1 Διανύσματα Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Διανύσματα 3.1 Έννοια διανύσματος Ορισμός 1 Ονομάζουμε Διάνυσμα ΑΒ ένα προσανατολισμένο ευθύγραμμο τμήμα ΑΒ με αρχή το Α και πέρας
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H
 Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
Εισαγωγή 1. Εξωτερικά του παραλληλογράμμου ΑΒΓΔ κατασκευάζουμε τα τετράγωνα ΑΒΕΖ και ΔΓΘΗ. Να αποδείξετε ότι : α. ZH E, H, Z,. Τα τμήματα ΑΓ και ΗΕ έχουν κοινό μέσο γ. Το κέντρο του παραλληλογράμμου είναι
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου. 4 ο ΘΕΜΑ. Εκφωνήσεις Λύσεις των θεμάτων. Έκδοση 1 η (19/11/2014)
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου 4 ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (9//4) Θέματα 4 ης Ομάδας Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP_4_866 [παράγραφος
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου 4 ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (9//4) Θέματα 4 ης Ομάδας Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP_4_866 [παράγραφος
Μαθηματικά προσανατολισμού Β Λυκείου. ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ α φάση. Διανύσματα
 Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
Μαθηματικά προσανατολισμού Β Λυκείου wwwaskisopolisgr ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΟΕΦΕ 00-018α φάση Διανύσματα 1 Σε σύστημα συντεταγμένων Oxy θεωρούμε τρία σημεία Α, Β, Γ του μοναδιαίου κύκλου, για τα οποία υπάρχει
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ 3 Ο : ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΠΑΡΑΔΕΙΓΜΑΤΑ η Κατηγορία : Ο Κύκλος και τα στοιχεία
ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
Ασκήσεις στην ευθεία. 2. Θεωρούµε την γραµµή µε εξίσωση x 2 +y 2-2x+y-5=0. Βρείτε τα σηµεία της καµπύλης, αν υπάρχουν, µε τετµηµένη -1.
 Ασκήσεις στην ευθεία 1. Να βρείτε τα σηµεία τοµής των γραµµών µε εξισώσεις : α) 7x-11y+1=0, x+y-=0 β) y-3x-=0, x +y =4 γ) x +y =α, 3x+y+α=0. Θεωρούµε την γραµµή µε εξίσωση x +y -x+y-5=0. Βρείτε τα σηµεία
Ασκήσεις στην ευθεία 1. Να βρείτε τα σηµεία τοµής των γραµµών µε εξισώσεις : α) 7x-11y+1=0, x+y-=0 β) y-3x-=0, x +y =4 γ) x +y =α, 3x+y+α=0. Θεωρούµε την γραµµή µε εξίσωση x +y -x+y-5=0. Βρείτε τα σηµεία
Μαθηµατικά Κατεύθυνσης Β Λυκείου Ευθεία. Ασκήσεις Ευθεία
 Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
Ασκήσεις Ευθεία 1. Να βρεθεί η εξίσωση της ευθείας η οποία διέρχεται από το σηµείο τοµής των ευθειών 3x + 4y 11 = 0 και 2x 3y + 21 = 0 και να γίνει η γραφική της παράσταση όταν είναι: i) παράλληλη στην
1 η δεκάδα θεµάτων επανάληψης
 1 1 η δεκάδα θεµάτων επανάληψης 1. Α. Έστω α = (x 1, y 1 ) και β = (x, y ) δύο διανύσµατα Να γράψετε την αναλυτική έκφραση του εσωτερικού γινοµένου τους i Αν τα διανύσµατα δεν είναι παράλληλα προς τον
1 1 η δεκάδα θεµάτων επανάληψης 1. Α. Έστω α = (x 1, y 1 ) και β = (x, y ) δύο διανύσµατα Να γράψετε την αναλυτική έκφραση του εσωτερικού γινοµένου τους i Αν τα διανύσµατα δεν είναι παράλληλα προς τον
ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ. ΘΕΜΑ 2ο
 Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
Β ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΝΥΣΜΑΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΘΕΜΑ ο ΘΕΜΑ 8603 Δίνεται τρίγωνο και σημεία και του επιπέδου τέτοια, ώστε 5 και 5. α) Να γράψετε το διάνυσμα ως γραμμικό
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ. Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου. 2 ο ΘΕΜΑ. Εκφωνήσεις Λύσεις των θεμάτων. Έκδοση 1 η (18/11/2014)
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (8//04) Θέματα ης Ομάδας ο ΘΕΜΑ Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP 8556
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Μαθηματικά Προσανατολισμού Β Γενικού Ημερησίου Λυκείου ο ΘΕΜΑ Εκφωνήσεις Λύσεις των θεμάτων Έκδοση η (8//04) Θέματα ης Ομάδας ο ΘΕΜΑ Μαθηματικά Προσανατολισμού Β Λυκείου GI_V_MATHP 8556
Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων
 Αρσάκεια Τοσίτσεια Σχολεία Μαθηματικά Κατεύθυνσης Β Λυκείου Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων ) α β α β α//β ) α β α β α β ) α β α β α β 4)
Αρσάκεια Τοσίτσεια Σχολεία Μαθηματικά Κατεύθυνσης Β Λυκείου Να χαρακτηρίσετε κάθε μία από τις παρακάτω προτάσεις ως Σωστή ή Λανθασμένη: Πράξεις διανυσμάτων ) α β α β α//β ) α β α β α β ) α β α β α β 4)
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Ποιες είναι οι ιδιότητες της πρόσθεσης των φυσικών; Το άθροισμα ενός φυσικού αριθμού με το 0 ισούται με τον ίδιο αριθμό. α+0=α Αντιμεταθετική ιδιότητα. Με βάση την οποία
3 ΚΩΝΙΚΕΣ ΤΟΜΕΣ ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Νρεθεί η εξίσωση του κύκλου σε καθεμιά από τις παρακάτω περιπτώσεις: α) έχει κέντρο την αρχή των αξόνων και ακτίνα β) έχει κέντρο το σημείο (3, - ) και ακτίνα 5 γ) έχει κέντρο το σημείο
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ. Νρεθεί η εξίσωση του κύκλου σε καθεμιά από τις παρακάτω περιπτώσεις: α) έχει κέντρο την αρχή των αξόνων και ακτίνα β) έχει κέντρο το σημείο (3, - ) και ακτίνα 5 γ) έχει κέντρο το σημείο
Επαναληπτικά συνδυαστικα θέµατα
 Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
Επαναληπτικά συνδυαστικα θέµατα A. Αν α, β i. αβ Θέµα ο µη µηδενικά διανύσµατα και ισχύει α+ β + α β =, τότε να δείξετε ότι: και ii. Αν α β τότε ισχύει α + β =. B. Να βρεθούν οι τιµές του λ ώστε η εξίσωση
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ - ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1. Δίνεται παραλληλόγραμμο ΑΒΓΔ με τρεις κορυφές τα σημεία Α (1,1), Γ (4,3) και Δ (,3). α) Να υπολογίσετε τα μήκη
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΗΣ Β ΛΥΚΕΙΟΥ Διανύσματα Πολλαπλασιασμός αριθμού με διάνυσμα ο Θέμα _8603 Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε 5 και
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Πρόλογος... 7 Περιεχόµενα... 9 Κεφάλαιο ο (του σχολικού βιβλίου) Μάθηµα 1 ο : Βασικά γεωµετρικά σχήµατα... 11 Μάθηµα ο : Γωνίες - κύκλος... 3 Κεφάλαιο 3 ο Μάθηµα 3
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Πρόλογος... 7 Περιεχόµενα... 9 Κεφάλαιο ο (του σχολικού βιβλίου) Μάθηµα 1 ο : Βασικά γεωµετρικά σχήµατα... 11 Μάθηµα ο : Γωνίες - κύκλος... 3 Κεφάλαιο 3 ο Μάθηµα 3
) = Απόσταση σημείου από ευθεία. Υπολογισμός Εμβαδού Τριγώνου. και A
 [Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
[Επιλογή Ιαν.. Εμβαδόν Τριγώνου ΣΤΟΧΟΙ: Ο µαθητής ϖρέϖει: να είναι ικανός να υϖολογίζει την αϖόσταση σηµείου αϖό ευθεία να είναι ικανός να υϖολογίζει το εµβαδό ενός τριγώνου αϖό τις συντεταγµένες των κορυφών
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβίου Μαθηµατικών Προσαναταισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός ποαπασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβίου
Παραουσίαση βιβίου Μαθηµατικών Προσαναταισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός ποαπασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβίου
1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: ii. Το ύψος ΒΚ
 Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
Ερωτήσεις ανάπτυξης 1. ** Σε ισοσκελές τρίγωνο ΑΒΓ µε κορυφή το Α, έχουµε ΒΓ = 4 cm και ΑΒ = 7 cm. Να υπολογίσετε: i. Το ύψος ΑΗ ii. Το ύψος ΒΚ. ** Σε ένα τετράγωνο ΑΒΓ ισχύει ΑΒ + ΑΓ = +. Να υπολογίσετε:
1.3 Εσωτερικό Γινόμενο
 1 Εσωτερικό Γινόμενο 1 Αν α = ( 1, ) i α β iii και β = ( 1, ), να υπολογίσετε τα εσωτερικά γινόμενα: ii ( α )( β ) α β α + β α iv Αν α =, β = 1 και ( αβ, ) = 15 ο, να υπολογίσετε το α β Με βάση το διπλανό
1 Εσωτερικό Γινόμενο 1 Αν α = ( 1, ) i α β iii και β = ( 1, ), να υπολογίσετε τα εσωτερικά γινόμενα: ii ( α )( β ) α β α + β α iv Αν α =, β = 1 και ( αβ, ) = 15 ο, να υπολογίσετε το α β Με βάση το διπλανό
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 3ο Παραλληλόγραµµα - Τραπέζια
 ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 3ο Παραλληλόγραµµα - Τραπέζια 184 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Να αντιστοιχίσετε κάθε στοιχείο της στήλης (Α) µε ένα µόνο στοιχείο της στήλης (Β): στήλη (Α) τετράπλευρα
ΓΕΩΜΕΤΡΙΑ - ΚΕΦΑΛΑΙΟ 3ο Παραλληλόγραµµα - Τραπέζια 184 ΕΡΩΤΗΣΕΙΣ ΑΝΑΠΤΥΞΗΣ ΚΑΙ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ 1. Να αντιστοιχίσετε κάθε στοιχείο της στήλης (Α) µε ένα µόνο στοιχείο της στήλης (Β): στήλη (Α) τετράπλευρα
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΒΑΣΙΚΟΙ ΤΥΠΟΙ ΑΠΟ ΤΗΝ ΘΕΩΡΙΑ ΔΙΑΝΥΣΜΑΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΔΙΑΝΥΣΜΑΤΟΣ Αρχή και Πέρας Φορέας Διεύθυνση (Συγγραμμικά διανύσματα) Μέτρο Κατεύθυνση (Ομόρροπα Αντίρροπα διανύσματα)
Β Λυκείου- Μαθηματικά Κατεύθυνσης. Μέρος Α Θεωρία. (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις)
 1 Μέρος Α Θεωρία (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις) Η έννοια του διανύσματος Ορισμός του Διανύσματος Διάνυσμα ονομάζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα του
1 Μέρος Α Θεωρία (Ορισμοί, θεωρήματα, αποδείξεις, παρατηρήσεις) Η έννοια του διανύσματος Ορισμός του Διανύσματος Διάνυσμα ονομάζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα του
1.3 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ
 . ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣ ΘΕΩΡΙΑ. Ορισµός Γινόµενο πραγµατικού αριθµού λ µε διάνυσµα α 0 λέγεται νέο διάνυσµα λα, που έχει µέτρο λα = λ α και είναι οµόρροπο του α όταν λ > 0 αντίρροπο του α όταν
. ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΙΑΝΥΣ ΘΕΩΡΙΑ. Ορισµός Γινόµενο πραγµατικού αριθµού λ µε διάνυσµα α 0 λέγεται νέο διάνυσµα λα, που έχει µέτρο λα = λ α και είναι οµόρροπο του α όταν λ > 0 αντίρροπο του α όταν
1 ΔΙΑΝΥΣΜΑΤΑ. Εισαγωγή
 1 ΙΝΥΣΜΤ Εισαγωγή Το διάνυσμα είναι ένα χαρακτηριστικό παράδειγμα έννοιας που αναπτύχθηκε μέσα από τη στενή αλληλεπίδραση Μαθηματικών και Φυσικής. κανόνας του παραλληλόγραμμου, σύμφωνα με τον οποίο το
1 ΙΝΥΣΜΤ Εισαγωγή Το διάνυσμα είναι ένα χαρακτηριστικό παράδειγμα έννοιας που αναπτύχθηκε μέσα από τη στενή αλληλεπίδραση Μαθηματικών και Φυσικής. κανόνας του παραλληλόγραμμου, σύμφωνα με τον οποίο το
9o Γεν. Λύκειο Περιστερίου ( 3.1) ΚΥΚΛΟΣ. ΚΕΦΑΛΑΙΟ 3 ο : KΩΝΙΚΕΣ ΤΟΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙ 3 ο : KΩΝΙΚΕΣ ΤΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΥ ( 3.) ΚΥΚΛΣ Γνωρίζουµε ότι ένας κύκλος (, ρ) είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου τα οποία απέχουν µια ορισµένη απόσταση ρ από ένα
ΚΕΦΑΛΑΙ 3 ο : KΩΝΙΚΕΣ ΤΜΕΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΝΣΗΣ Β ΛΥΚΕΙΥ ( 3.) ΚΥΚΛΣ Γνωρίζουµε ότι ένας κύκλος (, ρ) είναι ο γεωµετρικός τόπος των σηµείων του επιπέδου τα οποία απέχουν µια ορισµένη απόσταση ρ από ένα
4 η δεκάδα θεµάτων επανάληψης
 1 4 η δεκάδα θεµάτων επανάληψης 1. Έστω τα διανύσµατα u = ( 6, 8) και v = (9, 1) είξτε ότι είναι αντίρροπα Να βρείτε την εξίσωση της έλλειψης που έχει ηµιάξονες τα µέτρα των διανυσµάτων, κέντρο την αρχή
1 4 η δεκάδα θεµάτων επανάληψης 1. Έστω τα διανύσµατα u = ( 6, 8) και v = (9, 1) είξτε ότι είναι αντίρροπα Να βρείτε την εξίσωση της έλλειψης που έχει ηµιάξονες τα µέτρα των διανυσµάτων, κέντρο την αρχή
και ω η γωνία που σχηµατίζει το διάνυσµα OA (1) x = ρσυν(ω+ θ) = ρσυνωσυνθ ρηµωηµθ και και
 ΣΤΡΟΦΗ ΙΝΥΣΜΤΟΣ Νίκος Ιωσηφίδης, Μαθηµατικός Φροντιστής, έροια e-mail: iossifid@yahoo.gr Στο άρθρο που ακολουθεί, όλα τα αναφερόµενα σηµεία θα θεωρούµε ότι βρίσκονται στο ίδιο επίπεδο. Ορισµοί: 1) Ονοµάζουµε
ΣΤΡΟΦΗ ΙΝΥΣΜΤΟΣ Νίκος Ιωσηφίδης, Μαθηµατικός Φροντιστής, έροια e-mail: iossifid@yahoo.gr Στο άρθρο που ακολουθεί, όλα τα αναφερόµενα σηµεία θα θεωρούµε ότι βρίσκονται στο ίδιο επίπεδο. Ορισµοί: 1) Ονοµάζουµε
1.4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ 4 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Κάθε διάνυσμα του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή : i j όπου i, j μοναδιαία διανύσματα με κοινή αρχή το
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ 4 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ 4 ΣΥΝΤΕΤΑΓΜΕΝΕΣ ΣΤΟ ΕΠΙΠΕΔΟ Κάθε διάνυσμα του επιπέδου γράφεται κατά μοναδικό τρόπο στη μορφή : i j όπου i, j μοναδιαία διανύσματα με κοινή αρχή το
β = (9, x) να είναι ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ Αµυραδάκη 20, Νίκαια ( ) ΤΑΞΗ...Β ΛΥΚΕΙΟΥ... ΜΑΘΗΜΑ...ΜΑΘΗΜΑΤΙΚΑ ΚΑΤ/ΣΗΣ...
 Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
Αµυραδάκη 0, Νίκαια (104903576) ΝΟΕΜΒΡΙΟΣ 01 ΘΕΜΑ 1 ο i) Αν Α( x 1, y 1 ) και Β(x, y ) δυο σηµεία του καρτεσιανού επιπέδου και (x, y) οι συντεταγµένες του µέσου Μ του ΑΒ, να αποδείξετε ότι : x 1 + x x
Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ
 8 Παραβολή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισµός Παραβολή είναι ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου τα οποία ισαπέχουν από µια σταθερή ευθεία (δ) που λέγεται διευθετούσα της παραβολής και από
8 Παραβολή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισµός Παραβολή είναι ο γεωµετρικός τόπος των σηµείων Μ του επιπέδου τα οποία ισαπέχουν από µια σταθερή ευθεία (δ) που λέγεται διευθετούσα της παραβολής και από
1.5. Ασκήσεις σχολικού βιβλίου σελίδας A Oµάδας ( )
 .5 Ασκήσεις σχολικού ιλίου σελίδας 47 50 A Oµάδας. Αν α (, 3) και (, 5), τότε Να ρείτε τα εσωτερικά γινόµενα α, (α ).(-3 ) και (α ). (3α + ) Να ρείτε τη σχέση που συνδέει τους κ, λ R, ώστε το εσωτερικό
.5 Ασκήσεις σχολικού ιλίου σελίδας 47 50 A Oµάδας. Αν α (, 3) και (, 5), τότε Να ρείτε τα εσωτερικά γινόµενα α, (α ).(-3 ) και (α ). (3α + ) Να ρείτε τη σχέση που συνδέει τους κ, λ R, ώστε το εσωτερικό
3.1. Ασκήσεις σχολικού βιβλίου σελίδας A Οµάδας
 3. Ασκήσεις σχολικού βιβλίου σελίδας 87 89 Οµάδας. Να βρείτε την εξίσωση του κύκλου µε κέντρο την αρχή των αξόνων σε καθεµιά από τις παρακάτω περιπτώσεις : (i) Όταν διέρχεται από το σηµείο Α(, 3 ) (ii)
3. Ασκήσεις σχολικού βιβλίου σελίδας 87 89 Οµάδας. Να βρείτε την εξίσωση του κύκλου µε κέντρο την αρχή των αξόνων σε καθεµιά από τις παρακάτω περιπτώσεις : (i) Όταν διέρχεται από το σηµείο Α(, 3 ) (ii)
Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ. Ηµιεπίπεδο Κάθε ευθεία ε επιπέδου Π χωρίζει τα σηµεία του επιπέδου που δεν ανήκουν στην ε σε δύο σηµειοσύνολα Π 1
 2 Η γωνία - Ο κύκλος Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ηµιεπίπεδο Κάθε ευθεία ε επιπέδου Π χωρίζει τα σηµεία του επιπέδου που δεν ανήκουν στην ε σε δύο σηµειοσύνολα Π 1, Π 2 τα οποία ονοµάζονται ηµιεπίπεδα
2 Η γωνία - Ο κύκλος Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ηµιεπίπεδο Κάθε ευθεία ε επιπέδου Π χωρίζει τα σηµεία του επιπέδου που δεν ανήκουν στην ε σε δύο σηµειοσύνολα Π 1, Π 2 τα οποία ονοµάζονται ηµιεπίπεδα
1 ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ. α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β
 O A M B ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ Ο ΘΕΜΑ ον : α α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β. Μονάδες 5 β. Αν α, ν
O A M B ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Β ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΔΙΑΓΩΝΙΣΜΑ Ο ΘΕΜΑ ον : α α. Τι ονομάζουμε εσωτερικό γινόμενο δύο διανυσμάτων, β. Μονάδες 5 β. Αν α, ν
Ασκήσεις Πράξεις ιανυσµάτων
 Ασκήσεις Πράξεις ιανυσµάτων 1 ίνονται τα διανύσµατα α,, x, y για τα οποία ισχύουν: x+ y= α+ 4 και 4x y= α+ Nδο τα διανύσµατα x, y είναι οµόρροπα Αν ισχύει η ισότητα MA+ 5ΡΑ = 3ΡΜ+ ΡΒ 4ΓΜ νδο τα σηµεία
Ασκήσεις Πράξεις ιανυσµάτων 1 ίνονται τα διανύσµατα α,, x, y για τα οποία ισχύουν: x+ y= α+ 4 και 4x y= α+ Nδο τα διανύσµατα x, y είναι οµόρροπα Αν ισχύει η ισότητα MA+ 5ΡΑ = 3ΡΜ+ ΡΒ 4ΓΜ νδο τα σηµεία
Επιμέλεια: Σακαρίκος Ευάγγελος 108 Θέματα - 24/1/2015
 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Επιμέλεια: Σακαρίκος Ευάγγελος 08 Θέματα - 4//05 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσαν. Κεφάλαιο
Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Επιμέλεια: Σακαρίκος Ευάγγελος 08 Θέματα - 4//05 Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσανατολισμού Τράπεζα Θεμάτων Β Λυκείου Μαθηματικά Προσαν. Κεφάλαιο
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΠΡΟΛΟΓΟΣ Αγαπητοί συνάδελφοι, Φίλοι µαθητές και µαθήτριες Η καινούργια µας σειρά βιβλίων µε τον τίτλο ΒΙΒΛΙΟµαθήµατα δηµιουργήθηκε από µια ιδέα µας για το περιοδικό
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΠΡΟΛΟΓΟΣ Αγαπητοί συνάδελφοι, Φίλοι µαθητές και µαθήτριες Η καινούργια µας σειρά βιβλίων µε τον τίτλο ΒΙΒΛΙΟµαθήµατα δηµιουργήθηκε από µια ιδέα µας για το περιοδικό
1.3 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
Μαθηματικά Θετικής και Τεχνολογικής κατεύθυνσης Διανύσματα
 Μαθηματικά Θετικής και Τεχνολογικής κατεύθυνσης Διανύσματα Περιεχόμενα Η Εννοια του διανύσματος Ομόρροπα-Αντίρροπα Διανύσματα Ισα Αντίθετα διανύσματα Πρόσθεση και Αφαίρεση Διανυσμάτων Διάνυσμα θέσεως Συντεταγμένες
Μαθηματικά Θετικής και Τεχνολογικής κατεύθυνσης Διανύσματα Περιεχόμενα Η Εννοια του διανύσματος Ομόρροπα-Αντίρροπα Διανύσματα Ισα Αντίθετα διανύσματα Πρόσθεση και Αφαίρεση Διανυσμάτων Διάνυσμα θέσεως Συντεταγμένες
Διανύσματα. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Kατεύθυνση κεφάλαιο ασκήσεις. Kglykos.gr. εκδόσεις. Καλό πήξιμο. Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α
 Διανύσματα Κώστας Γλυκός Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7 0 0 8 8 8 8 Kglykosgr / 9 / 0 1 6 Kατεύθυνση κεφάλαιο 1 44 ασκήσεις και τεχνικές σε 1 σελίδες εκδόσεις Καλό πήξιμο Τα πάντα για τα διανύσματα
Διανύσματα Κώστας Γλυκός Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7 0 0 8 8 8 8 Kglykosgr / 9 / 0 1 6 Kατεύθυνση κεφάλαιο 1 44 ασκήσεις και τεχνικές σε 1 σελίδες εκδόσεις Καλό πήξιμο Τα πάντα για τα διανύσματα
Τράπεζα Θεμάτων Διαβαθμισμένης Δυσκολίας-Μαθηματικά Ομάδας Προσανατολισμού Θετικών Σπουδών ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Ι Κ Α ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Σχολικό έτος : 04-05 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων
Μ Α Θ Η Μ Α Τ Ι Κ Α ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Β Λ Υ Κ Ε Ι Ο Υ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΔΙΑΒΑΘΜΙΣΜΕΝΗΣ ΔΥΣΚΟΛΙΑΣ Σχολικό έτος : 04-05 Τα θέματα εμπλουτίζονται με την δημοσιοποίηση και των νέων θεμάτων
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΟΡΙΣΜΟΣ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ 1. Να υπολογιστεί το εσωτερικό γινόμενο a δύο διανυσμάτων a και αν: ι) a a 5, 7,(, ) 5, ιι) a 5,,( a, ). 6 6. Το διάνυσμα
ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΟΡΙΣΜΟΣ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ 1. Να υπολογιστεί το εσωτερικό γινόμενο a δύο διανυσμάτων a και αν: ι) a a 5, 7,(, ) 5, ιι) a 5,,( a, ). 6 6. Το διάνυσμα
Μονάδες 5,5 γ) Αν τα διανύσματα a, είναι μη μηδενικά και θ είναι η γωνία των a. λ 0. Για ποια από τις παρακάτω τιμές του λ τα διανύσματα a.
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΘΕΜΑ 1 ο (Πανελλήνιες θετικής κατεύθυνσης Β Λυκείου 1999) Α. Έστω a ( x1,) y1 και ( x,) y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. α) Να εκφράσετε (χωρίς απόδειξη) το
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΘΕΜΑ 1 ο (Πανελλήνιες θετικής κατεύθυνσης Β Λυκείου 1999) Α. Έστω a ( x1,) y1 και ( x,) y δύο διανύσματα του καρτεσιανού επιπέδου Οxy. α) Να εκφράσετε (χωρίς απόδειξη) το
v Α. Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων, β
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ o α Α Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων, β Μονάδες 4 Β Να αποδείξετε ότι το εσωτερικό γινόµενο
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ o α Α Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων, β Μονάδες 4 Β Να αποδείξετε ότι το εσωτερικό γινόµενο
Σχόλιο. Παρατηρήσεις. Παρατηρήσεις. p q p. , p1 p2
 A. ΠΡΟΤΑΣΕΙΣ Στα Μαθηµατικά χρησιµοποιούµε προτάσεις οι οποίες µπορούν να χαρακτηριστούν ως αληθείς (α) ή ψευδείς (ψ). Τις προτάσεις συµβολίζουµε µε τα τελευταία µικρά γράµµατα του Λατινικού αλφαβήτου:
A. ΠΡΟΤΑΣΕΙΣ Στα Μαθηµατικά χρησιµοποιούµε προτάσεις οι οποίες µπορούν να χαρακτηριστούν ως αληθείς (α) ή ψευδείς (ψ). Τις προτάσεις συµβολίζουµε µε τα τελευταία µικρά γράµµατα του Λατινικού αλφαβήτου:
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ o Α. Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων α, β. Μονάδες 4 Β. Να αποδείξετε ότι το εσωτερικό γινόµενο δύο διανυσµάτων
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ o Α. Τι ονοµάζουµε εσωτερικό γινόµενο δύο διανυσµάτων α, β. Μονάδες 4 Β. Να αποδείξετε ότι το εσωτερικό γινόµενο δύο διανυσµάτων
Ερωτήσεις ανάπτυξης 1. ** 2. ** 3. ** 4. ** 5. ** 6. **
 Ερωτήσεις ανάπτυξης 1. ** ίνονται επίπεδο p και τρία µη συνευθειακά σηµεία του Α, Β και Γ καθώς και ένα σηµείο Μ, που δεν συµπίπτει µε το Α. Αν η ευθεία ΑΜ τέµνει την ευθεία ΒΓ, να δείξετε ότι το Μ είναι
Ερωτήσεις ανάπτυξης 1. ** ίνονται επίπεδο p και τρία µη συνευθειακά σηµεία του Α, Β και Γ καθώς και ένα σηµείο Μ, που δεν συµπίπτει µε το Α. Αν η ευθεία ΑΜ τέµνει την ευθεία ΒΓ, να δείξετε ότι το Μ είναι
3 η δεκάδα θεµάτων επανάληψης
 η δεκάδα θεµάτων επανάληψης. Έστω η υπερβολή x y. Να βρείτε Tις ασύµπτωτες και την εκκεντρότητα της υπερβολής. i Tις εφαπτόµενες της υπερβολής που είναι παράλληλες στην ευθεία (ε) : x + y + 0 ii Tο εµβαδόν
η δεκάδα θεµάτων επανάληψης. Έστω η υπερβολή x y. Να βρείτε Tις ασύµπτωτες και την εκκεντρότητα της υπερβολής. i Tις εφαπτόµενες της υπερβολής που είναι παράλληλες στην ευθεία (ε) : x + y + 0 ii Tο εµβαδόν
Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ
 2ο κεφάλαιο: Ευθείες Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος Αποστόλου
2ο κεφάλαιο: Ευθείες Β ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΟΣΤΟΛΟΥ ΓΙΩΡΓΟΣ ΜΑΘΗΜΑΤΙΚΟΣ ) Μαθηµατικά Προσανατολισµού Β Λυκείου Αποστόλου Γιώργος Μαθηµατικός Copyright 2015 Αποστόλου Γιώργος Αποστόλου
 Κεφάλαιο 6 Παράλληλες Ευθείες και Τετράπλευρα Ορισμός. Δύο ευθείες ονομάζονται παράλληλες όταν ανήκουν στο ίδιο επίπεδο και δεν τέμνονται. Δύο παράλληλες ευθείες ε και ζ συμβολίζονται ε ζ. Γωνίες δύο ευθειών
Κεφάλαιο 6 Παράλληλες Ευθείες και Τετράπλευρα Ορισμός. Δύο ευθείες ονομάζονται παράλληλες όταν ανήκουν στο ίδιο επίπεδο και δεν τέμνονται. Δύο παράλληλες ευθείες ε και ζ συμβολίζονται ε ζ. Γωνίες δύο ευθειών
1.5 ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ.. ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Αν είναι δυο μη μηδενικά διανύσματα τότε ονομάζουμε εσωτερικό γινόμενο των και τον αριθμό : όπου φ είναι η γωνία των
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ.. ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Αν είναι δυο μη μηδενικά διανύσματα τότε ονομάζουμε εσωτερικό γινόμενο των και τον αριθμό : όπου φ είναι η γωνία των
ΜΑΘΗΜΑ 8. B 2.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία
 ΜΑΘΗΜΑ 8. B.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία Θεωρία Ασκήσεις γ. τόπου και µεγιστο ελάχιστου Στις ασκήσεις αυτού του µαθήµατος χρησιµοποιούµε ανισωτικές σχέσεις από την Ευκλείδεια Γεωµετρία. Θυµίζουµε
ΜΑΘΗΜΑ 8. B.3 Χρησιµοποιώντας Ευκλείδεια Γεωµετρία Θεωρία Ασκήσεις γ. τόπου και µεγιστο ελάχιστου Στις ασκήσεις αυτού του µαθήµατος χρησιµοποιούµε ανισωτικές σχέσεις από την Ευκλείδεια Γεωµετρία. Θυµίζουµε
ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ
 1.1.. ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΕΜΑ ΟΝ ΤΡΙΓΩΝΟΥ ΘΕΩΡΙΑ 1. Εξίσωση γραµµής C Μια εξίσωση µε δύο αγνώστους x, y λέγεται εξίσωση µιας γραµµής C, όταν οι συντεταγµένες των σηµείων της C, και µόνον αυτές, την επαληθεύουν..
1.1.. ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΚΑΙ ΕΜΑ ΟΝ ΤΡΙΓΩΝΟΥ ΘΕΩΡΙΑ 1. Εξίσωση γραµµής C Μια εξίσωση µε δύο αγνώστους x, y λέγεται εξίσωση µιας γραµµής C, όταν οι συντεταγµένες των σηµείων της C, και µόνον αυτές, την επαληθεύουν..
Β.1.8. Παραπληρωματικές και Συμπληρωματικές γωνίες Κατά κορυφήν γωνίες
 Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
