... λέγονται στοιχεία του πίνακα Α και οι δείκτες i και j δηλώνουν τη γραμμή και τη στήλη, αντίστοιχα, που ανήκει το στοιχείο α
|
|
|
- Ἐμμανουήλ Αποστόλου
- 10 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούε ε το ορισό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθώ ή άλλω στοιχείω Οι πίακες εφαίζοται στη θεωρία τω γραικώ συστηάτω, στη θεωρία τω γραικώ απεικοίσεω και σήερα πλέο χρησιοποιούται σε όλους τους κλάδους τω αθηατικώ Θα ορίσουε τις πράξεις εταξύ τω πιάκω και θα ελετήσουε τις ιδιότητές τους Οι πίακες που θα θεωρήσουε στη συέχεια έχου στοιχεία πραγατικούς ή ιγαδικούς αριθούς Ότα ααφερόαστε στο σώα Κ, εοούε ότι Κ= ή Κ= 2 Βασικοί ορισοί Ορισός 2 Μία ορθογώια παράταξη στοιχείω από το σώα Κ σε οριζότιες σειρές, που λέγοται γραές, και σε κατακόρυφες σειρές, που λέγοται στήλες, της ορφής α α2 α 2 22 α α α 2 α α2 α λέγεται πίακας τύπου Συήθως συβολίζεται ε έα από τα κεφαλαία γράατα ή ε το γεικό στοιχείο α σε παρέθεση, δηλαδή γράφουε Α= ( α ή ( α Α=, α ο τύπος του πίακα είαι γωστός Οι αριθοί α λέγοται στοιχεία του πίακα Α και οι δείκτες i και j δηλώου τη γραή και τη στήλη, ατίστοιχα, που αήκει το στοιχείο α Για παράδειγα, οι πίακες Α=, Β= είαι τύπου 2 3 και 2 2, ατίστοιχα, και έχουε
2 8 Κεφάλαιο 2 Πίακες α =, α2 = 2, α23 = 5, β 2 = 4, β 22 = 5, κλπ Ότα είαι =, τότε ο πίακας λέγεται τετραγωικός Έας πίακας τύπου (ατ, λέγεται πίακας-γραή (ατ, πίακας - στήλη Το σύολο όλω τω πιάκω τύπου ε στοιχεία από το σώα Κ συ- βολίζεται ε Μ ( Κ ή Μ τω τετραγωικώ πιάκω συβολίζεται ε (, α το σώα Κ θεωρείται γωστό Το σύολο Μ Μ Κ ή απλά Τα στοιχεία α, α22,, α ορίζου τη κύρια διαγώιο του τετραγωικού πίακα Α= ( α Ο τετραγωικός πίακας ( α Α= λέγεται τριγωικός άω, α όλα τα στοιχεία του που βρίσκοται κάτω από τη κύρια διαγώιο είαι 0, δηλαδή είαι α = 0, για i j Α= α λέγεται > Οοίως ο πίακας ( τριγωικός κάτω, α όλα τα στοιχεία του που βρίσκοται πάω από τη κύρια διαγώιο είαι 0, δηλαδή ισχύει ότι α = 0, για i < j Η σχέση της ισότητας στο σύολο ( ( β Β=, ορίζεται ως εξής: Μ Κ, α είαι ( α Α=Β α = β, για κάθε i =, 2,,, j =, 2,, Α= και 22 Πράξεις στο σύολο τω πιάκω Η πρόσθεση πιάκω Ορισός 2 2 Στο σύολο Μ τω πιάκω ε στοιχεία στο σώα Κ= ή η πρόσθεση είαι ία εσωτερική πράξη, που ορίζεται ως εξής: ( a b + : Μ Μ Μ,( Α, Β Α+Β : = +, όπου Α= ( a και Β= ( b Ο πίακας Α +Β λέγεται άθροισα τω πιάκω Α, Β και κάθε του στοιχείο προκύπτει ως άθροισα τω ατίστοιχω στοιχείω τω πιάκω Α και Β Για παράδειγα, α είαι 0 2 Α= 3 3, Β= , τότε Α+Β=
3 22 Οι πράξεις στο σύολο τω πιάκω 9 Θεώρηα 22 Η πράξη της πρόσθεσης ικαοποιεί τις ακόλουθες ιδιότητες: (i Α+Β=Β+Α, για κάθε ΑΒ Μ, (ατιεταθετική ιδιότητα (ii ( Α+Β +Γ=Α+ ( Β+Γ, για κάθε ΑΒΓ Μ,, (προσεταιριστική ιδιότητα (iii Υπάρχει το ουδέτερο στοιχείο για τη πρόσθεση και είαι ο ηδεικός πίακας Ο= (0, που όλα τα στοιχεία του είαι 0 Ισχύει ότι (iv Για κάθε πίακα ( a Α +Ο=Ο+Α=Α, για κάθε Α Μ Α= υπάρχει ο ατίθετος πίακας Α = ( a που είαι τέτοιος ώστε Α+ ( Α = ( Α +Α=Ο Έτσι, το σύολο Απόδειξη Μ γίεται αβελιαή προσθετική οάδα Α= Β=, (i Σύφωα ε το ορισό της πρόσθεσης, α είαι ( a, ( b έχουε Α+Β= ( a + b = ( b a + =Β+Α (ii Α Α= ( a, Β= ( b και Γ= ( c είαι ( a b c ( a b c (iii Α Α= ( a τότε: Ο+Α=Α+Ο= ( a + 0 = ( a =Α (iv Α Α= ( a τότε: ( ( (( a a ( 0 πίακες, τότε ( Α+Β +Γ= ( + + = + ( + =Α+ ( Β+Γ Α+ Α = Α +Α= + = =Ο Η πράξη της αφαίρεσης στο σύολο Μ ορίζεται έσω της πρόσθεσης από τη ισότητα Α Β : =Α+ ( Β Από το ορισό και τις ιδιότητες της πρόσθεσης εύκολα προκύπτει ότι το άθροισα τριώ ή περισσότερω πιάκω του ιδίου τύπου είαι το ίδιο ε οποιαδήποτε σειρά και α εκτελεστού οι επιέρους προσθέσεις Για παράδειγα, ισχύει Α+Β+Γ+Δ= ( Α+Β + ( Γ+Δ = [( Α+Β +Γ ] +Δ=Δ+ [ Β+ ( Γ+Α ] Η εξίσωση πιάκω Α+Χ=Β έχει οαδική λύση Χ =Β Α, αφού Α+Χ=Β Α+ ( Α+Χ = ( Α +Β [( Α +Α ] +Χ =Β+ ( Α Ο+Χ=Β Α Χ=Β Α
4 20 Κεφάλαιο 2 Πίακες Ο πολλαπλασιασός αριθού ε πίακα Ορισός Στο σύολο Μ τω πιάκω ε στοιχεία στο σώα Κ= ή ο πολλαπλασιασός αριθού ε πίακα είαι ία εξωτερική πράξη ε συτελεστές στο σώα Κ, που, α Α= ( a και λ Κ, ορίζεται ως εξής: λ Α= ( λa Συήθως γράφουε λα, ατί του τυπικού συβόλου λ Α Για παράδειγα, α είαι Θεώρηα Για κάθε, ισχύου: (i λ ( Α+Β = λ Α+ λ Β, (ii ( λ + Α= λ Α+ Α, (iii λ ( Α = ( λ Α, 0 2 Α= 3 3, τότε Α= Α = a, Β= b Μ ( Κ λ Κ και ( ( (iv Α=Α, όπου είαι η οάδα τω πραγατικώ αριθώ Απόδειξη λ ( Α+Β = λ( a + b = λa + λb = λa + λb = λ Α+ λ Β (i ( ( ( ( (ii ( (( a ( a a ( a ( a (iii λ ( Α = λ ( a ( ( ( ( = λ a = λ a = ( λ Α (iv ( a ( a λ + Α = λ + = λ + = λ + = λ Α+ Α Α= = =Α Παρατήρηση Το σύολο Μ ( Κ εφοδιασέο ε τις πράξεις της πρόσθεσης και του πολλαπλασιασού αριθού ε πίακα, όπως θα άθουε στο κεφάλαιο 8, αποκτά τη δοή διαυσατικού χώρου πάω στο σώα Κ Πολλαπλασιασός πιάκω Η πράξη του πολλαπλασιασού πιάκω δε είαι εσωτερική πράξη στο σύολο Μ ( Κ, είαι όως εσωτερική πράξη στο σύολο Μ ( Κ Η αφετηρία του ορισού του πολλαπλασιασού πιάκω είαι η θεωρία τω γρα-
5 22 Οι πράξεις στο σύολο τω πιάκω 2 ικώ απεικοίσεω που θα ελετήσουε στο κεφάλαιο 9 Θα δούε ότι σε κάθε γραική απεικόιση ατιστοιχίζεται έας πίακας και ατιστρόφως Επιπλέο, α οι πίακες Α και Β είαι ατίστοιχοι τω γραικώ απεικοίσεω f και g, τότε ο πίακας που ορίζουε ως γιόεο ΑΒ είαι ο ατίστοιχος της απεικόισης f g Έτσι οδηγούεθα στο ακόλουθο ορισό: Α= Μ ( Κ, Β= Μ ( Κ, το γιόεο Ορισός 223 Α ( a ( b ρ Α Β ή απλά ΑΒ είαι έας πίακας τύπου ρ ε γεικό στοιχείο c a b a b a b a b = =, i j i2 2 j i j ik kj k = που προκύπτει από το πολλαπλασιασό τω στοιχείω της i- γραής του πίακα Α ε τα ατίστοιχα στοιχεία της j στήλης του πίακα Β και άθροιση τω γιοέω που προκύπτου 0 2 Για παράδειγα, α Α= , Β= 2, τότε ΑΒ = , εώ ορίζεται και ο πίακας 2 + ( ( ( ΒΑ = = Παρατηρήσεις Το γιόεο ΑΒ ορίζεται όο ότα ο αριθός τω στηλώ του πίακα Α ισούται ε το αριθό τω γραώ του πίακα Β Σχηατικά έχουε Α Β ΑΒ, ρ ρ εώ για τους παραπάω πίακες το γιόεο ΒΑ ορίζεται, όο ότα = ρ και ε γέει έχουε ΑΒ ΒΑ Θεώρηα Α οι πίακες Α, ΒΓ, είαι κατάλληλου τύπου, ώστε α ορίζοται οι πράξεις που εφαίζοται, τότε ισχύου: (i ( ΑΒ Γ = Α( ΒΓ (προσεταιριστική ιδιότητα ΑΒ+Γ ( =ΑΒ+ΑΓ ii, (επιεριστικές ιδιότητες ( Β+Γ Α=ΒΑ+ΓΑ (iii ΑΒ = Ο Α =Οή Β= Ο
6 22 Κεφάλαιο 2 Πίακες Απόδειξη (i Α είαι ( a, ( b, ( c Α= Β= Γ=, και γράψουε ρ ρ τ το γεικό στοιχείο του πίακα Α ως a ( Α = κλπ, τότε έχουε ρ ρ ρ ( ΑΒ Γ = ( ΑΒ ik c kj = a i σbσ k c kj = a i σ bσ k c kj k= k= σ= σ= k= = a i σ( ΒΓ σ j = Α( ΒΓ σ = (ii Α είαι ( a, ( b, ( c Α= Β= Γ=, τότε έχουε ρ ρ ΑΒ+Γ ( = a ( b + c = a b + a c =ΑΒ+ΑΓ ik kj kj ik kj ik kj k= k= k= Οοίως, α Α= ( a, Β= ( b, Γ= ( c, τότε έχουε ρ ( Β+Γ Α= ( b + c a = b a + c a =ΒΑ+ΓΑ ik ik kj ik kj ik kj k= k= k= (iii Αρκεί α βρούε έα ατιπαράδειγα ε πίακες για τους οποίους ισχύει ότι ΑΒ = Ο ε Α Ο και Β Ο Τέτοιοι είαι, για παράδειγα, οι πίακες Α= και Β= Ο οαδιαίος πίακας Ο πίακας Ι = ( δ =, όπου δ 0 0, α i = = 0, α i j j είαι η συάρτηση δέλτα του Kronecker, οοάζεται οαδιαίος πίακας και έχει τις ιδιότητες: ΑΙ =ΙΑ = Α, για κάθε πίακα Α τύπου, ΑΙ = Α,για κάθε πίακα Α τύπου, Ι Α=Α, για κάθε πίακα Α τύπου ρ
7 22 Οι πράξεις στο σύολο τω πιάκω 23 Ο ατίστροφος πίακας Ορισός 224 Α ο πίακας Α είαι τετραγωικός τύπου και υπάρχει πίακας Χ τέτοιος ώστε ΑΧ = ΧΑ = Ι, τότε λέε ότι ο πίακας Α είαι ατιστρέψιος και ο πίακας Χ είαι ο ατίστροφος πίακας του Α Γράφουε τότε Χ =Α Θεώρηα 224 Α οι πίακες Α, Β είαι ατιστρέψιοι, τότε ισχύου: (i ( Α = Α (ii ( ΑΒ =Β Α Απόδειξη (i Από το ορισό 224 έχουε ότι ΑΑ = Α Α =Ι, οπότε προκύπτει άεσα το ζητούεο (ii ( ΑΒ( Β Α = Α( ΒΒ Α = ΑΙ Α = ΑΑ = Ι και οοίως αποδεικύεται ότι: ( Β Α ( ΑΒ =Ι Στα επόεα κεφάλαια θα θεωρήσουε δύο τρόπους εύρεσης του ατίστροφου εός πίακα, α αυτός υπάρχει Σηειώουε ότι δε έχου όλοι οι τετραγωικοί πίακες ατίστροφο πίακα Στο παρό κεφάλαιο θα δώσουε έα τύπο για το υπολογισό του ατίστροφου εός 2 2 πίακα 2 Α είαι Α= a a a2 a 22 και Χ= x y z w είαι ο ζητούεος ατίστροφος του πίακα Α,τότε από τις ισότητες ΑΧ =ΧΑ=Ι 2 και τη επίλυση τω γραικώ συστηάτω ε δύο εξισώσεις και δύο αγώστους που προκύπτου, ε τη προϋπόθεση ότι aa22 a2a2 0, λαβάουε: a a2 a22 a2 Χ= a a = a a a a a a Οι δυάεις εός πίακα Για κάθε τετραγωικό πίακα Α ορίζουε τις δυάεις του ως εξής: 0 Α =Ι, Α =Α και n Α = Α n Α, για κάθε * n ε 2 n
8 24 Κεφάλαιο 2 Πίακες Επιπλέο, α πίακας Α είαι ατιστρέψιος, τότε ορίζουε ( Α n * Α =, για κάθε n Με βάση τις ιδιότητες που ικαοποιεί η πράξη του πολλαπλασιασού πιάκω προκύπτου αέσως οι ιδιότητες: m n n m m+ n Α Α = Α Α = Α, για κάθε mn, m 2 ( n mn n Α = Α, για κάθε mn, λα = λ Α, για κάθε n 3 ( n n n n < απαιτείται η ισότητα ( λ λ (Για 0 4 ( Α ( Α =, για κάθε n n n Α = Α, για κάθε λ 0 5 ( Α+Β = ( Α+Β ( Α+Β =Α +ΑΒ+ΒΑ+Β 6 Α ΑΒ = ΒΑ, τότε ισχύου: ( Α±Β =Α ± 2ΑΒ+Β ( Α±Β =Α ± 3Α Β+ 3ΑΒ ±Β 2 2 ( Α+Β ( Α Β =Α Β n n n n k k * ( Α+Β = Α Β k = 0 k, για κάθε n Ο αάστροφος πίακας Ορισός Α ( a Α= Μ, τότε ο πίακας που προκύπτει από το Α ε εαλλαγή εταξύ γραώ και στηλώ του λέγεται αάστροφος πίακας του Α και συβολίζεται ε Α, έχουε δηλαδή Α = a Μ Για παράδειγα, α είαι ( ji 2 Α= 3, 0 5 Β = 2, τότε 3 Α = και [ 2 3] Β = Από το ορισό του αάστροφου πίακα άεσα προκύπτου οι ιδιότητες:
9 22 Οι πράξεις στο σύολο τω πιάκω 25 ( Α+Β =Α +Β, γιακάθε Α, Β Μ, 2 ( λα = λα, για κάθε λ Κ, Α Μ, 3 ( ΑΒ = Β Α, για κάθε Α Μ, Β Μ, 4 Ι =Ι, 5 ( Α = Α, για κάθε Α Μ και 6 ( Α = ( Α ρ Απόδειξη Η απόδειξη τω περισσοτέρω από τις παραπάω ιδιότητες είαι απλή εφαρογή του ορισού Ειδικότερα για τη 3, α ε ( Α συβολίσουε το γεικό στοιχείο του πίακα Α, έχουε : (( ΑΒ = ( ΑΒ ( ( ( ji = ajkbki = Β ik Α kj = Β Α Για τη 6 έχουε k= k= ( ( ( ( ΑΑ = Α Α = Ι ΑΑ = Α Α = Ι Α Α = Α Α = Ι, οπότε, λόγω της οαδικότητας του ατίστροφου εός πίακα, θα ισχύει ότι ( ( Ορισός 226 Ο τετραγωικός πίακας Α = ( a (i συετρικός, α (ii ατισυετρικός, α i, j =,2,, Για παράδειγα, από τους πίακες Α = Α Α = Α, δηλαδή, α a aji, Μ λέγεται: Α = Α, δηλαδή α ji Α= 2 3, Β= 2 0, = για κάθε i, j =,2,,, a = a, για κάθε ο Α είαι συετρικός, εώ ο Β είαι ατισυετρικός Παρατηρούε ότι τα στοιχεία της κυρίας διαγωίου του πίακα Β είαι όλα ηδέ Αυτό δε είαι τυχαίο, αλλά ισχύει σε κάθε ατισυετρικό πίακα, αφού από τη ισότητα a = aji για i= j προκύπτει ότι a ii = 0, για κάθε i =, 2,,
10 26 Κεφάλαιο 2 Πίακες 2 3 Ειδικοί τύποι πιάκω Κατ αρχή σηειώουε ότι, σε ία γραή που δε έχει όλα τα στοιχεία της 0 (η ηδεική γραή, το ηγετικό στοιχείο της είαι το πρώτο, από αριστερά προς τα δεξιά, η ηδεικό στοιχείο της Ορισός 2 3 (α Ο πίακας ( a Α= Μ λέγεται κλιακωτός ή κλιακωτής ορφής, ότα ισχύου τα ακόλουθα: (i οι ηδεικές γραές, α υπάρχου, βρίσκοται στη σειρά ετά τις η ηδεικές γραές και (ii α γ, γ2,, γκ, κ είαι οι η ηδεικές γραές του πίακα Α, τότε το ηγετικό στοιχείο της γ i + - γραής βρίσκεται δεξιότερα από το ηγετικό στοιχείο της γ i -γραής (β Ο πίακας ( a Α= Μ λέγεται αηγέος κλιακωτός ή αηγ- έης κλιακωτής ορφής, α ισχύου τα ακόλουθα: (i είαι κλιακωτός, (ii το ηγετικό στοιχείο κάθε η ηδεικής γραής είαι και (iii σε ία στήλη που περιέχει το ηγετικό στοιχείο κάποιας γραής, όλα τα άλλα στοιχεία της είαι 0 Για παράδειγα, οι παρακάτω πίακες είαι κλιακωτοί Α= και Β=, εώ αηγέοι κλιακωτοί είαι οι πίακες Γ= 0 2 και Δ= Στοιχειώδεις πράξεις και πίακες Στο σύολο τω πιάκω θεωρούε απεικοίσεις της ορφής τ: Μ Μ, Α τ( Α, που λέγοται στοιχειώδεις πράξεις γραώ ή γραοπράξεις Ο πίακας τ ( Α προκύπτει από το πίακα Α ε εφαρογή ιας από τις ακόλουθες διαδικασίες:
11 23 Ειδικοί τύποι πιάκω 27 γ γ, εαλλαγή της i γραής ε τη j γραή I i j II γ λγ, λ 0, πολλαπλασιασός της i γραής επί λ 0 i i III γ γ + λγ, λ 0, ατικατάσταση της i γραής από το άθροισα i i j αυτής και του λ πλασίου της j γραής Οι πίακες Α και τ ( Α λέγοται γραοϊσοδύαοι Όοια, ορίζοται και οι στοιχειώδεις πράξεις στηλώ ή στηλοπράξεις και συβολίζοται ε σ: Μ Μ, Α σ( Α σ σ, σ λσ, σ σ + λσ, λ 0 i j i i i i j Σε κάθε ία από τις στοιχειώδεις πράξεις γραώ (ατίστοιχα, στηλώ ατιστοιχίζουε έα στοιχειώδη πίακα Έτσι, στη στοιχειώδη πράξη γραώ τ που εφαρόζεται σε πίακα, ατιστοιχίζουε το στοιχειώδη πίακα τ ( Ι που προκύπτει από τη εφαρογή της τ στο οαδιαίο πίακα Ι, εώ στη στοιχειώδη πράξη στηλώ σ που εφαρόζεται σε πίακα, ατιστοιχίζουε το στοιχειώδη πίακα σ ( Ι που προκύπτει από τη εφαρογή της σ στο οαδιαίο πίακα Ι Για παράδειγα, στις στοιχειώδεις πράξεις γ γ2, σ2 3 σ2, γ3 γ3 + 2γ, ότα εφαρόζοται σε 3 4 πίακα, ατιστοιχίζοται οι παρακάτω στοιχειώδεις πίακες: ,, Ααγωγή πίακα σε αηγέο κλιακωτό Θεωρούε έα πίακα ( a Α= Μ Αυτός ε διαδοχική εφαρογή στοιχειωδώ πράξεω γραώ αάγεται αρχικά σε κλιακωτό και στη συέχεια σε αηγέο κλιακωτό πίακα Η διαδικασία ααγωγής είαι αλγοριθική (αλγόριθος τω Gauss-Jordan και περιγράφεται ως εξής:
12 28 Κεφάλαιο 2 Πίακες Ι Με εαλλαγή γραώ, α είαι αάγκη, κάουε το πρώτο στοιχείο της πρώτης η ηδεικής στήλης διάφορο του 0 Το στοιχείο αυτό το οοάζουε βασικό (pivot, όπως και το ηγετικό στοιχείο κάθε η ηδεικής γραής ΙΙ Με εφαρογή της γραοπράξης γ ( a γ το στοιχείο a γίεται ίσο ε Στη συέχεια ε εφαρογή τω γραοπράξεω γ γ a γ,, γ γ a γ ηδείζουε όλα τα στοιχεία της πρώτης στήλης εκτός του βασικού Α όλα τα στοιχεία της πρώτης στήλης είαι 0, τότε εφαρόζουε τη διαδικασία που περιγράψαε στη πρώτη από τις επόεες στήλες που έχει η ηδεικά στοιχεία, κοκ ΙΙΙ Αγοώτας τη πρώτη γραή και τη πρώτη στήλη του πίακα που έχει προκύψει, επααλαβάουε τη παραπάω διαδικασία για α κάουε το στοιχείο a22 ίσο ε και τα στοιχεία a32,, a 2 της δεύτερης στήλης που βρίσκοται κάτω από το a 22 ίσα ε 0 Συεχίζουε τη ίδια διαδικασία έχρις ότου ο πίακας Α γίει κλιακωτός και ε τα ηγετικά στοιχεία τω γραώ του ίσα ε ΙVΜε στοιχειώδεις πράξεις γραώ τύπου ΙΙΙ ετατρέπουε τα η ηδεικά στοιχεία κάθε στήλης που περιέχει το ηγετικό ιας γραής σε ηδεικά αρχίζοτας από αυτή που είαι δεξιότερα Παρατηρήσεις Με τα βήατα Ι και ΙΙ ο πίακας ετατρέπεται σε κλιακωτό, χωρίς α είαι ααγκαίο α γίου τα ηγετικά στοιχεία τω γραώ ίσα ε Γεικά ο κλιακωτός πίακας που προκύπτει δε είαι οαδικός έχει όως πάτοτε το ίδιο αριθό η ηδεικώ γραώ Ο αριθός αυτός έχει εγάλη σηασία για έα πίακα και στα επόεα κεφάλαια θα δούε ότι οοάζεται βαθός του πίακα 2 Ο αηγέος κλιακωτός πίακας που προκύπτει ε το παραπάω αλγόριθο είαι οαδικός 3 Τα τρία πρώτα βήατα της παραπάω εθόδου αποτελού τη έθοδο απαλοιφής του Gauss, εώ η πλήρης έθοδος είαι η έθοδος απαλοιφής τω Gauss-Jordan Η ααγωγή πίακα σε αηγέο κλιακωτό είαι πολύ χρήσιη για τη εύρεση του βαθού πίακα, αλλά και για τη επίλυση γραικώ συστηάτω Παράδειγα 24 Να ετατραπεί σε αηγέο κλιακωτό ο πίακας Α=
13 24 Ααγωγή πίακα σε αηγέο κλιακωτό 29 Λύση Ο πίακας Α γίεται: γ γ γ γ γ γ4 γ4 3γ ( 4 γ γ3 0 2 γ3 γ3 4γ γ2 γ3 γ4 γ4 8γ γ3 γ γ4 γ4 0γ γ3 ( γ3 4 ( γ 4 γ γ2 γ2 γ γ γ + γ3 γ γ+ 5γ4 γ γ 2γ Στη συέχεια θα δούε ερικές προτάσεις σχετικές ε τις στοιχειώδεις πράξεις, τους στοιχειώδεις πίακες και τη εύρεση του ατίστροφου εός πίακα Πρόταση 24 (α Α τ : Μ Μ είαι ία στοιχειώδης πράξη γραώ και Α Μ, τότε ( τ( Α = τ Ι Α (β Α σ : Μ Μ είαι ία στοιχειώδης πράξη στηλώ και Α Μ, τότε σ( Α =Ασ( Ι Απόδειξη (α Θα εξετάσουε όο τις στοιχειώδεις πράξεις τύπου Ι, ( γ i γ j Οι άλλες δύο περιπτώσεις και το ερώτηα (β αποδεικύοται αάλογα Ο στοιχειώδης πίακας που ατιστοιχεί στη γραοπράξη τ ( γi γ j είαι
14 30 Κεφάλαιο 2 Πίακες όπου ( ii jj ji, τ Ι =Ι Ε Ε +Ε +Ε Ε είαι πίακας που έχει το στοιχείο του ίσο ε και όλα τα υπόλοιπα στοιχεία του είαι 0 Έστω ότι ο πίακας ( a γραές γ = a a 2 a, k Τότε θα είαι Επίσης έχουε k k k k i jγ i+, j i j+ τ( Α = γ γ γ γ γ γ γ τ ( Ι Α = ( Α= έχει ii jj ji ii jj ji Ι Ε Ε +Ε +Ε Α=Α Ε Α Ε Α+Ε Α+Ε Α γ γ γi γ 0 a i j 0 γ j = + + = = τ ( Α γ j 0 γ j 0 γ i γ i γ 0 a γ 0 γ Παρατήρηση Σηειώουε ότι οι στοιχειώδεις πίακες που ατιστοιχίζοται στις στοιχειώδεις πράξεις γ i λγ i και γ γ + λγ, λ 0 είαι οι diag(,, λ, και Ι + λε, ατίστοιχα i i j Πρόταση 242 Κάθε στοιχειώδης πίακας είαι ατιστρέψιος Απόδειξη Έστω P και Q οι στοιχειώδεις πίακες που ατιστοιχού σε ία γραοπράξη τ και στη ατίστροφή της, έστω τ Σύφωα ε τη πρόταση 24 έχουε ( ( ( ( ( τ τ τ τ Ι = Ι = PΙ = Q PΙ = QP, ( ( ( Ι = τ τ Ι = QΙ = P QΙ = PQ Άρα έχουε τη ισότητα PQ = QP =Ι, οπότε ο πίακας P είαι ατιστρέψιος ε P = Q
15 25 Εύρεση του ατίστροφου πίακα Εύρεση του ατίστροφου πίακα Από τις προτάσεις 24 και 242 έπεται ότι ο πίακας που προκύπτει ε διαδοχική εφαρογή γραοπράξεω σε έα πίακα Α είαι της ορφής PΑ, όπου ο P είαι ατιστρέψιος πίακας ως γιόεο στοιχειωδώ πιάκω Ειδικότερα, για τετραγωικούς πίακες έχουε: Πρόταση 2 5 Έστω ότι ο πίακας Α Μ ( Κ ε διαδοχική εφαρογή γραοπράξεω τ, τ2,, τ s ε ατίστοιχους στοιχειώδεις πίακες P,, P2 ετασχηατίζεται στο αηγέο κλιακωτό πίακα Α R Τότε ισχύου:, P s I Α ο Α R έχει ία τουλάχιστο ηδεική γραή, τότε ο πίακας Α είαι η ατιστρέψιος II Α ο Α R δε έχει ηδεικές γραές, τότε Α R =Ι, ο πίακας Α είαι ατιστρέψιος και Α = P PPΙ s 2 Απόδειξη Ι Έστω ότι ο πίακας Α R έχει ία τουλάχιστο ηδεική γραή και ας υποθέσουε ότι ο πίακας Α είαι ατιστρέψιος Τότε θα υπάρχει πίακας Χ τέτοιος ώστε ΑΧ = ΧΑ = Ι ( Από τη πρόταση 24, θα υπάρχει ατιστρέψιος πίακας P = Ps PP 2 τέτοιος, ώστε α ισχύει P PPΑ = PΑ = Α (2 s 2 Από τις ( και (2 έχουε Ι = PP = PΑΧ P = Α Χ P R R Ι = ΧΑ = ΧP PΑ = ΧP Α R, από τις οποίες προκύπτει ότι ΑR ( Χ P = ( ΧP Α =Ι, δηλαδή ο πίακας Α R είαι ατιστρέψιος, που είαι άτοπο, γιατί ο πίακας Α R έχει ία τουλάχιστο ηδεική γραή και το γιόεό του ε οποιοδήποτε πίακα θα περιέχει επίσης ία τουλάχιστο ηδεική γραή και έτσι δε πορεί α είαι ο οαδιαίος πίακας Άρα ο πίακας Α δε είαι ατιστρέψιος
16 32 Κεφάλαιο 2 Πίακες ΙΙ Α ο πίακας Α R δε έχει ηδεική γραή, τότε αυτός θα περιέχει ηγετικά καταεηέα σε η ηδεικές γραές, που το καθέα βρίσκεται δεξιότερα από το ηγετικό της προηγούεης γραής, οπότε θα είαι Α =Ι Επιπλέο θα ισχύει R s 2 R s 2 P PPΑ= PΑ=Α =Ι Α = P PP = P Κ το οαδιαίο πίακα Ι και εφαρόσουε και στους δύο ταυτόχροα τις ίδιες στοιχειώδεις πράξεις γραώ, ώστε ο πίακας Α α ετασχηατιστεί στο αηγέο κλιακωτό πίακα Α, τότε θα έχουε Α γράψουε δίπλα στο πίακα Α Μ ( R [ ] Α Ι ΑR Β Από τη πρόταση 25 συπεραίουε ότι: Α ΑR Ι, τότε ο πίακας Α δε ατιστρέφεται Α Α R =Ι, τότε ο πίακας Α ατιστρέφεται και Α =Β Παράδειγα 2 5 Να βρεθεί ο ατίστροφος του πίακα 2 3 Α= Λύση Έχουε [ Α Ι γ γ γ 3] = γ3 γ3 3γ γ3 γ3 2γ2 γ2 γ2 2γ γ2 ( γ2 γ γ 3γ γ γ 2γ = Ι3 Β Άρα ο πίακας Α είαι ατιστρέψιος και ο ατίστροφός του είαι ο 2 0 Α =Β=
17 26 Εισαγωγή στα γραικά συστήατα Εισαγωγή στα γραικά συστήατα Κάθε εξίσωση της ορφής λx+ λ2x2 + + λx = β, (,,, όπου λ, λ2,, λ, β Κ = ή και x x2 x άγωστοι αριθοί από το σώα Κ, λέγεται γραική εξίσωση ε αγώστους Ο αριθός β λέγεται σταθερός όρος της εξίσωσης, εώ οι αριθοί λ, λ2,, λ λέγοται συτελεστές τω αγώστω Λύση της γραικής εξίσωσης ( λέγεται κάθε διατεταγέη -άδα ω, ω,, ω Κ τέτοια ώστε ( 2 λω+ λ2ω2 + + λω = β, δηλαδή επαληθεύεται η εξίσωση, α θέσουε xi = ωi, i =,2,, Γραικό σύστηα ε εξισώσεις και αγώστους ή - γραικό σύστηα είαι έα (πεπερασέο πλήθος γραικώ εξισώσεω ε αγώστους, δηλαδή έχει τη ορφή αx + α2x2 + + α x = β 2x 22x2 2x α + α + + α = β2 α x+ α2x2+ + αx = β Α θεωρήσουε τους πίακες (2 α α2 α 2 22 α α α2 Α=, α α2 α x β x β 2 2 Χ=, Β= x β τότε το γραικό σύστηα (2 γράφεται ως ία εξίσωση πιάκω ΑΧ =Β, (3 όπου ο πίακας Α είαι πίακας τω συτελεστώ, ο πίακας Χ είαι ο πίακας τω αγώστω και ο πίακας Β είαι πίακας τω σταθερώ όρω Λύση της γραικού συστήατος (2 λέγεται κάθε διατεταγέη -άδα (,,, 2 ξ ξ ξ Κ που επαληθεύει και τις εξισώσεις του συστήατος (2
18 34 Κεφάλαιο 2 Πίακες Το γραικό σύστηα (2 λέγεται συβιβαστό, α έχει ία τουλάχιστο λύση, εώ λέγεται αδύατο, α δε έχει λύση Για λόγους συβατότητας ε τους συβολισούς ας θα συβολίζουε τη λύση ( ξ, ξ2,, ξ και ε το πίακα-στήλη [ ] ξ ξ ξ2 ξ = Δύο γραικά συστήατα ε εξισώσεις και αγώστους ΑΧ=Β και 2 2 Α Χ=Β, λέγοται ισοδύαα, α έχου ακριβώς τις ίδιες λύσεις Η επίλυση εός γραικού συστήατος, δηλαδή η διαδικασία εύρεσης όλω τω λύσεω του συστήατος, βασίζεται στη εύρεση άλλω γραικώ συστηάτω ισοδυάω προς το αρχικό, αλλά απλούστερης ορφής Α ο πίακας Β τω σταθερώ όρω είαι ο ηδεικός πίακας, δηλαδή α είαι Β= [ 0 0 0], τότε το γραικό σύστηα γίεται ΑΧ =Ο (4 και λέγεται οογεές Ο πίακας ΑΒ Μ ( + που είαι ο πίακας Α συπληρωέος ε ία τελευταία στήλη, αυτή που ορίζει ο πίακας Β τω σταθερώ όρω λέγεται επαυξηέος πίακας του συστήατος ΑΧ =Β 2 7 Η έθοδος απαλοιφής του Gauss Η βασική έθοδος επίλυσης του γραικού συστήατος ΑΧ =Β, (Σ όπου Α= ( α Μ, Χ= [ x x2 x ], Β= β β2 β, είαι η έθοδος απαλοιφής του Gauss Η έθοδος αυτή ουσιαστικά συίσταται στο ετασχηατισό του επαυξηέου πίακα ΑΒ του συστήατος (Σ σε αηγέο κλιακωτό ε χρήση όο στοιχειωδώ πράξεω γραώ, ακολουθώτας το αλγόριθο τω Gauss-Jordan που περιγράψαε παραπάω στη παράγραφο 24, ως εξής: Ι Με εαλλαγή γραώ, α είαι αάγκη κάουε το πρώτο στοιχείο της πρώτης η ηδεικής στήλης διάφορο του 0 Το στοιχείο αυτό το οοάζουε βασικό (pivot, όπως και το ηγετικό στοιχείο κάθε η ηδεικής γραής
19 27 Η έθοδος απαλοιφής του Gauss 35 ΙΙ Με εφαρογή της γραοπράξης γ ( a γ το στοιχείο a γίεται ίσο ε Στη συέχεια ε εφαρογή τω γραοπράξεω γ γ a γ,, γ γ a γ, ηδείζουε όλα τα στοιχεία της πρώτης στήλης εκτός του βασικού Α όλα τα στοιχεία της πρώτης στήλης είαι 0, τότε η διαδικασία που περιγράψαε εφαρόζεται στη πρώτη από τις επόεες στήλες που έχει η ηδεικά στοιχεία, κοκ III Αγοώτας τη πρώτη γραή και τη πρώτη στήλη του πίακα που έχει προκύψει, επααλαβάουε τη παραπάω διαδικασία για α κάουε το στοιχείο a22 ίσο ε και τα στοιχεία a32,, a 2 της δεύτερης στη- λης που βρίσκοται κάτω από το a 22 ίσα ε 0 Συεχίζουε τη ίδια διαδικασία έχρις ότου ο πίακας Α γίει κλιακωτός και ε τα ηγετικά στοιχεία τω γραώ του ίσα ε IV Με στοιχειώδεις πράξεις γραώ τύπου ΙΙΙ ετατρέπουε τα η ηδεικά στοιχεία κάθε στήλης που περιέχει το ηγετικό ιας γραής σε ηδεικά, αρχίζοτας από αυτή που είαι δεξιότερα Είαι φαερό ότι ε διαδοχική εφαρογή στοιχειωδώ πράξεω γραώ στο επαυξηέο πίακα του συστήατος (Σ, τα προκύπτοτα συστήατα έχου εξισώσεις που είαι γραικοί συδυασοί τω εξισώσεω του αρχικού συστήατος (Σ Έτσι, τα συστήατα που προκύπτου είαι ισοδύαα προς το αρχικό σύστηα, δηλαδή έχου το ίδιο σύολο λύσεω ε το σύστηα (Σ Μετά τη ααγωγή του επαυξηέου πίακα [ Α Β ] σε αηγέο κλιακωτό διακρίουε τις περιπτώσεις: Α στο αηγέο κλιακωτό πίακα υπάρχει γραή της ορφής β, β 0, τότε το σύστηα είαι αδύατο Α δε υπάρχου γραές της ορφής β, β 0 και έχουε συολικά κ η ηδεικές γραές, κ min{, }, τότε θεωρούε τους κ αγώστους που ατιστοιχού σε στήλες του αηγέου κλιακωτού πίακα, που δε περιέχου κάποιο από τα ηγετικά, ως αυθαίρετους και εκφράζουε τους υπόλοιπους αγώστους ως συαρτήσεις τω αυθαίρετω αγώστω Παράδειγα Να προσδιορίσετε το σύολο τω λύσεω του γραικού συστήατος: x+ 2y+ 3z+ w= 3, y z+ 2w= 4, x+ 3y+ 2z+ 3w= 7 { }
20 36 Κεφάλαιο 2 Πίακες Λύση Με στοιχειώδεις πράξεις γραώ ετασχηατίζουε το επαυξηέο πίακα του συστήατος σε αηγέο κλιακωτό Έχουε: γ γ γ γ3 γ3 γ2 γ γ 2γ Από τη ορφή του αηγέου κλιακωτού πίακα που προκύπτει συπεραίουε ότι το σύστηα είαι συβιβαστό Οι άγωστοι z και w που ατιστοιχού στις δύο τελευταίες στήλες, οι οποίες δε περιέχου κάποιο από τα ηγετικά τω η ηδεικώ γραώ, επιλέγοται ως αεξάρτητοι (αυθαίρετοι άγωστοι, εώ οι άγωστοι x και y που ατιστοιχού στις δύο πρώτες στήλες, οι οποίες περιέχου τα ηγετικά τω η ηδεικώ γραώ, είαι οι εξαρτηέοι άγωστοι Έτσι έχουε το ισοδύαο σύστηα x+ 5z 3w= 5 x = 5 5z+ 3w y z + 2w = 4 y = 4 + z 2 w, z, w Εποέως, η τυχούσα από τις άπειρες λύσεις του συστήατος είαι ( xyzw,,, = ( 5 5κ + 3 λ,4+ κ 2 λ, κ, λ = ( 5, 4, 0, 0 + κ( 5,,, 0 + λ(3, 2, 0,, κ, λ, εώ το σύολο τω λύσεω του συστήατος είαι το Λ= ( 5 5κ+ 3 λ,4+ κ 2 λκλ,, : κλ, { } Παράδειγα 2 Να προσδιορίσετε το σύολο τω λύσεω του οογεούς συστήατος: x+ 2x2 + 3x3 + 4x4 = 0 x + 3x + 4x + 5x = Λύση Ο επαυξηέος πίακας του συστήατος γίεται : γ2 γ γ γ γ 2γ και το σύστηα είαι ισοδύαο ε το
21 27 Η έθοδος απαλοιφής του Gauss 37 x + x + 2x = 0 x = x 2x x2 + x3 + x4 = 0 x2 = x3 x4, x3, x4 Εποέως το σύολο τω λύσεω του δεδοέου οογεούς συστήατος είαι Λ= ( κ 2 λ, κ λκλ,, : κλ, { } { κ λ κ λ } = (,,, 0 + ( 2,, 0,:, Παράδειγα 3 Να προσδιορίσετε τις τιές της παραέτρου a για τις οποίες έχει λύση το σύστηα x+ 3y+ 5z = 2x+ 4z = x y+ z = a, a και στη συέχεια α βρείτε τη λύση του συστήατος Λύση Ο επαυξηέος πίακας του συστήατος γίεται: γ2 γ2 2γ ΑΒ = γ3 γ3 γ a a γ2 γ2 6 γ3 γ3+ 4γ γ γ 3γ a a 3 Εποέως το σύστηα είαι συβιβαστό, ότα a = 0 a = 3 3 Για a =, το σύστηα είαι ισοδύαο ε το σύστηα 3 x+ 2z = x = z 2 2, z y+ z = y = z 6 6 οπότε το σύολο τω λύσεω του είαι Λ= c, c, c : c 2 6
22 38 Κεφάλαιο 2 Πίακες 28 Η LU παραγοτοποίηση πίακα Όπως ξέρουε, η έθοδος απαλοιφής του Gauss για τη επίλυση του γραικού συστήατος ΑΧ =Β (Σ βασίζεται στη ετατροπή του επαυξηέου πίακα [ Α Β ] σε αηγέο κλιακωτό Στη παράγραφο αυτή θα περιγράψουε ία διαφορετική εθοδο επίλυσης του γραικού συστήατος (Σ η οποία βασίζεται στη παραγοτοποίηση του πίακα Α τω συτελεστώ σε γιόεο δύο πιάκω, εός κάτω τριγωικού και εός κλιακωτού πίακα Η έθοδος αυτή είαι ιδιαίτερα χρήσιη ότα έχουε α λύσουε πολλά γραικά συστήατα ε το ίδιο πίακα συτελεστώ και διαφορετικό πίακα σταθερώ όρω, είαι κατάλληλη για ηλεκτροικούς υπολογιστές και αποτελεί τη βάση πολλώ υπολογιστικώ πακέτω Ας υποθέσουε ότι έχουε α λύσουε το γραικό σύστηα (Σ και ότι έχουε παραγοτοποιήσει το πίακα Α Μm n( Κ, Κ = ή τω συτελεστώ σε γιόεο δύο πιάκω της ορφής Α = LU, ( όπου ο L είαι m m κάτω τριγωικός ε τα στοιχεία της κυρίας διαγωίου ίσα ε, εώ ο U είαι κλιακωτός m n πίακας Έχουε ΑΧ=Β ( LU Χ=Β L( U Χ =Β, οπότε, α θέσουε Y = U Χ, τότε έχουε α επιλύσουε τα απλά γραικά συστήατα ε πίακα κλιακωτής ορφής L Y =Β και U Χ = Y Επιλύουε το σύστηα L Y =Β ε ατικατάσταση προς τα επρός και στη συέχεια επιλύουε το σύστηα U Χ = Y ε ατικατάσταση προς τα πίσω Για παράδειγα, ας υποθέσουε ότι έχουε προς λύση το σύστηα x x2 ΑΧ = = = Β x x4 και ότι έχουε βρει τη παραγοτοποίηση Α= = = LU Επιλύουε πρώτα το σύστηα
23 28 Η LU- παραγοτοποίηση πίακα 39 y y y2 = Y= y2 = 3 3 y y 3 Στη συέχεια προκύπτει το σύστηα x x 7,75 + 0,5α x2 x = 3 Χ = =, α x 3, 5 3 x + α x4 x α 4 Ο αλγόριθος της LU -παραγοτοποίησης Θεωρούε πίακα Α Μ ( m n Κ και ε διαδοχικές στοιχειώδεις πράξεις γραώ, χωρίς α κάουε εαλλαγή γραώ, ετατρέπουε το πίακα σε κλιακωτό, οπότε έχουε Ρs Ρ2ΡΑ = U, (2 όπου Ρ, Ρ2, Ρ s είαι οι ατίστοιχοι στοιχειώδεις πίακες Επειδή όλοι οι στοιχειώδεις πίακες είαι ατιστρέψιοι έχουε Α=Ρ U LU Ρ2 Ρ s =, (3 όπου έχουε θέσει L =Ρ Ρ2 Ρ s Επιπλέο λαβάουε Ρs Ρ2Ρ L =Ι, (4 οπότε παρατηρούε ότι οι ίδιες γραοπράξεις ετατρέπου το πίακα L στο οαδιαίο πίακα Για παράδειγα, ας θεωρήσουε το πίακα 2 0 Α= τω συτελεστώ του συστήατος που λύσαε προηγουέως Έχουε γ2 γ2 γ γ3 γ3 γ Μέχρι τώρα χρησιοποιήσαε ως βασικό (pivot στοιχείο το a = 2 (συβολίζεται ε παχύ αύρο και παρατηρούε ότι οι ίδιες στοιχειώδεις πράξεις δίου
24 40 Κεφάλαιο 2 Πίακες γ γ 2γ 0 0 γ3 γ3 γ * 0 * Στη συέχεια έχουε γ3 γ2+ γ = U, όπου χρησιοποιήσαε ως βασικό το στοιχείο a 22 = Παρατηρούε ότι η ίδια στοιχειώδης πράξη δίει γ γ + γ 0 0, οπότε πλέο είαι φαερό ότι ο κατάλληλος πίακας L που ε τις ίδιες γραοπράξεις ετατρέπεται στο οαδιαίο πίακα είαι ο 0 0 L = Μπορούε πλέο α περιγράψουε τη διαδικασία παραγοτοποίησης του πίακα Α ως εξής: (i (ii Μετατρέπουε το πίακα Α ε στοιχειώδεις πράξεις γραώ, χωρίς εαλλαγές γραώ, σε κλιακωτό, οπότε προκύπτει ο πίακας U Διαορφώουε κάθε στήλη του Α που έχει βασικό στοιχείο, κάθε φορά που εφαίζεται, ε ηδεικά πάω από το βασικό στοιχείο και διαιρώτας τα υπόλοιπα στοιχεία της ε το βασικό στοιχείο Οι στήλες που διαορφώοται αζί ε ία τελευταία στήλη της ορφής [ 0 0 ] αποτελού τις στήλες του πίακα L 29 Διαερίσεις πιάκω Θεωρούε πίακα ( a Α= και τους φυσικούς αριθούς, 2,, r,, 2,, s έτσι, ώστε r = και s =
25 29 Διαερίσεις πιάκω 4 Στη συέχεια ε διακεκοέες οριζότιες και κατακόρυφες γραές απoκόβουε τις πρώτες γραές ετά τις 2 επόεες γραές κοκ, τις πρώτες στήλες κοκ Έτσι από το πίακα Α σχηατίζουε rs πίακες, έστω Α, κ =, 2,, r, λ = κλ, 2,, s, τύπου κ λ Οι πίακες Α κλ αποτελού ία r s διαέριση του πίακα Α που ατιστοιχεί στους αριθούς (, 2,, και ( r, 2,, s Συβολικά γράφουε Α= ( Α κλ r s Για παράδειγα, ο 3 5 πίακας Α= πορεί α διαεριστεί σε 6 υποπίακες ως εξής Α Α2 Α3 Α= ( Αλ = = Α2 Α22 Α 23 0 Ας θεωρήσουε τώρα το 5 4πίακα Β ε ία 3 2 διαέριση Β Β2 4 Β= Β2 Β22 = Β Β Το γιόεο τω δύο πιάκω Α και Β είαι ο πίακας ΑΒ = ΑikΒkj = k = Σηειώουε ότι για α είαι γεικά δυατός ο παραπάω πολλαπλασιασός διαερισέω πιάκω πρέπει και αρκεί α είαι δυατός ο πολλαπλασιασός όλω τω ατίστοιχω υποπιάκω Α ik και Β kj Με κατάλληλη επιλογή τω διαερίσεω, συήθως γίεται ευκολότερα ο πολλαπλασιασός δύο πιάκω Στο προηγούεο παράδειγα, ατί α κάουε απ ευθείας το πολλαπλασιασό τω δύο πιάκω, πολλαπλασιάζουε υποπίακες που έχου ικρότερο αριθό γραώ και στηλώ Αυτό
26 42 Κεφάλαιο 2 Πίακες είαι σηατικό, κυρίως ότα οι δεδοέοι πίακες έχου εγάλο αριθό γραώ και στηλώ Μία ιδιαίτερη περίπτωση έχουε, ότα ο πίακας Α πορεί α διαεριστεί σε υποπίακες Α, Α2,, Α r, πιθαώς διαφορετικώ τάξεω, έτσι ώστε Α Ο Ο Ο Α2 Ο Α= = diag ( Α, Α2,, Αr Ο Ο Α r Επιπλέο, α [ ], Α= Α Α Β= 2 Β 2 Β, τότε ΑΒ =ΑΒ +Α2Β 2, ότα βέβαια ορίζοται οι πολλαπλασιασοί και οι προσθέσεις υποπιάκω που εφαίζοται, π χ = = + = και = + = Πίακες ε στοιχεία συαρτήσεις [ ] Πολλές φορές θεωρούε πίακες ε στοιχεία συαρτήσεις ιας ή περισσοτέρω πραγατικώ εταβλητώ, όπως οι πίακες a( t a2 ( t a ( t x ( t a2( t a22 ( t a2 ( t x2 ( t Α ( t =, Χ ( t = a( t a2( t a( t x ( t
27 20 Πίακες ε στοιχεία συαρτήσεις 43 Ορισός 2 0 (i Ο πίακας ( t ( a ( t Α = είαι συεχής για t = t0, α κάθε συάρτηση a ( t είαι συεχής για t = t0 Ο πίακας Α ( είαι συεχής στο διάστηα [ α, β ], α είαι συεχής σε κάθε σηείο του διαστήατος [ α, β ] (ii Ο πίακας ( t ( a ( t Α = είαι παραγωγίσιος στο διάστηα [ α, β ], α κάθε ία από τις συαρτήσεις a ( t είαι παραγωγίσιη στο διάστηα [ α, β ] και η παράγωγός του είαι ο πίακας dα Α ( t : = ( a ( t dt (iii Όοια ορίζουε το ολοκλήρωα του πίακα Α ( t = ( a ( t β β α Α ( tdt: = ( α a ( tdt Για παράδειγα, ο πίακας t 2t Α e e t = ( cos t sin t είαι συεχής στο και ισχύει 2π t 2t e e 2e Α ( t = sin t cos t και e π π Α( tdt = Μερικές από τις βασικές ιδιότητες της παραγώγισης πιάκω ε στοιχεία συαρτήσεις παραθέτουε παρακάτω, όπου ( a ( t, ( b ( t ( c ( t Α= Β= και Γ= (σταθερός πίακας είαι πίακες κατάλληλου τύπου, ώστε α ορίζοται οι εφαιζόεες πράξεις πιάκω : d dα dt dt d dα dβ dt dt dt ( ΓΑ = Γ 3 ( 2 ( Α+Β = + 4 ( d dα dβ ΑΒ = Β + Α dt dt dt d dα Α = Α Α dt dt t
... λέγονται στοιχεία του πίνακα Α και οι δείκτες δηλώνουν τη γραµµή και τη στήλη, αντίστοιχα, που ανήκει το στοιχείο α. . Για παράδειγµα, οι πίνακες
 ΚΕΦΑΛΑΙΟ ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούµε µε το ορισµό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθµώ ή άλλω στοιχείω Οι πίακες εµφαίζοται στη θεωρία τω γραµµικώ
ΚΕΦΑΛΑΙΟ ΠΙΝΑΚΕΣ Στο Κεφάλαιο αυτό θα ασχοληθούµε µε το ορισµό και τις στοιχειώδεις ιδιότητες τω πιάκω, που είαι ορθογώιες παρατάξεις αριθµώ ή άλλω στοιχείω Οι πίακες εµφαίζοται στη θεωρία τω γραµµικώ
Παράδειγμα Το γνωστό παράδειγμα με τα βάρη 30 ατόμων ταξινομημένα σε 5 ομάδες. Η μέση τιμή για το δείγμα έχει βρεθεί x = 77. = =
 Παράδειγα Το γωστό παράδειγα ε τα βάρη 0 ατόω ταξιοηέα σε 5 οάδες. Η έση τιή για το δείγα έχει βρεθεί 77. Τάξη Απόλυτες συχότητες Κετρική τιή τάξης Απόκλιση από το έσο 65-69 67,5 9,5 70-7 6 7,5,5 75-79
Παράδειγα Το γωστό παράδειγα ε τα βάρη 0 ατόω ταξιοηέα σε 5 οάδες. Η έση τιή για το δείγα έχει βρεθεί 77. Τάξη Απόλυτες συχότητες Κετρική τιή τάξης Απόκλιση από το έσο 65-69 67,5 9,5 70-7 6 7,5,5 75-79
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
1. Το σύνολο των μιγαδικών αριθμών
 Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Ι δ ι ο τ η τ ε ς Π ρ ο σ θ ε σ η ς - Π ο λ λ α π λ α σ ι α σ μ ο υ ΙΔΙΟΤΗΤΑ ΠΡΟΣΘΕΣΗ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
2.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
β± β 4αγ 2 x1,2 x 0.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω
Ε 1. Διαφορικός λογισμός (Κανόνες παραγώγισης)
 Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεων
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Θεωρία - Μέθοδοι
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
ΛΥΚΕΙΟ ΜΕΤΑΜΟΡΦΩΣΗΣ 2014 ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ. 1. Εισαγωγικά. Υποθέτουµε ότι ο αναγνώστης γνωρίζει τα περιεχόµενα στην ενότητα Γραµµικές Μορφές.
 ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ Εισαγωγιά Υποθέτουε ότι ο ααγώστης γωρίζει τα περιεχόεα στη εότητα Γραιές Μορφές Γειές υποθέσεις Συβοισοί Ο χώρος, στοιχεία του οποίου χρησιοποιούε, είαι έας γραιός (αυσατιός) χώρος V
ΑΛΓΕΒΡΑ ΤΑΝΥΣΤΩΝ Εισαγωγιά Υποθέτουε ότι ο ααγώστης γωρίζει τα περιεχόεα στη εότητα Γραιές Μορφές Γειές υποθέσεις Συβοισοί Ο χώρος, στοιχεία του οποίου χρησιοποιούε, είαι έας γραιός (αυσατιός) χώρος V
Λύση. Λύση Άσκηση 3. Λύση. ( Α Α Α Ι ) Α. Α Α=Ιν. Άσκηση 4. επαληθεύει τη σχέση Χ. Λύση.
 Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ = Γ. β1 = β2
 Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικών αριθµών. Μιγαδικό επίπεδο. Γεωµετρική παράσταση του αθροίσµατος µιγαδικών αριθµών.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
ν ν Άσκηση 1. Α =Α, Β =Β. Λύση Άσκηση Α Β =Β Α, Α Β=ΒΑ. Β Α= ( Β Β)( ΑΒ ) Β Α=Ι( ΑΒ ) Β Α=ΑΒ. Άσκηση = Α Α Α Α=.
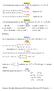 Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
1.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ
 ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηµα ασκήσεων 11/12/2006
 Τήα Επιστήης και Τεχολογίας Υλικώ Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηα ασκήσεω //006 Μελέτη οοδιάστατου στοιχειακού στερεού ε δύο τροχιακά αά άτοο ε χρήση υβριδικώ ατοικώ τροχιακώ Θεωρούε δύο τροχιακά
Τήα Επιστήης και Τεχολογίας Υλικώ Εισαγωγή στη Φυσική Στερεάς Κατάστασης Μάθηα ασκήσεω //006 Μελέτη οοδιάστατου στοιχειακού στερεού ε δύο τροχιακά αά άτοο ε χρήση υβριδικώ ατοικώ τροχιακώ Θεωρούε δύο τροχιακά
ΜΑΘΗΜΑ 9 Γενικές ασκήσεις µιγαδικών
 ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
Λυµένες Ασκήσεις * * *
 Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
Αάλυση Πιάκω και Εφαρµογές Σελίδα 1 από 6 Μάθηµα 9 ο ΓΙΝΟΜΕΝΟ KRONECKER Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 15 Λυµέες Ασκήσεις Άσκηση 91 Α AB, είαι πίακες τύπου µ µ και ατίστοιχα, υπολογίσατε τη
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» TAΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΥΝΑΜΕΙΣ - ΤΑΥΤΟΤΗΤΕΣ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ (Μέρος πρώτο) ΒΑΣΙΚΗ ΘΕΩΡΙΑ
 ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» TAΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΥΝΑΜΕΙΣ - ΤΑΥΤΟΤΗΤΕΣ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ (Μέρος πρώτο) ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΥΝΑΜΕΙΣ Α είι ές πργτικός ριθός κι ές φυσικός εγλύτερος
ΠΡΟΤΥΠΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» TAΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΥΝΑΜΕΙΣ - ΤΑΥΤΟΤΗΤΕΣ ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ (Μέρος πρώτο) ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΥΝΑΜΕΙΣ Α είι ές πργτικός ριθός κι ές φυσικός εγλύτερος
είναι οι τιμές μιας μεταβλητής Χ, που αφορά τα άτομα ενός δείγματος μεγέθους v,. Συχνότητα (απόλυτη) νi
 ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός λέγεται έα σύολο που θέλουμε α εξετάσουμε τα στοιχεία του ως προς έα ή περισσότερα χαρακτηριστικά τους Μεταβλητές λέγοται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε
ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός λέγεται έα σύολο που θέλουμε α εξετάσουμε τα στοιχεία του ως προς έα ή περισσότερα χαρακτηριστικά τους Μεταβλητές λέγοται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε
Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ Ασκήσεις : 1, 2, 3, σελ. 107.
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Μαθηματικά κατεύθυνσης Γ Λυκείου. Όλη η θεωρία και οι ασκήσεις των πανελλαδικών εξετάσεων. Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς
 Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 19/03/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίνος Ιωάννου, Στέφανος Γεροντόπουλος, Σταυρούλα Γκιτάκου
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 19/03/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίος Ιωάου, Στέφαος Γεροτόπουλος, Σταυρούλα Γκιτάκου ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α5 α γράψετε στο
ΜΑΘΗΜΑ / ΤΑΞΗ : ΧΗΜΕΙΑ / Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 19/03/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: Μαρίος Ιωάου, Στέφαος Γεροτόπουλος, Σταυρούλα Γκιτάκου ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Για τις ερωτήσεις Α1 έως και Α5 α γράψετε στο
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος
 Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
αναφέρετε τις θεµελιώδεις υποθέσεις της ειδικής θεωρίας της σχετικότητας προσδιορίσετε πώς µετασχηµατίζεται ένας τανυστής 2ης τάξης
 Σηειώσεις Ηλεκτροαγητισός και Σχετικότητα, Λ. Περιβολαρόπουλος Σκοπός ΣΗΜΕΙΩΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΚΑΙ ΣΧΕΤΙΚΟΤΗΤΑ Λ. Περιβολαρόπουλος Σκοπός του κεφαλαίου είαι ια σύτοη αασκόπηση της ειδικής θεωρίας
Σηειώσεις Ηλεκτροαγητισός και Σχετικότητα, Λ. Περιβολαρόπουλος Σκοπός ΣΗΜΕΙΩΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΚΑΙ ΣΧΕΤΙΚΟΤΗΤΑ Λ. Περιβολαρόπουλος Σκοπός του κεφαλαίου είαι ια σύτοη αασκόπηση της ειδικής θεωρίας
στους μιγαδικούς αριθμούς
 Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
Τι είναι εκτός ύλης. Σχολικό έτος
 Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 79 ος ΠΑΝΕΛΛΗΝΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ο ΘΑΛΗΣ 10 Νοεμβρίου 2018 Β ΓΥΜΝΑΣΙΟΥ
 Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: 3 3 ( 8) ( 12) ( 8) ( 12) Α= + + 10 + 22. 3 3 2 2 2 ( 3) 2 ( 3) Στο διπλαό σχήμα το τρίγωο ΑΒΓ είαι ισοσκελές (ΑΒ = ΑΓ), με, και ΑΔ είαι η
Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: 3 3 ( 8) ( 12) ( 8) ( 12) Α= + + 10 + 22. 3 3 2 2 2 ( 3) 2 ( 3) Στο διπλαό σχήμα το τρίγωο ΑΒΓ είαι ισοσκελές (ΑΒ = ΑΓ), με, και ΑΔ είαι η
+ + = + + α ( β γ) ( )
 ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]
![ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β] ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]](/thumbs/20/426829.jpg) ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
z = =5 ενώ z 1 z 2. (µε απόδειξη) z = z z I. z = z. z 1 z z όπου z 1 =x 1 +y 1 i και z 2 =x 2 +y 2 i σταθεροί z παριστάνει υπερβολή µε z 2
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΕΡΓΑΣΙΑ 2 (Παράδοση:.) Λύση Ι. Το πεδίο ορισµού Α, θα προκύψει από την απαίτηση ο παρονοµαστής να είναι διάφορος του µηδενός.
 ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
ΕΡΓΑΣΙΑ (Παράδοση:.) Σηείωση: Οι ασκήσεις είναι βαθολογικά ισοδύναες Άσκηση Να προσδιορίσετε τα όρια: sin( ) I. lim, II. lim sin, III. lim ( ln ) sin z Όπου χρειαστεί να θεωρήσετε γνωστό ότι lim z z Ι.
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
1. * Δύο κανονικά οκτάγωνα είναι όμοια. Σ Λ 2. * Δύο κανονικά πολύγωνα με τον ίδιο αριθμό πλευρών είναι όμοια.
 Κεφάλαιο 11: ΚΑΝΟΝΙΚΑ ΠΟΥΓΩΝΑ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Δύο καοικά οκτάγωα είαι όμοια.. * Δύο καοικά πολύγωα με το ίδιο αριθμό πλευρώ είαι όμοια.. * Έα κυρτό πολύγωο που έχει όλες του τις
Κεφάλαιο 11: ΚΑΝΟΝΙΚΑ ΠΟΥΓΩΝΑ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Δύο καοικά οκτάγωα είαι όμοια.. * Δύο καοικά πολύγωα με το ίδιο αριθμό πλευρώ είαι όμοια.. * Έα κυρτό πολύγωο που έχει όλες του τις
ΜΙΓΑΔΙΚΟΙ 9o ΓΕΛ ΠΕΡΙΣΤΕΡΙΟΥ είναι τέλεια, να υπολογίσετε την τιμή της παράστασης: Α = (1 + i) v - (1 - i) v. 15. Αν z μιγαδικός και f (ν) = i
 Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
ΟΡΙΑ. 0 : Παραγοντοποιώ αριθµητή και παρονοµαστή και διώχνω τους παράγοντες x, x 0 που προκύπτουν.
 ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΟΡΙΑ Πηλίκα πολυωυµικώ µε µορφή 0 0 : Παραγοτοποιώ αριθµητή και παροοµαστή και διώχω τους παράγοτες, 0 που προκύπτου Περιπτώσεις µε ρίζες µορφής 0 0 Περιπτώσεις στις οποίες χρειάζεται α πολλαπλασιάσω µε
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ( ) Να αποδείξετε ότι για κάθε θετικό ακέραιο ν ισχύει : ! + 2 2! + 3 3! + +ν ν! = (ν + 1)!
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
(c f (x)) = c f (x), για κάθε x R
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α. Α η συάρτηση f είαι
ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συνδυασμός ν στοιχείων ανά κ είναι μια μη διατεταγμένη συλλογή κ στοιχείων από τα ν.
 13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
Ασαφής Λογική και Αναγνώριση Προτύπων
 Ασαφής Λογική και Αναγνώριση Προτύπων Ορισός Έστω Χ ένα τυπικό σύνολο αντικειένων, που το καλούε σύπαν, του οποίου τα στοιχεία τα συβολίζουε ε. Η σχέση του περιέχεσθε για ένα τοπικό υποσύνολο του Α του
Ασαφής Λογική και Αναγνώριση Προτύπων Ορισός Έστω Χ ένα τυπικό σύνολο αντικειένων, που το καλούε σύπαν, του οποίου τα στοιχεία τα συβολίζουε ε. Η σχέση του περιέχεσθε για ένα τοπικό υποσύνολο του Α του
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 04 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
Δ/νση Β /θµιας Εκπ/σης Φλώρινας Κέντρο ΠΛΗ.ΝΕ.Τ. (Πρόοδοι) ΠΡΟΟΔΟΙ
 ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ AA A A
 Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Αάλυση Πιάκω και Εφαρµογές Σελίδα από 0 Μάθηµα 7 ο ΚΑΝΟΝΙΚΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : Από τη σχέση (54) µέχρι τέλος του εδαφίου, σελ 5, Πρόταση 6, σελ 45, Πρόταση 66 (θεώρηµα Schur), σελ 54
Μαθηµατική Επαγωγή 175.
 Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
Μαθηµατική Επαγωγή 75. Μαθηµατική Επαγωγή Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Στο κεφάλαιο τω προόδω έχει αποδειχθεί ότι ο ισχυρισµός v( v+ ) P( v ):+ + 3 +... + v, v N είαι αληθής (ως άθροισµα
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
5 η ΕΚΑ Α ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 41.
 ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 5 η ΕΚΑ Α 4. Έστω Ω { ω, ω, ω, ω 4 } ο δειγµατικός χώρος εός πειράµατος τύχης και τα εδεχόµεα Α {ω, ω }, Β {ω, ω 4 } + Α είαι P(A B) και Ρ( Β Α ), όπου θετικός ακέραιος τότε + 4 Να αποδείξετε
0..1 ΒΑΣΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΝΝΟΙΕΣ
 Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
Πανελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γενικης Παιδειας
 ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΑΛΓΕΒΡΑ Α' ΛΥΚΕΙΟΥ. Η ΕΞΙΣΩΣΗ αx+β=0
 Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
4.6. Μη γραµµικοί ταξινοµητές Ν Back error propagation
 ΑΤΕΙ Σερρώ 4.6. Μη γραιοί ταξιοητές Back error propagaon Μία ιαφορετιή τεχιή χειαού εός πολυεπίπεου percepron για τη ταξιόηη η γραιά ιαχωριοέω λάεω βαίεται τη ατιατάταη της υάρτηης dx από ία υεχή αι ιαφορίιη
ΑΤΕΙ Σερρώ 4.6. Μη γραιοί ταξιοητές Back error propagaon Μία ιαφορετιή τεχιή χειαού εός πολυεπίπεου percepron για τη ταξιόηη η γραιά ιαχωριοέω λάεω βαίεται τη ατιατάταη της υάρτηης dx από ία υεχή αι ιαφορίιη
ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ
 ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ Α. ΑΣΦΑΛΙΣΕΙΣ ΕΠΙ ΠΟΛΛΩΝ ΚΕΦΑΛΩΝ Ορισένες φορές ένα ασφαλιστήριο καλύπτει περισσότερες από ία ζωές. Ένα προφανές παράδειγα είναι η ασφάλιση θανάτου για δύο συζύγους, καθένας
ΧΙΙ. ΑΠΟ ΚΟΙΝΟΥ ΑΣΦΑΛΙΣΕΙΣ Α. ΑΣΦΑΛΙΣΕΙΣ ΕΠΙ ΠΟΛΛΩΝ ΚΕΦΑΛΩΝ Ορισένες φορές ένα ασφαλιστήριο καλύπτει περισσότερες από ία ζωές. Ένα προφανές παράδειγα είναι η ασφάλιση θανάτου για δύο συζύγους, καθένας
c f(x) = c f (x), για κάθε x R
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 30 ΜΑΪΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΠΛΗ 12 - Πρόσθεση πινάκων, βαθμωτός πολλαπλασιασμός, γινόμενο πινάκων, ανάστροφος ενός πίνακα
 1.1 Πρόσθεση πινάκων, βαθμωτός πολλαπλασιασμός, γινόμενο πινάκων, ανάστροφος ενός πίνακα Η έννοια του πίνακα. Ένας πίνακας Α με διαστάσεις mxn, δηλαδή με m γραμμές και n στήλες, με στοιχεία πραγματικούς
1.1 Πρόσθεση πινάκων, βαθμωτός πολλαπλασιασμός, γινόμενο πινάκων, ανάστροφος ενός πίνακα Η έννοια του πίνακα. Ένας πίνακας Α με διαστάσεις mxn, δηλαδή με m γραμμές και n στήλες, με στοιχεία πραγματικούς
Επαναληπτικό Διαγώνισμα Μαθηματικών Γενικής Παιδείας Γ Λυκείου
 Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Στατιστική Συμπερασματολογία
 4. Εκτιητική Στατιτική Συπεραατολογία εκτιήεις τω αγώτω παραέτρω ιας γωτής από άποψη είδους καταοής έλεγχο τω υποθέεω που γίοται ε χέη ε τις παραέτρους ιας καταοής και ε χέη ε το είδος της καταοή. ΒΙΟ309-Εκτιητική
4. Εκτιητική Στατιτική Συπεραατολογία εκτιήεις τω αγώτω παραέτρω ιας γωτής από άποψη είδους καταοής έλεγχο τω υποθέεω που γίοται ε χέη ε τις παραέτρους ιας καταοής και ε χέη ε το είδος της καταοή. ΒΙΟ309-Εκτιητική
www.fr-anodos.gr (, )
 ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ. Το lim f ( ) έχει όηµα σε γειτοικά σηµεία µε το δηλαδή ότα ( a, ) (, β ) a. Δε µε εδιαφέρει α το ίδιο το αήκει η όχι στο πεδίο ορισµού της f αλλά µε εδιαφέρει α υπάρχου στο πεδίο ορισµού
lim f (x) = +. ΣΗΜΕΙΩΣΕΙΣ Μη πεπερασμένο όριο στο x 0 R
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμέο Όριο στο R - Κεφ..7: Όρια Συάρτησης
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓ(α) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία: Κυριακή 7 Απριλίου 0 ιάρκεια Εξέτασης: ώρες Α.. Σχολικό βιβλίο Σελίδες
Κλασικός Ορισμός Πιθανοτήτας. Κανόνες Λογισμού των Πιθανοτήτων
 P(A) Κλσικός Ορισός Πιθοτήτς Πλήθος Ευοϊκώ Περιπτώσεω Πλήθος Δυτώ Περιπτώσεω P(Ω) = Ρ() = 0 Γι κάθε εδεχόεο Α ισχύει: 0 Ρ(Α) Ν(Α) Ν(Ω) Κόες Λογισού τω Πιθοτήτω Γι συίστ / ξέ εδεχόε:. Ρ(ΑΒ) = Ρ(Α) + Ρ(Β)
P(A) Κλσικός Ορισός Πιθοτήτς Πλήθος Ευοϊκώ Περιπτώσεω Πλήθος Δυτώ Περιπτώσεω P(Ω) = Ρ() = 0 Γι κάθε εδεχόεο Α ισχύει: 0 Ρ(Α) Ν(Α) Ν(Ω) Κόες Λογισού τω Πιθοτήτω Γι συίστ / ξέ εδεχόε:. Ρ(ΑΒ) = Ρ(Α) + Ρ(Β)
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ. 1. Τι ονομάζουμε σύνολο Μιγαδικών Αριθμών; Τι ονομάζουμε πραγματικό μέρος - φανταστικό μέρος ενός μιγαδικού αριθμού z = α + βi.
 ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
 015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
Η παραπάνω ιδιότητα γενικεύεται και για περισσότερους από δύο πραγµατικούς αριθµούς. Έτσι έχουµε: αβγ α β γ = β β. d a β = α
 ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ. Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες,
 ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
78 Ερωτήσεις Θεωρίας Στα Μαθηματικά Γενικής Παιδείας
 Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 77 ος ΠΑΝΕΛΛΗΝΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ο ΘΑΛΗΣ 12 Νοεμβρίου 2016 Β ΓΥΜΝΑΣΙΟΥ ˆ ΑΔΒ.
 Τηλ 361653-3617784 - Fax: 364105 Tel 361653-3617784 - Fax: 364105 1 Νοεμβρίου 016 Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: ( ) ( 5) ( ) 3 3 3 0 15 8 3 Α= + + 3 5 3 9 Πρόβλημα Δίεται
Τηλ 361653-3617784 - Fax: 364105 Tel 361653-3617784 - Fax: 364105 1 Νοεμβρίου 016 Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: ( ) ( 5) ( ) 3 3 3 0 15 8 3 Α= + + 3 5 3 9 Πρόβλημα Δίεται
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ. όπου ν θετικός ακέραιος κ) z = 2 ( 3i 2. > να δείξετε ότι Re( )
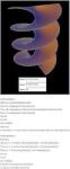 ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
4. Δεσμευμένη Πιθανότητα - Ανεξαρτησία Ενδεχομένων
 Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
Δεσμευμέη Πιθαότητα Αεξαρτησία Εδεχομέω 4 Δεσμευμέη Πιθαότητα - Αεξαρτησία Εδεχομέω 4 Γιατί δεσμευμέη πιθαότητα Το όημα της δεσμευμέης πιθαότητας Η πιθαότητα, ως έα μέτρο του βαθμού βεβαιότητας που έχουμε
ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ
 ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ 1. Α. Να βρεθού οι κ,λ R για τους οποίους είαι ίσα τα πολυώυµα ( λ + 1) x ( κ ) x λ + 1 (x) = και Q(x) = κx λx + κ Β. Να βρείτε τους πραγµατικούς αριθµούς α, β, γ R για τους
ΒΑΣΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ 1. Α. Να βρεθού οι κ,λ R για τους οποίους είαι ίσα τα πολυώυµα ( λ + 1) x ( κ ) x λ + 1 (x) = και Q(x) = κx λx + κ Β. Να βρείτε τους πραγµατικούς αριθµούς α, β, γ R για τους
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΜΕΘΟΔΟΛΟΓΙΑ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ
 ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Ρωτήσαμε 50 μαθητές μιας τάξης για το αριθμό τω αδελφώ τους Οι απατήσεις που πήραμε είαι: 0,,,,4,5 Α v, v, v, v4, v5, v 6 είαι οι ατίστοιχες συχότητες τους
ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Ρωτήσαμε 50 μαθητές μιας τάξης για το αριθμό τω αδελφώ τους Οι απατήσεις που πήραμε είαι: 0,,,,4,5 Α v, v, v, v4, v5, v 6 είαι οι ατίστοιχες συχότητες τους
Γραπτές ανακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις
 Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Γραπτές αακεφαλαιωτικές προαγωγικές και απολυτήριες εξετάσεις Δρ. Πααγιώτης Λ. Θεοδωρόπουλος Σχολικός Σύμβουλος κλάδου ΠΕ03 www.p-theodoropoulos.gr Για το υπολογισμό του βαθμού της ετήσιας επίδοσης τω
Ιγνάτιος Ιωαννίδης. Στατιστική Όριο - Συνέχεια συνάρτησης Παράγωγοι Ολοκληρώματα
 Ιγάτιος Ιωαίδης Στατιστική Όριο - Συέχεια συάρτησης Παράγωγοι Ολοκληρώματα Περιέχει: Συοπτική Θεωρία Μεθοδολογία Λύσης τω Ασκήσεω Λυμέα Παραδείγματα Ασκήσεις με τις απατήσεις τους ΘΕΣΣΑΛΟΝΙΚΗ Το βιβλίο
Ιγάτιος Ιωαίδης Στατιστική Όριο - Συέχεια συάρτησης Παράγωγοι Ολοκληρώματα Περιέχει: Συοπτική Θεωρία Μεθοδολογία Λύσης τω Ασκήσεω Λυμέα Παραδείγματα Ασκήσεις με τις απατήσεις τους ΘΕΣΣΑΛΟΝΙΚΗ Το βιβλίο
ΑΠΑΝΤΗΣΕΙΣ. ευτέρα, 17 Μα ου 2010 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ. Οµάδα Μαθηµατικών της Ώθησης. Επιµέλεια:
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 ευτέρα, 7 Μα ου 00 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ
ΑΠΑΝΤΗΣΕΙΣ. Επιµέλεια: Οµάδα Μαθηµατικών της Ώθησης
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 ΑΠΑΝΤΗΣΕΙΣ Επιµέλεια: Οµάδα Μαθηµατικώ της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 0 Τετάρτη, 3 Μα ου 0 Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α Α. Α οι συαρτήσεις f, g είαι παραγωγίσιμες στο
Παρατηρήσεις 1 Για α ααζητήσουµε το όριο της f στο, πρέπει η f α ορίζεται όσο θέλουµε κοτά στο, δηλαδή η f α είαι ορισµέη σ έα σύολο της µορφής ( α, )
 Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
ΒΑΣΙΚΕΣ ΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ
 ΚΕΦΑΛΑΙΟ 3 ΒΑΣΙΚΕΣ ΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ ΕΙΣΑΓΩΓΙΚΑ Η καταοή πιθαότητας η έση τιή και η διασπορά ιας τυχαίας εταβλητής εξετάσθηκα στο Κεφάλαιο Στο κεφάλαιο αυτό ελετώται διεξοδικά οι σηατικότερες διακριτές
ΚΕΦΑΛΑΙΟ 3 ΒΑΣΙΚΕΣ ΙΑΚΡΙΤΕΣ ΚΑΤΑΝΟΜΕΣ ΕΙΣΑΓΩΓΙΚΑ Η καταοή πιθαότητας η έση τιή και η διασπορά ιας τυχαίας εταβλητής εξετάσθηκα στο Κεφάλαιο Στο κεφάλαιο αυτό ελετώται διεξοδικά οι σηατικότερες διακριτές
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
Α. Οι Πραγματικοί Αριθμοί
 ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
xf(y) + yf(x) = (x + y)f(x)f(y)
 ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Η. ΑΣΚΗΣΕΙΣ ( T) ( 1) ( 2) 3 x =
 Αν είναι "εκ προοιίου φανερό" ότι η παραπάνω διαδικασία είναι συνεπής προς τον υπολογισό της Παραγράφου ΣΤ το προηγούενο παράδειγα επελέγη ε στόχο την επίδειξη αυτής της συνέπειας Η ΑΣΚΗΣΕΙΣ Σε ένα πίνακα
Αν είναι "εκ προοιίου φανερό" ότι η παραπάνω διαδικασία είναι συνεπής προς τον υπολογισό της Παραγράφου ΣΤ το προηγούενο παράδειγα επελέγη ε στόχο την επίδειξη αυτής της συνέπειας Η ΑΣΚΗΣΕΙΣ Σε ένα πίνακα

 ΜΑΘΗΜΑΤΙΚΑ α x +β
ΜΑΘΗΜΑΤΙΚΑ α x +β