ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ
|
|
|
- Νέμεσις Γεωργίου
- 10 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΠΕΡΙΛΗΨΗ ΣΥΜΒΟΛΙΣΜΩΝ NOTATION ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ -Bd, Steat and Lghtfoot "Tanpot Phenomena" -Bd, Amtong and Haage "Dynamc of Polymec Lqd" Οι υσικές ποσόηες σην εωρία ων αινοµένων µααοράς µπορούν να αξινοµηούν σε - Αριµηικά µονόµερα ή βαµωά µεγέη Scala, όπως ερµοκρασία, ενέργεια, όγκος - ιανυσµαικά µεγέη Vecto, όπως αχύηα, ορµή, ύναµη - Τανυσές ή ανυσικά µεγέη Second-ode teno, όπως ιαµηική άση, ρυµός ροής ορµής Με α αριµηικά µονόµερα ή βαµωά µεγέη υπάρχει µόνο ένας ρόπος πολλαπλασιασµού, όµως µε α ιανυσµαικά και ανυσικά µεγέη υπάρχουν οι εξής ρόποι: - ngle dot εσωερικό γινόµενο - doble dot : ιπλό γινόµενο - co : εξωερικό γινόµενο Οι παρακάω ύποι παρένεσης α χρησιµοποιηούν για να ηλώσουν α αποελέσµαα ων ιαορεικών πράξεων Αριµηικό µέγεος, σ : ] ιανυσµαικό µέγεος ], ] { } Τανυσικό µέγεος {σ } Το σύµβολο πολλαπλασιασµού µπορεί να ερµηνευεί σύνωνα µε α παρακάω: Σηµείο ή σύµβολο πολλαπλασιασµού Mltplcaton gn None Τάξη Ode of Relt Σ- Σ- : Σ-4 Σ
2 Παραείγµαα: η άξη είναι εύερης άξης ανυσής η άξη είναι - πρώης άξης ιάνυσµα σ: η άξη είναι -4 µηενικής άξης αριµηικό µέγεος Ορισµός ιανύσµαος: Μία ποσόηα που έχει ένα συγκεκριµένο µέγεος και ιεύυνση είναι ο µέγεος ου ιανύσµαος ύο ιανύσµαα είναι ίσα όαν α µεγέη ους είναι ίσα και οι ιευύνσεις ους συµπίπουν Πρόσεση και ααίρεση ιανυσµάων: Εσωερικό γινόµενο ngle dot ύο ιανυσµάων: co Μεαεικός commtatve v v Μη-προσεαιρισικός not aocatve v v Επιµερισικός dtbtve v ] v
3 Εξωερικό γινόµενο Co Podct ύο ιανυσµάων: ] n n όπου n είναι ένα µοναιαίο η κανονικό ιάνυσµα nt vecto κάεο nomal σο επίπεο που περιέχει α and και έχει έοια ιεύυνση, που ένας εξιόσροος κοχλίας ght-handed ce α µεακινόαν εάν σρέαµε ο προς ο µε ον συνοµόερο ρόπο Μη-µεαεικός not commtatve ] -] Μη-προσεαιρισικός not aocatve v ]] v] ] Επιµερισικός dtbtve v] ] ] v ]
4 4 ΙΑΝΥΣΜΑΤΙΚΕΣ ΠΡΑΞΕΙΣ ΑΠΟ ΑΝΑΛΥΤΙΚΗ ΠΛΕΥΡΑ ANALYTICAL VIEWPOINT Καρεσιανές συνεαγµένες,,, y, ανίσοιχα Πολλές εξισώσεις µπορούν να γραούν εύκολα χρησιµοποιώνας ο έλα ου Κonece και ον εναλλασσόµενο µοναιαίο ανυσή altenatng nt teno ε, α οποίο ορίζοναι σαν: και f f ε εάν,, ε - εάν,, ε εάν ύο ή περισσόεροι είκες είναι ίιοι Εύκολα µπορεί κάποιος να αποείξει: ε ε h h και ε ε mn m n - n m Σύµωνα µε α ανωέρω η ορίζουσα detemnant µίας µήρας µπορεί να γραεί: α α α α α α ε α α α α α α
5 5 ΟΡΙΣΜΟΣ ΙΑΝΥΣΜΑΤΟΣ ΚΑΙ ΤΟΥ ΜΕΓΕΘΟΥΣ ΤΟΥ - ΜΟΝΑ ΙΑΙΑ Ή ΚΑΝΟΝΙΚΑ ΙΑΝΥΣΜΑΤΑ Ενα ιάνυσµα ορίζεαι από ις ρεις συνισώσες ου component ή α µεγέη ων προβολών ου the magntde of t poecton,, and επάνω σους άξονες,, and, ανίσοιχα Εσι µπορούµε να γράψουµε, όπου,, and είναι α ανίσοιχα κανονικά ιανύσµαα Οι παρακάω αυόηες µπορούν να αποειχούν εύκολα: ] ] ] Ολες οι ανωέρω σχέσεις µπορούν να γραούν σαν: - ] ] - ] - ε ]
6 6 Πρόσεση ιανυσµάων: Βαµωός πολλαπλασιασµός ιανύσµα µε αριµηικό µέγεος: ] Εσωερικό γινόµενο ιανυσµάων: ] ] Εξωερικό γινόµενο ιανυσµάων: ] ] ] ε
7 7 Απόειξη Ταυόηας Παράειγµα: Απόειξε ην παρακάω αυόηα v ] v - v Η αυόηα µπορεί να αποειχεί για ην -συνισώσα -component, έσι ο άροισµα mmaton Σ µπορεί να παραληεί για λόγους απλούσευσης v ] Σ Σ ε v ] Σ Σ ε Σ l Σ m ε lm v l m ] Σ Σ Σ l Σ m ε ε lm v l m Σ Σ Σ l Σ m ε ε lm v l m Σ Σ l Σ m l m - m l v l m Σ Σ l Σ m l m v l m - Σ Σ l Σ m m l v l m Ανικαισούµε l σον πρώο όρο και m σον εύερο όρο v Σ Σ m m m - Σ Σ l l v l Ανικαισούµε m σον πρώο όρο και l σον εύερο όρο v Σ - Σ v v - v v - v
8 8 ΙΑΝΥΣΜΑΤΙΚΕΣ ΙΑΦΟΡΙΚΕΣ ΠΡΑΞΕΙΣ VECTOR DIFFERENTIAL OPERATIONS Ο ελεσής ανάελα del opeato ορίζεαι είναι ιάνυσµα ως: Η κλίση αριµηικού βαµωού πείου gadent of a cala feld: Μη-µεαεικός not commtatve L Μη-προσεαιρισικός not aocatve Επιµερισικός dtbtve Η απόκλιση ιανυσµαικού πείου dvegence of a vecto feld: ] ] Μη-µεαεικός not commtatve Μη-προσεαιρισικός not aocatve Επιµερισικός dtbtve
9 9 O σροβιλισµός ιανυσµαικού πείου cl of a vecto feld: ] ] ] ] cl ot Είναι µόνο επιµερισική Ο ελεσής ου Laplace The Laplacan Opeato: Ο ελεσής ου Laplace ορίζεαι ως: Ο ελεσής ου Laplace για ένα ιάνυσµα είναι: ] ] - Η ουσιασική παράγωγος The Sbtantal Devatve: Εάν είναι η οπική αχύηα ου ρευσού local fld velocty όε: t Dt D
10 Η ουσιασική παράγωγος btantal devatve για µια αριµηική ποσόηα είναι: D Dt t Η ουσιασική παράγωγος btantal devatve για µία ιανυσµαική ποσόηα είναι: D Dt t t Οι παραπάνω ποσόηες µπορούν να χρησιµοποιηούν για καρεσιανές συνεαγµένες Για όλες ις άλλες συνεαγµένες: ]]
11 ΤΑΝΥΣΤΕΣ Ενα ιάνυσµα,, ορίζεαι απο ις ρείς συνισώσες ου,, and Οµοια, ένας ανυσής ορίζεαι από εννέα συνισώσες ή σοιχεία nne component Τα σοιχεία,, και λέγοναι ιαγώνια, ενώ α άλλα µη-ιαγώνια Εάν,, και όε ο ανυσής λέγεαι συµµερικός ymmetc Ο ανάσροος ανυσής tanpoe ου ορίζεαι ως: * Εάν είναι συµµερικός, όε * υαικό γινόµενο ύο ιανυσµάων Dyadc Podct of To Vecto:
12 Ταυοικός ή µοναιαίος ανυσής Unt Teno: Οι συνισώσες ου µοναιαίου ανυσή είναι Κonece delta fo,, Μοναιαία υάα Unt Dyad: Είναι απλώς α υαικά γινόµενα ων µοναιαίων ιανυσµάων, m n σα οποία m,n,, Εσι, ένας ανυσής µπορεί να γραεί ως: Και ο υαικό γινόµενο ύο ιανυσµάων ως: Επίσης επισηµαίνουµε και ις εξής αυόηες:
13 cala : l l vecto ] vecto ] teno l l Αροισµα ανυσών: σ σ σ Πολλαπλασιασµός ενός ανυσή µε ένα αριµηικό µέγεος: ιπλό γινόµενο Doble Dot Podct ύο ανυσών: : : l l l σ σ σ l l : l σ l l l Ανικαισούµε l και για να απλοποιηεί ως: 4 - a cala hch σ
14 4 Εσωερικό γινόµενο ύο ανυσών Dot Podct of To Teno: l l l σ σ σ l l l σ l l l l l σ l Εσωερικό γινόµενο Dot Podct ενός ανυσή µε ένα ιάνυσµα: ] ] ιαορικές Πράξεις Dffeental Opeaton: ] ] ] Μερικές άλλες αυόηες που µπορούν εύκολα να αποειχούν: :
15 ΟΛΟΚΛΗΡΩΤΙΚΑ ΘΕΩΡΗΜΑΤΑ ΓΙΑ ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ INTEGRAL THEOREMS FOR VECTORS AND TENSORS 5 Θεώρηµα απόκλισης καά Ga - Otogad Dvegence Theoem: Εάν V είναι µια κλεισή περιοχή η οποία εσωκλείεαι από µία επιάνεια S όε dv n ds n ds n ds V S S S όπου n είναι ο κάεο µοναιαίο ιάνυσµα µε ιεύυνση προς α έξω otadly dected nomal vecto dv n ds όπου είναι ένα αριµηικό µέγεος V S όπου είναι ένας ανυσής ] dv V n ] ds S Θεώρηµα σροβιλισµού καά Stoe Cl Theoem: Εάν S είναι µία επιάνεια η οποία εσωκλείεαι από µία κλεισή καµπύλη C, όε: ] S n ds t C dc όπου t είναι ο µοναιαίο εαπόµενο ιάνυσµα σην καεύυνση ολοκλήρωσης και n είναι ο µοναιαίο κάεο ιάνυσµα σο S σην καεύυνση όπου ένας εξιόσροος κοχλίας α µεακινόαν εάν η κεαλή ου περισρεόαν σην καεύυνση ολοκλήρωσης καά µήκος ου C
16 ιαόριση ή παραγώγιση ριπλού ολοκληρώµαος καά Lebnt The Lebnt Fomla fo Dffeentatng a Tple Integal: 6 d dt dv V V dv t S n ds όπου είναι η αχύηα ενός σοιχείου ης επιάνειας face element, και είναι µία αριµηική ποσόηα, η οποία µπορεί να είναι συνάρηση έσης και χρόνου, πχ,,y,,t Επίσης VVt και SSt Εάν η επιάνεια ου όγκου κινείαι µε µια οπική αχύηα ου ρευσού local fld velocty, όε d dt D ρ dv ρ dv Dt V V όπου ρ είναι η πυκνόηα ου ρευσού
17 7 ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΣΥΝΤΕΤΕΓΜΕΝΕΣ CURVILINEAR COORDINATES Mέχρι ώρα έχουµε εωρήσει καρεσιανές συνεαγµένες,, y and Οµως πολλές ορές είναι πιο υσικό βολικό να λύσουµε προβλήµαα σε καµπυλόγραµµες συνεαγµένες Οι πιο γνωσές καµπυλόγραµµες συνεαγµένες είναι οι κυλινρικές cylndcal και οι σαιρικές phecal Σην παρούσα ανάπυξη ενιαερόµασε σο πως να γράψουµε ιαορικά, όπως, v], και :v σε καµπυλόγραµµες συνεαγµένες Για να ο κάνουµε αυό χρειαζόµασε ύο εργαλεία α Την παράσαση epeon για σε καµπυλόγραµµες συνεαγµένες β Τα ιαορικά ως προς ον χώρο patal devatve ων µονοιάσαων ιανυσµάων σε καµπυλόγραµµες συνεαγµένες Κυλινρικές Συνεαγµένες Cylndcal Coodnate Οι ιµές ων,, and ανί ων, y, and Από απλή γεωµερία οι εξής παρασάσεις µπορούν να γραούν: co y y n actan y/ Για να µεαρέψουµε ιαορικά ως προς, y, and σε ιαορικά ως προς,, and, µπορούµε να χρησιµοποιήσουµε ον κανόνα ης αλυσίας σην παραγώγιση chan le of dffeentaton Εσι, n co -
18 8 co n y Με αυές ις παρασάσεις, α ιαορικά οποιωνήποε αριµηικών παρασάσεων ως προς, y and µπορούν να εκρασούν ως προς α, and αλλάζουν Χρησιµοποιώνας ριγωνοµερία, co n -n co y y y Τώρα σρέουµε ην προσοχή µας σις σχέσεις µεαξύ ων µονοιάσαων ιανυσµάων Σε καρεσιανές συνεαγµένες, y, and και σε κυλινρικές συνεαγµένες,, and Σο Σχήµα βλέπουµε όι όπως ο σηµείο P µεακινείαι οι καευύνσεις ων, Οαν λυούν οι παραπάνω σχέσεις ως προς, y, and, α εξής αποελέσµαα µπορούν να παραχούν: co - n n co y Τα ιανύσµαα και οι ανυσές µπορούν να αναλυούν σις συνισώσες ους σε όλα α συσήµαα συνεαγµένων, όπως και σην περίπωση ων καρεσιανών συνεαγµένων που έχουµε εξεάσει Για παράειγµα: v ] v - v v - v v - v
19 9 σ σ σ σ Σαιρικές Συνεαγµένες Sphecal Coodnate εξής σχέσεις: Οι σαιρικές συνεαγµένες συσχείζοναι µε ις ανίσοιχες καρεσιανές σύµωνα µε ις Σχήµα: Σαιρικές συνεαγµένες n co y y n n actan y / co actany/ Οι ιαορικές πράξεις devatve opeato είναι: co co n n co - - n co n co n n y n n co - Οι σχέσεις µεαξύ ων µοναιαίων ιανυσµάων είναι: n co n n co co co co n -n - n co Οι παραπάνω σχεσεις µπορούν να λυούν για, y, and : y y y
20 n co co co -n n n co n co y co -n Μερκά παραείγµαα πράξεων σε σαιρικές συνεαγµένες είναι: σ : σ σ σ σ σ σ σ σ σ v ] v v v
21 ΙΑΦΟΡΙΚΕΣ ΠΡΑΞΕΙΣ ΣΕ ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΣΥΝΤΕΤΑΓΜΕΝΕΣ DIFFERENTIAL OPERATIONS IN CURVILINEAR COORDINATES Ο ελεσής opeato α παραχεί σε κυλινρικές και σαιρικές συνεαγµένες Κυλινρικές: Οι εξής σχέσεις µπορούν να εξαχούν µε ιαορισµό ων σχέσεων µεαξύ ων µοναιαίων ιανυσµάων σε κυλινρικές συνεαγµένες και καρεσιανές συνεαγµένες - Ο ορισµός ου σε καρεσιανές συνεαγµένες είναι: y y Ανικαισώνας, y, and σαν συναρήσεις ων,, and και απλοποιώνας, ο ελεσής σε κυλινρικές συνεαγµένες µπορεί να γραεί:
22 Σαιρικές συνεαγµένες Οι εξής σχέσεις µπορούν να εξαχούν µε ιαορισµό ων σχέσεων µεαξύ ων µοναιαίων ιανυσµάων σε σαιρικές συνεαγµένες και καρεσιανές συνεαγµένες co - n - co n - Ο ορισµός ου ελεσή σε καρεσιανές συνεαγµένες είναι: y y Ανικαισώνας, y, and σαν συναρήσεις ων,, and, και απλοποιώνας, ο ελεσής σε σαιρικές συνεαγµένες µπορεί να γραεί: ϕ n Fo moe detal ee: RB Bd, WE Steat and EN Lghtfoot, "Tanpot Phenomena," Wley, Ne Yo, 96 RB Bd, RC Amtong and O Haage, "Dynamc of Polymec Lqd," Vol, "Fld Mechanc," Wley, Ne Yo, 977
23
24 4
25 5
26 6
27 7
_Σχήµα 2_. Σελίδα 1 από 5. τον οποίο γίνεται η µεταπτωτική κίνηση. Άξονας περιστροφής τροχού. Άξονας γύρω από. τον οποίο γίνεται η µεταπτωτική κίνηση
 ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ιονύσης Μηρόπουλος Κίνηση σερεού Παραηρήσεις ση µεαπωική κίνηση ενός σρεφόµενου ροχού Η ανάρηση αυή έγινε µε αφορµή: 1) Την πολύ καλή και ενδιαφέρουσα ανάρηση ου συναδέλφου Νίκου αµαόπουλου µε ίλο «Μεαπωική
ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ
 Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
Ε. Μ. ΠΟΛΥΤΕΧΝΕΙΟ Τµήµα Αγρονόµων-Τοπογράφων Μηχανικών Εργασήριο Συγκοινωνιακής Τεχνικής ΣΗΜΕΙΩΣΕΙΣ ΜΑΘΗΜΑΤΟΣ: ΣΧΕ ΙΑΣΜΟΣ ΣΥΓΚΟΙΝΩΝΙΑΚΩΝ ΕΡΓΩΝ - ΟΙΚΟΝΟΜΙΚΑ ΣΤΟΙΧΕΙΑ ΤΟΞΑ ΣΥΝΑΡΜΟΓΗΣ ΣΙ ΗΡΟ ΡΟΜΙΚΗΣ 1. Τόξο
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ
 ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
ΣΥΝΕΛΙΞΗ ΣΤΟ ΠΕ ΙΟ ΤΟΥ ΧΡΟΝΟΥ Για κάθε γραµµικό και χρονικά αναλλοίωο σύσηµα συνεχούς χρόνου ισχύει όι η απόκριση y() ου όαν αυό διεγείρεαι από είσοδο x() δίνεαι από η σχέση: y () = x( ) h ( ) d = x ()
Εισαγωγή στη Θεωρία Σημάτων και Συστημάτων
 Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
Εισαγωγή ση Θεωρία Σημάων και Συσημάων Ιωάννης Χαρ. Κασαβουνίδης Τμήμα Μηχ. Η/Υ Τηλεπ. & Δικύων Πανεπισήμιο Θεσσαλίας ΦΘινοπωρινό Εξάμηνο 9/ Άσκηση Να υπολογίσεε ο παρακάω άθροισμα: Θυμίζουμε ην ανάπυξη
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ. LT και μονάδες στο SI, kgm/s 2 ή N. υνισταμένη. υνισταμένη. d dt. d dt.
 ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
ΙΙΙ. ΔΙΑΤΗΡΗΣΗ (ΙΣΟΖΥΓΙΟ) ΓΡΑΜΜΙΚΗΣ ΟΡΜΗΣ ΑΣΥΜΠΙΕΣΤΗ ΡΟΗ Έσω ένα υδραυλικό σύσημα ο οποίο περιέχεαι σε έναν όγκο ελέγχου C συνολικού όγκου και ο οποίο αναλλάσει μάζα με ο περιβάλλον με ρυθμούς (παροχές
13. Συνήθεις διαφορικές εξισώσεις
 Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κ Χρισοδολίδης: Μαθηµαικό Σµπλήρµα για α Εισαγγικά Μαθήµαα Φσικής 67 3 Σνήθεις διαφορικές εξισώσεις 3 Ορισµοί Μια εξίσση πο περιέχει παραγώγος κάποιας σνάρησης, ονοµάζεαι διαφορική εξίσση ( Ε) Αν η σνάρηση
Κεφάλαιο 5 Πολλαπλοί χημικοί αντιδραστήρες
 Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Κεφάλαιο 5 Πολλαπλοί χημικοί ανιδρασήρες Σε ορισμένες περιπώσεις, σε μια χημική βιομηχανία, η χρήση ενός μόνο χημικού ανιδρασήρα δεν είναι όσο αποελεσμαική όσο θα ήαν επιθυμηό. Συνεπώς, είναι απαραίηο
Εργαστήριο Ηλεκτρικών κυκλωμάτων
 Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Εργασήριο Ηλεκρικών κυκλωμάων Αυό έργο χορηγείαι με άδεια Creaive Commons Aribuion-NonCommercial-ShareAlike Greece 3.. Σκοπός ων πειραμάων Ονομ/νυμο: Μηρόπουλος Σπύρος Τμήμα: Ε6 Το εργασήριο πραγμαοποιήθηκε
Θέματα Περασμένων Εξετάσεων και Απαντήσεις
 Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
Θέμαα Περασμένων Εξεάσεων και Απανήσεις Εξεάσεις Ιουνίου. ΘΕΜΑ.,5 μονάδα Δίνεαι ο ΓΧΑ σύσημα με κρουσική απόκριση iπ h co8 π π Να βρεθεί η έξοδός ου αν η είσοδός είναι co π co 6π co 8π i W, < Εφαρμόζονας
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ
 ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
ΜΗΧΑΝΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ ΥΛΙΚΩΝ V. ΜΙΚΡΟΠΛΑΣΤΙΚΟΤΗΤΑ ΤΩΝ ΚΡΥΣΤΑΛΛΩΝ 1. Εισαγωγή Ση µέχρι ώρα συζήησή µας για ην µηχανική συµπεριφορά ων µεαλλικών υλικών, όπου εξεάσαµε ην ελασική και ην πλασική ους συµπεριφορά
Πως λύνεται ένα πρόβληµα.
 Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
Πως λύνεαι ένα πρόβληµα. Όπως έχουµε ήδη αναφέρει, α βήµαα για ην παραγωγή λογισµικού είναι: 1. Καανόηση προβλήµαος 2. Επίλυση ου προβλήµαος 3. Λογικός έλεγχος ης λύσης (αν υπάρχουν λάθη πήγαινε σο 1.)
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ
 ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
ΚΕΦΑΛΑΙΟ 4: ΤΥΠΟΠΟΙΗΣΗ ΠΡΟΪΟΝΤΩΝ ΚΑΙ ΤΕΧΝΙΚΗ ΠΡΟΟ ΟΣ 4.1 Η ΥΙΟΘΕΤΗΣΗ ΝΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ: ΣΤΑΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ Όαν η εχνολογία εξελίσσεαι η πρώη ερώηση µας είναι καά πόσο θα υιοθεηθεί δεδοµένου ης µεγάλης εγκαεσηµένης
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ
 Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
Κεφάλαιο 8 ΑΝΑΛΥΣΗ ΒΙΟΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ ΣΤΟ ΠΕ ΙΟ ΤΗΣ ΣΥΧΝΟΤΗΤΑΣ Θεωρούµε όι Έσω X µία διακριή χρονοσειρά 0 ± ±. µ x Ε{X } και γ { X X } E { [ X µ ][ X µ ] } ( 0 ± cov + + x x Το φάσµα ισχύος ης X ορίζεαι
ΕΛΕΓΧΟΣ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΕΦΑΛΑΙΟ 2 ΚΕΦΑΛΑΙΟ 2. Πλεονεκτήματα ψηφιακού ελέγχου
 ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
ΚΕΦΑΛΑΙΟ Πλεονεκήμαα ψηφιακού ελέγχου Ικανόηα για επεξεργασία αλγορίθμων με λογισμικό ανί για harwar. Αλλαγή ου σχεδιασμού χωρίς αλλαγές σο harwar. Μείωση μεγέθους, βάρους, ισχύος καθώς και χαμηλό κόσος.
Γιάννη Σ. Μπούταλη Αναπληρωτή Καθηγητή Δ.Π.Θ. ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθητικές σημειώσεις στο μάθημα ΣΑΕ ΙΙ
 Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Γιάννη Σ Μπούαλη Αναπληρωή Καθηγηή ΔΠΘ ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ βοηθηικές σημειώσεις σο μάθημα ΣΑΕ ΙΙ Ξάνθη, Μάιος 7 Ι Μπούαλη Λύση ων εξισώσεων καάσασης ΛΥΣΗ ΤΩΝ ΕΞΙΣΩΣΕΩΝ ΚΑΤΑΣΤΑΣΗΣ Σε αυό ο κεφάλαιο
Δυναμική συμπεριφορά των λογικών κυκλωμάτων MOS. Διάλεξη 10
 Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
Δυναμική συμπεριφορά ων λογικών κυκλωμάων MOS Διάλεξη 10 Δομή ης διάλεξης Εισαγωγή Ανισροφέας NMOS με φορίο ύπου αραίωσης Ανισροφέας CMOS Διάφορα ζηήμαα Ασκήσεις Δυναμική συμπεριφορά ων λογικών κυκλωμάων
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ-I ΕΙΣΑΓΩΓΗ ΒΑΣΙΚΑ ΣΗΜΑΤΑ Μοναδιαία βηµαική συνάρηση (Ui Sep Fucio) U () =, U () =, .5 - -
ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ. Το δέλτα του Kronecker. Το σύµβολο µετάθεσης. Χρήσιµες σχέσεις ΟΡΙΣΜΟΙ (3.133) = 1 =+1. εijk. αν ijk = 123 ή 231 ή 312 (3.
 ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ ΟΡΙΣΜΟΙ Το δέλτα του Konece δ δ + 1 αν 0 αν (3.133 Το σύµβολο µετάεσης ε +1 ε 1 ε 0 αν 13 ή 31 ή 31 αν 13 ή 13 ή 31 αν οποιοιδήποτε δείκτες είναι ίδιοι (3.134 Χρήσιµες σχέσεις εεh
ΙΑΝΥΣΜΑΤΑ ΚΑΙ ΤΑΝΥΣΤΕΣ ΟΡΙΣΜΟΙ Το δέλτα του Konece δ δ + 1 αν 0 αν (3.133 Το σύµβολο µετάεσης ε +1 ε 1 ε 0 αν 13 ή 31 ή 31 αν 13 ή 13 ή 31 αν οποιοιδήποτε δείκτες είναι ίδιοι (3.134 Χρήσιµες σχέσεις εεh
ΙΑΛΕΞΕΙΣ ΜΗΧΑΝΙΚΗΣ. Την Κινηµατική (µελετάει την κίνηση των σωµάτων χωρίς να ενδιαφέρεται για τις δυνάµεις που ενεργούν στα σώµατα)
 ΙΑΛΕΞΕΙΣ ΜΗΧΑΝΙΚΗΣ ΤΕΙ / Λ, ΤΜΗΜΑ: ΜΗΧΑΝΙΚΗΣ ΒΙΟΣΥΣΤΗΜΑΤΩΝ Η Μηχανική, εκτός απο θεωρητικός, είναι και εφηρµοσµένος κλάδος της Φυσικής. Αποτελεί την ραχοκοκαλιά της σύγχρονης Μηχανολογίας και διαιρείται
ΙΑΛΕΞΕΙΣ ΜΗΧΑΝΙΚΗΣ ΤΕΙ / Λ, ΤΜΗΜΑ: ΜΗΧΑΝΙΚΗΣ ΒΙΟΣΥΣΤΗΜΑΤΩΝ Η Μηχανική, εκτός απο θεωρητικός, είναι και εφηρµοσµένος κλάδος της Φυσικής. Αποτελεί την ραχοκοκαλιά της σύγχρονης Μηχανολογίας και διαιρείται
Ροπή δύναμης. Τι προκαλεί την επιτάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω του. Τι προκαλεί την γωνιακή επιτάχυνση ενός στερεού σώματος;
 Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
Τι προκαλεί ην επιάχυνση ενός υλικού σημείου; Η άσκηση δύναμης F πάνω ου Τι προκαλεί ην γωνιακή επιάχυνση ενός σερεού σώμαος; Η ροπή δύναμης F Για να αλλάξουμε ην περισροφική καάσαση ενός σώμαος παίζουν
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ε. Στυλιάρης
 (Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
(Με ιδέες και υλικό από ΔΙΑΝΥΣΜΑΤΑ ΣΤΟΝ ΤΡΙΣΔΙΑΣΤΑΤΟ ΧΩΡΟ Καρεσιανές Συνεαγμένες Εσωερικό Γινόμενο Διανυσμάων Εξωερικό Γινόμενο Διανυσμάων Βαθμωό Γινόμενο Τριών Διανυσμάων ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης
Κεφάλαιο 3 ο. Κυκλώματα με στοιχεία αποθήκευσης ενέργειας
 Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
Κεφάλαιο 3 ο Κυκλώμαα με σοιχεία αποθήκευσης ενέργειας Η διαφορά μεαξύ ης ανάλυσης ων ωμικών κυκλωμάων, που μελεήσαμε ως ώρα, και ων κυκλωμάων που ακολουθούν είναι όι οι εξισώσεις που προκύπουν από ην
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ 1 ΣΕΙΡΑΣ FOURIER. Ανάπτυξη σειράς Dirac σε σειρά Fourier (Εκθετική Fourier):
 ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΘΕΩΡΙΑ ΣΗΜΑΤΩΝ - ΣΥΣΤΗΜΑΤΩΝ 7-5-7 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ FOURIER ΠΑΡΑ ΕΙΓΜΑ ΣΕΙΡΑΣ FOURIER Ανάπυξη σειράς Dirac σε σειρά Fourier (Εκθεική Fourier): s () = δ ( k) k = c s e d e inω inω () n = = = ιόι f () δ (
ΦΥΣΙΚΗ Ι. ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ ΣΩΜΑΤΟΣ Ισορροπία Σωματιδίου Στατική Ισορροπία Στερεού Σώματος
 ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
ΔΥΝΑΜΕΙΣ Διανυσμαική Φύση ης Δύναμης Σύνθεση Δυνάμεων ΡΟΠΗ Η Έννοια ης Ροπής Ροπή Πολλών Δυνάμεων Ζεύγος Δυνάμεων ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Α. Καραμπαρμπούνης, Ε. Συλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ,, 4 5 ΣΤΑΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
fysikoblog.blogspot.com
 fysoblog.blogspot.com Πανεπιστήμιο Αηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις ΙΙ: Αλλαγή Συστήματος Συντεταγμένων Στις σημειώσεις αυτές δίνομε την αναπαράσταση των τελεστών
fysoblog.blogspot.com Πανεπιστήμιο Αηνών Τμήμα Φυσικής Κβαντομηχανική ΙI Α. Καρανίκας και Π. Σφήκας Σημειώσεις ΙΙ: Αλλαγή Συστήματος Συντεταγμένων Στις σημειώσεις αυτές δίνομε την αναπαράσταση των τελεστών
Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ
 Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ TΑ TΡΙΑ ΣΥΝΗΘΗ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ O P(,, ) O φ φ φ P(, φ, ) P(,, φ) O φ (α) (β) (γ) (α) Κατεσιαό σύστηµα συτεταγµέω,,. (σχήµα (α)) (β) Σύστηµα
Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ TΑ TΡΙΑ ΣΥΝΗΘΗ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ O P(,, ) O φ φ φ P(, φ, ) P(,, φ) O φ (α) (β) (γ) (α) Κατεσιαό σύστηµα συτεταγµέω,,. (σχήµα (α)) (β) Σύστηµα
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ
 ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
ΚΙΝΗΤΗΡΕΣ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ Οι κινηήρες αυής ης καηγορίας ροφοδοούναι από κάποια πηγή συνεχούς άσης. Από καασκευασικής απόψεως, δεν παρουσιάζουν καμία διαφορά σε σχέση με ις γεννήριες ΣΡ. Βασικό πλεονέκημά
Μεγαλύτερες περιπέτειες
 Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Μεγαλύερες εριέειες Μεά ην ανάρηση «Ένα σύσημα σωμάων σε εριέειες» ας άμε ένα βήμα αρακάω, ση μελέη ου συσήμαος σωμάων και ης εφαρμογής ου γενικευμένου νόμου ου Νεύωνα. --------------------------------------
Που ασκείται η δύναμη στήριξης;
 Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Που σκείι η δύνμη σήριξης; Θεωρούμε μι πρισμική ράβδο μήκους l η οποί θεωρείι ιδνικό σερεό σώμ. Υποθέουμε όι η ράβδος βρίσκει «υπό κθεσώς κπόνησης». Θεωρούμε μι νοηή ομή η οποί διιρεί ην ράβδο σε δύο μέρη
Καμπυλόγραμμα Συστήματα Συντεγμένων
 Καμπυλόγραμμα Συστήματα Συντεγμένων Προσδιορίστε την αναπαράσταση των τελεστών και σε ένα καμπυλόγραμμο σύστημα συντεταγμένων. Εξειδικεύστε τα αποτέλεσματά σας στις περιπτώσεις : (α) πολικών συντεταγμένων
Καμπυλόγραμμα Συστήματα Συντεγμένων Προσδιορίστε την αναπαράσταση των τελεστών και σε ένα καμπυλόγραμμο σύστημα συντεταγμένων. Εξειδικεύστε τα αποτέλεσματά σας στις περιπτώσεις : (α) πολικών συντεταγμένων
ΦΥΣ 145 Υπολογιστικές Μέθοδοι στη Φυσική. Τελική εξέταση 5 Μάη 2007 Ομάδα 2 η
 ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
ΦΥΣ 145 Υπολογισικές Μέθοδοι ση Φυσική Τελική εξέαση 5 Μάη 2007 Ομάδα 2 η Γράψε ο ονομαεπώνυμο, αριθμό αυόηας και ο password σας σο πάνω μέρος ης αυής ης σελίδας. Πρέπει να απανήσεε και σα 5 προβλήμαα
13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ
 ETION 1 13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 13.1 Ορισµοί Μεγέθη Μια ποσότητα που εκφράζεται από ένα µόνο πραγµατικό αριθµό καλείται βαθµωτό µέγεθος. Μια ποσότητα που εκφράζεται από περισσότερους από έναν πραγµατικούς
ETION 1 13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 13.1 Ορισµοί Μεγέθη Μια ποσότητα που εκφράζεται από ένα µόνο πραγµατικό αριθµό καλείται βαθµωτό µέγεθος. Μια ποσότητα που εκφράζεται από περισσότερους από έναν πραγµατικούς
Εργαστηριακή Άσκηση Το σύστημα αναμονής M/G/1
 Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Εργασηριακή Άσκηση 4 5 Το σύσημα αναμονής M/G/ Γιάννης Γαροφαλάκης, Καθηγηής Αθανάσιος Ν.Νικολακόπουλος, Phd(c) Σκοπός ης παρούσας εργασίας είναι η εξερεύνηση ων βασικών ιδιοήων ενός από α κλασικόερα μονέλα
Νόμος Αmpere. i r. Β dl = Β(dl ακτ +dl τοξ ) = Β rdθ = 2π. Β dl = μ ο i
 Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Νόος Αmpee = o Τυχαία κλεισή διαδροή προσεγγιζεαι από ακινικά ευθ. ήαα και κυκλικά όξα dθ dθ dl ακινικά = 0 dl όξα = dθ dl = (dl ακ +dl οξ ) = dθ = o dθ = o dθ Ρευαοφόρο ς αγωγός dl = ο Νόος Αmpee Το ολοκλήρωα
Η Έννοια της τυχαίας ιαδικασίας
 Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
Η Έννοια ης υχαίας ιαδικασίας Η έννοια ης υχαίας διαδικασίας, βασίζεαι σην επέκαση ης έννοιας ης υχαίας µεαβληής, ώσε να συµπεριλάβει ο χρόνο. Σεκάθεαποέλεσµα s k ενόςπειράµαοςύχης ανισοιχούµε, σύµφωναµεκάποιοκανόνα,
ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ
 Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
Σ. Η. ΔΡΙΤΣΟΣ, 07 ΚΑΜΠΤΙΚΗ ΕΝΙΣΧΥΣΗ ΜΕ ΠΡΟΣΘΕΤΕΣ ΣΤΡΩΣΕΙΣ ΣΚΥΡΟ ΕΜΑΤΟΣ Ε ΟΜΕΝΑ οκός Οπλισµένου Σκυροέµαος Ενισχυµένη µε Σρώση Οπλισµένου Σκυροέµαος Φ0 Φ0 η ΑΡΙΘΜΗΤΙΚΗΕΦΑΡΜΟΓΗ Yλικά : C5/30, Φ0 S Άνοιγµαοκού:
, e + Σε ένα δείγμα ίδιων ραδιενεργών πυρήνων η πιθανότητα διάσπασης για κάποιο συγκεκριμένο πυρήνα είναι τυχαία.
 ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΚΕΦΑΛΑΙΟ 6 : ΠΥΡΗΝΙΚΕΣ ΔΙΑΣΠΑΣΕΙΣ Πυρηνικοί Μεασχημαισμοί Οι δυναοί πυρηνικοί μεσχημαισμοί είναι : Εκπομπή σωμαιδίων-α : 4 2 H Εκπομπή σωμαιδίων-β : - ν, + Εκπομπή ακίνων-γ : φωόνιο Σχάση : διάσπαση πυρήνα
ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ 90º. 180º ω. Οι απαντήσεις και τα σχετικά σχόλια
 Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Φυσική καεύθυνσης Γ Σερεό σώµα ΑΛΛΑΓΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΟΥ ΑΞΟΝΑ ΠΕΡΙΣΤΡΟΦΗΣ ΣΤΡΕΦΟΜΕΝΟΥ ΣΩΜΑΤΟΣ άξονας 9º 18º Ο ροχός ου σχήµαος έχει ροπή αδράνειας Ι και σρέφεαι γύρ από ον άξονά ου µε γνιακή αχύηα µέρου.
Digital Integrated Circuits, 2 nd edition, J. M. Rabaey, A. Chandrakasan, B. Nikolic
 Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
Πρόβληµα 4. gital Itegrated Circuits, d editio, J. M. abaey, A. Chadrakasa, B. Nikolic You are desigig a clock distributio etwork i which it is critical to miimize skew betwee local clocks (CLK, CLK, ad
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ
 ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΚΙΝΗΤΙΚΗ ΑΛΥΣΩΤΩΝ ΑΝΤΙΔΡΑΣΕΩΝ ΠΟΛΥΜΕΡΙΣΜΟΥ ΚΑΙ ΜΟΡΙΑΚΗ ΚΑΤΑΝΟΜΗ ΤΩΝ ΛΑΜΒΑΝΟΜΕΝΩΝ ΠΡΟΪΟΝΤΩΝ Η ρόοδος ης ανίδρασης μορί να υολογισί: Τιλοδόηση διλών δσμών Μαβολή ου όγκου ου μέσου ης ανίδρασης Μέρηση ης
ΠΕΡΙΕΧΟΜΕΝΑ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ...23 ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...15 ΚΕΦΑΛΑΙΟ 3 ΕΥΘΕΙΕΣ...32 ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...43
 ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ. ΑΠΟΛΥΤΗ ΤΙΜΗ. ΑΝΙΣΟΤΗΤΕΣ...5 ΚΕΦΑΛΑΙΟ ΣΥΣΤΗΜΑΤΑ ΟΡΘΟΓΩΝΙΩΝ ΣΥΝΤΕΤΑΓΜΕΝΩΝ... ΚΕΦΑΛΑΙΟ ΕΥΘΕΙΕΣ... ΚΕΦΑΛΑΙΟ 4 ΚΥΚΛΟΙ...4 ΚΕΦΑΛΑΙΟ 5 ΕΞΙΣΩΣΕΙΣ ΚΑΙ ΟΙ
5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών
 Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
Κεφάλαιο 5 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 5.1 Συναρτήσεις δύο ή περισσοτέρων µεταβλητών Οταν ένα µεταβλητό µέγεθος εξαρτάται αποκλειστικά από τις µεταβολές ενός άλλου µεγέθους, τότε η σχέση που συνδέει
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 3ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ
 ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ
 Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
Η ΜΑΘΗΜΑΤΙΚΗ ΜΟΥΣΙΚΗ ΕΙΣΑΓΩΓΗ Όπως είαι γωσό, η Μουσική είαι Μαθημαικά και (σο βάθος) υπάρχει, μία «αδιόραη αρμοία» μεαξύ αυώ ω δύο. Έα μουσικό έργο, διέπεαι από μαθημαικούς όμους, σε ό,ι αφορά ις σχέσεις
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ
 1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
1η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΘΕΡΜΟΚΡΑΣΙΑ ΑΕΡΑ ΚΑΙ ΜΕΤΑΦΟΡΑ ΑΙΣΘΗΤΗΣ ΘΕΡΜΟΤΗΤΑΣ ΜΕΘΟΔΟΙ ΜΕΤΡΗΣΗΣ ΘΕΡΜΟΚΡΑΣΙΑΣ Δισολή (θερμική δισολή σερεών-υγρών-ερίων) Ηλεκρική νίσση (εξάρησή ης πό θερμοκρσί) Θερμοηλεκρικό
TO MONTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (Reptation Model)
 TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
TO MOTEΛΟ ΤΗΕ ΕΡΠΙΣΗΣ (epttion Moel) Η έννοια ου σωλήνα (tube) σις περιελίξεις (entglements). Αλληλεπιδράσεις-interpenetrtion Τοπολογικοί περιορισμοί (σην lterl/κάθεη κίνηση) Tube moel [e Gennes ; Ewrs
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών :
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών :
u u u u u u u u u u u x x x x
 Βασικοί συµβολισµοί και σχέσεις ϕ ϕ ui & ϕ=, ϕ, i=, ui, j= t x x u1 u1 u1 x1 x2 x u 3 1, 1 ui, j ui, j u1, 1 ui, j ui, j u u u u u u u u u u u i 2 2 2 i, j= = i, j 2, 2 i, j = i, j 2, 2 i, j = x j x1 x2
Βασικοί συµβολισµοί και σχέσεις ϕ ϕ ui & ϕ=, ϕ, i=, ui, j= t x x u1 u1 u1 x1 x2 x u 3 1, 1 ui, j ui, j u1, 1 ui, j ui, j u u u u u u u u u u u i 2 2 2 i, j= = i, j 2, 2 i, j = i, j 2, 2 i, j = x j x1 x2
k ) 2 P = a2 x 2 P = 2a 2 x y 2 Q = b2 y 2 Q = 2b 2 y z 2 R = c2 z 2 R = 2c 2 z P x = 2a 2 Q y = 2b 2 R z = 2c 2 3 (a2 +b 2 +c 2 ) I = 64π
 Γενικά Μαθηματικά ΙΙΙ Πέμπτο σετ ασκήσεων, Λύσεις Άσκηση 1 Το θεώρημα Gauss γενικά διατυπώνεται ως: F dv = ( F η)dσ (1) V Για την άσκηση όπου μας δίνεται η σφαίρα x + y + z 4 = Φ, το κάθετο διάνυσμα η,
Γενικά Μαθηματικά ΙΙΙ Πέμπτο σετ ασκήσεων, Λύσεις Άσκηση 1 Το θεώρημα Gauss γενικά διατυπώνεται ως: F dv = ( F η)dσ (1) V Για την άσκηση όπου μας δίνεται η σφαίρα x + y + z 4 = Φ, το κάθετο διάνυσμα η,
10. Παραγώγιση διανυσµάτων
 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 51 10 Παραγώγιση διανυσµάτων 101 Παράγωγος διανυσµατικής συνάρτησης Αν οι συνιστώσες ενός διανύσµατος = είναι συνεχείς συναρτήσεις
Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 51 10 Παραγώγιση διανυσµάτων 101 Παράγωγος διανυσµατικής συνάρτησης Αν οι συνιστώσες ενός διανύσµατος = είναι συνεχείς συναρτήσεις
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών :
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών :
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ. 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διατμητικής Αντοχής Εδάφους. Διδάσκοντες: Β. Χρηστάρας Καθηγητής Β. Μαρίνος, Αν.
 ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
ΤΕΧΝΙΚΗ ΓΕΩΛΟΓΙΑ 3 η Σειρά Ασκήσεων (3B) 1. Υπολογισμός Διαμηικής Ανοχής Εδάφους Συνοχή (c) Γωνία ριβής (φ ο ) Διδάσκονες: Β. Χρησάρας Καθηγηής Β. Μαρίνος, Αν. Καθηγηής Εργασήριο Τεχνικής Γεωλογίας και
Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο ολοκλήρωμα α είδους
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 29 Σφαιρικές συντεταγμένες- Εφαρμογές διπλού και τριπλού ολοκληρώματος- -Επικαμπύλιο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ. Μέρος Α (2007-08)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ ETY-445 ΡΕΥΣΤΟ ΥΝΑΜΙΚΗ ΣΗΜΕΙΩΣΕΙΣ Μέρος Α (2007-08) ΕΙΣΑΓΩΓΗ I-1 Ρευσοµηχανική (Fluid Mechanics) είναι ο κλάδος ης εφαρµοσµένης µηχανικής (applied
Εφαρμοσμένα Μαθηματικά ΙΙ 4ο Σετ Ασκήσεων (Λύσεις) Διπλά Ολοκληρώματα Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διπλά Ολοκληρώματα Επιμέλεια: Ι. Λυχναρόπουλος. Προσεγγίστε τo ολοκλήρωμα ( + ) I d d με αθροίσματα iemann χωρίζοντας το πεδίο ολοκλήρωσης σε ίσα ορθογώνια.
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διπλά Ολοκληρώματα Επιμέλεια: Ι. Λυχναρόπουλος. Προσεγγίστε τo ολοκλήρωμα ( + ) I d d με αθροίσματα iemann χωρίζοντας το πεδίο ολοκλήρωσης σε ίσα ορθογώνια.
- Ομοιότητα με βάση τις εξισώσεις Νavier-Stokes - 2- διάστατη ασυμπίεστη Ροή
 ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΚΕΦΑΛΑΙΟ 8 ΡΟΗ ΠΡΑΓΜΑΤΙΚΟΥ ΡΕΥΣΤΟΥ-ΣΥΝΕΚΤΙΚΗ ΡΟΗ - Ιξώδες - Ομοιόηα με βάση ις εξισώσεις Νaier-Stkes - - διάσαη ασυμπίεση Ροή ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ 0 ΕΞΙΣΩΣΕΙΣ ΟΡΜΗΣ t 1 μ 1 g μ t - Οιακές Συνθήκες B σο -
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ.
 ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΙΕΡΕΥΝΗΣΗ ΚΑΙ ΑΝΑΛΥΤΙΚΗ ΠΑΡΟΥΣΙΑΣΗ ΥΠΟΛΟΓΙΣΜΩΝ ΚΛΩΘΟΕΙ ΟΥΣ, Ι ΙΑΙΤΕΡΑ ΣΕ ΜΗ ΤΥΠΙΚΕΣ ΕΦΑΡΜΟΓΕΣ. Ν. Ε. Ηλιού Επίκουρος Καθηγητής Τµήµατος Πολιτικών Μηχανικών Πανεπιστηµίου Θεσσαλίας Γ.. Καλιαµπέτσος Επιστηµονικός
ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ
 ΠΑΡΑΡΤΗΜΑ ΙΙ ΠΑΡΑΡΤΗΜΑ ΙΙ ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ ΠΙΝΑΚΑΣ ΜΟΝΑ ΕΣ ΜΕΓΕΘΩΝ ΣΤΟ MK ΣΥΜΒΟΛΟ ΜΕΓΕΘΟΥΣ M (ή L ) Αλληλεπαγωγή (hen) H ΟΝΟΜΑ ΜΕΓΕΘΟΥΣ (ΜΟΝΑ Α) ΣΥΜΒΟΛΟ ΜΟΝΑ ΑΣ ΙΑΣΤΑΣΕΙΣ L Αυτεπαγωγή
ΠΑΡΑΡΤΗΜΑ ΙΙ ΠΑΡΑΡΤΗΜΑ ΙΙ ΜΟΝΑ ΕΣ, ΣΤΑΘΕΡΕΣ, ΧΡΗΣΙΜΕΣ ΣΧΕΣΕΙΣ ΠΙΝΑΚΑΣ ΜΟΝΑ ΕΣ ΜΕΓΕΘΩΝ ΣΤΟ MK ΣΥΜΒΟΛΟ ΜΕΓΕΘΟΥΣ M (ή L ) Αλληλεπαγωγή (hen) H ΟΝΟΜΑ ΜΕΓΕΘΟΥΣ (ΜΟΝΑ Α) ΣΥΜΒΟΛΟ ΜΟΝΑ ΑΣ ΙΑΣΤΑΣΕΙΣ L Αυτεπαγωγή
6. ΙΑΦΟΡΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΡΟΗΣ
 6.1 ΚΙΝΗΜΑΤΙΚΗ ΡΟΪΚΟΥ ΣΤΟΙΧΕΙΟΥ 6. ΙΑΦΟΡΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΡΟΗΣ -Λεπτοµέρειες της ροής Απειροστός όγκος ελέγχου - ιαφορική Ανάλυση Περιγραφή πεδίων ταχύτητας και επιτάχυνσης Euleian, Lagangian U U(x,y,,t)
6.1 ΚΙΝΗΜΑΤΙΚΗ ΡΟΪΚΟΥ ΣΤΟΙΧΕΙΟΥ 6. ΙΑΦΟΡΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΡΟΗΣ -Λεπτοµέρειες της ροής Απειροστός όγκος ελέγχου - ιαφορική Ανάλυση Περιγραφή πεδίων ταχύτητας και επιτάχυνσης Euleian, Lagangian U U(x,y,,t)
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
11. Βαθµίδα, Απόκλιση, Στροβιλισµός
 56 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής Βαθµίδα, Απόκλιση, Στροβιλισµός Βαθµίδα Έστω µια συνεχής βαθµωτή συνάρτηση,, Αν σε ένα σηµείο διατηρήσουµε σταθερά τα και και
56 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής Βαθµίδα, Απόκλιση, Στροβιλισµός Βαθµίδα Έστω µια συνεχής βαθµωτή συνάρτηση,, Αν σε ένα σηµείο διατηρήσουµε σταθερά τα και και
Μαθηματική Εισαγωγή - Διανύσματα 25/7/2014
 Κωνσταντίνος Χ. Παύλου Φυσικός Ραδιοηλεκτρολόγος (MSc) 2 ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορή Επίλυση βασικών μορών εξισώσεων Συναρτήσεις
Κωνσταντίνος Χ. Παύλου Φυσικός Ραδιοηλεκτρολόγος (MSc) 2 ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορή Επίλυση βασικών μορών εξισώσεων Συναρτήσεις
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ
 ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
ΡΟΗ ΠΟΛΥΜΕΡΙΚΩΝ ΤΗΓΜΑΤΩΝ ΣΕ ΑΓΩΓΟΥΣ. Ιξώδες Έσω ροή µεαξύ δύο παράλληλων πλακών εµβαδού Α και ανοίγµαος Η (Σχ. ). Σχ. du ιαµηική άση: =η =η γ dy () όπου: γ ο ρυθµός διάµησης, η ο ιξώδες. Παραηρήσεις για
Καρτεσιανό Σύστηµα y. y A. x A
 Στη γενική περίπτωση µπορούµε να ορίσουµε άπειρα συστήµατα συντεταγ- µένων τα οποία να µας επιτρέπουν να προσδιορίσουµε τη θέση ενός σηµείου. Στη Φυσική χρησιµοποιούνται αρκετά. Τα βασικά από αυτά θα εξετάσουµε
Στη γενική περίπτωση µπορούµε να ορίσουµε άπειρα συστήµατα συντεταγ- µένων τα οποία να µας επιτρέπουν να προσδιορίσουµε τη θέση ενός σηµείου. Στη Φυσική χρησιµοποιούνται αρκετά. Τα βασικά από αυτά θα εξετάσουµε
Σχήµα 1. . Μητρόπουλος Στερεό. Άξονας Β. Άξονας Α. ίσκος 2. ίσκος 1. Βάση στήριξης. Σύστηµα στήριξης του δίσκου 1. Κοχλίες σύσφιξης.
 ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
ύο δίσοι µε ιµάν ι πιχνίδι ης σροφορµής () Άξονς Άξονς ίσος ίσος Σχήµ άση σήριξης Η ειονιζόµενη διάξη σο σχήµ είνι έν σύσηµ δύο οριζόνιων δίσων µε µάζες Μ, Μ ι ίνες,, συνεζευγµένων µε ιµάν, που µπορούν
Διανύσματα. ! Ο απλούστερος ορισμός διανύσματος είναι ότι μετρά μετατοπίσεις. ! Διανύσματα περιγράφουν μέτρο αλλά και κατεύθυνση
 Επισκόπιση Θα µελετήσουµε την κίνηση σωµάτων και πώς οι αλληλεπιδράσεις τους µε άλλα σώµατα επηρεάζουν τη κίνηση αυτή Η µελέτη αυτή στηρίζεται σε µετρηµένο αριµό εµελιωδών αρχών που συσχετίζουν αιτία και
Επισκόπιση Θα µελετήσουµε την κίνηση σωµάτων και πώς οι αλληλεπιδράσεις τους µε άλλα σώµατα επηρεάζουν τη κίνηση αυτή Η µελέτη αυτή στηρίζεται σε µετρηµένο αριµό εµελιωδών αρχών που συσχετίζουν αιτία και
Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος (Λύσεις) Ι. Λυχναρόπουλος
 3/4/6 Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος (Λύσεις) Ι. Λυχναρόπουλος Άσκηση (Μονάδες.5) Έστω το ολοκλήρωμα: I da {(, ) :, } 3 ( + 3 ) Να εκφράσετε το ολοκλήρωμα σε νέες συντεταγμένες, οι οποίες ορίζονται
3/4/6 Εφαρμοσμένα Μαθηματικά ΙΙ Πρόοδος (Λύσεις) Ι. Λυχναρόπουλος Άσκηση (Μονάδες.5) Έστω το ολοκλήρωμα: I da {(, ) :, } 3 ( + 3 ) Να εκφράσετε το ολοκλήρωμα σε νέες συντεταγμένες, οι οποίες ορίζονται
( ) { } ( ) ( ( ) 2. ( )! r! e j ( ) Κίνηση στερεών σωμάτων. ω 2 2 ra. ω j. ω i. ω = ! ω! r a. 1 2 m a T = T = 1 2 i, j. I ij. r j. d 3! rρ. r! e!
 Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Εργαστήριο Ανώτερης Γεωδαισίας Μάθημα 7ου Εξαμήνου (Ακαδ. Έτος ) «Εισαγωγή στο Γήινο Πεδίο Βαρύτητας»
 Εργαστήριο Ανώτερης Γεωδαισίας Μάθημα 7ου Εξαμήνου (Ακαδ. Έτος 018 19 «Εισαγωγή στο Γήινο Πεδίο Βαρύτητας» ΟΝΟΜΑΤΕΠΩΝΥΜΟ... ΕΞΑΜΗΝΟ... Ημερομηνία Παράδοσης : 6/11/018 ΑΣΚΗΣΗ 3 Σκοπός: Η παρούσα εργασία
Εργαστήριο Ανώτερης Γεωδαισίας Μάθημα 7ου Εξαμήνου (Ακαδ. Έτος 018 19 «Εισαγωγή στο Γήινο Πεδίο Βαρύτητας» ΟΝΟΜΑΤΕΠΩΝΥΜΟ... ΕΞΑΜΗΝΟ... Ημερομηνία Παράδοσης : 6/11/018 ΑΣΚΗΣΗ 3 Σκοπός: Η παρούσα εργασία
, της οποίας το µέτρο ικανοποιεί τη σχέση:
 Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Στην κορυφή της κεκλιµένης έδρας µιας ορθογώνιας σφήνας µάζας M, η οποία ισορροπεί πάνω σε λείο οριζόντιο έδαφος, αφήνεται µικ ρός κύβος µάζας m. Nα δείξετε ότι η σφήνα κινείται στο σύστη µα αναφοράς του
Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να:
 6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις
 ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
Στροφορµή. υο παρατηρήσεις: 1) Η στροφορµή ενός υλικού σηµείου, που υπολογίζουµε µε βάση τα προηγούµενα, αναφέρεται. σε µια ορισµένη χρονική στιγµή.
 Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
Κανονισμός Πυροπροστασίας Κτιρίων (π.δ. 41/2018)
 Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
Κανονισμός Πυροπροσασίας Κιρίων (π.δ. 41/2018) Πεδίο Εφαρμογής Πεδίο Εφαρμογής Α. Σα κίρια ή μήμαα κιρίων, που ανεγείροναι μεά ην έναρξη ισχύος ου και ων οποίων οι χρήσεις εμπίπουν σε μία από ις περιπώσεις
ιάνυσµα ονοµάζεται το µαθηµατικό µέγεθος που περιγράφεται από µιατριάδαστοιχείων: το
 Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων ΜΑΘΗΜΑΤΙΚΑ Ι Μαθηµατικά Ι Ακαδ. Έτος 2008-9 1/44 1. Ορισµοί 2. Είδη διανυσµάτων 3. Πράξεις διανυσµάτων 4. Εσωτερικό, εξωτερικό και µικτό γινόµενο
Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων ΜΑΘΗΜΑΤΙΚΑ Ι Μαθηµατικά Ι Ακαδ. Έτος 2008-9 1/44 1. Ορισµοί 2. Είδη διανυσµάτων 3. Πράξεις διανυσµάτων 4. Εσωτερικό, εξωτερικό και µικτό γινόµενο
ιονύσης Μητρόπουλος νόµος του Νεύτωνα έχει για το σωµατίδιο τη µορφή F = (2), (3).
 ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ιούσης Μηρόπουλος Σερεό ΣΥΣΤΗΜΑ ΣΩΜΑΤΙ ΙΩΝ, ΣΤΕΡΕΟ ΣΩΜΑ ΟΣ ΝΟΜΟΣ ΤΟΥ ΝΕΥΤΩΝΑ Έα σωµαίδιο, Ορµή, Σροφορµή Ο ος όµος ου Νεύωα σε αδραειακό και µη αδραειακό σύσηµα Γωρίζουµε όι η ορµή εός σωµαιδίου µάζας
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ. Μερικές βασικές έννοιες διανυσματικού λογισμού
 ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 7 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ o ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Λ 4. Λ. Σ. Σ 4. Λ. Λ. Σ 4. Σ 4. Σ 4. Σ 44. Σ 5. Σ 5. Σ 45. Σ 6. Σ 6.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 7 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ o ΜΕΡΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Λ 4. Λ. Σ. Σ 4. Λ. Λ. Σ 4. Σ 4. Σ 4. Σ 44. Σ 5. Σ 5. Σ 45. Σ 6. Σ 6.
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός.
 1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
Παντελής Μπουμπούλης, M.Sc., Ph.D. σελ. 2 math-gr.blogspot.com, bouboulis.mysch.gr
 VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
Θεματική ενότητα : Βασικά εργαλεία και Μέθοδοι για τον έλεγχο της ποιότητας.
 Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Εργασία 5 Θεμαική ενόηα : Βασικά εργαλεία και Μέθοδοι για ον έλεγχο ης ποιόηας. Άσκηση 1 (η άσκηση έχει λυθεί βάσει ων διευκρινίσεων που δόθηκαν από ον καθηγηή ) α) Το καάλληλο σαισικό εργαλείο που θα
Λύσεις στο επαναληπτικό διαγώνισμα 3
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Λύσεις στο επαναληπτικό διαγώνισμα Διπλά Ολοκληρώματα Άσκηση (Υπολογισμός διπλού ολοκληρώματος- Αλλαγή
5 ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ
 48 49 5 ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ 5 ΕΙΣΑΓΩΓΗ ΟΡΙΣΜΟΣ: Κάθε συνάρτηση : A B με Α R n και Β R ονομάζεται πραγματική συνάρτηση n μεταβλητών ΠΑΡΑΤΗΡΗΣΕΙΣ: Ι Αν Α R n και Β R n τότε έχουμε διανυσματική συνάρτηση
48 49 5 ΣΥΝΑΡΤΗΣΕΙΣ ΔΥΟ ΜΕΤΑΒΛΗΤΩΝ 5 ΕΙΣΑΓΩΓΗ ΟΡΙΣΜΟΣ: Κάθε συνάρτηση : A B με Α R n και Β R ονομάζεται πραγματική συνάρτηση n μεταβλητών ΠΑΡΑΤΗΡΗΣΕΙΣ: Ι Αν Α R n και Β R n τότε έχουμε διανυσματική συνάρτηση
m e j ω t } ja m sinωt A m cosωt
 ΕΝΟΤΗΤΑ IV ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 26 Στρεόµενα διανύσµατα Σε κυκλώµατα όπου η διέγερση είναι περιοδική και ηµιτονοειδής οι τάσεις και τα ρεύµατα αναπαρίστανται µε µιγαδικούς αριθµούς, ή όπως συνήθως λέµε
ΕΝΟΤΗΤΑ IV ΕΝΑΛΛΑΣΣΟΜΕΝΟ ΡΕΥΜΑ 26 Στρεόµενα διανύσµατα Σε κυκλώµατα όπου η διέγερση είναι περιοδική και ηµιτονοειδής οι τάσεις και τα ρεύµατα αναπαρίστανται µε µιγαδικούς αριθµούς, ή όπως συνήθως λέµε
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not deined. Σκοποί Μαθήματος (Επικεφαλίδα
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 015 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση... Error! Bookmark not deined. Σκοποί Μαθήματος (Επικεφαλίδα
Multi Post. Ενδοριζικοί άξονες ανασύστασης
 Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Multi Post Ενδορζοί άξς ανασύσασης MultiPost Σύσηµα νδορζών αξόνων α αποαάσαση µ ρηνώδη υλά Το σύσηµα Multi Post ης D+Z που πρλαµβάν άξς αασυασµένους από αθαρό άνο ίνα ένα ύολο σο χρσµό α δοµασµένο σύσηµα
Τα θέματα συνεχίζονται στην πίσω σελίδα
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΚΑΤΕΥΘΥΝΣΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΞΕΤΑΣΤΙΚΗ ΙΑΝΟΥΑΡΙΟΥ ΑΚΑΔ. ΕΤΟΣ 16-17 Διδάσκων : Χ. Βοζίκης Τ. Ε. Ι. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΚΑΤΕΥΘΥΝΣΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΞΕΤΑΣΤΙΚΗ ΙΑΝΟΥΑΡΙΟΥ ΑΚΑΔ. ΕΤΟΣ 16-17 Διδάσκων : Χ. Βοζίκης Τ. Ε. Ι. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ. Βιβλίο διδάσκοντα με λύσεις προβλημάτων. Κεφάλαιο 1. ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγητής
 ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
ΑΝΤΟΧΗ ΥΛΙΚΩΝ ΚΑΙ ΔΟΜΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Βιβλίο διδάσκονα με λύσεις ροβλημάων Κεφάλαιο ΕΥΡΙΠΙΔΗΣ ΠΑΠΑΜΙΧΟΣ Καθηγηής epapamic@civil.auth.gr ΝΙΚΟΣ ΧΑΡΑΛΑΜΠΑΚΗΣ Καθηγηής charalam@civil.auth.gr Αρισοέλειο Πανισήμιο
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
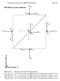 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
 1 ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 3 1.1 Γενικά.......................... 3 1.2 Ορισµοί......................... 4 1.3 Στοιχειώδεις Πράξεις Μεταξύ ιανυσµάτων....... 8 1.3.1 Γινόµενο Αριθµού επί ιάνυσµα.........
1 ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 3 1.1 Γενικά.......................... 3 1.2 Ορισµοί......................... 4 1.3 Στοιχειώδεις Πράξεις Μεταξύ ιανυσµάτων....... 8 1.3.1 Γινόµενο Αριθµού επί ιάνυσµα.........
Κεφάλαιο 4. Θεωρήµατα οµής
 Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
Κεφάαιο 4 Θεωρήαα οής Σ' αυό ο εφάαιο θ αποδείξουε α Θεωρήαα οής για πεπερασένα παραγόενα R-πρόυπα, όπου R αέραια περιοχή υρίων ιδεωδών, (απι) 4 Ανάυση σε άθροισα περιοδιού αι εεύθερου, ανάυση σοιχείο
( ) ( ) ( )! r a. Στροφορμή στερεού. ω i. ω j. ω l. ε ijk. ω! e i. ω j ek = I il. ! ω. l = m a. = m a. r i a r j. ra 2 δ ij. I ij. ! l. l i.
 Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 1. Σχήµα 1 Σχήµα 2
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
c(2x + y)dxdy = 1 c 10x )dx = 1 210c = 1 c = x + y 1 (2xy + y2 2x + y dx == yx = 1 (32 + 4y) (2x + y)dxdy = 23 28
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-7: Πιθανότητες-Χειµερινό Εξάµηνο 5 ιδάσκων : Π. Τσακαλίδης Λύσεις 6ης Σειρά Ασκήσεων Ασκηση. (α) Εχουµε ότι : 6 5 x= y= 6 x= 6 x= c(x + y)dxdy = ) c
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-7: Πιθανότητες-Χειµερινό Εξάµηνο 5 ιδάσκων : Π. Τσακαλίδης Λύσεις 6ης Σειρά Ασκήσεων Ασκηση. (α) Εχουµε ότι : 6 5 x= y= 6 x= 6 x= c(x + y)dxdy = ) c
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών f
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Βαθμωτές Συναρτήσεις Πολλών Μεταβλητών f
ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
 ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ A u B Μέτρο Διεύθυνση Κατεύθυνση (φορά) Σημείο Εφαρμογής Διανυσματικά Μεγέθη : μετάθεση, ταχύτητα, επιτάχυνση, δύναμη Μονόμετρα Μεγέθη : χρόνος, μάζα, όγκος, θερμοκρασία,
ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ A u B Μέτρο Διεύθυνση Κατεύθυνση (φορά) Σημείο Εφαρμογής Διανυσματικά Μεγέθη : μετάθεση, ταχύτητα, επιτάχυνση, δύναμη Μονόμετρα Μεγέθη : χρόνος, μάζα, όγκος, θερμοκρασία,
