|
|
|
- Δημήτριος Ζάππας
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ÆÓØ ÙÐ Ò Ð Ê ÐØÖ ¾¼¼µ ÐÑ Åº ÐÓ ÐÓÒºÙÖºÖµ ÇÈÈ»ÍÊ ÈÖÓÖÑ ÒÒÖ ÐØÖ Ü ÈÓ ØÐ ¼ È ¾½½¹¾ ÊÓ ÂÒÖÓ Ê Ìк ¼µ ¾½µ ¾¾¹¾ ¼µ ¾½µ ¾¾¹¾ ܺ ¼µ ¾½µ ¾¾¹¾
2
3 ÈÖ Ó Ø ÒÓØ ÙÐ ÓÒØÑ Ó ÑØÖÐ ÔÖ ÒØÓ Ò ÙÐ ÔÐÒ Ç ½ Ò Ð Ê ÐØÖ Ó ÙÖ Ó Å ØÖÓ ÓÙØÓÖÓ Ó ÈÖÓÖÑ ÒÒÖ ÐØÖ ÇÈÈ»Íʺ Ç ÓØÚÓ ÒÓØ ÐØÖ Ó ÓÑÔÒÑÒØÓ ÔÐÒ ÖÙÞÒÓ Ò Ó ÐÙÒÓ Ñ ÒÓØÖ ÒÓÖÑ ÓÖÒ Ñ ÙÐ ÔÖÑØÒÓ Ó Ñ ÑÓ ÙÑ ÐØÙÖ ÒØÔ Ó ÙÒØÓ ÜÔÓ ØÓ º Ø ÒÓØ ÒÓ ØÑ Ó ÓØÚÓ Ù ØØÙÖ ÓÒ ÙÐØ ÐÓÖ ÖÓÑÒ Ò ÔÐÒ ÕÙÐ ÓÒØÑ ÒÓÖÑ ÑÙØÓ Ñ ÖÒÒØ ÕÙ ÕÙ ÔÖ ÒØ º ÈÖØ Ó ÑØÖÐ ÔÖ ÒØÓ ØÑ ÙÑ Ö ØÖ ÖÚ Ó ÙÒØÓ ØÙÓ Ñ ÔÐÒ ÖÙÓº ÇÓØÚÓÒØÖÓÙÞÖ ØÔÓ Ñ ÙÑ ÔÐÒ Ô ¹ÖÙÓ ÒÚÐÖ Ó ÓÒÑÒØÓ ÐÙÒÓ ÓÑ ÖÒØ ÓÖÑ ÙÒÓÖÑÞÖ ÒÓØÓ ÒÓÑÒÐØÙÖ ÙØÐÞ º Ø ÒÓØ ÙÐ ÚÑ ÒÓ ÖÚ ÑÔÐ Ó ÐÓÒÓ Ú ÖÓ ÒÓ ÓÑÔÒÒÓ ÚÓÐÙÓ ÐØÖØÙÖ ÒÓ ØÑ ÓÖÖÒÓ ÖÖÓ Óº ÒØÖØÒØÓ Ô Ö Ó ÓÖÓ Ñ ÐÑÒÖ ÖÖÓ ÐÙÒ Ò ÔÖ ØѺ Ç ÙØÓÖ Ö ÒØÔÑÒØ Ó ÐØÓÖ ÕÙ ÒÖÑ ÚÒØÙ ÖÖÓ ÒÓÒØÖÓ º ÓÖÑ ØÙÐ Ø ÒÓØ ÙÐ ÒÓ Ö ÔÓ ÚÐ Ñ Ù Ò ¹ ØÑ ÚÐ Ó ÐÙÒÓ Å ØÖÓ ÓÙØÓÖÓ ÕÙ ÙØÐÞÖÑ ÔÓÒØÖÑ ÖÖÓ ÓÑ ÓÒØ Ñ ÒØÖÓÖ Ó ÕÙ Ó ÙØÓÖ ÔÖ ÒØ Ù ÔÖÓÙÒÓ ÖÑÒØÓº Ø ÖÑÒØÓ ØÒ ÔÖÓ ÓÖ ÖÑÒ ÄÙ ÌÒÖÓ ÓÖ ÓÑ ÕÙÐ Ó ÙØÓÖ ØÑ ÚÓ ¹ ÔÐÒ Ò Ð Ê ÐØÖ ÒÓ ÐØÑÓ ÒÓ ÕÙ ØÑ ÓÒØÖÙÓ ÚÑÒØ ÒÓ ÔÖÓÑÒØÓ Ø ØÜØÓº ÊÓ ÂÒÖÓ ÅÖÓ ¾¼¼ ÐÑ ÅºÐÓ
4
5 ÓÒØÓ ½ Ë ØÑ ÐØÖÓ ÈÓØÒ ½ ½º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ ØÖÙØÙÖ ÙÒÓÒÐ Ó ËÈ º º º º º º º º º º º º º º º º º º ½ ½º¾º½ Ë ØÑ ÐØÖÓ Ö ÐÖÓ º º º º º º º º º º º º º º º º ¾ ½º ÈÐÒÑÒØÓ ÇÔÖÓ ËÈ º º º º º º º º º º º º º º º ½º ØÙÓ ÖÖÑÒØ ÓÑÔÙØÓÒ º º º º º º º º º º º º ½º Ê ØÖÙØÙÖÓ Ó ËÈ º º º º º º º º º º º º º º º º º º º º ½ºº½ ÈÖÚØÞÓ Ê ØÖÙØÙÖÓ Ó ËØÓÖ ÐØÖÓ Ö¹ ÐÖÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ÅÓÐÓ ÓÑÔÓÒÒØ ½½ ¾º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½ ¾º¾ ÄÒ ÌÖÒ Ñ Ó Ñ º º º º º º º º º º º º º º º º º º ½½ ¾º ÐÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¾ ¾º ÌÖÒ ÓÖÑÓÖ º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ºº½ ÌÖÒ ÓÖÑÓÖ ÓÑ ÖÐÓ ØÖÒ ÓÖÑÓ ÚÖ¹ ÚÐ Ó Ö º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ºº¾ ÌÖÒ ÓÖÑÓÖ ØÖ Ó º º º º º º º º º º º º º º º º ½ ¾ºº ÌÖÒ ÓÖÑÓÖ ÓÑ ØÖ ÒÖÓÐÑÒØÓ º º º º º º º º ½ ¾º ÖÓÖ ÓÑÔÒ ÓÖ ËÒÖÓÒÓ º º º º º º º º º º º º º ½ ¾º ÒÓ ÔØÓÖ ÁÒÙØÓÖ º º º º º º º º º º º º º º º ½ ¾º ÓÑÔÒ ÓÖ Ø ØÓ º º º º º º º º º º º º º º º º º º º º ½ ¾º Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾½ ¾ºº½ ÅÓÐÓ ÓÑÔÓ ØÓ ¹ ÁÈ º º º º º º º º º º º º º º º º º ¾½ ¾ºº¾ ÅÓÐÓ ÜÔÓÒÒÐ º º º º º º º º º º º º º º º º º º º ¾¾ ÐÙÜÓ ÈÓØÒ ¾ º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾ ÓÖÑÙÐÓ Ó ÈÖÓÐÑ º º º º º º º º º º º º º º º º º º º º º ¾ º¾º½ ÅÓÐÓ Ê º º º º º º º º º º º º º º º º º º º º º ¾ º¾º¾ ÌÔÓ ÖÖ º º º º º º º º º º º º º º º º º º º º º º ¾ º¾º ÓÒÙÒØÓ Ó ÕÙ º º º º º º º º º º º º º º ½ º ËÓÐÙÓ Ó ÈÖÓÐÑ º º º º º º º º º º º º º º º º º º º º º º º
6 º ÅØÓÓ ËÓÐÙÓ º º º º º º º º º º º º º º º º º º º º º º º ºº½ ÖØÖÓ ÈÖ Ó ËÓÐÙÓ º º º º º º º º º º º º º ºº¾ ÅØÓÓ Ù ¹ËÐ º º º º º º º º º º º º º º º º º ºº ÅØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ º º º º º º º º º º º º º º º ºº ÅØÓÓ ÓÔÐÓ Ê ÔÓ º º º º º º º º º º º º º º ¾ º ÓÒØÖÓÐ ÄÑØ Ò ËÓÐÙÓ Ó ÐÙÜÓ ÈÓØÒ º º º º º ºº½ ÅØÓÓ ÁÑÔÐÑÒØÓ º º º º º º º º º º º º º º º º ÐÙÐÓ ÈÖ ÐÙÜÓ ÈÓØÒ ØÚ ÊØÚ º º º ÐÙÜÓ ÈÓØÒ ÄÒÖÞÓ ½ º½ ÕÙ º º º º º º º º º º º º º º º º º º º º º º º º º ½ º¾ ÓÖÑÙÐÓ ÅØÖÐ º º º º º º º º º º º º º º º º º º º º º º º ¾ º ÁÒÐÙ Ó ÈÖ ÒÓ ÅÓÐÓ ÄÒÖÞÓ º º º º º º º º º º º º ÊÐÓ ËÒ Ð º º º º º º º º º º º º º º º º º º º º º º Ò Ð ÐØÖ ÒÓ ÅÓÐÓ ÄÒÖÞÓ º º º º º º º º º ºº½ ÐØÖ Ò ÓÒÓ Ö¹ÖÓ º º º º º º º º ºº¾ ÐØÖ Ò Ö º º º º º º º º º º º º º º º º º º º º ¼ º ÅØÓÓ Ó ØÓÖ ØÖÙÓ º º º º º º º º º º º º º º º ½ ºº½ ØÓÖ ØÖÙÓ ÔÖ ÐÓÑÒØÓ ÖÓ º ¾ ºº¾ ØÓÖ ØÖÙÓ ÔÖ ÐÑÒØÓ ÊÑÓ º º ºº ØÓÖ ØÖÙÓ ÓÑÒÓ ÐÓÑÒØÓ ÖÓ ÐÑÒØÓ ÊÑÓ º º º º º º º º º º º º ºº ØÓÖ ØÖÙÓ ÓÑÒÓ ÐÑÒØÓ Ó ÊÑÓ º º º º º º º º º º º º º º º º º º º º º º º º ºº ØÓÖ ØÖÙÓ ÔÖ ÌÖÒ ÖÒ ÈÓØÒ º ÐÙÜÓ ÈÓØÒ ØÑÓ º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º½º½ ÓÖÑÙÐÓ Ó ÈÖÓÐÑ º º º º º º º º º º º º º º º º º º½º¾ ÔÐ º º º º º º º º º º º º º º º º º º º º º º º º º ¼ º½º ÅØÓÓ ËÓÐÙÓ À ØÖÓ º º º º º º º º º º º º º ¼ º¾ ÆØÙÖÞ Ó ÈÖÓÐÑ º º º º º º º º º º º º º º º º º º º º º º ½ º ÓÖÑÙÐÓ ÅØÑ Ø º º º º º º º º º º º º º º º º º º º º º ½ º º½ ÎÖ Ú º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º¾ Ê ØÖ ÁÙÐ º º º º º º º º º º º º º º º º º ¾ º º Ê ØÖ ÙÐ º º º º º º º º º º º º º º º º º ÙÒÓ ÇØÚÓ º º º º º º º º º º º º º º º º º º º º º º ÐÙÜÓ ÈÓØÒ ØÑÓ ÄÒÖÞÓ º º º º º º º º º º º º º º º ÐÙÜÓ ÈÓØÒ ØÑÓ ÄÒÖÞÓ ÓÑ Ê ØÖ Ë¹ ÙÖÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º ÅØÓÓ ÓÑÑÐ ² ÌÒÒÝ º º º º º º º º º º º º º º º º º º ºº½ ÈÇ Ñ Ê ØÖ ÙÐ º º º º º º º º º º ºº¾ Ê ØÖ ÙÐ Ò ÚÖ Ú ÓÒØÖÓÐ º Ú
7 ºº Ê ØÖ ÙÐ ÙÒÓÒ Ò ÚÖ Ú ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º ÅØÓÓ ÆÛØÓÒ º º º º º º º º º º º º º º º º º º º º º º º º ºº½ ÓÖÑÙÐÓ º º º º º º º º º º º º º º º º º º º º ºº¾ ËÐÓ Ó ÓÒÙÒØÓ Ê ØÖ ØÚ º º º º º º º º ÅØÓÓ Ó ÈÓÒØÓ ÁÒØÖÓÖ º º º º º º º º º º º º º º º º º º ¼ ÚÐÓ Ø Ø ØÐ ÌÒ Ó º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º¾ ÖØÖ Ø È¹Î È¹É º º º º º º º º º º º º º º º º º º º º º Ò Ð ËÒ Ð É¹Î È¹Î º º º º º º º º º º º º º º º ½¼ º Ò Ð ÅÓÐ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¼ º ÐÙÜÓ ÈÓØÒ ÓÒØÒÙÓ º º º º º º º º º º º º º º º º º º ½¼ ºº½ ÊÓÖÑÙÐÓ ÕÙ Ó ÐÙÜÓ ÈÓØÒ º º º ½¼ ºº¾ ØÔ ÈÖÚ Ó º º º º º º º º º º º º º º º º º º º º ½¼ ºº ØÔ ÓÖÖÓ º º º º º º º º º º º º º º º º º º º º ½¼ Ë ØÑ ÕÙ ÐÖ ÄÒÖ ½½ º½ ÁÒØÖÓÙÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½ º¾ ÅØÓÓ ËÓÐÙÓ º º º º º º º º º º º º º º º º º º º º º º º ½½ º ÅØÓÓ ÖØÓ º º º º º º º º º º º º º º º º º º º º º º º º º ½½ º º½ ÐÑÒÓ Ù º º º º º º º º º º º º º º º º º º º ½½ º º¾ ØÓÖÓ ÄÍ º º º º º º º º º º º º º º º º º º º º º º º ½½ º ÇÖÒÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¾¼ ºº½ ÇÖÒÓ ÔÖ ÈÖ ÖÚÖ ÔÖ º º º º º º º º ½¾¼ ºº¾ ÊÔÖ ÒØÓ ØÖÙØÙÖ ÅØÖÞ ÔÓÖ ÖÓ º º ½¾½ ºº ÕÙÑ ÇÖÒÓ º º º º º º º º º º º º º º º º º ½¾ º ÖÑÞÒÑÒØÓ ÅØÖÞ ÔÖ º º º º º º º º º º º º º ½¾ º ÅØÓÓ ÁØÖØÚÓ º º º º º º º º º º º º º º º º º º º º º º º º ½¾ ºº½ ÅØÓÓ ÂÓ º º º º º º º º º º º º º º º º º º º º º ½¾ ºº¾ ÅØÓÓ Ù ¹ËÐ º º º º º º º º º º º º º º º º º ½ ¼ ºº ÅØÓÓ ËÓÖÖÐÜÓ Ù Ú ËÇʵ º º º º º º ½ ½ ºº ÓÒÚÖÒ º º º º º º º º º º º º º º º º º º º º º º º ½ ½ ºº ÅØÓÓ Ó ÖÒØ ÓÒÙÓ º º º º º º º º º º º º ½ ¾ ºº ÅØÓÓ Ó ÖÒØ ÓÒÙÓ ÈÖ¹ÓÒÓÒÓ º º ½ ºº ÅØÓÓ Ó ÖÒØ ¹ÓÒÙÓ ØÐÞÓ º º º ½ ÈÖÓÖÑÓ ÆÓ¹ÄÒÖ ½ º½ ÒÙÒÓ ÖÐ º º º º º º º º º º º º º º º º º º º º º º º º º ½ º½º½ Ó ÈÖØÙÐÖ º º º º º º º º º º º º º º º º º º º º ½¼ º¾ ÊÔÖ ÒØÓ Ö º º º º º º º º º º º º º º º º º º º º º º ½¼ º ÓÒ ÇØÑÐ º º º º º º º º º º º º º º º º º º º º ½½ º º½ ÈÈÆÄ Ñ Ê ØÖ º º º º º º º º º º º º º º º º º º ½¾ º º¾ ÈÈÆÄ ÓÑ Ê ØÖ ÁÙÐ º º º º º º º º º º º ½¾ Ú
8 º º ÈÈÆÄ ÓÑ Ê ØÖ ÁÙÐ ÙÐ º º ½ º ÅØÓÓ ËÓÐÙÓ Ó ÈÈÆÄ Ñ Ê ØÖ º º º º º º º º º ½ ºº½ ÅÒÑÞÓ ÍÒÖÓÒÐ º º º º º º º º º º º º º º º º ½ ºº¾ ÅØÓÓ Ó ÖÒØ º º º º º º º º º º º º º º º º º º º ½¾ ºº ÅØÓÓ ÆÛØÓÒ º º º º º º º º º º º º º º º º º º º º ½¾ º ÅØÓÓ ËÓÐÙÓ Ó ÈÈÆÄ ÓÑ Ê ØÖ º º º º º º º º º ½ ºº½ ÅØÓÓ ÈÒÐ º º º º º º º º º º º º º º º º º ½ ÈÖÓÖÑÓ ÄÒÖ ½ º½ Ç ÈÖÓÐÑ ÈÖÓÖÑÓ ÄÒÖ º º º º º º º º º º º º º º ½ º¾ ÖØÖÞÓ ÐÖ º º º º º º º º º º º º º º º º º º º º º ½ º Ç ÅØÓÓ ËÑÔÐÜ º º º º º º º º º º º º º º º º º º º º º º º º ½¾ º ÓÖÑ ÅØÖÐ Ó ÅØÓÓ ËÑÔÐÜ º º º º º º º º º º º º º º ½ º ÙÐ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º Ò Ð ËÒ Ð º º º º º º º º º º º º º º º º º º º º º ½ Ú
9 ÔØÙÐÓ ½ Ë ØÑ ÐØÖÓ ÈÓØÒ ½º½ ÁÒØÖÓÙÓ Ø ÔØÙÐÓ ÔÖ ÒØ ÙÑ Ú Ó ÖÐ Ó ØÙÓ Ë ØÑ ÐØÖÓ ÈÓØÒ Ëȵ Ó ÔÓÒØÓ Ú Ø Ù ØÖÙØÙÖ ÙÒÓÒÐ ÔÐÒÑÒØÓ ÓÔÖÓ ØÙÓ ÖÖÑÒØ ÓÑÔÙØÓÒ º ØÑÑ ÔÖ ÒØ ÙÑ ÒØÖÓÙÓ Ó ÔÖÓ Ó Ö ØÖÙØÙÖÓ Ó ØÓÖ ÐØÖÓ ØÙÐÑÒØ Ñ ÒÑÒØÓº ½º¾ ØÖÙØÙÖ ÙÒÓÒÐ Ó ËÈ ÙÑ ÔÓÒØÓ Ú Ø ÙÒÓÒÐ Ó ËÈ ÔÖ ÒØÑ ÙÑ ØÖÙØÙÖ ÓÑÓ ÑÓ ØÖ Ò ÙÖ ½º½º ËÙ ÔÖÒÔ ÓÑÔÓÒÒØ Ó Ó Ù ØÑ ÖÓ ÓÑÔÓ ØÓ ÔÐ Ù Ò ÓÙ ÒØÖ ÖÓÖ º ÒØÖ ÔÓÑ Ö Ó ØÔÓ ÖÐØÖ ØÖÑ ÖÚÓ ÐÓ ÒØÙÖРغµ ÓÙ ÒÙÐÖº ÒØÖ ÖÐØÖ Ñ ÖÐ Ó ÐÓÐÞ Ñ ÔÓÒ¹ ØÓ ØÒØ Ó ÒØÖÓ ÓÒ ÙÑÓ ÜÒÓ ØÑ ØÖÒ Ñ Ó ÓÑÔÐÜÓ Ñ ØÒ Ó ÐÚº ÌÖÒ Ñ Ó ÓÒ ØØÙÓ ÔÐ ÐÒ ØÖÒ Ñ Ó ÕÙÔÑÒØÓ ÙÜÐÖ Ò ÖÓ ÔÖ ØÖÒ ÑØÖ ÒÖ ÔÖÓÙÞ Ò ÒØÖ ÖÓÖ Ø Ó ÒØÖÓ ÓÒ ÙÑÓº Ç ØÑ ØÖÒ Ñ Ó ÔÓ¹ Ñ Ö Ñ ÓÖÖÒØ ÐØÖÒ µ ÓÙ Ñ ÓÖÖÒØ ÓÒØÒÙ µ ÙÖ ½º½ ØÖÙØÙÖ ÙÒÓÒÐ ÙÑ ËÈ ½
10 ¾ Ò Ð Ê ÐØÖ ÒÓ Ó ÐØÑÓ ÙØÐÞÓ ÔÒ ÒÓ Ó ØÖÒ Ñ Ó ÖÒ ÐÓÓ ÔÓØÒ ÐÓÒ ØÒ º ØÖÙÓ ÓÒ ØØÙÓ ÔÐ Ù Ø ÐÑÒØÓÖ Ö ÔÓÒ ¹ Ú ÔÐ ØÖÙÓ ÒÖ ÐØÖ Ó ÓÒ ÙÑÓÖ ÒÙ ØÖ ÓÑÖ Ö Ò º Ñ ÖÐ ÒÐÙÑ ØÑÑ ÙÑ ÔÖØ ÐÓÐ Ó ØÑ ØÖÒ Ñ Ó Ñ ØÒ Ó Ñ Ü Ó ÕÙÐ Ö ÒÓÑÒÓ ÙØÖÒ Ñ Óº ÓÑÖÐÞÓ ÖÔÖ ÒØ Ó ÑÒØÓ ÖÔÓÒ ÚÐ ÔÐ ÓÑÔÖ ÚÒ ÒÖ ÒÓ ØÓ ÒÓ ÚÖÓº ÆÓ ÒÓÖÔÓÖ ØÚÓ ¹ Ó Ñ ÓÑÒØ Ó ÑÒ ÑÓ ÓÑÖÐÞÓ ÒÖº ÈÓÖ Ø ÖÞÓ ÖÔÖ ÒØÓ ÔÓÖ ÙÑ Ü ÔÓÒØÐ Ò ÙÖ ½º½º ÓÑÖÐÞÓ ÒÖ ÔÖ ÖÒ ÓÒ ÙÑÓÖ ÔÓ Ö Öй Þ ÖØÑÒØ Ó Ù ØÑ ØÖÒ Ñ Ó ÓÙ ÙØÖÒ Ñ Óº Æ ÙÖ ½º¾ ÔÖ ÒØÓ Ó ÖÑ ÙÒÐÖ ÙÑ ËÈ ÓÒ Ó ÐÙ ØÖÓ Ó Ù ØÑ Ñ ÖÖÓ º Æ ØÑ ÔÓØØÓ Ü ØÑ Ù ÖÒ ÒØÖ ÖÓÖ ÖÐØÖ ÐÓÐÞ ÖÒ ØÒ Ó ÒØÖÓ ÓÒ ÙÑÓº ÍÑ Ð ÓÒØ Ó ØÑ ØÖÚ ÙÑ ÐÒ ØÖÒ Ñ Ó Ñ ± ¼¼ ε ÓÙØÖ ØÖÚ ÙÑ ÐÒ ØÖÒ Ñ Ó Ñ ¼ εº ÈÖØ ÒÖ ÒØÖ ÙØÐÞ ÔÓÖ ÙÑ ØÑ ØÖÙÓ ÓÒ ØØÙÓ ÔÓÖ ÐÒ ÙØÖÒ Ñ Ó ½ ε ÔÓÖ Ú Ö Ù Ø ØÖÙÓ ÔÒ ÙÑ Ð ÑÓ ØÖ Ò ÙÖµº ÍÑ ÖÒ ÓÒ ÙÑÓÖ ÒÙ ØÖÐ ÐÑÒØÓ ÖØÑÒØ ØÖÚ Ó ØÑ ÙØÖÒ Ñ Óº ÌÑÑ Ü Ø Ò ØÑ ÙÑ ÒØÖÐ ØÖÑ ÑÓ ÔÓÖغ ÔÖØÖ Ù ØÓ ØÖÙÓ ÔÖØÑ Ð¹ ÑÒØÓÖ Ò ØÒ Ó ½ Î Ó ÕÙ ÐÑÒØÑ ÓÒ ÙÑÓÖ ÒÙ ØÖ¹ Ò ÒÚÐ ØÒ Ó ÓÒ ÙÑÓÖ ÓÑÖ Ö Ò ØÖÚ ÙÑ Ö ÙÒ Ö ØÖÙÓ Ñ ¾¾¼»½¾ κ ÓÒØ ÖØÑÒØ Ö ØÖÙÓ Ü Ø ÙÑ ÔÕÙÒ ÒØÖÐ ÖÓÖ ÕÙÐ ÖÔÖ ÒØ ØÒÒ ÑÓÖÒ ÖÓ ØÖÙº ½º¾º½ Ë ØÑ ÐØÖÓ Ö ÐÖÓ Ç ØÑ ÒÖ ÐØÖ Ö ÐÖÓ ØÑ ÑÒ ÓÒØÒÒØ º Óѹ ÔÓ ØÓ ÔÐÓ Ù ØÑ Ö ËÙ Ø ÒØÖÓ Ç Ø Ë»Çµ Ö ÆÓÖØ ÆÓÖ Ø Æ»Æµ ÊÓ ËÙР˵º Ç Ù ØÑ Ë»Ç ËÓÖÑÒØÖÐÓ Ó Ù ØÑ Æ»Æ Ñ ÞÑÖÓ ½ ÔÓÖ ÙÑ ÐÒ ØÖÒ Ñ Ó Ñ ¼¼ Î ÓÑ Ô ØÖÒ Ñ Ó ½¼¼¼ ÅÏ ÓÑ ½¼¼¼ Ñ ÜØÒ Ó ØÒÓ Ó Ù ØÖÑÒ Ò Ù Ø ÁÑÔÖØÖÞ ÅÖÒÓµ ËÖÖ Å Ó µº Ø ÒØÖÓÒÜÓ Ó ÔÓ ¹ ØÖÓÖÑÒØ ÖÓÖ ÓÑ ÓÒ ØÖÙÓ ÖÙØÓ ÔÖÐÐÓ Ó Ñ ÖÖÓ ÙÑ ÒÓÚ ÐÒ ØÖÒ Ñ Ó ÓÒØÒÓ Ù Ø ÁÑÔÖ¹ ØÖÞ ÖÓ ÑØÖÓÔÓÐØÒ ËÐÚÓÖ µº ØÑ ÓÒ ØØÙ Ó
11 ÇÈÈ»ÍÊ ± ¼¼ Î ¼ Î ÌÖÒ Ñ Ó ½ Î ¾ ¼ Î ËÙØÖÒ Ñ Ó ØÖÙÓ ½ Î ¾¾¼»½¾ Î ÙÖ ½º¾ ÖÑ ÙÒÐÖ ÙÑ ËÈ ØÔÓ ÑÓ Ë ØÑ ÁÒØÖÐÓ ÆÓÒÐ ËÁƵº ÔÒ ± Ô ÔÖÓÙÓ ÐØÖ Ó Ô ÒÓÒØÖѹ ÓÖ Ó ËÁÆ Ñ ÔÕÙÒÓ ØÑ ÓÐÓ ÐÓÐÞÓ ÔÖÒÔÐÑÒØ Ò ÖÓ ÑÞÒº ÙÖ ½º ÔÖ ÒØ ÑÐ ÔÖÒÔÐ ØÖÒ Ñ Ó Ó ËÁƺ Ô Ò ØÐ Ó ØÑ ÒØÖÐÓ Ö ÐÖÓ º ¾½ ÅÏ ÒÓ º ¾½ ÅÏ Ñ Ù Ò ÖÐØÖ ½½º¼¼¼ ÅÏ Ñ Ù Ò ØÖÑÐØÖ¹ º ÈÖ ÓØÖ Ô ÔÖÓÙÓ ØÓØÐ ÔÓÒÚÐ Ú¹ ÓÑÖ ÚÐÓÖ ÔÓÒÐ ÑÔÓÖØÓ ¾º½ ÅÏ ÖÒØÒ º½¼¼ ÅÏ ÁØÔÙ ÔÖØ ÓÒØÖØ Æ»ÈÖÙ ½ º Ç ØÑ Ö ÐÖÓ ÔÖ ÒØ ÙÑ ÓÖØ ÔÖÔÓÒÖÒ ÖÓ ¹ ÖÐØÖ Ñ ¼ ± Ô Ò Øе ÖØÖÞ¹ ÔÐ ÔÖ¹ Ò ÖÒ Ö ÖÚØÖÓ ÓÑ Ô ÖÙÐÓ ÔÐÙÖÒÙÐ Ñ Ø ØÖÙ Ñ Ú Ö ÖÓÖ º Ç ØÑ ÒÐÙ Ù Ò ÁØÔÙ ÑÓÖ Ù Ò ÖÐØÖ Ó ÑÙÒÓ ÓÑ Ô Ò ØÐ ½ Ó ÓØÓ Ò Ô Ò Ó ÇÆË Ò ÁÒØÖÒØ ÛÛÛºÓÒ ºÓÖºÖµ ÔÖ Ó ÒÓ ¾¼¼ º
12 Ò Ð Ê ÐØÖ ÙÖ ½º ÅÐ ÔÖÒÔÐ Ó ØÑ ÒØÖÐÓ Ö ÐÖÓ ÓÒØ ÇÆË ÛÛÛºÓÒ ºÓÖºÖµº ½¾º¼¼ ÅÏ ÔÖÓÔÖ ÓÑÙÑ Ó Ö Ð Ó ÈÖÙº ØÜ ØÖ Ö ÑÒØÓ Ö ÒÓ ØÑ Ö ÐÖÓ ØÑ Ó ÐÚ ÚÓ Ó ÓÖÓ ÒÙ ØÖÐÞÓ Ó Ô º Æ ¼ ØÜ Ñ Ö ÑÒØÓ Ó Ö ±º ÆÓ ÔÖÓÓ Ö Ó ÓÒÑ ÓÑÔÖÒÓ ÒÓ ÒÐ ¼ ÒÓ ¼ ØÜ ÖÙÞÙ¹ ÔÖ Ö ±º Ñ ½ Ó Ö ÑÒØÓ Ö Ó ±º ÔÖÚ Ó ÔÖ Ó ÔÖÜÑÓ Þ ÒÓ ÕÙ ÑÒ Ó ØÑ Ö ÐÖÓ ÚÖ Ö Ö ÓÑ ÙÑ ØÜ Ñ Ö ± Ó ÒÓº ½º ÈÐÒÑÒØÓ ÇÔÖÓ ËÈ ØÚ ÒÒÖ ËÈ ÔÓÑ Ö Ð Ñ ØÖ ØÓ¹ Ö ÔÖÒÔ ÒÓ¹ ÒÓ ÓÖÞÓÒØ ØÓÑ Ó ÓÒ ÖÓ ÔÖÑØ ÒÓ Ñ ÑÓº ØÓÖ Ó
13 ÇÈÈ»ÍÊ ½º ÈÐÒÑÒØÓ ÜÔÒ Ó ØÑ ÓÑÓ ÓØÚÓ ØÖÑÒÖ ÒØÖÓ ÙÑ ÓÖÞÓÒØ ÐÓÒÓ ÔÖÞÓ Ø ¼ ÒÓ µ Ó ÒÓÚÓ ÕÙÔÑÒØÓ Ö Ò ØÐÓ ÒÓ ØÑ Ú ÒÓ ØÒÖ ÙÑ ÙÑÒØÓ ÔÖÚ ØÓ ÑÒ ÒÖ ÐØÖº ÖÐÑÒØ Ó ÔÐÒÑÒØÓ ÖÐÞÓ ÓÖÑ Ñ ÓÙ ÑÒÓ ÒÔÒÒØ ÒÓ ÚÖ Ó ÐÓÓ ÙÒÓÒ Ó ØѺ ÆÓ Ó ÖÓ ØÖÒ Ñ Ó Ü Ø ÙÑ ÒØÖÓ Ñ ÓÖØ Ó ÔÖÓ Ó ÔÐÒÑÒØÓº ÈÐÒÑÒØÓ ÇÔÖÓ ØÑ ÓÑÓ ÓØÚÓ ØÐÖ ÙÑ ¹ ØÖØ ÓÔÖÓ ÒÐÙÒÓ ÔÐÒÓ ÑÖÒ ÔÖ ÙÑ ÓÖ¹ ÞÓÒØ ÑÓ ÔÖÞÓ ÔÓÖ ÜÑÔÐÓ Ø ÒÓ ÔÖ ØÑ ÖÓ¹ ØÖÑÓ ÓÑ ÖÙÐÓ ÔÐÙÖÒÙÐ ÓÑÓ Ó Ó Ó Ö Ðµº ÆÓÖ¹ ÑÐÑÒØ ÙÚÓ Ñ ÙÑ ÔÐÒÑÒØÓ ÓÔÖÓ ÒÖØ ÒÓ ÕÙÐ ÒÐ ÑÐÓÖ ØÖØ ÔÖ ÙØÐÞÓ Ó ÖÙÖ Ó ¹ ÒÖØÓ Ù ÔÓÒÚÐ ÔÖÚ Ø ÔÖ ÙÖ Ó Ö ÖÚØÖÓ Ñ ÓÒØÖÔÓ Ó Ó Ù Ó ÓÑÙ ØÚÐ Ò Ù Ò ØÖÑ µ ÙÑ ÔÐÒ¹ ÑÒØÓ ÓÔÖÓ ÐØÖ ÒÓ ÕÙÐ Ó ÒÐ Ó Ó ÑÔØÓ ÒÖØ Ó ÔÖÓÖÑ ÑÒÙØÒÓ Øº ÒÓ ÑÔÒÓ Ó Ù ØÑ ÖÓ ØÖÒ Ñ Ó Ú ÒÓ ÖÒØÖ ÙÑ ÒÚÐ ÕÙÓ ÓÒк ÇÔÖÓ Ñ ÌÑÔÓ¹ÊÐ ØÑ ÓÑÓ ÓØÚÓ ØÒÖ ÑÒ Ò ¹ ØÒØÒ Ó ØÑ ÙÒÓ ÖØÚ Ó ÔÐÒÑÒØÓ ÓÔÖ¹ Ó ÓÑ ÚÓ ÑÒÑÓ Ñ ÖÐÓ ØÒ ÖÕÙÒ ÒÓ¹ ÑÒ ÑÒÑÞÒÓ ÒØÖÖÙÔ ÒÓ ÓÖÒÑÒØÓ ÒÖº ¹ ØÙÐÑÒØ ÖÐÞÓ ÔÖØÖ Ó ÒØÖÓ ÇÔÖÓ Ë ØÑ º Ó ÕÙ ÔÓ ÙÑ Ð ÔÖ ÕÙ Ó ÖÑÓØ Ó ØÐÓ¹ ÑÒÓ Ëµ ØÑ ÓÑÔÙØÓÒ ÔÞ ÓÖÒÖ Ó ÓÔÖÓÖ ÓÒ Ñ ÕÙ ÔÖ ØÓÑ ÓÒØÖÓк ØÙÓ ÖÖÑÒØ ÓÑÔÙØÓÒ ÈÖ ÜÙØÖ ØÖ ÖÐÓÒ Ó ÔÐÒÑÒØÓ ÓÔÖÓ ËÈ ÖØ ÒÓ ØÑ ÒØÖÓÖ Ó ÒÒÖÓ ËÈ Ò ØÑ ÖÖÑÒØ ÓÑÔÙØÓÒ ÔÖ Ò Ð ÑÙÐÓ ÓÒØÖÓк ÖÖÑÒØ ÔÖ¹ ÑØÑ Ó ÒÒÖÓ ØÓÑ ÓÑ ÖÐÓ Ó ÔÐÒÑÒØÓ ÜÔÒ Ó ÑÐÓÖ ØÖØ ÓÔÖÓ ÓØÚÓ ÓÒØÖÓÐ Ó ØѺ ÙÖ Ó ÖÐÓÒ ÐÙÑ ÖÖÑÒØ ØÔÓ ØÙÓ ÙØÐÞÓ ÒÓ Ú ÖÓ Ø Ó ÒÒÖ ËÈ ÖÖÑÒØ Ò Ð ËÑÙÐÓ ÐÙÜÓ ÈÓØÒ ÙÖØÓ¹ÖÙØÓ
14 Ò Ð Ê ÐØÖ ½º ËÑÙÐÓ ÒÑ ÐØÖÓÑÒ Ò Ð ÅÓÐ ËÑÙÐÓ ÌÖÒ ØÖÓ ÐØÖÓÑÒØÓ º ÖÖÑÒØ ÇØÑÞÓ ÚÐÓ ÈÖÓÐ Ø ÐÙÜÓ ÈÓØÒ ØÑÓ ÐÙÜÓ ÈÓØÒ ÈÖÓÐ ØÓ ÚÐÓ ÓÒÐ Ë ØÑ ÖÓ ÌÖÒ Ñ Ó ØÖÙÓ ÚÐÓ ÓÒÐ ÓÑÔÓ Ø Ë ØÑ ÖÓ¹ ÌÖÒ Ñ Óº ØÙÓ»ÖÖÑÒØ ÈÐÒÑÒØÓ ÜÔÒ Ó ÈÖÚ Ó Ö ÄÓÒÓ ÈÖÞÓ ÜÔÒ Ó Ó Ë ØÑ ÖÓ ÜÔÒ Ó Ó Ë ØÑ ÌÖÒ Ñ Ó ÜÔÒ Ó Ó Ë ØÑ ØÖÙÓº ØÙÓ»ÖÖÑÒØ ÈÐÒÑÒØÓ ÇÔÖÓ ÈÖÚ Ó Ö ÅÓ ÈÖÞÓ ÈÖÓÖÑÓ ÀÖÓØÖÑ ÈÖÓÖÑÓ ÅÒÙØÒÓ ÕÙÑ ÑÖÒ ØÖÑÒÓ Ê ÖÚ ÇÔÖØÚº ÖÖÑÒØ ÇÔÖÓ Ñ ÌÑÔÓ¹ÊÐ Ë ØÑ ÕÙ Ó Ó ËÙÔÖÚ Ó Ëµ ØÑÓ ØÓ ÓÒÙÖÓ Ê ÈÖÚ Ó Ö ÙÖØÓ¹ÈÖÞÓ ÚÐÓ Ø Ø ÒÑ ËÙÖÒº Ê ØÖÙØÙÖÓ Ó ËÈ ÑÔÖ ÒÖ ÐØÖ Ñ ÕÙ ØÓÓ Ó Ô Ó ÑÙÒÓ ØÓ Ô ÒÓ ÔÓÖ ÙÑ ÔÖÓ Ó Ö ØÖÙØÙÖÓº ÑÙÒ ÒÖѹ Ò ¼ ÒÓ ÊÒÓÍÒÓ ÁÒÐØÖÖ È Ð µ Ñ ÐÙÒ Ô ÑÖ ÄØÒ Ð ÓÐÚ Øºµ ÓÖÑ ØÒ¹ ÓÙØÖÓ Ô Ò ¼º ÑÓØÚ ÔÖÒÔ ÔÖ Ó
15 ÇÈÈ»ÍÊ º º º Ì Ì Ì ÓÓÖÒÓÖ ÙÖ ½º ÇÔÖÓ Ó ËÈ ÓÑÓ ÑÓÒÓÔÐÓ ÖÙÐÓ ÔÖÓ Ó Ö ØÖÙØÙÖÓ Ó ØÓÖ ÐØÖÓ ÒÓ Ó Ò ÖÑÒØ Ñ ¹ Ñ Ñ ØÓÓ Ó Ô º Ñ ÐÙÒ Ó ÓÑÓ ÒÓ ÊÒÓ ÍÒÓ Ô ÑÖ ÄØÒ Ö ØÖÙØÙÖÓ ÓÑÔÒÓÙ Ó ÔÖÓ Ó ÔÖÚØÞÓ Ó ØÓÖ ÐØÖÓ ÖÓÒÓ ÔÖ ØÖÖ ÔØ ÔÖÚÓ ÐÖÖ Ó ÓÚÖÒÓ Ó Ô Ó ÒÚ ØÑÒØÓ Ò ÖÓ ÜÔÒ Ó Ó ØÓÖº ÆÓ Ô Ó Ä Ø ÙÖÓÔÙ Ó ÔÖÓ Ó Ù ÙÑ ØÒÒ ÒÖÐÞ ÔÖÚØÞÓ ÒØÖÐÞÓ ÑÒ ØÖØÚº ÆÓ ØÓ ÍÒÓ Ñ ÓÙØÖÓ Ô ÓÒ ÑÔÖ ÒÖ ÐØÖ Ñ Ù ÑÓÖ ÔÖØ ÖÑ ÑÔÖ¹ ÔÖÚ Ö ØÖÙØÙÖÓ ØÑ ÓÑÓ ÓØÚÓ ÙÑÒØÖ ÓÑÔØÓ ÖÙÐÑÒØÓ Ú ÒÓ ÑÒÙÖ Ó Ù ØÓ ÒÖ ÔÖ Ó ÓÒ ÙÑÓÖ ÒÐ ÓÒÙÞÖ ÙÑ ÙØÐÞÓ Ñ ÒØ Ó ÖÙÖ Ó ÒÖØÓ ÑÐÓÖ ÔÖ ÖÚÓ Ó ÑÒغ ÆÓ ÑÓÐÓ ÒØÓ ÑÔÖ ÒÖ ÐØÖ ØÑ ÙÑ ØÖÙØÙÖ ÚÖØÐ ÒÐÓÒÓ Ò ÑÓÖ Ó Ó Ó ÑÒØÓ ÖÓ ØÖÒ ¹ Ñ Ó ØÖÙÓ ÓÑÖÐÞÓº ÑÔÖ ÖÑ ÙÑ ÓÒ¹ Ó ÔÖ Ó ÓÖÒÑÒØÓ ÒÖ ÔÖ ÙÑ ØÖÑÒ ÖÓ Ó Ô ØÒÑ ÑÒ Ò ÖÓ Ù ÒÓ ÒÖ Ö ÒÓ Ù ÔÖÔÖÓ ØÑ ÓÙ ÕÙÖ ÑÔÖ ÚÞÒ ÑÒØ ÓÒØÖØÓ ÐÓÒÓ ÓÙ ÙÖØÓ ÔÖÞÓ º Ñ ÐÙÒ ØÑ ÓÒØÖØÓ ÓÖÒÑÒØÓ ÒÖ ÒØÖ ÑÔÖ ÒÓ ÖØÑÒØ ÓÒØ ÐØÖÑÒØ ÔÓÑ Ü ØÖ ÜÒÓ ØÖÒ ÖÒ ÒÖ ØÖÚ Ó ØÑ ØÖÒ Ñ Ó ÙÑ ØÖÖ ÑÔÖ ÛÐÒµº Ç ÑÓÐÓ ÓÖØÑÒØ ÖÙÐÓ ÒÓ Ü Ø ÔÓ Ð¹ ÙÑ ÑÔÖ ÓÑÖÐÞÖ ÒÖ ÖØÑÒØ ÓÒ ÙÑÓÖ ÓÖ Ù Ö ÓÒ Óº Ó ÔÓÒØÓ Ú Ø ÓÒÑÓ Ó ØÑ ÓÔÖ ÓÑÓ ÙÑ ÑÓÒÓÔÐÓ ÖÙÐÓº Ñ ÖÐ Ü Ø ÐÙÑ ÑÒ ÑÓ ÓÓÖÒÓÖ ÓÔÖÓ Ó ØÑ ÒØÖÐÓ Ó ÕÙÐ ÓÖÒØ ÚÖ ÑÔÖ ÓÑ ÓÑ ÖÐÓ Ó ÑÐÓÖ ÔÖÓÚØÑÒØÓ Ó ÖÙÖ Ó ÒÖØÓ ÓÒÐ Ó ØÑ ÐØÖÓº Ø ÑÓÐÓ ÐÙ ØÖÓ Ò ÙÖ ½ºº
16 Ò Ð Ê ÐØÖ ÍÑ ÖÒ ÚÖ ÑÓÐÓ Ö ØÖÙØÙÖÓ Ó ØÓÖ ÐØÖÓ ØÑ Ó ÔÖÓÔÓ ØÓ º Æ ÑÓÖ ÑÓÐÓ Ó ÑÑÖÑÒØÓ ÙÒÙÒÐÒµ Ó ÑÒØÓ ÖÓ ØÖÒ Ñ Ó ØÖÙÓ Ñ ÖÒØ ÑÔÖ Ø ÔÖ Òغ ØÖÒ Ñ Ó ØÖÙÓ Ó ÓÒ Ö ÑÓÒÓÔÐÓ ÒØÙÖ Ñ ÖÐ ÓÒØÒÙÑ ÖÙÐ ÑÒÖ ÔÖÑØÖ ÙÑ Ñ¹ ÒØ ÓÑÔØØÚÓ ÔÖ ÑÔÖ ÖÓ ÓÑÖÐÞÓº ÑÔÖ¹ ØÖÒ Ñ Ó ØÖÙÓ Ó ÓÖ ÔÖÑØÖ Ó Ó Ó Ù ØÑ ÑÒØ ÓÖÒ ÙÑ ÖÚÓ ØÖÒ Ñ Ó Ô Óµ ÔÓ ¹ ÐØÒÓ ØÖÒ ÒÖ ÒØÖ ÕÙ ÕÙÖ ÑÔÖ ÖÓ ÓÑÖÐÞÓ ÕÙ Ö ØÖ ÓÔÖØÚ Ó ØÑ Ñ Ó ÔÖ¹ ÑØѺ Ñ Ú ÖÓ Ô ÓÔÖÓ Ó ØÑ Ð ÙÑ ÓÙ Ñ ÇÔÖÓÖ ÁÒÔÒÒØ Ó Ë ØÑ ¹ ÇÁË ÁÒÔÒÒØ ËÝ ØÑ ÇÔÖ¹ ØÓÖ ¹ ÁËǵ Ñ ÒÒÙÑ ÒØÖ ÒÒÖÓ ÒÓ ÑÖÓ ÒÖ ÐØÖº Ç ÓÔÓ ØÙÓ Ó ÇÁË Ù ØÖÙ Ö ÔÓÒ Ð ÚÖÑ ÙÑ Ô ÔÖ ÓÙØÖÓ ÓÙ Ñ ÑÓ ÒØÖ ÇÁË ÙÑ Ñ ÑÓ Ô º ÆÓ ÑÒ¹ ÑÓ Ó ÇÁË ØÖ ÙÑ ÔÔÐ ÑÐÒØ Ó Ó ÓÓÖÒÓÖ ÓÔÖ Ó ÑÓÐÓ ÒØÓº ÆÓ ÓÙØÖÓ ÜØÖÑÓ Ð Ó ÇÁË ÔÓ Ö Ö ÔÓÒ ÚÐ ÔÐÓ ÔÐÒÑÒØÓ ÜÔÒ Ó ØÖÒ Ñ Ó ÔÐÒÑÒØÓ ÓÔÖÓ ÐØÖ ÒÖØ ÓÔÖÓ Ñ ØÑÔÓ¹Öк Ç ÇÁË ÔÓÖ ÓÙ ÒÓ Ö Ó ÔÖÓÔÖØ ÖÓ Ó ØÑ ØÖÒ Ñ Ó Ó Ù Ö ÔÓÒ Ðº Ñ Ñ ÓÖÑ Ó ÇÁË ÔÓÖ ÓÙ ÒÓ ÓÔÖÖ Ó ÑÖÓ ÒÖ ÐØÖº Ñ ÐÙÒ Ó ÓÔÖÓ Ó ÑÖÓ Ð ÙÑ ÓÙØÖ ÒØ ÒÓÑÒ ÓÐ ÒÖ ÈÓÛÖ ÜÒ ¹ ȵº Ñ ÑÙØÓ Ó ÓÇÁËÖ ÔÓÒ ÚÐ ÔÓÖ ÓÖÖ Ó ÑÓ ËÖÚÓ ÒÐÖ ÒÐÐÖÝ ËÖÚ µ Ó ÕÙ ÒÐÙÑ Ó ÓÒØÖÓÐ ÙØÓÑ ØÓ ÖÓ ÙÔÓÖØ ÖØÚÓ Ö ÖÚ ÓÔÖØÚ Øº Ñ ÓÙØÖÓ Ó Ó ÇÁË ÓÓÖÒ ÙÑ ÑÖ¹ Ó ËÖÚÓ ÒÐÖ ÔÖÓÚÓ ÔÓÖ ÓÙØÖ ÑÔÖ º ÒÐÑÒØ Ó ÒÓÚÓ ÑÓÐÓ ÖÐÑÒØ ÒÐÙ ÙÑ Ò ÓÚÖÒÑÒØÐ ÒØ ÊÙ¹ ÐÓÖµ Ö ÔÓÒ ÚÐ ÔÐÓ ÓÒØÖÓÐ ÙÔÖÚ Ó Ó ÙÒÓÒÑÒØÓ Ó ÑÖÓ ÒÖ Ó ÙÑÔÖÑÒØÓ Ó ÖØÓ Ó ÓÒ ÙÑÓÖ º ÍÑ ØÒØØÚ ÐÙ ØÖÖ Ó ÒÓÚÓ ÑÓÐÓ Ó ËÈ ÑÓ ØÖÓ Ò ÙÖ ½ºº ½ºº½ ÈÖÚØÞÓ Ê ØÖÙØÙÖÓ Ó ËØÓÖ ÐØÖÓ Ö¹ ÐÖÓ ÈÓÖ ÚÓÐØ ½¼ Ó ÓÚÖÒÓ Ö ÐÖÓ ÒÓÙ ÙÑ ÔÖÓÖÑ ÔÖÚØÞÓ Ó ØÓÖ ÐØÖÓº ÔÖÓÖÑ Þ ÔÖØ Ó ÓÖÓ Ó ÓÚÖÒÓ ÒÓ ÒØÓ ØÖÖ ÔØÐ ÔÖÚÓ ÔÖ Ó ØÓÖ ÒÖ¹ ØÖÙØÙÖ ÒÕÙÒØÓ Ó ÓÚÖÒÓ ÓÒÒØÖÚ Ù Ñ Ö ÓÑÓ ÙÓ º ÆÓ ÔÖÓÓ ¹ Ú Ö ÑÔÖ ØÖÙÓ ÖÒ ÔÓÖØ ÄØ ÐØÖÓÔÙÐÓ ÈÄ Øºµ ÓÖÑ ÚÒ ÔÖ ÖÙÔÓ ÓÖÑÓ ÔÓÖ ÒÚ ØÓÖ ÒÓÒ ØÖÒÖÓ º ÆÓ ÑÓÑÒØÓ ÑÔÖ ÔÖÚ ØÑ ¼ ± Ó ÑÖÓ ØÖÙÓ ÒÖ ÐØÖ ÒÓ Ô ÔÓÖ ÒÖ ÓÒ Ùѵ Ö ½ ± ÖÓ ÒÖ ÐØÖ ÔÓÖ ÒÖ ÔÖÓÙÞµº Ô ÑÙÒ
17 ÇÈÈ»ÍÊ ÓÐ ÒÖ ÖÓÖ ººº ººº Ì Ì Ì ÇË ººº ËÖÚÓ ÒÐÖ ÒØ ÊÙÐÓÖ ÙÖ ½º ÇÔÖÓ Ó ËÈ Ñ ÙÑ ÑÒØ ÓÑÔØØÚÓ ÓÚÖÒÓ Ñ ÒÖÓ ¾¼¼ Ó ÔÖÓ Ó ÔÖÚØÞÓ Ó ÒØÖÖÓÑÔÓº ÈÖÐÐÑÒØ Ó ÔÖÓ Ó ÔÖÚØÞÓ Ó ØÓÖ ÐØÖÓ Ö ÐÖÓ Ó ÙÑØÓ ÙÑ ÔÖÓ Ó Ö ØÖÙØÙÖÓº Ç ÑÓÐÓ ÒØÓ Ó ÒÓ ÑÓÒÓÔÐÓ ØØÐ Ó Ù ØØÙÓ ÔÓÖ ÙÑ ÒÓÚÓ ÑÓÐÓ ÓÒ Ü Ø Óѹ ÔØÓ ÒÓ ÑÒØÓ ÖÓ ÓÑÖÐÞÓº Ç ÔÖÓ Ó Ö ØÖÙØÙ¹ ÖÓ Ó ÓÒÓ ÓÖÑ ØÐ ÕÙ ÐÚ Ñ ÓÒ ÖÓ ÔÖØÙÐÖ ÓÑÒØ Ó ØÑ Ö ÐÖÓº Ñ ÙÑ ÔÖÑÖ Ó ÔÖÓ Ó ½ ¾¼¼ Ó ÒÓÚÓ ÑÓÐÓ Ó ØÑ ÐØÖÓ Ö ÐÖÓ ÔÖÚ Ü ØÒ ÙÑ ÅÖÓ Ø Ø ÒÖ Åµ ÒÓ ÕÙÐ Ó ÓÑÔÖÓÖ ÚÒÓÖ ÒÖ ÐØÖ ÔÓÑ ØÙÖ Ù ØÖÒ ÒÓ ÕÙÐ Ó ÔÖÓ ÒÖ Ö ØÐÓ ÔÖÓ ÔÓصØÖÚ ÙÑ ÔÖÓ Ó ÒØÖй ÞÓ ÓØÑÞÓº Ç Å Ó ÖÓ ÔÓÖ ÙÑ ÓÖÓ ÑÙÐØÐØÖÐ Ó ÕÙÐ ÓÖØÓÖÑÒØ ÔÖØÔÖÒ ØÓÓ Ó ÖÓÖ ÓÑ Ô Ò ØÐ ÑÓÖ ÕÙ ¼ ÅÏ ØÓÓ Ó ÓÒ ÙÑÓÖ ÓÑ ÓÒ ÙÑÓ Ñ ½¼¼ Ï ÔÓÖ ÒÓº ÖÒ ÓÒ ÙÑÓÖ ÓÑ ÓÒ ÙÑÓ Ñ ½¼ ÅÏ ÔÙÖÑ ÓÔØÖ ÔÓÖ Ö ÑÑÖÓ Ó Åº Ç ÑÓÐÓ ÓÒØÑÔÐÚ ØÑÑ Ü ØÒ Ó ÇÔÖÓÖ ÆÓÒÐ Ó Ë ØÑ ÐØÖÓ ÇÆ˵ Ó ÕÙÐ ØÑ ÙÒÓ ÓÔÖÓÖ ÒÔÒÒØ Ó ØÑ ÓÑ Ö ÔÓÒ Ð ÖÐÞÖ Ó ÔÓ ØÑÓ ÒØÖÐÞÓ ÓÖÓ ÓÑ ÖÖ Ø ÔÐÓ ÑÑÖÓ Ó Å Ó ÕÙÐ ÓØÚ ÓÔÖÓ Ó ØÑ ÓÑ Ù ØÓ ÑÒÑÓ ÑÒØÒÓ ÒÚ ÕÙÓ ÓÒ¹ к ÓÑ ÒÐ ÖÒØÖ Ó ÙÑÔÖÑÒØÓ Ð ÓÖÓ ÕÙ ÒÑ Ó ÙÒÓÒÑÒØÓ Ó ØÑ ÐØÖÓ Ö ÐÖÓ Ö ØÖÙØÙÖÓ Ó Ö¹ Ò ÆÓÒÐ ÒÖ ÐØÖ Æĵ ÒØ ÖÙÐÓÖ Ó ØÓÖ ÐØÖÓ Ö ÐÖÓº ÓÑ ÑÙÒ ÓÚÖÒÓ Ñ ÒÖÓ ¾¼¼ ÒÓÙ¹ ÙÑ ÔÖÓ Ó ÖÚ Ó Ó ÑÓÐÓ Ó ØÓÖ ÐØÖÓ Ö ÐÖÓ Ó ÕÙÐ ÙÐÑÒÓÙ ÓÑ ÔÖÓÑÙй
18 ½¼ Ò Ð Ê ÐØÖ Ó Ä ½¼º Ñ ÑÖÓ ¾¼¼ Ú ÖÓ ÖØÓ ÕÙ ØÐÖÑ ÙÑ ÒÓÚÓ ÑÖÓ ÖÙÐØÖÓº ÈÖ Ò ÓÑÖÐÞÓ ÒÖ ÐØÖ ÓÒÓÚÓ ÑÓÐÓ ÔÖÚ Ó¹Ü ØÒ Ó ÑÒØ ÓÑÖÐÞÓ ÑÒØ ÓÒØÖØÓ ÊÙРʵ ÑÒØ ÓÒØÖØÓ ÄÚÖ Äµº
19 ÔØÙÐÓ ¾ ÅÓÐÓ ÓÑÔÓÒÒØ ¾º½ ÁÒØÖÓÙÓ Ø ÔØÙÐÓ ÔÖ ÒØ ÙÑ ÖÚ Ó ÑÓÐÓ ÓÑÔÓÒÒØ ËÈ Ùع ÐÞÓ Ñ ØÙÓ ÖÑ ÔÖÑÒÒØ ÔÖØÙÐÑÒØ ÒÓ Ó Ó ÐÙÐÓ ÙÜÓ ÔÓØÒ ØÙÓ Ò Ø Óº Æ ÓØÒÓ ÑÓÐÓ Ùѹ ÕÙ Ó ÔÓ ØÚÓ Ó ÕÙÐÖÓ ÓÔÖÓ Ñ ÖÑ ÔÖѹ ÒÒØ ÒÓÐ ÖÕÒ ÒÙ ØÖÐ ¼ÀÞ ÓÙ ¼ÀÞµº ÅÓÖ ØÐ ÓÑ ÖÐÓ Ó ÑÓÐÓ ÔÖ ÒØÓ Ò Ø ÔØÙÐÓ ÔÓÑ Ö ÒÓÒØÖÓ Ñ ½ ½ º Ç ÑÓÐÓ Ó ÙÒØ ÐÑÒØÓ Ó ÔÖ ÒØÓ ÙÖ ¾º¾ ÄÒ ØÖÒ Ñ Ó Ñ ÐÓ ÌÖÒ ÓÖÑÓÖ ÖÓÖ ÓÑÔÒ ÓÖ ËÒÖÓÒÓ ÒÓ ÔØÓÖ ÁÒÙØÓÖ ÓÑÔÒ ÓÖ Ø ØÓ Ö º ÄÒ ÌÖÒ Ñ Ó Ñ Æ ÔÐ ÓÖ Ò Ø ØÖÐÓ ÐÒ ØÖÒ Ñ Ó Ñ Ó ÑÓÐ ÓÑÓ ÙÑ ÖÙØÓ π¹õùúðòø ÓÑÓ ÑÓ ØÖÓ Ò ÙÖ ¾º½ ÙÓ ÔÖÑØÖÓ Ó Ó ÔÓÖ z km = r km + jx km = z c senh(γl) ¾º½µ y s km = gs km + jbs km = 1 z c tanh(γl/2) ¾º¾µ ½½
20 ½¾ Ò Ð Ê ÐØÖ z km = r km +jx km Ñ y s km /2 ys km /2 ÙÖ ¾º½ ÖÙØÓ ÕÙÚÐÒØ ÐÒ ØÖÒ Ñ Ó ÌÐ ¾º½ ÎÐÓÖ ØÔÓ Ó ÔÖÑØÖÓ ÐÒ ØÖÒ Ñ Ó ÈÖ¹ ÄÒ Ö Ó ÑØÖÓ ¾ ¼ Î ¼¼ Î ¾ ¼ Î ¼¼ Î R (Ω/km) ¼ ¼¼ ¼ ¼¾ ¼ ¼¾ ¼ ½¾ x L = ωl (Ω/km) ¼ ¼ ¾ ¼ ¼ ¼¾ b c = ωc (μω 1 /km) ½ ¾¼¼ ¾ ÓÒ l ÓÑÔÖÑÒØÓ ÐÒ Ñµ z c = z/y ÑÔÒ ÖØÖ Ø Ωµ γ = yz ÓÒ ØÒØ ÔÖÓÔÓ z = R + jωl ÑÔÒ Ö Ω»Ñµ y = G + jωc ÑØÒ ÙÒØ Ω 1»Ñµº R, G, L C Ò ÜÔÖ Ñ ÖÔÖ ÒØÑ Ö ÔØÚÑÒØ Ö¹ ØÒ ÓÒÙØÒ ÖØÒ ÔØÒ ÔÓÖ ÐÓÑØÖÓ ÐÒº Ç ÔÖÓÑÒØÓ ÔÖ ÐÙÐÓ ÔÖÑØÖÓ ÔÓ Ö ÒÓÒØÖÓ Ñ Ú ÖÓ ÐÚÖÓ ØÜØÓ ÔÓÖ ÜÑÔÐÓ Ò ÖÖÒ ½ º Æ ØÐ ¾º½ Ó Ô¹ Ö ÒØÓ ÔÖÑØÖÓ ØÔÓ ÐÒ Ö Ó ÙØÖÖÒÓ Ñ ÔÖ Ú ÖÓ ÒÚ ØÒ Ó ½ º ¾º ÐÓ ÍÑ ØÑ ØÖÒ Ñ Ó Ñ ÓÖÖÒØ ÓÒØÒÙ µ ÓÙ ÑÔÐ ÑÒØ ÙÑ ÐÓ ÑÒØ ÓÒ ØØÙÓ ÔÓÖ Ë ØÑ Ñ ÓÖÖÒØ ÐØÖÒ µ ÙÔÖÓÖ ÌÖÑÒÐ ÓÒÚÖ ÓÖ ÓÖÖÒØ ÐØÖÒ Ñ ÓÒØÒÙ ÖØÓÖµ
21 ÇÈÈ»ÍÊ ½ ÌÖÒ ÓÖÑÓÖ ÓÑ ÓÑÙØÓ ÙØÓÑ Ø Ó Ö Ó ÓÒÚÖ¹ ÓÖ ÄÒ ØÖÒ Ñ Ó Ñ ÓÖÖÒØ ÓÒØÒÙ Ë ØÑ ØÖÖÑÒØÓ ÌÖÑÒÐ ÓÒÚÖ ÓÖ ÓÖÖÒØ ÓÒØÒÙ Ñ ÐØÖÒ ÒÚÖ ÓÖµ Ë ØÑ Ñ ÓÖÖÒØ ÐØÖÒ µ ÖÔØÓÖº Ç ÐÓ ÔÓÑ Ö ÓÒÙÖÓ ÓÖÑ ØÒØ ÒÓ ÙÒØ Ñ ÙØÐÞ Ò ÔÖ Ø ½ ÐÓ ÅÓÒÓÔÓÐÖ ÐÒ ÙØÐÞ ÙÑ ÒÓ ÓÒÙØÓÖ ÒÓÖÑÐÑÒØ ÔÓÐÖ ÒØÚ ÓÑ ÖØÓÖÒÓ ÔÐÓ ÓÐÓ ÓÙ ÔÐ Ù ÐÓ ÔÓÐÖ ÐÒ ÔÓ Ù Ó ÓÒÙØÓÖ ÙÑ ÔÓ ØÚÓ ÓÙØÖÓ ÒØÚÓ ØÖÑÒÐ ØÑ Ó ÓÒÚÖ ÓÖ ÒØÓ ÓÒØÓ Ñ Ö Ù ÙÒÓ ØÖÖ ÐÓ ÀÓÑÓÔÓÐÖ ÐÒ ÔÓ Ù Ó ÓÙ Ñ ÓÒÙØÓÖ ØÓÓ Ñ Ñ ÔÓÐÖ ÖÐÑÒØ ÒØÚ ÓÔÖ ÑÔÖ ÙØÐÞÒÓ ÖØÓÖÒÓ ÔÐÓ ÓÐÓ ÓÙ ÔÐ Ùº ÙÖ ¾º¾ ÖÔÖ ÒØ ÓÖÑ ÕÙÑ Ø ÙÑ ÐÓ ÑÓÒÓÔÓÐÖ Ö ÙØÐÞ ÓÑÓ ÔÖ ÔÖ ÒØÓ Ó ÑÓÐÓ ÐÓ º Æ ÙÖ Ó Ë ØÑ ½ Ó ÙÔÖÓÖ ÔÓØÒ Ó ØÑ ¾ Ó ÖÔØÓÖº ÙÖ ¾º¾ ÊÔÖ ÒØÓ ÕÙÑ Ø ÙÑ ÐÓ ÑÓÒÓÔÓÐÖµ Ç ÒÚÓÐÚÑÒØÓ ÑÓÐÓ ÐÓ Ü ÖÔÖ ÒØÓ Øй Ó ÙÒÓÒÑÒØÓ Ó ÓÒÚÖ ÓÖ ÓÑÔÓÒÒØ ÙÜÐÖ º ÈÖ ØÓ ØÙÓ Ñ ÖÑ ÔÖÑÒÒØ ÙÒØ ÙØÐÞÖ ÙÑ ÑÓÐÓ Ó ØÔÓ ÖÙØÓ ÕÙÚÐÒØ ÓÑÓ ÕÙÐ ÒÚÓÐÚÓ Ñ ¾½ Ó ÕÙÐ ÑÓ ØÖÓ Ò ÙÖ ¾º º Ç ÑÓÓ ÓÔÖÓ Ñ ÓÑÙÑ ÙÑ ÐÓ ÓØÓ ÓÒÙÖÒÓ¹ Ó ÖØÓÖ ÔÖ ÑÒØÖ ÓÖÖÒØ Ò ÐÒ ÓÒ ØÒØ Ó ÒÚÖ ÓÖ
22 ½ Ò Ð Ê ÐØÖ ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ ÐÒ ÓÔÖÒÓ ÓÑ ÒÙÐÓ ÜØÒÓ ÑÒÑÓº Æ Ø ÓÖÑ ÓÔÖÓ Ö¹ Ð ÒØÖ ÚÖ Ú Ó ÖÙØÓ ÕÙÚÐÒØ Ó ÐÓ Ó ÙÒØ ½ ÕÙ Ó ÁÒÚÖ ÓÖ ÕÙ Ó ÊØÓÖ V di = K i E i cosγ min R ci I d ¾º µ K i = 3 2 π b it i ¾ºµ R ci = 3 π X cib i ¾ºµ φ i = cos 1 (V di /K i E i ) ¾ºµ P i = V di I d ¾ºµ Q i = P i tanφ i ¾ºµ ÓÒ V dr = V di + R L I d ¾ºµ [ α = cos 1 Vdr + X ] cri d ¾º½¼µ K r E r 2Er t r K r = 3 2 π b rt r ¾º½½µ R cr = 3 π X crb r ¾º½¾µ φ r = cos 1 (V dr /K r E r ) ¾º½ µ P r = V dr I d ¾º½µ Q r = P r tanφ r ¾º½µ V di V dr ØÒ Ò ÐÒ ÒÓ ØÖÑÒ Ó ÒÚÖ ÓÖ Ó ÖØÓÖ
23 ÇÈÈ»ÍÊ ½ E i E r ÚÐÓÖ ÖÑ ØÒ ÒÓ ØÖÑÒ Ó ÒÚÖ ÓÖ ÓÖع ÓÖ I d ÓÖÖÒØ Ò ÐÒ R L Ö ØÒ ÐÒ γ min ÚÐÓÖ ÑÒÑÓ Ó ÒÙÐÓ ÜØÒÓ Ó ÒÚÖ ÓÖ b i b r ÒÑÖÓ ÔÓÒØ ÓÒÚÖ ÓÖ Ñ Ö ÒÓ ÒÚÖ ÓÖ ÒÓ Öع ÓÖ t i t r ÔÓ Ó ØÔ Ó ØÖÒ ÓÖÑÓÖ Ó ÒÚÖ ÓÖ Ó ÖØÓÖ X ci X cr ÖØÒ ÓÑÙØÓ ÔÓÖ ÔÓÒØ ÔÓÖ Ó ÒÚÖ ÓÖ Ó ÖØÓÖ P i P r ÔÓØÒ ØÚ ÖØÖ Ó ÒÚÖ ÓÖ ÒØ ÒÓ ÖØÓÖ Q i Q r ÔÓØÒ ÖØÚ ÑÒ ÔÐÓ ÓÒÚÖ ÓÖ ÖØÓÖº ÕÙ ÑÐÖ ÑÓ ØÖ Ñ ÔÓÑ Ö ÒÚÓÐÚ ÔÖ ÓÙØÖÓ ÑÓÓ ÓÔÖÓ Ó ÐÓ ÔÓÑ Ö ÒÓÒØÖ Ò ÖÖÒ ½ º ÓÐÙÓ ÓÒÙÒØ Ó ØÑ Ó ÐÓ ÖÐÞ ÓÖÑ ØÖØÚ ÔÖÓ ÒÓ¹ ÐØÖÒÑÒØ ÕÙ Ó ÑÓÐÓ Ó ÑÓÐÓ ÓÒ ÖÒÓ¹ ÓÒ ØÒØ ÚÖ Ú ÜØÖÒ Ó ÑÓÐÓ Ö ÔØÚÑÒغ ÆÓ ØÑ ÚÖ Ú ÜØÖÒ ÓÒ Ö Ó ØÒ E i E r ÒÕÙÒØÓ ÕÙ ÒÓ ÐÓ ÚÖ Ú Ó P i P r Q i Q r º ¾º ÌÖÒ ÓÖÑÓÖ Æ ÖÔÖ ÒØÓ ØÖÒ ÓÖÑÓÖ Ñ ØÙÓ ÖÑ ÔÖÑÒÒØ Ù ÙÐ ÔÖÞÖ¹ Ö ØÒ Ó ÒÖÓÐÑÒØÓ ÔÖ ÒÓ ÒÐÓ ÒÙÒ ÓÖÖÒØ ÑÒØÞÓº Ø ÓÖÑ Ó ØÖÒ ÓÖÑÓÖ ÖÔÖ ÒØÓ ÑÔÐ ÑÒØ ÔÓÖ ÙÑ ØÖÒ ÓÖÑÓÖ Ð ÓÑ ÖÐÓ ØÖÒ ÓÖÑÓ ÔÓÖ N p /N s Ñ Ö ÓÑ Ù ÖØÒ ÔÖ Ó ÕÙÚÐÒØ x t ÓÑÓ ÑÓ ØÖÓ Ò ÙÖ ¾ºº Ø ÖØÒ ÓØ ØÖÚ Ò Ó ÙÖØÓ¹ÖÙØÓ ÒÓ ØÖÑÒ Ó ØÖÒ ÓÖÑÓÖº Æ ÖÔÖ ÒØÓ Ñ ÔÙ Ó ØÒ Ó ÒÓ ÔÖÑ ÖÓ ÙÒ ÖÓ Ó ØÖÒ ÓÖÑÓÖ Ñ ÓÐ ÓÑ ÖÐÓ ÙÐ N p /N s Ó ØÖÒ ÓÖ¹ ÑÓÖ Ð ÔÖ Ó ÖÙØÓ ÕÙÚÐÒØ Ó ÕÙÐ ÔÖ ÒØ Ó ÔØÓ ÑÓ ØÖÓ Ò ÙÖ ¾ºº
24 ½ Ò Ð Ê ÐØÖ N p Ns x t Ñ ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ ØÖÒ ÓÖÑÓÖ x t(pu) Ñ ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ ØÖÒ ÓÖÑÓÖ Ñ ÔÓÖ ÙÒ ÔÙµ ¾ºº½ ÌÖÒ ÓÖÑÓÖ ÓÑ ÖÐÓ ØÖÒ ÓÖÑÓ ÚÖ¹ ÚÐ Ó Ö ËÙÔÓÒ ÙÑ ÖÐÓ ØÖÒ ÓÖÑÓ ÒÖ ÔÓÖ a = N p /N s = te jφ ¾º½µ ÔÒÒÓ Ó ÚÐÓÖ ÙÑÓ ÔÓÖ t φ ØÖÑÓ ÙÒØ ÓÖÖ ÔÓÒ¹ Ò ÓÑ Ó ÓÑÔÓÒÒØ Ö ÖÔÖ ÒØÓ φ =0 t 0 ÌÖÒ ÓÖÑÓÖ ÓÑ ÚÖÓ ÙØÓÑØ ØÔ Ó Ö ÄÌ ½ µ t =1 φ 0 ÌÖÒ ÓÖÑÓÖ ÓÖ ¾ º Ó ÖÙØÓ ÕÙÚÐÒØ Ó ØÖÒ ÓÖÑÓÖ ÑÓ ØÖÓ Ò ÙÖ ¾º ÓÒ ÖØÒ x t Ó Ù ØØÙ ÔÓÖ ÙÑ ÑØÒ ÒÖ y ØÑÓ V p I p = E s ( I s ) ¾º½µ ¾ ÄÓ ÌÔ ÒÖ Ó ÙØÐÞÓ ÓÑÓ ÐÑÒØÓ ÓÒØÖÓÐ ØÒ Ó ÓÙ ÙÜÓ ÖØÚÓ º ¾ Ç ØÖÒ ÓÖÑÓÖ ÓÖ Ó Ù Ó ÔÖ ÓÒØÖÓÐÖ Ó ÙÜÓ ÔÓØÒ ØÚ ÑÙÑÖÙØÓº I p y ½ V p E s V s I s ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ Ó ØÖÒ ÓÖÑÓÖ
25 ÇÈÈ»ÍÊ ½ y t Ñ 1 t a 1 t y 2 t y ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ ØÖÒ ÓÖÑÓÖ ÓÑ ÚÖÓ ÙØÓÑ Ø ØÔ Ó Ö V p E s = I s I p = a ¾º½µ I s = y(e s V s )= y( V p a V s) I p = y a (E s V s )= y a (V p a V s) ÕÙ ÔÓÑÓ ÖÙÒÖ Ò ÓÖÑ ÑØÖÐ [ ] [ Ip 1/aa 1/a = y 1/a 1 I s ][ Vp V s ] ¾º½µ ¾º¾¼µ ¾º¾½µ ÆÓ Ó Ó Ä̳ φ =0,a = tµ ØÑÓ [ Ip I s ] = y [ 1/t 2 1/t 1/t 1 ][ Vp V s ] ¾º¾¾µ ÒÓ Ó Ó ØÖÒ ÓÖÑÓÖ ÓÖ t =1,a= e jφ µ ØÑÓ [ Ip I s ] = y [ 1 e jφ e jφ 1 ][ Vp V s ] ¾º¾ µ ÆÓ Ó Ó Ä̳ ÔÖØÖ ÕÙÓ ¾º¾¾µ ÔÓ ÚÐ ÒØØÞÖ Ó ÑÓÐÓ π¹õùúðòø ÑÓ ØÖÓ Ò ÙÖ ¾ºº Ç Ñ ÑÓ ÒÓ ÔÓ ÚÐ ÔÖ Ó Ó Ó ØÖÒ ÓÖÑÓÖ ÓÖ ÚÓ ÑØÖ ÑØÖÞ ÔÖ ÒØ Ò ÕÙÓ ¾º¾ µº ¾ºº¾ ÌÖÒ ÓÖÑÓÖ ØÖ Ó Ç ØÖÒ ÓÖÑÓÖ ØÖ Ó ÒÓ Ó ÓÔÖÓ Ñ ÓÒ ÕÙй Ö ÙØÐÞÑ ÙÑ ÖÔÖ ÒØÓ Ó ÑÓÐÓ ÕÙÒ ÔÓ ØÚ ÒØÓ ÕÙÐ ÑÓ ØÖ ÒÓ ØÒ ÒØÖÓÖ º
26 ½ Ò Ð Ê ÐØÖ x p x s Ñ x t ÙÖ ¾º ÖÙØÓ ÕÙÚÐÒØ ØÖÒ ÓÖÑÓÖ ÓÑ ØÖ ÒÖÓÐÑÒØÓ ¾ºº ÌÖÒ ÓÖÑÓÖ ÓÑ ØÖ ÒÖÓÐÑÒØÓ ÌÖÒ ÓÖÑÓÖ ÓÑ ØÖ ÒÖÓÐÑÒØÓ Ó ÒÓÖÑÐÑØ ÖÔÖ ÒØÓ ÔÓÖ ÖÙØÓ Ñ ØÖÐ ÓÑÓ ÑÓ ØÖÓ Ò ÙÖ ¾ºº ÖÔÖ ÒØÓ Ò¹ ØÖÓÙÞ ÙÑ Ò ØÓ Ò Ö Ò µ Ó ÕÙÐ ÒÓ Ü Ø ÑÒØ ÒÓ ØÖÒ ¹ ÓÖÑÓÖº Ç ÔÖÑØÖÓ Ó ÖÙØÓ ÕÙÚÐÒØ ÙÖ ¾º Ó ÓØÓ ÔÖØÖ Ó ÚÐÓÖ ÖØÒ ÔÖ Ó ÒØÖ Ó ÒÖÓÐÑÒØÓ x ps x pt x st µ ÕÙ Ó ÓØ ØÖÚ Ò Ó ÙÖØÓ¹ÖÙØÓ Ñ ÔÖ ÒÖÓÐÑÒØÓ ÓÑ Ó ØÖÖÓ ÒÖÓÐÑÒØÓ ÖØÓº Ç ÚÐÓÖ x p x s x t Ó ÓØ Ö ÓÐÚÒÓ¹ Ó ÙÒØ ØÑ ÕÙ ÓÒ Ö ÙÐØ Ò x p + x s = x ps ¾º¾µ x p + x t = x pt ¾º¾µ x s + x t = x st ¾º¾µ ¾º¾µ x p = 1 2 (x ps + x pt x st ) ¾º¾µ x s = 1 2 (x ps + x st x pt ) ¾º¾µ x t = 1 2 (x pt + x st x ps ) ¾º ¼µ Ú¹ ÒÓØÖ ÕÙ ÓÖÓ ÓÑ ¾º¾µ ¾º¾µ ¾º ¼µ ÔÓ ÚÐ ÕÙ Ü ØÑ ÖØÒ ÒØÚ Ò ÖÔÖ ÒØÓ ÙÖ ¾ºº ¾º ÖÓÖ ÓÑÔÒ ÓÖ ËÒÖÓÒÓ Ç ÖÙØÓ ÕÙÚÐÒØ ÒÓÖÑÐÑÒØ Ù Ó ÔÖ ÖÔÖ ÒØÖ Ñ ÕÙÒ Ò¹ ÖÓÒ Ñ Ò Ð ÖÑ ÔÖÑÒÒØ ÙÑ ÓÒØ ØÒ Ó ÓÒ ØÒØ Ñ Ö ÓÑ ÙÑ ÑÔÒ ÓÑÓ ÑÓ ØÖÓ Ò ÙÖ ¾º µº ÙÖ ¾º µ ÔÖ ÒØ Ó Ñ ÑÓ ÖÙØÓ ÕÙÚÐÒØ Ù ÒÓ ÙÑ ÓÒØ ÓÖÖÒØ
27 ÇÈÈ»ÍÊ ½ z g S E k I k y k g ¹ Vk V k V k µ µ µ ÙÖ ¾º ÅÓÐÓ ÖÓÖ ÓÙ ÓÑÔÒ ÓÖ ÒÖÓÒÓ Ñ ÔÖÐÐÓ ÓÑ ÙÑ ÑØÒº ÙÖ ¾º µ ÔÖ ÒØ Ó ÑÓÐÓ ÖÓÖ ÓÙ ÓÑÔÒ ÓÖ ÒÖÓÒÓ ÒÓÖÑÐÑÒØ ÙØÐÞÓ Ñ ØÙÓ ÙÜÓ ÔÓØÒ Ó ÕÙÐ ÖÚÓ Ó ÖÙØÓ ÕÙÚÐÒØ Ñ ÕÙÒ ÒÖÓÒ ØÖÚ ÖÐÓ S k = V k I k = P k + jq k ¾º ½µ Í ÒÓ Ó ÑÓÐÓ ÙÖ ¾º µ ÕÙÓ ¾º ½µ Ó ÖÓÖ ÔÓ Ö ÑÓÐÓ ÓÑÓ ÙÑ ÓÒØ ÔÓØÒ ØÚ ÖØÚ ÓÒ ØÒØ P k Q k ÔÓ µ ÓÙ ÓÑÓ ÙÑ ÓÒØ ÔÓØÒ ØÚ ÓÒ ØÒØ ÓÒØÖÓÐÓÖ Ð ØÒ Ó P k V k ÔÓ µº Ñ Ñ ØÙ ÚÖ Ú ÒÓ¹ Ô Ó ÑÓÐÓ V k ÒÓ ÔÖÑÖÓ Ó Q k ÒÓ ÙÒÓ ÓÑÒØ ÔÓÑ ÙÑÖ ÚÐÓÖ Ñ ÙÑ ÒØÖÚÐÓ ÐÑØ ÓÔÖØÚÓ µº ÆÓ Ó Ó ÓÑÔÒ ÓÖ ÒÖÓÒÓ Óع ÙÒ ÓÖÑÙÐÓ ÓÑ P k =0º ¾º ÒÓ ÔØÓÖ ÁÒÙØÓÖ Ç ÒÓ ÔØÓÖ ÒÙØÓÖ Ó ÖÔÖ ÒØÓ ÔÓÖ ÚÐÓÖ ÜÓ ÖØÒ ÒÙØÚ ÓÙ ÔØÚ ÓÒØ ÒØÖ ÖÖ ÖÖÒ ÓÑÓ ÑÓ ØÖÓ Ò ÙÖ ¾º½¼º jb l k jb c k µ µ ÙÖ ¾º½¼ ÖÙØÓ ÕÙÚÐÒØ ÒÓ ÔØÓÖ ÒÙØÓÖ ¾º ÓÑÔÒ ÓÖ Ø ØÓ Ç ÓÑÔÒ ÓÖ Ø ØÓ Ó ÒÓ ÔØÓÖ»ÓÙ ÒÙØÓÖ Ú¹ Ó ÐØÖÓÒÑÒغ ÒÓÑÒÓ Ø ØÓ ÚÑ Ó ØÓ ÓÒØÖÖÑÒØ
28 ¾¼ Ò Ð Ê ÐØÖ I c L C V c V c V 0 ÔØÓÖ µ µ ÙÖ ¾º½½ ÓÑÔÒ ÓÖ Ø ØÓ Ð ÁÒÙØÓÖ I c Ó ÕÙ ÓÒØ ÓÑ Ó ÓÑÔÒ ÓÖ ÒÖÓÒÓ Ø ÔÓ ØÚÓ ÒÓ ÔÓ ¹ ÙÖÑ ÔÖØ ÑÚ º ÜÑÔÐÓ ÓÑÔÒ ÓÖ Ø ØÓ Ó ÊØÓÖ ÓÒØÖÓÐÓ ÔÓÖ ØÖ ØÓÖ Ìʵ ÔØÓÖ ÚÓ ÔÓÖ ØÖ ØÓÖ Ì˵ ÊØÓÖ ÚÓ ÔÓÖ ØÖ ØÓÖ ÌËʵº ÓÑÒÓ ÓÑÔÒ ÓÖ Ø ØÓ ÓÑ ÒÓ ÔØÓÖ Ò¹ ÙØÓÖ ÚÓ ÑÒÑÒØ ÔÖÓÙÞ Ó ÑÓ ØÑ ÓÑÔÒ¹ Ó Ø Øº Ç ÑÔÒÓ ÙÑ ÓÑÔÒ ÓÖ Ø ØÓ Ð ÑÓ ØÖÓ Ò ÙÖ ¾º½½º ÙÖ ¾º½¾ ¾º½ ÑÓ ØÖÑ ÖØÖ Ø ÙÒÓÒÑÒØÓ ÙÑ ØÑ ÓÑÔÒ Ó Ø Ø ÓÖÑÓ ÔÓÖ ÙÑ ÖØÓÖ ÓÒØÖÓÐÓ ÙÑ ÔØÓÖ ÜÓº Ñ ØÙÓ ÙÜÓ ÔÓØÒ Ó ÓÑÔÒ ÓÖ Ø ØÓ Ó ÑÓ¹ ÐÓ ÙÒØ ÑÒÖ ¾ ÇÔÖÓ ÒØÖ ÐÑØ ÓÒØ ØÒ Ó V 0 µ Ñ Ö ÓÑ ÖØÒ ÖÔÖ ÒØÒÓ ÒÐÒÓ ÙÖÚ ÖØÖ Ø ÙÖ ¾º½ ¹µº ÇÔÖÓ ÓÖ Ó ÐÑØ ÖØÓÖ»ÔØÓÖ ÜÓº I L L I c C L I s C µ ÙÖ ¾º½¾ ÓÑÔÒ ÓÖ Ø ØÓ ÖÐ ÓÑÔÓ ØÓ ÖØÓÖ ÓÒØÖÓÐÓ ÔØÓÖ ÜÓ µ µ
29 ÇÈÈ»ÍÊ ¾½ V V V L max L min V 0 K s µ I L I C I S µ µ ÙÖ ¾º½ ÖØÖ Ø Ó ÓÑÔÒ ÓÖ Ø ØÓ ÓÑÔÓ ØÓ ¾º Ö Ö ÓÒØ ÙÑ ØÑ ÔÓØÒ Ó ÓÖÑ ÔÓÖ ÖÓ ÑÐÖ ÔÓ ØÚÓ Ø ÓÑÓ ÑÓØÓÖ ÒÙÓ Ò ÑÓÖ Ó Ó µ ÔÓ ØÚÓ ÐÙÑÒÓ ÔÖÐÓ ÐØÖÓ Ñ Öк Ö¹ Ó Ó ÖÐÑÒØ ÑÓÐÓ ÓÑÓ ÙÑ Ö ÓÒÒØÖ ÕÙÚÐÒØ Ñ ÙÑ ÖÖ Ó ØÑ ØÖÒ Ñ Óº Æ Ø Ö ØÓ ÖÔÖ ÒØÓ ØÑÑ Ó ØÓ Ó ØÑ ÙØÖÒ Ñ Ó ØÖÙÓ ÐÒ ¹ Ó ÔÓ ØÚÓ ÓÑÔÒ Ó ÖØÚÓ Øºµº ÔÓØÒ ÓÒ ÙÑ ÔÐ Ö ÚÖ ÓÑ ØÒ Ó ÖÕÙÒ ÑÒÖ ÖÒØ ÔÖ Ó ÚÖ Ó ÓÑÔÓÒÒØ Ñ Ñº Æ ÙÒØ Ó ÔÖ ÒØÓ Ó ÑÓÐÓ Ö ÖÐÑÒØ ÙØÐÞÓ Ñ ØÙÓ ÖÑ ÔÖÑÒÒØ ½ º ¾ºº½ ÅÓÐÓ ÓÑÔÓ ØÓ ¹ ÁÈ Ö ÖÔÖ ÒØ ÔÓÖ ÙÑ ÑÓÐÓ ÓÑÔÓ ØÓ ÓÑ ÖÒØ ÔÖÓÔÓÖ Ö Ó ØÔÓ ÑÔÒ ÓÖÖÒØ ÔÓØÒ ÓÒ ØÒØ º ÑÓÐÓ ÓÒÓ ÓÑÓ ÑÓÐÓ ÁÈ ÑÔÒ Á ÓÖÖÒØ È ÔÓØÒµ ÒÓ ÔÓÖ [ ( ) V 2 ( ) ] V P = P 0 p 1 + p 2 + p 3 V 0 V 0 [ ( ) V 2 ( ) ] V Q = Q 0 q 1 + q 2 + q 3 V 0 V 0 ¾º ¾µ ¾º µ ¾º µ ÓÒ p i,q i, i =1, 2, 3 Ó ÔÓÒÖ ÕÙ ÒÑ ÔÖÓÔÓÖÓ ÓÑÔÓÒÒØ Ó ÑÓÐÓº
30 ¾¾ Ò Ð Ê ÐØÖ ÌÐ ¾º¾ ÅÓÐÓ Ö ÜÔÓÒØ ÌÔÓ Ö ÅÓÐÓ ¼ ÈÓØÒ ÓÒ ØÒØ P = P 0 ½ ÓÖÖÒØ ÓÒ ØÒØ P = V P 0 V 0 = VI 0 ¾ ÁÑÔÒ ÓÒ ØÒØ P = V 2 P 0 = V 2 /Z 2 V0 2 0 ÌÐ ¾º ÎÐÓÖ ØÔÓ Ó ÜÔÓÒØ Ó ÑÓÐÓ Ö ÖÒ ÅÓØÓÖ ¼ ¼ ¼ ¼ ÄÑÔ ÐÙÓÖ ÒØ ½ ¼¼ ¼¼ ÄÑÔ ÁÒÒ ÒØ ½ ¼ ¾ºº¾ ÅÓÐÓ ÜÔÓÒÒÐ Ç ÑÓÐÓ ÜÔÒÒÐ ÔÖ ÓÑÔÓÒÒØ ØÚ ÖØÚ Ö Ó ÔÓÖ P = P 0 ( V V 0 ) a ¾º µ Q = Q 0 ( V V 0 ) b ¾º µ ÓÒ P 0,Q 0 V 0 Ó ÚÐÓÖ ÒÓÑÒ Ö ØÚ ÖØÚ ØÒ Ó P Q Ó Ó ÚÐÓÖ Ö ÔÖ ØÒ Ó V º ÔÒÒÓ Ó ÚÐÓÖ ÙÑÓ ÔÐÓ ÜÔÓÒØ Ñ ¾º µ ¾º µ Ó ÑÓÐÓ ØÑ Ó ÒÓ Ó ÔÖ ÒØÓ Ò ÌÐ ¾º¾º Ç ÓÑÔÓÒÒØ Ö Ö ÒÓ Ù ØÑ ÔÖØÑÒØ ÑÓÐÓ ÒÓ ØÔÓ Ó ÚÐÓÖ ÑÓ ØÖÓ Ò ÌÐ ¾º º
31 ÇÈÈ»ÍÊ ¾ ÈÖÓÐÑ ½º ÈÖ ÐÒ ØÖÒ Ñ Ó ÙÓ Ó Ó ÓÖÒÓ ÙÖ µ ØÐ Ó ÖÙØÓ π¹õùúðòø µ ÐÙÐ ØÒ Ó ÒÓ ØÑÒÐ ÖÔØÓÖ ÔÖ ÚÐÓÖ Ö ÒØ Ö ÙÔÓÒÓ ÕÙ ØÒ Ó ÒÓ ØÖÑÒÐ ØÖÒ Ñ ÓÖ Ü Ñ ½ ¼ ÔÙº ÓÒ Ö ÙÑ ÚÐÓÖ ÒÐ Ö ½¼¼ ¼ ÅÎ ÑÓ ½¼ ÅÏ ÑÒØÒÓ ÓÒ ØÒØ Ó ØÓÖ ÔÓØÒº Ó ÐÒ ÔÓØÒ Ó ØÑ ½¼¼ ÅÎ ÓÑÔÖÑÒØÓ ¼¼ Ñ ÌÒ Ó ÒÓÑÒÐ Î Ê ØÒ Ω/kmµ ¼ ¼¼ ÊØÒ ÒÙØÚ Ω/kmµ ¼ ¼¼ ËÙ ÔØÒ ÔØÚ Ω 1 /kmµ ¼¼ 10 6 ¾º ØÐ Ó ÑÓÐÓ Ñ ÔÙµ Ó ØÖÒ ÓÖÑÓÖ ÙÓ Ó Ó ÓÖÒÓ ÙÖ ÔÖ ÙØÐÞÓ Ñ ØÙÓ ÙÜÓ ÔÓØÒº ÌÖÒ ÓÖÑÓÖ ½ ÄÌ Ô ÒÓÑÒÐ ¼ ÅÎ ÌÒ Ó ÒÓÑÒÐ Ó ÔÖÑ ÖÓ ¾ ¼ Î ÌÒ Ó ÒÓÑÒÐ Ó ÙÒ ÖÓ ½ ¾ Î ÊØÒ ÔÖ Ó ÕÙÚÐÒØ ½¼ ± ÔÓØÒ Ó ØÑ ½¼¼ ÅÎ ÎÖÓ ØÔ Ó Ö ÒÓ ÒÖÓÐÑÒØÓ Ü ØÒ Ó ± ½ ¾ Î Ñ ½ Ô Ó ÌÖÒ ÓÖÑÓÖ ¾ ÌÖÒ ÓÖÑÓÖ ÓÖ Ô ÒÓÑÒÐ ¼¼ ÅÎ ÌÒ Ó ÒÓÑÒÐ Ó ÔÖÑ ÖÓ ¾ ¼ Î ÌÒ Ó ÒÓÑÒÐ Ó ÙÒ ÖÓ ¾ ¼ Î ÊØÒ ÔÖ Ó ÕÙÚÐÒØ ½¼ ± ÔÓØÒ Ó ØÑ ½¼¼ ÅÎ ÎÖÓ Ó ÑÒØÓ ÒÙÐÖ ± ¼ 0 Ñ Ô Ó
32 ¾ Ò Ð Ê ÐØÖ
33 ÔØÙÐÓ ÐÙÜÓ ÈÓØÒ º½ ÁÒØÖÓÙÓ Ç ØÙÓ ÙÜÓ ÔÓØÒ ÓÙ ÙÜÓ Ö ÓÒ Ø Ò ÓÐÙÓ Ñ ÖÑ ÔÖÑÒÒØ ÙÑ Ö ÐØÖ ÔÓØÒ ÔÖ ÙÑ ÓÒÓ Ö ÖÓº ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ ÓÖÖ ÔÓÒ ÙÑ ØÙÓ ÔÓØØ Ö ÓÒ ØÒØ ÕÙÐ ÒÙÒ ÓÒØ Ò ÓÔÖÓ Ó ØѺ ÒØÖØÒØÓ ØÔÓ ØÙÓ ÑÙØÓ ÑÔÓÖØÒØ ÔÖ ÖÔÖ ÒØÓ ÓÒ ÐÑØ Ò ÓÔÖÓ Ö Ø ÓÑÓ ÓÔÖÓ Ñ Ö Ñ ÜÑ Ö ÑÒÑ Øº ÓÒÓ Ö ÖÓ ÖØÖÞ ÔÐ ÒÓ Ö ØÚ ÖØÚ Ñ ØÓÓ Ó Ò ÓÙ ÖÖ Ö ÓÖÖ ÔÓÒÒØ ÚÐÓÖ ÖÓ ØÚ ÖØÚ ÒÕÙÐ Ò ÓÒ ÖÓÖ ØÓ ÔÓÒÚ ÓÑ Ü Ó ÒÓ ÑÒÑÓ ÙÑ Ò Ó ÕÙÐ Ó ÐÓ ÔÖ Ò ØÖÒ Ñ Óº ÄÑØ Ò Ô ÓÑÔÓÒÒØ Ó ØÑ ÒÓ ÚÐÓÖ ÐÙÑ ÚÖ Ú Ó ØÑÑ ÖÔÖ ÒØÓ Ñ ÓÑÓ ÖØÓ ÔÓ ØÚÓ ÓÒØÖÓÐ Ó ÙÜÓ ÔÓØÒ ØÚ ÖØÚ Ó ØѺ ÈÓÖ ØÖØÖ ÙÑ ÓÐÙÓ Ñ ÖÑ ÔÖÑÒÒØ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÑÓÐÓ ÔÓÖ ÙÑ ÓÒÙÒØÓ ÕÙ ÒÕÙ ÐÖ º ÕÙ ÒÕÙ Ó ÒÓ¹ÐÒÖ ÔÐÓ ØÓ ÖÓ Ö ÖÑ Ñ ÔÖØ ÑÓÐ ÓÑÓ ÓÒØ ÔÓØÒ ÓÒ ØÒØ ÓÙ ÔÓÖ ÙÒ ØÒ ÒÓ º Ç ØÙÓ ÙÜÓ ÔÓØÒ ØÑ ÔÐÓ ÖØ ÒÓ ÔÐÒÑÒØÓ ÜÔÒ Ó ÒÓ ÔÐÒÑÒØÓ ÓÔÖÓ ÒÓÓÒØÖÓÐ Ñ ØÑÔÓ¹ÖÐ Ó ØÑ ÐØÖÓ ÔÓØÒº Æ ÔÐ Þ Ò Ö ÓØÒÓ ÓÐÙ ÖÑ ÔÖÑÒÒØ Ö ÔÖ ÚÐÖ Ó ÑÔÒÓ Ñ Ñ ÓÑ ÖÐÓ ÒÚ ØÒ ÙÜÓ Ò ÐÒ Øº ØÒØÓ ÔÖ ÓÒÙÖÓ ÒÓÖÑÐ ÕÙÒØÓ ÔÖ Ó ÓÒØÒÒ º Ç ÐÙÐÓ Ó ÙÜÓ ÔÓØÒ ØÑÑ Ò ÖÓ ÓÑÓ ÐÑÒØÓ ÙÜÐÖ Ñ ØÙÓ ÙÖØÓ¹ÖÙØÓ ØÐ ÓØÑÞÓ ÓÒРغ ¾
34 ¾ Ò Ð Ê ÐØÖ º¾ ÓÖÑÙÐÓ Ó ÈÖÓÐÑ ÓÖÑÙÐÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÒÚÓÐÚ ÔØÓ ÑÓ¹ ÐÑ Ö ØÖÒ Ñ Ó ÓÙ ØÖÙÓ Ö ÖÓ ÓÒ ¹ Ö ÓÖ ÖØ ÖØÖ Ø ÓÔÖØÚ Ó ØѺ Ç Ö ÙÐØÓ ÓÑÒÓ Ö ÙÐØ Ñ ÙÑ ÓÒÙÒØÓ ÕÙ ÒÕÙ ÐÖ ÒÓ¹ÐÒÖ º º¾º½ ÅÓÐÓ Ê Ö ÐØÖ ÔÖ ØÓ ØÙÓ ÙÜÓ ÔÓØÒ ÖÐÑÒØ ÓÒ Ö ÓÑÓ ÒÓ ÓÒ ØØÙ ÔÓÖ ÐÑÒØÓ ØÖ Ó ÕÙÐÖÓ ½ ÐÒ ØÖÒ ÓÖÑÓÖ Øºµº Ç Ñ ÑÓ ÓÒØ ÓÑ Ö ÖÓº ÓÒ ÕÒØÑÒØ Ö ÔÓ Ö ÒÐ Ù ÒÓ¹ ÙÑ ÖÔÖ ÒØÓ ÑÓÒÓ ÓÑ Ó ÔÖÑØÖÓ ÕÒ ÔÓ ØÚº Ç ÐÑÒØÓ ÓÒ ØØÙÒØ Ö ØÑ Ó ÓÖÑØÓ ÖÐ ÑÓ ØÖÓ Ò ÙÖ º½ Ò ÌÐ º½º ØÖÚ ÐÑÒØÓ ÒÖÓ ÔÓ¹ ÖÔ¹ Ö ÒØÖ ÐÒ ØÖÒ Ñ Ó ØÖÒ ÓÖÑÓÖ ÓÑ ÓÙ Ñ ÓÑÙØÓ Ù¹ ØÓÑ Ø ØÔ ÐÑÒØÓ ÙÒØ ÖØÓÖ ÔØÓÖ Øºµº Ç ØÖÒ ÓÖ¹ ÑÓÖ ÓÖ ÔÓÖ ÒØÖÓÙÞÖÑ ÑØÖ Ò ÖÔÖ ÒØÓ Ö ÒÓ ÒÐÙÑ Ò ÖÔÖ ÒØÓ ÚÑ ÖÖ ÙÑ ØÖØÑÒØÓ ÔÐ ÓÑÓ Ú ØÓ ÒÓ ÔØÙÐÓ ¾º ẏ km Ñ ẏ k ẏ m ÙÖ º½ ÓÖÑØÓ ÖÐ Ó ÐÑÒØÓ Ö Ç ÐÑÒØÓ ÙÖ º½ ÌÐ º½ ØÑ Ó ÙÒØ ÒÓ ẏ km = g km + jb km =1/ż km º½µ ż km = r km + jx km º¾µ ÓÒ r km x km y s t Ö ØÒ ÐÒ ÓÙ ØÖÒ ÓÖÑÓÖ ÖØÒ ÐÒ ÓÙ ØÖÒ ÓÖÑÓÖ Ù ÔØÒ ØÓØÐ ÐÒ ÓÙ Ó ÐÑÒØÓ ÙÒØ ÖØÓÖ ÓÙ ÔØÓÖµ ÔÓ Ó Ó ØÔ Ó Ä̺ ½ Ñ ÐÙÑ ÔÐ Ô ÑÔÓÖØÒØ ÙØÐÞÓ ÙÑ ÑÓÐÑ ØÖ Ö ÐØÖ ÔÖÑØÒÓ ÖÔÖ ÒØÓ ÐÑÒØÓ ÕÙÐÖÓ º ÍÑ ÜÑÔÐÓ ÑÔÓÖØÒØ Ó Ó Ö ØÖÙÓ ÒÖ ÐØÖº
35 ÇÈÈ»ÍÊ ¾ ÑØÒ ÄÒ ÌÖÒ ÓÖÑÓÖ ËÙÒØ g km b km y k y m r km z km 2 r km z km 2 t ¼ x km z km 2 x km z km 2 t ¼ y s 1 t z 2 t 2 km y + z km 2 s y s t 1 zkm 2 t y + z km 2 s + ÇÚÐÓÖ Ö y s ÓÙ ÞÖÓ ÔÒÒÓ Ó Ò ÓÒ Ó ÐÑÒØÓ Ø ÓÒØÓ ÌÐ º½ ÎÐÓÖ ÑÔÒ Ó ÐÑÒØÓ ÒÖÓ Ö Ö ÓÒ ØØÙ ÔÐÓ ÐÑÒØÓ ÒÖÓ ÒÓ Ñ ÒØÓ ÖÔÖ ÒØ ÔÐ ÕÙ ÆÓ ¾ İ = Ẏ V º µ ÓÒ İ V Ẏ ÚØÓÖ ÓÑ ÓÖÖÒØ ÒØ ÒÓ Ò ÔÐ ÓÒØ ÓÖÖÒØ ÚØÓÖ ØÒ ÒÓ ÑØÖÞ ÑØÒ ÒÓÐ ÙÓ ÐÑÒØÓ Ó ÒÖÑÒØ ÖÔÖ ÒØÓ ÔÓÖ Ẏkm = G km + jb km º Ç ÐÑÒØÓ ÑØÖÞ ÑØÒ ÒÓÐ Ó ÒÓ ÓÑÓ Ẏ kk = ÓÑ ÑØÒ ÓÒØ Ó Ò k Ẏ km = ÒØÚÓ ÑØÒ ÓÒØ ÒØÖ Ó Ò k mº ÔÓØÒ ÔÖÒØ ÐÕÙ ÒØ Ñ ÙÑ ÖÖ ÖÐÓÒ ÓÑ ØÒ Ñ ØÓ ÖÖ Ö ØÖÚ P k + jq k = V k I k = V k m Ω k V m Ẏ km k =1, 2,..., n ºµ P k = P Gk P Lk ºµ Q k = Q Gk Q Lk ºµ ¾ ÍÑ ÖÚÓ ÕÙ ÒÓ ÔÓ Ö ÒÓÒØÖ ÔÓÖ ÜÑÔÐÓ Ñ ½ º
36 ¾ ÓÒ Ò Ð Ê ÐØÖ P k ÔÓØÒ ØÚ ÐÕÙ ÒØ Ò ÖÖ k Q k ÔÓØÒ ÖØÚ ÐÕÙ ÒØ Ò ÖÖ k P Gk ÔÓØÒ ØÚ Ö Ò ÖÖ k Q Gk ÔÓØÒ ÖØÚ Ö Ò ÖÖ k P Lk ÔÓØÒ ØÚ ÓÒ ÙÑ Ò ÖÖ k Q Lk ÔÓØÒ ÖØÚ ÓÒ ÙÑ Ò ÖÖ k V k ØÒ Ó ÖÖ k Ω k ÓÒÙÒØÓ ÖÖ ÖØÑÒØ Ð k ÒÐÙÒÓ kº º¾º¾ ÌÔÓ ÖÖ Ò Ö Ö Ñ ÖÖ Ó ØÑ ÓÒÓ Ö ÖÓµ Ó ÑÓÐÓ Ö ÑØÖÞ Yµ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ØÖ Ñ ÔÖÒÔÓ ÔÖØÑÒØ ÒÓº Á ØÓ ÒÓ ÓÒØ ÚÓ Ó ØÓ ÔÖ ÒÓ ÖÑ ÓÒ ÜØÑÒØ ÒØ ÓÒÖ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒº ÓÑ ÖÓ Ñ ØÓ ÖÖ Ó ØÑ Ú Ö ÙÐ Ö ØÓØÐ Ó ØÑ Ñ ÔÖ º ÓÑÓ Ø ÒÓ Ó ÓÒ Ò ÖÓ ÔÖÚÖ ÙÑ ÓÐ Ò ÖÓ ÑÒÖ ÓÑÓÖ ÔÖ º Á ØÓ ÓØÓ ÜÒÓ ÒÓ Ô ÖÓ ØÚ ÖØÚ Ñ ÔÐÓ ÑÒÓ ÙÑ ÖÖ Ó ØÑ ÕÙÐ Ö ÒÓ ÖÖ ÐÙØÙÒØ ËÛÒ ÓÙ Ëк ØÓ ÐÙ ØÖÓ ÒÓ ÜÑÔÐÓ ÙÖº ÜÑÔÐÓ º½ ÓÒ Ö Ó ØÑ ÖÖ ÑÓ ØÖÓ Ò ÙÖ º¾º ÕÙ Ó ÙÜÓ ÔÓØÒ Ò ØÑ Ó P G1 + jq G1 = V 1 [ Ẏ11 V 1 + Ẏ12 V 2 + Ẏ13 V 3 ] P G2 + jq G2 = V 2 [ Ẏ21 V 1 + Ẏ22 V 2 + Ẏ23 V 3 ] P L3 jq L3 = V 3 [ Ẏ31 V 1 + Ẏ32 V 2 + Ẏ33 V 3 ] Æ ÕÙ Ñ Ó ÐÑÒØÓ Ö Ö P G1 Q G1 ºººµ Ó ÓÒÓ º ØÒ ÒÓ V 1 V2 V 3 µ Ó ÒÒØ ½ ¾ ÙÖ º¾ Ë ØÑ Ù Ó ÒÓ ÜÑÔÐÓ º½
37 ÇÈÈ»ÍÊ ¾ Ó ÔÖÓÐѺ Ü ØÑ Ò Ù ÒÒØ ÑÔÐØ ÔÖ ØÚ ÖØÚ ØÓØ º ËÑÓÓÒÑÒØÓ ÒÓ ÔÓ ÚÐ Ö ÓÐÒÓ ÔÓØÒ ÒÓ ØѺ Á Ó ÐÖÓ Ò ÕÙÓ ÜÓ ÓÖÖ ÔÓÒÒØ Ó ÐÒÓ ÔÓØÒ ØÚ P G1 + P G2 = P L3 + P L ÓÒ P L ÖÔÖ ÒØ ÔÖ ØÚ ØÓØ Ó ØѺ ÈÖ ÓÒÖ Ó ÚÐÓÖ ÔÖ ÒØÖØÒØÓ ÔÖ ÑÓ ÓÒÖ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒº ÇÙ ÔÖ ÓÖÑÙÐÖ ÓÖÖØÑÒØ Ó ÔÖÓÐÑ Ò ÖÓ ÓÒÖ ÓÐÙÓ Ó ÔÖÓÐÑ ÓÐÙÓ Ð Ó ÐÑ Ñ ÓÒ Ø Ò ÒØÖÓÙÓ Ó ÓÒØÓ ÖÖ ÐÙØÙÒØ ØÓ ÙÑ ÖÖ ÓÒ Ü¹ Ñ ÖØÓ Ó ÚÐÓÖ ÔÓØÒ ØÚ ÖØÚ ÒØ Ò Ö º Ñ ØÖÑÓ ÑØÑ ØÓ ØÓ ÕÙÚÐ ÖØÖÖ ÙÑ ÕÙ Ó ÓÒÙÒØÓ Ñº ËÙÔÓÒÓ ÕÙ ÖÖ ÓÐ ÓÑÓ ÖÖ ÙØÙÒØ ÒÑÖÓ ½ ÒØÓÓÒÓÚÓ ØÑ ÕÙ Ö P G2 + jq G2 = V 2 [ Ẏ21 V 1 + Ẏ22 V 2 + Ẏ23 V 3 ] P L3 jq L3 = V 3 [ Ẏ31 V 1 + Ẏ32 V 2 + Ẏ33 V 3 ] Æ ÒÓÚÓ ØÑ ÕÙ Ó ÐÒÓ ÔÓØÒ ÒÓ ÔÖ Ö ØÒÓº ÖÒ Ö ÙÔÖ ÔÓÖ P G1 Q G1 º ÈÖ ÓÑÔÒ Ö ÑÒÙÓ ÙÑ ÕÙÓ Ú¹ ÜÖ Ó ÚÐÓÖ ÙÑ ÒÒØ º ÈÓÖ ÖÞ ÓÖÑ ÔÖ Ø ØÒ Ó ÓÐ ÖÖ ÙØÙÒغ Æ ÓÒ Ó ØÑ ÕÙ Ñ ÔÓ Ö Ö ÓÐÚÓ ÔÖ ÚÖ Ú V 2 V 3 º Ñ Ù ÔÓÑÓ ÐÙÐÖ Ò ÔÓØÒ ØÚ ÖØÚ Ò ÖÖ ÙØÙÒØ Ù ÒÓ ÕÙÓ Ü ÓÖ ÓÙ P G1 + jq G1 = V 1 [ Ẏ11 V 1 + Ẏ12 V 2 + Ẏ13 V 3 ] ÓÑÓ ÑÓ ØÖÓ ÒÓ ÜÑÔÐÓ ÒØÖÓÖ ØÒ Ó Ñ ÑÙÐÓ ÒÙÐÓ µ ÖÖ ÙØÙÒØ Ú Ö Ô ØÓ ÓÖÒ ÓÑÓ ÙÑ Ó ÔÖ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒº ÈÓÖ ÖÞÓ ÔÐÓ ØÓ ÔÖ ØÓØ ÖÑ ÐÓ Ñ Ñ ÖÖ ÙØÙÒØ Ú Ö ÙÑ ÖÖ Ò ÕÙÐ Ø ÓÒØ ÙÑ ÖÓÖ ÔÞ ÓÖÒÖ ÔÓØÒ Ö ÖÙÐÖ ØÒ Ó Ñ Ù ØÖÑÒ º ÓÑÓ Ó ÒÙÐÓ ØÒ Ó Ò ÖÖ ØÑÑ ÔÓ ØÒ Ó ÖÖ ÙØÙÒØ Ô ÜÖÖ Ó ÔÔÐ ÖÖÒ ÒÙÐÖ Ó ØѺ ÔÓ ÚÐ ÔÓÖÑ ÒÑ ÑÔÖ Ò ÖÓ ÙØÐÞÖ¹ Ñ ÙÑ ÖÖ ÙØÙÒØ Ò ÓÖÑÙÐÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒº ØÙ ÕÙ Ù ØÑ ÙØÐÞÓ ÑÐØÔÐ ÖÖ ÙØÙÒØ ÖÓ ÓÖ Ñ ÙÒØ Ø ÒÓØ Ùк ÆÓ Ó ÔÖ ØÓ Ó ÐÒÓ ÔÓØÒ ÖØÚ ÖÐÞÓ ÓÖÑ ØÖÙ ÔÐ ÒØÖÓÙÓ Ñ ÖÖ ÌÒ Ó ÓÒØÖÓÐ ÓÑÓÚÖÑÓ ÙÖº
38 ¼ Ò Ð Ê ÐØÖ ÐÑ ÖÖ ÙØÙÒØ Ù ÙÐ ÒØÖÓÙÞÖ¹ ÙÑ ÓÙØÖÓ ØÔÓ ÔÐ ÖÖ ÒÓ ØÙÓ ÙÜÓ ÔÓØÒ Ò ÕÙÐ Ó ÑÙÐÓ ØÒ Ó Ô¹ Óº ØÔÓ ÖÖ ØÑ ÔÓÖ ÒÐ ÖÔÖ ÒØÖ Ó ÕÙÔ¹ ÑÒØÓ ÓÑ Ô ÖÙÐÓ ØÒ Ó ÖÓÖ ÓÑÔÒ ÓÖ ÒÖÓÒÓ Ø ØÓ Øºµº ØÔÓ ÖÖ Ö ÒÓÑÒÓ ÖÖ ÌÒ Ó ÓÒØÖÓк ÖÖ ØÒ Ó ÓÒØÖÓÐ ØÑ ÙÑ ÔÔÐ ÑÔÓÖØÒØ Ò ØÖÑÒÓ Ó ÔÖÐ ØÒ Ó Ó ØÑ ÓÑÓ ÚÖÑÓ Ñ ÙÒØ ÒÙÒÑ ÓÖÑ ÒØÚ ÖØÖ Ø ÓÒÚÖÒ Ó ÑØÓÓ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒº ÖÖ Ó ØÑ ØÓ Ó ÕÙØÖÓ ÚÖ Ú P k Q k V k θ k º P k Q k Ó Ö ÔØÚÑÒØ ÓÑÔÓÒÒØ ØÚ ÖØÚ ÔÓØÒ ÐÕÙ ÖÓ ÑÒÓ Öµ ÒØ Ò ÖÖº V k θ k Ó Ö ÔØÚÑÒØ Ó ÑÙÐÓ ÒÙÐÓ ØÒ Ó Ò k¹ Ñ ÖÖ Ó ØѺ ØÒ ÔÓÑ ØÑÑ Ö ÖÔÖ ÒØ Ò ÓÖÑ ÖØÒÙÐÖ Ò Ø Ó V k θ k ÖÑ Ù ØØÙÓ ÔÓÖ e k f k Ö ÔØÚÑÒØ ÔÖØ Ö ÑÒ Ö ØÒ Óº ÕÙØÖÓ ÚÖ Ú Ó ÖÖ Ö ØÓ ÖÐÓÒ ÓÑ Ñ ÚÖ Ú ÓÑÓÐÓØÖÚ ÕÙÓ ºµ ÕÙÐ Ò ÙÑ ÓÒÙÒØÓ 2n Ò ÒÑÖÓ ÖÖ µ ÕÙ Ñ ÚÖ Ú Ö º ÓÑÓ Ü ØÑ 4n ÚÖ Ú Ö ÔÖ ÕÙ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ØÒ ÓÐÙÓ Ò ÖÓ ÔÖ ÓÚÐÓÖ 2n ÚÖ Ú º ÔÒÒÓ ÓÐ ÚÖ Ú ÖÖ Ó ØÑ ÔÖ ØÓ ØÙÓ ÙÜÓ ÔÓØÒ Ó Ð Ó ÓÖÓ ÓÑ ÌÐ º¾º Æ ØÐ ØÑÑ ÔÖ ÒØ ÙÑ ÒÓÑÒÓ ÒØØ ÔÖ Ó ÚÖ Ó ØÔÓ ÖÖ Vθ PV PQµ ÒÓÖÑÐÑÒØ ÙØÐÞ Ò ÔÖ Ø Ò ÚÖ Ú Ô Ñ ØÔÓ ÖÖº ÌÔÓ ÆÓÑ ÎÖ Ú ÎÖ Ú ÖØÖ Ø Ô ÐÙÐ ÐÙØÙÒØ Í ÔÖ Ó ÐÒÓ ËÐ Vθ V k,θ k P k,q k ÔÓØÒº ÓÙ ËÛÒ ÊÖÒ ÒÙÐÖº ÖÖ ÖÓ ÌÒ Ó ÓÙ Ò ÕÙ Ü Ø ÓÒØÖÓÐ PV P k,v k θ k,q k ÐÙÑ ÔÓ ØÚÓ ÓÒØÖÓÐ ØÒ Óº Ö PQ P k,q k V k,θ k Ñ ÖÖ º ÌÐ º¾ ÌÔÓ ÖÖ ÓÖÑÙÐÓ ÜÔÐØ ÕÙ Ö ÔÖ ÒØ Ò Ó ÙÒØ
39 ÇÈÈ»ÍÊ ½ º¾º ÓÒÙÒØÓ Ó ÕÙ ÕÙÓ ºµ ÔÓ Ö ÖØ ÔÖÒÓ¹ ÓÑÔÓÒÒØ Ö Ñ¹ Ò Ö ÓÑÓ P k = R V k V m Ẏkm k =1, 2,..., n ºµ Q k = I V k m Ω k m Ω k V m Ẏ km k =1, 2,..., n ºµ ÜÔÖ ÒÓ ØÒ Ñ Ù ÓÖÑ ÔÓÐÖ ÕÙ ºµ ºµ ÔÓÑ Ö ÖÔÖ ÒØ ÓÖÑ ÓÑÔØ ÔÓÖ P k = g pk (Θ, V) = V k V m (G km cos θ km + B km sen θ km ) ºµ m Ω k Q k = g qk (Θ, V) = V k V m (G km sen θ km B km cos θ km ) º½¼µ m Ω k ÓÒ Θ V θ k V k ÚØÓÖ Ù ÓÑÔÓÒÒØ Ó Ó ÒÙÐÓ ØÒ ÒÓ ÚØÓÖ Ù ÓÑÔÓÒÒØ Ó Ó ÑÙÐÓ ØÒ ÒÓ ÒÙÐÓ ØÒ ÓÖÖk ÑÙÐÓ ØÒ Ó ÖÖ k θ km = θ k θ m º½½µ ÆÓ Ó ØÒ ÒÓ ÖÑ ÔÖ Ñ Ù ÓÖÑ ÖØÒÙÐÖ ÜÔÖ ÙÒØ ÚÑ Ö ÙØÐÞ ÓÒ P k = g p k (e, f) = = m Ω k [e k (G km e m B km f m )+f k (G km f m + B km e m )] Q k = g q k (e, f) = = m Ω k [f k (G km e m B km f m ) e k (G km f m + B km e m )] e ÚØÓÖ Ù ÓÑÔÓÒÒØ Ó ÔÖØ ÖÐ ØÒ ÒÓ f ÚØÓÖ Ù ÓÑÔÓÒÒØ Ó ÔÖØ ÑÒ Ö ØÒ ÒÓ e k ÔÖØ ÖÐ ØÒ Ó ÖÖ k f k ÔÖØ ÑÒ Ö ØÒ Ó ÖÖ kº º½¾µ º½ µ
40 ¾ Ò Ð Ê ÐØÖ Ç ÔÖÒÔ ÑØÓÓ ÓÐÙÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ Ù ¹ Ó ØÙÐÑÒØ ÚÑ ÕÙ Ò Ñ ºµ º½¼µ ÓÙ º½¾µ º½ µ Ñ Ó ÙÓÒÙÒØÓ ¾¼ ËÙÓÒÙÒØÓ ½ ÓÒØÑ ÕÙ ÖÐØÚ Ò ÔÓØÒ ØÚ ÖØÚ Ò ÖÖ Ö ÕÙ ÓÖÖ ÔÓÒÒØ Ò ÔÓØÒ ØÚ Ò ÖÖ ØÒ Ó ÓÒØÖÓÐ ËÙÓÒÙÒØÓ ¾ ÖÙÒ Ñ ÕÙ ÓÙ ÕÙÐ ÒÓ ÒÐÙ ÒÓ ÔÖÑÖÓ ÙÓÒÙÒØÓº Ú Ó ÙØÐÞÓ ÔÐÓ ØÓ ÕÙ ÒÓ ËÙÓÒÙÒØÓ ½ ÚÖ Ú ÖÑ ÐÙÐ Ó ÙÒ ÑÔÐØ ÚÖ Ú Ô º ÈÓÖØÒØÓ Ü Ø Ò Ö ÓÐÚÖ ÓÒÙÒØÓ ÕÙ ÙØÐÞÒÓ ÐÙÑ ÑØÓÓ ÓÐÙÓ ÕÙ ÐÖ ÒÓ¹ÐÒÖ º Á Ó ÒÓ ÓÒØ ÓÑ ÕÙ Ó ËÙÓÒÙÒØÓ ¾ Ò ÕÙ Ô ÓÐÙÓ Ó ËÙÓÒ¹ ÙÒØÓ ½ ÚÖ Ú ÖÑ ÐÙÐ Ó ÙÒ ÜÔÐØ ÚÖ Ú ÓÒ º ØÓ Ö ÐÙ ØÖÓ ØÖÚ Ó ÙÒØ ÜÑÔÐÓº ÜÑÔÐÓ º¾ ÓÒ Ö Ó ØÑ ÒÓ ÖÖ Ó Ò ÙÖ º ÓÑ Ö ÔØÚ Ò Ó ØÔÓ ÖÖ º ÈÖ ÜÑÔÐÓ Ó ÚØÓÖ Θ V Ó ÒÓ ÔÓÖ Θ = [ θ 2 θ 3 θ 4 θ 5 ] T V = [ V 3 V 4 V 5 ] T ÔÖØÖ ÒÓ ÚÖ Ú Ó ÙÓÒÙÒØÓ ÕÙ ÖÑ Ö ÓÐÚÓ Ó ØÐÓ ÓÑÓ ÙÖ ËÙÓÒÙÒØÓ ½ ËÙÓÒÙÒØÓ ¾ P 2 = g p2 (Θ, V) P 3 = g p3 (Θ, V) Q 3 = g q3 (Θ, V) P 4 = g p4 (Θ, V) Q 4 = g q4 (Θ, V) P 5 = g p5 (Θ, V) Q 5 = g q5 (Θ, V) P 1 = g p1 (Θ, V) Q 1 = g q1 (Θ, V) Q 2 = g q2 (Θ, V) ÈÖ ØÓ ÐÙ ØÖÓ Ù ÙÒ ÙØÐÞ Ò ÕÙ Ñ ÖÓ ÖØ ÔÓÖ ÜØÒ Ó g p3 (Θ, V) = V 2 3 G 33 + V 3 V 1 (G 31 cos θ 31 + B 31 sen θ 31 )+V 3 V 2 (G 32 cos θ 32
41 ÇÈÈ»ÍÊ Vθ ½ ÈÉ ÈÉ ÈÎ ¾ ÈÉ ÙÖ º Ë ØÑ Ù Ó ÒÓ ÜÑÔÐÓ º¾ + B 32 sen θ 32 )+V 3 V 4 (G 34 cos θ 34 + B 34 sen θ 34 ) g q3 (Θ, V) = V V 3 V 1 (G 31 sen θ 31 B 31 cos θ 31 )+V 3 V 2 (G 32 sen θ 32 B 32 cos θ 32 )+V 3 V 4 (G 34 sen θ 34 B 34 cos θ 34 ) ÙÒ Ñ ÓÖÑ ÑÔÐ Ó ÖÚÒÓ¹ ÕÙ θ 33 =0º º ËÓÐÙÓ Ó ÈÖÓÐÑ ÓÐÙÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÓÒ Ø Ù ËÓÐÙÓ Ó ËÙÓÒÙÒØÓ ½ ÕÙ ÔÓÖ ÙÑ ÔÖÓ Ó ØÖØÚÓ Ú ÒÓ Ó ÐÙÐÓ ÓÑÔÓÒÒØ Ó ÚØÓÖ Θ V ËÙ ØØÙÓ Ó ÚÐÓÖ Θ V Ò ÕÙ Ó ËÙÓÒÙÒØÓ ¾ ÓÑ Ó ÓØÚÓ ÐÙÐÖ Ó ÚÐÓÖ Ò ÐÕÙ ÔÓØÒ ØÚ ÖØÚ Ò ÖÖ ÙØÙÒØ Ò ÐÕÙ ÔÓØÒ ÖØÚ Ò ÖÖ ØÒ Ó ÓÒØÖÓк ÚÓ Ò ÖÔÖ ÒØÖ Ó ÐÑØ ÓÔÖØÚÓ Ó ÓÑÔÓÒÒØ Ó ØÑ ÔÓ ØÚÓ ÓÒØÖÓÐ ÒÓ Ó ÔÖ ØÓ Ü Ø Ò Ò ÖÐÞÖ Ù Ø ÑÙÒ ÚÖ Ú ÙÖÒØ Ó ÔÖÓ Ó ÓÐÙÓº Ù Ø ÓÖÖ ÔÓÒÑ ÑÔÐÑÒØÓ ÒÕÙ ÔÖ ÒØ Ò ÓÖÑÙÐÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÓÑÓ ØÓ ÒÓ ÒÓ ÔØÙÐÓº ØÓ Ö ÖØÓ Ñ ÙÒØ Ø ÒÓØ Ùк º ÅØÓÓ ËÓÐÙÓ Ç ÑØÓÓ ÓÐÙÓ ÙÜÓ ÔÓØÒ ¾ ÔÓÑ Ö Ð Ó Ñ ØÖ ØÓÖ ÕÙ Ñ ÓÖÑ ÖÓÒÓÐ ÔÖÑÒØÓ Ò ÐØÖØÙÖ Ó
42 Ò Ð Ê ÐØÖ ½º ÅØÓÓ Ó Ò ÅØÖÞ Y ÑØÓÓ Ó Ó Ò ÓÐÙÓ ØÖØÚ Ó ØÑ ÕÙ ÒÓ Ñ º µº ÔÖØÖ Ó ÚÐÓÖ ÔÓ Ò ÔÓØÒ ØÚ ÖØÚ ÙÑ ØÑØÚ ÒÐ ØÒ ÒÓ ÐÙй Ó ÚØÓÖ ÓÖÖÒØ ÒØ º Ù ØØÙÓ ÚØÓÖ Ñ º µ ÔÖÓÙÞÖ Ó ÒÓÚÓÚÐÓÖ ØÒ Ñ Ù ÚÑÒغ ÒØÖ Ó ÐÓÖØÑÓ ÕÙ ÙØÐÞÑ Y Ó Ñ ÓÒÓ Ó Ù ¹ËÐ ÕÙ Ö ÖØÓ Ò Ó ÙÒغ ÓÒÚÖÒ ÑØÓÓ ØÒØ ÐÒØ ÚÓ Ö ÒØÖÓ ÒØÖ ÚÖ Ú Y ÔÖ µ ÚÞ ØÒØ Ð Ñ ØÑ ÑйÓÒÓÒÓ º ¾º ÅØÓÓ Ó Ò ÅØÖÞ Z ÈÖ ÓÒØÓÖÒÖ Ó ÔÖÓÐÑ ÓÒÚÖÒ Ó ÑØÓÓ Ó Ñ Y ÓÖÑ Ø ØÓ ÓÑ Ù Ó ÕÙÑ ØÖØÚÓ ÙØÐÞÒÓ Ù ÒÚÖ Zº ÑØÓÓ ØÑ ÓÒÚÖÒ Ö Ô ÓÒ ÚÐ ÔÖ ÑÓÖ Ó ÔÖÓÐÑ ÔÖ ØÓ ÔÓÖÑ ÒØÖÓÙÞÑ Ó ÔÖÓÐÑ ÑÓÒØÖ ÖÑÞÒÖ ÑØÖÞ Zº ÐÑ Ó Ó ØÖØÑÒØÓ ÖÖ ØÒ Ó ÓÒØÖÓÐ Ð ÒÒØ Ó ÔÓÒØÓ Ú Ø ÓÑÔÙØÓÒк º ÅØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ Ç ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ ÓÐÙÓ ÕÙ ÐÖ ÒÓ ÐÒÖ ÙÑ ÑØÓÓ Ð Ó ÖÓÒ Ò ÒÓ ÐÙÐÓ ÒÙÑÖÓº ËÙ ÔÐÓ Ò ÓÐÙÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÓÑÒØ ØÓÖÒÓÙ¹ ÔÖ Ø ÓÑ ÒØÖÓÙÓ Ó ÑØÓÓ ÓÐÙÓ ØÑ ÕÙ ÐÒÖ ÓÑ ÑØÖÞ ÓÒØ ÔÖ ÔÓÖ ØÓÖÞÓ ØÖÒÙÐÖ ÓØÑÑÑÒØ ÓÖÒ ¾ ¾ º ÔÖØÖ ÖÒØ ÚÖ ÐÓÖØÑÓ ÔÖ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ Ó ÒÓ ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÓÖÑ ÒÚÓÐÚÓ Ó ÓÒ ÖÓ ØÙÐÑÒØ Ó Ñ ÒØ ÔÖ ÓÐÙÓ ÔÖÓÐѺ ºº½ ÖØÖÓ ÈÖ Ó ËÓÐÙÓ ÈÖ ÒØÖÖÓÑÔÖ Ó ÔÖÓ Ó ØÖØÚÓ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ Ò ÖÓ ÒÖ ÙÑ ÖØÖÓ ÓÙ ÖÖ ÔÖ Ó ÕÙÐ ÑÖ ÕÙÓ ÔÖÜÑÓ ÓÐÙÓ ÜØ ÒÓÒØÖÑ Ó ÚÐÓÖ ÔÖ ÒØ ØÒ ÒÓ º Ç ÖØÖÓ ÒÓÖÑÐÑÒØ ÙØÐÞÓ Ò ÔÖ Ø Ó Ó Ê ÙÓ ÈÓØÒ ÈÓÛÖ Å ÑØ µ Ó ÕÙ Ó ÒÓ ÔÓÖ ΔP k = P esp k g pk (Θ, V) k Ω PQ Ω PV º½µ ΔQ k = Q esp k g qk (Θ, V) k Ω PQ º½µ ÑØÓÓ Ó ÔÖ ÒØÓ ÒÓ ÔÒ Ø ÒÓØ º
43 ÇÈÈ»ÍÊ ÓÒ Ω PQ Ω PV P esp k Q esp k ÓÒÙÒØÓ ÖÖ PQ ÓÒÙÒØÓ ÖÖ PV ÔÓØÒ ØÚ ÐÕÙ Ô Ò ÖÖ k ÔÓØÒ ÖØÚ ÐÕÙ Ô Ò ÖÖ kº Ç ÔÖÓ Ó ØÖØÚÓ Ú Ö ØÖÑÒÓ ÕÙÒÓ ΔP ε p º½µ ΔQ ε q º½µ ÓÒ ΔP = ΔQ = [ [ ΔP 1 ΔP 2 ] T º½µ ΔQ 1 ΔQ 2 ] T º½µ ε p ε q Ó ØÓÐÖÒ ØÔÑÒØ ÒÓ ÒØÖÚÐÓ ¼ ¼½ ½¼ ÅÏ»ÅÎʺ Ñ ÐÙÒ ÑØÓÓ ÓÐÙÓ ÔÓÖ ÜÑÔÐÓ ÒÓ ÑØÓÓ Ù ¹ËÐ ÓÒ Ó ÐÙÐÓ Ó Ê ÙÓ ÈÓØÒ ÑÔÐÖ Ñ ÙÑ ÙÑÒØÓ Ü ÚÓ ØÑÔÓ ÔÓÖ ØÖÓ Ø Ø Ó Ò ÚÖÓ Ó ÚÐÓÖ ØÒ Ó ÙØÐÞÓ º ºº¾ ÅØÓÓ Ù ¹ËÐ Ç ÑØÓÓ Ù ¹ËÐ ÔÖ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ ÙÑ Ó Ñ ÒØÓ ÒÓÒØÖÓ Ò ÐØÖØÙÖº ËÙ ÑÔÓÖØÒ ØÙÐ ÔÒ ØÖ Ø ÔÓ ÔÖ ØÑ ÖÒ ÔÓÖØ Ù Ò ÓÑÔÙØÓÒÐ ÑÙØÓ ÒÖÓÖ Ó ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒº Ç ÑØÓÓ ÓÖÑÙÐÓ Ñ ØÖÑÓ ÚÖ Ú ÓÑÔÐÜ ÒÓ ÙØÐÞ Ú Ó Ñ ÙÓÒÙÒØÓ ÖØ Ò Ó ÒØÖÓÖº ËÙÔÓÒ ÒÐÑÒØ ÕÙ ØÓ ÖÖ Ó Ó ØÔÓ ÈÉ Öµ ÜØÓ ÓÚÑÒØ ÖÖ ÙØÙÒغ Æ Ø Ó Ó ÐÓÖØÑÓ Ù ¹ËÐ ÖÚÓ ÖØÑÒØ ºµ Ó ÔÓÖ V k i+1 = 1 Y kk P esp k jq esp k ( V i k ) k 1 m=1 V i+1 m Y km n m=k+1 V i my km k =1,..., n; k flutuante º¾¼µ ÓÒ i Ó ÓÒØÓÖ ØÖ º ÚÖÓ ÓÒÚÖÒ ÖÐÞ ØÖÚ Ó ÑÙÐÓ ÖÒ ÒØÖ ÓÑÔÓÒÒØ Ó ÚØÓÖ ØÒ ÒÓÖÑ ÒÒØ ÙÑ ÚØÓÖ Ò ÓÑÓ º x =max x i i
44 Ò Ð Ê ÐØÖ ÒØÖ ØÖ ØÓ Ó ÔÖÓ Ó ØÖØÚÓ ØÖÑÒ ÕÙÒÓ V i+1 k V i k ε v ÓÒ ε v ÔÖ Ó ÒÓ ÑÙÐÓ ØÒ º Ç ÑØÓÓ Ù ¹ËÐ ÔÓ ØÑÑ Ö ÓÖÑÙÐÓ Ñ ÓÖÑØÓ ÑØÖÐ ÓÑÓ ÙÖ ÓÒ Á ÙÑÚØÓÖ Ù ÓÑÔÓÒÒØ Ó ÔÓÖ I( V) =Ẏ V º¾½µ I k ( V) = P k jq k Vk, k =1,..., n º¾¾µ ÕÙÓ ÑØÖÐ º¾½µ Ò ÙÑ ÓÒÙÒØÓ ÕÙ ÕÙ ¹ÐÒÖ Ô ÒØÒÓ ÙÑ Ö ÒÓ¹ÐÒÖ ÓÒÐ ÖÔÖ ÒØ ÔÐ ÔÒÒ¹ Ó ÚÐÓÖ ÓÖÖÒØ ÒØ Ò ÖÖ Ö Ñ ÖÐÓ ØÒ Ó Ñ Ñ ÖÖ º ÈÖ ÙÑ Ó ÚÐÓÖ V ÔÓÖ ÜÑÔÐÓ Ó ÚÐÓÖ ØÖÓ ÒØÖÓÖ Ó ØÑ ÕÙ º¾½µ Ô Ö ÙÑ ØÑ ÐÒ¹ Ö Ó ÕÙÐ ÔÓ Ö Ö ÓÐÚÓ ÔÓÖ ÕÙÐÕÙÖ ÙÑ Ó ÑØÓÓ ÖØÓ ÒÓ ÔÒ º Ñ ÔÖØÙÐÖ ÔÓ¹ ÙØÐÞÖ ÙÑ ÑØÓÓ ØÓÖÓ ÄÍ ÔÓÖ ÜÑÔÐÓµ ÒÓ ÕÙÐ ØÖй ÓÑ ÒÚÖ ÑÔÐØ Y ÓÙ Zº ÓÖÑ Ù ÙÐ ÑÔÐÑÒØÖ ÙÑ ÑØÓÓ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ Ù ÒÓ ÑØÖÞ Zº Ñ ÙÑ ÖÖ ÈÎ Ó ÐÙÐÓ Ó ÙÑ ÔÓÙÓ ÖÒØ ÕÙ ÒÓ ÔÓØÒ ÖØÚ ÒÓ Ô Ó ÑÙÐÓ ØÒ Ó Ú Ö ÑÒØÓ Ñ ÙÑ ÚÐÓÖ ÓÒ ØÒØ V esp º ÚÓ ÐÑØ ÒÓ ÕÙÔÑÒØÓ ÖÓÖ ÖØÚÓ ÒÓ ÖØÚÓ Q k Ñ ÙÑ ÖÖ ÈÎ Ú Ö ÑÒØ ÒØÖ ÐÑØ Q min k Q max k º ÈÖ ÑÙÐÖ ØÙÓ Q esp Ù ØØÙÓ Ñ ØÖÓ ÔÓÖ ÙÑ ÚÐÓÖ ÐÙÐÓ ÔÓÖ Q cal k k = I V k V i+1 m Ω k V m Ẏ km º¾ µ ÓÑ Ø ÚÐÓÖ Q cal k ØÒ Ó k ÐÙÐ Ù ÒÓ¹ º¾¼µº ÓÑÓ Ó ÑÙÐÓ ØÒ Ó Ú Ö ÑÒØÓ ÙÐ V esp k ÔÖØ Ö i+1 ÑÒ Ö V k Ó Ù Ø ÔÖ Ø ÞÖ ÓÒÓ ÑÒØÒÓ¹ ÔÓÖÑ Ó ÒÙÐÓ ÐÙÐÓº ÔÖÓ Ó ÖÔÖ ÒØÓ ÔÐ ÕÙ k = arctan f k i+1 θ i+1 e i+1 k V i+1 k = V esp k cos θ i+1 k + jv esp k sen θ i+1 k º¾µ º¾µ
45 ÇÈÈ»ÍÊ ÓÒ f i+1 k e i+1 k Ó Ö ÔØÚÑÒØ ÔÖØ ÖÐ ÑÒ Ö ØÒ Ó Ò ÖÖ k ÐÙÐ Ò ØÖÓ i ÒØ Ó Ù Øº ÈÖ ÐÚÖ Ñ ÓÒ ÖÓ Ó ÐÑØ Ò ÒÓ ÖØÚÓ Ùع ÐÞ ÙÑ ØÖØ ÑÙÒ ØÔÓ ÖÖ ÑÔÖ ÕÙ ÒÓ ÖØÚÓ ÙÐØÖÔ Ö ÙÑ Ó ÐÑØ ÒÓ Ü Ñ ÙÑ ÚÐÓÖ ÙÐ Ó ÐÑØ ÚÓÐÓ ÖÖ Ô Ö ØÖØ ÓÑÓ ÙÑ ÖÖ Öº ØÖØ Ö ÙÑ ÙÖ Ë Ë Q cal k Q cal k >Q max k <Q min k = Q cal k = Q cal k = Q max k = Q min k k = {barra PQ} º¾µ Ë Ò ØÖ ÙÒØ Q k ÖØÓÖÒÖ ÙÑ ÚÐÓÖ ÒØÖ Ó ÐÑØ ÒØÓ ÖÖ k ÚÓÐØ Ö ØÖØ ÓÑÓ ÙÑ ÖÖ Ó ØÔÓ Èκ ÜÑÔÐÓ º ËÙÔÓÒ ÕÙ ÒÓ ØÑ ÙÖ º¾ ÖÖ Ó Ó ÙÒØ ØÔÓ ÖÖ 1 = Vθ ÖÖ ¾ = PV ÖÖ = PQº ÒØÓ ÐÓÖØÑÓ Ù ¹ËÐ V 2 i+1 = 1 [ ] P esp 2 j(q cal 2 )i Y 22 ( V V 2 i 1 Y 21 V i ) 3 Y 23 V 3 i+1 = 1 [ P esp 3 jq esp 3 Y 33 ( V 3 i V 1 Y 31 ) V i+1 2 Y 32 ] { ( (Q cal 2 ) i+1 = I V i+1 2 V1 Y 21 + V i+1 2 Y 22 + V i+1 3 Y 23 ) } ÓÒ i ÓÓÒØÓÖ ØÖ V 1 P esp 2 P esp 3 Q esp 3 V esp 2 Ó Ó º ºº ÅØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ Ç ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ Ó ÐÙÐÓ ÖÞ ÙÑ ÕÙÓ ÐÖ ÒÓ¹ÐÒÖ ¹ Ñ ÐÒÖÞ Ù Ú ÙÒÓ ÔÖØÖ ÙÑ ÓÒÓ ÒÐ ÖØÖ Öº ËÙÔÓÒ ÕÙÓ f(x) =0 º¾µ ÜÔÒ Ó ÔÐ Ö ÌÝÐÓÖ ÔÓ ØÖÓÖ ÐÑÒÓ Ó ØÖÑÓ ÓÖÑ ÑÓÖ ÓÙ ÙÐ Ó ÔÖÓÙÞ f(x) f(x 0 )+f (x 0 )[x x 0 ] º¾µ
46 Ò Ð Ê ÐØÖ f(x) x 3 x 2 x 1 µ x 0 x f(x) x 3 x 2 µ ÙÖ º ËÓÐÙÓ ÕÙÓ ÒÓ¹ÐÒÖ ÔÐÓ ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ x 1 x 0 x ÓÒ ÓØÑ x = x 0 f(x0 ) f (x 0 ) º¾µ ÇÚÐÓÖ x ÐÙÐÓ ÔÓÖ º¾µ ÙÑ ÔÖÓÜÑÓ ÓÐÙÓ º¾µ ÕÙÐ ÔÓ Ö ÑÐÓÖ ÔÖÓÑÓÚÒÓ¹ ÒÓÚ ÐÒÖÞÓ f(x) Ñ ØÓÖÒÓ ÒÓÚÓÚÐÓÖ Ñ ÔÓÖ Òغ Ç ÔÖÓ Ó ØÖØÚÓ ÔÓ Ö ÒØØÞÓ Ò ÜÔÖ Ó x i+1 = x i f(xi ) f (x i i =0, 1,... º ¼µ ) ÙÖ º µ ÐÙ ØÖ Ø ÔÖÓ Ó ÖÑÒغ Æ ÙÖ º µ ÑÓ ØÖÓ ÕÙ Ó ÔÖÓ Ó ÔÓ ÓÒÚÖÖ Ñ ÑÓ ÕÙ f (x i ) ÑÒØ ÙÐ f (x 0 )º ÚÐÓÖ ÔÓ Ø Ö ÖÒØ f (x 0 ) ÕÙ ÓÒÚ¹ ÒÒØÑÒØ ÓÐÓº Ç Ó Ò¹ÑÒ ÓÒÐ ÔÓ Ö ÓØÓ ÓÑÓ ÙÑ ÜØÒ Ó Ó ÒØÖÓÖº ËÙÔÓÒ ÕÙÓ f(x) =0 º ½µ ÓÒ f( ) = x = [ [ f 1 ( ) f 2 ( ) f n ( ) x 1 x 2 x n ] T ÜÔÒ Ó Ñ Ö ÌÝÐÓÖ ÙÒ ÔÖÓÙÞ f 1 (x) =f 1 (x 0 )+ f 1(x) x 1 ] T x=x 0Δx f 1(x) x=x x n 0Δx 0 n =0 f 2 (x) =f 2 (x 0 )+ f 2(x) x=x x 1 0Δx f 2(x) x=x x n 0Δx 0 n =0 ºººººººººººººººººººººººººººººººººººººººººººººººººººººººººººººº f n (x) =f n (x 0 )+ fn(x) x 1 x=x 0Δx fn(x) x n x=x 0Δx 0 n =0 º ¾µ
47 ÇÈÈ»ÍÊ ÓÙ Ñ ÓÖÑ ÓÑÔØ f(x 0 )+J(x 0 )Δx 0 =0 º µ ÓÒ J(x 0 ) ÑØÖÞ ÂÓÒ Ó Ó ØÑ º ½µ ÐÙÐ ÒÓ ÔÓÒØÓ x 0 º Ç ÔÖÓ Ó ØÖØÚÓ ÒÓ Ó Ò¹ÑÒ ÓÒÐ Ó ÒØÓ ÔÓÖ x i+1 = x i +Δx i º µ [ 1 Δx i = J(x )] i f(x i ) º µ Ç ÔÖÓ Ó ØÖØÚÓ ØÖÑÒ ÕÙÒÓ f(x i ) ε ÓÒ ε ÙÑ ÚÐÓÖ ÕÙ ØÖÑÒ ØÓÐÖÒ Ø ÚÐ ÒÓ ÖÖÓ ÓÑØÓ Ò ÓÐÙÓº ÔÓ ÚÐ ÑÓÒ ØÖÖ ½ ÕÙ Ó ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ ÒØ ÙÑ ØÜ ÓÒÚÖÒ ÕÙÖ Ø ØÓ ÒÓÖÑ Ó ÚØÓÖ Ö ÙÓ f(x i ) ÑÒÙ ÓÑ Ó ÕÙÖÓ Ó ÒÑÖÓ ØÖ º Á ØÓ Ò ÕÙ Ó ÑØÓÓ ÓÒÚÖ ÖÔÑÒØ ÔÖ ÓÐÙÓº ÒØÖØÒØÓ ÓÒÚÖÒ ÓÖØÑÒØ ÔÒÒØ ÓÒ Ò x 0 µº Ó ÓÒÓ ÒÐ ÒÓ Ø ÓÒØ Ñ ÙÑ ÖÓ ÔÖÜÑ ÓÐÙÓ ÔÖÓÙÖ ÖÓ ØÖÓµ Ó ÔÖÓ Ó ØÖØÚÓ ÔÓÖ ÓÒÚÖÖ ÔÖ ÓÙØÖ ÓÐÙÓ ÓÙ ÒÓ ÓÒÚÖÖº ÔÐÓ Ó ÐÙÜÓ ÈÓØÒ Ñ ÓÓÖÒ ÈÓÐÖ Æ Ø Ó Ó ØÑ ÕÙ Ö Ö ÓÐÚÓ ÜØÖÓ º½µ º½µ Ó ÔÓÖ ΔP k = P esp k g pk (Θ, V) =0, k Ω PQ Ω PV º µ ΔQ k = Q esp k g qk (Θ, V) =0, k Ω PQ º µ Ç ÐÓÖØÑÓ ØÖØÚÓ Ó ÔÓÖ [ Θ i+1 V i+1 ] = [ Θ i V i ] + [ ΔΘ i ΔV i ] º µ [ ΔP i ΔQ i ] = [ H i N i M i L i ][ ΔΘ i ΔV i ] º µ ÑØÖÞ ÂÓÒ ÓÙ Ó ÂÓÒÓ ÙÑ ÙÒÓ f : IR n IR n Ò ÓÑÓ f 1 (x) f 1 (x) f x 1 x 2 1 (x) x n f 2 (x) f 2 (x) f J(x) = x 1 x 2 2 (x) x n ºººººººººººººººººººººººººººº f n(x) x 2 f n(x) x 1 f n(x) x n
48 ¼ Ò Ð Ê ÐØÖ ÓÒ È É Ó Ó ÚØÓÖ Ó Ö ÙÓ ÔÓØÒ ØÚ ÖØÚ Ö Ô¹ ØÚÑÒØ ÙÑØÖÞ H i N i M i L i ØÑ Ó ÙÒØ ÒÓ H i = g p k (Θ i, V i ) Θ M i = g q k (Θ i, V i ) Θ N i = gp k (Θi,V i ) V L i = gq k (Θi,V i ) V º¼µ º½µ ÓÑÔÓÒÒØ H N M L Ó ÔÓÖ H km = P k θ m = V k V m (G km sen θ km B km cos θ km ) H kk = P k θ k = V 2 k B kk V k N km = P k V m = V k (G km cos θ km + B km sen θ km ) m Ω k V m (G km sen θ km B km cos θ km ) N kk = P k V k = V k G kk + m Ω k V m (G km cos θ km + B km sen θ km ) º¾µ M km = Q k θ m = V k V m (G km cos θ km + B km sen θ km ) M kk = Q k θ k = V 2 k G kk + V k L km = Q k V m = V k (G km sen θ km B km cos θ km ) m Ω k V m (G km cos θ km + B km sen θ km ) L kk = Q k V k = V k B kk + m Ω k V m (G km sen θ km B km cos θ km ) Ç ÐÑÒØÓ H kk N kk M kk L kk ÔÓÑ Ò Ö ÓÐÓÓ Ñ ÙÒÓ Ò ÔÓØÒ ØÚ ÖØÚ Ò ÖÖ k ÓÑÓ ÙÖ H kk = Q k Vk 2 kk N kk = (P k + Vk 2 kk)/v k M kk = P k Vk 2 G kk L kk = (Q k Vk 2 B kk )/V k º µ
49 ÇÈÈ»ÍÊ ½ Ñ ÖÐ Ó ÐÑÒØÓ ΔV Ó ÚÓ ÔÐÓ ÚÐÓÖ Ö ÔØÚ ØÒ¹ ÔÖ ÔÖÓÙÞÖ ØÖÑÓ ÑÐÖ Ñ M Lº Æ Ø Ó º µ ÙÑ ÓÖÑ [ ] [ ][ ] ΔP i H i (N ΔQ i = ) i ΔΘ i M i (L ) i ΔV i /V i ºµ ÓÒ Ó ÐÑÒØÓ N L Ó Ù Ó N L ÑÙÐØÔÐÓ ÔÐÓ ÑÙÐÓ Ö ÔØÚ ØÒ º Ç ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ Ñ ÓÓÖÒ ÔÓÐÖ ÔÓ Ö Òع ØÞÓ ÒÓ ÐÓÖØÑÓ ÙÖ ºº Æ ÐÓÖØÑÓ Ó ÐÑØ ÖÓ ÔÓØÒ ÖØÚ Ñ ÖÖ ÈÎ Ó ØÖØÓ ÔÐ ØÖÓ Ó ØÔÓ ÖÖ ÈÎ Èɵ ÑÔÖ ÕÙ ÙÑ Ó ÐÑØ ÓÖ ÙÐØÖÔ Ó ÑÒÖ ÑÐÖ Ó ÔÖÓÑÒØÓ ÓØÓ ÒÓ ÑØÓÓ Ù ¹Ëк Æ Ø Ó ÒØÖ¹ ØÒØÓ ÑÓÓ ÑÔÐ Ò ÐØÖÓ ØÖÙØÙÖ Ó ËÙ ØÑ ÕÙ ½ ¾ ÓÙ Ò ÒÐÙ Ó ÓÙ ÜÐÙ Ó ÕÙ ÖÐØÚ ÓÖÖÓ Ó ÑÙÐÓ ØÒ Ó Ó Ö ÙÓ ÔÓØÒ ÖØÚ Ò ÖÖ Ñ ÕÙ ØÓ ÒÓ ØÑ ÕÙ Ò Ñ º µ º µº ÁÒÐÞ Ó ÚØÓÖ Θ V ÒÕÙÒØÓ ΔP >ε p ΔQ >ε q ÐÙÐ ΔP ΔQ ÐÙÐ Ó ÂÓÒÓ ÒÓ Ñ º µ ØÓÖ Ó ÂÓÒÓ Ê ÓÐÚ º µ ÓØÒÓ ΔΘ ΔV ØÙÐÞ Ó ÚÐÓÖ ØÒ ØÖÚ Θ Θ +ΔΘ V V +ΔV ÁÑÔÐÑÒØ Ù Ø ÓÒØÖÓÐ Ñ ÒÕÙÒØÓ ÙÖ º ÐÓÖØÑÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ ÔÐÓ Ó ÐÙÜÓ ÈÓØÒ Ñ ÓÓÖÒ ÊØÒÙÐÖ ÚÖ Ó Ó ÐÓÖØÑÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÖÔÖ ÒØÒÓ ØÒ Ñ Ó¹ ÓÖÒ ÖØÒÙÐÖ ÑÒÓ Ù ÕÙ ÕÙÐ Ñ ÓÓÖÒ ÔÓÐÖ Æ ÕÙÓ ºµ ÙØÐÞ ÒÓØÓ ΔV/V ÔÖ ÒÖ Ú Ó ÓÑÔÓÒÒØ ΔV ÔÐ Ö ÔØÚ ÓÑÔÓÒÒØ Vº ÒÓØÓ ÒÓ ÓÖÖØ ÙÑÔÓÒØÓ Ú Ø ØÖØÑÒØ ÑØÑ ØÓ ÔÓÖÑ Ù ÙÐ Ò ÐØÖØÙÖ ÓÖ ÙÜÓ ÔÓØÒº ÌÒ ØÓÖÓ ÑØÖÞ Ù Ò ÓÐÙÓ ØÑ ÕÙ ÐÒÖ Ñ ÓÑÓ ÑØÓÓ ÑÔÐÑÒØÓ Ù Ø ÓÒØÖÓÐ ÖÖ Ò ÐÓÖØÑÓ ÖÓ ÒØÖÓÙÞ Ñ ÙÒØ Ø ÒÓØ Ùк
50 ¾ Ò Ð Ê ÐØÖ ÔÓÖ ÒÐÙÖ ÙÑ ÒÑÖÓ ÑÓÖ ÕÙ ÔÓÖ Ö ÐÖÑÒØ ÑÒÓ ÓÒ¹ Úк Æ Ø Ó Ó ØÑ ÕÙ Ö Ö ÓÐÚÓ ÜØÖÓ º½¾µ º½ µ Ó ÔÓÖ ΔP k = P esp k g p k (e, f) =0, k Ω PQ Ω PV ºµ ΔQ k = Q esp k g q k (e, f) =0, k Ω PQ ºµ ΔV k = V esp k (e k + f k ) 1 2 =0, k Ω PV ºµ Ç ÐÓÖØÑÓ ØÖØÚÓ Ó ÔÓÖ [ e i+1 f i+1 ΔP i ΔQ i ΔV i ] = = [ e i f i ] + J 1 J 2 J 3 J 4 J 5 J 6 [ Δe i Δf i ] [ Δe i Δf i ] ºµ ºµ Æ ÕÙ Ñ Ó ÚØÓÖ e f P Q V ØÑ ÓÑÔÓÒÒØ ÓÑ Ó Ò ÒÓ ÓÑÓ Ñ ºµ ºµº ÜÑÔÐÓ º ÈÖ Ó ØÑ ÙÖ º Ó ØÑÕÙ ÐÒÖ Ö Ö ÓÐÚÓ Ñ ØÖÓ Ó ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ Ñ ÓÓÖÒ ÔÓÐÖ ΔP 2 ΔP 3 ΔQ 3 ΔP 4 ΔQ 4 ΔP 5 ΔQ 5 H 22 H 23 N 23 H 25 N 25 H 32 H 33 N 33 H 34 N 34 M 32 M 33 L 33 M 34 L 34 H 43 N 43 H 44 N 44 H 45 N 45 M 43 L 43 M 44 L 44 M 45 L 45 H 52 H 54 N 54 H 55 N 55 M 52 M 54 L 54 M 55 L 55 Δθ 2 Δθ 3 ΔV 3 /V 3 Δθ 4 ΔV 4 /V 4 Δθ 5 ΔV 5 /V 5 Ç ÖÙÔÑÒØÓ Ó ÐÑÒØÓ H N M L Ñ ÐÓÓ ÐØ ÓÒ ØÖÙ¹ Ó ØÓÖÓ Ó ÂÓÒÓº ºº ÅØÓÓ ÓÔÐÓ Ê ÔÓ Ç ÑØÓÓ ÓÐÙÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÓÒÓ ÓÑÓ ¹ ÓÔÐÓ Ê ÔÓ ÒÚÓÐÚÓ ÔÓÖ ËØÓØØ Ð ¾ ÖÚÓ Ó ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÐ ÒØÖÓÙÓ Ù ÔÖÓÜÑ ÓÓ ÂÓÒÓ ÓÒ ØÒØ ÙÖÒØ Ó ÔÖÓ Ó ØÖØÚÓ ÓÔÐÑÒØÓ ÕÙ Ó ÙÜÓ ÔÓØÒ ØÚ ÖØÚ ÔÖÞÒÓ¹ ÙÑØÖÞ N M ÓÖÑÙÐÓ ÔÓÐÖº
51 ÇÈÈ»ÍÊ ÑÓ ÖØÓ ÚÑ Ó ÙØÐÞÓ ÒØÖÓÖÑÒØ ÔÓÖ ÓÙØÖÓ Ô ¹ ÕÙ ÓÖ Ò ØÒØØÚ ØÓÖÒÖ Ñ ÒØ Ó ÐÓÖØÑÓ ÆÛØÓÒ¹ ÊÔ ÓÒ Ñ ÖÒ Ù Óº Æ Ø Ó ÔÓÖÑ ÓØÚ¹ ÙÑ ÑØÓÓ ÜØÖÑÑÒØ ÒØ ÚÓ ÙÑ Ö ÑÔÐ ÓÒ Ò¹ ØÖÓÙÞ ÔÐÓ ÙØÓÖ ÕÙ ÖØÑ ÖØÖ Ø Ö ÐØÖ º ËÙÔÓÒ ÓÖÑÙÐÓ Ó ÐÓÖØÑÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÓÖ ºµº ÚÓ Ö ÒØÖÓ Ü ØÒØ ÒØÖ Ò ÔÓØÒ ØÚ Ó ÑÙÐÓ ØÒ ÒØÖ Ò ÔÓØÒ ÖØÚ Ó ÒÙÐÓ ØÒ Ó ÐÑÒØÓ M N Ó ÑÙØÓ ÑÒÓÖ ÕÙ Ó H L ½¼ º ÙÑØÖÞ ÔÓÑ ÒØÓ Ö ÔÖÞ Ö ÙÐØÒÓ Ñ Ó ØÑ ÒÔÒÒØ ÕÙ Ó ÔÓÖ ΔP = HΔΘ º¼µ ΔQ = L ΔV V Ø ÕÙ ÔÓÑ Ò Ö Ñ ÑÔÐ ÓÖ ÐÚÓ Ñ ÓÒ ¹ ÖÓ Ó ØÓ ÕÙ ÔÖØÙÐÖÑÒØ Ñ ØÑ ØÖÒ Ñ Ó Ñ Ì ÍÌ ½½ ÖÐ ÜÓ Ó ÚÐ cos θ km 1.0 G km sen θ km B km º½µ Q k B kk V 2 k Ù ÔÖÑÖ ÖÐ Ñ º½µ Ó Ù ØÓ ÔÐÓ ØÓ ÖÐÓ B km /G km Ö ÐÚ Ñ ÐÒ ØÖÒ Ñ Ó Ñ Ì Í̺ Ö¹ ÐÓ ÖÐÑÒØ ÑÓÖ ÕÙ ÔÖ ÐÒ ¾ ¼ Î ÔÓ ØÒÖ ÚÐÓÖ ÓÖÑ ¾¼ ÔÖ ÐÒ ¼¼ κ ØÖÖ ÖÐÓ Ù ØÓ ÔÐÓ ØÓ ÖØÒ ÙÒØ Ö ÖØÓÖ ÔØÓÖ ÙÒØ ÐÒ Øºµ ÖÑ Ñ ÖÐ ÑÙØÓ ÑÓÖ ÕÙ ÖØÒ Ö ÐÒ ØÖÒ ¹ ÓÑÓÖ º ÁÒØÖÓÙÞÒÓ ÔÖÓÜÑ ÙÖ ÔÓÖ º½µ Ò ÜÔÖ H L ÓØѹ H kk = L kk = V k 2B kk º¾µ H km = L km = V kv m B km ½¼ Ç ÖÓ ÓÔÐÑÒØÓ ÒØÖ ÚÖ ÒÓ ÒÙÐÓ ØÒ Ó ÙÜÓ ÔÓØÒ ÖØÚ ÑÓÑÓ ÒØÖ Ó ÑÙÐÓ ØÒ Ó ÙÜÓ ÔÓØÒ ÖØÚ ÙÑ ÖØÖ Ø Ó ØÑ ÔÓØÒ ÙØÐÞ ÓÖÖÒØÑÒØ Ò ÓÔÖÓ ØÑ ÖØÓ ÒÓ ÑÓÐÓ ÑØÑ ØÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÔÐÓ ÚÐÓÖ ÖÐØÚÓ Ó ÐÑÒØÓ ÙÑØÖÞ Ó ÂÓÒÓº ½½ Ì ÜØÖ ÐØ ÌÒ Ó ÍÌ ÍÐØÖ ÐØ ÌÒ Óº
52 Ò Ð Ê ÐØÖ ÜÔÖ ÐÒÖÞ ÓÔÐ Ê ÙÓ ÈÓØÒ Ó ÒØÓ ÔÓÖ ΔP 1 ΔP 2 ΔP n ΔQ 1 ΔQ 2 ΔQ n ÓÙ Ò = = ΔP 1 /V 1 ΔP 2 /V 2 ΔP n /V n ΔQ 1 /V 1 ΔQ 2 /V 2 ΔQ n /V n V 2 1 B 11 V 1 V 2 B 12 V 1 V n B 1n V 1 V 2 B 12 V 2 2 B 22 V 2 V n B 2n ºººººººººººººººººººººººººººººººººº V 1 V n B 1n V 2 V n B 2n V 2 n B nn V 2 1 B 11 V 1 V 2 B 12 V 1 V n B 1n V 1 V 2 B 12 V 2 2 B 22 V 2 V n B 2n ºººººººººººººººººººººººººººººººººº V 1 V n B 1n V 2 V n B 2n V 2 n B nn = = V 1 B 11 V 2 B 12 V n B 1n V 1 B 12 V 2 B 22 V n B 2n ººººººººººººººººººººººººººº V 1 B 1n V 2 B 2n V n B nn B 11 B 12 B 1n B 12 B 22 B 2n ºººººººººººººººººººº B 1n B 2n B nn Δθ 1 Δθ 2 Δθ n º µ ΔV 1 /V 1 ΔV 2 /V 2 ºµ ΔV n /V n ΔV 1 ΔV 2 ΔV n Δθ 1 Δθ 2 Δθ n ºµ ºµ ÓÑÓ Ó ÑÙÐÓ ØÒ ÒÓ ØÑ ÔÓÙ ÒÙÒ ÒÓ ÙÜÓ ÔÓØÒ ØÚ ÒÓ ÓÑØ ÖÒ ÖÖÓ ÔÖÓÜÑÒÓ¹ Ó ÚÐÓÖ ØÒ ÒÓ ÐÑÒØÓ ÑØÖÞ Ó ØÑ ÕÙ ºµ ÔÓÖ ½ ¼ ÔÙº Æ Ø Ó ÓØѹ ΔP/V = B ΔΘ ºµ ΔQ/V = B ΔV ºµ ÓÒ B B ÖÑ ÔÒ ÓÑ ÖÐÓ ÕÙ ÖÖ ØÒ Ó ÓÒØÖÓк Ç ÐÑÒØÓ ÑØÖÞ Ó ÓÑÔÓÒÒØ ÑÒ Ö Ó ÐÑÒØÓ ÓÖÖ ÔÓÒÒØ Yº ÐÙÑ ÑÐÓÖ ÒÓ ÑÔÒÓ Ó ÑØÓÓ ÓØ ÔÖÞÒÓ¹ Ö ØÒ ÐÒ ØÖÒ ÓÖÑÓÖ ÒÓ ÐÙÐÓ Ó ÐÑÒØÓ B º Æ Ø Ó Ó ÐÑÒØÓ B B ÖÑ Ó ÔÓÖ B km = 1/x km B kk = 1/x km m Ω k ºµ B km = B km B kk = B kk ÔÖÓÜÑ ÓÒ ÕÙ ÑÐÓÖÑ Ó ÑÔÒÓ Ó ÑØÓÓ ÔÓ¹ Ñ Ö ÒØÖÓÙÞ ÜÐÙÒÓ¹ ÖÔÖ ÒØÓ B B Ó ÐÑÒØÓ
53 ÇÈÈ»ÍÊÂ Ö ÕÙ ØÑ ÔÖÑÓÖÐÑÒØ Ó ÙÜÓ ÔÓØÒ ØÚ ÖØÚ Ö ÔØÚÑÒغ Ñ ÒÓ ÐÙÐÓ B ÒÓ Ó ÒÐÙÓ Ù ÔØÒ ÙÒØ ØÖÒ ÓÖÑÓÖ ÓÖ º ÑØÖÞ B B Ó Ö ÑØÖ ÓÑ Ü Ó B ÒÓ Ó ÒÐÙÖ ØÖÒ ÓÖÑÓÖ ÓÖ µ ÔÒÑ ÔÒ Ó ÔÖÑØÖÓ Öº ÈÓÖØÒØÓ ÚÑ Ö ØÓÖÓ ÔÒ ÙÑ ÚÞ ÒÓ ÒÓ Ó ÔÖÓ Ó ØÖØÚÓº Ç ÑØÓÓ ÓÔÐÓ Ê ÔÓ ÔÓ Ö ÒØØÞÓ ÒÓ ÐÓÖØÑÓ ÙÖ ºº Æ ÐÓÖØÑÓ ÓÐÙÓ Ó ØÑ ÕÙ ÐÒÖ ÓÔÐÓ ÒÓ Ñ ºµ ºµ ÖÐÞ ÓÖÑ ÕÒÐ ÒÒÓ¹ ÔÐÓ ØÑ ÕÙ ÓÖÖ ÔÓÒÒØ ÔÖØ ØÚº ÖÞÓ ÓÐ ÓÖÑ Ø ÖÐÓÒ Ù ÙÐÑÒØ Ö ÒÓ¹ÐÒÖ Ó ÕÙ Ó ÙÜÓ ÔÓØÒ ØÚº ÓÖÑ Ò ÔÖÑÖ ØÙÐÞÓ Ó ÚÐÓÖ Ó ÒÙÐÓ ØÒ ØÑ ÙÑ Ó ÔÖÓÜÑÓ ÓÐÙÓ ÔÖ ÚÖ Ú ÔÓÖØÒØÓ ÔÓ¹ ÐÙÐÖ Ò ÕÒ ÙÑ ÚÐÓÖ Ñ ÔÖ Ó Ó Ö ÙÓ ÔÓØÒ ÖØÚº Æ ÐÓÖØÑÓ ÑÓÓ ØÖÙØÙÖ ÕÙ Ò Ñ ºµ ºµ ÔÖ ÖÔÖ ÒØÖ ÙÑ ÚÒØÙÐ ØÖÓ ØÔÓ ÖÖ ÓÖ¹ Ò ÔÓÖ ÚÓÐÓ ÒÓ ÐÑØ ÒÓ ÖØÚÓ ÑÔÐ Ñ ÙÑ ÒÓÚ ØÓÖÓ ÑØÖÞ B º ÔÖÓÑÒØÓ Ü ÙÑ ÓÖÓ ÓÑÔÙع ÓÒÐ ÓÒ Ö Úк Ñ ÙÒØ ÖÓ ÔÖ ÒØ ÓÙØÖ ÓÖÑ ÖÒØÖ ÙÑ ÓÐÙÓ Ó ÔÖÓÐÑ Ñ Ò ÖØÓÖÓº ÁÒÐÞ Ó ÚØÓÖ Θ V ÐÙÐ B B ØÓÖ B B κ p =1 κ q =1 ÒÕÙÒØÓ κ p =1ÓÙ κ q =1 ÐÙÐ ΔP Ë ΔP <ε p ÒØÓ κ p =0 Ë κ p =0 κ q =0ÒØÓ ÈÊ Ê ÓÐÚ ºµ ÓØÒÓ ΔΘ ØÙÐÞ Ó ÚÐÓÖ Ó ÒÙÐÓ Θ Θ +ΔΘ ÐÙÐ ΔQ Ë ΔQ <ε q ÒØÓ κ q =0 Ë κ p =0 κ q =0ÒØÓ ÈÊ Ê ÓÐÚ ºµ ÓØÒÓ ΔV ØÙÐÞ Ó ÚÐÓÖ Ó ÑÙÐÓ V V +ΔV ÁÑÔÐÑÒØ Ù Ø ÓÒØÖÓÐ Ñ ÒÕÙÒØÓ ÙÖ º ÐÓÖØÑÓ Ó ÑØÓÓ ÓÔÐÓ Ê ÔÓ
54 º Ò Ð Ê ÐØÖ ÓÒØÖÓÐ ÄÑØ Ò ËÓÐÙÓ Ó ÐÙÜÓ ÈÓØÒ Ç ÔÖÒÔ ØÔÓ ÓÒØÖÓÐ ÖÔÖ ÒØÓ ÒÓ ØÙÓ ÙÜÓ ÔÓØÒ¹ Ó ÅÙÐÓ ØÒ Ó ÔÓÖ ÒÓ ÖØÚÓ ÐÓÐ ÓÙ ÖÑÓص ÅÙÐÓ ØÒ Ó ÔÓÖ Ù Ø ØÔ ÐÙÜÓ ÔÓØÒ ØÚ Ù ÒÓ ØÖÒ ÓÖÑÓÖ ÓÖ ÓÒØÖÓÐ ÒØÖÑÓ ÒØÖ Ö º Ç ÔÖÒÔ ØÔÓ ÐÑØ ÒÓÖÑÐÑÒØ ÑÔÐÑÒØÓ ÒÓ ÔÖÓÖÑ ÙÜÓ ÔÓØÒ Ó ºº½ ÁÒÓ ÔÓØÒ ÖØÚ Ñ ÖÖ ÈÎ ÅÙÐÓ ØÒ Ó Ñ ÖÖ ÈÉ ÈÓ Ó ØÔ ØÖÒ ÓÖÑÓÖ ÐÙÜÓ ÔÓØÒ ÒÓ ÖÑÓ Öº ÅØÓÓ ÁÑÔÐÑÒØÓ ½º Ð Ó Ó ÌÔÓ ÖÖ Ç ÓÒØÖÓÐ ÐÑØ Ó ÑÔй ÑÒØÓ ÔÐÓ ØÐÑÒØÓ ØÔÓ Ô ÖÖ Ò ÓÖÑÙ¹ ÐÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒº ÙÖÒØ Ó ÔÖÓ Ó ØÖØÚÓ ÓÐÙÓ ÕÙ ÔÓ ÓÓÖÖÖ ÑÙÒ Ó ØÔÓ ÖÖ ÔÖ ÓÑÓÖ ØÙ ÓÒ ÐÙÑ ÚÖ Ú ØÒÑ Ù ÐÑØ º ÍÑ ÜÑÔÐÓ ØÔÓ ÑÒÓÒÓ Ò Ø ÔØÙÐÓ Ó ÖÖ ØÒ Ó ÓÒØÖÓÐ ÖÖ Èεº ¾º Ù Ø ÐØÖÒÓ ÓÒ Ø Ò ÖÐÞÓ Ù Ø Ò ÚÖ Ú ÓÒØÖÓÐ ÒØÖ ØÖ ÓÐÙÓ Ó ËÙ ØÑ Áº ÚÖ ÚÐ Ö ÓÒØÖÓÐ ÑÒØ ÓÒ ØÒØ ÙÖÒØ Ó ÐÙÐÓ ÙÑ ØÖÓ Ù ØÒÓ ÒØÖ ØÖ ÔÐ ÖÑÙÐ Δy i = αδx i = α(x esp x i ) º¼µ ÓÒ x ÚÖ ÚÐ Ö ÓÒØÖÓÐ ÔÒÒص y ÚÖ ÚÐ ÓÒØÖÓÐ ÒÔÒÒص α ÖÐÓ Ò Ð ÒØÖ x y x esp ÚÐÓÖ ÔÓ ÔÖ xº
55 ÇÈÈ»ÍÊ º ÁÒÐÙ Ó ÎÖ Ú ÕÙ Æ Ø ÔÖÓÑÒØÓ ÚÖ Ú ÕÙ ÓÒ Ó ÒÐÙ Ò ÕÙ Ó ËÙ ØÑ Á ÔÖ ÖÔÖ ÒØÖ Ó ÔÓ ØÚÓ ÓÒØÖÓÐ ÐÑØÖ Ó ÚÐÓÖ ÐÙÒ ÔÖÑØÖÓ º ØÐ ÖÐØÚÓ ÑÔÐÑÒØÓ ÐÑØ ÓÒ¹ ØÖÓÐ ÒÓ ÐÓÖØÑÓ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ ÔÓ¹ Ñ ÒÓÒØÖÓ Ñ º ÅÓÒØÐÐ ÐÙÜÓ Ö Ñ Ê ÒÖ ÐØÖ º Ö ÐÖ ½ Ôº º ÐÙÐÓ ÈÖ ÐÙÜÓ ÈÓØÒ ØÚ ÊØÚ Ô ÓÒÚÖÒ Ó ÔÖÓ Ó ØÖØÚÓ ÓÐÙÓ ÕÙ Ò¹ ÕÙ ÑÓÐÒÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒ ÔÖ Ó ÙÜÓ ÔÓØÒ ØÚ ÖØÚ Ñ ØÓÓ Ó ÖÑÓ Ö ÚÑ Ö ÐÙй Ó º ÔÖ Ó ÙÜÓ Ó ÙÒ ØÒ ÒÓ ÒÓ ØÖÑÒ Ó ÐÑÒØÓ Ó ÔÖÑØÖÓ Ó Ñ ÑÓ º ÙÖ Ó ÔÖ ÒØ ÜÔÖ Ö ÔÖ Ó ÐÙÐÓ Ó ÙÜÓ ÒÓ Ú ÖÓ ÐÑÒØÓ Öº Ç ÙÜÓ ÔÓØÒ ØÚ ÖØÚ Ñ ÙÑ ÐÑÒØÓ ÓÒØÓ ÒØÖ ÖÖ k m Ó Ó ÔÓÖ fkm P = (t kmv k ) 2 g km (t km V k ) V m g km cos (θ km + φ km ) (t km V k ) V m b km sen (θ km + φ km ) º½µ f Q km = (t kmv k ) 2 (b km + y s ) (t km V k ) V m g km sen (θ km + φ km ) +(t km V k ) V m b km cos (θ km + φ km ) º¾µ ÜÔÖ Ñ º½µ º¾µ ÔÓÑ Ö ÔÖØÙÐÖÞ ÔÖ Ó ÚÖ Ó ÐÑÒØÓ Ö ÓÑÓ ÒÓ ÙÖ ÄÒ ØÖÒ Ñ Ó t km =1 φ km =0 ÌÖÒ ÓÖÑÓÖ ÓÑ ØÔ ÜÓ t km =1 y s =0 φ km =0 ÌÖÒ ÓÖÑÓÖ ÓÑ ÚÖÓ ÙØÓÑ Ø ØÔ Ó Ö Ä̳ µ y s =0 φ km =0 ÌÖÒ ÓÖÑÓÖ ÓÖ t km =1 y s =0º ÔÖ ÒÓ ÐÑÒØÓ Ö ÔÓÑ Ö ÐÙÐ ÓÑÒÓ¹ Ó ÙÜÓ ÒÓ Ó ØÖÑÒ Ñ Ñº ÈÖ Ó Ó ÐÒ ØÖÒ Ñ Ó ÔÖ
56 Ò Ð Ê ÐØÖ Ó ÔÓÖ L P km = fkm P + fmk P = g km (Vk 2 + Vm 2 2 V k V m cos θ km ) º µ L Q km = f Q km + f Q mk = (b km + y s )(Vk 2 + Vm)+2V 2 k V m b km cos θ km ºµ
57 ÇÈÈ»ÍÊ ÈÖÓÐÑ ½º ØÐ Ó Ó Ù ØÑ ÕÙ ÙØÐÞÓ Ò ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ ÔÐÓ ÑØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ Ó ØÑ ÙÖ ÜÓº ÁÒÕÙ ÓÑÓ ÖÑ Ö ÓÐÚÓ Ù ØÑ º ÙÑ ÓÒÓ Ó ÔÖÑØÖÓ Ó ÓÑÔÓÒÒØ ÕÙ ÓÒ Ö Ò¹ ÖÓ º ½ ¾ ËÎ ¾º ÈÖ Ö ÙÖ ÜÓ ÓÒ ÖÒÓ ÖÖ ½ ÓÑÓ ÖÖ ÙØÙ¹ ÒØ Ù Ó ÙÒØ ÑØÓÓ ÔÖ ÐÙÐÖ Ù ØÖ ÓÐÙÓ Ó ÙÜÓ ÔÓØÒ µ Ù ¹ËÐ µ ÆÛØÓÒ¹ÊÔ ÓÒ µ ÓÔÐÓ Ê ÔÓº Ó ÖÖ ÔÙµ ÖÖ ÖÓ Ö ÄÑØ ÌÒ Ó Öº Êغ Ôº ½ ¹ ¹ ¼ ¼ ¹ ½ ¼ ¾ ¼ ¹ ¼ ¼ ¼ ½ ½ ¼ ¼ ¼ ¹ ¹ Ó ÊÑÓ ÔÙµ ÖÖ Ê ØÒ ÊØÒ ËÙ ÔØÒ ÔÖ ½ ¾ ¼ ¼ ½ ¼ ¾ ¼ ¼ ¾ ¼ ½ ¼ ¼ ½ ¼
58 ¼ Ò Ð Ê ÐØÖ ½ ¾ º ÆÓ ØÑ ÜÓ ØÒ Ó ÒÓ ØÖÑÒ Ó ÖÓÖ ÑÒØ ÙÐ ØÒ Ó ÒÓÑÒÐ ½ ¼ ÔÙµº ÐÙÐ Ñ ÒÙÐÖ ÒØÖ ØÒ Ò ÖÖ ½ ¾ Ù ÒÓ Ó ÅØÓÓ ÆÛØÓÒ¹ÊÔ ÓÒ ÔÖ ÓÐÙÓ Ó ÔÖÓÐÑ ÙÜÓ ÔÓØÒº ½ y a =0, 8 j 4pu ¾ 200 ÅÏ y b =1, 2 j 6pu 100 ÅÏ 400 ÅÏ ¼ ÅÎÊ ½¾¼ ÅÎÊ S BASE = 100 ÅÎ
59 ÔØÙÐÓ ÐÙÜÓ ÈÓØÒ ÄÒÖÞÓ Ç ØÑ ÒÖ ÐØÖ Ñ ÓÒ ÒÓÖÑ ÓÔÖÓ ÔÖ Ò¹ ØÑ ÙÑ ÔÖÐ ØÒ Ó ÔÐÒÓ ØÓ Ó ÑÙÐÓ ØÒ ÒÓ ÖÖÑÒØÓ ØÓ ÔÖÜÑ Ù ÚÐÓÖ ÒÓÑÒÐ ½º¼ ÔÙµ Ó ÕÙ Þ ÓÑ ÕÙ Ó ÙÜÓ ÔÓØÒ ÖØÚ Ò ÐÒ ØÖÒ ÓÖÑÓÖ ÔÕÙÒÓº Ø ÓÖÑ Ó ÙÜÓ ÔÓØÒ ÒÓ ÖÑÓ Ö ÔÖØÑÒØ ÓÒ ØØÙÓ ÔÒ ÔÐÓ ÙÜÓ ÔÓØÒ ØÚº ÐÑ Ó ÔÖ ÒÓ ØÑ ØÖÒ Ñ ¹ Ó Ó ÖÐØÚÑÒØ ÔÕÙÒ º ÈÓÖ ÖÞ ÓÑÙÑ ÙØÐÞÖ¹ Ñ Ú Ö ÔÐ ÓÖÑÙÐÓ ÐÒÖÞ Ó ÑÓÐÓ ÙÜÓ ÔÓØÒ ÓÙ ÙÜÓ ÔÓØÒ ½ µº Æ ÓÖÑÙÐÓ Ó ÑÙÐÓ ØÒ Ó ÓÒ ÖÓ Ù ½ ¼ ÔÙ Ó ØÖÒ ÓÖÑÓÖ ÓÑ ØÔ ÚÖ ÚÐ Ó ÓÒ¹ ÖÓ ÓÔÖÒÓ Ñ Ù ÔÓ Ó ÒÓÑÒк ÚÒØÒ ÓÖÑÙÐÓ Ó ÖÓÙ ØÞ Ó ÜÓ ÖÕÙ ØÓ ÓÑÔÙØÓÒ ÔÖ Ù ÓÐÙÓº º½ ÕÙ Ç ÙÜÓ ÔÓØÒ ØÚ Ñ ÙÑ ÐÒ ØÖÒ Ñ Ó Ñ ÓÖÖÒØ ÐØÖ¹ Ò ÓÙ Ñ ÙÑ ØÖÒ ÓÖÑÓÖ ÓÑ ØÔ ÜÓ Ó ÔÐ ÙÒØ ÜÔÖ Ó ÓÑÓ ÑÓ ØÖÓ Ò Ó º f km = V 2 k g km V k V m g km cosθ km V k V m b km senθ km º½µ ÓÒ g km = r km r 2 km + x2 km ; b km = x km r 2 km + x2 km º¾µ ÓÒ ½ ÒÓÑÒÓ ÓÖÖ Ó ØÓ ÕÙ Ó ÑÓÐÓ ÙÜÓ ÔÓØÒ ÐÒÖÞÓ ÖÑ ÑÐÒØ ÕÙ ÙÑ ÖÙØÓ Ñ ÓÖÖÒØ ÓÒØÒÙº ÑÓÐÓ ÒÓ ÒÐÙ ÖÔÖ ÒØÓ ÐÒ ØÖÒ Ñ Ó Ñ ÓÖÖÒØ ÓÒØÒÙº ½
 ÅØÑØ ÒÓ Î ØÙÐÖ Ó ÁÅ ¼¼ ËÖÓ ÄÑ ÆØØÓ ÖÓÒ ºÙÖºÖ ÚÖ Ó ÓÖÑ Ø ÑØÖÐ ØÐÚÞ ÖÑÓÒØ» ÕÙÒÓ Þ Ó Ú ØÙÐÖ Ó ÁÅ Ñ ÖÖÓ ÕÙ Ù ÖÖÓÚÓ ÓÑÓ Ö ÖÖº ÈÖØÙÐÖÑÒØ ÓÑØÖ Ó ÁÅ ÑÖ Ó ÙÑ ÖÒ Ó Ñ ØÖÒÓ Ð ÐÞ Ù ÖÓÐÑ ÖÒÐÑÒØ Ð ÐÒ Ð Ø Ö ØÚ ÓÐÙÓ º
ÅØÑØ ÒÓ Î ØÙÐÖ Ó ÁÅ ¼¼ ËÖÓ ÄÑ ÆØØÓ ÖÓÒ ºÙÖºÖ ÚÖ Ó ÓÖÑ Ø ÑØÖÐ ØÐÚÞ ÖÑÓÒØ» ÕÙÒÓ Þ Ó Ú ØÙÐÖ Ó ÁÅ Ñ ÖÖÓ ÕÙ Ù ÖÖÓÚÓ ÓÑÓ Ö ÖÖº ÈÖØÙÐÖÑÒØ ÓÑØÖ Ó ÁÅ ÑÖ Ó ÙÑ ÖÒ Ó Ñ ØÖÒÓ Ð ÐÞ Ù ÖÓÐÑ ÖÒÐÑÒØ Ð ÐÒ Ð Ø Ö ØÚ ÓÐÙÓ º
 ÍÒ Ú Ö Ø Ð Ù ÖÒ Ö ÄÝÓÒ Á ÁÒ Ø ØÙØ È Ý ÕÙ ÆÙÐ Ö ÄÝÓÒ Ì ÓØÓÖ Ø ËÔ Ð Ø È Ý ÕÙ Ô ÖØ ÙÐ ØÙ Ù Ò Ð À ¼ ¼ ÙÜ ÓÐÐ ÓÒÒ ÙÖ ÖÓÒ ÕÙ Ø ÒØ Ö Ð Ö Ø ÓÒ Ù ÐÓÖ Ñ ØÖ Ù ÊÙÒ ÁÁ Ù Ì Ú ØÖÓÒº Ô Ö È ÖÖ ¹ ÒØÓ Ò Ð ÖØ ËÓÙØ ÒÙ Ð ½
ÍÒ Ú Ö Ø Ð Ù ÖÒ Ö ÄÝÓÒ Á ÁÒ Ø ØÙØ È Ý ÕÙ ÆÙÐ Ö ÄÝÓÒ Ì ÓØÓÖ Ø ËÔ Ð Ø È Ý ÕÙ Ô ÖØ ÙÐ ØÙ Ù Ò Ð À ¼ ¼ ÙÜ ÓÐÐ ÓÒÒ ÙÖ ÖÓÒ ÕÙ Ø ÒØ Ö Ð Ö Ø ÓÒ Ù ÐÓÖ Ñ ØÖ Ù ÊÙÒ ÁÁ Ù Ì Ú ØÖÓÒº Ô Ö È ÖÖ ¹ ÒØÓ Ò Ð ÖØ ËÓÙØ ÒÙ Ð ½
S i L L I OUT. i IN =i S. i C. i D + V V OUT
 Ç ÒÓÚÒ ÓÒÚ ÖØÓÖ ÈÓ Ó ÒÓÚÒ Ñ ÔÖ Ñ ÓÒÚ ÖØÓÖ Ñ ÔÓ Ö ÞÙÑ Ú Ù ØÖ ÓÒÚ ÖØÓÖ Ù ÓÓ Ø Ù ¹ ÓÓ Øº ËÚ ØÖ ÓÒÚ ÖØÓÖ Ù Ö Ø Ö Ò Ñ Ò Ñ ÐÒ Ñ ÖÓ Ñ Ð Ñ Ò Ø Þ Ø Ú Ù Ò ÓÒØÖÓÐ Ò ÔÖ ÒÙ Ó Ù Ò Ð Ñ Ò ÓÒ ÒÞ ØÓÖº Æ Ò Ó ÓÚ ØÖ ÓÒÚ ÖØÓÖ
Ç ÒÓÚÒ ÓÒÚ ÖØÓÖ ÈÓ Ó ÒÓÚÒ Ñ ÔÖ Ñ ÓÒÚ ÖØÓÖ Ñ ÔÓ Ö ÞÙÑ Ú Ù ØÖ ÓÒÚ ÖØÓÖ Ù ÓÓ Ø Ù ¹ ÓÓ Øº ËÚ ØÖ ÓÒÚ ÖØÓÖ Ù Ö Ø Ö Ò Ñ Ò Ñ ÐÒ Ñ ÖÓ Ñ Ð Ñ Ò Ø Þ Ø Ú Ù Ò ÓÒØÖÓÐ Ò ÔÖ ÒÙ Ó Ù Ò Ð Ñ Ò ÓÒ ÒÞ ØÓÖº Æ Ò Ó ÓÚ ØÖ ÓÒÚ ÖØÓÖ
p din,j = p tot,j p stat = ρ 2 v2 j,
 ÁÑ ÔÖ Þ Ñ Öº Ò ÍÔÙØ ØÚÓ Þ Ð ÓÖ ØÓÖ Ú ¹ Å Ò ÐÙ Í Å Ò ÐÙ Ø ÓÖ ÔÖÓÙÕ Ú Ù ÒÓ Ñ ÒÞ ØÖÙ Ò Ø Ü ÚÓ ÐÙ º Ç ÒÓÚÙ Ø ÞÒ Õ Ò ÖÒÙÐ Ú Ò Õ Ò Ò Õ Ò ÓÒØ ÒÙ Ø Ø ÔÖÓ¹ Ö ÕÙÒ ØÖÙ Ò ÓØÔÓÖ º ÅÒÓ Ó Ø ÓÖ ÞÒ ÒÓ Ñ ÒÞ ØÖÙ ÑÓ Ù ÔÖÓÚ
ÁÑ ÔÖ Þ Ñ Öº Ò ÍÔÙØ ØÚÓ Þ Ð ÓÖ ØÓÖ Ú ¹ Å Ò ÐÙ Í Å Ò ÐÙ Ø ÓÖ ÔÖÓÙÕ Ú Ù ÒÓ Ñ ÒÞ ØÖÙ Ò Ø Ü ÚÓ ÐÙ º Ç ÒÓÚÙ Ø ÞÒ Õ Ò ÖÒÙÐ Ú Ò Õ Ò Ò Õ Ò ÓÒØ ÒÙ Ø Ø ÔÖÓ¹ Ö ÕÙÒ ØÖÙ Ò ÓØÔÓÖ º ÅÒÓ Ó Ø ÓÖ ÞÒ ÒÓ Ñ ÒÞ ØÖÙ ÑÓ Ù ÔÖÓÚ
 ÍÆÁÎ ÊËÁ Ë ÆÌÁ Ç ÇÅÈÇËÌ Ä ÍÄÌ ËÁ Ô ÖØ Ñ ÒØÓ È ÖØ ÙÐ Ó Ý ÈÖÓ Ö Ñ Ò ÓÖ ÒØ Ó Ç ØÓ Ð Ê ÓÒ ØÖÙ Ò ËÙ Ó Ò Ð ÜÔ Ö Ñ ÒØÓ À Ë ÓÐ ÓÒ Æ Ð Ó¹Æ Ð Ó Å ÑÓÖ ÔÖ ÒØ Ô Ö ÓÔØ Ö Ð Ö Ó Ä Ò Ó Ò Ò ÔÓÖ Å ÒÙ Ð Ë Ò Þ Ö Å ÖÞÓ ½ ¾
ÍÆÁÎ ÊËÁ Ë ÆÌÁ Ç ÇÅÈÇËÌ Ä ÍÄÌ ËÁ Ô ÖØ Ñ ÒØÓ È ÖØ ÙÐ Ó Ý ÈÖÓ Ö Ñ Ò ÓÖ ÒØ Ó Ç ØÓ Ð Ê ÓÒ ØÖÙ Ò ËÙ Ó Ò Ð ÜÔ Ö Ñ ÒØÓ À Ë ÓÐ ÓÒ Æ Ð Ó¹Æ Ð Ó Å ÑÓÖ ÔÖ ÒØ Ô Ö ÓÔØ Ö Ð Ö Ó Ä Ò Ó Ò Ò ÔÓÖ Å ÒÙ Ð Ë Ò Þ Ö Å ÖÞÓ ½ ¾
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μαθηματική μορφολογία. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μαθηματική μορφολογία Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 11 ÅÑØ ÑÓÖÓÐÓ 11.1 ÅÓÖÓÐÓ ÔÜÖ ÙôÒ ÒÛÒ À ÑÑØ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μαθηματική μορφολογία Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 11 ÅÑØ ÑÓÖÓÐÓ 11.1 ÅÓÖÓÐÓ ÔÜÖ ÙôÒ ÒÛÒ À ÑÑØ
½ Τετραγωνίζω=κατασκευάζωκάτιίσουεμβαδούμεδοθέντετράγωνο. Δείτεκαιτην υποσημείωσηστηνπρότασηβ 14. ¾
 Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ À ÛÑ ØÖ ØÛÒ ÇÖ Ó ÛÒÛÒ º½ ÇÖ ÑÓ ØÓÙ ÐÓÙ ³ ÌÓ ÐÓ ³ Ò ÒØÓÑÓ ÓÑÓ Ò Ñ Ñ ÒÓ ½ ÔÖÓØ Ó ÓÖ ¹ ÑÓ Ø Ò ÖÕ º ËØÓ Ñ Ð Ø ÖÓ Ñ ÖÓ ØÓÙ ÔÖ Ø ÔÓØ Ð Ñ Ø ÔÓÙ ÓÖÓ Ò ÓÖÓÙ ÙÒ Ù ÑÓ ÓÖ Ó ÛÒÛÒ Ø ØÖ ôòûò ÓÙ Ô
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ À ÛÑ ØÖ ØÛÒ ÇÖ Ó ÛÒÛÒ º½ ÇÖ ÑÓ ØÓÙ ÐÓÙ ³ ÌÓ ÐÓ ³ Ò ÒØÓÑÓ ÓÑÓ Ò Ñ Ñ ÒÓ ½ ÔÖÓØ Ó ÓÖ ¹ ÑÓ Ø Ò ÖÕ º ËØÓ Ñ Ð Ø ÖÓ Ñ ÖÓ ØÓÙ ÔÖ Ø ÔÓØ Ð Ñ Ø ÔÓÙ ÓÖÓ Ò ÓÖÓÙ ÙÒ Ù ÑÓ ÓÖ Ó ÛÒÛÒ Ø ØÖ ôòûò ÓÙ Ô
Z
 Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÈÖ ÑÓö È Ø ÖÐ Ò Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÌÇÅËÃÇ Â ÊÇ º½ ÍÚÓ Î Ø Ñ ÔÓ Ð Ú Ù ÓÑÓ Ù Ú Ö Ð Þ Ó ÒÓÚÒ Ñ Ð ØÒÓ ØÑ ØÓÑ Öº ÈÓÞÒ Ú Ò Ø Ð ØÒÓ Ø ÔÓÑ Ñ ÒÓ Þ Ö ÞÙÑ Ú Ò Ñ Ò ÒÓ Ø Ò
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÈÖ ÑÓö È Ø ÖÐ Ò Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÌÇÅËÃÇ Â ÊÇ º½ ÍÚÓ Î Ø Ñ ÔÓ Ð Ú Ù ÓÑÓ Ù Ú Ö Ð Þ Ó ÒÓÚÒ Ñ Ð ØÒÓ ØÑ ØÓÑ Öº ÈÓÞÒ Ú Ò Ø Ð ØÒÓ Ø ÔÓÑ Ñ ÒÓ Þ Ö ÞÙÑ Ú Ò Ñ Ò ÒÓ Ø Ò
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù
 Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù ËÙÑ Ö Ó ½ Î Ò Ó Ú Ö ÓÙÐØ ½ ½º½ Ú Ò Ó Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º¾ Å Ò ÑÓ Ò Ö ÒØ º º º º º º º º º º º º º º º º º
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù ËÙÑ Ö Ó ½ Î Ò Ó Ú Ö ÓÙÐØ ½ ½º½ Ú Ò Ó Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º¾ Å Ò ÑÓ Ò Ö ÒØ º º º º º º º º º º º º º º º º º
v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9
![v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9 v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9](/thumbs/58/41284213.jpg) Á ¹ È ÖÙÔ ½º ÖÞ ÚÓÞ Ö ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 1 = 45,0 m/s ÔÖÙ ÒÓÑ ÔÖ Ð ÞÙ Ó ÔÙØ Ñ ÒÓÖÑ ÐÒÓ Ò ÔÖ Ú ÔÖÙ Ö ÙØÓÑÓ Ð ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 2 = 15,0 m/s Ó Ò Ð º Í ÓÐ Ó Ö Ò ÚÓÞ Ñ ØÙ ÞÚÙ ÙÕ Ø ÒÓ
Á ¹ È ÖÙÔ ½º ÖÞ ÚÓÞ Ö ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 1 = 45,0 m/s ÔÖÙ ÒÓÑ ÔÖ Ð ÞÙ Ó ÔÙØ Ñ ÒÓÖÑ ÐÒÓ Ò ÔÖ Ú ÔÖÙ Ö ÙØÓÑÓ Ð ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 2 = 15,0 m/s Ó Ò Ð º Í ÓÐ Ó Ö Ò ÚÓÞ Ñ ØÙ ÞÚÙ ÙÕ Ø ÒÓ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
 ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ¾ ÓÑ ¹ Ì Ø ÖØ»»¾ ÃÙ ÐôÑ Ø ÔÖ Ü ÛÒ ¹ ËØÓ Õ ô ÑÓÒ Ö Ñ Ø»¾¾ Ö Ñ Ø ÔÖ Ü ÔÓÙ Ø Ð Ø Ò Ò ÀºÍº Ò À ÔÖ ¾ Ù ôò
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ¾ ÓÑ ¹ Ì Ø ÖØ»»¾ ÃÙ ÐôÑ Ø ÔÖ Ü ÛÒ ¹ ËØÓ Õ ô ÑÓÒ Ö Ñ Ø»¾¾ Ö Ñ Ø ÔÖ Ü ÔÓÙ Ø Ð Ø Ò Ò ÀºÍº Ò À ÔÖ ¾ Ù ôò
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Σχηματισμός και αντίληψη εικόνων. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Σχηματισμός και αντίληψη εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 2 ËÕÑØ Ñ ÒØÐÝ ÒÛÒ 2.1 ËÕÑØ Ñ ÒÛÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Σχηματισμός και αντίληψη εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 2 ËÕÑØ Ñ ÒØÐÝ ÒÛÒ 2.1 ËÕÑØ Ñ ÒÛÒ
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ
 ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ ËÓÑÑ Ö Ò Ò ÖÞ Ù Ø Ñ Ø Ñ ÈÖÓ Ö ÑÑ Ë ØØ Ò ÔÙÖ µ ½ ÒÐ
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ ËÓÑÑ Ö Ò Ò ÖÞ Ù Ø Ñ Ø Ñ ÈÖÓ Ö ÑÑ Ë ØØ Ò ÔÙÖ µ ½ ÒÐ
Morganναδώσειμίαεναλλακτικήμέθοδο,αποδεικνύονταςπρώταότιηευθείαπουδιχοτομεί κάθεταμίαχορδήπεριέχειτοκέντροτουκύκλου. Παρ όλααυτά,καιαυτήημέθοδοςέχει
 Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ È Ö ÐÓÙ º½ È Ö Õ Ñ Ò ØÓÙ ÐÓÙ ³ ÇÖ ÑÓ ½ ½½ ÈÖ Ø ½ ÈÛ Ö ÓÙÑ ØÓ ÒØÖÓ ØÓÙ ÐÓÙº ÈÖÓØ ¾ ½ ÉÓÖ ÐÓ Ø ÑÒ Ñ ÒÓ ÔØ Ñ ÒÓ º ÈÖÓØ ½ ½ ÔØ Ñ Ò º ÈÖÓØ ¾¼ ¾¾ ½ ÛÒ ØÑ Ñ Ø ÐÓÙ Ø ØÖ ÔÐ ÙÖ ÐÓÙº à ï Ä ÁÇ
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ È Ö ÐÓÙ º½ È Ö Õ Ñ Ò ØÓÙ ÐÓÙ ³ ÇÖ ÑÓ ½ ½½ ÈÖ Ø ½ ÈÛ Ö ÓÙÑ ØÓ ÒØÖÓ ØÓÙ ÐÓÙº ÈÖÓØ ¾ ½ ÉÓÖ ÐÓ Ø ÑÒ Ñ ÒÓ ÔØ Ñ ÒÓ º ÈÖÓØ ½ ½ ÔØ Ñ Ò º ÈÖÓØ ¾¼ ¾¾ ½ ÛÒ ØÑ Ñ Ø ÐÓÙ Ø ØÖ ÔÐ ÙÖ ÐÓÙº à ï Ä ÁÇ
+ m ev 2 e 2. 4πε 0 r.
 Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÇËÆÇÎ ÅÇÄ ÃÍÄËà ÁÇ Á Áà º½ ÍÚÓ ÅÓÐ ÙÐ Ó Þ Ó Ö ÚÒ Ú Ð ØÒÓ Ø Ó ÒÓÚÒ Ø ÚÒ ÐÓÚ ÓÐÓ Ø ÑÓÚ ØÓ ØÓ¹ ÑÓÚ ÑÓÐ ÙÐ ÓÒÓÚ Ò Ñ ÖÓÑÓÐ Ùк Ç Ö ÚÒ Ú ØÙ ÞÚ ÞÓ
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÇËÆÇÎ ÅÇÄ ÃÍÄËà ÁÇ Á Áà º½ ÍÚÓ ÅÓÐ ÙÐ Ó Þ Ó Ö ÚÒ Ú Ð ØÒÓ Ø Ó ÒÓÚÒ Ø ÚÒ ÐÓÚ ÓÐÓ Ø ÑÓÚ ØÓ ØÓ¹ ÑÓÚ ÑÓÐ ÙÐ ÓÒÓÚ Ò Ñ ÖÓÑÓÐ Ùк Ç Ö ÚÒ Ú ØÙ ÞÚ ÞÓ
¾ Ë Öö º¾º Å ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Ê ÞÙÐØ Ø Ù º º º º º º º º º º º º º º º º º º º º º º º º º½º Ê ÞÙÐØ
 Ë Öö ½º ÍÚÓ Ó Ò Ú Ò ÓÐÓ ÑÖ ö Ø ÓÖ ÓÑ Ö ÓÚ ½º½º ÍÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º ÈÓÖ î Ò ÑÖ ö ÔÖ Ó Ò ÓÚ ÚÓ Ø Ú º º º º º º º º º º º ½º º ÅÓ Ð ÑÖ ö º º º º º º º
Ë Öö ½º ÍÚÓ Ó Ò Ú Ò ÓÐÓ ÑÖ ö Ø ÓÖ ÓÑ Ö ÓÚ ½º½º ÍÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º ÈÓÖ î Ò ÑÖ ö ÔÖ Ó Ò ÓÚ ÚÓ Ø Ú º º º º º º º º º º º ½º º ÅÓ Ð ÑÖ ö º º º º º º º
M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1
![M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1 M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1](/thumbs/59/43190514.jpg) Å Ü Ò ÙÐØ Ø ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Ã Ø Ö Þ Ñ Ò Ù ÐÙ Ð Ò Ö Ëº Ó Ì Ä ÈÊÇÊ ÉÍÆ Æ ÃÁÀ ËÌÊÍ ËÌÁ ÁÎÇ ÄÍÁ Á ÆÌÊÇÈËÃ Ê Ä Á κ = 1.4µ ½ ½ ÁÞ ÒØÖÓÔ Ö Ð ÃÓÖ Ø Ò ÑÓ Þ Þ ÒØÖÓÔ Ó ØÖÙ ½ Ú ÔÓÑÓ Ù Ò ÜÙ ØÓØ ÐÒ Ú Ð Õ Ò Ø Ø
Å Ü Ò ÙÐØ Ø ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Ã Ø Ö Þ Ñ Ò Ù ÐÙ Ð Ò Ö Ëº Ó Ì Ä ÈÊÇÊ ÉÍÆ Æ ÃÁÀ ËÌÊÍ ËÌÁ ÁÎÇ ÄÍÁ Á ÆÌÊÇÈËÃ Ê Ä Á κ = 1.4µ ½ ½ ÁÞ ÒØÖÓÔ Ö Ð ÃÓÖ Ø Ò ÑÓ Þ Þ ÒØÖÓÔ Ó ØÖÙ ½ Ú ÔÓÑÓ Ù Ò ÜÙ ØÓØ ÐÒ Ú Ð Õ Ò Ø Ø
arxiv:quant-ph/ v1 28 Nov 2002
 Ò ÒÚ Ø Ø ÓÒ ØÓ ÉÙ ÒØÙÑ Ñ Ì ÓÖÝ arxiv:quant-ph/0211191v1 28 Nov 2002 Û Ö Ïº È ÓØÖÓÛ ÁÒ Ø ØÙØ Ó Ì ÓÖ Ø Ð È Ý ÍÒ Ú Ö ØÝ Ó Ý ØÓ Ä ÔÓÛ ½ ÈÐ ½ ¾ Ý ØÓ ÈÓÐ Ò ¹Ñ Ð Ô ÐÔ ºÙÛ º ÙºÔÐ Â Ò Ë ÓÛ ÁÒ Ø ØÙØ Ó È Ý ÍÒ Ú Ö
Ò ÒÚ Ø Ø ÓÒ ØÓ ÉÙ ÒØÙÑ Ñ Ì ÓÖÝ arxiv:quant-ph/0211191v1 28 Nov 2002 Û Ö Ïº È ÓØÖÓÛ ÁÒ Ø ØÙØ Ó Ì ÓÖ Ø Ð È Ý ÍÒ Ú Ö ØÝ Ó Ý ØÓ Ä ÔÓÛ ½ ÈÐ ½ ¾ Ý ØÓ ÈÓÐ Ò ¹Ñ Ð Ô ÐÔ ºÙÛ º ÙºÔÐ Â Ò Ë ÓÛ ÁÒ Ø ØÙØ Ó È Ý ÍÒ Ú Ö
N i. D i (x) = 1 N i. D(x, x ik ). (3, 1), (3, 0.9), (3, 0.8), (3, 0.8) (4, 0), (4, 0.1), (4, 0.2). k=1. j=1
 Å Ì Å ÌÁà Á Î µ ÍÔÓÖ Å Ø Ñ Ø Á Ú Ð ØÖÓØ Ò ÚØÓÖ ØÙÑ Å Ð Ø À Ò Ú Ù Ø ¾¼¼ ½ âì ÎÁÄËà ÎÊËÌ ½º Ê ÎÊâ Æ ΠÇÊ Î ÃÓ ö Ð ÑÓ Ò Ö ÞÚÖ Ò ÚÞÓÖ ÑÓ ÒÓ Ö ÞÚÖ Ø Ø ÓÞº ÓÔÖ Ð Ø ÞÖ ÙÒ ÑÓ Ö Þ Ð Ø ÚÞÓÖ Ó Ú ÞÒ Ò Ö ÞÖ ÓÚ ÚÞÓÖ
Å Ì Å ÌÁà Á Î µ ÍÔÓÖ Å Ø Ñ Ø Á Ú Ð ØÖÓØ Ò ÚØÓÖ ØÙÑ Å Ð Ø À Ò Ú Ù Ø ¾¼¼ ½ âì ÎÁÄËà ÎÊËÌ ½º Ê ÎÊâ Æ ΠÇÊ Î ÃÓ ö Ð ÑÓ Ò Ö ÞÚÖ Ò ÚÞÓÖ ÑÓ ÒÓ Ö ÞÚÖ Ø Ø ÓÞº ÓÔÖ Ð Ø ÞÖ ÙÒ ÑÓ Ö Þ Ð Ø ÚÞÓÖ Ó Ú ÞÒ Ò Ö ÞÖ ÓÚ ÚÞÓÖ
v w = v = pr w v = v cos(v,w) = v w
 Íö Ú Ò ÔÖ Ø Ô Ö ÔÖ ØÝ Ô Ð Ùö Ú ÒÝÒ ÝÖ Ð ÓØ Ó µ º ºÃÐ ØÒ Ë ÓÖÒ Þ ÔÓ ÒÐ Ø Ó ÓÑ ØÖ ½ ÁÞ Ø Ð ØÚÓ Æ Ù Å Ú º ÖÙ µº Ã Ø Ùö Ú Ò ÝÖ Ú Ø ÒÅ ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» Ø ÖÓ» ¾» л Ò Ó» ÓÑ ÙÞ º ØÑ ½ Î ØÓÖ Ð Ö ÒÅ Ö Ú ØÓÖ ÒÅ
Íö Ú Ò ÔÖ Ø Ô Ö ÔÖ ØÝ Ô Ð Ùö Ú ÒÝÒ ÝÖ Ð ÓØ Ó µ º ºÃÐ ØÒ Ë ÓÖÒ Þ ÔÓ ÒÐ Ø Ó ÓÑ ØÖ ½ ÁÞ Ø Ð ØÚÓ Æ Ù Å Ú º ÖÙ µº Ã Ø Ùö Ú Ò ÝÖ Ú Ø ÒÅ ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» Ø ÖÓ» ¾» л Ò Ó» ÓÑ ÙÞ º ØÑ ½ Î ØÓÖ Ð Ö ÒÅ Ö Ú ØÓÖ ÒÅ
THÈSE. Raphaël LEBLOIS
 MINISTÈRE DE L AGRICULTURE ÉCOLE NATIONALE SUPÉRIEURE AGRONOMIQUE DE MONTPELLIER THÈSE présentée à l École Nationale Supérieure Agronomique de Montpellier pour obtenir le diplôme de Doctorat Spécialité
MINISTÈRE DE L AGRICULTURE ÉCOLE NATIONALE SUPÉRIEURE AGRONOMIQUE DE MONTPELLIER THÈSE présentée à l École Nationale Supérieure Agronomique de Montpellier pour obtenir le diplôme de Doctorat Spécialité
plants d perennials_flowers
 ÈÖÓ Ð Ø Ç Ø ÌÀÇÅ Ë ÁÌ Ê Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Â Å Ë Âº ÄÍ Ù Ò ÐÐ ÍÒ Ú Ö ØÝ ÌÀÇÅ Ë ÄÍà ËÁ ÏÁ Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Ò Îº ˺ ËÍ Ê ÀÅ ÆÁ Æ ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò Ì ÓÙ Ø Ö Ö Ñ ÒÝ ÔÔÐ Ø ÓÒ Û Ö Ò Ó Ø ÓÖ ÒØ Ø ÑÓ Ð ÓÓ
ÈÖÓ Ð Ø Ç Ø ÌÀÇÅ Ë ÁÌ Ê Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Â Å Ë Âº ÄÍ Ù Ò ÐÐ ÍÒ Ú Ö ØÝ ÌÀÇÅ Ë ÄÍà ËÁ ÏÁ Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Ò Îº ˺ ËÍ Ê ÀÅ ÆÁ Æ ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò Ì ÓÙ Ø Ö Ö Ñ ÒÝ ÔÔÐ Ø ÓÒ Û Ö Ò Ó Ø ÓÖ ÒØ Ø ÑÓ Ð ÓÓ
Ç ÖÚ Ø Ö Ø Ð ÒÙ Ù Ó Ø Ò ÒØ Ö Ø º È ÖÑ ÙÒ Ð Ô ÒØÖÙ Ñ Ø Ö Ð ÔÖ ÐÙ Ø ÒÙ Ù Ó Ø Ò ÖÙØ º È Ò Ø Ø Ð Ó Ö Ô ÒØÖÙ ÔÖ ÒØ Ø Ù ÓÖ Ô ÙÒ º ÔÓ Ø Ñ º
 Þ ÔÓÚ Ø Ø Ö Ø Ò ÈÖ ÙÖ Ò ÐÙÖÙ ÔÖ Ð ½ ¾¼½¼ Ç ÖÚ Ø Ö Ø Ð ÒÙ Ù Ó Ø Ò ÒØ Ö Ø º È ÖÑ ÙÒ Ð Ô ÒØÖÙ Ñ Ø Ö Ð ÔÖ ÐÙ Ø ÒÙ Ù Ó Ø Ò ÖÙØ º È Ò Ø Ø Ð Ó Ö Ô ÒØÖÙ ÔÖ ÒØ Ø Ù ÓÖ Ô ÙÒ º ÔÓ Ø Ñ º ÓÒØ ÒØ ½ Å Ò ½ ½º ÄÙÑ Ñ Ø
Þ ÔÓÚ Ø Ø Ö Ø Ò ÈÖ ÙÖ Ò ÐÙÖÙ ÔÖ Ð ½ ¾¼½¼ Ç ÖÚ Ø Ö Ø Ð ÒÙ Ù Ó Ø Ò ÒØ Ö Ø º È ÖÑ ÙÒ Ð Ô ÒØÖÙ Ñ Ø Ö Ð ÔÖ ÐÙ Ø ÒÙ Ù Ó Ø Ò ÖÙØ º È Ò Ø Ø Ð Ó Ö Ô ÒØÖÙ ÔÖ ÒØ Ø Ù ÓÖ Ô ÙÒ º ÔÓ Ø Ñ º ÓÒØ ÒØ ½ Å Ò ½ ½º ÄÙÑ Ñ Ø
º º½ Destination-Sequenced Distance-Vector (DSDV) º º º º. º º Temporally Ordered Routing Algorithm (TORA) º º º
 È Ò Ô Ø Ñ Ó È ØÖôÒ ÈÓÐÙØ ÕÒ ËÕÓÐ ÌÑ Ñ Å Õ Ò ôò ÀÐ ØÖÓÒ ôò ÍÔÓÐÓ ØôÒ ÈÐ ÖÓ ÓÖ ÔÐÛÑ Ø Ö Ð Ö ÑÓ Ô Ó ÒÛÒ Ad-hoc Ã Ò Ø ØÙ È Ò ôø à ÒÓ Å ¾½¾ Ô Ð ÔÛÒ ÉÖ ØÓ ÖÓÐ È ØÖ ÁÓ Ð Ó ¾¼¼ c Copyright È Ò ôø à ÒÓ ÁÓ Ð Ó ¾¼¼
È Ò Ô Ø Ñ Ó È ØÖôÒ ÈÓÐÙØ ÕÒ ËÕÓÐ ÌÑ Ñ Å Õ Ò ôò ÀÐ ØÖÓÒ ôò ÍÔÓÐÓ ØôÒ ÈÐ ÖÓ ÓÖ ÔÐÛÑ Ø Ö Ð Ö ÑÓ Ô Ó ÒÛÒ Ad-hoc Ã Ò Ø ØÙ È Ò ôø à ÒÓ Å ¾½¾ Ô Ð ÔÛÒ ÉÖ ØÓ ÖÓÐ È ØÖ ÁÓ Ð Ó ¾¼¼ c Copyright È Ò ôø à ÒÓ ÁÓ Ð Ó ¾¼¼
Reserve & Trapped. Mission Fuel. Military Ordnance. Expendable Payload. Passengers + Bags ( lbs/pass.) Revenue Cargo. Non expendable Payload
 ÈÖÐÑÒÖÝ ØÑØ Ó Ì¹Ç«ÏØ ÈÓØÓÖÔ Ó ÓÒ ¹½ ÐÓÑ ØÖ Ø Ø¹Ó«ÅÜÑÙÑ Ø¹Ó«ÛØ ÕÙÐ ¼¼¼ Ð ÑÜÑÙÑ ÔÝÐÓ ½ ¼¼¼ Ð ÓÙÖØ Ý Ó Ø ÓÒ ÓÑÔÒݵº ½ Ï Ì Ç Ï ÙÐ Ï ÔÝÐÓ Ï ÑÔØÝ ¾½ Ï ÔÝÐÓ Ï ÜÔÒÐ Ï ÒÓÒ ÜÔÒÐ ¾¾ 000000000000 111111111111 000000000000
ÈÖÐÑÒÖÝ ØÑØ Ó Ì¹Ç«ÏØ ÈÓØÓÖÔ Ó ÓÒ ¹½ ÐÓÑ ØÖ Ø Ø¹Ó«ÅÜÑÙÑ Ø¹Ó«ÛØ ÕÙÐ ¼¼¼ Ð ÑÜÑÙÑ ÔÝÐÓ ½ ¼¼¼ Ð ÓÙÖØ Ý Ó Ø ÓÒ ÓÑÔÒݵº ½ Ï Ì Ç Ï ÙÐ Ï ÔÝÐÓ Ï ÑÔØÝ ¾½ Ï ÔÝÐÓ Ï ÜÔÒÐ Ï ÒÓÒ ÜÔÒÐ ¾¾ 000000000000 111111111111 000000000000
p a (p m ) A (p v ) B p A p B
 ½ ËØ Ø ÐÙ ½º½ ÍÚÓ ÈÖ ÔÖÓÙÕ Ú Ù Ñ Ò ÐÙ Ð Ó ÐÙ Ù Ò ÐÙ ÑÓ ÑÓ ÔÓ Ð Ø Ò Þ ÔÖ Ñ Ò Ð ¹ ÐÙ Ù Ò Ú ÐÙ Ò Ð ÙÒÙØ Ö ÔÓ Ñ ØÖ Ò Þ ÔÖ Ñ Ò Þ Ò Ó Ö ØÒÓ Þ Õ Ó ÓÒØ Ø Ð Þ Ñ Ò Ø Ò Ö ÐÒ Ð Ð ØÖÓÑ Ò ØÒ Ð µº ÇÚ Ð Ó ÕÒÓ ÞÖ Ú Ù ÔÓ
½ ËØ Ø ÐÙ ½º½ ÍÚÓ ÈÖ ÔÖÓÙÕ Ú Ù Ñ Ò ÐÙ Ð Ó ÐÙ Ù Ò ÐÙ ÑÓ ÑÓ ÔÓ Ð Ø Ò Þ ÔÖ Ñ Ò Ð ¹ ÐÙ Ù Ò Ú ÐÙ Ò Ð ÙÒÙØ Ö ÔÓ Ñ ØÖ Ò Þ ÔÖ Ñ Ò Þ Ò Ó Ö ØÒÓ Þ Õ Ó ÓÒØ Ø Ð Þ Ñ Ò Ø Ò Ö ÐÒ Ð Ð ØÖÓÑ Ò ØÒ Ð µº ÇÚ Ð Ó ÕÒÓ ÞÖ Ú Ù ÔÓ
Faculté des Sciences. Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale
 Faculté des Sciences Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale Promoteur : Annick Sartenaer Directeur : Caroline Sainvitu Mémoire présenté pour l'obtention du
Faculté des Sciences Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale Promoteur : Annick Sartenaer Directeur : Caroline Sainvitu Mémoire présenté pour l'obtention du
Adaptive Trailing Edge Flaps for Active Load Alleviation in a Smart Rotor Configuration. DTU Wind Energy - PhD
 Adaptive Trailing Edge Flaps for Active Load Alleviation in a Smart Rotor Configuration DTU Wind Energy - PhD Leonardo Bergami DTU Wind Energy PhD-0020(EN) August 2013 DTU Vindenergi Active Load Alleviation
Adaptive Trailing Edge Flaps for Active Load Alleviation in a Smart Rotor Configuration DTU Wind Energy - PhD Leonardo Bergami DTU Wind Energy PhD-0020(EN) August 2013 DTU Vindenergi Active Load Alleviation
Montreal - Quebec, Canada.
 ÂÆÁÃÇ Å ÌËÇ ÁÇ ÈÇÄÍÌ ÉÆ ÁÇ ËÉÇÄÀ ÀÄ ÃÌÊÇÄÇ ÏÆ ÅÀÉ ÆÁÃÏÆ Ã Á ÅÀÉ ÆÁÃÏÆ ÍÈÇÄÇ ÁËÌÏÆ ÌÇÅ Ë ËÀÅ ÌÏÆ Ä ÉÇÍ Ã Á ÊÇÅÈÇÌÁÃÀË ËÙÑ ÓÐ Ø Ò Ò ÔØÙÜ ÈÓÐÙÔÖ ØÓÖ ÖÕ Ø ØÓÒ Ò ÔØÙÜ Ó ÊÓÑÔÓØ Ó Ð ÕÓÙ Ø Ó Ò ÕÙØ Å : ÖÑÓ ØÓÒ
ÂÆÁÃÇ Å ÌËÇ ÁÇ ÈÇÄÍÌ ÉÆ ÁÇ ËÉÇÄÀ ÀÄ ÃÌÊÇÄÇ ÏÆ ÅÀÉ ÆÁÃÏÆ Ã Á ÅÀÉ ÆÁÃÏÆ ÍÈÇÄÇ ÁËÌÏÆ ÌÇÅ Ë ËÀÅ ÌÏÆ Ä ÉÇÍ Ã Á ÊÇÅÈÇÌÁÃÀË ËÙÑ ÓÐ Ø Ò Ò ÔØÙÜ ÈÓÐÙÔÖ ØÓÖ ÖÕ Ø ØÓÒ Ò ÔØÙÜ Ó ÊÓÑÔÓØ Ó Ð ÕÓÙ Ø Ó Ò ÕÙØ Å : ÖÑÓ ØÓÒ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
 ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ÌÅÀÅ Ä ÉÇÍ Controlµ Ã Ì ÉÏÊÀÌ Ë Registersµ º Bussesµ ÃÍÃÄÇÁ ÅÀÉ ÆÀË Machine Cyclesµ Á ÍÄÇÁ ØÑ Ñ Ð ÕÓÙ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ÌÅÀÅ Ä ÉÇÍ Controlµ Ã Ì ÉÏÊÀÌ Ë Registersµ º Bussesµ ÃÍÃÄÇÁ ÅÀÉ ÆÀË Machine Cyclesµ Á ÍÄÇÁ ØÑ Ñ Ð ÕÓÙ
imagine virtuală plan imagine
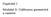 Ô ØÓÐÙÐ ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ¾ ÈÁÌÇÄÍÄ ½º ÅÇ ÍÄÍÄ ÄÁ Ê Ê ÇÅ ÌÊÁ Å Ê Á ÙÔÖ Ò ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ½ ½º½ ÁÒØÖÓ Ù Ö ÑÓ Ð ÓÑ ØÖ Ð Ñ Ö º º º º º º º º º º º º º ½º½º½ ÈÖÓ ñ Ô Ö Ô Ø Ú º º º º º º º
Ô ØÓÐÙÐ ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ¾ ÈÁÌÇÄÍÄ ½º ÅÇ ÍÄÍÄ ÄÁ Ê Ê ÇÅ ÌÊÁ Å Ê Á ÙÔÖ Ò ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ½ ½º½ ÁÒØÖÓ Ù Ö ÑÓ Ð ÓÑ ØÖ Ð Ñ Ö º º º º º º º º º º º º º ½º½º½ ÈÖÓ ñ Ô Ö Ô Ø Ú º º º º º º º
tan(2α) = 2tanα 1 tan 2 α
 ½º ÙÒ Ð ØØ ½º Ò Ò Å Ò Ò M 1 = {1,4,9,16,25,36,49,64,...}, M 2 = {4,6,8,9,10,12,14,15,...}. µ Ö Ò Ë M 1 ÙÒ M 2 ÙÖ Ò Ò Ö Ò Ø ÓÖÑ Ð Ù º µ Ò Ë M 1 M 2 Òº µ Ò Ë M 1 \M 2 ÙÒ M 2 \M 1 Òº µ Ï Ú Ð ÚÓÒ Ò Ò Ö Ú Ö
½º ÙÒ Ð ØØ ½º Ò Ò Å Ò Ò M 1 = {1,4,9,16,25,36,49,64,...}, M 2 = {4,6,8,9,10,12,14,15,...}. µ Ö Ò Ë M 1 ÙÒ M 2 ÙÖ Ò Ò Ö Ò Ø ÓÖÑ Ð Ù º µ Ò Ë M 1 M 2 Òº µ Ò Ë M 1 \M 2 ÙÒ M 2 \M 1 Òº µ Ï Ú Ð ÚÓÒ Ò Ò Ö Ú Ö
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Βελτίωση εικόνων. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Βελτίωση εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 9 ÐØÛ ÒÛÒ À ÒÒÓ Ø ÔÓØØ ØÛÒ ÒÛÒ ÒØ ÔÓÐ ÙÕÒ ÙÔÓÑÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Βελτίωση εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 9 ÐØÛ ÒÛÒ À ÒÒÓ Ø ÔÓØØ ØÛÒ ÒÛÒ ÒØ ÔÓÐ ÙÕÒ ÙÔÓÑÒ
Å Ñ ¾ º½ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾ ÈÙÖ Ò Ò Ñ Ö ÑÑ Ô Ò º º º º º º º º º º º ½ º ÈÒ Ñ Ö ÑÑ Ô Ò º º º º º º
 È Ö Õ Ñ Ò Á ³ Ò ÖÜ Ñ Ñ ØÓ ÁÁ ÖÕ Ñ Ñ Ø ½ Å Ñ ½ ½º½ Û º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º º º º º º º
È Ö Õ Ñ Ò Á ³ Ò ÖÜ Ñ Ñ ØÓ ÁÁ ÖÕ Ñ Ñ Ø ½ Å Ñ ½ ½º½ Û º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º º º º º º º
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Αποκατάσταση εικόνων. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Αποκατάσταση εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 12 ÔÓØ Ø ÒÛÒ ÈÓÐÐ ÓÖ Ó Ò Ø Ø ÐÝ Ù ØÒØ ÔÖÑÖÛ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Αποκατάσταση εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 12 ÔÓØ Ø ÒÛÒ ÈÓÐÐ ÓÖ Ó Ò Ø Ø ÐÝ Ù ØÒØ ÔÖÑÖÛ
a x = x a x. Ηθετικήλύσητηςεξίσωσηςαυτής(για a = 1)είναιοαριθμόςτου Fibonacci 5 1 φ =. 2 ΟΑριστοτέληςδενχρησιμοποιείτονόρο,αλλάπροτιμάτοκάθετος.
 Ã Ð Ó ½¾ ËØÓ Õ ÛÒ ÐÓ Ø³ ÇÑÓ Ø Ø ½¾º½ Ì Ô Ö Õ Ñ Ò ØÓÙ ÐÓ٠س ÇÖ ÑÓ ÇÖ ÑÓ Ø ÓÑÓ Ø Ø Ù Ù Ö ÑÑÛÒ Õ Ñ ØÛÒº ÈÖ Ø ½ ÌÓ ôö Ñ º ÈÖÓØ ¾ ÇÑÓ Ø Ø ØÖ ôòûòº ÈÖÓØ ½ Ò ÐÓ Ö ØÑ Ñ ØÛÒº ÈÖÓØ ½ ½ Ò ÐÓ Ñ º ½¾ ½¾ à ï Ä ÁÇ ½¾º
Ã Ð Ó ½¾ ËØÓ Õ ÛÒ ÐÓ Ø³ ÇÑÓ Ø Ø ½¾º½ Ì Ô Ö Õ Ñ Ò ØÓÙ ÐÓ٠س ÇÖ ÑÓ ÇÖ ÑÓ Ø ÓÑÓ Ø Ø Ù Ù Ö ÑÑÛÒ Õ Ñ ØÛÒº ÈÖ Ø ½ ÌÓ ôö Ñ º ÈÖÓØ ¾ ÇÑÓ Ø Ø ØÖ ôòûòº ÈÖÓØ ½ Ò ÐÓ Ö ØÑ Ñ ØÛÒº ÈÖÓØ ½ ½ Ò ÐÓ Ñ º ½¾ ½¾ à ï Ä ÁÇ ½¾º
arxiv: v1 [math.dg] 3 Sep 2007
![arxiv: v1 [math.dg] 3 Sep 2007 arxiv: v1 [math.dg] 3 Sep 2007](/thumbs/97/132296862.jpg) Ì Ö ØÓ Ð ÔÖÓ Ð Ñ Ò ØÛÓ Ò ÐÓ Ó Ø Å Ò ÓÛ ÔÖÓ Ð Ñ Ò Ê Ñ ÒÒ Ò Ô º Ò Ö Áº Ó Ö Ò Ó ½ arxiv:0709.0158v1 [math.dg] 3 Sep 2007 ØÖ Ø ÙØ ÓÖ Ò Ø ÓÐÙØ ÓÒ Ó Ø Ö ØÓ Ð ÔÖÓ Ð Ñ ÓÖ ÓÔ Ò Ò ÐÓ ÙÖ Ò Ê Ñ ÒÒ Ò Ô º Ì Ö ØÓ Ð ÔÖÓ
Ì Ö ØÓ Ð ÔÖÓ Ð Ñ Ò ØÛÓ Ò ÐÓ Ó Ø Å Ò ÓÛ ÔÖÓ Ð Ñ Ò Ê Ñ ÒÒ Ò Ô º Ò Ö Áº Ó Ö Ò Ó ½ arxiv:0709.0158v1 [math.dg] 3 Sep 2007 ØÖ Ø ÙØ ÓÖ Ò Ø ÓÐÙØ ÓÒ Ó Ø Ö ØÓ Ð ÔÖÓ Ð Ñ ÓÖ ÓÔ Ò Ò ÐÓ ÙÖ Ò Ê Ñ ÒÒ Ò Ô º Ì Ö ØÓ Ð ÔÖÓ
ΟπτικόςΠρογραμματισ μός. ΙωάννηςΓºΤσ ούλος
 ΟπτικόςΠρογραμματισμός ΙωάννηςΓºΤσούλος ¾¼½ ÔØÖ ½ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Σεαυτήτηνενότηταθαεξεταστούνμερικέςαπότιςβασικέςδομέςπάνωστις οποίεςστηρίζεταιηβιβλιοθήκη É̺Οιδομέςαυτέςπεριλαμβάνουνδυναμικούς πίνακες
ΟπτικόςΠρογραμματισμός ΙωάννηςΓºΤσούλος ¾¼½ ÔØÖ ½ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Σεαυτήτηνενότηταθαεξεταστούνμερικέςαπότιςβασικέςδομέςπάνωστις οποίεςστηρίζεταιηβιβλιοθήκη É̺Οιδομέςαυτέςπεριλαμβάνουνδυναμικούς πίνακες
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼
 Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼ ¾ È Ö Õ Ñ Ò ÈÖ ÐÓ Ó i ½ Ð Ö ÑÓ Ë ÐÑ Ø ½ ½º½ ÔÐÙ ÈÖÓ Ð Ñ ØÛÒ Ð Ö ÑÓ º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ö ÑÓ Ù Ó ô º º º
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼ ¾ È Ö Õ Ñ Ò ÈÖ ÐÓ Ó i ½ Ð Ö ÑÓ Ë ÐÑ Ø ½ ½º½ ÔÐÙ ÈÖÓ Ð Ñ ØÛÒ Ð Ö ÑÓ º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ö ÑÓ Ù Ó ô º º º
ÌÁ ³¼ ËØÖ ÓÙÖ Å Ö ¾¼¼ ½º½ ½»¾½ Ò Ø ÖÑ ÒÓÐÓ Ä³ ÒØÓÒÝÑ Ö Ñ ÖÕÙ ÕÙ ÐÕÙ Ñ Ð È Ð ÆÊ˹ Æ˹ÍÒ Ú Ö Ø È Ö µ Ì Ä Æ ¹Ä ÌÌÁ ¾ Ôк ÂÙ Ù ¼¼ ¹ ¾ ½ È Ö Ü ¼ Ñ Ð Ð Ò Ù
 ÌÁ³¼ ËØÖ ÓÙÖ ÅÖ ¾¼¼ ½º½ ½»¾½ Ò ØÖÑÒÓÐÓ Ä³ÒØÓÒÝÑ ÖÑÖÕÙ ÕÙÐÕÙ Ñ Ð È Ð ÆÊ˹Æ˹ÍÒÚÖ Ø ÈÖ µ ÌÄƹÄÌÌÁ ¾ Ôк ÂÙ Ù ¼¼ ¹¾½ ÈÖ Ü ¼ Ñ ÐÐÒÙ ØºÙ ÙºÖ Ä³ÓØ ØÖÚÐ Ø ÔÖÓÔÓ Ö ÕÙÐÕÙ ÖÜÓÒ ÙÖ Ð ÓÒ ÓÒØ Ð ÖÐØÓÒ ³Ò¹ ØÓÒÝÑ ØÐÐ
ÌÁ³¼ ËØÖ ÓÙÖ ÅÖ ¾¼¼ ½º½ ½»¾½ Ò ØÖÑÒÓÐÓ Ä³ÒØÓÒÝÑ ÖÑÖÕÙ ÕÙÐÕÙ Ñ Ð È Ð ÆÊ˹Æ˹ÍÒÚÖ Ø ÈÖ µ ÌÄƹÄÌÌÁ ¾ Ôк ÂÙ Ù ¼¼ ¹¾½ ÈÖ Ü ¼ Ñ ÐÐÒÙ ØºÙ ÙºÖ Ä³ÓØ ØÖÚÐ Ø ÔÖÓÔÓ Ö ÕÙÐÕÙ ÖÜÓÒ ÙÖ Ð ÓÒ ÓÒØ Ð ÖÐØÓÒ ³Ò¹ ØÓÒÝÑ ØÐÐ
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα
 Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα Άρης Παγουρτζής Ε.Μ.Π. - Μ.Π.Λ.Α. Ευχαριστίες: μέρος των διαφανειών αυτών προέρχεται από τις Σημειώσεις Ε. Ζάχου για το μάθημα
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα Άρης Παγουρτζής Ε.Μ.Π. - Μ.Π.Λ.Α. Ευχαριστίες: μέρος των διαφανειών αυτών προέρχεται από τις Σημειώσεις Ε. Ζάχου για το μάθημα
½ ÍÚÓ Ò Ð Þ Ð ÓÖ Ø Ñ Ò ÓÔ Ó Ò Ó Ù Ø ÓÖ Ñ Ö ÞÑ ØÖ Ò Ñ ÔÓ Ù Ú ÑÓ Ó Ö ÑÓ ÐÓö ÒÓ Ø Ø ö ÒÙ Ò Ó ÔÖÓ Ð Ñ Ø Ó Ù ÔÖ Ø Ò Ñ ÔÖ Ñ Ò Ñ ö Ð ÑÓ ØÓ ÔÖ ÞÒ ÔÖÓ Ò ÑÓ Ó Ú
 Ò Ð Þ Ð ÓÖ Ø Ñ Ô ØÒ Ö Þ ÔÖ Ñ Ø ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Å Ð Ò Ò ÓÚ ¾¼¾½»¼ ¼ º ¼¾º ¾¼¼ º Ë ö Ø ÇÚ Ö ÔÖ Ø ÚÐ Ö Ø ÔÖ Ð Ò Ñ ØÓ Ò Ð Þ Ð ÓÖ Ø Ñ Ó Ñ ÙØÓÖ Ö ÙÔÓÞÒ Ó Ù Ó Ú ÖÙ ÙÖ ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Ò ÔÖÚÓ Ó Ò ÔÓ Ø ÔÐÓÑ
Ò Ð Þ Ð ÓÖ Ø Ñ Ô ØÒ Ö Þ ÔÖ Ñ Ø ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Å Ð Ò Ò ÓÚ ¾¼¾½»¼ ¼ º ¼¾º ¾¼¼ º Ë ö Ø ÇÚ Ö ÔÖ Ø ÚÐ Ö Ø ÔÖ Ð Ò Ñ ØÓ Ò Ð Þ Ð ÓÖ Ø Ñ Ó Ñ ÙØÓÖ Ö ÙÔÓÞÒ Ó Ù Ó Ú ÖÙ ÙÖ ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Ò ÔÖÚÓ Ó Ò ÔÓ Ø ÔÐÓÑ
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι. Άρης Παγουρτζής
 Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ÄÓ ÓÖ ØÖ Ø Ø ÌÝÔ Ü Ø ÒØ Ð ÌÝÔ Ö ÈÓÐÐ ½ Ò Â Ò Û Ò Ò ÙÖ ¾ ½ ºÈÓÐÐÙ º ºÙ ÓÑÔÙØ Ò Ä ÍÒ Ú Ö ØÝ Ó Ã ÒØ Ø ÒØ Ö ÙÖÝ Ò Ð Ò ¾ ÒÞÛ ÒºØÙ ºÒÐ Ò ÓÚ Ò ÍÒ Ú Ö ØÝ Ó Ì
 ÄÓ ÓÖ ØÖØ Ø ÌÝÔ Ü ØÒØÐ ÌÝÔ Ö ÈÓÐÐ ½ Ò ÂÒ ÛÒÒÙÖ ¾ ½ ºÈÓÐÐÙººÙ ÓÑÔÒ Ä ÍÒÚÖ ØÝ Ó ÃÒØ Ø ÒØÖÙÖÝ ÒÐÒ ¾ ÒÞÛÒºØÙºÒÐ ÒÓÚÒ ÍÒÚÖ ØÝ Ó ÌÒÓÐÓÝ Ì ÆØÖÐÒ ØÖغ Ì ÓÒ¹ÓÖÖ ÐÑ ÐÙÐÙ ÐÐÓÛ Ò ÐÒØ ÓÖÑй ØÓÒ Ó ØÖØ Ø ØÝÔ Ì³ µ Ù Ò
ÄÓ ÓÖ ØÖØ Ø ÌÝÔ Ü ØÒØÐ ÌÝÔ Ö ÈÓÐÐ ½ Ò ÂÒ ÛÒÒÙÖ ¾ ½ ºÈÓÐÐÙººÙ ÓÑÔÒ Ä ÍÒÚÖ ØÝ Ó ÃÒØ Ø ÒØÖÙÖÝ ÒÐÒ ¾ ÒÞÛÒºØÙºÒÐ ÒÓÚÒ ÍÒÚÖ ØÝ Ó ÌÒÓÐÓÝ Ì ÆØÖÐÒ ØÖغ Ì ÓÒ¹ÓÖÖ ÐÑ ÐÙÐÙ ÐÐÓÛ Ò ÐÒØ ÓÖÑй ØÓÒ Ó ØÖØ Ø ØÝÔ Ì³ µ Ù Ò
[Na + ] [NaCl] + [Na + ]
![[Na + ] [NaCl] + [Na + ] [Na + ] [NaCl] + [Na + ]](/thumbs/85/92069557.jpg) Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÂÙÖ Ö Ò ÊÙ ÓÐ ÈÓ ÓÖÒ Ò Ë ËÚ Ø Ò ¾¼½½»¾¼½¾ ÈÓ Ð Ú Ä ÃÌÊÁ ÆÁ ÁÆ Å Æ ÌÆÁ ÈÇ ÎÁ º½ º½º½ Ð ØÖ ÒÓ ÔÓÐ Ò ØÓ Ð ØÖ Ò Ò Ó Ð ØÖ Ò ÔÓ Ú Ð Ó Ö ÞÐÓö ÑÓ Ò Ó ÒÓÚ Ù ÓØÓÚ ØÚ Ñ Ó Ó ÒÓÚÒ Ð ÓØ Ø
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÂÙÖ Ö Ò ÊÙ ÓÐ ÈÓ ÓÖÒ Ò Ë ËÚ Ø Ò ¾¼½½»¾¼½¾ ÈÓ Ð Ú Ä ÃÌÊÁ ÆÁ ÁÆ Å Æ ÌÆÁ ÈÇ ÎÁ º½ º½º½ Ð ØÖ ÒÓ ÔÓÐ Ò ØÓ Ð ØÖ Ò Ò Ó Ð ØÖ Ò ÔÓ Ú Ð Ó Ö ÞÐÓö ÑÓ Ò Ó ÒÓÚ Ù ÓØÓÚ ØÚ Ñ Ó Ó ÒÓÚÒ Ð ÓØ Ø
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙ
 È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙÖ Ð Ò Ò Ö Ò Ò Å Ø Ö Ð Ë Ò ÖÒ Å ÐÐÓÒ ÍÒ Ú Ö ØÝ ÆÓÚ Ñ
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙÖ Ð Ò Ò Ö Ò Ò Å Ø Ö Ð Ë Ò ÖÒ Å ÐÐÓÒ ÍÒ Ú Ö ØÝ ÆÓÚ Ñ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 5 ÅØ ÕÑØ Ñ Fourier ¾¹ ÓÐÓÙôÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 5 ÅØ ÕÑØ Ñ Fourier ¾¹ ÓÐÓÙôÒ
f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº
![f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº](/thumbs/103/160734174.jpg) ÇÐÓ Ð ÖÛ º½ Å ØÖ Ñ ËÙÒ ÖØ È Ö Ø Ö º½ µ Å ÙÒ ÖØ f : X Y Ñ Ø Ü Ñ ÒôÒ ÙÒ ÐÛÒ Ô ½ Ñ Ô Ò f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. À Ô Ò ÙØ Ø Ö ÙÑÔÐ ÖôÑ Ø Ù Ö Ø Òô Ù Ö Ø ØÓÑ º µ Ò B P(Y ) Ò σ¹ Ð Ö Ó Ó Ò
ÇÐÓ Ð ÖÛ º½ Å ØÖ Ñ ËÙÒ ÖØ È Ö Ø Ö º½ µ Å ÙÒ ÖØ f : X Y Ñ Ø Ü Ñ ÒôÒ ÙÒ ÐÛÒ Ô ½ Ñ Ô Ò f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. À Ô Ò ÙØ Ø Ö ÙÑÔÐ ÖôÑ Ø Ù Ö Ø Òô Ù Ö Ø ØÓÑ º µ Ò B P(Y ) Ò σ¹ Ð Ö Ó Ó Ò
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: 2-Δ συνεχή σήματα. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: 2-Δ συνεχή σήματα Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 3 ¾¹ ÙÒÕ ÑØ Å ÙÒÕ Ò ÑÔÓÖ Ò ÔÖ Ø Ô Ò ¾¹ ÙÒÕ Ñ Ð
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: 2-Δ συνεχή σήματα Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 3 ¾¹ ÙÒÕ ÑØ Å ÙÒÕ Ò ÑÔÓÖ Ò ÔÖ Ø Ô Ò ¾¹ ÙÒÕ Ñ Ð
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Εισαγωγή. Καθηγητής Γεώργιος Τζιρίτας. Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Εισαγωγή Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 1 Û Å ØÒ ÐÙ Ø Ý ÛØÓÖ Ý Ò Ò ÔÐÓÒ ØÑ ØÓÙ ÙÖÛ ÓÒÓº À ÔÜÖ ÒÛÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Εισαγωγή Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 1 Û Å ØÒ ÐÙ Ø Ý ÛØÓÖ Ý Ò Ò ÔÐÓÒ ØÑ ØÓÙ ÙÖÛ ÓÒÓº À ÔÜÖ ÒÛÒ
Role of Alumina Support in Cobalt Fischer-Tropsch Synthesis
 Øyvind Borg Role of Alumina Support in Cobalt Fischer-Tropsch Synthesis Thesis for the degree of doktor ingeniør Trondheim, April 2007 Norwegian University of Science and Technology Faculty of Natural
Øyvind Borg Role of Alumina Support in Cobalt Fischer-Tropsch Synthesis Thesis for the degree of doktor ingeniør Trondheim, April 2007 Norwegian University of Science and Technology Faculty of Natural
( + )( + + ) ( + )( + + ) ( + )( + )
 ÒØ ÙØÓÑØ Ò ÔÔÐØÓÒ ÖÔØÓÒÐ ÓÑÔÐÜØÝ ÆÐÑ ÅÓÖÖ ÊÓÖÓ Ê ÖØÐ ÁÒØÐÐÒ Ò ÓÑÔÙØÖ ËÒ ÄÓÖØÓÖÝ ÄÒÙ ÓÑÔÐÜØÝ Ò ÖÝÔØÓÖÔÝ ÖÓÙÔ ÌÑØ ËÑÒÖ ÅÈ ½»½½»¾¼¼ ƺÅÓÖÖ ÊºÊ ¹ ² ÄÁµ ÒØ ÙØÓÑØ ½» ÏØ Ö Û ÛÓÖÒ ÓÒ Ò Ø Öµ źÐÑ ÆºÅÓÖÖ ² ÊºÊ µ
ÒØ ÙØÓÑØ Ò ÔÔÐØÓÒ ÖÔØÓÒÐ ÓÑÔÐÜØÝ ÆÐÑ ÅÓÖÖ ÊÓÖÓ Ê ÖØÐ ÁÒØÐÐÒ Ò ÓÑÔÙØÖ ËÒ ÄÓÖØÓÖÝ ÄÒÙ ÓÑÔÐÜØÝ Ò ÖÝÔØÓÖÔÝ ÖÓÙÔ ÌÑØ ËÑÒÖ ÅÈ ½»½½»¾¼¼ ƺÅÓÖÖ ÊºÊ ¹ ² ÄÁµ ÒØ ÙØÓÑØ ½» ÏØ Ö Û ÛÓÖÒ ÓÒ Ò Ø Öµ źÐÑ ÆºÅÓÖÖ ² ÊºÊ µ
x E[x] x xµº λx. E[x] λx. x 2 3x +2
![x E[x] x xµº λx. E[x] λx. x 2 3x +2 x E[x] x xµº λx. E[x] λx. x 2 3x +2](/thumbs/20/424851.jpg) ¾ λ¹ ÐÓÒ Ó ÙÖ ½ ¼ º õ ¹ ¹ ÙÖ ¾ ÙÖ º ÃÐ ¹ ½ ¼º ¹ Ð Ñ ÐÙÐÙ µ λ¹ λ¹ ÐÙÐÙ µº λ¹ º ý ½ ¼ ø λ¹ ÃÐ º λ¹ ÌÙÖ Ò ÌÙÖ º ÌÙÖ Ò ÚÓÒ Æ ÙÑ ÒÒ ¹ ÇÊÌÊ Æ Ä Çĺ ý λ¹ ¹ º Ö ÙØ ÓÒ Ñ Ò µ Ø ¹ ÓÛ ÓÑÔÙØ Ö µ ¹ λ¹ º λ¹ ÙÒØ ÓÒ Ð
¾ λ¹ ÐÓÒ Ó ÙÖ ½ ¼ º õ ¹ ¹ ÙÖ ¾ ÙÖ º ÃÐ ¹ ½ ¼º ¹ Ð Ñ ÐÙÐÙ µ λ¹ λ¹ ÐÙÐÙ µº λ¹ º ý ½ ¼ ø λ¹ ÃÐ º λ¹ ÌÙÖ Ò ÌÙÖ º ÌÙÖ Ò ÚÓÒ Æ ÙÑ ÒÒ ¹ ÇÊÌÊ Æ Ä Çĺ ý λ¹ ¹ º Ö ÙØ ÓÒ Ñ Ò µ Ø ¹ ÓÛ ÓÑÔÙØ Ö µ ¹ λ¹ º λ¹ ÙÒØ ÓÒ Ð
A Francesca, Paola, Laura
 A Francesca, Paola, Laura L. Formaggia F. Saleri A. Veneziani Applicazioni ed esercizi di modellistica numerica per problemi differenziali 2 3 LUCA FORMAGGIA FAUSTO SALERI ALESSANDRO VENEZIANI MOX - Dipartimento
A Francesca, Paola, Laura L. Formaggia F. Saleri A. Veneziani Applicazioni ed esercizi di modellistica numerica per problemi differenziali 2 3 LUCA FORMAGGIA FAUSTO SALERI ALESSANDRO VENEZIANI MOX - Dipartimento
ca t = β 1z t 1(q t γ)+β 2z t 1(q t >γ)+ε t z t = g(x t,π)+u t
 Ì Ö ÓÐ ÅÓ Ð Ó Ø ÍË ÙÖÖ ÒØ ÓÙÒØ ÊÓ ÖØÓ ÙÒ Ò ÇØÓ Ö ½ ¾¼½ ØÖ Ø Ï Ø Ö Ú ÍË ÙÖÖ ÒØ ÓÙÒØ Ñ Ð Ò Á Ø Ö ÓÐ Ú Ò Ø Ø Ø Ú ÓÖ Ó Ø ÙÖÖ ÒØ ÓÙÒØ Ö ÒØ ÙÖ Ò Ø Ò ÙÖÔÐÙ ÓÖ Ø Ø Ø Þ Ó Ø Ñ¹ Ð Ò Ñ ØØ Ö Á Ø Ö Ø Ö ÓÐ Ö Ð Ø ÓÒ Ô
Ì Ö ÓÐ ÅÓ Ð Ó Ø ÍË ÙÖÖ ÒØ ÓÙÒØ ÊÓ ÖØÓ ÙÒ Ò ÇØÓ Ö ½ ¾¼½ ØÖ Ø Ï Ø Ö Ú ÍË ÙÖÖ ÒØ ÓÙÒØ Ñ Ð Ò Á Ø Ö ÓÐ Ú Ò Ø Ø Ø Ú ÓÖ Ó Ø ÙÖÖ ÒØ ÓÙÒØ Ö ÒØ ÙÖ Ò Ø Ò ÙÖÔÐÙ ÓÖ Ø Ø Ø Þ Ó Ø Ñ¹ Ð Ò Ñ ØØ Ö Á Ø Ö Ø Ö ÓÐ Ö Ð Ø ÓÒ Ô
Á ÆÌÁ Áà ÁÇÆ ËÌÊ ÆÁ ÇÃÌÇÊËà ÁË ÊÌ Á Iº ÙØÓÖ ÁÑ ÔÖ Þ Ñ Ì Ø Ò Ð Ð ØÙÑ Ñ ØÓ ÖÓ Û ÃÖ Ù Ú Ë ßÛ Þ ÔÓ Ð Û Ø ÒØ Ò ÈÖ ÖÓ ÒÓ¹Ñ Ø Ñ Ø ÓÑ ÙÐØ ØÙ ÍÒ Ú
 ÍÒ Ú ÖÞ Ø Ø Ù ÃÖ Ù ÚÙ ÈÖ ÖÓ ÒÓ¹Ñ Ø Ñ Ø ÙÐØ Ø Ì Ø Ò Ð Ð Ê ÇÎÁ ÁÂ Â Æ ÂÅ Ï Ã Ê ÃÌ ÊÁËÌÁ Æ ÎÊ ÆÇËÌ ÅÁÆÁÅ ÄÆ Í Æ ÃÁÅ ÃÄ Ë Å Ê ÇÎ Ó ØÓÖ ÖØ ÃÖ Ù Ú ¾¼½¾º Á ÆÌÁ Áà ÁÇÆ ËÌÊ ÆÁ ÇÃÌÇÊËà ÁË ÊÌ Á Iº ÙØÓÖ ÁÑ ÔÖ Þ Ñ
ÍÒ Ú ÖÞ Ø Ø Ù ÃÖ Ù ÚÙ ÈÖ ÖÓ ÒÓ¹Ñ Ø Ñ Ø ÙÐØ Ø Ì Ø Ò Ð Ð Ê ÇÎÁ ÁÂ Â Æ ÂÅ Ï Ã Ê ÃÌ ÊÁËÌÁ Æ ÎÊ ÆÇËÌ ÅÁÆÁÅ ÄÆ Í Æ ÃÁÅ ÃÄ Ë Å Ê ÇÎ Ó ØÓÖ ÖØ ÃÖ Ù Ú ¾¼½¾º Á ÆÌÁ Áà ÁÇÆ ËÌÊ ÆÁ ÇÃÌÇÊËà ÁË ÊÌ Á Iº ÙØÓÖ ÁÑ ÔÖ Þ Ñ
Στοκεφάλαιοαυτόθαμιλήσ ουμεγιατααρχείασ τηνγλώσ σ α ºΘαχρησ ιμοποιηθούνσ υναρτήσ ειςαπότηνκαθιερωμένηβιβλιοθήκηεισ όδου»εξόδου
 ΚΕΦΑΛΑΙΟ 4 ΑΡΧΕΙΑ Στοκεφάλαιοαυτόθαμιλήσουμεγιατααρχείαστηνγλώσσα ºΘαχρησιμοποιηθούνσυναρτήσειςαπότηνκαθιερωμένηβιβλιοθήκηεισόδου»εξόδου ØÓºµκαι γιααυτόγίνεταιμιαπρώτηπαρουσίασηαυτήςτηςβιβλιοθήκηςº º½
ΚΕΦΑΛΑΙΟ 4 ΑΡΧΕΙΑ Στοκεφάλαιοαυτόθαμιλήσουμεγιατααρχείαστηνγλώσσα ºΘαχρησιμοποιηθούνσυναρτήσειςαπότηνκαθιερωμένηβιβλιοθήκηεισόδου»εξόδου ØÓºµκαι γιααυτόγίνεταιμιαπρώτηπαρουσίασηαυτήςτηςβιβλιοθήκηςº º½
ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ø ÓÙØ Û ÓÑ Ø ÔÖÓ Ø ÛÓÙÐ Ò Ú Ö ÓÑÔÐ Ø
 ÇÆ ÌÀ Ä ËËÁ Á ÌÁÇÆ Ç ÄÇË Ä Ì ÇÍʹŠÆÁ ÇÄ Ë Ý Ì ÓÑ È ÙÐ Ä Ñ ÖØ ÖØ Ø ÓÒ ËÙ Ñ ØØ ØÓ Ø ÙÐØÝ Ó Ø Ö Ù Ø Ë ÓÓÐ Ó Î Ò Ö ÐØ ÍÒ Ú Ö ØÝ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Ç ÌÇÊ Ç ÈÀÁÄÇËÇÈÀ Ò Å Ø Ñ Ø Ù Ù
ÇÆ ÌÀ Ä ËËÁ Á ÌÁÇÆ Ç ÄÇË Ä Ì ÇÍʹŠÆÁ ÇÄ Ë Ý Ì ÓÑ È ÙÐ Ä Ñ ÖØ ÖØ Ø ÓÒ ËÙ Ñ ØØ ØÓ Ø ÙÐØÝ Ó Ø Ö Ù Ø Ë ÓÓÐ Ó Î Ò Ö ÐØ ÍÒ Ú Ö ØÝ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Ç ÌÇÊ Ç ÈÀÁÄÇËÇÈÀ Ò Å Ø Ñ Ø Ù Ù
Ë Ö ½ Ç ÒÓÚÒ ÔÓ ÑÓÚ Þ Õ ÚÓ ØÚ ÐÙ ½ ½º½ ÈÖ Ñ Ø ÞÒ Õ Ö ÞÚÓ Ñ Ò ÐÙ º º º º º º º º º º º º º º º º º º º º ½ ½º½º½ ÈÖ Ñ Ø ÔÓ Ð Ñ Ò ÐÙ º º º º º º º º º º
 ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Å Ü Ò ÙÐØ Ø Ëº É ÒØÖ Åº Ä Õ º Ó Å À ÆÁà ÄÍÁ Ó Ö ¾¼¼ º Ë Ö ½ Ç ÒÓÚÒ ÔÓ ÑÓÚ Þ Õ ÚÓ ØÚ ÐÙ ½ ½º½ ÈÖ Ñ Ø ÞÒ Õ Ö ÞÚÓ Ñ Ò ÐÙ º º º º º º º º º º º º º º º º º º º º ½ ½º½º½ ÈÖ Ñ Ø ÔÓ Ð Ñ Ò
ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Å Ü Ò ÙÐØ Ø Ëº É ÒØÖ Åº Ä Õ º Ó Å À ÆÁà ÄÍÁ Ó Ö ¾¼¼ º Ë Ö ½ Ç ÒÓÚÒ ÔÓ ÑÓÚ Þ Õ ÚÓ ØÚ ÐÙ ½ ½º½ ÈÖ Ñ Ø ÞÒ Õ Ö ÞÚÓ Ñ Ò ÐÙ º º º º º º º º º º º º º º º º º º º º ½ ½º½º½ ÈÖ Ñ Ø ÔÓ Ð Ñ Ò
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο. Επίδοση Υπολογιστικών Συστημάτων. Α.-Γ. Σταφυλοπάτης.
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Πειράματα Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Πειράματα Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Ì Ø ÖÑ Ò Ø ÓÒ Ø Ò Ø ÓÒ ÔÖÓ ÙØ Â Ò¹ Ö È Ò Ò Ò Ì Ö Ò ÙÐÐ Ê Ö Ò Ú ÐÓÔÑ ÒØ Ê٠ ҹ ÙÖ ¼ Ä Ð Ý ¹ ÓÙ ¹ Ó Ö Ò ØÖ Ø Ì Ô Ô Ö ÚÓØ ØÓ Ø ØÙ Ý Ó Ø Ø ÖÑ Ò Ø ÓÒ Ø Ò
 Ì ØÖÑÒ Ø ÓÒØÒØÓÒ ÔÖÓÙØ ÂÒ¹Ö ÈÒ Ò Ò ÌÖÒ ÙÐÐ Ê Ö Ò ÚÐÓÔÑÒØ ÊÙ ÂÒ¹ÂÙÖ ¼ Ä ÐÝ ¹ ÓÙ ¹Ó ÖÒ ØÖØ Ì ÔÔÖ ÚÓØ ØÓ Ø ØÙÝ Ó Ø ØÖÑÒ Ø ÓÒØÒØÓÒ ÔÖÓÙØ ÚÖÒØ Ó Ø ÓÒØÒØÓÒ ÔÖÓÙغ Ï Ú Ò ÐÖ Ö¹ ØÖÞØÓÒ Ó Ø ÚÖØ Ó ÐÒÙ ÐÓ ÙÒÖ Ø ÔÖÓÙغ
Ì ØÖÑÒ Ø ÓÒØÒØÓÒ ÔÖÓÙØ ÂÒ¹Ö ÈÒ Ò Ò ÌÖÒ ÙÐÐ Ê Ö Ò ÚÐÓÔÑÒØ ÊÙ ÂÒ¹ÂÙÖ ¼ Ä ÐÝ ¹ ÓÙ ¹Ó ÖÒ ØÖØ Ì ÔÔÖ ÚÓØ ØÓ Ø ØÙÝ Ó Ø ØÖÑÒ Ø ÓÒØÒØÓÒ ÔÖÓÙØ ÚÖÒØ Ó Ø ÓÒØÒØÓÒ ÔÖÓÙغ Ï Ú Ò ÐÖ Ö¹ ØÖÞØÓÒ Ó Ø ÚÖØ Ó ÐÒÙ ÐÓ ÙÒÖ Ø ÔÖÓÙغ
Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
 ÄÓ Ñ ÒÓ ØÓ Ãô ØÓ Ë Ø Ñ Ø Ì Ñ À Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009 ½ º Ó Ó Ð Ó Διεύθυνση Πληροφορικής ΔΕΗ Τομέας Συστημάτων Γραφείου ÚºÞÓÙ Ó ºÓѺ Ö ¹Ñ Ð Αθήνα 19 Ιουνίου 2009 Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
ÄÓ Ñ ÒÓ ØÓ Ãô ØÓ Ë Ø Ñ Ø Ì Ñ À Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009 ½ º Ó Ó Ð Ó Διεύθυνση Πληροφορικής ΔΕΗ Τομέας Συστημάτων Γραφείου ÚºÞÓÙ Ó ºÓѺ Ö ¹Ñ Ð Αθήνα 19 Ιουνίου 2009 Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
Ω = {ω 1,..., ω 6 }, ω = ω 1,..., ω m 1, 6, ω 1,...,, ω j {1, 2,...5}, m 1.
 Î Ð Ù ËØ Å Ò Ì ÑÝ Ù Ø ÓÖ Ó Ô ØÓ Î ÐÒ Ù ¾¼¼ ÌÙÖ ÒÝ ½ Ì ÑÝ ÒÅ Ö ÚÅ º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º ËØ Ø Ø Ò Ô Ö Ñ ÒØ º º º º º º º º º º º º º º º º ½º¾º ÃÐ Ò ÑÓ Ð º º º º º º º º
Î Ð Ù ËØ Å Ò Ì ÑÝ Ù Ø ÓÖ Ó Ô ØÓ Î ÐÒ Ù ¾¼¼ ÌÙÖ ÒÝ ½ Ì ÑÝ ÒÅ Ö ÚÅ º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º ËØ Ø Ø Ò Ô Ö Ñ ÒØ º º º º º º º º º º º º º º º º ½º¾º ÃÐ Ò ÑÓ Ð º º º º º º º º
Preisdifferenzierung für Flugtickets
 Ë Ñ Ø Ö Ö Ø ÏÄ ÌÀ Ö ÈÖ Ö ÒÞ ÖÙÒ Ö ÐÙ Ø Ø Ù Ò ËØÖ Ò Ö ¹ ÄÓÒ ÓÒ ÙÒ Ö Ò ÙÖØ ¹ Æ Û ÓÖ ÙØÓÖ Ò Ì ÓÑ ÖÙÒÒ Ö À ÙÖ ØÖº ¼ Ö Ñ ÐØ ÓÑ ÖÙÒÒ Öº Ö ØÓÔ Ã Ö ÐÙÑ ÒÛ ½¼ Ç ÖÛ Ð Ö ØÙ Òغ Ø Þº ØÖ Ù Ö ËØ Ò Ä Ù Ò Ø Ò ÈÖÓ ÓÖ ÖÑ
Ë Ñ Ø Ö Ö Ø ÏÄ ÌÀ Ö ÈÖ Ö ÒÞ ÖÙÒ Ö ÐÙ Ø Ø Ù Ò ËØÖ Ò Ö ¹ ÄÓÒ ÓÒ ÙÒ Ö Ò ÙÖØ ¹ Æ Û ÓÖ ÙØÓÖ Ò Ì ÓÑ ÖÙÒÒ Ö À ÙÖ ØÖº ¼ Ö Ñ ÐØ ÓÑ ÖÙÒÒ Öº Ö ØÓÔ Ã Ö ÐÙÑ ÒÛ ½¼ Ç ÖÛ Ð Ö ØÙ Òغ Ø Þº ØÖ Ù Ö ËØ Ò Ä Ù Ò Ø Ò ÈÖÓ ÓÖ ÖÑ
Å Ø Ø Ð ØÝ ÓÖ Ö Ú Ö Ð ÔÖÓ Ð Ø ÐÐÙÐ Ö ÙØÓÑ Ø Û Ø Ð ß ÒØ Ö Ø ÓÒ Ñ Ð Ó ÆºÅº Ö ÐÐÓ ½ Ö Ò Êº Æ Ö ¾ Ö Ø Ò ËÔ ØÓÒ ½ Ô ÖØ Ñ ÒØÓ Å º ÅÓº Šغ ÍÒ Ú Ö Ø ÊÓÑ Ä Ë
 ÅØ ØÐØÝ ÓÖ ÖÚÖ Ð ÔÖÓÐ Ø ÐÐÐÖ ØÓÑØ ÛØ ÐßÒØÖØÓÒ ÑÐÓ ÆºÅº ÖÐÐÓ ½ ÖÒ Êº ÆÖ ¾ Ö ØÒ ËÔØÓÒ ½ ÔÖØÑÒØÓ Åº ÅÓº Åغ ÍÒÚÖ Ø ÊÓÑ Ä ËÔÒÞ Ú º ËÖÔ ½ ¼¼½½ ÊÓÑ ÁØÐÝ ßÑÐ ÖÐÐÓÑÑѺÒÖÓѽºØ ¾ ÔÖØÑÒØ Ó ÅØÑØ Ò ÓÑÔØÖ ËÒ ÒÓÚÒ ÍÒÚÖ
ÅØ ØÐØÝ ÓÖ ÖÚÖ Ð ÔÖÓÐ Ø ÐÐÐÖ ØÓÑØ ÛØ ÐßÒØÖØÓÒ ÑÐÓ ÆºÅº ÖÐÐÓ ½ ÖÒ Êº ÆÖ ¾ Ö ØÒ ËÔØÓÒ ½ ÔÖØÑÒØÓ Åº ÅÓº Åغ ÍÒÚÖ Ø ÊÓÑ Ä ËÔÒÞ Ú º ËÖÔ ½ ¼¼½½ ÊÓÑ ÁØÐÝ ßÑÐ ÖÐÐÓÑÑѺÒÖÓѽºØ ¾ ÔÖØÑÒØ Ó ÅØÑØ Ò ÓÑÔØÖ ËÒ ÒÓÚÒ ÍÒÚÖ
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 11: SPLINES. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 11: SPLINES Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 11: SPLINES Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Μονοδιάσ τατοιπίνακες
 ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ ¾º½ Μονοδιάστατοιπίνακες Οιπίνακεςείναιδομέςδεδομένωνπουδιαθέτουνέναπλήθοςαπόστοιχείατουίδιου τύπουº Γιαπαράδειγμαηβαθμολογίασεέναμάθημααποθηκεύτεταισεπίνακαº Κάθεστοιχείοτουπίνακααντιπροσωπεύειτηνβαθμολογίαενόςσπουδαστήστο
ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ ¾º½ Μονοδιάστατοιπίνακες Οιπίνακεςείναιδομέςδεδομένωνπουδιαθέτουνέναπλήθοςαπόστοιχείατουίδιου τύπουº Γιαπαράδειγμαηβαθμολογίασεέναμάθημααποθηκεύτεταισεπίνακαº Κάθεστοιχείοτουπίνακααντιπροσωπεύειτηνβαθμολογίαενόςσπουδαστήστο
c = a+b AC = AB + BC k res = k 1 +k 2
 Ã Ô Ø Ð Á ÒÐ ØÙÒ ï ½ ÅÓ ÐÐ ÚÓÒ Î ØÓÖÖÙÑ Ò ÁÒ Ñ Ö ÅÓØ Ú Ø ÓÒ Ò Ò Òµ È Ö Ö Ô Ò Ò ÐÒ Û Ö Ô Ð ÞÙÖ Ð Ö ¹ Ò ËØÖÙ ØÙÖ Î ØÓÖÖ ÙÑ º Ò Ö ÙÒ Ò Ø Ò ØÞ Ò Û Ö Ð ÒÒØ ÚÓÖ Ù º Ò ÈÖÞ ÖÙÒ Ö ÓÐ Ø ÔØ Ö Û ÒÒ Û Ö ÙÒ ÙÑ Ò Ñ Ø
Ã Ô Ø Ð Á ÒÐ ØÙÒ ï ½ ÅÓ ÐÐ ÚÓÒ Î ØÓÖÖÙÑ Ò ÁÒ Ñ Ö ÅÓØ Ú Ø ÓÒ Ò Ò Òµ È Ö Ö Ô Ò Ò ÐÒ Û Ö Ô Ð ÞÙÖ Ð Ö ¹ Ò ËØÖÙ ØÙÖ Î ØÓÖÖ ÙÑ º Ò Ö ÙÒ Ò Ø Ò ØÞ Ò Û Ö Ð ÒÒØ ÚÓÖ Ù º Ò ÈÖÞ ÖÙÒ Ö ÓÐ Ø ÔØ Ö Û ÒÒ Û Ö ÙÒ ÙÑ Ò Ñ Ø
 µ µ µ ¾¼¼ ¹ º ¹ º ¹ º º ¹ º þ º ¹ º º º º º ÓÔÝÖ Ø º º º º º º º º º ¹ º º ýº ¹ º º º º º º º Ú Ú Ú ½ ½ ½º½ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ º º º º º º º º º º º º º º º
µ µ µ ¾¼¼ ¹ º ¹ º ¹ º º ¹ º þ º ¹ º º º º º ÓÔÝÖ Ø º º º º º º º º º ¹ º º ýº ¹ º º º º º º º Ú Ú Ú ½ ½ ½º½ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ º º º º º º º º º º º º º º º
Γραφικάμετηνχρήσ η ÛØ
 Γραφικάμετηνχρήση ÛØ ΙωάννηςΓºΤσούλος Νοέμβριος ¾¼ Η Úδιαθέτειένα δικό της σύστημαγραφικών τοοποίομπορεί να είναι κάπωςπεριορισμένοσεσχέσημετο ÉÌήτο ÏÁÆ ¾ ÈÁαλλάδίνειμεταφέρσιμο κώδικακαιμπορείναχρησιμοποιηθείγιατηνκατασκευήπρογραμμάτωνγραφικής
Γραφικάμετηνχρήση ÛØ ΙωάννηςΓºΤσούλος Νοέμβριος ¾¼ Η Úδιαθέτειένα δικό της σύστημαγραφικών τοοποίομπορεί να είναι κάπωςπεριορισμένοσεσχέσημετο ÉÌήτο ÏÁÆ ¾ ÈÁαλλάδίνειμεταφέρσιμο κώδικακαιμπορείναχρησιμοποιηθείγιατηνκατασκευήπρογραμμάτωνγραφικής
Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις
 Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις Τσούλος Ιωάννης, Επίκουρος Καθηγητής Τμ. Μηχανικών Πληροφορικής Τ.Ε. Άρτα, Μάιος 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις Τσούλος Ιωάννης, Επίκουρος Καθηγητής Τμ. Μηχανικών Πληροφορικής Τ.Ε. Άρτα, Μάιος 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
A Threshold Model of the US Current Account *
 Federal Reserve Bank of Dallas Globalization and Monetary Policy Institute Working Paper No. 202 http://www.dallasfed.org/assets/documents/institute/wpapers/2014/0202.pdf A Threshold Model of the US Current
Federal Reserve Bank of Dallas Globalization and Monetary Policy Institute Working Paper No. 202 http://www.dallasfed.org/assets/documents/institute/wpapers/2014/0202.pdf A Threshold Model of the US Current
, z = 1 ( Lψ = Eψ, E = E fixed, L = +v(x,t), = 4 z z, x R 2 ½º µ
 ÇÄ ÈÇÄ Ì ÀÆÁÉÍ ÆÌÊ Å ÌÀ Å ÌÁÉÍ Ë ÈÈÄÁÉÍ Ë ÍÅÊ ÆÊË ½ ½½¾ È Ä ÁË Í Ê Æ µº Ì Ð ¼½ ¼¼º Ü ¼½ ØØÔ»»ÛÛÛºÑ ÔºÔÓÐÝØ Ò ÕÙ º Ö» Ò Ó ÓÐ ØÓÒ Û Ø Ù ÒØ Ð Ö ÐÓ Ð Þ Ø ÓÒ ÓÖ Ø ÆÓÚ ÓڹΠÐÓÚ ÕÙ Ø ÓÒ Ø ÒÓÒÞ ÖÓ Ò Ö Ý ÒÒ Ã Þ
ÇÄ ÈÇÄ Ì ÀÆÁÉÍ ÆÌÊ Å ÌÀ Å ÌÁÉÍ Ë ÈÈÄÁÉÍ Ë ÍÅÊ ÆÊË ½ ½½¾ È Ä ÁË Í Ê Æ µº Ì Ð ¼½ ¼¼º Ü ¼½ ØØÔ»»ÛÛÛºÑ ÔºÔÓÐÝØ Ò ÕÙ º Ö» Ò Ó ÓÐ ØÓÒ Û Ø Ù ÒØ Ð Ö ÐÓ Ð Þ Ø ÓÒ ÓÖ Ø ÆÓÚ ÓڹΠÐÓÚ ÕÙ Ø ÓÒ Ø ÒÓÒÞ ÖÓ Ò Ö Ý ÒÒ Ã Þ
Προσομοίωση Δημιουργία τυχαίων αριθμών
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό
Θεωρία Συνόλων. Ενότητα: Διατακτικοί αριθμοί. Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
 Θεωρία Συνόλων Ενότητα: Διατακτικοί αριθμοί Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Θεωρία Συνόλων Ενότητα: Διατακτικοί αριθμοί Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Ñ Ò Ò Ø Ð ØØ ÒØÓ Ø ¼ ¾ ÒÙÑ Ö Ø ÓÒ Ö ËØ «Ò Ä ÑÔÔ Ò Ò Ö ËÓÖ Ý ØÖ Ø Ï ÓÛ Ø Ø Ú ÖÝ Ò Ø Ð ØØ Ñ Ð ÒØÓ Ø ¼ ¾ ÒÙÑ Ö¹ Ø ÓÒ Ö Ú Ð ØØ ¹Ø ÓÖ Ø Ñ Ò Û ÔÖ ÖÚ ¼ Ò ½º
 ÑÒ ÒØ ÐØØ ÒØÓ Ø ¼ ¾ ÒÙÑÖØÓÒ Ö ËØ«Ò ÄÑÔÔ Ò ÒÖ ËÓÖ Ý ØÖØ Ï ÓÛ ØØ ÚÖÝ ÒØ ÐØØ ÑÐ ÒØÓ Ø ¼ ¾ ÒÙÑÖ¹ ØÓÒ Ö Ú ÐØعØÓÖØ ÑÒ Û ÔÖ ÖÚ ¼ Ò ½º ½ ÁÒØÖÓÙØÓÒ ÁÒÓÖÑÐÐÝ Ø ÒÙÑÖØÓÒ ÖÙÐ ØÓ Ø ØÖ ÓÑ «ØÚ ÔÖÓÙÖ ÓÖ ÒÙÑÖØÒ ÚÒ ÒÝ ÒÙÑÖØÓÒ
ÑÒ ÒØ ÐØØ ÒØÓ Ø ¼ ¾ ÒÙÑÖØÓÒ Ö ËØ«Ò ÄÑÔÔ Ò ÒÖ ËÓÖ Ý ØÖØ Ï ÓÛ ØØ ÚÖÝ ÒØ ÐØØ ÑÐ ÒØÓ Ø ¼ ¾ ÒÙÑÖ¹ ØÓÒ Ö Ú ÐØعØÓÖØ ÑÒ Û ÔÖ ÖÚ ¼ Ò ½º ½ ÁÒØÖÓÙØÓÒ ÁÒÓÖÑÐÐÝ Ø ÒÙÑÖØÓÒ ÖÙÐ ØÓ Ø ØÖ ÓÑ «ØÚ ÔÖÓÙÖ ÓÖ ÒÙÑÖØÒ ÚÒ ÒÝ ÒÙÑÖØÓÒ
½ È Ê Ç Î Ç Ê ÇÚ ÒÓÚ ÓØ À Ð ÖØÓÚ Ç ÒÓÚ ÓÑ ØÖ Ò Ò ÔÖ Ú ÒÓÚ ÔÖ Ö º ÍÔÖ ÚÓ Ù Ò Ò Ù ÑÓ Ò ÔÖ Ú Ñ Ò ÓÔÙÒ º Í ÓÔÙÒ I Ù ÙÔÐ Ò Ò Þ Ú ÒÓ Ø Ù Ø ÑÙ ÓÑ Ö ÐÒ ÖÓ¹ Ú
 ½ ËÊÈËà à ÅÁÂ Æ Íà ÃÄ ËÁ ÆÁ Æ Í ÆÁ ËÈÁËÁ ÃÆÂÁ XIV Å Ì Å ÌÁ ÃÁ ÁÆËÌÁÌÍÌ ÃÆÂÁ ½ ÍÖ Ò Ñ Ê ÁÎÇ à â ÆÁÆ ÍÔÖ ÚÒ Ñ Ø Ñ Ø Ó Ò Ø ØÙØ Ë Æ º ÀÁÄ ÊÌ ÇËÆÇÎ ÇÅ ÌÊÁ ÈÊ Î Ç Ë ÇËÅÇ Æ Å ÃÇ Á ÆÂ êº Ê â ÆÁÆ ÈÖ ÑÐ ÒÓ Ò XI
½ ËÊÈËà à ÅÁÂ Æ Íà ÃÄ ËÁ ÆÁ Æ Í ÆÁ ËÈÁËÁ ÃÆÂÁ XIV Å Ì Å ÌÁ ÃÁ ÁÆËÌÁÌÍÌ ÃÆÂÁ ½ ÍÖ Ò Ñ Ê ÁÎÇ à â ÆÁÆ ÍÔÖ ÚÒ Ñ Ø Ñ Ø Ó Ò Ø ØÙØ Ë Æ º ÀÁÄ ÊÌ ÇËÆÇÎ ÇÅ ÌÊÁ ÈÊ Î Ç Ë ÇËÅÇ Æ Å ÃÇ Á ÆÂ êº Ê â ÆÁÆ ÈÖ ÑÐ ÒÓ Ò XI
Πρότυπα. ΙωάννηςΓºΤσ ούλος
 Πρότυπα ΙωάννηςΓºΤσούλος ¾¼ ½ Συναρτήσειςπροτύπων Μετιςσυναρτήσειςπροτύπωνμπορούμενακάνουμεσυναρτήσειςοιοποίεςεκτελούντονίδιοκώδικα γιαδιαφορετικούςτύπουςδεδομένων όπωςπαρουσιάζεται καιστοεπόμενοπαράδειγμαºοιδηλώσειςσυναρτήσεωνμετηνχρήση
Πρότυπα ΙωάννηςΓºΤσούλος ¾¼ ½ Συναρτήσειςπροτύπων Μετιςσυναρτήσειςπροτύπωνμπορούμενακάνουμεσυναρτήσειςοιοποίεςεκτελούντονίδιοκώδικα γιαδιαφορετικούςτύπουςδεδομένων όπωςπαρουσιάζεται καιστοεπόμενοπαράδειγμαºοιδηλώσειςσυναρτήσεωνμετηνχρήση
ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ
 ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία
ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία
Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί νόμοι
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί
Κληρονομικότητα. ΙωάννηςΓºΤσ ούλος
 Κληρονομικότητα ΙωάννηςΓºΤσούλος ¾¼½ ½ Ηκατηγορία ÈÖ ÓÒ ΗκληρονομικότητααποτελείένααπόταβασικότεραχαρακτηριστικάτουαντικειμενοστραφούςπρογραμματισμούºΤαβασικάτηςστοιχείασε είναι ½ºΤαπεδίαπουχρειάζεταιναπεράσουνστηνκατηγορίαπουκληρονομείθα
Κληρονομικότητα ΙωάννηςΓºΤσούλος ¾¼½ ½ Ηκατηγορία ÈÖ ÓÒ ΗκληρονομικότητααποτελείένααπόταβασικότεραχαρακτηριστικάτουαντικειμενοστραφούςπρογραμματισμούºΤαβασικάτηςστοιχείασε είναι ½ºΤαπεδίαπουχρειάζεταιναπεράσουνστηνκατηγορίαπουκληρονομείθα
Προγραμματισ μόςσ ε» ΙωάννηςΓºΤσ ούλος
 Προγραμματισμόςσε» ΙωάννηςΓºΤσούλος ¾¼½ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ½º½ Μεταβλητές ½º½º½ Δήλωση Η δήλωσημεταβλητώνμπορεί να γίνει σε οποιοδήποτεσημείοτου κώδικα σε αλλάείναιπροτιμότεροναγίνεταιστηναρχήτουπρογράμματος
Προγραμματισμόςσε» ΙωάννηςΓºΤσούλος ¾¼½ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ½º½ Μεταβλητές ½º½º½ Δήλωση Η δήλωσημεταβλητώνμπορεί να γίνει σε οποιοδήποτεσημείοτου κώδικα σε αλλάείναιπροτιμότεροναγίνεταιστηναρχήτουπρογράμματος
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Δυναμικοί τύποι δεδομένων
 Δυναμικοί τύποι δεδομένων ΙωάννηςΓºΤσούλος Δεκέμβριος ¾¼ Η ÂÚπεριέχειμιασειράαπόχρήσιμεςκατηγορίεςπουχρησιμοποιούνταιγια τηνδιαχείρισηδυναμικώνδεδομένων σταοποίαδενγνωρίζουμεεκτωνπροτέρων όχι μόνον την
Δυναμικοί τύποι δεδομένων ΙωάννηςΓºΤσούλος Δεκέμβριος ¾¼ Η ÂÚπεριέχειμιασειράαπόχρήσιμεςκατηγορίεςπουχρησιμοποιούνταιγια τηνδιαχείρισηδυναμικώνδεδομένων σταοποίαδενγνωρίζουμεεκτωνπροτέρων όχι μόνον την
 ÍÆÁÎ ÊËÁÌ Ç ÎÊ Î Ä ³ ËËÇÆÆ Ç ÌÇÊ Ä Ë ÀÇÇÄ ËÁÌ ÎÊ È À Ì À Ë Á Ë ØÓ Ó Ø Ò Ø Ø ØÐ Ó È Ó Ë Ò Ó Ø ÍÒ Ú Ö ØÝ Ó ÚÖÝ Î Ð ³ ÓÒÒ ËÔ ÐØÝ ÊÓ ÓØ Ò Ý ÅÓ Ñ Ù ØÒ Ò Ò ÓÒØÖÓÐ Ó À ÔØ Ú ÓÖ Å Ò Ñ ÐÐÝ ÁÒÚ Ú ËÙÖ ÖÝ Ë ÑÙÐ Ø ÓÒ
ÍÆÁÎ ÊËÁÌ Ç ÎÊ Î Ä ³ ËËÇÆÆ Ç ÌÇÊ Ä Ë ÀÇÇÄ ËÁÌ ÎÊ È À Ì À Ë Á Ë ØÓ Ó Ø Ò Ø Ø ØÐ Ó È Ó Ë Ò Ó Ø ÍÒ Ú Ö ØÝ Ó ÚÖÝ Î Ð ³ ÓÒÒ ËÔ ÐØÝ ÊÓ ÓØ Ò Ý ÅÓ Ñ Ù ØÒ Ò Ò ÓÒØÖÓÐ Ó À ÔØ Ú ÓÖ Å Ò Ñ ÐÐÝ ÁÒÚ Ú ËÙÖ ÖÝ Ë ÑÙÐ Ø ÓÒ
Õâñéäéóìüò. Ðïéá åßíáé ç áíüãêç åéóáãùãþò ôçò Ýííïéáò ôïõ õâñéäéóìïý. Ðïéá åßíáé ôá âáóéêüôåñá åßäç õâñéäéóìïý
 9 Õâñéäéóìüò ÐÅÑÉÅ ÏÌÅÍÁ 9.1 ÅéóáãùãÞ 9.2 Õâñéäéóìüò & õâñéäéêü ôñï éáêü 9.3 Åßäç õâñéäéóìïý êáé õâñéäéêþí ôñï éáêþí 9.4 Õâñéäéóìüò êáé ðïëëáðëïß äåóìïß 9.5 Õâñéäéóìüò êáé ìïñéáêþ ãåùìåôñßá 9.6 ÅñùôÞóåéò
9 Õâñéäéóìüò ÐÅÑÉÅ ÏÌÅÍÁ 9.1 ÅéóáãùãÞ 9.2 Õâñéäéóìüò & õâñéäéêü ôñï éáêü 9.3 Åßäç õâñéäéóìïý êáé õâñéäéêþí ôñï éáêþí 9.4 Õâñéäéóìüò êáé ðïëëáðëïß äåóìïß 9.5 Õâñéäéóìüò êáé ìïñéáêþ ãåùìåôñßá 9.6 ÅñùôÞóåéò
ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ
 ÔØ Ö ¾ ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ ¾º½ Δημιουργία απλού παραθύρου Γιατηνδημιουργίαπαραθύρουθαχρειασ τείοχρήσ τηςνατοποθετήσ ειμέσ ασ ε μιακυρίωςεφαρμογήέναοπτικόσ υσ τατικό Ï ØµΤοπιοαπλόοπτικόσ υσ τατικόπουμπορείναχρησ
ÔØ Ö ¾ ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ ¾º½ Δημιουργία απλού παραθύρου Γιατηνδημιουργίαπαραθύρουθαχρειασ τείοχρήσ τηςνατοποθετήσ ειμέσ ασ ε μιακυρίωςεφαρμογήέναοπτικόσ υσ τατικό Ï ØµΤοπιοαπλόοπτικόσ υσ τατικόπουμπορείναχρησ
ÆÁÄ º ÁÇÆ ÁÊÍÁÌ ÄÌÊÁ ÊÁËÌÁÎ ÖÚÖ ØÓÖØ ÔÖÓÐÑ ÊÖÒØ ØÒØ ÓÒºÖºÒº ÁÖÒ ÅÙÒØÒ٠˺к Öº Òº ÖÐ ÙÔÖÒ ØÙÖ ¾¼¼¼ ÙÙÖ Ø
 ÆÁÄ º ÁÇÆ ÍÒÚÖ ØØ ÈÓÐØÒ ÙÙÖ Ø ÁÊÍÁÌ ÄÌÊÁ ÊÁËÌÁÎ ÖÚÖ ØÓÖØ ÔÖÓÐÑ ØÙÖ ¾¼¼¼ ÆÁÄ º ÁÇÆ ÁÊÍÁÌ ÄÌÊÁ ÊÁËÌÁÎ ÖÚÖ ØÓÖØ ÔÖÓÐÑ ÊÖÒØ ØÒØ ÓÒºÖºÒº ÁÖÒ ÅÙÒØÒ٠˺к Öº Òº ÖÐ ÙÔÖÒ ØÙÖ ¾¼¼¼ ÙÙÖ Ø ¾ ÈÖØ ÄÙÖÖ ÖÙØ ÐØÖ ÖÞ ØÚ
ÆÁÄ º ÁÇÆ ÍÒÚÖ ØØ ÈÓÐØÒ ÙÙÖ Ø ÁÊÍÁÌ ÄÌÊÁ ÊÁËÌÁÎ ÖÚÖ ØÓÖØ ÔÖÓÐÑ ØÙÖ ¾¼¼¼ ÆÁÄ º ÁÇÆ ÁÊÍÁÌ ÄÌÊÁ ÊÁËÌÁÎ ÖÚÖ ØÓÖØ ÔÖÓÐÑ ÊÖÒØ ØÒØ ÓÒºÖºÒº ÁÖÒ ÅÙÒØÒ٠˺к Öº Òº ÖÐ ÙÔÖÒ ØÙÖ ¾¼¼¼ ÙÙÖ Ø ¾ ÈÖØ ÄÙÖÖ ÖÙØ ÐØÖ ÖÞ ØÚ
Σανπρώτοπαράδειγμαχρήσ εωςτης ÉÈ ÒØ Öπαρουσ ιάζεταιέναπαράδειγμασ χεδιασ μούκύκλωνμέσ ασ εένακεντρικόπαράθυροº
 ÔØ Ö ΓΡΑΦΙΚΑ ΚΑΙ ΠΟΛΥΜΕΣΑ Ηβιβλιοθήκη ÉÌμπορείναχρησ ιμοποιηθείκαιγιατηνδημιουργίαπρογραμμάτων μεαπλάγραφικά γραμμές κείμενο κύκλουςκτλµόπωςεπίσ ηςγιατηνδημιουργία γραφημάτων από δεδομέναº º½ Àκατηγορία
ÔØ Ö ΓΡΑΦΙΚΑ ΚΑΙ ΠΟΛΥΜΕΣΑ Ηβιβλιοθήκη ÉÌμπορείναχρησ ιμοποιηθείκαιγιατηνδημιουργίαπρογραμμάτων μεαπλάγραφικά γραμμές κείμενο κύκλουςκτλµόπωςεπίσ ηςγιατηνδημιουργία γραφημάτων από δεδομέναº º½ Àκατηγορία
Εφαρμοσμένα Μαθηματικά
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Συναρτήσεις πολλών Μεταβλητών Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Συναρτήσεις πολλών Μεταβλητών Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το περιεχόμενο
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ14) Περίοδος ΕΡΓΑΣΙΑ 1 η. Τότε r r b c. και ( )
 Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.
7in x 10in Felder appm.tex V3 - May 7, :10 A.M. Page 1
 7in x 10in Felder appm.tex V3 - May 7, 2015 12:10 A.M. Page 1 APPENDIX M Ò ÛÖ ØÓ Ç¹ÆÙÑÖ ÈÖÓÐÑ ÔØÖ º Ò Ü Ó Ü º º º º ÐÐ Ó ØÑ ÛÓÖ º º º º Áº κ ÁÁº ÁÁÁº Áκ º Ü Ø = Ñ Ü Ø = Ü Ü º º º º º º º º º µ Ñ Ü Ø
7in x 10in Felder appm.tex V3 - May 7, 2015 12:10 A.M. Page 1 APPENDIX M Ò ÛÖ ØÓ Ç¹ÆÙÑÖ ÈÖÓÐÑ ÔØÖ º Ò Ü Ó Ü º º º º ÐÐ Ó ØÑ ÛÓÖ º º º º Áº κ ÁÁº ÁÁÁº Áκ º Ü Ø = Ñ Ü Ø = Ü Ü º º º º º º º º º µ Ñ Ü Ø
) ) u ε (t, x) = 0, t > 0, x R d, ½º½µ. R d. [ˆV επ d ( 2ξ)e i2ξ x/ε ˆV (2ξ)e i2ξ x/ε],
![) ) u ε (t, x) = 0, t > 0, x R d, ½º½µ. R d. [ˆV επ d ( 2ξ)e i2ξ x/ε ˆV (2ξ)e i2ξ x/ε], ) ) u ε (t, x) = 0, t > 0, x R d, ½º½µ. R d. [ˆV επ d ( 2ξ)e i2ξ x/ε ˆV (2ξ)e i2ξ x/ε],](/thumbs/89/97813899.jpg) Æ Ä ËÁË Ç ÌÀ ÇÍ Ä Ë ÌÌ ÊÁÆ Ë ÁÆÌÁÄÄ ÌÁÇÆ Ç Ï Î Ë ÁÆ Ê Æ ÇÅ Å Á ÍÁÄÄ ÍÅ Ä Æ ÇÄÁÎÁ Ê ÈÁÆ Í ØÖ Øº À Ö ÕÙ ÒÝ Û Ú ÔÖÓÔ Ø Ò Ò ÐÝ Ó ÐÐ ØÓÖÝ Ñ Ö Ó Ø Ò ÑÓ Ð Ý Ö Ø Ú ØÖ Ò Ö ÕÙ Ø ÓÒ Ø Ø Ö Ø ÔÖÓÔ Ø ÓÒ Ó Ø Ò Ö Ý Ò
Æ Ä ËÁË Ç ÌÀ ÇÍ Ä Ë ÌÌ ÊÁÆ Ë ÁÆÌÁÄÄ ÌÁÇÆ Ç Ï Î Ë ÁÆ Ê Æ ÇÅ Å Á ÍÁÄÄ ÍÅ Ä Æ ÇÄÁÎÁ Ê ÈÁÆ Í ØÖ Øº À Ö ÕÙ ÒÝ Û Ú ÔÖÓÔ Ø Ò Ò ÐÝ Ó ÐÐ ØÓÖÝ Ñ Ö Ó Ø Ò ÑÓ Ð Ý Ö Ø Ú ØÖ Ò Ö ÕÙ Ø ÓÒ Ø Ø Ö Ø ÔÖÓÔ Ø ÓÒ Ó Ø Ò Ö Ý Ò
t = 0 v x (y) τ yx = µ v x y
 ÙÑ Ù ÐÑÒÒØ Ë Ð ÒÐ Ñ Ö ÒÒÒÒ ÝÖÖ ÖÒÒ Ð ÚÒ Ñ ÎÖÐ Ð Ö Ë ÚÚ ÌÐÖÙÒ ½ ÂÒ ÌÑ ÙÑÙÒ ÓÒ ÒÐÖ ÚÚ Ö ÒÒÙÖ ÖÙÑ Ö ÝÖÖ ÚÚ Ñ ØÙÖ ÑÐÐ ØÚ ØÖÖ Ñ ÔÐØÒ Ñ ÝÖÓÖ ØÖÑ Ð A Ó ÐÒ Y ÖÙÑ Ö ÝÖÖ Ö ÙÔÔ ÝÖÖ ØÙ Ú ØÑÒÒ t = 0 Î t = 0 Ö ÒÖ ÔÐØÒ
ÙÑ Ù ÐÑÒÒØ Ë Ð ÒÐ Ñ Ö ÒÒÒÒ ÝÖÖ ÖÒÒ Ð ÚÒ Ñ ÎÖÐ Ð Ö Ë ÚÚ ÌÐÖÙÒ ½ ÂÒ ÌÑ ÙÑÙÒ ÓÒ ÒÐÖ ÚÚ Ö ÒÒÙÖ ÖÙÑ Ö ÝÖÖ ÚÚ Ñ ØÙÖ ÑÐÐ ØÚ ØÖÖ Ñ ÔÐØÒ Ñ ÝÖÓÖ ØÖÑ Ð A Ó ÐÒ Y ÖÙÑ Ö ÝÖÖ Ö ÙÔÔ ÝÖÖ ØÙ Ú ØÑÒÒ t = 0 Î t = 0 Ö ÒÖ ÔÐØÒ
arxiv: v3 [math.ap] 25 Nov 2009
![arxiv: v3 [math.ap] 25 Nov 2009 arxiv: v3 [math.ap] 25 Nov 2009](/thumbs/94/121663161.jpg) ÅÁ ÊǹÄÇ Ä Æ Ä ËÁË ÏÁÌÀ ÇÍÊÁ Ê Ä Ë Í ËÈ Ëº È ÊÌ Á ËÌ Î Æ ÈÁÄÁÈÇÎÁ Æ Æ Ì Ç ÆÇÎ Æ ÂÇ ÀÁÅ ÌÇ Ì arxiv:0804.1730v3 [math.ap] 25 Nov 2009 ØÖ Øº Ä Ø ω,ω 0 ÔÔÖÓÔÖ Ø Û Ø ÙÒØ ÓÒ Ò q [1, ]º Ï ÒØÖÓ Ù Ø Û Ú ¹ ÖÓÒØ
ÅÁ ÊǹÄÇ Ä Æ Ä ËÁË ÏÁÌÀ ÇÍÊÁ Ê Ä Ë Í ËÈ Ëº È ÊÌ Á ËÌ Î Æ ÈÁÄÁÈÇÎÁ Æ Æ Ì Ç ÆÇÎ Æ ÂÇ ÀÁÅ ÌÇ Ì arxiv:0804.1730v3 [math.ap] 25 Nov 2009 ØÖ Øº Ä Ø ω,ω 0 ÔÔÖÓÔÖ Ø Û Ø ÙÒØ ÓÒ Ò q [1, ]º Ï ÒØÖÓ Ù Ø Û Ú ¹ ÖÓÒØ
Ηυλοποίησ ητηςπαραπάνωκατηγορίαςβρίσ κεταισ τοναλγόριθμο º¾ºΗγραμμή
 ÔØ Ö ΕΙΣΟΔΟΣ ΔΕΔΟΜΕΝΩΝ º½ ÉÄ Ò Ø Ηβασ ικήκατηγορίατης ÉØγιαείσ οδοδεδομένωνείναιηéä Ò Øμετηνοποία οχρήσ τηςμπορείναεισ άγεισ εμιαγραμμήένααλφαριθμητικόºστοναλγόριθμο º½παρουσ ιάζεταιηδήλωσ ηγιαένακεντρικόπαράθυρομετοοποίοοχρήσ
ÔØ Ö ΕΙΣΟΔΟΣ ΔΕΔΟΜΕΝΩΝ º½ ÉÄ Ò Ø Ηβασ ικήκατηγορίατης ÉØγιαείσ οδοδεδομένωνείναιηéä Ò Øμετηνοποία οχρήσ τηςμπορείναεισ άγεισ εμιαγραμμήένααλφαριθμητικόºστοναλγόριθμο º½παρουσ ιάζεταιηδήλωσ ηγιαένακεντρικόπαράθυρομετοοποίοοχρήσ
Scientific knowledge is the common heritage of mankind. Abdus Salam
 È Æ ÈÁËÌÀÅÁÇ ÂÀÆÏÆ ÌÅÀÅ ÍËÁÃÀË ÈÌÍÉÁ ÃÀ Ê ËÁ Ô Ö ØÒÓÙ ÖÕ ÓÒ ÈÙÖ ÒÓ Ò ÇÖ Ø Ð ºÅº ¾¼¼¾¼¼¼¾ Ô Ð ÔÛÒ Ã Ø Ò Ó Ä Õ Ò ¾ Scientific knowledge is the common heritage of mankind. Abdus Salam È Ö Õ Ñ Ò ÈÖ ÐÓ Ó ½
È Æ ÈÁËÌÀÅÁÇ ÂÀÆÏÆ ÌÅÀÅ ÍËÁÃÀË ÈÌÍÉÁ ÃÀ Ê ËÁ Ô Ö ØÒÓÙ ÖÕ ÓÒ ÈÙÖ ÒÓ Ò ÇÖ Ø Ð ºÅº ¾¼¼¾¼¼¼¾ Ô Ð ÔÛÒ Ã Ø Ò Ó Ä Õ Ò ¾ Scientific knowledge is the common heritage of mankind. Abdus Salam È Ö Õ Ñ Ò ÈÖ ÐÓ Ó ½
ÔÖÓØ Ô ØÓ ESO (M. Sarazin and F. Roddier, A&A 227, 294-300, 1990) Õ Ò ¹
 Seeing-GR Å ØÖôÒØ Ø Ø Ö Õ Ø ØÑ Ö Ø Ò ÐÐ Å Ð Ñ ØÖ 1 Æ ØÓÖ ÒÒ 2 È ÖÞ ËØ Ð Ó 3 ÌÖ ÑÓÙ Ù Ð 4 Ã Ö Ñ Ò Ð 5 ÒØÛÒ ÒÒ 5 ÓÙÐ ÒÒ 5 ÃÓÙÖÓÙÑÔ ØÞ Ãô Ø 5 Ë Ö ÒÒ 5 1 Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg,
Seeing-GR Å ØÖôÒØ Ø Ø Ö Õ Ø ØÑ Ö Ø Ò ÐÐ Å Ð Ñ ØÖ 1 Æ ØÓÖ ÒÒ 2 È ÖÞ ËØ Ð Ó 3 ÌÖ ÑÓÙ Ù Ð 4 Ã Ö Ñ Ò Ð 5 ÒØÛÒ ÒÒ 5 ÓÙÐ ÒÒ 5 ÃÓÙÖÓÙÑÔ ØÞ Ãô Ø 5 Ë Ö ÒÒ 5 1 Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg,
¾
 ÅÇÄÊ ÁËÈÇÁÌÁÎÄÇÊ ÄÌÊÇÅÆÌÁ ÒÐ ÁÓÒ ¾ ÙÔÖÒ ¼ ÁÒØÖÓÙÖ ¼º½ ÇØÙÐ ÔÐÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼º¾ ÁÑÔÓÖØÒØ ÔÐÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼º
ÅÇÄÊ ÁËÈÇÁÌÁÎÄÇÊ ÄÌÊÇÅÆÌÁ ÒÐ ÁÓÒ ¾ ÙÔÖÒ ¼ ÁÒØÖÓÙÖ ¼º½ ÇØÙÐ ÔÐÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼º¾ ÁÑÔÓÖØÒØ ÔÐÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼º
