SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD
|
|
|
- Ιανός Δασκαλόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek, Marko Srdanović
2 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD TEMA: TORZIJA RAVNOG ŠTAPA Osijek, Marko Srdanović 1
3 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZNANSTVENO PODRUČJE: ZNANSTVENO POLJE: ZNANSTVENA GRANA: TEMA: PRISTUPNIK: NAZIV STUDIJA: TEHNIČKE ZNANOSTI TEMELJNE TEHNIČKE ZNANOSTI TEHNIČKA MEHANIKA TORZIJA RAVNOG ŠTAPA MARKO SRDANOVIĆ PREDDIPLOMSKI SVEUČILIŠNI STUDIJ Tekst zadatka U radu treba analizirati naprezanja i deformaciju za ravne štapove opterećene momentom torzije. Analizirati štapove kružnog poprečnog presjeka, prstenastog, neokuruglog te tankostjenog poprečnog presjeka. Za odabrane oblike poprečnih presjeka usporediti veličine naprezanja kao i pripadajuću deformaciju. U uvodu treba opisati problem, u teoretskom dijelu izvesti temeljne jednadžbe za rješavanje zadanog problema. Analizu provesti na primjerima različitih poprečnih presjeka. Rad treba sadržavati sažetak na izvornom jeziku. Rad treba predati u 3 primjerka (original + 2 kopije), spiralno uvezana u A4 formatu i cjelovitu elektroničku datoteku na CD-u. Osijek, 26. svibanj Mentor/ica: Predsjednik/ica Odbora za završne i diplomske ispite: Izv. prof. dr. sc. Mirjana Bošnjak-Klečina Izv. prof. dr. sc. Mirjana Bošnjak-Klečina 2
4 S A D R Ž A J 1. UVOD ŠTAPOVI OKRUGLOG PRESJEKA (OSOVINE) OPTEREĆENI TORZIJOM ŠTAPOVI NEOKRUGLOG PRESJEKA TANKOSTIJENI ŠTAPOVI OPTEREĆENI TORZIJOM TANKOSTIJENI ŠTAPOVI OTVORENOG PRESJEKA OPTEREĆENI TORZIJOM TANKOSTIJENI ŠTAPOVI ZATVORENOG PRESJEKA OPTEREĆENI TORZIJOM RIJEŠENI PRIMJERI ZAKLJUČAK LITERATURA..29 3
5 TORZIJA RAVNIH ŠTAPOVA Sažetak: U završnom radu se obrađuje problem uvijanja ravnih štapova. Analizirana su naprezanja i deformacije ravnih štapova opterećenih momentom torzije. Kod štapova kružnog poprečnog presjeka pri deformiranju poprečni presjeci ostaju ravni i okomiti na uzdužnu os štapa. Kod neokruglih i tankostijenih štapova ne vrijede bernoulijeve hipoteze. U radu su analizirani štapovi kružnog, prstenastog, neokruglog i tankostijenog poprečnog presjeka. Za odabrane oblike poprečnih presjeka napravljena je usporedba naprezanja i pripadajućih deformacija. 4
6 1. UVOD Pri opterećenju ravnog štapa momentima M i koji djeluju u ravnini okomito na os štapa u bilo kojem poprečnom presjeku štapa postoji samo moment torzije (moment uvijanja) M t, dok su sve ostale unutarnje sile jednake nuli. Ovakav slučaj opterećenja štapa nazivamo torzija ili uvijanje štapa. Da bismo odredili moment torzije u nekom presjeku štapa koristimo metodu prereza, tada nam od šest uvjeta ravnoteže ostaje samo uvjet: M x = 0 Ostali uvjeti ravnoteže su zadovoljeni te iz toga slijedi da je k M t = - M i i=i Moment torzije u nekom poprečnom presjeku štapa jednak je sumi svih momenata koji djeluju s jedne ili druge strane štapa. Slika 1.1 Ordinata M t predstavlja veličinu momenta torzije. Karakter deformacije štapova opterećenih torzijom zavisi od oblika poprečnog presjeka. Štapove dijelimo u 3 grupe: Štapovi kružnog poprečnog presjeka Slika 1.2 5
7 Štapovi neokruglog poprečnog presjeka Slika 1.3 Štapovi tankostijenog poprečnog presjeka Slika 1.4 Rezultati eksperimentalnih istraživanja pokazala su da se samo kod štapova kružnog presjeka primjenjuje se hipoteza ravnih poprečnih presjeka. Kod štapova neokruglog poprečnog presjeka ne vrijedi Bernoulijeva hipoteza te se problemi promatraju u teoriji elastičnosti. Kod štapova tankostijenog presjeka uvodimo niz pretpostavki što omogućuje rješavanje problema torzije metodama znanosti o otpornosti materijala. Iz tih razloga za svaku grupu štapova analizu deformacija i naprezanja radimo drugačije. 2. ŠTAPOVI OKRUGLOG PRESJEKA (OSOVINE) OPTEREĆENI TOR- ZIJOM Pri djelovanju momenta torzije na slobodnome kraju štapa neki presjek na udaljenosti x zaokrenut će se u odnosu na ukliješteni presjek za kut ϕ koji još nazivamo i kutom uvijanja ili kutom torzije. Što je veći moment torzije veći je i kut torzije ϕ te vrijedi ϕ = ϕ (M t ). Grafički to možemo prikazati dijagramom ϕ-m t, a posebno zanimljiv dio dijagrama je dio u elastičnom području, odnosno početni pravocrtni dio dijagrama koji predstavlja linearnu ovisnost između momenta torzije i kuta uvijanja. (slika 2.1) Slika 2.1 6
8 U presjeku štapa djeluje samo moment torzije te iz toga zaključujemo da u ravnini poprečnoga presjeka djeluju samo posmična naprezanja. Slika 2.2 Na mali element djeluje posmično naprezanje τ koje možemo rastaviti na dvije komponente u smjeru normale na τ n i u smjeru tangente na τ t. Prema zakonu o uzajamnosti posmičnih naprezanja komponenta τ n =τ n ' na plaštu štapa, a ona su jdenaka nuli jer na plaštu štapa ne djeluje uzdužno tangencijalno opterećenje. Prema tome vektor posmičnog naprezanja okomit je na polumjer kruga. Iz toga slijedi da su u bilo kojoj točki naprezanja τ upravljena okomito na odgovarajući polumjer odnosno da imaju smjer tangente na koncentrične kružnice. Slika 2.3 Iz uvjeta ravnoteže dobivamo da M t mora biti jednak zbroju momenata unutarnjih sila τda s obzirom na os ordinata te iz toga slijedi: M t= A Pretpostavke (slika 2.4) : Kod deformacije štapa poprečni presjeci ostaju ravni i okomiti na os štapa odnosno vrijedi hipteza ravnih poprečnih presjeka. 7
9 Poprečni presjeci se rotiraju oko osi štapa kao kruti diskovi odnosno oni se ne deformiraju u svojoj ravnini, a polumjeri u tim presjecima ostaju pravci i rotiraju se za isti kut odnosno u prijevodu vrijedi hipoteza krutosti presjeka Pri samoj deformaciji štapa razmak između poprečnih presjeka se ne mijenja te u smjeru osi štapa normalna naprezanja jednaka su nuli. Slika 2.4 Uslijed djelovanja momenta torzije desni presjek elementa štapa se zakrene u odnosu na lijevi za neki kut dφ a taj kut se naziva kut uvijanja.beskonačno mali pravokutnik ABCD prelazi u paralelogram A'B'CD. Prvobitni pravi kut ACD postaje oštri i mijenja se za veličinu γ te nastaje smicanje elementa AB u odnosu na CD te iz toga slijedi da iz trokuta OAA' dobivamo da je AA' = ρdφ Slika 2.5 Relativno smicanje dano je izrazom : S obzirom da je dφ kut uvijanja a dx duljina elementa štapa, odnos predstavlja kut uvijanja na jedinicu dužine štapa i naziva se relativni kut uvijanja a mjeri se u rad/m. Ako izraz (relativni kut uvijanja) zamjenimo s Θ tada dobivamo S obzirom da je riječ o čistome posmiku Hookeov zakon ima oblik: 8
10 Iz gornje jednadžbe vidimo da za ρ = 0 naprezanje τ = 0, a s povećanjem ρ naprezanje raste linearno. Najveće naprezanje je u točkama koje su najudaljenije od središta odnosno osi štapa što je vidljivo na slici ispod. Slika 2.6 Ako u uvjet ravnoteže umjesto τ uvrstimo izraz GΘρ u kojemu modul posmika G i relativni kut torzije Θ ne ovise o površini poprečnoga presjeka tada dobivamo izraz: Integral da je polarni moment tromosti poprečnog presjeka Iz izraza M t slijedi da je : Uvrstimo li Θ u τtada ćemo dobiti konačan izraz za raspodjelu naprezanja u poprečnome presjeku štapa: Najveće naprezanje se pojavljuje na rubnim vlaknima poprečnog presjeka te je dano izrazom: Iz čega slijedi da je : 9
11 Kada u izraz Θ= uvrstimo izraz za relativni kut uvijanja koji ovisi o kutu uvijanja na jedinicu dužine štapa dobit ćemo kut uvijanja elementa štapa duljine dx: dφ=θ dx= Kut zaokreta krajnjih presjeka: φ= Ako je moment torzije M t (x) konstantan kao i polarni moment tromosti I p (x), duljine l i od homogenog i izotropnog materijala tada kut uvijanja glasi: φ= [rad] Nazivnik G I p naziva se torzijska krutost presjeka štapa a cjelokupni izraz za kut uvijanja daje vezu između momenta torzije i samog kuta uvijanja te je osnova Hookeovog zakona za torziju. - Polarni moment tromosti I p = Slika 2.7 p 10
12 Prstenasti kružni presjek Slika 2.8 Ako izraz γ p =ρ uvrstimo u Hookeov zakon tada slijedi: τ p =G γ p =G ρ θ ako bi pak u ovaj izraz uvrstili vrijednost za kut θ u kojemu kut θ ovisi o momentu torzije i torzijskoj krutosti tada slijedi: τ p = G ρ odakle je τ= t p Uvedemo li izraz za polarni moment otpora W p =I p /R tada dobivamo slijedeći oblik: τ t = p Za prstenasti kružni presjek polarni moment otpora dan je izrazom: W p =
13 3. ŠTAPOVI NEOKRUGLOG PRESJEKA Za početak ćemo razmotriti deformaciju štapa neokruglog presjeka opterećenog na uvijanje iz čega ćemo moći zaključiti gdje su deformacije najveće te kakvo je naprezanje u elementima neokruglog presjeka. Prvo promotrimo štap pravokutnog presjeka koji nije opterećen Sama mreža je pravilna te je vidljivo da nema nikakvih deformacija. Slika 3.1 Ukoliko taj štap opteretimo momentum torzije M t mreža na stranama štapa će se zakrenuti u smjeru djelovanja momenta torzije, poprečne linije štapa se pri uvijanju iskrivljuju a najveće deformacije nastaju u sredini strana poprečnoga presjeka. U uglovima deformacija nema. Iz toga možemo zaključiti kako nastaje deplanacija presjeka odnosno ne vrijedi hipoteza ravnih poprečnih presjeka i to vrijedi za sve štapove neokruglog poprečnog presjeka. Proračun naprezanja I deformacija kod štapova neokruglog presjeka kako smo već naveli u uvodu malo je složeniji te se provodi metodama teorije elastičnosti. Za slučaj sa slike 3.2 izbočavanje poprečnih presjeka nije spriječeno te takav slučaj torzije nazivamo čistom ili slobodnom torzijom. Svi poprečni presjeci jednako se deformiraju te se udaljenost među njima ne mijenja, iz čega možemo zaključiti kako su normalna naprezanja jednaka nuli. Uzimajući u obzir diferencijalne jednadžbe ravnoteže, jednadžbe neprekinutosti deformacija, fizikalnih jednadžbi I rubnih uvjeta, metodama teorije elastičnosti dolazi se do Poissonove diferencijalne jednadžbe problema torzije: = -2 G Θ pri čemu je G modul posmika, Φ relativni kut torzije te Φ = Φ(x,y) funkcija naprezanja koja ima konstantnu vrijednost u točkama konture, odnosno: = 0 2 Slika
14 Slika 3.3 Uvjet na konturi koji je ograničen jednom zatvorenom konturom glasi Φ = 0 Uvjet na čelnim pobočkama štapa glasi: M t =2 Φ(x,y) dxdy A Parcijalne derivacije funkcije Φ(x,y) po koordinatama daju komponente posmičnog naprezanja τ zx i τ zy. Veličina ukupnog posmičnog naprezanja jednaka je gradijentu funkcije Φ(x,y): τ = τ zx = τ zy = - zx 2 zy 2 Vidljivo je da se problem torzije svodi na određivanje funkcije naprezanja Φ(x,y) koja mora zadovoljavati Poissonovu diferencijalnu jednadžbu problema torzije u svim točkama poprečnoga presjeka, kao i jednadžbu za uvjete na konturi (Φ = 0) te jednažbu za uvjete na čelnim pobočkama štapa. Slika
15 Dijagram posmičnih naprezanja za štap pravokutnoga presjeka gdje je b<h, iz dijagrama je vidljivo da su naprezanja u uglovima jednaka nuli, dok je najveće posmično naprezanje u sredini stranice h, odnosno veće stranice u ovome slučaju točka A. τ A =τ max = t 2 τ B =η τ max Relativni kut torzije glasi: Θ = t 3 Iz relativnog kuta torzije možemo dobiti kut zaokreta s obzirom na duljinu štapa l te on glasi: t φ= l 3 Slika 3.5 Kako je vidljivo u tablici koeficijenti α,β, η ovise o odnosu visine i širine poprečnog presjeka. Slika 3.6 Na gornjoj slici nam je prikazan dijagram posmičnih naprezanja za štap eliptičnoga presjeka, te je vidljivo da se najveće posmično naprezanje pojavljuje u točkama A na krajevima male osi eliptičnoga presjeka. Naprezanje u točki A dano je izrazom: τ A = τ max t 2 14
16 Naprezanje u točki B dano je izrazom: τ B = t 2 a,b - poluosi elipse Kut zaokreta krajnjih presjeka štapa eliptičnoga presjeka dan je izrazom: φ= Kut zaokreta krajnjih presjeka štapa trokutastog istostraničnog presjeka neke duljine l dan je izrazom: Izraze za naprezanja I deformacije koje smo naveli možemo zapisati u općem obliku kao: τ max = φ= M t =G I t Θ Prikaz torzijskih momenata inercije i otpornih torzijskih momenata ovisno o obliku poprečnog presjeka Slika
17 4. TANKOSTIJENI ŠTAPOVI OPTEREĆENI TORZIJOM Štapovi odnosno tankostijeni gredni nosači kod kojih je jedna dimenzija poprečnog presjeka debljine stijenke manja od ostalih. Kao orijentacijsku granicu koristimo vrijednost da je t max 0,1b gdje je t max najveća debljina stijenke poprečnog presjeka dok je b neka druga dimenzija poprečnog presjeka. Tankostijeni nosači s obzirom na oblik poprečnog presjeka dijele se na : otvorene, zatvorene i otvoreno-zatvorene. Slika 4.1 Veličina i raspodjela tangencijalnih naprezanja uzrokovana čistom torzijom znatno se razlikuje kod tankostijenih nosača otvorenih i zatvorenih poprečnih presjeka. Dolazi do pojave smičnog toka po poprečnome presjeku. Slika 4.2 Kod otvorenih presjeka vanjskom momentu uvijanja ravnotežu drži moment unutrašnjih sila koje djeluju na malom kraku (slika a) Slika 4.3 Kod zatvorenih presjeka krak unutrašnjih sila djelovanja znatno veći (slika b) te stoga možemo zaključiti da zatvoreni presjeci imaju znatno veću čvrstoću i krutost od otvorenih presjeka. 16
18 4.1 TANKOSTIJENI ŠTAPOVI OTVORENOG POPREČNOG PRESJEKA Kao i prije promatramo slučaj slobodne torzije, koristeći membransku analogiju najlakše ćemo odrediti karakter naprezanja u poprečnome presjeku tankostijenog štapa. Slika 4.4 Zamislimo izrezan otvor u ravnoj ploči oblika poprečnog presjeka i na njemu napetu membranu opterećenu jednolikim pritiskom, očito je da se oblik membrane kao I naprezanje u štapu neće znatno izmjeniti ako se profile presjeka razvije. Iz toga slijedi da je naprezanje u promatranome otvorenom profilu približno jednako kao I u uskom pravokutnom presjeku, prema tome naprezanja I deformacije u otvorenom presjeku mogu se približno odrediti izrazima: Gore navedeni izrazi vrijede općenito za sve otvorene profile koji se mogu razviti u pravokutnik. Ukoliko je tankostijeni presjek sastavljen od dijelova različite debljine presjek podijelimo na pojedine dijelove konstantne debljine. Slika 4.5 Na osnovu izraza τ max i Θ za svaki pravokutni dio presjeka dobivamo : 17
19 gdje je b i debljina a s i duljina pravokutnika, s time da vrijedi b i << s i. moment torzije M t u presjeku možemo prikazati kao zbroj memenata M ti Ukoliko u gore navedeni izraz uvrstimo izraz za M ti i uzmemo u obzir da je relativni kut uvijanja Θ jednak za sve dijelove presjeka tada dobivamo: gdje je : Koristeći gore navedene formule te uvrštavanjem jedne u drugu dobivamo izraz za maksimalno naprezanje u i-tom elementu : Slijedi da je najveće naprezanje u presjeku nastaje u sredini stranica elementa koji ima najveću debljinu, odnosno maksimalno naprezanje dano je izrazom: Torzijski moment otpora poprečnog presjeka Membranskom analogijom može se lako pokazati da na unutarnjim uglovima izlomljenog profila dolazi do pojave koncentracije naprezanja jer je kut nagiba membrane α u točki A veći nego u ostlaim točkama unutarnje konture. Maksimalno naprezanje u unutarnjim uglovima ne možemo odrediti nego ih možemo samo analizirati detaljnom primjenom membranske analogije. Maksimalno posmično naprezanje dano izrazom τ max odnosi se na dijelove presjeka koji su dovoljno udaljeni od unutarnjih uglova. 18
20 Kako bismo smanjili koncentraciju naprezanja na mjestu unutarnjeg ugla zaobljuje se kontura presjeka, odnosno što je polumjer zaobljenja veći, koncentracija naprezanja biti će manja. Slika 4.6 Primjeri Torzijski moment tromosti i torzijski moment otpora za: Kružni tankostijeni otvoreni poprečni presjek Kutijasti otvoreni poprečni presjek Slika 4.7 Slika
21 4.2 TANKOSTIJENI ŠTAPOVI ZATVORENOG PRESJEKA OPTEREĆENI TORZIJOM Promatramo slučaj slobodne torzije cilindričnog štapa s tankim stijenkama zatvorenog profila, gdje se debljina stijenke t postupno mijenja uzduž konture presjeka tako da se može zanemariti koncentracija naprezanja. Središnjom linijom presjeka nazivamo skup točaka jednako udaljenih od vanjske i unutarnje konture poprečnoga presjeka. Slika 4.9 Prilikom deformacije štapa poprečni presjeci mogu se slobodno vitoperiti bez iskrivljavanja u svojoj ravnini, zbog čega nam oblik poprečnoga presjeka ostaje nepromijenjen. U krajnjim točkama normale n-n na središnju liniju presjeka vector naprezanja ima smjer tangente na vanjsku i unutarnju konturu presjeka, ali zbog male debljine presjeka elementa ti vektori su gotovo paralelni te zbog toga uzimamo da su nam vektori naprezanja τ paralelni s tangentom na središnju liniju presjeka. Ako s dva poprečna i dva uzdužna presjeka okomita na konturu iz štapa izrežemo element duljine dx te razmak između točaka odaberemo proizvoljno s time da je debljina u točki 1 t 1 a u točki 2 t 2. Ako vrijedi zakon o uzajamnosti poprečnih naprezanja u uzdužnim presjecima djeluju posmična naprezanja koja su jednaka, τ 1 i τ 2. Jednadžba ravnoteže u smjeru osi štapa daje: τ 1 t 1 dx τ 2 t 2 dx=0 τ 1 t 1= τ 2 t 2 budući da su točke 1 i 2 odabrane proizvoljno, to je produkt τ t=const. i naziva se tok posmičnih naprezanja. Obzirom da nam je tok posmičnih naprezanja τ t=const. iz uvjeta ravnoteže oko osi x koja je usporedna s osi štapa dobivamo: Krivolinijski integral uzet je duž zatovrene središnje linije presjeka duljine s. 20
22 Slika 4.10 prilikom integracije izraza za M t po središnjoj liniji presjeka produkt τ t=const te ga možemo izvući ispred integrala: Produkt ρ ds dvostruka je površina trokuta s vrhom u točki O, osnovice ds i visine ρ, a integral jednak je dvostrukoj površini obuhvaćenoj središnjom linijom presjeka, te ukoliko označimo tu površinu A 0 dobivamo: prva Bredtova for- Te naposlijetku dobivamo izraz za posmično naprezanje koje se naziva i mula : Pri konstantnoj debljini presjeka t, naprezanja τ u svim točkama presjeka jednaka su po veličini. U presjeku promenjive debljine najveće naprezanje će biti na mjestu gdje je debljina presjek najmanja: gdje je W torzijski moment otpora poprečnog presjeka. W t = 2 A 0 t min Slika
23 Pri konstantnoj debljini t presjeka, naprezanja τ u svim točkama presjeka jednaka su po veličini. U presjeku promjenjljive debljine najveće naprezanje τ bit će na mjestu gdje je debljina stijenke presjeka najmanja te je dano izrazom: τ max = gdje je W t =2 A 0 t min torzijski moment otpora poprečnoga presjeka. Zamislimo da smo s dva poprečna presjeka izdvojili element štapa duljine dx. Momenti torzije u tim presjecima pojavljuju se kao vanjsko opterećenje za izdvojeni dio štapa. Na kutu torzije dφ promatranog štapa moment torzije obavlja rad: dw= Specifična je potencijalna energija pri čistome posmiku dana izrazom u=t 2 /2 G Potencijalna energija akumulirana u elementarnom volumenu s površinom osnovice t ds i visine dx jednaka je: u t dsdx Energiju akumuliranu u čitavome promatranom dijelu štapa dobit ćemo integriranjem gornjeg izraza po dužini zatvorene središnje linije presjeka: Pri integriranju po središnjoj liniji presjeka produkt τ t, te G i dx konstantne su veličine pa se mogu izvući ispred znaka integrala: Uzimajući u obzir prvu Bredtovu formulu dobivamo: Ukoliko u izraz gore unesemo izraz za kut torzije promatranog štapa koji obavlja rad: Tada dobivamo relativni kut torzije : 22
24 Ovaj izraz poznat je kao druga Bredtova formula. Ako uvedemo oznaku: koja se pojavljuje kao geometrijska karakteristika tankostijenog presjeka pri torziji I naziva se torzijski moment krutosti onda dobivamo konačni oblik za relativni kut torzije Θ : 5. RIJEŠENI PRIMJERI Treba odrediti kut zaokreta i maksimalno posmično naprezanje nosača opterećenog momentom torzije M t = 5 knm. Poznat je modul elastičnosti E = MPa i Poissonov koeficijent υ=0,3. Tražene vrijednosti odrediti za različite poprečne presjeke te usporediti rezultate. (svi promjeri i polumjeri dani su u milimetrima) E MPa υ 0,3 G= = 0, MPa a) Kružni poprečni presjeci 1) Puni kružni poprečni presjek d=70 mm M t =5 knm G= MPa τ, Θ=? Ip= = = mm
25 3 70 Wp= = 3 = mm τ W p. = 74.3 MPa Θ = = rad/m p,. 2) Prstenasti poprečni presjek D=70 mm d=30 mm M t = 5 knm G= MPa τ, Θ=? D I p = = mm W p = = = mm 3 D 70 τ = = = MPa W p. Θ p.. = rad/m 24
26 3) Tankostijeni zatvoreni poprečni presjek D=70 mm d=50 mm R=35 mm r=25 mm R sr = 30 mm M t = 5 knm G=0.769*10 5 MPa R r Rsr= = = 30 mm 2 2 τ, Θ=? A0= Rsr 2 π 30 2 π 2827,43 mm 2 It 2 Rsr 3 π t π mm 4 W t 2 A t 2 Rsr 2 π t π mm 3 τ = = MPa 2 A 0 t. Θ = = rad/m.. 4) Tankostijeni otvoreni poprečni presjek D=70 mm d=50 mm M t = 5 knm G=0.769*10 5 MPa τ, Θ=? Dsr=60 mm s= Dsr π 60 π 88.5 mm It /3 t 3 /3 Ds π t π 10 3 = mm 4 25
27 τ= t 0 = MPa t. Wt 2/3 Rst π t π 0 2 = mm 3 Θ.. = rad/m b) Pravokutni poprečni presjeci 1) Pravokutni puni presjek h=50 mm b=50 mm M t = 5 knm G=0.769*10 5 MPa τ, Θ=? h/b=1 α β 0. 4 t τ = = MPa α 2. t Θ = rad/m β 4.. 2) Pravokutni tankostijeni zatvoreni presjek h=46 mm b=46 mm M t = 5 knm G=0.769*10 5 MPa τ, Θ=? 26
28 A0=46 2 =2116 mm h It= = = mm 4 h W 2 t t= mm 3 Θ = rad/m. τ = = MPa 2 0 t min 3) Pravokutni tankostijeni otvoreni presjek h=46 mm b=46 mm M t = 5 knm G=0.769*10 5 MPa τ, Θ=? It= (46+46)= mm τ t 4= MPa Θ= = = rad/m.. 27
29 6. ZAKLJUČAK U riješenim primjerima su izraćunate vrijednosti posmičnih naprezanja i deformacija određenih poprečnih presjeka za opterećenje ravnih štapova momentom torzije. a) Riješavani su : a) Kružni poprečni presjeci: Puni presjek Prstenasti presjek Tankostijeni zatvoreni poprečni presjek Tankostijeni otvoreni poprečni presjek Vanjski promjer svih poprečnih presjeka je isti. b) Pravokutni poprečni presjeci: Puni presjek Tankostijeni zatvoreni poprečni presjek Tankostijeni otvoreni poprečni presjek Vanjska širina i visina svih pravokutnih poprečnih presjeka je ista. Tablična usporedba rezultata izračunatih vrijednosti naprezanja i deformacija: 28
30 Razmotrimo prvo kružne poprečne presjeke: Kružni presjeci: Puni τ=74.3 MPa Θ= rad/m Prstenasti τ=76.92 MPa Θ= rad/m Tankostijeni zatvoreni τ=89.29 MPa Θ= rad/m Tankostijeni otvoreni τ= MPa Θ= rad/m Kod kružnih presjeka najmanje posmično naprezanje nam daje puni presjek τ=74.3 MPa, zatim prstenasti τ=76.92 MPa, zatim tankostijeni zatvoreni poprečni presjek τ=89.29 MPa te naposlijetku tankostijeni otvoreni presjek τ= MPa. Kada gledamo relativni kut zaokreta najmanji kut zaokreta daje nam puni presjek Θ= rad/m, zatim prstenasti presjek Θ= rad/m, tankostijeni otvoreni Θ= rad/m te najveći kut zaokreta daje tankostijeni zatvoreni presjek Θ= rad/m. Uzimajući u obzir navedene rezultate najbolji presjek koji možemo iskoristiti je puni presjek. Pravokutni presjeci: Puni τ= MPa Θ= rad/m Tankostijeni zatvoreni τ= MPa Θ= rad/m Tankostijeni otvoreni τ= MPa Θ= rad/m Iz rezultata je vidljivo da nam je za jednak iznos opterećenja posmično naprezanje najmanje kod punog presjeka te iznosi τ= MPa, zatim kod tankostijenog zatvorenog presjeka gdje posmično naprezanje iznosi τ= MPa te na posljednjem mjestu tankostijeni otvoreni presjek koji daje posmično naprezanje τ= MPa. Uzimajući u obzir kut zaokreta poredak je jednak. Odnosno puni presjek Θ= rad/m, zatim tankostijeni zatvoreni Θ= rad/m te najlošiji presjek tankostijeni otvoreni Θ= rad/m. Uzimajući u obzir navedene rezultate najbolji presjek koji možemo iskoristiti je puni presjek. Ako u obzir uzimamo iskorištenost i količinu potrebnog materijala tada možemo reći da je u štapu šupljeg poprečnog presjeka materijal bolje iskorišten odnosno za jednake momente otpora prstenastog i punog presjeka štap prstenastog presjeka može izdržati jednako opterećenje s manjim utroškom materijala. Najpovoljniji su poprečni presjeci cijevnog oblika. 7. LITERATURA 1. Šimić, V.:Otpornost materijala I, Školska knjga, Zagreb, Alfirević, I.:Nauka o čvrstoći I, Tehnička knjiga, Zagreb, Brnić, J.; Turkalj, G.:Nauka o čvrstoći I, Tehnički fakultet Sveučilišta u Rijeci,
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD Osijek, 15. rujan 2017. Ivan Kovačević SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD Osijek, 15. rujan 2017. Ivan Kovačević SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET ZAVRŠNI RAD
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA
 ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
ČVRSTOĆA 13. GEOMETRIJSKE KARAKTERISTIKE RAVNIH PRESJEKA ŠTAPA STATIČKI MOMENTI I MOMENTI INERCIJE RAVNIH PLOHA Kao što pri aksijalnom opterećenju štapa apsolutna vrijednost naprezanja zavisi, između ostalog,
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek, 15. rujan 2015. Marija Vidović SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJE
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek, 15. rujan 2015. Marija Vidović SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJE
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Geometrijske karakteristike poprenih presjeka nosaa. 9. dio
 Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Geometrijske karakteristike poprenih presjeka nosaa 9. dio 1 Sile presjeka (unutarnje sile): Udužna sila N Poprena sila T Moment uvijanja M t Moment savijanja M Napreanja 1. Normalno napreanje σ. Posmino
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
6 Primjena trigonometrije u planimetriji
 6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
6 Primjena trigonometrije u planimetriji 6.1 Trgonometrijske funkcije Funkcija sinus (f(x) = sin x; f : R [ 1, 1]); sin( x) = sin x; sin x = sin(x + kπ), k Z. 0.5 1-6 -4 - -0.5 4 6-1 Slika 3. Graf funkcije
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
 Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek 25. rujan 2015. Siniša Ivković SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek 25. rujan 2015. Siniša Ivković SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
ISPITNI ZADACI FORMULE. A, B i C koeficijenti (barem jedan A ili B različiti od nule)
 FORMULE Implicitni oblik jednadžbe pravca A, B i C koeficijenti (barem jedan A ili B različiti od nule) Eksplicitni oblik jednadžbe pravca ili Pravci paralelni s koordinatnim osima - Kada je u općoj jednadžbi
FORMULE Implicitni oblik jednadžbe pravca A, B i C koeficijenti (barem jedan A ili B različiti od nule) Eksplicitni oblik jednadžbe pravca ili Pravci paralelni s koordinatnim osima - Kada je u općoj jednadžbi
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Prof. dr. sc. Vedrana Kozulić TEHNIČKA MEHANIKA 2 Predavanja Akad. god. 2008/09
 Prof. dr. sc. Vedrana Koulić EHNČK EHNK Predavanja kad. god. 008/09 OPORNOS ERJL Otpornost materijala je grana tehničke mehanike koja proučava probleme čvrstoće, krutosti i stabilnosti pojedinih dijelova
Prof. dr. sc. Vedrana Koulić EHNČK EHNK Predavanja kad. god. 008/09 OPORNOS ERJL Otpornost materijala je grana tehničke mehanike koja proučava probleme čvrstoće, krutosti i stabilnosti pojedinih dijelova
Savijanje nosaa. Savijanje ravnog štapa prizmatinog poprenog presjeka. a)isto savijanje. b) Savijanje silama. b) Savijanje silama.
 Štap optereen na savijanje naivamo nosa ili grea. Savijanje nosaa a) Napreanja ( i τ) b) Deformacije progib (w) Os štapa se ko savijanja akrivljuje to je elastina ili progibna linija nosaa. Savijanje ravnog
Štap optereen na savijanje naivamo nosa ili grea. Savijanje nosaa a) Napreanja ( i τ) b) Deformacije progib (w) Os štapa se ko savijanja akrivljuje to je elastina ili progibna linija nosaa. Savijanje ravnog
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek, 15. rujna 2015. Dragana Zekić SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD Osijek, 15. rujna 2015. Dragana Zekić SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK
2.7 Primjene odredenih integrala
 . INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
. INTEGRAL 77.7 Primjene odredenih integrala.7.1 Računanje površina Pořsina lika omedenog pravcima x = a i x = b te krivuljama y = f(x) i y = g(x) je b P = f(x) g(x) dx. a Zadatak.61 Odredite površinu
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
PROSTA GREDA (PROSTO OSLONJENA GREDA)
 ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ROS GRED (ROSO OSONJEN GRED) oprečna sila i moment savijanja u gredi y a b c d e a) Zadana greda s opterećenjem l b) Sile opterećenja na gredu c) Određivanje sila presjeka grede u presjeku a) Unutrašnje
ISPIT GRUPA A - RJEŠENJA
 Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
Pismeni ispit iz OTPORNOSTI MATERIJALA I - grupa A 1. Kruta poluga AB oslonjena je na dva čelična štapa u A i B i opterećena trouglastim opterećenjem, kao na slici desno. Ako su oba štapa iste dužine L,
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami
 BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
BETONSKE KONSTRUKCIJE 3 M 1/r dijagrami Izv. prof. dr.. Tomilav Kišiček dipl. ing. građ. 0.10.014. Betonke kontrukije III 1 NBK1.147 Slika 5.4 Proračunki dijagrami betona razreda od C1/15 do C90/105, lijevo:
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
MATEMATIKA 1 8. domaća zadaća: RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Neka je a 3 x 3 + a 2 x 2 + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka.
 Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
Neka je a 3 x 3 + a x + a 1 x + a 0 = 0 algebarska jednadžba trećeg stupnja. Rješavanje ove jednadžbe sastoji se od nekoliko koraka. 1 Normiranje jednadžbe. Jednadžbu podijelimo s a 3 i dobivamo x 3 +
Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu
 Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
Osječki matematički list 000), 5 9 5 Više dokaza jedne poznate trigonometrijske nejednakosti u trokutu Šefket Arslanagić Alija Muminagić Sažetak. U radu se navodi nekoliko različitih dokaza jedne poznate
BETONSKE KONSTRUKCIJE 2
 BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona.
 Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
l = l = 0, 2 m; l = 0,1 m; d = d = 10 cm; S = S = S = S = 5 cm Slika1.
 . U zračnom rasporu d magnetnog kruga prema slici akumulirana je energija od,8 mj. Odrediti: a. Struju I; b. Magnetnu energiju akumuliranu u zračnom rasporu d ; Poznato je: l = l =, m; l =, m; d = d =
. U zračnom rasporu d magnetnog kruga prema slici akumulirana je energija od,8 mj. Odrediti: a. Struju I; b. Magnetnu energiju akumuliranu u zračnom rasporu d ; Poznato je: l = l =, m; l =, m; d = d =
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
SVEUČILIŠTE JOSIPA JURAJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKULTET OSIJEK ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURAJA STROSSMAYERA U OSIJEKU ZAVRŠNI RAD Osijek, 15.09.2015. SVEUČILIŠTE JOSIPA JURAJA STROSSMAYERA U OSIJEKU ZAVRŠNI RAD TEMA: USPOREDBA REZULTATA PRORAČUNA STATIČKI NEODREĐENIH SUSTAVA
SVEUČILIŠTE JOSIPA JURAJA STROSSMAYERA U OSIJEKU ZAVRŠNI RAD Osijek, 15.09.2015. SVEUČILIŠTE JOSIPA JURAJA STROSSMAYERA U OSIJEKU ZAVRŠNI RAD TEMA: USPOREDBA REZULTATA PRORAČUNA STATIČKI NEODREĐENIH SUSTAVA
RADIJVEKTORI. ALGEBARSKE OPERACIJE S RADIJVEKTORIMA. LINEARNA (NE)ZAVISNOST SKUPA RADIJVEKTORA.
 Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
Napomena: U svim zadatcima O označava ishodište pravokutnoga koordinatnoga sustava u ravnini/prostoru (tj. točke (0,0) ili (0, 0, 0), ovisno o zadatku), označava skalarni umnožak, a vektorski umnožak.
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKKULTET ZAVRŠNI RAD
 SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKKULTET ZAVRŠNI RAD SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKKULTET ZAVRŠNI RAD TEMA: IZRAČUN UNUTRAŠNJIH SILA I PLANOVA
SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKKULTET ZAVRŠNI RAD SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU GRAĐEVINSKI FAKKULTET ZAVRŠNI RAD TEMA: IZRAČUN UNUTRAŠNJIH SILA I PLANOVA
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
VAŽNO. Posmino naprezanje τ
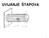 UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
UVIJANJE ŠTAPOVA 1 VAŽNO Posmino naprezanje τ τ ρ I o 2 aksimalno posmino naprezanja τ za: ρ r d 2 τ maks W 0 3 Polarni momen romosi: I o 4 d π 32 [ ] 4 cm Polarni momen opora: W o 3 d π 16 cm [ ] 3 4
, 81, 5?J,. 1o~",mlt. [ BO'?o~ ~Iel7L1 povr.sil?lj pt"en:nt7 cf~ ~ <;). So. r~ ~ I~ + 2 JA = (;82,67'11:/'+2-[ 4'33.10'+ 7M.
 J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
J r_jl v. el7l1 povr.sl?lj pt"en:nt7 cf \ L.sj,,;, ocredz' 3 Q),sof'stvene f1?(j'me")7e?j1erc!je b) po{o!.aj 'i1m/' ce/y11ra.[,p! (j'j,a 1lerc!/e
( ) ( ) Zadatak 001 (Ines, hotelijerska škola) Ako je tg x = 4, izračunaj
 Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Zadaak (Ines, hoelijerska škola) Ako je g, izračunaj + 5 + Rješenje Korisimo osnovnu rigonomerijsku relaciju: + Znači svaki broj n možemo zapisai n n n ( + ) + + + + 5 + 5 5 + + + + + 7 + Zadano je g Tangens
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
2. Ako je funkcija f(x) parna onda se Fourierov red funkcije f(x) reducira na Fourierov kosinusni red. f(x) cos
 . KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
. KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
20 mm. 70 mm i 1 C=C 1. i mm
 MMENT NERJE ZDTK. Za površinu prema datoj slici odrediti: a centralne težišne momente inercije, b položaj glavnih, centralnih osa inercije, c glavne, centralne momente inercije, d glavne, centralne poluprečnike
MMENT NERJE ZDTK. Za površinu prema datoj slici odrediti: a centralne težišne momente inercije, b položaj glavnih, centralnih osa inercije, c glavne, centralne momente inercije, d glavne, centralne poluprečnike
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
Dinamika tijela. a g A mg 1 3cos L 1 3cos 1
 Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
Linearna algebra I, zimski semestar 2007/2008
 Linearna algebra I, zimski semestar 2007/2008 Predavanja: Nenad Bakić, Vježbe: Luka Grubišić i Maja Starčević 22. listopada 2007. 1 Prostor radijvektora i sustavi linearni jednadžbi Neka je E 3 trodimenzionalni
Linearna algebra I, zimski semestar 2007/2008 Predavanja: Nenad Bakić, Vježbe: Luka Grubišić i Maja Starčević 22. listopada 2007. 1 Prostor radijvektora i sustavi linearni jednadžbi Neka je E 3 trodimenzionalni
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
Algebra Vektora. pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske
 Algebra Vektora 1 Algebra vektora 1.1 Definicija vektora pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske veličine za opis skalarne veličine trebamo zadati samo njezin iznos (npr.
Algebra Vektora 1 Algebra vektora 1.1 Definicija vektora pri rješavanju fizikalnih problema najčešće susrećemo skalarne i vektorske veličine za opis skalarne veličine trebamo zadati samo njezin iznos (npr.
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Sume kvadrata. mn = (ax + by) 2 + (ay bx) 2.
 Sume kvadrata Koji se prirodni brojevi mogu prikazati kao zbroj kvadrata dva cijela broja? Propozicija 1. Ako su brojevi m i n sume dva kvadrata, onda je i njihov produkt m n takoder suma dva kvadrata.
Sume kvadrata Koji se prirodni brojevi mogu prikazati kao zbroj kvadrata dva cijela broja? Propozicija 1. Ako su brojevi m i n sume dva kvadrata, onda je i njihov produkt m n takoder suma dva kvadrata.
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
4. poglavlje (korigirano) LIMESI FUNKCIJA
 . Limesi funkcija (sa svim korekcijama) 69. poglavlje (korigirano) LIMESI FUNKCIJA U ovom poglavlju: Neodređeni oblik Neodređeni oblik Neodređeni oblik Kose asimptote Neka je a konačan realan broj ili
. Limesi funkcija (sa svim korekcijama) 69. poglavlje (korigirano) LIMESI FUNKCIJA U ovom poglavlju: Neodređeni oblik Neodređeni oblik Neodređeni oblik Kose asimptote Neka je a konačan realan broj ili
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
