Integracija funkcija više promenljivih
|
|
|
- Ξάνθιππος Λιάπης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Integrcij funkcij više promenljivih Drgn S. Djordjević Univerzitet u Nišu, Prirodno-mtemtički fkultet Niš, Srbij Februry 18, 216
2 ii
3 Predgovor Predvnj su nmenjen studentim, koji polžu ispit iz predmet Mtemtičk nliz 4. Tekst nije kompletn, i konstntno se rdi n poboljšnju mterijl nmenjenog studentim (obrtiti pžnju n dtum upisn n prvoj strni). Studenti su u obvezi d konsultuju dodtnu literturu, koj je nveden u spisku referenci. Obvezno posetiti bilioteku Fkultet. Celine koje nije neophodno nučiti, počinju simbolom, zvršvju simbolom. iii
4 iv
5 Sdržj Predgovor iii 1 Prostor R n Vektorski prostor R n Sklrni proizvod Norm u prostoru R n Metrički prostori Integrcij Žordnov mer u R n Mer prvougonik u R Mer n-intervl u R n Unutršnj i spoljn mer Rimnov integrl Rimnov sum Drbuove sume Oznke i terminologij Klse integrbilnih funkcij Svojstv Rimnovog integrl eometrijski i fizički smiso integrl Interpretcij dvostrukog integrl Interpretcij trostrukog integrl Specifičnosti integrl u R n z n Izrčunvnje integrl Slučj prostor R Slučj prostor R n, n Smen promenljivih Polrn smen u rvni Uopšten polrn smen v
6 vi SADRŽAJ Cilindričn smen u trostrukom integrlu Sfern smen u trostrukom integrlu Nesvojstveni integrli Pojmovi u mehnici Moment inercije mterijlne rvne figure Elips inercije Moment inercije mterijlne figure Težište mterijlne rvne figure Težište mterijlne figure u prostoru Krivolinijski integrli Krive u R n Krivolinijski integrl prvog red Rimnov sum i geometrijsk interpretcij krivolinijskog integrl prvog red Krivolinijski integrl drugog red rinov formul u rvni Slučj višestruko poveznih oblsti Primen krivolinijskog integrl drugog red n izrčunvne površine skup u rvni Nezvisnost integrl od putnje integrcije Mehnički smiso krivolinijskog integrl Površinski integrli Površi u R Prv kvdrtn form površi i površin površi Površinski integrli prvog red Površinski integrli drugog red Teorij polj Formul us Ostrogrdskog Formul Stoks Prmetrski integrli Funkcij gornje grnice Svojstveni prmetrski integrli Nesvojstveni prmetrski integrli m funkcij (Ojlerov integrl drugog red) Bet funkcij (Ojlerov integrl prvog red) Litertur 159
7 lv 1 Prostor R n 1.1 Vektorski prostor R n Skup relnih brojev oznvčvmo s R, skup prirodnih brojev oznčvmo s N. Ako je n N, ond je R n = R } {{ R } = {x = (x 1,..., x n ) : x 1,..., x n R}. n put Skup R n je veom vžn u dljim rzmtrnjim, te ćemo opisćemo njegov lgebrsk i metričk svojstv. Podsećmo n definiciju Abelove 1 (komuttivne) grupe i polj. Definicij Nek je binrn opercij n neprznom skupu, odnosno :. Ako je x, y, piše se češće x y umesto (x, y). Pretpostvimo d vže sledeć svojstv: (1) ( x, y, z ) x (y z) = (x y) z (socijtivnost); (2) ( e )( x ) x e = e x = x (postojnje neutrlnog element e ); (3) ( x )( x 1 ) x x 1 = x 1 x = e (postojnje inverznog element x 1 z x ); (4) ( x, y ) x y = y x (komuttivnost). Td je (, ) Abelov (komuttivn) grup, ili krće je Abelov grup (u odnosu n ). Element e je neutrlni element z operciju, x 1 je inverzni element z x. Ako je skup Abelov grup, i pri tome je rzmtrn opercij oznčen s +, td je trdicionlno neutrlni element u odnosu n operciju + 1 Niels Henrik Abel ( ), norveški mtemtičr 1
8 2 LAVA 1. PROSTOR R N oznčen s. Ako je x, ond je suprotn element od x u odnosu n operciju + oznčen s x. Ov konvencij se nziv ditivn notcij. U mnogim slučjevim je prirodno s oznčiti operciju n Abelovoj grupi. Td je neutrlni element u odnosu n operciju oznčen s 1. Ako je x, td je suprotn element od x u odnosu n oznčen s x 1. Definicij Nek su n skupu F definisne opercije + i, tko d vže sledeć svojstv: (1) (F, +) je Abelov grup; (2) (F \ {}) je polje; (3) ( x, y, z F) x (y + z) = (x y) + (x z) (distributivnost opercije u odnosu n operciju +). Td je F polje u odnosu n nvedene opercije. Skup R je polje u odnosu n stndrdne opercije + i. Tko de, skup kompleksnih brojev C je polje u odnosu n uobičjene opercije. Definicij Nek je V neprzn skup n kome je definisn binrn opercij +, tko d je (V, +) Abelov grup. Oznčimo s neutrlni element ove Abelove grupe. Nek je F skup relnih ili kompleksnih brojev. Nek je, osim tog, definisn funkcij p : F V V, u krćem zpisu p(λ, x) = λx z λ F i x V, koj ispunjv osobine: (1) ( λ, µ F)( x V ) (λ + µ)x = λx + µx; (2) ( λ F)( x, y V ) λ(x + y) = λx + λy; (3) ( λ, µ F)( x V ) (λµ)x = λ(µx); (4) ( x V ) 1x = x. Td je V vektorski prostor nd poljem F. Elementi vektorskog prostor jesu vektori, elementi polj F jesu sklri. Opercij + u skupu V jeste sbirnje vektor. Neutrlni element u skupu V u odnosu n ovu operciju jeste nul vektor. Opercije + i u skupu F jesu sbirnje i množenje sklr. Funkcij p(λ, x) = λx jeste množenje vektor sklrom. Vektorski prostor nd poljem R nziv se reln vektorski prostor. Vektorski prostor nd poljem C je kompleksn vektorski prostor. Nije teško dokzti sledeće tvr denje. Teorem Ako je V vektorski prostor nd poljem F, td vži: (1) ( x V ) x = ; (2) ( λ F) λ = ; (3) ( x V ) ( 1)x = x, gde je x inverzni z x u odnosu n + u V.
9 1.1. VEKTORSKI PROSTOR R N 3 Nek je x = (x 1,..., x n ), y = (y 1,..., y n ) R n. Sbirnje je definisno koordintno, odnosno x + y = (x 1 + y 1,..., x n + y n ). U odnosu n ovko definisnu operciju + skup R n je Abelov grup, pri čemu je nul-vektor = (,..., ), inverzni element od x je x = ( x 1,..., x n ). je Množenje sklrom je tko de definisno koordintno. Ako je λ R, td λx = (λx 1,..., λx n ). Teorem Skup R n je vektorski prostor nd poljem R. Moguće je svki vektor x = (x 1,..., x n ) R n poistovetiti s tčkom čije su koordinte uprvo dte ko n-tork (x 1,..., x n ). U tom slučju vektor x interpretirmo ko vektor s početkom u = (,, ) i krjem u (x 1,..., x n ). Uprvo opisn procedur jeste prelz s vektorskog prostor R n n fini prostor R n. Smtrmo d je procedur jsn, te ćemo o skupu R n rvnoprvno govoriti ko o vektorskom prostoru (skupu vektor), i o finom prostoru (skupu tčk). U slučju n = 2 ili n = 3, jednostvn je geometrijsk interpretcij prostor R n. Primer (Slik 1) Nek je n = 2. Ako je x = (x 1, x 2 ) R 2, td x identifikujemo s geometrijskim vektorom Ox. Ako je y = (y 1, y 2 ) R 2, ond je očigledno x+y = Ox+ Oy. Dužin vektor x y je u stvri rstojnje izme du krjnjih tčk vektor x i y. Primetimo sledeću konvenciju: prv koordint vektor x je n horizontlnoj osi, drug koordint vektor x je n vertiklnoj osi; mogli smo uzeti i obrnut redosled, li ko prihtimo jedn redosled os, ond se tog ndlje i pridržvmo. Ov konvencij je u vezi s orijentcijom prostor R 2. Podsećmo d se ov orijentcij poklp s orijentcijom trigonometrijske kružnice.
10 4 LAVA 1. PROSTOR R N Slik 1. Slik 2. Primer (Slik 2) Nek je n = 3. Sd uzimmo desnu orijentciju, ko n Slici 2. Preostli detlji geometrijske interpretcije poklpju se s interpretcijom u prostoru R 2. U ovom slučju treb obrtiti pžnju n redosled koordintnih os. Postoje dv osnovn redosled (permutcije): x 1, x 2, x 3, ili x 2, x 1, x 3. Ostli redosledi se mogu dobiti cikličnim rotirnjem os u prethodne dve premutcije. Ovj redosled se, ko i u prethodnom
11 1.2. SKALARNI PROIZVOD 5 primeru, odnosi n orijentciju prostor R 3. Koristićemo smo desnu orijentciju. Anlogno prethodnom rzmtrnju, skup C n je vektorski prostor nd poljem C, opercije su definisne n isti nčin ko u prostoru R n. Nvodimo druge primere, koji nemju geometrijsku interpretciju. Primer Skup C[, b] relnih neprekidnih funkcij n segmentu [, b] je reln vektorski prostor. Z x, y C[, b], λ R i t [, b], sbirnje funkcij i množenje sklrom definisno je uobičjeno: (x y)(t) = x(t) + y(t), (λ x)(t) = λx(t). 1.2 Sklrni proizvod Uvodimo pojm sklrnog proizvod n relnim vektorskim prostorim. Definicij Nek je V vektorski prostor nd poljem relnih brojev R. Nek preslikvnje s : V V R im sledeć svojstv: (1) ( x V ) s(x, x) ; (2) ( x V ) (s(x, x) = x = ); (3) ( λ, µ R)( x, y, z V ) s(λx + µy, z) = λs(x, z) + µs(y, z); (4) ( x, y V ) s(x, y) = s(y, x). Td je funkcij s sklrni proizvod n vektorskom prostoru V. Primer Ako je x = (x 1,..., x n ) R n i y = (y 1,..., y n ) R n, td je njihov sklrni proizvod definisn n sledeći nčin: x, y = n x i y i. i=1 Lko je proveriti sve osobine sklrnog proizvodd. Z n = 2, 3 nije teško utvrditi d se ov definicij sklrnog proizvod poklp s pozntom definicijim n skupu geometrijskih vektor u rvni ili prostoru. Primer U skupu C[, b] sklrni prozivod se definiše n sledeći nčin: z sve funkcije f, g C[, b]. f, g = b f(t)g(t)dt
12 6 LAVA 1. PROSTOR R N Primer Nek je p C[, b] dt nenegtivn neprekidn funkcij. Opštiji sklrni proizvod u skupu C[, b] definisn je n sledeći nčin: x, y = b f(t)g(t)p(t)dt, z svko f, g C[, b]. Ako je p(t) = 1 z svko t [, b], ond uprvo uvedeni sklrni proizvod postje odgovrjući iz prethodnog primer. Teorem (Nejednkost Koši-Švrz-Bunjkovskog) Nek je (V, s) unitrn prostor. Td z svko x, y V vži x, y x, x 1/2 y, y 1/2. Dokz. Nk je x, y V. Z svko t R vži: x ty, x ty = x, x 2t x, y + t 2 y, y. S desne strne je nenegtivn kvdrtn funkcij po t, te je diskriminnt ove kvdrtne funkcije mnj ili jednk od nule, odnosno Odvde sledi tvr denje. x, y 2 x, x y, y. 1.3 Norm u prostoru R n Postoji više normi u vektorskom prostoru. Nvodimo definiciju proizvoljne norme Pret- Definicij Nek je V vektorski prostor nd C ili nd R. postvimo d funkcij : V R im svojstv: (1) ( x V ) x ; (2) ( x V ) ( x = x = ); (3) ( x V )( λ C ( ili λ R) ) λx = λ x ; (4) ( x, y V ) x + y x + y (nejednkost trougl). Td je norm n V. Ure den pr (V, ) jeste normirn prostor, ili krće V je normirn prostor. Posebno je interesntn norm indukovn sklrnim proizvodom.
13 1.3. NORMA U PROSTORU R N 7 Teorem Nek je V unitrn prostor, n kome je definisn sklrni proizvod,. Definišemo funkciju n skupu V n sledeći nčin: x = x, x, x V. Td je norm n unitrnom prostoru V. Dokz. Jedini problem je dokzti nejednkost trogl. Z proizvoljne x, y V, n osnovu nejednkosti Koši-Švrc-Bunjkovskog, vži x + y 2 = x + y, x + y = x, x + 2 x, y + y, y = ( x + y ) 2. Iz prethodne nejednkosti sledi nejednkost trougl z normu definisnu sklrnim proizvodom. Primer (Euklidksk norm) Imjući u vidu d je sklrni proizvod u R n definisn ko x, y = b x j y x, x = (x 1,..., x n ), y = (y 1,..., y n ) R n, j=1 proizilzi d je norm indukovn ovim sklrnim proizvodom odre den ko n x = x 2 j. Ov norm se nziv euklidsk norm. Prostor R n je euklidski prostor. Primer U prostoru R n norm može biti uveden n sledeće nčine: x = x 2 = n x i 2, Euklidov norm x 1 = n i=1 i=1 j=1 x i, x = mx 1 i n x i Euklidov norm jeste intenzitet geometrijskog vektor u slučju n = 1, 2, 3. Primer U skupu C[, b] norm može biti definisn n sledeći nčin: x = mx t [,b] x(t).
14 8 LAVA 1. PROSTOR R N Primer Nek je dt skup C[, b] s rnije definisnim sklrnim proizvodom. Td je norm funkcje f C[, b] dt s b f = f(t) 2 dt. Norm, smim tim i sklrni proizvod, n prirodn nčin odre duju rstojnje u vektorskom prostoru. Teorem Ako je norm n vektorskom prostoru V, ond je rstojnje n skupu V, koje je indukovno normom, definisno ko d(x, y) = x y, x, y V. 1.4 Metrički prostori Pojm rstojnj izme du element nekog skup je veom vžn u mtemtici. Stog detljno rzmtrmo ovo pitnje. U jednom skupu se n više nčin može definisti rstojnje. Definicij Nek je X proizvoljn neprzn skup, i nek je d : X X R preslikvnje, tko d z svko x, y, z X vži (1) d(x, y) ; (2) d(x, y) = d(y, x); (3) d(x, y) = ko i smo ko x = y; (4) d(x, y) d(x, z) + d(z, y) (nejednkost trougl). Td je d metrik, ili rstojnje n skupu X. Ure den pr (X, ρ) jeste metrički prostor. Jednostvnije, X je metrički prostor, i podrzumevmo d je n skupu X definisn nek metrik. Elementi metričkog prostor nzivju se tčke. Ako je x, y X, td je broj d(x, y) rstojnje izme du tčk x i y. Primer () N skupu relnih brojev R metrik je definisn n uobičjeni nčin: ko su x, y R, ond je d(x, y) = x y. (b) Nek je R 2 = {(x 1, x 2 ) : x 1, x 2 R} skup svih ure denih prov relnih brojev, koji geometrijski interpretirmo ko rvn. Ako je x = (x 1, x 2 ) R 2 i y = (y 1, y 2 ) R 2, ond je njihovo Euklidovo rstojnje odre deno s d(x, y) = (x 1 y 1 ) 2 + (x 2 y 2 ) 2.
15 1.4. METRIČKI PROSTORI 9 (c) Slično je i u trodimenzionlnom prostoru R 3. Ako je x = (x 1, x 2, x 3 ) R 3 i y = (y 1, y 2, y 3 ) R 3, td je Euklidovo rstojnje izme du ovih tčk d(x, y) = (x 1 y 1 ) 2 + (x 2 y 2 ) 2 + (x 3 y 3 ) 2. (d) Nek je R n = {(x 1,..., x n ) : x 1,..., x n R} skup ure denih n-torki relnih brojev. Ako je x = (x 1,..., x n ) R n i y = (y 1,..., y n ) R n, ond je Euklidovo rstojnje izme du tčk x i y definisno ko: ( n ) 1/2 d(x, y) = (x k y k ) 2. k=1 Dokz. Svojstv (1), (2) i (3) iz Definicije je jednostvno proveriti, dok je osobin (4) iste definicije posledic sledećeg tvr denj: Teorem Ako su 1,..., n, b 1,... b n proizvoljni relni brojevi, td vži ( n ) 1/2 ( n ) 1/2 ( n ) 1/2 ( i + b i ) 2 2 i + b 2 i. i=1 i=1 Ako je i = x i z i, b i = z i y i (i = 1,..., n) u prethodnoj Teoremi 1.4.1, sledi d z x = (x 1,..., x n ), y = (y 1,..., y n ) i z = (z 1,..., z n ) vži: ( n ) 1/2 ( n ) 1/2 ( n ) 1/2 d(x, y) = (x i y i ) 2 (x i z i ) 2 + (z i y i ) 2 i=1 d(x, z) + d(z, y), i=1 Ovim je dokzn nejednkost trougl z funkciju d. Definicij Prostor R n s rstojnjem iz Primer nziv se Euklidov prostor. U skupu R n mogu se definisti rstojnj i n neki drugi nčin, ko što pokzuju sledeći primeri. Primer () Nek je x = (x 1,..., x n ) i y = (y 1,..., y n ) R n. Td su n d 1 (x, y) = mx x i y i, d 2 (x, y) = x i y i i=1,n metrike n skupu R n i vži d(x, y) n i=1 i=1 i=1 d 1 (x, y) d(x, y) d 2 (x, y) n d 1 (x, y),
16 1 LAVA 1. PROSTOR R N gde je d Euklidovo rstojnje n R n. (b) Nek je B[, 1] skup svih relnih funkcij koje su definisne i ogrničene n segmentu [, 1]. Z proizvoljne funkcije x, y B[, 1], funkcij d definisn je n sledeći nčin: d (x, y) = sup x(t) y(t). t [,1] Očigledno, funkcij d ispunjv uslove (1) (3) Definicije Neposredno iz definicije funkcije d sledi: x(t) y(t) ρ(x, y) z svko t [, 1]. N osnovu nejednkosti trougl z relne brojeve, z proizvoljne funkcije x, y, z B[, 1] i svko t [, 1] vži sledeć procen: x(t) y(t) x(t) z(t) + z(t) y(t) d (x, z) + d (z, y). Prem tome vži d (x, y) = sup x(t) y(t) d (x, z) + d (z, y), t [,1] što predstvlj nejednkost trougl z funkciju d. Tčke ovog metričkog prostor jesu ogrničene relne funkcije n skupu [, 1]. (c) Nek je C[, b] skup svih relnih funkcij, koje su definisne i neprekidne n segmentu [, b]. Td se u skupu C[, b] metrik može definisti n sledeći nčin: d (x, y) = mx x(t) y(t), t [,b] z svko x, y C[, b]. (d) Skup kompleksnih brojev oznčen je s C. Svki broj z C predstvlj se ko z = x + iy, gde su x i y relni brojevi, x = Re z i y = Im z, i je imginrn jedinic. Skup kompleksnih brojev predstvljen je jednom rvni, pri čemu vži z = x + iy = (x, y). Stog je rstojnje u C definisno n isti nčin ko u prostoru R 2. Ako je z = x + iy i w = u + iv, gde su x, y, u, v R, td je d(z, w) = (x u) 2 + (y v) 2. Iz činjenice d je modul kompleksnog broj z = x + iy definisn ko z = d(z, ), sledi d(z, w) = z w.
17 1.4. METRIČKI PROSTORI 11 (e) U prostoru C n ure denih n-torki kompleksnih brojev definisn je metrik n sledeći nčin. Ako je z = (z 1,..., z n ) C n i w = (w 1,..., w n ) C n, pri čemu je z i, w i C z svko i = 1,..., n, td je ( n ) 1/2 d(z, w) = z i w i 2. i=1 Sd podrzumevmo d je konvergencij nizov u skupu R dobro poznt. N osnovu ovog, definiše se konvergencij nizov u proizvoljnom metričkom prostoru. Definicij Nek je (x n ) n niz tčk u metričkom prostoru X. Niz (x n ) n konvergir k tčki X (u oznci lim x n = ), ko brojni niz n (d(x n, )) n konvergir k, odnosno ( ϵ > )( n N)( n N)(n n = d(x n, ) < ϵ). Drugim rečim, lim x n = ko i smo ko lim d(x n, ) =. n n Ako je lim x n =, td je tčk grničn vrednost niz (x n ) n. n Ogrničeni nizovi čine širu klsu od konvergentnih nizov u metričkom prostoru. Definicij Niz tčk (x n ) n metričkog prostor X je ogrničen, ko postoje X i broj C >, tko d z svko n N vži uslov d(x n, ) C. Sledi nekoliko osnovnih tvr denj koj se odnose n konvergentne i ogrničene nizove. Teorem Ako je niz (x n ) n konvergentn u metričkom prostoru X, ond je on i ogrničen. Dokz. Nek je lim x n =, odnosno lim d(x n, ) =. Niz (d(x n, )) n je n n konvergentn niz relnih brojev, te je ogrničen. Stog postoji neki broj C >, tko d z svko n N vži d(, x n ) C. Ovim je pokzn ogrničenost niz (x n ) n u metričkom prostoru X. Teorem Niz (x n ) n u metričkom prostoru X ne može konvergirti dvem rzličitim tčkm. Dokz. Nek je lim x n = i lim x n = b. N osnovu nejednkosti trougl n n vži d(, b) d(, x n ) + d(x n, b).
18 12 LAVA 1. PROSTOR R N Obzirom d nizovi d(, x n ) i d(x n, b) teže k kd n, sledi d je d(, b) =, odnosno = b. Otvoren kugl poluprečnik r (r > ) s centrom u tčki metričkog prostor X jeste skup B(; r) = {x X : d(x, ) < r}. Kugl s centrom u R poluprečnik r > n relnoj prvoj jeste intervl ( r, + r). Ako je = ( 1, 2 ) R 2, ond je B(; r) = {x = (x 1, x 2 ) : (x 1 1 ) 2 + (x 2 2 ) 2 < r} krug s centrom u tčki poluprečnik r. Kugl u R 3 je kugl, ili lopt u uobičjenom smislu. Koristeći pojm kugle u metričkom prostoru, moguće je dti još jednu krkterizciju konvergencije niz tčk. Teorem Niz tčk (x n ) n metričkog prostor X konvergir k tčki X, ko i smo ko svk kugl B(; r) sdrži sve tčke niz (x n ) n, osim eventulno končno mnogo tčk tog niz. Dokz. Nek je lim n x n = i nek je B(; r) proizvoljn kugl. Z dti broj r > postoji n N, tko d z svko n N s svojstvom n n vži d(x n, ) < r. Proizilzi d kugl B(; r) sdrži sve člnove niz (x n ) n n. Obrnuto, pretpostvimo d svk kugl B(; ϵ) sdrži sve člnove niz (x n ) n, osim eventulno neki končn broj tčk tog niz. Nek je ϵ > proizvoljn broj i x n1 tčk s njvećim indeksom niz (x n ) n koj ne pripd kugli B(; ϵ). Sve ostle tčke morju pripdti ovoj kugli, odnosno z svki prirodn broj n, ko je n > n 1, ond je d(x n, ) < ϵ. Sledi lim n x n =. Konvergencij niz tčk prostor R n ekvivlentn je konvergenciji svkog niz koordint. Teorem Niz tčk (x m ) m prostor R n, pri čemu je x m = (x m 1,..., xm n ), konvergir k tčki = ( 1,..., n ), ko i smo ko svki koordintni niz (x m i ) m konvergir k tčki i (i = 1,..., n). Drugim rečim, i = 1,..., n. lim m xm = ko i smo ko je lim m xm i = i z svko Dokz. Dovoljno je dokzti tvr denje u slučju n = 2. U slučju n 2 tehničke detlje dokz prepuštmo čitocu. Nek je lim m xm =, gde je
19 1.4. METRIČKI PROSTORI 13 x m = (x m 1, xm 2 ) i = ( 1, 2 ). Td je lim m d(xm, ) =. Vži x m 1 1 (x m 1 1) 2 + (x m 2 2) 2 = d(x m, ), m. Ovim je pokzno lim m xm 1 lim m xm 2 = 2. S druge strne, pretpostvimo d vži Td je d(x m, ) = = 1. N potpuno isti nčin može se dokzti lim m xm 1 = 1 i lim m xm 2 = 2. (x m 1 1) 2 + (x m 2 2) 2 kd m, odkle sledi lim m xm =. Nek je M podskup metričkog prostor X. Tčk x M je unutršnj tčk skup M, ko postoji nek kugl B(x ; r) M. Skup svih unutršnjih tčk skup M oznčen je s int M, ili M. Iz definicije skup unutršnjih tčk sledi int M M. Skup M je otvoren ko je int M = M. Otvoren kugl u metričkom prostoru je otvoren skup. Nrvno, intervl je otvoren skup u R, otvoren krug je otvoren skup u R 2, otvoren lopt je otvoren skup u R 3. Obzirom d je int[, b] = (, b), skup [, b] nije otvoren. Tčk x X je rubn tčk skup M X, ko svk kugl B(x ; r) im neprzn presek i s skupom M i s skupom X \ M. Skup svih rubnih tčk skup M nziv se rub skup M i oznčv s M, ili M. Očigledno vži int M M =. Nek je, b, c R, < b < c i M = (, b) {c}. Td je M = {, b, c}. Rub krug u rvni jeste kružnic. Rub lopte u prostoru jeste sfer. Svk tčk skup M mor biti ili unutršnj, ili rubn (nikd i jedno i drugo). Tčk x X je tčk ngomilvnj skup M X, ko postoji niz rzličitih tčk (x n ) n, x n M, tko d je lim x n = x. Skup svih tčk n ngomilvnj skup M oznčen je s cc M, ili M. Sve tčke skup M koje nisu tčke ngomilvnj skup M, jesu izolovne tčke skup M. Skup izolovnih tčk skup M oznčen je s iso M. Očigledno vži iso M = M \ cc M. Nek je, b, c R, < b < c i M = (, b) {c}. Td je cc M = [, b], iso M = {c}. Ztvorenje skup M jeste skup cl M = M cc M. Često se ztvorenje skup M oznčv s M. Skup M je ztvoren ko je M = cl M, odnosno ko je cc M M.
20 14 LAVA 1. PROSTOR R N Skup M = [, b] {c} (, b, c, R, < b < c) je ztvoren. Skup M 1 = (, b) {c} nije ni otvoren ni ztvoren. Skup M 2 = (, b) je otvoren u R. Przn skup i ceo prostor X su jedini skupovi koji su istovremeno otvoreni i ztvoreni u metričkom prostoru. Odnos izme du otvorenih i ztvorenih skupov dt je sledećom teoremom. Teorem Podskup M metričkog prostor X je otvoren, ko i smo ko je skup X \ M ztvoren. Dokz. Nek je M otvoren podskup u X. Treb dokzti d je skup X \ M ztvoren, odnosno cc(x \ M) X \ M. Nek je cc(x \ M). Td postoji niz rzličitih tčk (x n ) n, x n X \ M, tko d je lim x n =. n Pretpostvimo d je / X \ M, odnosno M. Postoji kugl B(; r), z koju vži B(; r) M. Kugl B(; r) sdrži sve tčke niz (x n ) n, osim eventulno končn broj tih tčk. Sledi d skup M sdrži sve tčke niz (x n ) n, osim eventulno neki končn broj tih tčk. Ovo je nemoguće, n osnovu pretpostvke x n X \ M z svko n N. Zključk je X \ M, odnosno X \ M je ztvoren. Nek je X \ M ztvoren skup i nek je M proizvoljn tčk. Treb dokzti d je int M. Pretpostvimo d nije unutršnj tčk skup M, odnosno M. Td svk kugl B(; r) im neprzn presek s skupom M i s skupom X \ M. Posmtrjmo kuglu poluprečnik ϵ 1 = 1, odnosno kuglu B(; 1). Postoji tčk x 1 X \ M, tko d je d(, x 1 ) < 1. Nek je ϵ 2 = d(, x 1 )/2. Kugl B(; ϵ 2 ) im neprzn presek s skupom X \ M, te stog postoji x 2 X \ M tko d je d(, x 2 ) < ϵ 2 < d(, x 1 ). Vži x 2 x 1. Nek je ϵ 3 = d(, x 2 )/2. U kugli K(; ϵ 3 ) postoji nek tčk x 3 X \M. Očigledno je x 3 x 2 i x 3 x 1. Nstvljjući ovj postupk, formir se niz rzličitih tčk (x n ) n, x n X \ M, z koji vži lim d(, x n) =, n odnosno lim x n =. Ovim je pokzno cc(x \ M)ıX \ M. Me dutim, n polzn pretpostvk je M, što je nemoguće. Zključk je d svk tčk M mor biti unutršnj tčk skup M, odnosno M je otvoren skup.
21 lv 2 Integrcij 2.1 Žordnov mer u R n U definiciji Rimnovog 1 integrl funkcije jedne relne promenljive n segmentu suštinski je iskorišćen pojm dužine (mere) intervl. U skupu R 2 pojmu mere odgovr pojm površine, u skupu R 3 pojmu mere odgovr pojm zpremine nekog skup. Postoji više rzličitih mer n prostoru R n, izučvćemo smo Žordnovu2. Nek je, b R, < b. Dužin intervl I = (, b) (ili bilo kog intervl [, b), (, b], [, b]) jeste b. Dkle, jednodimenzionln mer intervl I je m 1 (I) = b. Nebitno je d li krjnje tčke tčke i b intervl I pripdju tom intervlu, ili ne. Time se prihvt činjenic d je dužin tčke jednk nuli (tj. mer jednoelemetnog skup jednk je nuli) Mer prvougonik u R 2 Nek su, b, c, d R, tko d vži < b i c < d. Td je ovim brojevim odre den prvougonik P u R 2 s koordintm temen: A = (, c), B = (b, c), C = (b, d) i D = (, d) (Slik 3). Prvougonik P izržen preko Dekrtovog 3 proizvod jeste P = (, b) (c, d). Mer ovog prvougonik (površin, preciznije dvodimenzionln mer) izrčunv se n sledeći nčin m 2 (P ) = (b )(d c). 1 eorg Friedrich Bernhrd Riemnn ( ), nemčki mtemtičr 2 Mrie Ennemond Cmille Jordn ( ), frncuski mtemtičr 3 René Descrtes (ltinski: Rentus Crtesius; ), frncuski mtemtičr i filozof 15
22 16 LAVA 2. INTERACIJA Broj 2 u simbolu m 2 oznčv dimenzuju prostor, odnosno nglšv d se rdi o prostoru R 2. Nije vžno d li rubne strnice tog prvougonik pripdju prvougoniku, ili ne. Ovim se usvj činjenic d je dvodimenzionln mer duži jednk nuli. Specijlno, dvodimenzionln mer tčke jednk je nuli. Dkle, ko je P 1 = [, b] [c, d], ond je m 2 (P 1 ) = (b )(d c). Tko de, ko je = b i P 2 = {} [c, d], ond je m 2 (P 2 ) =. Slik 3. Nek su sd P 1,..., P n prvougonici u R 2, s svojstvom d je P i P j (i j) ili przn skup, ili neki deo rubov ovih prvougonik. Drugim rečim, P i i P j nemju zjedničkih unutršnjih tčk. Prirodno je sd definisti meru unije ovih prvougonik ko zbir njihovih mer, odnosno ( n ) m 2 P i = i=1 n m 2 (P i ). i=1 Skupovi oblik E = n i=1 P i jesu elementrni skupovi (podrzumev se d rzličiti skupovi P i i P j nemju zjedničkih unutršnjih tčk). Ako su P, Q prvougonici koji imju zjedničkih unutršnjih tčk, td je jednostvno proveriti d se skup P Q može prikzti ko unij končno mnogo prvougonik koji uzjmno nemju zjedničkih unutršnjih tčk.
23 2.1. ŽORDANOVA MERA U R N 17 Anlogno, ko su A i B dv elementrn skup, td je A B = P 1 P k, pri čemu su P 1,... P k prvougonici koji u provim nemju zjedničkih unutršnjih tčk (Slik 4). Sledi d je A B elementrn skup. Slično, A B i A \ B tko de jesu elementrni skupovi. Slik 4. Ako su A, B uzjmno disjunktni elementrni skupovi, ond je m 2 (A B) = m 2 (A) m 2 (B). Ako su A i B elementrni skupovi i A B, ond n osnovu disjunktne unije B = A (B \ A) sledi d je m 2 (B) = m 2 (A) + m 2 (B \ A). Dkle, m 2 (A) m 2 (B) Mer n-intervl u R n Anlogn je situcij u prostoru R n. Nek je 1,..., n R i b 1,..., b n R n, tko d je i < b i z svko i = 1,..., n. Skup I = n ( i, b i ) = (b 1 1 ) (b n n ) i=1
24 18 LAVA 2. INTERACIJA je n-intervl u R n. Ako je n = 2, ond je I prvougonik. Ako je n = 3, ond je I kvdr. Primetimo d su strnice n-intervl uvek prlelne koordintnim osm. n-dimenzionln mer n-intervl I odre den je s m n (I) = n (b i i ) = (b 1 1 )... (b n n ). i=1 Nije vžno d li delovi hiper-rvni koje ogrničvju prvougonik, pripdju smom prvougoniku, ili ne: veličin m n (I) se ne menj. Ako je J neki (n 1)-intervl koji ogrničv n-intervl I, (dkle, J pripd hiperrvni dimenzije n 1), td je m n (J) =. Specijlno, n-dimenzionln mer jednoelementnog skup jedk je. Primetimo d ko je J bilo koji (n 1)-intervl, ond J može biti posmtrn ko degenerisni n-intervl, odnosno j = b j z neko j. Ako su I 1,..., I k n-intervli, koji nemju zjedničkih unutršnjih tčk, ond je k E = elementrn skup u R n. Mer ovog elementrnog skup E odre den je s m n (E) = j=1 I j n m n (I j ). j=1 Ako su E, F elementrni skupovi, td su E F, E F i E \ F tko de elementrni skupovi. Nime, svki od ovih skupov može biti prikzn ko unij n-intervl, koji me dusobno nemju zjedničkih unutršnjih tčk. Ako su E, F elementrni skupovi i E F =, jednostvno je proveriti d vži m n (E F ) = m n (E) m n (F ). Ov osobin se nziv končn ditivnost mere m n n fmiliji elementrnih skupov. Ako su A, B elementrni skupovi i A B, n osnovu disjunktne unije B = A (B \ A) sledi m n (B) = m n (A) + m n (B \ A) m n (A). Ov osobin se nziv monotonost mere n fmiliji elementrnih skupov Unutršnj i spoljn mer Potrebno je meru definisnu u prethodnoj sekciji, proširiti n opštiju fmiliju podskupv od R n. Nek je skup R 2 ogrničen. Td postoje elementrni skupovi koji su sdržni u, i postoje elementrni skupovi koji
25 2.1. ŽORDANOVA MERA U R N 19 sdrže. Nek je m i n() = sup{m(a) : A i A je elementrn skup} m e n() = inf{m(b) : B i B je elementrn skup}. Obzirom d je ogrničen skup, sledi d su m i n() i m e n() relni nenegtivni brojevi. Broj m i n() jeste unutršnj mer, broj m e n() jeste spoljn mer skup. Očigledno, uvek vži m i n() m e n(). Definicij Ogrničen skup R n je merljiv u Žordnovom smislu ko i smo ko je m i n() = m e n(). U tom slučju broj m n () (= m i n() = m e n()) jeste (n-dimenzionln) Žordnov mer skup. Koristićemo smo Žordnovu meru, te ubuduće umesto Žordnov mer pišemo mer. Z svki merljiv skup vži m n (). Dokzujemo nekoliko osnovnih tvr denj o merljivim skupovim i meri. Teorem Nek su A i B merljivi skupovi. Td vži: (1) Ako je A B, ond je m n (A) m n (B) (monotonost mere); (2) Ako je A R n otvoren skup, td je m n (A) > ; (3) m n (A) = ko i smo ko z svko ϵ > postoji elementrn skup F, tko d je A F i m n (F ) < ϵ (krkterizcij skup mere nul); (4) Unij dv skup mere nul jeste skup mere nul; (5) Ogrničen skup H R n je merljiv ko i smo ko je m n ( H) = ; (6) Skupovi A B, A B i A \ B su merljivi; (7) Ako je A B A B, ond je m n (A B) = m n (A) + m n (B) (končn ditivnost mere); (8) Ako je A B, td je m n (B \ A) = m n (B) m n (A). Dokz. Sve nvedene osobine očigledno vže z n-intervle i elementrne skupove. Dokzujemo ove osobine z proizvoljne merljive skupove. (1) Sledi n osnovu skupovne inkluzije elementrnih figur skupov upisnih u A, smim tim i u B. (2) Ako je A otvoren i merljiv, ond z svko x A postoji neki otvoren n-intervl I, tko d je x I A, te je m n (A) >. (3) Sledi iz definicije infimum. (4) Sledi n osnovu svojstv (3). (5)Nek je F proizvoljn otvoren elementrn skup, sdržn u H i nek je proizvoljn ztvoren elementrn skup koji sdrži H.
26 2 LAVA 2. INTERACIJA Očigledno vži H \F, odnosno \F je elementrn skup koji sdrži H. S druge strne, ko je K proizvoljn elementrn skup koji sdrži H, ond postoje elementrni skupovi F i, koji zdovoljvju F H i \ F = K. Pretpostvimo d je H merljiv skup i nek je ϵ > proizvoljno. Postoji elementrn skup F H tko d je m(h) m(f ) > m(h) ϵ/2. Tko de postoji elementrn skup H, tko d vži m n (H) m n () < m n (H)+ ϵ/2. Prem tome, m e n( H) m n () m n (F ) < ϵ. N osnovu svojstv (3) sledi d je H merljiv i njegov mer je jednk nuli. Sd pretpostvimo d je m n ( H) =. Z ϵ > postoje elementrni skupovi F i d vži F H, H \ F i m n () m n (F ) < ϵ. Td je, n osnovu m e n(h) m n () i m i n(h) m(f ), ispunjeno m e n(h) m i n(h) < ϵ. Kko je ϵ > proizvoljno, sledi d je H merljiv skup. (6) Sledi n osnovu svojstv (4), (5), ko i jednostvnih skupovnih inkluzij (A B) A B, (A B) A B i (A \ B) A B. (7) Sledi n osnovu svojstv (5) i (6). (8) Sledi n osnovu (7). Nvodimo primer ogrničenog skup koji nije merljiv. Primer Nek je Q 1 skup svih tčk skup [, 1] [, 1], čije su koordinte rcionlni brojevi. Skup Q 1 ne sdrži ni jedn netrivijln 2- intervl, već sdrži smo degenerisne intervle koji se svode n jednoelementne skupove. Stog je m i 2 (Q 1) =. Skup Q 1 je gust u [, 1] [, 1]. Stog ne postoji mnj elementrn figur od [, 1] [, 1] koj sdrži Q 1. Stog je m e 2 (Q 1) = 1. Dkle, skup Q 1 nije merljiv. 2.2 Rimnov integrl Rimnov sum Nek je Euklidov 4 norm u prostoru R n, odnosno ko je x = (x 1,..., x n ) ( n ) 1/2 R n, ond je x = x i 2. Ako je x, y R n i y = (y 1,..., y n ), ond i=1 je ( n ) 1 2 d(x, y) = x y = (x i y i ) 2 Euklidovo rstojnje izme du tčk x i y. 4 Euklid iz Aleksndrije, Eυκλειδηζ (oko 325. p.n.e p.n.e.), grčki mtemtičr i=1
27 2.2. RIMANOV INTERAL 21 Nek je merljiv (prem tome i ogrničen) skup u R n. Nek su 1,..., k merljivi i uzjmno disjunktni skupovi, z koje vži = k i=1 i. Td se fmilij skupov P = { 1,..., k } nziv rzbijnje (podel) skup. Nek je dim( i ) dijmetr skup i, odnosno dim( i ) = sup{d(u, v) : u, v i }, i = 1,..., k. Njveći od tih dijmetr nziv se dijmetr rzbijnj P skup, odnosno d(p) = mx{dim( 1 ),..., dim( k )}. Jednostvno je uočiti d z svki merljiv skup postoji neko rzbijnje P. Nek su T P = { 1,..., k } i T P = {E 1,..., E l } dv rzbijnj merljivog skup R n. Rzbijnje P je finije od rzbijnj P, u oznci P P, ko z svko E j P postoji s T P, tko d je E j s. Ako su P = { 1,..., k } i P = {E 1,..., E l } dv rzbijnj merljivog skup, td postoji rzbijnje P P, koje je finije i od P i od P. Rzbijnje P P je definisno ko P P = { s E j : s = 1,..., k, j = 1,..., l}. Ako je P proizvoljno rzbijnje merljivog skup R n, uvek postoji finije rzbijnje P istog skup. Ako je, recimo, P = { 1,..., k }, ond se može posmtrti rzbijnje P j = { j 1,..., j k } svkog skup j, te je P = { i j } i,j rzbijnje skup, s osobinom P P. Ako je P = { 1,..., k } rzbijnje merljivog skup, i ko je P = {E 1,..., E l } rzbijnje merljivog skup E, td je P P = { 1,..., k, E 1,..., E l } rzbijnje merljivog skup E. Nek je f : R reln funkcij, i nek je ξ i i proizvoljn tčk z svko i = 1, 2,..., k. Koristimo oznku ξ = (ξ 1,..., ξ k ). Sum σ(f,, P, ξ) = k f(ξ i ) m n ( i ) (2.1) i=1 je Rimnov integrln sum funkcije f n skupu, koj odgovr podeli P i izboru tčk ξ = (ξ 1,..., ξ k ). Činjenic d se svk podel P merljivog skup može učiniti finijom, omogućv uvo denje sledeće definicije.
28 22 LAVA 2. INTERACIJA Definicij (Rimnov integrl funkcije n skupu) Nek je merljiv skup u R n, i nek je f : R funkcij. Broj I je Rimnov integrl funkcije f n skupu, u oznci f, ko z svko ϵ > postoji δ ϵ >, tko d z svko rzbijnje P = { 1,..., k } skup, koje im svojstvo d(p) < δ, i z svki izbor tčk ξ 1 1,..., ξ k k vži I σ(f,, P, ξ) < ϵ. Ako postoji integrl f, ond je funkcij f integrbiln n skupu (u Rimnovom smislu). Rzmtrćemo smo Rimnov integrl funkcij, te pišemo integrl umesto Rimnov integrl. Formulišemo očigledn ekvivlent uslov integrbilnosti funkcije n merljivom skupu. Teorem Nek je merljiv skup u R n i nek je f : R funkcij. Rimnov integrl I funkcije f n skupu je grničn vrednost I = f = lim σ(f,, P, ξ), d(t ) ukoliko ov grničn vrednost postoji nezvisno od rzbijnj P skup i nezvisno od izbor tčk ξ. Skup svih relnih funkcij, koje su integrbilne n merljivom skupu R n, oznčv se s R() Drbuove sume Nek je merljiv skup u R n, i nek je P = { 1,..., k } rzbijnje skup. Nek je f : R ogrničen funkcij. Posmtrmo infimum i supremum funkcije f n svkom skupu i : m i = inf x i f(x) i M i = sup x i f(x), z svko i = 1, 2,..., k. Funkcij f je ogrničen, te je m i R i M i R z svko i. Donj i gornj Drbuov 5 sum definisne su, redom: s(f,, P) = k m i m n ( i ) i S(f,, P) = i=1 5 Jen-ston Drboux ( ), frncuski mtemtičr k M i m n ( i ). i=1
29 2.2. RIMANOV INTERAL 23 Nek je σ(f,, P, ξ) jedn Rimnov sum funkcije f n skupu u odnosu n istu podelu P. Td očigledno vže nejednkosti: s(f,, P) σ(f,, P, ξ) S(f,, P). (2.2) Nek je P = { 1,..., l } rzbijnje skup s svojstvom d z svko j {1,..., l} postoji neko i {1,..., k} tko d je j i, odnosno nek je podel P finij od podele P. N osnovu j i sledi d vži m i m j M j M i. Nek je, jednostvnosti rdi, i = 1 s, s l. Td je s(f,, P ) = s(f, i, P ) = s m t m n ( t), t=1 l m t m n ( t) = t=1 k s(f, i, P ). Iz t i z svko t {1,..., s}, sledi d je m t m i z svko t {1,..., s}. Stog je Sledi s(f, i, P ) = s(f,, P ) = s m t m n ( t) m i t=1 n s T (f, i ) i=1 i=1 s m n ( t) = m i m n ( i ). t=1 n m i m n ( i ) = s(f,, P ). i=1 Z gornje Drubove sume, pod uslovom P pokzti suprotn nejednkost: S(f,, P ) S(f,, P). Dkle, dokzli smo sledeći rezultt. P, može se nlogno Teorem Nek je merljiv podskup od R n, nek je f : R ogrničen funkcij, i nek su P i P dv rzbijnj skup, tko d je P P. Td z svki izbor tčk ξ (svk tčk ξ i pripd odgovrjućim elementu i rzbijnj P )vži: s(f,, P) s(f,, P ) σ(f,, P, ξ) S(f,, P ) S(f,, P). (2.3)
30 24 LAVA 2. INTERACIJA Definicij Broj I f = sup s(f,, P), gde je supremum uzet po svim P rzbijnjim P skup, nziv se donji integrl funkcije f n skupu. Broj I f = inf S(f,, P), gde je infimum uzet po svim rzbijnjim skup P P, nziv se gornji integrl funkcije f n skupu. N osnovu nejednkosti (2.3), sledi d vži I f I f. Dokzćemo osnovnu teoremu, kojom su odre deni ekvivlentni uslovi integrbilnosti funkcije n nekom merljivom skupu. Teorem Nek je funkcij f ogrničen n merljivom skupu R n. Td su sledeć tvr denj ekvivlentn: (1) I f = I f ; (2) Z svko ϵ > postoji rzbijnje T skup, tko d vži S T (f, ) s T (f, ) < ϵ; (3) Z svko ϵ > postoji δ >, tko d z svko rzbijnje T skup dijmetr mnjeg od δ, vži S T (f, ) s T (f, ) < ϵ; (4) Postoji integrl f = I. Ako vži bilo koje od prethodnih tvr denj, ond je I = I f = I f. Dokz. (1) = (2): Nek je ϵ >. Donji integrl I f je supremum donjih Drbuovih sum. Stog z ϵ > postoji nek podel T 1, tko d z odgovrjuću donju Drbuovu sumu vži s T1 (f, ) > I f ϵ 2. ornji integrl If je infimum gornjih Drbuovih sum. Prem tome, z ϵ > postoji podel T 2 s svojstvom S T2 (f, ) < I f + ϵ 2. Postoji podel T, koj je finij od podel T 1 i T 2 (n primer, T = T 1 T 2 ). Td je I f ϵ 2 < s T 1 (f, ) s T (f, ) I f I f S T (f, ) S T2 (f, ) < I f + ϵ 2. N osnovu pretpostvke I f = I f, sledi d vži S T (f, ) s T (f, ) < ϵ. (2) = (1): Tvr denje sledi n osnovu očiglednih nejednkosti s T (f, ) I f I f S T (f, ). (4) = (3): Pretpostvimo d postoji integrl I = f. Nek je ϵ >. Td postoji broj δ >, tko d z svku podelu T skup dijmetr mnjeg od δ, vži I ϵ 2 σ T (f,, ξ) < I + ϵ 2,
31 2.2. RIMANOV INTERAL 25 nezvisno od izbor tčk ξ i i. U prethodnim nejednkostim se može uzeti, jedn z drugim, supremum ili infimum sume σ T (f,, ξ) po svim ξ i i. Odtle neposredno sledi I ϵ 2 s T (f, ) S T (f, ) I + ϵ 2, smim tim i S T (f, ) s T (f, ) < ϵ. (3) = (2): Ov implikcij je trivijln. (3) = (4): Iz pretpostvke d vži tvr denje (3) sledi d vže tvr denj (1) i (2). Nek je ϵ >. Td postoji δ >, tko d z svko rzbijnje T skup dijmetr mnjeg od δ vži S T (f, ) s T (f, ) < ϵ. Z proizvoljn izbor tčk ξ i i vži s T (f, ) σ T (f,, ξ) S T (f, ). Tko de vži i s T (f, ) I f = I f S T (f, ). Prem tome, sledi d vži I f σ T (f,, ξ) < ϵ, z svku podelu T s osobinom d je dijmetr podele T mnji od δ i z proizvoljn izbor tčk ξ i i. Sledi d je I f jednk integrlu funkcije f n skupu, odnosno I f = f. (2) = (3): Ov implikcij je njinteresntnij. Nek je funkcij f ogrničen konstntom M n skupu, odnosno z svko x nek je f(x) M. Nek je ϵ >. Iz činjenice d vži tvr denje (2) sledi d postoji rzbijnje T = { 1,..., k } skup s svojstvom S T (f, ) s T (f, ) < ϵ. Nek je n i = inf f(x) i N i = sup f(x), i = 1,..., k. N osnovu merljivosti x i x i skupov i sledi d je mer njihovog rub jednk nuli, odnsono m n ( i ) = z svko i = 1,..., k. Nek je Γ = k i. Td je m n (Γ) =. Postoji elementrn skup σ, s svojstvim Γ σ i m n (σ) < 2M. Ne gubeći od opštosti može se pretpostviti d je σ otvoren skup. Postoji otvoren skup σ s svojstvim: Γ σ σ i σ σ =. Td je m n (σ ) < ϵ 2M i δ = inf{d(x, y) : x σ, y σ} >. Nek je T 1 = {F 1,..., F l } proizvoljno rzbijnje skup dijmetr d s svojstvom d < δ. Td je S T1 (f, ) s T1 (f, ) = i=1 l (M i m i ) m(f i ), pri čemu je m i = inf f(x) i M i = sup f(x), z svko i = 1,..., l. Nek su x F i x F i I i J podskupovi skup {1,..., l} s svojstvim: i I ko i smo ko F i im neprzn presek s Γ, j J ko i smo ko F j Γ =. Ako je i I, td vži F i σ. Stog je m(f i ) < ϵ. i=1 i I (M i m i ) m(f i ) 2M i I ϵ
32 26 LAVA 2. INTERACIJA Ako je j J, td F j Γ = i po konstrukciji skup Γ sledi d mor biti F j i z neko i. Sve tkve skupove obeležimo s 1,..., t. Tko de nek je F 1,..., F s1 1,...,F st 1,..., F st s. Td vži N krju, s s i (M j m j ) m(f j ) = (M j m j ) m(f j ) j J i=1 j=s i 1 s s i s (N i n i ) m(f j ) (N i m i ) m( i ) < ϵ. i=1 j=s i 1 i=1 S T1 (f, ) s T1 (f, )= i I (M i m i ) m(f i ) + j J(M j m j ) m(f j )<2ϵ. Time je dokzno tvr denje (3) Oznke i terminologij Ako je merljiv skup u R 2 i f R(), ond je čest oznk f = f = f(x, y) dx dy. Integrl f nziv se dvostruki integrl funkcije f n skupu. Ako je merljiv skup u R 3 i f R(), ond je f = f = f(x, y, z) dx dy dz. Integrl f je trostruki integrl funkcije f n skupu. Končno, ko je merljiv skup u R n i f R(), ond je f = f = f(x 1,..., x n ) dx 1 dx n. }{{} n put }{{} n put Integrl f je n-integrl funkcije f n skupu.
33 2.3. KLASE INTERABILNIH FUNKCIJA Klse integrbilnih funkcij Nek je R n proizvoljn merljiv skup. Nisu sve funkcije, koje su definisne n skupu, obvezno integrbilne n skupu. S druge strne, ko je R n proizvoljn merljiv skup i ko je g(x) = z svko x, td je g(ξ i ) = z svku tčku ξ i i. Stog vži g(x) dx =. Sledi d je nul-funkcij integrbiln n svkom merljivom skupu i njen integrl n tom skupu je jednk nuli. Skup intergbilnih funkcij, pod odre denim uslovim, sdrži sve neprekidne funkcije. Preciznije, vži sledeć teorem. Teorem Ako je reln funkcij f definisn i neprekidn n ztvorenom i merljivom skupu u R n, td je funkcij f integrbiln n. Dokz. Skup je merljiv i stog je ogrničen. Sledi d je kompktn skup. Prem Kntorovoj 6 teoremi, funkcij f je rvnomerno neprekidn n skupu. Nek je ϵ >. N osnovu rvnomerne neprekidnosti funkcije f sledi d postoji broj δ >, tko d z svke dve tčke x 1, x 2 s svojstvom ϵ d(x 1, x 2 ) < δ vži f(x 1 ) f(x 2 ) < m n (). Nek je T = { 1,..., k } proizvoljno rzbijnje skup dijmetr mnjeg od δ. Imjuću u vidu stndrdne oznke m i i m i, sledi d vži M i m i = sup x i f(x) inf x i f(x) = sup x i f(x) + sup x i ( f(x)) = sup x 1,x 2 i (f(x 1 ) f(x 2 )) sup f(x 1 ) f(x 2 ) x 1,x 2 i ϵ m n (). Z odgovrjuće Drbuove sume funkcije f n skupu, ispunjeno je S T (f, ) s T (f, ) < ϵ. Prem Teoremi 2.2.3, postoji integrl f. Ako je R n, td je skup relnih i neprekidnih funkcij n oznčen s C(). N osnovu prethodne teoreme, ko je merljiv i ztvoren (tj. je merljiv kompkt), ond je C() R(). Teorem Nek je reln funkcij f definisn i ogrničen n merljivom i ztvorenom skupu R n, tkv d je mer skup tčk prekid funkcije f jednk nuli. Td je funkcij f integrbiln n skupu. Dokz. Nek je M = sup f(x) <, nek je E skup tčk prekid funkcije x f u skupu, i nek je ϵ >. N osnovu m(e) =, sledi d postoji otvoren 6 eorg Ferdinnd Ludwig Philipp Cntor ( ), nemčki mtemtičr
34 28 LAVA 2. INTERACIJA elementrn skup F, tko d je E F i m(f ) < 4M. Skup \F je ztvoren i merljiv. N osnovu Teoreme funkcij f je integrbiln n skupu \F. Prem tome, postoji rzbijnje T = { 1,..., k } skup \ F, z koje vži S T (f, \ F ) s T (f, \ F ) < ϵ 2. Nek je k+1 = F. Td je T 1 = T { k+1 } rzbijnje skup i vži m( k+1 ) m(f ) < ϵ 4M. Stog, uz prirodne oznke M i i m i, vži S T1 (f, ) s T1 (f, ) (M k+1 m k+1 ) m( k+1 ) + 2M ϵ 4M + ϵ 2 = ϵ. ϵ k (M i m i ) m( i ) N osnovu Teoreme (2) sledi d je funkcij f integrbiln n skupu. i=1 2.4 Svojstv Rimnovog integrl Dokzujemo osnovn svojstv Rimnovog integrl. Nek je merljiv skup u R n, i nek je f : R funkcij definisn n. (1) Ako je m n () =, ond je f =. Dokz. N osnovu m n () = sledi σ T (f,, ξ) =, te je i f =. (2) 1 = m n (), pri čemu je 1 konstnt funkcij x 1 z svko x. Dokz. Z proizvoljno rzbijnje T merljivog skup vži σ T (f,, ξ) = ( m m ) 1 m n ( i ) = m n i = m n (). i=1 i=1 Posledic Ako je merljiv skup u R 2, ond je Ako je V merljiv skup u R 3, ond je V dx dy dz = m 3 (V ). dx dy = m 2 (). (3) Ako je f(x) z svko x, i ko je f integrbiln funkcij n, ond je f.
35 2.4. SVOJSTVA RIMANOVO INTERALA 29 Dokz sledi n osnovu nejednkosti σ T (f,, ξ) = n f(ξ i ) m( i ) i=1 i definicije Rimnovog integrl. (4) Ako su f i g integrbilne funkcije n, i ko je α, β R, ond je funkcij αf + βg integrbiln n i vži (αf + βg) = α f + β g. Dokz ovog tvr denj sledi n osnovu jednkosti σ T (αf + βg,, ξ) = α σ T (f,, ξ) + β σ T (f,, ξ). (5) Ako su f i g integrbilne funkcije n, i ko z svko x vži f(x) g(x), td je f g. Dokz sledi neposredno n osnovu (3) i (4), imjući u vidu d je g f n. (6) Nek su A i B merljivi skupovi u R n, A B, i nek je f ogrničen i integrbiln funkcij n B. Td je f integrbiln funkcij n A. Dokz. Skup C = B \ A je merljiv. Svko rzbijnje skupov A i C indukuje jedno rzbijnje skup B. Obrnuto, svko rzbijnje skup B može se učiniti finijijm, tko d je to rzbijnje unij rzbijnj skup A i rzbijnj skup C. Stog, nek je T rzbijnje skup B, koje se sstoji od rzbijnj T 1 skup A i rzbijnj T 2 skup C. Vži očigledn nejednkost: S T1 (f, A) s T1 (f, A) S T (f, B) s T (f, B). Nek je ϵ >. Kko je f R(B), sledi d postoji rzbijnje T skup B tko d je S T (f, B) s T (f, B) < ϵ. Prem prethodnom, T = T 1 T 2, pri čemu je T 1 rzbijnje skup A, dok je T 2 rzbijnje skup B \ A. Sledi d je S T1 (f, A) s T1 (f, A) < ϵ, te je f R(A). (7) Nek je i m n ( ) =. Funkcij f je integrbiln n ko i smo ko je f integrbiln n \ ; u tom slučju je f = f. \ Dokz. Svko rzbijnje skupov i \ dovodi do rzbijnj skup. Obrnuto, ko je T rzbijnje skup, ond postoje rzbijnj: T 1 skup \ i T 2 skup 1, tko d T 1 T 2 jeste finije rzbijnje of T. Dkle,
36 3 LAVA 2. INTERACIJA bez gubljenj opštosti, posmtrmo rzbijnje T = T 1 T 2, pri čemu je T 1 rzbijnje skup \, T 2 je rzbijnje skup. Kko je σ T (f,, ξ) = z svki izbor tčk ξ, sledi d je σ T (f,, ξ) = σ T (f, \, ξ). Odvde sledi rezultt, prelskom n grničnu vrednost kd d(t ). (8) Nek su A i B merljivi skupovi u R n s svojstvim: m n (A B) =, A B =, i nek je funkcij f ogrničen n skupu. Td je funkcij f integrbiln n skupu, ko i smo ko je f integrbiln n skupovim A i B. U tom slučju vži jednkost f = f + f. (2.4) A Dokz. Svko rzbijnje skupov A i B proizvodi rzbijnje skup. S druge strne, svko rzbijnje skup može se učiniti finijim tko, d su skupovi novog rzbijnj sdržni i u polznom rzbijnju skup A i u polznom rzbijnju skup skup B. Činjenic m n (A B) = grntuje d je integrl n skupu bilo koje integrbilne funkcije jednk integrlu te iste funkcije n skupu \ (A B). Prem tome, posmtrmo rzbijnje T skup koje indukuje rzbijnje T 1 skup A i rzbijnje T 2 skup B, pri čemu znemrujemo skup A B. Sledi očigledn jednkost σ T (f, ) = σ T1 (f, A) + σ T2 (f, B). (2.5) Ukoliko postoje integrli f i f, td postoji i integrl f, te sledi A B A B tržen jednkost integrl (2.4). Obrnuto, iz ogrničenosti i integrbilnosti funkcije f n skupu, sledi integrbilnost funkcije f n skupovim A i B. (9) Ako su f i g ogrničene i integrbilne funkcije n merljivom skupu R n, td je i fg integrbiln n skupu. Dokz. Obzirom d su funkcije f i g ogrničene n skupu, postoji neki broj L >, tko d z svko x vži f(x) L i g(x) L. Nek je ϵ > proizvoljn broj. N osnovu ogrničenosti i integrbilnosti funkcij f i g n skupu, sledi d postoji rzbijnje T = { 1,..., l } skup, tko d vži B S T (f, ) s T (f, ) = S T (g, ) s T (g, ) = l i=1 l i=1 (M i m i ) m( i ) < ϵ 2L (N i n i ) m( i ) < ϵ 2L. i
37 2.4. SVOJSTVA RIMANOVO INTERALA 31 Pri tome koristimo oznke: M i = sup f(x), m i = inf f(x), x i x i N i = sup g(x), n i = inf g(x), x i x i K i = sup f(x)g(x), k i = inf f(x)g(x). x i x i N osnovu osobin supremum i infimum, vži sledeć procen: K i k i = sup fg inf i i fg sup i f sup g inf f inf g i i i = M i N i m i n i = M i N i m i N i + m i N i m i n i = N i (M i m i ) + m i (N i n i ) L[(M i m i ) + (N i n i )]. N osnovu poslednje nejednkosti, sledi d vži: S T (fg, ) s T (fg, ) = l (K i k i ) m( i ) i=1 L [(S T (f, ) s T (f, )) + S T (g, ) s T (g, ))] < ϵ. Prem tome, funkcij fg je integrbiln n skupu. (1) Ako je funkcij f ogrničen i integrbiln n, ond je funkcij f tko de integrbiln n i vži f f. Dokz. Nek je ϵ >. N osnovu ogrničenosti i integrbilnosti funkcije f n skupu, postoji podel T = { 1,..., l } skup, tko d vži nejednkost S T (f, ) s T (f, ) = l (M i m i ) m( i ) < ϵ. i=1 Koristimo oznke
38 32 LAVA 2. INTERACIJA M i = sup f(x), m i = inf f(x), x i x i N i = sup f(x), n i = inf f(x). x i x i N osnovu nejednkosti f(x) f(y) f(x) f(y), sledi nejednkost N i n i M i m i, z svko i = 1,..., l. N osnovu ove nejednkosti proizilzi procen S T ( f, ) s T ( f, ) S T (f, ) s T (f, ) < ϵ. Prem tome, funkcij f je integrbiln n skupu. Nek su sd σt 1 (f,, ξ) = t f(ξ i ) m n ( i ) i σt 2 (f,, ξ) = t i=1 f(ξ i ) m( i ) Rimnove sume z integrle f i f redom. N osnovu očigledne nejednkosti σt 1 (f,, ξ) σ2 T ( f,, ξ), sledi odgovrjuć nejednkost integrl. (11) (Teorem o srednjoj vrednosti interl) Nek je merljiv skup u R n, f, g : R integrbilne funkcije, m f(x) M z svko x, i g(x) z svko x. Td postoji tčk λ [m, M], tko d je fg = λ g. Ako je uz to povezn i kompktn skup, i ko je f neprekidn funkcij n, td postoje tčke ν, ξ tko d je 1 fg = f(ν) g i f(ξ) = f. m n () Dokz. N osnovu g i m f M, sledi mg f g M g, te je m g fg M g. Ako je g =, ond λ može biti bilo koji reln broj. Ako je g >, td n osnovu prethodne procene vži fg λ = [m, M]. g i=1
39 2.5. EOMETRIJSKI I FIZIČKI SMISAO INTERALA 33 Ako je povezn i kompktn skup i f neprekidn funkcij n, td f dostiže svoj minimum i mksimum n. Stog se može uzeti m = min x f(x), M = mx x f(x). N osnovu poveznosti skup sledi d postoji ν s svojstvom f(ν) = λ [m, M]. Poslednj jednkost sledi ko se posmtr funkcij g(x) = x z svko x. 2.5 eometrijski i fizički smiso integrl Dokzujemo sledeće tvr denje, koje je relevntno z geometrijsko shvtnje integrl. Teorem Nek je R n merljiv skup, i nek je funkcij f ogrničen i integrbiln n skupu. Td grfik funkcije f, odnosno skup Γ r (f) = {(x, f(x)) : x } R n+1, jeste merljiv u R n+1 i njegov mer jeste nul, odnosno m n+1 (Γ r (f)) =. Dokz. Nek je k N. U prostoru R n (koji sdrži ) posmtrmo hiper-rvni koje su normlne n svku koordintnu osu (dkle, prlelne 1 svim preostlim koordintnim osm) i tu osu seku u tčki l, pri čemu 2 k je l Z. N tj nčin se dobij 1 -mrež prostor R n. 2 k Dkle, ko je k = 1, ond postoji fmilij hiper-rvni, tko d je odre den potfmilij tih rvni normln n jednu koordintnu osu i tu osu pomenut potfmilih hiper-rvni seče u tčkm:, 1, 1, 2, 2,.... Ako je k = 2, ond hiper-rvni seku koordintnu osu (onu osu kojoj su hiper-rvni normlne) u tčkm, 1 2, 1 2, 1, 1, 3 2, 3 2, 2, 2,.... Dkle, 1 2 -mrež je finij od 1-mreže, 1 4 -mrež je finij od 1 2-mreže, i tko redom. Z svko k N posmtrmo n-intervle odre dene 1 -mrežnom, koji su 2 k sdržni u. Nek su to skupovi {E1 k, Ek 2,..., Ek l k }. Td je te je i m n (F k ) = F k = l k i=1 l k i=1 E k i, m n (E k i ) m n ().
40 34 LAVA 2. INTERACIJA Skup je merljiv, te je lim m n(f k ) = m i n() = m n (). k Nek je ϵ >. Postoji k N, tko d je m n () ϵ < m n (F k ) m n (). Posmtrjmo sd skup ko podskup prostor R n+1. Svki skup Ei k je n-intervl, li je to istovremeno degenerisni n + 1-intervl, koji im 2 k temen, i temen su oznčen s T 1,..., T 2 k. Nek je ξ i Ei k. Kroz svko teme posmtrmo prvu prlelnu dodtoj osi, koj je n + 1 po redu (tj. prv je prleln koordintnoj osi koj ne pripd polznom prostoru R n ). Posmtrmo duži n toj prvoj, koje polz od temen T j, zvršvju, redom, u tčkm s vrednostim m j, f(ξ j ), M j. Ako je k dovoljno veliki broj, ond su m j, f(ξ j ), M j istog znk (osim ko je f(ξ j ) =, li ovj specijln slučj ne predstvlj suštinksu prepreku u rzmtrnju). Nek je, n primer m j, f(ξ j ), M j >. Posmtrjmo (n + 1)-intervle Td je K j = E k j (, m j ), L j = E k j [, M j ]. m n+1 (K j ) = m n (E k j ) m j, m n+1 (L j ) = m n (E k j ) M j. rfik funkcije f n skupu E j je sdržn u skupu L j \ K j. Stog je grfik funkcije f n skupu F k sdržn u skupu l k (K j \ L j ). Vži m n+1 l k j=1 j=1 k l (K j \ L j ) = (M j m j )m n (Ej k ). Poslednj sum je rzlik gornje i donje Drbuove sume funkcije f n skupu F k. Funkcij f je integrbiln n, p je integrbiln i n F k. Stog postoji novi broj k N (veći od prethodnog k), tko d je Sd je k l j=1 (M j m j )m n (Ej k ) < ϵ. j=1 S(f, ) s(f, ) = S(f, F k ) s(f, F k ) + S(f, \ F k ) s(f, \ F k ).
41 2.5. EOMETRIJSKI I FIZIČKI SMISAO INTERALA 35 Funkcij f je ogrničen, te je f N n skupu. Dkle, z unpred zdni broj ϵ > postoji broj k N (odnosno, postoji mrež 1 koj 2 k indukuje rzbijnje skup ), tko d je S(f, ) s(f, ) ϵ + Nϵ. Immo u vidu d je grfik funkcije f sdržn u (n + 1)-intervlim čij je (n + 1)-mer mnj od ϵ + 2Mϵ. Sledi d je m n+1 (Γ r (f)) = Interpretcij dvostrukog integrl Rzmotrimo dvostruki integrl. Nek je merljiv skup u R 2, i nek je f : R nenegtivn, ogrničen i integrbiln funkcij. Unutršnjost skup oznčimo s, rub skup oznčimo s. Iz merljivosti skup sledi d je m 2 ( ) =. Stog je f = f. rfik Γ r (f) = {(x, y, z) : (x, y), z = f(x, y)} je grfik površi u R 3. Posmtrjmo cilindr V odre den skupom, skupom Γ r (f), čije su izvodnice prlelne z-osi, i sve izvodnice prolze kroz. N ovj nčin je ogrničen skup u prostoru R 3. N osnovu prethodne teoreme, m 3 (Γ r (f)) =. Tko de je m 3 () =, jer je ogrničen i degenerisn skup u R 3. Procenimo meru cilindrske površi, oznčene s K. Kko je m 2 ( ) =, skup je pokriven elementrnim 2-intervlim čij je ukupn mer proizvoljno ml (tj. može se učiniti mnjom od bilo kog unpred zdnog broj ϵ > ). Stog je cilindrsk površ K sdržn u uniji končno mnogo 3-intervl, čij se ukupn trodimenzionln mer može učiniti proizvoljno mlom. Stog je m 3 (K) =. Dkle, m 3 (V ) ne zvisi od trodimenzionlnih mer skupov, Γ r (f), K. Posmtrjmo proizvoljnu 1 -mrežu prostor R 2, koj indukuje rzbijnje 2 k T skup. Donje i gornje Drbuove sume funkcije f n skupu, indukovne rzbijnjem T, sd čine trodimenzionlne mere cilindr upisnih u V, i cilindr opisnih oko V. Funkcij f je integrbiln n, te je f = m 3 (V ). Ukoliko bi funkcij f bil negtivn n, ond bi bilo f = m 3 (V ).
42 36 LAVA 2. INTERACIJA Interpretcij trostrukog integrl Trostruki integrl im jednostvnu fizičku interpretciju. Nek je merljiv skup u R 3, koji je model nekog tel u prostoru. Pretpostvimo d je f nenegtivn, ogrničen i integrbiln funkcij n, koju smtrmo funkcijom rspodele gustine tel. Posmtrmo rzbijnje T = { 1,..., m } skup, koje je dovoljno fino, odnosno dovoljno mlog dijmetr, d se funkcij rspodele gustine f u skupu (telu) i nezntno rzlikuje od konstnte. Td je z svko ξ i i veličin f(ξ i ) m( i ) približno jednk msi tel i. Prem tome, Rimnov sum σ T (f, ) približno je jednk msi tel. Očigledno, grešk u rčunu se smnjuje ukoliko se smnjuje i dijmetr podele T. Dkle, pod pretpostvkom d je funkcij f rspodel gustine tel, sledi d je f ms tel. 2.6 Specifičnosti integrl u R n z n 2 Rimnov integrl funkcije f n skupu je prirodno uopštenje integrl n [, b]. Definicij integrl, kko smo do sd pokzli, zhtev uvo denje pojm mere u R n. Bogtij geometrijsk struktur prostor R n u odnosu n R donosi izvesne specifične osobine integrl, koje se ne zsnivju smo n rzličitoj interpretciji mere. U slučju integrl b f(x) dx funkcije jedne promenljive, u smoj definiciji je sdržn uslov ogrničenosti funkcije f. U suprotnom rdi se o nesvojstvenom integrlu, koji se posebno rzmtr. Me dutim, ko je merljiv skup u R n, n 2, i f R(), ond funkcij f ne mor biti obvezno ogrničen. Primer Nek je = [, 1] {} segment u R 2. Očigledno, m 2 () =. Bilo koj reln funkcij f s domenom, mor biti integrbiln n. N primer, nek je z svko y R: f(x, y) = { 1 x, x (, 1],, x =. Funkcij f očigledno nije ogrničen, li je f = (Slik 5).
43 2.6. SPECIFIČNOSTI INTERALA U RN ZA N 2 37 O Slik 5. 1 Definicij Merljiv skup R n je jednostvn, ko z svko ϵ > postoji rzbijnje T skup, tko d je d(t ) < ϵ i d je svki skup iz T pozitivne n-dimenzionlne mere. Skup u Primeru nije jednostvn, jer z bilo koju podelu T skup, svki element iz im dvodimenzionlnu meru jednku nuli. S druge strne, mnogi skupovi zist jesu jednostvni. Teorem Ako je otvoren i merljiv skup u R n, ond je jednostvn skup. Dokz. Nek je otvoren merljiv skup, i nek je ϵ >. Posmtrjmo 1 -mrežu prostor R n. Ako je E k 2 k j jedn n-intervl odre den ovom mrežom, ond je njegov dijmetr d(ej k) = n. Postoji k N tko d je d(e k 2 2k j ) < ϵ. Z ovko odbrno k, posmtrjmo rzbijnje T = {Ej k : j} skup, pri čemu posmtrmo smo neprzne skupove Ej k. Pretpostvimo d postoji neki Ej k, tko d je m n(ej k ) =. Td skup Ej k ne sdrži ni jedn otvoreni n-intervl. Stog im przn presek s (Ej k). Prem tome, seče smo rub skup Ej k u nekoj tčki x. Ako bi x bil unutršnj tčk skup, ond bi skup seko unutršnost skup Ej k, što je nemoguće. Dkle, x. Poslednj činjenic je nemoguć, jer je otvoren, p ne sdrži ni jednu svoju rubnu tčku. Sledi d je m n (Ej k ) > z svki skup Ek j. Ako je merljiv podskup od R n, i ko je skup jednostvn, ond je i skup jednostvn. Stog su i ztvorenj otvorenih merljivih skupov tko de jednostvni skupovi. Teorem Ako je merljiv i jednostvn skup u R n, i ko je f R(), ond je f ogrničen n.
44 38 LAVA 2. INTERACIJA Dokz. Pretpostvimo d je f neogrničen n. Z proizvoljno δ > postoji rzbijnje T = { 1,..., k } skup, tko d je d(t ) < δ i m( j ) > z svko j = 1,..., k. Funkcij f nije ogrničen n br jednom elementu iz T, recimo f nije ogrničen n 1. Posmtrjmo proizvoljne tčke ξ j j z j = 1,..., k, i odgovrjuću Rimnovu sumu σ T (f,, ξ) = f(ξ 1 )m n ( 1 ) + k f(ξ j )m n ( j ). Fiksirjmo vrednosti ξ 2,..., ξ k. Td z svko M > možemo odbrti tčku ξ 1 1, tko d je σ T (f,, ξ) M. Ovo je u suprotnosti s pretpostvkom f R(). Sledi d je f ogrničen n. 2.7 Izrčunvnje integrl Integrle funkcij n merljivivm skupovim iz R n izrčunvmo njčešće njihovim svodjenjem n ponovljene integrle Slučj prostor R 2 j=2 Dokzćemo njpre osnovne rezultte u prostoru R 2. Teorem Pretpostvimo d vži: (1) Funkcij (x, y) f(x, y) je integrbiln u prvougoniku Π = {(x, y) : x b, c y d}; d (2) Z svko x [, b] postoji integrl f(x, y) dy. Td integrl x segmentu [, b] i vži Π f(x, y) dx dx = c d f(x, y) dy definiše integrbilnu funkciju po x n c b d c f(x, y) dy dx b d dx c f(x, y) dy. Dokz. Odberimo tčke c = y < y 1 < y 2 < < y n = d i = x < x 1 < x 2 < < x m = b s svojstvom y i y i 1 = h z svko i i x j x j 1 h z svko j. Odberimo proizvoljne tčke α j [x j 1, x j ] i β i [y i 1, y i ]. N ovj nčin postigli smo rzbijnje segment [c, d] i [, b], ko i rzbijnje
45 2.7. IZRAČUNAVANJE INTERALA 39 prvougonik Π mnjim prvougonicim s temenim u tčkm (x j, y i ). Z proizvoljno x [, b] vži d je n n s h (x) = f(x, β i )(y i y i 1 ) = f(x, β i )h i=1 Rimnov sum integrl σ h = = n d f(x, y) dy. Tko de, c i=1 j=1 n i=1 j=1 i=1 m f(α j, β i )(x i x i 1 )(y j y j 1 ) m f(α j, β i )(x i x i 1 )h je Rimnov sum koj odgovr integrlu f(x, y) dx dy. Posmtrjmo Rimnovu sumu integrl S h = b Π s h (x) dx, koj je jednk m s h (α j )(x j x j 1 ) = σ h. j=1 Zbog uslov x j x j 1 h z svko j, sledi d ko dijmetr podele skup Π teži nuli, ond teže nuli i dijmetri podele segment [c, d] i [, b], ov činjenic se jednostvno opisuje ko h. N osnovu jednkosti dvojne i ponovljene grnične vrednosti funkcij dve promenljive, proizilzi i jednkost integrl: b d f(x, y) dx dy = f(x, y) dy dx. Time je teorem dokzn. Primer Izrčunti Π Π c xy dx dy, gde je Π = [, 1] [2, 3]. Rešenje. Funkcij (x, y) f(x, y) = xy je neprekidn, te stog i integrbiln n skupu Π. N osnovu Teoreme 2.7.1, sledi Π xy dx dy = 1 3 x dx y dy =
46 4 LAVA 2. INTERACIJA Definicij Nek su φ i ψ neprekidne funkcije n segmentu [, b] i z svko x [, b] nek vži φ(x) ψ(x). Skup Ω = {(x, y) : φ(x) y ψ(x), x b} jeste elementrn skup u odnosu n y-osu (Slik 6). Slik 6. Teorem Skup Ω u prethodnoj Definiciji je merljiv u R 2. Dokz. Nek je I duž u rvni koj spj tčke (, φ()) i (, ψ()). Nek je J duž koj spj tčke (b, φ(b)) i (b, ψ(b)). Td je rub skup Ω Ω = I J Γ r (φ) Γ r (ψ), gde je Γ r (φ) grfik funkcije φ, Γ r (ψ) grfk funkcije ψ. rfik integrbilne funkcije, smim tim i neprekidne funkcije, im dvodimenzionlnu meru jednku nuli. Dkle, m 2 ( Ω) =, odkle proizilzi d je skup Ω merljiv u R 2. Teorem Nek je Ω elementrn skup u odnosu n y-osu, odre den Definicijom Nek je (x, y) f(x, y) integrbiln funkcij n skupu ψ(x) Ω, pri čemu z svko x [, b] postoji integrl f(x, y) dy. Td vži sledeć formul φ(x) Ω f(x, y) dx dy = b ψ(x) dx f(x, y) dy. φ(x) Dokz. Funkcije φ i ψ su neprekidne n segmentu [, b] i dostižu, redom, svoj minimum i mksimum n ovom segmentu. Nek je c = min x [,b] φ(x), d = mx x [,b] ψ(x).
47 2.7. IZRAČUNAVANJE INTERALA 41 Očigledno je Ω Π = [, b] [c, d]. Skup Ω je merljiv, p je i skup Π \ Ω tko de merljiv. Nek je funkcij F definisn n skupu Π sledeći nčin: { f(x, y), (x, y) Ω, F (x, y) =, (x, y) Π \ Ω. Sledi Π F (x, y) dx dy = Ω = Prem Teoremi 2.7.1, proizilzi d vži Ω F (x, y) dx dy + f(x, y) dx dy. Π\Ω F (x, y) dx dy Ω f(x, y) dx dy = = = b b b d dx c dx dx F (x, y) dy φ(x) c ψ(x) φ(x) dy + ψ(x) φ(x) f(x, y) dy. f(x, y) dy + d ψ(x) dy Time je teorem dokzn. Primer Izrčunti integrl x 1, x 2 y 1} (Slik 7). x 2 dx dy n skupu = {(x, y) : 1 Slik 7.
48 42 LAVA 2. INTERACIJA Rešenje. N osnovu Teoreme 2.7.3, vži: x 2 dx dy = dx x 2 1 x 2 dy = 1 x 2 (1 x 2 ) dx = Primer Nek je skup ogrničen kružnicm x 2 + y 2 = 4 i x 2 2x+y 2 =. Prikzti dvostruki integrl f(x, y) dx dy ko dv uzstopn integrl (Slik 8). Slik 8. Rešenje. Skup je unij tri elemtrn skup u odnosu n y-osu: Ω 1 = {(x, y) : 2 x, 4 x 2 y 4 x 2 } Ω 2 = {(x, y) : x 2, 4 x 2 y 2x x 2 }, Ω 3 = {(x, y) : x 2, 2x x 2 y 4 x 2 }. Prem Teoremi sledi f(x, y) dx dy = dx dx 4 x 2 4 x 2 f(x, y) dy + 4 x 2 2x x 2 f(x, y) dy. 2 2x x 2 dx f(x, y) dy 4 x 2
49 2.7. IZRAČUNAVANJE INTERALA 43 Slik 9. Primer Izrčunti integrl (Slik 9) I = π/2 dy π/2 y sin x x dx. Rešenje. Poznto je d neodre deni integrl sin x x sin x u končnom obliku. Vži lim x sin x x = ogrničen i neprekidn n posmtrnom skupu x dx ne može biti izrčunt = 1, odkle sledi d je funkcij (x, y) { (x, y) : y π 2, y x π } = {(x, y) : x π } 2 2, y x. Prem Teoremi 2.7.3, vži: I = = π/2 π/2 dy π/2 y sin x x sin x x dx = x dy dx = sin x x π/2 dx dy = π/2 sin x dx = 1. x dx sin x x dy Slučj prostor R n, n 3 Nije teško dokzti rezultt nlogn Teoremi u prostoru veće dimenzije.
50 44 LAVA 2. INTERACIJA Teorem Nek su = k (b i i ) i K = m (d i c i ) prvougonici, i=1 redom, u R k i R m. Nek je funkcij f integrbiln n prvougoniku K. Ako z svko x postoji integrl f(x, y) dy, td vži formul K f(x, y) dx dy = dx f(x, y) dy. K Definicij Nek je merljiv skup u R n i nek su φ, ψ : R neprekidne funkcije s svojstvom φ(x) ψ(x) z svko x = (x 1,..., x n ). Skup K j=1 Ω = {(x 1,..., x n, x n+1 ) : x, φ(x) x n+1 ψ(x)} R n+1 jeste elementrn skup u odnosu n osu x n+1. Teorem Elementrn skup Ω, odre den Definicijom je merljiv u prostoru R n+1. Teorem Nek je Ω merljiv i elementrn skup u odnosu n osu x n+1, opisn u 2.21 Definiciji. Nek je (x, x n+1 ) f(x, x n+1 ) integrbiln ψ(x) funkcij n Ω i nek z svko x postoji interl f(x, x n+1 ) dx n+1. Td vži formul Ω f(x, x n+1 ) dx dx n+1 = dx ψ(x) φ(x) φ(x) f(x, x n+1 ) dx n+1. Primer Izrčunti trostruki integrl I = xyz dx dy dz ko je skup = [, 1] [2, 3] [4, 5]. Rešenje. Prem Teoremi vži I = 1 3 x dx 2 5 y dy 4 z dz = Primer Izrčunti trostruki integrl I = z dx dy dz n skupu Ω ogrničenom rvnim x + y + z = 1, x =, y =, z = (Slik 2.7.2). Ω
51 2.8. SMENA PROMENLJIVIH 45 Rešenje. Skup Ω prikzn je n sledeći nčin: Ω = {(x, y, z) : x 1, y 1 x, z 1 x y}. Ω je elementrn u odnosu n z-osu. Nek je skup u rvni ogrničen prvm x + y = 1, x = i y =. Skup je elementrn u odnosu n y-osu. Prem Teoremi vži Ω z dx dy dz = = = x dx dx dy 1 x y z dz = 1 2 (1 x y) 2 dy = dx (1 x y) 2 dx dy 1 x t 2 dt 2.8 Smen promenljivih U opštem slučju, potrebno je integrl neke funkcije izrčunti n skupu koji nije elementrn u odnosu n neku koordintnu osu. Stog se uvodi smen promenljivih. Skup ( R n ) je povezn ko z svke dve tčke A, B, postoji neprekidno preslikvnje γ : [, b] s svojstvom d je γ() = A i γ(b) = B. Otvoren i povezn skup jeste oblst. Ako je oblst, ond je ztvorenje oblsti. Posmtrmo preslikvnj definisn n oblstim u R n. Nek je R n oblst i nek su definisne funkcije (ξ 1,..., ξ n ) φ 1 (ξ 1,..., ξ n ),..., φ n (ξ 1,..., ξ n )
52 46 LAVA 2. INTERACIJA z ξ = (ξ 1,..., ξ n ). Td je φ(ξ) = (φ 1 (ξ 1,..., ξ n ),..., φ n (ξ 1,..., ξ n )) D, gde je D neki novi skup u R n. Preciznije, D je slik skup koordintnim preslikvnjim φ 1,..., φ n. Zhtev se d svi prcijlni izvodi prvog red φ i (i, j = 1,..., n) budu neprekidne funkcije n. Tko de, pretpostvlj ξ j se d je jkobijn 7 ovog koordintnog preslikvnj rzličit od nule, odnosno J = D(φ 1,..., φ n ) D(ξ 1,..., ξ n ) = φ 1 ξ 1. φ n ξ 1 φ 1 φ n. φ n ξ n z svko (ξ 1,..., ξ n ). Td je preslikvnje φ = (φ 1,..., φ n ) : R n regulrno (ili dopustiv trnsformcij odnosno smen). Preslikvnje φ je bijektivno iz n D. Osim tog, φ je otvoreno preslikvnje, odnosno φ() = D, pri čemu je D oblst (videti dogovrjuće rezultte iz predmet Mtemtičk nliz 3). Formulišemo bez dokz tvr denje, koje ilustruje ulogu jkobijn preslikvnj. Teorem Nek je φ : R n regulrno preslikvnje, pri čemu je oblst u R n. Nek je Π n-dimenzionln kock u strnice h, kojoj pripd tčk M i nek je Π = φ(π). Td je Π merljiv skup u R n i m n (Π ) lim h m n (Π) = lim m n (Π ) h h n = J(M) i ov konverencij je rvnomern po M. Ovde je s J(M) oznčen vrednost jkobijn preslikvnj φ u tčki M. Sd dokzujemo vžnu teoremu o smeni promenljivih u višestrukom integrlu. Teorem Nek je merljiv oblst u prostoru promenljivih ξ 1,..., ξ n, D nek je merljiv oblst u prostoru promenljivih x 1,..., x n. Nek je φ = (φ 1,..., φ n ) : D regulrno preslikvnje, odnosno x 1 = φ 1 (ξ 1,..., ξ n ),..., x n = φ n (ξ 1,..., ξ n ), J = D(φ 1,..., φ n ) D(ξ 1,..., ξ n ), (ξ 1,..., ξ n ). 7 Crl ustv Jcob Jcobi ( ), nemčki mtemtičr
53 2.8. SMENA PROMENLJIVIH 47 Ako je (x 1,..., x n ) f(x 1,..., x n ) neprekidn funkcij n skupu D, ond vži jednkost D f(x 1,..., x n ) dx 1 dx n = (2.6) = f(x 1 (ξ 1,..., ξ n ),..., x n (ξ 1,..., ξ n )) J (2.7) dξ 1 dξ n. (2.8) Dokz. Poznto je d je kompozicij neprekidnih funkcij tko de neprekidn funkcij. Oblsti D i su merljive, prem tome i ogrničene. Skupovi i D su kompktni. Neprekidne funkcije n kompktnim skupovim jesu integrbilne. Stog ob integrl u (2.6) postoje. Dokzujemo njihovu jednkost. Funkcij f je neprekidn n kompktnom skupu D, te je stog ogrničen n D. Postoji broj L >, tko d z svko x D vži f(x) L. Jkobijn J je neprekidno preslikvnje n kompktu. Stog postoji broj K, tko d z svko ξ vži J(ξ) K. Posmtr se podel prostor R n promenljivih ξ 1,..., ξ n prvm prlelnim koordintnim osm, pri čemu su susedne prlelne prve uvek n rstojnju h. Sve kocke koje imju neprzn presek s oznčimo s 1,..., l. Skup {1,..., l} podelimo n dv disjunktn skup I i J n sledeći nčin: i I ko i smo ko i = ; j J ko i smo ko j. Sd je j. j J Nek je D i = φ( i ), pri čemu je φ = (φ 1,..., φ n ). N osnovu Teoreme postoje tčke M i i, i I, tko d vži m n (D i ) = J(M i ) m n ( i ) + ϵ(h)m n ( i ), pri čemu je lim ϵ(h) = rvnomerno po M i i. Nek je N i = φ(m i ) D i, h i I. Nek je ϵ > proizvoljn broj. N osnovu činjenice ( m n )( ) = sledi d se h može odbrti dovoljno mlo, tko d je m n j < ϵ 4LK. Td je j J f(n i ) J(M i ) m n ( i ) < ϵ 4. (2.9) j J
54 48 LAVA 2. INTERACIJA Očigledno vži f(n i )m n (D i ) = f(n i ) J(M i ) m n ( i ) + f(n i )ϵ(h)m n ( i ), i I i I i I (2.1) Obzirom d je konvergencij ϵ(h) kd h rvnomern po M i, sledi ϵ d postoji dovoljno mlo h, tko d je ispunjeno ϵ(h) < 4L m(). Prem tome, f(n i )ϵ(h)m n ( i ) L ϵ 4L m n () m n() = ϵ 4. (2.11) i I N osnovu integrbilnosti funkcije f n skupu D sledi d postoji dovoljno mli broj h, s svojstvom l f(x) dx f(n i ) m n (D i ) < ϵ 4. (2.12) f(n i ) J(M i ) m n ( i ) je Rimnov sum koj odgovr integrlu Sum l i=1 D i=1 f(φ(ξ)) J(ξ) dξ. (2.13) Preslikvnje φ : D je regulrno, specijlno i neprekidno, te je ogrničeno. Postoji broj S >, tko d z svko ξ vži φ(ξ) S. Skupovi { 1,..., l } čine rzbijnje skup dijmetr h n (u n- dimenzionlnom prostoru). Prem tome, dijmetr rzbijnj { i } teži nuli ko i smo ko h. I fmilij {D 1,..., D l } čini rbijnje skup D dijmetr ne većeg od Sh n. Prem tome, ko h, ond i dijmetr rzbijnj {D i } teži nuli. Inverzno preslikvnje φ 1 : D je tkodje regulrno (i neprekidno). Prem tome, ko dijmetr rzbijnj {D i } teži nuli, ond i h. Regulrno preslikvnje φ : D je otvoreno, odnosno slik tčke skup u tčke skup D. Obzirom d je i inverzno preslikvnje regulrno (smim tim i otvoreno), sledi d φ preslikv rub skup n rub skup D. Prem tome, skup E = D j sdrži rub skup D i m(e) M n h n ( n) n. j J Z dto ϵ > postoji dovoljno mlo h, tko d vži m(e) ϵ 4L. Sd je f(n j ) m(d j ) < ϵ 4. (2.14) j J
55 2.8. SMENA PROMENLJIVIH 49 Sd dolzimo do procene: l f dx f(n i ) J(M i ) m n ( i ) D i=1 l f dx f(n i )m n (D i ) D i=1 + l l + f(n i )m n (D i ) f(n i ) J(M i ) m n ( i ) i=1 i=1 l f dx f(m i )m(d i ) D i=1 + + f(n i )m(d i ) f(n i ) J(M i ) m n ( i ) i I i I + f(n j )m n (D j ) + f(n j ) J(M j ) m n ( j ) j J ϵ 4 + ϵ 4 + ϵ 4 + ϵ 4 = ϵ Pri tome, prv psolutn vrednost je mnj od ϵ 4 n osnovu (2.12), drug psolutn vrednost je mnj od ϵ 4 n osnovu formule (2.1) i nejednkosti (2.11). Treć psolutn vrednost je mnj od ϵ 4 n osnovu nejednkosti (2.14). Četvrt psolutn vrednost je mnj od ϵ 4 n osnovu nejednkosti (2.9). Sd, imjući u vidu Rimnovu sumu integrl u (2.13), sledi tržen jednkost integrl f dx = f(φ(ξ)) J(ξ) dξ. D j J Prethodn teorem im primene u mnogim konkretnim slučjevim Polrn smen u rvni Dobro je poznto d svk tčk P = (x, y) (, ) u rvni n jedinstven nčin može biti prikzn korišćenjem polrnog rdijus i polrnog ugl.
56 5 LAVA 2. INTERACIJA Polrni rdijus je intenzitet vektor OP, polrni ugo je ugo koji pozitivni deo x-ose zklp s vektorom OP, počev od pozitivnog del x-ose suprotno kretnju kzljke n čsovniku (Slik 1). Slik 1. U ovom slučju z svku tčku (x, y) (, ) postoje jedinstveni brojevi r > i φ < 2π, tko d vži x = r cos φ, y = r sin φ. Nrvno, ko je x = y =, ond je r =, φ može biti bilo koji ugo. Inverzne trnsformcije jesu r = x 2 + y 2, φ = rctg y x. Jkobijn uvedenog preslikvnj jeste J = cos φ sin φ r sin φ r cos φ = r. Očigledno je J zbog uslov r >.
57 2.8. SMENA PROMENLJIVIH 51 Slik 11. Ako je skup cel rvn s izuzetkom koordintnog početk, nlizirmo št je skup D, odnosno domen promenljivih r i φ. Očigledno, r-os pripd skupu, li ne i ostli deo rub (Slik 11). Ovj nedosttk neće biti presudn prilikom izrčunvnj višestrukih integrl. Rzlog leži u činjenici d je površin tčke ili duži jednk nuli. Primer Ispitti koju oblst u prostoru promenljivih r i φ polrn smen preslikv n krug : x 2 +y 2 R 2. Koristeći ovu smenu, izrčunti integrl I = (x 2 + y 2 ) dx dy. Rešenje. U nejednkosti x 2 + y 2 R, kojom je odre den unutršnost krug zmenimo promenljive x i y preko r i φ. Proizilzi r 2 R 2. Pri tome z promenljivu φ nem nikkvih ogrničenj, odnosno uslovi koji opisuju skup u ovom primeru jesu < r R i φ < 2π. Drugim rečim, vži D = {(r, φ) : < r R, φ < 2π}. Sd, koristeći Teoremu o smeni promenljivih, proizilzi d vži I = (r 2 cos 2 φ + r 2 sin 2 φ)r dr dφ = D 2π dφ R r 2 r dr = 1 2 R4 π. U ovom primeru ignorisn je centr krug, u koju se ne slik ni jedn tčk skup D, zbog uslov r >. Me dutim, to u ovom slučju nije od presudnog znčj z rčunnje integrl. Nime, integrl posmtrne funkcije
58 52 LAVA 2. INTERACIJA (x, y) f(x, y) = x 2 + y 2 n skupu može se izrčunti ko zbir integrl n skupu 1 i n skupu 2. Pri tome 1 nek sdrži smo centr krug, odnosno 1 = {(, )}, 2 = \ 1. Kko je mer skup 1 jednk nuli, to će i integrl funkcije po tom skupu biti jednk nuli, i dovoljno je posmtrti integrl funkcije f n skupu 2. Sd je slik skup D = {(r, φ) : < r R, φ < 2π} polrnom smenom jednk skupu 2. Ko što se vidi, izuzeće skup 1 ne utiče n vrednost integrl. Ov nedorečenost koristi se u svim nrednim primerim bez posebnog obrzloženj Uopšten polrn smen Uopštene polrne koordinte se koriste kd je polzni domen integrcije elips, ne krug. Posmtr se preslikvnje x = r cos φ, y = br sin φ, φ < 2π, r >, gde su, b neke konstnte rzličite od nule. Td je jkobijn preslikvnj J = cos φ b sin φ r sin φ br cos φ = br. eometrijsk interpretcij ove trnsformcije sličn je interpretciji polrne smene. Nime, ko su dte vrednosti z x i y, pri čemu je (x, y) (, ), ond su jedinstveni r i φ odre deni n sledeći nčin: r = x y2 b 2 >, y φ = rctg [, 2π). xb Obrnuto, ko su poznte vrednosti r > i φ [, 2π), ond je formulm x = r cos φ, y = br sin φ odre den jedinstven tčk rvni s izuzetkom koordintnog početk. Ko i u slučju polrnih koordint, izuzeće koordintnog početk neće predstvljti poteškoće u izrčunvnju integrl. U izvesnim specijlnim slučjevim koristi se uopšten polrn smen x = r α cos β φ, y = br α sin β φ, φ [, 2π), r > (, b, α, β ). Primer Izrčunti integrl I = x 2 + y2 2 b 2 unutršnjost elipse, odnosno : x y2 b 2 1,, b >. dx dy, gde je skup
59 2.8. SMENA PROMENLJIVIH 53 Rešenje. Uvodimo uopštene polrne koordinte x = r cos φ, y = br sin φ, r >, φ [, 2π). Zmenom promenljvih r i φ u nejednkost koj odre duje unutršnjost elipse, sledi r 2 1. Obzirom d ne postoje ogrničenj z promenljvu φ, domen D promenljivih r i φ dt je n sledeći nčin: Sd je trženi integrl D = {(r, φ) : φ < 2π, < r 1}. I = 2π dφ 1 r brdr = 2 3 bπ. Primer Izrčunti površinu figure u rvni, koj je ogrničen krivom 4 x y + 4 = 1 i prvm x =, y =, pri čemu je, b > (Slik 12). b Slik 12. Rešenje. Uvodimo uopštenu polrnu smenu x = r 4 cos 8 φ, y = br 4 sin 8 φ, φ [, 2π), r >. Jkobijn uvedene smene je J = 32br 7 cos 7 φ sin 7 φ. Iz činjenice, b > sledi d mor biti x > i y >, te se nmeće uslov φ (, π/2). Zmenom uopštenih polrnih koordint u jednčinu krive koj odre duje rub skup, dobij se jednčin r = 1. Prem tome, domen promenljive r je
60 54 LAVA 2. INTERACIJA intervl (, 1). U ovom domenu promenljivih r i φ jkobijn preslikvnj je pozitivn. Prem tome, tržen površin jednk je sledećem integrlu: I = 32b π/2 cos 7 φ sin 7 φ dφ 1 r 7 dr = b Cilindričn smen u trostrukom integrlu Cilindrične koordinte u prostoru R 3 predstvljju neposredno uopštenje polrnih koordint. Preciznije, u rvni promenljivih x, y uvodi se polrn smen, promenljiv z ostje nepromenjen: x = r cos φ, y = r sin φ, z = ξ, pri čemu je φ < 2π, r >, ξ R. Lko utvr dujemo d je z ovko uzet domen promenljive (r, φ, ξ) jkobijn preslikvnj dt n sledeći nčin: cos φ r sin φ J = sin φ r cos φ 1 = r >. eometrijsk interpretcij ovih smen je sledeć. Nek je P tčk u trodimenzionlnom prostoru s koordintm (x, y, z), nek je P ortogonln projekcij tčke P n rvn xoy. Td je ξ jednko z koordinti tčke P, r je rstojnje tčke P od koordintnog početk, φ je ugo meren od pozitivnog del x-ose do vektor OP, suprotno kretnju kzljke n čsovniku (Slik 13).
61 2.8. SMENA PROMENLJIVIH 55 Slik 13. Moguće je uvesti uopštenu cilindričnu smenu x = r cos φ, y = br sin φ, z = ξ, r >, φ [, 2π), ξ R, z proizvoljne, b. Td je jkobijn preslikvnj J = br. U izvesnim slučjevim uvodi se smen oblik x = r α cos β φ, y = br α sin β φ, z = ξ, r >, φ [, 2π), ξ R (, b, α, β ). Primer Nći zpreminu tel, čij je grnic dt jednčinom (x 2 + y 2 + z 2 ) 2 = x 2 + y 2 (Slik 14).
62 56 LAVA 2. INTERACIJA Slik 14. Rešenje. Uvodimo cilindrične koordinte. Koristeći činjenicu r >, proizilzi d vži r 2 + ξ 2 = r, odnosno ξ = ± r(1 r). Veličin r(1 r) mor biti nenegtivn, odkle sledi < r 1. Z φ nem nikkvih ogrničenj, te je φ < 2π. Sd je očigledno d skup čij je grnic dt nvedenom jednčinom, dobijmo z ξ r(1 r). Stog vži m 3 () = 2π dφ 1 = 4π 1 dr r(1 r) r(1 r) r dξ r r 2 + r dr = π2 4. Poslednji integrl se može rešiti, n primer, Ojlerovom smenom r 2 + r = tr, odkle sledi r = 1 1+t 2 i t [, + ). Primer Odrediti zpreminu tel ogrničenog površim z = x 2 + y 2, x 2 + y 2 = x, x 2 + y 2 = 2x i z = (Slik 15).
63 2.8. SMENA PROMENLJIVIH 57 Slik 15. Rešenje. Uvodimo cilindričnu smenu x = r cos φ, y = r sin φ, z = ξ, pri čemu je r >, ξ R i φ ( π/2, π/2). Zmenom cilindričnih koordint u jednčine površi, dolzimo do sledećih jednčin u polrnom obliku: ξ = r 2, r = cos φ, r = 2 cos φ, ξ =. Iz prve i poslednje jednčine proizilze grnice promenljive ξ: ξ (, r 2 ). Iz druge (ko i treće) jednčine, iz uslov r > sledi uslov φ ( π/2, π/2). N krju, iz druge i treće jednčine proizilzi uslov z promenljivu r: r (cos φ, 2 cos φ). Prem tome, tržen zpremin jednk je integrlu I = π/2 π/2 dφ 2 cos φ cos φ r dr r2 dξ = 45π 32. Primer Izrčunti zpreminu tel koje je ogrničeno površim x2 2 + y 2 b 2 + z2 c 2 = 1 i x2 2 + y2 b 2 = z, pri tome se im u vidu deo u unutršnjosti c prboloid (, b, c > ) (Slik 16).
64 58 LAVA 2. INTERACIJA Slik 16. Rešenje. Uvodimo uopštenu cilindričnu smenu: x = r cos φ, y = br sin φ, z = cξ, pri čemu je r >, φ (, 2π) i ξ R. Jkobijn ovko uvedenog preslikvnj jeste J = bcr. Skup koji je u unutršnjosti elipsoid i prboloid, dt je sistemom nejednčin u cilindričnom obliku: r 2 + ξ 2 1 i r 2 ξ. Zbog poslednje nejednčine mor biti ξ, zbog prve nejednčine ( je ξ 1. Nek je ξ (, 1). Td je ξ 1 ξ 2 ko i smo ko je ) ( ) ξ, Prem tome, ko je ξ, 5 1 2, ond je r (, ξ). Ako ( 5 1 ) je ξ 2, 1, ond je r (, 1 ξ 2 ). Z φ nem nikkvih ogrničenj. Prem tome, tržen zpremin jednk je sledećem integrlu: 2π ξ 1 1 ξ 2 I = bc dφ dξ r dr + dξ r dr = bcπ = 4 15 bcπ. ξ 2 dξ + Time smo došli do krj rešenj (1 ξ 2 ) 2 dξ
65 2.8. SMENA PROMENLJIVIH Sfern smen u trostrukom integrlu Mnogi trostruki integrli izrčunvju se uvo denjem sferne smene. Nek je Jkobijn ove smene je x = r cos φ sin ψ, y = r sin φ sin ψ, z = r cos ψ, r >, φ < 2π, < ψ < π. cos φ sin ψ r sin φ sin ψ r cos φ cos ψ J = sin φ sin ψ r cos φ sin ψ r sin φ cos ψ cos ψ r sin ψ = r2 sin ψ. Prem tome, J = r 2 sin ψ. eometrijsko tumčenje ove smene je sledeće. Ako je P tčk u prostoru R 3 s koordintm (x, y, z), nek je P ortogonln projekcij tčke P n Oxy rvn. Td je r rstojnje tčke P od koordintnog početk O, φ je ugo u rvni Oxy meren počev od pozitivnog del x-ose do vektor OP suprotno kretnju kzljke n čsovniku, ψ je ugo koji vektor OP zklp s pozitivnim delom z-ose, meren počev od pozitivnog del z-ose. Primer Izrčunti msu kugle x 2 + y 2 + z 2 2, ko je rspodel gustine dt funkcijom f(x, y, z) = x 2 + y 2 + z 2. Dokz. Ako je skup n kome se vrši integrcij kugl, ond je to krkterističn primer potrebe z uvo denjem sfernih koordint. U ovom primeru prelskom n sferne koordinte sledi d je funkcij rspodele gustine f(x(r, φ, ψ), y(r, φ, ψ), z(r, φ, ψ)) = r. Zmenom sfernih koordint u nejednčinu koj u Dekrtovim koordintm odre duje kuglu, sledi d je nejednčin koj u sfernim koordintm opisuje kuglu, dt ko r 2 2, odnosno r. Pri tome nem nikkvih dodtnih ogrničenj z φ i ψ. Stog se ms tel rčun n sledeći nčin: I = 2π dφ π dψ r 3 sin ψdr = 4 π.
66 6 LAVA 2. INTERACIJA 2.9 Nesvojstveni integrli Od interes je rzmtrti nesvojstvene integrle. Integrl može biti nesvojstven u dv slučj. Moguće je d domen integrcije jeste neogrničen skup, ili je funkcij neogrničen u okolini neke tčke rub domen. Nek je oblst u R m, m 2. Niz otvorenih i izmerljivih skupov ( n ) n je monotoni pokrivč otvorenog skup, ko je = k i n n+1 z svko n N. Definicij Nek je f funkcij definisn n otvorenom skupu, tko d je f integrbiln n svkom merljivom (prem tome i ogrničenom) podskupu od. Ako postoji grničn vrednost lim f(x) dx = I n n z svki monotoni pokrivč ( n ) n skup, ond je I nesvojstven višestruki integrl funkcije f n skupu, u oznci I = f f(x) dx. Vžno je uočiti d uveden definicij vži smo u slučju m 2. Nime, Definicij n prvoj ne poklp se s rnijim pojmom nesvojstvenog integrl funkcije jedne promenljive, već je specijlnij. Rzlog leži u činjenici d je monotoni pokrivč u Definiciji proizvoljn, dok u slučju funkcij jedne promenljive to nije bio slučj. N primer, z funkcije jedne promenljive posmtrn je grničn vrednost oblik + f(x) dx = n lim n + k=1 f(x) dx (2.15) i rdi se o specijlnom monotonom pokrivnju intervl (, + ) skupovim oblik n = (, n), n N. Ovo je suštinsk rzlik u integrciji funkcij više promenljivih u odnosu n integrciju funkcij jedne promenljive. Nvodimo i primer kojim ilustrujemo prethodn rzmtrnj. Primer Pokzti d je integrl + f(x) dx, gde je f(x) = ( 1)n+1, x [n 1, n), n N, n
67 2.9. NESVOJSTVENI INTERALI 61 konvergentn integrl u nesvojstvenom smislu n prvoj (odnosno u smislu grnične vrednosti (2.15) ), li nije konvergentn u smislu Definicije Rešenje. Prem Košijevom kriterijumu, nvedeni integrl kovergir u smislu grnične vrednosti (2.15), ko i smo ko konvergir red ( 1) n+1 n. Nrvno, pomenuti red je uslovno konvergentn, i stog integrl postoji u smislu grnične vrednosti (2.15). S druge strne, prem Rimnovoj teoremi, postoji neki rspored člnov red ( 1) n+1 n, tko d je sum novog red jednk +. Nek je to red n s novim rsporedom člnov. Ovom redu odgovr novi monotoni pokričc skup (, + ). Rčunjući grničnu vrednost integrl po novom monotonom pokrivču, sledi d je vrednost integrl u smislu 2.41 Definicije jednk +. Prem tome, funkcij nije integrbiln u smislu Definicije U ovom primeru eventulno prihvtnje mogućih grničnih vrednosti + ili nije od posebnog znčj, stog što promen monotonog pokrivč dovodi do promene grnične vrednosti. Sledeći vžn rezultt je očekivn i posledic je proizvoljnog izbor monotonog pokrivč otvorenog skup. Teorem Funkcij f je integrbiln n otvorenom skupu R m, m 2, ko i smo ko je f integrbiln n. Teorem je suštinski rzličit od odgovrjućeg rezultt z integrle funkcij jedne promenljive. U slučju nesvojstvenog integrl funkcije jedne promenljive, iz psolutne konvergencije integrl sledi običn konvergencij ovog integrl, dok obrnuto ne vži. N krju, nvodimo očekivno tvr denje z nenegtivne funkcije. Teorem Ako je f nenegtivn funkcij n otvorenom skupu R m, td z svki monotoni pokrivč ( n ) n skup postoji lim f(x) dx n n ko končn broj, ili je ov grničn vrednost jednk +. Primer Ispitti konvergenciju i odrediti vrednost integrl (x I = e 2 +y 2) dx dy. R 2 Rešenje. Funkcij f(x, y) = e (x2 +y 2) je nenegtivn i stog je integrl konvergentn, ili je njegov vrednost +. Skupovi n = {(x, y) : x 2 + y 2 <
68 62 LAVA 2. INTERACIJA n 2 } čine monotoni pokrivč rvni R 2. x = r cos φ, y = r sin φ) Sledi d vži (korišćenjem smene I n = e (x2+y2) dx dy = n 2π n dφ re r2 dr = π(1 e n2 ) i I = lim n I n = π. Prem tome, polzni integrl je konvergentn i njegov vrednost je jednk π. Primer Dokzti d vži Pusonov 1 integrl). + e x2 dx = π (usov integrl 8 ; Ojler 9 - Rešenje. Nek je F n = ( n, n) ( n, n) monotoni pokrivč skup R 2. Prem prethodnom primeru je Prem tome, π = lim n = lim n + F n +n n e (x2+y2) dx dy = lim e x2 dx e x2 dx = π. 2. +n n n e x2 dx +n n e y2 dy 2.1 Pojmovi u mehnici U ovoj sekciji povezujemo integrle i rzne pojmove u mehnici. 8 Johnn Crl Friedrich uss ( ), nemčki mtemtičr i fizičr 9 Leonhrd Euler ( ), švjcerski mtemtičr i fizičr 1 Siméon Denis Poisson ( ), frncuski mtemtičr, geometr i fizičr
69 2.1. POJMOVI U MEHANICI Moment inercije mterijlne rvne figure Nek je M mterijln tčk mse m i nek je O proizvoljn tčk prostor. Moment inercije mterijlne tčke M u odnosu n tčku O jeste veličin I = mr 2, gde je r rstojnje izme du tčk O i M. Ako je dt sistem mterijlnih tčk M 1,..., M n, čije su mse redom jednke m 1,..., m n, ond je moment inercije ovog sistem mterijlnih tčk jednk I = n m i ri 2, gde je r i rstojnje tčke M i od tčke O. i=1 Nek je mterijln rvn figur pozitivne mse. Smtrmo d je figur u rvni Oxz. Nek je funkcij (x, y) f(x, y) gustine rspodele mse rvne figure. Funkcij f je nenegtivn i neprekidn n. Nek je T = { 1,..., n } proizvoljno rzbijnje skup i nek su M i = (x i, y i ) i proizvoljne tčke. Elementrn moment inercije n delu i u odnosu n koordintni početk O jeste proizvod kvdrt rstojnj tčke M i od koordintnog početk i mse tel i. Ms tel i jednk je proizvodu gustine i površine (degenerisne dvodimenzionlne zpremine). Prem tome, I i = (x 2 i + y2 i )f(x i, y i ) m 2 ( i ). Po nlogiji s sistemom od končno mnogo mterijlnih tčk, moment inercije tel u odnosu n koordintni početk približno je jednk sumi n (x 2 i + yi 2 )f(x i, y i ) m 2 ( i ). i=1 Odstupnje od tčnog moment inercije je utoliko mnje ukoliko je dijmetr podele mnji. Obzirom d je prethodn sum u stvri Rimnov sum funkcije (x, y) (x 2 + y 2 )f(x, y) n skupu, sledi d je moment inercije tel u odnosu n koordintni početk jednk I O = (x 2 + y 2 )f(x, y) dx dy. Moment inercije u odnosu n koordintni početk nziv se i polrni moment inercije. Anlogno se može definisti moment inercije mterijlne rvne figure u odnosu n bilo koju koordintnu osu. Td se koristi kvdrt rstojnj od te koordintne ose. Integrli I x = y 2 f(x, y) dx dy i I y = x 2 f(x, y) dx dy jesu momenti inercije rvne figure u odnosu n x- i y-koordintne ose redom.
70 64 LAVA 2. INTERACIJA Primer Nći moment inercije rvne mterijlne figure u odnosu n obe ose i koordintni početk, ko je ogrničen krivm y 2 = x 1, x = 2 i y =, u delu rvni y, gustin rspodele mse dt je funkcijom f(x, y) = y. Rešenje. Presek krivih koje ogrničvju oblst jesu tčke A(1, ), B(2, ) i C(2, 1). Momenti inercije tel u odnosu n koordinntne ose jesu 1 2 I y = y dy y 2 +1 x 2 dx = , I x = y 3 dy 2 y 2 +1 dx = 1 12, moment inercije u odnosu n koordinntni početk jeste I O = I x + I y = Elips inercije Nek je rvno telo u koordintnoj rvni Oxy, čij je gustin rspodele mse dt nenegtivnom neprekidnom funkcijom (x, y) f(x, y) n skupu. Nek je l prv koj prolzi kroz koordintni početk i zklp ugo φ s pozitivnim delom x-ose. Td je jednčin prve l dt ko y = x tg φ, odnosno x sin φ y cos φ =. Nek je M(x, y) proizvoljn tčk rvni. Lko se proverv d je rstojnje tčke M od prve l jednko r = x sin φ y cos φ. Moment inercije tel u odnosu n prvu l jednk je I l = (x sin φ y cos φ) 2 f(x, y) dx dy = sin 2 φ + cos 2 φ x 2 f(x, y) dx dy 2 sin φ cos φ y 2 f(x, y) dx dy = I y sin 2 φ 2I xy sin φ cos φ + I x cos 2 φ, xyf(x, y) dx dy
71 2.1. POJMOVI U MEHANICI 65 uz prirodnu oznku I xy = xyf(x, y) dx dy. Veličin I l definisn je integrlom nenegtivne funkcije, te je I l > (osim u ekstremnim slučjevim koji sd nisu od interes). Stog se prethodn formul može zpisti u obliku ( ) cos φ 2 ( ) ( ) ( ) sin φ cos φ sin φ 2 1 = I x 2I xy + I y. (2.16) Il Il Il Il Uočimo n prvoj l tčku A(x, y), koj je n rstojnju od O jednkom 1. Položj tčke A uslovljen je prvom l, odnosno uslovljen je uglom Il φ. Tržimo geometrijsko mesto svih tkvih tčk A u zvisnosti od ugl φ. Drugim rečim, rotirmo prvu l oko koordintnog početk i prtimo kretnje tčke A. Očigledno, koordinte (x, y) tčke A zdovoljvju uslove: x = cos φ Il, y = sin φ Il. N osnovu jednkosti 2.16 sledi rezultt 1 = x 2 I x 2xyI xy + y 2 I y. (2.17) Veličine I x, I y i I xy ne zvise od ugl φ, već smo koordinte (x, y) tǩce A. Prem tome geometrijsko mesto svih tčk A(x, y), koje se dobij promenom ugl φ, jeste kriv drugog red, čij je jednčin dt formulom 2.17.Formulom s, t = s(x, y)t(x, y)f(x, y) dx dy definisn je sklrni proizvod u skupu C() svih neprekidnih funkcij n komptu. N osnovu nejednkosti Koši 11 -Bunjkovskog 12 -Švrc13 : s, t s t, pri čemu je (videti 1.32 Primer iz prve glve) s = (s(x, y)) 2 f(x, y) dx dy 11 Augustin-Louis Cuchy ( ), frncuski mtemtičr 12 Viktor Ykovych Bunykovsky ( ), ukrjinsko-ruski mtemtičr) 13 Krl Hermnn Amndus Schwrz ( ), nemčki mtemtičr 1 2.
72 66 LAVA 2. INTERACIJA N osnovu ove nejednkosti sledi procen 2 xyf(x, y) dx dy x 2 f(x, y) dx dy koj se krće može zpisiti I x I y I 2 xy >. y 2 f(x, y) dx dy, Prem tome, diskrimnt krive (2.49.2) je pozitivn i t kriv je elips. Kriv (2.49.2) je elips inercije mterijlnog rvnog tel Moment inercije mterijlne figure Nek je M(x, y, z) tčk u prostoru mse m. Td su momenti inercije tčke M u odnosu n sve tri koordintne ose i koordintni početk dti formulm: I x = (y 2 + z 2 )m, I y = (x 2 + z 2 )m, I z = (x 2 + y 2 )m, I O = (x 2 + y 2 + z 2 )m. Nek je dt končn sistem tčk M 1 (x 1, y 1, z 1 ),..., M n (x n, y n, z n ), čije su mse redom m 1,..., m n. Kvdrti njihovih rstojnj od, n primer, ose Ox jesu y1 2 + z2 1,..., y2 n + zn. 2 Td je moment inercije ovog sistem tčk u odnosu n x-osu jednk n I x = (yi 2 + zi 2 )m i. i=1 Nek je telo predstvljen ko merljiv oblst u prostoru. ustin rspodele tel dt je funkcijom f(x, y, z) koj je nenegtivn i neprekidn n. Po nlogiji s rnijim rzmtrnjim, momenti inercije oblsti u odnosu n koordintne ose i kordintni početk jesu redom: I x = (y 2 + z 2 )f(x, y, z) dx dy dz, I y = (x 2 + z 2 )f(x, y, z) dx dy dz I z = (x 2 + y 2 )f(x, y, z) dx dy dz I O = (x 2 + y 2 + z 2 )f(x, y, z) dx dy dz.
73 2.1. POJMOVI U MEHANICI 67 Primer Dto je telo oblik vljk visine 2h, poluprečnik osnove R, konstntne gustine c. Izrčunti moment inercije vljk u odnosu n osu vljk, ko i n prvu koj polovi osu vljk i normln je n nju. Rešenje. Jednostvnosti rdi, nek je središte vljk koordintni početk, os vljk nek je n z-osi. Sd treb izrčunti moment inercije vljk u odnosu n z-osu i u odnosu n bilo koju prvu u rvni Oxy, koj prolzi kroz koordintni početk: n primer u odnosu n x-osu. Td je I z = c (x 2 + y 2 ) dx dy dz. Uvedimo cilindrične koordinte: z = r cos φ, y = r sin φ, z = ξ. Td je domen novih promenljivih r (, R), ξ ( h, h) i φ (, 2π). Stog je 2π h I z = c dφ h R dξ r 3 dr = πchr 4. Tko de je I x = c 2π dφ R r dr = cπhr 2 ( 2h 2 h h 3 + R2 2 (r 2 sin 2 φ + ξ 2 ) dξ ) Težište mterijlne rvne figure Nek je dt končn sistem tčk P i (x i, y i ), čije su mse jednke m i, i = 1,..., n. Td težište T (x t, y t ) ovog sistem tčk im sledeće koordinte: x t = n x i m i i=1, y n t = m i i=1 n y i m i. n m i i=1 i=1 Nek je rvn figur, odnosno merljiv oblst u R 2, i nek je dt gustin rspodele mse tel funkcijom f(x, y), koj je nenegtivn i neprekidn n. Nek je T = { 1,..., n } rzbijnje skup i nek
74 68 LAVA 2. INTERACIJA su M i (x i, y i ) i proizvoljne tčke. Td su približne koordinte težist T (x t, y t ) tel dte n sledeći nčin: x t n x i f(x i, y i ) m( i ), y n t f(x i, y i ) m( i ) i=1 i=1 n y i f(x i, y i ) m( i ). n f(x i, y i ) m( i ) i=1 i=1 Prelskom n grničnu vrednost kd dijmetr podele teži nuli, sledi d su koordinte težišt precizno: xf(x, y) dx dy yf(x, y) dx dy x t = f(x, y) dx dy, y t = f(x, y) dx dy. Izrzi M y = xf(x, y) dx dy, M x = yf(x, y) dx dy nzivju se sttički momenti rvne figure u odnosu n ose Oy i O x redom. Veličin f(x, y) dx dy je, nrvno, ms rvnog tel. Primer Izrčunti koordinte težišt tel oblik četvrtine elipse x 2 + y2 = 1, x, y, ko je gustin rspodele mse dt s f(x, y) = 1. 2 b 2 Rešenje. Prem rnije dtim formulm, vži x t = dx dx b 2 x 2 b 2 x 2 x dy dy = 4 3π i y t = 4b 3π Težište mterijlne figure u prostoru Nek je telo u prostoru predstvljeno ko oblst u R 3. ustin rspodele mse tel dt je nenegtivnom i neprekidnom funkcijom f(x, y, z) n
75 2.1. POJMOVI U MEHANICI 69 skupu. Td su koordinte težišt tel T (x t, y t, z t ) dte formulm xf(x, y, z) dx dy dz yf(x, y, z) dx dy dz x t = f(x, y, z) dx dy dz, y t = f(x, y, z) dx dy dz zf(x, y, z) dx dy dz z t = f(x, y, z) dx dy dz. Izrzi M yz = M xy = xf(x, y, z) dx dy dz, M xz = zf(x, y, z) dx dy dz yf(x, y, z) dx dy dz, nzivju se sttički momenti rvne figure u odnosu n rvni Oyz, Oxz i Oxy redom. Primer Dto je telo oblik polulopte poluprečnik R i konstntne gustine c. Odrediti težište tel. Rešenje. Bez gubljenj opštosti, pretpostvimo d je telo ogrničeno polusferom z = R 2 x 2 y 2 i Oxy rvni. Očigledno su poznte koordinte x t = i y t =. Prelskom n sferne koordinte: x = r cos φ sin ψ, y = R sin φ sin ψ, z = r cos ψ, uz uslove r (, R), φ (, 2π), ψ (, π/2), sledi d vži 2π R π/2 dφ r 3 dr sin ψ cos ψ dψ z t = = 3 8 R. 2 3 R3 π
76 7 LAVA 2. INTERACIJA
77 lv 3 Krivolinijski integrli 3.1 Krive u R n Kriv u prostoru R n je neprekidno preslikvnje γ : [, b] R n, pri čemu je, b R i < b. Skup γ = {γ(t) : t [, b]} je grfik krive γ. Immo u vidu d je neprekidn slik kompktnog skup uvek kompktn skup, [, b] je kompkt u R i γ je neprekidno preslikvnje n [, b]. Stog proizilzi d je γ kompktn skup u R n. Ako je γ : [, b] R n kriv, td postoje koordintne funkcije x 1,..., x n : [, b] R n, tko d z svko t [, b] vži γ(t) = (x 1 (t),..., x n (t)). Koristi se i oznk γ = (x 1,..., x n ). Podsećmo d je neprekidnost funkcije γ n [, b] ekvivlentn neprekidnosti svih koordintnih funkcij x 1,..., x n n [, b]. Kriv γ je uvek orijentism u smislu rst prmetr. Dkle, z svko t 1, t 2 [, b] i t 1 < t 2, vži d je kriv γ orijentisn od tčke γ(t 1 ) k tčki γ(t 2 ). Specijlno, γ() je početk krive γ, dok je γ(b) krj krive γ, i kriv γ je orijentisn od tčke γ() k tčki γ(b). Ako postoje tčke t 1, t 2 [, b], tko d je t 1 t 2 i γ(t 1 ) = γ(t 2 ) = T, ond je T tčk smopresek krive γ. Izuzetno, ko je γ() = γ(b) = T, ond je T istovremeno početk i krj krive γ, li nije tčk smopresek. Ako je γ() = γ(b), ond je γ ztvoren kriv. Kriv γ je prost, ko ov kriv nem tčk smopresek. Nek je P : = t 1 < t 1 < < t k = b proizvoljn podel segment [, b]. Td je k l(γ P ) = γ(t j ) γ(t j 1 ) j=1 71
78 72 LAVA 3. KRIVOLINIJSKI INTERALI dužin poligonlne linije γ P čij su temen γ(t ), γ(t 1 ),..., γ(t k ) u skupu γ, i ov temen su odre den podelom P. U upotrebi je termin: poligonln linij γ P je upisn u krivu γ. Nek je d(p) = mx t j t j 1 dijmetr j podele P. Ako podeli P pridružimo nekoliko podeonih tčk, dobijmo finiju podelu P, u oznci P P. Očidgledno je d(p) d(p ). Finijoj podeli odgovr nov poligonln linij γ P, čij je dužin l(γ P ). N osnovu očigledne geometrijske nejednkosti trougl, sledi d je l(γ P ) l(γ P ) (videti Sliku 17). Slik 17. Dkle, finije podele segment [, b] proizvode poligonlne linije veće dužine, koje su upisne u krivu γ. Kriv γ je rektificijbiln (odnosno, kriv γ im dužinu), ko postoji pozitivn broj M tko d je k γ(t j ) γ(t j 1 ) M j=1 z sve podele P : = t < t 1 < < t k = b segment [, b]. Ako je γ rektificijbiln kriv, ond je l(γ) = sup P k γ(t j ) γ(t j 1 ) j=1 dužin krive γ, pri čemu je supremum uzet po svim podelm P segment [, b]. Rektificijbilne krive se nzivju još i krive ogrničene vrijcije, pri čemu je totln vrijcij krive (n segmentu [, b]) uprvo jednk dužini te krive. Ako je γ rektificijbiln kriv, imjući u vidu d su dužine poligonlnih linij nenegetivne, dolzimo do jednkosti: lim k d(p) j=1 γ(t j ) γ(t j 1 ) = sup P k γ(t j ) γ(t j 1 ). j=1
79 3.1. KRIVE U R N 73 Pri tome, lim d(p) j=1 k γ(t j ) γ(t j 1 ) = A R, ko i smo ko z svko ϵ > postoji δ >, tko d z svku podelu P segment [, b] vži implikcij k d(p) < δ = γ(t j ) γ(t j 1 ) A < ϵ. j=1 Kriv (funkcij) γ = (x 1,..., x n ) je diferencijbiln, ko i smo ko su sve koordintne funkcije x 1,..., x n diferencijbilne. U tom slučju je γ = (x 1,..., x n). Ako je γ (t) z neko t [, b], ond je γ (t) je tngent krive γ u tčki γ(t). Kriv (funkcij) γ je neprekidno diferencijbiln, ko i smo ko γ postoji i γ je neprekidn funkcij. Ekvivlentno, γ je neprekdino diferencijbiln ko i smo ko su sve funkcije x 1,..., x n neprekidno diferencijbilne. Kriv γ je gltk, ko je γ neprekidn funkcij n [, b] i γ (t) z svko t [, b]. Imjući u vidu d je γ (t) vektor tngente krive γ u tčki γ(t), proizilzi d je kriv γ je gltk, ko i smo ko je vektor tngente krive γ rzličit od nul-vektr u svkoj tčki, i osim tog kretnje vektor tngente je neprekidno. Ekvivlentno, γ = (x 1,..., x n ) je gltk kriv, ko i smo ko su sve funkcije x 1,..., x n neprekidno diferencijbilne n [, b], i pri tome je γ (t) = (x 1 (t))1 + + (x n(t)) 2, z svko t [, b]. ( b b Ako je γ = (x 1,..., x n ) kriv, td je po definiciji γ(t)dt = Svi integrli postoje, jer su po pretpostvci funkcije x 1,..., x n neprekidne n [, b]. Teorem Nek je γ : [, b] R n neprekidno diferencijbiln funkcij. Td vži formul Njutn-Ljbnic: b γ (t)dt = γ(b) γ(). ) b x 1 (t)dt,, x n (tdt.
80 74 LAVA 3. KRIVOLINIJSKI INTERALI Dokz. Nek je γ = (x 1,..., x n ). Primenimo odgovrjuću teoremu z sklrne funkcij x 1,..., x n, koje su neprekidno diferencijbilne n [, b]: b γ (t)dt = = b b x 1(t)td,..., x n(t)dt ( ) x 1 (b) x 1 (),..., x n (b) x n () = γ(b) γ(). Dokzujemo sledeću teoremu o integrlim krivih (vektorskih funkcij sklrnog rgument). Teorem Nek je γ : [, b] R n neprekidno preslikvje. Td je t γ(t) reln integrbiln funkcij n [, b] i pri time je b b γ(t)dt γ(t) dt. Dokz. Nek je γ = (x 1,..., x n ). Sve funkcije γ, x 1,..., x n su neprekidne n [, b]. Funkcij x x je neprekidn n R n. Stog je i funkcij t γ(t) = (x 1 (t)) (x n (t)) 2 neprekidn n [, b]. Dkle, postoji b γ(t) dt. Nek je y = y = (y 1,..., y n ). Vži y 2 = b n yi 2 = i=1 γ(t)dt R n i y i = n i=1 y i b x i (t)dt = b b x i (t)dt, j = 1,..., n. Td je ( n ) y i x i (t) dt. N osnovu nejednkosti Koši-Švrc-Bunjkovskog, sledi d je z svko t [, b] ispunjeno: ( n n y i x i (t) i=1 i=1 y 2 i i=1 ) 1/2 ( n ) 1/2 (x i (t)) 2 = y γ(t). Integrlimo poslednju nejednkost po t n segmentu [, b]: y 2 = b i=1 i=1 ( n ) b y i x i (t) dt y γ(t) dt.
81 3.1. KRIVE U R N 75 Ako je y =, tržen nejednkost sledi trivijlno, Ako je y, ond je b b γ(t)dt = y γ(t) dt. Rezultt ove teoreme trivijlno vži i pod opštijom pretpostvkom, d su sve funkcije x 1,..., x n Rimn integrbilne n segmentu [, b]. Koristeći prethodno dokznu nejednkost dokzujemo teoremu o rektificijbilnosti gltke krive. Teorem Nek je γ : [, b] R n gltk kriv. Td je γ rektificijbiln kriv i njen dužin je l(γ) = b γ (t) dt = b (x 1 (t))2 + + (x n(t)) 2 dt. Dokz. Nek je P : = t < t 1 < t k = b proizvoljn podel segment [, b]. N osnovu neprekidnosti funkcij x 1,..., x n sledi d vži: γ(t j ) γ(t j 1 ) = t j γ (t)dt t j γ (t) dt. t j 1 t j 1 Sumirnjem svih nejednkosti z j = 1,..., k, sledi d je k γ(t j ) γ(t j 1 ) j=1 b γ (t) dt. N krju, posmtrmo supremum leve strne nejednkosti po svim podelm P segment [, b]: l(γ) b γ (t) dt. Potrebno je dokzti suprotnu nejednkost. Funkcij γ je neprekidn n [, b], te je ov funkcij rvnomerno neprekidn n [, b]. Nek je ϵ >. Postoji δ >, tko d z svko s, t [, b], ko je s t < δ, ond je γ (s) γ (t) < ϵ. Nek je P : = t 1 < t 1 < < t k = b podel segment [, b], tko d je t i t j 1 < δ z svko j = 1,..., k. Stog, ko je t [t j 1, t j ], ond je i γ (t) γ (t j < ϵ, odnosno γ (t) γ (t j ) + ϵ.
82 76 LAVA 3. KRIVOLINIJSKI INTERALI Sd je t j t j 1 t j γ (t) dt ( γ (t j ) + ϵ)dt = ( γ (t j ) + ϵ)(t j t j 1 ) t j 1 t j = (γ (t) + γ (t j ) γ (t))dt + ϵ(t j t j 1 ) t j 1 t j t j γ (t)dt + (γ (t j ) γ (t))dt + ϵ(t j t j 1 ) t j 1 t j 1 γ(t j 1 ) γ(t j ) + t j γ(t j 1 ) γ(t j ) + 2ϵ(t j t j 1 ). t j 1 γ (t j ) γ (t) dt + ϵ(t j t j 1 ) Sberemo sve prethodne nejednkosti z j = 1,..., k: b γ (t) dt k γ(t j ) γ(t j 1 ) + 2ϵ(b ). j=1 Lev strn nejednkosti je konstntn broj, dok desn strn zvisi od podele P i broj ϵ >. Dkle, posmtrmo prvo infimum desne strne po svim ϵ >, ztim posmtrmo supremum po svim podelm P segment [, b]. Sledi tržen nejednkost b γ (t) dt l(γ). Uzimjući u obzir d smo pokzli i obrnutu nejednkost, teorem je dokzn. Kriv γ je deo po deo gltk, ko postoji podel P : = s 1 < s 1 < < s m = b segment [, b], tko d je kriv γ gltk n svkom od segment [s j 1, s j ], j = 1,..., m. U ovom slučju lev tngent krive γ u tčki s j n segmentu [s j 1, s j ] ne mor biti jednk desnoj tngenti krive γ u tčki s j n segmentu [s j, s j+1 ]. Dkle, jedine tčke koje remete neprekidnost kretnj tngente γ jesu s 1,..., s m 1. Deo po deo gltk kriv nziv se putnj. Ako je γ prost ztvoren putnj u rvni, td je γ kontur u rvni.
83 3.1. KRIVE U R N 77 Teorem Ako je γ deo po deo gltk kriv u R n, td je γ rektificijbiln. Tko de l(γ) = b γ (t) dt = b (x 1 (t))2 + + (x n(t)) 2 dt, pri čemu znemrujemo končno mnogo tčk s j u kojim ne postoji γ (s j ). Dokz. Nek je = s < s 1 < < s m = b, tko d je γ gltk n svkom segmentu [s j 1, s j ]. Td je γ rektificijbiln n [s j 1, s j ]. Jednostvno sledi d je dužin krive γ (n segmentu [, b]) jednk zbiru dužin krive γ n svkom od segment [s j 1, s j ]. Formul z izrčunvnje dužine krive b sledi n osnovu γ (t) dt = m s j γ (t) dt. j=1s j 1 Definicij Nek je, b, c, d R tko d je < b i c < d. Preslikvnje µ : [, b] [c, d] je difeomorfizm, ko je µ strogo monoton bijekcij, i pri tome su µ i µ 1 neprekidno diferencijbilne funkcije. Definicij Nek su γ 1 : [, b] R n i γ 2 : [c, d] R n dve putnje. Putnje γ 1 i γ 2 su medjusobno ekvivlentne i iste orijentcije, ko postoji strogo rstući difeomorfizm µ : [, b] [c, d], tko d je γ 1 = γ 2 µ. U tom slučju koristimo oznku γ 1 γ 2. Sledeće tvr denje je očigledno. Teorem Ako je γ 1 γ 2, ond je γ 1 = γ 2. Teorem Relcij je relcij ekvivlencije n skupu svih putnj u R n. Dokz. Nek su γ 1 : [, b] R n, γ 2 : [c, d) R n i γ 3 : [e, f] R n putnje. Identičko preslikvnje id : [, b] [, b] je strogo rstući difeomorfizm, te n osnovu γ 1 = γ 1 id sledi γ 1 γ 1, odnosno je refleksivn relcij. Nek je γ 1 γ 2 i nek je µ : [, b] [c, d] strogo rstući difeomorfizm tko d vži γ 1 = γ 2 µ. Td je µ 1 : [c, d] [, b] tko de strogo rstući difeomorfizm i γ 2 = γ 1 µ 1. Sledi d je γ 2 γ 1. Time dokzujemo simetričnost relcije. Nek je γ 1 γ 2, γ 2 γ 3, i nek su µ : [, b] [c, d], ν : [c, d] [e, f] strogo rstući difeomorfizmi, tko d je γ 1 = γ 2 µ i γ 2 = γ 3 ν. Td je ν µ : [, b] [e, f] strogo rstući difeomorfizm i γ 1 = γ 3 (ν µ). Sledi γ 1 γ 3. Time je dokzn trnzitivnost relcije.
84 78 LAVA 3. KRIVOLINIJSKI INTERALI Ako su [, b] i [c, d] dv netrivijln segment relne prve ( < b i c < d), td postoji strogo rstući difeomorfizm µ : [, b] [c, d]. Jednostvno je proveriti d linerni preslikvnje µ(t) = d c b t + c d c b ispunjv tržene uslove. Definicij Nek su γ 1 [, b] R n i γ 2 : [c, d] R n dve putnje, i nek je µ : [, b] [c, d] strogo opdjući difeomorfizm. Ako je γ 1 = γ 2 µ, td su γ 1 i γ 2 ekvivlentne i suprotnih orijentcij. Oznk je γ 1 γ 2. Teorem Nek su γ 1 : [, b] R n, γ 2 : [c, d] R n i γ 3 : [e, f] R n putnje. (1) Ako je γ 1 γ 2, td je γ 2 γ 1 ; (2) Ako je γ 1 γ 2 i γ 2 γ 3, td je γ 1 γ 3. Dokz. (1) Nek je γ 1 γ 2 i nek je µ : [, b] [c, d] strogo opdjući difeomorfizm tko d vži γ 1 = γ 2 µ. Td je µ 1 : [c, d] [, b] strogo opdjući difeomorfizm i vži γ 2 = γ 1 µ 1. Stog je γ 2 γ 1. (2) Nek je, uz uslove (1), ν : [c, d] [e, f] strogo opdjući difeomorfizm tko d je γ 2 = γ 3 ν. Td je ν µ : [, b] [e, f] strogo rstući difeomorfizm i vži γ 1 = γ 3 (ν µ). Stog je γ 1 γ 3. Nek je γ 1 : [, b] R n putnj. Posmtrmo preslikvnje µ : [, b] [, b] definisno s µ(t) = +b t. Td je µ strogo opdjući difeomorfizm. Ako je γ 2 : [, b] R n putnj definisn ko γ 2 (t) = γ 1 (s + b t) = γ 1 µ, td je γ 2 γ 1. N krju, često se koristi sbirnje putnj koje se nstvljju. Nek su γ 1 : [, b] R n i γ 2 : [c, d] R n dve putnje, tko d je γ 1 (b) = γ 2 (c). Nek je e > b. Postoji strogo rstući difeomorfizm µ : [b, e] [c, d]. Nek je γ 3 : [b, e] R n putnj odre den ko γ 3 (t) = γ 2 (µ(t). Td je γ 3 γ 2. Definišemo putnju γ : [, e] R n n sledeći nčin: { γ 1 (t), t [, b], γ(t) = γ 3 (t) = γ 2 (µ(t)), t [b, e]. Td je putnj γ jednk zbiru putnj γ 1 i γ 2, u oznci γ = γ 1 + γ 2 (vidi Sliku 18). Slik 18.
85 3.2. KRIVOLINIJSKI INTERAL PRVO REDA 79 N krju formulišemo Žordnovu teoremu o prostim ztvorenim krivm u rvni. Teorem (Žordn) Nek je γ prost ztvoren kriv u rvni R2. Td postoje uzjmno disjunktne oblsti γ i γ, tko d vži: (1) γ γ = ; (2) γ je ogrničen oblst, γ je neogrničen oblst u R 2 ; (3) γ = γ = γ ; (4) R 2 = γ γ γ. Dokz ove teoreme prevzilzi okvire rukopis iz mtemtičke nlize n uobičjenom nivou. Žordnov teorem može biti dokzn, izme du ostlog, korišćenjem Bruerove teoreme o fiksnoj tčki, ili metodm lgebrske topologije. Skup γ je ogrničen oblst odre den konturom γ, ili kontur γ ogrničv oblst γ. S druge strne, γ je neogrničen oblst odre den konturom γ. Intuitivno, kontur γ je orijentisn pozitivno, ko pri obilstku konture γ u smeru orijentcije, oblst γ ostje s leve strne konture. Precizn definicij pozitivne orijentcije konture uvodi se primenom homotopije: kružnic γ 1 (t) = (cos t, sin t), t [, 2π] neprekidnom trnsformcijom u rvni R 2 može biti preveden u krivu γ. Pri tome, pozitivn orijentcij kružnice (u smeru rst prmetr t) postje pozitivn orijentcij konture γ. Ovkv nepekidn trnsformcij je homotopn ekvivlencij, i izučv se detljno u okviru topologije. Ako je γ kontur u rvni, ond je njen pozitivn orijencij oznčen s γ +, dok je negtivn orijentcij oznčen s γ. 3.2 Krivolinijski integrl prvog red Definicij Nek je γ = (x 1,..., x n ) : [, b] R n putnj, i nek je f : γ R funkcij. Ako je funkcij (f γ) γ integrbiln u Rimnovom smislu n [, b], td je funkcij f integrbiln n γ, i krivolinijski integrl prvog red funkcije f po putnji γ definisn je ko
86 8 LAVA 3. KRIVOLINIJSKI INTERALI γ f = γ fds = = b b (f γ)(t) γ (t) dt f(x 1 (t),..., x n (t)) (x 1 (t))2 + (x n(t)) 2 dt. U prethodnoj formuli jvlju se izvodi x j, koji su neprekidne funkcije svud n [, b], osim evenutlno u končno mnogo tčk. Tčke u kojim izvodi x j ne postoje, jednostvno znemrimo u prethodnoj definiciji krivolinijskog integrl prvog red. Jsno je d znemrivnje končno mnogo tčk ne utiče n vrednost integrl. N primer, ko je funkcij f neprekidn n γ osim eventulno u končno mnogo tčk, ond postoji f. γ Teorem Nek su γ 1 : [, b] R n i γ 2 : [c, d] R n dve putnje, tko d je γ 1 γ 2, ili γ 1 γ 2. Ako je f : γ1 R funkcij koj je integrbiln n γ 1, td je f integrbiln i n γ 2 i γ 1 f = γ 2 f. Dokz. Nek je γ 1 = γ 2 µ, pri čemu je µ : [, b] [c, d] strogo rstući difeomorfizm. Td je µ n [, b]. Vži: f = γ 1 = = b b d c b f(γ 1 (t)) γ 1(t) dt = f(γ 2 (µ(t))) γ 2(µ(t))µ (t) dt f(γ 2 (µ(t))) γ 2(µ(t)) µ (t)dt f(γ 2 (s)) γ 2(s) ds = f. γ 2 Pretpostvimo sd d je µ strogo opdjući difeomorfizm. µ n [, b], i stog je Td je
87 3.2. KRIVOLINIJSKI INTERAL PRVO REDA 81 γ 1 f = = b b = f(γ 1 (t)) γ 1(t) dt = b f(γ 2 (µ(t))) γ 2(µ(t)) ( µ (t))dt c d f(γ 2 (s)) γ 2(s) ds = f. γ 2 f(γ 2 (µ(t))) γ 2(µ(t))µ (t) dt Time je teorem dokzn. Formulišemo sledeće očigledno svojstvo krivolinijskih integrl. Teorem Krivolinijski integrl prvog red je linern u odnosu n funkciju. Drugim rečim, ko su f i g integrbilne funkcije n putnji γ u R n, i ko je α, β R, td je αf + βg tko de integrbiln n γ, i vži formul Dokz. Sledi n osnovu γ (αf + βg)ds = α γ fds + β γ gds. α γ f + β γ b g = α = b b f(γ(t) γ (t) dt + β g(γ(t) γ (t) dt (αf(γ(t)) + βg(γ(t)) γ (t) dt = (αf + βg). γ N krju, formulišemo tvr denje o ditivnosti integrl u odnosu n putnju integrcije. γ 1 2 Teorem Nek je funkcij f integrbiln n putnjm γ 1 i γ 2 u R n. Td je f integrbiln i n putnji γ 1 + γ 2, pri čemu vži formul +γ γ 1 γ 2 f = f + f.
88 82 LAVA 3. KRIVOLINIJSKI INTERALI Dokz. Nek su γ 1 : [, b] R n i γ 2 : [c, d] R n putnje. Nek je e > b. Postoji rstući difeomorfizm µ : [b, e] [c, d] tko d je γ 2 : [b, e] Rn odre den s γ 3 = γ 2 µ. Td je γ 3 γ 2. Nek je f integrbiln n γ 1 i n γ 2. Td je f integrbiln n γ 3. Nek je γ = γ 1 + γ 2 (videti odeljk o zbiru putnj). Td je γ [,b] = γ 1 i γ [b,e] = γ 3. Vži: γ 1 f + γ 2 f = = = γ 1 γ 3 f + f = b b b e (f(γ 1 (t)) γ 1(t) dt + (f(γ 3 (t)) γ 3(t) dt e b e (f(γ(t)) γ (t) dt + (f(γ(t)) γ (t) dt (f(γ(t)) γ (t) dt = γ 1 +γ 2 f. Time je tvr denje dokzno. Teorem Nek je γ putnj u R n. Td je γ 1 = γ ds = l(γ). Dokz. Sledi n osnovu definicije krivolinijskog interl prvog red, ko i dokzne formule z izrčunvnje dužine putnje: γ b 1 = γ (t) dt = l(γ). Primer Izrčunti dužinu kružnice poluprečnik r >. Dokz. Dovoljno je posmtrti kružnicu u rvni poluprečnik r s centrom u kooridntnom početku. Prmetrske jednčine ove kručnice su x = r cos t, y = r sin t, t [, 2π]. Prem dokznoj formuli, dužin kružnice je l = 2π r 2 sin 2 t + r 2 cos 2 tdt = 2rπ.
89 3.2. KRIVOLINIJSKI INTERAL PRVO REDA Rimnov sum i geometrijsk interpretcij krivolinijskog integrl prvog red Rzmtrmo krivolinijski integrl prvog red ko grničnu vrednost odgovrjućih Rimnovih sum. Pretpostvimo d je γ = (x 1,..., x n ) : [, b] R n putnj, i nek je f : γ R funkcij integrbiln n γ. Nek je = t < t 1 < < t k = b proizvoljno rzbijnje segment [, b], i nek su η j [t j 1, t j ] (j = 1,..., k) proizvoljne tčke u tim segmentim. Oznčimo s l j dužin putnje γ izme du tčk γ(t j 1 ) i γ(t j ). Ov dužin postoji, jer je po pretpostvci γ putnj u R n, smim tim postoji l(γ). Primetimo d je ξ j = γ(η j ) n pomenutom delu putnje γ izme du γ(t j 1 ) i γ(t j ). Nek je ξ = (ξ 1,..., ξ k ). Posmtrjmo integrlnu sumu S(f, γ, P, ξ) = k f(ξ j )l j. (3.1) Imjući u vidu d je dužin l k približno jednk γ(t j ) γ(t j 1 ) = (x 1 (t j ) x 1 (t j 1 )) (x n (t j ) x n (t j 1 )) 2, sledi d je S(f, γ, P, ξ) = j=1 k j=1 j=1 f(γ(η j )) (x 1 (t j ) x 1 (t j 1 )) (x n (t j ) x n (t j 1 )) 2 k ( ) 2 ( ) 2 x1 xn f(γ(η j )) + + (t j t j 1), t j t j 1 t j t j 1 pri čemu je x i = x i (t j ) x i (t j 1 ) z i = 1,..., n. rešk u proksimciji se smnjuje ukoliko je d(p). Sledi d je lim S(f, γ, P, ξ) = f, d(p) γ pri čemu ov grničn vrednost postoji nezvisno od podele P i nezvisno od izbor tčk ξ. N osnovu sveg izloženog, do krivolinijskog integrl prvog red funkcije f po putnji γ, može se doći rzmtrnjem grničnih vrednosti odgovrjućih Rimnovih sum (3.1).
90 84 LAVA 3. KRIVOLINIJSKI INTERALI U cilju dobijnj geometrijske interpretcije krivolinijskog integrl prvog red, nek je γ : [, b] R 2, pri čemu je R 2 prostor promenljivih x i y. Nek je z = f(x, y) neprekidn funkcij definisn n γ. Pretpostvimo d je f n γ i d je f integrbiln n γ. Td je Rimnov sum (3.1) jednk približno površini cilindrske površi C u prostoru R 3 promenljivih x, y, z, pri čemu je cilindrsk površ odre den n sledeći nčin: genertris površi C je putnj γ, izvodnice površi C su prlelne z-osi, dok je gornj grnic površi C grfik krive f γ (videti Sliku 19). Slik 19. Specijlno, ko je f = 1 n γ, ond je integrl γ ds = l(γ) jednk dužini krive γ, ovj zključk smo izveli i rnije. Primer Izrčunti integrl γ x 2 + y 2 = 1, y. y 2 x ds, ko je kriv γ polovin kružnice Rešenje. U ovom zdtku, ko i u svim nrednim zdcim, ko se posebno ne nglsi, treb uzek uzimti tkvu prmetrsku reprezentciju krive, d je posmtrni grfik krive opisn tčno jednom. N primer, krug x 2 +y 2 = 1 može biti opisn prmetrskim jednčinm x = cos t, y = sin t, t [, 2π], ko i jednčinm x = cos t, y = sin t,
91 3.2. KRIVOLINIJSKI INTERAL PRVO REDA 85 t [, 4π]. Prvom reprezentcijom svk tčk grfik opisn je tčno jednom, osim tčke (1, ) koj je i početk i krj krive, te je stog opisn dv put. U drugom slučju je svk tčk grfik krive opisn po dv put, početn odnosno krjnj tčk je opisn tri put. Prv reperezentcij dje prostu krivu γ, drug dje krivu γ 1, koj im tčke smopresek. Ako se drugčije ne zhtev, pod kružnicom se podrzumev prost kriv, dt prvom reprezentcijom. Vrtimo se sd konkretnom problemu. Polukružnic u ovom zdtku opisn je prmetrskim jednčinm: x = cos t, y = sin t, t [, π]. Sd je trženi integrl I = γ π y 2 x ds = sin 2 t cos t dt. Funkcij cos t menj znk n segmentu [, π], i stog se ovj segment deli n dv del. Prethodni integrl postje: I = π/2 π sin 2 t cos t dt sin 2 t cos t dt = 2 3. π/2 Primer Nek je dt deo eliptičkog cilindr x2 5 + y2 9 = 1, y, z, i nek je dt rvn z = y. Nći površinu del cilindr izme du rvni Oxy i rvni z = y (Slik 2). Rešenje. Nek je γ presek cilindr s rvni xoy, odnosno deo elipse x2 1, y. Treb izrčunti integrl I = γ yds. 5 + y2 9 = Prmetrske jednčine del elipse jesu x = 5 cos t, y = 3 sin t, t [, π]. Površin trženog del cilindr jeste je I = π 3 sin t 5 sin 2 t + 9 cos 2 t dt.
92 86 LAVA 3. KRIVOLINIJSKI INTERALI Smenom cos t = u proizilzi d vži I = 3 1 4u du = u du = ln 5. Slik 2. Primer Izrčunti krivolinijski integrl prvog red γ xy ds, ko je γ dt ko presek sfere x 2 + y 2 + z 2 = 2 i rvni x + y + z =. Rešenje. Iz jednčine rvni neposredno sledi z = x y. Zmenom ovog izrz u jednčinu sfere, dolzimo do jednčine Dobijen kriv je kružnic u rvni x + y + z =. Dokzćemo d svk kriv drugog red oblik gde je B, im ekvivlentn oblik x 2 + xy + y 2 = 1. (3.2) Ax 2 + 2Bxy + Cy 2 = D (3.3) λ(y αx) 2 + µ(y βx) 2 = D, (3.4) pri čemu je αβ = 1. Slučj B = je smo kd je kriv već u elementrnom obliku.
93 3.2. KRIVOLINIJSKI INTERAL PRVO REDA 87 Jednostvnim upore divnjem koeficijent dolzi se do sistem jednčin λα 2 + µβ 2 A = λα + µβ + B = λ + µ C =. Poslednji sistem jednčin se može shvtiti ko homogeni sistem jednčin s netrivijlnim rešenjem (λ, µ, 1), odkle sledi d determinnt tog sistem mor biti jednk nuli, odnosno α 2 β 2 A α β B 1 1 C =. Prv kolon se pomnoži s 1 i dod drugoj koloni, te se dobij α 2 β 2 α 2 A α β α B 1 C =. Uslov αβ = 1 grntuje α β, te se drug kolon podeli s β α i dobij se α 2 α + β A α 1 B 1 C =. Drug kolon se pomnoži s α i dod prvoj, pri čemu se uzim u obzir αβ = 1. Dobij se jednčin 1 α + β A 1 B 1 C =. Poslednj jednčin dje uslov α + β = C A, uz pretpostvku B. B Zjedno s pretpostvkom αβ = 1, dolzi se do vrednosti z α i β. Ztim se jednostvno odre duju λ i µ. U ovom konkretnom slučju (3.2) je A = C = 1 i B = 1 2. Stog je α + β =, što zjedno s αβ = 1 dje α = 1,β = 1. Ztim sledi λ = 1 4 i µ = 3 4. Ekvivlentn oblik krive (3.2) je ( ) y x 2 ( ) (y + x) =
94 88 LAVA 3. KRIVOLINIJSKI INTERALI Stog se uvodi smen promenljivih inverzne trnsformcije su u = y x 3 3, v = 2 2 y + x, w = 2 z, x = v 3u 3u + v, y =, z = 2 w Kružnic u novim koordintm je dt sistemom jednčin: u 2 + v 2 = 1, w = v. Stog se uvode cilindrične koordinte, u kojim je jednčin kručnice dt s: u = cos φ, v = sin φ, w = sin φ, φ [, 2π]. Vrćnjem n polzne koordinte x, y i z, sledi d je jednčin kružnice: φ [, 2π]. x = sin φ 3 cos φ 3 cos φ + sin φ, y =, z = 2 sin φ, Polzni integrl je I = = γ 2 3 xy ds = 1 3 2π 2π (sin 2 φ 3 cos 2 φ) (x φ) 2 + (y φ) 2 + (z φ) 2 dφ (sin 2 φ 3 cos 2 φ) dφ = 2π Krivolinijski integrl drugog red U ovoj lekciji definišemo krivolinijski integrl koji zvisi od orijentcije putnje. Nek je oblst u R 3. Vektorsko polje je svko preslikvnje iz u R 3. Ako ovo preslikvnje oznčimo s F : R 3, ond postoje koordintne funkcije P, Q, R : R, tko d vži F = (P, Q, R).
95 3.3. KRIVOLINIJSKI INTERAL DRUO REDA 89 Vektorsko polje F je rvno, ko postoji koordintni sitetm u R 3 u odnosu n koji je R =. Specijlno, ko postoji koordinnti sistem u R 3 tko d je Q = i R =, ond polje F = (P,, ) jeste sklrno polje. Podsetimo d je polje F je neprekidno, ko i smo ko je F neprekidn funkcij, odnosno ko i smo ko su relne funkcije P, Q, R neprekidne. Polje F je diferencijbilno, ko i smo ko su funkcije P, Q, R diferencijbilne. Polje F je neprekidno diferencijbilno, ko i smo ko su funkcije P, Q, R neprekidno diferencijbilne. Nek je γ : [, b] R 3 putnj u R 3, pri čemu je A = γ() početk, γ, B = γ(b) krj putnje γ. Putnj γ orijentisn od tčke A k tčki B. Ako je γ = (x, y, z), ond je γ = (x, y, z ) i dγ = γ (t)dt = ( dx, dy, dz). Sklrni proizvod vektor F i dγ jeste: F dγ = F, dγ = P dx + Q dy + R dz. Krivolinijski integrl drugog red neprekidnog vektorskog polj F po orijentisnoj putnji γ (od tčke A k tčki B), definisn je ko F F, γ P dx + Q dy + R dz γ := γ b b γ (F γ)(t), dγ(t) b (F γ)(t), γ (t) dt [P (x(t), y(t), z(t))x (t) + Q(x(t), y(t), z(t))y (t) + R(x(t), y(t), z(t))z (t)]dt. Integrl n desnoj strni je odre deni integrl neprekidne funkcije jedne relne promenljive, te stog krivolinijski integrl drugog red neprekidnog polj F po putnji γ uvek postoji. I u ovom slučju znemrujemo tčke u kojim izvodi x, y, z ne postoje. Integrl može biti definisn i opštije. Nime, dovoljno je pretpostviti d postoje Rimnovi integrli funkcij P x, Q y i R z n [, b]. U tom slučju je F integrbilno vektorsko polje po orijentisnoj putnji γ. Teorem Ako su γ 1 i γ 2 ekvivlentne putnje iste orijentcije, odnosno γ 1 γ 2, i ko je F integrbilno polje n γ 1, td je F integrbilno i n γ 2, pri čemu vži γ 1 γ 2 F = F.
96 9 LAVA 3. KRIVOLINIJSKI INTERALI Dokz. Nek su γ 1 : [, b] R 3 i γ 2 : [c, d] R 3 putnje, i nek je µ : [, b] [c, d] strogo rstući difeomorfizm (tj. µ ) tko d je γ 1 = γ 2 µ. Nek je F vektorsko polje integrbilno n γ1. Td je, korišćenjem smene s = µ(t): F = γ 1 = b d c b (F γ 1 )(t), γ 1(t) dt = (F(γ 2 (µ(t))), (γ 2(µ(t))µ (t) dt F(γ 2 (s)), γ 2(s) ds = F. γ 2 Teorem Ako su γ 1 i γ 2 ekvivlentne putnje suprotnih orijentcij, odnosno ko je γ 1 γ 2, i ko je vektorsko polje F integrbilno n γ 1, ond je F integrbilno n γ 2 i vži γ 1 F = F. γ 2 Dokz. Nek su dte putnje γ 1 : [, b] R 3, γ 2 : [c, d] R 3, i nek je µ : [, b] [c, d] opdjući difeomorfizm (µ ) tko d je γ 1 = γ 2 µ. Nek je F vektorsko polje definisno n γ1. Td je γ 1 F = b = (F(γ 1 (t)), γ 1(t) dt = d c b F(γ 2 (s)), γ 2(s)) ds = F. γ 2 (F(γ 2 (µ(t))), (γ 2(µ(t)) µ (t)dt Posledic Krivolinijski integrl drugog red menj znk ukoliko se promeni orijendtcije putnje. Formulišemo sledeći jednostvn rezultt, koji se može dokzti nlogno odgovrjućem rezulttu z krivolinijske integrle drugog red.
97 3.3. KRIVOLINIJSKI INTERAL DRUO REDA 91 Teorem Ako su γ 1 i γ 2 orijentisne putnje koje se mogu nstviti u smislu orijentcije, i ko je vektorsko polje F integrbilno n γ 1 i γ 2, td je vektorsko polje F integrbilno n γ 1 + γ 2 i vži F = F + F. γ 1 +γ 2 γ 1 γ 2 Ako su vektorsk polj F i integrbiln n orijenitsnoj putnji γ, i ko je α, β R, td je αf + β polje integrbilno n putnji γ i vži αf + β = α F + β. γ Drugim rečim, krivolinijski integrl drugog red je ditivn u odnosu n krivu i linern u odnosu n vektorsko polje. N krju, nvodimo primere koji ilustruju prezentovne rezultte. Primer Izrčunti y dx x dy, gde je kriv γ sum kružnog luk γ x 2 + y 2 = 1 od tčke A(1, ) do tčke B(, 1) i duži od B do A (Slik 21). B γ γ Slik 21. Rešenje. Jednčin orijentisnog luk AB jeste x = cos t, y = sin t, t [, π/2]. Sd je π/2 I 1 = y dx x dy = [ sin 2 t cos 2 t]dt = π 2. γ 1 Jednčin orijentisne duži BA jeste x + y = 1, odnosno x = t, y = 1 t, t [, 1]. Stog je I 2 = γ 2 y dx x dy = 1 A [(1 t) t( 1)]dt = 1.
98 92 LAVA 3. KRIVOLINIJSKI INTERALI N krju, trženi integrl je I = I 1 + I 2 = π Primer Izrčunti integrl γ y 2 dx + z 2 dy + x 2 dz, gde je γ Vivinijev 1 kriv (Slik 22): x 2 + y 2 + z 2 = 2, x 2 + y 2 = x, z, pozitivno orijentisn, posmtrn odozgo. Rešenje. Ekvivlentn oblik jednčin cilindr je ( x ) y 2 = 2 4. Uvodimo cilindrične koordinte x = 2 + r cos φ, y = r sin φ, z = ξ. Sd jednčin cilindr u novim koordintm glsi r = /2. Zmenom ovih uslov u jednčinu sfrere, dobijmo 2 2 cos φ + ξ2 = 2 2. N osnovu uslov ξ, jednčin krive jeste x = cos φ, y = sin φ, z = cos φ, φ [, 2π]. Iz činjenice d je z rstuć funkcij po φ [, π] i opdjuć funkcij po φ [π, 2π], sledi d je orijentcij krive uprvo on tržen: pri rstu prmetr φ gornji deo sfere ostje s leve strne krive. Sd je trženi integrl jednk: I = 3 8 2π sin 3 φ dφ π 2π (1 cos φ) cos φ dφ (1 + cos φ) 2 sin φ 1 cos φ dφ. Jednostvnom smenom φ = ψ + π, uz korišćenje jednkosti sin(ψ + π) = sin ψ i cos(ψ+π) = cos ψ, prvi i treći integrl se redom svode n integrle π π sin 3 ψ dψ i π π (1 cos ψ) 2 sin ψ 1 + cos ψ dψ. Ob integrl su jednk nuli, iz rzlog što je domen integrcije simetričn u odnosu n koordintni početk, funkcije koje se integrle jesu neprne. Stog je I = 3 4 2π (1 cos φ) cos φ dφ = 3 π 4. 1 Vincenzo Vivini ( ), itlijnski mtemtičr
99 3.4. RINOVA FORMULA U RAVNI 93 Slik rinov formul u rvni Oblst V u rvni R 2 je prosto povezn, ko z svku konturu γ u skupu V vži γ V. Ekvivlentno, V je prosto povezn oblst, ko je svk kontur u V homotopno ekvivlentn tčki u V. Ako oblst V nije prosto povezn, ond je oblst V višestruko povezn. Nek je γ + pozitivno orijentisn kontur u rvni R, koj ogrničv oblst γ. Dokzćemo vezu izme du krivolinijskih integrl drugog red vektorskog polj F po konturi, i dvostrukog integrl odre dene funkcije po oblsti γ. Oblst V u R 2 je elementrn u odnosu n koordintne ose, ko postoje deo po deo neprekidno diferencijbilne funkcije f, g : [, b] R i h, k : [c, d] R, tko d je f < g n [, b], ko i h < k n [c, d], i pri tome je (Slik 23): V = {(x, y) R 2 : x [, b], f(x) < y < g(x)} = {(x, y) R 2 : y [c, d], h(y) < x < k(y)}.
Matematička analiza 4
 Mtemtičk nliz 4 Drgn S. Dor dević 14.5.214. 2 Sdržj Predgovor 5 1 Integrcij 7 1.1 Žordnov mer u R n....................... 7 1.1.1 Mer prvougonik u R 2................ 7 1.1.2 Mer n-intervl u R n..................
Mtemtičk nliz 4 Drgn S. Dor dević 14.5.214. 2 Sdržj Predgovor 5 1 Integrcij 7 1.1 Žordnov mer u R n....................... 7 1.1.1 Mer prvougonik u R 2................ 7 1.1.2 Mer n-intervl u R n..................
2.6 Nepravi integrali
 66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
66. INTEGRAL.6 Neprvi integrli Definicij. Nek je f : [, R funkcij koj je Riemnn integrbiln n svkom podsegmentu [, ] od [,. Ako postoji končn es f() (.4) ond se tj es zove neprvi integrl funkcije f n [,
Mera, integral i izvod
 Mer, integrl i izvod Drgn S. Dor dević 3.1.2014. 2 Sdržj Predgovor 5 1 Uvod 7 1.1 Osnovni pojmovi......................... 7 1.2 Topološki prostori......................... 8 1.3 Metrički prostori.........................
Mer, integrl i izvod Drgn S. Dor dević 3.1.2014. 2 Sdržj Predgovor 5 1 Uvod 7 1.1 Osnovni pojmovi......................... 7 1.2 Topološki prostori......................... 8 1.3 Metrički prostori.........................
 IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
IZVOD FUNKCIJE Predpostvimo d je unkcij deinisn u nekom intervlu, i d je tčk iz intervl, iksirn. Uočimo neku proizvoljnu tčku iz tog intervl,. Ov tčk može d se pomer levo desno, p ćemo je zvti promenljiv
Odred eni integrali. Osnovne osobine odred enog integrala: f(x)dx = 0, f(x)dx = f(x)dx + f(x)dx.
 Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Odred eni integrli Osnovne osobine odred enog integrl: fx), fx) fx) b c fx), fx) + c fx), 4 ) b αfx) + βgx) α fx) + β gx), 5 fx) F x) b F b) F ), gde je F x) fx), 6 Ako je f prn funkcij fx) f x), x R ),
Integralni raqun. F (x) = f(x)
 Mterijl pripremio Benjmin Linus U mterijlu su e definicije, teoreme, dokzi teorem (rđenih n predvƭu i primeri. Dodo sm i neke done primere d bih ilustrovo prikznu teoriju. Integrlni rqun Definicij. Nek
Mterijl pripremio Benjmin Linus U mterijlu su e definicije, teoreme, dokzi teorem (rđenih n predvƭu i primeri. Dodo sm i neke done primere d bih ilustrovo prikznu teoriju. Integrlni rqun Definicij. Nek
DIPLOMSKI RAD. Nesvojstveni integral. Univerzitet u Kragujevcu Prirodno matematički fakultet. Kandidat: Marta Milošević 47/00
 Univerzitet u Krgujevu Prirodno mtemtički fkultet IPLOMSKI RA Nesvojstveni integrl Mentor: r Mirjn Pvlović Kndidt: Mrt Milošević 47/ KRAGUJEVAC,. Sdržj. Nesvojstveni jednostruki integrl 3.. efiniij, primeri
Univerzitet u Krgujevu Prirodno mtemtički fkultet IPLOMSKI RA Nesvojstveni integrl Mentor: r Mirjn Pvlović Kndidt: Mrt Milošević 47/ KRAGUJEVAC,. Sdržj. Nesvojstveni jednostruki integrl 3.. efiniij, primeri
SLIČNOST TROUGLOVA. kažemo da su slične ( sa koeficijentom sličnosti k ) ako postoji transformacija sličnosti koja figuru F prevodi u figuru F
 SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
SLIČNOST TROUGLOV Z dve figure F i F kžemo d su slične ( s koefiijentom sličnosti k ) ko postoji trnsformij sličnosti koj figuru F prevodi u figuru F. Činjeniu d su dve figure slične obeležvmo s F F. Sličnost
7 Odreženi integrali. Neka je funkcija f(x) definisana na intervalu [a, b]. Ako ovaj interval podelimo
![7 Odreženi integrali. Neka je funkcija f(x) definisana na intervalu [a, b]. Ako ovaj interval podelimo 7 Odreženi integrali. Neka je funkcija f(x) definisana na intervalu [a, b]. Ako ovaj interval podelimo](/thumbs/89/98520281.jpg) 7 Odreženi integrli 63 7 Odreženi integrli Nek je funkcij f(x) definisn n intervlu [, ]. Ako ovj intervl podeo n n delov tčkm = x < x < x
7 Odreženi integrli 63 7 Odreženi integrli Nek je funkcij f(x) definisn n intervlu [, ]. Ako ovj intervl podeo n n delov tčkm = x < x < x
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
1 Odredeni integral. Integrabilnost ograničene funkcije
 Odredeni integrl. Integrbilnost ogrničene funkcije Njprije uvedimo dvije pretpostvke. Prv, d je reln funkcij segment[, b] končne dužine ( < < b < + ). Definicij 2. Podjel segment [, b], u oznci P, je svki
Odredeni integrl. Integrbilnost ogrničene funkcije Njprije uvedimo dvije pretpostvke. Prv, d je reln funkcij segment[, b] končne dužine ( < < b < + ). Definicij 2. Podjel segment [, b], u oznci P, je svki
SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE
 SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE Do sd smo već definisli skup Ω elementrnih dogđj Ako se elementrni dogđji ω mogu predstviti ko relni brojevi, ond se eksperiment može zmisliti ko izbor jedne promenljive
SLUČAJNE PROMENLJIVE-FUNKCIJA RASPODELE Do sd smo već definisli skup Ω elementrnih dogđj Ako se elementrni dogđji ω mogu predstviti ko relni brojevi, ond se eksperiment može zmisliti ko izbor jedne promenljive
= + injekcija. Rješenje 022 Kažemo da funkcija f ima svojstvo injektivnosti ili da je ona injekcija ako vrijedi
 Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
Zdtk 0 (Anstzij, gimnzij) Provjeri je li funkcij f log( 5) + + injekcij Rješenje 0 Kžemo d funkcij f im svojstvo injektivnosti ili d je on injekcij ko vrijedi f ( ) f ( ) Dkle, funkcij je injekcij ko rzličitim
B I O M A T E M A T I K A
 Mterijli z predmet B I O M A T E M A T I K A Biologij Zorn Rkić Beogrd, 03. godine i S A D R Ž A J. UVOD. Skupovi. Funkcije 4.3 Relcije 6.4 Brojevi: celi, rcionlni i relni 8.5 Kompleksni brojevi 7.6 Elementi
Mterijli z predmet B I O M A T E M A T I K A Biologij Zorn Rkić Beogrd, 03. godine i S A D R Ž A J. UVOD. Skupovi. Funkcije 4.3 Relcije 6.4 Brojevi: celi, rcionlni i relni 8.5 Kompleksni brojevi 7.6 Elementi
4. Relacije. Teorijski uvod
 VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
VI, VII i VIII dvoqs veжbi Vldimir Blti 4. Relije Teorijski uvod Podsetimo se n neke od pojmov veznih z skupove, koji su nm potrebni z uvođeƭe pojm relije. Dekrtov proizvod skup iniemo n slede i nqin:
M A T E M A T I K A 1
 Mterijli z predmet M A T E M A T I K A 1 Fizičk hemij Zorn Rkić Beogrd, 010 godine i S A D R Ž A J 1 UVOD 1 11 Skupovi 1 1 Funkcije 4 13 Relcije 6 14 Brojevi: celi, rcionlni i relni 8 15 Kompleksni brojevi
Mterijli z predmet M A T E M A T I K A 1 Fizičk hemij Zorn Rkić Beogrd, 010 godine i S A D R Ž A J 1 UVOD 1 11 Skupovi 1 1 Funkcije 4 13 Relcije 6 14 Brojevi: celi, rcionlni i relni 8 15 Kompleksni brojevi
NEKE POVRŠI U. Površi koje se najčešće sreću u zadacima su: 1. Elipsoidi. 2. Hiperboloidi. 3. Paraboloidi. 4. Konusne površi. 5. Cilindrične površi
 NEKE POVŠI U Pvrši kje se njčešće sreću u dcim su:. Elipsidi. Hiperlidi. Prlidi 4. Knusne pvrši 5. Cilindrične pvrši. Elipsidi Osnvn jednčin elipsid ( knnsk) je : + + = c, i c su dsečci n, i si. Presek
NEKE POVŠI U Pvrši kje se njčešće sreću u dcim su:. Elipsidi. Hiperlidi. Prlidi 4. Knusne pvrši 5. Cilindrične pvrši. Elipsidi Osnvn jednčin elipsid ( knnsk) je : + + = c, i c su dsečci n, i si. Presek
VALJAK. Valjak je geometrijsko telo ograničeno sa dva kruga u paralelnim ravnima i delom cilindrične površi čije su
 ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
ALJAK ljk je geometijsko telo ogničeno s dv kug u plelnim vnim i delom ilindične povši čije su izvodnie nomlne n vn ti kugov. Os vljk je pv koj polzi koz ente z. Nvno ko i do sd oznke su: - je povšin vljk
M A T E M A T I Č K A A N A L I Z A
 Miloš Miličić M A T E M A T I Č K A A N A L I Z A Akdemsk miso Beogrd, 2012 Dr Miloš Miličić redovni profesor Držvnog univerzitet u Novom Pzru MATEMATIČKA ANALIZA Recenzenti Dr Ćeml Dolićnin redovni profesor
Miloš Miličić M A T E M A T I Č K A A N A L I Z A Akdemsk miso Beogrd, 2012 Dr Miloš Miličić redovni profesor Držvnog univerzitet u Novom Pzru MATEMATIČKA ANALIZA Recenzenti Dr Ćeml Dolićnin redovni profesor
4 INTEGRALI Neodredeni integral Integriranje supstitucijom Parcijalna integracija Odredeni integral i
 Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Sdržj 4 INTEGRALI 64 4. Neodredeni integrl........................ 64 4. Integrirnje supstitucijom.................... 68 4. Prcijln integrcij....................... 7 4.4 Odredeni integrl i rčunnje površine
Krivolinijski integral
 Poglvlje 4 Krivolinijski integrl 4.1 Vektorsko polje U ovom i nrednom poglvlju, osim sklrnih, rdićemo i s vektorskim funkcijm više promenljivih, F : R n R m, F = (F1,...,F m ), F i : R n R, i = 1,...,m,
Poglvlje 4 Krivolinijski integrl 4.1 Vektorsko polje U ovom i nrednom poglvlju, osim sklrnih, rdićemo i s vektorskim funkcijm više promenljivih, F : R n R m, F = (F1,...,F m ), F i : R n R, i = 1,...,m,
Rešavanje diferencijalnih jednačina pomoću redova. Specijalne funkcije. Ortogonalne funkcije
 Glv 1 Rešvnje diferencijlnih jednčin pomoću redov. Specijlne funkcije. Ortogonlne funkcije 1.1 Neke druge specijlne funkcije Skoro bez izuzetk, njčešće korišćene specijlne funkcije su trigonometrijske
Glv 1 Rešvnje diferencijlnih jednčin pomoću redov. Specijlne funkcije. Ortogonlne funkcije 1.1 Neke druge specijlne funkcije Skoro bez izuzetk, njčešće korišćene specijlne funkcije su trigonometrijske
GRANIČNE VREDNOSTI FUNKCIJA zadaci II deo
 GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
GRANIČNE VREDNOSTI FUNKCIJA zdci II deo U sledećim zdcim ćemo korisii poznu grničnu vrednos: li i mnje vrijcije n i 0 n ( Zdci: ) Odredii sledeće grnične vrednosi: Rešenj: 4 ; 0 g ; 0 cos v) ; g) ; 4 ;
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
dužina usmjerena (orijentirana) dužina (zna se koja je točka početna, a koja krajnja) vektor
 I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
I. VEKTORI d. sc. Min Rodić Lipnović 009./010. 1 Pojm vekto A B dužin A B usmjeen (oijentin) dužin (n se koj je točk početn, koj kjnj) A B vekto - kls ( skup ) usmjeenih dužin C D E F AB je epeentnt vekto
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
U n i v e r z i t e t u B e o g r a d u. Matematički fakultet ITOOV STOHASTIČKI INTEGRAL I PRIMENE
 U n i v e r z i t e t u B e o g r d u Mtemtički fkultet ITOOV STOHASTIČKI INTEGRAL I PRIMENE M s t e r r d Mentor: dr Jelen Jocković Student: Jelen R. Suzić B e o g r d, 2015 S d r ž j Predgovor 1 1 Integrlni
U n i v e r z i t e t u B e o g r d u Mtemtički fkultet ITOOV STOHASTIČKI INTEGRAL I PRIMENE M s t e r r d Mentor: dr Jelen Jocković Student: Jelen R. Suzić B e o g r d, 2015 S d r ž j Predgovor 1 1 Integrlni
LAPLASOVA TRANSFORMACIJA
 Mster rd LAPLASOVA TRANSFORMACIJA Snježn Mksimović Mentor: Akdemik dr Stevn Pilipović Novi Sd, pril 211. iii Sdržj Predgovor vi 1. Osnovn Lplce-ov trnsformcij 1 1.1. Egzistencij Lplce-ove trnsformcije...............
Mster rd LAPLASOVA TRANSFORMACIJA Snježn Mksimović Mentor: Akdemik dr Stevn Pilipović Novi Sd, pril 211. iii Sdržj Predgovor vi 1. Osnovn Lplce-ov trnsformcij 1 1.1. Egzistencij Lplce-ove trnsformcije...............
Osnove elektrotehnike I parcijalni ispit VARIJANTA A. Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti.
 Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Osnove elektrotehnike I prcijlni ispit 3..23. RIJNT Prezime i ime: roj indeks: Profesorov prvi postult: Što se ne može pročitti, ne može se ni ocijeniti... U vzdušni pločsti kondenztor s rstojnjem između
Matematički osnovi Z transformacije
 Mtemtiči osnovi Z trnsformcije Uvod u Z-trnsformciju: Z-trnsformcij i njen invern trnsformcij se u mtemtici rmtrju i rlog što ovve trnsformcije imju neposrednu primenu u eletrotehnici i to prvenstveno
Mtemtiči osnovi Z trnsformcije Uvod u Z-trnsformciju: Z-trnsformcij i njen invern trnsformcij se u mtemtici rmtrju i rlog što ovve trnsformcije imju neposrednu primenu u eletrotehnici i to prvenstveno
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Neodreeni integrali. Glava Teorijski uvod
 Glv Neodreeni integrli. Teorijski uvod Nek je funkcij f :, b R. Definicij: ϕ- primitivn funkcij funkcije f ϕ f, b Teorem: ϕ- primitivn funkcij funkcije f ϕ+c- primitivn funkcij funkcije f Definicij: f
Glv Neodreeni integrli. Teorijski uvod Nek je funkcij f :, b R. Definicij: ϕ- primitivn funkcij funkcije f ϕ f, b Teorem: ϕ- primitivn funkcij funkcije f ϕ+c- primitivn funkcij funkcije f Definicij: f
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Rijeseni neki zadaci iz poglavlja 4.5
 Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
Rijeseni neki zdci iz poglvlj 4.5 Prije rijesvnj zdtk prisjetimo se itnih stvri koje ce ns prtiti tijekom njihovog promtrnj. Definicij: (Trigonometrij prvokutnog trokut) ktet nsuprot kut ϕ sin ϕ hipotenuz
d(o,1) = i = 1. Uvođenjem koordinatizacije operacije s vektorima sveli smo na operacije s brojevima: ako je [ ] [ ]
![d(o,1) = i = 1. Uvođenjem koordinatizacije operacije s vektorima sveli smo na operacije s brojevima: ako je [ ] [ ] d(o,1) = i = 1. Uvođenjem koordinatizacije operacije s vektorima sveli smo na operacije s brojevima: ako je [ ] [ ]](/thumbs/75/72220779.jpg) -- 71 -- 7.2. KOORDINATNI SISTEM-KOORDINATIZACIJA Podsjetimo se pojmov dimenzij i bz prostor: ''Njveći'' broj linerno nezvisnih vektor u nekom vektorskom prostoru zovemo dimenzijom tog prostor. Ako je
-- 71 -- 7.2. KOORDINATNI SISTEM-KOORDINATIZACIJA Podsjetimo se pojmov dimenzij i bz prostor: ''Njveći'' broj linerno nezvisnih vektor u nekom vektorskom prostoru zovemo dimenzijom tog prostor. Ako je
Matematika za ekonomiste Časlav Pejdić, (064)
 Mtemtik z ekonomiste Čslv Pejdić, (06) 09 0 SADRŽAJ SADRŽAJ UVOD DEO RELACIJE I FUNKCIJE DEO ALGEBRA 6 DEO NIZOVI I REDOVI DEO NEPREKIDNOST I DIFERENCIJABILNOST FUNKCIJE 7 5 DEO LIMESI I IZVODI 9 6 DEO
Mtemtik z ekonomiste Čslv Pejdić, (06) 09 0 SADRŽAJ SADRŽAJ UVOD DEO RELACIJE I FUNKCIJE DEO ALGEBRA 6 DEO NIZOVI I REDOVI DEO NEPREKIDNOST I DIFERENCIJABILNOST FUNKCIJE 7 5 DEO LIMESI I IZVODI 9 6 DEO
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Izvodi i integrali necelog reda
 UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ntš Durković Izvodi i integrli necelog red -mster rd- Mentor: Docent dr Snj Konjik Novi Sd, 2. Predgovor Frkcioni
UNIVERZITET U NOVOM SADU PRIRODNO-MATEMATIČKI FAKULTET DEPARTMAN ZA MATEMATIKU I INFORMATIKU Ntš Durković Izvodi i integrli necelog red -mster rd- Mentor: Docent dr Snj Konjik Novi Sd, 2. Predgovor Frkcioni
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Matematiqki fakultet. Univerzitet u Beogradu. Domai zadatak
 Matematiqki fakultet Univerzitet u Beogradu Domai zadatak Zlatko Lazovi 30. decembar 2016. verzija 1.1 Sadraj 1 METRIQKI PROSTORI 2 1 1 METRIQKI PROSTORI a) Neka je (M, d) metriqki prostor i neka je (x
Matematiqki fakultet Univerzitet u Beogradu Domai zadatak Zlatko Lazovi 30. decembar 2016. verzija 1.1 Sadraj 1 METRIQKI PROSTORI 2 1 1 METRIQKI PROSTORI a) Neka je (M, d) metriqki prostor i neka je (x
OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA
 OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
OSNOVE TRIGONOMETRIJE PRVOKUTNOG TROKUT - DEFINIIJ TRIGONOMETRIJSKIH FUNKIJ - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKIJ KUTOV OD - PRIMJEN N PRVOKUTNI TROKUT - PRIMJEN U PLNIMETRIJI 4.1. DEFINIIJ TRIGONOMETRIJSKIH
c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]
![c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata] c = α a + β b, [sustav rješavamo metodom suprotnih koeficijenata]](/thumbs/92/108578155.jpg) Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
Zdtk (Tihomir, tehničk škol) c = 8 i. Rješenje Prikži vektor c ko linernu kombinciju vektor i b ko je = i + 3 j, b = 4 i 3 j, Nek su i b vektori i α, β relni brojevi. Vektor c = α + β b nzivmo linernom
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
TROUGAO. - Stranice a,b,c ( po dogovoru stranice se obeležavaju nasuprot temenu, npr naspram temena A je stranica a, itd) 1, β
 TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
TRUG Mngug kji im ti stnie zve se tug. snvni elementi tugl su : - Temen,, - Stnie,, ( p dgvu stnie se eležvju nsupt temenu, np nspm temen je stni, itd) - Uglvi, unutšnji α, β, γ i spljšnji α, β, γ γ α
1 Ekstremi funkcija više varijabli
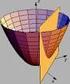 1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
1 Ekstremi funkcij više vrijbli Definicij ekstrem funkcije: Funkcij u = f(x 1, x 2,, x n ) im u točki T ( 1, 2,, n ) A) LOKALNI MINIMUM f( 1, 2,, n ) ko z svku točku T vrijedi nejednkost: T ( 1 + dx 1,
1.1 Neodre deni integral
 . Neodre deni integrl.. Površinski problem Uvod u površinski problem Iko većin rzmišlj o integrlu isključivo ko o obrtu izvod, osnove integrlnog rčun sežu mnogo dlje u prošlost od modernih vremen. Jedn
. Neodre deni integrl.. Površinski problem Uvod u površinski problem Iko većin rzmišlj o integrlu isključivo ko o obrtu izvod, osnove integrlnog rčun sežu mnogo dlje u prošlost od modernih vremen. Jedn
Odredjeni integral je granicna vrijednost sume beskonacnog broja clanova a svaki clan tezi k nuli i oznacava se sa : f x dx f x f x f x f x b a f
 Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
Mte ijug: Rijeseni zdci iz vise mtemtike 8. ODREDJENI INTEGRALI 8. Opcenito o odredjenom integrlu Odredjeni integrl je grnicn vrijednost sume eskoncnog roj clnov svki cln tezi k nuli i ozncv se s : n n
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA
 SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
SINUSNA I KOSINUSNA TEOREMA REŠAVANJE TROUGLA Sinusn terem glsi: Strnie trugl prprinlne su sinusim njim nsprmnih uglv. R sinβ sinγ Odns dužine strni i sinus nsprmng ugl trugl je knstnt i jednk je dužini
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
 27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
Metrički prostori i Riman-Stiltjesov integral
 Metrički prostori i Riman-Stiltjesov integral Dragan S. Djordjević Niš, 2009. 0 Sadržaj Predgovor 3 1 Metrički prostori 5 1.1 Primeri metričkih prostora................. 5 1.2 Konvergencija nizova i osobine
Metrički prostori i Riman-Stiltjesov integral Dragan S. Djordjević Niš, 2009. 0 Sadržaj Predgovor 3 1 Metrički prostori 5 1.1 Primeri metričkih prostora................. 5 1.2 Konvergencija nizova i osobine
Relativno mirovanje tečnosti. Translatorno kretanje suda sa tečnošću
 Reltivno irovnje tečnosti Trnsltorno kretnje sud s tečnošću Zdtk Cistern čiji je orečni resek elis oluos i b nunjen je tečnošću ustine i kreće se rvolinijski jednklo ubrzno ubrznje w o orizontlnoj rvni
Reltivno irovnje tečnosti Trnsltorno kretnje sud s tečnošću Zdtk Cistern čiji je orečni resek elis oluos i b nunjen je tečnošću ustine i kreće se rvolinijski jednklo ubrzno ubrznje w o orizontlnoj rvni
Uvod Newton-Leibnizova formula Glavne metode integriranja. Integrali. Franka Miriam Brückler
 Integrli Frnk Mirim Brückler Antiderivcije Koj je vez izmedu x 2 i 2x? Antiderivcije Koj je vez izmedu x 2 i 2x? Antiderivcij (primitivn funkcij) zdne funkcije f : I R (gdje je I otvoren intervl) je svk
Integrli Frnk Mirim Brückler Antiderivcije Koj je vez izmedu x 2 i 2x? Antiderivcije Koj je vez izmedu x 2 i 2x? Antiderivcij (primitivn funkcij) zdne funkcije f : I R (gdje je I otvoren intervl) je svk
MEHANIKA FLUIDA. Pritisak tečnosti na ravne površi
 MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
MEHANKA FLUDA Pritisk tečnosti n rvne površi. zdtk. Tešk brn dimenzij:, b i α nprvljen je od beton gustine ρ b. Kosi zid brne smo s jedne strne kvsi vod, gustine ρ, do visine h. Odrediti ukupni obrtni
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА
 ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
ТЕМПЕРАТУРА СВЕЖЕГ БЕТОНА empertur sežeg beton menj se tokom remen i zisi od ećeg broj utijnih prmetr: Početne temperture mešine (n izsku iz mešie), emperture sredine, opote hidrtije ement, Rzmene topote
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
NEJEDNAKOSTI I PRIMENE
 NEJEDNAKOSTI I PRIMENE dr Jele Mojlović Prirodo-mtemtički fkultet Niš SADRŽAJ Nejedkosti izmed u brojih sredi Prime ejedkosti izmed u brojih sredi 6 Geometrijske ejedkosti Nejedkosti z elemete trougl Stereometrijske
NEJEDNAKOSTI I PRIMENE dr Jele Mojlović Prirodo-mtemtički fkultet Niš SADRŽAJ Nejedkosti izmed u brojih sredi Prime ejedkosti izmed u brojih sredi 6 Geometrijske ejedkosti Nejedkosti z elemete trougl Stereometrijske
1. zadatak , 3 Dakle, sva kompleksna re{ewa date jedna~ine su x 1 = x 2 = 1 (dvostruko re{ewe), x 3 = 1 + i
 PRIPREMA ZA II PISMENI IZ ANALIZE SA ALGEBROM. zadatak Re{avawe algebarskih jedna~ina tre}eg i ~etvrtog stepena. U skupu kompleksnih brojeva re{iti jedna~inu: a x 6x + 9 = 0; b x + 9x 2 + 8x + 28 = 0;
PRIPREMA ZA II PISMENI IZ ANALIZE SA ALGEBROM. zadatak Re{avawe algebarskih jedna~ina tre}eg i ~etvrtog stepena. U skupu kompleksnih brojeva re{iti jedna~inu: a x 6x + 9 = 0; b x + 9x 2 + 8x + 28 = 0;
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Matematika 2. Boris Širola
 Mtemtik 2 (. Riemnnov integrl) Boris Širol predvnj . Riemnnov integrl 3 Pretpostvimo d immo neku neprekidnu relnu funkciju f, definirnu n nekom segmentu; tj., nek je dn neprekidn funkcij f : [, b] R.
Mtemtik 2 (. Riemnnov integrl) Boris Širol predvnj . Riemnnov integrl 3 Pretpostvimo d immo neku neprekidnu relnu funkciju f, definirnu n nekom segmentu; tj., nek je dn neprekidn funkcij f : [, b] R.
4. Trigonometrija pravokutnog trokuta
 4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
4. Trigonometrij prvokutnog trokut po školskoj ziri od Dkić-Elezović 4. Trigonometrij prvokutnog trokut Formule koje koristimo u rješvnju zdtk: sin os tg tg ktet nsuprot kut hipotenuz ktet uz kut hipotenuz
KUPA I ZARUBLJENA KUPA
 KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
KUPA I ZAUBLJENA KUPA KUPA Povšin bze B Povšin omotč M P BM to jet P B to jet S O o kupe Oni peek Obim onog peek O op Povšin onog peek P op Pimen pitgoine teoeme vnotn jednkotn kup je on kod koje je, p
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE
 1 SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE Neka je (V, +,, F ) vektorski prostor konačne dimenzije i neka je f : V V linearno preslikavanje. Definicija. (1) Skalar
1 SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE Neka je (V, +,, F ) vektorski prostor konačne dimenzije i neka je f : V V linearno preslikavanje. Definicija. (1) Skalar
1.PRIZMA ( P=2B+M V=BH )
 .RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
.RIZMA ( =+M = ).Izrčunti površinu i zpreminu kvr čij je ijgonl ug 0m, užine osnovnih ivi su m i m. D 0m m b m,? D 00 b 00 8 8 b b 87 87 0 87 8 87 b 87 87 87 8 87. Ivie kvr onose se ko :: ijgonl je ug.oreiti
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
MATEMATIKA 2. seminari. studij: Prehrambena tehnologija i Biotehnologija
 MATEMATIKA seminri studij: Prehrmben tehnologij i Biotehnologij Sdržj Integrlni rčun funkcije jedne vrijble. Uvod................................. Odredeni (Riemnnov) integrl. Problem površine........
MATEMATIKA seminri studij: Prehrmben tehnologij i Biotehnologij Sdržj Integrlni rčun funkcije jedne vrijble. Uvod................................. Odredeni (Riemnnov) integrl. Problem površine........
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA
 TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
TRIGONOMETRIJSKE FUNKCIJE OŠTROG UGLA Trignmetrij je prvitn predstvlj lst mtemtike kje se vil izrčunvnjem nepzntih element trugl pmću pzntih. Sm njen nziv ptiče d dve grčke reči TRIGONOS- št znči trug
A MATEMATIKA Zadana je z = x 3 y + 1
 A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
A MATEMATIKA (.5.., treći kolokvij). Zdn je z 3 + os. () Izrčunjte ngib plohe u pozitivnom smjeru -osi. (b) Izrčunjte ngib pod ) u točki T(, ). () Izrčunjte z u T(, ). (5 bodov). Zdn je z 3 ln. () Izrčunjte
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
1 Afina geometrija. 1.1 Afini prostor. Definicija 1.1. Pod afinim prostorom nad poljem K podrazumevamo. A - skup taqaka
 1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
FURIJEOVI REDOVI ZADACI ( II
 FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
FURIJEOVI REDOVI ZADACI ( II deo Primer. Fukciju f ( = rzviti u Furijeov red segmetu [,] ztim izrčuti sumu red. ( Rešeje: Kko je f ( = = = f ( zkjučujemo d je fukcij pr. Koristimo formue: = f ( = + ( cos
PIRAMIDA I ZARUBLJENA PIRAMIDA. - omotač se sastoji od bočnih strana(najčešće jednakokraki trouglovi), naravno trostrana piramida u omotaču
 PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
PIRAMIDA I ZARULJENA PIRAMIDA Slično ko i kod pizme i ovde ćemo njpe ojniti oznke... - oeležvmo dužinu onovne ivice - oeležvmo dužinu viine pimide - oeležvmo dužinu viine očne tne ( potem) - oeležvmo dužinu
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA
 FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
FORMULE VEZANE UZ MATEMATIČKE KOLEGIJE PREDDIPLOMSKOG STUDIJA Vrijednoti inu i koinu π π π π ϕ 6 4 3 in ϕ 3 co ϕ 3 Trigonometrijke funkcije polovičnih rgument in x = co x co x = + co x Trigonometrijke
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Zadaća iz kolegija Metrički prostori 2013./2014.
 Zadaća iz kolegija Metrički prostori 2013./2014. Zadaća nosi 5 bodova. Sve tvrdnje u zadacima obrazložiti! Renato Babojelić 31 Lea Božić 13 Ana Bulić 7 Jelena Crnjac 5 Bernarda Dragin 19 Gabriela Grdić
Zadaća iz kolegija Metrički prostori 2013./2014. Zadaća nosi 5 bodova. Sve tvrdnje u zadacima obrazložiti! Renato Babojelić 31 Lea Božić 13 Ana Bulić 7 Jelena Crnjac 5 Bernarda Dragin 19 Gabriela Grdić
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Zadatak 2 Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z 3 z 4 i objasniti prelazak sa jedne na drugu granu.
 Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
Granične vrednosti realnih funkcija i neprekidnost
 Granične vrednosti realnih funkcija i neprekidnost 1 Pojam granične vrednosti Naka su x 0 R i δ R, δ > 0. Pod δ okolinom tačke x 0 podrazumevamo interval U δ x 0 ) = x 0 δ, x 0 + δ), a pod probodenom δ
Granične vrednosti realnih funkcija i neprekidnost 1 Pojam granične vrednosti Naka su x 0 R i δ R, δ > 0. Pod δ okolinom tačke x 0 podrazumevamo interval U δ x 0 ) = x 0 δ, x 0 + δ), a pod probodenom δ
8 Funkcije više promenljivih
 8 Funkcije više promenljivih 78 8 Funkcije više promenljivih Neka je R skup realnih brojeva i X R n. Jednoznačno preslikavanje f : X R naziva se realna funkcija sa n nezavisno promenljivih čiji je domen
8 Funkcije više promenljivih 78 8 Funkcije više promenljivih Neka je R skup realnih brojeva i X R n. Jednoznačno preslikavanje f : X R naziva se realna funkcija sa n nezavisno promenljivih čiji je domen
Dru{tvo matemati~ara Srbije. Republi~ki seminar 2011, Novi Sad, Srbija. Pripremawe u~enika osnovnih {kola za takmi~ewa iz matematike
 Dru{tvo mtemti~r Srije Repuli~ki seminr 0, Novi Sd, Srij Pripremwe u~enik osnovnih {kol z tkmi~ew iz mtemtike \or e Brli}, Mtemti~ki institut SANU, Beogrd, Srij Zdrvko Cvetkovski, Evropski univerzitet,
Dru{tvo mtemti~r Srije Repuli~ki seminr 0, Novi Sd, Srij Pripremwe u~enik osnovnih {kol z tkmi~ew iz mtemtike \or e Brli}, Mtemti~ki institut SANU, Beogrd, Srij Zdrvko Cvetkovski, Evropski univerzitet,
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).
![PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ). PID: Domen P je glavnoidealski [PID] akko svaki ideal u P je glavni (generisan jednim elementom; oblika ap := {ab b P }, za neko a P ).](/thumbs/74/70316766.jpg) 0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
0.1 Faktorizacija: ID, ED, PID, ND, FD, UFD Definicija. Najava pojmova: [ID], [ED], [PID], [ND], [FD] i [UFD]. ID: Komutativan prsten P, sa jedinicom 1 0, je integralni domen [ID] oblast celih), ili samo
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
