ASPECTE CANTITATIVE ALE MANAGEMENTULUI CALITĂŢII PRODUSELOR ŞI SERVICIILOR DIN TURISM
|
|
|
- Αναστασούλα Δαμασκηνός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 6 Maagemetul caltăţ prouselor ş servclor î tursm Captolul ASPECTE CANTITATIVE ALE MANAGEMENTULUI CALITĂŢII PRODUSELOR ŞI SERVICIILOR DIN TURISM.. Preczare PRECIZĂM CĂ FIRMELE CITATE ÎN PREZENTUL MATERIAL NU EXISTĂ, ORICE CONCORDANŢĂ DE NUME CU FIRME ÎNREGIST- RATE FIIND PUR ACCIDENTALĂ. Numărul staarulu Deumrea staarulu Verfcarea caltăţ loturlor e prouse pe baza velulu e 36/3-84 caltate acceptabl (AQL). Regul e utlzare a proceeelor ş tabelelor statstce - matematce petru verfcarea caltăţ pr măsurare Verfcarea caltăţ loturlor e prouse. Metoe e prelevare a eşatoaelor petru prouse î bucăţ. 874/ - 77 Fabltate, meteabltate ş spobltate. Fabltate. Termologe Caltatea prouselor. Termologe Fabltatea prouselor ustrale. Icator e fabltate. Stueţ vor cosulta, la Bbloteca Uverstăţ Poltehca Tmşoara aceste staare ş îş vor ota prcpalele preveer ale acestora... Prcpalele staare româeşt care reglemetează cotrolul caltăţ servclor ş prouselor Î tabelul. sut eumerate prcpalele staare e stat - STAS-ur - care reglemetează caltatea ş fabltatea prouselor ş servclor. Aceste staare auc reglemetăr specfce, completâ staarele teraţoale meţoate î paragrafele.6. ş.. Tabelul. Numărul Deumrea staarulu staarulu Cotrolul statstc al caltăţ. Cotrolul î tmpul procesulu e fabrcaţe. Prcp e bază Aplcaţ ale metoelor statstce. Termologe ş smbolur. Verfcarea caltăţ loturlor e prouse pe baza velulu e caltate acceptabl (AQL). Regul e utlzare a proceeelor ş 36/ - 84 tabelelor statstce - matematce petru verfcarea caltăţ pr atrbute ş pr măsurare. Verfcarea caltăţ loturlor e prouse pe baza velulu e caltate acceptabl (AQL). Regul e utlzare a proceeelor ş 36 /- 84 tabelelor statstce - matematce petru verfcarea caltăţ pr atrbute..3. Defţ Mărme caracterstcă a caltăţ Caltatea lmtă (LQ) Caltatea mee a uu proces e fabrcaţe Caltatea mee rezultată (AOQ) Tabelul. Defţe Nvelul e caltate care corespue ue probabltăţ e acceptare relatv reusă. Repreztă caltatea lmtă a lotulu petru care beefcarul ar putea să accepte, cu o mcă probabltate (e mamum 5 - %), că u lot e o astfel e caltate ar putea să apară. Se eprmă pr fracţuea efectvă mee sau pr umărul meu e efecte pe utăţ e prous, estmată pe baza eşatoaelor succesve prelevate rect petru acest scop, sau lotur verfcate la prma prezetare. Se eprmă pr fracţuea efectvă, sau pr umărul meu e efecte pe utăţ e prous, a ue cattăţ obţută î urma verfcăr caltăţ uu şr e lotur succesve, cluzâ î această colectvtate u uma loturle acceptate, c ş loturle î care, ca urmare a respger lor coform aceluaş pla, efectvele găste pr verfcare % au fost îlocute cu utăţ e prous coforme caltatv.
2 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm Mărme caracterstcă a caltăţ Caracterstca operatvă Defectv (utate e prous cu efecte) Defectv crtc Defectv major Defectv mor Defectul crtc Defectul major Defectul mor Defectul Efectvul eşatoulu () Efectvul lotulu (N) Eşatoarea (prelevarea) Eşatoarea multplă Eşatoarea smplă Eşatoul Defţe Caracterstca uu pla e verfcare at, care că probabltatea e acceptare a uu lot î fucţe e caltatea sa reală. Această caracterstcă poate f reprezetată tabelar sau grafc, sub forma curbe CO. Utatea e prous cu uul sau ma multe efecte. Defectvul care preztă uul sau ma multe efecte crtce. Defectvul care preztă uul sau ma multe efecte majore. Defectvul care preztă uul sau ma multe efecte more. Defectul care este susceptbl să coucă la lpsă e securtate sau la rscur e accetare a utlzatorlor, sau care ar putea să împece îeplrea fucţe uu prous fal mportat. Defectul care, fără să fe crtc, este susceptbl să provoace o efectare sau să reucă î mo substaţal posbltatea e utlzare a prousulu respectv î scopul petru care a fost esemat. Defectul care u este susceptbl să reucă prea mult posbltatea e utlzare a prousulu respectv î scopul petru care a fost esemat sau care, faţă e specfcaţle stablte, costtue o abatere care afectează oar î mcă măsură utlzarea sau fucţoarea efcetă a prousulu respectv. Necoformtatea utăţ e prous cu coţle stablte petru ua caracterstcle sale. Numărul e utăţ e prous prezete î eşato. Î aumte cazur, poate f egal cu efectvul lotulu. Numărul e utăţ e prous prezete î lot. Proceura folostă petru etragerea sau costturea uu eşato. Moul e eşatoare care presupue posbltatea prelevăr pâă la = 7 eşatoae succesve, ecza e prelevare a eşatoulu "" ( ) f î fucţe e formaţle furzate e cele "-" eşatoae preceete. Moul e eşatoare care costă î prelevarea uu sgur eşato pe lot. Ua sau ma multe utăţ e prous, prelevate aleatoru tr-u lot, estate furzăr e formaţ asupra lotulu ş, evetual, servr rept bază ue ecz refertoare la lotul e prouse sau la procesul care a geerat lotul respectv. Mărme caracterstcă Defţe a caltăţ Raportul ître umărul e efectve ş umărul total e Fracţuea efectvă (p) utăţ e prous coserate. Se eprmă î procete. Lmta caltăţ me Valoarea mamă a caltăţ me rezultate, aşa cum a rezultate (AOQL) fost eftă ma sus. Smbolul e eare al efectvelor eşatoaelor î Ltera e co (LC) raport cu efectvul lotulu ş velul e verfcare a caltăţ utlzat. Cattatea eftă tr-o aumtă marfă, fabrcată î coţ presupuse uforme, care trebue etras u Lotul [supus verfcăr eşato spre a f supus verfcăr caltatve, acă petru caltăţ] care se etermă îcararea sa î crterul / crterle e acceptare. Lotul poate fer e o mulţme e utăţ. Nvelul e caltate care corespue ue probabltăţ e acceptare specfcate relatv rcate. Repreztă Nvelul e caltate fracţuea efectvă mamă care, î scopul verfcăr acceptabl (AQL) caltăţ pr eşatoare, poate f coserată î mo satsfăcător rept caltate mee a procesulu e fabrcaţe la furzor. Nvelul e verfcare Caracterstca uu pla e verfcare, aleasă apror, care (Nv) leagă efectvul eşatoulu e cele al loturlor. Numărul e acceptare (A) Numărul e efecte (pe utăţ e prous - u) Numărul e respgere (R) Plaul e verfcare a caltăţ Este, î verfcarea caltăţ pr atrbute, valoarea mamă a umărulu e efectve sau e efecte găste î eşato care ma permte luarea ecze e acceptare a lotulu. Raportul ître umărul e efecte ş umărul total e utăţ e prous coserate. Se eprmă î procete. Este, î verfcarea caltăţ pr atrbute, valoarea mmă a umărulu e efectve sau e efecte găste î eşato, care couce la ecza e respgere a lotulu. Asamblul format plaul e eşatoare ş regulle specfce care trebue urmate petru luarea ecze e acceptare sau e respgere a uu lot, î fucţe e velul caltăţ acestua. Plaul e verfcare este: a.) vualzat pr elemetele varate e trare staar (vel e caltate acceptabl, vel e verfcare, efectvul lotulu, tpul plaulu e eşatoare - smplu, ublu sau multplu), elemete care se stablesc î cotractul ecoomc e aprovzoare, b.) costtut elemete ca: efectvul eşatoulu, umărul e acceptare, umărul e respgere.
3 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm Mărme caracterstcă a caltăţ Probabltatea e acceptare (Pa) Proceeul e verf-care a caltăţ Utatea e prous Utatea verfcată Verfcarea caltăţ la prma prezetare Verfcarea caltăţ pr atrbute Verfcarea caltăţ pr eşatoare Verfcarea caltăţ Defţe Probabltatea ca u lot e o aumtă caltate să fe acceptat pe baza uu pla e verfcare at. Se costtue totaltatea plaurlor e verfcare suboroate setulu stablt al celor patru elemete varate e trare î staar ş corespuzătoare ecestăţlor refertoare la mofcarea severtăţ e verfcare sau la mofcarea temporară a claselor efectvelor loturlor lvrate. Obectul supus verfcăr caltăţ, cu scopul e a f clasfcat ca efectv sau eefectv, sau petru a se eterma umărul e efecte pe care îl coţe. Poate f u sgur artcol, o pereche, u asamblu e artcole, o lugme, o suprafaţă, u volum, o operaţe, o compoetă a uu asamblu - prous ft sau îsuş pro-usul ft. Nu este oblgatoru ca utatea e prous să cocă cu utatea e achzţoare, lvrare, proucţe sau trasport. O utate e prous, u lot e prouse, u proces e fabrcaţe. Este u terme aplcabl loturlor supuse petru prma ată verfcăr caltăţ, î scopul e a le stge e loturle care ar trebu presupuse verfcăr î urma remeerlor efectuate ca ş rept cosecţă a respger lor la prma verfcare. Metoă e verfcare a caltăţ pr costatarea, pe fecare utate e prous tr-u eşato prelevat tru lot, a prezeţe sau a abseţe ue caracterstc caltatve (atrbut) oarecare ş coserarea, upă moul e eprmare a caltăţ lotulu, fe a umărulu total e utăţ care poseă sau u această caracterstcă, fe a umărulu total e efecte găste la utăţle e prous tr-u eşato. Verfcarea uu umăr restrâs e utăţ e prous, prelevate aleatoru tr-u lot sau tr-u proces e fabrcaţe, coform uu pla. Procesul e măsurare, eamare, îcercare, etaloare, sau orce altă moaltate e comparare a utăţ verfcate cu specfcaţle care î sut aplcable..4. Prelucrarea statstcă a atelor î tursm.4.. Parametr statstc Fe u şr e ate,, =, ( eumu-se ş varablă aleatoare, ar mulţmea a căre elemete sut - şrul propru-zs - efeşte populaţa). Prelucrarea statstcă a acestor ate presupue etermarea: a) parametrlor statstc prcpal: parametr e teţă: mea artmetcă e soaj (mometul e soaj e orul îtâ): =, (.) = meaa e soaj (valoarea faţă e care 5% valor sut ma mar, ar 5% sut ma mc, valorle şrulu e ate f arajat î ore crescătoare sau escrescătoare): M M e e = =, + + +, mpar, par, (.) moul (moa) e soaj (valoarea care apare cel ma frecvet î şrul e valor): M = + 3 ( M e ), (.3) valoarea cetrală: c ma + m = (.4) (ue ma ş m valoarea mamă, respectv mmă şr), c e împrăştere: mometul e soaj e orul p : = p Mp, (.5) = mometul cetrat e soaj e orul p : p ( f ( ) µ p = ), (.6) = î care f este frecveţa absolută asocată valor,
4 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm spersa e soaj (abaterea staar emprcă) (mometul cetrat e orul al olea): ( ) = f ( ) s =, (.7.) = = sau, luâ ca reper valoarea aevărată X: σ = = ( ) ( X) = f ( X) =, (.7.) abaterea mee pătratcă (abaterea staar) (măsura varabltăţ varable aleatoare, respectv măsura tuturor abaterlor aleatoare îtâmplătoare e la valoarea mee, ): s = s, (.8.) respectv măsura tuturor abaterlor aleatoare îtâmplătoare e la valoarea aevărată: ampltuea şrulu e ate: σ = σ, (.8.) R = ma m, (.9) coefcetul e varaţe al şrulu: s C v =, (.) coefcetul e asmetre al şrulu: coefcetul e boltre al şrulu: 3 ) 3 mărmea tervalulu e grupare (coform H. A. Sturges): R a =. (.4) frecveţa absolută (f ) este repreztă umărul e mărm şrul e varable; se eprmă î utăţ cocrete e măsură; * f frecveţa relatvă ( ), eumtă ş poere sau greutate specfcă, repreztă probabltatea e aparţe a ue aumte varable ş se obţe ca mărme relatvă, raportâ frecveţa varable la totalul frecveţelor: * f * f f =, sau f [%] = f f = frecveţa cumulată: F( ) = f j j= = * * j j= ; (.5), respectv F ( ) = f. (.6) Utlzâu-se oţuea e frecveţă, cu sesul e poere, se trouc următor cator a teţe cetrale: mea artmetcă poerată: ( f ) = =, (.7) f (µ β =, (.) mea armocă (utlzablă la calculul velulu meu al ue caracterstc (s ) ervate cu caracter e mărme mee parţală, sau mărme relatvă parţală, e eemplu: la calculul celu meu e grup al preţurlor, câ u estă formaţ refertoare la volumul fzc al mărfurlor): µ 4 β =, (.) (s ) cu observaţle: - acă β < 3, estatea e repartţe este ma ascuţtă ecât cea ată e repartţa ormală, - acă β = 3, estatea e repartţe coce cu repartţa ormală, - acă β > 3, estatea e repartţe este ma aplatzată ecât cea ată e repartţa ormală; b) verfcarea ormaltăţ şrulu e ate: stablrea umărulu e clase î care se subve şrul e ate: = + 3,3 log(), (.3) sau, utlzâ frecveţa (poerea), = h =, = f = h =, (.8) f =
5 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 69 7 Maagemetul caltăţ prouselor ş servclor î tursm mea pătratcă (utlzată atuc câ preomă valorle mar ale varable ş se oreşte acorarea ue mportaţe ma mar aceste categor e valor): p = = sau ( f ) = p =, (.9) f = mea geometrcă (se utlzează î cazul serlor cu amcă rcată): g = =, respectv = f ( f ) g ; (.) = = - abaterea mee pătratcă: s =,4957, - mometul cetrat e orul 3: µ 3 = -,576, - mometul cetrat e orul 4: µ 4 =,4753, - ampltuea şrulu: R = 4, - coefcetul şrulu: C v =,9546, - coefcetul e asmetre: β =,566, - coefcetul e boltre: β =,475. Î fgura. este reprezetată estatea e repartţe petru populaţa stuată, apromată cu o repartţe ormală..4.. Icator statstc specfc actvtăţlor turstce Ître mărmle me efte pr relaţle (.), (.7), (.8), (.9), (.) estă relaţa: a) Icator macroecoomc Capactatea e cazare h < g < < p. capactatea e cazare estetă (stalată) repreztă umărul e locur e folosţă turstcă îscrse î cel ma recet act e recepţe, sau e STUDIU DE CAZ ) Fe populaţa eftă e: 8, 8, 7, 9, 9, 9, 9, 5, 5, 9, 8, 5, 8, 7, 9, 8, 5, 6, 9, 8, 9, 7, 9. Să se stablească parametr statstc prcpal e teţă. Petru cele 3 e valor: - mea artmetcă este 7,657, - umarul e ate şr: 3 mpar, ş atuc meaa este: M e = 8, petru (+)/ =, - moul e soaj este: M o = 8,69565, - valoarea cetrală: c = 7, - spersa: s =,375, omologare, sau e clasfcare, a utăţ turstce respectve, capactatea e cazare î fucţue (spoblă) repreztă umărul e locur e cazare e care pot beefca turşt, ţâ cot e umărul e zle cât este eschsă utatea turstcă respectvă. Crculaţa turstcă umărul total e turşt (ΣT) repreztă umărul persoaelor care călătoresc î afara localtăţlor î care îş au omclul stabl, petru o peroaă ma mcă e lu ş stau cel puţ o oapte îtr-o utate e cazare turstcă; motvul călătore trebue să fe fert e acela e a esfăşura o actvtate retrbută, îoptarea repreztă fecare oapte petru care o persoaă este îregstrată îtr-o utate e cazare turstcă, umărul total e zle-turst (Σ(z T)), (z ma = umărul e zle), umărul meu e turşt: urata mee a sejurulu: estatea crculaţe turstce: ( z T) T =, (.) T P aut ( z T) z =, (.) T T (z T) Dt =, D't =, (.) P aut Fg... Varaţa estăţ e repartţe ormală (P aut = populaţa autohtoă totală a ţăr aalzate).
6 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 7 7 Maagemetul caltăţ prouselor ş servclor î tursm b) Icator facar cele cotrbuţe tursmulu la îcasărle valutare: îcasăr valutare tursm îcasăr valutare totale c c f_ f_ El_c = :, (.9) c f_, cele cotrbuţe tursmulu la cheltuelle valutare: cheltuel î valută efectuate î străătate cheltuel valutare totale (.3) ue pr "c" s-a otat cererea turstcă, ar rept factor e flueţă (f_) au fost coseraţ preţurle, populaţa, veturle obţute actvtăţ turstce, cheltuel cu publctatea, etc. (cu ce "" s-a coserat mărmea respectvă e referţă). sau mport e buur, servc sau captal petru tursm mport total catorul îcasărlor fscale: îcasăr fscale tursm îcasăr fscale totale, (.4) Icator oferte turstce: oferta turstcă se costtue poteţalul turstc atural ş atropc, baza tehco-materală ş forţa e mucă,, (.5) c) Icator mcroecoomc (caracterstc socetăţlor turstce) Icator cerer turstce: cererea turstcă repreztă totaltatea persoaelor care îş mafestă orţa e a se eplasa î afara localtăţ e reşeţă, cosumul turstc repreztă cheltuelle efectuate e cererea turstcă petru achzţoarea uor buur ş servc legate e motvaţa turstcă, realzată îatea sau î tmpul eplasăr sau la locul e estaţe. Icator cerer turstce pot f grupaţ, î fucţe e tpul cerer, î: catorul cerer totale: (cerere totală) = (cerere eteră) + (cerere teră), catorul e proveeţă a cerer: - cererea eteră: - cererea teră: cererea eteră ţara "" total cerere eteră cerere reguea "j" total cerere teră proucţa turstcă se efeşte rept asamblul e servc care moblzează forţa e mucă, echpametele ş buurle materale care se materalzează îtr-u cosum efectv î tursm. Icator oferte turstce se clasfcă î:, (.6) - cator a baze materale: + cator fourlor fe: ++ cator e uzură a fourlor fe: valoare four fe uzate I uz = valoare totală e vetar, (.3) ++ cator e îore a fourlor fe (cu referre la o aumtă peroaă e tmp - semestru, a, etc): valoare four fe o I = valoare totală e vetar, (.3) ++ cator e scoatere fucţue a fourlor fe (e regulă, se referă la o aumtă peroaă e tmp - semestru, a, etc, raportat la îceputul peroae): valoare four fe scoase fucţue valoare totală e vetar, (.3) (.7) - cator capactăţ e cazare: se referă la umărul total e locur e cazare ş repreztă oferta teoretcă mamă - î utăţ-zle, sau oferta efectvă (reală) - î utăţ-zle; - cator mjloacelor e agreemet, aalzate î fucţe e felul lor, sau (.8) e locur e agreemet la e locutor; + cator specfc stalaţlor e trasport: - cerere pe mjloace e cazare: graul e satsfacere a cerer turstce a ue stalaţ e trasport: cerere cazare hotel cerere cazare vle cerere cazare ha,, cerere totală cerere totală cerere totală capactate mee orară stalaţe e trasport umăr e locur e cazare - cerere pe mjloace e trasport, graul e otare a ue stalaţ e trasport: - cerere sezoeră (aual, trmestral, luar, ), (capactate mee orară stalaţe e trasport) (fereţa e vel a stalaţe) - elastctatea cerer:, (.34) umăr e locur e cazare (.33)
7 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm graul e aglomerare a ue pârt e sch: Icator poteţalulu turstc al peţe lugmea pârte Fe "" proucător P ( =, ) e servc turstce, "m" cosumator ; (.35) umărul e locur e cazare C j ( j =,m ) a acestor servc ş N j om-zle solctate e către cosumatorul Icator ocupăr forţe e mucă C j e la proucătorul P ; relaţa tre aceşt parametr poate f prezetată catorul structur forţe e mucă, aceasta f grupată pe j =,m stetc î tabelul.3: categor e agajaţ (ag) Tabelul.3 catorul utlzăr tmpulu e lucru: urata mee a zle e lucru: agj sfm j =, (.36) ag j ho zm =, (.37) zo ue ho = umăr e ore-om lucrate ş zo = umăr e zle-om lucrate, - urata mee a lu "j" lucrate: j lmj = zo, (.38) tma Cosumator P P C N N C j Proucător P P Cerere solvablă N NT N j NT j C m N m N m N m NT m Cerere G G G G Cu aceste ate, se efesc: cota e paţă a proucătorulu e servc turstce: (tma j = total meu e agajaţ î lua "j"), G catorul prouctvtăţ muc: P =, (.43) G valoare totală îcasăr î jua "j" Pm j = (.39) tma probabltatea ca u cosumator să achzţoeze prousul turstc e la j proucătorul P : Icator cerere - ofertă Nj coefcetul e utlzare a capactăţ e cazare: a j =, (.44) NTj N Nt Ds Ucc = =, (.4) Lc z Lc z poerea cerer cosumatorulu "j" î totalul cerer solvable, G: cu N = umărul e îoptăr, NTj qj =, (.45) Lc = umărul e locur e cazare, G z = umărul e zle luate î calcul, probabltatea e atracţe a cosumatorulu "j" faţă e proucătorul "" - Nt = umărul e turşt î peroaa coserată, este o varablă care epe e tmp ş e efectul uor factor e atracţe, Ds = urata mee a sejurulu, cum ar f: coefcetul e aalză a actvtăţ ue ageţ e voaj: cerere comercalzată pr ageţe Cag = (.4) cerere turstcă totală Cag = locur comercalzate pr ageţe umăr total e locur (.4) cele e caltate a servclor - etermată pe baza compoetelor prcpale ale caltăţ; se stableşte u puctaj al prousulu turstc furzat e proucătorul "" la mometul t: I calt = puctaj atcpat puctaj realzat G, (.4)
8 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm cele e atractvtate al preţulu: I pret = preţ atcpat preţ realzat ezvoltarea reţele e strbuţe a prouselor turstce (fecare proucător e servc turstce va căuta să-ş ezvolte o reţea propre e strbuţe, pr termeul cărea îş va atrage cosumator) uce u ce e atracţe al cosumatorulu "j" petru prousul turstc "" î fucţe e staţa j tre e: I st = staţa efectvă tre cosumator ş prousul turstc staţa estmată tre cosumator ş prousul turstc - volumul îcasărlor valutare prestaţa turstcă, - volumul proucţe ustrale e atură turstcă,, (.47) - proucţa etă e buur (ş servc) turstce, - vetul et actvtăţ turstce,, (.48) î care staţa estmată ( est ) tre cosumator ş prousul turstc cosumat/ ofert este ată e: est = m ( ) + h jh < (staţa efectvă), (.49) cu = eroarea e estmare a staţe, jh = staţa e la cosumatorul "j" la strbutorul "h" al prousulu turstc "", la mometul t. Dacă ( est (staţa efectvă)) (I st = ). (.5) Icele e atracţe al cosumatorulu se poate apreca ş upă costul trasportulu; cele e prompttue a eservr cosumatorlor se eprmă pr: t str Iprompt =, (.5) t prompt î care prompttuea cu care este eservt cosumatorul este: t = <, (.5) prompt mh (t jh ) + t t str - acumulărle băeşt provete surse legate e actvtatea turstcă, - proftul, etc. Î veerea etermăr ş aalze efceţe actvtăţlor tursm se calculează - cator tehco - ecoomc e fuametare a efceţe ecoomce a vestţlor î tursm, care se costtue : valoarea vestţe, capactatea e cazare sau e almetaţe publcă, urata e realzare a vestţe, e la emarare ş pâă la falzarea e, vestţa specfcă, acă volumul e vestţ ecesar petru u loc e cazare sau e masă, volumul îcasărlor totale, cheltuelle totale, cheltuelle efectuate la e le îcasaţ, vetul et (volumul acumulărlor totale), beefcul - B: B = (totalul îcasărlor estmate) - (totalul cheltuellor), (.54) rata retabltăţ (rata beefculu) R b = beefcul totalul îcasărlor, (.55) urata e recuperare a vestţe totale, coefcetul margal al vestţe, reprezetat pr umărul e procete cu care cresc, î peroaa "t" e tmp îcasărle, raportat la creşterea cu uu la sută a volumulu vestţlor, - cator e efceţă ecoomcă a baze e cazare: coefcetul e utlzare (e ocupare) a capactăţ e cazare: î care - t str este tmpul efectv e strbuţe a prousulu turstc, - t prompt este urata mee e aşteptare petru ca prousul turstc "" îoptăr realzate îoptăr realzate să fe strbut cosumatorulu "j", C u.cazare = = umăr e patur îoptăr poable, (.55) - t jh este tmpul e aşteptare petru cosumatorul "j" petru ca să fe î care "îoptăr posble = umăr e patur 365", sau servt e strbutorul "h" cu prousulu turstc "", la mometul t, îcasarea mee pe pat, - t este toleraţa e estmare a tmpulu e aşteptare; cheltuala mee pe pat, Dacă - cator e efceţă ecoomcă, a baze e almetaţe publcă, la vel ( tprompt tstr ) (Iprompt = ). (.53) mcroecoomc: Icator efceţe ecoomce, la vel mcroecoomc, a tursmulu se îcasăr proucţa propre pe m spaţu e proucţe, aprecază pr: prouctvtatea muc persoalulu prouctv: - volumul e marfă turstcă esfăcută, valoarea proucţe vâute ş îcasate P pers.pro =, (.57) - volumul e îcasăr prestaţa turstcă, umăr meu e persoal
9 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm valoarea îcasărlor pe u loc e mucă, beefcul pe u loc e mucă, coefcetul e utlzare a capactăţ săl e mese: C utl.ca.sala = umărul meu e locur ocupate zlc umărul total e locur, (.58) afluul e cosumator pe u loc e masă, umărul cosumatorlor pe ospătar, îcasarea mee pe clet, cheltuel la le îcasăr, rata retabltăţ, efă ca raportul tre beefc ş îcasăr, prouctvtatea orară a muc, eftă ca volumul total al îcasărlor, raportat la umărul e ore lucrate, - cator e efceţă ecoomcă a baze e agremet: graul e ocupare a capactăţ e agremet, rata retabltăţ, cheltuel la le îcasăr, - cator e efceţă ecoomcă a parculu propru e utlaje e trasport: coefcetul e utlzare: C utlz = utlaje zlce î eploatare, (.58) total utlaje î vetar coefcet e ocupare, sau frecveţa e utlzare a uu aumt mjloc e trasport, coefcetul e utlzare a tmpulu e lucru, îcasarea mee pe utlaj-zle, vual, îcasarea mee pe utlaj-zle vetar. ) Icator caltăţ actvtăţ turstce Laturle caltatve ale tursmulu se costtue : - coţle e servc, - ptorescul zoe, - valorle storce ş culturale ale zoe, - velul poluăr, - coţle e clmă, - obectve culturale ş ustrale, - satsfacţa persoală a turstulu. Icator caltăţ oferte se evaluează pr creşterea/scăerea cerer ca urmare a îmbuătăţr/îrăutătr ş versfcăr/eversfcăr servclor turstce. Î acest scop, se vor lua î calcul: - velul caltăţ prestaţlor, - velul versfcăr servclor, - graul e cofort ş otare a utăţ turstce, - cator e compettvtate, - cator specfc e păstrare a echlbrulu ecologc, - refacerea ş fortfcarea forţe e mucă a turştlor, - efecte culturale, cum ar f: umărul e moumete storce la e locutor, umărul e vztator la e locutor, frecveţa vztăr obectvelor turstce, grupate pe sezoae, - umărul e turşt: care vztează zoa petru prma ată, care repetă vzta (e - 3 or, e 4-5 or, e ma mult e 5 or). Icator meţoaţ ma sus se vor aplca petru atele culese î tmpul efectuăr practc tehologce..5. Sstemul e cator a caltăţ Icator caltăţ sut epres cattatve ale caracterstclor prouselor sau servclor la care se referă. Sstemul e cator a caltăţ este costrut sub forma ue prame î trepte: treapta îtâ, stuată la baza prame, cupre cel ma larg spectru e cator e caltate, eumţ cator aaltc, (smpl) a caltăţ ş se referă la o sgură caracterstcă, treapta a oua, stuată î zoa meaă a prame, cupre grupa catorlor stetc a caltăţ, caracterstc fecăre grupe e caracterstc, treapta a trea, costtu vârful prame, cupre catorul comple (tegral) al caltăţ..5.. Icator aaltc (smpl) e caltate Ca ş caracterstcle e caltate, cator aaltc a caltăţ care repreztă aceste caracterstc se eprmă î utăţ aturale, atural-coveţoale, e tmp e mucă ş valorce. Î fucţe e atura lor, cator aaltc e caltate se eprmă: cator aaltc a caracterstclor tehce, ecoomce ş e utlzare se eprmă umerc, cator aaltc a caracterstclor socale se eprmă atât umerc cât ş pr calfcatve, cator aaltc a caracterstclor estetce se eprmă pr calfcatve trasformable î mărm umerce, coform ue scale alese e către utlzator, cum ar f, e eemplu: foarte be =, be = 8, satsfăcător = 6, esatsfăcător = 4.
10 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 79 8 Maagemetul caltăţ prouselor ş servclor î tursm Icator aaltc se eprmă sub forma e cator relatv, calculaţ cu relaţa: b =, (.6) ue: =, umărul e ore a caracterstclor e caltate luate î coserare, mărmea catorulu smplu al caracterstc a prousulu sau servculu aalzat, b mărmea catorulu e bază (e comparare) al caracterstc, mărmea relatvă a catorulu e caltate; asupra valor acestu cator se fac următoarele observaţ: acă <, atuc velul caltăţ caracterstc este feror velulu luat ca bază e aprecere, acă =, atuc velul caltăţ caracterstc este egal cu velul luat ca bază e aprecere, catorul stetc al caracterstclor socale este eft pe baza prcpulu utltăţ î ses Neuma-Morgerster. Coform acestu prcpu, caracterstcle socale se trasformă î utltăţ, eprmat pr mea artmetcă, rect: sau pr mea artmetcă poerată: s s = I s = u, (.63.) s I s = (u ), (.63.) s = = ue s umărul e caracterstc socale luate î coserare, u utltatea caracterstc socale, coefcetul e poere (e mportaţă) al caracterstc socale ; catorul stetc al caracterstclor e eploatare este etc cu catorul e spobltate Icatorul comple (tegral) e caltate acă, > atuc velul caltăţ caracterstc este superor velulu luat ca bază e aprecere. Acest cator eprmă legătura tre caracterstcle efectve ale prousulu/ servculu ş parametr e etermare a evo socale cărea î corespue..5.. Icator stetc e caltate Dacă urata e fucţoare a prousulu este e pâă la u a, catorul comple e caltate este at e: Aceşt cator corespu prcpalelor grupe e caracterstc e caltate: catorul stetc al caracterstclor tehce se coseră a f at e velul tehc al prousulu; catorul stetc al caracterstclor estetce este coserat a f mea artmetcă a calfcatvelor acorate petru fertele caracterstc estetce luate î coserare; se calculează cu relaţa: e I es = N, (.6) e = ue: e umărul e caracterstc estetce luate î coserare, N calfcatvul (ota) acorat(ă) caracterstc estetce ; catorul stetc al caracterstclor ecoomce este at e costul specfc al caltăţ, (costul, raportat la utatea e efect utl E u ): I ec Eu I =, (.64) C + C r ue: E u efectul utl (rezultatul) obţut pr prousul/servcul respectv, C r cheltuelle efectuate petru materalzarea prousulu/serv-culu, C e cheltuelle e eploatare. Dacă urata e fucţoare este ma mare e u a, catorul comple e caltate este at e: Eu(t) I = C + C r e = C r e f e) e = e Eu ( + = Eu =, (.65.) f Cr f() + C ( + ) + C (+ e ue: f umărul alor e fucţoare, C Cp + Cc + C + C tot p = =, (.6) e ( =,5) coefcet ormatv e efceţă ecoomcă, E E u ue: C p costul e preverea efectelor ş e asgurare a caltăţ, C c costul cotrolulu e caltate, C costul îtreţer prousulu la beefcar ş costul servce-ulu, C p costul pererlor atorate lpse / efectelor e caltate; C r cheltuelle efectuate petru materalzarea prousulu respectv a servculu, C e cheltuelle auale e eploatare (îtrebuţare). ( + e ) ( ) e) f() =. (.65.) f + = e
11 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 8 8 Maagemetul caltăţ prouselor ş servclor î tursm Î cazul ue aalze cocrete, se calculează câte u cator comple atât petru prousul / servcul ou, cât ş petru prousul / servcul e bază; ce o cator se compară ş, apo, se trag cocluz refertoare la caltatea precozată a prousulu / servculu ou. Petru aprecerea velulu e caltate, se foloseşte, î cazul ue proucţ omogee, coefcetul meu al caltăţ, coefcet obţut ca mea artmetcă (sau mea artmetcă poerată) a coefceţlor, grupaţ î clase e caltăţ; î cazul meer poerate, poerle sut ate e cattatea e prouse fabrcate, grupate e asemeea pe clase e caltăţ. (î cele ce urmează prezetăm moul e calcul al acestor coefceţ, folos oar apelatvul prouse ; î cazul servclor, coefceţ respectv se folosesc î acelaş mo, cu observaţa că se vor folos calfcatve trasformable î mărm umerce, coform ue scale alese e către utlzator, î coformtate cu observaţle paragraful.5.). Coefcetul meu al caltăţ este at e: ( q ) = =, (.66) q = ue. umărul e prouse clasa aalzată, coefcetul clase e caltate (e eemplu: = - caltate etra, = - caltatea îtâ, = - caltatea a oua, ), q cattatea e prouse clasa. Utlzâ cele petru peroaa e bază e comparaţe - ş cele j petru peroaa luată î coserare (luă, trmestru, a, ), se obţ coefceţ me e caltate petru peroaa coserată: cele sarc e pla î omeul caltăţ: cele e îeplre a plaulu: ( q = qpl pl = I = = (.67) pl/ ( q ) q = q = pl ) cele e amcă a caltăţ: j I = ; (.69) coefcetul meu e caltate geeralzat, calculat î cazul proucţe omogee ş obţut ca mee artmetcă poerată a coefceţlor me e caltate a prouselor aalzate, poerle f ate e valoarea prousulu respectv (p q ): ( p q ) = * = = ( v ), (.7) = (p q ) = ue: umărul e ore al prousulu aalzat, * p q v = greutatea specfcă a valor prousulu aalzat. (p q ) = Coefcetul meu e caltate geeralzat se foloseşte aceleaş coţ ca ş coefcetul meu e caltate ş aume: coefcetul meu geeralzat al caltăţ plafcate: ( pl p q pl) = * pl = = ( pl v pl), (.7) = (p q ) = coefcetul meu geeralzat al caltăţ realzat î peroaa e bază: pl ( p q ) = * = = ( v ), (.7) = (p q ) = coefcetul meu geeralzat al caltăţ efectv realzate: ( p q) ( qj) = * = = ( v ). (.73) = (p = q) j = q j = I = = (.68) pl/j Pr termeul acestor coefceţ se vor putea, acum, apreca pl ( q ) coefcetul e amcă a caltăţ: = pl = pl =, (.74)
12 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm cele e amcă a caltăţ: N cr umărul efectelor crtce, N pr umărul efectelor prcpale, I =, (.75) N sec umărul efectelor secuare, coefcetul e mofcare a caltăţ: ue m * =, (.76) * arată care ar f fost caltatea mee geeralzată î coţle caltăţ vuale peroaa curetă ( coţoat), cele e mofcare a caltăţ: coefcetul schmbărlor structurale ale caltăţ: cele schmbărlor structurale ale caltăţ: * I =, (.77) (v) s = *, (.78) I (v*).5.4. Icator urmărţ î scopul realzăr uu sstem e ormatve metoologce e aplcare a caltăţ N m umărul efectelor more. Petru etermarea acestu cator, trebue prestabltă o lstă a efectelor posble ş clasfcarea lor upă gravtate (crtce, prcpale, secuare, more), î fucţe e mplcaţle aparţe lor asupra capactăţ e utlzare; fecărea tre aceste categor se acoră câte u puctaj, respectv, 5,,, coform otaţlor relaţa (.83);.) coefcetul emertelor (coefcetul e pealzare), care permte efectuarea e comparaţ ître verş furzor: K = total pucte e pealzare umăr prouse aalzate, (.83) e.) poerea proucţe fără efecte e caltate recepţoate proucţa propre (Q pr ) totalul proucţe totale: Qpr I4 = ; (.84) Q f.) poerea valor prouselor fără efecte e caltate recepţoate e beefcar î valoarea proucţe marfă: V =, (.79) pml Vpr I5 =, (.85) * V a.) poerea proucţe e caltate superoară î totalul proucţe realzate: Qf I =, (.8) Q ue: Q f proucţa fzcă (valorc) e caltate superoară, Q t proucţa totală realzată, pe clase e caltate; t b.) poerea proucţe fără efecte (Q f ) e caltate î totalul proucţe realzate: c.) puctajul efectelor: I Qf = ; (.8) Q t ( N + 5 N + N ) I 3 = cr pr sec + Nm, (.8) ue: umărul e prouse cotrolate, t pmr ue: V pml valoarea proucţe marfă lvrată î peroaa e tmp aalzată, V pr valoarea prouselor reclamate ca efecte ş valate ca atare, V pmr valoarea proucţe marfă realzată peroaa e tmp aalzată; g.) poerea proucţe fzce fără efecte e caltate î valoarea totală a proucţe fzce realzate: I Vpft Vpfr =, (.86) V 6 pfl ue: V pfl valoarea proucţe fzce totale lvrată, V pfr valoarea prouselor fzce reclamate ca efecte ş valate ca atare, V pft valoarea totală a proucţe fzce realzate; STUDIU DE CAZ ) Se cere să se apreceze, prtr-u cator comple, caltatea esparlelor prouse e S. C. "Casa albastră" S. R. L., pr comparaţe cu cele cofecţoate e S. C. Răchta S.R.L., coform tabelulu.4.:
13 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm Tabelul.4 Tabelul.5 INDICATORI MĂRIME INDICATORI SIMPLI DE CALITATE S. C. Casa Albastră S.R.L. S. C. Răchta S.R.L. Proucţa auală (m bucăţ) Cheltuele pt. realzarea prousulu (m le) Cheltuele auale pt. reparaţ (m le) Cheltuele auale e eploatare (m le) Durata e fucţoare a prousulu (a) Coform formule (.65.), f(t) Icatorul comple I, coform formule (.65.) ( +,5) f(t) = ( +,5) + ( +,5), I 9 = CA 65, , ,5, I 8 = R 63, , ,5 ( +,5) f(t) = ( +,5) + (+,5) Se poate cosera, coform calculelor efectuate, că esparlele prouse e Socetatea comercală Casa Albastră sut ma performate puct e veere caltatv, eoarece catorul comple e caltate I CA =, > > I R =, OBSERVAŢIE: acă egaltatea I CA > I R u este satsfăcută, trebue găsţ, pr apromaţ succesve, ace cator smpl e caltate a căror mofcare couce la o sporre a caltăţ prouselor realzate e socetatea comercală aalzată. 3) Să se calculeze caltatea mee plafcată, realzată ş cele e realzare (îeplre) a plaulu prvtor la caltatea esparlelor prouse e Socetatea comercală "Casa albastră", pe baza atelor tabelul.5,5 Clasa e caltate Etra I II Esparle lvrate [m bucăţ] Plafcat Î peroaa aalzată Î peroaa e bază TOTAL Σq pl = = 9 Σq = = Σq = = 9 Caltatea mee se aprecază pr termeul coefceţlor me e caltate, calculabl cu ajutorul relaţlor (.66): caltatea mee plafcată (coefcetul meu e caltate plafcat): pl = =,473684, 9 caltatea mee realzată (coefcetul meu e caltate realzat): = =,, cele e epăşre a plaulu, coform relaţe (.68), va f: I / pl, = = =,885., pl Cocluze: se obţe o epăşre a îeplr sarc e pla cu prvre la caltatea mee e : % - 8,85 % = 9,5 %. 4) Să se eterme amca caltăţ petru peroaa aalzată. Apelâ, ou, la relaţa (.66), rezultă coefcetul meu e caltate e bază: = =,358, 9 cele e amcă a caltăţ, coform relaţe (.69): I, = =,6333.,358 = 5) Petru ouă peroae e tmp, Socetatea comercală "Casa albastră" preztă următoarele ate refertoare la caltatea mee ş valoarea proucţe petru tre prouse, coform tabelulu.5.
14 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm Prous Relaţa e calcul A B C TOTAL Coefcet meu e caltate q (.66) Tabelul.5 Valoarea proucţe [m le] p q p * v Cattate prousă, total (structura proucţe) [%] * v (.66) (.7) (.7) (.7) (.7),358, 79, 666,7 7,73 66,67,9474,545 47,3 66,7 8,8 6,67,4734,455 3,6 666,6 9,9 6, ,, (petru peroaa e bază, poerea pe prousul A a fost e 8,995 le/bucată, rezultă: q = 8,995 9, ar petru peroaa aalzată) p 79, v * A) = ( petru prousul Nvelul e caltate acceptabl Nvelul e caltate acceptabl (AQL = Acqure Qualty Level), împreuă cu ltera e co (LC), se utlzează î scopul eăr plaelor e verfcare. Î mometul î care u beefcar preczează o aumtă valoare petru velul e caltate acceptabl petru u aumt efectv (sau efect), sau petru u grup e efetve (efecte), el că furzorulu că pr plaul e verfcare utlzat acceptă marea majortate a loturlor lvrate, atâta tmp cât fracţuea efectvă mee (sau umărul meu e efecte pe e utăţ e prous) a procesulu e fabrcaţe care prov loturle u este ma mare ecât o valoare acceptată e beefcar. U aumt pla e verfcare trebue astfel costrut, îcât probabltatea e acceptare a uu lot cu o caltate egală cu valoarea specfcată a velulu e caltate acceptabl epe e efectvul eşatoulu. Petru u vel e caltate acceptabl at, probabltatea e acceptare este, î geeral, ma mare petru eşatoae cu efectve ma mar. Valoarea, sau valorle, velulu e caltate acceptabl utlzate se stablesc pr cotracte ecoomce e aprovzoare, cu specfcarea caltăţ loturlor e prouse. Se poate stabl fe o sgură valoare petru velul e caltate acceptabl, petru o clasă e efecte, fe ma multe valor petru subclasele e efecte clasa respectvă. Valorle efectve ale velulu e caltate acceptabl, coform STAS 36/ - 86, se preztă sub forma ue progres geometrce cu raţa ( ) =,585. Şrul valorlor velulu e caltate acceptabl este:,,,5,,5,,4,,65,,,,5,,5,,4,,65,,,,5,,5, 4,, 6,5,, 5, 5, 4, 65,, 5, 5, 4, 65,. După clasfcarea efectelor caracterstclor e caltate î clase e gravtate, se alcătuesc plaur e cotrol petru fecare clasă î parte. Cea ma smplă clasfcare costă î stablrea uma a ouă clase e gravtate a efectelor: majore ş more. Fecăre clase se atrbue câte o valoare a velulu e caltate acceptabl, e eemplu, petru efectele majore AQL =,65 %, ar petru efectele more AQL =,5 %, rezultâ câte u pla e verfcare a caltăţ petru recepţa prousulu petru fecare clasă e efecte î parte. U lot va f acceptat acă corespue ambelor plaur e verfcare ş va f resps acă este ecorespuzător petru cel puţ uul plaur. Cel ma es, caltatea uu lot se eprmă pr fracţuea efectvă, sau prtr-u umăr e efecte pe e utăţ e prous. Î cazul î care prousele pot prezeta efecte e gravtăţ ferte, velul e caltate acceptabl se stableşte fereţat, î fucţe e clasfcarea efectelor, e eemplu: Tabelul.6 Tpul efectulu Nvelul e caltate acceptabl Descrerea efectelor CRITIC -,65 CRITIC -,,5 MAJOR -,4,65 MAJOR -, MINOR -,5 MINOR - Î cazul î care estă u umăr mare () e caracterstc ş petru fecare se stableşte câte o valoare a velulu e caltate acceptabl ş u umăr e acceptare, A, velul global e caltate se stableşte cu relaţa: respectv A g = (A ), (.87) = ( AQL ) AQL = =. (.88) Petru efectele crtce, este mposbl e ales o fracţue efectvă acceptablă. Î aumte stuaţ, se poate mesoa mărmea eşatoulu astfel îcât petru o valoare aleasă β a rsculu să poată f etermată o fracţue efectvă P, prestabltă; coserâ o repartţe Posso a efectelor crtce, rezultă: ( log ( β )) 3,6 =. (.89) P
15 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 89 9 Maagemetul caltăţ prouselor ş servclor î tursm Coform STAS 36/ - 84, se pot lua următoarele valor: petru AQL,5, ecza e alegere a ue cele ouă varate e eprmare a caltăţ lotulu (pr P sau u * ) este flueţată ma mult e elemete e or amstratv, eoarece u flueţează sesbl plaurle e cotrol, petru AQL (,5, ], coserâ caltatea lotulu eprmată pr u *, plaul e verfcare (este ma sever), petru AQL >, petru eprmarea caltăţ loturlor se foloseşte eclusv u *. Î etermarea valor velulu e caltate acceptabl este ecesar să se ţă seama că este u cator al caltăţ solctate fabrcaţe. Totoată, este ecesar să se ţă cot e moul î care urmează să fe foloste prousele lvrate, e cosecţele ce ecurg î urma efectăr prouselor ş e umărul compoetelor prouselor: X =, (.9) ue: valoarea velulu e caltate acceptabl petru compoete, X valoarea velulu e caltate acceptabl petru asamblu, umărul compoetelor asamblulu. STUDIU DE CAZ 6) Fe, petru clasa efectelor majore tr-u lot e N = 55 prouse (utăţ e prous), sut 5 prouse fără efecte, 7 prouse cu câte u efect, prouse cu câte ouă efecte ş tre prouse cu câte tre efecte. Să se apreceze caltatea lotulu. aprecerea caltăţ, ca fracţue efectvă, p = = = 5,45, aprecerea caltăţ, ca umăr e efecte pe utăţ e prous: u * = = = = = 8,36 efecte / (utăţ e prous) Moelarea matematcă a cotrolulu e caltate ş.7.. Moelarea cotrolulu pr termeul repartţe ormale Pr efţe, o varablă aleatoare cotuă X se supue ue leg ormale N(,s), acă are o estate e repartţe ată pr: f(,,s) = ep π, (.9) s s cu R ş parametr repartţe R ş s >. Fucţa e repartţe va f ată e: F(,,s) = ep = π f(,,s). (.9) s s Curba e repartţe ormală, prezetată î fgura., are următoarele propretăţ: amte u puct e mam, petru f( ) =, scăzâ la stâga ş la s π reapta acestua ş tzâ asmptotc la aa abscselor, este smetrcă faţă e oroata corespuzătoare valor me,, are formă e clopot, cu covetatea îreptată î sus ş ouă pucte e fleue, stuate la staţa = ± s e aa e smetre, oroata mamă este cu atât ma mare, cu cât spersa s este ma mcă, ar câ aceasta creşte, curba "se turteşte", luâ o formă ce î ce ma plată. Petru a uşura calculele, se trouce varabla aleatoare ormată z =, s astfel îcât parametr repartţe ev: = ş s =. Ca urmare, estatea repartţe ormale ormată eve: z f(z,,) = ep, (.93) π ar fucţa e repartţe ormală ormată va f: F(z ) = p z p f(z,,) z = π z p z ep z. (.94) recepţe Deoarece fucţa e repartţe ormală ormată este smetrcă faţă e aa oroatelor (vez fgura.), se poate scre: Moelarea matematcă a feomeelor care urmăresc caltatea prouselor ş servclor, respectv moelează cotrolul e caltate se preztă sub forma repartţlor z F(z = ) = P(z < ) = f(z) z = ep z =, (.95) statstce. π
16 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 9 9 Maagemetul caltăţ prouselor ş servclor î tursm respectv Fg... Destatea repartţe ormale Fg... Destatea repartţe ormate z p z F(z p) = f(z) z + f(z) z =,5 + ep z, (.96) π î care tegrala z p z p z Φ (z p) = ep z (.97) π se umeşte fucţa ormală ormată Laplace sau, pe scurt, fucţa Laplace. STUDIU DE CAZ 7) S. C. "Casa Albastră" S. R. L. cumpără e becur. Durata mee e fucţoare garatată e proucător este e e ore, cu o abatere mee pătratcă e e ore. Să se eterme: a) umărul e becur care se vor are, probabl, î prmele 7 e ore e fucţoare, b) umărul e becur care se vor are, probabl, ître 9 ş 3 e ore e fucţoare, c) umărul e ore e fucţoare upă care se vor are, probabl, % becur. a) Notâ cu urata e fucţoare a uu bec ş avâ, atele probleme, mea artmetcă = ş abaterea staar s =, varabla ormală ormată este: 7 z p = = = 3. s Destatea e repartţe ormală (relaţa (.93)), î care s-a făcut abstracţe e epresa e sub racal (f'(z,,) = ep(-z,5)) va avea valorle tabelul.7:.z.f(z) Tabelul.7,5,,5,,5 3,,,885,6653,3465,3534,4394, Fucţa ormală ormată Laplace (.97) va avea valoarea Ф =,49838; ar eoarece valoarea varable ormale ormate z p este egatvă, e plasăm la stâga ae oroatelor ş fucţa e repartţe ormală ormată va avea valoarea: F =,5 -,49838 =,6. Numărul e becur care, probabl, se vor are upă 7 e ore e fucţoare este,6 = 3,4. Î cocluze, se aprecază că, î coţle ate, upă 7 e ore e fucţoare se vor are, probabl, 3 becur. OBSERVAŢIE: coform efţe (.97), fucţa ormală ormată rezultă pr tegrarea valorlor tabel: z p z,5 Φ(zp ) = ep z = ( (, +,+ (,885 + π π +,6653 +,3465 +,3534 +,4394))) =,4953 =, π b) Ca ş î cazul preceet, varabla ormală ormată este 9 z p = = =. σ Destatea e repartţe ormală (relaţa (.93)), î care s-a făcut abstracţe e epresa e sub racal (f'(z,,) = ep(-z /)) va avea valorle tabelul.8:
17 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm.z.f(z) Tabelul.8,,4,6,8,,,98,93,8357,765,6653 Fucţa ormală ormată Laplace (.97) va avea valoarea Ф =,3454; ar eoarece valoarea varable ormale ormate z p este egatvă, e plasăm la stâga ae oroatelor ş fucţa e repartţe ormală ormată va avea valoarea: F =,5 -,3454=,5946. Numărul e becur care, probabl, se vor are upă 9 e ore e fucţoare este,5946 = 38,96. Î cocluze, se aprecază că, î coţle ate, upă 9 e ore e fucţoare se vor are, probabl, 39 becur. Petru estmarea umărulu e becur care se vor are, probabl, upă 3 e ore e fucţoare, varabla ormală ormată este z 3 = = 3 p s =. Destatea e repartţe ormală (relaţa (.93)), î care s-a făcut abstracţe e epresa e sub racal (f'(z,,) = ep(-z,5)) va avea valorle tabelul.9:.z.f(z) Tabelul.9,5,,5,,5 3,,885,6653,3465,3534,4394, Fucţa ormală ormată Laplace (.97) va avea valoarea Ф =,49838; ar eoarece valoarea varable ormale ormate z p este poztvă, e plasăm la reapta ae oroatelor ş fucţa e repartţe ormală ormată va avea valoarea: F =,5 +,49838 =, Numărul e becur care, probabl, se vor are upă 3 e ore e fucţoare este,99838 = 996,76. Î cocluze, se aprecază că, î coţle ate, upă 9 e ore e fucţoare se vor are, probabl, 997 becur. Dec, ître 9 ş 3 e ore e fucţoare se vor are, probabl, î coţle ate = 679 becur. c) Probabltatea ca să se ară % becur este P = -, =,9, ar P(z ) =,9 =,5 + Φ (z ) Φ (z ),4. p p p = D fgura.3, se obţe z p =,85. Cu această valoare:,85 = = 87,5. Pe baza acestu rezultat, se poate apreca că, î coţle coserate, % becur ( e becur) se vor are upă 87 e ore..7.. Moelarea matematcă a cotrolulu cu repartţa bomală Repartţa bomală se poate eplca pr termeul "scheme" lu Beroull: ("schema" lu Beroull costă î etragerea ue ble tr-o ură î care se află ble albe ş egre, ar, upă cosemarea rezultatulu etrager, bla se retrouce î ură) realzarea uu aumt evemet (e eemplu, etragerea ue ble e culoare prestabltă) este epeetă e realzarea celorlalte evemete. Î cazul cotrolulu prouselor, se presupue că u lot coţe Co prouse corespuzătoare ş Ne prouse ecorespuzătoare (cu efecte). Probabltatea aleger uu prous ecorespuzător este P(Ne) = p, ar probabltatea aleger uu prous corespuzător este P(Co) = q = - p. Se vor efectua aleger (etrager) succesve e prouse lot, urmate e retroucerea prouselor î lot, upă verfcarea acestora. Varabla aleatoare bomală, varablă e tp scret, a aparţe uu prous cu efecte, X, este eftă rept umărul prouselor efecte obţute pe parcursul a etrager, varablă ce a valor tervalul [, ]. La a - a etragere, probabltatea ca evemetul "prous ecorespuzător" - Ne - să apară e or este P(,) = p, ar probabltatea aparţe evemetulu "prous corespuzător" - Co - este P(,) = q. Numărul combaţlor posble e prouse care evemetul De se îtâleşte e or, [, ], este egal cu etrager a prouse ecorespuzătoare este: P C, ar probabltatea! = P(X = ) = C p q = p q, (.98)! ( )! care repreztă terme ezvoltăr bomulu (e ue prove eumrea e lege e repartţe bomală) lu Newto (p+q). Fucţa e repartţe este:! F() = P(X < ) = P(,) = p ( p). (.99)! ( )! Probabltatea ca î îcercăr succesve să se proucă u evemet Ne cu o probabltate ată p, costată, respectv probabltatea ca varabla aleatoare scretă X, care are o repartţe bomală, să a o valoare oarecare X = + este: p P(, + ) = P(,). (.) + q
18 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm +,5 p,5 p P( Ne ) = Φ Φ. (.5) p ( p) p ( p) STUDIU DE CAZ 8) S. C. "Casa Albastră" S. R. L. cumpără u lot e becur espre care se şte că % u îeplesc ormele e caltate. D acest lot, se prelevează aleator 5 becur. Se cere: a) Determarea valor me ş a sperse; b) Probabltatea găsr a,,, 3, 4, 5 becur e caltate ecorespuzătoare. a) Volumul eşatoulu este = 5, ar p =,. Rezultă: q = - p = -, =,99. Mea artmetcă va f: = p = 5,=, 5, ar spersa: s = p q = 5,,99 =,495. Fg..3. Valoarea mee a varable aleatoare screte X, care urmează legea e repartţe bomală este: = p, (.) ar spersa aceste varable este: î care s (X) = p q Î cazul î care este îepltă coţa. (.) < P <, atuc + P(,) = f(z) p ( p), (.3) p z =. (.4) p ( p) Respectv, acă 5 ş p 4, se poate utlza fucţa Laplace, eftă pr relaţa (.97): +,5 p,5 p P(,) = Φ Φ, (.4) p ( p) p ( p) ar probabltatea ca u aumt umăr e prouse ecorespuzătoare să se afle î tervalul [, ] este: b) Probabltatea ca ître cele 5 becur să u se găsească vreuul ecorespuzător este: 5 5 P(5,) = C5 p q = q =,99 =,9599. Utlzâ, î cotuare, relaţa e recureţă (.), se obţe: 5 p P (5,) = P(5,) =,483, + q 5 p 4 P(5,) = P(5,) = 9,73, + q 5 p 6 P(5,3) = P(5,) = 9,896, + q 5 p 8 P(5,4) = P(5,3) = 4,94997, 3 + q 5 p P(5,5) = P(5,4) = 9, q 9) La verfcarea cotorulu e apă rece petru S. C. "Casa Albastră" S. R. L., s- au efectuat ser e măsurător petru etermarea curbe ebtmetrulu. Probabltatea ca o sere cele să ea rezultate ecorespuzătoare este,. Să se calculeze probabltatea ca umărul serlor e măsurător care au eror să fe ma mc sau cel mult egal cu 3 ş să se reprezte grafc repartţa umărulu e ser cu eror. D atele oferte, rezultă =, p =,, q = - p = -, =,8, mea artmetcă a măsurătorlor cu eror este: = p =, =, ar 5
19 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm spersa: s = p q =,,8 =,6. Probabltatea ca ître cele măsurător u se găsească vreua ecorespuzătoare este P(,) = C p q = q = =,8,7374. Utlzâ, î cotuare, relaţa e recureţă (.), se obţ rezultatele tabelul., prezetate grafc î fgura.4: P(,) (formula (.3)) Tabelul. ar probabltatea ca umărul serlor e măsurător ecorespuzătoare să fe ma mare ecât 4 este: P(X > 4) = P(X 4) =,8796 =, 874 (respectv e,9 %). p = λ = cost F() = P(,) (formula (.99)),7374,7374,68435,3758,399,6778 3,37,8796 4,888,9677 5,644, ,555, ,786,9999 8,74, ,4,,, Probabltatea ca ma mult e 3 măsurător să u corespuă este: P(X 3) =,8796, Fg..4. Probabltatea ş fucţa e repartţe bomală Parametr repartţe sut: Coform leg Posso, probabltatea este ată e.7.3. Moelarea cotrolulu cu repartţa Posso fucţa e frecveţă Posso este: Moelul e cotrol e tp Posso se realzează plecâ e la repartţa bomală, î coţle î care probabltatea e aparţe a evemetulu urmărt este mcă, ar volumul eşatoulu este mare, astfel îcât să se realzeze coţa. (.6) Legea e repartţe Posso se ma umeşte ş legea evemetelor rare. = λ ş s = λ. (.7) P(.) = C p ( p) ar relaţa e recureţă petru fucţa e frecveţă este:, (.8) λ f(, λ) = ep( λ), (.9)! λ f( +, λ) = f(, λ), cu f( = ) = ep( λ). (.)
20 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 99 3 Maagemetul caltăţ prouselor ş servclor î tursm Fucţa e repartţe va f ată e: STUDIU DE CAZ F(, λ) = P(X < ) = ep( λ) λ. (.) m! m= ) S.C. "Casa Albastră" S. R. L. cumpără u lot e e becur. D aalza esfăşurăr procesulu e fabrcaţe, se cuoaşte că fracţuea efectvă probablă (rata efectelor) este e,5 %. Se cere să se eterme probabltatea ca î lotul achzţoat să se găsească a) 5 becur ecorespuzătoare, b) ma mult e becur ecorespuzătoare. a) D atele probleme, rezultă: =, p =,5, λ = p =,5 =. Apelâ relaţa (.9), fucţa e frecveţă va f: 5 λ f(, λ) = ep( λ) = e =,3478.! 5! b) Se calculează, ma îtâ probabltatea aparţe evemetulu opus, coform atelor tabelul.: Tabelul..f(,λ) * F(, λ) (relaţa (.)) ,53999E-5,45 4,53999E-4,499,7E-3,769 7,56665E-3,336,8966E-,953 3,78333E-,6786 6,3555E-,34 9,79E-,,599E-,338,5E-,45793,5E-,5834 m Petru calculul prme valor, s-a folost relaţa (.9), ar petru celelalte, relaţa e recureţă (.). Rezultă, î urma efectuăr calculelor, P( ) = = f(,) = F(,) =,5834 (ultma valoare coloaa reapta a tabelulu e calcule), probabltatea cerută f: P (X > ) =,5834 =,4696, respectv 4,696 % Moelul cotrolulu cu repartţa hpergeometrcă Moelul repartţe hpergeometrce se recomaă să se utlzeze atuc câ ecza e acceptare sau e respgere se a pe baza umărulu e prouse rebutate proba efectuată, î coţle îeplr ş a uelor coţ refertoare la volumul lotulu, al probe ş a proporţe tre aceşt o cator. Se coseră că: lotul e prouse supuse cotrolulu este ft, e volum N, prousele cotrolate u se retrouc î lot (ec, este evtată coţa fuametală a "scheme" Beroull), volumul eşatoulu este, fracţuea efectvă a eşatoulu este p. Petru stablrea elemetelor plaurlor e cotrol (rscur, umere e acceptare, umere e respgere etc.) se va lua î coserare atât volumul îtregulu lot, cât ş volumul eşatoulu. Se utlzează otaţle tabelul.: Icator Tabelul. î lot Smbol folost.î eşato Numărul prouselor N. Numărul rebuturlor D. Numărul prouselor corespuzătoare G.g Fracţuea efectvă P.p Numărul prouselor ecorespuzătoare Q q Ître aceşt cator estă relaţle: D G N = D + G; P + Q = ; D = N P; G = N Q; P = ; Q = (.) N N
21 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm 3 3 Maagemetul caltăţ prouselor ş servclor î tursm g = + g; p + q = ; = p; g = q; p = ; q =. (.3) Probabltatea ca eşatoul etras să coţă "" rebutur ş "g" prouse corespuzătoare este ată e: P(,; D,N) = C D N C C g G N relaţe care, coform propretăţlor combărlor, poate f scrsă: D N g G C C C =, (.4) C C CD CG D! G!! (N )! P(,; D,N) = =. (.5) C! g! N! (D )! (G g)! STUDIU DE CAZ N g ) Să se stueze parametr repartţe hpergeometrce utlzate la recepţa efectuată asupra uu lot e 3 e prouse, eşatoul f e 6 prouse. Se costată că umărul prouselor rebutate lot este e 7 prouse. D atele probleme, rezultă că N = 3, D = 7, G = N - D = 3, = 6, 6 CN = C3 = , ar rezultatele calculelor sut prezetate î tabelul.3 ş î fgura.5. Fg..5. Rezultatele calculelor, coform tabelulu.3..g D C g C G Tabelul.3 g C D C G P(,; D,N) (relaţa (.4)) P(, ;D, N) ,7, ,39669, ,337, ,439, ,49, ,8, ,,.7.5. Stablrea rscurlor Eseţa cotrolulu statstc costă î aceea că aprecerea caltăţ uu lot e volum N se face pe baza uu eşato ( < N), etras aleator lot, ma precs pe baza uu parametru e eşatoare. D cauza faptulu că parametr eşatoulu (mea artmetcă, abaterea mee pătratcă, fracţuea efectvă etc.) se abat aleator e la parametr lotulu, aceşta se vor estma (apreca) cu o aumtă probabltate. Ca urmare, orce ecze e acceptare sau respgere a lotulu comportă u aumt rsc e a f eroată. Cotrolul statstc poate couce la ouă felur e ecz eroate: a.) respgerea uu lot care coţe o fracţue efectvă P ma mcă ecât fracţuea efectvă amsă P, ş care ar trebu acceptat - poteza H : P P. Îtru asemeea caz, eroarea comsă se umeşte eroare e geul I. Probabltatea comter ue eror e geul I se umeşte rsc al furzorulu ş se otează cu α. De regulă, se amte α,5, b.) acceptarea uu lot care coţe o fracţue efectvă P ma mare ecât velul fat P, ş care ar trebu acceptat, eroarea comsă î acest caz umu-se eroare e geul II. Probabltatea comter ue eror e geul al II - lea poartă umele e rsc al beefcarulu, ş se otează cu β. De regulă, se amte β [,5,,]. Rezultă că: prtre fracţule efectve P [, P ] estă o valoare P, petru care acorarea calfcatvulu (calfcarea) rept ecorespuzătoare, ec respgerea, lotulu etermă perer ecoomce mame, prtre fracţule efectve P (P, ] estă o valoare P, petru care ecza e acceptare a lotulu etermă perer ecoomce mame. Fracţuea efectvă P se umeşte fracţue efectvă acceptată, sau vel e caltate acceptabl (AQL). De asemeea, P = - α.
22 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm Fracţuea efectvă P se umeşte fracţue efectvă tolerată sau caltate lmtă. Fracţuea efectvă P a (P ) =,5 se umeşte fracţue efectvă probablă. Ître mărmle efte ma sus estă relaţle: STUDII DE CAZ > α > > β >, < P < P <, P P > N. (.6) ) Rscul proucătorulu. Petru u lot e e becur, cotrolul ş ecza e achzţe se a pe baza verfcăr uu eşato e e becur. Preveerle cotractuale stablesc că lotul este corespuzător acă velul procetulu e rebutur este e cel mult P = 4 % ş că velul rsculu, la proucător, e se respge u lot corespuzător este α = 5 %.. Coţle stablte se îcarează î coţle mpuse petru repartţa hpergeometrcă. Pr urmare: N =, D = N P =,4 = 4, G = N - -D = - 6 = 96, P = D/N = 4/ =,4, Q = G/N = 96/ =,96, =, = 6. Rezultatele sut prezetate î tabelul.4. P(,; D,N) (relaţa (.5)) Tabelul.4 P(,;D,N) α = ( - ) % P(,;D,N),4793, ,89,4449, ,47,59538, ,5 3,8567,99748,99 4,84-3, ,44 5,498-4, ,7-4 Se costată că acă, î urma cotrolulu, umărul becurlor rebutate este ma mc sau egal cu o (petru =, rscul proucătorulu este α = 3,5 %), lotul se acceptă (A = ), ar acă este ma mare ecât ouă becur efecte, lotul se respge (R = 3). 3) Rscul beefcarulu. Petru u lot e 5 e becur, cotrolul ş ecza e achzţe se a pe baza verfcăr uu eşato e e becur (reluarea stuulu e caz.), juecat pr prsma beefcarulu). Preveerle cotractuale stablesc că lotul este corespuzător acă velul procetulu e rebutur este e cel mult P = %. Coţle stablte se îcarează î coţle mpuse petru repartţa hpergeometrcă. Pr urmare: N = 5, D = N P = 5, = 5, G = N - -D = 5-5 = 35, P = D/N = 5/5 =,, Q = G/N = 35/5 =,9, =, = 5. Rezultatele sut prezetate î tabelul P(,; D,N) (relaţa (.5)) Tabelul.5 P(,;D,N) = β β P %,956,956,956,67933,3635 3,635,387,68 6,8,98,8943 8,943,847, ,7454,53, ,9697,3544, ,9968,3679, , ,996-5, ,763-7,,673-8, 9,99999,, Petru atele calculate î tabel, se observă că î cazul ue fracţu efectve A = (cel mult ouă prouse efecte) rscul proucătorulu este β =,68, acă e 68, %, stuaţe care este acceptablă. Petru o amelorare a stuaţe, trebue crescut procetul P. Î fgura.6. este prezetat prousul β P î procete, avâ ca parametru parametrul P. Petru a e îcara î coţa petru rscul beefcarulu (β %) ş î coţa coform cărea umărul e prouse efecte să fe cel mult A, trebue mofcată valoarea mărm P, î mo succesv. Se ajuge, astfel, ca să fe îepltă coţa cerută petru valoarea P = 4 %, rezultatele f prezetate î tabelul.6. Se costată că, î acest caz, β = 8,368 %.
23 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm coţe o fracţue efectvă P = D/N. Curba caracterstc operatve este reprezetată e varaţa lu ΣP a (p) î fucţe e P, aşa cum este prezetat î fgurle.7. ş.8. Nvelul P al fracţu efectve stableşte fereţa tre loturle corespuzătoare ş cele ecorespuzătoare, astfel: acă P P, atuc lotul este acceptat cu certtue, acă P > P, atuc lotul este resps î totaltate (coform curbe caracterstce teoretce - vez fgura.7. Σ a (p) teoretc Fg..6. practc Tabelul.6 P(,; D,N) (relaţa (.5)) P(,;D,N) = β β P %,34,34,488,76,96,4598,6456,8368,8,4434,8 5,474,479,4473,65,568,668 6,3,7584,846,74 4) Rscul proucătorulu ş al beefcarulu. Pe baza eemplelor e ma sus să se eterme smulta rscul proucătorulu ş al beefcarulu, petru u lot e 75 e prouse, care s-a ales u eşato e 5 prouse, luâu-se P = 4 %, ar umărul prouselor ecorespuzătoare acceptabl volumul eşatoulu A = Determarea caracterstc operatve a plaulu e cotrol al caltăţ Caracterstca operatvă eprmă, îtr-o formă matematcă, probabltatea acceptăr loturlor î fucţe e mărmea fracţu efecte. Caracterstca operatvă se eprmă pr fucţa P a (p), care este probabltatea e acceptare a lotulu ce α. Σ Fg..7. Alurle curbe caracterstce operatve P a β α. (p) P α. P P P P P. β. β Fg..7. Mărmle specfce ale curbe caracterstce operatve Î realtate, atortă erorlor e reprezetatvtate, se comt eror e ecze, a căror estmare probablstcă se realzează pr termeul rsculu proucă-torulu, α ş pr termeul rsculu beefcarulu, β, cele ouă egaltăţ terpretâu-se:
24 Cap.. Aspecte cattatve ale maagemetul caltăţ prouselor ş servclor tursm Maagemetul caltăţ prouselor ş servclor î tursm acă P P, atuc lotul este e caltate acceptablă, putâ f, totuş, resps, acă P > P, atuc lotul este e caltate ecorespuzătoare, ar poate f, totuş, acceptat. Zoa P (P, P ) repreztă o zoă e fereţă, î care eczle sut echvalete. Mărmle caracterstce ale curbe operatve escrse e fgura.8 se terpretează astfel: rscul proucătorulu, α, măsoară probabltatea respger uu lot corespuzător caltatv. Loturle corespuzătoare, cu P P sut acceptate cu o probabltate rcată, e P = - α, îsă, atortă erorlor e eşatoare, vor f ş lotur respse î mo ejustfcat, cu o probabltate P = α, lotur ecorespuzătoare, cu P P sut respse cu o probabltate rcată, e P = - β, estâ, îsă, ş lotur acceptate cu o probabltate egală cu rscul beefcarulu P = β, acă P (P, P ), u lot poate f resps cu o probabltate P = - α - β. STUDIU DE CAZ 5) Fe plaul e cotrol eft prtr-u umăr e e prouse, care se etrage u eşato e e prouse ş se ma mpue ca umărul prouselor ecorespuzătoare acceptabl î volumul eşatoulu să fe ă =. Să se eterme curba operatvă, f ate valorle fracţu efectve: P = {,,,4,,8,,,,5,,} (la care se aaugă, evet, P =, ş P =,). Se va folos moelul repartţe hpergeometrce, petru care vom avea N =, =, D = P, G = - D, = {,,,3,4,5,6,7,8,9}, g = 9 - (se va veea, coform tabelulu.7, că petru valor a, calculele u îş ma au rostul). Calculele sut prezetate î tabelul.7. P 7 8,,4,8,,5,,368,887,45579,58,46 9 Σ P,383,,,,,, Fg..8. Curba operatva petru stuul e caz 5 Curba operatvă se va obţe făcâ suma probabltăţlor aflate easupra valorlor =, ş f reprezetată î fgura.8. P Tabelul.7,,4,8,,5,,638384,43338,55773,956,694,6596,333,4953,344,67933,96,435,38384,535,3688,387,36347,599,358,477,98,74,586,478,847,38,43688,6845,53,763,995,354,3548,963
Sondajul statistic- II
 08.04.011 odajul statstc- II EŞATIOAREA s EXTIDEREA REZULTATELOR www.amau.ase.ro al.sac-mau@cse.ase.ro Data : 13 aprle 011 Bblografe : ursa I,cap.VI,pag.6-70 11.Aprle.011 1 odajul aleator smplu- cu revere
08.04.011 odajul statstc- II EŞATIOAREA s EXTIDEREA REZULTATELOR www.amau.ase.ro al.sac-mau@cse.ase.ro Data : 13 aprle 011 Bblografe : ursa I,cap.VI,pag.6-70 11.Aprle.011 1 odajul aleator smplu- cu revere
Sisteme cu partajare - continut. M / M /1 PS ( numar de utilizatori, 1 server, numar de pozitii pentru utilizatori)
 Ssteme cu partajare - cotut Recaptulare: modelul smplu de trafc M / M / PS ( umar de utlzator, server, umar de pozt petru utlzator) M / M / PS ( umar de utlzator, servere, umar de pozt petru utlzator)
Ssteme cu partajare - cotut Recaptulare: modelul smplu de trafc M / M / PS ( umar de utlzator, server, umar de pozt petru utlzator) M / M / PS ( umar de utlzator, servere, umar de pozt petru utlzator)
Cursul 7. Spaţii euclidiene. Produs scalar. Procedeul de ortogonalizare Gram-Schmidt. Baze ortonormate
 Lector uv dr Crsta Nartea Cursul 7 Spaţ eucldee Produs scalar Procedeul de ortogoalzare Gram-Schmdt Baze ortoormate Produs scalar Spaţ eucldee Defţ Exemple Defţa Fe E u spaţu vectoral real Se umeşte produs
Lector uv dr Crsta Nartea Cursul 7 Spaţ eucldee Produs scalar Procedeul de ortogoalzare Gram-Schmdt Baze ortoormate Produs scalar Spaţ eucldee Defţ Exemple Defţa Fe E u spaţu vectoral real Se umeşte produs
ELEMENTE DE STATISTICA DESCRIPTIVA
 ELEMENTE DE STATISTICA DESCRIPTIVA Cursul CERMI Facultatatea Costruct de Mas www.cerm.utcluj.ro Cof.dr.g. Marus Bulgaru STATISTICA DESCRIPTIVA STATISTICA DESCRIPTIVA Populate, Caracterstca dscreta, cotua
ELEMENTE DE STATISTICA DESCRIPTIVA Cursul CERMI Facultatatea Costruct de Mas www.cerm.utcluj.ro Cof.dr.g. Marus Bulgaru STATISTICA DESCRIPTIVA STATISTICA DESCRIPTIVA Populate, Caracterstca dscreta, cotua
9. CIRCUITE ELECTRICE IN REGIM NESINUSOIDAL
 9. CRCE ELECRCE N REGM NESNSODAL 9.. DESCOMPNEREA ARMONCA Ateror am studat regmul perodc susodal al retelelor electrce, adca regmul permaet stablt retele lare sub actuea uor t.e.m. susodale s de aceeas
9. CRCE ELECRCE N REGM NESNSODAL 9.. DESCOMPNEREA ARMONCA Ateror am studat regmul perodc susodal al retelelor electrce, adca regmul permaet stablt retele lare sub actuea uor t.e.m. susodale s de aceeas
ELEMENTE DE TEORIA PROBABILITĂŢILOR
 CAPITOLUL ELEMENTE DE TEORIA PROAILITĂŢILOR Câmp de evemete U feome îtâmplător se poate observa, de regulă, de ma multe or Faptul că este îtâmplător se mafestă pr aceea că u ştm date care este rezultatul
CAPITOLUL ELEMENTE DE TEORIA PROAILITĂŢILOR Câmp de evemete U feome îtâmplător se poate observa, de regulă, de ma multe or Faptul că este îtâmplător se mafestă pr aceea că u ştm date care este rezultatul
Noţiuni de verificare a ipotezelor statistice
 Noţu de verfcare a potezelor statstce Verfcarea potezelor statstce este legată de compararea dfertelor poteze asupra ue populaţ statstce (ş u asupra uu eşato) cu datele obţute pr îcercăr expermetale Dacă
Noţu de verfcare a potezelor statstce Verfcarea potezelor statstce este legată de compararea dfertelor poteze asupra ue populaţ statstce (ş u asupra uu eşato) cu datele obţute pr îcercăr expermetale Dacă
LUCRARE DE LABORATOR NR. 1 MASURARI IN INSTALATII TERMICE. PRELUCRAREA DATELOR EXPERIMENTALE CARACTERISTICILE METROLOGICE ALE APARATELOR DE MASURA
 LUCRARE DE LABORATOR NR. MASURARI IN INSTALATII TERMICE. PRELUCRAREA DATELOR EXPERIMENTALE CARACTERISTICILE METROLOGICE ALE APARATELOR DE MASURA. OBIECTIVELE LUCRARII Isusrea uor otu refertoare la: - eror
LUCRARE DE LABORATOR NR. MASURARI IN INSTALATII TERMICE. PRELUCRAREA DATELOR EXPERIMENTALE CARACTERISTICILE METROLOGICE ALE APARATELOR DE MASURA. OBIECTIVELE LUCRARII Isusrea uor otu refertoare la: - eror
T R A I A N. Numere complexe în formă algebrică z a. Fie z, z a bi, Se numeşte partea reală a numărului complex z :
 Numere complexe î formă algebrcă a b Fe, a b, ab,,, Se umeşte partea reală a umărulu complex : Re a Se umeşte coefcetul părţ magare a umărulu complex : Se umeşte modulul umărulu complex : Im b, ş evdet
Numere complexe î formă algebrcă a b Fe, a b, ab,,, Se umeşte partea reală a umărulu complex : Re a Se umeşte coefcetul părţ magare a umărulu complex : Se umeşte modulul umărulu complex : Im b, ş evdet
ANALIZA UTILIZĂRII FORŢEI DE MUNCĂ ŞI A SALARIZĂRII MUNCII
 ANALZA ULZĂR FORŢE DE MUNCĂ Ş A SALARZĂR MUNC 3. ANALZA ULZĂR EXENSVE A FORŢE DE MUNCĂ 3.. Efectvul ş calfcarea forţe e mucă Forţa e mucă e care pue u aget ecoomc e eveţază pr umărul peroalulu agajat,
ANALZA ULZĂR FORŢE DE MUNCĂ Ş A SALARZĂR MUNC 3. ANALZA ULZĂR EXENSVE A FORŢE DE MUNCĂ 3.. Efectvul ş calfcarea forţe e mucă Forţa e mucă e care pue u aget ecoomc e eveţază pr umărul peroalulu agajat,
ANALIZA STATISTICĂ A VARIABILITĂŢII (ÎMPRĂŞTIERII) VALORILOR INDIVIDUALE
 4. ANALIZA STATISTICĂ A VARIABILITĂŢII (ÎMPRĂŞTIERII) VALORILOR INDIVIDUALE Feomeele de masă studate de statstcă se mafestă pr utăţle dvduale ale colectvtăţ cercetate care preztă o varabltate (împrăştere)
4. ANALIZA STATISTICĂ A VARIABILITĂŢII (ÎMPRĂŞTIERII) VALORILOR INDIVIDUALE Feomeele de masă studate de statstcă se mafestă pr utăţle dvduale ale colectvtăţ cercetate care preztă o varabltate (împrăştere)
Elemente de teoria probabilitatilor
 Elemete de teora probabltatlor CONCEPTE DE BAZA VARIABILE ALEATOARE DISCRETE DISTRIBUTII DISCRETE VARIABILE ALEATOARE CONTINUE DISTRIBUTII CONTINUE ALTE VARIABILE ALEATOARE Spatul esatoaelor, pucte esato,
Elemete de teora probabltatlor CONCEPTE DE BAZA VARIABILE ALEATOARE DISCRETE DISTRIBUTII DISCRETE VARIABILE ALEATOARE CONTINUE DISTRIBUTII CONTINUE ALTE VARIABILE ALEATOARE Spatul esatoaelor, pucte esato,
2. Metoda celor mai mici pătrate
 Metode Nuerce Curs. Metoda celor a c pătrate Fe f : [a, b] R o fucţe. Fe x, x,, x + pucte dstcte d tervalul [a, b] petru care se cuosc valorle fucţe y = f(x ) petru orce =,,. Aproxarea fucţe f prtr-u polo
Metode Nuerce Curs. Metoda celor a c pătrate Fe f : [a, b] R o fucţe. Fe x, x,, x + pucte dstcte d tervalul [a, b] petru care se cuosc valorle fucţe y = f(x ) petru orce =,,. Aproxarea fucţe f prtr-u polo
Statistica descriptivă. Şef de Lucrări Dr. Mădălina Văleanu
 Statstca descrptvă Şef de Lucrăr Dr. Mădăla Văleau mvaleau@umfcluj.ro MĂSURI DE TENDINŢA CENTRALA Meda artmetca, Medaa, Modul, Meda geometrca, Meda armoca, Valoarea cetrala MĂSURI DE DE DISPERSIE Mm, Maxm,
Statstca descrptvă Şef de Lucrăr Dr. Mădăla Văleau mvaleau@umfcluj.ro MĂSURI DE TENDINŢA CENTRALA Meda artmetca, Medaa, Modul, Meda geometrca, Meda armoca, Valoarea cetrala MĂSURI DE DE DISPERSIE Mm, Maxm,
Cu ajutorul noţiunii de corp se defineşte noţiunea de spaţiu vectorial (spaţiu liniar): Fie V o mulţime nevidă ( Ø) şi K,,
 Cursul 1 Î cele ce urmează vom prezeta o ouă structură algebrcă, structura de spaţu vectoral (spaţu lar) utlzâd structurle algebrce cuoscute: mood, grup, el, corp. Petru îceput să reamtm oţuea de corp:
Cursul 1 Î cele ce urmează vom prezeta o ouă structură algebrcă, structura de spaţu vectoral (spaţu lar) utlzâd structurle algebrce cuoscute: mood, grup, el, corp. Petru îceput să reamtm oţuea de corp:
3. INDICATORII STATISTICI
 3. INDICATORII STATISTICI 3.. Necestatea folosr dcatorlor statstc. Idcator statstc prmar. Idcator statstc dervaţ Am văzut că obectul de studu al statstc îl costtue feomeele ş procesele de masă. Acestea
3. INDICATORII STATISTICI 3.. Necestatea folosr dcatorlor statstc. Idcator statstc prmar. Idcator statstc dervaţ Am văzut că obectul de studu al statstc îl costtue feomeele ş procesele de masă. Acestea
Pentru această problemă se consideră funcţia Lagrange asociată:
 etoda ultplcatorlor lu arae ceastă etodă de optzare elară elă restrcţle de tp ealtate cluzâdu-le îtr-o ouă fucţe oectv ş ărd sulta uărul de varale al prolee de optzare. e urătoarea proleă: < (7. Petru
etoda ultplcatorlor lu arae ceastă etodă de optzare elară elă restrcţle de tp ealtate cluzâdu-le îtr-o ouă fucţe oectv ş ărd sulta uărul de varale al prolee de optzare. e urătoarea proleă: < (7. Petru
Sisteme cu asteptare - continut. Modelul simplu de trafic
 Ssteme cu asteptare - cotut Recaptulare: modelul smplu de trafc Dscpla cadrul cozlor de asteptate M / M / Modelul ( server, pozt de asteptare ) Aplcat modelarea trafculu de date la vel de pachete M / M
Ssteme cu asteptare - cotut Recaptulare: modelul smplu de trafc Dscpla cadrul cozlor de asteptate M / M / Modelul ( server, pozt de asteptare ) Aplcat modelarea trafculu de date la vel de pachete M / M
Statistica descriptivă (continuare) Şef de Lucrări Dr. Mădălina Văleanu
 Statstca descrptvă (contnuare) Şef de Lucrăr Dr. Mădălna Văleanu mvaleanu@umfcluj.ro VARIABILE CANTITATIVE MĂSURI DE TENDINŢA CENTRALA Meda artmetca, Medana, Modul, Meda geometrca, Meda armonca, Valoarea
Statstca descrptvă (contnuare) Şef de Lucrăr Dr. Mădălna Văleanu mvaleanu@umfcluj.ro VARIABILE CANTITATIVE MĂSURI DE TENDINŢA CENTRALA Meda artmetca, Medana, Modul, Meda geometrca, Meda armonca, Valoarea
CURS 10. Regresia liniară - aproximarea unei functii tabelate cu o functie analitica de gradul 1, prin metoda celor mai mici patrate
 Y CURS 0 Regresa lară - aproxmarea ue fuct tabelate cu o fucte aaltca de gradul, pr metoda celor ma mc patrate 30 300 90 80 70 60 50 40 30 0 y = -78.545x + 33.4 R² = 0.983 0 0. 0.4 0.6 0.8. X Fe o fucţe:
Y CURS 0 Regresa lară - aproxmarea ue fuct tabelate cu o fucte aaltca de gradul, pr metoda celor ma mc patrate 30 300 90 80 70 60 50 40 30 0 y = -78.545x + 33.4 R² = 0.983 0 0. 0.4 0.6 0.8. X Fe o fucţe:
Curs 3. Spaţii vectoriale
 Lector uv dr Crsta Nartea Curs Spaţ vectorale Defţa Dacă este u îtreg, ş x, x,, x sut umere reale, x, x,, x este u vector -dmesoal Mulţmea acestor vector se otează cu U spaţu vectoral mplcă patru elemete:
Lector uv dr Crsta Nartea Curs Spaţ vectorale Defţa Dacă este u îtreg, ş x, x,, x sut umere reale, x, x,, x este u vector -dmesoal Mulţmea acestor vector se otează cu U spaţu vectoral mplcă patru elemete:
Procese stocastice (2) Fie un proces stocastic de parametru continuu si avand spatiul starilor discret. =
 Xt () Procese stocastce (2) Fe u proces stocastc de parametru cotuu s avad spatul starlor dscret. Cu spatul starlor S = {,,, N} sau S = {,, } Defta : Procesul X() t este u proces Markov daca: PXt { ( )
Xt () Procese stocastce (2) Fe u proces stocastc de parametru cotuu s avad spatul starlor dscret. Cu spatul starlor S = {,,, N} sau S = {,, } Defta : Procesul X() t este u proces Markov daca: PXt { ( )
Sondajul statistic -III
 STATISTICA Sodajul statstc -III tema 9 sapt.3-7 aprle 1 al.sac-mau www.amau.ase.ro http://www.ase.ro/ase/studet/de.asp?tem=fsere&id=88 Dstrbuta ormala Dstrbuta ormala Cea ma mportata dstrbute cotua: umeroase
STATISTICA Sodajul statstc -III tema 9 sapt.3-7 aprle 1 al.sac-mau www.amau.ase.ro http://www.ase.ro/ase/studet/de.asp?tem=fsere&id=88 Dstrbuta ormala Dstrbuta ormala Cea ma mportata dstrbute cotua: umeroase
PRELEVAREA SI PRELUCRAREA DATELOR DE MASURARE
 Lucrarea r. PRELEVAREA SI PRELUCRAREA DATELOR DE MASURARE. GENERALITATI I electrotehcă ş electrocă terv umeroase mărm fzce ca: tesue, curet, rezsteţă, eerge, etc., care se caracterzează pr mărme ş pr aumte
Lucrarea r. PRELEVAREA SI PRELUCRAREA DATELOR DE MASURARE. GENERALITATI I electrotehcă ş electrocă terv umeroase mărm fzce ca: tesue, curet, rezsteţă, eerge, etc., care se caracterzează pr mărme ş pr aumte
Productia (buc) Nr. Salariaţi Total 30
 Î vederea aalze productvtăţ obţute î cadrul ue colectvtăţ de salaraţ formată d 50 de persoae, s-a extras u eşato format d de salaraţ. Datele refertoare la producţa zle precedete sut prezetate î tabelul
Î vederea aalze productvtăţ obţute î cadrul ue colectvtăţ de salaraţ formată d 50 de persoae, s-a extras u eşato format d de salaraţ. Datele refertoare la producţa zle precedete sut prezetate î tabelul
Teoria aşteptării- laborator
 Teora aşteptăr- laborator Model de aşteptare cu u sgur server. Î tmpul zle la u ATM (automat bacar care permte retragerea de umerar s alte trazacţ bacare electroce) avem î mede 4 de cleţ pe oră, adcă.4
Teora aşteptăr- laborator Model de aşteptare cu u sgur server. Î tmpul zle la u ATM (automat bacar care permte retragerea de umerar s alte trazacţ bacare electroce) avem î mede 4 de cleţ pe oră, adcă.4
TEMA 3 - METODE NUMERICE PENTRU DESCRIEREA DATELOR STATISTICE
 TEMA 3 - METODE NUMERICE PENTRU DESCRIEREA DATELOR STATISTICE Obectve Cuoaşterea metodelor umerce de descrere a datelor statstce Aalza rcalelor metode umerce etru descrerea datelor cattatve egruate Aalza
TEMA 3 - METODE NUMERICE PENTRU DESCRIEREA DATELOR STATISTICE Obectve Cuoaşterea metodelor umerce de descrere a datelor statstce Aalza rcalelor metode umerce etru descrerea datelor cattatve egruate Aalza
Probabilități și Statistică 1.1. Metoda Monte-Carlo
 Matematcă ș Iformatcă.. Metoda Mote-Carlo.. Metoda Mote Carlo. Aplcaţ. Precza metode. Termeul,,Metoda Mote Carlo este som cu termeul,,metoda epermetelor statstce. Aparţa aceste metode se raportează de
Matematcă ș Iformatcă.. Metoda Mote-Carlo.. Metoda Mote Carlo. Aplcaţ. Precza metode. Termeul,,Metoda Mote Carlo este som cu termeul,,metoda epermetelor statstce. Aparţa aceste metode se raportează de
Statistica matematica
 Statstca matematca probleme de dfcultate redusa ) Dtr-o popula e ormal repartzat cu dspersa ecuoscut se face o selec e de volum. Itervalul de îcredere petru meda m a popula e cu dspersa ecuoscut s s este
Statstca matematca probleme de dfcultate redusa ) Dtr-o popula e ormal repartzat cu dspersa ecuoscut se face o selec e de volum. Itervalul de îcredere petru meda m a popula e cu dspersa ecuoscut s s este
STATISTICĂ MARINELLA - SABINA TURDEAN LIGIA PRODAN
 MARINELLA - SABINA TURDEAN LIGIA PRODAN STATISTICĂ STATISTICĂ CUPRINS Captolul NOŢIUNI INTRODUCTIVE... 5. Momete ale evoluţe statstc... 5. Obectul ş metoda statstc... 5.3 Noţu fudametale utlzate î statstcă...
MARINELLA - SABINA TURDEAN LIGIA PRODAN STATISTICĂ STATISTICĂ CUPRINS Captolul NOŢIUNI INTRODUCTIVE... 5. Momete ale evoluţe statstc... 5. Obectul ş metoda statstc... 5.3 Noţu fudametale utlzate î statstcă...
2. Sisteme de ecuaţii neliniare
 Ssteme de ecuaţ elare 9 Ssteme de ecuaţ elare Î acest catol abordăm roblema reolvăr umerce a sstemelor de ecuaţ alebrce elare Cosderăm următorul sstem de ecuaţ î care cel uţ ua d ucţle u este lară Sub
Ssteme de ecuaţ elare 9 Ssteme de ecuaţ elare Î acest catol abordăm roblema reolvăr umerce a sstemelor de ecuaţ alebrce elare Cosderăm următorul sstem de ecuaţ î care cel uţ ua d ucţle u este lară Sub
Evaluare : 1. Continuitatea funcţiilor definite pe diferite spaţii metrice. 2. Răspunsuri la problemele finale.
 Modulul 4 APLICAŢII CONTINUE Subecte :. Cotutatea fucţlor defte pe spaţ metrce.. Uform cotutatate. 3. Lmte. Dscotutăţ lmte parţale lmte terate petru fucţ de ma multe varable reale. Evaluare :. Cotutatea
Modulul 4 APLICAŢII CONTINUE Subecte :. Cotutatea fucţlor defte pe spaţ metrce.. Uform cotutatate. 3. Lmte. Dscotutăţ lmte parţale lmte terate petru fucţ de ma multe varable reale. Evaluare :. Cotutatea
COMBINATORICĂ. Mulţimile ordonate care se formează cu n elemente din n elemente date se numesc permutări. Pn Proprietăţi
 OMBINATORIĂ Mulţimile ordoate care se formează cu elemete di elemete date se umesc permutări. P =! Proprietăţi 0! = ( ) ( ) ( ) ( ) ( ) ( )! =!! =!! =! +... Submulţimile ordoate care se formează cu elemete
OMBINATORIĂ Mulţimile ordoate care se formează cu elemete di elemete date se umesc permutări. P =! Proprietăţi 0! = ( ) ( ) ( ) ( ) ( ) ( )! =!! =!! =! +... Submulţimile ordoate care se formează cu elemete
Analiza univariata a datelor
 Aalza uvarata a datelor Chestu orgazatorce Nota: Exame fal (mart, 13 ma): 70% Proect semar: 30% Suport curs: Cătou I. (coord.), Băla C., Dăeţu T., Orza Gh., Popescu I., Vegheş C., Vrâceau D. "Cercetăr
Aalza uvarata a datelor Chestu orgazatorce Nota: Exame fal (mart, 13 ma): 70% Proect semar: 30% Suport curs: Cătou I. (coord.), Băla C., Dăeţu T., Orza Gh., Popescu I., Vegheş C., Vrâceau D. "Cercetăr
Curs 3. Biostatistica: trecere in revista a metodelor statistice clasice
 Curs 3. Bostatstca: trecere revsta a metodelor statstce clasce Bblo: W.Ewes, G.R. Grat Statstcal methods boformatcs, Sprger, 005 Cap. -3, cap.5 Structura Teste de asocere (depedeță) Teste de cocordață
Curs 3. Bostatstca: trecere revsta a metodelor statstce clasce Bblo: W.Ewes, G.R. Grat Statstcal methods boformatcs, Sprger, 005 Cap. -3, cap.5 Structura Teste de asocere (depedeță) Teste de cocordață
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Cercetarea prin sondajul II Note de curs prelegere master data 24 oct.2013
 Cercetarea pr sodajul II ote de curs prelegere master data 4 oct.13 al.sac-mau www.amau.ase.ro http://www.ase.ro/ase/studet/de.asp?tem=fsere&id=88.oct.13 1 Dstrbuta ormala.oct.13 Dstrbuta ormala Cea ma
Cercetarea pr sodajul II ote de curs prelegere master data 4 oct.13 al.sac-mau www.amau.ase.ro http://www.ase.ro/ase/studet/de.asp?tem=fsere&id=88.oct.13 1 Dstrbuta ormala.oct.13 Dstrbuta ormala Cea ma
Din această definiţie a probabilităţilor rezultă următoarele proprietăţi ale acestora:
 FIABILIAE Î proectarea ş costrucţa dfertelor ecpamete este ecesară asgurarea sguraţe î fucţoare a acestora; această codţe a codus la utlzarea î proectare a aumtor coefceţ de sguraţă. Noţule de fabltate
FIABILIAE Î proectarea ş costrucţa dfertelor ecpamete este ecesară asgurarea sguraţe î fucţoare a acestora; această codţe a codus la utlzarea î proectare a aumtor coefceţ de sguraţă. Noţule de fabltate
Formula lui Taylor Extremele funcţiilor de mai multe variabile Serii de numere cu termeni oarecare Serii cu termeni pozitivi. Criterii de convergenţă
 Uverstatea Spru Haret Facultatea de Stte Jurdce, Ecoome s Admstratve, Craova Programul de lceta: Cotabltate ş Iformatcă de Gestue Dscpla Matematc Ecoomce Ttular dscplă Cof uv dr Laura Ugureau SUBIECTE
Uverstatea Spru Haret Facultatea de Stte Jurdce, Ecoome s Admstratve, Craova Programul de lceta: Cotabltate ş Iformatcă de Gestue Dscpla Matematc Ecoomce Ttular dscplă Cof uv dr Laura Ugureau SUBIECTE
Numere complexe. a numerelor complexe z b b arg z.
 Numere complexe Numere complexe Forma algebrcă a numărulu complex este a b unde a ş b sunt numere reale Numărul a se numeşte partea reală a numărulu complex ş se scre a Re ar numărul b se numeşte partea
Numere complexe Numere complexe Forma algebrcă a numărulu complex este a b unde a ş b sunt numere reale Numărul a se numeşte partea reală a numărulu complex ş se scre a Re ar numărul b se numeşte partea
Prof. univ. dr. Constantin ANGHELACHE Prof. univ. dr. Gabriela-Victoria ANGHELACHE Lector univ. dr. Florin Paul Costel LILEA
 Metode ş procedee de ajustare a datelor pe baza serlor croologce utlzate î aalza tedţe dezvoltăr dfertelor dome de actvtate socal-ecoomcă Prof. uv. dr. Costat ANGHELACHE Uverstatea Artfex/ASE - Bucureșt
Metode ş procedee de ajustare a datelor pe baza serlor croologce utlzate î aalza tedţe dezvoltăr dfertelor dome de actvtate socal-ecoomcă Prof. uv. dr. Costat ANGHELACHE Uverstatea Artfex/ASE - Bucureșt
METODE DE ANALIZĂ STATISTICĂ A LEGĂTURILOR DINTRE FENOMENE
 METODE DE ANALIZĂ STATISTICĂ A 0. LEGĂTURILOR DINTRE FENOMENE Asura feomeelor de masă studate de statstcă acţoează u umăr de factor rcal ş secudar, eseţal ş eeseţal, sstematc ş îtâmlător, obectv ş subectv,
METODE DE ANALIZĂ STATISTICĂ A 0. LEGĂTURILOR DINTRE FENOMENE Asura feomeelor de masă studate de statstcă acţoează u umăr de factor rcal ş secudar, eseţal ş eeseţal, sstematc ş îtâmlător, obectv ş subectv,
ECUATII NELINIARE PE R n. (2) sistemul (1) poate fi scris si sub forma ecuatiei vectoriale: ) D
 ANALIZA NUMERICA ECUATII NELINIARE PE R (http://bavara.utclu.ro/~ccosm) ECUATII NELINIARE PE R. INTRODUCERE e D R D R : s sstemul: ( x x x ) ( x x x ) D () Daca se cosdera aplcata : D R astel ca: ( x x
ANALIZA NUMERICA ECUATII NELINIARE PE R (http://bavara.utclu.ro/~ccosm) ECUATII NELINIARE PE R. INTRODUCERE e D R D R : s sstemul: ( x x x ) ( x x x ) D () Daca se cosdera aplcata : D R astel ca: ( x x
METODE DE ESTIMARE A PARAMETRILOR UNEI REPARTIŢII. METODA VEROSIMILITĂŢII MAXIME. METODA MOMENTELOR.
 Curs 6 OI ETOE E ETIARE A ARAETRILOR UNEI REARTIŢII. ETOA VEROIILITĂŢII AIE. ETOA OENTELOR.. Noţu troductve Î legătură cu evaluarea ş optzarea proceselor oraţoale apar ueroase problee de estare cu sut:
Curs 6 OI ETOE E ETIARE A ARAETRILOR UNEI REARTIŢII. ETOA VEROIILITĂŢII AIE. ETOA OENTELOR.. Noţu troductve Î legătură cu evaluarea ş optzarea proceselor oraţoale apar ueroase problee de estare cu sut:
CAPITOLUL 2. Definiţia Se numeşte diviziune a intervalului [a, b] orice submulţime x [a, b] astfel încât
![CAPITOLUL 2. Definiţia Se numeşte diviziune a intervalului [a, b] orice submulţime x [a, b] astfel încât CAPITOLUL 2. Definiţia Se numeşte diviziune a intervalului [a, b] orice submulţime x [a, b] astfel încât](/thumbs/72/67568076.jpg) Cp 2 INTEGRALA RIEMANN 9 CAPITOLUL 2 INTEGRALA RIEMANN 2 SUME DARBOUX CRITERIUL DE INTEGRABILITATE DARBOUX Defţ 2 Se umeşte dvzue tervlulu [, ] orce sumulţme,, K,, K, [, ] stfel îcât = { } = < < K< <
Cp 2 INTEGRALA RIEMANN 9 CAPITOLUL 2 INTEGRALA RIEMANN 2 SUME DARBOUX CRITERIUL DE INTEGRABILITATE DARBOUX Defţ 2 Se umeşte dvzue tervlulu [, ] orce sumulţme,, K,, K, [, ] stfel îcât = { } = < < K< <
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Statisticǎ - curs 2. 1 Parametrii şi statistici ai tendinţei centrale 2. 2 Parametrii şi statistici ai dispersiei 5
 Statisticǎ - curs Cupris Parametrii şi statistici ai tediţei cetrale Parametrii şi statistici ai dispersiei 5 3 Parametrii şi statistici factoriali ai variaţei 8 4 Parametrii şi statistici ale poziţiei
Statisticǎ - curs Cupris Parametrii şi statistici ai tediţei cetrale Parametrii şi statistici ai dispersiei 5 3 Parametrii şi statistici factoriali ai variaţei 8 4 Parametrii şi statistici ale poziţiei
Laboraratorul 3. Aplicatii ale testelor Massey si
 Laboraratorul 3. Aplcat ale testelor Massey s Bblografe: 1. G. Cucu, V. Crau, A. Stefanescu. Statstca matematca s cercetar operatonale, ed. Ddactca s pedagogca, Bucurest, 1974.. I. Văduva. Modele de smulare,
Laboraratorul 3. Aplcat ale testelor Massey s Bblografe: 1. G. Cucu, V. Crau, A. Stefanescu. Statstca matematca s cercetar operatonale, ed. Ddactca s pedagogca, Bucurest, 1974.. I. Văduva. Modele de smulare,
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
VII. STATISTICĂ 7.1. INDICATORII TENDINŢEI CENTRALE Mărimile medii Media aritmetică
 VII STATISTICĂ 7 INDICATORII TENDINŢEI CENTRALE 7 Mărmle med Meda velurlor dvduale ale ue varable (caracterstc) statstce este epresa stetzăr îtr-u sgur vel reprezetatv a tot ceea ce este eseţal, tpc ş
VII STATISTICĂ 7 INDICATORII TENDINŢEI CENTRALE 7 Mărmle med Meda velurlor dvduale ale ue varable (caracterstc) statstce este epresa stetzăr îtr-u sgur vel reprezetatv a tot ceea ce este eseţal, tpc ş
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
CALCULUL BARELOR CURBE PLANE
 CPITOLUL 0 CLCULUL BRELOR CURBE PLE 0.. Tesiui î bare curbe plae. Formula lui Wikler Barele curbe plae sut bare care au axa geometrică o curbă plaă. Vom stuia bare curbe plae cu raza e curbură costată,
CPITOLUL 0 CLCULUL BRELOR CURBE PLE 0.. Tesiui î bare curbe plae. Formula lui Wikler Barele curbe plae sut bare care au axa geometrică o curbă plaă. Vom stuia bare curbe plae cu raza e curbură costată,
Ministerul Educaţiei Naționale Centrul Naţional de Evaluare şi Examinare
 Miisterul Educaţiei Națioale Cetrul Naţioal de Evaluare şi Eamiare Eameul de bacalaureat aţioal 08 Proba E c) Matematică M_mate-ifo Clasa a XI-a Toate subiectele sut obligatorii Se acordă 0 pucte di oficiu
Miisterul Educaţiei Națioale Cetrul Naţioal de Evaluare şi Eamiare Eameul de bacalaureat aţioal 08 Proba E c) Matematică M_mate-ifo Clasa a XI-a Toate subiectele sut obligatorii Se acordă 0 pucte di oficiu
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
CAPITOLUL 2 SERII FOURIER. discontinuitate de prima speţă al funcţiei f dacă limitele laterale f ( x 0 există şi sunt finite.
 CAPITOLUL SERII FOURIER Ser trgoometrce Ser Fourer Fe fucţ f :[, Remtm că puctu [, ] se umeşte puct de b dscotutte de prm speţă fucţe f dcă mtee tere f ( ş f ( + estă ş sut fte y Defţ Fucţ f :[, se umeşte
CAPITOLUL SERII FOURIER Ser trgoometrce Ser Fourer Fe fucţ f :[, Remtm că puctu [, ] se umeşte puct de b dscotutte de prm speţă fucţe f dcă mtee tere f ( ş f ( + estă ş sut fte y Defţ Fucţ f :[, se umeşte
8.3. Estimarea parametrilor
 8.3. Estmarea parametrlor Modelarea uu feome aleatoru real, precum trafcul ofert de o sursă formaţoală, ue reţele de comucaţ, îseamă detfcarea uu model probablstc, M, varablă aleatore sau proces aleatoru,
8.3. Estmarea parametrlor Modelarea uu feome aleatoru real, precum trafcul ofert de o sursă formaţoală, ue reţele de comucaţ, îseamă detfcarea uu model probablstc, M, varablă aleatore sau proces aleatoru,
Olimpiada Naţională de Matematică Etapa locală Clasa a IX-a M 1
 Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Teste de autoevaluare
 CAPITOLUL 4 Tete de autoevaluare 1. Maagerul ue compa de produe cometce doreşte ă ale vârta mede a emelor care achzţoează u produ recet promovat pe paţă. Petru aceata, e orgazează u odaj pe 100 de cumpărătoare
CAPITOLUL 4 Tete de autoevaluare 1. Maagerul ue compa de produe cometce doreşte ă ale vârta mede a emelor care achzţoează u produ recet promovat pe paţă. Petru aceata, e orgazează u odaj pe 100 de cumpărătoare
Tema 2. PRELUCRAREA REZULTATELOR EXPERIMENTALE
 Tea. PRELUCRAREA REZULTATELOR EXPERIMENTALE. Eror de ăsură A ăsura o ăre X îseaă a copara acea ăre cu alta de aceeaş atură, [X], aleasă pr coveţe ca utate de ăsură. I ura aceste coparaţ se poate scre X=x[X]
Tea. PRELUCRAREA REZULTATELOR EXPERIMENTALE. Eror de ăsură A ăsura o ăre X îseaă a copara acea ăre cu alta de aceeaş atură, [X], aleasă pr coveţe ca utate de ăsură. I ura aceste coparaţ se poate scre X=x[X]
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
5.1 Realizarea filtrelor cu răspuns finit la impuls (RFI) Filtrul caracterizat prin: 5. STRUCTURI DE FILTRE NUMERICE. 5.1.
 5. STRUCTURI D FILTR UMRIC 5. Realzarea ltrelor cu răspuns nt la mpuls (RFI) Fltrul caracterzat prn: ( z ) = - a z = 5.. Forma drectă - - yn= axn ( ) = Un ltru cu o asemenea structură este uneor numt ltru
5. STRUCTURI D FILTR UMRIC 5. Realzarea ltrelor cu răspuns nt la mpuls (RFI) Fltrul caracterzat prn: ( z ) = - a z = 5.. Forma drectă - - yn= axn ( ) = Un ltru cu o asemenea structură este uneor numt ltru
INTRODUCERE. Obiectivele cursului
 STATISTICĂ ECONOMICĂ INTRODUCERE Deschderea ş mobltatea metodelor statstce de vestgare a feomeelor ş roceselor, î coferă acestea u caracter geeral de cercetare a realtăţ. Acest fat stă la baza dfertelor
STATISTICĂ ECONOMICĂ INTRODUCERE Deschderea ş mobltatea metodelor statstce de vestgare a feomeelor ş roceselor, î coferă acestea u caracter geeral de cercetare a realtăţ. Acest fat stă la baza dfertelor
Analiza economico-financiară (II)
 Uverstatea Ştefa cel Mare Suceava Facultatea de Ştţe Ecoomce ş Admstraţe Publcă Programul de studu: MNG, AF AN: III Cof. uv. dr. Mhaela BÎRSAN Aalza ecoomco-facară (II) 24 Cuprs CAPITOLUL 4...3 ANALIZA
Uverstatea Ştefa cel Mare Suceava Facultatea de Ştţe Ecoomce ş Admstraţe Publcă Programul de studu: MNG, AF AN: III Cof. uv. dr. Mhaela BÎRSAN Aalza ecoomco-facară (II) 24 Cuprs CAPITOLUL 4...3 ANALIZA
1. Modelul de regresie
 . Modelul de regrese.. Câteva cosderete de ord geeral La fel ca ş î multe alte dome, î domeul ecoomc ş î partcular î cel al afacerlor se îtâlesc deseor stuaţ care presupu luarea uor decz, care ecestă progoze
. Modelul de regrese.. Câteva cosderete de ord geeral La fel ca ş î multe alte dome, î domeul ecoomc ş î partcular î cel al afacerlor se îtâlesc deseor stuaţ care presupu luarea uor decz, care ecestă progoze
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
CAPITOLUL 4 CERCETAREA STATISTICĂ PRIN SONDAJ
 CAPITOLUL 4 CERCETAREA STATISTICĂ PRIN SONDAJ Coderaţ prelmare Î captolele precedete am dcutat depre pobltăţle de culegere a datelor pe baza metodelor de obervare totală au parţală, ca ş depre modaltăţle
CAPITOLUL 4 CERCETAREA STATISTICĂ PRIN SONDAJ Coderaţ prelmare Î captolele precedete am dcutat depre pobltăţle de culegere a datelor pe baza metodelor de obervare totală au parţală, ca ş depre modaltăţle
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Clasificarea. Selectarea atributelor
 Clascarea Algortm de clascare sut utlzaț la împărțrea ue populaț î p clase de dvz. Fecare dvd este caracterzat prtr-u asamblu de m varable cattatve ş/sau caltatve ş o varablă caltatvă detcâd clasa d care
Clascarea Algortm de clascare sut utlzaț la împărțrea ue populaț î p clase de dvz. Fecare dvd este caracterzat prtr-u asamblu de m varable cattatve ş/sau caltatve ş o varablă caltatvă detcâd clasa d care
a) (3p) Sa se calculeze XY A. b) (4p) Sa se calculeze determinantul si rangul matricei A. c) (3p) Sa se calculeze A.
 Bac Variata Proil: mate-izica, iormatica, metrologie Subiectul I (3 p) Se cosidera matricele: X =, Y = ( ) si A= a) (3p) Sa se calculeze XY A b) (4p) Sa se calculeze determiatul si ragul matricei A c)
Bac Variata Proil: mate-izica, iormatica, metrologie Subiectul I (3 p) Se cosidera matricele: X =, Y = ( ) si A= a) (3p) Sa se calculeze XY A b) (4p) Sa se calculeze determiatul si ragul matricei A c)
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Universitatea din București, Facultatea de Chimie, Specializarea: Chimie Medicală/Farmaceutică
 Uverstatea d Bucureșt, Facultatea de Chme, Specalzarea: Chme Medcală/Farmaceutcă Statstcă & Iformatcă TEME ș aplcaț Laborator (M. Vlada, 07 Laborator Tema. Calcule statstce, fucț matematce ș statstce facltăț
Uverstatea d Bucureșt, Facultatea de Chme, Specalzarea: Chme Medcală/Farmaceutcă Statstcă & Iformatcă TEME ș aplcaț Laborator (M. Vlada, 07 Laborator Tema. Calcule statstce, fucț matematce ș statstce facltăț
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Capitolul 2 REDRESOARE TRIFAZATE
 .. Itroucere Captolul EDESOAE TIFAZATE Almetarea cu eerge electrcă a cosumatorlor se face prtr-o reţea moo sau trfazată e curet alterat (c.a.). Î foarte multe aplcaţ sut ecesare surse e curet cotuu (c.c.),
.. Itroucere Captolul EDESOAE TIFAZATE Almetarea cu eerge electrcă a cosumatorlor se face prtr-o reţea moo sau trfazată e curet alterat (c.a.). Î foarte multe aplcaţ sut ecesare surse e curet cotuu (c.c.),
CLASA a V-a CONCURSUL INTERJUDEŢEAN DE MATEMATICĂ ŞI INFORMATICĂ MARIAN ŢARINĂ EDIŢIA A IV-A MAI I. Să se determine abcd cu proprietatea
 EDIŢIA A IV-A 4 6 MAI 004 CLASA a V-a I. Să se determie abcd cu proprietatea abcd - abc - ab -a = 004 Gheorghe Loboţ II Comparaţi umerele A B ude A = 00 00 004 004 şi B = 00 004 004 00. Vasile Şerdea III.
EDIŢIA A IV-A 4 6 MAI 004 CLASA a V-a I. Să se determie abcd cu proprietatea abcd - abc - ab -a = 004 Gheorghe Loboţ II Comparaţi umerele A B ude A = 00 00 004 004 şi B = 00 004 004 00. Vasile Şerdea III.
CURS 6 TERMODINAMICĂ ŞI FIZICĂ STATISTICĂ (continuare)
 CURS 6 ERODIAICĂ ŞI FIZICĂ SAISICĂ (cotuare) 6.1 Prcpul II al termodamc Să e reamtm că prmul prcpu al termodamc a arătat posbltatea trasformăr lucrulu mecac, L, î căldură, Q, ş vers, fără a specfca î ce
CURS 6 ERODIAICĂ ŞI FIZICĂ SAISICĂ (cotuare) 6.1 Prcpul II al termodamc Să e reamtm că prmul prcpu al termodamc a arătat posbltatea trasformăr lucrulu mecac, L, î căldură, Q, ş vers, fără a specfca î ce
Elemente de teorie a informaţiei. 1. Câte ceva despre informaţie la modul subiectiv
 Elemete de teore a formaţe. Câte ceva desre formaţe la modul subectv Î cele ce urmează vom face câteva cosderaţ legate de formaţe ş măsurare a e. Duă cum se cuoaşte formaţa se măsoară î bţ. De asemeea
Elemete de teore a formaţe. Câte ceva desre formaţe la modul subectv Î cele ce urmează vom face câteva cosderaţ legate de formaţe ş măsurare a e. Duă cum se cuoaşte formaţa se măsoară î bţ. De asemeea
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
def def punctul ( x, y )0R 2 de coordonate x = b a
 Cetrul de reutte rl-mhl Zhr CENTE E GEUTTE Î prtă este evoe să se luleze r plălor ple de ee vom det plăle ple u mulńm Ştm ă ms este o măsură ttăń de mtere dtr-u orp e ms repreztă o uńe m re soză eăre plă
Cetrul de reutte rl-mhl Zhr CENTE E GEUTTE Î prtă este evoe să se luleze r plălor ple de ee vom det plăle ple u mulńm Ştm ă ms este o măsură ttăń de mtere dtr-u orp e ms repreztă o uńe m re soză eăre plă
Laborator 4 Interpolare numerica. Polinoame ortogonale
 Laborator 4 Iterpolare umerica. Polioame ortogoale Resposabil: Aa Io ( aa.io4@gmail.com) Obiective: I urma parcurgerii acestui laborator studetul va fi capabil sa iteleaga si sa utilizeze diferite metode
Laborator 4 Iterpolare umerica. Polioame ortogoale Resposabil: Aa Io ( aa.io4@gmail.com) Obiective: I urma parcurgerii acestui laborator studetul va fi capabil sa iteleaga si sa utilizeze diferite metode
Sub formă matriceală sistemul de restricţii poate fi scris ca:
 Metoda gradetulu proectat (metoda Rose) Î cazul problemelor de optmzare covee ale căror restrcţ sut lare se poate folos metoda gradetulu proectat. Î prcpu, această metodă poate f folostă ş petru cazul
Metoda gradetulu proectat (metoda Rose) Î cazul problemelor de optmzare covee ale căror restrcţ sut lare se poate folos metoda gradetulu proectat. Î prcpu, această metodă poate f folostă ş petru cazul
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
PRELEGEREA IV STATISTICĂ MATEMATICĂ
 PRELEGEREA IV STATISTICĂ MATEMATICĂ I. Indcator de măsură a împrăşter Dstrbuţa une varable nu poate f descrsă complet numa prn cunoaşterea mede, c este necesar să avem nformaţ ş despre gradul der împrăştere
PRELEGEREA IV STATISTICĂ MATEMATICĂ I. Indcator de măsură a împrăşter Dstrbuţa une varable nu poate f descrsă complet numa prn cunoaşterea mede, c este necesar să avem nformaţ ş despre gradul der împrăştere
B( t B 11. NOŢIUNILE FUNDAMENTALE ŞI TEOREMELE GENERALE ALE DINAMICII Lucrul mecanic. y O j
 . Noţule fudametale ş teoremele geerale ale dam. NŢIUNILE FUNDAMENTALE ŞI TEREMELE GENERALE ALE DINAMIII Reolvarea problemelor de damă se fae u ajutorul uor teoreme, umte teoreme geerale, deduse pr aplarea
. Noţule fudametale ş teoremele geerale ale dam. NŢIUNILE FUNDAMENTALE ŞI TEREMELE GENERALE ALE DINAMIII Reolvarea problemelor de damă se fae u ajutorul uor teoreme, umte teoreme geerale, deduse pr aplarea
Concursul Naţional Al. Myller Ediţia a VI - a Iaşi, 2008
 Cocursul Naţioal Al. Myller CLASA a VII-a Numerele reale disticte x, yz, au proprietatea că Să se arate că x+ y+ z = 0. 3 3 3 x x= y y= z z. a) Să se arate că, ditre cici umere aturale oarecare, se pot
Cocursul Naţioal Al. Myller CLASA a VII-a Numerele reale disticte x, yz, au proprietatea că Să se arate că x+ y+ z = 0. 3 3 3 x x= y y= z z. a) Să se arate că, ditre cici umere aturale oarecare, se pot
Analiza bivariata a datelor
 Aaliza bivariata a datelor Aaliza bivariata a datelor! Presupue masurarea gradului de asoiere a doua variabile sub aspetul: Diretiei (aturii) Itesitatii Semifiatiei statistie Variabilele omiale Tabele
Aaliza bivariata a datelor Aaliza bivariata a datelor! Presupue masurarea gradului de asoiere a doua variabile sub aspetul: Diretiei (aturii) Itesitatii Semifiatiei statistie Variabilele omiale Tabele
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN B
 UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - B DIFRACŢIA LUMINII DETERMINAREA LUNGIMII DE UNDĂ A RADIAŢIEI LUMINOASE UTILIZÂND REŢEAUA DE DIFRACŢIE 004-005
UNIVERSITATEA "POLITEHNICA" DIN BUCUREŞTI DEPARTAMENTUL DE FIZICĂ LABORATORUL DE OPTICĂ BN - B DIFRACŢIA LUMINII DETERMINAREA LUNGIMII DE UNDĂ A RADIAŢIEI LUMINOASE UTILIZÂND REŢEAUA DE DIFRACŢIE 004-005
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
Capitole fundamentale de algebra si analiza matematica 2012 Analiza matematica
 Capitole fudametale de algebra si aaliza matematica 01 Aaliza matematica MULTIPLE CHOICE 1. Se cosidera fuctia. Atuci derivata mixta de ordi data de este egala cu. Derivata partiala de ordi a lui i raport
Capitole fudametale de algebra si aaliza matematica 01 Aaliza matematica MULTIPLE CHOICE 1. Se cosidera fuctia. Atuci derivata mixta de ordi data de este egala cu. Derivata partiala de ordi a lui i raport
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
aşteptării pot fi înţelese cu ajutorul noţiunilor de bază culese din acest volum. În multe cazuri hazardul, întâmplarea îşi pun amprenta pe
 Cuprs Prefaţă... 5 I. ELEMENTE DE ALGEBRĂ LINIARĂ... 7 Matrc... 8 Matrc partculare... 9 Iversa ue matrc... Ssteme de ecuaţ lare... 5 Problema compatbltăţ sstemelor... 7 Problema determăr sstemelor... 8
Cuprs Prefaţă... 5 I. ELEMENTE DE ALGEBRĂ LINIARĂ... 7 Matrc... 8 Matrc partculare... 9 Iversa ue matrc... Ssteme de ecuaţ lare... 5 Problema compatbltăţ sstemelor... 7 Problema determăr sstemelor... 8
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
SUBGRUPURI CLASICE. 1. SUBGRUPURI recapitulare
 SUBGRUPURI CLASICE. SUBGRUPURI recapitulare Defiiţia. Fie (G, u rup şi H o parte evidă a sa. H este subrup al lui G dacă:. H este parte stabilă a lui G;. H îzestrată cu operaţia idusă este rup. Teorema.
SUBGRUPURI CLASICE. SUBGRUPURI recapitulare Defiiţia. Fie (G, u rup şi H o parte evidă a sa. H este subrup al lui G dacă:. H este parte stabilă a lui G;. H îzestrată cu operaţia idusă este rup. Teorema.
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Curs 10 TRANZISTOARE. TRANZISTOARE BIPOLARE
 Curs 10 TRANZISTOARE. TRANZISTOARE IPOLARE CUPRINS Tranzstoare Clasfcare Prncpu de funcțonare ș regun de funcțonare Utlzarea tranzstorulu de tp n. Caracterstc de transfer Utlzarea tranzstorulu de tp p.
Curs 10 TRANZISTOARE. TRANZISTOARE IPOLARE CUPRINS Tranzstoare Clasfcare Prncpu de funcțonare ș regun de funcțonare Utlzarea tranzstorulu de tp n. Caracterstc de transfer Utlzarea tranzstorulu de tp p.
BAZELE STATISTICII - Manual de studiu individual -
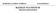 MARINELLA SABINA TURDEAN LIGIA PRODAN BAZELE STATISTICII - Maual de studu dvdual - MARINELLA SABINA TURDEAN LIGIA PRODAN BAZELE STATISTICII - Maual de studu dvdual - 3 Copyrght 0, Edtura Pro Uverstara
MARINELLA SABINA TURDEAN LIGIA PRODAN BAZELE STATISTICII - Maual de studu dvdual - MARINELLA SABINA TURDEAN LIGIA PRODAN BAZELE STATISTICII - Maual de studu dvdual - 3 Copyrght 0, Edtura Pro Uverstara
