Sprendinio kompleksinis pavidalas: z = a exp(iϕ) = a (cos ϕ + i sin ϕ). Plokščiosios bangos lygtis:
|
|
|
- ᾍιδης Σκλαβούνος
- 5 χρόνια πριν
- Προβολές:
Transcript
1 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 7 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 1.1. HARMONINIAI VIRPSIAI. MONOCHROMATINĖS BANGOS Hrmoninii virpesii r periodinii fizikinio ddžio kitimi like, nuskomi sinuso (rb kosinuso) dėsniu, kurio išrišk gunm išsprendus diferencilinę lgtį: d m = f + P ; dt či P sunkis, f elstinė jėg, nuokrpis nuo pusiusvros pdėties, f elstinio ršio koeficients. Šios lgties sprendins: = sin(ω t + δ) rb = cos(ω t + δ); či = P/f, virpesių mplitudė, ω kmpinis džnis, δ prdinė virpesių fzė. Šiomis lgtimis nuskomos sistemos vdinmos hrmoniniis oscilitoriis. Hrmoninio oscilitorius modelis suvidino svrbų vidmenį tomų ir molekulių spektroskopijoje. Oscilitorius virpesių periods T = π m f, o pilnutinė energij f =. Sprendinio kompleksinis pvidls: z = ep(iϕ) = (cos ϕ + i sin ϕ). Plokščiosios bngos lgtis:
2 8 s = cosω t = cos ν v či k = π /λ kmpinis bngos skičius. Sferinės bngos lgtis: ( ω t k ) = cos ( π t k ) r s = cos ω t ; r v či r bngos pviršius kreivumo spinduls. Bet kokios bngos lgtis r diferencilinės lgties, vdinmos bngine lgtimi, sprendins. Bendrsis bnginės lgties pvidls r toks: s s + s + = z 1 s ; t d ω λ či fzinis greitis v = = =. d t k T Šią bnginę lgtį tenkin ne tik funkcij s(,, z, t) = cos( ω t k k k z), v z ; (1.1.1) t bet ir funkcij pvidlo f (,, z, t) = f ( ωt k k k z) z b c pv. Nemonochromtinės bngos ( bngos vor, b gęstnčioji bng, c mūš) t t t nusknti bngą be sinuso rb kosinuso išriškos. Monochromtinė bng išreiškim toki periodine funkcij, ki ne tik periods, bet ir mplitudė bei prdinė fzė, nekint like. Griežti žiūrint, pv. pvizduotos bngos nėr monochromtinės. Bngos voros mplitudė (1.1.1 pv.) už t ribų lgi nuliui. Jei sinusinės dlies ilgis r geroki didesnis už bngos ilgį, turime ilgą bngos vorą. Kuo mplitudė mžiu kint like, tuo bng monochromtiškesnė. Prktiški niekuomet neturime visiški monochromtinių bngų, nes tokis
3 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 9 bngs nuskntieji virpesii r bstrkcij. Optikoje ngrinėjmos bngos, glinčios tik tm tikru rtiniu būti monochromtinėmis. Todėl įvedm kvzimonochromtinės bngos smprt. [ ω t + δ ( )] s = ( t) cos t. Reliose sąlgose džniusii r ne tskir bng, bet bngų grupė. Psitenkindmi vienmčiu uždviniu, bngų grupę glim išreikšti eilės hrmoninių bngų, kurių džnii sugrupuoti pie pgrindinį džnį, tstojmąj. Jei grupės nrių džnii skirisi nuo pgrindinio dugiu nei mž jo dlis, ti jų mplitudės r geroki mžesnės už mplitudę tų bngų, kurių džnii rtimi pgrindinim. Todėl beveik vis energij telkisi džniuose, rtimuose pgrindinim. Trumpoje bngų voroje nėr vrujnčiojo džnio ir, skirstnt tokią vorą į hrmonines bngs, skirstins pgl džnius pltus. Jei bngos vor ilg, ti viens džnis r vrujntis ir kuo ji ilgesnė, tuo mžiu skirisi nuo monochromtinės bngos. Td bngos džnių intervls siurėj ir riboje susidro griežti pstovios mplitudės monochromtinė bng. Glim įsivizduoti ir kitą ribinį tvejį, ki bngos vor toki trump ir netisklingos formos, kd nė vieno džnio neglim likti vrujnčiuoju. Tokios rūšies virpesii vdinmi bngų impulsu. Tigi pprstųjų hrmoninių (monochromtinių) bngų smprt r lbi svrbi, nes dugelis rezulttų gli būti išreikšti ptogioje formoje. Tčiu, kd ptenkinmi piškinti dugelį eksperimento detlių optikoje, džni tenk netgi monochromtinę šviesą likti bngų grupe. 1.. SUPRPOZICIJOS PRINCIPAS. SUPRATIMAS API FURJĖ SKLIDIMĄ Bendroji užduotis pie lisvojo pvidlo bngų grupės sklidimą geroki supprstėj dėl to, kd bet kokią funkciją glim išreikšti tm tikrų funkcijų sum. Fiziški ti reiški, kd lisvoji bngų grupė gli būti išreikšt bngų rb bngos impulsų sum. Trkim, kd kokime nors erdvės tške fiksuojms vienu metu beglinio bngų skičius poveikis. Pprsčiusi hipotezė, kurią glim tikti bendrojo jų poveikio tžvilgiu, r toki. Jei s 1, s, s 3, tskirų bngų trikdžii kokime nors erdvės tške tm tikru liko momentu, ti tstojmsis trikds r jų lgebrinė sum: s = s 1 + s + s 3 + (1..1)
4 Jei tstojmsis judess pršoms bngos lgtimi (1.1.1), ti būtin, kd s būtų tos lgties sprendins. Bngos lgties sprendinii r ditvūs ir td s r bngos lgties sprendins. Superpozicijos princips r fizikinė hipotezė, pgl kurią šviesos bngos trikds kokime nors tške ir tm tikru liko momentu susidrntis pereinnt eilei bngų r lgus tskirų bngų trikdžių lgebrinei sumi. Mtemtiški ti užršom (1..1). Superpozicijos princips nudojms td, ki sistemos svbės neprikluso nuo to, r ji veikim trikdžio, r ne. Toki nepriklusombė bus td, ki poveikis nelbi stiprus. Jei superpozicijos princips r tenkinms, ti lisvąją bngų grupę glim pkeisti jos dedmosiomis ir kiekvienos dedmosios poveikį ngrinėti tskiri. Rcionlus šių dedmųjų prinkims, t.. skleidimo metodo prinkims, gli geroki supprstinti užduotį. Toks rcionlus skleidims r skleidims į monochromtines bngs, t.. lisvoji funkcij pteikim kip hrmoninių funkcijų visum. Tm geri tink Furjė (Fourier) teorem nesinusinės formos bng visuomet gli būti išreikšt hrmoninių bngų sum. Furjė eilutės pč ptogios td, ki norim išreikšti funkcijs, kurių neglim išreikšti koki nors pprst lgebrine išrišk, tčiu kurią glim suskirstti į dlis, tenkinnčis Dirichle sąlgs. Trkim, kd funkcij s = f () skleidžim Furjė eilute intervle nuo l 0 iki + l 0. Jei = π l/l 0, ti Furjė eilutė bus toki: f ) = + cos + cos + + b sin + b sin + ( ; či Furjė koeficienti b 0 n = 1 π 1 = π π π π π f ( ) d; f ( ) sin n d; n 1 = π π π f ( ) cos n d; n = 1,, 3,. Įvedus pstoviuosius A 0, A 1, ir δ 1, δ,, nuskomus sąršiis A 0 = 0 ; A 1 sin δ 1 = 1 ; A 1 cos δ 1 = b 1, funkcij f () = A 0 + A 1 sin ( +δ 1) + A sin ( +δ ) +. Kiekviens nrs, išskrus pirmąjį, nusko sinusinę bngą. Toks skleidims vdinms hrmonine nlize. Jei skleidimo intervls nuo - iki +, ti hrmoninių dedmųjų sek bus ištisinis spektrs.
5 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 11 Amplitudės kitims like nusko intensvumo kitimą ir vdinms modulivimu. Moduliuoti glim ne tik bngos mplitudę (mplitudės modulivims), bet ir fzę (fzės modulivims) LKTRINIO DIPOLIO SPINDULIAVIMAS lektrinio dipolio modelis plčii nudojms įviriose optinėse užduotse. Šiuo modeliu glim ptenkinmi nuskti šviesos sklidimą medžigose, sugertį, spindulivimą, šviesos sklidą ir kitus reiškinius. lektrinis dipolis r sistem, sudrt iš dviejų vienodo didumo ir priešingų ženklų krūvininkų q, trp kurių tstums r. Pgrindinė dipolio chrkteristik r dipolinis moments p = q r. Jei dipolio krūvininki (rb viens krūvininks) hrmoningi virp plei šį, toki sistem vdinm tiesiniu hrmoniniu oscilitoriumi. Oscilitorius kintntsis dipolinis moments lgus p = p 0 cos ωt (či ω krūvininko virpesių džnis). Reiki pbrėžti, kd p = q r kitims gli vkti kip dėl e = e 0 cos ω t, tip ir dėl r = r cos ω t kitimo. Krūvio kitims relizuojms rdijotechnikoje, o tstumo kitims r dugelio fizikinių reiškinių pgrinds. Optikoje džniusii ngrinėjm, ki r = r cos ω t, r << λ ir tirim dideliuose tstumuose l (l >> r). Vektorius l brėžims iš oscilitorius centro O į ngrinėjmąjį tšką A (1.3.1 pv.). Sritis, kurioje kint l, vdinm bngos zon. lektrodinmikoje įrodom, kd pirmuoju rtiniu neutrlios sistemos judnčiųjų krūvininkų luks bngos zonoje sutmp su luku oscilitorius, kurio elektrinis moments lgus suminim sistemos momentui. Kdngi elektromgnetinis trikds sklind į viss puses nuo dipolio vienodu greičiu c (ki dipolis r vkuume), ti bngos sklidimo liks į visus tškus, nutolusius nuo dipolio vienodu tstumu l, toks pts. Todėl visuose sferos, kurios centre r dipolis, tškuose virpesių fzės r vienodos, t.. dipolio skleidžimoji bng r sferinė. Kdngi į greiti kintntį šviesos luką reguoj tik tomų ir molekulių elektroni, jų virpesius veikint lukui glim modeliuoti hrmoniniis oscilitoriis. Izotropinėje molekulėje (t.. veikint elektrinim lukui, elektrons pslenk vienodi visomis molekulės krptimis) elektrono virpez H O θ pv. Dipolio spinduliuojmos sferinės bngos elektromgnetinis luks l A N
6 1 sių krptis sutmp su krintnčiosios šviesos bngos elektrinio vektorius virpesių krptimi. Antrinės bngos elektrinio vektorius krptį lemi elektrono, kuris sukeli šią bngą, virpesių krptis, t.. r toje pčioje plokštumoje, kip ir p. Kdngi elektromgnetinės bngos r skersinės, vektorius turi būti sttmens bngos sklidimo krpčii. Šios dvi sąlgos, leminčios vektorius pdėtį, leidži susidrti įvizdį pie virpnčiojo elektrono spindulivimą (1.3.1 pv.). Hrmoninio oscilitorius vidutinė energij proporcing virpesių džnio ketvirtjm lipsniui ω 4 ir prikluso nuo spinduliuotės linkmės (sin θ): 4 ω p0 S = sin θ ; 3 8π c l pv. lementrus oscilitorius spinduliuotės digrm P či p 0 mplitudinė dipolinio momento vertė. Dipolio spinduliuotės energijos skirstins (spinduliuotės digrm) pvizduot 1.3. pv. nergij r didžiusi krptimis, sttmenomis elektrono virpesių liniji (elementrus spinduliuotojo šii), ir lgi nuliui krptimis plei šį (išilginė elektromgnetinė bng neglim!). rdvinis vizds susidrtų suknt figūrą, pvizduotą 1.3. pv., pie dipolio šį. Dėsningums, kd oscilitorius spinduliuojm gli proporcing džnio ketvirtjm lipsniui, lbi svrbus šviesos sklidos teorijoje. Toki rški priklusombe nuo bngos ilgio iškinm, pvzdžiui, dngus ždr splv (trumposios bngos sklidomos stipriu negu ilgosios) ir rudon Sulės splv sulėldžio metu, ki pereinnt spindulims storus tmosferos sluoksnius melsvieji spindulii iš tiesioginio sruto išsklidomi stipriu negu rudonieji LKTROMAGNTINIŲ BANGŲ POLIARIZACIJA Polirizuotoji ir ntūrlioji švies. lektromgnetinės bngos polirizcij ti šinės simetrijos pžeidims (bngos sklidimo krpties tžvilgiu) skersinėje bngoje, kuris psireiški tuo, kd elektrinio luko stiprio (rb mgnetinio luko H) poktis įviriomis krptimis plokštumoje, sttmenoje sklidimo krpčii, r skirtings. Kitip trint, polirizuotoji elektromgnetinė bng r toki bng, kurioje elektrinio luko (rb
7 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 13 mgnetinio) stiprio konkretus didumo vektorius gls jud tm tikru dėsningumu. Jei vektorius projekcijos į plokštumą, sttmeną sklidimo krpčii, gls jud tiese, turėsime tiesii polirizuotą bngą (1.4.1 pv.). Apskriti polirizuotoje bngoje tm tikros fzės vektorius (krtu ir H) b c z z z pv. Tiesii (), pskriti (b) ir elipsiški (c) polirizuotoji bng bėgnčioje bngoje brėži erdvines pskrits spirles, o sttmenoje plokštumoje pskritimą (1.4.1 b pv.). Ki bėgnčioje bngoje brėžimos erdvinės elipsinės spirlės, o sklidimo krpčii sttmenoje plokštumoje elipsę turėsime elipsiški polirizuotą bngą (1.4.1 c pv.). Ki ngrinėjmjme srute visos bngos, sklindnčios iš skirtingų elementriųjų mikroskopinių spinduolių, polirizuotos vienodi, toki polirizcij vdinm pilnutine. Pprsčiusiose plokščiose vienltėse elektromgnetinėse bngose (pvz., šviesos bngose skidrioje izotropinėje terpėje) vektorii ir H virp tskirose plokštumose, sttmenose bngos sklidimo krpčii, t.. bngos griežti skersinės. Vektorių ir H glis brėžimos figūros pnšios, bet psuktos vien kitos tžvilgiu 90 0 ; fzės ir sukimosi krpts vienodos. Šiuo tveju glim klbėti pie tm tikrą bngos polirizciją visumoje. Sudėtingesnėse nevienltėse bngose (pvz., bngose metluose rb esnt visiškjm vidus tspindžiui skidrioje terpėje) vektorii ir H virp skirtingose plokštumose, jų brėžimos kreivės skirtingos, skirtingos ir fzės. Klbėti pie bngos polirizciją visumoje neglim, reiki nurodti ir H polirizciją tskiri.
8 14 Jei vektorius dedmosios nesusietos fze (nekoherentinės) ir skirtingų elementriųjų mikrospinduolių skleidžimose bngose virpesii r skirtingų vienodi tikimų orientcijų, švies ntūrlioji (rb nepolirizuotoji). Jos sudėtje gli būti elipsiški, tiesii bei pskriti polirizuotų bngų. Švies, kurioje r vrujnts lbiusii tikimų krpčių virpesii, vdinm iš dlies polirizuot. Kiekbiški ji nuskom polirizcijos lipsniu. Atskiri silpni sąveikujnts elementrieji mikrospinduliuotoji (tomi, molekulės) spinduliuoj polirizuotą šviesą. Jos polirizcijos pobūdį nusko sistemos spinduolis šviesos luks judėjimo kiekio momento tvermės dėsnis iki ir po spindulivimo kto. Kiekvienm tskirm spindulivimo modeliui būding tm tikr polirizcij. Pvzdžiui, hrmoninis dipolinis oscilitorius spinduliuoj tiesii polirizuots bngs, elektrinis rb mgnetinis rottorius elipsiški polirizuots. Jei spinduolis r išorinime elektrinime rb mgnetinime luke, šviesos polirizcij tmp sudėtingesne kiekvien spinduliuotės spektro linij skl į kelis skirtingos polirizcijos linijs. Mkroskopinių kūnų spinduliuojm švies sudrt iš didelio elementriųjų spinduolių skičius. Jos polirizcij nuskom spinduolių prigimtimi ir jų orientcij. Ki spinduolii išsidėstę visiški netvrkingi, švies ntūrlioji, o, pvz., kristluose gli būti ženkli polirizcij. Pusiusvrusis šiluminis spindulivims, kip visiški izotropinis, r ntūrlusis. Tempertūrinių spinduolių spinduliuotė r silpni polirizuot dėl pviršinių sluoksnių poveikio, kuriuose nėr visiškos pusiusvros trp spinduliuotės ir medžigos. Pvzdžiui, kitrinės lempos volfrmo siūlelio spinduliuojm švies r polirizuot iki (15 0)%, gvsidbrio lempos iki (5 8)%. Dienos švies prktiški r ntūrlioji, nors tskirų dngus plotų švies visuomet r šiek tiek polirizuot. Stiprii polirizuotą šviesą spinduliuoj liuminescuojnts sksčii ir kietieji kūni, pč ždinnt polirizuot švies. Šviesos polirizcijos pobūdis turi esminės įtkos šviesos sąveiki su medžig. Optiški izotropinėse medžigose, o krtis ir metluose, nuo šviesos polirizcijos prikluso šviesos sklidimo greitis ir krptis (dvejops spindulių lūžis), o tip pt sugertis (dichroizms). Sklindnt šviesi medžigoje polirizcijos pobūdis gli keistis: pkint virpesių plokštum (tsispindint, lūžtnt, optiški ktviose terpėse); tiesii polirizuot švies gli tpti elipsiški polirizuot (visiškojo vidus tspindžio tveju; tsispindint nuo sugerinčių pviršių, pvz., metlų).
9 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 15 Terpės sklidom švies tip pt keiči svo polirizciją. Sklindnt terpėse polirizuoti šviesi išsklidtoji visuomet tm tikru lipsniu depolirizuojsi. Indikuotosios spinduliuotės polirizcijos pobūdis visuomet toks pt kip ir sktinmosios. Kvntinėje elektrodinmikoje šviesos trikds ngrinėjms kip fotonų, kurių sukins (vidinis impulso moments) lgus vienetui, sruts. Šviesos polirizcij ngrinėjm kip įvirių sukinio orientcijų psireiškimo glimbių, t.. šviesos polirizciją lemi šviesos kvntų fotonų struktūros svbės. Sukinio projekcij į kokią nors išskirtą fizikinę krptį (pvz., šviesos sklidimo krptį) gli įgti vertes: +1; 0 ir 1. Antroji iš jų skersinims šviesos fotonms (titinkntiems skersinėms bngoms bngų įvizdžiuose) nerelizuojm, o pirmji ir trečiji titink dešinioji ir kirioji pskritiminės polirizcijos. Glim teigti, kd tiesii polirizuot švies r dviejų vienodi tikimų būsenų fotonų superpozicij; vienoje būsenoje sukins orientuots išilgi sklidimo krpties, o kitoje prieš ją. lipsinę polirizciją glim suprsti kip pskritiminės ir tiesinės polirizcijų sumą, ks iškinm fotonų sukinių orientcijų psireiškimu. snt dipolinim spindulivimui, polirizuot švies perneš impulso momentą lgų h/π kiekvienm fotonui (h Plnko pstovioji). Polirizuotoji švies leidži išiškinti dugelį medžigos sndros ptumų. Pgl šviesos polirizcijos pobūdį glim drti išvds pie spinduliuotojų buvimo suždintoje būsenoje trukmę. Išsklidtos šviesos depolirizcij pteiki žinis pie šilumines fluktucijs terpėje, koncentrcines fluktucijs tirpluose ir t. t. Veikint medžigs polirizuotąj švies, glim keisti jos svbes: sukurti priemišinius tm tikros orientcijos centrus, perkelti tomus į norimos momento orientcijos būsens (optinis kupinims), orientuoti sugerties centrus. Šviesos polirizcij, kip nizotropinė svbė, leidži tirti viss medžigos nizotropijos rūšis. Kristlų optikoje tirim jų struktūr. Virpesių ir bngų sudėtis. Trkim, kd vien krptimi z sklind dvi tiesii polirizuotos trpusvje sttmenose plokštumose monochromtinės bngos = sin (ω t k z), (1.4.1) = 0 sin (ω t k z + δ) ; (1.4.) či δ prdinis fzių skirtums trp virpesių k bngos skičius. Dėl superpozicijos = +. Sudrkime tstojmąjį virpesį nuskomos kreivės lgtį. (1.4.) išrišką glim užršti tip:
10 16 = 0 sin (ω t k z) cos δ + 0 cos (ω t k z) sin δ. Pnudojus (1.4.1) išrišką užršom: = 0 cosδ sinδ. Iš či pv. Dviejų trpusvje sttmenųjų virpesių sudėtis (bendrsis tvejis) b pv. Dviejų trpusvje sttmenųjų virpesių sudėtis ( vienodos fzės, b priešingos fzės) 0 cosδ = sin δ. (1.4.3) Ti elipsės lgtis, kurios grfiks pvizduots pv. Jei cos δ = 0 ir sin δ = ± 1, ti + 0 = 1 ir elipsės šs sutmp su koordinčių ir šimis. Sumuojnt dvi tiesii trpusvje sttmeni polirizuots bngs, ki fzių skirtums trp jų δ = π / + mπ (či m = 0, 1,, ), sukurim tstojmoji elipsiški polirizuot bng. Ki = 0, elipsė tmp pskritimu ir sukurim pskriti polirizuot švies. Ki cos δ 0, ti (1.4.3) lgtis irgi nusko elipsę, bet jos šs nesutmp su koordinčių šimis. lipsė bus ir tuo tveju, ki = 0. Ki cos δ = ± 1 ir sin δ = 0, ti (1.4.3) lgtis bus tokio pvidlo: = 0, 0 t.. gunmos tiesių lgts:
11 ĮVADAS Į BANGINĘ ŠVISOS TORIJĄ 17 0 = 0 ir + 0 = 0. Atstojmojo vektorius gls jud tiese (1.4.3 pv.). Susidriusi tiesinės polirizcijos bng r ribinis elipsinės polirizcijos tvejis. Iš to išpluki, kd bet kokios polirizcijos elektromgnetinė bng r dviejų tiesinės polirizcijos bngų, kurių vektorius virp trpusvje sttmenose plokštumose, superpozicijos pdrins Glim įrodti, kd tiesinės polirizcijos bng tsirnd dėl pskritiminės polirizcijos bngų superpozicijos. Trkim, kd r kirinės ir dešininės pskritiminės polirizcijos bngos, kurių elektrinio vektorius projekcijos į koordinčių šis ir (1.4.4 pv.) reiškimos tip: 1 = 0 cos ω t; 1 = 0 sin ω t; = 0 cos ω t; = 0 sin ω t. Dėl superpozicijos gunm: = 1 + = 0 cos ω t; = 1 + = 0, t.. susidro tiesinės polirizcijos bng. Atstojmsis vektorius nukreipts šies krptimi. Jei trp tskirų virpesių būtų fzių skirtums, ti tstojmųjų virpesių linij sudrtų su šimi tm tikrą kmpą. 0 ωt pv. Dviejų pskriti polirizuotų bngų sudėtis
Plokštumų nusakymas kristale
 Kristlų struktūrinės nlizės metodi Plokštumų nuskyms kristle Kristlų nizotropij dro didelę įtką puslidininkinių prietisų prmetrms. Nuo puslidininkinių plokštelių kristlogrfinės orientcijos prikluso tokie
Kristlų struktūrinės nlizės metodi Plokštumų nuskyms kristle Kristlų nizotropij dro didelę įtką puslidininkinių prietisų prmetrms. Nuo puslidininkinių plokštelių kristlogrfinės orientcijos prikluso tokie
Matematinės analizės egzamino klausimai MIF 1 kursas, Bioinformatika, 1 semestras,
 MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
MIF kurss, Bioinformtik, semestrs, 29 6 Tolydžios tške ir intervle funkciju pibrėžimi Teorem Jei f C[, ], f() = A , ti egzistuoj toks c [, ], kd f(c) = 2 Konverguojnčios ir diverguojnčios eikutės
2015 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija. I dalis
 PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
PATVIRTINTA Ncionlinio egzminų centro direktorius 0 m. birželio d. įskymu Nr. (..)-V-7 0 M. MATEMATIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pgrindinė sesij I dlis Užd. Nr. 4 7
5 paskaita. 5.1 Kompaktiškosios aibės Sąvokos
 5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
5 pskit 5.1 Kompktiškosios ibės 5.1.1 Sąvokos Iš mtemtinės nlizės kurso žinome dvi svrbis prėžtu reliu ju skičiu ibiu svybes. Pirmoji Bolcno-Vejerštrso teorem: bet kuri beglinė prėžt reliu ju skičiu ibė
Matematika 1 4 dalis
 Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Matematika 1 4 dalis Analizinės geometrijos elementai. Tiesės plokštumoje lygtis (bendroji, kryptinė,...). Taško atstumas nuo tiesės. Kampas tarp dviejų tiesių. Plokščiosios kreivės lygtis Plokščiosios
Labai svarbi tiesiniu operatoriu šeima kompaktiškieji operatoriai. Jiems skirtas paskutinysis?? skyrelis.
 13 pskit 13.1 Tiesinii opertorii Šime skyriuje ngrinėjmos normuotu ju erdviu tiesinės funkcijos tiesinii opertorii. Bigtinės dimensijos erdvėms, kip mtysime, jie pršomi mtricomis. Tigi tiesiniu opertoriu
13 pskit 13.1 Tiesinii opertorii Šime skyriuje ngrinėjmos normuotu ju erdviu tiesinės funkcijos tiesinii opertorii. Bigtinės dimensijos erdvėms, kip mtysime, jie pršomi mtricomis. Tigi tiesiniu opertoriu
2.7. VIDURINIŲ REIKŠMIŲ TEOREMOS, JŲ TAIKYMAI
 .7. VIDURINIŲ REIKŠMIŲ TEOREMOS, JŲ TAIKYMAI 7.. Ferm teorem. (Pierre de Fermt, 6-665, http://www-history.mcs.std.c.uk/~history/mthemticis/fermt.html). Jei fukcij, pibrėžt itervle I vidiime jo tške turi
.7. VIDURINIŲ REIKŠMIŲ TEOREMOS, JŲ TAIKYMAI 7.. Ferm teorem. (Pierre de Fermt, 6-665, http://www-history.mcs.std.c.uk/~history/mthemticis/fermt.html). Jei fukcij, pibrėžt itervle I vidiime jo tške turi
FDMGEO4: Antros eilės kreivės I
 FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
FDMGEO4: Antros eilės kreivės I Kęstutis Karčiauskas Matematikos ir Informatikos fakultetas 1 Koordinačių sistemos transformacija Antrosios eilės kreivių lgtis prastinsime keisdami (transformuodami) koordinačių
K F = F 2 /F 1 = l 1 /l 2. (1)
 Stiprinims 1. Mechninės jėgos F stiprinims 1.1. Archimedo sverts. O l 2 F 2 T l 1 m P = m g F 1 1 pv. K F = F 2 /F 1 = l 1 /l 2. (1) či: P sunkio jėg; T įtempimo (tmprumo) jėg; F 1, 2 titinkmi poveikio
Stiprinims 1. Mechninės jėgos F stiprinims 1.1. Archimedo sverts. O l 2 F 2 T l 1 m P = m g F 1 1 pv. K F = F 2 /F 1 = l 1 /l 2. (1) či: P sunkio jėg; T įtempimo (tmprumo) jėg; F 1, 2 titinkmi poveikio
I.4. Laisvasis kūnų kritimas
 I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
I4 Laisvasis kūnų kitimas Laisvuoju kitimu vadinamas judėjimas, kuiuo judėtų kūnas veikiamas tik sunkio jėos, nepaisant oo pasipiešinimo Kūnui laisvai kintant iš nedidelio aukščio h (dau mažesnio už Žemės
Matematiniai modeliai ir jų korektiškumas
 1 skyrius Mtemtinii modelii ir jų korektiškums 1.1. Mtemtinių uždvinių klsifikcij Mtemtinis modelivims yr svrbus nujs žinių gvimo būds, kuris vis džniu nudojms sprendžint technologinius uždvinius, tirint
1 skyrius Mtemtinii modelii ir jų korektiškums 1.1. Mtemtinių uždvinių klsifikcij Mtemtinis modelivims yr svrbus nujs žinių gvimo būds, kuris vis džniu nudojms sprendžint technologinius uždvinius, tirint
1 SKYRIUS. Laplaso transformacija 2 SKYRIUS. Integralinės lygtys
 1 SKYRIUS. Lplo trnformcij 3 1. Integrlinė trnformcijo..................... 3 2. Lplo trnformcij........................ 3 2.1. Lplo trnformcijo vybė.............. 4 2.2. Lplo trnformcijo tikym prendžint
1 SKYRIUS. Lplo trnformcij 3 1. Integrlinė trnformcijo..................... 3 2. Lplo trnformcij........................ 3 2.1. Lplo trnformcijo vybė.............. 4 2.2. Lplo trnformcijo tikym prendžint
2.6. IŠVESTINĖ, DIFERENCIJAVIMAS
 6 IŠVESTINĖ DIFERENCIJAVIMAS 61 Išvestiės sąvok Fukcijos išvestiės sąvok yr mtemtikos istrumets kurio reikšmę suku įvertiti Glbūt ti glim plygiti su vidus degimo vriklio sukūrimu Diferecijuoti pprsčiusis
6 IŠVESTINĖ DIFERENCIJAVIMAS 61 Išvestiės sąvok Fukcijos išvestiės sąvok yr mtemtikos istrumets kurio reikšmę suku įvertiti Glbūt ti glim plygiti su vidus degimo vriklio sukūrimu Diferecijuoti pprsčiusis
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 6 tem. SĄLYGINĖS TAPATYBĖS IR NELYGYBĖS 009 0 Teorinę medžigą prengė ei šeštąją užduotį sudrė Vilnius pedgoginio universiteto doents Juos Šinkūns Įrodmo uždvinii r vieni
LIETUVOS JAUNŲJŲ MATEMATIKŲ MOKYKLA 6 tem. SĄLYGINĖS TAPATYBĖS IR NELYGYBĖS 009 0 Teorinę medžigą prengė ei šeštąją užduotį sudrė Vilnius pedgoginio universiteto doents Juos Šinkūns Įrodmo uždvinii r vieni
ANALIZINĖ GEOMETRIJA III skyrius (Medžiaga virtualiajam kursui)
 ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
ngelė aškienė NLIZINĖ GEMETRIJ III skrius (Medžiaga virtualiajam kursui) III skrius. TIESĖS IR PLKŠTUMS... 5. Tiesės lgts... 5.. Tiesės [M, a r ] vektorinė lgtis... 5.. Tiesės [M, a r ] parametrinės lgts...
Matematika PIRMOJI KNYGA. Išplėstinis kursas. Vadovėlis gimnazijos IV klasei
 Mtemtik Išplėstinis kurss Vdovėlis gimnzijos IV klsei PIRMOJI KNYGA Turinys Trigonometrinės funkcijos 5 Rdininis kmpo mts Posūkio kmpi 5 Bet kokio kmpo sinuss, kosinuss, tngents ir kotngents 9 Funkcijos
Mtemtik Išplėstinis kurss Vdovėlis gimnzijos IV klsei PIRMOJI KNYGA Turinys Trigonometrinės funkcijos 5 Rdininis kmpo mts Posūkio kmpi 5 Bet kokio kmpo sinuss, kosinuss, tngents ir kotngents 9 Funkcijos
Diržinė perdava. , mm;
 6.. Diržinė erdv Šime oskyryje diržinės erdvos greiteigio skriemlio (mžojo) geometrinii ir jėginii rmetri žymimi tini indeks, o lėteigio (didžiojo) tini indeks. Šime oskyryje teikt trecinių diržinių erdvų
6.. Diržinė erdv Šime oskyryje diržinės erdvos greiteigio skriemlio (mžojo) geometrinii ir jėginii rmetri žymimi tini indeks, o lėteigio (didžiojo) tini indeks. Šime oskyryje teikt trecinių diržinių erdvų
NEAPIBRĖŽTINIS INTEGRALAS su MAPLE. Aleksandras KRYLOVAS
 NEAPIBRĖŽTINIS INTEGRALAS su MAPLE Aleksndrs KRYLOVAS TURINYS. PIRMYKŠTĖ FUNKCIJA IR NEAPIBRĖŽTINIS INTEGRALAS 6.. PIRMYKŠTĖS FUNKCIJOS APIBRĖŽIMAS 6.. NEAPIBRĖŽTINIO INTEGRALO SAVOKA 7.. NEAPIBRĖŽTINIO
NEAPIBRĖŽTINIS INTEGRALAS su MAPLE Aleksndrs KRYLOVAS TURINYS. PIRMYKŠTĖ FUNKCIJA IR NEAPIBRĖŽTINIS INTEGRALAS 6.. PIRMYKŠTĖS FUNKCIJOS APIBRĖŽIMAS 6.. NEAPIBRĖŽTINIO INTEGRALO SAVOKA 7.. NEAPIBRĖŽTINIO
1. Individualios užduotys:
 IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
IV. PAPRASTOSIOS DIFERENCIALINĖS LYGTYS. Individualios užduots: - trumpa teorijos apžvalga, - pavzdžiai, - užduots savarankiškam darbui. Pirmosios eilės diferencialinių lgčių sprendimas.. psl. Antrosios
I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI ATSAKYMAI
 008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
008 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO VERTINIMO INSTRUKCIJA Pagrindinė sesija Kiekvieno I dalies klausimo teisingas atsakymas vertinamas tašku. I dalis KLAUSIMŲ SU PASIRENKAMUOJU ATSAKYMU TEISINGI
P. Kasparaitis. Vaizdų ir signalų apdorojimas. Filtrai
 P Ksritis Vidų ir signlų dorojims Filtri 8 Filtri Sitmeninii filtri Aibrėžims Sitmeninis filtrs ti mtemtiši ibrėžt sistem, sirt sitmeninim signlui modifiuoti Sitmeninio signlo [ tvidvimą į žymėime ti:
P Ksritis Vidų ir signlų dorojims Filtri 8 Filtri Sitmeninii filtri Aibrėžims Sitmeninis filtrs ti mtemtiši ibrėžt sistem, sirt sitmeninim signlui modifiuoti Sitmeninio signlo [ tvidvimą į žymėime ti:
ŠVIESOS SKLIDIMAS IZOTROPINĖSE TERPĖSE
 ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
ŠVIESOS SKLIDIMAS IZOTROPIĖSE TERPĖSE 43 2.7. SPIDULIUOTĖS IR KŪO SPALVOS Spinduliuotės ir kūno optiniam apibūdinimui naudojama spalvos sąvoka. Spalvos reiškinys yra nepaprastas. Kad suprasti spalvos esmę,
06 Geometrin e optika 1
 06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
06 Geometrinė optika 1 0.1. EIKONALO LYGTIS 3 Geometrinėje optikoje įvedama šviesos spindulio sąvoka. Tai leidžia Eikonalo lygtis, kuri išvedama iš banginės lygties monochromatinei bangai - Helmholtco
X galioja nelygyb f ( x1) f ( x2)
 Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Monotonin s funkcijos Tegul turime funkciją f : A R, A R. Apibr žimas. Funkcija y = f ( x) vadinama monotoniškai did jančia (maž jančia) aib je X A, jei x1< x2 iš X galioja nelygyb f ( x1) f ( x2) ( f
Dviejų kintamųjų funkcijos dalinės išvestinės
 Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Dviejų kintamųjų funkcijos dalinės išvestinės Dalinės išvestinės Tarkime, kad dviejų kintamųjų funkcija (, )yra apibrėžta srityje, o taškas 0 ( 0, 0 )yra vidinis srities taškas. Jei fiksuosime argumento
Spalvos. Šviesa. Šviesos savybės. Grafika ir vizualizavimas. Spalvos. Grafika ir vizualizavimas, VDU, Spalvos 1
 Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Spalvos Grafika ir vizualizavimas Spalvos Šviesa Spalvos Spalvų modeliai Gama koregavimas Šviesa Šviesos savybės Vandens bangos Vaizdas iš šono Vaizdas iš viršaus Vaizdas erdvėje Šviesos bangos Šviesa
Feromagnetinis rezonansas feritiniame rutuliuke
 VILNIAUS UNIVERSITETAS Rdiofiikos ktedr Ferognetinis reonnss feritinie rutuliuke Mikrobngų fiikos lbortorinis drbs Nr. 12 Pruošė doc. V. Klesinsks Vilnius 25 2 MIKROBANGŲ FIZIKOS LABORATORIJA Turinys Metodinii
VILNIAUS UNIVERSITETAS Rdiofiikos ktedr Ferognetinis reonnss feritinie rutuliuke Mikrobngų fiikos lbortorinis drbs Nr. 12 Pruošė doc. V. Klesinsks Vilnius 25 2 MIKROBANGŲ FIZIKOS LABORATORIJA Turinys Metodinii
KAIP VYKSTA FOTOSENSIBILIZACIJA BIOLOGINĖSE SISTEMOSE?
 2 skyrius KAIP VYKSTA FOTOSENSIBILIZACIJA BIOLOGINĖSE SISTEMOSE? Trumpai pateikiami svarbiausi šviesos parametrai, reikalavimai efektyviems fotosensibilizatoriams ir esminiai fotosenibilizacijos reakcijų
2 skyrius KAIP VYKSTA FOTOSENSIBILIZACIJA BIOLOGINĖSE SISTEMOSE? Trumpai pateikiami svarbiausi šviesos parametrai, reikalavimai efektyviems fotosensibilizatoriams ir esminiai fotosenibilizacijos reakcijų
Vilniaus universitetas. Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS
 Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Vilniaus universitetas Edmundas Gaigalas A L G E B R O S UŽDUOTYS IR REKOMENDACIJOS Vilnius 1992 T U R I N Y S 1. Vektorinė erdvė............................................. 3 2. Matricos rangas.............................................
Kengura Tarptautinio matematikos konkurso užduotys ir sprendimai. Junioras
 Kengur 013 Trptutinio mtemtikos konkurso užduotys ir sprendimi Juniors KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS KENGŪRA 013 TARPTAUTINIO MATEMATIKOS KONKURSO UŽDUOTYS IR SPRENDIMAI Autorius ir sudrytojs
Kengur 013 Trptutinio mtemtikos konkurso užduotys ir sprendimi Juniors KENGŪROS KONKURSO ORGANIZAVIMO KOMITETAS KENGŪRA 013 TARPTAUTINIO MATEMATIKOS KONKURSO UŽDUOTYS IR SPRENDIMAI Autorius ir sudrytojs
1 TIES ES IR PLOK TUMOS
 G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
G E O M E T R I J A Gediminas STEPANAUSKAS 1 TIES ES IR PLOK TUMOS 11 Plok²tumos ir ties es plok²tumoje normalin es lygtys 111 Vektorin e forma Plok²tumos α padetis koordina iu sistemos Oxyz atºvilgiu
Matematika 1 3 dalis
 Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
Matematika 1 3 dalis Vektorių algebros elementai. Vektorių veiksmai. Vektorių skaliarinės, vektorinės ir mišriosios sandaugos ir jų savybės. Vektoriai Vektoriumi vadinama kryptinė atkarpa. Jei taškas A
taip: Q m : m Z, n N, t.y. aibę sudaro trupmenos n
 SKYRIUS AIBĖS IR FUNKCIJOS Aibės ir jų veiksmi Kiekvieme gmtos moksle esm tiek tiesos, kiek esm mtemtikos IKts Aibės sąvok mtemtikoje likom pirmie, es legvi suvokim ir eturi pibrėţimo Ji vrtojm ir ksdieiime
SKYRIUS AIBĖS IR FUNKCIJOS Aibės ir jų veiksmi Kiekvieme gmtos moksle esm tiek tiesos, kiek esm mtemtikos IKts Aibės sąvok mtemtikoje likom pirmie, es legvi suvokim ir eturi pibrėţimo Ji vrtojm ir ksdieiime
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai
 1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
1. Įvadas. Laisvųjų dalelių kvantinės mechanikos elementai 1.1. Branduolio nukleonų energijos diskretumo aiškinimas. Dalelė stačiakampėje potencialo duobėje Dalelės banginė funkcija tai koordinačių ir
Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas
 Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
Pirmasis uždavinys Temos. Intervalinės statistinės eilutės sudarymas. Santykinių dažnių histogramos brėžimas. Imties skaitinių charakteristikų skaičiavimas Uždavinio formulavimas a) Žinoma n = 50 tiriamo
2014 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA Pagrindinė sesija
 PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 04 m. birželio 6 d. Nr. (.)-V-69birželio 4 04 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA I dalis Kiekvieno I dalies klausimo
PATVIRTINTA Nacionalinio egzaminų centro direktoriaus 04 m. birželio 6 d. Nr. (.)-V-69birželio 4 04 M. FIZIKOS VALSTYBINIO BRANDOS EGZAMINO UŽDUOTIES VERTINIMO INSTRUKCIJA I dalis Kiekvieno I dalies klausimo
Elektronų ir skylučių statistika puslaidininkiuose
 lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
lktroų ir skylučių statistika puslaidiikiuos Laisvų laidumo lktroų gracija, t.y. lktroų prėjimas į laidumo juostą, gali vykti kaip iš dooriių lygmų, taip ir iš valtiės juostos. Gracijos procsas visuomt
Molekulių energijos lygmenys Atomų Spektrai
 Kas ta spektroskopija? Biomolekulių spektroskopija: Įvadas Spektroskopija tai mokslas, kuris tiria medžiagą, panaudodamas EM spinduliuotės sąveiką su ja. Pavyzdys matomos (VIS) srities spektroskopija tai
Kas ta spektroskopija? Biomolekulių spektroskopija: Įvadas Spektroskopija tai mokslas, kuris tiria medžiagą, panaudodamas EM spinduliuotės sąveiką su ja. Pavyzdys matomos (VIS) srities spektroskopija tai
04 Elektromagnetinės bangos
 04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
04 Elektromagnetinės bangos 1 0.1. BANGINĖ ŠVIESOS PRIGIMTIS 3 Šiame skyriuje išvesime banginę lygtį iš elektromagnetinio lauko Maksvelo lygčių. Šviesa yra elektromagnetinė banga, kurios dažnis yra optiniame
Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 1 Teiginio
Skysčiai ir kietos medžiagos
 Skysčiai ir kietos medžiagos Dujos Dujos, skysčiai ir kietos medžiagos Užima visą indo tūrį Yra lengvai suspaudžiamos Lengvai teka iš vieno indo į kitą Greitai difunduoja Kondensuotos fazės (būsenos):
Skysčiai ir kietos medžiagos Dujos Dujos, skysčiai ir kietos medžiagos Užima visą indo tūrį Yra lengvai suspaudžiamos Lengvai teka iš vieno indo į kitą Greitai difunduoja Kondensuotos fazės (būsenos):
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Diferencialinių lgčių ir skaičiavimo matematikos katedra Naugarduko g. 24, LT-3225 Vilnius,
Biologinių pigmentų fluorescencijos tyrimas
 VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS KVANTINĖS ELEKTRONIKOS KATEDRA BIOFOTONIKOS LABORATORIJA Laboratorinis darbas (BPFT) Biologinių pigmentų uorescencijos tyrimas VILNIUS 24 1. Darbo tikslas Ištirti
VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS KVANTINĖS ELEKTRONIKOS KATEDRA BIOFOTONIKOS LABORATORIJA Laboratorinis darbas (BPFT) Biologinių pigmentų uorescencijos tyrimas VILNIUS 24 1. Darbo tikslas Ištirti
Statistinė termodinamika. Boltzmann o pasiskirstymas
 Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
Statistinė termodinamika. Boltzmann o pasiskirstymas DNR molekulių vaizdas DNR struktūros pakitimai. Keičiantis DNR molekulės formai keistųsi ir visos sistemos entropija. Mielėse esančio DNR struktūros
MATEMATINĖ LOGIKA. Įžanginių paskaitų medžiaga iš knygos
 MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
MATEMATINĖ LOGIKA Įžanginių paskaitų medžiaga iš knygos Aleksandras Krylovas. Diskrečioji matematika: vadovėlis aukštųjų mokyklų studentams. Vilnius: Technika, 2009. 320 p. ISBN 978-9955-28-450-5 Teiginio
Ištirti dujų spinduliuotės spektrų ypatumus ir spalvoto tirpalo šviesos sugertį.
 1 Darbo tikslai Ištirti dujų spinduliuotės spektrų ypatumus ir spalvoto tirpalo šviesos sugertį. Užduotys 1. Sugraduoti monochromatorių. 2. Išmatuoti vandenilio dujų spinduliuotės spektro Balmerio serijos
1 Darbo tikslai Ištirti dujų spinduliuotės spektrų ypatumus ir spalvoto tirpalo šviesos sugertį. Užduotys 1. Sugraduoti monochromatorių. 2. Išmatuoti vandenilio dujų spinduliuotės spektro Balmerio serijos
FRANKO IR HERCO BANDYMAS
 VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
VILNIAUS UNIVERSITETAS Kietojo kūno elektronikos katedra Atomo ir branduolio fizikos laboratorija Laboratorinis darbas Nr. FRANKO IR HERCO BANDYMAS Parengė A. Poškus 013-08-31 Turinys Darbo tikslas 1.
GEOMETRINĖS OPTIKOS PAGRINDAI
 OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
OPTINĖS SISTEMOS GEOMETRINĖS OPTIKOS PAGRINDAI sites.google.com/site/optinessistemos/ I. ĮVADAS Ženklai geometrinėje optikoje LABAI SVARBU! Fizikinė optika ir geometrinė optika Fizikinė optika - bangų
Lituoti plokšteliniai šilumokaičiai XB
 Apršyms XB yr vriu lituoti plokštelinii šilumokičii, skirti nudoti centrlizuoto šildymo ir vėsinimo sistemose, pvyzdžiui, uitinio kršto vndens ruošimo sistemoje, šilumos punkte tskirti šilumos tinklus
Apršyms XB yr vriu lituoti plokštelinii šilumokičii, skirti nudoti centrlizuoto šildymo ir vėsinimo sistemose, pvyzdžiui, uitinio kršto vndens ruošimo sistemoje, šilumos punkte tskirti šilumos tinklus
9. Sukimas Bendrosios žinios
 9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
9. Sukimas 9.. Benrosios žinios Sukimas ra eformavimo tias, aibūinamas skersjūvių asisukimu stro ašies atžvilgiu nuo sukimo momento (9. av.). Jis susijęs su kaminėmis eformacijomis (žr. 8. oskrį). ai eformuojasi
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
III.Termodinamikos pagrindai
 III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
III.ermodinamikos pagrindai III.. Dujų plėtimosi darbas egu dujos yra cilindre su nesvariu judančiu stūmokliu, kurio plotas lygus S, ir jas veikia tik išorinis slėgis p. Pradinius dujų parametrus pažymėkime
Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes.
 Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes. Ji susideda iš vienodų arba skirtingų atomų. Molekulėje
Atomų sąveikos molekulėje rūšys (joninis ir kovalentinis ryšys). Molekulė mažiausia medžiagos dalelė, turinti esmines medžiagos chemines savybes. Ji susideda iš vienodų arba skirtingų atomų. Molekulėje
KRŪVININKŲ JUDRIO PRIKLAUSOMYBĖS NUO ELEKTRINIO LAUKO STIPRIO TYRIMAS
 VILNIAUS UNIVERSITETAS Puslaidininkių fizikos katedra Puslaidininkių fizikos mokomoji laboratorija Laboratorinis darbas Nr. 5 KRŪVININKŲ JUDRIO PRIKLAUSOMYBĖS NUO ELEKTRINIO LAUKO STIPRIO TYRIMAS 013-09-0
VILNIAUS UNIVERSITETAS Puslaidininkių fizikos katedra Puslaidininkių fizikos mokomoji laboratorija Laboratorinis darbas Nr. 5 KRŪVININKŲ JUDRIO PRIKLAUSOMYBĖS NUO ELEKTRINIO LAUKO STIPRIO TYRIMAS 013-09-0
8. LENKIAMŲ PLOKŠTELIŲ ELEMENTAI
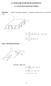 8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
8. LENKIAMŲ PLOKŠELIŲ ELEMENAI 8.1. LENKIAMŲ PLOKŠELIŲ EORIJA Įtempimai: storį: paprastai operuojama įrąžomis įtempimų atstojamosiomis per plokštelės z τ z t τ z M t = zdz, M =...., M =.. t t = τzdz, =
KURKIME ATEITĮ DRAUGE! FIZ 414 APLINKOS FIZIKA. Laboratorinis darbas SAULĖS ELEMENTO TYRIMAS
 EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
EUROPOS SĄJUNGA Europos socialinis fondas KURKIME ATEITĮ DRAUGE! 2004-2006 m. Bendrojo programavimo dokumento 2 prioriteto Žmogiškųjų išteklių plėtra 4 priemonė Mokymosi visą gyvenimą sąlygų plėtra Projekto
15 darbas ŠVIESOS DIFRAKCIJOS TYRIMAS
 15 daras ŠVIESOS DIFRKCIJOS TYRIMS Užduotys 1. Išmatuoti plyšio plotį.. Išmatuoti atstumą tarp dviejų plyšių. 3. Nustatyti šviesos angos ilgį iš difrakcinio vaizdo pro apskritą angą. 4. Nustatyti kompaktinio
15 daras ŠVIESOS DIFRKCIJOS TYRIMS Užduotys 1. Išmatuoti plyšio plotį.. Išmatuoti atstumą tarp dviejų plyšių. 3. Nustatyti šviesos angos ilgį iš difrakcinio vaizdo pro apskritą angą. 4. Nustatyti kompaktinio
VI SKYRIUS VI SKYRIUS OPTINĖ HOLOGRAFIJA
 180 OPTINĖ HOLOGRAFIJA Holografija vadinamas šviesos bangų struktūros užrašymo ir atgaminimo metodas, grindžiamas koherentinių šviesos pluoštelių difrakcija ir interferencija. Kaip ir fotografijoje, ji
180 OPTINĖ HOLOGRAFIJA Holografija vadinamas šviesos bangų struktūros užrašymo ir atgaminimo metodas, grindžiamas koherentinių šviesos pluoštelių difrakcija ir interferencija. Kaip ir fotografijoje, ji
PNEUMATIKA - vožtuvai
 Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
Mini vožtuvai - serija VME 1 - Tipas: 3/2, NC, NO, monostabilūs - Valdymas: Mechaninis ir rankinis - Nominalus debitas (kai 6 barai, Δp = 1 baras): 60 l/min. - Prijungimai: Kištukinės jungtys ø 4 žarnoms
BRANDUOLIO FIZIKOS EKSPERIMENTINIAI METODAI
 VILNIAUS UNIVERSITETAS Andrius Poškus ATOMO FIZIKA IR BRANDUOLIO FIZIKOS EKSPERIMENTINIAI METODAI (20 ir 21 skyriai) Vilnius 2008 Turinys 20. Blyksimieji detektoriai 381 20.1. Įvadas 381 20.2. Blyksnio
VILNIAUS UNIVERSITETAS Andrius Poškus ATOMO FIZIKA IR BRANDUOLIO FIZIKOS EKSPERIMENTINIAI METODAI (20 ir 21 skyriai) Vilnius 2008 Turinys 20. Blyksimieji detektoriai 381 20.1. Įvadas 381 20.2. Blyksnio
Kompiuterinė lazerių fizika. Viktorija Pyragaitė
 Kompiuterinė lazerių fizika Viktorija Pyragaitė VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS Viktorija Pyragaitė KOMPIUTERINĖ LAZERIŲ FIZIKA Elektroninis leidinys Mokomoji knyga Vilnius 2013 Apsvarstė ir
Kompiuterinė lazerių fizika Viktorija Pyragaitė VILNIAUS UNIVERSITETAS FIZIKOS FAKULTETAS Viktorija Pyragaitė KOMPIUTERINĖ LAZERIŲ FIZIKA Elektroninis leidinys Mokomoji knyga Vilnius 2013 Apsvarstė ir
Matematinės analizės konspektai
 Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Matematinės analizės konspektai (be įrodymų) Marius Gedminas pagal V. Mackevičiaus paskaitas 998 m. rudens semestras (I kursas) Realieji skaičiai Apibrėžimas. Uždarųjų intervalų seka [a n, b n ], n =,
Specialieji analizės skyriai
 Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Specialieji analizės skyriai. Trigonometrinės Furje eilutės Moksle ir technikoje dažnai susiduriame su periodiniais reiškiniais, apibūdinamais periodinėmis laiko funkcijomis: f(t). 2 Paprasčiausia periodinė
Taikomoji branduolio fizika
 VILNIAUS UNIVERSITETAS Taikomoji branduolio fizika Parengė A. Poškus Vilnius 2015-05-20 Turinys 1. Neutronų sąveika su medžiaga...1 1.1. Neutronų sąveikos su medžiaga rūšys...1 1.2. Neutrono sukeltų branduolinių
VILNIAUS UNIVERSITETAS Taikomoji branduolio fizika Parengė A. Poškus Vilnius 2015-05-20 Turinys 1. Neutronų sąveika su medžiaga...1 1.1. Neutronų sąveikos su medžiaga rūšys...1 1.2. Neutrono sukeltų branduolinių
Kinetinė biomolekulių spektroskopija 1. Darbo tikslas šmatuoti BSA (jaučio serumo albumino) ir GFP (žaliai fluorescuojančio baltymo) baltymų fluoresce
 Laboratorinis darbas Kinetinė biomolekulių spektroskopija 2008 Vilnius Kinetinė biomolekulių spektroskopija 1. Darbo tikslas šmatuoti BSA (jaučio serumo albumino) ir GFP (žaliai fluorescuojančio baltymo)
Laboratorinis darbas Kinetinė biomolekulių spektroskopija 2008 Vilnius Kinetinė biomolekulių spektroskopija 1. Darbo tikslas šmatuoti BSA (jaučio serumo albumino) ir GFP (žaliai fluorescuojančio baltymo)
ELEKTRINIS KIETŲJŲ KŪNŲ LAIDUMAS
 II skyrius ELEKTRINIS KIETŲJŲ KŪNŲ LAIDUMAS 2.1. Kietųjų kūnų klasifikacija pagal laiduą Pagal gebėjią praleisti elektros srovę visos edžiagos gatoje yra skirstoos į tris pagridines klases: laidininkus,
II skyrius ELEKTRINIS KIETŲJŲ KŪNŲ LAIDUMAS 2.1. Kietųjų kūnų klasifikacija pagal laiduą Pagal gebėjią praleisti elektros srovę visos edžiagos gatoje yra skirstoos į tris pagridines klases: laidininkus,
Dijagrami: Greda i konzola. Prosta greda. II. Dijagrami unutarnjih sila. 2. Popre nih sila TZ 3. Momenata savijanja My. 1. Uzdužnih sila N. 11.
 Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
Dijagrami:. Udužnih sia N Greda i konoa. Popre nih sia TZ 3. Momenata savijanja My. dio Prosta greda. Optere ena koncentriranom siom F I. Reaktivne sie:. M A = 0 R B F a = 0. M B = 0 R A F b = 0 3. F =
MATEMATIKOS BRANDOS EGZAMINO PROGRAMA
 PATVIRTINTA Lietuvos Respublikos švietimo ir mokslo ministro 0 m. liepos d. įskymu Nr. V-97 MATEMATIKOS BRANDOS EGZAMINO PROGRAMA I. BENDROSIOS NUOSTATOS. Mtemtikos brndos egzmino progrmos (toliu Progrm)
PATVIRTINTA Lietuvos Respublikos švietimo ir mokslo ministro 0 m. liepos d. įskymu Nr. V-97 MATEMATIKOS BRANDOS EGZAMINO PROGRAMA I. BENDROSIOS NUOSTATOS. Mtemtikos brndos egzmino progrmos (toliu Progrm)
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos
 Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
Su pertrūkiais dirbančių elektrinių skverbtis ir integracijos į Lietuvos elektros energetikos sistemą problemos Rimantas DEKSNYS, Robertas STANIULIS Elektros sistemų katedra Kauno technologijos universitetas
RADIONAVIGACINĖS SISTEMOS IR ĮRANGA
 VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS Algimantas Jakučionis RADIONAVIGACINĖS SISTEMOS IR ĮRANGA Mokomoji knyga Vilnius 2007 UDK 656.7:621.396(075.8) Ja 248 Algimantas Jakučionis. Radionavigacinės sistemos
VILNIAUS GEDIMINO TECHNIKOS UNIVERSITETAS Algimantas Jakučionis RADIONAVIGACINĖS SISTEMOS IR ĮRANGA Mokomoji knyga Vilnius 2007 UDK 656.7:621.396(075.8) Ja 248 Algimantas Jakučionis. Radionavigacinės sistemos
DEFORMUOJAMO KŪNO MECHANIKA 1 dalis
 DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
DEFORMUOJAMO KŪNO MECHANIKA dalis T U R I N Y S. Deformuojamojo kūo mechaikos objektas ir jos ršs su kitais mokslais. Tamprumo teorijos sąvokos ir prielaidos 3. Įtempimų būvio teorija 4. Pusiausvros difereciali
4.1 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n. Priminsime, kad šios erdvės elementai yra vektoriai vektoriu
 IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
IV DEKARTO KOORDINAČIU SISTEMA VEKTORIAI 41 Skaliarinė sandauga erdvėje R n Tarkime, kad duota vektorinė erdvė R n Priminsime, kad šios erdvės elementai yra vektoriai α = (a 1,, a n ) Be mums jau žinomu
= 0.927rad, t = 1.16ms
 P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA
 LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
LIETUVOS JAUNŲ J Ų MATEMATIKŲ MOKYKLA tema. APSKRITIMŲ GEOMETRIJA (00 0) Teorinę medžiagą parengė bei antrąją užduotį sudarė Vilniaus pedagoginio universiteto docentas Edmundas Mazėtis. Apskritimas tai
Fizika. doc. dr. Vytautas Stankus. Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas
 Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
Fizika doc. dr. Vytautas Stankus Fizikos katedra Matematikos ir gamtos mokslų fakultetas Kauno Technologijos Universitetas Studentų 50 58 kab. Darbo tel.: 861033946 Vytautas.Stankus@ktu.lt Bendrosios fizikos
= γ. v = 2Fe(k) O(g) k[h. Cheminė kinetika ir pusiausvyra. Reakcijos greičio priklausomybė nuo temperatūros. t2 t
 Cheminė kineika ir pusiausyra Nagrinėja cheminių reakcijų greiį ir mechanizmą. Cheminių reakcijų meu kina reaguojančių iagų koncenracijos: c ų koncenracija, mol/l laikas, s c = Reakcijos greičio io ()
Cheminė kineika ir pusiausyra Nagrinėja cheminių reakcijų greiį ir mechanizmą. Cheminių reakcijų meu kina reaguojančių iagų koncenracijos: c ų koncenracija, mol/l laikas, s c = Reakcijos greičio io ()
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
 1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
VIII. FRAKTALINĖ DIMENSIJA. 8.1 Fraktalinės dimensijos samprata. Ar baigtinis Norvegijos sienos ilgis?
 VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
VIII FRAKTALINĖ DIMENSIJA 81 Fraktalinės dimensijos samprata Ar baigtinis Norvegijos sienos ilgis? Tarkime, kad duota atkarpa, kurios ilgis lygus 1 Padalykime šia atkarpa n lygiu daliu Akivaizdu, kad kiekvienos
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
5 klasė. - užduotys apie varniuką.
 5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
5 klasė - užduotys apie varniuką. 1. Varniukas iš plastilino lipdė raides ir iš jų sudėliojo užrašą: VARNIUKO OLIMPIADA. Vienodas raides jis lipdė iš tos pačios spalvos plastelino, o skirtingas raides
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

Papildomo ugdymo mokykla Fizikos olimpas. Mechanika Dinamika 1. (Paskaitų konspektas) 2009 m. sausio d. Prof.
 Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
Papildoo ugdyo okykla izikos olipas Mechanika Dinaika (Paskaitų konspektas) 9. sausio -8 d. Prof. Edundas Kuokštis Vilnius Paskaita # Dinaika Jei kineatika nagrinėja tik kūnų judėjią, nesiaiškindaa tą
d 2 y dt 2 xdy dt + d2 x
 y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
y t t ysin y d y + d y y t z + y ty yz yz t z y + t + y + y + t y + t + y + + 4 y 4 + t t + 5 t Ae cos + Be sin 5t + 7 5 y + t / m_nadjafikhah@iustacir http://webpagesiustacir/m_nadjafikhah/courses/ode/fa5pdf
Specialieji analizės skyriai
 Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
Specialieji analizės skyriai. Specialieji analizės skyriai Kompleksinio kinamojo funkcijų teorija Furje eilutės ir Furje integralai Operacinis skaičiavimas Lauko teorijos elementai. 2 Kompleksinio kintamojo
TEMA: Šviesos banginės savybės, apibendrinimas Fizika: 10 klasė Mokytoja: Rasa Armonienė 2014 m.
 TEMA: Šviesos banginės savybės, apibendrinimas Fizika: 10 klasė Mokytoja: Rasa Armonienė 2014 m. 1. Šviesos dispersija 2. Elektromagnetinių bangų skalė 3. Spektrai 4. Šviesos interferencija 5. Šviesos
TEMA: Šviesos banginės savybės, apibendrinimas Fizika: 10 klasė Mokytoja: Rasa Armonienė 2014 m. 1. Šviesos dispersija 2. Elektromagnetinių bangų skalė 3. Spektrai 4. Šviesos interferencija 5. Šviesos
Termochemija. Darbas ir šiluma.
 Termochemija. Darbas ir šiluma. Energija gyvojoje gamtoje. saulės šviesa CO 2 H 2 O O 2 gliukozė C 6 H 12 O 6 saulės šviesa Pavyzdys: Fotosintezė chloroplastas saulės 6CO 2 + 6H 2 O + šviesa C 6 H 12 O
Termochemija. Darbas ir šiluma. Energija gyvojoje gamtoje. saulės šviesa CO 2 H 2 O O 2 gliukozė C 6 H 12 O 6 saulės šviesa Pavyzdys: Fotosintezė chloroplastas saulės 6CO 2 + 6H 2 O + šviesa C 6 H 12 O
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
EUROPOS CENTRINIS BANKAS
 2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
2005 12 13 C 316/25 EUROPOS CENTRINIS BANKAS EUROPOS CENTRINIO BANKO NUOMONĖ 2005 m. gruodžio 1 d. dėl pasiūlymo dėl Tarybos reglamento, iš dalies keičiančio Reglamentą (EB) Nr. 974/98 dėl euro įvedimo
Παρασκευή 1 Νοεμβρίου 2013 Ασκηση 1. Λύση. Παρατήρηση. Ασκηση 2. Λύση.
 (, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
(, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
FUNKCIJOS. veiksmu šioje erdvėje apibrėžkime dar viena. a = {a 1,..., a n } ir b = {b 1,... b n } skaliarine sandauga
 VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
VII DAUGELIO KINTAMU JU FUNKCIJOS 71 Bendrosios sa vokos Iki šiol mes nagrinėjome funkcijas, apibrėžtas realiu skaičiu aibėje Nagrinėsime funkcijas, kurios apibrėžtos vektorinėse erdvėse Tarkime, kad R
MECHANINIS DARBAS, GALIA, ENERGIJA. TVERMĖS DĖSNIAI MECHANIKOJE. HIDRODINAMIKA
 LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS MECHANINIS DARBAS, GALIA, ENERGIJA TVERMĖS DĖSNIAI MECHANIKOJE HIDRODINAMIKA III KURSO III TURO METODINIAI NURODYMAI IR UŢDUOTYS
LIETUVOS FIZIKŲ DRAUGIJA ŠIAULIŲ UNIVERSITETO JAUNŲJŲ FIZIKŲ MOKYKLA FOTONAS MECHANINIS DARBAS, GALIA, ENERGIJA TVERMĖS DĖSNIAI MECHANIKOJE HIDRODINAMIKA III KURSO III TURO METODINIAI NURODYMAI IR UŢDUOTYS
!"#$ % &# &%#'()(! $ * +
 ,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
,!"#$ % &# &%#'()(! $ * + ,!"#$ % &# &%#'()(! $ * + 6 7 57 : - - / :!", # $ % & :'!(), 5 ( -, * + :! ",, # $ %, ) #, '(#,!# $$,',#-, 4 "- /,#-," -$ '# &",,#- "-&)'#45)')6 5! 6 5 4 "- /,#-7 ",',8##! -#9,!"))
1.4. Rungės ir Kuto metodas
 .4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
.4. RUNGĖS IR KUTO METODAS.4. Rungės ir Kuto metodas.4.. Prediktoriaus-korektoriaus metodas Palyginkime išreikštinį ir simetrinį Eulerio metodus. Pirmojo iš jų pagrindinis privalumas tas, kad išreikštinio
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA. Algoritmų teorija. Paskaitų konspektas
 VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
VILNIAUS UNIVERSITETAS MATEMATIKOS IR INFORMATIKOS FAKULTETAS PROGRAMŲ SISTEMŲ KATEDRA Algoritmų teorija Paskaitų konspektas Dėstytojas: lekt. dr. Adomas Birštunas Vilnius 2015 TURINYS 1. Algoritmo samprata...
Kodėl mikroskopija? Optinė mikroskopija: įvadas. Žmogaus akis. Žmogaus akis. Žmogaus akis. Vaizdo formavimasis žmogaus akyje
 Kodėl mikroskopija? Todėl, kad pamatyti reiškia patikėti... Optinė mikroskopija: įvadas Žmogaus akis Žmogaus akis Mato šviesą, kurios bangų ilgis nuo 400 nm (violetinė) iki 750 nm (mėlyna) Stiebelių ir
Kodėl mikroskopija? Todėl, kad pamatyti reiškia patikėti... Optinė mikroskopija: įvadas Žmogaus akis Žmogaus akis Mato šviesą, kurios bangų ilgis nuo 400 nm (violetinė) iki 750 nm (mėlyna) Stiebelių ir
Algoritmai. Vytautas Kazakevičius
 Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
Algoritmai Vytautas Kazakevičius September 2, 27 2 Turinys Baigtiniai automatai 5. DBA.................................. 5.. Abėcėlė............................ 5..2 Automatai..........................
STOGO ŠILUMINIŲ VARŽŲ IR ŠILUMOS PERDAVIMO KOEFICIENTO SKAIČIAVIMAS
 STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
STOGO ŠILUMINIŲ VAŽŲ I ŠILUMOS PEDAVIMO KOEFICIENTO SKAIČIAVIMAS ST 2.05.02:2008 2 priedas 1. Stogo suminė šiluminė varža s (m 2 K/W) apskaičiuojama pagal formulę [4.6]: s 1 2... n ( g q ); (2.1) čia:
Rimtautas Piskarskas. Fotodetektoriai
 Rimtautas Piskarskas Fotodetektoriai Vilnius 2003 Fotodetektorius kas tai? Fotodetektorius tai kietakūnis jutiklis, šviesos energiją paverčiantis elektros energija. hυ E g laidumo juosta Esant net ir silpam
Rimtautas Piskarskas Fotodetektoriai Vilnius 2003 Fotodetektorius kas tai? Fotodetektorius tai kietakūnis jutiklis, šviesos energiją paverčiantis elektros energija. hυ E g laidumo juosta Esant net ir silpam
Paprastosios DIFERENCIALINĖS LYGTYS
 Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Paprastosios DIFERENCIALINĖS LYGTYS prof. Artūras Štikonas Paskaitų kursas Matematikos ir informatikos fakultetas Taikomosios matematikos institutas, Diferencialinių lygčių katedra Naugarduko g. 24, LT-3225
Balniniai vožtuvai (PN 16) VRB 2 dviejų angų, vidiniai ir išoriniai sriegiai VRB 3 trijų angų, vidiniai ir išoriniai sriegiai
 Techninis aprašymas alniniai vožtuvai (PN 16) VR 2 dviejų angų, vidiniai ir išoriniai sriegiai VR 3 trijų angų, vidiniai ir išoriniai sriegiai prašymas Savybės: Padidinto sandarumo ( bubble tight ) konstrukcija
Techninis aprašymas alniniai vožtuvai (PN 16) VR 2 dviejų angų, vidiniai ir išoriniai sriegiai VR 3 trijų angų, vidiniai ir išoriniai sriegiai prašymas Savybės: Padidinto sandarumo ( bubble tight ) konstrukcija
